PSEB 10th Class Maths Solutions Chapter 13 Surface Areas and Volumes Ex 13.5

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 13 Surface Areas and Volumes Ex 13.5 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 13 Surface Areas and Volumes Ex 13.5

Question 1.
A copper wire 3 mm in diameter is wound about a cylinder whose length is 12 cm, and diameter 10 cm, so as to cover the curved surface of the cylinder. Find the length and mass of the wire, assuming the density of copper to 8.88 g per cm³.
Solution:
Diametcr of wire (d) = 3 mm
∴ Radius of wire (r) = \(\frac{3}{2}\) mm = \(\frac{3}{20}\) cm

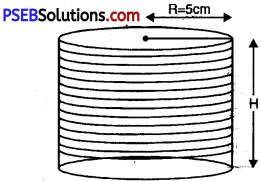
Diameter of cylinder = 10 cm
Radius of cylinder (R) = 5 cm
Height of cylinder (H) = 12 cm
Circumference of cylinder = length of wire used in one turn
2πR = length of wire used in one turn
2 × \(\frac{22}{7}\) × 5 = length of wire used in one turn
\(\frac{220}{7}\) = length of wire used in one turn
Number of turn used = \(\frac{\text { Height of cylinder }}{\text { Diameter of wire }}\)
= \(\frac{12 \mathrm{~cm}}{3 \mathrm{~mm}}=\frac{12}{3} \times 10\) [1 mm = \(\frac{1}{10}\) cm]
= \(\frac{120}{3}\) = 40

∴ length of wire used = Number of turns × length of wire used in one turn
H = 40 × \(\frac{220}{7}\) = 1257.14 cm
Volume of wire used = πr²H
= \(\frac{22}{7} \times \frac{3}{20} \times \frac{3}{20} \times 1257.14\) = 88.89 cm³
Mass of 1 cm³ = 8.88 gm
Mass of 88.89 cm³ = 8.88 × 88.89 = 789.41 gm
Hence, length of wire is 1257.14 cm
and mass of wire is 789.41 gm.

Question 2.
A right triangle, whose sides are 3 cm and 4 cm (other than hypotenuse) is made to revolve about its hypotenuse. Find the volume and surface area the double cone so formed. (Choose value of t as found
appropriate.)
Solution:
Let ∆ABC be the right triangle right angled at A whose sides AB and AC measure 3 cm and 4 cm respectively.
The length of the side BC (hypotenuse) = \(\sqrt{3^{2}+4^{2}}=\sqrt{9+16}\) = 5 cm
Here, AO (or A’O) is the radius of the common base of the double cone formed revolving the right triangle about BC.
Height of the cone BAA’ is BO and slant height is 3 cm.
Height of the cone CAA’ is CO and slant height is 4 cm.
Now, ∆AOB ~ ∆CAB (AA similarity)

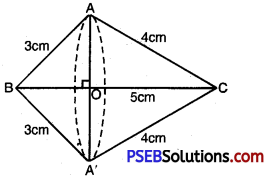
∴ \(\frac{\mathrm{AO}}{4}=\frac{3}{5}\)

⇒ AO = \(\frac{4 \times 3}{5}=\frac{12}{5}\) cm

Also \(\frac{\mathrm{BO}}{3}=\frac{3}{5}\)

⇒ BO = \(\frac{\mathrm{BO}}{3}=\frac{3}{5}\) cm
Thus CO = BC – OB
= 5 – \(\frac{9}{5}\) = \(\frac{16}{5}\) cm
Now, Volume of double cone = [Volume of Cone ABA’] + [Volume of cone ACA’]

∴ Volume of double cone = 30 cm³.
Also, surface area of double cone = [Surface area of Cone ABA’] + [surface area of Cone ACA’]
= π .AO.AB + π. AO.A’C
= \(\left(\frac{22}{7} \times \frac{12}{5} \times 3\right)+\left(\frac{22}{7} \times \frac{12}{5} \times 4\right)\)

= \(\left(\frac{792}{35} \times \frac{1056}{35}\right)\)
= \(\frac{1848}{35}\) = 52.75 cm²

Question 3.
A cistern, Internally measuring 150 cm × 120 cm × 110 cm, has 129600 cm3 of water in it. Porous bricks are placed in the water until the cistern is full to the brim. Each brick absorbs one-seventeenth of its own volume of water. How many bricks can be put in without the water overflowing, each brick being 22.5 cm × 7.5 cm × 6.5 cm?
Solution:
Volume of one brick = 22.5 × 7.5 × 6.5 cm³ = 1096.87 cm³
Volume of cistern = 150 × 120 × 110 cm³ = 1980000 cm³
Let number of bricks used = n
Total volume of n bricks = n (volume of one brick) = n [1096.871] cm³
Volume of water = 129600 cm³
Volume of water available for bricks = 1980000 – 129600 = 1850400 cm³

Each bricks absorb \(\frac{1}{17}\)th of its volume in water
Volume of water available for bricks = \(\frac{17}{16}\) × volume of water available for bricks
= \(\frac{17}{10}\) × 1850400
Volume of water available for bricks = 1966050 cm³
Total volume of n bricks = Volume of water available for bricks
n[1096.87] cm³ = 1966050 cm³

n = \(\frac{1966050}{1096.87}\)
n = 1792.42
Hence, Number of bricks used = 1792.

Question 4.
In one fortnight of a given month, there was a rainfall of 10 cm in a river valley. If the area of the valley is 97280 km², show that the total rainfall was approximately equivalent to the addition to the normal water of three rivers each 1072 km long, 75 m wide and 3 m deep.
Solution:
Area of valley = 97280 km²
Rainfall in valley = 10 cm
∴ Volume of total rainfall = 97280 × \(\frac{10}{100}\) × \(\frac{1}{1000}\) km³
= 9.728 km³

Question 5.
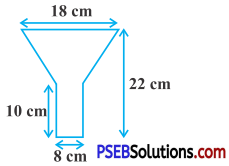
An oil funnel made of tin sheet consists of a cylindrical portion 10 cm long attached to a frust.un of a cone. if the total height is 22 cm, diameter of the cylindrical portion is 8 cm and the diameter of the top of the funnel is 18 cm, find the area of the tin sheet required to make the funnel.

Solution:
Diameter of top of funnel = 18 cm
∴ Radius of top of funnel (R) = \(\frac{18}{2}\) cm = 9 cm
Diameter of bottom of funnel = 8 cm
Radius of bottom of funnel (r) = 4 cm
Height of cylindrical portion (h) = 10 cm
Height of frustum (H) = (22 – 10) = 12 cm
Slant height of frustum (l)
= \sqrt{\mathrm{H}^{2}+(\mathrm{R}-r)^{2}}\(\)

= \(\sqrt{(12)^{2}+(9-4)^{2}}\)

= \(\sqrt{144+(5)^{2}}\)

= \(\sqrt{144+25}\) = \(\sqrt{169}\)
Slant height of frustum (l) = 13 cm
Area of metal sheet required curved
surface area of cylindrical base + curved surface of frustum = 2πrh + πL [R + r]
= 2 × \(\frac{22}{7}\) × 4 × 10 + \(\frac{212}{7}\) × 13 [9 + 4] cm²
= 251.42 + 531.14 = 782.56 cm²

Question 6.
Derive the formula for the curved surface area and total surface area of a frustum of a cone, given to you in Section 13.5, using the symbols as explamed.
Solution:
A frustum of a right circular cone has two unequal flat circular bases and a curved surface. Let ACDB be the frustum of the cone obtained by removing the portion VCÐ. The line-segment OP joining the centres of two bases is called the height of the frustum. Each of the line-segments AC and BD of frustum ACDB is called its slant height.

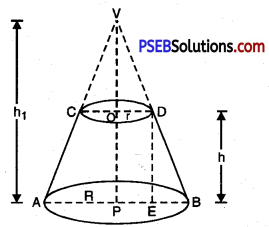
Let R and r be the radii of the circular end faces (R > r) of the frustum ACDB of the cone (V, AB). We complete the conical part VCD. Let h and l be the vertical height and slant height respectively. Then OP = h and AC = BD = l.

The frustum of the right circular cone can be viewed as the difference of the two right circular VAB and VCD.
Let the height of the cone VAB be h₁ and its slant height l₁ i.e. VP = h₁ and VA = VB = l₁.

Now from right ∆DEB, we have
DB² = DE² + BE²

⇒ l² = h² + (R – r)²
⇒ l = \(\sqrt{h^{2}+(\mathrm{R}-r)^{2}}\)
Again ∆VOD ~ ∆VPB

⇒ \(\frac{V D}{V B}=\frac{O D}{P B}\)

⇒ \(\frac{l_{1}-l}{l_{1}}=\frac{r}{R}\)

⇒ 1 – \(\frac{l}{l_{1}}=\frac{r}{\mathrm{R}}\)

⇒ \(\frac{l}{l_{1}}=1-\frac{r}{\mathrm{R}}=\frac{\mathrm{R}-r}{\mathrm{R}}\)

⇒ l₁ = \(\frac{l \mathrm{R}}{\mathrm{R}-r}\)

⇒ Now, l₁ – l₁ = \(\frac{l \mathrm{R}}{\mathrm{R}-r}-l=\frac{l r}{\mathrm{R}-r}\)

Curved surface area of the frustum of cone = πRl₁ – πr(l₁ – l)
[Curved surface area of a cone = π × r × 1]

= πR. \(\frac{l R}{R-r}\) – πr. \(\frac{l r}{\mathrm{R}-r}\)

= πl (\(\frac{\mathrm{R}^{2}-r^{2}}{\mathrm{R}-r}\)) = \(\frac{\pi l(\mathrm{R}-r)(\mathrm{R}+r)}{(\mathrm{R}-r)}\)
= πl (R + r) sq. units.
∴ Curved snafaue area of the frustum of right circular cone = πl (R + r) sq. units,
where l = \(\sqrt{h^{2}+(\mathrm{R}-r)^{2}}\)
and total surface area of frustum of right circular cone = Curved surface area + Area of base + Area of top
= πl (R + r) + πR² + πr²
∴ π [R² + r² + l (R + r)] sq. units.

Question 7.
Derive the formula for the volume of the frustum of a cone, given to you in section 13.5, using the symbols as explained.
Solution:
A frustum of a right circular cone has two unequal flat circular bases and a curved surface. Let ACDB be the frustum of the cone obtained by removing the portion VCD. The line-segment OP joining the centres of two bases is called the height of the frustum. Each of the line-segments AC and BD of frustum ACDB is called its slant height.

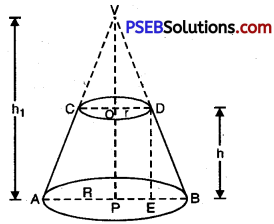
Ler R and r be the radii of the circular end faces (R > r) of the fnistum ACDB of the cone (V, AB). We complete the conical part VCD. Let h and l be the vertical height and slant height respectively. Then OP = h and AC = BD = l. The frustum of the right circular cone can be viewed as the difference of the two right circular VAB and VCD.
Let theheight of the cone VAB be h₁ and its slant height l₁ i.e.VP = h₁ and VA = VB = l₁.
∴ The height of the cone VCD = VP – OP = h₁ – h
Since right ∆s VOD and VPB are similar
⇒ \(\frac{\mathrm{VO}}{\mathrm{VP}}=\frac{\mathrm{OD}}{\mathrm{PB}}=\frac{h_{1}-h}{h_{1}}=\frac{r}{\mathrm{R}}\)

⇒ 1 – \(\frac{h}{h_{1}}=\frac{r}{\mathrm{R}}\)

⇒ \(\frac{h}{h_{1}}=1-\frac{r}{\mathrm{R}}=\frac{\mathrm{R}-r}{\mathrm{R}}\)

⇒ h₁ = \(\frac{h \mathrm{R}}{\mathrm{R}-r}\)

⇒ Height of the cone VCD = \(\frac{h \mathrm{R}}{\mathrm{R}-r}-h=\frac{h \mathrm{R}-h \mathrm{R}+h r}{\mathrm{R}-r}=\frac{h r}{\mathrm{R}-r}\)

Volume of the frustrum ACDB of the cone (V,AB) = Volume of the cone (V, AB) – Volume of the cone (V, CD)
= \(\)

= \(\frac{\pi}{3}\left(\mathrm{R}^{2} \cdot \frac{h \mathrm{R}}{\mathrm{R}-r}-r^{2} \cdot \frac{h r}{\mathrm{R}-r}\right)\)

= \(\frac{\pi h}{3}\left(\frac{\mathrm{R}^{3}-r^{3}}{\mathrm{R}-r}\right)\)

= \(\frac{1}{3} \pi h \times \frac{(\mathrm{R}-r)\left(\mathrm{R}^{2}+\mathrm{R} r+r^{2}\right)}{(\mathrm{R}-r)}\)

= \(\frac{1}{3}\) πh (R² + Rr + r²)
Hence, volume of the frustum of cone is \(\frac{1}{3}\) πh (R² + Rr + r²).

Again if A₁ and A₂ (A₁ > A₂) are the surface areas of the two circular bases, then A₁ = πR² andA₂ = πr²

Now volume of the frustum of cone,

= \(\frac{1}{3}\) πh (R² + r² + Rr)

= \(\frac{h}{3}\) (πR² + πr² + \(\sqrt{\pi \mathrm{R}^{2}} \sqrt{\pi r^{2}}\))

= \(\frac{h}{3}\) (A₁ + A₂ + \(\sqrt{A_{1} A_{2}}\))