PSEB 10th Class Maths Solutions Chapter 15 ਸੰਭਾਵਨਾ Ex 15.1

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 15 ਸੰਭਾਵਨਾ Ex 15.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 15 ਸੰਭਾਵਨਾ Exercise 15.1

1. ਹੇਠ ਲਿਖੇ ਕਥਨਾਂ ਨੂੰ ਪੂਰਾ ਕਰੋ :

ਪ੍ਰਸ਼ਨ (i).
ਘਟਨਾ E ਦੀ ਸੰਭਾਵਨਾ + ਘਟਨਾ ‘E ਨਹੀਂ” ਦੀ ਸੰਭਾਵਨਾ = …….. ਹੈ ।
ਉੱਤਰ:
ਘਟਨਾ E + ਸੰਭਾਵਿਤ ਘਟਨਾ ‘ਨਹੀਂ E’ ਦੀ ਸੰਭਾਵਨਾ = 1 ਹੈ ।

ਪ੍ਰਸ਼ਨ (ii).
ਉਸ ਘਟਨਾ ਦੀ ਸੰਭਾਵਨਾ ਜੋ ਵਾਪਰ ਨਹੀਂ ਸਕਦੀ ……….. ਹੈ | ਅਜਿਹੀ ਘਟਨਾ ……… ਕਹਾਉਂਦੀ ਹੈ ।
ਉੱਤਰ:
ਉਸ ਘਟਨਾ ਦੀ ਸੰਭਾਵਨਾ ਜੋ ਵਾਪਰ ਨਹੀਂ ਸਕਦੀ 0 ਹੈ । ਅਜਿਹੀ ਘਟਨਾ ਅਸੰਭਵ ਘਟਨਾ ਕਹਾਉਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ (iii).
ਉਸ ਘਟਨਾ ਦੀ ਸੰਭਾਵਨਾ ਜਿਸਦਾ ਵਾਪਰਨਾ ਨਿਸ਼ਚਿਤ ਹੈ ……… ਹੈ | ਅਜਿਹੀ ਘਟਨਾ…….. ਕਹਾਉਂਦੀ ਹੈ ।
ਉੱਤਰ:
ਉਸ ਘਟਨਾ ਦੀ ਸੰਭਾਵਨਾ ਜਿਸਦਾ ਵਾਪਰਨਾ | ਨਿਸ਼ਚਿਤ ਹੈ, 1 ਹੈ | ਅਜਿਹੀ ਘਟਨਾ ਨਿਸ਼ਚਿਤ ਘਟਨਾ ਕਹਾਉਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ (iv).
ਕਿਸੇ ਪ੍ਰਯੋਗ ਦੀਆਂ ਸਾਰੀਆਂ ਆਰੰਭਿਕ ਘਟਨਾਵਾਂ ਦੀਆਂ ਸੰਭਾਵਨਾਵਾਂ ਦਾ ਜੋੜ …….. ਹੈ ।
ਉੱਤਰ:
ਕਿਸੇ ਪ੍ਰਯੋਗ ਦੀਆਂ ਸਾਰੀਆਂ ਆਰੰਭਿਕ ਘਟਨਾਵਾਂ ਦੀਆਂ ਸੰਭਾਵਨਾਵਾਂ ਦਾ ਜੋੜ 1 ਹੈ ।

ਪ੍ਰਸ਼ਨ (v).
ਕਿਸੇ ਘਟਨਾ ਦੀ ਸੰਭਾਵਨਾ …….. ਤੋਂ ਵੱਡੀ ਜਾਂ ਉਸਦੇ ਬਰਾਬਰ ਹੁੰਦੀ ਹੈ ਅਤੇ ………. ਤੋਂ ਛੋਟੀ ਜਾਂ ਉਸਦੇ ਬਰਾਬਰ ਹੁੰਦੀ ਹੈ ।
ਉੱਤਰ:
ਕਿਸੇ ਘਟਨਾ ਦੀ ਸੰਭਾਵਨਾ 0 ਤੋਂ ਵੱਡੀ ਜਾਂ ਉਸਦੇ ਬਰਾਬਰ ਹੁੰਦੀ ਹੈ ਅਤੇ 1 ਤੋਂ ਛੋਟੀ ਜਾਂ ਉਸਦੇ ਬਰਾਬਰ ਹੁੰਦੀ ਹੈ ।

2. ਹੇਠਾਂ ਦਿੱਤੇ ਪ੍ਰਯੋਗਾਂ ਵਿੱਚੋਂ ਕਿਹੜੇ-ਕਿਹੜੇ ਪ੍ਰਯੋਗਾਂ ਦੇ ਪਰਿਣਾਮ ਸਮਸੰਭਾਵੀ ਹਨ ? ਸਪੱਸ਼ਟ ਕਰੋ ।

ਪ੍ਰਸ਼ਨ (i).
ਇੱਕ ਡਰਾਈਵਰ ਕਾਰ ਚਲਾਉਣ ਦਾ ਯਤਨ ਕਰਦਾ ਹੈ । ਕਾਰ ਚੱਲਣੀ ਸ਼ੁਰੂ ਹੋ ਜਾਂਦੀ ਹੈ ਜਾਂ ਕਾਰ ਚੱਲਣੀ ਸ਼ੁਰੂ | ਨਹੀਂ ਹੁੰਦੀ ਹੈ ।
ਉੱਤਰ:
ਜਦੋਂ ਇੱਕ ਡਰਾਈਵਰ ਕਾਰ ਚਲਾਉਣ ਦਾ ਯਤਨ ਕਰਦਾ ਹੈ ਤਾਂ ਆਮ ਸਥਿਤੀ ਵਿੱਚ ਕਾਰ ਚੱਲਣ ਲੱਗ ਜਾਂਦੀ ਹੈ ਪਰ ਜੇਕਰ ਕਾਰ ਵਿੱਚ ਕੋਈ ਦੋਸ਼ ਹੈ ਤਾਂ ਕਾਰ ਨਹੀਂ ਚਲਦੀ । ਇਸ ਲਈ ਇਹ ਨਤੀਜਾ ਸਮਸੰਭਾਵੀ ਨਹੀਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ (ii).
ਇੱਕ ਖਿਡਾਰੀ ਬਾਸਕਟਬਾਲ ਨੂੰ ਬਾਸਕਟ ਵਿੱਚ ਪਾਉਣ ਦਾ ਯਤਨ ਕਰਦੀ ਹੈ । ਉਹ ਬਾਸਕਟ ਵਿੱਚ ਗੋਂਦ ਪਾ ਸਕਦੀ | ਹੈ ਜਾ ਨਹੀਂ ਪਾ ਸਕਦੀ ਹੈ ।
ਉੱਤਰ:
ਜਦੋਂ ਇੱਕ ਖਿਡਾਰੀ ਬਾਸਕੱਟਵਾਲ ਨੂੰ ਬਾਸਕਟ ਵਿੱਚ ਪਾਉਣ ਦਾ ਯਤਨ ਕਰਦਾ ਹੈ ਤਾਂ ਇਸ ਸਥਿਤੀ ਵਿੱਚ ਨਤੀਜਾ ਸਮ ਸੰਭਾਵੀ ਨਹੀਂ ਹੈ ਕਿਉਂਕਿ ਨਤੀਜਾ ਕਈ ਤੱਥਾਂ ‘ਤੇ ਨਿਰਭਰ ਕਰਦਾ ਹੈ ਜਿਵੇਂ ਕੀ ਖਿਡਾਰੀ ਦੀ ਸਿੱਖਿਆ, ਪ੍ਰਯੋਗ ਕੀਤੀ ਜਾਣ ਵਾਲੀ ਬੰਦੂਕ ਦੀ ਪ੍ਰਕ੍ਰਿਤੀ ਆਦਿ ।

ਪ੍ਰਸ਼ਨ (iii).
ਇੱਕ ਸੱਚ ਜਾਂ ਝੂਠ ਪ੍ਰਸ਼ਨ ਦਾ ਅਨੁਮਾਨ ਲਗਾਇਆ ਜਾਂਦਾ ਹੈ ।ਉੱਤਰ ਸਹੀ ਹੈ ਜਾਂ ਗ਼ਲਤ ਹੋਵੇਗਾ ।
ਉੱਤਰ:
ਕਿਉਂਕਿ ਇੱਕ ਪ੍ਰਸ਼ਨ ਲਈ ਦੋ ਸੰਭਾਵਨਾਵਾਂ ਜਾਂ ਤਾਂ ਸਹੀ ਜਾਂ ਗ਼ਲਤ ਹੈ । ਠੀਕ-ਗਲਤ ਦੇ ਇਸ ਪ੍ਰਸ਼ਨ ਦੇ ਇਸ ਪ੍ਰਯੋਗ ਵਿੱਚ ਇੱਕ ਹੀ ਨਤੀਜਾ ਹੋ ਸਕਦਾ ਹੈ ਜਾਂ ਤਾਂ ਠੀਕ ਜਾਂ ਗਲਤ ਭਾਵ ਦੋਵਾਂ ਵਿੱਚੋਂ ਇੱਕ ਅਤੇ ਦੋਵਾਂ ਦੇ ਘੱਟਣ ਦੇ ਮੌਕੇ ਬਰਾਬਰ ਹਨ । ਇਸ ਲਈ ਦੋਵੇਂ ਪਰਿਣਾਮ ਸਮਸੰਭਾਵੀ ਹਨ ।

ਪ੍ਰਸ਼ਨ (iv).
ਇੱਕ ਬੱਚੇ ਦਾ ਜਨਮ ਹੁੰਦਾ ਹੈ ।ਉਹ ਇੱਕ ਲੜਕਾ ਹੈ ਜਾਂ ਇੱਕ ਲੜਕੀ ਹੈ ।
ਉੱਤਰ:
ਇੱਕ ਨਵਾਂ ਜੰਮਿਆ ਬੱਚਾ (ਭਾਵ ਜਿਸਦਾ ਜਨਮ ਇਸੇ ਸਮੇਂ ਹੋਇਆ ਹੈ । ਇੱਕ ਲੜਕਾ ਵੀ ਹੋ ਸਕਦਾ ਹੈ ਅਤੇ ਇੱਕ ਲੜਕੀ ਵੀ ਹੋ ਸਕਦੀ ਹੈ । ਇਸ ਲਈ ਦੋਵੇਂ ਨਤੀਜੇ ਸਮ ਸੰਭਾਵੀ ਹਨ ।

ਪ੍ਰਸ਼ਨ 3.
ਫੁੱਟਬਾਲ ਦੇ ਖੇਡ ਨੂੰ ਆਰੰਭ ਕਰਦੇ ਸਮੇਂ ਇਹ ਫੈਸਲਾ ਲੈਣ ਲਈ ਕਿ ਕਿਹੜੀ ਟੀਮ ਪਹਿਲਾਂ ਗੇਂਦ ਲਵੇਗੀ, ਇਸ ਦੇ ਲਈ ਸਿੱਕਾ ਉਛਾਲਣਾ ਇੱਕ ਨਿਆਸੰਗਤ ਵਿਧੀ ਕਿਉਂ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ ?
ਹੱਲ:
ਜਦੋਂ ਸਿੱਕੇ ਨੂੰ ਉਛਾਲਿਆਂ ਜਾਂਦਾ ਹੈ ਤਾਂ ਕੇਵਲ ਦੋ ਹੀ ਸੰਭਾਵਨਾਵਾਂ ਹੁੰਦੀਆਂ ਹਨ । ਭਾਵ ਚਿੱਤ ਜਾਂ ਪੱਟ । ਇੱਕ ਸਿੱਕਾ ਉਛਾਲਣ ਦੇ ਨਤੀਜੇ ਦੀ ਪਹਿਲਾਂ ਭਵਿਖਵਾਣੀ ਨਹੀਂ ਕੀਤੀ ਜਾ ਸਕਦੀ ।

ਪ੍ਰਸ਼ਨ 4.
ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ਕਿਹੜੀ ਸੰਖਿਆ ਕਿਸੇ ਘਟਨਾ ਦੀ ਸੰਭਾਵਨਾ ਨਹੀਂ ਹੋ ਸਕਦੀ ?
(A) \(\frac{2}{3}\)
(B) -1.5
(C) 15%
(D) 0.7.
ਹੱਲ:
ਜਿਵੇਂ ਕਿ ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ ਕਿ ਕਿਸੇ ਘਟਨਾ ਦੀ ਸੰਭਾਵਨਾ 0 ਤੋਂ ਘੱਟ ਜਾਂ 1 ਤੋਂ ਜ਼ਿਆਦਾ ਨਹੀਂ ਹੋ ਸਕਦੀ ਭਾਵ 0 ≤ P (E) ≤ 1
∴ (B) – 1.5 ਸੰਭਵ ਨਹੀਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ 5.
ਜੇਕਰ P(E) = 0.05 ਹੈ, ਤਾਂ E ਨਹੀਂ’ ਦੀ ਸੰਭਾਵਨਾ ਕੀ ਹੈ ?
ਹੱਲ:
ਜਿਵੇਂ ਕਿ ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ
P (E) + P (\(\bar{E}\)) = 1
P (\(\bar{E}\)) = 1 – P (E)
= 1 – 0.05
= 0.95.

ਪ੍ਰਸ਼ਨ 6.
ਇੱਕ ਥੈਲੇ ਵਿੱਚ ਕੇਵਲ ਨਿਬ ਦੀ ਮਹਿਕ ਵਾਲੀਆਂ | ਮਿੱਠੀਆਂ ਗੋਲੀਆਂ ਹਨ | ਮਾਲਿਨੀ ਬਿਨ੍ਹਾਂ ਥੈਲੇ ਵਿੱਚ ਦੇਖੇ ਉਸ | ਵਿੱਚੋਂ ਇੱਕ ਗੋਲੀ ਬਾਹਰ ਕੱਢਦੀ ਹੈ । ਇਸ ਦੀ ਕੀ ਸੰਭਾਵਨਾ ਹੈ ਕਿ ਉਹ ਕੱਢੀ ਗਈ ਗੋਲੀ
(i) ਸੰਤਰੇ ਦੀ ਮਹਿਕ ਵਾਲੀ ਹੈ ?
(ii) ਨਿੰਬੂ ਦੀ ਮਹਿਕ ਵਾਲੀ ?
ਹੱਲ:
(i) ਕਿਉਂਕਿ ਇੱਕ ਥੈਲੇ ਵਿਚ ਕੇਵਲ ਨਿੰਬੂ ਦੀ ਮਹਿਕ ਵਾਲੀਆਂ ਮਿਠੀਆਂ ਗੋਲੀਆਂ ਹਨ ।
∴ ਸੰਤਰੇ ਦੀ ਮਹਿਕ ਵਾਲੀ ਕੋਈ ਗੋਲੀ ਨਹੀਂ ਹੈ ।
∴ ਇਹ ਅਸੰਭਵ ਘਟਨਾ ਹੈ ।
(ii) ਕਿਉਂਕਿ ਥੈਲੇ ਵਿਚ ਕੇਵਲ ਨਿੰਬੂ ਦੀ ਮਹਿਕ ਵਾਲੀਆਂ ਗੋਲੀਆਂ ਹਨ ।
∴ ਇਹ ਨਿਸ਼ਚਿਤ ਘਟਨਾ ਹੈ ।
∴ ਨਿੰਬੂ ਦੀ ਮਹਿਕ ਵਾਲੀਆਂ ਗੋਲੀਆਂ ਕੱਢਣ ਦੀ ਸੰਭਾਵਨਾ = \(\frac{1}{1}\) = 1 ਹੈ ।

ਪ੍ਰਸ਼ਨ 7.
ਇਹ ਦਿੱਤਾ ਹੋਇਆ ਹੈ ਕਿ 3 ਵਿਦਿਆਰਥੀਆਂ ਦੇ ਇੱਕ ਸਮੂਹ ਵਿੱਚੋਂ 2 ਵਿਦਿਆਰਥੀਆਂ ਦੇ ਜਨਮ ਦਿਨ ਇੱਕ ਹੀ ਦਿਨ ਨਾ ਹੋਣ ਦੀ ਸੰਭਾਵਨਾ 0.992 ਹੈ । ਇਸ ਦੀ ਕੀ ਸੰਭਾਵਨਾ ਹੈ ਕਿ ਇਨ੍ਹਾਂ 2 ਵਿਦਿਆਰਥੀਆਂ ਦਾ ਜਨਮ ਦਿਨ ਇੱਕ ਹੀ ਦਿਨ ਹੋਵੇ ?
ਹੱਲ:
ਦੋ ਵਿਦਿਆਰਥੀਆਂ ਦੇ ਜਨਮ ਦਿਨ ਇੱਕ ਹੀ ਦਿਨ ਜਨਮ ਦਿਨ ਹੋਣ ਦੀ ਘਟਨਾ ਨੂੰ ਲੈ ਮੰਨ ਲਉ ।
∴ ਦੋ ਵਿਦਿਆਰਥੀਆਂ ਦਾ ਜਨਮ ਦਿਨ ਇੱਕ ਹੀ ਦਿਨ ਨਾ ਹੋਣ ਦੀ ਘਟਨਾ \(\bar{A}\) ਹੈ । ,
∴ P (\(\bar{A}\)) = 0.992
P (A) = 1 – P(\(\bar{A}\)) (P (A) +P (\(\bar{A}\)) = 1)
= 1 – 0.992 = 0.008
∴ ਦੋ ਵਿਦਿਆਰਥੀਆਂ ਦਾ ਜਨਮ ਦਿਨ ਇੱਕ ਹੀ ਦਿਨ ‘ ਹੋਣ ਦੀ ਸੰਭਾਵਨਾ 0.008 ਹੈ ।

ਪ੍ਰਸ਼ਨ 8.
ਇੱਕ ਥੈਲੇ ਵਿੱਚ 3 ਲਾਲ ਅਤੇ 5 ਕਾਲੀਆਂ ਗੇਂਦਾ ਹਨ । ਇਸ ਥੈਲੇ ਵਿੱਚੋਂ ਇੱਕ ਗੇਂਦ ਅਚਾਨਕ ਬਾਹਰ ਕੱਢੀ | ਗਈ ਹੈ । ਇਸ ਦੀ ਸੰਭਾਵਨਾ ਕੀ ਹੋਵੇਗੀ ਕਿ ਗੇਂਦ
(i) ਲਾਲ ਹੋਵੇ ?
(ii) ਲਾਲ ਨਹੀਂ ਹੋਵੇ ?
ਹੱਲ:
ਲਾਲ ਗੇਂਦਾਂ ਦੀ ਸੰਖਿਆ = 3
ਕਾਲੀਆਂ ਗੇਂਦਾ ਦੀ ਸੰਖਿਆ = 5
ਕੁੱਲ ਗੇਂਦਾ ਦੀ ਸੰਖਿਆ = 3 + 5 = 8
ਇੱਕ ਗੇਂਦ ਅਚਾਨਕ ਕੱਢੀ ਜਾਂਦੀ ਹੈ ।
(i) ਲਾਲ ਗੇਂਦ ਕੱਢਣ ਦੀ ਸੰਭਵਾਨਾਂ

P(ਲਾਲ ਗੇਂਦ) = \(\frac{3}{8}\)

(ii) ਲਾਲ ਗੇਂਦ ਨਾ ਕੱਢਣ ਦੀ ਸੰਭਾਵਨਾ
= 1 – P (ਲਾਲ ਗੇਂਦ)
= 1 – \(\frac{3}{8}\) = \(\frac{5}{8}\)
[P(\(\bar{A}\)) = 1 – P(E)]

ਪ੍ਰਸ਼ਨ 9.
ਇੱਕ ਡੱਬੇ ਵਿੱਚ 5 ਲਾਲ ਬੰਟੇ, 8 ਚਿੱਟੇ ਬੰਟੇ ਅਤੇ 4 ਹਰੇ ਬੰਟੇ ਹਨ ।ਇਸ ਡੱਬੇ ਵਿੱਚੋਂ ਇੱਕ ਬੰਟਾ ਅਚਾਨਕ ਬਾਹਰ ਕੱਢਿਆ ਜਾਂਦਾ ਹੈ ।ਇਸਦੀ ਕੀ ਸੰਭਾਵਨਾ ਹੈ ਕਿ ਕੱਢਿਆ ਗਿਆ ਬੰਦਾ
(i) ਲਾਲ ਹੈ ?
(ii) ਚਿੱਟਾ ਹੈ ?
(iii) ਹਰਾ ਨਹੀਂ ਹੈ ?
ਹੱਲ:
ਲਾਲ ਬੰਟਿਆਂ ਦੀ ਸੰਖਿਆ = 5
ਚਿੱਟੇ ਬੰਟਿਆਂ ਦੀ ਸੰਖਿਆ = 8
ਹਰੇ ਬੰਟਿਆਂ ਦੀ ਸੰਖਿਆ =4
ਕੁੱਲ ਬੰਟੇ = 5 + 8 + 4 = 17
ਕਿਉਂਕਿ ਇਕ ਬੰਟਾ ਕੱਢਿਆ ਗਿਆ ਹੈ
(i) ਕਿਉਂਕਿ ਲਾਲ ਬੰਟੇ 5 ਹਨ
ਲਾਲ ਬੰਟੇ ਦੇ ਕੱਢਣ ਦੀ ਸੰਭਾਵਨਾ

= \(\frac{5}{17}\)

(ii) ਕਿਉਂਕਿ ਚਿੱਟੇ ਬੰਟੇ 8 ਹਨ ।
ਚਿੱਟਾ ਬੰਟਾ ਕੱਢਣ ਦੀ ਸੰਭਾਵਨਾ

= \(\frac{8}{17}\)

(iii) ਕਿਉਂਕਿ ਹਰੇ ਬੰਟੇ 4 ਹਨ ।
ਹਰਾ ਬੰਟਾ ਕੱਢਣ ਦੀ ਸੰਭਾਵਨਾ

= \(\frac{4}{17}\)
∴ ਹਰਾ ਬੰਟਾ ਨਾ ਕੱਢਣ ਦੀ ਸੰਭਾਵਨਾ = 1 – ਹਰਾ ਬੰਟਾ ਕੱਢਣ ਦੀ ਸੰਭਾਵਨਾ ।
= 1 – \(\frac{4}{17}\) = \(\frac{17-4}{17}\) = \(\frac{13}{17}\)

ਪ੍ਰਸ਼ਨ 10.
ਇੱਕ ਪਿੱਗੀ ਬੈਂਕ (piggy bank) ਵਿੱਚ, 50 ਪੈਸੇ ਦੇ ਸੌ ਸਿੱਕੇ ਹਨ, ₹ 1 ਦੇ ਪੰਜਾਹ ਸਿੱਕੇ ਹਨ, ₹ 2 ਦੇ ਵੀਹ ਸਿੱਕੇ ਅਤੇ ₹ 5 ਦੇ ਦਸ ਸਿੱਕੇ ਹਨ | ਜੇਕਰ ਪਿੱਗੀ ਬੈਂਕ ਨੂੰ ਹਿਲਾ ਕੇ ਉਲਟਾ ਕਰਨ ਤੇ ਕੋਈ ਇੱਕ ਸਿੱਕਾ ਬਾਹਰ ਡਿੱਗਣ ਦੇ ਪਰਿਣਾਮ ਸਮਸੰਭਾਵੀ ਹਨ ਬਰਾਬਰ ਦੀ ਸੰਭਾਵਨਾ ਵਾਲੇ) ਤਾਂ ਉਸਦੀ ਸੰਭਾਵਨਾ ਕੀ ਹੈ ਕਿ ਉਹ ਡਿੱਗਿਆ ਹੋਇਆ ਸਿੱਕਾ
(i) 50 ਪੈਸੇ ਦਾ ਹੋਵੇਗਾ
(ii) ਤੋਂ 5 ਦਾ ਨਹੀਂ ਹੋਵੇਗਾ ?
ਹੱਲ:
50 ਪੈਸੇ ਦੇ ਸਿੱਕਿਆਂ ਦੀ ਸੰਖਿਆ = 100
₹ 1 ਦੇ ਸਿੱਕਿਆਂ ਦੀ ਸੰਖਿਆ = 50
₹ 2 ਦੇ ਸਿੱਕਿਆਂ ਦੀ ਸੰਖਿਆ = 20
₹ 5 ਦੇ ਸਿੱਕਿਆਂ ਦੀ ਸੰਖਿਆ = 10
∴ ਸਿੱਕਿਆਂ ਦੀ ਕੁੱਲ ਸੰਖਿਆ = 100 + 50 + 20 + 10 = 180
50 ਪੈਸੇ ਦੇ 100 ਸਿੱਕੇ ਹਨ ।
50 ਪੈਸੇ ਦੇ ਸਿੱਕੇ ਨਿਕਲਣ ਦੀ ਸੰਭਾਵਨਾ

= \(\frac{100}{180}\)
p (50 ਪੈਸੇ ਦੇ ਸਿੱਕੇ) = \(\frac{5}{9}\)

(ii) ₹ 5 ਦੇ ਸਿੱਕਿਆਂ ਦੀ ਸੰਖਿਆ = 10
∴ ₹ 5 ਦੇ ਸਿੱਕੇ ਕੱਢਣ ਦੀ ਸੰਭਾਵਨਾ

P (₹ 5 ਦੇ ਸਿੱਕੇ) = \(\frac{10}{180}\) = \(\frac{1}{18}\)
P (₹ 5 ਦੇ ਸਿੱਕੇ ਨਾ ਨਿਕਲਣ) = 1 – P (5)
= 1 – \(\frac{1}{18}\) = \(\frac{18-1}{18}\) = \(\frac{17}{18}\)

ਪ੍ਰਸ਼ਨ 11.
ਗੋਪੀ ਆਪਣੇ ਜਲ-ਜੀਵ-ਕੁੰਡ (aquarium) ਦੇ ਲਈ ਇੱਕ ਦੁਕਾਨ ਤੋਂ ਮੱਛੀਆਂ ਖਰੀਦਦੀ ਹੈ । ਦੁਕਾਨਦਾਰ ਇੱਕ ਟੈਂਕੀ ਜਿਸ ਵਿੱਚ 5 ਨਰ ਮੱਛੀਆਂ ਅਤੇ 8 ਮਾਦਾ ਮੱਛੀਆਂ ਹਨ, ਵਿਚੋਂ ਇੱਕ ਮੱਛੀ ਪੱਖਪਾਤ ਰਹਿਤ ਉਸਨੇ ਬਾਹਰ ਕੱਢੀ ਹੈ। (ਦੇਖੋ ਚਿੱਤਰ) । ਇਸਦੀ ਕੀ ਸੰਭਾਵਨਾਂ ਹੈ ਕਿ ਬਾਹਰ ਕੱਢੀ। ਗਈ ਮੱਛੀ ਨਰ ਮੱਛੀ ਹੈ ?

ਹੱਲ:
ਨਰ ਮੱਛੀਆਂ ਦੀ ਸੰਖਿਆ = 5
ਮਾਦਾ ਮੱਛੀਆਂ ਦੀ ਸੰਖਿਆ = 8
ਕੁੱਲ ਮੱਛੀਆਂ ਦੀ ਸੰਖਿਆ = 5 + 8 = 13
ਨਰ ਮੱਛੀ ਕੱਢਣ ਦੀ ਸੰਭਾਵਨਾ

P (ਨਰ ਮੱਛੀ) = \(\frac{5}{13}\)

ਪ੍ਰਸ਼ਨ 12.
ਸੰਯੋਗ (chance) ਦੇ ਇੱਕ ਖੇਡ ਵਿੱਚ ਇੱਕ ਤੀਰ ਨੂੰ ਘੁਮਾਇਆ ਜਾਂਦਾ ਹੈ, ਜੋ ਵਿਰਾਮ ਵਿੱਚ ਆਉਣ ਤੋਂ ਬਾਅਦ ਸੰਖਿਆਵਾਂ 1, 2, 3, 4, 5, 6, 7, 8 ਵਿੱਚੋਂ ਕਿਸੇ ਇੱਕ ਸੰਖਿਆਂ ਵੱਲ ਸੰਕੇਤ ਕਰਦਾ ਹੈ । (ਦੇਖੋ ਚਿੱਤਰ) । ਜੇਕਰ ਇਹ ਸਾਰੇ ਪਰਿਣਾਮ ਸਮਸੰਭਾਵੀ ਹਨ ਤਾਂ ਇਸਦੀ ਕੀ ਸੰਭਾਵਨਾ ਹੈ ਕਿ ਇਹ ਤੀਰ ਸੰਕੇਤ

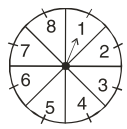
(i) 8 ਨੂੰ ਕਰੇਗਾ ?
(ii) ਇੱਕ ਟਾਂਕ ਸੰਖਿਆਂ ਨੂੰ ਕਰੇਗਾ ?
(iii) 2 ਤੋਂ ਵੱਡੀ ਸੰਖਿਆ ਨੂੰ ਕਰੇਗਾ ?
(iv) 9 ਤੋਂ ਛੋਟੀ ਸੰਖਿਆ ਨੂੰ ਕਰੇਗਾ ?
ਹੱਲ:
(i) ਪਰਿਣਾਮਾਂ ਦੀ ਕੁੱਲ ਸੰਖਿਆ
= {1, 2, 3, 4, 5, 6, 7, 8}
‘8’ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾਂ = \(\frac{1}{8}\)
∴ P (8) = \(\frac{1}{8}\)

(ii) ਟਾਂਕ ਸੰਖਿਆ = {1, 3, 5, 7}
ਟਾਂਕ ਸੰਖਿਆ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾਂ
= \(\frac{4}{2}\) = \(\frac{1}{2}\)
P (ਟਾਂਕ ਸੰਖਿਆ) = \(\frac{1}{2}\)

(iii) 2 ਤੋਂ ਵੱਡੀਆਂ ਸਿਖਿਆਵਾਂ = {3, 4, 5, 6, 7, 8}
2 ਤੋਂ ਵੱਡੀ ਸੰਖਿਆ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾਂ
= \(\frac{6}{8}\) = \(\frac{3}{4}\)
P (2 ਤੋਂ ਵੱਡੀ ਸੰਖਿਆ) = \(\frac{3}{4}\)

(iv) 9 ਤੋਂ ਛੋਟੀ ਸੰਖਿਆਵਾਂ
{1, 2, 3, 4, 5, 6, 7, 8}
∴ 9 ਤੋਂ ਛੋਟੀ ਸੰਖਿਆ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ
= \(\frac{8}{8}\)
P (9 ਤੋਂ ਛੋਟੀ ਸੰਖਿਆ) = 1

ਪ੍ਰਸ਼ਨ 13.
ਇੱਕ ਪਾਸੇ ਨੂੰ ਇੱਕ ਵਾਰ ਸੁੱਟਿਆ ਜਾਂਦਾ ਹੈ । ਹੇਠ ਲਿਖਿਆਂ ਦੀ ਸੰਭਾਵਨਾ ਪਤਾ ਕਰੋ :
(i) ਇੱਕ ਅਭਾਜ ਸੰਖਿਆ
(ii) 2 ਅਤੇ 6 ਦੇ ਵਿਚਕਾਰ ਸਥਿਤ ਕੋਈ ਸੰਖਿਆ
(iii) ਇੱਕ ਟਾਂਕ ਸੰਖਿਆ
ਹੱਲ:
ਜਦੋਂ ਪਾਸੇ ਨੂੰ ਇੱਕ ਵਾਰ ਸੁੱਟਿਆ ਜਾਂਦਾ ਹੈ ਤਾਂ ਸੰਭਵ ਪਰਿਣਾਮ ਹਨ :
S = {1, 2, 3, 4, 5, 6}
(i) ਅਭਾਜ ਸੰਖਿਆਵਾਂ ਹਨ :
{2, 3, 5}
∴ ਅਭਾਜ ਸੰਖਿਆ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ
= \(\frac{3}{6}\) = \(\frac{1}{2}\)
P (ਇੱਕ ਅਭਾਜ ਸੰਖਿਆ) = \(\frac{1}{2}\)

(ii) 2ਅਤੇ 6 ਦੇ ਵਿਚਕਾਰ ਸਥਿਤ ਸੰਖਿਆਵਾਂ= {3,4,5}
2 ਅਤੇ 6 ਦੇ ਵਿਚਕਾਰ ਸਥਿਤ ਸੰਖਿਆਵਾਂ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ = \(\frac{3}{6}\) = \(\frac{1}{2}\)
P (2 ਅਤੇ 6 ਵਿੱਚ ਸੰਖਿਆ) = \(\frac{1}{2}\)

(iii) ਟਾਂਕ ਸੰਖਿਆਵਾਂ ਹਨ = { 1, 3, 5}
ਟਾਂਕ ਸੰਖਿਆ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ
= \(\frac{3}{6}\) = \(\frac{1}{2}\)
P (ਟਾਂਕ ਸੰਖਿਆ) = \(\frac{1}{2}\)

ਪ੍ਰਸ਼ਨ 14.
52 ਪੱਤਿਆਂ ਦੀ ਚੰਗੀ ਤਰ੍ਹਾਂ ਫੈਂਟੀ ਗਈ ਤਾਸ਼ ਦੀ ਗੁੱਟੀ ਵਿੱਚੋਂ ਇੱਕ ਪੱਤਾ ਬਾਹਰ ਕੱਢਿਆ ਜਾਂਦਾ ਹੈ | ਹੇਠਾਂ ਲਿਖਿਆਂ ਨੂੰ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ ਪਤਾ ਕਰੋ :
(i) ਲਾਲ ਰੰਗ ਦਾ ਬਾਦਸ਼ਾਹ
(ii) ਇੱਕ ਤਸਵੀਰ ਵਾਲਾ ਪੱਤਾ ।
(iii) ਲਾਲ ਰੰਗ ਦਾ ਤਸਵੀਰ ਵਾਲਾ ਪੱਤਾ |
(iv) ਪਾਨ ਦਾ ਗੁਲਾਮ
(v) ਹੁਕਮ ਦਾ ਪੱਤਾ
(vi) ਇੱਕ ਇੱਟ ਦੀ ਬੇਗਮ
ਹੱਲ:
52 ਪੱਤਿਆਂ ਵਾਲੀ ਗੁੱਟੀ ਵਿੱਚ 52 ਪੱਤੇ ਹਨ ।
(i) ਲਾਲ ਰੰਗ ਦੇ ਦੋ ਬਾਦਸ਼ਾਹ ਭਾਵ ਪਾਨ ਦਾ ਬਾਦਸ਼ਾਹ ਅਤੇ ਇੱਟ ਦਾ ਬਾਦਸ਼ਾਹ ।
∴ ਲਾਲ ਰੰਗ ਦਾ ਬਾਦਸ਼ਾਹ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ
= \(\frac{2}{52}\) = \(\frac{1}{26}\)
P (ਲਾਲ ਰੰਗ ਦਾ ਬਾਦਸ਼ਾਹ ) = \(\frac{1}{26}\)

(ii) 12 ਤਸਵੀਰ ਵਾਲੇ ਪੱਤੇ ਦਾ ਭਾਵ 4 ਗੁਲਾਮ, 4 ਬੇਗਮ ਅਤੇ 4 ਬਾਦਸ਼ਾਹ
ਤਸਵੀਰ ਵਾਲੇ ਪੱਤੇ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ = \(\frac{12}{52}\)
∴ P (ਤਸਵੀਰ ਵਾਲਾ ਪੱਤਾ) = \(\frac{2}{13}\)

(iii) ਕਿਉਂਕਿ ਲਾਲ ਰੰਗ ਦੇ ਤਸਵੀਰ ਵਾਲੇ 6 ਪੱਤੇ ਭਾਵ 2 ਗੁਲਾਮ, 2 ਬੇਗ਼ਮ ਅਤੇ 2 ਬਾਦਸ਼ਾਹ ਹਨ ।
∴ 6 ਲਾਲ ਰੰਗ ਦੇ ਤਸਵੀਰ ਵਾਲੇ ਪੱਤੇ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ = \(\frac{6}{52}\)
P (ਲਾਲ ਤਸਵੀਰ ਵਾਲਾ ਪੱਤਾ) = \(\frac{3}{26}\)

(iv) ਕਿਉਂਕਿ ਪਾਨ ਦਾ ਕੇਵਲ ਇੱਕ ਹੀ ਗੁਲਾਮ ਹੈ ।
∴ ਪਾਨ ਦਾ ਗੁਲਾਮ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ = \(\frac{1}{52}\)
P (ਇੱਕ ਪਾਨ ਦਾ ਗੁਲਾਮ) = \(\frac{1}{52}\)

(v) ਕਿਉਂਕਿ ਹੁਕਮ ਦੇ 13 ਪੱਤੇ ਹਨ ।
∴ ਹੁਕਮ ਦਾ ਪੱਤਾ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ = \(\frac{13}{52}\)
P(ਹੁਕਮ ਦਾ ਪੱਤਾ) = \(\frac{1}{4}\)

(vi) ਕਿਉਂਕਿ ਇੱਟ ਦੀ ਕੇਵਲ ਇੱਕ ਹੀ ਬੇਗਮ ਹੈ
∴ ਇੱਟ ਦੀ ਬੇਗ਼ਮ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ = \(\frac{1}{52}\)
P (ਇੱਟ ਦੀ ਬੇਗਮ) = \(\frac{1}{52}\)

ਪ੍ਰਸ਼ਨ 15.
ਤਾਸ਼ ਦੇ ਪੰਜ ਪੱਤਿਆਂ -‘ਇੱਟ ਦਾ ਦਹਿਲਾ , ਗੁਲਾਮ, ਬੇਗ਼ਮ, ਬਾਦਸ਼ਾਹ ਅਤੇ ਧੱਕੇ ਨੂੰ ਪਲਟ ਕੇ ਚੰਗੀ ਤਰ੍ਹਾਂ ਫੈਂਟਿਆਂ ਗਿਆ ਹੈ । ਫਿਰ ਇਹਨਾਂ ਵਿੱਚੋਂ ਅਚਾਨਕ ਇੱਕ ਪੱਤਾ ਬਾਹਰ ਕੱਢਿਆ ਜਾਂਦਾ ਹੈ ।
(i) ਇਸਦੀ ਕੀ ਸੰਭਾਵਨਾ ਹੈ ਕਿ ਇਹ ਪੱਤਾ ਇੱਕ ਬੇਗ਼ਮ ਹੈ ?
(ii) ਜੇਕਰ ਬੇਗ਼ਮ ਆਉਂਦੀ ਹੈ ਤਾਂ, ਉਸਨੂੰ ਅੱਲਗ ਰੱਖ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ਅਤੇ ਇੱਕ ਹੋਰ ਪੱਤਾ ਬਾਹਰ ਕੱਢਿਆ ਜਾਂਦਾ ਹੈ । ਇਸਦੀ ਕੀ ਸੰਭਾਵਨਾ ਹੈ ਕਿ ਦੂਸਰਾ ਕੱਢਿਆ ਗਿਆ ਪੱਤਾ
(a) ਇੱਕ ਯੁੱਕਾ ਹੈ ?
(b) ਇੱਕ ਬੇਗ਼ਮ ਹੈ ?
ਹੱਲ:
ਪੰਜ ਪੱਤੇ ਇੱਟ ਦਾ ਦਹਿਲਾ, ਗੁਲਾਮ, ਬੇਗਮ, ਬਾਦਸ਼ਾਹ ਅਤੇ ਇੱਟ ਹਨ ।
(i) ਬੇਗ਼ਮ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ = \(\frac{1}{5}\)
∴ P (ਇੱਕ ਬੇਗ਼ਮ) = \(\frac{1}{5}\)

(ii) ਜੇਕਰ ਬੇਗ਼ਮ ਆਉਂਦੀ ਹੈ ਤਾਂ ਉਸ ਨੂੰ ਅਲੱਗ ਰੱਖ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ਤਾਂ ਬਾਕੀ ਚਾਰ ਪੱਤੇ ਬੱਚ ਜਾਂਦੇ ਹਨ । ਇੱਟ ਦਾ ਦਹਿਲਾ, ਗੁਲਾਮ, ਬਾਦਸ਼ਾਹ ਅਤੇ ਧੱਕਾ
(a) ਯੱਕਾ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ = \(\frac{1}{4}\)
|P (ਇੱਕ ਯੱਕਾ) = \(\frac{1}{4}\)
ਕੋਈ ਬੇਗ਼ਮ ਨਹੀਂ ਬਚੀ ।
(b) ਬੇਗ਼ਮ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ = \(\frac{0}{4}\) = 0
P (ਬੇਗ਼ਮ) = 0

ਪ੍ਰਸ਼ਨ 16.
ਕਿਸੇ ਕਾਰਨ 12 ਖਰਾਬ ਪੈੱਨ 132 ਚੰਗੇ ਪੈਂਨਾਂ ਵਿੱਚ ਮਿਲ ਗਏ ਹਨ । ਕੇਵਲ ਵੇਖ ਕੇ ਨਹੀਂ ਦੱਸਿਆ ਜਾ ਸਕਦਾ ਕਿ ਕੋਈ ਪੈੱਨ ਖਰਾਬ ਹੈ ਜਾਂ ਠੀਕ ਹੈ ।ਇਸ ਮਿਸ਼ਰਣ ਵਿੱਚੋਂ, ਇੱਕ ਪੈਂਨ ਅਚਾਨਕ ਬਾਹਰ ਕੱਢਿਆ ਜਾਂਦਾ ਹੈ । ਬਾਹਰ ਕੱਢੇ ਗਏ ਪੈਂਨ ਦੇ ਠੀਕ ਹੋਣ ਦੀ ਸੰਭਾਵਨਾ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਖਰਾਬ ਪੈਂਨਾਂ ਦੀ ਸੰਖਿਆਂ = 12
ਚੰਗੇ ਪੈਂਨਾਂ ਦੀ ਸੰਖਿਆਂ = 132
∴ ਐੱਨਾਂ ਦੀ ਕੁੱਲ ਸੰਖਿਆਂ = 12 + 132 = 144
ਚੰਗੇ ਪੈੱਨ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ = \(\frac{132}{144}\) = \(\frac{11}{12}\)
P (ਇੱਕ ਚੰਗਾ ਪੈਂਨ) = \(\frac{11}{12}\)

ਪ੍ਰਸ਼ਨ 17.
(i) 20 ਬਲਬਾਂ ਦੇ ਇੱਕ ਸਮੂਹ ਵਿੱਚ 4 ਬਲਬ ਖਰਾਬ ਹਨ ।ਇਸ ਸਮੂਹ ਵਿੱਚੋਂ ਇੱਕ ਬਲਬ ਅਚਾਨਕ ਬਾਹਰ ਕੱਢਿਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਦੀ ਕੀ ਸੰਭਾਵਨਾ ਹੈ ਕਿ ਇਹ ਬਲਬ ਖ਼ਰਾਬ ਹੋਵੇਗਾ ?
(ii) ਮੰਨ ਲਓ (i) ਵਿੱਚ ਬਾਹਰ ਕੱਢਿਆ ਗਿਆ ਬਲਬ | ਖ਼ਰਾਬ ਨਹੀਂ ਹੈ ਅਤੇ ਨਾ ਹੀ ਇਸਨੂੰ ਦੁਬਾਰਾ ਬਲਬਾਂ ਦੇ ਨਾਲ ਮਿਲਾਇਆ ਜਾਂਦਾ ਹੈ । ਹੁਣ ਬਾਕੀ ਬਲਬਾਂ ਵਿੱਚੋਂ ਇੱਕ ਬਲਬ ਅਚਾਨਕ ਕੱਢਿਆ ਜਾਂਦਾ ਹੈ ।ਇਸਦੀ ਕੀ ਸੰਭਾਵਨਾ ਹੈ ਕਿ ਇਹ ਬਲਬ ਖ਼ਰਾਬ ਨਹੀਂ ਹੋਵੇਗਾ?
ਹੱਲ:
(i) ਖ਼ਰਾਬ ਬਲਬਾਂ ਦੀ ਸੰਖਿਆਂ = 4
ਚੰਗੇ ਬਲਬਾਂ ਦੀ ਸੰਖਿਆਂ = 16
ਬਲਬਾਂ ਦੀ ਕੁੱਲ ਸੰਖਿਆਂ = 4 + 16 = 20
ਖ਼ਰਾਬ ਬਲਬ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ = \(\frac{4}{20}\)

(ii) ਜਦੋਂ ਕੱਢਿਆ ਗਿਆ ਬਲਬ ਦੁਬਾਰਾ ਬਲਬਾਂ ਵਿਚ ਨਹੀਂ ਮਿਲਾਇਆ ਜਾਂਦਾ, ਤਾਂ 19 ਬਲਬ ਬਾਕੀ ਬਚਦੇ ਹਨ ।
ਹੁਣ ਖ਼ਰਾਬ ਬਲਬ ਪ੍ਰਾਪਤ ਨਾ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ = \(\frac{15}{19}\)
∴ P (ਬਲਬ ਖ਼ਰਾਬ ਨਹੀਂ) = \(\frac{15}{19}\)

ਪ੍ਰਸ਼ਨ 18.
ਇੱਕ ਪੇਟੀ ਵਿੱਚ 90 ਪਲੇਟਾਂ (discs) ਹਨ , ਜਿਹਨਾਂ ਉੱਤੇ 1 ਤੋਂ 90 ਤੱਕ ਸੰਖਿਆਵਾਂ ਲਿਖੀਆਂ ਹਨ । ਜੇਕਰ ਇਸ ਪੇਟੀ ਵਿੱਚੋਂ ਇੱਕ ਪਲੇਟ ਅਚਾਨਕ ਬਾਹਰ ਕੱਢੀ ਜਾਂਦੀ ਹੈ ਤਾਂ ਕੀ ਇਸਦੀ ਸੰਭਾਵਨਾ ਪਤਾ ਕਰੋ ਕਿ ਇਸ ਪਲੇਟ ਉੱਤੇ ਅੰਕਿਤ ਹੋਵੇਗੀ ।
(i) ਦੋ ਅੰਕਾਂ ਦੀ ਇੱਕ ਸੰਖਿਆ
(ii) ਇੱਕ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ
(iii) 5 ਨਾਲ ਵੰਡੀ ਜਾਣ ਵਾਲੀ ਇੱਕ ਸੰਖਿਆ ।
ਹੱਲ:
1 ਤੋਂ 90 ਤੱਕ ਕੁੱਲ 90 ਸੰਖਿਆਵਾਂ ਹਨ ਅਤੇ 10 ਤੋਂ 90 ਤੱਕ 80 ਸੰਖਿਆਵਾਂ 2 ਅੰਕਾਂ ਵਾਲੀਆਂ ਹਨ ।
(i) ਦੋ ਅੰਕਾਂ ਵਾਲੀ ਸੰਖਿਆਂ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ = \(\frac{81}{90}\)
∴ P (ਦੋ ਅੰਕਾਂ ਦੀ ਇੱਕ ਸੰਖਿਆ) = \(\frac{81}{90}\)

(ii) ਪੂਰਨ ਵਰਗ ਸੰਖਿਆਵਾਂ ਹਨ :{1, 4, 9, 16, 25, 36, – 49, 64, 81} 1 ਤੋਂ 90 ਤੱਕ 9 ਪੁਰਨ ਵਰਗ ਸੰਖਿਆਵਾਂ ਹਨ ।
∴ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ
= \(\frac{9}{90}\) = \(\frac{1}{10}\)
P (ਇੱਕ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ) = \(\frac{1}{10}\)

(iii) 5 ਨਾਲ ਵੰਡੀਆਂ ਜਾਣ ਵਾਲੀਆਂ ਸੰਖਿਆਵਾਂ ਹਨ : {5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90}
5 ਨਾਲ ਵੰਡਣ ਯੋਗ 18 ਸੰਖਿਆਵਾਂ ਹਨ ।
∴ 5 ਨਾਲ ਵੰਡੀ ਜਾਣ ਵਾਲੀ ਸੰਖਿਆਦੀ ਸੰਭਾਵਨਾ
= \(\frac{18}{90}\) = \(\frac{1}{5}\)
∴ ਲੋੜੀਂਦੀ ਸੰਭਾਵਨਾ = \(\frac{1}{5}\)

ਪ੍ਰਸ਼ਨ 19.
ਇੱਕ ਬੱਚੇ ਦੇ ਕੋਲ ਇੱਕ ਅਜਿਹਾ ਪਾਸਾ ਹੈ ਜਿਸਦੇ ਫਲਕਾਂ ਉੱਤੇ ਹੇਠ ਲਿਖੇ ਅੱਖਰ ਅੰਕਿਤ ਹਨ ।

ਇਸ ਪਾਸੇ ਨੂੰ ਇੱਕ ਵਾਰ ਸੁੱਟਿਆ ਜਾਂਦਾ ਹੈ । ਇਸਦੀ ਕੀ ਸੰਭਾਵਨਾ ਹੈ ਕਿ
(i) A ਪ੍ਰਾਪਤ ਹੋਵੇ ?
(ii) D ਪ੍ਰਾਪਤ ਹੋਵੇ ?
ਹੱਲ:
ਪਾਸੇ ਦੇ ਫਲਕਾਂ ਦੀ ਸੰਖਿਆ = 6
S = {A, B, C, D, E, A}
n (S) = 6
(1) ਕਿਉਂਕਿ ਦੋ ਫਲਕਾਂ ਉੱਤੇ A ਹੈ ।
∴ A ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ = \(\frac{2}{6}\) = \(\frac{1}{3}\)
P(A) = \(\frac{1}{3}\)
(2) ਕਿਉਂਕਿ ਕੇਵਲ ਇੱਕ ਫਲਕ ਉੱਤੇ D ਹੈ ।
D ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ = \(\frac{1}{6}\)
∴ P(D) = \(\frac{1}{6}\)

ਪ੍ਰਸ਼ਨ 20.
ਮੰਨ ਲਓ ਤੁਸੀਂ ਇੱਕ ਪਾਸੇ ਨੂੰ ਚਿੱਤਰ ਵਿੱਚ ਦਰਸਾਏ ਆਇਤਾਕਾਰ ਖੇਤਰ ਵਿੱਚ ਅਚਾਨਕ ਸੁੱਟਦੇ ਹੋ । ਇਸਦੀ ਕੀ ਸੰਭਾਵਨਾ ਹੈ ਕਿ ਇਹ ਪਾਸਾ 1m ਵਿਆਸ ਵਾਲੇ ਚੱਕਰ ਦੇ ਅੰਦਰ ਡਿੱਗੇਗਾ ?

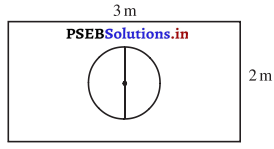
ਹੱਲ:
ਆਇਤ ਦੀ ਲੰਬਾਈ (1) = 3 m
ਆਇਤ ਦੀ ਚੌੜਾਈ (b) = 2 m
∴ ਆਇਤ ਦਾ ਖੇਤਰਫਲ = 3 m × 2 m = 6 m²
ਚੱਕਰ ਦਾ ਵਿਆਸ = 1 m
ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ (R) = \(\frac{1}{2}\) m
∴ ਚੱਕਰ ਦਾ ਖੇਤਰਫਲ = πR²
= π\(\left(\frac{1}{2}\right)^{2}\) = \(\frac{\pi}{4}\) m²
ਚੱਕਰ ਦੇ ਅੰਦਰ ਡਿੱਗਣ ਵਾਲੇ ਪਾਸੇ ਦੀ ਸੰਭਾਵਨਾ

∴ ਲੋੜੀਂਦੀ ਸੰਭਾਵਨਾ = \(\frac{\pi}{24}\)

ਪ੍ਰਸ਼ਨ 21.
144 ਬਾਲ ਪੈਂਨਾਂ ਦੇ ਇੱਕ ਸਮੂਹ ਵਿੱਚ 20 ਬਾਲ ਪੈੱਨ ਖ਼ਰਾਬ ਹਨ ਅਤੇ ਬਾਕੀ ਠੀਕ ਹਨ |ਤੁਸੀਂ ਉਹੀ ਪੈਂਨ ਖ਼ਰੀਦਣਾ ਚਾਹੋਗੇ ਜਿਹੜਾ ਠੀਕ ਹੈ, ਪਰੰਤੂ ਖ਼ਰਾਬ ਪੈੱਨਤੁਸੀਂ ਖਰੀਦਣਾ ਨਹੀਂ ਚਾਹੋਗੇ !ਦੁਕਾਨਦਾਰ ਇਹਨਾਂ ਪੈਂਨਾਂ ਵਿੱਚੋਂ ਅਚਾਨਕ ਇੱਕ ਪੈਂਨ ਬਾਹਰ ਕੱਢ ਕੇ ਤੁਹਾਨੂੰ ਦਿੰਦਾ ਹੈ ।ਇਸਦੀ ਕੀ ਸੰਭਾਵਨਾ ਹੈ ਕਿ
(i) ਤੁਸੀਂ ਉਹ ਪੈਂਨ ਖਰੀਦੋਗੇ ?
(ii) ਤੁਸੀਂ ਉਹ ਪੈਂਨ ਨਹੀਂ ਖਰੀਦੋਗੇ ?
ਹੱਲ:
ਸਮੂਹ ਦੇ ਬਾਲ ਪੈਂਨਾਂ ਦੀ ਕੁੱਲ ਸੰਖਿਆ = 144
ਖਰਾਬ ਪੈਂਨਾਂ ਦੀ ਸੰਖਿਆ = 20
∴ ਚੰਗੇ ਪੈਂਨਾਂ ਦੀ ਸੰਖਿਆ = 144 – 20
= 124
(i) ਮੰਨ ਲਉ ਤੁਸੀਂ ਉਹ ਪੈਂਨ ਖਰੀਦਣ ਦੀ ਘਟਨਾ ਨੇ ਹੈ
∴ ਐੱਨ ਖਰੀਦਣ ਦੀ ਸੰਭਾਵਨਾ = \(\frac{124}{144}\)
P(A) = \(\frac{31}{36}\)

(ii) ਉਹ ਪੈਂਨ ਨਹੀਂ ਖਰੀਦਣ ਦੀ ਘਟਨਾ ਨੇ ਹੋਵੇਗੀ ।
P(\(\overline{\mathrm{A}}\)) = 1 – P (A)
= 1 – \(\frac{31}{36}\)
= \(\frac{36-31}{36}\)
∴ P (ਪੈਂਨ ਨਹੀਂ ਖਰੀਦਣਾ) = \(\frac{5}{36}\)

ਪ੍ਰਸ਼ਨ 22.
ਇੱਕ ਸਲੇਟੀ ਪਾਸੇ ਅਤੇ ਨੀਲੇ ਪਾਸੇ ਨੂੰ ਇੱਕਠੇ ਸੁੱਟਿਆ ਜਾਂਦਾ ਹੈ । ਸਾਰੇ ਸੰਭਾਵਿਤ ਪਰਿਣਾਮਾਂ ਨੂੰ ਲਿਖੋ ।
(i) ਹੇਠ ਲਿਖੀ ਸਾਰਣੀ ਨੂੰ ਪੂਰਾ ਕਰੇ :

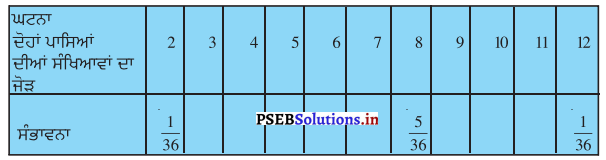
(ii) ਇਕ ਵਿਦਿਆਰਥੀ ਇਹ ਤਰਕ ਦਿੰਦਾ ਹੈ ਕਿ ‘ਇੱਥੇ ਕੁੱਲ 11 ਪਰਿਣਾਮ 2, 3, 4, 5, 6, 7, 8, 910, 11 ਅਤੇ 12 ਹਨ । ਇਸ ਕਰਕੇ ਹਰੇਕ ਦੀ ਸੰਭਾਵਨਾ \(\frac{1}{11}\) ਹੈ । ਕੀ ਤੁਸੀਂ ਇਸ ਤਰਕ ਨਾਲ ਸਹਿਮਤ ਹੋ ? ਕਾਰਨ ਸਹਿਤ ਉੱਤਰ ਦਿਓ ।
ਹੱਲ:
ਜਦੋਂ ਦੋ ਪਾਸੇ ਸੁੱਟੇ ਜਾਂਦੇ ਹਨ ਤਾਂ ਸੰਭਾਵਿਤ ਪਰਿਣਾਮਾਂ ਦੀ ਕੁੱਲ ਸੰਖਿਆ ਹੈ :
S = {(1,1) (1, 2) (1, 3) (1, 4) (1,5) (1,6)
(2, 1) (2, 2) (2, 3) (2, 4) (2,5) (2, 6)
(3, 1) (3, 2) (3, 3) (3, 4) (3, 5) (3,6)
(4, 1) (4, 2) (4, 3) (4, 4) (4, 5) (4, 6)
(5, 1) (5, 2) (5, 3) (5, 4) (5, 5) (5, 6)
(6, 1) (6, 2) (6, 3) (6,4) (6,5) (6, 6)}
n (S) = 36
ਮੰਨ ਲਉ ਜੋੜ 3 ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਘਟਨਾ ਨੇ ਹੈ ।
∴ A = {1, 2) (2, 1)}
n (A) = 2
∴ ਜੋੜ ਤੇ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ = \(\frac{2}{36}\) = \(\frac{1}{18}\)
P(A) = \(\frac{1}{18}\)
ਮੰਨ ਲਓ ਜੋੜ ‘4 ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਘਟਨਾ B ਹੈ ।
B = {(1, 3), (3, ; (2, 2)}
n(B) = 3
∴ P(B) = \(\frac{3}{36}\) = \(\frac{1}{12}\)
ਮੰਨ ਲਓ ਜੋੜ ‘5 ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ ਹੈ ।
C = {(1, 4) (4, 1) (2, 3) (3, 2)}
n (C) = 4
P(C) = \(\frac{4}{36}\) = \(\frac{1}{9}\)
ਮੰਨ ਲਓ ਜੋੜ ‘ੴ’ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਘਟਨਾ ਹੈ ।
D= {(1, 5) (5, 1) (2, 4) (4, 2) (3, 3)}
n (D) = 5
∴ P (D) = \(\frac{5}{36}\)
ਮੰਨ ਲਓ ਜੋੜ ‘7′ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਘਟਨਾ E ਹੈ ।
E = {(1, 6) (6, 1) (2, 5) (5, 2) (4, 3) (3, 4)}
n (E) = 6
∴ P (E) = P (ਜੋੜ 7 ਪ੍ਰਾਪਤ ਕਰਨਾ) = \(\frac{6}{36}\) = \(\frac{1}{6}\)
ਜਦੋਂ ਦੋਵੇਂ ਪਾਸਿਆਂ ਨੂੰ ਸੁੱਟਿਆਂ ਜਾਂਦਾ ਹੈ ਤਾਂ
ਮੰਨ ਲਓ ਜੋੜ ‘8’ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਘਟਨਾ F ਹੈ !
F= {(2, 6) (6, 2) (3, 5) (4, 4) (5, 3)}
∴ n (F) = 5
P (F) = P (ਜੋੜ 8 ਪ੍ਰਾਪਤ ਕਰਨਾ) = \(\frac{5}{36}\)
ਮੰਨ ਲਓ ਜੋੜ ‘9′ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਘਟਨਾ G ਵੈ
G = {(4, 5) (5, 4) (3, 6) (6, 3)}
n(G) = 4
∴ P (G) = P (ਜੋੜ 9 ਪ੍ਰਾਪਤ ਕਰਨਾ) = \(\frac{4}{36}\) = \(\frac{1}{9}\)
ਮੰਨ ਲਓ ਜੋੜ ‘10′ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਘਟਨਾ H ਵੈ
H = {(6, 4) (4, 6) (5, 5)}
n (H) = 3
∴ P(H) = P (ਜੋੜ 10 ਪ੍ਰਾਪਤ ਕਰਨਾ) = \(\frac{3}{36}\) = \(\frac{1}{12}\)
ਮੰਨ ਲਉ ਜੋੜ ‘11′ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਘਟਨਾ I ਹੈ ।
I = {(5, 6) (6, 5)}
n (I) = 2
∴ P(I) = P (ਜੋੜ 11 ਪ੍ਰਾਪਤ ਕਰਨਾ) = \(\frac{2}{36}\) = \(\frac{1}{18}\)
ਮੰਨ ਲਓ ਜੋੜ ’12’ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਘਟਨਾ J ਹੈ ।
J = {(6, 6}; n (J) = 1
∴ P (J) = \(\frac{1}{36}\)

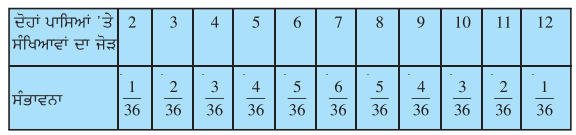
(ii) ਨਹੀਂ ਸਾਰੇ 11 ਸਮ ਸੰਭਾਵੀ ਸੰਭਾਵਿਤ ਪਰਿਣਾਮ ਨਹੀਂ ਹਨ । ਕਿਉਂਕਿ ਉਨ੍ਹਾਂ ਦੀ ਸੰਭਾਵਨਾ ਭਿੰਨ-ਭਿੰਨ ਹੈ ।

ਪ੍ਰਸ਼ਨ 23.
ਇੱਕ ਖੇਡ ਵਿੱਚ ਇੱਕ ਰੁਪਏ ਦੇ ਸਿੱਕੇ ਨੂੰ ਤਿੰਨ ਵਾ ਉਛਾਲਿਆ ਜਾਂਦਾ ਹੈ ਅਤੇ ਹਰੇਕ ਵਾਰ ਦਾ ਪਰਿਣਾਮ ਲਿ ॥ ਲਿਆ ਜਾਂਦਾ ਹੈ ।ਤਿੰਨੋ ਪਰਿਣਾਮ ਸਮਾਨ ਹੋਣ ਤੇ, ਭਾਵ ਤਿੰਨ ਚਿੱਤ ਜਾਂ ਤਿੰਨ ਪੱਟ ਪ੍ਰਾਪਤ ਹੋਣ ਤੇ, ਹਨੀਫ਼ ਖੇਡ ਵਿੱਚ ਜਿੱਤ ਜਾਏਗਾ, ਨਹੀਂ ਤਾਂ ਉਹ ਹਾਰ ਜਾਏਗਾ | ਹਨੀਫ਼ ਦੇ ਖੇਡ ਵਿੱਚ ਹਾਰ ਜਾਣ ਦੀ ਸੰਭਾਵਨਾ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਜਦੋਂ ਇੱਕ ਰੁਪਏ ਦੇ ਸਿੱਕੇ ਨੂੰ ਤਿੰਨ ਵਾਰ ਉਛਾਲਿਆ ਜਾਂਦਾ ਹੈ ਤਾਂ ਸੰਭਾਵਿਤ ਪਰਿਣਾਮ
S = {HHH, HHT HTH, THH, HTT, THT, TTH, TTT}
n (S) = 8
ਮੰਨ ਲਓ ਤਿੰਨ ਪਰਿਣਾਮ ਸਮਾਨ ਹੋਣ ਦੀ ਘਟਨਾ A ਹੈ। ਭਾਵ {HHH, TTT}
∴ P (A) = \(\frac{2}{8}\) = \(\frac{1}{4}\)
ਹਾਰ ਜਾਣ ਦੀ ਸੰਭਾਵਨਾ = 1 – P (A)
P(\(\overline{\mathrm{A}}\)) = 1 – \(\frac{1}{4}\)
= \(\frac{4-1}{4}\)
= \(\frac{3}{4}\)
∴ ਹਾਰ ਜਾਣ ਦੀ ਸੰਭਾਵਨਾ = \(\frac{3}{4}\)

ਪ੍ਰਸ਼ਨ 24.
ਇੱਕ ਪਾਸੇ ਨੂੰ ਦੋ ਬਾਰ ਸੁੱਟਿਆ ਜਾਂਦਾ ਹੈ । ਇਸਦੀ ਕੀ ਸੰਭਾਵਨਾ ਹੈ ਕਿ
(i) 5 ਕਿਸੇ ਵੀ ਵਾਰ ਨਹੀਂ ਆਏਗਾ ?
(ii) 5 ਘੱਟੋ ਘੱਟ ਇੱਕ ਵਾਰ ਆਏਗਾ ?
ਹੱਲ:
ਜਦੋਂ ਪਾਸੇ ਨੂੰ ਦੋ ਵਾਰ ਸੁੱਟਿਆਂ ਜਾਂਦਾ ਹੈ ਤਾਂ ਸੰਭਾਵਿਤ ਪਰਿਣਾਮ
S = {(1, 1) (1, 2) (1, 3) (1, 4) (1, 5) (1,6)
(2, 1) (2, 2) (2, 3) (2, 4) (2, 5) (2, 6)
(3, 1) (3, 2) (3, 3) (3, 4) (3, 5) (3, 6)
(4,1) (4, 2) (4, 3) (4, 4) (4, 5) (4, 6)
(5, 1) (5, 2) (5, 3) (5, 4) (5, 5) (5, 6)
(6, 1) (6, 2) (6, 3) (6, 4) (6, 5) (6,6)}
n (S) = 36
ਮੰਨ ਲਓ ‘5’ ਹਰੇਕ ਵਾਰ ਆਏਗਾ ਘਟਨਾ A ਹੈ
A = {(1, 5) (2, 5) (3, 5) (4, 5) (5, 5) (6, 5) (5, 1) (5, 2) (5, 3) (5, 4) (5, 5)}
n (A) = 11
∴ ‘5’ ਇੱਕ ਵਾਰ ਵੀ ਨਹੀਂ ਆਏਗਾ ਘਟਨਾ \(\overline{\mathrm{A}}\) ਹੈ ।
n (\(\overline{\mathrm{A}}\)) = 36 – 11 = 25
(i) ∴ ‘5’ ਇਕ ਵਾਰ ਵੀ ਨਹੀਂ ਆਏਗਾ ਦੀ ਸੰਭਾਵਨਾ = \(\frac{25}{36}\), P(\(\overline{\mathrm{A}}\)) = \(\frac{25}{36}\)
‘5 ‘ ਘੱਟੋ ਘੱਟ ਇਕ ਵਾਰ ਆਏਗਾ = \(\frac{11}{36}\)
∴ P (A) = \(\frac{11}{36}\)

ਪ੍ਰਸ਼ਨ 25.
ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ਕਿਹੜਾ ਤਰਕ ਸੱਚ ਹੈ ਅਤੇ ਕਿਹੜਾ ਤਰਕ ਸੱਚ ਨਹੀਂ ਹੈ ? ਕਾਰਨ ਸਹਿਤ ਉੱਤਰ ਦਿਓ :
(i) ਜੇਕਰ ਦੋ ਸਿੱਕਿਆਂ ਨੂੰ ਇੱਕੋ ਵਾਰ ਉਛਾਲਿਆਂ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਇਸਦੇ ਤਿੰਨ ਸੰਭਾਵਿਤ ਪਰਿਣਾਮ ਦੋ ਚਿੱਤ, ਦੋ ਪੱਟ ਜਾਂ ਹਰੇਕ ਇੱਕ ਵਾਰ ਹੈ । ਇਸ ਕਰਕੇ ਇਹਨਾਂ ਵਿੱਚੋਂ ਹਰੇਕ ਪਰਿਣਾਮ ਦੀ ਸੰਭਾਵਨਾ \(\frac{1}{3}\) ਹੈ ।
(ii) ਜੇਕਰ ਇੱਕ ਪਾਸੇ ਨੂੰ ਸੁੱਟਿਆ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਉਸਦੇ ਸੰਭਾਵਿਤ ਪਰਿਣਾਮ-ਇੱਕ ਟਾਂਕ ਸੰਖਿਆ ਜਾਂ ਇੱਕ ਜਿਸਤ ਸੰਖਿਆ ਹੈ । ਇਸ ਕਰਕੇ ਇੱਕ ਟਾਂਕ ਸੰਖਿਆ ਪਤਾ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ \(\frac{1}{2}\) ਹੈ ।
ਹੱਲ:
(i) ਜਦੋ ਦੋ ਸਿੱਕਿਆਂ ਨੂੰ ਉਛਾਲਿਆਂ ਜਾਂਦਾ ਹੈ ਤਾਂ ਸੰਭਾਵਿਤ ਪਰਿਣਾਮ ਹਨ :
S = {HH, HT, TH, TT}
ਦੋ ਚਿੱਤ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ = \(\frac{1}{4}\)
P (HH) = \(\frac{1}{4}\)
ਦੋ ਪੱਟ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ = \(\frac{1}{4}\)
P (TT) = \(\frac{1}{4}\)
ਇਕ ਚਿੱਤ ਅਤੇ ਇੱਕ ਪੱਟ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ
= \(\frac{2}{4}\) = \(\frac{1}{2}\)
∴ (i) ਤਰਕ ਠੀਕ ਨਹੀਂ ਹੈ ।

(ii) ਜਦੋ ਪਾਸੇ ਨੂੰ ਸੁਣਿਆਂ ਜਾਂਦਾ ਹੈ ਤਾਂ ਸੰਭਾਵਿਤ ਪਰਿਣਾਮ ਹਨ :
S = {1, 2, 3, 4, 5, 6}
n (S) = 6
ਟਾਂਕ ਸੰਖਿਆ : 1, 3, 5
∴ ਟਾਂਕ ਸੰਖਿਆ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ = \(\frac{3}{6}\) = \(\frac{1}{2}\)
ਜਿਸਤ ਸੰਖਿਆ : 2, 4, 6
∴ ਜਿਸਤ ਦੀ ਸੰਖਿਆ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ = \(\frac{3}{6}\) = \(\frac{1}{2}\)
(ii) ਤਰਕ ਠੀਕ ਹੈ ।