Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 15 ਸੰਭਾਵਨਾ Ex 15.2 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 10 Maths Chapter 15 ਸੰਭਾਵਨਾ Exercise 15.2
ਪ੍ਰਸ਼ਨ 1.
ਦੋ ਗਾਹਕ ਸ਼ਾਮ ਅਤੇ ਏਕਤਾ ਇੱਕ ਵਿਸ਼ੇਸ਼ ਦੁਕਾਨ ਉੱਤੇ ਇੱਕ ਹੀ ਹਫ਼ਤੇ ਵਿੱਚ ਜਾ ਰਹੇ ਹਨ । (ਮੰਗਲਵਾਰ ਤੋਂ ਸ਼ਨੀਵਾਰ ਤੱਕ) ਹਰੇਕ ਦੁਆਰਾ ਦੁਕਾਨ ਉੱਤੇ ਕਿਸੇ ਦਿਨ ਜਾਂ ਕਿਸੇ ਹੋਰ ਦਿਨ ਜਾਣ ਦੇ ਪਰਿਣਾਮ ਸਮਸੰਭਾਵੀ (ਬਰਾਬਰ ਸੰਭਾਵਨਾ ਵਾਲੇ) ਹਨ । ਇਸਦੀ ਕੀ ਸੰਭਾਵਨਾ ਹੈ ਕਿ ਦੋਨੋਂ ਉਸ ਦੁਕਾਨ ਤੇ
(i) ਇੱਕ ਹੀ ਦਿਨ ਜਾਣਗੇ ?
(ii) ਕ੍ਰਮਵਾਰ (ਨਾਲ-ਨਾਲ ਵਾਲੇ ਦਿਨਾਂ ਵਿੱਚ ਜਾਣਗੇ ?
(iii) ਭਿੰਨ-ਭਿੰਨ ਦਿਨਾਂ ਵਿੱਚ ਜਾਣਗੇ ?
ਹੱਲ:
ਜਦੋਂ ਸ਼ਾਮ ਅਤੇ ਏਕਤਾ ਇੱਕ ਦੁਕਾਨ ਉੱਤੇ ਇੱਕ ਹਫ਼ਤੇ ਜਾਣਗੇ ਤਾਂ ।
S = {(T, T) (T, W) (T, Th) (T, F) (T, S)
(W, T) (W, W) (W, Th) (W, F) (W, S)
(Th, T) (Th, W) (Th, Th) (Th, F) (Th, S)
(F, T) (F, W) (F, Th) (F, F) (F, S)
(S, T) (S, W) (S, Th) (S, F) (S, S)}
ਇੱਥੇ T ਮੰਗਲਵਾਰ ਲਈ, W ਬੁੱਧਵਾਰ, Th ਵੀਰਵਾਰ,
F ਸ਼ੁਕਰਵਾਰ, S ਸ਼ਨੀਵਾਰ ਲਈ ਹੈ।
n(S) = 25
(i) ਮੰਨ ਲਓ ਸ਼ਾਮ ਅਤੇ ਏਕਤਾ ਦੀ ਦੁਕਾਨ ਤੇ ਜਾਣ ਦੀ ਘਟਨਾ A ਹੈ ।
A = {(T, T), (W, W) (Th, Th) (F, F), (S, S)}
n (A) = 5
ਦੋਵੇਂ ਇੱਕ ਹੀ ਦਿਨ ਜਾਣਗੇ ਦੀ ਸੰਭਾਵਨਾ ਹੈ।
= \(\frac{5}{25}\) = \(\frac{1}{5}\)
∴ P(A) = \(\frac{1}{5}\)
(ii) ਮੰਨ ਲਉ ਸ਼ਾਮ ਅਤੇ ਏਕਤਾ ਉਸ ਦੁਕਾਨ ਤੇ ਕ੍ਰਮਵਾਰ ਦਿਨਾਂ ਵਿਚ ਜਾਣਗੇ ਦੀ ਘਟਨਾ B ਹੈ .
(B) = [(T, W) (W, T) (W, Th), (Th, W) (Th, F) (F, Th) (F, S) (F, S)]
n (B) = 8
∴ “ਦੋਵੇਂ ਕ੍ਰਮਵਾਰ ਦਿਨਾਂ ਵਿੱਚ ਦੁਕਾਨ ਤੇ ਜਾਣਗੇ’ ਦੀ ਸੰਭਾਵਨਾ ਹੈ = \(\frac{8}{25}\)
(iii) ਸੰਭਾਵਨਾ ਕਿ ਦੋਵੇਂ ਉਸ ਦੁਕਾਨ ਤੇ ਭਿੰਨ ਭਿੰਨ ਦਿਨਾਂ ਵਿੱਚ ਜਾਣਗੇ
= 1 – ਸੰਭਾਵਨਾ ਕਿ ਦੋਵੇਂ ਉਸ ਦਾਕਾਨ ਤੇ ਇੱਕ ਹੀ ਦਿਨ ਜਾਣਗੇ
= 1 – \(\frac{1}{5}\) ∵[∴ P(\(\overline{\mathrm{A}}\)) = 1 – P(A)]
= \(\frac{5-1}{5}\)
= \(\frac{4}{5}\)
![]()
ਪ੍ਰਸ਼ਨ 2.
ਇੱਕ ਪਾਸੇ ਦੇ ਫਲਕਾਂ ਉੱਤੇ ਸੰਖਿਆਂਵਾਂ 1, 2, 2, 3, 6 ਲਿਖੀਆਂ ਹੋਈਆਂ ਹਨ ? ਇਸ ਨੂੰ ਦੋ ਵਾਰ ਸੁੱਟਿਆ ਜਾਂਦਾ ਹੈ ਅਤੇ ਦੋਨੋਂ ਵਾਰ ਪ੍ਰਾਪਤ ਹੋਈਆਂ ਸੰਖਿਆਂਵਾਂ ਦਾ ਜੋੜ ਲਿਖ ਲਿਆ ਜਾਂਦਾ ਹੈ । ਦੋਨੋਂ ਵਾਰ ਸੁੱਟਣ ਤੋਂ ਬਾਦ, ਪ੍ਰਾਪਤ ਜੋੜ ਦੇ ਕੁੱਝ ਸੰਭਾਵਿਤ ਮੁੱਲ ਹੇਠਾਂ ਦਿੱਤੀ ਸਾਰਨੀ ਵਿੱਚ ਦਿੱਤੇ ਹਨ । | ਇਸ ਸਾਰਨੀ ਨੂੰ ਪੂਰਾ ਕਰੋ ।
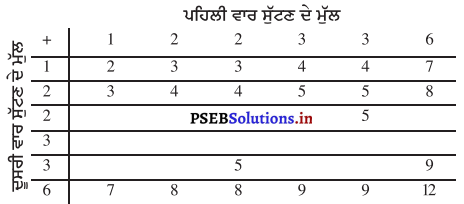
ਇਸ ਦੀ ਕੀ ਸੰਭਾਵਨਾ ਹੈ ਕਿ ਕੁੱਲ ਜੋੜ
(i) ਇੱਕ ਜਿਸਤ ਸੰਖਿਆ ਹੋਵੇਗਾ ?
(ii) 6 ਹੈ ?
(iii) ਘੱਟ ਤੋਂ ਘੱਟ 6 ਹੈ ?
ਹੱਲ:
ਪੂਰਨ ਸਾਰਨੀ : ਪਹਿਲੀ ਵਾਰ ਸੁੱਟਣ ਦੇ ਮੁੱਲ
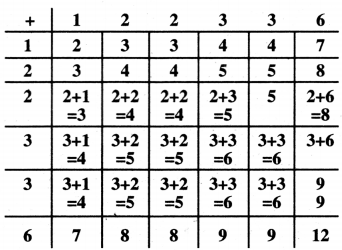
ਦੂਸਰੀ ਵਾਰ ਸੁੱਟਣ ਦੇ ਮੁੱਲ
ਸੰਭਾਵਿਤ ਪਰਿਣਾਮਾਂ ਦੀ ਸੰਖਿਆ ਹੈ 6 × 6 = 36
(i) ਮੰਨ ਲਓ ‘ਕੁੱਲ ਜੋੜ, ਇਕ ਸੰਖਿਆ’ ਪ੍ਰਾਪਤ ਕਰਨਾ ਘਟਨਾ A ਹੈ ।
A = {2, 4, 4, 4, 4, 4, 4, 4, 4, 6, 6, 6, 6, 8, 8, 8, 8, 12}
n (A) = 18
∴ ਇਕ ਜਿਸਤ ਸੰਖਿਆ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ
= \(\frac{18}{36}\) = \(\frac{1}{2}\)
P (ਜਿਸਤ ਸੰਖਿਆ) = \(\frac{1}{2}\)
(ii) ਮੰਨ ਲਓ ‘ਜੋੜ 6 ਪ੍ਰਾਪਤ ਕਰਨਾ’ ਘਟਨਾ B ਹੈ ।
B = {6, 6, 6, 6}
n (B) = 4,
∴ ਕੁਲ ਜੋੜ 6 ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ = \(\frac{4}{36}\)
∴ P (B) = \(\frac{1}{9}\)
(iii) ਮੰਨ ਲਓ ‘ਕੁਲ ਜੋੜ ਘੱਟ ਤੋਂ ਘੱਟ 6′ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਘਟਨਾ ‘C’ ਹੈ ।
C = {6, 6, 6, 6, 7, 7, 8, 8, 8, 8, 9, 9, 9, 9, 12}
n (C) = 15
∴ ਜੋੜ ਘੱਟ-ਤੋਂ-ਘੱਟ 6 ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ
= \(\frac{15}{36}\) = \(\frac{5}{12}\)
∴ P (C) = \(\frac{5}{12}\)
ਪ੍ਰਸ਼ਨ 3.
ਇੱਕ ਥੈਲੇ ਵਿੱਚ 5 ਲਾਲ ਗੇਂਦਾਂ ਅਤੇ ਕੁੱਝ ਨੀਲੀਆਂ ਗੇਦਾਂ ਹਨ | ਜੇਕਰ ਇਸ ਥੈਲੇ ਵਿੱਚੋਂ ਨੀਲੀ ਗੇਂਦ ਕੱਢਣ ਦੀ ਸੰਭਾਵਨਾ ਲਾਲ ਗੇਂਦ ਬਾਹਰ ਕੱਢਣ ਦੀ ਸੰਭਾਵਨਾ ਤੋਂ ਦੁੱਗਣੀ ਹੈ, ਤਾਂ ਥੈਲੇ ਵਿੱਚ ਨੀਲੀਆਂ ਗੇਦਾਂ ਦੀ ਸੰਖਿਆ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਗੇਂਦਾਂ ਦੀ ਸੰਖਿਆ = 5
ਮੰਨ ਲਓ ਨੀਲੀਆਂ ਗੋਂਦਾਂ ਦੀ ਸੰਖਿਆ = x
∴ ਗੇਂਦਾਂ ਦੀ ਕੁੱਲ ਸੰਖਿਆ = 5 + x
ਨੀਲੀਆਂ ਗੇਂਦਾ ਕੱਢਣ ਦੀ ਸੰਭਾਵਨਾ = \(\frac{x}{5+x}\)
ਲਾਲ ਗੇਂਦ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ = \(\frac{5}{5+x}\)
ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ
ਨੀਲੀਆਂ ਗੇਂਦਾਂ ਦੀ ਸੰਭਾਵਨਾ = 2 ਲਾਲ ਗੇਂਦਾਂ ਦੀ ਸੰਭਾਵਨਾ
\(\frac{x}{5+x}\) = 2[latex]\frac{5}{5+x}[/latex]
x = 10
∴ ਨੀਲੀ ਗੇਂਦਾਂ ਦੀ ਸੰਖਿਆ = 10
![]()
ਪ੍ਰਸ਼ਨ 4.
ਇੱਕ ਪੇਟੀ ਵਿਚ 12 ਗੇਂਦਾਂ ਹਨ, ਜਿਹਨਾਂ ਵਿੱਚ 1 ਕਾਲੀਆਂ ਹਨ । ਜੇਕਰ ਇਸ ਵਿੱਚੋਂ ਇੱਕ ਗੇਂਦ ਅਚਾਨਕ | ਬਾਹਰ ਕੱਢੀ ਜਾਂਦੀ ਹੈ ਤਾਂ ਇਸਦੀ ਸੰਭਾਵਨਾ ਪਤਾ ਕਰੋ ਕਿ | ਇਹ ਗੇਂਦ ਕਾਲੀ ਹੈ । ਜੇਕਰ ਇਸ ਪੇਟੀ ਵਿੱਚ 6 ਕਾਲੀਆਂ | ਗੇਦਾਂ ਹੋਰ ਪਾ ਦਿੱਤੀਆਂ ਜਾਣ, ਤਾਂ ਕਾਲੀ ਗੇਂਦ ਨਿਕਲਣ ਦੀ ਸੰਭਾਵਨਾ ਪਹਿਲੀ ਸੰਭਾਵਨਾ ਨਾਲੋਂ ਦੁੱਗਣੀ ਹੋ ਜਾਂਦੀ ਹੈ । x ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਥੈਲੇ ਵਿਚ ਕੁੱਲ ਗੇਂਦਾਂ = 12
ਕਾਲੀ ਗੇਂਦਾਂ ਦੀ ਸੰਖਿਆ = x
∴ ਕਾਲੀ ਗੇਂਦਾਂ ਦੀ ਸੰਭਾਵਨਾ = \(\frac{x}{12}\)
ਜੇਕਰ ਥੈਲੇ ਵਿੱਚ 6 ਕਾਲੀ ਗੇਂਦਾਂ ਹੋਰ ਪਾ ਦਿੱਤੀਆਂ
ਜਾਣ ਤਾਂ ਕੁੱਲ ਗੇਂਦਾਂ = 12 + 6 = 18
ਕਾਲੀ ਗੇਂਦਾਂ ਦੀ ਸੰਖਿਆ = x + 6
ਕਾਲੀ ਗੇਂਦਾਂ ਦੀ ਸੰਭਾਵਨਾ = \(\frac{x+6}{18}\)
ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ
ਕਾਲੀ ਗੇਂਦਾਂ ਦੀ ਸੰਭਾਵਨਾ = 2 ਪਹਿਲਾਂ ਵਾਲੀ ਕਾਲੀ ਗੇਂਦ ਦੀ ਸੰਭਾਵਨਾ
\(\frac{x+6}{18}\) = \(\frac{2x}{12}\)
\(\frac{x+6}{3}\) = \(\frac{2x}{2}\)
\(\frac{x+6}{3}\) = x
x + 6 = 3x
6 = 3x – x
6 = 2x
x = 3
∴ ਕਾਲੀ ਗੇਂਦਾਂ ਦੀ ਸੰਖਿਆ = 3
![]()
ਪ੍ਰਸ਼ਨ 5.
ਇੱਕ ਡੱਬੇ ਵਿੱਚ 24 ਬੰਟੇ ਹਨ ਜਿਨ੍ਹਾਂ ਵਿੱਚੋਂ ਕੁੱਝ ਹਰੇ । ਹਨ ਅਤੇ ਬਾਕੀ ਨੀਲੇ ਹਨ । ਜੇਕਰ ਇਸ ਡੱਬੇ ਵਿੱਚੋਂ ਅਚਾਨਕ ਇੱਕ ਬੰਟਾ ਬਾਹਰ ਕੱਢਿਆ ਜਾਂਦਾ ਹੈ ਤਾਂ ਇਸ ਬੰਟੇ ਦੇ ਹਰਾ ਹੋਣ ਦੀ ਸੰਭਾਵਨਾ \(\frac{2}{3}\) ਹੈ । ਡੱਬੇ ਵਿੱਚ ਨੀਲੇ ਬੰਟਿਆਂ ਦੀ ਸੰਖਿਆ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਜਾਰ ਵਿੱਚ ਕੁੱਲ ਬੰਟੇ = 24
ਮੰਨ ਲਓ ਹਰੇ ਬੰਟੇ = x
∴ ਨੀਲੇ ਬੰਟੇ = 24 – x
ਜਦੋਂ ਇੱਕ ਬੰਟਾ ਬਾਹਰ ਕੱਢਿਆ ਜਾਂਦਾ ਹੈ, ਤਾਂ
ਹਰਾ ਬੰਟਾ ਬਾਹਰ ਨਿਕਲਣ ਦੀ ਸੰਭਾਵਨਾ = \(\frac{2}{3}\)
\(\frac{x}{24}\) = \(\frac{2}{3}\)
x = \(\frac{24×2}{3}\)
x = 16
∴ ਨੀਲੇ ਬੰਟਿਆਂ ਦੀ ਸੰਖਿਆਂ = 24 – x
= 24 – 16 = 8.
