Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 3 ਦੋ ਚਲਾਂ ਵਿੱਚ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਜੋੜੇ Ex 3.1 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 10 Maths Chapter 3 ਦੋ ਚਲਾਂ ਵਿੱਚ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਜੋੜੇ Exercise 3.1
ਪ੍ਰਸ਼ਨ 1.
ਬਲਦੇਵ ਆਪਣੀ ਲੜਕੀ ਨੂੰ ਕਹਿੰਦਾ ਹੈ, “ਸੱਤ ਸਾਲ ਪਹਿਲਾਂ ਮੈਂ ਤੇਰੇ ਨਾਲੋਂ ਸੱਤ ਗੁਣਾ ਉਮਰ ਦਾ ਸੀ । ਹੁਣ ਤੋਂ ਤਿੰਨ ਸਾਲ ਬਾਅਦ ਮੈਂ ਤੇਰੇ ਤੋਂ ਸਿਰਫ਼ ਤਿੰਨ ਗੁਣਾ ਉਮਰ ਦਾ ਰਹਿ ਜਾਵਾਂਗਾ । ਕੀ ਇਹ ਮੰਨੋਰੰਜਕ ਹੈ ?) ਇਸ ਸਥਿਤੀ ਨੂੰ ਬੀਜ ਗਣਿਤਿਕ ਅਤੇ ਗ੍ਰਾਫੀ ਰੂਪਾਂ ਵਿੱਚ ਵਿਅਕਤ ਕਰੋ (ਦਰਸਾਉ) ।
ਹੱਲ:
ਮੰਨ ਲਉ ਬਲਦੇਵ ਦੀ ਵਰਤਮਾਨ ਉਮਰ ਹੈ।
= x ਸਾਲ
ਅਤੇ ਬਲਦੇਵ ਦੀ ਲੜਕੀ ਦੀ ਵਰਤਮਾਨ ਉਮਰ = y ਸਾਲ
ਬੀਜ ਗਣਿਤਿਕ ਸਥਿਤੀ ਵਿੱਚ
ਪ੍ਰਸ਼ਨ ਦੀ ਪਹਿਲੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
x – 7 = 7 (y – 7)
ਜਾਂ x – 7 = 7y – 49
ਜਾਂ x – 7y + 42 = 0
ਪ੍ਰਸ਼ਨ ਦੀ ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
x + 3 = 3 (y + 3)
ਜਾਂ x + 3 = 3y + 9
ਜਾਂ x – 3y – 6 = 0
∴ ਦੋ ਚਲਾਂ ਵਿੱਚ ਰੇਖੀ ਸਮੀਕਰਣ ਜੋੜਾ ਹੈ :
x – 7y + 42 = 0
ਅਤੇ x – 3y – 6 = 0
ਗ੍ਰਾਫੀ ਸਥਿਤੀ ਵਿਚ
x – 7y + 42 = 0
x = 7y – 42 …..(1)
y = 5. ਨੂੰ (1) ਵਿਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = 7 × 5 – 42
= 35 – 42 = – 7
y = 6 ਨੂੰ (1) ਵਿਚ , ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x = 7 × 6 – 42
= 42 – 42 = 0
y = 7 ਨੂੰ (1) ਵਿਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x = 7 × 7 – 42
= 49 – 42 = 7
ਸਾਰਣੀ
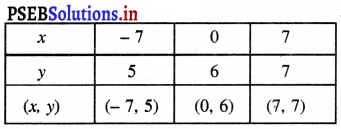
ਬਿੰਦੂਆਂ A (- 7, 5), B (0, 6), C (7, 7) ਨੂੰ ਅੰਕਿਤ ਕਰਨ ‘ਤੇ ਅਤੇ ਉਨ੍ਹਾਂ ਨੂੰ ਮਿਲਾਉਂਦੇ ਹੋਏ ਖਿਚਣ ‘ਤੇ ਸਾਨੂੰ ਸਮੀਕਰਣ x – 7y + 42 = 0 ਦਾ ਆਲੇਖ ਮਿਲਦਾ ਹੈ :
x – 3y – 6 = 0
x = 3y + 6 ….(2)
y = 0 ਨੂੰ (2), ਵਿਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = 3 × 0 + 6
= 0 + 6 = 6.
y = 3 ਨੂੰ (2) ਵਿਚ ਰੱਖਣ ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x = 3 × 3 + 6
= 9 + 6 = 15
y = – 2 ਨੂੰ (2) ਵਿੱਚ ਰੱਖਣ ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x = 3 × -2 + 6
= – 6 + 6 = 0
ਸਾਰਣੀ
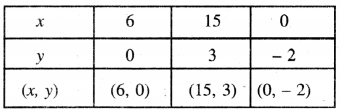
ਬਿੰਦੁਆਂ D (6, 0), E (15, 3), F (0, – 2) ਨੂੰ | ਆਲੇਖਿਤ ਕਰਨ ‘ਤੇ ਉਨ੍ਹਾਂ ਦੀ ਰੇਖਾ ਨੂੰ ਮਿਲਾਉਣ ‘ਤੇ ਸਾਨੂੰ | ਸਮੀਕਰਣ x – 3y – 6 = 0 ਦਾ ਆਲੇਖ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
ਆਲੇਖ ਤੋਂ ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਕਿ ਦੋਵੇਂ ਰੇਖਾਵਾਂ
G (42, 12) ਉੱਤੇ ਕੱਟਦੀਆਂ ਹਨ ।
ਇਸ ਲਈ, x = 42 ਅਤੇ y = 12 ਸਮੀਕਰਣਾਂ ਦੇ ਜੋੜੇ ਦਾ ਹੱਲ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 2.
ਕ੍ਰਿਕੇਟ ਟੀਮ ਦੇ ਇੱਕ ਕੋਚ ਨੇ ₹ 3900 ਵਿੱਚ 3 ਬੱਲੇ ਅਤੇ 6 ਗੇਂਦਾਂ ਖ਼ਰੀਦੀਆਂ । ਬਾਅਦ ਵਿਚ ਉਸਨੇ ਇਕ ਹੋਰ ਬੱਲਾ ਅਤੇ ਉਸੇ ਤਰ੍ਹਾਂ ਦੀਆਂ 3 ਗੇਂਦਾਂ ₹ 1300 ਵਿਚ ਖ਼ਰੀਦੀਆਂ । ਇਸ ਸਥਿਤੀ ਨੂੰ ਬੀਜ ਗਣਿਤਿਕ ਅਤੇ ਜਿਮਾਇਤੀ ਰੂਪਾਂ ਵਿੱਚ ਵਿਅਕਤ ਕਰੋ
ਹੱਲ:
ਮੰਨ ਲਉ ਇੱਕ ਬੱਲੇ ਦਾ ਮੁੱਲ = ₹ x
ਇੱਕ ਗੇਂਦ ਦਾ ਮੁੱਲ = ₹ y
ਬੀਜ ਗਣਿਤਿਕ ਹੱਲ:
ਪ੍ਰਸ਼ਨ ਦੀ ਪਹਿਲੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
3x +6y = 3900
ਜਾਂ x+ 2y = 1300
ਪ੍ਰਸ਼ਨ ਦੀ ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
1x + 3y = 1300
∴ ਦੋ ਚਲਾਂ ਵਿੱਚ ਰੇਖੀ ਸਮੀਕਰਣ ਜੋੜਾ ਹੈ :
1 + 2y = 1300
ਅਤੇ + 3y = 1300
ਆਲੇਖ ਸਥਿਤੀ ਵਿਚ
x + 2y = 1300
x = 1300 – 2y …..(1)
y = 0 ਨੂੰ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = 1300 – 2 × 0
x = 1300
y = 500 ਨੂੰ (1) ਵਿਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x = 1300 – 2 × 500
= 1300 – 1000 = 300
y = 650 ਨੂੰ (1) ਵਿਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x = 1300 – 2 × 650
x = 1300 – 1300 = 0
ਸਾਰਣੀ
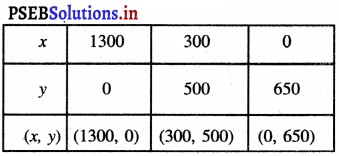
ਬਿੰਦੂਆਂ A (1300, 0), B (300, 500) ਅਤੇ C (0, 650) ਨੂੰ ਆਲੇਖਿਤ ਕਰਨ ਅਤੇ ਉਨ੍ਹਾਂ ਨੂੰ ਮਿਲਾਉਣ ਵਾਲੀ ਰੇਖਾ ਖਿਚਣ ‘ਤੇ ਸਾਨੂੰ ਸਮੀਕਰਣ x + 2y = 1300 ਦਾ ਆਲੇਖ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x + 3y = 1300
x = 1300 – 3y ……..(2)
y = 0 ਨੂੰ (2) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = 1300 – 3 × 0
= 1300
y = 500 ਨੂੰ (2) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x = 1300 – 3 × 500
= 1300 – 1500 = – 200
y = 300 ਨੂੰ (2) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x = 1300 – 3 × 300
= 1300 – 900 = 400
ਸਾਰਣੀ

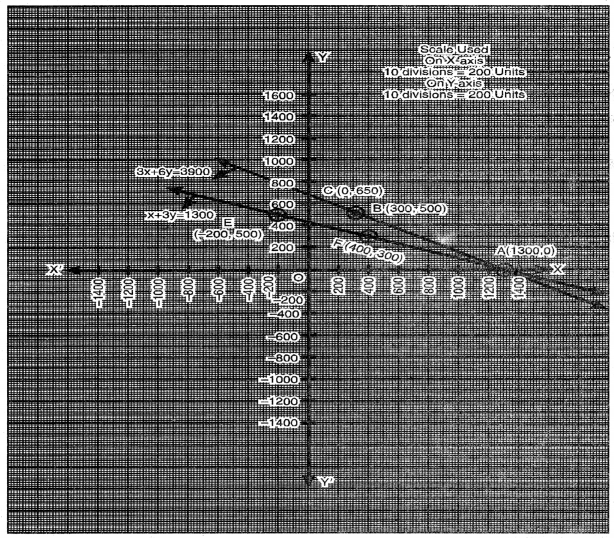
ਬਿੰਦੁਆਂ A (1300, 0), E – 200, 500), F (400, 300) ਨੂੰ ਆਲੇਖਿਤ ਕਰਨ ਤੇ ਅਤੇ ਉਨ੍ਹਾਂ ਨੂੰ ਮਿਲਾਉਣ ਵਾਲੀ ਰੇਖਾ ਖਿਚਣ ‘ਤੇ ਸਾਨੂੰ ਸਮੀਕਰਣ x + 3y =1300 ਦਾ ਆਲੇਖ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
ਆਲੇਖ ਤੋਂ ਇਹ ਸਪੱਸ਼ਟ ਹੁੰਦਾ ਹੈ ਕਿ ਦੋਵੇਂ ਰੇਖਾਵਾਂ A (1300, 0) ਉੱਤੇ ਕਟੰਦੀਆਂ ਹਨ ।
ਇਸ ਲਈ x = 1300 ਅਤੇ y = 0 ਦਿੱਤੇ ਗਏ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਜੋੜੇ ਦੇ ਹੱਲ ਹਨ ।
![]()
ਪ੍ਰਸ਼ਨ 3.
2 ਕਿ. ਗ੍ਰਾਮ ਸੇਬ ਅਤੇ 1 ਕਿ. ਗ੍ਰਾਮ ਅੰਗੂਰ ਦਾ ਮੁੱਲ ਕਿਸੇ ਦਿਨ ਤੋਂ 160 ਸੀ । ਇਕ ਮਹੀਨੇ ਬਾਅਦ 4 ਕਿ.ਗ੍ਰਾਮ ਸੇਬ ਅਤੇ 2 ਕਿ. ਗ੍ਰਾਮ ਅੰਗੂਰ ਦਾ ਮੁੱਲ ₹ 300 ਹੋ ਜਾਂਦਾ ਹੈ । ਇਸ ਸਥਿਤੀ ਨੂੰ ਬੀਜ ਗਣਿਤਿਕ ਅਤੇ ਜਿਮਾਇਤੀ ਰੂਪ ਵਿਚ ਦਰਸਾਉ ਵਿਅਕਤ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ 1 ਕਿ.ਗਾਮ ਸੇਬਾਂ ਦਾ ਮੁੱਲ = ₹ x
1 ਕਿ.ਗ੍ਰਾਮ ਅੰਗੂਰ ਦਾ ਮੁੱਲ = ₹ y
ਬੀਜ ਗਣਿਤਿਕ ਰੂਪ ਵਿੱਚ
ਪ੍ਰਸ਼ਨ ਦੀ ਪਹਿਲੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
2x + 2y = 160
ਪ੍ਰਸ਼ਨ ਦੀ ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
4x + 2y = 300
∴ ਦੋ ਚਲਾਂ ਵਿੱਚ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
2x + y = 160
ਅਤੇ 4x + 2y = 300
ਜਿਮਾਇਤੀ ਰੂਪ
2 + y = 160
2x = 160 – y
x = \(\frac{160-y}{2}\) ……(1)
y = 0 ਨੂੰ (1) ਵਿਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x = \(\frac{160-0}{2}\) = \(\frac{160}{2}\)
= 80.
y = 60 ਨੂੰ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = \(\frac{160-60}{2}\) = \(\frac{100}{2}\)
= 50
y= 160 ਨੂੰ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = \(\frac{160-160}{2}\)
= \(\frac{0}{2}\)
= 0
ਸਾਰਣੀ
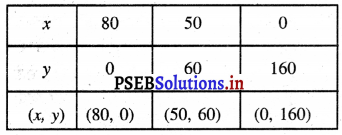
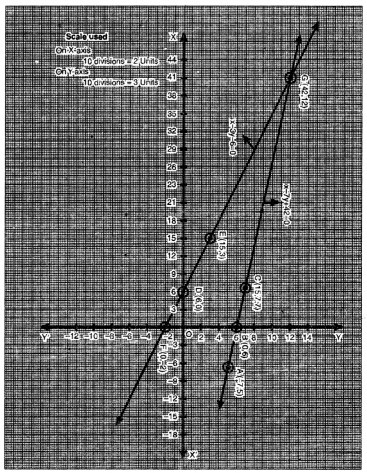
ਬਿੰਦੁਆਂ A (80, 0), B (50, 60), C (0, 160) ਨੂੰ ਅੰਕਿਤ ਕਰਨ ’ਤੇ ਅਤੇ ਉਨ੍ਹਾਂ ਨੂੰ ਮਿਲਾਉਂਦੇ ਹੋਏ ਰੇਖਾ ਖਿੱਚਣ ’ਤੇ ਸਮੀਕਰਣ 2x + y = 160 ਦਾ ਆਲੇਖ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
4x + 2y = 300
2x + y = 150
2x = 150 – y
x = \(\frac{150-y}{2}\) …(2)
y = 0 ਨੂੰ (2), ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x = \(\frac{150-0}{2}\) = \(\frac{150}{2}\)
= 75
y = 50 ਨੂੰ (2) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x = \(\frac{150-50}{2}\) = \(\frac{100}{2}\) = 50
y = 150 ਨੂੰ (2) ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x = \(\frac{150-150}{2}\) = \(\frac{=}{2}\)
= 0
ਸਾਰਣੀ
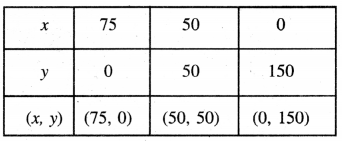
ਬਿੰਦੁਆਂ D (75, 0), E (50, 50), F (0, 150) ਨੂੰ | ਅੰਕਿਤ ਕਰਨ ਅਤੇ ਉਨ੍ਹਾਂ ਨੂੰ ਮਿਲਾਉਂਦੇ ਹੋਏ ਰੇਖਾ ਖਿੱਚਣ ‘ਤੇ ਸਮੀਕਰਣ 4x + 2y = 300 ਦਾ ਆਲੇਖ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
ਇਸ ਤੋਂ ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਕਿ ਦੋਵੇਂ ਰੇਖਾਵਾਂ ਕਿਸੇ ਵੀ ਬਿੰਦੂ ‘ਤੇ ਨਹੀਂ ਕੱਟਦੀਆਂ ਹਨ ਇਸ ਲਈ ਉਹ ਸਮਾਂਤਰ ਹਨ ।