PSEB 10th Class Maths Solutions Chapter 3 दो चर वाले रैखिक समीकरण युग्म Ex 3.2

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 3 दो चर वाले रैखिक समीकरण युग्म Ex 3.2 Textbook Exercise Questions and Answers

PSEB Solutions for Class 10 Maths Chapter 3 दो चर वाले रैखिक समीकरण युग्म Ex 3.2

प्रश्न 1.
निम्न समस्याओं में रैखिक समीकरणों के युग्म बनाइए और उनके ग्राफीय विधि से हल ज्ञात कीजिए।
(i) कक्षा X के 10 विद्यार्थियों ने एक गणित की पहेली प्रतियोगिता में भाग लिया। यदि लड़कियों की संख्या लड़कों की संख्या से 4 अधिक हो, तो प्रतियोगिता में भाग लिए लड़कों और लड़कियों की संख्या ज्ञात कीजिए।
(ii) 5 पेंसिल तथा 7 कलमों का कुल मूल्य ₹ 50 है, जबकि 7 पेंसिल तथा 5 कलमों का मूल्य ₹ 46 है। एक पेंसिल और एक कलम का मूल्य ज्ञात कीजिए।
हल :
(i) मान लीजिए .
प्रतियोगिता में लड़कों की संख्या = x
और प्रतियोगिता में लड़कियों की संख्या = y
प्रतियोगिता में भाग लेने वाले कुल विद्यार्थी = 10
∴ x + y = 10
या x + y – 10 = 0
प्रश्न अनुसार,
y = x + 4
या x = y – 4
अब रैखिक समीकरणों
x + y = 10
और x – y + 4 = 0 का आलेख खींचिए।
x + y = 10
या x = 10 – y..(1)
y = 0 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है।
x = 10 – 0 = 10
y = 7 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है
x = 10 – 7 = 3
y = 10 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है
x = 10 – 10 = 0

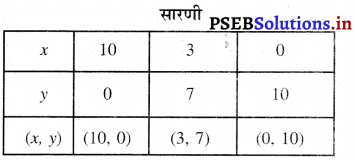
बिंदुओं A (10, 0), B (3, 7), C (0, 10) को आलेखित करने और उनको मिलाते हुए रेखा खींचने पर हमें समीकरण x + y = 10 का आलेख प्राप्त होता है।
x – y + 4 = 0
या x = y – 4 …………..(2)
y = 0 को (2) में प्रतिस्थापित करने पर हमें प्राप्त होता है।
x = 0 – 4 = – 4
y = 7 को (2) में प्रतिस्थापित करने पर हमें प्राप्त होता है।
x = 7 – 4 = 3
y = 4 को (2) में प्रतिस्थापित करने पर हमें प्राप्त होता है।
x = 4 – 4 = 0

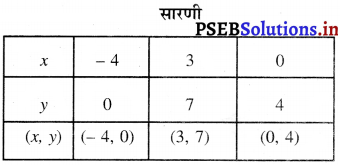
बिंदुओं D (- 4,0), B (3, 7), E (0, 4) को आले खित करने और उनको मिलाते हुए रेखा खींचने पर हमें समीकरण x-y +4= 0 का आलेख प्राप्त होता है।

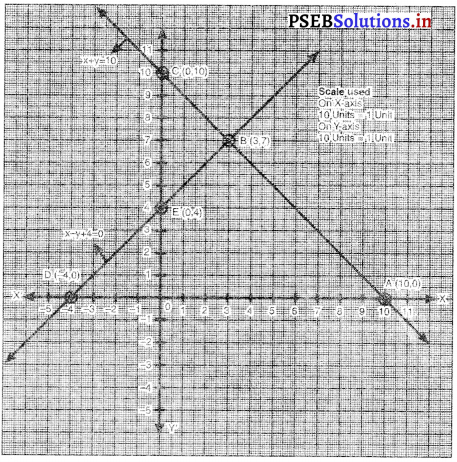
आलेख से यह स्पष्ट है कि दोनों रैखिक समीकरण बिंदु B (3, 7) पर मिलते हैं।
∴ बिंदु B (3, 7) आलेखीय स्थिति है।
अतः प्रतियोगिता में लड़कों की संख्या = 3
प्रतियोगिता में लड़कियों की संख्या = 7

(ii) मान लीजिए 1 पेंसिल का मूल्य = ₹ x
और 1 कलम का मूल्य = ₹ y
पहली शर्त अनुसार,
5x + 7y = 50
दूसरी शर्त अनुसार,
7x + 5y = 46
∴ रैखित समीकरण युग्म है :
5x + 7y = 50
7x + 5y = 46
अब इन रैखिक समीकरणों का आलेख खींचिए :
5x + 7y = 50
या 5x = 50 – 7y
या x = \(\frac{50-7 y}{5}\) ……………(1)
y = 0 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है।
x = \(\frac{50-7 \times 0}{5}=\frac{50}{5}\)
x = 10
y = 5 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है।

x = \(\frac{50-7 \times 5}{5}=\frac{50-35}{5}\)

= \(\frac{15}{5}\) = 3

y = 7 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है।

x = \(\frac{50-7 \times 7}{5}=\frac{50-49}{5}\)

= \(\frac{1}{5}\) = 0.2

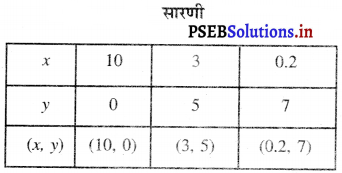
बिंदुओं A (10, 0), B (3, 5), C (0.2, 7) को आलेखित करने और उनको मिलाते हुए रेखा खीचने पर हमें समीकरण 5x + 7y = 50 का आलेख प्राप्त होता
7x+ 5y = 46
या 7x = 46 – 5y
या \(\frac{46-5 y}{7}\) …………….(2)
y = 0 को (2) में प्रतिस्थापित करने पर हमें प्राप्त होता है।

x = \(\frac{46-5 \times 0}{7}=\frac{46}{7}\) = 6.5

y = 5 को (2) में प्रतिस्थापित करने पर हमें प्राप्त होता है।

x = \(\frac{46-5 \times 5}{7}=\frac{46-25}{7}\)

= \(\frac{21}{7}\) = 3

y = – 4 को (2) में प्रतिस्थापित करने पर हमें प्राप्त होता है।

x = \(\frac{46-5 \times(-4)}{7}=\frac{46+20}{7}\)

= \(\frac{66}{7}\) = 9.5

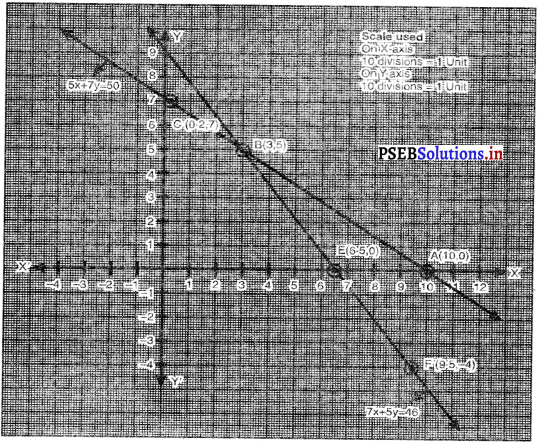
बिंदुओं E (6.5, 0), B (3, 5), F (9.5, – 4) को आलेखित करने और उनको मिलाते हुए रेखा खीचने पर हमें समीकरण 7x + 5y = 46 का आलेख प्राप्त होता है।
आलेख से यह स्पष्ट है कि दोनों रैखिक समीकरण बिंदु B (3, 5) पर मिलते हैं
∴ बिंदु B (3, 5) आलेखीय स्थिति है।
अतः, एक पेंसिल का मूल्य = 3 रु
एक कलम का मूल्य = 5 रु

प्रश्न 2.
अनुपातों \(\frac{a_{1}}{a_{2}}\), \(\frac{b_{1}}{b_{2}}\) और \(\frac{c_{1}}{c_{2}}\) की तुलना कर ज्ञात कीजिए कि निम्न समीकरण युग्म द्वारा निरूपित रेखाएँ एक बिंदु पर प्रतिच्छेद करती हैं, समांतर हैं अथवा संपाती हैं:
(i) 5x – 4y + 8 = 0
7x + 6y – 9 = 0

(ii) 9x + 3y + 12 = 0
18x + 6y + 24 = 0

(iii) 6x – 3y + 10 = 0
2x – y + 9 = 0
हल :
(i) दी गई रैखिक समीकरण युग्म है :
5x – 4y + 8 = 0
और 7x + 6y – 9 = 0
यहाँ a₁ = 5, b₁ = – 4, c₁ = 8
a₂ = 7, b₂ = 6, c₂ = – 9
अब, \(\frac{a_{1}}{a_{2}}=\frac{5}{7} ; \frac{b_{1}}{b_{2}}\);

\(\frac{b_{1}}{b_{2}}=\frac{-4}{6}=\frac{-2}{3}\);

\(\frac{c_{1}}{c_{2}}=\frac{8}{-9}\) \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)

अतः, दी गई रैखिक समीकरण युग्म एक बिंदु पर प्रतिच्छेद करती हैं।

(ii) दी गई रैखिक समीकरण युग्म हैं :
9x + 3y + 12 = 0
और 18x + 6y + 24 = 0
a₁ = 9, b₁ = 3, c₁ = 12
a₂ = 18, b₂ = 6, c₂ = 24
अब \(\frac{a_{1}}{a_{2}}=\frac{9}{18}=\frac{1}{2}\);

\(\frac{b_{1}}{b_{2}}=\frac{3}{6}=\frac{1}{2}\);

\(\frac{c_{1}}{c_{2}}=\frac{12}{24}=\frac{1}{2}\)

∴ \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
अतः, दी गई समीकरण-युग्म संपाती हैं।

(iii) दी गई रैखिक समीकरण-युग्म है
6x – 3y + 10 = 0
और 2x – y + 9 = 0
यहाँ a₁ = 6, b₁ = – 3, c₁ = 10
a₂ = 2, b₂ = – 1, c₂ = 9

अब \(\frac{a_{1}}{a_{2}}=\frac{6}{2}\) = 3;

\(\frac{b_{1}}{b_{2}}=\frac{-3}{-1}\) = 3;

\(\frac{c_{1}}{c_{2}}=\frac{10}{9}\)

∴ \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)

अतः, दी गई रैखिक समीकरण-युग्म एक दूसरे समांतर है

प्रश्न 3.
अनुपातों \(\), \(\) और \(\) की तुलना कर ज्ञात कीजिए कि निम्न रैखिक समीकरणों के युग्म संगत हैं या असंगत :
(i) 3x + 2y = 5; 2x – 3y = 7
(ii) 2r – 3y = 8; 4x – 6y = 9
(iii) x+5y = 7; 9x – 10y = 14
(iv) 5x – 3y = 11; – 10x + 6y = – 22
(v) x +2y = 8; 2x + 3y = 12
हलः
(i) दी गई रैखिक समीकरण-युग्म है
3x + 2y = 5 और 2x – 3y = 7
या 3x + 2y – 5 = 0
और 2r – 3y – 7 = 0
यहाँ a₁ = 3, b₁ = 2, c₁ = – 5
a₂ = 2, b₂ = – 3, c₂ = – 7

अब \(\frac{a_{1}}{a_{2}}=\frac{3}{2}\);

\(\frac{b_{1}}{b_{2}}=\frac{2}{-3}\);

\(\frac{c_{1}}{c_{2}}=\frac{-5}{-7}=\frac{5}{7}\);

∴ \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)

अतः दी गई रैखिक समीकरण-युग्म संगत है।

(ii) दी गई रैखिक समीकरण-युग्म है
2x – 3Y = 8 और 4x – 6y = 9
या 2x – 3y – 8 = 0
4x – 6y – 9 = 0
यहाँ a₁ = 2, b₁ = – 3, c₁ = – 8
a₂ = 4, b₂ = – 6, c₂ = – 9
अब \(\frac{a_{1}}{a_{2}}=\frac{2}{4}=\frac{1}{2}\);

\(\frac{b_{1}}{b_{2}}=\frac{-3}{-6}=\frac{1}{2}\);

\(\frac{c_{1}}{c_{2}}=\frac{-8}{-9}=\frac{8}{9}\);

∴ \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)

अतः, दी गई रैखिक समीकरण-युग्म असंगत है

(iii) दी गई रैखिक समीकरण-युग्म है
\(\frac{3}{2}\) x + \(\frac{5}{3}\) y = 7
और 9x – 10y = 14
या \(\frac{3}{2}\) x + \(\frac{4}{4}\) y – 7 = 0
और 9 x – 10y – 14 = 0
यहाँ a₁ = \(\frac{3}{2}\), b₁ = \(\frac{5}{3}\), c₁ = – 7
a₂ = 9, b₂ = – 10, c₂ = – 14

अतः, दी गई रैखिक समीकरण-युग्म असंगत है।

(iv) दी गई रैखिक समीकरण-युग्म है :
5x – 3y = 11 और – 10x + 6y = – 22
या 5x – 3y – 11 = 0 और – 10x + 6y + 22 = 0
a₁ = 5, b₁ = – 3, c₁ = – 11
a₂ = – 10, b₂ = 6, c₂ = 22
अब \(\frac{a_{1}}{a_{2}}=\frac{5}{-10}=\frac{1}{2}\);

\(\frac{b_{1}}{b_{2}}=\frac{3}{6}=-\frac{1}{2}\);

\(\frac{c_{1}}{c_{2}}=\frac{-11}{22}=\frac{-1}{2}\)

∵ \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)

अतः, दी गई रैखिक समीकरण-युग्म संगत है

(v) दी गई रैखिक समीकरण-युग्म है :
\(\frac{4}{3}\)x + 2y = 8 और 2x + 3y = 12
और \(\frac{4}{3}\)x + 2y – 8 = 0 या 2x + 3y – 12 = 0
यहाँ a₁ = \(\frac{4}{3}\), b₁ = 2, c₁ = – 12
a₂ = 2, b₂ = 3, c₂ = – 12

अतः, दी गई रैखिक समीकरण-युग्म संगत है।

प्रश्न 4.
निम्न रैखिक समीकरणों के युग्मों में से कौन युग्म संगत/असंगत हैं ? यदि संगत हैं, तो ग्राफीय विधि से हल ज्ञात कीजिए :
(i) x + y = 5, 2x + 2y = 10
(ii) x – y = 8, 3x – 3y = 16
(iii) 2x + y – 6 = 0, 4x – 2y -4 = 0
(iv) 2x – 2y – 2 = 0, 4x – 4y – 5 = 0
हल :
(i) दी गई रैखिक समीकरण-युग्म है :
x + y = 5 और 2x + 2y = 10
या x + y – 5 = 0 2x + 2y – 10 = 0
यहाँ a₁ = 1, b₁ = 1, c₁ = – 5
a₂ = 2, b₂ = 2, c₂ = – 10
अब \(\frac{a_{1}}{a_{2}}=\frac{1}{2}\);

\(\frac{b_{1}}{b_{2}}=\frac{1}{2}\);

\(\frac{c_{1}}{c_{2}}=\frac{-5}{-10}=\frac{1}{2}\)

∴ \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
∴ दी गई रैखिक समीकरण युग्म इसका आलेख खींचिए
x + y = 5
x = 5 – y ……………..(1)
y = 0 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है
x = 5 – 0 = 5
y = 3 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है
x = 5 – 3 = 2
y = 5 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है।
x = 5 – 5 = 0

बिंदुओं A (5, 0), B (2, 3), C (0, 5) को आलेखित करने और उनको मिलाते हुए रेखा खींचने पर हमें समीकरण x + y = 5 का आलेख प्राप्त होता है।
2x + 2y = 10. या 2 (x + y) = 10
x + y = 5
या x = 5 – y ……………(2)
y = 0 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है
x = 5 – 0 = 5
y = 2 को (2) में प्रतिस्थापित करने पर हमें प्राप्त होता है
x = 5 – 2 = 3
y = 5 को (2) में प्रतिस्थापित करने पर हमें प्राप्त होता है
x = 5 – 5 = 0

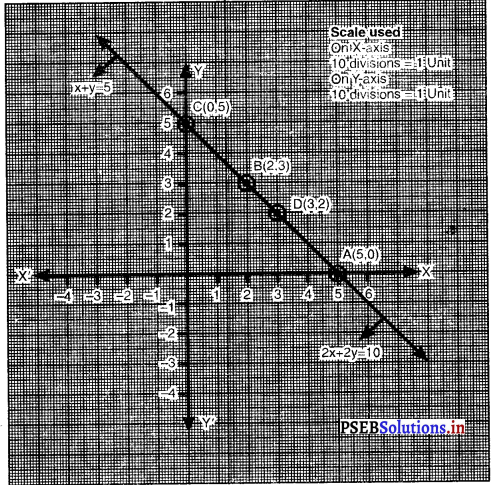
बिंदुओं A (5, 0), D (3, 2), C (0, 5) को आलेखित करने और उनको मिलाते हुए रेखा खींचने पर हमें समीकरण 2x + 2y = 10 का आलेख प्राप्त होता है।
आलेख से यह स्पष्ट है कि दी गई रैखिक समीकरण युग्म संपाती रेखाएँ हैं या इनके अपरिमित रूप से अनेकों हल हैं।

(ii) दी गई रैखिक समीकरण-युग्म है :
x – y = 8 और 3x – 3y = 16
या x – y – 8 = 0 और 3x – 3y – 16 = 0
यहाँ a = 1, b = – 1, c = 8
a = 3, b = – 3, c = – 16

अब \(\frac{a_{1}}{a_{2}}=\frac{1}{3}\);

\(\frac{b_{1}}{b_{2}}=\frac{-1}{-3}=\frac{1}{3}\);

\(\frac{c_{1}}{c_{2}}=\frac{-8}{-16}=\frac{1}{2}\)

∴ \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)

अतः, दी गई रैखिक समीकरण-युग्म असंगत है।

(iii) दी गई रैखिक समीकरण-युग्म है :
2x + y -6 = 0
और 4x – 2y – 4 = 0
यहाँ a₁ = 2, b₁ = 1, c₁ = – 6
a₂ = – 4, b₂ = – 2, c₂ = – 4

अब, \(\frac{a_{1}}{a_{2}}=\frac{2}{4}=\frac{1}{2}\);

\(\frac{b_{1}}{b_{2}}=\frac{1}{-2}\);

\(c_{1}=\frac{-6}{-4}=\frac{3}{2}\)

∴ \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
∴ दी गई रैखिक समीकरण–युग्म इस रैखिक समीकरणों का आलेख खींचिए
2x + y – 6 = 0
या 2x = 6 – y
x = \(\frac{6-y}{2}\) …………….(1)

y = 0 को (1) में प्रतिस्थापित करने पर, हमें प्राप्त होता है :

x = \(\frac{6-0}{2}=\frac{6}{2}\) = 3

y = 2 को (1), में प्रतिस्थापित करने पर, हमें प्राप्त होता है :

x = \(\frac{6-2}{2}\)

= \(\frac{4}{2}\) = 2

y = – 2 को (1) में प्रतिस्थापित करने पर, हमें प्राप्त होता है

x = \(\frac{6-(-2)}{2}=\frac{6+2}{2}\)

= \(\frac{8}{2}\) = 4

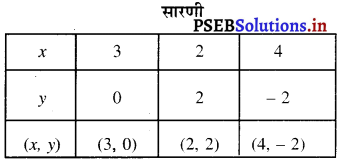
बिंदुओं A (3, 0), B (2, 2), C (4, – 2) को आले खित करने और उनको मिलाते हुए रेखा खींचने पर हमें समीकरण 2x + y – 6 = 0 का आलेख प्राप्त होता है।
4x – 2y – 4 = 0
या 2[2x – y – 2] = 0
या 2x – y – 2 = 0
या 2x = y + 2
या x = \(\fracy+2}{2}\) …………(2)

y = 0 को (2) में प्रतिस्थापित करने पर, हमें प्राप्त होता है

x = \(\frac{0+2}{2}\)

= \(\frac{2}{2}\) = 1

y = 2 को (2) में प्रतिस्थापित करने पर, हमें प्राप्त होता है

x = \(\frac{2+2}{2}\)
= \(\frac{4}{2}\) = 2

y = – 2 को (2) में प्रतिस्थापित करने पर, हमें प्राप्त होता है :

x = \(\frac{-2+2}{2}\)

= \(\frac{0}{2}\) = 0

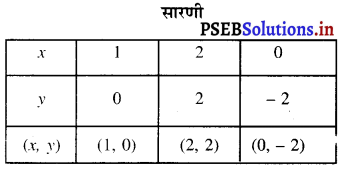
बिंदुओं D (1,0), B (2, 2), E (0, -2) को आलेखित करने और उनको मिलाते हुए रेखा खींचने पर हमें समीकरण 4x – 2y – 4 = 0 का आलेख प्राप्त होता है।

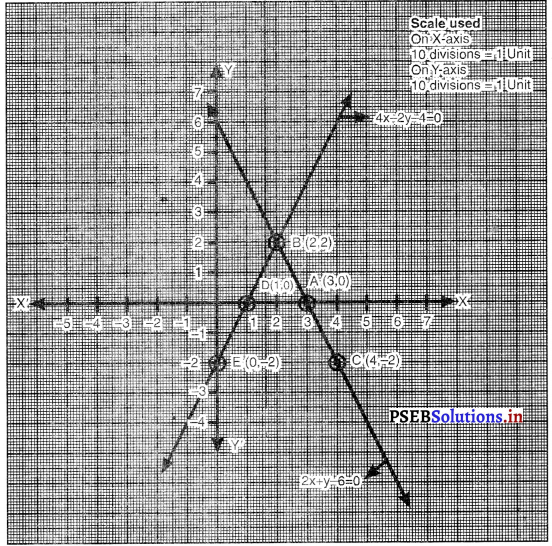
आलेख से यह स्पष्ट है कि दी गई समीकरण-युग्म बिंदु B (2, 2) पर मिलती है।
अतः, दी गई रैखिक समीकरण-युग्म अद्वितीय है।

(iv) दी गई रैखिक किरण-युग्म है
2x – 2y – 2 = 0 और 4x – 4y – 5 = 0
यहाँ a₁ = 2, b₁ = – 2, c₁ = – 2
a₂ = 4, b₂ = – 4, c₂ = – 5
अब \(\frac{a_{1}}{a_{2}}=\frac{2}{4}=\frac{1}{2}\);

\(\frac{b_{1}}{b_{2}}=\frac{-2}{-4}=\frac{1}{2}\);

\(\frac{c_{1}}{c_{2}}=\frac{-2}{-5}=\frac{2}{5}\)

∴ \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)

अतः, दी गई समीकरण युग्म असंगत है। उत्तर

प्रश्न 5.
एक आयताकार बाग, जिसकी लंबाई, चौड़ाई से 4 m अधिक है, का अर्धपरिमाप 36 m है। बाग की विमाएँ ज्ञात कीजिए।
हल :
मान लीजिए बाग की लंबाई = x m
बाग की चौड़ाई = y m
बाग का परिमाप = 2 [x + y] m
बाग के परिमाप का आधा = (x + y) m
प्रश्न की पहली शर्त अनुसार,
x = y + 4
प्रश्न की दूसरी शर्त का अनुसार,
x + y = 36
∴ रैखिक समीकरण-युग्म है:
x = y + 4 और x + y = 36
x = y + 4 …………..(1)

y = 0 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
x = 0 + 4 = 4
y = – 4 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
x = – 4 + 4 = 0
y = 16 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
x = 16 + 4 = 20

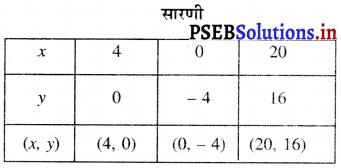
बिंदुओं A (4, 0), B (0, – 4), C (20, 16) को आलेखित करने और उनको मिलाते हुए रेखा खींचने पर हमें समीकरण x = y + 4 का आलेख प्राप्त होता है।

x + y = 36
x = 36 – y …………….(2)
y = 12 को (2) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
x = 36 – 12 = 24
y = 24 को (2) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
x = 36 – 24 = 12
y = 16 को (2) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
x = 36 – 16 = 20

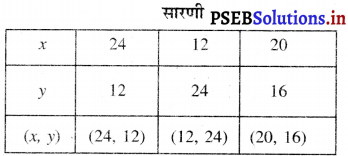
बिंदुओं D (24, 12), E (12, 24), C (20, 16) को आलेखित करने और उनको मिलाते हुए रेखा खींचने पर हमें समीकरण x + y = 36 का आलेख प्राप्त होता है।

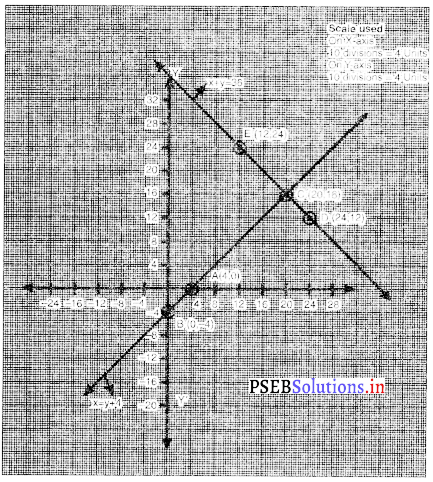
आलख स यह स्पष्ट ह क राखक समाकरणा का युग्म बिंदु C (20, 16) पर मिलता है।
∴ C (20, 16) अर्थात् x = 20 और y = 16 रैखिक समीकरण युग्म का हल है।
अतः, बाग की लंबाई = 20 m
बाग की चौड़ाई = 16 m

एक अन्य विधि:
मान लीजिए बाग बाग की चौड़ाई = x m
बाग की लंबाई = (x + 4) m
बाग का परिमाप = 2 [लंबाई + चौड़ाई]
= 2 [x + x + 4] m
= [2x + 4] m
∴ बाग के परिमाप का आधा = (2x + 4) m
प्रश्न अनुसार,
2x + 4 = 36
2x = 36 – 4
2x = 32
x = \(\frac{32}{2}\) = 16
अतः, बाग की चौड़ाई = 16 m
और बाग की लंबाई = (16 + 4) m = 20 m

प्रश्न 6.
एक रैखिक समीकरण 2x + 3y – 8 = 0 दी गई है। दो चरों में एक ऐसी और रैखिक समीकरण लिखिए ताकि प्राप्त युग्म का ज्यामितीय निरूपण जैसा कि :
(i) प्रतिछेद रेखाएँ हों।
(ii) समांतर रेखाएँ हों।
(iii) संपाती रेखाएँ हों।
हल :
स्थिति I. प्रतिच्छेद करती रेखाएँ:
दी गई रैखिक समीकरण है :
2x + 3y – 8 = 0 ……………(1)
यहा पर प्रातप्छा५त रखाए का शता का पूरा करम फ लिए अनेक मान है
अर्थात् \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
इनमें से एक है।
3x – 2y – 6 = 0 ………….(2)
अब रैखिक समीकरण (1) और (2) का आलेख खींचिए।
2x + 3y – 8 = 0 या 2x = 8 – 3y
या x = \(\frac{8-3 y}{2}\) ………….(1)

y = 0 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :

x = \(\frac{8-3 \times 0}{2}=\frac{8}{2}\) = 4

y = – 2 को (1) में प्रतिस्थापित __करने पर हमें प्राप्त होता है :

x = \(\frac{8-3(-2)}{2}=\frac{14}{2}\) = 7

y = 2 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :

x = \(\frac{8-3 \times 2}{2}=\frac{8-6}{2}=\frac{2}{2}=1\) = 1

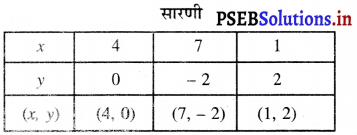
बिंदुओं A (4,0), B (7, — 2), C (1, 2) को आलेखित करने और उनको मिलाने पर प्राप्त रेखा खींचने पर हमें समीकरण 2x + 3y – 8 = 0 का आलेख प्राप्त होता है।
3x – 2y – 6 = 0 या 3x = 6 + 2y
या x = \(\frac{6+2 y}{3}\) ………….(2)

y = 0 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :

x = \(\frac{6+2 \times 0}{3}=\frac{6}{3}=2\)

y = – 3 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
x = \(\frac{6+2(-3)}{3}\)

= \(\frac{6-6}{3}\) = 0

y = 3 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :

x = \(\frac{6+2 \times 3}{3}=\frac{6+6}{3}\)

= \(\frac{12}{3}\) = 4

बिंदुओं D (2, 0), E (0, – 3), F (4, 3) को आलेखित करने और उनको मिलाने पर प्राप्त रेखा खींचने पर हमें समीकरण 3x – 2y – 6 = 0 का आलेख प्राप्त होता है।
आलेख से यह स्पष्ट है कि रैखिक किरण युग्म बिंदु G पर प्रतिच्छेद करता है।

बिंदुओं G (2.5, 0), H (- 2, 3), I (7, – 3) को आलेखित करने और उनको मिलाकर रेखा खींचने से हमें समीकरण 2x + 3y – 5 = 0 का आलेख प्राप्त होता है।

स्थिति III.
संपाती रेखाओं के लिए
दी गई रैखिक समीकरण है
2x + 3y – 8 = 0 …………..(1)
दो चरों में ऐसे और भी अधिकतम अन्य रैखिक समीकरण हो सकते हैं जो संपाती रेखाओं की शर्त को संतुष्ट करते हों अर्थात् \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
अतः उनमें से एक इस प्रकार है :
6x + 9y – 24 = 0 ……………(4)

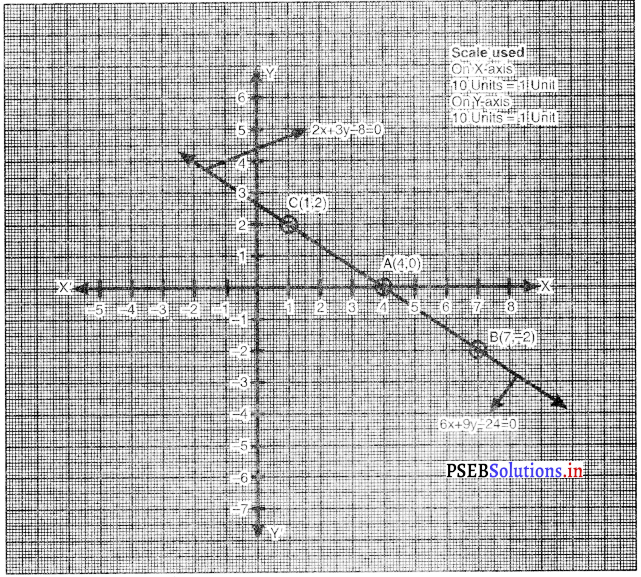
अब रैखिक समीकरणों (1) और (4) का आलेख खींचिए।
रैखिक समीकरण (4) लीजिए
6x + 9y – 24 = 0
‘या 3 [2x + 3y – 8] = 0
या 2x + 3y – 8 = 0
∴ दोनों में बिंदु एक समान है और दोनों समीकरणों की एक ही रेखा है।

प्रश्न 7.
समीकरणों x -y + 1 = 0 और 3x + 2y – 12 = 0 का ग्राफ खींचिए।x-अक्ष और इन रेखाओं से बने त्रिभुज के शीर्षों के निर्देशांक ज्ञात कीजिए और त्रिभुजाकार पटल को छायांकित कीजिए।
हल :
एक रैखिक समीकरण-युग्म लीजिए
x – y + 1 = 0 और 3x + 2y – 12= 0
x – y + 1 = 0
या x = y – 1 …………(1)
y = 0 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
x = 0 – 1 = – 1
y = 3 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
x = 3 – 1 = 2 y = 1 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
x = 1 – 1 = 0

बिंदुओं A (- 1, 0), B (2, 3), C (0, 1) को आलेखित करने और उनको मिला कर रेखा खींचने पर हमें समीकरण x – y + 1 = 0 का आलेख प्राप्त होता है।
3x + 2y – 12 = 0
या 3x = 12 – 2y
या x = \(\frac{12-2 y}{3}\) ………..(2)
y = 0 को (2) में प्रतिस्थापित करने पर हमें प्राप्त होता है :

x = \(\frac{12-2 \times 0}{3}=\frac{12}{3}\) = 4

y = 3 को (2), में प्रतिस्थापित करने पर हमें प्राप्त होता है :

x = \(\frac{12-2 \times 3}{3}=\frac{12-6}{3}=\frac{6}{3}\) = 2

y = 6 को (2) में प्रतिस्थापित करने पर हमें प्राप्त होता है :

x = \(\frac{12-2 \times 6}{3}=\frac{12-12}{3}\) = 0

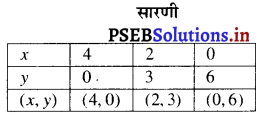
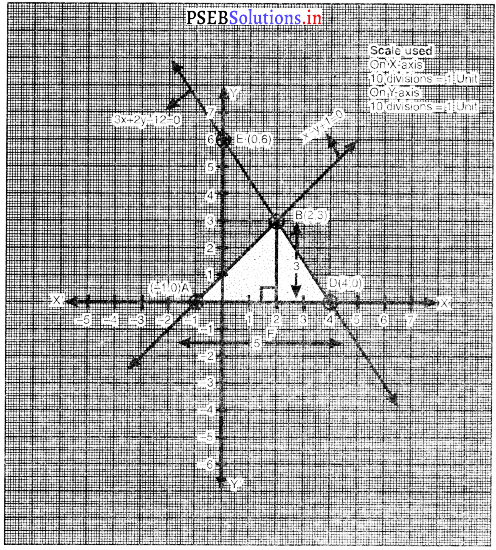
बिंदुओं D (4,0), B (2, 3), E (0, 6) को आलेखित करने और उनको मिलाकर रेखा खींचने पर हमें समीकरण 3x + 2y – 12 = 0 आलेख प्राप्त होता है।

रैखिक समीकरणों के युग्म और .x-अक्ष द्वारा बनाए गए त्रिभुज के शीर्षों को आलेख में छायांकित किया गया है।

∆ABD इस प्रकार बनी त्रिभुज है।
∆ABD के शीर्षों के निर्देशांक हैं : A (- 1, 0), B (2, 3) और D (4,0).
अब, आधार AD की लंबाई = AO + OD
= 1 + 4 = 5 मात्रक
लंब BF की लंबाई = 3 मात्रक
∴ ∆ABD का क्षेत्रफल = \(\frac{1}{2}\) × आधार × लंब
= \(\frac{1}{2}\) × AD × BF
= (\(\frac{1}{2}\) × 5 × 3) वर्ग मात्रक
= \(\frac{15}{2}\) = 7.5 वर्ग मात्रक