Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 6 ਤ੍ਰਿਭੁਜ Ex 6.2 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 10 Maths Chapter 6 ਤ੍ਰਿਭੁਜ Exercise 6.2
ਪ੍ਰਸ਼ਨ 1.
ਚਿੱਤਰ (i) ਅਤੇ (ii) ਵਿੱਚ, DE || BC ਹੈ।
(i) ਵਿੱਚ EC ਅਤੇ (i) ਵਿੱਚ AD ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ ।
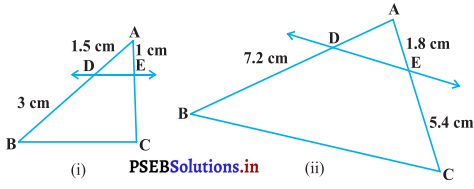
ਹੱਲ:
(i) △ABC ਵਿੱਚ DE || BC …(ਦਿੱਤਾ ਹੈ )
∴ \(\frac{\mathrm{AD}}{\mathrm{BD}}\) = \(\frac{\mathrm{AE}}{\mathrm{EC}}\)
[ਮੂਲ ਸਮਾਨ ਅਨੁਪਾਤਤਾ ਮੇਯ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ]
\(\frac{1.5}{3}\)= \(\frac{1}{EC}\)
EC = \(\frac{3}{1.5}\)
EC = \(\frac{3×10}{15}\) = 2
∴ EC = 2 cm
(ii) △ABC ਵਿੱਚ,
DE || BC … (ਦਿੱਤਾ ਹੈ।)
∴ \(\frac{\mathrm{AD}}{\mathrm{BD}}\) = \(\frac{\mathrm{AE}}{\mathrm{EC}}\)
[ਮੂਲ ਸਮਾਨ ਅਨੁਪਾਤ ਪ੍ਰਮੇਯ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ਤੇ]
\(\frac{AD}{7.2}\) = \(\frac{1.8}{5.4}\)
AD = \(\frac{1.8×7.2}{5.4}\)
= \(\frac{18}{10}\) × \(\frac{72}{10}\) × \(\frac{10}{54}\)
= \(\frac{24}{10}\) = 2.4
∴ AD = 2.4 cm
![]()
ਪ੍ਰਸ਼ਨ 2.
ਕਿਸੇ △PQR ਦੀਆਂ ਭੁਜਾਵਾਂ PQ ਅਤੇ PR ਉੱਤੇ ਕੁਮਵਾਰ ਬਿੰਦੂ E ਅਤੇ 7 ਸਥਿਤ ਹਨ । ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ਹਰੇਕ ਸਥਿਤੀ ਵਿੱਚ ਦੱਸੋ ਕਿ, ਕੀ EF ||QR ਹੈ :
(i) PE = 3.9 cm, EQ=3 cm,
PF = 3.6 cm ਅਤੇ FR = 2.4 cm
(ii) PE = 4 cm, QE = 4.5 cm,
PF = 8 cm ਅਤੇ RF = 9 cm
(iii) PQ = 1.28 cm, PR = 2.56 cm,
PE = 0.18 cm ਅਤੇ PF = 0.36 cm.
ਹੱਲ:
△PQR ਵਿੱਚ ਦੋ ਬਿੰਦੂ ਕੁਮਵਾਰ E ਅਤੇ F ਭੁਜਾ PQ ਅਤੇ PR ਉੱਤੇ ਸਥਿਤ ਹਨ ।
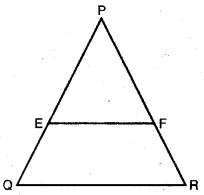
(i) PE = 3.9 cm, EQ = 3 cm
PF = 3.6 cm, FR = 2.4 cm
\(\frac{PE}{EQ}\) = \(\frac{3.9}{3}\) = \(\frac{39}{30}\) = \(\frac{13}{10}\) = 1.3
\(\frac{PF}{FR}\) = \(\frac{3.6}{2.4}\) = \(\frac{36}{24}\) = \(\frac{3}{2}\) = 1.5
\(\frac{PE}{EQ}\) ≠ \(\frac{PF}{FR}\)
∴ EF, QR ਦੋ ਸਮਾਂਤਰ ਨਹੀਂ ਹੈ
(ii) PE = 4 cm, QE = 4.5 cm
PF = 8 cm, RF = 9 cm
\(\frac{PE}{QE}\) = \(\frac{4}{4.5}\) = \(\frac{40}{45}\) = \(\frac{8}{9}\) … (1)
\(\frac{PF}{RF}\) = \(\frac{8}{9}\) …(2)
(1) ਅਤੇ (2) ਤੋਂ,
\(\frac{PE}{QE}\) = \(\frac{PF}{RF}\)
∴ ਮੂਲ ਸਮਾਨ ਅਨੁਪਾਤਤਾ ਪ੍ਰਮੇਯ ਦੇ ਵਿਲੋਮ ਤੋਂ EF || QR.
(iii) PQ = 1.28 cm, PR = 2.56 cm
PE = 0.18 cm, PF = 0.36 cm
EQ = PQ – PE = 1.28 – 0.18 = 1.10 cm
ER = PR – PF = 2.56 -0.36 = 2.20 cm
ਇੱਥੇ \(\frac{PE}{EQ}\) = \(\frac{0.18}{1.10}\) = \(\frac{18}{110}\) = \(\frac{9}{55}\) … (1)
ਅਤੇ \(\frac{PF}{FR}\) = \(\frac{0.36}{2.20}\) = \(\frac{36}{220}\) = \(\frac{9}{55}\) …..(2)
(1) ਅਤੇ (2) ਤੋਂ, \(\frac{PE}{EQ}\) = \(\frac{PF}{FR}\)
∴ ਮੂਲ ਸਮਾਨ ਅਨੁਪਾਤਤਾ ਪ੍ਰਮੇਯ ਦੇ ਵਿਲੋਮ ਤੋਂ
EF || QR.
![]()
ਪ੍ਰਸ਼ਨ 3.
ਚਿੱਤਰ ਵਿੱਚ ਜੇਕਰ LM || CB ਅਤੇ
LN || CD ਹੋਵੇ, ਤਾਂ ਸਿੱਧ ਕਰੇ ਕਿ \(\frac{AM}{AB}\) = \(\frac{AN}{AD}\) ਹੈ
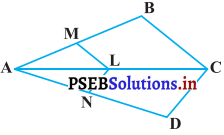
ਹੱਲ:
△ABC ਵਿਚ
LM || CB (ਦਿੱਤਾ ਹੈ।)
∴ \(\frac{AM}{MB}\) = \(\frac{AL}{LC}\)
(ਮੂਲ ਸਮਾਨ ਅਨੁਪਾਤ ਪ੍ਰਮੇਯ ਅਨੁਸਾਰ)
ਦੁਬਾਰਾ △ACD ਵਿੱਚ,
LN || CD (ਦਿੱਤਾ ਹੈ।)
∴ \(\frac{AN}{ND}\) = \(\frac{AL}{LC}\) …(2)
ਮੂਲ ਸਮਾਨ ਅਨੁਪਾਤਤਾ ਪ੍ਰਮੇਯ ਅਨੁਸਾਰ)
(1) ਅਤੇ (2) ਤੋਂ,
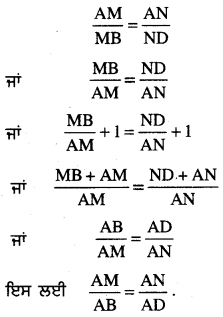
ਪ੍ਰਸ਼ਨ 4.
ਚਿੱਤਰ ਵਿਚ DE || A ਅਤੇ DF || AE ਹੈ । ਸਿੱਧ ਕਰੋ ਕਿ \(\frac{BF}{FE}\) = \(\frac{BE}{EC}\) ਹੈ ॥
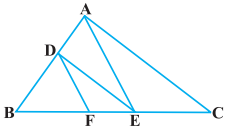
ਹੱਲ:
△ABC ਵਿੱਚ
DE || AC (ਦਿੱਤਾ ਹੈ।)
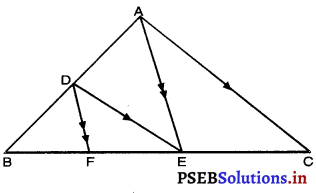
∴ \(\frac{BD}{DA}\) = \(\frac{BE}{EC}\) …(1)
ਮੂਲ ਸਮਾਨ ਅਨੁਪਾਤ ਪ੍ਰਮੇਯ ਅਨੁਸਾਰ △ABE ਵਿੱਚ,
DF || AE (ਦਿੱਤਾ ਹੈ।)
∴ \(\frac{BD}{DA}\) = \(\frac{BF}{FE}\) …(2)
ਮੂਲ ਸਮਾਨ ਅਨੁਪਾਤਤਾ ਪ੍ਰਮੇਯ ਅਨੁਸਾਰ
(1) ਅਤੇ (2) ਤੋਂ,
\(\frac{BE}{EC}\) = \(\frac{BF}{FE}\)
![]()
ਪ੍ਰਸ਼ਨ 5.
ਚਿੱਤਰ ਵਿਚ DE || OQ ਅਤੇ DF | OR ਹੈ । ਦਿਖਾਉ ਕਿ EF ||QR ਹੈ ।
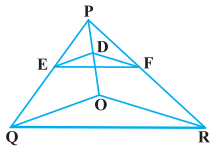
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △PQR ਵਿੱਚ, DE||OQ ਅਤੇ
DF || OR.
ਸਿੱਧ ਕਰਨਾ ਹੈ : EF|QR.
ਸਬੂਤ : △PQO ਵਿਚ,
ED || QO (ਦਿੱਤਾ ਹੈ।)
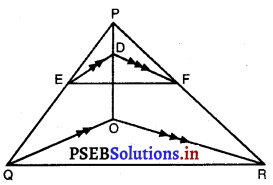
∴ \(\frac{PD}{DO}\) = \(\frac{PF}{EQ}\) …(1)
[ਮੂਲ ਸਮਾਨ ਅਨੁਪਾਤਤਾ ਪ੍ਰਮੇਯ ਤੋਂ।]
ਦੁਬਾਰਾ △POR ਵਿੱਚ,
DF || OR (ਦਿੱਤਾ ਹੈ )
∴ \(\frac{PD}{DO}\) = \(\frac{PF}{FR}\) …(2)
[ਮੂਲ ਸਮਾਨ ਅਨੁਪਾਤਤਾ ਪ੍ਰਮੇਯ ਤੋਂ ]
(1) ਅਤੇ (2) ਤੋਂ,
\(\frac{PE}{EQ}\) = \(\frac{PF}{FR}\)
△PQR ਵਿੱਚ ਮੂਲ ਸਮਾਨ ਅਨੁਪਾਤਤਾ ਪ੍ਰਮੇਯ ਦੇ ਵਿਲੋਮ ,
EF || QR.
ਪ੍ਰਸ਼ਨ 6.
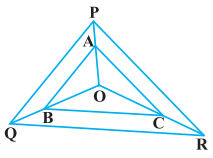
ਚਿੱਤਰ ਵਿਚ ਕੁਮਵਾਰ OP, OQ ਅਤੇ OR ਉੱਤੇ ਸਥਿਤ ਬਿੰਦੂ A, B ਅਤੇ Cਇਸ ਤਰ੍ਹਾਂ ਹਨ ਕਿ AB || PQ ਅਤੇ AC|| PR ਹੈ । ਦਰਸਾਉ ਕਿ BC|QR ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △PQR ਵਿਚ ਬਿੰਦੂ A, B ਅਤੇ C ਕੁਮਵਾਰ OP, 0Q ਅਤੇ OR ਉੱਤੇ ਇਸ ਤਰ੍ਹਾਂ ਸਥਿਤ ਹਨ ਕਿ AB || PQ ਅਤੇ AC || PR ਹੈ ।
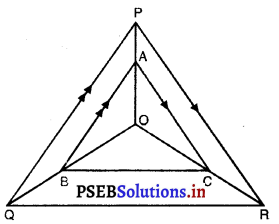
ਸਿੱਧ ਕਰਨਾ ਹੈ : BC || QR.
ਸਬੂਤ : △OPQ ਵਿੱਚ,
AB || PQ (ਦਿੱਤਾ ਹੈ।)
∴ \(\frac{OA}{AP}\) = \(\frac{OB}{BQ}\) …(1)
[ਮੂਲ ਸਮਾਨ ਅਨੁਪਾਤ ਪ੍ਰਮੇਯ ਤੋਂ]
ਦੁਬਾਰਾ △OPR ਵਿੱਚ,
AC || PR (ਦਿੱਤਾ ਹੈ।)
∴ \(\frac{OA}{AP}\) = \(\frac{OC}{CR}\) …(2)
[ਮੂਲ ਸਮਾਨ ਅਨੁਪਾਤ ਪ੍ਰਮੇਯ ਤੋਂ]
(1) ਅਤੇ (2) ਤੋਂ,
\(\frac{OB}{BQ}\) = \(\frac{OC}{CR}\)
∴ ਮੂਲ ਸਮਾਨ ਅਨੁਪਾਤਤਾ ਮੇਯ ਦੇ ਉਲਟ ਤੋਂ △OQR ਵਿੱਚ BC || QR ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 7.
ਮੇਯ 6.1 ਦਾ ਪ੍ਰਯੋਗ ਕਰਦੇ ਹੋਏ ਸਿੱਧ ਕਰੋ ਕਿ ਇਕ ਤ੍ਰਿਭੁਜ ਦੀ ਇਕ ਭੁਜਾ ਦੇ ਮੱਧ ਬਿੰਦੂ ਵਿਚੋਂ ਦੂਸਰੀ ਭੁਜਾ ਦੇ ਸਮਾਂਤਰ ਖਿੱਚੀ ਗਈ ਰੇਖਾ ਤੀਸਰੀ ਭੁਜਾ ਨੂੰ ਸਮਦੁਭਾਜਿਤ ਕਰਦੀ ਹੈ । (ਯਾਦ ਕਰੋ ਕਿ ਤੁਸੀਂ ਇਸ ਨੂੰ ਜਮਾਤ IX ਵਿੱਚ ਸਿੱਧ ਕਰ ਚੁੱਕੇ ਹੋ ॥
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △ABC ਵਿੱਚ D, AB ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ ਭਾਵ AD = DB ਹੈ ।
BC ਦੇ ਸਮਾਂਤਰ ਰੇਖਾ AC ਨੂੰ E ਉੱਤੇ ਕੱਟਦੀ ਹੈ ਜਿਵੇਂ ਕਿ ਚਿੱਤਰ ਵਿੱਚ ਦਿਖਾਇਆ ਗਿਆ ਹੈ ਭਾਵ DE || BC ਹੈ ।
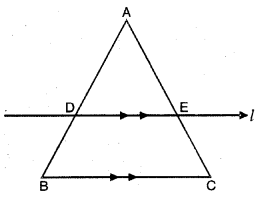
ਸਿੱਧ ਕਰਨਾ ਹੈ : E, AC ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ ।
ਸਬੂਤ : D, AB ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ ।
ਭਾਵ AD = DB (ਦਿੱਤਾ ਹੈ।)
\(\frac{AD}{BD}\) = 1 …(1)
ਦੁਬਾਰਾ △ABC ਵਿੱਚ DE || BC
∴ \(\frac{AD}{DB}\) = \(\frac{AE}{EC}\)
[ਮੂਲ ਸਮਾਨ ਅਨੁਪਾਤਤਾ ਪ੍ਰਮੇਯ ਤੋਂ।]
∴ 1 = \(\frac{AE}{EC}\) [(1) ਤੋਂ।]
∴ AE = EC
∴ E, AC ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ ।
ਪ੍ਰਸ਼ਨ 8.
ਮੇਯ 6.2 ਦਾ ਪ੍ਰਯੋਗ ਕਰਦੇ ਹੋਏ ਸਿੱਧ ਕਰੋ ਕਿ ਇਕ ਤ੍ਰਿਭੁਜ ਦੀਆਂ ਕਿਸੇ ਤੋਂ ਭੁਜਾਵਾਂ ਦੇ ਮੱਧ ਬਿੰਦੂਆਂ ਨੂੰ ਮਿਲਾਉਣ ਵਾਲੀ ਰੇਖਾ ਤੀਸਰੀ ਭੁਜਾ ਦੇ ਸਮਾਂਤਰ ਹੁੰਦੀ ਹੈ । (ਯਾਦ ਕਰੋ ਕਿ ਤੁਸੀਂ ਜਮਾਤ IX ਵਿਚ ਅਜਿਹਾ ਕਰ ਚੁੱਕੇ |
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △ABC ਵਿੱਚ, D ਅਤੇ E ਕ੍ਰਮਵਾਰ AB ਅਤੇ AC ਦੇ ਮੱਧ ਬਿੰਦੂ ਹਨ ਜਿਸ ਨਾਲ AD = BD ਅਤੇ AE = EC ਹਨ ID ਅਤੇ E ਨੂੰ ਮਿਲਾਇਆ ਗਿਆ ਹੈ ।
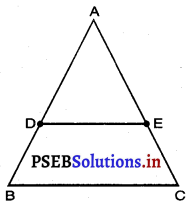
ਸਿੱਧ ਕਰਨਾ ਹੈ : DE || BC
ਸਬੂਤ : D, AB ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ , (ਦਿੱਤਾ ਹੈ।)
ਭਾਵ AD = BD
\(\frac{AD}{BD}\) = 1 …(1)
E, AC ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ (ਦਿੱਤਾ ਹੈ।)
∴ AE = EC
\(\frac{AE}{EC}\) = 1 …(2)
(1) ਅਤੇ (2) ਤੋਂ, \(\frac{AB}{BD}\) = \(\frac{AE}{EC}\)
ਮੂਲ ਸਮਾਨ ਅਨੁਪਾਤਤਾ ਮੇਯ ਦੇ ਪ੍ਰਯੋਗ ਤੋਂ,
DE || BC
![]()
ਪ੍ਰਸ਼ਨ 9.
ABCD ਇੱਕ ਸਮਲੰਬ ਚਤੁਰਭੁਜ ਹੈ ਜਿਸ ਵਿੱਚ AB || DC ਹੈ ਅਤੇ ਇਸਦੇ ਵਿਕਰਣ ਆਪਸ ਵਿੱਚ ਬਿੰਦੁ O ‘ਤੇ ਕੱਟਦੇ ਹਨ । ਦਿਖਾਓ ਕਿ \(\frac{AO}{BO}\) = \(\frac{CO}{DO}\) ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ABCD ਇੱਕ ਸਮਲੰਬ ਚਤੁਰਭੁਜ ਹੈ । ਜਿਸ ਵਿੱਚ AB || DC ਹੈ । ਵਿਕਰਣ AC ਅਤੇ BD ਇੱਕ-ਦੂਜੇ ਨੂੰ ਬਿੰਦੂ O ਉੱਤੇ ਕੱਟਦੇ ਹਨ ।
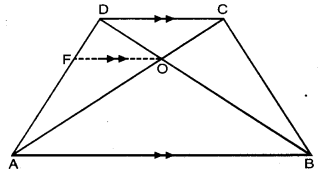
ਸਿੱਧ ਕਰਨਾ ਹੈ : \(\frac{AO}{BO}\) = \(\frac{CO}{DO}\)
ਰਚਨਾਂ : O ਤੋਂ FO || DC || AB ਖਿੱਚੋ ।
ਸਬੂਤ : △DAB ਵਿੱਚ
FO || AB (ਰਚਨਾ)
∴ \(\frac{DF}{FA}\) = \(\frac{DO}{BO}\) …(1)
[ਮੂਲ ਸਮਾਨ ਅਨੁਪਾਤਤਾ ਪ੍ਰਮੇਯ ਦੇ ਪ੍ਰਯੋਗ ਨਾਲ]
△DCA ਵਿੱਚ
FO || DC (ਰਚਨਾ)
\(\frac{DF}{FA}\) = \(\frac{CO}{AO}\) …(2)
[ਮੂਲ ਸਮਾਨ ਅਨੁਪਾਤਤਾ ਪ੍ਰਮੇਯ ਦੇ ਪ੍ਰਯੋਗ ਦੁਆਰਾ]
(1) ਅਤੇ (2) ਤੋਂ, \(\frac{DO}{BO}\) = \(\frac{CO}{AO}\) ⇒ \(\frac{AO}{BO}\) = \(\frac{CO}{DO}\)
ਪ੍ਰਸ਼ਨ 10.
ਇਕ ਚਤੁਰਭੁਜ ABCD ਦੇ ਵਿਕਰਣ ਆਪਸ ਵਿੱਚ ਬਿੰਦੂ O ਉੱਤੇ ਇਸ ਤਰ੍ਹਾਂ ਕੱਟਦੇ ਹਨ ਕਿ \(\frac{AO}{BO}\) = \(\frac{CO}{DO}\) ਹੈ । ਦਿਖਾਓ ਕਿ ABCD ਇੱਕ ਸਮਲੰਬ ਚਤੁਰਭੁਜ ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਚਤੁਰਭੁਜ ABCD ਵਿੱਚ ਵਿਕਰਣ AC ਅਤੇ BD ਆਪਸ ਵਿੱਚ ਬਿੰਦੂ O ਉੱਤੇ ਇਸ ਤਰ੍ਹਾਂ ਕੱਟਦੇ ਹਨ ਕਿ \(\frac{AO}{BO}\) = \(\frac{CO}{DO}\) ਹੈ ।
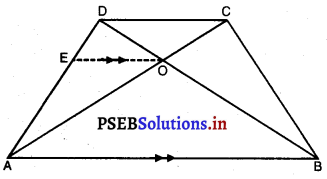
ਸਿੱਧ ਕਰਨਾ ਹੈ : ਚਤੁਰਭੁਜ ABCD ਇੱਕ ਸਮਲੰਬ ਚਤੁਰਭੁਜ ਹੈ।
ਰਚਨਾ : ‘O’ ਤੋਂ ਇੱਕ ਰੇਖਾ EO || AB ਖਿੱਚੋ ਜੋ AD ਨੂੰ E ਉੱਤੇ ਮਿਲਦੀ ਹੈ ।
ਸਬੂਤ : △DAB ਵਿੱਚ
EO || AB
∴ \(\frac{DE}{EA}\) = \(\frac{DO}{OB}\) …(1)
[ਮੂਲ ਸਮਾਨ ਅਨੁਪਾਤਤਾ ਪ੍ਰਮੇਯ ਦੇ ਪ੍ਰਯੋਗ ਦੁਆਰਾ]
ਪਰ \(\frac{AO}{BO}\) = \(\frac{CO}{DO}\) (ਦਿੱਤਾ ਹੈ।)
ਜਾਂ \(\frac{AO}{CO}\) = \(\frac{BO}{DO}\)
ਜਾਂ \(\frac{CO}{AO}\) = \(\frac{DO}{BO}\)
⇒ \(\frac{DO}{OB}\) = \(\frac{CO}{AO}\) …(2)
(1) ਅਤੇ (2) ਤੋਂ, \(\frac{DE}{EA}\) = \(\frac{CO}{AO}\)
∴ ਮੂਲ ਸਮਾਨ ਅਨੁਪਾਤਤਾ ਪ੍ਰਮੇਯ ਦੇ ਪ੍ਰਯੋਗ ਦੁਆਰਾ
EO || DC
ਨਾਲ ਹੀ, EO || AB
⇒ AB || DC
∴ ਚਤੁਰਭੁਜ ABCD ਇਕ ਸਮਲੰਬ ਚਤੁਰਭੁਜ ਹੈ ਜਿਸ AB || CD.
