PSEB 10th Class Maths Solutions Chapter 6 ਤ੍ਰਿਭੁਜ Ex 6.4

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 6 ਤ੍ਰਿਭੁਜ Ex 6.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 6 ਤ੍ਰਿਭੁਜ Exercise 6.4

ਪ੍ਰਸ਼ਨ 1.
ਮੰਨ ਲਉ △ABC ~ △DEF ਹੈ ਅਤੇ ਇਨ੍ਹਾਂ ਦੇ ਖੇਤਰਫਲ ਕੁਮਵਾਰ 64 cm² ਅਤੇ 121 cm² ਜੇਕਰ EF = 15.4 cm ਹੋਵੇ ਤਾਂ BC ਪਤਾ ਕਰੋ ।
ਹੱਲ:
△ABC ~ △DEF, △ABC ਦਾ ਖੇਤਰਫਲ = 64 cm² ਅਤੇ △DEF ਦਾ ਖੇਤਰਫਲ = 121 cm² ਅਤੇ EF = 15.4 cm ਹੈ ।

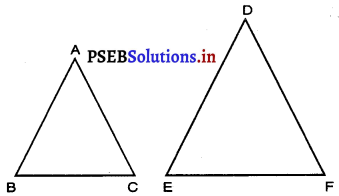
△ABC ~ △DEF
∴ \(\frac{ar(△ABC)}{ar(△DEF}\) = \(\left(\frac{\mathrm{AB}^{2}}{\mathrm{DE}^{2}}\right)\) = \(\left(\frac{\mathrm{AC}^{2}}{\mathrm{DF}^{2}}\right)\) = \(\left(\frac{\mathrm{BC}^{2}}{\mathrm{EF}^{2}}\right)\)
[ਜੇਕਰ ਦੋ ਤ੍ਰਿਭੁਜਾਂ ਸਮਰੂਪ ਹੋਣ ਤਾਂ ਉਨ੍ਹਾਂ ਦੇ ਖੇਤਰਫਲ ਦਾ ਅਨੁਪਾਤ ਸੰਗਤ ਭੁਜਾਵਾਂ ਦੇ ਅਨੁਪਾਤ ਦੇ ਵਰਗ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ।]

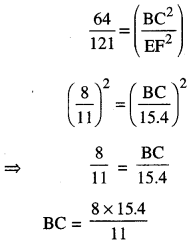
BC = 8 × 14
BC = 11.2 cm.

ਪ੍ਰਸ਼ਨ 2.
ਇੱਕ ਸਮਲੰਬ ਚਤੁਰਭੁਜ ABCD ਜਿਸ ਵਿੱਚ AB || DC ਹੈ, ਦੇ ਵਿਕਰਣ ਆਪਸ ਵਿੱਚ ਬਿੰਦੁ 0 ਉੱਤੇ ਕੱਟਦੇ ਹਨ । ਜੇਕਰ AB = 2 CD ਹੋਵੇ ਤਾਂ ਤ੍ਰਿਭੁਜਾਂ AOB ਅਤੇ COD ਦੇ ਖੇਤਰਫਲਾਂ ਦਾ ਅਨੁਪਾਤ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ABCD ਇਕ ਸਮਲੰਬ ਚਤੁਰਭੁਜ ਹੈ ਜਿਸ ਵਿੱਚ AB || DC ਹੈ, ਦੇ ਵਿਕਰਣ AC ਅਤੇ BD ਆਪਸ ਵਿੱਚ O ਬਿੰਦੂ ਉੱਤੇ ਕੱਟਦੇ ਹਨ ਅਤੇ AB = 2 CD ਹੈ ।

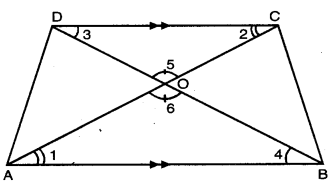
△AOB ਅਤੇ △COD ਵਿੱਚ,
∠1 = ∠2 (ਇਕਾਂਤਰ ਕੋਣ)
∠3 = ∠4 (ਇਕਾਂਤਰ ਕੋਣ)
∠5 = ∠6 (ਸਿਖ਼ਰ ਸਨਮੁੱਖ ਕੋਣ)
∴ △AOB ~ △COD
∴ \(\frac{ar(△AOB)}{ar(△COD}\) = \(\left(\frac{\mathrm{AB}^{2}}{\mathrm{CD}^{2}}\right)\)

[ਜੇਕਰ ਦੋ ਤ੍ਰਿਭੁਜਾਂ ਸਮਰੂਪ ਹੋਣ, ਤਾਂ ਉਨ੍ਹਾਂ ਦੇ ਖੇਤਰਫਲਾਂ ਦਾ ਅਨੁਪਾਤ ਉਨ੍ਹਾਂ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਦੇ ਅਨੁਪਾਤ ਦੇ ਵਰਗ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ]
= \(\left(\frac{2 \mathrm{CD}}{\mathrm{CD}}\right)^{2}\) (∵ AB = 2CD)
\(\frac{ar(△AOB)}{ar(△COD}\) = \(\frac{4 \mathrm{CD}^{2}}{\mathrm{CD}^{2}}\) = \(\frac{4}{1}\)
∵ ਲੋੜੀਂਦਾ ar △AOB ਅਤੇ ar △COD ਦਾ ਅਨੁਪਾਤ = 4 : 1

ਪ੍ਰਸ਼ਨ 3.
ਚਿੱਤਰ ਵਿੱਚ ਇੱਕੋ ਆਧਾਰ BC ਉੱਤੇ ਦੋ ਤਿਭੁਜ ABC ਅਤੇ DBC ਬਣੇ ਹੋਏ ਹਨ । ਜੇਕਰ AD, BC ਨੂੰ O’ ਤੇ ਕੱਟੇ ਤਾਂ ਦਰਸਾਉ ਕਿ
\(\frac{ar(△ABC)}{ar(△DBC}\) = \(\frac{\mathrm{AO}}{\mathrm{DO}}\) ਹੈ।

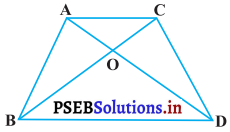
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △ABC ਅਤੇ △DBC ਇਕ ਹੀ ਆਧਾਰ BC ਉੱਤੇ ਬਣੇ ਹੋਏ ਹਨ ਅਤੇ AD, BC ਨੂੰ O ਉੱਤੇ ਕੱਟਦੀ ਹੈ !

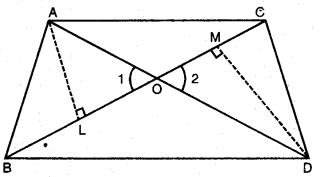
ਸਿੱਧ ਕਰੋ : \(\frac{ar(△ABC)}{ar(△DBC}\) = \(\frac{\mathrm{AO}}{\mathrm{DO}}\)
ਰਚਨਾ : AL ⊥ BC, DM ⊥ BC ਖਿੱਚੋ ।
ਸਬੂਤ : △ALO ਅਤੇ △DMO ਵਿੱਚ,
∠1 = ∠2 (ਸਿਖ਼ਰ ਸਨਮੁਖ ਕੋਣ)
∠L = ∠M (ਹਰੇਕ 90°)
∴ △ALO ~ △DMO [AA ਸਮਰੂਪਤਾ ਕਸੌਟੀ]
∴ \(\frac{\mathrm{AL}}{\mathrm{DM}}\) = \(\frac{\mathrm{AO}}{\mathrm{DO}}\) …(1)
[ਜੇਕਰ ਦੋ ਤਿਭੁਜਾਂ ਸਮਰੂਪ ਹੋਣ, ਤਾਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਸਮਾਨ ਅਨੁਪਾਤੀ ਹੁੰਦੀਆਂ ਹਨ]

ਪ੍ਰਸ਼ਨ 4.
ਜੇਕਰ ਦੋ ਸਮਰੂਪ ਤ੍ਰਿਭੁਜਾਂ ਦੇ ਖੇਤਰਫਲ ਬਰਾਬਰ ਹੋਣ ਤਾਂ ਸਿੱਧ ਕਰੋ ਕਿ ਉਹ ਤ੍ਰਿਭੁਜ ਸਰਬੰਗਸਮ ਹੁੰਦੇ ਹਨ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਦੋ ਤਿਭੁਜਾਂ △ABC ਅਤੇ △DEF ਦੇ ਸਮਰੂਪ ਹਨ ਅਤੇ ਖੇਤਰਫਲ ਬਰਾਬਰ ਹਨ ।
ਸਿੱਧ ਕਰਨਾ : △ABC ~ △DEF

ਸਬੂਤ : ਕਿਉਂਕਿ △ABC ~ △DEF,
∴ \(\frac{ar(△ABC)}{ar(△DEF}\) = \(\left(\frac{\mathrm{BC}^{2}}{\mathrm{EF}^{2}}\right)\)
⇒ \(\left(\frac{\mathrm{BC}^{2}}{\mathrm{EF}^{2}}\right)\) = 1
[∵ ar (△ABC) = ar (△DEF)
⇒ (BC)² = (EF)²
⇒ BC = EF
ਨਾਲ ਹੀ, ਕਿਉਂਕਿ △ABC ~ △DEF, ਇਸ ਲਈ ਉਹ ਸਮਕੋਣੀ ਹਨ ।
ਅਤੇ ∠B = ∠E
ਅਤੇ ∠C = ∠F
ਹੁਣ ਤ੍ਰਿਭੁਜਾਂ △ABC ਅਤੇ △DEF ਵਿੱਚ,
∠B = ∠E, ∠C = ∠F
ਅਤੇ BC = EF
∴ △ABC ≅ △DEF (ASA ਸਰਬੰਗਸਮ ਪਰਿਮੇਯ)

ਪ੍ਰਸ਼ਨ 5.
ਇੱਕ ਤ੍ਰਿਭੁਜ ABC ਦੀਆਂ ਭੁਜਾਵਾਂ AB, BC ਅਤੇ CA ਦੇ ਮੱਧ ਬਿੰਦੂ ਕੁਮਵਾਰ D, E ਅਤੇ F ਹਨ △DEF ਅਤੇ △ABC ਦੇ ਖੇਤਰਫਲਾਂ ਦਾ ਅਨੁਪਾਤ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਇੱਕ △ABC ਦੀਆਂ ਭੁਜਾਵਾਂ AB, BC ਅਤੇ CA ਦੇ ਮੱਧ ਬਿੰਦੂ ਕੁਮਵਾਰ D, E ਅਤੇ F ਹਨ ।

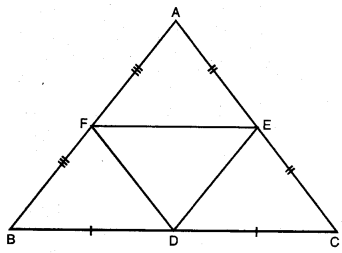
ਸਿੱਧ ਕਰਨਾ : ਖੇਤਰਫਲ (△DEF) : ਖੇਤਰਫਲ (△ABC) ਪਤਾ ਕਰਨਾ ।
ਸਬੂਤ : △ABC ਵਿਚ,
F, AB ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ । …(ਦਿੱਤਾ ਹੈ।)
E, AC ਦਾ ਮੱਧ ਬਿੰਦੁ ਹੈ । …(ਦਿੱਤਾ ਹੈ।)
ਇਸ ਲਈ ਮੱਧ ਬਿੰਦੂ ਪ੍ਰਮੇਯ ਤੋਂ,
FE || BC ਅਤੇ FE = \(\frac{1}{2}\)BC
⇒ FE || BD
ਅਤੇ FE = BD [∵ BD = \(\frac{1}{2}\)BC]
∴ BDEF ਇਕ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਹੈ ।
(∵ ਸਨਮੁੱਖ ਭੁਜਾਵਾਂ ਸਮਾਂਤਰ ਅਤੇ ਸਮਾਨ ਹਨ)
△FBD ਅਤੇ △DEF ਵਿੱਚ,
FB = DE
…(|| gm BDEF ਦੀਆਂ ਸਨਮੁੱਖ ਭੁਜਾਵਾਂ)
FD = FD (ਇਕੋ ਜਿਹੇ।
…(|| gm BDEF ਦੀਆਂ ਸਨਮੁੱਖ ਭੁਜਾਵਾਂ)
BD = FE
∴ △FBD ≅ △DEF
… (SSS ਸਰਬੰਗਸਮ ਪ੍ਰਯੋਗ)
ਇਸ ਤਰ੍ਹਾਂ ਅਸੀਂ ਸਿੱਧ ਕਰ ਸਕਦੇ ਹਾਂ ।
△AFE ≅ △DEF
ਅਤੇ △EDC ≅ △DEF
ਜੇਕਰ ਤ੍ਰਿਭੁਜਾਂ ਸਰਬੰਗਸਮ ਹੋਵੇ ਤਾਂ ਖੇਤਰਫਲ ਬਰਾਬਰ ਹੁੰਦੇ ਹਨ।
∴ ar (△FBD) = ar (△DEF) …(1)
ar (△AFE) = ar (△DEF) . …(2)
ar (△EDC) = ar (△DEF) …(3)
ਹੁਣ ar △(ABC) = ar (△FBD) + ar (△DEF) + ar (△AFE) + ar (△EDC)
= ar (△DEF) + ar (△DEF) + ar (△DEF) + ar (△DEF)
[(1), (2) ਅਤੇ (3) ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ਤੇ]
= 4 ar (△DEF)
⇒ ar (△DEF) = \(\frac{1}{4}\)ar (△ABC)
⇒ \(\frac{ar(△DEF)}{ar(△ABC}\) = \(\frac{1}{4}\)
∴ ar (△DEF) : ar(△ABC) = 1 : 4.

ਪ੍ਰਸ਼ਨ 6.
ਸਿੱਧ ਕਰੋ ਕਿ ਦੋ ਸਮਰੂਪ ਤਿਭੁਜਾਂ ਦੇ ਖੇਤਰਫਲਾਂ ਦਾ ਅਨੁਪਾਤ ਇਨ੍ਹਾਂ ਦੀਆਂ ਸੰਗਤ ਮੱਧਿਕਾਵਾਂ ਦੇ ਅਨੁਪਾਤ ਦਾ ਵਰਗ ਹੁੰਦਾ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △ABC ~ △DEF.
AX ਅਤੇ DY ਮਵਾਰ ਭੁਜਾ BC ਅਤੇ EF ਮੱਧਿਕਾਵਾਂ ਹਨ ।

ਕਿਉਂਕਿ ਦੋ ਸਮਰੂਪ ਤ੍ਰਿਭੁਜਾਂ ਦੇ ਖੇਤਰਫਲਾਂ ਦਾ ਅਨੁਪਾਤ ਉਨ੍ਹਾਂ ਦੀ ਸੰਗਤ ਭੁਜਾਵਾਂ ਦੇ ਅਨੁਪਾਤ ਦੇ ਵਰਗ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ ।
∴ \(\frac{ar(△ABC)}{ar(△DEF}\) = \(\left(\frac{\mathrm{AB}^{2}}{\mathrm{DE}^{2}}\right)\) = \(\left(\frac{A X^{2}}{D Y^{2}}\right)\)

ਪ੍ਰਸ਼ਨ 7.
ਸਿੱਧ ਕਰੋ ਕਿ ਇਕ ਵਰਗ ਦੀ ਕਿਸੇ ਭੁਜਾ ਉੱਤੇ ਬਣਾਏ ਗਏ ਸਮਭੁਜੀ ਤ੍ਰਿਭੁਜ ਦਾ ਖੇਤਰਫਲ ਉਸੇ ਵਰਗ ਦੇ ਇੱਕ ਵਿਕਰਣ ‘ਤੇ ਬਣੇ ਸਮਭੁਜੀ ਤ੍ਰਿਭੁਜ ਦੇ ਖੇਤਰਫਲ ਦਾ ਅੱਧਾ ਹੁੰਦਾ ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ABCD ਇਕ ਵਰਗ ਹੈ।
ਸਮਭੁਜੀ △ABC ਵਰਗ ਦੀ ਭੁਜਾ AB ਉੱਤੇ ਸਥਿਤ ਹੈ ਅਤੇ ਸਮਭੁਜੀ △ACF ਵਿਕਰਣ AC ਉੱਤੇ ਬਣੀ ਹੈ ।

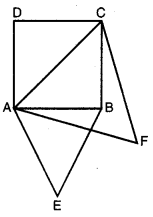
ਸਿਪ ਕਰਨਾ ਹ : \(\frac{ar(△ABC)}{ar(△ACF}\) = \(\frac{1}{2}\)
ਸਬੂਤ : ਸਮਕੋਣ △ABC ਵਿੱਚ
AB² + BC² = AC
[ਪਾਇਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਦੁਆਰਾ]
⇒ AB² + AB² = AC²
[∵ AB = BC, ਇਕ ਹੀ ਵਰਗ ਦੀਆਂ ਭੁਜਾਵਾਂ ]
⇒ 2AB² = AC² ….(1)
ਹੁਣ ਹਰੇਕ △ABE ਅਤੇ △ACE ਸਮਭੁਜੀ ਹਨ ਅਤੇ ਇਸ ਲਈ ਸਮਕੋਣੀ ਹਨ । ਇਸ ਲਈ ਸਮਰੂਪ ਹਨ ।
ਭਾਵ △ABE ~ △ACF.
ਇੱਥੇ ਪਹਿਲੀ 4 ਦੀ ਕੋਈ ਭੁਜਾ ਦੂਸਰੀ ਤ੍ਰਿਭੁਜ ਦੀ ਕਿਸੇ ਭੁਜਾ ਦੇ ਸਮਾਂਤਰ ਹੈ ।
∴ \(\frac{ar(△ABE)}{ar(△ACF}\) = \(\left(\frac{\mathrm{AB}^{2}}{\mathrm{AC}^{2}}\right)\).
[∵ ਦੋ ਸਮਰੂਪ ਤਿਭੁਜਾ ਦੇ ਖੇਤਰਫਲ ਦਾ ਅਨੁਪਾਤ ਉਨ੍ਹਾਂ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਦੇ ਅਨੁਪਾਤ ਦੇ ਵਰਗ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ ॥]
= \(\frac{\mathrm{AB}^{2}}{2 \mathrm{AB}^{2}}\) = \(\frac{1}{2}\). [(1) ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ਤ]
ਸਹੀ ਉੱਤਰ ਚੁਣੋ ਅਤੇ ਆਪਣੇ ਉੱਤਰ ਦਾ ਸਪਸ਼ਟੀਕਰਣ ਵੀ ਦਿਉ ।

ਪ੍ਰਸ਼ਨ 8.
ABC ਅਤੇ BDE ਦੋ ਸਮਭੁਜੀ ਤ੍ਰਿਭੁਜਾਂ ਇਸ ਪ੍ਰਕਾਰ ਹਨ ਕਿ ॥ ਭੁਜਾ BC ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ । ਤ੍ਰਿਭੁਜਾਂ ABC ਅਤੇ BDE ਦੇ ਖੇਤਰਫਲਾਂ ਦਾ ਅਨੁਪਾਤ ਹੈ :
(A) 2 : 1
(B) 1 : 2
(C) 4 : 1
(D) 1 : 4.
ਹੱਲ:
△ABC ਅਤੇ △BDE ਦੋ ਸਮਭੁਜੀ ਤ੍ਰਿਭੁਜ ਇਸ ਤਰ੍ਹਾਂ ਹਨ ਕਿ D ਭੁਜਾ BC ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ ।
∴ BD = DC = \(\frac{1}{2}\) BC,
ਮੰਨ ਲਉ ਸਮਭੁਜੀ ਤ੍ਰਿਭੁਜ ਦੀ ਭੁਜਾ 2a ਹੈ ।
∴ △ABC ~ △BDE
∴ \(\frac{ar(△ABC)}{ar(△BDE}\) = \(\frac{\mathrm{AB}^{2}}{\mathrm{BD}^{2}}\)
= \(\frac{(2 a)^{2}}{(a)^{2}}\) = \(\frac{4 a^{2}}{a^{2}}\)
= \(\frac{4}{1}\)
∴ (C) ਸਹੀ ਵਿਕਲਪ ਹੈ ।

ਪ੍ਰਸ਼ਨ 9.
ਦੋ ਸਮਰੂਪ ਤ੍ਰਿਭੁਜਾਂ ਦੀਆਂ ਭੁਜਾਵਾਂ 4 : 9 ਦੇ ਅਨੁਪਾਤ ਵਿੱਚ ਹਨ । ਇਨ੍ਹਾਂ ਤ੍ਰਿਭੁਜਾਂ ਦੇ ਖੇਤਰਫਲਾਂ ਦਾ ਅਨੁਪਾਤ ਹੈ :
(A) 2 : 3
(B) 4 : 9
(C) 81 : 16
(D) 16 : 81
ਹੱਲ:

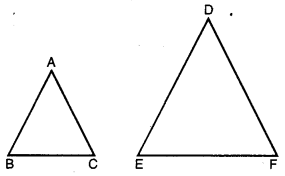
△ABC ~ △DEF (ਦਿੱਤਾ ਹੈ।)
\(\frac{\mathrm{AB}}{\mathrm{DE}}\) = \(\frac{\mathrm{AC}}{\mathrm{DF}}\) = \(\frac{\mathrm{BC}}{\mathrm{EF}}\) = \(\frac{4}{9}\)
∴ \(\frac{ar(△ABC)}{ar(△DEF}\) = \(\frac{\mathrm{AB}^{2}}{\mathrm{DE}^{2}}\)
[ਦੋ ਸਮਰੂਪ ਤ੍ਰਿਭੁਜਾਂ ਦੇ ਖੇਤਰਫਲਾਂ ਦਾ ਅਨੁਪਾਤ ਉਨ੍ਹਾਂ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਦੇ ਅਨੁਪਾਤ ਦੇ ਵਰਗ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ।]
\(\frac{ar(△ABC)}{ar(△DEF}\) = \(\left(\frac{4}{9}\right)^{2}\) = \(\frac{16}{81}\)
∴ (D) ਸਹੀ ਵਿਕਲਪ ਹੈ ।