PSEB 10th Class Maths Solutions Chapter 6 ਤ੍ਰਿਭੁਜ Ex 6.5

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 6 ਤ੍ਰਿਭੁਜ Ex 6.5 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 6 ਤ੍ਰਿਭੁਜ Exercise 6.5

1. ਕੁੱਝ ਤ੍ਰਿਭੁਜਾਂ ਦੀਆਂ ਭੁਜਾਵਾਂ ਹੇਠਾਂ ਦਿੱਤੀਆਂ ਗਈਆਂ ਹਨ । ਨਿਰਧਾਰਿਤ ਕਰੋ ਕਿ ਇਹਨਾਂ ਵਿੱਚੋਂ ਕਿਹੜੀ-ਕਿਹੜੀ | ਤਿਭੁਜ ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ ਹੈ । ਇਸ ਸਥਿਤੀ ਵਿੱਚ ਕਰਣ ਦੀ ਲੰਬਾਈ ਵੀ ਲਿਖੋ :

ਪ੍ਰਸ਼ਨ (i).
7 cm, 24 cm, 25 cm
ਉੱਤਰ:
ਮੰਨ ਲਉ △ABC ਵਿੱਚ,
AB = 7 cm
BC = 24 cm, AC = 25 cm
AB² + BC² = (7)² + (24)²
= 49 + 576 = 625
AC² = (25)² = 625
ਹੁਣ AB² + BC² = AC²
∴ △ABC ਇੱਕ ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ ਹੈ ।

ਪ੍ਰਸ਼ਨ (ii).
3 cm, 8 cm, 6 cm
ਉੱਤਰ:
ਮੰਨ ਲਉ △PQR ਵਿੱਚ,
PQ = 3 cm, QR = 8 cm
PR = 6 cm
PQ² + PR² = (3)² + (6)²
= 9 + 36 = 45
QR² = (8)² = 64
ਇੱਥੇ PQ² + PR² ≠ QR²
∴ △PQR ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ ਨਹੀਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ (iii).
50 cm, 80 cm, 100 cm
ਉੱਤਰ:
ਮੰਨ ਲਉ AMNP ਵਿੱਚ, MN = 50 cm,
NP = 80 cm, MP = 100 cm
MN² + NP² = (50)² + (80)²
= 2500 + 6400 = 8900
MP² = (100)² = 1000
ਇੱਥੇ, MP² ≠ MN² + NP²
∴ △MNP ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ ਨਹੀਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ (iv).
13 cm, 12 cm, 5 cm.
ਉੱਤਰ:
ਮੰਨ ਲਉ △ABC ਵਿੱਚ,
AB = 13 cm, BC = 12 cm, AC = 5 cm
BC² + AC² = (12)² + (5)²
= 144 + 25 = 169
AB² = (13)² = 169
AB² = BC² + AC²
∴ △ABC ਸਮਕੋਣ ਤਿਭੁਜ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
PQR ਇੱਕ ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸਦਾ ਕੋਣ ? ਸਮਕੋਣ ਹੈ ਅਤੇ OR ‘ਤੇ ਬਿੰਦੁ M ਇਸ ਤਰ੍ਹਾਂ ਸਥਿਤ ਹੈ। ਕਿ PM ⊥ QR ਹੈ । ਦਰਸਾਉ ਕਿ PM² = QM.MR ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਸਮਕੋਣ △PQR ਵਿੱਚ ਕੋਣ P ਸਮਕੋਣ ਹੈ । QR ‘ਤੇ ਬਿੰਦੂ M ਇਸ ਤਰ੍ਹਾਂ ਸਥਿਤ ਹੈ ਕਿ PM ⊥ QR ਹੈ । | ਵੋ
ਸਿੱਧ ਕਰਨਾ : PM² = QM × MR

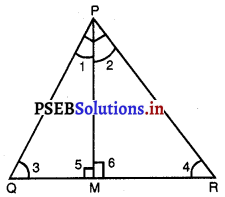
ਸਬੂਤ : ∠P = 90° (ਦਿੱਤਾ ਹੈ।)
∴ ∠1 + ∠2 = 90° …(1)
∠M = 90°
△PMQ ਵਿਚ
∠1 + ∠3 + ∠5 = 180°
∠1 + ∠3 = 90° …(2)
[∠M = 90°]
(1) ਅਤੇ (2) ਤੋਂ
∠1 + ∠2 = ∠1 + ∠3
∠2 = ∠3
△QPM ਅਤੇ △RPM ਵਿੱਚ
∠3 = ∠2 (ਸਿੱਧ ਕੀਤਾ)
∠5 = ∠6 (ਹਰੇਕ 90)
∴ △QMP ~ △PMR [AA ਸਮਰੂਪਤਾ ਕਸੌਟੀ]
\(\frac{ar(△QMP)}{ar(△PMR)}\) = \(\frac{\mathrm{PM}^{2}}{\mathrm{MR}^{2}}\)
[ਜੇਕਰ ਦੋ ਤ੍ਰਿਭੁਜਾਂ ਸਮਰੂਪ ਹਨ ਤਾਂ ਉਨ੍ਹਾਂ ਦੇ ਖੇਤਰਫਲਾਂ ਦਾ ਅਨੁਪਾਤ ਉਨ੍ਹਾਂ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਦੇ ਵਰਗਾਂ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ ]

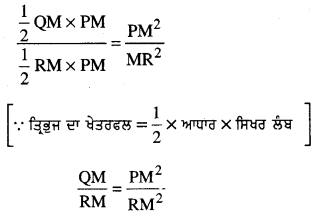
PM² = OM.RM

ਪ੍ਰਸ਼ਨ 3.
ਚਿੱਤਰ ਵਿਚ ABD ਇਕ ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ ਹੈ ਇਸਦਾ ਕੋਣ A ਸਮਕੋਣ ਹੈ ਅਤੇ AC ⊥ BD ਹੈ ।ਦਿਖਾਉ ਕਿ

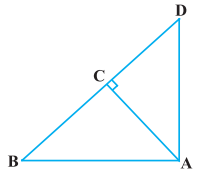
(i) AB² = BC.BD
(ii) AC² = BC.DC
(iii) AD² = BD.CD.
ਹੱਲ:
△DAB ਅਤੇ △DCA ਵਿੱਚ,
∠D = ∠D (ਸਾਂਝਾ)
∠A = ∠C (ਹਰੇਕ 90°)
∴ △DAB ~ △DCA [AA ਸਮਰੂਪਤਾ]
△DAB ਅਤੇ △ACB ਵਿੱਚ, …(1)
∠B = ∠B (ਸਾਂਝਾ)
∠A =∠C (ਹਰੇਕ 90°)
∴ △DAB ~ △ACB …(2)
(1) ਅਤੇ (2) ਤੋਂ
△DAB ~ △ACB ~ △DCA.

(i) △ACB ~ △DAB (ਸਿੱਧ ਕੀਤਾ।)
∴ \(\frac{ar(△ACB)}{ar(△DAB)}\) = \(\frac{\mathrm{AB}^{2}}{\mathrm{DB}^{2}}\)
[ਜੇਕਰ ਦੋ ਭੁਜਾਂ ਸਮਰੂਪ ਹਨ ਤਾਂ ਉਨ੍ਹਾਂ ਦੇ ਖੇਤਰਫਲਾਂ ਦਾ ਆਨੁਪਾਤ ਉਨ੍ਹਾਂ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਦੇ ਵਰਗਾਂ ਦੇ ਅਨੁਪਾਤ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ।]

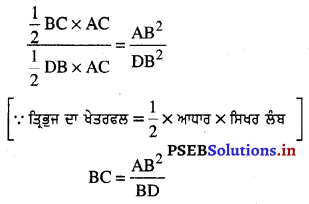
AB² = BC × BD.

(ii) △ACB ~ △DCA (ਸਿੱਧ ਕੀਤਾ)
\(\frac{ar(△ACB)}{ar(△DCA)}\) = \(\frac{A C^{2}}{D C^{2}}\)
[ਜੇਕਰ ਦੋ ਤ੍ਰਿਭੁਜਾਂ ਸਮਰੂਪ ਹਨ ਤਾਂ ਉਨ੍ਹਾਂ ਦੇ ਖੇਤਰਫਲਾਂ ਦਾ ਅਨੁਪਾਤ ਸੰਗਤ ਭੁਜਾਵਾਂ ਦੇ ਅਨੁਪਾਤ ਦੇ | ਵਰਗਾਂ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ।]

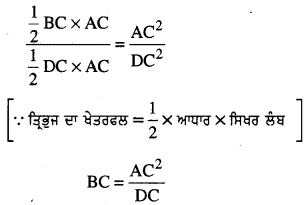
AC² = BC × DC

(iii) △DAB ~ △DCA (ਸਿੱਧ ਕੀਤਾ)
\(\frac{ar(△DAB)}{ar(△DCA)}\) = \(\frac{\mathrm{DA}^{2}}{\mathrm{DB}^{2}}\)
[ਜੇਕਰ ਦੋ ਤ੍ਰਿਭੁਜਾਂ ਸਮਰੂਪ ਹਨ ਤਾਂ ਉਨ੍ਹਾਂ ਦੇ ਖੇਤਰਫਲਾਂ ਦਾ ਅਨੁਪਾਤ ਸੰਗਤ ਭੁਜਾਵਾਂ ਦੇ ਅਨੁਪਾਤ ਦੇ ਵਰਗਾਂ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ।]

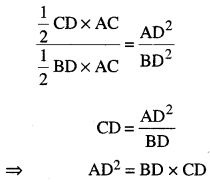
ਪ੍ਰਸ਼ਨ 4.
ABC ਇੱਕ ਸਮਦੋਭੁਜੀ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸ ਦਾ ਕੋਣ ? | ਸਮਕੋਣ ਹੈ । ਸਿੱਧ ਕਰੋ ਕਿ AB² = 2AC² ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △ABC ਇਕ ਸਮਦੋਭੁਜੀ ਤਿਭੁਜ ਹੈ ਜਿਸਦਾ ਕੋਣ C ਸਮਕੋਣ ਹੈ ।
ਸਿੱਧ ਕਰਨਾ : AB² = AC²

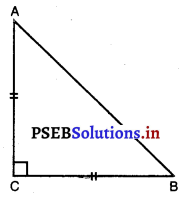
ਸਬੂਤ : △ACB ਵਿੱਚ, ∠C = 90°
AC = BC (ਦਿੱਤਾ ਹੈ।)
AB² = AC² + BC²
[ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਤੋਂ]
= AC² + AC² [BC = AC]
ਇਸ ਲਈ AB² = 2AC²

ਪ੍ਰਸ਼ਨ 5.
ABC ਇੱਕ ਸਮਦੋਭੁਜੀ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸ ਵਿਚ | AC = BC ਹੈ । ਜੇਕਰ AB² = 2AC² ਹੈ ਤਾਂ ਸਿੱਧ ਕਰੋ ਕਿ ABC ਇੱਕ ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △ABC ਇਕ ਸਮਦੋਭੁਜੀ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸ ਵਿੱਚ AC = BC ਹੈ ।
AB² = 2AC²
ਸਿੱਧ ਕਰਨਾ : △ABC ਇਕ ਸਮਕੋਣ ਤਿਭੁਜ ਹੈ ।

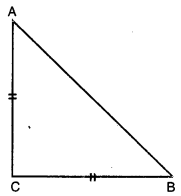
ਸਬੂਤ : AB² = 2AC² ਦਿੱਤਾ ਹੈ।)
AB² = AC² + AC²
AB² = AC² + BC² [AC = BC]
∴ ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਦੇ ਉਲਟ ਤੋਂ △ABC ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ ਹੈ ।

ਪ੍ਰਸ਼ਨ 6.
ਇੱਕ ਸਮਭੁਜੀ ਤ੍ਰਿਭੁਜ ABC ਦੀ ਭੁਜਾ 2a ਹੈ । ਇਸਦੇ ਹਰੇਕ ਸਿਖਰ ਲੰਬ ਦੀ ਲੰਬਾਈ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
△ABC ਸਮਭੁਜੀ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸਦੀ ਭੁਜਾ 2a ਹੈ ।
AD ⊥ BC
AB = AC= BC = 2a
△ADB ≅ △ADC [RHS ਸਰਬੰਰਾਮਮ ਤੋਂ]
∴ BD = DC = a

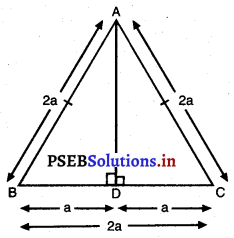
ਸਮਕੋਣ △ADB ਤੋਂ,
AB² = AD² + BD²
(2a)² = AD² + (a)²
4a² – a² = AD²
AD² = 3a²
AD = \(\sqrt {3}\) a.

ਪ੍ਰਸ਼ਨ 7.
ਸਿੱਧ ਕਰੋ ਕਿ ਇੱਕ ਸਮਚਤੁਰਭੁਜ ਦੀਆਂ ਭੁਜਾਵਾਂ ਦੇ ਵਰਗਾਂ ਦਾ ਜੋੜ ਉਸਦੇ ਵਿਕਰਣਾਂ ਦੇ ਵਰਗਾਂ ਦੇ ਜੋੜ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ : ਸਮਚਤੁਰਭੁਜ ABCD ਦੇ ਵਿਕਰਣ AC ਅਤੇ BD ਇਕ-ਦੂਜੇ ਨੂੰ O ਉੱਤੇ ਕੱਟਦੇ ਹਨ !
ਸਿੱਧ ਕਰਨਾ :
AB² + BC² + CD² + AD = AC² + BD²
ਸਬੂਤ : ∵ ਸਮਚਤੁਰਭੁਜ ਦੇ ਵਿਕਰਣ ਆਪਸ ਵਿਚ ਸਮਕੋਣ ਉੱਤੇ ਸਮਦੁਭਾਜਿਤ ਹੁੰਦੇ ਹਨ ।

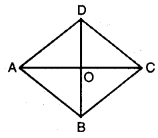
∴ AO = CO, BO = DO
∴ O ਉੱਤੇ ਕੋਣ ਸਮਕੋਣ ਹੈ।
△AOB ਵਿੱਚ, ∠AOB = 90°
∴ AB² = AO² + BO² …(1)
[ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਯ ਤੋਂ]
ਇਸ ਤਰ੍ਹਾਂ, BC² = CO² + B0² ….(2)
CD² = CO² + DO² …(3)
ਅਤੇ DA² = DO² + AO² …(4)
(1), (2), (3) ਅਤੇ (4) ਨੂੰ ਜੋੜਨ ਤੇ
AB² + BC² + CD² + DA²
= 2AO² + 2CO² + 2BO² + 2DO²
= 4AO² + 4BO²
[∵ AO = CO ਅਤੇ BO = DO]
= (2AO)² + (2BO)² = AC² + BD².

ਪ੍ਰਸ਼ਨ 8.
ਚਿੱਤਰ ਵਿੱਚ, △ABC ਦੇ ਵਿੱਚ ਸਥਿਤ ਕੋਈ ਬਿੰਦੂ 0 ਹੈ ਅਤੇ AD ⊥ BC, OE ⊥ AC ਅਤੇ OF ⊥ AB ਹੈ । ਦਿਖਾਉ ਕਿ
(i) OA² + OB² + OC²– OD² – OE² – OF²
= AF² + BD² + CE²
(ii) AF² + BD² + CE²
= AE² + CD² + BF².

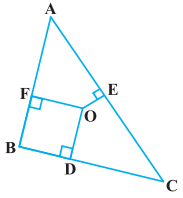
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △ABC ਜਿਸ ਵਿਚ
OD ⊥ BC, OE ⊥ AC ਅਤੇ OF ⊥ AB ਹੈ ।
ਸਿੱਧ ਕਰਨਾ :
(i) AF² + BD² + CE²
= OA² + OB² + OC² – OD² – OE² – OF²

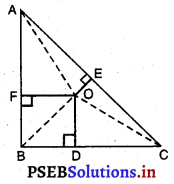
(ii) AF² + BD² + CE²
= AE² + CD² + BF².
ਰਚਨਾ : OB, OC ਅਤੇ OA ਨੂੰ ਮਿਲਾਉ
ਸਬੂਤ (i) ਸਮਕੋਣ △AFO ਵਿੱਚ,
OA² = OF² + AF² [ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਤੋਂ]
ਜਾਂ AF² = OA² – OF² ….(1)
ਸਮਕੋਣ △BDO ਵਿੱਚ,
OB² = BD² + OD²
[ਪਾਈਥਾਗੋਰਸ ਮੇਯ ਤੋਂ]
⇒ BD² = OB² – OD² …(2)
ਸਮਕੋਣ △CEO ਵਿੱਚ,
OC² = CE² + OE² [ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਤੋਂ।]
⇒ CE² = OC² – OE² …(3)
∴ AF² + BD² + CE² = OA² – OF² + OB² – OD² + OC² – OE²
[(1), (2), ਅਤੇ (3) ਨੂੰ ਜੋੜਨ ਤੇ]
= OA² + OB² + OC² – OD² – OE² – OF²
ਜੋਕਿ (1) ਨੂੰ ਸਿੱਧ ਕਰਦਾ ਹੈ ।
ਦੁਬਾਰਾ AF² + BD² + CE²
= (OA² – OE²) + (OC² – OD²) + (OB² – OF²)
= AE² + CD² + BE²
: AE² = AO² – OE²
CD² = OC² – OD²
BF² = OB² – OF²

ਪ੍ਰਸ਼ਨ 9.
10 m ਲੰਬੀ ਇੱਕ ਪੌੜੀ ਇਕ ਕੰਧ ਨਾਲ ਲਗਾਉਣ ‘ਤੇ ਜ਼ਮੀਨ ਨਾਲੋਂ 8 m ਦੀ ਉੱਚਾਈ ‘ਤੇ ਸਥਿਤ ਇੱਕ ਖਿੜਕੀ ਤੱਕ ਪਹੁੰਚਦੀ ਹੈ । ਕੰਧ ਦੇ ਅਧਾਰ ਤੋਂ ਪੌੜੀ ਦੇ ਹੇਠਲੇ ਸਿਰੇ ਦੀ ਦੂਰੀ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਖਿੜਕੀ ਦੀ ਧਰਤੀ ਤੋਂ ਉਚਾਈ (AB) = 8 m

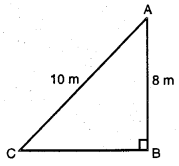
ਪੌੜੀ ਦੀ ਲੰਬਾਈ (AC) = 10 m
ਪੌੜੀ ਦੇ ਹੇਠਲੇ ਸਿਰੇ ਅਤੇ ਕੰਧ ਦੇ ਅਧਾਰ ਵਿਚਲੀ ਦੂਰੀ (BC) = ?
△ABC ਵਿੱਚ,
AB² + BC² = AC² [ਪਾਈਥਾਗੋਰਸ ਮੇਯ ਤੋਂ]
(8)² + (BC)² = (10)²
64 + BC² = 100
BC² = 100 – 64
BC = \(\sqrt {36}\)
BC = 6 m.
∴ ਪੌੜੀ ਦੇ ਹੇਠਲੇ ਸਿਰੇ ਅਤੇ ਕੰਧ ਦੇ ਅਧਾਰ ਵਿਚਲੀ | ਦੂਰੀ = 6 m.

ਪ੍ਰਸ਼ਨ 10.
18 m ਉੱਚੇ ਇਕ ਸਿੱਧੇ ਖੜੇ ਖੰਭੇ ਦੇ ਉੱਪਰਲੇ ਸਿਰੇ | ਨਾਲ ਤਾਰ ਦਾ ਇੱਕ ਸਿਰਾ ਜੁੜਿਆ ਹੋਇਆ ਹੈ ਅਤੇ ਤਾਰ ਦਾ | ਦੂਸਰਾ ਸਿਰਾ ਇਕ ਕਿੱਲੇ ਨਾਲ ਜੁੜਿਆ ਹੋਇਆ ਹੈ । ਖੰਬੇ ਦੇ | ਅਧਾਰ ਤੋਂ ਕਿੱਲੇ ਨੂੰ ਕਿੰਨੀ ਦੂਰੀ ‘ਤੇ ਗੱਡਿਆ ਜਾਵੇ ਕਿ ਤਾਰ ਤਣੀ ਰਹੇ ਜਦੋਂ ਕਿ ਤਾਰ ਦੀ ਲੰਬਾਈ 24 m ਹੈ ।
ਹੱਲ:
ਮੰਨ ਲਉ ਖੰਬੇ ਦੀ ਉਚਾਈ AB = 18 m
ਤਾਰ ਦੀ ਲੰਬਾਈ Ac = 24 m

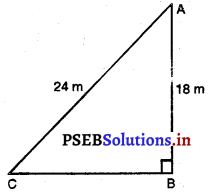
C, ਤੇ ਕਿੱਲਾ ਗੱਡਿਆ ਹੋਇਆ ਹੈ । ਖੰਬੇ ਤੋਂ ਦੂਰੀ BC = ਹੈ ।
ਸਮਕੋਣ △ABC,
AB² + BC² = AC²
[ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਤੋਂ।]
(18)² + (BC)² = (24)²
324 + (BC)² = 576
BC² = 576 – 324
BC = \(\sqrt {252}\) = 6\(\sqrt {7}\)
BC = 6\(\sqrt {7}\) m

ਪ੍ਰਸ਼ਨ 11.
ਇੱਕ ਹਵਾਈ ਜਹਾਜ਼ ਇੱਕ ਹਵਾਈ ਅੱਡੇ ਤੋਂ ਉੱਤਰ ਵੱਲ 1000 km/h ਦੀ ਚਾਲ ਨਾਲ ਉੱਡਦਾ ਹੈ । ਉਸੇ ਸਮੇਂ ਇੱਕ ਹੋਰ ਹਵਾਈ ਜਹਾਜ਼ ਉਸੇ ਹਵਾਈ ਅੱਡੇ ਤੋਂ ਪੱਛਮ ਵੱਲ 1200 km/h ਦੀ ਚਾਲ ਨਾਲ ਉੱਡਦਾ ਹੈ । 1\(\frac{1}{2}\) ਘੰਟੇ ਬਾਦ ਦੋਵਾਂ ਹਵਾਈ ਜਹਾਜ਼ਾਂ ਦੀ ਵਿਚਕਾਰਲੀ ਦੂਰੀ ਕਿੰਨੀ ਹੋਵੇਗੀ ।
ਹੱਲ:
ਪਹਿਲੇ ਹਵਾਈ ਜਹਾਜ਼ ਦੀ ਚਾਲ = 1000 km/h

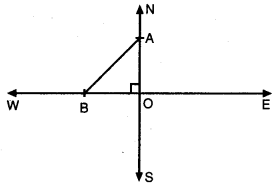
ਪਹਿਲੇ ਹਵਾਈ ਜਹਾਜ਼ ਦੁਆਰਾ ਉੱਤਰ ਵੱਲ 1\(\frac{1}{2}\) ਘੰਟੇ ਵਿਚ ਤੈਅ ਕੀਤੀ ਦੂਰੀ = 1000 × \(\frac{3}{2}\)
OA = 1500 km
ਦੂਸਰੇ ਹਵਾਈ ਜਹਾਜ ਦੀ ਚਾਲ = 1200 km/h
ਦੂਸਰੇ ਹਵਾਈ ਜਹਾਜ ਦੁਆਰਾ 1\(\frac{1}{2}\) ਘੰਟੇ ਵਿਚ ਤੈਅ ਕੀਤੀ ਦੂਰੀ
=1200 × \(\frac{3}{2}\) km
OB = 1800 km
ਸਮਕੋਣ △AOB ਵਿੱਚ, .
AB² = AO² + OB²
AB² = (1500)² + (1800)²
AB = \(\sqrt {2250000+3240000}\)
= \(\sqrt {5490000}\)
AB = 300\(\sqrt {61}\) km
∴ ਦੋਹਾਂ ਹਵਾਈ ਜਹਾਜ਼ਾਂ ਵਿਚਲੀ ਦੂਰੀ
= 300\(\sqrt {61}\) km

ਪ੍ਰਸ਼ਨ 12.
ਦੋ ਖੰਭੇ ਜਿਨ੍ਹਾਂ ਦੀਆਂ ਉੱਚਾਈਆਂ ਭੂਮੀ ‘ਤੇ 6 m ਅਤੇ 11 m ਹਨ ਅਤੇ ਸਮਤਲ ਭੂਮੀ ‘ਤੇ ਖੜ੍ਹੇ ਹਨ । ਜੇਕਰ ਉਹਨਾਂ ਦੇ ਹੇਠਲੇ ਸਿਰਿਆਂ ਦੇ ਵਿਚਕਾਰਲੀ ਦੂਰੀ 12m ਹੋਵੇ ਤਾਂ ਉਹਨਾਂ ਦੇ ਉੱਪਰਲੇ ਸਿਰਿਆਂ ਦੇ ਵਿਚਕਾਰਲੀ ਦੂਰੀ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਖੰਭੇ ਦੀ ਉੱਚਾਈ (AB) = 11m
ਖੰਭੇ ਦੀ ਉੱਚਾਈ (CD) = 6 m

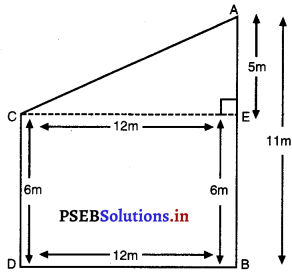
ਖੰਭੇ ਦੇ ਅਧਾਰਾਂ ਦੇ ਵਿਚਕਾਰਲੀ ਦੂਰੀ = 12 m
C ਤੋਂ CE ⊥ AB ਖਿੱਚੋ
BE = DC = 6m
AE = AB – BE
= (11 – 6) m = 5 m
ਸਮਕੋਣ △AEC ਵਿੱਚ,
AC² = AE² + EC²
AC = \(\sqrt{(5)^{2}+(12)^{2}}\)
= \(\sqrt {25+144}\)
= \(\sqrt {169}\) = 13.
∴ ਖੰਭੇ ਦੇ ਉੱਪਰਲੇ ਸਿਰਿਆਂ ਵਿਚਕਾਰਲੀ ਦੂਰੀ = 13m.

ਪ੍ਰਸ਼ਨ 13.
ਇੱਕ ਤ੍ਰਿਭੁਜ ABC ਜਿਸਦਾ ਕੋਣ C ਸਮਕੋਣ ਹੈ, ਦੀਆਂ ਭੁਜਾਵਾਂ CA ਅਤੇ CB ‘ਤੇ ਕੁਮਵਾਰ ਬਿੰਦੂ D ਅਤੇ L ਸਥਿਤ ਹਨ । ਸਿੱਧ ਕਰੋ ਕਿ
AE² + BD² = AB² + DE²
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △ABC ਇੱਕ ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸ ਵਿਚ C ਸਮਕੋਣ ਹੈ ਭੁਜਾ CA ਅਤੇ CB ਤੇ ਕ੍ਰਮਵਾਰ ਬਿੰਦੂ D ਅਤੇ E ਸਥਿਤ ਹਨ ।
∴ CD = AD = \(\frac{1}{2}\)AC
BE = EC = \(\frac{1}{2}\)BC
ਸਿੱਧ ਕਰਨਾ :
AE² + BD² = AB² + DE²
ਸਬੂਤ : ਸਮਕੋਣ △BCA ਵਿੱਚ,
AB² = BC² + CA² …..(1) [
ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਤੋਂ]

ਸਮਕੋਣ △ECD ਵਿੱਚ,
DE² = EC² + DC² …(2)
[ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ]
ਸਮਕੋਣ △ACE ਵਿੱਚ
AE² = AC² + CE² …(3)
ਸਮਕੋਣ △BCD ਵਿੱਚ
BD² = BC² + CD² …(4)
(3) ਅਤੇ (4) ਨੂੰ ਜੋੜਣ ਤੇ,
AE² + BD² = AC² + CE² + BC² + CD²
= [AC² + CB²] + [CE² + DC²]
= AB² + DE²
[(3) ਅਤੇ (4) ਤੋਂ]
ਇਸ ਲਈ AE² + BD² = AB² + DE².

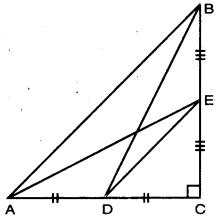
ਪ੍ਰਸ਼ਨ 14.
ਕਿਸੇ ਤ੍ਰਿਭੁਜ ABC ਦੇ ਸਿਖ਼ਰ A ਤੋਂ BC ‘ਤੇ ਸੁੱਟਿਆ ਗਿਆ ਲੰਬ BC ਨੂੰ ਬਿੰਦੂ ‘ਤੇ ਇਸ ਤਰ੍ਹਾਂ ਕੱਟਦਾ ਹੈ ਕਿ DB = 3 CD ਹੈ (ਦੇਖੋ ਚਿੱਤਰ) ।
ਸਿੱਧ ਕਰੋ ਕਿ 2AB² = 2AC² + BC² ਹੈ ।

ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △ABC ਵਿੱਚ, AD ⊥ BC
DB = 3CD ਹੈ ।
ਸਿੱਧ ਕਰਨਾ :
2AB² = 2AC² + BC².
ਸਬੂਤ : ਸਮਕੋਣ ਭੁਜ ADB ਅਤੇ ADC ਵਿੱਚ
AB² = AD² + BD² ;
AC² = AD² + DC²
[ਪਾਈਥਾਗੋਰਸ ਮੇਯ ਤੋਂ ]
∴ AB² – AC² = BD² – DC²
= 9CD² – CD²;
[∵ BD = 3CD]
= 8CD² = 8\(\left(\frac{\mathrm{BC}}{4}\right)^{2}\)
[∵ BC = DB + CD
=3CD + CD
= 4CD
∴ CD = \(\frac{1}{2}\)BC]
∴ AB² – AC² = \(\frac{\mathrm{BC}^{2}}{2}\)
⇒ 2(AB² – AC²) = BC²
⇒ 2AB² – 2AC² = BC²
∴ AB² = 2AC² + BC².

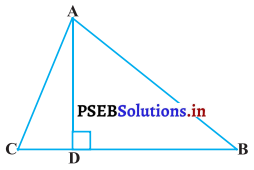
ਪ੍ਰਸ਼ਨ 15.
ਕਿਸੇ ਸਮਭੁਜੀ ਤ੍ਰਿਭੁਜ ABC ਦੀ ਭੁਜਾ BC ‘ਤੇ ਇੱਕ ਬਿੰਦੂ ) ਇਸ ਤਰ੍ਹਾਂ ਸਥਿਤ ਹੈ ਕਿ BD = \(\frac{1}{3}\)BC ਹੈ । ਸਿੱਧ ਕਰੇ ਕਿ 9AD² = 7AB² ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਸਮਭੁਜੀ ਤ੍ਰਿਭੁਜ ABC ਦੀ ਭੁਜਾ BC ‘ਤੇ ਇਕ ਬਿੰਦੂ ) ਇਸ ਤਰ੍ਹਾਂ ਸਥਿਤ ਹੈ ਕਿ BD = \(\frac{1}{3}\)BC ਹੈ ।
ਸਿੱਧ ਕਰਨਾ : 9AD² = 7AB².

ਰਚਨਾ : AM ⊥ BC ਖਿੱਚੋ
ਸਬੂਤ : △AMB ≅ △AMC [R.H.S. ਨਿਯਮ ਨਾਲ AM = AM ਅਤੇ AB = AC]
∴ BM = MC = \(\frac{1}{2}\)BC
ਦੁਬਾਰਾ BD = \(\frac{1}{3}\)BC
ਅਤੇ DC = \(\frac{2}{3}\)BC
(∵ BC, D ਤੇ ਤਿੰਨ ਭਾਗਾਂ ਵਿਚ ਵਿਭਾਜਿਤ ਕਰਦਾ ਹੈ ॥)
ਹੁਣ △ADC ਵਿੱਚ, ∠C ਨਿਊਣ ਕੋਣ ਹੈ
∴ AD² = AC² + DC² – 2DC × MC

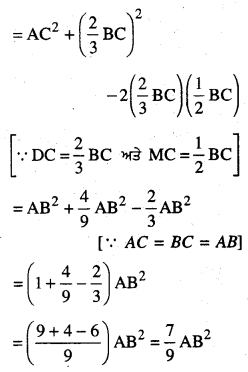
∴ AD² = AB²
⇒ 9AD² = 7AB².

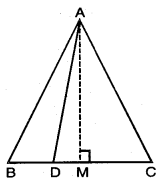
ਪ੍ਰਸ਼ਨ 16.
ਕਿਸੇ ਸਮਭੁਜੀ ਤ੍ਰਿਭੁਜ ਵਿੱਚ, ਸਿੱਧ ਕਰੋ ਕਿ ਉਸਦੀ ਇਕ ਭੁਜਾ ਦੇ ਵਰਗ ਦਾ ਤਿਗੁਣਾ ਤਿੰਨ ਗੁਣਾ) ਉਸ ਦੇ ਇਕ ਸਿਖਰ ਲੰਬ ਦੇ ਵਰਗ ਦੇ ਚਾਰ ਗੁਣਾ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △ABC ਇੱਕ ਸਮਭੁਜੀ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸ ਵਿੱਚ AB = BC = AC

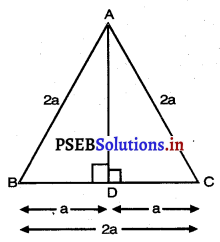
AD ⊥ DC
ਸਿੱਧ ਕਰਨਾ : 3AB² = 4AD²
ਸਬੂਤ : △ABC ਸੈਂ,
ਮੰਨ ਲਉ : AB = BC = AC = 2a
AD ⊥ BC
∴ BD = DC = \(\frac{1}{2}\)BC = a
ਸਮਕੋਣ ਤਿਭੁਜ ਵਿਚ,
AB² = AD² + BD²
(2a)² = AD² + (a)²
4a² = AD² + a²
4a² – a² = AD²
AD² = 3a²
= 3\(\left[\frac{\mathrm{AB}}{2}\right]^{2}\)
[AB = 2a
a = \(\frac{\mathrm{AB}}{2}\)]
AD² = 3\(\frac{\mathrm{AB}^{2}}{4}\)
3AB² = 4AD².

ਪ੍ਰਸ਼ਨ 17.
ਸਹੀ ਉੱਤਰ ਚੁਣ ਕੇ ਉਸਦਾ ਕਾਰਣ ਦੱਸੋ : △ABC ਵਿੱਚ AB = 6\(\sqrt {3}\) cm, AC = 12 cm ਅਤੇ BC = 6 cm ਹੈ । ਕੋਣ B ਹੈ :
(A) 120°
(B) 60°
(C) 90°
(D) 45°
ਹੱਲ:
AC = 12 cm
AB= 6\(\sqrt {3}\) cm
BC = 6 cm
AC² = (12)² = 144
AB² + BC² = (6\(\sqrt {3}\))² + (6)²
= 108 + 36
AB² + BC² = 144
∴ AB² + BC² = AC²
ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਤੋਂ,
△ABC ਵਿੱਚ B ਸਮਕੋਣ ਹੈ ।
∴ ∠B = 90°
∴ ਵਿਕਲਪ (C) ਸਹੀ ਹੈ ।