PSEB 10th Class Maths Solutions Chapter 6 ਤ੍ਰਿਭੁਜ Ex 6.6

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 6 ਤ੍ਰਿਭੁਜ Ex 6.6 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 6 ਤ੍ਰਿਭੁਜ Exercise 6.6

ਪ੍ਰਸ਼ਨ 1.
ਚਿੱਤਰ ਵਿੱਚ, PS ਕੋਣ ∠PR ਦਾ ਸਮਦੋਭਾਜਕ ਹੈ । ਸਿੱਧ ਕਰੋ ਕਿ \(\frac{QS}{SR}\) = \(\frac{PQ}{PR}\) ਹੈ ।

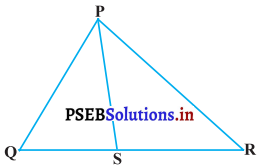
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △PQR, PS ਕੋਣ ∠QPR ਦਾ ਸਮਦੋਭਾਜਕ ਹੈ ਭਾਵ ∠1 = ∠2
ਸਿੱਧ ਕਰਨਾ : \(\frac{QS}{SR}\) = \(\frac{PQ}{PR}\)

ਰਚਨਾ : R ਤੋਂ ਇੱਕ ਰੇਖਾ PS ਦੇ ਸਮਾਂਤਰ ਖਿੱਚੋ ਜੋ QP ਨੂੰ ਵਧਾਉਣ ਤੇ Tਉੱਤੇ ਮਿਲਦੀ ਹੈ ।
ਸਬੂਤ : △QRT ਵਿੱਚ,
PS || TR
∠2 = ∠3 (ਇਕਾਂਤਰ ਕੋਣ)
∠1 = ∠4 (ਸੰਗਤ ਕੋਣ)
ਪਰ ∠1 = ∠2 (ਦਿੱਤਾ ਹੈ।)
∴ ∠3 = ∠4
△PRT ਵਿੱਚ
∠3 = ∠4 (ਸਿੱਧ ਕੀਤਾ)
PT = PR [ਸਮਾਨ ਭੁਜਾਵਾਂ ਦੇ ਸਨਮੁੱਖ ਕੋਣ ਵੀ ਬਰਾਬਰ ਹੁੰਦੇ ਹਨ ]
△QRT ਵਿੱਚ
PS || TR

ਪ੍ਰਸ਼ਨ 2.
ਚਿੱਤਰ ਵਿਚ D ਤ੍ਰਿਭੁਜ ABC ਦੇ ਕਰਣ AC ਉੱਤੇ ਇਕ ਬਿੰਦੂ ਹੈ ਜਦ ਕਿ BD ⊥ AC ਅਤੇ DM ⊥ BC ਅਤੇ DN ⊥ AB ਹੈ । ਸਿੱਧ ਕਰੋ ਕਿ
(i) DM² = DN.MC
(ii) DN² = DM.AN

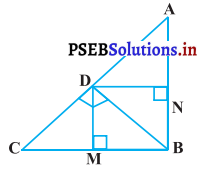
ਦਿੱਤਾ ਹੈ : △ABC ਵਿੱਚ, DM ⊥ BC,
DN ⊥ AB ਹੈ ।
ਸਿੱਧ ਕਰਨਾ : DM² = DN.AC
DN = DM.AN.
ਹੱਲ:
BD ² AC (ਦਿੱਤਾ ਹੈ।)
⇒ ∠BDC= 90°
⇒ ∠BDM + ∠MDC = 90° …(1)
△DMC ਵਿੱਚ
∠DMC = 90°
[∵ DM ⊥ BC (ਦਿੱਤਾ ਹੈ)]
⇒ ∠C + ∠MDC = 90° ..(2)
(1) ਅਤੇ (2) ਤੋਂ
∠BDM + ∠MDC = ∠C + ∠MDC
⇒ ∠BDM =∠C
[ਦੋਵੇਂ ਪਾਸਿਉਂ ∠MDC ਨੂੰ ਕੱਟਣ ਤੇ]
ਹੁਣ △BMD ਅਤੇ △MDC ਵਿੱਚ,
∠BDM = ∠C [ਸਿੱਧ ਕੀਤਾ]
∠BMD = ∠MDC [ਹਰੇਕ 90°]
∴ ∠BMD ~ ∠MDC [AA ਕਮੇਟੀ]
⇒ \(\frac{\mathrm{DM}}{\mathrm{BM}}\) = \(\frac{\mathrm{MC}}{\mathrm{DM}}\)
[∵ ਸਮਰੂਪ ਤ੍ਰਿਭੁਜਾਂ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਸਮਾਨ ਅਨੁਪਾਤੀ ਹੁੰਦੀਆਂ ਹਨ |]
⇒ DM² = BM × MC
⇒ DM² = DN × MC
[∵ BM = DN]
ਇਸੇ ਤਰ੍ਹਾਂ △NDA ~ △NBD
⇒ \(\frac{\mathrm{DN}}{\mathrm{BN}}\) = \(\frac{\mathrm{AN}}{\mathrm{DN}}\)
[∵ ਸਮਰੂਪ ਤ੍ਰਿਭੁਜਾਂ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਸਮਾਨ ਅਨੁਪਾਤੀ ਹੁੰਦੀਆਂ ਹਨ |]
⇒ DN² = BN × AN
⇒ DN² = DM × AN

ਪ੍ਰਸ਼ਨ 3.
ਚਿੱਤਰ ਵਿੱਚ ABC ਇੱਕ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸ ਵਿਚ ∠ABC > 90° ਹੈ ਅਤੇ AD ⊥ CB ਹੈ ਸਿੱਧ ਕਰੋ ਕਿ AC² = AB² + BC² + 2BC.BD ਹੈ ।

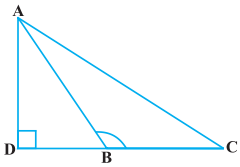
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △ABC ਵਿੱਚ AD ⊥ BC ਜਦੋਂ BC ਨੂੰ ਵਧਾਇਆ ਜਾਂਦਾ ਹੈ ∠ABC > 90° ਹੈ ।
ਸਿੱਧ ਕਰਨਾ : AC² = AB² + BC² + 2BC.BD.
ਸਬੂਤ : ਮੰਨ ਲਉ : BC = a,
CA = b,
AB = C,
AD = h
ਅਤੇ BD = x.
ਸਮਕੋਣ ਤਿਭੁਜ △ADB ਵਿੱਚ, ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਤੋਂ,
AB² = BD² + AD
ਭਾਵ c² = x² + h²
ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ △ADC ਵਿੱਚ
AC² = CD² + AD²
ਭਾਵ b² = (a + x)² + h²
= a² + 2ax + x² + h²
= a² + 2ax + c²;
[(1) ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ਤੇ]
b² = a² + c² + 2ax
ਹੁਣ . , AC² = AB² + BC² + 2BC × BD.

ਪ੍ਰਸ਼ਨ 4.
ਚਿੱਤਰ ਵਿੱਚ ABC ਇੱਕ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸ ਵਿੱਚ ∠ABC < 90° ਹੈ ਅਤੇ AD ⊥ BC ਹੈ ।
ਸਿੱਧ ਕਰੋ ਕਿ
AC² = AB² + BC² – 2BC.BD ਹੈ ।

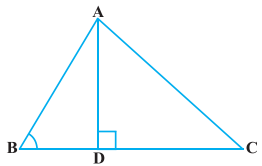
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △ABC ਜਿਸ ਵਿਚ ∠ABC <90° ਅਤੇ AD ⊥ BC ਹੈ ।
ਸਿੱਧ ਕਰਨਾ : AC² = AB² + BC² – 2BC.BD.
ਸਬੂਤ : ADC ਇੱਕ ਸਮਕੋਣ ਹੈ ਜਿਸ ਵਿਚ D ਇੱਕ ਸਮਕੋਣ ਹੈ ।
AC² = CD² + DA² ….(1)
(ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਤੋਂ।)
ਨਾਲ ਹੀ, △ADB ਸਮਕੋਣ △ ਹੈ D ਇਕ ਸਮਕੋਣ ਹੈ ।
AB² = AD² +DB² ….(2)
(1) ਤੋਂ ।
AC² = AD² +(CB – BD)²
= AD² + CB² + BD² – 2CB × BD
ਜਾਂ AC² = (BD² + AD²) + CB² – 2CB × BD
AC² = AB² + BC² – 2BC × BD.
[(2) ਦੇ ਪ੍ਰਯੋਗ ਤੋਂ।

ਪ੍ਰਸ਼ਨ 5.
ਚਿੱਤਰ ਵਿੱਚ AD ਤ੍ਰਿਭੁਜ ABC ਦੀ ਇਕ ਮੱਧਕਾ ਹੈ . ਅਤੇ AM ⊥ BC ਹੈ । ਸਿੱਧ ਕਰੋ ਕਿ :
(i) AC² = AD² + BC.DM + \(\left(\frac{\mathrm{BC}}{2}\right)^{2}\)
(ii) AB² = AD² – BC.DM + \(\left(\frac{\mathrm{BC}}{2}\right)^{2}\)
(iii) AC² + AB² = 2AD² + \(\frac{1}{2}\)BC²

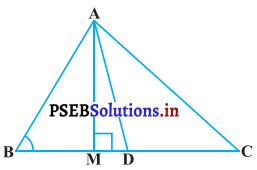
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △ABC ਵਿੱਚ, AM ⊥ BC, AD, △ABC ਦੀ ਇੱਕ ਮੱਧਕਾ ਹੈ ।
ਸਿੱਧ ਕਰਨਾ :
(i) AC² = AD² + BC.DM + \(\left(\frac{\mathrm{BC}}{2}\right)^{2}\)
(ii) AB² = AD² – BC.DM + \(\left(\frac{\mathrm{BC}}{2}\right)^{2}\)
(iii) AC² + AB² = 2AD² + \(\frac{1}{2}\)BC²
ਸਬੂਤ : △AMC ਵਿੱਚ,
AC² = AM² + MC²
= AM² + (MD +DC)²
AC² = AM² + MD² + DC² + 2MD × DC
AC² = (AM² + MD²) + \(\left(\frac{\mathrm{BC}}{2}\right)^{2}\) + 2.MD\(\left(\frac{\mathrm{BC}}{2}\right)\)
AC² = AD² + BC × MD + \(\frac{\mathrm{BC}^{2}}{4}\)
[ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ △AMD
AD² = AM² + MD²]
∴ AC² = AD² + BC.MD + \(\frac{\mathrm{BC}^{2}}{4}\) …(1)

(ii) ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ AMB ਵਿੱਚ,
AB² = AM² + BM²
= AM² + (BD – MD)²
= AM² + BD² + MD² – 2BD × MD
= (AM² + MD²) + BD² – 2(\(\frac{1}{2}\)BC) MD
= AD² + (\(\frac{1}{2}\)BC)² – BC.MD
[∵ △AMD ਸੇਂ, AD² = MA² + MD²]
AB² = AD² + \(\left(\frac{\mathrm{BC}}{2}\right)^{2}\) – BC.MD …2

(iii) (1) ਅਤੇ (2) ਨੂੰ ਜੋੜਨ ਤੇ,
AB² + AC² = AD² + BC.MD + \(\left(\frac{B C}{2}\right)^{2}\) + AD² + \(\left(\frac{B C}{2}\right)^{2}\) – BC.MD
= 2AD² + \(\frac{\mathrm{BC}^{2}}{4}\) + \(\frac{\mathrm{BC}^{2}}{4}\)
= 2AD² + 2\(\frac{\mathrm{BC}^{2}}{4}\)
AB² + AC² = 2AD² + \(\frac{\mathrm{BC}^{2}}{2}\)

ਪ੍ਰਸ਼ਨ 6.
ਸਿੱਧ ਕਰੋ ਕਿ ਇੱਕ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਦੇ ਵਿਕਰਣਾਂ ਦੇ ਵਰਗਾਂ ਦਾ ਜੋੜ ਉਸ ਦੀਆਂ ਭੁਜਾਵਾਂ ਦੇ ਵਰਗਾਂ ਦੇ ਜੋੜ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ ।
ਹੱਲ:

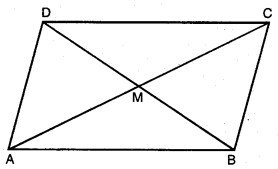
ਦਿੱਤਾ ਹੈ : ਮੰਨ ਲਉ ABCD ਇਕ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਹੈ ਜਿਸ ਦੇ ਵਿਕਰਣ AC ਅਤੇ BD ਪਰਸਪਰ ਬਿੰਦੂ M ਉੱਤੇ ਕੱਟਦੇ ਹਨ ।
ਸਿੱਧ ਕਰਨਾ : AB² + BC² + CD² + DA²
= AB² + BC²
ਸਬੂਤ : ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਦੇ ਵਿਕਰਣ ਇਕ ਦੂਸਰੇ ਨੂੰ ਪਰਸਪਰ ਕੱਟਦੇ ਹਨ ।
ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ABCD ਵਿੱਚ, ਵਿਕਰਣ BD ਅਤੇ AC ਇਕ-ਦੂਸਰੇ ਨੂੰ ਕੱਟਦੇ ਹਨ ।
ਜਾਂ MB ਅਤੇ MD ਕ੍ਰਮਵਾਰ △ABC ਅਤੇ △ADC ਦੀ ਮੱਧਕਾ ਹੈ ।
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ AD, △ABC ਦੀ ਮੱਧਕਾ ਹੈ ।
∴ AB² + AC² = 2AD² + \(\frac{1}{2}\)BC²
ਇਸ ਦਾ ਪ੍ਰਯੋਗ ਕਰਦੇ ਹੋਏ,
AB² + BC² = 2BM² + \(\frac{1}{2}\)BC² …(1)
ਅਤੇ AD² + CD² = 2DM² + \(\frac{1}{2}\)AC² …(2)
(1) ਅਤੇ (2), ਨੂੰ ਜੋੜਨ ਤੇ
AB² + BC² + AD² + CD²
= 2(BM² + DM²) + \(\frac{1}{2}\)(AC² + AC²)
AB² + BC² + AD² + CD²
= 2(\(\frac{1}{4}\)BD² + \(\frac{1}{4}\)BD²) + AC²
AB² + BC² + AD² + CD² = BD² + AC²
ਇੱਕ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਦੇ ਵਿਕਰਣਾਂ ਦੇ ਵਰਗਾਂ ਦਾ ਜੋੜ ਉਸਦੀ ਭੁਜਾਵਾਂ ਦੇ ਵਰਗਾਂ ਦੇ ਜੋੜ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 7.
ਚਿੱਤਰ ਵਿਚ ਇਕ ਚੱਕਰ ਦੀਆਂ ਦੋ ਜੀਵਾਵਾਂ (ਵਤਰਾਂ) AB ਅਤੇ CD ਆਪਸ ਵਿੱਚ P ਬਿੰਦੂ ‘ਤੇ ਕੱਟਦੀਆਂ ਹਨ ।
ਸਿੱਧ ਕਰੋ ਕਿ :
(i) △AFC ~ △DPB
(ii) AP.PB = CP.DP.

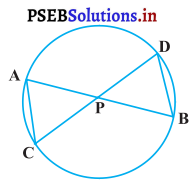
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਇੱਕ ਚੱਕਰ ਦੀਆਂ ਦੋ ਜੀਵਾਵਾਂ AB ਅਤੇ CD ਇਕ-ਦੂਜੇ ਨੂੰ ਮਾਂ ਉੱਤੇ ਕੱਟਦੀਆਂ ਹਨ ।
ਸਿੱਧ ਕਰਨਾ : (i) △APC ~ △DPB
(ii) AP.PB = CP.DP.
ਸਬੂਤ : (i) △APC ਅਤੇ △DPB ਵਿੱਚ,
∠1 = ∠2 (ਸਿਖਰ ਸਨਮੁੱਖ ਕੋਣ)
∠3 = ∠4 (ਇੱਕ ਹੀ ਖੰਡ ਵਿੱਚ ਬਣੇ ਕੋਣ)
∴ △APC ~ △DPB [AA ਸਮਰੂਪਤਾ ਕਸੌਟੀ]

(ii) △APC ~ △DPB (ਸਿੱਧ ਕੀਤਾ)
\(\frac{AD}{DP}\) = \(\frac{PC}{PB}\)
(ਜੇਕਰ ਦੋ ਤ੍ਰਿਭੁਜਾਂ ਸਮਰੂਪ ਹੋਣ ਤਾਂ ਸੰਗਤ ਕੋਣ ਸਮਾਨ ਅਨੁਪਾਤੀ ਹੁੰਦੇ ਹਨ ॥)
AP.PB = PC.DP

ਪ੍ਰਸ਼ਨ 8.
ਚਿੱਤਰ ਵਿੱਚ ਇੱਕ ਚੱਕਰ ਦੀਆਂ ਦੋ ਵਤਰਾਂ AB ਅਤੇ CD ਵਧਾਉਣ ਤੇ ਆਪਸ ਵਿੱਚ ਬਿੰਦੂ ‘ਤੇ ਕੱਟਦੀਆਂ ਹਨ । निय व वि
(i) △PAC ~ △PDB
(ii) PA.PB = PC.PD.

ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਇਕ ਚੱਕਰ ਦੀਆਂ ਦੋ ਜੀਵਾਵਾਂ AB ਅਤੇ CD ਵਧਾਉਣ ਤੇ ਪਰਸਪਰ P ਬਿੰਦੁ ਤੇ ਕੱਟਦੇ ਹਨ ।
ਸਿੱਧ ਕਰਨਾ : (i) △PAC ~ △PDB
(ii) PA.PB = PC.PD.
ਸਬੂਤ : (i) △PAC ਅਤੇ △PDB ਤੋਂ,
∠P = ∠P
∠PAC = ∠PDB (ਚੱਕਰੀ ਚਤੁਰਭੁਜ ਦਾ ਬਾਹਰੀ ਕੋਣ ਅੰਦਰਲੇ ਕੋਣ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ।)
∴ △PAC ~ △PDB [AA ਸਮਰੂਪਤਾ ਕਸੋਟੀ ਤੋਂ।]

(iii) △PAB ~ △PDB
\(\frac{PA}{PD}\) = \(\frac{PC}{PB}\)
[ਜੇ ਦੋ ਸਮਰੂਪ ਤ੍ਰਿਭੁਜ ਹਾਂ ਤਾਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਸਮਾਨੁਪਾਤੀ ਹੁੰਦੀਆਂ ਹਨ |]
PA × PB = PC × PD.

ਪ੍ਰਸ਼ਨ 9.
ਚਿੱਤਰ ਵਿੱਚ,ਤ੍ਰਿਭੁਜ ABC ਦੀ ਭੁਜਾ BC ‘ਤੇ ਇੱਕ ਬਿੰਦੂ D ਇਸ ਤਰ੍ਹਾਂ ਸਥਿਤ ਹੈ ਕਿ \(\frac{BD}{DC}\) = \(\frac{AB}{AC}\) ਹੈ । ਸਿੱਧ ਕਰੋ ਕਿ AD, ਕੋਣ ∠BAC ਦਾ ਸਮਦੋਭਾਜਕ ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △ABC, ਵਿਚ ਭੁਜਾ BC ਉੱਤੇ ਇੱਕ ਬਿੰਦੂ D ਇਸ ਪ੍ਰਕਾਰ ਸਥਿਤ ਹੈ ਕਿ \(\frac{BD}{DC}\) = \(\frac{AB}{AC}\)
ਸਿੱਧ ਕਰਨਾ AD ਕੋਣ ∠BAC ਦਾ ਸਮਦੋਭਾਜਕ ਹੈ ।
ਅਰਥਾਤ, ∠1 = ∠2
ਰਚਨਾ : C ਵਿੱਚ CE || DA ਖਿੱਚੋ ਜੋ BA ਨੂੰ E ਤੇ ਮਿਲੇ ।

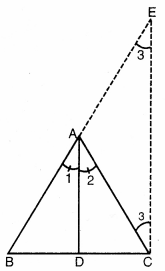
ਸਬੂਤ : △BCE ਵਿੱਚ,
AD || CE …(ਚਨਾ)
ਸਮਾਨੁਪਾਤ ਪ੍ਰਮੇਯ ਤੋਂ,

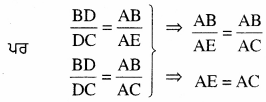
△ACE ਵਿੱਚ,
AE = AC
⇒ ∠3 = ∠4 … (ਬਰਾਬਰ ਭੁਜਾਵਾਂ ਦੇ ਸਨਮੁੱਖ ਕੋਣ)
ਕਿਉਂਕਿ CE || DA ਅਤੇ AC ਉਨ੍ਹਾਂ ਨੂੰ ਕੱਟਦੀ ਹੈ ।
∠2 = ∠4 ..(ਇਕਾਂਤਰ ਕੋਣ)
ਨਾਲ ਹੀ CE || DA ਅਤੇ BAE ਉਨ੍ਹਾਂ ਨੂੰ ਕੱਟਦੀ ਹੈ ।
∠1 = ∠3 …(ਸੰਗਤ ਕੋਣ)
ਇਸ ਤਰ੍ਹਾਂ ਸਾਨੂੰ ਮਿਲਦਾ ਹੈ :
∠3 = ∠4
⇒ ∠4 = ∠1
∠3 = ∠1
ਪਰ ∠4 = ∠2
⇒ ∠1 = ∠2.
AD, ∠BAC ਨੂੰ ਸਮਦੁਭਾਜਿਤ ਕਰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 10.
ਨਾਜ਼ਿਮਾ ਇੱਕ ਨਦੀ ਦੇ ਧਾਰਾ ਵਿੱਚ ਮੱਛੀਆਂ ਪਕੜ ਰਹੀ ਹੈ । ਉਸ ਦੀ ਮੱਛੀਆਂ ਫੜਣ ਵਾਲੀ ਛੜ ਦਾ ਸਿਰਾ ਪਾਣੀ ਦੀ ਸਤਾ ਤੋਂ 1.8 mਉੱਪਰ ਹੈ ਅਤੇ ਡੋਰੀ ਦੇ ਹੇਠਲੇ ਸਿਰੇ ਤੇ ਲੱਗਿਆ ਕੁੰਡਾ, ਪਾਣੀ ਦੀ ਸਤ੍ਹਾ ‘ਤੇ ਇਸ ਤਰ੍ਹਾਂ ਸਥਿਤ ਹੈ ਕਿ ਉਸਦੀ ਨਾਜ਼ਿਮਾ ਤੋਂ ਦੂਰੀ 3.6 m ਹੈ ਅਤੇ ਛੜ ਦੇ ਸਿਰੇ ਦੇ ਠੀਕ ਹੇਠਾਂ ਪਾਣੀ ਦੀ ਸੜਾ’ ਤੇ ਸਥਿਤ ਬਿੰਦੂ ਤੋਂ ਉਸਦੀ ਦੂਰੀ | 2.4 m ਹੈ । ਇਹ ਮੰਨਦੇ ਹੋਏ ਕਿ ਉਸਦੀ ਡੋਰੀ (ਉਸ ਦੀ ਛੜ ਦੇ ਸਿਰੇ ਤੋਂ ਕੁੰਡੇ ਤੱਕ) ਤਣੀ ਹੋਈ ਹੈ, ਉਸਨੇ ਕਿੰਨੀ ਡੋਰੀ ਬਾਹਰ ਕੱਢੀ ਹੋਈ ਹੈ । (ਦੇਖੋ ਚਿੱਤਰ) ਜੇਕਰ ਉਹੀ ਡੋਰੀ ਨੂੰ 5 | cms ਦੀ ਦਰ ਨਾਲ ਅੰਦਰ ਖਿੱਚੇ ਤਾਂ 12 ਸੈਕਿੰਡਾਂ ਬਾਦ ਨਜ਼ਿਮਾ ਦੀ ਕੁੰਡੇ ਤੋਂ ਖਿਤਿਜ਼ੀ ਦੀ ਦੁਰੀ ਕਿੰਨੀ ਹੋਵੇਗੀ ।

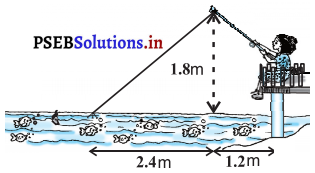
ਹੱਲ:
ਸਮਕੋਣ ABC ਵਿੱਚ,
AB = 1.8 m,
BC = 2.4 m, ∠B = 90°
ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਤੋਂ,
AC² = AB² + BC²
AC² = (1.8)² + (2.4)²
AC² = 3.24 + 5.76 = 9
AC² = (3)²
AC = 3 m
ਹੁਣ ਨਾਜ਼ਿਮਾ ਡੋਰੀ ਨੂੰ 5 cm/s ਦੀ ਦਰ ਨਾਲ ਬਾਹਰ | ਖਿੱਚੇ, ਤਾਂ ਡੋਰੀ ਦੀ ਲੰਬਾਈ ਘੱਟ ਹੁੰਦੀ ਹੈ ।
= 5 × 12 m = 60 cm
= 0.6 m : 12 ਸੈਕਿੰਡ ਵਿੱਚ
ਮੰਨ ਲਉ, 12 ਸੈਕਿੰਡ ਬਾਦ ਕਾਂਟੇ ਦੀ ਸਥਿਤੀ D ਹੈ ।
∴ AD = AC – (12 ਸੈਕਿੰਡ ਵਿਚ ਤੈਅ ਕੀਤੀ ਦੂਰੀ)
= (3 – 0.6) m = 2.4 m
ਹੁਣ, ਸਮਕੋਣ ਤਿਭੁਜ △ABD ਵਿੱਚ ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਤੋਂ
AD² = AB² + BD²
(2.4)² = (1.8)² + BD²
BD² = 5.76 – 3.24
BD² = 2.52 m
BD = 1.587 m
∴ ਨਾਜ਼ਿਮਾ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ
= BD + 1.2 m
= (1.587 + 1.2) m
= 2.787 m
= 2.79 m
ਹੁਣ, ਡੋਰੀ ਦੀ ਲੰਬਾਈ ਅਤੇ ਨਾਜ਼ਿਮਾ ਦੁਆਰਾ ਤੈਅ | ਕੀਤੀ ਗਈ ਦੂਰੀ 3m ਅਤੇ 2.79 m