PSEB 10th Class Maths Solutions Chapter 7 ਨਿਰਦੇਸ਼ ਅੰਕਜਿਮਾਇਤੀ Ex 7.3

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 7 ਨਿਰਦੇਸ਼ ਅੰਕਜਿਮਾਇਤੀ Ex 7.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 7 ਨਿਰਦੇਸ਼ ਅੰਕਜਿਮਾਇਤੀ Exercise 7.3

ਪ੍ਰਸ਼ਨ 1.
ਉਸ ਤ੍ਰਿਭੁਜ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ਜਿਸਦੇ ਸਿਖਰ ਹਨ :
(i) (2, 3); (-1, 0); (2, – 4)
(ii) (-5, -1); (3, – 5); (5, 2)
ਹੱਲ:
(i) ਮੰਨ ਲਉ △ABC ਦੇ ਸਿਖਰ A (2, 3); B (-1, 0) ਅਤੇ C (2, – 4) ਹਨ ।
ਇੱਥੇ , x₁ = 2, x₂ = -1, x₃ = 2
y₁ =3, y₂ = 0, y₃ = – 4
∴ △ABC ਦਾ ਖੇਤਰਫਲ
= \(\frac{1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂]
= \(\frac{1}{2}\)[2 × (0 + 4) – 1 × -4, -3) + 2 × (3 – 0)]
= \(\frac{1}{2}\)[18 + 7 + 6] = \(\frac{21}{2}\)
= 10.5 ਵਰਗ ਇਕਾਈਆਂ ।

(ii) ਮੰਨ ਲਉ BABC ਦੇ ਸਿਖਰ ਹਨ A (-5, -1) ; B (3, -5) ਅਤੇ C (5, 2) ਹਨ
ਇੱਥੇ , x₁ = -5, x₂ = 3, x₃ = 5
y₁ = -1, y₂ = -5, y₃ = 2
∴ △ABC ਦਾ ਖੇਤਰਫਲ
= \(\frac{1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]
= \(\frac{1}{2}\)[(-5(-5 – 2) + 3 (2 + 1) + 5 (-1 + 5)]
= \(\frac{1}{2}\)[35 + 9 + 120] = \(\frac{1}{2}\) × 64
= 32 ਵ. ਇਕਾਈਆਂ

ਪ੍ਰਸ਼ਨ 2.
ਹੇਠਾਂ ਦਿੱਤੀਆਂ ਵਿੱਚੋਂ ਹਰੇਕ ਵਿਚ “k’ ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ ਤਾਂ ਕਿ ਤਿੰਨੇ ਬਿੰਦੂ ਸਮਰੇਖੀ ਹੋਣ :
(i) (7, -2); (5, 1); (3, k).
(ii) (8, 1); (k, -4); (2, – 5)
ਹੱਲ:
(i) ਮੰਨ ਲਉ ਦਿੱਤੇ ਗਏ ਬਿੰਦੂ A (7, – 2); B (5, 1) ਅਤੇ C (3, k) ਹਨ ।
ਇੱਥੇ x₁ = 7, x₂ = 5, x₃ = 3
y₁ = -2, y₂ = 1, y₃ = k
ਤਿੰਨ ਬਿੰਦੂ ਸਮਰੇਖੀ ਹੁੰਦੇ ਹਨ ਜੇਕਰ
= \(\frac{1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]
= \(\frac{1}{2}\)[7 (1 – k) + 5 (k + 2) + 3 (-2 – 1)] = 0
7 – 7k + 5k + 10 – 9 = 0
-2k + 8 = 0
-2k = -8
k = 4

(ii) ਮੰਨ ਲਉ ਦਿੱਤੇ ਗਏ ਬਿੰਦੂ A(8, 1) B (k, -4) ਅਤੇ C (2, -5) ਹਨ ।
ਇੱਥੇ x₁ = 8, x₂ = k, x₃ = 2
y₁ = 1, y₂ = -4, y₃ = -5
ਤਿੰਨ ਬਿੰਦੁ ਸਮਰੇਖੀ ਹਨ ਜੇਕਰ
= \(\frac{1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)] = 0
ਜਾਂ \(\frac{1}{2}\)[8(-4 + 5) + k (-5 – 1) + 2 (1 + 4)] = 0
8 – 6k + 10 = 0
-6k = – 18
k = 3

ਪ੍ਰਸ਼ਨ 3.
ਸਿਖਰਾਂ (0, -1), (2, 1) ਅਤੇ (0, 3) ਵਾਲੇ ਤ੍ਰਿਭੁਜ ਦੀਆਂ ਭੁਜਾਵਾਂ ਦੇ ਮੱਧ ਬਿੰਦੂਆਂ ਤੋਂ ਬਣਨ ਵਾਲੇ ਤ੍ਰਿਭੁਜ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।ਇਸ ਖੇਤਰਫਲ ਦਾ ਦਿੱਤੇ ਹੋਏ ਤ੍ਰਿਭੁਜ ਦੇ ਖੇਤਰਫਲ ਨਾਲ ਅਨੁਪਾਤ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ ਦਿੱਤੀ ਹੋਈ ਤ੍ਰਿਭੁਜ ABCਦੇ ਸਿਖਰ A(0, – 1); B (2, 1) ਅਤੇ C (0, 3) ਹਨ ।
D, E, F ਕੁਮਵਾਰ AB, BC, CA ਦੇ ਮੱਧ ਬਿੰਦੂ ਹਨ ।
∴ ਮੱਧ ਬਿੰਦੂ ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਕੇ

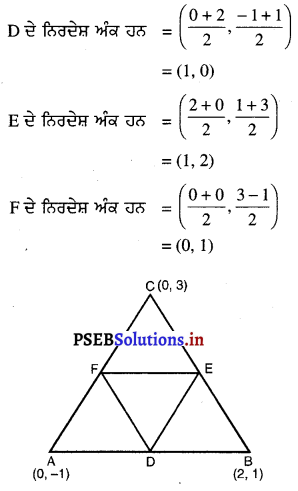
∴ △DEF ਦੇ ਸਿਖਰਾਂ ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ D (1, 0); E(1, 2); F (0, 1) ਹਨ ।
ਇੱਥੇ , x₁ = 1, x₂ = 1, x₃ = 0
y₁ = 0, y₂ = 2, y₃ = 1
∴ △DEF ਦਾ ਖੇਤਰਫਲ
= \(\frac{1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]
= \(\frac{1}{2}\)[1(2 – 1) + 1(1 – 0) + 0(0 – 2)]
= \(\frac{1}{2}\)[1 + 1 + 0] = \(\frac{2}{2}\)
= 1 ਵ. ਇਕਾਈਆਂ
△ABC ਵਿਚ
x₁ = 0, x₂ = 2, x₃ = 0
y₁ = – 1, y₂ = 1, y₃ = 3
△ABC ਦਾ ਖੇਤਰਫਲ
= \(\frac{1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]
= \(\frac{1}{2}\)[0 (1 – 3) + 2 (3 + 1) + 0 (-1 – 1)]
= \(\frac{1}{2}\)[0 + 8 + 0] = \(\frac{8}{2}\) = 4 ਵ. ਇਕਾਈਆਂ

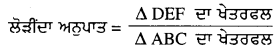
= \(\frac{1}{4}\)

ਪ੍ਰਸ਼ਨ 4.
ਉਸ ਚਤੁਰਭੁਜ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ਜਿਸਦੇ | ਸਿਖਰ, ਇਸੇ ਕੂਮ ਵਿੱਚ (4, -2); (-3, -5); (3, – 2) ਵ ਅਤੇ (2, 3) ਹਨ ।
ਹੱਲ:
ਮੰਨ ਲਉ ਦਿੱਤੀ ਹੋਈ ਚਤੁਰਭੁਜ ABCD ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਹਨ A (-4, – 2); B (-3, – 5) ; c (3, -2) ਅਤੇ D (2, 3) ਹਨ ।
AC ਨੂੰ ਮਿਲਾਓ, ਚਤੁਰਭੁਜ ABCD, ਦੋ ਤ੍ਰਿਭੁਜਾਂ ਵਿਚ ਵਿਭਾਜਿਤ ਹੋ ਜਾਂਦੀ ਹੈ ।
ਭਾਵ △ABC ਅਤੇ △CDA ਵਿਚ

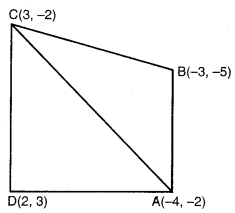
△ABC ਵਿਚ
x₁ = -4, x₂ = 3, x₃ = 3
y₁ = -2, y₂ = -5, y₃ = -2
△ABC ਦਾ ਖੇਤਰਫਲ
= \(\frac{1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₃)]
= \(\frac{1}{2}\)[-4(-5 + 2) + (-3)(-2 + 2) + 3(-2 + 5)]
= \(\frac{1}{2}\)[12 + 0 + 9] = \(\frac{21}{2}\) ਵਰਗ ਇਕਾਈਆਂ
△CDA ਵਿਚ
x₁ = 3, x₂ = 2, x₃ = -4
y₁ = -2, y₂ = 3, y₃ = -2
△CDA ਦਾ ਖੇਤਰਫਲ
= \(\frac{1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]
= \(\frac{1}{2}\)[3 (3 + 2) + 2 (2 + 2) + (-4) (-2 – 3)]
= \(\frac{1}{2}\)[20 + 15 + 0] = \(\frac{35}{2}\) ਵਰਗ ਇਕਾਈਆਂ
ਹੁਣ, ਚਤੁਰਭੁਜ ABCD ਦਾ ਖੇਤਰਫਲ
= (△ABC ਦਾ ਖੇਤਰਫਲ) + (△ACD ਦਾ ਖੇਤਰਫਲ)
= \(\frac{21}{2}\) + \(\frac{35}{2}\)
= \(\frac{56}{2}\) = 28 ਵਰਗ ਇਕਾਈਆਂ

ਪ੍ਰਸ਼ਨ 5.
ਜਮਾਤ IX ਵਿਚ ਤੁਸੀਂ ਪੜ੍ਹਿਆ ਹੈ (ਪਾਠ 9, ਉਦਾਹਰਣ 3) ਕਿ ਕਿਸੇ ਤ੍ਰਿਭੁਜ ਦੀ ਇੱਕ ਮੱਧਕਾ (Median) ਉਸਨੂੰ ਬਰਾਬਰ ਖੇਤਰਫਲਾਂ ਵਾਲੇ ਦੋ ਤ੍ਰਿਭੁਜਾਂ ਵਿਚ ਵੰਡਦੀ ਹੈ । ਇਸ ਨਤੀਜੇ ਦੀ ਪੜਤਾਲ ਉਸ ਤ੍ਰਿਭੁਜ ABC ਦੇ ਲਈ ਕਰੋ ਜਿਸਦੇ ਸਿਖਰ A(4, -6), B(3, -2) ਅਤੇ C(5, 2) ਹਨ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ △ABC ਦੇ ਸਿਖਰਾਂ ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ A(4, – 6) ; B (3, – 2) ਅਤੇ C (5, 2)
ਮੰਨ ਲਉ CD ਇਕ ਮੱਧਿਕਾ ਹੈ । ਅਰਥ D, AB ਦਾ ਮੱਧ ਬਿੰਦੁ ਹੈ ਜੋ △ABC ਨੂੰ ਦੋ ਭਾਗਾਂ ਵਿਚ ਵੰਡਦਾ ਹੈ।

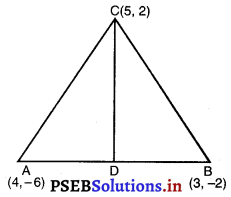
(5, 2)
△ADC ਅਤੇ △CDB
D ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ = (\(\frac{4+3}{2}\), \(\frac{-6-2}{2}\))
= (\(\frac{7}{2}\), \(\frac{-8}{2}\))
= (3.5, 4)
△ADC ਵਿੱਚ,
x₁ = 4, x₂ = 3.5, x₃ = 5
y₁ = -6, y₂ = -4, y₃ = 2
△ADC ਦਾ ਖੇਤਰਫਲ
= \(\frac{1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]
= \(\frac{1}{2}\)[4 (-4 – 2) + 3.5 (2 + 6) + 5 (-6 + 4)]
= \(\frac{1}{2}\)[-24 + 28 – 10]
= \(\frac{1}{2}\) × -6 = -3 = 3 ਵ. ਇਕਾਈਆਂ
(∵ ਖੇਤਰਫਲ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੋ ਸਕਦਾ ਹੈ।)
△CDB ਵਿਚ,
x₁ = 5, x₂ = 3.5, x₃ = 3
y₁ = 2, y₂ = -4, y₃ = -2
△CDB ਦਾ ਖੇਤਰਫਲ = \(\frac{1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]
= \(\frac{1}{2}\)[5 (-4 + 2) + 3.5 (-2 – 2) + 3 (2 + 4)]
= \(\frac{1}{2}\)[-10 – 14 + 18] = \(\frac{1}{2}\) × – 6 = -3
= 3 ਵ. ਇਕਾਈਆਂ
(∵ ਖੇਤਰਫਲ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੋ ਸਕਦਾ)
ਇਸ ਲਈ ਇਹ ਸੱਪਸ਼ਟ ਹੈ ਕਿ △ADC ਦਾ ਖੇਤਰਫਲ = △CDB ਦਾ ਖੇਤਰਫਲ = 3 ਵ. ਇਕਾਈਆਂ
∴ ਤ੍ਰਿਭੁਜ ਦੀ ਮੱਧਿਕਾ ਇਸਨੂੰ ਬਰਾਬਰ ਖੇਤਰਫਲ ਵਾਲੇ ਦੋ ਤਿਭੁਜਾਂ ਵਿੱਚ ਵੰਡਦੀ ਹੈ ।