PSEB 10th Class Maths Solutions Chapter 7 निर्देशांक ज्यामिति Ex 7.4

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 7 निर्देशांक ज्यामिति Ex 7.4 Textbook Exercise Questions and Answers

PSEB Solutions for Class 10 Maths Chapter 7 निर्देशांक ज्यामिति Ex 7.4

प्रश्न 1.
बिंदुओं A(2, – 2) और B (3, 7) को जोड़ने वाले रेखाखंड को रेखा 2x + y – 4 = 0 जिस अनुपात में विभाजित करती है उसे ज्ञात कीजिए।
हल:
मान लीजिए रेखा 2x + y – 4 = 0 बिंदुओं A (2, – 2) और B (3, 7) को मिलाने वाले रेखाखंड को C (x, y) पर k : 1 के अनुपात में विभाजित करता है।

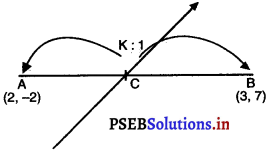
∴ C के निर्देशांक हैं :
x = \(\frac{3 k+2 \times 1}{k+1}=\frac{3 k+2}{k+1}\)

और y = \(\frac{7 k+(-2) \times 1}{k+1}=\frac{7 k-2}{k+1}\)

∴ C\(\left[\frac{3 k+2}{k+1}, \frac{7 k-2}{k+1}\right]\) रेखा 2x + y – 4 = 0 पर स्थित होगा।
अर्थात् \(2\left(\frac{3 k+2}{k+1}\right)+\left(\frac{7 k-2}{k+1}\right)\) – 4 = 0
या \(\frac{6 x+4+7 k-2-4 k-4}{k+1}\) = 0
या 9k – 2 = 0
या 9k = 2
या k = \(\frac{2}{9}\)
∴ अनुपात k : 1 = \(\frac{2}{9}\) : 1 = 2 : 9
अतः अभीष्ट अनुपात 2 :9 है।

प्रश्न 2.
x और y में एक संबंध ज्ञात कीजिए, यदि बिंदु (x, y); (1, 2) और (7, 0) सरेखी हैं।
हल :
दिए गए बिंदु A (x, y); B (1, 2) और C (7, 0) हैं।
यहाँ x₁ = x, x₂ = 1, x₃ = 7
y₁ = y, y₂ = 2, y₃ = 0
∵ तीन बिंदु सरेखी होते हैं :
यदि \(\frac{1}{2}\) [x₁ (y₂ – y₃) + x₂ (y₃ – y₁) + x₃ (y₁ – y₂)] = 0
या \(\frac{1}{2}\) [x(2 – 0) + 1 (0 – 9) +7 (y – 2)] = 0
या 2x – y + 7y – 14=0
या 2x + 6y – 14 = 0
या x + 3y – 7 = 0 अभीष्ट संबंध हैं।

प्रश्न 3.
बिंदुओं (6, – 6), (3, – 7) और (3, 3) से होकर जाने वाले वृत्त का केंद्र ज्ञात कीजिए।
हल :
मान लीजिए 0 (x, y) अभीष्ट केंद्र है जो कि बिंदुओं P(6, – 6); Q (3, – 7) और R (3, 3) में से गुजरता है।
∵ वृत्त की त्रिज्याएँ समान होती हैं।

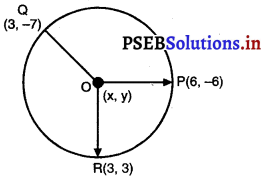
∴ OP = OQ = OR
(OP)² = (OQ)² = (OR)²
अब, (OP)² = (OQ)²
(x – 6)² + (y + 6)² = (x – 3)² + (y + 7)²
या x² + 36 – 12x + y + 36 + 12y = x² + 9 – 6x + y + 49 + 14y
या – 12x + 12y+ 72 = – 6x + 14y + 58
या – 6x – 2y + 14 = 0
या 3x + y – 7 = 0
साथ ही, (OQ)² = (OR)²
या (x – 3)² + (y + 7)² = (x – 3)² + (y – 3)²
या (y + 7)² = (y – 3)²
या y² + 49 + 14y = y² + 9 – 6y
20y = – 40
y = \(\frac{-40}{20}\) = – 2
yके इस मान को (1) में प्रतिस्थापित करने पर हमें प्राप्त | होता है :
3x – 2 – 7 = 0
3x – 9 = 0
या 3x = 9
या x = \(\frac{9}{3}\) = 3
∴ अभीष्ट केंद्र (3, – 2) है।

प्रश्न 4.
किसी वर्ग के दो सम्मुख शीर्ष (- 1, 2) और (3, 2) हैं। वर्ग के अन्य दोनों शीर्ष ज्ञात कीजिए।
हल :
मान लीजिए वर्ग ACBD के दो सम्मुख शीर्ष A (- 1, 2) और B (3, 2) हैं तथा C का निर्देशांक (x, y) है। –
∵ वर्ग की प्रत्येक भुजा की लंबाई समान होती है।
∴ AC = BC
या (AC)² = (BC)²
या (x + 1)² + (y – 2)² = (x – 3)² + (y – 2)²

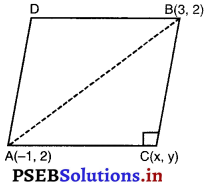
या (x + 1)² = (x – 3)²
या x² + 1 + 2x = x +9-6x
या 8x = 8
या x = \(\frac{8}{8}\) = 1 ……………(1)
अब समकोण ∆ACB में, पाइथागोरस प्रमेय का उपयोग करने पर
(AC)² + (BC)² = (AC)²
(x + 1)² + (y – 2)² + (x – 3)² + (y – 2)² = (3 + 1)² + (2 – 2)²
या x² + 1 + 2x + y² + 4 – 4y + 12 + 9 – 6x + y² + 4 – 4y = 16
या 2x + 2y² – 4x – 8y + 2 = 0
या x + y² – 2x – 4y + 1 = 0
x = 1
(1) से प्राप्त x के मान को प्रतिस्थापित करने पर हमें प्राप्त होता है :
(1)² + y² – 2 (1) – 4y + 1 = 0
या y² – 4y = 0
या y (y – 4) = 0
या y = 0 या y – 4 = 0
या y = 0 या y = 4
∴ y = 0, 4
∴ अभीष्ट बिंदु (1, 0) और (4, 0) हैं।

प्रश्न 5.
कृष्णानगर के एक सैकेंडरी स्कूल के कक्षा X के विद्यार्थियों को उनके बागवानी क्रियाकलाप के लिए, एक आयाताकर भूखंड दिया गया है। गुलमोहर की पौध (sapling) को परस्पर 1 m की दूरी पर इस भूखंड की परिसीमा (boundary) पर लगाया जाता है। इस भूखंड के अंदर एक त्रिभुजाकार घास लगा हुआ लॉन (lawn) है, जैसा कि आकृति में दर्शाया गया है। विद्यार्थियों को भूखंड के शेष भाग में फूलों के पौधे के बीज बोने हैं।
(i) A को मूलबिंदु मानते हुए, त्रिभुज के शीर्षों के निर्देशांक ज्ञात कीजिए।
(ii) यदि मूलबिंदु C हो, तो APQR के शीर्षों के निर्देशांक क्या होंगे ?
साथ ही, उपरोक्त दोनों स्थितियों में, त्रिभुजों के क्षेत्रफल ज्ञात कीजिए। आप क्या देखते हैं ?

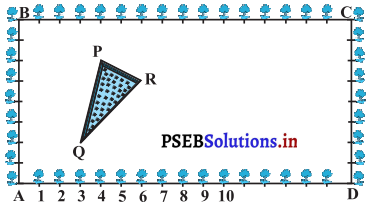
हल:
स्थिति I. जब A को मूल बिंदु लें तो AD’; X-अक्ष और AB ; Y-अक्ष हैं।
∴ त्रिभुजाकार घास के लॉन PQR के निर्देशांक P (4, 6); Q (3, 2) और R( 6, 5) हैं।
यहां x₁ = 4, x₂ = 3, x₃ = 6
y₁ = 6, y₂ = 2, y₃ = 5
अब ∆PQR का क्षेत्रफल
= \(\frac{1}{2}\) [x₁ (y₂ – y₃) + x₂ (y₃ – y₁) + x₃ (y₁ – y₂)]
= \(\frac{1}{2}\) [4 (2 – 5) + 3 (5 – 6) + 6 (6 – 2)]
= \(\frac{1}{2}\) [- 12 – 3 + 24]
= \(\frac{9}{2}\) = 4.5 वर्गमात्रक

स्थिति II.
जब C को मूल बिंदु लें तो CB ; X-अक्ष है और CD ; Y-अक्ष लेते हैं।
∴ त्रिभुजाकार घास के लॉन PQR के निर्देशांक हैं : P (12, 2); Q (13, 6) और R (10, 3) हैं।
यहाँ x₁ = 12, x₂ = 13, x₃ = 10
y₁ = 2, y₂ = 6, y₃ = 3
अब ∆PQR का क्षेत्रफल
= \(\frac{1}{2}\) [x₁ (y₂ – y₃) + x₂ (y₃ – y₁) + x₃ (y₁ – y₂)]
= \(\frac{1}{2}\) [12 (6 – 3) + 13 (3 – 2) + 10 (2 – 6)]
= \(\frac{1}{2}\) [36 + 13 – 40]
= \(\frac{9}{2}\) = 4.5 वर्गमात्रक
उपर्युक्त दोनों स्थितियों से स्पष्ट है कि त्रिभुजाकार घास के लॉन का क्षेत्रफल एक समान है।

प्रश्न 6.
एक त्रिभुज ABC के शीर्ष A(4,6), B(1, 5) और C(7, 2) हैं। भुजाओं AB और AC को क्रमशः D और E पर प्रतिच्छेद करते हुए एक रेखा इस प्रकार खींची गई है कि \(\frac{\mathrm{AD}}{\mathrm{AB}}=\frac{\mathrm{AE}}{\mathrm{AC}}=\frac{1}{4}\) है। ∆ADE का क्षेत्रफल परिकलित कीजिए और इसकी तुलना ∆ABC के क्षेत्रफल से कीजिए।(प्रमेय 6.2 और प्रमेय 6.6 का स्मरण कीजिए।)
हल :
∆ABC के शीर्ष A (4, 6); B (1, 5) और C (7, 2) हैं।

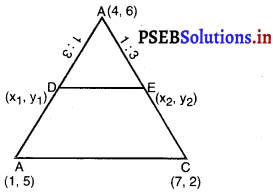
भुजाओं AB और AC को क्रमशः D (x, y) और E (x, y) पर काटती हुई रेखा इस प्रकार खींचिए ताकि \(\frac{\mathrm{AD}}{\mathrm{AB}}=\frac{\mathrm{AE}}{\mathrm{AC}}=\frac{1}{4}\)
∴ D और E, AB और AC को अनुपात 1 : 3 में | विभाजित करते हैं।
∴ D के निर्देशांक हैं :
x₁ = \(\frac{1(1)+3(4)}{1+3}=\frac{1+12}{4}=\frac{13}{4}\)

और y = \(\frac{1(5)+3(6)}{1+3}=\frac{5+18}{4}=\frac{23}{4}\)
∴ D के निर्देशांक हैं : (\(\frac{13}{4}\), \(\frac{23}{4}\))

अब E के निर्देशांक हैं :
x₂ = \(\frac{1(7)+3(4)}{1+3}=\frac{7+12}{4}=\frac{19}{4}\)

और y₂ = \(\frac{1(2)+3(6)}{1+3}=\frac{2+18}{4}=\frac{20}{4}=5\)

∴ E के निर्देशांक हैं (\(\frac{19}{4}\), 5)

∆ADE में, x₁ = 4, x₂ = 4, x₃
y₁ = 6, y₂ = 1, y₃ = 5

∆ADE का क्षेत्रफल

∆ABC में,
x₁ = 4, x₂ = 1, x₃ = 37
y₁ = 6, y₂ = 5, y₃ = 2
∆ABC का क्षेत्रफल = \(\frac{1}{2}\) [x₁ (y₂ – y₃) + x₂ (y₃ – y₁) + x₃ (y₁ – y₂)]
= \(\frac{1}{2}\) [4 (5 – 2) + 1 (2 – 6) + 7 (6 – 5)]
अब,
= \(\frac{1}{16}=\left(\frac{1}{4}\right)^{2}=\left(\frac{\mathrm{AD}}{\mathrm{AB}}\right)^{2}\) या \(\left(\frac{\mathrm{AE}}{\mathrm{AC}}\right)^{2}\)

प्रश्न 7.
मान लीजिए A (4, 2), B (6, 5) और C (1, 4) एक त्रिभुज ABC के शीर्ष हैं।
(i) A से होकर जाने वाली माध्यिका BC से D पर मिलती है। बिंदु D के निर्देशांक ज्ञात कीजिए।
(ii) AD पर स्थित ऐसे बिंदु P के निर्देशांक ज्ञात कीजिए कि AP : PD = 2 : 1 हो।
(iii) माध्यिकाओं BE और CF पर ऐसे बिंदुओंQ और R के निर्देशांक ज्ञात कीजिए कि BQ : QE = 2 : 1 हो और CR: RF = 2 : 1 हो।
(iv) आप क्या देखते हैं ?
[नोट : वह बिंदु जो तीनों माध्यिकाओं में सार्वनिष्ठ हो, उस त्रिभुज का केंद्रक (centroid) कहलाता है और यह प्रत्येक माध्यिका को 2 : 1 के अनुपात में विभाजित करता है।
(v) यदि A(x,y), B(xy) और C (x,ys) त्रिभुज ABC के शीर्ष हैं, तो इस त्रिभुज के केंद्रक के निर्देशांक ज्ञात कीजिए।
हल :
दिया गया है कि AABC के शीर्ष A (4, 2); B (6, 5) और C (1, 4) हैं।
(i) AD, शीर्ष A से माध्यिका है।
∴ D, EC का मध्य बिंदु है।

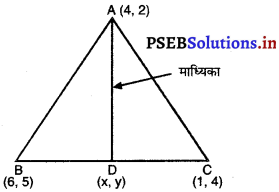
तब x = \(\frac{6+1}{2}=\frac{7}{2}\)

y = \(\frac{5+4}{2}=\frac{9}{2}\)

अत: D के निर्देशांक (\(\frac{9}{2}\), \() हैं।

(ii) मान लीजिए P (x, y), AD पर कोई बिंदु इस प्रकार है कि AP : PD = 2 : 1

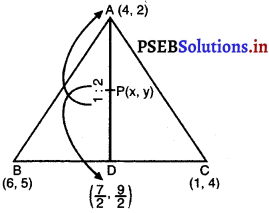
तब x = [latex]\frac{2\left(\frac{7}{2}\right)+1(4)}{2+1}=\frac{7+4}{3}=\frac{11}{3}\)

y = \(\frac{2\left(\frac{9}{2}\right)+1(2)}{2+1}=\frac{9+2}{3}=\frac{11}{3}\)

अत: P के निर्देशांक (\(\frac{11}{3}\), \(\frac{11}{3}\)) हैं।

(iii) मान लीजिए BE और CF, AABC की क्रमशः AC और AB पर माध्यिकाएँ हैं। . E और F क्रमश: AC और AB के मध्यबिंदु हैं।

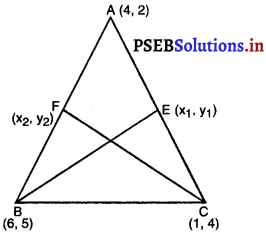
E के निर्देशांक हैं :
x₁ = \(\frac{4+1}{2}=\frac{5}{2}\)

और y₁ = \(\frac{4+2}{2}=\frac{6}{2}\) = 3
E के निर्देशांक हैं : (\(\frac{5}{2}\), 3)

F के निर्देशांक हैं :
x₂ = \(\frac{4+6}{2}=\frac{10}{2}\) = 5
और y₂ = \(\frac{5+2}{2}=\frac{7}{2}\)
∴ F के निर्देशांक हैं : (5, \(\frac{7}{2}\))
अब, Q, BE को इस तरह विभाजित करता है कि : BQ : QE = 2 : 1

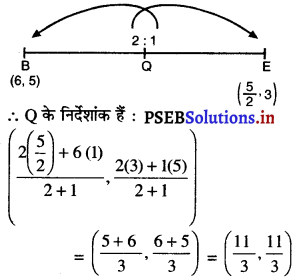
साथ ही, R, CF को इस तरह विभाजित करता है कि CR : RF = 2 : 1

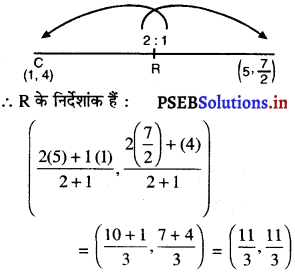
(iv) उपर्युक्त चर्चा से यह स्पष्ट है कि P, Q और R के निर्देशांक एक समान हैं और एक बिंदु पर संपाती हैं।
यह बिंदु त्रिभुज का केंद्रक कहलाता है, जो कि प्रत्येक माध्यिका को 2 : 1 के अनुपात में विभाजित करता है।

(v) दी गई ∆ABC के शीर्ष A (x₁, y₁); B (x₂, y₂) और C (x₃, y₃) हैं।

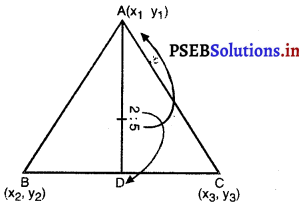
मान लीजिए AD, ∆ABC की माध्यिका है।

∴ D, BC का मध्य-बिंदु है तब D के निर्देशांक हैं : \(\left(\frac{x_{2}+x_{3}}{2}, \frac{y_{2}+y_{3}}{2}\right)\)
मान लीजिए AD, AABC की माध्यिका है। :: D, BC का मध्य-बिंदु है तब D के निर्देशांक हैं :
अब G, ∆ABC का केंद्रक है जो माध्यिका AD को 2 : 1 के अनुपात में विभाजित करता है।
∴ G के निर्देशांक हैं : [(iv) का प्रयोग करने पर]

प्रश्न 8.
बिंदुओंA (- 1, – 1), B (- 1, 4), C (5, 4) और D (5, – 1) से एक आयत ABCD बनता है। P, Q, R और S क्रमशः भुजाओं AB, BC, CD और DA के मध्य बिंदु हैं। क्या चतुर्भुज PQRS एक वर्ग है ? क्या यह एक आयत है ? क्या यह एक समचतुर्भुज है ? सकारण उत्तर दीजिए।
हल :
दिया है : दी गई आयत ABCD के शीर्ष हैं : A(-1, – 1); B (-1,4); C (5, 4) और D (5, — 1).

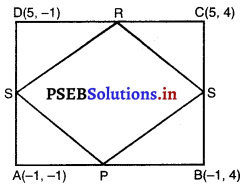
∵ P, AB का मध्य-बिंदु है
∴ P के निर्देशांक हैं : \(\left(\frac{-1-1}{2}, \frac{-1+4}{2}\right)=\left(-1, \frac{3}{2}\right)\)

∵ Q, BC का मध्य-बिंदु है
∴ Q के निर्देशांक हैं : \(\left(\frac{-1+5}{2}, \frac{4-4}{2}\right)\) = (2, 4)

∵ R, CD का मध्य-बिंदु है
∴ R के निर्देशांक हैं : \(\left(\frac{5+5}{2}, \frac{4+1}{2}\right)=\left(5, \frac{3}{2}\right)\)

∵ S, AD का मध्य-बिंदु है
∴ S के निर्देशांक हैं : \(\left(\frac{5-1}{2}, \frac{-1-1}{2}\right)\) = (2, 0)

अब, PQ = \(\sqrt{(2+1)^{2}+\left(4-\frac{5}{2}\right)^{2}}\)
= \(\sqrt{(3)^{2}+\left(\frac{8-5}{2}\right)^{2}}\)
= \(\sqrt{9+\frac{9}{4}}=\sqrt{\frac{36+9}{4}}=\sqrt{\frac{45}{4}}\)

उपर्युक्त चर्चा से यह स्पष्ट है कि PQ = RS और QR = SP
साथ ही, PR ≠ QS
⇒ चतुर्भुज PQRS की सम्मुख भुजाएँ बराबर हैं परंतु विकर्ण बराबर नही हैं।
⇒ चतुर्भुज PQRS एक समांतर चतुर्भुज है।