PSEB 10th Class Maths Solutions Chapter 7 ਨਿਰਦੇਸ਼ ਅੰਕਜਿਮਾਇਤੀ Ex 7.4

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 7 ਨਿਰਦੇਸ਼ ਅੰਕਜਿਮਾਇਤੀ Ex 7.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 7 ਨਿਰਦੇਸ਼ ਅੰਕਜਿਮਾਇਤੀ Exercise 7.4

ਪ੍ਰਸ਼ਨ 1.
ਬਿੰਦੂਆਂ A(2, – 2) ਅਤੇ B (3, 7) ਨੂੰ ਮਿਲਾਉਣ ਵਾਲੇ ਰੇਖਾਖੰਡ ਨੂੰ ਰੇਖਾ 2x + y – 4 = 0 ਕਿਸ ਅਨੁਪਾਤ ਵਿਚ ਵੰਡਦੀ ਹੈ, ਉਹ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ ਰੇਖਾ 2x + y – 4 = 0 ਬਿੰਦੂ A (2, – 2) ਅਤੇ B(3, 7) ਨੂੰ ਮਿਲਾਉਣ ਵਾਲੇ ਰੇਖਾਖੰਡ ਨੂੰ C(x, y) ਉੱਤੇ k : 1 ਅਨੁਪਾਤ ਵਿਚ ਵੰਡਦੀ ਹੈ ।

∴ C [\(\frac{3 k+2}{k+1}\), \(\frac{7 k-2}{k+1}\)] ਰੇਖਾ 2x + y – 4 = 0 ਉੱਤੇ ਹੋਵੇਗਾ ।
ਭਾਵ 2 \(\left(\frac{3 k+2}{k+1}\right)\) + \(\left(\frac{7 k-2}{k+1}\right)\) – 4 = 0
\(\frac{6 x+4+7 k-2-4 k-4}{k+1}\) = 0
9k – 2 = 0
9k = 2
k = \(\frac{2}{9}\)
∴ ਅਨੁਪਾਤ k : 1 = \(\frac{2}{9}\) : 1 = 2 : 9
∴ ਲੋੜੀਂਦਾ ਅਨੁਪਾਤ 2:9 ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
x ਅਤੇ y ਵਿਚਕਾਰ ਇਕ ਸੰਬੰਧ ਪਤਾ ਕਰੋ ਜੇਕਰ ਬਿੰਦੂ | (x, y) ; (1, 2) ਅਤੇ (7, 0) ਸਮਰੇਖੀ ਹਨ ।
ਹੱਲ:
ਦਿੱਤੇ ਗਏ ਬਿੰਦੂ A(x, y) ; B (1, 2) ਅਤੇ C (7, 0) ਹੈ ।
ਇੱਥੇ x₁ = 1, x₂ = 1, x₃ = 7
y₁ = y, y₂ = 2, y₃ = 0
∵ ਤਿੰਨ ਬਿੰਦੂ ਸਮਰੇਖੀ ਹਨ ਜੇਕਰ
= \(\frac{1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)] = 0
\(\frac{1}{2}\)[x (2 – 0) + 1 (0 – y) + 7 (y – 2)] = 0
2x – y + 7y – 14 = 0
2x + 6y – 14 = 0
ਜਾਂ x + 3y – 7 = 0 ਲੋੜੀਂਦਾ ਸੰਬੰਧ ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਬਿੰਦੂਆਂ (6, – 6), (3, – 7) ਅਤੇ (3, 3) ਤੋਂ ਹੋ ਕੇ ਜਾਣ ਵਾਲੇ ਚੱਕਰ ਦਾ ਕੇਂਦਰ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਓ O (x, y) ਲੋੜੀਂਦਾ ਕੇਂਦਰ ਹੈ ਜੋ ਕਿ ਬਿੰਦੂ P(6, – 6) ; Q (3, – 7) ਅਤੇ R (3, 3) ਵਿਚੋਂ ਲੰਘਦਾ ਹੈ
∵ ਚੱਕਰ ਦੇ ਅਰਧ ਵਿਆਸ ਸਮਾਨ ਹੁੰਦੇ ਹਨ

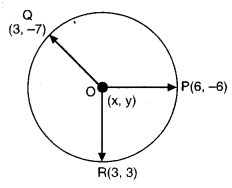
∴ OP = OQ = OR
ਜਾਂ (OP)² = (OQ)² = (OR)²
(OP)² = (OQ)²
(x – 6)² + (y + 6)² = (x – 3)² + (y + 7)²
x² + 36 – 12 x + y² + 36 + 12y = x² +²9 – 6 + y² + 49 + 14y
-12x + 12y + 72 = -6x + 14y + 58
-6x – 2y + 14 = 0
3x + y -7 = 0 ….(1)
(OQ)² = (OR)²
(x – 3)² + (y + 7)² = (x – 3)² + (y – 3)²
(y + 7)² = (y – 3)²
y² + 49 + 14y = y² + 9 – 6y
20y = – 40
y = \(\frac{-40}{20}\) = -2
y ਦਾ ਮੁੱਲ (1) ਵਿਚ ਰੱਖਣ ਤੇ ਅਸੀਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ ।
3x – 2 – 7 = 0
3x – 9 = 0
3x = 9
x = 3
∴ ਲੋੜੀਂਦਾ ਕੇਂਦਰ ਹੈ (3, – 2)

ਪ੍ਰਸ਼ਨ 4.
ਜੇਕਰ ਇੱਕ ਵਰਗ ਦੇ ਦੋ ਸਾਹਮਣੇ (Opposite) ਦੇ ਸਿਖਰ (-1, 2) ਅਤੇ (3, 2) ਹਨ ਤਾਂ ਵਰਗ ਦੇ ਦੋਵੇਂ ਸਿਖਰ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ ਵਰਗ ABCD ਦੇ ਦੋ ਸਨਮੁੱਖ ਸਿਖਰ A (-1, 2) ਅਤੇ C (3, 2) ਅਤੇ B ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ (x, y) ਹਨ ।
∵ ਵਰਗ ਦੀ ਹਰੇਕ ਭੁਜਾ ਦੀ ਲੰਬਾਈ ਬਰਾਬਰ ਹੈ
∴ AB = BC
(AB)² = (BC)²
(x + 1)² + (y – 2)² = (x – 3)² + (y – 2)²

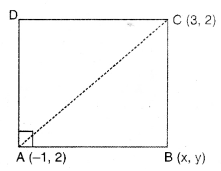
(x + 1)² = (x – 3)²
x² + 1 + 2x = x² + 9 – 6x
8x = 8
x = 1 …(1)
ਹੁਣ ਸਮਕੋਣ △ABC ਵਿਚ,
ਪਾਇਥਾਗੋਰਸ ਦਾ ਪਰਿਮੇਯ ਪ੍ਰਯੋਗ ਕਰਕੇ
(AB)² + (BC)² = (AC)²
(x + 1)² + (y – 2)² + (x – 3)² + (y – 2)²
= (3 + 1)² + (2 – 2)²
x² + 1 + 2x + y² + 4 – 4y + x² +9 – 6x + y² + 4 – 4y = 16
2x² + 2y² – 4x – 8y + 2 = 0
x² + y² – 2x – 4y + 1 = 0 …(2)
x = 1 ਦਾ ਮੁੱਲ (2) ਵਿਚ ਰੱਖਣ ਤੇ
(1)² + y² – 2 (1) – 4y + 1 = 0
y² – 4y = 0
y (y – 4) = 0
y = 0 ਜਾਂ y = 4
∴ ਲੋੜੀਂਦਾ ਬਿੰਦੁ (1, 0) ਅਤੇ (4, 0) ਹਨ ।

ਪ੍ਰਸ਼ਨ 5.
ਕ੍ਰਿਸ਼ਨਾ ਨਗਰ ਦੇ ਇਕ ਸੈਕੰਡਰੀ ਸਕੂਲ ਦੀ X ਜਮਾਤ ਦੇ ਵਿਦਿਆਰਥੀਆਂ ਨੂੰ ਬਾਗਬਾਨੀ ਕਿਰਿਆਵਾਂ ਕਰਨ ਲਈ ਇੱਕ ਆਇਤਾਕਾਰ ਜਮੀਨ ਦਾ ਟੁੱਕੜਾ ਦਿੱਤਾ ਗਿਆ ਹੈ । ਗੁਲਮੋਹਰ ਦੇ ਪੌਦੇ ਇਸ ਦੀ ਸੀਮਾਂ ‘ ਤੇ ਆਪਸ ਵਿਚ 1m ਦੀ ਦੂਰੀ ‘ਤੇ ਲਗਾਏ ਗਏ ਹਨ । ਜ਼ਮੀਨ ਦੇ ਇਸ ਟੁੱਕੜੇ ਦੇ ਅੰਦਰ ਇੱਕ ਤਿਭੁਜ ਅਕਾਰ ਦਾ ਘਾਹ ਲੱਗਿਆ ਹੋਇਆ ਲਾਅਨ (Law) ਹੈ ਜਿਸ ਤਰ੍ਹਾਂ ਕਿ ਚਿੱਤਰ ਵਿੱਚ ਦਿਖਾਇਆ ਗਿਆ ਹੈ । ਵਿਦਿਆਰਥੀਆਂ ਨੇ ਜ਼ਮੀਨ ਦੇ ਬਾਕੀ ਹਿੱਸੇ ਵਿਚ ਫੁੱਲਾਂ ਦੇ ਪੌਦਿਆਂ ਦੇ ਬੀਜ ਬੀਜਣੇ ਹਨ ।
(i) A ਨੂੰ ਮੂਲ ਬਿੰਦੂ ਮੰਨਦੇ ਹੋਏ, ਤਿਭੁਜ ਦੇ ਸਿਖਰਾਂ ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਪਤਾ ਕਰੋ ।
(ii) ਜੇਕਰ ਮੂਲ ਬਿੰਦੂ ਹੋਵੇ ਤਾਂ APR ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਕੀ ਹੋਣਗੇ ? ਨਾਲ ਹੀ, ਉਪਰੋਕਤ ਦੋਹਾਂ ਸਥਿਤੀਆਂ ਵਿੱਚ ਤਿਭੁਜਾਂ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ । ਤੁਸੀਂ ਕੀ ਦੇਖਦੇ ਹੋ ?

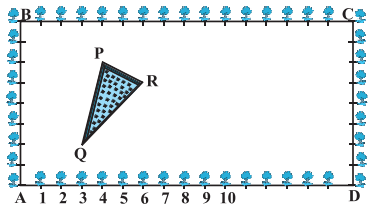
ਹੱਲ:
ਸਥਿਤੀ I ਜਦੋਂ A ਮੂਲ ਬਿੰਦੂ ਹੈ ਤਾਂ AD ; X-ਧੁਰੇ ਅਤੇ AB; Y-ਧੁਰਾ ਹੈ ।
∴ ਤਿਭੁਜਾਕਾਰ ਘਾਹ ਦੇ ਲਾਨ POR ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ P (4, 6); Q (3, 2) ਅਤੇ R( 6, 5) ਹੈ ।
ਇੱਥੇ x₁ = 4, x₂ = 3, x₃ = 6
y₁ = 6, y₂ = 2, y₃ = 5
ਹੁਣ, △PQR ਦਾ ਖੇਤਰਫਲ
= \(\frac{1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]
= \(\frac{1}{2}\)[4 (2 – 5) + 3 (5 – 6) + 6 (6 – 2)]
= \(\frac{1}{2}\)[-12 – 3 + 24] = \(\frac{9}{2}\)
= 4.5 ਵ. ਇਕਾਈਆਂ
ਸਥਿਤੀ II. ਜਦੋਂ c ਮੂਲ ਬਿੰਦੂ ਹੈ ਤਾਂ CB ; X-ਧੁਰਾ । CD ; Y-ਧੁਰਾ ਹੈ
∴ ਤ੍ਰਿਭੁਜਾਕਾਰ ਘਾਹ ਦਾ ਲਾਨ PQR ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ : P (12, 2); Q (13, 6) ਅਤੇ R (10, 3) ਹੈ ।
ਇੱਥੇ x₁ = 12, x₂ = 13, x₃ = 10
y₁ = 2, y₂ = 6, y₃ = 3
ਹੁਣ △POR ਦਾ ਖੇਤਰਫਲ
= \(\frac{1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]
= \(\frac{1}{2}\)[12 (6 – 3) + 13 (3 – 2) + 10 (2 – 6)]
= \(\frac{1}{2}\)[36 + 13 – 40] = \(\frac{9}{2}\)
= 4.5 ਵ. ਇਕਾਈਆਂ
ਇਸ ਤੋਂ ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਕਿ ਤਿਭੁਜਾਕਾਰ ਘਾਹ ਦੇ ਲਾਨ ਦਾ ਖੇਤਰਫਲ ਸਮਾਨ ਹੈ ।

ਪ੍ਰਸ਼ਨ 6.
ਇਕ ਤ੍ਰਿਭੁਜ ABC ਦੇ ਸਿਖਰ A(4, 6), B(1, 5) ਅਤੇ C(7, 2) ਹਨ । ਭੁਜਾਵਾਂ AB ਅਤੇ AC ਨੂੰ ਕ੍ਰਮਵਾਰ D ਅਤੇ E ਉੱਤੇ ਕੱਟਦੀ ਹੋਈ ਇਕ ਰੇਖਾ ਇਸ ਤਰ੍ਹਾਂ ਖਿੱਚੀ ਗਈ ਹੈ ਕਿ \(\frac{AD}{AB}\) = \(\frac{AE}{AC}\) = \(\frac{1}{4}\) ਹੈ । △ADE ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ਅਤੇ ਇਸਦੀ ਤੁਲਨਾ △ABC ਦੇ ਖੇਤਰਫਲ ਨਾਲ ਕਰੋ ਥਿਊਰਮ (ਮੇਯ 6.2 ਅਤੇ ਥਿਊਰਮ (ਮੇਯ) 6.6 ਨੂੰ ਯਾਦ ਕਰੋ ।
ਹੱਲ:
△ABC ਦੇ ਸਿਖਰ ਹਨ A (4, 6); B (1, 5) ਅਤੇ C (7, 2) ਹਨ ।

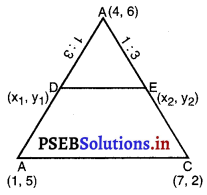
ਭੁਜਾ AB ਅਤੇ AC ਨੂੰ ਕ੍ਰਮਵਾਰ D (x, y) ਅਤੇ E (x₂, y₂) ਉੱਤੇ ਕੱਟਦੀ ਹੋਈ ਰੇਖਾ ਇਸ ਤਰ੍ਹਾਂ ਖਿੱਚੋ ਕਿ
\(\frac{AD}{AB}\) = \(\frac{AE}{AC}\) = \(\frac{1}{4}\)
∴ D ਅਤੇ E, AB ਅਤੇ AC ਨੂੰ ਅਨੁਪਾਤ 1 : 3 ਵਿੱਚ ਵੰਡਦੇ ਹਨ ।
∴ D ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਹਨ

△ADE ਵਿੱਚ,
= \(\frac{1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]

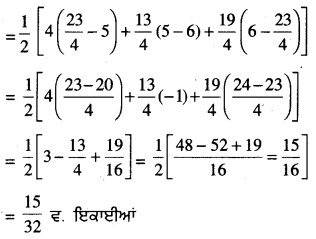
△ABC ਵਿੱਚ,
x₁ =4, x₂ = 1, x₃ = 7
y₁ = 6, y₂ = 5, y₃ = 2
△ABC ਦਾ ਖੇਤਰਫਲ
= \(\frac{1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]
= \(\frac{1}{2}\)[4 (5 – 2) + 1 (2 – 6) + 7 (6 – 5)]
= \(\frac{15}{2}\) ਵ. ਇਕਾਈਆਂ

ਪ੍ਰਸ਼ਨ 7.
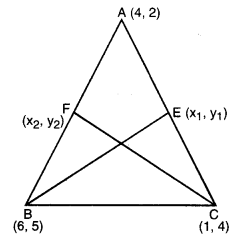
ਮੰਨ ਲਉ A (4, 2), B (6, 5) ਅਤੇ C (1, 4) ਇਕ ਤ੍ਰਿਭੁਜ ABC ਦੇ ਸਿਖਰ ਹਨ ।
(i) A ਤੋਂ ਹੋ ਕੇ ਜਾਣ ਵਾਲੀ ਮੱਧਿਕਾ BC ਨੂੰ D’ਤੇ ਮਿਲਦੀ ਹੈ । ਬਿੰਦੁ D ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਪਤਾ ਕਰੋ ।
(ii) AD ‘ਤੇ ਸਥਿਤ ਅਜਿਹੇ ਬਿੰਦੂ P ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਪਤਾ ਕਰੋ ਕਿ AP : PD = 2 : 1 ਹੋਵੇ ।
(ii) ਮੱਧਿਕਾਵਾਂ BE ਅਤੇ CF ਉੱਤੇ ਅਜਿਹੇ ਬਿੰਦੂਆਂ Q ਅਤੇ R ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਪਤਾ ਕਰੋ ਕਿ BQ : QE = 2 : 1 ਹੋਵੇ ਅਤੇ CR : RF = 2 : 1 ਹੋਵੇ
(iv) ਤੁਸੀਂ ਕੀ ਦੇਖਦੇ ਹੋ ?
[ਨੋਟ : ਉਹ ਬਿੰਦੂ ਜੋ ਤਿੰਨਾਂ ਮੱਧਿਕਾਵਾਂ ਦਾ ਸਾਂਝਾ ਹੋਵੇ, ਉਸ 1 ਨੂੰ ਤ੍ਰਿਭੁਜ ਦਾ ਕੇਂਦਰਕ (Centroid) ਕਹਿੰਦੇ ਹਨ ਅਤੇ ਇਹ | ਹਰ ਇੱਕ ਮੱਧਿਕਾ ਨੂੰ 2:1 ਦੇ ਅਨੁਪਾਤ ਵਿੱਚ ਵੰਡਦਾ ਹੈ ।]
(v) ਜੇਕਰ A(x₁, y₁), B(x₂, y₂) ਅਤੇ C (x₃, y₃) ਤ੍ਰਿਭੁਜ ABC ਦੇ ਸਿਖਰ ਹੋਣ ਤਾਂ ਇਸ ਤ੍ਰਿਭੁਜ ਦੇ ਕੇਂਦਰਕ ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ ਕਿ △ABC ਦੇ ਸਿਖਰ A (4, 2); B (6, 5) ਅਤੇ C (1, 4) ਹੈ ।
(i) AD, ਸਿਖਰ A ਤੋਂ ਮੱਧਕਾ ਹੈ
∴ D, BC ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ ।

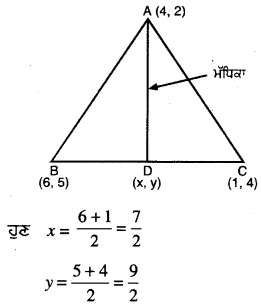
∴ D ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਹਨ (\(\frac{7}{2}\), \(\frac{9}{2}\))

(ii) ਮੰਨ ਲਓ P (x, y), AD ਉੱਤੇ ਕੋਈ ਬਿੰਦੂ ਇਸ ਤਰ੍ਹਾਂ ਹੈ ਕਿ AP : PD = 2 : 1


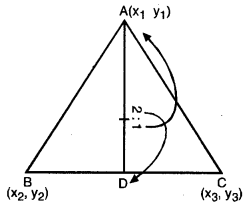
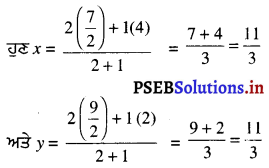
∴ P ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ (\(\frac{11}{3}\), \(\frac{11}{3}\)) ਹਨ ।

(iii) ਮੰਨ ਲਉ BE ਅਤੇ CF, AABC ਦੀਆਂ ਕ੍ਰਮਵਾਰ AC ਅਤੇ AB ਉੱਤੇ ਮੱਧਿਕਾਵਾਂ ਹਨ
∴ E ਅਤੇ F, ਮਵਾਰ AC ਅਤੇ AB ਦੇ ਮੱਧ ਬਿੰਦੂ ਹਨ

E ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ
x₁ = \(\frac{4+1}{2}\) = \(\frac{5}{2}\)
ਅਤੇ y₁ = \(\frac{4+2}{2}\) = \(\frac{6}{2}\) = 3
∴ E ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਹਨ : (\(\frac{5}{2}\), 3)
F ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ
x₂ = \(\frac{4+6}{2}\) = \(\frac{10}{2}\) = 5
y₂ = \(\frac{5+2}{2}\) = \(\frac{7}{2}\)
∴ F ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਹਨ (5, \(\frac{7}{2}\))
ਹੁਣ, Q, BE ਨੂੰ ਇਸ ਤਰ੍ਹਾਂ ਕੱਟਦਾ ਹੈ ਕਿ BQ : QE = 2 : 1

ਨਾਲ ਹੀ R, CF ਨੂੰ ਇਸ ਤਰ੍ਹਾਂ ਵਿਭਾਜਤ ਕਰਦਾ ਹੈ ਕਿ CR : RF = 2 : 1

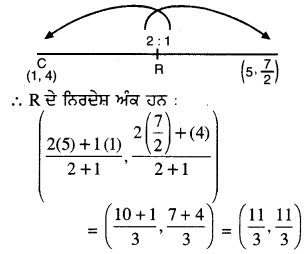
(iv) ਇਸ ਤੋਂ ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਕਿ P, Q ਅਤੇ R ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਇਕ ਸਮਾਨ ਹਨ ਅਤੇ ਇਕੋ ਬਿੰਦੂ ਉੱਤੇ ਕੱਟਦੇ ਹਨ ।ਇਹ ਬਿੰਦੁ ਤਿਭੁਜ ਦਾ ਕੇਂਦਰਿਕ ਕਹਿਲਾਉਂਦਾ ਹੈ । ਹਰੇਕ ਮੱਧਕਾ ਨੂੰ 2 : 1 ਵਿਚ ਵਿਭਾਜਤ ਕਰਦਾ ਹੈ ।

(v) ਦਿੱਤੀ ਹੋਈ △ABC ਦੇ ਸਿਖਰ A (x₁, y₁); B (x₂, y₂) ਅਤੇ C (x₃, y₃) ਹੈ ।

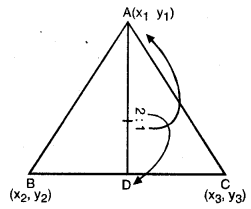
ਮੰਨ ਲਉ AD, △ABC ਦੀ ਮੱਧਕਾ ਹੈ :
∴ D, BC ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ ਤਾਂ D ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ।
(\(\frac{x_{2}+x_{3}}{2}\), \(\frac{y_{2}+y_{3}}{2}\))
ਹੁਣ, G, △ABC ਦਾ ਕੇਂਦਰ ਹੈ ਜੋ ਮੱਧਿਕਾ AD ਨੂੰ 2 : 1 ਵਿਚ ਵਿਭਾਜਤ ਕਰਦਾ ਹੈ
∴ G ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਹਨ :

ਪ੍ਰਸ਼ਨ 8.
ਬਿੰਦੂਆਂ A (-1, -1), B (-1, 4), C (5, 4) ਅਤੇ D (5, -1) ਤੋਂ ਇਕ ਆਇਤ ABCD ਬਣਦਾ ਹੈ । P,Q,R ਅਤੇ 5 ਕੁਮਵਾਰ ਭੁਜਾਵਾਂ AB, BC, CD ਅਤੇ DA ਦੇ ਮੱਧ ਬਿੰਦੂ ਹਨ । ਕੀ ਚਤੁਰਭੁਜ PORS ਇੱਕ ਵਰਗ ਹੈ ? ਕੀ ਇਹ ਇੱਕ ਆਇਤ ਹੈ ? ਕੀ ਇਹ ਇਕ ਸਮਚਤੁਰਭੁਜ ਹੈ ? ਕਾਰਣ ਸਹਿਤ ਉੱਤਰ ਦਿਉ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ ABCD ਦੇ ਸਿਖਰ ਹਨ ।
A(-1, – 1); B (-1, 4); C (5, 4) ਅਤੇ D (5, – 1).

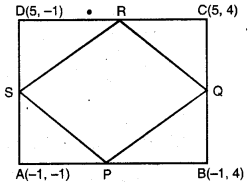
∵ P, AB ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ
∴ P ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਹਨ ।
(\(\frac{-1-1}{2}\), \(\frac{-1+4}{2}\)) = (1, \(\frac{3}{2}\))
∵ Q, BC ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ
∴ Q ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਹਨ
(\(\frac{-1+5}{2}\), \(\frac{4+4}{2}\)) = (2, 4)
∵ R, CD ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ
∴ R ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਹਨ
(\(\frac{5+5}{2}\), \(\frac{4-1}{2}\)) = (5, \(\frac{3}{2}\))
∵ S, AD ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ
∴ S ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਹਨ



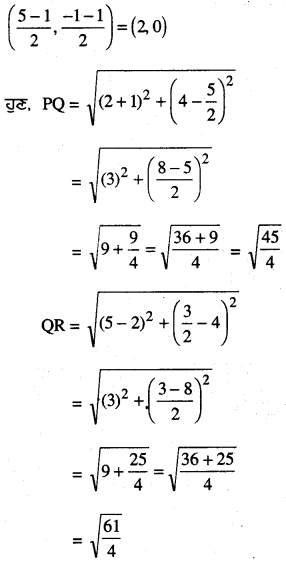
ਹੁਣ ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਕਿ
PQ = Rs ਅਤੇ QR = SP
ਨਾਲ ਹੀ, PR ≠ QS
PQRS ਦੀਆਂ ਭੁਜਾਵਾਂ ਬਰਾਬਰ ਹਨ ਪਰ ਬਰਾਬਰ ਨਹੀਂ ਹਨ ।
∴ PQRS ਇਕ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਹੈ ।