Punjab State Board PSEB 10th Class Science Book Solutions Chapter 12 ਬਿਜਲੀ Textbook Exercise Questions and Answers.
PSEB Solutions for Class 10 Science Chapter 12 ਬਿਜਲੀ
PSEB 10th Class Science Guide ਬਿਜਲੀ Textbook Questions and Answers
ਪ੍ਰਸ਼ਨ 1.
ਪ੍ਰਤਿਰੋਧ R ਦੇ ਕਿਸੇ ਤਾਰ ਦੇ ਟੁਕੜੇ ਨੂੰ ਪੰਜ ਬਰਾਬਰ ਭਾਗਾਂ ਵਿੱਚ ਕੱਟਿਆ ਗਿਆ ਹੈ। ਇਨ੍ਹਾਂ ਟੁਕੜਿਆਂ ਨੂੰ ਫਿਰ ਸਮਾਨਾਂਤਰ ਵਿੱਚ ਜੋੜਿਆ ਗਿਆ ਹੈ ਜੇਕਰ ਸੰਯੋਗ ਦਾ ਡੁੱਲ-ਪ੍ਰਤਿਰੋਧ R’ ਹੈ ਤਾਂ \(\frac{\mathbf{R}}{\mathbf{R}^{\prime}}\) ਅਨੁਪਾਤ ਦਾ ਮਾਨ ਹੈ :
(a) \(\frac {1}{25}\)
(b) \(\frac {1}{5}\)
(c) 5
(d) 25.
ਹੱਲ :
ਹਰੇਕ ਕੱਟੇ ਹੋਏ ਭਾਗ ਦਾ ਪ੍ਰਤਿਰੋਧ \(\frac{R}{5}\)
ਤਿਰੋ
∴ R1 = R2 = R3 = R4 = R5 = \(\frac{R}{5}\) ਹੋਵੇਗਾ
ਪੰਜਾਂ ਕੱਟੇ ਹੋਏ ਟੁਕੜਿਆਂ ਨੂੰ ਸਮਾਨਾਂਤਰ ਵਿੱਚ ਜੋੜਨ ਤੇ
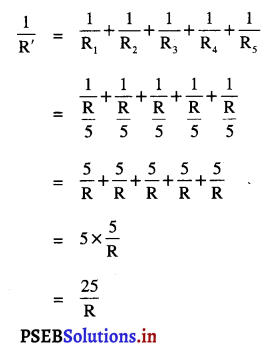
∴ R’ = \(\frac{\mathrm{R}}{25}\)
ਜਾਂ = \(\frac{\mathrm{R}}{\mathrm{R}^{\prime}}\) = 25
∴ ਸਹੀ ਉੱਤਰ (d) 25 ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 2.
ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ਕਿਹੜਾ ਪਦ ਬਿਜਲਈ ਸਰਕਟ ਵਿੱਚ ਬਿਜਲਈ ਸ਼ਕਤੀ ਨੂੰ ਨਹੀਂ ਦਰਸਾਉਂਦਾ ?
(a) I2R
(b) IR2
(c) VI
(d) V2/R.
ਹੱਲ :
ਬਿਜਲਈ ਸ਼ਕਤੀ P = V × I
= (IR) × I
= I2R
= (\(\frac{\mathrm{V}}{\mathrm{R}}\))2 × R (∵\(\frac{\mathrm{V}}{\mathrm{I}}\) = R)
= \(\frac{V^{2}}{R}\)
ਸਿਰਫ਼ IR2 ਬਿਜਲਈ ਸਰਕਟ ਵਿੱਚ ਬਿਜਲਈ ਸ਼ਕਤੀ ਨੂੰ ਨਹੀਂ ਦਰਸਾਉਂਦਾ ਹੈ ।
∴ ਸਹੀ ਉੱਤਰ ਹੋਵੇਗਾ (b) IR2
ਪ੍ਰਸ਼ਨ 3.
ਕਿਸੇ ਬਿਜਲਈ ਬੱਲਬ ਉੱਤੇ 220 V ਅਤੇ 100 ਅੰਕਿਤ ਹੈ। ਜਦੋਂ ਇਸਨੂੰ 110V ਉੱਤੇ ਚਾਲੂ ਕਰਦੇ ਹਨ ਤਾਂ ਇਸ ਦੁਆਰਾ ਵਰਤੀ ਸ਼ਕਤੀ ਹੋਵੇਗੀ :
(a) 100W
(b) 75W
(c) 50W
(d) 25 W.
ਹੱਲ :
ਸੂਤਰ P = \(\frac{\mathrm{V}^{2}}{\mathrm{R}}\) miss
ਬੱਲਬ ਦਾ ਪ੍ਰਤਿਰੋਧ R = \(\frac{\mathrm{V}^{2}}{\mathrm{P}}\)
= \(\frac{(220)^{2}}{100}\)
= \(\frac{220 \times 220}{100}\)
= 484Ω
∴ ਦੂਜੀ ਅਵਸਥਾ ਵਿੱਚ 110v ਤੇ ਚਾਲੂ ਕਰਨ ਨਾਲ ਬੱਲਬ ਦੁਆਰਾ ਖ਼ਪਤ ਕੀਤੀ ਗਈ ਸ਼ਕਤੀ
p1 = \(\frac{\mathrm{V}_{1}^{2}}{\mathrm{R}}\)
= \(\frac{(110)^{2}}{484}\)
= \(\frac{110 \times 110}{484}\)
= 25 W
ਇਸ ਲਈ ਸਹੀ ਉੱਤਰ (d) 25 ਹੈ ।
ਪ੍ਰਸ਼ਨ 4.
ਦੋ ਚਾਲਕ ਤਾਰਾਂ ਜਿਨ੍ਹਾਂ ਦੇ ਪਦਾਰਥ, ਲੰਬਾਈ ਅਤੇ ਵਿਆਸ ਬਰਾਬਰ ਹਨ ਕਿਸੇ ਬਿਜਲਈ ਸਰਕਟ ਵਿੱਚ ਜਿਸਦੇ ਸਿਰਿਆਂ ਤੇ ਟੈਂਸ਼ਲ ਅੰਤਰ ਉਹੀ ਹੋਵੇ, ਪਹਿਲਾਂ ਲੜੀ ਵਿੱਚ ਅਤੇ ਫਿਰ ਸਮਾਨਾਂਤਰ ਵਿੱਚ ਜੋੜੀਆਂ ਗਈਆਂ । ਲੜੀ ਅਤੇ ਸਮਾਨਾਂਤਰ ਸੰਯੋਗ ਵਿੱਚ ਉਤਪੰਨ ਤਾਪ ਦਾ ਅਨੁਪਾਤ ਹੋਵੇਗਾ :
(a) 1 : 2
(b) 2 : 1
(c) 1 : 4
(d) 4 : 1.
ਹੱਲ :
ਕਿਉਂਕਿ ਸਾਰੇ ਚਾਲਕ ਇੱਕ ਸਮਾਨ ਪਦਾਰਥ, ਲੰਬਾਈ ਅਤੇ ਵਿਆਸ ਦੇ ਹਨ, ਇਸ ਲਈ ਸਾਰਿਆਂ ਦਾ ਪ੍ਰਤਿਰੋਧ ਬਰਾਬਰ ਹੋਵੇਗਾ। ਮੰਨ ਲਓ ਇਹ R ਹੈ।
ਦੋਨਾਂ ਚਾਲਕ ਤਾਰਾਂ ਨੂੰ ਲੜੀਕਮ ਵਿੱਚ ਸੰਯੋਜਿਤ ਕਰਨ ‘ਤੇ ਪ੍ਰਤਿਰੋਧ Rs = R + R = 2R
ਦੋਨਾਂ ਚਾਲਕ ਤਾਰਾਂ ਨੂੰ ਸਮਾਨਾਂਤਰ ਕ੍ਰਮ ਵਿੱਚ ਸੰਯੋਜਿਤ ਕਰਨ ‘ਤੇ ਪ੍ਰਤਿਰੋਧ \(\frac{1}{R_{p}}=\frac{1}{R}+\frac{1}{R}=\frac{2}{R}\)
ਲੜੀਕਮ ਵਿੱਚ ਸੰਯੋਜਿਤ ਹੋਣ ‘ਤੇ ਉਤਪੰਨ ਹੋਇਆ ਤਾਪ H1 = Ps = \(\frac{\mathrm{V}^{2}}{\mathrm{R}_{s}}\)
ਸਮਾਨਾਂਤਰ ਕੂਮ ਵਿੱਚ ਸੰਯੋਜਿਤ ਹੋਣ ‘ਤੇ ਉਤਪੰਨ ਹੋਇਆ ਤਾਪ H2 = pp = \(\frac{\mathrm{V}^{2}}{\mathrm{R}_{p}}\)
ਜੇਕਰ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ V ਹੈ ਤਾਂ ਦੋਨਾਂ ਸੰਯੋਜਨਾਂ ਵਿੱਚ ਉਤਪੰਨ ਤਾਪ ਦਾ ਅਨੁਪਾਤ
\(\frac{\mathrm{H}_{1}}{\mathrm{H}_{2}}\) = \(\frac{\mathrm{V}^{2} / \mathbf{R}_{s}}{\mathrm{~V}^{2} / \mathbf{R}_{p}}=\frac{\mathbf{R}_{p}}{\mathbf{R}_{s}}=\frac{\mathbf{R} / 2}{2 \mathbf{R}}\) = \(\frac{1}{4}\)
ਇਸ ਲਈ ਸਹੀ ਉੱਤਰ (c) 1 : 4 ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 5.
ਕਿਸੇ ਬਿਜਲਈ ਸਰਕਟ ਵਿੱਚ ਦੋ ਬਿੰਦੂਆਂ ਦੇ ਵਿੱਚ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ ਮਾਪਣ ਲਈ ਵੋਲਟਮੀਟਰ ਨੂੰ ਕਿਸ ਪ੍ਰਕਾਰ ਜੋੜਿਆ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਕਿਸੇ ਬਿਜਲਈ ਸਰਕਟ ਦੇ ਦੋ ਬਿੰਦੂਆਂ ਵਿੱਚ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ ਮਾਪਣ ਲਈ ਵੋਲਟਮੀਟਰ ਨੂੰ ਦੋ ਬਿੰਦੂਆਂ ਵਿਚਲੇ ਸਮਾਨਅੰਤਰ ਵਿੱਚ ਜੋੜਿਆ ਜਾਂਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 6.
ਇੱਕ ਤਾਂਬੇ ਦੀ ਤਾਰ ਦਾ ਵਿਆਸ 0.5 mm ਅਤੇ ਪ੍ਰਤਿਰੋਧਕਤਾ 1.6 × 10-8Ωm ਹੈ। 10Ω ਪ੍ਰਤਿਰੋਧ ਦਾ ਪ੍ਰਤਿਰੋਧਕ ਬਣਾਉਣ ਲਈ ਕਿੰਨੀ ਲੰਬੀ ਤਾਰ ਦੀ ਜ਼ਰੂਰਤ ਹੋਵੇਗੀ ? ਜੇਕਰ ਇਸ ਤੋਂ ਦੁੱਗਣੇ ਵਿਆਸ ਦੀ ਤਾਰ ਲਈ ਜਾਵੇ ਤਾਂ ਪ੍ਰਤਿਰੋਧ ਵਿੱਚ ਕੀ ਅੰਤਰ ਆਵੇਗਾ ?
ਹੱਲ :
ਦਿੱਤਾ ਹੈ, ਤਾਰ ਦੀ ਪ੍ਰਤਿਰੋਧਕਤਾ (ρ) = 1.6 × 10-8Ωm
ਤਾਰ ਦਾ ਪ੍ਰਤਿਰੋਧ (R) = 10Ω
ਤਾਰ ਦਾ ਵਿਆਸ (2r) = 0.5 mm
= 5 × 10-4m
∴ ਤਾਰ ਦਾ ਅਰਧ-ਵਿਆਸ (r) = 25 × 10-4 m
ਤਾਰ ਦੇ ਪਰਿਖੇਤਰ ਕਾਟ ਦਾ ਖੇਤਰਫਲ (A) = πr2
= 3.14 × (2.5 × 10-4)2 m2
= 19.625 × 10-8 m2
:: ਸੂਤਰ R = ρ\(\frac{l}{\mathrm{~A}}\) ਤੋਂ
ਤਾਰ ਦੀ ਲੰਬਾਈ (l) = \(\frac{\mathrm{R} \times \mathrm{A}}{\rho}\)
= = \(\frac{10 \times 19.625 \times 10^{-8}}{1.6 \times 10^{-8}}\)
= 12.26 × 103 m
= 12260m
ਵਿਆਸ ਦੁੱਗਣਾ ਕਰਨ ਨਾਲ ਤਾਰ ਦਾ ਅਰਧ-ਵਿਆਸ ਵੀ ਦੁਗਣਾ ਅਤੇ ਪਰਿਖੇਤਰ ਕਾਟ ਦਾ ਖੇਤਰਫਲ (A = πr2). ਚੌਗੁਣਾ ਹੋ ਜਾਵੇਗਾ ।
∴ R ∝ \(\frac{1}{\mathrm{~A}}\)
∴ ਖੇਤਰਫਲ ਚੌਗੁਣਾ ਹੋਣ ਕਾਰਨ ਤਾਰ ਦਾ ਪ੍ਰਤਿਰੋਧ \(\frac{1}{4}\) ਰਹਿ ਜਾਏਗਾ।
ਅਰਥਾਤ ਪ੍ਰਤਿਰੋਧ R’ = \(\frac{1}{4}\)R
= \(\frac{1}{4}\) × 10
= 2.5Ω
ਪ੍ਰਸ਼ਨ 7.
ਕਿਸੇ ਤਿਰੋਧਕ ਦੇ ਸਿਰਿਆਂ ਤੇ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ vਦੇ ਭਿੰਨ ਮਾਨਾਂ ਲਈ ਉਸ ਤੋਂ ਪ੍ਰਭਾਵਿਤ ਬਿਜਲਈ ਧਾਰਾਵਾਂ V ਦੇ ਸੰਗਤ ਮਾਨ ਹੇਠ ਦਿੱਤੇ ਗਏ
ਹਨ :

V ਅਤੇ I ਦੇ ਵਿੱਚ ਗ੍ਰਾਫ਼ ਖਿੱਚ ਕੇ ਇਸ ਪ੍ਰਤਿਰੋਧਕ ਦਾ ਤਿਰੋਧ ਗਿਆਤ ਕਰੋ ।
ਹੱਲ :
ਲੋੜੀਂਦੇ ਗ੍ਰਾਫ਼ ਦੇ ਲਈ ਨਾਲ ਦਿੱਤਾ ਹੋਇਆ ਚਿੱਤਰ ਵੇਖੋ ।
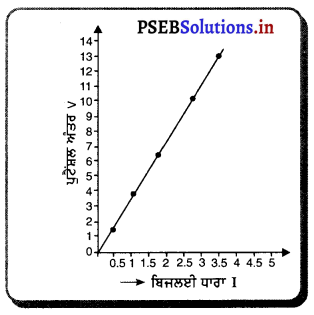
ਪ੍ਰਤਿਰੋਧਕ ਦਾ ਪ੍ਰਤਿਰੋਧ = ਗ੍ਰਾਫ਼ ਦੀ ਢਲਾਨ
ਅਰਥਾਤ R = \(\frac{\Delta V}{\Delta I}\)
ਦਿੱਤੇ ਹੋਏ ਅੰਕੜਿਆਂ ਤੋਂ
V1 = 3.4V, V2 = 10.2 V
ਸੰਗਤ I1 = 1.0A, I2 = 3.4
∴ ΔV = V2 – V1
= 10.2 – 3.4
= 6.8V
ਅਤੇ ΔI = I2 – I1
= 3.0A – 1.0A
= 2.0 A
∴ ਪ੍ਰਤਿਰੋਧ R = \(\frac{\Delta \mathrm{V}}{\Delta \mathrm{I}}\)
= \(\frac{6.8 \mathrm{~V}}{2.0 \mathrm{~A}}\)
= 3.4Ω
ਪ੍ਰਸ਼ਨ 8.
ਕਿਸੇ ਅਗਿਆਤ ਪ੍ਰਤਿਰੋਧਕ ਦੇ ਸਿਰਿਆਂ ਤੇ 12V ਦੀ ਬੈਟਰੀ ਜੋੜਨ ਤੇ ਸਰਕਟ ਵਿੱਚ 2.5mA ਬਿਜਲਈ ਧਾਰਾ ਪ੍ਰਵਾਹਿਤ ਹੁੰਦੀ ਹੈ। ਤਿਰੋਧਕ ਦੇ ਪ੍ਰਤਿਰੋਧ ਦੀ ਗਣਨਾ ਕਰੋ ।
ਹੱਲ :
ਦਿੱਤਾ ਹੈ, ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ V = 12V
ਪ੍ਰਵਾਹਿਤ ਧਾਰਾ I = 2.5 mA
= 2.5 × 10-3 A
ਪ੍ਰਤਿਰੋਧਕ ਦਾ ਪ੍ਰਤਿਰੋਧ R = \(\frac{\mathrm{V}}{\mathrm{I}}\)
= \(\frac{12}{2.5 \times 10^{-3}}\)
= \(\frac{12 \times 10^{3}}{2.5}\)
= 4.8 × 103Ω
= 4.8KΩ
![]()
ਪ੍ਰਸ਼ਨ 9.
9V ਦੀ ਬੈਟਰੀ ਨੂੰ 0.2Ω, 0.3Ω, 0.4Ω, 0.5Ω ਅਤੇ 12Ω ਪ੍ਰਤਿਰੋਧਕਾਂ ਨਾਲ ਲੜੀ ਵਿੱਚ ਜੋੜਿਆ ਗਿਆ ਹੈ। 12Ω ਦੇ ਤਿਰੋਧਕ ਵਿੱਚ ਕਿੰਨੀ ਬਿਜਲਈ ਧਾਰਾ ਪ੍ਰਵਾਹਿਤ ਹੋਵੇਗੀ ?
ਹੱਲ :
ਦਿੱਤਾ ਹੈ, R1 = 0.2Ω, R2 = 0.3Ω, R3 = 0.4Ω, R4 = 0.5Ω, R5 = 12Ω
ਲੜੀ ਸੰਯੋਜਨ ਦਾ ਕੁੱਲ ਪ੍ਰਤਿਰੋਧ R = R1 + R2 + R3 + R4 + R5
= 0.2 + 0.3 + 0.4 + 0.5 + 12
= 13.4Ω
ਬਿਜਲਈ ਸਰਕਟ ਵਿੱਚ ਪ੍ਰਵਾਹਿਤ ਹੋ ਰਹੀ ਕੁੱਲ ਧਾਰਾ I = \(\frac{\mathrm{V}}{\mathrm{R}}\)
= \(\frac{9 \mathrm{~V}}{13.4 \Omega}\)
= 0.67A
ਲੜੀ ਸੰਯੋਜਨ ਵਿੱਚ ਹਰੇਕ ਪ੍ਰਤਿਰੋਧ ਵਿੱਚੋਂ 0.67A ਦੀ ਧਾਰਾ ਹੀ ਪ੍ਰਵਾਹਿਤ ਹੋਵੇਗੀ।
∴ 12Ω ਦੇ ਤਿਰੋਧਕ ਵਿੱਚ ਪ੍ਰਵਾਹਿਤ ਹੋਣ ਵਾਲੀ ਧਾਰਾ = 0.67A
ਪ੍ਰਸ਼ਨ 10.
176Ω ਪ੍ਰਤਿਰੋਧ ਦੇ ਕਿੰਨੇ ਪ੍ਰਤਿਰੋਧਕਾਂ ਨੂੰ ਸਮਾਨਾਂਤਰ ਕੂਮ ਵਿੱਚ ਜੋੜਿਆ ਜਾਵੇ ਤਾਂ ਕਿ 220v ਦੇ ਬਿਜਲਈ ਸਰੋਤ ਤੋਂ 5A ਬਿਜਲਈ ਧਾਰਾ ਪ੍ਰਵਾਹਿਤ ਹੋਵੇ ।
ਹੱਲ :
ਦਿੱਤਾ ਹੈ, ਸਰੋਤ ਦਾ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ V = 220 V
ਪ੍ਰਵਾਹਿਤ ਬਿਜਲਈ ਧਾਰਾ ਦੀ ਮਾਤਰਾ I = 5A
∴ ਸੰਯੋਜਨ ਦਾ ਤੁੱਲ-ਪ੍ਰਤਿਰੋਧ R = \(\frac{\mathrm{V}}{\mathrm{I}}\)
= \(\frac{220 \mathrm{~V}}{5 \mathrm{~A}}\)
ਜਾਂ R = 44Ω
R1 = R2 = R3 ……………….. = Rn = 176Ω
ਮੰਨ ਲਓ ਅਜਿਹੇ n ਪ੍ਰਤਿਰੋਧਕ ਸਮਾਨਾਂਤਰ ਜੋੜੇ ਗਏ ਹਨ, ਤਾਂ

= \(\frac{176}{44}\) = 4
ਇਸ ਲਈ 4 ਪ੍ਰਤਿਰੋਧਕ ਹੀ ਸਮਾਨਾਂਤਰ ਜੋੜੇ ਜਾਣਗੇ ।
ਪ੍ਰਸ਼ਨ 11.
ਇਹ ਦਰਸਾਓ ਕਿ ਤੁਸੀਂ 6Ω ਪ੍ਰਤਿਰੋਧ ਦੇ ਤਿੰਨ ਪ੍ਰਤਿਰੋਧਕਾਂ ਨੂੰ ਕਿਸ ਪ੍ਰਕਾਰ ਜੋੜੋਗੇ ਕਿ ਸੰਯੋਗ ਦਾ ਤਿਰੋਧ : (i) 9Ω (ii) 4Ω ਹੋਵੇ।
ਹੱਲ :
(i) 9Ω ਦਾ ਪ੍ਰਤਿਰੋਧ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ ਪਹਿਲੇ ਦੋ ਪ੍ਰਤਿਰੋਧਕਾਂ ਨੂੰ ਸਮਾਨਾਂਤਰ ਵਿੱਚ ਅਤੇ ਤੀਸਰੇ ਪ੍ਰਤਿਰੋਧ ਨੂੰ ਇਸ ਸੰਯੋਜਨ ਨਾਲ ਲੜੀ ਵਿੱਚ ਜੋੜਨਾ ਹੋਵੇਗਾ ।
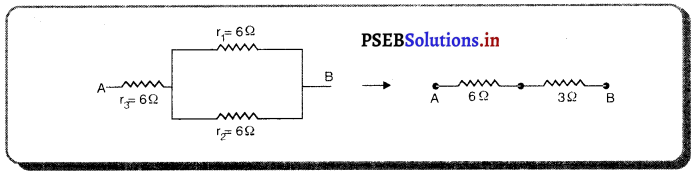
ਮੰਨ ਲਓ ਸਮਾਨਾਂਤਰ ਸੰਯੋਗ ਦਾ ਪ੍ਰਤਿਰੋਧ R ਹੈ ।
∴ = \(\frac{1}{\mathrm{R}}=\frac{1}{r_{1}}+\frac{1}{r_{2}}\)
= \(\frac{1}{6}+\frac{1}{6}\)
= \(\frac{2}{6}\)
∴ R = \(\frac{6}{2}\) = 3Ω
ਇਹ 3Ω ਦਾ ਤੁੱਲ-ਪ੍ਰਤਿਰੋਧ, 6Ω ਦੇ ਤੀਸਰੇ ਪ੍ਰਤਿਰੋਧ ਨਾਲ ਲੜੀ ਵਿੱਚ ਜੁੜ ਕੇ ਕੁੱਲ ਪ੍ਰਤਿਰੋਧ = r3 + R
= 6Ω + 3Ω
= 92 ਹੋ ਜਾਵੇਗਾ ਉੱਤਰ
(ii) ਸੰਯੋਜਨ ਦਾ ਤੁੱਲ-ਪ੍ਰਤਿਰੋਧ 4Ω ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ ਪਹਿਲੇ 6Ω ਦੇ ਦੋ ਪ੍ਰਤਿਰੋਧਕਾਂ ਨੂੰ ਲੜੀ ਵਿੱਚ ਜੋੜਨਾ ਹੋਵੇਗਾ ਅਤੇ ਉਸ ਤੋਂ ਬਾਅਦ ਇਸ ਨਾਲ ਤੀਸਰਾ ਤਿਰੋਧਕ ਸਮਾਨਾਂਤਰ ਜੋੜਿਆ ਜਾਵੇਗਾ ।
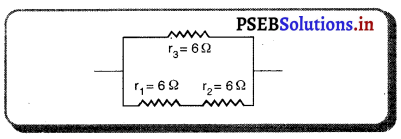
6Ω ਤੇ 6Ω ਦੇ ਦੋ ਪ੍ਰਤਿਰੋਧਕਾਂ ਨੂੰ ਲੜੀ ਵਿੱਚ ਜੋੜਨ ਤੇ
ਸੰਯੋਜਨ ਦਾ ਤੁੱਲ-ਪ੍ਰਤਿਰੋਧ R = r1 + r2
= 6 + 6
= 12Ω ਹੋਵੇਗਾ |
ਇਹ 12Ω ਦਾ ਪ੍ਰਤਿਰੋਧ ਤੀਸਰੇ 6Ω ਦੇ ਪ੍ਰਤਿਰੋਧ ਨਾਲ ਸਮਾਨਅੰਤਰ ਵਿੱਚ ਜੋੜਨ ਨਾਲ ਕੁੱਲ ਪ੍ਰਤਿਰੋਧ R’ ਪ੍ਰਾਪਤ ਹੋਵੇਗਾ ।
∴ \(\frac{1}{\mathrm{R}^{\prime}}=\frac{1}{6}+\frac{1}{12}\)
= \(\frac{2+1}{12}\)
= \(\frac{3}{12}\)
= \(\frac{1}{4}\)
∴ R’ = 4Ω
ਪ੍ਰਸ਼ਨ 12.
220 v ਦੀ ਬਿਜਲਈ ਲਾਇਨ ਉੱਤੇ ਉਪਯੋਗ ਕੀਤੇ ਜਾਣ ਵਾਲੇ ਬਹੁਤ ਸਾਰੇ ਬਲਬਾਂ ਨੂੰ 10W ਅੰਕਿਤ ਕੀਤਾ ਗਿਆ ਹੈ। ਜੇਕਰ 220v ਲਾਇਨ ਵਿੱਚ ਅਨੁਮਾਨਤ ਅਧਿਕਤਮ ਬਿਜਲਈ ਧਾਰਾ 5A ਹੈ ਤਦ ਇਸ ਲਾਇਨ ਦੀਆਂ ਦੋ ਤਾਰਾਂ ਵਿੱਚ ਕਿੰਨੇ ਬੱਲਬ ਸਮਾਨਾਂਤਰ ਵਿੱਚ ਜੋੜੇ ਜਾ ਸਕਦੇ ਹਨ ?
ਹੱਲ :
ਮੰਨ ਲਓ n ਬੱਲਦਾਂ ਨੂੰ ਸਮਾਨਾਂਤਰ ਵਿੱਚ ਜੋੜਿਆ ਹੈ,
ਤਾਂ ਬਿਜਲਈ ਸਰਕਟ ਦੀ ਸ਼ਕਤੀ p = n × ਇੱਕ ਬੱਲਬ ਦੀ ਸ਼ਕਤੀ
n × 10
= 10n ਵਾਟ (W)
ਦਿੱਤਾ ਹੈ, V = 220V
I = 5A
P = V × 1 ਤੋਂ
10n = 220 × 5
∴ n = \(\frac{220 \times 5}{10}\)
= 110
ਅਰਥਾਤ 110 ਬੱਲਦਾਂ ਨੂੰ ਸਮਾਨਾਂਤਰ ਵਿੱਚ ਜੋੜਿਆ ਜਾ ਸਕਦਾ ਹੈ
ਵਿਕਲਪਿਕ ਤਰੀਕਾ
ਹਰੇਕ ਬੱਲਬ ਦਾ ਪ੍ਰਤਿਰੋਧ (r) = \(\frac{V^{2}}{P}\)
= \(\frac{(220)^{2}}{10}\)
= \(\frac{220 \times 220}{10}\)
= 4840Ω
ਸਰਕਟ ਦੀ ਕੁੱਲ ਤਿਰੋਧਕਤਾ (R) =\(\frac{220 \mathrm{~V}}{5 \mathrm{~V}}\)
= 44Ω
ਮੰਨ ਲਓ ਬੱਲਬਾਂ ਦੀ ਕੁੱਲ ਸੰਖਿਆ n ਹੈ, ਤਾਂ
ਪ੍ਰਤਿਰੋਧਕਤਾ (R) = \(\frac{r}{n}\)
⇒ ਬੱਲਬਾਂ ਦੀ ਸੰਖਿਆ n = \(\frac{r}{\mathrm{R}}\)
= \(\frac{4840}{44}\)
= 110
![]()
ਪ੍ਰਸ਼ਨ 13.
ਇੱਕ ਬਿਜਲਈ ਭੱਠੀ ਦੀ ਤਪਤ ਪਲੇਟ ਦੀਆਂ ਪ੍ਰਤਿਰੋਧਕ ਕੁੰਡਲੀਆਂ A ਅਤੇ B ਦੀਆਂ ਬਣੀਆਂ ਹੋਈਆਂ ਹਨ ਜਿਨ੍ਹਾਂ ਵਿੱਚ ਹਰ ਇੱਕ ਦਾ ਤਿਰੋਧ 24Ω ਹੈ। ਇਨ੍ਹਾਂ ਨੂੰ ਵੱਖ-ਵੱਖ ਲੜੀ ਵਿੱਚ ਜਾਂ ਸਮਾਨਾਂਤਰ ਵਿੱਚ ਜੋੜ ਕੇ ਉਪਯੋਗ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ। ਜੇਕਰ ਇਹ ਭੱਠੀ 220 V ਬਿਜਲਈ ਸਰੋਤ ਨਾਲ ਜੋੜੀ ਜਾਵੇ ਤਾਂ ਤਿੰਨਾਂ ਕੇਸਾਂ ਵਿੱਚ ਪ੍ਰਵਾਹਿਤ ਬਿਜਲਈ ਧਾਰਾਵਾਂ ਕੀ ਹਨ ?
ਹੱਲ :
ਦਿੱਤਾ ਹੈ, ਪੁਟੈਂਸ਼ਲ V = 220 V
ਕੁੰਡਲੀਆਂ ਦਾ ਪ੍ਰਤਿਰੋਧ R1 = R2 = 24Ω
ਪਹਿਲੀ ਅਵਸਥਾ ਵਿੱਚ-ਜਦੋਂ ਕਿਸੇ ਇੱਕ ਕੁੰਡਲੀ ਨੂੰ ਲਗਾਇਆ ਜਾਂਦਾ ਹੈ ਤਾਂ
ਕੁੱਲ ਤਿਰੋਧ
R = R1 = 24Ω
∴ ਪ੍ਰਵਾਹਿਤ ਬਿਜਲਈ ਧਾਰਾ I = \(\frac{V}{R}\)
= \(\frac{220}{24}\)
= 9.17A
ਦੂਜੀ ਅਵਸਥਾ ਵਿੱਚ – ਜਦੋਂ ਦੋਨਾਂ ਕੁੰਡਲੀਆਂ ਨੂੰ ਲੜੀਬੱਧ ਲਗਾਇਆ ਜਾਂਦਾ ਹੈ, ਤਾਂ
ਕੁੱਲ ਤਿਰੋਧ R = R1 + R2
= 24 + 24 = 48Ω
ਲੜੀਬੱਧ ਵਿੱਚ ਜੁੜੀਆਂ ਹੋਈਆਂ ਕੁੰਡਲੀਆਂ ਵਿੱਚੋਂ ਪ੍ਰਵਾਹਿਤ ਧਾਰਾ I = \(\frac{V}{R}\)
= \(\frac{220}{48}\)
= 4.58A
ਤੀਸਰੀ ਅਵਸਥਾ ਵਿੱਚ – ਜਦੋਂ ਕੁੰਡਲੀਆਂ ਨੂੰ ਸਮਾਨਾਂਤਰ ਜੋੜਿਆ ਜਾਂਦਾ ਹੈ, ਤਾਂ

I = 18.3A
ਪ੍ਰਸ਼ਨ 14.
ਹੇਠ ਲਿਖੇ ਸਰਕਟਾਂ ਵਿੱਚ ਹਰ ਇੱਕ ਵਿੱਚ 2Ω ਪ੍ਰਤਿਰੋਧਕ ਦੁਆਰਾ ਖਪਤ ਸ਼ਕਤੀਆਂ ਦੀ ਤੁਲਨਾ ਕਰੋ-
(i) 6V ਦੀ ਬੈਟਰੀ ਨਾਲ ਲੜੀ ਵਿੱਚ ਜੋੜੇ ਗਏ 1Ω ਅਤੇ 2Ω ਦੇ ਤਿਰੋਧਕ
(ii) 4V ਦੀ ਬੈਟਰੀ ਨਾਲ ਸਮਾਨਾਂਤਰ ਜੋੜੇ ਗਏ 12Ω ਅਤੇ 2Ω ਦੇ ਪ੍ਰਤਿਰੋਧਕ ॥
ਹੱਲ :
(i) ਦਿੱਤਾ ਹੈ, V = 6V
1Ω ਅਤੇ 2Ω ਦੇ ਲੜੀ ਸੰਯੋਜਨ ਦਾ ਪ੍ਰਤਿਰੋਧ R = 1Ω + 2Ω
= 3Ω
ਬਿਜਲਈ ਸਰਕਟ ਵਿੱਚੋਂ ਗੁਜ਼ਰ ਰਹੀ ਬਿਜਲਈ ਧਾਰਾ I = \(\frac{V}{R}\)
= \(\frac{6}{3}\)
∴ I = 2A
ਲੜੀ ਵਿੱਚ ਜੋੜੇ ਗਏ ਹਰੇਕ ਪ੍ਰਤਿਰੋਧ ਵਿੱਚੋਂ 2A ਦੀ ਧਾਰਾ ਪ੍ਰਵਾਹਿਤ ਹੋਵੇਗੀ।
∴ 2Ω ਦੇ ਪ੍ਰਤਿਰੋਧਕ ਦੁਆਰਾ ਖ਼ਪਤ ਸ਼ਕਤੀ P1 = I2R
= (2)2 × 2
= 4 × 2
∴ P1 = 8 ਵਾਟ (W)
(ii) ∵ ਦੋਨੋਂ ਪ੍ਰਤਿਰੋਧ ਸਮਾਨਾਂਤਰ ਕੂਮ ਵਿੱਚ ਜੁੜੇ ਹੋਏ ਹਨ। ਇਸ ਲਈ ਹਰੇਕ ਪ੍ਰਤਿਰੋਧ ਦੇ ਸਿਰਿਆਂ ਵਿਚਾਲੇ ਇੱਕ ਸਮਾਨ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ 4V ਹੋਵੇਗਾ ।
∴ 2Ω ਦੇ ਪ੍ਰਤਿਰੋਧ ਦੁਆਰਾ ਖ਼ਪਤ ਹੋਈ ਸ਼ਕਤੀ p2 = \(\frac{\mathrm{V}^{2}}{\mathrm{R}}\)
= \(\frac{(4)^{2}}{2}\)
= \(\frac{16}{2}\)
P2= 8 ਵਾਟ (W)
ਇਸ ਲਈ ਦੋਨਾਂ ਅਵਸਥਾਵਾਂ ਵਿੱਚ 2Ω ਪ੍ਰਤਿਰੋਧਕ ਵਿੱਚ ਇੱਕ ਸਮਾਨ ਸ਼ਕਤੀ ਖ਼ਰਚ ਹੋਵੇਗੀ ।
ਪ੍ਰਸ਼ਨ 15.
ਦੋ ਬਿਜਲਈ ਲੈਂਪ ਜਿਨ੍ਹਾਂ ਵਿੱਚੋਂ ਇੱਕ ਤੇ 100w; 220V ਅੰਕਿਤ ਹੈ ਅਤੇ ਦੂਜੇ ਤੇ 60W, 220V ਹੈ, ਬਿਜਲਈ ਮੁੱਖ ਲਾਇਨ ਨਾਲ ਸਮਾਨਾਂਤਰ ਵਿੱਚ ਜੋੜੇ ਗਏ ਹਨ। ਜੇਕਰ ਬਿਜਲੀ ਦੀ ਪੂਰਤੀ ਦੀ ਵੋਲਟਤਾ 220 V ਹੈ ਤਾਂ ਬਿਜਲੀ ਦੀ ਮੁੱਖ ਲਾਇਨ ਤੋਂ ਕਿੰਨੀ ਧਾਰਾ ਲਈ ਜਾਂਦੀ ਹੈ ?
ਹੱਲ :
ਪਹਿਲੇ ਬਿਜਲਈ ਲੈਂਪ ਲਈ, ਟੈਂਸ਼ਲ ਅੰਤਰ V1 = 220 V,
ਲੈਂਪ ਦੀ ਸ਼ਕਤੀ P1 = 100W
ਮੰਨ ਲਓ ਇਸ ਦਾ ਪ੍ਰਤਿਰੋਧ R1 ਹੈ, ਤਾਂ P = \(\frac{\mathrm{V}^{2}}{\mathrm{R}}\) ਤੋਂ
ਪਹਿਲੇ ਲੈਂਪ ਦਾ ਪ੍ਰਤਿਰੋਧ R1 = \(\frac{V_{1}^{2}}{P_{1}}\)
= \(\frac{(220)^{2}}{100}\)
= \(\frac{220 \times 220}{100}\)
∴ R1 = 484Ω
ਦੂਜੇ ਲੈਂਪ ਲਈ, ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ V2 = 220V,
ਲੈਂਪ ਦੀ ਸ਼ਕਤੀ P2 = 60W
ਦੂਜੇ ਲੈਂਪ ਦਾ ਪ੍ਰਤਿਰੋਧ R2 = \(\frac{\mathrm{V}_{2}^{2}}{\mathrm{p}_{2}}\)
= \(\frac{(220)^{2}}{60}\)
= \(\frac{220 \times 220}{60}\)
∴ R1 = \(\frac{2420}{3}\)Ω
ਦੋਨਾਂ ਲੈਂਪਾਂ ਨੂੰ ਸਮਾਨਾਂਤਰ ਜੋੜਨ ਨਾਲ ਸੰਯੋਜਨ ਦਾ ਪ੍ਰਤਿਰੋਧ R ਹੋਵੇ, ਤਾਂ

∵ ਲਾਇਨ ਵੋਲਟਤਾ V = 220V
∴ ਲਾਇਨ ਤੋਂ ਲਈ ਜਾਣ ਵਾਲੀ ਬਿਜਲਈ ਧਾਰਾ I = \(\frac{\mathrm{V}}{\mathrm{R}}\)
= \(\frac{220}{302.5}\)
∴ I = 0.73A
ਪ੍ਰਸ਼ਨ 16.
ਕਿਸ ਵਿੱਚ ਵਧੇਰੇ ਬਿਜਲਈ ਊਰਜਾ ਵਰਤੀ ਜਾਂਦੀ ਹੈ :
250W ਦਾ ਟੀ. ਵੀ. ਸੈਂਟ (TV) ਜੋ ਇੱਕ ਘੰਟੇ ਤੱਕ ਚਲਾਇਆ ਜਾਂਦਾ ਹੈ ਜਾਂ 1200W ਦਾ ਬਿਜਲਈ ਟੋਸਟਰ ਜੋ 10 ਮਿੰਟ ਲਈ ਚਲਾਇਆ ਜਾਂਦਾ ਹੈ ?
ਹੱਲ :
ਟੀ.ਵੀ. ਸੈਂਟ (TV) ਲਈ P1 = 250W
= 250 JS-1
t1 = 1h
= 60 × 60s
ਟੀ.ਵੀ. ਸੈਂਟ ਦੁਆਰਾ ਵਰਤੀ ਗਈ ਊਰਜਾ = P1 × t1
= 250 × (60 × 60)
= 900000 J
= 9 × 105 J ਟੋਸਟਰ ਲਈ, …………… (i)
P2 = 1200W
= 1200 JS-1
t2 = 10 ਮਿੰਟ
= 10 × 60s
ਟੋਸਟਰ ਦੁਆਰਾ ਵਰਤੀ ਗਈ ਊਰਜਾ = P2 × t2
= 1200 × (10 × 60)
= 720000 J
= 7.2 × 105J ………..(ii)
ਸਮੀਕਰਨ (i) ਅਤੇ (ii) ਤੋਂ ਸਪੱਸ਼ਟ ਹੈ ਕਿ T.V. ਸੈਂਟ ਦੁਆਰਾ ਖ਼ਪਤ ਹੋਈ ਊਰਜਾ ਵੱਧ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 17.
8Ω ਪ੍ਰਤਿਰੋਧ ਦਾ ਇੱਕ ਬਿਜਲਈ ਹੀਟਰ ਬਿਜਲਈ ਮੁੱਖ ਲਾਇਨ ਤੋਂ 2 ਘੰਟੇ ਤੱਕ 15A ਬਿਜਲਈ ਧਾਰਾ ਲੈਂਦਾ ਹੈ। ਹੀਟਰ ਵਿੱਚ ਉਤਪੰਨ ਤਾਪ ਦੀ ਦਰ ਦੀ ਗਣਨਾ ਕਰੋ।
ਹੱਲ :
ਦਿੱਤਾ ਹੈ, . R = 8 Ω
I = 15A
ਬਿਜਲਈ ਹੀਟਰ ਵਿਚ ਤਾਪ ਉਤਪੰਨ ਹੋਣ ਦੀ ਦਰ ਅਰਥਾਤ ਬਿਜਲਈ ਹੀਟਰ ਦੀ ਸ਼ਕਤੀ
P = I2R
= (15)2 × 8
= 225 × 8
= 1800 W
ਪ੍ਰਸ਼ਨ 18.
ਹੇਠ ਲਿਖਿਆਂ ਦੀ ਵਿਆਖਿਆ ਕਰੋ :
(a) ਬਿਜਲੀ-ਲੈਂਪਾਂ ਦੇ ਫਿਲਾਮੈਂਟ ਦੇ ਨਿਰਮਾਣ ਵਿੱਚ ਇੱਕ ਮਾਤਰ ਟੰਗਸਟਨ ਦਾ ਹੀ ਉਪਯੋਗ ਕਿਉਂ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ?
(b) ਬਿਜਲਈ ਤਾਪਨ ਯੰਤਰਾਂ ਜਿਵੇਂ ਕਿ ਬੈਂਡ ਟੋਸਟਰ ਅਤੇ ਬਿਜਲਈ ਪ੍ਰੈੱਸ ਦੇ ਚਾਲਕ ਸ਼ੁੱਧ ਧਾਤੁਆਂ ਦੇ ਸਥਾਨ ਤੇ ਮਿਸ਼ਰਤ ਧਾਤਾਂ ਦੇ ਕਿਉਂ ਬਣਾਏ ਜਾਂਦੇ ਹਨ ?
(c) ਘਰੇਲੂ ਬਿਜਲਈ ਸਰਕਟਾਂ ਵਿੱਚ ਲੜੀ ਸੰਯੋਜਨ ਦਾ ਉਪਯੋਗ ਕਿਉਂ ਨਹੀਂ ਕੀਤਾ ਜਾਂਦਾ ?
(d) ਇੱਕ ਤਾਰ ਦਾ ਪ੍ਰਤਿਰੋਧ ਉਸਦੀ ਪਰਿਖੇਤਰ ਕਾਟ ਦੇ ਖੇਤਰਫਲ ਵਿੱਚ ਪਰਿਵਰਤਨ ਨਾਲ ਕਿਸ ਪ੍ਰਕਾਰ ਬਦਲਦਾ ਹੈ ?
(e) ਬਿਜਲੀ ਸੰਚਾਰਣ ਦੇ ਲਈ ਕਾਪਰ ਅਤੇ ਐਲੂਮੀਨੀਅਮ ਦੀਆਂ ਤਾਰਾਂ ਦਾ ਉਪਯੋਗ ਕਿਉਂ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
(a) ਕਿਉਂਕਿ ਟੰਗਸਟਨ ਦੀ ਉੱਚ ਪ੍ਰਤਿਰੋਧਕਤਾ (5.2 × 10-8 ਓਹਮ-ਮੀਟਰ) ਹੈ ਅਤੇ ਟੰਗਸਟਨ ਦਾ ਪਿਘਲਾਓ ਦਰਜਾ ਵੀ ਹੋਰਨਾਂ ਧਾਤਾਂ ਦੀ ਤੁਲਨਾ ਵਿੱਚ ਬਹੁਤ ਉੱਚਾ (3400°C) ਹੈ, ਇਸ ਲਈ ਬਿਜਲਈ ਲੈਪਾਂ ਦੇ ਫਿਲਾਮੈਂਟ ਦੇ ਨਿਰਮਾਣ ਲਈ ਆਮ ਤੌਰ ਤੇ ਸਿਰਫ ਟੰਗਸਟਨ ਧਾਤੂ ਦਾ ਉਪਯੋਗ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।
(b) ਮਿਸ਼ਰਤ ਧਾਤਾਂ ਦੀ ਪ੍ਰਤਿਰੋਧਕਤਾ ਸ਼ੁੱਧ ਧਾਤੂਆਂ ਦੀ ਤੁਲਨਾ ਵਿੱਚ ਜ਼ਿਆਦਾ ਹੈ ਅਤੇ ਤਪ ਵੱਧਣ ਨਾਲ ਇਸ ਦੀ ਤਿਰੋਧਕਤਾ ਵਿੱਚ ਨਾਂ ਦੇ ਬਰਾਬਰ ਪਰਿਵਰਤਨ ਹੁੰਦਾ ਹੈ। ਇਸ ਤੋਂ ਛੁਟ ਮਿਸ਼ਰਤ ਧਾਤਾਂ ਦਾ ਆਕਸੀਕਰਨ ਵੀ ਬਹੁਤ ਘੱਟ ਹੁੰਦਾ ਹੈ ਜਿਸਦੇ ਪਰਿਣਾਮਸਰੂਪ ਮਿਸ਼ਰਤ ਧਾਤਾਂ ਤੋਂ ਬਣੇ ਚਾਲਕਾਂ ਦੀ ਉਮਰ ਸ਼ੁੱਧ ਧਾਤ ਚਾਲਕਾਂ ਦੀ ਉਮਰ ਦੀ ਤੁਲਨਾ ਤੋਂ ਵੱਧ ਹੁੰਦੀ ਹੈ। ਇਸੇ ਲਈ ਬੈਂਡ ਟੋਸਟਰ ਅਤੇ ਬਿਜਲਈ ਪੈਂਸਾਂ ਦੇ ਫ਼ਿਲਾਮੈਂਟ ਮਿਸ਼ਰਤ ਧਾਤਾਂ ਦੇ ਬਣਾਏ ਜਾਂਦੇ ਹਨ ।
(c) ਲੜੀਕਮ ਸੰਯੋਜਨ ਵਿੱਚ ਜਿਵੇਂ-ਜਿਵੇਂ ਹੋਰ ਪ੍ਰਤਿਰੋਧਕ ਜੁੜਦੇ ਹਨ, ਸਰਕਟ ਦਾ ਕੁੱਲ ਪ੍ਰਤਿਰੋਧ ਵੱਧਦਾ ਜਾਂਦਾ ਹੈ ਅਤੇ ਵੱਖ-ਵੱਖ ਪਤਿਰੋਧਕਾਂ ਦੇ ਸਿਰਿਆਂ ਵਿਚਕਾਰ ਪ੍ਰਾਪਤ ਪੁਟੈਂਸ਼ਲ ਘੱਟਦਾ ਜਾਂਦਾ ਹੈ। ਇਸ ਲਈ ਸਰਕਟ ਵਿਚ ਧਾਰਾ ਦੀ ਮਾਤਰਾ ਵੀ ਘੱਟ ਜਾਂਦੀ ਹੈ। ਜੇਕਰ ਘਰਾਂ ਨੂੰ ਪ੍ਰਕਾਸ਼ਿਤ ਕਰਨ ਲਈ ਲੜੀਮ ਵਿੱਚ ਵਿਵਸਥਾ ਕਰੀਏ ਤਾਂ ਸਰਕਟ ਵਿੱਚ ਜਿੰਨੇ ਜ਼ਿਆਦਾ ਲੈਂਪ ਸੰਯੋਜਿਤ ਹੋਣਗੇ, ਓਨਾ ਹੀ ਉਨ੍ਹਾਂ ਦਾ ਪ੍ਰਕਾਸ਼ ਘੱਟ ਜਾਵੇਗਾ। ਇਸ ਤੋਂ ਇਲਾਵਾ ਲੜੀਮ ਵਿਵਸਥਾ ਦੀ ਵਰਤੋਂ ਕਰਨ ਨਾਲ ਸਵਿੱਚ ਆਂਨ ਕਰਨ ਤੇ ਸਾਰੇ ਬਲਬ ਇੱਕੋ ਸਮੇਂ ਚਮਕਣਗੇ ਅਤੇ ਸਵਿੱਚ ਆਫ’ ਕਰਨ ਤੇ ਵੀ ਸਾਰੇ ਬਲਬ ਇਕੱਠੇ ਬੁਝ ਜਾਣਗੇ ਜਦੋਂ ਕਿ ਸਮਾਨੰਤਰ ਕੂਮ ਵਿਵਸਥਾ ਕਰਨ ਤੇ ਸੁਤੰਤਰਤਾ ਪੂਰਵਕ ਕਿਸੇ ਵੀ ਬਲਬ ਨੂੰ ਜਗਾਇਆ ਜਾਂ ਬੁਝਾਇਆ ਜਾ ਸਕਦਾ ਹੈ ।
(d) ਤਾਰ ਦਾ ਤਿਰੋਧ ਉਸਦੀ ਪਰਿਖੇਤਰ ਕਾਟ ਦੇ ਖੇਤਰਫਲ ਦੇ ਉਲਟ ਹੁੰਦਾ ਹੈ (R ∝ \(\frac{1}{\mathrm{~A}}\)) ਅਰਥਾਤ ਮੋਟੀ ਤਾਰ ਦਾ ਪਰਿਖੇਤਰ ਕਾਟ ਦਾ ਖੇਤਰਫਲ ਵੱਧ ਹੋਵੇਗਾ ਅਤੇ ਉਸਦਾ ਪ੍ਰਤਿਰੋਧ ਘੱਟ ਹੋਵੇਗਾ ।
(e) ਬਿਜਲੀ ਦੇ ਸਭ ਤੋਂ ਵਧੀਆ ਚਾਲਕਾਂ ਵਿੱਚ ਪਹਿਲੀ ਥਾਂ ਤੇ ਚਾਂਦੀ, ਦੁਸਰੀ ਥਾਂ ਤੇ ਤਾਂਬਾ ਅਤੇ ਤੀਸਰੀ ਥਾਂ ਤੇ ਐਲੂਮੀਨੀਅਮ ਹੈ। ਚਾਂਦੀ ਇੱਕ ਕੀਮਤੀ ਧਾਤ ਹੈ, ਪਰੰਤੂ ਤੁਲਨਾ ਵਿੱਚ ਬਹੁਤ ਘੱਟ ਮਾਤਰਾ ਵਿੱਚ ਉਪਲੱਬਧ ਹੈ। ਇਸ ਲਈ ਬਿਜਲੀ ਚਾਲਨ ਵਿਵਸਥਾ ਵਿੱਚ ਚਾਂਦੀ ਦੀ ਜਗ੍ਹਾ ਤੇ ਸਸਤੀ ਅਤੇ ਕਾਫ਼ੀ ਮਾਤਰਾ ਵਿੱਚ ਮਿਲਣ ਵਾਲੀਆਂ ਧਾਤਾਂ ਤਾਂਬਾ ਅਤੇ ਐਲੂਮੀਨੀਅਮ ਪ੍ਰਯੋਗ ਕੀਤੀਆਂ ਜਾਂਦੀਆਂ ਹਨ ।
Science Guide for Class 10 PSEB ਬਿਜਲੀ InText Questions and Answers
ਅਧਿਆਇ ਦੇ ਅੰਦਰ ਦਿੱਤੇ ਗਏ ਪ੍ਰਸ਼ਨ ਅਤੇ ਉਨ੍ਹਾਂ ਦੇ ਉੱਤਰ
ਪ੍ਰਸ਼ਨ 1.
ਬਿਜਲਈ ਸਰਕਟ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ?
ਉੱਤਰ-
ਬਿਜਲਈ ਸਰਕਟ – ਬਿਜਲੀ ਸਰੋਤ ਤੋਂ ਵੱਖ-ਵੱਖ ਘਟਕਾਂ ਤੋਂ ਹੋ ਕੇ ਬਿਜਲਈ ਧਾਰਾ ਦੇ ਲਗਾਤਾਰ ਅਤੇ ਬੰਦ ਪੱਥ ਨੂੰ ਬਿਜਲਈ ਸਰਕਟ ਕਹਿੰਦੇ ਹਨ ।
ਬਿਜਲਈ ਧਾਰਾ ਦੇ ਘਟਕ – ਬਿਜਲਈ ਧਾਰਾ ਦੇ ਹੇਠ ਲਿਖੇ ਮੁੱਖ ਘਟਕ ਹਨ-
- ਬਿਜਲੀ ਸਰੋਤ (ਬੈਟਰੀ ਜਾਂ ਸੈੱਲ)
- ਚਾਲਕ ਤਾਰ
- ਸਵਿੱਚ (ਕੁੰਜੀ)
- ਕੋਈ ਹੋਰ ਉਪਕਰਨ ਜਿਹੜਾ ਬਿਜਲਈ ਸਰਕਟ ਵਿੱਚ ਜੋੜਿਆ ਗਿਆ ਹੋਵੇ ।
ਪ੍ਰਸ਼ਨ 2.
ਬਿਜਲਈ ਧਾਰਾ ਦੀ ਇਕਾਈ ਦੀ ਪਰਿਭਾਸ਼ਾ ਦਿਓ ।
ਜਾਂ
ਬਿਜਲੀ ਧਾਰਾ ਦੀ ਇਕਾਈ ਦਾ ਨਾਂ ਅਤੇ ਪਰਿਭਾਸ਼ਾ ਦਿਓ ।
ਉੱਤਰ-
ਬਿਜਲਈ ਧਾਰਾ ਦਾ S.I ਮਾਤ੍ਰਿਕ ਐਮਪੀਅਰ ਹੈ ਜਿਸਨੂੰ ‘A’ ਨਾਲ ਪ੍ਰਗਟਾਇਆ ਜਾਂਦਾ ਹੈ ।
ਐਮਪੀਅਰ-ਜਦੋਂ ਕਿਸੇ ਚਾਲਕ ਵਿੱਚੋਂ 1 ਸੈਕਿੰਡ ਵਿੱਚ 1 ਭੂਲਾਂਮ ਚਾਰਜ ਪ੍ਰਵਾਹਿਤ ਹੁੰਦਾ ਹੈ ਤਾਂ ਪ੍ਰਯੋਗ ਕੀਤੀ ਗਈ ਬਿਜਲਈ ਧਾਰਾ ਦੀ ਮਾਤਰਾ ਨੂੰ 1 ਐਮਪੀਅਰ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।
∴ 1A= \(\frac{1 \mathrm{C}}{1 s}\)
![]()
ਪ੍ਰਸ਼ਨ 3.
ਇੱਕ ਕੂਲਾਂਮ ਚਾਰਜ ਦੀ ਰਚਨਾ ਕਰਨ ਵਾਲੇ ਇਲੈੱਕਟ੍ਰਾਨਾਂ ਦੀ ਸੰਖਿਆ ਦੀ ਗਣਨਾ ਕਰੋ ।
ਹੱਲ :
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ, 1 ਇਲੈਂਕਨ ਚਾਰਜ = 1.6 × 10-19C
ਮੰਨ ਲਓ 1 ਕੂਮ ਰਚਨਾ ਕਰਨ ਵਾਲੇ ਇਲੈਕਟ੍ਰਾਨਾਂ ਦੀ ਸੰਖਿਆ = n
∴ n × 1.6 × 10-19C = 1C
ਜਾਂ n = \(\frac{1}{1.6 \times 10^{-19}}\)
= \(\frac{1 \times 10^{19}}{1.6}\)
= \(\frac{10}{16}\) × 1019
= 0.625 × 1019
= 6.25 × 1018
ਇਸ ਲਈ 1 ਕੂਲਾਂਮ ਚਾਰਜ (C) = 6.25 × 1018 ਇਲੈੱਕਟੂਨ ਉੱਤਰ
ਪ੍ਰਸ਼ਨ 4.
ਉਸ ਯੁਕਤੀ ਦਾ ਨਾਂ ਲਿਖੋ ਜੋ ਕਿਸੇ ਚਾਲਕ ਦੇ ਸਿਰਿਆਂ ਉੱਤੇ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ ਬਣਾਏ ਰੱਖਣ ਵਿੱਚ ਸਹਾਇਤਾ ਕਰਦੀ ਹੈ।
ਉੱਤਰ-
ਸੈੱਲ ਇੱਕ ਅਜਿਹੀ ਯੁਕਤੀ (ਜੁਗਤ) ਹੈ ਜੋ ਕਿਸੇ ਚਾਲਕ ਦੇ ਸਿਰਿਆਂ ਉੱਤੇ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ ਬਣਾਏ ਰੱਖਣ ਵਿੱਚ ਸਹਾਇਤਾ ਕਰਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 5.
ਇਹ ਕਹਿਣ ਦਾ ਕੀ ਭਾਵ ਹੈ ਕਿ ਦੋ ਬਿੰਦੁਆਂ ਵਿਚਕਾਰ ਟੈਂਸ਼ਲ ਅੰਤਰ 1v ਹੈ ?
ਉੱਤਰ-
ਦੋ ਬਿੰਦੂਆਂ ਵਿਚਕਾਰ ਟੈਂਸ਼ਲ ਅੰਤਰ 1 ਵੋਲਟ (V) ਤੋਂ ਭਾਵ ਹੈ ਕਿ ਦੋ ਬਿੰਦੂਆਂ ਵਿਚਕਾਰ 1 ਕੂਲਾਮ ਚਾਰਜ ਲਿਜਾਣ ਵਿੱਚ 1 ਜੂਲ ਕਾਰਜ ਹੁੰਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 6.
6 v ਵੋਲਟ ਬੈਟਰੀ ਵਿੱਚੋਂ ਲੰਘਣ ਵਾਲੇ ਹਰ ਇੱਕ ਕੂਲਾਂਮ ਚਾਰਜ ਨੂੰ ਕਿੰਨੀ ਊਰਜਾ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ ?
ਹੱਲ :
ਇੱਥੇ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ (V) = 6 ਵੋਲਟ
ਚਾਰਜ ਦੀ ਮਾਤਰਾ (Q) = 1 ਕੂਲਾਂਮ
ਦਿੱਤੀ ਗਈ ਊਰਜਾ (ਕੀਤਾ ਗਿਆ ਕਾਰਜ) (W) = ?

ਅਰਥਾਤ V = \(\frac{\mathrm{W}}{\mathrm{Q}}\)
:: ਦਿੱਤੀ ਗਈ ਊਰਜਾ W = V × Q
= 6 ਵੋਲਟ × 1 ਕੂਲਾਂਮ
= 6 ਜੂਲ (J)
ਪ੍ਰਸ਼ਨ 7.
ਕਿਸੇ ਚਾਲਕ ਦਾ ਤਿਰੋਧ ਕਿਹੜੇ ਕਾਰਕਾਂ ਉੱਤੇ ਨਿਰਭਰ ਕਰਦਾ ਹੈ ?
ਉੱਤਰ-
ਚਾਲਕ ਦੇ ਪ੍ਰਤਿਰੋਧ ਦੀ ਨਿਰਭਰਤਾ – ਕਿਸੇ ਚਾਲਕ ਦਾ ਤਿਰੋਧ ਹੇਠ ਲਿਖੇ ਕਾਰਕਾਂ ਤੇ ਨਿਰਭਰ ਕਰਦਾ ਹੈ-
(i) ਚਾਲਕ ਦੀ ਲੰਬਾਈ (l)-ਕਿਸੇ ਚਾਲਕ ਦਾ ਪ੍ਰਤਿਰੋਧ ਚਾਲਕ ਦੀ ਲੰਬਾਈ (l) ਦੇ ਸਿੱਧਾ ਅਨੁਪਾਤੀ ਹੁੰਦਾ ਹੈ ।
ਅਰਥਾਤ R ∝ l ………(1)
(ii) ਚਾਲਕ ਦੀ ਪਰਿਖੇਤਰ ਕਾਟ ਦਾ ਖੇਤਰਫਲ (A)-ਕਿਸੇ ਚਾਲਕ ਦਾ ਤਿਰੋਧ ਉਸਦੀ ਪਰਿਖੇਤਰ ਕਾਟ (A) ਦੇ ਖੇਤਰਫਲ ਦਾ ਉਲਟ ਅਨੁਪਾਤੀ ਹੁੰਦਾ ਹੈ ।
ਅਰਥਾਤ R ∝ \(\frac{1}{\mathrm{~A}}\) ………(2)
(iii) ਚਾਲਕ ਦੇ ਪਦਾਰਥ ਦੀ ਪ੍ਰਕਿਰਤੀ-ਕਿਸੇ ਚਾਲਕ ਦਾ ਪ੍ਰਤਿਰੋਧ ਉਸ ਚਾਲਕ ਦੇ ਪਦਾਰਥ ਦੀ ਪ੍ਰਕਿਰਤੀ ਤੇ ਨਿਰਭਰ ਕਰਦਾ ਹੈ ।
ਇਨ੍ਹਾਂ ਸਾਰੇ ਕਾਰਕਾਂ ਨੂੰ ਜੋੜਨ (ਸੰਯੋਜਿਤ) ਨਾਲ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
R ∝ \(\frac{l}{\mathrm{~A}}\)
ਜਾਂ R = ρ × \(\frac{l}{\mathrm{~A}}\) ਜਿੱਥੇ ਏ ਅਨੁਪਾਤੀ ਸਥਿਰ ਅੰਕ ਹੈ ।
ਪ੍ਰਸ਼ਨ 8.
ਸਮਾਨ ਪਦਾਰਥ ਦੀਆਂ ਦੋ ਤਾਰਾਂ ਵਿੱਚ ਜੇਕਰ ਇੱਕ ਪਤਲੀ ਅਤੇ ਦੂਜੀ ਮੋਟੀ ਹੋਵੇ ਤਾਂ ਇਨ੍ਹਾਂ ਵਿੱਚੋਂ ਕਿਸ ਵਿੱਚ ਬਿਜਲੀ ਦੀ ਧਾਰਾ ਆਸਾਨੀ ਨਾਲ ਪ੍ਰਵਾਹਿਤ ਹੋਵੇਗੀ, ਜਦੋਂ ਇਨ੍ਹਾਂ ਨੂੰ ਸਮਾਨ ਬਿਜਲਈ ਸਰੋਤ ਨਾਲ ਜੋੜਿਆ ਜਾਂਦਾ ਹੈ ਕਿਉਂ ?
ਉੱਤਰ-
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ ਕਿ ਚਾਲਕ ਤਾਰ ਦਾ ਪ੍ਰਤਿਰੋਧ ਉਸ ਤਾਰ ਦੀ ਪਰਿਖੇਤਰ ਕਾਟ (Area of cross-section) ਦੇ ਉਲਟ ਅਨੁਪਾਤੀ ਹੁੰਦਾ ਹੈ ਅਰਥਾਤ ਮੋਟੀ ਤਾਰ ਦਾ ਪ੍ਰਤਿਰੋਧ ਘੱਟ ਅਤੇ ਪਤਲੀ ਤਾਰ ਦਾ ਪ੍ਰਤਿਰੋਧ ਵੱਧ ਹੋਵੇਗਾ।
ਹੁਣ R ∝ \(\frac{1}{l}\)
ਇਸ ਲਈ ਮੋਟੀ ਤਾਰ ਦਾ ਪ੍ਰਤਿਰੋਧ ਪਤਲੀ ਤਾਰ ਦੀ ਤੁਲਨਾ ਵਿੱਚ ਘੱਟ ਹੋਣ ਦੇ ਕਾਰਨ ਉਸ ਵਿੱਚੋਂ ਬਿਜਲਈ ਧਾਰਾ ਦਾ ਬਹਾਓ ਅਧਿਕ ਅਤੇ ਸੌਖ ਨਾਲ ਹੁੰਦਾ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 9.
ਮੰਨ ਲਓ ਕਿਸੇ ਬਿਜਲਈ ਪਦਾਰਥ ਦੇ ਘਟਕ ਦੇ ਦੋ ਸਿਰਿਆਂ ਵਿੱਚ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ ਨੂੰ ਉਸ ਦੇ ਪਹਿਲੇ ਟੈਂਸ਼ਲ ਅੰਤਰ ਦੀ ਤੁਲਨਾ ਵਿੱਚ ਘਟਾ ਕੇ ਅੱਧਾ ਕਰ ਦੇਣ ਤੇ ਵੀ ਉਸ ਦਾ ਪ੍ਰਤਿਰੋਧ ਨਿਸਚਿਤ ਰਹਿੰਦਾ ਹੈ। ਤਾਂ ਉਸ ਪਦਾਰਥ ਵਿੱਚ ਪ੍ਰਵਾਹਿਤ ਹੋਣ ਵਾਲੀ ਬਿਜਲਈ ਧਾਰਾ ਵਿੱਚ ਕੀ ਪਰਿਵਰਤਨ ਹੋਵੇਗਾ ?
ਉੱਤਰ-
ਮੰਨ ਲਓ ਪਹਿਲੀ ਅਵਸਥਾ ਵਿੱਚ ਬਿਜਲਈ ਪਦਾਰਥ ਦੇ ਦੋ ਸਿਰਿਆਂ ਵਿੱਚ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ V, ਤਿਰੋਧ R ਅਤੇ Q ਗੁਜ਼ਰ ਰਹੀ ਬਿਜਲਈ ਧਾਰਾ I ਹੈ, ਤਾਂ
ਓਮ ਦੇ ਨਿਯਮ ਅਨੁਸਾਰ I = \(\frac{\mathrm{V}}{\mathrm{R}}\) ………..(1)
ਜੇਕਰ ਬਿਜਲਈ ਪਦਾਰਥ ਦੇ ਦੋਨਾਂ ਸਿਰਿਆਂ ਵਿਚਾਲੇ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ ਪਹਿਲੀ ਅਵਸਥਾ ਤੋਂ ਅੱਧਾ ਕਰ ਦੇਈਏ (ਅਰਥਾਤ \(\frac{\mathrm{V}}{2}\) ਕਰੀਏ) ਜਦੋਂ ਕਿ ਤਿਰੋਧ ਨੀਯਤ (ਸਥਿਰ ਰਹੇ ਤਾਂ ਬਿਜਲਈ ਧਾਰਾ ਦੀ ਮਾਤਰਾ ਪਰਿਵਰਤਿਤ ਹੋ ਕੇ I’ ਹੋ ਜਾਵੇਗੀ ।

ਅਰਥਾਤ ਬਿਜਲਈ ਧਾਰਾ ਪਹਿਲੀ ਅਵਸਥਾ ਤੋਂ ਅੱਧੀ ਰਹਿ ਜਾਵੇਗੀ ।
ਪ੍ਰਸ਼ਨ 10.
ਬਿਜਲਈ ਟੋਸਟਰਾਂ ਅਤੇ ਬਿਜਲਈ ਪ੍ਰੈੱਸਾਂ ਦੇ ਤਾਪਨ ਫਿਲਾਮੈਂਟ ਬੁੱਧ ਧਾਤ ਦੇ ਨਾ ਬਣਾ ਕੇ ਮਿਸ਼ਰਤ ਧਾਤ ਦੇ ਕਿਉਂ ਬਣਾਏ ਜਾਂਦੇ ਹਨ ?
ਉੱਤਰ-
ਬਿਜਲਈ ਟੋਸਟਰਾਂ ਅਤੇ ਬਿਜਲਈ ਪ੍ਰੈੱਸਾਂ ਦੇ ਤਾਪਨ ਫਿਲਾਮੈਂਟ ਸ਼ੁੱਧ ਧਾਤ ਦੇ ਨਾ ਬਣਾ ਕੇ ਕਿਸੇ ਮਿਸ਼ਰਤ ਧਾਤ ਦੇ ਬਣਾਏ ਜਾਂਦੇ ਹਨ। ਇਸਦੇ ਹੇਠ ਲਿਖੇ ਕਾਰਨ ਹਨ-
- ਮਿਸ਼ਰਤ ਧਾਤ ਦੀ ਪ੍ਰਤਿਰੋਧਕਤਾ ਸ਼ੁੱਧ ਧਾਤ ਦੀ ਤੁਲਨਾ ਵਿੱਚ ਅਧਿਕ ਹੁੰਦੀ ਹੈ ।
- ਮਿਸ਼ਰਤ ਧਾਤ ਦਾ ਉੱਚ ਤਾਪ ਤੇ ਦਹਿਨ (ਆਕਸੀਕਨ) ਨਹੀਂ ਹੁੰਦਾ ਹੈ ।
- ਮਿਸ਼ਰਤ ਧਾਤ ਦਾ ਪਿਘਲਾਓ ਦਰਜਾ ਉੱਚਾ ਹੁੰਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 11.
ਹੇਠ ਲਿਖੇ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਉੱਤਰ ਸਾਰਨੀ 12:2 ਵਿੱਚ ਦਿੱਤੇ ਅੰਕੜਿਆਂ ਦੇ ਆਧਾਰ ਤੇ ਦਿਓ :
(a) ਆਇਰਨ (Fe) ਅਤੇ ਮਰਕਰੀ (Hg) ਵਿੱਚੋਂ ਕਿਹੜਾ ਚੰਗਾ ਚਾਲਕ ਹੈ ?
(b) ਕਿਹੜਾ ਪਦਾਰਥ ਸਭ ਤੋਂ ਵਧੀਆ ਚਾਲਕ ਹੈ ?
ਉੱਤਰ-
(a) ਆਇਰਨ (Fe), ਮਰਕਰੀ (Hg) ਦੀ ਤੁਲਨਾ ਵਿੱਚ ਚੰਗਾ ਚਾਲਕ ਹੈ, ਕਿਉਂਕਿ ਆਇਰਨ ਦੀ ਪ੍ਰਤਿਰੋਧਕਤਾ ਮਰਕਰੀ ਦੇ ਮੁਕਾਬਲੇ ਵਿੱਚ ਘੱਟ ਹੈ।
(b) ਚਾਂਦੀ (ਸਿਲਵਰ) ਸਭ ਤੋਂ ਵਧੀਆ ਚਾਲਕ ਹੈ ਕਿਉਂਕਿ ਇਸ ਦੀ ਪ੍ਰਤਿਰੋਧਕਤਾ (16.0 × 10-8Ω m) ਸਭ ਤੋਂ ਘੱਟ ਹੈ ।
ਪ੍ਰਸ਼ਨ 12.
ਕਿਸੇ ਬਿਜਲਈ ਸਰਕਟ ਦਾ ਯੋਜਨਾਬੱਧ ਚਿੱਤਰ ਖਿੱਚੋ ਜਿਸ ਵਿੱਚ 2 – 2v ਦੇ ਤਿੰਨ ਸੈੱਲਾਂ ਦੀ ਬੈਟਰੀ, ਇੱਕ 5Ω ਪ੍ਰਤਿਰੋਧਕ, ਇੱਕ 8Ω ਪ੍ਰਤਿਰੋਧਕ, ਇੱਕ 12Ω ਪ੍ਰਤਿਰੋਧਕ ਅਤੇ ਇੱਕ ਪਲੱਗ ਕੁੰਜੀ ਸਾਰੇ ਲੜੀ ਵਿੱਚ ਸੰਯੋਜਿਤ ਹੋਣ ।
ਹੱਲ :
ਬਿਜਲਈ ਸਰਕਟ ਦਾ ਯੋਜਨਾਬੱਧ ਚਿੱਤਰ-
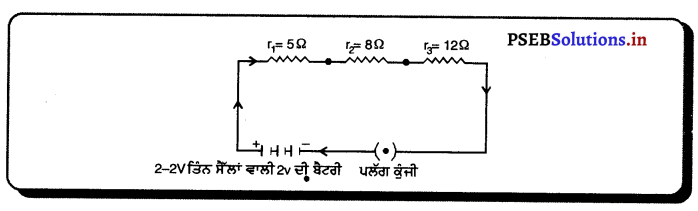
ਪ੍ਰਸ਼ਨ 13.
ਪ੍ਰਸ਼ਨ 1 ਦਾ ਸਰਕਟ ਦੁਬਾਰਾ ਖਿੱਚੋ ਅਤੇ ਇਸ ਵਿੱਚ ਪ੍ਰਤਿਰੋਧਕਾਂ ਤੋਂ ਪ੍ਰਵਾਹਿਤ ਬਿਜਲਈ ਧਾਰਾ ਨੂੰ ਮਾਪਣ ਲਈ ਐਮਮੀਟਰ ਅਤੇ 12Ω ਦੇ ਪ੍ਰਤਿਰੋਧਕ ਦੇ ਸਿਰਿਆਂ ਵਿੱਚ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ ਮਾਪਣ ਲਈ ਵੋਲਟਮੀਟਰ ਲਗਾਓ। ਐਮਮੀਟਰ ਅਤੇ ਵੋਲਟਮੀਟਰ ਦੇ ਕੀ ਮਾਨ ਹੋਣਗੇ ?
ਹੱਲ :
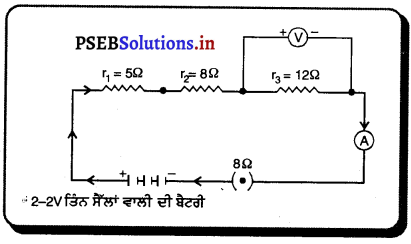
r1 = 5Ω
r2 = 8Ω
r3 = 12Ω
ਸਰਕਟ ਦਾ ਕੁੱਲ ਪ੍ਰਤਿਰੋਧ (R) = ?
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ ਪ੍ਰਤਿਰੋਧਕਾਂ ਨੂੰ ਲੜੀ ਵਿੱਚ ਸੰਯੋਜਿਤ ਕਰਨ ਨਾਲ ਸਰਕਟ ਦਾ ਕੁੱਲ ਤਿਰੋਧ
R = r1 + r2 + r3
R = 5Ω + 8Ω + 12Ω
∴ R = 25Ω
ਬੈਟਰੀ ਦੇ ਟਰਮੀਨਲਾਂ ਦੇ ਵਿਚਕਾਰ ਕੁੱਲ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ V = 6V
ਹੁਣ ਓਹਮ ਦੇ ਨਿਯਮ ਅਨੁਸਾਰ I = \(\frac{V}{R}\)
I = \(\frac{6 V}{25 \Omega}\)
∴ I = 0.24 ਐਮਪੀਅਰ (A)
12Ω ਦੇ ਪ੍ਰਤਿਰੋਧਕ ਦੇ ਸਿਰਿਆਂ ਵਿਚਕਾਰ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ = I × r3
= 0.24 × 12
= 2.88 ਵੋਲਟ (V)
ਇਸ ਲਈ ਐਮਮੀਟਰ ਅਤੇ ਵੋਲਟਮੀਟਰ ਦੀ ਪੜ੍ਹਤ ਦਾ ਮਾਨ ਕ੍ਰਮਵਾਰ 0.24A ਅਤੇ 2.88v ਹੋਵੇਗਾ ।
![]()
ਪ੍ਰਸ਼ਨ 14.
ਜਦੋਂ
(a) 1Ω ਅਤੇ 106Ω
(b) 1Ω, 103Ω ਅਤੇ 106Ω ਦੇ ਪ੍ਰਤਿਰੋਧਾਂ ਨੂੰ ਸਮਾਨਾਂਤਰ ਵਿੱਚ ਜੋੜਿਆ ਜਾਂਦਾ ਹੈ ਤਾਂ ਇਨ੍ਹਾਂ ਦੇ ਕੁੱਲ ਤਿਰੋਧ ਦੇ ਸੰਬੰਧ ਵਿੱਚ ਤੁਸੀਂ ਕੀ ਨਿਰਣਾ ਕਰੋਗੇ ?
ਹੱਲ :
ਦਿੱਤਾ ਹੈ, r1 = 1Ω
ਅਤੇ r2 = 106Ω
ਮੰਨ ਲਓ ਇਨ੍ਹਾਂ ਦਾ ਤੁੱਲ-ਤਿਰੋਧ R ਹੈ ਜਦੋਂ ਇਨ੍ਹਾਂ ਤਿਰੋਧਾਂ ਨੂੰ ਸਮਾਨਾਂਤਰ ਬੱਧ ਵਿਵਸਥਾ ਵਿੱਚ ਸੰਯੋਜਿਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ, ਤਾਂ

∴ R = 0.9Ω (ਲਗਪਗ)
(b) ਇੱਥੇ,
r1 = 1Ω
r2 = 103Ω
r3 = 106Ω
ਮੰਨ ਲਓ ਇਨ੍ਹਾਂ ਦਾ ਤੁੱਲ-ਪ੍ਰਤਿਰੋਧ R ਹੈ ਜਦੋਂ ਇਨ੍ਹਾਂ ਤਿਰੋਧਾਂ ਨੂੰ ਸਮਾਨਾਂਤਰ ਬੱਧ ਜੋੜਿਆ ਜਾਂਦਾ ਹੈ, ਤਾਂ

∴ R = 0.9Ω (ਲਗਪਗ)
ਪ੍ਰਸ਼ਨ 15.
100Ω ਦਾ ਇੱਕ ਬਿਜਲਈ ਬੱਲਬ, 50Ω ਦਾ ਇੱਕ ਬਿਜਲਈ ਟੋਸਟਰ, 500Ω ਦਾ ਇੱਕ ਪਾਣੀ ਫਿਲਟਰ 220v ਦੇ ਬਿਜਲਈ ਸਰੋਤ ਨਾਲ ਸਮਾਨਾਂਤਰ ਕੂਮ ਵਿੱਚ ਜੋੜੇ ਗਏ ਹਨ । ਉਸ ਬਿਜਲਈ ਪੈਂਸ ਦਾ ਪਤਿਰੋਧ ਕੀ ਹੈ, ਜਿਸ ਨੂੰ ਜੇਕਰ ਸਮਾਨ ਸਰੋਤ ਦੇ ਨਾਲ ਜੋੜ ਦੇਈਏ ਉਹ ਓਨੀ ਹੀ ਬਿਜਲਈ ਧਾਰਾ ਲੈਂਦੀ ਹੈ ਜਿੰਨੀ ਤਿੰਨੋਂ ਯੰਤਰ ਲੈਂਦੇ ਹਨ। ਇਹ ਵੀ ਗਿਆਤ ਕਰੋ ਕਿ ਇਸ ਬਿਜਲਈ ਪੈਂਸ ਤੋਂ ਕਿੰਨੀ ਬਿਜਲਈ ਧਾਰਾ ਪ੍ਰਵਾਹਿਤ ਹੁੰਦੀ ਹੈ ?
ਹੱਲ :
100Ω ਦਾ ਬਿਜਲਈ ਬੱਲਬ, 50Ω ਦਾ ਬਿਜਲਈ ਟੋਸਟਰ ਅਤੇ 500Ω ਦਾ ਪਾਣੀ ਫ਼ਿਲਟਰ ਸਮਾਨਾਂਤਰ ਕੁਮ ਵਿੱਚ ਜੋੜਿਆ ਗਿਆ ਹੈ ਅਤੇ R ਉਨ੍ਹਾਂ ਦਾ ਤੱਲ-ਤਿਰੋਧ ਹੈ, ਤਾਂ
ਓਹਮ ਦੇ ਨਿਯਮ ਅਨੁਸਾਰ, \(\frac{1}{R}\) = \(\frac{1}{100}+\frac{1}{50}+\frac{1}{500}\)
= \(\frac{5+10+1}{500}\)
= \(\frac{16}{500}\)
R = \(\frac{500}{16}\)
= 31.25Ω
ਇਸ ਲਈ ਬਿਜਲਈ ਐੱਸ ਦਾ ਡੁੱਲ-ਪ੍ਰਤਿਰੋਧ, (R) = 31.25Ω
ਟੈਂਸ਼ਲ ਅੰਤਰ (V) = 220V
ਬਿਜਲਈ ਧਾਰਾ ਦੀ ਮਾਤਰਾ (I) = ?
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ, I = \(\frac{V}{R}\)
= \(\frac{200}{\frac{500}{16}}\)
= \(\frac{220 \times 16}{500}\)
= \(\frac{352}{50}\)
∴ I = 7.04 A
ਪ੍ਰਸ਼ਨ 16.
ਲੜੀ ਵਿੱਚ ਜੋੜਨ ਦੀ ਥਾਂ, ਬਿਜਲਈ ਯੰਤਰਾਂ ਨੂੰ ਸਮਾਨਾਂਤਰ ਵਿੱਚ ਜੋੜਨ ਤੇ ਕੀ ਲਾਭ ਹਨ ?
ਉੱਤਰ-
ਬਿਜਲਈ ਯੁਕਤੀਆਂ ਨੂੰ ਲੜੀ ਕੁਮ ਦੀ ਤੁਲਨਾ ਵਿੱਚ ਸਮਾਨਾਂਤਰ ਕੂਮ ਵਿੱਚ ਜੋੜਨ ਦੇ ਲਾਭ
(1) ਕਿਸੇ ਲੜੀਕੂਮ ਵਿੱਚ ਜੋੜੇ ਗਏ ਬਿਜਲਈ ਸਰਕਟ ਵਿੱਚ ਸ਼ੁਰੂ ਤੋਂ ਅੰਤ ਤਕ ਬਿਜਲਈ ਧਾਰਾ ਸਥਿਰ ਨੀਯਤ) ਰਹਿੰਦੀ ਹੈ ਜਿਹੜਾ ਕਿ ਵਿਵਹਾਰਿਕ ਨਹੀਂ ਹੈ। ਜੇਕਰ ਅਸੀਂ ਕਿਸੇ ਬਿਜਲਈ ਸਰਕਟ ਵਿੱਚ ਬਿਜਲਈ ਬੱਲਬ ਅਤੇ ਬਿਜਲਈ ਹੀਟਰ ਨੂੰ ਲੜੀਕਮ ਵਿੱਚ ਜੋੜਾਂਗੇ ਤਾਂ ਇਹ ਸਹੀ ਢੰਗ ਨਾਲ ਕਾਰਜ ਨਹੀਂ ਕਰ ਸਕਣਗੇ। ਕਿਉਂਕਿ ਇਨ੍ਹਾਂ ਨੂੰ ਵੱਖ-ਵੱਖ ਮਾਨ ਦੀ ਬਿਜਲਈ ਧਾਰਾ ਵੱਖ-ਵੱਖ ਬਿਜਲਈ ਧਾਰਾ ਦੀ ਲੋੜ ਪੈਂਦੀ ਹੈ। ਇਸ ਤੋਂ ਉਲਟ ਸਮਾਨਾਂਤਰ ਕੂਮ ਵਿਵਸਥਿਤ ਸਰਕਟ ਵਿੱਚ ਬਿਜਲਈ ਧਾਰਾ ਵਿਭਿੰਨ ਜੁਗਤਾਂ ਵਿੱਚ ਵੰਡੀ ਜਾਂਦੀ ਹੈ ।
(2) ਲੜੀਬੱਧ ਸੰਯੋਜਨ ਬਿਜਲਈ ਸਰਕਟ ਵਿੱਚ ਜੇਕਰ ਇੱਕ ਬਿਜਲੀ ਦੀ ਜੁਗਤਾਂ ਕਾਰਜ ਕਰਨਾ ਬੰਦ ਕਰ ਦਿੰਦੀ ਹੈ ਤਾਂ ਬਿਜਲਈ ਪੱਥ ਟੁੱਟ ਜਾਂਦਾ ਹੈ ਤਾਂ ਹੋਰ ਜੁਗਤਾਂ ਕੰਮ ਕਰਨਾ ਬੰਦ ਕਰ ਦਿੰਦੀਆਂ ਹਨ। ਇਸ ਤੋਂ ਵਿਪਰੀਤ ਸਮਾਨਾਂਤਰ ਕੂਮ ਵਾਲੇ ਸਰਕਟ ਵਿੱਚ ਬਿਜਲਈ ਧਾਰਾ ਵਿਭਿੰਨ ਬਿਜਲਈ ਜੁਗਤਾਂ ਵਿਚ ਵਿਭਾਜਿਤ ਹੋਣ ਤੇ ਵੀ ਹੋਰ ਬਿਜਲਈ ਜੁਗਤਾਂ ਕੰਮ ਕਰਦੀਆਂ ਰਹਿੰਦੀਆਂ ਹਨ ।
(3) ਪ੍ਰਤਿਰੋਧਕਾਂ ਨੂੰ ਸਮਾਨਾਂਤਰ ਵਿੱਚ ਜੋੜਨ ਨਾਲ ਕਿਸੇ ਵੀ ਚਾਲਕ ਵਿੱਚ ਸਵਿੱਚ ਦੀ ਸਹਾਇਤਾ ਨਾਲ ਬਿਜਲਈ ਧਾਰਾ ਸੁਤੰਤਰਤਾ ਪੁਰਵਕ ਪ੍ਰਵਾਹਿਤ ਹੋਣ ਦਿੱਤੀ ਜਾਂ ਰੋਕੀ ਜਾ ਸਕਦੀ ਹੈ ਜਿਸ ਕਰਕੇ ਬਿਜਲਈ ਜੁਗਤਾਂ ਨੂੰ ਸੁਤੰਤਰਤਾ ਪੂਰਵਕ ਕੰਮ ਵਿੱਚ ਲਿਆਇਆ ਜਾ ਸਕਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 17.
2Ω, 3Ω ਅਤੇ 6Ω ਦੇ ਤਿੰਨ ਪ੍ਰਤਿਰੋਧਕਾਂ ਨੂੰ ਕਿਸ ਪ੍ਰਕਾਰ ਜੋੜਿਆ ਜਾਵੇ ਕਿ ਕੁੱਲ ਤਿਰੋਧ :
(a) 4Ω
(b) 1Ω ਹੋਵੇ ।
ਹੱਲ :
(a) ਕੁੱਲ ਪ੍ਰਤਿਰੋਧ 4Ω ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ- ਅਜਿਹਾ ਕਰਨ ਲਈ 3Ω ਅਤੇ 6Ω ਦੇ ਪ੍ਰਤਿਰੋਧਕਾਂ ਨੂੰ ਸਮਾਨਾਂਤਰ ਜੋੜ ਕੇ 2Ω ਦੇ ਪ੍ਰਤਿਰੋਧਕ ਨਾਲ ਲੜੀਬੱਧ ਵਿੱਚ ਜੋੜਿਆ ਜਾਂਦਾ ਹੈ ।
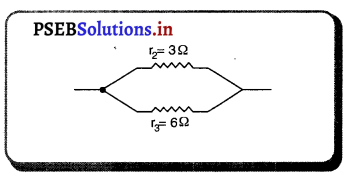
ਮੰਨ ਲਓ r2 = 3Ω ਅਤੇ r3 = 6Ω ਨੂੰ ਸਮਾਨਾਂਤਰ ਵਿੱਚ ਜੋੜਨ ਤੇ ਕੁੱਲ ਤਿਰੋਧ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ, ਤਾਂ
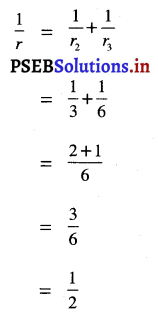
∴ r = 2Ω
ਹੁਣ = r1 = 2Ω ਅਤੇ r2 ਅਤੇ r3 ਦਾ ਕੁੱਲ ਪ੍ਰਤਿਰੋਧ r = 2Ω ਨੂੰ ਲੜੀਬੱਧ ਜੋੜਨ ਨਾਲ ਕੁੱਲ ਪ੍ਰਤਿਰੋਧ R ਹੈ, ਤਾਂ
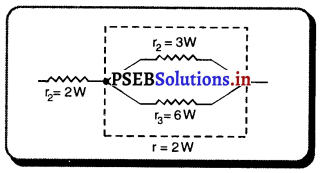
R = r1 + r
= 2Ω + 2Ω
∴ R = 4Ω
(b) ਕੁੱਲ ਤਿਰੋਧ 1Ω ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ ਸੰਯੋਜਨ-1Ω ਦਾ ਕੁੱਲ ਪ੍ਰਤਿਰੋਧ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ r1 = 2Ω, r2 = 3Ω ਅਤੇ r3 = 6Ω ਨੂੰ ਸਮਾਨਾਂਤਰ ਵਿੱਚ ਜੋੜਨਾ ਹੋਵੇਗਾ ।
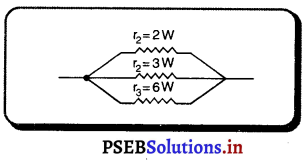
ਮੰਨ ਲਓ ਕੁੱਲ ਤਿਰੋਧ R ਹੈ, ਤਾਂ ਸਮਾਨਾਂਤਰ ਸੰਯੋਜਨ ਦੇ ਸੂਤਰ ਤੋਂ
\(\frac{1}{R}\) = \(\frac{1}{r_{1}}+\frac{1}{r_{2}}+\frac{1}{r_{3}}\)
= \(\frac{1}{2}+\frac{1}{3}+\frac{1}{6}\)
= \(\frac{3+2+1}{6}\)
= \(\frac{6}{6}\)
= 1
∴ R = 1Ω
![]()
ਪ੍ਰਸ਼ਨ 18.
4Ω, 8Ω, 12Ω ਅਤੇ 24Ω ਪ੍ਰਤਿਰੋਧ ਦੀਆਂ ਚਾਰ ਕੁੰਡਲੀਆਂ ਨੂੰ ਜੋੜਨ ਤੇ (a) ਅਧਿਕਤਮ (b) ਨਿਊਨਤਮ ਪ੍ਰਤਿਰੋਧ ਕਿੰਨਾ ਪ੍ਰਾਪਤ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ?
ਹੱਲ :
(a) ਅਧਿਕਤਮ ਪ੍ਰਤਿਰੋਧ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ ਸੰਯੋਜਨ – ਜੇਕਰ ਇਨ੍ਹਾਂ ਚਹੁੰ ਤਿਰੋਧਕਾਂ ਨੂੰ ਲੜੀਬੱਧ ਜੋੜਿਆ ਜਾਵੇ ਤਾਂ ਅਧਿਕਤਮ ਕੁੱਲ ਪ੍ਰਤਿਰੋਧ ਪ੍ਰਾਪਤ ਹੋਵੇਗਾ ।
RS = r1 + r2 + r3 + r4
= 4Ω + 8Ω + 12Ω + 24Ω
= 48Ω
(b) ਨਿਊਨਤਮ ਪ੍ਰਤਿਰੋਧ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ ਸੰਯੋਜਨ ਵਿਵਸਥਾ – ਜੇਕਰ ਦਿੱਤੇ ਗਏ ਚਹੁੰ ਪ੍ਰਤਿਰੋਧਕਾਂ ਨੂੰ ਸਮਾਨਾਂਤਰ ਵਿਚ ਜੋੜਿਆ ਜਾਵੇ ਤਾਂ ਨਿਊਨਤਮ ਕੁੱਲ ਪ੍ਰਤਿਰੋਧ ਪ੍ਰਾਪਤ ਹੋਵੇਗਾ ।

∴ Rp = 2Ω
ਪ੍ਰਸ਼ਨ 19.
ਬਿਜਲੀ ਲੰਘਾਉਣ ਨਾਲ ਕਿਸੇ ਬਿਜਲਈ ਹੀਟਰ ਦੀ ਡੋਰੀ ਕਿਉਂ ਨਹੀਂ ਚਮਕਦੀ ਜਦੋਂ ਕਿ ਉਸ ਦੀ ਕੁੰਡਲੀ ਚਮਕਦੀ ਹੈ ?
ਉੱਤਰ-
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ, H = I2Rt
⇒ H = R
ਤਾਪਨ ਕੁੰਡਲੀ ਦਾ ਉੱਚ ਪ੍ਰਤਿਰੋਧ ਹੁੰਦਾ ਹੈ ਜਿਸ ਕਾਰਨ ਅਧਿਕ ਬਿਜਲਈ ਊਰਜਾ, ਤਾਪ ਊਰਜਾ ਵਿੱਚ ਪਰਿਵਰਤਿਤ ਹੋ ਜਾਂਦੀ ਹੈ ਜਿਸ ਕਾਰਨ ਤਾਪਨ ਕੁੰਡਲੀ ਚਮਕਣ ਲੱਗ ਪੈਂਦੀ ਹੈ। ਦੂਜੇ ਪਾਸੇ ਬਿਜਲਈ ਹੀਟਰ ਦੀ ਡੋਰੀ ਦਾ ਤਿਰੋਧ ਬਹੁਤ ਘੱਟ ਹੁੰਦਾ ਹੈ ਜਿਸ ਕਰਕੇ ਉਹ ਨਹੀਂ ਚਮਕਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 20.
ਇੱਕ ਘੰਟੇ ਵਿੱਚ 50v. ਦੇ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ ਤੇ 96000 ਕੂਲਾਂਮ ਚਾਰਜ ਭੇਜਣ ਨਾਲ ਉਤਪੰਨ ਹੁੰਦੇ ਤਾਪ ਦੀ ਗਣਨਾ ਕਰੋ ।
ਹੱਲ :
ਦਿੱਤਾ ਹੈ, Q = 96000 ਕੂਲਾਮ
t = 1 ਘੰਟਾ
= 60 × 60 ਸੈਕਿੰਡ
V = 50 ਵੋਲਟ
H = Q × V
= 96000 × 50
= 4.825 × 106 ਜੂਲ
= 4.825 × 103 ਕਿਲੋ-ਜੂਲ ਉੱਤਰ
ਪ੍ਰਸ਼ਨ 21.
20Ω ਤਿਰੋਧ ਦੀ ਕੋਈ ਬਿਜਲਈ ਐੱਸ 5A ਬਿਜਲਈ ਧਾਰਾ ਲੈਂਦੀ ਹੈ।30s ਵਿੱਚ ਉਤਪੰਨ ਤਾਪ ਦੀ ਗਣਨਾ ਕਰੋ ।
ਹੱਲ :
ਦਿੱਤਾ ਹੈ, ਤਿਰੋਧ (R) = 20Ω
ਬਿਜਲਈ ਧਾਰਾ (I) = 5A
ਸਮਾਂ (t) = 30s
ਉਤਪੰਨ ਹੋਈ ਊਰਜਾ (H) = ?
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ, ਉਤਪੰਨ ਹੋਈ ਤਾਪ ਊਰਜਾ (H) = I2Rt
= (5)2 × 20 × 30
= 25 × 20 × 30 J
= 15000 J (ਜੂਲ)
= 1.5 × 104
ਪ੍ਰਸ਼ਨ 22.
ਬਿਜਲਈ ਧਾਰਾ ਦੁਆਰਾ ਦਿੱਤੀ ਊਰਜਾ ਦੀ ਦਰ ਦਾ ਨਿਰਧਾਰਨ ਕਿਵੇਂ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਬਿਜਲਈ ਧਾਰਾ ਦੁਆਰਾ ਦਿੱਤੀ ਊਰਜਾ ਦੀ ਦਰ ਦਾ ਨਿਰਧਾਰਨ ਬਿਜਲਈ ਸਮਰੱਥਾ (ਸ਼ਕਤੀ ਦੁਆਰਾ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 23.
ਇੱਕ ਬਿਜਲਈ ਮੋਟਰ 220v ਦੇ ਬਿਜਲਈ ਸਰੋਤ ਤੋਂ 5.0 A ਬਿਜਲਈ ਧਾਰਾ ਲੈਂਦੀ ਹੈ। ਮੋਟਰ ਦੀ ਸ਼ਕਤੀ ਨਿਰਧਾਰਿਤ ਕਰੋ ਅਤੇ 2 ਘੰਟੇ ਵਿੱਚ ਮੋਟਰ ਦੁਆਰਾ ਖ਼ਪਤ ਊਰਜਾ ਦੀ ਗਣਨਾ ਕਰੋ ।
ਹੱਲ :
ਦਿੱਤਾ ਹੈ, ਬਿਜਲਈ ਧਾਰਾ (I) = 5.0 A
ਬਿਜਲਈ ਪੁਟੈਂਸ਼ਲ ਅੰਤਰ (V) = 220 V
ਸਮਾਂ (t) = 2 ਘੰਟੇ
= 2 × 60 × 60 ਸੈਕਿੰਡ
ਮੋਟਰ ਦੀ ਸ਼ਕਤੀ (P) = V × I
ਖ਼ਪਤ ਹੋਈ ਊਰਜਾ (E) = ?
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ, ਸ਼ਕਤੀ (P) = V × I
= 220 × 5
= 1100 W (ਵਾਟ) ਉੱਤਰ
2 ਘੰਟੇ ਵਿੱਚ ਖ਼ਪਤ ਹੋਈ ਊਰਜਾ (E) = P × t
= 1100 ਵਾਟ × 2 ਘੰਟੇ
= 2200 ਵਾਟ ਘੰਟੇ (Wh)
= 2.2 ਕਿਲੋਵਾਟ ਘੰਟਾ (Kwh)
