PSEB 11th Class Maths Solutions Chapter 8 Binomial Theorem Miscellaneous Exercise

Punjab State Board PSEB 11th Class Maths Book Solutions Chapter 8 Binomial Theorem Miscellaneous Exercise Questions and Answers.

PSEB Solutions for Class 11 Maths Chapter 8 Binomial Theorem Miscellaneous Exercise

Question 1.
Find a, b and n in the expansion of (a + b)ⁿ if the first three terms of the expansion are 729, 7290 and 30375, respectively.
Answer.
It is known that (r + 1)th term, (T_{r + 1}), in the binomial expansion of (a + b)ⁿ is given by T_{r + 1} = \({ }^{n} C_{r}\) a^{n – r r= a}
The first three terms of the expansion are given as 729, 7290, and 30375 respectively.
Therefore, we obtain
T₁ = \({ }^{2} C_{0} a^{n-0} b^{0}\)
= aⁿ = 729 ……………..(i)

T₂ = \({ }^{n} C_{1} a^{n-1} b^{1}\)
= n a^{n – 1} b = 7290 …………….(ii)

T₃ = \({ }^{n} C_{2} a^{n-2} b^{2}\)
= \(\frac{n(n-1)}{2} a^{n-2} b^{2}\) = 30375 ……………….(iii)

Dividing eq. (ii) by eq. (i), we obtain \(\frac{n a^{n-1} b}{a^{n}}=\frac{7290}{729}\)
⇒ \(\frac{n b}{a}\) = 10 ……………….(iv)

Dividing eq. (iii) by eq. (ii), we obtain

Question 2.
Find a if the coefficient of x² and x³ in the expansion of (3 + ax)⁹ are equal.
Answer.
It is known that (r + 1)th term, (T_{r + 1}), in the binomial expansion of (a + b)ⁿ is given by T_{r + 1} = \({ }^{n} C_{r} a^{n-r} b^{r}\)

Assuming that x² occurs in the (r + 1)th term in the expansion of (3 + ax)⁹, we obtain
T_{r + 1} = \({ }^{9} C_{r}(3)^{9-r}(a x)^{r}\)
= \({ }^{9} C_{r}(3){ }^{9-r} a^{r} x^{r}\)

Comparing the indices of x in x² and in T_{r + 1} we obtain r = 2
Thus, the coefficient of x² is
\({ }^{9} C_{2}(3)^{9-2} a^{2}=\frac{9 !}{2 ! 7 !}(3)^{7} a^{2}=36(3)^{7} a^{2}\)

Assuming that x³ occurs in the (k + 1)th term in the expansion of (3 + ax)⁹, we obtain
T_{k + 1} = \({ }^{9} C_{k}(3)^{9-k}(a x)^{k}={ }^{9} C_{k}(3)^{9-k} a^{k} x^{k}\)

Comparing the indices of x in x³ in T_{r + 1}, we obtain k = 3
Thus, the coefficient of x³ is
\({ }^{9} C_{3}(3)^{9-3} a^{3}=\frac{9 !}{3 ! 6 !}(3)^{6} a^{3}=84(3)^{6} a^{3}\)

It is given that the coefficients of x² and x³ are same.
84 (3)⁶ a³ = 36 (3)⁷ a²
⇒ 84a = 36 × 3
⇒ a = \(\frac{36 \times 3}{84}=\frac{108}{84}\)
⇒ a = \(\frac{9}{7}\)

Thus, the required value of a is \(\frac{9}{7}\).

Question 3.
Find the coefficient of x5 in the product (1 + 2x)⁶(1 – x)⁷ using binomial theorem.
Answer.
Using Binomial Theorem, the expressions, (1 + 2x)⁶ and (1 – x)⁷, can be expanded as

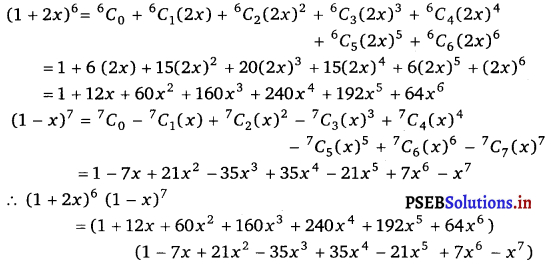
The complete multiplication of the two brackets is not required to be carried out.
Only those terms, which involve x⁵, are required.
The terms containing x⁵ are
1 (- 21x⁵) + (12x) (35x⁴) + (60x²) (- 35x³) + (160x³) (21x²) + (240x⁴) (- 7x) + (192 x⁵)(1)
= 171 x⁵
Thus, the coefficient of x⁵ in the given product.
= – 21 + 420 – 2100 + 3360 -1 680 +192 = 171.

Question 4.
If a and b are distinct integers, prove that a – b is a factor of aⁿ – bⁿ, whenever n is a positive integer.
[Hint : write aⁿ = (a – b + b)ⁿ and expand]
Answer.
In order to prove that (a – b) is a factor of (aⁿ – bⁿ), it has to be proved that
aⁿ – bⁿ = k(a – b), where k is some natural number
It can be written that, a = a – b + b
∴ aⁿ = (a – b + b)ⁿ = [(a – b) + b]ⁿ
= \({ }^{n} C_{0}(a-b)^{n}+{ }^{n} C_{1}(a-b){ }^{n-1} b+\ldots+{ }^{n} C_{n-1}(a-b) b^{n-1}+{ }^{n} C_{n} b^{n}\)

= \((a-b)^{n}+{ }^{n} C_{1}(a-b)^{n-1} b+\ldots+{ }^{n} C_{n-1}(a-b) b^{n-1}+b^{n}\)

\(a^{n}-b^{n}=(a-b)\left[(a-b)^{n-1}+{ }^{n} C_{1}(a-b)^{n-2} b+\ldots+{ }^{n} C_{n-1} b^{n-1}\right]\)

aⁿ – bⁿ = k (a -b)

where k = \(\left[(a-b)^{n-1}+{ }^{n} C_{1}(a-b)^{n-2} b+\ldots+{ }^{n} C_{n-1} b^{n-1}\right]\) is a natural number
This shows that (a – b) is a factor of (aⁿ – bⁿ), where n is a positive integer.

Question 5.
Evaluate (√3 + √2)⁶ – (√3 – √2)⁶.
Answer.
Firstly, the expression (a + b)⁶ – (a – b)⁶ is simplified by using Binomial Theorem.
This can be done as
(a + b)⁶ = \({ }^{6} C_{0}\) a⁶ + \({ }^{6} C_{1}\) a⁵ b + \({ }^{6} C_{2}\) a⁴ b² + \({ }^{6} C_{3}\) a³b³ + \({ }^{6} C_{4}\) a²b⁴ + \({ }^{6} C_{5}\) ab⁵ + \({ }^{6} C_{6}\) b⁶

= a⁶ + 6 a⁵b + 15 a⁴b² + 20 a³b³ + 15 a²b⁴ + 6 ab⁵ + b⁶ (a – b)⁶

= \({ }^{6} C_{0}\) a⁶ – \({ }^{6} C_{1}\) a⁵b + \({ }^{6} C_{2}\) a⁴b² – \({ }^{6} C_{3}\) a³b³ + \({ }^{6} C_{4}\) a²b⁴ – \({ }^{6} C_{5}\) a¹b⁵ + \({ }^{6} C_{6}\) b⁶

= a⁶ – 6 a⁵b + 15 a⁴b² – 20 a³b³ + 15 a²b⁴ – 6ab⁵ + b⁶

.-. (a + b)⁶ – (a – b)⁶ = 2[6a⁵b + 20a³b³ + 6ab⁵]

Putting a = √3 and b = √2, we obtain (√3 + √2)⁶ – (√3 – √2)⁶
= 2[6(√3)⁵ (√2) + 20 (√3)³ (√2)³ + 6 (√3) (√2)⁵]
= 2[54 √6 +120 √6 + 24 √6]
= 2 × 198 √6 = 396√6.

Question 6.
Find the value of (a² + \(\sqrt{a^{2}-1}\))⁴ + (a² – \(\sqrt{a^{2}-1}\))⁴.
Answer.
Firstly, the expression (x + y)⁴ + (x – y)⁴ is simplified by using Binomial Theorem.
This can be done as
(x + y)⁴ = \({ }^{4} C_{0}\) x⁴ + \({ }^{4} C_{1}\) x³y + \({ }^{4} C_{2}\) x²y² + \({ }^{4} C_{3}\) xy³ + \({ }^{4} C_{4}\) y⁴
= x⁴ + 4x³y + 6x²y² + 4xy³ + y⁴

(x – y)⁴ = \({ }^{4} C_{0}\) x⁴ – \({ }^{4} C_{1}\) x³y + \({ }^{4} C_{2}\) x²y² – \({ }^{4} C_{3}\) xy³ + \({ }^{4} C_{4}\) y⁴
= x⁴ – 4x³y + 6x²y² – 4xy³ + y⁴

∴ (x + y)⁴ + (x – y)⁴ = 2(x⁴ + 6x²y² + y⁴).

Putting x = a² and y = \(\sqrt{a^{2}-1}\), we obtain
(a² + \(\sqrt{a^{2}-1}\))⁴ + (a² – \(\sqrt{a^{2}-1}\))⁴
= 2 [(a²)⁴ + 6(a²)² (Ja2 -l)² + \(\left(\sqrt{a^{2}-1}\right)\)⁴]
= 2 [a⁸ + 6a⁴ (a² – 1) + (a² – 1)²]
= 2 [a⁸ + 6a⁶ – 6a⁴ + a⁴ – 2a² + 1]
= 2 [a⁸ + 6a⁶ – 5a⁴ – 2a² + 1]
= 2a⁸ + 12a⁶ – 10a⁴ – 4a² + 2.

Question 7.
Find an approximation of (0.99)⁵ using the first three terms of its expansion.
Answer.
We have, (0.99)⁵ = (1 – 0.01)⁵
= 1 – \({ }^{5} C_{1}\) × (0.01) + \({ }^{5} C_{2}\) × (0.01)² – ……….
= 1 – 0.05 + 10 × 0.0001 – ………..
= 1.001 – 0.05 = 0.951.

Question 8.
Find n, if the ratio of the fifth term from the beginning to the fifth term from the end in the expression of \(\left(\sqrt[4]{2}+\frac{1}{\sqrt[4]{3}}\right)^{n}\) is √6 : 1.
Answer.

2n – 16 = 4
⇒ 2n = 20
⇒ n = \(\frac{20}{2}\)
⇒ n = 10.

Question 9.
Expand using Binomial Theorem \(\left(1+\frac{x}{2}-\frac{2}{x}\right)^{4}\), x ≠ 0.
Answer.
Using Binomial Theorem, the given expression \(\left(1+\frac{x}{2}-\frac{2}{x}\right)^{4}\) can be expanded as \(\left[\left(1+\frac{x}{2}\right)-\frac{2}{x}\right]^{4}\),

= \(1+2 x+\frac{3}{2} x^{2}+\frac{x^{3}}{2}+\frac{x^{4}}{16}-\frac{8}{x}-12-6 x\) – \(x^{2}+\frac{8}{x^{2}}+\frac{24}{x}+6-\frac{32}{x^{3}}+\frac{16}{x^{4}}\)

= \(\frac{16}{x}+\frac{8}{x^{2}}-\frac{32}{x^{3}}+\frac{16}{x^{4}}-4 x+\frac{x^{2}}{2}+\frac{x^{3}}{2}+\frac{x^{4}}{16}-5\).

Question 10.
Find the expansion of (3x² – 2ax + 3a²)³ using binomial theorem.
Answer.
Using Binomial Theorem, the given expression (3x² – 2ax + 3a²)³ can be expanded as [(3x² – 2ax) + 3a²]³

= \({ }^{3} C_{0}\) (3x² – 2ax)3 + \({ }^{3} C_{1}\) (3x² – 2ax)² (3a²) + \({ }^{3} C_{2}\) (3x² – 2ax) (3a²)² + \({ }^{3} C_{3}\) (3a²)³

= (3x² – 2ax)³ + 3 (9x⁴ – 12ax³ + 4a²x²) (3a²) + 3 (3x² – 2ax) (9a⁴) + 27a⁶

= (3x² – 2ax)³ + 81a²x⁴ – 108a³x³ + 36a⁴x² + 81a⁴x² – 54a⁵x + 27a⁶

= (3x² -2ax)³ + 81 a²x⁴ – 108a³x³ + 117a⁴x² – 54a⁵x + 27a⁶ …………….(i)

Again by using Binomial Theorem, we obtain (3x² – 2ax)³
= \({ }^{3} C_{0}\) (3x²)³ – \({ }^{3} C_{1}\) (3x²)² (2ax) + \({ }^{3} C_{2}\) (3x²) (2ax)² – \({ }^{3} C_{3}\)(2ax)³
= 27x⁶ – 3(9x⁴) (2ax) + 3(3x²) (4a²x²) – 8a³x³
= 27x⁶ – 54ax⁵ + 36a²x⁴ – 8a³x³ ………….(ii)

From eqs. (i) and (ii), we obtain (3x² – 2ax + 3a²)³
= 27x⁶ – 54ax⁵ + 36a² x⁴ – 8a³x³ + 81a²x⁴ – 108a³x³ + 117a⁴x² – 54a⁵x + 27a⁶
= 27x⁶ – 54ax⁵ + 117a²x⁴ – 116a³x³ + 117a⁴x² – 54a⁵x + 27a⁶.