PSEB 12th Class Economics Solutions Chapter 30 सह-सम्बन्ध

Punjab State Board PSEB 12th Class Economics Book Solutions Chapter 30 सह-सम्बन्ध Textbook Exercise Questions, and Answers.

PSEB Solutions for Class 12 Economics Chapter 30 सह-सम्बन्ध

PSEB 12th Class Economics सह-सम्बन्ध Textbook Questions and Answers

I. वस्तुनिष्ठ प्रश्न (Objective Type Questions)

प्रश्न 1.
सह-सम्बन्ध किसे कहते हैं ?
उत्तर-
जब दो या दो से अधिक मात्राएं सहानुभूति में परिवर्तित होती हैं जिससे एक में परिवर्तन के कारण दूसरे में भी परिवर्तन होता है तो वे सह-सम्बन्धित कहलाती हैं।

प्रश्न 2.
सह-सम्बन्ध (Correlation) तथा प्रतीपगमन (Regression) में क्या भेद हैं ?
उत्तर-
सह-सम्बन्ध से दो या दो से अधिक चरों में परस्पर सम्बन्ध की मात्रा (Degree) का ज्ञान होता है जबकि प्रतीपगमन द्वारा इस सम्बन्ध की प्रकृति (Nature) का पता चलता है।

प्रश्न 3.
दो अथवा दो से अधिक चरों अथवा समूहों में निश्चित सम्बन्ध पाया जाता है तो इसको ………. कहते हैं।
(a) अपकिरण
(b) प्रमाप विचलन
(c) सह-सम्बन्ध
(d) कोई भी नहीं।
उत्तर-
(c) सह-सम्बन्ध ।

प्रश्न 4.
जब दो चरों में एक ही दिशा में परिवर्तन होता है तो इसको …………. सह-सम्बन्ध कहते हैं।
(a) धनात्मक
(b) ऋणात्मक
(c) एक दिशाई
(d) कोई भी नहीं।
उत्तर-
(a) धनात्मक।

प्रश्न 5.
जब दो चरों में परिवर्तन विपरीत दिशा में होता है तो इसको ……….. सह-सम्बन्ध कहते हैं।
(a) धनात्मक
(b) ऋणात्मक
(c) विपरीत दिशाई
(d) कोई भी नहीं।
उत्तर-
(b) ऋणात्मक।

प्रश्न 6.
जब दो चरों में स्थाई रूप में समान अनुपात में परिवर्तन होता है तो इसको ……….. कहते हैं।
उत्तर-
समरेखीय सह-सम्बन्ध।

प्रश्न 7.
जब दो चरों में अस्थाई और असमान रूप में परिवर्तन हो तो इसको ………………… कहते हैं।
उत्तर-
वक्र रेखीय सह-सम्बन्ध।

प्रश्न 8.
सह-सम्बन्ध गुणांक विधि का निर्माण …………….. ने किया था।
(a) कार्ल पीयर्सन
(b) स्पीयर मैन
(c) बाऊले
(d) उपरोक्त में से कोई नहीं।
उत्तर-
(a) कार्ल पीयर्सन।

प्रश्न 9.
पद सह-सम्बन्ध विधि का निर्माण ……………….. ने किया था।
उत्तर-
चार्ल्स एडवर्ड स्पीयर मैन। (1904)।

प्रश्न 10.
सह-सम्बन्ध गुणांक तथा पद सह-सम्बन्ध गुणांक में कोई अन्तर नहीं।
उत्तर-
ग़लत।

प्रश्न 11.
जब दो चरों में परिवर्तन एक ही दिशा में होता है इसको धनात्मक सह-सम्बन्ध कहते हैं।
उत्तर-
सही।

प्रश्न 12.
जब दो चरों में परिवर्तन विपरीत दिशा में होता है तो इसको ऋणात्मक सह-सम्बन्ध कहते हैं।
उत्तर-
सही।

प्रश्न 13.
जब दो चरों में सम्बन्ध का अध्ययन किया जाता है तो इसको सह-सम्बन्ध कहा जाता है।
उत्तर-
सही।

प्रश्न 14.
जब तीन अथवा इससे अधिक चरों के सम्बन्ध का अध्ययन किया जाता है तो इसको बहुमुखी सहसम्बन्ध कहा जाता है।
उत्तर-
सही।

प्रश्न 15.
सह-सम्बन्ध का मूल्य + 1 से – 1 के बीच में हो सकता है।
उत्तर-
सही।

प्रश्न 16.
कार्ल पीयर्सन के सह-सम्बन्ध गुणांक का सूत्र लिखो।
उत्तर-
r= \(\frac{\Sigma x y}{\sqrt{\Sigma x^{2} \times \Sigma y^{2}}}\)

प्रश्न 17.
लघु विधि अनुसार सह-सम्बन्ध गुणांक का सूत्र लिखो।
उत्तर-
r= \(\frac{\Sigma d x^{\prime} d y^{\prime}-\frac{\Sigma d x^{\prime} \times \Sigma d y^{\prime}}{\mathrm{N}}}{\sqrt{\Sigma d x^{2}-\left(\frac{\Sigma d x}{\mathrm{~N}}\right)^{2} \sqrt{\Sigma d y^{2}-\frac{(\Sigma d y)^{2}}{\mathrm{~N}}}}}\)

प्रश्न 18.
स्पीयरमैन द्वारा दिये गए श्रेणी अन्तर के सह-सम्बन्ध का सूत्र लिखो।
उत्तर-
rk = \(1-\frac{6\left(\Sigma D^{2}\right)}{N^{3}-N}\)

प्रश्न 19.
श्रेणी सह-सम्बन्ध का प्रयोग गुणात्मक सम्बन्ध को प्रकट करने के लिए किया जाता है।
उत्तर-
सही।

प्रश्न 20.
सह-सम्बन्ध की मात्राएं पांच प्रकार की होती हैं।
उत्तर-
सही।

II. अति लघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
कार्ल पीयर्सन के सह-सम्बन्ध गुणांक से क्या अभिप्राय है ?
उत्तर-
सह-सम्बन्ध तकनीक ऐसी सांख्यिकी तकनीक है, जिसकी मदद से दिए गए चरों के सह-सम्बन्ध के आकार, स्वभाव, दिशाओं तथा महत्त्व का अध्ययन किया जाता है। सह-सम्बन्ध द्वारा इस बात की पढ़ाई की जाती है कि क्या दिए गए चरों में सह-सम्बन्ध है ? यदि सह-सम्बन्ध है तो कितनी मात्रा में है ? क्या यह सम्बन्ध धनात्मक है अथवा ऋणात्मक है। इसलिए यूले तथा कैंडल अनुसार, “सह-सम्बन्ध विश्लेषण का सम्बन्ध इस बात से होता है कि दो चरों में सम्बन्ध किस तरह का है।”

प्रश्न 2.
सह-सम्बन्ध के कोई दो गुण बताएँ।
उत्तर-
गुण अथवा महत्त्व-कार्ल पीयर्सन के सह-सम्बन्ध गुणांक के मुख्य गुण निम्नलिखित हैं –

1. दो चरों के सम्बन्ध की दिशा का पता लगता है। इस द्वारा स्पष्ट कर सकते हैं कि दो चरों में सम्बन्ध धनात्मक है अथवा ऋणात्मक है।
2. दो चरों में सह-सम्बन्ध की मात्रा का ज्ञान होता है। दो चरों में पूर्ण धनात्मक, ऊँचे दर्जे का धनात्मक कम दर्जे का धनात्मक सम्बन्ध पाया जाता है अथवा कि पूर्ण ऋणात्मक, ऊँचे दर्जे का धनात्मक, कम दर्जे का धनात्मक सम्बन्ध है अथवा कोई सम्बन्ध नहीं है। इसका ज्ञान सह-सम्बन्ध गुणांक द्वारा होता है।

प्रश्न 3.
सह-सम्बन्ध के कोई दो दोष बताएँ।
उत्तर-
दोष (Demerits)

• साधारण तौर पर रेखीय सम्बन्ध की कल्पना करके सह-सम्बन्ध का माप किया जाता है, परंतु यह भी सम्भव है कि सम्बन्ध गैर-रेखीय हों। इस स्थिति में सह-सम्बन्ध की कल्पना गलत हो जाती है।
• सीमान्त मूल्यों अर्थात् बहुत बड़ी अथवा बहुत छोटी मदों का प्रभाव सह-सम्बन्ध पर बहुत अधिक होता है।

प्रश्न 4.
स्पीयरमैन की दर्जा सह-सम्बन्ध विधि से क्या अभिप्राय है ? ।
उत्तर-
इंग्लैंड के प्रसिद्ध मनोवैज्ञानिक चार्ल्स एडवर्ड स्पीयरमैन ने 1904 में गुणात्मक तथ्यों के बीच सह-सम्बन्ध का पता करने के लिए एक विधि का निर्माण किया जिस विधि को स्पीयरमैन की दर्जा सह-सम्बन्ध गुणांक विधि कहा जाता है। इस विधि को स्पीयरमैन की दर्जा अन्तर विधि भी कहा जाता है। स्पीयरमैन के अनुसार कुछ तथ्य ऐसे होते हैं जिनका अंकों में माप नहीं किया जा सकता। उदाहरणस्वरूप सुन्दरता, भाषण मुकाबला, वीरता इत्यादि चरों को अंकों में नहीं दर्शाया जा सकता, बल्कि ऐसी स्थिति में प्राथमिकता क्रम दिए जाते हैं।

प्रश्न 5.
जब दर्जे दिए हों तो दर्जा सह-सम्बन्ध गुणांक के माप का सूत्र बताएँ।
उत्तर-
rk = \(1-\frac{6 \Sigma D^{2}}{N^{3}-N}\)

प्रश्न 6.
जब दर्जे न दिए गए हों तो दर्जा सह-सम्बन्ध गुणांक के माप सूत्र बताएँ। जब दर्जे एक-दूसरे के सामान्य हों।
उत्तर-
rk =\(1-\frac{6\left[\Sigma\mathrm{D}^{2}+\frac{1}{12}\left(m^{3}-m\right)+\frac{1}{12}\left(m^{3}-m\right) \cdots \cdots \cdots\right]}{\mathrm{N}^{3}-\mathrm{N}}\)

III. लघु उत्तरीय प्रश्न | (Short Answer Type Questions)

प्रश्न 1.
कार्ल पीयर्सन के सह-सम्बन्ध गुणांक से क्या अभिप्राय है ? इसके मुख्य लक्षण बताओ।
उत्तर-
सह-सम्बन्ध तकनीक ऐसी सांख्यिकी तकनीक है, जिसकी मदद से दिए गए चरों के सह-सम्बन्ध के आकार, स्वभाव, दिशाओं तथा महत्त्व का अध्ययन किया जाता है। सह-सम्बन्ध द्वारा इस बात की पढ़ाई की जाती है कि क्या दिए गए चरों में सह-सम्बन्ध है ? यदि सह-सम्बन्ध है तो कितनी मात्रा में है ? क्या यह सम्बन्ध धनात्मक है-
अथवा
ऋणात्मक है। इसलिए यूले तथा कैंडल अनुसार, “सह-सम्बन्ध विश्लेषण का सम्बन्ध इस बात से होता है कि दो चरों में सम्बन्ध किस तरह का है।”मुख्य लक्ष्ण (Main Features)-कार्ल पीयर्सन के सह-सम्बन्ध के मुख्य लक्ष्ण अथवा विशेषताएं इस प्रकार हैं_-

1. दिशा का ज्ञान-सह-सम्बन्ध द्वारा दो चरों की परिवर्तन की दिशा का ज्ञान प्राप्त होता है। इस प्रकार यह स्पष्ट किया जा सकता है कि दो चरों में धनात्मक अथवा ऋणात्मक सह-सम्बन्ध है।
2. मात्रा का ज्ञान-दो चरों में यदि सम्बन्ध है तो कितना है। इसकी मात्रा में परिवर्तन – 1 से + 1 के बीच हो सकता है।
3. अच्छा माप-सह-सम्बन्ध में सांख्यिकी का अच्छा माप होता है, क्योंकि यह समान्तर औसत तथा प्रमाप विचलन पर आधारित है।
4. एकरूपता-सह-सम्बन्ध का गुणांक एकरूपता की विशेषता रखता है अर्थात् RXY = RYX होता है।

प्रश्न 2.
कार्ल पीयर्सन के सह-सम्बन्ध गुणांक के गुण तथा दोष बताओ।
अथवा
सह-सम्बन्ध का महत्त्व बताओ।
उत्तर-
गुण अथवा महत्त्व-कार्ल पीयर्सन के सह-सम्बन्ध गुणांक के मुख्य गुण अग्रलिखित हैं-

1. दो चरों के सम्बन्ध की दिशा का पता लगता है। इस द्वारा स्पष्ट कर सकते हैं कि दो चरों में सम्बन्ध धनात्मक है अथवा ऋणात्मक है।
2. दो चरों में सह-सम्बन्ध की मात्रा का ज्ञान होता है। दो चरों में पूर्ण धनात्मक, ऊँचे दर्जे का धनात्मक कम दर्जे का धनात्मक सम्बन्ध पाया जाता है अथवा कि पूर्ण ऋणात्मक, ऊँचे दर्जे का धनात्मक, कम दर्जे का धनात्मक सम्बन्ध है अथवा कोई सम्बन्ध नहीं है। इसका ज्ञान सह-सम्बन्ध गुणांक द्वारा होता है।
3. सह-सम्बन्ध गुणांक एक आदर्श माप है, क्योंकि यह समान्तर औसत तथा प्रमाप विचलन पर आधारित है।
4. सह-सम्बन्ध गुणांक न केवल सैद्धान्तिक समस्याओं का, बल्कि व्यावहारिक समस्याओं का हल करने के लिए भी लाभदायक होता है।
5. सह-सम्बन्ध पर अन्य सांख्यिकी विधियां भी आधारित हैं।

दोष (Demerits) –

• साधारण तौर पर रेखीय सम्बन्ध की कल्पना करके सह सम्बन्ध का माप किया जाता है, परंतु यह भी सम्भव है कि सम्बन्ध गैर-रेखीय हों। इस स्थिति में सह-सम्बन्ध की कल्पना गलत हो जाती है।
• सीमान्त मूल्यों अर्थात् बहुत बड़ी अथवा बहुत छोटी मदों का प्रभाव सह-सम्बन्ध पर बहुत अधिक होता है।
• सह-सम्बन्ध का प्रयोग सावधानी से करने की आवश्यकता होती है नहीं तो परिणाम गलत प्राप्त हो जाते
• इस द्वारा गुणात्मक तत्त्वों ईमानदारी, सुन्दरता इत्यादि का अध्ययन नहीं किया जाता।

प्रश्न 3.
कार्ल पीयर्सन के सह-सम्बन्ध की गणना के लिए प्रत्यक्ष विधि की व्याख्या करो।
उत्तर-
प्रत्यक्ष विधि (Direct Method)-कार्ल पीयर्सन के सह-सम्बन्ध की गणना प्रत्यक्ष विधि द्वारा इस प्रकार की जाती है-

1. दो श्रेणियों X तथा Y की समान्तर औसत (\(\overline{\mathrm{X}}\) तथा \(\bar{Y}\)) का पता किया जाता है।
2. दोनों श्रेणियों के मूल्यों के समान्तर औसतों का विचलन निकाला जाता है अर्थात् X = (x –\(\overline{\mathrm{X}}\) ) तथा Y = (Y – \(\overline{\mathrm{Y}}\) ) का पता किया जाता है।
3. विचलनों X तथा Y के वर्ग बनाकर इन वर्गों का जोड़ Σx² तथा Σy² प्राप्त किया जाता है।
4. दोनों श्रेणियों के विचलनों X तथा Y को गुणा करके गुणनफल XY प्राप्त किया जाता है। इस गुणनफल के जोड़ को Σxy द्वारा प्रकट किया जाता है।
5. सह-सम्बन्ध गुणांक की गणना निम्नलिखित सूत्र द्वारा की जाती है। r = \(\frac{\Sigma x y}{\sqrt{\Sigma x^{2} \times \Sigma y^{2}}} \)

प्रश्न 4.
सह-सम्बन्ध गुणांक का अर्थशास्त्र के लिए विशेषकर क्या महत्त्व है ?
उत्तर-
अर्थशास्त्र में महत्त्व
1. नियमों की परख के लिए-अर्थशास्त्र के बहुत-से नियमों की परख सह-सम्बन्ध गुणांक से की जाती है। उदाहरणस्वरूप मांग के नियम में वस्तु की कीमत तथा वस्तु की मांग के ऋणात्मक सम्बन्ध को दिखाया जाता है। इस प्रकार पूर्ति के नियम में वस्तु की कीमत तथा इसकी पूर्ति का सीधा तथा धनात्मक सह-सम्बन्ध होता है। इस प्रकार अर्थशास्त्र के नियमों की परख सह-सम्बन्ध द्वारा की जाती है।

2. अनुसन्धान के लिए-अर्थशास्त्र के क्षेत्र में अनुसन्धान के कार्य के लिए भी सह-सम्बन्ध की सहायता प्राप्त की जाती है। अनुसन्धान द्वारा नियमों का निर्माण किया जाता है। उन नियमों की परख सह-सम्बन्ध द्वारा की जाती है।

3. नीति निर्माण के लिए-सह-सम्बन्ध विश्लेषण न केवल सैद्धान्तिक तौर पर ही महत्त्वपूर्ण होता है बल्कि यह तो व्यावहारिक तौर पर भी लाभदायक है। गरीबों को दी गई सहायता से उनकी आर्थिक स्थिति में कितना सुधार हुआ है इसका ज्ञान सह-सम्बन्ध की विधि द्वारा किया जा सकता है।

4. आर्थिक समस्याओं के लिए-आर्थिक समस्याएं निर्धनता, बेरोज़गारी, मुद्रा-स्फीति का हल सह-सम्बन्ध द्वारा किया जा सकता है। मुद्रा के फैलाव से रोज़गार में कितनी वृद्धि होती है तथा कीमत स्तर पर क्या प्रभाव पड़ता है, इसका ज्ञान सह-सम्बन्ध द्वारा प्राप्त किया जा सकता है।

प्रश्न 5.
प्रतीपगमन (Regression) से क्या अभिप्राय है ?
उत्तर-
प्रतीपगमन विश्लेषण वह क्रिया है जिस द्वारा एक चर का अनुमान दूसरे चरों से लगा सकते हैं। उदाहरणस्वरूप जब कीमत में विशेष दर पर परिवर्तन होता है तो मांग में कितना परिवर्तन होगा। इस तरह हमारे पास किसी देश की जनसंख्या के आंकड़े प्राप्त हैं उनमें से कोई एक अंक स्पष्ट नहीं तो प्रतीपगमन विश्लेषण की सहायता से उस अंक की खोज की जा सकती है।

इस प्रकार दो अथवा दो से अधिक चरों के लिए कारणात्मक सम्बन्ध को स्थापित करने के लिए इस विधि का निर्माण किया गया है। इससे भविष्य के बारे अनुमान लगाया जा सकता है। इस विधि की सहायता से देश की सरकार यह बताती है कि पिछले वर्ष कितनी गेहूँ की पैदावार हुई है तथा अगले वर्ष कितनी गेहूँ उत्पन्न होने की सम्भावना है। इस प्रकार आंकड़ों के सह-सम्बन्ध से प्रतीपगमन किया जाता है। प्रतीपगमन विश्लेषण सह-सम्बन्ध विश्लेषण पर आधारित है।

प्रश्न 6.
सह-सम्बन्ध तथा प्रतीपगमन में अंतर बताओ।
उत्तर-
सह-सम्बन्ध तथा प्रतीपगमन में मुख्य अन्तर निम्नलिखित हैं –

1. मात्रा तथा स्वरूप का ज्ञानसह-सम्बन्ध-इस विश्लेषण से दो अथवा दो से अधिक चरों में सम्बन्ध की मात्रा (Degree) का ज्ञान प्राप्त होता प्रतीपगमन-इस विश्लेषण से दो अथवा दो से अधिक चरों के स्वरूप का ज्ञान प्राप्त होता है। सह-सम्बन्ध विश्लेषण दो अथवा दो से अधिक चरों के सह-परिवर्तन की जाँच करता है, जबकि प्रतीपगमन इन चरों के परिवर्तन के स्वरूप तथा मात्रा की गणना करके भविष्य सम्बन्धी अनुमान लगाने की योग्यता प्रदान करता है।
2. कारण परिणाम का सम्बन्ध सह-सम्बन्ध-सह-सम्बन्ध विश्लेषण में एक चर में परिवर्तन कारण होती है तथा दूसरे चर में परिवर्तन उसका परिणाम होता है। यह अनिवार्य नहीं। सह-सम्बन्ध में कारण तथा परिणाम के सम्बन्ध को स्पष्ट नहीं किया जाता बल्कि दो चरों में परिवर्तन की दिशा की अभिव्यक्ति की जाती है। प्रतीपगमन-इस विश्लेषण में कारण तथा परिणाम के सम्बन्ध को विशेष तौर पर स्पष्ट किया जाता है। इस द्वारा चरों के मूल्यों में सह-सम्बन्ध मात्रा तथा दिशा का माप किया जाता है।

IV. दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)

प्रश्न 1.
सह-सम्बन्ध का अर्थ बताओ। सह-सम्बन्ध के महत्त्व को स्पष्ट कीजिए।
(Explain the meaning of Correlation. Discuss the importance or significance of Correlation.)
उत्तर-
अब तक जिन सांख्यिकी विधियों का अध्ययन किया गया है, उन का सम्बन्ध एक चर से सम्बन्धित था, परन्तु व्यावहारिक जीवन में दो अथवा दो से अधिक चरों का परस्पर सम्बन्ध पाया जाता है। उदाहरणस्वरूप-

1. कीमत में परिवर्तन से मांग में परिवर्तन हो जाता है।
2. आय में परिवर्तन से व्यय में परिवर्तन होता है।
3. किसी वस्तु के विज्ञापन से बिक्री में परिवर्तन होता है, इत्यादि।

इस प्रकार दो चरों में उस समय सह-सम्बन्ध कहा जाता है, जब दोनों में एक समय ही परिवर्तन हो जाता है। एक चर में परिवर्तन कारण दूसरे चर में परिणामस्वरूप में सम्बन्ध पाया जाता है। इस सम्बन्धित सांख्यिकी तकनीक को सह-सम्बन्ध कहते हैं। दो चरों में उससे सह-सम्बन्ध कहा जाता है, जब दोनों चरों में एकत्रित परिवर्तन आएं।
परिभाषाएं (Definitions) –

1. यूले तथा कैंडल के अनुसार, “सह-सम्बन्ध विश्लेषण का सम्बन्ध यह बताता है कि दो चरों में सम्बन्ध किस तरह का है।” (“Correlation analysis deals with the study of the way in which the two variables are related.”-Yule & Kendall)
2. प्रो० ए० एम० टयूटल के अनुसार, “दो अथवा दो से अधिक चरों के सह-परिवर्तनों के विश्लेषण को सह-सम्बन्ध कहा जाता है।” (“Correlation is an analysis of the variance between two or more variables.” -A.M. Tuttle)

सह-सम्बन्ध की विशेषताएं (Characteristics of Correlation)-
अथवा
सह-सम्बन्ध का महत्त्व-
(Importance of Correlation) सह-सम्बन्ध की विशेषताओं द्वारा इसके महत्त्व का पता लगता है –

1. सह-सम्बन्ध द्वारा दो अथवा दो से अधिक चरों में पाए जाने वाले सम्बन्धों की मात्रा तथा दिर.. को स्पष्ट किया जाता है।
2. सह-सम्बन्ध के कारण तथा परिणाम का सम्बन्ध नहीं बताता, बल्कि दो चरों के परस्पर सम्बन्ध को प्रकट करता है कि उसका उद्देश्य मात्र तथा दिशा का प्रगटावा करना होता है।
3. प्रतीपगमन विधि सह-सम्बन्ध विधि पर आधारित है, यदि चरों में सह-सम्बन्ध हों तो एक चर के मूल्य का पता होने की स्थिति में दूसरे चर के मूल्य का अनुमान लगाया जा सकता है।
4. व्यापारिक क्षेत्रों में भविष्य के लिए अनुमान लगाने के लिए सह-सम्बन्ध विश्लेषण लाभदायक होता है।
5. सह-सम्बन्ध का प्रभाव हमारी भविष्यवाणी की अनिश्चितता के विस्तार को कम करता है।
6. सह-सम्बन्ध की सैद्धान्तिक तथा व्यावहारिक महत्ता होने के कारण इसका प्रयोग वैज्ञानिक अनुसन्धानों में दिन प्रतिदिन बढ़ रहा है।
7. सह-सम्बन्ध द्वारा चरों सम्बन्धी ज्ञान प्राप्त हो जाता है। इस द्वारा स्वतन्त्र तथा आधारित चरों का पता लगता है। इस प्रकार सह-सम्बन्ध की विशेषताएं ही सह-सम्बन्ध विश्लेषण के महत्त्व को स्पष्ट करती हैं।

प्रश्न 2.
सह-सम्बन्ध की मात्राओं की व्याख्या करो। (Discuss the degrees of Correlation.)
अथवा
सह-सम्बन्ध गुणांक से क्या अभिप्राय है ? सह-सम्बन्ध की मात्राओं को स्पष्ट करो।
(What is meant by Co-efficient of Correlation ? Discuss the degrees of Correlation.)
उत्तर-
सह-सम्बन्ध गुणांक का अर्थ-वह गुणांक जोकि सह-सम्बन्ध की मात्रा तथा दिशा को मापता है उसको सह-सम्बन्ध गुणांक कहा जाता है। सह-सम्बन्ध गुणांक को अंग्रेजी भाषा के अक्षर (r) द्वारा प्रकट किया जाता है। यदि X तथा Y दो चर हैं तो rxy इन दोनों चरों की मात्रा तथा दिशा को दर्शाता है।

सह-सम्बन्ध गुणांक की मुख्य विशेषताएं इस प्रकार हैं-
1. सह-सम्बन्ध के गुणांक का विस्तार – 1 से + 1 तक है अर्थात् सह-सम्बन्ध गुणांक का मूल्य – 1 से कम अथवा + 1 से अधिक नहीं हो सकता।

गुणांक का विस्तार – 1 से + 1 तक होता है।

2. सह-सम्बन्ध का गुणांक आरम्भ में परिवर्तनों से स्वतन्त्र है अर्थात् किसी भी स्थिर को X अथवा Y अथवा दोनों के मूल्यों से घटा दिया जाए तो इसका सह-सम्बन्ध गुणांक पर कोई प्रभाव नहीं पड़ता।

3. सह-सम्बन्ध गुणांक एक शुद्ध अंक होता है अर्थात् इसकी कोई भी इकाई नहीं होती।

4. सह-सम्बन्ध गुणांक एकरूपता की विशेषता रखता है, अर्थात्,
rxy = ryx
यदि हम X तथा Y को किसी स्थिर में विभाजित करते हैं तो इससे सह-सम्बन्ध गुणांक पर कोई प्रभाव नहीं पड़ता।

सह-सम्बन्ध की मात्राएं-
सह-सम्बन्ध गुणांक से सह-सम्बन्ध की दिशा तथा मात्रा का अध्ययन किया जाता है। इस प्रकार दिशा तथा मात्रा के आधार पर सह-सम्बन्ध गुणांक निम्नलिखित वर्गों में विभाजित किया जा सकता है-

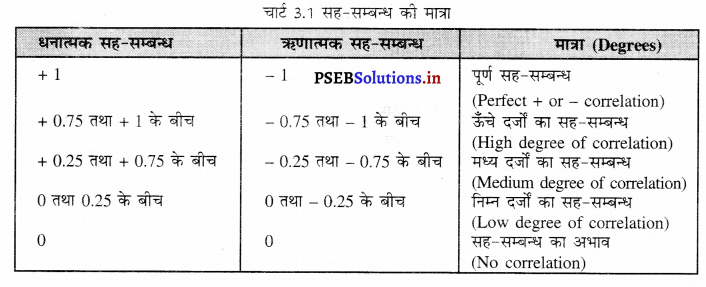
ऊपर दिए गए चार्ट के आधार पर सह-सम्बन्ध की मात्राओं की व्याख्या इस प्रकार की जा सकती है-
1. पूर्ण सह-सम्बन्ध (Perfect Correlation)-सह-सम्बन्ध उस स्थिति में पूर्ण सह-सम्बन्ध कहा जाता है, जब दोनों चरों में समान दर पर परिवर्तन होता है, पूर्ण सह-सम्बन्ध दो प्रकार का होता है –

• पूर्ण धनात्मक (Perfect Positive)-सह-सम्बन्ध को पूर्ण धनात्मक कहा जाता है जब सह सम्बन्ध गुणांक (+ 1) होता है।
• पूर्ण ऋणात्मक (Perfect of Negative)-सह-सम्बन्ध को पूर्ण ऋणात्मक कहा जाता है, जब सह-सम्बन्ध गुणांक (- 1) होता है।

2. ऊँचे दों का सह-सम्बन्ध (High degree of Correlation)-जब दो चरों के सह-सम्बन्ध की बहुत अधिक मात्रा हो तो इसको ऊँचे दों का सह-सम्बन्ध कहा जाता है। यह भी दो प्रकार का होता है

• ऊँचे दों का धनात्मक सह-सम्बन्ध (High degree of Positive Correlation)-इस स्थिति में सह-सम्बन्ध गुणांक + 0.75 से + 1 के बीच होता है।
• ऊँचे दों का ऋणात्मक सह-सम्बन्ध (High degree of Negative Correlation)-जब दो शृंखलाओं में सह-सम्बन्ध गुणांक – 0.75 से – 1 के बीच होता है तो इसको ऊँचे दों का ऋणात्मक सह-सम्बन्ध कहा जाता है।

3. मध्य दों का सह-सम्बन्ध (Medium Correlation)-जब चरों के बीच सह-सम्बन्ध की मात्रा न तो बहुत अधिक तथा न ही बहुत कम हो तो ऐसी स्थिति में सह-सम्बन्ध को मध्य दों वाला कहा जाता है।
यह भी दो प्रकार का होता है-

• मध्य दों का धनात्मक सह-सम्बन्ध (Medium degree of Positive Correlation) इस स्थिति में सह-सम्बन्ध गुणांक – 0.25 से – 0.75 के बीच होता है।
• मध्य दों का ऋणात्मक सह-सम्बन्ध (Medium degree of Negative Correlation) इस स्थिति में सह-सम्बन्ध गुणांक – 0.25 से – 0.75 के बीच होता है।

4. निम्न दों का सह-सम्बन्ध (Low degree of Correlation)-जब दो चरों में सह-सम्बन्ध कम मात्रा में पाया जाता है तो इसको निम्न दों का सह-सम्बन्ध कहा जाता है।
यह दो प्रकार का हो सकता-

• निम्न दर्जी का धनात्मक सह-सम्बन्ध (Low degree of Positive Correlation)-जब इस स्थिति में सह-सम्बन्ध गुणांक 0 से + 0.25 के बीच होता है।
• निम्न दों का ऋणात्मक सह-सम्बन्ध (Low degree of Negative Correlation)-इस स्थिति में सह-सम्बन्ध गुणांक 0 से – 0.25 के बीच होता है| (a) निम्न दों का धनात्मक सह-सम्बन्ध

5. सह-सम्बन्ध का अभाव (No Correlation)-जब दो चरों में कोई सम्बन्ध न पाया जाए अर्थात् एक चर में परिवर्तन से दूसरे चर पर पड़ने वाला प्रभाव कोई न हो तो इसको सह-सम्बन्ध का अभाव कहा जाता है। इस स्थिति में सह-सम्बन्ध गुणांक शून्य (0) होता है।

प्रश्न 3.
सह-सम्बन्ध पता लगाने की कौन-सी विधियां हैं ? बिखरे बिन्दु चित्र विधि की व्याख्या करो। इस विधि के गुण तथा दोष बताओ।
उत्तर-
दो चरों के परस्पर सम्बन्ध का पता लगाने के लिए मुख्य तौर पर निम्नलिखित विधियां हैं

1. बिखरे बिन्दु चित्र विधि (Scatter Diagram Method)
2. कार्ल पीयर्सन की सह-सम्बन्ध गुणांक विधि (Karl Pearsons co-efficient of correlation)
3. सपीयरमैन की दर्जा सह-सम्बन्ध गुणांक विधि (Spearman’s co-efficient of Rank correlation method) चाहे सह-सम्बन्ध का पता करने के लिए कुछ अन्य विधियां भी हैं, परन्तु हम इन तीन विधियों का अध्ययन करेंगे।

1. बिखरे बिन्दु चित्र विधि (Scatter Diagram Method)-दो चरों में सह-सम्बन्ध का पता करने के लिए यह सबसे सरल विधि है। बिखरे बिन्दु चित्र द्वारा दो चरों के परस्पर सह-सम्बन्ध की दशा तथा मात्रा का ज्ञान प्राप्त हो जाता है। ग्राफ पेपर पर स्वतन्त्र चरों को X अक्ष पर तथा आधारित चरों को Y अक्ष पर प्रदर्शित किया जाता है।

X श्रेणी तथा Y श्रेणी के जोड़े को एक बिन्दु द्वारा अंकित किया जाता है। इस प्रकार सभी जोड़ों के बिन्दु चित्र में बनाए जाते हैं। इस तरह X तथा Y के जितने जोड़े होते हैं, उनते ही बिन्दु अंकित हो जाते हैं। यह सभी बिन्दु एक निश्चित प्रवृत्ति को प्रकट करते हैं। इन बिन्दुओं की दिशा को देखकर धनात्मक अथवा ऋणात्मक सह-सम्बन्ध का पता लगता है, जबकि इन बिन्दुओं के बिखराव को देखकर सह-सम्बन्ध की मात्रा का ज्ञान प्राप्त होता है। बिखरे बिन्दु चित्र निम्नलिखित किस्म के हो सकते हैं।

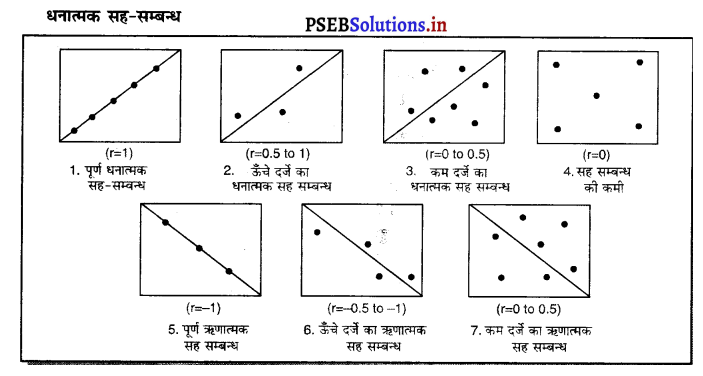
1. पूर्ण धनात्मक सह-सम्बन्ध (Perfect Positive Correlation)-जब बिन्दु एक सीधी रेखा का रूप धारण कर लेते हैं तथा उनकी ढाल धनात्मक होती है तो इस स्थिति में सह-सम्बन्ध गुणांक + 1 होगा।

2. ऊँचे दों का धनात्मक सह-सम्बन्ध (High degree of Positive Correlation)-जब भिन्न भिन्न मूल्यों के बिन्दु नीचे से ऊपर अर्थात् बाएं से दाएं ओर ऊपर की ओर बढ़ते हैं तथा सीधी रेखा के नज़दीक होते हैं तो इस स्थिति में ऊँचे दों का धनात्मक सह-सम्बन्ध होता है तथा सह-सम्बन्ध गुणांक (r) 0.5 से 1 तक होगा।

3. कम दों का धनात्मक सह-सम्बन्ध (Low degree of Positive Correlation)-जब दो चरों के बिन्दु बाएं से दाएं ओर ऊपर की ओर बढ़ते हैं, परन्तु रेखा से बिन्दुओं का बिखराव अधिक होता है तो इसको कम दों का सह-सम्बन्ध कहा जाता है। इस स्थिति में सह-सम्बन्ध गुणांक 0 से 0.5 तक होता

4. सह-सम्बन्ध की कमी (No Correlation)-जिस समय बिन्दुओं का फैलाव अनियत होता है, एक चर में परिवर्तन से दूसरा चर बहुत अधिक अथवा घट जाता है या स्थिर रहता है तो बिन्दु बिखरे होते हैं तथा उनमें कोई निश्चित प्रवृत्ति नज़र नहीं आती तो इस स्थिति को सह-सम्बन्ध की कमी कहा जाता है तथा सह-सम्बन्ध गुणांक 0 (शून्य) होता है।

5. पूर्ण ऋणात्मक सह-सम्बन्ध (Perfect Negative Correlation)-जब दो चरों का सम्बन्ध एक सीधी रेखा का रूप धारण कर लेता है तो वह रेखा बाईं ओर से दाईं ओर नीचे झुकी होती है तो इस स्थिति को पूर्ण ऋणात्मक सह-सम्बन्ध कहा जाता है, जैसे कि मांग वक्र होती है। इस स्थिति में सह-सम्बन्ध गुणांक r = – 1 होता है।

6. ऊँचे दों का ऋणात्मक सह-सम्बन्ध (High degree of Negative Correlation)-जब भिन्न भिन्न मूल्यों के बिन्दु बाईं ओर से दाईं ओर को नीचे की ओर जाते हैं तथा ऋणात्मक ढाल वाली रेखा के नज़दीक होते हैं तो इस स्थिति को ऊँचे दों का ऋणात्मक सह-सम्बन्ध कहा जाता है। इस स्थिति में सह-सम्बन्ध गुणांक r = – 0.5 से – 1 तक होता है।

7. कम दों का ऋणात्मक सह-सम्बन्ध (Low degree of Negative Correlation)-जब दो चरों के बिन्दु बाईं से दाईं ओर नीचे की ओर जाते हैं तो सीधी रेखा से उन बिन्दुओं की अधिक दूरी होती है तो इस सह-सम्बन्ध को कम दों का ऋणात्मक सह-सम्बन्ध कहा जाता है। इस स्थिति में सहसम्बन्ध गुणांक 0 से – 0.5 तक होता है।

कार्ल पीयर्सन की सह-सम्बन्ध गुणांक विधि (Karl Pearson’s Co-efficient of Correlation) –

प्रश्न 4.
कार्ल पीयर्सन की सह-सम्बन्ध गुणांक विधि से क्या अभिप्राय है ? इस विधि द्वारा सह-सम्बन्ध की गणना कैसे की जाती है ?
(What is Karl Pearson’s Coefficient of Correlation Method? How co-efficient of correlation is calculated with this method ?)
उत्तर-
कार्ल पीयर्सन महत्त्वपूर्ण सांख्यिकी शास्त्री हुए हैं। उन्होंने 1870 में सह-सम्बन्ध गुणांक की गणना के लिए वैज्ञानिक तथा गणितीय विधि का निर्माण किया। कार्ल पीयर्सन अनुसार दो चरों के परस्पर सम्बन्ध को अंग्रेज़ी के अक्षर r द्वारा प्रकट किया जा सकता है। इस विधि के अनुसार r का मूल्य निश्चित तथा स्थाई होता है। यह विधि समान्तर औसत तथा प्रमाप विचलन पर आधारित है। इसलिए इस विधि को सबसे अच्छी विधि कहा जाता है। इस विधि से दो चरों की दिशा तथा मात्रा दोनों का ही ज्ञान प्राप्त हो जाता है। इस विधि को कार्ल पीयर्सन के नाम पर ही कार्ल पीयर्सन की सह-सम्बन्ध गुणांक विधि कहा जाता है।

मुख्य विशेषताएं (Main Characteristics) –
1. दिशा का ज्ञान-दो श्रृंखलाओं में सह-सम्बन्ध की दिशा का नाम कार्ल पीयर्सन की इस विधि द्वारा प्राप्त हो जाता है। जब हमारे पास जवाब धनात्मक आता है तो दोनों श्रृंखलाओं का सम्बन्ध धनात्मक होता है, जब जवाब ऋणात्मक होता है तो सह-सम्बन्ध ऋणात्मक होगा।

2. मात्रा का ज्ञान-कार्ल पीयर्सन की इस विधि द्वारा दो चरों में कितना सम्बन्ध है इस का ज्ञान भी प्राप्त होता है। सह-सम्बन्ध गुणांक का माप हमेशा (-)1 से (0) शून्य तथा (+) 1 के बीच होता है। यदि जवाब (-) है तो पूर्ण ऋणात्मक सह-सम्बन्ध होगा। + 1 की स्थिति में पूर्ण धनात्मक सह-सम्बन्ध होता है। इसी तरह ऊँचे दों, मध्य दों अथवा कम दों के सह-सम्बन्ध का पता लग जाता है। इस प्रकार सहसम्बन्ध की मात्रा का ज्ञान भी इस विधि द्वारा हो जाता है। शून्य (0) की स्थिति में सह-सम्बन्ध की कमी होती है।

3. उत्तम विधि-यह विधि गणित औसत तथा प्रमाप विचलनों पर आधारित है। इसलिए सह-सम्बन्ध गुणांक के परिणाम शुद्ध तथा उचित होते हैं। इस विधि द्वारा व्यावहारिक तथा सैद्धान्तिक समस्याओं का हल किया जा सकता है। इसलिए सह-सम्बन्ध की गणना के लिए इस विधि को उत्तम विधि कहा जाता है।

कार्ल पीयर्सन के सह-सम्बन्ध की गणना (Calculation of Karl Pearson’s Co-efficient of Correlation)-
कार्ल पीयर्सन की इस विधि अनुसार सह-सम्बन्ध के गुणांक का माप करने के लिए दोनों चरों की समान्तर औसत में से लिए गए विचलनों के गुणनफल के योग को दोनों चरों के प्रमाप विचलनों के गुणनफल तथा सम्बन्धित चरों की संख्या (N) से विभाजित कर प्राप्त किया जाता है। इसलिए कार्ल पीयर्सन ने निम्नलिखित सूत्र दिया-

प्रत्यक्ष विधि अथवा वास्तविक समान्तर औसत विधि
r = \(\frac{\Sigma x y}{N \sigma_{x} \times \sigma y}\)
इस सूत्र में,
r = सह-सम्बन्ध गुणांक सिगमा Σ = जोड़
X = X- \(\bar{X}\)
Y = Y- \(\bar{Y} \)
N = मदों की संख्या oX = X मदों का प्रमाप विचलन
OY = Y मदों का प्रमाप विचलन
कार्ल पीयर्सन के ऊपर दिए सूत्र को निम्नलिखित रूप में लिखा जा सकता है-
r = \(\frac{\Sigma x y}{\sqrt{\Sigma x^{2} \times \Sigma y^{2}}}\)
क्योंकि r = \(\frac{\Sigma x y}{N \sigma \times \sigma y}=\frac{\Sigma x y}{\sqrt{\frac{\Sigma x^{2}}{N} \times \frac{\Sigma y^{2}}{N}}}=\frac{\Sigma x y}{\sqrt{\Sigma x^{2} \times y^{2}}}\)
यहां X = (x- \(\bar{X}\) ) तथा Y = (Y – \(\bar{Y}\) )

इस प्रकार सह-सम्बन्ध गुणांक (r) का मूल्य हमेशा – 1 तथा + के बीच रहता है।
माप विधि-

1. दो श्रेणियों X तथा Y का समान्तर औसत (\(\bar{X}\) तथा \(\bar{Y}\) ) पता करो।
2. दोनों श्रेणियों की समान्तर औसत से व्यक्तिगत मूल्यों का विचलन निकालो।
   (x = X-\(\bar{X}\) ) तथा (y = Y – \(\bar{X}\) )
3. दोनों श्रेणियों के विचलनों x तथा ) का वर्ग (x² तथा y² ) निकालो तथा इनके वर्गों का अलग-अलग जोड़
   (Σx² तथा Σy²) पता करो।
4. दोनों श्रेणियों के विचलनों x तथा y को गुणा करके गुणनफल xy प्राप्त करो तथा गुणनफल जोड़ (Σxy) पता करो।
5. निम्नलिखित सूत्र का प्रयोग करो।
   r = \(\frac{\Sigma x y}{\sqrt{\Sigma x^{2} \times \Sigma y^{2}}}\)
   इससे सह-सम्बन्ध गुणांक (r) का पता लग जाता है।

प्रश्न 5.
निम्नलिखित आंकड़ों का सह-सम्बन्ध गुणांक पता करो।

हल (Solution) :

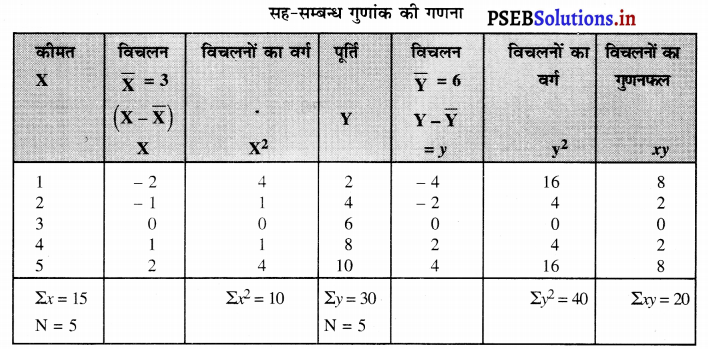
समान्तर औसत (Mean)
\(\bar{X}\) = \(\frac{\Sigma X}{N}=\frac{15}{5}\) = 3
\(\overline{\mathrm{Y}}\) = \(\frac{\Sigma Y}{N}=\frac{30}{5}\) = 6

सह-सम्बन्ध गुणांक
r = \(\frac{\Sigma x y}{\sqrt{\Sigma x^{2} \times \Sigma y^{2}}}\)
Σxy = 20, Σx²= 10,Σy²= 40
∴ r = \( \frac{20}{\sqrt{10 \times 40}}=\frac{20}{\sqrt{400}}=\frac{20}{20}\) = 1
1 = 1 उत्तर
इसलिए सह-सम्बन्ध गुणांक पूर्ण धनात्मक है। इससे पता चलता है कि जब कीमतों में वृद्धि होती है तो पूर्ति में भी वृद्धि हो रही है। कीमत में वृद्धि 1, 1 रु० है तथा पूर्ति में वृद्धि 2, 2 वस्तुओं की है। वृद्धि का अनुपात कीमत तथा पूर्ति में समान होने के कारण सह-सम्बन्ध गुणांक पूर्ण धनात्मक है।

प्रश्न 6.
निम्नलिखित आंकड़ों से शादी के समय पति-पत्नी की आयु का सह-सम्बन्ध गुणांक कार्ल पीयर्सन विधि द्वारा ज्ञात करो।

पति की आयु :	20	25	28	30	32	45
पत्नी की आयु :	18	20	22	32	28	42

हल (Solution) :
कार्ल पीयर्सन का सह-सम्बन्ध पति की आयु

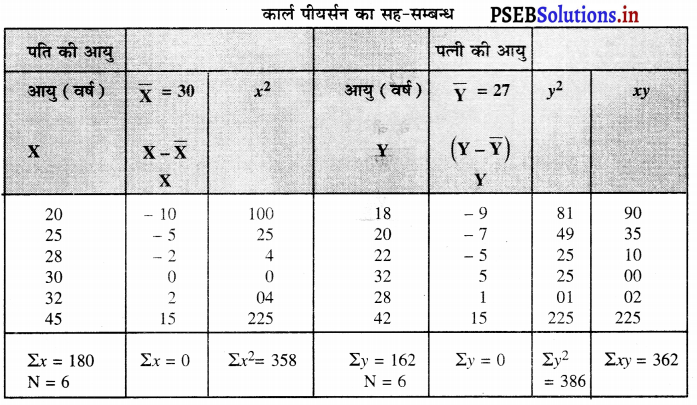
\(\bar{X}\) = \(\frac{\Sigma X}{N}=\frac{180}{6}\) = 30
\(\overline{\mathrm{Y}}\) = \(\frac{\Sigma Y}{N}=\frac{162}{6}\) = 27
r = \(\frac{\Sigma x y}{\sqrt{\Sigma x^{2} \times \Sigma y^{2}}}=\frac{362}{\sqrt{358 \times 386}}=\frac{362}{371.34}\) = 0.975
सह-सम्बन्ध 0.975 ऊंचे दों का धनात्मक सम्बन्ध है। इसका अर्थ है कि पति-पत्नी की आयु में सम्बन्ध सीधा तथा नज़दीकी है।

दूसरा सुत्र (Second Method)-
r = \(\frac{\Sigma d x d y-\frac{\Sigma d x \times \Sigma d y}{\mathrm{~N}}}{\sqrt{\Sigma d x^{2}-\frac{(\Sigma d x)^{2}}{N}} \sqrt{\Sigma d y^{2}-\frac{(\Sigma d y)^{2}}{N}}}\)

इस सूत्र में
r = सह-सम्बन्ध गुणांक
dx = x श्रेणी की मदों का उस श्रेणी की कल्पित औसत पर विचलन (X – A)
Σdx = X श्रेणी के विचलनों dx का जोड़
dy = Y श्रेणी की मदों का उस श्रेणी की कल्पित औसत से विचलन (Y – A)
Σdy = Y श्रेणी के विचलनों dy का जोड़।
Σdxdy = dx तथा dy के गुणनफल का जोड़
Σdr² = dx के वर्गों का जोड़
Σdy² = dy के वर्गों का जोड़
N = मदों की संख्या।

प्रश्न 7.
निम्नलिखित आंकड़ों का सह-सम्बन्ध गुणांक पता करो।

हल (Solution) :
कीमत तथा मांग के बीच सह-सम्बन्ध गुणांक की गणना कामत | A = 12

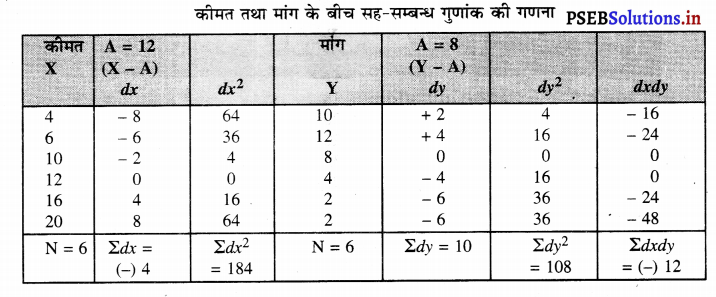
कार्ल पीयर्सन का सह-सम्बन्ध गुणांक

r = \(\frac{(-) 105.33}{\sqrt{184-2.67} \sqrt{108-16.67}}\)
r = \(\frac{(-) 105.33}{\sqrt{181.33 \times 91.33}}\)
r = \(\frac{(-) 105.33}{\sqrt{16560.87}}\)
r = \(\frac{(-) 105.33}{128.69}\)
r = (-) 0.818 इसमें ऊँचे दों का ऋणात्मक सह-सम्बन्ध है। इससे अभिप्राय है कि दी गई सूचना में कीमत तथा मांग में ऊँचे दों का ऋणात्मक सह-सम्बन्ध है।

स्पीयरमैन की दर्जा सह-सम्बन्ध गुणांक विधि
(Spearman’s Co-efficient of Rank Correlation)

प्रश्न 8.
स्पीयरमैन की दर्जा सह-सम्बन्ध गुणांक विधि को स्पष्ट करो। (Explain Spearman’s Co-efficient of rank Correlation Method) ।
उत्तर-
इंग्लैंड के प्रसिद्ध मनोवैज्ञानिक चार्ल्स एडवर्ड स्पीयरमैन ने 1904 में गुणात्मक तथ्यों के बीच सह-सम्बन्ध का पता करने के लिए एक विधि का निर्माण किया जिस विधि को स्पीयरमैन की दर्जा सह-सम्बन्ध गुणांक विधि कहा जाता है। इस विधि को स्पीयरमैन की दर्जा अन्तर विधि भी कहा जाता है। स्पीयरमैन के अनुसार कुछ तथ्य ऐसे होते हैं जिनका अंकों में माप नहीं किया जा सकता। उदाहरणस्वरूप सुन्दरता, भाषण मुकाबला, वीरता इत्यादि चरों को अंकों में नहीं दर्शाया जा सकता, बल्कि ऐसी स्थिति में प्राथमिकता क्रम दिए जाते हैं। भाषण प्रतियोगिता में 10 बुलारे भाग लेते हैं। निर्णय करने के लिए दो न्यायाधीश हैं।

ये न्यायाधीश अपनी काबलीयत तथा समझ अनुसार प्रतियोगियों को प्राथमिकता क्रम देते हैं। इन दोनों न्यायाधीशों के निर्णय को दर्जा सह-सम्बन्ध गुणांक द्वारा परख कर यह बताया जाता है कि इनके निर्णय में धनात्मक सम्बन्ध है अथवा ऋणात्मक सम्बन्ध है। इस प्रकार दोनों न्यायाधीशों के फैसले की दिशा का पता लगता है। इससे दोनों के निर्णय की मात्रा का भी पता किया जा सकता है। इन उद्देश्यों की पूर्ति के लिए स्पीयरमैन ने निम्नलिखित सूत्र का निर्माण किया, जिस द्वारा दर्जा सह-सम्बन्ध गुणांक का पता किया जा सकता है
rk = \(1-\frac{6 \Sigma D^{2}}{N^{3}-N}\)
इस सूत्र में
rk = दर्जा सह-सम्बन्ध गुणांक
D² = दो न्यायाधीशों द्वारा दिए गए प्राथमिकता क्रम का अंतर (R₁ – R₂) = D होता है, इसके वर्ग को D² कहा जाता है तथा जोड़ को Σd² कहा जाता है।
N = प्राथमिकता क्रम की संख्या
नोट : दर्जा सह-सम्बन्ध गुणांक का मूल्य – 1 से + के बीच होता है।
(1) यदि rk = (-) है तो इस स्थिति में दिए गए चरों के दर्जे एक-दूसरे के विपरीत होते हैं।
प्रथम न्यायाधीश द्वारा प्राथमिकता क्रम : 1. 2, 3, 4, 5, 6
द्वितीय न्यायाधीश द्वारा प्राथमिकता क्रम : 6, 5, 4. 3, 2, 1
इसको ऋणात्मक सह-सम्बन्ध दर्जा गुणांक कहा जाएगा।

(2) यदि rk = + 1 है तो इस स्थिति में दिए गए चरों के दर्जे एक-दूसरे के समरूप हैं तो इस स्थिति में प्राथमिकता क्रम एक-समान होता है। प्रथम न्यायाधीश द्वारा प्राथमिकता क्रम = 123456
द्वितीय न्यायाधीश द्वारा प्राथमिकता क्रम = 123456
इस स्थिति को पूर्ण धनात्मक दर्जा सह-सम्बन्ध गुणांक कहा जाता है।

(3) यदि rk = 0 है तो इस स्थिति में दो न्यायाधीशों द्वारा प्राथमिकता क्रम में कोई सम्बन्ध नहीं होता। दर्जा सह-सम्बन्ध के गुणांक की गणना दर्जा सह-सम्बन्ध गुणांक की गणना तीन स्थितियों में की जाती है –

• जब दर्जे दिए हों।
• जब दर्जे न दिए हों
• जब श्रेणी मूल्य एक-दूसरे के समान हों।

(A) जब दर्जे दिए हों (When Ranks are Given)
दर्जा सह-सम्बन्ध गुणांक की गणना करते समय यदि दोनों श्रेणियों में भिन्न-भिन्न मदों के क्रम अथवा दर्जे दिए हों तो निम्नलिखित माप विधि का प्रयोग किया जाता है।

• दिए गए दो दों का अन्तर (R₁ – R₂) की गणना करो तथा इन अन्तरों को D द्वारा लिखा जाता है।
• इन अंतरों (D) का वर्ग निकालो इससे D प्राप्त हो जाएगा। इसका जोड़ कर लो जिसको ΣD द्वारा प्रकट किया जाता है।
• इस प्रकार प्राप्त मूल्यों को निम्न सूत्र से भाग करो जिससे दर्जा सह-सम्बन्ध गुणांक (rk) का पता लग जाता है। rk = \(1-\frac{6 \Sigma D^{2}}{N^{3}-N}\)

प्रश्न 9.
सुन्दरता मुकाबले में दो न्यायाधीशों ने प्रतियोगियों को निम्नलिखित अनुसार प्राथमिकता क्रम प्रदान किए। इन न्यायाधीशों के फैसले में सह-

सम्बन्ध को स्पष्ट करो। प्रतियोगी	A	B	C	D	E	F
न्यायाधीश I द्वारा क्रम (Ranks)	1	2	3	4	5	6
न्यायाधीश II द्वारा क्रम (Ranks)	2	3	1	5	4	6

हल (Solution) :
दर्जा सह-सम्बन्ध गुणांक की गणना

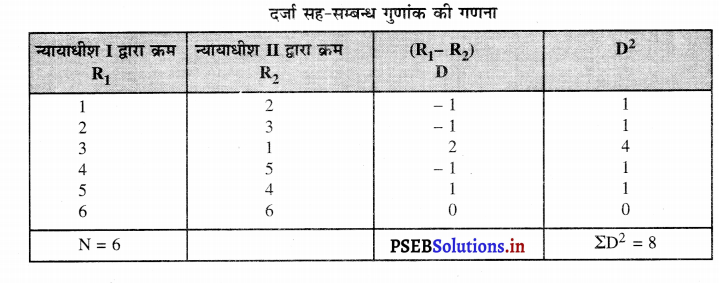
दर्जा सह-सम्बन्ध गुणांक
rk = \(1-\frac{6 \Sigma D^{2}}{N^{3}-N}\)
rk = \(1-\frac{6(8)}{(6)^{3}-6} \) = \(1-\frac{48}{216-6}\)
rk = \(1-\frac{48}{210}\)
rk = 1 – 0.229
rk = 0.771 उत्तर

न्यायाधीशों के निर्णय में ऊँचे दर्जे का धनात्मक सह-सम्बन्ध है अर्थात् दोनों न्यायाधीशों द्वारा जो निर्णय दिया गया है उस निर्णय में काफ़ी हद तक सहमति पाई जाती है।

(B) जब दर्जे न दिए हों (When Ranks are not Given)
माप विधि

1. दोनों श्रेणियों की मदों को घटते क्रमानुसार तथा बढ़ते क्रमानुसार लिखो। मान लो घटते क्रमानुसार लिखा जाता है तो सबसे बड़ी मद को दर्जा 1, उससे छोटी को दर्जा 2, उससे छोटी को 3 से तथा इस तरह अन्य की मदों के दर्जे लिख लो।
2. दर्जा देने के पश्चात् दोनों श्रेणियों को मूल रूप में लिख लो तथा सम्बन्धित दर्जे प्रदान करो।
3. प्रथम श्रेणी के दों तथा द्वितीय श्रेणी के दों का अंतर (D = R₁ – R₂) पता करो।
4. दों के अन्तर D के वर्ग बनाओ (D²) तथा इनका जोड़ करो (ΣD²)
5. निम्नलिखित सूत्र का प्रयोग करके दर्जा सह-सम्बन्ध गुणांक प्राप्त किया जा सकता है-
   rk = \(1-\frac{6 \Sigma D^{2}}{N^{3}-N}\)

प्रश्न 10.
अर्थशास्त्र तथा सांख्यिकी की परीक्षा में 10 विद्यार्थियों ने निम्नलिखित अनुसार अंक प्राप्त किए हैं।

अर्थशास्त्र :	30	42	25	55	38	65	40	18	60	28
सांख्यिकी :	60	35	40	75	80	48	50	55	62	70

हल (Solution) : पहले प्राप्त किए अंकों को घटते क्रमानुसार लिखो तथा दर्जा दो।

अर्थशास्त्र :	65	60	55	42	40	38	30	28	25	16
क्रम (Ranks) :	1	2	3	4	5	6	7	8	9	10
सांख्यिकी :	80	75	70	62	60	55	50	48	40	35
क्रम (Ranks):	1	2	3	4	5	6	7	8	9	10

अब सारणी की मदों को मूल रूप में लिखकर ऊपर दिए क्रम उनके सामने अंकित करके दर्जा सह-सम्बन्ध पता करते हैं।
दर्जा सह-सम्बन्ध गुणांक की गणना

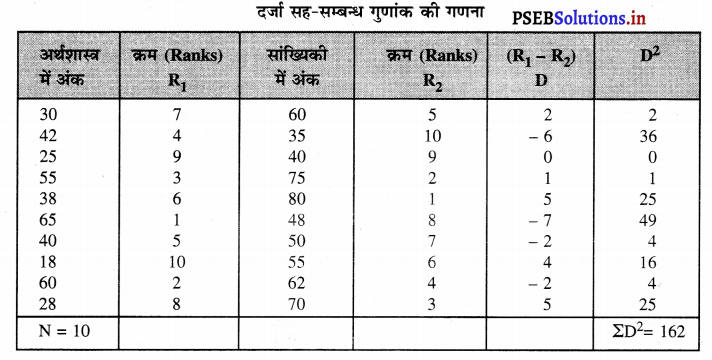
दर्जा सह-सम्बन्ध गुणांक
rk = \(1-\frac{6 \Sigma D^{2}}{N^{3}-N}\)
rk = \(1-\frac{6(162)}{(10)^{3}-10}\)
rk = \(1-\frac{972}{1000-10}\)
rk = \(1-\frac{972}{990}\) = 1 – 0.982 = 0.018 उत्तर
इससे अभिप्राय है कि 10 विद्यार्थियों द्वारा अर्थशास्त्र तथा सांख्यिकी में प्राप्त किए अंकों में बहुत कम दर्जे का धनात्मक सह-सम्बन्ध है। जब एक विद्यार्थी के अर्थशास्त्र में अंक अधिक हैं तो सांख्यिकी में कम हैं, जब अर्थशास्त्र के विषय में अंकों की वृद्धि होती है तो सांख्यिकी में वृद्धि है परन्तु यह सम्बन्ध हमेशा नहीं रहता। |

(C) जब श्रेणी मूल्य एक दूसरे के समान हों (When the Values of series are same or when Ranks are Repeated) कई बार श्रेणी में दो अथवा दो से अधिक मदों के मूल्य समान होते हैं। इस स्थिति में समान मूल्य की मदों को औसत दर्जा दिया जाता है। उदाहरणस्वरूप प्रथम तथा द्वितीय मद का मूल्य समान है। इनको 1 तथा 2 दर्जा मिलना था, परन्तु अब समान होने के कारण दोनों मदों को औसत दर्जा \(\frac{1+2}{2}\) = 1.5 दिया जाएगा। इसी तरह यदि कोई मूल्य तीन बार समान आते हैं जिनको 3, 4, 5 दर्जा मिलना था। इन तीन मदों के समान होने के कारण औसत दर्जा \(\frac{3+4+5}{3} \) = \(\frac{12}{3}\) = 4 दर्जा प्रत्येक मूल्य को दिया जाएगा। इस प्रकार दर्जा प्रदान करने के पश्चात् पहले दिए सूत्र का समायोजन किया जाता है।

समायोजन विधि (Adjustment Method)-इस स्थिति में ΣD² में +\(\frac{1}{12}\) (m³ – m) पद को जमा किया जाता है। जब दो मदों के मूल्य समान है तो ΣD² में \(\frac{1}{12}\) = (2³ – 2) = 0.5 शामिल करते हैं , यदि तीन मदें समान हैं तो \(\frac{1}{12}\) [(3)³-3] = 2 को शामिल किया जाता है जितनी मदों के मूल्य समान होते हैं उतनी बार ΣD² में (m³ -m) का मूल्य शामिल किया जाता है। इस प्रकार जब श्रेणी मूल्य एक-दूसरे के समान होते हैं तो दर्जा सह-सम्बन्ध गुणांक का सूत्र इस प्रकार प्रयोग किया जाता है।
rk =1 \(-\left[\frac{\left.6 \Sigma \mathrm{D}^{2}+\frac{1}{12}\left(m^{3}-m\right)+\frac{1}{12}\left(m^{3}-m\right)\right)+\frac{1}{12}\left(m^{3}-m\right)+\ldots \ldots \ldots}{\mathrm{N}^{3}-\mathrm{N}}\right] \)

प्रश्न 11.
कविता प्रतियोगिता में 7 प्रतियोगियों ने भाग लिया। दो न्यायाधीश द्वारा इन प्रतियोगियों को 100 में से निम्नलिखित अंक दिए गए। न्यायाधीश के निर्णय में दर्जा सह-सम्बन्ध गुणांक ज्ञात करो।

X :	82	80	70	70	68	67	50
Y:	17	25	25	40	16	20	10

हल (Solution) :
प्रथम X तथा Y श्रेणी के आँकड़ों को घटते क्रमानुसार लिखकर दर्जा प्रदान करते हैं।

X:	82	80	70	70	68	67	50
Ranks :	1	2	3.5	3.5	5	6	7

= \(\frac{3+4}{2}\) = 3.5

Y:	40	25	25	20	17	16	10
Ranks:	1	2.5	2.5	4	5	6	7

= \(\frac{2+3}{2}\) = 2.5
अब इनको मौलिक रूप में लिखकर प्रदान किए प्राथमिक क्रम लिखते हैं, परन्तु जितनी मदें समान हैं उस श्रेणी के ऊपर उनकी संख्या को अंकित किया जाता है। जैसे कि X श्रेणी में 70, 70 मदें समान हैं, उस श्रेणी के ऊपर m = 2 (item = 2) लिखा जाएगा। इसी तरह Y श्रेणी में 25, 25 दो मदें समान हैं तो इस स्थिति में Y श्रेणी के ऊपर m = 2 लिखा जाएगा। समायोजन सूत्र में m का मूल्य भर देते हैं।

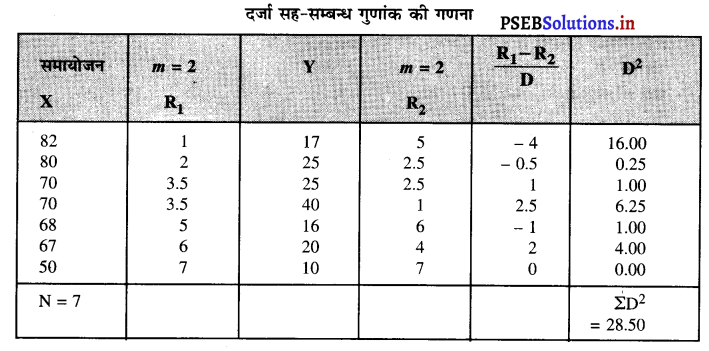
दर्जा सह-सम्बन्ध गुणांक

rk = \(1-\frac{6(29.5)}{336} \)
rk = \(1-\frac{177}{336}\)
rk = 1 – 0.527 = 0.473 उत्तर
दोनों न्यायाधीशों द्वारा निर्णय में धनात्मक दर्जा सह-सम्बन्ध है, परन्तु इस सह-सम्बन्ध में मध्य दर्जा के लगभग सह-सम्बन्ध पाया जाता है। परिणाम में पूर्ण सहमति नहीं है।