PSEB 12th Class Maths Solutions Chapter 11 Three Dimensional Geometry Ex 11.3

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 11 Three Dimensional Geometry Ex 11.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 11 Three Dimensional Geometry Ex 11.3

Question 1.
In each of the following cases, determine the direction cosines of the normal to the plane and the distance from the origin.
(a) z = 2
(b) x + y + z = 1
(c) 2x + 3y – z = 5
(d) 5y + 8 = 0
Solution.
(a) The equation of the plane is z = 2 or 0x + 0y + z = 2 ……………..(i)
The direction ratios of normal are 0, 0 and 1.
∴ \(\sqrt{0^{2}+0^{2}+1^{2}}\) = 1
Dividing both sides of equation (i) by 1, we get
0 . x + 0 . y + 1 . z = 2
This is of the form lx + my + nz = d, where 1, m, n are the direction cosines of normal to the plane and d is the distance of the perpendicular drawn from the origin.
Therefore, the direction cosines are 0, 0 and 1 and the distance of the plane from the origin is 2 units.

(b) x + y + z = 1 ……………..(i)
The direction ratios of normal are 1, 1 and 1.
∴ \(\sqrt{(1)^{2}+(1)^{2}+(1)^{2}}\) = √3
Dividing both sides of equation (1) by we get
\(\frac{1}{\sqrt{3}} x+\frac{1}{\sqrt{3}} y+\frac{1}{\sqrt{3}} z=\frac{1}{\sqrt{3}}\) ………………(ii)
This equation is of the form lx + my + nz = d, where l, m, n are the direction cosines of normal to the plane and d is the distance of normal from the origin.
Therefore, the direction cosines of the normal are and and the \(\frac{1}{\sqrt{3}}\), \(\frac{1}{\sqrt{3}}\), \(\frac{1}{\sqrt{3}}\) distance of normal from the origin is \(\frac{1}{\sqrt{3}}\) units.

(c) 2x + 3y – z = 5 ………………(i)
The direction ratios of normal are 2, 3 and – 1.
∴ \(\sqrt{(2)^{2}+(3)^{2}+(-1)^{2}}=\sqrt{14}\)
Dividing both sides of equation (i) by √14, we get

\(\frac{2}{\sqrt{14}} x+\frac{3}{\sqrt{14}} y-\frac{1}{\sqrt{14}} z=\frac{5}{\sqrt{14}}\)

This equation is of the form lx + my + nz = d, where l, m, n are the direction cosines of normal to the plane and d is the distance of normal from the origin.

Therefore, the direction cosines of the normal are \(\frac{2}{\sqrt{14}}\), \(\frac{3}{\sqrt{14}}\) and \(\frac{- 1}{\sqrt{14}}\) and the distance of normal from the origin is \(\frac{5}{\sqrt{14}}\) units.

(d) 5y + 8 = 0
⇒ 0x – 5y + 0z = – 8 ………………..(i)
The direction ratios of normal are 0, – 5 and 0.
∴ \(\sqrt{0+(-5)^{2}+0}\) = 5
Dividing both sides of equation (i) by 5, we get – y = \(\frac{8}{5}\)
This equation is of the form lx + my + nz = d, where l, m, n are the direction cosines of normal to the plane and d is the distance of normal from the origin.
Therefore, the direction cosines of the normal to the plane are 0,- 1 and 0 and the distance of normal from the origin is \(\frac{8}{5}\) units.

Question 2.
Find the vector equation of a plane which is at a distance of 7 units from the origin and normal to the vector 3î + 5ĵ – 6k̂.
Solution.
The normal vector is, \(\vec{n}\) = 3î + 5ĵ – 6k̂

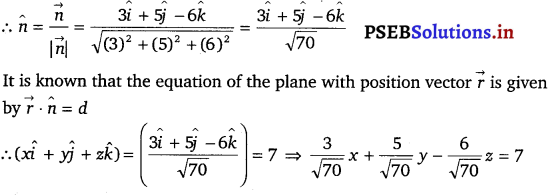
This is the vector equation of the required plane.

Question 3.
Find the Cartesian equation of the following planes
(a) \(\vec{r}\) (î + ĵ – k̂) = 2
(b) \(\vec{r}\) (2î + 3ĵ – 4k̂) = 1
(c) \(\vec{r}\) [(s – 2t) î + (3 – t) ĵ + (2s + t) k̂] = 15
Solution.
(a) It is given that equation of the plane is \(\vec{r}\) (î + ĵ – k̂) = 2 …………. (i)
For any arbitrary point P(x, y, z) on the plane, position vector \(\vec{r}\) is given by,
\(\vec{r}\) = xî + yĵ – zk̂
Substituting the value, of \(\vec{r}\) in equation (i), we get
(xî + yĵ – zk̂) (î + ĵ- k̂) = 2
⇒ x + y – z = 2
This is the Cartesian equation of the plane.

(b) Given vector equation is \(\vec{r}\) . (2î +3ĵ – 4k̂) = 1
For any arbitrary point P(x, y, z) on the plane, position vector \(\vec{r}\) is given by
\(\vec{r}\) = xî + yĵ – zk̂
Substituting the value of r in equation (i), we get
(xî + yĵ – zk̂ ) . (2î +3ĵ – 4k̂) = 1
⇒ 2x + 3y – 4z = 1
This is the Cartesian equation of the plane.

(c) Given vector equation is \(\vec{r}\) . [(s – 2t) î + (3 – t ) ĵ + (2s + t) k̂] = 15 ………….. (i)
For any arbitrary point P (x, y, z) on the plane, position vector is given by
\(\vec{r}\) = xî + yĵ – zk̂
Substituting the value, of in equation (i), we get
(xî + yĵ – zk̂) . [(s – 2t) î + (3 – t) k̂ + (2s + t) k̂] = 15
⇒ (s – 2t) x + (3 – t) y + (2s + t) z = 15
This is the Cartesian equation of the plane.

Question 4.
In the following cases, find the coordinates of the foot of the perpendicular drawn from the origin.
(a) 2x + 3y + 4z – 12 = 0
(b) 3y + 4z – 6 = 0
(c) x + y + z = 1
(d) 5y + 8 = 0
Solution.
(a) Let the coordinates of the foot of perpendicular P from the origin to the plane be (x, y, z).
2x + 3y + 4z – 12 = 0
⇒ 2x + 3y + 4z = 12 ………..(i)
The direction ratios of normal are 2, 3 and 4.
∴ \(\sqrt{(2)^{2}+(3)^{2}+(4)^{2}}=\sqrt{29}\)

Dividing both sides of equation (i) by we get
∴ \(\frac{2}{\sqrt{29}} x+\frac{3}{\sqrt{29}} y+\frac{4}{\sqrt{29}} z=\frac{12}{\sqrt{29}}\)

This equation is of the form lx + my + nz = d, where 1, m, n are the direction cosines of normal to the plane and d is the distance of normal from the origin.

The coordinates of the foot of the perpendicular are given by (ld, md, nd)
Therefore, the coordinates of the foot of perpendicular are
\(\left(\frac{2}{\sqrt{29}}, \frac{12}{\sqrt{29}}, \frac{3}{\sqrt{29}}, \frac{12}{\sqrt{29}}, \frac{4}{\sqrt{29}}, \frac{12}{\sqrt{29}}\right)\) i.e., \(\left(\frac{24}{29}, \frac{36}{49}, \frac{48}{29}\right)\).

(b) Let the coordinates of the foot of perpendicular P from the origin to the plane be (x₁, y₁, z₁).
3y + z – 6 = 0
⇒ 0x + 3y + 4z = 6 ………………(i)
The direction ratios of normal are 0, 3 and 4.
∴ \(\sqrt{0+3^{2}+4^{2}}\) = 5
Dividing the both sides of equation (i) by 5, we get
0 . x + \(\frac{3}{5}\) y + \(\frac{4}{5}\) z = \(\frac{6}{5}\)
This equation is of the form lx + my + nz = d, where l, m, n are the direction cosines of normal to the plane and d is the distance of normal from the origin.
The coordinates of the foot of the perpendicular are given by (ld, md, nd).
Therefore, the coordinates of the foot of the perpendicular are \(\left(0, \frac{3}{5} \cdot \frac{6}{5}, \frac{4}{5} \cdot \frac{6}{5}\right)\) i.e., \(\left(0, \frac{18}{25}, \frac{24}{25}\right)\)

(c) Let the coordinates of the foot of perpendicular P from the origin to the plane be (x₁, y₁, z₁).
x + y + z = 1 ………………(i)
The direction ratios of normal are 1, 1 and 1.
∴ \(\sqrt{1^{2}+1^{2}+1^{2}}=\sqrt{3}\)

Dividing the both sides of equation (i) by √3, we get
\(\frac{1}{\sqrt{3}} x+\frac{1}{\sqrt{3}} y+\frac{1}{\sqrt{3}} z=\frac{1}{\sqrt{3}}\)

This equation is of the form lx + my + nz = d, where l, m, n are the direction cosines of normal to the plane and d is the distance of normal from the origin.

The coordinates of the foot of the perpendicular are given by (ld, md, nd).
Therefore, the coordinates of the foot of the perpendicular are \(\left(\frac{1}{\sqrt{3}} \cdot \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}} \cdot \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}} \cdot \frac{1}{\sqrt{3}}\right)\) i.e., \(\left(\frac{1}{3}, \frac{1}{3}, \frac{1}{3}\right)\).

(d) Let the coordinates of the foot of perpendicular P from the origin to the plane be (x₁, y₁, z₁).
5y + 8 = 0
⇒ 0 . x – 5y + 0 . z = 8 ……………(i)
The direction ratios of normal are 0, – 5 and 0.
∴ \(\sqrt{0+(-5)^{2}+0}\) = 5
Dividing both sides of equation (i) by 5, we get
– y = \(\frac{8}{5}\)
This equation is of the form lx + my + nz = d, where l, m, n are the direction cosines of normal to the plane and d is the distance of normal from the origin.
The coordinates of the foot of the perpendicular are given by (ld, md, nd) Therefore, the coordinates of the foot of the perpendicular are (0, – 1 (\(\frac{8}{5}\), 0) i.e., (0, – \(\frac{8}{5}\), 0).

Question 5.
Find the vector and Cartesian equations of the planes
(a) that passes through the point (1, 0, – 2) and the normal to the plane is î + ĵ – k̂.
(b) that passes through the point (1, 4, 6) and the normal vector to the plane is î – 2 ĵ + k̂.
Solution.
(a) The position vector of point (1, 0, – 2) is \(\vec{a}\) = î – 2 k̂
The normal vector N perpendicular to the plane is \(\vec{N}\) = î + ĵ – k̂
The vector equation of the plane is given by, \((\vec{r}-\vec{a}) \cdot \vec{N}\) = 0
⇒ [\(\vec{r}\) – (î – 2k̂)] . (î + ĵ – k̂) = 0 ……………(i)
\(\vec{r}\) is the position vector of any point P(x, y, z) in the plane.
∴ \(\vec{r}\) = xî + yĵ + zk̂
Therefore, equation (i) becomes
[(xî + yĵ + zk̂) – (î – 2k̂) . {î + ĵ – k̂) = 0
⇒ [(x – 1)î + yĵ + (z + 2)k̂] . (î + ĵ – k̂) = 0
⇒ (x – 1) + y – (z + 2) = 0
⇒ x + y – z – 3 = 0
⇒ x + y – z = 3
This is the Cartesian equation of the required plane.

(b) The position vector of the point (1, 4, 6) is \(\vec{a}\) = î + 4ĵ + 6k̂
The normal vector N perpendicular to the plane is \(\vec{N}\) = î – 2ĵ + k̂
The vector equation of the plane is given by, (\(\vec{r}\) – \(\vec{a}\)) . \(\vec{N}\) = 0
⇒ [\(\vec{r}\) – ( î + 4ĵ + 6k̂)] + 4; +6fc)] . (î – 2ĵ + k̂ ) = 0 ……………(i)
\(\vec{r}\) is the position vector of any point P(x, y, z) in the plane.
∴ \(\vec{r}\) = xî + yĵ + zk̂
Therefore, equation (i) becomes
[(xî + yĵ + zk̂) – (î + 4ĵ + 6k̂)] (î – 2ĵ + k̂) = 0
⇒ [(x – 1)î +(y – 4)ĵ + (z – 6)k̂] . (î – 2ĵ + k̂) = 0
⇒ (x – 1) – 2 (y – 4) + (z – 6) = 0
⇒ x – 2y + z + 1 = 0
This is the Cartesian equation of the required plane.

Question 6.
Find the equations of the planes that passes through three points.
(a) (1, 1, – 1), (6, 4, – 5), (- 4, – 2, 3)
(b) (1, 1, 0),(1, 2, 1), (- 2, 2, – 1)
Solution.
Solution.
(a) The given points are A(1, 1, – 1), B(6, 4, – 5) and C(- 4, – 2, 3).
\(\left|\begin{array}{ccc}
1 & 1 & -1 \\
6 & 4 & -5 \\
-4 & -2 & 3
\end{array}\right|\) =(12 – 10) – (18 – 20) – (- 12 + 16)
= 2 + 2 – 4 = 0
Since, A, B, C are collinear points, there will be infinite number of planes passing through the given points.

(b) The given points are A(1, 1, 0), B(1, 2, 1) and C(- 2, 2, – 1)
\(\left|\begin{array}{ccc}
1 & 1 & 0 \\
1 & 2 & 1 \\
-2 & 2 & -1
\end{array}\right|\) = (- 2 – 2) – (2 + 2) = – 8 ≠ 0
Therefore, a plane will pass through the points A, B and C.
It is known that the equation of the plane through the points, (x₁, y₁, z₁),
(x₂, y₂, z₂)and (x₃, y₃, z₃) is

\(\left|\begin{array}{ccc}
x-x_{1} & y-y_{1} & z-z_{1} \\
x_{2}-x_{1} & y_{2}-y_{1} & z_{2}-z_{1} \\
x_{3}-x_{1} & y_{3}-y_{1} & z_{3}-z_{1}
\end{array}\right|\) = 0

\(\left|\begin{array}{ccc}
x-1 & y-1 & z \\
0 & 1 & 1 \\
-3 & 1 & -1
\end{array}\right|\) = 0
⇒ (- 2) (x – 1) – 3 (y – 1) + 3z = 0
⇒ – 2x – 3y + 3z + 2 + 3 = 0
⇒ – 2x – 3y + 3z = – 5
⇒ 2x + 3y – 3z = 5
This is the Cartesian equation of the required plane.

Question 7.
Find the intercepts cut off by the plane 2x + y – z = 5.
Sol.
Given plane, 2x + y – z = 5 ……………(i)
Dividing both sides of equation (i) by 5, we get
\(\frac{2}{5} x+\frac{y}{5}-\frac{z}{5}\) = 1

\(\frac{x}{\frac{5}{2}}+\frac{y}{5}+\frac{z}{-5}\) = 1 ………………….(ii)

It is known that the equation of a plane in intercept form is \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\) = 1,
where a, b, c are the intercepts cut off by the plane at x, y and z axes respectively.
Therefore, for the given equation, a = \(\frac{5}{2}\), b = 5 and c = – 5.

Question 8.
Find the equation of the plane with intercept 3 on the y-axis and parallel to ZOX plane.
Solution.
The equation of the plane ZOX is y = 0
Any plane parallel to it is of the form, y = a
Since, the y-intercept of the plane is 3,
∴ a = 3
Thus, the equation of the required plane y = 3.

Question 9.
Find the equation of the plane through the intersection of the planes 3x – y + 2z – 4 = 0 and x + y + z – 2 = 0 and the point (2, 2, 1).
Solution.
The equation of any plane through the intersection of the planes, 3x – y + 2z – 4 = 0 and x + y + z- 2 = 0 is
(3x- y + 2z – 4) + α (x + y + z -2) = 0 where α ∈ R ……………..(i)
The plane passes through the point (2, 2, 1).
Therefore, this point will satisfy equation (i).
∴ (3 × 2 – 2 + 2 × 1 – 4) + α (2 + 2 + 1 – 2) = 0
⇒ 2 + 3α = 0
⇒ α = – \(\frac{2}{3}\)
Substituting α = – \(\frac{2}{3}\) in equation (i), we get
(3x – y + 2z – 4) – \(\frac{2}{3}\) (x + y + z – 2) = 0
⇒ 3 (3x -y + 2z – 4) – 2 (x + y + z – 2) = 0
⇒ (9x – 3y + 6z – 12) – 2(x + y + z – 2) = 0
⇒ 7x – 5y + 4z – 8 = 0
This is the required equation of the plane.

Question 10.
Find the vector equation of the plane passing through the intersection of the planes \(\overrightarrow{\boldsymbol{r}}\) . (2î + 7ĵ – 3k̂) = 7, \(\overrightarrow{\boldsymbol{r}}\) . (2î + 5ĵ + 3k̂) = 9 and through the point (2,1, 3).
Solution.
The equations of the planes are \(\overrightarrow{\boldsymbol{r}}\) . (2î + 7ĵ – 3k̂) = 7 and \(\overrightarrow{\boldsymbol{r}}\) . (2î + 5ĵ + 3k̂) = 9

⇒ \(\overrightarrow{\boldsymbol{r}}\) . (2î + 2ĵ – 3k̂) – 7 = 0 …………..(i)

⇒ \(\overrightarrow{\boldsymbol{r}}\) . (2î + 5ĵ + 3k̂) – 9 = 0 …………..(ii)

The equation of any plane through the intersection of the planes given in equations (i) and (ii) is given by
⇒ [\(\vec{r}\) . (2î + 2ĵ – 3k̂)] – 7] + λ [\(\vec{r}\) . (2î + 5ĵ + 3k̂) – 9] = 0, where λ ∈ R
\(\vec{r}\) . [(2î + 2ĵ – 3k̂) + λ (2î + 5ĵ + 3k̂)] = 9λ. + 7
\(\vec{r}\) . [(2 + 2λ) î + (2 + 5λ) ĵ + (3λ – 3) k̂] = 9λ + 7 ………………(iii)
The plane passes through the point (2, 1, 3).
Therefore, its position vector is given by, \(\vec{r}\) = 2î + 2ĵ – 3k̂
Substituting in equation (iii), we get
(2î + ĵ – 3k̂) . [(2 + 2λ)î + (2 + 5λ)ĵ + (3λ – 3)k̂] = 9λ + 7
(2 + 2λ) + (2 + 5λ) + (3λ – 3) = 9λ + 7
⇒ 18λ – 3 = 9λ + 7
⇒ 9λ = 10
⇒ λ = \(\frac{10}{9}\)
Substituting λ = \(\frac{10}{9}\) in equation (iii), we get
\(\vec{r} \cdot\left(\frac{38}{9} \hat{i}+\frac{68}{9} \hat{j}+\frac{3}{9} \hat{k}\right)\) = 17
⇒ \(\vec{r}\) = (38î +68ĵ + 3k̂) = 153
This is the vector equation of the required plane.

Question 11.
Find the equation of the plane through the line of intersection of the planes x + y + z = 1 and 2x + 3y + 4z = 5 which is perpendicular to the plane x – y + z = 0.
Solution.
The equation of the plane through the intersection of the planes, x + y + z = 1 and 2x + 3y + 4z = 5 is
(x + y + z – 1) + λ (2x + 3y + 4z – 5) = 0
⇒ (2λ + 1) x + (3λ + 1) y + (4λ + 1) z – (5λ + 1) = 0 ……………..(i)
The direction ratios, a₁, b₁, c₁ of this plane are (2λ + 1), (3λ + 1) and (4λ + 1).
The plane in equation (i) is perpendicular to x – y + z = 0
Its direction ratios, a₂, b₂, c₂ are 1, – 1 and 1.
Since the planes are perpendicular, a₁a₂ + b₁b₂ + c₁c₂ = 0
⇒ (2λ + 1) – (3λ + 1) + (4λ + 1) = 0
⇒ 3λ + 1 = 0
⇒ λ = – \(\frac{1}{3}\)
Substituting λ = – \(\frac{1}{3}\) in equation (i), we get
\(\frac{1}{3} x-\frac{1}{3} z+\frac{2}{3}\) = 0
⇒ x – z + 2 = 0
This is the required equation of the plane.

Question 12.
Find the angle between the planes whose vector equations are \(\overrightarrow{\boldsymbol{r}}\) . (2î + 3ĵ – 3k̂) = 5 and \(\overrightarrow{\boldsymbol{r}}\) . (3î – 3ĵ + 5k̂) = 3.
Solution.
We know that the angle 0 between the planes

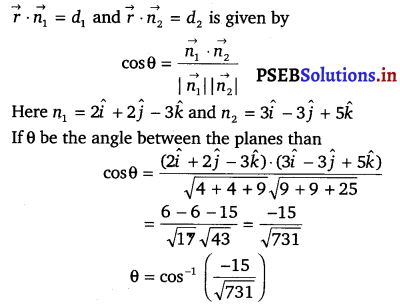
Question 13.
In the following cases, determine whether the given planes are parallel or perpendicular, and in case they are neither, find the angles between them.
(a) 7x + 5y + 6z + 30 = 0 and 3x – y – 10z + 4=0
(b) 2x + y + 3z – 2 = 0 and x – 2y + 5 = 0
(c) 2x – 2y + 4z + 5 = 0 and 3x – 3y + 62 -1 = 0
(d) 2x – y + 3z – 1 = 0 and 2x – y + 3z + 3 = 0
(e) 4x + 8y + z – 8 = 0 and y + z – 4 = 0
Solution.
(a) The equations of the planes are 7x + 5y + 6z + 30 = 0 and 3x – y – 10z + 4 = 0
Here, a₁ = 7, b₁ = 5, c₁ = 6 and a₂ = 3, b₂ = – 1, c₂ = – 10
∴ a₁a₂ + b₁b₁ + c₁c₂ = 7 × 3 + 5 × (- 1) + 6 × (- 10) = – 44 ≠ 0
Therefore, the given planes are not perpendicular each other

(b) The equations of the planes are 2x + y + 3z – 2 = 0 and x – 2y + 5 = 0
Here, a₁ = 2, b₁ = 1, c₁ = 3 and a₂ = 1, b₂ = – 2, c₂ = 0
∴ a₁a₂ + b₁b₂ + c₁c₂ = 2 × 1 + 1 × (- 2) + 3 × 0 = 0
Therefore, the given planes are perpendicular to each other.

(c) The equations of the planes are 2x – 2y + 4z + 5 = 0 and 3x – 3y + 6z – 1 = 0
Here, a₁ = 2, b₁ = – 2, c₁ = 4 and a₂ = 3, b₂ = – 3, c₂ = 6
∴ a₁a₂ + b₁b₂ + c₁c₂ = 2 × 3 + (- 2) (- 3) + 4 × 6
= 6 + 6 + 24 = 36 ≠ 0
Thus, the given planes are not perpendicular to each other.

(d) The equation of the planes are 2x – y + 3z – 1 = 0 and 2x – y + 3z + 3 = 0
Here, a₁ = 2, b₁ = – 1, C₁ = 3 and a₂ = 2, b₂ = – 1, c₂
∴ a₁a₂ + b₁b₂ + c₁c₂ = 2 × 2 + (- 1) × (- 1) + 3 × 3 = 14 ≠ 0
Thus, the given planes are not perpendicular to each other.
\(\frac{a_{1}}{a_{2}}=\frac{2}{2}\) = 1,

\(\frac{b_{1}}{b_{2}}=\frac{-1}{-1}\) = 1 and

\(\frac{c_{1}}{c_{2}}=\frac{3}{3}\) = 1

∴ \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
Thus, the given lines are parallel to each other.

(e) The equations of the planes are 4x + 8y + z – 8 = 0 and y + z – 4 = 0
Here a₁ = 4, b₁ = 8, c₁ = 1 and a₂ = 0, b₂ = 1, c₂ = 1
a₁a₂ + b₁b₂ + c₁c₂ = 0
Therefore, the given lines are not perpendicular to each other.
\(\frac{a_{1}}{a_{2}}=\frac{4}{0}\),

\(\frac{b_{1}}{b_{2}}=\frac{8}{1}\) = 8,

\(\frac{c_{1}}{c_{2}}=\frac{1}{1}\) = 1,

∴ \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
Therefore, the given lines are not parallel to each other.
The angle between the planes is given by,
θ = cos^-1 \(\left|\frac{4 \times 0+8 \times 1+1 \times 1}{\sqrt{4^{2}+8^{2}+1^{2}} \times \sqrt{0^{2}+1^{2}+1^{2}}}\right|\)

θ = cos^-1 \(\left|\frac{9}{9 \times \sqrt{2}}\right|\)

θ = cos^-1 \(\left(\frac{1}{\sqrt{2}}\right)\)

θ = 45.

Question 14.
In the following cases, find the distance of each of the given points from the corresponding given plane.

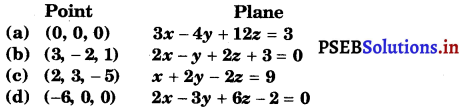
Solution.
We know that the distance between a point P(x₁, y₁, z₁) and a plane, Ax + By + Cz = D, is given by
d = \(\left|\frac{A x_{1}+B y_{1}+C z_{1}-D}{\sqrt{A^{2}+B^{2}+C^{2}}}\right|\) …………………(i)

(a) The given point is (0, 0, 0) and the plane is 3x – 4y + 12z = 3

∴ d = \(\left|\frac{3 \times 0-4 \times 0+12 \times 0-3}{\sqrt{(3)^{2}+(-4)^{2}+(12)^{2}}}\right|=\frac{3}{\sqrt{169}}=\frac{3}{13}\)

(b) The given point is(3,- 2, 1) and the plane is 2x – y + 2z – 3 = 0

∴ d = \(\left|\frac{2 \times 3-(-2)+2 \times 1+3}{\sqrt{(2)^{2}+(-1)^{2}+(2)^{2}}}\right|=\left|\frac{13}{3}\right|=\frac{13}{3}\)

(c) The given point is (2, 3, – 5) and the plane is x + 2y – 2z = 9

∴ d = \(\left|\frac{2+2 \times 3-2(-5)-9}{\sqrt{(1)^{2}+(2)^{2}+(-2)^{2}}}\right|=\frac{9}{3}\) = 3

(d) The given point is (- 6, 0, 0) and the plane is lx – 3y + 6z – 2 = 0.

∴ d = \(\left|\frac{2(-6)-3 \times 0+6 \times 0-2}{\sqrt{(2)^{2}+(-3)^{2}+(6)^{2}}}\right|=\left|\frac{-14}{\sqrt{49}}\right|=\frac{14}{7}\) = 2