Punjab State Board PSEB 5th Class Maths Book Solutions Chapter 4 Fractions Ex 4.4 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 5 Maths Chapter 4 Fractions Ex 4.4
Question 1.
Check whether the following fractions are in its lowest form or not :
(a) \(\frac{12}{14}\)
(b) \(\frac{21}{3}\)
(c) \(\frac{13}{17}\)
(d) \(\frac{25}{50}\)
(e) \(\frac{14}{21}\)
(f) \(\frac{8}{13}\)
(g) \(\frac{7}{15}\)
(h) \(\frac{14}{27}\)
(i) \(\frac{25}{35}\)
(j) \(\frac{18}{23}\)
Solution:
(a) To find whether the fraction \(\frac{12}{14}\) is in its lowest term or not, we will find the HCF of 12 and 14.
Now, HCF of 12 and 14 = 2
Because the HCF of numerator and denominator is not 1.
∴ The fraction is not in its lowest term. To change the fraction into its lowest term, we will divide the numerator (12) and denominator (14) by HCF (2)
Fraction = \(\frac{12}{14}\) = \(\frac{12 \div 2}{14 \div 2}\) = \(\frac{6}{7}\)
∴ The lowest form of \(\frac{12}{14}\) is \(\frac{6}{7}\).
(b) To find whether the fraction \(\frac{21}{35}\) in its lowest term or not, we will find the HCF of 21 and 35 Now, HCF of 21 and 35 = 7
Now, HCF of 21 and 35 = 7

Because the HCF of numerator and denominator is not 1
∴ The fraction is not in its lowest terms. To change the fraction into its lowest terms, we will divide the numerator (21) and denominator (35) by their HCF (7)
Fraction = \(\frac{21}{35}\) = \(\frac{21 \div 7}{35 \div 7}\) = \(\frac{3}{5}\)
∴ The lowest form of \(\frac{21}{35}\) is \(\frac{3}{5}\)
(c) To find whether the fraction \(\frac{13}{17}\) is in its lowest terms or not, we will find the HCF of 13 and 17 Now, HCF of 13 and 17 = 1
Therefore, the fraction \(\frac{13}{17}\) is in its lowest terms.
(d) To find whether the fraction \(\frac{25}{50}\) is in its lowest terms or not, we will find the HCF of 25 and 50.
Now, HCF of 25 and 50 = 25
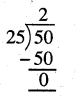
Because, the HCF of numerator and denominator is not 1, therefore, the fraction is not in its lowest terms. To change the fraction into its lowest terms, we will divide the numerator (25) and denominator (50) by their HCF (25)
Fraction = \(\frac{25}{50}\) = \(\frac{25 \div 25}{50 \div 25}\) = \(\frac{1}{2}\)
∴The lowest form of \(\frac{25}{50}\) is \(\frac{1}{2}\)
(e) In \(\frac{14}{21}\), HCF of numerator (14) and denominator (21) = 7

The fraction \(\frac{14}{21}\) is not in its lowest terms because HCF of numerator (14) and denominator (21) is not 1. To change, the fraction, into its lowest terms we will divide the numerator (14) and denominator (21) by their HCF (7)
\(\frac{14}{21}\) = \(\frac{14 \div 7}{21 \div 7}\) = \(\frac{2}{3}\)
∴ The lowest form of fraction \(\frac{14}{21}\) is \(\frac{2}{3}\).
(f) To find whether the fraction \(\frac{8}{13}\) is in its lowest terms or not, we will find the HCF of numerator (8) and denominator (13)
Now, HCF of 8 and 13 = 1

Therefore, the fraction \(\frac{8}{13}\) is in its lowest form.
(g) To find whether the fraction \(\frac{7}{15}\) is in its lowest terms or not, we will find the HCF of numerator 7 and denominator 15.
Now, HCF of 7 and 15 = 1
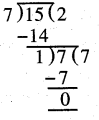
Therefore, the fraction is in its lowest form.
(h) To find whether the fraction \(\frac{14}{27}\) is in its lowest terms or not, we will find the HCF of numerator (14) and denominator (27).
Now, HCF of 14 and 27 = 1

Therefore, the fraction \(\frac{14}{27}\) is in its lowest terms.
(i) To find whether the fraction \(\frac{25}{35}\) is in its lowest term or not, we will find the HCF of numerator (25) and denominator (35).
Now, the HCF of 25 and 35 = 5

Because, the HCF of numerator and denominator is not 1, therefore, the fraction \(\frac{25}{35}\) is not m its lowest terms.
To change the fraction into its lowest terms, we will divide the numerator and denominator by their HCF (5).
\(\frac{25}{35}\) = \(\frac{25 \div 5}{35 \div 5}\) = \(\frac{5}{7}\)
Therefore, the lowest form of \(\frac{25}{35}\) is \(\frac{5}{7}\).
(j) To find whether the fraction \(\frac{18}{23}\) is in its lowest terms or not, we will find the HCF of numerator (18) and denominator (23).
Now, HCF of 18 and 23 = 1

Therefore, the fraction \(\frac{18}{23}\) is in its lowest terms.
![]()
Question 2.
Write the lowest form of following fractions :
(a) \(\frac{4}{8}\)
(b) \(\frac{12}{18}\)
(c) \(\frac{15}{20}\)
(d) \(\frac{35}{45}\)
(e) \(\frac{24}{36}\)
(f) \(\frac{8}{12}\)
(g) \(\frac{18}{21}\)
(h) \(\frac{25}{45}\)
(i) \(\frac{6}{12}\)
(j) \(\frac{9}{27}\)
Solution:
(a) HCF of 4 and 8 = 4
Therefore, the lowest form of \(\frac{4}{8}\)
= \(\frac{4 \div 4}{8 \div 4}\) = \(\frac{1}{2}\)
(b) HCF of 12 and 18 = 6
Therefore, the lowest form of \(\frac{12}{18}\)
= \(\frac{12 \div 6}{18 \div 6}\) = \(\frac{2}{3}\)
(c) HCF of 15 and 20 = 5
Therefore, the lowest form of \(\frac{15}{20}\)
= \(\frac{15 \div 5}{20 \div 5}\) = \(\frac{3}{4}\)
(d) HCF of 35 and 45 = 5
Therefore, the lowest form of \(\frac{35}{45}\)
= \(\frac{35 \div 5}{45 \div 5}\) = \(\frac{7}{9}\)
(e) HCF of 24 and 36 = 12
Therefore, the lowest form of \(\frac{24}{36}\)
= \(\frac{24 \div 12}{36 \div 12}\) = \(\frac{2}{3}\)
(f) HCF of 8 and 12 = 4
Therefore, the lowest form of \(\frac{8}{12}\)
= \(\frac{8 \div 4}{12 \div 4}\) = \(\frac{2}{3}\)
(g) HCF of 18 and 21 = 3
Therefore, the lowest form of \(\frac{18}{21}\)
= \(\frac{18 \div 3}{21 \div 3}\) = \(\frac{6}{7}\)
(h) HCF of 25 and 45 = 5
Therefore, the lowest form of \(\frac{25}{45}\)
= \(\frac{25 \div 5}{45 \div 5}\) = \(\frac{5}{9}\)
(i) HCF of 6 and 12 = 6
Therefore, the lowest form of \(\frac{6}{12}\)
= \(\frac{6 \div 6}{12 \div 6}\) = \(\frac{1}{2}\)
(j) HCF of 9 and 27 = 9
Therefore, the lowest form of \(\frac{9}{27}\)
= \(\frac{9 \div 9}{27 \div 9}\) = \(\frac{1}{3}\)
