Punjab State Board PSEB 11th Class Economics Book Solutions Chapter 25 अपकिरण के माप Textbook Exercise Questions, and Answers.
PSEB Solutions for Class 11 Economics Chapter 25 अपकिरण के माप
PSEB 11th Class Economics अपकिरण के माप Textbook Questions and Answers
I. वस्तुनिष्ठ प्रश्न (Objective Type Questions)
प्रश्न 1.
अपकिरण (Dispersion) किसे कहते हैं ?
उत्तर-
संख्यात्मक आंकड़े एक माध्य मूल्य के दोनों ओर फैलने की जिस सीमा तक प्रवृत्ति रखते हैं, उस सीमा को उन आंकड़ों का विचरण या अपकिरण कहते हैं।
प्रश्न 2.
प्रमाप विचलन (Standard Deviation) की एक विशेषता लिखिए।
उत्तर-
प्रमाप विचलन के अन्तर्गत मूल्यों से विचलन सदैव समान्तर माध्य से ही लिए जाते हैं क्योंकि यह माध्य केन्द्रीय प्रवृत्ति का सर्वश्रेष्ठ माप समझा जाता है। माध्यका एवं भूयिष्ठक का प्रयोग नहीं किया जाता है।
प्रश्न 3.
प्रमाप विचलन (Standard Deviation) किसे कहते हैं?
उत्तर-
प्रमाप विचलन किसी श्रेणी के विभिन्न पदों के समान्तर माध्य से लिए गए विचलन के वर्गों का समान्तर माध्य वर्गमूल होता है।
प्रश्न 4.
विचरण गुणांक का प्रयोग किस लिए किया जाता है?
उत्तर-
विचरण गुणांक का प्रयोग दो श्रेणियों की विचरणशीलता, स्थिरता, एकरूपता तथा संगति (Consistency) की तुलना करने के लिए किया जाता है।
प्रश्न 5.
माध्य विचलन से क्या अभिप्राय है?
उत्तर-
एक श्रृंखला के किसी माध्य से निकाले गये विचलनों के जोड़ को समान्तर माध्य विचलन कहा जाता है।
प्रश्न 6.
विचरण गुणांक (Co-efficient of Variation) किसे कहते हैं?
उत्तर-
दो या दो से अधिक श्रृंखलाओं में अपकिरण (Dispersion) या विचरण (Variation) की तुलना करने के लिए विचरण गुणांक का प्रयोग किया जाता है। यह विचरण का सापेक्ष (Relative) माप है।

प्रश्न 7.
प्रमाप विचलन के दो लाभ लिखिए।
उत्तर-
- सभी मूल्यों पर आधारित प्रमाप विचलन श्रृंखला के सभी मूल्यों पर आधारित है। इसमें किसी मूल्य की अवहेलना नहीं की जाती।
- स्पष्ट व निश्चित माप-प्रमाप विचलन अपकिरण का एक स्पष्ट व निश्चित माप है जो प्रत्येक स्थिति में ज्ञात किया जा सकता है।
प्रश्न 8.
लारेन्ज़ वक्र क्या है?
उत्तर-
लारेन्ज़ वक्र, समान रेखा से वास्तविक वितरण के विचलन का बिन्दु रेखीय माप है। लारेन्ज़ वक्र एक संचयी प्रतिशत वक्र होता है।
प्रश्न 9.
किसी श्रेणी की भिन्न-भिन्न मदों में तथा उनका औसत से कितना अन्तर है इसको …………. कहते हैं।
(a) औसत विचलन
(b) प्रमाप विचलन
(c) अपकिरण
(d) उपरोक्त सभी।
उत्तर-
(c) अपकिरण।
प्रश्न 10.
अपकिरण को. ……………… श्रेणी का माप कहा जाता है।
(a) पहली
(b) दूसरी
(c) तीसरी
(d) चौथी।
उत्तर-
(b) दूसरी।
प्रश्न 11.
श्रेणी की समान्तर औसत, माध्यका तथा बहुलक से लिए गए भिन्न-भिन्न मूल्यों से विचलन की औसत को ……………….. कहते हैं।
उत्तर-
मध्य विचलन।
प्रश्न 12.
किसी श्रेणी के भिन्न-भिन्न मूल्यों की समान्तर औसत से लिए गए विचलनों की समान्तर औसत को ……………….. कहते हैं।
(a) माध्य विचलन
(b) प्रमाप विचलन
(c) विचलन गुणांक
(d) उपरोक्त कोई नहीं।
उत्तर-
(b) प्रमाप विचलन।
प्रश्न 13.
माध्य विचलन को समान्तर औसत, माध्यका अथवा बहुलक की सहायता से मापते हैं जबकि प्रमाप विचलन को ……………… की सहायता से मापते हैं।
(a) समान्तर औसत
(b) माध्यका
(c) बहुलक
(d) उपरोक्त सभी।
उत्तर-
(a) समान्तर औसत।
प्रश्न 14.
दो श्रेणियों के उपकिरण की तुलना के लिए सापेक्ष माप को …………… कहते हैं।
उत्तर-
विचलन गुणांक।
प्रश्न 15.
अपकिरण के माप की दो मुख्य किस्में बताएं।
उत्तर-
- निरपेक्ष माप
- सापेक्ष माप।
प्रश्न 16.
विस्तार से क्या अभिप्राय है ?
उत्तर-
किसी श्रेणी के सबसे बड़े और सब से छोटे मूल्य के अन्तर को विस्तार कहते हैं।
प्रश्न 17.
चतुर्थक विचलन का माप सूत्र लिखें।
उत्तर-
चतुर्थक विचलन = \(\frac{\mathrm{Q}_{3}-\mathrm{Q}_{1}}{2}\)
प्रश्न 18.
चतुर्थक विचलन गुणांक का सूत्र लिखें।
उत्तर:-
चतुर्थक विचलन गुणाक = \(\frac{\mathrm{Q}_{3}-\mathrm{Q}_{1}}{\mathrm{Q}_{3}+\mathrm{Q}_{1}}\)
प्रश्न 19.
लारेन्ज़ वक्र से क्या अभिप्राय है ?
उत्तर-
लारेन्ज़ वक्र वह वक्र है जो कि वास्तविक वितरण का विचलन सम्मान वितरण रेखा पर दिखाता है।
प्रश्न 20.
लारेन्ज़ वक्र का प्रयोग सबसे पहले किसने किया था ?
उत्तर-
डॉक्टर मैक्स लारेन्ज़।

प्रश्न 21.
लारेन्ज़ वक्र डॉक्टर बाऊले की देन है।
उत्तर-
ग़लत।
प्रश्न 22.
विस्तार किसी श्रृंखला की सबसे बड़ी तथा सबसे छोटी मद का अन्तर होता है।
उत्तर-
सही।
प्रश्न 23.
मध्य विचलन तथा प्रमाप विचलन में कोई अन्तर नहीं होता।
उत्तर-
ग़लत।
प्रश्न 24.
विस्तार (Range) तका माप सूत्र लिखो।
उत्तर-
R = L- S.
प्रश्न 25.
विस्तार गुणांक (Co-efficient of Range) का माप सूत्र लिखो।
उत्तर-
Co-efficient of Range = \(\frac{L-S}{L+S}\)
प्रश्न 26.
चतुर्थक विचलन गुणांक का सूत्र लिखो।
उत्तर-
Co-efficient of Q.D. = \(\frac{\mathrm{Q}_{3}-\mathrm{Q}_{1}}{\mathrm{Q}_{3}+\mathrm{Q}_{1}}\)
प्रश्न 27.
मध्य विचलन गुणांक का सूत्र लिखो।
उत्तर-
M.D.\((\overline{\mathbf{X}})\) = \(\frac{\Sigma|D \bar{X}|}{N}\)
प्रश्न 28.
प्रमाप विचलन गुणांक का सूत्र लिखो।
उत्तर-
प्रमाप विचलन गुणांक = \(\frac{\sigma}{\overline{\mathbf{X}}}\)
प्रश्न 29.
लघु विधि द्वारा प्रमाप विचलन गुणांक का सूत्र लिखो।
उत्तर-
σ = \(\sqrt{\frac{\Sigma d x^{2}}{\mathrm{~N}}-\left(\frac{\Sigma d x}{\mathrm{~N}}\right)^{2}}\)
प्रश्न 30.
पद विचलन विधि द्वारा प्रमाप विचलन गुणांक का सूत्र लिखो।
उत्तर-
σ = \(\sqrt{\frac{\Sigma f d x^{2}}{\mathrm{~N}}-\left(\frac{\Sigma f d x}{\mathrm{~N}}\right)^{2}}\)

प्रश्न 31.
विचलन गुणांक का सूत्र लिखें।
उत्तर-
विचलन गुणांक CV = \(\frac{\sigma}{\bar{X}} \times 100=\left(\frac{\text { Standard Deviation }}{\text { Mean }} \times 100\right)\)
प्रश्न 32.
चतुर्थक किसे कहते हैं ?
उत्तर-
यदि एक श्रेणी को चार समान भागों में विभाजित किया जाए तो प्रत्येक भाग को चतुर्थक कहा जाता है।
प्रश्न 33.
चतुर्थक कितने होते हैं ?
उत्तर-
(Q1) = प्रथम चतुर्थक को निचला चतुर्थक (Q1) कहा जाता है।
(Q2) = द्वितीय चतुर्थक मध्यका कहा जाता है।
(Q3) = ऊपरी चतुर्थक (Q3) होता है।
प्रश्न 34.
यदि किसी श्रेणी को सौ भागों में बराबर बांटा जाए तो प्रत्येक अन्तिम इकाई को ………. कहते
(a) दशमक
(b) शतमक
(c) चतुर्थक
(d) इनमें से कोई नहीं।
उत्तर-
(b) शतमक।
प्रश्न 35.
चतुर्थक को स्थिति का औसत कहा जाता है।
उत्तर-
सही।
प्रश्न 36.
निचले चतुर्थक का अखण्डित श्रेणी के लिए माप सूत्र लिखें।
उत्तर-
(Q1) = \(\mathbf{L}_{1}+\frac{\frac{\mathrm{N}}{4}-c f p}{f} \times i\)
प्रश्न 37.
चतुर्थक का अखण्डित श्रेणी के लिए माप सूत्र लिखें।
उत्तर-
(Q3) = \(\mathrm{L}_{1}+\frac{\frac{3 \mathrm{~N}}{4}-c f p}{f} \times i\)

II. अति लघु उत्तरीय प्रश्न (Very Short Answer Type Questions)
प्रश्न 1.
अपकिरण से क्या अभिप्राय है ?
उत्तर-
एक श्रेणी की मदों में अन्तर को अपकिरण कहा जाता है। अपकिरण का माप इस बात को स्पष्ट करता है कि किसी श्रेणी वितरण की भिन्न-भिन्न मदें उस श्रेणी के मध्य से कितनी दूरी पर हैं अर्थात् उन मदों में फैलाव अथवा प्रसार कितना है। उस प्रकार अथवा फैलाव को अपकिरण कहा जाता है। सूर्य की किरणें धरती तक पहुंचते समय फैल जाती हैं, इस प्रकार मदों का आपस में कितना प्रसार है, उसको अपकिरण कहते हैं। अपकिरण को दो अर्थों में स्पष्ट किया जाता है।
प्रश्न 2.
मध्य विचलन से क्या अभिप्राय है ?
उत्तर-
श्रेणी के किसी सांख्यिकी औसत (समान्तर मध्य, मध्यका, बहुलक) से निकाले गए भिन्न-भिन्न मूल्यों के विचलनों के समान्तर औसत को मध्य विचलन कहा जाता है। मूल्य के विचलन निकालते समय गणित चिह्नों (+) तथा (-) को छोड़ दिया जाता है। मध्य विचलन की मुख्य विशेषताएं इस प्रकार हैं- .
- मध्य विचलन सभी मदों पर आधारित होता है।
- सीमान्त मदों का प्रभाव मध्य विचलन पर बहुत कम होता है।
प्रश्न 3.
मध्य विचलन के कोई दो गुण बताएँ।
उत्तर-
- समझने में आसान-मध्य विचलन को आसानी से समझा जा सकता है।
- सीमान्त मूल्यों से कम प्रभावित-सीमान्त मूल्यों अर्थात् बहुत बड़ी अथवा बहुत छोटी मदों से मध्य विचलन अधिक प्रभावित नहीं होता।
प्रश्न 4.
मध्य विचलन के दोष बताएँ।
उत्तर-
मध्य विचलन के दोष-
- विश्वसनीय नहीं-मध्य विचलन की धारणा विश्वसनीय नहीं है। विशेष तौर पर बहुलक के अनिश्चित होने पर बहुलक द्वारा ज्ञात किया गया मध्य विचलन भी अनिश्चित होता है।
- गणितीय शुद्धि नहीं-मध्य विचलन का सबसे बड़ा दोष यह है कि इसमें गणितीय शुद्धि नहीं है। इसमें (+) तथा (-) चिह्नों को छोड़ दिया जाता है। इस प्रकार उचित परिणाम प्राप्त नहीं होते।
- बीज गणित का प्रयोग नहीं-मध्य विचलन में गणितीय अशद्धि होती है। इसीलिए इसका प्रयोग बीज गणित प्रयोगों के लिए नहीं किया जा सकता। परिणामस्वरूप इसको अन्य सूत्रों का आधार नहीं बनाया जा सकता।
प्रश्न 5.
प्रमाप विचलन से क्या अभिप्राय है ? इसकी विशेषताएं बताओ।
उत्तर-
प्रो० सपीगल अनुसार, “प्रमाप विचलन समान्तर औसत से किसी श्रेणी के भिन्न-भिन्न मूल्यों के विचलनों । के वर्ग का वर्गमूल होता है।” प्रमाप विचलन की विशेषताएं इस प्रकार हैं –
- प्रमाप विचलन में हमेशा समान्तर औसत द्वारा विचलन निकाला जाता है। समान्तर औसत दूसरी औसतों, मध्यकों तथा बहुलक से अधिक विश्वसनीय औसत है।
- प्रमाप विचलन में बीज गणित चिह्नों (+) तथा (-) को छोड़ा नहीं जाता बल्कि विचलनों के वर्ग लिए जाते हैं। इससे ऋणात्मक विचलन अपने आप धनात्मक बन जाते हैं।
- यह एक वैज्ञानिक विधि है, जिसकी बीज गणित प्रयोग की जा सकती है। सांख्यिकी के बहुत से सूत्र प्रमाप विचलन पर ही आधारित हैं।
प्रश्न 6.
प्रमाप विचलन के गुण लिखो।
उत्तर-
प्रमाप विचलन के गुण –
- सभी मूल्यों पर आधारित-प्रमाप विचलन श्रेणी के सभी मूल्यों पर आधारित होता है। इसलिए किसी मूल्य को भी आँखों से ओझल नहीं किया जा सकता।
- स्पष्ट धारणा-प्रमाप विचलन की धारणा स्पष्ट है इसीलिए इसका माप प्रत्येक स्थिति में किया जा सकता है।
- बीज गणित विवेचन-प्रमाप विचलन में गणित चिह्नों (+) तथा (-) को आँखों से ओझल नहीं किया जाता। इसीलिए इसका बीज गणित विवेचन सम्भव होता है। प्रमाप विचलन का प्रयोग अन्य रीतियों में भी किया जा सकता है।

प्रश्न 7.
प्रमाप विचलन के कोई दो दोष बताएँ।
उत्तर-
दोष (Demerits)
- सीमान्त मूल्यों का अधिक प्रभाव-किसी श्रेणी की बहुत बड़ी मदों अथवा बहुत लघु मदों का प्रभाव प्रमाप विचलन पर बहुत अधिक पड़ता है।
- जटिल विधि-प्रमाप विचलन का माप करना एक कठिन विधि है। इसलिए दूसरी विधियों की तुलना में इसको कठिन माना जाता है।
प्रश्न 8.
लॉरेंज़ वक्र से क्या अभिप्राय है ?
उत्तर-
लॉरेंज़ वक्र-अमेरिका के अर्थशास्त्री डॉक्टर लॉरेंज़ ने अपकिरण का माप करने के लिए बिन्दु रेखीय विधि का निर्माण किया। इसलिए इस विधि को लॉरेंज़ वक्र कहा जाता है। लॉरेंज़ वक्र में श्रेणी के मूल्यों को रेखाचित्र द्वारा प्रकट किया जाता है। इसमें कहीं मूल्यों तथा आवृत्ति का संचीय प्रतिशत वक्र बनाया जाता है। यह वक्र समान वितरण रेखा से जितना दूर होता है, श्रेणी की मदों में असमानता उतनी ही अधिक होती है। इसलिए “लॉरेंज़ वक्र समान वितरण रेखा से असल विचलन के विचलन का बिन्दु रेखीय माप होता है।”
प्रश्न 9.
निम्नलिखित आंकड़ों से Q1 ज्ञात करें।
अंक : 5 8 10 15 16 18 20
हल (Solution) :
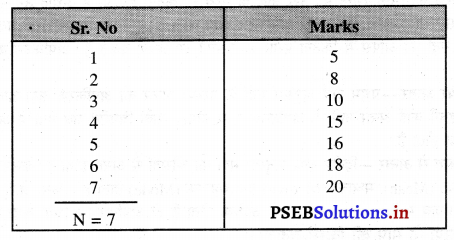
q1 = \(\left(\frac{\mathrm{N}+1}{4}\right)\) th size of the item
= \(\frac{7+1}{4}=\frac{8}{4}\) = 2nd size of the item
q1 = 8 Ans.
प्रश्न 10.
निम्नलिखित आंकड़ों से Q3 ज्ञात करें।
अंक : 8 9 12 15 18 20 25
हल (Solution) :
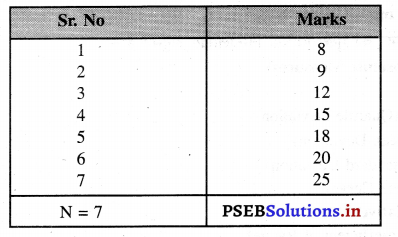
q3 = 3\(\left(\frac{N+1}{4}\right)\) th size of the item
q3 = \(\frac{3(7+1)}{4}=\frac{3(8)}{4}=\frac{24}{4}\) = 6th size of the item
Q3 = 20 Marks Ans.
III. लघु उत्तरीय प्रश्न (Short Answer Type Questions)
प्रश्न 1.
अपकिरण से क्या अभिप्राय है ?
उत्तर-
एक श्रेणी की मदों में अन्तर को अपकिरण कहा जाता है। अपकिरण का माप इस बात को स्पष्ट करता है कि किसी श्रेणी वितरण की भिन्न-भिन्न मदें उस श्रेणी के मध्य से कितनी दूरी पर हैं अर्थात् उन मदों में फैलाव अथवा प्रसार कितना है। उस प्रसार अथवा फैलाव को अपकिरण कहा जाता है। सूर्य की किरणें धरती तक पहुंचते समय फैल जाती हैं, इस प्रकार मदों का आपस में कितना प्रसार है, उसको अपकिरण कहते हैं। अपकिरण को दो अर्थों में स्पष्ट किया जाता है-
1. मदों में परस्पर अन्तर-प्रथम अर्थ अनुसार मदों के परस्पर अन्तर को अपकिरण कहा जाता है। यदि सभी मदें एक समान हैं तथा इनमें कोई अन्तर नहीं तो अपकिरण शून्य होगा। इसके विपरीत जब मदों में अन्तर अधिक होता है तो अपकिरण अधिक होता है।
2. मदों का औसत से अन्तर-द्वितीय अर्थ अनुसार मदों का औसतों से अन्तर होता है। केन्द्रीय प्रवृत्तियों की मुख्य औसतें समान्तर औसत (Mean), मध्यका (Median) तथा बहुलक (Mode) होती हैं। किसी श्रेणी की मदों का औसतों से कितना अन्तर है। जब मदों का अन्तर औसत से अधिक होता है तो अपकिरण अधिक कहा जाता है।
प्रश्न 2.
अपकिरण के माप की किस्में बताओ।
उत्तर-
अपकिरण के माप दो प्रकार के होते हैं –
(1) निरपेक्ष माप
(2) सापेक्ष माप।
1. निरपेक्ष माप-किसी श्रेणी के आंकड़ों का माप उस समय में ही किया जाए जिस रूप में आंकड़े दिए गए हैं तो अपकिरण के इस प्रकार के माप को निरपेक्ष माप कहा जाता है। उदाहरणस्वरूप मदें क्विटलों, रुपयों इत्यादि में दी हुई हैं तथा जवाब भी क्विटलों के रूप में प्रकट किया जाता है तो इस प्रकार के माप को अपकिरण का निरपेक्ष माप कहते हैं।
2. सापेक्ष माप-जब किसी श्रेणी के माप को अनुपात अथवा प्रतिशत के रूप में प्रकट किया जाता है, इसको सापेक्ष माप कहा जाता है। उदाहरणस्वरूप एक स्कूल में ग्यारहवीं कक्षा के विद्यार्थियों में 50% विद्यार्थी प्रथम डिवीजन प्राप्त करते हैं। इस प्रकार आंकड़ों को प्रतिशत रूप में अंकित किया जाता है तो इसको सापेक्ष माप कहा जाता है।

प्रश्न 3.
अपकिरण के माप की विधियां बताओ।
उत्तर-
अपकिरण के माप की मुख्य विधियां निम्नलिखित अनुसार हैं
(A) निरपेक्ष माप (Absolute Measures)
- विस्तार (Range)
- चतुर्थक विचलन (Quartile Deviation)
- मध्य विचलन (Mean Deviation)
- प्रमाप विचलन (Standard Deviation)
- लारेंज वक्र (Lorenz Curve)
(B) सापेक्ष माप (Relative Measures)
- विस्तार गुणांक (Co-efficient of Range)
- चतुर्थक विचलन गुणांक (Co-efficient of Quartile Deviation)
- मध्य विचलन गुणांक (Co-efficient of Mean Deviation)
- प्रमाप विचलन गुणांक। (Co-efficient of Standard Deviation)
प्रश्न 4.
मध्य विचलन की विशेषताएं बताओ।
उत्तर-
श्रेणी के किसी सांख्यिकी औसत (समान्तर मध्य, मध्यका, बहुलक) से निकाले गए भिन्न-भिन्न मूल्यों के विचलनों के समान्तर औसत को मध्य विचलन कहा जाता है। मूल्य के विचलन निकालते समय गणित चिह्नों (+) तथा (-) को छोड़ दिया जाता है। मध्य विचलन की मुख्य विशेषताएं इस प्रकार हैं-
- मध्य विचलन सभी मदों पर आधारित होता है।
- सीमान्त मदों का प्रभाव मध्य विचलन पर बहुत कम होता है।
- मध्य विचलन का माप केन्द्रीय प्रवृत्तियों समान्तर औसत, मध्यका तथा बहुलक द्वारा किया जा सकता है।
- मध्य विचलन में विचलन निकालते समय गणित चिह्नों (+) तथा (-) को आंखों से ओझल किया जाता है।
प्रश्न 5.
मध्य विचलन के गुण तथा दोष बताओ।
उत्तर-
मध्य विचलन के मुख्य गुण निम्नलिखित हैं-
- सरल गणना-मध्य विचलन की गणना सरलता से की जा सकती है। इसका माप समान्तर औसत, मध्यका अथवा बहुलक द्वारा किया जा सकता है।
- सभी मूल्यों पर आधारित-मध्य विचलन श्रृंखला के सभी मूल्यों पर आधारित होता है। इसलिए इसका रूप विस्तृत होता है।
- समझने में आसान-मध्य विचलन को आसानी से समझा जा सकता है।
- सीमान्त मूल्यों से कम प्रभावित-सीमान्त मूल्यों अर्थात् बहुत बड़ी अथवा बहुत छोटी मदों से मध्य विचलन अधिक प्रभावित नहीं होता।
मध्य विचलन के दोष-
- विश्वसनीय नहीं-मध्य विचलन की धारणा विश्वसनीय नहीं है। विशेष तौर पर बहुलक के अनिश्चित होने पर बहुलक द्वारा ज्ञात किया गया मध्य विचलन भी अनिश्चित होता है।
- गणितीय शुद्धि नहीं-मध्य विचलन का सबसे बड़ा दोष यह है कि इसमें गणितीय शुद्धि नहीं है। इसमें (+) तथा (-) चिह्नों को छोड़ दिया जाता है। इस प्रकार उचित परिणाम प्राप्त नहीं होते।
- बीज गणित का प्रयोग नहीं-मध्य विचलन में गणितीय अशुद्धि होती है। इसीलिए इसका प्रयोग बीज गणित प्रयोगों के लिए नहीं किया जा सकता। परिणामस्वरूप इसको अन्य सूत्रों का आधार नहीं बनाया जा सकता।
प्रश्न 6.
प्रमाप विचलन से क्या अभिप्राय है ? इसकी विशेषताएं बताओ।
उत्तर-
प्रो० सपीगल अनुसार, “प्रमाप विचलन समान्तर औसत से किसी श्रेणी के भिन्न-भिन्न मूल्यों के विचलनों के वर्ग का वर्गमूल होता है।” प्रमाप विचलन की विशेषताएं इस प्रकार हैं
- प्रमाप विचलन में हमेशा समान्तर औसत द्वारा विचलन निकाला जाता है। समान्तर औसत दूसरी औसतों, मध्यकों तथा बहुलक से अधिक विश्वसनीय औसत है।
- प्रमाप विचलन में बीज गणित चिह्नों (+) तथा (-) को छोड़ा नहीं जाता बल्कि विचलनों के वर्ग लिए जाते हैं। इससे ऋणात्मक विचलन अपने आप धनात्मक बन जाते हैं।
- यह एक वैज्ञानिक विधि है, जिसकी बीज गणित प्रयोग की जा सकती है। सांख्यिकी के बहुत से सूत्र प्रमाप विचलन पर ही आधारित हैं।”
प्रश्न 7.
प्रमाप विचलन के गुण तथा दोष लिखो।
उत्तर-
प्रमाप विचलन के गुण –
- सभी मूल्यों पर आधारित-प्रमाप विचलन श्रेणी के सभी मूल्यों पर आधारित होता है। इसलिए किसी मूल्य को भी आँखों से ओझल नहीं किया जा सकता।
- स्पष्ट धारणा-प्रमाप विचलन की धारणा स्पष्ट है इसीलिए इसका माप प्रत्येक स्थिति में किया जा सकता है।
- बीज गणित विवेचन-प्रमाप विचलन में गणित चिह्नों (+) तथा (-) को आँखों से ओझल नहीं किया जाता। इसीलिए इसका बीज गणित विवेचन सम्भव होता है। प्रमाप विचलन का प्रयोग अन्य रीतियों में भी किया जा सकता है।
- नमूना परिवर्तन का कम प्रभाव-नमूने में परिवर्तन हो जाता है तो प्रमाप विचलन के परिणाम पर इसका अधिक प्रभाव नहीं पड़ता।
दोष (Demerits)
- सीमान्त मूल्यों का अधिक प्रभाव-किसी श्रेणी की बहुत बड़ी मदों अथवा बहुत लघु मदों का प्रभाव प्रमाप विचलन पर बहुत अधिक पड़ता है।
- जटिल विधि-प्रमाप विचलन का माप करना एक कठिन विधि है। इसलिए दूसरी विधियों की तुलना में इसको कठिन माना जाता है।
- साधारण मनुष्य के लिए मुश्किल-प्रमाप विचलन का अध्ययन सांख्यिकी ज्ञान के बिना सम्भव नहीं होता। साधारण मनुष्य इस धारणा को आसानी से समझकर प्रयोग नहीं कर सकता।

प्रश्न 8.
लॉरेंज़ वक्र से क्या अभिप्राय है ? इसके गुण तथा दोष बताओ।
उत्तर-
लॉरेंज़ वक्र-अमेरिका के अर्थशास्त्री डॉक्टर लॉरेंज़ ने अपकिरण का माप करने के लिए बिन्दु रेखीय विधि का निर्माण किया। इसलिए इस विधि को लॉरेंज़ वक्र कहा जाता है। लॉरेंज़ वक्र में श्रेणी के मूल्यों को रेखाचित्र द्वारा प्रकट किया जाता है। इसमें कहीं मूल्यों तथा आवृत्ति का संचीय प्रतिशत वक्र बनाया जाता है। यह वक्र समान वितरण रेखा से जितना दूर होता है, श्रेणी की मदों में असमानता उतनी ही अधिक होती है। इसलिए, “लॉरेंज़ वक्र समान वितरण रेखा से असल विचलन के विचलन का बिन्दु रेखीय माप होता है।”
गुण (Merits)
- यह अपकिरण के माप के लिए सरल तथा आकर्षक विधि है।
- इस विधि द्वारा तुलना की जा सकती है। विशेष तौर पर आयु, मजदूरी, लाभ इत्यादि के वितरण की असमानताओं को एक नज़र में परखने के लिए यह अधिक उपयोगी है।
दोष (Demerits)
- अपकिरण की इस विधि को बनाते समय संचित प्रतिशत का माप करना पड़ता है। इसलिए इसको समझना कठिन है।
- अपकिरण का प्रकटीकरण ही किया जा सकता है। आंकड़ों के रूप में अपकिरण को स्पष्ट नहीं किया जा सकता।
प्रश्न 9.
चतुर्थक की गणना कैसे की जाती है ?
उत्तर-
चतुर्थक का माप विभिन्न शृंखलाओं में विभिन्न प्रकार से किया जाता है।
(i) व्यक्तिगत तथा खण्डित श्रृंखला (Individual and Discrete Series)—व्यक्तिगत तथा खण्डित श्रृंखला में चतुर्थक का माप करने के लिये निम्नलिखित सूत्रों का प्रयोग किया जाता है
Qı = Size of the \(\left(\frac{N+1}{4}\right)\) th item of the series
Q3 = Size of the \(\left(\frac{3(N+1)}{4}\right)\) th item of the series
(ii) आवृत्ति वितरण श्रृंखला (Frequency Distribution Series)-आवृत्ति वितरण शृंखला में चतुर्थक का माप निम्नलिखित सूत्र से लिया जाता है-
Q1 = Size of the \(\left(\frac{N}{4}\right)\) th item
Q3 = Size of the 3\(\left(\frac{N}{4}\right)\) th item
तथा निम्नलिखित सूत्र का प्रयोग किया जाता है-
Q1 = L1+\(\left[\frac{\frac{N}{4}-c f_{p}}{f}\right] \times i\)
Q3 = L1 + \(\left[\frac{\frac{3 \mathrm{~N}}{4}-c f_{p}}{f}\right] \times i\)
IV. दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)
प्रश्न 1.
अपकिरण से क्या अभिप्राय है ? अपकिरण के महत्त्व को स्पष्ट करें। (What is dispersion ? Why is the study of dispersion essential ?)
उत्तर-
अपकिरण का अर्थ (Meaning of Dispersion)-एक श्रेणी की मदों में अन्तर को अपकिरण कहा जाता है। अपकिरण का माप इस बात को स्पष्ट करता है कि किसी श्रेणी की भिन्न-भिन्न मदें उस मध्य से कितनी दूरी पर हैं। उन मदों में प्रसार अथवा फैलाव कितना है। उस प्रसार अथवा फैलाव को अपकिरण कहा जाता है। अपकिरण की तुलना सूर्य की किरणों अथवा बैटरी की रोशनी से की जा सकती है। सूर्य की किरणें धरती पर पहुंचने तक बहुत फैल जाती हैं। बैटरी को जगाने से इसकी रोशनी फैलती जाती है। इसी प्रकार मदों का फैलाव अथवा प्रसार कितना है, उसको अपकिरण कहते हैं।
अपकिरण का महत्त्व तथा उद्देश्य (Importance of Objectives of Dispersion)-अपकिरण का मुख्य उद्देश्य अथवा महत्त्व निम्नलिखित बातों से स्पष्ट होता है-
1. श्रेणी विभाजन की बनावट का ज्ञान-किसी श्रेणी विभाजन की बनावट का ज्ञान अपकिरण के माप से स्पष्ट होता है। उदाहरणस्वरूप तीन श्रेणियों की समान्तर औसत समान हो सकती है, परन्तु उनकी मदों में अन्तर भिन्न-भिन्न हो सकता है। इसलिए औसतें किसी श्रेणी की मदों की उचित प्रतिनिधिता नहीं करतीं। किसी श्रेणी की बनावट की उचित जानकारी अपकिरण के माप से की जा सकती है। इसलिए अपकिरण का माप महत्त्वपूर्ण है।
2. तुलना में सहायक-अपकिरण का माप तुलना के लिए भी लाभदायक होता है। जैसे कि देश A की राष्ट्रीय आय दोगुनी हो जाती है। जनसंख्या भी दोगुनी हो जाती है. तो प्रति व्यक्ति आय समान रहती है। देश B में राष्ट्रीय आय 4 गुणा बढ़ गई है, जबकि जनसंख्या में वृद्धि भी चार गुणा है। इसलिए प्रति व्यक्ति आय समान रहती है। औसत आय की तुलना से हम यह परिणाम निकालते हैं कि दोनों देशों ने कोई उन्नति नहीं की। परन्तु देश A से देश B में उन्नति की दर अधिक है। इसलिए अपकिरण का माप दो अथवा दो से अधिक श्रेणियों में तुलना के लिए सहायक होता है।
3. पदों के मूल्यों का विस्तार-किसी श्रेणी में दिए गए पदों के मूल्यों का विस्तार कितना है ? इसकी जानकारी अपकिरण के माप द्वारा की जा सकती है। पदों के मूल्यों का विस्तार इस बात की जानकारी प्रदान करता है कि सबसे ऊंचे तथा सबसे नीचे पद मूल्यों का अन्तर कितना है ? इस अन्तर का ज्ञान प्राप्त करके मदों सम्बन्धी ठीक जानकारी प्राप्त की जा सकती है।
4. औसत की प्रतिनिधिता का ज्ञान-अपकिरण के माप का एक उद्देश्य इस बात की जानकारी प्रदान करना भी होता है कि औसत मूल्य, मदों की ठीक प्रतिनिधिता कर रहे हैं अथवा नहीं। अपकिरण का माप, औसत के सम्बन्ध में किसी श्रेणी की मदों में एक समानता की सीमा को स्पष्ट करती है। दी गई मदों तथा औसत में जितना अन्तर अधिक होता है, मदों में उतनी एक समानता कम होती है। एक औसत को प्रतिनिधि कहा जाएगा। यदि यह एक समान तथा विश्वसनीय परिणाम स्वीकार करती है।
5. सांख्यिकी विधियों का आधार-अपकिरण का माप अन्य सांख्यिकी विधियों के माप के लिए लाभदायक होता है। सह-सम्बन्ध, परिकल्पना की परख, प्रतीपगमन इत्यादि विधियां अपकिरण के माप पर आधारित हैं। इसलिए आंकड़ा शास्त्र में अपकिरण का माप महत्त्वपूर्ण स्थान रखता है।
प्रश्न 2.
अपकिरण के माप की किस्में बताओ। अपकिरण के माप की विधियों को स्पष्ट करो।(Explain the types of the measures of dispersion. Describe the methods of Absolute Measures of Dispersion.)
उत्तर-
अपकिरण के माप दो प्रकार के होते हैं –
(1) निरपेक्ष माप
(2) सापेक्ष माप।
1. निरपेक्ष माप (Absolute Measure)-किसी श्रेणी के आंकड़ों का माप प्राथमिक इकाइयों में भी बताया जाए, जिस रूप में उस श्रेणी के मूल्य दिए होते हैं तो अपकिरण का निरपेक्ष माप कहा जाता है। उदाहरणस्वरूप मजदूरों की मज़दूरी रुपयों में दी हुई है तथा अपकिरण का माप रुपयों में किया जाता है। इस तरह वस्तुओं की कीमत रुपयों में, लम्बाई मीटरों में तथा भार किलोग्रामों में ही किया जाए तो इसको निरपेक्ष माप कहा जाता है।
2. सापेक्ष माप (Relative Measure)-जब किसी श्रेणी के अपकिरण के माप को अनुपात अथवा प्रतिशत के रूप में प्रकट किया जाता है तो इसको सापेक्ष माप कहा जाता है। जैसे कि ग्यारहवीं कक्षा के विद्यार्थियों में से 70% विद्यार्थी प्रथम दर्जे में पास हुए हैं। इसको सापेक्ष माप कहा जाएगा। इसको अपकिरण गुणांक भी कहा जाता है।
अपकिरण के माप की विधियां (Methods of Measuring Disperrion)-अपकिरण के माप को दो भागों में विभाजित किया जाता है-
| अपकिरण के निरपेक्ष माप (Absolute Measures of Dispersion) |
अपकिरण के सापेक्ष माप (Relative Measures of Dispersion) |
| A. स्थिति के माप- 1. विस्तार (Range) |
1. विस्तार गुणांक (Co-efficient of Range) |
| 2. चतुर्थक विचलन (Quartile Deviation) |
2. चतुर्थक विचलन गुणांक (Co-efficient of Quartile Deviation) |
| B. गणित का माप-3. औसत विचलन (Mean Deviation) |
3. औसत विचलन गुणांक (Co-efficient of Mean Devaition) |
| 4. प्रमाप विचलन (Standard Deviation) |
4. प्रमाप विचलन गुणांक (Co-efficient of Standard Deviation) |
| C. ग्राफ द्वारा माप – 5. लॉरेंज़ वक्र (Lorenz Curve) |
|
प्रश्न 3.
चतुर्थक से क्या अभिप्राय है ? इसकी माप विधि को स्पष्ट करें। (What do you mean by Quartile ? Explain its measure method.)
उत्तर-
हम देख चुके हैं कि मध्यका दिए गए आंकड़ों को दो समान भागों में विभाजित करती है, जब आंकड़ों को बढ़ते अथवा घटते क्रम अनुसार लिखा जाता है तो विभाजन के तीन बिन्दु प्राप्त होते हैं। केन्द्र वाले बिन्दु को मध्यका कहा जाता है। पहले चौथाई भाग को निम्न चतुर्थक (Q1) तथा तीसरे चौथाई भाग को ऊपरी चतुर्थक (Q3) कहा जाता है। चतुर्थक को समझने के लिए मध्यका को रेखाचित्र द्वारा स्पष्ट करते हैं-
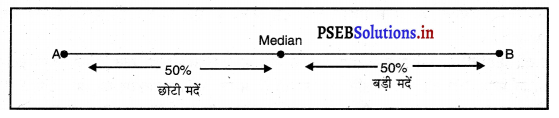
AB रेखा का मध्य M है जो कि रेखा को दो समान भागों में विभाजित करता है। M बिन्दु वाली मद को मध्यका कहा जाता है। अब चतुर्थक को समझना आसान होगा, जब आंकड़ों को बढ़ते अथवा घटते क्रमानुसार करके इसको चार बराबर भागों में विभाजित करते हैं। विभाजन के तीन बिन्दु प्राप्त होते हैं, इनको निम्न चतुर्थक, मध्य चतुर्थक तथा ऊपरी चतुर्थक कहा जाता है। मध्य चतुर्थक हमेशा बीच में स्थित होता है। इसको मध्यका कहते हैं। निम्न चतुर्थक Q1 से 25% मदें कम होती हैं तथा ऊपरी चतुर्थक Q3 से 25% मदें अधिक होती हैं।
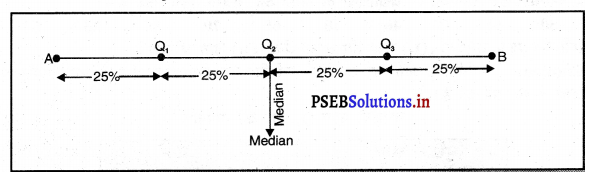
रेखाचित्र में AB रेखा को तीन बिन्दु Q1, Q2, Q3, चार भागों में विभाजित करते हैं। इसलिए चतुर्थक तीन होते हैं।
Q1 = प्रथम चतुर्थक (Lower Quartile or First Quartile)
Q2= द्वितीय चतुर्यक (Second Quartile or Median)
Q3 = तीसरा चतुर्थक (Upper Quartile or Third Quartile)
क्योंकि दूसरा चतुर्थक मध्यका होती है इसलिए प्रथम चतुर्थक तथा निम्न चतुर्थक (Q1) तथा तीसरे चतुर्थक अथवा ऊपरी चतुर्थक का माप किया जाता है। .
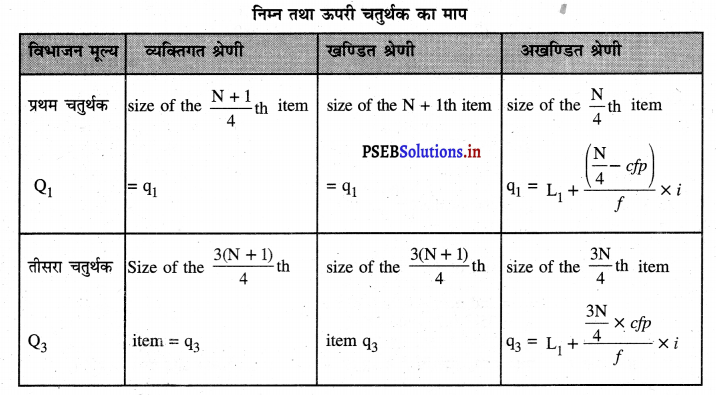
व्यक्तिगत श्रेणी में माप विधि-
- व्यक्तिगत श्रेणी के आंकड़ों को बढ़ते क्रमानुसार अथवा घटते क्रमानुसार लिखना अनिवार्य होता है। मदों की श्रृंखला नम्बर लिखकर कुल संख्या (N) का पता करो।
- प्रथम चतुर्थक के मूल्य का पता करने के लिए निम्नलिखित सूत्र का प्रयोग किया जाता है।
q1 = \(\frac{N+1}{4}\) th size of the item
- तीसरे चतुर्थक के मूल्य का पता करने के लिए निम्नलिखित सूत्र का प्रयोग किया जाता है।
q3 = \(\frac{3(\mathrm{~N}+1)}{4}\) th Size of the item
- हमारे पास जो मद का आकार प्राप्त होता है, उसके सामने वाली मद Q1 अथवा Q3 होती है।

प्रश्न 4.
निम्नलिखित तालिका में विद्यार्थियों के अंकों का विवरण दिया गया है –
अंक : 50 55 60 40 20 65 70 80 35 52 इस श्रेणी का प्रथम चतुर्थक (Q1) तथा तीसरा चतुर्थक (Q3) ज्ञात कीजिए।
हल (Solution) :
विद्यार्थियों के अंक बढ़ते क्रमानुसार नहीं दिए गए। इसलिए पहले इनको बढ़ते क्रमानुसार लिखते हैं तथा श्रृंखला नम्बर स्वयं देते हैं।
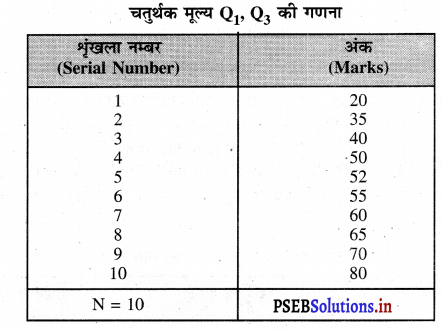
Q1 की गणना
q1 = size of the \(\left(\frac{\mathrm{N}+1}{4}\right)\) th item.
q1 = size of the \(\left(\frac{10+1}{4}\right)\) th item.
q1 = size of the \(\left(\frac{11}{4}\right)\) = 2.75 th item.
q1 = 2nd item + 0.75 (3rd item – 2nd item)
q1 = 35 + 0.75 (40 – 35)
q1 = 35 + 3.75 = 38.75 अंक
(इससे ज्ञात होता है कि प्रथम 25% विद्यार्थियों ने 38.75 अंक अथवा इससे कम अंक प्राप्त किए हैं।) Q3 की गणना
Q3 = size of the \(\left(\frac{3(\mathrm{~N}+1)}{4}\right)\) th item
Q3 = size of the \(\left[\frac{3(10+1)}{4}\right]\) th item
\(\frac{33}{4}\) =8.25th item
Q3 = 8th item + 0.25 (9th item – 8th item)
Q3 = 65 + 0.25 (70 – 65)
Q3 = 65 + 1.25 = 66.25 अंक ऊपरी चतुर्थक से ज्ञात होता है कि प्रथम 75% विद्यार्थियों के अंक 66.25 अथवा इससे कम हैं।
खण्डित श्रेणी में चतुर्थक का माप (Measurement of Quartiles in Discrete Series)
मापी विधि
- खण्डित श्रेणी में दी मदों की संचयी आवृत्ति निकालो।
- आवृत्ति का जोड़ करो इससे कुल संख्याओं की संख्या (N) प्राप्त हो जाती है।
- प्रथम चतुर्थक के लिए निम्न सूत्र का प्रयोग करो
Q1 = \(\frac{\mathrm{N}+1}{4}\) size of the item
तीसरे चतुर्थक के लिए इस सूत्र का प्रयोग करो
Q3 = \(\frac{3(N+1)}{4}\) size of the item
प्रथम तथा तीसरे चतुर्थक का आकार (size of the item) को संचयी आवृत्ति में देखो। जिस संचयी आवृत्ति में यह आकार प्राप्त होता है उसके सामने वाली मद को Q1 अथवा Q3 कहा जाता है।
प्रश्न 5.
ग्यारहवीं कक्षा के विद्यार्थियों के भार (weight) का विवरण इस प्रकार दिया है। इनका Q1, Q3, ज्ञात कीजिए।
| भार (किलोग्राम) : |
40 |
42 |
45 |
46 |
48 |
50 |
51 |
53 |
55 |
| विद्यार्थियों की संख्या : |
5 |
11 |
14 |
8 |
10 |
12 |
6 |
4 |
2 |
हल (Solution) :
प्रथम चतुर्थक (Q1) तथा तीसरा चतुर्थक (Q3) की गणना कीजिए।
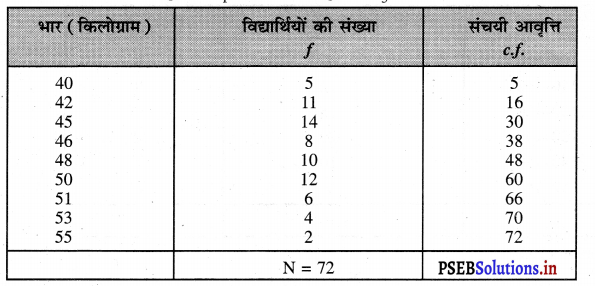
Q1 की गणना
q1 = size of the \(\left(\frac{\mathrm{N}+1}{4}\right)\)th item
q2 = size of the \(\left(\frac{72+1}{4}\right)=\frac{73}{4}\)
= 18.25th item
यह संचयी आवृत्ति 30 में शामिल है।
q1 = 45 kg Ans.
इससे यह ज्ञात होता है कि प्रथम 25% विद्यार्थियों का भार 45 किलोग्राम अथवा इससे कम है। Q3 की गणना
q3 = size of the \(\left(\frac{3(\mathrm{~N}+1)}{4}\right)\) in item
q3 = size of the \(\left(\frac{3(72+1)}{4}\right)\) th item
= 54.75th item यह संचयी आवृत्ति 60 में शामिल है। इसके सामने मद 50 है।
q3= 50 kg Ans.
कुल विद्यार्थियों में से प्रथम 75% विद्यार्थियों का भार 50 किलोग्राम अथवा इससे कम है।
अखण्डित श्रृंखला में चतुर्थक का माप (Measurement of Quartiles in Continuous Series)

प्रश्न 6.
‘निम्नलिखित तालिका की प्रथम चतुर्थक तथा तीसरे चतुर्थक का माप करो।
| मज़दूरी (₹): |
100-110 |
110-120 |
120-130 |
130-140 |
140-150 |
| मज़दूरों की संख्या : |
8 |
12 |
15 |
20 |
10 |
हल (Solution) :
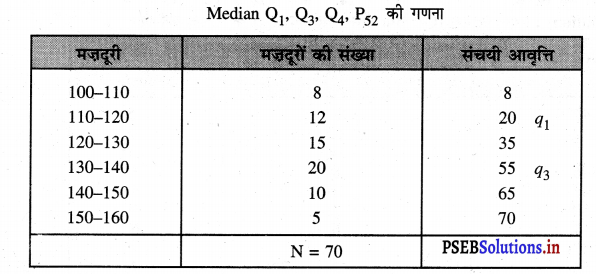
Calculation of Q1
q1 = size of the\(\left(\frac{\mathrm{N}}{4}\right)\) th = \(\frac{70}{4}\) = 17.5 item
q1 = \(\mathrm{L}_{1}+\frac{\frac{\mathrm{N}}{4}-c f p}{f} \times i\)
q1 = 110+ \(\frac{17.5-8}{12} \times 10\) = 110+7.92
q1 = 117.92
इससे स्पष्ट होता है कि प्रथम 25% मज़दूरों की मज़दूरी ₹ 117.92 के समान अथवा इससे कम है। Q3 का माप
q3 = \(\mathrm{L}_{1}+\frac{\frac{3 \mathrm{~N}}{4}-c f p}{f} \times i \)
q3 = size of the \(\frac{3 \mathrm{~N}}{4}\) th item = \(\frac{3 \times 70}{4}\) = 52.5th item
q3 = 130+ \(\frac{52.5-35}{20} \times 10\)
= 130+ 8.75
= ₹ 138.75
इससे ज्ञात होता है कि प्रथम 75% मज़दूरों की मजदूरी ₹ 138.75 अथवा इससे कम है।
प्रश्न 7.
निम्नलिखित आंकड़ों से चतुर्थकों का माप करें।
| अंक : |
20-30 |
30-40 |
40-50 |
50-60 |
60-70 |
70-80 |
80-90 |
| विद्यार्थियों की संख्या : |
7 |
13 |
24 |
20 |
16 |
12 |
8 |
हल (Solution) :
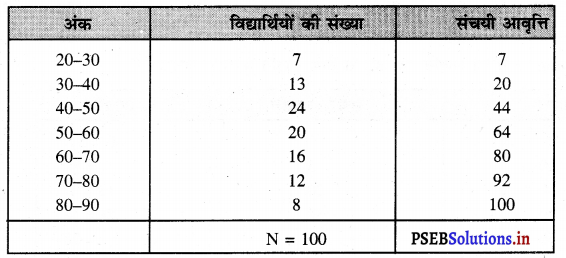
Calculation of Q1
q1 = size of the \(\left(\frac{\mathrm{N}}{4}\right)\) th item
वर्गान्तर = \(\frac{100}{4}\) = 25th item.
Q1 वर्गान्तर 40-50 के वर्ग में है
∴ Q1 = \(\mathrm{L}_{1}+\frac{\frac{\mathrm{N}}{4}-c f p}{f} \times i\)
= 40+ \(\frac{25-20}{24} \times 10\)
= 40 + 2.08 = 42.08 उत्तर
q3 is the value \(\frac{3 \mathrm{~N}}{4}\) = \(\frac{300}{4}\) = 75th item
q3 वर्गान्तर 60-70 में है ..
Q3 = \(\mathrm{L}_{1}+\frac{\frac{3 \mathrm{~N}}{4}-c p f}{f} \times i\)
= 60 + \(\frac{75-64}{16} \times 10\)
= 60 + 6.875
∴ Q3 = 66.875 उत्तर
प्रश्न 8.
निम्नलिखित आंकड़ों के आधार पर चतुर्थकों का माप करें :
| से कम प्राप्तांक : |
80 |
70 |
60 |
50 |
40 |
30 |
| छात्रों की संख्या : |
100 |
90 |
80 |
60 |
32 |
20 |
हल (Solution) :
संचयी आवृत्ति को पहले साधारण आवृत्ति में बदला जाएगा।
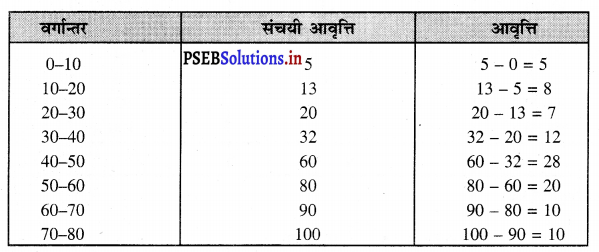
Calculation of
Q1 is the value of \(\left(\frac{\mathrm{N}}{4}\right)\) th = \(\frac{100}{4}\) = 25th item
Q1 वर्गान्तर (30 – 40) में है।
∴ Q1 = \(\mathrm{L}_{1}+\frac{\frac{\mathrm{N}}{4}-c f p}{f} \times i\)
= 30+\(\frac{25-20}{12} \times 10\)
= 30 + \(\frac{5}{12} \times 10\)
= 30 + 4.17
Q1 = 34.17 उत्तर
Calculation of Q3
Q3 is the value of \(\left(\frac{3 \mathrm{~N}}{4}\right)\) th = \(\frac{100 \times 3}{4} \) = 75th item
Q3 वर्गान्तर (50 – 60) में है
Q3 = \(\mathrm{L}_{1}+\frac{\frac{3 \mathrm{~N}}{4}-c f p}{f} \times i\)
= 50+ \(\frac{75-60}{20} \times 10\)
= 50 + \(\frac{15}{2}\)
= 50 + 7.5
Q3 = 57.5 उत्तर
दशमक और प्रतीशतक (Deciles And Percentiles)

प्रश्न 9.
दशमक और प्रतीशतक की माप विधि स्पष्ट करें।
उत्तर-
दशमक (Decile) और प्रतिशतक (Percentiles)-जब एक श्रेणी को 10 भागों में बांट कर D1 से D9 तक माप किया जाता है तो इस को दशमक कहा जाता है।

कुल 9 दशमक होते हैं D5 को माध्यका (Median) कहा जाता है।
व्यक्तिगत श्रेणी और खण्डित श्रेणी में दशमक का माप
D1 = Size of \(\left(\frac{\mathrm{N}+1}{10}\right)\) th item
D2 = Size of \(\left[\frac{2(N+1)}{10}\right]\) th item
D3 = Size of \(\left[\frac{3(N+1)}{10}\right]\) an item
D9 = Size of \(\left[\frac{9(N+1)}{10}\right]\) an item
अखण्डित श्रेणी में दशमक का माप अखण्डित श्रेणी (Continuous Series) में दशमक वर्ग अन्तर के माप का सूत्र इस प्रकार है
D1 = Size of \(\left(\frac{N}{10}\right)\) th item
D2 = Size of 2\(\left(\frac{\mathrm{N}}{10}\right)\) th item
D3 = Size of 3\(\left(\frac{N}{10}\right)\) th item
D9 = Size of 9(\left(\frac{N}{10}\right))th item
यदि दशमक का माप करना हो तो सूत्र इस प्रकार है-
D1 = \(\mathrm{L}_{1}+\frac{\frac{\mathrm{N}}{10}-C f p}{f} \times i\)
D2 = \(\mathrm{L}_{1}+\frac{\frac{2 \mathrm{~N}}{10}-C f p}{f} \times i\)
D3 = \(\mathrm{L}_{1}+\frac{\frac{3 \mathrm{~N}}{10}-C f p}{f} \times i\)
D9 = \(\mathrm{L}_{1}+\frac{\frac{9 \mathrm{~N}}{10}-C f p}{f} \times i\)
प्रतिशतक (Percentiles)
जब श्रृंखला को 100 बराबर हिस्सों में बांट कर P से P तक का माप किया जाता है तो इसको प्रतिशतक कहा जाता है। P50 = Median, P23 = Q1 और P75 = Q3 होता है।

व्यक्तिगत तथा खण्डित श्रेणी में प्रतिशतक का माप-व्यक्तिगत तथा खण्डित श्रेणी में माप का सूत्र
P1 = Size of the \(\left(\frac{\mathrm{N}+1}{100}\right)\) th item.
P2 = Size of the 2 \(\left(\frac{\mathrm{N}+1}{100}\right)\) th item.
P3 = Size of the 3 \(\left(\frac{\mathrm{N}+1}{100}\right)\) th item
P99 = Size of the 99 \(\left(\frac{\mathrm{N}+1}{100}\right)\) th item
अखण्डित श्रेणी में प्रतिशतक वर्ग के माप का सूत्र
P1 = Size of the \(\left(\frac{\mathrm{N}+1}{100}\right)\) th item
P2 = Size of the 2 \(\left(\frac{\mathrm{N}+1}{100}\right)\) th item.
P3 = Size of the 3 \(\left(\frac{\mathrm{N}+1}{100}\right)\)th item.
P99 = Size of the 99\(\left(\frac{\mathrm{N}+1}{100}\right)\) th item
प्रतिशतक के माप का सूत्र :
P1 = \(L_{1}+\left(\frac{\frac{N}{100}-C f p}{f}\right) \times i\)
P99 = \(\mathrm{L}_{1}+\left(\frac{\frac{99 N}{100}-\mathrm{C} f p}{f}\right) \times i\)
प्रश्न 10.
व्यक्तिगत श्रेणी में दशमक और प्रतिशतक का माप
उदाहरण : विद्यार्थियों द्वारा प्राप्त किये गए अंक इस प्रकार हैं
10, 18, 20, 25, 28, 40, 50, 60, 70, 88, D3 और P67 का माप करें :
हल (Solution) :
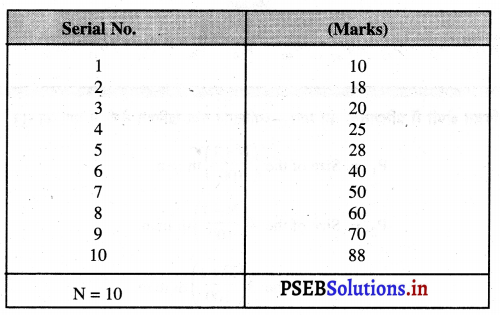
D3 का माप
D3 = Size of the 3 \(\left(\frac{\mathrm{N}+1}{100}\right)\) th item.
= Size of the 3\(\left(\frac{10+1}{10}\right)\) th item.
= Size of the \(\frac{3(11)}{10}=\frac{33}{10}\) = 3.3 rd item.
D3 = Size of the 3(4th-3rd item)
= 20 + 3(25-20)
= 20+ 1.5
D3 = 21.5
P67 का माप
P67 = Size of the 67 \(\left(\frac{\mathrm{N}+1}{100}\right)\)th item
= Size of the 67\(\left(\frac{10+1}{10}\right)\) in item
= Size of the 67\(\left(\frac{11}{100}\right)=\frac{737}{100}\) = 7.371 item
P67= 7th item + .37(8th – 7th item) th item
= 50 + :37 (60 – 50)
= 50 + 3.7
P= 53.7

खण्डित श्रेणी में माप
प्रश्न 11.
मज़दूरों की मजदूरी के आंकड़े दिए गए हैं :
D2, D7, P21, P84 का माप करें।
| मज़दूरी |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
800 |
900 |
| मजदूरों की संख्या |
3 |
7 |
15 |
20 |
25 |
10 |
8 |
7 |
4 |
हल (Solution) : .
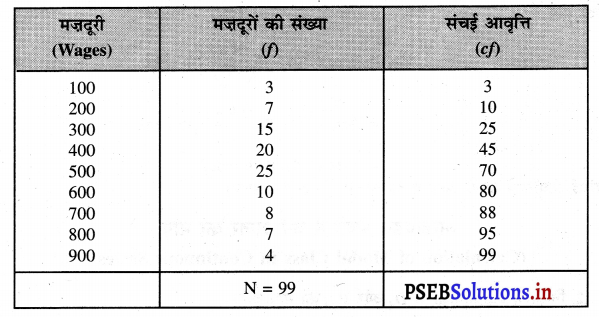
D2 का माप
D2 = Size of the 2 \(\left(\frac{\mathrm{N}+1}{100}\right)\) th item
= Size of the 2 \(\left(\frac{99+1}{10}\right)\) th item
= Size of 20th item.
यह संचई आवृत्ति में 25 में स्थित है जोकि ₹ 300 मज़दूरी को प्रकट करती है।
D2= ₹ 300 उत्तर।
D7 का माप
D7 = Size of the 7\(\left(\frac{\mathrm{N}+1}{100}\right)\) th item.
= Size of the 7\(\left(\frac{99+1}{10}\right)\)th item.
= Size of the 70th item.
यह संचई आवृत्ति में 70 में स्थित है जो कि ₹ 500 मज़दूरी को प्रकट करती है।
D7 = ₹ 500 उत्तर।
P21 का माप
P21 = Size of the 21\(\left(\frac{\mathrm{N}+1}{100}\right)\)th item.
= Size of the 21 \(\left(\frac{99+1}{10}\right)\)
= Size of the 21st item.
Size of the 21st item यह (C.f.) में 25 में आती है।
∴ P21 = ₹ 300 उत्तर
P84 का माप
P84 = Size of the 84\(\left(\frac{\mathrm{N}+1}{100}\right)\) th item.
= Size of the 84\(\left(\frac{99+1}{10}\right)\) th item.
= Size of the 84th item.
यह संचई आवृत्ति में 88 में आती है इसलिए P84 = ₹ 700 उत्तर।
अखण्डित श्रेणी में वर्ग अन्तर का माप (Calculation of Modal Class in Continuous Series)
प्रश्न 12.
निम्नलिखित आंकड़ों से D4 और P70 का माप करें।
| अंक : |
0- 10 |
10-20 |
20 – 30 |
30 – 40 |
40 – 50 |
| आवृत्ति : |
5 |
15 |
25 |
20 |
5 |
हल (Solution):
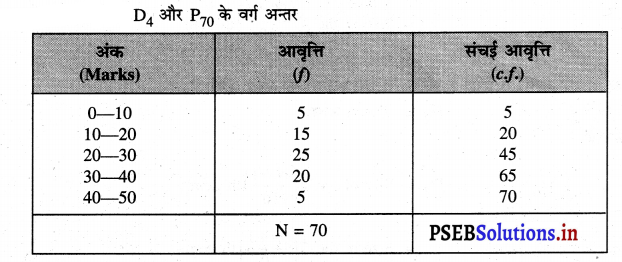
D4 के वर्ग अन्तर का माप
D4 = Size of the 4 \(\left(\frac{\mathrm{N}}{10}\right)\) in item
= Size of the 4\(\left(\frac{70}{10}\right)\) th item.
= Size of the 28th item.
यह संचई आवृत्ति में 45 में आएगी इसलिए D4 का वर्ग-अन्तराल = 20 – 30 उत्तर।
D4 का माप
यदि D4 का माप करना हो तो
D4 = \(\mathrm{L}_{1}+\left(\frac{\frac{4(N)}{10}-c f p}{f}\right) \times i\)
= 20 + \(\left(\frac{\frac{4(70)}{10}-20}{25}\right) \times 10\)
= 20 + \(\frac{28-20}{25} \times 10\)
= 20 + \(\frac{8 \times 10}{25}\)
= 20 + 3.2
= 23-2 अंक उत्तर।
P70 प्रतिशतक के वर्ग-अन्तर का माप
P70 = Size of the \(\left(\frac{70(N)}{100}\right)\) th item.
= Size of the \(\left(\frac{70(70)}{100}\right)\) th item.
= Size of the 49th item.
यह संचई आवृत्ति (cf) 65 में आती है।
∴ P70 का वर्ग अन्तराल = 30 – 40 उत्तर।
P70 का माप
P70 = \(\mathrm{L}_{1}+\left(\frac{\frac{70(\mathrm{~N})}{100}-c f p}{f}\right) \times i\)
= 30 + \(\left[\frac{\left(\frac{70 \times 70}{100}\right)-45}{20}\right] \times 10\)
= 30 + \(\frac{49-45}{20} \times 10\)
= 30 + \( \frac{4}{20} \times 10\)
= 30 + 2 = 32 अंक
P70 = 32 अंक उत्तर।
.
विस्तार (Range)
प्रश्न 13.
विस्तार का माप कैसे किया जाता है ?
उत्तर-
1. विस्तार का अर्थ-किसी श्रेणी में सबसे बड़े मूल्य तथा सबसे लघु मूल्य के अन्तर को विस्तार कहा जाता है। विस्तार के माप की यह सबसे सरल विधि है, जिसमें निम्नलिखित सूत्र का प्रयोग किया जाता है-
Range = L-S
यहां L = सबसे बड़ा मूल्य (Largest value)
S = सबसे लघु मूल्य (Smallest value)
2. विस्तार गुणांक-ऊपर दिए निरपेक्ष माप में दो अथवा दो से अधिक श्रेणियों की तुलना नहीं की जा सकती। इसलिए विस्तार के तुलनात्मक माप करने के लिए विस्तार गुणांक का प्रयोग किया जाता है। इसका माप करने के लिए निम्नलिखित सूत्र का प्रयोग किया जाता है
Co-efficient of Range = \(\frac{\mathrm{L}-\mathrm{S}}{\mathrm{L}+\mathrm{S}}\)

विस्तार तथा विस्तार गुणांक की गणना (Calculation of Range and Co-efficient of Range)
विस्तार की गणना तीन प्रकार की श्रेणियों में निम्नलिखित अनुसार की जाती है
(A) व्यक्तिगत श्रेणी (Individual Series)
विधि-व्यक्तिगत श्रेणी में दी गई मदों में से सबसे बड़ी मद के मूल्य तथा सबसे लघु मद के मूल्य का अन्तर निकाल लिया जाता है। इस अन्तर को विस्तार कहते हैं।
प्रश्न 14.
निम्नलिखित दो खिलाडियों के स्कोर का विवरण दिया गया है, विस्तार तथा विस्तार गणांक ज्ञात करो। यह बताओ कि किस खिलाड़ी की बल्लेबाजी ज्यादा स्थिर है।

हल (Solution) :
I. युवराज सिंह
(i) विस्तार = अधिकतम मूल्य – न्यूनतम मूल्य
= 104 – 12 = 92 दौड़ें
(ii) 
= \(\frac{104-12}{104+12}=\frac{92}{116}\) = 0.793
II. महेन्द्र सिंह धोनी
(i) विस्तार = अधिकतम मूल्य – न्यूनतम मूल्य
= 82 – 45 = 37
(ii) विस्तार गुणांक = 
विस्तार गुणांक = \(\frac{82-45}{82+45}=\frac{37}{127}\)
तुलना करने के लिए विस्तार गुणांक का प्रयोग करते हैं। विस्तार गुणांक महेन्द्र सिंह धोनी का कम है। महेन्द्र सिंह धोनी की दौड़ों में विचरण कम है। इसलिए महेन्द्र सिंह धोनी की बल्लेबाजी अधिक स्थिर अथवा विश्वसनीय है।
(B) खण्डित श्रेणी (Discrete Series) विधि-खण्डित श्रेणी की मदों के साथ आवृत्ति दी होती है। गणना करते समय सबसे बड़ी मद तथा सबसे छोटी मद का अन्तर निकाला जाता है। इसमें आवृत्ति में कोई ध्यान नहीं दिया जाता। विस्तार तथा विस्तार गुणांक की गणना विधि व्यक्तिगत श्रेणी वाली ही है।
प्रश्न 15.
निम्नलिखित आंकड़ों का विस्तार तथा विस्तार गुणांक पता करो।
| अंक (X) : |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
| आवृत्ति (f) : |
2 |
8 |
60 |
40 |
35 |
19 |
11 |
हल (Solution) :
(i) विस्तार (R) = L – S
L = 40, S = 10
R = 40 – 10 = 30 अंक उत्तर
विस्तार 30 अंक यह स्पष्ट करता है कि अधिक अंक तथा कम अंक प्राप्त करने वालों में अन्तर अधिक है।
(ii) विस्तार गुणांक = \(\frac{\mathrm{L}-\mathrm{S}}{\mathrm{L}+\mathrm{S}}\)
Co-efficient of Range = \(\frac{40-10}{40+10}=\frac{30}{50}\) = 0.6 उत्तर
विस्तार अधिक होने के कारण विस्तार गुणांक का मूल्य अधिक है।
(C) अखण्डित श्रेणी (Continuous Series)
प्रश्न 16.
निम्नलिखित आंकड़ों का विस्तार तथा विस्तार गुणांक पता करो
| अंक: |
10-19 |
20-29 |
30-39 |
40-49 |
50-59 |
60-69 |
| विद्यार्थियों की संख्या: |
8 |
15 |
20 |
53 |
31 |
16 |
हल (Solution) :
इस प्रश्न में वर्गान्तर समावेशी श्रेणी में दिए गए हैं। इनको प्रथम अपवर्जी श्रेणी में बदलो। नोट-प्रथम वर्ग की ऊपरी सीमा 19 है तथा द्वितीय वर्ग की निचली सीमा 20 का अन्तर 20-19 = 1 का अर्ध =\(\frac{1}{2}\) = 0.5 है। प्रत्येक वर्ग की निचली सीमा में से 0.5 घटाओ तथा प्रत्येक वर्ग की ऊपरी सीमा में 0.5 जोड़ो।
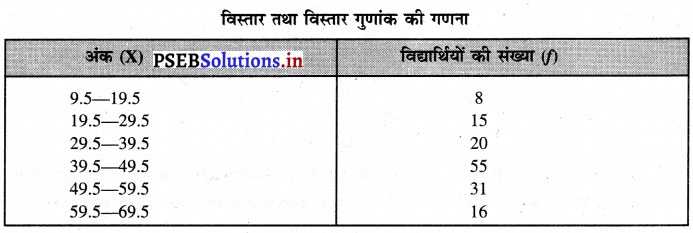
(i) विस्तार (Range) = L-S
R = 69:5 – 9.5 = 60 अंक उत्तर
सबसे अधिक अंकों तथा सबसे कम प्राप्त किए गए अंकों का अन्तर 60 है अर्थात् अंकों का विस्तार बहुत अधिक है |
(ii) विस्तार गुणांक (Co-efficient of Range) = \(\frac{\mathrm{L}-\mathrm{S}}{\mathrm{L}+\mathrm{S}}\)
C.R = \(\frac{69.5-9.5}{69.5+9.5}=\frac{60}{79}\) = 0.759 उत्तर
विस्तार अधिक होने के कारण विस्तार गुणांक अधिक है।

द्वितिय विधि (Second Method)
मध्य बिन्दुओं की विधि-इस विधि अनुसार अखण्डित श्रेणी में अपवर्जी वर्गान्तर दिए हों तो मध्य बिन्दु ज्ञात किए जाते हैं। सबसे बड़े अथवा सबसे लघु मध्य मूल्यों के अन्तर को विस्तार कहा जाता है।
प्रश्न 17.
एक स्कूल में पढ़ने वाले विद्यार्थियों के भार का विवरण दिया गया है। विस्तार तथा विस्तार गुणांक ज्ञात करो।
| भार (किलोग्राम): |
0-20 |
20-40 |
40-60 |
60-80 |
80-100 |
| विद्यार्थियों की संख्या: |
15 |
58 |
129 |
43 |
25 |
हल (Solution) :
विस्तार तथा विस्तार गुणांक की गणना ।
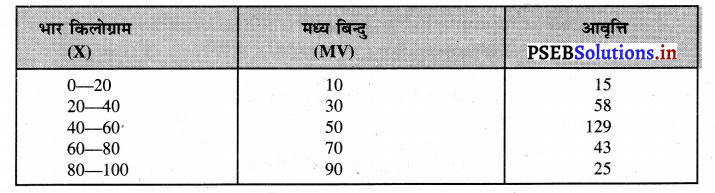
(i) विस्तार (Range) = LMV – SMV
R = 90 – 10 – 80 किलोग्राम उत्तर
विद्यार्थियों के मध्य मूल्य अधिकतम भार 90 किलोग्राम तथा मध्य मूल्य न्यूनतम भार 10 किलोग्राम का अन्तर 80 किलोग्राम है।
(ii) विस्तार गुणांक (Co-efficient of Range) = \(\frac{\mathrm{LMV}-\mathrm{SMV}}{\mathrm{LMV}+\mathrm{SMV}}\)
C.R. = \(\frac{90-10}{90+10}=\frac{80}{100}\) = 0.8 उत्तर
विस्तार अधिक होने के कारण विस्तार गुणांक अधिक है, जोकि एक के नज़दीक है।
3. चतुर्थक विचलन (Quartile Deviation)
प्रश्न 18.
चतुर्थक विचलन तथा चतुर्थक विचलन गुणांक का अर्थ बताओ।
उत्तर-
चतुर्थक विचलन-विस्तार की तरह चतुर्थक की स्थिति से सम्बन्धित अपकिरण का माप होता है। चतुर्थक विचलन किसी भी श्रेणी के तीसरे चतुर्थक (Q3) तथा प्रथम चतुर्थक (Q1) के अन्तर का अर्थ होता है। चतुर्थक विचलन को अर्ध चतुर्थक विचलन विस्तार भी कहते हैं। इसकी गणना के लिए निम्नलिखित सूत्र का प्रयोग किया जाता है-
चतुर्थक विचलन (Quartile Deviation) = \(\frac{\mathrm{Q}_{3}-\mathrm{Q}_{1}}{2}\)
यदि हम तीसरे चतुर्थक तथा प्रथम चतुर्थक का अन्तर निकाल लेते हैं तो इसको अन्तर चतुर्थक विचलन (InterQuartile Range) कहते हैं। यदि अन्तर चतुर्थक विचलन का अर्ध कर लिया जाए तो यह अर्ध चतुर्थक विचलन कहा जाता है, इसको चतुर्थक विचलन कहते हैं।
चतर्थक विचलन गुणांक (Co-efficient of Quartile Deviation)-चतुर्थक विचलन गुणांक अपकिरण का सापेक्ष माप (Relative Measure of Dispersion) होता है। इसका गुणांक ज्ञात करने के लिए तीसरे चतुर्थक तथा प्रथम चतुर्थक के अन्तर को तीसरे चतुर्थक तथा प्रथम चतुर्थक के जोड़ से विभाजित किया जाता है।
चतुर्थक विचलन गुणांक = \(\frac{\mathrm{Q}_{3}-\mathrm{Q}_{1}}{\mathrm{Q}_{3}+\mathrm{Q}_{1}}\)
इस प्रकार चतुर्थक विचलन गुणांक का पता चल जाता है।
चतर्थक विचलन की गणना (Calculation of Quartile Deviation),माप विधि
1. निम्नलिखित चतुर्थक का माप करो
Q1 = Size of the \(\frac{(\mathrm{N}+1)}{4}\) th item
2. ऊपरी चतुर्थक का माप करो
Q3 = Size of the \(\frac{3(\mathrm{~N}+1)}{4} \) item.
3. निम्नलिखित सूत्र द्वारा माप करो –
चतुर्थक विचलन (Q.D.) = \(\frac{\mathrm{Q}_{3}-\mathrm{Q}_{1}}{2}\)
चतुर्थक विचलन गुणांक = \(\frac{\mathrm{Q}_{3}-\mathrm{Q}_{1}}{\mathrm{Q}_{3}+\mathrm{Q}_{1}}\)
A. व्यक्तिगत श्रेणी (Individual Series)
प्रश्न 19.
निम्नलिखित सारणी का चतुर्थक विचलन तथा चतुर्थक विचलन गुणांक पता करो।
अंक : 8 10 20 15 3 0 40 25
हल (Solution) :
दिए आंकड़ों को बढ़ते क्रमानुसार लिखा जाता है। चतुर्थक विचलन तथा चतुर्थक विचलन गुणांक की गणना
q1 = size of the \(\frac{(\mathrm{N}+1)}{4}\) th item
q1= size of the \(\frac{(7+1)}{4}\) th = \(\frac{8}{4}\) = 2nd item.
q1 = 10 अंक
q3 = size of the \(\frac{3(N+1)}{4}\) th item.
q3 = size of the \(\frac{3(7+1)}{4}=\frac{3 \times 8}{4}\) = 6th item.
= \(\frac{24}{4}\) = 6th item.
q3 = 30 अंक
(i) चतुर्थक विचलन (Q.D.) = \(\frac{\mathrm{Q}_{3}-\mathrm{Q}_{1}}{2}\)
Q.D. = \(\frac{30-10}{2}=\frac{20}{2}\) = 10 अंक उत्तर
चतुर्थक विचलन 10 अंक है। चतुर्थक विचलन जितना अधिक होता है, यह तीसरे चतुर्थक Q3 तथा प्रथम चतुर्थक Q1 में आंकड़ों के अधिक विस्तार को प्रकट करता है। चतुर्थक विचलन जितना कम होता है, यह आंकड़ों की कम भिन्नता को प्रकट करता है।
(ii) चतुर्थक विचलन गुणांक (Co-efficient of Q.D.)
= \(\frac{\mathrm{Q}_{3}-\mathrm{Q}_{1}}{\mathrm{Q}_{3}+\mathrm{Q}_{1}}\)
Co-efficient of Q.D. = \(\frac{30-10}{30+10}=\frac{20}{40}\) = 0.5 उत्तर
इससे ज्ञात होता है कि प्रथम चतुर्थक तथा तीसरा चतुर्थक विचलन गुणांक 0.5 है, जितना चतुर्थक गुणांक अधिक होता है, उतनी विषमता अधिक होती है।
B. खण्डित श्रेणी (Discrete Series)
निम्न चतुर्थक Q1 तथा ऊपरी चतुर्थक Q3 का माप संचीय आवृत्ति की सहायता से पता किया जाता है।
प्रश्न 20.
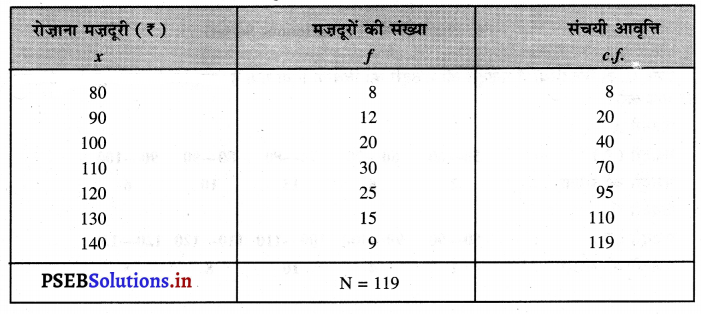
निम्नलिखित आंकड़ों का चतुर्थक विचलन तथा चतुर्थक विचलन गुणांक पता करो।
| रोज़ाना मज़दूरी (रु०) : |
80 |
90 |
100 |
110 |
120 |
130 |
140 |
| मज़दूरों की संख्या : |
8 |
12 |
20 |
30 |
25 |
15 |
10 |
हल (Solution):
चतुर्थक विचलन तथा चतुर्थक विचलन गुणांक की गणना
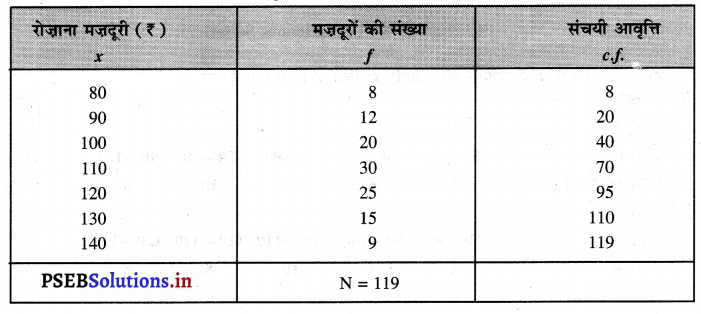
q1 = size of the \(\left(\frac{N+1}{4}\right)\)th item
q1 = size of the \(\left(\frac{119+1}{4}\right)\)th item
= \(\frac{120}{4}\) = 30th item.
q1 = ₹ 100
q3 = size of the \(\frac{3(\mathrm{~N}+1)}{4}\) th item.
= \(\frac{3 \times 120}{4}\) = 90th item.
Q3 = ₹ 120
(i) चतुर्थक विचलन (Q.D.) = \(\frac{\mathrm{Q}_{3}-\mathrm{Q}_{1}}{2}=\frac{120-100}{2}=\frac{20}{2}\) = = ₹ 10 उत्तर
मज़दूरों की मजदूरी में भिन्नता कम है।
(ii) चतुर्थक विचलन गुणांक = \(\frac{\mathrm{Q}_{3}-\mathrm{Q}_{1}}{\mathrm{Q}_{3}+\mathrm{Q}_{1}}\)
(Co-efficient of Q.D.) = \(\frac{120-100}{120+100}=\frac{20}{220} \) = 0.09 उत्तर
जब चतुर्थक विचलन कम होता है तो चतुर्थक विचलन गुणांक का मूल्य कम होता है।
C. अखण्डित श्रेणी (Continuous Series)

प्रश्न 21.
दो फैक्टरियों में मजदूरों की मजदूरी का विवरण दिया गया है। चतुर्थक विचलन द्वारा अपकिरण का माप करो।
फैक्टरी A मज़दूरी (₹) : 50-60 60-70 70-80 80-90 90-100
मज़दूरों की संख्या : 2 8 15 106
फैक्टरी B मज़दूरी (₹) : 80-90 . 90-100 100-110 110-120 120-130
मजदूरों की संख्या : 1 4 108
हल (Solution) :
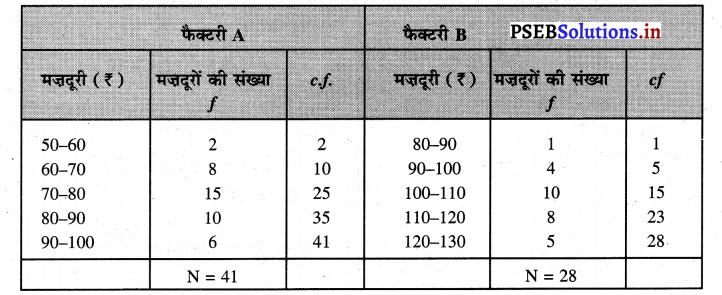
फैक्टरी A
Q1 का माप
q1 = \(\frac{n}{4}=\frac{41}{4}\) = 10.25th item
(70-80) के वर्ग अन्तराल में है)
∴ Q1 = \( \mathrm{L}_{1}+\frac{n / 4-\mathrm{C} f p}{f} \times i\)
= 70 + \(\frac{10.25-10}{15} \times 10\)
= 70 +\(\frac{.25}{3} \times 2\)
= 70 + \(\frac{.50}{3}\)
Q1 = 70 +0.167
Q3 का माप
q3 = \( \frac{3 n}{4}=\frac{3(41)}{4}=\frac{123}{4}\) = 30.75th Item
(80-90 वर्ग-अन्तराल में है)
∴ Q3 = \(L_{1}+\frac{\frac{3 n}{4}-C f p}{f} \times i\)
= 80 + \(\frac{30.75-25}{10} \times 10\)
= 80 + 5.75
Q3 = 85.75
चतुर्थक विचलन (Q.D.)
QD = \(\frac{\mathrm{Q}_{3}-\mathrm{Q}_{1}}{2}\)
= \(\frac{87.75-70.167}{2}=\frac{17.583}{2}\)
QD = 8.792 उत्तर
चतुर्थक विचलन गुणांक = \(\frac{\mathrm{Q}_{3}-\mathrm{Q}_{1}}{\mathrm{Q}_{3}+\mathrm{Q}_{1}}\)
= \(\frac{87.75-70.167}{87.75+70.167}=\frac{8.792}{157.917}\) = 0.055
Co-efficient of Q.D. = 0.055 उत्तर
फैक्टरी B
Q1 का माप
q1 = \(\frac{n}{4}=\frac{28}{4}\) = 7th Item
(100-110) के वर्ग अन्तराल में है)
Q1 = \(\mathrm{L}_{1}+\frac{n / 4-\mathrm{C} f p}{f} \times i\)
= 100 + \(\frac{7-5}{10} \times 10\)
= 100 + 2 = 102
Q1 = 102
Q3 का माप
q3 = \(\frac{3 n}{4}=\frac{3(28)}{4}=\frac{84}{4}\) = 21st Item
(110-120) वर्ग अन्तराल में है)
Q3 = \(\mathrm{L}_{1}+\frac{\frac{3 n}{4}-C f p}{f} \times i\)
= 110 + \(\frac{21-15}{8} \times 10\)
= 110 + \(\frac{21-15}{8} \times 10\)
= 110 + \(\frac{6}{8} \times 10\)
= 110 + 7.5 = 117.5
Q3 = 117.5
चतुर्थक विचलन (Q.D.) = \(\frac{\mathrm{Q}_{3}-\mathrm{Q}_{1}}{2}\)
= \(\frac{117.5-102}{2}=\frac{15.5}{2}\) = 7.75
Q.D. = 7.75 Ans.
चतुर्थक विचलन गुणांक = \(\frac{\mathrm{Q}_{3}-\mathrm{Q}_{1}}{\mathrm{Q}_{3}+\mathrm{Q}_{1}}\)
= \(\frac{117.5-102}{117.5+102}\)
= \(\frac{15.5}{219.5}\) = 0.071
Co-efficient of Q.D. = 0.071 Ans.
चतुर्थक विचलन गुणांक फैक्टरी A में फैक्टरी B से अधिक है। इसलिए फैक्टरी A में फैक्टरी B की तुलना में अधिक विषमता (Variability) पाई जाती है।
प्रश्न 22.
चतुर्थक विचलन के गुण तथा दोष बताओ।
उत्तर-
चतुर्थक विचलन के गुण (Merits of Quartile Deviation)
1. सरल-चतुर्थक का माप करना आसान है।
2. माप-इस का माप करना भी सरल है।
3. सीमान्त मूल्यों का कम प्रभात-चतुर्थक द्वारा अपकिरण का माप करते समय सीमान्त मूल्यों का बहुत कम प्रभाव पड़ता है।
चतर्थक विचलन के दोष (Demerits of Quartile Deviation)
1. अस्थिरता-चतुर्थक विचलन में अस्थिरता का दोष होता है क्योंकि साँपल में परिवर्तन होने से इसके मूल्य पर काफ़ी प्रभाव पड़ता है।
2. सभी मूल्यों पर आधारित नहीं-चतुर्थक में श्रेणी के सभी मूल्यों को ध्यान में रख कर इनका माप नहीं किया जाता। 3. श्रृंखला का ज्ञान-चतुर्थक द्वारा श्रृंखला की बनावट का पूरा ज्ञान प्राप्त नहीं होता।
3. मध्य विचलन (Mean Deviation)
प्रश्न 23.
मध्य विचलन का अर्थ बताओ। मध्य विचलन की गणना किस विधि द्वारा की जा सकती है ? (Explain the meaning of Mean Deviation. How is Mean Deviation calculated ?)
उत्तर-
मध्य विचलन का अर्थ (Meaning of Mean Deviation)-मध्य विचलन को औसत विचलन भी कहा जाता है। औसतें मुख्य तीन प्रकार की होती हैं-समान्तर औसत, मध्यका तथा बहुलक। किसी श्रेणी की औसत निकालकर मदों में से औसत का विचलन निकाला जाता है। विचलन निकालते समय बीज गणित चिह्न (+) तथा (-) को छोड़ दिया जाता है। इस प्रकार विचलनों के मध्य को मध्य विचलन कहा जाता है।
परिभाषा-
कलार्क तथा सकेड के अनुसार, “श्रेणी की किसी औसत समान्तर मध्य, मध्यका अथवा बहुलक से निकाले गए विचलनों का समान्तर मध्य उस श्रेणी का मध्य विचलन कहा जाता है, परन्तु विचलनों के चिह्नों (+), (-) को छोड़ दिया जाता है।”
(“Average Deviation is the average amount of scatter of items is a distribution from either mean, or median or the mode, ignoring signs of deviation.”-Clark and Schkade)
गणित चिह्नों (+) तथा (-) को छोड़ने का मुख्य कारण यह है कि समान्तर औसत से मदों का विचलन निकाला जाए तो जवाब शून्य (Zero) होता है।
माप विधि-
- सबसे पहले दी श्रेणी की औसत (समान्तर मध्य, मध्यका अथवा बहुलक) ज्ञात करो।
- प्राप्त की औसत से भिन्न-भिन्न मदों का विचलन ज्ञात करो। बीज गणित चिह्न (+), (-) को छोड़ दो।
- विचलनों को |D| इसको D मोडलस पढ़ा जाता है। चिह्न द्वारा प्रकट करो।
- विचलनों को मदों की संख्या से विभाजित करो। इससे मध्य विचलन प्राप्त हो जाता है।
- चाहे मध्य विचलन समान्तर औसत, मध्यका तथा बहुलक द्वारा निकाला जा सकता है।
साधारण तौर पर समान्तर औसत (X) तथा मध्यका (M) का ही प्रयोग किया जाता है। बहुलक (Z) का प्रयोग नहीं किया जाता। परन्तु प्रश्न में जिस औसत द्वारा मध्य विचलन पूछा जाए उस औसत का प्रयोग करो।

माप सूत्र (Formula) –
माप विचलन के माप दो तरह के होते हैं-
I. निरपेक्ष माप (Absolute Measure)-निरपेक्ष माप द्वारा मध्य विचलन की गणना निम्नलिखित श्रेणियों में इस प्रकार की जाती है
1. व्यक्तिगत श्रेणी (Individual Series)-मध्य विचलन का माप समान्तर औसत, मध्यका अथवा बहुलक से पता किया जाता है। इसलिए जिस औसत से मध्य विचलन की गणना करनी हो उस औसत द्वारा माप का सूत्र निम्नलिखित अनुसार है –
- यदि विचलन समान्तर औसत से लिया जाए तो
M.D. \((\bar{X})=\frac{\Sigma|X-\bar{X}|}{N}\) OR = \(\frac{\Sigma\left|\mathrm{D}_{\overline{\mathrm{X}}}\right|}{\mathrm{N}}\)
- यदि विचलन मध्यका से लिया जाए तो
M.D (M) = \(\frac{\Sigma|\mathbf{X}-\mathrm{M}|}{\mathrm{N}} \mathrm{OR}=\frac{\Sigma\left|\mathrm{D}_{\mathrm{M}}\right|}{\mathrm{N}}\)
- यदि विचलन बहुलक से लिया जाए तो
M.D. (Z) = \(\frac{\Sigma|\mathbf{X}-\mathbf{Z}|}{\mathrm{N}} \mathrm{OR}=\frac{\Sigma\left|\mathrm{D}_{\mathrm{Z}}\right|}{\mathrm{N}} \)
यहां M.D. \((\bar{X})\) = समान्तर मध्य से मध्य विचलन
|D|x = इसको पढ़ा जाता जाता है D मोडलस समान्तर मध्य से मदों का विचलन (+), (-) चिह्नों को छोड़कर।
|D|M = मध्यक से मदों का विचलन (+1), (-) चिह्नों को छोड़कर
|D|Z = बहुलक से मदों का विचलन (+1), (-) चिह्नों को छोड़कर
N मदों की संख्या
2. खण्डित तथा अखण्डित श्रेणी (Discrete and Continuous Series)-खण्डित तथा अखण्डित श्रेणी में निम्नलिखित सूत्र का प्रयोग किया जाता है –
समान्तर मध्य, मध्यका तथा बहुलक द्वारा मध्य विचलन
(i) M.D. \(\bar{X}\) = \(\frac{\Sigma f|D \overline{\mathrm{X}}|}{\mathrm{N}}\)
(ii) M.D.M = \(\frac{\Sigma f\left|\mathrm{D}_{\mathrm{M}}\right|}{\mathrm{N}}\)
(iii) M.D.Z = \(\frac{\Sigma f\left|D_{Z}\right|}{N}\)
साधारण तौर पर मध्य विचलन का माप मध्यका द्वारा किया जाता है। कई बार समान्तर औसत (mean) का प्रयोग भी किया जाता है।
परन्तु बहुलक (mode) का प्रयोग कभी-कभी ही किया जाता है।
- सबसे पहले समान्तर मध्य, मध्यका तथा बहुलक की गणना करो।
- औसत से मदों का विचलन निकालो (+) तथा (-) चिह्नों को छोड़ दो। इसको (D) द्वारा लिखो।
- प्रत्येक मद के सामने वाली आवृत्ति (f) को |D| से गुणा करके गुणनफल को f|D| लिखो।
- प्राप्त हुए गुणनफल का जोड़ Σf |D| करके इनकी संख्या |N| पर विभाजित करो। इस प्रकार मध्य विचलन (M.D.) प्राप्त हो जाता है।
II. सापेक्ष माप (Relative Measure)-अपकिरण के सापेक्ष माप को मध्य विचलन का गुणांक कहा जाता है। मध्य विचलन के गुणांक की गणना करने के लिए मध्य विचलन को समान्तर औसत, मध्यका अथवा बहुलक द्वारा निकालने के पश्चात् जिस औसत से मध्य विचलन की गणना की गई है, उस औसत से भाग कर दिया जाता है। इस प्रकार मध्य विचलन प्राप्त हो जाता है। मध्य विचलन गुणांक का सूत्र निम्नलिखित अनुसार है-
(i) Co-efficient of MD\(\bar{X}\) = \(\frac{\mathrm{MD}_{\overline{\mathrm{X}}}}{\overline{\mathrm{X}}} \)
(ii) Co-efficient of M.D.M = \(\frac{\text { M.D.M }}{\text { Median }}\)
(iii) Co-efficient of M.D.Z = \(\frac{\text { M.D.Z }}{\text { Mode }}\)
व्यक्तिगत श्रेणी (Individual Series)
प्रश्न 24.
निम्नलिखित आंकड़ों की सहायता से मध्य विचलन तथा उसके गुणांक का पता करो।
अंक : 8 10 12 15 18 . 20 25 इसकी गणना मध्यका द्वारा करो।
हल (Solution):
मध्यक द्वारा मध्य विचलन तथा उसके गुणांक की गणना
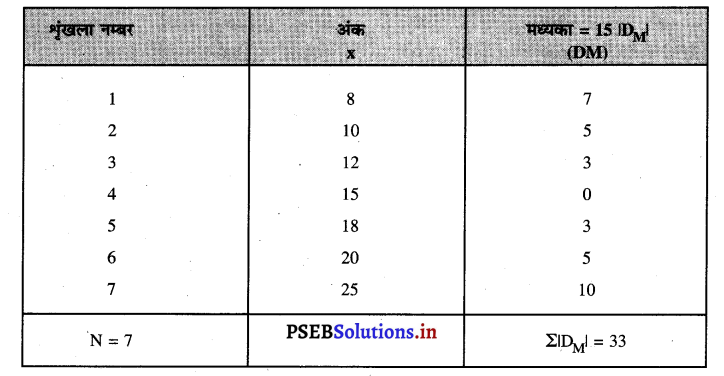
मध्यका द्वारा मध्य विचलन
m = size of the \(\frac{(\mathrm{N}+1)}{2}\) th item.
M = size of the \(\left(\frac{7+1}{2}\right) \mathrm{th}=\frac{8}{2}\) = 4th item.
Median = 15 marks
M.D.M= \(\frac{\Sigma\left|D_{M}\right|}{N}=\frac{33}{7}\) = 4.714 अंक उत्तर
Co-efficient of M.D. = \(\frac{\text { M.D.M. }}{\text { Median }}=\frac{4.714}{15} \) = 0.314 उत्तर
मध्य विचलन गुणांक 1 की अनुपात में जितना कम है वह समंकों के कम उत्तर को प्रकट करता है।
प्रश्न 25.
फैक्टरी A तथा फैक्टरी B में मजदूरी सम्बन्धी आंकड़े दिए गए हैं। मध्यका तथा मध्य विचलन ज्ञात करो तथा तुलना करो।
हल (Solution):
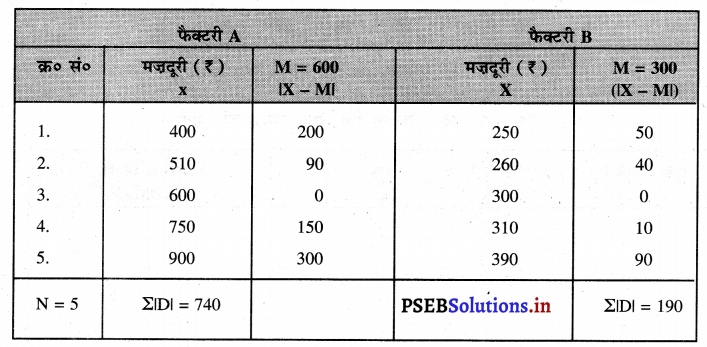
m= \(\frac{\mathrm{N}+1}{2}=\frac{5+1}{2}=\frac{6}{2}\) = 3rd item.
M (Median)= 600
MDM = \(\frac{\Sigma|\mathrm{D}|}{\mathrm{N}}=\frac{740}{5}\) = ₹ 148
मध्य विचलन गुणांक = \(\frac{\mathrm{MD}_{\mathrm{M}}}{\text { Median }}\) = \(\frac{148}{600} \) = 0.247
m = \(\frac{N+1}{2}=\frac{5+1}{2}=\frac{6}{2}\) = 3rd item
M (मध्यका )= ₹300
MDM = \(\frac{\Sigma|\mathrm{D}|}{\mathrm{N}}=\frac{300}{5}\) = ₹60
मध्य विचलन गुणांक = \(\frac{\mathrm{MD}_{\mathrm{M}}}{\text { Median }}\)
= \(\frac{\mathrm{MD}_{\mathrm{M}}}{\text { Median }}\) = \(\frac{60}{300}\) = 0.200
फैक्टरी A का मध्य विचलन गुणांक फैक्टरी B के मध्य विचलन गुणांक से अधिक है। इसलिए फैक्टरी A की मज़दूरी में भिन्नता अधिक है।
प्रश्न 26.
आठवीं कक्षा में पढ़ने वाले विद्यार्थियों की आयु का विवरण इस प्रकार है। औसत विचलन तथा औसत विचलन गुणांक ज्ञात करो।
| आयु (वर्ष) : |
11 |
12 |
13 |
14 |
15 |
| विद्यार्थियों की संख्या : |
2 |
8 |
15 |
3 |
2 |
हल (Solution) :
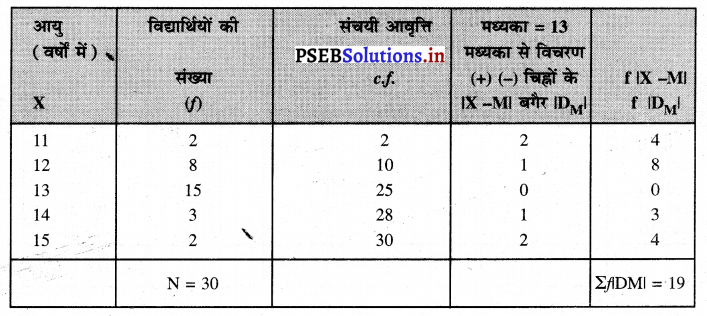
(i) मध्यका (Median) का माप
m = \(\frac{\mathrm{N}+1}{2}=\frac{30+1}{2}=\frac{31}{2}\) = 15.5th item.
यह संचयी आवृत्ति 25 में पाई जाती है।
∴ मध्यका = 13 वर्ष ।
(ii) औसत विचलन (Mean Deviation) का माप –
मध्यका से माप विचलन = \(\frac{\Sigma f\left|\mathrm{D}_{\mathrm{M}}\right|}{\mathrm{N}}=\frac{19}{30}\) = 0.633
औसत विचलन से ज्ञात होता है कि मध्यका से दूरी कम है।
(iii) औसत विचलन गुणांक (Co-efficient of Mean Deviation)
Co-efficient of M.D. =\(\frac{\text { M.D. }}{\text { Median }}=\frac{0.63}{13}\) = 0.049
मध्य विचलन गुणांक काफ़ी कम है, इसलिए मध्यका से आयु की कम दूरी पाई जाती है।
अखण्डित श्रेणी में मध्य विचलन की गणना (Calculation of Mean Deviation in Continuous Series)
अखण्डित श्रेणी वर्गों के अन्तर के मध्य मूल्य निकाल लेते हैं। इससे अखण्डित श्रेणी, खण्डित श्रेणी का रूप धारण कर लेती है। इसके पश्चात् खण्डित श्रेणी जैसे ही मध्य विचलन की गणना की जाती है।

प्रश्न 27.
निम्नलिखित आंकड़ों का समान्तर मध्य द्वारा मध्य विचलन के गुणांक का माप करो।
| अंक: |
0-10 |
10-20 |
20-30 |
30-40 |
40-50 |
| विद्यार्थियों की संख्या : |
2 |
8 |
10 |
15 |
5 |
हल (Solution) :
मध्य विचलन तथा मध्य विचलन के गुणांक की गणना
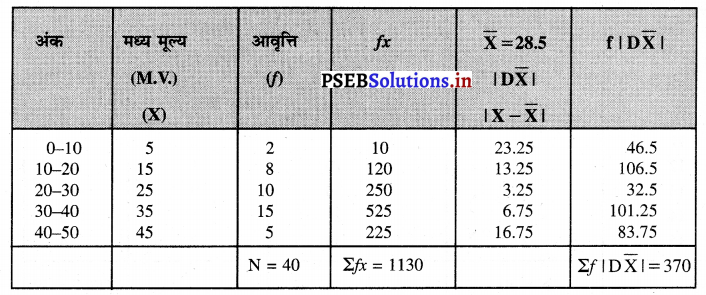
(i) समान्तर मध्य (Mean) \(\bar{X} \) = \(\frac{\Sigma f x}{\mathrm{~N}}=\frac{1130}{40}\) = 28.25
(ii) मध्य विचलन (Mean Deviation)
M.D. = \(\frac{\Sigma(f|\mathrm{D} \overline{\mathrm{x}}|)}{\mathrm{N}}=\frac{370}{40}\) = 9.25 अंक उत्तर
समान्तर औसत से भिन्नता 9.25 अंक है।
(iii) मध्य विचलन का गुणांक Coefficient of M.D.= \(\frac{\mathrm{MD} \overline{\mathrm{X}}}{\text { Mean }}=\frac{9.25}{28.25}\) = 0.327 उत्तर
मध्य विचलन गुणांक 0.327 है अथवा 32.7% है जोकि काफ़ी कम है इसलिए अंकों में अन्तर कम है।
4. प्रमाप विचलन (Standard Deviation)
प्रश्न 28.
प्रमाप विचलन से क्या अभिप्राय है? प्रमाप विचलन तथा मध्य विचलन में अन्तर बताओ। (What is meant by Standard Deviation ? Distinguish between Mean Deviation and Standard Deviation.)
उत्तर-
अपकिरण के माप के लिए इस विधि की सबसे पहले कार्ल पीयर्सन (Karl Pearson) ने 1893 में व्याख्या की थी। इसको अपकिरण के माप की सबसे अधिक महत्त्वपूर्ण, उपयोगी तथा विश्वसनीय विधि माना जाता है। प्रमाप विचलन को विचलन वर्ग मध्य मूल्य भी कहा जाता है। इसको ग्रीक भाषा के अक्षर (0) सिगमा द्वारा प्रकट किया जाता है। जितनी आंकड़ों में अपकिरण अथवा भिन्नता अधिक होगी, उतना ही प्रमाप विचलन अधिक होगा अर्थात्-
- यदि प्रमाप विचलन छोटा है तो इसका अर्थ आंकड़ों में भिन्नता कम है अथवा एक समानता पाई जाती है।
- यदि प्रमाप विचलन बड़ा है तो इसका अर्थ है कि आंकड़ों में भिन्नता अधिक है अथवा एक समानता नहीं है।
प्रमाप विचलन का अर्थ (Meaning of Standard Deviation)-किसी श्रेणी के मध्यमान में से उसकी भिन्न-भिन्न मदों के निकाले गए विचलनों के वर्गों की औसत के वर्गमूल को प्रमाप विचलन कहा जाता है।
प्रमाप विचलन हमेशा समान्तर मध्य में से ही विचलनों द्वारा लिया जाता है क्योंकि समान्तर मध्य में से लिए गए विचलनों के वर्गों का जोड़ किसी अन्य औसत में से लिए गए विचलनों के वर्गों की आवश्यकता से न्यूनतम होता है।
प्रमाप विचलन की विशेषताएं (Characteristics of Standard Deviation)-
- प्रमाप विचलन में मदों से विचलन समान्तर मध्य से लिए जाते हैं।
- प्रमाप विचलन में गणित चिह्न जमा (+) तथा घटाओ ( – ) को छोड़ा नहीं जाता। हासिल किए गए विचलनों के वर्ग कर लिए जाते हैं, जिससे ऋणात्मक विचलन भी धनात्मक बन जाते हैं।
- प्रमाप विचलन की गणना करने के लिए उन वर्गों का जिनका वर्ग किया गया है इसका मध्य प्राप्त करके वर्गमूल निकाला जाता है। इसको प्रमाप विचलन कहते हैं।
प्रमाप विचलन तथा मध्य विचलन में अन्तर (Difference between Mean Deviation and Standard Deviation)-प्रमाप विचलन तथा मध्य विचलन में मुख्य अन्तर इस प्रकार हैं-
- प्रमाप विचलन (S.D.)-प्रमाप विचलन की गणना केवल समान्तर मध्य द्वारा ही की जाती है। मध्य विचलन (M.D.)-मध्य विचलन की गणना केन्द्रीय प्रवृत्तियां समान्तर मध्य (Mean), मध्यक (Median) अथवा बहुलक के आधार पर की जा सकती है।
- प्रमाप विचलन (S.D.)-प्रमाप विचलन में श्रेणी की मदों की समान्तर औसत (Mean) से मदों के विचलन निकाले जाते हैं। प्राप्त किए विचलनों के वर्ग करके (+) तथा (-) चिह्नों को धनात्मक (+) बना लिया जाता है। इस प्रकार विचलनों की औसत पता करके वर्गमूल निकाला जाता है। इस प्रकार (+) तथा (-) चिह्नों को ध्यान में रखा जाता हैं |
मध्य विचलन (M.D.)-मध्य विचलन में गणित चिह्नों (+) तथा (-) को छोड़ दिया जाता है। यह मध्य विचलन का सबसे बड़ा दोष है।
A.व्यक्तिगत श्रेणी (Individual Series)
प्रमाप विचलन गणना की विधियाँ (Method of Measuring Standard Deviation)
- प्रत्यक्ष विधि(1) किसी श्रेणी के मूल्यों की समान्तर औसत ज्ञात कीजिए।
- प्रत्येक मूल्य में से समान्तर औसत (X̄) को घटाओ तथा विचलन को छोटी X द्वारा अंकित करो।
(x-X̄=x)
- प्राप्त किए विचलनों (x) का वर्ग पता करो तथा विचलनों के वर्गों (x2) का जोड़ (Σx2) कर लें।
- निम्नलिखित सूत्र का प्रयोग करो
(i) σ = \(\sqrt{\frac{\Sigma x^{2}}{N}}=\sqrt{\frac{(\mathrm{X}-\overline{\mathrm{X}})^{2}}{\mathrm{~N}}}\)

σ (सिगमा) = प्रमाप विचलन
Σx2 = मदों से समान्तर औसत के विचलनों के वर्गों का जोड़
N = मदों की संख्या
√ = वर्गमूल
5. प्रमाप विचलन के वर्ग को वेरीअँस अथवा प्रसारण कहा जाता है अथवा प्रसारण कहा जाता
Variance or V = σ2 अथवा \(\frac{\Sigma x^{2}}{\mathrm{~N}}\) जहां x = x = x – X̄
6. सापेक्ष माप-प्रमाप विचलन के सापेक्ष माप को प्रमाप विचलन गुणांक कहा जाता है। इसकी गणना का सूत्र निम्नलिखित अनुसार है

प्रश्न 29.
निम्नलिखित आंकड़ों का प्रमाप विचलन तथा प्रमाप विचलन का गुणांक ज्ञात करो –
अंक : 6, 9, 10, 13, 17, 19, 21, 25
हल (Solution) :
प्रमाप विचलन की गणना ( प्रत्यक्ष विधि)
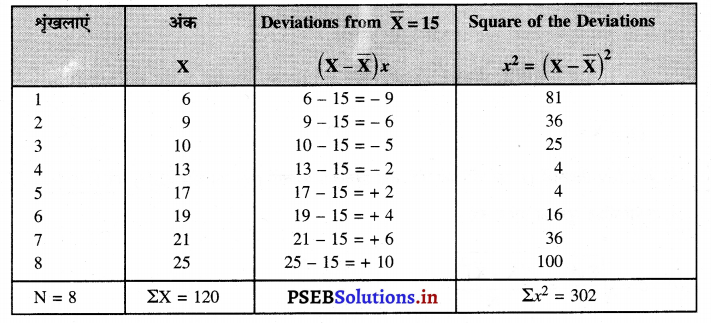
समान्तर औसत (Mean)
X̄ = \(\frac{\Sigma x}{N}=\frac{120}{8}\)
प्रमाप विचलन (Standard Deviation)
σ = \( \sqrt{\frac{(\mathrm{X}-\overline{\mathrm{X}})^{2}}{\mathrm{~N}}}=\sqrt{\frac{\Sigma x^{2}}{\mathrm{~N}}}=\sqrt{\frac{302}{8}}=\sqrt{37.75}\)
σ = 6.14 उत्तर
(Standard Deviation gives us the absolute value of variation. By this, we cannot measure the variability of two or more series. We have to study the relative measure of dispersion.)
अपकिरण गुणांक (Co-efficient of Variation)
Co-efficient of Variation = \( \frac{\text { S.D. }}{\bar{X}} \times 100=\frac{6.14}{15} \times 100\)
or Co-efficient of variation = 40.9%
It shows that the variation of the items from Mean is 40.9%.

प्रश्न 30.
निम्न सारणी का प्रमाप विचलन ज्ञात करो –
| आकार : |
5 |
10 |
15 |
20 |
25 |
30 |
| आवृत्ति : |
2 |
8 |
10 |
15 |
8 |
7 |
हल (Solution) :
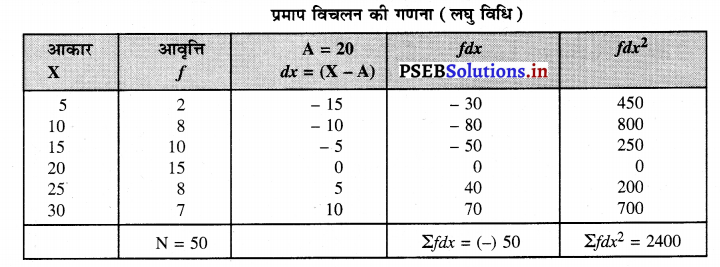
प्रमाप विचलन
S.D. or σ = \(\sqrt{\frac{\Sigma f d x^{2}}{N}-\left(\frac{\Sigma f d x}{N}\right)^{2}}\)
σ = \(\sqrt{\frac{2400}{50}-\left[\frac{(-50)}{50}\right]^{2}}\)
σ = \(\sqrt{48-1}=\sqrt{47}\) 6.85 उत्तर
निरपेक्ष प्रमाप विचलन 6.85 है।
प्रश्न 31.
निम्नलिखित सारणी का पद विचलन विधि द्वारा प्रमाप विचलन ज्ञात करो।
| अंक : |
20 |
30 |
40 |
50 |
60 |
| विद्यार्थियों की संख्या |
6 |
10 |
20 |
55 |
10 |
हल (Solution) :
प्रमाप विचलन की गणना (पद विचलन विधि)
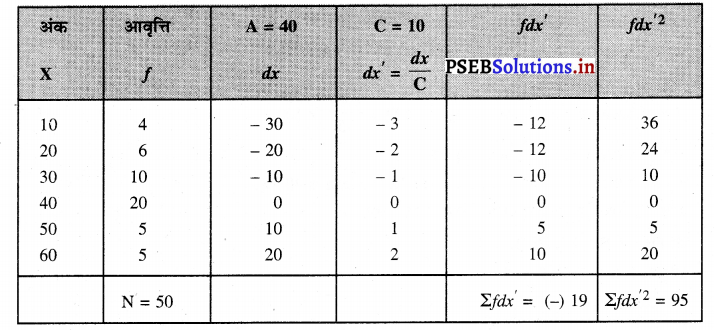
प्रमाप विचलन
S.D. or σ = \(\sqrt{\frac{\Sigma f d x^{\prime 2}}{N}-\left(\frac{\Sigma f d x^{\prime}}{N}\right)^{2}} \times C\)
σ = \(\sqrt{\frac{95}{50}-\left(\frac{(-) 19}{50}\right)^{2}} \times 10\)
σ = \(\sqrt{1.9-0.144} \times 10\)
σ = \(\sqrt{1.756} \times 10\)
σ = 1.325 x 10 = 13.25 उत्तर
निरपेक्ष प्रमाप विचलन 13.25 है।
प्रश्न 32.
निम्नलिखित सारणी का प्रमाप विचलन प्रत्यक्ष विधि द्वारा ज्ञात करो।
| मज़दूरी (२) |
0-10 |
10-20 |
20-30 |
30-40 |
40-50 |
| मज़दूरों की संख्या |
2 |
3 |
10 |
4 |
1 |
हल (Solution) :
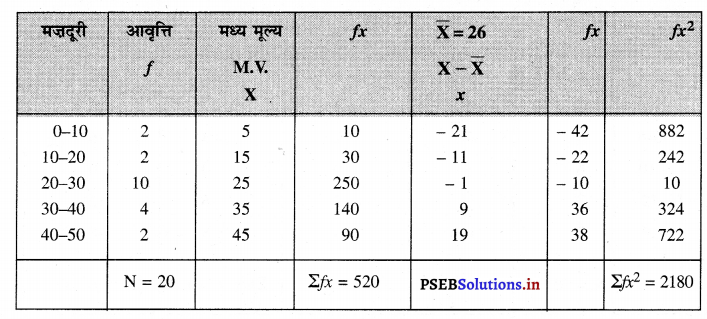
समान्तर औसत की गणना
X̄ = \(\frac{\sum f x}{\mathrm{~N}}=\frac{520}{20}\) = 26
प्रमाप विचलन
S.D. or σ = \(\sqrt{\frac{\Sigma f x^{2}}{\mathrm{~N}}}\)
σ = \(\sqrt{\frac{2180}{20}}=\sqrt{109}\) = ₹ 10.44 उत्तर
निरपेक्ष प्रमाप विचलन 10.44 है।
(B) लघु विधि (Short Cut Method)
अखण्डित श्रेणी में प्रमाप विचलन की गणना करते समय खण्डित श्रेणी में प्रयोग की जाने वाली विधि का प्रयोग किया जाता है। अखण्डित श्रेणी के मध्य मूल्य (Mid values) निकाले जाते हैं। इस प्रकार अखण्डित श्रेणी अपने-आप ही खण्डित श्रेणी का रूप धारण कर लेती है। इस विधि में निम्नलिखित सूत्र का प्रयोग किया जाता है –
σ = \(\sqrt{\frac{\Sigma f d x^{2}}{N}-\left(\frac{\Sigma f d x^{\prime}}{N}\right)^{2}}\)
प्रश्न 33.
निम्नलिखित आंकड़ों द्वारा प्रमाप विचलन ज्ञात करो –
| आकार : |
2-4 |
4-6 |
6-8 |
8-10 |
10-12 |
12-14 |
| आवृत्ति : |
1 |
2 |
3 |
4 |
6 |
3 |
हल (Solution) :
प्रमाप विचलन की गणना (लघु विधि)
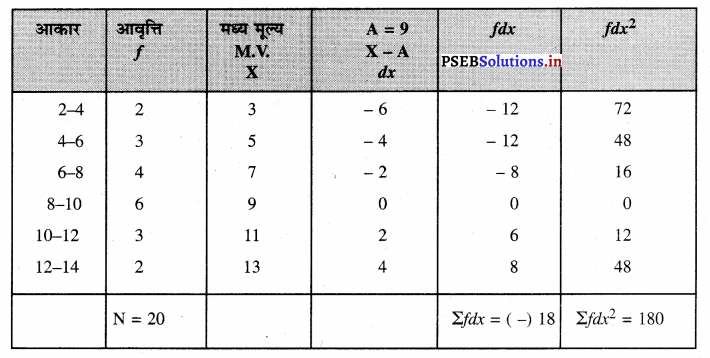
प्रमाप विचलन (Standard Deviation)
S.D. or σ = \(\sqrt{\frac{\Sigma f d x^{2}}{\mathrm{~N}}-\left(\frac{\Sigma f d x}{\mathrm{~N}}\right)^{2}}\)
σ = \(\sqrt{\frac{180}{20}-\left(\frac{(-) 18}{20}\right)^{2}}\)
σ = \(\sqrt{9-(0.9)^{2}}=\sqrt{8.19}\)
σ = 2.86 उत्तर
(C) पद विचलन विधि यदि पद विचलन लिए जाएं तो गणना का कार्य और आसान हो जाता है। इस विधि में निम्नलिखित सूत्र का प्रयोग किया जाता है
σ = \( \sqrt{\frac{\Sigma f d x^{2}}{\mathrm{~N}}-\left(\frac{\Sigma f d x}{\mathrm{~N}}\right)^{2}} \times \mathrm{C}\)
प्रश्न 34.
निम्नलिखित आंकड़ों से प्रमाप विचलन ज्ञात करो –
| अंक : |
0-5 |
5-10 |
10-15 |
15-20 |
20-25 |
25-30 |
30-35 |
| विद्यार्थियों की संख्या: |
8 |
12 |
20 |
25 |
22 |
10 |
3 |
हल (Solution):
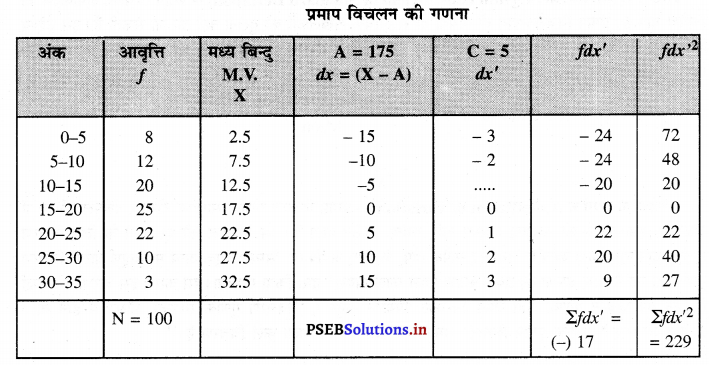
प्रमाप विचलन (Standard Deviation)
S.D. or σ = \( \sqrt{\frac{\Sigma f d x^{\prime 2}}{\mathrm{~N}}-\left(\frac{\Sigma f d x^{\prime}}{\mathrm{N}}\right)^{2}} \times \mathrm{C}\)
σ = \(\sqrt{\frac{229}{100}-\left(\frac{(-) 17}{100}\right)^{2}} \times 5\)
σ = \(\sqrt{2.29-0.0289} \times 5 \)
σ = \(\sqrt{2.2611} \times 5\)
σ = 1.504 × 5
σ = 7.52 उत्तर
निरपेक्ष प्रमाप विचलन 7.520 है।
प्रमाप विचलन गुणांक तथा विचरण गुणांक (Co-efficient of Standard Deviation and Co-efficient of Variation)
प्रश्न 35.
प्रमाप विचलन गुणांक, विचरण गुणांक तथा प्रसरण का अर्थ बताओ। (Explain the meaning of Co-efficient of Standard Deviation, Co-efficient of Valuable and Variance.)
उत्तर-
. प्रमाप विचलन गुणांक (Co-efficient of Standard Deviation)-प्रमाप विचलन अपकिरण का निरपेक्ष माप है। प्रमाप विचलन द्वारा दो अथवा दो से अधिक शृंखलाओं की तुलना नहीं की जा सकती है। इस उद्देश्य के लिए प्रमाप विचलन गुणांक की गणना की जाती है। इसको अपकिरण का सापेक्ष माप कहा जाता है तथा इसका सूत्र निम्नलिखित अनुसार है
प्रमाप विचलन गुणांक (Co-efficient of S.D.) = \(\frac{\text { Standard Dèviation }}{\text { Mean }} \)
= \(\frac{\sigma}{\overline{\mathrm{X}}}\)
2. विचरण गुणांक (Co-efficient of variation)-प्रमाप विचरण गुणांक साधारण तौर पर दशमलव भिन्न में आता है। इसलिए इसको समझना आसान नहीं, बल्कि कठिन होता है। इस मुश्किल को दूर करने के लिए विचरण गुणांक का प्रयोग किया जाता है। इसलिए सापेक्ष माप के लिए अपकिरण सम्बन्धी एक अन्य महत्त्वपूर्ण धारणा विचरण गुणांक दी गई है। इस धारणा का प्रयोग सबसे पहले कार्ल पियर्सन द्वारा किया गया था। इस कारण इस धारणा को कार्ल पियर्सन का विचरन गुणांक कहा जाता है। कार्ल पियर्सन अनुसार, “विचरण गुणांक समान्तर औसत में होने वाला प्रतिशत विचरण है जबकि प्रमाप विचलन समान्तर औसत में होने वाला कुल विचरण है।”
विचरण गुणांक or CV = \(\frac{\delta}{\bar{X}} \times 100\)
विचरण गुणांक प्रमाप विचलन का प्रतिशत रूप है। इसका प्रयोग भिन्न-भिन्न श्रृंखलाओं में तुलना के लिए किया जाता है, जिस समूह का विचरण गुणांक (C.V.) अधिक होगा, उस समूह में कम एक समानता पाई जाएगी। जिस समूह का विचरण गुणांक (C.V.) कम होगा, उस समूह में अधिक एक समानता पाई जाएगी।
अर्थात्
(i) C.V. अधिक है – कम समानता
(ii) C.V. कम है – अधिक समानता
3. प्रसरण (Variance)-प्रमाप विचलन के वर्ग को प्रसरण कहा जाता है। प्रसरण के माप के लिए निम्नलिखित सूत्र का प्रयोग किया जाता है
(Direct Method) व्यक्तिगत श्रेणी
प्रसरण (Variance) or V = \(\frac{\Sigma x^{2}}{\mathrm{~N}}\) or σ2
खण्डित तथा अखण्डित श्रेणी
प्रसरण (Variance) or V = \(\frac{\Sigma f x^{2}}{\mathrm{~N}}\)
लघु विधि (Short Cut Method)
प्रसरण (Variance)
V = \(\frac{\Sigma f d x}{\mathrm{~N}}-\left(\frac{\Sigma f d x}{\mathrm{~N}}\right)^{2}\)
– अथवा
V = σ2

A. व्यक्तिगत श्रेणी (Individual Series) :
प्रश्न 36.
पंचवर्षीय योजना में दो नगरों की कीमतों में परिवर्तन का विवरण इस प्रकार है। बताओ कौन-से नगर में कीमतें स्थिर रहीं।
नगर A की कीमतें : 10 18 20 15 12
नगर B की कीमतें : 20 21 19 23 – 17
हल (Solution):
विचरण गुणांक की गणना
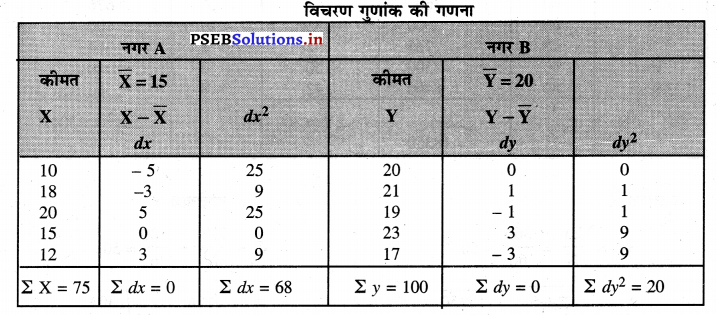
नगर A
X̄ = \(\frac{\Sigma x}{N}=\frac{75}{5}\) = 15
σ = \(\sqrt{\frac{\Sigma d x^{2}}{\mathrm{~N}}}=\sqrt{\frac{68}{5}}=\sqrt{13.6}\) = 3.69
विचरण गुणांक
C.V. = \(\frac{\sigma}{\bar{X}} \times 100 \)
= \(\frac{3.69}{15} \times 100\) = 24.58 उत्तर
नगर B
Ȳ = \(\frac{\Sigma Y}{N}=\frac{100}{5}\) = 20
σ = \(\sqrt{\frac{\Sigma d y^{2}}{N}}=\sqrt{\frac{20}{5}}=\sqrt{4}\) = 2
(Co-efficient of variation)
C.V. = \(\frac{\sigma}{\overline{\mathrm{X}}} \times 100\)
= \(\frac{2}{20} \times 100\) = 10 उत्तर
विचरण गुणांक नगर A की तुलना में B नगर का कम है। इसलिए कीमतें B नगर में अधिक स्थिर रहती हैं।
प्रश्न 37.
दो बल्लेबाजों x तथा Y द्वारा भिन्न-भिन्न पारियों में रनों का विवरण इस प्रकार है?
x : 15 1200 75 10 140 Y : 60 76 30 42 5 0 42.
बताओ-
(i) दोनों में कौन-सा खिलाड़ी अधिक रन बनाने वाला है ?
(ii) कौन-सा खिलाड़ी अधिक स्थिर है?
हल (Solution) :
यह पता करने के लिए कि कौन-सा खिलाड़ी अधिक रन बनाने वाला है औसत रनों की तुलना करनी पड़ेगी तथा यह जानने के लिए कि कौन-सा खिलाड़ी अधिक स्थिर है विचरण गुणांक (C.V.) की तुलना करनी पड़ेगी।
समान्तर औसत तथा विचरण गुणांक का माप
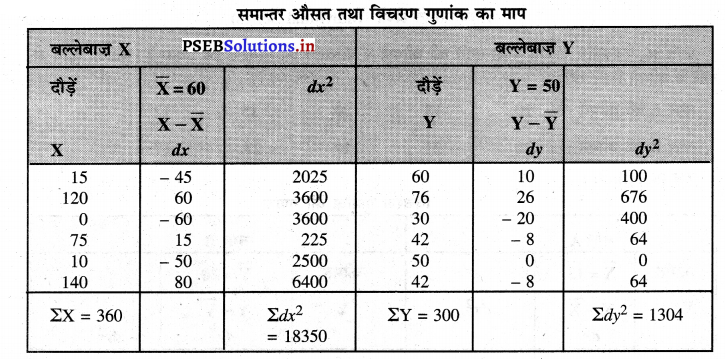
बल्लेबाज़ X
X̄ = \(\frac{\Sigma x}{N}=\frac{360}{60}\) = 60
σx = \( \sqrt{\frac{\Sigma d x^{2}}{\mathrm{~N}}}=\sqrt{\frac{18350}{6}}\)
= 66.05 दौड़ें
Co-efficient of variation
CVx = \(\frac{\sigma}{\bar{X}} \times 100\)
= \(\frac{66.05}{60} \times 100\)
= 101.08
बल्लेबाज़ Y
Ȳ = \(\frac{\Sigma Y}{N}=\frac{300}{6}\) = 50
σ = \(\sqrt{\frac{\Sigma d y^{2}}{N}}=\sqrt{\frac{1304}{6}}\)
= 14.74 दौड़ें
Co-efficient of variation Cvy = Fx 100
CVy = \(\frac{\sigma}{\overline{\mathbf{Y}}} \times 100\)
= \(\frac{14.74}{50} \times 100\)
= 29.48
(i) X बल्लेबाज़ की औसत दौड़ें 60, Y बल्लेबाज़ की औसत दौड़ें 50 की तुलना में अधिक हैं। इसलिए X बल्लेबाज़ अच्छा खिलाड़ी है।
(ii) विचरण गुणांक (C.V.) बल्लेबाज़ Y का 29.48, बल्लेबाज़ X के विचरण गुणांक 101.08 से कम है। इसलिए बल्लेबाज़ Y अधिक स्थिर है।
प्रश्न 38.
फैक्टरी A तथा फैक्टरी B में मजदूरों की औसत मज़दूरी तथा प्रमाप विचलन का विवरण निम्नलिखित अनुसार दिया हुआ है। विचरण गुणांक पता करो।

हल (Solution) :
फैक्टरी A का विचरण गुणांक
Co-efficient of variation of factory X = \(\frac{\sigma}{\overline{\mathrm{X}}}\) x 100
C.V.= \(\frac{6}{40}\) x 100 = 15
फैक्टरी B का विचरण गुणांक
Co-efficient of variation of factory Y = \( \frac{\sigma}{\overline{\mathrm{Y}}}\) x 100
C.V. = \(\frac{9}{30}\) x 100 = 30
फैक्टरी B का विचरण गुणांक 30 फैक्टरी A के विचरण गुणांक 15 से अधिक है। इसलिए फैक्टरी B में विचरण अधिक है।
प्रश्न 39.
प्रमाप विचलन के गुण एवं दोष बताएं।
उत्तर-
प्रमाप विचलन के गुण (Merits of Standard Deviation)
- सभी मूल्यों पर आधारित-प्रमाप विचलन श्रृंखला के सभी मूल्यों पर आधारित होता है।
- निश्चित परिभाषा-प्रमाप विचलन की परिभाषा निश्चित होती है।
- निश्चित माप-प्रमाप विचलन का माप स्पष्ट तथा निश्चित होता है। इसका प्रयोग हरेक स्थिति में किया जा सकता है।
- बीज गणित अध्ययन-प्रमाप विचलन का बीज गणित विधियों में काफी प्रयोग संभव होता है।
- तुलना-इस विधि के द्वारा दो या दो से अधिक श्रृंखलाओं की तुलना की जा सकती है।
प्रमाप विचलन के दोष (Demerits of Standard Deviation)
- कठिन माप-प्रमाप विचलन का माप करना कठिन होता है।
- सीमान्त मल्यों का प्रभाव-इस विधि में सीमान्त मूल्यों का अधिक प्रभाव पड़ता है।
- खुले वर्गान्तर-खुले वर्गान्तर में प्रमाप विचलन का माप नहीं किया जा सकता।
5. लॉरेंज़ वक्र (Lorenz Curve)
प्रश्न 40.
लॉरेंज़ वक्र से क्या अभिप्राय है? लॉरेंज़ वक्र की निर्माण विधि स्पष्ट करो। (What is Lorenz Curve ? Explain the method for the formulation of Lorenz Curve.)
अथवा
अपकिरण की ग्राफ विधि से क्या अभिप्राय है ? ग्राफ विधि द्वारा अपकिरण के माप का निर्माण कैसे किया जाता है?
(What is meant by Graphic Method of dispersion? How is dispersion measured with Graphic Method ?)
अथवा
अपकिरण के माप की बिन्दु रेखीय विधि से क्या अभिप्राय है? इस विधि द्वारा अपकिरण का माप कैसे किया जाता है?
(What is meant by outline Method of dispersion? How is dispersion measured with it ?)
उत्तर-
लॉरेंज वक्र का अर्थ (Meaning of Larenz Curve) अपकिरण के माप के लिए एक ढंग का निर्माण अमेरिका के अर्थशास्त्री डॉक्टर मैक्स लॉरेंज (Dr. Max Lorenz) ने किया। उन्होंने एक वक्र से आय तथा धन के वितरण में असमानताओं का अध्ययन किया। इस वक्र को लॉरेंज़ वक्र (Lorenz curve) कहा जाता है। आजकल के अर्थशास्त्री इस वक्र का प्रयोग आय, धन, लाभ, मजदूरी इत्यादि आर्थिक दरों के प्रकटावे के लिए करते हैं। लॉरेंज़ वक्र को संचयी प्रतिशत वक्र भी कहा जाता है। इसलिए लॉरेंज़ वक्र समान वितरण रेखा से जितना दूर होता है, उतनी ही असमानता अधिक होती है। लॉरेंज़ वक्र वितरण रेखा के नज़दीक होगा, उतना ही असमानता कम होती है।
लॉरेंज़ वक्र की निर्माण विधि(Method to draw Lorenz Curve) –
लॉरेंज़ वक्र की निर्माण विधि निम्नलिखित अनुसार हैं-
- दिए हुए मूल्यों तथा आवृत्ति को संचित रूप में बदलो। वर्ग अन्तराल की स्थिति में मध्य मूल्य निकालकर संचयी जोड़ करो।
- संचित किए हुए मूल्यों तथा आवृत्तियों को प्रतिशत में बदलो।
- ग्राफ पेपर पर OX तथा OY रेखाएं बनाओ। 10X अक्ष सभी प्रतिशत संचयी आवृत्तियां, 100 से 0 तक तथा OY अक्ष पर सभी प्रतिशत संचयी मदों 0 से 100 तक लिया जाता है।
- OX अक्ष के शून्य (0) मापदण्ड को OY अक्ष के 100 मापदण्ड से मिलाओ। इसको करने अथवा समान वितरण रेखा कहा जाता है।
- मूल्यों तथा आवृत्तियों की प्रतिशत संचयी आंकड़ों को ग्राफ पर बिन्दुओं द्वारा अंकित किया जाता है तथा इन बिन्दुओं को आपस में मिला देते हैं, जिससे लॉरेंज़ वक्र प्राप्त होता है। इसलिए लॉरेंज़ वक्र को बिन्दु विधि अथवा ग्राफ विधि भी कहा जाता है।
- लॉरेंज़ वक्र, समान वितरण रेखा से जितना नज़दीक होता है, अपकिरण की मात्रा उतनी कम होती है। लॉरेंज़ वक्र जितना अधिक दूर होगा, अपकिरण उतना अधिक होगा।

प्रश्न 41.
दो फैक्टरियों द्वारा मजदूरों को दी जाने वाली मजदूरी का विवरण इस प्रकार है
| मज़दूरी (₹): |
0-20 |
20-40 |
40-60 |
60-80 |
80-100 |
| फैक्टरी A में मजदूरों की संख्या : |
60 |
80 |
120 |
90 |
150 |
| फैक्टरी B में मजदूरों की संख्या : |
150 |
100 |
90 |
110 |
50 |
हल : मजदूरी वितरण से समानताओं की तुलना करने के लिए लॉरेंज़ वक्र का निर्माण करो।
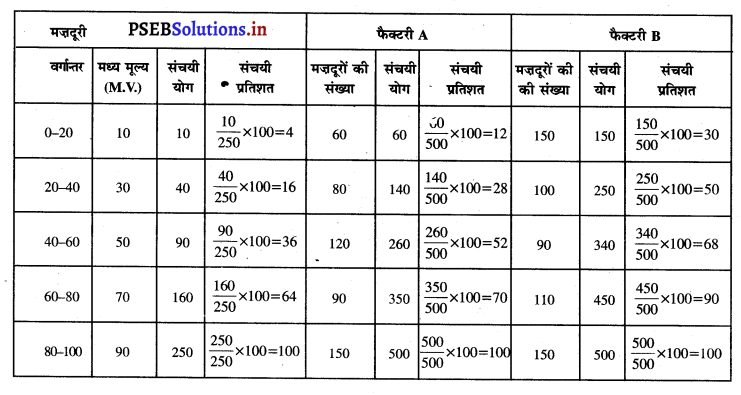
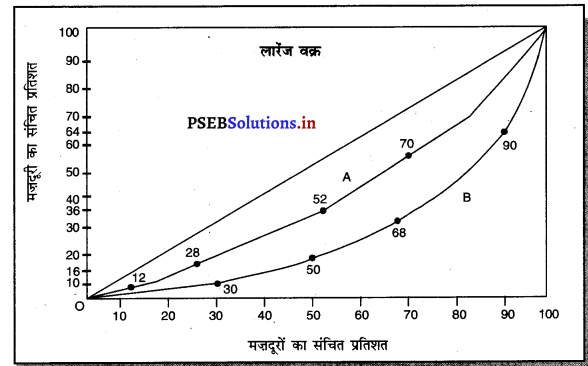
समान विभाजन वक्र (Line of Equal Distribution) से लॉरेंज़ वक्र जितना दूर होगा, उतनी ही आंकड़ों में असमानता ज्यादा होगी। इस उदाहरण में फैक्टरी A की तुलना में फैक्टरी B में लॉरेंज़ वक्र अधिक दूर है। इसलिए फैक्टरी B के मजदूरों की मजदूरी में असमानता अधिक है।
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()

![]()