Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 11 रचनाएँ Ex 11.1 Textbook Exercise Questions and Answers
PSEB Solutions for Class 10 Maths Chapter 11 रचनाएँ Ex 11.1
निम्न में से प्रत्येक के लिए रचना का औचित्य भी दीजिए :
प्रश्न 1.
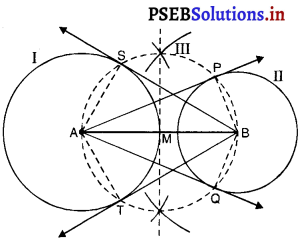
7.6 cm लंबा एक रेखाखंड खींचिए और इसे 5 : 8 के अनुपात में विभाजित कीजिए। दोनों भागों को मापिए।
हल :
एक 7.6 cm लंबाई का रेखाखंड।
रचना के चरण :
1. एक रेखाखंड AB = 7.6 cm लीजिए।
2. न्यून कोण ∠BAX बनाती हुई कोई किरण AX खींचिए।
3. किरण AX पर 5 + 8 = 13 (दिया गया अनुपात 5 : 8) बिन्दु A1, A2, A3, A4, A5 …………… A, A11, A12, A13
इस प्रकार अंकित कीजिए कि A1A2 = A2A3 = A3A4 = …………… = A11A12 = A12 A13 हो।
4. BA13 को मिलाइए।
5. बिंदु A5, से होकर जाने वाली A5C || A13B (A5 पर ∠AA13B के बराबर कोण बनाकर) AB को एक बिंदु ‘C’ प्रतिच्छे द करती हुई खींचिए। तब AC : CB = 5 : 8
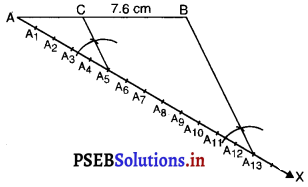
औचित्य :
आइए हम देखें कि यह विधि कैसे हमें अभीष्ट विभाजन प्रदान करती है।
∆AA4313B में,
क्योंकि A5C || A13B है।
∴ आधारभूत समानुपातिकता प्रमेय द्वारा
\(\frac{\mathrm{AA}_{5}}{\mathrm{~A}_{5} \mathrm{~A}_{13}}=\frac{\mathrm{AC}}{\mathrm{CB}}\)
रचना से, \(\frac{\mathrm{AA}_{5}}{\mathrm{~A}_{5} \mathrm{~A}_{13}}=\frac{5}{8}\)
∴ \(\frac{\mathrm{AC}}{\mathrm{CB}}=\frac{5}{8}\)
यह दर्शाता है कि ‘C’, AB को 5 : 8 के अनुपात में विभाजित करता है।
दोनों भागों को मापने पर, AC = 2.9 cm, CB = 4.7 cm
वैकल्पिक विधि :
रचना के चरण :
1. एक रेखाखंड AB = 7.6 cm लीजिए।
2. एक न्यून कोण ZBAX खींचिए।
3. ∠ABY इस प्रकार खींचिए कि ∠ABY = ∠BAX.
4. बिंदु A1, A2, A3, A4, A5 किरण AX पर अंकित कीजिए ताकि A1A2 = A2A3 = A3A4 = A4A5.
5. बिंदु B1, B2, B3, B4, B5, B6, B7, B8 किरण BY पर इस प्रकार अंकित कीजिए कि B1B2 = B2B3 = B3B4 = B4B5 = B5B6 = B6B7 = B7B8
6. A5B8 को मिलाइए मानो यह AB को बिंदु ‘C’ पर प्रतिच्छेद करती है।
तब AC : CB = 5 : 8
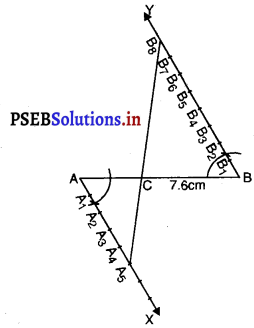
औचित्य : ∆ACA, और ∆ BCBg में,
∠ACAF = ∠BCBg [शीर्षाभिमुख कोण]
∠BAAT = ∠ABBg [रचना]
∴ ∆ACAS ~ ∆BCBg [AA-समरूपता कसौटी] |
∆ उनकी संगत भुजाएँ एक ही अनुपात में होंगी।

अत: AC : CB = 5 : 8.

प्रश्न 2.
4 cm, 5 cm और 6 cm भुजाओं वाले एक त्रिभुज की रचना कीजिए और फिर इसके समरूप एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की \(\frac{2}{3}\) गुनी हों।
हल :
रचना के चरण :
1. दी गई शर्तों और मापों से एक त्रिभुज की रचना कीजिए।
मान लीजिए ∆ABC है। ABC AB = 5 cm, AC = 4 cm और BC = 6 cm.
2. भुजा BC के नीचे कोई कोण ZCBX बनाइए।
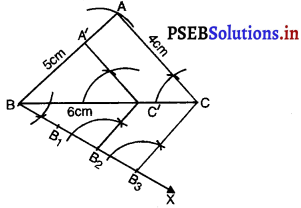
3. तीन बिंदु (ई में 2 और 3 में से बड़ी संख्या) B1, B2, B3, BX पर इस प्रकार अंकित कीजिए कि | BB1 = B1B2 = B2B3 हो।
4. B3C को मिलाइए।
5. B2 (\(\frac{2}{3}\)में और 3 में छोटी संख्या) में से एक रेखा B3C के समांतर खींचिए जो BC को C’ पर प्रतिच्छेद करती है।
6. C’, में से होकर जाने वाली CA के समांतर एक रेखा खींचिए जो BA को A’ पर मिले।
अतः, ∆A’BC’ अभीष्ट त्रिभुज है जिसकी भुजाएँ। ∆ABC की संगत भुजाओं की \(\frac{2}{3}\) गुनी हैं।
रचना का औचित्य :
पहले हम यह दिखाएंगे कि पहली त्रिभुज और रचना की गई त्रिभुज समरूप हैं।
अर्थात् ∆ABC’ ~ ∆ABC.
∆A’BC’ और ∆ABC लीजिए
∠B = ∠B [उभयनिष्ठ]
∠A’C’B = ∠ACB [रचना से]
∆A’C’B ~ ∆ACB [AA-समरूपता]
∴ उनकी संगत भुजाएँ एक समान अनुपात में होंगी।
\(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{A}^{\prime}}{\mathrm{CA}}\) ……………..(1)
अब ∆B2BC’ और ∆B3BC लीजिए
∠B = ∠B [उभयनिष्ठ]
∴ ∠B2C’B = ∠B2CB [रचना]
∴ ∆B2BC’ ~ ∆B3BC [AA-समरूप]
उनकी संगत भुजाएँ एक समान अनुपात में होंगी।

⇒ A’B = \(\frac{2}{3}\) AB
और BC’ = \(\frac{2}{3}\) BC;
C’A’ = \(\frac{2}{3}\) CA.
अतः, रचना औचित्य पूर्ण है।

प्रश्न 3.
5 cm, 6 cm और 7 cm भुजाओं वाले एक त्रिभुज की रचना कीजिए और फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिये हुए त्रिभुज की संगत भुजाओं की = गुनी हों।
हल :
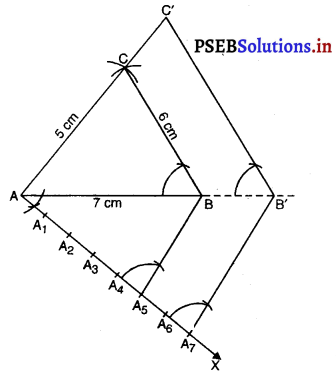
रचना के चरण :
1. ∆ABC की रचना कीजिए जिसमें AB = 7 cm, BC = 6 cm और AC = 5 cm हैं।
2. आधार AB के नीचे कोई न्यून कोण ∠BAX बनाइए।
3. सात बिंदु A1, A2, A3, A4, A5, A6, A7, किरण AX पर इस प्रकार अंकित कीजिए कि
AA1 = A1A2 = A2A3 = A3A4 = A4A5 = A5A6 = A6A7
4. BA5 को मिलाइए।
5. A7, से A5B के समांतर एक रेखा खींचिए। मान लीजिए यह AB को बढ़ाने पर B’ पर इस प्रकार मिलती है कि AB’ = \(\frac{7}{5}\) AB.
6. B’ में से एक रेखा BC के समांतर एक रेखा खींचिए जो AC को बढ़ाने पर C’ पर मिलती है।
∆AB’C’ अभीष्ट त्रिभुज है।
रचना का औचित्य:
∆ABC और ∆AB’C’ में,
∠A = ∠A [उभयनिष्ठ]
∠ABC = ∠AB’C’ [रचना]
∴ ∠ABC ~ ∠AB’C’ [AA-समरूपता]
∴ उनकी संगत भुजाएँ एक ही अनुपात में होंगी।
\(\frac{\mathrm{AB}}{\mathrm{AB}^{\prime}}=\frac{\mathrm{BC}}{\mathrm{B}^{\prime} \mathrm{C}^{\prime}}=\frac{\mathrm{CA}}{\mathrm{C}^{\prime} \mathrm{A}}\) …………(1)
पुन: ∆ AA5B और ∆AA7B’ में,
∠A = ∠A [उभयनिष्ठ]
∠AAB = ∠AA,B’ [संगत कोण]
∴ ∆ AA5BB ~ ∆ AA7B’ [AA-समरूपता]
∴ उनकी संगत भुजाएँ एक ही अनुपात में होंगी।

अत: ∆AB’C’ की भुजाएँ ∆ABC की संगत भुजाओं की \(\frac{7}{5}\) गुनी हैं।

प्रश्न 4.
आधार 8 cm तथा ऊँचाई 4 cm के एक समद्विबाहु त्रिभुज की रचना कीजिए और फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ इस समद्विबाहु त्रिभुज की संगत भुजाओं की 13, गुनी हों।
हल :
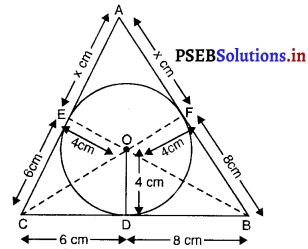
दिया है : समद्विबाहु त्रिभुज का आधार = 8 cm और ऊँचाई = 4 cm
रचना करना :
एक त्रिभुज जिसकी भुजाएँ समद्विबाहु त्रिभुज की संगत भुजाओं का 1\(\frac{1}{2}\) गुनी है।
रचना के चरण :
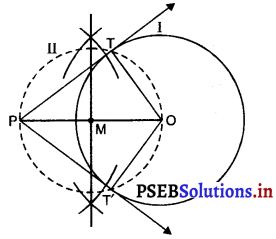
1. आधार AB = 8 cm लीजिए।
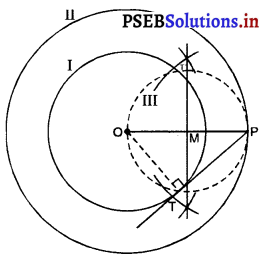
2. AB का लंब समद्विभाजक खींचिए जो AB को ‘M’ पर प्रतिच्छेद करे।
3. M को केन्द्र मानकर और त्रिज्या 4 cm, लेकर एक चाप लगाइए जो लंब समद्विभाजक को ‘C’ पर प्रतिच्छेद करे।
4. CA और CB को मिलाइए।
5. ∆ABC समद्विबाहु त्रिभुज है जिसमें CA = CB.
6. भुजा BC के नीचे कोई न्यून कोण ∠BAX बनाइए।
7. तीन बिंदु (1\(\frac{1}{2}\) या \(\frac{3 }{2}\) में 2 या 3 में से बड़ी संख्या)
A1, A2, A3, ‘AX’ पर इस प्रकार अंकित कीजिए कि AA1 = A1A2 = AA3 हो।
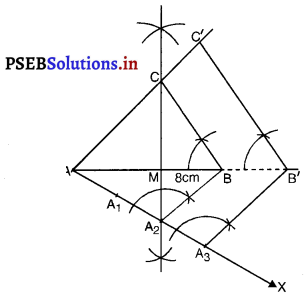
8. A2 (\(\frac{3 }{2}\) में ‘2’ और ‘3’ से छोटी संख्या) और B को मिलाइए।
9. A3, में से एक रेखा A2B के समांतर खींचिए जो AB को बढ़ाने पर B’ पर मिले।
10. B’, में से एक रेखा BC के समांतर खींचिए जो AC को बढ़ाने पर C’ पर मिले। ∆A B’C’ अभीष्ट त्रिभुज है जिसकी भुजाएँ ∆ABC की संगत भुजाओं की
1\(\frac{1}{2}\) गुनी हैं।
रचना का औचित्य :
सर्वप्रथम हम सिद्ध करेंगे कि ∆AB’C’ और ∆ABC समरूप हैं।
∆ AB’C’ और ∆ ABC लीजिए
∠A = ∠A [उभयनिष्ठ]
∠AB’C’ = ∠ABC [रचना से]
∆AB’C’ ~ ∆ABC [AA-समरूपता से)
∴ उनकी संगत भुजाएँ एक ही अनुपात में हैं।
\(\frac{\mathrm{AB}^{\prime}}{\mathrm{AB}}=\frac{\mathrm{B}^{\prime} \mathrm{C}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{A}}{\mathrm{CA}}\) ……………(1)
अब ∆ A3AB’ और ∆ A2AB लीजिए।
∠A = ∠A [उभयनिष्ठ]
∠B’A3A = ∠B’A2A [रचना से]
∴ ∆ A3A B’ ~ ∆ A2AB [AA-समरूपता]
∴ उनकी संगत भुजाएँ एक ही अनुपात में होंगी।

⇒ AB’ = 1 \(\frac{1}{2}\) (AB)
⇒ B’C’ = 1\(\frac{1}{2}\) (BC)
और C’A = 1\(\frac{1}{2}\) (CA)
अतः रचना औचित्य है।

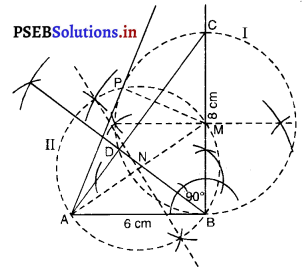
प्रश्न 5.
एक त्रिभुज ABC बनाइए जिसमें BC = 6 cm, AB = 5 cm और ∠ABC = 60° हो। फिर एक त्रिभुज की रचना कीजिए, जिसकी भुजाएँ ∆ABC की संगत भुजाओं की – गुनी हों।
हल :
रचना के चरण :
1. रेखा खंड BC = 6 cm लीजिए।
2. B पर 60° का कोण बनाइए अर्थात् ∠BAX = 60° बनाइए।
3. B को केन्द्र मानकर और 5 cm त्रिज्या लेकर एक चाप खींचिए जो BX को ‘A पर प्रतिच्छेद करे।
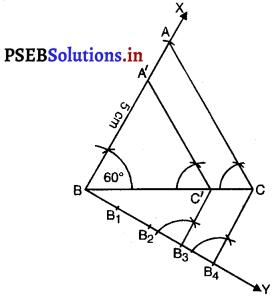
4. A और C को मिलाइए।
5. BC के नीचे B पर कोई न्यून कोण बनाइए।
6. चार बिंदु ( में 3 और 4 में से बड़ी संख्या) B1, B2, B3, B4, रेखा BY पर इस प्रकार अंकित कीजिए कि BB1 = B1B2 = B2B3 = B3B4 हो।
7. B4 और C को मिलाइए।
8. B3 (में \(\frac{3}{4}\) 3 और 4 से छोटी संख्या) में से एक रेखा B4C के समांतर संगत कोण बनाती हुई खींचिए। मान लीजिए B3 में से खींची रेखा BC को C’ पर प्रतिच्छेद करती है।
9. C’, में से एक रेखा CA के समांतर खींचिए जो BA को. A’ पर प्रतिच्छेद करती है।
∆A’BC’ अभीष्ट त्रिभुज है जिसकी संगत भुजाएँ ∆ABC की संगत भुजाओं के \(\frac{3}{4}\) गुनी हैं।
रचना के औचित्य :
∆A’BC’ और ∆ABC लीजिए।
∠B = ∠B [उभयनिष्ठ]
∠A’C’B = ∠ACB [संगत कोण]
∴ ∆A’BC’ ~ ∆ABC [AA-समरूपता]
∴ उनकी संगत भुजाएँ एक ही अनुपात में होंगी।
∆ \(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{A}^{\prime}}{\mathrm{CA}}\) ……………(1)
अब ∆B,BC’ और ∆B,BC लीजिए।
∠B = ∠B [उभयनिष्ठ]
∠C’B3B = ∠CB4B [संगत कोण]
∆B3BC’ ~ ∆B4BC [AA-समरूपता]
∴ उनकी संगत भुजाएँ एक ही अनुपात में होंगी।
\(\frac{\mathrm{B}_{3} \mathrm{~B}}{\mathrm{~B}_{4} \mathrm{~B}} \approx \frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{B}_{3}}{\mathrm{CB}_{4}}\) ………………..(2)
(I) और (II) सें,
\(\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{B}_{3} \mathrm{~B}}{\mathrm{~B}_{4} \mathrm{~B}}\)
पर, \(\frac{\mathrm{B}_{3} \mathrm{~B}}{\mathrm{~B}_{4} \mathrm{~B}}=\frac{3}{4}\) [रचना]
\(\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{3}{4}\) …………….(3)
(1) और (3) से,
\(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{A}^{\prime}}{\mathrm{CA}}=\frac{3}{4}\)
अर्थात् ∆A’BC’ की भुजाएँ ∆ABC की संगत भुजाओं का \(\frac{4}{4}\) गुनी हैं।
⇒ A’B = \(\frac{3}{4}\) AB;
BC’ = \(\frac{3}{4}\) BC
और C’A’ = \(\frac{3}{4}\) CA
प्रश्न 6.
एक त्रिभुज ABC बनाइए, जिसमें BC = 7 cm, ∠B = 45°, ∠A = 105° हो। फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ ∆ABC की संगत भुजाओं की \(\frac{4}{3}\) गुनी हों।
हल :
रचना के चरण :
1. दिए गए मापों से त्रिभुज ABC की रचना कीजिए।
2. भुजा BC के नीचे बिंदु B पर कोई न्यून कोण ∠CBX खींचिए।
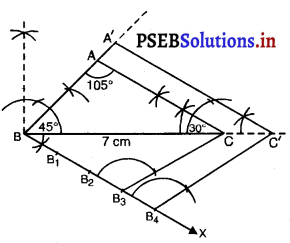
त्रिभुज के कोण योग गुणधर्म से
∠A + ∠B + ∠C = 180°
105° + 45° + ∠C = 180°
∠C = 180 – 150° = 30°
3. चार बिंदु ( में 3 और 4 में से बड़ी संख्या) B1, B2, B3, B4, ‘BX’ पर इस प्रकार अंकित कीजिए कि BB1 = B1B2 = B2B3 = B3B4 हो।
4. B3C (\(\frac{4}{3}\) में 3 और 4 में से छोटी) मिलाइए।
5. B4 में से एक रेखा B3C के समांतर खींचिए जो BC को बढ़ाने पर C’ पर प्रतिच्छेद करे।
6. C’ में से एक अन्य रेखा CA के समांतर खींचिए जो BA को बढ़ाने पर A’ पर प्रतिच्छेद करे।
7. ∆A’BC’ अभीष्ट त्रिभुज है जिसकी भुजाएँ त्रिभुज ABC की संगत भुजाओं की \(\frac{4}{3}\) गुनी हैं।
रचना का औचित्य :
∆ ABC’ और ∆ ABC लीजिए।
∠B = ∠B [उभयनिष्ठ]
∠A’C’B = ∠ACB [रचना]
∴ ∆A’B’C – ∆ABC [AA-समरूपता]
∴ उनकी संगत भुजाएँ एक ही अनुपात में होंगी।
∴ \(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{A}^{\prime}}{\mathrm{CA}}\) ……………….(1)
पुनः ∆B4BC’ और ∆B3BC लीजिए।
∠B = ∠B [उभयनिष्ठ]
∠C’B4B = ∠CB3B [रचना से]
∆ BBC’ ~ ∆BBC [AA-समरूपता]
∴ उनकी संगत भुजाएँ एक ही अनुपात में होंगी।

⇒ A’B = \(\frac{4}{3}\) AB ;
BC’ = \(\frac{4}{3}\) BC
और C’A’ = \(\frac{4}{3}\) CA
अतः रचना का औचित्य है।
प्रश्न 7.
एक समकोण त्रिभुज की रचना कीजिए, जिसकी भुजाएँ (कर्ण के अतिरिक्त)4cm तथा 3 cm लंबाई की हों। फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की \(\frac{5}{3}\) गुनी हों।
हल :
रचना के चरण :
1. दी गई शर्तों से समकोण त्रिभुज खींचिए। मान लीजिए यह ∆ABC है। BC = 4 cm; AB = 3 cm और ∠B = 90°.
2. भुजा BC के नीचे कोई न्यून कोण ∠CBX खींचिए।
3. पाँच बिंदु (\(\frac{5}{3}\) में 5 और 3 में से बड़ी संख्या) B1, B2, B3, B4, B5, B6 पर इस प्रकार अंकित कीजिए कि BB1 = B1B2 = B2B3 = B3B4 = B4B5 हो।
4. B3 (\(\frac{5}{3}\) में ‘5’ और ‘3’ से एक छोटी संख्या) और ‘C’ को मिलाइए।
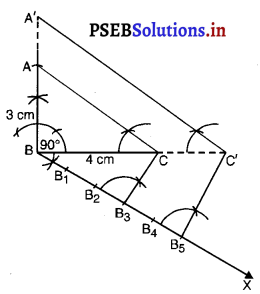
5. B5 में से एक रेखा BC के समांतर खींचिए जो BC को बढ़ाने पर C’ पर प्रतिच्छेद करे।
6. पुन: C’ में से एक रेखा CA के समांतर खींचिए जो BA को बढ़ाने पर A’ पर मिले।
∆ ABC’ अभीष्ट त्रिभुज है जिसकी भुजाएँ ∆ABC की संगत भुजाओं का \(\frac{5}{3}\) गुनी हैं।
रचना का औचित्य :
∆A BC’ और ∆ABC लीजिए।
∠B = ∠B [उभयनिष्ठ]
∠A’C’B = ∠ACB [रचना से]
∴ ∆A’BC’ ~ ∆ABC [AA-समरूपता कसौटी]
∴ उनकी संगत भुजाएँ एक ही अनुपात में हैं।
\(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{A}^{\prime}}{\mathrm{CA}}\) ……….(1)
पुनः ∆B5C’ B और ∆B3CB में,
∠B = ∠B [उभयनिष्ठ]
∠C’B5B = ∠CB3B [रचना से]
∴ ∆B5C’B ~ AB3CB [AA-समरूपता]
∴ उनकी संगत भुजाएँ एक ही अनुपात में हैं।

⇒ A’B = \(\frac{5}{3}\) AB;
BC’ = \(\frac{5}{3}\) BC
और C’A’ = \(\frac{5}{3}\) CA
![]()
![]()
![]()
![]()
![]()