Class 10

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 7 ਨਿਰਦੇਸ਼ ਅੰਕਜਿਮਾਇਤੀ Ex 7.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 7 ਨਿਰਦੇਸ਼ ਅੰਕਜਿਮਾਇਤੀ Exercise 7.2

ਪ੍ਰਸ਼ਨ 1.
ਉਸ ਬਿੰਦੁ ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਪਤਾ ਕਰੋ ਜੋ ਬਿੰਦੂਆਂ (-1,7) ਅਤੇ (4,-3) ਨੂੰ ਮਿਲਾਉਣ ਵਾਲੇ ਰੇਖਾਖੰਡ ਨੂੰ 2: 3 ਦੇ ਅਨੁਪਾਤ ਵਿਚ ਵੰਡਦਾ ਹੈ ।
ਹੱਲ:
ਮੰਨ ਲਉ P (x, y) ਲੋੜੀਂਦਾ ਬਿੰਦੂ ਹੈ, ਜੋ ਦਿੱਤੇ ਗਏ ਬਿੰਦੁਆਂ A(-1, 7) ਅਤੇ B (4, – 3) ਨੂੰ ਮਿਲਾਉਣ ਵਾਲੇ ਰੇਖਾਖੰਡ ਨੂੰ 2 : 3 ਵਿਚ ਵੰਡਦਾ ਹੈ ।

∴ x = \(\frac{2 \times 4+3 \times-1}{2+3}\) = \(\frac{8-3}{5}\) = \(\frac{5}{5}\) = 1
ਅਤੇ y = \(\frac{2 \times-3+3 \times 7}{2+3}\) = \(\frac{-6+21}{5}\) = \(\frac{15}{5}\) = 3
∴ ਲੋੜੀਂਦਾ ਬਿੰਦੂ ਹੈ (1, 3)

ਪ੍ਰਸ਼ਨ 2.
ਬਿੰਦੂਆਂ (4, – 1) ਅਤੇ (-2, – 3) ਨੂੰ ਮਿਲਾਉਣ ਵਾਲੇ ਰੇਖਾਖੰਡ ਨੂੰ ਤਿੰਨ ਸਮਾਨ ਭਾਗ (Trisection) ਕਰਨ ਵਾਲੇ ਬਿੰਦੂਆਂ ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ P (x₁, y₁) ਅਤੇ Q (x₂, y₂) ਲੋੜੀਂਦੇ ਬਿੰਦੂ ਹਨ ਜੋ ਬਿੰਦੁ A (4, – 1) ਅਤੇ (-2, – 3) ਨੂੰ ਮਿਲਾਉਣ ਵਾਲੇ ਰੇਖਾਖੰਡ ਦੇ ਤਿੰਨ ਸਮਾਨ ਭਾਗ ਕਰਦੇ ਹਨ । ਭਾਵ P (x₁, y₁) AB ਨੂੰ 1 : 2 ਦੇ ਅਨੁਪਾਤ ਵਿਚ ਅਤੇ Q (x₂, y₂) AB ਨੂੰ 2 : 1 ਦੇ ਅਨੁਪਾਤ ਵਿਚ ਵੰਡਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਤੁਹਾਡੇ ਸਕੂਲ ਵਿਚ ਖੇਡਣ ਦੇ ਮੁਕਾਬਲੇ ਕਰਵਾਉਣ ਦੇ ਲਈ ਇਕ ਆਇਤਾਕਾਰ ਮੈਦਾਨ ABCD ਵਿੱਚ, ਚੂਨੇ ਦੇ ਨਾਲ 1m ਦੀ ਦੂਰੀ ‘ਤੇ ਕਤਾਰਾਂ ਬਣਾਈਆਂ ਗਈਆਂ ਹਨ । AD ਦੇ ਅਨੁਸਾਰ ਆਪਸ ਵਿਚ 1m ਦੀ ਦੂਰੀ ਤੇ 100 ਗਮਲੇ ਰੱਖੇ ਗਏ ਹਨ, ਜਿਸ ਤਰ੍ਹਾਂ ਕਿ ਚਿੱਤਰ ਵਿਚ ਦਰਸਾਇਆ ਗਿਆ ਹੈ । ਨਿਹਾਰਿਕਾ ਦੂਸਰੀ ਕਤਾਰ ਵਿੱਚ AD ਦੇ \(\frac{1}{4}\) ਭਾਗ ਦੇ ਬਰਾਬਰ ਦੀ ਦੂਰੀ ਤੇ ਦੌੜਦੀ ਹੈ ਅਤੇ ਉੱਥੇ ਇੱਕ ਹਰਾ ਝੰਡਾ ਗੱਡ ਦਿੰਦੀ ਹੈ । ਪ੍ਰੀਤ ਅੱਠਵੀਂ ਕਤਾਰ ਵਿਚ AD ਦੇ \(\frac{1}{5}\) ਭਾਗ ਦੇ ਬਰਾਬਰ ਦੀ ਦੂਰੀ ਤੇ ਦੌੜਦੀ ਹੈ ਅਤੇ ਉੱਥੇ | ਇੱਕ ਲਾਲ ਝੰਡਾ ਗੱਡ ਦਿੰਦੀ ਹੈ । ਦੋਹਾਂ ਝੰਡਿਆਂ ਦੀ | ਵਿਚਕਾਰਲੀ ਦੁਰੀ ਕੀ ਹੈ ? ਜੇਕਰ ਰਸ਼ਿਮ ਨੂੰ ਇਕ ਨੀਲਾ ਝੰਡਾ ਇਹਨਾਂ ਦੋਹਾਂ ਝੰਡਿਆਂ ਨੂੰ ਮਿਲਾਉਣ ਵਾਲੇ ਰੇਖਾਖੰਡ ਦੇ ਠੀਕ ਅੱਧੀ ਦੂਰੀ (ਵਿਚਕਾਰ) ‘ਤੇ ਗੱਡਣਾ ਹੋਵੇ ਤਾਂ ਉਸਨੂੰ ਆਪਣਾ ਝੰਡਾ ਕਿੱਥੇ ਗੱਡਣਾ ਚਾਹੀਦਾ ਹੈ ?

ਹੱਲ:
ਦਿੱਤੇ ਗਏ ਚਿੱਤਰ ਵਿਚ A ਨੂੰ ਮੂਲ ਬਿੰਦੂ ਮੰਨ ਲੈਂਦੇ ਹਨ | AB ਨੂੰ ਧੁਰਾ ਅਤੇ AD ਨੂੰ y-ਧੁਰਾ ਮੰਨ ਲੈਣ ਤੇ ਹਰੇ ਝੰਡੇ ਦੀ ਸਥਿਤੀ
= ਨਿਹਾਰਿਕਾ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਦੂਰੀ
= ਨਿਹਾਰਿਕਾ ਦੂਸਰੀ ਕਤਾਰ ਵਿਚ AD ਦੇ \(\frac{1}{4}\) ਭਾਗ ਦੇ ਬਰਾਬਰ ਦੀ ਦੂਰੀ ਦੌੜਦੀ ਹੈ
= \(\frac{1}{4}\) × 100 = 25m
∴ ਹਰੇ ਝੰਡੇ ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ (2, 25) ਹੈ ।
ਹੁਣ, ਲਾਲ ਝੰਡੇ ਦੀ ਸਥਿਤੀ
= ਪ੍ਰੀਤ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਦੂਰੀ
= ਪੀਤ ਅੱਠਵੀਂ ਕਤਾਰ ਵਿਚ AD ਦੇ \(\frac{1}{5}\)
ਭਾਗ ਦੇ ਬਰਾਬਰ ਦੂਰੀ ਦੌੜਦੀ ਹੈ
= \(\frac{1}{5}\) × 100 = 20m.
∴ ਹਰੇ ਅਤੇ ਲਾਲ ਝੰਡੇ ਦੇ ਵਿੱਚ ਦੀ ਦੂਰੀ
= \(\sqrt{(8-2)^{2}+(20-25)^{2}}\)
= \(\sqrt {36+25}\) = \(\sqrt {61}\) m .
ਨੀਲੇ ਝੰਡੇ ਦੀ ਸਥਿਤੀ
= ਹਰੇ ਝੰਡੇ ਅਤੇ ਲਾਲ ਝੰਡੇ ਨੂੰ ਮਿਲਾਉਣ ਵਾਲੇ ਰੇਖਾਖੰਡ ਦਾ ਅੱਧਾ
= (\(\frac{2+8}{2}\), \(\frac{25+20}{2}\))
= (5, 22.5).
ਨੀਲਾ ਝੰਡਾ 5ਵੀਂ ਕਤਾਰ ਵਿਚ ਅਤੇ AD ਤੋਂ 22.5 ਮੀ. ਦੀ ਦੂਰੀ ਉੱਤੇ ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
ਬਿੰਦੂਆਂ (-3, 10) ਅਤੇ (6, -8) ਨੂੰ ਮਿਲਾਉਣ ਵਾਲੇ ਰੇਖਾਖੰਡ ਨੂੰ ਬਿੰਦੂ (-1, 6) ਕਿਸ ਅਨੁਪਾਤ ਵਿਚ ਵੰਡਦਾ ਹੈ ।
ਹੱਲ:
ਮੰਨ ਲਉ ਬਿੰਦੁ P (-1, 6) ਬਿੰਦੁ A (-3, 10) | ਅਤੇ B (6, – 8) ਨੂੰ ਮਿਲਾਉਣ ਵਾਲੇ ਰੇਖਾਖੰਡ | ਨੂੰ K : 1 ਦੇ ਅਨੁਪਾਤ ਵਿਚ ਵੰਡਦਾ ਹੈ ।

∴ -1 = \(\frac{6 \times K-3 \times 1}{K+1}\)
ਜਾਂ -K – 1 = 6K – 3
-K – 6K = – 3 + 1
– 7K = -2
ਜਾਂ K = \(\frac{2}{7}\)
∴ K : 1 = \(\frac{2}{7}\) = 2 : 7
∴ ਲੋੜੀਂਦਾ ਅਨੁਪਾਤ 2 : 7. ਹੈ ।

ਪ੍ਰਸ਼ਨ 5.
ਬਿੰਦੁਆਂ A (1, – 5) ਅਤੇ B (- 4, 5) ਨੂੰ ਮਿਲਾਉਣ ਵਾਲੇ ਰੇਖਾਖੰਡ ਨੂੰ 7-ਧੁਰਾ ਕਿਸ ਅਨੁਪਾਤ ਵਿੱਚ ਵੰਡਦਾ ਹੈ । ਇਸ ਵੰਡਣ ਵਾਲੇ ਬਿੰਦੂ ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਵੀ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ x-ਧੁਰੇ ਉੱਤੇ ਲੋੜੀਂਦਾ ਬਿੰਦੂ P (x, 0) ਹੈ ਜੋ A (1, – 5) ਅਤੇ B (-4, 5) ਨੂੰ ਮਿਲਾਉਣ ਵਾਲੇ ਰੇਖਾਖੰਡ ਨੂੰ K : 1 ਦੇ ਅਨੁਪਾਤ ਵਿਚ ਵੰਡਦਾ ਹੈ ।

P ਦਾ y ਨਿਰਦੇਸ਼ ਅੰਕ ਹੈ
0 = \(\frac{5 \times K+(-5) \times 1}{K+1}\)
0 = \(\frac{5 K-5}{K+1}\)
5K – 5 = 0
5K = 5
K = 1
∴ ਲੋੜੀਂਦਾ ਅਨੁਪਾਤ K : 1 = 1 : 1
ਹੁਣ, P ਦਾ x ਨਿਰਦੇਸ਼ ਅੰਕ ਹੈ
x = \(\frac{-4 \times K+1 \times 1}{K+1}\)
K = 1, ਦਾ ਮੁੱਲ ਰੱਖਣ ਤੇ
x = \(\frac{-4 \times 1+1 \times 1}{1+1}\) = \(\frac{-4+1}{2}\)
x = \(-\frac{3}{2}\)
∴ ਲੋੜੀਂਦਾ ਬਿੰਦੂ ਹੈ : (\(-\frac{3}{2}\), 0)

ਪ੍ਰਸ਼ਨ 6.
ਜੇਕਰ ਬਿੰਦੂ (1, 2) ; (4, y) ; (x, 6) ਅਤੇ (3, 5) ਇਸੇ ਕੂਮ ਵਿਚ ਲੈਣ ‘ਤੇ ਇੱਕ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਦੇ ਸਿਖਰ ਹੋਣ ਤਾਂ 1 ਅਤੇ y ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ABCD ਦੇ ਸਿਖਰ ਹਨ : A (1, 2) ; B (4, y) ; C (x, 6) ਅਤੇ D (3, 5)
ਪਰ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਦੇ ਵਿਕਰਣ ਇਕ ਦੂਜੇ ਨੂੰ ਸਮਦੁਭਾਜਿਤ ਕਰਦੇ ਹਨ :
ਸਥਿਤੀ I : ਜਦੋਂ E, A (1, 2) ਅਤੇ C (x, 6) ਦਾ ਮੱਧ ਬਿੰਦੁ ਹੋਵੇ ।
∴ E ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਹਨ
E = (\(\frac{x+1}{2}\), \(\frac{6+2}{2}\))
E = (\(\frac{x+1}{2}\), 4) …(1)

ਸਥਿਤੀ II : ਜਦੋਂ E, B (4, y) ਅਤੇD (3, 5) ਦਾ ਮੱਧ ਬਿੰਦੁ ਹੋਵੇ ।
E ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਹਨ :
E = (\(\frac{3+4}{2}\), \(\frac{5+y}{2}\))
E = (\(\frac{7}{2}\), \(\frac{5+y}{2}\)) …(2)
ਪਰ (1) ਅਤੇ (2) ਵਿਚ E ਦੇ ਮੁੱਲ ਸਮਾਨ ਹਨ ਇਸ ਲਈ ਨਿਰਦੇਸ਼ ਅੰਕਾਂ ਦੀ ਤੁਲਨਾ ਕਰਨ ਤੇ
\(\frac{x+1}{2}\) = \(\frac{7}{2}\) ਅਤੇ 4 = \(\frac{5+y}{2}\)
x + 1 = 7 ਅਤੇ 8 = 5 + y
x = 6 ਅਤੇ y = 3
∴ x ਅਤੇ y ਦੇ ਮੁਲ ਹਨ 6 ਅਤੇ 3 ਹਨ ।

ਪ੍ਰਸ਼ਨ 7.
ਬਿੰਦੂ A ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਪਤਾ ਕਰੋ, ਜਿੱਥੇ AB ਇੱਕ | ਚੱਕਰ ਦਾ ਵਿਆਸ ਹੈ । ਜਿਸਦਾ ਕੇਂਦਰ (2, – 3) ਹੈ ਅਤੇ B ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ (1, 4) ਹਨ ।
ਹੱਲ:
ਮੰਨ ਲਉ A ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ (x, y) ਹੈ ।
ਪਰ, ਵਿਆਸ ਦੇ ਸਿਖਰਾਂ ਦਾ ਮੱਧ ਬਿੰਦੂ ਕੇਂਦਰ ਹੁੰਦਾ ਹੈ ।

∴ O, A (x, y) ਅਤੇ B (1, 4) ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ ।
∴ (\(\frac{x+1}{2}\), \(\frac{y+4}{2}\)) = (2, -3)
ਤੁਲਨਾ ਕਰਨ ‘ਤੇ,
\(\frac{x+1}{2}\) = 2 ਅਤੇ \(\frac{y+4}{2}\) = -3
x + 1 = 4 ਅਤੇ y + 4 = – 6
x = 4 – 1 ਅਤੇ y = – 6 – 4
x = 3 ਅਤੇ y = – 10
∴ ਲੋੜੀਂਦਾ ਬਿੰਦੂ ਹੈ (3 – 10)

ਪ੍ਰਸ਼ਨ 8.
ਜੇਕਰ ਅਤੇ B ਕੁਮਵਾਰ (-2, -2) ਅਤੇ (2, 4) | ਹੋਣ ਤਾਂ P ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਪਤਾ ਕਰੋ ਤਾਂ ਕਿ AP = \(\frac{3}{7}\)AB ਹੋਵੇ ਅਤੇ P ਰੇਖਾਖੰਡ AB ‘ਤੇ ਸਥਿਤ ਹੋਵੇ ।
ਹੱਲ:
ਮੰਨ ਲਉ ਲੋੜੀਂਦਾ ਬਿੰਦੂ ਹੈ P(x, y).
ਨਾਲ ਹੀ AP = \(\frac{3}{7}\)AB … ਦਿੱਤਾ ਹੈ।
ਪਰ PB = AB – AP
= AB – \(\frac{3}{7}\)AB = (\(\frac{7-3}{7}\))AB
= \(\frac{4}{7}\)AB
∴ \(\frac{\mathrm{AP}}{\mathrm{PB}}=\frac{\frac{3}{7} \mathrm{AB}}{\frac{4}{7} \mathrm{AB}}=\frac{3}{4}\)
∴ P ਦਿੱਤੇ ਗਏ ਬਿੰਦੂ A ਅਤੇ B ਨੂੰ 3:4 ਦੇ ਅਨੁਪਾਤ ਵਿਚ ਵੰਡਦਾ ਹੈ ।

∴ ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਹਨ : (\(-\frac{2}{7}\), \(-\frac{20}{7}\)

ਪ੍ਰਸ਼ਨ 9.
ਬਿੰਦੂਆਂ A (-2, 2) ਅਤੇ B (2, 8) ਨੂੰ ਮਿਲਾਉਣ ਵਾਲੇ ਰੇਖਾਖੰਡ AB ਨੂੰ ਚਾਰ ਬਰਾਬਰ ਭਾਗਾਂ ਵਿਚ ਵੰਡਣ ਵਾਲੇ ਬਿੰਦੂਆਂ ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ C, D ਅਤੇ E ਲੋੜੀਂਦੇ ਬਿੰਦੂ ਹਨ ਜੋ ਬਿੰਦੂ A ( 2, 2) ਅਤੇ B (2, 8) ਨੂੰ ਮਿਲਾਉਣ ਵਾਲੇ ਰੇਖਾਖੰਡ ਨੂੰ ਚਾਰ ਬਰਾਬਰ ਭਾਗਾਂ ਵਿੱਚ ਵੰਡਦੇ ਹਨ ।
ਤਾਂ D, A ਅਤੇ B ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ ; C, A ਅਤੇ D ਦਾ | ਮੱਧ ਬਿੰਦੂ ਹੈ; E, D ਅਤੇ B ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ ਤਾਂ ਕਿ
AC = CD = DE = EB
ਹੁਣ, A ਅਤੇ B ਦਾ ਮੱਧ ਬਿੰਦੂ ( D ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ)
= (\(\frac{-2+2}{2}\), \(\frac{2+8}{2}\) = (0, 5)
A ਅਤੇ D ਦਾ ਮੱਧ ਬਿੰਦੂ (C ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ)
(\(\frac{-2+0}{2}\), \(\frac{-2+5}{2}\) = (1, \(\frac{7}{2}\)
D ਅਤੇ B ਦਾ ਮੱਧ ਬਿੰਦੂ (E ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ)
(\(\frac{2+0}{2}\), \(\frac{8+5}{2}\)) = (-1, \(\frac{13}{2}\))
∴ ਲੋੜੀਂਦੇ ਬਿੰਦੂ ਹਨ :
(0, 5), (-1, \(\frac{7}{2}\)) ਅਤੇ (1, \(\frac{13}{2}\))

ਪ੍ਰਸ਼ਨ 10.
ਇਕ ਸਮਚਤੁਰਭੁਜ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ | ਜਿਸਦੇ ਸਿਖਰ, ਇਸੇ ਕੂਮ ਵਿਚ (3, 0), (4, 5), (-1, 4) ਅਤੇ (-2, – 1) ਹਨ ।
ਸੰਕੇਤ : ਸਮਚਤੁਰਭੁਜ ਦਾ ਖੇਤਰਫਲ = \(\frac{1}{2}\) (ਉਸਦੇ ਵਿਕਰਣਾਂ ਦਾ ਗੁਣਨਫਲ)]
ਹੱਲ:
ਮੰਨ ਲਉ ਸਮਚਤੁਰਭੁਜ ABCD ਦੇ ਸਿਖਰ ਬਿੰਦੂ ਹਨ : A (3, 0) ; B (4, 5) ; C (- 1, 4) ਅਤੇ D (-2, – 1).
ਵਿਕਰਣ AC = \(\sqrt{(-1-3)^{2}+(4-0)^{2}}\)
= \(\sqrt {16+16}\) = \(\sqrt {32}\)
= 4\(\sqrt {2}\)

ਵਿਕਰਣ BD
BD = \(\sqrt{(-2-4)^{2}+(-1-5)^{2}}\)
= \(\sqrt {36+36}\) = \(\sqrt {72}\)
= 6\(\sqrt {2}\)
∴ ਸਮਚਤੁਰਭੁਜ ABCD ਦਾ ਖੇਤਰਫਲ
= \(\frac{1}{2}\) × AC × BD
= [\(\frac{1}{2}\) × 4\(\sqrt {2}\) × 6\(\sqrt {2}\)]
= (\(\frac{1}{2}\) × 24 × 2)
= 24 ਵ.ਮੀ.
∴ ਸਮਚਤੁਰਭੁਜ ਦਾ ਖੇਤਰਫਲ 24 ਵ.ਮੀ. ਹੈ ।

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 7 ਨਿਰਦੇਸ਼ ਅੰਕਜਿਮਾਇਤੀ Ex 7.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 7 ਨਿਰਦੇਸ਼ ਅੰਕਜਿਮਾਇਤੀ Exercise 7.1

ਪ੍ਰਸ਼ਨ 1.
ਬਿੰਦੂਆਂ ਦੇ ਹੇਠ ਦਿੱਤਿਆਂ ਜੋੜਿਆਂ ਦੀ ਵਿਚਕਾਰਲੀ ਦੂਰੀ ਪਤਾ ਕਰੋ :
(i) (2, 3) ; (4, 1)
(ii) (-5, 7) ; (-1, 3)
(iii) (a, b) ; (-a, – b).
ਹੱਲ:
(i) ਦਿੱਤੇ ਗਏ ਬਿੰਦੂ ਹੈਂ : (2, 3) ; (4, 1)
ਲੋੜੀਂਦੀ ਦੂਰੀ = \(\sqrt{(4-2)^{2}+(1-3)^{2}}\)
= \(\sqrt{4+4}\) = \(\sqrt {8}\) = 2\(\sqrt {2}\)

(ii) ਦਿੱਤੇ ਗਏ ਬਿੰਦੂ ਹਨ : (-5, 7) ; (-1, 3)
ਲੋੜੀਂਦੀ ਦੂਰੀ = \(\sqrt{(-1+5)^{2}+(3-7)^{2}}\)
= \(\sqrt{16+16}\) = \(\sqrt{32}\) =4\(\sqrt{2}\)

(iii) ਦਿੱਤੇ ਗਏ ਬਿੰਦੂ ਹਨ : (a, b); (-a,-b)
ਲੋੜੀਂਦੀ ਦੂਰੀ = \(\sqrt{(-a-a)^{2}+(-b-b)^{2}}\)
= \(\sqrt{(-2 a)^{2}+(-2 b)^{2}}\)
= \(\sqrt{4 a^{2}+4 b^{2}}\)
= 2\(\sqrt{a^{2}+b^{2}}\)

ਪ੍ਰਸ਼ਨ 2.
ਬਿੰਦੂਆਂ (0, 0) ਅਤੇ (36, 15) ਦੀ ਵਿਚਕਾਰਲੀ ਦੂਰੀ ਪਤਾ ਕਰੋ। ਕੀ ਤੁਸੀ ਹੁਣ ਭਾਗ 7.2 ਵਿੱਚ ਦਿੱਤੇ ਦੋਹਾਂ ਸ਼ਹਿਰਾਂ A ਅਤੇ B ਵਿਚਕਾਰਲੀ ਦੂਰੀ ਪਤਾ ਕਰ ਸਕਦੇ ਹੋ ?
ਹੱਲ:
ਦਿੱਤੇ ਗਏ ਬਿੰਦੂ ਹਨ :
A (0, 0) ਅਤੇ B (36, 15)
ਦੂਰੀ AB = \(\sqrt{(0-36)^{2}+(0-15)^{2}}\)
= \(\sqrt{1296+225}\) = \(\sqrt{1521}\)
= 39
ਭਾਗ 7.2 ਦੇ ਅਨੁਸਾਰ
ਬਿੰਦੂ A (0, 0) ਅਤੇ B (36, 15) ਚਿੱਤਰ ਵਿਚ – ਦਿਖਾਏ ਅਨੁਸਾਰ

BC ⊥X-ਧੁਰੇ ਤੇ ਖਿੱਚੋ ।
ਹੁਣ ਸਮਕੋਣ ACB ਵਿੱਚ,
AB = \(\sqrt{A C^{2}+B C^{2}}\)
= \(\sqrt{(36)^{2}+(15)^{2}}\)
= \(\sqrt{1296+225}\) = \(\sqrt{1521}\)
= 39.
∴ ਬਿੰਦੂਆਂ ਵਿਚ ਲੋੜੀਂਦੀ ਦੂਰੀ 39 ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਨਿਰਧਾਰਿਤ ਕਰੋ ਕਿ ਕੀ ਬਿੰਦੂ (1, 5), (2, 3) ਅਤੇ (-2, – 11) ਸਮਰੇਖੀ ਹਨ ।
ਹੱਲ:
ਦਿੱਤੇ ਗਏ ਬਿੰਦੂ ਹਨ : A (1, 5) ; B (2, 3) ਅਤੇ C (-2 – 11).

ਉਪਰੋਕਤ ਦੂਰੀਆਂ ਤੋਂ ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਕਿ ਕਿਸੇ ਦੋ ਦਾ ਜੋੜਫਲ ਤੀਸਰੇ ਦੇ ਬਰਾਬਰ ਨਹੀਂ ਹੈ । ਇਸ ਲਈ ਇਹ ਬਿੰਦੂ ਸਮਰੇਖੀ ਨਹੀਂ ਹਨ ।

ਪ੍ਰਸ਼ਨ 4.
ਜਾਂਚ ਕਰੋ ਕਿ ਕੀ ਬਿੰਦੂ (5, – 2) (6, 4) ਅਤੇ (7, -2) ਇੱਕ ਸਮਦੋਭੁਜੀ ਤ੍ਰਿਭੁਜ ਦੇ ਸਿਖਰ ਹਨ ।
ਹੱਲ:
ਦਿੱਤੇ ਗਏ ਬਿੰਦੂ ਹਨ A (3, – 2) ; B (6, 4) ਅਤੇ c (7, – 2).

ਉਪਰੋਕਤ ਦੂਰੀ ਤੋਂ ਸਪੱਸ਼ਟ ਹੈ ਕਿ
AB = BC = \(\sqrt{37}\).
∴ ਦਿੱਤੇ ਗਏ ਬਿੰਦੂ ਸਮਦੋਭੁਜੀ ਤ੍ਰਿਭੁਜ ਦੇ ਸਿਖਰ ਹਨ ।

ਪ੍ਰਸ਼ਨ 5.
ਕਿਸੇ ਜਮਾਤ ਵਿੱਚ, ਚਾਰ ਮਿੱਤਰ ਬਿੰਦੂਆਂ A, B, C ਅਤੇ D ‘ਤੇ ਬੈਠੇ ਹੋਏ ਹਨ, ਜਿਸ ਤਰ੍ਹਾਂ ਕਿ ਚਿੱਤਰ ਵਿਚ ਦਰਸਾਇਆ ਗਿਆ ਹੈ । ਚੰਪਾ ਅਤੇ ਚਮੇਲੀ ਜਮਾਤ ਦੇ ਅੰਦਰ ਆਉਂਦੀਆਂ ਹਨ ਅਤੇ ਕੁਝ ਸਮਾਂ ਦੇਖਣ ਤੋਂ ਬਾਅਦ ਚੰਪਾ, ਚਮੇਲੀ ਨੂੰ ਪੁੱਛਦੀ ਹੈ, “ਕੀ ਤੂੰ ਨਹੀਂ ਸੋਚਦੀ ਕਿ ABCD ਇੱਕ ਵਰਗ ਹੈ ?” ਚਮੇਲੀ ਇਸ ਨਾਲ ਸਹਿਮਤ ਨਹੀਂ ਹੈ । ਦੂਰੀ ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਕੇ, ਦੱਸੋ ਕਿ ਇਹਨਾਂ ਵਿੱਚੋਂ ਕੌਣ ਸਹੀ ਹੈ ।

ਹੱਲ:
ਦਿੱਤੇ ਗਏ ਚਿੱਤਰ ਵਿਚ ਸਿਖਰ ਬਿੰਦੂ ਹਨ : A (3, 4) ; B (6, 7) ; C (9, 4) ਅਤੇ D (6, 1).

ਸਪੱਸ਼ਟ ਹੈ ਕਿ
AB = BC = CD = DA = \(\sqrt{18}\)
ਅਤੇ AC = BD = 6.
∴ ABCD ਇਕ ਵਰਗ ਬਣਦਾ ਹੈ ਚੰਪਾ ਦੀ ਸੋਚ ਸਹੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 6.
ਹੇਠਾਂ ਦਿੱਤੇ ਬਿੰਦੂਆਂ ਦੁਆਰਾ ਬਣਨ ਵਾਲੇ ਚਤੁਰਭੁਜ ਦੀ ਕਿਸਮ ਜੇਕਰ ਕੋਈ ਹੈ ਤਾਂ ਦੱਸੋ ਅਤੇ ਆਪਣੇ ਉੱਤਰ ਦਾ ਕਾਰਣ ਵੀ ਦੱਸੋ :
(i) (-1, -2), (1, 0), (-1, 2), (-3, 0)
(ii) (-3, 5), (3, 1), (0, 3), (-1, – 4)
(iii) (4, 5), (7, 6), (4, 3), (1, 2).
ਹੱਲ:
(i) ਦਿੱਤੇ ਗਏ ਬਿੰਦੂ ਹਨ : A (-1, – 2) ; B (1, 0) ; C (-1, 2) ਅਤੇ D (-3, 0).


ਹੁਣ ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਕਿ
AB = BC = CD = DA = \(\sqrt{8}\)
AC = BD = 4.
∴ ਇਹ ਚਤੁਰਭੁਜ ABCD ਇੱਕ ਵਰਗ ਹੈ ।

(ii) ਦਿੱਤੇ ਗਏ ਬਿੰਦੂ ਹਨ : A (-3, 5); B (3, 1); (0, 3) ਅਤੇ D (-1, – 4)

ਹੁਣ, BC + CA = \(\sqrt{13}\) + \(\sqrt{13}\)
= 2\(\sqrt{13}\) = AB
∴ A, B ਅਤੇ C ਇਕ ਰੇਖਾ ਵਿਚ ਹਨ ਅਤੇ A, B, C ਅਤੇ D ਚਤੁਰਭੁਜ ਨਹੀਂ ਬਣਾਉਂਦੇ ।

(iii) ਦਿੱਤੇ ਗਏ ਬਿੰਦੂ : A (4, 5) ; B (7, 6) ; C (4, 3) ਅਤੇ D (1, 2)
AB = \(\sqrt{(7-4)^{2}+(6-5)^{2}}\)

ਹੁਣ ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਕਿ
AB = CD ਅਤੇ BC = DA
ਅਤੇ AC ≠ BD.
∴ ਸਨਮੁਖ ਭੁਜਾਵਾਂ ਬਰਾਬਰ ਹਨ ਪਰ ਉਹਨਾਂ ਦੇ ਵਿਕਰਣ ਬਰਾਬਰ ਨਹੀਂ ਹਨ ।
∴ ਦਿੱਤੀ ਹੋਈ ਚਤੁਰਭੁਜ ABCD ਇਕ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਹੈ ।

ਪ੍ਰਸ਼ਨ 7.
x-ਧੁਰੇ ‘ਤੇ ਉਹ ਬਿੰਦੂ ਪਤਾ ਕਰੋ ਜੋ (2, – 5) ਅਤੇ (-2, 9) ਤੋਂ ਬਰਾਬਰ ਦੂਰੀ ‘ਤੇ ਹੈ।
ਹੱਲ:
ਮੰਨ ਲਓ ਲੋੜੀਂਦਾ ਬਿੰਦੂ ਹੈ P (x, 0) ਅਤੇ ਦਿੱਤੇ ਗਏ ਬਿੰਦੂ ਹਨ A (2, -5) ਅਤੇ B (-2, 9). ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ,
PA = PB
(PA)² = (PB)²
(2 – x)² + (-5 – 0)² = (-2 – x)² + (9 – 0)²
4 + x – 4x + 25 = 4 + x² + 4x + 81
– 8x = 56
x = \(\frac{56}{8}\) = -7
∴ਲੋੜੀਂਦਾ ਬਿੰਦੂ (-7, 0) ਹੈ ।

ਪ੍ਰਸ਼ਨ 8
y ਦਾ ਉਹ ਮੁੱਲ ਪਤਾ ਕਰੋ ਜਿਸਦੇ ਲਈ ਬਿੰਦੂ P (2, – 3) ਅਤੇ Q (10, y) ਦੇ ਵਿਚਕਾਰ ਦੀ ਦੂਰੀ 10 ਇਕਾਈਆਂ ਹੈ ।
ਹੱਲ:
ਦਿੱਤੇ ਗਏ ਬਿੰਦੂ ਹਨ : P (2, – 3) ਅਤੇ Q (10, y)
PQ = \(\sqrt{(10-2)^{2}+(y+3)^{2}}\)
= \(\sqrt{64+y^{2}+9+6 y}\)
= \(\sqrt{y^{2}+6 y+73}\)
ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ, PQ = 10
\(\sqrt{y^{2}+6 y+73}\) = 10
y² + 6y + 73 = 100
y² + 6y – 27 = 0
y² + 9y – 3y – 27 = 0
y (y + 9) – 3 (y + 9) = 0
(y +9) (y – 3) = 0.
y + 9 = 0 ਜਾਂ y – 3 =0
y = -9 ਜਾਂ y = 3
y = -9 ਅਤੇ 3

ਪ੍ਰਸ਼ਨ 9.
ਜੇਕਰ Q (0, 1) ਬਿੰਦੁਆਂ P (5, -3) ਅਤੇ R (x, 6) ਤੋਂ ਬਰਾਬਰ ਦੂਰੀ ‘ਤੇ ਹੈ ਤਾਂਝ ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ । ਦੂਰੀਆਂ QR ਅਤੇ PR ਵੀ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਦਿੱਤੇ ਗਏ ਬਿੰਦੂ ਹਨ : Q (0, 1) ;
P (5, – 3) ਅਤੇ R (x, 6)
QP = \(\sqrt{(5-0)^{2}+(-3-1)^{2}}\)
= \(\sqrt{25+16}\) = \(\sqrt{41}\)
QR = \(\sqrt{(x-0)^{2}+(6-1)^{2}}\)
= \(\sqrt{x^{2}+25}\)
ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ
QP = QR
\(\sqrt{41}\) = \(\sqrt{x^{2}+25}\)
41 = x² + 25 ਜਾਂ x² = 16
x = ±\(\sqrt{16}\) = ±4.
ਜਦੋਂ = 4 ਤਾਂ R (4, 6).
QR = \(\sqrt{(4-0)^{2}+(6-1)^{2}}\)
= \(\sqrt{16+25}\) = \(\sqrt{41}\)
PR = \(\sqrt{(4-5)^{2}+(6+3)^{2}}\)
= \(\sqrt{1=81}\) = \(\sqrt{82}\)
ਜਦੋਂ = -4 ਤਾਂ R (-4, 6).
QR = \(\sqrt{(-4-0)^{2}+(6-1)^{2}}\)
= \(\sqrt{16+25}\) = \(\sqrt{41}\)
PR = \(\sqrt{(-4-5)^{2}+(6+3)^{2}}\)
= \(\sqrt{81+81}\) = \(\sqrt{162}\).

ਪ੍ਰਸ਼ਨ 10.
x ਅਤੇ y ਵਿੱਚ ਇੱਕ ਅਜਿਹਾ ਸੰਬੰਧ ਪਤਾ ਕਰੋ ਕਿ ਬਿੰਦੂ (x, y) ਬਿੰਦੂਆਂ (3, 6) ਅਤੇ (-3, 4) ਤੋਂ ਬਰਾਬਰ ਦੀ ਦੂਰੀ ‘ਤੇ ਹੋਵੇ ।
ਹੱਲ:
ਮੰਨ ਲਓ ਲੋੜੀਂਦਾ ਬਿੰਦੂ P (x, y) ਹੈ ।
ਦਿੱਤੇ ਗਏ ਬਿੰਦੂ ਹਨ A (3, 6) ਅਤੇ B (-3, 4)

ਦੋਵੇਂ ਪਾਸੇ ਵਰਗ ਕਰਨ ਤੇ
x² + y² – 6x – 12y +45
= x² + y² + 6x – 8y + 25
– 12x – 4y + 20 = 0
3x + y – 5 = 0
ਲੋੜੀਂਦਾ ਸੰਬੰਧ ਹੈ ।

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 6 ਤ੍ਰਿਭੁਜ Ex 6.6 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 6 ਤ੍ਰਿਭੁਜ Exercise 6.6

ਪ੍ਰਸ਼ਨ 1.
ਚਿੱਤਰ ਵਿੱਚ, PS ਕੋਣ ∠PR ਦਾ ਸਮਦੋਭਾਜਕ ਹੈ । ਸਿੱਧ ਕਰੋ ਕਿ \(\frac{QS}{SR}\) = \(\frac{PQ}{PR}\) ਹੈ ।

ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △PQR, PS ਕੋਣ ∠QPR ਦਾ ਸਮਦੋਭਾਜਕ ਹੈ ਭਾਵ ∠1 = ∠2
ਸਿੱਧ ਕਰਨਾ : \(\frac{QS}{SR}\) = \(\frac{PQ}{PR}\)

ਰਚਨਾ : R ਤੋਂ ਇੱਕ ਰੇਖਾ PS ਦੇ ਸਮਾਂਤਰ ਖਿੱਚੋ ਜੋ QP ਨੂੰ ਵਧਾਉਣ ਤੇ Tਉੱਤੇ ਮਿਲਦੀ ਹੈ ।
ਸਬੂਤ : △QRT ਵਿੱਚ,
PS || TR
∠2 = ∠3 (ਇਕਾਂਤਰ ਕੋਣ)
∠1 = ∠4 (ਸੰਗਤ ਕੋਣ)
ਪਰ ∠1 = ∠2 (ਦਿੱਤਾ ਹੈ।)
∴ ∠3 = ∠4
△PRT ਵਿੱਚ
∠3 = ∠4 (ਸਿੱਧ ਕੀਤਾ)
PT = PR [ਸਮਾਨ ਭੁਜਾਵਾਂ ਦੇ ਸਨਮੁੱਖ ਕੋਣ ਵੀ ਬਰਾਬਰ ਹੁੰਦੇ ਹਨ ]
△QRT ਵਿੱਚ
PS || TR

ਪ੍ਰਸ਼ਨ 2.
ਚਿੱਤਰ ਵਿਚ D ਤ੍ਰਿਭੁਜ ABC ਦੇ ਕਰਣ AC ਉੱਤੇ ਇਕ ਬਿੰਦੂ ਹੈ ਜਦ ਕਿ BD ⊥ AC ਅਤੇ DM ⊥ BC ਅਤੇ DN ⊥ AB ਹੈ । ਸਿੱਧ ਕਰੋ ਕਿ
(i) DM² = DN.MC
(ii) DN² = DM.AN

ਦਿੱਤਾ ਹੈ : △ABC ਵਿੱਚ, DM ⊥ BC,
DN ⊥ AB ਹੈ ।
ਸਿੱਧ ਕਰਨਾ : DM² = DN.AC
DN = DM.AN.
ਹੱਲ:
BD ² AC (ਦਿੱਤਾ ਹੈ।)
⇒ ∠BDC= 90°
⇒ ∠BDM + ∠MDC = 90° …(1)
△DMC ਵਿੱਚ
∠DMC = 90°
[∵ DM ⊥ BC (ਦਿੱਤਾ ਹੈ)]
⇒ ∠C + ∠MDC = 90° ..(2)
(1) ਅਤੇ (2) ਤੋਂ
∠BDM + ∠MDC = ∠C + ∠MDC
⇒ ∠BDM =∠C
[ਦੋਵੇਂ ਪਾਸਿਉਂ ∠MDC ਨੂੰ ਕੱਟਣ ਤੇ]
ਹੁਣ △BMD ਅਤੇ △MDC ਵਿੱਚ,
∠BDM = ∠C [ਸਿੱਧ ਕੀਤਾ]
∠BMD = ∠MDC [ਹਰੇਕ 90°]
∴ ∠BMD ~ ∠MDC [AA ਕਮੇਟੀ]
⇒ \(\frac{\mathrm{DM}}{\mathrm{BM}}\) = \(\frac{\mathrm{MC}}{\mathrm{DM}}\)
[∵ ਸਮਰੂਪ ਤ੍ਰਿਭੁਜਾਂ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਸਮਾਨ ਅਨੁਪਾਤੀ ਹੁੰਦੀਆਂ ਹਨ |]
⇒ DM² = BM × MC
⇒ DM² = DN × MC
[∵ BM = DN]
ਇਸੇ ਤਰ੍ਹਾਂ △NDA ~ △NBD
⇒ \(\frac{\mathrm{DN}}{\mathrm{BN}}\) = \(\frac{\mathrm{AN}}{\mathrm{DN}}\)
[∵ ਸਮਰੂਪ ਤ੍ਰਿਭੁਜਾਂ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਸਮਾਨ ਅਨੁਪਾਤੀ ਹੁੰਦੀਆਂ ਹਨ |]
⇒ DN² = BN × AN
⇒ DN² = DM × AN

ਪ੍ਰਸ਼ਨ 3.
ਚਿੱਤਰ ਵਿੱਚ ABC ਇੱਕ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸ ਵਿਚ ∠ABC > 90° ਹੈ ਅਤੇ AD ⊥ CB ਹੈ ਸਿੱਧ ਕਰੋ ਕਿ AC² = AB² + BC² + 2BC.BD ਹੈ ।

ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △ABC ਵਿੱਚ AD ⊥ BC ਜਦੋਂ BC ਨੂੰ ਵਧਾਇਆ ਜਾਂਦਾ ਹੈ ∠ABC > 90° ਹੈ ।
ਸਿੱਧ ਕਰਨਾ : AC² = AB² + BC² + 2BC.BD.
ਸਬੂਤ : ਮੰਨ ਲਉ : BC = a,
CA = b,
AB = C,
AD = h
ਅਤੇ BD = x.
ਸਮਕੋਣ ਤਿਭੁਜ △ADB ਵਿੱਚ, ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਤੋਂ,
AB² = BD² + AD
ਭਾਵ c² = x² + h²
ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ △ADC ਵਿੱਚ
AC² = CD² + AD²
ਭਾਵ b² = (a + x)² + h²
= a² + 2ax + x² + h²
= a² + 2ax + c²;
[(1) ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ਤੇ]
b² = a² + c² + 2ax
ਹੁਣ . , AC² = AB² + BC² + 2BC × BD.

ਪ੍ਰਸ਼ਨ 4.
ਚਿੱਤਰ ਵਿੱਚ ABC ਇੱਕ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸ ਵਿੱਚ ∠ABC < 90° ਹੈ ਅਤੇ AD ⊥ BC ਹੈ ।
ਸਿੱਧ ਕਰੋ ਕਿ
AC² = AB² + BC² – 2BC.BD ਹੈ ।

ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △ABC ਜਿਸ ਵਿਚ ∠ABC <90° ਅਤੇ AD ⊥ BC ਹੈ ।
ਸਿੱਧ ਕਰਨਾ : AC² = AB² + BC² – 2BC.BD.
ਸਬੂਤ : ADC ਇੱਕ ਸਮਕੋਣ ਹੈ ਜਿਸ ਵਿਚ D ਇੱਕ ਸਮਕੋਣ ਹੈ ।
AC² = CD² + DA² ….(1)
(ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਤੋਂ।)
ਨਾਲ ਹੀ, △ADB ਸਮਕੋਣ △ ਹੈ D ਇਕ ਸਮਕੋਣ ਹੈ ।
AB² = AD² +DB² ….(2)
(1) ਤੋਂ ।
AC² = AD² +(CB – BD)²
= AD² + CB² + BD² – 2CB × BD
ਜਾਂ AC² = (BD² + AD²) + CB² – 2CB × BD
AC² = AB² + BC² – 2BC × BD.
[(2) ਦੇ ਪ੍ਰਯੋਗ ਤੋਂ।

ਪ੍ਰਸ਼ਨ 5.
ਚਿੱਤਰ ਵਿੱਚ AD ਤ੍ਰਿਭੁਜ ABC ਦੀ ਇਕ ਮੱਧਕਾ ਹੈ . ਅਤੇ AM ⊥ BC ਹੈ । ਸਿੱਧ ਕਰੋ ਕਿ :
(i) AC² = AD² + BC.DM + \(\left(\frac{\mathrm{BC}}{2}\right)^{2}\)
(ii) AB² = AD² – BC.DM + \(\left(\frac{\mathrm{BC}}{2}\right)^{2}\)
(iii) AC² + AB² = 2AD² + \(\frac{1}{2}\)BC²

ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △ABC ਵਿੱਚ, AM ⊥ BC, AD, △ABC ਦੀ ਇੱਕ ਮੱਧਕਾ ਹੈ ।
ਸਿੱਧ ਕਰਨਾ :
(i) AC² = AD² + BC.DM + \(\left(\frac{\mathrm{BC}}{2}\right)^{2}\)
(ii) AB² = AD² – BC.DM + \(\left(\frac{\mathrm{BC}}{2}\right)^{2}\)
(iii) AC² + AB² = 2AD² + \(\frac{1}{2}\)BC²
ਸਬੂਤ : △AMC ਵਿੱਚ,
AC² = AM² + MC²
= AM² + (MD +DC)²
AC² = AM² + MD² + DC² + 2MD × DC
AC² = (AM² + MD²) + \(\left(\frac{\mathrm{BC}}{2}\right)^{2}\) + 2.MD\(\left(\frac{\mathrm{BC}}{2}\right)\)
AC² = AD² + BC × MD + \(\frac{\mathrm{BC}^{2}}{4}\)
[ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ △AMD
AD² = AM² + MD²]
∴ AC² = AD² + BC.MD + \(\frac{\mathrm{BC}^{2}}{4}\) …(1)

(ii) ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ AMB ਵਿੱਚ,
AB² = AM² + BM²
= AM² + (BD – MD)²
= AM² + BD² + MD² – 2BD × MD
= (AM² + MD²) + BD² – 2(\(\frac{1}{2}\)BC) MD
= AD² + (\(\frac{1}{2}\)BC)² – BC.MD
[∵ △AMD ਸੇਂ, AD² = MA² + MD²]
AB² = AD² + \(\left(\frac{\mathrm{BC}}{2}\right)^{2}\) – BC.MD …2

(iii) (1) ਅਤੇ (2) ਨੂੰ ਜੋੜਨ ਤੇ,
AB² + AC² = AD² + BC.MD + \(\left(\frac{B C}{2}\right)^{2}\) + AD² + \(\left(\frac{B C}{2}\right)^{2}\) – BC.MD
= 2AD² + \(\frac{\mathrm{BC}^{2}}{4}\) + \(\frac{\mathrm{BC}^{2}}{4}\)
= 2AD² + 2\(\frac{\mathrm{BC}^{2}}{4}\)
AB² + AC² = 2AD² + \(\frac{\mathrm{BC}^{2}}{2}\)

ਪ੍ਰਸ਼ਨ 6.
ਸਿੱਧ ਕਰੋ ਕਿ ਇੱਕ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਦੇ ਵਿਕਰਣਾਂ ਦੇ ਵਰਗਾਂ ਦਾ ਜੋੜ ਉਸ ਦੀਆਂ ਭੁਜਾਵਾਂ ਦੇ ਵਰਗਾਂ ਦੇ ਜੋੜ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ ।
ਹੱਲ:

ਦਿੱਤਾ ਹੈ : ਮੰਨ ਲਉ ABCD ਇਕ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਹੈ ਜਿਸ ਦੇ ਵਿਕਰਣ AC ਅਤੇ BD ਪਰਸਪਰ ਬਿੰਦੂ M ਉੱਤੇ ਕੱਟਦੇ ਹਨ ।
ਸਿੱਧ ਕਰਨਾ : AB² + BC² + CD² + DA²
= AB² + BC²
ਸਬੂਤ : ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਦੇ ਵਿਕਰਣ ਇਕ ਦੂਸਰੇ ਨੂੰ ਪਰਸਪਰ ਕੱਟਦੇ ਹਨ ।
ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ABCD ਵਿੱਚ, ਵਿਕਰਣ BD ਅਤੇ AC ਇਕ-ਦੂਸਰੇ ਨੂੰ ਕੱਟਦੇ ਹਨ ।
ਜਾਂ MB ਅਤੇ MD ਕ੍ਰਮਵਾਰ △ABC ਅਤੇ △ADC ਦੀ ਮੱਧਕਾ ਹੈ ।
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ AD, △ABC ਦੀ ਮੱਧਕਾ ਹੈ ।
∴ AB² + AC² = 2AD² + \(\frac{1}{2}\)BC²
ਇਸ ਦਾ ਪ੍ਰਯੋਗ ਕਰਦੇ ਹੋਏ,
AB² + BC² = 2BM² + \(\frac{1}{2}\)BC² …(1)
ਅਤੇ AD² + CD² = 2DM² + \(\frac{1}{2}\)AC² …(2)
(1) ਅਤੇ (2), ਨੂੰ ਜੋੜਨ ਤੇ
AB² + BC² + AD² + CD²
= 2(BM² + DM²) + \(\frac{1}{2}\)(AC² + AC²)
AB² + BC² + AD² + CD²
= 2(\(\frac{1}{4}\)BD² + \(\frac{1}{4}\)BD²) + AC²
AB² + BC² + AD² + CD² = BD² + AC²
ਇੱਕ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਦੇ ਵਿਕਰਣਾਂ ਦੇ ਵਰਗਾਂ ਦਾ ਜੋੜ ਉਸਦੀ ਭੁਜਾਵਾਂ ਦੇ ਵਰਗਾਂ ਦੇ ਜੋੜ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 7.
ਚਿੱਤਰ ਵਿਚ ਇਕ ਚੱਕਰ ਦੀਆਂ ਦੋ ਜੀਵਾਵਾਂ (ਵਤਰਾਂ) AB ਅਤੇ CD ਆਪਸ ਵਿੱਚ P ਬਿੰਦੂ ‘ਤੇ ਕੱਟਦੀਆਂ ਹਨ ।
ਸਿੱਧ ਕਰੋ ਕਿ :
(i) △AFC ~ △DPB
(ii) AP.PB = CP.DP.

ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਇੱਕ ਚੱਕਰ ਦੀਆਂ ਦੋ ਜੀਵਾਵਾਂ AB ਅਤੇ CD ਇਕ-ਦੂਜੇ ਨੂੰ ਮਾਂ ਉੱਤੇ ਕੱਟਦੀਆਂ ਹਨ ।
ਸਿੱਧ ਕਰਨਾ : (i) △APC ~ △DPB
(ii) AP.PB = CP.DP.
ਸਬੂਤ : (i) △APC ਅਤੇ △DPB ਵਿੱਚ,
∠1 = ∠2 (ਸਿਖਰ ਸਨਮੁੱਖ ਕੋਣ)
∠3 = ∠4 (ਇੱਕ ਹੀ ਖੰਡ ਵਿੱਚ ਬਣੇ ਕੋਣ)
∴ △APC ~ △DPB [AA ਸਮਰੂਪਤਾ ਕਸੌਟੀ]

(ii) △APC ~ △DPB (ਸਿੱਧ ਕੀਤਾ)
\(\frac{AD}{DP}\) = \(\frac{PC}{PB}\)
(ਜੇਕਰ ਦੋ ਤ੍ਰਿਭੁਜਾਂ ਸਮਰੂਪ ਹੋਣ ਤਾਂ ਸੰਗਤ ਕੋਣ ਸਮਾਨ ਅਨੁਪਾਤੀ ਹੁੰਦੇ ਹਨ ॥)
AP.PB = PC.DP

ਪ੍ਰਸ਼ਨ 8.
ਚਿੱਤਰ ਵਿੱਚ ਇੱਕ ਚੱਕਰ ਦੀਆਂ ਦੋ ਵਤਰਾਂ AB ਅਤੇ CD ਵਧਾਉਣ ਤੇ ਆਪਸ ਵਿੱਚ ਬਿੰਦੂ ‘ਤੇ ਕੱਟਦੀਆਂ ਹਨ । निय व वि
(i) △PAC ~ △PDB
(ii) PA.PB = PC.PD.

ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਇਕ ਚੱਕਰ ਦੀਆਂ ਦੋ ਜੀਵਾਵਾਂ AB ਅਤੇ CD ਵਧਾਉਣ ਤੇ ਪਰਸਪਰ P ਬਿੰਦੁ ਤੇ ਕੱਟਦੇ ਹਨ ।
ਸਿੱਧ ਕਰਨਾ : (i) △PAC ~ △PDB
(ii) PA.PB = PC.PD.
ਸਬੂਤ : (i) △PAC ਅਤੇ △PDB ਤੋਂ,
∠P = ∠P
∠PAC = ∠PDB (ਚੱਕਰੀ ਚਤੁਰਭੁਜ ਦਾ ਬਾਹਰੀ ਕੋਣ ਅੰਦਰਲੇ ਕੋਣ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ।)
∴ △PAC ~ △PDB [AA ਸਮਰੂਪਤਾ ਕਸੋਟੀ ਤੋਂ।]

(iii) △PAB ~ △PDB
\(\frac{PA}{PD}\) = \(\frac{PC}{PB}\)
[ਜੇ ਦੋ ਸਮਰੂਪ ਤ੍ਰਿਭੁਜ ਹਾਂ ਤਾਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਸਮਾਨੁਪਾਤੀ ਹੁੰਦੀਆਂ ਹਨ |]
PA × PB = PC × PD.

ਪ੍ਰਸ਼ਨ 9.
ਚਿੱਤਰ ਵਿੱਚ,ਤ੍ਰਿਭੁਜ ABC ਦੀ ਭੁਜਾ BC ‘ਤੇ ਇੱਕ ਬਿੰਦੂ D ਇਸ ਤਰ੍ਹਾਂ ਸਥਿਤ ਹੈ ਕਿ \(\frac{BD}{DC}\) = \(\frac{AB}{AC}\) ਹੈ । ਸਿੱਧ ਕਰੋ ਕਿ AD, ਕੋਣ ∠BAC ਦਾ ਸਮਦੋਭਾਜਕ ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △ABC, ਵਿਚ ਭੁਜਾ BC ਉੱਤੇ ਇੱਕ ਬਿੰਦੂ D ਇਸ ਪ੍ਰਕਾਰ ਸਥਿਤ ਹੈ ਕਿ \(\frac{BD}{DC}\) = \(\frac{AB}{AC}\)
ਸਿੱਧ ਕਰਨਾ AD ਕੋਣ ∠BAC ਦਾ ਸਮਦੋਭਾਜਕ ਹੈ ।
ਅਰਥਾਤ, ∠1 = ∠2
ਰਚਨਾ : C ਵਿੱਚ CE || DA ਖਿੱਚੋ ਜੋ BA ਨੂੰ E ਤੇ ਮਿਲੇ ।

ਸਬੂਤ : △BCE ਵਿੱਚ,
AD || CE …(ਚਨਾ)
ਸਮਾਨੁਪਾਤ ਪ੍ਰਮੇਯ ਤੋਂ,

△ACE ਵਿੱਚ,
AE = AC
⇒ ∠3 = ∠4 … (ਬਰਾਬਰ ਭੁਜਾਵਾਂ ਦੇ ਸਨਮੁੱਖ ਕੋਣ)
ਕਿਉਂਕਿ CE || DA ਅਤੇ AC ਉਨ੍ਹਾਂ ਨੂੰ ਕੱਟਦੀ ਹੈ ।
∠2 = ∠4 ..(ਇਕਾਂਤਰ ਕੋਣ)
ਨਾਲ ਹੀ CE || DA ਅਤੇ BAE ਉਨ੍ਹਾਂ ਨੂੰ ਕੱਟਦੀ ਹੈ ।
∠1 = ∠3 …(ਸੰਗਤ ਕੋਣ)
ਇਸ ਤਰ੍ਹਾਂ ਸਾਨੂੰ ਮਿਲਦਾ ਹੈ :
∠3 = ∠4
⇒ ∠4 = ∠1
∠3 = ∠1
ਪਰ ∠4 = ∠2
⇒ ∠1 = ∠2.
AD, ∠BAC ਨੂੰ ਸਮਦੁਭਾਜਿਤ ਕਰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 10.
ਨਾਜ਼ਿਮਾ ਇੱਕ ਨਦੀ ਦੇ ਧਾਰਾ ਵਿੱਚ ਮੱਛੀਆਂ ਪਕੜ ਰਹੀ ਹੈ । ਉਸ ਦੀ ਮੱਛੀਆਂ ਫੜਣ ਵਾਲੀ ਛੜ ਦਾ ਸਿਰਾ ਪਾਣੀ ਦੀ ਸਤਾ ਤੋਂ 1.8 mਉੱਪਰ ਹੈ ਅਤੇ ਡੋਰੀ ਦੇ ਹੇਠਲੇ ਸਿਰੇ ਤੇ ਲੱਗਿਆ ਕੁੰਡਾ, ਪਾਣੀ ਦੀ ਸਤ੍ਹਾ ‘ਤੇ ਇਸ ਤਰ੍ਹਾਂ ਸਥਿਤ ਹੈ ਕਿ ਉਸਦੀ ਨਾਜ਼ਿਮਾ ਤੋਂ ਦੂਰੀ 3.6 m ਹੈ ਅਤੇ ਛੜ ਦੇ ਸਿਰੇ ਦੇ ਠੀਕ ਹੇਠਾਂ ਪਾਣੀ ਦੀ ਸੜਾ’ ਤੇ ਸਥਿਤ ਬਿੰਦੂ ਤੋਂ ਉਸਦੀ ਦੂਰੀ | 2.4 m ਹੈ । ਇਹ ਮੰਨਦੇ ਹੋਏ ਕਿ ਉਸਦੀ ਡੋਰੀ (ਉਸ ਦੀ ਛੜ ਦੇ ਸਿਰੇ ਤੋਂ ਕੁੰਡੇ ਤੱਕ) ਤਣੀ ਹੋਈ ਹੈ, ਉਸਨੇ ਕਿੰਨੀ ਡੋਰੀ ਬਾਹਰ ਕੱਢੀ ਹੋਈ ਹੈ । (ਦੇਖੋ ਚਿੱਤਰ) ਜੇਕਰ ਉਹੀ ਡੋਰੀ ਨੂੰ 5 | cms ਦੀ ਦਰ ਨਾਲ ਅੰਦਰ ਖਿੱਚੇ ਤਾਂ 12 ਸੈਕਿੰਡਾਂ ਬਾਦ ਨਜ਼ਿਮਾ ਦੀ ਕੁੰਡੇ ਤੋਂ ਖਿਤਿਜ਼ੀ ਦੀ ਦੁਰੀ ਕਿੰਨੀ ਹੋਵੇਗੀ ।

ਹੱਲ:
ਸਮਕੋਣ ABC ਵਿੱਚ,
AB = 1.8 m,
BC = 2.4 m, ∠B = 90°
ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਤੋਂ,
AC² = AB² + BC²
AC² = (1.8)² + (2.4)²
AC² = 3.24 + 5.76 = 9
AC² = (3)²
AC = 3 m
ਹੁਣ ਨਾਜ਼ਿਮਾ ਡੋਰੀ ਨੂੰ 5 cm/s ਦੀ ਦਰ ਨਾਲ ਬਾਹਰ | ਖਿੱਚੇ, ਤਾਂ ਡੋਰੀ ਦੀ ਲੰਬਾਈ ਘੱਟ ਹੁੰਦੀ ਹੈ ।
= 5 × 12 m = 60 cm
= 0.6 m : 12 ਸੈਕਿੰਡ ਵਿੱਚ
ਮੰਨ ਲਉ, 12 ਸੈਕਿੰਡ ਬਾਦ ਕਾਂਟੇ ਦੀ ਸਥਿਤੀ D ਹੈ ।
∴ AD = AC – (12 ਸੈਕਿੰਡ ਵਿਚ ਤੈਅ ਕੀਤੀ ਦੂਰੀ)
= (3 – 0.6) m = 2.4 m
ਹੁਣ, ਸਮਕੋਣ ਤਿਭੁਜ △ABD ਵਿੱਚ ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਤੋਂ
AD² = AB² + BD²
(2.4)² = (1.8)² + BD²
BD² = 5.76 – 3.24
BD² = 2.52 m
BD = 1.587 m
∴ ਨਾਜ਼ਿਮਾ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ
= BD + 1.2 m
= (1.587 + 1.2) m
= 2.787 m
= 2.79 m
ਹੁਣ, ਡੋਰੀ ਦੀ ਲੰਬਾਈ ਅਤੇ ਨਾਜ਼ਿਮਾ ਦੁਆਰਾ ਤੈਅ | ਕੀਤੀ ਗਈ ਦੂਰੀ 3m ਅਤੇ 2.79 m

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 6 ਤ੍ਰਿਭੁਜ Ex 6.5 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 6 ਤ੍ਰਿਭੁਜ Exercise 6.5

1. ਕੁੱਝ ਤ੍ਰਿਭੁਜਾਂ ਦੀਆਂ ਭੁਜਾਵਾਂ ਹੇਠਾਂ ਦਿੱਤੀਆਂ ਗਈਆਂ ਹਨ । ਨਿਰਧਾਰਿਤ ਕਰੋ ਕਿ ਇਹਨਾਂ ਵਿੱਚੋਂ ਕਿਹੜੀ-ਕਿਹੜੀ | ਤਿਭੁਜ ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ ਹੈ । ਇਸ ਸਥਿਤੀ ਵਿੱਚ ਕਰਣ ਦੀ ਲੰਬਾਈ ਵੀ ਲਿਖੋ :

ਪ੍ਰਸ਼ਨ (i).
7 cm, 24 cm, 25 cm
ਉੱਤਰ:
ਮੰਨ ਲਉ △ABC ਵਿੱਚ,
AB = 7 cm
BC = 24 cm, AC = 25 cm
AB² + BC² = (7)² + (24)²
= 49 + 576 = 625
AC² = (25)² = 625
ਹੁਣ AB² + BC² = AC²
∴ △ABC ਇੱਕ ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ ਹੈ ।

ਪ੍ਰਸ਼ਨ (ii).
3 cm, 8 cm, 6 cm
ਉੱਤਰ:
ਮੰਨ ਲਉ △PQR ਵਿੱਚ,
PQ = 3 cm, QR = 8 cm
PR = 6 cm
PQ² + PR² = (3)² + (6)²
= 9 + 36 = 45
QR² = (8)² = 64
ਇੱਥੇ PQ² + PR² ≠ QR²
∴ △PQR ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ ਨਹੀਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ (iii).
50 cm, 80 cm, 100 cm
ਉੱਤਰ:
ਮੰਨ ਲਉ AMNP ਵਿੱਚ, MN = 50 cm,
NP = 80 cm, MP = 100 cm
MN² + NP² = (50)² + (80)²
= 2500 + 6400 = 8900
MP² = (100)² = 1000
ਇੱਥੇ, MP² ≠ MN² + NP²
∴ △MNP ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ ਨਹੀਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ (iv).
13 cm, 12 cm, 5 cm.
ਉੱਤਰ:
ਮੰਨ ਲਉ △ABC ਵਿੱਚ,
AB = 13 cm, BC = 12 cm, AC = 5 cm
BC² + AC² = (12)² + (5)²
= 144 + 25 = 169
AB² = (13)² = 169
AB² = BC² + AC²
∴ △ABC ਸਮਕੋਣ ਤਿਭੁਜ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
PQR ਇੱਕ ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸਦਾ ਕੋਣ ? ਸਮਕੋਣ ਹੈ ਅਤੇ OR ‘ਤੇ ਬਿੰਦੁ M ਇਸ ਤਰ੍ਹਾਂ ਸਥਿਤ ਹੈ। ਕਿ PM ⊥ QR ਹੈ । ਦਰਸਾਉ ਕਿ PM² = QM.MR ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਸਮਕੋਣ △PQR ਵਿੱਚ ਕੋਣ P ਸਮਕੋਣ ਹੈ । QR ‘ਤੇ ਬਿੰਦੂ M ਇਸ ਤਰ੍ਹਾਂ ਸਥਿਤ ਹੈ ਕਿ PM ⊥ QR ਹੈ । | ਵੋ
ਸਿੱਧ ਕਰਨਾ : PM² = QM × MR

ਸਬੂਤ : ∠P = 90° (ਦਿੱਤਾ ਹੈ।)
∴ ∠1 + ∠2 = 90° …(1)
∠M = 90°
△PMQ ਵਿਚ
∠1 + ∠3 + ∠5 = 180°
∠1 + ∠3 = 90° …(2)
[∠M = 90°]
(1) ਅਤੇ (2) ਤੋਂ
∠1 + ∠2 = ∠1 + ∠3
∠2 = ∠3
△QPM ਅਤੇ △RPM ਵਿੱਚ
∠3 = ∠2 (ਸਿੱਧ ਕੀਤਾ)
∠5 = ∠6 (ਹਰੇਕ 90)
∴ △QMP ~ △PMR [AA ਸਮਰੂਪਤਾ ਕਸੌਟੀ]
\(\frac{ar(△QMP)}{ar(△PMR)}\) = \(\frac{\mathrm{PM}^{2}}{\mathrm{MR}^{2}}\)
[ਜੇਕਰ ਦੋ ਤ੍ਰਿਭੁਜਾਂ ਸਮਰੂਪ ਹਨ ਤਾਂ ਉਨ੍ਹਾਂ ਦੇ ਖੇਤਰਫਲਾਂ ਦਾ ਅਨੁਪਾਤ ਉਨ੍ਹਾਂ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਦੇ ਵਰਗਾਂ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ ]

PM² = OM.RM

ਪ੍ਰਸ਼ਨ 3.
ਚਿੱਤਰ ਵਿਚ ABD ਇਕ ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ ਹੈ ਇਸਦਾ ਕੋਣ A ਸਮਕੋਣ ਹੈ ਅਤੇ AC ⊥ BD ਹੈ ।ਦਿਖਾਉ ਕਿ

(i) AB² = BC.BD
(ii) AC² = BC.DC
(iii) AD² = BD.CD.
ਹੱਲ:
△DAB ਅਤੇ △DCA ਵਿੱਚ,
∠D = ∠D (ਸਾਂਝਾ)
∠A = ∠C (ਹਰੇਕ 90°)
∴ △DAB ~ △DCA [AA ਸਮਰੂਪਤਾ]
△DAB ਅਤੇ △ACB ਵਿੱਚ, …(1)
∠B = ∠B (ਸਾਂਝਾ)
∠A =∠C (ਹਰੇਕ 90°)
∴ △DAB ~ △ACB …(2)
(1) ਅਤੇ (2) ਤੋਂ
△DAB ~ △ACB ~ △DCA.

(i) △ACB ~ △DAB (ਸਿੱਧ ਕੀਤਾ।)
∴ \(\frac{ar(△ACB)}{ar(△DAB)}\) = \(\frac{\mathrm{AB}^{2}}{\mathrm{DB}^{2}}\)
[ਜੇਕਰ ਦੋ ਭੁਜਾਂ ਸਮਰੂਪ ਹਨ ਤਾਂ ਉਨ੍ਹਾਂ ਦੇ ਖੇਤਰਫਲਾਂ ਦਾ ਆਨੁਪਾਤ ਉਨ੍ਹਾਂ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਦੇ ਵਰਗਾਂ ਦੇ ਅਨੁਪਾਤ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ।]

AB² = BC × BD.

(ii) △ACB ~ △DCA (ਸਿੱਧ ਕੀਤਾ)
\(\frac{ar(△ACB)}{ar(△DCA)}\) = \(\frac{A C^{2}}{D C^{2}}\)
[ਜੇਕਰ ਦੋ ਤ੍ਰਿਭੁਜਾਂ ਸਮਰੂਪ ਹਨ ਤਾਂ ਉਨ੍ਹਾਂ ਦੇ ਖੇਤਰਫਲਾਂ ਦਾ ਅਨੁਪਾਤ ਸੰਗਤ ਭੁਜਾਵਾਂ ਦੇ ਅਨੁਪਾਤ ਦੇ | ਵਰਗਾਂ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ।]

AC² = BC × DC

(iii) △DAB ~ △DCA (ਸਿੱਧ ਕੀਤਾ)
\(\frac{ar(△DAB)}{ar(△DCA)}\) = \(\frac{\mathrm{DA}^{2}}{\mathrm{DB}^{2}}\)
[ਜੇਕਰ ਦੋ ਤ੍ਰਿਭੁਜਾਂ ਸਮਰੂਪ ਹਨ ਤਾਂ ਉਨ੍ਹਾਂ ਦੇ ਖੇਤਰਫਲਾਂ ਦਾ ਅਨੁਪਾਤ ਸੰਗਤ ਭੁਜਾਵਾਂ ਦੇ ਅਨੁਪਾਤ ਦੇ ਵਰਗਾਂ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ।]

ਪ੍ਰਸ਼ਨ 4.
ABC ਇੱਕ ਸਮਦੋਭੁਜੀ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸ ਦਾ ਕੋਣ ? | ਸਮਕੋਣ ਹੈ । ਸਿੱਧ ਕਰੋ ਕਿ AB² = 2AC² ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △ABC ਇਕ ਸਮਦੋਭੁਜੀ ਤਿਭੁਜ ਹੈ ਜਿਸਦਾ ਕੋਣ C ਸਮਕੋਣ ਹੈ ।
ਸਿੱਧ ਕਰਨਾ : AB² = AC²

ਸਬੂਤ : △ACB ਵਿੱਚ, ∠C = 90°
AC = BC (ਦਿੱਤਾ ਹੈ।)
AB² = AC² + BC²
[ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਤੋਂ]
= AC² + AC² [BC = AC]
ਇਸ ਲਈ AB² = 2AC²

ਪ੍ਰਸ਼ਨ 5.
ABC ਇੱਕ ਸਮਦੋਭੁਜੀ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸ ਵਿਚ | AC = BC ਹੈ । ਜੇਕਰ AB² = 2AC² ਹੈ ਤਾਂ ਸਿੱਧ ਕਰੋ ਕਿ ABC ਇੱਕ ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △ABC ਇਕ ਸਮਦੋਭੁਜੀ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸ ਵਿੱਚ AC = BC ਹੈ ।
AB² = 2AC²
ਸਿੱਧ ਕਰਨਾ : △ABC ਇਕ ਸਮਕੋਣ ਤਿਭੁਜ ਹੈ ।

ਸਬੂਤ : AB² = 2AC² ਦਿੱਤਾ ਹੈ।)
AB² = AC² + AC²
AB² = AC² + BC² [AC = BC]
∴ ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਦੇ ਉਲਟ ਤੋਂ △ABC ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ ਹੈ ।

ਪ੍ਰਸ਼ਨ 6.
ਇੱਕ ਸਮਭੁਜੀ ਤ੍ਰਿਭੁਜ ABC ਦੀ ਭੁਜਾ 2a ਹੈ । ਇਸਦੇ ਹਰੇਕ ਸਿਖਰ ਲੰਬ ਦੀ ਲੰਬਾਈ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
△ABC ਸਮਭੁਜੀ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸਦੀ ਭੁਜਾ 2a ਹੈ ।
AD ⊥ BC
AB = AC= BC = 2a
△ADB ≅ △ADC [RHS ਸਰਬੰਰਾਮਮ ਤੋਂ]
∴ BD = DC = a

ਸਮਕੋਣ △ADB ਤੋਂ,
AB² = AD² + BD²
(2a)² = AD² + (a)²
4a² – a² = AD²
AD² = 3a²
AD = \(\sqrt {3}\) a.

ਪ੍ਰਸ਼ਨ 7.
ਸਿੱਧ ਕਰੋ ਕਿ ਇੱਕ ਸਮਚਤੁਰਭੁਜ ਦੀਆਂ ਭੁਜਾਵਾਂ ਦੇ ਵਰਗਾਂ ਦਾ ਜੋੜ ਉਸਦੇ ਵਿਕਰਣਾਂ ਦੇ ਵਰਗਾਂ ਦੇ ਜੋੜ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ : ਸਮਚਤੁਰਭੁਜ ABCD ਦੇ ਵਿਕਰਣ AC ਅਤੇ BD ਇਕ-ਦੂਜੇ ਨੂੰ O ਉੱਤੇ ਕੱਟਦੇ ਹਨ !
ਸਿੱਧ ਕਰਨਾ :
AB² + BC² + CD² + AD = AC² + BD²
ਸਬੂਤ : ∵ ਸਮਚਤੁਰਭੁਜ ਦੇ ਵਿਕਰਣ ਆਪਸ ਵਿਚ ਸਮਕੋਣ ਉੱਤੇ ਸਮਦੁਭਾਜਿਤ ਹੁੰਦੇ ਹਨ ।

∴ AO = CO, BO = DO
∴ O ਉੱਤੇ ਕੋਣ ਸਮਕੋਣ ਹੈ।
△AOB ਵਿੱਚ, ∠AOB = 90°
∴ AB² = AO² + BO² …(1)
[ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਯ ਤੋਂ]
ਇਸ ਤਰ੍ਹਾਂ, BC² = CO² + B0² ….(2)
CD² = CO² + DO² …(3)
ਅਤੇ DA² = DO² + AO² …(4)
(1), (2), (3) ਅਤੇ (4) ਨੂੰ ਜੋੜਨ ਤੇ
AB² + BC² + CD² + DA²
= 2AO² + 2CO² + 2BO² + 2DO²
= 4AO² + 4BO²
[∵ AO = CO ਅਤੇ BO = DO]
= (2AO)² + (2BO)² = AC² + BD².

ਪ੍ਰਸ਼ਨ 8.
ਚਿੱਤਰ ਵਿੱਚ, △ABC ਦੇ ਵਿੱਚ ਸਥਿਤ ਕੋਈ ਬਿੰਦੂ 0 ਹੈ ਅਤੇ AD ⊥ BC, OE ⊥ AC ਅਤੇ OF ⊥ AB ਹੈ । ਦਿਖਾਉ ਕਿ
(i) OA² + OB² + OC²– OD² – OE² – OF²
= AF² + BD² + CE²
(ii) AF² + BD² + CE²
= AE² + CD² + BF².

ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △ABC ਜਿਸ ਵਿਚ
OD ⊥ BC, OE ⊥ AC ਅਤੇ OF ⊥ AB ਹੈ ।
ਸਿੱਧ ਕਰਨਾ :
(i) AF² + BD² + CE²
= OA² + OB² + OC² – OD² – OE² – OF²

(ii) AF² + BD² + CE²
= AE² + CD² + BF².
ਰਚਨਾ : OB, OC ਅਤੇ OA ਨੂੰ ਮਿਲਾਉ
ਸਬੂਤ (i) ਸਮਕੋਣ △AFO ਵਿੱਚ,
OA² = OF² + AF² [ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਤੋਂ]
ਜਾਂ AF² = OA² – OF² ….(1)
ਸਮਕੋਣ △BDO ਵਿੱਚ,
OB² = BD² + OD²
[ਪਾਈਥਾਗੋਰਸ ਮੇਯ ਤੋਂ]
⇒ BD² = OB² – OD² …(2)
ਸਮਕੋਣ △CEO ਵਿੱਚ,
OC² = CE² + OE² [ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਤੋਂ।]
⇒ CE² = OC² – OE² …(3)
∴ AF² + BD² + CE² = OA² – OF² + OB² – OD² + OC² – OE²
[(1), (2), ਅਤੇ (3) ਨੂੰ ਜੋੜਨ ਤੇ]
= OA² + OB² + OC² – OD² – OE² – OF²
ਜੋਕਿ (1) ਨੂੰ ਸਿੱਧ ਕਰਦਾ ਹੈ ।
ਦੁਬਾਰਾ AF² + BD² + CE²
= (OA² – OE²) + (OC² – OD²) + (OB² – OF²)
= AE² + CD² + BE²
: AE² = AO² – OE²
CD² = OC² – OD²
BF² = OB² – OF²

ਪ੍ਰਸ਼ਨ 9.
10 m ਲੰਬੀ ਇੱਕ ਪੌੜੀ ਇਕ ਕੰਧ ਨਾਲ ਲਗਾਉਣ ‘ਤੇ ਜ਼ਮੀਨ ਨਾਲੋਂ 8 m ਦੀ ਉੱਚਾਈ ‘ਤੇ ਸਥਿਤ ਇੱਕ ਖਿੜਕੀ ਤੱਕ ਪਹੁੰਚਦੀ ਹੈ । ਕੰਧ ਦੇ ਅਧਾਰ ਤੋਂ ਪੌੜੀ ਦੇ ਹੇਠਲੇ ਸਿਰੇ ਦੀ ਦੂਰੀ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਖਿੜਕੀ ਦੀ ਧਰਤੀ ਤੋਂ ਉਚਾਈ (AB) = 8 m

ਪੌੜੀ ਦੀ ਲੰਬਾਈ (AC) = 10 m
ਪੌੜੀ ਦੇ ਹੇਠਲੇ ਸਿਰੇ ਅਤੇ ਕੰਧ ਦੇ ਅਧਾਰ ਵਿਚਲੀ ਦੂਰੀ (BC) = ?
△ABC ਵਿੱਚ,
AB² + BC² = AC² [ਪਾਈਥਾਗੋਰਸ ਮੇਯ ਤੋਂ]
(8)² + (BC)² = (10)²
64 + BC² = 100
BC² = 100 – 64
BC = \(\sqrt {36}\)
BC = 6 m.
∴ ਪੌੜੀ ਦੇ ਹੇਠਲੇ ਸਿਰੇ ਅਤੇ ਕੰਧ ਦੇ ਅਧਾਰ ਵਿਚਲੀ | ਦੂਰੀ = 6 m.

ਪ੍ਰਸ਼ਨ 10.
18 m ਉੱਚੇ ਇਕ ਸਿੱਧੇ ਖੜੇ ਖੰਭੇ ਦੇ ਉੱਪਰਲੇ ਸਿਰੇ | ਨਾਲ ਤਾਰ ਦਾ ਇੱਕ ਸਿਰਾ ਜੁੜਿਆ ਹੋਇਆ ਹੈ ਅਤੇ ਤਾਰ ਦਾ | ਦੂਸਰਾ ਸਿਰਾ ਇਕ ਕਿੱਲੇ ਨਾਲ ਜੁੜਿਆ ਹੋਇਆ ਹੈ । ਖੰਬੇ ਦੇ | ਅਧਾਰ ਤੋਂ ਕਿੱਲੇ ਨੂੰ ਕਿੰਨੀ ਦੂਰੀ ‘ਤੇ ਗੱਡਿਆ ਜਾਵੇ ਕਿ ਤਾਰ ਤਣੀ ਰਹੇ ਜਦੋਂ ਕਿ ਤਾਰ ਦੀ ਲੰਬਾਈ 24 m ਹੈ ।
ਹੱਲ:
ਮੰਨ ਲਉ ਖੰਬੇ ਦੀ ਉਚਾਈ AB = 18 m
ਤਾਰ ਦੀ ਲੰਬਾਈ Ac = 24 m

C, ਤੇ ਕਿੱਲਾ ਗੱਡਿਆ ਹੋਇਆ ਹੈ । ਖੰਬੇ ਤੋਂ ਦੂਰੀ BC = ਹੈ ।
ਸਮਕੋਣ △ABC,
AB² + BC² = AC²
[ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਤੋਂ।]
(18)² + (BC)² = (24)²
324 + (BC)² = 576
BC² = 576 – 324
BC = \(\sqrt {252}\) = 6\(\sqrt {7}\)
BC = 6\(\sqrt {7}\) m

ਪ੍ਰਸ਼ਨ 11.
ਇੱਕ ਹਵਾਈ ਜਹਾਜ਼ ਇੱਕ ਹਵਾਈ ਅੱਡੇ ਤੋਂ ਉੱਤਰ ਵੱਲ 1000 km/h ਦੀ ਚਾਲ ਨਾਲ ਉੱਡਦਾ ਹੈ । ਉਸੇ ਸਮੇਂ ਇੱਕ ਹੋਰ ਹਵਾਈ ਜਹਾਜ਼ ਉਸੇ ਹਵਾਈ ਅੱਡੇ ਤੋਂ ਪੱਛਮ ਵੱਲ 1200 km/h ਦੀ ਚਾਲ ਨਾਲ ਉੱਡਦਾ ਹੈ । 1\(\frac{1}{2}\) ਘੰਟੇ ਬਾਦ ਦੋਵਾਂ ਹਵਾਈ ਜਹਾਜ਼ਾਂ ਦੀ ਵਿਚਕਾਰਲੀ ਦੂਰੀ ਕਿੰਨੀ ਹੋਵੇਗੀ ।
ਹੱਲ:
ਪਹਿਲੇ ਹਵਾਈ ਜਹਾਜ਼ ਦੀ ਚਾਲ = 1000 km/h

ਪਹਿਲੇ ਹਵਾਈ ਜਹਾਜ਼ ਦੁਆਰਾ ਉੱਤਰ ਵੱਲ 1\(\frac{1}{2}\) ਘੰਟੇ ਵਿਚ ਤੈਅ ਕੀਤੀ ਦੂਰੀ = 1000 × \(\frac{3}{2}\)
OA = 1500 km
ਦੂਸਰੇ ਹਵਾਈ ਜਹਾਜ ਦੀ ਚਾਲ = 1200 km/h
ਦੂਸਰੇ ਹਵਾਈ ਜਹਾਜ ਦੁਆਰਾ 1\(\frac{1}{2}\) ਘੰਟੇ ਵਿਚ ਤੈਅ ਕੀਤੀ ਦੂਰੀ
=1200 × \(\frac{3}{2}\) km
OB = 1800 km
ਸਮਕੋਣ △AOB ਵਿੱਚ, .
AB² = AO² + OB²
AB² = (1500)² + (1800)²
AB = \(\sqrt {2250000+3240000}\)
= \(\sqrt {5490000}\)
AB = 300\(\sqrt {61}\) km
∴ ਦੋਹਾਂ ਹਵਾਈ ਜਹਾਜ਼ਾਂ ਵਿਚਲੀ ਦੂਰੀ
= 300\(\sqrt {61}\) km

ਪ੍ਰਸ਼ਨ 12.
ਦੋ ਖੰਭੇ ਜਿਨ੍ਹਾਂ ਦੀਆਂ ਉੱਚਾਈਆਂ ਭੂਮੀ ‘ਤੇ 6 m ਅਤੇ 11 m ਹਨ ਅਤੇ ਸਮਤਲ ਭੂਮੀ ‘ਤੇ ਖੜ੍ਹੇ ਹਨ । ਜੇਕਰ ਉਹਨਾਂ ਦੇ ਹੇਠਲੇ ਸਿਰਿਆਂ ਦੇ ਵਿਚਕਾਰਲੀ ਦੂਰੀ 12m ਹੋਵੇ ਤਾਂ ਉਹਨਾਂ ਦੇ ਉੱਪਰਲੇ ਸਿਰਿਆਂ ਦੇ ਵਿਚਕਾਰਲੀ ਦੂਰੀ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਖੰਭੇ ਦੀ ਉੱਚਾਈ (AB) = 11m
ਖੰਭੇ ਦੀ ਉੱਚਾਈ (CD) = 6 m

ਖੰਭੇ ਦੇ ਅਧਾਰਾਂ ਦੇ ਵਿਚਕਾਰਲੀ ਦੂਰੀ = 12 m
C ਤੋਂ CE ⊥ AB ਖਿੱਚੋ
BE = DC = 6m
AE = AB – BE
= (11 – 6) m = 5 m
ਸਮਕੋਣ △AEC ਵਿੱਚ,
AC² = AE² + EC²
AC = \(\sqrt{(5)^{2}+(12)^{2}}\)
= \(\sqrt {25+144}\)
= \(\sqrt {169}\) = 13.
∴ ਖੰਭੇ ਦੇ ਉੱਪਰਲੇ ਸਿਰਿਆਂ ਵਿਚਕਾਰਲੀ ਦੂਰੀ = 13m.

ਪ੍ਰਸ਼ਨ 13.
ਇੱਕ ਤ੍ਰਿਭੁਜ ABC ਜਿਸਦਾ ਕੋਣ C ਸਮਕੋਣ ਹੈ, ਦੀਆਂ ਭੁਜਾਵਾਂ CA ਅਤੇ CB ‘ਤੇ ਕੁਮਵਾਰ ਬਿੰਦੂ D ਅਤੇ L ਸਥਿਤ ਹਨ । ਸਿੱਧ ਕਰੋ ਕਿ
AE² + BD² = AB² + DE²
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △ABC ਇੱਕ ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸ ਵਿਚ C ਸਮਕੋਣ ਹੈ ਭੁਜਾ CA ਅਤੇ CB ਤੇ ਕ੍ਰਮਵਾਰ ਬਿੰਦੂ D ਅਤੇ E ਸਥਿਤ ਹਨ ।
∴ CD = AD = \(\frac{1}{2}\)AC
BE = EC = \(\frac{1}{2}\)BC
ਸਿੱਧ ਕਰਨਾ :
AE² + BD² = AB² + DE²
ਸਬੂਤ : ਸਮਕੋਣ △BCA ਵਿੱਚ,
AB² = BC² + CA² …..(1) [
ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਤੋਂ]

ਸਮਕੋਣ △ECD ਵਿੱਚ,
DE² = EC² + DC² …(2)
[ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ]
ਸਮਕੋਣ △ACE ਵਿੱਚ
AE² = AC² + CE² …(3)
ਸਮਕੋਣ △BCD ਵਿੱਚ
BD² = BC² + CD² …(4)
(3) ਅਤੇ (4) ਨੂੰ ਜੋੜਣ ਤੇ,
AE² + BD² = AC² + CE² + BC² + CD²
= [AC² + CB²] + [CE² + DC²]
= AB² + DE²
[(3) ਅਤੇ (4) ਤੋਂ]
ਇਸ ਲਈ AE² + BD² = AB² + DE².

ਪ੍ਰਸ਼ਨ 14.
ਕਿਸੇ ਤ੍ਰਿਭੁਜ ABC ਦੇ ਸਿਖ਼ਰ A ਤੋਂ BC ‘ਤੇ ਸੁੱਟਿਆ ਗਿਆ ਲੰਬ BC ਨੂੰ ਬਿੰਦੂ ‘ਤੇ ਇਸ ਤਰ੍ਹਾਂ ਕੱਟਦਾ ਹੈ ਕਿ DB = 3 CD ਹੈ (ਦੇਖੋ ਚਿੱਤਰ) ।
ਸਿੱਧ ਕਰੋ ਕਿ 2AB² = 2AC² + BC² ਹੈ ।

ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △ABC ਵਿੱਚ, AD ⊥ BC
DB = 3CD ਹੈ ।
ਸਿੱਧ ਕਰਨਾ :
2AB² = 2AC² + BC².
ਸਬੂਤ : ਸਮਕੋਣ ਭੁਜ ADB ਅਤੇ ADC ਵਿੱਚ
AB² = AD² + BD² ;
AC² = AD² + DC²
[ਪਾਈਥਾਗੋਰਸ ਮੇਯ ਤੋਂ ]
∴ AB² – AC² = BD² – DC²
= 9CD² – CD²;
[∵ BD = 3CD]
= 8CD² = 8\(\left(\frac{\mathrm{BC}}{4}\right)^{2}\)
[∵ BC = DB + CD
=3CD + CD
= 4CD
∴ CD = \(\frac{1}{2}\)BC]
∴ AB² – AC² = \(\frac{\mathrm{BC}^{2}}{2}\)
⇒ 2(AB² – AC²) = BC²
⇒ 2AB² – 2AC² = BC²
∴ AB² = 2AC² + BC².

ਪ੍ਰਸ਼ਨ 15.
ਕਿਸੇ ਸਮਭੁਜੀ ਤ੍ਰਿਭੁਜ ABC ਦੀ ਭੁਜਾ BC ‘ਤੇ ਇੱਕ ਬਿੰਦੂ ) ਇਸ ਤਰ੍ਹਾਂ ਸਥਿਤ ਹੈ ਕਿ BD = \(\frac{1}{3}\)BC ਹੈ । ਸਿੱਧ ਕਰੇ ਕਿ 9AD² = 7AB² ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਸਮਭੁਜੀ ਤ੍ਰਿਭੁਜ ABC ਦੀ ਭੁਜਾ BC ‘ਤੇ ਇਕ ਬਿੰਦੂ ) ਇਸ ਤਰ੍ਹਾਂ ਸਥਿਤ ਹੈ ਕਿ BD = \(\frac{1}{3}\)BC ਹੈ ।
ਸਿੱਧ ਕਰਨਾ : 9AD² = 7AB².

ਰਚਨਾ : AM ⊥ BC ਖਿੱਚੋ
ਸਬੂਤ : △AMB ≅ △AMC [R.H.S. ਨਿਯਮ ਨਾਲ AM = AM ਅਤੇ AB = AC]
∴ BM = MC = \(\frac{1}{2}\)BC
ਦੁਬਾਰਾ BD = \(\frac{1}{3}\)BC
ਅਤੇ DC = \(\frac{2}{3}\)BC
(∵ BC, D ਤੇ ਤਿੰਨ ਭਾਗਾਂ ਵਿਚ ਵਿਭਾਜਿਤ ਕਰਦਾ ਹੈ ॥)
ਹੁਣ △ADC ਵਿੱਚ, ∠C ਨਿਊਣ ਕੋਣ ਹੈ
∴ AD² = AC² + DC² – 2DC × MC

∴ AD² = AB²
⇒ 9AD² = 7AB².

ਪ੍ਰਸ਼ਨ 16.
ਕਿਸੇ ਸਮਭੁਜੀ ਤ੍ਰਿਭੁਜ ਵਿੱਚ, ਸਿੱਧ ਕਰੋ ਕਿ ਉਸਦੀ ਇਕ ਭੁਜਾ ਦੇ ਵਰਗ ਦਾ ਤਿਗੁਣਾ ਤਿੰਨ ਗੁਣਾ) ਉਸ ਦੇ ਇਕ ਸਿਖਰ ਲੰਬ ਦੇ ਵਰਗ ਦੇ ਚਾਰ ਗੁਣਾ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △ABC ਇੱਕ ਸਮਭੁਜੀ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸ ਵਿੱਚ AB = BC = AC

AD ⊥ DC
ਸਿੱਧ ਕਰਨਾ : 3AB² = 4AD²
ਸਬੂਤ : △ABC ਸੈਂ,
ਮੰਨ ਲਉ : AB = BC = AC = 2a
AD ⊥ BC
∴ BD = DC = \(\frac{1}{2}\)BC = a
ਸਮਕੋਣ ਤਿਭੁਜ ਵਿਚ,
AB² = AD² + BD²
(2a)² = AD² + (a)²
4a² = AD² + a²
4a² – a² = AD²
AD² = 3a²
= 3\(\left[\frac{\mathrm{AB}}{2}\right]^{2}\)
[AB = 2a
a = \(\frac{\mathrm{AB}}{2}\)]
AD² = 3\(\frac{\mathrm{AB}^{2}}{4}\)
3AB² = 4AD².

ਪ੍ਰਸ਼ਨ 17.
ਸਹੀ ਉੱਤਰ ਚੁਣ ਕੇ ਉਸਦਾ ਕਾਰਣ ਦੱਸੋ : △ABC ਵਿੱਚ AB = 6\(\sqrt {3}\) cm, AC = 12 cm ਅਤੇ BC = 6 cm ਹੈ । ਕੋਣ B ਹੈ :
(A) 120°
(B) 60°
(C) 90°
(D) 45°
ਹੱਲ:
AC = 12 cm
AB= 6\(\sqrt {3}\) cm
BC = 6 cm
AC² = (12)² = 144
AB² + BC² = (6\(\sqrt {3}\))² + (6)²
= 108 + 36
AB² + BC² = 144
∴ AB² + BC² = AC²
ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਤੋਂ,
△ABC ਵਿੱਚ B ਸਮਕੋਣ ਹੈ ।
∴ ∠B = 90°
∴ ਵਿਕਲਪ (C) ਸਹੀ ਹੈ ।

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 6 ਤ੍ਰਿਭੁਜ Ex 6.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 6 ਤ੍ਰਿਭੁਜ Exercise 6.4

ਪ੍ਰਸ਼ਨ 1.
ਮੰਨ ਲਉ △ABC ~ △DEF ਹੈ ਅਤੇ ਇਨ੍ਹਾਂ ਦੇ ਖੇਤਰਫਲ ਕੁਮਵਾਰ 64 cm² ਅਤੇ 121 cm² ਜੇਕਰ EF = 15.4 cm ਹੋਵੇ ਤਾਂ BC ਪਤਾ ਕਰੋ ।
ਹੱਲ:
△ABC ~ △DEF, △ABC ਦਾ ਖੇਤਰਫਲ = 64 cm² ਅਤੇ △DEF ਦਾ ਖੇਤਰਫਲ = 121 cm² ਅਤੇ EF = 15.4 cm ਹੈ ।

△ABC ~ △DEF
∴ \(\frac{ar(△ABC)}{ar(△DEF}\) = \(\left(\frac{\mathrm{AB}^{2}}{\mathrm{DE}^{2}}\right)\) = \(\left(\frac{\mathrm{AC}^{2}}{\mathrm{DF}^{2}}\right)\) = \(\left(\frac{\mathrm{BC}^{2}}{\mathrm{EF}^{2}}\right)\)
[ਜੇਕਰ ਦੋ ਤ੍ਰਿਭੁਜਾਂ ਸਮਰੂਪ ਹੋਣ ਤਾਂ ਉਨ੍ਹਾਂ ਦੇ ਖੇਤਰਫਲ ਦਾ ਅਨੁਪਾਤ ਸੰਗਤ ਭੁਜਾਵਾਂ ਦੇ ਅਨੁਪਾਤ ਦੇ ਵਰਗ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ।]

BC = 8 × 14
BC = 11.2 cm.

ਪ੍ਰਸ਼ਨ 2.
ਇੱਕ ਸਮਲੰਬ ਚਤੁਰਭੁਜ ABCD ਜਿਸ ਵਿੱਚ AB || DC ਹੈ, ਦੇ ਵਿਕਰਣ ਆਪਸ ਵਿੱਚ ਬਿੰਦੁ 0 ਉੱਤੇ ਕੱਟਦੇ ਹਨ । ਜੇਕਰ AB = 2 CD ਹੋਵੇ ਤਾਂ ਤ੍ਰਿਭੁਜਾਂ AOB ਅਤੇ COD ਦੇ ਖੇਤਰਫਲਾਂ ਦਾ ਅਨੁਪਾਤ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ABCD ਇਕ ਸਮਲੰਬ ਚਤੁਰਭੁਜ ਹੈ ਜਿਸ ਵਿੱਚ AB || DC ਹੈ, ਦੇ ਵਿਕਰਣ AC ਅਤੇ BD ਆਪਸ ਵਿੱਚ O ਬਿੰਦੂ ਉੱਤੇ ਕੱਟਦੇ ਹਨ ਅਤੇ AB = 2 CD ਹੈ ।

△AOB ਅਤੇ △COD ਵਿੱਚ,
∠1 = ∠2 (ਇਕਾਂਤਰ ਕੋਣ)
∠3 = ∠4 (ਇਕਾਂਤਰ ਕੋਣ)
∠5 = ∠6 (ਸਿਖ਼ਰ ਸਨਮੁੱਖ ਕੋਣ)
∴ △AOB ~ △COD
∴ \(\frac{ar(△AOB)}{ar(△COD}\) = \(\left(\frac{\mathrm{AB}^{2}}{\mathrm{CD}^{2}}\right)\)

[ਜੇਕਰ ਦੋ ਤ੍ਰਿਭੁਜਾਂ ਸਮਰੂਪ ਹੋਣ, ਤਾਂ ਉਨ੍ਹਾਂ ਦੇ ਖੇਤਰਫਲਾਂ ਦਾ ਅਨੁਪਾਤ ਉਨ੍ਹਾਂ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਦੇ ਅਨੁਪਾਤ ਦੇ ਵਰਗ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ]
= \(\left(\frac{2 \mathrm{CD}}{\mathrm{CD}}\right)^{2}\) (∵ AB = 2CD)
\(\frac{ar(△AOB)}{ar(△COD}\) = \(\frac{4 \mathrm{CD}^{2}}{\mathrm{CD}^{2}}\) = \(\frac{4}{1}\)
∵ ਲੋੜੀਂਦਾ ar △AOB ਅਤੇ ar △COD ਦਾ ਅਨੁਪਾਤ = 4 : 1

ਪ੍ਰਸ਼ਨ 3.
ਚਿੱਤਰ ਵਿੱਚ ਇੱਕੋ ਆਧਾਰ BC ਉੱਤੇ ਦੋ ਤਿਭੁਜ ABC ਅਤੇ DBC ਬਣੇ ਹੋਏ ਹਨ । ਜੇਕਰ AD, BC ਨੂੰ O’ ਤੇ ਕੱਟੇ ਤਾਂ ਦਰਸਾਉ ਕਿ
\(\frac{ar(△ABC)}{ar(△DBC}\) = \(\frac{\mathrm{AO}}{\mathrm{DO}}\) ਹੈ।

ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △ABC ਅਤੇ △DBC ਇਕ ਹੀ ਆਧਾਰ BC ਉੱਤੇ ਬਣੇ ਹੋਏ ਹਨ ਅਤੇ AD, BC ਨੂੰ O ਉੱਤੇ ਕੱਟਦੀ ਹੈ !

ਸਿੱਧ ਕਰੋ : \(\frac{ar(△ABC)}{ar(△DBC}\) = \(\frac{\mathrm{AO}}{\mathrm{DO}}\)
ਰਚਨਾ : AL ⊥ BC, DM ⊥ BC ਖਿੱਚੋ ।
ਸਬੂਤ : △ALO ਅਤੇ △DMO ਵਿੱਚ,
∠1 = ∠2 (ਸਿਖ਼ਰ ਸਨਮੁਖ ਕੋਣ)
∠L = ∠M (ਹਰੇਕ 90°)
∴ △ALO ~ △DMO [AA ਸਮਰੂਪਤਾ ਕਸੌਟੀ]
∴ \(\frac{\mathrm{AL}}{\mathrm{DM}}\) = \(\frac{\mathrm{AO}}{\mathrm{DO}}\) …(1)
[ਜੇਕਰ ਦੋ ਤਿਭੁਜਾਂ ਸਮਰੂਪ ਹੋਣ, ਤਾਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਸਮਾਨ ਅਨੁਪਾਤੀ ਹੁੰਦੀਆਂ ਹਨ]

ਪ੍ਰਸ਼ਨ 4.
ਜੇਕਰ ਦੋ ਸਮਰੂਪ ਤ੍ਰਿਭੁਜਾਂ ਦੇ ਖੇਤਰਫਲ ਬਰਾਬਰ ਹੋਣ ਤਾਂ ਸਿੱਧ ਕਰੋ ਕਿ ਉਹ ਤ੍ਰਿਭੁਜ ਸਰਬੰਗਸਮ ਹੁੰਦੇ ਹਨ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਦੋ ਤਿਭੁਜਾਂ △ABC ਅਤੇ △DEF ਦੇ ਸਮਰੂਪ ਹਨ ਅਤੇ ਖੇਤਰਫਲ ਬਰਾਬਰ ਹਨ ।
ਸਿੱਧ ਕਰਨਾ : △ABC ~ △DEF

ਸਬੂਤ : ਕਿਉਂਕਿ △ABC ~ △DEF,
∴ \(\frac{ar(△ABC)}{ar(△DEF}\) = \(\left(\frac{\mathrm{BC}^{2}}{\mathrm{EF}^{2}}\right)\)
⇒ \(\left(\frac{\mathrm{BC}^{2}}{\mathrm{EF}^{2}}\right)\) = 1
[∵ ar (△ABC) = ar (△DEF)
⇒ (BC)² = (EF)²
⇒ BC = EF
ਨਾਲ ਹੀ, ਕਿਉਂਕਿ △ABC ~ △DEF, ਇਸ ਲਈ ਉਹ ਸਮਕੋਣੀ ਹਨ ।
ਅਤੇ ∠B = ∠E
ਅਤੇ ∠C = ∠F
ਹੁਣ ਤ੍ਰਿਭੁਜਾਂ △ABC ਅਤੇ △DEF ਵਿੱਚ,
∠B = ∠E, ∠C = ∠F
ਅਤੇ BC = EF
∴ △ABC ≅ △DEF (ASA ਸਰਬੰਗਸਮ ਪਰਿਮੇਯ)

ਪ੍ਰਸ਼ਨ 5.
ਇੱਕ ਤ੍ਰਿਭੁਜ ABC ਦੀਆਂ ਭੁਜਾਵਾਂ AB, BC ਅਤੇ CA ਦੇ ਮੱਧ ਬਿੰਦੂ ਕੁਮਵਾਰ D, E ਅਤੇ F ਹਨ △DEF ਅਤੇ △ABC ਦੇ ਖੇਤਰਫਲਾਂ ਦਾ ਅਨੁਪਾਤ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਇੱਕ △ABC ਦੀਆਂ ਭੁਜਾਵਾਂ AB, BC ਅਤੇ CA ਦੇ ਮੱਧ ਬਿੰਦੂ ਕੁਮਵਾਰ D, E ਅਤੇ F ਹਨ ।

ਸਿੱਧ ਕਰਨਾ : ਖੇਤਰਫਲ (△DEF) : ਖੇਤਰਫਲ (△ABC) ਪਤਾ ਕਰਨਾ ।
ਸਬੂਤ : △ABC ਵਿਚ,
F, AB ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ । …(ਦਿੱਤਾ ਹੈ।)
E, AC ਦਾ ਮੱਧ ਬਿੰਦੁ ਹੈ । …(ਦਿੱਤਾ ਹੈ।)
ਇਸ ਲਈ ਮੱਧ ਬਿੰਦੂ ਪ੍ਰਮੇਯ ਤੋਂ,
FE || BC ਅਤੇ FE = \(\frac{1}{2}\)BC
⇒ FE || BD
ਅਤੇ FE = BD [∵ BD = \(\frac{1}{2}\)BC]
∴ BDEF ਇਕ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਹੈ ।
(∵ ਸਨਮੁੱਖ ਭੁਜਾਵਾਂ ਸਮਾਂਤਰ ਅਤੇ ਸਮਾਨ ਹਨ)
△FBD ਅਤੇ △DEF ਵਿੱਚ,
FB = DE
…(|| gm BDEF ਦੀਆਂ ਸਨਮੁੱਖ ਭੁਜਾਵਾਂ)
FD = FD (ਇਕੋ ਜਿਹੇ।
…(|| gm BDEF ਦੀਆਂ ਸਨਮੁੱਖ ਭੁਜਾਵਾਂ)
BD = FE
∴ △FBD ≅ △DEF
… (SSS ਸਰਬੰਗਸਮ ਪ੍ਰਯੋਗ)
ਇਸ ਤਰ੍ਹਾਂ ਅਸੀਂ ਸਿੱਧ ਕਰ ਸਕਦੇ ਹਾਂ ।
△AFE ≅ △DEF
ਅਤੇ △EDC ≅ △DEF
ਜੇਕਰ ਤ੍ਰਿਭੁਜਾਂ ਸਰਬੰਗਸਮ ਹੋਵੇ ਤਾਂ ਖੇਤਰਫਲ ਬਰਾਬਰ ਹੁੰਦੇ ਹਨ।
∴ ar (△FBD) = ar (△DEF) …(1)
ar (△AFE) = ar (△DEF) . …(2)
ar (△EDC) = ar (△DEF) …(3)
ਹੁਣ ar △(ABC) = ar (△FBD) + ar (△DEF) + ar (△AFE) + ar (△EDC)
= ar (△DEF) + ar (△DEF) + ar (△DEF) + ar (△DEF)
[(1), (2) ਅਤੇ (3) ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ਤੇ]
= 4 ar (△DEF)
⇒ ar (△DEF) = \(\frac{1}{4}\)ar (△ABC)
⇒ \(\frac{ar(△DEF)}{ar(△ABC}\) = \(\frac{1}{4}\)
∴ ar (△DEF) : ar(△ABC) = 1 : 4.

ਪ੍ਰਸ਼ਨ 6.
ਸਿੱਧ ਕਰੋ ਕਿ ਦੋ ਸਮਰੂਪ ਤਿਭੁਜਾਂ ਦੇ ਖੇਤਰਫਲਾਂ ਦਾ ਅਨੁਪਾਤ ਇਨ੍ਹਾਂ ਦੀਆਂ ਸੰਗਤ ਮੱਧਿਕਾਵਾਂ ਦੇ ਅਨੁਪਾਤ ਦਾ ਵਰਗ ਹੁੰਦਾ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △ABC ~ △DEF.
AX ਅਤੇ DY ਮਵਾਰ ਭੁਜਾ BC ਅਤੇ EF ਮੱਧਿਕਾਵਾਂ ਹਨ ।

ਕਿਉਂਕਿ ਦੋ ਸਮਰੂਪ ਤ੍ਰਿਭੁਜਾਂ ਦੇ ਖੇਤਰਫਲਾਂ ਦਾ ਅਨੁਪਾਤ ਉਨ੍ਹਾਂ ਦੀ ਸੰਗਤ ਭੁਜਾਵਾਂ ਦੇ ਅਨੁਪਾਤ ਦੇ ਵਰਗ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ ।
∴ \(\frac{ar(△ABC)}{ar(△DEF}\) = \(\left(\frac{\mathrm{AB}^{2}}{\mathrm{DE}^{2}}\right)\) = \(\left(\frac{A X^{2}}{D Y^{2}}\right)\)

ਪ੍ਰਸ਼ਨ 7.
ਸਿੱਧ ਕਰੋ ਕਿ ਇਕ ਵਰਗ ਦੀ ਕਿਸੇ ਭੁਜਾ ਉੱਤੇ ਬਣਾਏ ਗਏ ਸਮਭੁਜੀ ਤ੍ਰਿਭੁਜ ਦਾ ਖੇਤਰਫਲ ਉਸੇ ਵਰਗ ਦੇ ਇੱਕ ਵਿਕਰਣ ‘ਤੇ ਬਣੇ ਸਮਭੁਜੀ ਤ੍ਰਿਭੁਜ ਦੇ ਖੇਤਰਫਲ ਦਾ ਅੱਧਾ ਹੁੰਦਾ ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ABCD ਇਕ ਵਰਗ ਹੈ।
ਸਮਭੁਜੀ △ABC ਵਰਗ ਦੀ ਭੁਜਾ AB ਉੱਤੇ ਸਥਿਤ ਹੈ ਅਤੇ ਸਮਭੁਜੀ △ACF ਵਿਕਰਣ AC ਉੱਤੇ ਬਣੀ ਹੈ ।

ਸਿਪ ਕਰਨਾ ਹ : \(\frac{ar(△ABC)}{ar(△ACF}\) = \(\frac{1}{2}\)
ਸਬੂਤ : ਸਮਕੋਣ △ABC ਵਿੱਚ
AB² + BC² = AC
[ਪਾਇਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਦੁਆਰਾ]
⇒ AB² + AB² = AC²
[∵ AB = BC, ਇਕ ਹੀ ਵਰਗ ਦੀਆਂ ਭੁਜਾਵਾਂ ]
⇒ 2AB² = AC² ….(1)
ਹੁਣ ਹਰੇਕ △ABE ਅਤੇ △ACE ਸਮਭੁਜੀ ਹਨ ਅਤੇ ਇਸ ਲਈ ਸਮਕੋਣੀ ਹਨ । ਇਸ ਲਈ ਸਮਰੂਪ ਹਨ ।
ਭਾਵ △ABE ~ △ACF.
ਇੱਥੇ ਪਹਿਲੀ 4 ਦੀ ਕੋਈ ਭੁਜਾ ਦੂਸਰੀ ਤ੍ਰਿਭੁਜ ਦੀ ਕਿਸੇ ਭੁਜਾ ਦੇ ਸਮਾਂਤਰ ਹੈ ।
∴ \(\frac{ar(△ABE)}{ar(△ACF}\) = \(\left(\frac{\mathrm{AB}^{2}}{\mathrm{AC}^{2}}\right)\).
[∵ ਦੋ ਸਮਰੂਪ ਤਿਭੁਜਾ ਦੇ ਖੇਤਰਫਲ ਦਾ ਅਨੁਪਾਤ ਉਨ੍ਹਾਂ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਦੇ ਅਨੁਪਾਤ ਦੇ ਵਰਗ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ ॥]
= \(\frac{\mathrm{AB}^{2}}{2 \mathrm{AB}^{2}}\) = \(\frac{1}{2}\). [(1) ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ਤ]
ਸਹੀ ਉੱਤਰ ਚੁਣੋ ਅਤੇ ਆਪਣੇ ਉੱਤਰ ਦਾ ਸਪਸ਼ਟੀਕਰਣ ਵੀ ਦਿਉ ।

ਪ੍ਰਸ਼ਨ 8.
ABC ਅਤੇ BDE ਦੋ ਸਮਭੁਜੀ ਤ੍ਰਿਭੁਜਾਂ ਇਸ ਪ੍ਰਕਾਰ ਹਨ ਕਿ ॥ ਭੁਜਾ BC ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ । ਤ੍ਰਿਭੁਜਾਂ ABC ਅਤੇ BDE ਦੇ ਖੇਤਰਫਲਾਂ ਦਾ ਅਨੁਪਾਤ ਹੈ :
(A) 2 : 1
(B) 1 : 2
(C) 4 : 1
(D) 1 : 4.
ਹੱਲ:
△ABC ਅਤੇ △BDE ਦੋ ਸਮਭੁਜੀ ਤ੍ਰਿਭੁਜ ਇਸ ਤਰ੍ਹਾਂ ਹਨ ਕਿ D ਭੁਜਾ BC ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ ।
∴ BD = DC = \(\frac{1}{2}\) BC,
ਮੰਨ ਲਉ ਸਮਭੁਜੀ ਤ੍ਰਿਭੁਜ ਦੀ ਭੁਜਾ 2a ਹੈ ।
∴ △ABC ~ △BDE
∴ \(\frac{ar(△ABC)}{ar(△BDE}\) = \(\frac{\mathrm{AB}^{2}}{\mathrm{BD}^{2}}\)
= \(\frac{(2 a)^{2}}{(a)^{2}}\) = \(\frac{4 a^{2}}{a^{2}}\)
= \(\frac{4}{1}\)
∴ (C) ਸਹੀ ਵਿਕਲਪ ਹੈ ।

ਪ੍ਰਸ਼ਨ 9.
ਦੋ ਸਮਰੂਪ ਤ੍ਰਿਭੁਜਾਂ ਦੀਆਂ ਭੁਜਾਵਾਂ 4 : 9 ਦੇ ਅਨੁਪਾਤ ਵਿੱਚ ਹਨ । ਇਨ੍ਹਾਂ ਤ੍ਰਿਭੁਜਾਂ ਦੇ ਖੇਤਰਫਲਾਂ ਦਾ ਅਨੁਪਾਤ ਹੈ :
(A) 2 : 3
(B) 4 : 9
(C) 81 : 16
(D) 16 : 81
ਹੱਲ:

△ABC ~ △DEF (ਦਿੱਤਾ ਹੈ।)
\(\frac{\mathrm{AB}}{\mathrm{DE}}\) = \(\frac{\mathrm{AC}}{\mathrm{DF}}\) = \(\frac{\mathrm{BC}}{\mathrm{EF}}\) = \(\frac{4}{9}\)
∴ \(\frac{ar(△ABC)}{ar(△DEF}\) = \(\frac{\mathrm{AB}^{2}}{\mathrm{DE}^{2}}\)
[ਦੋ ਸਮਰੂਪ ਤ੍ਰਿਭੁਜਾਂ ਦੇ ਖੇਤਰਫਲਾਂ ਦਾ ਅਨੁਪਾਤ ਉਨ੍ਹਾਂ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਦੇ ਅਨੁਪਾਤ ਦੇ ਵਰਗ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ।]
\(\frac{ar(△ABC)}{ar(△DEF}\) = \(\left(\frac{4}{9}\right)^{2}\) = \(\frac{16}{81}\)
∴ (D) ਸਹੀ ਵਿਕਲਪ ਹੈ ।

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 6 ਤ੍ਰਿਭੁਜ Ex 6.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 6 ਤ੍ਰਿਭੁਜ Exercise 6.3

ਪ੍ਰਸ਼ਨ 1.
ਦੱਸੋ ਕਿ ਚਿੱਤਰ ਵਿਚ ਦਿੱਤੇ ਗਏ ਤ੍ਰਿਭੁਜ ਦੇ ਜੋੜਿਆਂ ਵਿਚੋਂ ਕਿਹੜੇ-ਕਿਹੜੇ ਜੋੜੇ ਸਮਰੂਪ ਹਨ । ਉਸ ਸਮਰੂਪਤਾ ਕਸੌਟੀ ਨੂੰ ਲਿਖੋ ਜਿਸ ਦਾ ਪ੍ਰਯੋਗ ਤੁਸੀਂ ਉੱਤਰ ਦੇਣ ਲਈ ਕੀਤਾ ਹੈ ਅਤੇ ਸਮਰੂਪ ਤ੍ਰਿਭੁਜਾਂ ਨੂੰ ਸੰਕੇਤਨ ਰੂਪ ਵਿਚ ਵੀ ਦਰਸਾਓ ।

ਹੱਲ:
(i) △ABC ਅਤੇ △PQR ਵਿੱਚ
∠A = ∠P (ਹਰੇਕ 60°)
∠B = ∠Q (ਹਰੇਕ 800)
∠C = ∠R (ਹਰੇਕ 40°)
∴ △ABC ~ △PQR [AAA ਸਮਰੂਪਤਾ)

(ii) △ABC ਅਤੇ △PQR ਵਿੱਚ
\(\frac{AB}{RQ}\) = \(\frac{2}{4}\) = \(\frac{1}{2}\) …..(1)
\(\frac{AC}{PQ}\) = \(\frac{3}{6}\) = \(\frac{1}{2}\) …(2)
\(\frac{AB}{RQ}\) = \(\frac{2.5}{5}\) = \(\frac{1}{2}\) …(3)
(1), (2) ਅਤੇ (3) ਤੋਂ,
\(\frac{BC}{PR}\) = \(\frac{AC}{PQ}\) = \(\frac{BC}{PR}\) = \(\frac{1}{2}\)
∴ △ABC ~ △QRP
[SSS ਸਮਰੂਪਤਾ ਕਸੌਟੀ ਨਾਲ

(iii) △LMP ਅਤੇ △DEF ਵਿੱਚ,

∴ ਦੋ ਤ੍ਰਿਭੁਜਾਂ ਸਮਰੂਪ ਨਹੀਂ ਹਨ ।

(iv) △MNL ਅਤੇ △PQR ਵਿੱਚ,
\(\frac{ML}{QR}\) = \(\frac{5}{10}\) = \(\frac{1}{2}\)
∠M = ∠Q (ਹਰੇਕ 70°)
\(\frac{MN}{PQ}\) = \(\frac{2.5}{5}\) = \(\frac{1}{2}\)
∴ △MNL ~ △QPR
[SAS ਸਮਰੂਪਤਾ ਕਸੌਟੀ ਤੋਂ ]

(v) △ABC ਅਤੇ △DEF ਵਿੱਚ,

∴ △ABC ਅਤੇ △DEF ਸਮਰੂਪ ਨਹੀਂ ਹਨ ।

(vi) △DEE ਵਿੱਚ,
∠D = 70°, ∠E = 80°
∠D + ∠E + ∠F = 180°
(ਤਿਭੁਜ ਦੇ ਕੋਣਾਂ ਦਾ ਜੋੜਫਲ)
70° + 80° + ∠F = 180°
∠F = 180° – 70° – 80°
∠F = 30°
△PQR ਵਿੱਚ,
∠Q = 80°, ∠R = 30°
∠P + ∠Q + ∠R = 180°
(ਤਿਭੁਜ ਦੇ ਕੋਣਾਂ ਦਾ ਜੋੜਫਲ)
∠P + 80° + 30° = 180°
∠P = 180° – 80° – 30°
∠P = 70°
△DEF ਅਤੇ △PQR ਵਿੱਚ,
∠D = ∠P (70° ਹਰੇਕ)
∠E = ∠Q (80° ਹਰੇਕ)
∠F = ∠R (30° ਹੇਰਕ)
∴ △DEF ~ △PQR (AAA ਸਮਰੂਪਤਾ ਕਸੌਟੀ)

ਪ੍ਰਸ਼ਨ 2.
ਚਿੱਤਰ ਵਿਚ △ODC ~ △OBA, ∠BOC= 125° ਅਤੇ ∠CDO = 70° ਹੈ | ∠DOC, ∠DCO ਅਤੇ ∠OAB ਪਤਾ ਕਰੋ ।

ਹੱਲ:
∠BOC = 125°
∠CDO = 70°
DOC ਇਕ ਸਰਲ ਰੇਖਾ ਹੈ ।
∴ ∠DOC + /COB = 180°
∠DOC + 125° = 180°
∠DOC = 180° – 125
∠DOC = 55°
∠DOC = ∠AOB = 55°
[ਸਿਖ਼ਰ ਸਨਮੁੱਖ ਕੋਣੀ]
∴ △ODC ~ △OBA
∠D = ∠B = 70°
△DOC ਨੇਂ, ∠D + ∠O + ∠C = 180°
70° + 55° + ∠C = 180°
∠C = 180° – 70° – 55°
∠C = 55°
∠C = ∠A = 55°
∠DOC = 55°
∴ ∠DCO = 55°
∠OAB = 55°

ਪ੍ਰਸ਼ਨ 3.
ਸਮਲੰਬ ਚਤੁਰਭੁਜ ABCD, ਜਿਸ ਵਿਚ AB || DC ਹੈ, ਦੇ ਵਿਕਰਣ AC ਅਤੇ BD ਆਪਸ ਵਿੱਚ Q’ ਤੇ ਕੱਟਦੇ ਹਨ । ਦੋ ਤ੍ਰਿਭੁਜਾਂ ਦੀ ਸਮਰੂਪਤਾ ਕਸੌਟੀ ਦਾ ਪ੍ਰਯੋਗ ਕਰਦੇ ਹੋਏ ਦਿਖਾਉ ਕਿ \(\frac{OA}{OC}\) =\(\frac{OB}{OD}\) ਹੈ ।
ਹੱਲ:

ਦਿੱਤਾ ਹੈ : ਸਮਲੰਬ ਚਤੁਰਭੁਜ ABCD ਜਿਸ ਵਿਚ AB DC ਹੈ ਅਤੇ ਵਿਕਰਣ AC ਅਤੇ BD ਆਪਸ ਵਿਚ O ‘ਤੇ ਕੱਟਦੇ ਹਨ ।
ਸਿੱਧ ਕਰਨਾ ਹੈ :
ਸਿੱਧ ਕਰਨਾਂ ਹੈ : \(\frac{OA}{OC}\) = \(\frac{OB}{OD}\)
ਸਬੂਤ : AB || DC
△DOC ਅਤੇ △BOA ਵਿੱਚ
∠1 = ∠2 (ਇਕਾਂਤਰ ਕੋਣ )
∠5 = ∠6 (ਸਿਖ਼ਰ ਸਨਮੁੱਖ ਕੋਣ)
∠3 = ∠4 (ਇਕਾਂਤਰ ਕੋਣ)
∴ △DOC ~ △BOA
[AAA ਸਮਰੂਪਤਾ ਕਸੋ]
∴ \(\frac{DO}{BO}\) = \(\frac{OC}{OA}\)
[ਜੇਕਰ ਦੋ ਭੁਜਾਂ ਸਮਰੂਪ ਹੋਣ ਤਾਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਸਮਾਨੁਪਾਤੀ ਹੁੰਦੀਆਂ ਹਨ ]
⇒ \(\frac{OA}{OC}\) = \(\frac{BO}{DO}\)

ਪ੍ਰਸ਼ਨ 4.
ਚਿੱਤਰ ਵਿਚ, \(\frac{QR}{QS}\) = \(\frac{QT}{PR}\) ਅਤੇ ∠1 = ∠2 ਹੈ । ਦਿਖਾਉ ਕਿ △PQS ~ △TQR ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △TQR ਵਿੱਚ
\(\frac{QR}{QS}\) = \(\frac{QT}{PR}\) ਅਤੇ
∠1 = ∠2

ਸਿੱਧ ਕਰਨਾ ਹੈ : △PQS – △TOR
ਸਬੂਤ : △PQR ਵਿਚ,
∠1 = ∠2 (ਦਿੱਤਾ ਹੈ।)
∴ PR = PQ [ਬਰਾਬਰ ਕੋਣਾਂ ਦੀਆਂ ਸਨਮੁੱਖ ਭੁਜਾਵਾਂ ਬਰਾਬਰ ਹੁੰਦੀਆਂ ਹਨ]

∠1 = ∠1 (ਸਾਂਝਾ)
∴ △PQS ~ △TQR [SAS ਸਮਰੂਪਤਾ ਕਸੋਟੀ]

ਪ੍ਰਸ਼ਨ 5.
△PQR ਦੀਆਂ ਭੁਜਾਵਾਂ PR ਅਤੇ QR ਉੱਤੇ ਕ੍ਰਮਵਾਰ | ਬਿੰਦ S ਅਤੇ T ਇਸ ਤਰਾਂ ਸਥਿਤ ਹਨ ਕਿ ∠P = ∠RTS ਹੈ । ਦਿਖਾਉ ਕਿ △RPQ ~ △RTS ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △POR ਦੀਆਂ ਭੁਜਾਵਾਂ PR ਅਤੇ QR ਉੱਤੇ ਕ੍ਰਮਵਾਰ ਬਿੰਦੂ S ਅਤੇ T ਇਸ ਤਰ੍ਹਾਂ ਸਥਿਤ ਹਨ ∠P = ∠RTS ਹੈ ।

ਸਿੱਧ ਕਰਨਾ ਹੈ : △RPQ ~ △RTS
ਸਬੂਤ : △RPQ ਅਤੇ △RTS ਵਿਚ,
∠RPQ = ∠RTS (ਦਿੱਤਾ ਹੈ।)
∠R = ∠R
∴ △RPQ ~ △RTS [AA ਸਮਰੂਪਤਾ ਕਸੌਟੀ]

ਪ੍ਰਸ਼ਨ 6.
ਚਿੱਤਰ ਵਿੱਚ, ਜੇਕਰ △ABE ≅ △ACD ਹੈ, ਤਾਂ ਦਿਖਾਉ ਕਿ △ADE ~ △ABC ਹੈ ।

ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △ABC ਅਤੇ △ABE ≅ △ACD ਹੈ ।
ਸਿੱਧ ਕਰਨਾ ਹੈ : △ADE ~ △ABC
ਸਬੂਤ : △ABE ≅ △ACD (ਦਿੱਤਾ ਹੈ)
AB = AC (ਸਰਬੰਗਸਮ ਤ੍ਰਿਭੁਜਾਂ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ) ਅਤੇ AE = AD (ਸਰਬੰਗਮ ਤ੍ਰਿਭੁਜਾਂ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ)
\(\frac{AB}{AC}\) = 1 …(1)
\(\frac{AD}{AE}\) = 1 …(2)
(1) ਅਤੇ (2) ਤੋਂ, \(\frac{AB}{AC}\) = \(\frac{AD}{AE}\)
△ADE ਅਤੇ △ABC ਵਿਚ, \(\frac{AD}{AE}\) = \(\frac{AB}{AC}\)
∠A = ∠A (ਸਾਂਝਾ)
∴ △ADE ~ △ABC [SAS ਸਮਰੂਪਤਾ ਕਸੌਟੀ ਤੋਂ]

ਪ੍ਰਸ਼ਨ 7.
ਚਿੱਤਰ ਵਿੱਚ, △ABC ਦੇ ਸਿਖ਼ਰ ਲੰਬ AD ਅਤੇ CE ਆਪਸ ਵਿੱਚ ਬਿੰਦੂ Pਉੱਤੇ ਕੱਟਦੇ ਹਨ |ਦਿਖਾਉ ਕਿ :
(i) △AEP ~ △CDP
(ii) △ABD ~ △CBE
(iii) △AEP ~ △ADB
(iv) △PDC – △BEC.
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △ABC ਵਿੱਚ AD ⊥ BC
ਅਤੇ CE ⊥ AB,

ਸਿੱਧ ਕਰਨਾ ਹੈ : (i) △AEP ~ △CDP
(ii) △ABD ~ △CBE
(iii) △AEP ~ △ADB
(iv) △PDC ~ △BEC
ਸਬੂਤ : (i) △AEP ਅਤੇ △CDP ਵਿੱਚ,
∠E = ∠D (ਹਰੇਕ 90°)
∠APE = ∠CPD (ਸਿਖ਼ਰ ਸਨਮੁੱਖ ਕੋਣ)
∴ △AEP ~ △CDP [AA ਸਮਰੂਪਤਾ ਕਸੌਟੀ]

(ii) △ABD ਅਤੇ △CBE ਵਿੱਚ,
∠D = ∠E (ਹਰੇਕ 90°)
∠B = ∠B (ਸਾਂਝਾ ਕੋਣ)
∴ △ABD ~ △CBE [AA ਸਮਰੂਪਤਾ ਕਸੌਟੀ]

(iii) △AEP ਅਤੇ △ADB ਵਿੱਚ,
∠E = ∠D (ਹਰੇਕ 90°)
∠A = ∠A (ਸਾਂਝਾ ਕੋਣ)
∴ △AEP ~ △ADB [AA ਸਮਰੂਪਤਾ ਕਸੌਟੀ]

(vi) △PDC ਅਤੇ △BEC ਵਿੱਚ,
∠C = ∠C (ਸਾਂਝਾ ਕੋਣ)
∠D = ∠E (ਹਰੇਕ 90°)
∴ △PDC ~ △BEC [AA ਸਮਰੂਪਤਾ ਕਸੌਟੀ]

ਪ੍ਰਸ਼ਨ 8.
ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ABCD ਦੀ ਵਧਾਈ ਗਈ ਭੁਜਾ AD ਉੱਤੇ ਸਥਿਤ E ਕੋਈ ਬਿੰਦੂ ਹੈ ਅਤੇ BE ਭੁਜਾ CD ਨੂੰ F’ ਤੇ ਕੱਟਦੀ ਹੈ । ਦਿਖਾਉ ਕਿ ਮੈ △ABE ~ △CFB ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ABCD ਦੀ ਵਧਾਈ ਗਈ ਭੁਜਾ AD ਉੱਤੇ ਸਥਿਤ E ਇਕ ਬਿੰਦੂ ਹੈ ਅਤੇ BE ਅਤੇ CD ਨੂੰ F ਬਿੰਦੂ ਉੱਤੇ ਕੱਟਦੀ ਹੈ ।

ਸਿੱਧ ਕਰਨਾ ਹੈ : △ABE ~ △CFB
ਸਬੂਤ : △ABE ਅਤੇ △CFB ਵਿੱਚ
∠A = ∠C (|| gm ਦੇ ਸਨਮੁੱਖ ਕੋਣ)
∠ABE = ∠CFB (ਇਕਾਂਤਰ ਕੋਣ)
∴ △ABE ~ △CFB (AA ਸਮਰੂਪਤਾ ਕਸੌਟੀ)

ਪ੍ਰਸ਼ਨ 9.
ਚਿੱਤਰ ਵਿੱਚ, ABC ਅਤੇ AMP ਦੋ ਸਮਕੋਣ ਤ੍ਰਿਭੁਜਾਂ ਹਨ, ਜਿਨ੍ਹਾਂ ਦੇ ਕੋਣ B ਅਤੇ Mਸਮਕੋਣ ਹਨ । ਸਿੱਧ ਕਰੋ ਕਿ
(i) △ABC ~ △AMP
(ii) \(\frac{CA}{PA}\) = \(\frac{BC}{MP}\).

ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △ABC ਅਤੇ △AMP ਦੋ ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ ਹਨ । ਜਿਨ੍ਹਾਂ ਦੇ ਕੋਣ B ਅਤੇ M ਸਮਕੋਣ ਹਨ ।
ਸਿੱਧ ਕਰਨਾ ਹੈ : (i) △ABC ~ △AMP ਵਿਚ,
(ii) \(\frac{CA}{PA}\) = \(\frac{BC}{MP}\)
ਸਬੂਤ : △ABC ਅਤੇ △AMP ਵਿੱਚ,
∠A = ∠A (ਸਾਂਝਾ ਕੋਣ)
∠B = ∠M (ਹਰੇਕ 90°)
∴ △ABC ~ △AMP (AA ਸਮਰੂਪਤਾ ਕਸੌਟੀ)
∴ \(\frac{AC}{AP}\) = \(\frac{BC}{MP}\)
[ਜੇਕਰ ਦੋ ਤ੍ਰਿਭੁਜਾਂ ਸਮਰੂਪ ਹੋਣ, ਤਾਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਸਮਾਨੁਪਾਤੀ ਹੁੰਦੀਆਂ ਹਨ |]
⇒ \(\frac{CA}{PA}\) = \(\frac{BC}{MP}\)

ਪ੍ਰਸ਼ਨ 10.
CD ਅਤੇ GH ਕ੍ਰਮਵਾਰ ∠ACB ਅਤੇ ∠EGF ਦੇ | ਅਜਿਹੇ ਸਮਦੁਭਾਜਕ ਹਨ ਕਿ ਬਿੰਦੂ D ਅਤੇ ਸ਼ ਕੁਮਵਾਰ △ABC ਅਤੇ △FEG ਦੀਆਂ ਭੁਜਾਵਾਂ AB ਅਤੇ FE ਉੱਤੇ ਸਥਿਤ ਹਨ । ਜੇਕਰ △ABC ~ △FEG ਹੋਵੇ, ਤਾਂ ਦਿਖਾਉ ਕਿ
(i) \(\frac{CD}{GH}\) = \(\frac{AC}{FG}\)
(ii) △DCB ~ △HGE
(iii) △DCA ~ △HGF
ਹੱਲ:

ਦਿੱਤਾ ਹੈ : △ABC ਅਤੇ △EFG ਵਿੱਚ, CD ਅਤੇ GH ਮਵਾਰ ∠ACB ਅਤੇ ∠EGF ਦੇ ਸਮਦੁਭਾਜਕ ਹਨ ਅਰਥਾਤ ∠1 = ∠2 ਅਤੇ ∠3 = ∠4 ਹੈ ।
△ABC ~ △FEG
ਸਿੱਧ ਕਰਨਾ ਹੈ : (i) \(\frac{CD}{GH}\) = \(\frac{AC}{FG}\)
(ii) △DCB ~ △HGE
(iii) △DCA ~ △HGE
ਸਬੂਤ : (i) △ABC ~ △FEG (ਦਿੱਤਾ ਹੈ।)
∠C = ∠G
[ਜੇਕਰ ਦੋ ਤ੍ਰਿਭੁਜਾਂ ਸਮਰੂਪ ਹੋਣ, ਤਾਂ ਸੰਗਤ ਕੋਣ ਬਰਾਬਰ ਹੁੰਦੇ ਹਨ]
\(\frac{1}{2}\)C = \(\frac{1}{2}\)G
∠1 = ∠3 ਜਾਂ ∠2 = ∠4
ਹੁਣ, △ACD ਅਤੇ △FGH ਵਿੱਚ
∠A = ∠F
∠2 = ∠4 (ਸਿੱਧ ਕੀਤਾ ਹੈ।)
∴ △ACD ~ △FGH
[∵ AA ਪ੍ਰਮਾਣਿਤ ਸਮਰੂਪਤਾ ਕਸੌਟੀ ਤੇ]
∴ \(\frac{CD}{GH}\) = \(\frac{AG}{FG}\)
[∵ ਸਮਰੂਪ ਤ੍ਰਿਭੁਜਾਂ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਸਮਾਨੁਪਾਤੀ ਹੁੰਦੀਆਂ ਹਨ ।]

(ii) ਹੁਣ, △DCB ਅਤੇ △HGE ਵਿੱਚ,
∠B = ∠E (ਸਿੱਧ ਕੀਤਾ)
∠1 = ∠3 [ਸਿੱਧ ਕੀਤਾ]
∴ △DCB ~ △HGE
[∵ AA ਸਮਰੂਪਤਾ ਕਸੌਟੀ ਨਾਲ]

(iii) ਹੁਣ, △DCA ਅਤੇ △HGF ਵਿੱਚ,
∠A = ∠F [ਸਿੱਧ ਕੀਤਾ]
∠2 = ∠4 ਸਿੱਧ ਕੀਤਾ]
∴ △DCA ~ △HGF
[∵ AA ਸਮਰੂਪਤਾ ਕਸੌਟੀ ਨਾਲ]

ਪ੍ਰਸ਼ਨ 11.
ਚਿੱਤਰ ਵਿੱਚ AB = AC ਵਾਲੇ ਇੱਕ ਸਮਦੋਭੁਜੀ ਤਿਭੁਜ ABC ਦੀ ਵਧਾਈ ਗਈ ਭੁਜਾ CB ਉੱਤੇ ਸਥਿਤ E, ਇੱਕ ਬਿੰਦੁ ਹੈ । ਜੇਕਰ AD ⊥ BC ਅਤੇ EF ⊥ AC ਹੋਵੇ, ਤਾਂ ਸਿੱਧ ਕਰੋ ਕਿ △ABD ~ △ECF ਹੈ ।

ਹੱਲ:
ਦਿੱਤਾ ਹੈ : AB = AC ਵਾਲੇ ਇਕ ਸਮਦੋਭੁਜੀ △ABC ਦੀ ਵਧਾਈ ਗਈ ਭੁਜਾ CB ਉੱਤੇ ਸਥਿਤ E ਇੱਕ ਬਿੰਦੁ ਹੈ । AD ⊥ BC ਅਤੇ EF ⊥ AC ਹੈ ।
ਸਿੱਧ ਕਰਨਾ : △ABD ~ △ECF
ਸਬੂਤ : △ABC ਸਮਦੋਭੁਜੀ ਤ੍ਰਿਭੁਜ ਹੈ । (ਦਿੱਤਾ ਹੈ) |
AB = AC
ਤ੍ਰਿਭੁਜ ਵਿੱਚ ਸਮਾਨ ਭੁਜਾਵਾਂ ਦੇ ਸਨਮੁੱਖ ਕੋਣ
∴ ∠B = ∠C (ਬਰਾਬਰ ਕੋਣ)
△ABD ਅਤੇ △ECF ਵਿੱਚ
∠ABD = ∠ECF (ਸਿੱਧ ਕੀਤਾ।)
∠ADB = ∠EFC (ਹਰੇਕ 90°)
∴ △ABD ~ △ECF [AA ਸਮਰੂਪਤਾ ਕਸੌਟੀ]

ਪ੍ਰਸ਼ਨ 12.
ਇੱਕ ਤ੍ਰਿਭੁਜ ABC ਦੀਆਂ ਕ੍ਰਮਵਾਰ ਭੁਜਾਵਾਂ AB, BC ਅਤੇ ਮੱਧਿਕਾADਕਿਸੇ ਹੋਰ ਤ੍ਰਿਭੁਜ PQR ਦੀਆਂ ਕ੍ਰਮਵਾਰ ਭੁਜਾਵਾਂ, PO, OR ਅਤੇ ਮੱਧਿਕਾ PM ਦੇ ਸਮਾਨ-ਅਨੁਪਾਤੀ ਹਨ (ਦੇਖੋ ਚਿੱਤਰ) ।ਦਿਖਾਉ ਕਿ △ABC ~ △PQR ਹੈ ।

ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △ABC ਦੀਆਂ ਭੁਜਾਵਾਂ AB, BC ਅਤੇ ਮਧਿਕਾ AD ਇਕ ਹੋਰ ਤ੍ਰਿਭੁਜ PQR ਦੀਆਂ ਕ੍ਰਮਵਾਰ ਭੁਜਾਵਾਂ PQ ਅਤੇ QR ਅਤੇ ਮੱਧਿਕਾ PM ਦੇ ਸਮਾਨ ਅਨੁਪਾਤੀ ਹਨ !
\(\frac{AB}{PQ}\) = \(\frac{AC}{PR}\) = \(\frac{AD}{PM}\)
ਸਿੱਧ ਕਰਨਾ ਹੈ : △ABC ~ △PQR

ਰਚਨਾ : AD ਨੂੰ E ਤੱਕ ਵਧਾਉ ਤਾਂ ਕਿ AD = DE ਅਤੇ PM ਨੂੰ N ਤੱਕ ਵਧਾਉ ਤਾਂ ਕਿ PM = MN ਹੋ ਜਾਵੇ । BE, CE, QN ਅਤੇ RN ਨੂੰ ਮਿਲਾਉ ।
ਸਬੂਤ : \(\frac{AB}{PQ}\) = \(\frac{AC}{PR}\) = \(\frac{AD}{PM}\) (ਦਿੱਤਾ ਹੈ।) ……(1)
BD = DC (ਦਿੱਤਾ ਹੈ )
AD = DE (ਰਚਨਾ)
ਚਤੁਰਭੁਜ ABEC ਦੇ ਵਿਕਰਣ ਇਕ-ਦੂਸਰੇ ਨੂੰ ਸਮਦੁਭਾਜਿਤ ਕਰਦੇ ਹਨ ।
∴ ਚਤੁਰਭੁਜ ABEC ਇਕ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜੇ ਹੈ ।
ਇਸੇ ਤਰ੍ਹਾਂ PQNR ਇਕ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਹੈ ।
∴ BE = AC
[ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਦੀਆਂ ਸਨਮੁੱਖ ਭੁਜਾਵਾਂ।]
ਅਤੇ QN = PR
\(\frac{BE}{AC}\) …(i)
\(\frac{QN}{PR}\) ….(ii)
(i) ਅਤੇ (ii) ਤੋਂ,


∴ △ABE ~ △PQN [ਭੁਜਾਵਾਂ ਸਮਾਨੁਪਾਤੀ ਹਨ]
∴ ∠1 = ∠2 …(4)
[ਸਮਰੂਪ ਤ੍ਰਿਭੁਜਾਂ ਦੇ ਸੰਗਤ ਕੋਣ]
ਇਸੇ ਤਰ੍ਹਾਂ, △ACE ~ △PRN
∠3 = ∠4 …(5)
[ਸਮਰੂਪ ਤ੍ਰਿਭੁਜਾਂ ਦੇ ਸੰਗਤ ਕੋਣ]
(4) ਅਤੇ (5) ਨੂੰ ਜੋੜਨ ਤੇ
∠1 + ∠3 = ∠2 + ∠4
∠A = ∠P
ਹੁਣ △ABC ਅਤੇ △PQR ਨੇਂ,
∠A = ∠P (ਸਿੱਧ ਕੀਤਾ।)
\(\frac{AB}{PQ}\) = \(\frac{AC}{PR}\) (ਦਿੱਤਾ ਹੈ।)
∴ ABC ~ △PQR
[SAS ਸਮਰੂਪਤਾ ਕਸੌਟੀ ਦੇ ਪ੍ਰਯੋਗ ਨਾਲ]

ਪ੍ਰਸ਼ਨ 13.
ਇੱਕ ਤ੍ਰਿਭੁਜ ABC ਦੀ ਭੁਜਾ BC ਉੱਤੇ ਇੱਕ ਬਿੰਦੂ ) ਇਸ ਤਰ੍ਹਾਂ ਸਥਿਤ ਹੈ ਕਿ ∠ADC = ∠BAC ਹੈ । ਦਿਖਾਉ ਕਿ CA² = CB.CD ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △ABC ਦੀ ਭੁਜਾ BC ਉੱਤੇ ਇੱਕ ਬਿੰਦੁ ) ਇਸ ਤਰ੍ਹਾਂ ਸਥਿਤ ਹੈ ਕਿ ∠ADC = ∠BAC ਹੈ ।
ਸਿੱਧ ਕਰਨਾ ਹੈ : CA² = CB.CD
ਸਬੂਤ : △ABC ਅਤੇ △ADC ਵਿੱਚ,

∠C = ∠C (ਸਾਂਝਾ)
∠BAC = ∠ADC (ਦਿੱਤਾ ਹੈ।)
∴ △ABC ~ △DAC [AA ਸਮਰੂਪਤਾ ਕਸੌਟੀ ਤੋਂ।]
∴ \(\frac{AC}{DC}\) = \(\frac{BC}{AC}\) [ਜੇਕਰ ਦੋ ਭੁਜਾਂ ਸਮਰੂਪ ਹੋਣ ਤਾਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਸਮਾਨੁਪਾਤੀ ਹੁੰਦੀਆਂ ਹਨ]
AC² = BC. DC

ਪ੍ਰਸ਼ਨ 14.
ਇੱਕ ਤ੍ਰਿਭੁਜ ABC ਦੀਆਂ ਭੁਜਾਵਾਂ AB, AC ਅਤੇ ਮੱਧਿਕਾ AD, ਇੱਕ ਹੋਰ ਤ੍ਰਿਭੁਜ ਦੀਆਂ ਭੁਜਾਵਾਂ PQ, PR, ਮੱਧਿਆ PM ਦੇ ਕ੍ਰਮਵਾਰ ਸਮਾਨ-ਅਨੁਪਾਤੀ ਹਨ ।ਦਰਸਾਉ ਕਿ △ABC ~ △PQR ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਦੋ ਤਿਭੁਜ ABC ਅਤੇ PQR ਵਿੱਚ D, BC ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ M, QR ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ ।
ਅਤੇ \(\frac{AB}{PQ}\) = \(\frac{AC}{PR}\) = \(\frac{AD}{PM}\) …(1)

ਸਿੱਧ ਕਰਨਾ ਹੈ : △ABC ~ △PQR
ਰਚਨਾ : AD ਨੂੰ E ਤੱਕ ਵਧਾਉ ਤਾਂਕਿ AD = DE ਹੋਵੇ
BE ਅਤੇ CE ਨੂੰ ਮਿਲਾਉ ।
PM ਨੂੰ N ਤੱਕ ਵਧਾਉ ਤਾਂ ਕਿ PM = MN ਹੋਵੇ ।
QN ਅਤੇ NR ਨੂੰ ਮਿਲਾਉ ॥
ਸਬੂਤ : ਚਤੁਰਭੁਜ ABEC ਦੇ ਵਿਕਰਣ AE ਅਤੇ BC ਆਪਸ ਵਿੱਚ ਬਿੰਦੂ ) ਉੱਤੇ ਸਮਭਾਜਿਤ ਕਰਦੇ ਹਨ ।
∴ ਚਤੁਰਭੁਜ ABEC ਇਕ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਹੈ ।
ਇਸ ਤਰ੍ਹਾਂ ਇਹ ਦਿਖਾਇਆ ਜਾ ਸਕਦਾ ਹੈ ਚਤੁਰਭੁਜ PQNR ਇਕ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਹੈ ।
ਕਿਉਂਕਿ ABEC ਇੱਕ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਹੈ ।
∴ BE = AC …..(2)
ਇਸੇ ਤਰ੍ਹਾਂ PQNR ਇੱਕ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਹੈ ।
∴ QN = PR …(3)
(2) ਨੂੰ (3) ਨਾਲ ਭਾਗ ਕਰਨ ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ,

∴ △ABC ~ △PON
∴ ∠BAE = ∠QPN …(6)
ਇਸ ਤਰ੍ਹਾਂ, ਇਹ ਸਿੱਧ ਕੀਤਾ ਗਿਆ ਹੈ ਕਿ
△AEC ~ △PNR
∴ ∠EAC = ∠NPR …(7)
(6) ਅਤੇ (7) ਨੂੰ ਜੋੜਨ ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
∠BAE + ∠EAC = ∠QPN + ∠NPR
ਹੁਣ △ABC ਅਤੇ △PQR ਸੇਂ
\(\frac{AB}{PQ}\) = \(\frac{AC}{PR}\)
∴ △ABC ~ △QPR (SAS ਸਮਰੂਪਤਾ ਕਸੌਟੀ ਨਾਲ)

ਪ੍ਰਸ਼ਨ 15.
6 m ਲੰਬਾਈ ਵਾਲੇ ਇੱਕ ਲੰਬ ਰੂਪ ਵਿੱਚ ਖੜੇ ਖੰਭੇ ਦੀ ਜ਼ਮੀਨ ‘ਤੇ ਪਰਛਾਵੇਂ ਦੀ ਲੰਬਾਈ 4m ਹੈ, ਜਦੋਂ ਕਿ ਉਸੇ ਸਮੇਂ ਇੱਕ ਮੀਨਾਰ ਦੀ ਪਰਛਾਵੇਂ ਦੀ ਲੰਬਾਈ 28 m ਹੈ । ਮੀਨਾਰ ਦੀ ਉਚਾਈ ਪਤਾ ਕਰੋ । .
ਹੱਲ:

ਖੰਭੇ ਦੀ ਲੰਬਾਈ = 6 m
ਖੰਭੇ ਦੇ ਪਰਛਾਵੇਂ ਦੀ ਲੰਬਾਈ = 4 m
ਮੰਨ ਲਉ ਮੀਨਾਰ ਦੀ ਉਚਾਈ = Hm
ਮੀਨਾਰ ਦੇ ਪਰਛਾਵੇਂ ਦੀ ਲੰਬਾਈ = 28 m
△ABC ਅਤੇ △PMN ਵਿੱਚ,
∠C = ∠N (ਮੀਨਾਰ ਦੇ ਪਰਛਾਵੇਂ ਦੀ ਲੰਬਾਈ)
∠B = ∠M (ਹਰੇਕ 90°)
∴ △ABC ~ △PMN [AA ਸਮਰੂਪਤਾ ਕਸੌਟੀ]
∴ \(\frac{AB}{PM}\) = \(\frac{BC}{MN}\)
[ਜੇਕਰ ਦੋ ਤ੍ਰਿਭੁਜ ਸਮਰੂਪ ਹੋਣ, ਤਾਂ ਉਨ੍ਹਾਂ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਸਮਾਨ ਅਨੁਪਾਤੀ ਹੁੰਦੀਆਂ ਹਨ ]
∴ \(\frac{6}{H}\) = \(\frac{4}{28}\) ⇒ H = \(\frac{6× 28}{4}\)
H = 6 × 7
H = 42 m
∴ ਮੀਨਾਰ ਦੀ ਉਚਾਈ = 42 m.

ਪ੍ਰਸ਼ਨ 16.
AD ਅਤੇ PM ਤ੍ਰਿਭੁਜਾਂ ABC ਅਤੇ POR ਦੀਆਂ ਕੁਮਵਾਰ ਮੱਧਿਕਾਵਾਂ ਹਨ, ਜਦੋਂ ਕਿ △ABC ~ △PQR ਹੈ । ਸਿੱਧ ਕਰੋ ਕਿ \(\frac{AB}{PQ}\) = \(\frac{AD}{PM}\) ਹੈ ।

ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △ABC ਅਤੇ △PQR ਦੀ AD ਅਤੇ PM ਮੱਧਿਕਾਵਾਂ ਹਨ ਅਤੇ △ABC ~ △PQR ਹੈ ।
ਸਿੱਧ ਕਰਨਾ ਹੈ : \(\frac{AB}{PQ}\) = \(\frac{AD}{PM}\)
ਸਬੂਤ : △ABC ~ △PQR (ਦਿੱਤਾ ਹੈ )
∴ \(\frac{AB}{PQ}\) = \(\frac{BC}{QR}\) = \(\frac{AC}{PR}\)
{ਜੇਕਰ ਦੋ ਤਿਭੁਜਾਂ ਸਮਰੂਪ ਹਨ, ਤਾਂ ਉਨ੍ਹਾਂ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਸਮਾਨ-ਅਨੁਪਾਤੀ ਹੁੰਦੀਆਂ ਹਨ }
∠A = ∠P
[ਜੇਕਰ ਦੋ ਤਿਭੁਜਾਂ ਸਮਰੂਪ ਹਨ, ਤਾਂ ਸੰਗਤ ਕੋਣ ਬਰਾਬਰ ਹੁੰਦੇ ਹਨ]
∠B = ∠Q
∠C = ∠R
D, BC ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ ।
∴ BD = DC = \(\frac{1}{2}\)BC ..(2)
M, OR ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ ।
∴ QM = MR = \(\frac{1}{2}\)QR …(3)

[ਜੇਕਰ ਦੋ ਤ੍ਰਿਭੁਜਾਂ ਸਮਰੂਪ ਹਨ ਤਾਂ ਉਨ੍ਹਾਂ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਸਮਾਨ ਅਨੁਪਾਤੀ ਹੁੰਦੀਆਂ ਹਨ]

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 6 ਤ੍ਰਿਭੁਜ Ex 6.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 6 ਤ੍ਰਿਭੁਜ Exercise 6.2

ਪ੍ਰਸ਼ਨ 1.
ਚਿੱਤਰ (i) ਅਤੇ (ii) ਵਿੱਚ, DE || BC ਹੈ।
(i) ਵਿੱਚ EC ਅਤੇ (i) ਵਿੱਚ AD ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ ।

ਹੱਲ:
(i) △ABC ਵਿੱਚ DE || BC …(ਦਿੱਤਾ ਹੈ )
∴ \(\frac{\mathrm{AD}}{\mathrm{BD}}\) = \(\frac{\mathrm{AE}}{\mathrm{EC}}\)
[ਮੂਲ ਸਮਾਨ ਅਨੁਪਾਤਤਾ ਮੇਯ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ]
\(\frac{1.5}{3}\)= \(\frac{1}{EC}\)
EC = \(\frac{3}{1.5}\)
EC = \(\frac{3×10}{15}\) = 2
∴ EC = 2 cm

(ii) △ABC ਵਿੱਚ,
DE || BC … (ਦਿੱਤਾ ਹੈ।)
∴ \(\frac{\mathrm{AD}}{\mathrm{BD}}\) = \(\frac{\mathrm{AE}}{\mathrm{EC}}\)
[ਮੂਲ ਸਮਾਨ ਅਨੁਪਾਤ ਪ੍ਰਮੇਯ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ਤੇ]
\(\frac{AD}{7.2}\) = \(\frac{1.8}{5.4}\)
AD = \(\frac{1.8×7.2}{5.4}\)
= \(\frac{18}{10}\) × \(\frac{72}{10}\) × \(\frac{10}{54}\)
= \(\frac{24}{10}\) = 2.4
∴ AD = 2.4 cm

ਪ੍ਰਸ਼ਨ 2.
ਕਿਸੇ △PQR ਦੀਆਂ ਭੁਜਾਵਾਂ PQ ਅਤੇ PR ਉੱਤੇ ਕੁਮਵਾਰ ਬਿੰਦੂ E ਅਤੇ 7 ਸਥਿਤ ਹਨ । ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ਹਰੇਕ ਸਥਿਤੀ ਵਿੱਚ ਦੱਸੋ ਕਿ, ਕੀ EF ||QR ਹੈ :
(i) PE = 3.9 cm, EQ=3 cm,
PF = 3.6 cm ਅਤੇ FR = 2.4 cm
(ii) PE = 4 cm, QE = 4.5 cm,
PF = 8 cm ਅਤੇ RF = 9 cm
(iii) PQ = 1.28 cm, PR = 2.56 cm,
PE = 0.18 cm ਅਤੇ PF = 0.36 cm.
ਹੱਲ:
△PQR ਵਿੱਚ ਦੋ ਬਿੰਦੂ ਕੁਮਵਾਰ E ਅਤੇ F ਭੁਜਾ PQ ਅਤੇ PR ਉੱਤੇ ਸਥਿਤ ਹਨ ।

(i) PE = 3.9 cm, EQ = 3 cm
PF = 3.6 cm, FR = 2.4 cm
\(\frac{PE}{EQ}\) = \(\frac{3.9}{3}\) = \(\frac{39}{30}\) = \(\frac{13}{10}\) = 1.3
\(\frac{PF}{FR}\) = \(\frac{3.6}{2.4}\) = \(\frac{36}{24}\) = \(\frac{3}{2}\) = 1.5
\(\frac{PE}{EQ}\) ≠ \(\frac{PF}{FR}\)
∴ EF, QR ਦੋ ਸਮਾਂਤਰ ਨਹੀਂ ਹੈ

(ii) PE = 4 cm, QE = 4.5 cm
PF = 8 cm, RF = 9 cm
\(\frac{PE}{QE}\) = \(\frac{4}{4.5}\) = \(\frac{40}{45}\) = \(\frac{8}{9}\) … (1)
\(\frac{PF}{RF}\) = \(\frac{8}{9}\) …(2)
(1) ਅਤੇ (2) ਤੋਂ,
\(\frac{PE}{QE}\) = \(\frac{PF}{RF}\)
∴ ਮੂਲ ਸਮਾਨ ਅਨੁਪਾਤਤਾ ਪ੍ਰਮੇਯ ਦੇ ਵਿਲੋਮ ਤੋਂ EF || QR.

(iii) PQ = 1.28 cm, PR = 2.56 cm
PE = 0.18 cm, PF = 0.36 cm
EQ = PQ – PE = 1.28 – 0.18 = 1.10 cm
ER = PR – PF = 2.56 -0.36 = 2.20 cm
ਇੱਥੇ \(\frac{PE}{EQ}\) = \(\frac{0.18}{1.10}\) = \(\frac{18}{110}\) = \(\frac{9}{55}\) … (1)
ਅਤੇ \(\frac{PF}{FR}\) = \(\frac{0.36}{2.20}\) = \(\frac{36}{220}\) = \(\frac{9}{55}\) …..(2)
(1) ਅਤੇ (2) ਤੋਂ, \(\frac{PE}{EQ}\) = \(\frac{PF}{FR}\)
∴ ਮੂਲ ਸਮਾਨ ਅਨੁਪਾਤਤਾ ਪ੍ਰਮੇਯ ਦੇ ਵਿਲੋਮ ਤੋਂ
EF || QR.

ਪ੍ਰਸ਼ਨ 3.
ਚਿੱਤਰ ਵਿੱਚ ਜੇਕਰ LM || CB ਅਤੇ
LN || CD ਹੋਵੇ, ਤਾਂ ਸਿੱਧ ਕਰੇ ਕਿ \(\frac{AM}{AB}\) = \(\frac{AN}{AD}\) ਹੈ

ਹੱਲ:
△ABC ਵਿਚ
LM || CB (ਦਿੱਤਾ ਹੈ।)
∴ \(\frac{AM}{MB}\) = \(\frac{AL}{LC}\)
(ਮੂਲ ਸਮਾਨ ਅਨੁਪਾਤ ਪ੍ਰਮੇਯ ਅਨੁਸਾਰ)
ਦੁਬਾਰਾ △ACD ਵਿੱਚ,
LN || CD (ਦਿੱਤਾ ਹੈ।)
∴ \(\frac{AN}{ND}\) = \(\frac{AL}{LC}\) …(2)
ਮੂਲ ਸਮਾਨ ਅਨੁਪਾਤਤਾ ਪ੍ਰਮੇਯ ਅਨੁਸਾਰ)
(1) ਅਤੇ (2) ਤੋਂ,

ਪ੍ਰਸ਼ਨ 4.
ਚਿੱਤਰ ਵਿਚ DE || A ਅਤੇ DF || AE ਹੈ । ਸਿੱਧ ਕਰੋ ਕਿ \(\frac{BF}{FE}\) = \(\frac{BE}{EC}\) ਹੈ ॥

ਹੱਲ:
△ABC ਵਿੱਚ
DE || AC (ਦਿੱਤਾ ਹੈ।)

∴ \(\frac{BD}{DA}\) = \(\frac{BE}{EC}\) …(1)
ਮੂਲ ਸਮਾਨ ਅਨੁਪਾਤ ਪ੍ਰਮੇਯ ਅਨੁਸਾਰ △ABE ਵਿੱਚ,
DF || AE (ਦਿੱਤਾ ਹੈ।)
∴ \(\frac{BD}{DA}\) = \(\frac{BF}{FE}\) …(2)
ਮੂਲ ਸਮਾਨ ਅਨੁਪਾਤਤਾ ਪ੍ਰਮੇਯ ਅਨੁਸਾਰ
(1) ਅਤੇ (2) ਤੋਂ,
\(\frac{BE}{EC}\) = \(\frac{BF}{FE}\)

ਪ੍ਰਸ਼ਨ 5.
ਚਿੱਤਰ ਵਿਚ DE || OQ ਅਤੇ DF | OR ਹੈ । ਦਿਖਾਉ ਕਿ EF ||QR ਹੈ ।

ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △PQR ਵਿੱਚ, DE||OQ ਅਤੇ
DF || OR.
ਸਿੱਧ ਕਰਨਾ ਹੈ : EF|QR.
ਸਬੂਤ : △PQO ਵਿਚ,
ED || QO (ਦਿੱਤਾ ਹੈ।)

∴ \(\frac{PD}{DO}\) = \(\frac{PF}{EQ}\) …(1)
[ਮੂਲ ਸਮਾਨ ਅਨੁਪਾਤਤਾ ਪ੍ਰਮੇਯ ਤੋਂ।]
ਦੁਬਾਰਾ △POR ਵਿੱਚ,
DF || OR (ਦਿੱਤਾ ਹੈ )
∴ \(\frac{PD}{DO}\) = \(\frac{PF}{FR}\) …(2)
[ਮੂਲ ਸਮਾਨ ਅਨੁਪਾਤਤਾ ਪ੍ਰਮੇਯ ਤੋਂ ]
(1) ਅਤੇ (2) ਤੋਂ,
\(\frac{PE}{EQ}\) = \(\frac{PF}{FR}\)
△PQR ਵਿੱਚ ਮੂਲ ਸਮਾਨ ਅਨੁਪਾਤਤਾ ਪ੍ਰਮੇਯ ਦੇ ਵਿਲੋਮ ,
EF || QR.

ਪ੍ਰਸ਼ਨ 6.
ਚਿੱਤਰ ਵਿਚ ਕੁਮਵਾਰ OP, OQ ਅਤੇ OR ਉੱਤੇ ਸਥਿਤ ਬਿੰਦੂ A, B ਅਤੇ Cਇਸ ਤਰ੍ਹਾਂ ਹਨ ਕਿ AB || PQ ਅਤੇ AC|| PR ਹੈ । ਦਰਸਾਉ ਕਿ BC|QR ਹੈ ।

ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △PQR ਵਿਚ ਬਿੰਦੂ A, B ਅਤੇ C ਕੁਮਵਾਰ OP, 0Q ਅਤੇ OR ਉੱਤੇ ਇਸ ਤਰ੍ਹਾਂ ਸਥਿਤ ਹਨ ਕਿ AB || PQ ਅਤੇ AC || PR ਹੈ ।

ਸਿੱਧ ਕਰਨਾ ਹੈ : BC || QR.
ਸਬੂਤ : △OPQ ਵਿੱਚ,
AB || PQ (ਦਿੱਤਾ ਹੈ।)
∴ \(\frac{OA}{AP}\) = \(\frac{OB}{BQ}\) …(1)
[ਮੂਲ ਸਮਾਨ ਅਨੁਪਾਤ ਪ੍ਰਮੇਯ ਤੋਂ]
ਦੁਬਾਰਾ △OPR ਵਿੱਚ,
AC || PR (ਦਿੱਤਾ ਹੈ।)
∴ \(\frac{OA}{AP}\) = \(\frac{OC}{CR}\) …(2)
[ਮੂਲ ਸਮਾਨ ਅਨੁਪਾਤ ਪ੍ਰਮੇਯ ਤੋਂ]
(1) ਅਤੇ (2) ਤੋਂ,
\(\frac{OB}{BQ}\) = \(\frac{OC}{CR}\)
∴ ਮੂਲ ਸਮਾਨ ਅਨੁਪਾਤਤਾ ਮੇਯ ਦੇ ਉਲਟ ਤੋਂ △OQR ਵਿੱਚ BC || QR ਹੈ ।

ਪ੍ਰਸ਼ਨ 7.
ਮੇਯ 6.1 ਦਾ ਪ੍ਰਯੋਗ ਕਰਦੇ ਹੋਏ ਸਿੱਧ ਕਰੋ ਕਿ ਇਕ ਤ੍ਰਿਭੁਜ ਦੀ ਇਕ ਭੁਜਾ ਦੇ ਮੱਧ ਬਿੰਦੂ ਵਿਚੋਂ ਦੂਸਰੀ ਭੁਜਾ ਦੇ ਸਮਾਂਤਰ ਖਿੱਚੀ ਗਈ ਰੇਖਾ ਤੀਸਰੀ ਭੁਜਾ ਨੂੰ ਸਮਦੁਭਾਜਿਤ ਕਰਦੀ ਹੈ । (ਯਾਦ ਕਰੋ ਕਿ ਤੁਸੀਂ ਇਸ ਨੂੰ ਜਮਾਤ IX ਵਿੱਚ ਸਿੱਧ ਕਰ ਚੁੱਕੇ ਹੋ ॥
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △ABC ਵਿੱਚ D, AB ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ ਭਾਵ AD = DB ਹੈ ।
BC ਦੇ ਸਮਾਂਤਰ ਰੇਖਾ AC ਨੂੰ E ਉੱਤੇ ਕੱਟਦੀ ਹੈ ਜਿਵੇਂ ਕਿ ਚਿੱਤਰ ਵਿੱਚ ਦਿਖਾਇਆ ਗਿਆ ਹੈ ਭਾਵ DE || BC ਹੈ ।

ਸਿੱਧ ਕਰਨਾ ਹੈ : E, AC ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ ।
ਸਬੂਤ : D, AB ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ ।
ਭਾਵ AD = DB (ਦਿੱਤਾ ਹੈ।)
\(\frac{AD}{BD}\) = 1 …(1)
ਦੁਬਾਰਾ △ABC ਵਿੱਚ DE || BC
∴ \(\frac{AD}{DB}\) = \(\frac{AE}{EC}\)
[ਮੂਲ ਸਮਾਨ ਅਨੁਪਾਤਤਾ ਪ੍ਰਮੇਯ ਤੋਂ।]
∴ 1 = \(\frac{AE}{EC}\) [(1) ਤੋਂ।]
∴ AE = EC
∴ E, AC ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ ।

ਪ੍ਰਸ਼ਨ 8.
ਮੇਯ 6.2 ਦਾ ਪ੍ਰਯੋਗ ਕਰਦੇ ਹੋਏ ਸਿੱਧ ਕਰੋ ਕਿ ਇਕ ਤ੍ਰਿਭੁਜ ਦੀਆਂ ਕਿਸੇ ਤੋਂ ਭੁਜਾਵਾਂ ਦੇ ਮੱਧ ਬਿੰਦੂਆਂ ਨੂੰ ਮਿਲਾਉਣ ਵਾਲੀ ਰੇਖਾ ਤੀਸਰੀ ਭੁਜਾ ਦੇ ਸਮਾਂਤਰ ਹੁੰਦੀ ਹੈ । (ਯਾਦ ਕਰੋ ਕਿ ਤੁਸੀਂ ਜਮਾਤ IX ਵਿਚ ਅਜਿਹਾ ਕਰ ਚੁੱਕੇ |
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △ABC ਵਿੱਚ, D ਅਤੇ E ਕ੍ਰਮਵਾਰ AB ਅਤੇ AC ਦੇ ਮੱਧ ਬਿੰਦੂ ਹਨ ਜਿਸ ਨਾਲ AD = BD ਅਤੇ AE = EC ਹਨ ID ਅਤੇ E ਨੂੰ ਮਿਲਾਇਆ ਗਿਆ ਹੈ ।

ਸਿੱਧ ਕਰਨਾ ਹੈ : DE || BC
ਸਬੂਤ : D, AB ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ , (ਦਿੱਤਾ ਹੈ।)
ਭਾਵ AD = BD
\(\frac{AD}{BD}\) = 1 …(1)
E, AC ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ (ਦਿੱਤਾ ਹੈ।)
∴ AE = EC
\(\frac{AE}{EC}\) = 1 …(2)
(1) ਅਤੇ (2) ਤੋਂ, \(\frac{AB}{BD}\) = \(\frac{AE}{EC}\)
ਮੂਲ ਸਮਾਨ ਅਨੁਪਾਤਤਾ ਮੇਯ ਦੇ ਪ੍ਰਯੋਗ ਤੋਂ,
DE || BC

ਪ੍ਰਸ਼ਨ 9.
ABCD ਇੱਕ ਸਮਲੰਬ ਚਤੁਰਭੁਜ ਹੈ ਜਿਸ ਵਿੱਚ AB || DC ਹੈ ਅਤੇ ਇਸਦੇ ਵਿਕਰਣ ਆਪਸ ਵਿੱਚ ਬਿੰਦੁ O ‘ਤੇ ਕੱਟਦੇ ਹਨ । ਦਿਖਾਓ ਕਿ \(\frac{AO}{BO}\) = \(\frac{CO}{DO}\) ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ABCD ਇੱਕ ਸਮਲੰਬ ਚਤੁਰਭੁਜ ਹੈ । ਜਿਸ ਵਿੱਚ AB || DC ਹੈ । ਵਿਕਰਣ AC ਅਤੇ BD ਇੱਕ-ਦੂਜੇ ਨੂੰ ਬਿੰਦੂ O ਉੱਤੇ ਕੱਟਦੇ ਹਨ ।

ਸਿੱਧ ਕਰਨਾ ਹੈ : \(\frac{AO}{BO}\) = \(\frac{CO}{DO}\)
ਰਚਨਾਂ : O ਤੋਂ FO || DC || AB ਖਿੱਚੋ ।
ਸਬੂਤ : △DAB ਵਿੱਚ
FO || AB (ਰਚਨਾ)
∴ \(\frac{DF}{FA}\) = \(\frac{DO}{BO}\) …(1)
[ਮੂਲ ਸਮਾਨ ਅਨੁਪਾਤਤਾ ਪ੍ਰਮੇਯ ਦੇ ਪ੍ਰਯੋਗ ਨਾਲ]
△DCA ਵਿੱਚ
FO || DC (ਰਚਨਾ)
\(\frac{DF}{FA}\) = \(\frac{CO}{AO}\) …(2)
[ਮੂਲ ਸਮਾਨ ਅਨੁਪਾਤਤਾ ਪ੍ਰਮੇਯ ਦੇ ਪ੍ਰਯੋਗ ਦੁਆਰਾ]
(1) ਅਤੇ (2) ਤੋਂ, \(\frac{DO}{BO}\) = \(\frac{CO}{AO}\) ⇒ \(\frac{AO}{BO}\) = \(\frac{CO}{DO}\)

ਪ੍ਰਸ਼ਨ 10.
ਇਕ ਚਤੁਰਭੁਜ ABCD ਦੇ ਵਿਕਰਣ ਆਪਸ ਵਿੱਚ ਬਿੰਦੂ O ਉੱਤੇ ਇਸ ਤਰ੍ਹਾਂ ਕੱਟਦੇ ਹਨ ਕਿ \(\frac{AO}{BO}\) = \(\frac{CO}{DO}\) ਹੈ । ਦਿਖਾਓ ਕਿ ABCD ਇੱਕ ਸਮਲੰਬ ਚਤੁਰਭੁਜ ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਚਤੁਰਭੁਜ ABCD ਵਿੱਚ ਵਿਕਰਣ AC ਅਤੇ BD ਆਪਸ ਵਿੱਚ ਬਿੰਦੂ O ਉੱਤੇ ਇਸ ਤਰ੍ਹਾਂ ਕੱਟਦੇ ਹਨ ਕਿ \(\frac{AO}{BO}\) = \(\frac{CO}{DO}\) ਹੈ ।

ਸਿੱਧ ਕਰਨਾ ਹੈ : ਚਤੁਰਭੁਜ ABCD ਇੱਕ ਸਮਲੰਬ ਚਤੁਰਭੁਜ ਹੈ।
ਰਚਨਾ : ‘O’ ਤੋਂ ਇੱਕ ਰੇਖਾ EO || AB ਖਿੱਚੋ ਜੋ AD ਨੂੰ E ਉੱਤੇ ਮਿਲਦੀ ਹੈ ।
ਸਬੂਤ : △DAB ਵਿੱਚ
EO || AB
∴ \(\frac{DE}{EA}\) = \(\frac{DO}{OB}\) …(1)
[ਮੂਲ ਸਮਾਨ ਅਨੁਪਾਤਤਾ ਪ੍ਰਮੇਯ ਦੇ ਪ੍ਰਯੋਗ ਦੁਆਰਾ]
ਪਰ \(\frac{AO}{BO}\) = \(\frac{CO}{DO}\) (ਦਿੱਤਾ ਹੈ।)
ਜਾਂ \(\frac{AO}{CO}\) = \(\frac{BO}{DO}\)
ਜਾਂ \(\frac{CO}{AO}\) = \(\frac{DO}{BO}\)
⇒ \(\frac{DO}{OB}\) = \(\frac{CO}{AO}\) …(2)
(1) ਅਤੇ (2) ਤੋਂ, \(\frac{DE}{EA}\) = \(\frac{CO}{AO}\)
∴ ਮੂਲ ਸਮਾਨ ਅਨੁਪਾਤਤਾ ਪ੍ਰਮੇਯ ਦੇ ਪ੍ਰਯੋਗ ਦੁਆਰਾ
EO || DC
ਨਾਲ ਹੀ, EO || AB
⇒ AB || DC
∴ ਚਤੁਰਭੁਜ ABCD ਇਕ ਸਮਲੰਬ ਚਤੁਰਭੁਜ ਹੈ ਜਿਸ AB || CD.

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 6 ਤ੍ਰਿਭੁਜ Ex 6.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 6 ਤ੍ਰਿਭੁਜ Exercise 6.1

ਪ੍ਰਸ਼ਨ 1.
ਬਰੈਕਟਾਂ ਵਿੱਚ ਦਿੱਤੇ ਗਏ ਸ਼ਬਦਾਂ ਵਿਚੋਂ ਸਹੀ ਸ਼ਬਦਾਂ ਦਾ ਪ੍ਰਯੋਗ ਕਰਕੇ, ਖ਼ਾਲੀ ਸਥਾਨ ਭਰੋ :
(i) ਸਾਰੇ ਚੱਕਰ ………. ਹੁੰਦੇ ਹਨ । (ਸਰਬੰਗਸਮ , ਸਮਰੂਪ)
(ii) ਸਾਰੇ ਵਰਗ …………… ਹੁੰਦੇ ਹਨ । (ਸਮਰੂਪ, ਸਰਬੰਗਮ)
(iii) ਸਾਰੇ ……………. ਤ੍ਰਿਭੁਜ ਸਮਰੂਪ ਹੁੰਦੇ ਹਨ । (ਸਮਦੋਭੁਜੀ, ਸਮਭੁਜੀ)
(iv) ਭੁਜਾਵਾਂ ਦੀ ਇੱਕ ਸਮਾਨ ਸੰਖਿਆ ਵਾਲੇ ਦੋ ਬਹੁਭੁਜ ਸਮਰੂਪ ਹੁੰਦੇ ਹਨ ਜੇਕਰ
(i) ਉਨ੍ਹਾਂ ਦੇ ਸੰਗਤ ਕੋਣ ……….. ਹੋਣ ਅਤੇ
(ii) ਉਨ੍ਹਾਂ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ……. ਹੋਣ । (ਬਰਾਬਰ, ਸਮਾਨੁਪਾਤੀ)
ਹੱਲ:
(i) ਸਾਰੇ ਚੱਕਰ ਸਮਰੂਪ ਹੁੰਦੇ ਹਨ ।
(ii) ਸਾਰੇ ਵਰਗ ਸਮਰੂਪ ਹੁੰਦੇ ਹਨ ।
(iii) ਸਾਰੇ ਸਮਭੁਜੀ ਤ੍ਰਿਭੁਜ ਸਮਰੂਪ ਹੁੰਦੇ ਹਨ ।
(iv) ਭੁਜਾਵਾਂ ਦੀ ਇੱਕ ਸਮਾਨ ਸੰਖਿਆ ਵਾਲੇ ਦੋ ਬਹੁਭੁਜ ਸਮਰੂਪ ਹੁੰਦੇ ਹਨ, ਜੇਕਰ
(i) ਉਨ੍ਹਾਂ ਦੇ ਸੰਗਤ ਕੋਣ ਬਰਾਬਰ ਹੋਣ ਅਤੇ
(ii) ਉਨ੍ਹਾਂ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਸਮਾਨੁਪਾਤੀ ਹੋਣ ।

ਪ੍ਰਸ਼ਨ 2.
ਹੇਠ ਲਿਖੇ ਜੋੜਿਆਂ ਦੀਆਂ ਦੋ ਭਿੰਨ-ਭਿੰਨ ਉਦਾਹਰਣਾਂ ਦਿਉ ।
(i) ਸਮਰੂਪ ਚਿੱਤਰ
(ii) ਅਜਿਹੇ ਚਿੱਤਰ ਜੋ ਸਮਰੂਪ ਨਹੀਂ ਹਨ ।
ਹੱਲ:
(i) (a) ਸਮਭੁਜੀ ਤ੍ਰਿਭੁਜਾਂ ਦੇ ਜੋੜੇ ਸਮਰੂਪ ਆਕ੍ਰਿਤੀਆਂ ਹਨ ,
(b) ਵਰਗਾਂ ਦੇ ਜੋੜੇ ਸਮਰੂਪ ਆਕ੍ਰਿਤੀਆਂ ਹਨ ।
(ii) (a) ਇੱਕ ਤ੍ਰਿਭੁਜ ਅਤੇ ਇਕ ਚਤੁਰਭੁਜ ਇਹੋ ਜਿਹੀ ਅਕੂਤੀਆਂ ਹਨ ਜੋ ਸਮਰੂਪ ਨਹੀਂ ਹਨ ।
(b) ਇਕ ਵਰਗ ਅਤੇ ਸਮ ਚਤੁਰਭੁਜ ਅਜਿਹੇ ਜੋੜੇ ਹਨ ਜੋ ਸਮਰੂਪ ਨਹੀਂ ਹਨ ।

ਪ੍ਰਸ਼ਨ 3.
ਦੱਸੋ ਕਿ ਹੇਠ ਦਿੱਤੇ ਚਤੁਰਭੁਜ ਸਮਰੂਪ ਹਨ ਜਾਂ ਨਹੀਂ :

ਹੱਲ:
ਦੋਵੇਂ ਚਤੁਰਭੁਜ ਸਮਰੂਪ ਨਹੀਂ ਹਨ ਕਿਉਂਕਿ ਉਨ੍ਹਾਂ ਦੇ ਸੰਗਤ ਕੋਣ ਬਰਾਬਰ ਨਹੀਂ ਹਨ ।

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 5 ਅੰਕਗਣਿਤਕ ਲੜੀਆਂ Ex 5.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 5 ਅੰਕਗਣਿਤਕ ਲੜੀਆਂ Exercise 5.4

ਪ੍ਰਸ਼ਨ 1.
A.P. : 121, 117, 113, … ਦਾ ਕਿਹੜਾ ਸਭ ਤੋਂ ਪਹਿਲਾ ਰਿਣਾਤਮਕ ਪਦ ਹੋਵੇਗਾ ?
ਸਿੰਕੇਤ : a_n < 0 ਦੇ ਲਈ 1 ਪਤਾ ਕਰੋ ।
ਹਲ:
ਦਿੱਤੀ ਹੋਈ A.P. ਹੈ ।
121, 117, 113, …
ਇੱਥੇ a = T₁ = 121 ; T₂ = 117; T₃ = 113
d = T₂ = T₁ = 117 – 121 = -4
ਸੂਤਰ T_n = a + (n – 1) d ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ਤੇ
T_n = 121 + (n – 1) (-4)
= 121 – 4n + 4
= 125 – 4n
ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ
T_n < 0
125 – 4n < 0 4n > 125
n > \(\frac{125}{4}\)
n > 31\(\frac{1}{4}\)
ਪਰ ਪਹਿਲੇ ਰਿਣਾਤਮਕ ਪਦ ਲਈ n ਸੰਪੂਰਨ ਸੰਖਿਆ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ।
∴ n = 32
∴ ਦਿੱਤੀ ਗਈ A.P. ਦਾ 32ਵਾਂ ਪਦ ਪਹਿਲਾ ਰਿਣਾਤਮਕ ਪਦ ਹੋਵੇਗਾ ।

ਪ੍ਰਸ਼ਨ 2.
ਕਿਸੇ A.P. ਦੇ ਤੀਸਰੇ ਅਤੇ ਸੱਤਵੇਂ ਪਦਾਂ ਦਾ ਜੋੜ 6 ਹੈ ਅਤੇ ਉਨ੍ਹਾਂ ਦਾ ਗੁਣਨਫਲ 8 ਹੈ । ਇਸ A.P. ਦੇ ਪਹਿਲੇ 16 ਪਦਾਂ ਦਾ ਜੋੜਫਲ ਪਤਾ ਕਰੋ ।
ਹਲ:
ਮੰਨ ਲਉ ‘a’ ਅਤੇ ‘d’ ਦਿੱਤੀ ਹੋਈ A.P. ਦਾ ਪਹਿਲਾ ਪਦ ਅਤੇ ਸਾਂਝਾ ਅੰਤਰ ਹੈ ।
ਪਹਿਲੀ ਸ਼ਰਤ ਅਨੁਸਾਰ,
T₃ + T₇ = 6
[a + (3 – 1)d] + [a + (7 – 1) d] = 6
|∵ T_n = a + (n – 1)d
a + 2d + a + 6d = 6
2a + 8d = 6
a + 4d = 3 …(1)
ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ,
T₃(T₇) = 8
[a + (3 – 1) d] [a + (7 – 1) d] = 8
|∵ T_n = a + (n – 1) d
(a + 2d) (a + 6d) = 8
[3 – 4d + 2] [3 – 4d + 6d] = 8
[(1) ਤੋਂ a = 3 – 4d]
(3 – 2d) (3 + 2d) = 8
9 – 4d² = 8
4d² =9 – 8
d² = \(\frac{1}{4}\)
d = ±\(\frac{1}{2}\)
ਸਥਿਤੀ I. ਜਦੋਂ d = \(\frac{1}{2}\)
d = \(\frac{1}{2}\) ਦਾ ਮੁੱਲ (1) ਵਿਚ ਰੱਖਣ ‘ਤੇ ਮਿਲਦਾ ਹੈ
a + 4\(\left(\frac{1}{2}\right)\) = 3
a + 2 = 3
a = 3 – 2 = 1
ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਕੇ \(\frac{n}{2}\) = [2a + (n – 1) d]
S_n = \(\frac{16}{2}\)[2(1) + (16 – 1)\(\frac{1}{2}\)]
= 8[2 + \(\frac{15}{2}\)]
= 8[latex]\frac{4+15}{2}[/latex]
= 8 × \(\frac{19}{2}\)
S₁₆ = 76.
ਸਥਿਤੀ II. ਜਦੋਂ ਵੀ d = \(-\frac{1}{2}\)
d = \(-\frac{1}{2}\) ਦਾ ਮੁੱਲ (1) ਵਿਚ ਰੱਖਣ ‘ਤੇ

S₁₆ = 20.

ਪ੍ਰਸ਼ਨ 3.
ਇੱਕ ਪੌੜੀ ਦੇ ਲਗਾਤਾਰ ਡੰਡੇ ਆਪਸ ਵਿੱਚ 25 cm ਦੀ ਦੂਰੀ ‘ਤੇ ਹਨ (ਦੇਖੋ ਚਿੱਤਰ ( ਡੰਡਿਆਂ ਦੀ ਲੰਬਾਈ ਇਕ ਸਮਾਨ ਰੂਪ ਨਾਲ ਘੱਟਦੀ ਜਾਂਦੀ ਹੈ ਅਤੇ ਸਭ ਤੋਂ ਹੇਠਲੇ ਡੰਡੇ ਦੀ ਲੰਬਾਈ 45 cm ਅਤੇ ਸਭ ਤੋਂ ਉਪਰਲੇ ਡੰਡੇ ਦੀ ਲੰਬਾਈ 25 cm ਹੈ । ਜੇਕਰ ਉਪਰਲੇ ਅਤੇ ਹੇਠਲੇ ਡੰਡੇ ਦੇ ਵਿਚਕਾਰਲੀ ਦੂਰੀ 2\(\frac{1}{2}\) m ਹੈ ਤਾਂ ਡੰਡਿਆਂ ਨੂੰ ਬਣਾਉਣ ਲਈ ਲੱਕੜੀ ਦੀ ਕਿੰਨੀ ਲੰਬਾਈ ਦੀ ਲੋੜ ਹੋਵੇਗੀ ?

ਸੰਕੇਤ : ਡੰਡਿਆਂ ਦੀ ਸੰਖਿਆਂ = \(\frac{250}{25}\) + 1 ਹੈ ।
ਹਲ:
ਡੰਡਿਆਂ ਵਿਚਕਾਰਲੀ ਕੁਲ ਲੰਬਾਈ
= 2\(\frac{1}{2}\)m = \(\frac{5}{2}\)m
= (\(\frac{5}{2}\) × 100)m
= 250 cm
ਹਰੇਕ ਡੰਡੇ ਦੀ ਲੰਬਾਈ = 25 cm

= \(\frac{250}{25}\) = 10
ਪਹਿਲੇ ਡੰਡੇ ਦੀ ਲੰਬਾਈ = 45 cm
ਇੱਥੇ a = 45; l = 25 ; n = 10
ਡੰਡਿਆਂ ਦੇ ਲਈ ਲਕੜੀ ਦੀ ਲੰਬਾਈ = S₁₀
= \(\frac{n}{2}\)[a + l]
= \(\frac{10}{2}\)[45 + 25]
= 5 (70)
= 350.
ਡੰਡਿਆਂ ਲਈ ਲੋੜੀਂਦੀ ਲਕੜੀ ਦੀ ਲੰਬਾਈ 350 cm ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
ਇਕ ਕਤਾਰ ਵਿੱਚ ਮਕਾਨਾਂ ਨੂੰ ਲਗਾਤਾਰ ਸੰਖਿਆਂ ਤੋਂ 49 ਨਾਲ ਦਰਸਾਇਆ ਗਿਆ ਹੈ । ਦਿਖਾਉ ਕਿ 1 ਦਾ ਇੱਕ ਅਜਿਹਾ ਮੁੱਲ ਹੈ ਕਿ x ਨਾਲ ਦਰਸਾਏ ਮਕਾਨ ਤੋਂ ਪਹਿਲੇ ਦੇ ਮਕਾਨਾਂ ਦੀ ਸੰਖਿਆਵਾਂ ਦਾ ਜੋੜ ਉਸ ਤੋਂ ਬਾਅਦ ਵਾਲੇ ਮਕਾਨਾਂ ਦੀ ਸੰਖਿਆਵਾਂ ਦੇ ਜੋੜ ਦੇ ਬਰਾਬਰ ਹੈ । ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ । | [ਸੰਕੇਤ : S_x-1= S₄₉ – S_x ਹੈ ]
ਹਲ:
ਮੰਨ ਲਉ x’ ਕਿਸੇ ਮਕਾਨ ਦੀ ਸੰਖਿਆਂ ਨੂੰ ਦਰਸਾਉਂਦਾ ਹੈ ।
ਇੱਥ a = T₁ = 1; d = 1
ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ
S_x-1 = S₄₉ – S_x
= \(\frac{x-1}{2}\)[2(1) + (x – 1 – 1) (1)]
= \(\frac{49}{2}\)[1 + 49] – \(\frac{x}{2}\)[2 (1) + (x -1)(1)]
[ਸੂਤਰ S_n = \(\frac{n}{2}\)[2a + (n – 1)d]
ਅਤੇ \(\frac{n}{2}\)(a + l) ਦਾ ਪ੍ਰਯੋਗ ਕਰਕੇ

x² = 1225
x = 35

ਪ੍ਰਸ਼ਨ 5.
ਇੱਕ ਫੁੱਟਬਾਲ ਦੇ ਮੈਦਾਨ ਵਿਚ ਇੱਕ ਛੋਟਾ ਚਬੂਤਰਾ ਹੈ | ਜਿਸ ਵਿਚ 15 ਪੌੜੀਆਂ ਬਣੀਆਂ ਹੋਈਆਂ ਹਨ । ਇਨ੍ਹਾਂ ਪੌੜੀਆਂ ਵਿਚੋਂ ਹਰੇਕ ਦੀ ਲੰਬਾਈ 50 m ਹੈ ਅਤੇ ਠੋਸ ਕੰਕਰੀਟ ਦੀ ਬਣੀ ਹੋਈ ਹੈ । ਹਰੇਕ ਪੌੜੀ ਵਿੱਚ \(\frac{1}{4}\) m ਦੀ ਚੌੜਾਈ ਅਤੇ \(\frac{1}{2}\) m ਦਾ ਫੈਲਾਵ (ਚੌੜਾਈ) ਹੈ । (ਦੇਖੋ ਚਿੱਤਰ) । ਇਸ ਚਬੂਤਰੇ ਨੂੰ ਬਣਾਉਣ ਲਈ ਲੱਗੀ ਕੰਕਰੀਟ ਦਾ ਕੁਲ ਆਇਤਨ ਪਤਾ ਕਰੋ ।
[ਸੰਕੇਤ : ਪਹਿਲੀ ਪੌੜੀ ਨੂੰ ਬਣਾਉਣ ਲਈ ਲੱਗੀ ਕੰਕਰੀਟ ਦਾ ਆਇਤਨ \(\frac{1}{4}\) × \(\frac{1}{2}\) × 50 m²ਹੈ ॥]

ਹੱਲ :
ਪਹਿਲੀ ਪੌੜੀ ਬਣਾਉਣ ਵਿਚ ਲੱਗੀ ਕੰਕਰੀਟ ਦਾ
ਆਇਤਨ = (\(\frac{1}{4}\) × \(\frac{1}{2}\) × 50) m³
= \(\left(\frac{25}{4}\right)\) m³
ਦੂਸਰੀ ਪੌੜੀ ਬਣਾਉਣ ਵਿਚ ਲੱਗੀ ਕੰਕ੍ਰਿਟ ਦਾ ਆਇਤਨ
= (\(\frac{2}{4}\) × \(\frac{1}{2}\) × 50) m³
= \(\left(\frac{25}{2}\right)\) m³
ਤੀਸਰੀ ਪੌੜੀ ਬਣਾਉਣ ਵਿਚ ਲੱਗੀ ਕੰਕਰੀਟ ਦਾ ਆਇਤਨ
= (\(\frac{3}{4}\) × \(\frac{1}{2}\) × 50) m³
= \(\left(\frac{75}{4}\right)\) m³
ਇਸੇ ਤਰ੍ਹਾਂ ਅੱਗੋਂ 15 ਪੌੜੀਆਂ ਹਨ ।

ਚਬੂਤਰਾ ਬਣਾਉਣ ਵਿਚ ਲੱਗੇ ਕੰਕਰੀਟ ਦਾ ਆਇਤਨ
= S₁₅

∴ ਚਬੂਤਰਾ ਬਣਾਉਣ ਲਈ ਲੋਂੜੀਦਾ ਦਾ ਕੰਕਰੀਟ = 750 m³

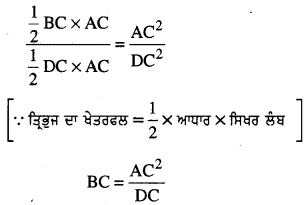
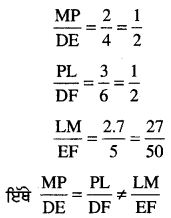
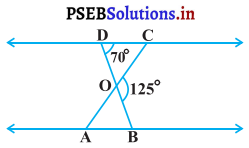
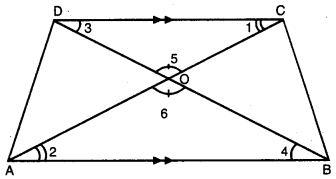
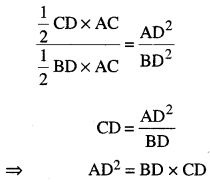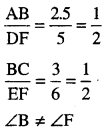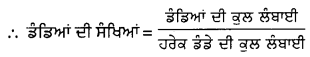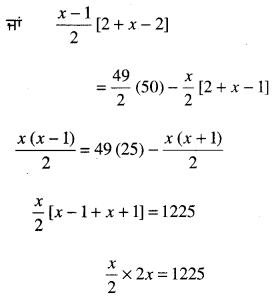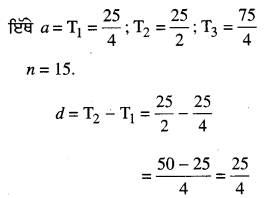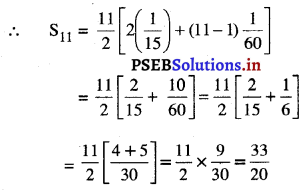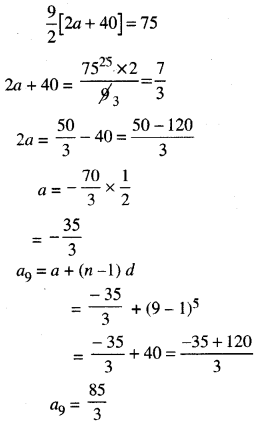Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 5 ਅੰਕਗਣਿਤਕ ਲੜੀਆਂ Ex 5.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 5 ਅੰਕਗਣਿਤਕ ਲੜੀਆਂ Exercise 5.3

1. ਹੇਠ ਦਿੱਤੀਆਂ ਅੰਕ ਗਣਿਤਕ ਲੜੀਆਂ ਦਾ ਜੋੜਫਲ ਪਤਾ ਕਰੋ :

ਪ੍ਰਸ਼ਨ (i).
2, 7, 12, … 10 ਪਦਾਂ ਤੱਕ
ਉੱਤਰ:
ਦਿੱਤੀ ਹੋਈ A.P. ਹੈ : 2, 7, 12, …
ਇੱਥੇ = 2, d = 7 – 2 = 5, n = 10
ਸੂਤਰ S_n = \(\frac{n}{2}\)[2a + (n – 1) d] ਦਾ ਪ੍ਰਯੋਗ ਕਰਕੇ
∴ S₁₀ = \(\frac{10}{2}\)[2 × 2 + (10 – 1) 5]
= 5 [4 + 45] = 95

ਪ੍ਰਸ਼ਨ (ii).
– 37, – 33, – 29… 12 ਪਦਾਂ ਤੱਕ
ਉੱਤਰ:
ਦਿੱਤੀ ਹੋਈ A.P. ਹੈ : 37, – 33, – 29…
ਇੱਥੇ a = – 37, d = – 33 + 37 = 4, n = 12
ਸੂਤਰ S_n = \(\frac{n}{2}\)[2a + (n – 1) d] ਦਾ ਪ੍ਰਯੋਗ ਕਰਕੇ
∴ S₁₂ = \(\frac{12}{2}\)[2(-37) + (12 – 1) 4]
= 6 [-74 + 44]
= – 180

ਪ੍ਰਸ਼ਨ (iii).
0.6, 1.7, 2.8, … 100 ਪਦਾਂ ਤੱਕ
ਉੱਤਰ:
ਦਿੱਤੀ ਹੋਈ A.P. ਹੈ 0.6, 1.7, 2.8,….
ਇੱਥੇ a = 0.6, d = 1.7 – 0.6 = 1.1
n = 100
ਇੱਥੇ S_n = \(\frac{n}{2}\)[2a + (n – 1) ] ਦਾ ਪ੍ਰਯੋਗ ਕਰਕੇ
∴ S₁₀₀ = \(\frac{100}{2}\)[2(0.6) + (100 – 1) 1.1]
= 50 [1.2 + 108.9]
= 5505

ਪ੍ਰਸ਼ਨ (iv).
\(\frac{1}{15}\), \(\frac{1}{12}\), \(\frac{1}{10}\), ….. 11 ਪਦਾਂ ਤੱਕ ।
ਉੱਤਰ:
ਦਿੱਤੀ ਹੋਈ A.P. ਹੈ :
\(\frac{1}{15}\), \(\frac{1}{12}\), \(\frac{1}{10}\), …..
ਇੱਥੇ a = \(\frac{1}{15}\),
d = \(\frac{1}{12}\) – \(\frac{1}{15}\) = \(\frac{5-4}{60}\)
= \(\frac{1}{60}\),
n = 11
ਸੂਤਰ S_n = \(\frac{n}{2}\)[2a + (n – 1)] ਦਾ ਪ੍ਰਯੋਗ ਤੋਂ

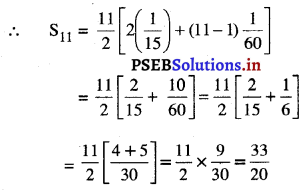
2. ਹੇਠ ਦਿੱਤਿਆਂ ਦਾ ਜੋੜਫਲ ਪਤਾ ਕਰੋ :

ਪ੍ਰਸ਼ਨ (i).
7 + 10\(\frac{1}{2}\) + 14 + … + 84
ਉੱਤਰ:
ਦਿੱਤੀ ਹੋਈ A.P. ਹੈ :
7 + 10\(\frac{1}{2}\) + 14 + … + 84
ਇੱਥੇ a = 7, d = 10\(\frac{1}{2}\) – 7 = \(\frac{21}{2}\) – 7
= \(\frac{21-14}{2}\) = \(\frac{7}{2}\)
ਅਤੇ l = T_n = 84
a + (n – 1) d = 84
7 + (n – 1)\(\frac{7}{2}\) = 84
(n – 1)\(\frac{7}{2}\) = 84 – 7 = 77
n – 1 = 77 × \(\frac{2}{7}\) = 22
n = 22 + 1 = 23
ਹੁਣ S₂₃ = \(\frac{23}{2}\)[7 + 84] |∵ S_n = \(\frac{n}{2}\)[a + l]
\(\frac{23}{2}\) × 91 = 2093

ਪ੍ਰਸ਼ਨ (ii).
34 + 32 + 30 + … + 10
ਉੱਤਰ:
ਦਿੱਤੀ ਹੋਈ A.P. ਹੈ
34 + 32 + 30 +… + 10
a = 34, d = 32 – 34 = – 2 l = T_n = 10
a + (n – 1) d = 10
34 + (n – 1) (-2) = 10
– 2(n – 1) = 10 – 34 = – 24
n – 1 = \(\frac{24}{2}\) = 12
n = 12 + 1 = 13
S₁₃ = \(\frac{13}{2}\)[34 + 10]
= \(\frac{13}{2}\) 44 |∵ S_n = \(\frac{n}{2}\)[a + l]
= 13 × 22 = 286

ਪ੍ਰਸ਼ਨ (iii).
– 5 +(-8) + (-11) + ….. + (-230)
ਉੱਤਰ:
ਦਿੱਤੀ ਹੋਈ A.P. ਹੈ
– 5 + (-8) + (-11) + … +(- 230)
a = -5, d = – 8 + 5 = – 3
l = T_n = – 230
a + (n – 1) d = – 230
-5 + (n – 1) (-3) = – 230
– 3 (n – 1) = – 230 + 5 = – 225
n – 1 = \(\frac{225}{3}\) = 75
n = 75 + 1 = 76
S₇₆ = \(\frac{76}{2}\)[-5 + (-230)] |∵ S_n = \(\frac{n}{2}\)[a + l]
= 38 (-235)
= – 8930

3. ਇੱਕ AP ਵਿੱਚ

ਪ੍ਰਸ਼ਨ (i).
a = 5, d = 3 ਅਤੇ a_n = 50 ਦਿੱਤਾ ਹੈ । n ਅਤੇ S_n ਪਤਾ ਕਰੋ
ਉੱਤਰ:
ਦਿੱਤਾ ਹੈ : a = 5, d = 3, a_n = 50
∵ a_n = 50
a + (n – 1) d = 50
5 + (n – 1) 3 = 50
3(n – 1) = 50 – 5 = 45
n – 1 = \(\frac{45}{3}\) = 15
n = 15 + 1 = 16
ਹੁਣ S_n = \(\frac{n}{2}\)[a + l]
= \(\frac{16}{2}\)[5 + 50] = 8 × 55
= 440

ਪ੍ਰਸ਼ਨ (ii).
a = 7 ਅਤੇ a₁₃ = 35 ਦਿੱਤਾ ਹੈ ।d ਅਤੇ S₁₃ ਪਤਾ ਕਰੋ ।
ਉੱਤਰ:
ਦਿੱਤਾ ਹੈ : a = 7, a₁₃ = 35
a₁₃ = 35
a + (n – 1) d = 35
7 + (13 – 1) d = 35
12d = 35 – 7 = 28
d = \(\frac{28}{12_{3}}\) = \(\frac{7}{3}\)
ਹੁਣ S₁₃ = \(\frac{13}{2}\)[7 + 35] = |∵ S_n = \(\frac{n}{2}\)[a + l]
= \(\frac{13}{2}\) × 42 = 13 × 21
= 273

ਪ੍ਰਸ਼ਨ (iii).
a₁₂ = 37 ਅਤੇ d = 3 ਦਿੱਤਾ ਹੈ a ਜੀਵ S₁₂ ਪਤਾ ਕਰੋ ।
ਉੱਤਰ:
ਦਿੱਤਾ ਹੈ : a₁₂ = 37, d = 3
∵ a₁₂ = 37
a + (n – 1) d = 37
a + (12 – 1) 3 = 37
a + 37 – 33 = 4
a + 33 = 37
a = 37 – 33 =4
S₁₂ = \(\frac{12}{2}\)[4 + 37] |S_n = \(\frac{n}{2}\)[a + l]
= 6 × 41 = 246

ਪ੍ਰਸ਼ਨ (iv).
a₃ = 15 ਅਤੇ S₁₀ = 125 ਦਿੱਤਾ ਹੈ । d ਅਤੇ a₁₀ ਪਤਾ ਕਰੋ ।
ਉੱਤਰ:
ਦਿੱਤਾ ਹੈ : a₃ = 15, S₁₀ = 125
∵ a₃ = 15
a + (n – 1) d = 15
a + (3 – 1) d = 15
a + 2d = 15 …(1)
∵ S₁₀ = 125
\(\frac{10}{2}\)[2n + (10 – 1) d] = 125
|∵ S_n = \(\frac{n}{2}\)[2a + (n – 1)d]
[24 + 9d] = 125
2a + 9d = \(\frac{125}{5}\) = 25
ਜਾਂ 2a +9d = 25 …(2)
‘a’ ਦਾ ਮੁੱਲ (2), ਵਿੱਚ ਰੱਖਣ ‘ਤੇ
2(15 – 2d) + 9d = 25
30 – 4d + 9d = 25
5d = 25 – 30
d = \(\frac{-5}{5}\) = -1
‘d’ ਦਾ ਮੁੱਲ (3) ਵਿਚ ਰੱਖਣ ‘ਤੇ
a = 15 – 2(-1)
= 15 + 2 = 17
a₁₀ = 17 + (10 – 1) (-1)
|∵ S_n = a + (n – 1) d
= 17 – 9 = 8

ਪ੍ਰਸ਼ਨ (v).
d = 5 ਅਤੇ S₉ = 75, ਦਿੱਤਾ ਹੈ । a ਅਤੇ a₉ ਪਤਾ ਕਰੋ ।
ਉੱਤਰ:
ਦਿੱਤਾ ਹੈ : d = 5, S₉ = 75
∵ S₉ = 75
\(\frac{9}{2}\)[2a + (9 – 1) 5) = 75
|∵ S_n = \(\frac{n}{2}\)[2a + (n – 1)d]

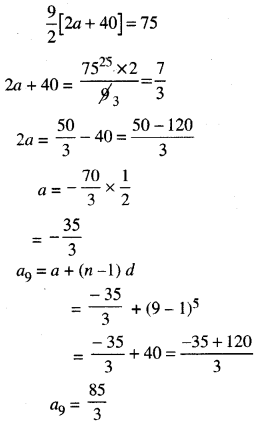
ਪ੍ਰਸ਼ਨ (vi).
a = 2, d = 8 ਅਤੇ S_n = 90 ਦਿੱਤਾ ਹੈ । n ਅਤੇ a_n ਪਤਾ ਕਰੋ ।
ਉੱਤਰ:
ਦਿੱਤਾ ਹੈ : a = 2, d = 8, S_n = 90,
∵ S_n = 90
\(\frac{n}{2}\)[2a + (n – 1) d] = 90
\(\frac{n}{2}\)[2 × 2 + (n – 1) 8] = 90
n[2 + 4n -4] = 90
n(4n – 2) = 90
4n² – 2n – 90 = 0
2n² – n – 45 = 0
2n² – 10n + 9n – 45 = 0
|S = – 2
|P = -45 × 2 = – 90
2n [n – 5] + 9 (n – 5) = 0
(2n + 9) (n – 5) = 0
2n + 9 = 0 or n – 5= 0
n = \(-\frac{9}{2}\) or n = – 5
∵ n ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੋ ਸਕਦਾ n = \(-\frac{9}{2}\) ਛਡ ਦਿੰਦੇ ਹਾਂ ।
∴ n = 5
ਹੁਣ a_n = a₅ = a + (5 – 1) d
= 2 + (5 – 1)8
= 2 + 32 = 34

ਪ੍ਰਸ਼ਨ (vii).
a = 8, a_n = 62 ਅਤੇ S_n = 210 ਦਿੱਤਾ ਹੈ । n ਅਤੇ d ਪਤਾ ਕਰੋ ।
ਉੱਤਰ:
ਦਿੱਤਾ ਹੈ : a = 8, a_n = 62, S_n = 210
∵ S_n = 210
\(\frac{n}{2}\)[a + a_n] = 210
\(\frac{n}{2}\)[8 + 6] = 210
\(\frac{n}{2}\) × 76 = 210
n = \(\frac{210}{35}\) = 6
a_n = 62
ਹੁਣ 8 + (6 – 1) d = 62
|∵ T_n = a + (n – 1) d
5d = 62 – 8 = 54
d = \(\frac{54}{5}\)

ਪ੍ਰਸ਼ਨ (viii).
a_n = 4, d = 2 ਅਤੇ S_n = – 14 ਦਿੱਤਾ ਹੈ । n ਅਤੇ a ਪਤਾ ਕਰੋ ।
ਉੱਤਰ:
ਦਿੱਤਾ ਹੈ : a_n =4, d = 2, S_n = – 14
∵ a_n = 4
a + (n – 1) d = 4
a + (n – 1)2 = 4
a + 2n – 2 = 4
a = 6 – 2n …(1)
S_n = – 14
\(\frac{n}{2}\)[a + a_n] = -14
\(\frac{n}{2}\)[6 – 2n + 4] = -14 ਦਾ ਪ੍ਰਯੋਗ ਕਰਕੇ
\(\frac{n}{2}\)[10 – 2n] = – 14
5n – n² + 14 = 0
n² – 5n – 14 = 0 |S = – 5
n² – 7n + 2n – 14 = 0 | P = 1 × – 14 = 14
n² – 7n + 2n – 14 = 0
n (n – 7) + 2 (n – 7) = 0
(n – 7) (n + 2) = 0
n = 7 ਜਾਂ n =-2
∵ n ਹਿਣਾਤਮਕ ਨਹੀਂ ਹੋ ਸਕਦਾ
∴ n = -2 ਨੂੰ ਛੱਡ ਦਿੰਦੇ ਹਾਂ ।
∴ n = 7
n ਦਾ ਮੁੱਲ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ
a = 6 – 2 × 7
= 6 – 14 = – 8

ਪ੍ਰਸ਼ਨ (ix).
a = 3, n = 8 ਅਤੇ S = 192 ਦਿੱਤਾ ਹੈ ।d ਪਤਾ ਕਰੋ ।
ਉੱਤਰ:
ਦਿੱਤਾ ਹੈ : a = 3, n = 8, S = 192
∵ S = 192
⇒ S₈ = 192 [∵ n = 8]
\(\frac{8}{2}\) [2 × 3 + (8 – 1) d]=192
|∵ S_n = \(\frac{n}{2}\)[2a + (n – 1) d]
4 [6 + 7d] = 192
6 + 7d = \(\frac{192}{4}\) =48
7d = 48 – 6 = 42
d = \(\frac{42}{7}\) = 6

ਪ੍ਰਸ਼ਨ (x).
l = 28, S = 144 ਅਤੇ ਕੁੱਲ 9 ਪਦ ਹਨ a ਪਤਾ ਕਰੋ ।
ਉੱਤਰ:
ਦਿੱਤਾ ਹੈ : l= 28, S = 144
ਹੁਣ ਕੁੱਲ ਪਦ 9 ਹਨ ।
∴ n = 9 ; l = a₉ = 28 ; S₉ = 144
∵ a₉ = 28
a + (9 – 1)d = 28
|∵ a_n = T_n = 9 + (n – 1)d
a + 8d = 28 …(1)
S₉ = 144
\(\frac{9}{2}\)[a + 28] = 144 (∵ S_n = \(\frac{n}{2}\)(a + 1))
a + 28 = \(\frac{144×2}{9}\) = 32
a = 32 – 28 = 4.

ਪ੍ਰਸ਼ਨ 4.
636 ਜੋੜ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ A.P.: 9, 17, 25 … ਦੇ ਕਿੰਨੇ ਪਦ ਲੈਣੇ ਚਾਹੀਦੇ ਹਨ ?
ਹੱਲ:
ਦਿੱਤਾ ਹੈ A.P. 9, 17, 25, ……
ਜਿੱਥੇ a = 9, d = 17 – 9 = 8
ਕਿਉਂਕਿ S_n = 636
\(\frac{n}{2}\)[2a+(n – 1) d] = 636
\(\frac{n}{2}\)[2(9) + (n – 1) 8] = 636
\(\frac{n}{2}\)[18+ 8n – 8] = 636
n[4n + 5] = 636
4n² + 5n – 636 = 0
a = 4, b = 5, c = – 636
D = (5)² – 4 × 4 × (-636)
= 25 + 10176
= 10201

∵ n ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੋ ਸਕਦਾ ।
n = \(-\frac{53}{4}\) ਨੂੰ ਛੱਡ ਦਿੰਦੇ ਹਨ ।
∴ n = 12
∴ ਦਿੱਤੀ ਗਈ A.P. ਦੇ 12 ਪਦਾਂ ਦਾ ਜੋੜ 636 ਹੈ ॥

ਪ੍ਰਸ਼ਨ 5.
ਕਿਸੇ AP. ਦਾ ਪਹਿਲਾ ਪਦ 5, ਅੰਤਿਮ ਪਦ 45 ਅਤੇ ਜੋੜਫਲ 400 ਹਨ । ਪਦਾਂ ਦੀ ਸੰਖਿਆ ਅਤੇ ਸਾਂਝਾ ਅੰਤਰ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : a = T₁ = 5; l = a_n = 45
S_n = 400
∵ T_n = 45
a + (n – 1) d = 45
5 + (n – 1)d = 45
(n – 1)d = 45 – 5 = 40
(n – 1)d = 40
S_n = 400
\(\frac{n}{2}\)[a + a_n] = 400
\(\frac{n}{2}\)[5 + 45] = 400
25n = 400
n = \(\frac{400}{25}\) = 16
n ਦਾ ਮੁੱਲ (1) ਵਿਚ ਰੱਖਣ ‘ਤੇ
(16 – 1) d = 40
15d = 40
d = \(\frac{40}{15}\) = \(\frac{8}{3}\)
n = 16, d = \(\frac{8}{3}\)

ਪ੍ਰਸ਼ਨ 6.
ਕਿਸੇ A.P. ਦਾ ਪਹਿਲਾ ਅਤੇ ਅੰਤਿਮ ਪਦ ਕੁਮਵਾਰ 17 ਅਤੇ 350 ਹਨ । ਜੇਕਰ ਸਾਂਝਾ ਅੰਤਰ 9 ਹੋਵੇ ਤਾਂ ਇਸ ਵਿੱਚ ਕਿੰਨੇ ਪਦ ਹੋਣਗੇ ਅਤੇ ਇਨ੍ਹਾਂ ਦਾ ਜੋੜਫਲ ਕਿੰਨਾ ਹੋਵੇਗਾ ?
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : a = T₁ = 17
l = a_n = 350, d = 9
∵ l = a_n = 350
a + (n -1) d = 350
17 + (n – 1) 9 = 350
9 (n – 1) = 350 – 17 = 333
n – 1 = \(\frac{333}{9}\) = 37
n = 37 + 1 = 38
ਹੁਣ S₃₈ = \(\frac{n}{2}\)[a + l]
= \(\frac{38}{2}\)[17 + 350]
= 19 × 367 = 6973
∵ ਦਿੱਤੀ ਹੋਈ A.P. ਦੇ 38 ਪਦਾਂ ਦਾ ਜੋੜ 6973 ਹੈ ।

ਪ੍ਰਸ਼ਨ 7.
ਉਸ A.P. ਦੇ ਪਹਿਲੇ 22 ਪਦਾਂ ਦਾ ਜੋੜਫਲ ਪਤਾ ਕਰੋ, ਜਿਸ ਵਿਚ d = 7 ਹੈ ਅਤੇ 22ਵਾਂ ਪਦ 149 ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : d = 7; T₂₂ = 149
n = 22
∵ T₂₂ = 149
a + (n – 1) d = 149
a + (22 – 1) 7 = 149
a + 147 = 149
a = 149 – 147 = 2
ਹੁਣ S₂₂ = \(\frac{n}{2}\)[a + T₂₂]
= \(\frac{22}{2}\)[2 + 149]
= 11 × 151 = 1661
∴ ਦਿੱਤੀ ਹੋਈ A.P. ਦੇ ਪਹਿਲੇ 22 ਪਦਾਂ ਦਾ ਜੋੜਫਲ 1661 ਹੈ ।

ਪ੍ਰਸ਼ਨ 8.
ਉਸ A.P. ਦੇ ਪਹਿਲੇ 51 ਪਦਾਂ ਦਾ ਜੋੜਫਲ ਪਤਾ ਕਰੋ, ਜਿਸਦੇ ਦੁਸਰੇ ਅਤੇ ਤੀਸਰੇ ਪਦ ਕੁਮਵਾਰ 14 ਅਤੇ 18 ਹਨ ।
ਹੱਲ:
ਮੰਨ ਲਉ ‘a’ ਅਤੇ ‘d’ ਪਹਿਲਾ ਪਦ ਅਤੇ ਸਾਂਝਾ ਅੰਤਰ ਹੈ ।
ਦਿੱਤਾ ਗਿਆ ਹੈ ਕਿ T₂ = 14; T₃ = 18
n = 51
∵ T₂ = 14
a + (n – 1) d = 14
a + (2 – 1) d = 14
a + d = 14
a = 14 – d …(1)
T₃ = 18
a + (n – 1) d = 18
a + (3 – 1) d = 18
a + 2d = 18
14 – d + 2d = 18
d = 18 – 14 = 4
d = 4
d ਦਾ ਮੁੱਲ (1) ਵਿਚ ਰੱਖਣ ‘ਤੇ
a = 14 – 4 = 10
ਹੁਣ S₅₁ = \(\frac{n}{2}\)[24 + (n – 1) d]
= \(\frac{51}{2}\)[2 × 10 + (51 – 1) 4]
= \(\frac{51}{2}\)[20 + 200]
= \(\frac{51}{2}\) × 220 = 51 × 110 = 5610
∴ ਦਿੱਤੀ ਹੋਈ A.P. ਦੇ ਪਹਿਲੇ 51 ਪਦਾਂ ਦਾ ਜੋੜ 5610 ਹੈ ।

ਪ੍ਰਸ਼ਨ 9.
ਜੇਕਰ ਕਿਸੇ A.P. ਦੇ ਪਹਿਲੇ 7 ਪਦਾਂ ਦਾ ਜੋੜਫਲ 49 ਹੈ ਅਤੇ ਪਹਿਲੇ 17 ਪਦਾਂ ਦਾ ਜੋੜ 289 ਹੈ ; ਤਾਂ ਇਸਦੇ ਪਹਿਲੇ ॥ ਪਦਾਂ ਦਾ ਜੋੜ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ a’ ਅਤੇ ‘d’ ਦਿੱਤੀ ਗਈ A.P. ਦਾ ਪਹਿਲਾ ਪਦ ਅਤੇ ਸਾਂਝਾ ਅੰਤਰ ਹੈ ।
ਪਹਿਲੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
S₇ = 49
\(\frac{n}{2}\)[2a + (n – 1) d] = 49
\(\frac{7}{2}\)[2a + (7 – 1) d] = 49
\(\frac{7}{2}\)[2a + 6d] = 49
\(\frac{7}{2}\)[2a + 6d]= 49
a + 3d = 7
a = 7 – 3d …(1)
ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
S₇ = 289
\(\frac{n}{2}\)[2a +(17 – 1) d] = 289
= \(\frac{17}{2}\)[2a + (17 – 1) d] = 289
a + 8d = \(\frac{289}{17}\) = 17
‘a’ ਦਾ ਮੁੱਲ (1) ਵਿਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਮਿਲਦਾ ਹੈ ।
7 – 3d + 8d = 17
5d = 17 – 7 = 10
d = \(\frac{10}{5}\) = 2
‘d’ ਦਾ ਮੁੱਲ (1), ਵਿਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਮਿਲਦਾ ਹੈ
a = 7 – 3 × 2
= 7 – 6 = 1
ਹੁਣ S_n = \(\frac{n}{2}\)[2a + (n – 1)d]
= \(\frac{n}{2}\)[2 × 1 + (n – 1)2]
= n[1 + n – 1] = n × n
= n²
∴ ਦਿੱਤੀ ਹੋਈ A.P. ਦੇ ਪਹਿਲੇ n ਪਦਾਂ ਦਾ ਜੋੜ n² ਹੈ ।

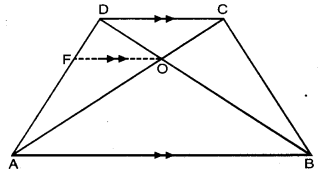
10. ਦਿਖਾਉ ਕਿ a₁, a₂, …a_n… ਤੋਂ ਇੱਕ A.P. ਬਣਦੀ ਹੈ, ਜੇਕਰ a_n ਹੇਠ ਦਿੱਤੇ ਅਨੁਸਾਰ ਪ੍ਰਭਾਸ਼ਿਤ ਹੋਵੇ ।

ਪ੍ਰਸ਼ਨ (i).
a_n = 3 + 4n
ਉੱਤਰ:
ਦਿੱਤਾ ਹੈ ਕਿ a_n = 3 + 4n …(1)
‘n’ ਦੇ ਭਿੰਨ-ਭਿੰਨ ਮੁੱਲ (1), ਵਿਚ ਰੱਖਣ ‘ਤੇ
a₁ = 3 + 4 (1) = 7
a₂ = 3 + 4 (2) = 11
a₃ = 3 + 4 (3) = 15,
ਹੁਣ a₂ – a₁, a₃ – a₂ = 15 – 11 = 4
∵ a₂ – a₁ = 11 – 7 = 4
a₃ – a₂ = 4 = d (ਮੰਨ ਲਉ)
∴ ਇਹ ਇੱਕ A.P. ਹੈ ।
ਇੱਥੇ a = 7, d = 4 ਅਤੇ n = 15
∴ S₁₅ = \(\frac{n}{2}\)[2a + (n – 1)d]
= \(\frac{15}{2}\)[2(7) + (15 – 1)4]
= \(\frac{15}{2}\)[14 + 56] = \(\frac{15}{2}\) × 70
= 15 × 35 = 525

ਪ੍ਰਸ਼ਨ (ii).
a_n = 9 – 5n ਨਾਲ ਹੀ, ਹਰੇਕ ਸਥਿਤੀ ਵਿੱਚ ਪਹਿਲੇ 15 ਪਦਾਂ ਦਾ ਜੋੜਫਲ ਪਤਾ ਕਰੋ ।
ਉੱਤਰ:
ਦਿੱਤਾ ਹੈ ਕਿ a_n = 9 – 5n …(1)
n ਦੇ ਭਿੰਨ-ਭਿੰਨ ਮੁੱਲ (1) ਵਿੱਚ ਭਰਨ ‘ਤੇ
a₁ = 9 – 5 (1) = 4
a₂ =² 9 – 5(2) = -1
a₃ = 9 – 5 (3) = – 6
ਹੁਣ a₂ – a₁ = -1 – 4 = – 5
ਇੱਥੇ a₃ – a₂ = – 6 + 1 = – 5
∴ a₂ – a₁ = a₃ – a₂ = -5 = d (ਮੰਨ ਲਉ)
∴ ਇਹ ਇਕ A.P. ਹੈ ।
ਇੱਥੇ a = 4, d = -5, n = 15
∴ S₁₅ = \(\frac{n}{2}\)[2a + (n – 1)a]
= \(\frac{15}{2}\)[2(4) + (15 – 1) (-5)]
= \(\frac{15}{2}\)[8 – 70] = \(\frac{15}{2}\)(-62)
= – 465

ਪ੍ਰਸ਼ਨ 11.
ਜੇਕਰ ਕਿਸੇ A.P. ਦੇ ਪਹਿਲੇ n ਪਦਾਂ ਦਾ ਜੋੜਫਲ 4n + n² ਹੋਵੇ ਤਾਂ ਇਸ ਦਾ ਪਹਿਲਾ ਪਦ (ਭਾਵ S₁) ਕੀ ਹੈ ? ਪਹਿਲੇ ਦੋ ਪਦਾਂ ਦਾ ਜੋੜਫਲ ਕੀ ਹੈ ? ਦੂਜਾ ਪਦ ਕੀ ਹੈ ? ਇਸੇ ਤਰ੍ਹਾਂ ਤੀਸਰਾ, 10ਵਾਂ ਅਤੇ ਵਾਂ ਪਦ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ ਕਿ A.P. ਦੇ ‘n’ ਪਦਾਂ ਦਾ ਜੋੜਫਲ ਹੈ
S_n = 4n – n² …(1)
n = 1 ਦਾ ਮੁੱਲ (1) ਵਿਚ ਰੱਖਣ ‘ਤੇ
S₂ = 4(2) – (2)² = 8 – 4
S₂ = 4
T₁ + T₂ = 4
3 + T₂ = 4
T₂ = 4 – 3 = 1
n = 3 ਦਾ ਮੁਲ (1) ਵਿਚ ਰੱਖਣ ‘ਤੇ
S₃ = 4 (3) – (3)² = 12 – 9 = 3
ਜਾਂ S₂ + T₃ = 3
4 + T₃ = 3
T₃ = 3 – 4 = -1
ਹੁਣ d = T₂ – T₁
= 1 – 3 = – 2
∴ T₁₀ = a + (n – 1) d
= 3 (10 – 1) (-2)
T₁₀ = 3 – 18 = -15
T_n = a + (n – 1) d
= 3 + (n – 1) (-2)
= 3 – 2n + 2
T_n = 5 – 2n

ਪ੍ਰਸ਼ਨ 12.
ਅਜਿਹੀਆਂ ਪਹਿਲੀਆਂ 40 ਧਨ ਸੰਪੂਰਨ ਸੰਖਿਆਵਾਂ ਦਾ ਜੋੜਫਲ ਪਤਾ ਕਰੋ ਜੋ 6 ਨਾਲ ਭਾਜਯੋਗ ਹਨ ।
ਹੱਲ:
6 ਨਾਲ ਭਾਜਯੋਗ ਸੰਪੂਰਨ ਸੰਖਿਆਵਾਂ ਹਨ
6, 12, 18, 24, 30, 36 42, …
ਇੱਥੇ a = T₁ = 6, T₂ = 12,
T₃ = 18, T₄ = 24
T₂ – T₁ = 12 – 6 = 6
T₃ – T₂ = 18 – 12 = 6
T₄ – T₃ = 24 – 18 = 6
∵ T₂ – T₁ = T₃ – T₂
= T₄ – T₃ = 6 = d (ਮੰਨ ਲਉ)
ਸੂਤਰ S_n = \(\frac{n}{2}\)[24 + (n – 1) d]
S₄₀ = \(\frac{40}{2}\)[2(6) + (40 – 1) 6]
= 20 [12 + 234]
= 20 (246) = 4920
∴ 6 ਨਾਲ ਭਾਜਯੋਗ 40 ਧਨ ਸੰਪੂਰਨ ਸੰਖਿਆਵਾਂ ਦਾ ਜੋੜਫਲ 4920 ਹੈ ।

ਪ੍ਰਸ਼ਨ 13.
8 ਦੇ ਪਹਿਲੇ 15 ਗੁਜਾਂ ਦਾ ਜੋੜਫਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
8 ਦੇ ਗੁਣ ਹਨ : 8, 16, 24, 32, 40, 48, …
ਇੱਥੇ a = T₁ = 8; T₂ = 16 ;
T₃ = 24 ; T₄ = 32
T₂ – T₁ = 16 – 8 = 8
T₃ – T₂ = 24 – 16 = 8
∵ T₂ – T₁ = T₃ – T₂ = 8 = d (ਮੰਨ ਲਉ।)
ਸੂਤਰ S_n = \(\frac{n}{2}\)[2a + (n – 1)d]
S₁₅ = \(\frac{15}{2}\)[2(8) + (15 – 1)8]
= \(\frac{15}{2}\)[16 + 112]
= \(\frac{15}{2}\) × 128 = 960
∴ 8 ਦੇ ਪਹਿਲੇ 15 ਗੁਣਕਾਂ ਦਾ ਜੋੜਫਲ 960 ਹੈ ।

ਪ੍ਰਸ਼ਨ 14.
0 ਅਤੇ 50 ਦੇ ਵਿਚ ਟਾਂਕ ਸੰਖਿਆਵਾਂ ਦਾ ਜੋੜਫਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
0 ਅਤੇ 50 ਦੇ ਵਿਚਕਾਰ ਟਾਂਕ ਸੰਖਿਆਵਾਂ ਹਨ 1, 3, 5, 7, 9, …, 49
ਇੱਥੇ a = T₁ = 1; T₂ = 3
T₃ = 5 ; T₄ = 7
l = T_n = 49
T₂ – T₁ = 3 – 1 = 2
T₃ – T₂ = 5 – 3 = 2
∵ T₂ – T₁ = T₃ – T₂ = 1 d (ਮੰਨ ਲਉ)
l = T_n = 49
a + (n – 1)d = 49
1 + (n – 1) 2 = 49
2(n – 1) = 49 – 1 = 48
n – 1 = \(\frac{48}{2}\) = 24
n = 24 + 1 = 25
ਸੂਤਰ S_n = \(\frac{n}{2}\)[2a + (n – 1)d]
S₂₅ = \(\frac{25}{2}\)[2(1) + (25 – 1) 2]
= \(\frac{25}{2}\)[2 + 48]
= \(\frac{25}{2}\) × 50 = 625
∴ 0 ਅਤੇ 50 ਦੇ ਵਿਚਕਾਰ ਟਾਂਕ ਸੰਖਿਆਵਾਂ ਦਾ ਜੋੜਫਲ 625 ਹੈ ।

ਪ੍ਰਸ਼ਨ 15.
ਨਿਰਮਾਣ ਕਾਰਜ ਨਾਲ ਸੰਬੰਧਤ ਕਿਸੇ ਠੇਕੇ ਵਿੱਚ ਕਿਸੇ ਨਿਸ਼ਚਿਤ ਮਿਤੀ ਤੋਂ ਬਾਅਦ ਕੰਮ ਦੇਰੀ ਨਾਲ ਪੂਰਾ ਕਰਨ ਲਈ, ਜ਼ੁਰਮਾਨਾ ਲਗਾਉਣ ਦੀ ਵਿਵਸਥਾ ਇਸ ਪ੍ਰਕਾਰ ਹੈ :
ਪਹਿਲੇ ਦਿਨ ਦੇ ਲਈ ₹ 200, ਦੂਸਰੇ ਦਿਨ ਲਈ ₹ 250, ਤੀਸਰੇ ਦਿਨ ਲਈ ₹ 300 ਆਦਿ ਭਾਵ ਹਰੇਕ ਅਗਲੇ ਦਿਨ ਦਾ ਜ਼ੁਰਮਾਨਾ ਆਪਣੇ ਤੋਂ ਠੀਕ ਪਹਿਲੇ ਦਿਨ ਦੇ ਜੁਰਮਾਨੇ ਨਾਲੋਂ ₹ 50 ਵੱਧ ਹੈ । ਇੱਕ ਠੇਕੇਦਾਰ ਨੂੰ ਜੁਰਮਾਨੇ ਦੇ ਰੂਪ ਵਿਚ ਕਿੰਨੀ ਰਕਮ ਦੇਣੀ ਪਵੇਗੀ, ਜੇਕਰ ਉਹ ਇਸ ਕੰਮ ਵਿੱਚ 30 ਦਿਨ ਦੀ ਦੇਰੀ ਕਰ ਦਿੰਦਾ ਹੈ ।
ਹੱਲ:
ਪਹਿਲੇ, ਦੁਸਰੇ ਅਤੇ ਤੀਸਰੇ ਦਿਨ ਲਈ ਜ਼ੁਰਮਾਨਾਂ ਹੈ : ₹ 200, ₹ 250, ₹ 300
ਜ਼ੁਰਮਾਨੇ ਵਿਚ ਅੰਤਰ ₹ 50 ਨਾਲ ਵੱਧਦਾ ਹੈ ।
∴ ਇਹ A.P. ਹੈ ।
₹ 200, ₹ 250, ₹ 300, ₹ 350
ਇੱਥੇ a = T₁ = 200 ; d = 50 ਅਤੇ n = 30
30 ਦਿਨਾਂ ਬਾਅਦ ਦੇਣਯੋਗ ਰਾਸ਼ੀ
S₃₀ = \(\frac{n}{2}\)[2a + (n – 1l) d]
= \(\frac{30}{2}\)[2(200) + (30 -1) 50]
= 15 [400 + 1450]
= 15 (1850) = 27750
∴ ਠੇਕੇਦਾਰ ਨੂੰ ਇਹ ਰਾਸ਼ੀ ₹ 27,750 ਜ਼ੁਰਮਾਨੇ ਦੇ ਰੂਪ ਵਿਚ ਦੇਣੀ ਪਵੇਗੀ ।

ਪ੍ਰਸ਼ਨ 16.
ਕਿਸੇ ਸਕੂਲ ਦੇ ਵਿਦਿਆਰਥੀਆਂ ਨੂੰ ਉਨ੍ਹਾਂ ਦੇ ਸਮੁੱਚੇ ਪ੍ਰਦਰਸ਼ਨ ਲਈ 7 ਨਕਦ ਇਨਾਮ ਦੇਣ ਲਈ ₹ 700 ਦੀ ਰਾਸ਼ੀ ਰੱਖੀ ਗਈ ਹੈ । ਜੇਕਰ ਹਰੇਕ ਇਨਾਮ ਆਪਣੇ ਤੋਂ ਠੀਕ ਪਹਿਲੇ ਇਨਾਮ ਤੋਂ ₹ 20 ਘੱਟ ਹੋਵੇ ਤਾਂ ਹਰੇਕ ਇਨਾਮ ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ ਪਹਿਲੇ ਵਿਦਿਆਰਥੀ ਨੂੰ ਦਿੱਤੀ ਗਈ ਇਨਾਮੀ ਦੀ ਰਾਸ਼ੀ = ₹ x
ਦੂਸਰੇ ਵਿਦਿਆਰਥੀ ਨੂੰ ਦਿੱਤੀ ਗਈ ਰਾਸ਼ੀ = ₹ (x – 20)
ਤੀਸਰੇ ਵਿਦਿਆਰਥੀ ਦੀ ਰਾਸ਼ੀ
= ₹ [x – 20 – 20}
= ₹ (-40)
∴ ਲੋੜੀਂਦਾ ਹੈ ।
₹ x, ₹ (x – 20), ₹ (x – 40)
∴ ਇਹ A.P. ਹੈ ।
a = ₹ x, d = – ₹ 20 n = 7
S_n = \(\frac{n}{2}\)[2a + (n – 1)d]
S₇ = \(\frac{7}{2}\)[2(x) + (7 – 1) (-20)
S₇ = \(\frac{7}{2}\)[2x – 120] = 7 (x – 60)
7 (x – 60) = 700
x – 60 = \(\frac{700}{7}\) = 100
x = 100 + 60.
x = 160
∴ 7 ਇਨਾਮ ਹਨ ₹ 160, ₹ 140, ₹ 120, ₹ 100, ₹ 80, ₹ 60, ₹ 40

ਪ੍ਰਸ਼ਨ 17.
ਇੱਕ ਸਕੂਲ ਦੇ ਵਿਦਿਆਰਥੀਆਂ ਨੇ ਹਵਾ ਪ੍ਰਦੂਸ਼ਣ ਘਟਾਉਣ ਲਈ ਸਕੂਲ ਦੇ ਅੰਦਰ ਅਤੇ ਬਾਹਰ ਪੌਦੇ ਲਗਾਉਣ ਬਾਰੇ ਸੋਚਿਆ । ਇਹ ਫੈਸਲਾ ਲਿਆ ਗਿਆ ਕਿ ਹਰੇਕ ਸ਼੍ਰੇਣੀ ਦਾ ਹਰੇਕ ਸੈਕਸ਼ਨ ਆਪਣੀ ਸ਼੍ਰੇਣੀ ਦੀ ਸੰਖਿਆ ਦੇ ਬਰਾਬਰ ਪੌਦੇ ਲਗਾਵੇਗਾ । ਉਦਾਹਰਣ ਦੇ ਲਈ ਪਹਿਲੀ ਸ਼੍ਰੇਣੀ ਦਾ ਇੱਕ ਸੈਕਸ਼ਨ 1 ਪੌਦਾ ਲਗਾਵੇਗਾ, ਸ਼੍ਰੇਣੀ II ਦਾ ਇੱਕ ਸੈਕਸ਼ਨ 2 ਪੌਦੇ ਲਗਾਵੇਗਾ, ਸ਼੍ਰੇਣੀ I ਦਾ ਇੱਕ ਸੈਕਸ਼ਨ 3 ਪੌਦੇ ਲਗਾਵੇਗਾ, ਆਦਿ, ਅਤੇ ਅਜਿਹਾ ਸ਼੍ਰੇਣੀ XII ਤੱਕ ਚਲਦਾ ਰਹੇਗਾ | ਹਰੇਕ ਸ਼੍ਰੇਣੀ ਦੇ 3 ਸੈਕਸ਼ਨ ਹਨ । ਇਸ ਸਕੂਲ ਦੇ ਵਿਦਿਆਰਥੀਆਂ ਦੁਆਰਾ ਲਗਾਏ ਗਏ ਪੌਦਿਆਂ ਦੀ ਕੁੱਲ ਸੰਖਿਆ ਕਿੰਨੀ ਹੋਵੇਗੀ ?
ਹੱਲ:
ਸ਼੍ਰੇਣੀ I ਦੇ ਤਿੰਨ ਸੈਕਸ਼ਨਾਂ ਦੁਆਰਾ ਲਗਾਏ ਗਏ ਪੌਦਿਆਂ ਦੀ ਸੰਖਿਆ = 3 × 1 = 3
ਸ਼੍ਰੇਣੀ II ਦੇ ਤਿੰਨ ਸੈਕਸ਼ਨਾਂ ਦੁਆਰਾ ਲਗਾਏ ਗਏ ਪੌਦਿਆਂ ਦੀ ਸੰਖਿਆ = 3 × 2 = 6
ਸ਼੍ਰੇਣੀ III ਦੇ ਤਿੰਨ ਸੈਕਸ਼ਨਾਂ ਦੁਆਰਾ ਲਗਾਏ ਗਏ ਪੌਦਿਆਂ ਦੀ ਸੰਖਿਆ = 3 × 3 = 9
……………………………………………..
……………………………………………..
……………………………………………..
ਸ਼੍ਰੇਣੀ XII ਦੇ ਤਿੰਨ ਸੈਕਸ਼ਨਾਂ ਦੁਆਰਾ ਲਗਾਏ ਗਏ ਪੌਦਿਆਂ ਦੀ ਸੰਖਿਆ = 3 × 12 = 36
∴ ਲੌੜੀਂਦਾ A.P. ਹੈ 3, 6, 9,…, 36
ਇੱਥੇ a = T₁ = 3 ; T₂ = 6; T₃ = 9
l = T_n = 36 ; n = 12
d = T₂ – T₁ = 6 – 3 = 3
ਵਿਦਿਆਰਥੀਆਂ ਦੁਆਰਾ ਲਗਾਏ ਗਏ ਪੌਦਿਆਂ ਦੀ ਸੰਖਿਆ
= S₁₂
= \(\frac{n}{2}\)[a + l]
= \(\frac{12}{2}\)[3 + 36] = 6 × 39 = 234
∴ ਵਾਯੂ ਪ੍ਰਦੂਸ਼ਣ ਰੋਕਣ ਲਈ ਲਗਾਏ ਗਏ ਪੋਦਿਆਂ ਦੀ ਸੰਖਿਆਂ 234 ਹੈ ।

ਪ੍ਰਸ਼ਨ 18.
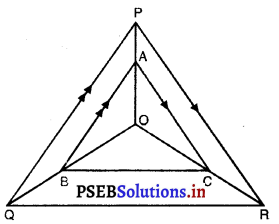
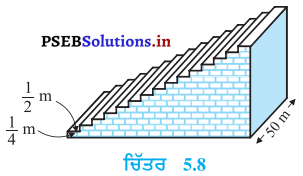
ਕੇਂਦਰ ਤੋਂ ਸ਼ੁਰੂ ਕਰਦੇ ਹੋਏ, ਵਾਰੀ-ਵਾਰੀ ਨਾਲ | A ਅਤੇ B ਨੂੰ ਕੇਂਦਰ ਮੰਨਦੇ ਹੋਏ ਅਰਧ ਵਿਆਸ 0.5 cm, 1.0 cm, 1.5 cm, 2.0 cm, …..ਵਾਲੇ ਲਗਾਤਾਰ ਅਰਧ ਚੱਕਰਾਂ ਨੂੰ ਖਿੱਚ ਕੇ ਇਕ ਕੁੰਡਲਦਾਰ (Spiral) ਬਣਾਇਆ | ਗਿਆ ਹੈ, ਜਿਵੇਂ ਕਿ ਚਿੱਤਰ ਵਿਚ ਦਿਖਾਇਆ ਗਿਆ ਹੈ । ਤੇਰਾਂ ਲਗਾਤਾਰ ਅਰਧ ਚੱਕਰਾਂ ਤੇ ਬਣੇ ਇਸ ਕੁੰਡਲਦਾਰ (Spiral) ਦੀ ਕੁੱਲ ਲੰਬਾਈ ਕੀ ਹੈ ? (π = \(\frac{22}{7}\) ਲਉ)
[ਸੰਕੇਤ : ਕ੍ਰਮਵਾਰ ਕੇਂਦਰ A, B, A, B… ਵਾਲੇ ਅਰਧ ( ਚੱਕਰਾਂ ਦੀਆਂ ਲੰਬਾਈਆਂ l₁, l₂, l₃, l₄ ਹਨ ]

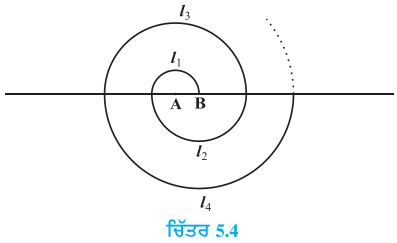
ਹੱਲ:
ਮੰਨ ਲਉ l₁ = ਪਹਿਲੇ ਅਰਧ ਚੱਕਰ ਦੀ ਲੰਬਾਈ
= πr₁ = π(0.5) = \(\frac{\pi}{2}\)
l₂ = ਦੂਸਰੇ ਅਰਧ ਚੱਕਰ ਦੀ ਲੰਬਾਈ
= πry = π(1) = π
l₃ = ਤੀਸਰੇ ਅਰਧ ਚੱਕਰ ਦੀ ਲੰਬਾਈ
= πr₃ = π(1.5) = \(\frac{3 \pi}{2}\)
l₄ = ਚੌਥੇ ਅਰਧ ਚੱਕਰ ਦੀ ਲੰਬਾਈ
= πr₄ = π(2) = 2π
∵ ਹਰੇਕ ਲੜੀ ਵਿਚ ਅਰਧ ਚੱਕਰਾਂ ਦੀ ਲੰਬਾਈ ਇਕ A.P. ਬਣਦੀ ਹੈ ।
ਇੱਥੇ a = T₁ = \(\frac{\pi}{2}\); T₂ = π
T₃ = \(\frac{3\pi}{2}\); T₄ = 2π …. ਅਤੇ n = 13
d = T₂ – T₁ = π – \(\frac{\pi}{2}\)
\(\frac{2 \pi-\pi}{2}\) = \(\frac{\pi}{2}\)
∴ ਕੁੰਡਲਦਾਰ (Spiral) ਦੀ ਕੁਲ ਲੰਬਾਈ = S₁₃

∴ ਕੁੰਡਲਦਾਰ (Spiral) ਦੀ ਕੁਲ ਲੰਬਾਈ = 143 ਸਮ

ਪ੍ਰਸ਼ਨ 19.
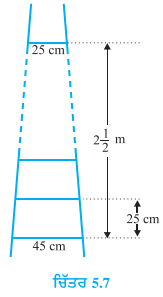
200 ਮੋਟੀਆਂ ਲੱਕੜਾਂ (Logs) ਦੀ ਢੇਰੀ ਨੂੰ ਇਸ ਤਰ੍ਹਾਂ ਰੱਖਿਆ ਜਾਂਦਾ ਹੈ ਕਿ ਸਭ ਤੋਂ ਹੇਠ ਵਾਲੀ ਕਤਾਰ ਵਿਚ 20 ਮੋਟੀਆਂ ਲੱਕੜਾਂ ਉਸ ਤੋਂ ਅਗਲੀ ਕਤਾਰ ਵਿਚ 19 ਮੋਟੀਆਂ ਲੱਕੜਾਂ ਉਸ ਤੋਂ ਅਗਲੀ ਕਤਾਰ ਵਿਚ 18 ਮੋਟੀਆਂ ਲੱਕੜਾਂ ਆਦਿ (ਦੇਖੋ ਚਿਤਰ)। ਇਹ 200 ਮੋਟੀਆਂ ਲੱਕੜਾਂ ਕਿੰਨੀਆਂ ਕਤਾਰਾਂ ਵਿੱਚ ਰੱਖੀਆਂ ਗਈਆਂ ਹਨ ਅਤੇ ਸਭ ਤੋਂ ਉਪਰਲੀ ਕਤਾਰ ਵਿੱਚ ਕਿੰਨੀਆਂ ਮੋਟੀਆਂ ਲੱਕੜਾਂ ਹਨ ?

ਹੱਲ:
ਸਭ ਤੋਂ ਹੇਠਲੀ ਕਤਾਰ ਵਿਚ ਮੋਟੀਆਂ ਲੱਕੜਾਂ ਦੀ ਸੰਖਿਆ = 20
ਦੂਸਰੀ ਕਤਾਰ ਵਿਚ ਮੋਟੀਆਂ ਲੱਕੜਾਂ ਦੀ ਸੰਖਿਆਂ = 19
ਤੀਸਰੀ ਕਤਾਰ ਵਿਚ ਮੋਟੀਆਂ ਲੱਕੜਾਂ ਦੀ ਸੰਖਿਆਂ = 18
ਇਸ ਤਰ੍ਹਾਂ ਅੱਗੇ ਵੀ ਹੈ
∴ ਹਰੇਕ ਕਤਾਰ ਵਿਚ ਰੱਖੀਆਂ ਗਈਆਂ ਮੋਟੀਆਂ ਲੱਕੜਾਂ ਦੀ ਸੰਖਿਆਂ ਇਕ A.P. ਬਣਾਂਦੀ ਹੈ ।
ਇੱਥੇ a = T₁ = 20 ;
T₂ = 19 ; T₃ = 18…
d = T₂ – T₁
= 19 – 20 = -1
ਮੰਨ ਲਓ S_n ਮੋਟੀਆਂ ਲੱਕੜਾਂ ਦੀ ਕੁਲ ਸਿੱਖਿਆ ਦੱਸਦੀ ਹੈ ।
∴ S_n = \(\frac{n}{2}\)[2a + (n – 1)d]
= \(\frac{n}{2}\)[2(20) + (n – 1) (-1)]
= \(\frac{n}{2}\)[40 – n + 1]
ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ
\(\frac{n}{2}\)[41 – n] = 200
41n – n² = 400
-n² + 41n – 400 = 0 | S = – 41
n² – 41n + 400 = 0 |P = 400
n² – 16n – 25n + 400 = 0
n (n – 16) – 25 (n – 16) = 0
(n – 16) (n – 25) = 0
n – 16 = 0 ਜਾਂ n – 25 = 0
n = 16, 25
ਸਥਿਤੀ I. ਜਦੋਂ n = 25
T₂₅ = a + (n – 1) d
= 20 + (25 – 1) (-1)
= 20 – 24 = -4 ਜੋ ਅਸੰਭਵ ਹੈ।
∴ n = 25 ਛਡ ਦਿੰਦੇ ਹਨ ।
ਸਥਿਤੀ II. ਜਦੋਂ n = 16
T₁₆ = a + (n – 1) d
= 20 + (16 – 1) (-1)
= 20 – 15 = 5
∴ ਕੁੱਲ 16 ਕਤਾਰਾਂ ਹਨ ਅਤੇ ਉਪਰਲੀ ਕਤਾਰ ਵਿਚ 5 ਮੋਟੀਆਂ ਲੱਕੜਾਂ ਹਨ ।

ਪ੍ਰਸ਼ਨ 20.
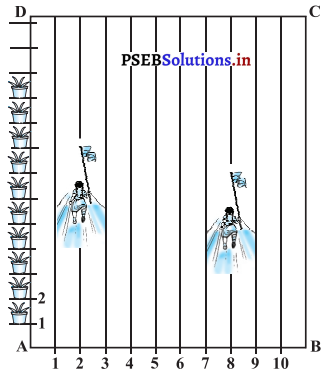
ਇੱਕ ਆਲੂ ਦੌੜ (potato race) ਵਿਚ ਆਰੰਭਿਕ ਸਥਾਨ ‘ਤੇ ਇੱਕ ਬਾਲਟੀ ਰੱਖੀ ਹੋਈ ਹੈ । ਜੋ ਪਹਿਲੇ ਆਲੂ ਤੋਂ 5 ਮੀਟਰ ਦੂਰ ਹੈ ਅਤੇ ਬਾਕੀ ਆਲੂਆਂ ਨੂੰ ਸਰਲ ਰੇਖਾ ਵਿਚ 3 m ਦੀ ਆਪਸੀ ਦੂਰੀ ਤੇ ਰੱਖਿਆ ਗਿਆ ਹੈ । ਇਸ ਰੇਖਾ ਉੱਤੇ 10 ਆਲੂ ਰੱਖੇ ਗਏ ਹਨ (ਦੇਖੋ ਚਿੱਤਰ)

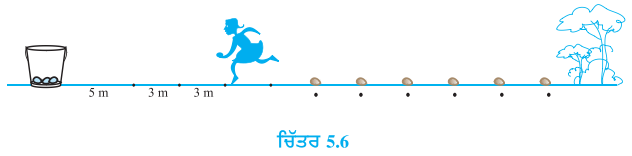
ਹਰੇਕ ਪ੍ਰਤਿਯੋਗੀ ਬਾਲਟੀ ਤੋਂ ਚਲਣਾ ਸ਼ੁਰੂ ਕਰਦੀ ਹੈ, ਨਜਦੀਕ ਤੋਂ ਨਜਦੀਕ ਵਾਲੇ ਆਲੂ ਨੂੰ ਚੁੱਕਦੀ ਹੈ, ਉਸਨੂੰ ਲੈਕੇ ਵਾਪਿਸ ਆ ਕੇ (ਦੌੜ ਕੇ) ਬਾਲਟੀ ਵਿੱਚ ਪਾ ਦਿੰਦੀ ਹੈ, ਦੂਸਰਾ ਆਲੂ ਚੁੱਕਣ ਲਈ ਵਾਪਸ ਦੌੜਦੀ ਹੈ, ਉਸ ਨੂੰ ਚੁੱਕ ਕੇ ਵਾਪਿਸ ਬਾਲਟੀ ਵਿਚ ਪਾ ਦਿੰਦੀ ਹੈ, ਅਤੇ ਉਹ ਅਜਿਹਾ ਉਦੋਂ ਤੱਕ ਕਰਦੀ ਹੈ ਜਦੋਂ ਤੱਕ ਸਾਰੇ ਆਲੂ ਬਾਲਟੀ ਵਿੱਚ ਨਾ ਆ ਜਾਣ । ਇਸ ਵਿੱਚ ਪ੍ਰਤੀਯੋਗੀ ਨੂੰ ਕੁੱਲ ਕਿੰਨੀ ਦੂਰੀ ਤੈਅ ਕਰਨੀ ਪਵੇਗੀ ?
[ਸੰਕੇਤ : ਪਹਿਲੇ ਅਤੇ ਦੂਜੇ ਆਲੂਆਂ ਨੂੰ ਚੁੱਕ ਕੇ ਬਾਲਟੀ ਵਿਚ ਪਾਉਣ ਲਈ ਦੌੜੀ ਗਈ ਦੂਰੀ = 2 × 5 + 2 × (5 + 3) ਹੈ ।]
ਹੱਲ:
ਪਹਿਲਾ ਆਲੂ ਚੁੱਕਣ ਲਈ ਤੈਅ ਕੀਤੀ ਦੂਰੀ = 2(5) ਮੀ. = 10 ਮੀ.
ਪਹਿਲੇ ਆਲੂਆਂ ਵਿਚ ਦੁਰੀ = 3 ਮੀ.
∴ ਦੂਜੇ ਆਲੂ ਲਈ ਤੈਅ ਕੀਤੀ ਦੂਰੀ
= 2 (5 +3) ਸਮ = 16 ਮੀ.
ਤੀਸਰਾ ਆਲੂ ਚੁੱਕਣ ਲਈ ਤੈਅ ਕੀਤੀ ਦੂਰੀ
= 2 (5 + 3 + 3) ਮੀ.
= 22 ਮੀ.
ਇਹ ਪ੍ਰਕਿਰਿਆ ਚਲਦੀ ਰਹੇਗੀ
∴ ਇਹ A.P. ਬਣ ਜਾਏਗੀ ।
10 ਮੀ., 16 ਮੀ., 22 ਮੀ., 28 ਮੀ., ……
a = T₁ = 10; T₂ = 16; T₃ = 22, …
d = T₂ – T₁ = 16 – 10 = 6
n = 10
∴ ਕੁਲ ਜਿੰਨੀ ਦੌੜ ਲਗਾਉਣੀ ਪਵੇਗੀ = S₁₀
= \(\frac{n}{2}\)[2a + (n – 1) d]
= \(\frac{10}{2}\)[2(10) + (10 – 1) 6]
=5 [20 + 54]
= 5 × 74 = 370
∴ ਪ੍ਰਤੀਯੋਗੀ ਨੂੰ ਕੁਲ 370 ਮੀ. ਦੀ ਦੁਰੀ ਦੌੜ ਕੇ ਤੈਅ ਕਰਨੀ ਹੈ ।