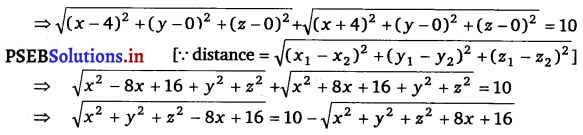Punjab State Board PSEB 11th Class Economics Book Solutions Chapter 4 उपभोगी का सन्तुलन Textbook Exercise Questions, and Answers.
PSEB Solutions for Class 11 Economics Chapter 4 उपभोगी का सन्तुलन
PSEB 11th Class Economics उपभोगी का सन्तुलन Textbook Questions and Answers
I. वस्तुनिष्ठ प्रश्न (Objective Type Questions)
प्रश्न 1.
कुल उपयोगिता की परिभाषा लिखें।
उत्तर-
एक वस्तु की सभी इकाइयों का उपभोग करने से प्राप्त होने वाली उपयोगिता के जोड़ को कुल उपयोगिता कहते हैं।
प्रश्न 2.
सीमान्त उपयोगिता की परिभाषा लिखें।
उत्तर-
एक वस्तु की एक और इकाई का उपयोग करने से प्राप्त होने वाली अतिरिक्त उपयोगिता को सीमान्त उपयोगिता कहते हैं।
अथवा
(MU = TUn TUn -1)
प्रश्न 3.
उपभोग से क्या अभिप्राय है ?
उत्तर-
उपभोग वह प्रक्रिया है जिस द्वारा वस्तुओं तथा सेवाओं के प्रयोग से आवश्यकताओं की सन्तुष्टि की जाती है।
प्रश्न 4.
उपयोगिता से क्या अभिप्राय है ?
उत्तर-
वस्तु या सेवा का वह गुण जिस द्वारा आवश्यकताएँ सन्तुष्ट होती हैं, उस गुण को उपयोगिता कहा जाता है।
प्रश्न 5.
सीमान्त उपयोगिता से कुल उपयोगिता का आंकलन कैसे किया जाता है ?
उत्तर-
सीमान्त उपयोगिता के जोड़ से कुल उपयोगिता प्राप्त हो जाती है।
प्रश्न 6.
जब कुल उपयोगिता अधिकतम होती है तो सीमान्त उपयोगिता कितनी होती है ?
उत्तर-
जब कुल उपयोगिता अधिकतम होती है तो सीमान्त उपयोगिता शून्य (Zero) होती है।
प्रश्न 7.
जब सीमान्त उपयोगिता ऋणात्मक होती है तो कुल उपयोगिता पर क्या प्रभाव पड़ता है ?
उत्तर-
जब सीमान्त उपयोगिता ऋणात्मक होती है तो कुल उपयोगिता गिरना शुरू हो जाती है।
प्रश्न 8.
जब सीमान्त उपयोगिता शून्य होती है तो कुल उपयोगिता की क्या स्थिति होती है ?
उत्तर-
जब सीमान्त उपयोगिता शून्य होती है तो कुल उपयोगिता अधिकतम होती है।
प्रश्न 9.
उपभोक्ता से क्या अभिप्राय है ?
उत्तर-
उपभोक्ता एक व्यक्ति, परिवार या सरकार हो सकती है जिस द्वारा आवश्यकताओं की पूर्ति के लिए वस्तुओं तथा सेवाओं का प्रयोग किया जाता है।
प्रश्न 10.
उपभोक्ता सन्तुलन क्या है ?
उत्तर-
उपभोक्ता सन्तुलन वह अवस्था है जब वह अपने व्यवहार को वर्तमान परिस्थितियों में सबसे अच्छा मानता है और उसमें कोई परिवर्तन नहीं करना चाहता।
प्रश्न 11.
घटती सीमान्त उपयोगिता के नियम से क्या अभिप्राय है ?
उत्तर-
घटती सीमान्त उपयोगिता के नियम अनुसार जब किसी वस्तु की इकाइयों का लगातार अधिक उपभोग किया जाता है तो प्रत्येक इकाई से प्राप्त होने वाली सीमान्त उपयोगिता घटती जाती है।
प्रश्न 12.
उपभोक्ता सन्तुलन की शर्त क्या होती है ?
उत्तर-
उपभोक्ता सन्तुलन = MUx = Price of X. MU of Money.
प्रश्न 13.
एक वस्तु के लिए उपभोक्ता सन्तुलन कैसे प्राप्त होता है ?
उत्तर–
प्राप्त उपयोगिता (MU) = त्यागी गई उपयोगिता (Price).
प्रश्न 14.
दो वस्तुओं के लिए उपभोक्ता सन्तुलन कैसे प्राप्त होता है ?
उत्तर-
X वस्तु की सीमान्त उपयोगिता (MU.) = Y वस्तु की सीमान्त उपयोगिता (MUy).
प्रश्न 15.
सीमान्त उपयोगिता (MU) = ………
उत्तर-
सीमान्त उपयोगिता (MU) = (TUn – TUn-1) Or \(\frac{\Delta \mathrm{TU}}{\Delta \mathrm{Q}}\)
प्रश्न 16.
MU1 + MU2 + MU3 = ……………….. + MUn = ……..
उत्तर-
Total Utility (T.U.)
प्रश्न 17.
जब कुल उपयोगिता अधिकतम होती है तो सीमान्त उपयोगिता ……. होती है।
(a) 1
(b) 2
(c) 3
(d) 0 (शून्य)
उत्तर-
(d) 0 (शून्य)।
प्रश्न 18.
एक वस्तु की स्थिति में उपभोगी का सन्तुलन तब होता है जब
(a) MUm
(b) MUr
(c) MUp
(d) इनमें से कोई नहीं।
उत्तर-
(a) MUm
प्रश्न 19.
दो वस्तुओं की खरीद में उपभोक्ता सन्तुलन उस समय होता है जब \(\frac{\mathbf{M U _ { x }}}{\mathbf{P}_{x}}=\frac{\mathbf{M U _ { y }}}{\mathbf{P}_{y}}\) ……………………… होती है।
(a) \(\frac{\mathrm{P}_{x}}{\mathrm{P}_{y}}\)
(b) \(\frac{P_{y}}{P_{x}}\)
(c) \(\frac{\mathrm{MU}_{x}}{\mathrm{MU}_{y}}\)
(d) MUm.
उत्तर-
(d) MUm.
प्रश्न 20.
किसी वस्तु की एक और इकाई का उपभोग करने से प्राप्त होने वाली अतिरिक्त उपयोगिता को …………….. कहते हैं।
उत्तर-
सीमान्त उपयोगिता।
प्रश्न 21.
जब सीमान्त उपयोगिता ऋणात्मक होती है तो कुल उपयोगिता अधिकतम होती है।
उत्तर-
सही।
प्रश्न 22.
एक वस्तु की स्थिति में उपभोगी को प्राप्त होने वाली सीमान्त उपयोगिता वस्तु की कीमत के बराबर हो जाती है तो इस को उपभोगी का सन्तुलन कहते हैं।
उत्तर-
सही।
प्रश्न 23.
जब एक मनुष्य के वस्तु भण्डार में वृद्धि होती है तो प्रत्येक वृद्धि के साथ प्राप्त होने वाला अतिरिक्त लाभ घटता जाता है। इस को घटती सीमान्त उपयोगिता का नियम कहते हैं।
उत्तर-
सही।
प्रश्न 24.
निम्नलिखित सारणी को पूरा करें-
| उपभोग की गई इकाइयाँ: |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| सीमान्त उपयोगिता : |
8 |
10 |
8 |
6 |
4 |
2 |
0 |
| कुल उपयोगिता : |
– |
– |
– |
– |
– |
– |
– |
उत्तर-
| उपभोग की गई इकाइयाँ : |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| सीमान्त उपयोगिता : |
8 |
10 |
8 |
6 |
4 |
2 |
0 |
| कुल उपयोगिता : |
8 |
18 |
26 |
32 |
36 |
38 |
38 |
प्रश्न 25.
घटती सीमान्त उपयोगिता का नियम ……. ने दिया।
(a) मार्शल
(b) एड्म स्मिथ
(c) गोसन
(d) कोई भी नहीं।
उत्तर-
(c) गोसन।
प्रश्न 26.
घटती सीमान्त उपयोगिता का नियम ………..से सम्बन्धित है।
(a) उपभोग
(b) विनिमय
(c) उत्पादन
(a) कोई भी नहीं।
उत्तर-
(a) उपभोग।
प्रश्न 27.
घटती सीमान्त उपयोगिता के नियम को ……….. भी कहा जाता है।
(a) अधिकतम सन्तुष्टि का नियम
(b) सन्तुष्टि का नियम
(c) गोसन का पहला नियम
(d) कोई भी नहीं।
उत्तर-
(c) गोसन का पहला नियम।
II. अति लघु उत्तरीय प्रश्न (Very Short Answer Type Questions)
प्रश्न 1.
उपभोगी से क्या अभिप्राय है ?
उत्तर-
उपभोगी उस व्यक्ति को कहा जाता है जोकि अपनी आवश्यकताओं की सन्तुष्टि के लिए वस्तुओं तथा सेवाओं का प्रयोग करता है। उपभोगी परिवार, सरकार अथवा फ़र्म भी हो सकती है। सरकार लोगों के लिए वस्तुओं तथा सेवाओं की खरीद करती है ताकि सामाजिक भलाई में वृद्धि हो सके।
प्रश्न 2.
उपभोगी के सन्तुलन से क्या अभिप्राय है ? ‘
उत्तर-
उपभोगी का सन्तुलन एक ऐसी अवस्था होती है, जब वह अपने वर्तमान व्यवहार को कुछ विशेष स्थितियों में सबसे अच्छा अनुभव करता है तथा उसमें कोई परिवर्तन नहीं करता, जब तक स्थितियों में कोई परिवर्तन नहीं होता।
प्रश्न 3.
उपयोगिता से क्या अभिप्राय है ?
उत्तर-
उपयोगिता का अर्थ वस्तु अथवा सेवा में उस गुण से होता है जिस द्वारा मानवीय आवश्यकताएं पूरी होती हैं अथवा हम यह कह सकते हैं कि किसी वस्तु में वह शक्ति जो आवश्यकताओं की पूर्ति करती है, उसको उपयोगिता कहा जाता है।(“’Utility is the want satisfying power of a good.”)
प्रश्न 4.
सीमान्त उपयोगिता को पारिभाषित करो।
उत्तर-
सीमान्त उपयोगिता किसी वस्तु की एक अन्य इकाई का उपभोग करने से जो अधिक तुष्टिगुण प्राप्त होता है उसको सीमान्त उपयोगिता कहा जाता है। उदाहरणस्वरूप एक वस्तु की पाँच इकाइयों का उपभोग करने से 100 युटिलज़ सन्तुष्टि प्राप्त होती है तथा छः इकाइयों का उपभोग करने से 110 युटिलज़ सन्तुष्टि मिलती है तो छठी इकाई का उपभोग करने से 110 – 100 = 10 युटिलज़ को सीमान्त उपयोगिता कहा जाता है।
MU = TUn – TUn-1) = 110 – 100 = 10 Utils.
प्रश्न 5.
कुल उपयोगिता से क्या अभिप्राय है ?
उत्तर-
किसी वस्तु की सभी इकाइयों के उपभोग से प्राप्त होने वाली उपयोगिता को कुल उपयोगिता कहा जाता है। मान लो एक उपभोगी तीन सेबों का उपभोग करता है। प्रथम सेब से 10 युटिल, द्वितीय सेब से 8 युटिल तथा तीसरे सेब से 6 युटिल उपयोगिता प्राप्त होती है तो कुल उपयोगिता 10 + 8 + 6 = 24 युटिल प्राप्त होगी।
प्रश्न 6.
टेबल की सहायता से बताइए कि जब सीमान्त तुष्टिगुण शून्य होता है तो कुल तुष्टिगुण अधिकतम होता है ?
उत्तर-
जब सीमान्त तुष्टिगुण शून्य होता है तो कुल तुष्टिगुण अधिकतम होता है। जैसा कि निम्नलिखित टेबल से स्पष्ट है –
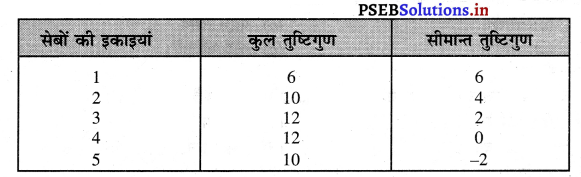
चार सेबों का उपभोग करने से सीमान्त तुष्टिगुण शून्य है और कुल तुष्टिगुण 12 अधिकतम है।
प्रश्न 7.
घटते सीमान्त तुष्टिगुण के नियम से क्या अभिप्राय है ?
उत्तर-
घटते सीमान्त तुष्टिगुण का नियम प्रोफैसर मार्शल की देन है। उनके अनुसार, “यदि अन्य बातें समान रहें जब एक निश्चित समय में एक उपभोगी किसी वस्तु का अधिक उपभोग करता है उस वस्तु की सीमान्त उपयोगिता घटती जाती है।” इसको घटते सीमान्त तुष्टिगुण का नियम कहते हैं।
III. लघु उत्तरीय प्रश्न (Short Answer Type Questions)
प्रश्न 1.
घटते सीमान्त उपयोगिता के नियम का संक्षेप में वर्णन करो।
उत्तर-
गोसन पहले अर्थशास्त्री थे जिन्होंने यह नियम दिया। इसलिए इस नियम को गोसन का पहला नियम भी कहते हैं। यह नियम लोगों की व्यावहारिक तथा मनोवैज्ञानिक स्थिति को ध्यान में रखकर बनाया गया है। प्रो० मार्शल के अनुसार, “जब किसी मनुष्य के वस्तु के भण्डार में वृद्धि होती है तो प्रत्येक वृद्धि से प्राप्त होने वाला लाभ घटता जाता है।” (“The additional benefit which a person derives from an increase of a stock of a thing diminishes with every increase in the stock that he already has.”) इस नियम को उपभोग का आधारपूर्वक नियम (Fundamental Law of Consumption) अथवा आधारपूर्वक मनोवैज्ञानिक नियम (Fundamental Psychological Law) भी कहा जाता है।
इस नियम अनुसार जब एक मनुष्य एक वस्तु की अधिक इकाइयों का उपभोग करता है तो उसको वस्तु से प्राप्त होने वाली सीमान्त उपयोगिता घटती जाती है अथवा कुल उपयोगिता में वृद्धि तो होती है परन्तु जिस अनुपात पर वृद्धि होती है, वह अनुपात घटता जाता है। उदाहरण-एक उपभोगी सेबों का उपभोग करता है, उसको प्राप्त M.U. तथा T.U. इस प्रकार है-
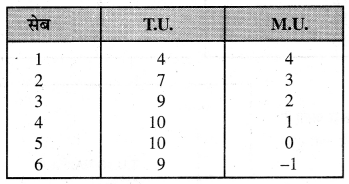
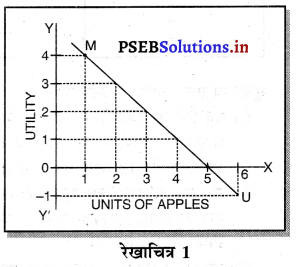
सूची-पत्र में तथा रेखाचित्र 1 में-
- सेबों का उपभोग करने से सीमान्त उपयोगिता 4, 3, 2, 1, 0 युटिलज़ घटता जाता है।
- जब सीमान्त उपयोगिता शून्य है तो. कुल उपयोगिता अधिकतम है।
- जब सीमान्त उपयोगिता ऋणात्मक है तो कुल उपयोगिता घटने लगता है, इसको घटते सीमान्त उपयोगिता का नियम कहते हैं।
प्रश्न 2.
उपयोगिता, सीमान्त उपयोगिता तथा कुल उपयोगिता के सम्बन्ध को स्पष्ट करें। कुल उपयोगिता तथा सीमान्त उपयोगिता के सम्बन्ध को स्पष्ट करें।
उत्तर-
उपयोगिता का अर्थ (Meaning of Utility)-अर्थशास्त्र में ‘उपयोगिता’ एक महत्त्वपूर्ण धारणा है। उपयोगिता का अर्थ किसी वस्तु या सेवा में उस गुण से होता है जो हमारी ज़रूरतों की पूर्ति करता है। इसीलिए किसी वस्तु में उस गुण या शक्ति को उपयोगिता कहा जाता है जिसके द्वारा मानवीय ज़रूरतों की सन्तुष्टि होती है। (Utility is the want satisfying power of a commodity.) उपयोगिता का माप संख्याओं 1, 2, 3, 4, 5 आदि द्वारा किया जाता है जिनको युटिल कहा जाता है।
सीमान्त उपयोगिता (Marginal Utility)-किसी वस्तु का एक बार और उपभोग करने से जिन कुल उपयोगिता में वृद्धि होती है उस वृद्धि को सीमान्त उपयोगिता कहा जाता है। उदाहरण के तौर पर एक वस्तु की 5 इकाइयों का उपभोग करने के साथ 100 युटिल प्राप्त होती है और छठी इकाई का उपभोग करने के साथ कुल उपयोगिता में वृद्धि 110 युटिल हो जाती है। तो छठी इकाई के उपभोग के साथ 110 -100 = 10 युटिल उपयोगिता की वृद्धि हुई है। इसीलिए सीमान्त उपयोगिता 10 युटिल होगी। इसका माप निम्नलिखित अनुसार किया जाता है।
MU = TUn – TUn-1
= TU6th Unit – TU5th Unit (110 – 100 = 10 युटिलज़)
कल उपयोगिता (Total Utility) किसी वस्तु की सभी इकाइयों के उपभोग से प्राप्त होने वाले उपयोगिता को कुल उपयोगिता कहा जाता है। मान लो एक आदमी ने तीन सेबों का उपभोग किया। पहले सेब से 10 युटिल, दूसरे सेब से 8 युटिल और तीसरे सेब से 6 युटिल उपयोगिता प्राप्त हुआ तो कुल उपयोगिता 10 + 8 + 6 = 24 युटिलज़ हुआ।
कुल उपयोगिता और सीमान्त उपयोगिता का सम्बन्ध (Relationship Between T.U. & M.U.)-
कुल उपयोगिता (T.U.) और सीमान्त उपयोगिता (M.U.) के सम्बन्ध को सूची-पत्र और रेखाचित्र द्वारा स्पष्ट करते हैं –
कुल उपयोगिता तथा सीमान्त उपयोगिता का सम्बन्ध –
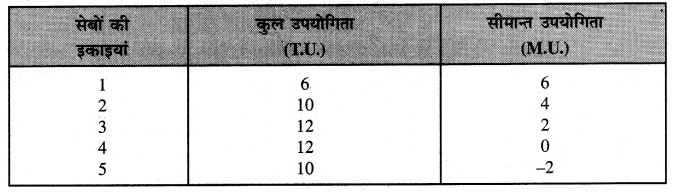
सूची-पत्र तथा रेखाचित्र 2 अनुसार –
- जब सेबों की इकाइयों का अधिक प्रयोग किया जाता है तो सीमान्त तुष्टिकरण (M.U.) घटता जाता है तथा कुल उपयोगिता में वृद्धि घटती दर पर होती है।
- जब सीमान्त उपयोगिता शून्य (zero) हो जाती है तो कुल उपयोगिता अधिकतम होती है, जैसे चौथे सेब के उपभोग में दिखाया गया है।
- जब पांचवें सेब का उपभोग किया जाता है तो सीमान्त उपयोगिता ऋणात्मक हो जाती है तो कुल उपयोगिता घटने लगती है, जैसे Mu द्वारा दिखाया गया है।
IV. दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)
प्रश्न 1.
घटती सीमान्त उपयोगिता के नियम की व्याख्या करो। इस नियम के अपवाद तथा महत्त्व को स्पष्ट करो।
(Explain the Law of Diminishing Marginals Utility. Give its Exceptions and Importance.)
उत्तर-
घटती सीमान्त उपयोगिता का नियम, उपयोगिता विश्लेषण का आधारपूर्वक नियम है। इस नियम को सबसे पहले एच० एच० गोसन (H.H. Gossen) ने 1854 में दिया था, परन्तु इस नियम की ठीक रूप में व्याख्या प्रो० मार्शल ने 1890 में अपनी पुस्तक “अर्थशास्त्र के सिद्धान्त” में की। प्रो० मार्शल के शब्दों में, “मनुष्य के पास किसी वस्तु की जितनी मात्रा होती है, उस वस्तु की मात्रा में जैसे-जैसे वृद्धि होती है, उसकी सीमान्त उपयोगिता घटती जाती है।” (“The additional benefit which a person dervies from a given stock of a thing, diminishes, with every increase in the stock that he already has.”-Marshall)
प्रो० चैपमैन के अनुसार, “जितनी कोई वस्तु हमारे पास अधिक मात्रा में होती है, उतनी ही कम मात्रा में हम अन्य प्राप्त करना चाहते हैं।” (“The more we have of a thing the less we want additional increament of it.”-Chapman) -उदाहरणस्वरूप एक मनुष्य को प्यास लगी है। पानी का पहला गिलास उस मनुष्य को बहुत उपयोगिता देगा। परन्तु दूसरे तथा तीसरे गिलास से प्राप्त होने वाली उपयोगिता घटती जाएगी। अन्य पानी पीने से उसको तकलीफ भी हो सकती है, अर्थात् वस्तु की वृद्धि से उपयोगिता घटती जाती है, परन्तु एक सीमा के पश्चात् यह उपयोगिता शून्य अथवा ऋणात्मक हो जाती है। इसको घटती उपयोगिता का नियम कहा जाता है।
मान्यताएं (Assumptions) –
- उपयोगिता का गणनावाचक माप हो सकता है।
- मुद्रा की सीमान्त उपयोगिता स्थिर रहती है।
- वस्तुओं की इकाइयां समान आकार तथा गुण वाली हैं।
- वस्तु का उपभोग एक समय तथा निरन्तर किया जाता है।
- उपभोगी की आय दी हुई है तथा यह स्थिर रहती है।
- वस्तु की कीमत तथा स्थानान्तरण वस्तुओं की कीमत स्थिर रहती है।
- उपभोक्ता की रुचि, फैशन, आदतें, रीति-रिवाज इत्यादि में कोई परिवर्तन नहीं होता।
नियम की व्याख्या (Explanation of the Law)-
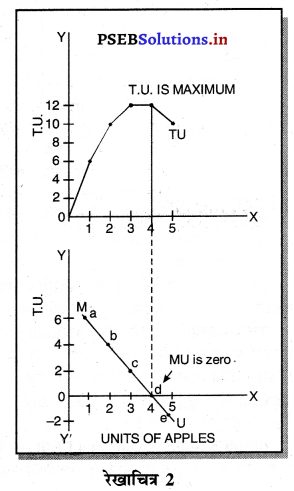
सीमान्त उपभोक्ता का नियम उपभोग का महत्त्वपूर्ण नियम है। एक मनुष्य के पास ₹ 7 हैं। इन पैसों से उपभोक्ता केले खरीदता है। जब यह पैसे केलों पर व्यय किए जाते हैं तो प्राप्त होने वाली सीमान्त उपयोगिता घटती जाती है। इसको सूचीपत्र तथा रेखाचित्र द्वारा दिखाया जा सकता है।
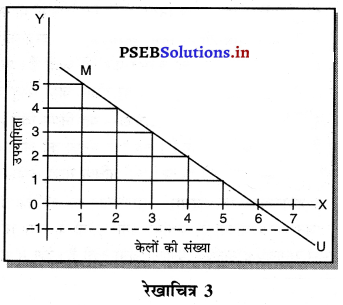
सूचीपत्र के अनुसार जब उपभोक्ता केलों पर व्यय करता है, तो प्राप्त होने वाली सीमान्त उपयोगिता 5, 4, 3, 2, 1 घटती जाती है। छठे केले से शून्य तथा सातवें केले से ऋणात्मक उपयोगिता प्राप्त होती है। रेखाचित्र 3 में दिखाया है कि उपभोक्ता को केलों से प्राप्त होने वाली सीमान्त उपयोगिता कम होती जाती है। छठी इकाई से शून्य तथा. सातवीं इकाई से ऋणात्मक उपयोगिता प्राप्त होती है। जिसको MU द्वारा दिखाया गया है। इसको घटती सीमान्त उपयोगिता का नियम कहा जाता है।
नियम के अपवाद (Exceptions of the Law)-घटती सीमान्त उपयोगिता का नियम निम्नलिखित स्थितियों में लागू नहीं होता है-
- दुर्लभ तथा अद्भुत वस्तुएं-दुर्लभ तथा अद्भुत वस्तुओं की मात्रा के बढ़ने से उपभोक्ता की उपयोगिता घटने की जगह पर बढ़ती जाती है।
- कंजूस मनुष्य-कंजूस मनुष्य के पास किसी वस्तु की मात्रा बढ़ने से वह मनुष्य उस वस्तु की अन्य मात्रा प्राप्त करना चाहता है।
- नशीले पदार्थ-यह नियम नशीले पदार्थों शराब, अफीम, तम्बाकू इत्यादि पर लागू नहीं होता। शराबी मनुष्य अधिक शराब पीकर अधिक उपयोगिता महसूस करता है।
- आरम्भिक इकाइयां-किसी वस्तु की आरम्भिक इकाइयों पर भी नियम लागू नहीं होता।
- अच्छी पुस्तकें-यह नियम अच्छी पुस्तकों, कविताओं, पुराने गानों के भण्डार पर भी लागू नहीं होता। .
नियम का महत्त्व (Importance of the Laws)-प्रो० टॉज़िग अनुसार, “घटती सीमान्त उपभोक्ता का नियम इतना व्यापक है कि इसको सर्वव्यापक कहना गलत नहीं होगा।” इसका महत्त्व इस प्रकार है –
1. नियमों का आधार-उपभोग के बहुत से नियम जैसे कि सम-सीमान्त उपयोगिता का नियम, मांग का नियम, उपभोक्ता की बचत का नियम इत्यादि इस नियम पर आधारित हैं।
2. उपभोक्ता के लिए लाभदायक-यह नियम उपभोक्ता के लिए महत्त्वपूर्ण है। एक उपभोक्ता अपनी सारी आय एक वस्तु पर ही व्यय नहीं करता; बल्कि विभिन्न प्रकार की वस्तुओं की खरीद करता है। इससे उस उपभोक्ता को अधिक उपभोक्ता प्राप्त होती है।
3. उत्पादकों के लिए लाभदायक-यह नियम उत्पादकों के लिए भी सहायक है। उत्पादक जब वस्तुओं का उत्पादन नहीं करते हैं तो एक प्रकार की वस्तुओं का ही उत्पादन नहीं किया जाता, बल्कि विभिन्न प्रकार की वस्तुएं विभिन्न वर्ग के लोगों के लिए बनाई जाती हैं। इससे उत्पादक को अधिकतम लाभ प्राप्त होता है।
4. मूल्य निर्धारण-यह नियम मूल्य निर्धारण में भी लाभदायक है। किसी वस्तु की मांग उस वस्तु से प्राप्त होने वाली सी :न्ति उपयोगिता पर निर्भर करती है, जब वस्तु की अधिक मात्रा की मांग की जाती है तो सीमान्त उपयोगिता कम होने के कारण वस्तु की कीमत कम दी जाती है। परन्तु कीमत के घटने से वस्तु की कम मात्रा बेची जाएगी। इसलिए कीमत निर्धारण उस बिन्दु पर होगा, जहां वस्तु की मांग, वस्तु की पूर्ति के समान होती है।
5. वित्त मंत्री के लिए लाभदायक-यह नियम वित्त मंत्री के लिए भी लाभदायक है। कर लगाते समय वित्त मंत्री इस नियम की सहायता लेता है। जब एक मनुष्य की आय बढ़ जाती है तो मुद्रा का सीमान्त उपयोगिता घटता जाता है, इस कारण अमीर मनुष्यों पर कर की अधिक मात्रा लगाई जाती है।
6. समाजवाद का आधार-समाजवाद वह आर्थिक प्रणाली है, जिसमें देश की सरकार आय तथा धन का समान विभाजन करना चाहती है, जबकि अमीर लोगों के पास अधिक धन होता है तो उन पर अधिक कर लगाया जाता है, जिससे समाजवाद आर्थिक प्रणाली जन्म लेती है। देश में साधनों का समान विभाजन होने के कारण प्रत्येक मनुष्य को लाभ प्राप्त होता है।
प्रश्न 2.
उपभोगी के सन्तुलन से क्या अभिप्राय है ?.एक वस्तु की स्थिति में उपभोगी सन्तुलन कैसे प्राप्त करता है ? (What is Consumer’s Equilibrium ? How does a consumer reach state of equilibrium in case of one commodity and two commodities ?)
उत्तर-
उपभोगी का सन्तुलन (Consumer’s Equilibrium)-उपभोगी का सन्तुलन उस स्थिति को कहा जाता है, जब एक उपभोगी अपनी आय तथा वस्तुओं की कीमतों अनुसार, अपना व्यय इस ढंग से करता है, जिससे उसको प्राप्त होने वाली सन्तुष्टि अधिक-से-अधिक होती है तथा इसमें वह कोई परिवर्तन नहीं करना चाहता, जब तक उपभोगी की आय, वस्तुओं की कीमतों, देश में फैशन, रीति-रिवाज इत्यादि में कोई परिवर्तन नहीं होता।
मान्यताएं (Assumptions) –
- विचारशील उपभोगी (Rational Consumer)-उपभोगी विचारशील है तथा अपनी आय से अधिक-सेअधिक सन्तुष्टि प्राप्त करना चाहता है।
- संख्यावाचक उपयोगिता (Cardinal Utility) -उपयोगिता का माप संख्यावाचक संख्याओं 1, 2, 3, 4 इत्यादि रूप में किया जा सकता है, जिनको युटिलज़ (Utils) कहा जाता है।
- मुद्रा का सीमान्त उपयोगिता स्थिर रहता है (Constant M.U. of money) – जब उपभोगी अपनी आय को व्यय करता है तो मुद्रा के सीमान्त उपयोगिता में कोई परिवर्तन नहीं होता।
- उपयोगिता स्वतन्त्र होती है (Utility is Independent)-वस्तु की उपयोगिता स्वतन्त्र होती है तथा अन्य वस्तुओं की उपयोगिता का इस पर कोई प्रभाव नहीं पड़ता।
- अन्य बातें समान रहती हैं (Other things being equal) – देश में फैशन, रीति-रिवाज, आदतें, दूसरी वस्तुओं की कीमतें स्थिर रहती हैं।
एक वस्तु की स्थिति में उपभोगी का सन्तुलन (Consumer’s Equilibrium in case of one Commodity)-मान लो एक उपभोगी ऐसी वस्तु की खरीद करता है, जिसका इस तरह से प्रयोग किया जा सकता है जब उपभोगी ऐसी वस्तु का उपभोग करता है तो घटते सीमान्त उपयोगिता का नियम (Law of Diminishing Marginal Utility) लागू होता है। इस नियम अनुसार जब एक उपभोगी एक वस्तु का निरन्तर उपभोग करता है तो अधिक उपभोग करने से प्राप्त होने वाली सीमान्त उपयोगिता घटती जाती है।
इसलिए विचारशील मनुष्य ऐसी वस्तु का उपभोग उस सीमा तक करेगा, जहां कि उस वस्तु की अन्तिम इकाई से प्राप्त सीमान्त उपयोगिता तथा उस इकाई के लिए दी जाने वाली कीमत के रूप में मुद्रा की उपयोगिता एक-दूसरे के समान हों अर्थात् उपभोगी का सन्तुलन निम्नलिखित स्थिति में होगा –
\(\frac{\mathrm{MU}_{x}}{\mathrm{MU}_{m}}=\mathrm{P}_{x}\)
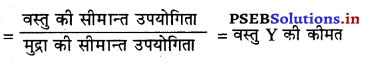
इसको सूची-पत्र द्वारा स्पष्ट किया जा सकता है –
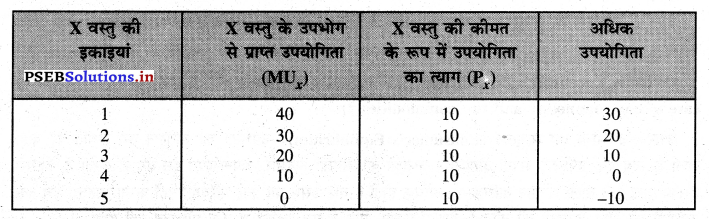
मान लो X वस्तु की कीमत 1 रुपया प्रति वस्तु दी हुई है। मुद्रा ₹ 1 की सीमान्त उपभोक्ता 10 युटिल के समान है (मुद्रा की सीमान्त उपभोक्ता का कोई विशेष मापदण्ड नहीं होता। यह तो लोगों की वस्तु सम्बन्धी पसन्द पर निर्भर करती है, जो स्थिर रहती है।) उपभोगी चार इकाइयों की खरीद करता है तो वस्तु की सीमान्त उपयोगिता तथा मुद्रा कीमत की सीमान्त उपयोगिता एक-दूसरे के समान है। इसको उपभोगी का सन्तुलन कहा जाता है।
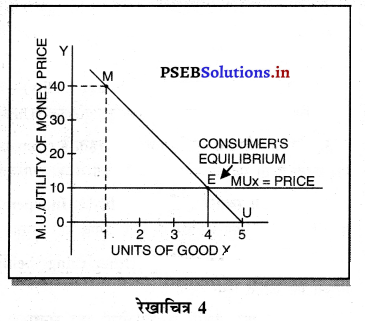
रेखाचित्र 4 में दिखाया है कि जब उपभोगी X वस्तु की अधिक इकाइयों का उपभोग करता है तो वस्तु से प्राप्त सीमान्त उपयोगिता (M.U.) घटती जाती है। ₹ 1 वस्तु की कीमत समान रहती है। एक रुपए की सीमान्त उपयोगिता 10 युटिल मानी गई है। सन्तुलन E बिन्दु पर स्थापित होगा, जिसको सन्तुलन का बिन्दु कहा जाता है।
उपभोगी का सन्तुलन = वस्तु से प्राप्त उपयोगिता = वस्तु की कीमत के रूप में उपयोगिता का त्याग।
V. संख्यात्मक प्रश्न (Numericals)
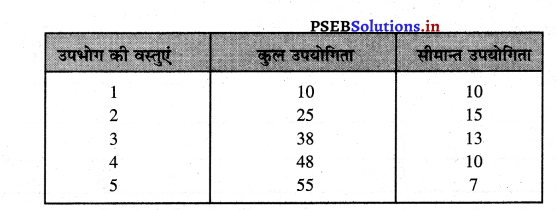
प्रश्न 1.
एक मनुष्य A की कुल उपयोगिता अनुसूची दी गई है। सीमान्त उपयोगिता अनुसूची ज्ञात करो।
उत्तर-
प्रश्न 2.
उत्तर
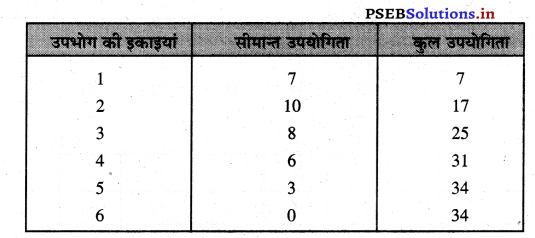
प्रश्न 3.
निम्नलिखित सारणी पूरी कीजिए :
| प्रयोग की गई इकाइयां : |
1 |
2 |
3 |
4 |
| कुल उपयोगिता : |
7 |
17 |
25 |
31 |
| सीमान्त उपयोगिता : |
– |
– |
– |
– |
उत्तर –
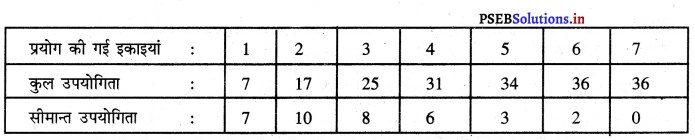
प्रश्न 4.
निम्नलिखित सारणी पूरी कीजिए :
| प्रयोग की गई इकाइयां : |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| कुल उपयोगिता |
10 |
25 |
38 |
48 |
55 |
60 |
63 |
| सीमान्त उपयोगिता : |
– |
– |
– |
– |
– |
– |
– |
उत्तर –
प्रश्न 5.
निम्नलिखित सारणी पूरी कीजिए :
| प्रयोग की गई इकाइयां : |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| कुल उपयोगिता : |
12 |
22 |
30 |
36 |
40 |
42 |
42 |
| सीमान्त उपयोगिता : |
– |
– |
– |
– |
– |
– |
– |
उत्तर –
प्रश्न 6.
निम्नलिखित सारणी को पूरा करें :
| प्रयोग की गई इकाइयां : |
0 |
1 |
2 |
3 |
4 |
5 |
| कुल उपयोगिता : |
1 |
15 |
30 |
42 |
52 |
61 |
| सीमान्त उपयोगिता : |
– |
– |
– |
– |
– |
– |
उत्तर-
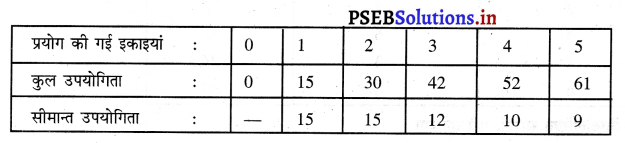
प्रश्न 7.
निम्नलिखित सारणी को पूरा करें :
| उपयोग की गई इकाइयां : |
0 |
1 |
2 |
3 |
4 |
5 |
| कुल उपयोगिता : |
0 |
10 |
25 |
38 |
48 |
55 |
| सीमान्त उपयोगिता : |
– |
– |
– |
– |
– |
– |
उत्तर –
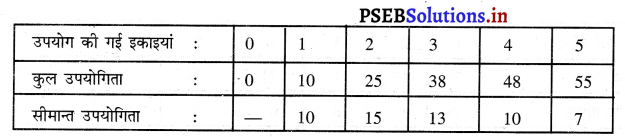
प्रश्न 8.
निम्नलिखित सारणी को पूरा करें :
| उपयोग की गई इकाइयां : |
0 |
1 |
2 |
3 |
4 |
5 |
| कुल उपयोगिता : |
0 |
20 |
35 |
47 |
57 |
65 |
| सीमान्त उपयोगिता : |
– |
– |
– |
– |
– |
|
उत्तर-
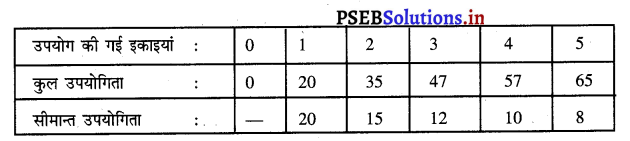
प्रश्न 9.
नीचे दिये हुए आंकड़ों से सीमान्त उपयोगिता मालूम करें :
| उपभोग की गई इकाइयां: |
1 |
2 |
3 |
4 |
5 |
| कुल उपयोगिता : |
10 |
25 |
38 |
48 |
55 |
उत्तर-
.
.
.
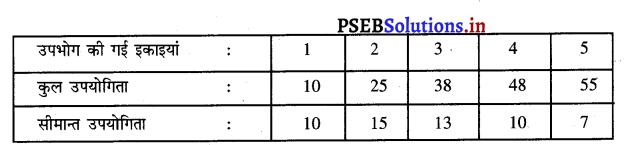
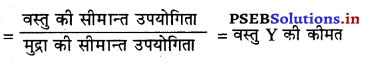
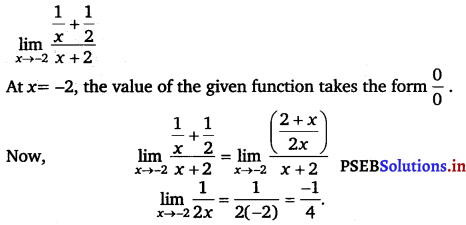
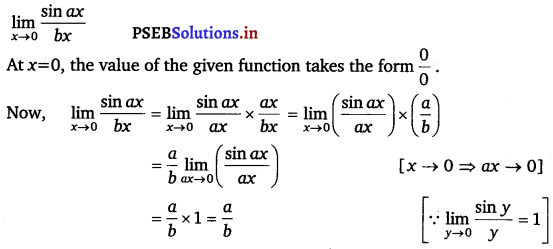
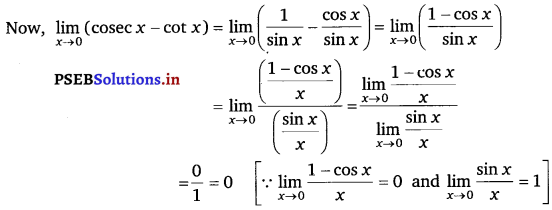
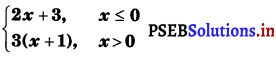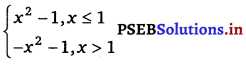
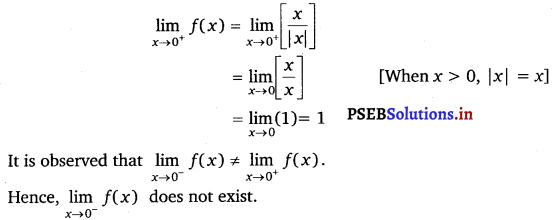
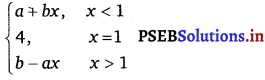and if \(\lim _{h \rightarrow 1}\) f(x) = f(1) what are possible values of a and b ?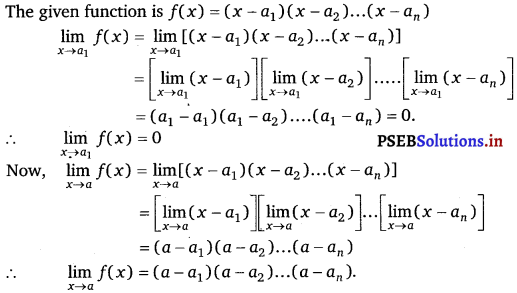
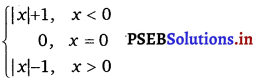For what value(s) of a does f(x) exists?
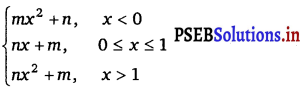For what integers m and n does \(\lim _{x \rightarrow 0}\) f(x) and \(\lim _{x \rightarrow 1}\) f(x) exist?
