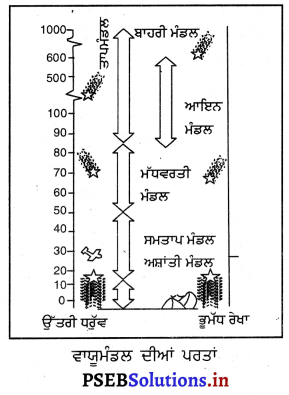
Punjab State Board PSEB 7th Class Social Science Book Solutions Geography Chapter 2 ਧਰਤੀ ਦਾ ਅੰਦਰੂਨੀ ਅਤੇ ਬਾਹਰਲਾ ਰੂਪ Textbook Exercise Questions and Answers.
PSEB Solutions for Class 7 Social Science Geography Chapter 2 ਧਰਤੀ ਦਾ ਅੰਦਰੂਨੀ ਅਤੇ ਬਾਹਰਲਾ ਰੂਪ
Social Science Guide for Class 7 PSEB ਧਰਤੀ ਦਾ ਅੰਦਰੂਨੀ ਅਤੇ ਬਾਹਰਲਾ ਰੂਪ Textbook Questions, and Answers
ਅਭਿਆਸ ਦੇ ਪ੍ਰਸ਼ਨ ਦੇ
(ਉ) ਹੇਠ ਲਿਖੇ ਹਰੇਕ ਪ੍ਰਸ਼ਨ ਦਾ ਉੱਤਰ ਇਕ ਸ਼ਬਦ/ਇਕ ਵਾਕ (1-15) ਸ਼ਬਦਾਂ ਵਿਚ ਲਿਖੋ –
ਪ੍ਰਸ਼ਨ 1.
ਧਰਤੀ ਦੇ ਕਿੰਨੇ ਖੋਲ ਹਨ ? ਇਨ੍ਹਾਂ ਦੇ ਨਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
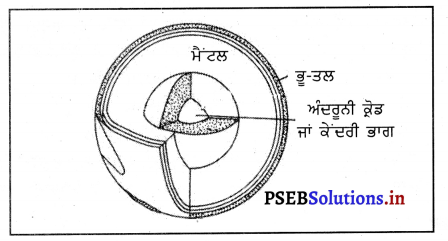
ਧਰਤੀ ਦੀਆਂ ਤਿੰਨ ਪਰਤਾਂ ਹਨ- ਥਲ ਮੰਡਲ, ਮੈਂਟਲ ਅਤੇ ਕੇਂਦਰੀ ਭਾਗ । ਇਨ੍ਹਾਂ ਨੂੰ ਕ੍ਰਮਵਾਰ ਸਿਆਲ, ਸੀਮਾ ਅਤੇ ਨਾਈਫ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 2.
ਧਰਤੀ ‘ਤੇ ਕਿੰਨੇ ਪ੍ਰਕਾਰ ਦੀਆਂ ਚੱਟਾਨਾਂ ਪਾਈਆਂ ਜਾਂਦੀਆਂ ਹਨ ?
ਉੱਤਰ-
ਧਰਤੀ ‘ਤੇ ਕਈ ਪ੍ਰਕਾਰ ਦੀਆਂ ਚੱਟਾਨਾਂ ਪਾਈਆਂ ਜਾਂਦੀਆਂ ਹਨ । ਨਿਰਮਾਣ ਦੇ ਆਧਾਰ ‘ਤੇ ਚੱਟਾਨਾਂ ਤਿੰਨ ਪ੍ਰਕਾਰ ਦੀਆਂ ਹੁੰਦੀਆਂ ਹਨ-ਅਰਾਨੀ ਚੱਟਾਨਾਂ, ਤਲਛੱਟੀ ਜਾਂ ਤਹਿਦਾਰ ਚੱਟਾਨਾਂ ਅਤੇ ਰੁਪਾਂਤਰਿਤ ਚੱਟਾਨਾਂ ।
ਪ੍ਰਸ਼ਨ 3.
ਧਰਤੀ ਦੇ ਮੈਂਟਲ ਭਾਗ ਬਾਰੇ ਲਿਖੋ ।
ਉੱਤਰ-
ਧਰਤੀ ਦੀ ਉੱਪਰਲੀ ਪਰਤ ਦੇ ਹੇਠਾਂ ਮੈਂਟਲ ਭਾਗ ਹੈ । ਇਸ ਦੀ ਔਸਤਨ ਮੋਟਾਈ 2900 ਕਿਲੋਮੀਟਰ ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
ਧਰਤੀ ਦੀ ਸਿਆਲ ਪਰਤ ਨੂੰ ਇਸ ਨਾਂ ਨਾਲ ਕਿਉਂ ਪੁਕਾਰਿਆ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਧਰਤੀ ਦੀ ਸਿਆਲ ਪਰਤ ਵਿਚ ਸਿਲੀਕਾਂ (Si) ਅਤੇ ਐਲੂਮੀਨੀਅਮ (Al) ਤੱਤਾਂ ਦੀ ਬਹੁਤਾਤ ਹੈ । ਇਸੇ ਕਾਰਨ ਇਸ ਪਰਤ ਨੂੰ ਸਿਆਲ (Si + Al = SIAL) ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 5.
ਧਰਤੀ ਦੇ ਅੰਦਰੂਨੀ ਭਾਗ ਨੂੰ ਕੀ ਆਖਦੇ ਹਨ ? ਇਹ ਕਿਹੜੇ-ਕਿਹੜੇ ਤੱਤਾਂ ਦੀ ਬਣੀ ਹੋਈ ਹੈ ?
ਉੱਤਰ-
ਧਰਤੀ ਦੇ ਅੰਦਰੂਨੀ ਭਾਗ ਨੂੰ “ਨਾਈਫ” ਕਹਿੰਦੇ ਹਨ । ਇਹ ਪਰਤ ਨਿੱਕਲ ਅਤੇ ਲੋਹੇ ਤੋਂ ਬਣੀ ਹੋਈ ਹੈ ।
ਪ੍ਰਸ਼ਨ 6.
ਧਰਤੀ ਨੂੰ ਭੋਂ-ਖੁਰਨ ਤੋਂ ਕਿਵੇਂ ਬਚਾਇਆ ਜਾ ਸਕਦਾ ਹੈ ?
ਉੱਤਰ-
ਧਰਤੀ ਨੂੰ ਹੇਠਾਂ ਲਿਖੇ ਢੰਗਾਂ ਦੁਆਰਾ ਭੋਂ-ਖੁਰਨ ਤੋਂ ਬਚਾਇਆ ਜਾ ਸਕਦਾ ਹੈ-
- ਵੱਧ ਤੋਂ ਵੱਧ ਦਰੱਖ਼ਤ ਲਗਾ ਕੇ,
- ਖੇਤੀਬਾੜੀ ਦੇ ਵਧੀਆ ਢੰਗ ਅਪਣਾ ਕੇ,
- ਪਸ਼ੂ ਚਰਾਉਣਾ ਘਟਾ ਕੇ ।
(ਅ) ਹੇਠ ਲਿਖੇ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਉੱਤਰ ਲਗਪਗ 50-60 ਸ਼ਬਦਾਂ ਵਿਚ ਦਿਓ
ਪ੍ਰਸ਼ਨ 1.
ਅਗਨੀ ਚੱਟਾਨਾਂ ਕਿਸ ਨੂੰ ਆਖਦੇ ਹਨ ? ਇਹ ਕਿੰਨੇ ਪ੍ਰਕਾਰ ਦੀਆਂ ਹਨ ? ਅੰਤਰਵੇਧੀ ਚੱਟਾਨਾਂ ਬਾਰੇ ਲਿਖੋ ।
ਉੱਤਰ-
ਅਗਨੀ ਚੱਟਾਨ ਉਹ ਚੱਟਾਨ ਹੈ ਜਿਸਦਾ ਨਿਰਮਾਣ ਮੈਗਮਾ ਅਤੇ ਲਾਵੇ ਦੇ ਠੰਢਾ ਹੋਣ ਨਾਲ ਹੋਇਆ ਹੈ । ਇਹ ਚੱਟਾਨਾਂ ਦੋ ਪ੍ਰਕਾਰ ਦੀਆਂ ਹਨ- ਅੰਤਰਵੇਧੀ ਚੱਟਾਨਾਂ ਅਤੇ ਬਾਹਰਵੇਧੀ ਚੱਟਾਨਾਂ ‘ ਅੰਤਰਵੇਧੀ ਚੱਟਾਨਾਂ-ਕਦੇ-ਕਦੇ ਮੈਗਮਾ ਧਰਤੀ ਦੇ ਅੰਦਰ ਹੀ ਹੌਲੀ-ਹੌਲੀ ਠੰਢਾ ਹੋ ਕੇ ਜੰਮ ਜਾਂਦਾ ਹੈ । ਇਸ ਪ੍ਰਕਾਰ ਬਣੀਆਂ ਚੱਟਾਨਾਂ ਨੂੰ ਅੰਤਰਵੇਧੀ ਚੱਟਾਨਾਂ ਕਹਿੰਦੇ ਹਨ । ਇਹ ਚੱਟਾਨਾਂ ਦੋ ਤਰ੍ਹਾਂ ਦੀਆਂ ਹੁੰਦੀਆਂ ਹਨ-ਪਾਤਾਲੀ ਅਗਨੀ ਚੱਟਾਨਾਂ ਅਤੇ ਮੱਧਵਰਤੀ ਅਗਨੀ ਚੱਟਾਨਾਂ ।
- ਪਾਤਾਲੀ ਅਗਨੀ ਚੱਟਾਨਾਂ-ਜਦੋਂ ਧਰਤੀ ਦੇ ਅੰਦਰੂਨੀ ਭਾਗ ਵਿਚ ਮੈਗਮਾ ਬਹੁਤ ਜ਼ਿਆਦਾ ਡੂੰਘਾਈ ‘ਤੇ ਚੱਟਾਨ ਦਾ ਰੂਪ ਧਾਰਨ ਕਰ ਲੈਂਦਾ ਹੈ, ਤਾਂ ਉਸ ਚੱਟਾਨ ਨੂੰ ਪਾਤਾਲੀ ਅਗਨੀ ਚੱਟਾਨ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਨਾਈਟ ਇਸੇ ਪ੍ਰਕਾਰ ਦੀ ਚੱਟਾਨ ਹੈ ।
- ਮੱਧਵਰਤੀ ਅਗਨੀ ਚੱਟਾਨਾਂ-ਕਦੀ-ਕਦੀ ਮੈਗਮਾ ਧਰਤੀ ਦੇ ਮੱਧ ਭਾਗਾਂ ਦੀਆਂ ਦਰਾੜਾਂ ਵਿਚ ਜੰਮ ਜਾਂਦਾ ਹੈ । ਇਸ ਪ੍ਰਕਾਰ ਜਿਹੜੀਆਂ ਚੱਟਾਨਾਂ ਬਣਦੀਆਂ ਹਨ ਉਨ੍ਹਾਂ ਨੂੰ ਮੱਧਵਰਤੀ ਅਗਨੀ ਚੱਟਾਨਾਂ ਕਹਿੰਦੇ ਹਨ । ਡਾਈਕ ਅਤੇ ਸਿਲ ਇਨ੍ਹਾਂ ਚੱਟਾਨਾਂ ਦੀਆਂ ਉਦਾਹਰਨਾਂ ਹਨ ।
ਪ੍ਰਸ਼ਨ 2.
ਤਹਿਦਾਰ ਚੱਟਾਨਾਂ ਕਿਸ ਨੂੰ ਆਖਦੇ ਹਨ ਅਤੇ ਇਹ ਕਿੰਨੇ ਪ੍ਰਕਾਰ ਦੀਆਂ ਹਨ ?
ਉੱਤਰ-
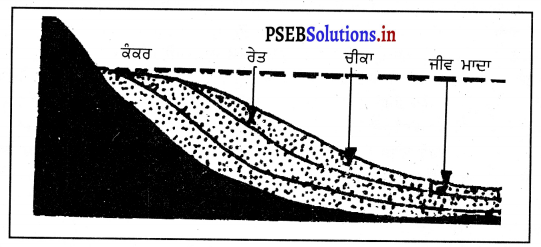
ਤਹਿਦਾਰ ਤਲਛੱਟੀ ਚੱਟਾਨਾਂ ਉਹ ਚੱਟਾਨਾਂ ਹਨ ਜਿਹੜੀਆਂ ਪਰਤਾਂ ਦੇ ਰੂਪ ਵਿਚ ਪਾਈਆਂ ਜਾਂਦੀਆਂ ਹਨ । ਇਹ ਅਨਾਛਾਦਨ ਦੇ ਕਾਰਕਾਂ ਦੀ ਜਮਾਂ ਕਿਰਿਆ ਨਾਲ ਬਣਦੀਆਂ ਹਨ । ਇਹ ਜਮਾਉ ਧਰਤੀ ਦੇ ਹੇਠਲੇ ਸਥਾਨਾਂ ‘ਤੇ ਪਾਏ ਜਾਂਦੇ ਹਨ । ਧਰਤੀ ਦੇ ਤਲ ‘ਤੇ ਵਰਖਾ, ਹਵਾ, ਗਰਮੀ, ਸਰਦੀ, ਨਦੀ ਅਤੇ ਹਿਮ ਨਦੀ ਦੇ ਕਾਰਨ ਚੱਟਾਨਾਂ ਟੁੱਟਦੀਆਂ ਰਹਿੰਦੀਆਂ ਹਨ।ਨਦੀਆਂ-ਨਾਲੇ ਇਨ੍ਹਾਂ ਟੁੱਟੀਆਂ ਹੋਈਆਂ ਚੱਟਾਨਾਂ ਦੇ ਮਾਦੇ ਨੂੰ ਆਪਣੇ ਨਾਲ ਰੋੜ ਕੇ ਲੈ ਜਾਂਦੇ ਹਨ । ਜਦੋਂ ਇਹ ਧਰਤੀ ਦਾ ਅੰਦਰੂਨੀ ਅਤੇ ਬਾਹਰਲਾ ਰੂਪ ਨਦੀਆਂ-ਨਾਲੇ ਸਮੁੰਦਰ ਵਿਚ ਜਾ ਕੇ ਡਿੱਗਦੇ ਹਨ ਤਾਂ ਸਾਰਾ ਤਲਛੱਟ ਸਮੁੰਦਰ ਦੀ ਤਹਿ ਵਿਚ ਜਮਾਂ ਹੋ ਜਾਂਦਾ ਹੈ |ਹਵਾ ਵੀ ਚੱਟਾਨੀ ਸਾਮੱਗਰੀ ਨੂੰ ਉਡਾ ਕੇ ਸਮੁੰਦਰ ਵਿਚ ਸੁੱਟਦੀ ਹੈ ।
ਸਮੁੰਦਰ ਵਿਚ ਜਮਾਂ ਹੋਣ ਵਾਲੀ ਇਸ ਸਾਮੱਗਰੀ ਨੂੰ ਤਲਛੱਟ ਜਾਂ ਤਹਿਦਾਰ (ਅਵਸਾਦ) ਕਹਿੰਦੇ ਹਨ । ਸਮਾਂ ਬੀਤਣ ਦੇਨਾਲ-ਨਾਲ ਨਦੀਆਂ ਤਲਛੱਟ ਦੀਆਂ ਪਰਤਾਂ ‘ਤੇ ਪਰਤਾਂ ਵਿਛਾਉਂਦੀਆਂ ਰਹਿੰਦੀਆਂ ਹਨ । ਲੱਖਾਂ ਸਾਲਾਂ ਦੇ ਬਾਅਦ ਦਬਾਅ ਦੇ ਕਾਰਨ ਤਲਛੱਟ ਦੀਆਂ ਪਰਤਾਂ ਕਠੋਰ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ਅਤੇ ਤਲਛੱਟੀ ਜਾਂ ਤਹਿਦਾਰ ਚੱਟਾਨਾਂ ਦਾ ਰੂਪ ਧਾਰਨ ਕਰ ਲੈਂਦੀਆਂ ਹਨ । ਰਚਨਾ ਦੇ ਆਧਾਰ ‘ਤੇ ਤਲਛੱਟੀ ਚੱਟਾਨਾਂ ਦੋ ਪ੍ਰਕਾਰ ਦੀਆਂ ਹੁੰਦੀਆਂ ਹਨ-ਜੈਵਿਕ ਅਤੇ ਅਜੈਵਿਕ ।
ਪ੍ਰਸ਼ਨ 3.
ਰੂਪਾਂਤਰਿਤ ਚੱਟਾਨਾਂ ਬਾਰੇ ਲਿਖੋ ਅਤੇ ਇਨ੍ਹਾਂ ਚੱਟਾਨਾਂ ਦੀਆਂ ਪ੍ਰਮੁੱਖ ਉਦਾਹਰਨਾਂ ਦਿਓ ।
ਉੱਤਰ-
ਧਰਤੀ ਦੇ ਅੰਦਰ ਪਾਏ ਜਾਣ ਵਾਲੇ ਤਾਪ ਅਤੇ ਦਬਾਓ ਜਾਂ ਦੋਨਾਂ ਦੇ ਸਾਂਝੇ ਪ੍ਰਭਾਵ ਦੇ ਕਾਰਨ ਅਗਨੀ ਅਤੇ ਤਹਿਦਾਰ ਚੱਟਾਨਾਂ ਦੇ ਰੰਗ, ਰੂਪ, ਬਨਾਵਟ, ਕਠੋਰਤਾ ਆਦਿ ਵਿਚ ਪਰਿਵਰਤਨ ਆ ਜਾਂਦਾ ਹੈ । ਇਨ੍ਹਾਂ ਪਰਿਵਰਤਨਾਂ ਦੇ ਕਾਰਨ ਮੂਲ ਤੌਰ ‘ਤੇ ਬਦਲ ਜਾਣ ਵਾਲੀਆਂ ਇਨ੍ਹਾਂ ਚੱਟਾਨਾਂ ਨੂੰ ਰੂਪਾਂਤਰਿਤ ਚੱਟਾਨਾਂ ਕਹਿੰਦੇ ਹਨ । ਰੂਪਾਂਤਰਨ ਦੋ ਤਰ੍ਹਾਂ ਦਾ ਹੁੰਦਾ ਹੈ, ਤਾਪੀ ਅਤੇ ਖੇਤਰੀ । ਤਾਪੀ ਰੂਪਾਂਤਰਨ-ਜਦੋਂ ਤਰੇੜਾਂ ਅਤੇ ਨਾਲੀਆਂ ਆਦਿ ਵਿਚ ਵਹਿੰਦਾ ਹੋਇਆ ਮੈਗਮਾ ਚੱਟਾਨਾਂ ਦੇ ਸੰਪਰਕ ਵਿਚ ਆਉਂਦਾ ਹੈ ਤਾਂ ਉਹ ਆਪਣੇ ਉੱਚ ਤਾਪਮਾਨ ਦੇ ਕਾਰਨ, ਉਨ੍ਹਾਂ ਨੂੰ ਪਿਘਲਾਂ ਦਿੰਦਾ ਹੈ ਇਸਨੂੰ ਤਾਪੀ ਰੂਪਾਂਤਰਨ ਕਹਿੰਦੇ ਹਨ । ਖੇਤਰੀ ਰੂਪਾਂਤਰਨ-ਕਿਸੇ ਵੱਡੇ ਖੇਤਰ ਵਿਚ ਉੱਪਰਲੀਆਂ ਚੱਟਾਨਾਂ ਦੇ ਬਹੁਤ ਜ਼ਿਆਦਾ ਦਬਾਓ ਦੇ ਕਾਰਨ ਚੱਟਾਨਾਂ ਦੇ ਮੂਲ ਰੂਪ ਵਿਚ ਜੋ ਪਰਿਵਰਤਨ ਹੁੰਦਾ ਹੈ ਇਸਨੂੰ ਖੇਤਰੀ ਰੂਪਾਂਤਰਨ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।

ਉਦਾਹਰਨ-
| ਮੂਲ ਚੱਟਾਨਾਂ |
ਰੂਪਾਂਤਰਿਤ ਚੱਟਾਨਾਂ |
| ਅਬਰਕ |
ਸ਼ਿਸ਼ਟ |
| ਬਿਮੀਨਸ ਕੋਲਾ |
ਐਂਥਰੇਸਾਈਟ ਕੋਲਾ |
| ਸ਼ੈਲ |
ਸਲੇਟ |
| ਗੈਬਰੇ |
ਸਰਪੈਨਟਾਈਨ |
| ਰੇਤ ਪੱਥਰ |
ਕਵਾਰਟਜ਼ਾਇਟ |
| ਪੀਟ |
ਕੋਲਾ |
ਪ੍ਰਸ਼ਨ 4.
ਧਰਤੀ ਵਿਚ ਮਿਲਣ ਵਾਲੇ ਖਣਿਜ ਪਦਾਰਥਾਂ ਦਾ ਵਰਗੀਕਰਨ ਕਰੋ ।
ਉੱਤਰ-
ਧਰਤੀ ਵਿਚ ਮਿਲਣ ਵਾਲੇ ਖਣਿਜਾਂ ਨੂੰ ਹੇਠ ਲਿਖੇ ਤਿੰਨ ਵਰਗਾਂ ਵਿਚ ਵੰਡਿਆ ਗਿਆ ਹੈ –
- ਧਾਤਵੀ ਖਣਿਜ-ਇਨ੍ਹਾਂ ਖਣਿਜਾਂ ਵਿਚ ਧਾਤੁ ਦੇ ਅੰਸ਼ ਹੁੰਦੇ ਹਨ , ਜਿਵੇਂ ਲੋਹਾ, ਤਾਂਬਾ, ਟਿਨ, ਐਲੂਮੀਨੀਅਮ, ਸੋਨਾ, ਚਾਂਦੀ ਆਦਿ ਖਣਿਜ ਧਾਤਵੀ ਖਣਿਜ ਹਨ ।
- ਅਧਾਤਵੀ ਖਣਿਜ-ਇਨ੍ਹਾਂ ਖਣਿਜਾਂ ਵਿਚ ਧਾਤੂ ਦੇ ਅੰਸ਼ ਨਹੀਂ ਹੁੰਦੇ ; ਜਿਵੇਂ ਸਲਫਰ, (ਗੰਧਕ), ਅਬਰਕ, ਜਿਪਸਮ, ਫ਼ਾਸਫੇਟ, ਪੋਟਾਸ਼ ਆਦਿ ਅਧਾਤਵੀ ਖਣਿਜ ਹਨ ।
- ਸ਼ਕਤੀ ਖਣਿਜ-ਇਨ੍ਹਾਂ ਖਣਿਜਾਂ ਨਾਲ ਬਾਲਣ ਸ਼ਕਤੀ ਅਤੇ ਊਰਜਾ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ । ਇਸ ਊਰਜਾ ਨਾਲ ਕਾਰਖ਼ਾਨੇ, ਮੋਟਰ ਗੱਡੀਆਂ ਆਦਿ ਚਲਾਈਆਂ ਜਾਂਦੀਆਂ ਹਨ । ਇਨ੍ਹਾਂ , ਖਣਿਜਾਂ ਵਿਚ ਕੋਲਾ, ਪੈਟਰੋਲੀਅਮ, ਕੁਦਰਤੀ ਗੈਸ ਆਦਿ ਸ਼ਾਮਲ ਹਨ ।
ਪ੍ਰਸ਼ਨ 5.
ਅਬਰਕ ਕਿਸ ਪ੍ਰਕਾਰ ਦਾ ਖਣਿਜ ਹੈ ? ਇਹ ਕਿਹੜੇ ਕੰਮ ਆਉਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਅਬਰਕ ਇਕ ਅਧਾਤਵੀ ਖਣਿਜ ਹੈ । ਇਸਦੇ ਬਹੁਤ ਸਾਰੇ ਲਾਭ ਹੋਣ ਦੇ ਕਾਰਨ ਇਹ ਇਕ ਮਹੱਤਵਪੂਰਨ ਖਣਿਜ ਬਣ ਗਿਆ ਹੈ ।
- ਇਸ ਖਣਿਜ ਦਾ ਜ਼ਿਆਦਾਤਰ ਪ੍ਰਯੋਗ ਬਿਜਲੀ ਦਾ ਸਾਮਾਨ ਬਣਾਉਣ ਵਿਚ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।
- ਇਸ ਦਾ ਉਪਯੋਗ ਲੈਂਪ ਦੀਆਂ ਚਿਮਨੀਆਂ, ਰੰਗ-ਰੋਗਨ, ਰਬੜ, ਕਾਗਜ਼, ਦਵਾਈਆਂ, ਮੋਟਰਾਂ, ਪਾਰਦਰਸ਼ੀ ਚਾਦਰਾਂ ਆਦਿ ਦੇ ਨਿਰਮਾਣ ਵਿਚ ਵੀ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।
- ਅਬਰਕ ਦੀਆਂ ਪਤਲੀਆਂ ਸ਼ੀਟਾਂ, ਬਿਜਲੀ ਦੀਆਂ ਮੋਟਰਾਂ ਅਤੇ ਗਰਮ ਕਰਨ ਵਾਲੀਆਂ ਵਸਤਾਂ ਵਿਚ ਤਾਪ ਨਸ਼ਟ ਹੋਣ ਅਤੇ ਕਰੰਟ ਲੱਗਣ ਤੋਂ ਬਚਾਅ ਲਈ ਵਰਤੀਆਂ ਜਾਂਦੀਆਂ ਹਨ ।
ਪ੍ਰਸ਼ਨ 6.
ਤਰਲ ਸੋਨਾ ਕਿਸ ਨੂੰ ਆਖਦੇ ਹਨ ? ਇਸ ਬਾਰੇ ਸੰਖੇਪ ਜਾਣਕਾਰੀ ਦਿਓ ।
ਉੱਤਰ-
ਤਰਲ ਸੋਨਾ ਖਣਿਜ ਤੇਲੇ ਨੂੰ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਇਸ ਨੂੰ ਇਹ ਨਾਂ ਇਸ ਲਈ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ਕਿਉਂਕਿ ਇਹ ਇਕ ਖਣਿਜ ਹੈ ਅਤੇ ਬਹੁਤ ਹੀ ਉਪਯੋਗੀ ਹੈ । ਇਸ ਨੂੰ ਪੈਟਰੋਲੀਅਮ ਜਾਂ ਚਾਲਕ ਸ਼ਕਤੀ ਵੀ ਕਹਿੰਦੇ ਹਨ । ਕਿਉਂਕਿ ਖਣਿਜਾਂ ਦੀ ਤਰ੍ਹਾਂ ਇਸ ਨੂੰ ਧਰਤੀ ਵਿਚੋਂ ਕੱਢਿਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਕਰਕੇ ਇਸਨੂੰ ਖਣਿਜ ਤੇਲ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਇਸ ਨੂੰ ਪੈਟਰੋਲੀਅਮ ਦਾ ਨਾਂ ਇਸ ਕਰਕੇ ਦਿੱਤਾ ਗਿਆ ਹੈ ਕਿਉਂਕਿ ਇਹ ਦੋ ਸ਼ਬਦਾਂ-‘ਪੈਟਰੋ’ ਅਤੇ ‘ਉਲੀਅਮ` ਦੇ ਜੋੜ ਨਾਲ ਬਣਿਆ ਹੈ । ਲਾਤੀਨੀ ਭਾਸ਼ਾ ਵਿਚ ਪੈਟਰੋ ਦਾ ਅਰਥ ਹੈ ਚੱਟਾਨ ਅਤੇ ਉਲੀਅਮ ਦਾ ਅਰਥ ਹੈ ਤੇਲ । ਇਸ ਪ੍ਰਕਾਰ ਪੈਟਰੋਲੀਅਮ ਦਾ ਸ਼ਬਦੀ ਅਰਥ ਚੱਟਾਨ ਤੋਂ ਪ੍ਰਾਪਤ ਹੋਣ ਵਾਲੇ ਖਣਿਜ ਤੇਲ ਤੋਂ ਹੈ । ਇਹ ਬਨਸਪਤੀ ਅਤੇ ਮਰੇ ਹੋਏ ਜੀਵਜੰਤੂਆਂ ਦੇ ਪਰਤਦਾਰ ਚੱਟਾਨਾਂ ਵਿਚਾਲੇ ਦੱਬੇ ਜਾਣ ਨਾਲ ਬਣਿਆ ਹੈ ।
ਸ਼ਨ 7.
ਧਰਤੀ ‘ਤੇ ਮਿੱਟੀ ਦੀ ਕੀ ਮਹੱਤਤਾ ਹੈ ? ਇਸ ਦੇ ਬਾਰੇ ਲਿਖੋ ।
ਉੱਤਰ-
ਮਿੱਟੀ ਇਕ ਬਹੁਤ ਹੀ ਮਹੱਤਵਪੂਰਨ ਭੂਮੀ ਸਾਧਨ ਹੈ । ਮਿੱਟੀ ਦੀ ਉਪਜਾਊ ਸ਼ਕਤੀ ਕਾਰਨ ਹੀ ਇਸ ਦਾ ਮਹੱਤਵ ਹੈ । ਉਪਜਾਊ ਮਿੱਟੀ ਦਾ ਮਨੁੱਖ ਨੂੰ ਆਪਣੇ ਵਲ ਖਿੱਚਦੀ ਰਹੀ ਹੈ ਕਿਉਂਕਿ ਮਨੁੱਖ ਨੂੰ ਭੋਜਨ ਦੀਆਂ ਵਸਤੂਆਂ ਇਸੇ ਤੋਂ ਪ੍ਰਾਪਤ ਹੁੰਦੀਆਂ ਹਨ । ਇਹੀ ਕਾਰਨ ਹੈ ਕਿ ਮਨੁੱਖ ਸ਼ੁਰੂ ਤੋਂ ਹੀ ਉਪਜਾਊ ਧਰਤੀਆਂ ‘ਤੇ ਰਹਿਣਾ ਪਸੰਦ ਕਰਦਾ ਰਿਹਾ ਹੈ । ਪ੍ਰਾਚੀਨ ਸਭਿਅਤਾਵਾਂ ਦਾ ਜਨਮ ਅਤੇ ਵਿਕਾਸ ਵੀ ਸੰਸਾਰ ਦੀਆਂ ਉਪਜਾਊ ਨਦੀ-ਘਾਟੀਆਂ ਵਿਚ ਹੀ ਹੋਇਆ ਹੈ । ਇਸ ਵਿਚ ਸਿੰਧ, ਨੀਲ, ਦਜਲਾ-ਫਰਾਤ, ਯੰਗਸੀ ਘਾਟੀਆਂ ਦਾ ਵਿਸ਼ੇਸ਼ ਯੋਗਦਾਨ ਰਿਹਾ ਹੈ | ਅੱਜ ਵੀ ਉਪਜਾਉ ਨਦੀ ਘਾਟੀਆਂ ਤੇ ਮੈਦਾਨਾਂ ਵਿਚ ਹੀ ਸੰਘਣੀ ਜਨਸੰਖਿਆ ਪਾਈ ਜਾਂਦੀ ਹੈ । ਭਾਰਤ ਆਪਣੀ ਉਪਜਾਊ ਮਿੱਟੀ ਦੇ ਕਾਰਨ ਹੀ ਇੰਨੀ ਵੱਡੀ ਜਨਸੰਖਿਆ ਲਈ ਭੋਜਨ ਪੈਦਾ ਕਰਨ ਵਿਚ ਸਮਰੱਥ ਹੋ ਸਕਿਆ ਹੈ ।
ਪ੍ਰਸ਼ਨ 8.
ਭਾਰਤ ਵਿਚ ਕੋਲਾ, ਲੋਹਾ ਅਤੇ ਪੈਟਰੋਲੀਅਮ ਕਿੱਥੇ-ਕਿੱਥੇ ਮਿਲਦਾ ਹੈ ?
ਉੱਤਰ-
ਭਾਰਤ ਵਿਚ ਕੋਲਾ, ਲੋਹਾ ਅਤੇ ਪੈਟਰੋਲੀਅਮ ਹੇਠ ਲਿਖੇ ਥਾਂਵਾਂ ਤੋਂ ਮਿਲਦਾ ਹੈ –
- ਕੋਲਾ-ਦਮੋਦਰ ਘਾਟੀ ਭਾਰਤ ਵਿਚ ਪ੍ਰਮੁੱਖ ਕੋਲਾ ਖੇਤਰ ਹੈ । ਬੰਗਾਲ ਅਤੇ ਮੱਧ ਪ੍ਰਦੇਸ਼ ਰਾਜਾਂ ਵਿਚ ਵੀ ਕੋਲਾ ਪਾਇਆ ਜਾਂਦਾ ਹੈ ।
- ਲੋਹਾ-ਲੋਹੇ ਦੇ ਭੰਡਾਰ ਔਡੀਸ਼ਾ, ਝਾਰਖੰਡ, ਬੰਗਾਲ, ਕਰਨਾਟਕ, ਮੱਧ ਪ੍ਰਦੇਸ਼ ਆਦਿ ਵਿੱਚ ਹਨ ।
- ਪੈਟਰੋਲੀਅਮ-ਭਾਰਤ ਵਿਚ ਪੈਟਰੋਲੀਅਮ ਆਸਾਮ, ਗੁਜਰਾਤ, ਬੰਬੇ ਹਾਈ ਆਦਿ ਤੋਂ ਮਿਲਦਾ ਹੈ ।
(ਈ) ਹੇਠ ਲਿਖੇ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਉੱਤਰ ਲਗਪਗ 125-130 ਸ਼ਬਦਾਂ ਵਿਚ ਦਿਓ –
ਪ੍ਰਸ਼ਨ 1.
ਧਰਤੀ ‘ਤੇ ਮਿਲਣ ਵਾਲੀਆਂ ਚੱਟਾਨਾਂ ਬਾਰੇ ਵਿਸਤਾਰ ਨਾਲ ਲਿਖੋ ।
ਉੱਤਰ-
ਧਰਤੀ ਦੀ ਉੱਪਰਲੀ ਪਰਤ ਜਿਨ੍ਹਾਂ ਪਦਾਰਥਾਂ ਨਾਲ ਬਣੀ ਹੋਈ ਹੈ, ਉਨ੍ਹਾਂ ਸਭ ਪਦਾਰਥਾਂ ਨੂੰ ਚੱਟਾਨਾਂ ਕਹਿੰਦੇ ਹਨ । ਚੱਟਾਨ ਪੱਥਰ ਵਾਂਗ ਕਠੋਰ ਵੀ ਹੁੰਦੀ ਹੈ ਅਤੇ ਰੇਤ ਵਾਂਗ ਨਰਮ ਵੀ । ਕੁੱਝ ਚੱਟਾਨਾਂ ਬਹੁਤ ਸਖ਼ਤ ਹੁੰਦੀਆਂ ਹਨ ਅਤੇ ਦੇਰ ਨਾਲ ਟੁੱਟਦੀਆਂ ਹਨ । ਕੁੱਝ ਚੱਟਾਨਾਂ ਨਰਮ ਹੁੰਦੀਆਂ ਹਨ ਅਤੇ ਛੇਤੀ ਟੁੱਟ ਜਾਂਦੀਆਂ ਹਨ 1 ਚੱਟਾਨਾਂ ਤਿੰਨ ਪ੍ਰਕਾਰ ਦੀਆਂ ਹੁੰਦੀਆਂ ਹਨ ।
1. ਅਗਨੀ ਚੱਟਾਨਾਂ-ਅਗਨੀ ਦਾ ਅਰਥ ਹੁੰਦਾ ਹੈ-ਅੱਗ ਜਾਂ ਅਗਨੀ ਨਾਲ ਸੰਬੰਧਿਤ । ਇੱਥੇ ਅਗਨੀ ਤੋਂ ਭਾਵ ਹੈਉੱਚਾ ਤਾਪਮਾਨ ਜਾਂ ਗਰਮੀ ਤੋਂ ਹੈ | ਅਗਨੀ ਚੱਟਾਨਾਂ ਧਰਤੀ ਦੀ ਅੰਦਰੂਨੀ ਗਰਮੀ ਤੋਂ ਬਣਦੀਆਂ ਹਨ । ਇਸ ਲਈ ਇਨ੍ਹਾਂ ਦਾ ਨਾਂ ਅਗਨੀ ਚੱਟਾਨਾਂ ਪੈ ਗਿਆ । ਧਰਤੀ ਦੇ ਅੰਦਰੂਨੀ ਭਾਗ ਵਿਚ ਬਹੁਤ ਗਰਮੀ ਹੁੰਦੀ ਹੈ । ਇੱਥੇ ਸਭ ਪਦਾਰਥ ਪਿਘਲੀ ਹੋਈ ਅਵਸਥਾ ਵਿਚ ਹੁੰਦੇ ਹਨ । ਇਨ੍ਹਾਂ ਪਿਘਲੇ ਹੋਏ ਪਦਾਰਥਾਂ ਨੂੰ ਮੈਗਮਾ ਕਹਿੰਦੇ ਹਨ । ਧਰਤੀ ਦੇ ਬਾਹਰ ਆਉਣ ਵਾਲੇ ਮੈਗਮਾ ਨੂੰ ਲਾਵਾ ਕਿਹਾ ਜਾਂਦਾ ਹੈ | ਬਾਹਰ ਨਿਕਲਣ ‘ਤੇ ਗਰਮ ਲਾਵਾ ਹੌਲੀ-ਹੌਲੀ ਠੰਢਾ ਹੋ ਕੇ ਠੋਸ ਬਣ ਜਾਂਦਾ ਹੈ । ਇਸ ਪਕਾਰ ਅਗਨੀ ਚੱਟਾਨਾਂ ਦਾ ਨਿਰਮਾਣ ਹੁੰਦਾ ਹੈ | ਅਗਨੀ ਚੱਟਾਨਾਂ ਦੋ ਪ੍ਰਕਾਰ ਦੀਆਂ ਹੁੰਦੀਆਂ ਹਨ –
ਅੰਤਰਵੇਧੀ ਚੱਟਾਨਾਂ ਅਤੇ ਬਾਹਰਵੇਧੀ ਚੱਟਾਨਾਂ –
(i) ਅੰਤਰਵੇਧੀ ਚੱਟਾਨਾਂ-ਇਹ ਚੱਟਾਨਾਂ ਧਰਾਤਲ ਦੇ ਅੰਦਰ ਬਣਦੀਆਂ ਹਨ । ਇਹ ਵੀ ਦੋ ਪ੍ਰਕਾਰ ਦੀਆਂ ਹੁੰਦੀਆਂ ਹਨਪਾਤਾਲੀ ਅਤੇ ਮਧਵਰਤੀ ।
(a) ਪਾਤਾਲੀ ਅਗਨੀ ਚੱਟਾਨਾਂ-ਕਈ ਵਾਰ ਲਾਵਾ ਧਰਾਤਲ ਦੇ ਹੇਠਾਂ ਹੀ ਠੰਢਾ ਹੋ ਕੇ ਜੰਮ ਜਾਂਦਾ ਹੈ । ਧਰਾਤਲ ਦੇ ਹੇਠਾਂ ਬਣੀਆਂ ਇਸ ਪ੍ਰਕਾਰ ਦੀਆਂ ਅਗਨੀ ਚੱਟਾਨਾਂ ਨੂੰ ਪਾਤਾਲੀ ਅਗਨੀ ਚੱਟਾਨਾਂ ਕਹਿੰਦੇ ਹਨ । ਗ੍ਰੇਨਾਈਟ ਇਸ ਪ੍ਰਕਾਰ ਦੀ ਚੱਟਾਨ ਹੈ ।
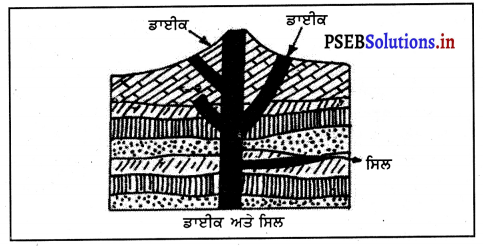
(b) ਮਧਵਰਤੀ ਅਗਨੀ ਚੱਟਾਨਾਂ-ਆਮ ਤੌਰ ‘ਤੇ ਲਾਵਾ ਧਰਤੀ ਦੇ ਧਰਾਤਲ ਨੂੰ ਪਾੜ ਕੇ ਬਾਹਰ ਨਿਕਲਣ ਦਾ ਯਤਨ ਕਰਦਾ ਹੈ । ਪਰੰਤੁ ਕਦੇ-ਕਦੇ ਇਹ ਧਰਾਤਲ ਤਕ ਨਹੀਂ ਪਹੁੰਚਦਾ ਅਤੇ ਧਰਾਤਲ ਦੀਆਂ ਤਰੇੜਾਂ ਵਿਚ ਹੀ ਠੰਡਾ ਹੋ ਕੇ ਕਠੋਰ ਰੂਪ ਧਾਰਨ ਕਰ ਲੈਂਦਾ ਹੈ । ਇਸ ਪ੍ਰਕਾਰ ਬਣੀਆਂ ਅਗਨੀ ਚੱਟਾਨਾਂ ਨੂੰ ਮਧਵਰਤੀ ਅਗਨੀ ਚੱਟਾਨਾਂ ਕਹਿੰਦੇ ਹਨ । ਡਾਈਕ, ਸਿਲ, ਡੋਲੋਰਾਈਟ ਅਗਨੀ ਚੱਟਾਨਾਂ ਦਾ ਨਿਰਮਾਣ ਇਸੇ ਪ੍ਰਕਾਰ ਹੁੰਦਾ ਹੈ ।
(ii) ਬਾਹਰਵੇਧੀ ਚੱਟਾਨਾਂ-ਇਹ ਚੱਟਾਨਾਂ ਧਰਾਤਲ ‘ਤੇ ਲਾਵਾ ਠੰਢਾ ਹੋਣ ਨਾਲ ਬਣਦੀਆਂ ਹਨ ।
2. ਤਲਛੱਟੀ ਜਾਂ ਤਹਿਦਾਰ ਚੱਟਾਨਾਂ-ਧਰਤੀ ਦੇ ਧਰਾਤਲ ਦੀਆਂ ਚੱਟਾਨਾਂ ਵਰਖਾ, ਹਵਾ, ਨਦੀ, ਹਿਮ ਨਦੀ ਅਤੇ ਗਰਮੀਸਰਦੀ ਦੇ ਕਾਰਨ ਟੁੱਟਦੀਆਂ ਰਹਿੰਦੀਆਂ ਹਨ । ਇਨ੍ਹਾਂ ਟੁੱਟੇ ਹੋਏ ਕਣਾਂ ਨੂੰ ਨਦੀਆਂ ਅਤੇ ਹਿਮ ਨਦੀਆਂ ਆਪਣੇ ਨਾਲ ਰੋੜ ਕੇ ਲੈ ਜਾਂਦੀਆਂ ਹਨ ਅਤੇ ਕਿਸੇ ਇਕ ਜਗ੍ਹਾ ‘ਤੇ ਇਕੱਠਾ ਕਰ ਦਿੰਦੀਆਂ ਹਨ |
ਹੌਲੀ-ਹੌਲੀ ਇਨ੍ਹਾਂ ਕਣਾਂ ਦੀਆਂ ਤਹਿਆਂ ਇਕ-ਦੂਜੇ ‘ਤੇ ਜਮਾਂ ਹੋਣ ਲੱਗਦੀਆਂ ਹਨ | ਹਜ਼ਾਰਾਂ ਸਾਲਾਂ ਤਕ ਦਬਾਅ ਦੇ ਕਾਰਨ ਇਹ ਤਹਿਆਂ ਕਠੋਰ ਹੋ ਜਾਂਦੀਆਂ ਹਨ । ਇਸ ਤਰ੍ਹਾਂ ਇਹ ਤਹਿਆਂ ਤਲਛੱਟੀ ਚੱਟਾਨਾਂ ਦਾ ਰੂਪ ਧਾਰਨ ਕਰ ਲੈਂਦੀਆਂ ਹਨ । ਇਨ੍ਹਾਂ ਚੱਟਾਨਾਂ ਨੂੰ ਤਹਿਦਾਰ ਜਾਂ ਪਰਤਦਾਰ ਚੱਟਾਨਾਂ ਵੀ ਕਹਿੰਦੇ ਹਨ । ਗੰਗਾ ਅਤੇ ਸਿੰਧ ਦਾ ਮੈਦਾਨ ਅਤੇ ਹਿਮਾਲਿਆ ਪਰਬਤ ਵੀ ਇਸ ਪ੍ਰਕਾਰ ਦੀਆਂ ਚੱਟਾਨਾਂ ਤੋਂ ਬਣਿਆ ਹੈ ।
3. ਰੂਪਾਂਤਰਿਤ ਚੱਟਾਨਾਂ-ਇਹ ਚੱਟਾਨਾਂ ਅਗਨੀ ਅਤੇ ਤਹਿਦਾਰ ਚੱਟਾਨਾਂ ਦੀ ਸੰਰਚਨਾ ਦੇ ਰੰਗ-ਰੂਪ, ਗੁਣ ਆਦਿ ਬਦਲਣ ਨਾਲ ਬਣਦੀਆਂ ਹਨ । ਇਹ ਰੂਪਾਂਤਰਨ ਧਰਤੀ ਦੇ ਅੰਦਰਲੀ ਗਰਮੀ ਅਤੇ ਦਬਾਅ ਦੇ ਕਾਰਨ ਹੁੰਦਾ ਹੈ । ਉਦਾਹਰਨ ਵਜੋਂ ਚੁਨੇ ਦਾ ਪੱਥਰ ਸੰਗਮਰਮਰ ਬਣ ਜਾਂਦਾ ਹੈ, ਜੋ ਇਕ ਰੁਪਾਂਤਰਿਤ ਚੱਟਾਨ ਹੈ । ਭਾਰਤ ਦਾ ਦੱਖਣੀ ਪਠਾਰ ਰੂਪਾਂਤਰਿਤ ਚੱਟਾਨਾਂ ਤੋਂ ਬਣਿਆ ਹੈ । ਰੂਪਾਂਤਰਿਤ ਚੱਟਾਨਾਂ ਧਰਾਤਲ ਦੇ ਹੇਠਾਂ ਬਹੁਤ ਡੂੰਘਾਈ ਵਿਚ ਪਾਈਆਂ ਜਾਂਦੀਆਂ ਹਨ ।
ਇਹ ਦੋ ਪ੍ਰਕਾਰ ਨਾਲ ਬਣਦੀਆਂ ਹਨ-ਤਾਪੀ ਰੂਪਾਂਤਰਨ ਦੁਆਰਾ ਅਤੇ ਖੇਤਰੀ ਰੂਪਾਂਤਰਨ ਦੁਆਰਾ ।
- ਤਾਪੀ ਰੂਪਾਂਤਰਨ ਦੁਆਰਾ-ਜਦੋਂ ਗਰਮ ਮੈਗਮਾ ਧਰਤੀ ਦੇ ਅੰਦਰ ਦੀਆਂ ਤਰੇੜਾਂ ਅਤੇ ਨਾਲੀਆਂ ਵਿਚੋਂ ਗੁਜ਼ਰਦਾ ਹੈ, ਤਾਂ ਇਹ ਆਪਣੇ ਸੰਪਰਕ ਵਿਚ ਆਉਣ ਵਾਲੀਆਂ ਚੱਟਾਨਾਂ ਨੂੰ ਪਕਾ ਦਿੰਦਾ ਹੈ । ਇਸ ਨੂੰ ਤਾਪੀ ਰੂਪਾਂਤਰ ਕਹਿੰਦੇ ਹਨ, ਜਿਸ ਤੋਂ ਰੁਪਾਂਤਰਿਤ ਚੱਟਾਨਾਂ ਬਣਦੀਆਂ ਹਨ ।
- ਖੇਤਰੀ ਰੂਪਾਂਤਰਨ ਦੁਆਰਾ-ਕਦੇ-ਕਦੇ ਇਕ ਵੱਡੇ ਖੇਤਰ ਵਿਚ ਉੱਪਰੀ ਚੱਟਾਨਾਂ ਦੇ ਦਬਾਅ ਕਾਰਨ ਹੇਠਲੀਆਂ ਚੱਟਾਨਾਂ ਦਾ ਮੂਲ ਰੂਪ ਬਦਲ ਜਾਂਦਾ ਹੈ । ਇਸ ਨੂੰ ਖੇਤਰੀ ਰੂਪਾਂਤਰਨ ਕਹਿੰਦੇ ਹਨ । ਰੂਪਾਂਤਰਿਤ ਚੱਟਾਨ ਵਿਚ ਮੂਲ ਚੱਟਾਨ ਦੇ ਕੁੱਝ ਗੁਣ ਜ਼ਰੂਰ ਰਹਿ ਜਾਂਦੇ ਹਨ । ਉਦਾਹਰਨ ਵਜੋਂ ਤਹਿਦਾਰ ਚੱਟਾਨ ਨਾਲ ਬਣੀ ਰੁਪਾਂਤਰਿਤ ਚੱਟਾਨ ਵੀ ਤਹਿਦਾਰ ਹੁੰਦੀ ਹੈ । ਇਸੇ ਪ੍ਰਕਾਰ ਅਗਨੀ ਚੱਟਾਨ ਨਾਲ ਬਣੀ ਪਰਿਵਰਤਿਤ ਰੂਪਾਂਤਰਿਤ ਚੱਟਾਨ ਦੇ ਕੁੱਝ ਗੁਣ ਮੂਲ ਚੱਟਾਨ ਨਾਲ ਮਿਲਦੇ-ਜੁਲਦੇ ਹੁੰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 2.
ਖਣਿਜ ਪਦਾਰਥ ਕਿਸ ਨੂੰ ਆਖਦੇ ਹਨ ? ਸਾਡੀ ਧਰਤੀ ‘ਤੇ ਕਿਹੜੇ ਖਣਿਜ ਪਦਾਰਥ ਮਿਲਦੇ ਹਨ ? ਇਨ੍ਹਾਂ ਦਾ ਵਰਗੀਕਰਨ ਕਰੋ । ਕਿਸੇ ਇਕ ਧਾਤਵੀ ਖਣਿਜ ਬਾਰੇ ਜਾਣਕਾਰੀ ਦਿਓ ।
ਉੱਤਰ-
ਚੱਟਾਨਾਂ ਦਾ ਨਿਰਮਾਣ ਕਰਨ ਵਾਲ਼ੇ ਪਦਾਰਥਾਂ ਨੂੰ ਖਣਿਜ ਪਦਾਰਥ ਕਹਿੰਦੇ ਹਨ । ਇਨ੍ਹਾਂ ਨੂੰ ਧਰਤੀ ਨੂੰ ਪੁੱਟ ਕੇ ਕੱਢਿਆ ਜਾਂਦਾ ਹੈ । ਸਾਡੀ ਧਰਤੀ ‘ਤੇ ਅਨੇਕ ਪ੍ਰਕਾਰ ਦੇ ਖਣਿਜ ਮਿਲਦੇ ਹਨ । ਖਣਿਜਾਂ ਦਾ ਵਰਗੀਕਰਨ-ਖਣਿਜਾਂ ਨੂੰ ਤਿੰਨ ਵਰਗਾਂ ਵਿਚ ਵੰਡਿਆ ਗਿਆ ਹੈ –
- ਧਾਤਵੀ ਖਣਿਜ-ਇਨ੍ਹਾਂ ਵਿਚ ਧਾਤੂ ਦੇ ਅੰਸ਼ ਹੁੰਦੇ ਹਨ । ਇਨ੍ਹਾਂ ਵਿਚ ਲੋਹਾ, ਤਾਂਬਾ, ਟਿਨ, ਐਲੂਮੀਨੀਅਮ, ਸੋਨਾ, ਚਾਂਦੀ ਆਦਿ ਖਣਿਜ ਸ਼ਾਮਿਲ ਹਨ ।
- ਅਧਾਤਵੀ ਖਣਿਜ-ਇਨ੍ਹਾਂ ਖਣਿਜਾਂ ਵਿਚ ਧਾਤੂ ਦਾ ਅੰਸ਼ ਨਹੀਂ ਹੁੰਦਾ । ਇਨ੍ਹਾਂ ਵਿਚ ਸਲਫਰ, ਅਬਰਕ, ਜਿਪਸਮ, ਫਾਸਫੇਟ, ਪੋਟਾਸ਼ ਆਦਿ ਖਣਿਜ ਸ਼ਾਮਿਲ ਹਨ ।
- ਸ਼ਕਤੀ ਖਣਿਜ-ਇਨ੍ਹਾਂ ਖਣਿਜਾਂ ਤੋਂ ਬਾਲਣ ਸ਼ਕਤੀ, ਉਰਜਾ ਆਦਿ ਮਿਲਦੇ ਹਨ । ਇਨ੍ਹਾਂ ਤੋਂ ਸਾਡੇ ਥਰਮਲ ਪਲਾਂਟ, ਕਾਰਖ਼ਾਨੇ, ਮੋਟਰ ਗੱਡੀਆਂ ਆਦਿ ਚਲਦੀਆਂ ਹਨ । ਕੋਲਾ, ਪੈਟਰੋਲੀਅਮ, ਕੁਦਰਤੀ ਗੈਸ ਆਦਿ ਮੁੱਖ ਸ਼ਕਤੀ ਖਣਿਜ ਹਨ ।
ਧਾਤਵੀ ਖਣਿਜ-ਮੁੱਖ ਧਾਤਵੀ ਖਣਿਜਾਂ ਦਾ ਵਰਣਨ ਇਸ ਪ੍ਰਕਾਰ ਹੈ –
1. ਲੋਹਾ-ਲੋਹੇ ਦਾ ਉਪਯੋਗ ਛੋਟੇ ਜਹੀ ਕਿੱਲ ਤੋਂ ਲੈ ਕੇ ਵੱਡੇ-ਵੱਡੇ ਸਮੁੰਦਰੀ ਬੇੜੇ ਬਣਾਉਣ ਵਿਚ ਹੁੰਦਾ ਹੈ | ਪੁਰੀ ਉਦਯੋਗਿਕ ਮਸ਼ੀਨਰੀ, ਮੋਟਰਕਾਰਾਂ, ਰੇਲਾਂ, ਖੇਤੀ ਲਈ ਮਸ਼ੀਨਰੀ ਆਦਿ ਦਾ ਨਿਰਮਾਣ ਵੀ ਇਸੇ ਖਣਿਜ ‘ਤੇ ਹੀ ਆਧਾਰਿਤ ਹੈ । ਲੋਹੇ ਅਤੇ ਇਸਪਾਤ ਨੇ ਉਦਯੋਗਿਕ ਖੇਤਰ ਵਿਚ ਕ੍ਰਾਂਤੀ ਲਿਆ ਦਿੱਤੀ ਹੈ । ਲੋਹਾ ਸੰਸਾਰ ਦੇ ਲਗਪਗ ਸਾਰੇ ਮਹਾਦੀਪਾਂ ਵਿਚ ਮਿਲਦਾ ਹੈ । ਭਾਰਤ ਵਿਚ ਉੜੀਸਾ, ਝਾਰਖੰਡ, ਬਿਹਾਰ, ਮੱਧਪ੍ਰਦੇਸ਼, ਛਤੀਸਗੜ, ਕਰਨਾਟਕ ਅਤੇ ਗੋਆ ਲੋਹੇ ਦੇ ਮੁੱਖ ਉਤਪਾਦਕ ਰਾਜ ਹਨ ।
2. ਤਾਂਬਾ-ਤਾਂਬਾ ਮਨੁੱਖ ਦੁਆਰਾ ਖੋਜੀ ਗਈ ਸਭ ਤੋਂ ਪਹਿਲੀ ਧਾਤ ਸੀ । ਇਸਦੇ ਉਦਯੋਗਿਕ ਮਹੱਤਵ ਨੂੰ ਦੇਖਦੇ ਹੋਏ ਲੋਹੇ ਤੋਂ ਬਾਅਦ ਤਾਂਬੇ ਦਾ ਸਥਾਨ ਆਉਂਦਾ ਹੈ । ਧਾਤੁ ਯੁੱਗ ਦਾ ਆਰੰਭ ਤਾਂਬੇ ਦੇ ਪ੍ਰਯੋਗ ਨਾਲ ਹੀ ਹੋਇਆ ਸੀ । ਇਸ ਤੋਂ ਕਈ ਤਰ੍ਹਾਂ ਦੇ ਬਰਤਨ ਬਣਾਏ ਜਾਂਦੇ ਹਨ | ਅੱਜ ਦੇ ਯੁੱਗ ਵਿਚ ਇਸਦਾ ਮਹੱਤਵ ਹੋਰ ਵੀ ਵੱਧ ਗਿਆ ਹੈ । ਇਸਦਾ ਉਪਯੋਗ ਬਿਜਲੀ ਦਾ ਸਮਾਨ ਬਣਾਉਣ ਲਈ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਇਸਨੂੰ ਬਿਜਲੀ ਦਾ ਸੂਚਾਲਕ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ । ਇਸੇ ਕਰਕੇ ਬਿਜਲੀ ਦੀਆਂ ਤਾਰਾਂ ਜ਼ਿਆਦਾਤਰ ਤਾਂਬੇ ਦੀਆਂ ਬਣਾਈਆਂ ਜਾਂਦੀਆਂ ਹਨ ।
ਟੈਲੀਫੋਨ-ਕੇਬਲ ਤਾਰਾਂ, ਰੇਲਵੇ ਇੰਜਨ, ਹਵਾਈ ਜਹਾਜ਼ ਅਤੇ ਘੜੀਆਂ ਵਿਚ ਵੀ ਇਸ ਦਾ ਪ੍ਰਯੋਗ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਚਿੱਲੀ (ਦੱਖਣੀ ਅਮਰੀਕਾ) ਸੰਸਾਰ ਵਿਚ ਸਭ ਤੋਂ ਵੱਧ ਤਾਂਬਾ ਪੈਦਾ ਕਰਦਾ ਹੈ । ਦੂਸਰੇ ਨੰਬਰ ਤੇ ਸੰਯੁਕਤ ਰਾਜ ਅਮਰੀਕਾ (ਯੁ.ਐੱਸ.ਏ.) ਆਉਂਦਾ ਹੈ | ਅਫ਼ਰੀਕਾ ਮਹਾਂਦੀਪ ਵਿਚ ਵੀ ਤਾਂਬੇ ਦੇ ਕਾਫ਼ੀ ਭੰਡਾਰ ਮਿਲਦੇ ਹਨ । ਇਸ ਤੋਂ ਇਲਾਵਾ ਭਾਰਤ, ਜਪਾਨ, ਆਸਟਰੇਲੀਆ ਵਿਚ ਵੀ ਤਾਂਬੇ ਦਾ ਉਤਪਾਦਨ ਹੁੰਦਾ ਹੈ । ਭਾਰਤ ਵਿਚ ਝਾਰਖੰਡ, ਮੱਧ ਪ੍ਰਦੇਸ਼, ਸੀਮਾਂਧਰ ਅਤੇ ਰਾਜਸਥਾਨ ਪ੍ਰਾਂਤਾਂ ਵਿਚ ਤਾਂਬੇ ਦੇ ਕਾਫ਼ੀ ਭੰਡਾਰ ਹਨ ।
3. ਬਾਕਸਾਈਟ-ਆਕਸਾਈਟ ਤੋਂ ਐਲੂਮੀਨੀਅਮ ਪ੍ਰਾਪਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ | ਐਲੂਮੀਨੀਅਮ ਹਲਕੇ ਭਾਰ ਵਾਲੀ ਧਾਤ ਹੈ, ਜਿਸਦਾ ਜ਼ਿਆਦਾਤਰ ਉਪਯੋਗ ਹਵਾਈ ਜਹਾਜ਼ ਬਣਾਉਣ ਵਿਚ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਰੇਲ ਗੱਡੀਆਂ, ਮੋਟਰਾਂ, ਬੱਸਾਂ, ਕਾਰਾਂ ਅਤੇ ਬਿਜਲੀ ਦੀਆਂ ਤਾਰਾਂ ਵਿਚ ਵੀ ਇਸ ਦਾ ਉਪਯੋਗ ਹੁੰਦਾ ਹੈ । ਇਸ ਤੋਂ ਬਰਤਨ ਵੀ ਬਣਾਏ ਜਾਂਦੇ ਹਨ । ਇਸ ਦੀਆਂ ਬਣੀਆਂ ਵਸਤੂਆਂ ਨੂੰ ਜੰਗਾਲ ਨਹੀਂ ਲੱਗਦਾ । ਇਸ ਕਰਕੇ ਇਹ ਵਸਤਾਂ ਬਹੁਤ ਦੇਰ ਤਕੂ ਪ੍ਰਯੋਗ ਵਿਚ ਲਿਆਈਆਂ ਜਾ ਸਕਦੀਆਂ ਹਨ । ਸੰਸਾਰ ਵਿਚ ਸਭ ਤੋਂ ਜ਼ਿਆਦਾ ਬਾਕਸਾਈਟ ਆਸਟਰੇਲੀਆ ਵਿਚ ਕੱਢਿਆ ਜਾਂਦਾ ਹੈ । ਭਾਰਤ ਵਿਚ ਬਾਕਸਾਈਟ, ਮਹਾਂਰਾਸ਼ਟਰ, ਮੱਧ ਪ੍ਰਦੇਸ਼, ਛਤੀਸਗੜ੍ਹ ਅਤੇ ਝਾਰਖੰਡ ਵਿਚ ਪਾਇਆ ਜਾਂਦਾ ਹੈ ।
4. ਮੈਂਗਨੀਜ਼-ਮੈਂਗਨੀਜ਼ ਵੀ ਇਕ ਬਹੁਤ ਮਹੱਤਵਪੂਰਨ ਖਣਿਜ ਪਦਾਰਥ ਹੈ । ਇਸਦਾ ਵਧੇਰੇ ਉਪਯੋਗ ਕੱਚੇ ਲੋਹੇ ਜੋ ਕਿ ਧਰਤੀ ਵਿਚੋਂ ਮਿਲਦਾ ਹੈ) ਤੋਂ ਸਟੀਲ ਬਣਾਉਣ ਵਿਚ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਇਹ ਬਲੀਚਿੰਗ ਪਾਉਡਰ, ਕੀਟਨਾਸ਼ਕ ਦਵਾਈਆਂ, ਰੰਗ-ਰੋਗਨ ਤੇ ਸ਼ੀਸ਼ਾ ਬਣਾਉਣ ਲਈ ਵੀ ਉਪਯੋਗ ਵਿਚ ਲਿਆਇਆ ਜਾਂਦਾ ਹੈ । ਰੂਸ, ਜਾਰਜੀਆ, ਯੂਕਰੇਨ, ਕਜ਼ਾਖਿਸਤਾਨ ਵਿਚ ਮੈਂਗਨੀਜ਼ ਦੇ ਕਾਫ਼ੀ ਭੰਡਾਰ ਮਿਲਦੇ ਹਨ । ਇਨ੍ਹਾਂ ਤੋਂ ਇਲਾਵਾ ਦੱਖਣੀ ਅਫ਼ਰੀਕਾ, ਬ੍ਰਾਜ਼ੀਲ (ਦੱਖਣੀ ਅਮਰੀਕਾ) ਅਤੇ ਭਾਰਤ ਵੀ ਮੈਂਗਨੀਜ਼ ਮੁੱਖ ਉਤਪਾਦਕ ਦੇਸ਼ ਹਨ । ਭਾਰਤ ਵਿਚ ਮੱਧ ਪ੍ਰਦੇਸ਼ ਵਿਚ ਸਭ ਤੋਂ ਜ਼ਿਆਦਾ ਮੈਂਗਨੀਜ਼ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ । ਤੇਲੰਗਾਨਾ, ਸੀਮਾਂਧਰ, ਕਰਨਾਟਕ, ਉੜੀਸਾ ਅਤੇ ਝਾਰਖੰਡ ਵਿਚ ਵੀ ਮੈਂਗਨੀਜ਼ ਮਿਲਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 3.
ਸ਼ਕਤੀ ਖਣਿਜ ਕਿਸ ਨੂੰ ਆਖਦੇ ਹਨ ? ਕਿਸੇ ਇਕ ਸ਼ਕਤੀ ਖਣਿਜ ਬਾਰੇ ਜਾਣਕਾਰੀ ਦਿਓ ।
ਉੱਤਰ-
ਉਹ ਖਣਿਜ ਜਿਨ੍ਹਾਂ ਨਾਲ ਕਾਰਖ਼ਾਨੇ, ਮੋਟਰ ਗੱਡੀਆਂ ਆਦਿ ਚਲਾਉਣ ਲਈ ਊਰਜਾ ਅਤੇ ਬਲਣ ਊਰਜਾ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ, ਸ਼ਕਤੀ ਖਣਿਜ ਕਹਾਉਂਦੇ ਹਨ। ਮੁੱਖ ਸ਼ਕਤੀ ਖਣਿਜ ਕੋਇਲਾ, ਖਣਿਜ ਤੇਲ, ਕੁਦਰਤੀ ਗੈਸ ਆਦਿ ਹਨ । ਇਨ੍ਹਾਂ ਵਿਚੋਂ ਕੋਇਲੇ ਅਤੇ ਖਣਿਜ ਤੇਲ ਦਾ ਉਦਯੋਗਿਕ ਦ੍ਰਿਸ਼ਟੀ ਤੋਂ ਵਿਸ਼ੇਸ਼ ਮਹੱਤਵ ਹੈ । ਇਨ੍ਹਾਂ ਦਾ ਸੰਖੇਪ ਵਰਣਨ ਇਸ ਪ੍ਰਕਾਰ ਹੈ –
1. ਕੋਇਲਾ-ਕੋਇਲਾ ਇਕ ਮੁੱਖ ਸ਼ਕਤੀ ਖਣਿਜ ਹੈ । ਹੁਣ ਕੋਇਲੇ ਦਾ ਸਿੱਧਾ ਸ਼ਕਤੀ ਦੇ ਰੂਪ ਵਿਚ ਉਪਯੋਗ ਘੱਟ ਗਿਆ ਹੈ । ਇਸ ਨਾਲ ਬਿਜਲੀ ਪੈਦਾ ਕਰਕੇ ਸ਼ਕਤੀ ਪ੍ਰਾਪਤ ਕੀਤੀ ਜਾਣ ਲੱਗੀ ਹੈ । ਇਸ ਉਦੇਸ਼ ਲਈ ਉਪਯੋਗ ਵਿਚ ਲਿਆਇਆ ਜਾਣ ਵਾਲਾ ਕੋਇਲੇ ਪੱਥਰੀ ਕੋਇਲਾ ਹੈ । ਇਹ ਕੋਇਲਾ ਹਜਾਰਾਂ ਸਾਲ ਪਹਿਲਾਂ ਜੰਗਲਾਂ ਦੇ ਧਰਤੀ ਦੀਆਂ ਡੂੰਘੀਆਂ ਪਰਤਾਂ ਵਿਚ ਦੱਬੇ ਰਹਿਣ ਅਤੇ ਧਰਤੀ ਦੀ ਗਰਮੀ ਅਤੇ ਉੱਪਰਲੀਆਂ ਤਹਿਆਂ ਦੇ ਦਬਾਅ ਕਰਕੇ ਬਣਿਆ ਸੀ । ਇਸ ਪ੍ਰਕਿਰਿਆ ਨੂੰ ਕਰੋੜਾਂ ਸਾਲ ਲੱਗ ਗਏ ।
ਸੰਸਾਰ ਵਿਚ ਕੋਇਲੇ ਦੇ ਜ਼ਿਆਦਾਤਰ ਭੰਡਾਰ 350 ਤੋਂ 650 ਅਕਸ਼ਾਂਸ਼ਾਂ ਵਿਚ ਪਾਏ ਜਾਂਦੇ ਹਨ। ਸੰਸਾਰ ਦੇ 90% ਕੋਇਲੇ ਦੇ ਭੰਡਾਰ ਚੀਨ, ਯੂ. ਐੱਸ.ਏ., ਰੂਸ ਅਤੇ ਯੂਰਪੀ ਦੇਸ਼ਾਂ ਵਿਚ ਮਿਲਦੇ ਹਨ । ਇਹਨਾਂ ਤੋਂ ਇਲਾਵਾ ਦੱਖਣੀ ਅਮਰੀਕਾ, ਅਫਰੀਕਾ, ਉੱਤਰੀ ਅਮਰੀਕਾ ਅਤੇ ਏਸ਼ੀਆ ਮਹਾਂਦੀਪ ਵਿਚ ਵੀ ਕੋਇਲਾ ਦੇ ਵਿਸ਼ਾਲ ਭੰਡਾਰ ਹਨ । ਜਾਪਾਨ ਅਤੇ ਥਾਈਲੈਂਡ ਵਿਚ ਵੀ ਕੋਇਲਾ ਮਿਲਦਾ ਹੈ । ਭਾਰਤ ਸੰਸਾਰ ਦਾ 5% ਕੋਇਲਾ ਪੈਦਾ ਕਰਦਾ ਹੈ । ਦਮੋਦਰ ਘਾਟੀ ਭਾਰਤ ਵਿਚ ਪ੍ਰਮੁੱਖ ਕੋਇਲਾ ਖੇਤਰ ਹੈ । ਪੱਛਮੀ ਬੰਗਾਲ ਅਤੇ ਮੱਧ ਪ੍ਰਦੇਸ਼ ਰਾਜਾਂ ਵਿਚ ਵੀ ਕੋਇਲਾ ਪਾਇਆ ਜਾਂਦਾ ਹੈ ।
2. ਖਣਿਜ ਤੇਲ-ਖਣਿਜ ਤੇਲ ਨੂੰ ਤਰਲ ਸੋਨਾ ਵੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਇਸ ਨੂੰ ਇਹ ਨਾਂ ਇਸਦੇ ਵਧਦੇ ਹੋਏ ਉਪਯੋਗ ਅਤੇ ਮਹੱਤਵ ਦੇ ਕਾਰਨ ਦਿੱਤਾ ਗਿਆ ਹੈ । ਇਸ ਨੂੰ ਪੈਟਰੋਲੀਅਮ ਅਤੇ ਚਾਲਕ ਸ਼ਕਤੀ ਵੀ ਕਹਿੰਦੇ ਹਨ ਕਿਉਂਕਿ ਖਣਿਜਾਂ ਵਾਂਗ ਹੀ ਇਸ ਨੂੰ ਵੀ ਧਰਤੀ ਵਿਚੋਂ ਕੱਢਿਆ ਜਾਂਦਾ ਹੈ, ਇਸ ਕਾਰਨ ਇਸ ਨੂੰ ਖਣਿਜ ਤੇਲ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਇਸ ਨੂੰ ਪੈਟਰੋਲੀਅਮ ਨਾਂ ਇਸ ਲਈ ਦਿੱਤਾ ਗਿਆ ਹੈ ਕਿਉਂਕਿ ਇਹ ਦੋ ਸ਼ਬਦਾਂ- ‘ਪੈਟਰੋ’ ਅਤੇ ‘ਉਲੀਅਮ” ਦੇ ਜੋੜ ਤੋਂ ਬਣਿਆ ਹੈ । ਲਾਤੀਨੀ ਭਾਸ਼ਾ ਵਿਚ ਪੈਟਰਾ ਦਾ ਅਰਥ ਹੈ ਚੱਟਾਨ ਅਤੇ ਉਲੀਅਮ ਦਾ ਅਰਥ ਹੈ-ਤੇਲ ।
ਇਸ ਪ੍ਰਕਾਰ ਪੈਟਰੋਲੀਅਮ ਦਾ ਸ਼ਾਬਦਿਕ ਅਰਥ ਚੱਟਾਨ ਤੋਂ ਪ੍ਰਾਪਤ ਖਣਿਜ ਤੇਲ ਹੈ –
1. ਇਹ ਬਨਸਪਤੀ ਅਤੇ ਮਰੇ ਹੋਏ ਜੀਵ-ਜੰਤੂਆਂ ਦੇ ਪਰਤਦਾਰ ਚੱਟਾਨਾਂ ਦੇ ਵਿਚਾਲੇ ਦੱਬ ਜਾਣ ਨਾਲ ਬਣਿਆ ਹੈ । ਜਿਹੜਾ ਪੈਟਰੋਲ ਸਾਨੂੰ ਧਰਤੀ ਦੇ ਹੇਠਾਂ ਤੋਂ ਮਿਲਦਾ ਹੈ, ਉਹ ਅਸ਼ੁੱਧ ਅਤੇ ਅਣਸੋਧਿਆ ਹੁੰਦਾ ਹੈ । ਇਸ ਨੂੰ ਕੱਚਾ ਤੇਲ ਹਨ । ਜਿਵੇਂ ਮਿੱਟੀ ਦਾ ਤੇਲ, ਡੀਜ਼ਲ, ਪੈਟਰੋਲ, ਗੈਸ, ਚਿਕਨਾਹਟ ਵਾਲੇ ਤੇਲ, ਗੀਸ, ਮੋਮ, ਵੈਸਲੀਨ ਆਦਿ । ਦੱਖਣਪੱਛਮੀ ਏਸ਼ੀਆ ਵਿਚ ਸੰਸਾਰ ਦੇ ਸਭ ਤੋਂ ਵੱਡੇ ਤੇਲ-ਭੰਡਾਰ ਹਨ । ਇਸ ਖੇਤਰ ਵਿਚ ਸਾਊਦੀ ਅਰਬ, ਈਰਾਨ, ਇਰਾਕ, ਕੁਵੈਤ ਅਤੇ ਯੂ.ਏ.ਈ. ਯੂਨਾਈਟਿਡ ਅਰਬ ਅਮੀਰੇਟਸ) ਸ਼ਾਮਿਲ ਹਨ ।
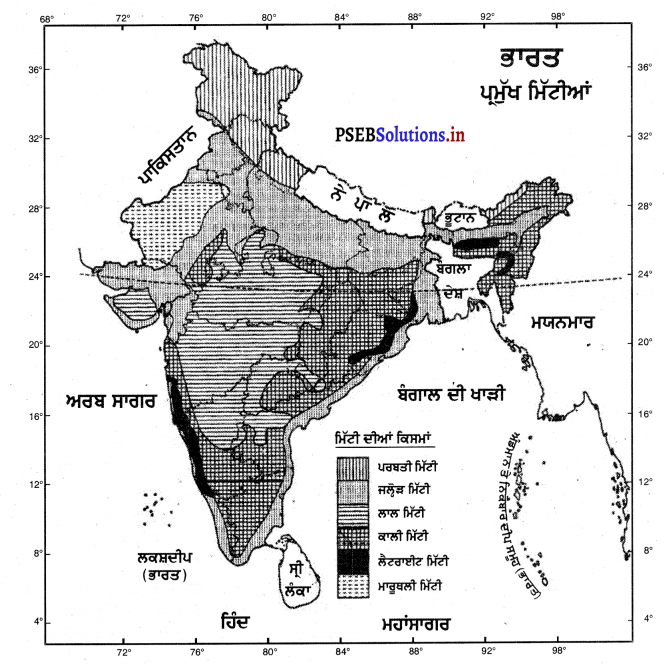
ਨੋਟ-ਵਿਦਿਆਰਥੀ ਦੋਨਾਂ ਵਿੱਚੋਂ ਕੋਈ ਇਕ ਲਿਖਣ – ਉੱਤਰ-ਮਿੱਟੀ ਇਕ ਮਹੱਤਵਪੂਰਨ ਸਾਧਨ ਹੈ । ਇਹ ਖੇਤੀ ਦਾ ਆਧਾਰ ਹੈ | ਭਾਰਤ ਵਿਚ ਮੁੱਖ ਰੂਪ ਵਿਚ ਛੇ ਪ੍ਰਕਾਰ ਦੀਆਂ ਮਿੱਟੀਆਂ ਪਾਈਆਂ ਜਾਂਦੀਆਂ ਹਨ, ਜਿਨ੍ਹਾਂ ਦਾ ਵਰਣਨ ਇਸ ਪ੍ਰਕਾਰ ਹੈ –
1. ਜਲੋੜ ਮਿੱਟੀ-ਜਲੋੜ ਮਿੱਟੀ ਉਹ ਮਿੱਟੀ ਹੈ ਜਿਹੜੀ ਨਦੀਆਂ ਦੁਆਰਾ ਲਿਆਂਦੀ ਗਈ ਤਲਛੱਟ ਦੇ ਜੰਮਣ ਨਾਲ ਬਣਦੀ ਹੈ । ਇਹ ਸੰਸਾਰ ਦੀਆਂ ਸਭ ਤੋਂ ਉਪਜਾਊ ਮਿੱਟੀਆਂ ਵਿਚੋਂ ਇਕ ਹੈ । ਭਾਰਤ ਵਿਚ ਇਹ ਮਿੱਟੀ ਸਤਲੁਜ-ਗੰਗਾ ਦੇ ਮੈਦਾਨ ਅਤੇ ਮਹਾਂਨਦੀ, ਗੋਦਾਵਰੀ, ਕਿਸ਼ਨਾ ਅਤੇ ਕਾਵੇਰੀ ਦੇ ਡੈਲਟਿਆਂ ਵਿਚ ਪਾਈ ਜਾਂਦੀ ਹੈ । ਜਲੋੜ ਮਿੱਟੀ ਉਪਜਾਊ ਦਾ ਹਰੇਕ ਸਾਲ ਨਵੀਨੀਕਰਨ ਹੁੰਦਾ ਰਹਿੰਦਾ ਹੈ । ਇਸ ਦਾ ਕਾਰਨ ਇਹ ਹੈ ਕਿ ਨਦੀਆਂ ਹਰ ਸਾਲ ਨਵੀਂ ਮਿੱਟੀ ਲਿਆ ਕੇ ਵਿਛਾਉਂਦੀਆਂ ਹਨ | ਨਵੀਂ ਜਲੋੜ ਮਿੱਟੀ ਨੂੰ ਖਾਦਰ ਅਤੇ ਪੁਰਾਣੀ ਜਲੋੜ ਮਿੱਟੀ ਨੂੰ ਬਾਂਗਰ ਕਹਿੰਦੇ ਹਨ ।
2. ਪੋਟਾਸ਼ ਅਤੇ – ਨਾਈਟ੍ਰੋਜਨ ਦੀ ਬਹੁਤ ਕਮੀ ਹੁੰਦੀ ਹੈ ਜਦਕਿ ਮੈਗਨੀਸ਼ੀਅਮ, ਲੋਹਾ, ਚੂਨਾ ਅਤੇ ਜੀਵ-ਅੰਸ਼ ਕਾਫ਼ੀ ਮਾਤਰਾ ਵਿਚ ਪਾਏ ਜਾਂਦੇ ਹਨ । ਇਹ ਮਿੱਟੀ ਨਮੀ ਨੂੰ ਕਾਫ਼ੀ ਸਮੇਂ ਤਕ ਸੁਰੱਖਿਅਤ ਰੱਖਦੀ ਹੈ । ਇਹ ਮਿੱਟੀ ਕਪਾਹ ਦੀ ਉਪਜ ਲਈ ਬਹੁਤ ਉਪਯੋਗੀ ਹੁੰਦੀ ਹੈ । ਇਸ ਲਈ ਇਸ ਨੂੰ ਕਪਾਹ ਦੀ ਮਿੱਟੀ ਦੇ ਨਾਂ ਨਾਲ ਵੀ ਪੁਕਾਰਿਆ ਜਾਂਦਾ ਹੈ । ਸਾਡੇ ਦੇਸ਼ ਵਿਚ ਕਾਲੀ ਮਿੱਟੀ ਉੱਤਰੀ ਮਹਾਂਰਾਸ਼ਟਰ, ਗੁਜਰਾਤ, ਪੱਛਮੀ ਮੱਧ ਪ੍ਰਦੇਸ਼ ਅਤੇ ਪੱਛਮੀ ਆਂਧਰਾ ਪ੍ਰਦੇਸ਼ ਵਿਚ ਪਾਈ ਜਾਂਦੀ ਹੈ ।
3. ਲਾਲ ਮਿੱਟੀ-ਇਸ ਮਿੱਟੀ ਦਾ ਨਿਰਮਾਣ ਅਗਨੀ ਚੱਟਾਨਾਂ ਤੋਂ ਹੋਇਆ ਹੈ । ਇਸ ਵਿਚ ਲੋਹੇ ਦਾ ਅੰਸ਼ ਵਧੇਰੇ ਹੁੰਦਾ ਹੈ । ਇਸੇ ਕਾਰਨ ਹੀ ਇਸਦਾ ਰੰਗ ਲਾਲ ਜਾਂ ਪੀਲਾ ਹੁੰਦਾ ਹੈ । ਇਹ ਮਿੱਟੀ ਵਧੇਰੇ ਉਪਜਾਊ ਨਹੀਂ ਹੁੰਦੀ । ਪਰੰਤੁ ਖਾਦਾਂ ਦੇ ਉਪਯੋਗ ਦੁਆਰਾ ਇਸ ਮਿੱਟੀ ਤੋਂ ਚੰਗੀ ਪੈਦਾਵਾਰ ਪ੍ਰਾਪਤ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ । ਭਾਰਤ ਵਿਚ ਲਾਲ ਮਿੱਟੀ ਪ੍ਰਾਇਦੀਪ ਦੇ ਦੱਖਣ ਅਤੇ ਪੁਰਬ ਦੇ ਗਰਮ-ਖੁਸ਼ਕ ਪ੍ਰਦੇਸ਼ਾਂ ਵਿਚ ਫੈਲੀ ਹੋਈ ਹੈ ।
4. ਲੈਟਰਾਈਟ ਮਿੱਟੀ-ਇਹ ਮਿੱਟੀ ਜ਼ਿਆਦਾ ਵਰਖਾ ਵਾਲੇ ਗਰਮ ਦੇਸ਼ਾਂ ਵਿਚ ਮਿਲਦੀ ਹੈ । ਭਾਰੀ ਵਰਖਾ ਅਤੇ ਉੱਚ ਤਾਪਮਾਨ ਦੇ ਕਾਰਨ ਇਸ ਮਿੱਟੀ ਦੇ ਪੋਸ਼ਕ ਤੱਤ ਘੁਲ ਕੇ ਮਿੱਟੀ ਦੇ ਹੇਠਾਂ ਚਲੇ ਜਾਂਦੇ ਹਨ । ਇਸ ਕਿਰਿਆ ਨੂੰ ਲਾਚਿੰਗ (Leaching) ਕਹਿੰਦੇ ਹਨ । ਪੋਸ਼ਕ ਤੱਤਾਂ ਦੀ ਕਮੀ ਦੇ ਕਾਰਨ ਇਹ ਮਿੱਟੀ ਖੇਤੀ ਲਈ ਵਧੇਰੇ ਉਪਯੋਗੀ ਨਹੀਂ ਹੁੰਦੀ । ਭਾਰਤ ਵਿਚ ਇਹ ਮਿੱਟੀ ਪੱਛਮੀ ਘਾਟ, ਛੋਟਾ ਨਾਗਪੁਰ ਦੇ ਪਠਾਰ ਅਤੇ ਉੱਤਰ-ਪੂਰਬੀ ਰਾਜਾਂ ਦੇ ਕੁੱਝ ਭਾਗਾਂ ਵਿਚ ਫੈਲੀ ਹੋਈ ਹੈ ।
Based upon Survey of India map with the permission of the Surveyor General of India. The territorial waters of India extend into the sea to a distance of twelve nautical miles from the appropriate baseline.
5. ਖੁਸ਼ਕ ਰੇਤਲੀ ਜਾਂ ਮਾਰੂਥਲੀ ਮਿੱਟੀ-ਇਸ ਮਿੱਟੀ ਵਿਚ ਰੇਤ ਦੇ ਕਣਾਂ ਦੀ ਬਹੁਤਾਤ ਹੁੰਦੀ ਹੈ ਪਰੰਤੂ ਇਸ ਵਿਚ ਹਿਊਮਸ ‘ ਦੀ ਘਾਟ ਹੁੰਦੀ ਹੈ । ਇਸ ਲਈ ਇਹ ਮਿੱਟੀ ਉਪਜਾਊ ਨਹੀਂ ਹੁੰਦੀ । ਭਾਰਤ ਵਿਚ ਇਹ ਮਿੱਟੀ ਰਾਜਸਥਾਨ ਅਤੇ ਗੁਜਰਾਤ ਦੇ ਮਾਰੂਥਲੀ ਖੇਤਰਾਂ ਵਿਚ ਪਾਈ ਜਾਂਦੀ ਹੈ ।
6. ਪਰਬਤੀ ਮਿੱਟੀ-ਪਰਬਤੀ ਮਿੱਟੀ ਘੱਟ ਡੂੰਘੀ ਅਤੇ ਪਤਲੀ ਤਹਿ ਵਾਲੀ ਹੁੰਦੀ ਹੈ । ਇਸ ਵਿਚ ਲੋਹੇ ਦਾ ਅੰਸ਼ ਵਧੇਰੇ ਹੁੰਦਾ ਹੈ । ਲੋੜੀਂਦੀ ਵਰਖਾ ਮਿਲਣ ‘ਤੇ ਇਸ ਮਿੱਟੀ ਵਿਚ ਚਾਹ ਦੀ ਖੇਤੀ ਕੀਤੀ ਜਾਂਦੀ ਹੈ । ਭਾਰਤ ਵਿਚ ਇਹ ਮਿੱਟੀ ਹਿਮਾਲਿਆ ਖੇਤਰ ਵਿਚ ਪਾਈ ਜਾਂਦੀ ਹੈ ।

ਹੋਰ ਮਹੱਤਵਪੂਰਨ ਪ੍ਰਸ਼ਨ ਦਾ
ਪ੍ਰਸ਼ਨ 1.
ਜਵਾਲਾਮੁਖੀ ਪਰਬਤ ਕਿਵੇਂ ਬਣਦਾ ਹੈ ? ਇਸਦਾ ਇਕ ਉਦਾਹਰਨ ਦਿਓ ।
ਉੱਤਰ-
ਜਵਾਲਾਮੁਖੀ ਪਰਬਤ ਧਰਾਤਲ ਵਿੱਚੋਂ ਬਾਹਰ ਨਿਕਲਣ ਵਾਲੇ ਲਾਵੇ ਦੇ ਇਕੱਠਾ ਹੋਣ ਤੇ ਬਣਦਾ ਹੈ । ਜਾਪਾਨ ਦਾ ਫਿਊਜੀਜਾਮਾ ਪਰਬਤ ਇਸ ਦਾ ਇਕ ਉੱਤਮ ਉਦਾਹਰਨ ਹੈ ।
ਪ੍ਰਸ਼ਨ 2.
ਮੁਸਾਮਦਾਰ (Porous) ਅਤੇ ਗ਼ੈਰ-ਮੁਸਾਮਦਾਰ (Non-Porous) ਚੱਟਾਨਾਂ ਵਿਚ ਕੀ ਅੰਤਰ ਹੈ ?
ਉੱਤਰ-
ਮੁਸਾਮਦਾਰ ਚੱਟਾਨਾਂ ਵਿਚ ਰੇਤ ਦੀ ਮਾਤਰਾ ਜ਼ਿਆਦਾ ਹੁੰਦੀ ਹੈ ਜਦੋਂ ਕਿ ਗੈਰ-ਮੁਸਾਮਦਾਰ ਚੱਟਾਨਾਂ ਵਿਚ ਚੀਨੀ ਮਿੱਟੀ ਦੀ ਮਾਤਰਾ ਵਧੇਰੇ ਹੁੰਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 3.
ਪਾਣੀ ਸਮਾ ਸਕਣ ਦੇ ਆਧਾਰ ‘ਤੇ ਚੱਟਾਨਾਂ ਦਾ ਵਰਗੀਕਰਨ ਕਰੋ ।
ਉੱਤਰ-
ਪਾਣੀ ਸਮਾ ਸਕਣ ਦੇ ਆਧਾਰ ‘ਤੇ ਚੱਟਾਨਾਂ ਦੋ ਪ੍ਰਕਾਰ ਦੀਆਂ ਹੁੰਦੀਆਂ ਹਨ-ਪਾਰਗਾਮੀ ਪਾਰਗੰਮ ਅਤੇ ਅਪਾਰਗਾਮੀ (ਅਪਾਰ-ਗੰਮ) । ਪਾਰਗਾਮੀ ਚੱਟਾਨਾਂ ਵਿਚ ਪਾਣੀ ਆਸਾਨੀ ਨਾਲ ਪ੍ਰਵੇਸ਼ ਕਰ ਜਾਂਦਾ ਹੈ ਪਰੰਤੂ ਅਪਾਰਗਾਮੀ ਚੱਟਾਨਾਂ ਵਿਚ ਪਾਣੀ ਪ੍ਰਵੇਸ਼ ਨਹੀਂ ਕਰ ਪਾਉਂਦਾ ।
ਪ੍ਰਸ਼ਨ 4.
ਰਸਾਇਣਿਕ ਰਚਨਾ ਦੇ ਆਧਾਰ ‘ਤੇ ਚੱਟਾਨਾਂ ਕਿਹੜੇ-ਕਿਹੜੇ ਦੋ ਪ੍ਰਕਾਰ ਦੀਆਂ ਹੁੰਦੀਆਂ ਹਨ ?
ਉੱਤਰ-
- ਖਾਰੀਆਂ ਚੱਟਾਨਾਂ ਅਤੇ
- ਤੇਜ਼ਾਬੀ ਜਾਂ ਅਮਲੀ ਚੱਟਾਨਾਂ ।
ਪ੍ਰਸ਼ਨ 5.
ਮੈਗਮਾ ਅਤੇ ਲਾਵਾ ਵਿਚ ਕੀ ਅੰਤਰ ਹੈ ?
ਉੱਤਰ-
ਧਰਾਤਲ ਦੇ ਅੰਦਰ ਪਿਘਲਿਆ ਹੋਇਆ ਪਦਾਰਥ ਮੈਗਮਾ ਕਹਾਉਂਦਾ ਹੈ। ਜਦੋਂ ਇਹ ਮੈਗਮਾ ਦਰਾਰਾਂ ਵਿਚੋਂ ਹੋ ਕੇ ਧਰਾਤਲ ‘ਤੇ ਆ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਇਸ ਨੂੰ ਲਾਵਾ ਕਹਿੰਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 6.
ਪ੍ਰਾਥਮਿਕ ਚੱਟਾਨਾਂ ਕਿਨ੍ਹਾਂ ਨੂੰ ਕਹਿੰਦੇ ਹਨ ਅਤੇ ਕਿਉਂ ? ਇਨ੍ਹਾਂ ਦੀਆਂ ਦੋ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਅਗਨੀ ਚੱਟਾਨਾਂ ਨੂੰ ਪ੍ਰਾਥਮਿਕ ਚੱਟਾਨਾਂ ਕਹਿੰਦੇ ਹਨ ਕਿਉਂਕਿ ਧਰਤੀ ‘ਤੇ ਸਭ ਤੋਂ ਪਹਿਲਾਂ ਇਨ੍ਹਾਂ ਹੀ ਚੱਟਾਨਾਂ ਦਾ ਨਿਰਮਾਣ ਹੋਇਆ ਸੀ ।
ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ-
- ਅਗਨੀ ਚੱਟਾਨਾਂ ਰਵੇਦਾਰ ਪਿੰਡਾਂ ਵਿਚ ਪਾਈਆਂ ਜਾਂਦੀਆਂ ਹਨ । ਇਸ ਲਈ ਇਨ੍ਹਾਂ ਵਿਚ ਤਹਿਆਂ ਜਾਂ ਪਰਤਾਂ ਨਹੀਂ ਹੁੰਦੀਆਂ ।
- ਇਨ੍ਹਾਂ ਚੱਟਾਨਾਂ ਵਿਚ ਬਨਸਪਤੀ ਅਤੇ ਜੀਵ-ਜੰਤੂਆਂ ਦੇ ਅਵਸ਼ੇਸ਼ ਵੀ ਨਹੀਂ ਪਾਏ ਜਾਂਦੇ ।
ਪ੍ਰਸ਼ਨ 7.
ਮਿੱਟੀ ਕਿਸ ਨੂੰ ਕਹਿੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਮਿੱਟੀ ਧਰਾਤਲ ਦਾ ਉੱਪਰਲਾ ਉਹ ਭਾਗ ਹੈ ਜਿਹੜਾ ਚੱਟਾਨਾਂ ਦੀ ਟੁੱਟ-ਭੱਜ ਤੋਂ ਬਣਦੀ ਹੈ । ਇਸ ਦੇ ਕਣ ਬਹੁਤੇ ਬਾਰੀਕ, ਨਰਮ ਅਤੇ ਅਲੱਗ-ਅਲੱਗ ਹੁੰਦੇ ਹਨ ਤਾਂ ਕਿ ਪੌਦਿਆਂ ਦੀਆਂ ਜੜ੍ਹਾਂ ਇਸ ਵਿਚ ਆਸਾਨੀ ਨਾਲ ਪ੍ਰਵੇਸ਼ ਕਰ ਸਕਣ ।

ਪ੍ਰਸ਼ਨ 8.
ਮਿੱਟੀ ਵਿਚ ਕਿਹੜੇ-ਕਿਹੜੇ ਦੋ ਪ੍ਰਕਾਰ ਦੇ ਤੱਤ ਹੁੰਦੇ ਹਨ ।
ਉੱਤਰ-
ਮਿੱਟੀ ਵਿਚ ਦੋ ਪ੍ਰਕਾਰ ਦੇ ਤੱਤ ਜਾਂ ਪਦਾਰਥ ਹੁੰਦੇ ਹਨ-ਖਣਿਜ ਅਤੇ ਕਾਰਬਨਿਕ ਪਦਾਰਥ । ਖਣਿਜ ਪਦਾਰਥ ਮਿੱਟੀ ਵਿਚ ਕਾਫ਼ੀ ਮਾਤਰਾ ਵਿਚ ਹੁੰਦੇ ਹਨ, ਜਿਹੜੇ ਇਸ ਨੂੰ ਮੂਲ ਚੱਟਾਨ ਤੋਂ ਮਿਲਦੇ ਹਨ । ਮਿੱਟੀ ਵਿੱਚ ਸ਼ਾਮਲ ਬਨਸਪਤੀ ਅਤੇ ਜੀਵ-ਜੰਤੂਆਂ ਦੇ ਗਲੇ-ਸੜੇ ਪਦਾਰਥ ਨੂੰ ਕਾਰਬਨਿਕ ਪਦਾਰਥ ਕਹਿੰਦੇ ਹਨ । ਇਹ ਮਿੱਟੀ ਦੀ ਉਪਜਾਊ ਸ਼ਕਤੀ ਨੂੰ ਵਧਾਉਂਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 9.
ਮਿੱਟੀ ਦੀ ਰਚਨਾ ਵਿਚ ਕਿਹੜੇ-ਕਿਹੜੇ ਕਾਰਕ ਸਹਾਇਕ ਹੁੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਮਿੱਟੀ ਦੀ ਰਚਨਾ ਵਿਚ ਹੇਠ ਲਿਖੇ ਕਈ ਕਾਰਕ ਸਹਾਇਕ ਹੁੰਦੇ ਹਨ-
- ਮੂਲ ਚੱਟਾਨ-ਮੂਲ ਚੱਟਾਨ ਤੋਂ ਭਾਵ ਉਸ ਚੱਟਾਨ ਤੋਂ ਹੈ ਜਿਸ ਤੋਂ ਮਿੱਟੀ ਦਾ ਨਿਰਮਾਣ ਹੁੰਦਾ ਹੈ । ਮਿੱਟੀ ਦੀਆਂ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਉਸ ਚੱਟਾਨ ਦੇ ਅਨੁਰੂਪ ਹੁੰਦੀਆਂ ਹਨ । ਉਦਾਹਰਨ ਵਜੋਂ ਚੱਟਾਨ (Shale) ਤੋਂ ਚੀਕਾ ਮਿੱਟੀ ਬਣਦੀ ਹੈ, ਜਦੋਂ ਕਿ ਰੇਤ ਪੱਥਰ ਤੋਂ ਰੇਤ ਦੇ ਕਣ ਪ੍ਰਾਪਤ ਹੁੰਦੇ ਹਨ ।
- ਜਲਵਾਯੂ-ਮਿੱਟੀ ਦੇ ਨਿਰਮਾਣ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਨ ਵਾਲੇ ਜਲਵਾਯੂ ਦੇ ਕਾਰਕਾਂ ਵਿਚ ਤਾਪਮਾਨ ਅਤੇ ਵਰਖਾ ਪ੍ਰਮੁੱਖ ਹਨ । ਤਾਪਮਾਨ ਵਿਚ ਵਾਰ-ਵਾਰ ਪਰਿਵਰਤਨ ਹੋਣ ਅਤੇ ਵਾਯੂਮੰਡਲ ਵਿਚ ਪਾਣੀ ਦੀ ਹੋਂਦ ਨਾਲ ਭੂਮੀ-ਕਟਾਓ ਦੀ ਦਰ ਵਧ ਜਾਂਦੀ ਹੈ । ਇਸ ਦੇ ਸਿੱਟੇ ਵਜੋਂ ਮਿੱਟੀ ਦੇ ਨਿਰਮਾਣ ਦੀ ਗਤੀ ਵਿਚ ਤੇਜ਼ੀ ਆ ਜਾਂਦੀ ਹੈ ।
- ਥਲ-ਆਕ੍ਰਿਤੀ-ਕਿਸੇ ਖੇਤਰ ਦੀ ਥਲ-ਆਕ੍ਰਿਤੀ ਉਸਦੇ ਅਪਵਾਹ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਦੀ ਹੈ । ਤਿੱਖੀ ਢਾਲ ‘ਤੇ ਟੁੱਟੀਆਂਭੱਜੀਆਂ ਚੱਟਾਨਾਂ ਦੇ ਕਣ ਟਿਕ ਨਹੀਂ ਪਾਉਂਦੇ ਅਤੇ ਪਾਣੀ ਦੁਆਰਾ ਤੇ ਗੁਰੁਤਾ ਬਲ ਦੇ ਪ੍ਰਭਾਵ ਨਾਲ ਇਹ ਕਣ ਢਾਲ ਤੋਂ ਹੇਠਾਂ ਵਲ ਖਿਸਕ ਜਾਂਦੇ ਹਨ । ਇਸਦੇ ਉਲਟ ਮੈਦਾਨਾਂ ਅਤੇ ਘੱਟ ਢਾਲਾਂ ‘ਤੇ ਮਿੱਟੀ ਬਿਨਾਂ ਕਿਸੇ ਰੁਕਾਵਟ ਤੋਂ ਟਿਕੀ ਰਹਿੰਦੀ ਹੈ ।
- ਮਿੱਟੀ ਵਿਚ ਮੌਜੂਦ ਮ੍ਰਿਤ ਪੌਦੇ ਅਤੇ ਜੀਵ-ਜੰਤੂ-ਮ੍ਰਿਤ ਪੌਦੇ ਅਤੇ ਜੀਵ-ਜੰਤੂਆਂ ਤੋਂ ਮਿੱਟੀ ਨੂੰ ਹਿਊਮਸ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ । ਹਿਊਮਸ ਵਾਲੀ ਮਿੱਟੀ ਜ਼ਿਆਦਾ ਉਪਜਾਊ ਹੁੰਦੀ ਹੈ ।
- ਸਮਾਂ-ਮਿੱਟੀ ਨਿਰਮਾਣ ਦੇ ਕਾਰਕ ਦੇ ਰੂਪ ਵਿਚ ਸਮਾਂ ਬਹੁਤ ਹੀ ਮਹੱਤਵਪੂਰਨ ਹੈ । ਮਿੱਟੀ ਦੇ ਨਿਰਮਾਣ ਵਿਚ ਜਿੰਨਾ ਸਮਾਂ ਵਧੇਰੇ ਲੱਗਦਾ ਹੈ, ਉੱਨੀ ਜ਼ਿਆਦਾ ਮੋਟੀ ਉਸ ਦੀ ਪਰਤ ਹੁੰਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 10.
ਮਿੱਟੀ ਦੇ ਅਪਰਦਨ ਜਾਂ ਭੂਮੀ-ਕਟਾਓ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ?
ਉੱਤਰ-
ਤੇਜ਼ ਹਵਾ ਅਤੇ ਵਗਦਾ ਹੋਇਆ ਪਾਣੀ ਮਿੱਟੀ ਦੀ ਉੱਪਰਲੀ ਸੜਾ ਨੂੰ ਆਪਣੇ ਨਾਲ ਵਹਾ ਕੇ ਲੈ ਜਾਂਦੇ ਹਨ । ਇਸ ਨੂੰ ਮਿੱਟੀ ਦਾ ਅਪਰਦਨ ਜਾਂ ਕਟਾਓ ਕਹਿੰਦੇ ਹਨ । ਇਸ ਦੇ ਕਾਰਨ ਮਿੱਟੀ ਖੇਤੀ ਯੋਗ ਨਹੀਂ ਰਹਿੰਦੀ । ਇਹ ਕਿਰਿਆ ਉਨ੍ਹਾਂ ਸਥਾਨਾਂ ‘ਤੇ ਵਧੇਰੇ ਹੁੰਦੀ ਹੈ ਜਿੱਥੇ ਭੂਮੀ ਦੀ ਢਾਲ ਬਹੁਤ ਤਿੱਖੀ ਹੋ ਜਾਂਦੀ ਹੈ ਅਤੇ ਜਿੱਥੇ ਵਰਖਾ ਤੇਜ਼ ਵਾਛੜ ਦੇ ਰੂਪ ਵਿਚ ਹੁੰਦੀ ਹੈ । ਭੂਮੀ-ਕਟਾਓ ਉਨ੍ਹਾਂ ਖੇਤਰਾਂ ਵਿਚ ਜ਼ਿਆਦਾ ਹੁੰਦਾ ਹੈ, ਜਿੱਥੇ ਬਨਸਪਤੀ ਘੱਟ ਹੋਵੇ, ਜਿਵੇਂ ਮਾਰੂਥਲੀ ਖੇਤਰ ਵਿਚ।
ਪ੍ਰਸ਼ਨ 11.
ਕਿਸ ਮਿੱਟੀ ਨੂੰ ਕਪਾਹ ਦੀ ਮਿੱਟੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ਅਤੇ ਕਿਉਂ ?
ਉੱਤਰ-
ਕਾਲੀ ਜਾਂ ਰੇਗੜ ਮਿੱਟੀ ਨੂੰ ਕਪਾਹ ਦੀ ਮਿੱਟੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਇਸ ਦਾ ਕਾਰਨ ਇਹ ਹੈ ਕਿ ਇਹ ਮਿੱਟੀ ਕਪਾਹ ਦੀ ਫ਼ਸਲ ਲਈ ਆਦਰਸ਼ ਹੁੰਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 12.
ਜਲੋੜ ਮਿੱਟੀ ਦੀਆਂ ਦੋ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
- ਇਸ ਮਿੱਟੀ ਵਿਚ ਪੋਟਾਸ਼, ਫਾਸਫੋਰਿਕ, ਐਸਿਡ ਅਤੇ ਚੂਨਾ ਉੱਚਿਤ ਮਾਤਰਾ ਵਿਚ ਹੁੰਦਾ ਹੈ ।
- ਇਸ ਮਿੱਟੀ ਵਿਚ ਨਾਈਟ੍ਰੋਜਨ ਅਤੇ ਜੈਵਿਕ ਪਦਾਰਥਾਂ ਦੀ ਘਾਟ ਹੁੰਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 13.
ਕਾਲੀ ਜਾਂ ਰੇਗੜ ਮਿੱਟੀ ਦੀਆਂ ਦੋ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
- ਕਾਲੀ ਮਿੱਟੀ ਲਾਵੇ ਦੇ ਪ੍ਰਵਾਹ ਤੋਂ ਬਣੀ ਹੁੰਦੀ ਹੈ ।
- ਇਹ ਮਿੱਟੀ ਕਪਾਹ ਦੀ ਫ਼ਸਲ ਲਈ ਵਧੇਰੇ ਉਪਯੋਗੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 14.
ਲੈਟਰਾਈਟ ਮਿੱਟੀ ਦੀਆਂ ਦੋ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
- ਲੈਟਰਾਈਟ ਮਿੱਟੀ ਘੱਟ ਉਪਜਾਉ ਹੁੰਦੀ ਹੈ ।
- ਇਹ ਮਿੱਟੀ ਘਾਹ ਅਤੇ ਝਾੜੀਆਂ ਪੈਦਾ ਕਰਨ ਲਈ ਉਪਯੋਗੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 15.
ਮਾਰੂਥਲੀ ਮਿੱਟੀ ਨੂੰ ਖੇਤੀ ਲਈ ਉਪਯੋਗੀ ਕਿਵੇਂ ਬਣਾਇਆ ਜਾ ਸਕਦਾ ਹੈ ?
ਉੱਤਰ-
ਸਿੰਚਾਈ ਦੀਆਂ ਸਹੂਲਤਾਂ ਜੁਟਾ ਕੇ ਮਾਰੂਥਲੀ ਮਿੱਟੀ ਨੂੰ ਖੇਤੀ ਲਈ ਉਪਯੋਗੀ ਬਣਾਇਆ ਜਾ ਸਕਦਾ ਹੈ ।
(ਉ) ਸਹੀ ਵਾਕਾਂ ਤੇ (✓) ਅਤੇ ਗਲਤ ਵਾਕਾਂ ਤੇ (✗) ਦਾ ਨਿਸ਼ਾਨ ਲਗਾਓ
ਪ੍ਰਸ਼ਨ 1.
ਅੱਜ ਤੱਕ ਵਿਸ਼ਵ ਇੱਕ ਗਲੋਬਲ ਪਿੰਡ ਨਹੀਂ ਬਣ ਸਕਿਆ ।
ਉੱਤਰ-
(✗)
ਪ੍ਰਸ਼ਨ 2.
ਜੀਵਮੰਡਲ ਵਿੱਚ ਪੇੜ-ਪੌਦੇ ਸ਼ਾਮਿਲ ਨਹੀਂ ਹਨ ।
ਉੱਤਰ-
(✗)
ਪ੍ਰਸ਼ਨ 3.
ਸਮੁੰਦਰ ਦਾ ਧਰਤੀ ਤੇ ਸਭ ਤੋਂ ਵਧੇਰੇ ਪ੍ਰਭਾਵ ਜਲਵਾਯੂ ਉੱਪਰ ਪੈਂਦਾ ਹੈ ।
ਉੱਤਰ-
(✓)
ਪ੍ਰਸ਼ਨ 4.
ਬੁੱਧ ਗ੍ਰਹਿ ਦੇ ਆਲੇ-ਦੁਆਲੇ ਵਾਯੂਮੰਡਲ ਨਹੀਂ ਹੈ ।
ਉੱਤਰ-
(✓)
(ਅ) ਸਹੀ ਮਿਲਾਨ ਕਰੋ
| 1. ਧਾਤੂ ਖਣਿਜ |
(i) ਬਹੁਤ ਜ਼ਿਆਦਾ ਉਪਜਾਊ |
| 2. ਅਧਾਤੂ ਖਣਿਜ |
(ii) ਸੋਨਾ, ਚਾਂਦੀ |
| 3. ਰੇਤਲੀ ਮਿੱਟੀ |
(iii) ਪੋਟਾਸ਼, ਫਾਸਫੇਟ |
| 4. ਜਲੋੜ ਮਿੱਟੀ |
(iv) ਹਿਊਮਸ ਦੀ ਕਮੀ ॥ |
ਉੱਤਰ-
| 1. ਧਾਤੂ ਖਣਿਜ |
(ii) ਸੋਨਾ, ਚਾਂਦੀ, |
| 2. ਅਧਾਤੂ ਖਣਿਜ |
(iii) ਪੋਟਾਸ਼, ਫਾਸਫੇਟ |
| 3. ਰੇਤਲੀ ਮਿੱਟੀ |
(iv) ਹਿਉਮਸ ਦੀ ਕਮੀ |
| 4. ਜਲੋੜ੍ਹ ਮਿੱਟੀ |
(i) ਬਹੁਤ ਜ਼ਿਆਦਾ ਉਪਜਾਊ |
(ਈ) ਸਹੀ ਉੱਤਰ ਚੁਣੋ ਧਰਤੀ ਦਾ ਅੰਦਰੂਨੀ ਅਤੇ ਬਾਹਰੀ ਸਰੂਪ –
ਪ੍ਰਸ਼ਨ 1.
ਜਾਪਾਨ ਦਾ ਫਿਊਜੀਜਾਮਾ ਪਰਬਤ ਲਾਵੇ ਤੋਂ ਬਣਿਆ ਹੈ। ਇਹ ਲਾਵਾ ਕਿੱਥੋਂ ਆਉਂਦਾ ਹੈ ?

(i) ਉੱਚੇ ਪਰਬਤਾਂ ਤੋਂ
(ii) ਧਰਤੀ ਦੇ ਅੰਦਰੂਨੀ ਭਾਗ ਤੋਂ
(iii) ਪਰਤਦਾਰ ਜਾਂ ਤਲਛੱਟੀ ਚੱਟਾਨਾਂ ਦੇ ਜੰਮਣ ਨਾਲ
(iv) ਲਾਵਾ
ਉੱਤਰ-
(iv) ਲਾਵਾ।
ਪ੍ਰਸ਼ਨ 2.
ਭਾਰਤ ਵਿਚ ਗੰਗਾ, ਸਤਲੁਜ ਦਾ ਮੈਦਾਨ ਇਕ ਵਿਸ਼ੇਸ਼ ਤਰ੍ਹਾਂ ਦੀ ਸਮੱਗਰੀ ਤੋਂ ਬਣਿਆ ਹੈ। ਇਸ ਸਮੱਗਰੀ ਦਾ ਜਮਾਵ ਕਿਵੇਂ ਹੁੰਦਾ ਹੈ ?
(i) ਵਹਿੰਦੇ ਹੋਏ ਪਾਣੀ ਦੁਆਰਾ
(ii) ਹਿਮ ਨਦੀ ਅਤੇ ਵਾਯੂ ਦੁਆਰਾ
(iii) ਇਨ੍ਹਾਂ ਸਭ ਦੇ ਦੁਆਰਾ।
ਉੱਤਰ-
(iii) ਇਨ੍ਹਾਂ ਸਭ ਦੇ ਦੁਆਰਾ।
![]()
![]()
![]()

![]()
![]()
![]()
![]()