Punjab State Board PSEB 8th Class Home Science Book Solutions Chapter 1 ਨਿੱਜੀ ਦੇਖ-ਭਾਲ Textbook Exercise Questions and Answers.
PSEB Solutions for Class 8 Home Science Chapter 1 ਨਿੱਜੀ ਦੇਖ-ਭਾਲ
Home Science Guide for Class 8 PSEB ਨਿੱਜੀ ਦੇਖ-ਭਾਲ Textbook Questions and Answers
ਅਭਿਆਸ ਦੇ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਉੱਤਰ
ਵਸਤੂਨਿਸ਼ਠ ਪ੍ਰਸ਼ਨ
ਪ੍ਰਸ਼ਨ 1.
ਊਰਜਾ ਪ੍ਰਦਾਨ ਕਰਨ ਵਾਲੇ ਤੱਤ ਕਿਹੜੇ ਹੁੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਕਾਰਬੋਹਾਈਡਰੇਟ ਅਤੇ ਚਿਕਨਾਈ ।
ਪ੍ਰਸ਼ਨ 2.
ਕੈਲਸ਼ੀਅਮ ਸਾਡੇ ਸਰੀਰ ਲਈ ਕਿਉਂ ਜ਼ਰੂਰੀ ਹੈ ?
ਜਾਂ
ਕੈਲਸ਼ੀਅਮ ਦੇ ਕੋਈ ਦੋ ਲਾਭ ਦੱਸੋ ।
ਉੱਤਰ-
- ਸਰੀਰ ਵਿਚ ਹੱਡੀਆਂ ਅਤੇ ਦੰਦਾਂ ਦਾ ਨਿਰਮਾਣ ਕਰਨਾ ।
- ਨਾੜੀਆਂ ਨੂੰ ਸਵਸਥ ਰੱਖਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 3.
ਖਾਣੇ ਨਾਲ ਜ਼ਿਆਦਾ ਪਾਣੀ ਕਿਉਂ ਨਹੀਂ ਪੀਣਾ ਚਾਹੀਦਾ ?
ਉੱਤਰ-
ਖਾਣੇ ਦੇ ਨਾਲ ਜ਼ਿਆਦਾ ਪਾਣੀ ਨਹੀਂ ਪੀਣਾ ਚਾਹੀਦਾ ਕਿਉਂਕਿ ਭੋਜਨ ਨੂੰ ਪਚਾਉਣ ਵਾਲੇ ਰਸ ਪਤਲੇ ਹੋ ਜਾਂਦੇ ਹਨ ਅਤੇ ਭੋਜਨ ਜਲਦੀ ਪਚਦਾ ਨਹੀਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
ਭਾਰਤੀ ਖੁਰਾਕ ਦੀ ਇੱਕ ਪ੍ਰਮੁੱਖ ਘਾਟ ਲਿਖੋ ।
ਉੱਤਰ-
ਭੋਜਨ ਵਿਚ ਕਲੋਰੀਆਂ ਦੀ ਮਾਤਰਾ ਦਾ ਘੱਟ ਹੋਣਾ ।
ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ
ਪਸ਼ਨ 5.
ਲੋੜ ਤੋਂ ਵੱਧ ਜਾਂ ਘੱਟ ਖਾਣ ਦੇ ਕੀ ਨੁਕਸਾਨ ਹਨ ?
ਉੱਤਰ-
ਜੇਕਰ ਜ਼ਰੂਰਤ ਤੋਂ ਵੱਧ ਖਾਣਾ ਖਾਧਾ ਜਾਏ ਤਾਂ ਮਿਹਦੇ ਅਤੇ ਅੰਤੜੀਆਂ ਨੂੰ ਜ਼ਿਆਦਾ ਮਿਹਨਤ ਕਰਨੀ ਪੈਂਦੀ ਹੈ । ਇਸ ਦੇ ਨਾਲ ਗੁਰਦਿਆਂ ‘ਤੇ ਵੀ ਜ਼ਿਆਦਾ ਬੋਝ ਪੈਂਦਾ ਹੈ ।ਖਾਧੇ ਹੋਏ ਭੋਜਨ ਵਿਚ ਉਬਾਲ ਜਿਹਾ ਆ ਜਾਂਦਾ ਹੈ, ਜਿਸ ਨਾਲ ਗੈਸ ਬਣਦੀ ਹੈ । ਇਸ ਨਾਲ ਪੇਟ ਖ਼ਰਾਬ ਹੋ ਜਾਂਦਾ ਹੈ । ਮੂੰਹ ਵਿਚੋਂ ਬਦਬੂ ਆਉਣ ਲੱਗ ਜਾਂਦੀ ਹੈ ਅਤੇ ਸਿਰ ਦੁੱਖਣ ਲੱਗ ਜਾਂਦਾ ਹੈ ।
ਜੇਕਰ ਜ਼ਿਆਦਾ ਦੇਰ ਤਕ ਜ਼ਰੂਰਤ ਤੋਂ ਵੱਧ ਭੋਜਨ ਖਾਧਾ ਜਾਏ ਤਾਂ ਪੇਟ ਦੀਆਂ ਬਿਮਾਰੀਆਂ ਹੋ ਜਾਂਦੀਆਂ ਹਨ, ਜਿਵੇਂ ਮਿਹਦੇ ਦੀਆਂ ਬਿਮਾਰੀਆਂ, ਗੁਰਦਿਆਂ ਵਿਚ ਖ਼ਰਾਬੀ ਅਤੇ ਖੂਨ ਦਾ ਦਬਾਉ ਵੱਧ ਸਕਦਾ ਹੈ । ਤੰਤੂਆਂ ਵਿਚ ਵਧੇਰੇ ਚਰਬੀ ਜੰਮ ਜਾਂਦੀ ਹੈ ਅਤੇ ਆਦਮੀ ਮੋਟਾ ਹੋ ਸਕਦਾ ਹੈ । ਪਿਸ਼ਾਬ ਵਿਚ ਸ਼ੱਕਰ ਆਉਣ ਦਾ ਰੋਗ ਹੋ ਸਕਦਾ ਹੈ ।
ਜੇਕਰ ਦੇਰ ਤਕ ਘੱਟ ਖਾਣਾ ਖਾਧਾ ਜਾਏ ਤਾਂ ਭਾਰ ਘੱਟ ਜਾਂਦਾ ਹੈ, ਕਮਜ਼ੋਰੀ ਆ ਜਾਂਦੀ ਹੈ। ਅਤੇ ਖੂਨ ਦੀ ਕਮੀ ਹੋ ਜਾਂਦੀ ਹੈ । ਘੱਟ ਖਾਣ ਨਾਲ ਬਿਮਾਰੀਆਂ ਦਾ ਸਾਹਮਣਾ ਕਰਨ ਦੀ ਸ਼ਕਤੀ ਘੱਟ ਜਾਂਦੀ ਹੈ ਅਤੇ ਖ਼ਾਸ ਕਰਕੇ ਤਪਦਿਕ ਹੋਣ ਦਾ ਡਰ ਰਹਿੰਦਾ ਹੈ । ਬੱਚੇ ਜੇਕਰ ਘੱਟ ਖਾਣਾ ਖਾਣ ਤਾਂ ਬੁੱਧੂ (Dull) ਜਿਹੇ ਹੋ ਜਾਂਦੇ ਹਨ ਅਤੇ ਜਲਦੀ ਥੱਕ ਜਾਂਦੇ ਹਨ । ਉਨ੍ਹਾਂ ਦੇ ਸਰੀਰ ਦਾ ਵਿਕਾਸ ਵੀ ਪੂਰਾ ਨਹੀਂ ਹੁੰਦਾ ਅਤੇ ਉਨ੍ਹਾਂ ਦਾ ਕੱਦ ਅਤੇ ਭਾਰ ਵੀ ਆਪਣੀ ਉਮਰ ਦੇ ਅਨੁਸਾਰ ਘੱਟ ਹੀ ਰਹਿੰਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 6.
ਕਰੀਮ ਅਤੇ ਤੇਲ ਕਿਉਂ ਵਰਤੇ ਜਾਂਦੇ ਹਨ ? ਇਨ੍ਹਾਂ ਦੀ ਥਾਂ ਹੋਰ ਕੀ ਵਰਤਿਆ ਜਾ ਸਕਦਾ ਹੈ ?
ਉੱਤਰ-
ਤੇਲ-ਰੋਜ਼ – ਰੋਜ਼ ਸਾਬਣ ਨਾਲ ਨਹਾਉਣ ਅਤੇ ਸਿਰ ਧੋਣ ਨਾਲ ਚਮੜੀ ਅਤੇ ਵਾਲ ਖ਼ੁਸ਼ਕ ਹੋ ਜਾਂਦੇ ਹਨ | ਸਾਡੀ ਚਮੜੀ ਦੀ ਉੱਪਰਲੀ ਤਹਿ ਦੇ ਤੰਤੂ ਵੀ ਝੜ ਕੇ ਚਮੜੀ ਤੇ ਜੰਮ ਜਾਂਦੇ ਹਨ ਅਤੇ ਚਮੜੀ ਨੂੰ ਖ਼ੁਸ਼ਕ ਕਰਦੇ ਹਨ ਇਹ ਸੈੱਲ: ਸਿਕਰੀ ਦੇ ਰੂਪ ਵਿਚ ਸਿਰ ਵਿਚ ਦੇਖੇ ਜਾ ਸਕਦੇ ਹਨ | ਪਤਝੜ ਤੇ ਸਰਦੀਆਂ ਵਿਚ ਚਮੜੀ ਵਧੇਰੇ ਖ਼ੁਸ਼ਕ ਹੋ ਜਾਂਦੀ ਹੈ ਜਿਸ ਲਈ ਇਹ ਜ਼ਰੂਰੀ ਹੋ ਜਾਂਦਾ ਹੈ ਕਿ ਚਮੜੀ ਨੂੰ ਚਮਕਦਾਰ ਅਤੇ ਲਚਕਦਾਰ ਬਣਾਉਣ ਲਈ ਸਿਰ ਅਤੇ ਸਰੀਰ ਤੇ ਕਿਸੇ ਤੇਲ ਨਾਲ ਮਾਲਿਸ਼ ਕੀਤੀ ਜਾਏ । ਸਿਰ ਅਤੇ ਚਮੜੀ ਤੇ ਤੇਲ ਸਿਰਫ਼ ਮਲਿਆ ਹੀ ਨਹੀਂ ਜਾਂਦਾ ਬਲਕਿ ਝੱਸਿਆ ਜਾਂਦਾ ਹੈ ਇਸ ਤਰ੍ਹਾਂ ਕਰਨ ਨਾਲ ਸਾਡੀ ਚਮੜੀ ਦੇ ਥੱਲੇ ਦੀਆਂ ਤੇਲ ਦੀਆਂ ਗ੍ਰੰਥੀਆਂ ਉਤੇਜਿਤ ਹੁੰਦੀਆਂ ਹਨ । ਜਿਨ੍ਹਾਂ ਤੋਂ ਕੁਦਰਤੀ ਤੇਲ ਨਿਕਲਦੇ ਹਨ । ਜਿਹੜੇ ਸਾਡੀ ਚਮੜੀ ਨੂੰ ਮੁਲਾਇਮ ਰੱਖਦੇ ਹਨ ।
ਕਰੀਮ – ਚਿਹਰੇ ਤੇ ਲਗਾਉਣ ਲਈ ਅੱਜ-ਕਲ੍ਹ ਕਈ ਤਰ੍ਹਾਂ ਦੀਆਂ ਕਰੀਮਾਂ ਬਜ਼ਾਰ ਵਿਚ ਮਿਲਦੀਆਂ ਹਨ । ਖ਼ਾਸ ਕਰਕੇ ਸਰਦੀਆਂ ਵਿਚ ਬੱਚਿਆਂ ਦੇ ਮੂੰਹ ਫਟ ਜਾਂਦੇ ਹਨ । ਇਸ ਨੂੰ ਠੀਕ ਕਰਨ ਲਈ ਵੀ ਥੰਧੀ ਕਰੀਮ ਲਗਾਈ ਜਾਣੀ ਚਾਹੀਦੀ ਹੈ | ਅੱਜ-ਕਲ੍ਹ ਬਜ਼ਾਰ ਵਿਚ ਹੋਰ ਵੀ ਕਈ ਤਰ੍ਹਾਂ ਦੀਆਂ ਕਰੀਮਾਂ ਮਿਲਦੀਆਂ ਹਨ ਜਿਨ੍ਹਾਂ ਦੇ ਲਗਾਉਣ ਨਾਲ ਚਿਹਰੇ ਤੋਂ ਕਿੱਲ, ਛਾਈਆਂ ਦੂਰ ਹੁੰਦੇ ਹਨ ਅਤੇ ਚਿਹਰੇ ‘ਤੇ ਨਿਖਾਰ ਆਉਂਦਾ ਹੈ । ਪੁਰਾਣੇ ਜ਼ਮਾਨੇ ਵਿਚ ਔਰਤਾਂ ਚਿਹਰੇ ਤੇ ਮੱਖਣ, ਗਲਿਸਰੀਨ ਜਾਂ ਗਲਿਸਰੀਨ ਵਿਚ ਨਿੰਬੂ ਦਾ ਰਸ ਮਿਲਾ ਕੇ ਮਲਦੀਆਂ ਸਨ । ਇਨ੍ਹਾਂ ਚੀਜ਼ਾਂ ਨਾਲ ਵੀ ਚਿਹਰਾ ਮੁਲਾਇਮ ਹੁੰਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 7.
ਟੈਲਕਮ ਪਾਊਡਰ ਦੇ ਕੀ ਲਾਭ ਹਨ ?
ਉੱਤਰ-
ਟੈਲਕਮ ਪਾਊਡਰ ਨਾਲ ਹੇਠ ਲਿਖੇ ਲਾਭ ਹਨ-
- ਟੈਲਕਮ ਪਾਊਡਰ ਪਸੀਨੇ ਨੂੰ ਸੋਖ ਲੈਂਦਾ ਹੈ ।
- ਇਸ ਨੂੰ ਲਗਾਉਣ ਨਾਲ ਪਸੀਨੇ ਦੀ ਬਦਬੂ ਨਹੀਂ ਆਉਂਦੀ ਹੈ ।
- ਟੈਲਕਮ ਪਾਊਡਰ ਦੇ ਇਸਤੇਮਾਲ ਨਾਲ ਕੱਪੜਿਆਂ ‘ਤੇ ਪਸੀਨੇ ਦਾ ਧੱਬਾ ਨਹੀਂ ਲਗਦਾ ।
- ਇਸ ਦਾ ਇਸਤੇਮਾਲ ਦਵਾਈਆਂ ਦੇ ਰੂਪ ਵਿਚ ਵੀ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 8.
ਕੱਪੜੇ ਕਿਉਂ ਪਹਿਨੇ ਜਾਂਦੇ ਹਨ ?
ਉੱਤਰ-
- ਗਰਮੀ, ਸਰਦੀ ਅਤੇ ਮੌਸਮ ਦੀਆਂ ਕਠਿਨਾਈਆਂ ਤੋਂ ਬਚਣ ਲਈ ਕੱਪੜੇ ਪਹਿਨੇ ਜਾਂਦੇ ਹਨ !
- ਕੱਪੜੇ ਪਹਿਨੇ ਹੋਣ ਤਾਂ ਮੱਛਰ, ਕੀਟ ਆਦਿ ਦੇ ਕੱਟਣ ਤੋਂ ਬਚਿਆ ਜਾ ਸਕਦਾ ਹੈ ।
- ਡਿਗਣ ਨਾਲ ਸਰੀਰ ‘ਤੇ ਚੋਟ ਦਾ ਅਸਰ ਘੱਟ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 9.
ਕੱਪੜੇ ਪਹਿਨਣ ਵੇਲੇ ਕਿਹੜੀਆਂ-ਕਿਹੜੀਆਂ ਗੱਲਾਂ ਦਾ ਧਿਆਨ ਰੱਖਣਾ ਜ਼ਰੂਰੀ ਹੈ ?
ਉੱਤਰ-
ਕੱਪੜੇ ਪਹਿਨਣ ਸਮੇਂ ਹੇਠ ਲਿਖੀਆਂ ਗੱਲਾਂ ਦਾ ਧਿਆਨ ਵਿਚ ਰੱਖਣਾ ਜ਼ਰੂਰੀ ਹੈ-
- ਮੌਸਮ ਅਨੁਸਾਰ ਇਸ ਤਰ੍ਹਾਂ ਦੇ ਕੱਪੜੇ ਪਹਿਨਣੇ ਚਾਹੀਦੇ ਹਨ ਜਿਨ੍ਹਾਂ ਨਾਲ ਸਰੀਰ ਦਾ ਤਾਪਮਾਨ ਠੀਕ ਰਹਿ ਸਕੇ ।
- ਗਰਮੀਆਂ ਵਿਚ ਹਲਕੇ, ਖੁੱਲ੍ਹੇ ਅਤੇ ਫਿੱਕੇ ਰੰਗਾਂ ਦੇ ਕੱਪੜੇ ਪਹਿਨਣੇ ਚਾਹੀਦੇ ਹਨ ।
- ਸਰਦੀਆਂ ਵਿਚ ਕਾਲੇ ਜਾਂ ਗੁੜੇ ਰੰਗ ਦੇ ਕੱਪੜੇ ਪਹਿਨਣਾ ਲਾਭਵੰਦ ਹੈ, ਕਿਉਂਕਿ ਇਹ ਰੰਗ ਸਭ ਤੋਂ ਵੱਧ ਸੂਰਜ ਦੀਆਂ ਕਿਰਨਾਂ ਨੂੰ ਰਚਾ ਲੈਂਦੇ ਹਨ ।
- ਹੇਠਲੇ ਕੱਪੜੇ ਜਿਹੜੇ ਜਿਸਮ ਨਾਲ ਲੱਗੇ ਰਹਿੰਦੇ ਹਨ ਹਰ ਰੋਜ਼ ਬਦਲਣੇ ਚਾਹੀਦੇ ਹਨ ।
- ਗਿੱਲੇ ਕੱਪੜੇ ਨਹੀਂ ਪਹਿਨਣੇ ਚਾਹੀਦੇ ।
- ਰਾਤ ਅਤੇ ਦਿਨ ਵਿਚ ਪਹਿਨਣ ਵਾਲੇ ਕੱਪੜੇ ਵੱਖ-ਵੱਖ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 10.
ਬੂਟ ਅਤੇ ਜੁਰਾਬਾਂ ਕਿਸ ਤਰ੍ਹਾਂ ਦੇ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ ?
ਉੱਤਰ-
ਬੂਟ ਅਤੇ ਜੁਰਾਬਾਂ ਨਾਪ ਦੇ ਅਨੁਸਾਰ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 11.
ਤੰਗ ਕੱਪੜੇ ਪਹਿਨਣ ਦੇ ਕੀ-ਕੀ ਨੁਕਸਾਨ ਹਨ ?
ਉੱਤਰ-
ਤੰਗ ਕੱਪੜੇ ਪਹਿਨਣ ਦੇ ਹੇਠ ਲਿਖੇ ਨੁਕਸਾਨ ਹਨ-
- ਤੰਗ ਕੱਪੜੇ ਪਹਿਨਣ ਨਾਲ ਖੂਨ ਦਾ ਦੌਰਾ, ਸਾਹ ਲੈਣ ਦੀ ਕਿਰਿਆ, ਪਾਚਨ ਕਿਰਿਆ ਅਤੇ ਮਾਸਪੇਸ਼ੀਆਂ ਦੀ ਹਿਲਜੁਲ ਠੀਕ ਤਰ੍ਹਾਂ ਨਹੀਂ ਹੋ ਸਕਦੀ ।
- ਤੰਗ ਕੱਪੜੇ ਪਹਿਨਣ ਨਾਲ ਠੀਕ ਢੰਗ ਨਾਲ ਉੱਠਣਾ, ਬੈਠਣਾ ਅਤੇ ਕੰਮ ਕਰਨਾ ਮੁਸ਼ਕਿਲ ਹੋ ਜਾਂਦਾ ਹੈ ।
- ਪੇਟੀਆਂ ਜ਼ਿਆਦਾ ਕੱਸ ਕੇ ਨਹੀਂ ਬੰਨ੍ਹਣੀਆਂ ਚਾਹੀਦੀਆਂ ਅਤੇ ਲਚਕਦਾਰ ਹਿੱਸੇ ਵੀ ਜ਼ਿਆਦਾ ਤੰਗ ਨਹੀਂ ਹੋਣੇ ਚਾਹੀਦੇ ।
- ਤੰਗ ਪੋਸ਼ਾਕ ਵਿਚ ਖੁੱਲ੍ਹੀ ਪੋਸ਼ਾਕ ਨਾਲੋਂ ਜ਼ਿਆਦਾ ਸਰਦੀ ਲੱਗਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 12.
ਨਿਸ਼ਾਸਤੇ ਵਾਲੇ ਭੋਜਨ ਪਦਾਰਥਾਂ ਤੋਂ ਕਿਹੜਾ ਪੌਸ਼ਟਿਕ ਤੱਤ ਮਿਲਦਾ ਹੈ ?
ਉੱਤਰ-
ਨਿਸ਼ਾਸਤੇ ਵਾਲੇ ਭੋਜਨ ਪਦਾਰਥਾਂ ਤੋਂ ਕਾਰਬੋਹਾਈਡਰੇਟ ਪੌਸ਼ਟਿਕ ਤੱਤ ਮਿਲਦਾ ਹੈ |
ਪ੍ਰਸ਼ਨ 13.
ਬਨਸਪਤੀ ਅਤੇ ਪਾਣੀਜਨ ਪ੍ਰੋਟੀਨ ਵਿਚ ਕੀ ਅੰਤਰ ਹੈ ?
ਜਾਂ
ਪ੍ਰੋਟੀਨ ਦੇ ਪ੍ਰਾਪਤੀ ਸਰੋਤ ਦੱਸੋ ।
ਉੱਤਰ-
ਬਨਸਪਤੀ ਅਤੇ ਪਾਣੀਜਨ ਪ੍ਰੋਟੀਨ ਵਿਚ ਅੰਤਰ
| (i) ਅਨਾਜ-ਕਣਕ, ਜੁਆਰ, ਬਾਜਰਾ, ਚੌਲ, ਮੱਕੀ, ਰਾਂਗੀ, ਜਈ ਤੋਂ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ | |
(i) ਜੰਤੂ ਪ੍ਰੋਟੀਨ-ਆਂਡਾ, ਮੀਟ, ਮੱਛੀ, ਕਲੇਜੀ ਆਦਿ ਤੋਂ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ । |
| (ii) ਦਾਲਾਂ-ਅਰਹਰ, ਮੂੰਗੀ, ਮਸਰ, ਮੋਠ, ਸੋਇਆਬੀਨ ਅਤੇ ਛੋਲਿਆਂ ਦੀ ਦਾਲ, ਚਪਟੀ ਸੇਮ, ਸੁੱਕੇ ਮਟਰ ਆਦਿ ਤੋਂ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ । |
(ii) ਦੁੱਧ ਅਤੇ ਦੁੱਧ ਤੋਂ ਬਣੇ ਪਦਾਰਥ ਗਾਂ, ਮੱਝ, ਬੱਕਰੀ ਅਤੇ ਮਾਂ ਦਾ ਦੁੱਧ, ਸੁੱਕਾ ਦੁੱਧ, ਪਨੀਰ ਆਦਿ ਤੋਂ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ । |
ਪ੍ਰਸ਼ਨ 14
ਤੰਤੂਆਂ ਦੀ ਮੁਰੰਮਤ ਅਤੇ ਨਵੇਂ ਤੰਤੂ ਬਣਾਉਣ ਲਈ ਭੋਜਨ ਦੇ ਕਿਹੜੇ ਪੌਸ਼ਟਿਕ ਤੱਤ ਲੋੜੀਂਦੇ ਹਨ ?
ਜਾਂ
ਸਰੀਰ ਦੇ ਵਿਕਾਸ ਲਈ ਭੋਜਨ ਦਾ ਕਿਹੜਾ ਪੋਸ਼ਣ ਤੱਤ ਜ਼ਰੂਰੀ ਹੈ ?
ਉੱਤਰ-
ਤੰਤੂਆਂ ਦੀ ਮੁਰੰਮਤ ਅਤੇ ਨਵੇਂ ਤੰਤੂ ਬਜਾਉਣ ਲਈ ਭੋਜਨ ਵਿਚਲੇ ਪ੍ਰੋਟੀਨ ਤੱਤ ਦੀ ਲੋੜ ਹੁੰਦੀ ਹੈ |ਇਹ ਸਾਨੂੰ ਦਾਲਾਂ, ਸੋਇਆਬੀਨ, ਫਲੀਦਾਰ ਸਬਜ਼ੀਆਂ, ਮੀਟ, ਅੰਡਾ, ਦੁੱਧ ਆਦਿ ਤੋਂ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 15.
ਕੋਈ ਅਜਿਹਾ ਭੋਜਨ ਦੱਸੋ, ਜਿਸ ਨੂੰ ਪੂਰਨ ਆਹਾਰ ਕਿਹਾ ਜਾ ਸਕੇ ?
ਉੱਤਰ-
ਪੂਰਨ ਆਹਾਰ ਅਜਿਹੇ ਭੋਜਨ ਨੂੰ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ਜਿਸ ਵਿੱਚ ਸਰੀਰ ਲਈ ਲੋੜੀਂਦੇ ਸਾਰੇ ਪੋਸ਼ਟਿਕ ਤੱਤ ਮੌਜੂਦ ਹੁੰਦੇ ਹਨ | ਅਜਿਹੇ ਤੱਤ ਹੇਠ ਲਿਖੇ ਹਨ-
- ਦੁੱਧ,
- ਅੰਡਾ ।
ਪ੍ਰਸ਼ਨ 16.
ਤੇਲ ਨਾਲ ਸਰੀਰ ‘ਤੇ ਮਾਲਿਸ਼ ਕਰਨ ਦਾ ਕੀ ਲਾਭ ਹੈ ?
ਉੱਤਰ-
ਤੇਲ ਨਾਲ ਸਰੀਰ ਉੱਤੇ ਮਾਲਿਸ਼ ਕਰਨ ਦਾ ਲਾਭ ਇਹ ਹੈ ਕਿ ਸਾਡੀ ਚਮੜੀ ਦੇ ਹੇਠਲੀਆਂ ਤੇਲ ਦੀਆਂ ਗ੍ਰੰਥੀਆਂ ਹਰਕਤ ਵਿਚ ਆ ਜਾਂਦੀਆਂ ਹਨ ਅਤੇ ਇਹਨਾਂ ਵਿਚੋਂ ਕੁਦਰਤੀ ਤੇਲ ਨਿਕਲਦੇ ਰਹਿੰਦੇ ਹਨ ਜੋ ਸਾਡੀ ਚਮੜੀ ਨੂੰ ਮੁਲਾਇਮ ਰੱਖਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 17.
ਚਮੜੀ ਦੇ ਥੱਲੇ ਦੀਆਂ ਤੇਲ ਰੀਥੀਆਂ ਨੂੰ ਉਤੇਜਿਤ ਕਰਨ ਲਈ ਕੀ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ?
ਉੱਤਰ-
ਚਮੜੀ ਹੇਠਲੀਆਂ ਤੇਲ ਗ੍ਰੰਥੀਆਂ ਨੂੰ ਉਤੇਜਿਤ ਕਰਨ ਲਈ ਤੇਲ ਨਾਲ ਮਾਲਿਸ਼ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 18.
ਕੋਲਡ ਕਰੀਮ ਅਤੇ ਵੈਨਜ਼ਿੰਗ ਕਰੀਮ ਵਿਚ ਕੀ ਅੰਤਰ ਹੈ ?
ਉੱਤਰ-
ਕੋਲਡ ਕਰੀਮ ਅਤੇ ਵੈਸ਼ਿੰਗ ਕਰੀਮ ਵਿਚ ਅੰਤਰ-
| ਕੋਲਡ ਕਰੀਮ |
ਵੈਸ਼ਿੰਗ ਕਰੀਮ |
| (i) ਕੋਲਡ ਕਰੀਮ ਸਰਦੀਆਂ ਵਿਚ ਇਸਤੇਮਾਲ ਕੀਤੀ ਜਾਂਦੀ ਹੈ । |
(i) ਵੈਸ਼ਿੰਗ ਕਰੀਮ ਕਿਸੇ ਵੀ ਰੁੱਤ ਵਿਚ ਇਸਤੇਮਾਲ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ । |
| (ii) ਕੋਲਡ ਕਰੀਮ ਵਿਚ ਚਿਕਨਾਈ ਹੁੰਦੀ ਹੈ | |
(ii) ਵੈਨਿਸ਼ਿੰਗ ਕਰੀਮ ਵਿਚ ਚਿਕਨਾਈ ਨਹੀਂ ਹੁੰਦੀ । |
ਪ੍ਰਸ਼ਨ 19.
ਠੀਕ ਢੰਗ ਦੇ ਕੱਪੜੇ ਪਹਿਨਣ ਦਾ ਕੀ ਮਹੱਤਵ ਹੈ ?
ਉੱਤਰ-
ਠੀਕ ਢੰਗ ਦੇ ਕੱਪੜੇ ਪਹਿਨਣ ਦਾ ਹੇਠ ਲਿਖਿਆ ਮਹੱਤਵ ਹੈ-
- ਇਹ ਸਰੀਰ ਨੂੰ ਗਰਮੀ, ਸਰਦੀ ਅਤੇ ਬਾਹਰਲੀਆਂ ਸੱਟਾਂ ਤੋਂ ਬਚਾਉਂਦੇ ਹਨ ।
- ਇਹ ਸਰੀਰ ਦੀ ਗਰਮੀ ਨੂੰ ਠੀਕ ਰੱਖਦੇ ਹਨ ।
- ਠੀਕ ਢੰਗ ਦੇ ਕੱਪੜੇ ਆਪਣੇ ਆਪ ਨੂੰ ਸਜਾਉਣ ਅਤੇ ਮਰਿਆਦਾ ਰੱਖਣ ਦੇ ਲਈ ਵੀ ਪਹਿਨਣੇ ਚਾਹੀਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 20.
ਪੈਰਾਂ ਦੇ ਬੂਟ ਨਾਪ ਦੇ ਹੀ ਕਿਉਂ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ ?
ਉੱਤਰ-
ਪੈਰਾਂ ਦੇ ਬੂਟ ਨਾ ਤੰਗ ਅਤੇ ਨਾ ਹੀ ਜ਼ਿਆਦਾ ਖੁੱਲ੍ਹੇ , ਸਗੋਂ ਨਾਪ ਦੇ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ । ਤੰਗ ਬੂਟਾਂ ਵਿਚ ਪੈਰ ਘੁੱਟੇ ਰਹਿੰਦੇ ਹਨ ਅਤੇ ਪੈਰਾਂ ਤੇ ਛਾਲੇ ਪੈ ਜਾਂਦੇ ਹਨ । ਜ਼ਿਆਦਾ ਖੁੱਲੇ ਬਟ ਵਿਚ ਵੀ ਪੈਰ ਹਿਲਦਾ ਰਹਿੰਦਾ ਹੈ ਜਿਸ ਨਾਲ ਜਖ਼ਮ ਹੋ ਸਕਦੇ ਹਨ । ਇਸ ਲਈ ਬੂਟ ਨਾਪ ਦੇ ਹੀ ਖਰੀਦਣੇ ਚਾਹੀਦੇ ਹਨ ।

ਨਿਬੰਧਾਤਮਕ ਪ੍ਰਸ਼ਨ
ਪ੍ਰਸ਼ਨ 21.
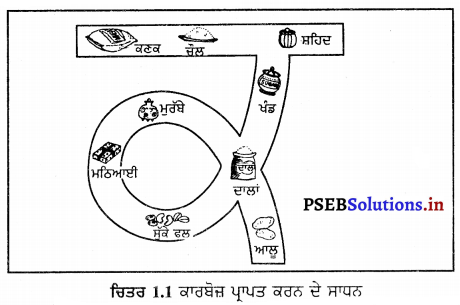
ਭੋਜਨ ਦੇ ਕਿਹੜੇ-ਕਿਹੜੇ ਤੱਤ ਹਨ ਅਤੇ ਇਹ ਕਿਹੜੇ ਸੋਮਿਆਂ ਤੋਂ ਮਿਲਦੇ ਹਨ ?
ਉੱਤਰ-
ਭੋਜਨ ਦੇ ਤੱਤ 6 ਪ੍ਰਕਾਰ ਦੇ ਹੁੰਦੇ ਹਨ-
- ਕਾਰਬੋਹਾਈਡਰੇਟ
- ਚਿਕਨਾਈ
- ਪ੍ਰੋਟੀਨ
- ਪਾਣੀ
- ਖਣਿਜ ਲੂਣ
- ਵਿਟਾਮਿਨ ।
ਪ੍ਰਾਪਤੀ ਦੇ ਸੋਮੇ-
- ਕਾਰਬੋਹਾਈਡਰੇਟ ਦੇ ਸੋਮੇ – ਚੌਲ, ਆਟਾ, ਆਲੂ, ਸ਼ਕਰਕੰਦੀ, ਕੇਲਾ, ਗੁੜ, ਖੰਡ, ਸ਼ਹਿਦ ਅਤੇ ਫਲ ॥
- ਚਿਕਨਾਈ ਦੇ ਸੋਮੇ – ਦੁੱਧ, ਘਿਓ, ਮੱਖਣ, ਤੇਲ, ਤੇਲਾਂ ਦੇ ਬੀਜ, ਸੁੱਕੇ ਮੇਵੇ, ਜਾਨਵਰਾਂ ਦੀ ਚਰਬੀ ਅਤੇ ਬਨਸਪਤੀ ਘਿਓ ।
- ਪ੍ਰੋਟੀਨ ਦੇ ਸੋਮੇ – ਬਨਸਪਤੀ ਪ੍ਰੋਟੀਨ-ਸੋਇਆਬੀਨ; ਰਾਜਮਾਂਹ, ਛੋਲੇ, ਦਾਲਾਂ, ਮਟਰ, ਫਲੀਆਂ ਤੋਂ ।
ਪਸ਼ੁ ਪ੍ਰੋਟੀਨ – ਆਂਡਾ, ਦੁੱਧ, ਮੀਟ, ਮੱਛੀ ਅਤੇ ਮੁਰਗੇ ਆਦਿ ।
- ਪਾਣੀ ਦੇ ਸੋਮੇ – ਭੋਜਨ ਜੋ ਅਸੀਂ ਖਾਂਦੇ ਹਾਂ ਅਤੇ ਪਾਣੀ ਜੋ ਅਸੀਂ ਪੀਂਦੇ ਹਾਂ ।
- ਖਣਿਜ ਲੂਣ ਦੇ ਸੋਮੇ-ਦੁੱਧ, ਕਲੇਜੀ, ਆਂਡੇ, ਹਰੀਆਂ ਸਬਜ਼ੀਆਂ, ਫਲ ਆਦਿ ।
- ਵਿਟਾਮਿਨ ਦੇ ਸੋਮੇ – ਦੁੱਧ, ਦਹੀਂ, ਆਂਡੇ ਦਾ ਪੀਲਾ ਭਾਗ, ਮੱਛੀ ਦੇ ਤੇਲ, ਮੱਛੀ, ਘਿਓ, ਮੱਖਣ, ਪੱਤੇਦਾਰ ਸਬਜ਼ੀਆਂ, ਟਮਾਟਰ, ਗਾਜਰ, ਪੱਕਿਆ ਪਪੀਤਾ, ਅੰਬ, ਕੱਦੂ, ਸੰਤਰਾ ਅਤੇ ਨਿੰਬੂ ਆਦਿ ।
ਪ੍ਰਸ਼ਨ 22.
ਭੋਜਨ ਖਾਣ ਸਮੇਂ ਕਿਹੜੀਆਂ ਗੱਲਾਂ ਦਾ ਧਿਆਨ ਰੱਖਣਾ ਜ਼ਰੂਰੀ ਹੈ ?
ਉੱਤਰ-
ਭੋਜਨ ਖਾਂਦੇ ਸਮੇਂ ਹੇਠ ਲਿਖੀਆਂ ਗੱਲਾਂ ਦਾ ਧਿਆਨ ਰੱਖਣਾ ਜ਼ਰੂਰੀ ਹੈ-
- ਭੋਜਨ ਹਮੇਸ਼ਾ ਤਾਜ਼ਾ ਅਤੇ ਖੁਸ਼ਬੂਦਾਰ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ਤਾਂ ਜੋ ਖਾਣ ਨੂੰ ਦਿਲ ਕਰੇ ।
- ਭੋਜਨ ਬਾਸੀ, ਜ਼ਰੂਰਤ ਨਾਲੋਂ ਘੱਟ ਜਾਂ ਜ਼ਿਆਦਾ ਪੱਕਿਆ ਹੋਇਆ ਨਹੀਂ ਖਾਣਾ ਚਾਹੀਦਾ ।
- ਸਵੇਰ ਅਤੇ ਸ਼ਾਮ ਦੇ ਭੋਜਨ ਵਿਚ ਭਿੰਨਤਾ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ।
- ਭੋਜਨ ਹਮੇਸ਼ਾ ਸਮੇਂ ‘ਤੇ ਖਾਣਾ ਚਾਹੀਦਾ ਹੈ ।
- ਲੋੜ ਤੋਂ ਵੱਧ ਭੋਜਨ ਖਾਣ ਨਾਲ ਪੇਟ ਖ਼ਰਾਬ ਹੋ ਸਕਦਾ ਹੈ ਕਿਉਂਕਿ ਮਿਹਦੇ ਨੂੰ ਜ਼ਿਆਦਾ ਕੰਮ ਕਰਨਾ ਪੈਂਦਾ ਹੈ ।
- ਖਾਣੇ ਦੇ ਨਾਲ ਜ਼ਿਆਦਾ ਪਾਣੀ ਨਹੀਂ ਪੀਣਾ ਚਾਹੀਦਾ ਕਿਉਂਕਿ ਭੋਜਨ ਨੂੰ ਪਚਾਉਣ ਵਾਲੇ ਰਸ ਪਤਲੇ ਹੋ ਜਾਂਦੇ ਹਨ ਅਤੇ ਭੋਜਨ ਜਲਦੀ ਪਚਦਾ ਨਹੀਂ ਹੈ |
- ਭੋਜਨ ਨੂੰ ਹੌਲੀ-ਹੌਲੀ ਚੰਗੀ ਤਰ੍ਹਾਂ ਚਬਾ ਕੇ ਖਾਣਾ ਚਾਹੀਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 23.
ਸਾਬਣ ਦਾ ਨਿੱਜੀ ਸਫ਼ਾਈ ਵਿਚ ਕੀ ਮਹੱਤਵ ਹੈ ?
ਉੱਤਰ-
ਸਾਡੇ ਸਰੀਰ ਦੀ ਚਮੜੀ ਦੇ ਥੱਲੇ ਤੇਲ ਦੀਆਂ ਗ੍ਰੰਥੀਆਂ ਹੁੰਦੀਆਂ ਹਨ, ਜਿਨ੍ਹਾਂ ਵਿਚੋਂ ਤੇਲ ਨਿਕਲ ਕੇ ਚਮੜੀ ‘ਤੇ ਆਉਂਦਾ ਰਹਿੰਦਾ ਹੈ । ਉੱਪਰਲੀ ਚਮੜੀ ਦੇ ਤੰਤੂ ਵੀ ਟੁੱਟਦੇ ਰਹਿੰਦੇ ਹਨ ਜੋ ਕਿ ਤੇਲ ਦੇ ਕਾਰਨ ਚਮੜੀ ਨਾਲ ਹੀ ਚਿਪਕੇ ਰਹਿੰਦੇ ਹਨ ।ਵਾਤਾਵਰਨ ਤੋਂ ਉੱਡ ਕੇ ਮਿੱਟੀ ਅਤੇ ਕੱਪੜਿਆਂ ਦੀ ਬੁਰ ਵੀ ਚਮੜੀ ਨਾਲ ਲੱਗ ਜਾਂਦੀ ਹੈ । ਗਰਮੀਆਂ ਵਿਚ ਸਰੀਰ ‘ਤੇ ਪਸੀਨਾ ਵੀ ਆਉਂਦਾ ਹੈ । ਜੇਕਰ ਇਨ੍ਹਾਂ ਸਾਰੀਆਂ ਚੀਜ਼ਾਂ ਨੂੰ ਸਰੀਰ ਤੋਂ ਨਾ ਉਤਾਰਿਆ ਜਾਏ ਤਾਂ ਚਮੜੀ ਨਾਲ ਹੀ ਚਿਪਕੀਆਂ ਰਹਿਣਗੀਆਂ ਤੇ ਇਨ੍ਹਾਂ ਵਿਚ ਬੈਕਟੀਰੀਆ ਪਲਣਗੇ । ਇਸ ਨਾਲ ਨਾ ਸਿਰਫ਼ ਸਰੀਰ ਵਿਚੋਂ ਬਦਬੂ ਆਉਣ ਲੱਗ ਜਾਂਦੀ ਹੈ ਬਲਕਿ ਕਈ ਤਰ੍ਹਾਂ ਦੀਆਂ ਚਮੜੀ ਦੀਆਂ ਬਿਮਾਰੀਆਂ ਵੀ ਲੱਗ ਜਾਂਦੀਆਂ ਹਨ । ਇਨ੍ਹਾਂ ਨੂੰ ਸਿਰਫ਼ ਪਾਣੀ ਨਾਲ ਨਹੀਂ ਉਤਾਰਿਆ ਜਾ ਸਕਦਾ ।
ਪਰ ਸਾਬਣ ਮਲਣ ਨਾਲ ਚਿਕਨਾਈ ਪਾਣੀ ਵਿਚ ਘੁਲ ਜਾਂਦੀ ਹੈ ਅਤੇ ਫਿਰ ਮੈਲ ਵੀ ਪਾਣੀ ਨਾਲ ਉਤਰ ਜਾਂਦੀ ਹੈ । ਸਾਰੇ ਸਰੀਰ ‘ਤੇ ਸਾਬਣ ਮਲਣ ਨਾਲ ਥੋੜੀ ਮਾਲਿਸ਼ ਵੀ ਹੁੰਦੀ ਹੈ, ਜਿਸ ਨਾਲ ਚਮੜੀ ਉਤੇਜਿਤ ਹੁੰਦੀ ਹੈ । ਨਹਾਉਣ ਲਈ ਹਮੇਸ਼ਾ ਨਰਮ ਸਾਬਣ ਦੀ ਵਰਤੋਂ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 24.
ਕੱਪੜੇ ਦੇ ਰੇਸ਼ੇ ਕਿੰਨੀ ਤਰ੍ਹਾਂ ਦੇ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ ? ਵਰਣਨ ਕਰੋ ।
ਜਾਂ
ਪਹਿਨਣ ਵਾਲੇ ਕੱਪੜੇ ਕਿਨ੍ਹਾਂ-ਕਿਨ੍ਹਾਂ ਰੇਸ਼ਿਆਂ ਤੋਂ ਬਣੇ ਹੁੰਦੇ ਹਨ ? ਵਰਣਨ ਕਰੋ ।
ਉੱਤਰ-
ਕੱਪੜੇ ਦੇ ਰੇਸ਼ੇ ਮੁੱਖ ਰੂਪ ਵਿਚ ਪੰਜ ਪ੍ਰਕਾਰ ਦੇ ਹੁੰਦੇ ਹਨ-
- ਸੂਤੀ ਕੱਪੜੇ
- ਲਿਨਨ
- ਰੇਸ਼ਮ
- ਉੱਨ
- ਟੈਰਾਲੀਨ, ਨਾਈਲੋਨ ਆਦਿ ।
1. ਸੂਤੀ ਕੱਪੜੇ – ਇਹ ਕਪਾਹ ਤੋਂ ਬਣਾਏ ਜਾਂਦੇ ਹਨ । ਸੂਤੀ ਕੱਪੜੇ ਗਰਮੀ ਦੇ ਚੰਗੇ ਸੁਚਾਲਕ ਹੁੰਦੇ ਹਨ ਅਤੇ ਪਾਣੀ ਨੂੰ ਬਹੁਤ ਜ਼ਿਆਦਾ ਨਹੀਂ ਚੁਸਦੇ । ਸੂਤੀ ਕੱਪੜਾ ਵਧੇਰੇ ਹੰਢਣਸਾਰ ਅਤੇ ਸਸਤਾ ਹੁੰਦਾ ਹੈ ਇਸ ਲਈ ਆਮ ਘਰਾਂ ਵਿਚ ਇਸ ਦੀ ਸਭ ਤੋਂ ਵੱਧ ਵਰਤੋਂ ਕੀਤੀ ਜਾਂਦੀ ਹੈ । ਗਰਮੀਆਂ ਵਿਚ ਹੇਠਲੇ ਅਤੇ ਬਾਹਰਲੇ ਕੱਪੜਿਆਂ ਲਈ ਅਤੇ ਸਰਦੀਆਂ ਵਿਚ ਹੇਠਲੇ ਕੱਪੜਿਆਂ ਲਈ ਇਸ ਦੀ ਵਰਤੋਂ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ।
2. ਲਿਨਨ – ਇਹ ਵੀ ਪੌਦਿਆਂ ਤੋਂ ਬਣਾਈ ਜਾਂਦੀ ਹੈ । ਇਹ ਸੂਤੀ ਕੱਪੜਿਆਂ ਨਾਲੋਂ ਮਹਿੰਗੀ ਹੁੰਦੀ ਹੈ । ਦੇਖਣ ਵਿਚ ਇਹ ਸੂਤੀ ਕੱਪੜੇ ਨਾਲੋਂ ਚਮਕਦਾਰ, ਛੂਹਣ ਵਿਚ ਨਰਮ ਅਤੇ ਸੁਤੀ ਤੋਂ ਵਧੀਆ ਲੱਗਦੀ ਹੈ । ਪਰ ਪਹਿਨਣ ਅਤੇ ਧੋਣ ਵਿਚ ਸੂਤੀ ਦੀ ਤਰ੍ਹਾਂ ਹੀ ਹੁੰਦੀ ਹੈ ।
3. ਰੇਸ਼ਮ – ਇਹ ਰੇਸ਼ਮ ਦੇ ਕੀੜਿਆਂ ਤੋਂ ਬਣਾਈ ਜਾਂਦੀ ਹੈ । ਇਹ ਗਰਮੀ ਦੀ ਚੰਗੀ ਸੂਚਾਲਕ ਨਹੀਂ ਹੁੰਦੀ ਅਤੇ ਪਾਣੀ ਵੀ ਜ਼ਿਆਦਾ ਨਹੀਂ ਚੁਸਦੀ । ਇਸ ਲਈ ਇਸ ਦੀ ਵਰਤੋਂ ਸਰਦੀਆਂ ਵਿਚ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ।ਸਿਲਕ ਨਰਮ ਅਤੇ ਚਮਕਦਾਰ ਹੋਣ ਦੇ ਕਾਰਨ ਪਹਿਨੀ ਹੋਈ ਸੋਹਣੀ ਲੱਗਦੀ ਹੈ । ਪਰ ਮਹਿੰਗੀ ਹੋਣ ਕਾਰਨ ਇਸ ਦੀ ਵਧੇਰੇ ਵਰਤੋਂ ਨਹੀਂ ਕੀਤੀ ਜਾਂਦੀ ।
4. ਉੱਨ – ਇਹ ਗਰਮੀ ਦੀ ਚੰਗੀ ਸੂਚਾਲਕ ਨਹੀਂ ਅਤੇ ਪਾਣੀ ਵੀ ਵੱਧ ਚੁਸਦੀ ਹੈ । ਇਸ ਲਈ ਊਨੀ ਕੱਪੜੇ ਸਰਦੀਆਂ ਵਿਚ ਹੀ ਪਹਿਨੇ ਜਾਂਦੇ ਹਨ । ਊਨੀ ਕੱਪੜੇ ਖੁੱਲ੍ਹੇ ਬੁਣੇ ਹੋਏ ਹੁੰਦੇ ਹਨ । ਇਨ੍ਹਾਂ ਦੀਆਂ ਵਿੱਥਾਂ ਵਿਚ ਹਵਾ ਭਰ ਜਾਂਦੀ ਹੈ ਜਿਹੜੀ ਸਰੀਰ ਦੀ ਗਰਮੀ ਨੂੰ ਬਾਹਰ ਨਹੀਂ ਜਾਣ ਦਿੰਦੀ । ਗਿੱਲੀ ਹੋਣ ਦੇ ਬਾਵਜੂਦ ਵੀ ਇਹ ਸਰੀਰ ਨਾਲ ਨਹੀਂ ਚਿਪਕਦੀ ਕਿਉਂਕਿ ਇਹ ਵਧੇਰੇ ਪਾਣੀ ਨੂੰ ਚੁਸਦੀ ਹੈ । ਇਸ ਲਈ ਬਹੁਤ ਕਸਰਤ ਕਰਨ ਮਗਰੋਂ ਝੱਟਪੱਟ ਉਨੀ ਕੱਪੜੇ ਪਹਿਨ ਲੈਣੇ ਚਾਹੀਦੇ ਹਨ । ਊਨੀ ਕੱਪੜੇ ਥੋੜੇ ਖੁਰਦਰੇ ਹੁੰਦੇ ਹਨ ਇਸ ਲਈ ਊਨੀ ਕੱਪੜੇ ਦੇ ਹੇਠਾਂ ਪਹਿਨਣ ਵਾਲੇ ਕੱਪੜੇ (Under garments) ਨਹੀਂ ਬਣਾਏ ਜਾਂਦੇ ।
5. ਟੈਰਾਲੀਨ, ਨਾਈਲੋਨ ਆਦਿ-ਇਹ ਕੱਪੜੇ ਪਹਿਨਣ ਵਿਚ ਹਲਕੇ, ਧੋਣ ਵਿਚ ਅਸਾਨ ਅਤੇ ਜ਼ਿਆਦਾ ਦੇਰ ਚੱਲਣ ਵਾਲੇ ਹੁੰਦੇ ਹਨ । ਇਹ ਕੱਪੜੇ ਪਾਣੀ ਨਹੀਂ ਚੂਸਦੇ ਅਤੇ ਗਰਮੀ ਦੇ ਚੰਗੇ ਸੁਚਾਲਕ ਨਹੀਂ ਹੁੰਦੇ । ਇਸ ਲਈ ਗਰਮੀਆਂ ਵਿਚ ਨਹੀਂ ਪਹਿਨੇ ਜਾ ਸਕਦੇ । ਧੋਣ ਵਿਚ ਅਸਾਨੀ ਅਤੇ ਬਿਨਾਂ ਪ੍ਰੈੱਸ ਕੀਤੇ ਵੀ ਪਹਿਨੇ ਜਾ ਸਕਣ ਕਾਰਨ ਅੱਜ-ਕਲ੍ਹ ਇਨ੍ਹਾਂ ਦੀ ਵਧੇਰੇ ਵਰਤੋਂ ਕੀਤੀ ਜਾਂਦੀ ਹੈ । ਇਨ੍ਹਾਂ ਦੇ ਜੁਰਾਬਾਂ ਅਤੇ ਜਾਂਘੀਏ ਆਦਿ ਵੀ ਬਣਦੇ ਹਨ ।

PSEB 8th Class Home Science Guide ਨਿੱਜੀ ਦੇਖ-ਭਾਲ Important Questions and Answers
ਹੋਰ ਮਹੱਤਵਪੂਰਨ ਪ੍ਰਸ਼ਨ
ਬਹੁਵਿਕਲਪੀ ਪ੍ਰਸ਼ਨ
ਪ੍ਰਸ਼ਨ 1.
ਵਿਟਾਮਿਨ B ਦੀ ਕਮੀ ਨਾਲ ਕਿਹੜਾ ਰੋਗ ਹੁੰਦਾ ਹੈ ?
(ਉ) ਬੇਰੀ-ਬੇਰੀ
(ਅ) ਸਕਰਵੀ
(ੲ) ਅੰਧਰਾਤਾ
(ਸ ਅਨੀਮੀਆ ।
ਉੱਤਰ-
(ਉ) ਬੇਰੀ-ਬੇਰੀ
ਪ੍ਰਸ਼ਨ 2.
ਵਿਟਾਮਿਨ ਸੀ ਦਾ ਸੋਮਾ ਨਹੀਂ ਹੈ-
(ੳ) ਆਂਵਲਾ
(ਅ) ਸੰਤਰਾ
(ੲ) ਨਿੰਬੂ
(ਸ) ਕੋਈ ਨਹੀਂ ।
ਉੱਤਰ-
(ਸ) ਕੋਈ ਨਹੀਂ ।
ਪ੍ਰਸ਼ਨ 3.
ਉੱਨ ਦੇ ਰੇਸ਼ਿਆਂ ਦੀ ਸਤਹਿ ਕਿਹੋ ਜਿਹੀ ਹੁੰਦੀ ਹੈ ?
(ੳ) ਖੁਰਦਰੀ
(ਅ) ਮੁਲਾਇਮ
(ੲ) ਚੀਨੀ
(ਸ) ਕੋਈ ਨਹੀਂ ।
ਉੱਤਰ-
(ੳ) ਖੁਰਦਰੀ
ਪ੍ਰਸ਼ਨ 4.
ਪਾਣੀ ਵਿਚ ਘੁਲਣਸ਼ੀਲ ਵਿਟਾਮਿਨ ਹੈ-
(ਉ) A
(ਅ) D
(ੲ) C
(ਸ) ਕੋਈ ਨਹੀਂ ।
ਉੱਤਰ-
(ੲ) C
ਪ੍ਰਸ਼ਨ 5.
ਕੋਲਡ ਕਰੀਮ ਦੀ ਵਰਤੋਂ …………………….. ਮੌਸਮ ਵਿਚ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ।
(ਉ) ਸਰਦ
(ਅ) ਗਰਮ
(ੲ) ਬਰਸਾਤੀ
(ਸ) ਕੋਈ ਨਹੀਂ ।
ਉੱਤਰ-
(ਉ) ਸਰਦ

ਪ੍ਰਸ਼ਨ 6.
ਦੁੱਧ ਕਿਹੋ ਜਿਹਾ ਆਹਾਰ ਹੈ ?
(ੳ) ਪੂਰਨ
(ਅ) ਅਰਧ
(ੲ) ਅਪੂਰਨ
(ਸ) ਸਾਦਾ ।
ਉੱਤਰ-
(ੳ) ਪੂਰਨ
ਪ੍ਰਸ਼ਨ 7.
ਸਰੀਰ ਦੀ ਸਫ਼ਾਈ ਲਈ ਜ਼ਰੂਰੀ ਹੈ-
(ਉ) ਸਾਬਣ
(ਅ) ਤੇਲ।
(ੲ) ਕਰੀਮ ਅਤੇ ਪਾਊਡਰ
(ਸ) ਉਪਰੋਕਤ ਸਾਰੇ ।
ਉੱਤਰ-
(ਉ) ਸਾਬਣ
ਸਹੀ/ਗਲਤ ਦੱਸੋ
1. ਸੋਇਆਬੀਨ ਵਿਚ ਪ੍ਰੋਟੀਨ ਤੱਤ ਮਿਲਦਾ ਹੈ ।
2. ਆਂਵਲੇ ਵਿਚ ਵਿਟਾਮਿਨ ਸੀ ਹੁੰਦਾ ਹੈ ।
3. ਕੋਲਡ ਕਰੀਮ ਵਿਚ ਚਿਕਨਾਈ ਹੁੰਦੀ ਹੈ ।
4. ਨਿਸ਼ਾਸ਼ਤੇ ਵਾਲੇ ਭੋਜਨ ਵਿਚ ਪ੍ਰੋਟੀਨ ਵੱਧ ਹੁੰਦਾ ਹੈ ।
5. ਤੰਗ ਕੱਪੜੇ ਪਹਿਣਨਾ ਵਧੀਆ ਹੁੰਦਾ ਹੈ ।
ਉੱਤਰ-
1. √
2. √
3. √
4. ×
5. × ।
ਖ਼ਾਲੀ ਥਾਂ ਭਰੋ
1. ………………… ਕਰੀਮ ਕਿਸੇ ਵੀ ਮੌਸਮ ਵਿਚ ਪ੍ਰਯੋਗ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ ।
2. ਸਰੀਰ ਦਾ ਨਿਰਮਾਣ ਕਰਨ ਵਾਲੇ ਤੱਤ ਪ੍ਰੋਟੀਨ ਅਤੇ …………………….. ਹੈ ।
3. ਬਨਸਪਤੀ ਵਾਲੀ ਖੁਰਾਕ ਵਿੱਚ ਵਧੇਰੇ ………………………….. ਹੁੰਦਾ ਹੈ ।
4. ਸਿਰ ਅਤੇ ਸਰੀਰ ਤੇ ……………………….. ਲਗਾਉਣ ਨਾਲ ਚਮੜੀ ਚਮਕਦਾਰ ਰਹਿੰਦੀ
ਉੱਤਰ-
1. ਵੈਨਿਸ਼ਿੰਗ,
2. ਖਣਿਜ ਲੂਣ,
3. ਫੋਕ,
4. ਤੇਲ ।

ਇਕ ਸ਼ਬਦ ਵਿੱਚ ਉੱਤਰ ਦਿਓ
ਪ੍ਰਸ਼ਨ 1.
ਨਿੰਬੂ ਅਤੇ ਸੰਤਰੇ ਵਿਚ ਕਿਹੜਾ ਵਿਟਾਮਿਨ ਪਾਇਆ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਵਿਟਾਮਿਨ ਸੀ ।
ਪ੍ਰਸ਼ਨ 2.
ਵਿਟਾਮਿਨ ਸੀ ਦੀ ਕਮੀ ਨਾਲ ਕਿਹੜਾ ਰੋਗ ਹੋ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਸਕਰਵੀ ।
ਪ੍ਰਸ਼ਨ 3.
ਦੁੱਧ ਨੂੰ ਕਿਹੋ ਜਿਹਾ ਆਹਾਰ ਕਿਹਾ ਜਾ ਸਕਦਾ ਹੈ ?
ਉੱਤਰ-
ਪੂਰਨ ਆਹਾਰ ।
ਪ੍ਰਸ਼ਨ 4.
ਬੇਰੀ-ਬੇਰੀ ਰੋਗ ਕਿਸ ਵਿਟਾਮਿਨ ਦੀ ਕਮੀ ਨਾਲ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਵਿਟਾਮਿਨ B ਦੀ ਕਮੀ ਨਾਲ ।
ਪ੍ਰਸ਼ਨ 5.
ਭੋਜਨ ਦੇ ਕਿਹੜੇ ਪੌਸ਼ਟਿਕ ਤੱਤ ਵਿੱਚ ਨਾਈਟਰੋਜਨ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਪੋਟੀਨ ਵਿਚ ।

ਪ੍ਰਸ਼ਨ 6.
ਵਿਟਾਮਿਨ B ਦੀ ਕਮੀ ਨਾਲ ਕਿਹੜਾ ਰੋਗ ਹੋ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਬੇਰੀ-ਬੇਰੀ ।
ਪ੍ਰਸ਼ਨ 7.
ਭੋਜਨ ਦਾ ਕਿਹੜਾ ਪੋਸ਼ਕ ਤੱਤ ਸੋਇਆਬੀਨ ਵਿਚ ਸਭ ਤੋਂ ਜ਼ਿਆਦਾ ਪਾਇਆ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਪ੍ਰੋਟੀਨ ਤੱਤ ।
ਪ੍ਰਸ਼ਨ 8.
ਨਿੰਬੂ ਅਤੇ ਆਂਵਲੇ ਵਿੱਚ ਕਿਹੜਾ ਵਿਟਾਮਿਨ ਪਾਇਆ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਵਿਟਾਮਿਨ ਸੀ ।
ਬਹੁਤ ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ
ਪ੍ਰਸ਼ਨ 1.
ਭੋਜਨ ਦੇ ਤੱਤਾਂ ਦੇ ਨਾਂ ਲਿਖੋ ।
ਉੱਤਰ-
ਕਾਰਬੋਜ਼, ਪ੍ਰੋਟੀਨ, ਚਿਕਨਾਈ, ਵਿਟਾਮਿਨ ਅਤੇ ਲਵਣ ।
ਪ੍ਰਸ਼ਨ 2.
ਭੋਜਨ ਦੇ ਤੱਤ ਸਰੀਰ ਲਈ ਕਿਉਂ ਜ਼ਰੂਰੀ ਹੁੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਸਰੀਰ ਨੂੰ ਜੀਵਤ ਰੱਖਣ ਅਤੇ ਸਰੀਰਕ ਵਿਕਾਸ ਲਈ ।

ਪ੍ਰਸ਼ਨ 3.
ਭੋਜਨ ਦੇ ਸਾਡੇ ਸਰੀਰ ਲਈ ਪ੍ਰਮੁੱਖ ਕੰਮ ਕੀ ਹਨ ?
ਉੱਤਰ-
ਸਰੀਰ ਨਿਰਮਾਣ, ਊਰਜਾ ਪ੍ਰਦਾਨ ਕਰਨਾ, ਸਰੀਰ ਵਿਚ ਹੋਣ ਵਾਲੀਆਂ ਕਿਰਿਆਵਾਂ ‘ਤੇ ਕੰਟਰੋਲ ਕਰਨਾ ਅਤੇ ਸਰੀਰ ਨੂੰ ਰੋਗ ਨਿਵਾਰਕ ਖਮਤਾ ਪ੍ਰਦਾਨ ਕਰਨਾ ।
ਪ੍ਰਸ਼ਨ 4.
ਸਾਡੇ ਸਰੀਰ ਦਾ ਪੋਸ਼ਣ ਕਰਨ ਵਾਲੇ ਤੱਤ ਕੀ ਕਹਾਉਂਦੇ ਹਨ ?
ਉੱਤਰ-
ਪੋਸ਼ਕ ਤੱਤ ।
ਪ੍ਰਸ਼ਨ 5.
ਸਰੀਰ ਦਾ ਨਿਰਮਾਣ ਕਰਨ ਵਾਲੇ ਤੱਤ ਕੀ ਹੁੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਪ੍ਰੋਟੀਨ ਅਤੇ ਖਣਿਜ ਲੂਣ ।
ਪ੍ਰਸ਼ਨ 6.
ਸਰੀਰ ਦੀ ਸੁਰੱਖਿਆ ਕਰਨ ਵਾਲੇ ਪਦਾਰਥ ਕਿਹੜੇ-ਕਿਹੜੇ ਹੁੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਵਿਟਾਮਿਨ ਅਤੇ ਖਣਿਜ ਲੂਣ ।
ਪ੍ਰਸ਼ਨ 7.
ਪਾਣੀ ਦਾ ਸਰੀਰ ਲਈ ਮੁੱਖ ਕੰਮ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਇਹ ਪੋਸ਼ਕ ਤੱਤਾਂ ਅਤੇ ਸਰੀਰਕ ਕਿਰਿਆਵਾਂ ਨੂੰ ਨਿਯਮਿਤ ਕਰਨ ਦਾ ਕੰਮ ਕਰਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 8.
ਕਾਰਬੋਜ਼ ਕਿਸ-ਕਿਸ ਤੱਤ ਤੋਂ ਮਿਲ ਕੇ ਬਣਦੇ ਹਨ ?
ਉੱਤਰ-
ਕਾਰਬਨ, ਹਾਈਡਰੋਜਨ ਅਤੇ ਆਕਸੀਜਨ ।

ਪ੍ਰਸ਼ਨ 9.
ਪ੍ਰੋਟੀਨ ਕਿਸ-ਕਿਸ ਤੱਤ ਤੋਂ ਮਿਲ ਕੇ ਬਣੇ ਹੁੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਕਾਰਬਨ, ਹਾਈਡਰੋਜਨ, ਆਕਸੀਜਨ, ਨਾਈਟਰੋਜਨ, ਫਾਸਫੋਰਸ ਅਤੇ ਗੰਧਕ ।
ਪ੍ਰਸ਼ਨ 10.
ਕਾਰਬੋਜ਼ ਦੇ ਦੋ ਪ੍ਰਮੁੱਖ ਪ੍ਰਾਪਤੀ ਸੋਮੇ ਦੱਸੋ । ਪੰਜਾਬ ਬੋਰਡ, 2004
ਉੱਤਰ-
ਅਨਾਜ ਅਤੇ ਰੀਨਾ ।
ਪ੍ਰਸ਼ਨ 11.
ਪ੍ਰੋਟੀਨ ਦੇ ਦੋ ਪ੍ਰਮੁੱਖ ਪ੍ਰਾਪਤੀ ਸੋਮੇ ਦੱਸੋ ।
ਉੱਤਰ-
ਆਂਡਾ ਤੇ ਦਾਲਾਂ ।
ਪ੍ਰਸ਼ਨ 12.
ਕਿਹੜੀਆਂ-ਕਿਹੜੀਆਂ ਬਨਸਪਤੀਆਂ ਵਿਚ ਪ੍ਰੋਟੀਨ ਜ਼ਿਆਦਾ ਮਿਲਦਾ ਹੈ ?
ਉੱਤਰ-
ਦਾਲਾਂ, ਅਨਾਜ, ਸੋਇਆਬੀਨ, ਅਖਰੋਟ, ਮੂੰਗਫ਼ਲੀ, ਬਦਾਮ, ਸੇਮ ਦੇ ਬੀਜ ਅਤੇ ਮਟਰ ਆਦਿ ।
ਪ੍ਰਸ਼ਨ 13.
ਜੰਤੂਆਂ ਤੋਂ ਪ੍ਰਾਪਤ ਕਿਹੜੇ-ਕਿਹੜੇ ਪਦਾਰਥਾਂ ਵਿਚ ਪ੍ਰੋਟੀਨ ਜ਼ਿਆਦਾ ਮਾਤਰਾ ਵਿਚ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਦੁੱਧ, ਦਹੀਂ, ਮੱਖਣ, ਪਨੀਰ, ਆਂਡੇ, ਮੀਟ, ਮੱਛੀ ।
ਪ੍ਰਸ਼ਨ 14.
ਕਿਹੜੇ-ਕਿਹੜੇ ਸਟਾਰਚ ਵਾਲੇ ਪਦਾਰਥਾਂ ਵਿਚ ਕਾਰਬੋਹਾਈਡਰੇਟ ਜ਼ਿਆਦਾ ਮਿਲਦਾ ਹੈ ?
ਉੱਤਰ-
ਚੌਲ, ਕਣਕ, ਸ਼ਕਰਕੰਦੀ, ਮੱਕੀ, ਸਾਬੂਦਾਨਾ, ਜੌ, ਅਖਰੋਟ, ਆਲੂ ਆਦਿ ।

ਪ੍ਰਸ਼ਨ 15.
ਚਿਕਨਾਈ ਦੇ ਦੋ ਮੁੱਖ ਸੋਮੇ ਦੱਸੋ ।
ਉੱਤਰ-
ਤੇਲ ਵਾਲੇ ਬੀਜ ਅਤੇ ਦੁੱਧ ।
ਪ੍ਰਸ਼ਨ 16.
ਸਰੀਰ ਦੇ ਲਈ ਲੋੜੀਂਦੇ ਪੰਜ ਖਣਿਜ ਤੱਤ ਦੱਸੋ ।
ਉੱਤਰ-
ਕੈਲਸ਼ੀਅਮ, ਫਾਸਫੋਰਸ, ਲੋਹਾ, ਆਇਉਡੀਨ ਅਤੇ ਸੋਡੀਅਮ ।
ਪ੍ਰਸ਼ਨ 17.
ਸਾਡੇ ਸਰੀਰ ਨੂੰ ਪਾਣੀ ਪ੍ਰਾਪਤ ਕਰਨ ਦੇ ਪ੍ਰਮੁੱਖ ਸੋਮੇ ਕੀ ਹਨ ?
ਉੱਤਰ-
- ਭੋਜਨ ਜੋ ਅਸੀਂ ਖਾਂਦੇ ਹਾਂ ਅਤੇ
- ਪਾਣੀ ਜੋ ਅਸੀਂ ਪੀਂਦੇ ਹਾਂ ।
ਪ੍ਰਸ਼ਨ 18.
ਕਾਰਬੋਹਾਈਡਰੇਟ ਦਾ ਮੁੱਖ ਕੰਮ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਸਰੀਰ ਦੀ ਕਿਰਿਆਸ਼ੀਲਤਾ ਲਈ ਊਰਜਾ ਪ੍ਰਦਾਨ ਕਰਨਾ ।
ਪ੍ਰਸ਼ਨ 19.
ਸਰੀਰ ਵਿਚ ਚਰਬੀ ਦਾ ਮੁੱਖ ਕੰਮ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਸਰੀਰ ਨੂੰ ਊਰਜਾ ਅਤੇ ਸ਼ਕਤੀ ਪ੍ਰਦਾਨ ਕਰਨਾ ।
ਪ੍ਰਸ਼ਨ 20.
ਲੋਹਾ ਪ੍ਰਾਪਤੀ ਦੇ ਮੁੱਖ ਸਾਧਨ ਕੀ ਹਨ ?
ਉੱਤਰ-
ਲੀਵਰ, ਮੀਟ, ਮੱਛੀ, ਆਂਡੇ, ਪੱਤੇਦਾਰ ਸਬਜ਼ੀਆਂ, ਅਨਾਜ, ਪੂਰਨ ਕਣਕ, ਦਾਲਾਂ, ਸੇਲਾ ਚੌਲ ਆਦਿ ।
ਪ੍ਰਸ਼ਨ 21.
(i) ਲੋਹਾ ਸਰੀਰ ਦੇ ਲਈ ਕਿਉਂ ਜ਼ਰੂਰੀ ਹੈ ?
(ii) ਲੋਹੇ ਦੀ ਕਮੀ ਨਾਲ ਕਿਹੜਾ ਰੋਗ ਹੋ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
(i) ਪ੍ਰੋਟੀਨ ਦੇ ਨਾਲ ਸੰਯੋਗ ਕਰਕੇ ਹੀਮੋਗਲੋਬਿਨ ਦਾ ਨਿਰਮਾਣ ਕਰਦਾ ਹੈ ।
(ii) ਅਨੀਮੀਆ ।

ਪ੍ਰਸ਼ਨ 22.
ਸਰੀਰ ਵਿਚ ਸੋਡੀਅਮ ਦਾ ਇਕ ਕੰਮ ਦੱਸੋ ।
ਉੱਤਰ-
ਸਰੀਰ ਵਿਚ ਖਾਰ ਅਤੇ ਤੇਜ਼ਾਬ ਦਾ ਸੰਤੁਲਨ ਬਣਾਈ ਰੱਖਣਾ ।
ਪ੍ਰਸ਼ਨ 23
(i) ਵਿਟਾਮਿਨ ਏ ਦੀ ਕਮੀ ਦੇ ਚਾਰ ਮੁੱਖ ਪ੍ਰਭਾਵ ਦੱਸੋ ।
ਜਾਂ
ਵਿਟਾਮਿਨ ਏ ਦੀ ਕਮੀ ਨਾਲ ਕਿਹੜਾ ਰੋਗ ਹੋ ਜਾਂਦਾ ਹੈ ?
ਜਾਂ
(ii) ਅੱਖਾਂ ਦੀ ਰੌਸ਼ਨੀ ਲਈ ਕਿਹੜਾ ਵਿਟਾਮਿਨ ਜ਼ਰੂਰੀ ਹੈ ?
ਜਾਂ
ਅੰਧਰਾਤਾ ਰੋਗ ਕਿਹੜੇ ਵਿਟਾਮਿਨ ਦੀ ਕਮੀ ਨਾਲ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
(i)
- ਅੰਧਰਾਤਾ ਰੋਗ,
- ਮਾਸਪੇਸ਼ੀਆਂ ਕਮਜ਼ੋਰ ਹੋ ਜਾਂਦੀਆਂ ਹਨ,
- ਸਰੀਰ ਕਮਜ਼ੋਰ ਹੋ ਜਾਂਦਾ ਹੈ
- ਰੋਗ ਖਮਤਾ ਘੱਟ ਹੋ ਜਾਂਦੀ ਹੈ ।
(ii) ਵਿਟਾਮਿਨ ‘ਏ’।
ਪ੍ਰਸ਼ਨ 24.
ਰਿਕਟਸ ਰੋਧੀ ਵਿਟਾਮਿਨ ਕਿਸ ਨੂੰ ਕਹਿੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਵਿਟਾਮਿਨ D ਨੂੰ ।
ਪ੍ਰਸ਼ਨ 25.
ਵਿਟਾਮਿਨ ਦੀ ਪ੍ਰਾਪਤੀ ਦੇ ਮੁੱਖ ਸਾਧਨ ਕੀ ਹਨ ?
ਉੱਤਰ-
ਖੱਟੇ ਰਸਦਾਰ ਫਲ ; ਜਿਵੇਂ-ਆਂਵਲੇ, ਸੰਤਰਾ, ਟਮਾਟਰ ਆਦਿ ।
ਪ੍ਰਸ਼ਨ 26.
ਕਿਹੜੇ-ਕਿਹੜੇ ਸ਼ੱਕਰ ਵਾਲੇ ਪਦਾਰਥਾਂ ਵਿਚ ਕਾਰਬੋਹਾਈਡਰੇਟ ਜ਼ਿਆਦਾ ਮਿਲਦਾ ਹੈ ?
ਉੱਤਰ-
ਸ਼ਹਿਦ, ਖੰਡ, ਗੁੜ, ਚੁਕੰਦਰ, ਅੰਗੂਰ ਅਤੇ ਹੋਰ ਮਿੱਠੇ ਫਲ ।
ਪ੍ਰਸ਼ਨ 27.
ਜੰਤੂਆਂ ਤੋਂ ਪ੍ਰਾਪਤ ਹੋਣ ਵਾਲੇ ਚਿਕਨਾਈ ਪਦਾਰਥ ਕਿਹੜੇ-ਕਿਹੜੇ ਹਨ ?
ਉੱਤਰ-
ਘਿਓ, ਮੱਖਣ, ਦੁੱਧ, ਕਰੀਮ,ਦਹੀਂ, ਪਨੀਰ, ਜਾਨਵਰਾਂ ਦੀ ਚਰਬੀ, ਮੱਛੀ, ਆਂਡੇ ਦੀ ਸਫ਼ੈਦੀ ।

ਪ੍ਰਸ਼ਨ 28.
ਬਨਸਪਤੀ ਤੋਂ ਪ੍ਰਾਪਤ ਹੋਣ ਵਾਲੇ ਚਿਕਨਾਈ ਵਾਲੇ ਪਦਾਰਥ ਕਿਹੜੇ-ਕਿਹੜੇ ਹਨ ?
ਉੱਤਰ-
ਮੂੰਗਫਲੀ, ਸਰੋਂ, ਤਿਲ, ਨਾਰੀਅਲ, ਬਦਾਮ, ਅਖਰੋਟ, ਚਿਲਗੋਜ਼ਾ ਆਦਿ ।
ਪ੍ਰਸ਼ਨ 29.
ਪ੍ਰੋਟੀਨ ਦੀ ਕਮੀ ਨਾਲ ਹੋਣ ਵਾਲੇ ਦੋ ਰੋਗ ਕਿਹੜੇ-ਕਿਹੜੇ ਹਨ ?
ਉੱਤਰ-
ਮਰਾਸਮਸ ਅਤੇ ਕਵਾਸ਼ਿਓਰਕਰ ।
ਪ੍ਰਸ਼ਨ 30.
ਲੋੜ ਨਾਲੋਂ ਜ਼ਿਆਦਾ ਮਾਤਰਾ ਵਿਚ ਕਾਰਬੋਜ਼ ਲੈਣ ਨਾਲ ਕਿਹੜੇ-ਕਿਹੜੇ ਰੋਗ ਹੋ ਜਾਂਦੇ ਹਨ ?
ਉੱਤਰ-
- ਮੋਟਾਪਾ ਅਤੇ
- ਸ਼ੂਗਰ (ਡਾਈਬਟੀਜ਼) ।
ਪ੍ਰਸ਼ਨ 31.
ਸਰੀਰ ਵਿਚ ਲੋੜ ਨਾਲੋਂ ਘੱਟ ਮਾਤਰਾ ਵਿਚ ਕਾਰਬੋਹਾਈਡਰੇਟ ਦਾ ਕੀ ਪ੍ਰਭਾਵ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
- ਕਮਜ਼ੋਰੀ
- ਸਰੀਰ ਦੀ ਕਿਰਿਆਸ਼ੀਲਤਾ ਘੱਟ ਹੋਣਾ
- ਚਮੜੀ ਵਿਚ ਝੁਰੜੀਆਂ ਪੈਣਾ
- ਚਮੜੀ ਦਾ ਲਟਕ ਜਾਣਾ
- ਅੰਦਰੂਨੀ ਅਵਸਥਾ ਦੇ ਵਿਕਾਸ ਵਿਚ ਰੁਕਾਵਟ :
ਪ੍ਰਸ਼ਨ 32.
ਸਰੀਰ ਵਿਚ ਆਇਓਡੀਨ ਦੀ ਕਮੀ ਨਾਲ ਕਿਹੜਾ ਰੋਗ ਹੋ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਗੋਈਟਰ (Goitre) ।
ਪ੍ਰਸ਼ਨ 33.
ਰੇਆਨ ਦੇ ਕੱਪੜਿਆਂ ਤੇ ਤੇਜ਼ਾਬ ਅਤੇ ਖਾਰ ਦਾ ਕੀ ਪ੍ਰਭਾਵ ਪੈਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਤੇਜ਼ ਤੇਜ਼ਾਬ ਅਤੇ ਖਾਰ ਦੋਵੇਂ ਹੀ ਰੇਆਨ ਦੇ ਕੱਪੜਿਆਂ ਨੂੰ ਹਾਨੀ ਪਹੁੰਚਾਉਂਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 34.
ਰੇਆਨ ਕਿਸ ਪ੍ਰਕਾਰ ਦਾ ਰੇਸ਼ਾ ਹੈ ?
ਉੱਤਰ-
ਸੈਲੂਲੋਜ਼ ਤੋਂ ਉਤਪਾਦਤ ਬਣਾਉਟੀ ਰੇਸ਼ਾ ।

ਪ੍ਰਸ਼ਨ 35.
ਰੇਆਨ ਦੇ ਕੱਪੜਿਆਂ ਨੂੰ ਧੋਂਦੇ ਸਮੇਂ ਕਿਹੜੀਆਂ ਗੱਲਾਂ ਦੀ ਮਨਾਹੀ ਹੈ ?
ਉੱਤਰ-
ਕੱਪੜਿਆਂ ਨੂੰ ਪਾਣੀ ਵਿਚ ਫੁਲਾਉਣਾ,ਤਾਪ, ਸ਼ਕਤੀਸ਼ਾਲੀ ਰਸਾਇਣਾਂ ਅਤੇ ਅਲਕੋਹਲ ਦੀ ਵਰਤੋਂ ।
ਪ੍ਰਸ਼ਨ 36.
ਰੇਆਨ ਦੇ ਕੱਪੜਿਆਂ ਦੀ ਧੁਆਈ ਲਈ ਕਿਹੜੀ ਵਿਧੀ ਠੀਕ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਗੁੰਨ੍ਹਣ ਅਤੇ ਨਪੀੜਨ ਦੀ ਵਿਧੀ ।
ਪ੍ਰਸ਼ਨ 37.
ਰੇਆਨ ਦੇ ਕੱਪੜਿਆਂ ਨੂੰ ਕਿੱਥੇ ਸੁਕਾਉਣਾ ਚਾਹੀਦਾ ਹੈ ?
ਉੱਤਰ-
ਛਾਂ ਵਾਲੀ ਥਾਂ ਤੇ ਬਿਨਾਂ ਲਟਕਾਏ ਚੌਰਸ ਥਾਂ ‘ਤੇ ।
ਪ੍ਰਸ਼ਨ 38.
ਰੇਆਨ ਦੇ ਕੱਪੜਿਆਂ ‘ਤੇ ਪੁੱਜ ਕਿਸ ਤਰ੍ਹਾਂ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ ?
ਉੱਤਰ-
ਘੱਟ ਗਰਮ ਪ੍ਰੈੱਸ ਕੱਪੜੇ ਦੇ ਉਲਟ ਪਾਸੇ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ । ਪ੍ਰੈੱਸ ਕਰਦੇ ਸਮੇਂ ਕੱਪੜੇ ਵਿਚ ਹਲਕੀ ਜਿਹੀ ਨਮੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 39.
ਉੱਨ ਦਾ ਤੰਤੂ ਕਿਹੋ ਜਿਹਾ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਕਾਫ਼ੀ ਕੋਮਲ, ਮੁਲਾਇਮ ਅਤੇ ਪਾਣੀਜਨ ।

ਪ੍ਰਸ਼ਨ 40.
ਉੱਨ ਦਾ ਰੇਸ਼ਾ ਆਪਸ ਵਿਚ ਕਿਨ੍ਹਾਂ ਕਾਰਨਾਂ ਨਾਲ ਜੁੜ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਨਮੀ, ਖਾਰ, ਦਬਾਅ ਅਤੇ ਗਰਮੀ ਦੇ ਕਾਰਨ ।
ਪ੍ਰਸ਼ਨ 41.
ਉੱਨ ਦੇ ਤੰਤੂਆਂ ਦੀ ਸੜਾ ਕਿਹੋ ਜਿਹੀ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਖੁਰਦਰੀ ।
ਪ੍ਰਸ਼ਨ 42.
ਉੱਨ ਦੇ ਰੇਸ਼ਿਆਂ ਦੀ ਸਤਹਿ ਖੁਰਦਰੀ ਕਿਉਂ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਕਿਉਂਕਿ ਉੱਨ ਦੀ ਸਤਹਿ ਤੇ ਪਰਸਪਰ ਵਿਆਪੀ ਰੇਸ਼ੇ ਹੁੰਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 43,
ਉੱਨ ਦੇ ਰੇਸ਼ਿਆਂ ਦੀ ਸਤਹਿ ਦੇ ਰੇਸ਼ਿਆਂ ਦੀ ਪ੍ਰਕਿਰਤੀ ਕਿਹੋ ਜਿਹੀ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਲਸਲਸੀ, ਜਿਸ ਨਾਲ ਰੇਸ਼ੇ ਜਦੋਂ ਪਾਣੀ ਦੇ ਸੰਪਰਕ ਵਿਚ ਆਉਂਦੇ ਹਨ ਤਾਂ ਫੁੱਲ ਕੇ . ਨਰਮ ਹੋ ਜਾਂਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 44.
ਉੱਨ ਦੇ ਰੇਸ਼ਿਆਂ ਦੇ ਦੁਸ਼ਮਣ ਕੀ ਹਨ ?
ਉੱਤਰ-
ਨਮੀ, ਤਾਪ ਅਤੇ ਖਾਰ ।
ਪ੍ਰਸ਼ਨ 45.
ਤਾਪ ਦੇ ਅਨਿਸ਼ਚਿਤ ਪਰਿਵਰਤਨ ਨਾਲ ਰੇਸ਼ਿਆਂ ‘ ਤੇ ਕੀ ਪ੍ਰਭਾਵ ਪੈਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਰੇਸ਼ਿਆਂ ਵਿਚ ਜਮਾਓ ਤੇ ਸੁੰਗੜਨ ਹੋ ਜਾਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 46.
ਉੱਨ ਦੇ ਕੱਪੜਿਆਂ ਨੂੰ ਕਿਸ ਪ੍ਰਕਾਰ ਦੇ ਸਾਬਣ ਨਾਲ ਧੋਣਾ ਚਾਹੀਦਾ ਹੈ ?
ਉੱਤਰ-
ਨਰਮ ਪ੍ਰਕਿਰਤੀ ਦੇ ਸ਼ੁੱਧ ਖਾਰ ਰਹਿਤ ਸਾਬਣ ਨਾਲ ।
ਪ੍ਰਸ਼ਨ 47.
ਧੁਆਈ ਨਾਲ ਕਦੀ-ਕਦੀ ਉੱਨ ਕਿਉਂ ਜੁੜ ਜਾਂਦੀ ਹੈ ?
ਉੱਤਰ-
ਊਨੀ ਕੱਪੜੇ ਨੂੰ ਧੋਂਦੇ ਸਮੇਂ ਜਦੋਂ ਪਾਣੀ ਜਾਂ ਸਾਬਣ ਦੇ ਘੋਲ ਵਿਚ ਹਿਲਾਇਆਜੁਲਾਇਆ ਜਾਂਦਾ ਹੈ ਤਾਂ ਉੱਨ ਦੇ ਤੰਤੂਆਂ ਦੇ ਰੇਸ਼ੇ ਆਪਸ ਵਿਚ ਇਕ-ਦੂਜੇ ਦੇ ਉੱਪਰ ਚੜ੍ਹ ਜਾਂਦੇ ਹਨ ਜਿਸ ਦੇ ਸਿੱਟੇ ਵਜੋਂ ਉੱਨ ਜੁੜ ਜਾਂਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 48.
ਸਰੀਰ ਦੇ ਵਾਧੇ ਲਈ ਭੋਜਨ ਦਾ ਕਿਹੜਾ ਪੋਸ਼ਕ ਤੱਤ ਜ਼ਰੂਰੀ ਹੈ ?
ਉੱਤਰ-
ਪ੍ਰੋਟੀਨ ।
ਪ੍ਰਸ਼ਨ 49.
ਸਾਬਣ ਦਾ ਨਿੱਜੀ ਸਫ਼ਾਈ ਵਿਚ ਕੀ ਮਹੱਤਵ ਹੈ ?
ਉੱਤਰ-
ਸਾਬਣ ਚਿਕਨਾਈ ਨੂੰ ਆਪਣੇ ਵਿਚ ਘੋਲ ਲੈਂਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਮੈਲ ਜੋ ਚਿਕਨਾਈ ਨਾਲ ਚਿੰਬੜੀ ਹੁੰਦੀ ਹੈ, ਵੀ ਪਾਣੀ ਪਾਉਣ ਤੇ ਉਤਰ ਜਾਂਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 50.
ਵਿਟਾਮਿਨ ‘ਸੀ’ ਦੀ ਕਮੀ ਨਾਲ ਕਿਹੜਾ ਰੋਗ ਹੋ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਸਕਰਵੀ ।

ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ
ਪ੍ਰਸ਼ਨ 1.
ਪੋਸ਼ਣ ਤੱਤ ਜਾਂ ਪੋਸ਼ਕ ਤੱਤ (Nutrients) ਕੀ ਹੁੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਉਹ ਤੱਤ ਜੋ ਸਾਡੇ ਸਰੀਰ ਦੀ ਪਾਲਣਾ ਕਰਦੇ ਹਨ, ਪੋਸ਼ਕ ਤੱਤ ਕਹਾਉਂਦੇ ਹਨ । ਇਹ ਭੋਜਨ ਦੇ ਘਟਕ (Components) ਹੁੰਦੇ ਹਨ । ਇਹ ਸਰੀਰ ਦੇ ਵਾਧੇ, ਜਣਨ ਅਤੇ ਸਵਸਥ ਜੀਵਨ ਬਿਤਾਉਣ ਲਈ ਜ਼ਰੂਰੀ ਹੁੰਦੇ ਹਨ |ਇਹ ਹਨ
- ਪ੍ਰੋਟੀਨ (Proteins)
- ਚਰਬੀ (Fats)
- ਕਾਰਬੋਜ਼ (Carbohydrates)
- ਖਣਿਜ ਲੂਣ (Minerals)
- ਵਿਟਾਮਿਨਜ਼ (Vitamins)
- ਪਾਣੀ (water) ।
ਪ੍ਰਸ਼ਨ 2.
ਪ੍ਰੋਟੀਨ ਕੀ ਹੈ ? ਭੋਜਨ ਵਿਚ ਇਸ ਦੀ ਕਮੀ ਨਾਲ ਕੀ ਹਾਨੀਆਂ ਹੁੰਦੀਆਂ ਹਨ ?
ਉੱਤਰ-
ਪ੍ਰੋਟੀਨ ਭੋਜਨ ਦੇ ਲੋੜੀਂਦੇ ਤੱਤਾਂ ਵਿਚੋਂ ਇਕ ਤੱਤ ਹੈ ।
ਜੀਵ ਦ੍ਰਵ ਦਾ ਨਿਰਮਾਣ ਕਰਨ ਵਾਲਾ ਮੁੱਖ ਪਦਾਰਥ ਪ੍ਰੋਟੀਨ ਹੈ | ਪਾਣੀ ਤੋਂ ਇਲਾਵਾ ਸਰੀਰ ਵਿਚ ਸਭ ਤੋਂ ਵੱਧ ਅੰਸ਼ ਪ੍ਰੋਟੀਨ ਦਾ ਹੈ । ਪ੍ਰੋਟੀਨ ਦੇ ਤੰਤੁ ਖ਼ੂਨ, ਐਨਜ਼ਾਈਮ, ਅੰਦਰੁਨੀ ਰੰਥੀਆਂ ਵਿਚੋਂ ਨਿਕਲਣ ਵਾਲੇ ਹਾਰਮੋਨ, ਕੋਮਲ ਤੰਤੂ ਅਤੇ ਹੱਡੀਆਂ ਵਿਚ ਹੁੰਦਾ ਹੈ ।
ਪ੍ਰੋਟੀਨ, ਕਾਰਬਨ, ਹਾਈਡਰੋਜਨ, ਆਕਸੀਜਨ, ਨਾਈਟਰੋਜਨ ਦੇ ਸੰਯੋਗ ਨਾਲ ਬਣਿਆ ਅਜਿਹਾ ਯੌਗਿਕ ਜੋ ਵੱਖ-ਵੱਖ ਪ੍ਰਕਾਰ ਦੇ ਅਮੀਨੋ ਅਮਲਾਂ ਦੇ ਸੰਯੋਜਨ ਤੋਂ ਬਣਦਾ ਹੈ ।
ਕਮੀ ਅਤੇ ਹਾਨੀਆਂ-
- ਬੱਚਿਆਂ ਦੇ ਭੋਜਨ ਵਿਚ ਪ੍ਰੋਟੀਨ ਦੀ ਕਮੀ ਹੋ ਜਾਣ ਨਾਲ ਉਸ ਦਾ ਵਿਕਾਸ ਰੁਕ ਜਾਂਦਾ ਹੈ ।
- ਸੋਕਾ ਅਤੇ ਕਵਾਸ਼ਿਓਰਕਰ ਰੋਗ ਹੋ ਜਾਂਦਾ ਹੈ ।
- ਬਾਲਗਾਂ ਵਿਚ ਇਸ ਦੀ ਕਮੀ ਨਾਲ ਭਾਰ ਘੱਟ ਹੋਣ ਦੇ ਨਾਲ ਅਨੀਮੀਆ ਰੋਗ ਵੀ ਹੋ ਜਾਂਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 3.
ਵੱਖ-ਵੱਖ ਪੌਸ਼ਟਿਕ ਤੱਤਾਂ (Nutrients) ਦੇ ਵਿਸ਼ੇਸ਼ ਕੰਮ ਦੱਸੋ ।
ਉੱਤਰ-
ਵੱਖ-ਵੱਖ ਪੌਸ਼ਟਿਕ ਤੱਤਾਂ ਦੇ ਵਿਸ਼ੇਸ਼ ਕੰਮ ਹੇਠ ਲਿਖੇ ਹਨ-
- ਕਾਰਬੋਜ਼ – ਇਨ੍ਹਾਂ ਦਾ ਮੁੱਖ ਕੰਮ ਊਰਜਾ ਪ੍ਰਦਾਨ ਕਰਨਾ ਹੈ । ਜਿਹੜੇ ਕਾਰਬੋਜ਼ਾਂ ਦਾ ਸਰੀਰ ਵਿਚ ਉਸੇ ਸਮੇਂ ਉਪਭੋਗ ਨਹੀਂ ਹੁੰਦਾ ਉਹ ਇਕੱਠੇ ਕਰ ਲਏ ਜਾਂਦੇ ਹਨ । ਇਹ ਚਿਕਨਾਈ ਵਿਚ ਬਦਲ ਕੇ ਇਕੱਠੇ ਹੁੰਦੇ ਹਨ । ਇਹ ਪਦਾਰਥ ਜਦੋਂ ਲੋੜ ਹੁੰਦੀ ਹੈ ਊਰਜਾ ਦਿੰਦੇ ਹਨ ।
- ਪੋਟੀਨ – ਪੋਟੀਨ ਦਾ ਮੁੱਖ ਕੰਮ ਨਵੇਂ ਟਿਸ਼ੂਆਂ ਦਾ ਨਿਰਮਾਣ ਅਤੇ ਪਹਿਲਾਂ ਬਣੀਆਂ ਕੋਸ਼ਿਕਾਵਾਂ ਦੀ ਮੁਰੰਮਤ ਕਰਨਾ ਹੁੰਦਾ ਹੈ । ਪ੍ਰੋਟੀਨ ਸੁਰੱਖਿਆ ਪ੍ਰਦਾਨ ਕਰਨ ਵਾਲੇ ਅਤੇ ਨਿਆਮਕ (Regulator) ਵੀ ਹੁੰਦੇ ਹਨ । ਲੋੜ ਨਾਲੋਂ ਵੱਧ ਮਾਤਰਾ ਵਿਚ ਹਿਣ ਕੀਤੇ ਗਏ ਪ੍ਰੋਟੀਨ, ਕਾਰਬੋਜ਼ ਅਤੇ ਚਿਕਨਾਈ ਵਿਚ ਬਦਲ ਕੇ ਸਰੀਰ ਵਿਚ ਇਕੱਠੇ ਹੋ ਜਾਂਦੇ ਹਨ ।
- ਚਿਕਨਾਈ – ਚਿਕਨਾਈ ਦਾ ਮੁੱਖ ਕੰਮ ਸਰੀਰ ਨੂੰ ਊਰਜਾ ਪ੍ਰਦਾਨ ਕਰਨਾ ਹੈ । ਇਹ ਚਿਕਨਾਈ ਘੁਲੇ ਵਿਟਾਮਿਨਾਂ ਅਤੇ ਲੋੜੀਂਦੇ ਚਿਕਨਾਈ ਅਮਲਾਂ ਦੇ ਵਾਹਕ ਵੀ ਹੁੰਦੇ ਹਨ । ਲੋੜ ਤੋਂ ਵੱਧ ਹਿਣ ਕੀਤੀ ਗਈ ਚਿਕਨਾਈ ਸਰੀਰ ਵਿਚ ਚਰਬੀ ਦੇ ਰੂਪ ਵਿਚ ਜਮਾਂ ਹੋ ਜਾਂਦੀ ਹੈ ।
- ਖਣਿਜ – ਇਨ੍ਹਾਂ ਦਾ ਕੰਮ ਸਰੀਰ ਨਿਰਮਾਣ (ਹੱਡੀ, ਦੰਦ ਅਤੇ ਕੋਮਲ ਕੋਸ਼ਿਕਾਵਾਂ ਦੇ ਰਚਨਾਤਮਕ ਭਾਗ) ਅਤੇ ਕੰਟਰੋਲ ਪੇਸ਼ੀ ਸੰਕੁਚਨ) ਹੁੰਦਾ ਹੈ ।
- ਵਿਟਾਮਿਨ – ਇਨ੍ਹਾਂ ਦਾ ਕੰਮ ਸਰੀਰ ਦੇ ਵਾਧੇ ਅਤੇ ਵੱਖ-ਵੱਖ ਕਿਰਿਆਵਾਂ ਦੇ ਕੰਮ ਕੰਟਰੋਲ ਦਾ ਹੁੰਦਾ ਹੈ ।
- ਪਾਣੀ – ਸਰੀਰ ਦਾ ਲੋੜੀਂਦਾ ਭਾਗ ਪਾਣੀ ਹੁੰਦਾ ਹੈ | ਪਾਣੀ ਪੋਸ਼ਕ ਤੱਤਾਂ ਦੇ ਸੰਵਹਿਣ ਅਤੇ ਸਰੀਰਕ ਕਿਰਿਆਵਾਂ ਦੇ ਕੰਟਰੋਲ ਦਾ ਕੰਮ ਕਰਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 4.
ਭੋਜਨ ਦਾ ਸਾਡੇ ਸਰੀਰ ਲਈ ਮੁੱਖ ਕੰਮ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਭੋਜਨ ਸਾਡੇ ਸਰੀਰ ਨੂੰ ਗਰਮੀ ਅਤੇ ਸ਼ਕਤੀ ਦਿੰਦਾ ਹੈ । ਨਵੇਂ ਸੈੱਲ ਬਣਾਉਂਦਾ ਹੈ ਅਤੇ ਪੁਰਾਣਿਆਂ ਦੀ ਮੁਰੰਮਤ ਕਰਦਾ ਹੈ ਅਤੇ ਸਾਡੇ ਸਰੀਰ ਵਿਚ ਅਜਿਹੇ ਹਾਰਮੋਨ ਅਤੇ ਐਨਜ਼ਾਈਮ ਬਣਾਉਂਦਾ ਹੈ ਜਿਸ ਨਾਲ ਸਾਡਾ ਸਰੀਰ ਠੀਕ ਅਵਸਥਾ ਵਿਚ ਰਹਿੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 5.
ਭੀਮ ਅਤੇ ਤੇਲ ਦਾ ਨਿੱਜੀ ਸਫ਼ਾਈ ਵਿਚ ਕੀ ਮਹੱਤਵ ਹੈ ?
ਉੱਤਰ-
ਸਿਰ ਅਤੇ ਸਰੀਰ ਤੇ ਤੇਲ ਲਗਾਉਣ ਨਾਲ ਚਮੜੀ ਦੀ ਖ਼ੁਸ਼ਕੀ ਦੂਰ ਹੋ ਜਾਂਦੀ ਹੈ ਤੇ ਇਕ ਚਮਕ ਆ ਜਾਂਦੀ ਹੈ ਅਤੇ ਕੀਮ ਨਾਲ ਚਿਹਰਾ ਚਮਕਦਾਰ ਅਤੇ ਨਿਖਰ ਜਾਂਦਾ ਹੈ । ਕਈ ਗ਼ਮਾਂ ਨਾਲ ਚਿਹਰੇ ਤੇ ਕਿੱਲ ਅਤੇ ਛਾਈਆਂ ਵੀ ਦੂਰ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ।
ਪ੍ਰਸ਼ਨ 6.
ਕੱਪੜੇ ਦੇ ਰੇਸ਼ੇ ਮੁੱਖ ਰੂਪ ਵਿਚ ਕਿੰਨੀ ਤਰ੍ਹਾਂ ਦੇ ਹੁੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਕੱਪੜੇ ਦੇ ਰੇਸ਼ੇ ਮੁੱਖ ਰੂਪ ਵਿਚ ਪੰਜ ਤਰ੍ਹਾਂ ਦੇ ਹੁੰਦੇ ਹਨ-ਸੂਤੀ, ਲਿਨਨ, ਰੇਸ਼ਮ, ਉੱਨ, ਟੈਰਾਲੀਨ ।
ਪ੍ਰਸ਼ਨ 7.
ਕੋਲਡ ਕਰੀਮ ਬਾਰੇ ਤੁਸੀਂ ਕੀ ਜਾਣਦੇ ਹੋ ?
ਉੱਤਰ-
ਕੋਲਡ ਕਰੀਮ ਦੀ ਵਰਤੋਂ ਸਰਦੀਆਂ ਦੇ ਮੌਸਮ ਵਿੱਚ ਹੁੰਦੀ ਹੈ ਅਤੇ ਇਸ ਵਿਚ ਚਿਕਨਾਈ ਹੁੰਦੀ ਹੈ, ਤਾਂ ਜੋ ਖੁਸ਼ਕੀ ਦੂਰ ਹੋ ਸਕੇ ।
ਪ੍ਰਸ਼ਨ 8.
ਭਾਰਤੀ ਖ਼ੁਰਾਕ ਦੀ ਆਮ ਘਾਟ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਭਾਰਤੀ ਖ਼ੁਰਾਕ ਦੀਆਂ ਆਮ ਘਾਟਾਂ ਹੇਠ ਲਿਖੀਆਂ ਹਨ-
- ਭੋਜਨ ਵਿਚ ਕੈਲੋਰੀ ਦੀ ਮਾਤਰਾ ਘੱਟ ਹੋਣਾ ।
- ਭੋਜਨ ਵਿਚ ਪ੍ਰੋਟੀਨ ਦੀ ਕਮੀ ।
- ਪ੍ਰਾਣੀਜਨ ਪ੍ਰੋਟੀਨ ਦਾ ਬਹੁਤ ਘੱਟ ਜਾਂ ਬਿਲਕੁਲ ਨਾ ਹੋਣਾ ।
- ਚਿਕਨਾਈ ਦਾ ਬਹੁਤ ਘੱਟ ਹੋਣਾ ਅਤੇ ਪਾਣੀਜਨ ਚਿਕਨਾਈ ਨਾ ਹੋਣਾ ।
- ਇਕ ਜਾਂ ਜ਼ਿਆਦਾ ਵਿਟਾਮਿਨ ਦੀ ਕਮੀ ਹੋਣਾ ।
- ਇਕ ਜਾਂ ਜ਼ਿਆਦਾ ਖਣਿਜ ਲੂਣਾਂ ਦੀ ਕਮੀ, ਖਾਸ ਕਰਕੇ ਚੂਨਾ ਅਤੇ ਲੋਹੇ ਦੀ ਕਮੀ ।
ਪ੍ਰਸ਼ਨ 9.
ਜੇ ਭੋਜਨ ਜ਼ਰੂਰਤ ਨਾਲੋਂ ਘੱਟ ਖਾਇਆ ਜਾਵੇ ਤਾਂ ਕੀ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਕਈ ਵਾਰ ਅਜਿਹੇ ਹਾਲਾਤ ਬਣ ਜਾਂਦੇ ਹਨ ਜਦੋਂ ਭੋਜਨ ਦੀ ਉਪਲੱਬਧਤਾ ਪੁਰੀ ਤਰ੍ਹਾਂ ਨਹੀਂ ਹੁੰਦੀ ਤੇ ਅਸੀਂ ਘੱਟ ਖਾ ਕੇ ਹੀ ਗੁਜ਼ਾਰਾ ਕਰਦੇ ਹਾਂ-ਜਿਵੇਂ ਹੜ੍ਹ ਆਉਣ, ਅਕਾਲ ਪੈ ਜਾਣ, ਲੜਾਈ ਹੋਣ ਦੀ ਸਥਿਤੀ । ਭੋਜਨ ਪੂਰੀ ਮਾਤਰਾ ਵਿਚ ਨਾ ਖਾਇਆ ਜਾਵੇ ਤਾਂ ਭਾਰ ਘੱਟ ਜਾਂਦਾ ਹੈ, ਕਮਜ਼ੋਰੀ ਹੋ ਜਾਂਦੀ ਹੈ ਅਤੇ ਖੂਨ ਦੀ ਕਮੀ ਹੋ ਜਾਂਦੀ ਹੈ । ਰੋਗਾਂ ਨਾਲ ਲੜਨ ਦੀ ਸ਼ਕਤੀ ਵੀ ਘੱਟ ਹੋ ਜਾਂਦੀ ਹੈ । ਬੱਚੇ ਜੇਕਰ ਲੋੜੀਂਦੀ ਮਾਤਰਾ ਵਿਚ ਖਾਣਾ ਨਾ ਖਾਣ ਤਾਂ ਬੁੱਧੂ ਜਿਹੇ ਹੋ ਜਾਂਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 10.
ਜ਼ਰੂਰਤ ਤੋਂ ਵੱਧ ਖਾਣਾ ਖਾਧਾ ਜਾਵੇ ਤਾਂ ਕੀ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਅਜਿਹੀ ਸਥਿਤੀ ਵਿਚ ਮਿਹਦੇ ਅਤੇ ਅੰਤੜੀਆਂ ਨੂੰ ਵਧੇਰੇ ਕੰਮ ਕਰਨਾ ਪੈਂਦਾ ਹੈ, ਗਰਦਿਆਂ ਤੇ ਵੀ ਵੱਧ ਬੋਝ ਪੈਂਦਾ ਹੈ । ਪੇਟ ਵਿਚ ਗੈਸ ਪੈਦਾ ਹੁੰਦੀ ਹੈ । ਮੁੰਹ ਵਿਚੋਂ ਬਦਬੂ ਆਉਣ ਲਗਦੀ ਹੈ ਅਤੇ ਸਿਰ ਦੁੱਖਣ ਲਗਦਾ ਹੈ | ਪੇਟ ਦੀਆਂ ਬੀਮਾਰੀਆਂ ਹੋ ਸਕਦੀਆਂ ਹਨ, ਖੂਨ ਦਾ ਦਬਾਉ ਵੱਧ ਸਕਦਾ ਹੈ ਤੇ ਕਈ ਹੋਰ ਰੋਗ ਹੋ ਸਕਦੇ ਹਨ ।

ਵੱਡੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ
ਪ੍ਰਸ਼ਨ 1.
ਕਾਰਬੋਜ਼ ਦੇ ਵੱਖ-ਵੱਖ ਸੋਮੇ ਤੇ ਕੰਮ ਦੱਸੋ ।
ਉੱਤਰ-
ਸਰੀਰ ਨੂੰ ਸ਼ਕਤੀ ਦੇਣ ਦਾ ਮੁੱਖ ਸਾਧਨ ਕਾਰਬੋਹਾਈਡਰੇਟ ਹੈ ।
ਸੋਮੇ ਜਾਂ ਸਾਧਨ – ਸਭ ਤੋਂ ਵੱਧ ਕਾਰਬੋਜ਼ ਅਨਾਜਾਂ ਤੋਂ ਮਿਲਦਾ ਹੈ, ਇਸ ਤੋਂ ਬਾਅਦ ਜੜ੍ਹ ਤੇ ਤਣੇ ਵਾਲੀਆਂ ਸਬਜ਼ੀਆਂ ਵਿਚੋਂ । ਕੁੱਝ ਮਾਤਰਾ ਵਿਚ ਦਾਲਾਂ ਤੇ ਫਲਾਂ ਵਿਚ ਵੀ ਮਿਲਦਾ ਹੈ ।
- ਸ਼ੁੱਧ ਕਾਰਬੋਹਾਈਡਰੇਟ ਭੋਜਨ ਪਦਾਰਥ-ਖੰਡ, ਗੁੜ, ਸ਼ਹਿਦ, ਸਾਬੂਦਾਨਾ ਅਤੇ ਅਖਰੋਟ ।
- ਅਨਾਜ-ਕਣਕ, ਚੌਲ, ਜਵਾਰ, ਬਾਜਰਾ, ਰੌਗੀ, ਜੌ, ਮੱਕੀ ।
- ਦਾਲਾਂ-ਮਾਂਹ, ਮੂੰਗੀ, ਅਰਹਰ, ਛੋਲਿਆਂ ਦੀ ਦਾਲ, ਮਸਰ, ਕੁਲਥ ਆਦਿ ।
- ਜੜ੍ਹ ਅਤੇ ਭੂਮੀ ਕੰਦ-ਆਲੂ, ਸ਼ਕਰਕੰਦੀ, ਚੁਕੰਦਰ ਆਦਿ ।
- ਤਾਜ਼ੇ ਤੇ ਸੁੱਕੇ ਫਲ-ਅੰਜ਼ੀਰ, ਖਜੂਰ, ਅੰਗੂਰ, ਕਿਸ਼ਮਿਸ਼, ਮੁਨੱਕਾ, ਖੁਰਮਾਨੀ ਆਦਿ ।
ਉਪਯੋਗ-
- (1) ਕਾਰਬੋਜ਼ ਸਰੀਰ ਨੂੰ ਸ਼ਕਤੀ ਦਿੰਦੇ ਹਨ । ਇਕ ਗ੍ਰਾਮ ਕਾਰਬੋਜ਼ ਦੇ ਬਲਣ ਨਾਲ ਸਾਨੂੰ ਚਾਰ ਕੈਲੋਰੀ ਸ਼ਕਤੀ ਮਿਲਦੀ ਹੈ ।
- ਇਹ ਪ੍ਰੋਟੀਨ ਦੁਆਰਾ ਪੈਦਾ ਹੋਈ ਵਾਧੂ ਉਰਜਾ ਨੂੰ ਨਸ਼ਟ ਹੋਣ ਤੋਂ ਬਚਾਉਂਦਾ ਹੈ ।
- ਇਹ ਵਿਟਾਮਿਨ ‘K’ ਅਤੇ ਨਿਆਸਿਨ ਦੇ ਨਿਰਮਾਣ ਵਿਚ ਸਰੀਰ ਵਿਚ ਪਾਏ ਜਾਣ ਵਾਲੇ ਜੀਵਾਣੂਆਂ ਦੀ ਸਹਾਇਤਾ ਕਰਦਾ ਹੈ ।
- ਕਾਰਬੋਜ਼ ਸਰੀਰ ਦੇ ਤਾਪ ਨੂੰ ਇਕੋ ਜਿਹਾ ਰੱਖਦੇ ਹਨ ।
- ਕਾਰਬੋਜ਼ ਨਲਿਕਾਹੀਨ ਗੰਥੀਆਂ ਦੇ ਰਸ ਕੱਢਣ ਵਿਚ ਸਹਾਇਕ ਹੈ ।
ਪ੍ਰਸ਼ਨ 2.
ਚਿਕਨਾਈ ਦੇ ਸੋਮੇ ਅਤੇ ਕੰਮ ਲਿਖੋ ।
ਉੱਤਰ-
ਸੋਮੇ-
- ਤੇਲ ਅਤੇ ਘਿਓ-ਮੂੰਗਫ਼ਲੀ, ਸਰੋਂ ਦਾ ਤੇਲ, ਨਾਰੀਅਲ ਦਾ ਤੇਲ, ਦੇਸੀ ਓ, ਬਨਸਪਤੀ ਘਿਓ ਅਤੇ ਮੱਖਣ ।
- ਮੇਵਾ ਤੇ ਬੀਜ-ਬਦਾਮ, ਕਾਜੂ, ਨਾਰੀਅਲ, ਮੂੰਗਫ਼ਲੀ, ਪਿਸਤਾ, ਅਖ਼ਰੋਟ, ਸੋਇਆਬੀਨ ਆਦਿ ।
- ਦੁੱਧ ਤੇ ਦੁੱਧ ਤੋਂ ਬਣੇ ਪਦਾਰਥ-ਗਾਂ-ਮੱਝ ਦਾ ਦੁੱਧ, ਖੋਇਆ, ਸੁੱਕਾ ਦੁੱਧ ਆਦਿ । ਮਾਸਾਹਾਰੀ ਭੋਜਨ-ਆਂਡਾ, ਮੀਟ, ਮੱਛੀ, ਲੀਵਰ ਆਦਿ ।
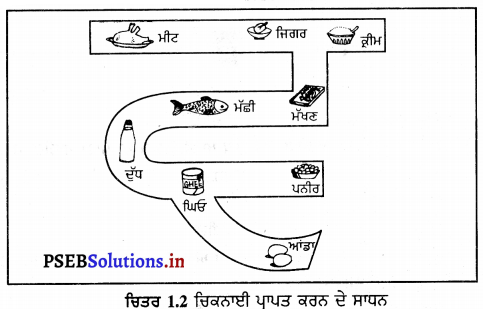
ਕੰਮ-
- ਚਿਕਨਾਈ ਦਾ ਮੁੱਖ ਕੰਮ ਸਾਡੇ ਸਰੀਰ ਨੂੰ ਊਰਜਾ ਅਤੇ ਸ਼ਕਤੀ ਪ੍ਰਦਾਨ ਕਰਨਾ ਹੈ । ਚਿਕਨਾਈ ਊਰਜਾ ਦੇ ਸਭ ਤੋਂ ਵੱਧ ਸਾਂਦਰਿਤ ਸੋਮੇ ਹਨ । ਇਕ ਗਾਮ ਚਿਕਨਾਈ ਤੋਂ ਸਾਨੂੰ 9 ਕੈਲੋਰੀ ਊਰਜਾ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ ।
- ਚਿਕਨਾਈ ਵਿਚ ਸਰੀਰ ਲਈ ਲੋੜੀਂਦੀ ਊਰਜਾ ਇਕੱਠੀ ਕਰਨ ਦਾ ਗੁਣ ਹੁੰਦਾ ਹੈ ।
- ਚਿਕਨਾਈਆਂ ਚਿਕਨਾਈ ਅਮਲਾਂ ਦਾ ਸੋਮਾ ਹੁੰਦੀਆਂ ਹਨ ਇਹ ਬਾਲ ਅਵਸਥਾ ਵਿਚ ਵਾਧੇ ਲਈ ਬਹੁਤ ਜ਼ਰੂਰੀ ਹੁੰਦੀਆਂ ਹਨ ਅਤੇ ਚਮੜੀ ਨੂੰ ਸਵਸਥ ਬਣਾਈ ਰੱਖਦੀਆਂ ਹਨ ।
- ਚਿਕਨਾਈਆਂ ਚਿਕਨਾਈ ਵਾਲੇ ਵਿਟਾਮਿਨਾਂ (A, D, E, K) ਨੂੰ ਸਰੀਰ ਵਿਚ ਪਹੁੰਚਾਉਂਦੀਆਂ ਹਨ ਅਤੇ ਇਨ੍ਹਾਂ ਵਿਟਾਮਿਨਾਂ ਦੇ ਅਵਸ਼ੋਸ਼ਣ ਵਿਚ ਸਹਾਇਤਾ ਕਰਦੀਆਂ ਹਨ ।
- ਚਿਕਨਾਈਆਂ ਸਰੀਰ ਦੇ ਅੰਗਾਂ ਦੇ ਚਾਰੇ ਪਾਸੇ ਗੱਦੀ ਦਾ ਕੰਮ ਕਰਦੀਆਂ ਹਨ । ਉਨ੍ਹਾਂ ਨੂੰ ਠੀਕ ਸਥਾਨ ਤੇ ਸਿੱਧੇ ਰੱਖਦੀਆਂ ਹਨ । ਉਨ੍ਹਾਂ ਨੂੰ ਸੱਟਾਂ ਤੋਂ ਬਚਾਉਂਦੀਆਂ ਹਨ ਅਤੇ ਨਾੜੀਆਂ ਦੀ ਰੱਖਿਆ ਵੀ ਕਰਦੀਆਂ ਹਨ ।
- ਚਿਕਨਾਈ ਤਾਪ ਦੀ ਅਲਪ ਚਾਲਕ ਹੋਣ ਕਾਰਨ ਸਰੀਰ ਨੂੰ ਊਰਜਾ ਦੀ ਹਾਨੀ ਤੋਂ ਰੋਕਦੀ ਹੈ ।
- ਚਿਕਨਾਈ ਦੀ ਮੌਜੂਦਗੀ ਨਾਲ ਭੋਜਨ ਦੇ ਸੁਆਦ ਅਤੇ ਪਰਿਪਤੀ ਵਿਚ ਵਾਧਾ ਹੁੰਦਾ ਹੈ ।
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()