Punjab State Board PSEB 8th Class Science Book Solutions Chapter 7 पौधे एवं जंतुओं का संरक्षण Textbook Exercise Questions and Answers.
PSEB Solutions for Class 8 Science Chapter 7 पौधे एवं जंतुओं का संरक्षण
PSEB 8th Class Science Guide पौधे एवं जंतुओं का संरक्षण Textbook Questions and Answers
अभ्यास
प्रश्न 1.
रिक्त स्थानों की उचित शब्दों द्वारा पूर्ति कीजिए-
(क) वह क्षेत्र जिसमें जंतु अपने प्राकृतिक आवास में संरक्षित होते हैं, …………… कहलाता है।
(ख) किसी क्षेत्र विशेष में पाई जाने वाली स्पीशीज़ ………………………. कहलाती है।
(ग) प्रवासी पक्षी सुदूर क्षेत्रों से ……………………….. परिवर्तन के कारण पलायन करते हैं।
उत्तर-
(क) चिड़ियाघर
(ख) विशेष क्षेत्री स्पीशीज
(ग) जलवायु
प्रश्न 2.
निम्नलिखित में अंतर स्पष्ट कीजिए-
(क) वन्य प्राणी उद्यान एवं जैवमंडलीय आरक्षित क्षेत्र
(ख) चिड़ियाघर एवं अभ्यारण्य
(ग) संकटापन्न एवं विलुप्त स्पीशीज़
(घ) वनस्पतिजात एवं प्राणिजात।
उत्तर-
(क) वन्यप्राणी उद्यान और जैवमंडलीय आरक्षित क्षेत्र में अंतर-
वन्य प्राणी उद्यान – एक ऐसा स्थान जहाँ जंगली जानवरों की सुरक्षा और संरक्षण किया जाता है।
जैवमंडलीय आरक्षित क्षेत्र – वन्य जीवन, पौधों और जंतु संसाधनों और उस क्षेत्र के आदिवासियों के पारंपरिक ढंग से जीवनयापन हेतु विशाल संरक्षित क्षेत्र।
(ख) चिड़ियाघर एवं अभ्यारण्य में अंतर-
चिड़ियाघर – ऐसा स्थान जहाँ जानवर अपने प्राकृतिक आवास में सुरक्षित रहते हैं।
अभ्यारण्य – वह क्षेत्र जहाँ जंतु और उनके आवास को संरक्षित रखा जाता है।
(ग) संकटापन्न एवं विलुप्त स्पीशीज़ में अंतर-
संकटापन्न स्पीशीज़ – वे जंतु जिनकी संख्या एक निर्धारित स्तर से कम होती जा रही है और वे विलुप्त हो सकते हैं।
विलुप्त स्पीशीज़ – वे जंतु जो पृथ्वी से विलुप्त हो चुके हैं।
(घ) वनस्पतिजात और प्राणिजात में अंतर-
वनस्पतिजात – किसी विशेष क्षेत्र में पाए जाने वाले पेड़-पौधों का समूह ।
प्राणिजात – किसी विशेष क्षेत्र में पाए जाने वाले जीव-जंतुओं का समूह ।

प्रश्न 3.
वनोन्मूलन का निम्न पर क्या प्रभाव पड़ता है, चर्चा कीजिए-
(क) वन्य प्राणी
(ख) पर्यावरण
(ग) गाँव ( ग्रामीण क्षेत्र)
(घ) शहर (शहरी क्षेत्र)
(ङ) पृथ्वी (च) अगली पीढ़ी।
उत्तर-
(क) वन्य प्राणियों पर वनोन्मूलन का प्रभाव-पेड़ – पौधे जंगली जानवरों को आवास और भोजन प्रदान करते हैं। वनोन्मूलन से प्राकृतिक आवास नष्ट हो जाते हैं और जानवर संकटापन्न स्पीशीज़ बन जाते हैं।
(ख) पर्यावरण पर वनोन्मूलन का प्रभाव – वनोन्मूलन से वातावरण में ऑक्सीजन की कमी आ जाती है। वर्षा और भूमि की उर्वरता में भी कमी आती है। इस कारण प्राकृतिक आपदाओं (बाढ़ और सूखा) की संभावनाएं बढ़ जाती हैं।
(ग ) गाँव ( ग्रामीण क्षेत्र) पर वनोन्मूलन का प्रभाव – अधिकतर कृषि गाँवों में होती है। जब वनोन्मूलन होता है तो भूमि की गुणवत्ता में परिवर्तन आता है।
(घ) शहर (शहरी क्षेत्र ) पर वनोन्मूलन का प्रभाव – शहरों में उद्योग और वाहन बहुत मात्रा में चलते हैं। यदि वनोन्मूलन होगा तो पर्यावरण दूषित हो जाएगा और शहरों में जिंदगी स्वस्थ नहीं रहेगी।
(ङ) पृथ्वी पर वनोन्मूलन का प्रभाव – वनोन्मूलन से प्राकृतिक आपदाओं की संभावना बढ़ती है। वनोन्मूलन से विश्व ऊष्मण में वृद्धि होती है। कम पेड़ों का अर्थ है, मृदा अपरदन।
(च) अगली पीढ़ी पर वनोन्मूलन का प्रभाव – वनोन्मूलन से पर्यावरण में परिवर्तन आते हैं जिससे अगली पीढ़ी पर बहुत प्रभाव पड़ता है। पर्यावरण प्रदूषित हो जाता है। इसलिए अगली पीढ़ी के लिए वन्य संपदा नहीं बचेगी।
प्रश्न 4.
क्या होगा यदि-
(क) हम वृक्षों की कटाई करते रहे ?
(ख) किसी जंतु का आवास बाधित हो ?
(ग) मिट्टी की ऊपरी परत अनावरित हो जाए ?
उत्तर-
(क) यदि वृक्षों की कटाई ऐसे ही होती रही तो वर्षा और भूमि की उर्वरकता में कमी आ जाएगी और प्राकृतिक आपदाओं (बाढ़ और सूखा) की संभावनाएँ बढ़ जाएँगी।
(ख) किसी जंतु के आवास के नष्ट होने से बढ़ती हुई जनसंख्या को जल और भोजन की उचित प्राप्ति नहीं होगी और वह स्पीशीज़, संकटापन्न जाति में आ सकती है।
(ग) मृदा की ऊपरी परत हटाने से मृदा में ह्यूमस की कमी होती है और उर्वरकता में कमी आ जाती है। धीरेधीरे उर्वर-भूमि मरुस्थल में परिवर्तित हो जाती है। इसे मरुस्थलीकरण कहते हैं।
प्रश्न 5.
संक्षेप में उत्तर दीजिए-
(क) हमें जैव विविधता का संरक्षण क्यों करना चाहिए ?
(ख) संरक्षित वन भी वन्य जंतुओं के लिए पूर्ण रूप से सुरक्षित नहीं है, क्यों ?
(ग) कुछ आदिवासी वन (जंगल) पर निर्भर करते हैं। कैसे ?
(घ) वनोन्मूलन के कारक और उनके प्रभाव क्या हैं ?
(ङ) रेड डाटा पुस्तक क्या है ?
(च) प्रवास से आप क्या समझते हैं ?
उत्तर-
(क) जैव विविधता का अर्थ है किसी क्षेत्र विशेष में पाए जाने वाले सभी पौधों, जंतुओं और सूक्ष्मजीवों को विभिन्न प्रजातियाँ। जंतु जो पौधों पर आश्रित हैं वे भी अपनी आदतों पर निर्भर करते हैं जैसे कि वाल पांडा बैंबू डंडी खाना पसंद करता है और ऑस्ट्रेलिया का कुळाला भालू सफेदे के पत्ते ही खाना पसंद करता है। पक्षी और बारहसिंघा की भी विशेष खाने की आदतें होती हैं। वन में विभिन्न पौधे प्रत्येक की आवश्यकता पूरी करने में समर्थ होते हैं। इससे शाकाहारी को भोजन मिलता है, भोजन श्रृंखला मज़बूत होती है। इसलिए जंतुओं के संरक्षण के लिए विविध पेड़-पौधों का संरक्षण भी अति आवश्यक है।
(ख) संरक्षित वन भी जीवों के लिए संरक्षित नहीं रहे क्योंकि इनके आस-पास के क्षेत्रों में रहने वाले लोग वनों का अतिक्रमण करके उन्हें नष्ट कर देते हैं।
(ग) कुछ आदिवासी जातियाँ वनों पर निर्भर होती हैं। सतपुड़ा राष्ट्रीय उद्यान की चट्टानों में आवास के प्रागैतिहासिक प्रमाण मिले हैं जिनसे आदिमानव के जीवनयापन के बारे में पता चलता है।
चट्टानों पर कुछ कलाकृतियाँ जैसे लड़ते हुए मनुष्य और जानवर का शिकार, नृत्य एवं वाद्ययंत्रों को बजाते हुए दर्शाया गया है। बाघ और लोगों के समूहों की कलाकृतियाँ भी इन चट्टानों पर पाई गई हैं। कई आदिवासी आज भी जंगलों में रहते हैं।
(घ) वनोन्मूलन के कारण – लोगों के बदलते जीवन स्तर और तकनीकी वृद्धि से वनों के उपयोग में अत्यधिक वृद्धि हुई है। अपने आराम और सुविधाओं के लिए वृक्षों की कटाई के निम्न उद्देश्य हैं-
- जनसंख्या वृद्धि के कारण घर बनाने की लकड़ी के लिए।
- कृषि भूमि के लिए।
- सड़कें और बाँधों के निर्माण के लिए।
- पशुओं के अतिचरण के लिए।
- खानों में वृद्धि के लिए।
वनोन्मूलन के प्रभाव – वनोन्मूलन के मुख्य दुष्प्रभाव हैं-
- ऑक्सीजन/कार्बन डाइऑक्साइड के अनुपात का असंतुलन
- अधिक बाढ़ें
- भू-स्ख लन
- जलवायु परिवर्तन
- वन में रहने वाले पशु-पक्षियों का नष्ट होना या प्रवास करना
- स्थलीय जल में कमी
- दवाइयों वाले पौधे नष्ट हो जाते हैं
- भूमि की उर्वरकता में कमी
- लकड़ी और रबड़ उद्योगों में गिरावट।
(ङ) रेड डाटा पुस्तक – यह पुस्तक संकटापन्न स्पीशीज़ के रिकार्ड का स्रोत है। पौधे, जंतुओं और अन्य स्पीशीज़ के लिए अलग-अलग रेड डाटा पुस्तकें हैं।
(च) प्रवास (Migration) – कुछ स्पीशीज़ों द्वारा अपने आवास से किसी निश्चित समय में बहुत दूर जाना प्रवास कहलाता है। प्रवास अधिकतर पक्षियों में पाया जाता है। पक्षी जलवायु परिवर्तन के कारण प्रवास करते हैं जैसे चपटे सिर वाली बतख, सुरखराब आदि प्रवासी पक्षी हैं।

प्रश्न 6.
फैक्टरियों एवं आवास की माँग की आपूर्ति हेतु वनों की अनवरत कटाई हो रही है। क्या इन परियोजनाओं के लिए वृक्षों की कटाई न्यायसंगत है ? इस पर चर्चा कीजिए तथा एक संक्षिप्त रिपोर्ट तैयार कीजिए।
उत्तर-
इन परियोजनाओं के लिए वृक्ष काटना न्यायपूर्वक नहीं है। बाकी विद्यार्थी स्वयं कक्षा में चर्चा करें।
प्रश्न 7.
अपने स्थानीय क्षेत्र में हरियाली बनाए रखने में आप किस प्रकार योगदान दे सकते हैं ? अपने द्वारा की जाने वाली क्रियाओं की सूची तैयार कीजिए।
उत्तर-
हरी संपदा का रख-रखाव-
- सड़कों के दोनों ओर वृक्ष लगाने चाहिएं।
- वनों के काटने पर रोकथाम लगानी चाहिएं।
- सरकार को अधिक वृक्ष काटने पर रोक लगाने के कानून बनाने चाहिएं।
- विशेष क्षेत्रों में पार्क (उदयान) बनाने चाहिएं।
प्रश्न 8.
वनोन्मूलन से वर्षा दर किस प्रकार कम हुई है ? समझाइए।
उत्तर-
वन वर्षा लाने में सहायक होते हैं। इसलिए वनोन्मूलन से वर्षा में कमी आती है और भूमि की उर्वरकता में कमी आती है। जिस कारण प्राकृतिक आपदाएँ आने की संभावनाएँ बढ़ गई हैं।
प्रश्न 9.
अपने राज्य के राष्ट्रीय उद्यानों के विषय में सूचना एकत्र कीजिए। भारत के रेखा मानचित्र में उनकी स्थिति दर्शाइए।
उत्तर-
विद्यार्थी स्वयं करें।
प्रश्न 10.
हमें कागज़ की बचत क्यों करनी चाहिए ? उन कार्यों की सूची बनाइए जिनके द्वारा आप कागज़ की बचत कर सकते हैं ?
उत्तर-
एक टन कागज़ की उत्पत्ति के लिए 17 हरे-भरे पेड़ चाहिएं। इसलिए हमें कागज़ की बचत करनी चाहिए। कागज़ का 5-7 बार पुनःचक्रण हो सकता है। हमें कागज़ को बचाना चाहिए, उपयोग में आए कागज़ को पुन:उपयोग में लाना चाहिए और पुनः चक्र करना चाहिए। इससे वनों के साथ-साथ पानी और ऊर्जा की बचत होती है। हानिकारक रसायनों के उपयोग में भी कमी आती है।
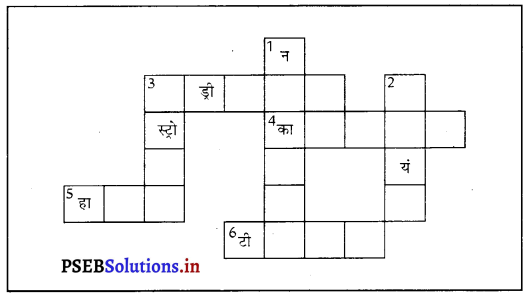
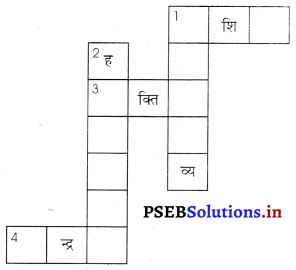
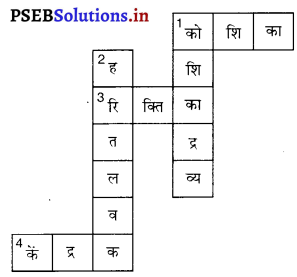
प्रश्न 11.
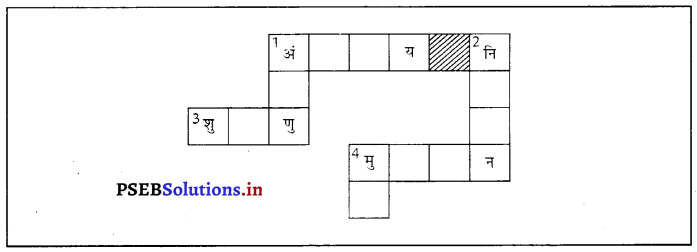
दी गई शब्द पहेली को पूरा कीजिएऊपर से नीचे की ओर
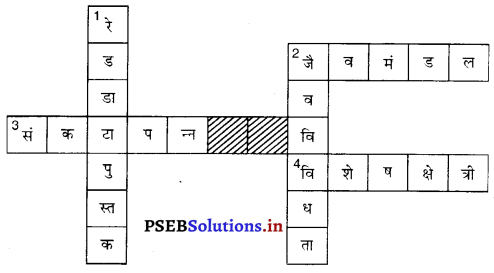
(1) विलुप्त स्पीशीज़ की सूचना वाली पुस्तकं
(2) पौधों, जंतुओं एवं सूक्ष्मजीवों की किस्में एवं विभिन्नताएँ।
बाईं से दाईं ओर-
(2) पृथ्वी का वह भाग, जिसमें सजीव पाए जाते हैं
(3) विलुप्त हुए स्पीशीज़
(4) एक विशिष्ट आवास में पाई जाने वाली।
स्पीशीज़
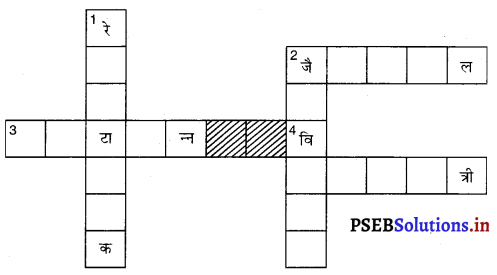
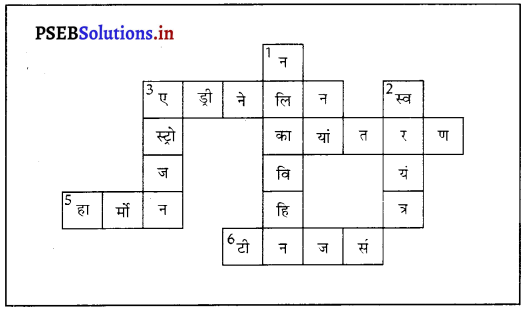
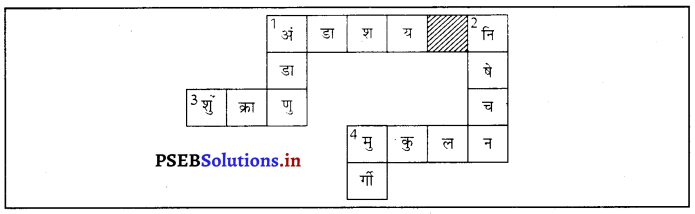
उत्तर-

PSEB Solutions for Class 8 Science पौधे एवं जंतुओं का संरक्षण Important Questions and Answers
TYPE-I
अति लघु उत्तरात्मक प्रश्न
प्रश्न 1.
रिक्त स्थान भरो-
(i) पृथ्वी की ऊपरी मिट्टी की परत का हटना …………………. कहलाता है।
उत्तर-
मृदा अपरदन
(ii) वन में पाए जाने वाले जंगली पौधे और जंतु ……………………. कहलाते हैं।
उत्तर-
वन्य जंतु
(iii) पौधों को …………………. गैस प्रकाश संश्लेषण के लिए चाहिए।
उत्तर-
कार्बन डाइऑक्साइड
(iv) उर्वर भूमि का रेगिस्तान में परिवर्तन होना …………………… कहलाता है।
उत्तर-
मरुस्थलीकरण
(v) ………………….. वह क्षेत्र है, जहाँ सजीवों का आवास है और जीवन को सहारा देता है।
उत्तर-
जैव-मंडल
(vi) ……………………. से तात्पर्य है पृथ्वी पर पाई जाने वाली विभिन्न प्रजातियाँ।
उत्तर-
जैव-विविधता
(vii) किसी विशेष क्षेत्र में पाए जाने वाले पशु-पक्षी और जीव-जंतु और ………………………. कहलाते हैं।
उत्तर-
वनस्पति जात, प्राणिजात
(viii) पंचमढ़ी जैवमंडल आरक्षित क्षेत्र में एक राष्ट्रीय उद्यान ………………….. , दो वन्य जंतु अभ्यारण्य और ……………………… आते हैं।
उत्तर-
सतपुड़ा, बोरी, पंचमढ़ी

(ix) एक विशेष क्षेत्र में पाए जाने वाले स्पीशीज़ को ……………………. कहते हैं।
उत्तर-
विशेष क्षेत्री स्पीशीज़
(x) …………………… सजीवों की समष्टि का समूह है, जो एक-दूसरे से अंतर्जनन करने में सक्षम होते हैं।
उत्तर-
स्पीशीज़।
प्रश्न 2.
वनोन्मूलन की परिभाषा दीजिए।
उत्तर-
वनों का काटना और उस भूमि का उपयोग दूसरे उद्देश्यों के लिए करना वनोन्मूलन कहलाता है।
प्रश्न 3.
वनोन्मूलन के प्राकृतिक कारक बताइए।
उत्तर-
दावानल और भीषण सूखा वनोन्मूलन के प्राकृतिक कारक हैं।
प्रश्न 4.
वर्षा और भूमि की उर्वरकता में कमी के क्या प्रभाव हैं ?
उत्तर-
इनसे प्राकृतिक आपदाओं (बाढ़ और सूखा) की संभावना बढ़ती है।
प्रश्न 5.
प्रकाश संश्लेषण के लिए पौधों को कौन-सी गैस की आवश्यकता होती है ?
उत्तर-
पौधों को कार्बन डाइऑक्साइड की आवश्यकता होती है।
प्रश्न 6.
पर्यावरण में कार्बन डाइऑक्साइड गैस की वृद्धि से क्या होगा ?
उत्तर-
इससे विश्व ऊष्मण होगा।

प्रश्न 7.
सूखा का क्या कारण है ?
उत्तर-
भूमि पर ताप में वृद्धि से सूखा पड़ता है।
प्रश्न 8.
मरुस्थलीकरण की परिभाषा लिखिए।
उत्तर-
मरुस्थलीकरण – उर्वर भूमि का रेगिस्तान में परिवर्तन, मरुस्थलीकरण कहलाता है।
प्रश्न 9.
उस स्थान का नाम लिखें जहाँ पौधे एवं जंतु ऊपरी हिमालय की श्रृंखलाओं एवं निचले पश्चिमी घाट के समान हैं।
उत्तर-
पंचमढ़ी जैवमंडलीय संरक्षित क्षेत्र।
प्रश्न 10.
सरकार वनों एवं वन्य जंतुओं के संरक्षण के लिए क्या करती है ?
उत्तर-
सरकार संरक्षण और सुरक्षा हेतु नियम, विधियाँ और नीतियाँ बनाती है।
प्रश्न 11.
जैवमंडल क्या है ?
उत्तर-
जैवमंडल – पृथ्वी का वह भाग जिसमें सजीव पाए जाते हैं अथवा जो जीवनयापन योग्य हैं।
प्रश्न 12.
जैव-विविधता की परिभाषा दीजिए।
उत्तर-
जैव-विविधता से तात्पर्य पृथ्वी पर पाए जाने वाले विभिन्न जीवों की प्रजातियों के पारस्परिक संबंध और पर्यावरण से संबंध है।
प्रश्न 13.
जैवमंडल आरक्षित क्षेत्र क्या है ?
उत्तर-
जैवमंडल आरक्षित क्षेत्र वे क्षेत्र हैं जहाँ जैव-विविधता की संरक्षणता होती है।

प्रश्न 14.
पंचमढ़ी में पाए जाने वाले एक राष्ट्रीय उद्यान और दो वन्यजंतु अभ्यारण्यों के नाम लिखिए।
उत्तर-
राष्ट्रीय उद्यान-सतपुड़ा।
वन्यजंतु अभ्यारण्य-बोरी एवं पंचमढ़ी।
प्रश्न 15.
वनस्पतिजात की परिभाषा लिखें।
उत्तर-
किसी विशेष क्षेत्र में पाए जाने वाले पेड़-पौधे वनस्पतिजात कहलाते हैं।
प्रश्न 16.
पंचमढ़ी जैवमंडल आरक्षित क्षेत्र के वनस्पतिजात के कुछ उदाहरण दो।
उत्तर-
साल, टीक, आम, जामुन, चाँदी, फर्ना, अर्जुन आदि।
प्रश्न 17.
प्राणिजात की परिभाषा लिखिए।
उत्तर-
किसी विशेष क्षेत्र में पाए जाने वाले जीव-जंतु प्राणिजात कहलाते हैं।
प्रश्न 18.
पंचमढ़ी जैवमंडल आरक्षित क्षेत्र के कुछ प्राणिजात के उदाहरण दीजिए।
उत्तर-
चिनकारा, नीला-बैल, भौंकने वाले हिरण, चीता, जंगली कुत्ता, भेड़िया आदि।
प्रश्न 19.
स्पीशीज़ की परिभाषा लिखिए।
उत्तर-
स्पीशीज़ – स्पीशीज़ सजीवों की समष्टि का वह समूह जो एक-दूसरे से अंतर्जनन करने में सक्षम है।
प्रश्न 20.
विशेष क्षेत्री स्पीशीज़ क्या है ?
उत्तर-
किसी विशेष क्षेत्र में पाए जाने वाले जीव-जंतु, पेड़-पौधे विशेष क्षेत्री स्पीशीज़ (Endemic) कहलाते हैं। यह भौगोलिक क्षेत्र, प्रांत, देश, राज्य कुछ भी हो सकता है।

प्रश्न 21.
पंचमढ़ी जैवमंडल आरक्षित क्षेत्र के दो विशेष क्षेत्री प्राणिजात के नाम लिखिए।
उत्तर-
- भारतीय विशाल गिलहरी,
- उड़ने वाली गिलहरी।
प्रश्न 22.
पंचमढ़ी जैवमंडल आरक्षित क्षेत्र के दो विशेष श्रेणी वनस्पतिजात के नाम लिखिए।
उत्तर-
- साल
- जंगली आम।
प्रश्न 23.
विशेष श्रेणी स्पीशीज़ के आवास को कौन-से कारक प्रभावित करते हैं और उनकी उपस्थिति को संकट में डालते हैं ?
उत्तर-
- आवास का नष्ट होना
- जनसंख्या वृद्धि
- नई स्पीशीज़ को शामिल करना।
प्रश्न 24.
वन्यप्राणी अभ्यारण्य (Wild Life Sanctuaries) क्या है ?
उत्तर-
वे क्षेत्र जहाँ वन्यप्राणी सुरक्षित एवं संरक्षित रखे जाते हैं, वन्यप्राणी अभ्यारण्य कहलाते हैं।
प्रश्न 25.
कुछ संकटापन्न मुख्य जंतुओं के नाम लिखो।
उत्तर-
काली बत्तख, सफेद आँख वाली बत्तख, हाथी, सुनहरी बिल्ली, गुलाबी सिर वाली बतख, घड़ियाल, मार्च मगरमच्छ, अजगर, राइनोसीरस आदि।
प्रश्न 26.
प्राणी उद्यान क्या है ?
उत्तर-
प्राणी उद्यान वे क्षेत्र हैं जहाँ जानवर सुरक्षित रखे जाते हैं।
प्रश्न 27.
राष्ट्रीय उद्यान (National Parks) क्या है ?
उत्तर-
राष्ट्रीय उद्यान, वे आरक्षित क्षेत्र हैं, जहाँ सभी प्रकार के पारितंत्रों की सुरक्षा की जाती है।

प्रश्न 28.
भारत के पहले आरक्षित क्षेत्र का नाम क्या है ?
उत्तर-
सतपुड़ा राष्ट्रीय उद्यान ।
प्रश्न 29.
सतपुड़ा राष्ट्रीय उद्यान में कौन-सा वनस्पतिजात पाया जाता है ?
उत्तर-
सबसे बढ़िया टीक।
प्रश्न 30.
चट्टान शरण (Rock Shelter) कहाँ पाए जाते हैं ?
उत्तर-
सतपुड़ा राष्ट्रीय उद्यान में चट्टान शरण पाए जाते हैं।
प्रश्न 31.
चट्टान शरण किस बात की जानकारी देते हैं ?
उत्तर-
आदिमानव के जीवनकाल की।
प्रश्न 32.
पंचमढ़ी जैवमंडल आरक्षित क्षेत्र में कितने चट्टान शरण पाए गए हैं ?
उत्तर-
55.
प्रश्न 33.
हमारी सरकार द्वारा ‘प्रोजेक्ट टाइगर’ कानून कब लागू हुआ ?
उत्तर-
प्रोजेक्ट टाइगर 1 अप्रैल, 1973 में सरकार द्वारा भारतीय टाइगरों की सुरक्षा हेतु लागू हुआ।
प्रश्न 34.
संकटापन्न स्पीशीज़ कौन-सी है ?
उत्तर-
वे स्पीशीज़ अथवा जंतु जिनकी संख्या में कमी हो रही है और विलुप्त होने की संभावना है, संकटापन्न स्पीशीज़ कहलाते हैं।
प्रश्न 35.
किसी एक विलुप्त जानवर का नाम लिखिए।
उत्तर-
डाइनोसॉर।

प्रश्न 36.
पारितंत्र (Ecosystem) की परिभाषा लिखिए।
उत्तर-
किसी क्षेत्र के सभी पेड़-पौधे, जीव-जंतु, सूक्ष्मजीव और अजैव घटक जैसे जलवायु, मिट्टी, नदियों के डेल्टा आदि से मिलकर बना तंत्र, पारितंत्र कहलाता है।
प्रश्न 37.
रेड डाटा पुस्तक की Website क्या है ?
उत्तर-
W.W.W./gov.in/envis/primates/page 102/htm/new/nwdc/plats. htm.
प्रश्न 38.
उस पक्षी का नाम बताओ जिसने मलेशिया से भारत तक प्रवास किया।
उत्तर-
सुरखाब।
प्रश्न 39.
कुछ प्रवासी पक्षियों के नाम लिखिए।
उत्तर-
सुरखाब, चपटे सिर वाली बत्तख़, ग्रेट कोमोनैट।
प्रश्न 40.
प्रवासी पक्षी क्या है ?
उत्तर-
प्रवाम पक्षी. वे पक्षी हैं, जो जलवायु परिवर्तन के कारण एक जगह से दूसरी जगह तक लंबा रास्ता तय पहनते हैं।
प्रश्न 41.
एक टन कागज़ की उत्पत्ति के लिए कितने पेड़ों की ज़रूरत होती है ?
उत्तर-
लगभग 17 पूरी तरह फैले हुए हरे-भरे पेड़।
प्रश्न 42.
पुनर्वनरोपण (Reforestation) क्या है ?
उत्तर-
पुनर्वनरोपण नष्ट किए गए पेड़ों की जगह नए पेड़ उगाना है।

प्रश्न 43.
वनोन्मूलन की दो हानियाँ लिखो। उत्तर-प्रदूषण का बढ़ना, वायुमंडल का तापमान बढ़ना, वायु में कार्बन डाईऑक्साइड की मात्रा बढ़ना।
प्रश्न 44.
विश्व ऊष्णन क्या है ?
उत्तर-
वायुमंडल में कार्बन डाइऑक्साइड की मात्रा बढ़ने से ताप में होने वाली वृद्धि को विश्व ऊष्णन कहते हैं।
प्रश्न 45.
वनों के काटने से वर्षा व जल-चक्र पर क्या प्रभाव होता है ?
उत्तर-
वनोन्मूलन से जल-चक्र का संतुलन बिगड़ता है, वर्षा में कमी आती है व सूखा पड़ता है।
प्रश्न 46.
मृदा अपरदन के दुष्प्रभाव लिखो।
उत्तर-
मिट्टी में ह्यूमस की कमी, उर्वरता में कमी व भूमि मरुस्थल बन जाती है।
प्रश्न 47.
मरुस्थलीकरण का मुख्य कारण क्या है ?
उत्तर-
भू-क्षरण।
TYPE-II
लघु उत्तरात्मक प्रश्न
प्रश्न 1.
मृदा अपरदन के कारक लिखिए।
उत्तर-
मृदा अपरदन के कारण-
- वायु द्वारा शुष्क ऋतु में हल चलाई हुई ऊपरी परत का उड़ाना।
- आंधियाँ।
- वनों का कटना और दावानल से मृदा अपरदन आरंभ होता है। मिट्टी नदियों और नालों द्वारा बहकर समुद्रों में एकत्रित हो जाती है।
- असुरक्षित खेत हवा और पानी से अपरदित हो जाते हैं।
- शहरीकरण से वनस्पति की हानि हुई है।
- बिल बनाने वाले जंतु भी मृदा अपरदन में सहायक हैं। यह मिट्टी को ढीला करते हैं जो पानी द्वारा बह सकती है।
- मानव क्रिया-कलाप जैसे पेड़ों को काटना, अतिचारण, फसलों का अधिक उगाना और गलत तरीके से खेतीबाड़ी करके मृदा अपरदन बढ़ता है।

प्रश्न 2.
मिट्टी का संरक्षण कैसे कर सकते हैं ?
उत्तर-
मिट्टी का संरक्षण-
- वनोन्मूलन को रोकना, अतिचारण को रोकना और नदियों तथा नालों द्वारा मिट्टी को बहने से रोकना।
- अधिक फसल उगाने से मृदा अपरदन रुक सकती है, क्योंकि फसल मृदा को बांधे रखती है।
- खेतों के इर्द-गिर्द बंध (Bunds) वर्षा के पानी को रोकते हैं और खनिजों के बहने पर भी रोक लगाते हैं।
- सिंचाई की नालियों में पानी की गति कम होनी चाहिए।
- वर्षा के पानी के लिए उत्सर्जित नहरें खेतों को मृदा अपरदन से बचाती हैं।
- सीढ़ीनुमा खेती भी मिट्टी का संरक्षण करती है।
- वायु से मिट्टी का संरक्षण पेड़ लगाकर और घास उगाकर किया जा सकता है। खेत के किनारे पेड़ों की कतार वायुरोधक का काम करती है।
प्रश्न 3.
वन्य जीवन की महत्ता लिखिए।
उत्तर-
वन्य जीवन की महत्ता-
- पौधे, जंतु और सूक्ष्मजीव कई वस्तुएँ देते हैं।
- भोजन श्रृंखला और प्राकृतिक चक्रों द्वारा पर्यावरण संतुलन बना रहता है।
- प्रजनन के लिए ‘जीन बैंक’ का रख-रखाव।
- वन्य जंतु मनोरंजन के साधन हैं।
- यह कवियों और कला प्रेमियों को उत्साहित करते हैं।
- नैतिक मूल्य के लिए।
प्रश्न 4.
संकटापन्न (Endangered) और सुमेय (Vulnerable) स्पीशीज़ में अंतर लिखिए।
उत्तर-
संकटापन्न और सुमेय स्पीशीज़ में अंतर-
| संकटापन्न स्पीशीज़ |
सुमेद्य स्पीशीज़ ( असुरक्षित) |
| (1) इनके खत्म होने और विलुप्त होने का डर अत्यधिक है। |
(1) इनका खत्म होने का डर है। |
| (2) ये विलुप्त हो चुके हैं। |
(2) यह संकटापन्न स्पीशीज़ में आ सकती है। |
प्रश्न 5.
जैवमंडल आरक्षित क्षेत्र का वर्णन करें।
उत्तर-
जैवमंडल आरक्षित क्षेत्र – यह विशेष क्षेत्र है जिसका उपयोग बहु-उद्देश्यों के लिए किया जाता है। इसके लिए इस क्षेत्र के विभिन्न भाग पृथक् करते हैं और प्रत्येक भाग एक विशेष कार्य के लिए निश्चित किया जाता है।
UNESCO के मानव और जैवमंडल प्रोग्राम (MBA) ने जैवमंडल आरक्षित क्षेत्र का संकल्प (Concept) दिया।
प्रश्न 6.
संकटापन्न स्पीशीज़ (Endangered Species) से क्या अभिप्राय है ?
उत्तर-
संकटापन्न स्पीशीज़-वह स्पीशीज़ जो विलुप्त होने की कगार पर हैं और इनका जीवन मुश्किल है। अब इन स्पीशीज़ की कुछ ही संख्या जीवित है। यह जल्दी ही विलुप्त हो सकते हैं जैसे कि विशाल भारतीय वसटर्ड पक्षी जो कि राजस्थान, गुजरात और महाराष्ट्र में रहता है, संकटापन्न पक्षी है।
प्रश्न 7.
विश्व ऊष्मण के कारण क्या हैं ?
उत्तर-
विश्व ऊष्मण के कारण-पर्यावरण में कार्बन डाइऑक्साइड और कुछ अन्य गैसों की वृद्धि के फलस्वरूप पर्यावरण के ताप में वृद्धि होने से धरती का वातावरण गर्म हो गया है अर्थात् विश्व ऊष्मण हुआ है।

प्रश्न 8.
वन महत्त्वपूर्ण प्राकृतिक स्त्रोत क्यों माने जाते हैं ?
उत्तर-
पृथ्वी पर वन महत्त्वपूर्ण प्राकृतिक स्रोत माने जाते हैं क्योंकि ये-
- वायु में ऑक्सीजन और CO2 का संतुलन रखते हैं और जीवन का आधार हैं।
- वर्षा लाने में सहायक हैं।
- जलवायु नियंत्रित करते हैं।
- भूमिगत जल की आपूर्ति करते हैं।
- बाढ़ें रोकते हैं।
- मृदा अपरदन रोकते हैं।
- कई दवाइयों के स्रोत हैं।
- वर्षा जल से मृदा को बहने से रोकते हैं।
- कई पादप उत्पाद जैसे रबड़, गोंद, रेसिन, शहद, लाख, कत्था आदि के स्रोत हैं।
- वन्य प्राणियों का आश्रय है, जो आदिवासियों के भोजन का मुख्य साधन हैं।
प्रश्न 9.
वनों के संरक्षण के लिए कौन-से उपाय करने चाहिए ?
उत्तर-
वनों के संरक्षण के उपाय – आधुनिक समय में मानव अपनी ज़रूरतों के आधार पर प्राकृतिक संसाधनों का अत्यधिक उपयोग कर रहा है। यदि वनों को अपने आराम के लिए पूरी तरह काट दिया तो पृथ्वी से मानव जाति हमेशा के लिए खत्म हो जाएगी। वनों के संरक्षण के लिए निम्नलिखित उपाय करने चाहिएं-
- अधिक पौधे लगाएँ।
- पादप उत्पादों का विवेकतापूर्ण उपयोग करें।
- पशुओं द्वारा अतिचारण रोकें।
- वनों में और वनों के इर्द-गिर्द खाने खोदने और उद्योग लगाने के नियम लागू करने चाहिए।
- वन पौधशालाएँ बना कर।
प्रश्न 10.
पौधे मृदा अपरदन कैसे रोकते हैं ?
उत्तर-
पौधों की जड़ें मिट्टी के कणों को बाँधकर रखती हैं। इसलिए यह कण पानी अथवा हवा के साथ नहीं बहते। इस तरह पौधे मृदा अपरदन को रोकते हैं।
प्रश्न 11.
वनों में विविध पौधों का होना क्यों आवश्यक है ?
उत्तर-
वनों में विविध पौधों की उपस्थिति के कारण हैं-
- जानवरों की विशेष भोजन आदतें।
- मानव और जानवरों दोनों की जरूरतों की आपूर्ति।
- कई जीवों का आवास।
- वनों में जानवरों के जीवन के लिए स्थित विविध भोजन शृंखला/भोजन जाल प्रदान करके।
प्रश्न 12.
पाँच राष्ट्रीय पार्कों के नाम लिखिए।
उत्तर-
- कार्बेट राष्ट्रीय पार्क – उत्तराखंड।
- कान्हा राष्ट्रीय पार्क – मध्यप्रदेश।
- संजय राष्ट्रीय पार्क – महाराष्ट्र।
- परियार राष्ट्रीय पार्क – केरल।
- बमुघाटा राष्ट्रीय पार्क – कर्नाटक।
प्रश्न 13.
वर्णन कीजिए कि वनोन्मूलन भूमिगत जल स्रोत की कमी में कैसे सहायक है ?
उत्तर-
वनस्पति में पानी को रोकने का सामर्थ्य होता है, जिससे भूमिगत जल की आपूर्ति होती है। आधुनिक समय में बड़े-बड़े वनों के क्षेत्रों को कई उद्देश्यों के लिए काटकर साफ कर दिया गया है। अतिचारण से भी वनस्पति नष्ट हुई है। इससे अनउपजाऊ भूमि बनी है जिसमें जल को पकड़कर रखने की क्षमता नहीं है। इस कारण भूमिगत जल स्रोतों में कमी आई है।
प्रश्न 14.
वनों के संरक्षण से अभिप्राय है वायु, जल और मिट्टी का संरक्षण। वर्णन करें।
उत्तर-
वन एक जटिल जैवमंडलीय तंत्र हैं। चाहे यह स्वयं (Sufficient) है फिर भी यह दूसरे निम्नीकरण पदार्थों पर अपने रख-रखाव के लिए निर्भर करता है। इसलिए वनों की सुरक्षा के लिए वायु, मिट्टी और जल का संरक्षण अति आवश्यक है। वन जलवायु परिस्थितियों पर निर्भर करते हैं। समय-समय पर भौगोलिक परिवर्तन जैसे बाँध बनाना और खाने खोदना। इससे उस क्षेत्र के वनों पर पर्यावरण नष्ट होने से बुरा प्रभाव पड़ता है। उद्योगों द्वारा फैले वायु प्रदूषण का दुष्प्रभाव वनों पर बहुत है, जवकि उद्योग मीलों दूर होते हैं।

प्रश्न 15.
आवास में व्यवधान वन्य जीवन को कैसे प्रभावित करते हैं ?
उत्तर-
जानवरों और पौधों का अपने आवास के साथ गहरा रिश्ता होता है। कई खास सजीव एक खास पर्यावरण में ही जीवित रह सकते हैं। सुनहरी शेर, ब्राज़ील के वर्षावनों के छोटे क्षेत्र पाए जाते थे। यह उनका प्राकृतिक आवास था। जब यह क्षेत्र नष्ट हो गया तो सुनहरा शेर बेघर हो गया। ब्राज़ील के कई और वर्षावन हैं, परंतु कुछ सुनहरी शेर प्राणी उद्यानों (Zoos) में जीवित हैं, लेकिन वे कभी भी अपने जंगली आवास में लौट नहीं पाएँगे। जब एक वन खत्म होता है तो बड़ी संख्या में जंतु संकटापन्न होते हैं अथवा विलुप्त हो जाते हैं।
प्रश्न 16.
कंचनजंगा राष्ट्रीय उद्यान के सात वन्य जंतुओं के नाम लिखो जो विलुप्त होने की कगार पर हैं।
उत्तर-
बर्फीला तेंदुआ, बदली तेंदुआ, मार्बल बिल्ली, हिमालय काला भालू, लाल पांडा, नीली भेड़, मस्क हिरण, सिरोड़ा हरा कबूतर आदि।
प्रश्न 17.
पारितंत्र (Ecosystem) क्या है ?
उत्तर-
पारितंत्र – जैविक घटक और भौतिक पर्यावरण (अजैविक घटकों) के पारस्परिक संयोग से बने तंत्र को पारितंत्र कहते हैं। यह प्राकृतिक और कृत्रिम हो सकता है। यह अस्थायी जैसे फसली खेत अथवा स्थायी जैसे जंगल हो सकता है। पारितंत्र बहुत विशाल जैसे समुद्र और वन अथवा इतना छोटा जैसे लकड़ी भी हो सकता है। अतः पारितंत्र पर्यावरण की संरचनात्मक और कार्यात्मक इकाई है, जिसकी एक पहचान है।
पारितंत्र जैविक और अजैविक घटकों का समूह है जहाँ दोनों एक-दूसरे से प्रभावित हैं।
प्रश्न 18.
सिल्वी कलचर (Silviculture) की क्या महत्ता है ?
उत्तर-
सिल्वी कलचर – यह एक मुख्य प्रोजेक्ट है जिसका आरंभ पुनर्वनरोपण से है। इसकी दो विशेषताएँ हैं-
- कच्ची सामग्री के उत्पादन में वृद्धि ।
- वन क्षेत्रों में वृद्धि।
प्रश्न 19.
जैवमंडल आरक्षित क्षेत्रों के कार्य क्या हैं ?
उत्तर-
जैवमंडल आरक्षित क्षेत्रों के कार्य-
- यह उस जगह की जैव विविधता का संतुलन रखते हैं।
- क्षेत्र की संस्कृति कायम रखते हैं।
- यह कई अन्य क्षेत्रों को भी आरक्षित करते हैं।
प्रश्न 20.
कुछ जानवरों के नाम लिखो, जिन्हें वन्यजीव अभ्यारण्य में संरक्षित किया जाता है ? भारतीय अभ्यारण्य क्या दर्शाते हैं ?
उत्तर-
कई संकटापन्न जंतु जैसे काली बत्तख, सफेद आँख वाली बत्तख, हाथी, सुनहरी बिल्ली, घड़ियाल, गुलाबी सिर वाली बत्तख, मार्श मगरमच्छ, अजगर, राइनोसीरस आदि वन्य जीवन अभ्यारण्य में सुरक्षित एवं संरक्षित रखे जाते हैं।
भारतीय अभ्यारण्य भूमि मज़ारे, चौड़े वन, पर्वतीय वन, झाड़ियाँ, नदियों के डैल्टा आदि का प्रदर्शन करते हैं।
प्रश्न 21.
प्रवासी पक्षियों पर संक्षिप्त नोट लिखें।
उत्तर-
प्रवासी पक्षी – वे पक्षी जो जलवायु परिवर्तन के कारण लंबे रास्ते तय करते हैं, प्रवासी पक्षी कहलाते हैं। चपटे सिर वाली बत्तख, विशाल कोओरैंट प्रवासी पक्षी हैं।
यह पक्षी सुदूर निश्चित स्थानों पर प्रत्येक वर्ष उड़कर पहुँचते हैं। यह पक्षी अपने प्राकृतिक आवास से दूर अंडे देने के लिए यहाँ आते हैं क्योंकि वहाँ जलवायु ठंडी और प्रतिकूल होती है।
प्रश्न 22.
पुनर्वनरोपण (Reforestation) पर नोट लिखें।
उत्तर-
पुनर्वनरोपण – यह नष्ट हो चुके वनों के स्थान पर नए बहुत अधिक पेड़ लगाने का प्रक्रम है। जितने पेड़ काटे जाएं, उतने तो अवश्य ही उगाने चाहिएं। यह प्रक्रम प्राकृतिक भी हो सकता है। यदि वन कटाई के बाद क्षेत्र को वैसे ही छोड़ दिया जाए तो यह अपने आप फिर उग जाता है। यदि हम हरित संपदा को अगली पीढ़ी के लिए बचाना चाहते हैं तो हमें अधिक पेड़ उगाने चाहिएं।
भारतीय सरकार ने 1952 में राष्ट्रीय वन कानून लागू किया। इसका लक्ष्य पूरी भूमि का 1/3 भाग वनों से ढ़ापना था, परंतु असफल होने पर 1980 में इसे फिर दोहराया गया। इसको वन संरक्षित कानून का नाम दिया गया। इसका उद्देश्य वनों की सुरक्षा और संरक्षण के साथ-साथ मानव की ज़रूरतों की आपूर्ति भी थी।

TYPE-III
दीर्घ उत्तरात्मक प्रश्न
प्रश्न 1.
वन्य जीवन के संरक्षण के उपाय लिखिए।
उत्तर-
वन्य जीवन के संरक्षण के उपाय-
- संकटापन्न स्पीशीज़ का संरक्षण।
- प्राकृतिक आवासों की सुरक्षा एवं संरक्षण हेतु भूमि और जल की योजना और रख-रखाव।
- जीन बैंक के लिए विविध किस्मों के खाद्य उपजें, पौधे, लकड़ी के पेड़, पानी के जीव और उनके रिश्तेदारों को संरक्षित करना।
- प्रत्येक देश को उपयोगी जीवों की पहचान कर उनकी सुरक्षा और संरक्षण के उपाय करना।
- वन्य क्षेत्रों को आरक्षित करना, प्रवासी पक्षियों और वन्य जंतुओं के लिए।
- लाभकारी जंतुओं के अति उपयोग को रोकना।
- वन्य पौधों और वन्य जंतुओं का अंतर्राष्ट्रीय व्यापार में वृद्धि करना।
- शिकारियों आदि से जंतुओं की रक्षा करनी। शिकार एक गैर-कानूनी कार्य है, इसको 1972 में वन्य जीवन सुरक्षा नियम बना कर लागू किया गया।
- उद्यानों और अभ्यारण्यों का निर्माण करना।
- ‘वन्य जीवन सप्ताह’ मनाना ताकि लोगों को जागरूक किया जा सके।
- संकटापन्न जंतुओं के लिए प्रजनन कार्यशालाओं का निर्माण करना।
प्रश्न 2.
वनों के कुछ लाभ लिखिए।
उत्तर-
वनों के लाभ-
- वन भूमि की उर्वरकता कायम रखते हैं।
- वन वर्षा लाने में सहायक हैं और जल चक्र का संतुलन रखते हैं।
- वनों से लकड़ी मिलती है। जैसे शीशम, टीक, साल, देवदार ।
- वनों से कागज़ मिलता है-कोणिय और बैंबू कागज़ निर्माण के उपयोग में आते हैं।
- दवाइयाँ-कई दवाइयों के पौधे वनों में पाए जाते हैं।
- वनों से कई उत्पाद जैसे रेज़िन, गोंद, लाख, रबड़, भोजन और कीटनाशक मिलते हैं।
- कार्क भी वनों से मिलता है जैसे ओक (क्वरकस)।
- कई अन्य उपयोगी वस्तुएँ जैसे प्राकृतिक रंग, मोम, शहद भी वनों से ही मिलती हैं।
- रेयान और कृत्रिम रेशम भी पेड़ों से मिलता है।
- नाइट्रेट सैलूलोज़ से प्लास्टिक तैयार किया जाता है।
- प्राकृतिक रबड़ भी वनों की देन है।
- लकड़ी ईंधन भी वनों से मिलता है।
- रेशा घास, रवस और संदल लकड़ी से कई उपयोगी तेल मिलते हैं जिनका उपयोग साबुन, शृंगार, दवाइयाँ, खाद्य पदार्थ, तंबाकू के निर्माण में किया जाता है।
- रीठा और शिकाकाई साबुन आदि औद्योगिक उत्पाद हैं।
- वनों का नैतिक मूल्य है।
प्रश्न 3.
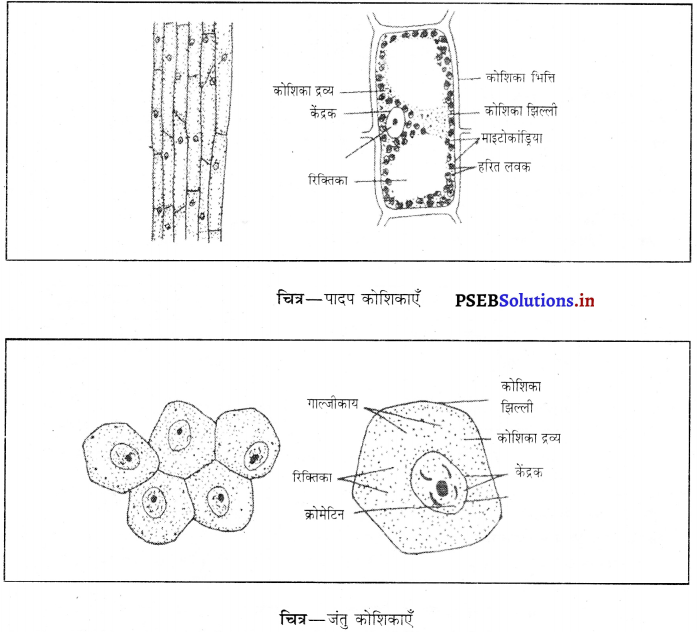
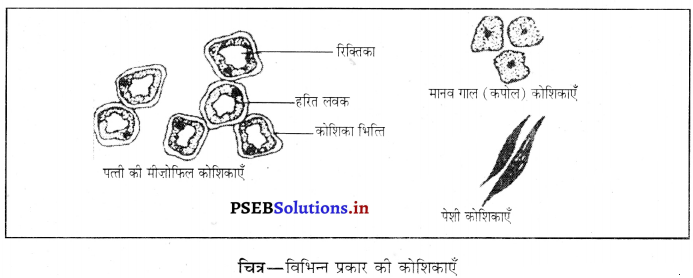
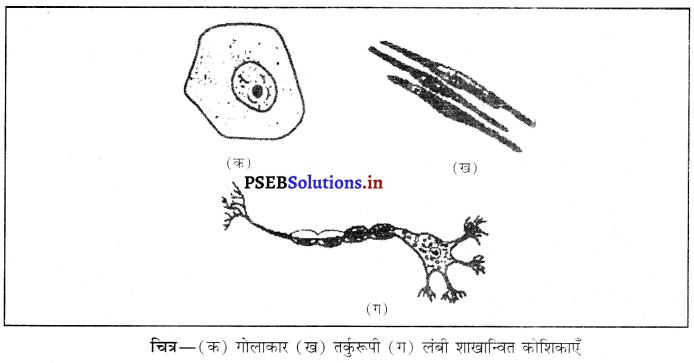
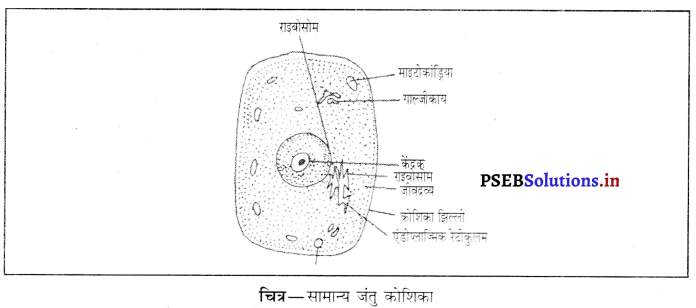
पंचमढ़ी जैवमंडल आरक्षित क्षेत्र के प्राणिजात एवं वनस्पतिजात के चित्र बनाएँ।
उत्तर-

![]()
![]()
![]()
![]()