PSEB 10th Class Maths Solutions Chapter 14 ਅੰਕੜਾਵਿਗਿਆਨ Ex 14.3

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 14 ਅੰਕੜਾਵਿਗਿਆਨ Ex 14.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 14 ਅੰਕੜਾਵਿਗਿਆਨ Exercise 14.3

ਪ੍ਰਸ਼ਨ 1.
ਹੇਠ ਦਿੱਤੀ ਬਾਰੰਬਾਰਤਾ ਵੰਡ ਕਿਸੇ ਮੁਹੱਲੇ ਦੇ 68 ਉਪਭੋਗਤਾਵਾਂ ਦੀ ਬਿਜਲੀ ਦੀ ਮਹੀਨੇਵਾਰ ਖਪਤ ਨੂੰ ਦਰਸਾਉਂਦਾ ਹੈ । ਇਹਨਾਂ ਅੰਕੜਿਆਂ ਦੀ ਮੱਧਕਾ, ਮੱਧਮਾਨ ਅਤੇ ਬਹੁਲਕ ਪਤਾ ਕਰੋ । ਇਸਦੀ ਤੁਲਨਾ ਵੀ ਕਰੋ ।

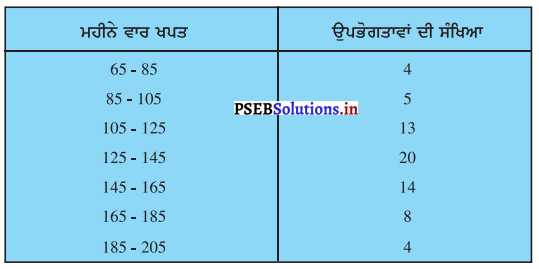
ਹੱਲ:

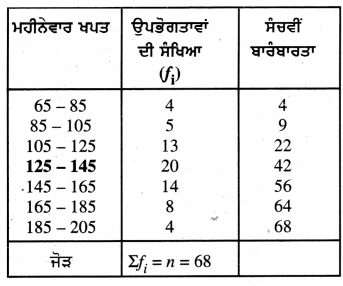
ਇੱਥੇ Σf_i = n = 68 ਤਾਂ \(\frac{n}{2}\) = \(\frac{68}{2}\) = 34
ਜੋ ਵਰਗ ਅੰਤਰਾਲ 125 – 145 ਵਿੱਚ ਸਥਿਤ ਹੈ।
∴ ਮੱਧਕਾ ਵਰਗ = 125 – 145 ਹੋਵੇਗਾ
∴ l = 125 ; n = 68 ; f = 20 ; cf = 22 ਅਤੇ h = 20
ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ, ਮੱਧਿਕਾ
= l + \(\left[\frac{\frac{n}{2}-c f}{f}\right]\) × h
= 125 + \(\left\{\frac{\frac{68}{2}-22}{20}\right\}\) × 20
= 125 + \(\frac{34-22}{20}\) × 20
= 125 + 12 = 37
ਮੱਧਮਾਨ ਲਈ

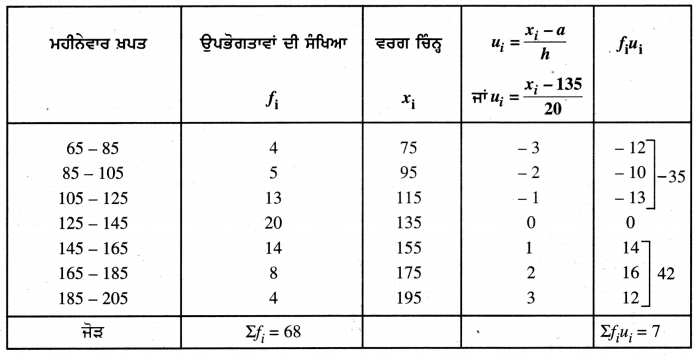
ਉਪਰੋਕਤ ਅੰਕੜਿਆਂ ਤੋਂ, ਕਾਲਪਨਿਕ ਮੱਧਮਾਨ (a) = 135
ਵਰਗ ਮਾਪ (h) = 20
∴ \(\bar{u}\) = \(\frac{\Sigma f_{i} u_{i}}{\Sigma f_{i}}\) = \(\frac{7}{8}\) = 0.102
ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ
ਮੱਧਮਾਨ (\(\bar{X}\)) = a + h\(\bar{u}\)
\(\bar{X}\) = 135 + 20 (0.102)
= 135 + 2.04 = 137.04
ਬਹੁਲਕ ਲਈ
ਦਿੱਤੇ ਗਏ ਅੰਕੜਿਆਂ ਵਿਚ ਅਧਿਕਤਮ ਬਾਰੰਬਾਰਤਾ 20 ਹੈ ਅਤੇ ਇਸ ਦਾ ਸੰਗਤ ਵਰਗ 125 – 145 ਹੈ
∴ ਬਹੁਲਕ ਵਰਗ = 125 – 145
∴ l = 125 ; f₁ = 20 ; f₀ = 13; f₂ = 14 ਅਤੇ h =20 ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ,
ਬਹੁਲਕ = l + \(\left(\frac{f_{1}-f_{0}}{2 f_{1}-f_{0}-f_{2}}\right)\) × h
= 125 + \(\left(\frac{20-13}{2(20)-13-14}\right)\) × 20
= 125 + \(\frac{7}{40-27}\) × 20
= 125 + \(\frac{140}{13}\)
= 125 + 10.76923
= 125 + 10.77 = 135.77.
∴ ਦਿੱਤੇ ਗਏ ਅੰਕੜਿਆਂ ਦਾ ਮੱਧਕ, ਮੱਧਮਾਨ ਅਤੇ ਬਹੁਲਕ ਹਨ : 137, 137.04 ਅਤੇ 135.77

ਪ੍ਰਸ਼ਨ 2.
ਜੇਕਰ ਹੇਠ ਦਿੱਤੀ ਗਈ ਵੰਡ ਦੀ ਮੱਧਿਕਾ 28.5 ਹੋਵੇ ਤਾਂ x ਅਤੇ y ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ :

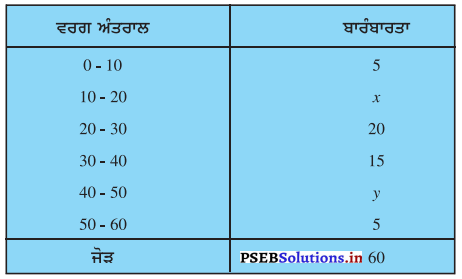
ਹੱਲ:

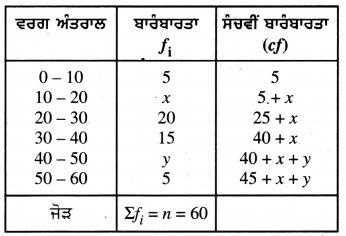
ਦਿੱਤੇ ਗਏ ਅੰਕੜਿਆਂ ਵਿੱਚ Σf_i = n = 60
∴ \(\frac{n}{2}\) = \(\frac{60}{2}\) = 30
ਵੰਡ ਦੀ ਮੱਧਿਕਾ = 28.5
ਜੋ ਕਿ ਵਰਗ਼ ਅੰਤਰਾਲ 20 – 30 ਵਿੱਚ ਸਥਿਤ ਹੈ ।
∴ ਮੱਧਿਆ ਵਰਗ = 20 – 30
∴ l = 20 ; f = 20; cf = 5 + x; h= 10
ਸਾਰਣੀ ਤੋਂ ਸਪੱਸ਼ਟ ਹੈ ਕਿ 45 + x + y = 60
x + y = 60 – 45 = 15
x + y = 15 …(1)
ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਕੇ ਮੱਧਿਕਾ = l + \(\left\{\frac{\frac{n}{2}-c f}{f}\right\}\) × h
28.5 = 20 + \(\left\{\frac{30-(5+x)}{20}\right\}\) × 10
28.5 = 20 + \(\frac{30-5-x}{2}\)
28.5 = \(\frac{40+25-x}{2}\)
2(28.5) = 65 – x
57.0 = 65 – x
x = 65 – 57 = 8
∴ x = 8
x ਦਾ ਇਹ ਮੁੱਲੇ (1) ਵਿੱਚ ਭਰਨ ਤੇ 8 + y = 15
y = 15 – 8 = 7
∴ x ਅਤੇ y ਦਾ ਮੁੱਲ 8 ਅਤੇ 7 ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
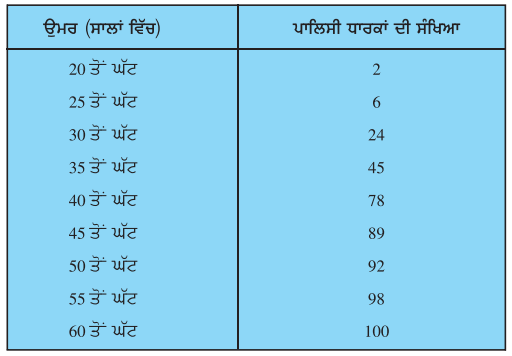
ਇੱਕ ਜੀਵਨ ਬੀਮਾ ਏਜੰਟ 100 ਪਾਲਿਸੀ ਧਾਰਕਾਂ ਦੀ | ਉਮਰ ਦੀ ਵੰਡ ਤੋਂ ਹੇਠ ਲਿਖੇ ਅੰਕੜੇ ਪ੍ਰਾਪਤ ਕਰਦਾ ਹੈ । | ਮੱਧਿਆ ਉਮਰ ਪਤਾ ਕਰੋ ਜੇਕਰ ਪਾਲਿਸੀ ਕੇਵਲ ਉਨ੍ਹਾਂ ਵਿਅਕਤੀਆਂ ਨੂੰ ਦਿੱਤੀ ਜਾਵੇ ਜਿਨ੍ਹਾਂ ਦੀ ਉਮਰ 18 ਸਾਲ ਜਾਂ । ਉਸ ਤੋਂ ਅਧਿਕ ਹੋਵੇ, ਪਰੰਤੂ 60 ਸਾਲ ਤੋਂ ਘੱਟ ਹੋਵੇ ।

ਹੱਲ:

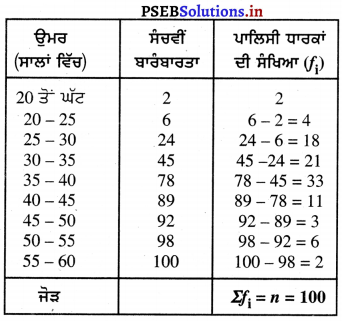
ਇੱਥੇ Σf_i = n = 100
ਤਾਂ \(\frac{n}{2}\) = \(\frac{100}{2}\) = 50, ਜੋ ਅੰਤਰਾਲ 35 – 40 ਵਿੱਚ ਸਥਿਤ ਹਨ ।
∴ ਮੱਧਕਾ ਵਰਗ = 35 – 40
∴ l = 35 ; n = 100 ; f = 33 ; cf = 45 ਅਤੇ h = 5
ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਕੇ, ਮੱਧਿਕਾ
= l + \(\left\{\frac{\frac{n}{2}-c f}{f}\right\}\) × h
= 35 + \(\left\{\frac{\frac{100}{2}-45}{33}\right\}\) × 5
= 35 + \(\frac{50-45}{33}\) × 5
= 35 + \(\frac{25}{33}\)
= 35 + 0.7575
= 35 +0.76 (ਲਗਭਗ) = 35.76
∴ ਮੱਧਿਕਾ ਉਮਰ 35.76 ਸਾਲ ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
ਇੱਕ ਪੌਦੇ ਦੀਆਂ 40 ਪੱਤਿਆਂ ਦੀ ਲੰਬਾਈ ਲਗਭਗ ਮਿਲੀਮੀਟਰ ਵਿੱਚ ਮਾਪੀ ਜਾਂਦੀ ਹੈ ਅਤੇ ਪ੍ਰਾਪਤ ਅੰਕੜਿਆਂ ਨੂੰ ਹੇਠਾਂ ਦਿੱਤੀ ਸਾਰਣੀ ਦੇ ਰੂਪ ਵਿੱਚ ਦਰਸਾਇਆ ਜਾਂਦਾ ਹੈ :

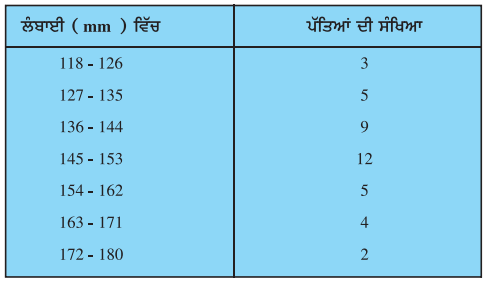
ਪੱਤਿਆਂ ਦੀ ਮੱਧਕਾ ਲੰਬਾਈ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਕਿਉਂਕਿ ਬਾਰੰਬਾਰਤਾ ਸਾਰਣੀ ਲਗਾਤਾਰ ਨਹੀਂ ਹੈ । ਇਸ ਲਈ ਇਸ ਨੂੰ ਪਹਿਲਾਂ ਲਗਾਤਾਰਤਾ ਵਰਗ ਅੰਤਰਾਲਾਂ ਵਿੱਚ ਬਦਲਣਾ ਪਵੇਗਾ,

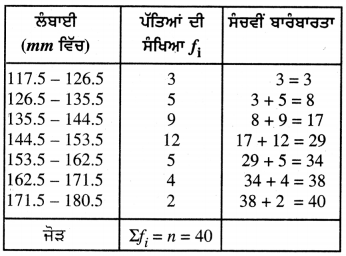
ਇੱਥੇ Σf_i = n = 40
ਤਾਂ, \(\frac{n}{2}\) = \(\frac{40}{2}\) = 20, ਜੋ ਅੰਤਰਾਲ 144.5 – 153.5 ਵਿੱਚ ਸਥਿਤ ਹੈ ।
∴ ਮੱਧਕਾ ਵਰਗ = 144.5 – 153.5
∴ l = 144.5 ; f = 12 ; cf = 17 ; h = 9
ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਦੇ ਹੋਏ,
ਮੱਧਿਆ = l + \(\left\{\frac{\frac{n}{2}-c f}{f}\right\}\) × h
ਮੱਧਿਆ = 144.5 + \(\left\{\frac{20-17}{12}\right\}\) × 9
= 144.5 + \(\frac{3×9}{12}\)
= 144.5 + 2.25 = 146.75
∴ ਪੱਤਿਆਂ ਦੀ ਮੱਧਿਕਾ ਲੰਬਾਈ 146.75 mm ਹੈ ।

ਪ੍ਰਸ਼ਨ 5.
ਹੇਠ ਲਿਖੀ ਸਾਰਣੀ 400 ਨਿਊਨ ਲੈਂਪਾਂ (lamp) ਦੇ ਜੀਵਨ ਕਾਲ (life time) ਨੂੰ ਦਰਸਾਉਂਦੀ ਹੈ :

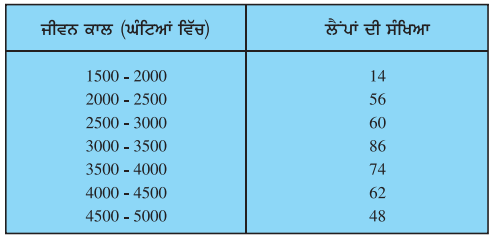
ਇੱਕ ਲੈਂਪ ਦਾ ਮੱਧਿਕਾ ਜੀਵਨ ਕਾਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:

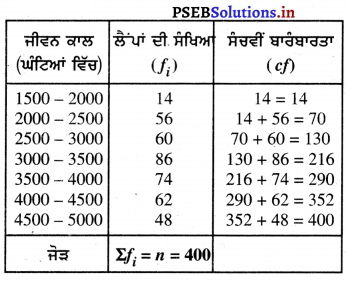
ਇੱਥੇ, Σf_i = n = 400
∴ \(\frac{n}{2}\) = \(\frac{400}{2}\) = 200 ; ਜੋ ਕਿ ਵਰਗ ਅੰਤਰਾਲ 3000 – 3500 ਵਿੱਚ ਸਥਿਤ ਹੈ ।
∴ ਮੱਧਿਆ ਵਰਗ = 3000 – 3500
l = 3000 ; n = 400 ; f = 86 ; cf = 130 ਅਤੇ h = 500
ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ,
ਮੱਧਕਾ = l + \(\left\{\frac{\frac{n}{2}-c f}{f}\right\}\) × h
ਮੱਧਿਕਾ = 3000 + \(\left\{\frac{\frac{400}{2}-130}{86}\right\}\) × 500
= 3000 + (\(\frac{200-130}{86}\) ) × 500
= 3000 + \(\frac{70×500}{86}\)
= 3000 + 406.9767441
= 3000 + 406.98 (ਲਗਭਗ
= 3406.98
∴ ਸੈਂਪ ਦਾ ਜੀਵਨਕਾਲ 3406.98 ਘੰਟੇ ਹੈ ।

ਪ੍ਰਸ਼ਨ 6.
ਇੱਕ ਸਥਾਨਕ ਟੈਲੀਫੋਨ ਡਾਇਰੈਕਟੀ ਤੋਂ 100 ਉੱਪ ਨਾਮ (surnames) ਦੀ ਸੂਚੀ ਲਈ ਗਈ ਅਤੇ ਉਨ੍ਹਾਂ ਵਿੱਚ ਵਰਤੇ ਗਏ ਅੰਗਰੇਜ਼ੀ ਵਰਣਮਾਲਾ ਦੇ ਅੱਖਰਾਂ ਦੀ ਸੰਖਿਆ ਦੀ ਹੇਠ ਲਿਖੀ ਬਾਰੰਬਾਰਤਾ ਵੰਡ ਪ੍ਰਾਪਤ ਹੋਈ :

ਉੱਪ-ਨਾਮਾਂ ਵਿਚ ਮੱਧਿ ਅੱਖਰਾਂ ਦੀ ਸੰਖਿਆ ਪਤਾ | ਕਰੋ । ਉੱਪ-ਨਾਮਾਂ ਵਿੱਚ ਮੱਧਮਾਨ, ਅੱਖਰਾਂ ਦੀ ਸੰਖਿਆ ਵੀ ਪਤਾ ਕਰੋ ਅਤੇ ਨਾਲ ਹੀ, ਉਪਨਾਮ ਦਾ ਬਹੁਲਕ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੱਧਕਾ ਲਈ

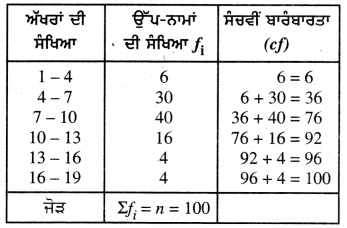
ਇੱਥੇ, Σf_i = n = 100
∴ \(\frac{n}{2}\) = \(\frac{100}{2}\) = 50, ਜੋ ਵਰਗ ਅੰਤਰਾਲ 7 – 10 ਵਿੱਚ ਹੈ।
∴ ਮੱਧਕਾ ਵਰਗ = 7 – 10
∴ l = 7; n = 100 ; f = 40 ; cf = 36 ਅਤੇ h = 3
ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ, ਮੱਧਿਕਾ = l + \(\left\{\frac{\frac{n}{2}-c f}{f}\right\}\) × h
= 7 + \(\left\{\frac{\frac{100}{2}-36}{40}\right\}\) × 3
= 7 + \(\left\{\frac{50-36}{40}\right\}\) × 3
= 7 + \(\frac{14×3}{40}\)
= 7 + \(\frac{21}{20}\)
= 7 + 1.05 = 8.05
ਮੱਧਿ ਅੱਖਰਾਂ ਦੀ ਸੰਖਿਆ 8.05 ਹੈ ।
ਮੱਧਮਾਨ ਲਈ ,

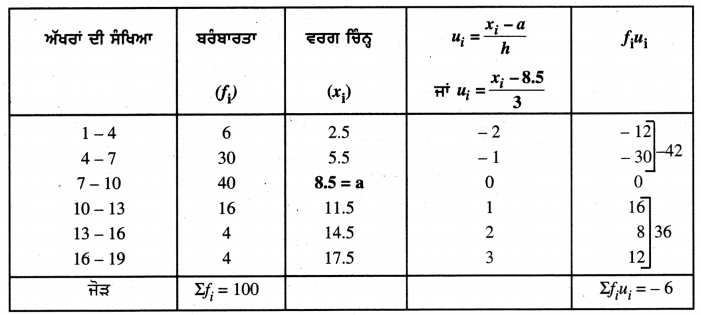
ਉਪਰੋਕਤ ਅੰਕੜਿਆਂ ਤੋਂ, ਕਾਲਪਨਿਕ ਮੱਧਮਾਨ (a) = 8.5
ਵਰਗ ਮਾਪ (h) = 3
∴ \(\bar{u}\) = \(\frac{\Sigma f_{i} u_{i}}{\Sigma f_{i}}\) = \(\frac{-6}{100}\) = -0.06
ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ, ‘ਤੇ, ਮੱਧਮਾਨ (\(\bar{u}\)) = a + h\(\bar{u}\)
\(\bar{x}\) = 8.5 + 3 (0.06) = 8.5 – 0.18 = 8.32
ਇਸ ਲਈ ਮੱਧਮਾਨ ਅੱਖਰਾਂ ਦੀ ਸੰਖਿਆ 8.32
ਬਹੁਲਕ ਲਈ
ਦਿੱਤੇ ਗਏ ਅੰਕੜਿਆਂ ਵਿਚ ਅਧਿਕਤਮ ਬਾਰੰਬਾਰਤਾ 40 ਹੈ ਅਤੇ ਸੰਗਤ ਅੰਤਰਾਲ 7 – 10 ਹੈ ।
∴ ਬਹੁਲਕ ਵਰਗ = 7 – 10
∴ l = 7; f₁ = 40 ; f₀ = 30 ; f₂ = 16 ਅਤੇ h = 3
ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ਤੇ,
ਬਹੁਲਕ = l + \(\left(\frac{f_{1}-f_{0}}{2 f_{1}-f_{0}-f_{2}}\right)\) × h
= 7 + \(\left(\frac{40-30}{2(40)-30-16}\right)\) × 3
= 7 + \(\frac{10}{80-46}\) × 3
= 7 + \(\frac{30}{34}\) = 7 + 0.882352941
=7 + 0.88 (ਲਗਭਗ)
= 7.88
∴ ਉੱਪਨਾਮਾਂ ਦਾ ਬਹੁਲਕ 7.88 ਅੱਖਰ ਹੈ

ਪ੍ਰਸ਼ਨ 7.
ਹੇਠ ਦਿੱਤੀ ਹੋਈ ਵੰਡ ਇੱਕ ਜਮਾਤ ਦੇ 30 ਵਿਦਿਆਰਥੀਆਂ ਦੇ ਵਜਨ (ਭਾਰ ਨੂੰ ਦਰਸਾਉਂਦੀ ਹੈ । ਵਿਦਿਆਰਥੀਆਂ ਦਾ ਮੱਧਕਾ ਭਾਰ ਪਤਾ ਕਰੋ ।

ਹੱਲ:

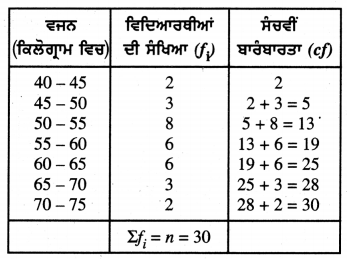
ਇੱਥੇ, Σf_i = n = 30
∴ \(\frac{n}{2}\) = \(\frac{30}{2}\) = 15; ਜੋ ਅੰਤਰਾਲ 55 – 60 ਵਿਚ ਸਥਿਤ ਹੈ
∴ ਮੱਧਕਾ ਵਰਗ = 55 – 60
∴ l = 55 ; n = 30; f = 6; cf = 13 ਅਤੇ h = 5
ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ਤੇ ਮੱਧਿਆ
ਮੱਧਕਾ = l + \(\left\{\frac{\frac{n}{2}-c f}{f}\right\}\) × h
ਮੱਧਿਕਾ = 55 + \(\left\{\frac{\frac{30}{2}-13}{6}\right\}\) × 5
= 55 + \(\left\{\frac{15-13}{6}\right\}\) × 5
= 55 + \(\frac{2×5}{6}\)
= 55 + \(\frac{5}{3}\)
= 55 + 1.6666
= 55 + 1.67 ਲਗਭਗ = 56.67
∴ ਮੱਧਿਕਾ ਭਾਰ 56.67 ਕਿਲੋਗ੍ਰਾਮ ਹੈ