Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 7 ਨਿਰਦੇਸ਼ ਅੰਕਜਿਮਾਇਤੀ Ex 7.1 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 10 Maths Chapter 7 ਨਿਰਦੇਸ਼ ਅੰਕਜਿਮਾਇਤੀ Exercise 7.1
ਪ੍ਰਸ਼ਨ 1.
ਬਿੰਦੂਆਂ ਦੇ ਹੇਠ ਦਿੱਤਿਆਂ ਜੋੜਿਆਂ ਦੀ ਵਿਚਕਾਰਲੀ ਦੂਰੀ ਪਤਾ ਕਰੋ :
(i) (2, 3) ; (4, 1)
(ii) (-5, 7) ; (-1, 3)
(iii) (a, b) ; (-a, – b).
ਹੱਲ:
(i) ਦਿੱਤੇ ਗਏ ਬਿੰਦੂ ਹੈਂ : (2, 3) ; (4, 1)
ਲੋੜੀਂਦੀ ਦੂਰੀ = \(\sqrt{(4-2)^{2}+(1-3)^{2}}\)
= \(\sqrt{4+4}\) = \(\sqrt {8}\) = 2\(\sqrt {2}\)
(ii) ਦਿੱਤੇ ਗਏ ਬਿੰਦੂ ਹਨ : (-5, 7) ; (-1, 3)
ਲੋੜੀਂਦੀ ਦੂਰੀ = \(\sqrt{(-1+5)^{2}+(3-7)^{2}}\)
= \(\sqrt{16+16}\) = \(\sqrt{32}\) =4\(\sqrt{2}\)
(iii) ਦਿੱਤੇ ਗਏ ਬਿੰਦੂ ਹਨ : (a, b); (-a,-b)
ਲੋੜੀਂਦੀ ਦੂਰੀ = \(\sqrt{(-a-a)^{2}+(-b-b)^{2}}\)
= \(\sqrt{(-2 a)^{2}+(-2 b)^{2}}\)
= \(\sqrt{4 a^{2}+4 b^{2}}\)
= 2\(\sqrt{a^{2}+b^{2}}\)
ਪ੍ਰਸ਼ਨ 2.
ਬਿੰਦੂਆਂ (0, 0) ਅਤੇ (36, 15) ਦੀ ਵਿਚਕਾਰਲੀ ਦੂਰੀ ਪਤਾ ਕਰੋ। ਕੀ ਤੁਸੀ ਹੁਣ ਭਾਗ 7.2 ਵਿੱਚ ਦਿੱਤੇ ਦੋਹਾਂ ਸ਼ਹਿਰਾਂ A ਅਤੇ B ਵਿਚਕਾਰਲੀ ਦੂਰੀ ਪਤਾ ਕਰ ਸਕਦੇ ਹੋ ?
ਹੱਲ:
ਦਿੱਤੇ ਗਏ ਬਿੰਦੂ ਹਨ :
A (0, 0) ਅਤੇ B (36, 15)
ਦੂਰੀ AB = \(\sqrt{(0-36)^{2}+(0-15)^{2}}\)
= \(\sqrt{1296+225}\) = \(\sqrt{1521}\)
= 39
ਭਾਗ 7.2 ਦੇ ਅਨੁਸਾਰ
ਬਿੰਦੂ A (0, 0) ਅਤੇ B (36, 15) ਚਿੱਤਰ ਵਿਚ – ਦਿਖਾਏ ਅਨੁਸਾਰ
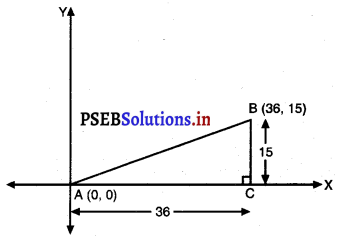
BC ⊥X-ਧੁਰੇ ਤੇ ਖਿੱਚੋ ।
ਹੁਣ ਸਮਕੋਣ ACB ਵਿੱਚ,
AB = \(\sqrt{A C^{2}+B C^{2}}\)
= \(\sqrt{(36)^{2}+(15)^{2}}\)
= \(\sqrt{1296+225}\) = \(\sqrt{1521}\)
= 39.
∴ ਬਿੰਦੂਆਂ ਵਿਚ ਲੋੜੀਂਦੀ ਦੂਰੀ 39 ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 3.
ਨਿਰਧਾਰਿਤ ਕਰੋ ਕਿ ਕੀ ਬਿੰਦੂ (1, 5), (2, 3) ਅਤੇ (-2, – 11) ਸਮਰੇਖੀ ਹਨ ।
ਹੱਲ:
ਦਿੱਤੇ ਗਏ ਬਿੰਦੂ ਹਨ : A (1, 5) ; B (2, 3) ਅਤੇ C (-2 – 11).
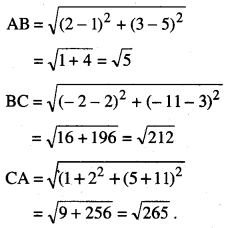
ਉਪਰੋਕਤ ਦੂਰੀਆਂ ਤੋਂ ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਕਿ ਕਿਸੇ ਦੋ ਦਾ ਜੋੜਫਲ ਤੀਸਰੇ ਦੇ ਬਰਾਬਰ ਨਹੀਂ ਹੈ । ਇਸ ਲਈ ਇਹ ਬਿੰਦੂ ਸਮਰੇਖੀ ਨਹੀਂ ਹਨ ।
ਪ੍ਰਸ਼ਨ 4.
ਜਾਂਚ ਕਰੋ ਕਿ ਕੀ ਬਿੰਦੂ (5, – 2) (6, 4) ਅਤੇ (7, -2) ਇੱਕ ਸਮਦੋਭੁਜੀ ਤ੍ਰਿਭੁਜ ਦੇ ਸਿਖਰ ਹਨ ।
ਹੱਲ:
ਦਿੱਤੇ ਗਏ ਬਿੰਦੂ ਹਨ A (3, – 2) ; B (6, 4) ਅਤੇ c (7, – 2).
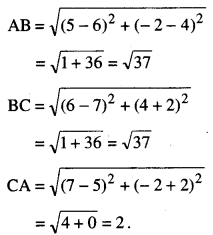
ਉਪਰੋਕਤ ਦੂਰੀ ਤੋਂ ਸਪੱਸ਼ਟ ਹੈ ਕਿ
AB = BC = \(\sqrt{37}\).
∴ ਦਿੱਤੇ ਗਏ ਬਿੰਦੂ ਸਮਦੋਭੁਜੀ ਤ੍ਰਿਭੁਜ ਦੇ ਸਿਖਰ ਹਨ ।
![]()
ਪ੍ਰਸ਼ਨ 5.
ਕਿਸੇ ਜਮਾਤ ਵਿੱਚ, ਚਾਰ ਮਿੱਤਰ ਬਿੰਦੂਆਂ A, B, C ਅਤੇ D ‘ਤੇ ਬੈਠੇ ਹੋਏ ਹਨ, ਜਿਸ ਤਰ੍ਹਾਂ ਕਿ ਚਿੱਤਰ ਵਿਚ ਦਰਸਾਇਆ ਗਿਆ ਹੈ । ਚੰਪਾ ਅਤੇ ਚਮੇਲੀ ਜਮਾਤ ਦੇ ਅੰਦਰ ਆਉਂਦੀਆਂ ਹਨ ਅਤੇ ਕੁਝ ਸਮਾਂ ਦੇਖਣ ਤੋਂ ਬਾਅਦ ਚੰਪਾ, ਚਮੇਲੀ ਨੂੰ ਪੁੱਛਦੀ ਹੈ, “ਕੀ ਤੂੰ ਨਹੀਂ ਸੋਚਦੀ ਕਿ ABCD ਇੱਕ ਵਰਗ ਹੈ ?” ਚਮੇਲੀ ਇਸ ਨਾਲ ਸਹਿਮਤ ਨਹੀਂ ਹੈ । ਦੂਰੀ ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਕੇ, ਦੱਸੋ ਕਿ ਇਹਨਾਂ ਵਿੱਚੋਂ ਕੌਣ ਸਹੀ ਹੈ ।
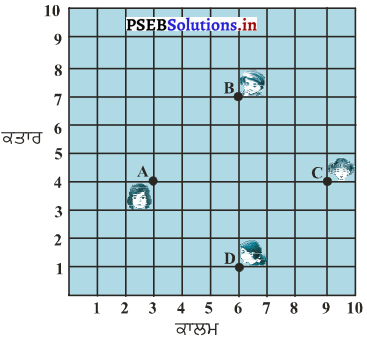
ਹੱਲ:
ਦਿੱਤੇ ਗਏ ਚਿੱਤਰ ਵਿਚ ਸਿਖਰ ਬਿੰਦੂ ਹਨ : A (3, 4) ; B (6, 7) ; C (9, 4) ਅਤੇ D (6, 1).
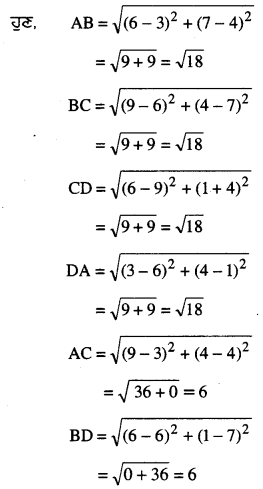
ਸਪੱਸ਼ਟ ਹੈ ਕਿ
AB = BC = CD = DA = \(\sqrt{18}\)
ਅਤੇ AC = BD = 6.
∴ ABCD ਇਕ ਵਰਗ ਬਣਦਾ ਹੈ ਚੰਪਾ ਦੀ ਸੋਚ ਸਹੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 6.
ਹੇਠਾਂ ਦਿੱਤੇ ਬਿੰਦੂਆਂ ਦੁਆਰਾ ਬਣਨ ਵਾਲੇ ਚਤੁਰਭੁਜ ਦੀ ਕਿਸਮ ਜੇਕਰ ਕੋਈ ਹੈ ਤਾਂ ਦੱਸੋ ਅਤੇ ਆਪਣੇ ਉੱਤਰ ਦਾ ਕਾਰਣ ਵੀ ਦੱਸੋ :
(i) (-1, -2), (1, 0), (-1, 2), (-3, 0)
(ii) (-3, 5), (3, 1), (0, 3), (-1, – 4)
(iii) (4, 5), (7, 6), (4, 3), (1, 2).
ਹੱਲ:
(i) ਦਿੱਤੇ ਗਏ ਬਿੰਦੂ ਹਨ : A (-1, – 2) ; B (1, 0) ; C (-1, 2) ਅਤੇ D (-3, 0).
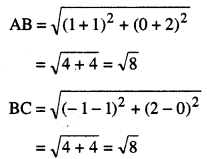
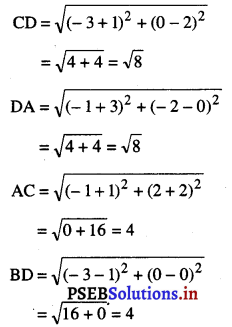
ਹੁਣ ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਕਿ
AB = BC = CD = DA = \(\sqrt{8}\)
AC = BD = 4.
∴ ਇਹ ਚਤੁਰਭੁਜ ABCD ਇੱਕ ਵਰਗ ਹੈ ।
(ii) ਦਿੱਤੇ ਗਏ ਬਿੰਦੂ ਹਨ : A (-3, 5); B (3, 1); (0, 3) ਅਤੇ D (-1, – 4)
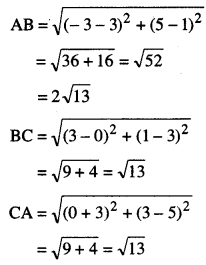
ਹੁਣ, BC + CA = \(\sqrt{13}\) + \(\sqrt{13}\)
= 2\(\sqrt{13}\) = AB
∴ A, B ਅਤੇ C ਇਕ ਰੇਖਾ ਵਿਚ ਹਨ ਅਤੇ A, B, C ਅਤੇ D ਚਤੁਰਭੁਜ ਨਹੀਂ ਬਣਾਉਂਦੇ ।
(iii) ਦਿੱਤੇ ਗਏ ਬਿੰਦੂ : A (4, 5) ; B (7, 6) ; C (4, 3) ਅਤੇ D (1, 2)
AB = \(\sqrt{(7-4)^{2}+(6-5)^{2}}\)
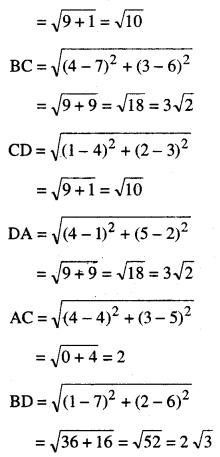
ਹੁਣ ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਕਿ
AB = CD ਅਤੇ BC = DA
ਅਤੇ AC ≠ BD.
∴ ਸਨਮੁਖ ਭੁਜਾਵਾਂ ਬਰਾਬਰ ਹਨ ਪਰ ਉਹਨਾਂ ਦੇ ਵਿਕਰਣ ਬਰਾਬਰ ਨਹੀਂ ਹਨ ।
∴ ਦਿੱਤੀ ਹੋਈ ਚਤੁਰਭੁਜ ABCD ਇਕ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 7.
x-ਧੁਰੇ ‘ਤੇ ਉਹ ਬਿੰਦੂ ਪਤਾ ਕਰੋ ਜੋ (2, – 5) ਅਤੇ (-2, 9) ਤੋਂ ਬਰਾਬਰ ਦੂਰੀ ‘ਤੇ ਹੈ।
ਹੱਲ:
ਮੰਨ ਲਓ ਲੋੜੀਂਦਾ ਬਿੰਦੂ ਹੈ P (x, 0) ਅਤੇ ਦਿੱਤੇ ਗਏ ਬਿੰਦੂ ਹਨ A (2, -5) ਅਤੇ B (-2, 9). ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ,
PA = PB
(PA)2 = (PB)2
(2 – x)2 + (-5 – 0)2 = (-2 – x)2 + (9 – 0)2
4 + x – 4x + 25 = 4 + x2 + 4x + 81
– 8x = 56
x = \(\frac{56}{8}\) = -7
∴ਲੋੜੀਂਦਾ ਬਿੰਦੂ (-7, 0) ਹੈ ।
ਪ੍ਰਸ਼ਨ 8
y ਦਾ ਉਹ ਮੁੱਲ ਪਤਾ ਕਰੋ ਜਿਸਦੇ ਲਈ ਬਿੰਦੂ P (2, – 3) ਅਤੇ Q (10, y) ਦੇ ਵਿਚਕਾਰ ਦੀ ਦੂਰੀ 10 ਇਕਾਈਆਂ ਹੈ ।
ਹੱਲ:
ਦਿੱਤੇ ਗਏ ਬਿੰਦੂ ਹਨ : P (2, – 3) ਅਤੇ Q (10, y)
PQ = \(\sqrt{(10-2)^{2}+(y+3)^{2}}\)
= \(\sqrt{64+y^{2}+9+6 y}\)
= \(\sqrt{y^{2}+6 y+73}\)
ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ, PQ = 10
\(\sqrt{y^{2}+6 y+73}\) = 10
y2 + 6y + 73 = 100
y2 + 6y – 27 = 0
y2 + 9y – 3y – 27 = 0
y (y + 9) – 3 (y + 9) = 0
(y +9) (y – 3) = 0.
y + 9 = 0 ਜਾਂ y – 3 =0
y = -9 ਜਾਂ y = 3
y = -9 ਅਤੇ 3
![]()
ਪ੍ਰਸ਼ਨ 9.
ਜੇਕਰ Q (0, 1) ਬਿੰਦੁਆਂ P (5, -3) ਅਤੇ R (x, 6) ਤੋਂ ਬਰਾਬਰ ਦੂਰੀ ‘ਤੇ ਹੈ ਤਾਂਝ ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ । ਦੂਰੀਆਂ QR ਅਤੇ PR ਵੀ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਦਿੱਤੇ ਗਏ ਬਿੰਦੂ ਹਨ : Q (0, 1) ;
P (5, – 3) ਅਤੇ R (x, 6)
QP = \(\sqrt{(5-0)^{2}+(-3-1)^{2}}\)
= \(\sqrt{25+16}\) = \(\sqrt{41}\)
QR = \(\sqrt{(x-0)^{2}+(6-1)^{2}}\)
= \(\sqrt{x^{2}+25}\)
ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ
QP = QR
\(\sqrt{41}\) = \(\sqrt{x^{2}+25}\)
41 = x2 + 25 ਜਾਂ x2 = 16
x = ±\(\sqrt{16}\) = ±4.
ਜਦੋਂ = 4 ਤਾਂ R (4, 6).
QR = \(\sqrt{(4-0)^{2}+(6-1)^{2}}\)
= \(\sqrt{16+25}\) = \(\sqrt{41}\)
PR = \(\sqrt{(4-5)^{2}+(6+3)^{2}}\)
= \(\sqrt{1=81}\) = \(\sqrt{82}\)
ਜਦੋਂ = -4 ਤਾਂ R (-4, 6).
QR = \(\sqrt{(-4-0)^{2}+(6-1)^{2}}\)
= \(\sqrt{16+25}\) = \(\sqrt{41}\)
PR = \(\sqrt{(-4-5)^{2}+(6+3)^{2}}\)
= \(\sqrt{81+81}\) = \(\sqrt{162}\).
ਪ੍ਰਸ਼ਨ 10.
x ਅਤੇ y ਵਿੱਚ ਇੱਕ ਅਜਿਹਾ ਸੰਬੰਧ ਪਤਾ ਕਰੋ ਕਿ ਬਿੰਦੂ (x, y) ਬਿੰਦੂਆਂ (3, 6) ਅਤੇ (-3, 4) ਤੋਂ ਬਰਾਬਰ ਦੀ ਦੂਰੀ ‘ਤੇ ਹੋਵੇ ।
ਹੱਲ:
ਮੰਨ ਲਓ ਲੋੜੀਂਦਾ ਬਿੰਦੂ P (x, y) ਹੈ ।
ਦਿੱਤੇ ਗਏ ਬਿੰਦੂ ਹਨ A (3, 6) ਅਤੇ B (-3, 4)

ਦੋਵੇਂ ਪਾਸੇ ਵਰਗ ਕਰਨ ਤੇ
x2 + y2 – 6x – 12y +45
= x2 + y2 + 6x – 8y + 25
– 12x – 4y + 20 = 0
3x + y – 5 = 0
ਲੋੜੀਂਦਾ ਸੰਬੰਧ ਹੈ ।
