PSEB 10th Class Maths Solutions Chapter 7 ਨਿਰਦੇਸ਼ ਅੰਕਜਿਮਾਇਤੀ Ex 7.2

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 7 ਨਿਰਦੇਸ਼ ਅੰਕਜਿਮਾਇਤੀ Ex 7.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 7 ਨਿਰਦੇਸ਼ ਅੰਕਜਿਮਾਇਤੀ Exercise 7.2

ਪ੍ਰਸ਼ਨ 1.
ਉਸ ਬਿੰਦੁ ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਪਤਾ ਕਰੋ ਜੋ ਬਿੰਦੂਆਂ (-1,7) ਅਤੇ (4,-3) ਨੂੰ ਮਿਲਾਉਣ ਵਾਲੇ ਰੇਖਾਖੰਡ ਨੂੰ 2: 3 ਦੇ ਅਨੁਪਾਤ ਵਿਚ ਵੰਡਦਾ ਹੈ ।
ਹੱਲ:
ਮੰਨ ਲਉ P (x, y) ਲੋੜੀਂਦਾ ਬਿੰਦੂ ਹੈ, ਜੋ ਦਿੱਤੇ ਗਏ ਬਿੰਦੁਆਂ A(-1, 7) ਅਤੇ B (4, – 3) ਨੂੰ ਮਿਲਾਉਣ ਵਾਲੇ ਰੇਖਾਖੰਡ ਨੂੰ 2 : 3 ਵਿਚ ਵੰਡਦਾ ਹੈ ।

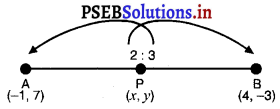
∴ x = \(\frac{2 \times 4+3 \times-1}{2+3}\) = \(\frac{8-3}{5}\) = \(\frac{5}{5}\) = 1
ਅਤੇ y = \(\frac{2 \times-3+3 \times 7}{2+3}\) = \(\frac{-6+21}{5}\) = \(\frac{15}{5}\) = 3
∴ ਲੋੜੀਂਦਾ ਬਿੰਦੂ ਹੈ (1, 3)

ਪ੍ਰਸ਼ਨ 2.
ਬਿੰਦੂਆਂ (4, – 1) ਅਤੇ (-2, – 3) ਨੂੰ ਮਿਲਾਉਣ ਵਾਲੇ ਰੇਖਾਖੰਡ ਨੂੰ ਤਿੰਨ ਸਮਾਨ ਭਾਗ (Trisection) ਕਰਨ ਵਾਲੇ ਬਿੰਦੂਆਂ ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ P (x₁, y₁) ਅਤੇ Q (x₂, y₂) ਲੋੜੀਂਦੇ ਬਿੰਦੂ ਹਨ ਜੋ ਬਿੰਦੁ A (4, – 1) ਅਤੇ (-2, – 3) ਨੂੰ ਮਿਲਾਉਣ ਵਾਲੇ ਰੇਖਾਖੰਡ ਦੇ ਤਿੰਨ ਸਮਾਨ ਭਾਗ ਕਰਦੇ ਹਨ । ਭਾਵ P (x₁, y₁) AB ਨੂੰ 1 : 2 ਦੇ ਅਨੁਪਾਤ ਵਿਚ ਅਤੇ Q (x₂, y₂) AB ਨੂੰ 2 : 1 ਦੇ ਅਨੁਪਾਤ ਵਿਚ ਵੰਡਦਾ ਹੈ ।

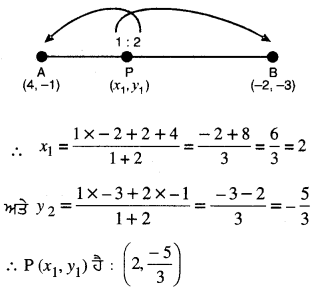
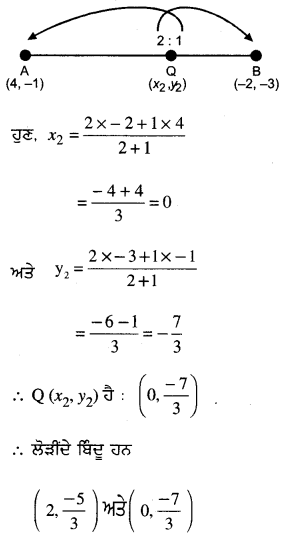
ਪ੍ਰਸ਼ਨ 3.
ਤੁਹਾਡੇ ਸਕੂਲ ਵਿਚ ਖੇਡਣ ਦੇ ਮੁਕਾਬਲੇ ਕਰਵਾਉਣ ਦੇ ਲਈ ਇਕ ਆਇਤਾਕਾਰ ਮੈਦਾਨ ABCD ਵਿੱਚ, ਚੂਨੇ ਦੇ ਨਾਲ 1m ਦੀ ਦੂਰੀ ‘ਤੇ ਕਤਾਰਾਂ ਬਣਾਈਆਂ ਗਈਆਂ ਹਨ । AD ਦੇ ਅਨੁਸਾਰ ਆਪਸ ਵਿਚ 1m ਦੀ ਦੂਰੀ ਤੇ 100 ਗਮਲੇ ਰੱਖੇ ਗਏ ਹਨ, ਜਿਸ ਤਰ੍ਹਾਂ ਕਿ ਚਿੱਤਰ ਵਿਚ ਦਰਸਾਇਆ ਗਿਆ ਹੈ । ਨਿਹਾਰਿਕਾ ਦੂਸਰੀ ਕਤਾਰ ਵਿੱਚ AD ਦੇ \(\frac{1}{4}\) ਭਾਗ ਦੇ ਬਰਾਬਰ ਦੀ ਦੂਰੀ ਤੇ ਦੌੜਦੀ ਹੈ ਅਤੇ ਉੱਥੇ ਇੱਕ ਹਰਾ ਝੰਡਾ ਗੱਡ ਦਿੰਦੀ ਹੈ । ਪ੍ਰੀਤ ਅੱਠਵੀਂ ਕਤਾਰ ਵਿਚ AD ਦੇ \(\frac{1}{5}\) ਭਾਗ ਦੇ ਬਰਾਬਰ ਦੀ ਦੂਰੀ ਤੇ ਦੌੜਦੀ ਹੈ ਅਤੇ ਉੱਥੇ | ਇੱਕ ਲਾਲ ਝੰਡਾ ਗੱਡ ਦਿੰਦੀ ਹੈ । ਦੋਹਾਂ ਝੰਡਿਆਂ ਦੀ | ਵਿਚਕਾਰਲੀ ਦੁਰੀ ਕੀ ਹੈ ? ਜੇਕਰ ਰਸ਼ਿਮ ਨੂੰ ਇਕ ਨੀਲਾ ਝੰਡਾ ਇਹਨਾਂ ਦੋਹਾਂ ਝੰਡਿਆਂ ਨੂੰ ਮਿਲਾਉਣ ਵਾਲੇ ਰੇਖਾਖੰਡ ਦੇ ਠੀਕ ਅੱਧੀ ਦੂਰੀ (ਵਿਚਕਾਰ) ‘ਤੇ ਗੱਡਣਾ ਹੋਵੇ ਤਾਂ ਉਸਨੂੰ ਆਪਣਾ ਝੰਡਾ ਕਿੱਥੇ ਗੱਡਣਾ ਚਾਹੀਦਾ ਹੈ ?

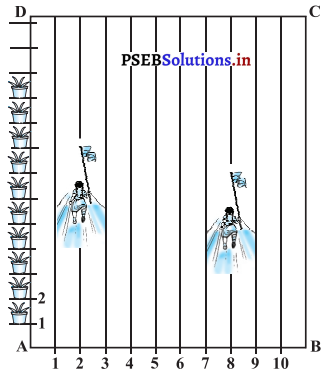
ਹੱਲ:
ਦਿੱਤੇ ਗਏ ਚਿੱਤਰ ਵਿਚ A ਨੂੰ ਮੂਲ ਬਿੰਦੂ ਮੰਨ ਲੈਂਦੇ ਹਨ | AB ਨੂੰ ਧੁਰਾ ਅਤੇ AD ਨੂੰ y-ਧੁਰਾ ਮੰਨ ਲੈਣ ਤੇ ਹਰੇ ਝੰਡੇ ਦੀ ਸਥਿਤੀ
= ਨਿਹਾਰਿਕਾ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਦੂਰੀ
= ਨਿਹਾਰਿਕਾ ਦੂਸਰੀ ਕਤਾਰ ਵਿਚ AD ਦੇ \(\frac{1}{4}\) ਭਾਗ ਦੇ ਬਰਾਬਰ ਦੀ ਦੂਰੀ ਦੌੜਦੀ ਹੈ
= \(\frac{1}{4}\) × 100 = 25m
∴ ਹਰੇ ਝੰਡੇ ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ (2, 25) ਹੈ ।
ਹੁਣ, ਲਾਲ ਝੰਡੇ ਦੀ ਸਥਿਤੀ
= ਪ੍ਰੀਤ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਦੂਰੀ
= ਪੀਤ ਅੱਠਵੀਂ ਕਤਾਰ ਵਿਚ AD ਦੇ \(\frac{1}{5}\)
ਭਾਗ ਦੇ ਬਰਾਬਰ ਦੂਰੀ ਦੌੜਦੀ ਹੈ
= \(\frac{1}{5}\) × 100 = 20m.
∴ ਹਰੇ ਅਤੇ ਲਾਲ ਝੰਡੇ ਦੇ ਵਿੱਚ ਦੀ ਦੂਰੀ
= \(\sqrt{(8-2)^{2}+(20-25)^{2}}\)
= \(\sqrt {36+25}\) = \(\sqrt {61}\) m .
ਨੀਲੇ ਝੰਡੇ ਦੀ ਸਥਿਤੀ
= ਹਰੇ ਝੰਡੇ ਅਤੇ ਲਾਲ ਝੰਡੇ ਨੂੰ ਮਿਲਾਉਣ ਵਾਲੇ ਰੇਖਾਖੰਡ ਦਾ ਅੱਧਾ
= (\(\frac{2+8}{2}\), \(\frac{25+20}{2}\))
= (5, 22.5).
ਨੀਲਾ ਝੰਡਾ 5ਵੀਂ ਕਤਾਰ ਵਿਚ ਅਤੇ AD ਤੋਂ 22.5 ਮੀ. ਦੀ ਦੂਰੀ ਉੱਤੇ ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
ਬਿੰਦੂਆਂ (-3, 10) ਅਤੇ (6, -8) ਨੂੰ ਮਿਲਾਉਣ ਵਾਲੇ ਰੇਖਾਖੰਡ ਨੂੰ ਬਿੰਦੂ (-1, 6) ਕਿਸ ਅਨੁਪਾਤ ਵਿਚ ਵੰਡਦਾ ਹੈ ।
ਹੱਲ:
ਮੰਨ ਲਉ ਬਿੰਦੁ P (-1, 6) ਬਿੰਦੁ A (-3, 10) | ਅਤੇ B (6, – 8) ਨੂੰ ਮਿਲਾਉਣ ਵਾਲੇ ਰੇਖਾਖੰਡ | ਨੂੰ K : 1 ਦੇ ਅਨੁਪਾਤ ਵਿਚ ਵੰਡਦਾ ਹੈ ।

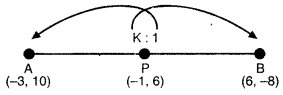
∴ -1 = \(\frac{6 \times K-3 \times 1}{K+1}\)
ਜਾਂ -K – 1 = 6K – 3
-K – 6K = – 3 + 1
– 7K = -2
ਜਾਂ K = \(\frac{2}{7}\)
∴ K : 1 = \(\frac{2}{7}\) = 2 : 7
∴ ਲੋੜੀਂਦਾ ਅਨੁਪਾਤ 2 : 7. ਹੈ ।

ਪ੍ਰਸ਼ਨ 5.
ਬਿੰਦੁਆਂ A (1, – 5) ਅਤੇ B (- 4, 5) ਨੂੰ ਮਿਲਾਉਣ ਵਾਲੇ ਰੇਖਾਖੰਡ ਨੂੰ 7-ਧੁਰਾ ਕਿਸ ਅਨੁਪਾਤ ਵਿੱਚ ਵੰਡਦਾ ਹੈ । ਇਸ ਵੰਡਣ ਵਾਲੇ ਬਿੰਦੂ ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਵੀ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ x-ਧੁਰੇ ਉੱਤੇ ਲੋੜੀਂਦਾ ਬਿੰਦੂ P (x, 0) ਹੈ ਜੋ A (1, – 5) ਅਤੇ B (-4, 5) ਨੂੰ ਮਿਲਾਉਣ ਵਾਲੇ ਰੇਖਾਖੰਡ ਨੂੰ K : 1 ਦੇ ਅਨੁਪਾਤ ਵਿਚ ਵੰਡਦਾ ਹੈ ।

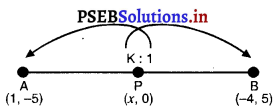
P ਦਾ y ਨਿਰਦੇਸ਼ ਅੰਕ ਹੈ
0 = \(\frac{5 \times K+(-5) \times 1}{K+1}\)
0 = \(\frac{5 K-5}{K+1}\)
5K – 5 = 0
5K = 5
K = 1
∴ ਲੋੜੀਂਦਾ ਅਨੁਪਾਤ K : 1 = 1 : 1
ਹੁਣ, P ਦਾ x ਨਿਰਦੇਸ਼ ਅੰਕ ਹੈ
x = \(\frac{-4 \times K+1 \times 1}{K+1}\)
K = 1, ਦਾ ਮੁੱਲ ਰੱਖਣ ਤੇ
x = \(\frac{-4 \times 1+1 \times 1}{1+1}\) = \(\frac{-4+1}{2}\)
x = \(-\frac{3}{2}\)
∴ ਲੋੜੀਂਦਾ ਬਿੰਦੂ ਹੈ : (\(-\frac{3}{2}\), 0)

ਪ੍ਰਸ਼ਨ 6.
ਜੇਕਰ ਬਿੰਦੂ (1, 2) ; (4, y) ; (x, 6) ਅਤੇ (3, 5) ਇਸੇ ਕੂਮ ਵਿਚ ਲੈਣ ‘ਤੇ ਇੱਕ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਦੇ ਸਿਖਰ ਹੋਣ ਤਾਂ 1 ਅਤੇ y ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ABCD ਦੇ ਸਿਖਰ ਹਨ : A (1, 2) ; B (4, y) ; C (x, 6) ਅਤੇ D (3, 5)
ਪਰ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਦੇ ਵਿਕਰਣ ਇਕ ਦੂਜੇ ਨੂੰ ਸਮਦੁਭਾਜਿਤ ਕਰਦੇ ਹਨ :
ਸਥਿਤੀ I : ਜਦੋਂ E, A (1, 2) ਅਤੇ C (x, 6) ਦਾ ਮੱਧ ਬਿੰਦੁ ਹੋਵੇ ।
∴ E ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਹਨ
E = (\(\frac{x+1}{2}\), \(\frac{6+2}{2}\))
E = (\(\frac{x+1}{2}\), 4) …(1)

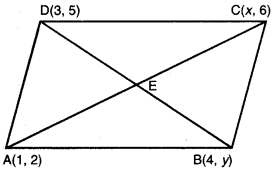
ਸਥਿਤੀ II : ਜਦੋਂ E, B (4, y) ਅਤੇD (3, 5) ਦਾ ਮੱਧ ਬਿੰਦੁ ਹੋਵੇ ।
E ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਹਨ :
E = (\(\frac{3+4}{2}\), \(\frac{5+y}{2}\))
E = (\(\frac{7}{2}\), \(\frac{5+y}{2}\)) …(2)
ਪਰ (1) ਅਤੇ (2) ਵਿਚ E ਦੇ ਮੁੱਲ ਸਮਾਨ ਹਨ ਇਸ ਲਈ ਨਿਰਦੇਸ਼ ਅੰਕਾਂ ਦੀ ਤੁਲਨਾ ਕਰਨ ਤੇ
\(\frac{x+1}{2}\) = \(\frac{7}{2}\) ਅਤੇ 4 = \(\frac{5+y}{2}\)
x + 1 = 7 ਅਤੇ 8 = 5 + y
x = 6 ਅਤੇ y = 3
∴ x ਅਤੇ y ਦੇ ਮੁਲ ਹਨ 6 ਅਤੇ 3 ਹਨ ।

ਪ੍ਰਸ਼ਨ 7.
ਬਿੰਦੂ A ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਪਤਾ ਕਰੋ, ਜਿੱਥੇ AB ਇੱਕ | ਚੱਕਰ ਦਾ ਵਿਆਸ ਹੈ । ਜਿਸਦਾ ਕੇਂਦਰ (2, – 3) ਹੈ ਅਤੇ B ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ (1, 4) ਹਨ ।
ਹੱਲ:
ਮੰਨ ਲਉ A ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ (x, y) ਹੈ ।
ਪਰ, ਵਿਆਸ ਦੇ ਸਿਖਰਾਂ ਦਾ ਮੱਧ ਬਿੰਦੂ ਕੇਂਦਰ ਹੁੰਦਾ ਹੈ ।

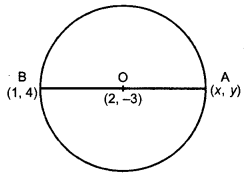
∴ O, A (x, y) ਅਤੇ B (1, 4) ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ ।
∴ (\(\frac{x+1}{2}\), \(\frac{y+4}{2}\)) = (2, -3)
ਤੁਲਨਾ ਕਰਨ ‘ਤੇ,
\(\frac{x+1}{2}\) = 2 ਅਤੇ \(\frac{y+4}{2}\) = -3
x + 1 = 4 ਅਤੇ y + 4 = – 6
x = 4 – 1 ਅਤੇ y = – 6 – 4
x = 3 ਅਤੇ y = – 10
∴ ਲੋੜੀਂਦਾ ਬਿੰਦੂ ਹੈ (3 – 10)

ਪ੍ਰਸ਼ਨ 8.
ਜੇਕਰ ਅਤੇ B ਕੁਮਵਾਰ (-2, -2) ਅਤੇ (2, 4) | ਹੋਣ ਤਾਂ P ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਪਤਾ ਕਰੋ ਤਾਂ ਕਿ AP = \(\frac{3}{7}\)AB ਹੋਵੇ ਅਤੇ P ਰੇਖਾਖੰਡ AB ‘ਤੇ ਸਥਿਤ ਹੋਵੇ ।
ਹੱਲ:
ਮੰਨ ਲਉ ਲੋੜੀਂਦਾ ਬਿੰਦੂ ਹੈ P(x, y).
ਨਾਲ ਹੀ AP = \(\frac{3}{7}\)AB … ਦਿੱਤਾ ਹੈ।
ਪਰ PB = AB – AP
= AB – \(\frac{3}{7}\)AB = (\(\frac{7-3}{7}\))AB
= \(\frac{4}{7}\)AB
∴ \(\frac{\mathrm{AP}}{\mathrm{PB}}=\frac{\frac{3}{7} \mathrm{AB}}{\frac{4}{7} \mathrm{AB}}=\frac{3}{4}\)
∴ P ਦਿੱਤੇ ਗਏ ਬਿੰਦੂ A ਅਤੇ B ਨੂੰ 3:4 ਦੇ ਅਨੁਪਾਤ ਵਿਚ ਵੰਡਦਾ ਹੈ ।

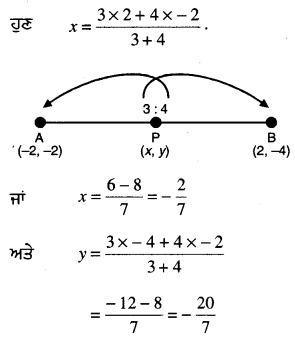
∴ ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਹਨ : (\(-\frac{2}{7}\), \(-\frac{20}{7}\)

ਪ੍ਰਸ਼ਨ 9.
ਬਿੰਦੂਆਂ A (-2, 2) ਅਤੇ B (2, 8) ਨੂੰ ਮਿਲਾਉਣ ਵਾਲੇ ਰੇਖਾਖੰਡ AB ਨੂੰ ਚਾਰ ਬਰਾਬਰ ਭਾਗਾਂ ਵਿਚ ਵੰਡਣ ਵਾਲੇ ਬਿੰਦੂਆਂ ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ C, D ਅਤੇ E ਲੋੜੀਂਦੇ ਬਿੰਦੂ ਹਨ ਜੋ ਬਿੰਦੂ A ( 2, 2) ਅਤੇ B (2, 8) ਨੂੰ ਮਿਲਾਉਣ ਵਾਲੇ ਰੇਖਾਖੰਡ ਨੂੰ ਚਾਰ ਬਰਾਬਰ ਭਾਗਾਂ ਵਿੱਚ ਵੰਡਦੇ ਹਨ ।
ਤਾਂ D, A ਅਤੇ B ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ ; C, A ਅਤੇ D ਦਾ | ਮੱਧ ਬਿੰਦੂ ਹੈ; E, D ਅਤੇ B ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ ਤਾਂ ਕਿ
AC = CD = DE = EB
ਹੁਣ, A ਅਤੇ B ਦਾ ਮੱਧ ਬਿੰਦੂ ( D ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ)
= (\(\frac{-2+2}{2}\), \(\frac{2+8}{2}\) = (0, 5)
A ਅਤੇ D ਦਾ ਮੱਧ ਬਿੰਦੂ (C ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ)
(\(\frac{-2+0}{2}\), \(\frac{-2+5}{2}\) = (1, \(\frac{7}{2}\)
D ਅਤੇ B ਦਾ ਮੱਧ ਬਿੰਦੂ (E ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ)
(\(\frac{2+0}{2}\), \(\frac{8+5}{2}\)) = (-1, \(\frac{13}{2}\))
∴ ਲੋੜੀਂਦੇ ਬਿੰਦੂ ਹਨ :
(0, 5), (-1, \(\frac{7}{2}\)) ਅਤੇ (1, \(\frac{13}{2}\))

ਪ੍ਰਸ਼ਨ 10.
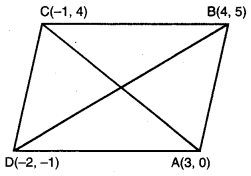
ਇਕ ਸਮਚਤੁਰਭੁਜ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ | ਜਿਸਦੇ ਸਿਖਰ, ਇਸੇ ਕੂਮ ਵਿਚ (3, 0), (4, 5), (-1, 4) ਅਤੇ (-2, – 1) ਹਨ ।
ਸੰਕੇਤ : ਸਮਚਤੁਰਭੁਜ ਦਾ ਖੇਤਰਫਲ = \(\frac{1}{2}\) (ਉਸਦੇ ਵਿਕਰਣਾਂ ਦਾ ਗੁਣਨਫਲ)]
ਹੱਲ:
ਮੰਨ ਲਉ ਸਮਚਤੁਰਭੁਜ ABCD ਦੇ ਸਿਖਰ ਬਿੰਦੂ ਹਨ : A (3, 0) ; B (4, 5) ; C (- 1, 4) ਅਤੇ D (-2, – 1).
ਵਿਕਰਣ AC = \(\sqrt{(-1-3)^{2}+(4-0)^{2}}\)
= \(\sqrt {16+16}\) = \(\sqrt {32}\)
= 4\(\sqrt {2}\)

ਵਿਕਰਣ BD
BD = \(\sqrt{(-2-4)^{2}+(-1-5)^{2}}\)
= \(\sqrt {36+36}\) = \(\sqrt {72}\)
= 6\(\sqrt {2}\)
∴ ਸਮਚਤੁਰਭੁਜ ABCD ਦਾ ਖੇਤਰਫਲ
= \(\frac{1}{2}\) × AC × BD
= [\(\frac{1}{2}\) × 4\(\sqrt {2}\) × 6\(\sqrt {2}\)]
= (\(\frac{1}{2}\) × 24 × 2)
= 24 ਵ.ਮੀ.
∴ ਸਮਚਤੁਰਭੁਜ ਦਾ ਖੇਤਰਫਲ 24 ਵ.ਮੀ. ਹੈ ।