Bhagya

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 5 Continuity and Differentiability Ex 5.4 Textook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 5 Continuity and Differentiability Ex 5.4

Question 1.
\(\frac{e^{x}}{\sin x}\)

Solution.
Let y = \(\frac{e^{x}}{\sin x}\)

By using the quotient rule, we get

\(\frac{d y}{d x}\) = \(\frac{\sin x \frac{d}{d x}\left(e^{x}\right)-e^{x} \frac{d}{d x}(\sin x)}{\sin ^{2} x}\)

= \(\frac{\sin x \cdot\left(e^{x}\right)-e^{x} \cdot(\cos x)}{\sin ^{2} x}\)

= \(\frac{e^{x}(\sin x-\cos x)}{\sin ^{2} x}\), x ≠ nπ, n ∈ Z.

Question 2.
e^sin-1 x.
Solution.
Let y = e^sin-1 x
By using the chain rule, we get

Question 3.
e^x3
Solution.
Let y = e^x3
By using the chain rule, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\) (e^x3)

= e^x3 . \(\frac{d}{d x}\) (x³)

= e^x3 . 3x²
= 3x² e^x3

Question 4.
sin(tan^-1 e^-x
Solution.
Let y = sin(tan^-1 e^-x
By using the chain rule, we get

Question 5.
log (cos e^x)
Solution.
Let y = log (cos e^x)
By using the chain rule, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\) [log (cos e^x)]

= \(\frac{1}{\cos e^{x}}\) . \(\frac{d}{d x}\) (cos e^x)

= \(\frac{1}{\cos e^{x}}\) . (- sin e^x) . \(\frac{d}{d x}\) (e^x)

= \(\frac{-\sin e^{x}}{\cos e^{x}}\) . e^x

= – e^x tan e^x, e^x ≠ (2n + 1) \(\frac{\pi}{2}\), n ∈ N.

Question 6.
\(e^{x}+e^{x^{2}}+\ldots+e^{x^{5}}\)
Solution.
\(e^{x}+e^{x^{2}}+\ldots+e^{x^{5}}\)
By using the chain rule, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\) (\(e^{x}+e^{x^{2}}+\ldots+e^{x^{5}}\))

= \(\frac{d}{d x}\) (e^x ) + \(\frac{d}{d x}\) (e^x2) + \(\frac{d}{d x}\) (e^x3) + \(\frac{d}{d x}\) (e^x4) + \(\frac{d}{d x}\) (e^x5)

= e^{x + [ex2 . \(\frac{d}{d x}\) (x2)] + [ ex3 . \(\frac{d}{d x}\) (x3)] + [ex4 . \(\frac{d}{d x}\) (x4)] + [ex5 . \(\frac{d}{d x}\) (x5)]}

= e^x + (e^x2 × 2x) + (e^x3 × 3x²) + (e^x4 × 4x³) + (e^x5 × 5x⁴)

= e^x + 2x e^x2 + 3x² e^x3 + 4x³ e^x4 + 5x⁴ e^x5

Question 7.
\(\sqrt{e^{\sqrt{x}}}\), x > 0
Solution.
Let y = \(\sqrt{e^{\sqrt{x}}}\)
Then, y² = e^√x
On differentiating w.r.t x, we get
y² = e^√x
⇒ 2y \(\frac{d y}{d x}\) = e^√x (√x)

⇒ 2y \(\frac{d y}{d x}\) = e^√x \(\frac{1}{2} \cdot \frac{1}{\sqrt{x}}\)

⇒ \(\frac{d y}{d x}=\frac{e^{\sqrt{x}}}{4 y \sqrt{x}}\)

⇒ \(\frac{d y}{d x}=\frac{e^{\sqrt{x}}}{4 \sqrt{e^{\sqrt{x}}} \sqrt{x}}\)

⇒ \(\frac{d y}{d x}=\frac{e^{\sqrt{x}}}{4 \sqrt{x e^{\sqrt{x}}}}\), x > 0

Question 8.
log (log x), x > 1
Solution.
Let y = log (log x)
By using the chain rule, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\) [log (log x)]
= \(\frac{1}{\log x} \cdot \frac{d}{d x}\) (log x)

= \(\frac{1}{\log x} \cdot \frac{1}{x}=\frac{1}{x \log x}\), x > 1.

Question 9.
\(\frac{\cos x}{\log x}\), x > 0
Solution.
Let y = \(\frac{\cos x}{\log x}\)
By using quotient rule, we get
\(\frac{d y}{d x}=\frac{\frac{d}{d x}(\cos x) \times \log x-\cos x \times \frac{d}{d x}(\log x)}{(\log x)^{2}}\)

= \(\frac{-\sin x \log x-\cos x \times \frac{1}{x}}{(\log x)^{2}}\)

= \(\frac{-[x \log x \sin x+\cos x]}{x(\log x)^{2}}\), x > 0.

Question 10.
cos (log x + e^x), x > 0
Solution.
Let y = cos (log x + e^x)
By using chain rule, we get
\(\frac{d y}{d x}\) = – sin (log x + e^x) + \(\frac{d}{d x}\) (log x + e^x)
= – sin (log x + e^x) . [\(\frac{d}{d x}\) (log x) + \(\frac{d}{d x}\) (e^x)]
= – sin (log x + e^x) . (\(\frac{1}{x}\) + e^x)
= – (\(\frac{1}{x}\) + e^x) sin (log x + e^x).

Punjab State Board PSEB 11th Class Chemistry Book Solutions Chapter 1 Some Basic Concepts of Chemistry Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Chemistry Chapter 1 Some Basic Concepts of Chemistry

PSEB 11th Class Chemistry Guide Some Basic Concepts of Chemistry InText Questions and Answers

Question 1.
Calculate the molecular mass of the following:
(i) H₂O (ii)CO₂ (iii) CH₄
Answer:
(i) H₂O
The molecular mass of water (H20)
= (2 x Atomic mass of hydrogen) + (1 x Atomic mass of oxygen)
= [2(1.008 u) +1(16.00 u)]
= 2.016u +16.00u = 18.016 u=18.02u

(ii) CO₂
The molecular mass of carbon dioxide (CO₂)
= (1 x Atomic mass of carbon) + (2 x Atomic mass of oxygen)
= [1(12.011u) + 2(16.00u)]
= 12.011u + 32.00u = 44.01u

(iii) CH₄
The molecular mass of methane (CH₄)
= (1 x Atomic mass of carbon) + (4 x Atomic mass of hydrogen)
– [1(12.011u) + 4(1.008u)]
= 12.011u + 4.032u = 16.043u

Question 2.
Calculate the mass per cent of different elements present in sodium sulphate (Na₂SO₄).
Answer:
The molecular formula of sodium sulphate is Na₂SO₄
Molar mass of Na₂SO₄ = 2 x Atomic mass of Na + 1 x Atomic mass of S + 4 x Atomic mass of O
= [(2 x 23.0) + (1 x 32.066) + (4 x 16.00)]
= 46.0 + 32.066 + 64.00 = 142.066 g
Mass per cent of sodium

Question 3.
Determine the empirical formula of an oxide of iron which has 69.9% iron and 30.1% dioxygen by mass.
Answer:

Question 4.
Calculate the amount of carbon dioxide that could be produced when
(i) 1 mol of carbon is burnt in air
(ii) 1 mole of carbon is burnt in 16g of dioxygen
(iii) 2 moles of carbon are burnt in 16g of dioxygen
Answer:

∵ 32.0g of O₂ produce 44.0 g of CO₂
∵ 16.0 g of O₂ produce = \(\frac{44}{32}\) x 16 = 22.0 g of CO₂
Amount of CO₂produced = 22.0g
(iii) Amount of CO₂produced when 2 moles (= 24 g) of C are burnt in 16.0g (limited amount ) of O₂ = 22.0g

Question 5.
Calculate the mass of sodium acetate (CH₃COONa) required to make 500mL of 0.375 molar aqueous solution. Molar mass of sodium acetate is 82.0.245 g mol^-1.
Answer:
0.375M aqueous solution of sodium acetate = 1000mL of solution containing 0.375 moles of sodium actate
∴ Number of moles of sodium acetate in 500 mL.
= \(\frac{0.375}{1000}\) x 500 = 0.1875 mole.
Molar mass of sodium acetate = 82.0245 g mol^-1
∴ Required mass of sodium acetate
= 82.0245 g mol^-1 x 0.1875 mole
= 15.38 g

Question 6.
Calculate the concentration of nitric acid in moles per litre in a sample which has a density, 1.41 gmLT1 and the mass per cent of nitric acid in it being 69%.
Answer:
Mass percent of nitric acid in the sample = 69%
Thus, 100 g of sample contains 69 g of nitric acid
Molar mass of nitric acid (HNO₃)
= {1 +14 + 3(16)} g mol^-1
= 1 +14 + 48 = 63 g mol^-1
∴ Number of moles in 69 g of HNO₃

Question 7.
How much copper can be obtained from 100 g of copper sulphate (CuSO₄)?
Answer:
1 mole of CuSO₄ contains 1 mole of copper.
Molar mass of CuSO₄
= (63.5) + (32.00) + 4(16.00)
= 63.5 + 32.00 + 64.00 = 159.5 g mol^-1
159.5 g of CuSO₄ contains = 63.5 g of copper
=> 100 g of CuSO₄ contains = \(\frac{63.5 \times 100 \mathrm{~g}}{159.5}\) = 39.81g
∴ Mass of copper that can be obtained from 100 g of CuSO₄ = 39.81 g

Question 8.
Determine the molecular formula of an oxide of iron in which the mass per cent of iron and oxygen are 69.9 and 30.1 respectively.
Answer:

Question 9.
Calculate the atomic mass (average) of chlorine using the following data:

	% Natural Abundance	Molar Mass
35cl	75.77	34.9689
37Cl	24.23	36.9659

Answer:
The average atomic mass of chlorine

= 26.4959 + 8.9568 = 35.4527
∴ The average atomic mass of chlorine = 35.4527

Question 10.
In three moles of ethane (C₂H₆), calculate the following:
(i) Number of moles of carbon atoms.
(ii) Number of moles of hydrogen atoms.
(iii) Number of molecules of ethane.
Answer:
(i) 1 mole of C₂H₆ contains 2 moles of carbon atoms.
∴ 3 moles of C₂H₆ will contain = 2 x 3 = 6 moles of carbon atoms
(ii) 1 mole of C₂H₆ contains 6 moles of hydrogen atoms.
∴ 3 moles of C₂H₆ will contain =3 x 6 = 18 moles of hydrogen atoms
(iii) 1 mole of C₂H₆ contains 6.022 x 10²³ molecules of ethane.
∴ 3 moles of C₂H₆ will contain = 3 x 6.022 x 10²³
= 18.066 x 10²³ molecules of ethane

Question 11.
What is the concentration of sugar (C₁₂H₂₂O₁₁) in mol L^-1 if 20 g of sugar are dissolved in enough water to make a final volume up to 2 L?
Answer:
Molar mass of sugar (C₁₂H₂₂O₁₁)
= 12 x 12 + 22 x 1 +11 x 16 = 342 g mol^-1
Molar concentration = \(\frac{\text { Moles of solute }}{\text { Volume of solution in L }}=\frac{0.0585}{2 \mathrm{~L}}\)
= 0.0293 mol L^-1 = 0.0293 M

Question 12.
If the density of methanol is 0.793 kg L^-1, what is its volume needed for making 2.5 L of its 0.25 M solution?
Answer:
Final volume, V₂ = 2.5 L
Final molarity, M₂ = 0.25 M
Density of methanol = 0.793 kg L^-1
Molarity of initial solution M₁ = ?
Initial volume, V₁ = ?
Molar mass of methanol (CH₃OH) = (1 x 12) + (4 x 1) + (1 x 16)
= 32 g mol^-1 = 0.032 kg mol^-1
Molarity of methanol solution, M₁ = \(\frac{0.793 \mathrm{~kg} \mathrm{~L}^{-1}}{0.032 \mathrm{~kg} \mathrm{~mol}^{-1}}\) = 24.78 mol L^-1
Applying,
M₁V₁ = M₂V₂
(24.78 mol L^-1)V₁ = (2.5L) (0.25mol L^-1)
V₁ = 0.02522 L
V₁ = 25.22 mL

Question 13.
Pressure is determined as force per unit area of the surface. The SI unit of pressure, pascal is as shown below :
1 Pa= IN m^-2
If mass of air at sea level is 1034 g cm-2, calculate the pressure in pascal.
Answer:
Pressure is defined as force acting per unit area of the surface.
i.e, P = F/A

= 101332.0 Nm^-2 [1N = 1kg ms^-2]
∴ Pressure = 1.01332 x 10⁵

Question 14.
What is the SI unit of mass? How is it defined?
Answer:
The SI unit of mass is kilogram (kg).
1 kilogram is defined as the mass equal to the mass of the international prototype of kilogram.

Question 15.
Match the following prefixes with their multiples :

	Prefixes	Multiples
(i)	micro	106
(ii)	deca	109
(iii)	mega	10-6
(iv)	giga	10-15
(v)	femto	10

Answer:

	Prefixes	Multiples
(i)	micro	10-6
(ii)	deca	10
(iii)	mega	106
(iv)	giga	109
(v)	femto	10-15

Question 16.
What do you mean by significant figures?
Answer:
The number of significant figures in a given data is the number of all certain digits plus one uncretain digit.
For example, if 15.6 mL is the result of an experiment, then 15 is certain while 6 is uncertain, and the total number of significant figures are 3.

Question 17.
A sample of drinking water was found to he severely contaminated with chloroform, CHC13, supposed to he carcinogenic in nature. The level of contamination was 15 ppm (by mass).
(i) Express this in per cent by mass.
(ii) Determine the molarity of chloroform in the water sample.
Answer:
(i) ∵ 10⁶ g of solution contains 15 g of CHCl₃
∴ 1 g of solution contains = \(\frac{15}{10^{6}}\) g of CHCl₃
100 g of solution contains = \(\frac{15}{10^{6}}\) x 10² = 15 x 10^-4 g of CHCl₃
∴ Percent by mass = 0.0015%

(ii) Molar mass of CHCl₃ = 12 +1 + 3 x 35.5 = 119.5 g mol^-1
0.0015% means 15 x 10^-4 g chloroform is present in 100 g sample.
Molarity = \(\frac{W \times 1000}{m \times \text { Volume of sample }}\)
[For water density = 1 g cm^-3; so mass = volume]
= \(\frac{15 \times 10^{-4} \times 1000}{119.5 \times 100}\)
= 1.25 x 10^-4 M

Question 18.
Express the following in the scientific notation :
(i) 0.0048
(ii) 234000
(iii) 8008
(iv) 500.0
(v) 6.0012
Answer:
(i) 0.0048 = 4.8 x 10^-3
(ii) 234000 = 2.34 x 10⁵
(iii) 8008 = 8.008 x 10³
(iv) 500.0 = 5.00 x 10²
(v) 6.0012 = 6.0012 x 10⁰

Question 19.
How many significant figures are present in the following?
(i) 0.0025
(ii) 208
(iii) 5005
(iv) 126000
(v) 500.0
(vi) 2.0034
Answer:
(i) 0.0025
There are 2 significant figures,
(ii) 208
There are 3 significant figures.
(iii) 5005
There are 4 significant figures.
(iv) 126000
There are 3 significant figures.
(v) 500.0
There are 4 significant figures.
(vi) 2.0034
There are 5 significant figures.

Question 20.
Round up the following upto three significant figures :
(i) 34.216 (ii) 10.4107
(iii) 0.04597 (iv) 2808
Answer:
(i) 34.2
(ii) 10.4
(iii) 0.0460
(iv) 2810

Question 21.
The following data are obtained when dinitrogen and dioxygen react together to form different compounds :

	Mass of dinitrogen	Mass of dioxygen
(i)	14 g	16 g
(ii)	14 g	32 g
(iii)	28 g	32 g
(iv)	28 g	80 g

(a) Which law of chemical combination is obeyed by the above experimental data? Give its statement.
(b) Fill in the blanks in the following conversions :
(i) 1 km = ………mm = ………pm
(ii) 1 mg = ………kg = ………ng
(iii) 1 mL = ………L = ………dm³
Answer:
On fixing the mass of dinitrogen as 14 g, then the masses of dioxygen which combines with the fixed mass (= 14 g) of dinitrogen will be 16, 32, 16, 40 which are in the simple whole number ratio of 1 : 2 : 1 : 2.5 or 2 : 4 : 2 : 5.

(a) Law of multiple proportions : This law was proposed by Dalton in 1803. According to this law, if tvo elements can combine to form two or more than two compounds, the masses of one element that combine with a fixed mass of the other element are in the ratio of small whole numbers.

Question 22.
If the speed of light is 3.0 x 10⁸ms^-1, calculate the distance covered by light in 2.00 ns.
Answer:
According to the question,
Time taken to cover the distance = 2.00 ns
2ns = 2.00 x 10^-9s [∵ 1ns = 10^-9s]
Speed of light = 3.0 x 10⁸ms^-1
Distance travelled by light in 2.00 ns
= Speed of light x Time taken
= (3.0 x 10⁸ms^-1)(2.00 x 10^-9s) = 6.00 x 10^-1 m = 0.6 m

Question 23.
In a reaction A + B₂ → AB₂
Identify the limiting reagent, if any, in the following reaction mixtures.
(i) 300 atoms of A + 200 molecules of B
(ii) 2 mol A + 3 mol B
(iii) 100 atoms of A + 100 molecules of B
(iv) 5 mol A + 2.5 mol B
(v) 2.5 mol A + 5 mol B
Answer:
(i) According to the given reaction, 1 atom of A reacts with 1 molecule of B.
Thus, 300 atoms of A will react with 200 molecules of B thereby, leaving 100 atoms of A unused. Hence, B is the limiting reagent.
(ii) According to the given reaction, 1 mol of A reacts with 1 mol of B. Thus, 2 mol of A will react with 2 mol of B. As a result, 1 mol of B will not be consumed. Hence, A is the limiting reagent.
(iii) According to the given reaction, 1 atom of A combines with 1 molecule of B. Thus, all 100 atoms of A will combine with all 100 molecules of B. Hence, the mixture is stoichiometric where no limiting reagent is present.
(iv) 1 mol of atom A combines with 1 mol of molecule B. Thus, 2.5 mol of B will combine only 2.5 mol of A. As a result, 2.5 mol of A will be left as such. Hence, B is the limiting reagent.
(v) 1 mol of atom A combines with 1 mql of molecule B. Thus, 2.5 mol of A will combine only 2.5 mol of B and the remaining 2.5 mol of B will be left as such. Hence, A is the limiting reagent.

Question 24.
Dinitrogen and dihydrogen react with each other to produce ammonia according to the following chemical equation: N2(g)+H2(g) → 2NH₃(g)
(i) Calculate the mass of ammonia produced if 2.00 x 10³ g dinitrogen reacts with 1.00 x 10³ g of dihydrogen.
(ii) Will any of the two reactants remain unreacted?
(iii) If yes, which one and what would be its mass?
On balancing the given chemical equation,
Answer:

⇒ 28 g N₂ reacts with 6 g H₂; 1 g N₂ reacts with \(\frac{6}{28}\) g H₂;
2.0 x 10³ g of N2 will react with \(\frac{2000 \times 6}{28}\) = 428.6 g of H₂.
Hence, N₂ is the limiting reagent.
∵ 28 g N2 produces 34 g NH3 34
∴ 1 g N2 produces \(\frac{34}{28}\) g NH₃
2.00 x 10³ f N₂ will produce = \(\frac{34 g}{28 g}\) x 2000g = 2428.57 g NH₃
(ii) N₂ is the limiting reagent and H₂ is the excess reagent. Hence, H₂ will remain unreacted.
(iii) Mass of H₂ remain unreacted = 1.00 x 10³ g – 428.6 g = 571.43 g

Question 25.
How are 0.50 mol Na₂CO₃ and 0.50 M Na₂CO₃ different?
Answer:
Molar mass of Na₂CO₃ = (2 x 23) +12.00 + (3 x 16) = 106 g mol^-1
Now, 1 mol Na₂CO₃ means 106 g Na₂CO₃
∴ 0.5 mol Na₂CO₃ = x °-5 mo1 Na₂C0₃ = 53 g Na₂C0₃
⇒ 0.50 M Na₂CO₃ = 0.50 mol/L Na₂CO₃
Hence, 0.50 mol Na₂CO₃ means 53 g Na₂CO₃ is present in 1 L of the solution.

Question 26.
If ten volumes of dihydrogen gas reacts with five volumes of dioxygen gas, how many volumes of water vapour would be produced?
Answer:
Reaction of dihydrogen with dioxygen can be written as:

Now, 2 volumes of dihydrogen react with 1 volume of O₂ to produce 2 volumes of water vapour.
Hence, 10 volumes of dihydrogen will react with 5 volumes of dioxygen to produce 10 volumes of water vapour.

Question 27.
Convert the following into basic units :
(i) 28.7 pm
(ii) 15.15 pm
(iii) 25365 mg
Answer:
(i) 28.7 pm :
∵ 1 pm = 10^-12 m
∴ 28.7pm = 28.7 x 10^-12 m = 2.87 x 10^-11 m

(ii) 15.15pm
∵ 1 pm =10 12 m
∴ 15.15 pm = 15.15 x 10^-12 m = 1.515 x 10^-11 m

(iii) 25365 mg :
1 mg = 10^-3 g
25365 mg = 2.5365 x 10⁴ x 10^-3 g
= 2.5365 x 10¹ g
Since,
1 g = 10^-3 kg
2.5365 x 10¹ g = 2.5365 x 10¹ x 10^-3 kg.
∴ 25365 mg = 2.5365 x 10^-2 kg

Question 28.
Which one of the following will have largest number of atoms?
(i) 1 g Au(s)
(ii) 1 g Na(s)
(iii) 1g Li (s)
(iv) 1 g of Cl₂(g)
Answer:
(i) 1 g Au (s) = \(\frac{1}{197}\) mol atoms of Au (s)
= \(\frac{6.022 \times 10^{23}}{197}\) mol atoms of Au (s)
= 3.06 x 10²¹ atoms of Au (s)

(ii) 1 g Na (s) = \(\frac{1}{23}\) mol atoms of Na (s)
= \(\frac{6.022 \times 10^{23}}{23}\) atoms of Na (s)
= 0.262 x 10²³ atoms of Na (s)
= 26.2 x 10²¹ atoms of Na (s)

(iii) 1 g Li (s) = \(\frac{1}{7}\) mol atoms of Li (s)
= \(\frac{6.022 \times 10^{23}}{23}\) atoms of Li (s)
= 86.0 x 1021 atoms of Li (s)

(iv) 1 gCl₂ (g) = \(\frac{1}{71}\) mol molecules of Cl₂ (g)
= \(\frac{6.022 \times 10^{23}}{71}\) molecules of Cl? (g)
= 0.0848 x 10²³ molecules of Cl₂ (g)
= 8.48 x 10²¹ molecules of Cl₂ (g)
(one molecule of Cl₂ contains two atoms of Cl)
Number of atoms of Cl = 2 x 8.48 x 10²¹ = 16.96 x 10²¹ atoms of Cl
Hence, 1 g of Li (s) has largest number of atoms.

Question 29.
Calculate the molarity of a solution of ethanol in water in which the mole fraction of ethanol is 0.040 (assume the density of water to be one).
Answer:
Mole fraction of ethanol (C₂H₅OH)

Number of moles present in 1L water;
ⁿH₂O = \(\)
ⁿH₂O = 55.55 moles
Substituting the value of ⁿH₂O in eq (i).
\(\frac{n_{\mathrm{C}_{2} \mathrm{H}_{5} \mathrm{OH}}}{n_{\mathrm{C}_{2} \mathrm{H}_{5} \mathrm{OH}}+55.55}\) = 0.040
ⁿC₂H₅OH – 0.040ⁿC₂H₅OH = 2.222mol
0.96 ⁿC₂H₅OH = 2.222 mol ⁿC₂H₅OH = \(\frac{2.222}{0.96}\) mol.
ⁿC₂H₅OH = 2.314 mol
∴ Molarity of solution = \(\frac{2.314 \mathrm{~mol}}{1 \mathrm{~L}}\) = 2.314M

Question 30.
What will be the mass of one 12C atom in g?
Answer:
1 mol of carbon atoms = 6.022 x 10²³ atoms of carbon = 12 g of carbon
∴ Mass of one ¹²C atom = \(\frac{\text { Atomic mass of } \mathrm{C}}{\text { Avogadro’s number }}=\frac{12 \mathrm{~g}}{6.022 \times 10^{23}}\)
= 1.993 x 10^-23 g

Question 31.
How many significant figures should be present in the answer of the following calculations?
(i) \(\frac{0.02856 \times 298.15 \times 0.112}{0.5785}\)
(ii) 5 x 5.364
(iii) 0.0125 + 0.7864 + 0.0215
Answer:
\(\frac{0.02856 \times 298.15 \times 0.112}{0.5785}\)
Least precise number of calculation = 0.112
Number of significant figures in the answer = Number of significant figures in the least precise number = 3 /*
(ii) 5 x 5.364
Least precise number of calculation = 5.364
Number of significant figures in the answer = Number of significant figures in 5.364 = 4
(iii) 0.0125 + 0.7864 + 0.0215
Since the least number of decimal places in each term is four, the number of significant figures in the answer is also 4.

Question 32.
Use the data given in the following table to calculate the molar mass of naturally occurring argon isotopes :

Isotope	Isotopic molar mass	Abundance
36 Ar	35.96755 g mol-1	0.337%
38 Ar	37.96272 g mol-1	0.063%
40 Ar	39.9624 g mol-1	99.600%

Answer:
Molar mass of argon

= 0.121 + 0.024 + 39.802 g mol^-1 = 39.947 g mol^-1

Question 33.
Calculate the number of atoms in each of the following
(i) 52 moles of Ar (ii) 52 u of He (iii) 52 g of He.
Answer:
(i) ∵ 1 mol of Ar = 6.022 x 10²³ atoms of Ar
∴ 52 moles of Ar = 52 x 6.022 x 10²³ atoms of Ar
= 3.131 x 10²⁵ atoms

(ii) ∵ 1 atom of He = 4 u of He
Or, 4 u of He = 1 atom of He
∴ 1 u of He = 1/4 atom of He
∴ 52 u of He = 52/4 atoms of He = 13 atoms

(iii) ∵ 4 g of He = 6.022 x 10²³ atoms
6022 1023 52
∴ 52 g of He = \(\frac{6.022 \times 10^{23} \times 52}{4}\) = 7.8286 x 10²⁴ atoms

Question 34.
A welding fuel gas contains carbon and hydrogen only. Burning a small sample of it in oxygen gives 3.38 g carbon dioxide, 0.690 g of water and no other products. A volume of 10.0 L (measured at STP) of this welding gas is found to weigh 11.6 g. Calculate (i) empirical formula, (ii) molar mass of the gas, and (iii) molecular formula.
Answer:
(i) 44 g CO₂ = 12 g carbon
3.38 g CO₂ = 12/44 x 3.38g = 0.9218 g carbon
18 g H₂O = 2g hydrogen
0.690 g H₂O = 2/18 x 0.690 g = 0.0767 g hydrogen
Total mass of compound = 0.9218+0.0767 = 0.9985 g (because compound contains only carbon and hydrogen)
% of C in the compound = \(\frac{0.9218}{0.9985}\) x 100 = 92.32
% of H in the compound = \(\frac{0.0767}{0.9985}\) x 100 = 7.68
Calculation for Empirical Formula

Hence, empirical formula = CH
(ii) Calculation for molar mass of the gas
10.0 L of the given gas at STP weigh = 11.6 g
∴ 22.4 L of the given gas at STP will weigh = \(\frac{11.6 \times 22.4}{10}\) = 25.984 g
Molar mass = 25.984 = 26 g mol^-1
(iii) Empirical formula mass (CH) =12 + 1 = 13
∴ n = \(\frac{\text { Molecular mass }}{\text { Empirical formula mass }}=\frac{26}{13}\) = 2
Hence, molecular formula = n x CH = 2 x CH = C₂H₂

Question 35.
Calcium carbonate reacts with aqueous HC1 to give CaCl₂ and CO₂ according to the reaction,
CaC0₃(s) + 2 HCl(aq) -» CaCl₂(aq) + C0₂(g) + H₂O(l) What mass of CaC0₃ is required to react completely with 25 mL of 0.75 M HC1?
Answer:
The given reaction is
CaC0₃(s) + 2HCl(aq) → CaCl₂(aq) + C0₂(g) + H₂0(l)
Let us find out the weight of HCl present in 25 mL of 0.75 M HCl
1000 mL of 1.0 M HCl contains = 36.5 g
25 mL of 0.75 M HCl contains = \(\frac{36.5}{1000}\) x 25 x 0.75
= 0.6844 g of HCl
According to the equation;
73 g of HCl [2(1 + 35.5)] reacts with 100.0 g of CaC0₃
0.6844 g of HCl reacts with = \(\frac{100}{73}\) x 0.6844 = 0.94 g of CaC0₃

Question 36.
Chlorine is prepared in the laboratory by treating manganese dioxide (MnO₂) with aqueous hydrochloric acid according to the reaction
4HCl(oq) + MnO₂(s) > 2H₂O(l) + MnCl₂(aq) + Cl₂(g)
How many grams of HCl react with 5.0 g of manganese dioxide?
Answer:

According to the balanced chemical equation,
∵ 87 g of MnO₂ react with 4 x 36.5 g HCl
∴ 5 g of MnO₂ will react \(\frac{4 \times 36.5 \times 5}{87}\) = 8.39 g HCl

Punjab State Board PSEB 12th Class Physical Education Book Solutions ਬੈਡਮਿੰਟਨ (Badminton) Game Rules.

ਬੈਡਮਿੰਟਨ (Badminton) Game Rules – PSEB 12th Class Physical Education

ਬੈਡਮਿੰਟਨ ਦਾ ਇਤਿਹਾਸ
(History of Badminton)

ਬੈਡਮਿੰਟਨ ਸ਼ਬਦ ਦੀ ਉਤਪੱਤੀ, ਗਲਾਉਸੇਸਟਰ ਸ਼ਾਇਰ (ਇੰਗਲੈਂਡ) ਵਿਚ ਇਕ ਐਸਟੇਟ, ‘ਬੈਡਮਿੰਟਨ’ ਸ਼ਹਿਰ ਦੇ ਨਾਂ ਤੋਂ ਹੋਇਆ ਹੈ । 1873 ਵਿਚ, ਪਹਿਲੇ ਬੈਡਮਿੰਟਨ ਕਲੱਬ ਦਾ ਆਰੰਭ ਇੰਗਲੈਂਡ ਵਿਚ ਹੋਇਆ ਸੀ । ਜਦਕਿ, ਇਸ ਤਰ੍ਹਾਂ ਦਾ ਵਿਸ਼ਵਾਸ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ਕਿ ਇਸ ਤਰ੍ਹਾਂ ਦਾ ‘ਬੈਟੇਡੋਕ’ ਨਾਮ ਦਾ ਇਕ ਖੇਡ, ਆਧੁਨਿਕ ਯੁੱਗ ਤੋਂ ਪਹਿਲਾਂ-ਚੀਨ ਦਾ ਇਕ ਭਾਗ ਸੀ ।

ਭਾਰਤ ਵਿਚ ਫਿਰ ਇਸ ਖੇਡ ਦਾ ਵਿਕਾਸ ਸੈਨਿਕ ਅਧਿਕਾਰੀਆਂ ਦੁਆਰਾ ਕੀਤਾ ਗਿਆ ਅਤੇ ਪੁਨੇ ਸ਼ਹਿਰ ਦੇ ਨਾਮ ‘ਤੇ ਇਸ ਨੂੰ ਪੁਨਾ ਕਿਹਾ ਗਿਆ। ਇੰਗਲੈਂਡ ਦੀ ਬੈਡਮਿੰਟਨ ਐਸੋਸੀਏਸ਼ਨ ਦਾ ਗਠਨ 1893 ਵਿਚ ਹੋਇਆ ਸੀ । ਅੰਤਰ ਰਾਸ਼ਟਰੀ ਬੈਡਮਿੰਟਨ ਫੈਡਰੇਸ਼ਨ ਦਾ ਗਠਨ 1934 ਵਿਚ ਹੋਇਆ | ਭਾਰਤ ਵਿਚ ਇਹ ਖੇਡ ਦੁਸਰੇ ਵਿਸ਼ਵ ਯੁੱਧ ਦੇ ਬਾਅਦ ਲੋਕਪ੍ਰਿਯ ਹੋਇਆ | ਭਾਰਤ ਦੀ ਬੈਡਮਿੰਟਨ ਐਸੋਸੀਏਸ਼ਨ ਦਾ ਗਠਨ 1935 ਵਿਚ ਹੋਇਆ । ਜਦਕਿ, ਪਹਿਲਾਂ ਨੈਸ਼ਨਲ ਬੈਡਮਿੰਟਨ ਚੈਂਪੀਅਨਸ਼ਿਪ 1936 ਵਿਚ ਹੋਈ । ਬੈਡਮਿੰਟਨ 1972 ਮਿਊਨਿਖ ਉਲੰਪਿਕ ਅਤੇ 1988 ਸੀਓਲ ਉਲੰਪਿਕ ਵਿਚ ਇਕ ਪ੍ਰਦਰਸ਼ਨੀ ਖੇਡ ਦੇ ਰੂਪ ਵਿਚ ਉਨ੍ਹਾਂ ਦਾ ਹਿੱਸਾ ਰਹੀ । ਬਾਰਸੀਲੋਨਾ ਦੇ 1992 ਉਲੰਪਿਕ ਖੇਡਾਂ ਵਿਚ ਇਹ ਇਕ ਪਦਕ ਖੇਡ ਬਣੀ ।

ਯਾਦ ਰੱਖਣ ਯੋਗ ਗੱਲਾਂ
(Tips to Remember)

1. ਡਬਲਜ਼ (Doubles) ਦੇ ਲਈ ਬੈਡਮਿੰਟਨ ਕੋਰਟ ਦਾ ਆਕਾਰ : 13.40 × 6.10 ਮੀ. ਜਾਂ 44’× 20 ਫੁੱਟ
2. ਸਿੰਗਲਜ਼ (Singles) ਦੇ ਲਈ ਬੈਡਮਿੰਟਨ ਕੋਰਟ ਦਾ ਆਕਾਰ : 13.40 × 5.18 ਮੀ. ਜਾਂ 44′ × 17′ ਫੁੱਟ
3. ਨੈੱਟ ਦੀ ਚੌੜਾਈ : 760 ਮਿ.ਮੀ. (76 ਸੈਂ. ਮੀ.).
4. ਵਿਚਕਾਰ ਤੋਂ ਨੈੱਟ ਦੀ ਉੱਚਾਈ : 1.524 ਮੀ.
5. ਪੋਸਟਸ (Posts) ਤੋਂ ਨੈੱਟ ਦੀ ਉੱਚਾਈ : 1.550 ਮੀ.
6. ਕੋਰਟ ਦਾ ਆਕਾਰ : ਆਇਤਾਕਾਰ ।
7. ਰੈਕਟ ਦਾ ਨਾਪ : ਲੰਬਾਈ 680 ਮਿ.ਮੀ. × ਚੌੜਾਈ 230 ਮਿ.ਮੀ.
8. ਸ਼ਟਲ ਦਾ ਭਾਰ : 4,73 ਗ੍ਰਾਮ ਤੋਂ 5.50 ਗ੍ਰਾਮ
9. ਸ਼ਟਲ ਦੇ ਪੱਖਾਂ ਦੀ ਸੰਖਿਆ : 14 ਤੋਂ 16
10. ਪੰਖਾਂ ਦੀ ਲੰਬਾਈ : 62 ਮਿ.ਮੀ. ਤੋਂ 70 ਮਿ.ਮੀ.
11. ਬੈਂਕ ਗੈਲਰੀ ਦੀ ਚੌੜਾਈ : 2′ – ” ( 76 ਮਿ.ਮੀ.)
12. ਸਾਈਡ ਗੈਲਰੀ ਦੀ ਚੌੜਾਈ : 1′ – 6″ ( 46 ” “)
13. ਮੱਧ ਤੋਂ ਸ਼ਾਰਟ ਸਰਵਿਸ ਦੀਆਂ ਰੇਖਾਵਾਂ : 6′ – 6″ (1.98 ਮੀ.)
14. ਅਧਿਕਾਰੀਆਂ ਦੀ ਸੰਖਿਆ : ਅੰਪਾਇਰ – 1, ਸਰਵਿਸ ਅੰਪਾਇਰ – 1, ਰੈਫ਼ਰੀ – 1, ਲਾਈਨਮੈਨ – 10.

ਬੈਡਮਿੰਟਨ ਕੋਰਟ

ਨਿਯਮ ਅਤੇ ਵਿਨਿਯਮ (Rules and Regulations)-
1. ਟਾਸ (Toss) – ਖੇਡ ਸ਼ੁਰੂ ਹੋਣ ਤੋਂ ਪਹਿਲਾਂ ਦੋਵੇਂ ਟੀਮਾਂ ਵੱਲੋਂ ਟਾਸ ਕੀਤਾ ਜਾਵੇਗਾ ਅਤੇ ਵਿਜੇਤਾ ਟੀਮ ਦੇ ਕੋਲ ਪਹਿਲਾਂ ਸਰਵ (Serve) ਕਰਨ ਅਤੇ ਰਸੀਵ (Receive) ਕਰਨ ਦਾ ਵਿਕਲਪ ਹੁੰਦਾ ਹੈ ।

2. ਸਕੋਰਿੰਗ (Scoring) –

• ਇਕ ਮੈਚ ਵਿਚ ਤਿੰਨ ਗੇਮਾਂ ਦੇ ਸਰਵੋਤਮ ਸ਼ਾਮਿਲ ਹੁੰਦੇ ਹਨ ।
• ਜਿਹੜੀ ਸਾਈਡ ਪਹਿਲੇ 21 ਪੁਆਇੰਟ ਸਕੋਰ ਕਰਦੀ ਹੈ, ਉਸ ਦੇ ਦੁਆਰਾ ਗੇਮ ਜਿੱਤੀ ਜਾਣੀ ਹੈ ।
• ਰੋਮ ਜਿੱਤਣ ਵਾਲੀ ਸਾਈਡ ਹੀ ਅਗਲੀ ਗੇਮ ਵਿਚ ਪਹਿਲੇ ਸਰਵ (Serve) ਕਰੇਗੀ ।
• ਰੈਲੀ (Rally) ਜਿੱਤਣ ਵਾਲੀ ਸਾਈਡ ਵਿਚ ਇਕ ਪੁਆਇੰਟ ਜੋੜਿਆ ਜਾਵੇਗਾ ।

3. ਇੰਡਸ ਵਿਚ ਪਰਿਵਰਤਨ (Change of Ends) – 11 ਪੁਆਇੰਟ ਦੇ ਬਾਅਦ ਪਹਿਲੀ ਗੇਮ ਅਤੇ ਤੀਸਰੀ ਗੇਮ ਦੇ ਅੰਤ ਵਿਚ ਇੰਡਸ ਵਿਚ ਪਰਿਵਰਤਨ ਹੁੰਦਾ ਹੈ ।

4. ਸਰਵਿਸ ਦੇ ਨਿਯਮ (Service Rules)-

• ਜੇਕਰ ਇਕ ਵਾਰ ਸਰਵਰ (Server) ਅਤੇ ਰਸੀਵਰ (Receiver) ਤਿਆਰ ਹੋਵੇ ਤਾਂ ਸਰਵ ਕਰਨ ਵਿਚ ਗ਼ੈਰ| ਜ਼ਰੂਰੀ ਦੇਰੀ ਕਰਨ ਦੀ ਪ੍ਰਵਾਨਗੀ ਨਹੀਂ ਹੁੰਦੀ ।
• ਸਰਵਿਸ ਦੇ ਦੌਰਾਨ ਸਰਵਰ ਅਤੇ ਰਸੀਵਰ ਕੋਰਟ ਦੇ ਸਾਹਮਣੇ ਤਿਰਛੇ ਖੜੇ ਹੋਣਗੇ ।
• ਸਰਵਰ ਅਤੇ ਰਸੀਵਰ ਦੇ ਦੋਵਾਂ ਪੈਰਾਂ ਦੇ ਕੁਝ ਭਾਗ ਸਥਿਰ ਅਵਸਥਾ ਵਿਚ ਕੋਰਟ ਦੇ ਧਰਾਤਲ ਦੇ ਸੰਪਰਕ ਵਿਚ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ ।
• ਸਰਵਿਸ ਦੇ ਦੌਰਾਨ ਸਰਵਰ ਦਾ ਰੈਕੇਟ ਪਹਿਲੇ ਸ਼ਟਲ ਦੇ ਆਧਾਰ ਨੂੰ ਹਿੱਟ ਕਰੇਗਾ ।
• ਸਰਵਿਸ ਦੇ ਦੌਰਾਨ ਸ਼ਟਲ ਪਹਿਲੇ ਕਮਰ ਦੀ ਪੱਧਰ ਦੇ ਹੇਠਾਂ ਹੋਵੇਗੀ ।
• ਡਬਲ ਵਿਚ, ਸਾਥੀ (Partner) ਆਪਣੇ ਕੋਰਟ ਦੇ ਅੰਦਰ ਕੋਈ ਵੀ ਪੋਜੀਸ਼ਨ ਲੈ ਸਕਦਾ ਹੈ ।
• ਸਰਵ ਕਰਦੇ ਹੋਏ ਜੇਕਰ ਸਰਵਰ ਸ਼ਟਲ ਮਿਸ ਕਰਦਾ ਹੈ, ਤਾਂ ਇਸਨੂੰ ਗਲਤੀ ਮੰਨਿਆ ਜਾਵੇਗਾ ।

5. ਗਲਤੀ (Fault)-

• ਜੇਕਰ ਸਰਵਿਸ ਦਾ ਸਹੀ ਸਰਵ ਨਹੀਂ ਹੈ, ਤਾਂ ਇਸਨੂੰ ਗਲਤੀ ਮੰਨਿਆ ਜਾਵੇਗਾ ।
• ਜੇਕਰ ਸ਼ਟਲ ਨੈੱਟ ਨੂੰ ਪਾਰ ਕਰਨ ਵਿਚ ਅਸਫਲ ਰਹਿੰਦੀ ਹੈ ਜਾਂ ਨੈੱਟ ਵਿਚੋਂ ਜਾਂ ਹੇਠਾਂ ਤੋਂ ਪਾਰ ਕਰਦੀ ਹੈ ।
• ਜੇਕਰ ਇਸ ਨੂੰ ਵਿਅਕਤੀ, ਖਿਡਾਰੀ ਜਾਂ ਕਿਸੇ ਹੋਰ ਪਦਾਰਥ ਨਾਲ ਸੰਪਰਸ਼ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।
• ਜੇਕਰ ਕੋਈ ਖਿਡਾਰੀ ਰੈਕੇਟ ਦੇ ਨਾਲ ਸੈੱਟ ਵਿਚੋਂ ਵਿਰੋਧੀ ਦੇ ਕੋਰਟ ’ਤੇ ਹਮਲਾ ਕਰਦਾ ਹੈ ਤਾਂ ਚੀਕਾਂ ਮਾਰਨ ਜਾਂ ਇਸ਼ਾਰਿਆਂ ਦੁਆਰਾ ਰੁਕਾਵਟ ਪੈਦਾ ਕਰਦਾ ਹੈ ।
• ਜੇਕਰ ਇਕ ਹੀ ਖਿਡਾਰੀ ਜਾਂ ਸਾਈਡ ਦੁਆਰਾ ਅਨੁਕੂਮ ਵਿਚ ਸ਼ਟਲ ਨੂੰ ਦੋ ਵਾਰ ਹਿੱਟ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।

ਲੈਂਟ ਨਿਯਮ (Let Rule)-
ਅੰਪਾਇਰ ਦੁਆਰਾ ‘ਲੈਟ’ (Let) ਸ਼ਬਦ ਦਾ ਪ੍ਰਯੋਗ ਖੇਡਾਂ ਨੂੰ ਰੋਕਣ ਦੇ ਲਈ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।

1. ਜੇਕਰ ਸ਼ਟਲ ਨੈੱਟ ਵਿਚ ਫਸ ਜਾਂਦੀ ਹੈ ਜਾਂ ਨੈੱਟ ‘ਤੇ ਲਟਕੀ ਰਹਿੰਦੀ ਹੈ, ਤਾਂ ਸਰਵਿਸ ਦੇ ਇਲਾਵਾ ਇਸਨੂੰ ਨੈੱਟ ਕਿਹਾ ਜਾਵੇਗਾ ।
2. ਜੇਕਰ ਸਰਵਿਸ ਦੇ ਦੌਰਾਨ, ਰਸੀਵਰ ਅਤੇ ਸਰਵਰ ਨਾਲ-ਨਾਲ ਗਲਤੀ ਕਰਦੇ ਹਨ, ਤਾਂ ਇਸਨੂੰ “ਲੈਂਟ’ ਕਿਹਾ ਜਾਵੇਗਾ ।
3. ਜੇਕਰ ਖੇਡ ਦੇ ਦੌਰਾਨ, ਸਰਵਿਸ ਕੋਰਟ ਵਿਚ ਗਲਤੀ ਹੁੰਦੀ ਹੈ, ਤਾਂ ਇਸਨੂੰ “ਲੈਂਟ ਕਿਹਾ ਜਾਵੇਗਾ |
4. ਜੇਕਰ ਖੇਡ ਦੇ ਦੌਰਾਨ ਸ਼ਟਲ ਪੂਰੀ ਤਰ੍ਹਾਂ ਨਾਲ ਟੁੱਟ ਜਾਂਦੀ ਹੈ, ਤਾਂ ਇਸਨੂੰ ਲੈਂਟ ਕਿਹਾ ਜਾਵੇਗਾ ।

ਮਹੱਤਵਪੂਰਨ ਸ਼ਬਦਾਵਲੀ
(Important Terminology)

1. ਲੌਂਟ (Let) ਅਚਾਨਕ ਵਾਪਰਨ ਵਾਲੀਆਂ (Unfareseen) ਪ੍ਰਸਥਿਤੀਆਂ ਦੇ ਪਰਿਣਾਮਸਵਰੂਪ ਗੇਮ ਨੂੰ ਰੋਕਣ ਦੇ ਲਈ ਅੰਪਾਇਰ ਦੁਆਰਾ ਉਪਯੁਕਤ ਸ਼ਬਦ ਹੈ ।
2. ਰੈਲੀ (Rally) – ਗੇਮ ਵਿਚ ਸ਼ਟਲ ਦੇ ਰੁਕ ਜਾਣ ਤਕ, ਸਰਵਿਸ ਤੋਂ ਆਰੰਭ ਕਰਕੇ ਇਕ ਜਾਂ ਵਧੇਰੇ ਸਟੋਕਸ ਦਾ ਕੁਮ ।
3. ਸਰਵ (Serve) – ਹਰੇਕ ਰੈਲੀ ਦੇ ਸ਼ੁਰੂ ਵਿਚ, ਸ਼ਟਲ ਕਾਕ ਨੂੰ ਖੇਡ ਵਿਚ ਲਿਆਉਣ ਦੇ ਲਈ ਪ੍ਰਯੋਗ ਕੀਤਾ ਗਿਆ ਸਟਰੋਕ ।
4. ਵੁੱਡ ਸ਼ਾਟ (Wood Shot) – ਇਕ ਨਿਯਮ ਅਨੁਸਾਰ ਖੇਡਿਆ ਗਿਆ ਸ਼ਾਟ, ਜਿਸ ਵਿਚ ਸ਼ਟਲ ਰੈਕਟ ਦੇ ਫਰੇਮ ਨੂੰ ਸਪੱਰਸ਼ ਕਰਦੀ ਹੈ ।
5. ਗਲਤੀ (Fault) – ਸਰਵਿਸ, ਰਸੀਵਿੰਗ ਜਾਂ ਖੇਡ ਦੇ ਦੌਰਾਨ ਖੇਡਣ ਦੇ ਨਿਯਮਾਂ ਦਾ ਉਲੰਘਣ ।
6. ਸ਼ਾਰਟ ਸਰਵਿਸ ਲਾਈਨ (Short Service line)-ਨੈੱਟ ਤੋਂ 1.98 ਮੀ. ਦੀ ਦੂਰੀ ਤੇ ਇਕ ਰੇਖਾ, ਜਿਸ ਵਿਚ ਨਿਯਮ ਅਨੁਸਾਰ ਸਰਵ ਕਰਨ ਦੇ ਲਈ ਸਰਵ ਨੂੰ ਕਰਾਸ ਜ਼ਰੂਰ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ।
7. ਡਿਉਸ (Deuce) – ਜਦੋਂ ਸਕੋਰ 20-20 ਤਕ ਪਹੁੰਚਦਾ ਹੈ, ਤਾਂ ਇਸ ਸ਼ਬਦ ਦਾ ਪ੍ਰਯੋਗ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਡਿਉਸ ਦੇ ਮਾਮਲੇ ਵਿਚ ਗੇਮ ਜਿੱਤਣ ਦੇ ਲਈ 2 ਪੁਆਇੰਟ ਦੀ ਲੀਡ (Lead) ਲੈਣੀ ਜ਼ਰੂਰੀ ਹੁੰਦੀ ਹੈ ।
8. ਸਮੈਸ਼ (Smash) – ਇਹ ਸਿਵਰ ਦੇ ਉਪਰ ਜ਼ੋਰ ਨਾਲ ਮਾਰਿਆ ਗਿਆ ਸਰੋਕ ਹੁੰਦਾ ਹੈ, ਜਿਸ ਵਿਚ ਸ਼ਟਲ ਤੇਜ਼ੀ ਨਾਲ ਹੇਠਾਂ ਡਿੱਗਦੀ ਹੈ ।

ਖੇਡ ਦੇ ਮੈਦਾਨ/ਕੋਰਟ ਜਾਂ ਉਪਕਰਨਾਂ ਦੇ ਮਾਪ
(Dimensions of Play Field/Court or Equipments)

1. ਕੋਰਟ (Court) – ਸਿੰਗਲਜ਼ ਅਤੇ ਡਬਲਜ਼ ਦੋਵਾਂ ਦੇ ਲਈ ਬੈਡਮਿੰਟਨ ਦੇ ਕੋਰਟ ਦਾ ਆਕਾਰ ਆਇਤਾਕਾਰ ਹੁੰਦਾ ਹੈ, ਜਿਸਦੀ ਲੰਬਾਈ 13.4 ਮੀਟਰ (44 ਫੁੱਟ) ਹੁੰਦੀ ਹੈ । ਡਬਲਜ਼ ਦੇ ਲਈ ਕੋਰਟ ਦੀ ਚੌੜਾਈ 6.1 ਮੀਟਰ (20 ਫੁੱਟ) ਹੁੰਦੀ ਹੈ ਅਤੇ ਸਿੰਗਲਜ਼ ਦੇ ਲਈ ਇਹ ਘੱਟ ਹੋ ਕੇ 5.18 ਮੀਟਰ (17 ਫੁੱਟ) ਰਹਿ ਜਾਂਦੀ ਹੈ ।

2. ਪੋਸਟਸ (Posts) – ਪੋਸ਼ਟਸ ਕੋਰਟ ਦੇ ਧਰਾਤਲ ਤੋਂ 1.55 ਮੀ. ਉੱਚੇ ਹੁੰਦੇ ਹਨ | ਭਾਵੇਂ ਸਿੰਗਲਜ਼ ਜਾਂ ਡਬਲਜ਼ ਖੇਡਿਆ ਜਾਵੇ, ਪੋਸਟਸ ਨੂੰ ਡਬਲਜ਼ ਸਾਈਡ ਰੇਖਾਵਾਂ ‘ਤੇ ਲਗਾਇਆ ਜਾਂਦਾ ਹੈ ।

3. ਨੈੱਟ (Net) – ਨੈੱਟ ਵਧੀਆ ਰੱਸੀ ਜਾਂ ਕੇਬਲ (Cable) ਦੀ ਬਣੀ ਹੋਵੇਗੀ । ਇਹ ਗੂੜ੍ਹੇ ਰੰਗ ਦੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ਜਿਸ ਦੀ ਜਾਲੀ 3/4″ ਤੋਂ 1” ਹੋਵੇਗੀ । ਨੈੱਟ ਦੀ ਚੌੜਾਈ 2’-6″ ਹੋਵੇਗੀ । ਨੈੱਟ ਦੀ ਉੱਚਾਈ ਮੱਧ ਤੋਂ ਜ਼ਮੀਨ ਤੋਂ 5 ਫੁੱਟ ਅਤੇ ਪੋਸਟਸ ਤੇ 5 ਫੁੱਟ 1 ਇੰਚ ਹੋਵੇਗੀ ।

4. ਰੈਕਟ (Racket) – ਰੈਕਟ ਦਾ ਫਰੇਮ ਰੈਕਟ ਦੀ ਸਹਾਇਤਾ ਨਾਲ ਜੁੜਿਆ ਹੋਵੇਗਾ । ਰੈਕਟ ਦੇ ਮੁੱਖ ਤੌਰ ਤੇ ਤਿੰਨ ਭਾਗ ਹੁੰਦੇ ਹਨ, ਸਿਰ, ਰੋਫਟ ਅਤੇ ਗਰਦਨ । ਸਿਰ ਲੰਬਾਈ ਵਿਚ 280 ਮਿ.ਮੀ. ਤੋਂ ਅਤੇ ਚੌੜਾਈ ਵਿਚ 220 ਮਿ.ਮੀ. ਤੋਂ ਅਧਿਕ ਨਹੀਂ ਹੋਵੇਗਾ | ਰੈਕਟ ਦੀ ਕੁੱਲ ਲੰਬਾਈ 680 ਮਿ.ਮੀ. ਅਤੇ ਚੌੜਾਈ 230 ਮਿ. ਮੀ. ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ।

5. ਸ਼ਟਲ (Shuttle) – ਸ਼ਟਲ ਆਮ ਜਾਂ ਸਿੰਥੈਟਿਕ ਪਦਾਰਥ ਦੀ ਬਣੀ ਹੋਵੇ । ਸ਼ਟਲ ਦਾ ਆਧਾਰ ਜਾਂ ਕਾਕ ਦਾ ਘੇਰਾ 25 ਤੋਂ 28 ਮਿ.ਮੀ. ਦੇ ਵਿਚ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ । ਖੰਭਾਂ (ਪੰਖਾਂ ਦੀ ਕੁੱਲ ਲੰਬਾਈ 62 ਤੋਂ 70 ਮਿ.ਮੀ. ਦੇ ਵਿਚ ਹੋਵੇਗੀ । ਸ਼ਟਲ ਦਾ ਭਾਰ 4.74 ਤੋਂ 5.50 ਗ੍ਰਾਮ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ।

ਬੁਨਿਆਦੀ ਗੁਣ (Fundamental Skills)-
1. ਰੈਕਟ ਨੂੰ ਪਕੜਨਾ (Holding the Racket) – ਇਸ ਖੇਡ ਵਿਚ ਸਭ ਤੋਂ ਮਹੱਤਵਪੂਰਨ ਅਤੇ ਬੁਨਿਆਦੀ ਕਾਰੀਗਰੀ ਰੈਕਟ ਨੂੰ ਪਕੜਨਾ ਹੁੰਦਾ ਹੈ । ਰੈਕਟ ਨੂੰ ਪਕੜਦੇ ਸਮੇਂ ਕਲਾਈ ਕਠੋਰ (Stiff) ਨਹੀਂ ਹੋਣੀ ਚਾਹੀਦੀ । ਰੈਕੇਟ ਨੂੰ ਪਕੜਣ ਦੀਆਂ ਮੁੱਖ ਤੌਰ ‘ਤੇ ਦੋ ਸ਼ੈਲੀਆਂ ਹੁੰਦੀਆਂ ਹਨ-ਫਰਾਇੰਗ ਪੈਂਨ ਪਕੜ ਅਤੇ ਬੈਕ ਹੈੱਡ ਪਕੜ ।

2. ਸਰਵਿਸ (Service) – ਹਰੇਕ ਰੈਲੀ (Rally) ਦੇ ਸ਼ੁਰੂ ਵਿਚ ਸ਼ਟਲ ਨੂੰ ਖੇਡ ਵਿਚ ਲਿਆਉਣ ਵਾਲੇ ਸਟ੍ਰੋਕ ਨੂੰ ਸਰਵਿਸ ਕਹਿੰਦੇ ਹਨ । ਮੁੱਖ ਤੌਰ ‘ਤੇ ਦੋ ਤਰ੍ਹਾਂ ਦੀ ਸਰਵਿਸ ਹੁੰਦੀ ਹੈ-ਹਾਈ ਸਰਵਿਸ (High Service) ਅਤੇ ਲੋ ਸਰਵਿਸ (Low Service) । ਹਾਈ ਸਰਵਿਸ ਵਿਚ ਖਿਡਾਰੀ ਸ਼ਟਲ ਨੂੰ ਕੋਰਟ ਦੇ ਪਿੱਛੇ ਗਹਿਰਾਈ ਵਿਚ ਕਰਨ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰਦਾ ਹੈ । ਦੂਸਰੇ ਪਾਸੇ, ਲੋ ਸਰਵਿਸ ਵਿਚ ਸਿਰਫ ਨੈੱਟ ਨੂੰ ਪਾਰ ਕਰਨਾ ਹੁੰਦਾ ਹੈ ਅਤੇ ਸ਼ਾਰਟ ਸਰਵਿਸ ਲਾਈਨ ਤੋਂ ਕੁਝ ਇੰਚ ਦੂਰ ਰੱਖਣਾ ਹੁੰਦਾ ਹੈ ।

3. ਸਟ੍ਰੋਕ (Stroke) – ਸ਼ਟਲ ਅਤੇ ਰੈਕਟ ਦੇ ਵਿਚ ਸੰਪਰਕ ਨੂੰ ਸਕ ਕਹਿੰਦੇ ਹਨ । ਵਿਭਿੰਨ ਸਕਾਂ ਨੂੰ ਮੁੱਖ ਤੌਰ ‘ਤੇ ਤਿੰਨ ਵਰਗਾਂ ਵਿਚ ਵੰਡਿਆ ਜਾ ਸਕਦਾ ਹੈ : (ੳ) ਫਾਰਹੁੱਡ ਸਟੋਕ (Forhead Stroke) (ਅ ਬੈਕ ਹੈੱਡ ਸਟ੍ਰੋਕ (Backhand Stroke) (ਈ ਔਵਰ ਹੈਡ ਸਟਰੋਕ (Overhead Stroke) ।

• ਫਾਰਹੁੱਡ ਸਟੂਕ Forehead Stroke) – ਇਸ ਦਾ ਪ੍ਰਯੋਗ ਖੇਡ ਵਿਚ ਅਕਸਰ ਹੁੰਦਾ ਹੈ । ਇਸ ਸਟ੍ਰੋਕ ਨੂੰ ਤਦ ਖੇਡਿਆ ਜਾਂਦਾ ਹੈ, ਜਦ ਸ਼ਟਲ ਰਸੀਵਰ ਦੇ ਅੱਗੇ ਡਿੱਗਦੀ ਹੈ । ਵਿਰੋਧੀ ਦੇ ਕੋਰਟ ਦੇ ਕਿਸੇ ਵੀ ਪੁਆਇੰਟ ਤੇ ਸ਼ਟਲ ਨੂੰ ਮਾਰਨਾ ਆਸਾਨ ਹੁੰਦਾ ਹੈ ।
• ਬੈਕ ਹੈੱਡ ਸਟਰੋਕ (Backhand Stroke) – ਇਹ ਸਧਾਰਨਤਾ ਮੁਸ਼ਕਿਲ ਸ਼ਾਟ ਹੁੰਦਾ ਹੈ ਕਿਉਂਕਿ ਸ਼ਟਲ ਖਿਡਾਰੀ ਦੇ ਉਸ ਪਾਸੇ ਡਿੱਗਦੀ ਹੈ, ਜਿਸ ਪਾਸੇ ਗਤੀਸ਼ੀਲਤਾ ਨਹੀਂ ਹੁੰਦੀ । ਇਸ ਸ਼ਾਟ ਨੂੰ ਜ਼ੋਰਦਾਰ ਢੰਗ ਨਾਲ ਵਾਪਿਸ ਦੇਣਾ ਮੁਸ਼ਕਿਲ ਹੁੰਦਾ ਹੈ ।
• ਝਾਪ ਸ਼ਾਟ (Drop Shot) – ਪ ਸ਼ਾਟਸ ਕਮਜ਼ੋਰ ਬੈਡਮਿੰਟਨ ਸ਼ਾਟਸ ਹੁੰਦੇ ਹਨ, ਜਿਸ ਵਿਚ ਇਕ ਪੁਆਇੰਟ ਜਿੱਤਣ ਦੇ ਲਈ ਚਕਮਾ ਦੇਣ ਵਾਲੇ ਢੰਗ ਨਾਲ ਖੇਡਿਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਸ਼ਾਟ ਦਾ ਉਦੇਸ਼ ਹੁੰਦਾ ਹੈ ਕਿ ਵਿਰੋਧੀ ਨੂੰ ਕਮਜ਼ੋਰ ਵਾਪਸੀ ਦੇ ਲਈ ਮਜ਼ਬੂਰ ਕੀਤਾ ਜਾਵੇ ।
• ਲੋਬ ਸ਼ਾਟ (Lob Shot) – ਇਸ ਵਿਚ ਸ਼ਟਲ ਨੂੰ ਵਿਰੋਧੀ ਦੀ ਆਧਾਰ ਲਾਈਨ ਤੇ ਉੱਚੇ ਅਤੇ ਡੂੰਘੇ ਵਿਚ ਹਿੱਟ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਇਸ ਵਿਚ ਹਾਈ ਸਰਵ ਨੂੰ ਪੂਰਨ ਵਿਸਤਾਰ ਨਾਲ ਖੇਡਿਆ ਜਾਂਦਾ ਹੈ ।
• ਸਮੈਸ਼ (Smash-ਇਹ ਔਵਰ ਹੈੱਡ ਤੇ ਹਮਲਾ ਕਰਨ ਵਾਲਾ ਸਟ੍ਰੋਕ ਹੁੰਦਾ ਹੈ । ਜੋ ਸ਼ਟਲ ਨੂੰ ਵਿਰੋਧੀ ਦੇ ਕੋਰਟ ਵਿਚ ਤੇਜ਼ੀ ਨਾਲ ਹੇਠਾਂ ਦੇ ਵੱਲ ਡਿੱਗਣ ਦੇ ਲਈ ਮਜ਼ਬੂਰ ਕਰ ਦਿੰਦੀ ਹੈ ।
• ਹੇਅਰ ਪਿੰਨ ਸ਼ਾਟ (Hair Pin Shot) – ਅਸੀਂ ਸ਼ਾਟ ਵਿਚ, ਸ਼ਟਲ ਨੂੰ ਨੈੱਟ ਦੇ ਬਿਲਕੁਲ ਕੋਲੋਂ ਤੇਜ਼ ਗਤੀ ਨਾਲ ਵਾਪਿਸ ਭੇਜਿਆ ਜਾਂਦਾ ਹੈ । ਸ਼ਟਲ ਦੀ ਗਤੀਵਿਧੀ ਇਕ ਹੇਅਰ ਪਿਨ ਦੀ ਤਰ੍ਹਾਂ ਹੁੰਦੀ ਹੈ । ਜਿਹੜੀ ਨੈੱਟ ਦੇ ਦੂਸਰੇ ਪਾਸੇ ਬਹੁਤ ਨੇੜੇ ਹੀ ਡਿੱਗਦੀ ਹੈ ।

ਮਹੱਤਵਪੂਰਨ ਟੂਰਨਾਮੈਂਟਸ
(Important Tournaments)

ਅੰਤਰ-ਰਾਸ਼ਟਰੀ ਪੱਧਰ (International Levely)-

1. ਥਾਮਸ ਕੱਪ
2. ਵਿਸ਼ਵ ਕੱਪ
3. ਵਿਲਸ ਕੱਪ
4. ਚਾਈਨਾ ਕੱਪ
5. ਉਬੇਰ ਕੱਪ
6. ਸ਼ਾਹ ਜੀ ਕੁਰੈਸ਼ੀ ਕੱਪ
7. ਉਲੰਪਿਕ ਖੇਡ ।
8. ਕਾਮਨਵੈਲਥ ਖੇਡ
9. ਏਸ਼ਿਆਈ ਖੇਡ
10. ਐਲਬਾ ਵਿਸ਼ਵ ਕੱਪ
11. ਆਲ ਇੰਗਲੈਂਡ ਚੈਂਪੀਅਨਸ਼ਿਪ
12. ਯੋਨੈਕਸ ਕੱਪ । ਰਾਸ਼ਟਰੀ ਪੱਧਰ (National Level)-
13. ਸੀਨੀਅਰ ਨੈਸ਼ਨਲ ਚੈਂਪੀਅਨਸ਼ਿਪ
14. ਅੱਗਰਵਾਲ ਕੱਪ
15. ਅੰਮ੍ਰਿਤ ਦੀਵਾਨ ਕੱਪ
16. ਆਲ ਇੰਡੀਆ ਇੰਟਰਵਰਸਿਟੀ ਚੈਂਪੀਅਨਸ਼ਿਪ

ਸਪਰੋਟਸ ਅਵਾਰਡ
(Sports Award)

ਅਰਜੁਨ ਪੁਰਸਕਾਰ ਜੇਤੂਆਂ ਦੀ ਸੂਚੀ (List of Arjuna Award Winners) – ਨੰਦ ਐੱਮ. ਨਾਟੇਕਰ ( 1961), ਮੀਨਾ ਸ਼ਾਹ (1962), ਦਿਨੇਸ਼ ਖੰਨਾ ( 1965), ਸੁਰੇਸ਼ ਗੋਇਲ (1967), ਦੀਪੂ ਘੋਸ਼ ( 1969), ਡੀ. ਵੀ. ਤਾਬੇ (1970), ਸ਼ੋਭਾ ਮੂਰਥੀ (1971), ਪ੍ਰਕਾਸ਼ ਪਾਦੂਕੋਨੋ (1972), ਰਮਨ ਘੋਸ਼ (1974), ਦੇਵੇਂਦਰ ਆਹੂਜਾ (1975), ਅਮੀ ਘੀਆ (1976), ਕੰਵਲ ਠਾਕੁਰ ਸਿੰਘ (1977-78), ਸੈੱਯਦ ਮੋਦੀ (1980-81), ਪਾਰਥੇ ਗਾਂਗੁਲੀ, ਕੁਮਾਰੀ ਮਧੂਮੀਤਾ ਗੋਸਵਾਮੀ (1981), ਰਾਜੀਵ ਬੱਗਾ (1991), ਅਰਪਣਾ ਪੋਪਟ (1999), ਵੀ.ਗੋਪੀਚੰਦ (2000), ਜਾਰਜ ਥਾਮਸ (2001), ਪਾਰੂਲ ਡੀ ਪਰਮਾਰ (2009), ਸੇਨਾ ਨੇਹਵਾਲ (2009), ਜਵਾਲਾ ਗੁੱਟਾ (2011) ।
ਦਰੋਣਾਚਾਰੀਆ ਅਵਾਰਡ-ਪੀ. ਗੋਪੀ ਚੰਦ (2009) ।

ਬੈਡਮਿੰਟਨ
(Badminton)

ਅਰਜੁਨ ਅਵਾਰਡ ਵਿਜੇਤਾ-ਨੰਦੂ ਨਾਟੇਕਰ (1961), ਮੀਨਾ ਸ਼ਾਹ (1962), ਦੀਨੇਸ਼ ਖੰਨਾ (1965), ਸੁਰੇਸ਼ ਗੋਇਲ (1967), ਦੀਪੂ ਘੋਸ਼ (1969), ਡੀ.ਵੀ. ਟਮਬੇ (1970), ਐੱਸ. ਊਰਥੀ (1971), ਪ੍ਰਕਾਸ਼ ਪਾਦੂਕੋਨ (1972), ਰਮਨ ਘੋਸ਼ (1974), ਦਵਿੰਦਰ ਅਹੂਜਾ (1975), ਅਮੀ ਘੀਆ (1976), ਕੇ.ਟੀ. ਸਿੰਘ (1977-78), ਸੱਯਦ ਮੋਦੀ (1980-81), ਪੀ. ਗਾਂਗੁਲੀ, ਮਧੁਮਿਤਾ ਬਿਸ਼ਟ (1982), ਰਾਜੀਵ ਬੱਗਾ (1991), ਪੁਲੇਲਾ ਗੋਪੀਚੰਦ (2000), ਜਾਰਜ ਥੋਮਸ (2000-01), ਮਦਾਸੂ ਸ੍ਰੀਨਿਵਾਸ ਰਾਓ (ਫਿਜ਼ਿਕਲੀ ਚੈਲੇਂਜਡ) (2003), ਅਭਿੰਨ ਸ਼ਾਮ ਗੁਪਤਾ (2004), ਅਪਰਨਾ ਪੋਪਟ (2005), ਚੇਤਨ ਆਨੰਦ (2006), ਰੋਹੀਤ ਭਾਕਰ (ਫਿਜ਼ਿਕਲੀ ਚੈਲੇਂਜਡ) (2006), ਅਨੂਪ ਸ਼੍ਰੀਧਰ (2008), ਸਾਇਨਾ ਨੇਹਵਾਲ (2009), ਅਸ਼ਵਨੀ ਪੋਨਅੱਪਾ, ਪਾਰੂਪਲੀਕੇਸ਼ਅਪ (2012), ਪੀ.ਵੀ. ਸਿੰਧੂ (2013), ਵੀ. ਦੀਜੂ (2014), ਕੇ. ਸੀਰੀਕਨਾਥ (2015)
ਦਰੋਣਾਚਾਰੀਆ ਅਵਾਰਡ ਵਿਜੇਤਾ-ਐੱਸ. ਐੱਮ. ਆਰਿਫ (2000), ਪੁਲੇਲਾ ਗੋਪੀਚੰਦ (2009) ।

PSEB 12th Class Physical Education Practical ਬੈਡਮਿੰਟਨ (Badminton)

ਪ੍ਰਸ਼ਨ 1.
ਅੰਤਰ-ਰਾਸ਼ਟਰੀ ਬੈਡਮਿੰਟਨ ਫੈਡਰੇਸ਼ਨ-ਕਦੋਂ ਸ਼ੁਰੂ ਹੋਇਆ ਸੀ ?
ਉੱਤਰ-
ਸਾਲ 1934 ਵਿਚ ।

ਪ੍ਰਸ਼ਨ 2.
ਉਲੰਪਿਕ ਖੇਡਾਂ ਵਿਚ ਬੈਡਮਿੰਟਨ ਨੂੰ ਇਕ ਪਦਕ ਖੇਡ ਦੇ ਰੂਪ ਵਿਚ ਕਦੋਂ ਸਵੀਕਾਰ ਕੀਤਾ ਗਿਆ ਸੀ ?
ਉੱਤਰ-
1992 ਉਲੰਪਿਕ ਖੇਡ ਬਰਸੀਲੋਨਾ ਵਿਚ ਇਹ ਇਕ ਪਦਕ ਖੇਡ ਬਣਿਆ ।

ਪ੍ਰਸ਼ਨ 3.
ਡਬਲਜ਼ ਦੇ ਲਈ ਬੈਡਮਿੰਟਨ ਕੋਰਟ ਦੇ ਪੜਾਅ ਕੀ ਹਨ ?
ਉੱਤਰ-
13.00 × 6.10 ਮੀ. ਜਾਂ 4 × 20 ਫੁੱਟ ।

ਪ੍ਰਸ਼ਨ 4.
ਨੈੱਟ ਦੀ ਚੌੜਾਈ ਕਿੰਨੀ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
760 ਕਿ.ਮੀ. (76 ਸੈਂ.ਮੀ.)

ਪ੍ਰਸ਼ਨ 5.
ਇਕ ਸ਼ਟਲ ਵਿਚ ਪੰਖਾਂ ਦੀ ਸੰਖਿਆ ਦੱਸੋ ।
ਉੱਤਰ-
14 ਤੋਂ 16 ਪੰਖ ।

ਪ੍ਰਸ਼ਨ 6.
ਬੈਡਮਿੰਟਨ ਮੈਚ ਦੇ ਲਈ ਕਿੰਨੇ ਅਧਿਕਾਰੀਆਂ ਦੀ ਜ਼ਰੂਰਤ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
1. ਅੰਪਾਇਰ, ਸਰਵਿਸ ਅੰਪਾਇਰ, 11 ਰੈਫ਼ਰੀ ਅਤੇ 10 ਲਾਈਨਮੈਨ ।

ਪ੍ਰਸ਼ਨ 7.
ਬੈਡਮਿੰਟਨ ਵਿਚ ਟੱਸ ਦੇ ਬਾਰੇ ਵਿਚ ਤੁਸੀਂ ਕੀ ਜਾਣਦੇ ਹੋ ?
ਉੱਤਰ-
ਖੇਡ ਦੇ ਸ਼ੁਰੂ ਹੋਣ ਤੋਂ ਪਹਿਲਾਂ ਟਾਸ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ਅਤੇ ਜਿੱਤੇ ਪਾਸੇ ਦੇ ਕੋਲ ਪਹਿਲੇ ਸਰਵ ਕਰਨ ਜਾਂ ਰਸੀਵ ਕਰਨ ਦਾ ਵਿਕਲਪ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 8.
ਮੱਧ ਤੋਂ ਸ਼ਾਰਟ ਸਰਵਿਸ ਲਾਈਨ ਦੀ ਦੂਰੀ ਕਿੰਨੀ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
6′-6″ (1.98 ਮੀ.) ।

ਪ੍ਰਸ਼ਨ 9.
ਡਿਊਸ (Deuce-ਸ਼ਬਦ ਤੋਂ ਤੁਸੀਂ ਕੀ ਸਮਝਦੇ ਹੋ ? ਉੱਤਰ-ਇਸ ਸ਼ਬਦ ਦਾ ਪ੍ਰਯੋਗ ਤਦ ਕੀਤਾ ਜਾਂਦਾ ਹੈ, ਜਦੋਂ ਸਕੋਰ 20-20 ਤਕ ਪਹੁੰਚਦਾ ਹੈ ।ਡਿਊਸ ਦੇ ਮਾਮਲੇ ਵਿਚ ਗੇਮ ਜਿੱਤਣ ਦੇ ਲਈ ਅਤੇ 2 ਪੁਆਇੰਟ ਸਕੋਰ ਕਰਨੇ ਜ਼ਰੂਰੀ ਹੁੰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 10.
ਪੋਸਟਸ (Posts) ਦੀ ਉੱਚਾਈ ਕਿੰਨੀ ਹੁੰਦੀ ਹੈ ? ਉੱਤਰ-ਪੋਸਟਸ ਕੋਰਟ ਦੇ ਧਰਾਤਲ ਤੋਂ 1.55 ਮੀ. ਉੱਚੇ ਹੁੰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 11.
ਬੈਡਮਿੰਟਨ ਵਿਚ ਮਹੱਤਵਪੂਰਨ ਅੰਤਰਰਾਸ਼ਟਰੀ ਪੱਧਰ ਦੇ ਟੂਰਨਾਮੈਂਟਸ ਦੇ ਨਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਥਾਮਸ ਕੱਪ, ਵਿਸ਼ਵ ਕੱਪ, ਵਿਲਸ ਵਿਸ਼ਵ ਕੱਪ, ਚਾਈਨਾ ਕੱਪ, ਉਬੇਰ ਕੱਪ, ਉਲੰਪਿਕ ਖੇਡ, ਏਸ਼ਿਆਈ ਖੇਡ, ਕਾਮਨਵੈਲਥ ਖੇਡ, ਆਲ ਇੰਡੀਆ ਚੈਂਪੀਅਨਸ਼ਿਪ, ਯੋਮੈਕਸ ਕੱਪ ।

Punjab State Board PSEB 12th Class Physical Education Book Solutions ਸਾਫਟ ਬਾਲ (Softball) Game Rules.

ਸਾਫਟ ਬਾਲ (Softball) Game Rules – PSEB 12th Class Physical Education

ਸਾਫਟ ਬਾਲ ਦਾ ਇਤਿਹਾਸ
(History of Soft Ball)

ਇਕ ਪੁਰਾਣੀ ਕਹਾਣੀ ਦੇ ਅਨੁਸਾਰ ਬੇਸਬਾਲ ਦੀ ਖੋਜ ਸੰਨ 1883 ਵਿੱਚ ਕੂਪਰਸਟਾਊਨ (Cooperstown) ਵਿਚ ਹੋਈ । | ਇਸ ਖੇਡ ਦੇ ਪਹਿਲੇ ਖਿਡਾਰੀ ਇਕ ਸੈਨਿਕ ਸਕੂਲ ਵਿਚ ਕੈਡੇਟ (Cadets) ਸਨ । ਇਸ ਖੇਡ ਦਾ ਆਯੋਜਨ ਐਬਰਾਨ ਡੇਬਲ ਡੇ (Abron Double Day) ਨੇ ਕੀਤਾ ਜੋ ਉਸੀ ਸਕੂਲ ਵਿਚ ਅਧਿਆਪਕ (Instructor) ਸੀ ਅਤੇ ਜਿਹੜਾ ਬਾਅਦ ਵਿਚ ਅਮਰੀਕੀ ਸੈਨਾ ਵਿਚ ‘‘ਜਨਰਲ’’ ਦੇ ਅਹੁਦੇ ਤੇ ਪਹੁੰਚ ਗਿਆ । ਸੰਨ 1845 ਵਿਚ ਪਹਿਲੀ ਟੀਮ ਖੇਡੀ ਜਿਸ ਵਿਚ ਨਿਯਮ ਲਗਭਗ ਅੱਜ ਵਰਗੇ ਸਨ ਅਤੇ ਇਸ ਖੇਡ ਦਾ ਆਯੋਜਨ ਅਲੈਗਜ਼ੈਂਡਰ ਕਾਰਟਰਾਈਟ ਦੀ ਲਾਅਨੀਅਰ (Alexander Cartwright the Clioneer) ਨੇ ਕੀਤਾ ਸੀ | ਅਗਲੇ 10 ਸਾਲਾਂ ਵਿਚ ਇਹ ਖੇਡ ਬਹੁਤ ਵਿਕਸਿਤ ਹੋਈ ਅਤੇ ਨਿਊਯਾਰਕ ਬੇਸਬਾਲ (New York Baseball) ਦੇ ਨਾਮ ਨਾਲ ਜਾਣੀ ਗਈ ਤਾਂਕਿ ਉਸਨੂੰ ‘‘ਸਾਫਟ ਬਾਲ’’ (Soft Ball) ਤੋਂ ਅਲੱਗ ਸਮਝਿਆ ਜਾਵੇ ਜਿਹੜਾ ਉਸ ਸਮੇਂ ਮੈਸਾ ਚੈਸੈਟਸ (Massa Chessets) ਵਿਚ ਬਹੁਤ ਲੋਕਪ੍ਰਿਅ ਸੀ । ਸੰਨ 1868 ਤੱਕ ਇਹ ਖੇਡ ਚੰਗੀ ਤਰ੍ਹਾਂ ਨਾਲ ਸਥਾਪਿਤ ਹੋ ਚੁੱਕੀ ਸੀ ।

ਉਦੋਂ 25 ਟੀਮਾਂ ਸਹਿਤ ਨੈਸ਼ਨਲ ਬੇਸਬਾਲ ਪਲੇਅਰ ਐਸੋਸੀਏਸ਼ਨ (National Baseball Association) ਦੀ ਨੀਂਹ ਰੱਖੀ ਗਈ । ਕਾਫ਼ੀ ਉਤਾਰ-ਚੜ੍ਹਾਅ ਦੇ ਬਾਵਜੂਦ ਇਹ ਖੇਡ ਕਾਫ਼ੀ ਲੋਕਪ੍ਰਿਅ ਰਹੀ । ਸੰਨ 1920 ਅਤੇ 1930 ਦੇ ਦੌਰਾਨ ਬੇਸਬਾਲ ਦੀ ਖੇਡ ਵਿਚ ਕੀਰਤੀਮਾਨ ਸਥਾਪਿਤ ਕਰਨ ਵਾਲੇ ਜਾਰਜ ਰੂਥ (George Ruth) ਜਿਹੇ ਖਿਡਾਰੀਆਂ ਦਾ ਉਦੈ ਹੋਇਆ, ਜਿਹੜਾ ਸਭ ਤੋਂ ਜ਼ਿਆਦਾ ਪ੍ਰਸਿੱਧ ਖਿਡਾਰੀ ਹੋਇਆ, ਉਸਨੇ ਇਕ ਪ੍ਰਖੇਪਕ (Pitcher) ਦੇ ਰੂਪ ਵਿਚ ਖੇਡ ਸ਼ੁਰੂ ਕੀਤੀ ਪਰੰਤੂ ਉਹ ਇੰਨਾ ਚੰਗਾ ਬੈਟਰ ਸੀ ਕਿ ਉਹ ਜਲਦੀ ਇਕ ਉੱਤਮ ਹਮਲਾਵਰ ਖਿਡਾਰੀ ਬਣ ਗਿਆ । ਰੂਸ ਨੇ ਬੇਸਬਾਲ ਦੇ ਪੁਰਾਣੇ ਤਰੀਕਿਆਂ ਨੂੰ ਇਕ ਨਵਾਂ ਆਯਾਮ ਦਿੱਤਾ ਸੀ । “ਹੋਮ ਰਨ’’ (Home Run) ਵਿਚ ਵਿਸ਼ੇਸ਼ ਯਤਨ ਕੀਤੇ ਜਿਸਨੇ ਭਾਰੀ ਜਨ ਸਮੂਹ ਨੂੰ ਆਕਰਸ਼ਿਤ ਕੀਤਾ ।

ਯਾਦ ਰੱਖਣ ਯੋਗ ਗੱਲਾਂ
(Tips to Remember)

1. ਹੋਮ ਪਲੇਟ ਅਤੇ ਫਸਟ ਬੇਸ ਵਿਚਕਾਰਲੀ ਦੂਰੀ= 60 ਫੁੱਟ
2. ਪਹਿਲੇ ਅਤੇ ਦੂਜੇ ਬੇਸ ਵਿਚਕਾਰਲੀ ਦੂਰੀ = 60 ਫੁੱਟ
3. ਦੂਜੇ ਬੇਸ ਤੋਂ ਤੀਜੇ ਬੇਸ ਵਿਚਕਾਰਲੀ ਦੂਜੀ = 60 ਫੁੱਟ
4. ਬੇਸ ਲਾਈਨ ਦੀ ਚੌੜਾਈ = 3 ਇੰਚ
5. ਪਹਿਲੇ ਬੇਸ ਤੇ ਤੀਜੇ ਬੇਸ ਦੀ ਲੰਬਾਈ = 84′ 10 ਫੁੱਟ
6. ਹੋਮ ਪਲੇਟ ਤੋਂ ਦੂਜੇ ਬੇਸ ਦੀ ਲੰਬਾਈ . = 84′ 10 ਫੁੱਟ
7. ਬੇਸ ਦੀ ਲੰਬਾਈ ਅਤੇ ਚੌੜਾਈ = 15 × 15 ਇੰਚ
8. ਬੇਸ ਦੀ ਮੋਟਾਈ = 3 ਤੋਂ 5 ਇੰਚ
9. ਬੈਟਰ ਬਾਕਸ ਦੀ ਲੰਬਾਈ = 7 ਫੁੱਟ
10. ਬੈਟਰ ਬਾਕਸ ਦੀ ਚੌੜਾਈ = 3 ਫੁੱਟ
11. ਕੈਚਰ ਬਾਕਸ ਦੀ ਲੰਬਾਈ ਅਤੇ ਚੌੜਾਈ = 10 × 8.5 ਫੁੱਟ ।
12. ਹੋਮ ਪਲੇਟ ਦੀ ਲੰਬਾਈ ਅਤੇ ਚੌੜਾਈ = 12 × 8.5 × 8.5 ਫੁੱਟ
13. ਪਿਚਿੰਗ ਰਬੜ ਦੀ ਲੰਬਾਈ ਅਤੇ ਚੌੜਾਈ = 24 × 6 ਇੰਚ
14. ਪਿੱਚਰ ਘੇਰੇ ਦਾ ਅਰਧ ਵਿਆਸ . = 8 ਫੁੱਟ
15. ਗੇਂਦ ਦਾ ਭਾਰ = 6 1/4 ਗ੍ਰਾਮ
16. ਗੇਂਦ ਦਾ ਘੇਰਾ = 12 ਇੰਚ
17. ਬੈਟ ਦੀ ਲੰਬਾਈ = 34 ਇੰਚ
18. ਬੈਟ ਦਾ ਭਾਰ = 38 ਆਉਂਸ
19. ਅਧਿਕਾਰੀਆਂ ਦੀ ਗਿਣਤੀ = 07
20. ਕੁੱਲ ਖਿਡਾਰੀ = 16 ਤੋਂ 18 (9 ਪੋਲਿੰਗ ਮੈਂਬਰ)

ਸਾਫਟ ਬਾਲ ਦੇ ਨਵੇਂ ਨਿਯਮ
(New Rules Related to Soft Ball)

1. ਸਾਫਟ ਬਾਲ ਡਾਇਮੰਡ ਦੀ ਹਿ ਰੇਖਾ 60 ਫੁੱਟ ਹੁੰਦੀ ਹੈ ।
2. ਹਿ ਰੇਖਾ ਵਿਚ ਪੁਰਸ਼ਾਂ ਦੇ ਲਈ ਪ੍ਰਖੇਪਣ ਦਾ ਫਾਸਲਾ 46 ਫੁੱਟ ਅਤੇ ਔਰਤਾਂ ਦੇ ਲਈ 40 ਫੁੱਟ ਹੁੰਦਾ ਹੈ ।
3. ਸਾਫ਼ਟ ਬਾਲ ਬੈਟ ਦੀ ਲੰਬਾਈ 34 ਇੰਚ ਹੁੰਦੀ ਹੈ ਅਤੇ ਇਸਦੇ ਸਭ ਤੋਂ ਵੱਡੇ ਭਾਗ ਦਾ ਘੇਰਾ 24 ਇੰਚ ਹੁੰਦਾ ਹੈ ।
4. ਸਾਫ਼ਟ ਬਾਲ ਵਿੱਚ ਸੁਰੱਖਿਆ ਹਿ ਦੀ ਅਧਿਕਤਮ ਲੰਬਾਈ 10 ਇੰਚ ਹੁੰਦੀ ਹੈ ।
5. ਸਾਫ਼ਟ ਬਾਲ ਦਾ ਅਧਿਕਤਮ ਘੇਰਾ 124 ਇੰਚ ਅਤੇ ਨਿਊਨਤਮ ਘੇਰਾ 11 ਇੰਚ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ।
6. ਸਾਫ਼ਟ ਬਾਲ ਵਿਚ ਪ੍ਰਖੇਪਣ ਪੱਟੀ ਦੀ ਲੰਬਾਈ ਅਤੇ ਚੌੜਾਈ 24 × 6 ਇੰਚ ਹੁੰਦੀ ਹੈ ।

ਸਾਫ਼ਟ ਬਾਲ ਦੇ ਸਾਧਾਰਨ ਨਿਯਮ
(General Rules of Soft Ball)

ਬੈਟਿੰਗ ਕ੍ਰਮ (Order of Batting) – ਅੰਪਾਇਰ ਵੱਲੋਂ ਦਿੱਤੇ ਗਏ ਬੈਟਿੰਗ ਕੂਮ ਦਾ ਪੂਰੀ ਖੇਡ ਦੇ ਦੌਰਾਨ ਪਾਲਣ ਕੀਤਾ ਜਾਣਾ ਚਾਹੀਦਾ ਹੈ । ਜੇਕਰ ਬੈਟਿੰਗ ਨਿਸਚਿਤ ਕੂਮ ਦੇ ਅਨੁਸਾਰ ਨਹੀਂ ਹੋ ਰਹੀ ਅਤੇ ਇਸ ਗਲਤੀ ਦਾ ਪਤਾ ਗਲਤ ਬੈਟਰ ਦੀ ਪਾਰੀ ਖ਼ਤਮ ਹੋਣ ਅਤੇ ਅਗਲੇ ਬੈਟਰ ਦੇ ਆਉਣ ਤੋਂ ਪਹਿਲਾਂ ਲਗਦਾ ਹੈ ਤਾਂ ਉਹ ਖਿਡਾਰੀ ਜਿਸ ਨੇ ਅਸਲ ਵਿਚ ਖੇਡਣਾ ਸੀ, ਆਊਟ ਮੰਨਿਆ ਜਾਵੇਗਾ, ਬਣਾਏ ਗਏ ਰਨ ਖਤਮ (Cancel) ਸਮਝੇ ਜਾਣਗੇ ਅਤੇ ਨ੍ਹੀ ਦੌੜਾਕ ਦੁਬਾਰਾ ਬੈਟਰ ਬਾਕਸ ਵਿਚ ਉਸ ਸਥਿਤੀ ਵਿਚ ਵਾਪਿਸ ਚਲੇ ਜਾਣਗੇ ਜਿੱਥੇ ਉਹ ਗਲਤ ਬੈਟਰ ਆਉਣ ਤੋਂ ਪਹਿਲਾਂ ਸਨ ।

ਜੇਕਰ ਇਸ ਗਲਤੀ ਦਾ ਪਤਾ ਉਦੋਂ ਲਗਦਾ ਹੈ ਜਦੋਂ ਗਲਤ ਬੈਟਰ ਬੈਟ ਤੇ ਹੈ ਤਾਂ ਸਹੀ ਬੈਟਰ ਗਲਤ ਬੈਟਰ ਦਾ ਸਥਾਨ ਲੈ ਸਕਦਾ ਹੈ । ਗਲਤ ਬੈਟਰ ਦੁਆਰਾ ਬਣਾਏ ਗਏ ਹਨ, ਸਾਈਕਾਂ ਦੀ ਸੰਖਿਆ, ਕੀਤੀ ਗਈ ਬਾਲਾਂ ਦੀ ਸੰਖਿਆ, ਬੇਸਾਂ ਦੀ ਸੰਖਿਆ ਆਦਿ ਸਹੀ ਬੈਟਰ ਦੇ ਖਾਤੇ ਵਿੱਚ ਪਾ ਦਿੱਤੀ ਜਾਵੇਗੀ ਅਤੇ ਖੇਡ ਨੂੰ ਸਹੀ ਮੰਨ ਕੇ ਜਾਰੀ ਰੱਖਿਆ ਜਾਵੇਗਾ ।
ਬੈਟਰ ਦੇ ਆਪਣੀ ਪਾਰੀ ਖ਼ਤਮ ਕਰਨ ਤੋਂ ਪਹਿਲਾਂ ਜੇਕਰ ਤੀਸਰਾ ਖਿਡਾਰੀ ਆਊਟ ਹੋ ਜਾਵੇ ਤਾਂ ਅਗਲੀ ਪਾਰੀ ਵਿਚ ਉਹ ਪਹਿਲਾ ਬੈਟਰ ਬਣੇਗਾ ।

ਬੈਟ (Bat) -ਇਹ ਠੋਸ ਲੱਕੜੀ ਦਾ ਅਤੇ ਗੋਲਾਕਾਰ ਹੋਵੇਗਾ । ਬੈਟ ਦੀ ਲੰਬਾਈ 34 ਇੰਚ ਅਤੇ ਸਭ ਤੋਂ ਵੱਡੇ ਭਾਗ | ਦਾ ਘੇਰਾ 21/4 ਇੰਚ ਤੋਂ ਜ਼ਿਆਦਾ ਨਹੀਂ ਹੋਵੇਗਾ । ਇਸਦੀ ਸੁਰੱਖਿਆ ਮੁੱਠ ਕਾਰਕ ਜਾਂ ਕਿਸੇ ਸੰਸ਼ਲਿਸ਼ਟ ਪਦਾਰਥ ਦੀ ਹੋਵੇਗੀ । ਇਹ ਸੁਰੱਖਿਆ ਮੁੱਠ 10 ਇੰਚ ਤੋਂ ਜ਼ਿਆਦਾ ਨਹੀਂ ਹੋਵੇਗੀ ਅਤੇ ਬੈਟ ਛੋਟੇ ਭਾਗ ਤੋਂ 15 ਇੰਚ ਤੋਂ ਜ਼ਿਆਦਾ ਅੱਗੇ ਨੂੰ ਨਹੀਂ ਨਿਕਲੇਗੀ ।

ਸਾਫ਼ਟ ਬਾਲ (Soft Ball) – ਪ੍ਰਮਾਣਿਕ ਸਾਫ਼ਟ ਬਾਲ ਚਪਟੇ ਧਰਾਤਲ ਵਾਲੀ ਜਾਂ ਟਾਂਕੇ ਛਿਪੇ ਹੋਏ ਚਿਕਨੀ ਉੱਨ ਵਾਲੀ ਹੋਵੇਗੀ । ਇਸਦਾ ਘੇਰਾ 121/4 ਇੰਚ ਤੋਂ ਜ਼ਿਆਦਾ ਅਤੇ 111/4 ਇੰਚ ਤੋਂ ਘੱਟ ਨਾ ਹੋਵੇ । ਇਸਦਾ ਭਾਰ 63/4 ਔਸ ਤੋਂ ਜ਼ਿਆਦਾ ਜਾਂ 6 ਔਸ ਤੋਂ ਘੱਟ ਨਾ ਹੋਵੇ।

ਹਿ ਪੱਟੀ (Home Plate) – ਹਿ ਪੱਟੀ ਰਬੜ ਜਾਂ ਕਿਸੇ ਹੋਰ ਢੁੱਕਵੇਂ ਪਦਾਰਥ ਦੀ ਬਣਾਈ ਜਾਵੇਗੀ । ਇਹ ਪੰਚਮੁਖੀ ਆਕਾਰ ਵਾਲੀ 17 ਇੰਚ ਚੌੜੀ ਕਿਨਾਰੇ ਦੇ ਕੋਲ ਖੇਪਕ ਸਥਲ ਦੇ ਸਾਹਮਣੇ ਵੱਲ ਹੋਵੇਗੀ । ਇਸ ਦੀਆਂ ਸਾਈਡਾਂ ਬੈਟਰ ਬਾਕਸ ਦੇ ਅੰਦਰ ਦੀਆਂ ਰੇਖਾਵਾਂ ਦੇ ਸਮਾਨਾਂਤਰ ਅਤੇ 8 ਇੰਚ ਲੰਬੀਆਂ ਹੋਣਗੀਆਂ । ਫੜਨ ਵਾਲਿਆਂ ਦੇ ਸਾਹਮਣੇ ਵਾਲੀਆਂ ਸਾਈਡਾਂ 12 ਇੰਚ ਲੰਬੀਆਂ ਹੋਣਗੀਆਂ ।

ਖੇਪਣ ਪੱਟੀ (Pitcher Plate) – ਲੱਕੜੀ ਜਾਂ ਰਬੜ ਦੀ ਖੇਪਣ ਪੱਟੀ 24 ਇੰਚ ਲੰਬੀ ਅਤੇ 6 ਇੰਚ ਚੌੜੀ ਹੋਵੇਗੀ । ਪੱਟੀ ਦੀ ਪਰੀ ਧਰਾਤਲ ਜ਼ਮੀਨ ‘ਤੇ ਹੋਵੇਗੀ ਅਤੇ ਪੱਟੀ ਦੀ ਅਗਰ ਰੇਖਾ ਗਹਿ ਪੱਟੀ ਦੇ ਬਾਹਰੀ ਕੋਣ ਤੋਂ ਔਰਤਾਂ ਦੇ ਲਈ 40 ਫੁੱਟ ਅਤੇ ਪੁਰਸ਼ਾਂ ਦੇ ਲਈ 46 ਫੁੱਟ ਹੋਵੇਗੀ ।

ਦਸਤਾਨੇ, ਜੁੱਤੇ ਆਦਿ ਸਮਾਨ (Gloves, Shoes etc.) – ਕੋਈ ਵੀ ਖਿਡਾਰੀ ਦਸਤਾਨੇ ਪਾ ਸਕਦਾ ਹੈ । ਕਿਰਮਿਚ ਜਾਂ ਚਮੜੇ ਦਾ ਜੁੱਤਾ ਪ੍ਰਮਾਣਿਕ ਸਮਝਿਆ ਜਾਵੇਗਾ । ਜੁੱਤਿਆਂ ਦਾ ਤਲਾ ਚਿਕਨਾ, ਨਰਮ ਜਾਂ ਸਖ਼ਤ ਰਬੜ ਦੇ ਪੰਚਰ ਵਾਲਾ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ । ਫੜਨ ਵਾਲਾ ਮਾਸਕ ਪਹਿਨ ਸਕਦਾ ਹੈ ।

ਬੈਟਿਡ ਗੇਂਦ (Batted Bally) – ਉਹ ਗੇਂਦ ਜੋ ਬੈਟ ਨਾਲ ਟਕਰਾਉਂਦੀ ਹੈ ਅਤੇ ਸਹੀ ਜਾਂ ਗਲਤ ਸੀਮਾ ਵਿਚ ਡਿੱਗਦੀ ਹੈ ।

ਰੁਕਾਵਟ ਬਾਲ (Blocked Ball) – ਇਹ ਉਹ ਗੇਂਦ ਹੈ ਜੋ ਬੈਟ ਕੀਤੀ ਗਈ ਹੈ ਜਾਂ ਸੁੱਟੀ ਗਈ ਹੈ, ਜਿਸ ਨੂੰ ਇਕ ਅਜਿਹਾ ਵਿਅਕਤੀ ਫੜ ਲੈਂਦਾ ਹੈ, ਛੂਹ ਲੈਂਦਾ ਹੈ ਜਾਂ ਰੋਕ ਲੈਂਦਾ ਹੈ ਜੋ ਨਾ ਤਾਂ ਖੇਡ ਰਿਹਾ ਹੈ, ਨਾ ਅਧਿਕਾਰਤ ਵਿਅਕਤੀ ਹੈ ਅਤੇ ਨਾ ਹੀ ਉਹ ਅਧਿਕਾਰਤ ਖੇਡ ਖੇਤਰ ਵਿਚ ਹੈ ।

ਬੰਟ (Bunt) – ਇਹ ਉਹ ਗੇਂਦ ਹੈ ਜੋ ਖੇਤਰ ਦੇ ਅੰਦਰ ਹੌਲੀ ਜਿਹੇ ਰੋਕੀ ਗਈ ਹੈ । ਜੇਕਰ ਉਹ ਦੂਸਰੇ ਸਟਾਈਕਰ ਦੇ ਬਾਅਦ ਇਸ ਤਰ੍ਹਾਂ ਕਰਦਾ ਹੈ, ਤਾਂ ਉਹ ਆਊਟ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ ।

ਪਕੜ ਜਾਂ ਕੈਚ (Catch) – ਇਹ ਵਿਧੀਪੂਰਵਕ ਫੜੀ ਗਈ ਗੇਂਦ ਹੈ, ਜਿਸ ਨੂੰ ਰੱਖਿਅਕ ਹੱਥਾਂ ਜਾਂ ਦਸਤਾਨਿਆਂ ਨਾਲ ਫੜ ਲੈਂਦਾ ਹੈ । ਜੇਕਰ ਗੇਂਦ ਰੱਖਿਅਕ ਦੀਆਂ ਬਾਹਾਂ ਵਿਚ ਅਟਕ ਕੇ ਰਹਿ ਜਾਵੇ ਜਾਂ ਉਸਦੇ ਸਰੀਰ ਜਾਂ ਕੱਪੜਿਆਂ ਵਿਚ ਫਸ ਕੇ ਥੱਲੇ ਨਾ ਡਿਗੇ ਤਾਂ ਪਕੜ ਜਾਂ ਕੈਚ ਉਦੋਂ ਤਕ ਪੂਰਨ ਨਹੀਂ ਮੰਨੀ ਜਾਵੇਗੀ ਜਦੋਂ ਤੱਕ ਰੱਖਿਅਕ ਉਸਨੂੰ ਹੱਥਾਂ ਜਾਂ ਦਸਤਾਨਿਆਂ ਨਾਲ ਫੜ ਨਾ ਲਵੇ ।

ਖਿਡਾਰੀ ਅਤੇ ਸਥਾਨਾਪੰਨ (Players and Substitutes) – ਇਕ ਟੀਮ ਵਿੱਚ ਨੌਂ (9) ਖਿਡਾਰੀ ਹੋਣਗੇ । ਇਹਨਾਂ ਦਾ ਪਦ ਨਿਮਨ ਪ੍ਰਕਾਰ ਹੋਵੇਗਾ : | ਖੇਪਕ, ਕੈਚਰ, ਪਹਿਲਾ ਹਿ ਰੱਖਿਅਕ, ਦੂਸਰਾ ਅਤੇ ਤੀਸਰਾ ਹਿ ਰੱਖਿਅਕ, ਨਿਕਟ ਰੱਖਿਅਕ, ਖੱਬਾ ਰੱਖਿਅਕ, ਕੇਂਦਰ ਰੱਖਿਅਕ, ਸੱਜਾ ਰੱਖਿਅਕ ।

ਖਿਡਾਰੀ ਖੇਡ ਵਿਚ ਉਸ ਸਮੇਂ ਮੰਨਿਆ ਜਾਵੇਗਾ ਜਦੋਂ ਉਸਦਾ ਨਾਂ ਫਲਾਂਕਨ-ਪੱਤਰ (Score Card) ਵਿਚ ਅੰਕਿਤ ਕਰ ਦਿੱਤਾ ਜਾਵੇਗਾ ।ਉਸਦੇ ਬੈਟਰ-ਕਾਸ ਵਿਚ ਜਿਸਦਾ ਨਾਂ ਅੰਕਿਤ ਹੋਵੇਗਾ, ਇਹ ਕਿਸੇ ਵੀ ਖਿਡਾਰੀ ਨੂੰ ਸਥਾਨਾਪਨ ਕਰ ਸਕਦਾ ਹੈ । ਸਥਾਨਾਪੰਨ ਖੇਡ ਵਿਚ ਹੇਠ ਲਿਖੇ ਰੂਪ ਮੰਨੇ ਜਾਣਗੇ ।

1. ਬੈਟਰ-ਜਦੋਂ ਉਹ ਬੈਟਰ-ਬਾਕਸ ਵਿਚ ਆਪਣਾ ਸਥਾਨ ਬ੍ਰਿਣ ਕਰ ਲਵੇ ।
2. ਰੱਖਿਅਕ-ਜਦੋਂ ਉਹ ਰੱਖਿਅਕ ਦੇ ਸਥਾਨ ਤੇ ਸਥਾਨਾਪੰਨ ਹੋ ਜਾਵੇ ।
3. ਦੌੜਾਕ-ਜਦੋਂ ਸਥਾਨਾਪੰਨ ਉਸਦੇ ਹਿ ਵਿਚ ਪ੍ਰਵੇਸ਼ ਕਰ ਲਵੇ ।
4. ਖੇਪਕ-ਜਦੋਂ ਉਹ ਖੇਪਣ ਪੱਟੀ ਵਿਚ ਆਪਣਾ ਸਥਾਨ ਗ੍ਰਹਿਣ ਕਰ ਲਵੇ ।

ਖੇਡ ਦੇ ਸੰਬੰਧ ਵਿਚ (About Play) – ਸਾਫਟ ਬਾਲ ਦੀ ਖੇਡ ਦੋ ਟੀਮਾਂ ਵਿਚ ਹੁੰਦੀ ਹੈ । ਇਕ ਖੇਡਦੀ ਅਤੇ ਦੂਜੀ ਖਿਡਾਉਂਦੀ ਹੈ । ਖਿਡਾਉਣ ਵਾਲੇ ਦੇ ਪੱਖ (ਪਾਸੇ) ਵਿਚ ਗੇਂਦ ਸੁੱਟਣ ਵਾਲਾ ਮੈਦਾਨ ਦੇ ਸਿਰੇ ਤੋਂ ਬੱਲੇਬਾਜ਼ ਦੇ ਵੱਲ ਗੇਂਦ ਸੁੱਟਦਾ ਹੈ । ਬੈਟਰ ਉਸਨੂੰ ਅਦ੍ਰਿਸ਼ਟ ਖੇਤਰ ਦੇ ਅੰਦਰ ਜਿੰਨੀ ਦੂਰ ਵੀ ਹੋ ਸਕੇ, ਹਿੱਟ ਕਰਕੇ ਸੁੱਟਦਾ ਹੈ । ਉਸਦੇ ਬਾਅਦ ਪੜਾਅ ਦੇ ਚਾਰੇ ਪਾਸੇ ਦੌੜਦਾ ਹੈ । ਖੇਪਕ ਅੰਡਰ ਹੈਂਡ ਗੇਂਦ ਸੁੱਟਦਾ ਹੈ । ਜੇਕਰ ਬੈਟਰ ਬਿਨਾਂ ਆਊਟ ਹੋਏ ਪਹਿਲੇ, ਦੂਸਰੇ ਅਤੇ ਤੀਸਰੇ ਪੜਾਅ ਨੂੰ ਫੜ ਕੇ ਦੌੜਦਾ ਹੋਇਆ ਮੂਲ ਪੜਾਅ (ਹੋਮ, ਬੇਸ) ਤੇ ਵਾਪਸ ਆ ਜਾਵੇ, ਤਾਂ ਉਸਨੂੰ ਇਕ ਰਨ (Run) ਮਿਲਦਾ ਹੈ । ਉਸਦੇ ਬਾਅਦ ਉਸਦੀ ਟੀਮ ਦੇ ਦੂਸਰੇ ਮੈਂਬਰ ਵਾਰੀ-ਵਾਰੀ ਨਾਲ ਆਉਂਦੇ ਹਨ । ਤਿੰਨ ਖਿਡਾਰੀਆਂ ਦੇ ਆਊਟ ਹੋ ਜਾਣ ਤੇ ਖਿਡਾਉਣ ਵਾਲਾ ਪੱਖ ਖੇਡਦਾ ਹੈ । ਇਸ ਪ੍ਰਕਾਰ ਖੇਡ ਪੰਜ ਇਨਿੰਗਜ਼ ਤੱਕ ਚੱਲਦੀ ਹੈ ।

ਗੇਂਦ ਸੁੱਟਦੇ ਸਮੇਂ ਗੇਂਦ ਸਰੀਰ ਦੇ ਸਾਹਮਣੇ ਰੱਖੀ ਜਾਂਦੀ ਹੈ ਅਤੇ ਦੋਨੋਂ ਹੱਥ ਠੀਕ ਢੰਗ ਨਾਲ ਜ਼ਮੀਨ ‘ਤੇ ਲੱਗੇ ਰਹਿੰਦੇ ਹਨ, ਨਾਲ ਹੀ ਪੈਰਾਂ ਨੂੰ Wind Up ਜਾਂ Back Swing ਦੇ ਸ਼ੁਰੂ ਹੋਣ ਤੇ ਗੇਂਦ ਤੋਂ ਇਕ ਹੱਥ ਹਟਾਉਣ ਤੋਂ ਪਹਿਲਾਂ ਘੱਟ ਤੋਂ ਘੱਟ ਸੈਕਿੰਡ ਤਕ ਗੇਂਦ ਖੇਪਣ ਪੱਟੀ (Pitcher Plate) ਦੇ ਨਾਲ ਲੱਗੇ ਰਹਿਣਾ ਚਾਹੀਦਾ ਹੈ । ਗੇਂਦ ਦੇ ਜਾਣ ਦੀ ਦਿਸ਼ਾ ਦੀ ਰੇਖਾ ਦੇ ਸਮਾਨਾਂਤਰ ਹੀ ਬਾਂਹ ਘੁਮਾਉਣੀ ਚਾਹੀਦੀ ਹੈ । ਬੈਟਰ ਨੂੰ ਬੈਟ ਸੱਜੇ ਮੋਢੇ ਦੇ ਪਿੱਛੇ ਵੱਲ ਖਿੱਚ ਕੇ ਥੱਲੇ ਰੱਖਣਾ ਚਾਹੀਦਾ ਹੈ | ਬਾਂਹ ਸਰੀਰ ਤੋਂ ਉੱਪਰ ਰਹੇ ਅਤੇ ਕੂਹਣੀ ਮੋਢਿਆਂ ਜਿੰਨੀ ਉੱਚੀ ਰੱਖੀ ਜਾਏ । ਹਿਟ ਲਗਾਉਂਦੇ ਸਮੇਂ ਬੈਟਰ ਨੂੰ ਬੈਟ ਅੱਗੇ ਨੂੰ ਘੁਮਾਉਣਾ ਚਾਹੀਦਾ ਹੈ ਅਤੇ ਹਿਟ ਦੇ ਬਾਅਦ ਉਸਨੂੰ ਪਹਿਲੇ ਵਾਲੀ ਦਿਸ਼ਾ ਵਿਚ ਲੈ ਜਾਣਾ ਚਾਹੀਦਾ ਹੈ ।

ਸਾਫਟ ਬਾਲ ਦੇ ਮੂਲ ਕੌਸ਼ਲ
(Fundamental Skill of Soft Ball)

1. ਬੈਟਿੰਗ (Batting)
2. ਗਿਪ (Grip) (ਬਾਲ ਨੂੰ ਫੜਨਾ।
3. ਸਟੀਸ (Stance)
4. ਸਟਰੋਕ (Stroke)
5. ਬੱਲਾ ਚੁੱਕਣਾ (Bat lift)
6. ਰੱਖਿਆਤਮਕ ਬੈਟਿੰਗ ਕਰਨਾ (Defence Batting)
7. ਸਟਰੋਕਸ (Strokes)
8. ਹੁਕ (Hook)
9. ਪੁਲ (Pull)
10. ਸਵੀਪ (Sweep)

ਬਾਲਿਗ (Bowling)
(ਉ) ਗੇਂਦ ਦੀ ਪਕੜ (Grip)

ਬਾਲਿਗ ਦੀਆਂ ਕਿਸਮਾਂ (Types of Bowling
(ਉ) ਫੁਲ ਟਾਸ (Full Toss)
(ਅ) ਗੁਡ ਲੈਂਥ : (Good Length)

ਖੇਤਰ-ਰੱਖਿਅਣ (Fielding)
(ਉ) ਕੈਚ (Catch)
(ਅ) ਗੇਂਦ ਰੋਕਣਾ (Stopping the Ball)
(ਇ) ਗੇਂਦ ਵਾਪਿਸ ਸੁੱਟਣਾ (Throwing the Ball Back)
(ਸ) ਪਿਚ ਕੀਪਿੰਗ (Pitch Keeping)

ਹਿ (ਘਰੇਲੂ) ਦਲ (Home Team) – ਇਹ ਉਹ ਟੀਮ ਹੈ ਜਿਸਦੇ ਖੇਤਰ ਵਿਚ ਖੇਡ ਹੋ ਰਹੀ ਸੀ ਜਾਂ ਜਿਸਨੇ ਖੇਡ ਖੇਤਰ ਦੀ ਵਿਵਸਥਾ ਕੀਤੀ ਹੋਵੇ ।

ਗੇਂਦ ਦੀ ਅਵੈਧ ਪਕੜ (Illegally Caught Ball) – ਗੇਂਦ ਦੀ ਅਵੈਧ ਪਕੜ ਉਦੋਂ ਹੋਵੇਗੀ ਜਦੋਂ ਕੋਈ ਰੱਖਿਅਕ ਪਖੇਪਿਤ ਜਾਂ ਬੈਟ ਕੀਤੀ ਹੋਈ ਗੇਂਦ ਨੂੰ ਉਸ ਸਮੇਂ ਆਪਣੀ ਟੋਪੀ, ਦਸਤਾਨਿਆਂ ਜਾਂ ਕੱਪੜਿਆਂ ਦੇ ਕਿਸੇ ਭਾਗ ਨਾਲ ਫੜ ਲਵੇ ਜਿਸ ਸਮੇਂ ਉਹ ਆਪਣੇ ਮੰਨਣ ਯੋਗ ਸਥਾਨ ਤੋਂ ਹਟੀ ਹੋਈ ਹੋਵੇ ।

ਉਛਾਲ ਵਿਚ (In Hight) – ਉਛਾਲ ਵਿਚ’ ਤੋਂ ਭਾਵ ਕਿਸੇ ਵੀ ਬੈਟ ਕੀਤੀ ਹੋਈ ਖੇਪਿਤ ਜਾਂ ਸੰਕ੍ਰਮਿਤ ਗੇਂਦ ਤੋਂ ਹੈ, ਜਿਸਨੇ ਰੱਖਿਅਕ ਦੇ ਇਲਾਵਾ ਜ਼ਮੀਨ ਜਾਂ ਹੋਰ ਵਸਤੂਆਂ ਨੂੰ ਛੂਹਿਆ ਨਾ ਹੋਵੇ ।

ਸੰਕਟ ਵਿਚ (In Teopardy) – ਇਹ ਸ਼ਬਦ ਇਸ਼ਾਰਾ ਕਰਦਾ ਹੈ ਕਿ ਗੇਂਦ ਖੇਡ ਵਿਚ ਹੈ ਪਰੰਤੂ ਹਮਲਾਵਰ ਖਿਡਾਰੀ ਆਉਟ ਕਰ ਦਿੱਤਾ ਗਿਆ ।

ਖੇਤਰ ਵਿਚ (In Field) – ਇਹ ਉਹ ਭਾਗ ਹੈ ਜਿਹੜਾ ਬੇਸ ਰੇਖਾਵਾਂ ਤੋਂ ਬਣੇ ‘ਡਾਇਮੰਡ’ ਵਿਚ ਆਉਂਦਾ ਹੈ ।

ਵੈਧ ਸਪਰਸ਼ (Legal Touch) – ਵੈਧ ਸਪਰਸ਼ ਉਦੋਂ ਹੁੰਦਾ ਹੈ ਜਦੋਂ ਕੋਈ ਘਾਤਕ ਬੈਟਰ ਜਾਂ ਹਿ ਦੌੜਾਕ ਨੂੰ ਹਿ ਨਹੀਂ ਛੂਹ ਰਿਹਾ, ਦਾ ਗੇਂਦ ਦੁਆਰਾ ਸਪਰਸ਼ ਹੋ ਜਾਵੇ ਜਦਕਿ ਰੱਖਿਅਕ ਗੇਂਦ ਨੂੰ ਮਜ਼ਬੂਤੀ ਨਾਲ ਫੜੇ ਹੋਇਆ ਹੈ । ਜੇਕਰ ਦੌੜਾਕ ਨੂੰ ਸਪਰਸ਼ ਕਰਦੀ ਹੋਈ ਗੇਂਦ ਨੂੰ ਰੱਖਿਅਕ ਦੁਆਰਾ ਸੁੱਟ ਦਿੱਤਾ ਜਾਵੇ ਤਾਂ ਉਹ ਮਜ਼ਬੂਤੀ ਨਾਲ ਫੜੀ ਹੋਈ ਹੀ ਮੰਨੀ ਜਾਵੇਗੀ ਜਦੋਂ ਤੱਕ ਕਿ ਦੌੜਾਕ ਰੱਖਿਅਕ ਦੇ ਹੱਥ ਨਾਲ ਜਾਣ-ਬੁੱਝ ਕੇ ਗੇਂਦ ਦੇ ਨਾਲ ਨਾ ਟਕਰਾ ਜਾਵੇ ।

ਗੇਂਦ ਦੀ ਵੈਧ ਪਕੜ (Legally Caught Ball) – ਗੇਂਦ ਦੀ ਵੈਧ ਪਕੜ ਉਦੋਂ ਹੁੰਦੀ ਹੈ ਜਦੋਂ ਕੋਈ ਰੱਖਿਅਕ ਬੈਟ ਕੀਤੀ ਹੋਈ ਜਾਂ ਸੰਮਿਤ ਗੇਂਦ ਨੂੰ ਫੜ ਲਵੇ ਪਰ ਉਹ ਪਕੜ ਰੱਖਿਅਕ ਦੀ ਟੋਪੀ, ਜੇਬ ਜਾਂ ਕੱਪੜਿਆਂ ਦੇ ਕਿਸੇ ਭਾਗ ਨਾਲ ਛੂਹੀ ਹੋਈ ਨਹੀਂ ਹੋਣੀ ਚਾਹੀਦੀ ।

ਰੇਖਾ ਤੇ ਅਗਰਸਰ (Line Drive) – ਇਹ ਉਹ ਗੇਂਦ ਹੁੰਦੀ ਹੈ ਜੋ ਖੇਡ ਖੇਤਰ ਵਿਚ ਤੀਬਰਤਾ ਨਾਲ ਜਾਂ ਸਿੱਧੇ ਬੈਟ ਨੂੰ ਜਾਵੇ ।

ਗੇਂਦ ਖੇਡੋ (Play Ball) – ਇਹ ਸ਼ਬਦ ਨਿਰਣਾਇਕ ਦੁਆਰਾ ਖੇਡ ਸ਼ੁਰੂ ਕਰਨ ਜਾਂ ਜਾਰੀ ਰੱਖਣ ਦੇ ਲਈ ਪ੍ਰਯੋਗ ਹੁੰਦਾ ਹੈ ।

ਬੈਟਰ ਅਪ (Batter up) – ਇਹ ਸ਼ਬਦ ਅੰਪਾਇਰ ਦੁਆਰਾ ਕਿਸੇ ਬਾਹਰ ਦੀ ਬੈਟਰ ਬਾਕਸ ਵਿਚ ਪ੍ਰਵੇਸ਼ ਕਰਨ ਦੇ ਸੰਕੇਤ ਦੇ ਰੂਪ ਵਿਚ ਪ੍ਰਯੋਗ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।

ਤੀਬਰ ਪ੍ਰਖੇਪਣ (Wild Pitch) – ਇਹ ਬਹੁਤ ਉੱਚੀ ਜਾਂ ਬਹੁਤ ਨੀਵੀਂ ਅਤੇ ਤੇਜ਼ ਸੁੱਟੀ ਹੋਈ ਗੇਂਦ ਹੁੰਦੀ ਹੈ ਜੋ ਕਿ ਕੈਚਰ ਸਾਧਾਰਨ ਕੋਸ਼ਿਸ਼ ਦੁਆਰਾ ਇਸਨੂੰ ਰੋਕ ਸਕਦਾ ਹੈ।

ਰੁਕਾਵਟ ਗੇਂਦ (Obstructed) – ਇਹ ਉਹ ਬੈਟ ਕੀਤੀ ਹੋਈ ਜਾਂ ਸੰਮਿਤ ਗੇਂਦ ਹੈ ਜੋ ਵਾੜ, ਸਤੰਭ, ਦਰੱਖ਼ਤ ਜਾਂ ਹਿ ਰੇਖਾ ਤੋਂ 25 ਫੁੱਟ ਅੰਦਰ ਸਥਿਤ ਕਿਸੇ ਵਸਤੂ ਤੇ ਹਮਲਾ ਕਰਦੀ ਹੈ ।

ਰੁਕਾਵਟ (Obstruction) – ਇਹ ਕਿਸੇ ਖਿਡਾਰੀ ਦੀ ਜੋ ਗੇਂਦ ਨਹੀਂ ਲਏ ਹੈ, ਉਹ ਕਿਰਿਆ ਹੈ ਅਤੇ ਹਿ ਦੌੜਾਕ ਦੇ ਸਹੀ ਮਾਰਗ ਵਿਚ ਰੁਕਾਵਟ ਪੈਦਾ ਕਰ ਰਿਹਾ ਹੈ ।

ਬੈਟਿੰਗ ਕੁਮ (Batting Order)- ਬੈਟਿੰਗ ਕਮ ਹਮਲਾਵਰ ਖਿਡਾਰੀਆਂ ਦਾ ਅਧਿਕਾਰਤ ਸੂਚੀਕਮ ਹੈ, ਜਿਸਦੇ ਅਨੁਸਾਰ ਦਲ ਦੇ ਮੈਂਬਰ ਬੈਟ ਕਰਨ ਜਾਣਗੇ । ਅੰਪਾਇਰ ਵਲੋਂ ਦਿੱਤੇ ਗਏ ਬੈਟਿੰਗ ਕ੍ਰਮ ਦਾ ਪੂਰੀ ਖੇਡ ਦੇ ਦੌਰਾਨ ਪਾਲਣ ਕੀਤਾ ਜਾਣਾ ਚਾਹੀਦਾ ਹੈ । ਜੇਕਰ ਬੈਟਿੰਗ ਕ੍ਰਮ ਦੇ ਅਨੁਸਾਰ ਨਹੀਂ ਹੋ ਰਹੀ ਅਤੇ ਗਲਤ ਬੈਟਰ ਪਾਰੀ ਖ਼ਤਮ ਹੋਣ ਅਤੇ ਅਗਲੇ ਬੈਟਰ ਦੇ ਆਉਣ ਤੋਂ ਪਹਿਲਾਂ ਇਸ ਗਲਤੀ ਦਾ ਪਤਾ ਲਗਦਾ ਹੈ ਤਦ ਜਿਸ ਖਿਡਾਰੀ ਨੇ ਅਸਲ ਵਿਚ ਬੈਟਿੰਗ ਕਰਨੀ ਸੀ ਉਹ ਆਉਟ ਮੰਨਿਆ ਜਾਵੇਗਾ ਅਤੇ ਬਣਾਏ ਗਏ ਰਨ ਖ਼ਤਮ ਸਮਝੇ ਜਾਣਗੇ ਅਤੇ ਹਿ ਦੌੜਾਕ ਆਪਣੇ ਬੈਟਕ ਬਾਕਸ ਵਿਚ ਉਸ ਸਥਾਨ ਤੇ ਵਾਪਸ ਚਲੇ ਜਾਣਗੇ, ਜਿਥੇ ਉਹ ਗਲਤ ਬੈਟਰ ਦੇ ਆਉਣ ਤੋਂ ਪਹਿਲਾਂ ਸਨ ।

ਦਖ਼ਲ-ਅੰਦਾਜ਼ੀ (Interference) – ਇਹ ਰੱਖਿਅਕ ਖਿਡਾਰੀ ਦੀ ਉਹ ਪ੍ਰਕਿਰਿਆ ਹੈ ਜਿਹੜੀ ਬੈਟਰ ਨੂੰ ਖੇਪਿਤ ਗੇਂਦ ਤੇ ਚੋਟ ਕਰਨ ਵਿਚ ਰੁਕਾਵਟ ਪੈਦਾ ਕਰਦੀ ਹੈ ਜਾਂ ਹਮਲਾਵਰ ਖਿਡਾਰੀ ਦੀ ਉਹ ਪ੍ਰਕਿਰਿਆ ਹੈ ਜੋ ਰੱਖਿਅਕ ਖਿਡਾਰੀ ਦੇ ਖੇਡਣ ਦੇ ਮਾਰਗ ਵਿਚ ਰੁਕਾਵਟ ਜਾਂ ਭਰਮ ਪੈਦਾ ਕਰਨ ਦੇ ਲਈ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ।

ਪਾਰੀ (Inning) – ਇਹ ਖੇਡ ਦਾ ਉਹ ਭਾਗ ਹੈ ਜਿਸਦੇ ਅੰਦਰ ਦਲ ਕ੍ਰਮ ਅਨੁਸਾਰ ਹਮਲਾ ਅਤੇ ਖੇਤਰ ਰੱਖਿਅਣ (ਫੀਲਡਿੰਗ) ਕਰਦੇ ਹਨ ।

ਬਾਹਰੀ ਖੇਤਰ (Out Field) – ਇਹ ਖੇਤਰ ਦਾ ਉਹ ਭਾਗ ਹੈ ਜੋ ਹਿ ਰੇਖਾਵਾਂ ਤੋਂ ਨਿਰਮਿਤ ਡਾਇਮੰਡ ਦੇ ਬਾਹਰ ਅਤੇ ਪਹਿਲੇ ਅਤੇ ਤੀਜੇ ਹਿ ਦੇ ਪਾਰ ਨਾ-ਮੰਨਣ ਯੋਗ ਰੇਖਾਵਾਂ ਅਤੇ ਮੈਦਾਨ ਦੀ ਸੀਮਾ ਦੇ ਅੰਦਰ ਹੈ ।

ਉੱਚਿਤ ਸਪੋਰਟਸ ਗਿਅਰਸ ਅਤੇ ਉਸਦਾ ਮਹੱਤਵ
(Proper Sports Gears and their Importance)

ਸਪੋਰਟਸ ਗਿਅਰਸ ਖੇਡ ਉਪਕਰਨ ਅਤੇ ਸਪੋਰਟਸ ਯੂਨੀਫਾਰਮ ਆਦਿ । ਸਾਫਟ ਬਾਲ ਦੀ ਖੇਡ ਵਿਚ ਭਿੰਨ-ਭਿੰਨ ਸਪੋਰਟਸ ਗਿਅਰਸ ਜਿਵੇਂ-ਬਾਲ, ਬੈਟ, ਸਾਫਟ ਬਾਲ, ਥਾਈ ਗਾਰਡ, ਐਬਡੋਮਿਨਲ ਗਾਰਡ, ਆਰਮ ਪੈਡਸ, ਲੈਂਗ ਪ੍ਰੋਟੈਕਟਰ, ਯੂਨੀਫਾਰਮ, ਸਾਫਟ ਬਾਲ ਕੀਪਿੰਗ ਦੇ ਦਸਤਾਨੇ ਆਦਿ ਦਾ ਪ੍ਰਯੋਗ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਉਦਾਹਰਨ ਦੇ ਲਈ ਬਾਲ ਦਾ ਭਾਰ 6% ਔਸ ਤੋਂ ਜ਼ਿਆਦਾ ਜਾਂ 6 ਔਸ ਤੋਂ ਘੱਟ ਨਾ ਹੋਵੇ | ਬਾਲ ਦਾ ਘੇਰਾ 122 ਇੰਚ ਤੋਂ ਜ਼ਿਆਦਾ ਜਾਂ 11 ਇੰਚ ਤੋਂ ਘੱਟ ਨਹੀਂ ਹੋਣਾ ਚਾਹੀਦਾ ।

ਇਹ ਸਪੋਰਟਸ ਗਿਅਰਸ ਖਿਡਾਰੀਆਂ ਦੇ ਪ੍ਰਦਰਸ਼ਨ ਦੇ ਲਈ ਬਹੁਤ ਮਹੱਤਵਪੂਰਨ ਭੂਮਿਕਾ ਨਿਭਾਉਂਦੇ ਹਨ । ਜੇਕਰ ਇਹ ਉਪਕਰਨ ਉੱਚਿਤ ਨਾ ਹੋਣ ਤਾਂ ਮੈਚ ਵਿਚ ਖਿਡਾਰੀਆਂ ਦੇ ਲਈ ਚੰਗਾ ਪ੍ਰਦਰਸ਼ਨ ਕਰਨਾ ਅਸੰਭਵ ਹੋ ਸਕਦਾ ਹੈ । ਇਸਦੇ ਨਾਲ-ਨਾਲ ਉੱਚਿਤ ਸੁਰੱਖਿਆਤਮਕ ਉਪਕਰਨ ਵੀ ਖੇਡ-ਸੱਟਾਂ ਤੋਂ ਬਚਾਓ ਕਰਨ ਵਿਚ ਮਹੱਤਵਪੂਰਨ ਹੁੰਦੇ ਹਨ ।

ਮਹੱਤਵਪੂਰਨ ਟੂਰਨਾਮੈਂਟਸ
(Important Tournaments)

1. ਉਪਿੰਕ ਸਾਫਟ ਬਾਲ ਚੈਂਪੀਅਨਸ਼ਿਪ
2. ਏਸ਼ੀਅਨ ਸਾਫਟ ਬਾਲ ਚੈਂਪੀਅਨਸ਼ਿਪ
3. ਨੈਸ਼ਨਲ ਸਾਫਟ ਬਾਲ ਚੈਂਪੀਅਨਸ਼ਿਪ
4. ਆਲ ਇੰਡੀਆ ਸਾਫਟ ਬਾਲ ਇੰਟਰ-ਯੂਨੀਵਰਸਿਟੀ ਚੈਂਪੀਅਨਸ਼ਿਪ

ਪਾਰੀ ਵਿਚ ਪਹਿਲਾਂ ਜਾਂ ਅੰਤਿਮ ਬੈਟ ਕਰਨ ਦੀ ਚੋਣ ਟਾਸ (Toss) ਦੁਆਰਾ ਕੀਤੀ ਜਾਵੇਗੀ । ਨਿਯਮਿਤ ਖੇਡ ਵਿੱਚ ਪੰਜ ਪਾਰੀਆਂ ਹੋਣਗੀਆਂ ।

1. ਜਦ ਕੋਈ ਬੈਟਰ ਬੇਸ ਰਨਰ ਬਣ ਜਾਂਦਾ ਹੈ ਤਾਂ ਉਹ ਬੈਟਰ ਦਾ ਕੰਮ ਪੂਰਾ ਕਰ ਸਕਦਾ ਹੈ ।
2. ਉੱਚਿਤ ਹਿਟ ਬਾਲ ਤੋਂ ਭਾਵ ਇਹ ਹੈ ਕਿ ਗੇਂਦ ਹੋਮ ਤੋਂ ਪਹਿਲੇ ਬੇਸ ਜਾਂ ਹੋਮ ਦੇ ਤੀਸਰੇ ਬੇਸ ਦੇ ਵਿਚ ਜ਼ਮੀਨ ‘ਤੇ ਆ ਕੇ ਰੁਕਦੀ ਹੈ ।
3. ਫਾਉਲੇ (Faul) ਹਿਟ ਬਾਲ ਉਹ ਹੈ ਜਦੋਂ ਉਹ ਹੋਮ ਦੇ ਪਹਿਲੇ ਬੇਸ ਜਾਂ ਹੋਮ ਦੇ ਤੀਸਰੇ ਬੇਸ ਦੇ ਮੱਧ ਗਲਤ ਸਥਾਨ ‘ਤੇ ਡਿਗਦੀ ਹੈ ।
4. ਨਿਮਨਲਿਖਿਤ ਦਸ਼ਾਵਾਂ ਵਿਚ ਬੈਟਰ ਆਊਟ ਮੰਨਿਆ ਜਾਵੇਗਾ :

• ਜੇਕਰ ਦੂਸਰੀ ਹਿਟ ਲਗਾਏ ਅਤੇ ਖੇਡਣ ਵਾਲਾ ਗੇਂਦ ਨੂੰ ਜ਼ਮੀਨ ਤੇ ਡਿੱਗਣ ਤੋਂ ਪਹਿਲਾਂ ਫੜ ਲਵੇ ।
• ਜੇਕਰ ਦੂਸਰੀ ਹਿਟ ਦੇ ਬਾਅਦ ਗੇਂਦ ਰੋਕਣ ਵਿਚ ਫਾਊਲ ਹੋ ਜਾਵੇ ।
• ਜੇਕਰ ਉਹਨਾਂ ਦੇ ਤਿੰਨ ਸਾਈਕ ਲੱਗ ਜਾਂਦੇ ਹਨ, ਤਾਂ ਉਸਦੇ ਛੇਤੀ ਪਿੱਛੇ ।
• ਹਿਟ ਦੇ ਤੁਰੰਤ ਬਾਅਦ ਜੇਕਰ ਬੈਟਰ ਦੇ ਪਹਿਲੇ ਬੇਸ ਦੇ ਛੁੱਟਣ ਤੋਂ ਪਹਿਲਾਂ ਬੇਸ ਮੈਨ (Base Man) ਦੇ ਹੱਥ ਆ ਜਾਵੇ ।

5. ਬੇਸ ਰਨਰ ਨੂੰ ਹਰੇਕ ਨਿਯਮ ਅਨੁਸਾਰ ਕੂਮਪੂਰਵਕ ਛੂਹਣਾ ਚਾਹੀਦਾ ਹੈ ਅਰਥਾਤ ਪਹਿਲੀ, ਦੂਸਰੀ, ਤੀਸਰੀ | ਅਤੇ ਹੋਮ ਬੇਸ ਆਪਣੇ ਤੋਂ ਪਹਿਲਾਂ ਬੇਸ ਰਨਰ ਤੋਂ ਪਹਿਲਾਂ ਕਿਸੇ ਵੀ ਬੇਸ ਰਨਰ ਦਾ ਰਨ ਨਹੀਂ ਗਿਣਿਆ ਜਾਵੇਗਾ । ਜੇਕਰ ਇਸ ਪਾਰੀ ਵਿਚ ਅਜਿਹਾ ਪਹਿਲੇ ਦਾ ਬੇਸ ਰਨਰ ਹੋਵੇ ਜੋ ਆਊਟ ਨਾ ਹੋਇਆ ਹੋਵੇ ।
6. ਜੇਕਰ ਕੋਈ ਰਨਰ ਬੇਸ ਦੇ ਵਿਚਕਾਰ ਦੌੜਦਾ ਹੋਇਆ ਆਊਟ ਕਰ ਦਿੱਤਾ ਜਾਵੇ ਅਤੇ ਪਿੱਛੇ ਵਾਲਾ ਦੂਸਰਾ ਰਨਰ ਉਹੀ ਬੇਸ ’ਤੇ ਆ ਜਾਵੇ, ਜਿਸ ਨੂੰ ਪਹਿਲੇ ਰਨਰ ਲਈ ਛੱਡ ਦਿੱਤਾ ਹੋਵੇ ।
7. ਠੀਕ ਗੇਂਦ ਹਿਟ ਕਰਨ ਤੋਂ ਬਾਅਦ ਬੈਟਰ ਬੇਸ ਰਨਰ ਬਣ ਜਾਂਦਾ ਹੈ ।
8. ਬੇਸ ਰਨਰ ਨੂੰ ਆਉਟ ਨਾ ਹੋਣ ਦਾ ਦੰਡ ਮਿਲਣ ਦੀ ਸੰਭਾਵਨਾ ਤੋਂ ਇਕ ਬੇਸ ਅੱਗੇ ਵਧਣ ਦਾ ਅਧਿਕਾਰ ਮਿਲੇਗਾ | ਪਰੰਤੂ ਹੇਠ ਲਿਖੀਆਂ ਦਸ਼ਾਵਾਂ ਵਿਚ ਉਸਨੂੰ ਇਕ ਤੋਂ ਵੱਧ ਬੇਸ ਅੱਗੇ ਵਧਣ ਦਾ ਅਧਿਕਾਰ ਹੋਵੇਗਾ ।

• ਜੇਕਰ ਬੈਟਰ ਚਾਰ ਗੇਂਦਾਂ ਦੇ ਮੱਧ ਬੇਸ ਰਨਰ ਬਣਦਾ ਹੈ ।
• ਉਸਦੀ ਛੁੱਟੀ ਹੋਈ ਗੇਂਦ ਲਗ ਜਾਂਦੀ ਹੈ ।
• ਸੁੱਟੀ ਹੋਈ ਗੇਂਦ ਨੂੰ ਹਿਟ ਕਰਨ ਵਿਚ ਰੁਕਾਵਟ ਪਹੁੰਚਾਏ ਜਾਣ ਤੇ ।

9. ਬੇਸ ਰਨਰ ਨਿਮਨਲਿਖਿਤ ਹਾਲਾਤਾਂ ਵਿਚ ਆਊਟ ਮੰਨਿਆ ਜਾਵੇਗਾ:
(ਉ) ਜਦੋਂ ਗੇਂਦ ਨੂੰ ਫੜਨ ਵਾਲਾ ਫੀਲਡਰ ਸਹੀ ਤਰੀਕੇ ਨਾਲ ਹਿਟ ਕੀਤੀ ਗਈ ਗੇਂਦ ਨੂੰ ਜ਼ਮੀਨ ਜਾਂ
ਫੀਲਡ ਦੇ ਇਲਾਵਾ ਕਿਸੇ ਹੋਰ ਚੀਜ਼ ਨੂੰ ਛੂਹੇ ਬਿਨਾਂ ਫੜ ਲਵੇ ।

• ਜੇਕਰ ਬੈਟ ਕਰਨ ਵਾਲਾ ਦੁਸਰਾ ਦਲ ਚਾਰ ਪਾਰੀਆਂ ਵਿੱਚ ਅਤੇ ਪੰਜਵੀਂ ਪਾਰੀ ਦੇ ਅੰਤ ਵਿੱਚ ਤੀਸਰੇ
  ਆਉਟ ਤੋਂ ਪਹਿਲਾਂ ਜ਼ਿਆਦਾ ਰਨ ਬਣਾ ਲਵੇ ਤਾਂ ਪੰਜ ਪਾਰੀਆਂ ਖੇਡਣ ਦੀ ਜ਼ਰੂਰਤ ਨਹੀਂ ਹੈ ।
• ਖੇਡ ਵਿਚ ਜੇਕਰ ਪੰਜਵੀਂ ਪਾਰੀ ਦੇ ਬਾਅਦ ਬਰਾਬਰ (Tie) ਹੋ ਜਾਵੇ ਤਾਂ ਜ਼ਿਆਦਾਤਰ ਪਾਰੀਆਂ ਦੁਆਰਾ ਖੇਡ ਤਦ ਤਕ ਜਾਰੀ ਰਹੇਗੀ ਜਦ ਤਕ ਪੂਰੀ ਪਾਰੀ ਦੇ ਬਾਅਦ ਪਹਿਲਾ ਦਲ ਜ਼ਿਆਦਾ ਰਨ ਨਾ ਬਣਾ ਲਵੇ ਜਾਂ ਬੈਟ ਕਰਨ ਵਾਲਾ ਦੂਸਰਾ ਦਲ ਪਾਰੀ ਦੇ ਅੱਧ ਵਿਚ ਤੀਸਰਾ ਆਊਟ ਹੋਣ ਤੋਂ ਪਹਿਲਾਂ ਜ਼ਿਆਦਾ ਰਨ ਨਾ ਬਣਾ ਲਵੇ ।
• ਨਿਰਣਾਇਕ ਦੁਆਰਾ ਘੋਸ਼ਿਤ ਪਾਰੀ ਨਿਯਮ ਅਨੁਸਾਰ ਮੰਨੀ ਜਾਵੇਗੀ ਜੇਕਰ ਤਿੰਨ ਜਾਂ ਜ਼ਿਆਦਾ ਪੂਰੀਆਂ ਪਾਰੀਆਂ ਖੇਡੀਆਂ ਜਾ ਚੁੱਕੀਆਂ ਹਨ ਜਾਂ ਬੈਟ ਕਰਨ ਵਾਲਾ ਦਲ ਪਹਿਲੇ ਦਲ ਦੁਆਰਾ ਤਿੰਨ ਜਾਂ ਜ਼ਿਆਦਾ ਪਾਰੀਆਂ ਵਿਚ ਬਣਾਏ ਗਏ ਰਨਾਂ ਤੋਂ ਜ਼ਿਆਦਾ ਰਨ ਬਣਾ ਚੁੱਕਾ ਹੈ ।
• ਜੇਕਰ ਤਿੰਨ ਜਾਂ ਜ਼ਿਆਦਾ ਪੁਨ ਪਾਰੀਆਂ ਦੇ ਬਾਅਦ ਘੋਸ਼ਿਤ ਬਾਜ਼ੀ ਹੋਵੇ ਤਾਂ ਫਲਾਂਕਨ (Score) ਸਮਾਨ ਹੋਣ ਤੇ ਨਿਯਮਿਤ ਜਾਂ ਬੈਟ ਕਰਨ ਵਾਲੇ ਦੂਸਰੇ ਦਲ ਦੁਆਰਾ ਪਹਿਲੇ ਦਲ ਦੀ ਅਪੂਰਨ ਪਾਰੀ ਦੇ ਬਰਾਬਰ ਅੰਕ ਬਣਾ ਲੈਣ ਤੇ ਵਿਨਿਯਮਿਤ ਬਰਾਬਰ (Tie) ਘੋਸ਼ਿਤ ਕੀਤੀ ਜਾਵੇਗੀ ।
• ਖੇਪਕ (ਗੇਂਦ ਸੁੱਟਣ ਵਾਲਾ ਬੈਟਰ ਨੂੰ ਗੇਂਦ ਦੇਣ ਦੀ ਕਿਰਿਆ ਇਕ ਕਦਮ ਤੋਂ ਜ਼ਿਆਦਾ ਨਹੀਂ ਲਵੇਗਾ। ਇਹ ਕਦਮ ਬੈਟਰ ਦੇ ਵਲ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ਅਤੇ ਕਦਮ ਗੇਂਦ ਸੁੱਟਣ ਦੇ ਨਾਲ ਹੀ ਲਿਆ ਜਾਣਾ ਚਾਹੀਦਾ ਹੈ ।
• ਖੇਪਕ ਆਪਣੀ ਇੱਛਾ ਅਨੁਸਾਰ ਗੇਂਦ ਸੁੱਟਣ ਦਾ ਕੋਈ ਵੀ ਢੰਗ (Wind up) ਅਪਣਾ ਸਕਦਾ ਹੈ, ਪਰੰਤੂ ਸ਼ਰਤ ਇਹ ਹੈ ਕਿ ਬੈਟਰ ਨੂੰ ਗੇਂਦ ਸੁੱਟਣ ਦੀ ਅੰਤਿਮ ਸਥਿਤੀ (Position) ਵਿਚ ਖੇਪਕ ਦੇ ਹੱਥ ਕੂਲ੍ਹਿਆਂ ਦੇ ਥੱਲੇ ਅਤੇ ਕਲਾਈ ਕੂਹਣੀ ਤੋਂ ਦੂਰ ਨਹੀਂ ਹੋਵੇਗੀ ।
• ਖੇਪਣ ਦੇ ਸਮੇਂ ਕੈਚਰ ਨੂੰ ਕੈਚਰਬਾਕਸ ਵਿਚ ਰਹਿਣਾ ਚਾਹੀਦਾ ਹੈ ।
• ਜੇਕਰ ਸੁੱਟੀ ਗਈ ਗੇਂਦ ਤੇ ਹਿੱਟ ਨਾ ਲੱਗੇ ਅਤੇ ਗੇਂਦ ਉਸਦੇ ਕਿਸੇ ਅੰਗ ਨੂੰ ਛੂਹ ਜਾਵੇ ਤਾਂ ਅੰਪਾਇਰ
  ਇਕ ਸਾਈਕ ਦੇਵੇਗਾ ।
• ਗਲਤ ਢੰਗ ਨਾਲ ਸੁੱਟੀ ਗਈ ਹਰ ਇਕ ਗੇਂਦ ਦੇ ਲਈ ਅੰਪਾਇਰ ਇਕ ‘‘ਬਾਲ’’ ਘੋਸ਼ਿਤ ਕਰੇਗਾ ।
• ਪਹਿਲੀ ਪਾਰੀ ਦੇ ਬਾਅਦ ਹਰੇਕ ਇਨਿੰਗ ਵਿਚ ਸਭ ਤੋਂ ਪਹਿਲਾਂ ਉਹ ਬੈਟਰ ਖੇਡੇਗਾ ਜਿਸਦਾ ਨਾਮ ਇਸ ਤੋਂ ਪਹਿਲੇ ਵਾਲੀ ਪਾਰੀ (Innings) ਵਿਚ ਖੇਡਣ ਵਾਲੇ ਅੰਤਿਮ ਖਿਡਾਰੀ ਦੇ ਬਾਅਦ ਹੋਵੇਗਾ, ਜਦੋਂ ਕਿਸੇ ਪਾਰੀ ਵਿਚ ਤੀਸਰਾ ਆਉਟ ਇਸ ਲਈ ਹੋਇਆ ਕਿ ਗੇਂਦ ਦੇ ਸੁੱਟੇ ਜਾਣ ਨਾਲ ਬੇਸ ਰਨਰ (Base Runner) ਨੇ ਬਹੁਤ ਜਲਦੀ ਆਪਣਾ ਬੇਸ ਛੱਡ ਦਿੱਤਾ ਹੋਵੇ ਤਾਂ ਬੈਟਰ ਨੂੰ ਆਊਟ ਨਹੀਂ ਕੀਤਾ ਜਾ ਸਕਦਾ, ਨਾ ਹੀ ਉਹ ਬੇਸ ਰਨਰ ਬਣੇਗਾ, ਇਸ ਲਈ ਅਗਲੀ ਪਾਰੀ ਵਿਚ ਵੀ ਉਹੀ ਪਹਿਲਾ ਬੈਟਰ, ਬੈਟਰ ਬਣੇਗਾ ।

(ਅ) ਜੇਕਰ ਸਹੀ ਹਿਟ ਤੋਂ ਬਾਅਦ ਗੇਂਦ ਹੱਥ ਵਿਚ ਫੜੇ ਹੋਏ ਫੀਲਡਰ ਬੇਸ ਰਨਰ ਨੂੰ ਇਹ ਬੇਸ ਛੁੱਟਣ ਤੋਂ ਪਹਿਲਾਂ ਛੂਹ ਲਵੇ ।
(ਈ) ਜੇਕਰ ਤੀਸਰੀ ਸਟ੍ਰਾਈਕ ਨੂੰ ਫੀਲਡਰ ਜ਼ਮੀਨ ਨੂੰ ਛੂਹਣ ਤੋਂ ਪਹਿਲਾਂ ਨਿਯਮ ਅਨੁਸਾਰ ਫੜ ਲਵੇ ।
(ਸ) ਜੇਕਰ ਉਹ ਬੈਟ ਨਾਲ ਲੱਗ ਕੇ ਛੁੱਟੀ ਗੇਂਦ ਨੂੰ ਰੋਕਣ ਆਦਿ ਦੇ ਯਤਨ ਵਿੱਚ ਲੱਗੇ ਫੀਲਡਰ ਦੇ ਨਾਲ ਟਕਰਾਉਣ ਨਾਲ ਆਪਣੇ ਆਪ ਨੂੰ ਬਚਾ ਸਕੇ ਜਾਂ ਉਹ ਕਿਸੇ ਵੀ ਤਰ੍ਹਾਂ ਫੀਲਡਰ ਦੇ ਦ ਆਦਿ ਰੋਕਣ ਵਿਚ ਰੁਕਾਵਟ ਪਾਉਣ ਜਾਂ ਸੁੱਟੀ ਗਈ ਗੇਂਦ ਨੂੰ ਜਾਣ-ਬੁਝ ਕੇ ਛੱਡ ਦੇਵੇ ।
(ਹ) ਗੇਂਦ ਸੁੱਟਣ ਵਾਲਾ ਗੇਂਦ ਸੁੱਟਣ ਦੀ ਹਾਲਤ ਵਿਚ ਹੀ ਰਹੇ ਅਤੇ ਉਸਦੇ ਨਿਯਮ ਅਨੁਸਾਰ ਗੇਂਦ ਸੁੱਟਣ ਤੱਕ ਬੇਸ ਛੱਡ ਦੇਵੇ ।

ਖਿਡਾਰੀ ਬਦਲਦੇ ਸਮੇਂ ਯਾਦ ਰੱਖਣ ਯੋਗ ਨਿਯਮ (The Rules which must be remembered in case of substitution of players) – ਸਾਫ਼ਟ ਬਾਲ ਦੇ ਬਾਕੀ ਸਾਰੇ ਖਿਡਾਰੀ ਕਿਸੇ ਵੀ ਸਮੇਂ ਖੇਡ ਤੋਂ ਬਾਹਰ ਕੱਢੇ ਜਾ ਸਕਦੇ ਹਨ ਸਿਵਾਇ ਖੇਪਕ (Pitcher) ਦੇ, ਜਿਸ ਦਾ ਨਾਮ ਘੋਸ਼ਿਤ ਹੋ ਚੁੱਕਾ ਹੈ ਜਾਂ ਜੋ ਖੇਪਣ ਪੱਟੀ (Pitcher Plate) ਦੇ ਸਥਾਨ ਹਿਣ ਕਰ ਚੁੱਕਾ ਹੋਵੇ । ਉਹ ਉਦੋਂ ਤੱਕ ਪ੍ਰਖੇਪਣ ਕਰੇਗਾ ਜਦੋਂ ਤੱਕ ਉਸਦੇ ਸਾਹਮਣੇ ਵਾਲਾ ਬੈਟਰ ਆਪਣੀ ਪਾਰੀ ਪੂਰੀ ਨਾ ਕਰ ਲਵੇ ਜਾਂ ਉਸਦਾ ਪੱਖ (ਪਾਸਾ) ਖ਼ਤਮ ਨਾ ਹੋ ਜਾਵੇ ।

PSEB 12th Class Physical Education Practical ਸਾਫਟ ਬਾਲ (Softball)

ਪ੍ਰਸ਼ਨ 1.
ਸਾਫਟ ਬਾਲ ਮੈਦਾਨ ਨੂੰ ਕੀ ਕਹਿੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਸਾਫਟ ਬਾਲ ਦੇ ਮੈਦਾਨ ਨੂੰ ਪਤੰਗ ਜਾਂ ਡਾਇਮੰਡ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਸਾਫਟ ਬਾਲ ਖੇਡ ਦੀ ਸ਼ੁਰੂਆਤ ਕਦੋਂ ਮੰਨੀ ਜਾਂਦੀ ਹੈ ?
ਉੱਤਰ-
ਸਾਲ 1926 ਤੋਂ ।

ਪ੍ਰਸ਼ਨ 3.
ਖੇਡ ਦੇ ਮੈਦਾਨ ਵਿਚ ਕਿੰਨੇ ਖਿਡਾਰੀ ਖੇਡਦੇ ਹਨ ?
ਉੱਤਰ-
9 ਖਿਡਾਰੀ ।

ਪ੍ਰਸ਼ਨ 4.
ਬੈਟਰ ਬਾਕਸ ਦੀ ਲੰਬਾਈ, ਚੌੜਾਈ ਬਾਰੇ ਦੱਸੋ ।
ਉੱਤਰ-
3′ × 71 × 2.30 ਮੀਟਰ ।

ਪ੍ਰਸ਼ਨ 5.
ਕਿਸ ਸਾਲ ਵਿਚ ਸਾਫਟ ਖੇਡ ਦਾ ਪ੍ਰਦਰਸ਼ਨ ਹੋਇਆ ?
ਉੱਤਰ-
ਸਾਲ 1936 ਵਿਚ ।

ਪ੍ਰਸ਼ਨ 6.
ਵੂਮੈਨ ਸਾਫਟ ਲੀਗ ਕਿਸ ਸਾਲ ਸ਼ੁਰੂ ਹੋਈ ?
ਉੱਤਰ-
ਸਾਲ 1953 ਵਿਚ ।

ਪ੍ਰਸ਼ਨ 7.
ਕੈਚਰ ਬਾਕਸ ਦੀ ਮਿਣਤੀ ਬਾਰੇ ਲਿਖੋ ।
ਉੱਤਰ-
10′ × 8.5 × 9.15 × 7.45 ਮੀਟਰ ।

ਪ੍ਰਸ਼ਨ 8.
ਬੈਟ ਦਾ ਕਿੰਨਾ ਭਾਰ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
34 ਆਊਂਸ ।

ਪ੍ਰਸ਼ਨ 9.
ਬੈਟ ਦੀ ਚੌੜਾਈ ਕਿੰਨੀ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
34′ ।

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 5 Continuity and Differentiability Ex 5.3 Textook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 5 Continuity and Differentiability Ex 5.3

Direction (1 – 15): Find \(\frac{d y}{d x}\) in the following :

Question 1.
2x + 3y = sin x
Solution.
Given, 2x + 3y = sin x
On differentiating w.r.t. x, we get
\(\frac{d}{d x}\) (2x + 3y) = \(\frac{d}{d x}\) (sin x)
⇒ \(\frac{d}{d x}\) (2x) + \(\frac{d}{d x}\) (3y) = cos x
⇒ 2 + 3 \(\frac{d y}{d x}\) = cos x dx
⇒ 3 \(\frac{d y}{d x}\) = cos x – 2
∴ \(\frac{d y}{d x}=\frac{\cos x-2}{3}\)

Question 2.
2x + 3y = sin y
Solution.
Given, 2x + 3y = sin y
On differentiating w.r.t. x, we get
\(\frac{d}{d x}\) (2x) + \(\frac{d}{d x}\) (3y) = \(\frac{d}{d x}\) (sin y)
⇒ 2 + 3 \(\frac{d y}{d x}\) = cos y \(\frac{d y}{d x}\)
⇒ 2 = (cos y – 3) \(\frac{d y}{d x}\)
∴ \(\frac{d y}{d x}\) = \(\frac{2}{\cos y-3}\)

Question 3.
ax + by² = cos y
Solution.
Given, ax + by² = cos y
On differentiating w.r.t. x, we get
\(\frac{d}{d x}\) (ax) + \(\frac{d}{d x}\) (y²) = \(\frac{d}{d x}\) (cos y)
⇒ a + b \(\frac{d}{d x}\) (y²) = \(\frac{d}{d x}\) (cos y) …………(i)
Using chain rule,
\(\frac{d}{d x}\) (y²) \(\frac{d y}{d x}\) and
\(\frac{d}{d x}\) (cos y) = – sin y \(\frac{d y}{d x}\) …………..(ii)
From (i) and (ii), we get
a + b × 2y \(\frac{d y}{d x}\) = – sin y \(\frac{d y}{d x}\)
⇒ (2by + sin y) \(\frac{d y}{d x}\) = – a
∴ \(\frac{d y}{d x}=\frac{-a}{2 b y+\sin y}\)

Question 4.
xy + y² = tanx + y
Solution.
Given, xy + y² = tanx + y
On differenating w.r.t. x, we get
\(\frac{d}{d x}\) (xy + y²) = \(\frac{d}{d x}\) (tanx + y)
⇒ \(\frac{d}{d x}\) (xy) + \(\frac{d}{d x}\) (y²) = \(\frac{d}{d x}\) (tanx) + \(\frac{d y}{d x}\)

⇒ [y . \(\frac{d}{d x}\) (x) + x . \(\frac{d y}{d x}\)] + 2y \(\frac{d y}{d x}\) = sec² x + \(\frac{d y}{d x}\)

⇒ y . 1 + x \(\frac{d y}{d x}\) + 2y \(\frac{d y}{d x}\) = sec² x + \(\frac{d y}{d x}\)

⇒ (x + 2y – 1) \(\frac{d y}{d x}\) = sec² x – y
∴ \(\frac{d y}{d x}=\frac{\sec ^{2} x-y}{(x+2 y-1)}\)

Question 5.
x² + xy + y² = 100
Sol.
Given, x² + xy + y² = 100
On differentiating w.r.t. x, we get
\(\frac{d}{d x}\) (x² + xy + y²) = \(\frac{d}{d x}\) (100)
⇒ \(\frac{d}{d x}\) (x²) + \(\frac{d}{d x}\) (xy) + \(\frac{d}{d x}\) (y²) = 0
⇒ 2x + [y . \(\frac{d}{d x}\) (x) + x . \(\frac{d y}{d x}\)] + 2y \(\frac{d y}{d x}\) = 0
⇒ 2x + y . 1 + x . \(\frac{d y}{d x}\) + 2y \(\frac{d y}{d x}\) = 0
⇒ 2x + y + (x + 2y) \(\frac{d y}{d x}\) = 0
⇒ \(\frac{d y}{d x}\) = – \(-\frac{2 x+y}{x+2 y}\)

Question 6.
x³ + x²y + xy² + y³ = 81
Solution.
Given, x³ + x²y + xy² + y³ = 81
On differentiating w.rt. x, we get
\(\frac{d}{d x}\) (x³ + x²y + xy² + y³) = \(\frac{d}{d x}\) (81)

⇒ \(\frac{d}{d x}\) (x³) + \(\frac{d}{d x}\) (x²y) + \(\frac{d}{d x}\) (xy²) + \(\frac{d}{d x}\) (y³) = 0

⇒ 3x² + [y \(\frac{d}{d x}\) x² + x² \(\frac{d y}{d x}\)] + [y² \(\frac{d}{d x}\) (x) + x \(\frac{d}{d x}\) (y²)] + 3 y² \(\frac{d}{d x}\) = 0

⇒ 3x² + [y . 2x + x² \(\frac{d y}{d x}\)] + [y² . 1 + x . 2y . \(\frac{d y}{d x}\)] + 3y² \(\frac{d y}{d x}\) = 0

⇒ (x² + 2xy + 3y²) \(\frac{d y}{d x}\) + (3x² + 2xy + y²)

∴ \(\frac{d y}{d x}=\frac{-\left(3 x^{2}+2 x y+y^{2}\right)}{\left(x^{2}+2 x y+3 y^{2}\right)}\)

Question 7.
sin² y + cos xy = k
Solution.
Given, sin² y + cos xy = k
On differentiating w.r.t. x, we get
⇒ \(\frac{d}{d x}\) (sin² y + cos xy) = \(\frac{d}{d x}\) (k)

⇒ \(\frac{d}{d x}\) (sin² y) + \(\frac{d}{d x}\) (cos xy) = 0 ……….(i)
Using chain rule, we get
\(\frac{d}{d x}\) (sin² y) = 2 sin y \(\frac{d}{d x}\) (sin y) = 2 sin y cos y \(\frac{d y}{d x}\) ………….(ii)

\(\frac{d}{d x}\) (cos xy) = – sin xy \(\frac{d}{d x}\) (xy) = – sin xy[y \(\frac{d}{d x}\) (x) + x \(\frac{d y}{d x}\)]

= – sin xy [y . 1 + x \(\frac{d y}{d x}\)] = – y sin xy – x sin xy \(\frac{d y}{d x}\) ………..(iii)
From Eq.s (i), (ii) and (iii), we get
2 sin y cos y \(\frac{d}{d x}\) – y sin xy – x sin xy \(\frac{d y}{d x}\) = 0
(2 sin y cos y – x sin xy) \(\frac{d y}{d x}\) = y sin xy
(sin 2y – x sin xy) \(\frac{d y}{d x}\) =y sin xy
∴ \(\frac{d y}{d x}\) = \(\frac{y \sin x y}{\sin 2 y-x \sin x y}\)

Question 8.
sin² x + cos² y = 1
Solution.
Given, sin² x + cos² y = 1
On differentiating w.r.t. x, we get
\(\frac{d}{d x}\) (sin² x + cos² y) = \(\frac{d}{d x}\) (1)
⇒ \(\frac{d}{d x}\) (sin² x) + \(\frac{d}{d x}\) (cos² y) = 0

⇒ 2 sin x . ⇒ (sin x) + 2 cos y . \(\frac{d}{d x}\) (cos y) = 0

⇒ 2 sin x cos x + 2 cos y (- sin y) . \(\frac{d y}{d x}\) = 0

⇒ sin 2x – sin 2y \(\frac{d y}{d x}\) = 0

∴ \(\frac{d y}{d x}=\frac{\sin 2 x}{\sin 2 y}\)

Question 9.
y = sin^-1 \(\left(\frac{2 x}{1+x^{2}}\right)\)
Solution.
Given, y = sin^-1 \(\left(\frac{2 x}{1+x^{2}}\right)\)
⇒ sin y = \(\left(\frac{2 x}{1+x^{2}}\right)\)
On differentiating w.r.t. x, we get
\(\frac{d}{d x}\) (sin y) = \(\frac{d}{d x}\) (\(\left(\frac{2 x}{1+x^{2}}\right)\))

cos y \(\frac{d y}{d x}\) = \(\frac{d}{d x}\) (\(\left(\frac{2 x}{1+x^{2}}\right)\)) …………(i)

The function \(\left(\frac{2 x}{1+x^{2}}\right)\) is of the form of \(f\frac{u}{v}\)

Therefore, by quotient rule, we get

Alternate method:
y = sin^-1 \(\left(\frac{2 x}{1+x^{2}}\right)\), put x = tan θ
θ = tan^-1 x
= sin^-1 \(\left(\frac{2 \tan \theta}{1+\tan ^{2} \theta}\right)\)
= sin^-1 sin 2θ
= 2θ = 2 tan^-1 x [∵ sin^-1 sin(θ) = θ]
∴ \(\frac{d y}{d x}=\frac{2}{1+x^{2}}\).

Question 10.
y = tan^-1 \(\left(\frac{3 x-x^{3}}{1-3 x^{2}}\right)\), \(-\frac{1}{\sqrt{3}}<x<\frac{1}{\sqrt{3}}\)
Solution.
Given, y = tan^-1 \(\left(\frac{3 x-x^{3}}{1-3 x^{2}}\right)\)

⇒ tan y = \(\left(\frac{3 x-x^{3}}{1-3 x^{2}}\right)\) …………(i)
It is known that, tan y = \(\frac{3 \tan \frac{y}{3}-\tan ^{3} \frac{y}{3}}{1-3 \tan ^{2} \frac{y}{3}}\) ………..(ii)
On comparing Eqs. (i) and (ii), we get

x = tan \(\frac{y}{3}\)

On differenating w.r.t x, we get

Question 11.
y = cos^-1 \(\left(\frac{1-x^{2}}{1+x^{2}}\right)\), 0 < x < 1
Solution.
Given, y = cos^-1 \(\left(\frac{1-x^{2}}{1+x^{2}}\right)\)
⇒ cos y = cos^-1 \(\left(\frac{1-x^{2}}{1+x^{2}}\right)\)

⇒ \(\frac{1-\tan ^{2} \frac{y}{2}}{1+\tan ^{2} \frac{y}{2}}=\frac{1-x^{2}}{1+x^{2}}\)

On comparing L.H.S. and R.H.S. of the above relationship, we get
tan \(\frac{y}{2}\) = x

On differentiating wr.t. x, we get

Question 12.
y = sin^-1 \(\left(\frac{1-x^{2}}{1+x^{2}}\right)\), 0 < x < 1
Solution.
Given, y = sin^-1 \(\left(\frac{1-x^{2}}{1+x^{2}}\right)\)

sin y = \(\left(\frac{1-x^{2}}{1+x^{2}}\right)\)

On differentiating wr.t. x, we get

\(\frac{d}{d x}\) (sin y) = \(\frac{d}{d x}\) \(\left(\frac{1-x^{2}}{1+x^{2}}\right)\)

Usin chain rule, we get

Question 13.
y = cos^-1 \(\left(\frac{2 x}{1+x^{2}}\right)\), – 1 < x < 1
Solution.
Given, y = cos^-1 \(\left(\frac{2 x}{1+x^{2}}\right)\)

cos y = \(\frac{2 x}{1+x^{2}\)

On differentiating wr.t. x, we get

Question 14.
y = sin^-1 \(\left(2 x \sqrt{1-x^{2}}\right)\), \(-\frac{1}{\sqrt{2}}<x<\frac{1}{\sqrt{2}}\)
Solution.
Given, y = sin^-1 \(\left(2 x \sqrt{1-x^{2}}\right)\), \(-\frac{1}{\sqrt{2}}<x<\frac{1}{\sqrt{2}}\)

⇒ sin y = 2x\(\sqrt{1-x^{2}}\)

On differentiating wr.t. x, we get

Question 15.
y = sec^-1 \(\left(\frac{1}{2 x^{2}-1}\right)\), 0 < x < \(\frac{1}{\sqrt{2}}\)
Solution.
Given, y = sec^-1 \(\left(\frac{1}{2 x^{2}-1}\right)\)
⇒ sec y = \(\frac{1}{2 x^{2}-1}\)
⇒ cos y = 2x² – 1
⇒ 2x² = 1 + cos y
⇒ 2x² = 2 cos² \(\frac{y}{2}\)
⇒ x = cos \(\frac{y}{2}\)
On differentiating wr.t. x, we get

Punjab State Board PSEB 12th Class Physical Education Book Solutions ਜੂਡੋ (Judo) Game Rules.

ਜੂਡੋ (Judo) Game Rules – PSEB 12th Class Physical Education

ਜੂਡੋ ਦਾ ਇਤਿਹਾਸ
(History of Judo)

ਜੂਡੋ, ਜਾਪਾਨ ਦਾ ਆਧੁਨਿਕ ਮਾਰਸ਼ਲ ਆਰਟਸ ਹੈ । ਪ੍ਰਾਚੀਨ ਕਾਲ ਵਿੱਚ ਇਸਨੂੰ ਜਿਝਸੂ (Jijsu) ਕਹਿੰਦੇ ਸਨ । | ਇਹ ਦਰਸ਼ਨ ਸ਼ਾਸਤਰ ਦੀ ਪੁਰਾਣੀ ਕਹਾਣੀ ਨਾਲ ਜੁੜਿਆ ਹੋਇਆ ਹੈ । ਇਹ ਕੋਮਲਤਾ, ਕਠੋਰਤਾ ਨੂੰ ਨਿਯੰਤਰਿਤ (Softmen, Controls Hardmen) ਕਰਦੀ ਹੈ । ਲੇਕ, ਕੇਲੀ, ਚਿਪ (Lake rounds Chip) ਮਾਰਸ਼ਲ ਆਰਟਸ ਦੇ | ਸਿਸਟਮ ਨਾਲ ਜੁੜਿਆ ਹੈ, ਜੋ 1532 ਵਿੱਚ ਸ਼ੁਰੂ ਹੋਇਆ ਸੀ । ਇਸ ਨੂੰ ਜਾਪਾਨ ਦੇ -ਜੂਝਸੂ ਦੀਆਂ ਕਿਸਮਾਂ ਦਾ ਸ਼ੁਰੂ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਸਿਸਟਮ ਦੇ ਸੰਸਥਾਪਕ ਨੇ ਜੂ-ਜੂਝਸੂ ਦੀ ਸਿੱਖਿਆ ਨੂੰ ਸਿਰਜਨਾਤਮਕ ਢੰਗ ਨਾਲ ਸਾਡੇ | ਸਾਹਮਣੇ ਰੱਖਿਆ । ਇਹ ਸੋਵਰਨਾਂ ਦੇ ਬਾਅਦ ਸਮੁਰਾਇ (Samurai) ਨੇ ਕਈ ਪ੍ਰਕਾਰ ਦੇ ਮਾਰਸ਼ਲ ਆਰਟਸ ਵਿੱਚ ਕਈ ਬਦਲਾਅ ਕੀਤੇ ਅਤੇ ਜੂ-ਜੂਝਸੂ ਹੀ ਜੋ ਬਿਨਾਂ ਕਿਸੇ ਹਥਿਆਰ ਦੇ ਆਤਮ ਸੁਰੱਖਿਆ ਤੇ ਆਧਾਰਿਤ ਸੀ, ਸੰਨ 1968 ਵਿੱਚ ਇੰਪੀਰੀਅਲ ਖੇਡ ਨੂੰ ਫੇਰ ਤੋਂ ਸ਼ੁਰੂ ਕੀਤਾ ਗਿਆ, ਜਿਸ ਵਿੱਚ ਸਮੁਰਾਇ ਦਾ ਪਤਨ ਸ਼ੁਰੂ ਹੋ ਗਿਆ, ਇਸ ਦੇ ਨਾਲ | ਮਾਰਸ਼ਲ ਆਰਟਸ ਵਿੱਚ ਗਿਰਾਵਟ ਆਉਣ ਲੱਗੀ ਅਤੇ ਸਾਰੇ ਸਕੂਲ ਖ਼ਤਮ ਹੋ ਗਏ ।

ਡਾ: ਜਿਗਾਰੇ ਕਾਨੋ (Jigaro Kano) ਨੇ ਇਸ ਕਲਾ ਨੂੰ ਸਰੀਰ ਦੇ ਪ੍ਰੀਖਿਅਣ ਦੇ ਲਈ ਉਪਯੋਗੀ ਮੰਨਿਆ । ਜਾਪਾਨ ਵਿੱਚ ਟੋਕੀਓ ਵਿੱਚ ਇਸ਼ਾਜੀ (Eishaji) ਬੁੱਧ ਧਰਮ ਦਾ ਇਕ ਮੰਦਿਰ ਦੇ ਬਹੁਤ ਹੀ ਛੋਟੇ ਕਸਬੇ ਵਿੱਚ ਇਸ ਕਲਾ ਨੂੰ ਸਿਖਾਉਣ ਦੇ 9 ਬੱਚਿਆਂ ਨੂੰ ਚੁਣਿਆ । ਉਨ੍ਹਾਂ ਨੇ ਇਸ ਦਾ ਨਾਂ ਬਦਲ ਕੇ ਕੋਡੋਕਾਨ ਜੂਡੋ (KodoKan Judo) ਰੱਖਿਆ । | ਇਸ ਨੂੰ Judo ਦੇ ਰੂਪ ਵਿਚ ਅਪਣਾਇਆ ਗਿਆ ਹੈ । ਸੰਨ 1951 ਵਿੱਚ ਅੰਤਰ-ਰਾਸ਼ਟਰੀ ਜੂਡੋ ਫੈਡਰੇਸ਼ਨ 1952 ਵਿੱਚ ਬਣਿਆ ਅਤੇ ਇਸ ਦੀ ਪਹਿਲੀ ਮੀਟਿੰਗ ਸੰਨ 1952 ਵਿੱਚ ਬੁਲਾਈ ਗਈ । ਜਿੱਥੇ Risei Kano ਨੂੰ ਪ੍ਰਧਾਨ ਬਣਾਇਆ ਗਿਆ । ਪੁਰਸ਼ਾਂ ਦੇ ਲਈ ਪਹਿਲੀ ਵਿਸ਼ਵ ਜੂਡੋ ਪ੍ਰਤੀਯੋਗਤਾ ਸੰਨ 1956 ਵਿੱਚ ਟੋਕੀਓ ਵਿੱਚ ਕਰਵਾਈ ਗਈ । ਸੰਨ 1964 ਵਿੱਚ ਟੋਕੀਓ ਉਲੰਪਿਕ ਖੇਡਾਂ ਵਿੱਚ ਜੂਡੋ ਨੂੰ ਸ਼ਾਮਿਲ ਕੀਤਾ ਗਿਆ । ਮਹਿਲਾਵਾਂ ਦੀ ਪਹਿਲੀ ਜੂਡੋ ਚੈਂਪੀਅਨਸ਼ਿਪ ਸੰਨ 1980 ਵਿੱਚ ਨਿਊਯਾਰਕ ਵਿਚ ਕਰਵਾਈ ਗਈ । ਮਹਿਲਾਵਾਂ ਦੀ ਪਹਿਲੀ ਜੂਡੋ ਚੈਂਪੀਅਨਸ਼ਿਪ ਸੰਨ 1980 ਵਿੱਚ ਨਿਊਯਾਰਕ ਵਿੱਚ ਕਰਵਾਈ ਗਈ । ਮਹਿਲਾਵਾਂ ਦੇ ਲਈ ਵੀ ਜੂਡੋ ਨੂੰ ਸੰਨ 1992 ਵਿੱਚ ਉਲੰਪਿਕ ਵਿੱਚ ਸਥਾਨ ਮਿਲਿਆ | ਸੀ, ਹੁਣ ਜੁਡੋ ਦੁਨੀਆ ਦਾ ਲੋਕਪ੍ਰਿਅ ਖੇਡ ਬਣ ਗਿਆ, ਜਾਪਾਨੀ | ਯਾਤਰੀਆਂ ਰਾਹੀਂ ਭਾਰਤ ਵਿੱਚ ਇਸ ਦੀ ਸ਼ੁਰੂਆਤ ਕੀਤੀ ਗਈ ।ਇਸਦਾ ਪ੍ਰਦਰਸ਼ਨ ਹਾਲੋਂ ਵਿੱਚ ਕੀਤਾ ਗਿਆ । ਇਹ ਹਾਲੋਂ ਜਾਪਾਨੀਆਂ | ਰਾਹੀਂ ਸਥਾਪਿਤ ਕੀਤੇ ਗਏ ਸਨ । ਇਹ ਪ੍ਰੀਖਿਅਣ ਹਾਲਾਂ ਨੂੰ ‘Dojos’ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਜੂਡੋ ਫੈਡਰੇਸ਼ਨ ਆਫ਼ ਇੰਡੀਆ ਦੀ ਸਥਾਪਨਾ ਸੰਨ 1965 ਵਿੱਚ ਕੀਤੀ ਗਈ ।ਕਈ ਸਾਲਾਂ ਦੇ ਬਾਅਦ ਇਸਨੂੰ ਅੰਤਰਰਾਸ਼ਟਰੀ | ਜੂਡੋ ਫੈਡਰੇਸ਼ਨ ਤੋਂ ਮਾਨਤਾ ਮਿਲੀ | ਭਾਰਤੀ ਖਿਡਾਰੀਆਂ ਨੇ ਸੰਨ 1986 ਵਿੱਚ ਸਿਉਲ ਗੇਮਸ ਵਿੱਚ ਭਾਗ ਲਿਆ ਸੀ । ਸੰਨ 1966 ਵਿੱਚ ਰਾਸ਼ਟਰੀ ਪਹਿਲੀ ਜੂਡੋ ਪ੍ਰਤੀਯੋਗਤਾ ਦਾ ਆਯੋਜਨ ਕੀਤਾ ਗਿਆ ਸੀ । ਹੁਣ ਇਹ ਖੇਡ ਸਕੂਲ ਗੇਮਸ ਆਫ਼ ਇੰਡੀਆ ਅਤੇ ਅੰਤਰ-ਰਾਸ਼ਟਰੀ ਵਿਦਿਆਲਿਆ ਵਿੱਚ ਵੀ ਖੇਡੀ ਜਾਂਦੀ ਹੈ ।

ਯਾਦ ਰੱਖਣ ਯੋਗ ਗੱਲਾਂ
(Tips to Remember)

1. ਜੂਡੋ ਮੈਦਾਨ ਦਾ ਆਕਾਰ = ਵਰਗਾਕਾਰ
2. ਜੁਡੋ ਮੈਦਾਨ ਦੀ ਇਕ ਭੁਜਾ ਦੀ ਲੰਬਾਈ = 10 ਮੀਟਰ
3. ਅਧਿਕਾਰਿਆਂ ਦੀ ਸੰਖਿਆ = ਤਿੰਨ
4. ਪੁਸ਼ਾਕ ਦਾ ਨਾਮ = ਜੁਡੋਗੀ
5. ਜੂਡੋ ਦੇ ਭਾਰ ਦੀ ਸੰਖਿਆ (ਪੁਰਸ਼ਾਂ ਦੇ ਲਈ) = ਅੱਠ
6. ਜੂਡੋ ਦੇ ਭਾਰ ਦੀ ਸੰਖਿਆ (ਔਰਤਾਂ ਦੇ ਲਈ) = ਸੱਤ
7. ਜੂਡੋ ਦੇ ਭਾਰ ਦੀ ਸੰਖਿਆ (ਜੂਨੀਅਰ ਦੇ ਲਈ = ਅੱਠ
8. ਜੂਡੋ ਖੇਡ ਦਾ ਸਮਾਂ = 10 ਮਿੰਟ ਤੋਂ 20 ਮਿੰਟ ।
9. ਜੁਡੋ ਦੇ ਮੈਦਾਨ ਦਾ ਨਾਮ = ਸ਼ਿਆਗੋ
10. ਪਲੇਟਫਾਰਮ ਨੂੰ ਕਵਰ ਕਰਨ ਲਈ ਟੁੱਕੜੀਆਂ ਦੀ ਗਿਣਤੀ = ਘੱਟ ਤੋਂ ਘੱਟ 50, 16 × 16 ਮੀ.
11. ਮੈਦਾਨ ਦਾ ਕੁੱਲ ਖੇਤਰ = ਜ਼ਿਆਦਾ ਤੋਂ ਜ਼ਿਆਦਾ 14 × 14 ਮੀ.
12. ਹਰੇਕ ਮੈਟ ਦੇ ਟੁੱਕੜੇ ਦਾ ਆਕਾਰ = 1 × 2 ਮੀ.
13. ਜੂਡੋ ਖਿਡਾਰੀਆਂ ਦੀ ਇਕ ਦੂਜੇ ਤੋਂ ਖੜ੍ਹੇ ਹੋਣ ਦੀ ਦੂਰੀ = 4 ਮੀ. 1

ਜੂਡੋ ਦੇ ਨਵੇਂ ਨਿਯਮ
(Latest Rules of Judo)

1. ਜੁਡੋ ਪ੍ਰਤੀਯੋਗਤਾ ਰੈਫ਼ਰੀ ਦੇ Hajime ਸ਼ਬਦ ਕਹਿਣ ਨਾਲ ਸ਼ੁਰੂ ਹੁੰਦੀ ਹੈ ।
2. ਖਿਡਾਰੀ ਅੰਗੂਠੀ, ਕੜਾ ਆਦਿ ਨਹੀਂ ਪਾ ਸਕਦਾ ਤੇ ਨਾ ਹੀ ਉਸਦੇ ਹੱਥਾਂ ਤੇ ਪੈਰਾਂ ਦੇ ਨਹੁੰ ਵਧੇ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ ।
3. ਰੈਫਰੀ ਦੇ ‘ਉਸਾਈ’ ‘ਮੰਮੀ-ਡੋਕੇਤ’ ਆਖਣ ਤੇ ਪਕੜ ਹਟ ਜਾਂਦੀ ਹੈ।
4. ਜੇਕਰ ਕਦੇ ਜੱਜ ਰੈਫਰੀ ਦੇ ਫੈਸਲੇ ਨਾਲ ਸਹਿਮਤ ਨਾ ਹੋਵੇ ਤਾਂ ਉਹ ਰੈਫਰੀ ਨੂੰ ਆਪਣਾ ਸੁਝਾਅ ਦੇ ਸਕਦਾ ਹੈ । ਰੈਫਰੀ ਠੀਕ ਸਮਝੇ ਤਾਂ ਜੱਜ ਜੇ ਫੈਸਲੇ ਨੂੰ ਮੰਨ ਸਕਦਾ ਹੈ ।
5. ਜੂਡੋ ਪ੍ਰਤੀਯੋਗਤਾ ਦੀ ਮਿਆਦ 3 ਮਿੰਟ ਤੋਂ 20 ਮਿੰਟ ਹੋ ਸਕਦੀ ਹੈ ।
6. ਜੂਡੋ ਮੁਕਾਬਲੇ ਵਿਚ ਪੇਟ ਨੂੰ ਘੁੱਟਣਾ ਜਾਂ ਸਿਰ ਜਾਂ ਧੌਣ ਨੂੰ ਸਿੱਧਾ ਲੱਤਾਂ ਨਾਲ ਘੁੱਟਣਾ ਫਾਊਲ ਹੈ ।
7. ਜੂਡੋ ਮੁਕਾਬਲੇ ਵਿਚ ਜੇ ਕੋਈ ਖਿਡਾਰੀ ਭਾਗ ਲੈਣ ਤੋਂ ਇਨਕਾਰ ਕਰ ਦੇਵੇ, ਤਾਂ ਉਸਦੇ ਵਿਰੋਧੀ ਖਿਡਾਰੀ ਨੂੰ ਤਰੁੱਟੀ ਦੇ ਕਾਰਨ (By Fusetcho) ਜੇਤੂ ਐਲਾਨ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।
8. ਜੇਕਰ ਕੋਈ ਖਿਡਾਰੀ ਮੁਕਾਬਲੇ ਵਿਚ ਆਪਣੇ ਵਿਰੋਧੀ ਖਿਡਾਰੀ ਦੀ ਗ਼ਲਤੀ ਨਾਲ ਜ਼ਖਮੀ ਹੋ ਜਾਵੇ, ਤਾਂ ਉਸ (ਜ਼ਖ਼ਮੀ) ਨੂੰ ਜੇਤੂ ਐਲਾਨ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।

ਜੂਡੋ ਦੇ ਖੇਡ ਦੇ ਖੇਤਰ ਅਧਿਕਾਰੀ, ਪੁਸ਼ਾਕ, ਖਿਡਾਰੀਆਂ ਦੇ ਮੁਕਾਬਲੇ ਦੀ ਮਿਆਦ, ਖਿਡਾਰੀਆਂ ਲਈ ਨਿਯਮ:
ਖੋਡ ਦਾ ਖੇਤਰ (Play ground) – ਜੁਡੋ ਦੇ ਖੇਡ ਦੇ ਮੈਦਾਨ ਨੂੰ ਸ਼ਿਆਗੋ’ ਆਖਿਆ ਜਾਂਦਾ ਹੈ । ਇਹ ਇਕ ਵਰਗਾਕਾਰ ਪਲੇਟਫਾਰਮ ਹੁੰਦਾ ਹੈ । ਇਸ ਦੀ ਹਰੇਕ ਭੁਜਾ 30 ਫੁੱਟ ਹੁੰਦੀ ਹੈ । ਇਹ ਪਲੇਟਫਾਰਮ ਭੂਮੀ ਤੋਂ ਕੁੱਝ ਉਚਾਈ ਤੇ ਹੁੰਦਾ ਹੈ । ਇਸ ਨੂੰ ਟਾਟ ਦੇ 50 ਟੁਕੜਿਆਂ ਜਾਂ ਕਨਵੇਸ ਨਾਲ ਢੱਕਿਆ ਜਾਂਦਾ ਹੈ । ਹਰੇਕ ਟੁਕੜੇ ਦਾ ਆਕਾਰ 3″ x 6″ ਹੁੰਦਾ ਹੈ ।

ਅਧਿਕਾਰੀ (Officials) – ਜੂਡੋ ਪ੍ਰਤੀਯੋਗਤਾ ਵਿਚ ਆਮ ਤੌਰ ਤੇ ਤਿੰਨ ਅਧਿਕਾਰੀ ਹੁੰਦੇ ਹਨ । ਇਹਨਾਂ ਵਿਚ ਇਕ ਰੈਫਰੀ ਤੇ ਦੋ ਜੱਜ ਹੁੰਦੇ ਹਨ । ਬਾਊਟ (Bout) ਨੂੰ ਰੈਫਰੀ ਆਯੋਜਿਤ ਕਰਦਾ ਹੈ । ਉਸਦਾ ਨਿਰਣਾ ਅੰਤਿਮ ਹੁੰਦਾ ਹੈ । ਇਸਦੇ ਵਿਰੁੱਧ ਅਪੀਲ ਨਹੀਂ ਹੋ ਸਕਦੀ । ਉਹ ਮੁਕਾਬਲੇ ਦੇ ਖੇਤਰ ਵਿਚ ਰਹਿ ਕੇ ਖੇਡ ਦੀ ਪ੍ਰਗਤੀ ਦਾ ਧਿਆਨ ਰੱਖਦਾ ਹੈ ।

ਪੁਸ਼ਾਕ (Costume) – ਖਿਡਾਰੀ ਦੀ ਪੁਸ਼ਾਕ ਨੂੰ ‘ਜੁਰੋਗੀ’ ਕਹਿੰਦੇ ਹਨ । ਜੇਕਰ ਜੁਡੋ ਨਾ ਹੋਏ, ਤਾਂ ਖਿਡਾਰੀ ਅਜਿਹੇ ਕੱਪੜੇ ਵੀ ਪਾ ਸਕਦੇ ਹਨ ਜਿਨ੍ਹਾਂ ਦੀ ਪੇਟੀ ਕਾਫ਼ੀ ਲੰਬੀ ਹੋਵੇ ਜੋ ਸਰੀਰ ਦੇ ਦੁਆਲੇ ਦੋ ਵਾਰ ਆ ਸਕੇ, ਵਰਗ ਆਕਾਰ ਗੰਢ (knot) ਵੀ ਦਿੱਤੀ ਜਾ ਸਕੇ ਅਤੇ ਫਿਰ 3” ਦੇ ਸਿਰੇ ਬਚ ਜਾਣ । ਜੈਕਟ ਵੀ ਇੰਨੀ ਲੰਬੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ਕਿ ਜਦੋਂ ਪੇਟੀ ਨੂੰ ਕਮਰ ਦੇ ਚਾਰੇ ਪਾਸੇ ਬੰਨਿਆ ਜਾਵੇ, ਤਾਂ ਹਿਪ ਲੁੱਕ ਜਾਵੇ । ਜੈਕਟ ਦੇ ਬਾਜੂ ਢਿੱਲੇ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ । ਇਸ ਦੇ ਬਿਨਾਂ ਜਿਸ ਪਜਾਮੇ ਦੀ ਵਰਤੋਂ ਕੀਤੀ ਜਾਵੇ, ਉਹ ਵੀ ਕਾਫ਼ੀ ਖੁੱਲ੍ਹਾ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ । ਕਫ ਅਤੇ ਬਾਹਵਾਂ ਦੇ ਵਿਚਕਾਰ 1′ ਦਾ ਫਾਸਲਾ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ਅਤੇ ਇਹ ਅੱਧੀ ਬਾਹਵਾਂ ਤੱਕ ਲਟਕਣੀ ਚਾਹੀਦੀ ਹੈ । ਖਿਡਾਰੀ ਅੰਗੁਠੀ, ਮਾਲਾ ਹਾਰ) ਆਦਿ ਨਹੀਂ ਪਹਿਨ ਸਕਦਾ, ਕਿਉਂਕਿ ਇਹਨਾਂ ਨਾਲ ਸੱਟ ਲੱਗਣ ਦਾ ਡਰ ਰਹਿੰਦਾ ਹੈ । ਖਿਡਾਰੀਆਂ ਦੇ ਹੱਥਾਂ ਦੀਆਂ ਉਂਗਲੀਆਂ ਦੇ ਨਹੁੰ ਕੱਟੇ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ ।

ਮੁਕਾਬਲੇ ਦੀ ਮਿਆਦ (Duration of the competition) – ਮੈਚ ਲਈ ਸਮੇਂ ਦੀ ਮਿਆਦ 3 ਮਿੰਟ ਤੋਂ 5 ਮਿੰਟ ਤੱਕ ਹੁੰਦੀ ਹੈ | ਖਾਸ ਹਾਲਤਾਂ ਵਿਚ ਇਸ ਮਿਆਦ ਵਿਚ ਕਮੀ ਜਾਂ ਵਾਧਾ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ।

ਖਿਡਾਰੀਆਂ ਲਈ ਨਿਯਮ (Rules of Judo Players) –

1. ਖਿਡਾਰੀਆਂ ਦੇ ਹੱਥਾਂ ਅਤੇ ਪੈਰਾਂ ਦੇ ਨਹੁੰ (Nails) ਕੱਟੇ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ ।
2. ਖਿਡਾਰੀ ਅੰਗੂਠੀ , ਕੜਾ ਆਦਿ ਨਹੀਂ ਪਾ ਸਕਦੇ ਹਨ, ਕਿਉਂਕਿ ਇਹਨਾਂ ਨਾਲ ਦੂਸਰੇ ਖਿਡਾਰੀ ਨੂੰ ਸੱਟ ਲੱਗਣ ਦੀ ਸੰਭਾਵਨਾ ਹੈ ।

ਜੂਡੋ ਮੁਕਾਬਲਾ ਕਿਸ ਤਰ੍ਹਾਂ ਆਰੰਭ ਹੁੰਦਾ ਹੈ । ਇਸ ਖੇਡ ਵਿਚ ਕਿਹੜੀਆਂ ਵਿਧੀਆਂ ਅਪਣਾਈਆਂ ਜਾਂਦੀਆਂ ਹਨ । ਜੂਡੋ ਮੁਕਾਬਲੇ ਦੇ ਵੱਖ-ਵੱਖ ਨਿਯਮਾਂ ਦਾ ਵਰਣਨ ਕਰੋ ।

ਜੂਡੋ ਮੁਕਾਬਲੇ ਦਾ ਆਰੰਭ (Start of Judo competition) – ਖਿਡਾਰੀ ਖੇਡ ਦੇ ਮੈਦਾਨ ਦੇ ਦਰਮਿਆਨ ਵਿਚ 13 ਫੁੱਟ ਦੀ ਦੂਰੀ ਤੇ ਖੜ੍ਹੇ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ । ਉਹਨਾਂ ਦੇ ਮੂੰਹ ਇਕ ਦੂਜੇ ਦੇ ਸਾਹਮਣੇ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ। ਉਹ ਇਕ ਦੂਜੇ ਨੂੰ ਖੜੇ-ਖੜੇ ਹੀ ਝੁਕ ਕੇ ਸਲਾਮ (Salute) ਕਰਦੇ ਹਨ । ਇਸ ਮਗਰੋਂ ਰੈਫ਼ਰੀ ‘ਹਾਜ਼ੀਮੇ’ (Hajime) ਸ਼ਬਦ ਕਹਿ ਕੇ ਬਾਊਟ ਆਰੰਭ ਕਰਵਾ ਦਿੰਦਾ ਹੈ । Hajime ਦਾ ਅਰਥ ਹੈ ‘ ਸ਼ੁਰੂ ਕਰੋ’ ।

ਜੂਡੋ ਦੀਆਂ ਵਿਧੀਆਂ (Judo Techniques) – ਜੂਡੋ ਵਿਚ ਹੇਠ ਲਿਖੀਆਂ ਵਿਧੀਆਂ ਅਪਣਾਈਆਂ ਜਾਂਦੀਆਂ ਹਨ-

1. ਨਾਗੇਵਾਜ਼ਾ (ਡੇਗਣ ਦੀ ਤਕਨੀਕ).
2. ਕਾਟਮੇਪਾਜ਼ਾ (ਗਰਾਊਂਡ-ਵਰਕ ਦੀ ਤਕਨੀਕ)

ਨਿਰਣਾ ਦਿੰਦੇ ਸਮੇਂ ਇਹਨਾਂ ਦੋਵੇਂ ਤਰ੍ਹਾਂ ਦੀਆਂ ਤਕਨੀਕਾਂ ਨੂੰ ਧਿਆਨ ਵਿਚ ਰੱਖਿਆ ਜਾਂਦਾ ਹੈ । ਆਮ ਤੌਰ ਤੇ ਨਿਰਣਾ ਇਕ ‘ਇੰਪਨ’ (ਅੰਕ) ਤੋਂ ਵੱਧ ਨਹੀਂ ਦਿੱਤਾ ਜਾਂਦਾ ।

ਨਿਯਮ (Rule)

1. ਡੇਗਣ ਦੀ ਤਕਨੀਕ ਵਿਚ ਕੁੱਝ ਪ੍ਰਗਤੀ ਕਰਨ ਮਗਰੋਂ ਖਿਡਾਰੀ ਨਿਰਸੰਕੋਚ ਲੇਟਣ ਦੀ ਸਥਿਤੀ ਹਿਣ ਕਰ ਸਕਦਾ ਹੈ ਅਤੇ ਇਸ ਤਰ੍ਹਾਂ ਉਹ Offensive ਵਿਚ ਆ ਸਕਦਾ ਹੈ ।
2. ਡੇਗਣ ਦੀ ਤਕਨੀਕ ਅਪਣਾਉਂਦੇ ਹੋਏ, ਜਦੋਂ ਕੋਈ ਪ੍ਰਤੀਯੋਗੀ ਡਿੱਗ ਜਾਂਦਾ ਹੈ ਜਾਂ ਪਤੀਯੋਗੀ Offensive ਲੈ | ਲੈਂਦਾ ਹੈ, ਅਤੇ ਜਦੋਂ ਵਿਰੋਧੀ ਖਿਡਾਰੀ ਡਿਗ ਜਾਂਦਾ ਹੈ ਤਾਂ ਵੀ ਖਿਡਾਰੀ ਲੋਟਣ ਦੀ ਸਥਿਤੀ ਲੈ ਸਕਦਾ ਹੈ ।
3. ਖੜੇ ਹੋਣ ਦੀ ਹਾਲਤ ਵਿਚ ਗਰਾਊਂਡ ਵਰਕ ਤਕਨੀਕ ਅਪਣਾਉਣ ਮਗਰੋਂ ਜਦੋਂ ਖਿਡਾਰੀ ਕੁੱਝ ਪ੍ਰਗਤੀ ਕਰ ਲੈਂਦਾ ਹੈ, ਤਾਂ ਉਹ ਵੀ ਨਿਰਸੰਕੋਚ ਲੇਟਵੀਂ ਸਥਿਤੀ ਹਿਣ ਕਰਕੇ Offensive ਵਿਚ ਆ ਸਕਦਾ ਹੈ।
4. ਜਦੋਂ ਇਕ ਜਾਂ ਦੋਵੇਂ ਖਿਡਾਰੀ ਮੁਕਾਬਲੇ ਦੇ ਖੇਤਰ ਤੋਂ ਬਾਹਰ ਹੋਣ ਤਾਂ ਕੋਈ ਵੀ ਵਰਤੀ ਗਈ ਤਕਨੀਕ-ਨਿਸਫਲ ਅਤੇ ਅਯੋਗ ਘੋਸ਼ਤ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ।
5. ਸੁੱਟਣ ਦੀ ਤਕਨੀਕ ਉਸ ਸਮੇਂ ਤੱਕ ਉੱਚਿਤ ਨਹੀਂ ਹੁੰਦੀ, ਜਦੋਂ ਤੱਕ ਸੁੱਟਣ ਵਾਲਾ ਅਤੇ ਉਸ ਦੇ ਵਿਰੋਧੀ ਦਾ ਅੱਧੇ
   ਤੋਂ ਵੱਧ ਸਰੀਰ ਮੁਕਾਬਲੇ ਦੇ ਖੇਤਰ ਵਿੱਚ ਰਹਿੰਦਾ ਹੈ ।

ਕੁਝ ਵਰਜਿਤ ਕੰਮ (Some Dont’s)-

1. ਪੇਟ ਨੂੰ ਘੁੱਟਣਾ (Do-Jine), ਸਿਰ ਜਾਂ ਧੌਣ ਨੂੰ ਸਿੱਧਾ ਲੱਤਾਂ ਨਾਲ ਘੁੱਟਣਾ ।
2. KASE TSUEWALA ਤਕਨੀਕ ਦਾ ਜੋੜਾਂ ਦੇ ਉੱਪਰ ਕੂਹਣੀ ਤੋਂ ਇਲਾਵਾ ਵਰਤੋਂ ਕਰਨਾ ।
3. ਜਿਸ ਲੱਤ ਉੱਤੇ ਹਮਲਾਵਰ ਖੜ੍ਹਾ ਹੋਵੇ, ਉਸ ਨੂੰ ਕੈਂਚੀ ਮਾਰਨੀ ।
4. ਵਿਰੋਧੀ ਖਿਡਾਰੀ ਉੱਤੇ ਜਾਣ-ਬੁਝ ਕੇ ਪਿੱਛੇ ਵੱਲ ਡੇਗਣਾ, ਜੋ ਕਿ ਪਿੱਛੋਂ ਉਸ ਨਾਲ ਚਿਪਟਿਆ ਜਾਵੇ ।
5. ਵਿਰੋਧੀ ਖਿਡਾਰੀ ਦੀ ਲੱਤ ਨੂੰ ਖੜੇ ਹੋਣ ਦੀ ਹਾਲਤ ਵਿਚ ਖਿੱਚਣਾ ਤਾਂ ਜੋ ਉਹ ਲੇਟਣ ਦੀ ਹਾਲਤ ਵਿਚ ਹੋ ਸਕੇ ।
6. ਵਿਰੋਧੀ ਖਿਡਾਰੀ ਦੇ ਕਮੀਜ਼ ਦੀਆਂ ਬਾਹਾਂ ਅਤੇ ਪਜਾਮੇ ਵਿਚ ਉਂਗਲਾਂ ਪਾ ਕੇ ਉਸ ਨੂੰ ਫੜਨਾ ।
7. ਕੋਈ ਵੀ ਅਜਿਹਾ ਕੰਮ ਜਿਸ ਨਾਲ ਵਿਰੋਧੀ ਨੂੰ ਸੱਟ ਨਾ ਲੱਗੇ ।
8. ਜਾਣ-ਬੁਝ ਕੇ ਪਕੜ ਤੋਂ ਬਚਣਾ ।
9. ਵਿਰੋਧੀ ਦੇ ਮੂੰਹ ਵੱਲ ਪੈਰ ਜਾਂ ਹੱਥ ਸਿੱਧਾ ਵਧਾਉਣਾ ।
10. ਰੈਫ਼ਰੀ ਦੀ ਆਗਿਆ ਦੇ ਬਿਨਾਂ ਪੇਟੀ ਨੂੰ ਖੋਲ੍ਹਣਾ ਜਾਂ ਬੰਣਾ ।
11. ਜਾਣ-ਬੁਝ ਕੇ ਖੇਡ ਦਾ ਮੈਦਾਨ ਵਿਚੋਂ ਬਾਹਰ ਨਿਕਲਣਾ ਜਾਂ ਬਿਨਾਂ ਕਾਰਨ ਵਿਰੋਧੀ ਖਿਡਾਰੀ ਨੂੰ ਬਾਹਰ ਧੱਕਣਾ ।
12. ਹਾਰਦੇ ਸਮੇਂ ਸੁਰੱਖਿਆ ਦਾ ਆਸਣ ਹਿਣ ਕਰਨਾ ।
13. ਅਜਿਹੀ ਪਕੜ ਜਾਂ ਲਾਕ ਲਗਾਉਣੀ ਜਿਸ ਨਾਲ ਵਿਰੋਧੀ ਖਿਡਾਰੀ ਦੀ ਰੀੜ੍ਹ ਦੀ ਹੱਡੀ ਨੂੰ ਖ਼ਤਰਾ ਪੈਦਾ ਹੋ ਜਾਵੇ ।
14. ਲਗਾਤਾਰ ਕਾਫ਼ੀ ਸਮੇਂ ਤੱਕ ਉਂਗਲੀਆਂ ਫਸਾ ਕੇ ਖੜ੍ਹੇ ਰਹਿਣਾ ।
15. ਗ਼ੈਰ-ਜ਼ਰੂਰੀ ਸੰਕੇਤ ਕਰਨਾ, ਆਵਾਜ਼ਾਂ ਕੱਸਣਾ ਜਾਂ ਚੀਕਣਾ ।

ਜੂਡੋ ਪ੍ਰਤੀਯੋਗਤਾ ਵਿਚ ਨਿਰਣਾ ਦੇਣ ਦੇ ਢੰਗ

ਨਿਰਣਾ (Judgement)-
1. ਜਦੋਂ ਕੋਈ ਖਿਡਾਰੀ ਆਪਣੇ ਵਿਰੋਧੀ ਨੂੰ ਉਸ ਦੀ ਹਾਲਤ ਵਿਧੀ ਤੋਂ ਵਿਰੋਧ ਲਈ ਪਿੱਠ ਦੇ ਭਾਰ ਸੁੱਟਦਾ ਹੈ ਤਾਂ ਉਸ ਨੂੰ ਇੰਪਨ (ਇਕ ਅੰਕ) ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ।
2. ਜਦ ਕੋਈ ਖਿਡਾਰੀ ਆਪ ਲੇਟਿਆ ਹੋਵੇ ਅਤੇ ਆਪਣੇ ਵਿਰੋਧੀ ਖਿਡਾਰੀ ਨੂੰ ਆਪਣੇ ਮੋਢਿਆਂ ਤੱਕ ਚੁੱਕ ਲਵੇ ਤਾਂ ਉਸ ਨੂੰ ਇੰਪਨ (ਇਕ ਅੰਕ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ।
3. ਜਦੋਂ ਨਿਸਚਿਤ ਸਮੇਂ ਤੱਕ ਕੋਈ ਫੈਸਲਾ ਨਾ ਹੋਵੇ ਤਾਂ ਬਰਾਬਰ ਦਾ ਫ਼ੈਸਲਾ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ । ਇਸ ਦੇ ਬਿਨਾਂ ਜਦੋਂ ਕਿਸੇ ਖਿਡਾਰੀ ਦੇ ਸੱਟ ਆਦਿ ਲੱਗ ਜਾਣ ਨਾਲ ਖੇਡ ਚਾਲੂ ਨਾ ਰੱਖੀ ਜਾ ਸਕੇ ਤਾਂ ਵੀ ਪ੍ਰਤੀਯੋਗਤਾ ਦੀ ਸਮਾਪਤੀ ਦਾ ਐਲਾਨ ਕਰ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ।
4. ਜਦੋਂ ਕੋਈ ਖਿਡਾਰੀ ਪ੍ਰਤੀਯੋਗਤਾ ਵਿਚ ਭਾਗ ਲੈਣ ਤੋਂ ਇਨਕਾਰ ਕਰ ਦੇਵੇ ਤਾਂ ਉਸਦੇ ਵਿਰੋਧੀ ਖਿਡਾਰੀ ਨੂੰ ਤਰੁੱਟੀ ਦੇ ਕਾਰਨ ਹਾਰਿਆ (By Fuset sho) ਜੇਤੂ ਐਲਾਨ ਕਰ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ।
5. ਜਦੋਂ ਕੋਈ ਖਿਡਾਰੀ ਕਿਸੇ ਰੈਫ਼ਰੀ ਦੀ ਚਿਤਾਵਨੀ ਦੀ ਵਾਰ-ਵਾਰ ਉਲੰਘਣਾ ਕਰਦਾ ਹੈ ਜਾਂ ਕਿਸੇ ਵਰਜਿਤ ਕੰਮ ਨੂੰ ਚਿਤਾਵਨੀ ਦੇ ਬਾਵਜੂਦ ਵੀ ਵਾਰ-ਵਾਰ ਕਰਦਾ ਹੈ ਤਾਂ ਉਸ ਨੂੰ ਨਿਯਮ ਉਲੰਘਣ ਕਰਨ ਕਾਰਨ ਹਾਰਿਆ (Honsaku Make) ਹੋਇਆ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ ।
6. ਜ਼ਖਮੀ ਹੋਣ ਕਾਰਨ ਜਦੋਂ ਕੋਈ ਖਿਡਾਰੀ ਪ੍ਰਤੀਯੋਗਤਾ ਵਿਚ ਭਾਗ ਲੈਣ ਵਿਚ ਅਸਮਰਥ ਹੋ ਜਾਂਦਾ ਹੈ ਤਾਂ ਫ਼ੈਸਲਾ ਇਸ ਪ੍ਰਕਾਰ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ-
(ਉ) ਜੇ ਕੋਈ ਖਿਡਾਰੀ ਵਿਰੋਧੀ ਖਿਡਾਰੀ ਦੀ ਗ਼ਲਤੀ ਦੇ ਕਾਰਨ ਜ਼ਖਮੀ ਹੋਇਆ ਹੋਵੇ ਤਾਂ ਉਸ (ਜ਼ਖਮੀ) ਨੂੰ ਜੇਤੂ ਐਲਾਨ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।
(ਅ) ਜੇ ਕੋਈ ਖਿਡਾਰੀ ਆਪਣੀ ਹੀ ਭੁੱਲ ਕਾਰਨ ਜ਼ਖਮੀ ਹੁੰਦਾ ਹੈ ਤਾਂ ਉਸ ਦੇ ਵਿਰੋਧੀ ਖਿਡਾਰੀ ਨੂੰ ਜੇਤੂ ਐਲਾਨ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।

JUDO WEIGHT CATEGORIES

MEN
Upto 50 kg
Upto 55 kg
Upto 60 kg
Upto 65 kg
Upto 71 kg
Upto 78 kg
Upto 86 kg
Upto + 86 kg

WOMEN
Upto 44 kg
Upto 48 kg
Upto 52 kg
Upto 56 kg
Upto 61 kg
Upto 66 kg
Upto 66 kg

JUNIOR
38 kg
40 kg
55 kg
50 kg
56 kg
63 kg
71 kg
Above 71 kg

Men = Total categories = Eight
Women = Total categories = Seven
Junior = Total categories = Eight

ਸਪਰੋਟਸ ਅਵਾਰਡ
(Sports Award)

ਅਰਜੁਨ ਪੁਰਸਕਾਰ ਜੇਤੂਆਂ ਦੀ ਸੂਚੀ (List of Arjuna Award Winners) – ਸੰਦੀਪ ਬਿਆਲਾ (1992), ਕਵਾਜ ਬਿੱਲੀ ਮੰਗਿਆ (1993), ਮਿਸ ਪੂਨਮ ਚੋਪੜਾ (1996), ਅੰਗਮ ਅਨੀਤਾ (1998), ਅਕਰਮ ਚਾਨੁ ਸ਼ਾਹ (2003), ਮਿਸ ਟੇਬੀ ਦੇਵੀ (2007) ਅਤੇ ਯਸ਼ਪਾਲ ਸੋਲੰਕੀ (2012) ।
ਦਰੋਣਾਚਾਰੀਆ ਐਵਾਰਡ-ਗੁਰਚਰਨ ਯੋਗੀ (2014) ਅਤੇ ਜੀਵਨ ਕੁਮਾਰ ਸ਼ਰਮਾ (2018) ।

PSEB 12th Class Physical Education Practical ਜੂਡੋ (Judo)

ਪ੍ਰਸ਼ਨ 1.
ਜੂਡੋ ਦਾ ਸ਼ਾਬਦਿਕ ਅਰਥ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਜੂਡੋ ਦੋ ਸ਼ਬਦਾਂ ਜੂ ਨਰਮ ਅਤੇ ਡੋ (ਤਰੀਕਾ) ਤੋਂ ਮਿਲ ਕੇ ਬਣਿਆ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਜੂਡੋ, ਦੇ ਜਨਮਦਾਤਾ ਕੌਣ ਸਨ ?
ਉੱਤਰ-
ਡਾ: ਜਗਾਰੋ ਕਾਨੋ ।

ਪ੍ਰਸ਼ਨ 3.
ਜੂਡੋ ਨੂੰ ਉਲੰਪਿਕ ਵਿਚ ਕਦੋਂ ਸ਼ਾਮਿਲ ਕੀਤਾ ਗਿਆ ਸੀ ?
ਉੱਤਰ-
1964 ਟੋਕੀਓ ਉਲੰਪਿਕ ਵਿਚ ।

ਪ੍ਰਸ਼ਨ 4.
ਅੰਤਰਰਾਸ਼ਟਰੀ ਜੂਡੋ ਫੈਡਰੇਸ਼ਨ ਦਾ ਗਠਨ ਕਦੋਂ ਹੋਇਆ ਸੀ ?
ਉੱਤਰ-
ਸਾਲ 1951 ਵਿਚ ।

ਪ੍ਰਸ਼ਨ 5. ਪ੍ਰਤੀਯੋਗਤਾ ਖੇਤਰ ਕਿੰਨੇ ਮੀਟਰ ਦਾ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
10 ਮੀਟਰ × 10 ਮੀਟਰ

ਪ੍ਰਸ਼ਨ 6.
ਜੂਡੋ ਪ੍ਰਤੀਯੋਗਤਾ ਵਿਚ ਕਿੰਨੇ ਅਧਿਕਾਰੀਆਂ ਦੀ ਲੋੜ ਪੈਂਦੀ ਹੈ ?
ਉੱਤਰ-
1 ਰੈਫਰੀ, 2 ਜੱਜ, 1 ਸਕੋਰਰ, 2 ਟਾਈਮ ਕੀਪਰ ।

ਪ੍ਰਸ਼ਨ 7.
ਓਬੀ (ਬੈਲਟ) ਦੀ ਚੌੜਾਈ ਕਿੰਨੀ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
4-5 ਸੈਂਮੀ. ।

ਪ੍ਰਸ਼ਨ 8.
ਪੁਰਸ਼ ਅਤੇ ਔਰਤਾਂ ਦੇ ਕਿੰਨੇ ਭਾਰ ਵਰਗ ਹੁੰਦੇ ਹਨ ?
ਉੱਤਰ-
7 ਭਾਰ ਵਰਗ ।

ਪ੍ਰਸ਼ਨ 9.
ਜੂਡੋ ਵਿਚ ਸਭ ਤੋਂ ਉੱਚਾ ਸਕੋਰ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਈਪੋਨ ।

ਪ੍ਰਸ਼ਨ 10.
ਆਦਮੀ ਵਰਗ ਵਿਚ ਪ੍ਰਤੀਯੋਗਤਾ ਸਮਾਂ ਕਿੰਨਾ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
4 ਮਿੰਟ ।

ਪ੍ਰਸ਼ਨ 11.
ਜੂਡੋ ਵਿਚ ‘‘ਰੇਈਂ’ ਸ਼ਬਦ ਦਾ ਕੀ ਅਰਥ ਹੈ ?
ਉੱਤਰ-
ਇਹ ਵਿਰੋਧੀਆਂ ਦੇ ਲਈ ਸਮਾਨ ਦਾ ਭਾਵ ਹੈ ।

ਪ੍ਰਸ਼ਨ 12.
ਪ੍ਰਤੀਯੋਗਤਾ ਸ਼ੁਰੂ ਕਰਨ ਤੋਂ ਪਹਿਲਾਂ ਰੈਫਰੀ ਕਿਸ ਸ਼ਬਦ ਦਾ ਇਸਤੇਮਾਲ ਕਰਦਾ ਹੈ ?
ਉੱਤਰ-
ਹਾਜਿਮੇ (Hajime) ।

Punjab State Board PSEB 12th Class Physical Education Book Solutions ਵੇਟ ਲਿਫਟਿੰਗ ਅਤੇ ਪਾਵਰ ਲਿਫਟਿੰਗ (Weight Lifting and Power Lifting) Game Rules.

ਵੇਟ ਲਿਫਟਿੰਗ ਅਤੇ ਪਾਵਰ ਲਿਫਟਿੰਗ (Weight Lifting and Power Lifting) Game Rules – PSEB 12th Class Physical Education

ਵੇਟ ਲਿਫਟਿੰਗ ਦਾ ਇਤਿਹਾਸ
(History of Weight Lifting)

ਇਹ ਤਾਕਤ ਦੇ ਮੁਕਾਬਲੇ ਬਹੁਤ ਪੁਰਾਣੇ ਯੁੱਗਾਂ ਤੋਂ ਚਲੇ ਆ ਰਹੇ ਹਨ । ਪਹਿਲੇ ਸਮੇਂ ਤੋਂ ਹੀ ਮਨੁੱਖ ਆਪਣੇ ਆਪ ਨੂੰ ਤਾਕਤਵਰ ਦੱਸਣ ਲਈ ਇਕ ਦੂਜੇ ਦੇ ਮੁਕਾਬਲੇ ਲਈ ਪੁਕਾਰਦੇ ਰਹੇ ਹਨ ਜਿਸ ਨਾਲ ਉਹ ਆਪਣੇ ਆਪ ਨੂੰ ਤਾਕਤਵਰ ਵਿਖਾ ਸਕੇ ।

ਪ੍ਰਾਚੀਨ ਇਤਿਹਾਸ-ਚਾਇਨਾ ਦੇ Zhou Dynasty ਵਿਚ ਵੇਟ ਲਿਫਟਿੰਗ ਨੂੰ ਦਰਸਾਇਆ ਗਿਆ ਹੈ ਜੋ 10ਵੀਂ ਸਦੀ ਤੋਂ ਆਰੰਭ ਹੁੰਦੀ ਹੈ । ਇਸ ਸਮੇਂ ਫ਼ੌਜ ਵਿਚ ਭਰਤੀ ਲਈ ਜਵਾਨਾਂ ਦੀ ਤਾਕਤ ਨੂੰ ਵੇਟ ਲਿਫਟਿੰਗ ਭਾਰ ਉਠਾਉਣਾ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ । 1896 ਵਿਚ ਓਲੰਪਿਕ ਖੇਡਾਂ ਵਿਚ ਭਾਰ ਉਠਾਉਣ ਲਈ ਖੇਡ ਮਹੱਤਤਾ ਮਿਲੀ ਜਿਸ ਵਿਚ ਬ੍ਰਿਟੇਨ ਦੇ Lavnceston Elliot ਨੇ ਇਕ ਹੱਥ ਦੇ ਲਿਫਟ ਇਸ ਪ੍ਰਤੀਯੋਗਿਤਾ ਨੂੰ ਜਿੱਤਿਆ | 1932 ਵਿਚ 5 ਭਾਰ ਪ੍ਰਤੀਯੋਗਿਤਾ ਵਿਚ ਸ਼ਾਮਿਲ ਕੀਤੇ ਗਏ । ਇਸ ਵਿਚ ਪ੍ਰੈੱਸ ਸਨੈਚ ਅਤੇ ਕਲੀਨ ਜ਼ਰਕ ਦਿੱਤਾ ਗਿਆ ।

Russell (England) ਦੇ ਵੇਟ ਲਿਫਟਿੰਗ ਨੂੰ ਉੱਨਤ ਕਰਨ ਦੇ ਲਈ ਉਨ੍ਹਾਂ ਦਾ ਬਹੁਤ ਯੋਗਦਾਨ ਹੈ । Russell ਨੇ ਪਹਿਲੇ ਵੇਟ ਲਿਫਟਿੰਗ ਵਿਚ ਜਿੱਤ ਪ੍ਰਾਪਤ ਕੀਤੀ । ਇਸਤਰੀਆਂ ਲਈ ਵੇਟ ਲਿਫ਼ਟਿੰਗ ਮੁਕਾਬਲੇ 2000 ਸਿਡਨੀ ਉਲੰਪਿਕ ਵਿਚ ਸ਼ਾਮਿਲ ਕੀਤੇ ਗਏ ।

ਯਾਦ ਰੱਖਣ ਯੋਗ ਗੱਲਾਂ
(Tips to Remember)

1. ਵੇਟ ਲਿਫ਼ਟਿੰਗ ਵਿੱਚ ਇਸਤਰੀਆਂ ਲਈ 11 ਭਾਰ ਅਤੇ ਮਰਦਾਂ ਦੇ 9 ਭਾਰ ਹੁੰਦੇ ਹਨ ।
2. ਪਾਵਰ ਲਿਫ਼ਟਿੰਗ ਵਿਚ ਮਰਦਾਂ ਲਈ 8 ਭਾਰ ਅਤੇ ਇਸਤਰੀਆਂ ਲਈ 7 ਭਾਰ ਹੁੰਦੇ ਹਨ ।
3. ਭਾਰ ਵਿੱਚ ਹਮੇਸ਼ਾਂ ਪੰਜ ਕਿਲੋ ਦਾ ਵਾਧਾ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।
4. ਵੇਟ ਲਿਫ਼ਟਿੰਗ ਵਿੱਚ ਸਨੈਚ, ਜਰਕ ਅਤੇ ਕਲੀਨ ਲਿਫਟ ਹੁੰਦੀ ਹੈ ।

ਵੇਟ ਲਿਫ਼ਟਿੰਗ ਅਤੇ ਪਾਵਰ ਲਿਫ਼ਟਿੰਗ ਦੇ ਨਵੇਂ ਨਿਯਮ
(Latest Rules of Weight Lifiting and Power Lifting)

1. ਭਾਰ ਚੁੱਕਣ ਦੀ ਪ੍ਰਤੀਯੋਗਤਾ ਲੱਕੜੀ ਦੇ ਵਰਗਾਕਾਰ ਪਲੇਟਫਾਰਮ ਉੱਤੇ ਕੀਤੀ ਜਾਂਦੀ ਹੈ, ਜਿਸ ਦੀ ਹਰੇਕ | ਸਾਈਡ 4 ਮੀਟਰ ਹੁੰਦੀ ਹੈ ।
2. ਬਾਰ ਦਾ ਵਜ਼ਨ 2 ਕਿਲੋ ਦੇ ਅਨੇਕਧਾ ਵਿਚ ਹੁੰਦਾ ਹੈ ।
3. ਮਰਦਾਂ ਲਈ ਬਾਰ ਦਾ ਭਾਰ 20 ਕਿਲੋ ਅਤੇ ਇਸਤਰੀਆਂ ਲਈ 15 ਕਿਲੋ ਹੁੰਦਾ ਹੈ ।
4. ਬਾਰ ਵਿਚ ਦੋ ਰੋਲਰ ਹੁੰਦੇ ਹਨ ਜਿਨ੍ਹਾਂ ਦਾ ਭਾਰ 2.5 kg ਹੁੰਦਾ ਹੈ ।
5. ਭਾਰ ਵਿਚ ਹਮੇਸ਼ਾ ਪੰਜ ਕਿਲੋ ਦਾ ਵਾਧਾ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।
6. ਹਰ ਭਾਰ ਦੇ ਵਰਗ ਵਿਚ ਹਰੇਕ ਘੰਟਾ ਪਹਿਲਾਂ ਖਿਡਾਰੀ ਹਿੱਸਾ ਲੈ ਸਕਦੇ ਹਨ ।
7. ਮੁਕਾਬਲਾ ਸ਼ੁਰੂ ਹੋਣ ਤੋਂ ਇਕ ਘੰਟਾ ਪਹਿਲਾਂ ਖਿਡਾਰੀਆਂ ਦਾ ਭਾਰ ਤੋਲਿਆ ਜਾਂਦਾ ਹੈ ।
8. ਭਾਰ ਸਿਰਫ਼ ਇਕ ਵਾਰ ਹੀ ਤੋਲਿਆ ਜਾਂਦਾ ਹੈ । ਪਰ ਜਿਹੜੇ ਖਿਡਾਰੀ ਉਸ ਵਰਗ ਦੇ ਭਾਰ ਤੋਂ ਵੱਧ ਹੁੰਦੇ ਹਨ, ਉਹਨਾਂ ਦਾ ਭਾਰ ਦੋ ਵਾਰੀ ਤੋਲਿਆ ਜਾਂਦਾ ਹੈ ।
9. ਭਾਰ ਨੂੰ ਝਟਕੇ ਨਾਲ ਮੋਢੇ ਤੱਕ ਲਿਆਉਣਾ ਗਲਤ ਕਿਰਿਆ ਹੈ ।
10. ਭਾਰ ਨੂੰ ਮੋਢਿਆਂ ਤੋਂ ਉੱਪਰ ਚੁੱਕਦੇ ਹੋਏ ਸਰੀਰ ਦੇ ਕਿਸੇ ਹਿੱਸੇ ਨਾਲ ਛੋਹਣਾ ਨਹੀਂ ਚਾਹੀਦਾ ।
11. ਜੇਕਰ ਕੋਈ ਖਿਡਾਰੀ ਚਿਤਾਵਨੀ ਦੇ ਬਾਵਜੂਦ ਮੰਦਾ ਵਿਹਾਰ ਕਰਨ ਤੋਂ ਬਾਜ ਨਹੀਂ ਆਉਂਦਾ, ਤਾਂ ਉਸ ਨੂੰ ਸਾਰੇ ਮੁਕਾਬਲੇ ਵਿਚ ਹਿੱਸਾ ਲੈਣ ਤੋਂ ਰੋਕਿਆ ਜਾ ਸਕਦਾ ਹੈ ।
12. ਜੇਕਰ ਕਿਸੇ ਭਾਰ ਚੁੱਕਣ ਵਾਲੇ ਖਿਡਾਰੀ ਨੇ ਨਸ਼ੇ ਆਦਿ ਦਾ ਪ੍ਰਯੋਗ ਕੀਤਾ ਹੋਵੇ,ਤਾਂ ਉਸਨੂੰ ਮੁਕਾਬਲੇ ਤੋਂ ਬਾਹਰ | ਕੱਢ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ।

ਭਾਰ ਚੁੱਕਣ ਦੇ ਮੁਕਾਬਲੇ ਲਈ ਭਾਰ ਦਾ ਵਰਗੀਕਰਨ

ਮੁਕਾਬਲੇ ਲਈ ਭਾਰ ਦਾ ਵਰਗੀਕਰਨ (Classification of Weight Lifting Competition) – ਮੁਕਾਬਲੇ ਹੇਠ ਲਿਖੇ ਵਰਗਾਂ ਵਿਚ ਹੁੰਦੇ ਹਨ


12. ਵੇਟ ਲਿਫਟਿੰਗ ਵਿਚ ਸਨੈਚ (Snatch) ਅਤੇ ਕਲੀਨ ਅਤੇ ਜਰਕ (Clean and Jerk) ਹੁੰਦਾ ਹੈ ।
13. ਪਾਵਰ ਲਿਫਟਿੰਗ ਵਿਚ ਸਕੈਟ (Squat), ਬੈਂਚ ਪਰੈਸ ਅਤੇ ਡੈਡ ਲਿਫਟ ਹੁੰਦਾ ਹੈ ।
14. ਹਰੇਕ ਵਰਗ ਵਿਚ ਹਰੇਕ ਟੀਮ ਦੇ ਦੋ ਖਿਡਾਰੀ ਹੀ ਭਾਗ ਲੈ ਸਕਦੇ ਹਨ । ਜੇਕਰ ਲੋੜ ਹੋਵੇ ਤਾਂ ਖਿਡਾਰੀ ਦੀ ਬਦਲੀ ਵੀ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ ।
15. ਮੁਕਾਬਲਾ ਆਰੰਭ ਹੋਣ ਤੋਂ ਇਕ ਘੰਟਾ ਪਹਿਲਾਂ ਖਿਡਾਰੀਆਂ ਦਾ ਭਾਰ ਤੋਲਿਆ ਜਾਂਦਾ ਹੈ । ਕੇਵਲ ਉਹਨਾਂ ਖਿਡਾਰੀਆਂ ਦਾ ਭਾਰ ਦੁਬਾਰਾ ਤੋਲਿਆ ਜਾਂਦਾ ਹੈ, ਜਿਹਨਾਂ ਦਾ ਭਾਰ ਉਸ ਭਾਰ ਦੇ ਵਰਗ ਤੋਂ ਵੱਧ ਹੁੰਦਾ ਹੈ ।

ਭਾਰ ਚੁੱਕਣ ਦੇ ਨਿਰਧਾਰਿਤ ਸਟਾਈਲਾਂ ਦਾ ਵਰਣਨ

ਭਾਰ ਚੁੱਕਣ ਲਈ ਨਿਰਧਾਰਿਤ ਸਟਾਈਲ (Styles for the Weight Lifting) – ਭਾਰ ਚੁੱਕਣ ਵਾਲੀ ਫੈਡਰੇਸ਼ਨ (Weight Lifting Federation) ਦੁਆਰਾ ਨਿਯਮਾਂ ਦੇ ਆਧਾਰ ਤੇ ਇਸ ਖੇਡ ਵਿਚ ਹੇਠ ਲਿਖੇ ਸਟਾਈਲ ਅਪਣਾਏ ਗਏ ਹਨ :

ਦੋ ਹੱਥ ਅਛੋਹ ਤੇ ਦਾਬ (Two hands clean and Press)

1. ਪਹਿਲੀ ਸਥਿਤੀ, ਮੋਢੇ ਉੱਤੇ ਚੁੱਕਣਾ (First Phase Shouldering) – ਇਸ ਸਥਿਤੀ ਵਿਚ ਬਾਰ ਖਿਤਿਜ ਰੂਪ ਵਿਚ (Horizontally) ਭਾਰ ਚੁੱਕਣ ਵਾਲੇ ਦੇ ਪੈਰਾਂ ਕੋਲ ਪਈ ਹੁੰਦੀ ਹੈ । ਇਸ ਨੂੰ ਖੁਲ੍ਹੇ ਹੱਥਾਂ ਨਾਲ ਫੜ ਕੇ ਇਕ ਹੀ ਝਟਕੇ ਨਾਲ ਪਹਿਲਾਂ ਮੋਢਿਆਂ ਤੱਕ ਲਿਆਇਆ ਜਾਂਦਾ ਹੈ । ਇਹ ਝਟਕਾ ਸਰੀਰ ਨੂੰ ਝੁਕਾ ਕੇ ਜਾਂ ਲੱਤਾਂ ਨੂੰ ਖੋਲ੍ਹ ਕੇ ਦਿੱਤਾ ਜਾ ਸਕਦਾ ਹੈ । ਜਦੋਂ ਬਾਰ ਚੁੱਕ ਲਈ ਜਾਵੇ, ਤਾਂ ਇਹ ਠੋਢੀ (Chin) ਦੇ ਹੇਠਾਂ ਪੂਰੀਆਂ ਝੁਕੀਆਂ ਹੋਈਆਂ ਭੁਜਾਵਾਂ ਤੇ ਰੁਕੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ । ਪੈਰ ਇਕੱਠੇ ਹੋਣ ਜਾਂ ਦੁਰ-ਦੁਰ ਹੋਣ ਤੇ ਇਹਨਾਂ ਦਾ ਤਲ (Level) ਇਕੋ ਜਿਹਾ ਹੋਵੇ ਅਤੇ ਲੱਤਾਂ ਬਿਲਕੁਲ ਸਿੱਧੀਆਂ ਹੋਣੀਆਂ ਚਾਹੀਦੀਆਂ ਹਨ । ਇਸ ਸਥਿਤੀ ਵਿਚ ਖੜ੍ਹੇ ਹੋ ਜਾਣ ਮਗਰੋਂ ਭਾਰ ਉਠਾਉਣ ਵਾਲਾ ਰੈਫਰੀ ਦੇ ਸੰਕੇਤ ਦੀ ਉਡੀਕ ਕਰਦਾ ਹੈ ।

2. ਦੂਜੀ ਸਥਿਤੀ, ਰੈਫਰੀ ਦੇ ਸੰਕੇਤ ਤੇ ਬਾਰ ਚੁੱਕਣਾ (Second Phase lifting the bar at the Signal of the Umpire) – ਦੂਜੀ ਸਥਿਤੀ ਉਹ ਹੈ, ਜਦੋਂ ਬਾਰ ਨੂੰ ਰੈਫਰੀ ਦਾ ਸੰਕੇਤ ਮਿਲਣ ਤੇ ਉਠਾਇਆ ਜਾਂਦਾ ਹੈ ਅਤੇ ਨਾਲ ਹੀ ਹੱਥਾਂ ਨੂੰ ਲੰਬਾਈ ਤੱਕ ਫੈਲਾਇਆ ਜਾਂਦਾ ਹੈ । ਉੱਪਰਲੀ ਕਿਰਿਆ ਅਤਿਅੰਤ ਸਾਦੀ ਅਤੇ ਸਪੱਸ਼ਟ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ, ਨਾ ਹੀ ਲੱਤਾਂ ਝਕਾਈਆਂ ਜਾਣ ਅਤੇ ਨਾ ਹੀ ਸਰੀਰ ਬਹੁਤ ਪਿੱਛੇ ਵੱਲ ਝੁਕਾਇਆ ਜਾਵੇ । ਕਿਸੇ ਤਰ੍ਹਾਂ ਦੀ ਹਿਲਜੁਲ ਨਹੀਂ ਹੋਣੀ ਚਾਹੀਦੀ ਅਤੇ ਨਾ ਹੀ ਪੈਰਾਂ ਦੀ ਸਥਿਤੀ ਵਿਚ ਪਰਿਵਰਤਨ ਹੋਵੇ | ਭਾਰ ਚੁੱਕਣ ਵਾਲੇ ਨੂੰ ਘੱਟ ਤੋਂ ਘੱਟ 2 ਸੈਕਿੰਡ ਇਸ ਸਥਿਤੀ ਵਿਚ ਬਿਨਾਂ ਹਿੱਲੇ ਖੜ੍ਹੇ ਰਹਿਣਾ ਚਾਹੀਦਾ ਹੈ । ਰੈਫਰੀ ਦਾ ਆਦੇਸ਼ ਮਿਲਣ ਤੇ ਬਾਰ ਨੂੰ ਹੇਠਾਂ ਮੈਟ ਤੇ ਰੱਖ ਦੇਣਾ ਚਾਹੀਦਾ ਹੈ ।

ਗ਼ਲਤ ਕਿਰਿਆਵਾਂ (Wrong Movements) – ਹੇਠ ਲਿਖੀਆਂ ਕਿਰਿਆਵਾਂ ਗਲਤ ਮੰਨੀਆਂ ਜਾਂਦੀਆਂ ਹਨ-

1. ਝਟਕੇ ਨਾਲ ਭਾਰ ਨੂੰ ਮੋਢਿਆਂ ਤਕ ਲੈ ਜਾਣਾ ।
2. ਰੈਫਰੀ ਦਾ ਸੰਕੇਤ ਮਿਲਣ ਤੋਂ ਪਹਿਲਾਂ ਹੀ ਬਾਰ ਚੁੱਕਣਾ ।
3. ਬਾਰ ਚੁੱਕਣ ਦੇ ਸਮੇਂ ਗੋਡਿਆਂ ਦਾ ਥੋੜ੍ਹਾ ਹੀ ਝੁਕਾਉਣਾ ।
4. ਭਾਰ ਦੇ ਹੇਠਾਂ ਬਹੁਤ ਜ਼ਿਆਦਾ ਝੁੱਕ ਜਾਣਾ ।
5. ਰੈਫਰੀ ਦੇ ਸੰਕੇਤ ਮਗਰੋਂ ਸ਼ੁੱਕ ਜਾਣਾ । (Flexing)
6. ਮੁੜ ਕੇ ਜਾਂ ਫੈਲਾ ਕੇ ਧੜ ਨੂੰ ਝੁਕਾਉਣਾ ।
7. ਵਾਰੀ-ਵਾਰੀ ਬਾਹਵਾਂ ਨੂੰ ਫੈਲਾਉਣਾ ।
8. ਧੜ ਨੂੰ ਘੁਮਾਉਣਾ ।
9. ਬਾਹਵਾਂ ਫੈਲਾਉਂਦੇ ਸਮੇਂ ਸੰਕੋਚ ਕਰਨਾ ।
10. ਅਪੂਰਨ ਬਾਹਵਾਂ ਦਾ ਪ੍ਰਸਾਰ ।
11. ਪੈਰਾਂ ਨੂੰ ਹਿਲਾਉਣਾ ।
12. ਪੈਰਾਂ, ਅੰਗੂਠਿਆਂ ਜਾਂ ਅੱਡੀਆਂ ਨੂੰ ਉਠਾਉਣਾ ।
13. ਰੈਫਰੀ ਦਾ ਸੰਕੇਤ ਮਿਲਣ ਤੋਂ ਪਹਿਲਾਂ ਬਾਰ ਹੇਠਾਂ ਕਰ ਲੈਣਾ ।

| ਦੋਵੇਂ ਹੱਥਾਂ ਨਾਲ ਸਨੈਚ (Two hands Snatch) – ਬਾਰ ਚੁਕਣ ਵੇਲੇ ਖਿਤਿਜ ਰੂਪ ਨਾਲ (Horizontally) ਭਾਰ ਚੁੱਕਣ ਵਾਲੇ ਦੀਆਂ ਲੱਤਾਂ ਦੇ ਅੱਗੇ ਰੱਖਿਆ ਜਾਂਦਾ ਹੈ । ਉਹ ਦੋਵੇਂ ਹੱਥਾਂ ਨਾਲ ਫੜ ਕੇ ਇਕ ਹੀ ਝਟਕੇ ਨਾਲ ਬਾਰ ਨੂੰ ਸਿਰ ਉੱਪਰ ਉਠਾ ਲੈਂਦਾ ਹੈ । ਇਸ ਸਮੇਂ ਉਸ ਦੀਆਂ ਲੱਤਾਂ ਵੱਖ-ਵੱਖ ਅਤੇ ਮੁੜੀਆਂ ਹੋਈਆਂ ਹੋ ਸਕਦੀਆਂ ਹਨ । ਬਾਰ ਦੀ ਗਤੀ ਨਿਰੰਤਰ ਅਤੇ ਸਰੀਰ ਦੇ ਨਾਲ-ਨਾਲ ਲਗਾਤਾਰ ਹੋਵੇਗੀ । ਇਸ ਗਤੀ ਦੇ ਸਮੇਂ ਪੈਰਾਂ ਤੋਂ ਇਲਾਵਾ ਸਰੀਰ ਦਾ ਕੋਈ ਵੀ ਅੰਗ ਧਰਤੀ ਨੂੰ ਨਹੀਂ ਛੂਹੇਗਾ | ਕਿਆ ਹੋਇਆ ਭਾਰ ਇਸ ਸਥਿਤੀ ਵਿਚ ਦੋ ਸੈਕਿੰਡ ਤਕ ਸਥਿਰ ਰਹਿਣਾ ਚਾਹੀਦਾ ਹੈ | ਬਾਹਵਾਂ ਅਤੇ ਲੱਤਾਂ ਫੈਲੀਆਂ ਹੋਣੀਆਂ ਚਾਹੀਦੀਆਂ ਹਨ ਅਤੇ ਪੈਰ ਵੱਧ ਤੋਂ ਵੱਧ 40 ਸੈਂਟੀਮੀਟਰ ਦੂਰ ਹੋਣ । ਇਸ ਦਿਸ਼ਾ ਵਿਚ ਗੁੱਟਾਂ ਨੂੰ ਮੋੜ ਲੈਣ ਮਗਰੋਂ ਲੱਤਾਂ ਜਾਂ ਬਾਹਵਾਂ ਨੂੰ ਫੈਲਾਉਣ ਦੀ ਆਗਿਆ ਨਹੀਂ ਹੁੰਦੀ । ਗੁਟਾਂ ਨੂੰ ਮੋੜਨ ਦੀ ਕਿਰਿਆ ਉਸ ਸਮੇਂ ਤੱਕ ਨਹੀਂ ਹੋਣੀ ਚਾਹੀਦੀ, ਜਦੋਂ ਤਕ ਕਿ ਬਾਰ ਸਪੱਸ਼ਟਤਾ ਨਾਲ ਭਾਰ ਚੁੱਕਣ ਵਾਲੇ ਦੇ ਸਿਰ ਤੋਂ ਉੱਪਰ ਨਾ ਪਹੁੰਚ ਚੁੱਕੀ ਹੋਵੇ ।

3. ਦੋ ਹੱਥ ਨਾਲ ਸਪੱਸ਼ਟ ਅਤੇ ਝਟਕਾ (Two hands clean and Jerk) – ਬਾਰ ਨੂੰ ਖਿਤਿਜ ਰੂਪ ਵਿਚ ਬਾਰ ਚੁੱਕਣ ਵਾਲੇ ਦੀਆਂ ਲੱਤਾਂ ਦੇ ਸਾਹਮਣੇ ਰੱਖਿਆ ਜਾਂਦਾ ਹੈ । ਉਹ ਇਸ ਨੂੰ ਦੋਵੇਂ ਹੱਥਾਂ ਨਾਲ ਫੜ ਕੇ ਇਕ ਹੀ ਝਟਕੇ ਨਾਲ ਧਰਤੀ ਤੋਂ ਚੁੱਕ ਕੇ ਮੋਢਿਆਂ ਤਕ ਲਿਆਉਂਦਾ ਹੈ । ਇਸ ਸਮੇਂ ਉਹ ਲੱਤਾਂ ਨੂੰ ਖੋਲ੍ਹ ਲੈਂਦਾ ਹੈ ਜਾਂ ਮੋੜ ਦਿੰਦਾ ਹੈ । ਜਦੋਂ ਤਕ ਬਾਂਹ ਆਪਣੀ ਅੰਤਿਮ ਸਥਿਤੀ ਵਿਚ ਨਹੀਂ ਪਹੁੰਚਦੀ, ਉਸ ਨੂੰ ਧਰਤੀ ਨਾਲ ਸਪਰਸ਼ ਨਹੀਂ ਕਰਨਾ ਚਾਹੀਦਾ । ਅੰਤਿਮ ਸਥਿਤੀ ਦੋ ਸੈਕਿੰਡ ਤਕ ਸਥਿਰ ਰਹਿੰਦੀ ਹੈ । ਇਸ ਦੌਰਾਨ ਕਿਸੇ ਤਰ੍ਹਾਂ ਦੀ ਹਿਲ-ਜੁਲ ਨਹੀਂ ਹੋਣੀ ਚਾਹੀਦੀ । ਇਸ ਸਥਿਤੀ ਵਿਚ ਪੈਰ ਇਕ ਰੇਖਾ ਵਿਚ ਅਤੇ ਵੱਧ ਤੋਂ ਵੱਧ 10 ਸੈਂਟੀਮੀਟਰ ਦੂਰ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ । | ਅਪੀਲ ਲਈ ਜਿਊਰੀ (Jury of appeal-ਜਿਊਰੀ ਨੂੰ ਅਧਿਕਾਰ ਹੈ ਕਿ ਉਹ ਕਿਸੇ ਜੱਜ ਜਾਂ ਰੈਫਰੀ ਨੂੰ ਬਦਲ ਦੇਣ । ਰੈਫਰੀ ਦੀ ਨਿਰਪੱਖਤਾ ਤੇ ਸ਼ੱਕ ਨਹੀਂ ਕੀਤਾ ਜਾ ਸਕਦਾ । ਰੈਫਰੀ ਦੇ ਫੈਸਲੇ ਦੇ ਖਿਲਾਫ ਲਿਖਤ ਅਪੀਲ ਹੋ ਸਕਦੀ ਹੈ, ਜਿਸ ਤੋਂ ਮਗਰੋਂ ਰੈਫਰੀ ਦੇ ਵਿਚਾਰ ਸੁਣ ਕੇ ਫ਼ੈਸਲਾ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।

ਗਲਤ ਕਿਰਿਆਵਾਂ (Incorrect Movements) – ਹੇਠ ਲਿਖੀਆਂ ਕਿਰਿਆਵਾਂ ਗਲਤ ਹਨ-

1. ਧਰਤੀ ਤੇ ਗੋਡਿਆਂ ਦੇ ਭਾਰ ਝੁਕਣਾ ।
2. ਬਾਰ ਦਾ ਮੋਢਿਆਂ ਤਕ ਪੁੱਜਣ ਤੋਂ ਪਹਿਲਾਂ ਸਰੀਰ ਦੇ ਕਿਸੇ ਅੰਗ ਨਾਲ ਛੂਹਣਾ ।
3. ਝਟਕੇ ਨੂੰ ਦੁਹਰਾਉਣਾ ।

ਖਿਡਾਰੀ ਦੀ ਪੁਸ਼ਾਕ (Costume) – ਖਿਡਾਰੀ ਤੈਰਾਕੀ ਵਾਲਾ ਸੂਟ ਅਤੇ ਤਣੀਆਂ ਵਾਲੀ ਪਹਿਲਵਾਨਾਂ ਦੀ ਪੁਸ਼ਾਕ (Jack Strap) ਹੀ ਧਾਰਨ ਕਰ ਸਕਦੇ ਹਨ ।

ਪਲੇਟਫ਼ਾਰਮ ਅਤੇ ਦੂਜਾ ਸਾਮਾਨ (Platform and other equipment) – ਭਾਰ ਚੁੱਕਣ ਦਾ ਮੁਕਾਬਲਾ ਲੱਕੜੀ ਦੇ ਇਕ ਵਰਗਾਕਾਰ ਪਲੇਟਫਾਰਮ ਤੇ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਜਿਸ ਦਾ ਹਰੇਕ ਪਾਸਾ 4 ਮੀਟਰ ਹੁੰਦਾ ਹੈ ਬਾਰ ਦਾ ਭਾਰ ਪੁਰਸ਼ਾਂ ਦੇ ਲਈ 20 ਕਿਲੋ ਅਤੇ ਔਰਤਾਂ ਦੇ ਲਈ 15 ਕਿਲੋਗ੍ਰਾਮ ਹੁੰਦਾ ਹੈ । ਭਾਰ ਵਿਚ ਸਦਾ 5 ਕਿਲੋ ਦਾ ਵਾਧਾ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਸਭ ਤੋਂ ਵੱਡੀ (Disc ) ਦਾ ਵਿਆਸ 45 c.m. ਹੁੰਦਾ ਹੈ ਅਤੇ ਬਾਰ ਦਾ ਵਿਆਸ ਹੱਥਾਂ ਦੁਆਰਾ ਫੜਨ ਦੀ ਥਾਂ ਤੇ 28 mm ਹੁੰਦਾ ਹੈ ।

ਸਾਧਾਰਨ ਨਿਯਮ (General Rules)-

1. ਸਾਰੇ ਕਲੀਨਜ਼ (Cleans), ਸਨੈਚਾਂ (Snatches) ਜਾਂ ਝਟਕਿਆਂ (Jerk) ਵਿਚ ਲੱਤਾਂ ਨੂੰ ਝੁਕਾਅ ਕੇ ਜਾਂ ਫੈਲਾਉਣ ਦੀ ਕਿਰਿਆ ਇੱਛੁਕ ਹੈ ਅਤੇ ਕਿਸੇ ਉੱਤੇ ਇਸ ਪ੍ਰਕਾਰ ਦੀ ਰੋਕ (restriction) ਨਹੀਂ ।
2. ਭਾਰ ਚੁੱਕਣ ਵਾਲਾ (Lifter) ਆਪਣੇ ਸਮੇਂ ਵਿਚ ਆਪਣੀਆਂ ਲੱਤਾਂ ਨੂੰ ਮੋੜ ਕੇ ਠੀਕ ਹਾਲਤ (Correct | Position) ਵਿਚ ਲਿਆ ਸਕਦਾ ਹੈ ।
3. ਹੁਕਿੰਗ (hooking) ਦੀ ਵਿਧੀ (technique) ਦੀ ਆਗਿਆ ਹੈ ।
4. ਕੂਹਣੀ ਮੋੜ (Hooking) ਦੀ ਆਗਿਆ ਨਹੀਂ ਹੈ ।
5. ਹੈਂਗ (Hang) ਨਾਲ ਸਪੱਸ਼ਟ ਕਿਰਿਆ (Clearing) ਮਨ੍ਹਾ ਹੈ ।
6. ਇਕ ਜਾਂ ਦੋ ਹੱਥਾਂ ਦੀ ਹਰੇਕ ਕਿਰਿਆ ਦੇ ਸਮੇਂ ਜਦੋਂ ਕਿ ਖਿਚਾਅ (Strain) ਅਨੁਭਵ ਹੁੰਦਾ ਹੋਵੇ ਉਸ ਨੂੰ ਇਕ ਯਤਨ (attempt) ਸਮਝਿਆ ਜਾਵੇਗਾ । ਵਿਸ਼ੇਸ਼ ਕਰਕੇ ਉਸ ਸਮੇਂ ਜਦੋਂ ਬਾਰ ਗੋਡਿਆਂ ਤੱਕ ਉੱਤੇ ਚੁੱਕੀ ਹੋਵੇ ।

ਭਾਰ ਮੁਕਾਬਲੇ ਦੇ ਨਿਯਮ (Ruiles of Competition)-

1. ਪਹਿਲੇ ਦਰਜੇ ਦੇ ਖਿਡਾਰੀ ਨੂੰ ਪੰਜ ਪੁਆਇੰਟ, ਦੂਜੇ ਨੂੰ ਤਿੰਨ ਅਤੇ ਤੀਜੇ ਨੂੰ ਇਕ ਪੁਆਇੰਟ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ।
2. ਟਾਈ ਦੀ ਦਸ਼ਾ ਵਿਚ ਹਲਕੇ ਸਰੀਰ ਵਾਲੇ ਖਿਡਾਰੀ ਨੂੰ ਭਾਰੇ ਸਰੀਰ ਵਾਲੇ ਖਿਡਾਰੀ ਤੋਂ ਪਹਿਲਾਂ ਰੱਖਿਆ ਜਾਂਦਾ ਹੈ ।
3. ਜਦੋਂ ਖਿਡਾਰੀਆਂ ਦਾ ਭਾਰ ਮੁਕਾਬਲੇ ਤੋਂ ਪਹਿਲਾਂ ਇਕੋ ਜਿਹਾ ਹੋਵੇ, ਤਾਂ ਮੁਕਾਬਲੇ ਮਗਰੋਂ ਵੀ ਉਹਨਾਂ ਦਾ ਭਾਰ | ਇਕੋ ਜਿਹਾ ਹੋਵੇ ਅਤੇ ਉਹ ਇਕੋ ਜਿਹਾ ਭਾਰ ਚੁੱਕਣ ਤਾਂ ਉਹਨਾਂ ਨੂੰ ਬਰਾਬਰ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ ਤੇ ਇਨਾਮ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ । ਇਸ ਦਸ਼ਾ ਵਿਚ ਦੂਜੇ ਦਰਜੇ ਦੇ ਖਿਡਾਰੀ ਨੂੰ ਇਨਾਮ ਨਹੀਂ ਦਿੱਤਾ ਜਾਂਦਾ । ਅਗਲੇ ਜੇਤੂ ਨੂੰ ਤੀਜੇ ਦਰਜੇ ਦਾ ਇਨਾਮ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ।
4. ਟੀਮਾਂ ਦੀ ਸਥਿਤੀ ਕੱਢਣ ਲਈ ਜ਼ਿਆਦਾ ਅੰਕ ਪ੍ਰਾਪਤ ਕਰਨ ਵਾਲੀ ਟੀਮ ਪਹਿਲੇ ਨੰਬਰ ਤੇ ਮੰਨੀ ਜਾਵੇਗੀ ।
5. ਪਲੇਟਫ਼ਾਰਮ ਤੇ ਕੇਵਲ ਹੇਠ ਲਿਖੇ ਵਿਅਕਤੀ ਹੀ ਮੁਕਾਬਲੇ ਦੌਰਾਨ ਮੌਜੂਦ ਰਹਿ ਸਕਦੇ ਹਨ-(ਉ) ਜਿਊਰੀ ਦੇ ਮੈਂਬਰ (ਅ) ਖੇਡ ਲਈ ਨਿਯੁਕਤ ਕੀਤੇ ਗਏ ਜੱਜ (ਇ) ਟੀਮਾਂ ਦੇ ਮੈਨੇਜਰ ਹਰੇਕ ਟੀਮ ਦਾ ਇਕ ਹੀ ਮੈਨੇਜਰ ਹੋ ਸਕਦਾ ਹੈ) (ਸ) ਮੁਕਾਬਲੇ ਵਿਚ ਭਾਗ ਲੈਣ ਵਾਲੇ ਖਿਡਾਰੀ ।
6. ਸੱਦੇ ਮਗਰੋਂ ਖਿਡਾਰੀਆਂ ਨੂੰ ਦੋ ਮਿੰਟਾਂ ਦੇ ਅੰਦਰ-ਅੰਦਰ ਭਾਰ ਚੁੱਕਣ ਲਈ ਤਿਆਰ ਰਹਿਣਾ ਪੈਂਦਾ ਹੈ। ਦੋ ਮਿੰਟਾਂ ਮਗਰੋਂ ਉਹਨਾਂ ਨੂੰ ਫਿਰ ਬੁਲਾਇਆ ਜਾਂਦਾ ਹੈ । ਜੇਕਰ ਦੇਰੀ ਤਿੰਨ ਮਿੰਟ ਤੋਂ ਵੱਧ ਹੋ ਜਾਵੇ, ਤਾਂ ਉਹਨਾਂ ਨੂੰ ਚੇਤਾਵਨੀ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ ।
7. ਜੋ ਖਿਡਾਰੀ ਪਲੇਟਫ਼ਾਰਮ ਦੇ ਬਾਹਰ ਪੈਰ ਰੱਖਦਾ ਹੈ, ਉਸਨੂੰ ਅਯੋਗ ਘੋਸ਼ਿਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।
8. ਜੋ ਖਿਡਾਰੀ ਦੁਰ-ਵਿਹਾਰ ਕਰਦਾ ਹੈ ਜਾਂ ਉੱਚੀ ਆਵਾਜ਼ ਵਿਚ ਬੋਲਦਾ ਹੈ, ਉਸਨੂੰ ਚੇਤਾਵਨੀ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ । ਦੂਜੀ ਵਾਰ ਚਿਤਾਵਨੀ ਮਗਰੋਂ ਉਸ ਨੂੰ ਅਯੋਗ ਘੋਸ਼ਿਤ ਕਰ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ।

ਸਪਰੋਟਸ ਅਵਾਰਡ
(Sports Award)

ਅਰਜੁਨ ਪੁਰਸਕਾਰ ਜੇਤੂਆਂ ਦੀ ਸੂਚੀ (List of Arjuna Award Winners) – ਐੱਲ. ਕੇ. ਦਾਸ (1962), ਕੇ.ਏ. ਰਾਓ (1963), ਬੀ.ਐੱਮ. ਭਾਟੀਆ (1965), ਐੱਮ.ਐੱਲ ਘੋਸ਼ (1966), ਏ.ਕੇ. ਮੰਡਲ (1972), ਦਲਵੀਰ ਸਿੰਘ (1975), ਤਾਰਾ ਸਿੰਘ (1982), ਵੀ.ਕੇ. ਦਾਰੂ (1983), ਐੱਸ.ਸੀ. ਭਾਸਕਰ (1985), ਆਰਚੰਦਰਾ (1990), ਭਾਰਤੀ ਸਿੰਘ (1993), ਕੇ. ਮਲੇਸ਼ਵਰੀ (1994), ਪਰਮਜੀਤ ਸ਼ਰਮਾ (1997), ਸਤੀਸ਼ ਰਾਏ (1998), ਟੀ. ਐੱਮ. ਮਥੁ (2002), ਗੀਤਾ ਰਾਣੀ (2006), ਕੇ.ਆਰ. ਕੁਮਾਰ (2011) ਅਤੇ ਐੱਨ. ਐੱਸ. ਚਾਨੂੰ (2012) ।

ਦਰੋਣਾਚਾਰੀਆ ਐਵਾਰਡ-ਪਾਲ ਸਿੰਘ ਸੰਧੂ (1996), ਅਜੈ ਕੁਮਾਰ ਸਿਰੋਹੀ (1999) ਅਤੇ ਹੰਸ ਸ਼ਰਮਾ (2000) |

PSEB 12th Class Physical Education Practical ਵੇਟ ਲਿਫਟਿੰਗ ਅਤੇ ਪਾਵਰ ਲਿਫਟਿੰਗ (Weight Lifting and Power Lifting)

ਪ੍ਰਸ਼ਨ 1.
ਭਾਰ ਚੁੱਕਣ ਦੇ ਨਿਰਧਾਰਿਤ ਸਟਾਲਾਂ ਦਾ ਵਰਣਨ ਕਰੋ ।
ਉੱਤਰ-
ਦੋ ਹੱਥ ਅਛੋਹ ਤੇ ਦਾਬ ਅਤੇ ਦੋਵਾਂ ਹੱਥਾਂ ਨਾਲ ਸਨੈਚ ।

ਪ੍ਰਸ਼ਨ 2.
ਭਾਰ ਚੁੱਕਣ ਵਿਚ ਖਿਡਾਰੀਆਂ ਦਾ ਭਾਰ ਕਦੋਂ ਤੋਲਿਆ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਮੁਕਾਬਲੇ ਤੋਂ ਇਕ ਘੰਟਾ ਪਹਿਲਾਂ ।

ਪ੍ਰਸ਼ਨ 3.
ਕੀ ਭਾਰ ਨੂੰ ਝਟਕੇ ਨਾਲ ਮੋਢੇ ਤਕ ਲਿਆਂਦਾ ਜਾ ਸਕਦਾ ਹੈ ?
ਉੱਤਰ-
ਨਹੀਂ ।

ਪ੍ਰਸ਼ਨ 4.
ਭਾਰ ਚੁੱਕਣ ਲਈ ਅਧਿਕਾਰੀਆਂ ਬਾਰੇ ਦੱਸੋ ।
ਉੱਤਰ-
ਰੈਫਰੀ-1, ਜੱਜ-3.

ਪ੍ਰਸ਼ਨ 5.
ਬਾਰ ਦੇ ਵਿਚ ਹਰ ਕਾਲਰ ਦਾ ਭਾਰ ਕਿੰਨਾ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
2.5 kg.

ਪ੍ਰਸ਼ਨ 6.
ਭਾਰਤ ਚੁੱਕਣ ਦੇ ਵਰਗਾਕਾਰ ਪਲੇਟਫਾਰਮ ਦਾ ਮਾਪ ਦੱਸੋ ।
ਉੱਤਰ-
4 ਮੀਟਰ ।

ਪ੍ਰਸ਼ਨ 7.
ਮਹਿਲਾ ਭਾਰ ਚੁੱਕਣ ਨੂੰ ਉਲੰਪਿਕ ਖੇਡਾਂ ਵਿਚ ਕਦੋਂ ਸ਼ਾਮਲ ਕੀਤਾ ਗਿਆ ?
ਉੱਤਰ-
2000 ਸਿਡਨੀ ਉਲੰਪਿਕ !

ਪ੍ਰਸ਼ਨ 8.
ਇੰਗਲੈਂਡ ਵਿਚ ਵੇਟ ਲਿਫ਼ਟਿੰਗ ਨੂੰ ਉੱਨਤ ਕਰਨ ਵਿਚ ਕਿਸ ਵਿਅਕਤੀ ਦਾ ਯੋਗਦਾਨ ਹੈ ?
ਉੱਤਰ-
ਰਸੇਲ (Russel) 1

ਪ੍ਰਸ਼ਨ 9.
ਭਾਰ ਚੁੱਕਣ ਵਿਚ ਇਸਤਰੀਆਂ ਲਈ ਕਿਹੜੇ ਭਾਰ ਵਰਗ ਹੁੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਗਿਆਰਾਂ (Eleven) ।

ਪ੍ਰਸ਼ਨ 10.
ਸਭ ਤੋਂ ਚੌੜੀ ਚੱਕੀ (ਡਿਸਕ) ਦਾ ਵਿਆਸ ਕਿੰਨਾ ਹੈ ?
ਉੱਤਰ-
45 ਸੈਂ.ਮੀ. ।

ਪ੍ਰਸ਼ਨ 11.
ਪਲੇਟਫਾਰਮ ਤੇ ਮੁਕਾਬਲੇ ਦੇ ਦੌਰਾਨ ਕਿਹੜੇ ਵਿਅਕਤੀ ਮੌਜੂਦ ਹੋ ਸਕਦੇ ਹਨ ?
ਉੱਤਰ-

1. ਜਿਊਰੀ ਦੇ ਮੈਂਬਰ
2. ਟੀਮ ਮੈਨੇਜਰ
3. ਰੈਫਰੀ
4. ਜੱਜ
5. ਖਿਡਾਰੀ ।

ਪ੍ਰਸ਼ਨ 12.
ਵੇਟ ਲਿਫਟਿੰਗ ਦੀਆਂ ਕਿਸੇ ਦੋ ਗ਼ਲਤ ਕਿਰਿਆਵਾਂ ਦੀ ਸੂਚੀ ਬਣਾਓ ।
ਉੱਤਰ-

1. ਧਰਤੀ ਤੇ ਗੋਡਿਆਂ ਦੇ ਭਾਰ ਝੁਕਣਾ
2. ਝਟਕੇ ਨੂੰ ਦੁਹਰਾਉਣਾ

ਪ੍ਰਸ਼ਨ 13.
ਮਰਦਾਂ ਲਈ ਬਾਰ ਦਾ ਭਾਰ ਕਿੰਨਾ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
20 ਕਿਲੋਗ੍ਰਾਮ ।

ਪ੍ਰਸ਼ਨ 14.
ਇਸਤਰੀਆਂ ਲਈ ਬਾਰ ਦਾ ਭਾਰ ਕਿੰਨਾ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
15 ਕਿਲੋਗ੍ਰਾਮ ।

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 3 Matrices Ex 3.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 3 Matrices Ex 3.1

Question 1.
In the matrix A = \(=\left[\begin{array}{cccc}
2 & 5 & 19 & -7 \\
35 & -2 & \frac{5}{2} & 12 \\
\sqrt{3} & 1 & -5 & 17
\end{array}\right]\), write:
(i) The order of the matrix
(ii) The number of elements,
(iii) The elements a₁₃, a₂₁, a₃₃, a₂₄, a₂₃.
Solution.
(i) In the given matrix, the number of rows is 3 and the number of columns is 4. Therefore, the order of the matrix is 3 × 4.
(ii) Since, the order of the matrix is 3 × 4, so there are 3 × 4 = 12 elements in it.
(iii) a₁₃ = 19, a₂₁ = 35, a₃₃= – 5, a₂₄ = 12, a₂₃ = \(\frac{5}{2}\).

Question 2.
If a matrix has 24 elements, what are the possible orders it can have? What, if it has 13 elements?
Solution.
We know that if a matrix is of the order m × n, it has mn elements. Thus, to find all the possible orders of a matrix having 24 elements, we have to find all the ordered pairs of natural numhers whose product is 24.
The ordered pairs are: (1, 24), (24,1), (2,12), (12, 2), (3, 8), (8, 3), (4, 6) and (6, 4).
Hence, the possible orders of a matrix having 24 elements are 1 × 24,24 × 1, 2 × 12,12 × 2, 3 × 8, 8 × 3, 4 × 6, and 6 × 4 (1, 13) and (13, 1) are the ordered pairs of natural numbers whose product is 13.
Hence, the possible orders of a matrix having 13 elements are 1 x 13 and 13×1.

Question 3.
If a matrix has 18 elements, what are the possible orders it can have? What, if it has 5 elements?
Solution.
We know that if a matrix is of the order m × n, it has mn elements. Thus, to find all the possible orders of a matrix having 18 elements, we have to find all the ordered pairs of natural numbers whose product is 18.
The ordered pairs are: (1, 18), (18, 1), (2, 9), (9, 2), (3, 6), and (6, 3)
Hence, the possible orders of a matrix having 18 elements are 1 × 18, 18 × 1, 2 × 9, 9 × 2, 3 × 6 and 6 × 3.
(1, 5)and (5, 1)are ordered pairs of natural numbers whose product is 5.
Hence, the possible orders of a matrix having 5 elements are 1 × 5 and 5 × 1.

Question 4.
Construct 2 × 2 matrix, A = [a_ij] whose elements are given by
(i) a_ij = \(\frac{(i+j)^{2}}{2}\)

(ii) a_ij = \(\frac{i}{j}\)

(iii) a_ij = \(\frac{(i+2 j)^{2}}{2}\)
Solution.
(i) The order of the given matrix is 2 × 2, so A = \(\left[\begin{array}{ll}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{array}\right]_{2 \times 2}\)
where a_ij = \(\frac{(i+2 j)^{2}}{2}\).
To find a₁₁, put i = 1 and j = 1
∴ a₁₁ = \(\frac{(1+1)^{2}}{2}\) = 2 Similarly

a₁₂ = \(\frac{(1+2)^{2}}{2}=\frac{9}{2}\)

a₂₁ = \(\frac{(2+1)^{2}}{2}=\frac{9}{2}\) and

a₂₂ = \(\frac{(2+2)^{2}}{2}\) = 8

(ii) Here, A = \(\left[\begin{array}{ll}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{array}\right]_{2 \times 2}\), where a_ij = \(\frac{i}{j}\).
∴ a₁₁ = \(\frac{1}{1}\) = 1,

a₁₂ = \(\frac{1}{2}\),

a₂₁ = \(\frac{2}{1}\) = 2 and

a₂₂ = \(\frac{2}{1}\) = 1

Hence, the required matrix is A = \(\left[\begin{array}{cc}
1 & 1 / 2 \\
2 & 1
\end{array}\right]_{2 \times 2}\)

(iii) Here, A = \(\left[\begin{array}{ll}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{array}\right]_{2 \times 2}\), where a_ij = \(\frac{(i+2 j)^{2}}{2}\)
∴ a₁₁ = \(\frac{(1+2)^{2}}{2}=\frac{9}{2}\)

a₁₂ = \(\frac{(1+4)^{2}}{2}=\frac{25}{2}\)

a₂₁ = \(\frac{(2+2)^{2}}{2}\) = 8

a₂₂ = \(\frac{(2+4)^{2}}{2}\) = 18

Hence, the required matrix is A = \(\left[\begin{array}{cc}
9 / 2 & 25 / 2 \\
8 & 18
\end{array}\right]_{2 \times 2}\).

Question 5.
Construct a 3 × 4 matrix, whose elements are given by:
(i) a_ij = \(\frac{4}{4}\) |- 3i + j|
(ii) a_ij = 2i – j
Solution.
In general, a 3 × 4 matrix is given by A = \(\left[\begin{array}{llll}
a_{11} & a_{12} & a_{13} & a_{14} \\
a_{21} & a_{22} & a_{23} & a_{24} \\
a_{31} & a_{32} & a_{33} & a_{34}
\end{array}\right]\)

(i) (i) a_ij = \(\frac{1}{2}\) |- 3i + j|, i = 1, 2, 3, 4 and j =1, 2, 3, 4
a₁₁ = \(\frac{1}{2}\) |- 3 × 1 + 1|
= \(\frac{1}{2}\) |- 3 + 1|
= \(\frac{1}{2}\) |- 2|
= \(\frac{21}{2}\) = 1

a₂₁ = \(\frac{1}{2}\) |- 3 × 2 + 1|
= \(\frac{1}{2}\) |- 6 + 1|
= \(\frac{1}{2}\) |- 5|
= \(\frac{5}{2}\)

a₃₁ = \(\frac{1}{2}\) |- 3 × 3 + 1|
= \(\frac{1}{2}\) |- 9 + 1|
= \(\frac{1}{2}\) |- 8|
= \(\frac{8}{2}\) = 4

a₁₂ = \(\frac{1}{2}\) |- 3 × 1 + 2|
= \(\frac{1}{2}\) |- 3 + 2|
= \(\frac{1}{2}\) |- 1|
= \(\frac{1}{2}\)

a₂₂ = \(\frac{1}{2}\) |- 3 × 2 + 2|
= \(\frac{1}{2}\) |- 6 + 2|
= \(\frac{1}{2}\) |- 4|
= \(\frac{4}{2}\) = 2

a₃₂ = \(\frac{1}{2}\) |- 3 × 3 + 2|
= \(\frac{1}{2}\) |- 9 + 2|
= \(\frac{1}{2}\) |- 7|
= \(\frac{7}{2}\)

a₁₃ = \(\frac{1}{2}\) |- 3 × 1 + 3|
= \(\frac{1}{2}\) |- 3 + 3| = 0

a₂₃ = \(\frac{1}{2}\) |- 3 × 2 + 3|
= \(\frac{1}{2}\) |- 6 + 3|
= \(\frac{1}{2}\) |- 3|
= \(\frac{3}{2}\)

a₃₃ = \(\frac{1}{2}\) |- 3 × 3 + 3|
= \(\frac{1}{2}\) |- 9 + 3|
= \(\frac{1}{2}\) |- 6|
= \(\frac{6}{2}\) = 3

a₁₄ = \(\frac{1}{2}\) |- 3 × 1 + 4|
= \(\frac{1}{2}\) |- 3 + 4|
= \(\frac{1}{2}\) |1|
= \(\frac{1}{2}\)

a₂₄ = \(\frac{1}{2}\) |- 3 × 2 + 4|
= \(\frac{1}{2}\) | – 6 + 4|
= \(\frac{1}{2}\) |- 2|
= \(\frac{2}{2}\) = 1

a₃₄ = \(\frac{1}{2}\) |- 3 × 3 + 4|
= \(\frac{1}{2}\) |- 9 + 4|
= \(\frac{1}{2}\) |- 5|
= \(\frac{5}{2}\)

Therfore, the required matrix is A = \(\left[\begin{array}{cccc}
1 & \frac{1}{2} & 0 & \frac{1}{2} \\
\frac{5}{2} & =2 & \frac{3}{2} & 1 \\
4 & \frac{7}{2} & 3 & \frac{5}{2}
\end{array}\right]_{3 \times 4}\)

(ii) a_ij = 2i – j, i = 1, 2, 3, 4 and j = 1, 2, 3, 4
a₁₁ = 2 × 1 – 1 = 2 – 1 = 1
a₁₂ = 2 × 2 – 1 = 4 – 1 = 3
a₁₃ = 2 × 3 – 1 = 6 – 1 = 5

a₂₁ = 2 × 1 – 2 = 2 – 2 = 0
a₂₂ = 2 × 2 – 2 = 4 – 2 = 2
a₂₃ = 2 × 3 – 2 = 6 – 2 = 4

a₃₁ = 2 × 1 – 3 = 2 – 3 = – 1
a₃₂ = 2 × 2 – 3 = 4 – 3 = 1
a₃₃ = 2 × 3 – 3 = 6 – 3 = 3

a₄₁ = 2 × 1 – 4 = 2 – 4 = – 2
a₄₂ = 2 × 2 – 4 = 4 – 4 = 0
a₄₃ = 2 × 3 – 4 = 6 – 4 = 0

Therfore, the required matrix is A = \(\left[\begin{array}{cccc}
1 & 0 & -1 & -2 \\
3 & 2 & 1 & 0 \\
5 & 4 & 3 & 2
\end{array}\right]_{3 \times 4}\).

Question 6.
Find the values of x, y, and z from the following equations:
(i) \(\left[\begin{array}{ll}
\mathbf{4} & \mathbf{3} \\
\boldsymbol{x} & 5
\end{array}\right]=\left[\begin{array}{ll}
\boldsymbol{y} & \boldsymbol{z} \\
\mathbf{1} & \mathbf{5}
\end{array}\right]\)

(ii) \(\left[\begin{array}{cc}
x+y & 2 \\
5+z & x y
\end{array}\right]=\left[\begin{array}{ll}
6 & 2 \\
5 & 8
\end{array}\right]\)

(iii) \(\left[\begin{array}{c}
x+y+z \\
x+z \\
y+z
\end{array}\right]=\left[\begin{array}{l}
9 \\
5 \\
7
\end{array}\right]\)
Solution.
(i) \(\left[\begin{array}{ll}
\mathbf{4} & \mathbf{3} \\
\boldsymbol{x} & 5
\end{array}\right]=\left[\begin{array}{ll}
\boldsymbol{y} & \boldsymbol{z} \\
\mathbf{1} & \mathbf{5}
\end{array}\right]\)
As the given matrices are equal, their corresponding elements are also equal.
Comparing the corresponding eleme nts, we get x = 1, y = 4, and z = 3.

(ii) \(\left[\begin{array}{cc}
x+y & 2 \\
5+z & x y
\end{array}\right]=\left[\begin{array}{ll}
6 & 2 \\
5 & 8
\end{array}\right]\)
As the given matrices are equal, their corresponding elements are also equal.
Comparing the corresponding elements, we get x + y = 6, xy = 8, 5 + z = 5
Now, 5 + z = 5
⇒ z = 0
We know that,
(x – y)² = (x + y)² – 4xy
⇒ (x – y)² = 36 – 32 = 4
⇒ x – y = ±2
Now, when x – y – 2 and x + y = 6, we get x = 4 and y = 2
When x – y = – 2 and x + y = 6, we get x = 2 and y = 4
∴ x = 4, y = 2, and z = 0 or x = 2, y = 4, and z = 0.

(iii) \(\left[\begin{array}{c}
x+y+z \\
x+z \\
y+z
\end{array}\right]=\left[\begin{array}{l}
9 \\
5 \\
7
\end{array}\right]\)
As the two matrices are equal, their corresponding elements are also equal.
Comparing the corresponding elements, we get
x + y + z = 9 ………..(i)
x + z = 5 ………….(ii)
y + z = 7
From Eqs. (i) and (ii), we have
y = 9 – 5
⇒ y = 4
Then, from Eq. (iii), we have:
4 + z = 7
⇒ z = 3
Now, x + z = 5
⇒ x = 5 – 3 = 2
∴ x – 2, y = 4 and z = 3.

Question 7.
Find the value of a, b, c and d from the following equation:
\(\left[\begin{array}{cc}
a-b & 2 a+c \\
2 a-b & 3 c+d
\end{array}\right]=\left[\begin{array}{cc}
-1 & 5 \\
0 & 13
\end{array}\right]\)
Solution.
We have,
\(\left[\begin{array}{cc}
a-b & 2 a+c \\
2 a-b & 3 c+d
\end{array}\right]=\left[\begin{array}{cc}
-1 & 5 \\
0 & 13
\end{array}\right]\)
As the two matrices are equal, their corresponding elements are also equal.
Comparing the corresponding elements, we get
a – b = – 1 ……………(i)
2a – b = 0 …………….(ii)
2a + c = 5 …………..(iii)
3c + d = 13 ………..(iv)
From Eq. (ii), we have
b = 2a
Then, from Eq. (i), we have
a – 2a = – 1
⇒ a -1
⇒ b = 2
Now, from Eq. (iii), we have
2 x 1 + c = 5
⇒ c = 5 – 2 = 3
From Eq. (iv) we have
3 × 3 + d = 13
⇒ 9 + d = 13
⇒ d = 13 – 9 = 4
Hence, a = 1, b = 2, c = 3 and d = 4.

Question 8.
A = [a_ij]_{m × n} is a square matrix, if
(A) m < n (B) m > n
(C) m = n
(D) None of these
Solution.
It is known that a given matrix is said to be a square matrix, if the number of rows is equal to the number of columns.
Therefore, A = [a_ij]_{m × n} is a square matrix, if m – n.
Hence, the correct answer is (C).

Question 9.
Which of the given values of x and y make the following pair of matrices equal?
\(\left[\begin{array}{cc}
3 x+7 & 5 \\
y+1 & 2-3 x
\end{array}\right]=\left[\begin{array}{cc}
0 & y-2 \\
8 & 4
\end{array}\right]\)
(A) x = \(\frac{-1}{3}\), y = 7

(B) Not possible to find

(C) y = 7, x = \(\frac{-2}{3}\)

(D) x = \(\frac{-1}{3}\), y = \(\frac{-2}{3}\)
Solution.
It is given that \(\left[\begin{array}{cc}
3 x+7 & 5 \\
y+1 & 2-3 x
\end{array}\right]=\left[\begin{array}{cc}
0 & y-2 \\
8 & 4
\end{array}\right]\)
On equating the corresponding elements, we get
3x + y = 0
⇒ x = – 3
5 = y – 2
⇒ y = 7
y + 1 = 8
⇒ y = 7
2 – 3x = 4
⇒ x = \(\frac{-2}{3}\)

We find that on comparing the corresponding elements of the two matrices, we get two different values of x, which is not possible.
Hence, it is not possible to find the values of x and y for which the given matrices are equal.
Hence, the correct answer is (B).

Q. 10.
The number of all possible matrices of order 3×3 with each entry 0 or 1 is
(A) 27
(B) 18
(C) 81
(D) 512
Solution.
The given matrix of the order 3 × 3 has 9 elements and each of these elements can be either 0 or 1.
Now, each of the 9 elements can be filled in two possible ways.
Therefore, by the multiplication principle, the required number of possible matrices is 2⁹ = 512.
Hence, the correct answer is (D).

Punjab State Board PSEB 6th Class Physical Education Book Solutions Chapter 4 ਪੰਜਾਬ ਦੀਆਂ ਲੋਕ ਖੇਡਾਂ Textbook Exercise Questions and Answers.

PSEB Solutions for Class 6 Physical Education Chapter 4 ਪੰਜਾਬ ਦੀਆਂ ਲੋਕ ਖੇਡਾਂ

Physical Education Guide for Class 6 PSEB ਪੰਜਾਬ ਦੀਆਂ ਲੋਕ ਖੇਡਾਂ Textbook Questions and Answers

 ਅਭਿਆਸ ਦੇ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਉੱਤਰ ।

ਪ੍ਰਸ਼ਨ 1.
ਬੱਚਿਆਂ ਦੀਆਂ ਕੋਈ ਦੋ ਖੇਡਾਂ ਦੇ ਨਾਂ ਲਿਖੋ ।
ਉੱਤਰ-

• ਬਾਂਦਰ ਕਿੱਲਾ
• ਗੁੱਲੀ ਡੰਡਾ ।

ਪ੍ਰਸ਼ਨ 2.
ਪੁੱਗਣ ਦੇ ਕਿੰਨੇ ਤਰੀਕੇ ਹੁੰਦੇ ਹਨ ? ਕਿਸੇ ਇੱਕ ਤਰੀਕੇ ਦਾ ਵਰਣਨ ਕਰੋ ।
ਉੱਤਰ-
ਪੁੱਗਣ ਦੇ ਤਿੰਨ ਤਰੀਕੇ ਹੁੰਦੇ ਹਨ ਪਹਿਲੀ ਵਿਧੀ-ਪਹਿਲਾਂ ਤਿੰਨ ਖਿਡਾਰੀ ਸੱਜਾ ਹੱਥ ਇਕ-ਦੂਜੇ ਦੇ ਹੱਥ ਤੇ ਰੱਖਦੇ ਹਨ ਤੇ ਇਕ ਸਮੇਂ ਹੱਥਾਂ ਨੂੰ ਹਵਾ ਵਿੱਚ ਉਛਾਲ ਕੇ ਉਲਟਾ ਦਿੰਦੇ ਹਨ । ਤਿੰਨਾਂ ਵਿੱਚ ਜੇਕਰ ਦੋ ਖਿਡਾਰੀ ਦੇ ਹੱਥ ਪੁੱਠੇ ਰੱਖੇ ਹੋਣ ਤੇ ਤੀਸਰੇ ਦਾ ਹੱਥ ਸਿੱਧਾ ਹੋਵੇ ਤਾਂ ਖਿਡਾਰੀ ਪੁੱਗ ਜਾਂਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਵਾਰੋ-ਵਾਰੀ ਇੱਕ ਨੂੰ ਛੱਡ ਕੇ ਸਾਰੇ ਖਿਡਾਰੀ ਪੁੱਗ ਜਾਂਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 3.
ਲੋਕ-ਖੇਡਾਂ ਦੀ ਮਹੱਤਤਾ ਬਾਰੇ ਨੋਟ ਲਿਖੋ ।
ਉੱਤਰ-
ਮਹੱਤਤਾ-

• ਸਰੀਰਕ ਬਲ, ਫੁਰਤੀ, ਦਿਮਾਗੀ ਚੁਸਤੀ ਆਦਿ ਇਨ੍ਹਾਂ ਖੇਡਾਂ ਨਾਲ ਆਉਂਦੇ ਹਨ । ਉਦਾਹਰਨ ਦੇ ਤੌਰ ‘ਤੇ ਜਦੋਂ ਖਿਡਾਰੀ ਠੀਕਰੀਆਂ ਤੇ ਨਿਸ਼ਾਨਾ ਲਾਉਣ ਦੀ ਖੇਡ ਖੇਡਦਾ ਹੈ, ਤਾਂ ਉਸਨੂੰ ਧਿਆਨ, ਏਕਾਗਰਤਾ ਕਰਨ ਦੀ ਸਿਖਲਾਈ ਮਿਲਦੀ ਹੈ । ‘ਕੋਟਲਾ ਛਪਾਕੀ ਖੇਡ ਤੋਂ ਚੌਕਸ ਰਹਿਣ ਦੀ ਸਿੱਖਿਆ ਮਿਲਦੀ ਹੈ । ਕਈ ਖੇਡਾਂ ਰਾਸ਼ਟਰੀ ਪੱਧਰ ਤੇ ਵੀ ਖੇਡੀਆਂ ਜਾਂਦੀਆਂ ਹਨ , ਜਿਵੇਂ-ਕੁਸ਼ਤੀ ਤੇ ਕਬੱਡੀ ।
• ਕੁਸ਼ਤੀ ਤੇ ਕਬੱਡੀ ਨਾਲ ਸਰੀਰਕ ਤਾਕਤ ਆਉਂਦੀ ਹੈ ॥
• ਖੇਡਾਂ ਨਾਲ ਦਿਮਾਗੀ ਚੁਸਤੀ ਵੀ ਵੱਧਦੀ ਹੈ ।
• ਇਹ ਖੇਡਾਂ ਬੱਚਿਆਂ ਵਿੱਚ ਆਪਸੀ ਸਾਂਝ ਨੂੰ ਵਧਾਉਂਦੀਆਂ ਹਨ ।
• ਸਾਡੇ ਵਿਰਸੇ ਅਤੇ ਸਭਿਆਚਾਰ ਨੂੰ ਕਾਇਮ ਰੱਖਣ ਵਿੱਚ ਸਹਾਇਕ ਹੁੰਦੀਆਂ ਹਨ ।

ਪ੍ਰਸ਼ਨ 4.
ਬਾਂਦਰ ਕਿੱਲਾ ਖੇਡ ਦੀ ਵਿਧੀ ਬਾਰੇ ਲਿਖੋ ।
ਉੱਤਰ-
ਮੁਹੱਲੇ ਦੇ ਸਾਰੇ ਬੱਚੇ ਇਕੱਠੇ ਹੋ ਕੇ ਬਾਂਦਰ ਕਿੱਲਾ ਖੇਡਣ ਦੇ ਲਈ ਕਿੱਲੇ ਲਈ । ਥਾਂ ਦੀ ਚੋਣ ਕਰਦੇ ਹਨ । ਖੇਡ ਸ਼ੁਰੂ ਕਰਨ ਤੋਂ ਪਹਿਲਾਂ ਬੱਚੇ ਗਾਉਂਦੇ ਹੋਏ ਇਕ-ਦੂਜੇ ਨੂੰ . ਕਹਿੰਦੇ ਹਨ

ਜੁੱਤੀਆਂ-ਚੱਪਲਾਂ ਦਾ,
ਕਰ ਲੋ ਵੀ ਹੀਲਾ |
ਹੁਣ ਆਪਾਂ ਰਲ ਕੇ,
ਖੇਡਣਾ ਬਾਂਦਰ ਕਿੱਲਾ ।

ਬਾਂਦਰ ਕਿੱਲਾ ਖੇਡਣ ਵਾਲੇ ਬੱਚੇ ਆਪਣੀਆਂ ਜੁੱਤੀਆਂ ਅਤੇ ਚੱਪਲਾਂ ਨੂੰ ਉਤਾਰ ਕੇ ਕਿੱਲੇ ਦੇ ਨੇੜੇ ਇਕੱਠੀਆਂ ਕਰ ਲੈਂਦੇ ਹਨ । ਕਿੱਲੇ ਦੇ ਹੇਠਲੇ ਪਾਸੇ 5 ਤੋਂ 7 ਮੀ : ਦੀ ਲੰਮੀ ਰੱਸੀ ਬੰਨ੍ਹ ਲੈਂਦੇ ਹਨ । ਬਾਂਦਰ ਕਿੱਲਾ ਖੇਡਣ ਵਾਲੇ ਬੱਚੇ ਵਾਰੀ ਦੇਣ ਵਾਲੇ ਬੱਚੇ ਨੂੰ ਪੁੱਗਦੇ ਹਨ । ਚੋਣ ਕਰਨ ਤੋਂ ਮਗਰੋਂ ਵਾਰੀ ਦੇਣ ਵਾਲਾ ਬੱਚਾ ਬਾਂਦਰ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ । ਬਾਂਦਰ ਬਣਿਆ ਬੱਚਾ ਕਿੱਲੇ ਨਾਲ ਬੰਨੀ ਰੱਸੀ ਨੂੰ ਫੜ ਕੇ ਸਾਰੀਆਂ ਜੁੱਤੀਆਂ ਅਤੇ ਚੱਪਲਾਂ ਦੀ ਰਾਖੀ ਕਰਦਾ ਹੈ ।

ਬਾਂਦਰ ਬਣਿਆ ਬੱਚਾ ਰੱਸੀ ਨੂੰ ਬਿਨਾਂ ਛੱਡ ਕਿਸੇ ਦੂਸਰੇ ਬੱਚੇ ਨੂੰ ਜੋ ਆਪਣੀਆਂ ਚੱਪਲਾਂ ਲੈਣ ਆਉਂਦਾ ਹੈ, ਉਸਨੂੰ ਛੂਹੇਗਾ। ਦੂਜੇ ਬੱਚੇ ਆਪਣੀਆਂ ਚੱਪਲਾਂ ਜਾਂ ਜੁੱਤੀਆਂ ਨੂੰ ਚੁੱਕਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰਦੇ ਹਨ । ਜੇਕਰ ਜੁੱਤੀਆਂ ਜਾਂ ਚੱਪਲਾਂ ਚੁੱਕਦੇ ਸਮੇਂ ਬਾਂਦਰ ਬਣਿਆ ਬੱਚਾ ਕਿਸੇ ਦੂਸਰੇ ਬੱਚੇ ਨੂੰ ਹੱਥ ਲਾਵੇ ਤਾਂ ਵਾਰੀ ਉਸ ਛੂਏ ਬੱਚੇ ਦੀ ਆ ਜਾਂਦੀ ਹੈ । ਜੇਕਰ ਸਾਰੇ ਬੱਚੇ ਬਿਨਾਂ ਛੂਏ ਆਪਣੀਆਂ ਚੱਪਲਾਂ ਤੇ ਜੁੱਤੀਆਂ ਚੁੱਕਣ ਵਿੱਚ ਕਾਮਯਾਬ ਹੋ ਜਾਂਦੇ ਹਨ, ਤਾਂ ਵਾਰੀ ਦੇਣ ਵਾਲਾ ਬਾਂਦਰ ਬੱਚਾ ਰੱਸੀ ਨੂੰ ਛੱਡ ਦੋੜੇਗਾ ਅਤੇ ਖ਼ਾਸ ਥਾਂ ਤੇ ਹੱਥ ਲਾਵੇਗਾ । ਨਿਸ਼ਚਿਤ ਜਗਾ ਤੇ ਪਹੁੰਚਣ ਤੋਂ ਪਹਿਲਾਂ-ਪਹਿਲਾਂ ਬਾਕੀ ਬੱਚੇ ਬਾਂਦਰ ਬੱਚੇ ਨੂੰ ਜੁੱਤੀਆਂ ਤੇ ਚੱਪਲਾਂ ਮਾਰਦੇ ਹਨ । ਬਾਂਦਰ ਦੇ ਨਿਸ਼ਚਿਤ ਜਗਾ ਤੇ ਪਹੁੰਚਣ ਤੇ ਜੁਤੀਆਂ ਮਾਰਨੀਆਂ ਬੰਦ ਕਰ ਦਿੰਦੇ ਹਨ । ਇਸਦੇ ਮਗਰੋਂ ਕਿਸੇ ਹੋਰ ਬੱਚੇ ਦੀ ਬਾਂਦਰ ਬਣਨ ਦੀ ਵਾਰੀ ਆ ਜਾਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 5.
ਤੁਹਾਨੂੰ ਕਿਹੜੀ ਲੋਕ-ਖੇਡ ਚੰਗੀ ਲੱਗਦੀ ਹੈ ? ਉਸ ਨੂੰ ਕਿਵੇਂ ਖੇਡਿਆ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਸਾਡੀ ਮਨਭਾਉਂਦੀ ਖੇਡ ‘ਕੋਟਲਾ ਛਪਾਕੀ ਹੈ । ਇਸ ਖੇਡ ਨੂੰ ਖੇਡਣ ਲਈ ਬੱਚਿਆਂ ਦੀ ਗਿਣਤੀ ਮਿਣਤੀ ਨਹੀਂ ਹੁੰਦੀ । ਇਸ ਖੇਡ ਦਾ ਦੂਸਰਾ ਨਾਮ ‘ਕਾਜੀ ਕੋਟਲੇ’ ਦੀ ਮਾਰ ਵੀ ਹੈ । ਇਸ ਖੇਡ ਨੂੰ ਖੇਡਣ ਲਈ 10-15 ਬੱਚੇ ਖੇਡਦੇ ਹਨ ਅਤੇ ਖੇਡਣ ਤੋਂ ਪਹਿਲਾਂ ਕਿਸੇ ਕੱਪੜੇ ਨੂੰ ਵੱਟ ਚੜਾ ਕੇ ਦੋਹਰਾ ਕਰਕੇ ਕੋਟਲਾ ਬਣਾ ਲੈਂਦੇ ਹਨ । ਫਿਰ ਬੱਚਾ ਜ਼ਮੀਨ ਤੇ ਕਿਸੇ ਤਿੱਖੀ ਜਿਹੀ ਚੀਜ਼ ਨਾਲ ਲਾਈਨ ਮਾਰ ਕੇ ਗੋਲਾ ਬਣਾਉਂਦਾ ਹੈ | ਬਾਕੀ ਸਾਰੇ ਬੱਚੇ ਚੱਕਰ ਦੀ ਖਿੱਚੀ ਲਾਈਨ ਤੇ ਮੁੰਹ ਅੰਦਰ ਕਰਕੇ ਬੈਠ ਜਾਂਦੇ ਹਨ । ਹੁਣ ਵਾਰੀ ਦੇਣ ਵਾਲਾ ਬੱਚਾ ਕੋਟਲੇ ਨੂੰ ਫੜ ਕੇ ਚੱਕਰ ਦੇ ਆਲੇ-ਦੁਆਲੇ ਦੌੜਦਾ ਹੈ । ਦੌੜਦਾ ਹੋਇਆ ਇਹ ਗੀਤ ਗਾਉਂਦਾ ਹੈ । ਕੋਟਲਾ ਛਪਾਕੀ ਜੁੰਮੇ ਰਾਤ ਆਈ ਜੇ। ਜਿਹੜਾ ਅੱਗੇ-ਪਿੱਛੇ ਦੇਖੇ, ਉਹਦੀ ਸ਼ਾਮਤ ਆਈ ਜੇ ।

ਗੋਲੇ ਵਿੱਚ ਬੈਠੇ ਬੱਚੇ ਗੀਤ ਗਾਉਣ ਵਾਲੇ ਬੱਚੇ ਦੇ ਪਿੱਛੇ ਗੀਤ ਗਾਉਂਦੇ ਹਨ । ਵਾਰੀ ਦੇਣ ਵਾਲਾ ਬੱਚਾ ‘ਕੋਟਲਾ ਛਪਾਕੀ ਜੁੰਮੇ ਰਾਤ ਆਈ ਜੇ’ ਅਤੇ ਗੋਲੇ ਦਾ ਚੱਕਰ ਲਗਾਉਂਦਾ ਹੈ । ਇਸ ਖੇਡ ਵਿੱਚ ਕੋਈ ਵੀ ਬੱਚਾ ਪਿੱਛੇ ਨਹੀਂ ਦੇਖ ਸਕਦਾ | ਸਾਰੇ ਬੱਚੇ ਜ਼ਮੀਨ ਵੱਲ ਦੇਖਦੇ ਹਨ । ਜੇ ਕੋਈ ਚੱਕਰ ਵਿੱਚ ਬੈਠਾ ਬੱਚਾ ਪਿੱਛੇ ਦੇਖਦਾ ਹੈ ਤਾਂ ਵਾਰੀ ਦੇਣ ਵਾਲਾ ਬੱਚਾ ਉਸਦੇ 4-5 ਕੋਟਲੇ ਮਾਰ ਦਿੰਦਾ ਹੈ । ਵਾਰੀ ਦੇਣ ਵਾਲਾ ਬੱਚਾ ਚੱਕਰ ਪੂਰਾ ਕਰਕੇ ਹੀ ਕਿਸੇ ਬੱਚੇ ਦੇ ਪਿੱਛੇ ਚੁੱਪ ਕਰਕੇ ਕੋਟਲਾ ਰੱਖ ਦਿੰਦਾ ਹੈ ਅਤੇ ਚੱਕਰ ਲਾ ਕੇ ਉਸ ਬੈਠੇ ਬੱਚੇ ਕੋਲ ਆ ਜਾਂਦਾ ਹੈ ।

ਜੇਕਰ ਬੈਠੇ ਹੋਏ ਬੱਚੇ ਨੂੰ ਕੋਟਲੇ ਦਾ ਪਤਾ ਨਹੀਂ ਚਲਦਾ ਤਾਂ ਵਾਰੀ ਦੇਣ ਵਾਲਾ ਬੱਚਾ ਕੋਟਲਾ ਚੁੱਕ ਕੇ ਉਸ ਬੱਚੇ ਨੂੰ ਮਾਰਨਾ ਸ਼ੁਰੂ ਕਰ ਦਿੰਦਾ ਹੈ | ਮਾਰ ਖਾਣ ਵਾਲਾ ਬੱਚਾ ਮਾਰ ਤੋਂ ਬਚਣ ਲਈ ਚੱਕਰ ਦੇ ਦੁਆਲੇ ਤੇਜ਼ੀ ਨਾਲ ਭੱਜਦਾ ਹੈ । ਜਦੋਂ ਤੱਕ ਉਹ ਬੱਚਾ ਆਪਣੀ ਜਗਾ ਤੇ ਦੁਬਾਰਾ ਨਹੀਂ ਪਹੁੰਚ ਜਾਂਦਾ ਉਦੋਂ ਤੱਕ ਬੱਚੇ ਨੂੰ ਕੋਟਲੇ ਦੀ ਮਾਰ ਸਹਿਣੀ ਪੈਂਦੀ ਹੈ । ਜੇਕਰ ਬੈਠੇ ਹੋਏ ਖਿਡਾਰੀ ਨੂੰ ਕੋਟਲਾ ਰੱਖਣ ਬਾਰੇ ਪਤਾ ਚੱਲ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਉਹ ਕੋਟਲਾ ਚੁੱਕ ਕੇ ਵਾਰੀ ਦੇਣ ਵਾਲੇ ਖਿਡਾਰੀ ਨੂੰ ਉਦੋਂ ਤੱਕ ਮਾਰਦਾ ਹੈ । ਜਦੋਂ ਤੱਕ ਉਹ ਚੱਕਰ ਲਗਾ ਕੇ ਬੈਠਣ ਵਾਲੇ ਦੀ ਖ਼ਾਲੀ ਜਗਾ ਤੇ ਆ ਬੈਠ ਨਹੀਂ ਜਾਂਦਾ । ਇਸ ਤਰ੍ਹਾਂ ਖੇਡ ਚੱਲਦੀ ਰਹਿੰਦੀ ਹੈ ।

PSEB 6th Class Physical Education Guide ਪੰਜਾਬ ਦੀਆਂ ਲੋਕ ਖੇਡਾਂ Important Questions and Answers

ਪ੍ਰਸ਼ਨ 1.
ਪੁੱਗਣ ਦੇ ਕਿੰਨੇ ਤਰੀਕੇ ਹਨ ?
(ਉ) ਦੋ
(ਅ) ਤਿੰਨ
(ੲ) ਚਾਰ
(ਸ) ਪੰਜ ।
ਉੱਤਰ-
(ਉ) ਦੋ

ਪ੍ਰਸ਼ਨ 2.
ਕਿਸੇ ਮਨ-ਪਸੰਦ ਖੇਡ ਦਾ ਨਾਂ ਲਿਖੋ ।
(ਉ) ਬਾਂਦਰ ਕਿੱਲਾ
(ਅ) ਕੋਟਲਾ ਛਪਾਕੀ
(ਈ) ਰੱਸੀ ਟੱਪਣਾ
(ਸ) ਉਪਰੋਕਤ ਕੋਈ ਨਹੀਂ ।
ਉੱਤਰ-
(ਉ) ਬਾਂਦਰ ਕਿੱਲਾ

ਪ੍ਰਸ਼ਨ 3.
ਵੱਡੀਆਂ ਦੋ ਖੇਡਾਂ ਦੇ ਨਾਂ ਲਿਖੋ ।
(ਉ) ਹਾਕੀ
(ਅ) ਫੁਟਬਾਲ
(ਬ) ਕ੍ਰਿਕੇਟ
(ਸ) ਉਪਰੋਕਤ ਸਾਰੇ |
ਉੱਤਰ-
(ਸ) ਉਪਰੋਕਤ ਸਾਰੇ |

ਪ੍ਰਸ਼ਨ 4.
ਲੋਕ ਖੇਡਾਂ ਵਿੱਚੋਂ ਕਿਸੇ ਦੋ ਦੇ ਨਾਂ ਲਿਖੋ ।
(ਉ) ਬਾਂਦਰ ਕਿੱਲਾ ਅਤੇ ਕੋਟਲਾ ਛਪਾਕੀ
(ਅ) ਚੋਰ ਸਿਪਾਹੀ
(ਇ) ਰੱਸੀ ਟੱਪਣਾ
(ਸ) ਖੋ-ਖੋ ।
ਉੱਤਰ-
(ਉ) ਬਾਂਦਰ ਕਿੱਲਾ ਅਤੇ ਕੋਟਲਾ ਛਪਾਕੀ

ਪ੍ਰਸ਼ਨ 5.
ਲੋਕ ਖੇਡਾਂ ਦੀ ਮਹੱਤਤਾ ਲਿਖੋ ।
(ਉ) ਸਰੀਰਕ ਬਲ ਵਧਦਾ ਹੈ
(ਅ) ਫੁਰਤੀ
(ਈ) ਦਿਮਾਗੀ ਚੁਸਤੀ ਆਉਂਦੀ ਹੈ
(ਸ) ਉਪਰੋਕਤ ਸਾਰੀਆਂ ।
ਉੱਤਰ-
(ਸ) ਉਪਰੋਕਤ ਸਾਰੀਆਂ ।

ਬਹੁਤ ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ

ਪ੍ਰਸ਼ਨ 1.
ਲੋਕ-ਖੇਡਾਂ ਦੇ ਕੋਈ ਦੋ ਨਾਂ ਲਿਖੋ ।
ਉੱਤਰ-

• ਕਿੱਕਲੀ
• ਕੋਟਲਾ ਛਪਾਕੀ ।

ਪ੍ਰਸ਼ਨ 2. ਕੋਟਲਾ ਛਪਾਕੀ ਦਾ ਗੀਤ ਲਿਖੋ ।
ਉੱਤਰ-
ਕੋਟਲਾ ਛਪਾਕੀ ਜੁੰਮੇ ਰਾਤ ਆਈ ਏ । ਜਿਹੜਾ ਅੱਗੇ ਪਿੱਛੇ, ਦੇਖੇ ਉਚੀ ਸ਼ਾਮਤ ਆਈ ਏ ।

ਪ੍ਰਸ਼ਨ 3.
ਬਾਂਦਰ ਕਿੱਲਾ ਦੀਆਂ ਚਾਰ ਲਾਈਨਾਂ ਲਿਖੋ ।
ਉੱਤਰ-
ਜੁੱਤੀਆਂ ਚੱਪਲਾ ਦਾ, ਕਰ ਲੋ ਵੀ ਹੀਲ੍ਹਾ: ਹੁਣ ਆਪਾਂ ਰਲ ਕੇ, ਖੇਡਣਾ ਬਾਂਦਰ ਕਿੱਲਾ ॥

ਪ੍ਰਸ਼ਨ 4.
ਪੁੱਗਣ ਦੇ ਕਿੰਨੇ ਤਰੀਕੇ ਹਨ ?
ਉੱਤਰ-
ਪੁੱਗਣ ਦੇ ਤਿੰਨ ਤਰੀਕੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 5.
ਕਿਸੇ ਮਨ-ਪਸੰਦ ਲੋਕ ਖੇਡ ਦਾ ਨਾਂ ਲਿਖੋ ।
ਉੱਤਰ-
ਬਾਂਦਰ ਕਿੱਲਾ ।

ਪ੍ਰਸ਼ਨ 6.
ਸਿਹਤ ਪੱਖੋਂ ਸਭ ਤੋਂ ਚੰਗੀ ਖੇਡ ਕਿਹੜੀ ਹੈ ?
ਉੱਤਰ-
ਰੱਸੀ ਟੱਪਣਾ |

ਪ੍ਰਸ਼ਨ 7. ਚੁਸਤੀ, ਫੁਰਤੀ ਤੇ ਏਕਾਗਰਤਾ ਕਿਸ ਖੇਡ ਨਾਲ ਆਉਂਦੀ ਹੈ ?
ਉੱਤਰ-
ਪਿੱਠੂ ਗਰਮ ਕਰਨ ਵਿੱਚ ।

ਪ੍ਰਸ਼ਨ 8.
ਵੱਡੀਆਂ ਤੇ ਲੋਕ ਖੇਡਾਂ ਦਾ ਇੱਕ-ਇੱਕ ਨਾਂ ਲਿਖੋ ।
ਉੱਤਰ-

• ਹਾਕੀ
• ਕੋਟਲਾ ਛਪਾਕੀ ।

ਪ੍ਰਸ਼ਨ 9. ਲੋਕ-ਖੇਡਾਂ ਦੀ ਇਕ ਮਹੱਤਤਾ ਲਿਖੋ ।
ਉੱਤਰ-
ਇਸ ਨਾਲ ਸਰੀਰ ਤੰਦਰੁਸਤ ਰਹਿੰਦਾ ਹੈ |

ਪ੍ਰਸ਼ਨ 10.
ਕਿੱਕਲੀ ਲੋਕ-ਖੇਡ ਨੂੰ ਕੌਣ ਖੇਡਦਾ ਹੈ ?
ਉੱਤਰ-
ਕੁੜੀਆਂ ਦੀ ਖੇਡ ਹੈ ।

ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ

ਪ੍ਰਸ਼ਨ 1.
ਖੇਡ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਖੇਡ ਉਹ ਕ੍ਰਿਆ ਹੈ ਜਿਸਨੂੰ ਮਨਪ੍ਰਚਾਵੇ ਲਈ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ਅਤੇ ਅਜਿਹੀਆਂ ਕਿਆ ਕਰਨ ਨਾਲ ਸਾਨੂੰ ਖੁਸ਼ੀ ਮਿਲਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਖੇਡਾਂ ਦੀਆਂ ਕਿਸਮਾਂ ਲਿਖੋ ।
ਉੱਤਰ-
ਖੇਡਾਂ ਦੀ ਵੰਡ ਕਈ ਤਰ੍ਹਾਂ ਨਾਲ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ ਜਿਵੇਂ ਕਿ ਸਰੀਰਕ ਖੇਡਾਂ ਅਤੇ ਦਿਮਾਗ਼ ਦੀਆਂ ਖੇਡਾਂ | ਅਜਿਹੀ ਇੱਕ ਵੰਡ ਹੈ, ਸਾਡੀਆਂ ਲੋਕ ਖੇਡਾਂ ਅਤੇ ਅਜੋਕੀਆਂ ਖੇਡਾਂ | ਜ਼ਿਕੇਟ, ਹਾਕੀ, ਵਾਲੀਬਾਲ, ਫੁਟਬਾਲ ਆਦਿ ਅਜੋਕੀਆਂ ਖੇਡਾਂ ਹਨ । ਇਨ੍ਹਾਂ ਨੂੰ ਖੇਡਣ ਲਈ ਖ਼ਾਸ ਸਮਾਨ, ਨਿਸ਼ਚਿਤ ਖੇਡ ਮੈਦਾਨ ਅਤੇ ਵਿਸ਼ੇਸ਼ ਖੇਡ ਨਿਯਮ ਹੁੰਦੇ ਹਨ । ਲੋਕ ਖੇਡਾਂ ਇਸ ਤੋਂ ਉਲਟ ਆਖੀਆਂ ਜਾ ਸਕਦੀਆਂ ਹਨ ।

ਪ੍ਰਸ਼ਨ 3.
ਖੇਡ ਕਿਸ ਉਮਰ ਦੇ ਲੋਕ ਖੇਡਦੇ ਹਨ ?
ਉੱਤਰ-
ਖੇਡ ਹਰ ਉਮਰ ਦੇ ਲੋਕ ਖੇਡਦੇ ਹਨ | ਬੱਚੇ, ਜਵਾਨ ਅਤੇ ਬਜ਼ੁਰਗ ਵੀ ਖੇਡਾਂ ਖੇਡਦੇ ਹਨ ਅਤੇ ਮੁੰਡੇ, ਕੁੜੀਆਂ ਵੀ ਖੇਡਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 4.
ਖੇਡਾਂ ਦੀ ਵੰਡ ਕਿਸ ਤਰ੍ਹਾਂ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ?
ਉੱਤਰ-
ਸਾਡੀਆਂ ਲੋਕ ਖੇਡਾਂ ; ਜਿਵੇਂ-ਕਿਤੇ, ਕੀ, ਵਾਲੀਵਾਲ, ਫੁਟਬਾਲ ਆਦਿ ।

ਪ੍ਰਸ਼ਨ 5.
ਲੋਕ ਖੇਡਾਂ ਵਿੱਚ ਕੀ ਨਿਯਮ ਇਚਿਤ ਹੁੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਅਜਿਹੀਆਂ ਖੇਡਾਂ ਖੇਡਣ ਲਈ ਕੋਈ ਸਮਾਨ ਜਾਂ ਨਿਯਮ ਨਿਸ਼ਚਿਤ ਨਹੀਂ ਹੁੰਦੇ ।

ਪ੍ਰਸ਼ਨ 6.
ਵੱਡੀਆਂ ਖੇਡਾਂ ਵਿੱਚ ਕੀ ਨਿਯਮ ਹੁੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਵੱਡੀਆਂ ਖੇਡਾਂ ਵਿਚ ਸਾਮਾਨ, ਖੇਡ ਦਾ ਮੈਦਾਨ ਤੇ ਨਿਯਮ ਨਿਸ਼ਚਿਤ ਹੁੰਦੇ ਹਨ । ਇਹ ਖੇਡਾਂ ਨਿਯਮਾਂ ਅਨੁਸਾਰ ਹੀ ਖੇਡੀਆਂ ਜਾਂਦੀਆਂ ਹਨ ।

ਪ੍ਰਸ਼ਨ 7.
ਲੋਕ ਖੇਡਾਂ ਖੇਡਣ ਲਈ ਵਾਰੀ ਪੁੱਗਣ ਦੀ ਵਿਧੀ ਦੱਸੋ ।
ਉੱਤਰ-
ਪਹਿਲਾਂ ਤਿੰਨ ਖਿਡਾਰੀ ਆਪਣਾ ਸੱਜਾ ਹੱਥ ਦੂਜੇ ਦੇ ਸੱਜੇ ਹੱਥ ਤੇ ਰੱਖਦੇ ਹਨ ਅਤੇ ਇੱਕੋ ਸਮੇਂ ਹੱਥਾਂ ਨੂੰ ਹਵਾ ਵਿੱਚ ਘੁਮਾ ਕੇ ਉਲਟਾ ਦਿੰਦੇ ਹਨ । ਤਿੰਨਾਂ ਵਿਚੋਂ ਜੇਕਰ ਦੋ ਖਿਡਾਰੀਆਂ ਦਾ ਹੱਥ ਉਲਟਾ ਹੁੰਦਾ ਹੈ ਤੇ ਇਕ ਖਿਡਾਰੀ ਦਾ ਸਿੱਧਾ ਹੁੰਦਾ ਹੈ, ਤਾਂ ਉਹ ਪੱਗ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 8.
ਪੁੱਗਣ ਦੀ ਦੂਜੀ ਵਿਧੀ ਦਾ ਗੀਤ ਲਿਖੋ ।
ਉੱਤਰ-
ਈਂਗਣ ਮੀਂਗਣ ਤਲੀ ਤਲੀਂਗਣ ਕਾਲਾ, ਪੀਲਾ, ਡੱਕਰਾ ਗੁੜ ਖਾਵਾਂ ਵੇਲ ਵਧਾਵਾਂ, ਮੂਲੀ ਪੱਤਰਾ । ਪਤਾ ਹੋ ਘੋੜੇ ਆਏ ਹੱਥ ਕੁਤਾੜੀ, ਪੈਰ ਕੁਤਾੜੀ ਨਿੱਕ ਬਾਲਿਆ ਤੇਰੀ ਵਾਰੀ |

ਪ੍ਰਸ਼ਨ 9.
ਕੀ ਲੋਕ ਖੇਡਾਂ ਵਿੱਚ ਟੀਮਾਂ ਦੀ ਵੰਡ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ?
ਉੱਤਰ-
ਹਾਂ, ਕਈ ਖੇਡਾਂ ਵਿੱਚ ਆਪਸ ਵਿੱਚ ਟੀਮਾਂ ਦੀ ਵੰਡ ਕੀਤੀ ਜਾਂਦੀ ਹੈ , ਜਿਵੇਂਕਬੱਡੀ, ਗੁੱਲੀ ਡੰਡਾ, ਰੱਸਾ ਕਸ਼ੀ ਆਦਿ ।

ਪ੍ਰਸ਼ਨ 10.
ਲੋਕ ਖੇਡਾਂ ਦੇ ਕੋਈ ਪੰਜ ਨਾਂ ਲਿਖੋ ।
ਉੱਤਰ-

1. ਬਾਂਦਰ ਕਿੱਲਾ
2. ਕੋਟਲਾ ਛਪਾਕੀ
3. ਕਿੱਕਲੀ
4. ਪਿੱਠੂ ਗਰਮ ਕਰਨਾ
5. ਰੱਸੀ ਟੱਪਣਾ ।

ਪ੍ਰਸ਼ਨ 11.
ਲੋਕ ਖੇਡਾਂ ਦੀ ਦੋ ਮਹੱਤਤਾ ਲਿਖੋ ।
ਉੱਤਰ-

• ਇਹਨਾਂ ਖੇਡਾਂ ਨੂੰ ਖੇਡਦੇ ਹੋਏ ਫੁਰਤੀ, ਸਰੀਰਕ ਬਲ ਅਤੇ ਦਿਮਾਗੀ ਚੁਸਤੀ ਆਦਿ ਦੇ ਗੁਣ ਆ ਜਾਂਦੇ ਹਨ ।
• ਜਦੋਂ ਖਿਡਾਰੀ ਠੀਕਰੀਆਂ ਨਾਲ ਨਿਸ਼ਾਨਾ ਲਾਉਣ ਦੀ ਖੇਡ ਖੇਡਦੇ ਹਨ । ਉਨ੍ਹਾਂ ਨੂੰ ਏਕਾਗਰਤਾ ਕਰਨ ਦੀ ਸਿਖਲਾਈ ਮਿਲਦੀ ਹੈ |

ਪ੍ਰਸ਼ਨ 12.
ਰੱਸੀ ਟੱਪਣਾ ਦੀ ਮਹੱਤਤਾ ਲਿਖੋ ।
ਉੱਤਰ-
ਇਹ ਖੇਡ ਕਸਰਤ ਪੱਖੋਂ ਬਹੁਤ ਹੀ ਵਧੀਆ ਖੇਡ ਹੈ । ਪੁੱਗਣ ਤੋਂ ਬਾਅਦ ਜਿਹੜੇ ਦੋ ਬੱਚੇ ਪਿੱਛੇ ਰਹਿ ਜਾਂਦੇ ਹਨ, ਉਹ ਇੱਕ ਦੂਜੇ ਦੇ ਸਾਹਮਣੇ ਖੜ੍ਹੇ ਹੋ ਕੇ ਇਕ ਹੱਥ ਰੱਸੀ ਨੂੰ ਜ਼ਮੀਨ ਨਾਲ ਛੁਹਾਉਂਦੇ ਹੋਏ, ਇਕ ਪਾਸੇ ਵੱਲ ਘੁਮਾਉਂਦੇ ਹਨ | ਬਾਕੀ ਬੱਚੇ ਲਾਈਨ ਬਣਾ ਕੇ ਇੱਕ-ਇੱਕ ਦੋ-ਦੋ ਟੱਪੇ ਲੈਂਦੇ ਹਨ । ਇਸ ਤਰ੍ਹਾਂ ਇਹ ਖੇਡ ਖੇਡੀ ਜਾਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 13.
ਪਿੱਠੂ ਗਰਮ ਕਰਨਾ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਪਿੱਠ ਗਰਮ ਕਰਨਾ ਵੀ ਪੰਜਾਬ ਦੇ ਬੱਚਿਆਂ ਲਈ ਬੜੀ ਦਿਲਚਸਪ ਖੇਡ ਹੈ । ਇਸ ਖੇਡ ਵਿੱਚ ਖੇਡਣ ਵਾਲੇ ਬੱਚੇ ਦੋ ਟੋਲੀਆਂ ਬਣਾ ਲੈਂਦੇ ਹਨ, ਅਤੇ 10-15 ਫੁੱਟ ਦੀ ਦੂਰੀ ਤੇ ਗੀਟੀਆਂ ਰੱਖ ਕੇ ਉਸ ਤੇ ਨਿਸ਼ਾਨਾ ਲਗਾਉਂਦੇ ਹਨ । ਇਸ ਤਰ੍ਹਾਂ ਇਹ ਖੇਡ ਖੇਡੀ ਜਾਂਦੀ

ਪ੍ਰਸ਼ਨ 14.
ਕਿੱਕਲੀ ਦੀ ਮਹੱਤਤਾ ਲਿਖੋ ।
ਉੱਤਰ-
ਕਿੱਕਲੀ ਪੰਜਾਬ ਦੀਆਂ ਕੁੜੀਆਂ ਦੀ ਬਹੁਤ ਹੀ ਹਰਮਨ-ਪਿਆਰੀ ਖੇਡ ਹੈ । ਕਿੱਕਲੀ ਖੇਡ ਅਤੇ ਗਿੱਧੇ ਦਾ ਸੁਮੇਲ ਹੈ । ਇਸ ਖੇਡ ਨੂੰ ਕੁੜੀਆਂ ਚਾਅ ਨਾਲ ਖੇਡਦੀਆਂ ਹਨ । ਇਸ ਖੇਡ ਵਿੱਚ ਕੁੜੀਆਂ ਇਕ ਥਾਂ ਤੇ ਇਕੱਠੀਆਂ ਹੋ ਕੇ ਆਪਸ ਵਿੱਚ ਜੋਟੇ ਬਣਾ ਕੇ ਇਕਦੂਜੀ ਦੇ ਹੱਥਾਂ ਵਿੱਚ ਕੰਘੀਆਂ ਪਾ ਕੇ ਘੁੰਮਦੀਆਂ ਹਨ । ਉਹਨਾਂ ਨੇ ਇਕ ਦੂਜੇ ਦਾ ਹੱਥ ਖੱਬੇ ਹੱਥ ਨਾਲ ਸੱਜਾ ਚ ਫੜਿਆ ਹੁੰਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਇਹ ਖੇਡ ਖੇਡੀ ਜਾਂਦੀ ਹੈ !

ਪ੍ਰਸ਼ਨ 15.
ਕੋਲਾ ਛਪਾਕੀ ਦੀ ਮਹੱਤਤਾ ਲਿਖੋ ।
ਉੱਤਰ-
ਛਪਾਕੀ ਪਿੰਡਾਂ ਵਿੱਚ ਖੇਡੀ ਜਾਣ ਵਾਲੀ ਛੋਟੀ ਉਮਰ ਦੇ ਮੁੰਡੇ-ਕੁੜੀਆਂ ਦੀ ਖੇਡ ਹੈ । ਇਸ ਡ ਨੂੰ ‘ਕਾਜੀ ਕੋਟਲੇ ਦੀ ਮਾਰ’ ਦੇ ਨਾਂ ਨਾਲ ਜਾਣਿਆ ਜਾਂਦਾ ਹੈ । ਕੋਲਾ ਛਪਾਕੀ ਜੁੰਮੇ ਰਾਤ ਆਈ ਜੇ । ਨੂੰ ਅੱਗੇ-ਪਿੱਛੇ ਦੇਖੇ, ਉਹਦੀ ਸ਼ਾਮਤ ਆ ਜੇ । ਗੋਲ ਚ ਤਾ ਵਿੱਚ ਬੈਠੇ ਹੋਏ ਬੱਚੇ ਵਾਰੀ ਦੇਣ ਵਾਲੇ ਦੇ ਪਿੱਛੇ-ਪਿੱਛੇ ਇਹ ਗੀਤ ਗਾਉਂਦੇ ਹਨ ।

ਵੱਡੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ

ਪ੍ਰਸ਼ਨ 1.
ਪੁੱਗਣ ਦੀ ਦੂਸਰੀ ਕੋਈ ਵਿਧੀ ਲਿਖੋ ।
ਉੱਤਰ-
ਪੁੱਗਣ ਦੀ ਦੂਜੀ ਵਿਧੀ-ਸਾਰੇ ਖਿਡਾਰੀ ਗੋਲ ਚੱਕਰ ਵਿੱਚ ਖੜ੍ਹੇ ਹੋ ਜਾਂਦੇ ਹਨ । ਉਨ੍ਹਾਂ ਵਿੱਚੋਂ ਇਕ ਖਿਡਾਰੀ ਵਾਰੀ-ਵਾਰੀ ਸਾਰੇ ਖਿਡਾਰੀਆਂ ਦੇ ਮੋਢੇ ਤੇ ਹੱਥ ਰੱਖ ਕੇ ਇਹ ਗੀਤ ਗਾਉਂਦਾ ਹੈ ।
ਈਂਗਣ ਮੀਂਗਣ ਤਲੀ ਤਲੀਂਗਣ
ਕਾਲਾ, ਪੀਲਾ, ਡੱਕਰਾ
ਗੁੜ ਖਾਵਾਂ, ਵੇਲ ਵਧਾਵਾਂ,
ਮੂਲੀ ਪੱਤਰਾ ।
ਪੱਤਾ ਵਾ, ਘੋੜੇ ਆਏ,
ਹੱਥ ਕੁਤਾੜੀ, ਪੈਰ ਕੁਤਾੜੀ
ਨਿੱਕੇ ਬਾਲਿਆ ਤੇਰੀ ਵਾਰੀ ।
ਜਿਸ ਖਿਡਾਰੀ ਨੂੰ ਆਖਰੀ ਸ਼ਬਦ ਤੇ ਹੱਥ ਲੱਗਦਾ ਹੈ । ਉਹ ਪੁੱਗ ਜਾਂਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਬਾਰ-ਬਾਰ ਕਰਦਿਆਂ ਅੰਤ ਵਿੱਚ ਰਹਿ ਜਾਣ ਵਾਲੇ ਦੀ ਵਾਰੀ ਤਹਿ ਹੋ ਜਾਂਦੀ ਹੈ । ਕਈ ਖੇਡਾਂ ਆਪਸ ਵਿੱਚ ਦੋ ਟੀਮਾਂ ਬਣਾ ਕੇ ਖੇਡੀਆਂ ਜਾਂਦੀਆਂ ਹਨ । ਜਿਵੇਂ-ਕਬੱਡੀ, ਗੁੱਲੀ ਡੰਡਾ, ਰੱਸਾ ਕਸ਼ੀ ਅਤੇ ਖੋ-ਖੋ ਆਦਿ ।

ਪ੍ਰਸ਼ਨ 2.
ਰੱਸੀ ਟੱਪਣਾ ਤੇ ਪਿੱਠੂ ਖੇਡ ਬਾਰੇ ਲਿਖੋ ।
ਉੱਤਰ-
ਰੱਸੀ ਟੱਪਣਾ-ਇਹ ਖੇਡ ਕਸਰਤ ਪੱਖੋਂ ਬਹੁਤ ਹੀ ਵਧੀਆ ਖੇਡ ਹੈ । ਪੁੱਗਣ ਤੋਂ ਬਾਅਦ ਜਿਹੜੇ ਦੋ ਬੱਚੇ ਪਿੱਛੇ ਰਹਿ ਜਾਂਦੇ ਹਨ, ਉਹ ਇੱਕ-ਦੂਜੇ ਦੇ ਸਾਹਮਣੇ ਖੜੇ ਹੋ ਕੇ ਹੱਥ ਰੱਸੀ ਨੂੰ ਜ਼ਮੀਨ ਨਾਲ ਛੁਹਾਉਂਦੇ ਹੋਏ, ਇੱਕ ਪਾਸੇ ਵੱਲ ਘੁੰਮਾਉਂਦੇ ਹਨ । ਬਾਕੀ ਬੱਚੇ ਲਾਈਨ ਬਣਾ ਕੇ ਇੱਕ-ਇਕ, ਦੋਦੋ ਟੱਪੇ ਲੈਂਦੇ ਹਨ । ਜਿਹੜੇ ਬੱਚੇ ਦੇ । ਪੈਰਾਂ ਨੂੰ ਰੱਸੀ ਛੂਹ ਜਾਵੇ ਉਹ ਆਉਟ ਹੋ ਜਾਂਦਾ ਹੈ ਅਤੇ ਰੱਸੀ ਘੁੰਮਾਉਣ ਦੀ ਵਾਰੀ ਦਿੰਦਾ ਹੈ । ਇਹ ਖੇਡ ਕੁੜੀਆਂ ਦੀ ਹਰਮਨ-ਪਿਆਰੀ ਖੇਡ ਰਹੀ ਹੈ ਪਰ ਅੱਜ-ਕਲ੍ਹ ਬਹੁਤ ਘੱਟ ਹੋ ਗਈ ਹੈ ।

ਪਿੱਠੂ ਗਰਮ ਕਰਨਾ-ਇਹ ਇੱਕ ਬੱਚਿਆਂ ਦੀ ਬੜੀ ਦਿਲਚਸਪ ਖੇਡ ਹੈ ਜਿਸ ਵਿੱਚ ਬੱਚਿਆਂ ਦੀ ਗਿਣਤੀ ਨਿਸ਼ਚਿਤ ਨਹੀਂ ਹੁੰਦੀ ਜਿਸ ਵਿਚ ਦੋ ਟੋਲੀਆਂ ਹੁੰਦੀਆਂ ਹਨ । ਖੇਡਣ ਵਾਲੀ ਜਗਾ ਤੇ ਸੱਤ ਠੀਕਰੀਆਂ ਇੱਕ-ਦੂਜੇ ਦੇ ਉੱਪਰ ਰੱਖ ਲਈਆਂ ਜਾਂਦੀਆਂ ਹਨ । ਇਨ੍ਹਾਂ ਚਿਣੀਆਂ ਹੋਈਆਂ ਠੀਕਰੀਆਂ ਤੋਂ ਲਗਭਗ 12 ਫੁੱਟ ਦੀ ਦੂਰੀ ‘ਤੇ ਇਕ ਲਾਈਨ ਖਿੱਚ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ । ਫਿਰ ਦੋਵੇਂ ਟੀਮਾਂ ਪੁੱਗਣ ਤੋਂ ਬਾਅਦ ਜਿਹੜੀ ਟੀਮ ਪੁੱਗ ਜਾਂਦੀ ਹੈ । ਉਸ ਟੀਮ ਦਾ ਇਕ ਖਿਡਾਰੀ ਲਾਈਨ ਤੇ ਖੜ੍ਹਾ ਹੋ ਕੇ ਰਬੜ ਦੀ ਗੇਂਦ ਨਾਲ ਚਿਣੀਆਂ ਹੋਈਆਂ ਗੀਟੀਆਂ ‘ਤੇ ਨਿਸ਼ਾਨਾ ਲਗਾਉਂਦਾ ਹੈ । ਇੱਕ ਖਿਡਾਰੀ ਨੂੰ ਨਿਸ਼ਾਨਾ ਲਗਾਉਣ ਦੇ ਤਿੰਨ ਮੌਕੇ ਦਿੱਤੇ ਜਾਂਦੇ ਹਨ । ਤਿੰਨ ਵਾਰ ਨਿਸ਼ਾਨਾ ਲਾਉਣ ਤੋਂ ਬਾਅਦ ਜੇਕਰ ਠੀਕਰੀਆਂ ਤੇ ਨਿਸ਼ਾਨਾ ਨਹੀਂ ਲੱਗਦਾ ਤਾਂ ਉਹ ਖਿਡਾਰੀ ਆਊਟ ਹੋ ਜਾਂਦਾ ਹੈ ।

ਜੇਕਰ ਗੇਂਦ ਨੂੰ ਠੱਪਾ ਪਾ ਕੇ ਸਾਹਮਣੇ ਵਾਲੇ ਖਿਡਾਰੀ ਪਕੜ ਲੈਂਦੇ ਹਨ, ਤਾਂ ਵੀ ਨਿਸ਼ਾਨੇ ਲਗਾਉਣ ਵਾਲਾ ਖਿਡਾਰੀ ਆਉਟ ਹੋ ਜਾਂਦਾ ਹੈ । ਜੇਕਰ ਨਿਸ਼ਾਨਾ ਲਗਾਉਣ ਵਾਲਾ ਖਿਡਾਰੀ ਠੀਕਰੀਆਂ ਤੇ ਸਹੀ ਨਿਸ਼ਾਨਾ ਲਗਾ ਦਿੰਦਾ ਹੈ, ਤਾਂ ਠੀਕਰੀਆਂ ਜ਼ਮੀਨ ਤੇ ਬਿਖਰ ਜਾਂਦੀਆਂ ਹਨ । ਨਿਸ਼ਾਨਾ ਲਗਾਉਣ ਵਾਲਾ ਖਿਡਾਰੀ ਜ਼ਮੀਨ ਤੇ ਬਿਖਰੀਆਂ ਠੀਕਰੀਆਂ ਨੂੰ ਜਲਦੀ-ਜਲਦੀ ਇਕੱਠੀਆਂ ਕਰਕੇ ਇੱਕ-ਦੂਜੀ ਤੇ ਰੱਖਦਾ ਹੈ ਤੇ ਵਿਰੋਧੀ ਟੀਮ ਦੇ ਖਿਡਾਰੀ ਉਨ੍ਹਾਂ ਠੀਕਰੀਆਂ ਨੂੰ ਚੁਣਨ ਵਾਲੇ ਖਿਡਾਰੀ ਨੂੰ ਗੇਂਦ ਦਾ ਨਿਸ਼ਾਨਾ ਬਣਾਉਂਦੇ ਹਨ । ਜੇਕਰ ਠੀਕਰੀਆਂ ਚਿਣਨ ਵਾਲੇ ਖਿਡਾਰੀ ਨੂੰ ਗੇਂਦ ਲੱਗ ਜਾਂਦੀ ਹੈ, ਤਾਂ ਉਹ ਆਉਟ ਹੋ ਜਾਂਦਾ ਹੈ । ਜੇਕਰ ਠੀਕਰੀਆਂ ਚਿਣਨ ਵਾਲਾ ਖਿਡਾਰੀ ਗੇਂਦ ਵੱਜਣ ਤੋਂ ਪਹਿਲਾਂ ਠੀਕਰੀਆਂ ਇਕੱਠੀਆਂ ਕਰ ਲੈਂਦਾ ਹੈ, ਤਾਂ ਉਸਨੂੰ ਹੋਰ ਵਾਰੀ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ । ਆਉਟ ਹੋਣ ਤੇ ਦੂਜੇ ਖਿਡਾਰੀ ਦੀ ਵਾਰੀ ਆ ਜਾਂਦੀ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਖੇਡ ਚੱਲਦੀ ਰਹਿੰਦੀ ਹੈ । ਠੀਕਰੀਆਂ ਦੇ ਨਿਸ਼ਾਨਾ ਲਾਉਣ ਵਾਲਾ ਖਿਡਾਰੀ |

ਪ੍ਰਸ਼ਨ 3.
ਕਿੱਕਲੀ ਦਾ ਵੇਰਵਾ ਦਿਉ ।
ਉੱਤਰ-
ਕਿੱਕਲੀ-ਪੰਜਾਬ ਵਿੱਚ ਕਿੱਕਲੀ ਕੁੜੀਆਂ ਦੀ ਹਰਮਨ-ਪਿਆਰੀ ਖੇਡ ਹੈ । ਕਿਲਕਿਲਾ ਦਾ ਅਰਥ ਖੁਸ਼ੀ ਅਤੇ ਚਾਅ ਦੀ ਆਵਾਜ਼ ਕਰਨਾ । ਕਿੱਕਲੀ ਖੇਡ ਅਤੇ ਗਿੱਧੇ ਦਾ ਜੋੜ ਹੈ । ਕਿੱਕਲੀ ਨੂੰ ਕੁੜੀਆਂ ਬੜੇ ਚਾਅ ਨਾਲ ਖੇਡਦੀਆਂ ਹਨ । ਇਕ ਜਗਾ ਤੇ ਇਕੱਠੀਆਂ ਹੋ ਕੇ ਕੁੜੀਆਂ ਜੋਟੇ ਬਣਾ ਲੈਂਦੀਆਂ ਹਨ ।
ਕਿੱਕਲੀ ਵਿੱਚ ਕੁੜੀਆਂ ਇਕ-ਦੂਜੇ ਦੇ ਹੱਥਾਂ ਵਿੱਚ ਕੰਘੀਆਂ | ਪਾ ਕੇ ਘੁੰਮਦੀਆਂ ਹਨ । ਉਨ੍ਹਾਂ ਨੇ ਇਕ-ਦੂਜੇ ਦਾ ਖੱਬਾ ਹੱਥ ਖੱਬੇ ਨਾਲ ਸੱਜਾ ਹੱਥ ਸੱਜੇ ਨਾਲ ਫੜਦੀਆਂ ਹਨ । ਦੋਵੇਂ ਕੁੜੀਆਂ ਦੀਆਂ ਬਾਹਾਂ ਦੀ ਸ਼ਕਲ 8 ਅੰਕ ਵਾਂਗ ਬਣ ਜਾਂਦੀ ਹੈ । ਘੁੰਮਣ ਵੇਲੇ ਕੁੜੀਆਂ ਕਿੱਕਲੀ ਦੇ ਗੀਤ ਗਾਉਂਦੀਆਂ ਹਨ ।
ਕਿੱਕਲੀ ਕਲੀਰ ਦੀ, |
ਪੱਗ ਮੇਰੇ ਵੀਰ ਦੀ,
ਦੁਪੱਟਾ ਭਰਜਾਈ ਦਾ,
ਫਿੱਟੇ ਮੂੰਹ ਜਵਾਈ ਦਾ ।

ਇਸ ਤਰ੍ਹਾਂ ਆਪਸ ਵਿੱਚ ਜੋੜੀਆਂ ਦਾ ਮੁਕਾਬਲਾ ਹੋਣ ਲੱਗ ਪੈਂਦਾ ਹੈ । ਦੇਸੀ ਖੇਡਾਂ ਵਿੱਚ ਟੂਰਨਾਮੈਂਟ ਨਹੀਂ ਕਰਾਇਆ ਜਾ ਸਕਦਾ ਹੈ । ਕਿੱਕਲੀ ਪਾਉਂਦੇ ਸਮੇਂ ਜੇਕਰ ਜੋੜੀ ਵਿੱਚੋਂ ਕਿਸੇ ਇੱਕ ਕੁੜੀ ਦਾ ਹੱਥ ਦੂਜੀ ਕੁੜੀ ਹੱਥੋਂ ਛੁੱਟ ਜਾਂਦਾ ਹੈ ਜਾਂ ਕਿੱਕਲੀ ਪਾਉਂਦੇ ਕੁੜੀ ਡਿੱਗ ਜਾਵੇ ਤਾਂ ਸਭ ਕੁੱਝ ਹਾਸੇ ਵਿੱਚ ਭੁੱਲ ਜਾਂਦਾ ਹੈ । ਇਸ ਵਿਚ ਕੁੜੀਆਂ ਖੇਡ ਦਾ ਬਹੁਤ ਆਨੰਦ ਪਾਉਂਦੀਆਂ ਹਨ ।

Punjab State Board PSEB 12th Class Physical Education Book Solutions Chapter 6 ਸਰੀਰਿਕ ਸਿੱਖਿਆ ਦੇ ਸਮਾਜਿਕ ਅਤੇ ਮਨੋਵਿਗਿਆਨਕ ਪੱਖ Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Physical Education Chapter 6 ਸਰੀਰਿਕ ਸਿੱਖਿਆ ਦੇ ਸਮਾਜਿਕ ਅਤੇ ਮਨੋਵਿਗਿਆਨਕ ਪੱਖ

Physical Education Guide for Class 12 PSEB ਸਰੀਰਿਕ ਸਿੱਖਿਆ ਦੇ ਸਮਾਜਿਕ ਅਤੇ ਮਨੋਵਿਗਿਆਨਕ ਪੱਖ Textbook Questions and Answers

ਇੱਕ ਅੰਕ ਵਾਲੇ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ (One Mark Question-Answers)

ਪ੍ਰਸ਼ਨ 1.
ਸਮਾਜ ਸ਼ਾਸਤਰ ਅੰਗਰੇਜ਼ੀ ਦੇ ਕਿਸ ਸ਼ਬਦ ਦਾ ਅਨੁਵਾਦ ਹੈ ?
ਉੱਤਰ:
ਸਮਾਜ ਸ਼ਾਸਤਰ ਦੋ ਸ਼ਬਦਾਂ ਦੇ ਸੁਮੇਲ ਤੋਂ ਬਣਿਆ ਹੈ ਜਿਸ ਵਿਚ ‘ “ਸੋਸੁਜ਼’’ (Socius) ਦਾ ਮਤਲਬ ਐਸੋਸਿਏਟ ਜਾਂ ਸਮਾਜਿਕ ਅਤੇ “ਲੋਗੋ’’ (Logos) ਤੋਂ ਭਾਵ ਵਿਗਿਆਨ ਜਾਂ ਅਧਿਐਨ ਤੋਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਕਿਹੜੇ ਦੇਸ਼ ਨੂੰ ਸੰਸਾਰ ਦੀਆਂ ਸਭ ਤੋਂ ਪੁਰਾਣੀਆਂ ਸੱਭਿਆਤਾਵਾਂ ਦੇ ਰੂਪ ਵਿੱਚ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ:
ਯੂਨਾਨ ।

ਪ੍ਰਸ਼ਨ 3.
ਕਿਹੜੀ ਖੇਡ ਨੂੰ ਸਭ ਖੇਡਾਂ ਦੀ ਮਾਂ ਦੇ ਰੂਪ ਵਿੱਚ ਜਾਣਿਆ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ:
ਜਿਮਨਾਸਟਿਕ ।

ਪ੍ਰਸ਼ਨ 4.
ਸਮਾਜ ਸ਼ਾਸਤਰ ਕਿਸ ਭਾਸ਼ਾ ਦਾ ਸ਼ਬਦ ਹੈ ?
ਉੱਤਰ:
ਇਹ ਦੋ ਸ਼ਬਦਾਂ ਤੋਂ ਮਿਲ ਕੇ ਬਣਿਆ ਹੈ-ਲਾਤੀਨੀ ਭਾਸ਼ਾ ਦੇ ਸ਼ਬਦ (Socius) ਜਿਸਦਾ ਅਰਥ ਹੈCompanion ਸਾਥੀ ਅਤੇ ਯੂਨਾਨੀ ਭਾਸ਼ਾ ਦੇ ਸ਼ਬਦ (Logos) ਜਿਸਦਾ ਅਰਥ ਹੈ-Knowledge ਗਿਆਨ ।

ਦੋ ਅੰਕਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ (Two Marks Question-Answers)

ਪ੍ਰਸ਼ਨ 5.
ਸਮਾਜ ਸ਼ਾਸਤਰ ਦੀ ਪਰਿਭਾਸ਼ਾ ਦਿਉ ।
ਉੱਤਰ:
ਗਰੇਟ (Garrett) ਦੇ ਅਨੁਸਾਰ, “ਸਮਾਜਿਕਤਾ ਇੱਕ ਅਜਿਹੀ ਪ੍ਰਕ੍ਰਿਆ ਹੈ ਜਿਸ ਦੁਆਰਾ ਜੀਵ ਜੰਤੂ ‘ ਵਿਅਕਤੀਗਤ ਮਨੁੱਖੀ ਜੀਵਨ ਵਿਚ ਤਬਦੀਲ ਹੋ ਜਾਂਦਾ ਹੈ।” ਔਗਬਰਨ (Ogburn) ਦੇ ਅਨੁਸਾਰ, “ਸਮਾਜੀਕਰਨ ਉਹ ਪ੍ਰਕ੍ਰਿਆ ਹੈ ਜਿਸ ਰਾਹੀਂ ਵਿਅਕਤੀ ਸਮੂਹ ਦੇ ਨਿਯਮਾਂ ਨੂੰ ਧਾਰਨ ਕਰਨਾ ਸਿੱਖਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 6.
ਸਮਾਜ ਸ਼ਾਸਤਰ ਦਾ ਕੀ ਅਰਥ ਹੈ ?
ਉੱਤਰ:
ਸਮਾਜ ਸ਼ਾਸਤਰ ਦੋ ਸ਼ਬਦਾਂ ਦੇ ਸੁਮੇਲ ਤੋਂ ਬਣਿਆ ਹੈ ਜਿਸ ਵਿਚ ‘ਸ਼ੋਸ਼ੂਜ” ਦਾ ਮਤਲਬ ਐਸੋਸਿਏਟ ਜਾਂ ਸਮਾਜਿਕ ਅਤੇ ‘‘ਲੋਗੋ” ਤੋਂ ਭਾਵ ਵਿਗਿਆਨ ਜਾਂ ਅਧਿਐਨ ਤੋਂ ਹੈ । ਇਸ ਲਈ ਸਮਾਜ ਸ਼ਾਸਤਰ ਸਮਾਜ ਦਾ ਵਿਗਿਆਨ ਹੈ । ਉਗਬਰਨ ਦੇ ਅਨੁਸਾਰ, “ਸਮਾਜੀਕਰਨ ਉਹ ਪ੍ਰਕਿਰਿਆ ਹੈ ਜਿਸ ਵਿਚ ਵਿਅਕਤੀ ਸਮੂਹ ਦੇ ਨਿਯਮਾਂ ਨੂੰ ਧਾਰਨਾ ਕਰਨਾ ਸਿੱਖਦਾ ਹੈ । ਸਰੀਰਕ ਸਿੱਖਿਆ ਅਤੇ ਖੇਡਾਂ ਇਕ ਵਿਅਕਤੀ ਵਿਚ ਸਮਾਜਿਕ ਗੁਣਾਂ ਦੇ ਰੁਝਾਨ ਨੂੰ ਬਣਾਉਣ ਲਈ ਇਕ ਬਲਾਕ ਦਾ ਕੰਮ ਕਰਦਾ ਹੈ । ਇਹ ਖੇਤਰ ਕਈ ਤਰ੍ਹਾਂ ਦੇ ਸਮਾਜਿਕ ਗੁਣ ਜਿਵੇਂ ਕਿ ਚਰਿੱਤਰ, ਗੁਣ, ਸਮੂਹ ਭਾਵਨਾਵਾਂ, ਜ਼ਿੰਮੇਵਾਰੀਆਂ, ਰੁਈਂਆਂ, ਸਮਰਪਣ ਅਤੇ ਸਮਾਜਿਕ ਸੰਚਾਰ ਆਦਿ ਭਿੰਨਤਾਵਾਂ ਪ੍ਰਦਾਨ ਕਰਦਾ ਹੈ :

ਪ੍ਰਸ਼ਨ 6.
ਆਪਸੀ ਭਾਈਚਾਰੇ ਦੀ ਸਾਂਝ ਬਾਰੇ ਲਿਖੋ ।
ਉੱਤਰ:
ਖੇਡਾਂ ਭਾਈਚਾਰੇ ਦੀ ਨੀਂਹ ਨੂੰ ਬੱਚਿਆਂ ਅਤੇ ਨੌਜਵਾਨਾਂ ਵਿਚ ਇਕ ਸਮਾਜਿਕ ਏਕਤਾ ਅਤੇ ਸਮਾਜਿਕ ਪੂੰਜੀ ਦੇ ਮਜ਼ਬੂਤ ਸੰਬੰਧ ਨੂੰ ਦਰਸਾਉਂਦੀਆਂ ਹਨ । ਖੇਡਾਂ ਇਹਨਾਂ ਬੱਚਿਆਂ ਅਤੇ ਨੌਜਵਾਨਾਂ ਨੂੰ ਕਈ ਮੌਕੇ ਪ੍ਰਦਾਨ ਕਰਦੀਆਂ ਹਨ, ਜਿੱਥੇ ਉਹ ਆਪਣੀ ਸਵੈ-ਇੱਛਾ ਨਾਲ ਭਾਗ ਲੈ ਸਕਦੇ ਹਨ ਅਤੇ ਜਿਸ ਕਾਰਨ ਉਹਨਾਂ ਵਿਚ ਲੀਡਰਸ਼ਿਪ ਦੇ ਗੁਣ, ਸਕਾਰਾਤਮਕ ਹੀਣੀ ਰਿਸਤੇ, ਸਨਮਾਨ ਅਤੇ ਨੈਤਿਕਤਾ ਦੇ ਗੁਣਾਂ ਦਾ ਵਿਕਾਸ ਹੁੰਦਾ ਹੈ ।

ਤਿੰਨ ਅੰਕਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ (Three Marks Question-Answers)

ਪ੍ਰਸ਼ਨ 7.
ਮਾਨਸਿਕ ਅਤੇ ਸਰੀਰਿਕ ਤਣਾਅ ਤੋਂ ਛੁਟਕਾਰਾ ਕਿਵੇਂ ਪਾਇਆ ਜਾ ਸਕਦਾ ਹੈ ?
ਉੱਤਰ:
ਹੇਠ ਦਿੱਤੇ ਅਨੁਸਾਰ ਮਾਨਸਿਕ ਅਤੇ ਸਰੀਰਕ ਤਣਾਅ ਤੋਂ ਛੁਟਕਾਰਾ ਪਾਇਆ ਜਾ ਸਕਦਾ ਹੈ-

• ਧਿਆਨ ਅਤੇ ਲੰਬੇ ਸਾਹ ਲੈ ਕੇ ।
• ਵਿਕਾਸਾਤਮਕ ਗਤੀਵਿਧੀਆਂ ਵਿਚ ਆਪਣੇ ਆਪ ਨੂੰ ਲਗਾ ਕੇ ।
• ਤਨਾਵ ਦੇ ਕਾਰਨਾਂ ਦਾ ਪਤਾ ਲਗਾ ਕੇ ।
• ਸਵੈ-ਮੁਲਾਂਕਣ ਕਰਕੇ ।
• ਸਮੂਹ ਵਿਚ ਗੱਲਾਂ-ਬਾਤਾਂ ਕਰਕੇ ਤਨਾਵ ਨੂੰ ਦੂਰ ਕਰਨਾ ।
• ਖੇਡਾਂ ਅਤੇ ਮਨੋਰੰਜਕ ਗਤੀਵਿਧੀਆਂ ਵਿਚ ਭਾਗ ਲੈ ਕੇ ।

ਪ੍ਰਸ਼ਨ 8.
ਸਮਾਜਿਕ ਭਾਵਨਾ ਦਾ ਵਿਕਾਸ ਕਿਵੇਂ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ:
ਖਿਡਾਰੀਆਂ ਵਲੋਂ ਜਦੋਂ ਕਿਸੇ ਖੇਡ ਮੁਕਾਬਲੇ ਵਿਚ ਇਕ ਟੀਮ ਦੇ ਤੌਰ ਤੇ ਹਿੱਸਾ ਲਿਆ ਜਾਂਦਾ ਹੈ ਤਾਂ ਉਹ ਆਪਣੀ ਟੀਮ ਨੂੰ ਜਿਤਾਉਣ ਲਈ ਪੂਰਾ ਜ਼ੋਰ ਲਾਉਂਦੇ ਹਨ ਤੇ ਆਪਸੀ ਸਹਿਯੋਗ ਤੇ ਤਾਲਮੇਲ ਕਰਦੇ ਹਨ । ਇਸ ਤਰ੍ਹਾਂ ਨਾਲ ਉਨ੍ਹਾਂ ਵਿਚ ਸਮਾਜਿਕ ਭਾਵਨਾ ਦਾ ਵਿਕਾਸ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 9.
ਰਾਸ਼ਟਰੀ ਏਕਤਾ ਵਿੱਚ ਖੇਡਾਂ ਦਾ ਕੀ ਯੋਗਦਾਨ ਹੈ ?
ਉੱਤਰ:
ਸਰੀਰਕ ਸਿੱਖਿਆ ਅਤੇ ਖੇਡਾਂ ਦੇ ਪ੍ਰੋਗਰਾਮ ਰਾਸ਼ਟਰੀ ਅਤੇ ਅੰਤਰਰਾਸ਼ਟਰੀ ਅਖੰਡਤਾ ਵਿਚ ਕੀਮਤੀ ਰੂਪ ਨਾਲ ਵਿਕਾਸ ਦਾ ਕੰਮ ਕਰਦੇ ਹਨ । ਇਹ ਅਜਿਹੀਆਂ ਗਤੀਵਿਧੀਆਂ ਪ੍ਰਦਾਨ ਕਰਦੇ ਹਨ, ਜੋ ਖੇਡਾਂ ਵਿਚ ਭਾਗ ਲੈਣ ਵਾਲਿਆਂ ਨੂੰ ਸੱਭਿਆਚਾਰ ਵਿਭਿੰਨਤਾਵਾਂ, ਵੱਖ-ਵੱਖ ਜਾਤਾਂ ਅਤੇ ਧਰਮ, ਉਸ ਦੇ ਸਮਾਜਿਕ ਨਿਯਮਾਂ, ਨੈਤਿਕ ਅਤੇ ਨੈਤਿਕ ਮੁੱਦੇ ਨੂੰ ਸਮਝਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰਦੇ ਹਨ । ਸਰੀਰਕ ਸਿੱਖਿਆ ਅਤੇ ਖੇਡਾਂ ਸਾਂਝੇ ਮੰਤਵ ਲਈ ਕੰਮ ਕਰਨ ਵਾਲਿਆਂ ਲੋਕਾਂ ਨੂੰ ਇੱਕ-ਜੁੱਟ ਕਰਕੇ ਇਕ ਸਾਂਝਾ ਪਲੇਟਫਾਰਮ ਪ੍ਰਦਾਨ ਕਰਦੀਆਂ ਹਨ । ਇਸ ਲਈ ਸਰੀਰਕ ਸਿੱਖਿਆ ਅਤੇ ਖੇਡਾਂ ਨੂੰ ਸਕੂਲੀ ਪ੍ਰੋਗਰਾਮ ਵਿਚ ਨੈਤਿਕ ਮੁੱਲ ਅਪਣਾਉਣ ਲਈ ਅਭਿਆਸ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ।

ਖੇਡਾਂ ਰਾਹੀਂ ਭਾਈਚਾਰਕ ਏਕਤਾ ਦੇ ਵਿਕਾਸ ਨੂੰ ਧਿਆਨ ਵਿੱਚ ਰੱਖਦੇ ਹੋਏ ਇਸ ਨੂੰ ਵਿੱਦਿਆ (Education) ਦਾ ਖਾਸ ਹਿੱਸਾ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ । ਉਲੰਪਿਕ ਖੇਡਾਂ ਦੀ ਉਤਪੱਤੀ ਦੇ ਵਿਚਾਰ ਪਿੱਛੇ ਯੂਨਾਨੀਆਂ ਦੁਆਰਾ ਖੇਡਾਂ ਵਿਚ ਭਾਈਚਾਰੇ ਅਤੇ ਸਹਿਯੋਗ ਦੀ ਭਾਵਨਾ ਦਾ ਵਿਕਾਸ ਕਰਨਾ ਸੀ । ਫਰਾਸ ਦੇ ਬੈਰਨ ਪਰੇਰੇ ਡੀ ਕੁਬਰਟਿਨ (Barran Pierre de Coubertin) ਨੇ ਇਸ ਵਿਚਾਰ ਨੂੰ ਅੱਗੇ ਵਧਾਇਆ ਅਤੇ ਉਲੰਪਿਕ ਖੇਡਾਂ ਨੂੰ 1896 ਵਿਚ ਫਿਰ ਤੋਂ ਸੁਰਜੀਤ ਕੀਤਾ ।

ਪ੍ਰਸ਼ਨ 10.
ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ਕਿਸੇ ਇੱਕ ‘ਤੇ ਨੋਟ ਲਿਖੋ ।
(ਉ) ਵਿੱਦਿਅਕ ਅਦਾਰਾ
(ਅ) ਮਿੱਤਰ ਮੰਡਲੀ
(ਇ) ਅਗਵਾਈ ਦਾ ਵਿਕਾਸ
(ਸ) ਉੱਚਿਤ ਖੇਡਾਂ ਦੀ ਚੋਣ ।
ਉੱਤਰ-
(ਉ) ਵਿੱਦਿਅਕ ਅਦਾਰਾ-ਵਿੱਦਿਅਕ ਸੰਸਥਾਵਾਂ ਜਿਵੇਂ ਕਿ ਸਕੂਲ ਬੱਚੇ ਦੇ ਜੀਵਨ ਵਿਚ ਮਹੱਤਵਪੂਰਨ ਭੂਮਿਕਾ ਨਿਭਾਉਂਦੇ ਹਨ । ਇਹ ਸੰਸਥਾਵਾਂ ਬੱਚਿਆਂ ਦੀ ਸ਼ਖਸੀਅਤ ਨੂੰ ਬਣਾਉਣ ਅਤੇ ਦੋਸਤ, ਪਰਿਵਾਰ ਅਤੇ ਅਧਿਆਪਕਾਂ ਨਾਲ ਸਕਾਰਾਤਮਕ ਗੱਲਬਾਤ ਕਰਨ ਵਿਚ ਮਦਦ ਕਰਦੀਆਂ ਹਨ । ਇਸ ਲਈ ਸਕੂਲ ਨੂੰ ਬੱਚੇ ਦਾ ਦੂਜਾ ਘਰ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਬੱਚਿਆਂ ਦਾ ਵਿਵਹਾਰ ਅਤੇ ਉਨ੍ਹਾਂ ਦੀ ਸ਼ਖਸੀਅਤ ਦਾ ਵਿਕਾਸ ਅਤੇ ਪਾਲਣ-ਪੋਸ਼ਣ ਸਿਰਫ ਮਾਪਿਆਂ ਤੇ ਨਿਰਭਰ ਨਹੀਂ ਕਰਦਾ ਹੈ, ਪਰ ਜਿਸ ਤਰੀਕੇ ਨਾਲ ਉਹ ਵਿਕਾਸ ਕਰਦੇ ਹਨ, ਸਕੂਲਾਂ ਲਈ ਵੀ ਇਕ ਚੁਣੌਤੀਪੂਰਨ ਕੰਮ ਹੈ ।

(ਅ) ਮਿੱਤਰ ਮੰਡਲੀ-ਬੱਚਿਆਂ ਦੇ ਵਿਹਾਰ ਤੇ ਹਾਣੀ ਗਰੁੱਪ ਦਾ ਪ੍ਰਭਾਵ ਪਰਿਵਾਰ ਦੀ ਤਰ੍ਹਾਂ ਮਹੱਤਵਪੂਰਨ ਹੈ । ਜਦੋਂ ਬੱਚੇ ਆਪਣੇ ਦੋਸਤਾਂ ਨਾਲ ਸਮਾਜਿਕ ਹੁਨਰ ਸਿੱਖਦੇ ਹਨ ਜਿਵੇਂ ਕਿ ਸਮੂਹ ਵਿਚ ਸੰਚਾਰ, ਸਹਾਇਕਤਾ, ਸਹਿਕਾਰਤਾ, ਭਾਈਚਾਰਾ ਆਦਿ, ਪਰ ਬਦਕਿਸਮਤੀ ਨਾਲ ਸਾਨੂੰ ਹਮੇਸ਼ਾ ਇਹ ਨਹੀਂ ਪਤਾ ਹੁੰਦਾ ਹੈ ਕਿ ਬੱਚੇ ਆਪਣੇ ਦੋਸਤਾਂ ਨਾਲ ਕਿਵੇਂ ਜੁੜੇ ਹੋਏ ਹਨ ਅਤੇ ਉਹਨਾਂ ਦੇ ਵਿਹਾਰ ਤੇ ਉਨ੍ਹਾਂ ਦਾ ਕੀ ਪ੍ਰਭਾਵ ਹੈ । ਇਸ ਲਈ ਜੇਕਰ ਕੋਈ ਬੱਚਾ ਬੁਰੀ ਸੰਗਤ ਵਿਚ ਰਹਿੰਦਾ ਹੈ, ਤਾਂ ਉਹ ਬੁਰੀਆਂ ਆਦਤਾਂ ਹੀ ਸਿੱਖੇਗਾ ਅਤੇ ਅਗਰ ਚੰਗੀ ਸੰਗਤ ਵਿਚ ਹੈ, ਤਾਂ ਚੰਗੇ ਪ੍ਰਭਾਵ ਉਸਦੀ ਸ਼ਖ਼ਸੀਅਤ ਤੇ ਦੇਖਣ ਨੂੰ ਮਿਲਣਗੇ ।

(ਬ) ਅਗਵਾਈ ਦਾ ਵਿਕਾਸ-ਖੇਡ ਅਤੇ ਕਿਰਿਆਵਾਂ ਵਿੱਚ ਕਈ ਅਜਿਹੇ ਮੌਕਾ ਆਉਂਦੇ ਹਨ, ਜਿੱਥੇ ਖਿਡਾਰੀ ਵਿੱਚ ਨੇਤਾ ਦੇ ਗੁਣਾਂ ਨੂੰ ਵਿਕਸਿਤ ਕਰਨ ਵਿੱਚ ਸਹਾਇਤਾ ਮਿਲਦੀ ਹੈ । ਕਿਸੇ ਵੀ ਟੀਮ ਜਾਂ ਸਮੂਹ ਨੂੰ ਨਿਰਦੇਸ਼ਿਤ | ਕਰਨਾ ਅਤੇ ਖੇਡ ਟੀਚੇ ਨੂੰ ਅਧਾਰ ਕਰਨਾ, ਖੇਡਾਂ ਵਿਦਿਆਵਾਂ ਦਾ ਮੁੱਖ ਅਧਾਰ ਹਨ : ਖੇਡ ਕਿਰਿਆਵਾਂ ਦੇ ਨਾਲ ਖਿਡਾਰੀਆਂ ਵਿੱਚ ਕਈ ਨੇਤਾ ਦੇ ਗੁਣ ਵਿਕਸਿਤ ਕੀਤੇ ਜਾ ਸਕਦੇ ਹਨ ।

(ਸ) ਉੱਚਿਤ ਖੇਡਾਂ ਦੀ ਚੋਣ-ਖੇਡਾਂ ਵਿਚ ਵਧੀਆ ਪ੍ਰਦਰਸ਼ਨ ਲਈ ਖਿਡਾਰੀ ਨੂੰ ਚਾਹੀਦਾ ਹੈ ਕਿ ਉਹ ਉੱਚਿਤ ਖੇਡ ਦੀ ਚੋਣ ਕਰੇ । ਜੇਕਰ ਖਿਡਾਰੀ ਖੇਡ ਦੀ ਚੋਣ ਮਨੋਵਿਗਿਆਨਕ ਪੱਖਾਂ ਨੂੰ ਧਿਆਨ ਵਿਚ ਰੱਖ ਕੇ ਕਰੇ ਤਾਂ ਇਸ ਦੇ ਸਾਰਥਕ ਨਤੀਜੇ ਨਿਕਲਦੇ ਹਨ ।

ਪੰਜ ਅੰਕਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ ਦੇ (Five Marks Question-Answers) 

ਪ੍ਰਸ਼ਨ 11.
ਸਿੱਖਣਾ ਕੀ ਹੈ ? ਇਸ ਦੀ ਪਰਿਭਾਸ਼ਾ ਅਤੇ ਨਿਯਮਾਂ ਦਾ ਵਰਣਨ ਕਰੋ ।
ਉੱਤਰ:
ਸਿੱਖਣ ਦੀ ਧਾਰਨਾ ਨੂੰ ਵਿਵਹਾਰ ਦੇ ਬਦਲਾਵ ਦੇ ਤਜ਼ਰਬਾ, ਨਵੀਆਂ ਆਦਤਾਂ ਅਤੇ ਹੁਨਰ ਪ੍ਰਾਪਤੀ ਵਜੋਂ ਸਮਝਿਆ ਜਾ ਸਕਦਾ ਹੈ । ਵਿਵਹਾਰ ਵਿਚ ਬਦਲਾਵ ਆਮ ਤੌਰ ਤੇ ਸਥਾਈ ਹੁੰਦਾ ਹੈ । ਇਹ ਵਿਸ਼ਵਾਸ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ਕਿ ਸਿੱਖਣਾ ਇਕ ਜੀਵਨ ਭਰ ਚੱਲਣ ਵਾਲੀ ਪ੍ਰਕਿਰਿਆ ਹੈ, ਜੋ ਕਿ ਪੰਘੂੜੇ ਵਿਚ ਸ਼ੁਰੂ ਹੁੰਦੀ ਹੈ ਅਤੇ ਕਬਰ ਵਿਚ ਖ਼ਤਮ ਹੋ ਜਾਂਦੀ ਹੈ । ਭਾਵ ਸਿੱਖਣਾ ਜਨਮ ਹੁੰਦਿਆਂ ਹੀ ਸ਼ੁਰੂ ਹੋ ਜਾਂਦਾ ਹੈ ਅਤੇ ਮਰਨ ਉਪਰੰਤ ਹੀ ਖ਼ਤਮ ਹੋ ਜਾਂਦਾ ਹੈ । ਇਹ ਦੇਖਿਆ ਜਾਂਦਾ ਹੈ ਕਿ ਇਕ ਵਿਅਕਤੀ ਆਪਣੇ ਆਪ ਨੂੰ ਬਚਾਉਣ ਭਾਵ ਜਿੰਦਾ ਰੱਖਣ ਲਈ ਸਮਾਜਿਕ ਹੁਨਰ ਅਤੇ ਵਾਤਾਵਰਣ ਨੂੰ ਗ੍ਰਹਿਣ ਕਰ ਲੈਂਦਾ ਹੈ । ਇਹ ਜ਼ਰੂਰੀ ਨਹੀਂ ਹੈ ਕਿ ਵਿਅਕਤੀ ਦੇ ਵਿਹਾਰ ਵਿਚ ਸਕਾਰਾਤਮਕ ਤਬਦੀਲੀ ਹੀ ਹੋਵੇ । ਵਿਹਾਰ ਵਿਚ ਢੁੱਕਵੀਂ ਤਬਦੀਲੀ ਸਮਾਜਿਕ ਸੰਤੁਸ਼ਟੀ ਅਤੇ ਸੰਪੂਰਨਤਾ ਤੇ ਵੀ ਨਿਰਭਰ ਕਰਦੀ ਹੈ ! ਇਸ ਲਈ ਕਿਹਾ ਜਾ ਸਕਦਾ ਹੈ ਕਿ ਸਿੱਖਣਾ ਵਿਹਾਰ ਵਿਚ ਬਦਲਾਵ ਕਰਨਾ, ਨਵੇਂ ਵਿਹਾਰ ਦਾ ਅਭਿਆਸ ਕਰਨਾ ਅਤੇ ਉਸਦੇ ਆਏ ਨਤੀਜਿਆਂ ਤੋਂ ਵਿਹਾਰ ਨੂੰ ਸਥਾਈ ਰੂਪ ਦੇਣਾ ਹੀ ਸਿੱਖਣਾ ਹੈ । ਸਿੱਖਣ ਨੂੰ ਕੁੱਝ ਅੱਗੇ ਦਿੱਤੀਆਂ ਪਰਿਭਾਸ਼ਾਵਾਂ ਦੁਆਰਾ ਵੀ ਸਮਝਿਆ ਜਾ ਸਕਦਾ ਹੈ ।

ਗੇਟਸ (Gates) ਦੇ ਅਨੁਸਾਰ, “ਸਿੱਖਣਾ, ਅਨੁਭਵ ਤੇ ਸਿਖਲਾਈ ਦੀ ਤਬਦੀਲੀ ਹੈ ।”. ਈ.ਆਰ. ਹਿਲਰਡ (E.R. Hilgard) ਦੇ ਅਨੁਸਾਰ, “ਸਿੱਖਣਾ ਵਿਹਾਰ ਵਿਚ ਇਕ ਸਥਾਈ ਤਬਦੀਲੀ ਹੈ ਜੋ ਕਿ ਪੁਰਾਣੇ ਅਨੁਭਵਾਂ ਦੇ ਅਨੁਸਾਰ ਵਾਪਰਦਾ ਹੈ ।”

ਸਿੱਖਣ ਦੇ ਨਿਯਮ (Rules of Learning)-
1. ਤਤਪਰਤਾ/ਤਿਆਰੀ ਦਾ ਨਿਯਮ (Law of Readiness)-ਸਿੱਖਣ ਨਾਲ ਸੰਬੰਧਿਤ ਸਭ ਤੋਂ ਮਹੱਤਵਪੂਰਨ · ਨਿਯਮ ਇਹ ਹੈ ਕਿ ਵਿਅਕਤੀ ਸਿੱਖਣ ਲਈ ਤਿਆਰ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ਭਾਵ ਉਸ ਦੀ ਉਸ ਕੰਮ ਨੂੰ ਸਿੱਖਣ ਦੇ ਪ੍ਰਤੀ ਦਿਲਚਸਪੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ । ਜੇਕਰ ਵਿਅਕਤੀ ਵਿਚ ਕੰਮ ਦੇ ਪਤੀ ਦਿਲਚਸਪੀ ਨਹੀਂ ਹੋਵੇਗੀ, ਤਾਂ ਉਹ ਕਦੇ ਵੀ ਉਸ ਕੰਮ ਨੂੰ ਸਿੱਖ ਨਹੀਂ ਸਕੇਗਾ । ਉਸ ਕੋਲ ਸਿੱਖਣ ਦਾ ਉਦੇਸ਼ ਤੇ ਸਥਿਤੀ ਸਾਫ਼ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ । ਉਦਾਹਰਣ ਦੇ ਤੌਰ ‘ਤੇ ਇਹ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ਕਿ ਤੁਸੀਂ ਇਕ ਘੋੜੇ ਨੂੰ ਤਲਾਅ ਵਿਚ ਲੈ ਜਾ ਸਕਦੇ ਹੋ, ਪਰ ਪਾਣੀ ਪੀਣ ਲਈ ਮਜ਼ਬੂਰ ਨਹੀਂ ਕਰ ਸਕਦੇ, ਜੇਕਰ ਉਹ ਪਿਆਸਾ ਨਾ ਹੋਏ । ਇਸੇ ਤਰ੍ਹਾਂ ਇੱਕ ਬੱਚਾ ਵੀ ਨਹੀਂ ਸਿੱਖਦਾ ਜੇਕਰ ਉਸ ਕੋਲ ਸਿੱਖਣ ਦਾ ਕੋਈ ਕਾਰਣ ਨਾ ਹੋਵੇ । ਬੌਰਨਡਾਈਕ ਅਨੁਸਾਰ (According to Thorndike) “ਜਦੋਂ ਕੋਈ ਵਾਹਨ ਚਾਲਕ ਇਕਾਈ ਸੰਚਾਲਨ ਕਰਨ ਲਈ ਤਿਆਰ ਹੁੰਦੀ ਹੈ, ਉਸ ਨੂੰ ਇਹ ਕੰਮ ਕਰਨ ਵਿਚ ਤਸੱਲੀ ਮਿਲਦੀ ਹੈ । ਜੇ ਕੋਈ ਵਾਹਕ ਇਕਾਈ ਸੰਚਾਲਨ ਕਰਨ ਲਈ ਤਿਆਰ ਹੀ ਨਹੀਂ, ਤਾਂ ਉਸ ਲਈ ਇਹ ਕੰਮ ਨਾਰਾਜ਼ਗੀ ਪੈਦਾ ਕਰਦਾ ਹੈ । ਜਦੋਂ ਕੋਈ ਵਾਹਕ ਇਕਾਈ ਸੰਚਾਲਨ ਕਰਨ ਲਈ ਰਜ਼ਾਮੰਦ ਹੁੰਦਾ ਹੈ, ਤਾਂ ਸੰਚਾਲਨ ਨਾ ਕਰ ਸਕਣਾ ਉਸ ਲਈ ਨਾਰਾਜ਼ਗੀ ਦਾ ਕਾਰਨ ਬਣਦਾ ਹੈ ।’’

2. ਪ੍ਰਭਾਵ ਦਾ ਨਿਯਮ (Law of Effect)-ਇਹ ਕੁਦਰਤੀ ਹੈ ਕਿ ਇਕ ਵਿਅਕਤੀ ਤਦ ਤੱਕ ਸਿੱਖਦਾ ਰਹਿੰਦਾ ਹੈ, ਜਦ ਤਕ ਉਸਦੇ ਸਿੱਖਣ ਦੇ ਨਤੀਜੇ ਸਕਾਰਾਤਮਕ ਪ੍ਰਭਾਵ ਪਾਉਂਦੇ ਹਨ ਜਾਂ ਫਿਰ ਸੁਆਰਥੀ ਸੰਤੋਸ਼ਜਨਕ ਅਤੇ ਖੁਸ਼ਹਾਲ ਮਹਿਸੂਸ ਕਰਦਾ ਹੈ । ਇਹ ਸਿੱਖਣ ਵਾਲੇ ਨੂੰ ਸਕਾਰਾਤਮਕ ਸ਼ਕਤੀ ਅਤੇ ਪ੍ਰੇਰਨਾ ਦਿੰਦਾ ਹੈ ਅਗਰ ਸਿੱਖਣ ਵਾਲਾ ਸੰਤੁਸ਼ਟ ਹੈ ਅਤੇ ਲਗਾਤਾਰ ਸੁਧਾਰ ਕਰਦਾ ਰਹਿੰਦਾ ਹੈ । ਦੂਜੇ ਪਾਸੇ ਜੇਕਰ ਸਿੱਖਣ ਵਾਲਾ ਅਸੰਤੁਸ਼ਟ ਹੈ ਅਤੇ ਬੁਰੀ ਭਾਵਨਾਵਾਂ ਦਾ ਸਾਹਮਣਾ ਕਰਦਾ ਹੈ, ਤਾਂ ਇਹ ਅਨੁਭਵ ਸਿੱਖਣ ਵਾਲੇ ਦੇ ਕੰਮ ਵਿਚ ਮੁਸ਼ਕਲ ਪੈਦਾ ਕਰ ਦੇਵੇਗਾ । ਇਸ ਲਈ ਇਹ ਇਕ ਅਧਿਆਪਕ ਅਤੇ ਟਰੇਨਰ ਲਈ ਚੁਣੌਤੀਪੂਰਨ ਕੰਮ ਹੈ ਕਿ ਉਹ ਸਿੱਖਣ ਵਾਲੇ ਦੀ ਸਿੱਖਣ ਦੀ ਸਥਿਤੀ ਤੋਂ ਸਕਾਰਾਤਮਕ ਨਤੀਜੇ ਬਰਕਰਾਰ ਰੱਖੇ | ਥੋਰਨਡਾਈਕ ਦੇ ਅਨੁਸਾਰ (Thorndike), “ਜੇ ਉੱਤੇਜਨਾ ਅਤੇ ਹੁੰਗਾਰੇ ਵਿਚਕਾਰ ਪਰਿਵਰਤਨਯੋਗ ਸੰਬੰਧ · ਸਥਾਪਿਤ ਹੋ ਜਾਣ ਤੇ ਤਸੱਲੀ ਦਾ ਪ੍ਰਭਾਵ ਪ੍ਰਗਟ ਹੋ ਜਾਵੇ ਤਾਂ ਇਹ ਸੰਬੰਧ ਮਜ਼ਬੂਤ ਹੋ ਜਾਂਦਾ ਹੈ, ਜੇ ਇਸ ਸੰਬੰਧ ਨਾਲ ਨਾਰਾਜ਼ਗੀ ਜਾਂ ਕੁੜੱਤਣ ਪੈਦਾ ਹੋ ਜਾਵੇ, ਤਾਂ ਸੰਬੰਧ ਦੀ ਤਾਕਤ ਕਮਜ਼ੋਰ ਹੋ ਜਾਂਦੀ ਹੈ ।”

3. ਅਭਿਆਸ ਦਾ ਨਿਯਮ (Law of Exercise-ਅਭਿਆਸ ਦਾ ਨਿਯਮ ਇਹ ਕਹਿੰਦਾ ਹੈ ਕਿ ਅਭਿਆਸ ਜਾਂ ਦੁਹਰਾਉਣਾ ਮਹੱਤਵਪੂਰਨ ਹੈ | ਕੁਝ ਚੀਜ਼ਾਂ ਨੂੰ ਚੰਗੀ ਅਤੇ ਸਟੀਕ ਤਰੀਕੇ ਨਾਲ ਯਾਦ ਰੱਖਣ ਲਈ ਦੁਹਰਾਓ ਜ਼ਰੂਰੀ ਹੈ । ਦੂਜੇ ਪਾਸੇ ਜੇਕਰ ਕਿਰਿਆ ਨੂੰ ਕੇਵਲ ਇਕ ਵਾਰ ਕੀਤਾ ਜਾਵੇ ਤਾਂ ਸਿੱਖਣ ਅਤੇ ਯਾਦ ਰਹਿਣ ਦੀ ਸੰਭਾਵਨਾ ਘੱਟ ਜਾਂਦੀ ਹੈ । ਇਹ ਨਿਯਮ ਅੱਗੇ ਲਿਖੇ ਦੋ ਭਾਗਾਂ ਵਿਚ ਵੰਡਿਆ ਹੋਇਆ ਹੈ –
(1) ਵਰਤੋਂ ਦਾ ਨਿਯਮ (Law of Use)-ਕਿਸੇ ਕਿਰਿਆ ਦੀ ਵਾਰ-ਵਾਰ ਵਰਤੋਂ ਕਰਨ ਨਾਲ ਸਿੱਖਣ ਪ੍ਰਕਿਰਿਆ ਜ਼ਿਆਦਾ ਹੁੰਦੀ ਹੈ ।
(2) ਗੈਰ ਵਰਤੋਂ ਦਾ ਨਿਯਮ (Law of Disuse-ਜੇਕਰ ਸਿੱਖੇ ਹੋਏ ਗੁਣ ਨੂੰ ਕਾਫੀ ਲੰਬਾ ਸਮਾਂ ਵਰਤੋਂ ਵਿੱਚ ਨਾ ਲਿਆਂਦਾ ਜਾਵੇ ਤਾਂ ਇਹ ਯਾਦ ਵਿਚੋਂ ਨਿਕਲ ਜਾਂਦਾ ਹੈ । ਇਸ ਲਈ ਸਿੱਖੀ ਹੋਈ ਗੱਲ ਦਾ ਦੁਹਰਾਓ ਅਤਿ ਜ਼ਰੂਰੀ ਹੈ । ਬਾਰਨਡਾਈਕ ਅਨੁਸਾਰ, “ਜਦੋਂ ਕਿਸੇ ਸਥਿਤੀ ਤੇ ਹੁੰਗਾਰੇ ਵਿਚਕਾਰ ਪਰਿਵਰਤਨ ਯੋਗ ਸੰਬੰਧ ਕਾਇਮ ਨਹੀਂ ਹੁੰਦਾ ਹੈ ਤਾਂ ਹੋਰ ਗੱਲਾਂ ਸਮਾਨ ਹੋਣ ਤੇ ਵੀ ਇਹ ਸੰਬੰਧ ਕਮਜ਼ੋਰ ਪੈ ਜਾਂਦਾ ਹੈ । ਜਦੋਂ ਕਿਸੇ ਸਥਿਤੀ ਤੇ ਹੁੰਗਾਰੇ ਵਿਚਕਾਰ ਪਰਿਵਰਤਨ ਯੋਗ ਸੰਬੰਧ ਕਾਇਮ ਨਹੀਂ ਹੁੰਦਾ ਤਾਂ ਹੋਰ ਗੱਲਾਂ ਸਮਾਨ ਹੋਣ ਤੇ ਵੀ ਇਹ ਸੰਬੰਧ ਕਮਜ਼ੋਰ ਪੈ ਜਾਂਦਾ ਹੈ ।”

ਪ੍ਰਸ਼ਨ 12.
ਕਿਸ਼ੋਰ ਅਵਸਥਾ ਦੀਆਂ ਸਮੱਸਿਆਵਾਂ ਬਾਰੇ ਤੁਸੀਂ ਕੀ ਜਾਣਦੇ ਹੋ ? ਵਿਸਥਾਰਪੂਰਵਕ ਲਿਖੋ ।
ਉੱਤਰ:
ਕਿਸ਼ੋਰ ਅਵਸਥਾ ਦੀਆਂ ਸਮੱਸਿਆਵਾਂ (Problems of Adolescents)-ਵਿਕਾਸ ਦੇ ਇਸ ਸਮੇਂ ਦੇ ਦੌਰਾਨ, ਕਿਸ਼ੋਰਾਂ ਵਿਚ ਬਹੁਤ ਸਾਰੇ ਸਰੀਰਕ, ਜੈਵਿਕ, ਮਾਨਸਿਕ ਅਤੇ ਵਿਵਹਾਰਿਕ ਤਬਦੀਲੀਆਂ ਦੇਖੀਆਂ ਜਾਂਦੀਆਂ ਹਨ । ਇਹ ਅਸ਼ ਅਤੇ ਤੇਜ਼ ਤਬਦੀਲੀਆਂ ਵਿਚ ਕਿਸ਼ੋਰਾਂ ਨੂੰ ਬਹੁਤ ਸਮੱਸਿਆਵਾਂ ਦਾ ਸਾਹਮਣਾ ਕਰਨਾ ਪੈਂਦਾ ਹੈ ਜੋ ਕਿ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਹੈ –
1. ਜੈਵਿਕ ਤਬਦੀਲੀਆਂ ਨਾਲ ਸੰਬੰਧਿਤ ਸਮੱਸਿਆਵਾਂ (Problems related to Biological Changes) ਸਰੀਰਕ ਜਾਂ ਜੈਵਿਕ ਬਦਲਾਵ ਦੋਵੇਂ ਮੁੰਡੇ ਅਤੇ ਕੁੜੀਆਂ ਵਿਚ ਦੇਖਣ ਨੂੰ ਮਿਲਦੇ ਹਨ । ਇਹ ਬਦਲਾਵ ਅੰਦਰੂਨੀ ਹੁੰਦੇ ਹਨ ਜਿਵੇਂ ਕਿ ਕੁੜੀਆਂ ਨੂੰ ਮਹਾਵਾਰੀ ਆਉਣਾ ਅਤੇ ਮੁੰਡਿਆਂ ਨੂੰ ਰਾਤ ਨੂੰ ਸਪਨੇ ਆਉਣਾ । ਬਿਨਾਂ ਅਚਾਨਕ ਹੋਣ ਵਾਲੇ ਸਰੀਰਕ ਬਦਲਾਵ ਉਹਨਾਂ ਨੂੰ ਬੇਚੈਨ ਕਰ ਦਿੰਦੇ ਹਨ ਅਤੇ ਉਹਨਾਂ ਨੂੰ ਇਹਨਾਂ ਦੇ ਅਨੁਕੂਲ ਹੋਣਾ ਔਖਾ ਲਗਦਾ ਹੈ । ਇਹ ਤਬਦੀਲੀਆਂ ਸਰੀਰ ਦੇ ਬਾਹਰ ਵੀ ਦੇਖੇ ਜਾਂਦੇ ਹਨ, ਜਿਵੇਂ ਮੁੰਡੇ ਕੁੜੀਆਂ ਦੇ ਸਰੀਰ ਤੇ ਵਾਲ ਆਉਣਾ ਆਦਿ ।

2. ਮਨੋਵਿਗਿਆਨਿਕ ਵਿਹਾਰ ਨਾਲ ਸੰਬੰਧਿਤ ਸਮੱਸਿਆਵਾਂ (Problems related to psychological Behaviour)-ਇਸ ਉਮਰ ਦੇ ਦੌਰਾਨ ਸਰੀਰਕ ਬਦਲਾਵ ਕਾਰਨ ਕਿਸ਼ੋਰ ਜ਼ਿਆਦਾ ਅਨਕੁਲ ਨਹੀਂ ਹੋ ਪਾਉਂਦੇ ਉਹ ਤਨਾਅ, ਚਿੰਤਾ, ਝਗੜਾ, ਵਾਲੇ ਵਿਵਹਾਰ ਆਦਿ ਚੇਤਨਾ ਵਿਚ ਘਿਰ ਜਾਂਦੇ ਹਨ । ਉਹ ਛੋਟੀ-ਛੋਟੀ ਗੱਲ ਉੱਪਰ ਆਪਣੇ ਵੱਡਿਆਂ ਨਾਲ ਝਗੜਾ ਕਰਦੇ ਹਨ । ਕਈ ਵਾਰ ਕਿਸ਼ੋਰ ਆਪਣੇ ਆਪ ਨੂੰ ਹਵਾ ਵਿਚ ਮਹਿਸੂਸ ਕਰਦੇ ਹਨ ਅਤੇ ਕਦੇ-ਕਦੇ ਖੁਦ ਨੂੰ ਡਿਪਰੈਸ਼ਨ ਵਿਚ ਪਾਉਂਦੇ ਹਨ ।

3. ਆਜ਼ਾਦੀ (Freedom)-ਇਸ ਉਮਰ ਵਿਚ ਨੌਜਵਾਨ ਆਪਣੇ ਵਿਚਾਰਾਂ ਅਤੇ ਕੰਮਾਂ ਤੋਂ ਅਜ਼ਾਦੀ ਚਾਹੁੰਦਾ ਹੈ । ਉਹ ਆਪਣੇ ਆਪ ਨੂੰ ਮਾਪਿਆਂ ਦੇ ਨਿਯੰਤਰਣ ਤੋਂ ਮੁਕਤ ਕਰਾਉਣਾ ਚਾਹੁੰਦਾ ਹੈ । ਉਹ ਆਪਣੇ ਆਪ ਨੂੰ ਨਾ ਹੀ ਜ਼ਿਆਦਾ ਸੁਰੱਖਿਆ ਵਿਚ ਰੱਖਣਾ ਤੇ ਨਾ ਹੀ ਘੱਟ ਸੁਰੱਖਿਆ ਵਿਚ ।

4. ਪਛਾਣ ਅਤੇ ਸਵੈ-ਨਿਰਣਾ (Recognition and Self Consciousness)-ਇਸ ਅੱਲ੍ਹੜ ਉਮਰ ਵਿਚ ਬੱਚਾ ਸਮਾਜ ਵਿਚ ਆਪਣੀ ਪਛਾਣ ਬਣਾਉਣਾ ਚਾਹੁੰਦਾ ਹੈ । ਉਹ ਚਾਹੁੰਦਾ ਹੈ ਕਿ ਸਭ ਉਸਨੂੰ ਸਿਆਣਾ ਅਤੇ ਸਮਾਜ ਨੂੰ ਸਮਝਣ ਵਾਲਾ ਸਮਝਣ । ਉਹ ਸਮੂਹ ਵਿਚ ਸਭ ਨੂੰ ਆਕਰਸ਼ਿਤ ਕਰਨ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰਦਾ ਹੈ । ਉਹ ਆਪਣੀ ਸਿਆਣਪ ਨਾਲ ਸਰੀਰਕ ਅਤੇ ਮਾਨਸਿਕ ਵਿਹਾਰ ਨੂੰ ਬਦਲਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰਦਾ ਹੈ ।

5. ਵਿਨਾਸ਼ਕਾਰੀ ਰੁਝਾਨ ਅਤੇ ਵਿਹਾਰ (Destructive Tendencies and Behaviour)-ਇਸ ਅੱਲ੍ਹੜ ਉਮਰ ਵਿਚ ਅਗਰ ਬਾਲਕ ਨੂੰ ਸਹੀ ਗਾਈਡ ਨਾ ਕੀਤਾ ਜਾਵੇ ਤਾਂ ਉਹ ਵਿਨਾਸ਼ਕਾਰੀ ਰੁਝਾਨਾਂ ਵਾਲੇ ਵਿਹਾਰ ਨੂੰ ਅਪਣਾ ਲੈਂਦਾ ਹੈ । ਉਹ ਕਈ ਵਾਰ ਹਮਲਾਵਰ ਵਾਲਾ ਵਿਵਹਾਰ ਕਰਦਾ ਜੋ ਉਸਨੂੰ ਆਪਣੀ ਇੱਛਾ ਦੇ ਵਿਰੁੱਧ ਕਰਨਾ ਪੈਂਦਾ ਹੈ । ਅਗਿਆਨਤਾ ਦੇ ਪ੍ਰਭਾਵ ਹੇਠ ਕਿਸ਼ੋਰ ਨਸ਼ੀਲੀਆਂ ਦਵਾਈਆਂ, ਸਿਗਰਟਾਂ, ਸ਼ਰਾਬ, ਗੰਦੀਆਂ ਫਿਲਮਾਂ ਦੇਖਣਾ ਆਦਿ ਕੰਮਾਂ ਦੀ ਲਤ ਵਿਚ ਫਸ ਜਾਂਦੇ ਹਨ ।

6. ਹਾਣੀ ਨਾਲ ਦੋਸਤੀ (Peer relationship-ਦੋਸਤ ਇਸ ਉਮਰ ਵਿਚ ਬਹੁਤ ਮਹੱਤਵਪੂਰਨ ਹੁੰਦੇ ਹਨ । ਉਹ ਆਪਣੇ ਮਾਤਾ-ਪਿਤਾ ਨਾਲੋਂ ਦੋਸਤਾਂ ਨਾਲ ਬਾਹਰ ਰਹਿਣਾ ਪਸੰਦ ਕਰਦੇ ਹਨ । ਸਮੂਹ ਵਿਚ ਸਤਿਕਾਰ ਅਤੇ ਮੁੱਲ ਵਾਸਤੇ ਉਹ ਆਪਣੇ ਆਪ ਨੂੰ ਦੂਜਿਆਂ ਨਾਲੋਂ ਬੇਹਤਰ ਬਣਾਉਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰਦੇ ਰਹਿੰਦੇ ਹਨ । ਇਹ ਉਮਰ ਸਮਾਜੀਕਰਨ ਲਈ ਬਹੁਤ ਵਧੀਆ ਉਮਰ ਹੁੰਦੀ ਹੈ ਜੇਕਰ ਉਹਨਾਂ ਨੂੰ ਸਹੀ ਸੇਧ ਦਿੱਤੀ ਜਾਵੇ ।

7. ਕੈਰੀਅਰ ਦੀ ਚੋਣ ਸੰਬੰਧੀ ਸਮੱਸਿਆਵਾਂ (Problems related to career Choices)-ਕੈਰੀਅਰ ਦੇ ਸੰਬੰਧ ਵਿਚ ਵਿਸ਼ਿਆਂ ਦੀ ਚੋਣ ਸੰਬੰਧਿਤ ਸਮੱਸਿਆਵਾਂ ਵੀ ਇਸ ਉਮਰ ਵਿਚ ਦੇਖੀਆਂ ਜਾਂਦੀਆ ਹਨ । ਉਹਨਾਂ ਨੂੰ ਸਕੂਲ ਵਿਚ ਰਹਿੰਦੇ ਆਪਣੇ ਕੈਰੀਅਰ ਸੰਬੰਧੀ ਵਿਸ਼ਿਆਂ ਦੀ ਚੋਣ ਕਰਨੀ ਪੈਂਦੀ ਹੈ । ਇਸ ਉਮਰ ਦੀ ਪਰਿਪੱਕਤਾ ਉਹਨਾਂ ਨੂੰ ਉਹਨਾਂ ਦੇ ਫੈਸਲੇ ਪ੍ਰਤੀ ਭਰਮ ਵਿੱਚ ਰੱਖਦੀ ਹੈ । ਉਹਨਾਂ ਨੂੰ ਸਮਝ ਨਹੀਂ ਆਉਂਦੀ ਕਿ ਜੋ ਫੈਸਲਾ ਉਹ ਲੈ ਰਹੇ ਹਨ ਉਹ ਸਹੀ ਹੈ ਜਾਂ ਗ਼ਲਤ ।

8. ਨਿਰਭਰਤਾ ਦੇ ਸੰਬੰਧ ਵਿਚ ਸਥਿਰਤਾ ਦੀ ਘਾਟ (Lack of Stability in relation to Dependency| ਇਹ ਉਮਰ ਬਚਪਨ ਅਤੇ ਜਵਾਨੀ ਵਿਚਕਾਰ ਇਕ ਪੁੱਲ ਹੈ । ਇਹ ਨਾ ਹੀ ਪਰਿਪੱਕਤਾ ਦੀ ਉਮਰ ਹੈ ਅਤੇ ਨਾ ਅਪਰਿਪੱਕਤਾ ਦੀ । ਉਹ ਨਿਰਭਰ ਤੇ ਸੁਤੰਤਰ ਵਿਹਾਰ ਵਿਚਕਾਰ ਹਮੇਸ਼ਾਂ ਸੰਘਰਸ਼ ਕਰਦਾ ਹੈ । ਇਕ ਪਾਸੇ ਉਹ ਕਿਸ਼ੋਰ ਅਵਸਥਾ ਨੂੰ ਜਾਣਨਾ ਨਹੀਂ ਚਾਹੁੰਦਾ ਤੇ ਦੂਜੇ ਪਾਸੇ ਜ਼ਿੰਮੇਵਾਰੀ ਲੈਣਾ ਚਾਹੁੰਦਾ ਹੈ । ਅਪਰਿਪੱਕਤਾ ਦੀ ਘਾਟ ਉਸ ਵਿਚ ਭਾਵਨਾਤਮਕ ਅਸੰਤੁਲਨ ਆ ਜਾਂਦਾ ਹੈ ।

9. ਸੈਕਸ ਸੰਬੰਧੀ ਸਮੱਸਿਆਵਾਂ (Sex related Problems)-ਇਸ ਉਮਰ ਵਿਚ ਬਹੁਤ ਸਰੀਰ ਬਦਲਾਅ ਆਉਂਦੇ ਹਨ ਉਹਨਾਂ ਵਿਚ ਸੈਕਸ ਪ੍ਰਤੀ ਇੱਛਾਵਾਂ ਦਾ ਵਾਧਾ ਹੁੰਦਾ ਹੈ ਜਿਸ ਕਾਰਨ ਮੁੰਡੇ ਕੁੜੀਆਂ ਇਕ ਦੂਜੇ ਪ੍ਰਤੀ | ਆਕਰਸ਼ਿਤ ਹੋ ਜਾਂਦੇ ਹਨ ਅਤੇ ਕਈ ਵਾਰ ਇਹ ਇੱਛਾਵਾਂ ਉਹਨਾਂ ਨੂੰ ਗੁੰਝਲਦਾਰ ਸਥਿਤੀ ਵਿਚ ਫਸਾ ਦਿੰਦੀਆਂ ਹਨ ।

ਪ੍ਰਸ਼ਨ 13.
ਮਨੋਵਿਗਿਆਨ ਦਾ ਕੀ ਅਰਥ ਹੈ ? ਖੇਡਾਂ ਵਿੱਚ ਮਨੋਵਿਗਿਆਨ ਦਾ ਕੀ ਮਹੱਤਵ ਹੈ ?
ਉੱਤਰ:
ਸਭ ਤੋਂ ਪਹਿਲਾਂ ਸਰੀਰਕ ਮਨੋਵਿਗਿਆਨੀਆਂ ਨੇ ਮਨੁੱਖੀ ਵਿਵਹਾਰ ਅਤੇ ਉਨ੍ਹਾਂ ਦੀਆਂ ਮਾਨਸਿਕ ਪ੍ਰਕਿਰਿਆਵਾਂ ਦਾ ਅਧਿਐਨ ਕਰਨ ਦੀ ਕੋਸ਼ਿਸ਼ ਕੀਤੀ ਸੀ । ਮਨੁੱਖੀ ਵਿਵਹਾਰ ਨੂੰ ਸਮਝਣ ਲਈ ਮਨੋਵਿਗਿਆਨ ਦਾ ਅਧਿਐਨ ਕਰਨਾ ਬਹੁਤ ਜ਼ਰੂਰੀ ਹੈ । ਮਨੋਵਿਗਿਆਨ ਸ਼ਬਦ ਲਾਤੀਨੀ (Latin) ‘ਭਾਸ਼ਾ ਦੇ ਦੋ ਸ਼ਬਦਾਂ ਦੇ ਸਾਈਕੇ (Psyche) ਅਤੇ ਲੋਗੋਜ਼ (Logos) ਦੇ ਸੁਮੇਲ ਤੋਂ ਬਣਿਆ ਹੈ । ਇੱਥੇ Psyche ਦਾ ਅਰਥ ਹੈ “ਆਤਮਾ’’ ਤੇ Logos ਦਾ ਅਰਥ ਹੈ ‘‘ਗੱਲ ਕਰਨੀ’ ਜਾਂ ‘ਅਧਿਐਨ ਕਰਨਾ’’ ਜਾਂ ਫਿਰ “ਵਿਗਿਆਨ’’ ਤੋਂ ਹੈ । ਭਾਵ ਮਨੋਵਿਗਿਆਨ ਦਾ ਅਰਥ ਸੀ ‘‘ਆਤਮਾ ਬਾਰੇ ਗੱਲ ਕਰਨੀ ।’’ ਪਰ ਸਮੇਂ ਨਾਲ ਮਨੋਵਿਗਿਆਨ ਦਾ ਅਰਥ ਅਤੇ ਧਾਰਨਾਵਾਂ ਬਦਲਦੀਆਂ ਗਈਆਂ | ਬਾਅਦ ਵਿਚ ਇਸ ਨੂੰ ਦਿਮਾਗ ਦਾ ਵਿਗਿਆਨ ਆਖਿਆ ਜਾਣ ਲੱਗਾ | ਅੰਤ ਵਿਚ ਮਨੋਵਿਗਿਆਨ ਨੂੰ ਵਿਵਹਾਰ ਦਾ ਵਿਗਿਆਨ’’ (Science of behaviour) ਪ੍ਰਵਾਨ ਕਰ ਲਿਆ ਗਿਆ ।

ਮਨੋਵਿਗਿਆਨ ਦੀਆਂ ਪਰਿਭਾਸ਼ਾਵਾਂ (Definitions of Psychology) ਵਾਰਨ (Warren) ਦੇ ਅਨੁਸਾਰ, “ਮਨੋਵਿਗਿਆਨ ਵਿਗਿਆਨ ਦਾ ਇਕ ਅਜਿਹਾ ਵਿਸ਼ਾ ਹੈ ਜੋ ਕਿ ਜੀਵਵਿਗਿਆਨ ਅਤੇ ਵਾਤਾਵਰਣ ਦੇ ਆਪਸ ਦੇ ਸੰਬੰਧ ਨੂੰ ਦਰਸਾਉਂਦਾ ਹੈ ।’’ ਵੁਡਵਰਥ (Woodworth) ਦੇ ਅਨੁਸਾਰ, “ਮਨੋਵਿਗਿਆਨ ਉਹਨਾਂ ਗਤੀਵਿਧੀਆਂ ਨਾਲ ਨਜਿੱਠਦਾ ਹੈ ਜਿਨ੍ਹਾਂ ਵਿਚ ਵਿਅਕਤੀ ਦਾ ਵਾਤਾਵਰਣ ਨਾਲ ਸੰਬੰਧ ਹੈ ।”

ਕਰੋਅ ਅਤੇ ਕਰੋਅ (Crow and Crow) ਦੇ ਅਨੁਸਾਰ, “ਮਨੋਵਿਗਿਆਨ, ਮਨੁੱਖੀ ਵਰਤਾਓ ਅਤੇ ਸੰਬੰਧਾਂ ਦਾ ਅਧਿਐਨ ਹੈ ।” | ਕਲਾਰਕ ਅਤੇ ਕਲਾਰਕ (Clark and Clark) ਦੇ ਅਨੁਸਾਰ, “ਖੇਡ ਮਨੋਵਿਗਿਆਨ ਇਕ ਪ੍ਰਭਾਵੀ ਮਨੋਵਿਗਿਆਨ ਹੈ । ਇਹ ਵਿਅਕਤਿਤੱਵ, ਭਾਵਨਾਤਮਕ ਅਤੇ ਪ੍ਰੇਰਕ ਪਹਿਲੂਆਂ ਅਤੇ ਸਰੀਰਕ ਗਤੀਵਿਧੀਆਂ ਨਾਲ ਸੰਬੰਧ ਰੱਖਦਾ ਹੈ । ਇਹ ਮਨੋਵਿਗਿਆਨ ਵਿਚ ਵਰਤੀਆਂ ਜਾਂਦੀਆਂ ਕਈ ਤਕਨੀਕਾਂ ਨਿਯੁਕਤ ਕਰਦਾ ਹੈ ।” ਮੌਕ ਡੋਊਗਾਲ (Mc. Dougall) ਦੇ ਅਨੁਸਾਰ, “ਮਨੋਵਿਗਿਆਨ, ਮਨੁੱਖੀ ਆਚਰਣ ਤੇ ਵਿਵਹਾਰ ਦਾ ਆਸ਼ਾਵਾਦੀ ਵਿਗਿਆਨ ਹੈ ।” ਵਾਟਸਨ (Watson) ਦੇ ਅਨੁਸਾਰ, “ਮਨੋਵਿਗਿਆਨ, ਮਨੁੱਖੀ ਵਰਤਾਉ ਦਾ ਰਚਨਾਤਮਕ ਵਿਗਿਆਨ ਹੈ ।

ਡਰੈਵਰ (Drever) ਦੇ ਅਨੁਸਾਰ, “ਵਰਤਾਉ, ਮਨੁੱਖੀ ਭਾਵਨਾਵਾਂ ਅਤੇ ਵਿਚਾਰਾਂ ਦੇ ਅੰਦਰੂਨੀ ਜੀਵਨ ਜਿਸ ਨੂੰ ਅਸੀਂ ਮਾਨਸਿਕ ਜੀਵਨ ਆਖਦੇ ਹਾਂ, ਦਾ ਪ੍ਰਗਟਾਉ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ ।” ਬਰਨਾਰਡ (Bernard) ਦੇ ਅਨੁਸਾਰ, “ਮਨੋਵਿਗਿਆਨ, ਜੀਵ ਦਾ ਆਪਣੇ ਵਾਤਾਵਰਣ ਵਿਚ ਢਲਣ ਦਾ ਅਧਿਐਨ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਅਸੀਂ ਕਹਿ ਸਕਦੇ ਹਾਂ ਕਿ ਮਨੋਵਿਗਿਆਨ ਮਨੁੱਖੀ ਵਿਹਾਰ ਦਾ ਅਧਿਐਨ ਹੈ ਜਿਸ ਦਾ ਸੰਬੰਧ ਅੰਦਰਲੇ ਵਾਤਾਵਰਣ ਨਾਲ ਹੈ ।

ਮਨੋਵਿਗਿਆਨ ਦਾ ਖੇਡ ਅਤੇ ਕਿਰਿਆਵਾਂ ਵਿੱਚ ਮਹੱਤਵ (Importance of Psychology in Games and Sports)-ਸਰੀਰਕ ਸਿੱਖਿਆ ਅਤੇ ਖੇਡਾਂ ਵਿਚ ਸਰੀਰਕ ਗਤੀਆਂ ਹੁੰਦੀਆਂ ਹਨ ਜੋ ਕਿ ਖੇਡ ਵਾਤਾਵਰਣ ਦੇ ਅਨੁਸਾਰ ਹੁੰਦੀਆਂ ਹਨ । ਸਿੱਖਿਆ ਦੇ ਵਿੱਚ ਮਨੋਵਿਗਿਆਨ ਦੇ ਸਿਧਾਂਤ ਨੂੰ ਲਾਗੂ ਕਰਨ ਲਈ ਮਨੋਵਿਗਿਆਨ ਦੀ ਲੋੜ ਪੈਂਦੀ ਹੈ । ਸਰੀਰਕ ਸਿੱਖਿਆ ਦੇ ਸੰਗਠਿਤ ਪ੍ਰੋਗਰਾਮ ਅਤੇ ਮੁਕਾਬਲਿਆਂ ਵਿਚ, ਜਿੱਥੇ ਹਰ ਕੋਈ ਜਿੱਤਣਾ ਚਾਹੁੰਦਾ ਹੈ, ਬਿਨਾਂ ਮਨੋਵਿਗਿਆਨ ਦੇ ਗਿਆਨ ਤੋਂ ਬਿਨਾਂ ਹੀ ਪ੍ਰਦਰਸ਼ਨ ਨਹੀਂ ਕਰ ਸਕਦਾ। ਇੱਥੇ ਖਿਡਾਰੀ ਦੇ ਮਨੋਵਿਗਿਆਨ ਵਿਹਾਰ ਜਿਵੇਂ ਕਿ ਉਸਦੀ ਰੁਚੀ, ਰਵੱਈਏ, ਪ੍ਰੇਰਨਾ ਅਤੇ ਭਾਵਨਾਤਮਕ ਵਿਹਾਰ ਦਾ ਗਿਆਨ ਹੋਣਾ ਜ਼ਰੂਰੀ ਹੈ । ਖੇਡਾਂ ਵਿਚ ਖੇਡ ਕੁਸ਼ਲਤਾ ਕਿਸੇ ਵੀ ਭੌਤਿਕ ਜਾਂ ਮਨੋਵਿਗਿਆਨ ਕਾਰਕਾਂ ਦੀ ਪ੍ਰਤੀਬੰਧਿਤ ਨਹੀਂ ਹੁੰਦੀ ਹੈ । ਇਹ ਗੱਲ ਵੀ ਚੰਗੀ ਤਰ੍ਹਾਂ ਸਮਝੀ ਜਾ ਚੁੱਕੀ ਹੈ ਕਿ ਖੇਡ ਕਾਰਜਕੁਸ਼ਲਤਾ ਤੇ ਕਈ ਮਨੋਵਿਗਿਆਨ ਤੱਤਾਂ ਦਾ ਪ੍ਰਭਾਵ ਪੈਂਦਾ ਹੈ ਜੋ ਕਿ ਖਿਡਾਰੀ ਦੇ ਪ੍ਰਦਰਸ਼ਨ ਦੇ ਪੱਧਰ ਨੂੰ ਸੁਧਾਰਦੇ ਹਨ । ਸਰੀਰਕ ਸਿੱਖਿਆ ਦੇ ਅਧਿਆਪਕ, ਕੋਚਾਂ ਅਤੇ ਟ੍ਰੇਨਰ ਨੂੰ ਵਿਅਕਤੀਗਤ ਵਿਕਾਸ ਅਤੇ ਪ੍ਰਾਪਤੀਆਂ ਲਈ ਮਨੋਵਿਗਿਆਨ ਦਾ ਗਿਆਨ ਲਾਗੂ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ।

ਮਨੋਵਿਗਿਆਨ ਦੀ ਮਹੱਤਤਾ ਨੂੰ ਹੇਠ ਲਿਖੀਆਂ ਮਹੱਤਵਪੂਰਨ ਗੱਲਾਂ ਦੁਆਰਾ ਵੀ ਸਮਝਿਆ ਜਾ ਸਕਦਾ ਹੈ –
1. ਸਭਾਅ ਨੂੰ ਜਾਨਣਾ ਅਤੇ ਸਮਝਣਾ (To Kiow and Understand the Behaviour-ਮਨੋਵਿਗਿਆਨ ਦਾ ਸਭ ਤੋਂ ਮਹੱਤਵਪੂਰਨ ਪਹਿਲੂ ਹੈ ਕਿ ਇਕ ਵਿਅਕਤੀ ਨੂੰ ਜਾਣਨਾ ਅਤੇ ਵਿਭਿੰਨ ਪਰਿਸਥਿਤੀਆਂ ਵਿਚ ਉਸਦੇ ਵਿਵਹਾਰ ਨੂੰ ਸਮਝਣਾ ।ਵਿਵਹਾਰ ਸੰਬੰਧੀ ਸਮਝ ਇਕ ਵਿਅਕਤੀ ਕਈ ਤਰ੍ਹਾਂ ਦੇ ਜਟਿਲ ਪਹਿਲੂਆਂ ਨੂੰ ਸਮਝਣ ਵਿਚ ਮਦਦਗਾਰ ਹੁੰਦੀ ਹੈ ਜਿਵੇਂ ਕਿ ਕਿਸੇ ਗਤੀਵਿਧੀ ਪ੍ਰਤੀ ਉਸਦੀ ਰੁਚੀ ਅਤੇ ਦੁੱਖ, ਵਿਭਿੰਨ ਪ੍ਰਤੀਯੋਗਤਾਵਾਂ ਦੇ ਸਮੇਂ ਉਸਦੀ ਭਾਵਨਾਤਮਕ ਸਥਿਤੀ ਆਦਿ । ਸੁਭਾਅ ਨੂੰ ਜਾਨਣਾ ਅਤੇ ਸਮਝਣ ਦੀ ਯੋਗਤਾ ਕਿਸੇ ਵੀ ਅਧਿਆਪਕ ਅਤੇ ਕੋਚ ਲਈ ਆਪਣੇ ਖਿਡਾਰੀ ਦੀ ਸਮਰੱਥਾ ਵਧਾਉਣ ਵਿਚ ਮੱਦਦ ਕਰੇਗੀ ।

2. ਭਾਵਨਾਵਾਂ ਨੂੰ ਸਹੀ ਦਿਸ਼ਾ ਅਤੇ ਕੰਟਰੋਲ ਕਰਨਾ (Channelization and Control of Emotions)- ਮਨੋਵਿਗਿਆਨ ਦਾ ਅਧਿਐਨ ਇਕ ਵਿਅਕਤੀ ਅਤੇ ਖਿਡਾਰੀ ਦੇ ਵਿਚਾਰਾਂ ਅਤੇ ਭਾਵਨਾਵਾਂ ਨੂੰ ਖਾਸ ਕਰਕੇ ਅਭਿਆਸ ਅਤੇ ਮੁਕਾਬਲੇ ਦੀ ਸਥਿਤੀ ਵਿਚ, ਸਮਝਣ ਵਿਚ ਮਦਦ ਕਰਦੀ ਹੈ ਜਿਵੇਂ ਕਿ ਡਰ, ਦਬਾਅ ਆਦਿ । ਮਨੋਵਿਗਿਆਨ ਦੇ ਗਿਆਨ ਨਾਲ ਪ੍ਰਤੀਯੋਗਤਾ ਵਿਚ ਆਈਆਂ ਕਈ ਤਰ੍ਹਾਂ ਦੀਆਂ ਸਥਿਤੀਆਂ ਨੂੰ ਸਮਝਣ ਅਤੇ ਸਹੀ ਦਿਸ਼ਾ ਦਿਖਾਉਣ ਵਿਚ ਮਦਦ ਕਰਦੀ ਹੈ ।

3. ਖਿਡਾਰੀਆਂ ਦਾ ਚੁਨਾਵ ਅਤੇ ਤਿਆਰੀ (Selection and Preparation of Athletics)-ਮਨੋਵਿਗਿਆਨ ਦੇ ਗਿਆਨ ਨਾਲ, ਕਿਸੇ ਵਿਸ਼ੇਸ਼ ਖੇਡ ਲਈ ਖਿਡਾਰੀਆਂ ਦੀ ਸਿਖਲਾਈ ਅਤੇ ਵਿਹਾਰ ਨੂੰ ਦੇਖਣ ਤੋਂ ਬਾਅਦ ਉਸਦੀ ਚੋਣ ਵਿਚ ਸਹਾਇਤਾ ਮਿਲਦੀ ਹੈ । ਖੇਡ ਖੇਤਰ ਵਿਚ ਚੰਗੀ ਤਿਆਰੀ ਲਈ ਕੁਝ ਮਨੋਵਿਗਿਆਨਿਕ ਲੱਛਣ ਜਿਵੇਂ ਕਿ ਸੰਕਲਪ ਸ਼ਕਤੀ, ਰੁਚੀ, ਪ੍ਰੇਰਣਾ, ਮੁਕਾਬਲੇ ਦੀ ਭਾਵਨਾ ਦਾ ਹੋਣਾ ਮਹੱਤਵਪੂਰਨ ਹੁੰਦਾ ਹੈ । ਇਸ ਲਈ ਟੀਮ ਦਾ ਚੁਨਾਵ ਕਰਦੇ ਸਮੇਂ ਮਨੋਵਿਗਿਆਨਿਕ ਵਿਵਹਾਰ ਦਾ ਗਿਆਨ ਲਾਭਕਾਰੀ ਹੁੰਦਾ ਹੈ ।

4. ਤਨਾਵ-ਮੁਕਤੀ ਦੇ ਰੂਪ ਵਿਚ ਮਹੱਤਵਪੂਰਨ (Important as a Relaxation Tool)-ਮਨੋਵਿਗਿਆਨ ਸਿਰਫ ਲੋਕਾਂ ਦੇ ਵਿਵਹਾਰ ਨੂੰ ਹੀ ਸਮਝਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਨਹੀਂ ਕਰਦਾ ਬਲਕਿ ਇਕ ਖਿਡਾਰੀ ਨੂੰ ਉਹਨਾਂ ਦੇ ਪ੍ਰਦਰਸ਼ਨ ਦੇ ਅਗਲੇ ਪੱਧਰ ਤੱਕ ਲੈ ਜਾਣ ਵਿਚ ਮਦਦ ਕਰਦਾ ਹੈ । ਇਹ ਸਿੱਖਣ ਦੀਆਂ ਵਿਪਰੀਤ ਪਰਿਣਾਮ ਆਉਣ ਤੇ ਉਦੇਸ਼ ਨਿਰਧਾਰਿਤ ਕਰਨ, ਕਲਪਨਾ ਸ਼ਕਤੀ ਅਤੇ ਕਈ ਮੁਸ਼ਕਿਲਾਂ ਨੂੰ ਨਿਪਟਣ ਵਿਚ ਮੱਦਦ ਕਰਦਾ ਹੈ ।

5. ਸੁਧਾਰ ਕਰਕੇ ਉਤਸ਼ਾਹ ਭਰਨਾ (Help in Inspiration to Improve-ਕੁਝ ਮਨੋਵਿਗਿਆਨਿਕ ਕਾਰਕ ਪ੍ਰਦਰਸ਼ਨ ਵਿਚ ਸੁਧਾਰ ਕਰਕੇ ਅਤੇ ਪ੍ਰੇਰਣਾ ਵਿਚ ਵਾਧਾ ਕਰਦਾ ਹੈ । ਇਸ ਨਾਲ ਖਿਡਾਰੀਆ ਨੂੰ ਮੁਸ਼ਕਿਲ ਪ੍ਰਸਥਿਤੀਆਂ ਵਿਚ ਵੀ ਕੰਮ ਕਰਨ ਦੀ ਪ੍ਰੇਰਣਾ ਮਿਲਦੀ ਹੈ ।

PSEB 12th Class Physical Education Guide ਸਰੀਰਿਕ ਸਿੱਖਿਆ ਦੇ ਸਮਾਜਿਕ ਅਤੇ ਮਨੋਵਿਗਿਆਨਕ ਪੱਖ Important Questions and Answers

ਇੱਕ ਅੰਕ ਵਾਲੇ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ (One Mark Question-Answers)

ਪ੍ਰਸ਼ਨ 1.
‘‘ਮਨੋਵਿਗਿਆਨ’’ ਸ਼ਬਦ ਕਿਸ ਭਾਸ਼ਾ ਤੋਂ ਲਿਆ ਗਿਆ ਹੈ ?
ਉੱਤਰ:
ਲਾਤੀਨੀ (Latin) ਭਾਸ਼ਾ ਤੋਂ।

ਪ੍ਰਸ਼ਨ 2.
ਸਮਾਜ ਸ਼ਾਸਤਰ ਦਾ ਅਰਥ ਸਮਝਾਓ ।
ਉੱਤਰ:
ਸਮਾਜ ਸ਼ਾਸਤਰ ਸ਼ਬਦ ਦੋ ਸ਼ਬਦਾਂ ਦੇ ਸੁਮੇਲ ਤੋਂ ਬਣਿਆ ਹੈ, ਜਿਸ ਵਿਚ ਸੋਸ਼ੂਜ਼ ਦਾ ਮਤਲਬ ‘ਐਸੋਸਿਏਟ ਜਾਂ ਸਮਾਜਿਕ’’ ਅਤੇ ‘ਲੋਗੋ’’ ਤੋਂ ਭਾਵ ਹੈ, ਵਿਗਿਆਨ ਜਾਂ ਅਧਿਐਨ ਕਰਨਾ । ਇਸ ਤਰ੍ਹਾਂ ਸਮਾਜ ਸ਼ਾਸਤਰ ‘ਸਮਾਜ ਦਾ ਵਿਗਿਆਨ ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਕੋਈ ਵੀ ਦੋ ਸਮਾਜਿਕ ਗੁਣਾਂ ਬਾਰੇ ਦੱਸੋ ।
ਉੱਤਰ:
ਭਾਈਚਾਰੇ ਦੀ ਨੀਂਹ ਅਤੇ ਚਰਿੱਤਰ ਅਤੇ ਨੈਤਿਕਤਾ ॥

ਪ੍ਰਸ਼ਨ 4.
ਮਨੁੱਖੀ ਵਤੀਰੇ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਨ ਵਾਲੀਆਂ ਦੋ ਸੰਸਥਾਵਾਂ ਦਾ ਨਾਮ ਦੱਸੋ ।
ਉੱਤਰ:
ਪਰਿਵਾਰ ਅਤੇ ਵਿੱਦਿਆਕ ਸੰਸਥਾਵਾਂ ।

ਪ੍ਰਸ਼ਨ 5.
ਆਧੁਨਿਕ ਉਲੰਪਿਕ ਖੇਡਾਂ ਦਾ ਪਿਤਾ ਕੌਣ ਹੈ ?
ਉੱਤਰ:
ਬੇਰਨ ਡੀ. ਕੁਬਰਟਿਨ ।

ਪਸ਼ਨ 6.
ਕਿਸ ਸਾਲ ਵਿਚ ਓਲੰਪਿਕ ਖੇਡਾਂ ਸ਼ੁਰੂ ਹੋਈਆਂ ?
ਉੱਤਰ:
1896 ਵਿਚ ।

ਪ੍ਰਸ਼ਨ 7.
ਵਿਅਕਤੀ ਦੇ ਨੈਤਿਕ ਅਤੇ ਚਰਿੱਤਰ ਗੁਣਾਂ ਨੂੰ ਉਜਾਗਰ ਕਰੋ ।
ਉੱਤਰ:
ਨੈਤਿਕ ਵਿਵਹਾਰ ਅਤੇ ਚਰਿਤਰ ਨਿਰਮਾਣ ਸਮਾਜਿਕ ਪਰਸਪਰ (Social interaction) ਤੇ ਨਿਰਭਰ ਕਰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 8.
ਮਨੋਵਿਗਿਆਨ ਨੂੰ ਪਰਿਭਾਸ਼ਿਤ ਕਰੋ !
ਉੱਤਰ:
ਮਨੋਵਿਗਿਆਨ ਦਾ ਅਰਥ ਹੈ “ਆਤਮਾ ਬਾਰੇ ਗੱਲ ਕਰਨੀ ।’’

ਪ੍ਰਸ਼ਨ 9.
ਮਨੋਵਿਗਿਆਨ ਦੇ ਦੋ ਮਹੱਤਤਾ ਨੂੰ ਉਜਾਗਰ ਕਰੋ ।
ਉੱਤਰ-ਸਰੀਰਕ ਸਿੱਖਿਆ ਅਤੇ ਖੇਡਾਂ ਵਿਚ ਸਰੀਰਕ ਗਤੀਆਂ ਹੁੰਦੀਆਂ ਹਨ ਜੋ ਕਿ ਖੇਡ ਵਾਤਾਵਰਣ ਦੇ ਅਨੁਸਾਰ ਹੁੰਦੀਆਂ ਹਨ । ਸਿੱਖਿਆ ਦੇ ਵਿੱਚ ਮਨੋਵਿਗਿਆਨ ਦੇ ਸਿਧਾਂਤ ਨੂੰ ਲਾਗੂ ਕਰਨ ਲਈ ਮਨੋਵਿਗਿਆਨ ਦੀ ਲੋੜ ਪੈਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 10.
ਸਿੱਖਣ ਦੀ ਧਾਰਨਾ ਨੂੰ ਸਪੱਸ਼ਟ ਕਰੋ ।
ਉੱਤਰ:
ਸਿੱਖਣ ਦੀ ਧਾਰਨਾ ਨੂੰ ਵਿਵਹਾਰ ਦੇ ਬਦਲਾਵ ਦੇ ਤਜ਼ਰਬਾ, ਨਵੀਆਂ ਆਦਤਾਂ ਅਤੇ ਹੁਨਰ ਪ੍ਰਾਪਤੀ ਵਜੋਂ ਸਮਝਿਆ ਜਾ ਸਕਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 11.
ਸਿੱਖਣ ਦੇ ਕੋਈ ਦੋ ਨਿਯਮ ਦੱਸੋ । ਉੱਤਰ-ਤਿਆਰੀ ਦਾ ਨਿਯਮ ਅਤੇ ਅਭਿਆਸ ਦਾ ਨਿਯਮ ।

ਪ੍ਰਸ਼ਨ 12.
ਸਿਖਲਾਈ ਦੀਆਂ ਸਥਾਨਾਂਤਰਣ ਕਿਸਮਾਂ ਕਿਹੜੀਆਂ ਹਨ ?
ਉੱਤਰ:
ਸਕਾਰਾਤਮਕ, ਨਕਾਰਾਤਮਕ ਅਤੇ ਜੀਰੋ ਸਥਾਨਾਂਤਰਣ ।

ਪ੍ਰਸ਼ਨ 13.
ਕਿਸ਼ੋਰ ਅਵਸਥਾ ਦਾ ਅਰਥ ਸਮਝਾਓ ।
ਉੱਤਰ:
ਸ਼ਬਦ “Adolescence’ ਯੂਨਾਨੀ ਭਾਸ਼ਾ ਦਾ ਸ਼ਬਦ ਹੈ ਜਿਸਦਾ ਭਾਵ ਹੈ ‘ਬਾਲਗ ਉਮਰ ਦਾ ਆਰੰਭ (To grow to maturity). ਆਮ ਤੌਰ ਤੇ ਇਹ ਸਰੀਰਕ ਅਤੇ ਮਾਨਸਿਕ ਤਬਾਦਲੇ ਦੀ ਉਮਰ ਹੁੰਦੀ ਹੈ । | ਜਸ਼ੈਲਡ (Jersield) ਦੇ ਅਨੁਸਾਰ, “ਅੱਲ੍ਹੜ ਉਮਰ ਉਹ ਉਮਰ ਹੈ ਜਿਸ ਵਿਚ ਵਿਅਕਤੀ ਬਚਪਨ ਤੋਂ ਪਰਿਪੱਕਤਾ ਵੱਲ ਵੱਧਦਾ ਹੈ ।”

ਪ੍ਰਸ਼ਨ 14.
ਕਿਸ਼ੋਰ ਅਵਸਥਾ ਦੀਆਂ ਕੋਈ ਦੋ ਸਮੱਸਿਆਵਾਂ ਬਾਰੇ ਦੱਸੋ ।
ਉੱਤਰ:
ਜੈਵਿਕ ਤਬਦੀਲੀਆਂ ਅਤੇ ਮਨੋਵਿਗਿਆਨਿਕ ਵਿਹਾਰ ਸੰਬੰਧੀ ਤਰੁੱਟੀਆਂ ।

ਪ੍ਰਸ਼ਨ 15.
ਕਿਸ਼ੋਰ ਅਵਸਥਾ ਨਾਲ ਸੰਬੰਧਿਤ ਸਮੱਸਿਆ ਨੂੰ ਹੱਲ ਕਰਨ ਲਈ ਉਪਾਅ ਦਿਓ ।
ਉੱਤਰ:

1. ਮਾਤਾ-ਪਿਤਾ ਦੁਆਰਾ ਮਾਰਗ-ਦਰਸ਼ਨ
2. ਲਿੰਗ ਸੰਬੰਧੀ ਜਾਣਕਾਰੀ ।

ਪ੍ਰਸ਼ਨ 16.
ਉਹਨਾਂ ਦੇਸ਼ਾਂ ਦਾ ਨਾਮ ਦੱਸੋ ਜਿਹਨਾਂ ਨੇ ਖੇਡਾਂ ਦੇ ਵਿਕਾਸ ਵਿਚ ਯੋਗਦਾਨ ਪਾਇਆ ਹੈ ?
ਉੱਤਰ:
ਯੂਨਾਨ, ਜਾਪਾਨ, ਅਮਰੀਕਾ, ਭਾਰਤ, ਚੀਨ, ਰੂਸ ਆਦਿ ।

ਪ੍ਰਸ਼ਨ 17.
ਸਿੱਖਣ ਦੇ ਸਥਾਨਾਂਤਰਣ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ? ‘
ਉੱਤਰ:
ਆਮ ਤੌਰ ਤੇ ਸਿੱਖਣ ਦੇ ਸਥਾਨਾਂਤਰਣ ਤੋਂ ਭਾਵ ਆਦਤਾਂ, ਹੁਨਰ ਅਤੇ ਰਵੱਈਏ ਨੂੰ ਇਕ ਖੇਤਰ ਤੋਂ ਦੂਜੇ ਖੇਤਰ ਵਿਚ ਲੈ ਕੇ ਜਾਣਾ | ਕਈ ਵਾਰ ਇਕ ਖੇਤਰ ਵਿਚ ਸਿੱਖਿਆ ਗਿਆ ਹੁਨਰ ਦੂਜੇ ਖੇਤਰ ਵਿਚ ਮੁਸ਼ਕਿਲ ਪੈਦਾ ਕਰਦਾ ਹੈ । ਇਸ ਕਰਕੇ ਸਿੱਖਣ ਦਾ ਸਥਾਨਾਂਤਰਣ ਦਾ ਪ੍ਰਭਾਵ ਬਹੁਤ ਪ੍ਰਭਾਵੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 18.
ਸਿੱਖਣ ਦੇ ਵੱਖ-ਵੱਖ ਨਿਯਮਾਂ ਨੂੰ ਉਜਾਗਰ ਕਰੋ ।
ਉੱਤਰ:
ਤਿਆਰੀ ਦਾ ਨਿਯਮ, ਪ੍ਰਭਾਵ ਦਾ ਨਿਯਮ ਅਤੇ ਅਭਿਆਸ ਦਾ ਨਿਯਮ ।

ਪ੍ਰਸ਼ਨ 19.
ਸਿੱਖਣ ਦੇ ਵੱਖ-ਵੱਖ ਨਿਯਮਾਂ ਦਾ ਜਨਮਦਾਤਾ ਕੌਣ ਹੈ ?
ਉੱਤਰ:
ਬੋਰਨਡਾਈਕ ।

ਪਸ਼ਨ 20.
ਸਮਾਜਿਕਤਾ ਤੋਂ ਤੁਸੀਂ ਕੀ ਸਮਝਦੇ ਹੋ ?
ਉੱਤਰ:
ਸਮਾਜਿਕ ਵਿਗਿਆਨ ਸਮਾਜ ਦਾ ਵਿਗਿਆਨ ਹੈ । ਇਹ ਸਮਾਜਿਕ ਰਿਸ਼ਤੇ, ਹਰ ਰੋਜ਼ ਦੀ ਜਿੰਦਗੀ ਦੇ ਮੇਲਜੋਲ ਅਤੇ ਸੱਭਿਆਚਾਰ ਦੇ ਅਧਿਐਨ ਦਾ ਇਕ ਪੈਟਰਨ ਹੈ । ਇਸ ਦਾ ਸੰਬੰਧ ਸਮਾਜ ਦੀ ਉਤਪੱਤੀ, ਕਾਰਜ ਅਤੇ ਸਮੱਸਿਆਵਾਂ ਦੇ ਸੰਬੰਧ ਵਿਚ ਮਨੁੱਖੀ ਸਮਾਜ ਦਾ ਅਧਿਐਨ ਕਰਨਾ ਹੈ । ਇਹ ਲੋਕਾਂ, ਸਮੂਹ, ਸੰਸਥਾਵਾਂ ਅਤੇ ਸੱਭਿਆਚਾਰ ਦੇ ਸੰਬੰਧ ਵਿਚ ਕੰਮ ਕਰਦਾ ਹੈ । ਇਹ ਪਰਿਵਾਰ, ਧਰਮ, ਸਿੱਖਿਆ, ਰਾਜਨੀਤੀ, ਮਨੁੱਖੀ ਵਤੀਰੇ ਅਤੇ ਸੱਭਿਆਚਾਰ ਨੂੰ ਸਮਝਣ ਵਿਚ ਵੀ ਮਦਦ ਕਰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 21.
ਸਮਾਜੀਕਰਨ ਤੋਂ ਤੁਸੀਂ ਕੀ ਸਮਝਦੇ ਹੋ ?
ਉੱਤਰ:
ਵਿਕਾਸ ਕਰਨ ਲਈ ਸਮਾਜਿਕ ਗੁਣ, ਹੁਨਰ, ਗਿਆਨ ਅਤੇ ਮੁੱਲ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਪ੍ਰਕਿਰਿਆ ਦੇ ਸਮਾਜਿਕ ਸੰਬੰਧਾਂ ਨੂੰ ਸਮਾਜੀਕਰਨ ਕਿਹਾ ਜਾਂਦਾ ਹੈ !

ਪ੍ਰਸ਼ਨ 22.
ਮਨੋਵਿਗਿਆਨ ਦਾ ਪਿਤਾ ਕੌਣ ਹੈ ?
ਉੱਤਰ:
ਸੰਗਮਡ ਫਾਊਂਡ ।

ਪ੍ਰਸ਼ਨ 23.
ਸਮਾਜ ਵਿਗਿਆਨ ਦਾ ਸ਼ਬਦੀ ਅਰਥ ਲਿਖੋ ।
ਉੱਤਰ:
ਸਮਾਜ ਸ਼ਾਸਤਰ ਸ਼ਬਦ ਦੋ ਸ਼ਬਦਾਂ ਦੇ ਸੁਮੇਲ ਤੋਂ ਬਣਿਆ ਹੈ, ਜਿਸ ਵਿਚ ਸੋਸ਼ਨ ਦਾ ਮਤਲਬ ‘‘ਐਸੋਸਿਏਜ ਜਾਂ ਸਮਾਜਿਕ’’ ਅਤੇ ‘‘ਲੋਗੋ” ਤੋਂ ਭਾਵ ਹੈ, ਵਿਗਿਆਨ ਜਾਂ ਅਧਿਐਨ ਕਰਨਾ । ਇਸ ਤਰ੍ਹਾਂ ਸਮਾਜ ਸ਼ਾਸਤਰ “ਸਮਾਜ ਦਾ ਵਿਗਿਆਨ’ ਹੈ ।

ਦੇ ਅੰਕਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ : (Two Marks Question-Answers)

ਪ੍ਰਸ਼ਨ 1.
ਸਮਾਜ ਸ਼ਾਸਤਰ ਤੋਂ ਤੁਸੀਂ ਕੀ ਸਮਝਦੇ ਹੋ ?
ਉੱਤਰ:
ਸਮਾਜ ਸ਼ਾਸਤਰ ਦਾ ਅਰਥ-ਸਮਾਜ ਸ਼ਾਸਤਰ ਸ਼ਬਦ ਦੋ ਸ਼ਬਦਾਂ ਦੇ ਸੁਮੇਲ ਤੋਂ ਬਣਿਆ ਹੈ, ਜਿਸ ਵਿਚ ਸੋਸ਼ੂਜ਼ ਦਾ ਮਤਲਬ ‘‘ਐਸੋਸਿਏਟ ਜਾਂ ਸਮਾਜਿਕ’’ ਅਤੇ ‘‘ਲੋਗੋ’’ ਤੋਂ ਭਾਵ ਹੈ, ਵਿਗਿਆਨ ਜਾਂ ਅਧਿਐਨ ਕਰਨਾ । ਇਸ ਤਰ੍ਹਾਂ ਸਮਾਜ ਸ਼ਾਸਤਰ ‘‘ਸਮਾਜ ਦਾ ਵਿਗਿਆਨ’’ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਸਮਾਜ ਸ਼ਾਸਤਰ ਨੂੰ ਪਰਿਭਾਸ਼ਿਤ ਕਰੋ ।
ਉੱਤਰ:
ਵਿਕਾਸ ਕਰਨ ਲਈ ਸਮਾਜਿਕ ਗੁਣ, ਹੁਨਰ, ਗਿਆਨ ਅਤੇ ਮੁੱਲ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਪ੍ਰਕ੍ਰਿਆ ਦੇ ਸਮਾਜਿਕ ਸੰਬੰਧਾਂ ਨੂੰ ਸਮਾਜੀਕਰਨ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਗਰੇਟ (Garrett) ਦੇ ਅਨੁਸਾਰ, “ਸਮਾਜਿਕਤਾ ਇੱਕ ਅਜਿਹੀ ਪ੍ਰਕ੍ਰਿਆ ਹੈ ਜਿਸ ਦੁਆਰਾ ਜੀਵ ਜੰਤੂ ਵਿਅਕਤੀਗਤ ਮਨੁੱਖੀ ਜੀਵਨ ਵਿਚ ਤਬਦੀਲ ਹੋ ਜਾਂਦਾ ਹੈ ।”

ਪ੍ਰਸ਼ਨ 3.
ਵੱਖ-ਵੱਖ ਸਮਾਜਿਕ ਗੁਣਾਂ ਨੂੰ ਉਜਾਗਰ ਕਰੋ ।
ਉੱਤਰ:

• ਭਾਈਚਾਰੇ ਦੀ ਨੀਂਹ ।
• ਚਰਿੱਤਰ ਅਤੇ ਨੈਤਿਕ ਗੁਣ
• ਸਮੂਹਿਕ ਅਹਿਸਾਸ ਅਤੇ ਜ਼ਿੰਮੇਵਾਰੀ
• ਊਰਜਾ ਦਾ ਚੈਨਲਾਈਜੇਸ਼ਨ ।

ਪ੍ਰਸ਼ਨ 4.
ਮਨੁੱਖੀ ਵਤੀਰੇ ਤੇ ਅਸਰ ਪਾਉਣ ਵਾਲੀਆਂ ਕਿਸੇ ਦੋ ਸੰਸਥਾਵਾਂ ਦਾ ਨਾਮ ਲਿਖੋ .
ਉੱਤਰ-

1. ਪਰਿਵਾਰ family)-ਮਨੁੱਖੀ ਵਤੀਰੇ ਨੂੰ ਪਰਿਵਾਰ ਸਭ ਤੋਂ ਪਹਿਲਾਂ ਪ੍ਰਭਾਵਿਤ ਕਰਦਾ ਹੈ ।
2. ਵਿੱਦਿਅਕ ਸੰਸਥਾਵਾਂ (Educational Institutions)-ਵਿੱਦਿਅਕ ਸੰਸਥਾਵਾਂ ਜਿਵੇਂ ਕਿ ਸਕੂਲ ਬੱਚੇ ਦੇ ਜੀਵਨ ਵਿਚ ਮਹੱਤਵਪੂਰਨ ਭੂਮਿਕਾ ਨਿਭਾਉਂਦੇ ਹਨ |

ਪ੍ਰਸ਼ਨ 5.
ਰਾਸ਼ਟਰੀ ਅਖੰਡਤਾ ਵਿਚ ਖੇਡਾਂ ਦੀ ਕੀ ਭੂਮਿਕਾ ਹੈ ?
ਉੱਤਰ:
ਸਰੀਰਕ ਸਿੱਖਿਆ ਅਤੇ ਖੇਡਾਂ ਦੇ ਪ੍ਰੋਗਰਾਮ ਰਾਸ਼ਟਰੀ ਅਤੇ ਅੰਤਰਰਾਸ਼ਟਰੀ ਅਖੰਡਤਾ ਵਿਚ ਕੀਮਤੀ ਰੂਪ ਨਾਲ ਵਿਕਾਸ ਦਾ ਕੰਮ ਕਰਦੇ ਹਨ । ਇਹ ਅਜਿਹੀਆਂ ਗਤੀਵਿਧੀਆਂ ਪ੍ਰਦਾਨ ਕਰਦੇ ਹਨ, ਜੋ ਖੇਡਾਂ ਵਿਚ ਭਾਗ ਲੈਣ ਵਾਲਿਆਂ ਨੂੰ ਸੱਭਿਆਚਾਰ ਵਿਭਿੰਨਤਾਵਾਂ, ਵੱਖ-ਵੱਖ ਜਾਤਾਂ ਅਤੇ ਧਰਮ, ਉਸ ਦੇ ਸਮਾਜਿਕ ਨਿਯਮਾਂ, ਨੈਤਿਕ ਅਤੇ ਨੈਤਿਕ ਮੁੱਦੇ ਨੂੰ ਸਮਝਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 6.
ਜਜਬਾਤਾਂ ਦੇ ਨਿਯੰਤਰਣ ਬਾਰੇ ਤੁਹਾਨੂੰ ਕੀ ਪਤਾ ਹੈ ?
ਉੱਤਰ:
ਮਨੋਵਿਗਿਆਨ ਦੇ ਅਧਿਐਨ ਨਾਲ ਇਕ ਵਿਅਕਤੀ ਅਤੇ ਖਿਡਾਰੀ ਦੇ ਵਿਚਾਰਾਂ ਅਤੇ ਭਾਵਨਾਵਾਂ ਨੂੰ ਖਾਸ ਕਰਕੇ ਅਭਿਆਸ ਅਤੇ ਮੁਕਾਬਲੇ ਦੀ ਸਥਿਤੀ ਨੂੰ ਸਮਝਣ ਵਿਚ ਮੱਦਦ ਮਿਲਦੀ ਹੈ , ਜਿਵੇਂ ਕਿ ਪਰੇਸ਼ਾਨੀ, ਡਰ, ਤਨਾਵ ਆਦਿ ।

ਪ੍ਰਸ਼ਨ 7.
ਸਿੱਖਣ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ?
ਉੱਤਰ:
ਸਿੱਖਣ ਦੀ ਧਾਰਨਾ ਨੂੰ ਵਿਵਹਾਰ ਦੇ ਬਦਲਾਵ ਦੇ ਤਜ਼ਰਬਿਆਂ, ਨਵੀਆਂ ਆਦਤਾਂ ਅਤੇ ਹੁਨਰ ਪ੍ਰਾਪਤੀ ਵਜੋਂ ਸਮਝਿਆ ਜਾ ਸਕਦਾ ਹੈ । ਵਿਵਹਾਰ ਵਿਚ ਬਦਲਾਵ ਆਮ ਤੌਰ ਤੇ ਸਥਾਈ ਹੁੰਦਾ ਹੈ । ਇਹ ਵਿਸ਼ਵਾਸ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ਕਿ ਸਿੱਖਣਾ ਇਕ ਜੀਵਨ ਭਰ ਚੱਲਣ ਵਾਲੀ ਪ੍ਰਕਿਰਿਆ ਹੈ, ਜੋ ਕਿ ਪੰਘੂੜੇ ਵਿਚ ਸ਼ੁਰੂ ਹੁੰਦੀ ਹੈ ਅਤੇ ਕਬਰ ਵਿਚ ਖ਼ਤਮ ਹੋ ਜਾਂਦੀ ਹੈ । ਭਾਵ ਸਿੱਖਣਾ ਜਨਮ ਹੁੰਦਿਆਂ ਹੀ ਸ਼ੁਰੂ ਹੋ ਜਾਂਦਾ ਹੈ ਅਤੇ ਮਰਨ ਉਪਰੰਤ ਹੀ ਖ਼ਤਮ ਹੋ ਜਾਂਦਾ ਹੈ । ਇਹ ਦੇਖਿਆ ਜਾਂਦਾ ਹੈ ਕਿ ਇਕ ਵਿਅਕਤੀ ਆਪਣੇ ਆਪ ਬਚਾਉਣ ਭਾਵ ਜਿੰਦਾ ਰੱਖਣ ਲਈ ਸਮਾਜਿਕ ਹੁਨਰ ਅਤੇ ਵਾਤਾਵਰਣ ਨੂੰ ਗ੍ਰਹਿਣ ਕਰ ਲੈਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 8.
ਸਿੱਖਣ ਦੇ ਵੱਖ-ਵੱਖ ਨਿਯਮਾਂ ਨੂੰ ਉਜਾਗਰ ਕਰੋ ।
ਉੱਤਰ:

• ਤਤਪਰਤਾ/ਤਿਆਰੀ ਦਾ ਨਿਯਮ
• ਪ੍ਰਭਾਵ ਦਾ ਨਿਯਮ ।
• ਅਭਿਆਸ ਦਾ ਨਿਯਮ ।

ਪ੍ਰਸ਼ਨ 9.
ਵਰਤੋਂ ਅਤੇ ਨਾ-ਵਰਤੋਂ ਦੇ ਨਿਯਮ ਵਿਚ ਕੀ ਅੰਤਰ ਹੈ ?
ਉੱਤਰ:
1. ਵਰਤੋਂ ਦਾ ਨਿਯਮ (Law of Use)-ਕਿਸੇ ਕਿਰਿਆ ਦੀ ਵਾਰ-ਵਾਰ ਵਰਤੋਂ ਕਰਨ ਨਾਲ ਸਿੱਖਣ ਪ੍ਰਕਿਰਿਆ ਜ਼ਿਆਦਾ ਹੁੰਦੀ ਹੈ ।
2. ਗੈਰ ਵਰਤੋਂ ਦਾ ਨਿਯਮ (Law of Disuse)–ਜੇਕਰ ਸਿੱਖੇ ਹੋਏ ਗੁਣ ਨੂੰ ਕਾਫੀ ਲੰਬਾ ਸਮਾਂ ਵਰਤੋਂ ਵਿੱਚ ਨਾ ਲਿਆਂਦਾ ਜਾਵੇ ਤਾਂ ਇਹ ਯਾਦ ਵਿਚੋਂ ਨਿਕਲ ਜਾਂਦਾ ਹੈ । ਇਸ ਲਈ ਸਿੱਖੀ ਹੋਈ ਗੱਲ ਦਾ ਦੁਹਰਾਓ ਅਤਿ ਜ਼ਰੂਰੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 10.
ਸਿਖਲਾਈ ਦੇ ਤਬਾਦਲੇ ਤੋਂ ਤੁਸੀਂ ਕੀ ਸਮਝਦੇ ਹੋ ?
ਉੱਤਰ:
ਆਮ ਤੌਰ ਤੇ ਸਿੱਖਣ ਦੇ ਸਥਾਨਾਂਤਰਣ ਤੋਂ ਭਾਵ ਆਦਤਾਂ, ਹੁਨਰ ਅਤੇ ਰਵੱਈਏ ਨੂੰ ਇਕ ਖੇਤਰ ਤੋਂ ਦੂਜੇ ਖੇਤਰ ਵਿਚ ਲੈ ਕੇ ਜਾਣਾ | ਕਈ ਵਾਰ ਇਕ ਖੇਤਰ ਵਿਚ ਸਿੱਖਿਆ ਗਿਆ ਹੁਨਰ ਦੂਜੇ ਖੇਤਰ ਵਿਚ ਮੁਸ਼ਕਿਲ ਪੈਦਾ ਕਰਦਾ ਹੈ । ਇਸ ਕਰਕੇ ਸਿੱਖਣ ਦਾ ਸਥਾਨਾਂਤਰਣ ਦਾ ਪ੍ਰਭਾਵ ਬਹੁਤ ਪ੍ਰਭਾਵੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 11.
ਸਿਖਲਾਈ ਦੇ ਵੱਖ-ਵੱਖ ਸਥਾਨਾਂਤਰਣ ਨੂੰ ਬਿਆਨ ਕਰੋ ।
ਉੱਤਰ:
ਸਿੱਖਣ ਦੇ ਸਥਾਨਾਂਤਰਣ ਦੇ ਪ੍ਰਕਾਰ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਹਨ –

1. ਸਕਾਰਾਤਮਕ ਸਥਾਨਾਂਤਰਣ
2. ਨਕਾਰਾਤਮਕ ਸਥਾਨਾਂਤਰਣ
3. ਜੀਰੋ ਸਥਾਨਾਂਤਰਣ ।

ਪ੍ਰਸ਼ਨ 12.
ਤੁਸੀਂ ਸਿਖਲਾਈ ਦੇ ਸਕਾਰਾਤਮਕ ਸਥਾਨਾਂਤਰਣ ਤੋਂ ਕੀ ਸਮਝਦੇ ਹੋ ? ..
ਉੱਤਰ:
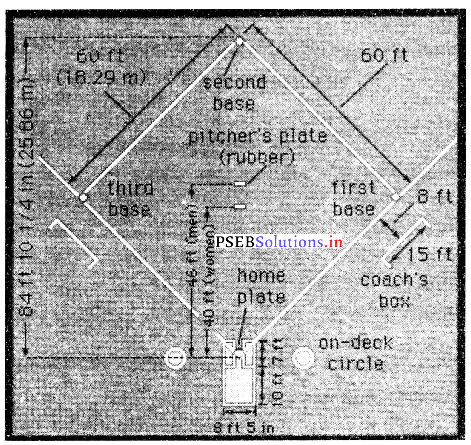
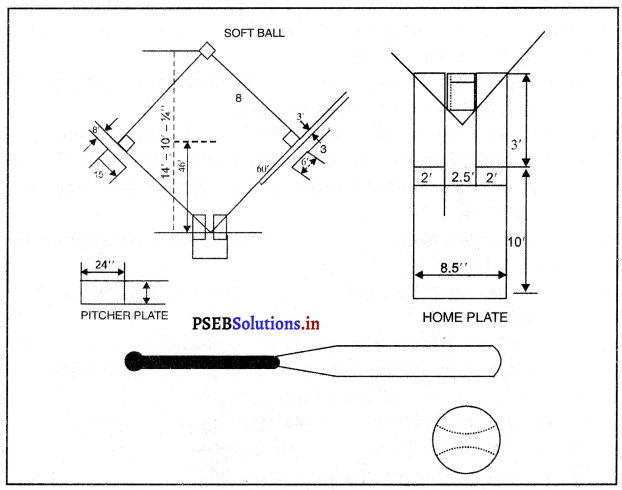
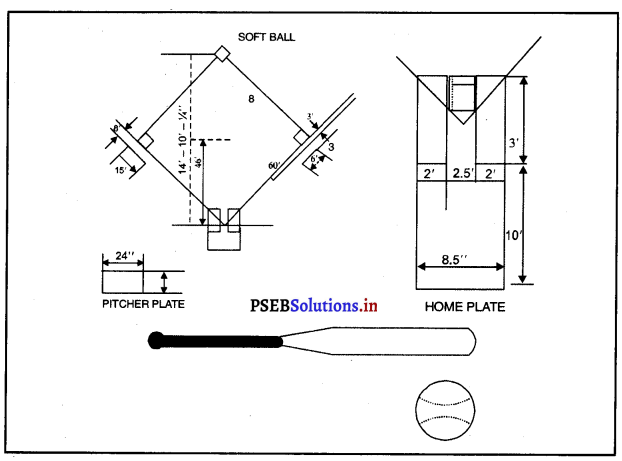
ਸਕਾਰਾਤਮਕ ਸਥਾਨਾਂਤਰਣ (Positive Transfer of Learning)-ਜਦ ਪਿਛਲਾ ਸਿੱਖਿਆ ਹੋਇਆ ਹੁਨਰ ਨਵੇਂ ਸਿੱਖਣ ਵਾਲੇ ਕੰਮ ਵਿਚ ਮਦਦ ਕਰਦਾ ਹੈ, ਤਾਂ ਉਸਨੂੰ ਸਕਾਰਾਤਮਕ ਸਥਾਨਾਂਤਰਣ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਜਿਵੇਂ ਲੰਬੇ ਸਮੇਂ ਤੱਕ ਦੌੜਨ ਵਾਲੀ ਸਹਿਣਸ਼ੀਲਤਾ, ਲੰਬੇ ਸਮੇਂ ਤੱਕ ਤੈਰਾਕੀ ਕਰਨ ਵਿਚ ਮਦਦ ਕਰੇਗਾ । ਇਸੇ ਤਰ੍ਹਾਂ ਯੋਗ ਆਸਣ, ਐਰੋਬਿਕਸ ਵਿਚ ਕੰਮ ਆਉਂਦੇ ਹਨ ਅਤੇ ਕ੍ਰਿਕਟ ਖੇਡਣ ਵਾਲੇ ਸਾਫਟਬਾਲ ਵਰਗੀਆਂ ਖੇਡਾਂ ਖੇਡ ਸਕਦੇ ਹਨ ਆਦਿ ।

ਪ੍ਰਸ਼ਨ 13.
ਸਿਖਲਾਈ ਦੋ ਜੀਰੋ ਸਥਾਨਾਂਤਰਣ ਤੋਂ ਤੁਸੀਂ ਕੀ ਸਮਝਦੇ ਹੋ ?
ਉੱਤਰ:
ਜੀਰੋ ਸਥਾਨਾਂਤਰਣ (Zero Transfer of Training)-ਇਸ ਸਥਿਤੀ ਵਿਚ ਪਹਿਲਾਂ ਸਿੱਖਿਆ ਹੁਨਰ, ਗਿਆਨ ਅਤੇ ਆਦਤਾਂ ਨਵੇਂ ਸਿੱਖਣ ਦੇ ਕੰਮ ਵਿਚ ਨਾ ਹੀ ਸਕਾਰਾਤਮਕ ਪ੍ਰਭਾਵ ਪਾਉਂਦੀ ਹੈ ਅਤੇ ਨਾ ਨਕਾਰਾਤਮਕ ਪ੍ਰਭਾਵ ਪੈਂਦਾ ਹੈ । ਇਸਨੂੰ ਜ਼ੀਰੋ ਸਥਾਨਾਂਤਰਣ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਉਦਾਹਰਣ ਦੇ ਤੌਰ ‘ਤੇ ਵਾਲੀਵਾਲ ਵਿਚ ਸਿੱਖੀ ਸਮੇਮਿੰਗ ਜਾਂ ਸਰਵਿਸ ਦਾ ਜਿਮਨਾਸਟਿਕ ਦੇ ਹੁਨਰ ਤੇ ਪ੍ਰਭਾਵ ਨਾ ਪਾਉਣਾ ।

ਪ੍ਰਸ਼ਨ 14.
ਕਿਸ਼ੋਰ ਅਵਸਥਾ ਦਾ ਅਰਥ ਸਮਝਾਓ ।
ਉੱਤਰ:
ਸ਼ਬਦ “Adolescence’’ ਯੂਨਾਨੀ ਭਾਸ਼ਾ ਦਾ ਸ਼ਬਦ ਹੈ ਜਿਸਦਾ ਭਾਵ ਹੈ ‘ਬਾਲਗ ਉਮਰ ਦਾ ਆਰੰਭ (To grow to maturity) ਆਮ ਤੌਰ ਤੇ ਇਹ ਸਰੀਰਕ ਅਤੇ ਮਾਨਸਿਕ ਤਬਾਦਲੇ ਦੀ ਉਮਰ ਹੁੰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 15.
ਕਿਸ਼ੋਰ ਅਵਸਥਾ ਦੀਆਂ ਵੱਖ-ਵੱਖ ਸਮੱਸਿਆਵਾਂ ਬਾਰੇ ਲਿਖੋ ।
ਉੱਤਰ:

• ਜੈਵਿਕ ਤਬਦੀਲੀਆਂ ਨਾਲ ਸੰਬੰਧਿਤ ਸਮੱਸਿਆਵਾਂ
• ਮਨੋਵਿਗਿਆਨਿਕ ਵਿਹਾਰ ਨਾਲ ਸੰਬੰਧਿਤ ਸਮੱਸਿਆਵਾਂ
• ਆਜ਼ਾਦੀ
• ਪਛਾਣ ਅਤੇ ਸਵੈ-ਨਿਰਣਾ
• ਵਿਨਾਸ਼ਕਾਰੀ ਰੁਝਾਨ ਅਤੇ ਵਿਹਾਰ
• ਹਾਣੀ ਨਾਲ ਦੋਸਤੀ ।

ਪ੍ਰਸ਼ਨ 16.
ਖੇਡਾਂ ਦੇ ਵਿਕਾਸ ਵਿਚ ਯੂਨਾਨੀ ਯੋਗਦਾਨ ਬਾਰੇ ਦੱਸੋ ।
ਉੱਤਰ:
ਯੂਨਾਨ ਦੀ ਸੱਭਿਅਤਾ ਸਭ ਤੋਂ ਪੁਰਾਣੀ ਸੱਭਿਅਤਾ ਵਿਚੋਂ ਇਕ ਹੈ । ਇਸ ਯੁੱਗ ਨੂੰ ਖੇਡ ਦੇ ਸੁਨਹਿਰੀ ਯੁੱਗ ਦੇ ਨਾਮ ਨਾਲ ਜਾਣਿਆ ਜਾਂਦਾ ਹੈ । ਖੇਡਾਂ ਦੇ ਸਭ ਦੇ ਵੱਡੇ ਖੇਡ ਮਹਾਂਉਤਸਵ ਯੂਨਾਨ ਤੋਂ 776 (BC) ਵਿਚ ਸ਼ੁਰੂ ਹੋਇਆ ਜਿਸ ਨੂੰ ਉਲੰਪਿਕ ਦੇ ਨਾਮ ਨਾਲ ਜਾਣਦੇ ਹਾਂ । ਇਹ ਖੇਡ ਯੂਨਾਨ ਦੇ ਦੇਵਤਾ ਯੂਯਸ ਦੇ ਸਨਮਾਨ ਵਿਚ ਖੇਡੀਆਂ ਜਾਂਦੀਆਂ ਹਨ ।

ਪ੍ਰਸ਼ਨ 17.
ਖੇਡਾਂ ਦੇ ਵਿਕਾਸ ਵਿੱਚ ਜਾਪਾਨ ਦੇ ਯੋਗਦਾਨ ਬਾਰੇ ਦੱਸੋ । |
ਉੱਤਰ:
ਜਾਪਾਨ ਦੇ ਇਤਿਹਾਸ ਨੂੰ ਦੋ ਕਾਲਾਂ ਵਿਚ ਵਰਗੀਕਰਣ ਕੀਤਾ ਜਾਂਦਾ ਹੈ, ਮੇਜ਼ੀ ਕਾਲ ( 1867) ਤੋਂ ਪਹਿਲਾ ਅਤੇ ਮੇਜ਼ੀਕਾਲ (1867) ਤੋਂ ਅੱਗੇ ਦਾ ਸਮਾਂ ।
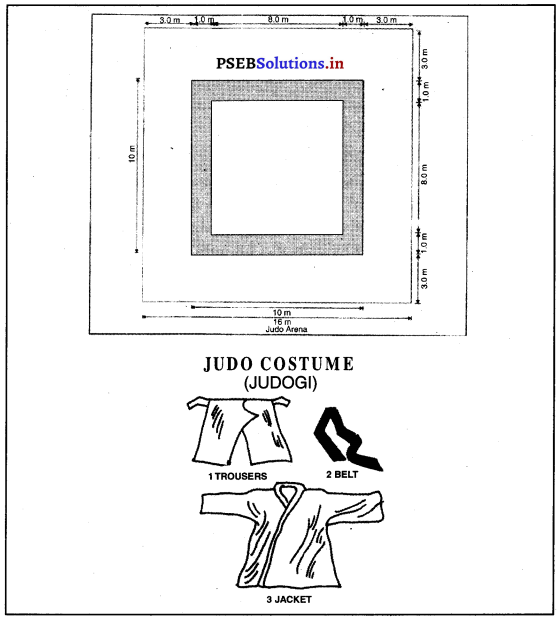
ਜਾਪਾਨ ਨੇ ਕਈ ਤਰ੍ਹਾਂ ਦੀਆਂ ਖੇਡਾਂ ਜਿਵੇਂ ਕਿ ਤੀਰ-ਅੰਦਾਜ਼ੀ, ਘੋੜਸਵਾਰੀ, ਕੁਸ਼ਤੀ ਅਤੇ ਜੂਡੋ ਆਦਿ ਵਰਗੀਆਂ ਖੇਡਾਂ ਸੰਸਾਰ ਨੂੰ ਦਿੱਤੀਆਂ ਹਨ ।

ਤਿੰਨ ਅੰਕਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ (Three Marks Question-Answers)

ਪ੍ਰਸ਼ਨ 1.
ਸਮਾਜ ਸ਼ਾਸਤਰ ਤੋਂ ਤੁਹਾਡਾ ਕੀ ਭਾਵ ਹੈ ?
ਉੱਤਰ:
ਮਨੁੱਖ ਨੂੰ ਕੁਦਰਤ ਦੁਆਰਾ ਇਕ ਸਮਾਜਿਕ ਜਾਨਵਰ (Social animal) ਵਜੋਂ ਜਾਣਿਆ ਜਾਂਦਾ ਹੈ । ਇਹ ਵੀ ਵਿਸ਼ਵਾਸ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ਕਿ ਵਿਅਕਤੀ ਆਪਣੀ ਅੰਦਰਲੇ ਝੁਕਾਵਾਂ ਅਤੇ ਸਮਾਜਿਕ ਗੁਣਾਂ ਦੀ ਮਦਦ ਨਾਲ ਸਵੈਵਾਤਾਵਰਣ ਦੀ ਸਿਰਜਨਾ ਕਰਦਾ ਹੈ । ਉਸਨੂੰ ਆਪਣੇ ਆਲੇ-ਦੁਆਲੇ ਦੇ ਸਹਾਇਕ ਵਾਤਾਵਰਣ ਵਿਚ ਜਿਊਣ ਲਈ ਸਮਾਜਿਕ ਹੁਨਰ ਨੂੰ ਸਿੱਖਣ ਦੀ ਲੋੜ ਪੈਂਦੀ ਹੈ ਜਿਸ ਲਈ ਉਸਨੂੰ ਸਮਾਜਿਕ ਸਿੱਖਿਆ ਦੇ ਰਾਹੀਂ ਜਾਣਾ ਪੈਂਦਾ ਹੈ । ਇਸ ਨੂੰ ਸਮਾਜ ਸ਼ਾਸਤਰ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਸਮਾਜ ਸ਼ਾਸਤਰ ਇੱਕ ਅਜਿਹਾ ਵਿਸ਼ਾ ਹੈ ਜੋ ਕਿ ਸਮਾਜ ਨੂੰ ਸਮਝਣ ਅਤੇ ਵਿਸ਼ਲੇਸ਼ਣ ਦਾ ਗਿਆਨ ਪ੍ਰਦਾਨ ਕਰਦਾ ਹੈ ।

ਸਮਾਜ ਸ਼ਾਸਤਰ ਦਾ ਅਰਥ-ਸਮਾਜ ਸ਼ਾਸਤਰ ਸ਼ਬਦ ਦੋ ਸ਼ਬਦਾਂ ਦੇ ਸੁਮੇਲ ਤੋਂ ਬਣਿਆ ਹੈ, ਜਿਸ ਵਿਚ ਸੋਸ਼ਨ ਦਾ ਮਤਲਬ ‘ਐਸੋਸਿਏਜ ਜਾਂ ਸਮਾਜਿਕ’’ ਅਤੇ ‘ਲੋਗੋ’’ ਤੋਂ ਭਾਵ ਹੈ, ਵਿਗਿਆਨ ਜਾਂ ਅਧਿਐਨ ਕਰਨਾ । ਇਸ ਤਰ੍ਹਾਂ ਸਮਾਜ ਸ਼ਾਸਤਰ “ਸਮਾਜ ਦਾ ਵਿਗਿਆਨ’ ਹੈ । | ਸਮਾਜਿਕ ਵਿਗਿਆਨ ਸਮਾਜ ਦਾ ਵਿਗਿਆਨ ਹੈ । ਇਹ ਸਮਾਜਿਕ ਰਿਸ਼ਤੇ, ਹਰ ਰੋਜ਼ ਦੀ ਜਿੰਦਗੀ ਦੇ ਮੇਲਜੋਲ ਅਤੇ ਸੱਭਿਆਚਾਰ ਦੇ ਅਧਿਐਨ ਦਾ ਇਕ ਪੈਟਰਨ ਹੈ । ਇਸ ਦਾ ਸੰਬੰਧ ਸਮਾਜ ਦੀ ਉਤਪੱਤੀ, ਕਾਰਜ ਅਤੇ ਸਮੱਸਿਆਵਾਂ ਦੇ ਸੰਬੰਧ ਵਿਚ ਮਨੁੱਖੀ ਸਮਾਜ ਦਾ ਅਧਿਐਨ ਕਰਨਾ ਹੈ । ਇਹ ਲੋਕਾਂ, ਸਮੂਹ, ਸੰਸਥਾਵਾਂ ਅਤੇ ਸੱਭਿਆਚਾਰ ਦੇ ਸੰਬੰਧ ਵਿਚ ਕੰਮ ਕਰਦਾ ਹੈ । ਇਹ ਪਰਿਵਾਰ, ਧਰਮ, ਸਿੱਖਿਆ, ਰਾਜਨੀਤੀ, ਮਨੁੱਖੀ ਵਤੀਰੇ ਅਤੇ ਸੱਭਿਆਚਾਰ ਨੂੰ ਸਮਝਣ ਵਿਚ ਵੀ ਮਦਦ ਕਰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਮਨੁੱਖੀ ਵਤੀਰੇ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਨ ਵਾਲੀਆਂ ਕੋਈ ਦੋ ਸੰਸਥਾਵਾਂ ਬਾਰੇ ਲਿਖੋ ।
ਉੱਤਰ :
1. ਪਰਿਵਾਰ (Family)-ਮਨੁੱਖੀ ਵਤੀਰੇ ਨੂੰ ਪਰਿਵਾਰ ਸਭ ਤੋਂ ਪਹਿਲਾਂ ਪ੍ਰਭਾਵਿਤ ਕਰਦਾ ਹੈ । ਪਰਿਵਾਰ ਮਨੁੱਖੀ ਵਤੀਰੇ ਦੀ ਨੀਂਹ ਹੁੰਦਾ ਹੈ । ਬੱਚੇ ਦੇ ਵਿਹਾਰ ਨੂੰ ਪਰਿਵਾਰਕ ਪਰੰਪਰਾਵਾਂ, ਕਦਰਾਂ, ਕੀਮਤਾਂ, ਵਿਸ਼ਵਾਸ, ਨੈਤਿਕਤਾ ਆਦਿ ਸਭ ਤੋਂ ਵੱਧ ਪ੍ਰਭਾਵਿਤ ਕਰਦੀਆਂ ਹਨ | ਪਰਿਵਾਰ ਪ੍ਰਾਇਮਰੀ ਸਮਾਜਿਕ ਸਮੂਹ ਹੋਣ ਕਾਰਣ ਬੱਚੇ ਦੇ ਵਿਹਾਰ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਦਾ ਹੈ । ਬੱਚੇ ਮਾਂ-ਬਾਪ ਦੁਆਰਾ ਦੱਸੀਆਂ ਗੱਲਾਂ ਦੀ ਪਾਲਣਾ ਕਰਦੇ ਹਨ ਪਰ ਸਭ ਤੋਂ ਜ਼ਿਆਦਾ ਉਹ ਰੋਜ਼ਾਨਾ ਜੀਵਨ ਦੇ ਨਿਰੀਖਣ ਤੋਂ ਸਿੱਖਦੇ ਹਨ । ਮਾਂ-ਬਾਪ ਦੇ ਸੰਬੰਧ ਬੱਚਿਆਂ ਦੇ ਜ਼ਿਆਦਾਤਰ ਪਹਿਲੂਆਂ ਉੱਤੇ ਵੱਡਾ ਪ੍ਰਭਾਵ ਹੁੰਦਾ ਹੈ ਇਸ ਕਰਕੇ ਆਮ ਤੌਰ ਤੇ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ਕਿ ਮਾਪੇ ਆਪਣੇ ਬੱਚੇ ਦੇ ਕੈਰੀਅਰ ਨੂੰ ਬਣਾ ਵੀ ਸਕਦੇ ਹਨ ਅਤੇ ਵਿਗਾੜ ਵੀ ਸਕਦੇ ਹਨ ।

2. ਵਿੱਦਿਅਕ ਸੰਸਥਾਵਾਂ (Educational Institutions)-ਵਿੱਦਿਅਕ ਸੰਸਥਾਵਾਂ ਜਿਵੇਂ ਕਿ ਸਕੂਲ ਬੱਚੇ ਦੇ ਜੀਵਨ ਵਿਚ ਮਹੱਤਵਪੂਰਨ ਭੂਮਿਕਾ ਨਿਭਾਉਂਦੇ ਹਨ । ਇਹ ਸੰਸਥਾਵਾਂ ਬੱਚਿਆਂ ਦੀ ਸ਼ਖਸੀਅਤ ਨੂੰ ਬਣਾਉਣ ਅਤੇ ਦੋਸਤ, ਪਰਿਵਾਰ ਅਤੇ ਅਧਿਆਪਕਾਂ ਨਾਲ ਸਕਾਰਾਤਮਕ ਗੱਲਬਾਤ ਕਰਨ ਵਿਚ ਮਦਦ ਕਰਦੀਆਂ ਹਨ । ਇਸ ਲਈ ਸਕੂਲ ਨੂੰ ਬੱਚੇ ਦਾ ਦੂਜਾ ਘਰ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਬੱਚਿਆਂ ਦਾ ਵਿਵਹਾਰ ਅਤੇ ਉਨ੍ਹਾਂ ਦੀ ਸ਼ਖਸੀਅਤ ਦਾ ਵਿਕਾਸ ਅਤੇ ਪਾਲਣ-ਪੋਸ਼ਣ ਸਿਰਫ ਮਾਪਿਆਂ ਤੇ ਨਿਰਭਰ ਨਹੀਂ ਕਰਦਾ ਹੈ, ਪਰ ਜਿਸ ਤਰੀਕੇ ਨਾਲ ਉਹ ਵਿਕਾਸ ਕਰਦੇ ਹਨ, ਸਕੂਲਾਂ ਲਈ ਵੀ ਇਕ ਚੁਣੌਤੀਪੂਰਨ ਕੰਮ ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਹੇਠ ਲਿਖਿਆਂ `ਤੇ ਨੋਟ ਲਿਖੋ ।
(ਉ) ਧਾਰਮਿਕ ਸੰਸਥਾਵਾਂ
(ਅ) ਰਾਸ਼ਟਰੀ ਸੱਭਿਆਚਾਰ ।
ਉੱਤਰ:
(ੳ) ਧਾਰਮਿਕ ਸੰਸਥਾਵਾਂ (Religious institutions)-ਇਹ ਇਕ ਅਜਿਹੀ ਥਾਂ ਹੈ ਜਿੱਥੇ ਸੰਯੁਕਤ ਪ੍ਰਣਾਲੀ ਹੈ ਜਿੱਥੇ ਪਵਿੱਤਰ ਵਿਸ਼ਵਾਸ, ਕਦਰਾਂ-ਕੀਮਤਾਂ ਅਤੇ ਰੀਤੀ-ਰਿਵਾਜ ਹਾਸਲ ਹੋ ਜਾਂਦੇ ਹਨ । ਇਹ ਸੰਸਥਾਵਾਂ ਨੈਤਿਕ ਕਦਰਾਂ-ਕੀਮਤਾਂ ਅਤੇ ਰੀਤੀ-ਰਿਵਾਜ ਹਾਸਲ ਹੋ ਜਾਂਦੇ ਹਨ । ਇਹ ਸੰਸਥਾਵਾਂ ਨੈਤਿਕ ਕਦਰਾਂ ਕੀਮਤਾਂ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਨ ਵਿਚ ਪ੍ਰਮੁੱਖ ਭੂਮਿਕਾ ਨਿਭਾਉਂਦੀ ਹੈ ਜਿਵੇਂ ਕਿ ਸੱਚ ਬੋਲਣਾ, ਨੁਕਸਾਨ ਨਾ ਪਹੁੰਚਾਉਣਾ, ਦੂਸਰਿਆਂ ਦਾ ਹਮਦਰਦੀ ਭਰਿਆ ਰਵੱਈਆ, ਬਜ਼ੁਰਗਾਂ ਦਾ ਆਦਰ ਕਰਨਾ ਆਦਿ ਮੂਲ ਬੱਚੇ ਦੇ ਵਿਹਾਰ ਵਿਚ ਮਹੱਤਵਪੂਰਨ ਭੂਮਿਕਾ ਨਿਭਾਉਂਦੇ ਹਨ ।

(ਅ) ਰਾਸ਼ਟਰੀ ਸੱਭਿਆਚਾਰ (National Culture)-ਰਾਸ਼ਟਰੀ ਸੱਭਿਆਚਾਰ ਬੱਚਿਆਂ ਦੀ ਜ਼ਿੰਦਗੀ ਤੇ ਭਾਰੀ ਪ੍ਰਭਾਵ ਪਾਉਂਦਾ ਹੈ । ਜਿਸ ਦੇਸ਼ ਵਿਚ ਬੱਚਾ ਜਨਮ ਲੈਂਦਾ ਹੈ, ਉੱਥੇ ਦੇ ਰੀਤੀ-ਰਿਵਾਜ, ਰਹਿਣ-ਸਹਿਣ, ਵਾਤਾਵਰਣ ਅਤੇ ਸੋਚ ਨੂੰ ਅਪਣਾਉਂਦਾ ਹੈ ਅਤੇ ਉਸਦਾ ਮਾਣ ਮਹਿਸੂਸ ਕਰਦਾ ਹੈ । ਇਹ ਹੀ ਸੋਚ ਰਾਸ਼ਟਰ ਦੀ ਤਾਕਤ ਬਣਦੀ ਹੈ ।ਅੱਜ ਦਾ ਬੱਚਾ ਕੱਲ੍ਹ ਕੌਮ ਦੀ ਉਮੀਦ ਹੈ ਅਤੇ ਅੱਜ ਉਸਦਾ ਵਿਕਾਸ, ਕੱਲ੍ਹ ਰਾਸ਼ਟਰ ਦਾ ਵਿਕਾਸ ਹੈ । ਸਵਾਮੀ ਵਿਵੇਕਾਨੰਦ ਦੇ ਅਨੁਸਾਰ, ਅੱਜ ਦਾ ਬੱਚਾ ਭਵਿੱਖ ਦਾ ਮਾਤਾ-ਪਿਤਾ, ਭਵਿੱਖ ਦਾ ਨਾਗਰਿਕ ਅਤੇ ਦੇਸ਼ ਦਾ ਭਵਿੱਖ ਹੈ । ਉਹਨਾਂ ਨੂੰ ਖਾਸ ਦੇਖਭਾਲ ਦੀ ਲੋੜ ਹੈ, ਉਹਨਾਂ ਦੇ ਅਧਿਕਾਰਾਂ ਦੀ ਰਾਖੀ ਦੀ ਲੋੜ ਹੈ ਕਿਉਂਕਿ ਉਹ ਕੱਲ ਦੇ ਜ਼ਿੰਮੇਵਾਰ ਨਾਗਰਿਕ ਹੋਣਗੇ ।

ਪ੍ਰਸ਼ਨ 4.
ਰਾਸ਼ਟਰੀ ਏਕਤਾ ਵਿਚ ਖੇਡਾਂ ਦੀ ਭੂਮਿਕਾ ਨੂੰ ਤੁਸੀਂ ਕਿਵੇਂ ਸਪੱਸ਼ਟ ਕਰੋਗੇ ?
ਉੱਤਰ:
ਸਰੀਰਕ ਸਿੱਖਿਆ ਅਤੇ ਖੇਡਾਂ ਦੇ ਪ੍ਰੋਗਰਾਮ ਰਾਸ਼ਟਰੀ ਅਤੇ ਅੰਤਰਰਾਸ਼ਟਰੀ ਅਖੰਡਤਾ ਵਿਚ ਕੀਮਤੀ ਰੂਪ ਨਾਲ ਵਿਕਾਸ ਦਾ ਕੰਮ ਕਰਦੇ ਹਨ । ਇਹ ਅਜਿਹੀਆਂ ਗਤੀਵਿਧੀਆਂ ਪ੍ਰਦਾਨ ਕਰਦੇ ਹਨ, ਜੋ ਖੇਡਾਂ ਵਿਚ ਭਾਗ ਲੈਣ ਵਾਲਿਆਂ ਨੂੰ ਸੱਭਿਆਚਾਰ ਵਿਭਿੰਨਤਾਵਾਂ, ਵੱਖ-ਵੱਖ ਜਾਤਾਂ ਅਤੇ ਧਰਮ ਉਸ ਦੇ ਸਮਾਜਿਕ ਨਿਯਮਾਂ, ਨੈਤਿਕ ਅਤੇ ਨੈਤਿਕ ਮੁੱਦੇ ਨੂੰ ਸਮਝਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰਦੇ ਹਨ |

ਸਰੀਰਕ ਸਿੱਖਿਆ ਅਤੇ ਖੇਡਾਂ ਸਾਂਝੇ ਮੰਤਵ ਲਈ ਕੰਮ ਕਰਨ ਵਾਲਿਆਂ ਲੋਕਾਂ ਨੂੰ ਇੱਕ-ਜੁੱਟ ਕਰਕੇ ਇਕ ਸਾਂਝਾ ਪਲੇਟਫਾਰਮ ਪ੍ਰਦਾਨ ਕਰਦੀਆਂ ਹਨ । ਇਸ ਲਈ ਸਰੀਰਕ ਸਿੱਖਿਆ ਅਤੇ ਖੇਡਾਂ ਨੂੰ ਸਕੂਲੀ ਪ੍ਰੋਗਰਾਮ ਵਿਚ ਨੈਤਿਕ ਮੁੱਲ ਅਪਣਾਉਣ ਲਈ ਅਭਿਆਸ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ । ਖੇਡਾਂ ਰਾਹੀਂ ਭਾਈਚਾਰਕ ਏਕਤਾ ਦੇ ਵਿਕਾਸ ਨੂੰ ਧਿਆਨ ਵਿੱਚ ਰੱਖਦੇ ਹੋਏ ਇਸ ਨੂੰ ਵਿੱਦਿਆ (education) ਦਾ ਖਾਸ ਹਿੱਸਾ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ । ਉਲੰਪਿਕ ਖੇਡਾਂ ਦੀ ਉਤਪੱਤੀ ਦੇ ਵਿਚਾਰ ਪਿੱਛੇ ਯੂਨਾਨੀ ਦੁਆਰਾ ਖੇਡਾਂ ਵਿਚ ਭਾਈਚਾਰੇ ਅਤੇ ਸਹਿਯੋਗ ਦੀ ਭਾਵਨਾ ਦਾ ਵਿਕਾਸ ਕਰਨਾ ਸੀ । ਫਰਾਸ ਦੇ ਬੈਰਨ ਪਰੇਰੇ ਡੀ ਕੁਬਰਟਿਨ (Baran Pierre de Coubertin) ਨੇ ਇਸ ਵਿਚਾਰ ਨੂੰ ਅੱਗੇ ਵਧਾਇਆ ਅਤੇ ਉਲੰਪਿਕ ਖੇਡਾਂ ਨੂੰ 1896 ਵਿਚ ਫਿਰ ਤੋਂ ਸੁਰਜੀਤ ਕੀਤਾ ।

ਪ੍ਰਸ਼ਨ 5.
ਮਨੋਵਿਗਿਆਨ ਸ਼ਬਦ ਦੀਆਂ ਦੋ ਪਰਿਭਾਸ਼ਾਵਾਂ ਦਿਉ !
ਉੱਤਰ:
ਕਰੋਅ ਅਤੇ ਕਰੋਅ (Crow and Crow) ਦੇ ਅਨੁਸਾਰ, “ਮਨੋਵਿਗਿਆਨ, ਮਨੁੱਖੀ ਵਰਤਾਓ ਅਤੇ ਸੰਬੰਧਾਂ ਦਾ ਅਧਿਐਨ ਹੈ । ਕਲਾਰਕ ਅਤੇ ਕਲਾਰਕ (Clark and Clark) ਦੇ ਅਨੁਸਾਰ, “ਖੇਡ ਮਨੋਵਿਗਿਆਨ ਇਕ ਪ੍ਰਭਾਵੀ ਮਨੋਵਿਗਿਆਨ ਹੈ । ਇਹ ਮੁਖਬੀਅਤਾ, ਭਾਵਨਾਤਮਕ ਅਤੇ ਪ੍ਰੇਕ ਪਹਿਲੂਆਂ ਅਤੇ ਸਰੀਰਕ ਗਤੀਵਿਧੀਆਂ ਨਾਲ ਸੰਬੰਧ ਰੱਖਦਾ ਹੈ । ਇਹ ਮਨੋਵਿਗਿਆਨ ਵਿਚ ਵਰਤੀਆਂ ਜਾਂਦੀਆਂ ਕਈ ਤਕਨੀਕਾਂ ਨਿਯੁਕਤ ਕਰਦਾ ਹੈ । ਮੌਕ ਡੋਊਗਾਲ (Mc. Dougall) ਦੇ ਅਨੁਸਾਰ, “ਮਨੋਵਿਗਿਆਨ, ਮਨੁੱਖੀ ਆਚਰਣ ਤੇ ਵਿਵਹਾਰ ਦਾ ਆਸ਼ਾਵਾਦੀ ਵਿਗਿਆਨ ਹੈ ।”

ਪ੍ਰਸ਼ਨ 6.
ਸਰੀਰਕ ਸਿੱਖਿਆ ਵਿਚ ਖੇਡ ਮਨੋਵਿਗਿਆਨ ਦੇ ਮਹੱਤਵ ਨੂੰ ਸਮਝਾਓ ।
ਉੱਤਰ:
ਮਨੋਵਿਗਿਆਨ ਦਾ ਮਹੱਤਵ (Importance of Psychology)-ਸਰੀਰਕ ਸਿੱਖਿਆ ਅਤੇ ਖੇਡਾਂ ਵਿਚ ਸਰੀਰਕ ਗਤੀਆਂ ਹੁੰਦੀਆਂ ਹਨ ਜੋ ਕਿ ਖੇਡ ਵਾਤਾਵਰਣ ਦੇ ਅਨੁਸਾਰ ਹੁੰਦੀਆਂ ਹਨ । ਸਿੱਖਿਆ ਦੇ ਵਿੱਚ ਮਨੋਵਿਗਿਆਨ ਦੇ ਸਿਧਾਂਤ ਨੂੰ ਲਾਗੂ ਕਰਨ ਲਈ ਮਨੋਵਿਗਿਆਨ ਦੀ ਲੋੜ ਪੈਂਦੀ ਹੈ । ਸਰੀਰਕ ਸਿੱਖਿਆ ਦੇ ਸੰਗਠਿਤ ਪ੍ਰੋਗਰਾਮ ਅਤੇ ਮੁਕਾਬਲਿਆਂ ਵਿਚ, ਜਿੱਥੇ ਹਰ ਕੋਈ ਜਿੱਤਣਾ ਚਾਹੁੰਦਾ ਹੈ, ਬਿਨਾਂ ਮਨੋਵਿਗਿਆਨ ਦੇ ਗਿਆਨ ਤੋਂ ਬਿਨਾਂ ਹੀ ਪ੍ਰਦਰਸ਼ਨ ਨਹੀਂ ਕਰ ਸਕਦਾ।

ਇੱਥੇ ਖਿਡਾਰੀ ਦੇ ਮਨੋਵਿਗਿਆਨ ਵਿਹਾਰ ਜਿਵੇਂ ਕਿ ਉਸਦੀ ਰੁਚੀ, ਰਵੱਈਏ, ਪ੍ਰੇਰਨਾ ਅਤੇ ਭਾਵਨਾਤਮਕ ਵਿਹਾਰ ਦਾ ਗਿਆਨ ਹੋਣਾ ਜ਼ਰੂਰੀ ਹੈ । ਖੇਡਾਂ ਵਿਚ ਖੇਡ ਕੁਸ਼ਲਤਾ ਕਿਸੇ ਵੀ ਭੌਤਿਕ ਜਾਂ ਮਨੋਵਿਗਿਆਨ ਕਾਰਕਾਂ ਦੀ ਪ੍ਰਤੀਬੰਧਿਤ ਨਹੀਂ ਹੁੰਦੀ ਹੈ । ਇਹ ਗੱਲ ਵੀ ਚੰਗੀ ਤਰ੍ਹਾਂ ਸਮਝੀ ਜਾ ਚੁੱਕੀ ਹੈ ਕਿ ਖੇਡ ਕਾਰਜਕੁਸ਼ਲਤਾ ਤੇ ਕਈ ਮਨੋਵਿਗਿਆਨ ਤੱਤਾਂ ਦਾ ਪ੍ਰਭਾਵ ਪੈਂਦਾ ਹੈ, ਜੋ ਕਿ ਖਿਡਾਰੀ ਦੇ ਪ੍ਰਦਰਸ਼ਨ ਦੇ ਪੱਧਰ ਨੂੰ ਸੁਧਾਰਦੇ ਹਨ | ਸਰੀਰਕ ਸਿੱਖਿਆ ਦੇ ਅਧਿਆਪਕ, ਕੋਚਾਂ ਅਤੇ ਟਰਨੇਰ ਨੂੰ ਵਿਅਕਤੀਗਤ ਵਿਕਾਸ ਅਤੇ ਪ੍ਰਾਪਤੀਆਂ ਲਈ ਮਨੋਵਿਗਿਆਨ ਦਾ ਗਿਆਨ ਲਾਗੂ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ । ਮਨੋਵਿਗਿਆਨ ਦੀ ਮਹੱਤਤਾ ਨੂੰ ਹੇਠ ਲਿਖੀਆਂ ਪਰਿਭਾਸ਼ਾਵਾਂ ਦੁਆਰਾ ਵੀ ਸਮਝਿਆ ਜਾ ਸਕਦਾ ਹੈ ,|

ਪ੍ਰਸ਼ਨ 7.
ਸਿੱਖਣ ਦਾ ਸੰਕਲਪ ਕੀ ਹੈ ?
ਉੱਤਰ:
ਸਿੱਖਣ ਦੀ ਧਾਰਨਾ ਨੂੰ ਵਿਵਹਾਰ ਦੇ ਬਦਲਾਵ ਦੇ ਤਜ਼ਰਬਾ, ਨਵੀਆਂ ਆਦਤਾਂ ਅਤੇ ਹੁਨਰ ਪ੍ਰਾਪਤੀ ਵਜੋਂ ਸਮਝਿਆ ਜਾ ਸਕਦਾ ਹੈ । ਵਿਵਹਾਰ ਵਿਚ ਬਦਲਾਵ ਆਮ ਤੌਰ ਤੇ ਸਥਾਈ ਹੁੰਦਾ ਹੈ । ਇਹ ਵਿਸ਼ਵਾਸ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ਕਿ ਸਿੱਖਣਾ ਇਕ ਜੀਵਨ ਭਰ ਚੱਲਣ ਵਾਲੀ ਪ੍ਰਕਿਰਿਆ ਹੈ, ਜੋ ਕਿ ਪੰਘੂੜੇ ਵਿਚ ਸ਼ੁਰੂ ਹੁੰਦੀ ਹੈ ਅਤੇ ਕਬਰ ਵਿਚ ਖ਼ਤਮ ਹੋ ਜਾਂਦੀ ਹੈ । ਭਾਵ ਸਿੱਖਣਾ ਜਨਮ ਹੁੰਦਿਆਂ ਹੀ ਸ਼ੁਰੂ ਹੋ ਜਾਂਦਾ ਹੈ ਅਤੇ ਮਰਨ ਉਪਰੰਤ ਹੀ ਖ਼ਤਮ ਹੋ ਜਾਂਦਾ ਹੈ ।

ਇਹ ਦੇਖਿਆ ਜਾਂਦਾ ਹੈ ਕਿ ਇਕ ਵਿਅਕਤੀ ਆਪਣੇ ਆਪ ਬਚਾਉਣ ਭਾਵ ਜਿੰਦਾ ਰੱਖਣ ਲਈ ਸਮਾਜਿਕ ਹੁਨਰ ਅਤੇ ਵਾਤਾਵਰਣ ਨੂੰ ਗ੍ਰਹਿਣ ਕਰ ਲੈਂਦਾ ਹੈ । ਇਹ ਜ਼ਰੂਰੀ ਨਹੀਂ ਹੈ ਕਿ ਵਿਅਕਤੀ ਦੇ ਵਿਹਾਰ ਵਿਚ ਸਕਾਰਾਤਮਕ ਤਬਦੀਲੀ ਹੀ ਹੋਵੇ । ਵਿਹਾਰ ਵਿਚ ਢੁੱਕਵੀਂ ਤਬਦੀਲੀ ਸਮਾਜਿਕ ਸੰਤੁਸ਼ਟੀ ਅਤੇ ਸੰਪੂਰਨਤਾ ਤੇ ਨਿਰਭਰ ਕਰਦੀ ਹੈ । | ਇਸ ਲਈ ਕਿਹਾ ਜਾ ਸਕਦਾ ਹੈ ਕਿ ਸਿੱਖਣਾ ਵਿਹਾਰ ਵਿਚ ਬਦਲਾਵ ਕਰਨਾ, ਨਵੇਂ ਵਿਹਾਰ ਦਾ ਅਭਿਆਸ ਕਰਨਾ ਅਤੇ ਉਸਦੇ ਆਏ ਨਤੀਜਿਆਂ ਤੋਂ ਵਿਹਾਰ ਨੂੰ ਸਥਾਈ ਰੂਪ ਦੇਣਾ ਹੀ ਸਿੱਖਣਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 8.
ਸਿਖਲਾਈ ਨੂੰ ਪਰਿਭਾਸ਼ਿਤ ਕਰੋ ।
ਉੱਤਰ:
ਗੇਟਸ (Gates) ਦੇ ਅਨੁਸਾਰ, “ਸਿੱਖਣਾ, ਅਨੁਭਵ ਤੇ ਸਿਖਲਾਈ ਦੀ ਤਬਦੀਲੀ ਹੈ।” ਈ. ਆਰ. ਹਿਲਗਰਡ (E.R. Hilgard) ਦੇ ਅਨੁਸਾਰ, “ਸਿੱਖਣਾ ਵਿਹਾਰ ਵਿਚ ਇਕ ਸਥਾਈ ਤਬਦੀਲੀ ਹੈ ਜੋ ਕਿ ਪੁਰਾਣੇ ਅਨੁਭਵਾਂ ਦੇ ਅਨੁਸਾਰ ਵਾਪਰਦਾ ਹੈ । ਮਿਟੌਲ (Mitchel) ਦੇ ਅਨੁਸਾਰ, “ਸਿਖਲਾਈ ਨੂੰ ਨਵੇਂ ਵਿਵਹਾਰ ਨੂੰ ਹਾਸਲ ਕਰਨ ਦੇ ਰੂਪ ਵਿਚ ਪਰਿਭਾਸ਼ਿਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਜੀ. ਮਰਫੀ (G. Murphy) ਦੇ ਅਨੁਸਾਰ, “ਸਿੱਖਣਾ ਵਿਹਾਰ ਵਿਚ ਉਸ ਹੋਰ ਸੋਧ ਨੂੰ ਸ਼ਾਮਲ ਕਰਦਾ ਹੈ ਜੋ ਵਾਤਾਵਰਨ ਦੀਆਂ ਜ਼ਰੂਰਤਾਂ ਨੂੰ ਪੂਰਾ ਕਰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 9.
ਸਿਖਲਾਈ ਦੇ ਤਬਾਦਲੇ ਦੀਆਂ ਕਿਸਮਾਂ ਨੂੰ ਦੱਸੋ ।
ਉੱਤਰ:
ਸਿੱਖਣ ਦੇ ਸਥਾਨਾਂਤਰਣ ਦੇ ਪ੍ਰਕਾਰ (Types of Transfer of training)-ਨਵਾਂ ਸਿੱਖਣਾ ਪਿਛਲੇ ਸਿੱਖੇ ਹੋਏ ਕੰਮ ਨੂੰ ਤਿੰਨ ਤਰੀਕਿਆਂ ਨਾਲ ਪ੍ਰਭਾਵਿਤ ਕਰਦਾ ਹੈ । ਜਿਵੇਂ ਹੁਨਰ, ਵਿਹਾਰ ਅਤੇ ਗਿਆਨ ।ਕਈ ਵੇਰ ਨਵਾਂ ਸਿੱਖਣਾ ਪੁਰਾਣੇ ਸਿੱਖੇ ਕੰਮ ਵਿਚ ਮੁਸ਼ਕਿਲਾਂ ਪੈਦਾ ਕਰਦਾ ਹੈ ਅਤੇ ਕਈ ਵਾਰ ਕਿਸੇ ਵੀ ਤਰੀਕੇ ਨਾਲ ਪ੍ਰਭਾਵਿਤ ਨਹੀਂ ਕਰਦਾ ।

ਇਸ ਲਈ ਇਸ ਨੂੰ ਸਮਝਣ ਲਈ ਇਸ ਨੂੰ ਤਿੰਨ ਭਾਗਾਂ ਵਿਚ ਵੰਡਿਆ ਜਾਂਦਾ ਹੈ ।
1. ਸਕਾਰਾਤਮਕ ਸਥਾਨਾਂਤਰਣ (Positive transfer of learning)-ਜਦ ਪਿੱਛਲਾ ਸਿੱਖਿਆ ਹੋਇਆ ਹੁਨਰ ਨਵੇਂ ਸਿੱਖਣ ਵਾਲੇ ਕੰਮ ਵਿਚ ਮਦਦ ਕਰਦਾ ਹੈ, ਤਾਂ ਉਸਨੂੰ ਸਕਾਰਾਤਮਕ ਸਥਾਨਾਂਤਰਣ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਜਿਵੇਂ ਲੰਬੇ ਸਮੇਂ ਤੱਕ ਦੌੜਨ ਵਾਲੀ ਸਹਿਣਸ਼ੀਲਤਾ, ਲੰਬੇ ਸਮੇਂ ਤੱਕ ਤੈਰਾਕੀ ਕਰਨ ਵਿਚ ਮਦਦ ਕਰੇਗਾ । ਇਸੇ ਤਰ੍ਹਾਂ ਯੋਗ ਆਸਣ, ਐਰੋਬਿਕਸ ਵਿਚ ਕੰਮ ਆਉਂਦੇ ਹਨ ਅਤੇ ਕ੍ਰਿਕਟ ਖੇਡਣ ਵਾਲੇ ਸਾਫਟਬਾਲ ਵਰਗੀਆਂ ਖੇਡਾਂ ਖੇਡ
ਸਕਦੇ ਹਨ ਆਦਿ ।

2. ਨਾਰਾਤਮਕ ਸਥਾਨਾਂਤਰਣ (Negative Transfer of Training-ਇਸ ਸਥਿਤੀ ਵਿਚ ਪਹਿਲਾਂ ਸਿੱਖਿਆ ਹੁਨਰ, ਆਦਤਾਂ ਅਤੇ ਗਿਆਨ ਨਵੇਂ ਕੰਮ ਨੂੰ ਸਿੱਖਣ ਵਿਚ ਮੁਸ਼ਕਿਲਾਂ ਪੈਦਾ ਕਰਦੇ ਹਨ, ਤਾਂ ਇਹਨਾਂ ਨੂੰ ਨਕਾਰਾਤਮਕ ਸਥਾਨਾਂਤਰਣ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਜਿਵੇਂ ਕਿ ਟੈਨਿਸ ਖਿਡਾਰੀ ਨੂੰ ਬੈਡਮਿੰਟਨ ਦਾ ਰੈਕਟ ਫੜਨ ਵਿਚ ਮੁਸ਼ਕਿਲ ਹੋਣਾ । ਕਿਉਂਕਿ ਟੈਨਿਸ ਵਿਚ ਹੱਥ ਦੀ ਗਰਿੱਪ ਸਖ਼ਤ ਹੁੰਦੀ ਹੈ ਜਦਕਿ ਬੈਡਮਿੰਟਨ ਵਿਚ ਰੈਕਟ ਪੋਲੇ ਹੱਥਾਂ ਨਾਲ ਫੜਨਾ ਹੁੰਦਾ ਹੈ ।

3. ਜੀਰੋ ਸਥਾਨਾਂਤਰਣ (Zero Transfer of Training-ਇਸ ਸਥਿਤੀ ਵਿਚ ਪਹਿਲਾਂ ਸਿੱਖਿਆ ਹੁਨਰ, ਗਿਆਨ ਅਤੇ ਆਦਤਾਂ ਨਵੇਂ ਸਿੱਖਣ ਦੇ ਕੰਮ ਵਿਚ ਨਾ ਹੀ ਸਕਾਰਾਤਮਕ ਪ੍ਰਭਾਵ ਪਾਉਂਦੀ ਹੈ ਅਤੇ ਨਾ ਨਕਾਰਾਤਮਕ ਪ੍ਰਭਾਵ ਪੈਂਦਾ ਹੈ । ਇਸਨੂੰ ਜ਼ੀਰੋ ਸਥਾਨਾਂਤਰਣ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਉਦਾਹਰਣ ਦੇ ਤੌਰ ‘ਤੇ ਵਾਲੀਵਾਲ ਵਿਚ ਸਿੱਖੀ ਸਮੇਮਿੰਗ ਜਾਂ ਸਰਵਿਸ ਦਾ ਜਿਮਨਾਸਟਿਕ ਦੇ ਹੁਨਰ ਤੇ ਪ੍ਰਭਾਵ ਨਾ ਪਾਉਣਾ ।

ਉਪੰਜ ਅੰਕਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ (Five Marks Question-Answers)

ਪ੍ਰਸ਼ਨ 1.
ਸਮਾਜ ਸ਼ਾਸਤਰ ਕੀ ਹੈ ਅਤੇ ਖੇਡਾਂ ਸਮਾਜਿਕ ਗੁਣਾਂ ਦੇ ਵਿਕਾਸ ਵਿਚ ਕਿਵੇਂ ਯੋਗਦਾਨ ਪਾਉਂਦੀਆਂ ਹਨ ?
ਜਾਂ
ਸਮਾਜ ਸ਼ਾਸਤਰ ਦੀ ਪਰਿਭਾਸ਼ਾ ਦਿਓ ਅਤੇ ਮਾਨਵੀ ਵਿਵਹਾਰ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਨ ਵਾਲੀ ਸੰਸਥਾਵਾਂ ਬਾਰੇ ਚਰਚਾ ਕਰੋ ।
ਉੱਤਰ:
(a) ਮਨੁੱਖ ਨੂੰ ਕੁਦਰਤ ਦੁਆਰਾ ਇਕ ਸਮਾਜਿਕ ਜਾਨਵਰ (Social animal) ਵਜੋਂ ਜਾਣਿਆ ਜਾਂਦਾ ਹੈ । ਇਹ ਵੀ ਵਿਸ਼ਵਾਸ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ਕਿ ਵਿਅਕਤੀ ਆਪਣੀ ਅੰਦਰਲੇ ਝੁਕਾਵਾਂ ਅਤੇ ਸਮਾਜਿਕ ਗੁਣਾਂ ਦੀ ਮਦਦ ਨਾਲ ਸਵੈ-ਵਾਤਾਵਰਣ ਦੀ ਸਿਰਜਨਾ ਕਰਦਾ ਹੈ । ਉਸਨੂੰ ਆਪਣੇ ਆਲੇ-ਦੁਆਲੇ ਦੇ ਸਹਾਇਕ ਵਾਤਾਵਰਣ ਵਿਚ ਜਿਉਣ ਲਈ ਸਮਾਜਿਕ ਹੁਨਰ ਨੂੰ ਸਿੱਖਣ ਦੀ ਲੋੜ ਪੈਂਦੀ ਹੈ ਜਿਸ ਲਈ ਉਸਨੂੰ ਸਮਾਜਿਕ ਸਿੱਖਿਆ ਦੇ ਰਾਹੀਂ ਜਾਣਾ ਪੈਂਦਾ ਹੈ । ਇਸ ਨੂੰ ਸਮਾਜ ਸ਼ਾਸਤਰ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਸਮਾਜ ਸ਼ਾਸਤਰ ਇੱਕ ਅਜਿਹਾ ਵਿਸ਼ਾ ਹੈ ਜੋ ਕਿ ਸਮਾਜ ਨੂੰ ਸਮਝਣ ਅਤੇ | ਵਿਸ਼ਲੇਸ਼ਣ ਦਾ ਗਿਆਨ ਪ੍ਰਦਾਨ ਕਰਦਾ ਹੈ । ਸਮਾਜ ਸ਼ਾਸਤਰ ਦਾ ਅਰਥ-ਸਮਾਜ ਸ਼ਾਸਤਰ ਸ਼ਬਦ ਦੋ ਸ਼ਬਦਾਂ ਦੇ ਸੁਮੇਲ ਤੋਂ ਬਣਿਆ ਹੈ, ਜਿਸ ਵਿਚ ਸੋਸੁਜ਼ ਦਾ ਮਤਲਬ ‘ਐਸੋਸਿਏਜ ਜਾਂ ਸਮਾਜਿਕ” ਅਤੇ “ਲੋਗੋ” ਤੋਂ ਭਾਵ ਹੈ, ਵਿਗਿਆਨ ਜਾਂ ਅਧਿਐਨ ਕਰਨਾ । ਇਸ ਤਰ੍ਹਾਂ ਸਮਾਜ ਸ਼ਾਸਤਰ ‘‘ਸਮਾਜ ਦਾ ਵਿਗਿਆਨ’ ਹੈ ।

ਸਮਾਜਿਕ ਵਿਗਿਆਨ ਸਮਾਜ ਦਾ ਵਿਗਿਆਨ ਹੈ । ਇਹ ਸਮਾਜਿਕ ਰਿਸ਼ਤੇ, ਹਰ ਰੋਜ਼ ਦੀ ਜਿੰਦਗੀ ਦੇ ਮੇਲਜੋਲ ਅਤੇ ਸੱਭਿਆਚਾਰ ਦੇ ਅਧਿਐਨ ਦਾ ਇਕ ਪੈਟਰਨ ਹੈ । ਇਸ ਦਾ ਸੰਬੰਧ ਸਮਾਜ ਦੀ ਉਤਪੱਤੀ, ਕਾਰਜ ਅਤੇ ਸਮੱਸਿਆਵਾਂ ਦੇ ਸੰਬੰਧ ਵਿਚ ਮਨੁੱਖੀ ਸਮਾਜ ਦਾ ਅਧਿਐਨ ਕਰਨਾ ਹੈ । ਇਹ ਲੋਕਾਂ, ਸਹ, ਸੰਸਥਾਵਾਂ ਅਤੇ ਸੱਭਿਆਚਾਰ ਦੇ ਸੰਬੰਧ ਵਿਚ ਕੰਮ ਕਰਦਾ ਹੈ । ਇਹ ਪਰਿਵਾਰ, ਧਰਮ, ਸਿੱਖਿਆ, ਰਾਜਨੀਤੀ, ਮਨੁੱਖੀ ਵਤੀਰੇ ਅਤੇ ਸੱਭਿਆਚਾਰ ਨੂੰ ਸਮਝਣ ਵਿਚ ਵੀ ਮਦਦ ਕਰਦਾ ਹੈ ।

(b) ਖੇਡਾਂ ਬੱਚਿਆਂ ਅਤੇ ਨੌਜਵਾਨਾਂ ਦੇ ਜੀਵਨ ਵਿਚ ਇੱਕ ਮਹੱਤਵਪੂਰਨ ਭੂਮਿਕਾ ਨਿਭਾਉਂਦੀਆਂ ਹਨ । ਜਿਸ ਦੀ ਸਹਾਇਤਾ ਨਾਲ ਉਹ ਸਮਾਜ ਵਿਚ ਇਕ ਲਾਭਦਾਇਕ ਮੈਂਬਰ ਵਜੋਂ ਵਿਕਾਸ ਕਰਦੇ ਸਨ ।

ਖੇਡਾਂ ਦੁਆਰਾ ਉਹਨਾਂ ਦੇ ਜੀਵਨ ਵਿਚ ਕੀ-ਕੀ ਸਮਾਜਿਕ ਗੁਣਾਂ ਦਾ ਵਿਕਾਸ ਹੁੰਦਾ ਹੈ ਉਸਦੀ ਚਰਚਾ ਅੱਗੇ ਲਿਖੇ ਅਨੁਸਾਰ ਦਿੱਤੀ ਗਈ ਹੈ-
1. ਡਾਈਚਾਰੇ ਦੀ ਨੀਂਹ (Community building-ਖੇਡਾਂ ਭਾਈਚਾਰੇ ਦੀ ਨੀਂਹ ਨੂੰ ਬੱਚਿਆਂ ਅਤੇ ਨੌਜਵਾਨਾਂ ਵਿਚ ਇਕ ਸਮਾਜਿਕ ਏਕਤਾ ਅਤੇ ਸਮਾਜਿਕ ਪੂੰਜੀ ਦੇ ਮਜ਼ਬੂਤ ਸੰਬੰਧ ਨੂੰ ਦਰਸਾਉਂਦੀਆਂ ਹਨ | ਖੇਡਾਂ ਇਹਨਾਂ ਬੱਚਿਆਂ ਅਤੇ ਨੌਜਵਾਨਾਂ ਨੂੰ ਕਈ ਮੌਕੇ ਪ੍ਰਦਾਨ ਕਰਦੀਆਂ ਹਨ, ਜਿੱਥੇ ਉਹ ਆਪਣੀ ਸਵੈ-ਇੱਛਾ ਨਾਲ ਭਾਗ ਲੈ ਸਕਦੇ ਹਨ ਅਤੇ ਜਿਸ ਕਾਰਣ ਉਹਨਾਂ ਵਿਚ ਲੀਡਰਸ਼ਿਪ ਦੇ ਗੁਣ, ਸਕਾਰਾਤਮਕ ਪੀਅਰ ਰਿਲੈਸ਼ਨ, ਸਨਮਾਨ ਅਤੇ ਨੈਤਿਕਤਾ ਦੇ ਗੁਣਾਂ ਦਾ ਵਿਕਾਸ ਹੁੰਦਾ ਹੈ । ‘

2. ਚਰਿੱਤਰ ਅਤੇ ਨੈਤਿਕ ਗੁਣ (Character and Moral Qualities)-ਨੈਤਿਕ ਵਿਵਹਾਰ ਅਤੇ ਚਰਿਤਰ ਨਿਰਮਾਣ ਸਮਾਜਿਕ ਪਰਸਪਰ (Social interaction) ਤੇ ਨਿਰਭਰ ਕਰਦਾ ਹੈ ਅਤੇ ਕਾਫੀ ਹੱਦ ਤੱਕ ਸਰੀਰਕ ਸਿੱਖਿਆ ਅਤੇ ਖੇਡ ਦ੍ਰਿਸ਼ ਦੇ ਪ੍ਰੋਗਰਾਮਾਂ ਤੇ ਨਿਰਭਰ ਕਰਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਸਰੀਰਕ ਸਿੱਖਿਆ ਦੇ ਅਧਿਆਪਕ, ਕੋਚ, ਵੇਨਿਕ ਆਦਿ ਬੱਚਿਆਂ ਅਤੇ ਨੌਜਵਾਨਾਂ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਨ ਲਈ ਇਕ ਨਿਰਣਾਇਕ ਭੂਮਿਕਾ ਅਦਾ ਕਰਦੇ ਹਨ । ਇਸ ਲਈ ਇਹ ਦੇਖਿਆ ਗਿਆ ਹੈ ਕਿ ਮੁਕਾਬਲੇ ਸੰਬੰਧੀ ਖੇਡਾਂ ਅਤੇ ਸਰੀਰਕ ਕ੍ਰਿਆਵਾਂ ਨੌਜਵਾਨਾਂ ਵਿਚ ਆਪਸੀ ਸਮਝ ਨੂੰ ਵਧਾਉਣ ਵਿਚ ਬਹੁਤ ਮਦਦਗਾਰ ਸਾਬਿਤ ਹੁੰਦੀਆਂ ਹਨ ।

3. ਸਮੂਹਿਕ ਅਹਿਸਾਸ ਅਤੇ ਜ਼ਿੰਮੇਵਾਰੀ (Group feeling and Responsibilities-ਟੀਮ ਖੇਡਾਂ ਸਮੂਹਿਕ ਅਹਿਸਾਸ ਅਤੇ ਜ਼ਿੰਮੇਵਾਰੀਆਂ ਨੂੰ ਜਨਮ ਦਿੰਦੀਆਂ ਹਨ । ਅਸੀ’ ਦੀ ਭਾਵਨਾ ਨੂੰ ਪੈਦਾ ਕਰਨ ਦਾ ਸਭ ਤੋਂ ਵਧੀਆ ਤਰੀਕਾ ਇਹ ਹੈ ਕਿ ਨੌਜਵਾਨਾਂ ਤੇ ਬੱਚਿਆਂ ਨੂੰ ਟੀਮ ਖੇਡਾਂ ਦਾ ਹਿੱਸਾ ਬਣਾਇਆ ਜਾਵੇ । ਇਹ ਟੀਮ ਮੈਂਬਰਾਂ ਅਤੇ ਸਮੂਹ ਵਿਚਕਾਰ ਭਾਈਚਾਰੇ, ਸਹਾਇਕ, ਸਤਿਕਾਰ, ਸਹਿਯੋਗ, ਹਮਦਰਦੀ ਵਰਗੇ ਸਮਾਜਿਕ ਗੁਣਾਂ ਦਾ ਵਿਕਾਸ ਕਰਦਾ ਹੈ ।

4. ਊਰਜਾ ਦਾ ਚੈਨਲਾਈਜੇਸ਼ਨ (Channelization of energy)-ਗੇਮਜ਼ ਅਤੇ ਖੇਡਾਂ ਊਰਜਾ ਨੂੰ ਸਹੀ ਤਰੀਕੇ ਨਾਲ ਪ੍ਰਵਾਹਿਤ ਕਰਨ ਵਿਚ ਅਹਿਮ ਭੂਮਿਕਾ ਨਿਭਾਉਂਦੀਆਂ ਹਨ । ਇਹ ਲੁਕੀਆ ਹੋਈਆਂ ਭਾਵਨਾਵਾਂ ਅਤੇ ਨਕਾਰਾਤਮਕ ਵਿਚਾਰਾਂ ਨੂੰ ਰਚਨਾਤਮਕ ਬਣਾਉਣ ਦਾ ਉਸਾਰੂ ਤਰੀਕਾ ਹੈ । ਇਹ ਵਿਅਕਤੀ ਦੇ ਵਿਵਹਾਰ ਵਿਚ , ਅਰਥਪੂਰਣ ਤਰੀਕੇ ਨਾਲ ਲੋੜੀਂਦੀਆਂ ਤਬਦੀਲੀਆਂ ਲਿਆਉਂਦਾ ਹੈ । ਇਹ ਵਿਅਕਤੀ ਦੇ ਸਾਰੇ ਨਕਾਰਾਤਮਕ ਵਿਚਾਰਾਂ ਨੂੰ ਬਾਹਰ ਕੱਢਣ ਵਿਚ ਉਪਯੋਗੀ ਹੈ ਨਹੀਂ ਤਾਂ ਅਜਿਹੇ ਵਿਅਕਤੀ ਸਮਾਜ ਲਈ ਖ਼ਤਰਾ ਬਣ ਜਾਂਦੇ ਹਨ ।

5. ਸਮੇਂ ਦੀ ਪਾਬੰਦ ਅਤੇ ਸਮਰਪਣ (Punctuality and dedication)-ਖੇਡਾਂ ਵਿਚ ਚੰਗੀ ਤਰ੍ਹਾਂ ਪ੍ਰਦਰਸ਼ਨ ਕਰਨ ਲਈ ਖੇਡ ਨਿਯਮਾਂ ਨੂੰ ਧਿਆਨ ਵਿਚ ਰੱਖਦੇ ਹੋਏ, ਬਹੁਤ ਸਮਰਪਣ ਦੀ ਲੋੜ ਪੈਂਦੀ ਹੈ । ਇਹ ਸਮਰਪਣ ਜ਼ਿੰਮੇਵਾਰੀ ਅਤੇ ਸਮੇਂ ਦੀ ਮਹੱਤਤਾ, ਸਮੇਂ ਦੀ ਪਾਬੰਦੀ ਅਤੇ ਹੋਰ ਟੀਮਾਂ ਦਾ ਸਤਿਕਾਰ ਕਰਨ ਵਾਲੇ ਗੁਣਾਂ ਦਾ ਸੰਚਾਰ ਕਰਦੀ ਹੈ । ਇਹ ਗੁਣ ਖੇਡਾਂ ਦੇ ਖੇਤਰ ਕਾਰਣ ਬੇਹਤਰ ਹੋ ਜਾਂਦੇ ਹਨ, ਜੋ ਵਿਅਕਤੀ ਸਮਾਜ ਦਾ ਚੰਗਾ ਮੈਂਬਰ ਬਣਨ ਵਿਚ ਮਦਦਗਾਰ ਸਾਬਿਤ ਹੁੰਦੇ ਹਨ । 6. ਸਮਾਜਿਕ ਮਾਨਤਾ ਅਤੇ ਸੰਚਾਰ (Social recognition and Communication)-ਹਰ ਵਿਅਕਤੀ ਸਮਾਜ ਦਾ ਭਾਈਚਾਰੇ ਦੀ ਮਾਨਤਾ ਅਤੇ ਭਾਵਨਾ ਨੂੰ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ ਸਰਗਰਮ ਮੈਂਬਰ ਬਣਨ ਦੀ ਇੱਛਾ ਰੱਖਦਾ ਹੈ । ਗੇਮਜ਼ ਅਤੇ ਖੇਡਾਂ ਸੰਚਾਰ ਅਤੇ ਸਮਾਜਿਕ ਰਿਸ਼ਤਿਆਂ ਦਾ ਬਹੁਤ ਵਧੀਆ ਮਾਧਿਅਮ ਹਨ । ਖੇਡਾਂ ਵਿਚ ਕਈ ਅਜਿਹੇ ਅਵਸਰ ਜਾਂ ਮੌਕੇ ਬਣਦੇ ਹਨ, ਜੋ ਸਮਾਜੀਕਰਣ ਵਿਚ ਅਹਿਮ ਭੂਮਿਕਾ ਨਿਭਾਉਂਦੇ ਹਨ । ਖੇਡਾਂ ਦੁਆਰਾ ਬੱਚਾ ਆਤਮ ਵਿਸ਼ਵਾਸ ਪ੍ਰਾਪਤ ਕਰਦਾ ਹੈ ਅਤੇ ਨੈਟਵਰਕਿੰਗ ਬਣਾਉਂਦਾ ਹੈ ਤਾਂ ਕਿ ਉਹ ਆਪਣੇ ਗੁਣਾਂ ਅਤੇ ਸੰਭਾਵਨਾਵਾਂ ਨੂੰ ਉਜਾਗਰ ਕਰ ਸਕੇ ਅਤੇ ਸਮਾਜ ਦਾ ਇੱਕ ਮਹੱਤਵਪੂਰਣ ਮੈਂਬਰ ਬਣ ਸਕੇ । ਇਸ ਲਈ ਖੇਡਾਂ ਸਿੱਖਿਆ ਪ੍ਰਣਾਲੀ ਦਾ ਅਨਿੱਖੜਵਾਂ ਹਿੱਸਾ ਹਨ, ਜੋ ਸਮਾਜੀਕਰਨ ਨੂੰ ਉਤਸਾਹਿਤ ਕਰਕੇ ਇੱਕ ਪਲੇਟਫਾਰਮ ਪ੍ਰਦਾਨ ਕਰਦੀਆਂ ਹਨ |

ਪ੍ਰਸ਼ਨ 2.
ਮਨੋਵਿਗਿਆਨ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ? ਪਰਿਭਾਸ਼ਾਵਾਂ ਦੀ ਸਹਾਇਤਾ ਨਾਲ ਸਮਝਾਓ ।
ਉੱਤਰ:
ਸਭ ਤੋਂ ਪਹਿਲਾਂ ਸਰੀਰਕ ਮਨੋਵਿਗਿਆਨੀਆਂ ਨੇ ਮਨੁੱਖੀ ਵਿਵਹਾਰ ਅਤੇ ਉਨ੍ਹਾਂ ਦੀਆਂ ਮਾਨਸਿਕ ਪ੍ਰਕਿਰਿਆਵਾਂ ਦਾ ਅਧਿਐਨ ਕਰਨ ਦੀ ਕੋਸ਼ਿਸ਼ ਕੀਤੀ ਸੀ । ਮਨੁੱਖੀ ਵਿਵਹਾਰ ਨੂੰ ਸਮਝਣ ਲਈ ਮਨੋਵਿਗਿਆਨ ਦਾ ਅਧਿਐਨ ਕਰਨਾ ਬਹੁਤ ਜ਼ਰੂਰੀ ਹੈ । ਮਨੋਵਿਗਿਆਨ ਸ਼ਬਦ ਗਰੀਕ ਭਾਸ਼ਾ ਦੇ ਦੋ ਸ਼ਬਦਾਂ ਦੇ ਸਾਈਕੇ (Psyche) ਅਤੇ ਲੋਗੋਜ਼ (Logos) ਦੇ ਸੁਮੇਲ ਤੋਂ ਬਣਿਆ ਹੈ ! ਇੱਥੇ Psyche ਦਾ ਅਰਥ ਹੈ “ਆਤਮਾ’’ ਤੇ Logos ਦਾ ਅਰਥ ਹੈ “ਗੱਲ ਕਰਨੀ’ ਜਾਂ ਅਧਿਐਨ ਕਰਨਾ’’ ਜਾਂ ਫਿਰ “ਵਿਗਿਆਨ’’ ਤੋਂ ਹੈ । ਭਾਵ ਮਨੋਵਿਗਿਆਨ ਦਾ ਅਰਥ ਸੀ “ਆਤਮਾ ਬਾਰੇ ਗੱਲ ਕਰਨੀ ।” ਪਰ ਸਮੇਂ ਨਾਲ ਮਨੋਵਿਗਿਆਨ ਦਾ ਅਰਥ ਅਤੇ ਧਾਰਨਾਵਾਂ ਬਦਲਦੀਆਂ ਗਈਆਂ | ਬਾਅਦ ਵਿਚ ਇਸ ਨੂੰ ਦਿਮਾਗ ਦਾ ਵਿਗਿਆਨ ਆਖਿਆ ਜਾਣ ਲੱਗਾ |

ਅੰਤ ਵਿਚ ਮਨੋਵਿਗਿਆਨ ਨੂੰ “ਵਿਵਹਾਰ ਦਾ ਵਿਗਿਆਨ’’ (Science of behaviour) ਪ੍ਰਵਾਨ ਕਰ ਲਿਆ ਗਿਆ । | ਮਨੋਵਿਗਿਆਨ ਦੀਆਂ ਪਰਿਭਾਸ਼ਾਵਾਂ (Definitions of Psychology) ਵਾਰਨ (Warren) ਦੇ ਅਨੁਸਾਰ, “‘ਮਨੋਵਿਗਿਆਨ ਵਿਗਿਆਨ ਦਾ ਇਕ ਅਜਿਹਾ ਵਿਸ਼ਾ ਹੈ ਜੋ ਕਿ ਜੀਵਵਿਗਿਆਨ ਅਤੇ ਵਾਤਾਵਰਣ ਦੇ ਆਪਸ ਦੇ ਸੰਬੰਧ ਨੂੰ ਦਰਸਾਉਂਦਾ ਹੈ ।” ਵੁਡਵਰਥ (Woodworth) ਦੇ ਅਨੁਸਾਰ, “ਮਨੋਵਿਗਿਆਨ ਉਹਨਾਂ ਗਤੀਵਿਧੀਆਂ ਨਾਲ ਨਜਿੱਠਦਾ ਹੈ ਜਿਨ੍ਹਾਂ ਵਿਚ ਵਿਅਕਤੀ ਦਾ ਵਾਤਾਵਰਣ ਨਾਲ ਸੰਬੰਧ ਹੈ ।”

ਪ੍ਰਸ਼ਨ 3.
ਸਿੱਖਣ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ਅਤੇ ਸਿੱਖਣ ਦੇ ਵੱਖ-ਵੱਖ ਸਥਾਨਾਂਤਰਣ ਨੂੰ ਸਮਝਾਓ ।
ਉੱਤਰ:
ਸਿੱਖਣ ਦੀ ਧਾਰਨਾ ਨੂੰ ਵਿਵਹਾਰ ਦੇ ਬਦਲਾਵ ਦੇ ਤਜ਼ਰਬਾ, ਨਵੀਆਂ ਆਦਤਾਂ ਅਤੇ ਹੁਨਰ ਪ੍ਰਾਪਤੀ ਵਜੋਂ ਸਮਝਿਆ ਜਾ ਸਕਦਾ ਹੈ । ਵਿਵਹਾਰ ਵਿਚ ਬਦਲਾਵ ਆਮ ਤੌਰ ਤੇ ਸਥਾਈ ਹੁੰਦਾ ਹੈ । ਇਹ ਵਿਸ਼ਵਾਸ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ਕਿ ਸਿੱਖਣਾ ਇਕ ਜੀਵਨ ਭਰ ਚੱਲਣ ਵਾਲੀ ਪ੍ਰਕਿਰਿਆ ਹੈ, ਜੋ ਕਿ ਪੰਘੂੜੇ ਵਿਚ ਸ਼ੁਰੂ ਹੁੰਦੀ ਹੈ ਅਤੇ ਕਬਰ ਵਿਚ ਖ਼ਤਮ ਹੋ ਜਾਂਦੀ ਹੈ । ਭਾਵ ਸਿੱਖਣਾ ਜਨਮ ਹੁੰਦਿਆਂ ਹੀ ਸ਼ੁਰੂ ਹੋ ਜਾਂਦਾ ਹੈ ਅਤੇ ਮਰਨ ਉਪਰੰਤ ਹੀ ਖ਼ਤਮ ਹੋ ਜਾਂਦਾ ਹੈ । ਇਹ ਦੇਖਿਆ ਜਾਂਦਾ ਹੈ ਕਿ ਇਕ ਵਿਅਕਤੀ ਆਪਣੇ ਆਪ ਬਚਾਉਣ ਭਾਵ ਜਿੰਦਾ ਰੱਖਣ ਲਈ ਸਮਾਜਿਕ ਹੁਨਰ ਅਤੇ ਵਾਤਾਵਰਣ ਨੂੰ ਗ੍ਰਹਿਣ ਕਰ ਲੈਂਦਾ ਹੈ । ਇਹ ਜ਼ਰੂਰੀ ਨਹੀਂ ਹੈ ਕਿ ਵਿਅਕਤੀ ਦੇ ਵਿਹਾਰ ਵਿਚ ਸਕਾਰਾਤਮਕ ਤਬਦੀਲੀ ਹੀ ਹੋਵੇ ।

ਵਿਹਾਰ ਵਿਚ ਢੁੱਕਵੀਂ ਤਬਦੀਲੀ ਸਮਾਜਿਕ ਸੰਤੁਸ਼ਟੀ ਅਤੇ ਸੰਪੂਰਨਤਾ ਤੇ ਨਿਰਭਰ ਕਰਦੀ ਹੈ ।
1. ਸਿੱਖਣ ਦੇ ਸਥਾਨਾਂਤਰਣ ਦੇ ਪ੍ਰਕਾਰ (Types of Transfer of training)-ਨਵਾਂ ਸਿੱਖਣਾ ਪਿਛਲੇ ਸਿੱਖੇ ਹੋਏ ਕੰਮ ਨੂੰ ਤਿੰਨ ਤਰੀਕਿਆਂ ਨਾਲ ਪ੍ਰਭਾਵਿਤ ਕਰਦਾ ਹੈ । ਜਿਵੇਂ ਹੁਨਰ, ਵਿਹਾਰ ਅਤੇ ਗਿਆਨ । ਕਈ ਵੇਰ ਨਵਾਂ ਸਿੱਖਣਾ ਪੁਰਾਣੇ ਸਿੱਖੇ ਕੰਮ ਵਿਚ ਮੁਸ਼ਕਿਲਾਂ ਪੈਦਾ ਕਰਦਾ ਹੈ ਅਤੇ ਕਈ ਵਾਰ ਕਿਸੇ ਵੀ ਤਰੀਕੇ ਨਾਲ ਪ੍ਰਭਾਵਿਤ ਨਹੀਂ ਕਰਦਾ । ਇਸ ਲਈ ਇਸ ਨੂੰ ਸਮਝਣ ਲਈ ਇਸ ਨੂੰ ਤਿੰਨ ਭਾਗਾਂ ਵਿਚ ਵੰਡਿਆ ਜਾਂਦਾ ਹੈ1. ਸਕਾਰਾਤਮਕ ਸਥਾਨਾਂਤਰਣ (Positive transfer of learning-ਜਦ ਪਿੱਛਲਾ ਸਿੱਖਿਆ ਹੋਇਆ ਹੁਨਰ ਨਵੇਂ ਸਿੱਖਣ ਵਾਲੇ ਕੰਮ ਵਿਚ ਮਦਦ ਕਰਦਾ ਹੈ, ਤਾਂ ਉਸਨੂੰ ਸਕਾਰਾਤਮਕ ਸਥਾਨਾਂਤਰਣ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਜਿਵੇਂ ਲੰਬੇ ਸਮੇਂ ਤੱਕ ਦੌੜਨ ਵਾਲੀ ਸਹਿਣਸ਼ੀਲਤਾ, ਲੰਬੇ ਸਮੇਂ ਤੱਕ ਤੈਰਾਕੀ ਕਰਨ ਵਿਚ ਮਦਦ ਕਰੇਗਾ । ਇਸੇ ਤਰਾਂ ਯੋਗ ਆਸਣ, ਐਰੋਬਿਕਸ ਵਿਚ ਕੰਮ ਆਉਂਦੇ ਹਨ ਅਤੇ ਕ੍ਰਿਕਟ ਖੇਡਣ ਵਾਲੇ ਸਾਫਟਬਾਲ ਵਰਗੀਆਂ ਖੇਡਾਂ ਖੇਡ ਸਕਦੇ ਹਨ ਆਦਿ ।

2. ਨਕਾਰਾਤਮਕ ਸਥਾਨਾਂਤਰਣ (Negative Transfer of Training)-ਇਸ ਸਥਿਤੀ ਵਿਚ ਪਹਿਲਾਂ ਸਿੱਖਿਆ ਹੁਨਰ, ਆਦਤਾਂ ਅਤੇ ਗਿਆਨ ਨਵੇਂ ਕੰਮ ਨੂੰ ਸਿੱਖਣ ਵਿਚ ਮੁਸ਼ਕਿਲਾਂ ਪੈਦਾ ਕਰਦੇ ਹਨ, ਤਾਂ ਇਹਨਾਂ ਨੂੰ ਨਕਾਰਾਤਮਕ ਸਥਾਨਾਂਤਰਣ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਜਿਵੇਂ ਕਿ ਟੈਨਿਸ ਖਿਡਾਰੀ ਨੂੰ ਬੈਡਮਿੰਟਨ ਦਾ ਰੈਕਟ ਫੜਨ ਵਿਚ ਮੁਸ਼ਕਿਲ ਹੋਣਾ । ਕਿਉਂਕਿ ਟੈਨਿਸ ਵਿਚ ਹੱਥ ਦੀ ਗਰਿੱਪ ਸਖ਼ਤ ਹੁੰਦੀ ਹੈ ਜਦਕਿ ਬੈਡਮਿੰਟਨ ਵਿਚ ਰੈਕਟ ਪੋਲੇ ਹੱਥਾਂ ਨਾਲ ਫੜਨਾ ਹੁੰਦਾ ਹੈ ।

3. ਜੀਰੋ ਸਥਾਨਾਂਤਰਣ (Zero Transfer of Training)-ਇਸ ਸਥਿਤੀ ਵਿਚ ਪਹਿਲਾਂ ਸਿੱਖਿਆ ਹੁਨਰ, , ਗਿਆਨ ਅਤੇ ਆਦਤਾਂ ਨਵੇਂ ਸਿੱਖਣ ਦੇ ਕੰਮ ਵਿਚ ਨਾ ਹੀ ਸਕਾਰਾਤਮਕ ਪ੍ਰਭਾਵ ਪਾਉਂਦੀ ਹੈ ਅਤੇ ਨਾ ਨਕਾਰਾਤਮਕ ਪ੍ਰਭਾਵ ਪੈਂਦਾ ਹੈ । ਇਸਨੂੰ ਜ਼ੀਰੋ ਸਥਾਨਾਂਤਰਣ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਉਦਾਹਰਣ ਦੇ ਤੌਰ ‘ਤੇਵਾਲੀਵਾਲ ਵਿਚ ਸਿੱਖੀ ਸਮੇਮਿੰਗ ਜਾਂ ਸਰਵਿਸ ਦਾ ਜਿਮਨਾਸਟਿਕ ਦੇ ਹੁਨਰ ਤੇ ਪ੍ਰਭਾਵ ਨਾ ਪਾਉਣਾ ।

ਪ੍ਰਸ਼ਨ 4.
ਖੇਡਾਂ ਮਨੁੱਖ ਦੀ ਸੰਸਕ੍ਰਿਤ ਵਿਰਾਸਤ ਹਨ । ਇਸ ਤੱਥ ਦੀ ਵਿਆਖਿਆ ਕਰੋ ।
ਉੱਤਰ:
ਸੱਭਿਆਚਾਰ ਨੂੰ ਉਸ ਵਿਵਹਾਰ ਦੇ ਰੂਪ ਵਿਚ ਪਰਿਭਾਸ਼ਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ, ਜੋ ਸਾਡੇ ਕੋਲ ਵਿਰਾਸਤ ਜਾਂ ਆਲੇ-ਦੁਆਲੇ ਤੋਂ ਆਉਂਦੀ ਹੈ । ਸੱਭਿਆਚਾਰ ਸਾਡੇ ਰਹਿਣ ਦੇ ਤਰੀਕੇ, ਖਾਣ ਦੀਆਂ ਆਦਤਾਂ, ਵਿਚਾਰਾਂ, ਰੀਤੀ-ਰਿਵਾਜ, ਰਵਾਇਤਾਂ, ਨੈਤਿਕ, ਕਲਾ, ਸਾਹਿਤ ਧਰਮ, ਖੇਡਾਂ ਅਤੇ ਜੀਵਨ ਦੇ ਹੋਰ ਕਈ ਪਹਿਲੂਆਂ ਤੋਂ ਮਿਲ ਕੇ ਬਣਦਾ ਹੈ । ਵਿਰਾਸਤੀ ਸ਼ਬਦ ਅਤੀਤ ਤੋਂ ਵਰਤਮਾਨ ਤੱਕ ਅਤੇ ਭੱਵਿਖ ਵਾਸਤੇ ਕਈ ਸੋਧਾਂ ਨਾਲ ਟਰਾਂਸਫਰ ਹੁੰਦਾ ਹੈ ।

ਵਿਰਾਸਤ ਅਤੀਤ ਵਰਤਮਾਨ ਵਿਚ ਇਕ ਪੁੱਲ ਵਾਂਗ ਕੰਮ ਕਰਦੀ ਹੈ | ਸਰੀਰਕ ਗਤੀਵਿਧੀਆਂ ਪੁਰਾਣੇ ਸਮੇਂ ਤੋਂ ਮੌਜੂਦ ਹਨ ਜਿਵੇਂ ਕਿ ਭੱਜਣਾ, ਫੜਨਾ, ਲੜਾਈ ਅਤੇ ਕੁੱਦਣ ਵਰਗੀਆਂ ਕਈ ਗਤੀਵਿਧੀਆਂ ਦੀ ਹੋਂਦ ਅੱਜ ਵੀ ਮੌਜੂਦ ਹੈ । ਹੌਲੀ-ਹੌਲੀ ਸਮਾਂ ਬੀਤਣ ਨਾਲ ਇਹਨਾਂ ਗਤੀਵਿਧੀਆਂ ਵਿਚ ਸੋਧ ਹੋਈ ਅਤੇ ਇਹ ਖੇਡਣ ਅਤੇ ਮਨੋਰੰਜ਼ਨ ਦੇ ਤੌਰ ਤੇ ਵਰਤੀਆਂ ਜਾਣ ਲੱਗ ਪਈਆਂ । ਖੇਡਾਂ ਨੂੰ ਵੱਖ-ਵੱਖ ਦੇਸ਼ਾਂ ਜਾਂ ਇਲਾਕਿਆਂ ਵਿਚ ਇਕ ਸੰਸਕ੍ਰਿਤੀ ਦੇ ਵਜੋਂ ਕਿਵੇਂ ਵਿਕਾਸ ਕੀਤਾ, ਇਸ ਦਾ ਵਿਵਰਣ ਹੇਠ ਦਿੱਤੇ ਅਨੁਸਾਰ ਹੈ|

ਯੂਨਾਨ (Greece)-ਯੂਨਾਨੀ ਸੱਭਿਅਤਾ ਸੰਸਾਰ ਦੀ ਸਭ ਤੋਂ ਪੁਰਾਣੀ ਸੱਭਿਅਤਾ ਸੀ । ਇਹ ਖੇਡਾਂ ਦੀ ਦੁਨੀਆਂ ਦਾ ‘‘ਗੋਲਡਨ ਏਰਾ’’ ਸੀ । ਖੇਡਾਂ ਦੇ ਸਭ ਤੋਂ ਉੱਚੇ ਈਵੈਂਟ ਯੂਨਾਨੀਆਂ ਵਲੋਂ ਇਜ਼ਾਦ ਕੀਤੇ ਗਏ ਸਨ, ਜਿਵੇਂ ਕਿ ਉਲੰਪਿਕ ਖੇਡਾਂ 776 ਈਸਵੀਂ ਵਿਚ ਸ਼ੁਰੂ ਕੀਤੀਆਂ ਗਈਆਂ । ਉਹਨਾਂ ਦੇ ਅਨੁਸਾਰ ਖੇਡਾਂ ਨੂੰ ਸੱਭਿਆਚਾਰ ਵਿਰਸੇ ਦੇ ਵਜੋਂ ਤੰਦਰੁਸਤੀ ਤੇ ਸਮੁੱਚੇ ਵਿਕਾਸ ਲਈ ਖੇਡਾਂ ਦੇ ਰੂਪ ਵਿਚ ਖੇਡਿਆ ਜਾਂਦਾ ਸੀ । ਖੇਡਾਂ ਲਈ ਮੁੱਖ ਰਾਜ ਏਥਨਜ ਅਤੇ ਸਪਾਰਟਾ ਸਨ ਜਿਨ੍ਹਾਂ ਨੇ ਖੇਡਾਂ ਦੀ ਸ਼ੁਰੂਆਤ ਕੀਤੀ ਅਤੇ ਖੇਡਾਂ ਨੂੰ ਉਹਨਾਂ ਦੇ ਪਰਮੇਸ਼ਵਰ ਜ਼ਸ ਦੇ ਸਨਮਾਨ ਵਿਚ ਇਕ ਤਿਉਹਾਰ ਦੇ ਰੂਪ ਵਿਚ ਮਨਾਇਆ ਜਾਂਦਾ ਸੀ । ਇਸ ਤਿਉਹਾਰ ਵਿਚ ਮੁੱਖ ਗਤੀਵਿਧੀਆਂ ਦੇ ਰੂਪ ਵਿਚ ਕੁਸ਼ਤੀ, ਘੋੜਿਆਂ ਦੀ ਦੌੜ, ਦੌੜਾਂ, ਸੁੱਟਣਾ, ਰੱਥਾਂ ਦੀ ਦੌੜ ਤੇ ਸ਼ਿਕਾਰ ਸ਼ਾਮਲ ਸਨ । 394 ਈਸਵੀਂ ਦੇ ਅੰਤ ਰੋਮਨ ਹਮਲਾਵਰਾਂ ਦੇ ਪ੍ਰਭਾਵ ਕਾਰਨ ਇਹਨਾਂ ਖੇਡਾਂ ਨੂੰ ਬੰਦ ਕਰ ਦਿੱਤਾ ਗਿਆ |

ਰੋਮ (Rome)-ਰੋਮ ਵਾਸੀ ਖੇਡ ਪ੍ਰੇਮੀ ਨਹੀਂ ਸਨ । ਉਹਨਾਂ ਦਾ ਵਿਸ਼ਵਾਸ ਸੀ ਕਿ ਤਾਕਤ ਅਤੇ ਸ਼ਕਤੀ ਨਾਲ ਸਰਵਉੱਚਤਾ ਹਾਸਿਲ ਕਰਨਾ { ਸਰੀਰਕ ਗਤੀਵਿਧੀਆਂ ਵਿਚ ਭਾਗ ਲੈਣ ਦਾ ਇਕੋ ਮਕਸਦ ਸੀ ਲੜਾਈ (ਸੈਨਾ) ਲਈ । ਆਪਣੇ ਆਪ ਨੂੰ ਤੰਦਰੁਸਤ ਰੱਖਣਾ । ਉਹ ਗਲੈਡੀਏਟਰ ਲੜਾਈ, ਆਦਮੀ ਨੂੰ ਲੜਾਈ ਕਰਾਉਣਾ ਅਤੇ ਪੰਛੀਆਂ ਦੀ ਲੜਾਈ ਆਦਿ ਗਤੀਵਿਧੀਆਂ ਕੀਤੀਆਂ ਜਾਂਦੀਆਂ ਸਨ ਅਤੇ ਇਹ ਤਦ ਤੱਕ ਕੀਤੀਆਂ ਜਾਂਦੀਆਂ ਸਨ, ਜਦ ਤਕ ਦੂਜੇ ਦੀ ਜ਼ਿੰਦਗੀ ਖਤਮ ਨਾ ਹੋ ਜਾਵੇ । ਉਹਨਾਂ ਨੇ ਕਈ ਖੇਡਾਂ ਜਿਵੇਂ ਕਿ ਰੇਸਿੰਗ, ਜੰਪਿੰਗ, ਤਲਵਾਰਵਾਦੀ ਅਤੇ ਲੜਾਈ ਝਗੜੇ (Combat) ਨੂੰ ਪੇਸ਼ ਕੀਤਾ ਸੀ ।

ਜਰਮਨੀ (Germany)-ਜਰਮਨੀ ਨੇ ਖੇਡਾਂ ਦੇ ਸੱਭਿਆਚਾਰ ਨੂੰ ‘‘ਆਸਟੈਸਿਸਿਜ਼ਮ” ਦੇ ਰੂਪ ਵਿੱਚ ਪੂਰੇ ਸੰਸਾਰ ਵਿਚ ਸਥਾਪਿਤ ਕੀਤਾ ਹੈ । 19ਵੀਂ ਸ਼ਤਾਬਦੀ ਵਿੱਚ, ਰਾਸ਼ਟਰਵਾਦ ਦੇ ਉਭਾਰ ਦੇ ਦੌਰਾਨ ਫਰੀਡਿਕ ਲੁੱਡਵਿੰਗ ਜਾਂਨ, ਜਿਨ੍ਹਾਂ ਨੂੰ ਜਿਮਨਾਸਟਿਕ ਦਾ ਪਿਤਾ ਕਿਹਾ ਜਾਂਦਾ ਹੈ, ਕਈ ਜਿਮਨਾਸਟਿਕ ਕਲੱਬਾਂ ਦੀ ਸਥਾਪਨਾ ਕੀਤੀ । ਉਹਨਾਂ ਨੇ ਕਈ ਈਵੈਂਟ ਨੂੰ ਜਨਮ ਦਿੱਤਾ ਜੋ ਅੱਜ ਉਲੰਪਿਕ ਖੇਡਾਂ ਦਾ ਹਿੱਸਾ ਹਨ । ਉਸੇ ਸਮੇਂ ਦੇ ਲੋਕਾਂ ਨੇ ਸਕੂਲ ਦੇ ਪ੍ਰੋਗਰਾਮਾਂ ਵਿਚ ਸਰੀਰਕ ਸਿੱਖਿਆ ਦੀ ਸ਼ੁਰੂਆਤ ਕੀਤੀ । ਜਰਮਨੀ ਦੇ ਯਤਨਾਂ ਵਜੋਂ ਜਿਮਨਾਸਟਿਕ ਦੀਆਂ ਕ੍ਰਿਆਵਾਂ ਸਾਡੇ ਕੋਲ ਆਈਆਂ ਹਨ । ਉਹਨਾਂ ਨੇ ਜਿਮਨਾਸਟਿਕ ਉਪਕਰਨ ਜਿਵੇਂ ਕਿ ਹੋਰੀਜੰਟਲ ਬਾਰ, ਵਾਲਟਿੰਗ ਕੋਰਸ ਆਦਿ ਦੁਨੀਆਂ ਨੂੰ ਦਿੱਤੇ ਹਨ ।

ਸਵੀਡਨ Sweden)-ਸਵੀਡਨ ਦੇ ਇਤਿਹਾਸ ਵਿਚ ਪਹਿੰਨਰਕ ਲਿਗ ਸਰੀਰਕ ਸਿੱਖਿਆ ਦੇ ਮੋਹਰੀ ਮੰਨੇ ਜਾਂਦੇ ਹਨ । ਉਹਨਾਂ ਨੇ ਜਿਮਨਾਸਟਿਕ ਦੀ ਇਕ ਪ੍ਰਣਾਲੀ ਜਿਸਨੂੰ ਸਵੀਡਨ ਜਿਮਨਾਸਟਿਕ ਕਿਹਾ ਜਾਂਦਾ ਹੈ, ਨੇ ਜਨਮ ਦਿੱਤਾ ਜੋ ਕਿ ਬਾਅਦ ਵਿਚ ਯੂਨਾਈਟਿਡ ਸਟੇਟ ਦੁਆਰਾ ਅਪਣਾਇਆ ਗਿਆ | ਇਸ ਤੋਂ ਇਲਾਵਾ ਉਹਨਾਂ ਨੇ ਨਵੇਂ ਉਪਕਰਨ ਜਿਵੇਂ ਕਿ ਸਟਾਲ ਹਾਲ, ਬਾਰ, ਸਟਿੰਗ ਰੈਸੇ ਆਦਿ ਵੀ ਪੇਸ਼ ਕੀਤੇ । ਸਵੀਡਸ ਜਿਮਨਾਸਟਿਕ ਵਿਚ ਸਰੀਰਕ ਗਤੀਵਿਧੀਆਂ ਦੇ ਪ੍ਰੋਗ੍ਰਾਮ ਇਸ ਤਰ੍ਹਾਂ ਬਣਾਏ ਜਾਂਦੇ ਸਨ ਤਾਂ ਕਿ ਹਰ ਗਰੁੱਪ ਆਪਣੀ ਸਮਰੱਥਾ ਅਨੁਸਾਰ ਉਸ ਵਿਚ ਭਾਗ ਲੈ ਸਕੇ । ਇਸ ਪ੍ਰਣਾਲੀ ਵਿੱਚ ਉਹਨਾਂ ਕਸਰਤਾਂ ਨੂੰ ਕਰਵਾਉਣ ਤੇ ਜ਼ੋਰ ਦਿੱਤਾ ਜਾਂਦਾ ਸੀ ਜੋ ਕਿ ਸਰੀਰਕ ਸਥਿਤੀ (Posture) ਨੂੰ ਠੀਕ ਰੱਖ ਸਕੇ | ਅੱਜ ਵੀ ਸਰੀਰਕ ਸਿੱਖਿਆ ਸਵੀਡਨ ਵਿਚ ਲਾਜ਼ਮੀ ਤੌਰ ਤੇ ਦੇਖੀ ਜਾਂਦੀ ਹੈ ।

ਡੈਨਮਾਰਕ (Denmark)-ਡੈਨਮਾਰਕ ਵਿਚ ਫਰਾਂਸ ਨਚੇਤਗਾਲ ਨੇ ਸਰੀਰਕ ਸਿੱਖਿਆ ਦੀ ਬੁਨਿਆਦ ਰੱਖੀ । ਉਹਨਾਂ ਦੇ ਨਿਰੰਤਰ ਯਤਨਾਂ ਕਾਰਨ ਸਰੀਰਕ ਸਿੱਖਿਆ ਸਕੂਲਾਂ ਦਾ ਹਿੱਸਾ ਬਣੀ । ਯੋਗ ਅਧਿਆਪਕਾਂ ਦੀ ਲੋੜ ਵੱਧੀ ਅਤੇ ਕਈ ਸਿਖਲਾਈ ਇਸ ਉਦੇਸ਼ ਨੂੰ ਮੁੱਖ ਰੱਖਦੇ ਹੋਏ ਸ਼ੁਰੂ ਕੀਤੇ ਗਏ । ਉਹਨਾਂ ਦੀ ਮੌਤ ਤੋਂ ਬਾਅਦ ਟੈਨਿਸ ਰਾਈਫਲ ਕਲੱਬ ਦੀ ਉਸਾਰੀ ਕੀਤੀ ਗਈ, ਜਿੱਥੇ ਸ਼ੂਟਿੰਗ ਅਤੇ ਮਿਲਟਰੀ ਡਿਲ ਦੀ ਸਿਖਲਾਈ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ ।

ਇੰਗਲੈਂਡ (England)-ਆਧੁਨਿਕ ਖੇਡਾਂ ਨੂੰ ਹਰਮਨ ਪਿਆਰਾ ਬਣਾਉਣ ਵਿਚ ਬ੍ਰਿਟਿਸ਼ ਦਾ ਯੋਗਦਾਨ ਬਹੁਤ ਵੱਡਾ ਹੈ । ਇੰਗਲੈਂਡ ਵਿਚ ਬਹੁਤ ਮਸ਼ਹੂਰ ਗਤੀਵਿਧੀਆਂ ਵਿਚ ਤੀਰ-ਅੰਦਾਜ਼ੀ, ਤੈਰਾਕੀ, ਹਾਕੀ, ਫੁੱਟਬਾਲ ਅਤੇ ਬਾਅਦ ਵਿਚ ਕ੍ਰਿਕਟ ਅਤੇ ਟੈਨਿਸ ਨੂੰ ਇਸ ਸਮੇਂ ਦੌਰਾਨ ਪੇਸ਼ ਕੀਤਾ । ਉਹਨਾਂ ਸਰੀਰਕ ਸਿੱਖਿਆ ਨੂੰ ਸਕੂਲੀ ਪਾਠਕ੍ਰਮ ਵਿਚ ਮਹੱਤਤਾ ਅਤੇ ਵਿਕਾਸ ਤੇ ਜ਼ੋਰ ਦਿੱਤਾ । ਉਹਨਾਂ ਨੇ ਖੇਡ ਮੈਦਾਨਾਂ ਅਤੇ ਜਿਮਨਾਸਟਿਕ ਹਾਲ ਦੇ ਰੱਖ ਰਖਾਵ ਤੇ ਵੀ ਜ਼ੋਰ ਦਿੱਤਾ ।