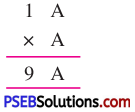Bhagya

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 3 Understanding Quadrilaterals Ex 3.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals Ex 3.2

Question 1.
(a)

Solution:
Sum of all the exterior angles of a polygon = 360°.
∴ x + 125° + 125° = 360°
∴ x + 250° = 360°
∴ x = 360° – 250° (Transposing 250° to RHS)
∴ x = 110°

(b)

Solution:
In this figure, two exterior angles are of 90° each. (one interior angle is 90°)
Sum of all exterior angles of a polygon = 360°.
∴ x + 90° + 60° + 90° + 70° = 360°
∴ x + 310° = 360°
∴ x = 360° – 310° (Transposing 310° to RHS)
∴ x = 50°

Question 2.
Find the measure of each exterior angle of a regular polygon of (i) 9 sides (ii) 15 sides
Solution:
(i) Number of sides (n) = 9
∴ Number of exterior angles = 9
The sum of all exterior angles = 360°.
The given polygon is a regular polygon.
∴ All the exterior angles are equal.
∴ Measure of an exterior angle = \(\frac{360^{\circ}}{9}\).
= 40°

(ii) Number of sides of regular polygon = 15
∴ Number of exterior angles = 15
The sum of all the exterior angles = 360°
The given polygon is a regular polygon.
∴ All the exterior angles are equal.
∴ The measure of each exterior angle = \(\frac{360^{\circ}}{15}\) = 24°

Question 3.
How many sides does a regular polygon have if the measure of an exterior angle is 24° ?
Solution:
Regular polygon is equiangular.
Sum of all the exterior angles = 360°
Measure of an exterior angle = 24°
∴ Number of sides = \(\frac{360^{\circ}}{24^{\circ}}\)
The polygon has 15 sides.

Question 4.
How many sides does a regular polygon have if each of its interior angles is 165° ?
Solution:
The given polygon is regular polygon.
Each interior angle = 165°
∴ Each exterior angle = 180° – 165° = 15°
∴ Number of sides = \(\frac{360^{\circ}}{15^{\circ}}\) = 24
The polygon has 24 sides.

Question 5.
(a) Is it possible to have a regular polygon with measure of each exterior angle as 22° ?
Solution:
Each exterior angle = 22°
∴ Number of sides = \(\frac{360^{\circ}}{22^{\circ}}=\frac{180^{\circ}}{11^{\circ}}\)
The number of sides of a regular polygon must be a whole number.
But, \(\frac {180}{11}\) is not a whole number.
∴ No, exterior angle of a regular polygon cannot be of measure 22°.

(b) Can it be an interior angle of a regular polygon ? Why ?
Solution:
If the measure of an interior angle of a polygon is 22°, then the measure of its exterior angle = 180° – 22° = 158°.
∴ Number of sides = \(\frac{360^{\circ}}{158^{\circ}}=\frac{180^{\circ}}{79^{\circ}}\)
\(\frac {180}{79}\)is not a whole number.
∴ No, 22° cannot be an interior angle of a regular polygon.

Question 6.
(a) What is the minimum interior angle possible for a regular polygon? Why ?
Solution:
The minimum number of sides of a polygon = 3
The regular polygon of 3-sides is an equilateral triangle.
Each interior angle of an equilateral triangle = 60°.
Hence, the minimum possible interior angle of a polygon = 60°.

(b) What is the maximum exterior angle possible for a regular polygon ?
Solution:
The sum of an exterior angle and its corresponding interior angle is 180°. (Linear pair)
And minimum interior angle of a regular polygon = 60°.
∴ The maximum exterior angle of a regular polygon = 180° – 60° = 120°.

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 16 Playing with Numbers Ex 16.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 16 Playing with Numbers Ex 16.1

Find the values of the letters in each of the following and give reasons for the steps involved:

Question 1.

Solution:
Here, we have two letters A and B, whose values are to be found.

By observing the ones column, we have A + 5 and we get 2 from this.
1. e., a number whose ones digit is 2, for this A has to be 7.
∴ A + 5 = 7 + 5 = 12

Now, for the sum in tens column, we have 1 + 3 + 2 = B
∴ B = 6
Thus,

Thus, A = 7 and B = 6

Question 2.

Solution:
Here, we have three letters A, B and C, whose values are to be found.

By observing the ones column, we have A + 8 and we get 3 from this.
i. e., a number whose ones digit is 3, for this A has to be 5.
∴ A + 8 = 5 + 8 = 13
Now, for the sum in tens column, we have 1 + 4 + 9 = CB
∴ CB = 14
Here, B = 4 and C = 1

Thus, A = 5, B = 4 and C = 1

Question 3.

Solution:
Here, we have A, whose value is to be found.

Since, product of ones digit
A × A = A, so it must be 1, 5 or 6.
When A = 1, then 1 1 But, the product is 9 A, so A = 1 is not possible.

When A = 5, then
But, the product is 9 A, so A = 5 is not possible.

When A = 6, then

Thus, A = 6

Question 4.

Solution:
Here, we have two letters A and B, whose values are to be found.

By observing the ones column, we have B + 7 and we get A from this, i. e., a number whose ones digit is A.
Now, for the sum in tens column, we have A + 3 and we get 6 from this. Therefore, the value of A must be 2. (Keeping in mind that carry over 1 is to be considered.)
If A = 2, then

Then B + 7 gives 2, so B + 37 must be 5 and sum in tens 6 2 column is 1 + 2 + 3 = 6, so it is correct.

Question 5.

Solution:
Here, we have three letters A, B and C, whose values are to be found.

Units digit of 3 × B is B, so B must be either 0 or 5.

When B = 0, then

When B = 5, then

Now, units digit of 3 × A is A. So A must be either 0 or 5, but A cannot be 0, because if A = 0, then AB becomes one-digit number. So A must be 5 and multiplication is either 55 × 3 or 50 × 3.
55 × 3 = 165, here A = 6, so this is not possible.
∴ 50 × 3 = 150

Thus, A = 5, B = 0 and C = 6

Question 6.

Solution:
Here, we have three letters A, B and C, whose values are to be found.

Units digit B × 5 = B, so B must be either 0 or 5.
When B = 0, then

When B = 5, then

Now, units digit of 5 × A = A, so A must be either 0 or 5.
There are three letters as a product. So A ≠ 0, but A = 5.
So multiplication is either 50 × 5 or 55 × 5.
50 × 5 = 250 and 55 × 5 = 275, so 55 × 5 is not correct.
So 50 × 5 = 250

Thus, A = 5, B = 0 and C = 2.

Question 7.

Solution:
Here, we have two letters A and B, whose values are to be found.

Units digit B × 6 = B, so B must be 2, 4, 6 or 8.
∴ Possible values of product BBB are 222, 444, 666 or 888.
If we divide these numbers by 6, then quotient should be A2, A4, A6 or A8.
Now, 222 ÷ 6 = 37, remainder = 0
But, the quotient is not as A2, so B = 2 is not possible.

Thus, A = 7 and B = 4

Question 8.

Solution:
Here, we have two letters A and B, whose values are to be found.

By observing the sum in unit column, we have 1 + B = 0. So here is a number whose unit digit is 0, so B must be 9.
Now, for sum in tens column, we have 1 + A + 1 = 9.
So A must be 7.

Thus, A = 7 and B = 9

Question 9.

Solution:
Here, we have two letters A and B, whose values are to be found.

By observing the sum in units column, we have B + 1 = 8.
∴ B must be 7.
Now,

By observing the sum in tens digit column, we have A + 7 = 1, i.e., whose unit’s digit is 1, so A must be 4.

Thus, A = 4 and B = 7

Question 10.

Solution:
Here, we have two letters A and B, whose values are to be found.

By observing the sum in tens column, we have 2 + A = 0, so A must be 8.
Then,

Now, by observing the sum in units column, we have 8 + B = 9, so B must be 1.

Thus, A = 8 and B = 1.

Punjab State Board PSEB 8th Class English Book Solutions English Letter/Application Writing Exercise Questions and Answers, Notes.

PSEB 8th Class English Letter/Application Writing

पत्र लिखना एक कला है। एक अच्छा पत्र लिख कर आप शत्रु का दिल भी जीत सकते हैं। पत्र मुख्यतः तीन प्रकार के होते हैं-व्यक्तिगत, व्यावसायिक अथवा अधिकारियों को लिखे गए पत्र।

व्यक्तिगत पत्र (Personal Letters)-व्यक्तिगत पत्र वे पत्र होते हैं जो हम अपने मित्रों या सगे-सम्बन्धियों को लिखते हैं। ऐसे पत्र प्रायः समाचारों से भरे होते हैं। इन पत्रों में हम अपने घर, परिवार, स्कूल या किसी अनुभव का वर्णन करते हैं। ये पत्र एक विशेष विधि द्वारा लिखे जाते हैं। इन्हें ऐसे लिखा जाता है जैसे कि आप किसी व्यक्ति से बातचीत कर रहे हों। पते के अतिरिक्त इन पत्रों के छ: भाग होते हैं।

1. लिखने वाले का पता (The address of the sender)
2. तिथि (Date)
3. सम्बोधन या अभिवादन (The salutation or greeting)
4. विषय-वस्तु (The body of letter)
5. विधिवत् अन्त (The subscription or complimentary close)
6. हस्ताक्षर (Signature)

प्रत्येक भाग को लिखने की अपनी अलग विधि होती है। आओ हम एक-एक करके इनका अध्ययन करें-
1. The Address of the Sender. पहले पत्र भेजने वाले का पता पृष्ठ पर सबसे ऊपर दायें कोने में लिखा जाता था। प्रत्येक लाइन में अन्त में Comma और आखिरी लाइन के अन्त में Full Stop लगाया जाता था।

परन्तु अब पता लिखते समय विराम चिन्ह लगाने की विधि में अन्तर आ गया है। अब पंक्तियों के अन्त में Commas और Full Stop का प्रयोग नहीं होता। इसके अतिरिक्त अब Sender’s Address दाहिने कोने की बजाये बाएं कोने में लिखा जाता है।

15 Model Town
Rajpura
2. Date. तिथि लिखने वाले के पते के बिल्कुल नीचे लिखी जाती है। तिथि लिखने की कई विधियां हैं, जैसे-
15 Model Town
Rajpura
March 12, 20……
या
12th March 20…..
या
12 March 20……
3. The Salutation or Greeting. (i) मित्र को पत्र लिखते समय उसे उसके नाम से सम्बोधित कीजिए; जैसे-Dear Mohan, जहां तक हो सके मित्र को उसी नाम (संक्षिप्त) से संबोधित कीजिए जिस नाम से आप बातचीत करते समय उसे सम्बोधित करते हैं; जैसे,
Dear Monu
Dear Sonu

(ii) माता-पिता, भाइयों, बहनों अथवा घनिष्ठ सगे सम्बन्धियों को आप यूं सम्बोधित कर सकते हैं-
My dear Father or Daddy/Dad
My dear Mother or Mamma/Mom
My dear Brother My dear Gopal
My dear Kamla
नोट-यदि आप Address में विराम चिन्ह नहीं लगाते तो आप सम्बोधन में भी इनका प्रयोग न करें।

4. The Body of the Letter-यह पत्र का सबसे महत्त्वपूर्ण भाग है। एक अच्छा पत्र वह माना जाता है जो सरल हो और जिसमें पाठक की रुचि बनी रहे। पत्र की प्रत्येक पंक्ति अर्थपूर्ण एवं रोचक हो। पत्र ऐसे लिखना चाहिए मानो आपका सम्बन्धी आपके सामने बैठा हो और आप से बातें कर रहा हो। पत्र का यह भाग लिखते समय विराम चिन्हों और Grammar के अन्य सभी नियमों का पूरा पालन करें।

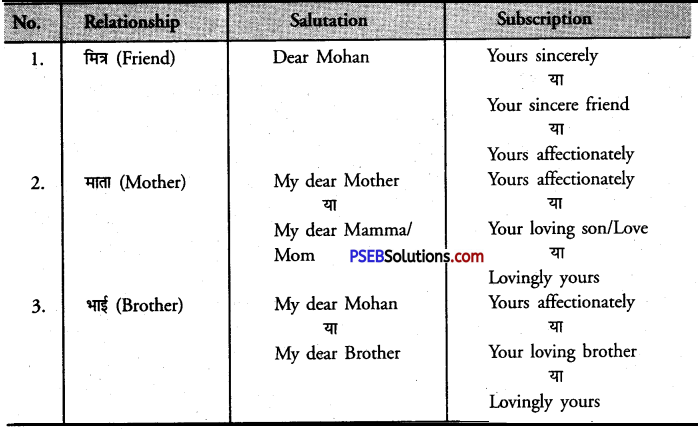
5. The Subscription or Complimentary Close-(i) मित्र को लिखे गए पत्र का अन्त इस प्रकार करें
Yours sincerely
या
Your sincere friend

(ii) सगे-सम्बन्धियों को लिखे गये पत्रों का अन्त इस प्रकार करें-
Yours affectionately

(iii) निम्नलिखित phrases के साथ भी व्यक्तिगत पत्रों का अन्त किया जा सकता है- . Ever sincerely yours
या
Your loving son/Love
या
Lovingly yours
नोट-यदि आपने सम्बोधन के समय comma नहीं लगाया तो आप पत्र का अन्त करने वाले phrase के साथ भी comma न लगायें।

6. Signature-व्यक्तिगत पत्र में आप को अपने पूरे हस्ताक्षर नहीं करने चाहिएं। आपको या तो नाम का पहला हिस्सा लिखना चाहिए या फिर वह नाम लिखें जिस नाम से आप अपने सगे-सम्बन्धियों या मित्रों द्वारा पुकारे जाते हैं। जैसे-
Sohan
या
Sonu आप Sohan Lal Gupta अर्थात् पूरा नाम न लिखें।

Salutation and Subscription at a Glance

Official Letters या Business Letters.
(i) ऐसे पत्रों में कोई विशेष अन्तर तो नहीं होता। अन्तर केवल इतना है कि इन पत्रों के प्राय: छ: की बजाए सात भाग होते हैं।

(ii) ऐसे पत्रों में पत्र लिखने वाले का पता और तिथि व्यक्तिगत पत्रों की तरह ही लिखे जाते हैं।’

(iii) ऐसे पत्रों में उस फर्म (Firm) या व्यक्ति का पूरा पता भी पत्र में लिखा जाता है जिसे पत्र लिखा जा रहा हो, जैसे-
Messrs Malhotra Book Depot
(Producers of Quality Books)
Railway Road
Jalandhar City

(iv) ऐसे पत्रों में सम्बोधन की विधि इस प्रकार होती है
Dear Sir
या
Dear Sirs
या
Madam
या
Sir
नोट-यदि व्यक्ति आप से परिचित है तो आप उसे यूं भी सम्बोधित कर सकते हैं-
Dear Mr. Sharma

(v) ऐसे पत्रों की विषय-वस्तु संक्षिप्त, स्पष्ट और विनम्र-भाषी होनी चाहिए।

(vi) ऐसे पत्रों का अन्त यूं करना चाहिए
Yours truly
या
Yours faithfully

(vii) आप माननीय व्यक्तियों अथवा उच्च पद पर आसीन व्यक्तियों को पत्र लिखते हुए Yours respectfully या Yours obediently का प्रयोग भी कर सकते हैं। नाम से सम्बोधित पत्रों का अन्त Yours sincerely से ही करना चाहिए।

(viii) ऐसे पत्रों में हस्ताक्षर पूरे होने चाहिएं और हस्ताक्षर के पश्चात् लिखने वाले का नाम या पद लिखा जाना चाहिए, जैसे-
Yours faithfully
Mohan Lal Sharma
Manager

Important Applications and Letters

1. Application for Marriage Leave
Write an application to the Headmistress of your school for marriage leave.

The Headmistress
Khalsa Public School
Nawanshahr
Madam

I beg to say that the marriage of my elder brother/sister takes place next week. I am to help my parents in making marriage arrangements. So I cannot come to school. Kindly grant me leave for five days. I shall be very thankful to you for this.

Yours obediently
Jaspinder Kaur
Roll No. 25
23. VIII A
March 15, 20 ………….

Word-Meanings-Marriage = विवाह, Takes place = होगी, Arrangements = व्यवस्थाएं, Much = अधिक.

2. Leave for Urgent Work
Write an application to the Principal of your school for leave for a day.

The Principal
A.B. Sen. Sec. School
Patiala Sir

I beg to say that I have an urgent piece of work at home. So I cannot come to school. Kindly grant me leave for today. I shall be thankful to you for this.

Yours obediently
Raman
Roll No. 25
VIII C
February 5, 20 ……

Word-Meanings-Urgent piece of work = आवश्यक कार्य, Grant = प्रदान करो

3. Application for a Testimonial
Imagine you are Kavita, a student of Govt. Sen. Sec School, Ludhiana. Write an application to the Principal of your school requesting him to send a testimonial as you are applying for the post of a clerk.

11 Happy House
Model Town
Jalandhar
The Principal
Govt. Sen. Sec. School
Ludhiana
Sir

I beg to say that I am an old student of your school. I have to apply for the post of a clerk in a bank. I need a testimonial from you for that. I am writing down the following details for reference.

I passed my Sen. Sec. Examination in 2001 with 600 marks. I stood first in the district. I was a member of the school hockey team. I took part in the debates also and won many trophies and cups for the school. I was in the good books of my teachers.

Kindly send me the testimonial as soon as possible and oblige.

Yours obediently
Kavita
March 14, 20……

Word-Meanings-Testimonial = अचरण पत्र, In the good books of = नजरों में अच्छा, Oblige = कृतार्थ करें।

4. Application for Change of Section
Write an application to the Principal of your school requesting him to change your section.

The Principal
Govt. Sen. Sec. School
Sirhind
Sir

I am a student of VIII B of your school. I live in Main Bazaar. All my friends are in VIII A Section of the school. So I feel very lonely in VIII B.

Besides, I have to do my home task alone at home. Whenever I am unable to attend the school, I cannot do my homework. There is none to tell me about the homework given by the class teacher. The boys of my street can help me in other ways also. I hope you will appreciate my problem and change my section.
Thanking you

Yours obediently
Kirpal Singh
Roll No. 46
VIII B
March 15, 20……

Word-Meanings- Feel = अनुभव करना, Ways = ढंग, Lonely = अकेला, Appreciate = समझना।

5. For Admission to the Next Class
Write an application to the Headmaster of your school requesting him for admission to the next class.

The Headmaster
Govt. High School
Phagwara
Sir

I beg to say that I am a student of 7th class of your school. I fell ill in March. Still I appeared in the annual examination. I failed but my class-fellows went to the next class.

I am a good student. I got first division in the half-yearly examination. Kindly give me a test on any day and admit me to the 8th class. I assure you that I shall get first division in Middle Standard Examination.
Thanking you

Yours obediently
Mohan Lal
VIII C
March 5, 20…….

Word-Meanings- Annual = वार्षिक, Division = श्रेणी.

6. Application for Late Fee
Write an application to the Headmaster of your school requesting him to permit you to pay your fee for the month late by ten days.

The Headmaster
Govt. High School
Hoshiarpur
Sir

I beg to say that I am a student of VIII A of your school. Tomorrow is fee day and I am unable to pay it. My father has gone to Delhi. He will come back in ten days. Kindly allow me to pay my fee late by ten days.

Thanking you

Yours obediently
Sohan Lal
VIII A
March 9, 20……..

Word-Meanings- Unable = असमर्थ, Allow = अनुमति देना

7. Permission to take part in Games
Write an application to the Headmaster of your school requesting him to permit you to take part in the evening games.

The Headmaster
A.B.C. High School
Moga
Sir

I am a student of VIII D of your school. Our school is preparing for the Distt. Sports Meet. There are regular games in the school in the evening. I am also fond of games. I am a good player of football. Last year I was a member of the school football team. But this year my name is not in the players’ list because I could not perform well in the final trial. I request you to give me another chance and permit me to take part in the evening games. I assure you that I will try my best to improve my performance.
Thanking you

Yours obediently
Vijay Kumar
Roll No. 25
VIII D
Dated : March 9, 20…………

Word Meanings-Take part = भाग लेना, Permit = अनुमति देना, Assure = विश्वास दिलाना।

8. Permission to go on a Historical Tour
Write an application to your Principal requesting him/her to permit you to go on a historical tour.

The Principal
Govt. Sen. Sec. School
Ladowal
Madam

We, the students of class VIII, beg to seek your permission for a historical tour. The school will close for the summer vacation next week. We want to see the Taj Mahal. We also want to go to Fatehpur Sikri. On our way back, we want to visit Delhi. The trip will be very useful for us. It will give us first hand knowledge of History. The trip will cost two hundred rupees per head. Our teacher of History has agreed to take us to these places. We are 30 girls in all. I hope you will arrange this trip.
Thanking you

Yours obediently
Manjit Kaur
VIII A
April 30, 20……

Word-Meanings- Summer = गर्मी, Trip = भ्रमण, Useful = उपयोगी, Knowledge = ज्ञान

11. On Recovery From Illness
Write a letter to your friend congratulating him on his recovery from long illness.

135 New Road
Nawanshahr
March 18, 20…..
Dear Mohan

I am glad to know that you have recovered from long illness. I congratulate you on your recovery. You worked very hard. So you fell ill. Now please take care of your health.

Take long walks in the morning. Drink milk and eat fruit. All this will make you healthy soon.
With best wishes.

Yours sincerely
Hardeep

Word-Meanings-Glad = प्रसन्न, Recovered = ठीक हो गये हो, Take care of = ध्यान रखो, Congratulate = बधाई देना

12. Invitation on Brother’s Marriage
Write a letter to your friend inviting him to your brother’s marriage.

Govt. High School
Amritsar
March 4, 20………
My dear Kamlesh

You will be glad to know that the marriage of my elder brother comes off on March 9, 20……. The marriage party will leave Amritsar for Delhi the same day. We invite you to join us in our joys.

You know that Delhi is a historical city. There are many buildings worth-seeing. You will see the Red Fort, the Qutab Minar and Jantar Mantar. Rina and Tina have also been invited. They will reach here on Sunday. We will have good time together.
I hope you will reach in time.

Yours sincerely
Mitlesh
Address:
Kumari Kamlesh
45 Mall Road
Shimla

Word-Meanings-Comes off = पड़ती है, Marriage party = बारात, Worth-seeing = दर्शनीय

13. Inviting a Friend to the Birthday Party
Suppose you are Harish. You live at 38 Manavta Park, Hoshiarpur. Invite your friend to come to your birthday party.

38 Manavta Park
Hoshiarpur
February 22, 20……
My dear Surinder

You will be glad to know that my birthday falls on next Monday. There will be a tea party in the evening. I have invited all my friends to the party. I cannot forget you on this day. Please reach here on Sunday evening. We will have a good time together.
Thanking you

Yours sincerely
Harish

Word-Meanings-Falls on = पड़ता है, Invited = आमन्त्रित किया है, Forget = भूलना।

14. To Uncle for a Birthday Gift
Suppose you are Poonam. You live at 232, Phase IX, Mohali. Your uncle has sent you a wrist-watch on your birthday. Write a letter of thanks to your uncle.

232 Phase
IX Mohali
March 8, 20……
My dear Uncle

It is very kind of you to remember me on my birthday. You have sent me a beautiful wrist-watch as a gift. It shows your love for me. I received many gifts that day but I liked your gift the most. Everybody praised it.

The watch will help me a lot. It will make my life regular. I shall never be late for school now. I thank you for this lovely gift. I assure you thar I shall keep this watch with great care.

With regards
Yours lovingly
Poonam
Address :
Shri Manohar Singh
Joginder Nagar
Rohtak

Word-Meanings-Gift = उपहार, The most = सबसे बढ़कर, Praised = प्रशंसा की, A lot = बहुत ज्यादा, Regular = नियमित, Care = ध्यान.

15. To Younger Brother to Take Interest in Studies
Write a letter to your younger brother/sister scolding him/her for neglecting studies.

18 Mohan Nagar
Batala
February 18, 20…….
My dear Suman

I received your progress report yesterday. You have failed in all the subjects. You are not working hard. You are neglecting your studies. It is very bad. Final examinations are drawing near. Be careful. Do not waste your time. Work hard. Finish your syllabus in time.
I hope you will act upon my advice.

Yours affectionately
Mohan

Word-Meanings Subjects = विषय, Neglecting = उपेक्षा कार रहे, Waste = नष्ट करना, Avoid = दूर रहना, Act upon = अमल करना।

16. Invitation for Summer Vacation
Write a letter to your friend asking him to spend a part of his summer vacation with you.

1407 Green Avenue
Amritsar
February 18, 20 ……
My dear Gopal

Your school has closed for the summer vacation. You are free now. I invite you to come to Amritsar. Amritsar is a holy city. Here are many places worth-seeing. You will see Sri Harmandar Sahib, the Durgayana Mandir, the Jallianwala Bagh and other important places.

We shall also study together. I hope you will reach here soon.

Yours sincerely
Ramesh

Word-Meanings-Invite = बुलाना, Holy = पठित्र, Worth-seeing = देखने योग्य।

17. To a Friend on his Failure
Write a letter to your friend who has failed in the examination, asking him not to lose heart but try again.

15 New Colony
Kotkapura
March 18, 20 ……
Dear Raman

Your result is out today. It is very sad that you have failed. It is your own fault. You never worked hard. You moved in a bad company. The result is before you.

Please act upon my advice. Don’t lose heart. Give up bad company and work hard. You will pass next time.

Yours sincerely
Kamal
Address:
Mr. Raman
370 Nai Basti
Ambala

Word-Meaning-Moved = घूमते रहे, Act upon = अमल करना, Lose heart = धैर्य छोड़ना।

18. Condolence Letter.
Suppose you are Satish. You live at 6 Soni Street, Khanna. Your friend has lost his mother. Write a letter of condolence to him.

6 Soni Street
Khanna
Feb. 20, 20 ……
My dear X

I got your letter yesterday. I was shocked to read it. The sudden death of your mother is. a great loss. I share your sorrow.

I met your mother last month. She looked healthy. Her death is untimely. It is the will of God. We must bow before His will. Please have courage.

Yours sincerely
Satish
Address:
Mr. X
15-New Chowk
ABC

Word Meanings-Shocked = आघात पहुंचा, Sudden = आकस्मिक, Great loss = बहुत बड़ी क्षति, Share = बांटना, Sorrow – दुःख, Untimely death = अकाल मृत्यु, Will = इच्छा।

19. To Avoid Bad Company
Write a letter to your younger brother, advising him to avoid bad company. Examination Hall

………City
March 15, 20…….
My dear Mukesh

I received a letter from your headmaster. I gather that you move in a bad company. Ramesh and Dinesh are your friends these days. Both of them smoke. They go to pictures everyday. You, too, have started smoking in their company. You have become a film-fan. Your headmaster is worried about you.

Dear brother, we have high hopes on you. You are the light of our home. The examinations are drawing near. Please give up your bad company.
I hope you will act upon my advice.

With love
Yours affectionately
Kamleshwar
Address:
Mr. Mukesh Verma
Boys’ Hostel
A.B.C. Sen. Sec. School
…….. City

Word-Meaning-Film-fan = फिल्म देखने के शौकीन, Draw near = निकट आना, Act upon = अमल करना।

20. To Father about Your Success in the Examination
You have passed the Middle Standard Examination. Write a letter to your father telling him about your good result.

36 Raj Nagar
Khanna
July 3, 20 ……
My dear Father

Our result was out yesterday. You will be glad to know that I have stood second in the state. I have secured 85% marks. My teacher and headmaster came to our house in the morning. They blessed and patted me. They congratulated the mother. All missed you badly on the occasion. When are you coming home?

Your loving son
Amit

Word-Meanings-Secure = प्राप्त करना, Missed = याद आई, Occasion = अवसर।

21. Letter about Hostel Life
You are Anil, a student of class VIII. You are residing in hostel. Write a letter to your mother about your hostel life.

Boys’ Hostel
A.B.C. Sen. Sec. School
Chandigarh
My dear Mother

Our new session has started. I have got a good room in the school hostel. My hostel life is well disciplined. There are fixed hours for study, meals and games. We get up in time and go to bed in time. Our hostel warden is kind as well as strict to us. He does not allow us to go out of the hostel after the main gate is closed.
Dear Mother, I miss you very badly. I wish I got wings to fly home.

With regards
Yours lovingly
Anil

Word-Meanings- Session = सत्र, Disciplined = अनुशासित, Fixed = निरिचत, Strict = सख्त

22. To Father About Your Papers
You are appearing in the Middle Standard Examination. Write a letter to your father telling him about your progress in the examination.

8 The Mall
Jalandhar Cantt
March 18, 20…….
My dear Father

I am taking my Middle Standard Examination these days. The English paper was very easy. I hope to get 80 marks in it. The paper in Mathematics was a little tough. But I did all the sums.

Punjabi and Social Studies are easy subjects. I hope to do well in them. I am sure that I shall get good marks. I may win a scholarship.
With regards to dear mother

Your loving son
Arun Kumar

Word-Meanings- Taking = दे रहा हृं, Over = समाप्त, Tough = कठिन, Do well = अच्छ करना

23. To Father for Change of School
Write a letter to your father asking him to allow you to change school.

512 Naya Nagar
…….. City
March 10, 20……..
My dear Father

I feel sad to tell you about my school. Once it was a great school. It was considered one of the best schools in the town. Now it is not. We have no Principal these days. We have no English teacher even. So I do not feel good at studies. I want to change my school. Jain High School is a good school. Kindly allow me to join it.

Your loving son
Raj Kumar
Address:
Mr. Mohan Lal Sharma
1 New Road
Patiala

Word Meanings-Considered = समझा जाता था, Feel good = मन लगना, Allow = अनुमति देना।

Punjab State Board PSEB 8th Class English Book Solutions English Grammar Sentence and its Types Exercise Questions and Answers, Notes.

PSEB 8th Class English Grammar Sentence and its Types

A sentence is a well arranged group of words which makes complete sense.
शब्दों का वह सुव्यवस्थित समूह जिससे पूरा अर्थ निकले कहलाता है, जैसे-

1. Lakhi Mal was very rich.
2. Where does the koel sit ?
3. Please bring him milk and fruit now.
4. Hurrah ! We have won the match.

Kinds of Sentence

वाक्य पांच प्रकार के होते हैं-

1. Assertive Sentences (साधारण वाक्य)
2. Interrogative Şentences (प्रश्नवाचक वाक्य)
3. Imperative Sentences (आजसयक वाक्य )
4. Exclamatory Sentences (विस्मया दिसूचक वाक्य)
5. Optative Sentences (इच्छासूचक वाक्य)

Parts of a Sentence

वाक्य के दो भाग होते है-

1. Subject (उद्देश्थ)
2. Predicate (विधेय)

1. वाक्य में जिस व्यक्ति पशु स्थान अथवा वस्तु के बारे में कुछ कहा जाता है उसे Subject कहते हैं।
2. Predicate. Subject के बारे में जो कुछ कहा जाता है उसे Predicate कहते हैं।

Sentence	Subject	Predicate
1. Amar lives in Allahabad.	Amar	lives in Allahabad.
2. How does a fish swim ?	a fish	How does swim.
3. May you live long !	you	May live long.
4. Mr. Verma is my teacher.	Mr. Verma	is my teacher.

विशेष- Imperative Sentences का Subject प्राय लुप्त रहता है जैसे-

1. Thank you. (I thank you.)
2. Come in. (You come in.)

Simple and Complex Sentences

What is a Simple Sentence?
(साधारण वाक्य की परिभाषा)

जिस वाक्य में केवल एक Finite Verb हो, वह Simple Sentence कहलाता है। साधारण वाक्य में एक Subject (उद्देश्य) और एक Predicate (विधेय). होता है; जैसे,-

1. Mohan loves his country.
2. Ram plays hockey.
3. Dogs bark.

Note. 1. जिस क्रिया का अपना subject (उद्देश्य) हो, वह Finite Verb (परिमित क्रिया) कहलाती है।
2. ऊपर के प्रत्येक वाक्य में एक-एक Finite Verb (loves, plays, bark) है।
3. प्रत्येक का अपना Subject (Mohan, Ram, Dogs) है और अपना Predicate (loves his country, plays hockey, bark) है।

What is a Complex Sentence?
(मिश्रित वाक्य की परिभाषा)

Complex Sentencé को जानने से पहले Clauses (उप-वाक्य) को समझ लेना आवश्यक है, क्योंकि Clauses के मेल से ही Complex Sentence बनता है।

Clause. शब्दों के ऐसे समूह को Clause (उप-वाक्य) कहते हैं जिसका अपना Subject तथा अपना Predicate हो और साथ में किसी अन्य वाक्य का उप-भाग भी हो।

Kinds of Clauses. Clauses के प्रकार को समझने के लिए हमें नीचे लिखे वाक्य को ध्यान से पढ़ना चाहिए-
I like him because he is brave.
नोट-1. इस वाक्य के दो भाग हैं।
2. प्रत्येक भाग में Subject और Predicate दोनों हैं। इसलिए दोनों ही clause हैं।

पहली Clause (I like him). पहली clause का पूरा अर्थ निकलता है। इसका अर्थ समझने के लिए दूसरी clause की आवश्यकता नहीं है। ऐसी clause को Principal Clause या Main Clause (प्रधान उप-वाक्य) कहते हैं।

दूसरी Clause (because he is brave). दूसरी clause का पूरा अर्थ नहीं निकलता। पूरा अर्थ देने के लिए यह Principal Clause पर depend (आश्रित) है। इसलिए इसे Dependent या Subordinate Clause (आश्रित उप-वाक्य) कहते हैं।

Complex Sentence की परिभाषा-जिस वाक्य में एक Principal Clause (प्रधान उप-वाक्य) तथा एक या एक से अधिक Subordinate Clauses (आश्रित उप-वाक्य) हों, उसे Complex Sentence कहते हैं।

Exercise (With Hints)

Pick out the complex sentences:
1. Rani is a nice girl.
2. I know that Mohan is a good boy.
3. He is the boy whom I saw in the market.
4. The man (who was) on the platform was my brother.
5. I met the girl with blue eyes.
6. I met the old man who had grey hair.
7. I went wherever he went.
8. I want to know where you found my watch.
9. He is the teacher of my choice.
10. Those whom the gods love, die young.
Hints:
2. I know that Mohan is a good boy.
3. He is the boy whom I saw in the market.
4. The man (who was) on the platform was my brother.
6. I met the old man who had grey hair.
7. I went wherever he went.
8. I want to know where you found my watch.
10. Those whom the gods love, die young.

Change of Sentences

A–Affirmative to Negative
नियम- (1) साधारणतया निर्षधात्मक (Negative) वाक्य बनाते समय not का प्रयोग होता है: जैसे-

Affirmative	Negative
1. I am a girl.	1. I am not a girl.
2. We are farmers.	2. We are not farmers.
3. You are a student.	3. You are not a student.
4. He was tall.	4. He was not tall.
5. They were proud.	5. They were not proud.
6. Radha was a fat girl.	6. Radha was not a fat girl.
7. I shall write a letter.	7. I shall not write a letter.
8. You will help me.	8. You will not help me.
9. I am reading a book.	9. I am not reading a book.
10. You are weeping.	10. You are not weeping.
11. I was buying a pen.	11. I was not buying a pen.
12. We were playing cards.	12. We were not playing cards.
13. He was swimming.	13. He was not swimming.
14. She had gone there before.	14. She hadn’t gone there before. Or She had not gone there before.
15. We should finish this job.	15. We should not finish this job.

(ii) Present Indefinite (पहली फार्म) में do not/does not + पहली फार्म तथा Past Indefinite (दूसरी फार्म) में did not + पहली फार्म का प्रयोग होता है: जैसे-

Affirmative	Negative
1. I like mangoes	1. I do not like mangoes.
2. We play hockey.	2. We do not play hockey.
3. You take exercise.	3. You do not take exercise.
4. She speaks the truth.	4. She does not speak the truth.
5. I do it.	5. I do not do it.
6. I took tea.	6. I did not take tea.
7. He read the book.	7. He did not read the book.
8. He sold milk.	8. He did not sell milk.
9. She lived in Delhi.	9. She did not live in Delhi.

(iii) Has, have, had यदि अधिकार (possession) अर्थात् किसी चीज़ का होना व्यक्त करते हों तो प्रायः negative sentences में ‘no’ का प्रयोग होता हैै परन्तु यदि संख्या दी हो तो not का प्रयोग होता है।

1. He has a coat.
He has no coat.

2. He had a book
He had no book.

3. Ram has three books.
Ram has not three books.

विशेष नोट-1. Negative बनाने के लिए isnt, wasn’t, haven’t, shan’t आदि का भी प्रयोग किया जा सकता है। इन छोटे रूपों का अध्ययन इस प्रकार करें

2. Can का Negative cannot में किया जाता है। cannot एक शब्द के रूप में लिखा जाता है।

3. Not का प्रयोग पहले शब्द के तुरन्त बाद करना चाहिए, जैसे, shall have been = shall not have been तथा shall be = shall not be.

4. Everybody का Negative nobody तथा either का neither होता है। जैसे,
Affirmative. Everybody is coming.
Negative. Nobody is coming.
Affirmative. Either he or his friend is coming.
Negative. Neither he nor his friend is coming.

मिश्चित वाक्य (Mixed Sentences)

Affirmative	Negative
1. He is a player.	He is not a player.
2. They were happy.	They were not happy.
3. He has many books.	He does not have many books.
4. We have four toys.	We do not have four toys.
5. The boys had a garland.	The boys had no garland.
6. I read a book.	I do not read a book.
7. He writes a letter.	He does not write a letter.
8. He does his work.	He does not do his work.
9. He went there.	He did not go there.
10. Mohan will tell a lie.	Mohan will not tell a lie.

B-Assertive to Interrogative

Assertive	Interrogative
1. I do my duty.	Do I do my duty ?
2. He can help you.	Can he help you?
3. They laughed at us.	Did they laugh at us ?
4. She is a girl.	Is she a girl ?
5. You are late.	Are you late ?
6. He was happy.	Was he happy?
7. We shall come soon.	Shall we come soon?
8. We built a house there.	Did we build a house there?
9. It may rain today.	May it rain today?
10. We must go there	Must we go there?
11. She does her work.	Does she do her work?

Exercise for Practice

Change the following sentences into Interrogative:
1. They can swim.
2. She has a gold ring.
3. These birds are pretty.
4. We have seen the Taj.
5. She helped me in my work.
6. The carpenter makes furniture.
7. This pen costs ten rupees.
8. The child fell from a tree.
9. He was brushing his teeth.
10. Our soldiers fought bravely.

C-Exclamatory to Assertive

Exclamatory	Assertive
1. What a lovely flower!	It is a very lovely flower.
2. Long live our king!	We wish that our king may live long.
3. Alas ! I shall never be able to meet her again.	It is very sad that I shall never be able to meet her again.
4. Hurrah ! I have won a scholarship.	I am very happy that I have won a scholarship.
5. What a pity you have lost everything!	It is very sad that you have lost everything.
6. Fie ! A soldier and afraid of death!	It is shameful for a soldier to be afraid of death.
7. How cold it is today!	It is very cold today. I am very glad to see you.
8. How glad I am to see you!	It is a very shameful act on your part.
9. What a shameful act on your part !	The traitors must be punished with death.
10. Death to the traitors!	Assertive

Exercise for Practice

I. Change the following Exclamatory sentences into Assertive sentences:
1. Bravo ! You have killed the enemy.
2. Alas ! I am undone.
3. How sweet the child is!
4. Alas ! How stupid I had been !
5. What a terrible noise !
6. How difficult the paper is !
7. May God bless you with a son!
8. What a beautiful wrist-watch!
9. Splendid ! You have won the day!
10. Alas! You have failed.

II. Change the following Affirmative (Declarative) sentences into Interrogative sentences (Questions):

1. He is clever.
2. He was simple.
3. Ram was feeling tired.
4. Sita was angry.
5. They were good friends.
6. I have two books.
7. She has three pencils.
8. We had a good time there.
9. I have to do it.
10. Sohan had finished his work.
11. I shall go there tomorrow.
12. He will play a match.
13. I can do it.
14. He may help you.
15. You could write.
16. The sun does not shine at night.
17. He beats his donkey with a stick.
18. He sees another dog.
19. The horse runs very fast.
20. They play a match.
21. He waited here for an hour.
22. The train started at ten.
23. He never lost heart.
24. I did not find him there.
25. The rose smelt sweet.
Answer:
1. Is he clever ?
2. Was he simple ?
3. Was Ram feeling tired ?
4. Was Sita angry?
5. Were they good friends ?
6. Have I two books ?
7. Has she three pencils ?
8. Had we a good time there ?
9. Have I to do it?
10. Had Sohan finished his work ?
11. Shall I go there tomorrow?
12. Will he play a match ?
13. Can I do it?
14. May he help you ?
15. Could you write ?
16. Does the sun not shine at night ?
17. Does he beat his donkey with a stick ?
18. Does he see another dog?
19. Does the horse run very fast ?
20. Do they play a match ?
21. Did he wait here for an hour ?
22. Did the train start at ten ?
23. Did he ever lose heart?
24. Did I not find him there ?
25. Did the rose smell sweet?

III. Convert the following Interrogative sentences into Assertive (Declarative) sentences:

1. Are you on leave today?
2. Was the train late ?
3. Were the boys not lazy ?
4. Am I strong?
5. Is your sister ill?
6. Has it been raining since morning ?
7. Have you fulfilled your promise ?
8. Had he a pen?
9. Have you a horse ?
10. Has she a lovely voice ?
11. Should I stick to my promise ?
12. Does your father like you?
13. Did she not sing a sweet song?
14. Did he paint the door blue?
15. Can you help me ?
16. Does she sing well ?
17. Do we love our country?
18. Did you have a nice holiday ?
19. Do birds build nests ?
Answer:
1. You are on leave today.
2. The train was late.
3. The boys were not lazy.
4. I am.. strong.
5. Your sister is ill.
6. It has been raining since morning.
7. You have fulfilled your promise.
8. He had a pen.
9. You have a horse.
10. She has a lovely voice.
11. I should stick to my promise.
12. Your father likes you.
13. She did not sing a sweet song.
14. He painted the door blue.
15. You can help me.
16. She sings well.
17. We love our country.
18. You had a nice holiday.
19. Birds build nests.

IV (a) Change the following Positive sentences into their Negative form:

1. Lotus is a very lovely flower.
2. His neighbour was quite well yesterday.
3. Sham has a garland of flowers in his hand.
4. I have a horse.
5. You had corrected me.
6. The cattle graze in the pasture.
7. I get up early in the morning.
8. We saw a snake in the grass.
9. Sit down.
10. Let him die.
Answer:
1. Lotus is not a very lovely flower.
2. His neighbour was not quite well yesterday.
3. Sham has not a garland of flowers in his hand.
4. I do not have a horse.
5. You had not corrected me.
6. The cattle do not graze in the pasture.
7. I do not get up early in the morning.
8. We did not see a snake in the grass.
9. Do not sit down.
10. Let him not die. (Or) Do not let him die.

(b) Change the following Negative sentences into their Positive form:

1. Sohan is not an idle boy.
2. We had not a book.
3. I do not have an umbrella with me.
4. He may not play well today.
5. She cannot tell a lie.
6. Do not bring me a second book of Hindi.
7. Do not let him go there.
8. Do not touch my chair.
9. I did not take the test.
10. You did not attend the class.
Answer:
1. Sohan is an idle boy.
2. We had a book.
3. I have an umbrella with me.
4. He may play well today.
5. She can tell a lie.
6. Bring me a second book of Hindi.
7. Let him go there.
8. Touch my chair.
9. I took the test.
10. You attended the class.

V. Change the following Exclamatory sentences into Assertive sentences:

1. Bravo! You have done well.
2. Alas! I have failed.
3. How beautiful the scenery is!
4. Alas! How foolish I had been!
5. What a disaster the earthquake is!
6. How stiff the paper is!
7. May God reward this act of yours!
8. What a terrible storm it is!
9. Wonderful! I have never seen the like of it earlier.
10. May God pardon this sinner!
Answer:
1. You have done very well.
2. It is very sad that I have failed
3. The scenery is very beautiful.
4. It is very sad that I had been very foolish.
5. The earthquake is a terrible disaster.
6. The paper is very stiff.
7. It is prayed that God may reward this act of yours.
8. It is a very terrible storm.
9. It is surprising that I have never seen the like of it earlier. (or) I wonder if I have ever seen the like of it.
10. It is prayed that God may pardon this sinner.

VI. Pick out the Subject and the Predicate in the following sentences:

1. The sun shines brightly.
2. You speak very hastily.
3. He plays cricket.
4. The rose smells sweet.
5. Children take after their parents.
6. Send it at once.
7. Tell me a story.
8. The old man was listening to the wireless.
9. Slow and steady wins the race:
10. Time and tide wait for nobody.
11. He did his work efficiently.
12. Barking dogs seldom bite.
Answer:

Subject	Predicate
1. The sun	shines brightly.
2. You	speak very hastily.
3. He	plays cricket.
4. The rose	smells sweet.
5. Children	take after their parents.
6. You	send it at once.
7. You	tell me a story.
8. The old man	was listening to the wireless.
9. Slow and steady	wins the race.
10. Time and tide	wait for nobody.
11. He	did his work efficiently.
12. Barking dogs	seldom bite.

Punjab State Board PSEB 6th Class Maths Book Solutions Chapter 14 Data Handling MCQ Questions with Answers.

PSEB 6th Class Maths Chapter 14 Data Handling MCQ Questions

Multiple Choice Questions.

Question 1.

(a) 30
(b) 40
(c) 50
(d) 5.
Answer:
(c) 50

Question 2.

(a) 1
(b) 14
(c) 21
(d) 28.
Answer:
(c) 21

Question 3.

(a) 6
(b) 1
(c) 5
(d) 8.
Answer:
(b) 1

Question 4.

(a) 200
(b) 2000
(c) 20
(d) 2.
Answer:
(a) 200

Question 5.
……….. represents data through picture of objects.
(a) Bar Graph
(b) Histogram
(c) Pictograph
(d) None of these.
Answer:
(c) Pictograph

Question 6.
Which tally marks represents 14?

Answer:

Question 7.

(a) 5
(b) 10
(c) 12
(d) 160.
Answer:
(b) 10

Question 8.
……………. is method of representing the data in uniform width size horizontal or vertical box with equal spacing.
(a) Histogram
(b) Bar Graph
(c) Pictograph
(d) Tally Marks.
Answer:
(b) Bar Graph

Question 9.
A …………… is a collection of numbers gathered to give some information:
(a) Frequency
(b) Data
(c) Tally mark
(d) None of these.
Answer:
(b) Data

Question 10.
If on a scale 1 unit = 200 then how much quantity does 5 units will represent?
(a) 100
(b) 1000
(c) 300
(d) 600.
Answer:
(b) 1000

Question 11.
In the adjoining bar graph the growth of population of India from 1951 to 2001 is shown. Observe the graph and find in which two consecutive years the population growth is maximum?

(a) Year 1951 to year 1961
(b) Year 1971 to year 1981.
(c) Year 1981 to year 1991
(d) Year 1991 to year 2001.
Answer:
(d) Year 1991 to year 2001.

Question 12.
The bar graph given alongside shows the amount of wheat purchased by government during the year 1998-2002. Read the bar graph and find in which year was the wheat production maximum?

(a) 1998
(b) 1999
(c) 2001
(d) 2002.
Answer:
(d) 2002

Question 13.

(a) 5
(b) 6
(c) 7
(d) 8.
Answer:
(c) 7

Question 14.

(a) 5
(b) 7
(c) 9
(d) 10.
Answer:
(d) 10

Question 15.
There is a circus in a village. The number of children came to see circus from Monday to Friday are shown by a pictograph. Read the following pictograph carefully and answer the questions below:

How many children came to see circus on Tuesday?
(a) 25
(b) 50
(c) 75
(d) 100.
Answer:
(c) 75

Fill in the blanks:

Question (i)

Answer:
Seven

Question (ii)
A data is a collection of …………… gathered to give some information.
Answer:
Numbers

Question (iii)
A diagram that represents stastieal data in the form of pictures is called …………….. .
Answer:
pictograph

Question (iv)
The initial step of any investigation is the ……………. of data.
Answer:
collection

Question (v)
The data can be arranged in a ……………. form using tally marks.
Answer:
tabular

Write True/False:

Question (i)
Pictograph represents the data in form of pictures. (True/False)
Answer:
True

Question (ii)
There are three types of data. (True/False)
Answer:
False

Question (iii)
The primary data is collected directly from of source. (True/False)
Answer:
True

Question (iv)

Answer:
False

Question (v)

Answer:
True

Punjab State Board PSEB 6th Class Maths Book Solutions Chapter 12 Perimeter and Area Ex 12.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 6 Maths Chapter 12 Perimeter and Area Ex 12.2

1. Find the approximate area of each of the following figures by countaing the number of squares – complete, more than half and exactly half.

Solution:
(i) Number of complete squares m = 7
Here we do not have any half square or more than half.
∴ n = 0, p = 0
∴ Area of plane figure = m + n + \(\frac {1}{2}\)p
= 7 + 0 + 0
= 7 sq. units

(ii) Number of complete squares m = 2
Number of more than half squares n = 4
Number of half squares p = 0
∴ Area of plane figure = m + n + \(\frac {1}{2}\)p
= 4 + 2 + 0
= 6 sq. units.

(iii) Number of complete squares m = 10
Number of more than half squares n = 0
Number of exactly half squares p = 2
∴ Area of plane figure = m + n + \(\frac {1}{2}\)p
= (10 + 0 + \(\frac {1}{2}\) × 2) sq. units
= (10 + 1) sq. units
= 11 sq. units

(iv) Number of complete squares m = 11
Number of more than half squares n = 0
Number of exactly half squares p = 2
∴ Area of plane figure = m + n + \(\frac {1}{2}\)p
= 11 + 0 + \(\frac {1}{2}\) × 2
= 11 + 1 = 12 sq. units

(v) Number of complete squares m = 10
Number of more than half squares n = 3
Number of exactly half squares p = 0
∴ Area of plane figure = m + n + \(\frac {1}{2}\)p
= 10 + 3 + 0
= 13 sq. units

2. Find the area of rectangle whose:

Question (i)
length = 12 cm, breadth = 16 cm
Solution:
Length of rectangle = 12 cm
and Breadth of rectangle = 16 cm.
∴ Area of rectangle = Length × Breadth
= 12 cm × 16 cm
= 192 sq. cm

Question (ii)
length = 25 m, breadth = 18 m
Solution:
Length of rectangle = 25 m
and Breadth of rectangle = 18 m
∴ Area of rectangle = Length × Breadth
= 25 m × 18 m
= 450 sq. m

Question (iii)
length = 2.7 m, breadth = 45 cm
Solution:
Length of rectangle = 2.7 m = 270 cm
and Breadth of rectangle = 45 cm
∴ Area of rectangle = Length × Breadth
= 270 cm × 45 cm
= 12150 sq. cm

Question (iv)
length 4.2 cm, breadth = 1.5 cm
Solution:
Length of rectangle = 4.2 cm
and Breadth of rectangle = 1.5 cm
∴ Area of rectangle = Length × Breadth
= 4.2 cm × 1.5 cm
= 6.3 sq. cm

Question (v)
length = 3.8 mm, breadth = 4 mm.
Solution:
Length of rectangle = 3.8 mm
and Breadth of rectangle = 4 mm
∴ Area of rectangle = Length × Breadth
= 3.8 mm × 4 mm
= 15.2 sq. mm

3. Find the area of the square with side:

Question (i)
19 cm
Solution:
Side of the square = 19 cm
∴ Area of the square = side × side
= 19 cm × 19 cm = 361 sq. cm.

Question (ii)
24 mm
Solution:
Side of square = 24 mm
∴ Area of square = side × side
= 24 mm × 24 mm
= 576 sq. mm

Question (iii)
3.5 cm
Solution:
Side of the square = 3.5 cm
Area of square = side × side
= 3.5 cm × 3.5 cm
= 12.25 sq. cm

Question (iv)
2.6 cm
Solution:
Side of the square = 2.6 cm
Area of square = side × side
= 2.6 cm × 2.6 cm
= 6.76 sq. cm

Question (v)
8.2 cm.
Solution:
Side of the square = 8.2 cm
Area of the square = side × side
= 8.2 cm × 8.2 cm
= 67.24 sq. cm.

4. The area of a rectangle is 216 sq. cm and its length is 12 cm. Find its breadth.
Solution:
The area of the rectangle = 216 sq. cm.
Length of the rectangle = 12 cm
Breadth of the rectangle = \(\frac{\text { Area }}{\text { Length }}\)
= \(\frac {216}{12}\) cm
= 18 cm.

5. The area of a rectangle is 225 sq. m and its breadth is 9 in. Find its length.
Solution:
The area of the rectangle = 225 sq. m
and Breadth of the rectangle = 9 m
∴ Length of the rectangle = \(\frac{\text { Area }}{\text { Breadth }}\)
= \(\frac {225}{9}\) m
= 25 m

6. The length and breadth of a ground are 32 m and 24 m. Find the cost of levelling the ground at the rate of ₹ 3 per sq. m.
Solution:
Length of ground = 32 m
and Breadth of ground = 24 m
Area of the ground = Length × Breadth
= 32 m × 24 m
= 768 sq. m.
Levelling cost of 1 sq. m = ₹ 3
Levelling cost of 768 sq. m = ₹ 3 × 768
= ₹ 2304

7. Find the perimeter of a rectangle whose area is 324 sq. cm and its one side is 36 cm.
Solution:
Area of rectangle = 324 sq. cm
One side of rectangle = 36 cm
∴ Other side of rectangle = \(\frac{\text { Area }}{\text { One side }}\)
= \(\frac {324}{36}\) = 9 cm
Perimeter of rectangle
= 2 × (1st side + 2nd side)
= 2 × (36 + 9) cm
= 2 × 45 cm
= 90 cm

8. The perimeter of a square field is 100 m. Find its area.
Solution:
The perimeter of square field = 100 m
∴ 4 × side of square = 100 m
∴ Side of a square = \(\frac {100}{4}\) = 25 m
Hence area of square field = side × side
= 25 m × 25 m
= 625 sq. m.

9. Area of a rectangle of length 20 cm is 340 sq. cm. Find its perimeter.
Solution:
Area of rectangle = 340 sq. cm
and Length of rectangle = 20 cm
Breadth of rectangle = \(\frac{\text { Area }}{\text { Length }}\)
= \(\frac {340}{20}\) cm = 17 cm
Perimeter of rectangle
= 2 × (Length + Breadth)
= 2 × (20 + 17) cm
= 2 × 37 cm
= 74 cm

10. A marble tile measure 15 cm × 20 cm. How many tiles will be required to cover a wall of size 4 m × 6 m?
Solution:
Area of the wall = 4 m × 6 m
= 400 cm × 600 cm
= 240000 sq. cm
Area of a marble tile = 15 cm × 20 cm
= 300 sq. cm
Number of tiles required to cover wall
= \(\frac{\text { Area of wall }}{\text { Area of tile }}=\frac{240000}{300}\) = 800
Hence number of tiles required to cover wall = 800

11. Find the cost of levelling the square field of side 75 m at rate of ₹ 5 per square metre.
Solution:
Side of the square field = 75 m
Area of square field = side × side
= 75 m × 75 m
= 5625 sq. m
Cost of levelling 1 sq. m = ₹ 5
Cost of levelling 5625 sq. m = ₹ 5 × 5625
= ₹ 28125

12. How many stamps of size 2 cm × 1.5 cm can be pasted on a sheet of paper of size 6 cm × 12 cm?
Solution:
Area of the sheet of paper
= 6 cm × 12 cm = 72 sq. cm
Area of one stamp = 2 cm × 1.5 cm = 3 sq cm
Number of stamps pasted on sheet of paper
= \(=\frac{\text { Area of paper sheet }}{\text { Area of stamp }}=\frac{72}{3}\) = 24.

13.

Question (i)
What will happen to the area of a square if its side is trebled (tripled)?
Solution:
Let side of the square = x cm
∴ Area of the square = (x × x) sq. m
Now, if the side is trebled, then side of new square = 3x cm
∴ Area of the new square
= [(3x) × (3x)] sq. m
= (3 × 3 × x × x) sq. m
= 9 (x × x) sq. cm
= 9 × (Area of original square)
∴ If side is trebled, then area becomes 9 times of original area.

Question (ii)
What will happen to the area of a rectangle if its length is halved and breadth is doubled?
Solution:
l cm and b cm be the length and breadth of the rectangle respectively.
∴ Area of rectangle = l × b
Now, If its length is halved and breadth is doubled.
∴ New length = \(\frac {1}{2}\) l
and new breadth = 2b
Thus area of new rectangle = length × breadth
= \(\frac {1}{2}\) × l × 2b
= \(\frac {1}{2}\) × 2 × (l × b)
= (l × b) = original area
Area will remain the same.

Question (iii)
What will happen to the area of a square if its side is halved?
Solution:
Let side of the square = x cm
∴ Area of the square = (x × x) sq. cm
Now, if side is halved, then
side of new square = \(\frac {1}{2}\)x cm
∴ Area of the new square sq.cm


Hence, if side is halved, then the area becomes one-fourth times original area.

14. Find the area of the following figures by splitting it into rectangles and squares:

Question (i)

Solution:
The given figure can be divided into 2 parts

Rectangle A of size 8 cm × 3 cm
Rectangle B of size 4 cm × 2 cm
∴ Area of rectangle A
= 8 cm × 3 cm = 24 sq. cm
and Area of rectangle B
= 4 cm × 2 cm
= 8 sq. cm
⇒ Total area of the figure
= 24 sq. cm + 8 sq. cm
= 32 sq. cm

Question (ii)

Solution:
The given figure can be divided into 2 parts

Rectangle A of size 10 cm × 2 cm
Rectangle B of size 8 cm × 2 cm
∴ Area of rectangle A
= 10 cm × 2 cm = 20 sq. cm
and Area of rectangle B
= 8 cm × 2 cm = 16 sq. cm
Total Area of the figure
= (20 + 16) sq. cm = 36 sq. cm

Question (iii)

Solution:
The given figure can be divided into 3 parts

Rectangle A of size 12 cm × 3 cm
Rectangle B of size 3 cm × 2 cm
Rectangle of size 12 cm × 3 cm
Area of rectangle A
= 12 cm × 3 cm = 36 sq. Cm
Area of rectangle B
= 3 cm × 2 cm = 6 sq. cm
Area of rectangle C
= 12 cm × 3 cm = 36 sq. cm
Total area of the figures
= (36 + 6 + 36) sq. cm
= 78 sq. cm

Question (iv)

Solution:
The given figure can be divided into 3 parts

Rectangle A of size 13 × 3 units
Rectangle B of size 5 × 3 units
Rectangle C of size 5 × 3
Area of rectangle A
= 13 × 3 = 39 sq. units
Area of rectangle B
= 5 × 3 = 15 sq. units
Area of rectangle C
= 5 × 3 = 15 sq. units
Hence total area of the figure
= (39 + 15 + 15) sq. units
= 69 sq. units Ans.

15. Fill in the blanks:

Question (i)
1 square metre = ……….. sq. cm.
Solution:
10000

Question (ii)
1 square cm = ………. sq. mm.
Solution:
100

Question (iii)
Area of Rectangle = …………. × ……………
Solution:
length, breadth

Question (iv)
Length = ………….. ÷ breadth.
Solution:
Area

Question (v)
Area of square = …………. × ……………
Solution:
side × side.

Punjab State Board PSEB 6th Class Maths Book Solutions Chapter 12 Perimeter and Area Ex 12.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 6 Maths Chapter 12 Perimeter and Area Ex 12.1

1. Find the perimeter of the following shapes:

Question (i)

Solution:
Perimeter = AB + BC + CD + DA
= 8 cm + 7 cm + 12 cm + 9 cm
= 36 cm

Question (ii)

Solution:
Perimeter = XY + YZ + ZX
= 10m + 10m + 8m
= 28m

Question (iii)

Solution:
Perimeter = PQ + QR + RS + SP
= 15 cm + 12 cm + 15 cm + 12 cm
= 54 cm

Question (iv)

Solution:
Perimeter = MN + NO + OP + PL + LM
= 8 cm + 7 cm + 5 cm + 6 cm + 7 cm
= 33 cm

Question (v)

Solution:
Perimeter = AB + BC + CD + DE + EF + FG + GM + MA
=8m + 2m + 6m + 4m + 6m + 2m + 8m + 8m
= 44 m

Question (vi)

Solution:
Perimeter = LM + MN + NO + OP + PQ + QR + RS + SL
= 3 cm + 3 cm + 3 cm + 3 cm + 3 cm + 3 cm + 3 cm + 3 cm
= 24 cm

2. Find the perimeter of the triangle with sides:

Question (i)
5 cm, 6 cm and 7 cm
Solution:
Perimeter of a triangle
= Sum of lengths of its sides
= 5 cm + 6 cm + 7 cm = 18 cm

Question (ii)
10 m, 12 m, 18 m
Solution:
Sides of triangle
= 10 m, 12 m, 18 m
∴ Perimeter of a triangle
= Sum of lengths of its sides
= 10 m + 12 m + 18 m = 40 m

Question (iii)
4.6 cm, 3.2 cm and 5.8 cm.
Solution:
Sides of triangle
= 4.6 cm, 3.2 cm and 5.8 cm
∴ Perimeter of triangle
= Sum of lengths of its sides
= 4.6 cm + 3.2 cm + 5.8 cm
= 13.6 cm

3. Find the perimeter of an isosceles triangle with 15 cm as length of equal side and 18 cm as base.
Solution:
Sides of isosceles triangle = 15 cm, 15 cm, 18 cm
Area of isosceles triangle = Sum of lengths of its sides
= (15 + 15 + 18) cm = 48 cm

4. Find the perimeter of a square with side:

Question (i)
16 cm
Solution:
Side of square = 16 cm
∴ Perimeter of square = 4 × side
= 4 × 16 cm
= 64 cm

Question (ii)
4.8 mm
Solution:
Side of square = 4.8 mm
∴ Perimeter of square = 4 × side
= 4 × 4.8 mm
= 19.2 mm

Question (iii)
125 cm
Solution:
Side of square = 125 cm
∴ Perimeter of square = 4 × side
= 4 × 125 cm
= 500 cm

Question (iv)
45 m
Solution:
Side of square = 45 m
∴ Perimeter of square = 4 × side
= 4 × 45 m
= 180 m

Question (v)
39 cm.
Solution:
Side of square = 39 cm
∴ Perimeter of square = 4 × side
= 4 × 39 cm
= 156 cm

5. Find the perimeter of a rectangle with:

Question (i)
Length 20 m and breadth 15 m
Solution:
Length of rectangle = 20 m
Breadth of rectangle = 15 m
∴ Perimeter of rectangle = 2 × (length + breadth)
= 2 × (20 + 15) m
= 2 × 35 m
= 70 m

Question (ii)
Length 25 m and breadth 35 m
Solution:
Length of rectangle = 25 m
Breadth of rectangle = 35 m
∴ Perimeter of rectangle = 2 × (length + breadth)
= 2 × (25 + 35) m
= 2 × 60 m
= 120 m

Question (iii)
Length 40 cm and breadth 28 cm
Solution:
Length of rectangle = 40 cm Breadth of rectangle = 28 cm
∴ Perimeter of rectangle = 2 × (length + breadth)
= 2 × (40 + 28) cm
= 2 × 68 cm
= 136 cm

Question (iv)
Length 18.3 cm and breadth 6.8 cm
Solution:
Length of rectangle = 18.3 cm
Breadth of rectangle = 6.8 cm
∴ Perimeter of rectangle
= 2 × (length + breadth)
= 2 × (18.3 + 6.8) cm
= 2 × 25.1 cm = 50.2 cm

Question (v)
Length 0.125 m and breadth 15 cm.
Solution:
Length of rectangle
= 0.125 m = 12.5 cm
Breadth of rectangle = 15 cm
∴ Perimeter of rectangle = 2 × (length + breadth)
= 2 × (12.5 + 15) cm
= 2 × 27.5 cm
= 55 cm

6. Find the perimeter of a regular hexagon with side:

Question (i)
5 cm
Solution:
Side of a regular hexagon = 5 cm
Perimeter of a regular hexagon = 6 × side
= 6 × 5 cm
= 30 cm

Question (ii)
12 cm
Solution:
Side of a regular hexagon = 12 cm
Perimeter of a regular hexagon = 6 × side
= 6 × 12 cm
= 72 cm

Question (iii)
7.2 cm.
Solution:
Side of a regular hexagon = 7.2 cm
Perimeter of a regular hexagon = 6 × side
= 6 × 7.2 cm
= 43.2 cm

7. Find the perimeter of an equilateral triangle with side:

Question (i)
10 cm
Solution:
Side of an equilateral triangle
= 10 cm
∴ Perimeter of an equilateral triangle = 3 × side
= 3 × 10 cm
= 30 cm

Question (ii)
8 m
Solution:
Side of an equilateral triangle = 8 m
∴ Perimeter of an equilateral triangle = 3 × side
= 3 × 8 m
= 24 m

Question (iii)
24 m
Solution:
Side of an equilateral triangle = 24 m
∴ Perimeter of an equilateral triangle = 3 × side
= 3 × 24 m
= 72 m

Question (iv)
5.6 m
Solution:
Side of an equilateral triangle = 5.6 m
∴ Perimeter of an equilateral triangle = 3 × side
= 3 × 5.6 m
= 16.8 m

Question (v)
12.1 cm.
Solution:
Side of an equilateral triangle = 12.1 cm
∴ Perimeter of an equilateral triangle = 3 × side
= 3 × 12.1 cm
= 36.3 cm

8. If the perimeter of a triangle is 48 cm and two sides are 12 cm and 17 cm. Find the third side.
Solution:
Perimeter of a triangle = 48 cm Sum of length of two sides = (12 + 17) cm = 29 cm
∴ Third side = 48 cm – 29 cm
= 19 cm

9. Find the side of an equilateral triangle, if the perimeter is:

Question (i)
45 cm
Solution:
Given perimeter of an equilateral triangle = 45 cm
Perimeter of an equilateral triangle = 3 × (side of the triangle)
⇒ 45 cm = 3 × side
⇒ Side of the triangle
= 15cm

Question (ii)
69 mm
Solution:
Given perimeter of an equilateral triangle = 69 mm
Perimeter of an equilateral triangle = 3 × (side of the triangle)
⇒ 69 = 3 × (side of the triangle)
⇒ Side of the triangle = \(\frac{69 \mathrm{~mm}}{3}\)
= 23 mm

Question (iii)
117 cm.
Solution:
Given perimeter of an equilateral triangle = 117 cm
Perimeter of an equilateral triangle = 3 × (side of the triangle)
⇒ 117 = 3 × (side of the triangle)
⇒ Side of the triangle = \(\frac{117 \mathrm{~cm}}{3}\)
= 39 cm

10. Find the side of a square if the perimeter is:

Question (i)
52 cm
Solution:
Given Perimeter of a square = 52 cm
Perimeter of a square = 4 × (side of square)
⇒ Side of square
= \(\frac{\text { perimeter of a square }}{\text { 4 }}\)
= \(\frac{52 \mathrm{~cm}}{4}\)
= 13 cm

Question (ii)
60 cm
Solution:
Given perimeter of a square = 60 cm
Side of a square
= \(\frac{\text { perimeter of a square }}{\text { 4 }}\)
= \(\frac{60 \mathrm{~cm}}{4}\)
= 15 cm

Question (iii)
112 cm.
Solution:
Given perimeter of a square = 112 cm
Side of a square
= \(\frac{\text { perimeter of a square }}{\text { 4 }}\)
= \(\frac{112 \mathrm{~cm}}{4}\)
= 28 cm

11.

Question (i)
The perimeter of rectangular field is 260 m. If its length is 80 m then find its breadth.
Solution:
Given perimeter of rectangular field = 260 m
and Length of the rectangular field = 80 m
∴ Perimeter of rectangular field = 2 × (length + breadth)
⇒ 260 = 2 × (80 + breadth)
⇒ \(\frac {260}{2}\) = 80 + breadth
⇒ 80 + breadth = 130
⇒ breadth = 130 – 80 = 50 m
Hence breadth of rectangular field = 50 m

Question (ii)
The perimeter of a rectangular garden is 140 m. If its breadth is 45 m then find its length.
Solution:
Given perimeter of rectangular garden = 140 m
and breadth of rectangular garden = 45 m
∴ Perimeter of rectangular garden = 2 × (length + breadth)
⇒ 140 = 2 × (length + 45)
⇒ \(\frac {260}{2}\) = length + 45
⇒ length = 70 – 45 = 25 m
Hence length of rectangular garden = 25 m

Question (iii)
The perimeter of a rectangle is 114 cm. If its length is 32 cm then find its breadth.
Solution:
Given perimeter of rectangle = 114 cm
and length of rectangle = 32 cm
∴ Perimeter of rectangle
= 2 × (length + breadth)
⇒ 114 = 2 × (32 + breadth)
⇒ \(\frac {114}{2}\) = 32 + breadth
⇒ breadth = 57 – 32 = 25 cm
Hence breadth of rectangle = 25 cm

12. The side of a triangular field are 15 m, 20 m and 18 m. Find the total distance travelled by a boy in taking 2 complete rounds of this field.
Solution:
Sides of a triangular fields = 15 m, 20 m and 18 m
Distance covered in one round of a triangular field = Perimeter of rectangular field = Sum of the length of the sides of a rectangular field
= 15 m + 20 m + 18 m
= 53 m
∴ Distance covered in taking 2 complete rounds of this field
= 2 × 53 m
= 106 m

13. Find the cost of fencing a square field of side 26 m at the rate of ₹ 3 per metre.
Solution:
Given side of the square field = 26 m
∴ Perimeter of the square field = 4 × side
= 4 × 26 m = 104 m
Perimeter of fencing = 104 m
Cost of 1 m of fencing = ₹ 3
Cost of 104 m of fencing
= 104 × ₹ 3
= ₹ 312

14. Mani runs around a square park of side 75 m. Kush runs around a rectangular park of length 60 m and breadth 45 m. Who covers less distance?
Solution:
Side of a square park = 75 m
Perimeter of square park = 4 × (side)
= 4 × (75 m) = 300 m
∴ Distance covered by Mani = 300 m
Length of rectangular park = 60 m
Breadth of rectangular park = 45 m
Perimeter of rectangular park = 2 (length + breadth)
= 2 × (60 + 45) m
= 2 × (105) m
= 210 m
∴ Distance covered by Kush = 210 m
Kush covers less distance.

15. Find the cost of framing a rectangular whiteboard with length 240 cm and breadth 150 cm at the rate of ₹ 6 per cm.
Solution:
Length of rectangular white board = 240 cm
Breadth of rectangular white board = 150 cm
Perimeter of rectangular white board = 2 × (length + breadth)
= 2 × (240 + 150) cm
= 2 × (390) cm
= 780 cm
Cost of fencing 1 cm = ₹ 6 × 780
= ₹ 4680

16. If length of a rectangle is ‘a’ units and breadth is 5 units. Find the perimeter of the rectangle.
Solution:
Given length of rectangle = ‘a’ units,
and Breadth of rectangle = 5 units
Perimeter of rectangle = 2 × (length + breadth)
= 2 × (a + 5) units
= 2 (a + 5) units

17. Fill in the blanks:

Question (i)
The sum of lengths of all sides of a polygon is called ……………. .
Solution:
perimeter

Question (ii)
Perimeter of Square = ……………. × side.
Solution:
4

Question (iii)
Perimeter of Rectangle = 2 × (………. +………) .
Solution:
length, breadth

Question (iv)
Side of a square = (……………) ÷ 4.
Solution:
perimeter

Question (v)
Perimeter of an equilateral triangle = …………….. × side.
Solution:
3.

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 10 Circles Ex 10.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 10 Circles Ex 10.1

Question 1.
How many tangents can a circle have?
Solution:
Since at any point on a circle, there can be one and only one tangeni. But circle is a collection of infinite points, so we can draw infinite number of tangents to a circle.

Question 2.
Fill in the blanks:
(i) A tangent to a circle intersects it in ………………. point(s).
Solution:
one

(ii) A line intersecting a circle in two points is called a ………………..
Solution:
secant.

(iii) A circle can have ……………. parallel tangents at the most.
Solution:
two

(iv) The common point of a lingent h, circle and the circit is called ………………
Solution:
point of contact.

Question 3.
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is:
(A) 12 cm
(B) 13 cm
(C) 8.5 cm
(D) \(\sqrt{119}\) cm.
Solution:
According to given information we draw the figure such that,

OP = 5 cm and OQ = 12 cm
∵ PQ is a tangent and OP is the radius
∵ ∠OPQ = 90°
Now, In right angled ∆OPQ.
By Pythagoras Theorem,
OQ² = OP² + QP²
Or (12)² = (5)² + QP²
Or QP² = (12)² – (5)²
Or QP² = 144 – 25 = 119
Or QP = \(\sqrt{119}\) cm.
Hence, option (D) is correct.

Question 4.
Draw a circle and two lines parallel to given line such that one is a tangent and other a secant to the circle.
Solution:
According to thc given information we draw a circle having O as centre and l is the given line.

Now, m and n be two lines parallel to a given line l such that m is tangent as well as parallel to l and n is secant to the circle as well as parallel to l.

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 9 Some Applications of Trigonometry Ex 9.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 9 Some Applications of Trigonometry Ex 9.1

Question 1.
A circus artist is climbing 220 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, ¡f the angle made by the rope with the ground level is 30° (see fig.).

Solution:
Let AB be the heignt of pole;
AC = 20 m be the length of rope.
The angle of elevation in this situation is 30°.
Various arrangements are as shown in figure.

In right angled ∆ABC,
\(\frac{\mathrm{AB}}{\mathrm{AC}}\) = sin 30°

or \(\frac{\mathrm{AB}}{20}=\frac{1}{2}\)

or AB = \(\frac{1}{2}\) × 20 = 10
Hence, height of pole is 10 m.

Question 2.
A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle 300 with it. The distance between the foot of the tree to the point where the top touches the ground is 8 rn Find the height of the tree.
Solution:
Let BD be length of tree before storm.
After storm AD = AC = length of broken part of tree.
The angle of elevation in this situation is 30°.
Various arrangements are as shown in the figure.

In right angled ∆ABC,

\(\frac{\mathrm{AB}}{\mathrm{AC}}\) = tan 30°

or \(\frac{h_{1}}{8}=\frac{1}{\sqrt{3}}\)
or h₁ = \(\frac{8}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}=\frac{8}{3} \sqrt{3}\) m ……….(1)

\(\frac{\mathrm{BC}}{\mathrm{AC}}\) = cos 30°

or \(\frac{8}{h_{2}}=\frac{\sqrt{3}}{2}\)

or \(h_{2}=\frac{8 \times 2}{\sqrt{3}}=\frac{16}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}\)

h₂ = \(\frac{16}{3}\) √3 …………..(2)

Total height of the tree = h₁ + h₂
= \(\frac{8}{3}\) √3 + \(\frac{16}{3}\) √3 [Using (1) & (2)]

= \(\left(\frac{8+16}{3}\right) \sqrt{3}=\frac{24}{3} \sqrt{3}\) = 8√3 m.
Hence, height of the tree is 8√3 m.

Question 3.
A contractor plants to install two slides for the children to play in a park. For the children below the age of 5 years, she
prefers to have a slide whose top is at a height of 1.5 m, and is inclined at an angle of 30° to the ground, whereas for elder children, she wants to have a steep slide at a height of 3 m, and inclined at an angle of 60° to the ground. What should be the length of the slide in each case?
Solution:
Case I:
For children below 5 years.
Let AC = l₁ m denote the length of slide and BC = 1.5 m be the height of slide. The angle of elevation is 30°.
Various arrangements are shown in figure.

In right angled ∆ABC,

\(\frac{\mathrm{BC}}{\mathrm{AC}}\) = sin 30°

or \(\frac{1 \cdot 5}{l_{1}}=\frac{1}{2}\)

or l₁ = 1.5 × 2 = 3 m.

Case II:
For Elder children
Let AC = 12 m represent the length of slide and BC = 3 m be the height of slide. The angle of elevation is 60°. Various arrangements are as shown in figure.

In right angled ∆ABC,

\(\frac{\mathrm{BC}}{\mathrm{AC}}\) = sin 60°

or \(\frac{3}{l_{2}}=\frac{\sqrt{3}}{2}\)

or l₂ = \(\frac{3 \times 2}{\sqrt{3}}=\frac{6}{\sqrt{3}}\)

= \(\frac{6}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}=\frac{6 \sqrt{3}}{3}\)

= 2√3 m.

Hence, length of slides for children below 5 years and elder children are 3 m and 2 m.

Question 4.
The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower, is 30°. Find the height of the tower.
Solution:
Let BC = h m be the height of tower and AB = 30 m be the distance at ground level. Various arrangements are as shown in figure.

In right angled ∆ABC,

\(\frac{\mathrm{BC}}{\mathrm{AB}}\) = tan 30°

or \(\frac{h}{30}=\frac{1}{\sqrt{3}}\)

or h = \(\frac{30}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}=\frac{30 \sqrt{3}}{3}\)

= 10√3 = 10 × 1.732
h = 17.32 (approx).
Hence, height of tower is 17.32 m.

Question 5.
A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
Solution:
Let us suppose position of the kite is at point CAC = l m be length of string with which kite is attached. The angle of elevation for this situation be 60°. Various arrangements are as shown in the figure.

In right angled ∆ABC,

\(\frac{\mathrm{CB}}{\mathrm{AB}}\) = sin 60°

or \(\frac{60}{l}=\frac{\sqrt{3}}{2}\)

or l = \(\frac{60 \times 2}{\sqrt{3}}=\frac{120}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}\)

= \(\frac{120 \sqrt{3}}{3}\) = 40√3 m.
Hence, length of the string be 40√3 m.

Question 6.
A 15 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.
Solution. Let ED = 30 m be the height of building and EC = l5 m be the height of boy.
The angle of elevation at different situation are 30° and 60° respectively.
Various arrangements are as shown in figure.

In right angled ∆ABC,

\(\frac{\mathrm{DC}}{\mathrm{AC}}\) = tan 30°

or \(\frac{28 \cdot 5}{x+y}=\frac{1}{\sqrt{3}}\)

or x + y = 28.5 × √3 m ………………(1)

Now, in right angled ∆BCD,

\(\frac{\mathrm{DC}}{\mathrm{BC}}\) = tan 60°

or \(\frac{28 \cdot 5}{y}=\sqrt{3}\)

or y = \(\frac{28 \cdot 5}{\sqrt{3}}\)

or y = \(\frac{28 \cdot 5}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}=\frac{28 \cdot 5 \times \sqrt{3}}{3}\) ……….(2)

Distance covered towards building = x = (x + y) – y
= (28.5 × √3) – (\(\frac{28.5}{3}\) × √3) m [sing (1) and (2)]

= 28.5 (1 – \(\frac{1}{3}\)) √3 m

= 28.5 (\(\frac{3-1}{4}\)) √3 m

= [28.5 × \(\frac{2}{3}\)]√3 m = 19√3 m.

Hence, distance covered by boy towards the building is 19√3 m.

Question 7.
From a point on the ground, the angles of elevation of the bottom and top of a transmission tower fixed at the top of a 20 m high building are 45° and 60° respectively. Find the height of the tower.
Solution:
Let BC = 20 m be the height of building and DC = h m be the height of transmission tower. The angle of elevation of
the bottom and top of a transmission tower are 45° and 60° respectively.
Various arrangements are as shown in the figure.

In right angled ∆ABC,
\(\frac{A B}{B C}\) = cot 45°

or \(\frac{\mathrm{AB}}{20}\) = 1
or AB = 20 m ………………..(1)
Also, in right angled ∆ABD,
\(\frac{A B}{B C}\) = cot 60°

or \(\frac{\mathrm{AB}}{20+h}=\frac{1}{\sqrt{3}}\)

AB = \(\frac{(20+h)}{\sqrt{3}}\) ………….(2)

From (1) and (2), we get

20 = \(\frac{(20+h)}{\sqrt{3}}\)
or 20√3 = 20 + h
or h = 20√3 – 20
or h = 20 (√3 – 1) m
= 20 (1.732 – 1) m
= 20 × 0.732 = 14.64 m.

Hence, height of the tower is 14.64 m.

Question 8.
A statue 1.6 m tall stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.
Solution. Let BC = h m be the height of Pedestal and CD = 1.6 m be the height of statue.
The angle of elevation of top of statue and top of pedestal are 60° and 45° respectively. Various arrangements are as shown in the figure.

In right angled ∆ABC,
\(\frac{A B}{B C}\) = cot 45°

or \(\frac{A B}{h}\) = 1

or AB = h m ………….(1)

In right angled ∆ABC,
\(\frac{\mathrm{AB}}{\mathrm{BD}}\) = cot 60°

or \(\frac{\mathrm{AB}}{h+1.6}=\frac{1}{\sqrt{3}}\)

or AB = \(\frac{h+1.6}{\sqrt{3}}\) ……….(2)

From (1) and (2), we get
h = \(\frac{h+1.6}{\sqrt{3}}\)
or √3h = h + 1.6
or (√3 – 1) h = 1.6
or (1.732 – 1) h = 16
or (0.732) h = 1.6
or h = \(\frac{1.6}{0.732}\) = 2.1857923
= 2.20 m (approx.)
Hence, height of pedestal is 2.20 m.

Question 9.
The angle of elevation of the top of a building from the foot of the tower is 300 and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the
building.
Solution:
Let BC = 50 m be height of tower and AD = h m be height of building. The angle of elevation of the top of a building from the foot of tower and top of tower from foot of the building are 30° and 60° respectively. Various arrangement are as shown in figure.

In right angled ∆ABC,
\(\frac{A B}{B C}\) = cot 60°

or \(\frac{\mathrm{AB}}{50}=\frac{1}{\sqrt{3}}\)

or AB = \(\frac{50}{\sqrt{3}}\) …………(1)

Also, in right angled ∆DAB,
\(\frac{\mathrm{AB}}{\mathrm{DA}}\) = cot 30°

or \(\frac{A B}{h}\) = √3
or AB = h√3 ……………(2)

From (1) and (2), we get
\(\frac{50}{\sqrt{3}}\) = h√3

or \(\frac{50}{\sqrt{3}} \times \frac{1}{\sqrt{3}}\) = h

or h = \(\frac{50}{3}\) = 16.6666

or h = 16.70 m (approx).
Hence, height of building is 16.70 m.

Question 10.
Two poles of equal heights are tanding opposite each other on either side of he road, which is 80 m wide. From a point
between them on the road the angles of elevation of the top of the poles are 60° and 30°, respectively. Find the height of the poles and the distances of the point from the poles.
Solution:
Let BC = DE = h m he height of two equal poles and point A be the required position where the angle of elevations of top of two poles are 30° and 60° respectively. Various arrangement are as shown in the figure.

In right angled ∆ADE,

\(\frac{E D}{D A}\) = tan 30°

or \(\frac{h}{x}=\frac{1}{\sqrt{3}}\)

or h = \(\frac{x}{\sqrt{3}}\) ……………(1)

In right angled ∆ABC,

\(\frac{\mathrm{BC}}{\mathrm{AB}}\) = tan 60°

or \(\frac{h}{80-x}\) = √3

or h = (80 – x) √3 …………(2)

From (1) and (2), we get
\(\frac{x}{\sqrt{3}}\) = (80 – x)
or x = (80 – x) √3 × √3
or x = (80 – x) 3
or x = 240 – 3x
or 4x = 240
or x = \(\frac{240}{4}\) = 60
Substitute this value of x in (I), we get
h = \(\frac{60}{\sqrt{3}}=\frac{60^{\circ}}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}\)

= \(\frac{60 \sqrt{3}}{3}=20 \sqrt{3}\)

= (20 × 1.732) m = 34.64 m
DA = x = 60 m
and AB = 80 – x = (80 – 60) m = 20 m.
Hence, heigth of the poles are 3464 m and the distances of the point from the poles are 20 m and 60 m respectively.

Question 11.
A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From a point 20 m away from this point on the same bank, the angle of elevation of the top of the tower is 30° (see fig.). Find the height of the tower and the width of the canal.

Solution:
Let BC = x m be the width of canal and CD = h m be height of TV tower. The angles of elevation of top of tower at different position are 30° and 60° respectively. Various arrangements are as shown in figure.

In right angled ∆ABC,

\(\frac{\mathrm{AB}}{\mathrm{BC}}\) = tan 60°

or \(\frac{h}{x}\) = √3
or h = √3x …………..(1)

Also, in right angled ∆ABD,
\(\frac{\mathrm{AB}}{\mathrm{BD}}\) = tan 30°

or \(\frac{h}{20+x}=\frac{1}{\sqrt{3}}\)

or h = \(\frac{20+x}{\sqrt{3}}\) ……………….(2)

From (1) and (2), we get

√3x = \(\frac{20+x}{\sqrt{3}}\)
or √3(√3x) = 20 + x
or 3x = 20 + x
or 2x = 20
or x = \(\frac{20}{2}\) = 10

Substitute this value of x in (1), we get
h = 10(√3)
= 10 × 1.732
h = 17.32 m
Hence, height of TV tower is 17.32 m and. width of the canal is 10 m.

Question 12.
From the top of a 7m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower.
Solution:
Let BD = hm be the height of cable tower and AE = 7 m be the height of building. The angle of elevation of the top of a cable tower and angle of depression of its foot from top of a building are 60° and 45° respectively.
Various arrangements are as shown in figure.

In right angled ∆ABC,

\(\frac{\mathrm{AB}}{\mathrm{AE}}\) = cot 45°

or \(\frac{\mathrm{AB}}{7}\) = 1

or AB = 7 m. ……………..(1)

Also, in right angled ∆DCE,

\(\) = cot 60°
or \(\frac{\mathrm{EC}}{h-7}=\frac{1}{\sqrt{3}}\)

or EC = \(\frac{h-7}{\sqrt{3}}\) ……………..(2)

But AB = EC ………….(Given)
7 = \(\frac{h-7}{\sqrt{3}}\) [Using (1) and (2)]
or 7√3 = h – 7
h = 7√3 + 7 = 7 (√3 + 1)
or h = 7 (1.732 + 1) = 7(2.732)
or h = 19.124
or h = 19.20 m (approx.)
Hence, height of the tower is 19.20 m.

Question 13.
As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
Solution:

Let CD = 75 m be the height of light house and point D be top of light house from w’here angles of depression of two ships are 30° and 45° respectively. Various arrangements are as shown in the figure.

In right angled ∆BCD,
\(\frac{\mathrm{BC}}{\mathrm{CD}}\) = cot 45°

or \(\frac{y}{75}\) = 1
or y = 75 m ……………(1)

Also, in right angled ∆ACD
\(\frac{\mathrm{AC}}{\mathrm{CD}}\) = cot 30°

or \(\frac{x+y}{75}\) = √3
or x + y = 75√3
or x + 75 = 75√3 [using (1)]
or x = 75√3 – 75
= 75 (√3 – 1)
= 75( 1.732 – 1)
= 75 (0.732)
or x = 54.90
Hence, distance between the two ships is 54.90 m.

Question 14.
A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant ¡s 60°. After some time, the angle of elevation reduces to 30° (see fig.). Find the distance travelled by the balloon during the interval.

Solution:
Let ‘AB’ be the position of 1.2 m tall girl, at the point of the angles of elevation of balloon at
different distances are 30° and 60° respectively. Various arrangements are as shwon in th figure.
According to question,
FG = ED = CE – CD
= 88.2 m – 1.2 m
= 87 m

In right angled ∆AGF,
\(\frac{A G}{G F}\) = cot 60°

or \(\frac{x}{87}=\frac{1}{\sqrt{3}}\)

or x = \(\frac{87}{\sqrt{3}}\) m.

Also, in right angled ∆ADE,
\(\frac{A D}{E D}\) = cot 30°

or \(\frac{x+y}{87}\) = √3

or x + y = 87√3
or \(\frac{87}{\sqrt{3}}\) + y = 87√3
or y = 87√3 – \(\frac{87}{\sqrt{3}}\)

or y = 87√3 – \(\frac{1}{\sqrt{3}}\)

or y = 87 \(\frac{3-1}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}\)

or y = \(\frac{87 \times 2 \times \sqrt{3}}{3}\)

or y = 58√3
or y = 58(1.732) = 100.456
or y = 100.456 m.
Hence, distance travelled by the balloon during the interval is 100.46 m.

Question 15.
A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the further t(me taken by the car to reach the foot of the tower.
Solution:
Let CD = h m. be the tower of height.
Let A be initial position of the car and after six seconds the car be at 13. The angles of depression at A and B are 30° and 60° respectively. Various arrangements are as shown in figure.

Let speed of the car be υ metre per second using formula, Distance = Speed x Time
AB = Distance covered by car in 6 seconds
AB = 6υ metre
Also, time taken by car to reach the tower be ‘n’ seconds.
∴ BC = nυ metre
In right angled ∆ACD.
\(\frac{\mathrm{CD}}{\mathrm{AC}}\) = tan 30°

or \(\frac{h}{6 v+n v}=\frac{1}{\sqrt{3}}\)

or h = \(\frac{6 v+n v}{\sqrt{3}}\) ……………….(1)

Also, in right angled ∆BCD,
\(\frac{C D}{B C}\) = tan 60°

or \(\frac{h}{n v}\) = √3
h = nv (√3) ……….(2)

From (1) and (2), we get
\(\frac{6 v+n v}{\sqrt{3}}\) = nυ(√3)
or 6υ + nυ = nυ(√3)
or 6υ + nυ = 3nυ
or 6υ = 2nυ
or n = \(\frac{6 v}{2 v}\) = 3
Hence, time taken by car to reach the foot of tower is 3 seconds.

Question 16.
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.
Solution:
Let CD = h m be the height of tower and B ; A be the required points which are at a distance of 4 m and 9 m from the tower respectively. Various arrangements are as shown in the figure.

In right angled ∆BCD
\(\frac{\mathrm{CD}}{\mathrm{BC}}\) = tan θ

or \(\frac{h}{4}\) = tan θ ………….(1)

Also, in right angled ∆ACD,
\(\frac{C D}{A C}\) = tan (90 – θ)

or \(\frac{h}{9}\) = cot θ

Multiplying (1) and (2), we get
\(\frac{h}{4} \times \frac{h}{9}\) = tan θ cot θ

or \(\frac{h^{2}}{36}=\tan \theta \times \frac{1}{\tan \theta}\)

or h² = 36 = (6)²
or h = 6
Hence, height of the tower is 6 m.

Punjab State Board PSEB 8th Class English Book Solutions English Grammar Tenses Exercise Questions and Answers, Notes.

PSEB 8th Class English Grammar Tenses

Tense शब्द लातीनी भाषा के शब्द tempus से बना है जिसका अर्थ है समय (Time) । अर्थात् Tense हमें किसी कार्य या घटना के समय या काल का ज्ञान कराता है। नीचे दिए गए वाक्य पढ़ें:

1. I play some game daily.
2. I played cricket yesterday.
3. I shall play hockey tomorrow.

पहले वाक्य के verb (play) से Present Time का बोध होता है। दूसरे वाक्य के verb (played) से Past. Time का बोध होता है। तीसरे वाक्य के verb (shall play) से Future Time का बोध होता है। इस तरह-
(1) जिस verb से Present Time का बोध होता है, वह Present Tense कहलाता है-
I take bath in the morning.
I go for a walk in the evening.

(2) जिस verb से Past Time का बोध होता है, वह Past Tense कहलाता है
I took bath in the,morning.
I went for a walk in the evening.

(3) जिस verb से Future Time का बोध होता है, वह Future Tense कहलाता है
I shall take bath in the morning.
I shall go for a walk in the evening.
इस प्रकार तीन मुख्य Tenses हैं-

1. The Present Tense
2. The Past Tense
3. The Future Tense.

अब यह जान लेना भी आवश्यक है कि प्रत्येक काल में कार्य अथवा क्रिया (verb) की स्थिति भिन्न-भिन्न होती है। हो सकता है कि काम चल रहा हो। यह भी सम्भव है कि कार्य पूरा हो चुका हो अथवा किसी अनिश्चित (indefinite) स्थिति में हो। इस तरह कार्य की मुख्य रूप से चार अवस्थाएं होती हैं। हम यूं भी कह सकते हैं कि प्रत्येक मुख्य Tense के चार रूप होते हैं और कुल मिला कर 12 Tenses होते हैं। यहां हम इन सभी Tenses का अलग-अलग अध्ययन करेंगे।

1. Simple Present Tense
OR
Present Indefinite Tense
Present Indefinite or Simple Present Tense का प्रयोग होता है-
(i) किसी आदत का वर्णन करने के लिए; जैसे,
He takes bath daily.
He goes for a walk everyday.

(ii) किसी सर्वमान्य सत्य को व्यक्त करने के लिए; जैसे,
The sun rises in the east.

(iii) किसी कहानी में किसी बीती हुई घटना को बताने में; जैसे,
The brave dog now kills the snake and waits for his master to come.

(iv) भविष्य में होने वाली किसी घटना को व्यक्त करने के लिए जो किसी योजना अथवा व्यवस्था का भाग हो; जैसे,
Our examination begins on Monday.

(v) Time तथा Condition की Clauses में साधारण Future Tense के स्थान पर; जैसे,
If it rains, we shall not go out for a walk.

(vi) कथनों को व्यक्त करने के लिए ; जैसे,
They say, “To err is human.

(vii) किसी ऐसी स्थिति को दर्शाने के लिए जो न बदलने वाली हो; जैसे,
Our house faces the east.

2. Present Continuous Tense
Present Continuous Tense का प्रयोग होता है-
(i) किसी ऐसे विशेष कार्य को प्रकट करने के लिए जो अभी पूरा न हुआ हो अथवा जारी हो; जैसे,
My brother is singing a song.

3. Present Perfect Tense
Present Perfect Tense का प्रयोग किया जाता है-
(i) ऐसे कार्य को प्रकट करने के लिए जो भूतकाल से अब तक जारी हो; जैसे,
I have never tasted tea. (I still do not drink it.)

(ii) किसी ऐसे पूर्ण कार्य अथवा घटना को प्रकट करने के लिए जो भूतकाल में विशेष समय को लेकर वर्तमान काल तक किया जाए; जैसे,
There have been two accidents on the road during 1984.

4. Present Perfect Continuous Tense.
यह Tense उस कार्य को व्यक्त करने के लिए प्रयोग होता है जो अतीत में किसी समय आरम्भ हुआ हो और अब भी चल रहा हो। समय को व्यक्त करने के लिए for (अनिश्चित समय) और since (निश्चित समय) का प्रयोग करते हैं; जैसे-
The match has been going on for an hour.
The man has been waiting for a reply.
You have been wasting your time since morning.

5. Past Indefinite Tense
OR
Simple Past Tense
Past Indefinite Tense का प्रयोग किया जाता है-
(i) भूतकाल की किसी आदत, लोकप्रिय कार्य अथवा सर्वमान्य तथ्य को प्रकट करने के लिए; जैसे,
People then believed that the sun moved round the earth.

(ii) ऐसे कार्य को व्यक्त करने के लिए जिस में भूतकाल में काफी समय लगा हो परन्तु जो अब समाप्त हो चुका हो; जैसे-
He lived in Delhi for ten years. (but he does not live there now)

(iii) भूतकाल में पूरे किए गए किसी कार्य को व्यक्त करने के लिए। इस प्रकार प्रायः बीते हुए समय को व्यक्त . करने के लिए किसी Adverb या Adverb phrase का प्रयोग किया जाता है: जैसे,
My father left for Delhi yesterday.

Note 1. कभी-कभी समय की अभिव्यक्ति Adverb की बजाये भाव (समय का) से भी हो सकती है; जैसे
I bought this watch in Mumbai.

Note 2. क्रमबद्ध घटनाओं में भी Time के Adverb की आवश्यकता नहीं पड़ती; जैसे,
He came. He saw. He conquered.

(iv) किसी प्रश्न का उत्तर देने में; जैसे,
How did he go to school ?
Answer:
He went on foot.

6. Past Continuous Tense
Past Continuous (Progressive) Tense का प्रयोग किया जाता है-
(i) किसी ऐसे कार्य को व्यक्त करने के लिए जो भूतकाल में किसी विशेष समय पर किया जा रहा हो, भले। ही कार्य करने का समय बताया गया हो, या न बताया गया हो; जैसे,-
At 7 a.m. this morning I was reading the newspaper.

7. Past Perfect Tense
Past Perfect Tense का प्रयोग किया जाता है-
(1) भूतकाल में एक साथ घटित होने वाले कार्यों में से पहले पूरा होने वाले कार्य के लिए; जैसे,
The patient had died before the doctor came.

8. Past Perfect Continuous Tense इस Tense का प्रयोग किसी ऐसे कार्य या घटना का वर्णन करने के लिए किया जाता है जो अतीत में किसी एक निश्चित समय (Point of Time) तक या किसी अवधि (Period of Time) में जारी रहे; जैसे,-
The phone had been ringing for a minute before Ram lifted it. वाक्य में स्पष्ट है कि जब राम ने फोन उठाया तब उससे पहले एक मिनट तक फोन की घण्टी बजती रही थी।

9. Future Indefinite Tense Simple Future Tense का प्रयोग ऐसे कार्य के लिए किया जाता है जो भविष्य में अभी किया जाना है; जैसे,
I shall finish the work tomorrow.
Tomorrow will be Monday.

10. Future Continuous Tense:
Future Continuous Tense का प्रयोग उस कार्य को करने के लिए किया जाता है जो भविष्य में किसी समय चल रहा हो; जैसे,
I shall be writing the letters then.
When I reach the station, the train will be moving.

11. Future Perfect Tense

• They will have heard the news by the time you reach.
• The teacher will have taken the roll-call before you enter the class.

12. Future Perfect Continuous Tense Future Perfect Continuous Tense का प्रयोग ऐसे कार्य का उल्लेख करने के लिए होता है जो भविष्य में किसी निश्चित समय के बाद भी जारी रहने का बोध कराता है; जैसे-

• The students will have been studying History since morning.
• He will have been studying Law for two years by next April.

Exercises From Board’s Grammar (Solved)

I. Fill in the blanks with the Simple Present or Present Continuous forms of the verbs given in the brackets:

1. The population of India ……………. very fast. (increase)
2. Water ……………. at 0° Celsius. (freeze)
3. The sun ……………. in the West. (not rise)
4. ……………. you ……………. Mr. Jain? (know)
5. ……………. he ever ……………… cricket? (play)
6. The Ganges …………… into the Bay of Bengal. (flow)
7. Why …………….. you ……………… this ? (eat)
8. She …………….. a bath. (have)
9. I …………… cricket everyday, but today I …………… tennis.. (play)
10. She usually ……………. a skirt but today she ……………… trousers. (wear)
Hints:
1. is increasing
2. freezes
3. does not rise
4. Do, know
5. Does, play
6. flows
7. are, eating
8. is having
9. play, am playing
10. wears, is wearing.

II. Fill in the blanks with the Present Perfect or Present Perfect Continuous forms of the verbs given in brackets:

1. Someone ……………. the window. (break)
2. Rita …………….. her pen. (lose)
3. The train ……………… just ………….. at the platform. (arrive)
4. We …………….. many medals. (win)
5. I ………. for a house for two months. (search)
6. …………. he ……………. a beard ? (grow)
7. ……………. you ……………. the Bible ? (read)
8. ……….. my uncle for months. (not visit)
9. She ……………… to China twice. (be)
10. We ……………. already ……………… our breakfast. (have)
Hints:
1. has broken
2. has lost
3. has, arrived
4. have won
5. have been searching
6. Has, grown
7. Have, read
8. have not visited
9. has been
10. have, had.

III. Fill in the blanks with the Simple Past Tense forms of the verbs given in the brackets:

Sher Singh smiled. He tossed his revolver in the air and ………… (catch) it by the handle. He ………… (take) careful aim at an empty sardine tin and …….3….. (fire) another six shots. The bullets ……4….. (go) through into the earth kicking up whiffs of dust. His Alsatian dog …….5….. (begin) to bark with excitement. He ………… (leap) up with a growl and ………… (run) down the canal embankment. He …….8….. (sniff) at the tin and …….9….. (take) it up in his mouth and …….10….. (run) back with it and ……. 11…. (lay) it at his master’s feet.
Hints:
1. caught
2. took
3. fired
4. went
5. began
6. leapt
7. ran
8. sniffed
9. took
10. ran
11. laid.

IV. Fill in the blanks with the Simple Past or Past Perfect forms of the verbs given in the brackets:

1. The plane ……………. When we reached the airport. (leave)
2. Ramesh …………… home when I phoned him. (return)
3. …………… he ……………. his old car before he bought a new one ? (sell)
4. The children ……………. before I came home. (sleep)
5. The film had already begun when we …………….. the theatre. (reach)
6. The teacher ……………. the book before the examination began. (finish)
7. The robber had run away before the police. (come)
8. Tom …………. sleepy after having a good lunch. (feel)
9. I ……………. the message before you came. (receive)
10. He ……………… for India last year. (play)
Hints:
1. had left
2. had returned
3. Had, sold
4. had slept
5. reached
6. had finished
7. came
8. felt
9. had received
10. played.

V. Correct the following sentences:

1. The rain has stopped yesterday.
2. He had been born in 1950.
3. He is suffering from fever since last night.
4. Stephenson has invented the steam engine.
5. He will reach home before the storm will come.
6. I left Bihar before the earthquake occurred.
7. She will reach the station before the train will go.
8. The great reformer had died in 1977.
9. I waited at home for her since 9 o’clock.
10. She finished her dinner when I saw her.
Hints:
1. The rain stopped yesterday.
2. He was born in 1950.
3. He has been suffering from fever since last night.
4. Stephenson invented the steam engine.
5. He will have reached home before the storm comes.
6. I had left Bihar before the earthquake occurred.
7. She will have reached the station before the train goes.
8. The great reformer died in 1977.
9. I had been waiting at home for her since 9 o’clock.
10. She had finished her dinner when I saw her.

Errors in the Use of Tenses

The Simple Past is often used wrongly for the Present Perfect Tense; as,

Incorrect : He did not write the letter yet.
Correct : He has not written the letter yet.
Incorrect : We did not hear from him for a week.
Correct : We have not heard from him for a week.
Incorrect : I lived in Ambala since 1990.
Correct : I have lived in Ambala since 1990.

The Present Perfect is often used wrongly for the Simple Past; as,

Incorrect – Columbus has discovered America.
Correct – Columbus discovered America.
Incorrect – Babar has won the First Battle of Panipat.
Correct – Babar won the First Battle of Panipat.
Incorrect – The servant has not answered when called.
Correct – The servant did not answer when called.

The Present Perfect Tense में Past Time को व्यक्त करने वाला adverb या कोई अन्य शब्द प्रयोग नहीं किया जा सकता जैसे-

Incorrect – I have made a call to him yesterday.
Correct – I made a call to him yesterday.
Incorrect – A new bookshop has been opened last Monday.
Correct – A new bookshop was opened last Monday.
Incorrect – I have finished my work last night.
Correct – I finished my work last night.

The Past Perfect is often used wrongly for the Simple Past; as,

Incorrect – I had visited her yesterday.
Correct – I visited her yesterday.
Incorrect – He had gone to Kolkata last year.
Correct – He went to Kolkata last year.
Incorrect – We had gone for a picnic last Sunday.
Correct – We went for a picnic last Sunday.
Incorrect – Nehru had died in 1964.
Correct – Nehru died in 1964.

The Simple Past is often used wrongly for the Past Perfect; as,

Incorrect – The patient died before the doctor came.
Correct – The patient had died before the doctor came.
Incorrect – The train left before we bought the tickets.
Correct – The train had left before we bought the tickets.
Incorrect – I finished my work before my father came.
Correct – I had finished my work before my father came.

The Past Perfect or Perfect Continuous, and not the Simple Past or Past Continuous, is used to express something that continued up to a past time after beginning at a still earlier time; as,

Incorrect – He told me that he was ill for four days.
Correct – He told me that he had been ill for four days.
Incorrect – She was writing a novel for six weeks when I visited her.
Correct – She had been writing a novel for six weeks when I visited her.

The Simple Future is often used wrongly for the Future Perfect; as;

Incorrect – We shall reach home before the sun will set.
Correct – We shall have reached home before the sun sets.
Incorrect – I shall leave for Ludhiana by the time he will come.
Correct – I shall have left for Ludhiana by the time he comes.