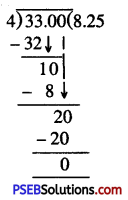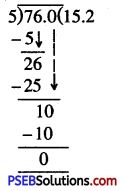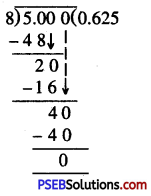Bhagya

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 10 Circles Ex 10.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Maths Chapter 10 Circles Ex 10.3

Question 1.
Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
Answer:

Thus, given a pair of circles, the maximum number of common points they have is 2.

Question 2.
Suppose you are given a circle. Give a construction to find its centre.
Answer:

• In the given circle, draw chords AB and BC with one endpoint B in common.
• Draw l-the perpendicular bisector of AB and m-the perpendicular bisector of BC.
• Let l and m intersect at O.
• Then, O is the centre of the given circle.

Note: Here, any two chords without an end-point in common can be drawn.

Question 3.
If two circles intersect at two points, prove that their centres lie on the perpendicular bisector of the common chord.
Answer:

Here, two circles with centre O and P intersect each other at points A and B.
AB and OP intersect at M.
In ∆ OAP and ∆ OBR
OA = OB (Radii of the circle with centre O)
PA = PB (Radii of the circle with centre P).
OP = OP (Common)
∴ ∆ OAP ≅ ∆ OBP (SSS rule)
∴ ∠ AOP = ∠ BOP (CPCT)
∴ ∠ AOM = ∠BOM
Now, in ∆ AOM and ∆ BOM,
AO = BO (Radii of the circle)
∠ AOM = ∠ BOM
OM = OM (Common)
∴ ∆ AOM = ∆ BOM (SAS rule)
∴ AM = BM and ∠ AMO = ∠ BMO (CPCT)
But, ∠AMO + ∠BMO = 180° (Linear pair)
∴ ∠ AMO = ∠ BMO = \(\frac{180^{\circ}}{2}\) = 90°
Thus, line OM is the perpendicular bisector of AB.
Hence, line OP is the perpendicular bisector of AB.
Thus, the centres O and P of the circle intersecting in points A and B lie on the perpendicular bisector of common chord AB.

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 10 Circles Ex 10.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Maths Chapter 10 Circles Ex 10.2

Question 1.
Recall that two circles are congruent if they have the same radii. Prove that equal chords of congruent circles subtend equal angles at their centres.
Answer:

Two circles with centres O and P are congruent. Moreover, chord AB of the circle with centre
O and chord CD of the circle with centre P are congruent.
In ∆ OAB and ∆ PCD,
OA = PC and OB = PD (Radii of congruent circles)
And, AB = CD (Given)
∴ ∆ OAB ≅ ∆ PCD (SSS rule)
∴ ∠AOB = ∠ CPD
Thus, equal chords of congruent circles subtend equal angles at their centres.

Question 2.
Prove that if chords of congruent circles subtend equal angles at their centres, then the chords are equal.
Answer:

Two circles with centres O and P are congruent. Moreover, ∠ AOB subtended by chord AB of the circle with centre O and ∠CPD subtended by chord CD of the circle with centre P at their respective centres are equal.
In ∆ OAB and ∆ PCD,
OA = PC and OB = PD (Radii of congruent circles)
And, ∠AOB = ∠CPD (Given)
∴ ∆ OAB ≅ ∆ PCD (SAS rule)
∴ AB = CD
Thus, if chords of congruent circles subtend equal angles at their centres, then the chords are equal.

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 10 Circles Ex 10.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Maths Chapter 10 Circles Ex 10.1

Question 1.
Fill in the blanks :
(i) The centre of a circle lies in ……………………….. of the circle, (exterior/interior)
Answer:
interior

(ii) A point, whose distance from the centre of a circle is greater than its radius lies in ………………….. of the circle, (exterior/interior)
Answer:
exterior

(iii) The longest chord of a circle is a ………………………. of the circle.
Answer:
diameter

(iv) An arc is a ……………….. when its ends are the ends of a diameter.
Answer:
semicircle

(v) Segment of a circle is the region between an arc and …………………………… of the circle.
Answer:
a chord

(vi) A circle divides the plane, on which it lies, in ………………………….. parts.
Answer:
three

Question 2.
Write True or False. Give reasons for your answers.
(i ) Line segment joining the centre to any point on the circle is a radius of the circle.
Answer:
The given statement is true, because according to the definition of a radius, a line segment joining the centre to any point on the circle is a radius of the circle.

(ii) A circle has only finite number of equal chords.
Answer:
The given statement is false, because a circle has infinitely many equal chords, e.g., all the diameters of a circle are chords and they are all equal and uncountable.

(iii) If a circle is divided into three equal arcs, each is a major arc.
Answer:
The given statement is false, because if a circle is divided into three equal parts, each part is a minor arc.

(iv) A chord of a circle, which is twice as long as its radius, is a diameter of the circle.
Answer:
The given statement is true, because a chord of a circle which is twice as long as its radius passes through the centre of the circle and a chord passing through the centre is called a diameter of the circle.

(v) Sector is the region between the chord and its corresponding arc.
Answer:
The given statement is false, because the region between a chord an corresponding arc is called a segment, not a sector.

(vi) A circle is a plane figure.
Answer:
The given statement is true, because circle is a collection of all the points in a plane which are at a fixed distance from a fixed point in the plane.

Punjab State Board PSEB 6th Class Maths Book Solutions Chapter 6 Decimals Ex 6.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 6 Maths Chapter 6 Decimals Ex 6.2

1. Convert the following decimal numbers into fractions and reduce it to lowest form.

Question (i)
1.4
Solution:
1.4 = \(\frac{14}{10}=\frac{14 \div 2}{10 \div 2}\)
(H.C.F. of 14 and 10 is 2)
= \(\frac {7}{5}\)

Question (ii)
2.25
Solution:
2.25 = \(\frac{225}{100}=\frac{225 \div 25}{100 \div 25}\)
(H.C.F. of 225 and 100 is 25)
= \(\frac {9}{4}\)

Question (iii)
18.6
Solution:
18.6 = \(\frac{186}{10}=\frac{186 \div 2}{10 \div 2}\)
(H.C.F. of 186 and 10 is 2)
= \(\frac {93}{5}\)

Question (iv)
4.04
Solution:
4.04 = \(\frac{404}{100}=\frac{404 \div 4}{100 \div 4}\)
(H.C.F. of 404 and 100 is 4)
= \(\frac {101}{25}\)

Question (v)
21.6
Solution:
21.6 = \(\frac{216}{10}=\frac{216 \div 2}{10 \div 2}\)
(H.C.F. of 216 and 10 is 2)
= \(\frac {108}{5}\)

2. Convert the following fractions into decimal numbers:

Question (i)
\(\frac {7}{100}\)
Solution:
\(\frac {7}{100}\) = 0.07
(Here denominator is 100)

Question (ii)
\(\frac {12}{10}\)
Solution:
\(\frac {12}{10}\) = 1.2
(Here denominator is 10)

Question (iii)
\(\frac {215}{100}\)
Solution:
\(\frac {215}{100}\) = 2.15
(Here denominator is 100)

Question (iv)
\(\frac {18}{1000}\)
Solution:
\(\frac {18}{1000}\) = 0.018
(Here denominator is 1000)

Question (v)
\(\frac {245}{10}\)
Solution:
\(\frac {245}{10}\) = 24.5
(Here denominator is 10)

3. Convert the following fractions into decimal numbers by equivalent fraction method:

Question (i)
\(\frac {5}{2}\)
Solution:
Here denominator is 2.
Convert into equivalent fraction with denominator 10 by multiplying it by 5.
∴ \(\frac{5}{2}=\frac{5 \times 5}{2 \times 5}=\frac{25}{10}\) = 2.5

Question (ii)
\(\frac {3}{4}\)
Solution:
Here denominator is 4.
Convert into equivalent fraction with denominator 100 by multiplying it by 25.
∴ \(\frac{3}{4}=\frac{3 \times 25}{4 \times 25}=\frac{75}{100}\) = 0.75

Question (iii)
\(\frac {28}{5}\)
Solution:
Here denominator is 5.
Convert into equivalent fraction with denominator 10 by multiplying it by 2.
∴ \(\frac{28}{5}=\frac{28 \times 2}{5 \times 2}=\frac{56}{10}\) = 5.6

Question (iv)
\(\frac {135}{20}\)
Solution:
Here denominator is 20.
Convert into equivalent fraction with denominator 100 by multiplying it by 5.
∴ \(\frac{135}{20}=\frac{135 \times 5}{20 \times 5}=\frac{675}{100}\)
= 6.75

Question (v)
\(\frac {17}{4}\)
Here denominator is 4.
Convert into equivalent fraction with denominator 100 by multiplying it by 25.
∴ \(\frac{17}{4}=\frac{17 \times 25}{4 \times 25}=\frac{425}{100}\)
= 4.25

4. Convert the following fractions into decimals by long division method:

Question (i)
\(\frac {17}{2}\)
Solution:

= 8.5

Question (ii)
\(\frac {33}{4}\)
Solution:

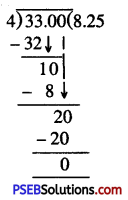
= 8.25

Question (iii)
\(\frac {76}{5}\)
Solution:

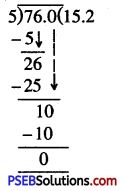
= 15.2

Question (iv)
\(\frac {24}{25}\)
Solution:

= 0.96

Question (v)
\(\frac {5}{8}\)
Solution:

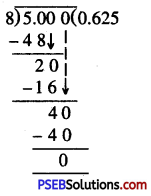
= 0.625

5. Represent the following decimals on number line:

Question (i)
(i) 0.7
(ii) 1.6
(iii) 3.7
(iv) 6.3
(v) 5.4
Solution:

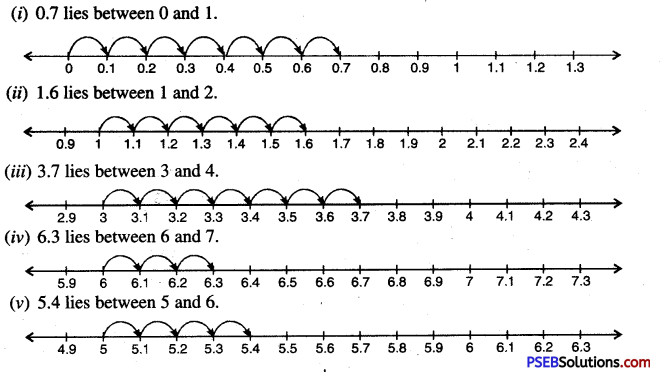
6. Write three decimal numbers between:

Question (i)
1.2 and 1.6
Solution:
Three decimal numbers between 1.2 and 1.6 are:
1.3, 1.4, 1.5

Question (ii)
2.8 and 3.2
Solution:
Three decimal numbers between 2.8 and 3.2 are:
2.9, 3, 3.1

Question (iii)
5 and 5.5.
Solution:
Three decimal numbers between 5 and 5.5 are:
5.1, 5.2, 5.3, 5.4.

7. Which number is greater:

Question (i)
0.4 or 0.7
Solution:

Since, 7 > 4
So, 0.7 > 0.4

Question (ii)
2.6 or 2.5
Solution:

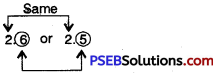
Since, 6 > 5
So, 2.6 > 2.5

Question (iii)
1.23 or 1.32
Solution:

Since, 3 > 2
So, 1.32 > 1.23

Question (iv)
12.3 or 12.4
Solution:

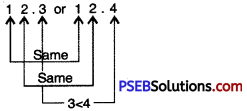
Since, 4 > 3
So, 12.4 > 12.3

Question (v)
18.35 or 18.3
Solution:

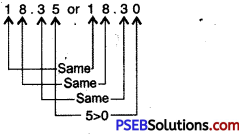
Since, 5 > 0
So, 18.35 > 18.30

Question (vi)
12 or 1.2
Solution:

Since, 12 > 1
So, 12 > 1.2

Question (vii)
5.06 or 5.061
Solution:

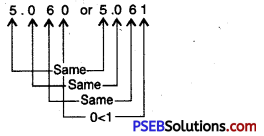
Since, 1 > 0
So, 5.061 > 5.060

Question (viii)
2.34 or 23.3
Solution:

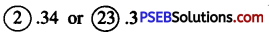
Since, 23 > 2
So, 23.3 > 2.34

Question (ix)
13.08 or 13.078
Solution:

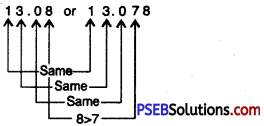
Since, 8 > 7
So, 13.08 > 13.078

Question (x)
2.3 or 2.03.
Solution:

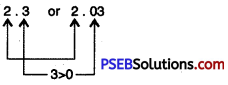
Since, 3 > 0
So, 2.3 > 2.03

8. Arrange the decimal numbers in ascending order:

Question (i)
2.5, 2, 1.8, 1.9
Solution:
Ascending order is :
1.8, 1.9, 2, 2.5

Question (ii)
3.4, 4.3, 3.1, 1.3
Solution:
Ascending order is :
1.3, 3.1, 3.4, 4.3

Question (iii)
1.24, 1.2, 1.42, 1.8.
Solution:
Ascending order is :
1.2, 1.24, 1.42, 1.8.

9. Arrange the decimal numbers in descending order:

Question (i)
4.1, 4.01, 4.12, 4.2
Solution:
Descending order is :
4.2, 4.12, 4.1, 4.01

Question (ii)
1.3, 1.03, 1.003, 13
Solution:
Descending order is :
13, 1.3, 1.03, 1.003

Question (iii)
8.02, 8.2, 8.1, 8.002.
Solution:
Descending order is :
8.2, 8.1, 8.02, 8.002.

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 9 Areas of Parallelograms and Triangles MCQ Questions with Answers.

PSEB 9th Class Maths Chapter 9 Areas of Parallelograms and Triangles MCQ Questions

Multiple Choice Questions and Answer

Answer each question by selecting the proper alternative from those given below each question to make the statement true:

Question 1.
Area of a parallelogram = ………………….
A. \(\frac{1}{2}\) × base × corresponding altitude
B. \(\frac{1}{2}\) × the product of diagonals
C. base × corresponding altitude
D. \(\frac{1}{2}\) × the product of adjacent sides.
Answer:
C. base × corresponding altitude

Question 2.
Area of a triangle = ……………………
A. base × corresponding altitude
B. base + corresponding altitude
C. \(\frac{1}{2}\) × base × corresponding altitude
D. 2 × base × corresponding altitude
Answer:
C. \(\frac{1}{2}\) × base × corresponding altitude

Question 3.
ABCD is a rectangle. If AB = 10 cm and ar (ABCD) = 150 cm², then BC = ………………….. cm.
A. 7.5
B. 15
C. 30
D. 12
Answer:
B. 15

Question 4.
ABCD is a square. If ar (ABCD) = 36 cm², then AB = ………………… cm.
A. 18
B. 9
C. 6
D. 12
Answer:
C. 6

Question 5.
In ∆ ABC, BC = 10 cm and the length of altitude AD is 5 cm. Then, ar (ABC) = …………………. cm².
A. 50
B. 100
C. 25
D. 15
Answer:
C. 25

Question 6.
In ∆ ABC, AD is an altitude. If BC = 8 cm and ar (ABC) = 40 cm², then AD = …………………. cm.
A. 5
B. 10
C. 15
D. 20
Answer:
B. 10

Question 7.
In ∆ PQR, QM is an altitude and PR is the hypotenuse. If PR = 12 cm and QM = 6 cm, then ar (PQR) = ……………………. cm².
A. 18
B. 72
C. 36
D. 24
Answer:
C. 36

Question 8.
In ∆ XYZ, XZ is the hypotenuse. If XY = 8cm and YZ = 12 cm, then ar (XYZ) = ……………….. cm².
A. 20
B. 40
C. 96
D. 48
Answer:
D. 48

Question 9.
In parallelogram ABCD, AM is an altitude corresponding to base BC. If BC = 8 cm and AM = 6 cm, then ar (ABCD) = …………………. cm².
A. 48
B. 24
C. 12
D. 96
Answer:
A. 48

Question 10.
In parallelogram PQRS, QR = 10 cm and ar (PQRS) = 120 cm². Then, the length of altitude PM corresponding to base QR is ……………………… cm.
A. 6
B. 12
C. 18
D. 24
Answer:
B. 12

Question 11.
For parallelogram ABCD, ar (ABCD) = 48 cm².
Then, ar (ABC) = …………………….. cm².
A. 96
B. 48
C. 24
D. 12
Answer:
C. 24

Question 12.
ABCD is a rhombus. If AC = 6 cm and BD = 9 cm, then ar (ABCD) = ………………….. cm².
A. 15
B. 7.5
C. 54
D. 27
Answer:
D. 27

Question 13.
PQRS is a rhombus. If ar (PQRS) = 40 cm² and PR = 8 cm, then QS = ………………….. cm.
A. 20
B. 10
C. 25
D. 40
Answer:
B. 10

Question 14.
In ∆ PQR, ∠Q = 90°, PQ = 5 cm and PR = 13 cm.
Then, ar (PQR) = …………………….. cm².
A. 15
B. 30
C. 45
D. 60
Answer:
B. 30

Question 15.
In ∆ ABC, P Q and R are the midpoints of AB, BC and CA respectively. If ar (ABC) = 32 cm²,
then ar (PQR) = ………………………. cm².
A. 128
B. 16
C. 8
D. 64
Answer:
C. 8

Question 16.
In ∆ ABC, P, Q and R are the midpoints of AB, BC and CA respectively. If ar (ABC) = 32 cm², then ar (PBCR) = ………………….. cm².
A. 10
B. 20
C. 30
D. 40
Answer:
C. 30

Question 17.
In ∆ ABC, P, Q and R are the midpoints of AB, BC and CA respectively. If ar (PBQR) = 36 cm², then ar (ABC) = ……………………….. cm².
A. 18
B. 36
C. 54
D. 72
Answer:
D. 72

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 9 Areas of Parallelograms and Triangles Ex 9.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Maths Chapter 9 Areas of Parallelograms and Triangles Ex 9.4

Question 1.
Parallelogram ABCD and rectangle ABEF are on the, same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.

Rectangle ABEF is a parallelogram too.
Now, parallelograms ABCD and ABEF are on the same base AB and they have equal areas. Hence, they are between the same parallels FC and AB.
In ∆ AFD, ∠F, being an angle of rectangle ABEF, is a right angle and so, AD is the hypotenuse.
∴ AD > AF
∴ AD + AB > AF + AB
∴ 2 (AD + AB) > 2 (AF + AB)
∴ Perimeter of parallelogram ABCD > Perimeter of rectangle ABEF

Question 2.
In the given figure, D and E are two points on BC such that BD = DE = EC. Show that ar (ABD) = ar (ADE) = ar (AEC).
Can you now answer the question that you have left in the ‘Introduction’ of this chapter, whether the field of Budhia has been actually divided into three parts of equal area?
[Remark : Note that by taking BD = DE = EC, the triangle ABC is divided into three triangles ABD, ADE and AEC of equal areas. In the same way, by dividing BC into n equal parts and joining the points of division so obtained to the opposite vertex of BC, you can divide AABC into n triangles of equal areas.]

Answer:
Here, in ∆ ABE, D is a point on BE such that BD = DE.
So, in ∆ ABE, D is the midpoint of BE and AD is a median.
∴ ar (ABD) = ar (ADE) ……………… (1)
Similarly, in A ADC, E is the midpoint of DC and AE is a median.
∴ ar (ADE) = ar (AEC) ……………. (2)
From (1) and (2),
ar (ABD) = ar (ADE) = ar (AEC)
Thus, in ∆ ABC, by joining the points of trisection of BC, i.e., D and E to vertex A, the triangle is divided into ∆ ABD, ∆ ADE and ∆ AEC which have the same area.

Now, the answer to the question which was left unanswered in the ‘Introduction’ is ‘Yes’. The manner in which Budhia divided her field, the area of all the three parts are equal.

Question 3.
In the given figure, ABCD, DCFE and ABFE are parallelograms. Show that ar (ADE) = ar (BCF).

Answer:
Opposite sides of a parallelogram are equal.
∴ In parallelogram ABCD, AD = BC, in parallelogram DCFE, DE = CF and in parallelogram ABFE, AE = BF.
Now, in ∆ ADE and ∆ BCE
AD = BC, DE = CF and AE = BE
∴ By SSS rule, ∆ ADE = ∆ BCF
∴ ar (ADE) = ar (BCF)

Question 4.
In the given figure, ABCD is a parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at E show that ar (BPC) = ar (DPQ).
[Hint: Join AC.]

Answer:
Join AC.
In parallelogram ABCD, BC || AD and BC = AD.
BC is produced to point Q such that AD = CQ.
Thus, AD = CQ and AD || CQ.
∴ Quadrilateral ACQD is a parallelogram.
Diagonals of a parallelogram divide it into four triangles of equal areas.
∴ ar (DPQ) = ar (DPA) = ar (APC) = ar (CPQ)
∴ ar (DPQ) = ar (APC) ……………. (1)
Now, ∆ APC and ∆ BPC are on the same base PC and between the same parallels PC and AB.
∴ ar (APC) = ar (BPC) ………….. (2)
From (1) and (2),
ar (BPC) = ar (DPQ)

Question 5.
In the given figure, ABC and BDE are two equilateral triangles such that D is the midpoint of BC. If AE intersects BC at F, show that
(i) ar (BDE) = \(\frac{1}{4}\)ar (ABC)
(ii) ar (BDE) = \(\frac{1}{2}\)ar (BAE)
(iii) ar (ABC) = 2ar (BEC)
(iv) ar (BFE) = ar (AFD)
(v ) ar (BFE) = 2ar (FED)
(vi) ar (FED) = \(\frac{1}{8}\)ar (AFC)
[Hint: Join EC and AD. Show that BE || AC and DE || AB, etc.]

Answer:
Join EC and AD.
In equilateral ∆ ABC, ∠ ACB = 60°
In equilateral ∆ BDE, ∠ DBE = 60°
∴ ∠ CBE = 60°
Thus, ∠ ACB = ∠ CBE
But, ∠ ACB and ∠ CBE are alternate angles formed by transversal BC of AC and BE and they are equal.
∴BE || AC .
Similarly, ∠ ABD = ∠ BDE = 60°
∴ DE || AB
Now, in ∆ ABC, D is the midpoint of BC.
Hence, AD is a median of ∆ ABC.
∴ ar (ADB) = ar (ADC) = \(\frac{1}{2}\)ar (ABC)
∆ ABC and AAEC are on the same base AC and between the same parallels AC and BE.
∴ ar (ABC) = ar (AEC)
∴ ar (ABC) = ar (ADC) + ar (EDC) + ar (AED) …………….. (1)
In ∆ EBC, ED is a median.
∴ ar (EDC) = ar (BDE) = \(\frac{1}{2}\)ar (EBC) ………………… (2)
∆ AED and ∆ BDE are on the same base DE and between the same parallels AB and DE.
∴ ar (AED) = ar (BDE) …………… (3)
From (1), (2) and (3),
ar (ABC) = \(\frac{1}{2}\)ar (ABC) + ar (BDE) + ar (BDE)
∴ ar (ABC) – \(\frac{1}{2}\) ar (ABC) = 2ar (BDE)
∴\(\frac{1}{2}\)ar (ABC) = 2ar (BDE)
∴ ar (BDE) = \(\frac{1}{4}\)ar (ABC) ….. Result (i)
∆ BAE and ∆ BCE are on the same base BE and between the same parallels BE and AC.
∴ ar (BAE) = ar (BCE) ……………. (4)
In ∆ BEC, ED is a median.
∴ ar (BDE) = \(\frac{1}{2}\)ar (BCE)
∴ ar (BDE) = \(\frac{1}{2}\)ar (BAE) [by (4)] ……. Result (ii)
The diagonals of trapezium ABED intersect at F.
∴ ar (AFD) = ar (BFE) ……………… (5)
The diagonals of trapezium ABEC intersect at F.
∴ ar (ABF) = ar (EFC) ………………….. (6)
In ∆ ABC, AD is a median. s
∴ ar (ABC) = 2ar (ADB) S
∴ ar (ABC) = 2[ar (ABF) + ar (AFD)l
∴ ar (ABC) = 2[ar (EFC) + ar (BFE)] [by (5) and (6)]
∴ ar (ABC) = 2ar (BEC) … Result (iii)
In trapezium ABED, AB || ED and diagonals intersect at F.
∴ ar (BFE) = ar (AFD) …….. Result (iv)
By result (i),
ar (BDE) = \(\frac{1}{4}\)ar (ABC)
∴ ar (BDE) = \(\frac{1}{4}\) 2ar (ABD)
∴ ar (BDE) = \(\frac{1}{2}\)ar (ABD)
∆ BDE and ∆ ABD have the common base s BD.
∴ Altitude on BD in ∆ BDE = \(\frac{1}{2}\) × altitude on BD in ∆ ABD.
Now, the altitude on base BD in ∆ BDE is the same as the altitude on base BF in ∆ BEF and the altitude on base BD in ∆ ABD is the same as the altitude on base FD in ∆ AFD.
∴ Altitude on base BF in ∆ BEF
= \(\frac{1}{2}\) × altitude on base FD in ∆ AFD.
But, ar (BFE) = ar (AFD) …Result (iv)]
∴ BF = 2 × FD
Now, in ∆ BFE and ∆ FED, the altitudes corresponding to base BF and FD respectively are the same.
∴ ar (BFE) = 2ar (FED) … Result (v)
Suppose, in ∆ ABD, the altitude on base BD = h.
∴ In ∆ AFC, the altitude on base FC = h.
Also, in ∆ BDE, the altitude on base BD = \(\frac{h}{2}\)
∴ In A FED, the altitude on base FD = \(\frac{h}{2}\).
Now, ar (FED) = \(\frac{1}{2}\) × FD × \(\frac{h}{2}\) = \(\frac{h \times \mathrm{FD}}{4}\).
∴ FD = \(\frac{4 {ar}(\mathrm{FED})}{h}\) ………….. (7)
and ar (AFC) = \(\frac{1}{2}\) × FC × h = \(\frac{h}{2}\) × FC
= \(\frac{h}{2}\) (CD + FD)
= \(\frac{h}{2}\) (BD + FD) [∵ BD = CD]
= \(\frac{h}{2}\) (BF + FD + FD)
= \(\frac{h}{2}\) (2FD + FD + FD) [∵ BF = 2FD]
= \(\frac{h}{2}\) × 4FD
∴ ar (AFC) = 2 × h × FD
= 2 × h × \(\frac{4 {ar}(\mathrm{FED})}{h}\) [by (7)]
∴ ar (AFC) = 8 ar (FED)
∴ ar (FED) = \(\frac{1}{8}\) ar (AFC) … Result (vi)

Question 6.
Diagonals AC and BD of a quadrilateral ABCD intersect each other at E Show that
ar (APB) × ar (CPD) = ar (APD) × ar (BPC).
[(Hint: From A and C, draw perpendiculars to BD.]
Answer:

Draw AM ⊥ BD and CN ⊥ BD, where M and N are points on BD.
∴ ar (APB) × ar (CPD)
= (\(\frac{1}{2}\) × PB × AM) × (\(\frac{1}{2}\) × PD × CN)
= (\(\frac{1}{2}\) × PB × CN) × (\(\frac{1}{2}\) × PD × AM)
Thus, ar (APB) × ar (CPD) = ar (APD) × ar (BPC)

Question 7.
P and Q are respectively the midpoints of sides AB and BC of a triangle ABC and R is the midpoint of AR show that
(i) ar (PRQ) = \(\frac{1}{2}\) ar (ARC)
(ii) ar (RQC) = \(\frac{3}{8}\) ar (ABC)
(iii) ar (PBQ) = ar (ARC)
Answer:

In ∆ ABC, AQ and CP are medians. In ∆ APC, CR is a median, In ∆ APQ, QR is a median. In ∆ PBC, PQ is a median, In ∆ RBC, RQ is a median.

(i) ar (PRQ) = ar(ARQ) }
= \(\frac{1}{2}\)ar (APQ)
= \(\frac{1}{2}\)ar (BPQ)
= \(\frac{1}{2}\)ar(PQC)
= \(\frac{1}{2}\) ∙ \(\frac{1}{2}\)ar (PBC)
= \(\frac{1}{4}\)ar (PBC)
= \(\frac{1}{4}\) ∙ \(\frac{1}{2}\)ar (ABC)
= \(\frac{1}{8}\)ar (ABC)
\(\frac{1}{2}\)ar (ARC) = \(\frac{1}{2}\) ∙ \(\frac{1}{2}\)ar(APC)
= \(\frac{1}{4}\)ar (APC)
= \(\frac{1}{4}\) ∙ \(\frac{1}{2}\)ar (ABC)
= \(\frac{1}{8}\)ar (ABC)
∴ar (PRQ) = \(\frac{1}{2}\)ar (ARC)

(ii) ar(RQC) = ar(RBQ)
= ar (PBQ) + ar (PRQ)
= \(\frac{1}{2}\)ar (PBC) + \(\frac{1}{8}\)ar (ABC)
= \(\frac{1}{2}\) ∙ \(\frac{1}{2}\)ar (ABC) + \(\frac{1}{8}\)ar (ABC)
= \(\frac{1}{4}\)ar (ABC) + \(\frac{1}{8}\)ar (ABC)
= \(\frac{3}{8}\)ar (ABC)

(iii) ar (PBQ) = \(\frac{1}{2}\)ar (PBC) = \(\frac{1}{2}\) ∙ \(\frac{1}{2}\)ar (ABC)
= \(\frac{1}{4}\)ar (ABC)
ar (ARC) = \(\frac{1}{2}\)ar (APC) = \(\frac{1}{2}\) ∙ \(\frac{1}{2}\)ar (ABC)
= \(\frac{1}{4}\)ar (ABC)
∴ ar (PBQ) = ar (ARC)

Question 8.
In the given figure, ABC is a right triangle right angled at A. BCED, ACFG and ABMN „ are squares on the sides BC, CA and AB respectively. Line segment AX ⊥ DE meets BC at Y. Show that:
(i) ∆ MBC S ∆ ABD
(ii) ar (BYXD) = 2ar (MBC)
(iii) ar (BYXD) = ar (ABMN)
(iv) ∆ FCB ≅ ∆ ACE
( v ) ar (CYXE) = 2ar (FCB)
(vi) ar (CYXE) = ar (ACFG)
(vii) ar (BCED) = ar (ABMN) + ar (ACFG)
Note: Result (vii) is the famous Theorem of Pythagoras. You shall learn a simpler j! proof of this theorem in Class X.

Answer:
(i) ∠ ABM = ∠ CBD = 90°
∴ ∠ABM + ∠ABC = ∠CBD + ∠ABC
∴ ∠ MBC = ∠ ABD
In ∆ MBC and ∆ ABD,
MB = AB, ∠ MBC = ∠ ABD and BC = BD
∴ By SAS rule, ∆ MBC ≅ ∆ ABD

(ii) ar (BYXD) = 2ar (ABD)
∴ ar (BYXD) = 2ar (MBC) [∆ MBC ≅ ∆ ABD]

(iii) ar (BYXD) = 2ar (ABD)
ar (ABMN) = 2ar (MBC)
But, ar (MBC) = ar (ABD)
∴ ar (BYXD) = ar (ABMN)

(iv) ∠ FCA = ∠ ECB = 90°
∴ ∠FCA + ∠ACB = ∠ECB + ∠ACB
∴ ∠FCB = ∠ACE
In ∆ FCB and ∆ ACE,
FC = AC, ∠ FCB = ∠ACE and CB = CE
∴By SAS rule, ∆ FCB ≅ ∆ ACE

(v) ar (CYXE) = 2ar (ACE)
∴ar (CYXE) = 2ar (FCB) [∵ ∆ FCB ≅ ∆ ACE]

(vi) ar (CYXE) = 2ar (FCB)
and ar (ACFG) = 2ar (FCB)
∴ ar (CYXE) = ar (ACFG)

(vii) ar (BCED) = ar (CYXE) + ar (BYXD)
∴ ar (BCED) = ar (ACFG) + ar (ABMN) [By result (iii) and (vi)]
∴ ar (BCED) = ar (ABMN) + ar (ACFG)

Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 12 Algebraic Expressions Ex 12.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 7 Maths Chapter 12 Algebraic Expressions Ex 12.1

1. Generate algebraic expressions for the following :

(i) The sum of a and b.
(ii) The number z multiplied by itself.
(iii) The product of x and y added to the product of m and n.
(iv) The quotient of p by 5 is multiplied by q.
(v) One half of z added to twice the number t.
(vi) Sum of squares of the number x and z.
(vii) Sum of the numbers x and z is subtracted from their product.
Solution:
(i) a + b
(ii) z²
(iii) xy + mn
(iv) \(\frac{p}{5} q\)
(v) \(2 t+\frac{z}{2}\)
(vi) x² + z²
(vii) xy – (x + y)

2. Separate constant terms and variable terms from the following :
7, xy, \(\frac{3 x^{2}}{2}, \frac{72}{3} z, \frac{-8 z}{3 x^{2}}\)
Solution:
Constant Terms 7, \(\frac {72}{3}\)
Variable Terms xy, \(\frac{3 x^{2}}{2}, \frac{72}{3} z, \frac{-8 z}{3 x^{2}}\)

3. Write the terms and factors for each of the following algebraic expression.
(a) 2x² + 3yz
(b) 15x²y + 3xy²
(c) -7xyz²
(d) 100pq + 10p²q²
(e) xy + 3x²y²
(f) -7x²yz + 3xy²z + 2xyz²
Solution:

Expression	Terms	Factors
(a) 2x2 + 3xy	2x2 3xy	2, x, x 3, x, y
(b) 15x2y + 3xy2	15x2y 3xy2	15, x, x, y 3, x, y, y
(c) -7xyz2	-7xyz2	-7, x, y, z, z
(d) 100pq + 10p2q2	100pq 10p2q2	100, p, q 10, p, p, q, q
(e) xy + 3x2y2	Xy 3x2y2	X, y 3, x, x, y, y
(f) -7x2yz + 3xy2z + 2 xyz2	-7x2yz 3xy2z 2xyz2	-7, x, x, y, z 3, x, y, y, z 2, x, y, z, z

4. Classify the following algebraic expression into monomial, binomial and trinomial.
(a) 7x + 3y
(b) 5 + 2x2y²z
(c) ax + by² + cz²
(d) 3x²y²
(e) 1 + x
(f) 10
(g) \(\frac {3}{2}\)p + \(\frac {7}{6}\)q
Solution:
(a) Binomial
(b) Binomial
(c) Trinomial
(d) Monomial
(e) Binomial
(f) Monomial
(g) Binomial.

5. Write numerical coefficient of each of the following algebraic expression.
(a) 2x
(b) \(\frac {-3}{2}\)xyz
(c) \(\frac {7}{2}\)x²p
(d) -p²q²
(e) -5mn²
Solution:
(a) 2
(b) \(\frac {-3}{2}\)
(c) \(\frac {7}{2}\)
(d) -1
(e) -5

6. State whether the given pairs of terms is of like or unlike terms.
(a) – 3y, \(\frac {7}{8}\)y
(b) – 32, – 32x
(c) 3x²y, 3xy²
(d) 14mn², 14mn²q
(e) 8pq, 32pq²
(f) 10, 15
Solution:
(a) Like
(b) Unlike
(c) unlike
(d) unlike
(e) unlike
(f) like

7. In the following algebraic expressions write the coefficient of :
(a) x in x²y
(b) xyz in 15x²yz
(c) 3pq² in 3p²q²r²
(d) m² in m² + n²
(e) xy in x²y² + 2x + 3
Solution:
(a) xy
(b) 15x
(c) pr²
(d) 1
(e) xy

8. Identify the terms and their factors in the following algebraic expressions by tree diagrams
(a) 12xy + 7x²
(b) p²q² + 3mn² – pqr
(c) 2x²y² + xyz² + zy
(d) \(\frac {3}{2}\)x³ + 2x²y² – 7y³
Solution:
(a)

(b)

(c)

(d)

9. Multiple Choice Questions :

Question (i).
An expression with only one term is called a
(a) Monomial
(b) Binomial
(c) Trinomial
(d) None of these
Answer:
(a) Monomial

Question (ii).
The coefficient of x in 8 – x + y is
(a) -1
(b) 1
(c) 8
(d) 0
Answer:
(a) -1

Question (iii).
Which of the following are like terms ?
(a) 7x, 12y
(b) 15x, 12x
(c) 3xy, 3x
(d) 2y, -2yx
Answer:
(c) 3xy, 3x

Question (iv).
Terms are added to form
(a) Expressions
(b) Variables
(c) Constants
(d) Factors
Answer:
(a) Expressions

Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 11 Perimeter and Area Ex 11.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 7 Maths Chapter 11 Perimeter and Area Ex 11.3

1. Find the circumference of circle whose
(i) Radius (r) = 21 cm
(ii) Radius (r) = 3.5 cm
(iii) Diameter = 84 cm
Solution:
(i) Given radius (r) = 21 cm
circumference of circle = 2πr
= 2 × \(\frac {22}{7}\) ×21
= 132 cm

(ii) Given radius (r) = 3.5 cm
Circumference = 2πl
= 2 × \(\frac {22}{7}\) × 3.5
= 22 cm

(iii) Given Diameter (d) = 84 cm
radius (r) = \(\frac{d}{2}=\frac{84}{2}\)
= 42 cm
Circumference = 2πr
= 2 × \(\frac {22}{7}\) × 42
= 264 cm

2. If the circumference of a circular sheet is 176 m, find its radius.
Solution:
Given circumference of circular sheet = 176 m
Let radius = r
So 2πr = 176
r = \(\frac{176}{2 \pi}\)
\(\frac{176}{2 \times \frac{22}{7}}\)
= 28 m

3. A circular disc of diameter 8.4 cm is divided into two parts what is the perimeter of each semicircular part ?
Solution:
Given diameter of a circular disc = 8.4 cm
radius (r) = \(\frac{8.4}{2}\) = 4.2 cm
Perimeter of semicircular part = πr + 2r
= \(\frac {22}{7}\) × 4.2 + 2 × 4.2
= 22 × 0.6 + 8.4
= 21.6 cm

4. Find the area of the circle having
(i) Radius r = 49 cm
(ii) Radius r = 2.8 cm
(iii) Diameter = 4.2 cm
Solution:
(i) Given radius (r) = 49 cm
Area of circle = πr²
= \(\frac {22}{7}\) × 49 × 49
= 7546 cm²

(ii) Given radius (r) = 2.8 cm
Area of circle = πr²
= \(\frac {22}{7}\) × 2.8 × 2.8
= 24.64 cm²

(iii) Given diameter (d) = 4.2 cm
radius (r) = \(\frac{d}{2}=\frac{4.2}{2}\)
Area of circle = πr²
= \(\frac {22}{7}\) × 2.1 × 2.1
= 13.86 cm²

5. A gardener wants to fence a circular garden of radius 15 m. Find the length of wire, if he makes three rounds offense. Also, find the cost of wire if it costs ₹ 5 per meter (Take π = 3.14).
Solution:
Given radius of circular garden (r) = 15 m
Circumference of the circular garden = 2πr
= 2 × 3.14 × 15
= 94.2 m
So, length of the wire to make three rounds offense
= 3 × 94.2
= 282.6 cm
Cost of wire= ₹ 5 × 282.6
= ₹ 1413

6. Which of the following has larger area and by how much ?
(a) Rectangle with length 15 cm and breadth 5.4 cm
(b) Circle of diameter 5.6 cm.
Solution:
(a) Given length of rectangle = 15 cm
breadth = 5.4 cm
Area of rectangle = length × breadth
= 15 × 5.4
= 81 cm2

(b) Given diameter of circle (d) = 5.6 cm
radius (r) = \(\frac{d}{2}=\frac{5.6}{2}\)
= 2.8 cm
Area of the circle = πr²
= \(\frac {22}{7}\) × (2.8)²
= 24.64 cm²
Hence, Rectangle has more area = 81 – 24.64
= 56.36 cm²

7. From a rectangular sheet of length 15 cm and breadth 12 cm a circle of radius 3.5 cm is removed. Find the area of remaining sheet.
Solution:
Given length of rectangular sheet = 15 cm
Breadth of rectangle sheet = 12 cm
Area of rectangular sheet = length × breadth
= 15 × 12
= 180 cm²
Given radius of circle (r) = 3.5 cm
Area of circle = πr²
= \(\frac {22}{7}\) × (3.5)²
= 38.5 cm²
Since circle is removed from rectangular sheet.
So, area of remaining sheet = Area of rectangular Sheet – Area of circle
= 180 – 38.5
= 141.5 cm2

8. From a circular sheet of radius 7 cm, a circle of radius 2.1 cm is removed, find the area of remaining sheet.
Solution:
Radius of the circular sheet = 7 cm
Area of the circular sheet = 1 cm
= πr2 = \(\frac {22}{7}\) × 7 × 7 cm²
=154 cm²
Radius of the circle = 2.1 cm
Area of the circle
\(\frac {22}{7}\) × 2.1 × 1.1 = \(\frac{22}{7} \times \frac{21}{10} \times \frac{21}{10}\)
= \(\frac {1386}{100}\)
= 13.86 cm²
Area of the remaining sheet = 154 cm² – 13.86 cm²
= 140.14 cm²

9. Smeep took a wire of length 88 cm and bent it into the shape of a circle, find the radius and area of the circle. If the same wire is bent into a square, what will be the side of the square ? Which figure encloses more area ?
Solution:
Given length of wire = 88 cm
The wire is bent into the shape of circle.
Circumference of circle = length of the
2πr = 88
r = \(\frac{88}{2 \pi}=\frac{44}{\pi} \mathrm{cm}\)
= 14 cm
Area of the circle = πr²
= π × (14)²
= \(\frac {22}{7}\) × 14 × 14
= 616 cm²
If the same wire is bent into the square
Let side of the square = a
Perimeter of square = length of the wire
4 × a = 88
a = \(\frac {88}{4}\)
= 22 cm
Area of the square = (side)²
= (22)²
= 484 cm²
Hence circle enclosed more area.

10. A garden is 120 m long and 85 m broad. Inside the garden, there is a circular pit of diameter 14 m. Find the cost of planting the remaining part of the garden at the rate of ₹ 5.50 per square meter.
Solution:
Given length of garden = 120 m
Breadth of garden = 85 m
Area of garden = length × breadth
= 120 × 85
= 10200 m²
Given diameter of circular pit (d) = 14 m
radius (r) = \(\frac{d}{2}=\frac{14}{2}\)
= 7 m
Area of circular pit = πr²
= \(\frac {22}{7}\) × 7 × 7
= 154 m²
Remaining part of garden = Area of garden for planting – Area of circular pit
= 10200 – 154
= 10046 m²
Cost of planting the remaining part of the garden
= ₹ 5.50 × 10046
= ₹ 55243

11. In the figure PQ = QR and PR = 56 cm. The radius of inscribed circle is 7 cm. Q is centre of semicircle. What is the area of shaded region ?

Solution:
Given PQ = QR
PR = 56 cm
Radius of inscribed circle = 7 cm
So PR = PQ + QR
= PQ + PQ = 2PQ
Hence, PQ = \(\frac{\mathrm{PR}}{2}=\frac{56}{2}\)
= 28 cm
So QR = PQ = 28 cm
Area of shaded region = Area of semicircle of diameter PR – Area of semicircle of diameter PQ – Area of semicircle of diameter QR – Area of inscribe circle

12. The minute hand of a circular clock is 18 cm long. How far does the tip of minute hand move in one hour ?
Solution:
Given minute hand of a circular clock = 18 cm
Distance covered by minute hand in 1 hour = 2πr
= 2 × 3.14 × 18
= 2 × \(\frac {314}{100}\) × 18
= \(\frac {11304}{100}\)
= 113.04 cm.

13. Multiple choice questions :

Question (i).
The circumference of a circle of diameter 10 cm is :
(a) 31.4 cm
(b) 3.14 cm
(c) 314 cm
(d) 35.4 cm
Answer:
(a) 31.4 cm

Question (ii).
The circumference of a circle with radius 14 cm is :
(a) 88 cm
(b) 44 cm
(c) 22 cm
(d) 85 cm
Answer:
(a) 88 cm

Question (iii).
What is the area of the circle of radius 7 cm ?
(a) 49 cm
(b) 22 cm²
(c) 154 cm²
(d) 308 cm²
Answer:
(c) 154 cm²

Question (iv).
Find the diameter of a circle whose area is 154 cm² ?
(a) 4 cm
(b) 6 cm
(c) 14 cm
(d) 12 cm
Answer:
(c) 14 cm

Question (v).
A circle has area 100 times the area of another circle. What is the ratio of their circumferences ?
(a) 10 : 1
(b) 1 : 10
(c) 1 : 1
(d) 2 : 1
Answer:
(a) 10 : 1

Question (vi).
Diameter of a circular garden is 9.8 cm. Which of the following is its area ?
(a) 75.46 cm²
(b) 76.46 cm²
(c) 74.4 cm²
(d) 76.4 cm²
Answer:
(a) 75.46 cm²

Punjab State Board PSEB 6th Class Maths Book Solutions Chapter 9 Understanding Elementary Shapes Ex 9.5 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 6 Maths Chapter 9 Understanding Elementary Shapes Ex 9.5

1. Which of the following are polygons and there is no polygon. Give the reason:

Solution:
(i) It is not a closed figure. Therefore it is not a polygon.
(ii) It is made up of lines segment. Therefore it is polygon.
(iii) It is not a polygon, because it is not made of line segments.
(iv) It is not closed by line segment. Therefore, it is not a polygon.
(v) It is not polygon because line segments are intersecting each other.
(vi) It is made up of line segments, therefore it is a polygon.

2. Classify the following as concave or convex polygons:

Solution:
(i) Concave Polygon
(ii) Convex Polygon
(iii) Concave Polygon
(iv) Concave Polygon
(v) Convex Polygon
(vi) Convex Polygon.

3. Tick in the boxes, if the property holds true for a particular quadrilateral otherwise eroes out ‘x’:

Quadrilateral Properties	Rectangle	Parallelogram	Rhombus	Trapezium	Square
All sides are equal
Only opposite sides are equal
Diagonals are equal
Diagonals bisect each other
Diagonals are perpendicular to each other
Each angle is 90°

Solution:

Quadrilateral Properties	Rectangle	Parallelogram	Rhombus	Trapezium	Square
All sides are equal	×	×	√	×	√
Only opposite sides are equal	√	√	×	×	×
Diagonals are equal	√	×	×	×	√
Diagonals bisect each other	√	√	√	×	√
Diagonals are perpendicular to each other	×	×	√	×	√
Each angle is 90°	√	×	X	×	√

4. Fill in the blanks:

Question (i)
…………… is a quadrilateral with only one pair of opposite sides parallel.
Solution:
Trapezium

Question (ii)
…………….. is a quadrilateral with all sides equal and diagonals of equal length.
Solution:
Square

Question (iii)
A polygon with atleast one angle is reflex is called ……………….. .
Solution:
Concave polygon

Question (iv)
………….. is a regular quadrilateral.
Solution:
Square

Question (v)
…………… is a quadrilateral with opposite sides equal and diagonals of unequal length.
Solution:
Parallelogram.

5. State True or False:

Question (i)
A rectangle is always a rhombus.
Solution:
False

Question (ii)
The diagonals of a rectangle are perpendicular to each other.
Solution:
False

Question (iii)
A square is a parallelogram.
Solution:
True

Question (iv)
A trapezium is a parallelogram.
Solution:
False

Question (v)
Opposite sides of a parallelogram are parallel.
Solution:
True.

Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 15 Visualising Solid Shapes Ex 15.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 7 Maths Chapter 15 Visualising Solid Shapes Ex 15.1

1. Match the two dimensional figure with the names.

Answer:
(i) (e)
(ii) (d)
(iii) (a)
(iv) (b)
(v) (c)

2. Match the three dimension shapes with the names.

Answer:
(i) (d)
(ii) (e)
(iii) (a)
(iv) (c)
(v) (b)

3. Identify the nets which can be used to make cubes (cut out copies of the nets and try it).


Answer:
(i), (iv)

4. Draw the net for a square pyramid with base as square of sides 5 cm and slant edges 7 cm.
Answer:

5. Draw a net for the following cylinder.

Answer:

6. Draw the net of the solid given in figure.

Answer:

7. Dice are cubes with dots on each face opposite faces of a die always have a total of seven dots on them following are two nets to make dice (cuber) the number inserted in each square indicate the number of dots in that box insert suitable number in the blank squares.


Solution:

8. Which solid will be obtained by folding the following net ?

Solution:

9. Complete the following table.


Solution:
(i) Faces : 6.
(ii) Edges : 2. vertices : NIL,
(iii) Faces : 7. Edges : 15.
(iv) faces : 5, vertices : 5.

10. Multiple Choice questions :

Question (i).
Out of following which is 3-D figure ?
(a) Square
(b) Triangle
(c) Sphere
(d) Circle
Answer:
(c) Sphere

Question (ii).
Total number of faces a cylinder has :
(a) 0
(b) 2
(c) 1
(d) 3
Answer:
(d) 3

Question (iii).
How many edges are there in a square pyramid ?
(a) 5
(b) 8
(c) 1
(d) 4
Answer:
(b) 8

Question (iv).
Sum of number on the opposite faces of a die is :
(a) 8
(b) 7
(c) 9
(d) 6
Answer:
(b) 7

Question (v).
Which is not a solid figure ?
(a) Cuboid
(b) Sphere
(c) Quadrilateral
(d) Pyramid
Answer:
(c) Quadrilateral