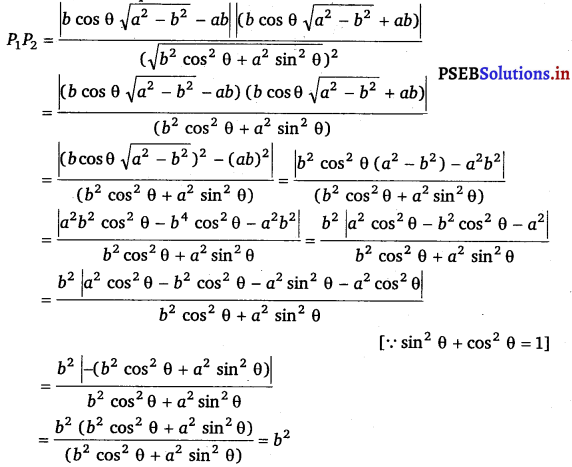Punjab State Board PSEB 11th Class Maths Book Solutions Chapter 10 Straight Lines Miscellaneous Exercise Questions and Answers.
PSEB Solutions for Class 11 Maths Chapter 10 Straight Lines Miscellaneous Exercise
Question 1.
Find the values of k for which the line (k – 3) x – (4 – k2)y + k2 – 7k + 6 = 0 is
(a) Parallel to the x-axis
(b) Parallel to the y-axis
(c) Passing through the origin.
Answer.
The given equation of line is
(k – 3) x – (4 – k2)y + k2 – 7k + 6 = 0
(a) If the given line is parallel to the x-axis, then
Slope of the given line = Slope of the x-axis The given line can be written as
(4 – k2)y = (k – 3)x + k2 – 7k + 6 = 0
y =\(\frac{(k-3)}{\left(4-k^{2}\right)} x+\frac{k^{2}-7 k+6}{\left(4-k^{2}\right)}\), which is of the form y = mx + c.
Slope of the given line = \(\frac{(k-3)}{\left(4-k^{2}\right)}\)
Slope of the x-axis = 0
\(\frac{(k-3)}{\left(4-k^{2}\right)}\) = 0
⇒ k – 3 = 0
⇒ k = 3
Thus, if the given line is parallel to the x-axis, then the value of k is 3.
(b) If the given line is parallel to the y-axis, it is vertical. Hence, its slope will be undefined.
The slope of the given line is \(\frac{(k-3)}{\left(4-k^{2}\right)}\)
Now, \(\frac{(k-3)}{\left(4-k^{2}\right)}\) is undefined at k2 = 4
k2 = 4
⇒ k = ± 2
Thus, if the given line is parallel to the y-axis, then the value of k is ± 2.
(c) If the given line is passing through the origin, then point (0, 0) satisfies the given equation of line.
(k – 3) (0) – (4 – k2) (0) + k2 – 7k + 6 = 0
k2 – 7k + 6 = 0
k2 – 6k – k + 6 = 0
(k – 6) (k – 1) = 0 k = 1 or 6
Thus, if the given line is passing through the origin, then the value of k is either 1 or 6.

Question 2.
Find the value of 6 and p, if the equation x cos θ + y sin θ = p is the normal form of the line √3x + y + 2 = 0.
Answer.
The equation of the given line is √3x + y + 2 = 0.
This equation can be reduced as √3x + y + 2 = 0
⇒ On dividing both sides by \(\frac{-\sqrt{3} x-y=2}{(-\sqrt{3})^{2}+(-1)^{2}}\) = 2, we obtain
\(-\frac{\sqrt{3}}{2} x-\frac{1}{2} y=\frac{2}{2}\)
⇒ \(\left(-\frac{\sqrt{3}}{2}\right) x+\left(-\frac{1}{2}\right) y\) = 1
On comparing equation (i) to x cos θ + y sin θ = p, we obtain
cos θ = – \(\frac{\sqrt{3}}{2}\), sin θ = – \(\frac{1}{2}\) and p = 1
Since the values of sin θ and cos θ are negative, θ = π + \(\frac{\pi}{6}\) = \(\frac{7 \pi}{6}\).
Thus, the respective values of θ and p are \(\frac{7 \pi}{6}\) and 1.
Question 3.
Find the equation of the lines, which cut-off intercepts on the axes whose sum and product are 1 and -6, respectively.
Answer.
Let the intercepts form of line be \(\frac{x}{a}+\frac{y}{b}\) = 1,
then a + b = 1 and ab = – 6.
b = 1 – a and a (1 – a) = – 6
⇒ a2 – a – 6 = 0
⇒ (a – 3) (a + 2) = 0
∴ a = 3, – 2
Case I:
If a = 3, then b = – \(\frac{6}{a}\)
= – \(\frac{6}{3}\) = – 2
∴ Equation of line is \(\frac{x}{3}+\frac{y}{-2}\) = 1
⇒ 2x – 3y – 6 = 0.
Case II:
If a = – 2, then b = \(\frac{-6}{-2}\) = 3
∴ Equation of line is \(\frac{x}{-2}+\frac{y}{3}\) = 1
⇒ 3x – 2y + 6 = 0.

Question 4.
What are the points on the y-axis whose distance from the line \(\frac{x}{3}+\frac{y}{4}\) = 1 is 4 units.
Answer.
Let (0, b) be the point on they-axis whose distance from line \(\frac{x}{3}+\frac{y}{4}\) = 1 is 4 units.
The given line can be written as 4x + 3y – 12 = 0 ……………..(i)
On comparing equation (i) to the general equation of line Ax + By + C = 0,we obtain A = 4, B = 3 and C = – 12.
It is known that the perpendicular distance (d) of a line Ax + By + C = 0 from a point (x1, y1) is given by
d = \(\)
Therefore, if (0, b) is the point on the y-axis whose distance from line \(\frac{x}{3}+\frac{y}{4}\) = 1 is 4 units, then:
4 = \(\frac{|4(0)+3(b)-12|}{\sqrt{4^{2}+3^{2}}}\)
4 = \(\frac{|3 b-12|}{5}\)
⇒ 20 = |3b – 12|
20 = ±(3b – 12)
20 = (3b – 12) or 20 = – (3b – 12)
3b = 20 + 12 or 3b = – 20 + 12
b = \(\frac{32}{3}\) or b = \(\frac{8}{3}\).
Thus, the required points are (o, \(\frac{32}{3}\)) and (o, \(\frac{8}{3}\)).
Question 5.
Find perpendicular distance from the origin of the line joining the points (cos θ, sin θ) and (cos Φ, sin Φ).
Answer.
Equation of the line joining the points (cos θ, sin θ) are (cos Φ, sin Φ) is given by


Question 6.
Find the equation of the line parallel to y-axis and drawn through the point of intersection of the lines x – 7y + 5 = 0 and 3x + y = 0.
Answer.
The point of intersection (x1, y1) of the lines x – 7y + 5 = 0 and 3x + y = 0 is obtained by solving these equations.
Putting y = – 3x in x – 7y + 5 = 0
⇒ x – 7 (- 3x) + 5 = 0,
⇒ x + 21x + 5 = 0
⇒ 22x + 5 = 0
⇒ x = \(\frac{5}{22}\)
Also, y = \(\frac{15}{12}\)
⇒ (x1, y1) = \(\left(\frac{-5}{22}, \frac{15}{12}\right)\)
Let a line parallel to y-axis through the point (x1, y1) is x = x1
Here x1 = – \(\frac{5}{22}\)
∴ The equation of the line parallel to y-axis passing through the point of intersection (x1, y1) of given lines is x = – \(\frac{5}{22}\) or 22x + 5 = 0.
Question 7.
Find the equation of a line drawn perpendicular to the line \(\frac{x}{4}+\frac{y}{6}\) = 1 through the point, where It meets the y-axis.
Answer.
Given equation of line is \(\frac{x}{4}+\frac{y}{6}\) = 1
\(\frac{3 x+12}{12}\) = 1
3x + 2y = 12 ……………..(i)
If line (i) meet the Y-axis, then put x = 0 in eq. (i), we get
0 + 2y = 12
⇒ y = 6
∴ Point is (0, 6).
Slope of line (i) is, m1 = – \(\frac{3}{2}\)
Slope of line perpendicular to line (i) is,
m2 = – \(-\frac{1}{m_{1}}=\frac{-1}{(-3 / 2)}=\frac{2}{3}\)
Now, equation of line having slope and passing through (0, 6) is given by
y – y1 = m (x – x1)
⇒ y – 6 = \(\frac{2}{3}\) (x – 0)
⇒ 3y – 18 = 2x
⇒ 2x – 3y + 18 = 0
Which is required equation of line.

Question 8.
Find the area of the triangle formed by the lines y – x = 0, x + y = 0 and x – k= 0.
Answer.
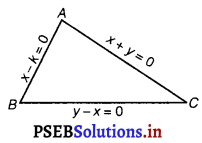
Let ABC be the triangle, whose sides are
AB: x – k = 0 ……………..(i)
BC: y – x = 0 ………………(ii)
and AC: x + y = 0 ………………(iii)
On solving eqs. (i) and (iii), we get Coordinates of A i.e.,(k, – k)
On solving eqs. (i) and (ii), we get Coordinates of B i.e.,(k, k)
On solving eqs. (ii) and (iii), we get Coordinates of C i.e. (0, 0)
∴ Area of ∆ABC = \(\frac{1}{2}\) {x1 (y2 – y3) + x2 (y3 – y1) + x3 (y1 – y2)
= \(\frac{1}{2}\) {k (k – 0) + k (0 + k) + 0 (- k – k)}
[∵ (x1, y1) = (k,- k), (x2, y2) = (k, k) and (x3, y3) = (0, 0)]
= \(\frac{1}{2}\) {k2 + k2} = \(\frac{1}{2}\) k2
= k2
Question 9.
Find the value of p so that the three lines 3x + y – 2 = 0 px + 2y – 3 = 0 and 2x – y – 3 = 0 may intersect at one point.
Answer.
The equations of the given lines are
3x + y – 2 = 0 …………(i)
px + 2y – 3 = 0 …………..(ii)
2x – y – 3 = 0 ……………..(iii)
On solving equations (i) and (iii), we obtain x = 1 and y = – 1.
Since these three lines may intersect at one point, the point of intersection of lines (i) and (iii) will also satisfy line (ii). p(1) + 2(- 1) – 3 = 0
p – 2 – 3 = 0
⇒ p = 5
Thus, the required value of p is 5.

Question 10.
If three lines whose equations are y = m1x + c1, y = m2x + c2 and y = m3x + c3 are concurrent, then show that m1 (c2 – c3) + m2 (c3 – c1) + m3 (c1 – c2) = 0.
Answer.
The equations of the given lines are
y = m1x + c1 ………………(i)
y = m2x + c2 ……………..(ii)
y = m3x + c3 ………………(iii)
On subtracting equation (i) from (ii), we obtain 0 = (m2 – m1) x + (c2 – c1)
⇒ (m1 – m2)x = c2 – c1
⇒ x = \(\frac{c_{2}-c_{1}}{m_{1}-m_{2}}\)
On substituting this value of x in eq. (i), we obtain
y = \(m_{1}\left(\frac{c_{2}-c_{1}}{m_{1}-m_{2}}\right)+c_{1}=\frac{m_{1} c_{2}-m_{1} c_{1}}{m_{1}-m_{2}}+c_{1}\)
= \(\frac{m_{1} c_{2}-m_{1} c_{1}+m_{1} c_{1}-m_{2} c_{1}}{m_{1}-m_{2}}=\frac{m_{1} c_{2}-m_{2} c_{1}}{m_{1}-m_{2}}\)
∴ \(\left(\frac{c_{2}-c_{1}}{m_{1}-m_{2}}, \frac{m_{1} c_{2}-m_{2} c_{1}}{m_{1}-m_{2}}\right)\) is the point of intersection of lines (i) and (ii).
It is given that lines (i), (ii) and (iii) are concurrent.
Hence the point of intersection of lines (i) and (ii) will also satisfy equation (iii).
\(\frac{m_{1} c_{2}-m_{2} c_{1}}{m_{1}-m_{2}}=m_{3}\left(\frac{c_{2}-c_{1}}{m_{1}-m_{2}}\right)+c_{3}\)
\(\frac{m_{1} c_{2}-m_{2} c_{1}}{m_{1}-m_{2}}=\frac{m_{3} c_{2}-m_{3} c_{1}+c_{3} m_{1}-c_{3} m_{2}}{m_{1}-m_{2}}\)
m1c2 – m2c1 – m3c1 – c3m1 + c3m2 = 0
m1 (c2 – c3) + m2 (c3 – c1) + m3 (c1 – c2) = 0.
Hence proved.

Question 11.
Find the equation of the lines through the point (3, 2) which make an angle of 45° with the line x – 2y = 3.
Answer.
Let the slope of the required line be m1.
The given line can be written as y = \(\frac{1}{2} x-\frac{3}{2}\) which is of the form y = mx + c.
Slope of the given line = m2 = \(\frac{1}{2}\)
It is given that the angle between the required line and line x – 2y = 3 is 45°
We know that if θ is the acute angle between lines l1 and l2 with slopes m1 and m2 respectively, then
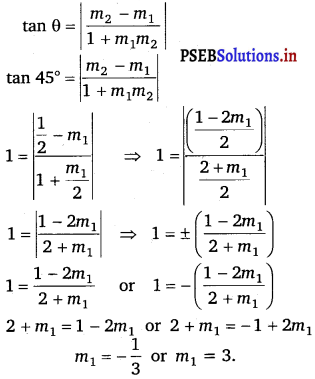
Case I : m1 = 3
The equation of the line passing through (3, 2) and having a slope of 3 is:
y – 2 = 3 (x – 3)
y – 2 = 3x – 9
3x – y = 7
Case II: m1 = – \(\frac{1}{3}\).
The equation of the line passing through (3, 2) and having a slope of – \(\frac{1}{3}\) is
y – 2 = – \(\frac{1}{3}\) (x – 3)
3y – 6 = – x + 3
x + 3y = 9.
Thus, the equations of the lines are 3x – y = 7 and x + 3y = 9.

Question 12.
Find the equation of the line passing through the point of intersection of the lines 4x + 7y – 3 = 0 and 2x – 3y + 1 = 0 that has equal intercepts on the axes.
Answer.
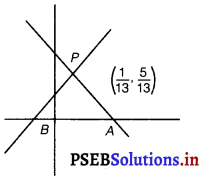
The given lines are
2x – 3y = – 1 …………….(i)
4x + 7y = 3 ……………(ii)
Multiplying eq. (i) by 2
4x – 6y = – 2 ………….(iii)
Subtracting eq. (iii) from eq. (ii), we get
13y = 5
⇒ y = \(\frac{13}{5}\)
Putting the value of y in eq. (i),
2x – \(\frac{3 \times 5}{13}\) = – 1
2x = – 1 + \(\frac{15}{13}=\frac{2}{13}\)
x = \(\frac{1}{13}\)
∴ Given lines intersect at P(\(\frac{1}{13}\), \(\frac{5}{13}\))
PA and PB are the lines that make equal intercepts on the axes.
They make angles of 135° with positive direction of x-axis.
Their slopes are tan 135° and tan 45° i.e., – 1 and 1 respectively.
∴ Equation of PA is y – \(\frac{5}{13}\) = (- 1) × (x – \(\frac{1}{13}\))
or 13y – 5 = – 13x + 1
13x + 13y – 6 = 0
Similarly, equation of PB is y – \(\frac{5}{13}\) = 1 × (x – \(\frac{5}{13}\))
⇒ 13y – 5 = 13x – 1
13x – 3y + 4 = 0.

Question 13.
Show that the equation of the line passing through the origin and nisildng an angle θ with the line y = mx + c is
\(\frac{y}{x}=\frac{m \pm \tan \theta}{1 \mp m \tan \theta}\)
Answer.
Slope of line y = mx + c is m.
Let M be the slope of required line, then
tan θ = \(\left|\frac{M-m}{1+m M}\right|=\pm\left(\frac{M-m}{1+M m}\right)\)
Case I:
Taking ‘+‘ sign,
tan θ = \(\frac{M-m}{1+m M}\)
Then, tan θ + Mm . tan θ = M – m

Question 14.
In what ratio, the line joining (- 1, 1) and (5, 7) is divided by the line x + y = 4?
Answer.
The equation of the line joining the points (- 1, 1) and (5, 7) is given by
y – 1 = \(\frac{7-1}{5+1}\) (x + 1)
= \(\frac{6}{6}\) (x + 1)
x – y + 2 = 0 ………….(i)
The equation of the given line is x + y – 4 = 0 ……………..(ii)
The point of intersection of lines (i) and (ii) is given by x = 1 and y = 3.
Let point (1, 3) divide the line segment joining (- 1, 1) and (5, 7) in the ratio 1 : k. Accordingly, by section formula.
(1, 3) = \(\left(\frac{k(-1)+1(5)}{1+k}, \frac{k(1)+1(7)}{1+k}\right)\)
(1, 3) = \(\left(\frac{-k+5}{1+k}, \frac{k+7}{1+k}\right)\)
\(\frac{-k+5}{1+k}\) = 1
∴ – k + 5 = 1 + k
⇒ 2k = 4
⇒ k = 2.
Thus, the line joining the points (- 1, 1) and (5, 7) is divided by line x + y = 4 in the ratio 1 : 2.

Question 15.
Find the distance of the line 4x + 7y + 5 = 0 from the point (1, 2) along the line 2x – y = 0.
Answer.
The given lines are
2x – y = 0 ………………..(i)
4x + 7y + 5 = 0 ………………..(ii)
A(1, 2) is a point on line (i).
Let B be the point of intersection of lines (i) and (ii).
On solving equations (i) and (ii), we obtain x = – \(\frac{5}{18}\) and y = – \(\frac{5}{9}\).
∴ Coordnates of point B = (- \(\frac{5}{18}\), – \(\frac{5}{9}\))
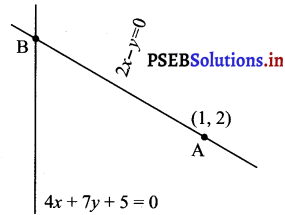

Thus, the required distance is \(\frac{23 \sqrt{5}}{18}\) units.

Question 16.
Find the direction in which a straight line must be drawn through the point (- 1, 2) so that its point of intersection with the line x + y = 4 may be at a distance of 3 units from this point.
Answer.
Any line passing through P(- 1, 2) is
y – 2 = m(x + 1)
where m is its slope
y = mx + m + 2 ……………(i)
Putting the value of ‘y’ in x + y = 4, we get
x + mx +m + 2 = 4
⇒ (1 + m) x = 4 – 2 – m
⇒ x = \(\frac{2-m}{1+m}\)
From eq.(i),
y = m (\(\frac{2-m}{1+m}\)) + m + 2
Now from the diagram, it is clear that the point of intersection of the other two legs of the right triangle having AB as the hypotenuse can be either P or Q.
Case I: When ∠APB is taken,
The perpendicular sides in ∠APB are AP and PB.
Now, side PB is parallel to x-axis and at a distance of 1 unit above x-axis.
So, equation of PB is y = 1 or y – 1 = 0.
The side AP is parallel to y-axis and at a distance of 1 unit on the right of y-axis.
So, equation of AP is x = 1 or x – 1 = 0.
Case II: When ∠AQB is taken.
The perpendicular sides in ∠AQB are AQ and QB.
Now, side AQ is parallel to x-axis and at a distance of 3 units above x – axis.
So, equation of AQ is y = 3 or y – 3 = 0.
The side QB is parallel to y-axis and at a distance of 4 units on the left of y-axis.
So, equation of QB is x = – 4 or x + 4 = 0.
Hence, the equation of the legs are: x = 1, y = 1 or x = – 4, y = 3.

Question 18.
Find the image of the point (3, 8) with respect to the line x + 3y = 7 assuming the line to be a plane mirror.
Answer.
Let AB be the line x + 3y = 7 and the image P(3, 8) of P(3, 8) be Q(x1, y1)middle point at PQ
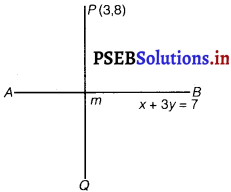
M \(\left(\frac{x_{1}+3}{2}, \frac{y_{1}+8}{2}\right)\) lies on AB.
∴ \(\left(\frac{x_{1}+3}{2}\right)+3\left(\frac{y_{1}+8}{2}\right)\) = 7
x1 + 3 + 3y1 + 24 = 14
⇒ x1 + 3y1 + 13 = 0 ……………….(i)
slope of AB = – \(\frac{1}{3}\),
Slope of PQ = \(\frac{y_{1}-8}{x_{1}-3}\)
AB ⊥ PQ
\(\left(-\frac{1}{3}\right)\left(\frac{y_{1}-8}{x_{1}-3}\right)\) = – 1
⇒ y1 – 8 = 3 (x1 – 3) = 3x1 – 9
⇒ y1 = 3x1 – 1 ………….(ii)
Putting the value of y1 in eq. (1), we get
x1 + 3 (3x1 – 1) + 13 = 0
10x1 + 10 = 0
x1 = – 1
Putting the value of x1 in (ii), we get
y1 = – 3 – 1 = – 4
∴ The point Q, the image of P is (- 1, 4).
Question 19.
If the lines y = 3x + 1 and 2y = x + 3 are equally inclined to the line y = mx + 4, find the value of m.
Answer.
The equations of the given lines are
y = 3x + 1
2y = x + 3 …………..(ii)
y = mx + 4 …………….(iii)
Slope of line (i), m1 = 3.
Slope of line (ii), m2 = \(\frac{1}{2}\)
Slope of line (iii), m3 = m.
It is given that lines (i) and (ii) are equally inclined to line (iii).
This means that the angle between lines (i) and (iii) equals the angles between lines (ii) and (iii).


Question 20.
If sum of the perpendicular distances of a variable point P(x, y) from the lines x + y – 5 = 0 and 3x – 2y + 7 = 0 is always 10. Show that P must move on a line.
Answer.
The equations of the given lines are
x + y – 5 = 0 …………….(i)
3x – 2y + 7 = 0 ………………(ii)
The perpendicular distances of P(x, y) from lines (j) and (ii) are respectively given by
d1 = \(\frac{|x+y-5|}{\sqrt{(1)^{2}+(1)^{2}}}\) and
d2 = \(\frac{|3 x-2 y+7|}{\sqrt{(3)^{2}+(-2)^{2}}}\)
i.e., d1 = \(\frac{|x+y-5|}{\sqrt{2}}\)
d2 = \(\frac{|3 x-2 y+7|}{\sqrt{13}} .\)
It is given that d1 + d2 = 10
∴ \(\frac{|x+y-5|}{\sqrt{2}}+\frac{|3 x-2 y+7|}{\sqrt{13}}\) = 10
⇒ √13 |x + y – 5| + √2 |3x – 2y + 7| – 10√26 = 0
⇒ √13 (x + y – 5) + √2 (3x – 2y + 7) – 10√26 = 0
[Assuming (x + y – 5) and (3x – 2y + 7) are positive]
⇒ √13x + √13y – 5√13 + 3√2x – 2√2y + 7√2 – 10√26 = 0
⇒ x (√13 + 3√2) + y (√13 – 2√2) + (7√2 – 5√13 – 10√26) = 0
which is the equation of a line.
Similarly, we can obtain the equation of line for any signs of (x + y – 5) and (3x – 2y + 7).
Thus, point P must move on a line.

Question 21.
Find equation of the line which is equidistant from parallel lines 9x+6y – 7 = 0 and 3x + 2y + 6 = 0.
Answer.
The given parallel lines are
9x + 6y – 7 = 0 …………….(i)
and 3x + 2y + 6 = 0 …………….(ii)
Multiplying (ii) by 3, we get
9x + 6y + 18 = 0 ………………….(iii)
Let the equations of (ii) line parallel to the lines (i) and (iii) is
9x + 6y + c = 0 …………..(iv)
Distance between (i) and (iv)
= \(\frac{|-7-c|}{\sqrt{9^{2}+6^{2}}}=\frac{|7+c|}{\sqrt{117}}\)
Distance between (iii) and (iv)
= \(\frac{|18-c|}{\sqrt{9^{2}+6^{2}}}\)
The third line being equidistant from the given two lines.
\(\frac{|7+c|}{\sqrt{117}}=\frac{|c+18|}{\sqrt{117}}\) or 2c = 11 or c = \(\frac{11}{2}\)
Putting this values of c in eq. (iv), we get
9x + 6y + \(\frac{11}{2}\) = 0
or 18x + 12y + 11 = 0
which is the equation of required line.
Question 22.
A ray of light passing through the point (1, 2) reflects on the x-axis at point A and the reflected ray passes through the point (5, 3). Find the coordinates of A.
Answer.
In the figure, PA is the incident ray and AR is the reflected ray, which makes an angle 0 from the X-axis.
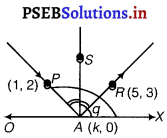
It is clear from the figure that AS ⊥ OX
It means AS bisect the ∠PAR.
Then, ∠PAS = ∠RAS
⇒ ∠RAX = ∠PAO = θ (let)
⇒ ∠XAP = 180° – θ
Slope of AR = tan θ
= \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
= \(\frac{3-0}{5-k}\) …………….(i)
[where, point A is (k, 0)]
Slope of AP = tan (180 – θ)
= – tan θ
= \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{2-0}{1-k}\) ……………(ii)
From eqs. (i) and (ii), we get
\(\frac{3}{5-k}=-\frac{2}{1-k}\)
⇒ 3 – 3k = – 10 + 2k
⇒ 5k = 13
⇒ k = \(\frac{13}{5}\)
Hence, the coordinates of A are (\(\frac{13}{5}\). 0).

Question 23.
Prove that the product of the lengths of the perpendiculars drawn from the points (\(\sqrt{a^{2}-b^{2}}\), 0) and (- \(\sqrt{a^{2}-b^{2}}\), 0) to the line \(\frac{x}{a}\) cos θ + \(\frac{y}{4}\) sin θ = 1 is b2.
Answer.
The equation of the given line is \(\frac{x}{a}\) cos θ + \(\frac{y}{4}\) sin θ = 1
or bx cos θ + ay sin θ – ab = 0 ……………….(i)
Length of the perpendicular from point (\(\sqrt{a^{2}-b^{2}}\), 0) to the line (i) is
P1 = \(\frac{\mid b \cos \theta\left(\sqrt{\left.a^{2}-b^{2}\right)}+a \sin \theta(0)-a b \mid\right.}{\sqrt{b^{2} \cos ^{2} \theta+a^{2} \sin ^{2} \theta}}\)
= \(\frac{\left|b \cos \theta \sqrt{a^{2}-b^{2}}-a b\right|}{\sqrt{b^{2} \cos ^{2} \theta+a^{2} \sin ^{2} \theta}}\) ……………….(ii)
Length of the perpendicular from point (- \(\sqrt{a^{2}-b^{2}}\), 0) to line (ii) is
P1 = \(\frac{b \cos \theta\left(-\sqrt{a^{2}-b^{2}}\right)+a \sin \theta(0)-a b}{\sqrt{b^{2} \cos ^{2} \theta+a^{2} \sin ^{2} \theta}}\)
= \(\frac{\left|b \cos \theta \sqrt{a^{2}-b^{2}}+a b\right|}{\sqrt{b^{2} \cos ^{2} \theta+a^{2} \sin ^{2} \theta}}\)
On multiplying equations (ii) and (iii), we obtain
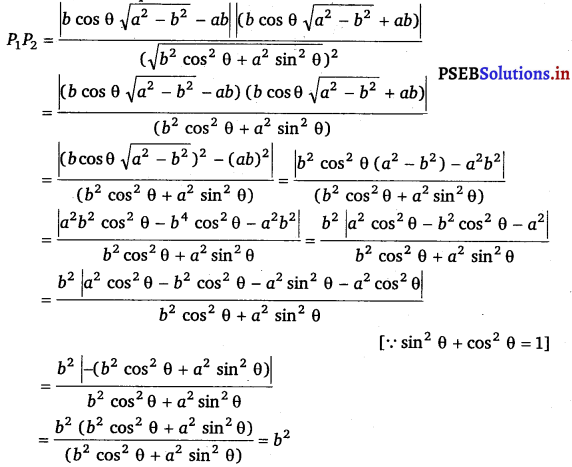

Question 24.
A person standfing at the junction (crossing) of two straight paths represented by the equations 2x – 3y + 4 = O and
3x + 4y – 5 = 0 wants to reach the path whose equation Is 6x – 7y + 8 = 0 in the least time. Find equation of the path that he should follow.
Answer.
The equations of the given lines are
2x – 3y + 4 = 0
3x + 4y – 5 = 0 …………..(ii)
6x – 7y + 8 = 0 …………(iii)
The person is standing at the junction of the paths represented by lines (i) and (ii).
On solving equations (i) and (ii), we obtain x = – \(\frac{1}{17}\) and y = \(\frac{22}{17}\)
Thus, the person is standing at point (- \(\frac{1}{17}\), \(\frac{22}{17}\))
The person can reach path (iii) in the least time if he walks along the perpendicular line to (iii) from point (- \(\frac{1}{17}\), \(\frac{22}{17}\)).
Slope of the line (iii) = \(\frac{6}{7}\).
∴ Slope of the line perpendicular to line (iii) = \(-\frac{1}{\left(\frac{6}{7}\right)}=-\frac{7}{6}\)
The equation of the line passing through and having a slope (- \(\frac{1}{17}\), \(\frac{22}{17}\)) and having a slope of – \(\frac{7}{6}\) is given by
\(\left(y-\frac{22}{17}\right)=-\frac{7}{6}\left(x+\frac{1}{17}\right)\)
6 (17y – 22) = – 7 (17x + 1)
102y – 132 = – 119x – 7
119x + 102y = 125
Hence, the path that the person should follow is 119x + 102y = 125.