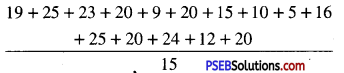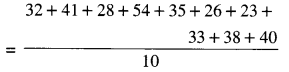Bhagya – Page 226 – PSEB Solutions

PSEB 12th Class Physical Education Notes Chapter 5 Disability

March 11, 2024March 11, 2024 by Bhagya

This PSEB 12th Class Physical Education Notes Chapter 5 Disability will help you in revision during exams.

PSEB 12th Class Physical Education Notes Chapter 5 Disability

→ The term disability is the state of being unable to use any part of the body properly, which may be due to injury or disease.

→ This restricts an individual to perform daily activities with comfort and ease.

→ The special ability or disability can be either structural disability or functional disability.

→ There are various causes of disability i.e. it can be inherited or caused by environmental factors.

→ The environmental factors are very vast. it can be due to disease, occupation, physical factors, social factors, chemical factors or psychological factors and accidents, etc.

→ There are many occupational diseases that may cause disability to a person.

→ These occupational diseases can be due to physical agents like dust, noise, radiation, and dust or chemical hazards, etc.

→ These diseases can be prevented to some extent by various means such as medical examination of the workers, maintenance of workplace, control of air or noise pollution, use of protective devices, etc.

→ Another term that has been discussed in this chapter is rehabilitation which means, “the act of restoring something to its original or normal state.

→ The literal meaning came from the Latin words ‘re’-mean again and ‘habitable meaning ‘make fit’. It is the process of keeping a person who suffered an injur}’ or illness to come to a self-sufficient state.

→ There are many societies that are actively engaged for the rehabilitation services such as the Indian Red Cross Society, All India Blind Relief Society, Tuberculosis Association of India, Indian Council for Child Welfare, etc.

→ Hence, these societies help people to return to their normal or near-normal way of living.

PSEB 12th Class Physical Education Notes Chapter 4 Sport Injuries

March 11, 2024March 11, 2024 by Bhagya

This PSEB 12th Class Physical Education Notes Chapter 4 Sport Injuries will help you in revision during exams.

PSEB 12th Class Physical Education Notes Chapter 4 Sport Injuries

→ The term sports injuries mean the injuries that occur during participation in sports activities or exercising.

→ It is also quite common especially for the people who tend to be active or exercise a lot in their routine.

→ The injuries in the field of sports can be due to direct or indirect impact on tissues i.e. soft tissues or hard tissues.

→ In the field, an athlete has to take part in terms of the process or training, or competition and seek medical treatment or first aid for the same.

→ The injuries in the field of sports can be due to poor physical fitness level, inadequate warming up or conditioning, lack of proper knowledge, poor quality sports equipment, bad conditions of the playfield, lack of nutritional diet, etc.

→ The chances of injuries can be avoided by adopting various preventive measures such as participation after proper warming up and conditioning, use of protective equipment, proper knowledge of rules and regulations and techniques, under the supervision of a coach, etc.

→ It is also important to know the basic first aid procedure in order to reduce the chances of further complications at the time of injuries on the field.

→ The sports injuries such as sprain, strain, abrasion, contusion, dislocation, and fracture can be managed with the help of first aid procedure and basic principles of RICE (Rest, Ice application, Compression, and Elevation).

→ But, it is well said that “Prevention is better than cure”.

→ Hence, the principle of ‘PRICE’ is more suitable to avoid the chances of injuries in the field of sports, where ‘P’ stands for ‘Protection’.

→ Hence, for the continuous improvement in the performance level, it is important to take care of each and every aspect related to injuries and their management.

PSEB 12th Class Physical Education Notes Chapter 3 Careers in Physical Education and Sports Awards

March 11, 2024March 11, 2024 by Bhagya

This PSEB 12th Class Physical Education Notes Chapter 3 Careers in Physical Education and Sports Awards will help you in revision during exams.

PSEB 12th Class Physical Education Notes Chapter 3 Careers in Physical Education and Sports Awards

→ Throughout history, sports have played a variety of important roles in society as recreation, preparation for war, and hunting.

→ The ancient Greeks were lovers of sports and taught their children to take part in these activities for health benefits.

→ The main activities at that time were wrestling, running, jumping, discus throw, javelin, and gymnastics, etc.

→ Later, during the modern era, the brief history of physical education revealed a focus on gymnastics, hygiene training, and the development of the human body.

→ In 1882, the Education Commission of India recommended introducing physical education in the school curriculum but did not succeed in their efforts.

→ In the year 1927, with the efforts of A.G. Noehren, H.C. Buck, and Dorabji Tata, IOA was established in order to promote physical education teachers in India.

→ LNCPE was established in Gwalior in the year 1957.

→ In the year 1984, the First National sports policy was introduced which laid the stress to include physical education as a compulsory subject in the school curriculum.

→ This laid foundation for the career options in the field of physical education to teach students at the school level.

→ With the implementation of the compulsory subjects in the school curriculum and with the development of competitive sports in India, career options were groomed in the field.

→ In order to teach at the school level various degree courses such as B.PE., B.P.Ed., D.P.Ed. were introduced for the school teacher.

→ In addition to this, to teach at the college level a teacher must possess, Masters’ Degree in Physical Education, UGC (NET), M.Phil, Ph.d.

→ With the advancement of physical education and sports in India, leading institutes provided various courses for the career options such as YMCA College Madras, LNIPE Gwalior, Shri Hanumans Parasarak Mandal (Amravati), Chennai University, Panjab University (Chandigarh), GNDU, Amritsar, etc.

→ The career options in the field of physical education and Sports also developed such as options to work as a school and college teacher, coaching, fitness trainer, sports journalism, sports physiotherapist, commentator, and official, etc.

→ In order to promote sportspersons, various sports awards were also introduced by the government of India such as the Rajiv Gandhi Khel Ratna Award, the highest sports award for the sports person i.e. Arjuna Award, in order to recognize the contribution of coaches, Dronacharya Award was also introduced, To encourage and improve sports at college or university level MAKA trophy was also introduced by the government of India in the year 1956.

→ Hence, It can be viewed that since the inception of physical education and sports, there has been continuous development in the field to engage youth and children in these activities.

PSEB 7th Class Maths Solutions Chapter 4 Simple Equations Ex 4.3

March 12, 2024March 11, 2024 by Bhagya

Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 4 Simple Equations Ex 4.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 7 Maths Chapter 4 Simple Equations Ex 4.3

1. Solve each of the following equation.

Question (i).
6x + 10 = – 2
Answer:
Given equation is 6x + 10 = – 2
Transposing + 10 from L.H.S to R.H.S
we get
6x = -2 – 10
or 6x = -12
Dividing both sides by 6, we get
\(\frac{6 x}{6}=\frac{-12}{6}\)
or x = – 2, which is the required solution.

To check Put x = – 2 in the LHS of the equation 6x + 10 = – 2
L.H.S. = 6x + 10
= 6 × -2 + 10
= -12 + 10
= – 2 = R.H.S.
∴ L.H.S. = R.H.S.

Question (ii).
2y – 3 = 2
Answer:
Given equation is 2y – 3 = 2
Transposing – 3 from L.H.S. to R.H.S,
we get
2y = 2 + 3
or 2y = 5
Dividing both sides by 2, we get:
\(\frac{2 y}{2}=\frac{5}{2}\)
or y = \(\frac {5}{2}\), which is the required solution

To check. Put y = \(\frac {5}{2}\) in the L.H.S of the equation 2y – 3 = 2
L.H.S = 2y – 3 = 2 × \(\frac {5}{2}\) – 3
= 5 – 3 = 2 = R.H.S.
∴ L.H.S. = R.H.S.

Question (iii).
\(\frac{a}{5}\) + 3 = 2
Answer:
Given equation is \(\frac{a}{5}\) + 3 = 2
Transposing + 3 from L.H.S to R.H.S., we get
\(\frac{a}{5}\) = 2 – 3
or \(\frac{a}{5}\) = -1
Multiplying both sides, by 5, we get
5 × \(\frac{a}{5}\) = 5 × – 1
or a = – 5, which is the required solution.

To Check: Put a = – 5 in the L.H.S of the equation
\(\frac{a}{5}\) + 3 = 2,
L.H.S. = \(\frac{a}{5}\) + 3
= \(\frac {-5}{5}\) + 3
= – 1 + 3
= 2 = R.H.S.
∴ L.H.S. = R.H.S.

Question (iv).
\(\frac{3 x}{2}=\frac{2}{3}\)
Answer:
Given equation is \(\frac{3 x}{2}=\frac{2}{3}\)
Multiplying both sides by 2, we get
2 × \(\frac{3 x}{2}\) = 2 × \(\frac {2}{3}\)
or 3x = \(\frac {4}{3}\)
Dividing both sides by 3 we get
\(\frac{3 x}{3}=\frac{4}{3} \times \frac{1}{3}\)
or x = \(\frac {4}{9}\), which is the required solution.

To Check. Put x = \(\frac {4}{9}\) in the L.H.S. of equation \(\frac{3 x}{2}=\frac{2}{3}\)
L.H.S. = \(\frac{3 x}{2}=\frac{3}{2} \times \frac{4}{9}\) = \(\frac {2}{3}\) = R.H.S.
∴L.H.S. = R.H.S.

Question (v).
\(\frac {5}{2}\)x = -5
Answer:
Given equation is \(\frac {5}{2}\) x = – 5
Multiplying both sides by 2, we get
2 × \(\frac {5}{2}\) x = 2 × – 5
or 5x = – 10
Dividing both sides by 5, we get
\(\frac{5 x}{5}=\frac{-10}{5}\)
or x = – 2, which is the required solution.

To Check. Put x = – 2 in L.H.S. of the equation \(\frac {5}{2}\)x = – 5
L.H.S. = \(\frac {5}{2}\)x = \(\frac {5}{2}\) × -2
= – 5 = R.H.S.
∴ L.H.S. = R.H.S.

Question (vi).
2x + \(\frac {5}{2}\) = \(\frac {37}{2}\)
Answer:
Given equation is 2x + \(\frac {5}{2}\) = \(\frac {37}{2}\)
Subtract \(\frac {5}{2}\) from both sides, we get
2x + \(\frac {5}{2}\) – \(\frac {5}{2}\)
= \(\frac {37}{2}\) – \(\frac {5}{2}\)
or 2x = \(\frac{37-5}{2}\)
or 2x = \(\frac {32}{2}\)
or 2x = 16
Dividing both sides by 2, we get
\(\frac{2 x}{2}=\frac{16}{2}\)
or x = 8, which is the required solution.

To Check. Put x = 8 in the L.H.S. of the equation 2x + \(\frac {5}{2}\) = \(\frac {37}{2}\)
L.H.S. = 2x + \(\frac {5}{2}\)
= 2 × 8 + \(\frac {5}{2}\)
= 16 + \(\frac {5}{2}\)
= \(\frac{32+5}{2}\)
= \(\frac {37}{2}\) = R.H.S.
∴ L.H.S. = R.H.S.

2. Solve the following equation

Question (i).
5 (x + 1) = 25
Answer:
Given equation is 5 (x + 1) = 25
Dividing both sides by 5 we get
\(\frac{5(x+1)}{5}=\frac{25}{5}\)
or x + 1 = 5
Transposing 1 from L.H.S. to R.H.S. we get
x = 5 – 1
or x = 4, which is the required solution.

To Check. Put x = 4 in the L.H.S. of the equation 5 (x + 1) = 25
L.H.S. = 5 (x + 1)
= 5 (4 + 1)
= 5 (5)
= 25 = R.H.S.
∴ L.H.S. = R.H.S.

Question (ii).
2 (3x – 1) = 10
Answer:
Given equation is 2 (3x – 1) = 10
Dividing both sides by 2, we get
\(\frac{2(3 x-1)}{2}=\frac{10}{2}\)
or 3x – 1 = 5
Transposing – 1 from L.H.S. to R.H.S we get
3x = 5 + 1
3x = 6
Dividing both sides by 3, we get \(\frac{3 x}{3}=\frac{6}{3}\)
or x = 2, which is the required solution.

To Check. Put x = 2, in the L.H.S. of the equation 2 (3x – 1) = 10
L.H.S. = 2 (3x – 1) = 10
L.H.S = 2 (3x – 1) = 2 (3 × 2 – 1)
= 2 (6 – 1)
= 2 × 5
= 10 = R.H.S.
∴L.H.S. = R.H.S.

Question (iii).
4 (2 – x) = 8
Answer:
Given equation is 4 (2 – x) = 8
Dividing both sides by 4, we get
\(\frac{4(2-x)}{4}=\frac{8}{4}\)
or 2 – x= 2
Transposing 2 from L.H.S. to R.H.S. we get
-x = 2 – 2
or – x = 0
Multiplying both sides by – 1, we get
-x × – 1 = x – 1
or x = 0, which is the required solution.

To Check. Put x = 0 in the L.H.S. of the equation 4 (2 – x) = 8
L.H.S. = 4 (2 – x) = 4 (2 – 0)
= 4 × 2
= 8 = R.H.S.
∴ L.H.S. = R.H.S.

Question (iv).
– 4 (2 + x) = 8.
Answer:
Given equation is – 4 (2 + x) = 8
Dividing both sides by – 4, we get
\(\frac{-4(2+x)}{-4}=\frac{8}{-4}\)
Transposing 2 from L.H.S. to R.H.S. we get :
x = – 2 – 2
or x = – 4, which is the required solution

To Check. Put x = – 4 in the L.H.S. of equation – 4 (2 + x) = 8
L.H.S. = – 4 (2 + x) = – 4 [2 + (- 4)]
= – 4 (2 – 4)
= – 4 (- 2)
= 8 = R.H.S.
∴ L.H.S. = R.H.S.

3. Solve the following equations :

Question (i).
4 = 5 (x – 2)
Answer:
Given equation is 4 = 5 (x – 2)
or 4 = 5x – 10
Transposing 5x to L.H.S. and 4 to R.H.S.,
we get
– 5x = – 4 – 10
or – 5x = – 14
Dividing both sides by – 5, we get
\(\frac{-5 x}{-5}=\frac{-14}{-5}\)
or, x = \(\frac {14}{5}\), which is the required solution.

To Check. Put x = \(\frac {14}{5}\) in the R.H.S. of the equation 4 = 5 (x – 2)
R.H.S. = 5 (x – 2) = 5\(\left(\frac{14}{5}-2\right)\)
= 5\(\left(\frac{14-10}{5}\right)\)
= 5 \(\left(\frac{4}{5}\right)\)
= 4 = L.H.S.
∴ L.H.S. = R.H.S.

Question (ii).
– 4 = 5 (x – 2)
Answer:
Given equation is – 4 = 5 (x – 2)
or – 4 = 5x – 10
Transposing -4 to R.H.S and 5x to L.H.S
we get
-5x = 4 – 10 or -5x = -6
Dividing both sides by – 5 we get
\(\frac{-5 x}{-5}=\frac{-6}{-5}\)
or x = \(\frac {6}{5}\), which is the required solution.

To Check. Put x = \(\frac {6}{5}\) in the R.H.S. of the equation – 4 = 5 (x – 2)
L.H.S. = 5 (x – 2)
= 5\(\left(\frac{6}{5}-2\right)\)
= 5\(\left(\frac{6-10}{5}\right)\)
= 5\(\left(\frac{-4}{5}\right)\)
= -4 = L.H.S.
L.H.S. = R.H.S.

Question (iii).
4 + 5 (p – 1) = 34
Answer:
Given equation is 4 + 5(p – 1) = 34
Transposing 4 to R.H.S. we get
5(p – 1) = 34 – 4
5(p – 1) = 30
Dividing both sides, by 5, we get
\(\frac{5(p-1)}{5}=\frac{30}{5}\)
p – 1=6
Transposing -1 to R.H.S. we get
p = 6 + 1
p = 7 which is the required solution.

To Check : Put p = 7 in L.H.S. of the equation 4 + 5 (p – 1) = 34
L.H.S. = 4 + 5 (p – 1)
= 4 + 5 (7 – 1)
= 4 + 5 (6)
= 4 + 30
= 34 = R.H.S.
∴ L.H.S. = R.H.S.

Question (iv).
6y – 1 = 2y + 1.
Answer:
Given equation is 6y – 1 = 2y + 1
Transposing – 1 to R.H.S. and 2y to L.H.S,
we get
6y – 2y = 1 + 1
or 4y = 2 or y = \(\frac {2}{4}\)
or y = \(\frac {1}{2}\), which is the required solution.

To Check Put y = \(\frac {1}{2}\) in both L.H.S. and R.H.S. of the equation
6y – 1 = 2y + 1
L.H.S. = 6y – 1 = 6 × \(\frac {1}{2}\) – 1 = 3 – 1 = 2
R.H.S. = 2y + 1 = 2 × \(\frac {1}{2}\) + 1 = 1 + 1 = 2.
∴ L.H.S. = R.H.S.

Question (i).
Construct 3 equations starting with x = 2
Answer:
First Equation.
(i) Start with x = 2
Multiplying both sides by 10
10x = 20
Adding 2 to both sides
10x + 2 = 20 + 2
or 10x + 2 = 22
This has resulted in an equation.

Second Equation. Start with x = 2
Divide both sides by 5
∴ \(\frac{x}{5}=\frac{2}{5}\)
This has resulted in an equation.

Third Equation. Start with x = 2
Multiply both sides by 5, we get
5x = 5 × 2
or 5x = 10
Subtracting 3 from both sides, we get
5x – 4 = 10 – 3
or 5x – 3 = 7
This has resulted in an equation.

Question (ii).
Construct 3 equation starting with x = – 2
Answer:
First Equation. Start with x = – 2
Multiplying both sides with 3, we get
3x = – 6
This has resulted in an equation

Second Equation. Start with x = – 2
Multiplying both sides with 3, we get 3x = -6
Adding 7 to both sides, we get 3x + 7
= -6 + 7 or 3x + 7 = 1
This has resulted in an equation.

Third Equation. Start with x = – 2
Multiplying both side with 2 we get 3x = – 6
Adding 10 to both sides we get
3x+ 10 = -6 + 10
or 3x + 10 = 4
This has resulted in an equation.

Multiple Choice Questions :

5. If 7x + 4 = 39, then x is equal to :
(a) 6
(b) -4
(c) 5
(d) 8
Answer:
(c) 5

6. If 8m – 8 = 56 then m is equal to :
(a) -4
(b) -2
(c) -14
(d) 8
Answer:
(d) 8

7. Which of the following number satisfies the equation – 6 + x = -18 ?
(a) 10
(b) – 13
(c) – 12
(d) – 16.
Answer:
(a) 10

8. If \(\frac{x}{2}\) = 14, then the value of 2x + 6 is equal to :
(a) 62
(b) -64
(c) 16
(d) -62.
Answer:
(a) 62

9. If 3 subtracted from twice a number is 5, then the number is :
(a) -4
(b) -2
(c) 2
(d) 4
Answer:
(d) 4

10. If 5 added to thrice an integer is – 7, then the integer is :
(a) – 6
(b) – 5
(c) -4
(d) 4
Answer:
(c) -4

PSEB 12th Class Physical Education Notes Chapter 2 Sports Training

March 11, 2024March 11, 2024 by Bhagya

This PSEB 12th Class Physical Education Notes Chapter 2 Sports Training will help you in revision during exams.

PSEB 12th Class Physical Education Notes Chapter 2 Sports Training

→ In today’s competitive world of sports, everyone aims at winning at all costs.

→ Hence, the concept of sports training has a vital role to play in the field of sports.

→ The concept of sports training deals with the systematic preparation of athletes to obtain peak performance at the time of competition.

→ The aim of sports training is to produce optimum performance during competition.

→ Hence, the training schedule is classified in such a way that a player gets complete recovery from the training load and feels fresh and energetic to take a fresh load to continue performance.

→ According to Martin, “Sports training is a planned and controlled process of achieving goals in which the changes of motor performance and behaviour are made through measures of content, method, and organisation”.

→ Hence, sports training implies a systematic and controlled way of imparting training to an athlete to produce an optimum performance at the time of competition.

→ In order to have fruitful results from the sports training programme various principles such as individual differences, the principle of use of disuse, load (overload), progression, safety, continuity, and rest or recovery must be followed, otherwise, the purpose of training will not be effective and useful for the trainees.

→ It is also important to perform the warm-up exercises to prepare an athlete physically, physiologically, or psychologically for the sports training programme or prior to competition.

→ It helps an athlete to perform with the least chances of injuries.

→ Similarly, limbering or cooling down plays a significant role to attain normal conditions after performing strenuous exercises.

→ Hence, sports training is the way and means of systematic training to develop various components of physical fitness to attain optimal performance during competition.

PSEB 7th Class Maths Solutions Chapter 3 Data Handling Ex 3.2

March 11, 2024March 11, 2024 by Bhagya

Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 3 Data Handling Ex 3.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 7 Maths Chapter 3 Data Handling Ex 3.2

1. Find the median of the following data :
3, 1, 5, 6, 3, 4, 5
Solution:
We arrange the data in ascending order.
1, 3, 3, 4, 5, 5, 6
Here, 3 and 5 both occur twice.
Therefore, both the numbers 3 and 5 are modes of the given data.

2. Find the mode of the following numbers :
2, 2, 2, 3, 4, 5, 5, 5, 6, 6, 8
Solution:
The given data is :
2, 2, 2, 3, 4, 5, 5, 5, 6, 6, 8
Median is the middle observation
∴ 5 is the median

3. The scores in mathematics test (out of 25) of 15 students are as follows :
19, 25, 23, 20, 9, 20, 15, 10, 5, 16, 25, 20, 24, 12, 20.
Find the mean, mode and median of this data ? Are they same ?
Solution:
Mean =
PSEB 7th Class Maths Solutions Chapter 3 Data Handling Ex 3.2 1
= \(\frac {263}{15}\)
= 17.53
Now we arrange the data in ascending order
5, 9, 10, 12, 15, 16, 19, 20, 20, 20, 20, 23, 24, 25, 25
Here 20 occurs more frequently
∴ Mode = 20
Median is the middle observation
∴ 20 is the median.
Yes, both Mode and Median are same.

4. The weight (in kg) of 15 students of class are :
38, 42, 35, 37, 45, 50, 32, 43, 43, 40, 36, 38, 43, 38, 47

Question (i).
Find the mode and median of this data.
Solution:
We arrange the data in ascending order
32, 25, 36, 37, 38, 38, 38, 40, 42, 43, 43, 43, 45, 47, 50
Mode. Here 38 and 43 occurs more frequently i.e. 3 times
∴ Mode = 38 and 43
Median is the middle observation
∴ 40 is median.

Question (ii).
Is there more than one mode ?
Solution:
Yes, there are two mode i.e. 38 and 43

5. Find the mode and median of the following data :
13, 16, 12, 14, 19, 12, 14, 13, 14
Solution:
We arrange the data in ascending order
12, 12, 13, 13, 14, 14, 14, 16, 19
Here 14 occurs more frequently
∴ Mode = 14
Median is middle observation
∴ 14 is median.

6. Find the mode of the following data :
12, 14, 12, 16, 15, 13, 14, 18, 19, 12, 14, 15, 16, 15, 16, 15, 16, 16, 15, 17, 13, 16, 16, 15, 15, 13, 15, 17, 15, 14, 15, 13, 15, 14.
Solution:
We arrange the data in ascending order
12, 12, 12, 13, 13, 13, 13, 14, 14, 14, 14, 14, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 16, 16, 16, 16, 16, 16, 16, 17, 17, 18, 19.
Here 15 occurs more frequently
∴ Mode =15

7. Multiple Choice Questions :

Question (i).
The mode of the data :
3, 5, 1, 2, 0, 2, 3, 5, 0, 2, 1, 6 is :
(a) 6
(b) 3
(c) 2
(d) 1.
Answer:
(c) 2

Question (ii).
A cricketer scored 38, 79, 25, 52, 0, 8, 100 runs in seven innings, the range of the runs scored is :
(a) 100
(b) 92
(c) 52
(d) 38.
Answer:
(a) 100

Question (iii).
Which of the following is not a central tendency of a data ?
(a) Mean
(b) Median
(c) Mode
(d) Range.
Answer:
(a) Mean

Question (iv).
The mean of 3, 1, 5, 7 and 9 is :
(a) 6
(b) 4
(c) 5
(d) 0.
Answer:
(c) 5

PSEB 12th Class Physical Education Notes Chapter 1 Physical Fitness

March 11, 2024March 11, 2024 by Bhagya

This PSEB 12th Class Physical Education Notes Chapter 1 Physical Fitness will help you in revision during exams.

PSEB 12th Class Physical Education Notes Chapter 1 Physical Fitness

→ The term Physical fitness has different notions for different segments of people.

→ It not only refers to being physically fit but also refers to a balanced state of mind.

→ A person can only be considered fit if he is able to function well without any undue fatigue or tiredness.

→ A person who is fit both on physical and mental aspects stays strong in every sphere of life.

→ Now, let’s discuss the definition of physical fitness.

→ It is the ability of an individual to work effectively and efficiently with joy and pleasure.

→ According to David R. Lamb, “Physical fitness is the capacity to meet the present and potential physical challenges of fife with success.”

→ In order to achieve the optimum level of physical fitness one must possess basic components such as strength, speed, endurance, agility, flexibility, and coordinative abilities.

→ If a person is having these components, then he will be considered to be physically fit.

→ But, there are various factors that may influence the physical fitness of an individual such as anatomical structure, physiological and psychological makeup, posture, diet, lifestyle, inactivity, injury, age and gender, etc.

→ So, these factors are responsible to have a major influence on the physical fitness of an individual.

→ Hence, physical fitness plays a vital role to live healthy, prosperous, and conducive life in the present scenario of technological advancement.

→ It helps in the proper growth and development with the efficient functioning of the physiological systems in the body.

→ These developments ultimately induce the feeling of a balanced state of mental health and physical health of a person.

PSEB 10th Class Science Notes Chapter 2 Acids, Bases and Salts

March 12, 2024March 11, 2024 by Bhagya

This PSEB 10th Class Science Notes Chapter 2 Acids, Bases and Salts will help you in revision during exams.

PSEB 10th Class Science Notes Chapter 2 Acids, Bases and Salts

→ The sour taste of foods is due to acids and the bitter taste is due to bases present in them. Acids turn blue litmus into red and bases turn the red litmus into the blue.

→ Acids and bases neutralize each other’s effects.

→ Acids and bases can be tested using litmus, turmeric, methyl orange, and phenolphthalein indicators.

→ On passing carbon dioxide gas through lime water, lime water turns milky.

→ On passing, excess carbon dioxide gas through lime water, its milky colour disappears due to the formation of soluble calcium bicarbonate.

→ Bases turn phenolphthalein pink in colour.

→ Acids and bases react to produce salt and water.

→ The flow of current in the solution is due to ions present in the solution.

→ In acids H+ ions are present. Acids produce hydrogen ion H⁺(aq) in a solution due to which solutions become acidic.

→ Bases produce hydroxide (OH^–) ions in water.

→ Alkali is a base that dissolves in water.

→ Bases are soapy to touch, bitter, and corrosive.

→ All acids produce H⁺(aq) and bases produce OH^–(aq) in an aqueous solution.

→ The process of the dissolving of acids or bases in water is highly exothermic, therefore to dilute them these should be added and mixed slowly in water. Never add water to concentrated acid.

→ A universal indicator is a mixture of several indicators.

→ Universal indicators show different colors for different concentrations of hydrogen ions in the solution.

→ A scale known as the pH scale has been developed for measuring the concentration of hydrogen ions present in the solution.

→ The ‘p’ in pH stands for ‘potenz’ this is a German word which means power.

→ On the pH scale, we can measure pH generally from 0 (very acidic) to 14 (very basic).

→ Higher is the concentration of hydronium ion, less is the value of pH. A neutral solution has a pH value of 7.

→ If the value of pH is less than 7 then the solution is acidic and if pH lies between 7 to 14 then the solution is basic.

→ Those acids which produce a large number of H⁺ ions are called strong acids and those acids which produce less H⁺ ions are weak acids.

→ Our body works in the range of 7.0 to 7.8.

→ When the pH value of rainwater is less than 5.6 it is called acid rain.

→ To get rid of acidity in the body, and antiacid like magnesium hydroxide which is a weak base is used.

→ If the pH value is less than 5.5 in the mouth, decay of teeth starts.

→ Nettle is a herbaceous plant that causes painful stings due to methanoic acid present in stinging hair. A traditional remedy is rubbing the area with the leaf of the dock plant.

→ Common salt (NaCl) is produced by the reaction between hydrochloric acid and sodium hydroxide.

→ Bleaching powder is produced by the action of chlorine on dry slaked lime.

→ Bleaching powder is used in the paper and textile industry for bleaching. It acts as an oxidant and as a disinfectant.

→ Baking soda (NaHCO₃) is produced from sodium chloride.

→ Sodium hydrogen carbonate is a mild non-corrosive base. It is used in the production of Baking powder and used in the preparation of cakes. It is also used in fire extinguishers.

→ Washing soda (NagCO₃.10H₂O) is prepared from sodium chloride. It is used in the glass, soap, paper industries. It is used to remove the permanent hardness of the water.

→ The chemical formula for hydrated copper sulfate is CuSO₄.5H₂O and of gypsum is CaSO₄.2H₂O.

→ Plaster of Paris is obtained from calcium sulphate hemihydrate (CaSO₄. \(\frac{1}{2}\) H₂O) by heating it at 373K.

→ Plaster of Paris is used for making toys and material for decoration.

→ Indicators: These are the substances that give different colors in acidic and basic solutions e.g. litmus, turmeric, phenolphthalein, methyl orange, etc.

→ Olfactory Indicators: There are some substances whose odour changes in acidic or basic media, which are known as olfactory indicators.

→ Acid: Those compounds which have one or more hydrogen atoms and which give hydrogen (H⁺) or hydronium (H₃O⁺) ions (H₃O⁺) ion in an aqueous solution are called acids. These are sour in taste.

→ Ionization: It is a process in which a substance produces ions in water, ionization.

→ Basicity of an acid: Basicity of an acid is the number of hydronium ions [H⁺] produced when one molecule of acid gets completely ionized in an aqueous solution.

→ Base: Bases are those compounds which are metal oxides or metal hydroxide or aqueous ammonia and these react with hydronium ion (H₃O⁺) of acids to produce salt and water.

→ Neutralization: Due to the reaction between acids and bases, salt and water are produced. This is called a neutralization reaction.

→ Alkali: Those basic hydroxides which on dissolving in water form hydroxyl (OH^–) ions, are called alkali.

→ Universal indicator: It is a mixture of various organic substances which show different colours with solutions having different pH values.

→ Dissociation: When a molecule or ionic compound dissociates into two or more atoms or ions, this is called dissociation.

→ Chemical dissociation: A reaction in which a molecule of a compound breaks into atoms or ions is called chemical dissociation.

→ The water of Crystallisation: Water, which is present in crystals of a substance is called water of crystallization. e.g., FeSO₄.7H₂O, Al₂O₃.2H₂O, CuSO₄.5H₂O, Na₂CO₃.10H₂O.

→ Efflorescence: The process of release of crystalline water from hydrated salts into the air is called efflorescence.

→ Deliquescence: This is a process in which a substance absorbs moisture from the atmosphere and dissolves in the absorbed water to form a solution.

→ Dilution: On mixing acid or base in water, the concentration of ions (H₃O⁺/OH^–) per unit volume becomes less. This is called dilution.

→ Chlor-alkali process: The electrolysis of sodium chloride solution is called chlor-alkali process.

PSEB 7th Class Maths Solutions Chapter 3 Data Handling Ex 3.1

March 11, 2024March 11, 2024 by Bhagya

Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 3 Data Handling Ex 3.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 7 Maths Chapter 3 Data Handling Ex 3.1

1. Find the mean of the following data :

Question (i).
3, 5, 7, 9, 11, 13, 15
Answer:
Mean = \(\frac{3+5+7+9+11+13+15}{7}\)
= \(\frac {63}{7}\)
= 9

Question (ii).
40, 30, 30, 0, 26, 60
Answer:
Mean = \(\frac{40+30+30+0+26+60}{6}\)
= \(\frac {183}{6}\)
= 9

2. Find the mean of the first five whole numbers.
Answer:
The first five whole numbers are : 0, 1, 2, 3, 4
Mean = \(\frac{0+1+2+3+4}{5}\)
= \(\frac {10}{5}\)
= 2
Hence, the mean of first five whole numbers = 2

3. A batsman scored the following number of runs in six innings :
36, 35, 50, 46, 60, 55
Calculate the mean runs scored by him in an inning.
Answer:
Mean runs
= \(\frac{36+35+50+46+60+55}{6}\)
= \(\frac {282}{6}\)
Hence, the mean runs scored by batsman in an innings = 47

4. The ages in years of 10 teachers of a school are :
32, 41, 28, 54, 35, 26, 23, 33, 38, 40
(i) What is the age of the oldest teacher and that of the youngest teacher ?
(ii) What is the range of the ages of the teachers ?
(iii) What is the mean age of these teachers ?
Answer:
Arranging the ages in ascending order, we get
23, 26, 28, 32, 33, 35, 38, 40, 41, 54
(i) Age of the oldest teacher = 54 years Age of the youngest teacher 23 years
(ii) Range of the ages = 54 – 23 = 31
(iii) Mean age of the teachers
PSEB 7th Class Maths Solutions Chapter 3 Data Handling Ex 3.1 1
= \(\frac {350}{10}\)
= 35 years.

5. The rain fall (in mm) ip a city on 7 days of a certain week was recorded as follows :
PSEB 7th Class Maths Solutions Chapter 3 Data Handling Ex 3.1 2
(i) Find the range of the rainfall in the above data.
(ii) Find the mean rainfall for the week.
(iii) How many days had the rainfall less than the mean rainfall ?
Answer:
(i) Arranging the rainfall (in mm) in ascending order, we get
Highest Rainfall = 20.5 mm
Lowest Rainfall = 0.0 mm
Range of the rainfall = 20.5 mm – 0.0 mm
= 20.5 mm.

(ii) Mean Rainfall
= \(\frac{0.01+12.2+2.1+0.0+20.5+5.5+1.0}{7}\)
= \(\frac {41.31}{7}\)
= 5.9 mm.

(iii) Number of days having rainfall less than mean rainfall = 5 days.

PSEB 10th Class Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1

March 11, 2024March 11, 2024 by Bhagya

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1

Question 1.
Aftab tells his daughter, “Seven years ago I was seven times as old as you were then. Also, three years from now, I shall
be three times as old as you will be” (Isn’t this interesting ?). Represent this situation algebraically and graphically.
Solution:
Let Aftabs present age = x years
and Aftab’s daughter’s present age = y years
Algebraical-Situation
According to 1st condition,
x – 7 = 7(y – 7)
or x – 7 = 7y – 49
or x – 7y + 42 = 0
According to 2nd condition,
x + 3 = 3(y + 3)
or x + 3 = 3y + 9
or x – 3y – 6 = 0
∴ Pair of Line’ar Equation in two variables are
x – 7y + 42 = 0
and x – 3y – 6 = 0

Graphical – Situation:
x – 7y + 42 = 0
x – 3y – 6 = 0

x = 7y – 42 ………….(1)
x = 3y + 6 …………..(2)
Putting y = 5 in (1), we get
Putting y = 0 in (2), we get

x = 7 × 5 – 42 = 35 – 42
x = -7
Putting y = 6 in (1), we get
x = 7 × 6 – 42 = 42 – 42 = 0
Putting y = 7 in (1), we get:
x = 7 × 7 – 42 = 49 – 42 = 7

Table

PSEB 10th Class Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1 1

Plotting the points A (-7, 5), B (0, 6), C (7, 7) and drawing a line joining them, we get the graph of the equation x – 7y + 42 = 0
x = 3 × 0 + 6
x = 0 + 6 = 6
Putting y = 3 in (2), we get:
x = 3 × 3 + 6
= 9 + 6 = 15
Putting y = -2 in (2), we get:
x = 3 × -2 + 6
= -6 + 6 = 0

Table:

PSEB 10th Class Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1 2

Plotting the points D (6, 0), E (15, 3), F (0, -2) and drawing a line joining them, we get the graph of the equation x – 3y – 6 = 0

PSEB 10th Class Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1 3

From the graph it is clear that the two lines intersect at G (42, 12).
Hence, x = 42 and y = 12 is the solution of given pair of linear equations.

Question 2.
The coach of a cricket team buys 3 bats and 6 balls for 3900. Later, she buys another bat and 3 more balls of the same kind for 1300. Represent this situation algebraically and geometrically. [Pb. 2019, Set-A, B, C]
Solution:
Let cost of one bat = x
Cost of one hail = y
Algehraical – Situation
According to 1st condition,
3x + 6y = 3900
or x + 2y = 1300
According to 2nd condition,
1x + 3y = 1300
∴ Pair of linear equations in two variables are:
x + 2y = 13001
and x + 3y = 1300

Graphical – Situation:
x + 2y = 1300
x = 1300 – 2y …………..(1)
Putting y = 0 in (1), we get
x = 1300 – 2 × 0
x= 1300
Putting y = 500 in (1), we get :
= 1300 – 2 × 500
= 1300 – 1000 = 300
Putting y = 650 in (1), we get :
x = 1300 – 2 × 650
1300 – 1300 = 0

Table:

PSEB 10th Class Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1 4

Plotting the points A (1300, 0), B (300, 500) and C (0, 650) drawing a line joining them we get the graph of the equation x + 2y = 1300.
x + 3y = 1300
x = 1300 – 3y …………….(2)
Putting y = 0 in (2), we get :
x = 1300 – 3 × 0 = 1300
Putting y = 500 in (2), we get :
x = 1300 – 3 × 500
= 1300 – 1500 = – 200
Putting y = 300 in (2), we get :
x = 1300 – 3 × 300
= 1300 – 900 = 400

Table:

PSEB 10th Class Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1 5

Plotting the points A (1300, 0), E (-200, 500), F (400, 300) and drawing a line joining them we get the graph of the
equation.
x + 3y = 1300

PSEB 10th Class Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1 6

From the graph it is clear that the two lines intersect at A (1300, 0).
Hence x = 1300 and y = 0 is the solution of given pair of linear equations.

Question 3.
The cost of 2 kg of apples and 1 kg of grapes on a day was found to be 160. After a month, the cost of 4 kg of apples and 2 kg of grapes is ₹ 300. Represent the situation algebraically and geometrically.
Solution:
Let cost of 1 kg apples = ₹ x
Cost of 1 kg grapes = ₹ y
Algebraical – Situation
According to 1st condition,
2x + 1y = 160
According to 2nd condition,
4x + 2y = 300
∴ Pair of linear equations in two variables
2x + y = 160
and 4x + 2y = 300
Graphical – Situation
2x + y = 160
2x = 160 – y
x = \(\frac{160-y}{2}\) ……………(1)
Putting y = 0 in (1), we get :
x = \(\frac{160-0}{2}=\frac{160}{2}\) = 80
Putting y = 60 in (1), we get :
x = \(\frac{160-60}{2}=\frac{100}{2}\) = 50
Putting y = 160 in (1), we get :
x = \(\frac{160-160}{2}=\frac{0}{2}\) = 0

PSEB 10th Class Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1 7

Plotting the points A (80, 0), B (50, 60), C (0, 160) and drawing a line joining them, we get the graph of the equation 2x + y = 160
Now 4x + 2y = 300
or 2x + y = 150
2x = 150 – y
x = \(\frac{160-y}{2}\) …………(2)
Putting y = 0 in (2), we get:
x = \(\frac{160-0}{2}=\frac{150}{2}\) = 75
Putting y = 50 in (2), we get:
x = \(\frac{150-50}{2}=\frac{100}{2}\) = 50
Putting y = 150 in (2), we get:
x = \(\frac{150-150}{2}=\frac{0}{2}\) = 0

PSEB 10th Class Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1 8

Plotting the points D (75, 0), E (50, 50), F (0, 150) and drawing a line joining them, we get the graph of equation
4x + 2y = 300

PSEB 10th Class Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1 9

From the graph, it is clear that the two lines do not intersect anywhere i.e. they are parallel.