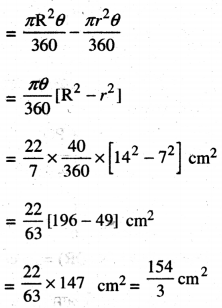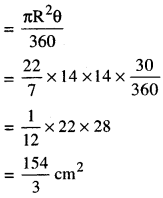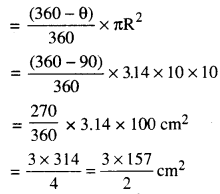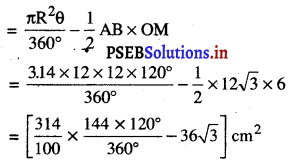Class 10

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 14 ਅੰਕੜਾਵਿਗਿਆਨ Ex 14.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 14 ਅੰਕੜਾਵਿਗਿਆਨ Exercise 14.1

ਪ੍ਰਸ਼ਨ 1.
ਵਿਦਿਆਰਥੀਆਂ ਦੇ ਇੱਕ ਸਮੂਹ ਦੁਆਰਾ ਆਪਣੇ ਵਾਤਾਵਰਨ ਚੇਤਨਾ ਅਭਿਆਨ ਦੇ ਅਧੀਨ ਇੱਕ ਸਰਵੇਖਣ ਕੀਤਾ ਗਿਆ ਜਿਸ ਵਿੱਚ ਉਹਨਾਂ ਨੇ ਇੱਕ ਮੁਹੱਲੇ ਦੇ 20 ਘਰਾਂ ਵਿੱਚ ਲੱਗੇ ਪੌਦਿਆਂ ਨਾਲ ਸੰਬੰਧਿਤ ਹੇਠਾਂ ਲਿਖੇ ਅੰਕੜੇ ਇਕੱਠੇ ਕੀਤੇ । ਪ੍ਰਤਿ ਘਰ ਦੀ ਮੱਧਮਾਨ (ਔਸਤ) ਪੌਦਿਆਂ ਦੀ ਸੰਖਿਆ ਪਤਾ ਕਰੋ ।

ਮੱਧਮਾਨ ਦਾ ਪਤਾ ਕਰਨ ਲਈ ਤੁਸੀਂ ਕਿਹੜੀ ਵਿੱਧੀ ਦਾ ਪ੍ਰਯੋਗ ਕੀਤਾ ਅਤੇ ਕਿਉਂ ?
ਹੱਲ:
ਕਿਉਂਕਿ ਪੌਦਿਆਂ ਦੀ ਸੰਖਿਆ ਅਤੇ ਘਰਾਂ ਦੀ ਸੰਖਿਆ ਦੇ ਮੁੱਲ ਘੱਟ ਹਨ ਇਸ ਲਈ ਅਸੀਂ ਪ੍ਰਤੱਖ ਵਿਧੀ ਦਾ ਪ੍ਰਯੋਗ ਕਰਾਂਗੇ

ਉਪਰੋਕਤ ਅੰਕੜਿਆਂ ਤੋਂ
ਮੱਧਮਾਨ \(\bar{X}\) = \(\frac{\Sigma f_{i} x_{i}}{\Sigma f_{i}}\)
= \(\frac{162}{20}\) = 8.1
ਇਸ ਲਈ ਪ੍ਰਤੀ ਘਰ ਪੌਦਿਆਂ ਦੀ ਮੱਧਮਾਨ ਸੰਖਿਆ 8.1 ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਕਿਸੇ ਫੈਕਟਰੀ ਦੇ 50 ਮਜਦੂਰਾਂ ਦੀ ਰੋਜ਼ਾਨਾ ਮਜ਼ਦੂਰੀ ਦੇ ਹੇਠਾਂ ਲਿਖੀ ਵੰਡ ਸਾਰਣੀ ਉੱਤੇ ਵਿਚਾਰ ਕਰੋ ।

ਇੱਕ ਸਹੀ (ਉਚਿਤ) ਵਿਧੀ ਦਾ ਪ੍ਰਯੋਗ ਕਰਦੇ ਹੋਏ, ਇਸ ਫੈਕਟਰੀ ਦੇ ਮਜ਼ਦੂਰਾਂ ਦੀ ਮੱਧਮਾਨ ਰੋਜ਼ਾਨਾ ਮਜ਼ਦੂਰੀ ਪੱਤਾ ਕਰੋ ।
ਹੱਲ:

ਦਿੱਤੇ ਗਏ ਅੰਕੜਿਆਂ ਤੋਂ
ਕਾਲਪਨਿਕ ਮੱਧਮਾਨ (a) = 150
ਵਰਗ ਮਾਪ (h) = 20
∴ \(\bar{u}\) = \(\frac{\Sigma f_{i} u_{i}}{\Sigma f_{i}}\)
= \(\frac{-12}{50}\) = -0.24
ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ (\(\bar{X}\)) = a + h\(\bar{u}\)
= 150 + (20)(-0.24)
= 150 – 4.8 =145.2
∴ ਫੈਕਟਰੀ ਦੇ ਮਜ਼ਦੂਰਾਂ ਦੀ ਮੱਧਮਾਨ ਰੋਜ਼ਾਨਾ ਮਜ਼ਦੂਰੀ ₹ 145.20 ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਹੇਠ ਦਿੱਤੀ ਵੰਡ ਸਾਰਣੀ ਇੱਕ ਮੁਹੱਲੇ ਦੇ ਬੱਚਿਆਂ ਦਾ ਰੋਜ਼ਾਨਾ ਜੇਬ ਖ਼ਰਚ ਨੂੰ ਦਰਸਾਉਂਦੀ ਹੈ । ਮੱਧਮਾਨ ਜੇਬ ਖ਼ਰਚਾ ₹ 18 ਹੈ | ਅਗਿਆਤ ਬਾਰੰਬਾਰਤਾ ‘f ‘ ਪਤਾ ਕਰੋ :

ਹੱਲ:

ਉਪਰੋਕਤ ਅੰਕੜਿਆਂ ਤੋਂ
ਕਾਲਪਨਿਕ ਮੱਧਮਾਨ (a) = 18
ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ, ਮੱਧਮਾਨ (\(\bar{X}\)) = a + \(\frac{\Sigma f_{i} d_{i}}{\Sigma f_{i}}\)
\(\bar{X}\) = 18 + \(\frac{2 f-40}{44+f}\)
ਪਰ, ਅੰਕੜਿਆਂ ਦਾ ਮੱਧਮਾਨ (\(\bar{x}\)) = 18 …….. (ਦਿੱਤਾ ਹੈ।)
∴ 18 = 18 + \(\frac{2 f-40}{44+f}\)
ਜਾਂ \(\frac{2 f-40}{44+f}\) = 18 – 18 = 0
ਜਾਂ 2f – 40 = 0
ਜਾਂ 2f = 40
ਜਾਂ f = \(\frac{40}{2}\) = 20
∴ ਅਗਿਆਤ ਬਾਰੰਬਾਰਤਾf = 20 ਹੈ । ਉੱਤਰ

ਪ੍ਰਸ਼ਨ 4.
ਕਿਸੇ ਹਸਪਤਾਲ ਵਿੱਚ, ਇੱਕ ਡਾਕਟਰ ਦੁਆਰਾ 30 ਇਸਤਰੀਆਂ ਦੀ ਜਾਂਚ ਕੀਤੀ ਗਈ ਅਤੇ ਉਨ੍ਹਾਂ ਦੀ ਦਿਲ ਦੀ ਧੜਕਣ (heart beat) ਪ੍ਰਤੀ ਮਿੰਟ ਨੋਟ ਕਰਕੇ ਹੇਠਾਂ ਦਰਸਾਉਂਦੀ ਵੰਡ ਸਾਰਣੀ ਵਿੱਚ ਸੰਖੇਪ ਰੂਪ ਨਾਲ ਲਿਖੀ ਗਈ । ਇੱਕ ਸਹੀ (ਉਚਿਤ) ਵਿਧੀ ਦੀ ਵਰਤੋਂ ਕਰਕੇ ਇਹਨਾਂ ਇਸਤਰੀਆਂ ਦੇ ਦਿਲ ਦੀ ਧੜਕਣ ਦੀ ਪ੍ਰਤੀ ਮਿੰਟ ਮੱਧਮਾਨ ਸੰਖਿਆ ਪਤਾ ਕਰੋ :

ਹੱਲ:

ਉਪ੍ਰੋਕਤ ਅੰਕੜਿਆਂ ਤੋਂ
ਕਾਲਪਨਿਕ ਮੱਧਮਾਨ (a) = 75.5
ਵਰਗ ਮਾਪ (h) = 3
∴ \(\bar{u}\) = \(\frac{\Sigma f_{i} u_{i}}{\Sigma f_{i}}\)
= \(\frac{4}{30}\) = 0.13 (ਲਗਭਗ)
ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ ਮੱਧਮਾਨ (\(\bar{X}\)) = a + h\(\bar{u}\)
= 75.5 + 3 (0.13)
= 75.5 + 0.39
\(\bar{X}\) = 7889
∴ ਇਸਤਰੀਆਂ ਦੇ ਦਿਲ ਦੀ ਧੜਕਣ ਦੀ ਪ੍ਰਤੀ ਮਿੰਟ ਮੱਧਮਾਨ ਸੰਖਿਆ 78.89 ਹੈ ।

ਪ੍ਰਸ਼ਨ 5.
ਕਿਸੇ ਬਜ਼ਾਰ ਵਿੱਚ, ਫਲ ਵਿਕੇਤਾ, ਪੇਟੀਆਂ ਵਿੱਚ ਰੱਖੇ ਅੰਬ ਵੇਚ ਰਹੇ ਸਨ । ਇਨ੍ਹਾਂ ਪੇਟੀਆਂ ਵਿੱਚ ਅੰਬਾਂ ਦੀ ਸੰਖਿਆ ਅਲੱਗ-ਅਲੱਗ ਸੀ । ਪੇਟੀਆਂ ਦੀ ਸੰਖਿਆ ਅਨੁਸਾਰ, ਅੰਬਾਂ ਦੀ ਵੰਡ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਸੀ :

ਇੱਕ ਪੇਟੀ ਵਿੱਚ ਰੱਖੀ ਅੰਬਾਂ ਦੀ ਮੱਧਮਾਨ ਸੰਖਿਆ ਪਤਾ ਕਰੋ । ਤੁਸੀਂ ਮੱਧਮਾਨ ਕੱਢਣ ਲਈ ਕਿਹੜੀ ਵਿੱਧੀ ਦਾ ਪ੍ਰਯੋਗ ਕੀਤਾ ਹੈ ?
ਹੱਲ:
ਕਿਉਂਕਿ ਅੰਬਾਂ ਦੀ ਸੰਖਿਆ ਅਤੇ ਪੇਟਿਆਂ ਦੀ ਸੰਖਿਆ ਦਾ ਮੁੱਲ ਜ਼ਿਆਦਾ ਹੈ । ਇਸ ਲਈ ਅਸੀਂ ਪਗ ਵਿਚਲਣ ਵਿਧੀ ਦਾ ਪ੍ਰਯੋਗ ਕਰਾਂਗੇ।

ਉਪਰੋਕਤ ਅੰਕੜਿਆਂ ਤੋਂ
ਕਾਲਪਨਿਕ ਮੱਧਮਾਨ (a) = 57
ਵਰਗ ਮਾਪ (h) = 3
∴ \(\bar{u}\) = \(\frac{\Sigma f_{i} u_{i}}{\Sigma f_{i}}\)
\(\bar{u}\) = \(\frac{25}{400}\) = 0.0625
ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ, (\(\bar{X}\)) = a + h\(\bar{u}\)
\(\bar{X}\) = 57 + 3 (0.0625)
= 57 + 0.1875
= 57.1875
= 57.19 ਲਗਭਗ
ਪੇਟੀ ਵਿੱਚ ਰੱਖੇ ਗਏ ਅੰਬਾਂ ਦੀ ਮੱਧਮਾਨ ਸੰਖਿਆ 57.19 ਹੈ ।

ਪ੍ਰਸ਼ਨ 6.
ਹੇਠਾਂ ਦਿੱਤੀ ਸਾਰਣੀ ਕਿਸੇ ਮੁਹੱਲੇ ਦੇ 25 ਪਰਿਵਾਰਾਂ ਦੇ ਭੋਜਨ ਉੱਪਰ ਹੋਏ ਰੋਜ਼ਾਨਾ ਖ਼ਰਚ ਨੂੰ ਦਰਸਾਉਂਦੀ ਹੈ :

ਇੱਕ ਉਚਿਤ ਵਿਧੀ ਦਾ ਪ੍ਰਯੋਗ ਕਰਕੇ ਭੋਜਨ ਉੱਪਰ ਹੋਏ ਖ਼ਰਚ ਦਾ ਮੱਧਮਾਨ ਪਤਾ ਕਰੋ ।
ਹੱਲ:

ਉਪਰੋਕਤ ਅੰਕੜਿਆਂ ਤੋਂ ।
ਕਾਲਪਨਿਕ ਮੱਧਮਾਨ (a) = 225
ਵਰਗ ਮਾਪ (h) = 50
∴ \(\bar{u}\) = \(\frac{\Sigma f_{i} u_{i}}{\Sigma f_{i}}\)
\(\bar{u}\) = \(-\frac{7}{25}\) = -0.28
ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ, ਮੱਧਮਾਨ (\(\bar{X}\)) = a + h\(\bar{u}\)
\(\bar{X}\) = 225 + 50 (0.28)
\(\bar{X}\) = 225 – 14
\(\bar{X}\) = 211
ਭੋਜਨ ਉੱਪਰ ਹੋਏ ਖ਼ਰਚ ਦਾ ਮੱਧਮਾਨ ₹211 ਹੈ ।

ਪ੍ਰਸ਼ਨ 7.
ਹਵਾ ਵਿੱਚ ਸਲਫਰ ਡਾਈਆਕਸਾਈਡ (SO₂) ਦੀ ਮਾਤਰਾ (Concentration) ਭਾਗ ਪ੍ਰਤੀ ਮਿਲਿਅਨ ਵਿੱਚ ਪਤਾ ਕਰਨ ਲਈ ਇੱਕ ਇਲਾਕੇ ਦੇ 30 ਮੁਹੱਲਿਆਂ ਵਿੱਚੋਂ ਅੰਕੜੇ ਇਕੱਠੇ ਕੀਤੇ ਗਏ । ਜਿਹਨਾਂ ਨੂੰ ਹੇਠ ਦਿੱਤੇ ਅਨੁਸਾਰ ਵਰਗੀਕ੍ਰਿਤ ਕੀਤਾ ਗਿਆ :

ਹਵਾ ਵਿੱਚ SO₂ ਦੀ ਮਾਤਰਾ ਦਾ ਮੱਧਮਾਨ ਪਤਾ ਕਰੋ ।
ਹੱਲ:

ਉਪਰੋਕਤ ਅੰਕੜਿਆਂ ਤੋਂ,
ਕਾਲਪਨਿਕ ਮੱਧਮਾਨ (a) = 0.10
ਵਰਗ ਮਾਪ (h) = 0.04
\(\bar{u}\) = \(\frac{\Sigma f_{i} u_{i}}{\Sigma f_{i}}\) = \(\frac{-1}{30}\) = -0.33 (ਲਗਭਗ)
ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ, (\(\bar{X}\)) = a + h\(\bar{u}\)
\(\bar{X}\) = 0.10 + 0.04(-0.33)
= 0.10 – 0.0013 = 0.0987 (ਲਗਭਗ)
ਹਵਾ ਵਿੱਚ SO₂ ਦੀ ਮਾਤਰਾ ਦਾ ਮੱਧਮਾਨ 0.0987 ppm ਹੈ ।

ਪ੍ਰਸ਼ਨ 8.
ਕਿਸੇ ਜਮਾਤ ਦੀ ਅਧਿਆਪਕਾ ਨੇ ਪੂਰੇ ਸਾਲ ਦੌਰਾਨ ਆਪਣੀ ਜਮਾਤ ਦੇ 40 ਵਿਦਿਆਰਥੀਆਂ ਦੀ ਗੈਰਹਾਜ਼ਰੀ ਨੂੰ ਹੇਠ ਲਿਖੇ, ਅਨੁਸਾਰ ਰਿਕਾਰਡ ਕੀਤਾ ਗਿਆ । ਇੱਕ ਵਿਦਿਆਰਥੀ ਜਿੰਨੇ ਦਿਨ ਗੈਰਹਾਜ਼ਿਰ ਰਿਹਾ ਉਸ ਦਾ ਮੱਧਮਾਨ ਪਤਾ ਕਰੋ :

ਹੱਲ:

ਉਪਰੋਕਤ ਅੰਕੜਿਆਂ ਤੋਂ
ਕਾਲਪਨਿਕ ਮੱਧਮਾਨ (a) = 17
ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ, ਮੱਧਮਾਨ (\(\bar{X}\)) = a + \(\frac{\Sigma f_{i} d_{i}}{\Sigma f_{i}}\)
\(\bar{X}\) = 17 + \(\frac{(-181)}{40}\)
= 17 – 4.52 = 12.48
∴ ਇੱਕ ਵਿਦਿਆਰਥੀ ਜਿੰਨੇ ਦਿਨ ਗ਼ੈਰ ਹਾਜ਼ਰ ਰਿਹਾ 12.48 ਹੈ ।

ਪ੍ਰਸ਼ਨ 9.
ਹੇਠਾਂ ਦਿੱਤੀ ਸਾਰਣੀ 35 ਸ਼ਹਿਰਾਂ ਦੀ ਸਾਖਰਤਾ ਦਰ (ਪ੍ਰਤੀਸ਼ਤ ਵਿੱਚ) ਦਰਸਾਉਂਦੀ ਹੈ । ਮੱਧਮਾਨ ਸਾਖਰਤਾ ਦਰ ਪਤਾ ਕਰੋ :

ਹੱਲ:

ਉਪਰੋਕਤ ਅੰਕੜਿਆਂ ਤੋਂ
ਕਾਲਪਨਿਕ ਮੱਧਮਾਨ (a) = 70
ਵਰਗ ਮਾਪ (h) = 10
\(\bar{u}\) = \(\frac{\Sigma f_{i} u_{i}}{\Sigma f_{i}}\) = \(\frac{-2}{35}\) = -0.057
ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ, (\(\bar{X}\)) = a + h\(\bar{u}\)
\(\bar{X}\) = 70 + 10(-0.057)
= 70 – 0.57 = 69.43
ਮੱਧਮਾਨ ਸਾਖਰਤਾ ਦਰ 69.43% ਹੈ ।

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 13 ਸਤੁਦਾ ਖੇਤਰਫਲ ਅਤੇ ਆਇਤਨ Ex 13.5 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 13 ਸਤੁਦਾ ਖੇਤਰਫਲ ਅਤੇ ਆਇਤਨ Exercise 13.5

ਪ੍ਰਸ਼ਨ 1.
3 mm ਵਿਆਸ ਵਾਲੇ ਤਾਂਬੇ ਦੇ ਇੱਕ ਤਾਰ ਨੂੰ 12 cm ਲੰਬੇ ਅਤੇ 10 cm ਵਿਆਸ ਵਾਲੇ ਇੱਕ ਬੇਲਣ ‘ਤੇ ਇਸ ਪ੍ਰਕਾਰ ਲਪੇਟਿਆ ਜਾਂਦਾ ਹੈ ਕਿ ਉਹ ਬੇਲਣ ਦੇ ਵਕਰ ਤਲ ਨੂੰ ਪੂਰੀ ਤਰ੍ਹਾਂ ਢੱਕ ਲੈਂਦਾ ਹੈ । ਤਾਰ ਦੀ ਲੰਬਾਈ ਅਤੇ ਮਾਨ (ਭਾਰ) ਪਤਾ ਕਰੋ, ਇਹ ਮੰਨਦੇ ਹੋਏ ਕਿ ਤਾਂਬੇ ਦੀ ਘਣਤਾ 8.88 gਤਿ cm³ ਹੈ ।
ਹੱਲ:
ਤਾਰ ਦਾ ਵਿਆਸ (d) = 3 mm
∴ ਤਾਰ ਦਾ ਅਰਧ ਵਿਆਸ (r) = \(\frac{3}{2}\) mm = \(\frac{3}{20}\) cm

ਬੇਲਣ ਦਾ ਵਿਆਸ = 10 cm
ਬੇਲਣ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 5 cm
ਬੇਲਣ ਦੀ ਉੱਚਾਈ (H) = 12 cm
ਬੇਲਣ ਦਾ ਪਰਿਮਾਪ = ਲਪੇਟੇ ਤਾਰ ਦੀ ਲੰਬਾਈ
2πR = ਇੱਕ ਲਪੇਟੇ ਤਾਰ ਦੀ ਲੰਬਾਈ
\(\frac{22}{7}\) × 2 × 5 = ਇੱਕ ਲਪੇਟੇ ਤਾਰ ਦੀ ਲੰਬਾਈ
\(\frac{220}{7}\) = ਲਪੇਟੇ ਤਾਰ ਦੀ ਲੰਬਾਈ

∴ ਪ੍ਰਯੋਗ ਕੀਤੀ ਤਾਰ ਦੀ ਲੰਬਾਈ = ਲਪੇਟਿਆਂ ਦੀ ਸੰਖਿਆ × ਇੱਕ ਲਪੇਟੇ ਵਿੱਚ ਪ੍ਰਯੋਗ ਕੀਤੀ ਤਾਰ ਦੀ ਲੰਬਾਈ
H = 40 × \(\frac{220}{7}\) cm
= 1257.14 cm
ਪ੍ਰਯੋਗ ਕੀਤੀ ਤਾਰ ਦਾ ਆਇਤਨ = πr²H
= \(\frac{22}{7}\) × \(\frac{3}{20}\) × \(\frac{3}{20}\) × 1257.14 cm³ = 88.89 cm³
1 cm³ ਤਾਰ ਦਾ ਮਾਨ = 8.88 gm
88.89 cm³ ਤਾਰ ਦਾ ਮਾਨ = 8.88 × 88.89
= 789.41 gm

ਪ੍ਰਸ਼ਨ 2.
ਇੱਕ ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ, ਜਿਸ ਦੀਆਂ ਭੁਜਾਵਾਂ 3 cm ਅਤੇ 4 cm ਹਨ (ਕਰਣ ਤੋਂ ਇਲਾਵਾ), ਨੂੰ ਉਸਦੇ ਕਰਣ ਦੇ ਅਨੁਸਾਰ ਘੁਮਾਇਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਪ੍ਰਾਪਤ ਦੋਹਰੇ ਥੰਕੂ (double cone) ਦੇ ਆਇਤਨ, ਅਤੇ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ । ( ਦਾ ਮੁੱਲ ਜੋ ਠੀਕ ਲੱਗੇ ਲੈ ਲਵੋ ॥
ਹੱਲ:
ਮੰਨ ਲਉ △ABC ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ ਹੈ, ਜਿਸਦਾ A ਉੱਤੇ ਸਮਕੋਣ ਹੈ । AB ਅਤੇ AC ਦਾ ਮਾਪ ਕ੍ਰਮਵਾਰ 3 cm ਅਤੇ 4 cm ਹੈ । ਭੁਜਾ BC (ਕਰਣ ਦੀ ਲੰਬਾਈ
= \(\sqrt{3^{2}+4^{2}}\) = \(\sqrt {9+16}\) = 5 cm
ਇੱਥੇ AO (ਜਾਂ A’O) ਪ੍ਰਾਪਤ ਦੋਵੇਂ ਪਾਸੇ ਸਾਂਝੇ ਅਧਾਰ ਦੀ ਅਰਧ ਵਿਆਸ ਸਮਕੋਣ ਤਿਭੁਜ ਭੁਜਾ BC ਦੇ ਆਸ-ਪਾਸ ਘੁੰਮ ਕੇ ਬਣੀ ਹੈ ।

ਸ਼ੰਕੂ BAA’ ਦੀ ਉੱਚਾਈ BO ਅਤੇ ਤਿਰਛੀ ਉੱਚਾਈ 3 cm ਹੈ ।
ਸ਼ੰਕੂ CAA’ ਦੀ ਉੱਚਾਈ CO ਅਤੇ ਤਿਰਛੀ ਉੱਚਾਈ 4 cm ਹੈ ।
ਹੁਣ △AOB ~ △CAB (AA ਸਮਰੂਪਤਾ)
∴ \(\frac{AO}{4}\) = \(\frac{3}{5}\)
⇒ AO = \(\frac{4×3}{5}\) = \(\frac{12}{5}\) cm
ਨਾਲ ਹੀ ਉਹ \(\frac{BO}{3}\) = \(\frac{3}{5}\)
⇒ BO = \(\frac{3×3}{5}\) = \(\frac{9}{5}\) cm
∴ CO = BC – OB
= 5 – \(\frac{9}{5}\)
= \(\frac{16}{5}\) cm
∴ ਦੋਹਰੇ ਦੋਹਰੇ ਸ਼ੰਕੂ ਦਾ ਆਇਤਨ
= ਸ਼ੰਕੂ ABA’ ਦਾ ਆਇਤਨ + ਸ਼ੰਕੂ ACA’ ਦਾ ਆਇਤਨ
= \(\frac{1}{3}\)π OA².OB + \(\frac{1}{3}\)π OA².OC
= \(\frac{1}{3}\)π OA²(OB + OC)
= \(\frac{1}{3}\) × \(\frac{22}{7}\) × \(\frac{12}{5}\) × \(\frac{12}{5}\) (\(\frac{9}{5}\) + \(\frac{16}{5}\) )
= \(\frac{22 \times 4 \times 12}{7 \times 5 \times 5}\) × \(\frac{25}{5}\)
= \(\frac{1056}{35}\) = 30\(\frac{6}{35}\) cm³
∴ ਦੋਹਰੇ ਸ਼ੰਕੂ ਦਾ ਆਇਤਨ = 30\(\frac{6}{35}\) cm³.
ਦੋਹਰੇ ਸ਼ੰਕੂ ਦੀ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ
= ਸ਼ੰਕੂ ABA ਦੀ ਸੜਾਂ ਦਾ ਖੇਤਰਫਲ + ਸ਼ੰਕੂ ACA ਦੀ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ
= π. AO. AB + π. AO.A’C

ਪ੍ਰਸ਼ਨ 3.
ਇੱਕ ਟੈਂਕੀ, ਜਿਸਦੇ ਅੰਦਰੂਨੀ ਮਾਪ 150 cm × 120 cm × 110 cm ਹਨ, ਵਿੱਚ 129600 cm³ ਪਾਣੀ ਹੈ । ਦੇ ਇਸ ਪਾਣੀ ਵਿੱਚ ਕੁੱਝ ਛੇਕਾਂ ਵਾਲੀਆਂ ਇੱਟਾਂ ਉਦੋਂ ਤੱਕ ਪਾਈਆਂ ਜਾਂਦੀਆਂ ਹਨ ਜਦੋਂ ਤੱਕ ਕਿ ਟੈਂਕੀ ਪੂਰੀ ਉੱਪਰ ਤੱਕ ਭਰ ਨਾ ਜਾਵੇ । ਹਰੇਕ ਇੱਟ ਆਪਣੇ ਆਇਤਨ ਦਾ \(\frac{1}{17}\) ਪਾਣੀ ਸੋਖ ਲੈਂਦੀ ਹੈ । ਜੇਕਰ ਹਰੇਕ ਇੱਟ ਦਾ ਮਾਪ 22.5 cm × 7.5 cm × 6.5 cm ਹੋਵੇ, ਤਾਂ ਟੈਂਕੀ ਵਿਚ ਕੁੱਲ ਕਿੰਨੀਆਂ ਇੱਟਾਂ ਪਾਈਆਂ ਜਾ ਸਕਦੀਆਂ ਹਨ, ਤਾਂ ਕਿ ਉਸ ਤੋਂ ਪਾਣੀ ਬਾਹਰ ਨਾ ਆਵੇ ?
ਹੱਲ:
ਇੱਟਾਂ ਦਾ ਆਇਤਨ = 22.5 × 7.5 × 6.5 cm³
= 1096.87 cm3
ਟੈਂਕੀ ਦਾ ਆਇਤਨ = 150 × 120 × 110 cm³
= 1980000
ਮੰਨ ਲਉ ਇੱਟਾਂ ਦੀ ਸੰਖਿਆ = n
ਇੱਟਾਂ ਦਾ ਆਇਤਨ = n [1096.87] cm³
ਇੱਟਾਂ ਲਈ ਲੋੜੀਂਦੇ ਪਾਣੀ ਦਾ ਆਇਤਨ
= (1980000 – 129600) cm³
= 1850400 cm³
ਹਰੇਕ ਇੱਟ ਆਪਣੇ ਆਇਤਨ ਦਾ \(\frac{1}{17}\) ਵਾਂ ਪਾਣੀ ਸੋਖ ਲੈਂਦੀ ਹੈ |
ਇੱਟਾਂ ਦੁਆਰਾ ਸੋਖਿਆ ਪਾਣੀ ਦਾ ਆਇਤਨ = \(\frac{17}{10}\) × ਇੱਟਾਂ ਲਈ ਲੋੜੀਂਦੇ ਪਾਣੀ ਦਾ ਆਇਤਨ
= \(\frac{17}{10}\) × 1850400 cm³
ਇੱਟਾਂ ਦੁਆਰਾ ਸੋਖੇ ਪਾਣੀ ਦਾ ਆਇਤਨ
= 1966050 cm³
n ਇੱਟਾਂ ਦਾ ਕੁੱਲ ਆਇਤਨ
= ਇੱਟਾਂ ਦੁਆਰਾ ਸੋਖੇ ਪਾਣੀ ਦਾ ਆਇਤਨ
n[1096.87] cm³ = 1966050 cm³
n = \(\frac{1966050}{1096.42}\)
n = 1792.42
ਪ੍ਰਯੋਗ ਕੀਤੀਆਂ ਇੱਟਾਂ ਦੀ ਸੰਖਿਆ = 1792

ਪ੍ਰਸ਼ਨ 4.
ਕਿਸੇ ਮਹੀਨੇ ਦੇ 15 ਦਿਨਾਂ ਵਿੱਚ, ਇੱਕ ਨਦੀ ਦੀ ਘਾਟੀ ਵਿੱਚ 10 cm ਵਰਖਾ ਹੋਈ । ਜੇਕਰ ਇਸ ਘਾਟੀ ਦਾ ਖੇਤਰਫਲ 97280 km2 ਹੈ, ਤਾਂ ਦਰਸਾਉ ਕਿ ਕੁੱਲ ਵਰਖਾ ਲਗਭਗ ਤਿੰਨ ਨਦੀਆਂ ਦੇ ਆਮ ਪਾਣੀ ਦੇ ਜੋੜ ਦੇ ਬਰਾਬਰ ਸੀ, ਜਦੋਂ ਕਿ ਹਰੇਕ ਨਦੀ 1072 km ਲੰਬੀ, 75 m ਚੌੜੀ ਅਤੇ 3 m ਡੂੰਘੀ ਹੈ ।
ਹੱਲ:
ਘਾਟੀ ਦਾ ਖੇਤਰਫਲ = 97280 km²
ਘਾਟੀ ਵਿਚ ਬਾਰਿਸ਼ = 10 cm
∴ ਕੁੱਲ ਵਰਖਾ ਦਾ ਆਇਤਨ
= 97280 × \(\frac{10}{100}\) × \(\frac{1}{1000}\) km³
= 9728 km³

ਪ੍ਰਸ਼ਨ 5.
ਟੀਨ ਦੀ ਬਣੀ ਹੋਈ ਇੱਕ ਤੇਲ ਦੀ ਕੁੱਪੀ 10 cm ਲੰਬੇ ਇੱਕ ਬੇਲਣ ਵਿੱਚ ਇੱਕ ਸ਼ੰਕੂ ਦੇ ਸ਼ੌਕ ਨੂੰ ਜੋੜਨ ਨਾਲ ਬਣੀ ਹੈ । ਜੇਕਰ ਇਸ ਦੀ ਕੁੱਲ ਉੱਚਾਈ 22 cm ਹੈ ਅਤੇ ਬੇਲਨਾਕਾਰ ਭਾਗ ਦਾ ਵਿਆਸ 8 cm ਹੈ ਅਤੇ ਕੁੱਪੀ ਦੇ ਉੱਪਰੀ ਸਿਰੇ ਦਾ ਵਿਆਸ 18 cm ਹੈ, ਤਾਂ ਇਸਦੇ ਬਣਾਉਣ ਵਿੱਚ ਲੱਗੀ ਟੀਨ ਦੀ ਚਾਦਰ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ (ਦੇਖੋ ਚਿੱਤਰ)।

ਹੱਲ:
ਕੁੱਪੀ ਦੇ ਉੱਪਰੀ ਸਿਰੇ ਦਾ ਵਿਆਸ = 18 cm
∴ ਕੁੱਪੀ ਦੇ ਉੱਪਰੀ ਸਿਰੇ ਦਾ ਅਰਧ ਵਿਆਸ (R) = \(\frac{18}{2}\) = 9 cm
ਕੁੱਪੀ ਦੇ ਆਧਾਰ ਦਾ ਵਿਆਸ = 8 cm
ਕੁੱਪੀ ਦੇ ਆਧਾਰ ਦਾ ਅਰਧ ਵਿਆਸ (r) = 4 cm
ਬੇਲਣਾਕਾਰ ਭਾਗ ਦੀ ਉੱਚਾਈ (h) = 10 cm
ਸ਼ੌਨਕ ਦੀ ਉੱਚਾਈ (H) = (22 – 10)
= 12 cm
ਸ਼ੌਨਕ ਦੀ ਤਿਰਛੀ ਉੱਚਾਈ (l)
= \(\sqrt{\mathrm{H}^{2}+(\mathrm{R}-r)^{2}}\)
= \(\sqrt{(12)^{2}+(9-4)^{2}}\)
= \(\sqrt{144+(5)^{2}}\)
= \(\sqrt {144+25}\) = \(\sqrt {169}\)
ਸ਼ੌਨਕ ਦੀ ਤਿਰਛੀ ਉੱਚਾਈ (l) = 13 cm
ਟੀਨ ਦੀ ਚੱਦਰ ਦਾ ਖੇਤਰਫਲ = ਬੇਲਣਾਕਾਰ ਆਧਾਰ ਦੀ ਵਕਰ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ + ਸ਼ੌਨਕ ਦੀ ਵਕਰ ਸੜਾ ਦਾ ਖੇਤਰਫਲ
= 2πrh + πL[R + r]
= 2 × \(\frac{22}{7}\) × 4 × 10 + \(\frac{212}{7}\) × 13[19 + 4] cm²
= 251.42 + 531.14 = 782.56 cm²
∴ ਪ੍ਰਯੋਗ ਕੀਤੀ ਧਾਤੂ ਦੀ ਚੱਦਰ ਦਾ ਕੁੱਲ ਖੇਤਰਫਲ
= 782.56 cm²

ਪ੍ਰਸ਼ਨ 6.
ਸ਼ੰਕੂ ਦੇ ਇੱਕ ਛਿਣਕ ਦੇ ਲਈ, ਪਹਿਲਾਂ ਸਪੱਸ਼ਟ ਕੀਤੇ ਸੰਕੇਤਾਂ ਦਾ ਪ੍ਰਯੋਗ ਕਰਦੇ ਹੋਏ, ਵਕਰ ਤਲ ਦਾ ਖੇਤਰਫਲ ਅਤੇ ਕੁੱਲ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ ਦੇ ਉਨ੍ਹਾਂ ਸੂਤਰਾਂ ਨੂੰ ਸਿੱਧ ਕਰੋ ਜੋ ਭਾਗ 13.5 ਵਿੱਚ ਦਿੱਤੇ ਗਏ ਹਨ ।
ਹੱਲ:
ਇਕ ਲੰਬ ਚੱਕਰਾਕਾਰ ਸ਼ੰਕੂ ਦੇ ਸ਼ੌਨਕ ਦੋ ਅਸਮਾਨ ਚੱਕਰਾਕਾਰ ਆਧਾਰ ਅਤੇ ਵਕਰ ਸਤਾ ਹਨ । ਮੰਨ ਲਉ ਭਾਗ VCD ਨੂੰ ਹਟਾ ਕੇ ਪ੍ਰਾਪਤ ਸ਼ੌਨਕ ACDB ਹੈ । ਦੋਹਾਂ ਦੇ ਆਧਾਰਾਂ ਦੇ ਕੇਂਦਰਾਂ ਨੂੰ ਮਿਲਾਉਣ ਵਾਲਾ ਰੇਖਾਖੰਡ OP ਛੰਨਕ ਦੀ ਉੱਚਾਈ ਕਹਾਉਂਦਾ ਹੈ । ਸ਼ੌਕ ACDB ਦਾ ਹਰੇਕ ਰੇਖਾਖੰਡ AC ਅਤੇ BD ਤਿਰਛੀ ਉੱਚਾਈ ਹੈ ।

ਮੰਨ ਲਉ R ਅਤੇ r (R > r) ਸ਼ੰਕੂ (VAB) ਦੇ ਸ਼ੌਣਕ ACDB ਦੇ ਚੱਕਰਾਕਾਰ ਸਿਰਿਆਂ ਦਾ ਅਰਧ ਵਿਆਸ ਹਨ । ਅਸੀਂ ਸ਼ੰਕੂ ਆਕਾਰ ਭਾਗ VCD ਨੂੰ ਪੂਰਾ ਕਰਦੇ ਹਾਂ । ਮੰਨ ਲਉ ਕਿ ਮੈਂ ਅਤੇ 1 ਕੁਮਵਾਰ ਸਿੱਧੀ ਉੱਚਾਈ ਅਤੇ ਤਿਰਛੀ ਉੱਚਾਈ ਹੈ । ਤਾਂ OP = h ਅਤੇ AC = BD = l.
ਲੰਬ ਚੱਕਰਾਕਾਰ ਸ਼ੰਕੂ ਦੇ ਸ਼ੌਣਕ ਨੂੰ ਦੋ ਲੰਬ ਚੱਕਰਾਕਾਰ ਸ਼ੰਕੂਆਂ ਦੇ ਬਰਾਬਰ VAB ਅਤੇ VCD ਦੇ ਅੰਤਰ ਦੇ ਰੂਪ ਵਿਚ ਦੇਖਿਆ ਜਾ ਸਕਦਾ ਹੈ ।
ਮੰਨ ਲਉ ਸ਼ੰਕੂ VAB ਦੀ ਉੱਚਾਈ h, ਅਤੇ ਤਿਰਛੀ ਉਚਾਈ l ਹੈ । ਭਾਵ VP = h₁ ਅਤੇ VA = VB = l₁.
ਹੁਣ ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ △DEB ਵਿਚ,
DB² = DE² + BE²
⇒ l² = h² + (R – r)²
⇒ l = \(\sqrt{h^{2}+(\mathrm{R}-r)^{2}}\)
ਦੁਬਾਗ △VOD ~ △VPB

= πl (R + r) ਵ. ਇਕਾਈਆਂ
∴ ਲੰਬ ਚੱਕਰਾਕਾਰ ਸ਼ੰਕੂ ਦੇ ਸ਼ੌਨਕ ਦੀ ਵਕਰ ਸਤਾ ਦਾ ਖੇਤਰਫਲ
= πl(R + r) ਵ. ਇਕਾਈਆਂ ਜਿੱਥੇ
l = \(\sqrt{h^{2}+(\mathrm{R}-r)^{2}}\)
ਲੰਬ ਚੱਕਰਾਕਾਰ ਸ਼ੰਕੂ ਦੇ ਸ਼ੌਨਕ ਦੀ ਕੁਲ ਸੜਾ ਦਾ ਖੇਤਰਫਲ
= ਵਕਰ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ+ਆਧਾਰ ਦਾ ਖੇਤਰਫਲ + ਉਪਰੀ ਸਿਰੇ ਦਾ ਖੇਤਰਫਲ
= πl(R + r) + πR² + πr²
= π[R² + r² + l(R + r)] ਵ. ਮੀ.

ਪ੍ਰਸ਼ਨ 7.
ਸ਼ੰਕੂ ਦੇ ਇੱਕ ਸ਼ੌਨਕ ਦੇ ਲਈ ਪਹਿਲਾਂ ਸਪੱਸ਼ਟ ਕੀਤੇ ਸੰਕੇਤਾਂ ਦਾ ਪ੍ਰਯੋਗ ਕਰਦੇ ਹੋਏ, ਆਇਤਨ ਦਾ ਉਹ ਸੂਤਰ | ਸਿੱਧ ਕਰੋ, ਜੋ ਭਾਗ 13.5 ਵਿਚ ਦਿੱਤਾ ਗਿਆ ਹੈ ।
ਹੱਲ:
ਇੱਕ ਲੰਬ ਚੱਕਰਾਕਾਰ ਸ਼ੰਕੂ ਦੇ ਸ਼ੌਨਕ ਦੇ ਅਸਮਾਨ ਚੱਕਰਾਕਾਰ ਆਧਾਰ ਅਤੇ ਵਕਰ ਸ਼ਤਾ ਹੁੰਦੀ ਹੈ । ਮੰਨ ਲਉ ਭਾਗ VCD ਨੂੰ ਹਟਾ ਕੇ ਪ੍ਰਾਪਤ ਸ਼ੌਨਕ ACDB ਹੈ ਦੋਹਾਂ ਦੇ ਆਧਾਰ ਨੂੰ ਮਿਲਾਉਣ ਵਾਲਾ ਰੇਖਾਖੰਡ OP ਸ਼ੌਨਕ ਦੀ ਲੰਬਾਈ ਕਹਾਉਂਦਾ ਹੈ ਸ਼ੌਨਕ ACDB ਦਾ ਹਰੇਕ ਰੇਖਾਖੰਡ AC ਅਤੇ BD ਤਿਰਛੀ ਉੱਚਾਈ ਕਹਾਉਂਦਾ ਹੈ ।

ਮੰਨ ਲਉ R ਅਤੇ r (R > r) ਸ਼ੰਕੂ (VAB) ਨੂੰ ਛਿੱਕ ACDB ਦੇ ਚੱਕਰਾਕਾਰ ਸਿਰਿਆਂ ਦੇ ਅਰਧ ਵਿਆਸ ਹਨ । ਅਸੀਂ ਸ਼ੰਕੂ ਵਾਲੇ ਭਾਗ VCD ਨੂੰ ਪੂਰਾ ਕਰਦੇ ਹਨ । ਮੰਨ ਲਉ ) ਅਤੇ ਕੁਮਵਾਰ ਸਿੱਧੀ ਅਤੇ ਤਿਰਛੀ ਉਚਾਈ ਹੈ । OP = h ਅਤੇ AC = BD = l.
ਲੰਬ ਚੱਕਰਾਕਾਰ ਸ਼ੰਕੂ ਦੇ ਸ਼ੌਨਕ ਦੇ ਦੋ ਲੰਬ ਚੱਕਰਕਾਰ ਸ਼ੰਕੂਆਂ ਦੇ ਬਰਾਬਰ VAB ਅਤੇ VCD ਦੇ ਅੰਤਰ ਰੂਪ ਵਿਚ ਦੇਖਿਆ ਜਾ ਸਕਦਾ ਹੈ ।
ਮੰਨ ਲਉ ਸ਼ੰਕੂ VAB ਦੀ ਉੱਚਾਈ h₁ ਅਤੇ ਤਿਰਛੀ ਉੱਚਾਈ l ਹੈ । ਭਾਵ VP = h₁ ਅਤੇ VA = VB = l₁.
∴ ਸ਼ੰਕੂ VCD ਦੀ ਉੱਚਾਈ = VP – OP
= h₁ – h
ਕਿਉਂਕਿ ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ VOD ਅਤੇ VPB ਸਮਰੂਪ ਹਨ ।
⇒ \(\frac{VO}{VP}\) = \(\frac{OD}{PB}\) = \(\frac{h_{1}-h}{h_{1}}\) \(\frac{r}{R}\)
⇒ 1 – \(\frac{h}{h_{1}}\) = \(\frac{r}{R}\)

ਪਰ ਜੇਕਰ A₁ ਅਤੇ A₂ (A₁ > A₂) ਦੋ ਚੱਕਰਾਕਾਰ ਆਧਾਰਾਂ ਦੀ ਕੁੱਲ ਸਤਾ ਦਾ ਖੇਤਰਫਲ ਹੈ
A₁ = πR² ਅਤੇ A₂ = πr²
ਹੁਣ ਸ਼ੰਕੂ ਦੇ ਸ਼ੌਨਕ ਦਾ ਆਇਤਨ
= \(\frac{1}{3}\) πh(R² + r² + Rr)
= \(\frac{h}{3}\) (πR² + πr² + \(\sqrt{\pi \mathrm{R}^{2}} \sqrt{\pi r^{2}}\))
= \(\frac{h}{3}\) (A₁ + A₂ + \(\sqrt{A_{1} A_{2}}\))

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 13 ਸਤੁਦਾ ਖੇਤਰਫਲ ਅਤੇ ਆਇਤਨ Ex 13.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 13 ਸਤੁਦਾ ਖੇਤਰਫਲ ਅਤੇ ਆਇਤਨ Exercise 13.2

(ਜਦੋਂ ਤੱਕ ਨਾ ਕਿਹਾ ਜਾਵੇ, π = \(\frac{22}{7}\) ਲਓ )

ਪ੍ਰਸ਼ਨ 1.
ਇੱਕ ਠੋਸ ਇੱਕ ਅਰਧ ਗੋਲੇ ‘ਤੇ ਖੜ੍ਹੇ ਸ਼ੰਕੂ ਦੇ ਆਕਾਰ ਦਾ ਹੈ । ਦੋਹਾਂ ਦਾ ਅਰਧ ਵਿਆਸ 1 cm ਹੈ ਅਤੇ ਸ਼ੰਕੂ ਦੀ ਉੱਚਾਈ ਉਸਦੇ ਅਰਧ ਵਿਆਸ ਦੇ ਬਰਾਬਰ ਹੈ । ਇਸ ਠੋਸ ਦਾ ਆਇਤਨ π ਦੇ ਪਦਾਂ ਵਿੱਚ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਸ਼ੰਕੁ ਦਾ ਅਰਧ ਵਿਆਸ = ਅਰਧਗੋਲੇ ਦਾ ਅਰਧ ਵਿਆਸ = 1 cm
R = 1 cm
∴ ਸ਼ੰਕੂ ਦੀ ਉੱਚਾਈ (H) = 1 cm

ਠੋਸ ਦਾ ਆਇਤਨ = ਸ਼ੰਕੂ ਦਾ ਆਇਤਨ + ਅਰਧਗੋਲੇ ਦਾ ਆਇਤਨ
= \(\frac{1}{3}\)πR²H + \(\frac{2}{3}\)πR³
= \(\frac{1}{3}\)πR²[H + 2R]
= \(\frac{1}{3}\)π × 1 × 1[1 + 2 × 1] cm²
= \(\frac{1}{3}\)π × 3 = \(\frac{3 \pi}{3}\) cm²
= π cm³
∴ ਠੋਸ ਦਾ ਆਇਤਨ = π cm³

ਪ੍ਰਸ਼ਨ 2.
ਇੱਕ ਇੰਜੀਨਿਅਰਿੰਗ ਦੇ ਵਿਦਿਆਰਥੀ ਮਨੋਹਰ ਨੂੰ ਇੱਕ ਪਤਲੀ ਐਲੂਮੀਨੀਅਮ ਦੀ ਸ਼ੀਟ ਦੀ ਵਰਤੋਂ ਕਰਦੇ ਹੋਏ ਇੱਕ ਮਾਡਲ ਬਣਾਉਣ ਲਈ ਕਿਹਾ ਗਿਆ ਜੋ ਇੱਕ ਅਜਿਹੇ ਬੇਲਣ ਦੇ ਆਕਾਰ ਦਾ ਹੋਵੇ ਜਿਸਦੇ ਦੋਨੋਂ ਸਿਰਿਆਂ ‘ਤੇ ਦੋ ਸ਼ੰਕੂ ਜੁੜੇ ਹੋਏ ਹੋਣ ।ਇਸ ਮਾਡਲ ਦਾ ਵਿਆਸ 3 cm ਹੈ ਅਤੇ ਇਸ ਦੀ ਲੰਬਾਈ 12 cm ਹੈ । ਜੇਕਰ ਹਰੇਕ ਸ਼ੰਕੂ ਦੀ ਉੱਚਾਈ 2 cm ਹੋਵੇ ਤਾਂ ਮਨੋਹਰ ਦੁਆਰਾ ਬਣਾਏ ਗਏ ਮਾਡਲ ਵਿੱਚ ਮੌਜੂਦ ਹਵਾ ਦਾ ਆਇਤਨ ਪਤਾ ਕਰੋ। (ਇਹ ਮੰਨ ਲਓ ਮਾਡਲ ਦੀਆਂ ਅੰਦਰੂਨੀ ਅਤੇ ਬਾਹਰੀ ਪਸਾਰਾਂ ਲਗਭਗ ਬਰਾਬਰ ਹਨ ।
ਹੱਲ:

ਸ਼ੰਕੂ ਦਾ ਅਰਧ ਵਿਆਸ = ਬੇਲਣ ਦਾ ਅਰਧ ਵਿਆਸ (R) = \(\frac{3}{2}\) cm
R = 5 cm
∴ R = 1.5 cm
ਹਰੇਕ ਸ਼ੰਕੂ ਦੀ ਉੱਚਾਈ (h) = 2 cm
∴ ਬੇਲਣ ਦੀ ਉਚਾਈ = (12 -2 – 2) cm
= 8 cm
ਬੇਲਣ ਵਿਚ ਮੌਜੂਦ ਹਵਾ ਦਾ ਆਇਤਨ = ਬੇਲਣ ਦਾ ਆਇਤਨ + 2 (ਸ਼ੰਕੂ ਦਾ ਆਇਤਨ)

ਬੇਲਣ ਵਿਚ ਹਵਾ ਦਾ ਆਇਤਨ
= \(\frac{22}{7}\) × \(\frac{3}{2}\) × \(\frac{3}{2}\) × \(\frac{28}{3}\) cm³
= 22 × 3 cm³
= 66 cm³
= 66 cm³

ਪ੍ਰਸ਼ਨ 3.
ਇੱਕ ਗੁਲਾਬਜਾਮਣ ਵਿੱਚ ਉਸਦੇ ਆਇਤਨ ਦੀ ਲਗਭਗ 30% ਖੰਡ ਦੀ ਚਾਸ਼ਣੀ ਹੁੰਦੀ ਹੈ | 45 ਗੁਲਾਬ ਜਾਮਣਾਂ ਵਿਚ ਲਗਭਗ ਕਿੰਨੀ ਚਾਸ਼ਣੀ ਹੋਵੇਗੀ, ਜੇਕਰ ਹਰੇਕ ਗੁਲਾਬਜਾਮਣ ਇੱਕ ਬੇਲਣ ਦੇ ਆਕਾਰ ਦਾ ਹੈ, ਜਿਸਦੇ ਦੋਨੋਂ ਸਿਰੇ ਅਰਧਗੋਲਾਕਾਰ ਹਨ ਅਤੇ ਉਸ ਦੀ ਲੰਬਾਈ 5 cm ਅਤੇ ਵਿਆਸ 2.8 cm ਹੈ (ਦੇਖੋ ਚਿੱਤਰ) ।

ਹੱਲ:
ਗੁਲਾਬ ਜਾਮਣ ਬੇਲਣ ਦੇ ਆਕਾਰ ਦਾ ਹੈ, ਜਿਸਦੇ ਦੋਵੇਂ ਸਿਰੇ ਅਰਧਗੋਲਾਕਾਰ ਹਨ ।
ਵੇਲਣ ਦਾ ਵਿਆਸ = ਅਰਧ ਗੋਲੇ ਦਾ ਵਿਆਸ = 2.8 cm
ਬੇਲਣ ਦਾ ਅਰਧ ਵਿਆਸ = ਅਰਧ ਗੋਲੇ ਦਾ ਅਰਧ ਵਿਆਸ (R)
= \(\frac{2.8}{2}\) = 1.4 cm
R = 1.4 cm

ਬੇਲਣਾਕਾਰ ਭਾਗ ਦੀ ਉੱਚਾਈ
= (5 – 14 – 1.4) cm
= (5 – 2.8) cm
= 2.2 cm
ਇੱਕ ਗੁਲਾਬ ਜਾਮਣ ਦਾ ਆਇਤਨ
= ਬੇਲਣ ਦਾ ਆਇਤਨ + 2 [ਅਰਧ ਗੋਲੇ ਦਾ ਆਇਤਨ]

= 22∙05 cm³
ਇਕ ਗੁਲਾਬ ਜਾਮਣ ਦਾ ਆਇਤਨ
= 25.05 cm³
ਹੁਣ, 45 ਗੁਲਾਬ ਜਾਮਣਾਂ ਦਾ ਆਇਤਨ
= 45 × 25.05 cm³
= 1127.25 cm³
∴ ਖੰਡ ਦੀ ਚਾਸ਼ਣੀ ਦਾ ਆਇਤਨ
= 45 ਗੁਲਾਬ ਜਾਮਣਾਂ ਦੇ ਆਇਤਨ ਦਾ 30%
= \(\frac{30 \times 1127.25}{100}\) cm³
= 338.175 cm³
∴ ਖੰਡ ਦੀ ਚਾਸ਼ਣੀ ਦੀ ਮਾਤਰਾ = 338 cm³

ਪ੍ਰਸ਼ਨ 4.
ਇੱਕ ਕਲਮਦਾਨ ਘਣਾਵ ਆਕਾਰ ਦੀ ਇੱਕ ਲੱਕੜੀ ਨਾਲ ਦਾ ਬਣਿਆ ਹੈ ਜਿਸ ਵਿੱਚ ਕਲਮ ਰੱਖਣ ਦੇ ਲਈ ਚਾਰ ਸ਼ੰਕੁ ਆਕਾਰ ਖੱਡੇ ਬਣੇ ਹੋਏ ਹਨ | ਘਣਾਵ ਦੀਆਂ ਪਸਾਰਾਂ (dimensions) 15 cm × 10 cm × 3.5 cm ਹਨ । ਹਰੇਕ ਖੰਡੇ ਦਾ ਅਰਧ ਵਿਆਸ 0.5 cm ਹੈ ਅਤੇ ਗਹਿਰਾਈ 1.4 cm ਹੈ । ਪੁਰੇ ਕਲਮਦਾਨ ਵਿੱਚ ਲੱਕੜੀ ਦਾ ਆਇਤਨ ਪਤਾ ਕਰੋ । (ਦੇਖੋ ਚਿੱਤਰ)

ਹੱਲ:
ਘਣਾਵ ਦੀ ਲੰਬਾਈ (L) = 15 cm
ਘਣਾਵ ਦੀ ਚੌੜਾਈ (B) = 10 cm
ਘਣਾਵ ਦੀ ਉੱਚਾਈ (H) = 3.5 cm
ਸ਼ੰਕੁ ਆਕਾਰ ਖੰਡੇ ਦਾ ਅਰਧ ਵਿਆਸ = 0.5 cm
ਸ਼ੰਕੂ ਆਕਾਰ ਖੱਡੇ ਦੀ ਉੱਚਾਈ h = 1.4 cm
ਕਲਮਦਾਨ ਵਿੱਚ ਲੱਕੜੀ ਦਾ ਆਇਤਨ
= ਘਣਾਵ ਦਾ ਆਇਤਨ – 4 [ਸ਼ੰਕੂ ਦਾ ਆਇਤਨ]

= (15 × 35 – \(\frac{22}{3×5}\) ) cm³
= (525 – 1.466) cm³
= 523.534 cm³.
ਕਲਮਦਾਨ ਵਿੱਚ ਲੱਕੜੀ ਦਾ ਆਇਤਨ
= 523.53 cm³

ਪ੍ਰਸ਼ਨ 5.
ਇੱਕ ਬਰਤਨ ਇੱਕ ਉਲਟੇ ਸ਼ੰਕੂ ਦੇ ਆਕਾਰ ਦਾ ਹੈ । ਇਸਦੀ ਉੱਚਾਈ 8 cm ਹੈ ਅਤੇ ਇਸਦੇ ਉੱਪਰੀ ਸਿਰੇ (ਜੋ ਖੁਲਿਆ ਹੋਇਆ ਹੈ) ਦਾ ਅਰਧ ਵਿਆਸ 5 cm ਹੈ । ਇਹ ਉੱਪਰ ਤੱਕ ਪਾਣੀ ਨਾਲ ਭਰਿਆ ਹੋਇਆ ਹੈ। ਜਦੋਂ ਇਸ ਬਰਤਨ ਵਿੱਚ ਸਿੱਕੇ ਦੀਆਂ ਕੁੱਝ ਗੋਲੀਆਂ ਜਿੰਨ੍ਹਾਂ ਵਿੱਚੋਂ ਹਰੇਕ 0:5 cm ਅਰਧ ਵਿਆਸ ਵਾਲਾ ਇੱਕ ਗੋਲਾ ਹੈ, ਪਾਈਆਂ ਜਾਂਦੀਆਂ ਹਨ ਤਾਂ ਇਸ ਵਿੱਚੋਂ ਭਰੇ ਹੋਏ ਪਾਣੀ ਦਾ ਇੱਕ ਚੌਥਾਈ ਭਾਗ ਬਾਹਰ ਨਿਕਲ ਜਾਂਦਾ ਹੈ | ਬਰਤਨ ਵਿਚ ਪਾਈਆਂ ਗਈਆਂ ਸਿੱਕੇ ਦੀਆਂ ਗੋਲੀਆਂ ਦੀ ਸੰਖਿਆ ਪਤਾ ਕਰੋ ।
ਹੱਲ:

ਸ਼ੰਕੂ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 5 cm
ਸ਼ੰਕੂ ਦੀ ਉੱਚਾਈ (H) = 8 cm
ਸਿੱਕੇ ਦੀ ਹਰੇਕ ਗੋਲੀ ਦਾ ਅਰਧ ਵਿਆਸ (r) = 0.5 cm
ਮੰਨ ਲਉ ਗੋਲੀਆਂ ਦੀ ਸੰਖਿਆ = N
ਤਾਂ ਪਾਣੀ ਦਾ ਇੱਕ ਚੌਥਾਈ ਭਾਗ ਬਾਹਰ ਨਿਕਲ ਜਾਂਦਾ ਹੈ ।
N [ਗੋਲੀਆਂ ਦਾ ਆਇਤਨ = \(\frac{1}{4}\) ਸ਼ੰਕੂ ਵਿੱਚ ਪਾਣੀ ਦਾ ਆਇਤਨ


= 10 × 10 = 100
ਗੋਲੀਆਂ ਦੀ ਸੰਖਿਆ = 100

ਪ੍ਰਸ਼ਨ 6.
ਉੱਚਾਈ 220 cm ਅਤੇ ਆਧਾਰ ਵਿਆਸ 24 cm ਵਾਲੇ ਇੱਕ ਬੇਲਣ ਜਿਸ ਤੇ ਉੱਚਾਈ 60 cm ਅਤੇ ਅਰਧ ਵਿਆਸ 8 cm ਵਾਲਾ ਇੱਕ ਹੋਰ ਬੇਲਣ ਰੱਖਿਆ ਹੋਇਆ ਹੈ, ਨਾਲ ਲੋਹੇ ਦਾ ਇੱਕ ਖੰਬਾ ਬਣਾਇਆ ਗਿਆ ਹੈ । ਇਸ ਖੰਬੇ ਦਾ ਮਾਨ (ਭਾਰ) ਪਤਾ ਕਰੋ, ਜਦੋਂ ਕਿ ਦਿੱਤਾ ਹੈ 1 cm³ ਲੋਹੇ ਦਾ ਮਾਣ (ਭਾਰ) 8g ਹੁੰਦਾ ਹੈ (π = 3∙14 ਲਓ) ।
ਹੱਲ:
ਹੇਠਾਂ ਵਾਲੇ ਬੇਲਣ ਦਾ ਵਿਆਸ = 24 cm
ਹੇਠਾਂ ਵਾਲੇ ਬੇਲਣ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 12 cm
ਹੇਠਾਂ ਵਾਲੇ ਬੇਲਣ ਦੀ ਉੱਚਾਈ (H) = 220 cm
ਉੱਪਰ ਵਾਲੇ ਬੇਲਣ ਦਾ ਅਰਧ ਵਿਆਸ (r) = 8 cm
ਉੱਪਰ ਵਾਲੇ ਬੇਲਣ ਦੀ ਉੱਚਾਈ (h) = 60 cm

ਖੰਬੇ ਦਾ ਆਇਤਨ = ਹੇਠਾਂ ਵਾਲੇ ਬੇਲਣ ਦਾ ਆਇਤਨ + | ਉੱਪਰ ਵਾਲੇ ਬੇਲਣ ਦਾ ਆਇਤਨ
= πR²H + πr²h
= [3.14 × 12 × 12 × 220 + 3.14 × 8 × 8 × 60] cm³
= [99475.2 + 12057.6] cm³
ਖੰਬੇ ਦਾ ਆਇਤਨ = 111532.8 cm³
1 cm³ ਦਾ ਦ੍ਰਵਸਾਨ = 8 gm
111532.8 cm³ ਦਾ ਦ੍ਰਵਸਾਨ = 8 × 111532. 8 gm
= 892262.4 gm
= \(\frac{892262.4}{1000}\) gm
= 892.2624 kg
= 892.2624 kg

ਪ੍ਰਸ਼ਨ 7.
ਇੱਕ ਠੋਸ ਵਿੱਚ, ਉੱਚਾਈ 120 cm ਅਤੇ ਅਰਧ ਵਿਆਸ 60 cm ਵਾਲਾ ਇੱਕ ਸ਼ੰਕੂ ਸ਼ਾਮਿਲ ਹੈ ਜੋ 60 cm ਅਰਧ ਵਿਆਸ ਵਾਲੇ ਇੱਕ ਅਰਧਗੋਲੇ ‘ਤੇ ਬਣਿਆ ਹੈ ਇਸ ਠੋਸ ਨੂੰ ਪਾਣੀ ਨਾਲ ਭਰੇ ਹੋਏ ਇੱਕ ਲੰਬ ਚੱਕਰੀ ਬੋਲਣ ਵਿੱਚ ਇਸ ਪ੍ਰਕਾਰ ਸਿੱਧਾ ਪਾ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ਕਿ ਇਹ ਬੋਲਣ ਦੇ ਤਲ ਨੂੰ ਸਪਰਸ਼ ਕਰੇ । ਜੇਕਰ ਬੇਲਣ ਦਾ ਅਰਧ ਵਿਆਸ 60 cm ਹੈ ਅਤੇ ਉੱਚਾਈ 180 cm ਹੈ ਤਾਂ ਬੇਲਣ ਵਿੱਚ ਬਾਕੀ ਬੱਚੇ ਪਾਣੀ ਦਾ ਆਇਤਨ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਸ਼ੰਕੂ ਦਾ ਅਰਧ ਵਿਆਸ = ਅਰਧ ਗੋਲੇ ਦਾ ਅਰਧ ਵਿਆਸ
= ਬੇਲਣ ਦਾ ਅਰਧ ਵਿਆਸ
= 60 cm

ਸ਼ੰਕੂ ਦੀ ਉੱਚਾਈ (h) = 120 cm
ਬੇਲਣ ਦੀ ਉੱਚਾਈ (H) = 180 cm
ਬੇਲਣਾਕਾਰ ਬਰਤਨ ਦਾ ਆਇਤਨ = πR²H
= \(\frac{22}{7}\) × 60 × 60 × 180 cm³
= 2036571.4 cm³
ਬੇਲਣ ਵਿਚ ਪਾਏ ਗਏ ਠੋਸ ਦਾ ਆਇਤਨ = ਅਰਧ ਗੋਲੇ ਦਾ ਆਇਤਨ + ਸ਼ੰਕੂ ਦਾ ਆਇਤਨ
= \(\frac{2}{3}\)πR³ + \(\frac{1}{3}\)πR²h
= \(\frac{1}{3}\)πR²[2R + h]
= \(\frac{1}{3}\) × \(\frac{22}{7}\) × 60 × 60 [2 × 60 +120] cm³
= \(\frac{1}{3}\) × \(\frac{22}{7}\) × 3600 [120 + 120] cm³
= \(\frac{1}{3}\) × \(\frac{22}{7}\) × 3600 × 40 cm³
= 905142.86 cm³
ਬਾਹਰ ਨਿਕਲੇ ਪਾਣੀ ਦਾ ਆਇਤਨ
= 905142.86 cm³
∴ ਬੇਲਣ ਵਿਚ ਬਚੇ ਬਾਕੀ ਪਾਣੀ ਦਾ ਆਇਤਨ = ਬੇਲਣ ਦਾ ਆਇਤਨ – ਬਰਤਨ ਵਿਚ ਪਾਏ ਗਏ ਠੋਸ ਦਾ ਆਇਤਨ
= (2036571.4 – 905142.86) cm³
= 1131428.5 cm³
= \(\frac{1131428.5}{100 \times 100 \times 100}\) m³
= 1.131 m³
∴ ਬੇਲਣ ਵਿੱਚ ਬਾਕੀ ਬਚੇ ਪਾਣੀ ਦਾ ਆਇਤਨ
= 1.131 m³

ਪ੍ਰਸ਼ਨ 8.
ਇੱਕ ਗੋਲਾਕਾਰ ਕੱਚ ਦੇ ਬਰਤਨ ਦੀ ਇੱਕ ਬੇਲਣ ਦੇ ਆਕਾਰ ਦੀ ਗਰਦਨ ਹੈ ਜਿਸ ਦੀ ਲੰਬਾਈ 8 cm ਹੈ ਅਤੇ ਵਿਆਸ 2 cm ਹੈ ਜਦੋਂ ਕਿ ਗੋਲਾਕਾਰ ਭਾਗ ਦਾ ਵਿਆਸ 8.5 cm ਹੈ । ਇਸ ਵਿੱਚ ਭਰੇ ਜਾ ਸਕਣ ਵਾਲੇ ਪਾਣੀ ਦੀ ਮਾਤਰਾ ਮਾਪ ਕੇ, ਇੱਕ ਬੱਚੇ ਨੇ ਇਹ ਪਤਾ ਕੀਤਾ ਕਿ ਇਸ ਬਰਤਨ ਦਾ ਆਇਤਨ 345 cm³ ਹੈ । ਜਾਂਚ ਕਰੋ ਕਿ ਉਸ | ਬੱਚੇ ਦਾ ਉੱਤਰ ਸਹੀ ਹੈ ਜਾਂ ਨਹੀਂ, ਇਹ ਮੰਨਦੇ ਹੋਏ ਕਿ ਉਪਰੋਕਤ ਮਾਪਣ ਅੰਦਰੂਨੀ ਮਾਪਣ ਹੈ ਅਤੇ π = 3.14।
ਹੱਲ:
ਗਰਦਨ ਦਾ ਵਿਆਸ ਬਿਲਣਾਕਾਰ ਭਾਗ) = 2 cm

∴ ਗਰਦਨ ਦਾ ਅਰਧ ਵਿਆਸ (r) = 1 cm
ਬੇਲਣਾਕਾਰ ਭਾਗ ਦੀ ਉੱਚਾਈ (H) = 8 cm
ਗੋਲਾਕਾਰ ਭਾਗ ਦਾ ਵਿਆਸ = 8.5 cm
ਗੋਲਾਕਾਰ ਭਾਗ ਦਾ ਅਰਧ ਵਿਆਸ (R) = \(\frac{8.5}{2}\) cm
= 4.25 cm
ਬਰਤਨ ਵਿਚ ਪਾਣੀ ਦਾ ਆਇਤਨ = ਗੋਲੇ ਦਾ ਆਇਤਨ + ਬੇਲਣ ਦਾ ਆਇਤਨ
= \(\frac{4}{3}\)πR³ + πr²h
= (\(\frac{4}{3}\) × 3.14 × 4.25 × 4.25 + 2.25 + 3.14 × 1 × 1 × 8) cm³
= (321.39 + 25.12) cm³
= 346.51 cm³
ਬਰਤਨ ਵਿਚ ਪਾਣੀ ਦਾ ਆਇਤਨ = 346.51 cm³ ਉਹ ਗਲਤ ਹੈ।

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 13 ਸਤੁਦਾ ਖੇਤਰਫਲ ਅਤੇ ਆਇਤਨ Ex 13.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 13 ਸਤੁਦਾ ਖੇਤਰਫਲ ਅਤੇ ਆਇਤਨ Exercise 13.4

(ਜਦੋਂ ਤੱਕ ਕਿਹਾ ਨਾ ਜਾਵੇ, π = \(\frac{22}{7}\) ਲਓ )

ਪ੍ਰਸ਼ਨ 1.
ਪਾਣੀ ਪੀਣ ਵਾਲਾ ਇੱਕ ਗਿਲਾਸ 14 cm ਉੱਚਾਈ | ਵਾਲੇ ਇੱਕ ਸ਼ੰਭੂ ਦੇ ਸ਼ੌਨਕ ਦੇ ਆਕਾਰ ਦਾ ਹੈ । ਦੋਨਾਂ ਚੱਕਰਾਕਾਰ ਸਿਰਿਆਂ ਦੇ ਵਿਆਸ 4 cm ਅਤੇ 2 cm ਹਨ । ਇਸ ਗਿਲਾਸ ਦੀ ਧਾਰਨ ਸਮਰੱਥਾ ਪਤਾ ਕਰੋ ।
ਹੱਲ:

ਉੱਪਰੀ ਸਿਰੇ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 2 cm
ਹੇਠਲੇ ਸਿਰੇ ਦਾ ਅਰਧ ਵਿਆਸ (r) = 1 cm
ਗਿਲਾਸ ਦੀ ਉੱਚਾਈ (H) = 14 cm
ਗਿਲਾਸ ਸ਼ੌਨਕ ਦੇ ਆਕਾਰ ਦਾ ਹੈ
ਸ਼ੌਨਕ ਦਾ ਆਇਤਨ
= \(\frac{1}{3}\)π[R² + r² + Rr]H
= \(\frac{1}{3}\) × \(\frac{22}{7}\)[(2)² + (1)² + 2 × 1]14 cm³
= \(\frac{1}{3}\) × \(\frac{22}{7}\)[4 + 1 + 2] 14 cm³
= \(\frac{1}{3}\) ×\(\frac{22}{7}\) × 7 × 14 cm³
= \(\frac{2214}{3}\) cm³ = 102.67 cm³
ਗਿਲਾਸ ਦੀ ਧਾਰਨ ਸਮਰੱਥਾ = 102.67 cm³

ਪ੍ਰਸ਼ਨ 2.
ਇੱਕ ਸ਼ੰਕੂ ਦੇ ਸ਼ੌਨਕ ਦੀ ਤਿਰਛੀ ਉੱਚਾਈ 4 cm ਹੈ ਅਤੇ ਇਸਦੇ ਚੱਕਰੀ ਸਿਰਿਆਂ ਦੇ ਪਰਿਮਾਪ (ਘੇਰਾ) 18 cm ਅਤੇ 6 cm ਹਨ ।ਇਸ ਛਿੰਕ ਦੀ ਵਕਰ ਸਤਾ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਛਿਨਕ ਦੀ ਤਿਰਛੀ ਉੱਚਾਈ (l) = 4 cm

ਮੰਨ ਲਉ ਉੱਪਰੀ ਸਿਰੇ ਅਤੇ ਹੇਠਲੇ ਸਿਰੇ ਦਾ ਅਰਧ ਵਿਆਸ R ਅਤੇ r ਹੈ ।
ਉੱਪਰਲੇ ਸਿਰੇ ਦਾ ਪਰਿਮਾਪੁ = 18 cm
2πR = 18
R = \(\frac{18}{2 \pi}\) = \(\frac{9}{\pi}\) cm
ਹੇਠਲੇ ਸਿਰੇ ਦਾ ਪਰਿਮਾਪ = 6 cm
2πr = 6 cm
r = \(\frac{6}{2 \pi}\) = \(\frac{3}{\pi}\) cm
ਜ਼ਿੰਕ ਦੀ ਵਕਰ ਸੜਾ ਦਾ ਖੇਤਰਫਲ
= π[R + r]l
= π[\(\frac{9}{\pi}\) + \(\frac{3}{\pi}\)] 4 cm²
= 4[latex]\frac{9+3}{\pi}[/latex] 4 cm²
= 12 × 4 cm²
= 48 cm²
ਸ਼ੌਨਕ ਦੀ ਵਕਰ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ
= 48 cm²

ਪ੍ਰਸ਼ਨ 3.
ਇੱਕ ਤੁਰਕੀ ਟੋਪੀ ਸ਼ੰਕੁ ਦੇ ਇੱਕ ਛਿਨਕ ਦੇ ਆਕਾਰ ਦੀ ਹੈ । (ਦੇਖੋ ਚਿੱਤਰ) ਜੇਕਰ ਇਸਦੇ ਖੁੱਲ੍ਹੇ ਸਿਰੇ ਦਾ ਅਰਧ ਵਿਆਸ 10 cm ਹੈ, ਉਪਰੀ ਸਿਰੇ ਦਾ ਅਰਧ ਵਿਆਸ 4 cm ਹੈ ਅਤੇ ਟੋਪੀ ਦੀ ਤਿਰਛੀ ਉੱਚਾਈ 15 cm ਹੈ, ਤਾਂ ਇਸ ਦੇ ਬਣਾਉਣ ਲਈ ਲੱਗੇ ਪਦਾਰਥ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।

ਹੱਲ:

15cm
ਸ਼ੌਨਕ ਦੇ ਹੇਠਲੇ ਸਿਰੇ ਦਾ ਅਰਧਵਿਆਸ (R) = 10 cm
ਸ਼ੌਨਕ ਉੱਪਰਲੇ ਸਿਰੇ ਦਾ ਅਰਧਵਿਆਸ (r) =4 cm
ਛਿਨਕ ਦੀ ਤਿਰਛੀ ਉੱਚਾਈ (l) = 15 cm
ਛਿਨਕ ਦੀ ਵਕਰ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ
= πl[R + r]
=\(\frac{22}{7}\) × 15[10 + 4] cm²
= \(\frac{22}{7}\) × 15 × 14 cm²
= 22 × 15 × 2 cm²
= 660 cm²
ਬੰਦ ਸਿਰੇ ਦਾ ਖੇਤਰਫਲ = πr² = \(\frac{22}{7}\) × (4)² cm²
= \(\frac{22}{7}\) × 4 × 4cm² = \(\frac{352}{7}\) cm
ਲੋੜੀਂਦੇ ਪਦਾਰਥ ਦਾ ਕੁੱਲ ਖੇਤਰਫਲ
= ਛਿਨਕ ਦੀ ਵਕਰ ਸਤਾ ਦਾ ਖੇਤਰਫਲ + ਬੰਦ ਸਿਰੇ ਦਾ ਖੇਤਰਫਲ
= (660 + 50.28) cm²
= 710.28 cm²

ਪ੍ਰਸ਼ਨ 4.
ਧਾਤੂ ਦੀ ਚਾਦਰ ਨਾਲ ਬਣਿਆ ਅਤੇ ਉੱਪਰ ਤੋਂ ਖੁਲਿਆ ਇੱਕ ਬਰਤਨ ਸ਼ੰਕੂ ਦੇ ਇੱਕ ਛਿਨਕ ਦੇ ਆਕਾਰ ਦਾ ਹੈ, ਜਿਸਦੀ ਉੱਚਾਈ 16 cm ਹੈ ਅਤੇ ਹੇਠਲੇ ਅਤੇ ਉੱਪਰੀ ਸਿਰਿਆਂ ਦੇ ਅਰਧ ਵਿਆਸ ਕੁਮਵਾਰ 8 cm ਅਤੇ 20 cm ਹਨ । ₹ 20 ਪ੍ਰਤਿ ਲਿਟਰ ਦੀ ਦਰ ਨਾਲ, ਇਸ ਬਰਤਨ ਨੂੰ ਪੂਰਾ ਭਰ ਸਕਣ ਵਾਲੇ ਦੁੱਧ ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ । ਨਾਲ ਹੀ, ਇਸ ਬਰਤਨ ਨੂੰ ਬਣਾਉਣ ਦੇ ਲਈ ਪ੍ਰਯੋਗ ਕੀਤੀ ਧਾਤੂ ਦੀ ਚਾਦਰ ਦਾ ਮੁੱਲ ₹ 8 ਤਿ 100 cm² ਦੀ ਦਰ ਨਾਲ ਪਤਾ ਕਰੋ । (π = 3.14 ਲਓ)
ਹੱਲ:

ਬਰਤਨ ਦੇ ਉੱਪਰੀ ਸਿਰੇ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 20 cm
ਹੇਠਲੇ ਸਿਰੇ ਦਾ ਅਰਧ ਵਿਆਸ (r) = 8 cm
ਬਰਤਨ ਦੀ ਉੱਚਾਈ (H) = 16 cm
ਤਿਰਛੀ ਉੱਚਾਈ (l) =\(\sqrt{\mathrm{H}^{2}+(\mathrm{R}-r)^{2}}\)
= \(\sqrt{(16)^{2}+(20-8)^{2}}\)
= \(\sqrt {256+144}\)
(l) = \(\sqrt {400}\) = \(\sqrt {20×20}\) cm
= 20 cm
ਬਰਤਨ ਦੀ ਧਾਰਿਤਾ = \(\frac{1}{3}\) πH[R² + r² + Rr²]
= \(\frac{1}{3}\) × 3.14 × 16[(20)² + (8)² + 20 × 8]
= \(\frac{3.14×16}{3}\)[400 + 64 + 160] cm³
= 3.14 × 16 × 624 cm³
= 10449.92 cm³
∴ ਬਰਤਨ ਵਿਚ ਦੁੱਧ ਦਾ ਆਇਤਨ
= 10449.92 cm³
= \(\frac{10449.92}{1000}\) ਲਿਟਰ
∴ ਬਰਤਨ ਵਿਚ ਦੁੱਧ ਦਾ ਆਇਤਨ = 10.45 ਲਿਟਰ
1 ਲਿਟਰ ਦਾ ਮੁੱਲ = ₹ 20
∴ 10.45 ਲਿਟਰ ਦਾ ਮੁੱਲ = ₹ 20 × 10.45
ਦੁੱਧ ਦਾ ਮੁੱਲ = ₹ 209
ਸ਼ੌਨਕ ਦੀ ਵਿਕਰ ਸਤਾ ਦਾ ਖੇਤਰਫਲ
= πL [R + r]
= 3:14 × 20 [20 + 8]
= 3.14 × 20 × 28 cm²
= 1758.4 cm²
ਬਰਤਨ ਦੇ ਆਧਾਰ ਦਾ ਖੇਤਰਫਲ = πr²
= 3.14 × (8)²
= 3.14 × 64
= 200.96 cm²
ਬਰਤਨ ਬਣਾਉਣ ਲਈ ਪ੍ਰਯੋਗ ਕੀਤੀ ਧਾਤੂ ਦੀ ਚਾਦਰ ਦਾ ਖੇਤਰਫਲ = ਸ਼ੌਨਕ ਦੀ ਵਕਰ ਸੜਾ ਦਾ ਖੇਤਰਫਲ + ਆਧਾਰ ਦਾ ਖੇਤਰਫਲ :
= (1758. 4 + 200.96) cm²
= 1959.36 cm²
100 cm² ਧਾਤੂ ਦੀ ਚਾਦਰ ਦਾ ਮੁੱਲ = ₹ 8
1 cm² ਧਾਤੂ ਦੀ ਚਾਦਰ ਦਾ ਮੁੱਲ = ₹ \(\frac{8}{10}\)
1959.36 cm² ਧਾਤੂ ਦੀ ਚਾਦਰ ਦਾ ਮੁੱਲ
= ₹ \(\frac{8}{100}\) × 1959.36
= ₹ 156.748
= ₹ 15675
ਧਾਤੂ ਦੀ ਚਾਦਰ ਦਾ ਕੁੱਲ ਮੁੱਲ
= ₹ 156.75
ਦੁੱਧ ਤੇ ਕੁੱਲ ਲਾਗਤ ਤੋਂ 209

ਪ੍ਰਸ਼ਨ 5.
20 cm ਉੱਚਾਈ ਅਤੇ ਸਿਖ਼ਰ ਕੋਣ (Vertical angle) 60° ਵਾਲੇ ਇੱਕ ਸ਼ੰਕੂ ਨੂੰ ਉਸਦੀ ਉੱਚਾਈ ਦੇ ਵਿੱਚਕਾਰ ਤੋਂ ਹੋ ਕੇ ਜਾਂਦੇ ਇੱਕ ਤਲ ਨਾਲ ਦੋ ਭਾਗਾਂ ਵਿੱਚ ਕੱਟਿਆ ਗਿਆ ਹੈ, ਜਦੋਂ ਕਿ ਤਲ ਸ਼ੰਕੂ ਦੇ ਆਧਾਰ ਦੇ ਸਮਾਂਤਰ ਹੈ । ਜੇਕਰ ਇਸ ਪ੍ਰਾਪਤ ਸ਼ੰਕੂ ਦੇ ਸ਼ੌਕ ਨੂੰ ਵਿਆਸ \(\frac{1}{16}\) cm ਵਾਲੇ ਇੱਕ ਤਾਰ ਦੇ ਰੂਪ ਵਿੱਚ ਬਦਲ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ਤਾਂ ਤਾਰ ਦੀ ਲੰਬਾਈ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਸ਼ੰਕੂ ਦੇ ਸਿਖਰ ਦਾ ਕੋਣ = 60°
ਸ਼ੰਕੂ ਦਾ ਸਿਖਰਲੰਬ ਸਿਖ਼ਰ ਕੋਣ ਨੂੰ ਸਮਦੁਭਾਜਿਤ ਕਰਦਾ ਹੈ
∠EOF = 30°

△ODB ਵਿਚ,
\(\frac{BD}{OD}\) = tan 30°
\(\frac{r}{10}\) = \(\frac{1}{\sqrt{3}}\)
r = \(\frac{1o}{\sqrt{3}}\) cm
△OEF ਵਿਚ,
\(\frac{EF}{OE}\) = tan 30°
\(\frac{R}{20}\) = \(\frac{1}{\sqrt{3}}\)
R = \(\frac{20}{\sqrt{3}}\) cm

ਛਿਨਕ ਦੀ ਤਾਰ ਬਣਾਈ ਗਈ ਹੈ ਜੋ ਬੇਲਣ ਆਕਾਰ ਦੀ ਹੈ ਜਿਸਦਾ ਵਿਆਸ \(\frac{1}{16}\) cm ਹੈ ।
∴ ਬੇਲਣਾਕਾਰ ਤਾਰ ਦਾ ਅਰਧ ਵਿਆਸ (r₁)
= \(\frac{1}{2}\) × \(\frac{1}{16}\) cm = \(\frac{1}{32}\) cm
ਮੰਨ ਲਉ ਇਸ ਤਰ੍ਹਾਂ ਬਣੇ ਬੇਲਣ ਦੀ ਉੱਚਾਈ = H cm
ਰੂਪ ਬਦਲਣ ‘ਤੇ ਆਇਤਨ ਬਰਾਬਰ ਰਹਿੰਦਾ ਹੈ
ਸ਼ੌਨਕ ਦਾ ਆਇਤਨ = ਬੇਲਣਾਕਾਰ ਤਾਰ ਦਾ ਆਇਤਨ
\(\frac{22}{7}\) × \(\frac{7000}{9}\) = πr₁²H
\(\frac{22}{7}\) × \(\frac{7000}{9}\) = \(\frac{22}{7}\) × \(\left(\frac{1}{32}\right)^{2}\) × H
H = \(\frac{\frac{22}{7} \times \frac{7000}{9}}{\frac{22}{7} \times \frac{1}{32} \times \frac{1}{32}}\) cm
= \(\frac{7000}{9}\) × 32 × 32 cm
H = \(\frac{796444.44}{100}\) m
H = 7964.44 m
∴ ਬੇਲਣਾਕਾਰ ਤਾਰ ਦੀ ਲੰਬਾਈ
H = 7964.44 m

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 13 ਸਤੁਦਾ ਖੇਤਰਫਲ ਅਤੇ ਆਇਤਨ Ex 13.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 13 ਸਤੁਦਾ ਖੇਤਰਫਲ ਅਤੇ ਆਇਤਨ Exercise 13.3

ਜਦੋਂ ਤੱਕ ਕਿਹਾ ਨਾ ਜਾਵੇ, π = \(\frac{22}{7}\) ਲਓ।

ਪ੍ਰਸ਼ਨ 1.
ਅਰਧ ਵਿਆਸ 4.2 cm ਵਾਲੇ ਧਾਤੂ ਦੇ ਇੱਕ ਗੋਲੇ ਨੂੰ ਪਿਘਲਾ ਕੇ ਅਰਧ ਵਿਆਸ 6 cm ਵਾਲੇ ਇੱਕ ਬੇਲਣ ਦੇ ਰੂਪ ਵਿੱਚ ਢਾਲਿਆ ਜਾਂਦਾ ਹੈ । ਬੇਲਣ ਦੀ ਉੱਚਾਈ ਪਤਾ ਕਰੋ ।
ਹੱਲ:

ਗੋਲੇ ਦਾ ਅਰਧ ਵਿਆਸ (r) = 4.2 cm
ਬੋਲਣ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 6 cm
ਮੰਨ ਲਉ ਬੇਲਣ ਦੀ ਉੱਚਾਈ = H cm
ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ,
ਗੋਲੇ ਦਾ ਆਇਤਨ = ਬੇਲਣ ਦਾ ਆਇਤਨ
\(\frac{4}{3}\)πr³ = πR²H
\(\frac{4}{3}\) × \(\frac{22}{7}\) × 4.2 × 4.2 × 4.2
= \(\frac{22}{7}\) × 6 × 6 × H

= \(\frac{2744}{1000}\) = 2.744 cm
ਬੇਲਣ ਦੀ ਉੱਚਾਈ (H) = 2744 cm

ਪ੍ਰਸ਼ਨ 2.
ਕ੍ਰਮਵਾਰ : 6 cm, 8 cm ਅਤੇ 10 cm ਅਰਧ ਵਿਆਸ ਵਾਲੇ ਧਾਤੂ ਦੇ ਤਿੰਨ ਠੋਸ ਗੋਲਿਆਂ ਨੂੰ ਪਿਘਲਾ ਕੇ ਇੱਕ ਵੱਡਾ ਠੋਸ ਗੋਲਾ ਬਣਾਇਆ ਜਾਂਦਾ ਹੈ ਇਸ ਗੋਲੇ ਦਾ ਅਰਧ ਵਿਆਸ ਪਤਾ ਕਰੋ ।
ਹੱਲ:

ਪਹਿਲੇ ਗੋਲੇ ਦਾ ਅਰਧ ਵਿਆਸ (r₁) = 6 cm
ਦੂਸਰੇ ਗੋਲੇ ਦਾ ਅਰਧ ਵਿਆਸ (r₂) = 8 cm
ਤੀਸਰੇ ਗੋਲੇ ਦਾ ਅਰਧ ਵਿਆਸ (r₃) = 10 cm
ਮੰਨ ਲਉ ਨਵੇਂ ਗੋਲੇ ਦਾ ਅਰਧ ਵਿਆਸ = R cm
ਤਿੰਨਾਂ ਗੋਲਿਆਂ ਦਾ ਆਇਤਨ = ਵੱਡੇ ਗੋਲੇ ਦਾ ਆਇਤਨ

= 2 × 2 × 3 cm
R = 12 cm
∴ ਗੋਲੇ ਦਾ ਅਰਧ ਵਿਆਸ = 12 cm

ਪ੍ਰਸ਼ਨ 3.
ਵਿਆਸ 7 m ਵਾਲਾ ਇੱਕ ਖੁਹ 20 m ਡੂੰਘਾ ਪੁੱਟਿਆ ਜਾਂਦਾ ਹੈ ਅਤੇ ਪੁੱਟਣ ਨਾਲ ਨਿਕਲੀ ਹੋਈ ਮਿੱਟੀ ਨੂੰ ਇੱਕੋ ਜਿਹੇ | ਰੂਪ ਵਿੱਚ ਫੈਲਾ ਕੇ 22 m × 14 m ਵਾਲਾ ਇੱਕ ਚਬੂਤਰਾ | ਬਣਾਇਆ ਗਿਆ ਹੈ | ਚਬੂਤਰੇ ਦੀ ਉੱਚਾਈ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਖੂਹ ਦਾ ਵਿਆਸ = 7 m
ਖੂਹ (ਬੇਲਣ ਦਾ ਅਰਧ ਵਿਆਸ) R = 6 m
ਖੂਹ ਦੀ ਉੱਚਾਈ (H) = 20 m
ਚਬੂਤਰੇ ਦੀ ਲੰਬਾਈ (L) = 22 m
ਦੇ ਚਬੂਤਰੇ ਦੀ ਚੌੜਾਈ (B) = 14 m
ਮੰਨ ਲਓ ਚਬੂਤਰੇ ਦਾ ਅਰਧ ਵਿਆਸ = H m

ਖੂਹ ਵਿਚੋਂ ਨਿਕਲੀ ਮਿੱਟੀ ਦਾ ਆਇਤਨ = ਬਣਾਏ ਗਏ ਚਬੂਤਰੇ ਦਾ ਆਇਤਨ

πR²H = L × B × H
\(\frac{22}{7}\) × \(\frac{7}{2}\) × \(\frac{7}{2}\) × 20 = 22 × 14 × h
∴ H = \(\frac{\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2} \times 20}{22 \times 14}\)
H = 2.5 cm
∴ ਚਬੂਤਰੇ ਦੀ ਉੱਚਾਈ H = 2.5 cm.

ਪ੍ਰਸ਼ਨ 4.
3 m ਵਿਆਸ ਦਾ ਇੱਕ ਖੁਹ 14 m ਦੀ ਗਹਿਰਾਈ ਡੂੰਘਾਈ) ਤੱਕ ਪੁੱਟਿਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਵਿੱਚੋਂ ਨਿਕਲੀ ਹੋਈ ਮਿੱਟੀ ਨੂੰ ਖੂਹ ਦੇ ਚਾਰੇ ਪਾਸੇ 4m ਚੌੜੀ ਇੱਕ ਚੱਕਰਾਕਾਰ ਚਬੂਤਰਾ (ring) ਬਣਾਉਂਦੇ ਹੋਏ, ਸਮਾਨ ਰੂਪ ਨਾਲ ਫੈਲਾ ਕੇ ਇੱਕ ਪ੍ਰਕਾਰ ਦਾ ਬੰਨ ਬਣਾਇਆ ਜਾਂਦਾ ਹੈ। ਬੰਨ ਦੀ ਉੱਚਾਈ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਖੂਹ ਦੀ ਗਹਿਰਾਈ (h) = 14
ਖੂਹ ਦਾ ਅਰਧ ਵਿਆਸ (P) = \(\frac{3}{2}\) m

ਬੰਨ ਖੋਖਲੇ ਬੇਲਣ ਦੇ ਆਕਾਰ ਦਾ ਹੈ ਜਿਸਦਾ ਅੰਦਰੂਨੀ ਅਰਧ ਵਿਆਸ ਖੂਹ ਦੇ ਅਰਧ ਵਿਆਸ ਦੇ ਬਰਾਬਰ ਹੈ ਅਤੇ ਬੰਨ ਦੀ ਚੌੜਾਈ 4 m ਹੈ ।
ਬੰਨ ਦੇ ਅੰਦਰਲਾ ਅਰਧ ਵਿਆਸ (r)
= ਖੂਹ ਦਾ ਅਰਧ ਵਿਆਸ (r) = \(\frac{3}{2}\) m
ਬੰਨ ਦਾ ਬਾਹਰੀ ਅਰਧ ਵਿਆਸ (R)
= (\(\frac{3}{2}\) + 4) m
R = \(\frac{11}{2}\) m
= 5.5 m
ਨਿਕਲੀ ਹੋਈ ਮਿੱਟੀ ਦਾ ਆਇਤਨ
= ਬਣੇ ਹੋਏ ਬੰਨਦਾ ਆਇਤਨ
πr²h = ਬਾਹਰੀ ਬੇਲਣ ਦਾ ਆਇਤਨ – ਅੰਦਰੂਨੀ ਬੇਲਣ ਦਾ ਆਇਤਨ
= πR²H – πr²H
= πH[R² – r²]
\(\frac{22}{7}\) × \(\frac{3}{2}\) × \(\frac{3}{2}\) × 14
= \(\frac{22}{7}\) × H[(5.5)² – (1.5)²]
H = \(=\frac{\frac{22}{7} \times \frac{3}{2} \times \frac{3}{2} \times 14}{\frac{22}{7} \times(5.5-1.5)(5.5+1.5)}\) m
= \(\frac{1.5 \times 1.5 \times 14}{4 \times 7}\) m
= 1.125 m
∴ ਬੰਨ ਦੀ ਉੱਚਾਈ H = 1.125 m

ਪ੍ਰਸ਼ਨ 5.
12 cm ਵਿਆਸ ਅਤੇ 15 cm ਉੱਚਾਈ ਵਾਲੇ ਇੱਕ । ਲੰਬ ਚੱਕਰੀ ਬੇਲਣ ਦੇ ਆਕਾਰ ਦਾ ਬਰਤਨ ਆਇਸਕੀਮ ਨਾਲ ਪੂਰਾ ਭਰਿਆ ਹੋਇਆ ਹੈ । ਇਸ਼ ਆਇਸਕ੍ਰੀਮ ਦੀ ਉੱਚਾਈ 12 cm ਅਤੇ ਵਿਆਸ 6 cm ਵਾਲੇ ਸ਼ੰਕੂਆਂ ਵਿੱਚ ਭਰਿਆ ਜਾਣਾ ਹੈ, ਜਿਨ੍ਹਾਂ ਦਾ ਉੱਪਰੀ ਸਿਰਾ ਅਰਧ ਗੋਲਾਕਾਰ ਹੋਵੇਗਾ । ਉਨ੍ਹਾਂ ਸ਼ੰਕੂਆਂ ਦੀ ਸੰਖਿਆ ਪਤਾ ਕਰੋ ਜੋ ਇਸ ਆਇਸਕੀਮ ਨਾਲ ਭਰੇ ਜਾ ਸਕਦੇ ਹਨ।
ਹੱਲ:

ਬੇਲਣ ਦਾ ਵਿਆਸ (D) = 12 cm
∴ ਬੇਲਣ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 6 cm
ਬੇਲਣ ਦੀ ਉੱਚਾਈ (H) = 15 cm
ਸ਼ੰਕੂ ਦਾ ਵਿਆਸ = 6 cm
ਸ਼ੰਕੂ ਦਾ ਅਰਧ ਵਿਆਸ (r) = 3 cm
ਅਰਧਗੋਲੇ ਦਾ ਅਰਧ ਵਿਆਸ (r) = 3 cm
ਸ਼ੰਕੂ ਦੀ ਉੱਚਾਈ (h) = 12 cm
ਮੰਨ ਲਉ ਸ਼ੰਕੂਆਂ ਦੀ ਸੰਖਿਆ = n
ਬਰਤਨ ਵਿਚ ਆਇਸਕ੍ਰਿਮ ਦਾ ਆਇਤਨ
= n [ਇੱਕ ਸ਼ੰਕੂ ਦਾ ਆਇਤਨ
πR²H = n
[ਸ਼ੰਕੂ ਦਾ ਆਇਤਨ + ਅਰਧਗੋਲੇ ਦਾ ਆਇਤਨ]

n = 10
ਸ਼ੰਕੂਆਂ ਦੀ ਸੰਖਿਆ = 10

ਪ੍ਰਸ਼ਨ 6.
5.5 cm × 10 cm × 3.5 cm ਪਸਾਰਾਂ ਵਾਲਾ ਇੱਕ ਘਣਾਵ ਬਣਾਉਣ ਦੇ ਲਈ 1.75 cm ਵਿਆਸ ਅਤੇ 2 mm ਮੋਟਾਈ ਵਾਲੇ ਕਿੰਨੇ ਚਾਂਦੀ ਦੇ ਸਿੱਕਿਆਂ (coins) ਨੂੰ ਪਿਘਲਾਉਣਾ ਪਏਗਾ ?
ਹੱਲ:
ਚਾਂਦੀ ਦਾ ਸਿੱਕਾ ਬੇਲਣ ਆਕਾਰ ਦਾ ਹੈ
ਚਾਂਦੀ ਦੇ ਸਿੱਕੇ ਦਾ ਵਿਆਸ = 1.75 cm
∴ ਚਾਂਦੀ ਦੇ ਸਿੱਕੇ ਦਾ ਅਰਧ ਵਿਆਸ (r) = \(\frac{1.75}{2}\) cm
ਚਾਂਦੀ ਦੇ ਸਿੱਕੇ ਦੀ ਮੋਟਾਈ
= ਬੇਲਣ ਦੀ ਉੱਚਾਈ (h) = 2 mm
ਅਰਥਾਤ h = \(\frac{2}{10}\) cm

ਘਣਾਵ ਦੀ ਲੰਬਾਈ (L) = 5.5 cm
ਘਣਾਵ ਦੀ ਚੌੜਾਈ (B) = 10 cm
ਘਣਾਵ ਦੀ ਉਚਾਈ (H) = 3.5 cm

ਮੰਨ ਲਉ ਚਾਂਦੀ ਦੇ ਸਿੱਕਿਆਂ ਨੂੰ ਪਿਘਲਾ ਕੇ ਨਵਾਂ ਘਣਾਵ ਬਣਾਇਆ ਗਿਆ ਹੈ
ਘਣਾਵ ਦਾ ਆਇਤਨ = n[ਚਾਂਦੀ ਦੇ ਸਿੱਕੇ ਦਾ ਆਇਤਨ]
= n[πr²h]

= 400
ਬਣੇ ਚਾਂਦੀ ਦੇ ਸਿੱਕਿਆਂ ਦੀ ਸੰਖਿਆ = 400

ਪ੍ਰਸ਼ਨ 7.
32 cm ਉੱਚੀ ਅਤੇ 18 cm ਆਧਾਰ ਦੇ ਅਰਧ ਵਿਆਸ ਵਾਲੀ ਇੱਕ ਬੇਲਣਾਕਾਰ ਬਾਲਟੀ ਰੇਤ ਨਾਲ ਭਰੀ ਹੋਈ ਹੈ । ਇਸ ਬਾਲਟੀ ਨੂੰ ਭੂਮੀ ‘ਤੇ ਖਾਲੀ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ਅਤੇ ਇਸ ਰੇਤ ਦੀ ਇੱਕ ਸ਼ੰਕੂ ਆਕਾਰ ਢੇਰੀ ਬਣਾਈ ਜਾਂਦੀ ਹੈ । ਜੇਕਰ ਸ਼ੰਕੁ ਆਕਾਰ ਢੇਰੀ ਦੀ ਉੱਚਾਈ 24 cm ਹੈ, ਤਾਂ ਇਸ ਢੇਰੀ ਦਾ ਅਰਧ ਵਿਆਸ ਅਤੇ ਤਿਰਛੀ ਉੱਚਾਈ ਪਤਾ ਕਰੋ ।
ਹੱਲ:

ਬੇਲਣਾਕਾਰ ਬਾਲਟੀ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 18 cm
ਬੇਲਣਾਕਾਰ ਬਾਲਟੀ ਦੀ ਉੱਚਾਈ (H) = 32 cm
ਸ਼ੰਕੂ ਦੀ ਉੱਚਾਈ (h) = 24 cm
ਮੰਨ ਲਉ ਸ਼ੰਕੂ ਦਾ ਅਰਧ ਵਿਆਸ ਅਤੇ ਢੇਰੀ ਦੀ ਤਿਰਛੀ ਉੱਚਾਈ ‘r’ cm ਅਤੇ ‘l’ cm ਹੈ ।
ਬਾਲਟੀ ਵਿਚ ਰੇਤ ਦਾ ਆਇਤਨ = ਸ਼ੰਕੂ ਵਿੱਚ ਰੇਤ ਦਾ ਆਇਤਨ

r² = 1296
r = \(\sqrt {1296}\) cm
r = 36 cm
∴ ਕੂ ਦਾ ਅਰਧ ਵਿਆਸ (r) = 36 cm
ਜਿਵੇਂ ਕਿ ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ
(ਤਿਰਛੀ ਉੱਚਾਈ)² = (ਅਰਧਵਿਆਸ)² + (ਉੱਚਾਈ)²
l² = r² + h²
l = \(\sqrt{(36)^{2}+(24)^{2}}\)
= \(\sqrt {1296+576}\)
= \(\sqrt {1872}\)
= \(\sqrt {12×12×13}\)
l = 12\(\sqrt {13}\) cm
∴ ਸ਼ੰਕੂ ਦੀ ਤਿਰਛੀ ਉੱਚਾਈ (l) = 12\(\sqrt {13}\) cm

ਪ੍ਰਸ਼ਨ 8.
6 m ਚੌੜੀ ਅਤੇ 1.5 m ਗਹਿਰੀ (ਡੂੰਘੀ) ਇੱਕ ਨਹਿਰ ਵਿੱਚ ਪਾਣੀ 10 km/h ਦੀ ਚਾਲ ਨਾਲ ਵਹਿ (ਚੱਲ) ਰਿਹਾ ਹੈ ।30 ਮਿੰਟ ਵਿੱਚ, ਇਹ ਨਹਿਰ ਕਿੰਨੇ ਖੇਤਰਫਲ ਦੀ ਸਿੰਚਾਈ ਕਰ ਸਕੇਗੀ, ਜਦਕਿ ਸਿੰਚਾਈ ਦੇ ਲਈ 8 cm ਡੂੰਘੇ ਪਾਣੀ ਦੀ ਜ਼ਰੂਰਤ ਹੁੰਦੀ ਹੈ ।
ਹੱਲ:
ਨਹਿਰ ਦੀ ਚੌੜਾਈ = 6 m
ਨਹਿਰ ਵਿੱਚ ਪਾਣੀ ਦੀ ਡੂੰਘਾਈ = 1.5 m
ਜਿਸ ਚਾਲ ਨਾਲ ਪਾਣੀ ਚਲ ਰਿਹਾ ਹੈ = 10 km/hr
ਇੱਕ ਘੰਟੇ ਵਿੱਚ ਨਿਕਲੇ ਪਾਣੀ ਦਾ ਆਇਤਨ = ਇਕ ਘੰਟੇ ਵਿੱਚ ਨਿਕਲੇ ਪਾਣੀ ਦੀ ਚਾਲ
= (6 × 1.5 m²) × 10 km
= 6 × 1.5 × 10 × 10 × 1000 m³.
∴ \(\frac{1}{2}\) ਘੰਟੇ ਵਿੱਚ ਨਿਕਲੇ ਪਾਣੀ ਦਾ ਆਇਤਨ
\(\frac{1}{2}\) × \(\frac{6×15}{10}\) × 100000
= 450000 m³
ਮੰਨ ਲਉ ਸਿੰਚਾਈ ਦਾ ਖੇਤਰਫਲ = (x) m²
ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ ਖੇਤ ਵਿੱਚ 8 cm ਗਹਿਰੇ ਪਾਣੀ ਦੀ ਲੋੜ
∴ \(\frac{1}{2}\) ਘੰਟੇ ਵਿਚ ਨਿਕਲੇ ਪਾਣੀ ਦਾ ਆਇਤਨ ਹੈ
= ਖੇਤ ਵਿੱਚ ਪਾਣੀ ਦਾ ਆਇਤਨ
450000 m³ = (ਖੇਤ ਦਾ ਖੇਤਰਫਲ) × ਪਾਣੀ ਦੀ ਉੱਚਾਈ
450000 m³ = x × (m)
\(\frac{450000}{8}\) × 100 = x
x = 562500 m²
x = \(\frac{562500}{10000}\) ਹੈਕਟੇਅਰ
[1 m² = \(\frac{1}{10000}\) ਹੈਕਟੇਅਰ]
x = 56.25 ਹੈਕਟੇਅਰ
∴ ਖੇਤ ਦਾ ਖੇਤਰਫਲ = 56.25 ਹੈਕਟੇਅਰ

ਪ੍ਰਸ਼ਨ 9.
ਇੱਕ ਕਿਸਾਨ ਆਪਣੇ ਖੇਤ ਵਿਚ ਬਣੀ 10 m ਵਿਆਸ ਵਾਲੀ ਅਤੇ 2 m ਡੂੰਘੀ ਇੱਕ ਬੇਲਣਾਕਾਰ ਟੈਂਕੀ ਨੂੰ ਅੰਦਰੂਨੀ ਵਿਆਸ 20 cm ਵਾਲੇ ਇੱਕ ਪਾਇਪ ਦੁਆਰਾ ਇੱਕ ਨਹਿਰ ਨਾਲ ਜੋੜਦਾ ਹੈ। ਜੇਕਰ ਪਾਇਪ ਵਿੱਚ ਪਾਣੀ 3 km/h ਦੀ । ਚਾਲ ਨਾਲ ਚੱਲ (ਵਹਿ ਰਿਹਾ ਹੈ ਤਾਂ ਕਿੰਨੇ ਸਮੇਂ ਬਾਅਦ ਟੈਂਕੀ ਭਰ ਜਾਵੇਗੀ ?
ਹੱਲ:
ਪਾਣੀ ਦੀ ਚਾਲ = 3 km/hr
ਪਾਇਪ ਦਾ ਅੰਦਰੂਨੀ ਵਿਆਸ = 20 cm
∴ ਪਾਇਪ ਦਾ ਅਰਧ ਵਿਆਸ (r) = 10 cm = \(\frac{10}{100}\) m
= \(\frac{1}{10}\) m
ਟੈਂਕੀ ਦਾ ਵਿਆਸ = 10 m
ਟੈਂਕੀ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 5 m
ਟੈਂਕੀ ਦੀ ਡੂੰਘਾਈ (H) = 2 m
ਮੰਨ ਲਉ ਪਾਇਪ n ਮਿੰਟਾਂ ਵਿਚ ਟੰਕੀ ਭਰਦੀ ਹੈ ਟੈਂਕੀ ਵਿਚ ਪਾਣੀ ਦਾ ਆਇਤਨ
= ਪਾਇਪ ਦੁਆਰਾ n ਮਿੰਟਾਂ ਵਿੱਚ ਚੱਕਿਆ ਪਾਣੀ
πR²H = n [ਅੰਦਰੂਨੀ ਕਾਟ ਦਾ ਖੇਤਰਫਲ × ਪਾਣੀ ਦੀ ਚਾਲੀ]
πR²H = n[(πr²) × 3 km/h]
\(\frac{22}{7}\) × (5)² × 2
= n[\(\frac{22}{7}\) × \(\frac{1}{10}\) × \(\frac{1}{10}\) × \(\frac{31000}{60}\)]
= 25 × 2
= n\(\frac{1}{10}\) × 50
⇒ n = 100 ਮਿੰਟ
∴ ਟੈਂਕੀ ਨੂੰ ਭਰਨ ਵਿਚ ਲੱਗਾ ਸਮਾਂ
= 100 ਮਿੰਟ

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 13 ਸਤੁਦਾ ਖੇਤਰਫਲ ਅਤੇ ਆਇਤਨ Ex 13.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 13 ਸਤੁਦਾ ਖੇਤਰਫਲ ਅਤੇ ਆਇਤਨ Exercise 13.1

ਜਦੋਂ ਤੱਕ ਨਾ ਕਿਹਾ ਜਾਵੇ, π = \(\frac{22}{7}\) ਲਓ ।

ਪ੍ਰਸ਼ਨ 1.
ਦੋ ਘਣ, ਜਿਨ੍ਹਾਂ ਵਿੱਚੋ ਹਰੇਕ ਦਾ ਆਇਤਨ 64 cm³ ਹੈ, ਦੇ ਸਮਾਨ ਫਲਕਾਂ ਨੂੰ ਮਿਲਾ ਕੇ ਇੱਕ ਠੋਸ ਬਣਾਇਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਨਾਲ ਪ੍ਰਾਪਤ ਘਣਾਵ ਦੀ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ ਹਰੇਕ ਘਣ ਦੀ ਭੁਜਾ = 1 cm
ਘਣ ਦਾ ਆਇਤਨ = 64 cm³
[ ਘਣ ਦਾ ਆਇਤਨ = (ਭੁਜਾ)³]

x³ = 64
x = \(\sqrt[3]{64}\)
= \(\sqrt[3]{4 \times 4 \times 4}\) cm
x = 4 cm
∴ ਘਣ ਦੀ ਭੁਜਾ = 4 cm
ਜਦੋਂ ਦੋ ਘਣਾਂ ਨੂੰ ਨਾਲ-ਨਾਲ ਜੋੜਿਆ ਜਾਂਦਾ ਹੈ ਤਾਂ ਘਣਾਵ ਬਣ ਜਾਂਦਾ ਹੈ ।
ਜਿਸਦੀ ਲੰਬਾਈ (L) = 2x cm = 2(4) = 8 cm
ਚੌੜਾਈ (B) = x cm = 4 cm
ਉੱਚਾਈ (H) = x cm = 4 cm

ਘਣਾਵ ਦੀ ਸੰਪੂਰਨ ਸੜਾ ਦਾ ਖੇਤਰਫਲ
= 2[LB + BH + HL]
= 2 [8 × 4 + 4 × 4 + 4 × 8] cm²
= 2 [ 32 + 16 + 32] cm²
= 2 [30] cm²
= 160 cm²

ਪ੍ਰਸ਼ਨ 2.
ਕੋਈ ਬਰਤਨ ਇੱਕ ਖੋਖਲੇ ਅਰਧ ਗੋਲੇ ਦੇ ਆਕਾਰ ਦਾ ਹੈ ਜਿਸਦੇ ਉਪਰ ਇੱਕ ਖੋਖਲਾ ਬੋਲਣ ਲੱਗਿਆ ਹੈ । ਅਰਧ ਗੋਲੇ ਦਾ ਵਿਆਸ 14 cm ਹੈ ਅਤੇ ਇਸ ਬਰਤਨ ਦੀ ਕੁੱਲ ਉੱਚਾਈ 13 cm ਹੈ । ਇਸ ਬਰਤਨ ਦੀ ਅੰਦਰੂਨੀ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਅਰਧ ਗੋਲੇ ਦਾ ਵਿਆਸ = ਬੇਲਣ ਦਾ ਵਿਆਸ
= 14 cm
2R = 14 cm
ਅਰਧ ਗੋਲੇ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 7 cm

ਬਰਤਨ ਦੀ ਕੁੱਲ ਉੱਚਾਈ = 13 cm
∴ ਬੇਲਣ ਦੀ ਉਚਾਈ = (13 – 7) = 6 cm
ਬਰਤਨ ਦੀ ਅੰਦਰੂਨੀ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ = ਬੇਲਣ ਦਾ ਅੰਦਰੂਨੀ ਸੜਾ ਦਾ ਖੇਤਰਫਲ + ਅਰਧ ਗੋਲੇ ਅੰਦਰੂਨੀ ਸਤਾ ਦਾ ਖੇਤਰਫਲ
= 2πRH + 2πR²
= 2πR [H + R]
= 2 × \(\frac{22}{7}\) × 7 (6 + 7) cm²
= 44 × 13 cm²
= 572 cm²
∴ ਬਰਤਨ ਦੀ ਅੰਦਰੂਨੀ ਸੜਾ ਦਾ ਖੇਤਰਫਲ
= 572 cm²

ਪ੍ਰਸ਼ਨ 3.
ਇੱਕ ਖਿਡੌਣਾ ਅਰਧ ਵਿਆਸ 3.5 cm ਵਾਲੇ ਇੱਕ ਸ਼ੰਕੁ ਆਕਾਰ ਦਾ ਹੈ ਜੋ ਉਸੇ ਅਰਧ ਵਿਆਸ ਵਾਲੇ ਇੱਕ ਅਰਧ ਗੋਲੇ ‘ਤੇ ਟਿਕਿਆ ਹੈ । ਇਸ ਖਿਡੌਣੇ ਦੀ ਕੁੱਲ ਉੱਚਾਈ 15.5 cm ਹੈ । ਇਸ ਖਿਡੌਣੇ ਦੀ ਕੁੱਲ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਸ਼ੰਕੁ ਦਾ ਅਰਧ ਵਿਆਸ = ਅਰਧ ਗੋਲੇ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 3.5 cm
ਖਿਡੌਣੇ ਦੀ ਕੁੱਲ ਉੱਚਾਈ = 15.5 cm
∴ ਸ਼ੰਕੂ ਦੀ ਉੱਚਾਈ (H) = (15.5 – 3.5) cm = 12 cm

ਸ਼ੰਕੂ. ਦੀ ਤਿਰਛੀ ਉੱਚਾਈ = \(\sqrt{\mathrm{R}^{2}+\mathrm{H}^{2}}\)
= \(\sqrt{(3.5)^{2}+(12)^{2}}\) cm
= \(\sqrt {1225+144}\) cm
= \(\sqrt {156.25}\) cm
ਸ਼ੰਕੂ ਦੀ ਤਿਰਛੀ ਉੱਚਾਈ (l) = 12.5 cm
ਖਿਡੌਣੇ ਦੀ ਕੁੱਲ ਸਤਾ ਦਾ ਖੇਤਰਫਲ
= ਸ਼ੰਕੁ ਦੀ ਕੁੱਲ ਸੜਾ ਦਾ ਖੇਤਰਫਲ + ਅਰਧ ਗੋਲੇ ਦੀ ਕੁੱਲ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ
= πRL + 2πR²
= πR [L + 2R]
= \(\frac{22}{7}\) × 35 [12.5 + 2 (3.5)] cm
= \(\frac{22}{7}\) × 35 [19.5] cm²
= \(\frac{1501.5}{7}\) cm²
= 214.5 cm²
∴ ਖਿਡੌਣੇ ਦੀ ਕੁੱਲ ਸੜਾ ਦਾ ਖੇਤਰਫਲ
= 214.5 cm²

ਪ੍ਰਸ਼ਨ 4.
ਭੁਜਾ 7 cm ਵਾਲੇ ਇੱਕ ਘਣਾਕਾਰ ਬਲਾਕ ਦੇ ਉੱਪਰ ਇੱਕ ਅਰਧ ਗੋਲਾ ਰੱਖਿਆ ਹੋਇਆ ਹੈ । ਅਰਧ ਗੋਲੇ ਦਾ ਵੱਧ ਤੋਂ ਵੱਧ ਵਿਆਸ ਕੀ ਹੋ ਸਕਦਾ ਹੈ ? ਇਸ ਤਰ੍ਹਾਂ ਬਣੇ ਠੋਸ ਦੀ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਘਣਾਕਾਰ ਬਲਾਕ ਦੀ ਭੁਜਾ = 7 cm

ਅਰਧ ਗੋਲੇ ਦਾ ਵਿਆਸ = ਘਣਾਕਾਰ ਬਲਾਕ ਦੀ ਭੁਜਾ = 7 cm
2R = 7
R = \(\frac{7}{2}\) cm = 3.5 cm
ਬਣੇ ਠੋਸ ਦੀ ਕੁੱਲ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ = ਘਣ ਦੀ ਕੁੱਲ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ + ਅਰਧ ਗੋਲੇ ਦੀ ਕੁੱਲ ਸੜਾ ਦਾ ਖੇਤਰਫਲ
= 6(ਭੁਜਾ)² + 2R²
= 6l² + R²
= 6(7)² + 2 × \(\frac{22}{7}\) × \(\frac{7}{2}\) × \(\frac{7}{2}\) cm²
= 294 + 77 = 371 cm²
ਠੋਸ ਦੀ ਕੁੱਲ ਸੜਾ ਦਾ ਖੇਤਰਫਲ = (ਘਣ ਦੀ ਕੁੱਲ ਸਤਾ ਦਾ ਖੇਤਰਫਲ) – (ਅਰਧ ਗੋਲੇ ਦੇ ਆਧਾਰ ਦਾ ਖੇਤਰਫਲ) + (ਅਰਧ ਗੋਲੇ ਦੀ ਵਕਰ ਸਤਾ ਦਾ ਖੇਤਰਫਲ )
= 6l² – πR² + 2πR²
= 6l² + πR²
= [6(7)² + \(\frac{22}{7}\) × \(\left(\frac{7}{2}\right)^{2}\) ] cm²
= [6(49) + 11 × \(\frac{7}{2}\)] cm²
= 332.5 cm²

ਪ੍ਰਸ਼ਨ 5.
ਇੱਕ ਘਣਾਕਾਰ ਲੱਕੜ ਦੇ ਬਲਾਕ ਦੇ ਇੱਕ ਫਲਕ ਨੂੰ ਅੰਦਰ ਵੱਲ ਕੱਟ ਕੇ ਇੱਕ ਅਰਧ ਗੋਲਾਕਾਰ ਖੱਡਾ ਇਸ ਤਰ੍ਹਾਂ ਬਣਾਇਆ ਗਿਆ ਹੈ ਕਿ ਅਰਧ ਗੋਲੇ ਦਾ ਵਿਆਸ ਘਣ ਦੇ ਇੱਕ ਕਿਨਾਰੇ l ਦੇ ਬਰਾਬਰ ਹੈ । ਬਾਕੀ ਬਚੇ ਠੋਸ ਦੀ ਸਤਾ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ ਘਣ ਦੀ ਭੁਜਾ = a
∴ ਅਰਧ ਗੋਲੇ ਦਾ ਵਿਆਸ = ਘਣ ਦੀ ਭੁਜਾ = a
2R = a
R = \(\frac{a}{2}\)

ਬਾਕੀ ਬਚੇ ਠੋਸ ਦੀ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ = ਘਣ ਦੀ ਕੁੱਲ ਸੜਾ ਦਾ ਖੇਤਰਫਲ – ਘਣ ਦੇ ਆਧਾਰ ਦਾ ਖੇਤਰਫਲ + ਅਰਧ ਗੋਲੇ ਦਾ ਅੰਦਰੂਨੀ ਵਕਰ ਸੜਾ ਦਾ
ਖੇਤਰਫਲ
= 6 (ਭੁਜਾ)² – πR² + 2πR²
= 6(a)² + πR²
= 6(a)² + π\(\left(\frac{a}{2}\right)^{2}\)
= 6a² + π\(\frac{a^{2}}{4}\)
= a²[6 + \(\frac{\pi}{4}\)]

ਪ੍ਰਸ਼ਨ 6.
ਦਵਾਈ ਦਾ ਇੱਕ ਕੈਪਸੂਲ (capsule) ਇੱਕ ਬੇਲਣ ਦੇ ਆਕਾਰ ਦਾ ਹੈ ਜਿਸ ਦੇ ਦੋਨਾਂ ਸਿਰਿਆਂ ‘ਤੇ ਇੱਕ-ਇੱਕ | ਅਰਧ ਗੋਲਾ ਲੱਗਿਆ ਹੋਇਆ ਹੈ । ਦੇਖੋ ਚਿੱਤਰ) ਪੁਰੇ ਕੈਪਸੂਲ ਦੀ ਲੰਬਾਈ 14 mm ਹੈ ਅਤੇ ਉਸ ਦਾ ਵਿਆਸ 5 mm ਹੈ । ਇਸ਼ਦੀ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।

ਹੱਲ:
ਕੈਪਸੁਲ ਦਾ ਵਿਆਸ = ਅਰਧ ਗੋਲੇ ਦਾ ਵਿਆਸ = ਬੇਲਣ ਦਾ ਵਿਆਸ = 5 mm
∴ 2R = 5 mm
R = \(\frac{5}{2}\) mm

ਕੈਪਸੂਲ ਦੀ ਅੰਦਰੂਨੀ ਲੰਬਾਈ = 14 mm
ਬੇਲਣਾਕਾਰ ਭਾਗ ਦੀ ਉੱਚਾਈ = (14 – \(\frac{5}{2}\) – \(\frac{5}{2}\)) mm
= (14 – 5) mm
H = 9 mm
ਕੈਪਸੂਲ ਦੀ ਕੁੱਲ ਸਤਾ ਦਾ ਖੇਤਰਫਲ
= ਬੇਲਣ ਦੀ ਕੁੱਲ ਸਤਾ ਦਾ ਖੇਤਰਫਲ + 2 ਅਰਧ ਗੋਲੇ ਦਾ ਕੁੱਲ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ
= 2πRH + 2(2πR²)
= 2πRH + 4πR²
= 2πR [H + 2R]
= 2 × \(\frac{22}{7}\) × \(\frac{5}{2}\)[9 + 5 ] mm²
= \(\frac{22}{7}\) × 5 × 14 mm²
= 22 × 5 × 2 mm²
= 220 mm²

ਪ੍ਰਸ਼ਨ 7.
ਕੋਈ ਤੰਬੂ ਇੱਕ ਬੇਲਣ ਦੇ ਆਕਾਰ ਦਾ ਹੈ ਜਿਸ ‘ਤੇ ਇੱਕ ਸ਼ੰਕੂ ਬਣਿਆ ਹੋਇਆ ਹੈ । ਜੇਕਰ ਬੇਲਣਾਕਾਰ ਭਾਗ ਦੀ ਉੱਚਾਈ ਅਤੇ ਵਿਆਸ ਕੁਮਵਾਰ 2.1 m ਅਤੇ 4m ਹਨ ਅਤੇ ਸ਼ੰਭ ਦੀ ਤਿਰਛੀ ਉੱਚਾਈ 2.8 m ਹੈ, ਤਾਂ ਇਸ ਤੰਬੂ ਨੂੰ ਬਣਾਉਣ ਲਈ ਵਰਤੇ ਜਾਣ ਵਾਲੇ ਕੈਨਵਸ (canvas) ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ । ਨਾਲ ਹੀ ਤੋਂ 500 ਪ੍ਰਤੀ m² ਦੀ ਦਰ ਨਾਲ ਇਸ ਵਿੱਚ ਵਰਤੋਂ ਹੋਣ ਵਾਲੇ ਕੈਨਵਸ ਦੀ ਲਾਗਤ ਪਤਾ ਕਰੋ । (ਧਿਆਨ ਦਿਉ ਕਿ ਤੰਬੂ ਦੇ ਆਧਾਰ ਨੂੰ ਕੈਨਵਸ ਨਾਲ ਨਹੀਂ ਢੱਕਿਆ ਜਾਂਦਾ ॥
ਹੱਲ:
ਸ਼ੰਕੂ ਦਾ ਵਿਆਸ = ਬੇਲਣ ਦਾ ਵਿਆਸ
2R = 4 m
R = 2 m

ਸ਼ੰਕੂ ਦਾ ਅਰਧ ਵਿਆਸ = ਬੇਲਣ ਦਾ ਅਰਧ ਵਿਆਸ
ਬੇਲਣ ਦੀ ਉੱਚਾਈ (H) = 2.1 m
ਸ਼ੰਕੂ ਦੀ ਤਿਰਛੀ ਉੱਚਾਈ(L) = 2.8m
ਤੰਬੂ ਦੀ ਵਕਰ ਸਤਾ ਦਾ ਖੇਤਰਫਲ
= ਬੇਲਣ ਦੀ ਵਕਰ ਸਤਾ ਦਾ ਖੇਤਰਫਲ + ਸ਼ੰਕੂ ਦੀ ਵਕਰ ਸੜਾ ਦਾ ਖੇਤਰਫਲ
= 2πRH + πRL
= πR [2H + L]
= \(\frac{22}{7}\) × 2[2(21) + 28]m²
= \(\frac{22}{7}\) × 2[42 + 2.8]m²
= \(\frac{22}{7}\) × 2 × 7 m²
= 44 m²
∴ ਤੰਬੂ ਦੀ ਵਕਰ ਸਤਾ ਦਾ ਖੇਤਰਫਲ = 44 m²
1m² ਕੈਨਵਸ ਦੀ ਲਾਗਤ = ₹ 500
44 m² ਕੈਨਵਸ ਦੀ ਲਾਗਤ = ₹ 44 × 500
= ₹ 22000
ਕੈਨਵਸ ਦੀ ਕੁਲ ਲਾਗਤ = ₹ 22000

ਪ੍ਰਸ਼ਨ 8.
ਉੱਚਾਈ 2.4 cm ਅਤੇ ਵਿਆਸ 1.4 cm ਵਾਲੇ ਇੱਕ ਠੋਸ ਬੇਲਣ ਵਿੱਚੋਂ ਇਸੇ ਉੱਚਾਈ ਅਤੇ ਇਸੇ ਵਿਆਸ ਵਾਲਾ ਇੱਕ ਸ਼ੰਕੂ ਆਕਾਰ ਦਾ ਖੋਲ (cavity) ਕੱਟ ਲਿਆ ਜਾਂਦਾ ਹੈ । ਬਾਕੀ ਬਚੇ ਠੋਸ ਦਾ ਨੇੜੇ ਤੋਂ ਨੇੜੇ ਵਰਗ ਸੈਂਟੀਮੀਟਰ (cm²) ਤੱਕ ਕੁੱਲ ਸੜਾ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਬੇਲਣ ਦਾ ਵਿਆਸ (D) = 1.4 cm
= ਸ਼ੰਕੂ ਦਾ ਵਿਆਸ
∴ ਬੇਲਣ ਦਾ ਅਰਧ ਵਿਆਸ =ਸ਼ੰਕੂ ਦਾ ਅਰਧ ਵਿਆਸ
(R) = 0.7 cm
ਬੇਲਣ ਦੀ ਉੱਚਾਈ (H) = 2.4 cm

ਜਿਵੇਂ ਕਿ ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ L² = R² + H²
L = \(\sqrt{(0.7)^{2}+(2.4)^{2}}\)
= \(\sqrt {0.49+5.76}\)
= \(\sqrt {6.25}\) = 2∙5
L = 2.5 cm
ਬਾਕੀ ਬਚੇ ਠੋਸ ਦੀ ਕੁੱਲ ਸੜਾ ਦਾ ਖੇਤਰਫਲ
= ਬੇਲਣ ਦੀ ਵਕਰ ਸਤਾ ਦਾ ਖੇਤਰਫਲ + ਬੇਲਣ ਦੇ ਆਧਾਰ ਦਾ ਖੇਤਰਫਲ + ਸ਼ੰਕੂ ਦੀ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ
= 2πRH + πR² + πRL
= πR [2R + R + L]
= \(\frac{22}{7}\) × 0.7 [2(24) + 0.7 + 25]
= \(\frac{22}{7}\) × \(\frac{7}{10}\) [48 + 3.2] cm²
= \(\frac{22}{10}\) × [8] cm²
= \(\frac{176}{10}\) = 17.6 cm²
ਬਾਕੀ ਬਚੇ ਠੋਸ ਦਾ ਖੇਤਰਫਲ = 17.6 cm²

ਪ੍ਰਸ਼ਨ 9.
ਲੱਕੜੀ ਦੇ ਇੱਕ ਠੋਸ ਬੇਲਣ ਦੇ ਹਰੇਕ ਸਿਰੇ ‘ਤੇ ਇਕ ਅਰਧ ਗੋਲਾ ਖੋਦ ਕੇ ਕੱਢਦੇ ਹੋਏ, ਇੱਕ ਵਸਤੂ ਬਣਾਈ ਗਈ ਹੈ, ਜਿਵੇਂ ਕਿ ਚਿੱਤਰ ਵਿੱਚ ਦਿਖਾਇਆ ਗਿਆ ਹੈ। ਜੇਕਰ ਬੇਲਣ ਦੀ ਉੱਚਾਈ 10 cm ਹੈ ਅਤੇ ਆਧਾਰ ਦਾ ਅਰਧ ਵਿਆਸ 3.5 cm ਹੈ ਤਾਂ ਇਸ ਵਸਤੂ ਦੀ ਕੁੱਲ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।

ਹੱਲ:
ਬੇਲਣ ਦੀ ਉੱਚਾਈ (H) = 10 cm
ਬੇਲਣ ਦਾ ਅਰਧ ਵਿਆਸ = ਅਰਧਗੋਲੇ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 3.5 cm

ਵਸਤੂ ਦੀ ਕੁੱਲ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ = ਬੇਲਣ ਦੀ ਵਕਰ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ + 2 (ਅਰਧ ਗੋਲੇ ਦੀ ਵਕਰ ਸੜਾ ਦਾ ਖੇਤਰਫਲ)
= 2πRH + 2(2πR²)
= 2πR[H + 2R]
= 2 × \(\frac{22}{7}\) × 35 [10 + (35)] cm²
= \(\frac{44}{7}\) × \(\frac{35}{10}\)[10 + 7]cm²
= 44 × \(\frac{5}{10}\) × 17 cm²
= 44 × \(\frac{1}{2}\) × 17 cm²
= 22 × 17 cm²
= 374 cm²
∴ ਵਸਤੂ ਦੀ ਕੁੱਲ ਸੜਾ ਦਾ ਖੇਤਰਫਲ
= 374 cm²

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 12 ਚੱਕਰ ਨਾਲ ਸੰਬੰਧਿਤ ਖੇਤਰਫਲ Ex 12.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 12 ਚੱਕਰ ਨਾਲ ਸੰਬੰਧਿਤ ਖੇਤਰਫਲ Exercise 12.3

(ਜਦੋਂ ਤੱਕ ਨਾ ਕਿਹਾ ਜਾਵੇ, π = \(\frac{22}{7}\) ਦਾ ਹੀ ਪ੍ਰਯੋਗ ਕਰੋ)

ਪ੍ਰਸ਼ਨ 1.
ਚਿੱਤਰ ਵਿਚ, ਰੰਗੀਨ ਭਾਗ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ, ਜੇਕਰ PO = 24 cm, PR = 7 cm ਅਤੇ O ਚੱਕਰ ਦਾ ਕੇਂਦਰ ਹੈ ।

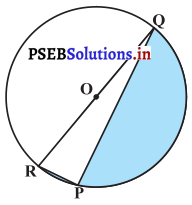
ਹੱਲ:
PQ = 24 cm
PR = 7 cm
RQ ਚੱਕਰ ਦਾ ਵਿਆਸ ਹੈ ।
∠RPQ = 90° [ ਅਰਧਚੱਕਰ ਵਿਚ ਬਣਿਆ ਕੋਣੀ △PQR]
QR² = RP² + PQ²
QR = \(\sqrt{(7)^{2}+(24)^{2}}\) = \(\sqrt {49+576}\)
= \(\sqrt {625}\)
QR = 25 cm
∴ ਚੱਕਰ ਦਾ ਵਿਆਸ (QR) = 25 cm
ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ (R) = \(\frac{25}{2}\) cm
ਛਾਇਆ ਅੰਕਿਤ ਭਾਗ ਦਾ ਖੇਤਰਫਲ = ਅਰਧ ਚੱਕਰ ਦਾ ਖੇਤਰਫਲ – △RPQ ਦਾ ਖੇਤਰਫਲ
= \(\frac{1}{2}\)πR² – \(\frac{1}{2}\)RP × PQ
= [\(\frac{1}{2}\) × \(\frac{22}{7}\) × \(\frac{25}{2}\) × \(\frac{25}{2}\) – \(\frac{1}{2}\) × 7 × 24] cm²
= [\(\frac{6875}{28}\) – 84] cm = \(\frac{4523}{28}\) cm²
= 161.53 cm²

ਪ੍ਰਸ਼ਨ 2.
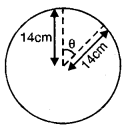
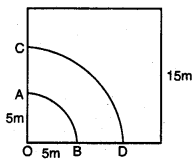
ਚਿੱਤਰ ਵਿਚ, ਰੰਗੀਨ ਭਾਗ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ, ਜੇਕਰ ਕੇਂਦਰ O ਵਾਲੇ ਦੋਵਾਂ ਸਮਕੇਂਦਰੀ ਚੱਕਰਾਂ (concentric) ਦੇ ਅਰਧ ਵਿਆਸ ਕ੍ਰਮਵਾਰ 7 cm ਅਤੇ 14 cm ਹਨ ਅਤੇ ∠AOC = 40° ਹੈ ।
ਹੱਲ:
ਛੋਟੇ ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ (r) = 7 cm
ਵੱਡੇ ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 14 cm
ਕੇਂਦਰੀ ਕੋਣ ∠AOC (θ) = 40°

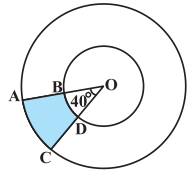
ਛਾਇਆ ਅੰਕਿਤ ਭਾਗ ਦਾ ਖੇਤਰਫਲ = ਦੀਰਘ ਅਰਧ ਵਿਆਸੀ ਖੰਡ OAC ਦਾ ਖੇਤਰਫਲ – ਲਘੂ ਅਰਧ ਵਿਆਸੀ ਖੰਡ OBD ਦਾ ਖੇਤਰਫਲ

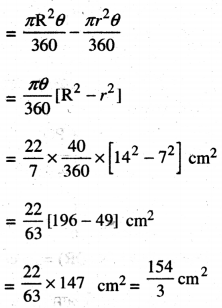
= 51.33 cm²
∴ ਛਾਇਆ ਅੰਕਿਤ ਭਾਰੀ ਦਾ ਖੇਤਰਫਲ
= 51.33 cm²

ਪ੍ਰਸ਼ਨ 3.
ਚਿੱਤਰ ਵਿਚ, ਰੰਗੀਨ ਭਾਗ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ, ਜੇਕਰ ABCD ਭੂਜਾ 14 cm ਵਾਲਾ ਇੱਕ ਵਰਗ ਹੈ ਅਤੇ APD ਅਤੇ BPC ਦੋ ਅਰਧ ਚੱਕਰ ਹਨ ।

ਹੱਲ:
ਵਰਗ ਦੀ ਭੁਜਾ = 14 cm
ਅਰਧ ਚੱਕਰ ਦਾ ਵਿਆਸ (AB = BC) = 14 cm
ਅਰਧ ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 7 cm
ਵਰਗ ਦਾ ਖੇਤਰਫਲ = (ਭੂਜਾ)²
= 14 × 14 cm²
= 196 cm²
ਅਰਧ ਚੱਕਰ ਦਾ ਖੇਤਰਫਲ = \(\frac{1}{2}\)πR²
= \(\frac{1}{2}\) × \(\frac{22}{7}\) × 7 × 7 cm²
= 77 cm²
ਦੋ ਅਰਧ ਚੱਕਰਾਂ ਦਾ ਖੇਤਰਫਲ = 2(77) cm²
= 154 cm²
ਰੰਗੀਨ ਭਾਗ ਦਾ ਖੇਤਰਫਲ = ਵਰਗ ABCD ਦਾ ਖੇਤਰਫਲ – ਦੋ ਅਰਧ ਚੱਕਰਾਂ ਦਾ ਖੇਤਰਫਲ
= (196 – 154) cm²
= 42 cm²
∴ ਛਾਇਆ ਵਾਲੇ ਭਾਗ ਦਾ ਖੇਤਰਫਲ = 42 cm²

ਪ੍ਰਸ਼ਨ 4.
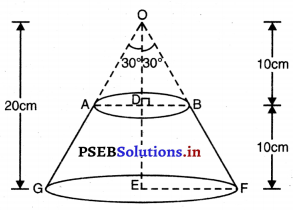
ਚਿੱਤਰ ਵਿੱਚ, ਰੰਗੀਨ ਭਾਗ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ, ਜਿੱਥੇ ਭੁਜਾ 12 cm ਵਾਲੇ ਇੱਕ ਸਮਭੁਜੀ ਤ੍ਰਿਭੁਜ OAB ਦੇ ਸਿਖਰ O ਨੂੰ ਕੇਂਦਰ ਮੰਨ ਕੇ 6 cm ਅਰਧ ਵਿਆਸ ਵਾਲਾ ਇੱਕ ਚੱਕਰੀ ਚਾਪ ਖਿੱਚਿਆ ਗਿਆ ਹੈ।

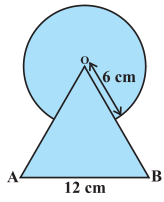
ਹੱਲ:
ਚਾਪ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 6 cm
ਸਮਭੁਜੀ ਤ੍ਰਿਭੁਜ OAB ਦੀ ਭੁਜਾ = 12 cm
OA = OB = AB = 12 cm
∴ ਕੇਂਦਰੀ ਕੋਣ (θ) = 60°
[ਸਿਮਭੁਜੀ ਤਿਭੁਜ ਦਾ ਹਰੇਕ ਕੋਣ 60°]
ਚੱਕਰ ਦੀ ਦੀਰਘ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ = ਚੱਕਰ ਦਾ ਖੇਤਰਫਲ – ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ

= 94.28 cm²
∴ ਦੀਰਘ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ
= 94.28 cm²
ਸਮਭੁਜੀ △OAB ਦਾ ਖੇਤਰਫਲ
= \(\frac{\sqrt{3}}{4}\)(ਭੁਜਾ²
= \(\frac{1.73}{4}\) × 12 × 12 cm²
= 1.73 × 36 cm²
= 62.28 cm²
ਰੰਗੀਨ ਭਾਗ ਦਾ ਖੇਤਰਫਲ = ਸਮਭੁਜੀ ਤਿਭੁਜ OAB ਦਾ ਖੇਤਰਫਲ + ਦੀਰਘ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ
= (62.28 +94.28) cm²
= 156.56 cm²
∴ ਰੰਗੀਨ ਭਾਗ ਦਾ ਖੇਤਰਫਲ = 156.56 cm²

ਪ੍ਰਸ਼ਨ 5.
ਭੁਜਾ 4 cm ਵਾਲੇ ਇੱਕ ਵਰਗ ਦੇ ਹਰੇਕ ਕੋਨੇ ਤੋਂ 1 cm ਅਰਧ ਵਿਆਸ ਵਾਲੇ ਚੱਕਰ ਦਾ ਇੱਕ ਚੌਥਾਈ ਕੱਟਿਆ ਗਿਆ ਹੈ ਅਤੇ ਵਿਚਾਲੇ 2 cm ਵਿਆਸ ਦਾ ਇੱਕ ਚੱਕਰ ਵੀ ਕੱਟਿਆ ਗਿਆ ਹੈ , ਜਿਵੇਂ ਕਿ ਚਿੱਤਰ ਵਿੱਚ ਦਰਸ਼ਾਇਆ ਗਿਆ ਹੈ | ਵਰਗ ਦੇ ਬਾਕੀ ਭਾਗ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।

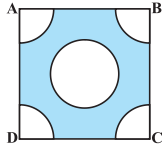
ਹੱਲ:
ਵਰਗ ਦੀ ਭੁਜਾ = 4 cm
ਕੱਟੇ ਗਏ ਹਰੇਕ ਚੌਥਾਈ ਦਾ ਅਰਧ ਵਿਆਸ (r) = 1 cm
ਚੱਕਰ ਦਾ ਵਿਆਸ (R) = 2 cm
∴ ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 1 cm
ਵਰਗ ਦਾ ਖੇਤਰਫਲ = (ਭੁਜਾ)²
= (4)² = 16 cm²
4 ਚੋਥਾਈਆਂ ਦਾ ਖੇਤਰਫਲ
= 4\(\left[\frac{\pi r^{2} \theta}{360^{\circ}}\right]\)] = \(\frac{4 \times 90^{\circ}}{360^{\circ}}\) × \(\frac{22}{7}\) × 1 × 1
= 1 × \(\frac{22}{7}\) × 1 × 1 cm²
= 3.14 cm²
ਚੱਕਰ ਦਾ ਖੇਤਰਫਲ = πR²
= \(\frac{22}{7}\) × 1 × 1 = \(\frac{22}{7}\) cm²
= 3.14 cm²
ਲੋੜੀਂਦਾ ਖੇਤਰਫਲ = (ਵਰਗ ਦਾ ਖੇਤਰਫਲ) – (4 ਚੌਥਾਈਆਂ ਦਾ ਖੇਤਰਫਲ) – (ਚੱਕਰ ਦਾ ਖੇਤਰਫਲ)
= (16 – 3.14 – 3.14) cm²
= 9.72 cm²
ਲੋੜੀਂਦਾ ਖੇਤਰਫਲ = 9.72 cm²

ਪ੍ਰਸ਼ਨ 6.
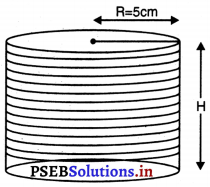
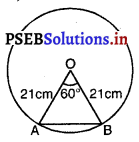
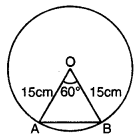
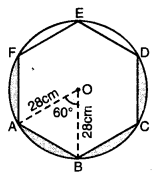
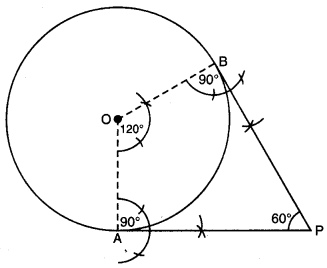
ਇੱਕ ਚੱਕਰਾਕਾਰ ਮੇਜਪੋਸ਼, ਜਿਸਦਾ ਅਰਧ ਵਿਆਸ 32 cm ਹੈ, ਵਿੱਚ ਇੱਕ ਸਮਭੁਜੀ ਤ੍ਰਿਭੁਜ ABC ਛੱਡਦੇ ਹੋਏ ਇੱਕ ਡਿਜ਼ਾਇਨ ਬਣਿਆ ਹੋਇਆ ਹੈ, ਜਿਵੇਂ ਕਿ ਚਿੱਤਰ ਵਿੱਚ ਦਰਸਾਇਆ ਗਿਆ ਹੈ ।ਇਸ ਡਿਜ਼ਾਇਨ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।

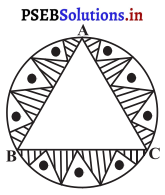
ਹੱਲ:
ਮੇਜਪੋਸ਼ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 32 cm
OA = OB = OC = 32 cm

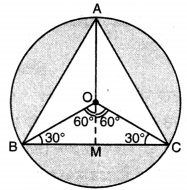
△ABC ਇਕ ਸਮਭੁਜੀ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸ ਵਿਚ
AB = AC = BC = 32 cm
∠A = ∠B = ∠C = 60°
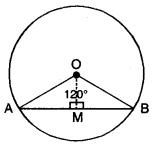
∠AOB = 120° = ∠BOC
OM ⊥ BC
BM = MC = \(\frac{1}{2}\)BC
△OBM ≅ △OMC [RHS ਸਰਬੰਗਸਮਤਾ]
ਹੁਣ △BOC ਵਿੱਚ,
ਬਿੰਦੂ O ਤੋਂ OM, ∠BOC ਅਤੇ BC ਦਾ ਲੰਬ ਸਮਦੁਭਾਜਕ ਖਿੱਚੋਂ ।
BM = MC = \(\frac{1}{2}\)BC
∴ ਪਰ OB = OC [ਚੱਕਰ ਦੇ ਅਰਧ ਵਿਆਸ]
∴ ∠B = ∠C
∴ ∠O + ∠B + ∠C = 180°
120° + 2∠B = 180°
∠B = 30°
ਅਤੇ ∠B = ∠C = 30°
ਪਰ ∠BOM ≅ ∠COM = 60°
△OMB ≅ △OMC [ਸਮਕੋਣ-ਕਣ-ਭੁਜਾ]
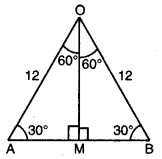
∴ △OMB ਵਿੱਚ
∠OBM = 30° [∠O = 60° ਅਤੇ ∠M = 90°]
∴ \(\frac{BM}{OB}\) = cos 30°
\(\frac{BM}{32}\) = \(\frac{\sqrt{3}}{2}\)
BM = 16\(\sqrt {3}\) cm
∴ BC = 2MB = 32\(\sqrt {3}\) cm
ਚੱਕਰ ਦਾ ਖੇਤਰਫਲ = πR² = \(\frac{22}{7}\) × (32)²
= \(\frac{22}{7}\) × 32 × 32
= 3218.28 cm²
△ ABC ਦਾ ਖੇਤਰਫਲ = \(\frac{\sqrt{3}}{4}\)(ਭੁਜਾ)²
= \(\frac{1.73}{4}\) × 32\(\sqrt {3}\) × 32\(\sqrt {3}\)
= 1328.64 cm²
∴ ਲੋੜੀਂਦਾ ਖੇਤਰਫਲ = ਚੱਕਰ ਦਾ ਖੇਤਰਫਲ – △ABC ਦਾ ਖੇਤਰਫਲ
= (3218.28 – 1328.64) cm²
= 1889.64 cm²

ਪ੍ਰਸ਼ਨ 7.
ਚਿੱਤਰ ਵਿੱਚ, ABCD ਭੁਜਾ 14 cm ਵਾਲਾ ਇੱਕ | ਵਰਗ ਹੈ । A,B,C ਅਤੇ D ਨੂੰ ਕੇਂਦਰ ਮੰਨ ਕੇ, ਚਾਰ ਚੱਕਰ ਇਸ ਤਰ੍ਹਾਂ ਖਿੱਚੇ ਗਏ ਹਨ ਕਿ ਹਰੇਕ ਚੱਕਰ ਤਿੰਨ ਬਾਕੀ ਚੱਕਰਾਂ ਵਿੱਚੋਂ ਦੋ ਚੱਕਰਾਂ ਨੂੰ ਬਾਹਰੀ ਰੂਪ ਵਿੱਚ ਸਪਰਸ਼ ਕਰਦਾ ਹੈ । ਰੰਗੀਨ ਭਾਗ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।

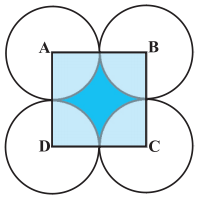
ਹੱਲ:
ਵਰਗ ABCD ਦੀ ਭੁਜਾ = 14 cm
ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 7 cm
ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਕੋਣ (θ) = 90°
[ਵਰਗ ਦਾ ਹਰੇਕ ਕੋਣ = 90°]
ਵਰਗ ਦਾ ਖੇਤਰਫਲ = (ਭੁਜਾ)²
= 14 × 14 = 196 cm²
ਚਾਰ ਚੌਥਾਈਆ ਦਾ ਖੇਤਰਫਲ = 4\(\left[\frac{\pi \mathrm{R}^{2} \theta}{360^{\circ}}\right]\)
= 4 × \(\frac{22}{7}\) × \(\frac{7×7×90}{360}\) cm²
= 22 × 7 = 154 cm²
∴ ਲੋੜੀਂਦਾ ਖੇਤਰਫਲ = ਵਰਗ ਦਾ ਖੇਤਰਫਲ- ਚਾਰ ਚੌਥਾਈਂਆ ਦਾ ਖੇਤਰਫਲ ।
= (196 – 154) cm²
= 42 cm²

ਪ੍ਰਸ਼ਨ 8.
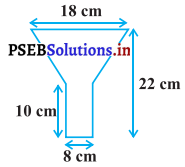
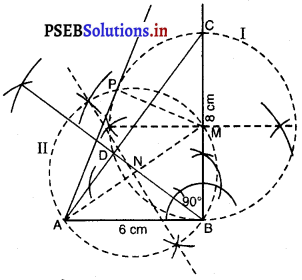
ਚਿੱਤਰ ਵਿੱਚ, ਇੱਕ ਦੌੜਨ ਦਾ ਰਸਤਾ (racing track) ਦਰਸਾਉਂਦੀ ਹੈ, ਜਿਸਦੇ ਸੱਜੇ ਅਤੇ ਖੱਬੇ ਸਿਰੇ ਅਰਧ ਚੱਕਰਾਕਾਰ ਹਨ। ਦੋਨਾਂ ਅੰਦਰੁਨੀ ਸਮਾਂਤਰ ਰੇਖਾਖੰਡਾਂ ਦੇ ਵਿਚਾਲੇ ਦੀ ਦੂਰੀ 60 m ਹੈ । ਉਨ੍ਹਾਂ ਵਿੱਚੋਂ ਹਰੇਕ ਰੇਖਾਖੰਡ 106 m ਲੰਬਾ ਹੈ । ਜੇਕਰ ਇਹ ਰਸਤਾ 10 m ਚੌੜਾ ਹੈ, ਤਾਂ ਪਤਾ ਕਰੋ ।
(i) ਰਸਤੇ ਦੇ ਅੰਦਰੂਨੀ ਕਿਨਾਰਿਆਂ ਦੇ ਅਨੁਸਾਰ ਇੱਕ ਪੂਰਾ ਚੱਕਰ ਲਗਾਉਣ ਵਿੱਚ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ
(ii) ਰਸਤੇ ਦਾ ਖੇਤਰਫਲ

ਹੱਲ:

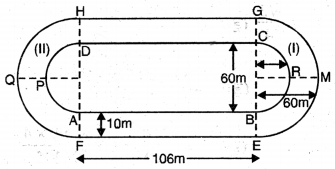
(i) ਇੱਥੇ AB = DC = 106 m
AF = BE = CG = HD = 10 m
ਅੰਦਰਲੇ ਅਰਧ ਚੱਕਰ (APD ਅਤੇ BRC) ਦਾ ਵਿਆਸ = 60 m
∴ ਅਰਧ ਚੱਕਰ (APD) ਦਾ ਅੰਦਰੂਨੀ ਅਰਧ ਵਿਆਸ (r) = 30 m
ਅਰਧ ਚੱਕਰ ਦਾ ਬਾਹਰੀ ਅਰਧ ਵਿਆਸ (R) = r + 10
= 30 + 10 = 40 m
ਰਸਤੇ ਦੇ ਅੰਦਰੂਨੀ ਕਿਨਾਰਿਆਂ ਦੇ ਅਨੁਸਾਰ ਇੱਕ ਪੂਰਾ ਚੱਕਰ ਲਗਾਉਣ ਵਿਚ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ
= AB + ਅਰਧ ਚੱਕਰ BRCਦਾ ਪਰਿਮਾਪ +CD + ਅਰਧ ਚੱਕਰ DPA ਦਾ ਪਰਿਮਾਪ
=2AB + 2 [ਅਰਧ ਚੱਕਰ BRC ਦਾ ਖੇਤਰਫਲ]
= 2 (106) + 2\(\left(\frac{2 \pi r}{2}\right)\)
= 212 + 2πr
= 212 + 2 × \(\frac{22}{7}\) × 30
= 212 + \(\frac{60×22}{7}\)
= 212 + 188.57
= 400.57 m
∴ ਰਸਤੇ ਦੇ ਅੰਦਰਲੇ ਕਿਨਾਰਿਆਂ ਦੇ ਅਨੁਸਾਰ ਪੂਰੇ ਚੱਕਰ ਵਿਚ ਤੈਅ ਦੂਰੀ
= 400.57 m

(ii) ਰਸਤੇ ਦਾ ਖੇਤਰਫਲ = ਆਇਤ ABEF ਦਾ ਖੇਤਰਫਲ + ਖੇਤਰ BEMGCRB ਦਾ ਖੇਤਰਫਲ+ਆਇਤ CGHD ਦਾ ਖੇਤਰਫਲ + ਖੇਤਰ CGRBMEB ਦਾ ਖੇਤਰਫਲ
= 2 ਆਇਤ ABCD ਦਾ ਖੇਤਰਫਲ +2 ਖੇਤਰਾਂ ਦਾ ਖੇਤਰਫਲ
= 2 (AB × AF) + 2 [ਅਰਧ ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ 60 cm – ਅਰਧ ਚੱਕਰ ਜਿਸਦਾ ਅਰਧ ਵਿਆਸ 30 cm ਹੈ ਦਾ ਖੇਤਰਫਲ]
= 2[106 ×10] + 2[\(\frac{\pi R^{2}}{2}\) – \(\frac{\pi r^{2}}{2}\)]
=2 × 1060 + \(\frac{2 \pi}{2}\)[R² – r²]
= 2120 + \(\frac{22}{7}\) × (40² – 30²)
= 2120 + \(\frac{22}{7}\)[1600 – 900]
= 2120 + \(\frac{22}{7}\)[700]
= 2120 + 2200
= 4320 m²
∴ ਰਸਤੇ ਦਾ ਖੇਤਰਫਲ = 4320 m²

ਪ੍ਰਸ਼ਨ 9.
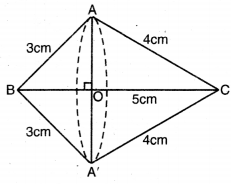
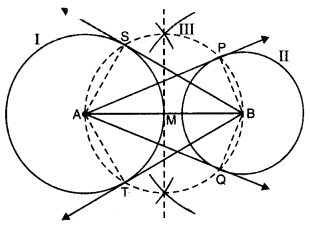
ਚਿੱਤਰ ਵਿੱਚ AB ਅਤੇ CD ਕੇਂਦਰ O ਵਾਲੇ ਇੱਕ ਚੱਕਰ ਦੇ ਦੋ ਪਰਸਪਰ ਆਪਸ ਵਿੱਚ) ਲੰਬ ਵਿਆਸ ਹਨ ਅਤੇ OD ਛੋਟੇ ਚੱਕਰ ਦਾ ਵਿਆਸ ਹੈ । ਜੇਕਰ OA = 7 cm ਹੈ, ਤਾਂ ਰੰਗੀਨ ਭਾਗ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।

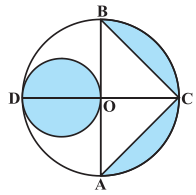
ਹੱਲ:
ਚੱਕਰ ਦਾ ਵਿਆਸ = 14 cm
ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ =7 cm
ਛੋਟੇ ਚੱਕਰ ਦਾ ਵਿਆਸ = 7 cm
∴ ਛੋਟੇ ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ = \(\frac{7}{2}\) cm
AB ਅਤੇ CD ਇਕ ਚੱਕਰ ਦੇ ਦੋ ਪਰਸਪਰ ਲੰਬ ਵਿਆਸ ਹਨ ।
AD ⊥ CD
ਵੱਡੇ ਚੱਕਰ ਦਾ ਖੇਤਰਫਲ = πR²
= \(\frac{22}{7}\) × 7 × 7 cm²
= 154 cm²
ਛੋਟੇ ਚੱਕਰ ਦਾ ਖੇਤਰਫਲ = πr²
= \(\frac{22}{7}\) × \(\frac{7}{2}\) × \(\frac{7}{2}\) cm²
= 38.50 cm²
△ABC ਦਾ ਖੇਤਰਫਲ = \(\frac{1}{2}\) ਦਾ ਆਧਾਰ × ਉੱਚਾਈ
= \(\frac{1}{2}\) × 14 × 7 cm²
= 49 cm²
∴ ਰੰਗੀਨ ਭਾਗ ਦਾ ਖੇਤਰਫਲ = ਵੱਡੇ ਚੱਕਰ ਦਾ ਖੇਤਰਫਲ-ਛੋਟੇ ਚੱਕਰ ਦਾ ਖੇਤਰਫਲ-ਤ੍ਰਿਭੁਜ ਦਾ ਖੇਤਰਫਲ
= (154 – 38.5 – 49) cm²
= 66.5 cm²

ਪ੍ਰਸ਼ਨ 10.
ਇੱਕ ਸਮਭੁਜੀ ਤ੍ਰਿਭੁਜ ABC ਦਾ ਖੇਤਰਫਲ 17320.5 cm² ਹੈ । ਇਸ ਤ੍ਰਿਭੁਜ ਦੇ ਹਰੇਕ ਸਿਖ਼ਰ ਨੂੰ ਕੇਂਦਰ ਮੰਨ ਕੇ ਤ੍ਰਿਭੁਜ ਦੀ ਭੁਜਾ ਦੇ ਅੱਧ ਦੇ ਬਰਾਬਰ ਅਰਧ ਵਿਆਸ ਲੈ ਕੇ ਇੱਕ ਚੱਕਰ ਖਿੱਚਿਆ ਜਾਂਦਾ ਹੈ(ਦੇਖੋ ਚਿੱਤਰ) । ਰੰਗੀਨ ਭਾਗ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।
(π = 3.14 ਅਤੇ \(\sqrt {3}\) = 1.73205 ਲਓ)

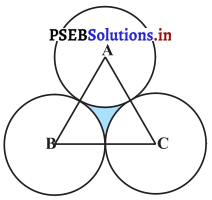
ਹੱਲ:
ਸਮਭੁਜੀ ਤ੍ਰਿਭੁਜ ABC ਦਾ ਖੇਤਰਫਲ
= 17320.5 cm²

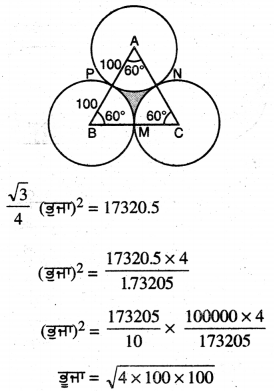
ਭੁਜਾ = 2 × 100 = 200 cm
∴ AB = BC = AC
ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ (R) = \(\frac{AB}{2}\) = \(\frac{200}{2}\) cm
= 100 cm
ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਕੋਣ, θ = 60°
ਅਰਧ ਵਿਆਸੀ ਖੰਡ APN ਦਾ ਖੇਤਰਫਲ = \(\frac{\pi R^{2} \theta}{360^{\circ}}\)
= \(\frac{3.14 \times 100 \times 100 \times 60^{\circ}}{360^{\circ}}\) cm²
= 5233.33 cm²
ਤਿੰਨਾਂ ਅਰਧ ਵਿਆਸੀ ਖੰਡਾਂ ਦਾ ਖੇਤਰਫਲ
= 3 × 5233.33 cm²
= 15699.99 cm²
= 15700 cm²
∴ ਲੋੜੀਂਦਾ ਖੇਤਰਫਲ = ਤ੍ਰਿਭੁਜ ਦਾ ਖੇਤਰਫਲ – ਤਿੰਨ ਅਰਧ ਵਿਆਸੀ ਖੰਡਾਂ ਦਾ ਖੇਤਰਫਲ
= 17320.5 – 15700 = 1620.5 cm²
∴ ਲੋੜੀਂਦਾ ਖੇਤਰਫਲ = 1620.5 cm²

ਪ੍ਰਸ਼ਨ 11.
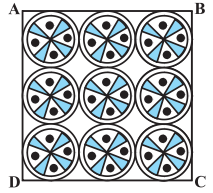
ਇੱਕ ਵਰਗਾਕਾਰ ਰੁਮਾਲ ‘ ਤੇ ਨੌ ਚੱਕਰਾਕਾਰ | ਡਿਜਾਇਨ ਬਣੇ ਹਨ, ਜਿਸ ਵਿੱਚੋਂ ਹਰੇਕ ਦਾ ਅਰਧ ਵਿਆਸ 7 cm ਹੈ । (ਦੇਖੋ ਚਿਤਰ), ਰੁਮਾਲ ਦੇ ਬਾਕੀ ਭਾਗ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।

ਹੱਲ:
ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 7 cm
ਚੱਕਰ ਦਾ ਵਿਆਸ = 2 × R
= 2 × 7
= 14 cm
ਕਿਉਂਕਿ ਵਰਗ ਦੀ ਭੁਜਾ ਦੇ ਅਨੁਸਾਰ ਤਿੰਨ ਚੱਕਰ ਹਨ।
∴ ਵਰਗ ਦੀ ਭੁਜਾ = 3 [14] cm = 42 cm
ਰੁਮਾਲ ਦਾ ਕੁੱਲ ਖੇਤਰਫਲ = ਵਰਗ ਦਾ ਖੇਤਰਫਲ
= (ਭੁਜਾ)²
= (42)² = 1764 cm²
ਨੌ ਚੱਕਰਾਕਾਰ ਡਿਜਾਈਨਾਂ ਦਾ ਖੇਤਰਫਲ = 9πR²
= 9 × \(\frac{22}{7}\) × (7)² cm²
= 9 × \(\frac{22}{7}\) × 7 × 7 cm²
=9 × 154 cm²
= 1386 cm²
∴ ਬਾਕੀ ਭਾਗ ਦਾ ਲੋੜੀਂਦਾ ਖੇਤਰਫਲ
= ਵਰਗ ਦਾ ਖੇਤਰਫਲ – 9 ਚੱਕਰਾਂ ਡਿਜਾਈਨਾਂ ਦਾ ਖੇਤਰਫਲ
= (1764 – 1386) cm²
= 378 cm²

ਪ੍ਰਸ਼ਨ 12.
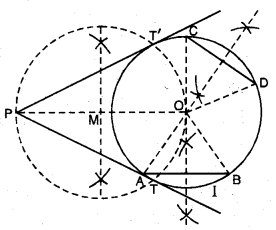
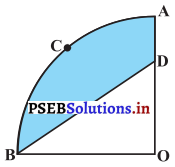
ਚਿੱਤਰ ਵਿੱਚ, OACB, ਕੇਂਦਰ O ਅਤੇ ਅਰਧ ਵਿਆਸ 3.5 cm ਵਾਲੇ ਇੱਕ ਚੱਕਰ ਦਾ ਚੌਥਾ ਭਾਗ ਹੈ । ਜੇਕਰ OD = 2 cm ਹੋਵੇ ਤਾਂ ਹੇਠਾਂ ਲਿਖਿਆਂ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ :
(i) ਚੌਥਾਈ OACB
(ii) ਰੰਗੀਨ ਭਾਗ ।

ਹੱਲ:
ਚੌਥਾਈ ਭਾਗ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 3.5 cm
ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਕੋਣ (θ) = 90°
OD = 2 cm.
(i) ਚੌਥਾਈ OACB ਦਾ ਖੇਤਰਫਲ = \(\frac{\pi R^{2} \theta}{360^{\circ}}\)
= \(\frac{22}{7}\) × \(\frac{3.5 \times 3.5 \times 90^{\circ}}{360^{\circ}}\) cm²
=9.625 cm²

(ii) △ODB ਦਾ ਖੇਤਰਫਲ = \(\frac{1}{2}\) ਆਧਾਰ × ਉਚਾਈ
= \(\frac{1}{2}\) × 3.5 × 2 cm² = 3.5 cm²
∴ ਰੰਗੀਨ ਭਾਗ ਦਾ ਖੇਤਰਫਲ = ਚੌਥਾਈ ਭਾਗ OACB ਦਾ ਖੇਤਰਫਲ – △ODB ਦਾ ਖੇਤਰਫਲ
= (9.625 – 3.5) cm²
= 6.125 cm²

ਪ੍ਰਸ਼ਨ 13.
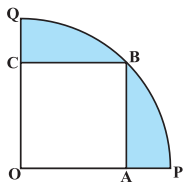
ਚਿੱਤਰ ਵਿਚ, ਇੱਕ ਚੌਥਾਈ OPBQ ਦੇ ਅੰਦਰ ਇੱਕ ਵਰਗ OABC ਬਣਿਆ ਹੋਇਆ ਹੈ । ਜੇਕਰ OA = 20 cm ਹੋਵੇ, ਤਾਂ ਰੰਗੀਨ ਭਾਗ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।
(π = 3.14 ਲਓ)

ਹੱਲ:
ਵਰਗ ABCO ਦੀ ਭੁਜਾ = 20 cm
∠AOC= 90°
AB = OA

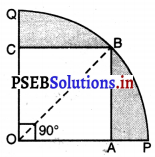
∴ △OAB ਵਿੱਚ
OB² = OA² + AB²
OB = \(\sqrt{(20)^{2}+(20)^{2}}\)
= \(\sqrt {400+400}\)
= \(\sqrt {800}\)
OB = 20\(\sqrt {2}\) cm
ਵਰਗ OABC ਦਾ ਖੇਤਰਫਲ = (ਭੁਜਾ)² = (20)²
∴ ਵਰਗ ਦਾ ਖੇਤਰਫਲ = 400 cm²
ਚੌਥਾਈ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 20\(\sqrt {2}\) cm
ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਕੋਣ (θ) = 90°
ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ = \(\frac{\pi \mathrm{R}^{2} \theta}{360^{\circ}}\)
= \(\frac{3.14 \times 20 \sqrt{2} \times 20 \sqrt{2} \times 90^{\circ}}{360^{\circ}}\)
= 2 × 314 cm²
= 628 cm²
∴ ਲੋੜੀਂਦਾ ਖੇਤਰਫਲ = ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ – ਵਰਗ ਦਾ ਖੇਤਰਫਲ
= (628 – 400) cm²
= 228 cm²

ਪ੍ਰਸ਼ਨ 14.
AB ਅਤੇ CD ਕੇਂਦਰ O ਅਤੇ ਅਰਧ ਵਿਆਸਾਂ 21 cm ਅਤੇ 7 cm ਵਾਲੇ ਦੋ ਸਮਕੇਂਦਰੀ ਚੱਕਰਾਂ ਦੇ ਕ੍ਰਮਵਾਰ ਦੋ ਚਾਪ ਹਨ (ਦੇਖੋ ਚਿੱਤਰ) । ਜੇਕਰ ∠OB = 30° ਹੈ, ਤਾਂ ਰੰਗੀਨ ਭਾਗ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।

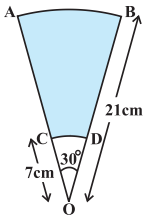
ਹੱਲ:
ਅਰਧ ਵਿਆਸੀ ਖੰਡ OBA ਦਾ ਅਰਧ ਵਿਆਸ (R) = 21 cm
ਅਰਧ ਵਿਆਸੀ ਖੰਡ ODCਦਾ ਅਰਧ ਵਿਆਸ (r) = 7 cm
ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਕੋਣ (θ) = 30°
ਦੀਰਘ ਅਰਧ ਵਿਆਸੀ ਖੰਡ (OAB) ਦਾ ਖੇਤਰਫਲ = \(\frac{\pi \mathrm{R}^{2} \theta}{360^{\circ}}\)
= \(\frac{22}{7}\) x \(\frac{21 \times 21 \times 30^{\circ}}{360^{\circ}}\) cm²
= 115.5 cm²
ਲਘੂ ਅਰਧ ਵਿਆਸੀ ਖੰਡ (ODC) ਦਾ ਖੇਤਰਫਲ = \(\frac{\pi r^{2} \theta}{360^{\circ}}\)
= \(\frac{22}{7}\) × \(\frac{7 \times 7 \times 30^{\circ}}{360^{\circ}}\) cm²
= 12.83 cm²
ਰੰਗੀਨ ਭਾਗ ਦਾ ਖੇਤਰਫਲ = ਦੀਰਘ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ (OAB) – ਲਘੂ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ (OCD)
= (115.5 – 12.83) cm²
= 102.66 cm²

ਪ੍ਰਸ਼ਨ 15.
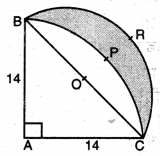
ਚਿੱਤਰ ਵਿੱਚ, ABC ਅਰਧ ਵਿਆਸ 14 cm ਵਾਲੇ ਇੱਕ ਚੱਕਰ ਦਾ ਚੌਥਾਈ ਹਿੱਸਾ ਹੈ ਅਤੇ BC ਨੂੰ ਬਿਆਸ ਮੰਨ ਕੇ ਇੱਕ ਅਰਧ ਚੱਕਰ ਖਿੱਚਿਆ ਗਿਆ ਹੈ । ਰੰਗੀਨ ਭਾਗ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।

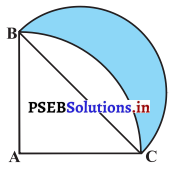
ਹੱਲ:
ਅਰਧ ਵਿਆਸੀ ਖੰਡ ACPB ਦਾ ਅਰਧ ਵਿਆਸ (r) = 14 cm
ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਕੋਣ (θ) = 90°
AB = AC = 7 cm

ਤ੍ਰਿਭੁਜ ਦਾ ਖੇਤਰਫਲ = \(\frac{1}{2}\) AB × AC
= \(\frac{1}{2}\) × 14 × 14 cm² = 98 cm²
ਅਰਧ ਵਿਆਸੀ ਖੰਡ ACPB ਦਾ ਖੇਤਰਫਲ = \(\frac{\pi r^{2} \theta}{360^{\circ}}\)
= \(\frac{22}{7}\) × \(\frac{14 \times 14 \times 90^{\circ}}{360^{\circ}}\)
= 154cm²
∴ BOCPB ਦਾ ਖੇਤਰਫਲ = ਅਰਧ ਵਿਆਸੀ ਖੰਡ ABPC ਦਾ ਖੇਤਰਫਲ – △ABC ਦਾ ਖੇਤਰਫਲ
= 154 cm² – 98 cm²
= 56 cm²
△BAC ਵਿੱਚ, AB² + AC² = BC²
(14)² + (14)² = BC²
BC = \(\sqrt {196+196}\) = \(\sqrt{2(196)}\)
= 14\(\sqrt {2}\) cm
∴ ਅਰਧ ਚੱਕਰ BOCR ਦਾ ਅਰਵਿਆਸ = \(\frac{14 \sqrt{2}}{2}\)
= 7\(\sqrt {2}\) cm
ਅਰਧ ਚੱਕਰ ਦਾ ਖੇਤਰਫਲ = \(\frac{\pi \mathrm{R}^{2}}{2}\)
= \(\frac{22}{7}\) × \(\frac{7 \sqrt{2} \times 7 \sqrt{2}}{2}\) cm²
= \(\frac{22}{7}\) × \(\frac{7 \times 7 \times 2}{2}\) cm²
= 154 cm²
ਲੋੜੀਂਦਾ ਖੇਤਰਫਲ = ਅਰਧ ਚੱਕਰ ਦਾ ਖੇਤਰਫਲ [ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ – △BAC ਦਾ ਖੇਤਰਫਲ
= 154 – [154 – 98]
= 154 – 56 = 98 cm²
ਰੰਗੀਨ ਭਾਗ ਦਾ ਖੇਤਰਫਲ = 98 cm²

ਪ੍ਰਸ਼ਨ 16.
ਚਿੱਤਰ ਵਿੱਚ, ਰੰਗੀਨ ਡਿਜਾਇਨ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ, ਜੋ 8 cm ਅਰਧ ਵਿਆਸਾਂ ਵਾਲੇ ਦੋ ਚੱਕਰਾਂ ਦੀਆਂ ਚੌਥਾਈਆਂ ਵਿੱਚ ਸਾਂਝਾ ਹੈ।

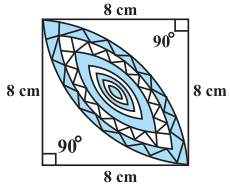
ਹੱਲ:
ਵਰਗ ਦੀ ਭੁਜਾ = 8 cm
ਵਰਗ ਦਾ ਖੇਤਰਫਲ = (8)² = 64 cm²
ਰੇਖਾ BD ਵਰਗ ABCD ਨੂੰ ਸਮਾਨ ਭਾਗਾਂ ਵਿੱਚ ਵੰਡਦੀ ਹੈ ।
△ABD ਦਾ ਖੇਤਰਫਲ = △BDC ਦਾ ਖੇਤਰਫਲ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਕੋਣ, θ = 90°
ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ = \(\)
= \(\frac{22}{7}\) × \(\frac{8 \times 8 \times 90^{\circ}}{360^{\circ}}\) cm²
= 50:28 cm²
ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ = 50.28 cm²
△ABD ਦਾ ਖੇਤਰਫਲ = \(\frac{1}{2}\) × AB × AD
= \(\frac{1}{2}\) × 8 × 8cm²
= 32 cm²
∴ ਚੱਕਰ ਖੰਡ DMBPD ਦਾ ਖੇਤਰਫਲ
= ABPD ਦਾ ਖੇਤਰਫਲ – △ABD ਦਾ ਖੇਤਰਫਲ
= 50.28 – 32
= 18.28 cm²
ਰੰਗੀਨ ਡਿਜ਼ਾਈਨਾਂ ਦਾ ਖੇਤਰਫਲ = 2 DMBPD ਦਾ ਖੇਤਰਫਲ
= 2(18.28) = 36.56 cm²

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 12 ਚੱਕਰ ਨਾਲ ਸੰਬੰਧਿਤ ਖੇਤਰਫਲ Ex 12.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 12 ਚੱਕਰ ਨਾਲ ਸੰਬੰਧਿਤ ਖੇਤਰਫਲ Exercise 12.2

(ਜਦੋਂ ਤੱਕ ਨਾ ਕਿਹਾ ਜਾਵੇ, π = \(\frac{22}{7}\) ਦਾ ਪ੍ਰਯੋਗ ਕਰੋ ।)

ਪ੍ਰਸ਼ਨ 1.
6 cm ਅਰਧ ਵਿਆਸ ਵਾਲੇ ਇੱਕ ਚੱਕਰ ਦੇ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ, ਜਿਸਦਾ ਕੋਣ 60° ਹੈ ।
ਹੱਲ:
ਚੱਕਰ ਦੇ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 6 cm

ਕੇਂਦਰ ਦਾ ਕੋਣ (θ) = 60°
∴ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ = \(\frac{\pi R^{2} \theta}{360}\)
= \(\frac{22}{7}\) × \(\frac{6×6×60}{360}\) cm²
= \(\frac{132}{7}\) cm²
∴ ਚੱਕਰ ਦੇ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ = 18.86 cm²

ਪ੍ਰਸ਼ਨ 2.
ਇੱਕ ਚੱਕਰ ਦੇ ਚੌਥੇ ਭਾਗ (quadrant) ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ, ਜਿਸਦਾ ਘੇਰਾ 22 cm ਹੈ ।
ਹੱਲ:
ਚੱਕਰ ਦਾ ਘੇਰਾ = 22 cm
2πR = 22
R = \(\frac{22×7}{2×22}\) = \(\frac{7}{2}\) cm
R = \(\frac{7}{2}\)
ਕੇਂਦਰ ਦਾ ਕੋਣ (θ) = 90°
∴ ਚੱਕਰ ਦੇ ਚੌਥੇ ਭਾਗ ਦਾ ਖੇਤਰਫਲ
= \(\frac{\pi R^{2} \theta}{360}\) = \(\frac{\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2} \times 90}{360}\) cm²
= \(\frac{77}{8}\) cm²
= 9.625 cm²

ਪ੍ਰਸ਼ਨ 3.
ਇੱਕ ਘੜੀ ਦੀ ਮਿੰਟਾਂ ਵਾਲੀ ਸੂਈ ਦੀ ਲੰਬਾਈ 14 cm ਹੈ । ਇਸ ਸੂਈ ਦੁਆਰਾ 5 ਮਿੰਟ ਵਿੱਚ ਤੈਅ ਕੀਤੇ ਖੇਤਰ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮਿੰਟਾਂ ਵਾਲੀ ਸੂਈ ਦੀ ਲੰਬਾਈ
= ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 14 cm

ਸਾਨੂੰ ਪਤਾ ਹੈ
60′ = 360°
1′ = \(\frac{360}{60}\) = 6°
5′ = 6° × 5 = 30°
ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਕੋਣ (θ) = 30°
∴ ਸੂਈ ਦੁਆਰਾ 5 ਮਿੰਟਾਂ ਵਿਚ ਬਣਾਏ ਗਏ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ

∴ ਸੂਈ ਦੁਆਰਾ 5 ਮਿੰਟਾਂ ਵਿਚ ਤੈਅ ਕੀਤੇ ਖੇਤਰ ਦਾ ਖੇਤਰਫਲ
= 51∙33 cm²

ਪ੍ਰਸ਼ਨ 4.
10 cm ਅਰਧ ਵਿਆਸ ਵਾਲੇ ਇੱਕ ਚੱਕਰ ਦੀ ਕੋਈ ਜੀਵਾ ਕੇਂਦਰ ‘ਤੇ ਇੱਕ ਸਮਕੋਣ ਬਣਾਉਂਦੀ ਹੈ । ਹੇਠਾਂ ਦਿੱਤਿਆਂ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ :
(i) ਸੰਗਤ ਲਘੂ ਚੱਕਰ ਖੰਡ
(ii) ਸੰਗਤ ਦੀਰਘ ਅਰਧ ਵਿਆਸੀ ਖੰਡ (π = 3.14 ਦਾ ਪ੍ਰਯੋਗ ਕਰੋ)
ਹੱਲ:
ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 10 cm
ਕੇਂਦਰ ਤੇ ਬਣਿਆ ਕੋਣ (θ) = 90°
∴ ਲਘੂ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ = \(\frac{\pi \mathrm{R}^{2} \theta}{360}\)
= 3∙14 × 10 × 10 × \(\frac{90}{360}\) = \(\frac{314}{4}\)
ਲਘੂ ਖੰਡ ਦਾ ਖੇਤਰਫਲ = \(\frac{314}{4}\) = 78.5 cm²
ਲਘੁ ਚੱਕਰ ਖੰਡ ਦਾ ਖੇਤਰਫਲ
= ਲਘੁ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ – △AOB ਦਾ ਖੇਤਰਫਲ
= 78.5 – \(\frac{1}{2}\) × ਆਧਾਰ × ਉਚਾਈ
= (78.5 – \(\frac{1}{2}\) × 10 × 10) cm²
= (78.5 – 50) cm²
= 28.5 cm²
∴ ਲਘੂ ਚੱਕਰ ਖੰਡ ਦਾ ਖੇਤਰਫਲ
= 28.5 cm²
ਵੱਡੇ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ

∴ ਵੱਡੇ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ
= 235.5 cm²

ਪ੍ਰਸ਼ਨ 5.
ਅਰਧ ਵਿਆਸ 21 cm ਵਾਲੇ ਚੱਕਰ ਦਾ ਇੱਕ ਚਾਪ ਕੇਂਦਰ ’ਤੇ 60° ਦਾ ਕੋਣ ਬਣਾਉਂਦਾ ਹੈ । ਪਤਾ ਕਰੋ :
(i) ਚਾਪ ਦੀ ਲੰਬਾਈ
(ii) ਚਾਪ ਦੁਆਰਾ ਬਣਾਏ ਗਏ ਅਰਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ
(iii) ਸੰਗਤ ਜੀਵਾ ਦੁਆਰਾ ਬਣਾਏ ਗਏ ਚੱਕਰ ਖੰਡ ਦਾ ਖੇਤਰਫਲ ।
ਹੱਲ:
(i) ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 21 cm

ਕੇਂਦਰ ਤੇ ਬਣਿਆ ਕੋਣ (θ) = 60°
ਚਾਪ ਦੀ ਲੰਬਾਈ = \(\frac{θ}{360}\) × 2πR
= \(\frac{60}{360}\) × 2 × \(\frac{22}{7}\) × 21
∴ ਚਾਪ ਦੀ ਲੰਬਾਈ = 22 cm

(ii) ਚਾਪ ਦੁਆਰਾ ਬਣਾਏ ਗਏ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ
= \(\frac{\pi R^{2} \theta}{360}\)
= \(\frac{22}{7}\) × \(\frac{21×21×60}{360}\)
= 231 cm²
ਕਿਉਂਕਿ △OAB ਸਮਭੁਜੀ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸ ਵਿਚ θ = 60°.

(iii) ਚੱਕਰ ਖੰਡ ਦਾ ਖੇਤਰਫਲ = ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ – vAOB ਦਾ ਖੇਤਰਫਲ
= \(\frac{\pi R^{2} \theta}{360}\) – \(\frac{\sqrt{3}}{4}\) (ਭੁਜਾ)²
= 231 – \(\frac{1∙73}{4}\) × 21 × 21 cm²
= 231 – 0.4325 × 441 cm²
= 231 – 190.7325 cm²
=4026 cm²
∴ ਚੱਕਰ ਖੰਡ ਦਾ = 40.26 cm²

ਪ੍ਰਸ਼ਨ 6.
15 cm ਅਰਧ ਵਿਆਸ ਵਾਲੇ ਇਕ ਚੱਕਰ ਦੀ ਕੋਈ ਜੀਵਾ ਕੇਂਦਰ ‘ਤੇ 60° ਦਾ ਕੋਣ ਬਣਾਉਂਦੀ ਹੈ। ਸੰਗਤ ਲਘੂ ਅਤੇ ਦੀਰਘ ਚੱਕਰ ਖੰਡਾਂ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।
(π = 3.14 ਅਤੇ \(\sqrt {3}\) = 1.73 ਦਾ ਪ੍ਰਯੋਗ ਕਰੋ ॥)
ਹੱਲ:
ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ = (R) = 15 cm
ਕੇਂਦਰ ਦਾ ਕੋਣ (θ) = 60°

△OAB ਵਿੱਚ ਕੇਂਦਰੀ ਕੋਣ θ = 60°
OA = OB = 15 cm
∴ ∠AZB = 60°
∴ △OAB ਸਮਭੁਜੀ ਤ੍ਰਿਭੁਜ ਹੈ ।
ਲਘੂ ਚੱਕਰ ਖੰਡ ਦਾ ਖੇਤਰਫਲ = (ਲਘੂ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ) – ਸਮਭੁਜੀ ਤਿਭੁਜ ਦਾ ਖੇਤਰਫਲ

∴ ਲਘੂ ਚੱਕਰ ਖੰਡ ਦਾ ਖੇਤਰਫਲ =20.43 cm²
ਦੀਰਘ ਚੱਕਰ ਖੰਡ ਦਾ ਖੇਤਰਫਲ = ਚੱਕਰ ਦਾ ਖੇਤਰਫਲ – ਲਘੂ ਚੱਕਰ ਖੰਡ ਦਾ ਖੇਤਰਫਲ
= πR² – 20.43
= 3.14 × 15 × 15 – 20.43
= (706.5 – 20.43) cm²
= 686.07 cm²
∴ ਦੀਰਘ ਚੱਕਰ ਖੰਡ ਦਾ ਖੇਤਰਫਲ = 686.07 cm²

ਪ੍ਰਸ਼ਨ 7.
12 cm ਅਰਧ ਵਿਆਸ ਵਾਲੇ ਇੱਕ ਚੱਕਰ ਦੀ ਕੋਈ ਜੀਵਾ ਕੇਂਦਰ ‘ ਤੇ 120° ਦਾ ਕੋਣ ਬਣਾਉਂਦੀ ਹੈ । ਸੰਗਤ ਚੱਕਰ ਖੰਡ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।
(π = 3.14 ਅਤੇ \(\sqrt {3}\) = 1.73 ਦਾ ਪ੍ਰਯੋਗ ਕਰੋ)
ਹੱਲ:
ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 12 cm
ਕੇਂਦਰ ਦਾ ਕੋਣ (θ) = 120°
△OAM ਵਿੱਚ, OM ⊥ AB
∴ AM = MB = \(\frac{1}{2}\) AB

∴ ∠OAM = 30° = ∠OBM

AB = 2AM
= 2\(\left(\frac{\mathrm{AM}}{\mathrm{OA}}\right)\)OA
= 2 (sin 60°) 12
AB = 2 × \(\frac{\sqrt{3}}{2}\) × 12 = 12\(\sqrt {3}\) cm
OM = OA\(\left(\frac{\mathrm{OM}}{\mathrm{OA}}\right)\) = 12 (cos 60°)
= 12 × \(\frac{1}{2}\) = 6 cm
∴ ਚੱਕਰ ਖੰਡ ਦਾ ਖੇਤਰਫਲ = ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ – △OAB ਦਾ ਖੇਤਰਫਲ
ਚੱਕਰ ਖੰਡ ਦਾ ਖੇਤਰਫਲ

= (150.72 – 36 × 1.73) cm²
= (150.72 – 62.28) cm²
= 8844 cm²
∴ ਚੱਕਰ, ਖੰਡ ਦਾ ਖੇਤਰਫਲ = 88.44 cm²

8. 15 m ਪੂਜਾ ਵਾਲੇ ਇੱਕ ਵਰਗਾਕਾਰ ਘਾਹ ਦੇ ਮੈਦਾਨ ਦੇ ਇੱਕ ਕੋਨੇ ‘ਤੇ ਲੱਗੇ ਕਿੱਲੇ ਨਾਲ ਘੋੜੇ ਨੂੰ 5 m ਲੰਬੀ ਰੱਸੀ ਨਾਲ ਬੰਨ੍ਹਿਆ ਹੋਇਆ ਹੈ । (ਦੇਖੋ ਚਿੱਤਰ ਪਤਾ ਕਰੋ ।

ਪ੍ਰਸ਼ਨ (i).
ਮੈਦਾਨ ਦੇ ਉਸ ਭਾਗ ਦਾ ਖੇਤਰਫਲ ਜਿੱਥੇ ਘੋੜਾ ਘਾਹ ਚਰ ਸਕਦਾ ਹੈ ।
ਹੱਲ:
ਵਰਗ ਦੀ ਭੁਜਾ = 15 m
ਕਿੱਲੇ ਨਾਲ ਬੰਨੀ ਰੱਸੀ ਦੀ ਲੰਬਾਈ = ਅਰਧ ਵਿਆਸੀ ਖੰਡ OAB ਦਾ ਅਰਧ ਵਿਆਸ (R) = 5 m
ਕੇਂਦਰੀ ਕੋਣ (θ) = 90°
[ਵਰਗ ਦਾ ਹਰੇਕ ਕੋਣ 90°]

ਅਰਧ ਵਿਆਸੀ ਖੰਡ OAB ਦਾ ਖੇਤਰਫਲ = \(\frac{\pi \mathrm{R}^{2} \theta}{360^{\circ}}\)
= \(\frac{3.14 \times 5 \times 5 \times 90^{\circ}}{360^{\circ}}\)
= \(\frac{3.14 \times 25}{4}\) = \(\frac{78.5}{4}\) m²
= 19.625 m²

ਪ੍ਰਸ਼ਨ (ii).
ਚਰੇ ਜਾਣ ਵਾਲੇ ਖੇਤਰਫਲ ਵਿੱਚ ਵਾਧਾ ਜੇਕਰ ਘੋੜੇ ਨੂੰ 5 m ਲੰਬੀ ਰੱਸੀ ਦੇ ਸਥਾਨ ‘ਤੇ 10 m ਲੰਬੀ ਰੱਸੀ ਨਾਲ ਬੰਨ ਦਿੱਤਾ ਜਾਵੇ। (π = 3.14 ਦਾ ਪ੍ਰਯੋਗ ਕਰੋ) !

ਹੱਲ:
ਜਦੋਂ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਅਰਧਵਿਆਸ ਵੱਧ ਕੇ 10 m ਹੋ ਜਾਂਦਾ ਹੈ ।
∴ ਅਰਧ ਵਿਆਸੀ ਖੰਡ OCD ਦਾ ਅਰਧ ਵਿਆਸ | (R₁) = 10 m
ਕੇਂਦਰੀ ਕੋਣ (θ) = 90°
∴ ਅਰਧ ਵਿਆਸੀ ਖੰਡ OCDP ਖੇਤਰਫਲ = \(\frac{\pi \mathrm{R}_{1}^{2} \theta}{360^{\circ}}\)

∴ ਚਰੇ ਜਾ ਸਕਣ ਵਾਲੇ ਖੇਤਰ ਦੇ ਖੇਤਰਫਲ ਵਿੱਚ ਵਾਧਾ
= ਅਰਧ ਵਿਆਸੀ ਖੰਡ OCD ਦਾ ਖੇਤਰਫਲ – ਅਰਧ ਵਿਆਸੀ ਖੰਡ OAB ਦਾ ਖੇਤਰਫਲ
= (78.5 – 19.625) cm²
= 58.875 m²
∴ ਚਰੇ ਜਾ ਸਕਣ ਵਾਲੇ ਖੇਤਰ ਦੇ ਖੇਤਰਫਲ ਵਿੱਚ ਵਾਧਾ
= 58.875 m²

ਪ੍ਰਸ਼ਨ 9.
ਇੱਕ ਚੱਕਰਾਕਾਰ ਬਰੂਚ (brooch) ਨੂੰ ਚਾਂਦੀ ਦੇ ਤਾਰ । ਨਾਲ ਬਣਾਇਆ ਜਾਣਾ ਹੈ ਜਿਸ ਦਾ ਵਿਆਸ 35 mm ਹੈ । ਤਾਰ ਨੂੰ ਚੱਕਰ ਦੇ 5 ਵਿਆਸਾਂ ਨੂੰ ਬਣਾਉਣ ਵਿੱਚ ਵਰਤਿਆ ਗਿਆ ਹੈ ਜੋ ਉਸ ਨੂੰ 10 ਬਰਾਬਰ ਅਰਧ ਵਿਆਸੀ ਖੰਡਾਂ ਵਿੱਚ ਵੰਡਦੀ ਹੈ ਜਿਵੇਂ ਕਿ ਚਿੱਤਰ ਵਿੱਚ ਦਰਸ਼ਾਇਆ ਗਿਆ ਹੈ । ਤਾਂ ਪਤਾ ਕਰੋ :
(i) ਕੁੱਲ ਲੋੜੀਂਦੀ ਚਾਂਦੀ ਦੇ ਤਾਰ ਦੀ ਲੰਬਾਈ
(ii) ਬਰੂਚ ਦੇ ਹਰੇਕ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ

ਹੱਲ:
ਚੱਕਰ ਦਾ ਵਿਆਸ (D) = 35 mm
ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ (R) = \(\frac{35}{2}\) mm
ਵਿਆਸਾਂ ਦੀ ਸੰਖਿਆ = 5
ਬਰਾਬਰ ਅਰਧ ਵਿਆਸੀ ਖੰਡਾਂ ਦੀ ਸੰਖਿਆ = 10
(i) ਪ੍ਰਯੋਗ ਕੀਤੀ ਗਈ ਤਾਰ ਦੀ ਲੰਬਾਈ = 5 ਵਿਆਸਾਂ ਦੀ ਲੰਬਾਈ + ਚੱਕਰ (ਬਚ) ਦਾ ਪਰਿਮਾਪ
= 5(35) + 2πR
= [175 + 2 × \(\frac{22}{7}\) × \(\frac{35}{2}\)] mm
= [175 + 110] mm
= 285 mm

(ii) ਬਰੂਚ ਦੇ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਕੋਣ

ਹਰੇਕ ਬਰੂਚ ਦਾ ਖੇਤਰਫਲ (ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ)
= \(\frac{\pi R^{2} \theta}{360}\)
= \(\frac{36}{360}\) × \(\frac{22}{7}\) × \(\frac{35}{2}\) × \(\frac{35}{2}\)
= \(\frac{1135}{4}\) = \(\frac{385}{4}\) mm²
= 96.25 mm²
∴ ਬਰੂਚ ਦੇ ਹਰੇਕ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ
= 96.25 mm²

ਪ੍ਰਸ਼ਨ 10.
ਇੱਕ ਛੱਤਰੀ ਵਿੱਚ ਅੱਠ ਤਾਰਾਂ ਹਨ, ਜੋ ਬਰਾਬਰ ਦੂਰੀ ‘ਤੇ ਲੱਗੀਆਂ ਹੋਈਆਂ ਹਨ (ਦੇਖੋ ਚਿੱਤਰ । ਛੱਤਰੀ ਨੂੰ 45 cm ਅਰਧ ਵਿਆਸ ਵਾਲਾ ਇੱਕ ਸਪਾਟ ਚੱਕਰ ਮੰਨਦੇ ਹੋਏ ਇਸ ਦੀਆਂ ਦੋ ਲਗਾਤਾਰ ਤਾਰਾਂ ਦੇ ਵਿਚਕਾਰ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।

ਹੱਲ:
ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ = 45 cm
ਤਾਰਾਂ ਦੀ ਸੰਖਿਆ = 8
ਕੇਂਦਰੀ ਕੋਣ (ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਕੋਣ) = \(\frac{360^{\circ}}{8}\)
= 45°
ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ = \(\frac{\pi R^{2} \theta}{360^{\circ}}\)
= \(\frac{45}{360^{\circ}}\) × \(\frac{22}{7}\) × 45 × 45 cm²
= \(\frac{1}{8}\) × \(\frac{22}{7}\) × 45 × 45 cm²
= \(\frac{22275}{28}\) cm²
= 795:53 cm²
∴ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ =795.53 cm²
∴ ਛੱਤਰੀ ਦੇ ਦੋ ਲਗਾਤਾਰ ਤਾਰਾਂ ਵਿਚਕਾਰ ਦਾ ਖੇਤਰਫਲ
= 795.53 cm²

ਪ੍ਰਸ਼ਨ 11.
ਕਿਸੇ ਕਾਰ ਦੇ ਦੋ ਵਾਇਪਰ (wipers) ਹਨ, ਆਪਸ ਵਿੱਚ ਕਦੇ ਵੀ ਇੱਕ ਦੂਸਰੇ ਨੂੰ ਛੂਹਦੇ ਨਹੀਂ । ਹਰੇਕ ਵਾਇਪਰ, ਜਿਸਦੀ ਪੱਤੀ ਦੀ ਲੰਬਾਈ 25 cm ਹੈ ਅਤੇ 115° ਦੇ ਕੋਣ ਤੱਕ ਘੁੰਮ ਕੇ ਸਫਾਈ ਕਰ ਸਕਦਾ ਹੈ । ਵਾਇਪਰਾਂ ਦੇ ਹਰੇਕ ਗੇੜੇ ਨਾਲ ਜਿੰਨਾ ਖੇਤਰਫਲ ਸਾਫ਼ ਹੋ ਜਾਂਦਾ ਹੈ, ਉਹ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਪੱਤੀ ਦੀ ਲੰਬਾਈ (R) = 25 cm
ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਕੋਣ (θ) = 115°
ਵਾਇਪਰ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦੇ ਰੂਪ ਵਿਚ ਘੁੰਮਦਾ ਹੈ ।

ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ = ਇਕ ਪੱਤੀ ਦੁਆਰਾ ਘੁੰਮਿਆ ਗਿਆ ਖੇਤਰਫਲ
= \(\frac{\pi \mathrm{R}^{2} \theta}{360^{\circ}}\)
= \(\frac{22}{7}\) × \(\frac{115}{360}\) × 25 × 25 cm²
= 27.48 cm²
ਵਾਇਪਰ ਦੀਆਂ ਦੋ ਪੱਤੀਆਂ ਦੁਆਰਾ ਘੁੰਮਿਆ ਗਿਆ ਖੇਤਰਫਲ = 2 ਖੰਡਾਂ ਦਾ ਖੇਤਰਫਲ
= 2 × 627.48 cm²
= 1254.96 cm²

ਪ੍ਰਸ਼ਨ 12.
ਜਹਾਜ਼ਾਂ ਨੂੰ ਸਮੁੰਦਰ ਜਲ ਸੜਾ ਦੇ ਹੇਠਾਂ ਸਥਿਤ ਚੱਟਾਨਾਂ ਦੀ ਚੇਤਾਵਨੀ ਦੇਣ ਦੇ ਲਈ, ਇੱਕ ਲਾਈਟ ਹਾਉਸ (light house) 80° ਕੋਣ ਵਾਲੇ ਇੱਕ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਵਿੱਚ 6.5 km ਦੀ ਦੂਰੀ ਤੱਕ ਲਾਲ ਰੰਗ ਦਾ ਪ੍ਰਕਾਸ਼ ਫੈਲਾਉਂਦਾ ਹੈ । ਸਮੁੰਦਰ ਦੇ ਉਸ ਭਾਗ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ਜਿਸ ਨਾਲ ਜਹਾਜ਼ਾਂ ਨੂੰ ਚੇਤਾਵਨੀ ਦਿੱਤੀ ਜਾ ਸਕੇ । (π = 3.14 ਦਾ ਪ੍ਰਯੋਗ ਕਰੋ ।)
ਹੱਲ:
ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਕੋਣ (θ) = 80°
ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਅਰਥਵਿਆਸ (R) = 16.5 km

ਸਮੁੰਦਰ ਦੇ ਉਸ ਭਾਗ ਦਾ ਖੇਤਰਫਲ ਜਿਥੋਂ ਤੱਕ ਜਹਾਜਾਂ ਨੂੰ ਚੇਤਾਵਨੀ ਦਿੱਤੀ ਜਾ ਸਕੇ
ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ = \(\frac{\pi \mathrm{R}^{2} \theta}{360^{\circ}}\)
= \(\frac{3.14 \times 16.5 \times 16.5 \times 80}{360}\) km²
= 189.97 km²
ਉਹ ਖੇਤਰ ਜਿੱਥੋਂ ਤੱਕ ਚੇਤਾਵਨੀ ਦਿੱਤੀ ਜਾ ਸਕੇ
= 189.97 km²

ਪ੍ਰਸ਼ਨ 13.
ਇੱਕ ਗੋਲ ਮੇਜਪੋਸ਼ ‘ਤੇ ਛੇ ਇੱਕੋ ਜਿਹੇ ਸਮਾਨ ਡਿਜਾਈਨ ਬਣੇ ਹੋਏ ਹਨ ਜਿਵੇਂ ਕਿ ਚਿੱਤਰ ਵਿੱਚ ਦਰਸਾਇਆ ਗਿਆ ਹੈ । ਜੇਕਰ ਮੇਜਪੋਸ਼ ਦਾ ਅਰਧ ਵਿਆਸ 28 cm ਹੈ ਤਾਂ ਤੋਂ 0.35 ਪ੍ਰਤੀ ਵਰਗ ਸੈਂਟੀਮੀਟਰ ਦੀ ਦਰ ਨਾਲ ਇਨ੍ਹਾਂ | ਡਿਜਾਈਨਾਂ ਨੂੰ ਬਣਾਉਣ ਦੀ ਲਾਗਤ ਪਤਾ ਕਰੋ ।
(\(\sqrt {3}\) = 1.7 ਲਓ)

ਹੱਲ:
ਸਮਾਨ ਡਿਜਾਈਨਾਂ ਦੀ ਸੰਖਿਆ = 6
ਡਿਜਾਈਨਾਂ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 28 cm
ਹਰੇਕ ਡਿਜਾਇਨ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦੇ ਆਕਾਰ ਦਾ ਹੈ, ਕੇਂਦਰੀ ਕੋਣ (θ) = \(\frac{360^{\circ}}{6}\) = 60°
ਕਿਉਂਕਿ ਕੇਂਦਰੀ ਕੋਣ 60° ਹੈ ਅਤੇ OA = OB ਹੈ ।
∴ △OAB ਇਕ ਸਮਭੁਜੀ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸਦੀ ਭੂਜਾ 28 cm ਹੈ ।

ਇੱਕ ਛਾਇਆ ਅੰਕਿਤ ਡਿਜਾਇਨ ਵਾਲੇ ਭਾਗ ਦਾ ਖੇਤਰਫਲ = ਚੱਕਰ ਖੰਡ ਦਾ ਖੇਤਰਫਲ = ਅਰਧ ਵਿਆਸੀ ‘ ਖੰਡ OAB ਦਾ ਖੇਤਰਫਲ – △OAB ਦਾ ਖੇਤਰਫਲ
= \(\frac{\pi \mathrm{R}^{2} \theta}{360^{\circ}}\) – \(\frac{\sqrt{3}}{4}\) (ਭੂਜਾ)²
= (\(\frac{22}{7}\) × \(\frac{2828}{360}\) × 60 – \(\frac{1.7}{4}\) × 28 × 28) cm²
= (410.66 – 333.2) cm²
= 77.46 cm²
∴ ਇਕ ਛਾਇਆ ਅੰਕਿਤ ਡਿਜਾਇਨ ਵਾਲੇ ਭਾਗ ਦਾ ਖੇਤਰਫਲ
= 77.46 cm²
ਛੇ ਡਿਜਾਈਨ ਭਾਗਾਂ ਦਾ ਖੇਤਰਫਲ = 6 [ਇਕ ਡਿਜਾਈਨ ਭਾਗ ਦਾ ਖੇਤਰਫਲ]
= 6 [77.46]
= 464.76 cm²
1 cm² ਡਿਜਾਈਨ ਬਣਾਉਣ ਦਾ ਖ਼ਰਚ = ₹ 0.35
464.76 cm² ਡਿਜਾਈਨ ਬਣਾਉਣ ਦਾ ਖ਼ਰਚ
= ₹0.35 × 464.76
= ₹ 162.67

ਪ੍ਰਸ਼ਨ 14.
ਹੇਠਾਂ ਦਿੱਤਿਆਂ ਵਿੱਚੋਂ ਸਹੀ ਉੱਤਰ ਚੁਣੋ :
ਅਰਧ ਵਿਆਸ Rਵਾਲੇ ਚੱਕਰ ਦੇ ਉਸ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ ਜਿਸਦਾ ਕੋਣ p° ਹੈ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਹੈ :
(A) \(\frac{p}{180}\) × 2πR
(B) \(\frac{p}{180}\) × πR²
(C) \(\frac{p}{360}\) × 2πR
(D) \(\frac{p}{720}\) × 2πR²
ਹੱਲ:
ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਕੋਣ (θ) = p°
ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ = R
ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ = \(\frac{\pi R^{2} \theta}{360}\)
= \(\frac{\pi \mathrm{R}^{2} \times p}{360}\)
∴ ਸਹੀ ਵਿਕਲਪ (D) ਹੈ ।

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 12 ਚੱਕਰ ਨਾਲ ਸੰਬੰਧਿਤ ਖੇਤਰਫਲ Ex 12.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 12 ਚੱਕਰ ਨਾਲ ਸੰਬੰਧਿਤ ਖੇਤਰਫਲ Exercise 12.1

ਜਦੋਂ ਤੱਕ ਹੋਰ ਕੁੱਝ ਨਾ ਕਿਹਾ ਜਾਵੇ, ਗ π = \(\frac{22}{7}\) ਪ੍ਰਯੋਗ ਕਰੋ !

ਪ੍ਰਸ਼ਨ 1.
ਦੋ ਚੱਕਰਾਂ ਦੇ ਅਰਧ ਵਿਆਸ ਕੁਮਵਾਰ 19cm ਅਤੇ 9cm ਹਨ । ਉਸ ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ ਪਤਾ ਕਰੋ ਜਿਸ ਦਾ ਘੋਰਾ ਇਨ੍ਹਾਂ ਦੋਨਾਂ ਚੱਕਰਾਂ ਦੇ ਘੇਰਿਆਂ ਦੇ ਜੋੜ ਦੇ ਬਰਾਬਰ ਹੈ।
ਹੱਲ:

ਪਹਿਲੇ ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ (r₁) = 19 cm
ਦੂਸਰੇ ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ (r₂) = 9 cm
ਮੰਨ ਲਉ ਤੀਸਰੇ ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ = R cm
ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ,
ਪਹਿਲੇ ਚੱਕਰ ਦਾ ਘੇਰਾ + ਦੂਸਰੇ ਚੱਕਰ ਦਾ ਘੇਰਾ = ਤੀਸਰੇ ਚੱਕਰ ਦਾ ਘੇਰਾ
2πr₁ + 2πr₂ = 2πR
2π [r₁ + r₂] = 2π R
19 + 9 = R
∴ R = 28
∴ ਤੀਸਰੇ ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ = 28 cm

ਪ੍ਰਸ਼ਨ 2.
ਦੋ ਚੱਕਰਾਂ ਦੇ ਅਰਧ ਵਿਆਸ ਕੁਮਵਾਰ 8 cm ਅਤੇ 6 cm ਹਨ । ਉਸ ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ ਪਤਾ ਕਰੋ ਜਿਸ ਦਾ ਖੇਤਰਫਲ ਇਨ੍ਹਾਂ ਦੋਨਾਂ ਚੱਕਰਾਂ ਦੇ ਖੇਤਰਫਲਾਂ ਦੇ ਜੋੜ ਦੇ ਬਰਾਬਰ ਹੈ ।
ਹੱਲ:
ਪਹਿਲੇ ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ (r₁) = 8 cm
ਦੂਸਰੇ ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ (r₂) = 6 cm
ਤੀਸਰੇ ਚੱਕਰ ਦਾ ਅਰਧਵਿਆਸ = R cm
ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ
ਤੀਸਰੇ ਚੱਕਰ ਦਾ ਖੇਤਰਫਲ = ਪਹਿਲੇ ਚੱਕਰ ਦਾ ਖੇਤਰਫਲ + ਦੂਸਰੇ ਚੱਕਰ ਦਾ ਖੇਤਰਫਲ
πR² = π\(r_{1}^{2}\) + π\(r_{2}^{2}\)
πR² = π[\(r_{1}^{2}\) + π\(r_{2}^{2}\)]
R² = (8)² + (6)²
R = \(\sqrt {64+36}\) = \(\sqrt {100}\)
R= 10 cm
∴ ਲੋੜੀਂਦਾ ਅਰਧ ਵਿਆਸ (R) = 10 cm

ਪ੍ਰਸ਼ਨ 3.
ਦਿੱਤਾ ਹੋਇਆ ਚਿੱਤਰ ਇੱਕ ਤੀਰ ਅੰਦਾਜ਼ੀ ਨਿਸ਼ਾਨੇ ਨੂੰ ਦਰਸਾਉਂਦਾ ਹੈ, ਜਿਸ ਵਿੱਚ ਕੇਂਦਰ ਦੇ ਬਾਹਰ ਵੱਲ ਪੰਜ ਖੇਤਰ GOLD,RED, BLUE, BLACK ਅਤੇ WHITE ਨੂੰ ਦਰਸਾਉਂਦੇ ਹਨ, ਜਿਨ੍ਹਾਂ ‘ਤੇ ਅੰਕ ਪ੍ਰਾਪਤ ਕੀਤੇ ਜਾ ਸਕਦੇ ਹਨ । GOLਅੰਕ ਵਾਲੇ ਖੇਤਰ ਦਾ ਵਿਆਸ 21 cm ਹੈ ਅਤੇ ਹਰੇਕ ਹੋਰ ਪੱਟੀ 10.5 cm ਚੌੜੀ ਹੈ । ਅੰਕ ਪ੍ਰਾਪਤ ਕਰਾਉਣ ਵਾਲੇ ਇਨ੍ਹਾਂ ਪੰਜਾਂ ਖੇਤਰਾਂ ਵਿੱਚੋਂ ਹਰੇਕ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।

ਹੱਲ:
Gold ਖੇਤਰ ਦਾ ਵਿਆਸ = 21 cm
Gold ਖੇਤਰ ਦਾ ਅਰਧ ਵਿਆਸ (R₁).
= \(\frac{21}{2}\) cm = 10.5 cm
∴ Gold ਖੇਤਰ ਦਾ ਖੇਤਰਫਲ
= π\(R_{1}^{2}\) = \(\frac{22}{7}\) × \(\frac{21}{2}\) × \(\frac{21}{2}\) = \(\frac{693}{2}\) cm²
= 346∙5 cm²
ਹਰੇਕ ਪੱਟੀ ਦੀ ਚੌੜਾਈ = 10.5 cm
∴ Red ਅਤੇ Gold ਖੇਤਰ ਦਾ ਅਰਧ ਵਿਆਸ (R₂)
= (10.5 + 10.5) cm
= 21 cm
Blue, Red ਅਤੇ Gold ਖੇਤਰ ਦਾ ਸੰਯੁਕਤ ਅਰਧ ਵਿਆਸ (R₃) = R₂ + 10.5 cm
= 21 + 10.5 = 31.5 cm
Black, Blue, Red ਅਤੇ Gold ਖੇਤਰ ਦਾ ਸਾਂਝਾ ਅਰਧ ਵਿਆਸ (R₄) = R₃ + 10.5
= (31.5 + 10.5) cm
= 42 cm
Black ਖੇਤਰ ਦਾ ਖੇਤਰਫਲ = Gold, Red, Blue ਅਤੇ Black ਖੇਤਰ ਦਾ ਖੇਤਰਫਲ – Gold, Red ਅਤੇ Blue ਖੇਤਰ ਦਾ ਸਾਂਝਾ ਅਰਧ ਵਿਆਸ
= π\(r_{4}^{2}\) – π\(r_{3}^{2}\)
= π[(42)² – (31.5)²] cm²
= \(\frac{22}{7}\) [1764 – 99225] cm²
= \(\frac{22}{7}\) [771.75] cm² = 2425.5 cm²
White, black, blue, red, gold ਖੇਤਰ ਦਾ ਸਾਂਝਾ | ਅਰਧ ਵਿਆਸ (R₅)
= R₄ + 15
R₅ = 42 + 10.5 = 52.5 cm
Black, blue, red ਅਤੇ gold ਖੇਤਰ ਦਾ ਅਰਧ | ਵਿਆਸ (R₄) = 42 cm
White ਅੰਕ ਲੈਣ ਵਾਲੇ ਖੇਤਰ ਦਾ ਖੇਤਰਫਲ = White, black, blue, red, gold ਖੇਤਰ ਦਾ ਖੇਤਰਫਲ – Black blue, red, gold ਦਾ ਖੇਤਰਫਲ
= π\(R_{5}^{2}\) – π\(R_{4}^{2}\)
= π[\(R_{5}^{2}\) – \(R_{4}^{2}\)]
= \(\frac{22}{7}\)[(525)² – (42)²] cm²
= \(\frac{22}{7}\)[2756.25 -1764] cm²
= \(\frac{22 \times 992.25}{7}\) = \(\frac{21829.5}{7}\) cm²
= 3118.5 cm²
∴ White ਅੰਕ ਵਾਲੇ ਖੇਤਰ ਦਾ ਖੇਤਰਫਲ
= 3118.5 cm²
∴ Red ਅੰਕ ਵਾਲੇ ਖੇਤਰ ਦਾ ਖੇਤਰਫਲ = Red or Gold ਦਾ ਖੇਤਰਫਲ – Gold ਦਾ ਖੇਤਰਫਲ

= 1039.5 cm²
∴ Red ਖੇਤਰ ਦਾ ਖੇਤਰਫਲ = 1039.5 cm²
Gold, Red ਅਤੇ Blue ਦਾ ਸਾਂਝਾ ਅਰਧਵਿਆਸ R,
= (10.5 + 10.5 + 10.5) = 31.5 cm
Blue ਅੰਕ ਵਾਲੇ ਖੇਤਰ ਦਾ ਖੇਤਰਫਲ
= Red, blue ਅਤੇ Gold ਦਾ ਖੇਤਰਫਲ – Gold ਅਤੇ Red ਦਾ ਖੇਤਰਫਲ
= π\(R_{3}^{2}\) – π\(R_{2}^{2}\)
= π[\(R_{3}^{2}\) – \(R_{2}^{2}\)]
= \(\frac{22}{7}\)[(31.52)² – (21)²] cm²
= \(\frac{22}{7}\)[99225 – 441] cm ²
= \(\frac{22}{7}\) × 551.25 cm² = \(\frac{12127.5}{7}\) cm²
= 1732.5 cm² .

ਪ੍ਰਸ਼ਨ 4.
ਕਿਸੇ ਕਾਰ ਦੇ ਹਰੇਕ ਪਹੀਏ ਦਾ ਵਿਆਸ 80 cm ਹੈ । ਜੇਕਰ ਇਹ ਕਾਰ 66 km/h ਦੀ ਚਾਲ ਨਾਲ ਚਲ ਰਹੀ ਹੈ । ਤਾਂ 10 ਮਿੰਟ ਵਿੱਚ ਹਰੇਕ ਪਹੀਆ ਕਿੰਨੇ ਚੱਕਰ ਲਗਾਉਂਦਾ ਹੈ ।
ਹੱਲ:
ਪਹੀਏ ਦਾ ਵਿਆਸ = 80 cm
ਪਹੀਏ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 40 cm
= \(\frac{4}{100}\) m = 0.04 m
ਪਹੀਏ ਦਾ ਘੇਰਾ = 2πr
= 2 × \(\frac{22}{7}\) × 0.04 m
ਮੰਨ ਲਉ ਕਾਰ ਦਾ ਪਹੀਆ ॥ ਪੂਰੇ ਚੱਕਰ ਲਗਾਉਣ ਵਿਚ 10 ਮਿੰਟ ਦਾ ਸਮਾਂ ਲੈਂਦਾ ਹੈ ।
= n[0.08 × \(\frac{22}{7}\)] m
ਕਾਰ ਦੀ ਚਾਲ = 66 km/h
60 ਮਿੰਟਾਂ ਵਿਚ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ
= 66 km = 66 × 1000 m
10 ਮਿੰਟ ਵਿਚ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ
= \(\) 10 m
= 11000 m
∴ n[\(\frac{22}{7}\) × 0.08] = 1100
n = \(\frac{11000}{0.08}\) × \(\frac{7}{22}\)
n = 4375
∴ ਕਾਰ ਦੇ ਪਹੀਏ ਦੁਆਰਾ 10 ਮਿੰਟਾਂ ਵਿਚ ਲਗਾਏ ਗਏ ਚੱਕਰਾਂ ਦੀ ਗਿਣਤੀ 4375 ਹੈ ।

ਪ੍ਰਸ਼ਨ 5.
ਹੇਠਾਂ ਲਿਖਿਆਂ ਵਿਚੋਂ ਸਹੀ ਉੱਤਰ ਚੁਣੋ ਅਤੇ ਆਪਣੇ ਉੱਤਰ ਦਾ ਸਪਸ਼ਟੀਕਰਨ ਦਿਓ :
ਜੇਕਰ ਇੱਕ ਚੱਕਰ ਦਾ ਪਰਿਮਾਪ ਅਤੇ ਖੇਤਰਫਲ ਸੰਖਿਆਤਮਕ ਰੂਪ ਵਿੱਚ ਬਰਾਬਰ ਹੈ, ਤਾਂ ਉਸ ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ ਹੈ ।
(A) 2 ਇਕਾਈਆਂ
(B) π ਇਕਾਈਆਂ
(C) 4 ਇਕਾਈਆਂ
(D) 7 ਇਕਾਈਆਂ
ਹੱਲ:
ਚੱਕਰ ਦਾ ਪਰਿਮਾਪ = ਚੱਕਰ ਦਾ ਖੇਤਰਫਲ
2πR = πR²
2R = R²
⇒ R = 2
∴ ਸਹੀ ਉੱਤਰ A ਹੈ (R) = 2 ਇਕਾਈਆਂ

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 11 ਰਚਨਾਵਾਂ Ex 11.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 11 ਰਚਨਾਵਾਂ Exercise 11.2

1. ਹੇਠਾਂ ਦਿੱਤੀ ਹਰੇਕ ਰਚਨਾ ਦੇ ਲਈ ਸਪੱਸ਼ਟੀਕਰਣ ਵੀ ਦਿਓ :

ਪ੍ਰਸ਼ਨ 1.
6 cm ਅਰਧ ਵਿਆਸ ਦਾ ਇੱਕ ਚੱਕਰ ਖਿੱਚੋ । ਕੇਂਦਰ ਤੋਂ 10 cm ਦੂਰ ਸਥਿਤ ਇੱਕ ਬਿੰਦੂ ਤੋਂ ਚੱਕਰ ’ਤੇ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਦੇ ਜੋੜੇ ਦੀ ਰਚਨਾ ਕਰੋ ਅਤੇ ਉਨ੍ਹਾਂ ਦੀਆਂ ਲੰਬਾਈਆਂ ਮਾਪੋ ।
ਹੱਲ:

ਰਚਨਾ ਦੇ ਪਰਾ :
1. ਇਕ ਚੱਕਰ (1) ਜਿਸਦਾ ਅਰਧ ਵਿਆਸ 6 cm ਹੈ, ਖਿੱਚੋ ।
2. ਕੇਂਦਰ ਤੋਂ 10 cm ਦੀ ਦੂਰੀ ਤੇ ਇਕ ਬਿੰਦੂ P ਲਉ OP ਨੂੰ ਮਿਲਾਉ ।
3. OP ਦਾ ਲੰਬ ਸਮਦੁਭਾਜਕ ਖਿੱਚੋ । ਮੰਨ ਲਉ ‘M’, OP ਦਾ ਮੱਧ ਬਿੰਦੁ ਹੈ !
4. “M’ ਨੂੰ ਕੇਂਦਰ ਮੰਨ ਕੇ ਅਤੇ MO ਨੂੰ ਅਰਧ ਵਿਆਸ ਲੈ ਕੇ ਇੱਕ ਚੱਕਰ (II) ਖਿੱਚੋ ਜੋ ਪਹਿਲੇ ਚੱਕਰ ਨੂੰ ਬਿੰਦੁ T ਅਤੇ T’ ਉੱਤੇ ਕੱਟਦਾ ਹੈ ।
5. ਹੁਣ PT ਅਤੇ PT’ ਨੂੰ ਮਿਲਾਉ ॥
ਰਚਨਾ ਦਾ ਸਪੱਸ਼ਟੀਕਰਣ :
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ ਕਿ ਕਿਸੇ ਬਿੰਦੁ ਉੱਤੇ ਸਪਰਸ਼ ਰੇਖਾ ਉਸ ਬਿੰਦੁ ਦੇ ਅਰਧ ਵਿਆਸ ਉੱਤੇ ਲੰਬ ਹੁੰਦੀ ਹੈ ਅਸੀਂ ਸਿੱਧ ਕਰਨਾ ਹੈ ਕਿ :
∠PTO = ∠PTO = 90°
OT ਨੂੰ ਮਿਲਾਇਆ ਗਿਆ ਹੈ ।
ਹੁਣ, PMO ਚੱਕਰ (II) ਦਾ ਵਿਆਸ ਹੈ ।
ਅਤੇ ∠PTO ਅਰਧ ਚੱਕਰ ਵਿੱਚ ਹੈ
∴ ∠PTO = 90°
[ਅਰਧ ਚੱਕਰ ਵਿਚ ਬਣਿਆ ਕੋਣ ਸਮਕੋਣ ਹੁੰਦਾ ਹੈ।]
ਇਸੇ ਤਰ੍ਹਾਂ ∠PTO’ = 90°
∴ PT ਅਤੇ PT’ ਚੱਕਰ ਦੀ ਅਤੇ T’ ਉੱਤੇ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਹਨ ।
ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਦੀ ਲੰਬਾਈ ਮਾਪਣ ਤੇ
ਇਸੇ ਤਰ੍ਹਾਂ PT = 8.1 cm
PT’ = 8.1 cm.

ਪ੍ਰਸ਼ਨ 2.
4 cm ਅਰਧ ਵਿਆਸ ਵਾਲੇ ਚੱਕਰ ’ਤੇ 6 cm ਅਰਧ ਵਿਆਸ ਦੇ ਇੱਕ ਸਮਕੇਂਦਰੀ ਚੱਕਰ ਦੇ ਕਿਸੇ ਬਿੰਦੁ ਤੋਂ ਇੱਕ ਸਪੱਰਸ਼ ਰੇਖਾ ਦੀ ਰਚਨਾ ਕਰੋ ਅਤੇ ਉਸਦੀ ਲੰਬਾਈ ਮਾਪੇ ॥ ਗਣਨਾ ਕਰਕੇ ਇਸ ਮਾਪ ਦੀ ਜਾਂਚ ਵੀ ਕਰੋ।
ਹੱਲ:
ਸਮਕੇਂਦਰੀ ਚੱਕਰ : ਦੋ ਜਾਂ ਵੱਧ ਚੱਕਰ ਜਿਨ੍ਹਾਂ ਦਾ ਇਕ ਹੀ ਕੇਂਦਰ ਹੋਵੇ ਪਰ ਅਰਧ ਵਿਆਸ ਅਲੱਗ-ਅਲੱਗ ਹੋਣ ਸਮਕੇਂਦਰੀ ਚੱਕਰ ਕਹਾਉਂਦੇ ਹਨ ।
ਰਚਨਾ ਦੇ ਪਗ :
1. ਇਕ ਚੱਕਰ ਜਿਸ ਦਾ ਕੇਂਦਰ “O’ ਅਤੇ ਅਰਧ ਵਿਆਸ 4 ਸਮ ਹੋਵੇ, ਖਿੱਚੋ । ਇਸਨੂੰ I ਅੰਕਿਤ ਕਰੋ ।

2. ਉਸੇ ਕੇਂਦਰ “O’ ਅਤੇ ਅਰਧ ਵਿਆਸ 6 cm ਦਾ ਇਕ ਹੋਰ ਚੱਕਰ ਖਿੱਚੋ ਜਿਸਨੂੰ II ਅੰਕਿਤ ਕਰੋ ।
3. ਚੱਕਰ II ਉੱਤੇ ਕੋਈ ਬਿੰਦੁ ‘P’ ਲਉ । OP ਨੂੰ ਮਿਲਾਓ ।
4. OP ਦਾ ਲੰਬ ਸਮਦੁਭਾਜਕ ਖਿੱਚੋ । ਮੰਨ ਲਉ ਇਹ ‘OP’ ਨੂੰ M ਉੱਤੇ ਕੱਟਦਾ ਹੈ ।
5. M ਨੂੰ ਕੇਂਦਰ ਮੰਨ ਕੇ ‘OM’ ਜਾਂ ‘MP’, ਨੂੰ ਅਰਧ ਵਿਆਸ ਲੈ ਕੇ ਚੱਕਰ III ਦੀ ਰਚਨਾ ਕਰੋ ਜੋ ਚੱਕਰ I ਨੂੰ T ਅਤੇ ‘ ਤੇ ਕੱਟਦਾ ਹੈ ।
6. PT ਨੂੰ ਮਿਲਾਓ । PT ਲੋੜੀਂਦੀ ਸਪਰਸ਼ ਰੇਖਾ ਹੈ ।
ਸਪੱਸ਼ਟੀਕਰਣ :
OT ਨੂੰ ਮਿਲਾਉ
ਹੁਣ OP ਚੱਕਰ III ਦਾ ਵਿਆਸ ਹੈ ।
∠OTP ਅਰਧ ਚੱਕਰ ਵਿਚ ਕੋਣ ਹੈ।
∴ ∠OTP = 90° …(1) ਹੁਣ
OT ⊥ PT [(1) ਦਾ ਪ੍ਰਯੋਗ ਕਰਕੇ]
∵ ਇਕ ਰੇਖਾ ਜੋ ਚੱਕਰ ਵਿਚ ਕਿਸੇ ਬਿੰਦੂ ਉੱਤੇ ਅਰਧ ਵਿਆਸ ਦੇ ਨਾਲ 90° ਦਾ ਕੋਣ ਬਣਾਉਂਦੀ ਹੈ ਉਹ ਚੱਕਰ ਦੀ ਸਪਰਸ਼ ਰੇਖਾ ਹੁੰਦੀ ਹੈ ।
∴ PT ਚੱਕਰ ‘I’ ਦੀ ਸਪਰਸ਼ ਰੇਖਾ ਹੈ
ਭਾਵ PT, 4 ਸਮ ਅਰਧ ਵਿਆਸ ਵਾਲੇ ਚੱਕਰ ਦੀ ਸਪਰਸ਼ ਰੇਖਾ ਹੈ ।
ਸਪਰਸ਼ ਰੇਖਾ ਦੀ ਲੰਬਾਈ :
△OTP ਲਉ ।
∠OTP = 90° ° [(i) ਦਾ ਪ੍ਰਯੋਗ ਕਰਕੇ]
∴ △OTP ਇਕ ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ ਹੈ।
OT = 4 cm
OP = 6 cm [ਚੱਕਰ I ਅਤੇ II ਦੇ ਅਰਧ ਵਿਆਸ]
PT = ?
ਸਮਕੋਣ △OTP ਵਿਚ
ਪਾਈਥਾਗੋਰਸ ਪਮੇਯ ਅਨੁਸਾਰ
OP² = OT² + PT²
[(ਕਰਣ)² = (ਅਧਾਰ)² + (ਲੰਬ)²]
PT² = OP² – OT² = 6² – 4²
= 36 – 16 = 20
PT = \(\sqrt {20}\) cm = 2\(\sqrt {5}\)
= 2 × 2.24 = 4.48 cm
∴ ਸਪਰਸ਼ ਰੇਖਾ ਦੀ ਲੰਬਾਈ
= 4.48 ਸਮ = 4.5 cm
ਮਾਪਣ ਤੇ ਸਪਸ਼ ਰੇਖਾ ਦੀ ਲੰਬਾਈ
= 4.5 cm
∴ ‘PT’ ਸਪਰਸ਼ ਰੇਖਾ ਦੀ ਲੰਬਾਈ ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
3 cm ਅਰਧ ਵਿਆਸ ਦਾ ਇੱਕ ਚੱਕਰ ਖਿੱਚੋ |ਇਸਦੇ ਕਿਸੇ ਵਧਾਏ ਗਏ ਵਿਆਸ ‘ਤੇ ਕੇਂਦਰ ਤੋਂ 7 cm ਦੀ ਦੂਰੀ ‘ਤੇ ਸਥਿਤ ਦੋ ਬਿੰਦੂ P ਅਤੇ Q ਲਓ । ਇਨ੍ਹਾਂ ਦੋਨਾਂ ਬਿੰਦੂਆਂ ਤੋਂ ਚੱਕਰ `ਤੇ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਖਿੱਚੋ ।
ਹੱਲ:
ਰਚਨਾ ਦੇ ਪਰੀ :
1. ਕੇਂਦਰ ‘O’ ਅਤੇ 3 cm ਅਰਧ ਵਿਆਸ ਵਾਲਾ ਇੱਕ ਚੱਕਰ ਖਿਚੋ ।
2. ਇਸਦਾ ਵਿਆਸ ‘AB’ ਖਿਚੋ ਅਤੇ ਦੋਵੇਂ ਪਾਸੇ ਵਧਾਓ ਜਿਵੇਂ OX ਅਤੇ OX’ ।
3. “OX” ਦਿਸ਼ਾ ਵਿਚ ਬਿੰਦੁ P’ ਅਤੇ ‘OX’ ਦਿਸ਼ਾ ਵਿੱਚ “Q’ ਬਿੰਦੂ ਇਸ ਤਰ੍ਹਾਂ ਲਉ |
ਤਾਂ ਕਿ OP = OQ = 7 cm.

4. OP ਅਤੇ OQ ਦਾ ਲੰਬ ਸਮਭਾਜਕ ਖਿੱਚੋ ਜੋ OP ਅਤੇ OQ ਨੂੰ ਕ੍ਰਮਵਾਰ ‘M’ ਅਤੇ ‘M’ ਉੱਤੇ ਕੱਟੇ ।
5. “M’ ਨੂੰ ਕੇਂਦਰ ਮੰਨ ਕੇ ਅਧਵਿਆਸ MO’ ਜਾਂ । M’O ਜਾਂ MQ ਲੈ ਕੇ ਚੱਕਰ ‘I’ ਖਿਚੋ ਜੋ ਚੱਕਰ ‘I’ ਨੂੰ T ਅਤੇ T’ ਉੱਤੇ ਕੱਟੇ ।
6. ਇਸੇ ਤਰ੍ਹਾਂ ‘M’ ਨੂੰ ਕੇਂਦਰ ਮੰਨ ਕੇ ਚੱਕਰ M’O ਜਾਂ MQ, ਲੈ ਕੇ ਚੱਕਰ (III) ਖਿਚੋ ਜੋ ਚੱਕਰ ‘I’ ਨੂੰ ‘S ਅਤੇ ‘S’ ਤੇ ਕੱਟੇ ।
7. PT, PT’ ਅਤੇ QS, QS’ ਨੂੰ ਮਿਲਾਓ।
ਰਚਨਾ ਦਾ ਸਪੱਸ਼ਟੀਕਰਣ :
‘OT’ ਅਤੇ ‘OT” ਅਤੇ ‘OS’ ਅਤੇ ‘OS’ ‘ ਨੂੰ ਮਿਲਾਓ ।
PT ਅਤੇ PT’ ਚੱਕਰ ਦੀਆਂ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਹਨ ਨੂੰ ਸਿੱਧ ਕਰਨ ਲਈ ਅਸੀਂ ਸਿੱਧ ਕਰਨਾ ਹੈ ਕਿ
∠PTO = ∠PTO = 90°
ਹੁਣ “OP ਚੱਕਰ ‘I’ ਦਾ ਵਿਆਸ ਹੈ ਅਤੇ ∠OTP | ਅਰਧ ਚੱਕਰ ਵਿਚ ਬਣਿਆ ਕੋਣ ਹੈ।
∴ ∠OTP = 90° …(1)
[∵ ਅਰਧ ਚੱਕਰ ਵਿਚ ਬਣਿਆ ਕੋਣ 90° ਹੁੰਦਾ ਹੈ]
ਪਰ “OT’ ਚੱਕਰ ‘I’ ਦਾ ਅਰਧ ਵਿਆਸ ਹੈ ਅਤੇ ਰੇਖਾ ‘PT’ ਚੱਕਰ ਨੂੰ “T’ ਤੇ ਸਪਰਸ਼ ਕਰਦੀ ਹੈ ।
∵ ਇਕ ਰੇਖਾ ਜੋ ਚੱਕਰ ਨੂੰ ਕਿਸੇ ਬਿੰਦੁ ਤੇ ਸਪਰਸ਼ ਕਰਦੀ ਹੈ ਅਤੇ ਉਸ ਬਿੰਦੁ ਉਤੇ ਅਰਧ ਵਿਆਸ ਦੇ ਨਾਲ 90 ਦਾ ਕੋਣ ਬਣਾਉਂਦੀ ਹੈ । ਚੱਕਰ ਦੀ ਸਪਰਸ਼ ਰੇਖਾ ਹੁੰਦੀ ਹੈ ।
∴ PT ਚੱਕਰ (1) ਬਿੰਦੂ (T) ਉੱਤੇ ਬਿੰਦੂ ‘P’ ਤੋਂ ਸਪਰਸ਼ ਰੇਖਾ ਹੈ । | ਇਸੇ ਤਰ੍ਹਾਂ PT’,QS ਅਤੇ QS’ ਚੱਕਰ I ਉੱਤੇ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਹਨ ।

ਪ੍ਰਸ਼ਨ 4.
5 cm ਅਰਧ ਵਿਆਸ ਦੇ ਇੱਕ ਚੱਕਰ ‘ਤੇ ਅਜਿਹੀਆਂ ਦੋ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਖਿੱਚੋ, ਜੋ ਆਪਸ ਵਿੱਚ 60° ਦੇ ਕੋਣ ‘ਤੇ ਝੁਕੀਆਂ ਹੋਣ ।
ਹੱਲ:
ਰਚਨਾ ਦੇ ਪਗ :
1. ਲੋੜੀਂਦੇ ਚਿੱਤਰ ਦਾ ਕੱਚਾ ਖਾਕਾ ਖਿੱਚੋ ।

∵ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ 60° ਦਾ ਕੋਣ ਬਣਾਉਂਦੀਆਂ ਹਨ
∠OTP = ∠OQT = 60°
[ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਅਰਧ ਵਿਆਸ ਉੱਤੇ ਲੰਬ ਹਨ ]
ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਦਾ ਝੁਕਾਅ ਪਤਾ ਕਰਨ ਲਈ ∠TOQ + ∠OTP + ∠OQT + ∠TPQ = 360°
[ਚਤੁਰਭੁਜ ਦੇ ਕੋਣਾਂ ਦਾ ਜੋੜ ਗੁਣੀ]
∠TOQ + 90° + 90° + 60° = 360°
∠TOQ = 360° – 90° – 90° – 60° = 120°
2. 5 cm ਅਰਧ ਵਿਆਸ ਦਾ ਇੱਕ ਚੱਕਰ ਖਿੱਚੋ
3. ਇਸ ਚੱਕਰ ਦੇ ਦੋ ਅਰਵਿਆਸ ਖਿਚੋ ਜੋ ਆਪਸ ਵਿੱਚ 120° ਦਾ ਕੋਣ ਬਣਾਉਣ ।
4. ਅਰਧ ਵਿਆਸ ਚੱਕਰ ਨੂੰ ‘A’ ਅਤੇ ‘B’ ਤੇ ਕੱਟਦੇ ਹਨ |
5. A ਅਤੇ B ਉੱਤੇ 90° ਦਾ ਕੋਣ ਬਣਾਉ ਜੋ ਇਕ-ਦੂਜੇ 1 ਨੂੰ ‘P’ ਉੱਤੇ ਕੱਟਣ ।

6. PA ਅਤੇ PB ਲੋੜੀਂਦੀਆਂ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਹਨ ।

ਪ੍ਰਸ਼ਨ 5.
8 cm ਲੰਬਾ ਇਕ ਰੇਖਾਖੰਡ AB ਖਿੱਚੋ | A’ ਨੂੰ ਕੇਂਦਰ ਮੰਨ ਕੇ 4 cm ਅਰਧ ਵਿਆਸ ਦਾ ਇੱਕ ਚੱਕਰ ਅਤੇ ‘B’ ਨੂੰ ਕੇਂਦਰ ਲੈ ਕੇ 3 cm ਅਰਧ ਵਿਆਸ ਦਾ ਇੱਕ ਹੋਰ ਚੱਕਰ ਖਿੱਚੋ | ਹਰੇਕ ਚੱਕਰ ’ਤੇ ਦੂਸਰੇ ਚੱਕਰ ਦੇ ਕੇਂਦਰ ਤੋਂ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਦੀ ਰਚਨਾ ਕਰੋ ।
ਹੱਲ:

ਰਚਨਾ ਦੇ ਪਗ :
1. ਇੱਕ ਰੇਖਾਖੰਡ AB = 8 cm ਖਿੱਚੋ।
2. ‘A’ ਨੂੰ ਕੇਂਦਰ ਮੰਨ ਕੇ 4 cm ਅਰਧ ਵਿਆਸ ਦਾ ਚੱਕਰ (I) ਖਿੱਚੋ ।
3. ‘B’ ਨੂੰ ਕੇਂਦਰ ਮੰਨ ਕੇ 3 cm ਅਰਧ ਵਿਆਸ ਦਾ ਚੱਕਰ ‘II’ ਖਿੱਚੋ ।
4. ਰੇਖਾਖੰਡ AB ਦਾ ਲੰਬ ਸਮਦੁਭਾਜਕ ਖਿੱਚੇ ਜੋ ‘AB’ ਨੂੰ ‘M’ ਉੱਤੇ ਕੱਟੇ ।
5. ‘M’ ਨੂੰ ਕੇਂਦਰ ਮੰਨ ਕੇ ਅਰਧ ਵਿਆਸ MA ਜਾਂ MB ਲੈ ਕੇ ਚੱਕਰ (III) ਖਿੱਚੋ ਜੋ ਚੱਕਰ (I) ਨੂੰ ‘S’ ਅਤੇ ‘T’ ਉੱਤੇ ਅਤੇ ਚੱਕਰ (II) ਨੂੰ ‘P’ ਅਤੇ ‘Q’ ਉੱਤੇ ਕੱਟੇ ।
6. ‘AP’ ਅਤੇ ‘AQ’ ਨੂੰ ਮਿਲਾਓ । ਇਹ ਬਿੰਦੁ “A” ਤੋਂ 3 cm ਅਰਵਿਆਸ ਵਾਲੇ ਚੱਕਰ ਤੇ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਹਨ |
7. ‘BS’ ਅਤੇ ‘BT’ ਨੂੰ ਮਿਲਾਓ । ਇਹ ਬਿੰਦੁ ‘B’ ਤੋਂ 4.cm ਅਰਧ ਵਿਆਸ ਵਾਲੇ ਚੱਕਰ ਤੇ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਹਨ ।
ਰਚਨਾ ਦਾ ਸਪੱਸ਼ਟੀਕਰਣ :
ਚੱਕਰ (III) ਵਿਚ AB ਵਿਆਸ ਹੈ ਤਾਂ ∠ASE ਅਤੇ ∠BPA ਅਰਧ ਚੱਕਰ ਦੇ ਕੋਣ ਹਨ
∴ ∠ASB = 90° …(1)
∠BPA = 90° …(2)
ਪਰ ∠ASB ਦਾ ਅਰਧ ਵਿਆਸ ਅਤੇ ਰੇਖਾਖੰਡ ‘BS ਦੇ ਵਿਚ ਦਾ ਕੋਣ ਹੈ ਅਤੇ ∠BPA ਅਰਧ ਵਿਆਸ ਅਤੇ ਰੇਖਾਖੰਡ ਚੱਕਰ (II) AP’ ਦੇ ਵਿਚ ਦਾ ਕੋਣ ਹੈ ।
∵ ਰੇਖਾਖੰਡ ਜੋ ਚੱਕਰ ਦੇ ਅਰਧ ਵਿਆਸ ਉੱਤੇ ਲੰਬ ਹੈ। ਉਸ ਬਿੰਦੂ ਤੇ ਚੱਕਰ ਦੀ ਸਪਰਸ਼ ਰੇਖਾ ਹੈ ।
∴ BS ਦਾ ਚੱਕਰ (I) ਦੀ ਬਿੰਦੁ ‘S’ ਉੱਤੇ ਸਪਰਸ਼ ਰੇਖਾ ਹੈ ਅਤੇ AP ਚੱਕਰ (II) ਦੀ ਬਿੰਦੂ ‘P’ ਉੱਤੇ ਸਪਰਸ਼ ਰੇਖਾ ਹੈ ।
ਇਸੇ ਤਰ੍ਹਾਂ AQ ਅਤੇ BT ਕ੍ਰਮਵਾਰ ਚੱਕਰ (II) ਚੱਕਰ (I) ਦੀਆਂ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਹਨ ।

ਪ੍ਰਸ਼ਨ 6.
ਮੰਨ ਲਓ ABC ਇੱਕ ਸਮਕੋਣ ਤਿਭੁਜ ਹੈ, ਜਿਸ ਵਿੱਚ AB = 6 cm, BC = 8 cm ਅਤੇ ∠B = 90° ਹੈ । B ਤੋਂ AC ‘ ਤੇ BD ਲੰਬ ਹੈ । ਬਿੰਦੁ B, C, D ਤੋਂ ਹੋ ਕੇ ਜਾਣ ਵਾਲਾ ਇੱਕ ਚੱਕਰ ਖਿੱਚਿਆ ਗਿਆ ਹੈ । ‘A’ ਤੋਂ ਇਸ ਚੱਕਰ `ਤੇ ਸਪਰਸ਼ ਰੇਖਾ ਦੀ ਰਚਨਾ ਕਰੋ ।
ਹੱਲ:

ਰਚਨਾ ਦੇ ਪਗ :
1. ਦਿੱਤੀਆਂ ਗਈਆਂ ਸ਼ਰਤਾਂ ਅਤੇ ਮਾਪ ਅਨੁਸਾਰ ਕੋਣ △ABC ਦੀ ਰਚਨਾ ਕਰੋ ।
2. BD ⊥ AC ਖਿੱਚੋ ।
3. ਭੁਜਾ BC ਦਾ ਮੱਧ ਬਿੰਦੁ ‘M’ ਲਉ ।
4. ‘M’ ਨੂੰ ਕੇਂਦਰ ਮੰਨ ਕੇ ਅਤੇ BC ਨੂੰ ਵਿਆਸ ਮੰਨ ਕੇ B, C, D ਵਿਚ ਅਰਧ ਚੱਕਰ ਵਿਚ ਬਣਿਆ ਕੋਣ 90° (∠BDC = 90°) ਹੁੰਦਾ ਹੈ | ਪਰਕਾਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਕੇ ਚੱਕਰ ਖਿੱਚੋ ਇਸਨੂੰ I ਮੰਨੋ ।
5. ‘A’ ਅਤੇ ‘M’ ਨੂੰ ਮਿਲਾਉ ।
6. AM ਦਾ ਲੰਬ ਸਮਦੁਭਾਜਕ ਖਿੱਚੋ ਜੋ AM ਨੂੰ ‘N’ ਉੱਤੇ ਕੱਟੇ । ‘N’ ਨੂੰ ਕੇਂਦਰ ਮੰਨ ਕੇ , ‘NA” ਜਾਂ ‘NM’ ਅਰਧ ਵਿਆਸ ਲੈ ਕੇ ਚੱਕਰ (II) ਖਿੱਚੋ ਜੋ ਚੱਕਰ (I) ਨੂੰ ‘B’ ਅਤੇ ‘P ਤੇ ਕੱਟੇ ।
7. AP ਨੂੰ ਮਿਲਾਉ ॥
8. AP ਅਤੇ AB ਲੋੜੀਂਦੀਆਂ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਹਨ ।
ਰਚਨਾ ਦਾ ਸਪੱਸ਼ਟੀਕਰਣ :
ਰੇਖਾਖੰਡ ‘AM’ ਨੂੰ ਵਿਆਸ ਲੈ ਕੇ ਚੱਕਰ (II) ਖਿੱਚੋ ।
∠APM ਅਰਧ ਚੱਕਰ ਹੈ।
∴ ∠APM = 90° [ਅਰਧ ਚੱਕਰ ਦਾ ਕੋਣ]
ਭਾਵ MP ⊥ AP ਪਰ ‘MP’ ਚੱਕਰ (I) ਦਾ ਅਰਧ ਵਿਆਸ ਹੈ
∴ AP ਚੱਕਰ (II) ਦੀ ਸਪਰਸ਼ ਰੇਖਾ ਹੈ ।
[∵ ਚੱਕਰ ਦੇ ਕਿਸੇ ਬਿੰਦੁ ਉੱਤੇ ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ ਦਾ ਲੰਬ ਕੋਈ ਰੇਖਾ ਉਸ ਚੱਕਰ ਦੀ ਸਪਰਸ਼ ਰੇਖਾ ਹੁੰਦੀ ਹੈ |]
ਇਸੇ ਤਰ੍ਹਾਂ ‘AB’ ਚੱਕਰ (I) ਦੀ ਸਪਰਸ਼ ਰੇਖਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 7.
ਕਿਸੇ ਵੰਗ ਦੀ ਸਹਾਇਤਾ ਨਾਲ ਇੱਕ ਚੱਕਰ ਖਿੱਚੋ । ਚੱਕਰ ਦੇ ਬਾਹਰ ਇੱਕ ਬਿੰਦੂ ਲਓ । ਇਸ ਬਿੰਦੂ ਤੋਂ ਚੱਕਰ ‘ਤੇ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਦੀ ਰਚਨਾ ਕਰੋ ।
ਹੱਲ:
ਕਿਸੇ ਵੰਗ ਦੀ ਸਹਾਇਤਾ ਨਾਲ ਚੱਕਰ ਖਿੱਚਣ ਦਾ ਭਾਵ ਹੈ ਚੱਕਰ ਦਾ ਕੇਂਦਰ ਨਹੀਂ ਪਤਾ ਹੈ। ਸਭ ਤੋਂ ਪਹਿਲਾਂ ਅਸੀਂ ਕੇਂਦਰ ਪਤਾ ਕਰਾਂਗੇ ।

ਰਚਨਾ ਦੇ ਪਗ :
1. ਚੂੜੀ ਦੀ ਸਹਾਇਤਾ ਨਾਲ ਚੱਕਰ ਖਿੱਚੋ ।
2. ਚੱਕਰ ਦੀਆਂ ਕੋਈ ਦੋ ਜੀਵਾਵਾਂ AB ਅਤੇ CD ਖਿੱਚੋ ।
3. ਜੀਵਾ AB ਅਤੇ CD ਦਾ ਲੰਬ ਸੰਮਦੁਭਾਜਕ ਖਿੱਚੋ ਜੋ , ਆਪਸ ਵਿੱਚ ਕੱਟਣ ।
[∵ ਰੇਖਾਖੰਡ ਦਾ ਲੰਬ ਸਮਦੁਭਾਜਕ ਉੱਤੇ ਸਥਿਤ ਕੋਈ ਬਿੰਦੂ ਇਸਦੇ ਸਿਰਿਆਂ ਦੇ ਬਿੰਦੂਆਂ ਤੋਂ ਸਮਾਨ ਦੂਰੀ ਤੇ ਹੁੰਦਾ ਹੈ ॥]
[∵ ‘O’, AB ਅਤੇ CD ਦੇ ਲੰਬ ਸਮਦੁਭਾਜਕ ਉੱਤੇ ਸਥਿਤ ਹੈ |
∴ OA = OB ਅਤੇ OC = OD
∴ OA = OB = OC = OD
(ਚੱਕਰ ਦੇ ਅਰਵਿਆਸ)
∴ ‘O’ ਚੱਕਰ ਦਾ ਕੇਂਦਰ ਹੈ ।
4. ਚੱਕਰ ਦੇ ਬਾਹਰ ਕੋਈ ਬਿੰਦੂ ‘P’ ਲਉ ॥
5. OP ਨੂੰ ਮਿਲਾਓ।
6. OP ਦਾ ਲੰਬ ਸਮਦੁਭਾਜਕ ਖਿੱਚੋ । ਮੰਨ ਲਓ ‘M’, OP ਦਾ ਮੱਧ ਬਿੰਦੁ ਹੈ ।
7. ‘M’ ਨੂੰ ਕੇਂਦਰ ਮੰਨ ਕੇ “MP” ਜਾਂ ‘MO’ ਅਰਵਿਆਸ ਲੈ ਕੇ ਚੱਕਰ II ਖਿੱਚੋ ਜੋ ਚੱਕਰ (I) ਨੂੰ T ਅਤੇ T’ ਤੇ ਕੱਟੇ ।
8. PT ਅਤੇ PT’ ਨੂੰ ਮਿਲਾਉ ਜੋ ਲੋੜੀਂਦੀਆਂ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਦਾ ਜੋੜਾ ਹਨ ।
ਰਚਨਾ ਦਾ ਸਪੱਸ਼ਟੀਕਰਣ :
ਅਰਧ ਵਿਆਸ ਸਪਰਸ਼ ਰੇਖਾ ਵਾਲੇ ਬਿੰਦੂ ਤੋਂ ਹਮੇਸ਼ਾ ਸਮਕੋਣ ਬਣਾਉਂਦੀ ਹੈ ।
∠PTO = PT’O = 90°.
OT ਨੂੰ ਮਿਲਾਉ ॥
ਹੁਣ ∠PTO ਅਰਧ ਚੱਕਰ 1 ਵਿੱਚ ਹੈ ।
∴ ∠PTO = 90°
[ਅਰਧ ਚੱਕਰ ਵਿੱਚ ਬਣਿਆ ਕੋਣ]
ਇਸੇ ਤਰ੍ਹਾਂ ∠PT’O = 90°
∴ PT ਅਤੇ PT’ ਚੱਕਰ ਉੱਤੇ ਬਿੰਦੂ ਅਤੇ T’ ਦੀਆਂ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਹਨ ।