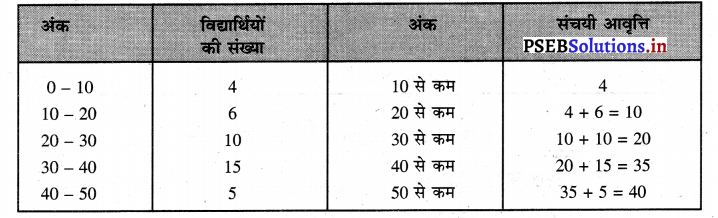
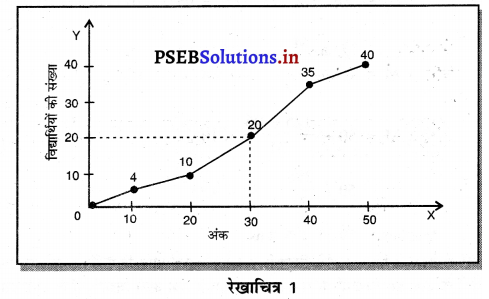
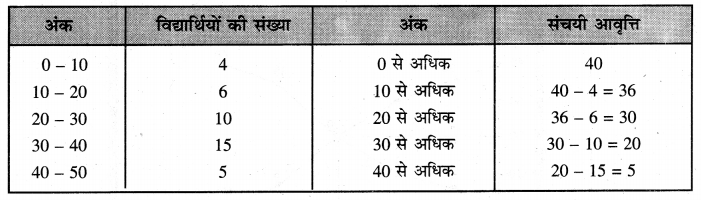
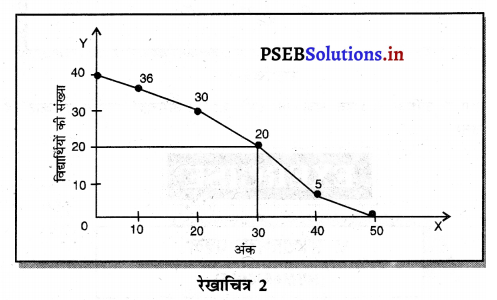
Punjab State Board PSEB 11th Class English Book Solutions Chapter 8 Water- A True Elixir Textbook Exercise Questions and Answers.
Class 11th English Book Chapter 8 Water- A True Elixir Question Answers
Water- A True Elixir Class 11 Questions and Answers
Short Answer Type Questions
Question 1.
Why is only one percent of the water available on our planet fit for drinking ?
Answer:
97 percent of the water available on our planet is salty ocean water. The remaining 3 percent water is fresh water, but 2 percent of it is frozen in glaciers and polar ice caps. This is the reason why only one percent of the water available on our planet is fit for drinking.
![]()
हमारे ग्रह पर उपलब्ध पानी का सत्तानबे प्रतिशत पानी समुद्र का खारा पानी है। बचा हुआ तीन प्रतिशत साफ पानी है, लेकिन इसका भी दो प्रतिशत हिमनदियों में तथा ध्रुवीय बर्फीली चोटियों पर जमा पड़ा है। यही कारण है कि हमारे ग्रह पर उपलब्ध पानी का सिर्फ एक प्रतिशत हिस्सा ही पीने योग्य है।
Question 2.
Why should we preserve the quality of water available to us ?
Answer:
Only one percent of the water available on our planet is fit for drinking. And moreover, the Earth’s water supply is also fixed. No new water is being made. So we must preserve the quality of water available to us.
हमारे ग्रह पर उपलब्ध पानी का सिर्फ एक प्रतिशत पानी ही पीने योग्य है। और इसके अतिरिक्त धरती की जलआपूर्ति सीमित है। कोई नया पानी पैदा नहीं हो रहा है। इसलिए हमें इसकी गुणवत्ता को अवश्य ही बनाए रखना होगा।
Question 3.
Why did civilizations generally grow on the banks of big rivers ?
Answer:
The most vital thing in our life is water. We cannot live without it. This is the reason that the civilizations generally grew on the banks of big rivers to fulfill their need of water. They did so to have easy access to water.
हमारे जीवन में सबसे महत्वपूर्ण चीज पानी है। हम इसके बिना जीवित नहीं रह सकते। यही कारण है कि अपनी पानी की आवश्यकता को पूरा करने के लिए सभ्यताएं प्राय: बड़ी नदियों के किनारों पर फली-फूलीं। उन्होंने ऐसा इसलिए किया ताकि पानी तक आसानी से पहुंचा जा सके।
Question 4.
What type of water supply and sewerage system prevailed during the Indus Valley Civilization period ?
Answer:
The Indus Valley Civilization flourished about 5000 years ago. The Indus Valley Civilization period had one of the most sophisticated urban water supply and sewerage systems in the world.
सिन्धु घाटी की सभ्यता लगभग 5000 वर्ष पहले विकसित हुई। सिन्धु घाटी की सभ्यता के काल में नगरीय जल आपूर्ति तथा गन्दे पानी के निकास की प्रणाली दुनिया की सबसे अत्याधुनिक प्रणालियों में से एक थी।
Question 5.
What role do forests play in the conservation of water ?
Answer:
Forests play a big role in the conservation of water. In the forests, water seeps gently into the ground as vegetation breaks the flow of water. This groundwater in turn feeds wells, lakes and rivers.
पानी के संरक्षण में जंगल बहुत बड़ी भूमिका निभाते हैं। जंगलों में पानी आसानी से धरती में रिस जाता है क्योंकि पेड़-पौधे पानी के बहाव को रोक देते हैं। बदले में यह ज़मीन का पानी कुओं, झीलों तथा नदियों को पानी की आपूर्ति करता है
Question 6.
Why is water conservation the need of the day?
Answer:
In the forests, water seeps gently into the ground as vegetation breaks the flow of water. This groundwater in turn feeds wells, lakes and rivers. Since the absence of water can turn fertile lands into dry, barren lifeless tracts of death, water conservation has become the need of the day. Forests play a big role in the conservation of water.
जंगलों में पानी आसानी से धरती में रिस जाता है क्योंकि पेड़-पौधे पानी के बहाव को रोक देते हैं। बदले में यह ज़मीन का पानी कुओं, झीलों तथा नदियों को पानी की आपूर्ति करता है। क्योंकि पानी का उपलब्ध न होना उपजाऊ भूमियों को सूखे, मौत के जीवन-रहित बंजर क्षेत्रों में परिवर्तित कर सकता है, इसलिए पानी को बचा कर रखना समय की ज़रूरत बन गई है। जंगल जल-सरंक्षण में बहुत बड़ी भूमिका निभाते हैं।
![]()
Question 7.
What did the Punjab Agriculture Minister admit on the floor of the house ?
Answer:
The writer says that the level of water is falling very fast in Punjab. It is estimated that there will be a great shortage of water in Punjab. The Punjab Agriculture Minister also admitted that the groundwater was continuously declining in 85% of areas of the state.
लेखक कहता है कि पंजाब में पानी का स्तर बहुत तेजी से गिर रहा है। यह अनुमान है कि पंजाब में पानी की बहुत कमी हो जाएगी। पंजाब के कृषि मंत्री ने भी स्वीकार किया कि राज्य के पचासी प्रतिशत इलाकों में जमीन के नीचे का पानी लगातार कम होता जा रहा है।
Question 8.
What is the result of the excessive decline in water table in the state ?
Answer:
Due to the excessive decline in water table in the Punjab state, nitrate presence in water has gone up by 10 times in the past four decades. It has increased to 5 mg/litre. The technologies related to soil and agronomic management can be used to save water.
पंजाब के राज्य में जल-स्तर में आई अत्यधिक गिरावट के कारण पिछले चार दशकों में पानी में नाइट्रेट की मौजूदगी दस गुणा ज्यादा बढ़ गई है। यह बढ़कर पांच मिलीग्राम प्रति लीटर हो गई है। भूमि तथा कृषि विज्ञान प्रबंधन से संबंधित तकनीकों का इस्तेमाल पानी को बचाने के लिए किया जा सकता है।
Question 9.
What technology can be used to save water?
Answer:
The water level is falling at very fast rate. So there is a great need to save water. The technologies related to soil and agronomic management can be used to save water. Planting and transplanting of crops, use of sprinklers, drip irrigation and furrow can help a lot in saving water.
पानी का स्तर बहुत तेजी से गिर रहा है। इसलिए पानी को बचाने की बहुत जरूरत है। भूमि तथा कृषि-विज्ञान प्रबंधन से संबंधित तकनीकों का इस्तेमाल पानी को बचाने के लिए किया जा सकता है। फसलों को लगाना और बदलना, स्प्रिंक्लरों (छिड़काव करने वाले यन्त्र), ड्रिप सिंचाई तथा फरो का प्रयोग पानी को बचाने में बहुत मदद कर सकता है।
Question 10.
How do the rural communities and the poor urban classes suffer due to the shortage of water?
Answer:
The rural communities and the poor urban classes suffer from a lack of clean and safe water. They have to bear the pain of walking miles at a time to gather water from ponds and streams. Thus they have to face a great suffering due to the shortage of water.
ग्रामीण समुदायों तथा गरीब शहरी वर्ग साफ तथा सुरक्षित पानी की कमी से पीड़ित हैं। उन्हें तालाबों तथा नदीनालों से पानी इकट्ठा करने के लिए लगातार मीलों पैदल चलने का कष्ट उठाना पड़ता है। इस प्रकार उन्हें पानी की कमी के कारण बहुत कष्ट उठाने पड़ते हैं।
![]()
Question 11.
How does the cropping pattern affect the water table ?
Answer:
The present cropping pattern is continually lowering the groundwater levels. It is a grave danger to mankind since water is the elixir of life. No life is possible without water. And in the absence of water, no cropping would be possible. The lands would become dry, barren lifeless tracts of death. So it is the need of the present situation that the traditional cropping pattern should be changed immediately.
वर्तमान फसल-प्रणाली जमीन के पानी के स्तर को निरंतर गिराती जा रही है। यह मानव-जाति के लिए एक गंभीर खतरा है क्योंकि पानी जीवन का अमृत है। पानी के बिना कोई जीवन संभव नहीं है। और पानी के उपलब्ध न होने से कोई फसल उगाना भी संभव नहीं होगा। ज़मीनें सूखे हुए, मौत के जीवन-रहित बंजर प्रदेश बन जाएंगी। इसलिए यह वर्तमान स्थिति की मांग है कि पारंपरिक फसल-प्रणाली को तुरंत बदल दिया जाए।
Question 12.
When did the Indus Valley Civilization flourish ? What type of water supply and sewerage system prevailed during the Indus Valley Civilization period ?
Answer:
The Indus Valley Civilization period had one of the most sophisticated urban water supply and sewerage systems in the world. The covered drains running beneath the streets of the ruins at both Mohenjodaro and Harappa show that the people were well acquainted with hygiene.
सिन्धु घाटी की सभ्यता में विश्व की सबसे अत्याधुनिक नगरीय जल आपूर्ति प्रणाली तथा गन्दे पानी की निकासी प्रणाली थी। मोहनजोदड़ो तथा हड़प्पा, दोनों ही शहरों के खण्डहरों की गलियों के नीचे से गुजरने वाली नालियां दर्शाती हैं कि लोग स्वास्थ्य-विज्ञान से भली भांति परिचित थे।
Question 13.
What comparison does a great writer and scientist draw between ‘water in a landscape and the eyes in a human face’ ?
Answer:
Eyes reflect the state of human mind. Their brightness reflects the joy and their shadows reflect the gloom of the human heart. Similarly, water seems to be bright and gay when the sun shines, But when it gets dark, water looks dull and gloomy.
आंखे मानवीय मन की स्थिति को प्रतिबिंबित करती हैं। उनकी चमक प्रसन्नता को प्रतिबिंबित करती हैं और उनकी छायाएं मानवीय हृदय की उदासी को प्रतिबिंबित करती हैं । उसी प्रकार जब सूर्य चमकता है, तो पानी शोख तथा प्रसन्न प्रतीत होता है। किंतु जब अंधेरा छा जाता है, तो पानी बेरंग और उदास प्रतीत होता है।
Question 14.
Water conservation has become the need of the day. Why?
Answer:
Water level is sinking year after year. If this continues, one day life would become impossible on this earth. To prevent that, every drop of water must be conserved.
जल स्तर वर्ष-प्रति-वर्ष गिरता जा रहा है। यदि यह जारी रहा, तो एक दिन इस धरती पर जीवन असंभव हो जाएगा। ऐसा होने से रोकने के लिए पानी की प्रत्येक बूंद को बचाना बहुत आवश्यक है।
Question 15.
How has cutting down of forests affected the water cycle and what should be done in this regard ?
Answer:
Cutting down of forests has disturbed the water cycle. Because of this, the water level is going down year after year. If this continues, a day will come when life on this earth will become impossible. To prevent such a situation, we should conserve every drop of water.
वनों की कटाई ने जल-चक्र को असंतुलित कर दिया है। इसके कारण जल-स्तर वर्ष-प्रति-वर्ष गिरता जा रहा है। यदि यह जारी रहा, तो एक दिन ऐसा आएगा जब धरती पर जीवन असंभव हो जाएगा। ऐसी स्थिति को रोकने के लिए हमें पानी की प्रत्येक बूंद को बचाना पड़ेगा।
Question 16.
What does C.V. Raman compare water to ?
Answer:
The great writer as well as scientist, C.V. Raman, compares water to the eyes in a human face. Eyes lend a unique beauty to the human face. Similarly, water in a landscape adds a unique beauty to the landscape.
महान् लेखक और वैज्ञानिक, सी० वी० रमन, किसी प्राकृतिक दृश्य में पानी की तुलना मानवीय चेहरे पर लगी आंखों से करता है। आंखें मानवीय चेहरे को अद्वितीय सुन्दरता प्रदान करती हैं। उसी प्रकार, पानी किसी प्राकृतिक दृश्य में एक अनोखी सुंदरता जोड़ देता है।
Long Answer Type Questions
Question 1.
How is water a source of beauty and joy ? Explain.
Answer:
Water is, no doubt, a source of beauty and joy. Little streams trickling down the rocks or big waterfalls give joy to our soul. Brooks or rivers present to our eyes a great feast. In other words, water presents a joy to our eyes and a freshening breath of beauty to our mind.
A great writer and scientist, C. V. Raman, compares water in a landscape to the eyes in a human face. Eyes lend a unique beauty to the human face. Similarly water in a landscape adds a unique beauty to the landscape.
पानी नि:संदेह सुन्दरता तथा प्रसन्नता का एक स्रोत है। चट्टानों तथा बड़े-बड़े झरनों से नीचे बहता हुआ पानी हमारी आत्मा को प्रसन्नता प्रदान करता है। छोटी-छोटी सरिताएँ और नदियां हमारी आँखों को भारी आनन्द प्रदान करती हैं। अन्य शब्दों में, पानी हमारी आंखों को सुख तथा हमारे मन को सुन्दरता की तरोताज़ा कर देने वाली सांस (हवा) प्रदान करता है।
एक महान् लेखक तथा वैज्ञानिक, सी० वी० रमन, प्राकृतिक दृश्य में पानी की तुलना मनुष्य के चेहरे पर लगी आँखों से करता है। आँखें मानवीय चेहरे को एक अद्वितीय सुन्दरता प्रदान करती हैं। उसी प्रकार, पानी किसी प्राकृतिक दृश्य में एक अद्वितीय सुन्दरता को जोड़ देता है।
![]()
Question 2.
Write a note on the necessity of conserving water.
Answer:
Today, there is great necessity of conserving water. Rising populations, growing industrialization and expanding agriculture have, no doubt, increased the consumption of water. But besides consuming, we are also wasting water. We are using it for wasteful purposes.
Moreover, by cutting down our forests, we have disturbed the water cycle also. As a result, the water level is sinking year after year. And if this continues, à day will come when life would become impossible on this earth. So to prevent that, we will have to conserve every drop of water.
आज पानी को बचाने की बहुत ज़्यादा ज़रूरत है। बढ़ती हुई जनसंख्या, बढ़ता हुआ औद्योगीकरण तथा विस्तृत होती खेतीबाड़ी ने नि:सन्देह पानी की खपत को बढ़ा दिया है। लेकिन पानी की खपत करने के अलावा हम पानी को बर्बाद भी कर रहे हैं। हम इसे फिजूल के उद्देश्यों के लिए इस्तेमाल कर रहे हैं।
इसके अलावा, अपने जंगलों को काटकर हमने जल-चक्र को असंतुलित कर दिया है। परिणामस्वरूप, जल-स्तर वर्ष-प्रति-वर्ष गिरता जा रहा है। अगर ऐसा ही चलता रहा, तो एक दिन ऐसा आएगा जब इस धरती पर जीवन असंभव हो जाएगा। इसलिए उस स्थिति को रोकने के लिए हमें पानी की हर एक बूंद को बचाना होगा।
Question 3.
How and why is the groundwater level falling in Punjab with every passing year ? Explain.
Answer:
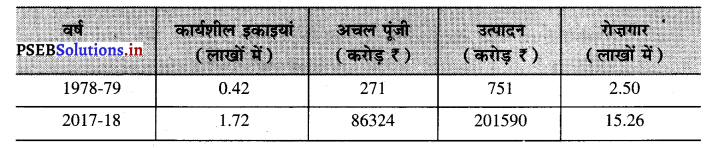
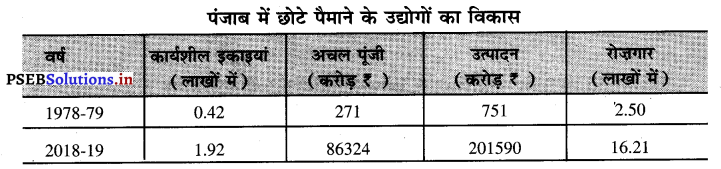
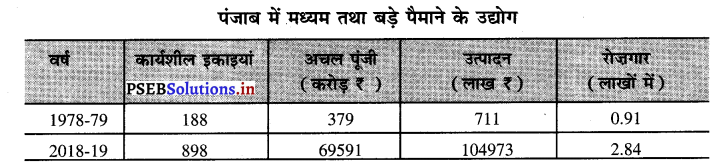
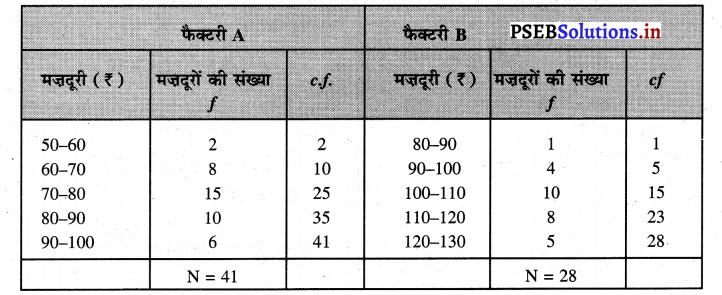
In Punjab, the groundwater level is falling due to overexploitation of water resources. It is going down by 60 cm every year. In less than 30 years, our state has used up groundwater reserves built up over the last 105 years.
Besides this, a major share of water is taken by rice-wheat cropping system in Punjab. It may be noticed that 1 kilogram of rice consumes about 3500 litres of water for its growth. Now in order to reach the water table, the farmers have to dig deeper and deeper into the ground and use more power to pump out water.
पंजाब में जलसंसाधनों के ज़रूरत से ज़्यादा इस्तेमाल के कारण ज़मीन के पानी का स्तर गिरता जा रहा है। यह प्रत्येक वर्ष साठ सेंटीमीटर नीचे जा रहा है। तीस से भी कम वर्षों में ही हमने पिछले एक सौ पांच वर्षों में बने ज़मीन के पानी के भण्डार को इस्तेमाल कर लिया है।
इसके अलावा पंजाब में पानी का ज़्यादातर हिस्सा चावल-गेहूं की फसल-प्रणाली की भेंट चढ़ जाता है। यह बात ध्यान देने लायक है कि एक किलोग्राम चावल को उगाने के लिए करीब 3500 लीटर पानी की खपत होती है। अब पानी के स्तर तक पहुंचने के लिए किसानों को ज़मीन के नीचे अधिक और अधिक गहराई तक खुदाई करनी पड़ती है तथा पानी को पम्प की सहायता से बाहर निकालने के लिए और ज्यादा बिजली का इस्तेमाल करना पड़ता है।
Question 4.
How does the cropping pattern affect the water table ?
Answer:
The present cropping pattern is continually lowering the groundwater levels. It is a grave danger to mankind since water is the elixir of life. No life is possible without water. And in the absence of water, no cropping would be possible also. The lands would become dry, barren lifeless tracts of death. So it is the need of the present situation that the traditional cropping pattern should be changed immediately.
वर्तमान फसल-प्रणाली ज़मीन के पानी के स्तर को निरंतर गिराती जा रही है। यह मानव-जाति के लिए एक गंभीर खतरा है क्योंकि पानी जीवन का अमृत है। पानी के बिना कोई जीवन संभव नहीं है। और पानी के उपलब्ध न होने से कोई फसल उगाना भी संभव नहीं होगा। ज़मीनें सूखे, मौत के जीवन-रहित बंजर प्रदेश बन जाएंगी। इसलिए यह वर्तमान स्थिति की मांग है कि पारंपरिक फसल-प्रणाली को तुरंत बदल दिया जाए।
![]()
Question 5.
Write a short paragraph on : ‘Water — a True Elixir”.
Answer:
Water is, no doubt, a true elixir of life. It is the basis of all life. We can live without food for a number of days, but we can’t do without water for a day even. But sadly, we are wasting and polluting this very source of life. We have disturbed the water cycle. Water keeps evaporating into the air. There are no trees to bring it back as rain because we have cut down our forests.
This is the reason that the water level is sinking year after year. And if this continues, a day will come when life would be impossible on this earth. To prevent that, we shall have to take urgent steps. We must conserve every drop of water to keep this earth liveable for our coming generations.
पानी नि:संदेह जीवन का सच्चा अमृत है। यह सारे जीवन का आधार है। हम भोजन के बिना कई दिनों तक जीवित रह सकते हैं। लेकिन पानी के बिना हम एक दिन भी काम नहीं चला सकते। किंतु दुःख की बात है कि हम जीवन के इस स्त्रोत को बर्बाद तथा प्रदूषित कर रहे हैं। हमने जल-चक्र को असंतुलित कर दिया है। पानी वाष्प बन कर हवा में उड़ता रहता है। इसे वर्षा के रूप में वापस लाने के लिए कोई पेड़ नहीं हैं क्योंकि हमने अपने जंगलों को काट डाला है।
यही कारण है कि जल-स्तर वर्ष-प्रति-वर्ष गिरता जा रहा है। यदि ऐसा ही चलता रहा, तो एक दिन ऐसा आएगा जब इस धरती पर जीवन असंभव हो जाएगा। उस स्थिति को रोकने के लिए हमें शीघ्र ही उपयुक्त कदम उठाने पड़ेंगे। आने वाली पीढ़ियों के लिए इस धरती को रहने लायक बनाए रखने के लिए हमें पानी की प्रत्येक बूंद को बचाना चाहिए।
Question 6.
Why does the author say that the food bowl of India, the state of Punjab, is fast drying up ?
Answer:
Punjab is on the verge of an economical disaster. The number of tubewells has grown up from 1.2 lakh in 1970 to about 13 lakh now. So the groundwater decline rate has reached an alarming level. And due to the excessive decline in the water table, presence of nitrate in water has gone up by 10 times in the past four decades.
In 1972, it was 0.5 mg/litre. But now it has increased to 5 mg/litre. And the excessive use of pesticides and insecticides by the farmers is multiplying the problem. And in the coming 20-25 years, water in Punjab will not remain fit for drinking.
पंजाब एक आर्थिक संकट की कगार पर खड़ा है। ट्यूबवेलों की गिनती 1970 में एक लाख बीस हजार से बढ़कर आज लगभग तेरह लाख हो गई है। इसलिए ज़मीन के पानी की गिरावट चिंताजनक स्तर पर पहुंच गई है। और जल-स्तर में अत्यधिक गिरावट के कारण पिछले चार दशकों में पानी में नाइट्रेट की मात्रा दस गुणा बढ़ गई है।
1972 में यह 0.5 मिलीग्राम प्रति लीटर थी। लेकिन अब यह बढ़कर पांच मिलीग्राम प्रति लीटर हो गई है। और किसानों के द्वारा कीटनाशक तथा कीड़ेमार दवाइयों का अत्यधिक इस्तेमाल समस्या को और ज्यादा बढ़ा रहा है और आने वाले बीस से पच्चीस वर्षों में पंजाब का पानी पीने लायक नहीं रह जाएगा।
Question 7.
How is the present cropping pattern lowering the groundwater levels ? What steps should be taken to save water ?
Answer:
The major share of water is taken by rice-wheat cropping system. It may be noticed that 1 kilogram of rice consumes about 3500 litres of water for its growth. So there is a great need to change the present cropping pattern which is continually lowering the groundwater levels.
The technologies related to soil and agronomic management should be adopted to save water. For using available water resources properly, water users’ associations should be constituted. Various technologies for enhancing artificial groundwater recharge should also be adopted.
पानी का एक बड़ा हिस्सा चावल-गेहूं फसल-प्रणाली की भेंट चढ़ जाता है। यह बात ध्यान देने लायक है कि एक किलोग्राम चावल को उगाने के लिए लगभग 3500 लीटर पानी की खपत होती है। इसलिए वर्तमान फसलप्रणाली को तुरंत बदल देने की ज़रूरत है जोकि ज़मीन के पानी के स्तर को लगातार गिराती जा रही है।
पानी की बचत करने के लिए भूमि तथा कृषि विज्ञान प्रबंधन से संबंधित तकनीकों को अपनाया जाना चाहिए। उपलब्ध जलसंसाधनों का उचित तरीके से इस्तेमाल करने के लिए पानी के उपभोक्ताओं की सभाओं का निर्माण किया जाना चाहिए। ज़मीन के पानी को कृत्रिम तरीके से दोबारा पूरा करने के लिए विभिन्न तकनीकों के इस्तेमाल को बढ़ावा देना चाहिए।
Objective Type Questions
Question 1.
Who wrote the chapter, ‘Water – a True Elixir’?
Answer:
Dr D.V. Jindal.
Question 2.
How much of the water available on earth is salty ocean water?
Answer:
Ninety-seven percent.
Question 3.
What has man sought in vain for ages ?
Answer:
The divine Amrita.
Question 4.
What is the basis of all life?
Answer:
Water.
![]()
Question 5.
What great role do forests play in case of water ?
Answer:
They help in the conservation of water.
Question 6.
What did the people in ancient India believe about the forests ?
Answer:
They believed that forests were the mothers of rivers.
Question 7.
What has increased the consumption of water ?
Answer:
Rising population, growing industrialisation and expanding agriculture.
Question 8.
What is known as the ‘food bowl of India’?
Answer:
The state of Punjab.
Question 9.
What is the true elixir of life?
Answer:
Water.
Question 10.
When did the Indus Valley Civilization flourish ?
Answer:
About 5000 years ago.
Question 11.
What provides freshening breath of beauty to the mind ?
Answer:
Water.
Question 12.
In the matter of water, which are the worst affected districts of Punjab ?
Answer:
Sangrur and Moga.
Question 13.
What takes the major share of water in Punjab ?
Answer:
Rice-wheat cropping system.
Question 14.
What technologies are related to soil and agronomic management ?
Answer:
Planting and transplanting time of crops, irrigation scheduling and new irrigation methods.
Vocabulary And Grammar
1. Match the words under column A with their meanings under column B :
А — в
1. plentiful — understanding
2. draught — sad
3. insight — twisting and turning
4. flourish — threatening, dangerous
5. acquainted — fall, decrease
6. gloomy — reach
7. serpentine — familiar with
8. alarming — prosper
9. decline — a small amount
10. access — sufficiently large with in quantity
Answer:
1. plentiful = sufficiently large in quantity
2. draught = a small amount
3. insight = understanding
4. flourish = prosper
5. acquainted with = familiar with
6. gloomy = sad
7. serpentine = twisting and turning
8. alarming = threatening, dangerous
9. decline = fall, decrease
0. access = reach.
2. Use prefixes to form the antonyms of the following words :
discipline, dependence, developed, secure, directly.
Answer:
1. discipline → indiscipline
2. dependence → independence
3. developed → underdeveloped
4. secure → insecure;
5. directly → indirectly.
3. Fill in each blank with a suitable modal :
1. The teacher said that he ……. be punished for his mistake. (will / would)
2. You …….. impose discipline on yourself first. (can / must)
3. Some of us are worrying about whether the stock market ……. crash. (will / should)
4. You …… be careful while driving. (must / need)
5. We …. preserve our forests. (must I need)
Answer:
1. would
2. must
3. will
4. must
5. must.
4. Change the form of narration :
1. Barb shouted, “Malcolm, hold on. I am going for help.”
2. I said, “What a mean act !”
3. “Most of you will be leaving school within six months,” said the teacher to his pupils.
4. I asked my guest, “Did you have a bad night ?”
5. She said, “I sold my car myself.”
Answer:
1. Barb shouted to Malcolm to hold on. She further told him that she was going for help.
2. I exclaimed that the act was very mean.
3. The teacher told his pupils that most of them would be leaving school within six months.
4. I asked my guest if he had a bad night.
5. She said that she had sold her car herself.
5. Use each of the following words as a noun and a verb :
treasure, order, attack, water, table, encounter.
Answer:
1. Treasure
(noun) – Good health is a valuable treasure that a man can possess.
(verb) – I treasure his friendship.
2. Order
(noun) – We must obey the orders of our seniors.
(verb) – I ordered him to leave my house.
3. Attack
(noun) – We are ready to face any attack.
(verb) – He attacked his enemy.
4. Water
(noun) – We cannot live without water.
(verb) – The gardener is watering the plants.
![]()
5. Table
(noun) – This is my office table
(verb) – He tabled the agenda for the meeting.
6. Encounter
(noun) – The criminal was shot dead in an encounter.
(verb) – She is the most beautiful woman I have ever encountered.
Water- A True Elixir Summary & Translation in English
Water- A True Elixir Summary in English:
This essay underlines the need of water conservation. Ninety-seven percent of water available on earth is salty ocean water. The remaining three percent water is fresh water, but most of it is frozen in glaciers and polar ice caps. Only one percent of water is available which is fit for drinking.
Besides this, the Earth’s water supply is fixed. No new water is being made. So we must preserve the quality of water available to us. Water is the basis of all life. We can live without food for a number of days. But we cannot live without water for a day even.
A great writer and scientist, C.V. Raman, has truly said that water is the real elixir of life available on earth. Without it, no life is possible. Today there is a great necessity of conserving water.
Forests play à vital role in the conservation of water.
In the forests, water seeps gently into the ground as vegetation breaks the flow of water. This groundwater in turn feeds wells, lakes and rivers. In ancient India, people believed that the forests were the ‘mothers of rivers. So they worshipped the forests. But modern man, in his greed, has cut down the trees and the forests.
Water is not only the real elixir of life, it is also a source of beauty and joy. Little streams trickling down the rocks give joy to our soul. And big rivers dancing down the hills present beautiful scenes to our eyes. Various water bodies like lakes, brooks, rivers, waterfalls, oceans have received rich tributes from many writers and poets.
The great writer and scientist, C.V. Raman, compares water in a landscape to the eyes in a human face. Eyes lend a unique beauty to the human face. Similarly, water in a landscape adds a unique beauty to the landscape.
However, this precious gift is in danger today. Rising populations, growing industrialization and expanding agriculture have, no doubt, increased the consumption of water. But besides consuming, we are also wasting it. We are using it for wasteful purposes.
Moreover, by cutting down our forests, we have disturbed the water cycle also. As a result, the water level is sinking year after year. And if this continues, a day will come when life would become impossible on this earth. To prevent that, we will have to conserve every drop of water.
The food bowl of India, the state of Punjab, is drying up very fast. It is on the verge of an economical disaster. The number of tubewells has grown up from 1.2 lakh in 1970 to about 13 lakh now. So the ground water decline rate has reached an alarming level.
And due to the excessive decline in water table, nitrate presence in water has gone up by 10 times in the past four decades. In 1972, it was 0.5 mg / litre. But now it has increased to 5 mg/litre. And the excessive use of pesticides and insecticides by the farmers is multiplying the problem. And in the coming 20-25 years, water in Punjab will not remain fit for drinking.
![]()
The groundwater level in Punjab is, no doubt, falling due to over-exploitation of water resources. It is going down by 60 cm every year. But besides this, the major share of water is taken by rice-wheat cropping system. It may be noticed that 1 kilogram of rice consumes about 3500 litres of water for its growth. So there is a great need to change the present cropping pattern which is continually lowering the groundwater levels.
The technologies related to soil and agronomic management should be adopted to save water. For using available water resources properly, water users’ associations should be constituted. Various technologies for enhancing artificial groundwater recharge should also be adopted. In short, we should conserve every drop of water to make this earth liveable for our coming generations.
Water- A True Elixir Translation in English:
Water is one of the most important gifts of Nature to Man. It is as essential to life as air. Life is not possible without air or water. But with the advation of civilization, it sometimes goes unnoticed that air and water, the two lifelines of this universe, are being polluted every day.
A day might come when this level of pollution increases so much that life becomes impossible. In that situation, air would become toxic to be breathed in and water would become poisonous.
Are we not thus robbing or disinheriting’ our future generations from their legitimate right to live We must set things right before it is too late. If the present generation does not read the writing on the waif, it would be willfully closing its eyes and pushing the future of mankind into jeopardy and extinction.
The author, Dr D. V. Jindal, is a senior lecturer, PES (I), retired from SCD Govt. College, Ludhiana. Having been a member of various academic bodies at various levels, he is presently a member of the External Faculty, English and Foreign Languages University, Hyderabad. A Ph.D. in Phonetics from Panjab University, Chandigarh, he is an author of several books on language and literature.
Water covers about 75 percent of our planet, so it appears plentiful. However, 97 percent of that water is salty ocean water, which we cannot drink. Of the 3 percent that is fresh water, most is frozen in glaciers and polar ice caps. As a result, only 1 percent of the Earth’s water may be available for drinking.
Moreover, the Earths water supply is fixed : no new water is being made. We have the same amount of water now as there was when the earth was created. This is the water we have, and we must preserve its quality. Water is the foundation of food and life. Next to air, water is our most precious resource. We cannot live without water.
C. V. Raman has rightly said, “’Man has through the ages sought in vain the imaginary elixir of life, the divine amrita, a draught of which was thought to confer immortality. But the true elixir of life lies near to our hands.
For it is the commonest of all liquids, plain water !” That is why most of our civilizations and important cities grew on the banks of big rivers only. Our ancient religious texts and epics give a good insight into the water storage and conservation systems that prevailed in those days.
The Indus Valley Civilization, that flourished along the banks of the river Indus and other parts of western and northern India about 5,000 years ago, had one of the most sophisticated urban water supply and sewerage systems in the world. The fact that the people were well acquainted with hygiene can be seen from the covered drains running beneath the streets of the ruins at both Mohenjodaro and Harappa.
In the forests, water seeps gently into the ground as vegetation breaks the flow of water. This groundwater in turn feeds wells, lakes, and rivers. Protecting forests means protecting water ‘catchments’. In ancient India, people believed that forests were the ‘mothers’ of rivers and worshipped the sources of these water bodies.
Water is a source of beauty and joy. It adds to the beauty of nature. It may be a little stream trickling down the rocks or a waterfall, big or small. It is a joy to the eyes and a freshening breath of beauty to the mind. Brooks and rivers dancing down the hills on their majestic journey to the sea in their serpentine ways add a touch of novelty to the scene.
Small tanks, lakes or big oceans earn rich tributes from sensitive poets. A great writer wrote : “Water in a landscape may be compared to the eyes in a human face. It reflects the mood of the hour, being bright and gay9 when the sun shines, turning to dark and gloomy when the sky is overcast.”
Over the years, rising populations, growing industrialization, and expanding agriculture have pushed up the demand for water. Efforts have been made to collect water by building dams and reservoirs and digging wells.
![]()
Some countries have also tried to recycle and desalinate (remove salts) water. Water conservation has become the need of the day. While the availability of water can turn millions of acres of uncultivated land into areas teeming with life and vegetation, the absence of water can convert fertile lands into dry, barren lifeless tracts of death.
Conservation of water in the agricultural sector is essential but depleting water table and a rise in salinity due to overuse of chemical fertilizers and pesticides is something serious. The food bowl of India, the state of Punjab, is fast drying up. It is on the verge of an ecological disaster.
The number of tubewells has grown up from 1.2 lakh in 1970 to about 13 lakh now and the groundwater decline rate has reached an alarming level. The worst affected districts are Sangrur and Moga where the water table is below 50 feet.
The Punjab Irrigation Minister admitted on the floor of the house in the Punjab Vidhan Sabha (29.06.12) that groundwater was continuously declining in 85% areas of the state. Worse, nitrate presence in water has gone up by 10 times in the past four decades. Another M.L.A. said, “The quality of water in 1972 was such that it had 0.5mg / litre of nitrate.
As of now, it has increased to 5mg / litre. And going by the excessive use of insecticides and pesticides by our farmers, it is expected to reach 10 mg / litre in the next 20 years. This means that water in the Punjab will cease to be potable for humans and animals in the next 20-25 years. Presence of nitrate up to 10 mg / litre renders it unfit for drinking.”
High levels of arsenic, nitrates and heavy metals in water are causing severe health problems across the whole of the Punjab. High nitrate levels in water can result in a reduced oxygen supply to vital tissues such as the brain. The state should, therefore, make a comprehensive policy on the issue on a top-priority basis. Departments of soil conservation, irrigation, electricity and agriculture should work in cohesion to meet this challenge.
According to the findings of the National Geophysical Research Institute, due to the over exploitation of water resources, the groundwater levels are going down by 60 cm every year.
The Punjab has, in less than 30 years, used up groundwater reserves built up over the last 105 years. In order to reach the water table, farmers are forced to dig deeper and deeper into the ground and use more power to pump out water. Even residents in cities using hand pump water are having to dig deeper than they did, say, 10 years ago.
The excessive decline in the water table is resulting in low discharge of tubewells, deepening of pits and tubewells, replacement of low-cost centrifugal pumps with costlier submersible pumps and increased energy cost, thereby affecting the socio-economic condition of small and marginal farmers of the state.
In the state, major share of water is taken by rice-wheat cropping system. It may be noticed that 1 kilogram of rice consumes 3500-4000 litres of water for its growth (depending upon its variety, sowing time, area, etc.). Therefore, it is the requirement of the present situation that the traditional cropping pattern should be changed immediately.
Moreover, there is a need to strictly switch over to the technologies related to soil and agronomic management that save water without a loss in crop yields leading to higher productivity per unit use of water. These technologies include planting and transplanting time of crops, irrigation scheduling and new irrigation methods, (e. g. sprinkler, drip, furrow, etc.) For using available water resources effectively and efficiently , water users’ associations / societies should be constituted.
Various measures technologies for enhancing artificial-5 groundwater recharge should also be adopted. We must hear the warning bells and act before it is too late. Every drop of water is precious and needs to be saved wherever and in whatever way it is possible.
Every day in rural communities and poor urban centres throughout India, hundreds of millions of people suffer from a lack of access to clean, safe water. Women and girls especially bear the burden of walking miles at a time to gather water from streams and ponds full of water-borne diseases that are making them and their families sick.
![]()
What each of us does in the world, how we live, does make a difference. We should learn the value of clean, safe water. We should take steps to protect it and to get it to the people who lack access to it today.
Water- A True Elixir Summary & Translation in Hindi
Water- A True Elixir Summary in Hindi:
लेख का विस्तृत सार यह लेख जल-संरक्षण की ज़रूरत को रेखांकित करता है । धरती पर उपलब्ध सत्तानबे प्रतिशत पानी समुद्र का खारा पानी है। बाकी तीन प्रतिशत साफ पानी है, लेकिन उसका भी अधिकतर भाग हिमनदियों में तथा ध्रुवीय बर्फीली चोटियों पर जमा पड़ा है। केवल एक प्रतिशत पानी ही पीने लायक है।
इसके अलावा, धरती का जलभण्डार सीमित है। कोई नया पानी नहीं बन रहा है। इसलिए हमारे पास जो पानी उपलब्ध है, हमें उसकी गुणवत्ता को बनाए रखना चाहिए। पानी सारे जीवन का आधार है। भोजन के बिना हम कई दिनों तक जीवित रह सकते हैं, लेकिन पानी के बिना हम एक दिन भी नहीं रह सकते।
एक महान लेखक तथा वैज्ञानिक, सी० वी० रमन, ने सच ही कहा है कि पानी धरती पर उपलब्ध जीवन का वास्तविक अमृत है। इसके बिना कोई जीवन संभव नहीं है। आज पानी को बचाने की बहुत अधिक आवश्यकता है।
जंगल जल-संरक्षण में एक महत्त्वपूर्ण भूमिका निभाते हैं। जंगलों में पानी आसानी से धरती में रिस जाता है क्योंकि पेड़-पौधे पानी के बहाव को रोक देते हैं। ज़मीन का यह पानी फिर कुओं, झीलों और नदियों को पानी की आपूर्ति करता है। प्राचीन भारत में लोगों का मानना था कि जंगल नदियों की ‘माताएं’ होते हैं। इसलिए वे जंगलों की पूजा किया करते थे। लेकिन आधुनिक मानव ने अपने लालच में पेड़ों और जंगलों को काट डाला है।
पानी सिर्फ जीवन का वास्तविक अमृत ही नहीं है, बल्कि सुन्दरता एवम् प्रसन्नता का स्रोत भी है। चट्टानों से नीचे बहते छोटे-छोटे झरने हमारी आत्मा को खुशी प्रदान करते हैं और पहाड़ों से नीचे नृत्य करती जाती बड़ीबड़ी नदियां हमारी आँखों के सामने खूबसूरत दृश्य पेश करती हैं। विभिन्न जल-स्रोत जैसे झीलें, नाले, नदियां, झरने, समुद्र, इत्यादि ने बहुत से लेखकों तथा कवियों से प्रशंसा बटोरी है।
महान् लेखक तथा वैज्ञानिक, सी० वी० रमन, किसी प्राकृतिक दृश्य में पानी की तुलना मानवीय चेहरे पर लगी आँखों से करता है। आँखें मनुष्य के चेहरे को अद्वितीय सुन्दरता प्रदान करती हैं। बिल्कुल उसी तरह ही किसी प्राकृतिक दृश्य में पानी प्राकृतिक दृश्य में अद्वितीय सुन्दरता को जोड़ देता है।
परंतु यह खूबसूरत उपहार आज खतरे में है। बढ़ती जनसंख्या, विकसित होते उद्योग तथा विस्तृत होती कृषि ने नि:संदेह पानी की खपत को बढ़ा दिया है। किन्तु इसकी खपत करने के अलावा हम इसे बर्बाद भी कर रहे हैं। हम इसे बेकार के कामों के लिए इस्तेमाल कर रहे हैं। इसके अलावा हमने जंगलों को काटकर जल-चक्र के संतुलन को बिगाड़ दिया है।
परिणामस्वरूप, वर्ष प्रति वर्ष जल-स्तर गिरता जा रहा है। अगर ऐसा ही चलता रहा तो एक दिन ऐसा आएगा जब इस धरती पर जीवन असंभव हो जाएगा। उस स्थिति को टालने के लिए हमें पानी की एकएक बूंद बचानी पड़ेगी।भोजन का कटोरा कहलाने वाला पंजाब का राज्य तेज़ी से सूखता जा रहा है। यह एक आर्थिक संकट की कगार पर खड़ा है।
![]()
ट्यूबवेलों की गिनती 1970 में एक लाख बीस हजार से बढ़कर आज लगभग तेरह लाख हो गई है। इसलिए ज़मीन के पानी की गिरावट चिंताजनक स्तर पर पहुंच गई है और जल-स्तर में अत्यधिक गिरावट के कारण पिछले चार दशकों में पानी में नाइट्रेट की मात्रा दस गुणा बढ़ गई है। 1972 में यह 0.5 मिलीग्राम प्रति लीटर थी।
लेकिन अब यह बढ़कर पांच मिलीग्राम प्रति लीटर हो गई है। और किसानों के द्वारा कीटनाशक तथा कीड़ेमार दवाइयों का अत्यधिक इस्तेमाल समस्या को और ज्यादा बढ़ा रहा है और आने वाले बीस से पच्चीस वर्षों में पंजाब का पानी पीने लायक नहीं रह जाएगा।
पंजाब में जमीन के पानी का स्तर निःसंदेह जल-संसाधनों के अत्यधिक इस्तेमाल के कारण गिर रहा है। यह प्रतिवर्ष साठ सेन्टीमीटर नीचे जा रहा है। लेकिन इसके अलावा, पानी का एक बड़ा हिस्सा चावल-गेहूं फसल प्रणाली की भेंट चढ़ जाता है।
यह ध्यान देने लायक बात है कि एक किलोग्राम चावल को उगाने के लिए लगभग 3500 लीटर पानी की खपत होती है। इसलिए वर्तमान फसल प्रणाली को तुरंत बदल देने की ज़रूरत है जोकि ज़मीन के पानी के स्तर को लगातार गिराती जा रही है। पानी की बचत करने के लिए भूमि तथा कृषि विज्ञान प्रबंधन से संबंधित तकनीकों को अपनाया जाना चाहिए।
उपलब्ध जल-संसाधनों का उचित तरीके से इस्तेमाल करने के लिए पानी के उपभोक्ताओं की सभाओं का निर्माण किया जाना चाहिए। ज़मीन के पानी को कृत्रिम तरीके से दोबारा पूरा करने के लिए विभिन्न तकनीकों के इस्तेमाल को बढ़ावा देना चाहिए। संक्षेप में, हमें इस धरती को अपनी आने वाली पीढ़ियों के रहने लायक बनाने के लिए पानी की हरेक बूंद को बचाना चाहिए।
Water- A True Elixir Translation in Hindi:
पानी प्रकृति के द्वारा मानव को दिए गए सबसे महत्त्वपूर्ण उपहारों में से एक है। यह जीवन के लिए उतना ही महत्त्वपूर्ण है, जितनी कि हवा। हवा अथवा पानी के बिना जीवन संभव नहीं है। लेकिन सभ्यता के विकास के साथ, कई बार इस ओर ध्यान ही नहीं दिया जाता कि हवा तथा पानी, जोकि इस दुनिया की दो जीवन-रेखाएं हैं, दिन प्रति दिन प्रदूषित हो रहे हैं। शायद एक दिन ऐसा भी आए जब प्रदूषण का यह स्तर इतना अधिक हो जाए कि जीवन ही असंभव हो जाए।
उस स्थिति में हवा इतनी विषैली हो जाएगी कि सांस भी नहीं ली जा सकेगी और पानी जहरीला हो जाएगा। इस तरह से क्या हम अपनी आने वाली पीढ़ियों को उनके जीने के न्यायसंगत अधिकार से वंचित अथवा बेदखल नहीं कर रहे हैं ? इससे पहले कि बहुत देर हो जाए, हमें सुधार कर लेना चाहिए। यदि वर्तमान पीढ़ी इस प्रत्यक्ष चेतावनी की तरफ ध्यान नहीं देगी तो इसका अर्थ होगा, अपनी आँखें जान-बूझ कर बन्द कर लेना और मानव-जाति के भविष्य को खतरे तथा विलुप्तीकरण के अंदर धकेल देना।
लेखक डा० डी० वी० जिन्दल जोकि एक वरिष्ठ प्राध्यापक, पी० ई० एस० (आई) है, वह ऐस० सी० डी० राजकीय कॉलेज, लुधियाना से रिटायर हुआ। विभिन्न स्तरों पर विभिन्न शैक्षणिक संस्थाओं के सदस्य के रूप में काम करने के बाद वर्तमान में वह इंग्लिश एण्ड फॉरेन लैंग्वेजिस युनिवर्सिटी, हैदराबाद के एक्स्टर्नल फैकल्टी का सदस्य है। उसने स्वर-विज्ञान के विषय में पंजाब विश्वविद्यालय, चंडीगढ़ से पी० एच० डी० को है, तथा वह भाषा तथा साहित्य पर लिखी गई कई पुस्तकों का लेखक है।
पानी ने हमारे ग्रह के 75 प्रतिशत भाग को ढक रखा है, इसलिए यह बहुत ज़्यादा मात्रा में प्रतीत होता है। किन्तु, उस पानी का 97 प्रतिशत भाग समुद्र का नमकीन (खारा) पानी है जिसे हम पी नहीं सकते हैं। जो तीन प्रतिशत ताज़ा पानी है उसमें से अधिकतर हिमनदियों तथा ध्रुवीय बफीर्ली चोटियों पर जमा पड़ा है।
![]()
परिणामस्वरूप, धरती का केवल एक प्रतिशत पानी ही शायद पीने के लिए उपलब्ध है। इसके अलावा. धरती की जल आपति सीमित है-कोई नया पानी उत्पन्न नहीं हो रहा है। हमारे पास अब भी पानी की उतनी ही मात्रा है जितनी तब थी जब इस धरती का निर्माण हुआ था। हमारे पास यही पानी है, और हमें इसकी गुणवत्ता को अवश्य ही बनाए रखना होगा। पानी भोजन एवम् जीवन का आधार है। हवा के पश्चात् पानी ही हमारी सबसे कीमती सम्पत्ति है।
हम पानी के बिना जीवित नहीं रह सकते।सी० वी० रमन ने ठीक ही कहा है, “मनुष्य कई युगों से व्यर्थ ही जीवन के काल्पनिक अमृत की तलाश करता रहा है, जोकि ईश्वरीय अमृत है, जिसकी एक बूंट भी, ऐसा सोचा जाता था कि, अमरता प्रदान करती थी।
लेकिन जीवन का वास्तविक अमृत तो हमारे हाथों के बिल्कुल समीप ही पड़ा है। क्योंकि यह सभी द्रवों में सबसे साधारण है, सादा जल !’ इसीलिए हमारी अधिकतर सभ्यताएं तथा महत्त्वपूर्ण नगर बड़ी नदियों के किनारे ही विकसित हुए।
हमारी प्राचीन धार्मिक पुस्तकें तथा महाकाव्य उन दिनों प्रचलित जल भण्डारण तथा संरक्षण प्रणालियों के बारे में अच्छी-खासी जानकारी देते हैं। सिन्धु घाटी की सभ्यता जोकि लगभग पाँच हजार वर्ष पूर्व सिन्धु नदी तथा भारत के अन्य पश्चिमी तथा उत्तरी भाग में फली फूली, में विश्व की सबसे अत्याधुनिक नगरीय जल आपूर्ति प्रणाली तथा गन्दे पानी की निकासी प्रणाली थी। इस सच्चाई को जानने के लिए कि लोगों को स्वास्थ्य विज्ञान की अच्छी-खासी जानकारी थी, मोहनजोदड़ो तथा हड़प्पा दोनों ही शहरों के खण्डहरों की गलियों के नीचे से गुजरने वाली ढकी हुई नालियों को देखा जा सकता है।
जंगलों में पानी आसानी से जमीन में रिस जाता है क्योंकि पेड़-पौधे पानी के बहाव को रोक देते हैं। फलस्वरूप ज़मीन का पानी कुओं, झीलों तथा नदियों को भरता है। जंगलों को बचाने का अर्थ है, जल ‘आवाह क्षेत्रों’ को बचाना। प्राचीन भारत में लोगों का मानना था कि जंगल नदियों की ‘मांऐं’ हैं और वे पानी के इन स्रोतों की पूजा किया करते थे।|
पानी सुन्दरता तथा प्रसन्नता का स्रोत है। यह प्रकृति की सुन्दरता में चार चांद लगाता है। यह किसी चट्टान या झरने, चाहे वह बड़ा हो अथवा छोटा, से नीचे बहकर आती हुई कोई छोटी धारा हो सकती है। यह आँखों को खुशी प्रदान करता है तथा दिमाग को तरोताज़ा कर देने वाली सुन्दर सांस (वायु) प्रदान करता है। अपने टेढ़े-मेढ़े रास्तों से होकर समुद्र में मिल जाने के लिए अपनी शाही यात्रा के लिए पहाड़ों से नीचे नृत्य करते हुए उतरते झरने तथा नदियां दृश्य को नवीनता प्रदान करते हैं। छोटे सरोवर, झीलें या विशाल समुद्र संवेदनशील कवियों की ्रशंसा के हकदार बनते हैं।
एक महान् लेखक ने लिखा “किसी प्राकृतिक दृश्य में जल की तुलना मनुष्य के चेहरे पर लगी आँखों से की जा सकती है। सूर्य के चमकने पर शोख तथा भड़कीला हो जाना, आकाश के बादलों से ढके होने पर गहरे रंग का तथा धुंधला-सा हो जाना, समय के
मिज़ाज को प्रतिबिंबित करता है।” कई सालों से, बढ़ती हुई जनसंख्या, बढ़ते हुए औद्योगीकरण तथा विस्तृत होती खेतीबाड़ी ने पानी की मांग को बढ़ा दिया है। बांध बनाकर तथा जलाशयों का निर्माण करके तथा कुएं खोदकर पानी का संग्रह करने की कोशिशें की गई हैं। कुछ देशों ने पानी को दोबारा प्रयोग के लायक बनाने की तथा इसमें से नमक को अलग करने की कोशिश भी की है।
पानी का संरक्षण आज के समय की जरूरत बन गया है। जबकि पानी की उपलब्धता लाखों एकड़ बंजर भूमि को जीवन तथा हरियाली से भरपूर क्षेत्रों में बदल सकती है, पानी की अनुपस्थिति उपजाऊ जमीनों को सूखे, मौत के जीवन-विहीन बंजर क्षेत्रों में बदल सकती है।
खेतीबाड़ी वाले इलाकों में पानी का संरक्षण आवश्यक है लेकिन कम होता जल-स्तर तथा रासायनिक खादों तथा कीटमार दवाइयों के अत्यधिक प्रयोग से खारेपन में बढ़ौतरी कुछ गंभीर किस्म की बात है। भारत का भोजन का कटोरा कहलाने वाला पंजाब का राज्य तेज़ी से सूखता जा रहा है। यह पर्यावरण आपदा की कगार पर खड़ा है।
![]()
ट्यूबवलों की संख्या जोकि 1970 में एक लाख बीस हजार थी, अब बढ़कर तेरह लाख हो गई है और ज़मीनी पानी की गिरावट की दर चौंका देने वाले स्तर पर पहुंच गई है। सबसे अधिक प्रभावित ज़िले संगरूर तथा मोगा हैं जहां जल-स्तर पचास फीट से भी नीचे है।
पंजाब के सिंचाई मन्त्री ने पंजाब विधान सभा के सदन के मंच पर स्वीकार किया कि धरती के नीचे का पानी राज्य के 85 प्रतिशत इलाकों में लगातार कम होता जा रहा है। इससे भी बुरी बात यह है कि पिछले चार दशकों में पानी में नाइट्रेट की मात्रा दस गुणा / तक बढ़ गई है। एक अन्य विधायक ने कहा, मे पानी की गुणवत्ता ऐसी थी कि इसमें 0.5 मिलीग्राम प्रति लीटर नाइट्रेट थी।
अब यह बढ़कर 5 मिलीग्राम प्रति लीटर हो गई है और अगर हमारे किसानों द्वारा की मार तथा खरपतवारनाशक दवाइयों के हद से ज्यादा इस्तेमाल को देखें तो अगले बीस वर्षों में इसके 10 मिलीग्राम प्रति लीटर तक पहुंच जाने की उम्मीद है। इसका अर्थ यह.हुआ कि अगले बीस से पच्चीस वर्षों में पंजाब का पानी मनुष्यों और पशुओं के पीने लायक नहीं रहेगा। मिलीग्राम प्रति लीटर तक नाइट्रेट की मौजूदगी इसे पीने के लिए अनुपयुक्त कर देती है।” पानी में संखिया, नाइट्रेट तथा भारी धातुओं की भारी मात्रा समूचे पंजाब में सेहत से संबंधित विकट समस्याओं का कारण बन रही है।
पानी में नाइट्रेट की भारी मात्रा हमारे महत्त्वपूर्ण तन्तुओं, जैसे कि दिमाग़, आदि में आक्सीजन की आपूर्ति को कम कर सकती है। इसलिए राज्य को इस विषय में उच्च प्राथमिकता के आधार पर एक विस्तृत नीति का निर्माण करना चाहिए। इस चुनौती का सामना करने के लिए भूमि-संरक्षण, सिंचाई, बिजली तथा खेतीबाड़ी विभागों को मिलकर काम करना चाहिए।
नैशनल जियोफिजीकल रिसर्च इंस्टिच्यूट की जांच पड़ताल के नतीजों के अनुसार, जल स्रोतों के अत्यधिक इस्तेमाल के कारण जमीन के नीचे का जल-स्तर सेंटीमीटर प्रतिवर्ष की दर से नीचे जा रहा है। पंजाब ने तीस से भी कम वर्षों में ही जमीन के पानी के उतने भण्डार को इस्तेमाल कर लिया है, जिसे बनने में पिछले 105 वर्ष लगे थे।
जल-स्तर तक पहुंचने के लिए किसान लोग जमीन को ज़्यादा से ज्यादा गहराई तक खोदने तथा पम्पों के द्वारा पानी बाहर निकालने के लिए अधिक बिजली इस्तेमाल करने के लिए मजबूर हैं। यहां तक कि शहरों के लोगों को हाथ का नल इस्तेमाल करने के लिए उससे भी अधिक गहराई तक खुदाई करनी पड़ रही है जितनी वे पहले करते थे, कह लीजिए दस वर्ष पहले।
जल-स्तर में अत्यधिक गिरावट का नतीजा यह निकला है-ट्यूबवेलों का कम पानी देना, गड्ढों तथा ट्यूबवेलों का और गहरा होना, कम लागत वाले अपकेन्द्री (सेन्ट्रीफ्यूगल) पंपों की जगह महंगे सबमर्सिबल पम्पों का आ जाना तथा बिजली की बढ़ी हुई कीमतें, और इसके कारण राज्य के छोटे तथा हाशिए पर बैठे (ग़रीब)
किसानों की सामाजिक-आर्थिक स्थिति का प्रभावित होना। राज्य में पानी का एक बड़ा हिस्सा चावल-गेहूं फसल प्रणाली की भेंट चढ़ जाता है। इस बात की तरफ ध्यान दिया जाए कि एक किलोग्राम चावल उगाने के लिए लीटर पानी की खपत होती है (यह इस बात पर निर्भर करता है कि इसकी किस्म, बिजाई का ) समय, इलाका, इत्यादि क्या हैं)।
इसलिए, वर्तमान स्थिति की मांग है कि पारंपरिक फसल उगाने वाले ढांचे को तुरंत बदल दिया जाए। इसके अलावा, इस बात की आवश्यकता है कि निश्चित तौर पर पुराने तौर-तरीकों को बदलकर भूमि तथा कृषि विज्ञान प्रबंधन से संबंधित तकनीकों को अपना लिया जाए जिससे फसल उत्पादन में बिना किसी नुक्सान के पानी की बचत होती है, जिसका परिणाम होता है पानी के प्रति यूनिट इस्तेमाल द्वारा पहले से अधिक उत्पादन।
इन तकनीकों में शामिल हैं – फसलों को बीजने तथा उनकी जगह दूसरी फसलों को बोने का समय, सिंचाई का समय नियत करना तथा नई सिंचाई प्रणालियों (जैसे-स्प्रिंकलर, ड्रिप, फरो, इत्यादि) का प्रयोग। उपलब्ध जल संसाधनों के प्रभावशाली तथा कुशलतापूर्ण इस्तेमाल के लिए पानी इस्तेमाल करने वालों की संस्थाओं/सभाओं का निर्माण किया जाना चाहिए।
ज़मीन के पानी को बनावटी तरीके से दोबारा पूरा करने के काम में तेजी लाने के लिए विभिन्न उपायों / तकनीकों को भी अपनाया जाना चाहिए। हमें खतरे की घंटियों को सुन लेना चाहिए और उसके अनुसार काम करना चाहिए इससे पहले कि बहुत देर हो जाए।
पानी की हर बूंद कीमती है और इसे बचाए जाने की आवश्यकता है-जहां भी और जैसे भी संभव हो। प्रतिदिन समूचे भारत में ग्रामीण समुदायों तथा ग़रीब शहरी केन्द्रों में सैंकड़ों-हज़ारों लोग साफ तथा सुरक्षित पानी तक पहुंच न हो पाने की कमी से ग्रस्त हैं। औरतों, तथा विशेष रूप से लड़कियों, को लगातार मीलों पैदल चलने का कष्ट उठाना पड़ता है, नदी-नालों तथा पानी से पैदा होने वाली बीमारियों से भरे तालाबों से पानी लाने के लिए, जो कि उन्हें तथा उनके परिवारों को बीमार बना रहा है।
![]()
हम में से हर कोई क्या करता है, हम कैसे रहते हैं, इन सब से फर्क पड़ता है। हमें साफ, सुरक्षित पानी के महत्त्व को जानना चाहिए। हमें, इसे बचाने के लिए तथा इसे उन लोगों तक पहुंचाने के लिए जिनकी आज इस तक पहुंच नहीं है, कदम उठाने चाहिएं।
A Panorama of Life PSEB Solutions Class 11
- Gender Bias Question Answer
- The Portrait of a Lady Question Answer
- Of Studies Question Answer
- Liberty and Discipline Question Answer
- A President Speaks Question Answer
- The Earth is not Ours Question Answer
- Let’s Not Forget the Martyrs Question Answer
- Water- A True Elixir Question Answer
- The First Atom Bomb Question Answer
- No Time for Fear Question Answer
















 img
img