Bhagya

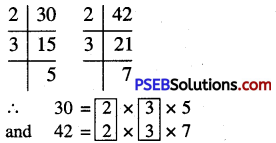
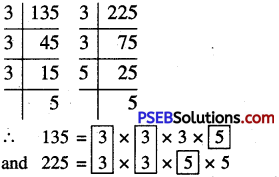
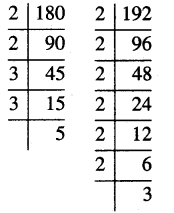
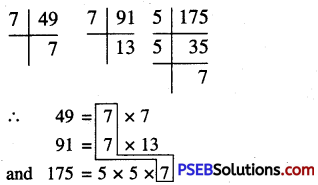Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 11 Constructions Ex 11.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 11 Constructions Ex 11.2

In each of the following, give also the justification of the construction.

Question 1.
Draw a circle of radius 6 cm from a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths.
Solution:

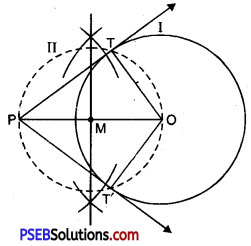
Steps of construction:
1. Draw a circle (1) of radius 6 cm.
2. Take a point ‘P’ at a distance of 10 m. from the centre of the circle. Join OP.
3. Draw perpendicular bisector of OP. Let ‘M’ be the mid point OP.
4. With ‘M’ as centre and radius MO, draw a circle (II) which intersects the circle (I) at T and T’.
5. Then FT and PT’ are two required tangents.

Justification of construction:
We know that tangent at a point is always perpendicular to the radius at the point. Now
we have to prove that ∠PTO = ∠PT’O = 90°.
OT is joined.
Now, PMO is the diameter of circle (II) and ∠PTO is in the semicircle.
∴ ∠PTO = 90° [Angle in semicircle is a right angle].
Similarly, ∠PT’O = 90°
∴ PT and PT’ has to be the tangents to the circle at T and T’.
(On measuring, the lengths of tangents
i.e., PT = 8.1 cm
PT’ = 8.1 cm.
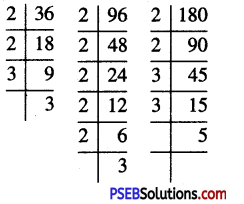
Co-centric circles. Two or more circles having same centre but different radii are called CO-CENTRIC circles.

Question 2.
Construct a tangent to a circle of radivs 4 cm from a point on the co-centric circle of radIus 6 cm and measure its length.
Also, erify the measurement by actual calculation.
Solution: Steps of construction:
STEPS OF CONSTRUCTION:
1. Draw a circle with cente O’ and radius 4 cm. Mark it as 1
2. Draw another circle with same centre ‘O’ and radius 6 cm and mark it as II.
3. Take any point ‘P’ on circle II. Join OP.
4. Draw pependicu1ar bisector of OP. Let it intersects ‘OP’ at M.
5. With M is centre and radius MO’ or ‘MP’, draw a circie III which intersects the circle ‘1’ at T and T’.
6. Join PT.
PT is the required tangent.

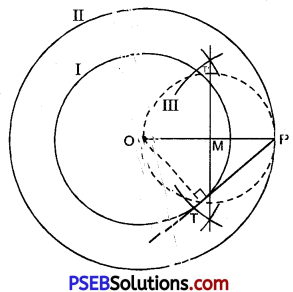
Justification of the construction :
Join OT.
Now OP is the diameter of the circle III.
∠OTP is in the semicircle.
∴ ∠OTP = 90° …………….(1)
[∴ Angle in a semicircle isa right angle]
Now OT ⊥ PT [using (I)]
∵ A line which makes an angle of 900 with radius at any point on the circle, the line is tangent to the circle.
∴ PT is tangent to the circle ‘I’
i.e. PT is tangent to the circle of radius 4.5 cm.

To calculate the length of tangent:
Consider ∆OTP,
∠OTP = 90° [using (i)]
∴ ∆OTP is a right angled triangle.
OT = 4 cm [Radius of I circle (given)]
OP = 6 cm [Radius of the II circle (given)]
PT = ? [to be calculated]
In rt. triangle ∆OTP,
By Pythagoras theorem
OP² = OT² + PT²
[(Hyp)² = (Base)² + (Perp.)²]
or PT² = OP² – OT²
= 6² – 4²
= 36 – 16 = 20
PT = \(\sqrt{20}\) cm
= 2√5 = 2 × 2.24 = 4.48 cm.
So, length of tangent by actual calculation = 4.48 cm = 4.5 cm.
Length of tangent by measurement = 4.5 cm
Hence, the length of tangent ‘PT’ is verified.

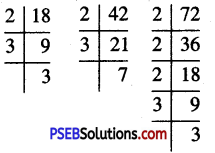
Question 3.
Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameter each at a distance of 7 cm from its centre. Draw tangents to the circle from these two points ‘P’ and ‘Q’.
Solution:
Steps of construction:
1. Draw a circle of radius 3 cm and centre ‘O’.

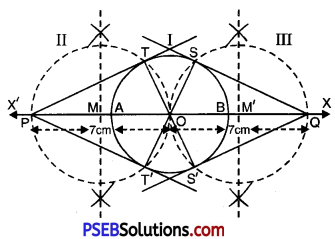
2. Draw its diameter ‘AB’ and extend it in both directions as OX and OX’.
3. Take a point P’ on OX” direction and ‘Q’ on OX’ direction such that OP = OQ = 7 cm.
4. Draw perpendicular bisectors of OP and OQ which intersects OP and OQ at ‘M’ and ‘M” respectively.
5. With ‘M’ as centre and radius = ‘MO’ or MP, draw a circle ‘II’ which intersects the circle ‘I’ at T and T’.
6. Similarly with ‘M’’ as centre and radius = M’O or MQ, draw a circle (III) which intersects the circle ‘I’ at S’ and ‘S’’.
7. Join PT, PT’ and QS and QS’.

Justification of construction :
Join OT’ and ‘OT” and ‘OS’ and OS’.
To prove ‘PT & PT’ tangents to the circle
we will prove that ∠PTO = ∠PT’O = 90°.
Now ‘OP’ acts as the diameter of circle ‘II’ and ∠OTP is in the semicircle.
∴ ∠OTP = 90° …………….(1) [∵ Angle in semicircle is 90°]
But ‘OT’ is the radius of circle ‘I’ and line ‘PT’ touches the circle at T’.
∵ The line which touches the circle at a point and makes an angle of 90° with radius at that point, is tangent to the circle.
∴ PT is tangent to the circle I at point T through point ‘P.
Similarly PT’, QS and QS’ are tangents to the circle I.

Question 4.
Draw a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60°
Solution:
Steps of construction:
1. Draw the rough sketch of required figure.

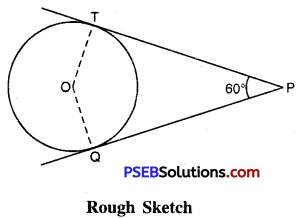
∵ the tangents make an angle of 60° with each other.
∠OTP = ∠OQT = 90°
[Tangent is perpendicular to the radius of circle]
1. To find inclination of radii with each other
∠TOQ + ∠OTP + ∠OQT + ∠TPQ = 360° [Angle sum property of quad.]
or ∠TOQ + 90° + 90° + 60 = 360°
or ∠TOQ = 360 – 90° – 90° – 60° = 120°
2. Draw a circle of radius 5 cm.
3. Draw two radii of circle which make an angle of 120° with each other.
4. The radii intersect the circle at ‘A’ and
5. Make an angle of 90° at each point A and B, which intersect each other at ‘P’.

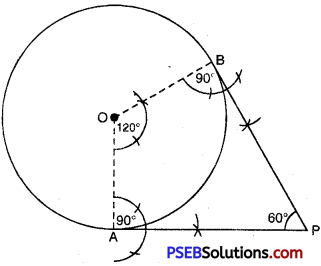
6. PA and PB are the required tangents.

Question 5.
Draw a line segment AB of length 8 cm. Taking ‘A’ as centre, draw a circle of radius 4 cm and taking ‘B’ as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.
Solution:

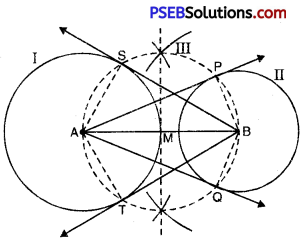
Steps of construction :
1. Draw a line segment AB = 8 cm.
2. With ‘A’ as centre and radius 4 cm, draw a circle (I)
3. With ‘B’ as centre and radius 3 cm, draw a circle ‘I’.
4. Draw the perpendicular bisector of line segment AB which inersects ‘AB’ at ‘M’.
5. With ‘M as centre and radius MA or MB. draw a circle (III) which intersects the circle (I) at ‘S’ and ‘T’ and circle (II) at ‘P’ and ‘Q’.
6. Join ‘AP’ and AQ’. These are required tangents to the circle with radius 3 cm. from point ‘A’.
7. Join ‘BS’ and ‘BT’. These are required tangents to the circle with radius 4 cm from point ‘B’.

Justification of Construction:
In circle (III), AB acts as diameter then ∠ASB and ∠BPA are in semicircle.
∴ ∠ASB = 90° ………………(1) [Angle in semicircle]
and ∠BPA = 90° .
But ∠ASB is angle between radius of circle (I) and line segment BS’ and ∠BPA is angle between radius of circle (II) and line segment ‘AP’.
∵ Line segment which is perpendicular to the radius of circle, is tangent to the circle through that point.
∴ BS is tangent to circle (I) at point ‘S’ and AP is tangent to circle (II) at point ‘P’.
Similarly AQ and BT are tangents to the circle (II) and (I) respectively.

Question 6.
Let ABC be a right triangle in which AB = 6 cm, BC = 5 cm and ∠B = 90°. BD is the perpendicular from B on AC. The circle through B, C, D is drawn. Construct the tangents from ‘A’ to this circle.
Solution:

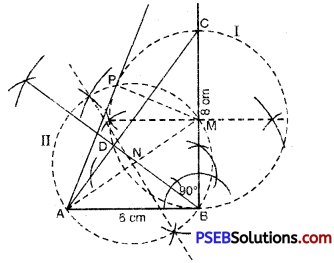
Steps of construction:
1. Construct rt. angled triangle. ABC according to given conditions and measurements.
2. Draw BD ⊥ AC.
3. Take mid point of side BC take it as
4. Take ‘M’ as centre and BC as diameter,
draw a circle through B. C, D using property, angle in semicircle is 90° (∠BDC 90°). Take this circle as I.
5. Now join ‘A’ and ‘M.
6. Draw perpendicular bisector of AM intersecting AM in point N. Now with ‘N’ as centre and ‘NA or ‘NM’ as radius, draw a circle (II) which intersects the circle (I) at ‘B’ and ‘P’.
7. Join AP.
8 AP and AB are the required tangents.

Justification of construction:
Line segment AM’ is diameter of circle (II)
∠APM is in semicircle
∴ ∠APM = 90° [Angle in semicircle]
i.e., MP ⊥ AP
But ‘MP’ is the radius of circle (I)
∴ AP is tangent to the circle (II)
[∵ Any line ⊥ to radius of circle at any point on the circle is tangent to the circle.]
Similarly AB is tangent to circle (I).

Question 7.
Draw a circle with the help of a bangle. Take a point outside the circle. Construct the pair of tangents from this poiñt
to the circle.
Solution:
To draw circle with bangle means the centre of circle is unknown. First find the centre of circle.

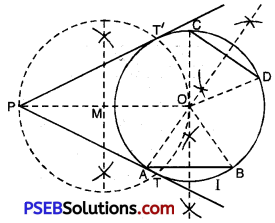
Steps of construction:
1. Draw a circle. using a bangle (I).
2. Take any two chords AB and CD (non parallel) on circle.
3. Draw the perpendicular bisectors of chords AB and CD. The perpendicular bisectors intersect each other
[∵ any point lying on perpendicular bisector of line segment is equidistant from its end points
[∵ ‘O’ lies on ⊥ bisector of AH and CD]
∴ OA = OB and OC = OD
∴ OA = OB = OC = OD (Radii of circle)
∴ ‘O’ is the centre of circle.
4. Take any point ‘P’ out side the circle.
5. Join OP.
6. Draw the perpcndicular bisector of OP let ‘M’ the mid point of OP.
7. With ‘M’ as centre and radius ‘MP’ or ‘MO’, draw a circle II which intersects the circle (I) at T and T’.
8. Join PT and PT’, which is required pair of tangents.

Justification of construction:
Tangent at a point is always perpendicular to the radius at the point. Now, we have to prove
that ∠PTO = PT’O = 90°
Join OT.
Now ∠PTO is in the semicircle I.
∵ ∠PTO = 90° [Angle in semicircle is a right angle]
Similarly ∠PT’O = 90°
∴ PT and PT’ has to be the tangents to the circle at T and T’.

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 11 Constructions Ex 11.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 11 Constructions Ex 11.1

In each of the questions, give the justification of the construction also.

Question 1.
Draw a line segment of length 7.6 cm and divide ¡tin the ratio 5 : 8. Measure the two parts.
Solution:
Given: A line segment of length of 7.6 cm.
Steps of construction:
1. Take a line segment AB = 7.6 cm.
2. Draw any ray AX, making an acute angle ∠BAX.
3. Locate 5 + 8 = 13 (given ratio 5: 8) points A₁, A₂, A₃, A₄, A₅, ………….., A₁₀, A₁₁, A₁₂, A₁₃ on ray AX such that A₁A₂ = A₂A₃ = A₃A₄ = …………. = A₁₁A₁₂ = A₁₂ A₁₃.
4. Join BA₁₃.
5. Through point A5, draw a line A₅C || A₁₃B (by making an angle equal to ∠A₁₃B) at A₅ intersecting AB at ‘C’. Then AC : CB = 5 : 8;

Justification:
Let us see how this method gives us the required division.
In ∆AA₁₃B,
Since A₅C || A₁₃B
∴ By Basic Proportionality Theorem
\(\frac{\mathrm{AA}_{5}}{\mathrm{~A}_{5} \mathrm{~A}_{13}}=\frac{\mathrm{AC}}{\mathrm{CB}}\)

By construction, \(\frac{\mathrm{AA}_{5}}{\mathrm{~A}_{5} \mathrm{~A}_{13}}=\frac{5}{8}\)

∴ \(\frac{\mathrm{AC}}{\mathrm{CB}}=\frac{5}{8}\)
This shows that ‘C’ divides AB in the ratio 5 : 8.
On measuring the two parts, AC = 2.9 cm and CB = 4.7 cm.

Alternative Method:
Steps of construction:
1. Take a line segment AB = 7.6 cm
2. Draw any acute angle ∠BAX
3. Draw angle ∠ABY such that ∠ABY = ∠BAX.
4. Locate the points A₁, A₂, A₃, A₄, A₅ on ray AX such that A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅.
5. Locate the points B₁, B₂, B₃, B₄, B₅, B₆, B₇, B₈ on ray BY such that B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅ = B₅B₆ = B₆B₇ = B₇B₈
6. Join A₅B₈ let it intersects AB at point Then AC : CB = 5 : 8.

justification:
In ∆ACA₅ and ∆BCB₈,
∠ACA₅ = ∠BCB₈ [vertically opp. ∠s]
∠BAA₅ = ∠ABB₈ [construction]
∴ AACA₅ ~ ABCB₈ [AA-similarity cond.]
∴ Their corresponding sides must be in the same ratio. ,
\(\frac{A C}{B C}=\frac{C A_{5}}{C B_{8}}=\frac{A_{5} A}{B_{8} B}\)
(I)(II) (III)
From I and III, \(\frac{A C}{B C}=\frac{A_{5} A}{B_{8} B}\)

But, \(\frac{A_{5} A}{B_{8} B}=\frac{5}{8}\) [construction]

\(\frac{A C}{C B}=\frac{5}{8}\).

Question 2.
Construct a triangle of sides 4 cm, 5 cm and 6 cm and then a triangle similar to it whose sides are \(\frac{2}{3}\) of corresponding sides of the first triangle.
Solution:
Steps of construction:
1. Construct a triangle ABC with given measurements. AB = 5 cm, AC = 4 cm and BC = 6 cm.
2. Make any acute angle ∠CBX below the side BC.

3. Locate three points (greater of 2 and 3 in \(\frac{2}{3}\))B₁, B₂, B₃ on BX such that BB₁ = B₁B₂ = B₂B₃.
4. Join B₃C.
5. Through B₂ (smaller of 2 and 3 in \(\frac{2}{3}\) draw a line parallel to B₃C, which intersect BC in C’.
6. Through C’, draw a line parallel to CA meeting BA is A’.
Thus ∆A’BC’ is the required triangle whose sides are of corresponding sides of ∆ABC.

Justification of construction :
First we will show that first triangle and constructed triangle are similar.
i.e. ∆A’BC’ ~ ∆ABC.
Consider ∆A’BC’ and ∆ABC.
∠B = ∠B [Common]
∠A’C’B= ∠ACB [By construction]
∆A’C’B ~ ∆ACB [AA – similarity]
∴ Their corresponding sides must be in the same ratio.
\(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{A}^{\prime}}{\mathrm{CA}}\) …………….(1)
Now, consider ∆B₂BC’ and ∆B₃BC,
∠B = ∠B [common]
∠B₂C’B = ∠B₂CB [construction]
∴ ∆B₂BC’ ~ ∆B₃BC [AA -similarity]
∴ Their corresponding sides must be in the same ratio.

\(\frac{\mathrm{B}_{2} \mathrm{~B}}{\mathrm{~B}_{3} \mathrm{~B}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{B}_{2}}{\mathrm{CB}_{3}}\)

I II III

Taking (I) and (II).
\(\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{B}_{2} \mathrm{~B}}{\mathrm{~B}_{3} \mathrm{~B}}\)

But, \(\frac{\mathrm{B}_{2} \mathrm{~B}}{\mathrm{~B}_{3} \mathrm{~B}}=\frac{2}{3}\) [construction]

\(\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{2}{3}\) ……………(2)

From (1) & (2),
\(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{A}^{\prime}}{\mathrm{CA}}=\frac{2}{3}\)

⇒ A’B = \(\frac{2}{3}\) AB and BC’ = \(\frac{2}{3}\) BC; C’A’ = \(\frac{2}{3}\) CA.
Hence, the construction is Justified.

Question 3.
Construct a triangle with sides 5 cm, 6 cm and 7 cm and then another triangle whose sides are of the corresponding sides of the first triangle.
Solution:

Steps of construction :
1. Construct a triangle ABC in which AB = 7 cm, BC 6 cm and AC =5 cm.
2. Make any acute angle ∠BAX below the base AB.
3. Locate seven points A₁, A₂, A₃, A₄, A₅, A₆, A₇ on the ray AX such that
AA₁ = A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅ = A₅A₆ = A₆A₇.
4. Join BA₅.
5. Through A₇, draw a line parallel A₅B. Let it meets AB at B’ on being produced such that AB’= \(\frac{7}{5}\) AB.
6. Through B’, draw a line parallel to BC which meets AC at C’ on being produced.
∆AB’C’ is the required triangle.

Justification of the construction.
In ∆ABC and ∆AB’C’,
∠A = ∠A [common]
∠ABC = ∠AB’C’ [corresponding ∠s]
∴ ∠ABC – ∠AB’C’ [AA-similarity]
∴ Their corresponding sides must be in the same ratio.
\(\frac{\mathrm{AB}}{\mathrm{AB}^{\prime}}=\frac{\mathrm{BC}}{\mathrm{B}^{\prime} \mathrm{C}^{\prime}}=\frac{\mathrm{CA}}{\mathrm{C}^{\prime} \mathrm{A}}\) ……………..(1)

Again, in ∆AA₅B and AA₇B’
∠A = ∠A [common]
∠AA5B = ∠AA7 B’ [corresponding ∠s]
∴ ∆AA5B ~ ∆AA7B’ [AA – similarity]
∴ Their corresponding sides must be in the same ratio.
\(\frac{\mathrm{AA}_{5}}{\mathrm{AA}_{7}}=\frac{\mathrm{A}_{5} \mathrm{~B}}{\mathrm{~A}_{7} \mathrm{~B}^{\prime}}=\frac{\mathrm{AB}}{\mathrm{AB}^{\prime}}\)

⇒ \(\frac{\mathrm{AB}}{\mathrm{AB}^{\prime}}=\frac{\mathrm{AA}_{5}}{\mathrm{AA}_{7}}\) [construction]

But, \(\frac{\mathrm{AB}}{\mathrm{AB}^{\prime}}=\frac{5}{7}\) …………….(2)

From (1) and (2),

\(\frac{\mathrm{AB}}{\mathrm{AB}^{\prime}}=\frac{\mathrm{BC}}{\mathrm{B}^{\prime} \mathrm{C}^{\prime}}=\frac{\mathrm{CA}}{\mathrm{C}^{\prime} \mathrm{A}}=\frac{5}{7}\)

or \(\frac{A B^{\prime}}{A B}=\frac{B^{\prime} C^{\prime}}{B C}=\frac{C^{\prime} A}{C A}=\frac{7}{5}\)

⇒ AB’ = \(\frac{7}{5}\) AB; B’C’ = \(\frac{7}{5}\) BC and C’A’ = \(\frac{7}{5}\) CA

Hence, the sides of ∆AB’C’ are \(\frac{4}{4}\) of ∆ABC.

Question 4.
Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then another triangle whose sides are 12 times
the corresponding sides of the isosceles triangle.
Solution:
Given: Base of isosceles triangle is 8 cm and Altitude = 4 cm
To construct: A triangle whose sides are times the sides of isosceles triangle.
Steps of construction:
1. Take base AB = 8 cm.
2. Draw perpendicular bisector of AB. Let it intersect AB at ‘M’.
3. With M as centre and radius = 4 cm, draw an arc which intersects the perpendicular bisector at ‘C’
4. Join CA and CB.
5. ∆ABC is an isosceles with CA = CB.
6. Make any acute angle ∠BAX below the side BC.
7. Locate three (greater of ‘2’ & ‘3’ in 1\(\frac{1}{2}\) or \(\frac{3}{2}\))
A₁, A₂, A₃ on ‘AX’ such that A A₁ = A₁ A₂ = A₂ A₃.

8. Join A₂ (2nd point smaller of ‘2 and ‘3’ in ) and B.
9. Through A₃, draw a line parallel to A₂B meet AB is B’ cm being produced.
10. Through B’, draw a line parallel to BC which meets AC in C’ on being produced. ∆AB’C’ is the required triangle whose sides are 1\(\frac{1}{2}\) times the corresponding sides of ∆ABC.

Justification of construction :
First we will prove ∆AB’C’ are ∆ABC and similar.
Consider ∆ AB’C’ and ∆ ABC
∠A = ∠A [Common]
∠AB’C’ = ∠ABC [By construction]
∠AB’C’ ~ ∠ABC [By AA – similarityj
∴ Their corresponding sides must be in the same ratio
\(\frac{\mathrm{AB}^{\prime}}{\mathrm{AB}}=\frac{\mathrm{B}^{\prime} \mathrm{C}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{A}}{\mathrm{CA}}\) ……………(1)

Now consider ∆ A₃AB’ and ∆ A,AB
∠A = ∠A [common]
∠B’A₃A = ∠BA₂A [By construction]
∴∆ A₃A B’ – ∆A₂AB [AA – similarity]
∴ Their corresponding sides must be in the same ratio
\(\frac{A_{3} A}{A_{2} A}=\frac{A B^{\prime}}{A B}=\frac{B^{\prime} A_{3}}{B A_{2}}\)
I II III
Taking (I) & (II),
\(\frac{A B^{\prime}}{A B}=\frac{A_{3} A}{A_{2} A}\)

But, \(\frac{A_{3} A}{A_{2} A}=\frac{3}{2}\) [construction]
⇒ \(\frac{\mathrm{AB}^{\prime}}{\mathrm{AB}}=\frac{3}{2}\) ……………..(2)
From (1) & (2)m
\(\frac{\mathrm{AB}^{\prime}}{\mathrm{AB}}=\frac{\mathrm{B}^{\prime} \mathrm{C}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{A}}{\mathrm{CA}}=\frac{3}{2}\left(1 \frac{1}{2}\right)\)

⇒ AB’ = 1\(\frac{1}{2}\) (AB); B’C’ = 1\(\frac{1}{2}\) BC and C’A’ = 1\(\frac{1}{2}\) (CA)
Hence, given result is justified.

Question 5.
Draw a triangle ABC with side BC = 6 cm, AB =5 cm and ¿ABC = 60°. Then construct a triangle whose sides are of the corresponding sides of the triangle ABC.
Solution:
Steps of construction :
1. Take a line segment BC = 6 cm
2. Construct an angle of measure 60° at point B. i.e., ∠CBX = 60°.
3. With B as centre and radius 5 cm draw an arc intersecting BX at ‘A’

4. Join A and C.
5. At B, make any acute angle ∠CBY below the side BC.
6. Locate four points (greater of 3 and 4 in \(\frac{3}{4}\)) B₁, B₂, B₃, B₄ on BY such that BB₁ = B₁B₂ = B₂B₃ = B₃B₄. .
7. Join B₄ and C.
8. Draw a line through B₃ (smaller of 3 and 4 in ) parallel to B₄C making corresponding angles. Let the line through B₃ intersects BC in C’.
9. Through C’, draw a line parallel to CA which intersects BA at A’.
The ∆A’BC’ is the required triangle whose sides are \(\frac{3}{4}\) of sides of ∆ABC.

Justification of the construction:
Consider ∆A’BC’ and ∆ABC
∠B = ∠B [commoni
∠A’C’B = ∠ACB [corresponding ∠s]
∴ ∆A’BC’ ~ ∆ABC [AA – similarity]
∴ Their corresponding sides must be in the same ratio.

∴ \(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{A}^{\prime}}{\mathrm{CA}}\) ……………..(1)

Now consider ∆B₃B C’ and ∆B₄BC.
∠B = ∠B [common]
∠ C’ B₃B = ∠CB₄B [corresponding ∠s]
∆B₃BC’ ~ ∆B₄BC [AA – similarity con.]
Their corresponding sides must be in the same ratio.
\(\frac{B_{3} B}{B_{4} B}=\frac{B C^{\prime}}{B C}=\frac{C^{\prime} B_{3}}{C B_{4}}\)
(I) (II) (III)

From (I) and (II),
\(\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{B}_{3} \mathrm{~B}}{\mathrm{~B}_{4} \mathrm{~B}}\)

But, = \(\frac{\mathrm{B}_{3} \mathrm{~B}}{\mathrm{~B}_{4} \mathrm{~B}}=\frac{3}{4}\) [construction]

\(\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{3}{4}\) ………..(3)

From (1) and (3)
\(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{A}^{\prime}}{\mathrm{CA}}=\frac{3}{4}\)

and C’A’= \(\frac{3}{4}\) CA.
∆A’BC’ is the required triangle whose sides are \(\frac{3}{4}\) sides of ∆ABC.

Question 6.
Draw a triangle ABC with side BC = 7 cm, ∠B = 45°. ∠A = 105°. Then construct a triangle whose sides are j- times
the corresponding sides of ∆ABC.
Solution:
Steps of construction:
1. Construct the triangle ABC with the given measurements.
BC = 7 cm; ∠B = 45, ∠A = 105°
By angle sum property of triangle
∠A + ∠B + ∠C= 180°
105° + 45° + ∠C = 180°
∠C = 180 – 150° = 30°
2. Make any acute angle ∠CBX at point B, below the sides BC.

3. Locate four points (greater of 3 and 4 in \(\frac{4}{3}\)) B₁, B₂, B₃, B₄ on ‘BX’ such that BB₁ = B₁B₂ = B₂B₃ = B₃B₄.
4. Join B₃C (smaller of 3 and 4 in \(\frac{4}{3}\)).
5. Through B₄, draw a line parallel to B₃C meeting BC in C’ on being produced.
6. Through C’, draw another line parallel to CA meeting BA in A’ on being produced.
7. ∆A’BC’ is the required triangle whose sides are times the triangle ABC.

Justification of construction:
Consider the ∆ A’BC’ and ∆ ABC,
∠B = ∠B [common]
∠A’C’B = ∠ACB [construction]
∴ ∆A’BC’ ~ ∆ABC [AA – similarity]
∴ Their corresponding sides must be in the same ratio

\(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{A}^{\prime}}{\mathrm{CA}}\) ………….(1)

Again, consider ∆B₄B C’ and ∆B₃BC,
∠B = ∠B [common]
∠C’B4B = ∠CB3B [By consiruction]
∴ BB C’ AB3BC [AA-si niilarity]
∴ Their corresponding sides must be in the same ratio
\(\frac{\mathrm{B}_{4} \mathrm{~B}}{\mathrm{~B}_{3} \mathrm{~B}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{B}_{4}}{\mathrm{CB}_{3}}\)
I II III

Taking I and II members.

\(\frac{B C^{\prime}}{B C}=\frac{B_{4} B}{B_{3} B}\)

But, \(\frac{B_{4} B}{B_{3} B}=\frac{4}{3}\) (construction)

or \(\frac{B C^{\prime}}{B C}=\frac{4}{3}\) ………….(2)

From (1) and (2),

\(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{A}^{\prime}}{\mathrm{CA}}=\frac{4}{3}\)

⇒ A’B = \(\frac{4}{3}\) AB; BC’ = \(\frac{4}{3}\) BC and C’A’ = \(\frac{4}{3}\) CA
Hence the construction is justified.

Question 7.
Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm. Then construct another triangle whose sides are \(\frac{5}{3}\) times the corresponding sides of the given triangle.
Solution:
Steps of construction:
1. Draw a right triangle using given conditions. Consider the triangle as ABC in which BC = 4 cm; AB = 3 cm and
∠B = 90°.
2. Make any acute angle ∠CBX below the line BC.
3. Locate five points (greater of 5 and 3 in \(\frac{5}{3}\)) B₁, B₂, B₃, B₄. B₅ on BX such that BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅.
4. Join B₃ (smaller of ‘5’ and ‘3’ in \(\frac{5}{3}\)) and ‘C’.

5. Through B₅. draw a line parallel to BC meeting BC is C’ on being produced.
6. Again draw a line through C’ parallel to CA meeting BA in A’ on being produced.
∆A’BC’ is the required triangle whose sides are \(\frac{5}{3}\) times the sides of ∆ABC.

Justification of construction :
Consider ∆A’BC’ and ∆ABC
∠B = ∠B [common]
∠A’C’B = ∠ACB [By construction]
∴ ∆A’BC’ ~ ∆ABC [AA-similarity condition]
∴ Their corresponding sides must be in the same ratio
\(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{A}^{\prime}}{\mathrm{CA}}\) ……………..(1)

Again, in ∆B₅C’B and ∆XB₃CB,
∠B = ∠B [common]
∠C’B₅B = ∠CB₃B [By construction]
∴ ∆B₅C’B ~ ∆B₃CB [AA-similarityj
∴ Their corresponding sidcs must be in the same ratio.

\(\frac{\mathrm{B}_{5} \mathrm{C}^{\prime}}{\mathrm{B}_{3} \mathrm{C}}=\frac{\mathrm{C}^{\prime} \mathrm{B}}{\mathrm{CB}}=\frac{\mathrm{BB}_{5}}{\mathrm{BB}_{3}}\)

I II III

Taking II and III members.
\(\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{B}_{5} \mathrm{~B}}{\mathrm{~B}_{3} \mathrm{~B}}\)

But, \(\frac{B_{5} B}{B_{3} B}=\frac{5}{3}\) [construction]

\(\frac{B C^{\prime}}{B C}=\frac{5}{3}\) ……………(2)
From (1) and (2),

\(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{A}^{\prime}}{\mathrm{CA}}=\frac{5}{3}\)

⇒ A’B = \(\frac{5}{3}\) AB; BC’ = \(\frac{5}{3}\) BC and C’A’ = \(\frac{5}{3}\) CA
Hence the construction is justified.

Punjab State Board PSEB 7th Class English Book Solutions English Grammar Noun Exercise Questions and Answers, Notes.

PSEB 7th Class English Grammar Noun

A Noun is the name of a person an animal place or a thing.
किसी व्यक्ति, पशु स्थान अथवा वस्तु के नाम को Noun (संज्ञा) कहते हैं; जैसे,

1. Mr. Amitabh Mukerjee is a Bengali.
2. Geeta went to Patiala.
3. A balloon was flying in the sky.

1. पहले वाक्य में व्यक्ति अर्थात् Mr. Amitabh Mukerjee, दूसरे में स्थान अर्थात् Patiala और तीसरे में वस्तु अर्थात् balloon का नाम दिया गया है। ये तीनों शब्द Nouns हैं।

Kinds:
Nouns चार प्रकार के होते हैं।

• Proper Noun. Proper Noun (व्यक्तिवाचक संज्ञा) किसी विशेष व्यक्ति या स्थान का नाम होता है, जैसे:
• Dinesh is a good boy.
• Chandigarh is the capital of Punjab.

2. Common Noun. जिस शब्द से किसी जाति के प्रत्येक व्यक्ति, स्थान, अथवा वस्तु का बोध हो, उसे Common Noun (जातिवाचक संज्ञा) कहते हैं; जैसे:

• She went to a lawyer.
• Amritsar is a big city.

3. Collective Noun. जिस संज्ञा से समूह का बोध होता है उसे Collective Noun (समुदायवाचक संज्ञा) कहते हैं; जैसे:

• A hockey team has eleven players.
• There are fifty boys in our class.
• She has lost her bunch of keys.

4. Abstract Noun. जिस संज्ञा से किसी वस्तु के गुण, कार्य अथवा अवस्था का बोध होता है, उसे Abstract Noun (भाववाचक संज्ञा) कहते हैं; जैसे:
गुण-Goodness, kindness, honesty, beauty.
कार्य-Laughter, hatred.
अवस्था-Boyhood, sleep, childhood, length, breadth.

Exercise 1

I. Underline the common nouns in the following sentences. Some sentences have more than one common noun. One has been done for you.
1. The baby was afraid of the dark.
2. Many people were being treated in the hospital.
3. The sky was full of dark clouds.
4. My house is very large.
5. I like to play with my favourite toys.
6. Books give us a lot of information.
7. Amarjit has injured his arm.
8. The old lady was very lonely.
9. The train to Jalandhar was late again.
10. The teacher spoke to her students.
11. Simran loves watching the television.
Hints:
2. people, hospital
3. clouds
4. house
5. toys
6. Books
7. arm
8. lady
9. train
10. teacher, students
11. television.

II. Fill in the blanks with suitable common nouns to form meaningful sentences:

1. Ravi could not find his ………….. in his bag.
2. Rahim fell into the
3. The ………… was late today.
4. Our ………….. is very beautiful.
5. We bought some …………. yesterday.
6. I saw a long
Hints:
1. pen
2. river
3. bus
4. garden
5. flowers
6. snake.

Exercise 2

I. Underline the proper nouns in the following sentences. Some sentences have more than one proper noun. The first one has been done for you:
1. Nutan was a great actress of India.
2. Ravana is a character from the Ramayana
3. The Ganges flows down from the Himalayas.
4. Children enjoyed at Appu Ghar.
5. The Esteem is an expensive car.
6. Prince Rana died in a tragic road accident.
7. Mr. Mohan uses a Videocon washing machine.
8. The Charminar is in Hyderabad.
9. The film Sholay was seen by a large number of people.
10. February is the shortest month of the year.
11. Verka ice-cream is available in many flavours.
Hints:
2. Ravana, Ramayana
3. Ganges, Himalayas
4. Appu Ghar
5. Esteem
6. Prince Rana
7. Mr. Mohan, Videocon washing machine
8. Charminar, Hyderabad
9. Sholay
10. February
11. Verka ice-cream.

II. Fill in the blanks with suitable proper nouns to form meaningful sentences.

1. My pet dog …………. is very lovable.
2. …………. is a popular hill station.
3. My favourite television programme is ………
4. The film ………… is running in four theatres.
5. The month of ………….. is very cold.
Hints:
1. Don
2. Shimla
3. Hungama
4. Sholay
5. January.

Exercise 3

I. Underline the collective nouns in the following sentences. The first one has been done for you.

1. The army marched forward to occupy the land.
2. Father bought a packet of sweets.
3. Our class is very noisy.
4. The mob destroyed the furniture.
5. We booked a suite of rooms in the hotel.
6. A herd of cattle was grazing in the field.
Hints:
2. packet
3. class
4. mob, furniture
5. suite
6. herd.

II. Fill in the blanks in the following phrases with collective nouns. Choose from the box given below:

soldiers
grapes
bananas
bees
stick
musicians
sailors
stones
puppies.
wolves
1. a band of musicians
2. a bundle of sticks
3. a heap of stones
4. a bunch of grapes
5. a regiment of soldiers
6. a pack of wolves
7. a swarm of bees
8. a bunch of bananas
9. a crew of sailors
10. a litter of puppies.

III. Choose from the following list of collective nouns to form meaningful sentences:

school
library
pride
audience
committee
1. The …………. held a two hour meeting.
2. The …………. enjoyed the film.
3. We saw a …………. of whales in the sea.
4. The ………….. of lions was an impressive sight.
5. The students collected books from the ………
Hints:
1. committee
2. audience
3. school
4. pride
5. library.

Exercise 4

I. Underline the abstract nouns in the following sentences. The first one has been done for you.

1. Soldiers are known for their bravery.
2. Books provide us with knowledge.
3. My grandfather enjoys good health.
4. We lost hope of finding our stolen jewellery.
5. Raj suffered a loss when he sold his house.
6. Navin was in a lot of pain after he fell.
7. The teacher told the parents about their son’s progress.
8. The little boy cried in fear on seeing the tiger.
9. It is our duty to respect our parents.
10. Most of us are afraid of failure.
Hints.
2. knowledge
3. health
4. hope
5. loss
6. pain
7. progress
8. fear
9. duty
10. failure.

II. Match abstract nouns from the given box that are opposite in meaning to those listed below. One has been done for you:

life
success
war
hatred
wealth
disagreement
cowardice
pain
cruelty
sorrow
noise
dishonesty.
Answer:
1. Silence – noise
2. kindness – cruelty
3. love – hatred
4. happiness – sorrow
5. agreement – disagreement
6. bravery – cowardice
7. peace – war
8. pleasure – pain
9. death – life
10. poverty – wealth
11. honesty – dishonesty
12. failure – success.
Note : A phrase doing the work of a noun is called a noun phrase.

Exercise 5

Underline the noun phrases in the following sentences:

1. I enjoy swimming in the river.
2. Serving our country is our duty.
3. Helping the poor gives me joy.
4. His dislike for me is unjustified.
5. My love for my friends is deep.
Answer:
1. I enjoy swimming in the river.
2. Serving our country is our duty.
3. Helping the poor gives me joy.
4. His dislike for me is unjustified.
5. My love for my friends is deep.
Note : A clause doing the work of a noun is called a noun clause.

Exercise 6

Underline the noun clause in the sentences.

1. I believe that he is honest.
2. Let me know where you are going.
3. No one doubts what he says.
4. I hope that he will pass his examination.
5. I do not know what he wants to do after graduation.
Answer:
1. I believe that he is honest.
2. Let me know where you are going.
3. No one doubts what he says.
4. I hope that he will pass his examination.
5. I do not know what he wants to do after graduation.

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 15 Introduction to Graphs Ex 15.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 15 Introduction to Graphs Ex 15.3

1. Draw the graphs for the following tables of values, with suitable scales on the axes.

Question (a)
Cost of apples

Number of apples	1	2	3	4	5
Cost (in ₹)	5	10	15	20	25

Solution:

1. Draw 2 lines perpendicular to each other as X-axis and Y-axis on graph paper.
2. Take scale :
On X-axis : 1 cm = 1 apple
On Y-axis 1 cm = ₹ 5
3. Plot the points (1, 5), (2, 10), (3, 15), (4, 20) and (5, 25) on graph paper.
4. Join these points and extend line.

(b) Distance travelled by a car

Time (in hours)	6 a.m.	7 a.m.	8 a.m.	9 a.m.
Distance (in km)	40	80	120	160

Solution:
1. Draw two lines perpendicular to each other as X-axis and Y-axis on graph paper.
2. Take scale:
On X-axis : 2 cm = 1 unit (Time in hours.)
On Y-axis : 1 cm = 10 km
3. Plot the points (6, 40), (7, 80), (8, 120) and (9, 160) on graph paper.
4. Join these points and extend line.

Question (i)
How much distance did the car cover during the period 7:30 a.m. to 8:00 a.m.?
Solution:
In the graph, draw a perpendicular at the point indicating 7:30 a.m. on the X-axis such that it meets the graph at P.
From P draw a line parallel to X-axis to meet Y-axis at 100 km.
∴ Distance travelled between 7:30 am and 8:00 am.
= (120 – 100) km
= 20 km

Question (ii)
What was the time when the car had covered a distance of 100 km since it’s start?
Solution:
When the car had covered a distance of 100 km, the time was 7 : 30 am.

(c) Interest on deposits for a year.

Deposit (in ₹)	1000	2000	3000	4000	5000
Simple Interest (in ₹)	80	160	240	320	400

Solution :
1. Draw two lines perpendicular to each other as X-axis and Y-axis on graph paper.
2. Take scale:
On X-axis : 2 cm = ₹ 1000 (deposit)
On Y-axis : 1 cm = ₹ 40 (simple interest)
3. Plot the points (1000, 80), (2000, 160), (3000, 240), (4000, 320) and (5000, 400) on graph paper.
4. Join these points and extend line.

Question (i)
Does the graph pass through the origin?
Solution:
Yes, it passes through the origin.

Question (ii)
Use the graph to find the interest on ₹ 2500 for a year.
Solution:
From the graph, the interest on ₹ 2500 for a year is ₹ 200.

Question (iii)
To get an interest of ₹ 280 per year, how much money should be deposited?
Solution:
From the graph an interest of ₹ 280 can be got by depositing ₹ 3500.

2. Draw a graph for the following:

Question (i)

Side of square (in cm)	2	3	3.5	5	6
Perimeter (in cm)	8	12	14	20	24

Is it a linear graph?
Solution:
1. Draw two lines perpendicular to each other as X-axis and Y-axis on graph paper.
2. Take scale:
On X-axis : 1 cm = 1 cm (Side of a square)
On Y-axis : 1 cm = 4 cm (Perimeter of a square) )
3. Plot the points (2, 8), (3, 12), (3.5, 14), (5, 20) and (6, 24) on graph paper.
4. Join these points and extend line.

Yes, it is a linear graph.

Question (ii)

Side of square (in cm)	2	3	4	5	6
Area (in cm2)	4	9	16	25	36

Is it a linear graph?
Solution:
1. Draw two lines perpendicular to each other as X-axis and Y-axis on graph paper.
2. Take scale:
On X-axis : 1 cm = 1 cm (Side of a square)
On Y-axis : 1 cm 5 cm (Area of a square)
3. Plot the points (2, 4), (3, 9), (4, 16), (5, 25) and (6, 36) on graph paper.
4. Join these points.

No, this graph is not a straight line. So it is not a linear graph.

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 4 Practical Geometry Ex 4.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 4 Practical Geometry Ex 4.2

1. Construct the following quadrilaterals:

Question (i).
Quadrilateral LIFT.
LI = 4 cm,
IF = 3 cm,
TL = 2.5 cm,
LF = 4.5 cm,
IT = 4 cm.
Solution:

Steps of construction:

• Draw a line segment LI = 4 cm.
• With L as centre and radius = 2.5 cm, draw an arc.
• With I as centre and radius = 4 cm, draw an arc to intersect the previous arc at T.
• With L as centre and radius = 4.5 cm draw an arc.
• With I as centre and radius 3 cm, draw an arc to intersect the previous, arc at F.
• Draw \(\overline{\mathrm{LT}}, \overline{\mathrm{IF}}, \overline{\mathrm{FT}}, \overline{\mathrm{LF}}\) and \(\overline{\mathrm{IT}}\).

Thus, LIFT is the required quadrilateral.

Question (ii).
Quadrilateral GOLD
OL = 7.5 cm,
GL = 6 cm,
GD = 6 cm,
LD = 5 cm,
OD = 10 cm.
Solution:

Steps of construction:

• Draw a line segment LD = 5 cm.
• With L as centre and radius = 7.5 cm, draw an arc.
• With D as centre and radius = 10 cm, draw another arc to intersect the previous arc at O.
• With L as centre and radius = 6 cm, draw an arc.
• With D as centre and radius = 6 cm, draw another arc to intersect previous arc at G.
• Draw \(\overline{\mathrm{LO}}, \overline{\mathrm{GO}}, \overline{\mathrm{DG}}, \overline{\mathrm{LG}}\) and \(\overline{\mathrm{DO}}\).

Thus, GOLD is the required quadrilateral.

Question (iii).
Rhombus BEND
BN = 5.6 cm,
DE = 6.5 cm.
Solution:

[Note: Diagonals of a rhombus are perpendicular bisectors of each another. Here, diagonals of □ BEND \(\overline{\mathrm{DE}}\) and \(\overline{\mathrm{BN}}\) intersect at A. So AN = 2.8 cm and AB = 2.8 cm (BN = 5.6 cm, \(\frac {1}{2}\) BN = AN and AB)]
Steps of construction:

• Draw a line segment DE = 6.5 cm.
• Draw perpendicular bisector \(\overleftrightarrow{X Y}\) of \(\overline{\mathrm{DE}}\), which intersects \(\overline{\mathrm{DE}}\) at A.
• With centre at A and radius = 5.6 × \(\frac {1}{2}\) = 2.8 cm, draw two arcs intersecting \(\overleftrightarrow{X Y}\) in points B and N.
• Draw \(\overline{\mathrm{DN}}, \overline{\mathrm{EN}}, \overline{\mathrm{EB}}\) and \(\overline{\mathrm{DB}}\).

Thus, BEND is the required quadrilateral.

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 15 Introduction to Graphs Ex 15.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 15 Introduction to Graphs Ex 15.2

1. Plot the following points on a graph sheet. Verify if they lie on a line:

Question (a)
A(4, 0), B (4, 2), C(4, 6), D(4, 2.5)
Solution:

Plotting the given points and then l joining them we find that they all S lie on the same line.

Question (b)
P(1, 1), Q(2, 2), R(3, 3), S(4, 4)
Solution:

Plotting the given points and then joining them we find that they all lie on the same line.

Question (c)
K(2, 3), L(5, 3), M(5, 5), N(2, 5)
Solution:

Plotting the given points and then joining them we find that all of them do not lie on the same line.

2. Draw the line passing through (2, 3) and (3, 2). Find the coordinates of the points at which this line meets the x-axis and y-axis.
Solution:

Plot the given points and join them to make a line. When you extend this line, it meets the X-axis at C (5, 0) and the Y-axis at D (0, 5).

3. Write the coordinates of the vertices of each of these adjoining figures:

Solution:
Figure:
(i) The coordinates of the vertices of quadrilateral OABC:
O are (0, 0)
A are (2, 0)
B are (2, 3)
C are (0, 3)

(ii) The coordinates of the vertices of quadrilateral PQRS:
P are (4, 3)
Q are (6, 1)
R are (6, 5)
S are (4, 7)

(iii) The coordinates of the vertices of triangle KLM:
K are (10, 5)
L are (7, 7)
M are (10, 8)

4. State whether True or False. Correct that are false:

Question (i)
A point whose x-coordinate is zero and y- coordinate is non-zero will lie on y-axis.
Solution:
True

Question (ii)
A point whose y-coordinate is zero and x-coordinate is 5 will lie on y- axis.
Solution:
False
Correct statement: A point whose y-coordinate is 0 and x-coordinate is 5 will lie on X-axis at a distance 5 units from origin.

Question (iii)
The coordinates of the origin are (0, 0).
Solution:
True

Punjab State Board PSEB 6th Class Maths Book Solutions Chapter 3 Playing with Numbers Ex 3.5 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 6 Maths Chapter 3 Playing with Numbers Ex 3.5

1. Find LCM of following numbers by prime factorization method:

Question (i)
45, 60
Solution:

∴ 45 = 3 × 3 × 5
60 = 2 × 2 × 3 × 5
We find that in these prime factorizations, 2 occurs maximum two times, 3 occurs maximum two times and 5 occurs maximum once
∴ L.C.M. of 45 and 60
= 2 × 2 × 3 × 3 × 5 = 180

Question (ii)
52, 56
Solution:

We find that in these prime fatorisation, 2 occurs maximum 3 times, 13 and 7 occurs maximum once.
∴ L.C.M. of 52 and 56
= 2 × 2 × 2 × 13 × 7 = 728

Question (iii)
96, 360
Solution:

∴ 96 = 2 × 2 × 2 × 2 × 2 × 3
360 = 2 × 2 × 2 × 3 × 3 × 5
We find that in these prime factorisation, 2 occurs maximum 5 times, 3 occurs maximum 2 times and 5 occurs maximum once.
∴ L.C.M. of 96 and 360
= 2 × 2 × 2 × 2 × 2 × 3 × 3 × 5 = 1440

Question (iv)
36, 96, 180
Solution:

∴ 36 = 2 × 2 × 3 × 3
96 = 2 × 2 × 2 × 2 × 2 × 3
and 180 = 2 × 2 × 3 × 3 × 5
We find that in these factorisation, 2 occurs maximum 5 times, 3 occurs maximum 2 times and 5 occurs maximum once.
∴ L.C.M. of 36, 96 and 182
= 2 × 2 × 2 × 2 × 2 × 3 × 3 × 5 = 1440

Question (v)
18, 42, 72.
Solution:

∴ 18 = 2 × 3 × 3
42 = 2 × 3 × 7
72 = 2 × 2 × 2 × 3 × 3
We find that in these factorization 2 occurs maximum 3 times, 3 occurs maximum 2 times and 7 occurs maximum once.
∴ L.C.M. of 18, 42 and 72
= 2 × 2 × 2 × 3 × 3 × 7 = 504

2. Find LCM of the following by common division method:

Question (i)
24, 64
Solution:

∴ L.C.M. of 24, 64
= 2 × 2 × 2 × 3 × 8 = 192

Question (ii)
42, 63
Solution:

∴ L.C.M. of 42 and 63
= 3 × 7 × 2 × 3 = 126

Question (iii)
108, 135, 162
Solution:

∴ L.C.M. of 108, 135 and 162
= 2 × 3 × 3 × 3 × 2 × 5 × 3 = 1620

Question (iv)
16, 18, 48
Solution:

∴ L.C.M. of 16, 18 and 48
= 2 × 2 × 2 × 2 × 3 × 3 = 144

Question (v)
48, 72, 108
Solution:

∴ L.C.M. of 48, 72 and 108
= 2 × 2 × 2 × 3 × 3 × 2 × 3 = 144

3. Find the smallest number which is divisible by 6, 8 and 10.
Solution:
We know that the smallest number divisible by 6, 8 and 10 is their L.C.M.
So, we calculate L.C.M. 6, 8 and 10

∴ L.C.M. = 2 × 3 × 4 × 5 = 120
Hence, required number =120

4. Find the least number when divided by 10,12 and 15 leaves remainder 7 in each case.
Solution:
We know that the least number divisible by 10, 12 and 15 is their L.C.M.

So, the required number will be 7 more than their L.C.M.
We calculate their L.C.M.
L.C.M of 10, 12 and 15 = 2 × 3 × 5 × 2 = 60
Hence, Required number = 60 + 7 = 67

5. Find the greatest 4-digit number exactly divisible by 12, 18 and 30.
Solution:
First find the L.C.M. of 12, 18, 30

∴ L.C.M. of 12, 18, 30
= 2 × 3 × 2 × 3 × 5 = 180
Now the greatest 4 digit number = 9999
We find that when 9999 is divided by 180, the remainder is 99.
Hence, the greatest number of 4 digits which is exactly divisible by 12, 18, 30
= 9999 – 99 = 9900

6. Find the sandiest 4-digit number exactly divisible by 15, 24 and 36.
Solution:
First find L.C.M. of 15, 24, 36

L.C.M. of 15, 24, 36
= 2 × 2 × 3 × 5 × 2 × 3 = 360 Now, 4 digit smallest number is 1000 We find that when 1000 is divided by 360, the remainder is 280.
∴ Smallest 4 digits number, which is exactly divisible by 15, 24 and 36
= 1000 + (360 – 280) = 1000 + 80 = 1080.
Hence, required number = 1080

7. Four bells toll at intervals of 4, 7, 12 and 14 seconds. The bells toll together at 5 a.m. When will they again toll together?
Solution:
The bells will toll together at a time which is multiple of four intervals 4, 7, 12 and 14 seconds
So, first we find L.C.M. of 4, 7, 12 and 14

∴ L.C.M. = 2 × 2 × 7 × 3 = 84
Thus the bells will toll together after 84 seconds or 1 minute 24 seconds.
First they toll together at 5 a.m., then they will toll together after 1 minutes 24 seconds i.e. 5 : 01 : 24 a.m.

8. Three boys step off together from the same spot their steps measures 56 cm, 70 cm and 63 cm respectively. At what distance from the starting point will they again step together?
Solution:
The distance covered by each one of them has to be same as well as minimum walk So, the minimum distance each should their steps will be L.C.M. of the distances L.C.M. of the measure of their steps.

∴ L.C.M. = 2 × 7 × 4 × 5 × 9 = 2520cm
Hence, the will again step to gether after a distance of 2520 cm.

9. Can two numbers have 15 as their HCF and 65 as their LCM. Give reasons in support of your answer.
Solution:
We know that H.C.F. of given numbers is a factor of their L.C.M.
But 15 is not a factor of 65
So, there can not be two numbers with H.C.F. 15 and L.C.M. 65.

10. Can two numbers have 12 as their HCF and 72 as their LCM. Give reasons in support of your answer.
Solution:
We know that H.C.F. of given numbers is a factor of their L.C.M.
Here, 12 divides 72 exactly. So 12 is a factor of 72
Hence, there can be two numbers with H.C.F. 12 and L.C.M 72.

11. The HCF and LCM of two numbers are 13 and 182 respectively. If one of the numbers is 26. Find other numbers.
Solution:
H.C.F. = 13 and L.C.M. = 182,
1st number = 25
Now, 1st number × 2nd number = H.C.F. × L.C.M.
26 × 2nd number = 13 × 182
∴ 2nd number = \(\frac {13×182}{26}\)
= 91

12. The LCM of two co-prime numbers is 195. If one number is 15 then find the other number.
Solution:
L.C.M. of two co-prime numbers = 195
H.C.F. of two co-prime numbers = 1
One number = 15
1st number × 2nd number = H.C.F. × L.C.M.
15 × 2nd number= 1 × 195
∴ 2nd number = \(\frac {1×195}{15}\)
= 13

13. The H.C.F. of two numbers is 6 and product of two numbers is 216. Find their L.C.M.
Solution:
H.C.F. of two numbers = 6
Product of two numbers = 216
We know that
H.C.F. × L.C.M. = Product of two numbers
∴ 6 × L.C.M. = 216
∴ L.C.M. = \(\frac {216}{6}\) = 36

Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 9 Rational Numbers MCQ Questions with Answers.

PSEB 7th Class Maths Chapter 9 Rational Numbers MCQ Questions

Multiple Choice Questions :

Question 1.
Look at the above number line and tell which of the following values is the greatest.
(a) a + b
(b) b – a
(c) a × b
(d) a ÷ b
Answer:
(a) a + b

Question 2.
The product of a rational number and its reciprocal is always :
(a) -1
(b) 0
(c) 1
(d) equal to itself.
Answer:
(c) 1

Question 3.
Which of the following is not an natural number ?
(a) 0
(b) 2
(c) 10
(d) 105.
Answer:
(a) 0

Question 4.
The ascending order of \(\frac{-3}{5}, \frac{-2}{5}, \frac{-1}{5}\) is :
(a) \(\frac{-1}{5}<\frac{3}{5}<\frac{2}{5}\)
(b) \(\frac{-3}{5}<\frac{-2}{5}<\frac{-1}{5}\)
(c) \(\frac{-3}{5}<\frac{-1}{5}<\frac{-2}{5}\)
(d) \(\frac{-2}{5}<\frac{-3}{5}<\frac{-1}{5}\)
Answer:
(b) \(\frac{-3}{5}<\frac{-2}{5}<\frac{-1}{5}\)

Question 5.
Write \(\frac {1}{4}\) as a rational number with 4 denominator 20.
(a) \(\frac{2}{20}\)
(b) \(\frac{3}{20}\)
(c) \(\frac{5}{20}\)
(d) \(\frac{4}{20}\)
Answer:
(c) \(\frac{5}{20}\)

Question 6.
The value of \(\frac{-13}{7}+\frac{6}{7}\) :
(a) \(\frac{19}{7}\)
(b) \(\frac{-7}{7}\)
(c) \(\frac{7}{7}\)
(d) None of these
Answer:
(b) \(\frac{-7}{7}\)

Question 7.
The additive inverse of \(\frac{-9}{11}\) is :
(a) \(\frac{9}{11}\)
(b) \(\frac{-9}{11}\)
(c) \(\frac{11}{9}\)
(d) \(\frac{-11}{9}\)
Answer:
(a) \(\frac{9}{11}\)

Question 8.
The additive inverse of \(\frac{5}{7}\) is :
(a) \(\frac{7}{5}\)
(b) \(\frac{-5}{7}\)
(c) \(\frac{-7}{5}\)
(d) \(\frac{5}{7}\)
Answer:
(b) \(\frac{-5}{7}\)

Fill in the blanks :

Question 1.
The smallest natural number is ………………..
Answer:
1

Question 2.
The numbers which are used for counting are called ………………..
Answer:
natural number

Question 3.
All natural number along with zero (0) are called ………………..
Answer:
whole number

Question 4.
Reciprocal of \(\frac {5}{3}\) is ………………..
Answer:
\(\frac {3}{5}\)

Question 5.
Additive inverse of –\(\frac {3}{4}\) is ………………..
Answer:
\(\frac {3}{4}\)

Write True or False :

Question 1.
The smallest natural number is zero (0). (True/False)
Answer:
False

Question 2.
0 is an integer which is neither negative nor positive. (True/False)
Answer:
True

Question 3.
The smallest whole number is 1. (True/False)
Answer:
False

Question 4.
–\(\frac {2}{5}\) is a fraction. (True/False)
Answer:
False

Question 5.
\(\frac {1}{0}\) not a rational number. (True/False)
Answer:
True

Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 9 Rational Numbers Ex 9.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 7 Maths Chapter 9 Rational Numbers Ex 9.2

1. Find the sum

Question (i).
\(\frac{6}{9}+\frac{2}{9}\)
Solution:
\(\frac{6}{9}+\frac{2}{9}\) = \(\frac{6+2}{9}\)
= \(\frac {8}{9}\)

Question (ii).
\(\frac{-15}{7}+\frac{9}{7}\)
Solution:
\(\frac{-15}{7}+\frac{9}{7}\) = \(\frac{-15+9}{7}\)
= \(\frac{-6}{7}\)

Question (iii).
\(\frac{17}{11}+\left(\frac{-9}{11}\right)\)
Solution:
\(\frac{17}{11}+\left(\frac{-9}{11}\right)\) = \(\frac{17-9}{11}\)
= \(\frac{8}{11}\)

Question (iv).
\(\frac{-5}{6}+\frac{3}{18}\)
Solution:
\(\frac{-5}{6}+\frac{3}{18}\)
Now, \(\frac{-5}{6}=\frac{-5}{6} \times \frac{3}{3}=\frac{-15}{18}\)

L.C.M. of 6 and 18
= 2 × 3 × 3 = 18
Thus, \(\frac{-5}{6}+\frac{3}{18}=\frac{-15}{18}+\frac{3}{18}\)
= \(\frac{-15+3}{18}\)
= \(\frac {-12}{18}\)
= \(\frac {-2}{3}\)

Question (v).
\(\frac{-7}{19}+\frac{-3}{38}\)
Solution:
\(\frac{-7}{19}+\frac{-3}{38}\)
Now, \(\frac{-7}{19}=\frac{-7}{19} \times \frac{2}{2}\)
= \(\frac {-14}{38}\)
\(\begin{array}{l|l}
2 & 19,38 \\
\hline 19 & 19,19 \\
\hline & 1,1 \\
\hline
\end{array}\)
L.C.M. = 2 × 19
= 38
Thus, \(\frac{-7}{19}+\frac{-3}{38}=\frac{-14}{38}+\frac{-3}{38}\)
= \(\frac{-14-3}{38}\)
= \(\frac{-17}{38}\)

Question (vi).
\(-3 \frac{4}{7}+2 \frac{3}{7}\)
Solution:
\(-3 \frac{4}{7}+2 \frac{3}{7}\)
= \(-\frac{25}{7}+\frac{17}{7}\)
= \(\frac{-25+17}{7}\)
= \(\frac{-8}{7}\)

Question (vii).
\(\frac{-5}{14}+\frac{8}{21}\)
Solution:
\(\frac{-5}{14}+\frac{8}{21}\)
Now, \(\frac{-5}{14}=\frac{-5}{14} \times \frac{3}{3}\)
= \(\frac{-15}{42}\)
\(\begin{array}{l|l}
2 & 14,21 \\
\hline 3 & 7,21 \\
\hline 7 & 7,7 \\
\hline & 1,1
\end{array}\)
L.C.M of 14, 21 = 2 × 3 × 7
= 42
\(\frac{8}{21}=\frac{8}{21} \times \frac{2}{2}\)
= \(\frac{16}{42}\)
Thus, \(\frac{-5}{14}+\frac{8}{21}\)
= \(\frac{-15}{42}+\frac{16}{42}\)
= \(\frac{-15+16}{42}\)
= \(\frac{1}{42}\)

Question (viii).
\(-4 \frac{1}{15}+3 \frac{2}{20}\)
Solution:

2. Find

Question (i).
\(\frac{7}{12}-\frac{11}{36}\)
Solution:
\(\frac{7}{12}-\frac{11}{36}\) = \(\frac{7}{12}\) + (Additive inverse of \(\frac{11}{36}\))
= \(\frac{7}{12}+\left(\frac{-11}{36}\right)\)
= \(\frac{21+(-11)}{36}\)
\(\begin{array}{l|l}
2 & 12,36 \\
\hline 2 & 6,18 \\
\hline 3 & 3,9 \\
\hline 3 & 1,3 \\
\hline & 1,1
\end{array}\)
L.C.M of 12 and 36
= 2 × 2 × 3 × 3
= 36
= \(\frac{10}{36}=\frac{5}{18}\)

Question (ii).
\(\frac{-5}{9}-\frac{3}{5}\)
Solution:
\(\frac{-5}{9}-\frac{3}{5}\) = \(\frac {-5}{9}\) + (additive inverse of \(\frac {3}{5}\))
= \(\frac{-5}{9}+\left(\frac{-3}{5}\right)\)
= \(\frac{-25+(-27)}{45}\)
L.C.M of 9 and 5 is 45 = \(\frac {-52}{45}\)

Question (iii).
\(\frac{-7}{13}-\left(\frac{-5}{91}\right)\)
Solution:
\(\frac{-7}{13}-\left(\frac{-5}{91}\right)\) = \(\frac {-7}{13}\) + (additive inverse of \(\frac {-5}{91}\))
= \(\frac{-7}{13}+\left(\frac{5}{91}\right)\)
= \(\frac{-49+(5)}{91}\)
L.C.M of 13 and 91 = 7 × 13 = 91
\(\begin{array}{l|l}
7 & 13,91 \\
\hline 13 & 13,13 \\
\hline & 1,1
\end{array}\)
= \(\frac {-44}{91}\)

Question (iv).
\(\frac{6}{11}-\frac{-3}{4}\)
Solution:
\(\frac{6}{11}-\frac{-3}{4}\) = \(\frac {6}{11}\) + (additive inverse of \(\frac {-3}{4}\))
= \(\frac{6}{11}+\left(\frac{3}{4}\right)\)
= \(\frac{24+33}{44}\)
L.C.M of 11 and 4 is 44 = \(\frac {57}{44}\)

Question (v).
\(3 \frac{4}{9}-\frac{28}{63}\)
Solution:

3. Find the product of :

Question (i).
\(\frac{5}{9} \times \frac{-3}{8}\)
Solution:
\(\frac{5}{9} \times \frac{-3}{8}\)
= \(\frac{5 \times-3}{9 \times 8}\)
= \(\frac {-5}{24}\)

Question (ii).
\(\frac{-3}{7} \times \frac{7}{-3}\)
Solution:
\(\frac{-3}{7} \times \frac{7}{-3}\)
= \(\frac{-3 \times 7}{7 \times-3}\)
= 1

Question (iii).
\(\frac{3}{13} \times \frac{5}{8}\)
Solution:
\(\frac{3}{13} \times \frac{5}{8}\)
= \(\frac{3 \times 5}{13 \times 8}\)
= \(\frac {15}{104}\)

Question (iv).
\(\frac {3}{10}\) × (-18)
Solution:
\(\frac {3}{10}\) × (-18)
= \(\frac{3 \times-18}{10}\)
= \(\frac{-27}{5}\)

4. Find the value of:

Question (i).
-9 ÷ \(\frac {3}{5}\)
Solution:
-9 ÷ \(\frac {3}{5}\)
= -9 × (Reciprocal of \(\frac {3}{5}\))
= -9 × \(\frac {5}{3}\)
= -15

Question (ii).
\(\frac {-4}{7}\) ÷ 4
Solution:
\(\frac {-4}{7}\) ÷ 4
= \(\frac {-4}{7}\) × (Reciprocal of 4)
= \(\frac{-4}{7} \times \frac{1}{4}\)
= \(\frac {-1}{7}\)

Question (iii).
\(\frac{7}{18} \div \frac{5}{6}\)
Solution:
\(\frac{7}{18} \div \frac{5}{6}\)
= \(\frac {7}{18}\) × (Reciprocal of \(\frac {5}{6}\))
= \(\frac{7}{18} \times \frac{6}{5}\)
= \(\frac {7}{15}\)

Question (iv).
\(\frac{-8}{35} \div\left(\frac{-2}{7}\right)\)
Solution:
\(\frac{-8}{35} \div\left(\frac{-2}{7}\right)\)
= \(\frac {-8}{35}\) × (Reciprocal of \(\frac {-2}{7}\))
= \(\frac{-8}{35} \times \frac{7}{-2}\)
= \(\frac {4}{5}\)

Question (v).
\(\frac {-9}{15}\) ÷ -18
Solution:
\(\frac {-9}{15}\) ÷ -18
= \(\frac {-9}{15}\) × (Reciprocal of -18)
= \(\frac{-9}{15} \times \frac{1}{-18}\)
= \(\frac {1}{30}\)

5. What ratonal number should be added to \(\frac {-5}{12}\) to get \(\frac {-7}{8}\)?
Solution:
Let the required number to be added be x.
then, \(\frac {-5}{12}\) + x = \(\frac {-7}{8}\)

L.C.M of 8, 12 = 2 × 2 × 2 × 3
= 24
= \(\frac{-7 \times 3+5 \times 2}{24}\)
= \(\frac{-21+10}{24}\)
= \(\frac {-11}{24}\)

6. What number should be subtracted from \(\frac {-2}{3}\) to get \(\frac {-5}{6}\) ?
Solution:
Let the required number to be subtracted be x, then
\(\frac{-2}{3}-x=\frac{-5}{6}\)
⇒ \(\frac{-2}{3}-\left(\frac{-5}{6}\right)\) = x
x = \(\frac{-2}{3}+\frac{5}{6}\)
= \(\frac{-4+5}{6}\)
= \(\frac {1}{6}\)

7. The product of two rational numbers is \(\frac {-11}{2}\). If one of them is \(\frac {33}{8}\), find the other number.
Solution:
Let the required number be x, then

8. Multiple Choice Questions

Question (i).
The sum of \(\frac{5}{4}+\left(\frac{25}{-4}\right)\) =
(a) -5
(b) 5
(c) 4
(d) -4
Answer:
(a) -5

Question (ii).
\(\frac{17}{11}-\frac{6}{11}\) =
(a) 1
(b) -1
(c) 6
(d) 3
Answer:
(a) 1

Question (iii).
\(\frac{2}{-5} \times \frac{-5}{2}\) =
(a) 1
(b) -1
(c) 2
(d) -5
Answer:
(a) 1

Question (iv).
\(\frac{7}{12} \div\left(\frac{-7}{12}\right)\) =
(a) 1
(b) -1
(c) 7
(d) -7
Answer:
(b) -1

Question (v).
Which of the following is value of (-4) × [(-5) + (-3)]
(a) -32
(b) 120
(c) 32
(d) -23
Answer:
(c) 32

Punjab State Board PSEB 6th Class Maths Book Solutions Chapter 3 Playing with Numbers Ex 3.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 6 Maths Chapter 3 Playing with Numbers Ex 3.4

1. Find H.C.F. of the following numbers by prime factorisation:

Question (i)
30, 42
Solution:
First we write the prime factorization of the given numbers

We find that 2 occurs two times and 3 occurs two times as common factors.
∴ HCF of 30 and 42 = 2 × 3 = 6

Question (ii)
135,225
Solution:
First we write the prime factorization of the given number

We find that 3 occurs two times and 5 occurs once as common factors
∴ HCF of 135 and 225 = 3 x 3 x 5 = 45

Question (iii)
180,192
Solution:
First we write the prime factorisation of the given numbers

We find that 2 occurs twice and 3 occurs once as common factors
HCF of 180 and 192
= 2 × 2 × 3 = 12

Question (iv)
49,91,175
Solution:
First we write the prime factorization of the given numbers

We find that 7 occurs once as a common factor.
∴ HCF of 49, 91 and 175 = 7

Question (v)
144, 252, 630.
Solution:
First we write the prime factorisation of the given numbers

We find that 2 occurs once and 3 occurs twice as common factors.
∴ HCF of 144, 252 and 630
= 2 × 3 × 3 = 18

2. Find H.C.F. of the following numbers using division method:

Question (i)
170, 238
Solution:
Given numbers are 170 and 238

Hence, H.C.F. of 170 and 238 = 34

Question (ii)
54, 144
Solution:
Given numbers are 54 and 144

Hence, H.C.F. of 54 and 144 = 18

Question (iii)
72, 88
Solution:
Given numbers are 72 and 88.

Hence, H.C.F. of 72 and 88 = 8

Question (iv)
96, 240, 336
Solution:
Given numbers are 96, 240 and 336 Consider any two numbers say 96 and 240

∴ H.C.F. of 96 and 240 = 48
Now, we find H.C.F. of 48 and 336
∴ H.C.F. of 48 and 336 = 48
Hence, H.C.F. of 96, 240 and 336 = 48

Question (v)
120, 156, 192.
Solution:
Given numbers are 120, 156 and 192 Consider any two numbers say 120 and 156

∴ H.C.F. of 12 and 192 = 12
Hence, H.C.F. of 120, 156 and 192 = 12

3. What is the H.C.F. of two prime numbers?
Solution:
H.C.F. of two prime numbers = 1.

4. What is the H.C.F. of two consecutive even numbers?
Solution:
The H.C.F. of two consecutive even numbers = 2.

5. What is the H.C.F. of two consecutive natural numbers?
Solution:
H.C.F. of two consecutive natural numbers = 1.

6. What is the H.C.F. of two consecutive odd numbers?
Solution:
H.C.F. of two conseutive odd numbers = 1.

7. Find the greatest number which divides 245 and 1029, leaving a remainder 5 in each case.
Solution:
Given that, required number when divides 245 and 1029, the remainder is 5 in each case.
⇒ 245 – 5 = 240 and 1029 – 5 = 1024 are completely divisible by the required number.
⇒ Required number is the highest common factor of 240 and 1024. Since it is given that required number is the greatest number.
∴ Required number is the H.C.F. 240 and 1024.

Hence, required number (H.C.F.) of 240 and 1024 = 16

8. Find the greatest number that can divide 782 and 460 leaving remainder 2 and 5 respectively.
Solution:
Required greatest number = H.C.F. of (782 – 2) and (460 – 5)
= H.C.F. of 780 and 455 = 65

Hence required greatest number = 65

9. Find the greatest number that will divide 398,437 and 540 leaving remainders 7,12 and 13 respectively.
Solution:
Required greatest number = H.C.F. of (398 – 7), (437 – 12) and (540 – 13)
= H.C.F. of 391, 425 and 527

∴ 391 = 17 × 23
425 = 5 × 5 × 17
and 527 = 17 × 31
∴ H.C.F. = 17
Hence, required greatest number = 17

10. Two different containers contain 529 litres and 667 litres of milk respectively. Find the maximum capacity of container which can measure the milk of both containers in exact number of times.
Solution:
We have to find, maximum capacity of a container which measure both conainers in exact number of times.
⇒ We required the maximum number which divides 529 and 667
⇒ Required number = H.C.F. of 529 and 667 = 23

Hence required capacity of container = 23 litres

11. There are 136 apples, 170 mangoes and 255 oranges. These are to be packed in boxes containing the same number of fruits. Find the greatest number of fruits possible in each box.
Solution:
We have to find the greatest number of fruits in each box ,
So, we required greatest numbers which divides 136, 170 and 255
∴ Required greatest number of fruits possible in each box
= H.C.F. of 136, 170 and 255
Now take any two numbers, say 136 and 170
H.C.F. of 136 and 170 = 34
Now find H.C.F. of 34 and 255
∴ H.C.F. of 34 and 255 = 17
H.C.F. of 136, 170 and 255 = 17

∴ Hence the greatest number of fruits possible in each box = 17

12. Three pieces of timber 54 m, 36 m and 24 m long, have to be divided into planks of the same length. What is the greatest possible length of each plank?
Solution:
We have to find the greatest possible length of each plank.
So, we required the maximum number which divides 54 m, 36 m and 24 m.
∴ Required length of each plank = H.C.F. of 54 m, 36 m and 24 m
Now, take any two numbers, say 54 and 36
H.C.F. of 54 and 36 = 18
Now find the H.C.F. of 18 and 24
H.C.F. 18 and 24 = 6
H.C.F. 54, 36 and 24 = 6

Hence, the greatest length of each plank = 6m

13. A room Measures 4.8 m and 5.04 m. Find the size of the largest square tile that can be used to tile the floor without cutting any tile.
Solution:
We have to find the size of largest square tile that can be used to the floor without cutting any tile.
∴ Required size of tile = H.C.F. of 4.8 and 5.04 m
= H.C.F. of 480 cm and 504 cm [1 m – 100 cm]
∴ H.C.F. of 480 cm and 504 cm = 24 cm

Hence size of each square tile = 24 cm

14. Reduce each of the following fractions to lowest forms:

Question (i)
\(\frac {85}{102}\)
Solution:
In order to reduce given fraction to the lowest terms,
We divide numerator and denominator by their H.C.F.
Now we find H.C.F. of 85 and 102 Clearly H.C.F. of 85 and 102 = 17

Question (ii)
\(\frac {52}{130}\)
Solution:
We find H.C.F. of 52 and 130
Clearly H.C.F. of 52 and 130 = 26

Question (iii)
\(\frac {289}{391}\)
Solution:
We find H.C.F. of 289 and 391
Clearly, H.C.F. of 289 and 391 = 17