Bhagya

This PSEB 7th Class Science Notes Chapter 3 ਰੇਸ਼ਿਆਂ ਤੋਂ ਕੱਪੜਿਆਂ ਤੱਕ will help you in revision during exams.

PSEB 7th Class Science Notes Chapter 3 ਰੇਸ਼ਿਆਂ ਤੋਂ ਕੱਪੜਿਆਂ ਤੱਕ

→ ਉੱਨ ਅਤੇ ਰੇਸ਼ਮ ਦੇ ਰੇਸ਼ੇ ਕੁਦਰਤ ਵਿੱਚ ਜੰਤੂਆਂ ਤੋਂ ਪ੍ਰਾਪਤ ਹੁੰਦੇ ਹਨ ।

→ ਉੱਨ ਦੇ ਰੇਸ਼ੇ ਭੇਡ, ਬੱਕਰੀ ਜਾਂ ਯਾਕ ਤੋਂ ਪ੍ਰਾਪਤ ਹੁੰਦੇ ਹਨ ।

→ ਭੇਡ ਦੀ ਪਤਲੀ ਚਮੜੀ ਉੱਪਰ ਦੋ ਤਰ੍ਹਾਂ ਦੇ ਰੇਸ਼ੇ ਹੁੰਦੇ ਹਨ

• ਦਾੜ੍ਹੀ ਦੇ ਰੁੱਖੇ ਵਾਲ ਅਤੇ
• ਚਮੜੀ ਦੇ ਨੇੜੇ ਮੌਜੂਦ ਤੰਤੂ ਰੂਪੀ ਮੁਲਾਇਮ ਵਾਲ ।

→ ਚੋਣਵੀਂ ਜਣਨ ਵਿਧੀ ਦੁਆਰਾ ਮਾਪਿਆਂ ਦੀ ਚੋਣ ਕਰਕੇ ਲੋੜੀਂਦੇ ਵਿਸ਼ੇਸ਼ ਗੁਣ ਜਿਵੇਂ ਮੁਲਾਇਮ ਵਾਲਾਂ ਵਾਲੀਆਂ ਭੇਡਾਂ ਜਾਂ ਸੰਘਣੀ ਜੱਤ ਵਾਲੀਆਂ ਭੇਡਾਂ ਪੈਦਾ ਕੀਤੀਆਂ ਜਾ ਸਕਦੀਆਂ ਹਨ ।

→ ਵਿਭਿੰਨ ਕਿਸਮ ਦੀ ਉੱਨ ਹੁੰਦੀ ਹੈ, ਜਿਵੇਂ ਭੇਡ ਦੀ ਉੱਨ, ਅੰਗੋਰਾ ਉੱਨ ਅਤੇ ਕਸ਼ਮੀਰੀ ਉੱਨ ।

→ ਉੱਨ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ ਭੇਡਾਂ ਨੂੰ ਪਾਲਿਆ ਜਾਂਦਾ ਹੈ । ਹੁ ਸੋਟਰਸ ਰੋਗ ਐਂਥਰੈਕਸ ਜੀਵਾਣੂ ਦੁਆਰਾ ਫੈਲਦਾ ਹੈ ।

→ ਰੇਸ਼ਮ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ ਰੇਸ਼ਮ ਦੇ ਕੀੜੇ ਨੂੰ ਪਾਲਣਾ ਸੇਰੀ ਕਲਚਰ ਅਖਵਾਉਂਦਾ ਹੈ । ਹੁ ਮਾਦਾ ਰੇਸ਼ਮ ਦੇ ਕੀੜੇ ਸੈਂਕੜੇ ਅੰਡੇ ਦਿੰਦੇ ਹਨ ।

→ ਅੰਡਿਆਂ ਵਿਚੋਂ ਨਿਕਲਣ ਵਾਲੇ ਲਾਰਵਾ ਕੇਟਰ ਪਿੱਲਰ ਅਖਵਾਉਂਦਾ ਹੈ ।

→ ਕੇਟਰ ਪਿੱਲਰ ਸਾਈਜ਼ ਵਿੱਚ ਵਾਧਾ ਕਰਦੇ ਹਨ ਅਤੇ ਪਿਊਪਾ (ਬਾਲਗ) ਬਣ ਜਾਂਦੇ ਹਨ ।

→ ਪਿਉਪਾ ਆਪਣੇ ਆਲੇ-ਦੁਆਲੇ ਇੱਕ 8 ਸ਼ਕਲ ਦਾ ਪ੍ਰੋਟੀਨ ਦਾ ਜਾਲ ਬੁਣ ਲੈਂਦਾ ਹੈ ਜੋ ਹਵਾ ਦੇ ਸੰਪਰਕ ਵਿੱਚ । ਆ ਕੇ ਸਖ਼ਤ ਹੋ ਕੇ ਰੇਸ਼ਮ ਦਾ ਫਾਈਬਰ ਬਣ ਜਾਂਦਾ ਹੈ ।

→ ਪਿਊਪਾ ਇਹਨਾਂ ਰੇਸ਼ਿਆਂ ਨਾਲ ਆਪਣੇ-ਆਪ ਨੂੰ ਢੱਕ ਲੈਂਦਾ ਹੈ ਅਤੇ ਇਸ ਆਕ੍ਰਿਤੀ ਨੂੰ ਕੋਕੂਨ ਆਖਦੇ ਹਨ ।

→ ਸਭ ਤੋਂ ਆਮ ਰੇਸ਼ਮ ਕੀੜਾ ਸ਼ਹਿਤੂਤ ਰੇਸ਼ਮ ਕੀੜਾ ਹੈ । ਰੇਸ਼ਮ ਦੀਆਂ ਹੋਰ ਕਿਸਮਾਂ ਟੱਸਰ ਰੇਸ਼ਮ, ਮੁਗਾ ਰੇਸ਼ਮ ਅਤੇ ਕੋਸਾ ਰੇਸ਼ਮ ਹਨ ।

→ ਜਿਸ ਪ੍ਰਕਿਰਿਆ ਦੁਆਰਾ ਕੋਕੂਨਾਂ ਨੂੰ ਪਾਣੀ ਵਿੱਚ ਉਬਾਲ ਕੇ ਜਾਂ ਭਾਫ਼ ਦੇ ਕੇ ਰੇਸ਼ੇ ਕੱਢੇ ਜਾਂਦੇ ਹਨ ਉਸਨੂੰ ਰੀਲਿੰਗ ਕਹਿੰਦੇ ਹਨ ।

→ ਰੀਲਿੰਗ ਵਿਸ਼ੇਸ਼ ਮਸ਼ੀਨਾਂ ਨਾਲ ਕੀਤੀ ਜਾਂਦੀ ਹੈ । ਰੇਸ਼ਮੀ ਕੱਪੜੇ ਬਣਨ ਲਈ ਰੇਸ਼ਮੀ ਧਾਗੇ ਦੀ ਵਰਤੋਂ ਕਰਦੇ ਹਨ ।

ਕੁੱਝ ਮਹੱਤਵਪੂਰਨ ਪਰਿਭਾਸ਼ਾਵਾਂ

1. ਜੱਤ-ਭੇਡ ਦੇ ਸਰੀਰ ਦੇ ਵਾਲਾਂ ਦਾ ਗੁੱਛਾ ।
2. ਰੀਲਿੰਗ-ਰੇਸ਼ਮ ਦੇ ਕੋਕੂਨ ਨੂੰ ਪਾਣੀ ਵਿੱਚ ਉਬਾਲ ਕੇ ਜਾਂ ਭਾਫ਼ ਦੇ ਕੇ ਰੇਸ਼ਮ ਦੇ ਰੇਸ਼ਿਆਂ ਨੂੰ ਕੱਢਣ ਦੀ ਪ੍ਰਕਿਰਿਆ ਨੂੰ ਰੀਲਿੰਗ ਆਖਦੇ ਹਨ ।
3. ਸਕੋਰਿੰਗ ਜਾਂ ਅਭਿਮਾਰਜਨ-ਕੱਟੀ ਹੋਈ ਚਮੜੀ ਸਮੇਤ ਵਾਲਾਂ ਨੂੰ ਟੈਂਕੀਆਂ ਵਿੱਚ ਪਾ ਕੇ ਚਿਕਨਾਈ (ਗਰੀਸ), ਧੂੜ, ਮੈਲ ਅਤੇ ਪਸੀਨਾ ਆਦਿ ਨੂੰ ਹਟਾਉਣ ਲਈ ਚੰਗੀ ਤਰ੍ਹਾਂ ਧੋਣਾ, ਸਕੋਰਿੰਗ ਕਹਾਉਂਦਾ ਹੈ ।
4. ਕੋਕੂਨ-ਰੇਸ਼ਮ ਦੇ ਰੇਸ਼ਿਆਂ ਨਾਲ ਬਣੀ ਹੋਈ ਪਰਤ ਜਿਹੜੀ ਕੇਟਰਪਿੱਲਰ ਨੂੰ ਢੱਕ ਲੈਂਦੀ ਹੈ, ਕੋਕੂਨ ਕਹਾਉਂਦੀ ਹੈ ।
5. ਸੇਰੀ-ਕਲਚਰ (ਰੇਸ਼ਮ ਦੇ ਕੀੜੇ ਨੂੰ ਪਾਲਣਾ)-ਰੇਸ਼ਮ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ ਰੇਸ਼ਮ ਦੇ ਕੀੜਿਆਂ ਨੂੰ ਪਾਲਣਾ ਸੇਰੀ ਕਲਚਰ ਕਹਾਉਂਦਾ ਹੈ ।
6. ਸ਼ੀਅਰਿੰਗ ਜਾਂ ਕਟਾਈ-ਭੇਡ ਦੇ ਵਾਲਾਂ ਅਤੇ ਚਮੜੀ ਦੀ ਪਤਲੀ ਪਰਤ ਨੂੰ ਭੇਡ ਦੇ ਸਰੀਰ ਤੋਂ ਹਟਾਉਣ ਦੀ ਪ੍ਰਕਿਰਿਆ ਨੂੰ ਸ਼ੀਅਰਿੰਗ ਜਾਂ ਉੱਨ ਦੀ ਕਟਾਈ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।
7. ਥਰੋਇੰਗ-ਕੱਚੇ ਰੇਸ਼ਮ ਨੂੰ, ਕੱਤੇ ਹੋਏ ਰੇਸ਼ਮ ਨੂੰ ਮਜ਼ਬੂਤ (ਮੋਟਾ) ਕਰਨ ਲਈ ਕੱਤਿਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਪ੍ਰਕਿਰਿਆ ਨੂੰ ਥਰੋਇੰਗ ਕਹਿੰਦੇ ਹਨ । ਇਹ ਅੱਡ-ਅੱਡ ਰੇਸ਼ਿਆਂ ਨੂੰ ਟੁੱਟਣ ਤੋਂ ਬਚਾਉਂਦਾ ਹੈ ।
8. ਕੌਂਬਿੰਗ ਜਾਂ ਕੰਘੀ ਕਰਨਾ-ਛੋਟੇ ਫੁੱਲੇ ਹੋਏ ਰੇਸ਼ੇ ਜਿਨ੍ਹਾਂ ਨੂੰ ਬੁਰ ਜਾਂ ਗੰਢਾਂ ਕਿਹਾ ਜਾਂਦਾ ਹੈ, ਨੂੰ ਹਟਾਉਣ ਦੀ ਪ੍ਰਕਿਰਿਆ ਕੌਂਬਿੰਗ ਜਾਂ ਕੰਘੀ ਕਰਨਾ ਕਹਿੰਦੇ ਹਨ ।
9. ਡਾਇੰਗ ਜਾਂ ਰੰਗਾਈ ਕਰਨਾ-ਭੇਡਾਂ ਦੀ ਉੱਨ ਨੂੰ ਵੱਖ-ਵੱਖ ਰੰਗਾਂ ਵਿੱਚ ਰੰਗਿਆ ਜਾ ਸਕਦਾ ਹੈ, ਕਿਉਂ ਜੋ ਕੁਦਰਤੀ ਰੰਗ ਤਾਂ ਸਿਰਫ਼ ਕਾਲਾ, ਭੂਰਾ ਜਾਂ ਚਿੱਟਾ ਹੁੰਦਾ ਹੈ ।
10. ਵਰਣਾਤਮਕ ਪ੍ਰਜਣਨ-ਵਿਸ਼ੇਸ਼ ਲੋੜੀਂਦੇ ਗੁਣਾਂ ਦੀਆਂ ਦੋ ਭੇਡਾਂ ਨੂੰ ਉਤਪੰਨ ਕਰਨ ਲਈ ਮਾਪਿਆਂ ਵਜੋਂ ਚੁਣ ਲਿਆ ਜਾਂਦਾ ਹੈ ਫਿਰ ਦੋਵਾਂ ਮਾਪਿਆਂ ਨੂੰ ਪ੍ਰਜਣਨ ਵਿੱਚ ਸ਼ਾਮਿਲ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ਇਸ ਪ੍ਰਕਿਰਿਆ ਨੂੰ ਚੋਣਵਾਂ ਪ੍ਰਜਣਨ ਕਹਿੰਦੇ ਹਨ ।

This PSEB 7th Class Science Notes Chapter 1 ਪੌਦਿਆਂ ਵਿੱਚ ਪੋਸ਼ਣ will help you in revision during exams.

PSEB 7th Class Science Notes Chapter 1 ਪੌਦਿਆਂ ਵਿੱਚ ਪੋਸ਼ਣ

→ ਸਾਰੇ ਜੀਵਾਂ (ਪੌਦਿਆਂ ਅਤੇ ਜੰਤੂਆਂ ਲਈ ਭੋਜਨ ਜ਼ਰੂਰੀ ਹੁੰਦਾ ਹੈ ।

→ ਭੋਜਨ ਦੇ ਮੁੱਖ ਅੰਸ਼-ਕਾਰਬੋਹਾਈਡਰੇਟਸ, ਚਰਬੀ, ਪ੍ਰੋਟੀਨ, ਵਿਟਾਮਿਨ ਅਤੇ ਖਣਿਜ ਹਨ, ਜੋ ਸਰੀਰ ਦੇ ਨਿਰਮਾਣ ਅਤੇ ਧੀ (ਵੱਧਣ ਲਈ ਜ਼ੂਰਰੀ ਹੁੰਦੇ ਹਨ ।

→ ਜੀਵ ਦੁਆਰਾ ਭੋਜਨ ਪ੍ਰਾਪਤ ਕਰਨ ਅਤੇ ਉਸਦੀ ਸਹੀ ਵਰਤੋਂ ਪੋਸ਼ਣ ਅਖਵਾਉਂਦੀ ਹੈ ।

→ ਵੱਖ-ਵੱਖ ਜੀਵਾਂ ਲਈ ਵੱਖ-ਵੱਖ ਪੋਸ਼ਣ ਹੁੰਦਾ ਹੈ ।

→ ਭੋਜਨ ਸੰਬੰਧੀ ਆਦਤਾਂ ਦੇ ਆਧਾਰ ‘ਤੇ ਪੋਸ਼ਣ ਨੂੰ ਦੋ ਸ਼੍ਰੇਣੀਆਂ ਵਿੱਚ ਵੰਡਿਆ ਜਾਂਦਾ ਹੈ-

• ਸਵੈਪੋਸ਼ੀ ਪੋਸ਼ਣ,
• ਪਰਪੋਸ਼ੀ ਪੋਸ਼ਣ

→ ਜਿਹੜੇ ਸਜੀਵ ਸਰਲ ਪਦਾਰਥਾਂ ਤੋਂ ਆਪਣਾ ਭੋਜਨ ਆਪ ਤਿਆਰ ਕਰਦੇ ਹਨ, ਉਨਾਂ ਨੂੰ ਸਵੈਪੋਸ਼ੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ਅਤੇ ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਪੋਸ਼ਣ ਨੂੰ ਸਵੈਪੋਸ਼ੀ ਪੋਸ਼ਣ ਆਖਦੇ ਹਨ ।

→ ਸਾਰੇ ਹਰੇ ਪੌਦੇ ਅਤੇ ਬੈਕਟੀਰੀਆ (ਜੀਵਾਣੂ ਸਵੈਪੋਸ਼ੀ ਹੁੰਦੇ ਹਨ ।

→ ਯੁਗਲੀਨਾ ਇੱਕ ਅਜਿਹਾ ਜੀਵ ਹੈ ਜੋ ਦੋਨੋਂ ਸਵੈਪੋਸ਼ਣ ਅਤੇ ਪਰਪੋਸ਼ਣ ਕਰ ਸਕਦਾ ਹੈ ।

→ ਪੱਤਿਆਂ ਨੂੰ ਪੌਦਿਆਂ ਦਾ ਭੋਜਨ ਤਿਆਰ ਕਰਨ ਦਾ ਕਾਰਖ਼ਾਨਾ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।

→ ਪੌਦੇ ਪ੍ਰਕਾਸ਼ ਸੰਸ਼ਲੇਸ਼ਣ ਦੀ ਕਿਰਿਆ ਦੁਆਰਾ ਆਪਣਾ ਭੋਜਨ ਤਿਆਰ ਕਰਦੇ ਹਨ । ਇਸ ਕਿਰਿਆ ਦੌਰਾਨ ਪੱਤਿਆਂ ਵਿਚ ਮੌਜੂਦ ਹਰੇ ਰੰਗ ਦਾ ਵਰਣਕ (ਕਲੋਰੋਫਿਲ, ਸੂਰਜੀ ਪ੍ਰਕਾਸ਼ ਦੀ ਉਪਸਥਿਤੀ ਵਿੱਚ ਹਵਾ ਦੀ ਕਾਰਬਨ-ਡਾਈਆਕਸਾਈਡ ਅਤੇ ਪਾਣੀ ਉਪਸਥਿਤੀ ਵਿਚ ਕਾਰਬੋਹਾਈਡਰੇਟਸ ਰੂਪੀ ਭੋਜਨ ਦਾ ਨਿਰਮਾਣ ਕਰਦੇ ਹਨ ।

→ ਪੌਦੇ ਦੇ ਪੱਤਿਆਂ ਦੀ ਸਤਹਿ ਉੱਪਰ ਛੋਟੇ-ਛੋਟੇ ਮੁਸਾਮ (ਛੇਕ) ਹੁੰਦੇ ਹਨ, ਜਿਨ੍ਹਾਂ ਰਾਹੀਂ ਹਵਾ ਦੀ ਕਾਰਬਨਡਾਈਆਕਸਾਈਡ ਅਤੇ ਨਿਰਮਿਤ ਆਕਸੀਜਨ ਦੀ ਅਦਲਾ-ਬਦਲੀ ਹੁੰਦੀ ਹੈ । ਇਨ੍ਹਾਂ ਨੂੰ ਸਟੋਮੈਟਾ ਦਾ ਨਾਂ ਦਿੱਤਾ ਗਿਆ ਹੈ ।

→ ਸਟੋਮੈਟਾ ਗਾਰਡ ਸੈੱਲਾਂ ਨਾਲ ਘਿਰੇ ਹੁੰਦੇ ਹਨ ।

→ ਮਿੱਟੀ ਵਿੱਚੋਂ ਪਾਣੀ ਅਤੇ ਖਣਿਜ ਪੌਦਿਆਂ ਦੀਆਂ ਜੜ੍ਹਾਂ ਰਾਹੀਂ ਸੋਖੇ ਜਾਂਦੇ ਹਨ ਅਤੇ ਫਿਰ ਜ਼ਾਈਲਮ ਟਿਸ਼ੂ ਰਾਹੀਂ | ਪੌਦੇ ਦੇ ਹੋਰ ਭਾਗਾਂ ਨੂੰ ਭੇਜੇ ਜਾਂਦੇ ਹਨ ।

→ ਸਾਰੇ ਜੀਵਾਂ ਲਈ ਸੂਰਜ ਹੀ ਊਰਜਾ ਦਾ ਮੂਲ ਸਰੋਤ ਹੈ ।

→ ਪ੍ਰਕਾਸ਼ ਸੰਸ਼ਲੇਸ਼ਣ ਕਿਰਿਆ ਵਿੱਚ ਸੂਰਜੀ ਪ੍ਰਕਾਸ਼ ਉਰਜਾ ਨੂੰ ਰਸਾਇਣਿਕ ਉਰਜਾ ਵਿੱਚ ਪਰਿਵਰਤਿਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।

→ ਕੁੱਝ ਅਜਿਹੇ ਪੌਦੇ ਹੁੰਦੇ ਹਨ ਜਿਨ੍ਹਾਂ ਦੇ ਪੱਤਿਆਂ ਦਾ ਰੰਗ ਹਰਾ ਨਹੀਂ ਹੁੰਦਾ ਪਰੰਤ ਕਿਸੇ ਹੋਰ ਰੰਗ ਦੇ ਵਰਣਕ ਹੁੰਦੇ ਹਨ ਜਿਵੇਂ ਕੌਲੀਅਸ ਵਿੱਚ ਲਾਲ ਰੰਗ ਦਾ ਵਰਣਕ ਅਤੇ ਲਾਲ ਬੰਦ ਗੋਭੀ ਵਿੱਚ ਬੈਂਗਨੀ ਰੰਗ ਦਾ ਵਰਣਕ ਹੁੰਦਾ ਹੈ । ਅਜਿਹੇ ਪੱਤਿਆਂ ਵਿੱਚ ਵੀ ਪ੍ਰਕਾਸ਼ ਸੰਸ਼ਲੇਸ਼ਣ ਹੁੰਦਾ ਹੈ, ਕਿਉਂਕਿ ਇਨ੍ਹਾਂ ਰੰਗਾਂ ਦੇ ਪੱਤਿਆਂ ਵਿੱਚ ਹਰੇ ਰੰਗ ਦਾ ਵਰਣਕ ਕਲੋਰੋਫਿਲ ਵੀ ਹੁੰਦਾ ਹੈ ।

→ ਪ੍ਰਕਾਸ਼ ਸੰਸ਼ਲੇਸ਼ਣ ਕਿਰਿਆ ਦੇ ਮੁੱਢਲੇ ਉਤਪਾਦ ਆਕਸੀਜਨ ਗੈਸ ਅਤੇ ਗੁਲੂਕੋਜ਼ ਹਨ ।

→ ਪਰਪੋਸ਼ੀਆਂ ਨੂੰ ਚਾਰ ਸ਼੍ਰੇਣੀਆਂ ਵਿੱਚ ਵੰਡਿਆ ਜਾਂਦਾ ਹੈ-

• ਮ੍ਰਿਤ ਆਹਾਰੀ,
• ਪਰਜੀਵੀ,
• ਕੀਟ ਆਹਾਰੀ ਅਤੇ
• ਸਹਿਜੀਵੀ ।

→ ਜਿਹੜੇ ਜੀਵ ਦੂਜੇ ਜੀਵਾਂ ਦੇ ਸਰੀਰ ਤੋਂ ਪੋਸ਼ਣ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਨ ਉਨ੍ਹਾਂ ਨੂੰ ਪਰਜੀਵੀ ਕਹਿੰਦੇ ਹਨ ।

→ ਜਿਹੜੇ ਜੀਵ ਪੋਸ਼ਣ ਲਈ ਮ੍ਰਿਤ ਸਰੀਰਾਂ ਅਤੇ ਗਲੇ-ਸੜੇ ਪਦਾਰਥਾਂ ‘ਤੇ ਨਿਰਭਰ ਕਰਦੇ ਹਨ ਉਨ੍ਹਾਂ ਨੂੰ ਮ੍ਰਿਤ ਆਹਾਰੀ ਕਹਿੰਦੇ ਹਨ । ਸਹਿਜੀਵੀ ਸੰਬੰਧ ਵਿੱਚ ਦੋ ਤਰ੍ਹਾਂ ਦੇ ਜੀਵ ਭੋਜਨ ਲਈ ਇੱਕ-ਦੂਜੇ ‘ਤੇ ਨਿਰਭਰ ਕਰਦੇ ਹਨ, ਜਿਸ ਵਿੱਚ ਦੋਵਾਂ ਨੂੰ ਲਾਭ ਹੁੰਦਾ ਹੈ । ਮ੍ਰਿਤ ਜੰਤੂਆਂ, ਗਲੇ-ਸੜੇ ਪੌਦਿਆਂ ਅਤੇ ਪੱਤਿਆਂ ਨੂੰ ਨਿਖੇੜਕਾਂ ਦੁਆਰਾ ਨਿਖੇੜਨ ਕਾਰਨ ਮਿੱਟੀ ਦੀ ਜ਼ਰੂਰੀ ਪੋਸ਼ਕ ਤੱਤਾਂ ਦੀ ਪ੍ਰਤੀ ਪੂਰਤੀ ਹੁੰਦੀ ਰਹਿੰਦੀ ਹੈ ।

ਕੁੱਝ ਮਹੱਤਵਪੂਰਨ ਪਰਿਭਾਸ਼ਾਵਾਂ

1. ਪੋਸ਼ਕ ਤੱਤ-ਭੋਜਨ ਦੇ ਮੁੱਖ ਅੰਸ਼ ਜਿਵੇਂ-ਕਾਰਬੋਹਾਈਡਰੇਟਸ, ਚਰਬੀ, ਪ੍ਰੋਟੀਨ, ਵਿਟਾਮਿਨ ਅਤੇ ਖਣਿਜ ਜਿਹੜੇ | ਸਰੀਰ ਦੇ ਨਿਰਮਾਣ ਵਿੱਚ ਸਹਾਈ ਹੁੰਦੇ ਹਨ, ਨੂੰ ਪੋਸ਼ਕ ਤੱਤ ਕਹਿੰਦੇ ਹਨ ।
2. ਸਵੈ-ਪੋਸ਼ਣ-ਜਿਹੜੇ ਸਜੀਵ ਸਰਲ ਪਦਾਰਥਾਂ ਤੋਂ ਆਪਣਾ ਭੋਜਨ ਆਪ ਤਿਆਰ ਕਰਦੇ ਹਨ ਉਨ੍ਹਾਂ ਨੂੰ ਸਵੈਪੋਸ਼ੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਪੋਸ਼ਣ ਨੂੰ ਸਵੈਪੋਸ਼ੀ ਕਹਿੰਦੇ ਹਨ ।
3. ਪਰਪੋਸ਼ਣ-ਜਿਹੜੇ ਜੀਵ ਆਪਣਾ ਭੋਜਨ ਆਪ ਤਿਆਰ ਨਹੀਂ ਕਰ ਸਕਦੇ ਪਰੰਤ ਆਪਣੇ ਭੋਜਨ ਲਈ ਦੂਜੇ ਜੀਵਾਂ ‘ਤੇ ਨਿਰਭਰ ਕਰਦੇ ਹਨ, ਉਨ੍ਹਾਂ ਨੂੰ ਪਰਪੋਸ਼ੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਪੋਸ਼ਣ ਨੂੰ ਪਰਪੋਸ਼ੀ ਪੋਸ਼ਣ ਕਹਿੰਦੇ ਹਨ ।
4. ਮਿਤ ਆਹਾਰ-ਅਜਿਹਾ ਪੋਸ਼ਣ ਜਿਸ ਵਿੱਚ ਮਰੇ ਹੋਏ ਜੀਵ ਜਾਂ ਗਲੇ-ਸੜੇ ਪਦਾਰਥ ਜਿਨ੍ਹਾਂ ਤੋਂ ਜੀਵਾਂ ਦਾ ਭੋਜਨ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
5. ਪਰਜੀਵੀ-ਉਹ ਜੀਵ ਜਿਹੜੇ ਭੋਜਨ ਲਈ ਦੂਜੇ ਪੌਦੇ ਅਤੇ ਜੀਵਾਂ ‘ਤੇ ਨਿਰਭਰ ਕਰਦੇ ਹਨ ਉਨ੍ਹਾਂ ਨੂੰ ਪਰਜੀਵੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।
6. ਪ੍ਰਕਾਸ਼-ਸੰਸ਼ਲੇਸ਼ਣ-ਇਹ ਇੱਕ ਅਜਿਹੀ ਕਿਰਿਆ ਹੈ ਜਿਸ ਵਿੱਚ ਪੌਦੇ ਦੀਆਂ ਪੱਤੀਆਂ ਜਿਨ੍ਹਾਂ ਵਿੱਚ ਹਰੇ ਰੰਗ ਦਾ ਵਰਣਕ ਕਲੋਰੋਫਿਲ ਹੁੰਦਾ ਹੈ, ਹਵਾ ਵਿੱਚ ਮੌਜੂਦ ਕਾਰਬਨ ਡਾਈਆਕਸਾਈਡ ਅਤੇ ਪਾਣੀ ਤੋਂ ਸੂਰਜੀ ਪ੍ਰਕਾਸ਼ ਉਰਜਾ ਦੀ ਮੌਜੂਦਗੀ ਵਿੱਚ ਭੋਜਨ ਕਾਰਬੋਹਾਈਡੇਟਸ (ਭੋਜਨ) ਦੇ ਰੂਪ ਵਿੱਚ ਤਿਆਰ ਕਰਦੇ ਹਨ । ਇੱਥੇ ਸੂਰਜੀ ਉਰਜਾ ਰਸਾਇਣਿਕ ਉਰਜਾ ਵਿੱਚ ਪਰਿਵਰਤਿਤ ਹੁੰਦੀ ਹੈ ।
7. ਕਲੋਰੋਫਿਲ-ਇਹ ਇੱਕ ਹਰੇ ਰੰਗ ਦਾ ਵਰਣਕ ਹੈ ਜਿਹੜਾ ਪੌਦਿਆਂ ਵਿੱਚ ਉਪਸਥਿਤ ਹੁੰਦਾ ਹੈ । ਇਹ ਪੌਦਿਆਂ ਨੂੰ ਆਪਣਾ ਭੋਜਨ ਤਿਆਰ ਕਰਨ ਲਈ ਜ਼ਰੂਰੀ ਹੁੰਦਾ ਹੈ ।
8. ਕਾਰਬੋਹਾਈਡਰੇਟਸ-ਇੱਕ ਕਿਸਮ ਦਾ ਸੂਖ਼ਮ ਪੋਸ਼ਕ ਹੈ ਜਿਹੜਾ ਕਈ ਖਾਧ ਪਦਾਰਥਾਂ, ਚੀਨੀ, ਸਟਾਰਚ ਅਤੇ ਰੇਸ਼ਿਆਂ ਵਿੱਚ ਮੌਜੂਦ ਹੁੰਦਾ ਹੈ । ਸਿਹਤਮੰਦ ਰਹਿਣ ਲਈ ਸਾਡੇ ਸਰੀਰ ਨੂੰ ਇਸ ਸੂਖ਼ਮ ਪੋਸ਼ਕ ਤੱਤ ਦੀ ਲੋੜ ਹੁੰਦੀ ਹੈ ।
9. ਸਟੋਮੈਟਾ-ਪੌਦਿਆਂ ਦੇ ਹਵਾ ਨਾਲ ਭਰਪੂਰ ਹਿੱਸਿਆਂ ਦੀ ਬਾਹਰਲੀ ਸਤਹਿ ’ਤੇ ਸਟੋਮੈਟਾ (ਛੇਕ) ਪਾਏ ਜਾਂਦੇ ਹਨ । ਪੱਤਿਆਂ ਉੱਪਰ ਸਟੋਮੈਟਾ ਦੀ ਸੰਖਿਆ ਸਭ ਤੋਂ ਵੱਧ ਹੁੰਦੀ ਹੈ । ਸਟੋਮੈਟਾ (ਜਾਂ ਛੇਕਾਂ) ਰਾਹੀਂ ਗੈਸਾਂ ਦੀ ਅਦਲਾ ਬਦਲੀ ਹੁੰਦੀ ਹੈ ।
10. ਮੇਜ਼ਬਾਨ-ਜਿਸ ਪੌਦੇ ਜਾਂ ਜੀਵ ਉੱਤੇ ਪਰਜੀਵੀ ਆਪਣੇ ਭੋਜਨ ਲਈ ਨਿਰਭਰ ਕਰਦਾ ਹੈ, ਉਸਨੂੰ ਮੇਜ਼ਬਾਨ (Host) ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।
11. ਰਸਾਇਣਿਕ ਖਾਦ-ਇਹ ਫੈਕਟਰੀ ਵਿੱਚ ਤਿਆਰ ਕੀਤੇ ਗਏ ਰਸਇਣਾਂ (ਅਕਾਰਬਨਿਕ ਲੂਣਾਂ ਦਾ ਮਿਸ਼ਰਣ ਹੁੰਦਾ ਹੈ । ਇਸ ਵਿੱਚ ਕਾਫ਼ੀ ਮਾਤਰਾ ਵਿੱਚ ਪੌਦਿਆਂ ਦੇ ਲਈ ਪੋਸ਼ਕ ਤੱਤ ਮੌਜੂਦ ਹੁੰਦੇ ਹਨ । ਇਹ ਮਿੱਟੀ ਦੇ ਵਿਚ ਮੌਜੂਦ ਪੋਸ਼ਕ ਤੱਤਾਂ ਦੀ ਘਾਟ ਨੂੰ ਦੁਬਾਰਾ ਪੂਰਾ ਕਰਦੀ ਹੈ ਤਾਂ ਜੋ ਮਿੱਟੀ ਦੀ ਉਪਜਾਊ ਸ਼ਕਤੀ ਬਣੀ ਰਹੇ ।
12. ਰਾਈਜ਼ੋਬੀਅਮ-ਇਹ ਇੱਕ ਬੈਕਟੀਰੀਆ ਹੈ ਜੋ ਫਲੀਦਾਰ ਪੌਦਿਆਂ ਦੀਆਂ ਜੜਾਂ ਤੇ ਗੰਢਾਂ ਵਿੱਚ ਹੁੰਦਾ ਹੈ । ਇਹ ਹਵਾ ਵਿਚਲੀ ਨਾਈਟ੍ਰੋਜਨ ਨੂੰ ਵਰਤੋਂ ਯੋਗ ਬਣਾ ਦਿੰਦਾ ਹੈ, ਜਿਸ ਦੀ ਵਰਤੋਂ ਪੌਦੇ ਕਰਦੇ ਹਨ ਅਤੇ ਇਸ ਦੇ ਬਦਲੇ ਵਿੱਚ ਪੌਦੇ ਇਸ ਬੈਕਟੀਰੀਆ ਨੂੰ ਆਸਰਾ ਅਤੇ ਭੋਜਨ ਪ੍ਰਦਾਨ ਕਰਦੇ ਹਨ ।

This PSEB 7th Class Science Notes Chapter 2 ਜੰਤੂਆਂ ਵਿੱਚ ਪੋਸ਼ਣ will help you in revision during exams.

PSEB 7th Class Science Notes Chapter 2 ਜੰਤੂਆਂ ਵਿੱਚ ਪੋਸ਼ਣ

→ ਜੰਤੁ ਪੌਦਿਆਂ ਵਾਂਗ ਆਪਣਾ ਭੋਜਨ ਆਪ ਨਹੀਂ ਤਿਆਰ ਕਰਦੇ ਹਨ । ਇਹ ਸਿੱਧੇ ਜਾਂ ਅਸਿੱਧੇ ਤੌਰ ‘ਤੇ ਆਪਣਾ ਭੋਜਨ ਪੌਦਿਆਂ ਤੋਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਨ ।

→ ਜੰਤੂ ਗੁੰਝਲਦਾਰ (ਜਟਿਲ) ਭੋਜਨ ਖਾਂਦੇ ਹਨ ਅਤੇ ਫਿਰ ਉਨ੍ਹਾਂ ਨੂੰ ਸਰਲ ਪਦਾਰਥਾਂ ਵਿੱਚ ਤੋੜਦੇ ਹਨ ।

→ ਵੱਖ-ਵੱਖ ਜੰਤੂਆਂ ਦੀ ਪੋਸ਼ਕਾਂ ਦੀ ਜ਼ਰੂਰਤ, ਭੋਜਨ ਗ੍ਰਹਿਣ ਦੇ ਢੰਗ ਅਤੇ ਸਰੀਰ ਵਿੱਚ ਭੋਜਨ ਦੀ ਵਰਤੋਂ ਦੇ ਢੰਗ ਵੱਖ-ਵੱਖ ਹੁੰਦੇ ਹਨ । ਜਿਹੜੇ ਜੰਤੂ ਕੇਵਲ ਪੌਦੇ ਖਾਂਦੇ ਹਨ ਉਨ੍ਹਾਂ ਨੂੰ ਸ਼ਾਕਾਹਾਰੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।

→ ਜਿਹੜੇ ਜੰਤੂ ਸਿਰਫ਼ ਦੂਜੇ ਜੰਤੂਆਂ ਨੂੰ ਆਪਣਾ ਭੋਜਨ ਬਣਾਉਂਦੇ ਹਨ, ਉਨ੍ਹਾਂ ਨੂੰ ਮਾਸਾਹਾਰੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।

→ ਜਿਹੜੇ ਜੰਤੂ ਪੌਦੇ ਅਤੇ ਦੂਜੇ ਜੰਤੂਆਂ ਦੋਵਾਂ ਨੂੰ ਖਾਂਦੇ ਹਨ, ਉਨ੍ਹਾਂ ਨੂੰ ਸਰਬਆਹਾਰੀ ਜੰਤੂ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।

→ ਵੱਖ-ਵੱਖ ਕਿਸਮ ਦੇ ਜੰਤੂਆਂ ਵਿੱਚ ਭੋਜਨ ਪ੍ਰਾਪਤ ਕਰਨ ਦੇ ਢੰਗ ਵੱਖ-ਵੱਖ ਹੁੰਦੇ ਹਨ ।

→ ਪਰਪੋਸ਼ੀ ਪੋਸ਼ਣ ਤਿੰਨ ਤਰ੍ਹਾਂ ਦਾ ਹੁੰਦਾ ਹੈ ।

• ਮ੍ਰਿਤ ਜੀਵੀ ਪੋਸ਼ਣ
• ਪਰਜੀਵੀ ਪੋਸ਼ਣ
• ਪਾਣੀਵਤ ਪੋਸ਼ਣ ।

→ ਪਾਣੀਵਤ ਪੋਸ਼ਣ ਦੌਰਾਨ ਗੁੰਝਲਦਾਰ ਜਟਿਲ) ਭੋਜਨ ਨੂੰ ਸਰੀਰ ਅੰਦਰ ਲਿਜਾਇਆ ਜਾਂਦਾ ਹੈ ਜਿੱਥੇ ਉਹ ਐਨਜ਼ਾਈਮਾਂ ਦੀ ਸਹਾਇਤਾ ਨਾਲ ਸਰਲ ਘੁਲਣਸ਼ੀਲ ਪਦਾਰਥਾਂ (ਯੌਗਿਕਾਂ ਵਿੱਚ ਤੋੜਿਆ ਜਾਂਦਾ ਹੈ, ਜਿਨ੍ਹਾਂ ਨੂੰ । ਸਰੀਰ ਦੁਆਰਾ ਸੋਖ ਲਿਆ ਜਾਂਦਾ ਹੈ ।

→ ਭੋਜਨ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਕਿਰਿਆ ਦੇ ਦੌਰਾਨ ਪੰਜ ਪੜਾਅ :

• ਭੋਜਨ ਗ੍ਰਹਿਣ ਕਰਨਾ,
• ਪਾਚਨ ਕਰਨਾ,
• ਸੋਖਣ,
• ਸਵੈਅੰਗੀਕਰਨ,
• ਮਲ ਨਿਕਾਸ ਕਿਰਿਆਵਾਂ ਹਨ ।

→ ਮਨੁੱਖ ਦੀ ਪਾਚਨ ਪ੍ਰਣਾਲੀ ਵਿੱਚ ਮੂੰਹ ਖੋੜ੍ਹ, ਭੋਜਨ ਨਲੀ, ਮਿਹਦਾ, ਛੋਟੀ ਆਂਦਰ, ਵੱਡੀ ਆਂਦਰ, ਮਲ ਨਲੀ ਅਤੇ ਮਲ ਦੁਆਰ ਸ਼ਾਮਲ ਹਨ । ਹੁ ਮਨੁੱਖ ਦੇ ਮੁੰਹ ਵਿੱਚ ਚਾਰ ਕਿਸਮ ਦੇ ਦੰਦ ਹੁੰਦੇ ਹਨ :

1. ਕੱਟਣ ਵਾਲੇ,
2. ਸੂਏ,
3. ਪੀ-ਮੋਲਰ ਅਤੇ
4. ਮੋਲਰ ਦਾੜਾਂ ।

→ ਭੋਜਨ ਦਾ ਪਾਚਨ ਮੁੰਹ ਤੋਂ ਸ਼ੁਰੂ ਹੋ ਕੇ ਅਤੇ ਛੋਟੀ ਆਂਦਰ ਤੱਕ ਹੁੰਦਾ ਹੈ । ਹੁ ਸੋਖਿਆ ਹੋਇਆ ਭੋਜਨ ਲਹ ਰਾਹੀਂ ਸਰੀਰ ਦੇ ਵੱਖ-ਵੱਖ ਭਾਗਾਂ ਤੱਕ ਭੇਜਿਆ ਜਾਂਦਾ ਹੈ ।

→ ਪਾਣੀ ਅਤੇ ਕੁੱਝ ਲਣਾਂ ਦਾ ਸੋਖਣ ਵੱਡੀ ਆਂਦਰ ਵਿੱਚ ਹੁੰਦਾ ਹੈ । ਹੁ ਅਣ-ਪਚਿਆ ਅਤੇ ਅਣ-ਸੋਖਿਆ ਭੋਜਨ ਮਲ ਦੇ ਰੂਪ ਵਿੱਚ ਮਲ ਨਲੀ ਵਿੱਚ ਰਹਿੰਦਾ ਹੈ ਅਤੇ ਫਿਰ ਮਲ ਨਲੀ ਦੁਆਰਾ ਗੁਦਾ ਰਾਹੀਂ ਉਸਦਾ ਤਿਆਗ ਹੁੰਦਾ ਹੈ ।

ਕੁੱਝ ਮਹੱਤਵਪੂਰਨ ਪਰਿਭਾਸ਼ਾਵਾਂ-

1. ਮਾਸਾਹਾਰੀ-ਅਜਿਹੇ ਜੰਤੂ ਜਿਹੜੇ ਕੇਵਲ ਦੂਜੇ ਜੰਤੂਆਂ ਨੂੰ ਆਪਣਾ ਭੋਜਨ ਬਣਾਉਂਦੇ ਹਨ, ਉਨ੍ਹਾਂ ਨੂੰ ਮਾਸਾਹਾਰੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।
2. ਸਰਬ-ਆਹਾਰੀ-ਜਿਹੜੇ ਜੰਤੂ ਪੌਦੇ ਅਤੇ ਦੂਜੇ ਜੰਤੂ ਨੂੰ ਭੋਜਨ ਵਜੋਂ ਖਾਂਦੇ ਹਨ, ਉਨ੍ਹਾਂ ਨੂੰ ਸਰਬਆਹਾਰੀ ਜੰਤੂ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।
3. ਭੋਜਨ ਗ੍ਰਹਿਣ ਕਰਨਾ-ਭੋਜਨ ਨੂੰ ਸਰੀਰ ਅੰਦਰ ਲਿਜਾਣ ਦੀ ਕਿਰਿਆ ਨੂੰ ਭੋਜਨ ਗ੍ਰਹਿਣ ਕਰਨਾ ਕਹਿੰਦੇ ਹਨ ।
4. ਪਾਚਨ-ਇਹ ਉਹ ਜੈਵ-ਪ੍ਰਕਿਰਿਆ ਹੈ ਜਿਸ ਦੌਰਾਨ ਗੁੰਝਲਦਾਰ (ਜਟਿਲ) ਪਦਾਰਥਾਂ ਨੂੰ ਸਰਲ ਪਦਾਰਥਾਂ ਵਿੱਚ ਤੋੜਿਆ ਜਾਂਦਾ ਹੈ | ਸਰੀਰ ਅੰਦਰ ਗੰਥੀਆਂ ਤੋਂ ਰਿਸਦੇ ਹੋਏ ਐਨਜ਼ਾਈਮ (ਰਸਾਇਣ) ਇਸ ਪਾਚਨ ਕਿਰਿਆ ਵਿੱਚ ਸਹਾਇਕ ਹੁੰਦੇ ਹਨ । ਪਾਚਨ ਮੂੰਹ ਖੋੜ੍ਹ ਤੋਂ ਸ਼ੁਰੂ ਹੋ ਕੇ ਛੋਟੀ ਆਂਦਰ ਵਿੱਚ ਪੂਰਾ ਹੁੰਦਾ ਹੈ ।
5. ਸੋਖਣ-ਇਹ ਭੋਜਨ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਕਿਰਿਆ ਦਾ ਇੱਕ ਪੜਾਅ ਹੈ ਜਿਸ ਵਿੱਚ ਪਚੇ ਹੋਏ ਭੋਜਨ ਨੂੰ ਛੋਟੀ ਆਂਦਰ ਦੀਆਂ ਅੰਦਰਲੀਆਂ ਕੰਧਾਂ ਰਾਹੀਂ ਸੋਖ ਲਿਆ ਜਾਂਦਾ ਹੈ ।
6. ਮਲ-ਤਿਆਗ-ਅਣ-ਪਚਿਆ ਭੋਜਨ, ਭੋਜਨ ਨਲੀ ਵਿੱਚੋਂ ਬਾਹਰ ਨਿਕਲ ਜਾਂਦਾ ਹੈ । ਇਸ ਪ੍ਰਕਿਰਿਆ ਨੂੰ ਮਲ ਤਿਆਗ ਕਹਿੰਦੇ ਹਨ |
7. ਮੂੰਹ ਖੋੜ੍ਹ-ਮੂੰਹ ਨਾਲ ਪ੍ਰਾਪਤ ਹੋਇਆ ਭੋਜਨ ਫਿਰ ਮੂੰਹ ਖੋੜ੍ਹ ਵਿੱਚ ਚਲਾ ਜਾਂਦਾ ਹੈ । ਇਹ ਦੰਦਾਂ ਤੋਂ ਅਗਾਂਹ ਵਾਲਾ ਖੇਤਰ ਹੈ ।
8. ਇਨੈਮਲ-ਦੰਦਾਂ ਉੱਤੇ ਮਜ਼ਬੂਤ ਸੁਰੱਖਿਅਕ ਪਦਾਰਥ ਇਨੈਮਲ ਦੀ ਪਰਤ ਹੁੰਦੀ ਹੈ ।
9. ਕੱਡ-ਜੰਤੂਆਂ (ਗਾਂ, ਮੱਝ ਅਤੇ ਉਠ) ਦੁਆਰਾ ਕਾਹਲੀ ਵਿੱਚ ਨਿਗਲਿਆ ਗਿਆ ਭੋਜਨ ਰੁਮੇਨ ਵਿੱਚ ਜਮ੍ਹਾਂ ਕਰ ਲਿਆ ਜਾਂਦਾ ਹੈ । ਇੱਥੇ ਭੋਜਨ ਦਾ ਅੰਸ਼ਿਕ ਪਾਚਨ ਹੁੰਦਾ ਹੈ । ਇਸ ਅੱਧ ਪਚੇ ਭੋਜਨ ਨੂੰ ਕੱਡ ਕਹਿੰਦੇ ਹਨ ।
10. ਭੋਜਨ ਨਲੀ-ਇਹ ਮਨੁੱਖੀ ਸਰੀਰ ਦੀ ਸਭ ਤੋਂ ਲੰਬੀ ਨਲੀ ਹੈ ਜੋ ਮੂੰਹ ਤੋਂ ਸ਼ੁਰੂ ਹੋ ਕੇ ਗੁਦਾ ਤੱਕ ਜਾਂਦੀ ਹੈ । ਇਸ ਵਿੱਚ ਐਨਜ਼ਾਈਮਾਂ ਦੁਆਰਾ ਗੁੰਝਲਦਾਰ (ਜਟਿਲ ਭੋਜਨ ਨੂੰ ਸਰਲ ਅਣੂਆਂ ਵਿੱਚ ਤੋੜਿਆ ਜਾਂਦਾ ਹੈ ।
11. ਪਿੱਤਾ-ਇਹ ਇੱਕ ਥੈਲੀ ਹੈ ਜਿਸ ਵਿੱਚ ਜਿਗਰ ਜੋ ਕਿ ਇੱਕ ਸਭ ਤੋਂ ਵੱਡੀ ਗੰਥੀ ਹੈ, ਦੁਆਰਾ ਰਿਸਾਵ ਹੋਇਆ ਰਸ ਜਮਾਂ ਹੁੰਦਾ ਹੈ ।
12. ਕਿਮੀ ਰੂਪੀ ਅੰਗ ਜਾਂ ਸੀਕਮ-ਇਹ ਜੰਤੂਆਂ ਦੀ ਭੋਜਨ ਨਲੀ ਦੀ ਛੋਟੀ ਆਂਦਰ ਅਤੇ ਵੱਡੀ ਆਂਦਰ ਦੇ ਵਿਚਕਾਰ ਥੈਲੀ ਵਰਗੀ ਰਚਨਾ ਹੈ ਜਿਸ ਨੂੰ ਕ੍ਰਿਮੀ ਰੂਪੀ ਅੰਗ ਜਾਂ ਸੀਕਮ (Caecum) ਕਹਿੰਦੇ ਹਨ ।
13. ਪਿੱਤਾ ਰਸ-ਜਿਗਰ ਸਾਡੇ ਸਰੀਰ ਦੀ ਸਭ ਤੋਂ ਵੱਡੀ ਗੰਥੀ ਹੈ ਜਿਸ ਵਿੱਚੋਂ ਰਿਸਾਵ ਹੁੰਦਾ ਹੈ ਜੋ ਪਿੱਤੇ ਵਿੱਚ ਜਮਾਂ ਰਹਿੰਦਾ ਹੈ । ਇਸ ਰਿਸਾਵ ਨੂੰ ਪਿੱਤਾ ਰਸ ਕਹਿੰਦੇ ਹਨ ।
14. ਜੁਗਾਲੀ ਕਰਨ ਵਾਲੇ ਰੂਮੀਨੈਂਟ)-ਘਾਹ ਖਾਣ ਵਾਲੇ ਜੰਤ ਜਿਵੇਂ ਗਾਂ, ਮੱਝ ਨੂੰ ਜੁਗਾਲੀ ਕਰਨ ਵਾਲੇ ਜਾਂ ਰੁਮੀਨੈਂਟ ਆਖਦੇ ਹਨ ।
15. ਸਵੈਅੰਗੀਕਰਣ-ਆਂਦਰ ਦੁਆਰਾ ਸੋਖਿਤ ਕੀਤਾ ਭੋਜਨ ਲਹੂ ਦੁਆਰਾ ਸਰੀਰ ਦੇ ਵੱਖ-ਵੱਖ ਭਾਗਾਂ ਤੱਕ ਪਹੁੰਚਾ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ । ਇਸ ਕਿਰਿਆ ਨੂੰ ਸਵੈਅੰਗੀਕਰਣ ਆਖਦੇ ਹਨ ।

Punjab State Board PSEB 9th Class Science Book Solutions Chapter 2 ਕੀ ਸਾਡੇ ਆਲੇ-ਦੁਆਲੇ ਦੇ ਪਦਾਰਥ ਸ਼ੁੱਧ ਹਨ? Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Science Chapter 2 ਕੀ ਸਾਡੇ ਆਲੇ-ਦੁਆਲੇ ਦੇ ਪਦਾਰਥ ਸ਼ੁੱਧ ਹਨ?

PSEB 9th Class Science Guide ਕੀ ਸਾਡੇ ਆਲੇ-ਦੁਆਲੇ ਦੇ ਪਦਾਰਥ ਸ਼ੁੱਧ ਹਨ? Textbook Questions and Answers

ਅਭਿਆਸ ਦੇ ਪ੍ਰਸ਼ਨ

ਪ੍ਰਸ਼ਨ 1.
ਹੇਠ ਲਿਖਿਆਂ ਨੂੰ ਨਿਖੇੜਨ ਲਈ ਤੁਸੀਂ ਕਿਹੜੀਆਂ ਵਿਧੀਆਂ ਨੂੰ ਅਪਣਾਉਗੇ ?
(ੳ) ਸੋਡੀਅਮ ਕਲੋਰਾਈਡ ਨੂੰ ਪਾਣੀ ਦੇ ਘੋਲ ਵਿੱਚ ਵੱਖ ਕਰਨ ਲਈ ।
(ਅ) ਅਮੋਨੀਅਮ ਕਲੋਰਾਈਡ ਨੂੰ ਸੋਡੀਅਮ ਕਲੋਰਾਈਡ ਅਤੇ ਅਮੋਨੀਅਮ ਕਲੋਰਾਈਡ ਦੇ ਮਿਸ਼ਰਣ ਵਿੱਚ ਵੱਖ ਕਰਨ ਲਈ ।
(ੲ) ਧਾਤ ਦੇ ਛੋਟੇ ਟੁਕੜੇ ਨੂੰ ਕਾਰ ਦੇ ਇੰਜਣ ਆਇਲ ਵਿੱਚੋਂ ਵੱਖ ਕਰਨ ਲਈ ।
(ਸ) ਦਹੀਂ ਵਿੱਚੋਂ ਮੱਖਣ ਕੱਢਣ ਲਈ ।
(ਹ) ਪਾਣੀ ਵਿੱਚੋਂ ਤੇਲ ਵੱਖ ਕਰਨ ਲਈ ।
(ਕ) ਚਾਹ ਵਿੱਚੋਂ ਚਾਹ-ਪੱਤੀ ਵੱਖ ਕਰਨ ਲਈ ।
(ਖ) ਰੇਤ ਵਿੱਚੋਂ ਲੋਹੇ ਦੀਆਂ ਪਿੰਨਾਂ ਨੂੰ ਵੱਖ ਕਰਨ ਲਈ ।
(ਗ) ਤੂੜੀ ਵਿੱਚੋਂ ਕਣਕ ਦੇ ਦਾਣਿਆਂ ਨੂੰ ਵੱਖ ਕਰਨ ਲਈ ।
(ਘ) ਪਾਣੀ ਵਿੱਚੋਂ ਤਰਦੇ ਹੋਏ ਬਾਰੀਕ-ਮਿੱਟੀ ਦੇ ਕਣਾਂ ਨੂੰ ਪਾਣੀ ਤੋਂ ਵੱਖ ਕਰਨ ਲਈ ।
(ਝ) ਫੁੱਲਾਂ ਦੀਆਂ ਪੱਤੀਆਂ ਦੇ ਨਿਚੋੜ ਵਿੱਚੋਂ ਵੱਖ-ਵੱਖ ਵਰਣਕਾਂ (pigments) ਨੂੰ ਵੱਖ ਕਰਨ ਲਈ ।
ਉੱਤਰ-
(ਉ) ਕਸ਼ੀਦਣ ਵਿਧੀ/ਵਾਸ਼ਪਨ ਨਾਲ ।
(ਅ) ਜੌਹਰ ਉਡਾਉਣਾ ਵਿਧੀ ।
(ੲ) ਫਿਲਟਰੀਕਰਨ ਜਾਂ ਛਾਣਨ ਵਿਧੀ ।
(ਸ) ਅਪਕੇਂਦਰਨ ਵਿਧੀ ।
(ਹ) ਨਿਖੇੜਕ ਵਿਧੀ (ਨਿਖੇੜਕ ਕੀਪ ਵਿਧੀ) ।
(ਕ) ਛਾਣਨ ਵਿਧੀ । (ਚੁੰਬਕੀ ਨਿਖੇੜਕ ਵਿਧੀ ।
(ਗ) ਫਟਕਣ ਵਿਧੀ ।
(ਘ) ਫਿਲਟਰੀਕਰਨ ਜਾਂ ਅਪਕੇਂਦਰਨ ਵਿਧੀ ।
(ਝ) ਕਰੋਮੈਟੋਗਰਾਫੀ ।

ਪ੍ਰਸ਼ਨ 2.
ਚਾਹ ਤਿਆਰ ਕਰਨ ਲਈ ਤੁਸੀਂ ਕਿਹੜੇ-ਕਿਹੜੇ ਪੜਾਵਾਂ ਦੀ ਵਰਤੋਂ ਕਰੋਗੇ । ਘੋਲ, ਘੋਲਕ, ਘੁਲਿਤ, ਘੁਲਣਸ਼ੀਲ, ਅਘੁਲਣਸ਼ੀਲ, ਫਿਲਟਰੇਟ ਅਤੇ ਰਹਿੰਦ-ਖੂੰਹਦ ਸ਼ਬਦਾਂ ਦੀ ਵਰਤੋਂ ਕਰੋ ।
ਉੱਤਰ-
ਘੋਲ ਦੀ ਚੋਣ – ਚਾਹ ਬਣਾਉਣ ਲਈ ਪਾਣੀ ਆਧਾਰਭੂਤ ਘੋਲਕ ਹੈ ਜਿਸ ਵਿੱਚ ਚੀਨੀ ਅਤੇ ਦੁੱਧ ਘੁਲਿਤ ਦੇ ਰੂਪ ਵਿੱਚ ਪਾਣੀ ਰੂਪੀ ਘੋਲਕ ਵਿੱਚ ਸਰਲਤਾ ਨਾਲ ਮਿਲ ਸਕਦੇ ਹਨ ।

ਉਬਾਲਣਾ – ਪਾਣੀ ਨੂੰ ਉਬਲਣ ਦਰਜੇ ਤਕ ਗਰਮ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਇਸ ਵਿਚ ਘੁਲਣਸ਼ੀਲ ਚੀਨੀ ਅਤੇ ਅਘੁਲਣਸ਼ੀਲ ਚਾਹ ਪੱਤੀ ਲੋੜ ਅਨੁਸਾਰ ਲੋੜੀਂਦੀ ਮਾਤਰਾ ਵਿੱਚ ਪਾ ਕੇ ਘੁਲਿਤ ਦੁੱਧ ਵਿੱਚ ਮਿਲਾਓ ।

ਛਾਣਨਾ – ਅਘੁਲਣਸ਼ੀਲ ਚਾਹ ਪੱਤੀ ਨੂੰ ਛਲਣੀ ਨਾਲ ਛਾਣੋ । ਘੁਲਣਸ਼ੀਲ ਚੀਨੀ ਅਤੇ ਦੁੱਧ ਚਾਹ ਬਣਾਉਣ ਵਿਚ ਵਰਤੇ ਗਏ ਰਹਿੰਦ-ਖੂੰਹਦ ਰੂਪ ਵਿੱਚ ਚਾਹ ਪੱਤੀ ਨੂੰ ਬਾਹਰ ਕੱਢ ਕੇ ਫਿਲਟਰੇਟ ਰੂਪ ਵਿੱਚ ਚਾਹ ਪ੍ਰਾਪਤ ਕਰ ਲਓ ।

ਪ੍ਰਸ਼ਨ 3.
ਸੀਮਾ ਨੇ ਤਿੰਨ ਵੱਖ-ਵੱਖ ਪਦਾਰਥਾਂ ਦੀਆਂ ਘੁਲਣਸ਼ੀਲਤਾਵਾਂ ਨੂੰ ਵੱਖ-ਵੱਖ ਤਾਪਮਾਨ ‘ਤੇ ਪਰਖਿਆ ਅਤੇ ਹੇਠਾਂ ਦਿੱਤੇ ਗਏ ਅੰਕੜੇ ਪ੍ਰਾਪਤ ਕੀਤੇ ਮਿਲਣ ਵਾਲੇ ਨਤੀਜਿਆਂ ਨੂੰ 100 ਗ੍ਰਾਮ ਪਾਣੀ ਵਿੱਚ ਘੁਲਿਤ ਪਦਾਰਥ ਦੀ ਮਾਤਰਾ, ਜਿਹੜੀ ਸੰਤ੍ਰਿਪਤ ਘੋਲ ਬਣਾਉਣ ਲਈ ਕਾਫ਼ੀ ਹੈ, ਹੇਠ ਲਿਖੀ ਸਾਰਣੀ ਵਿੱਚ ਦਰਸਾਇਆ ਗਿਆ ਹੈ-

(ਉ) 50 ਗ੍ਰਾਮ ਪਾਣੀ ਵਿੱਚ 313 K ਤੇ ਪੋਟਾਸ਼ੀਅਮ ਨਾਈਟ੍ਰੇਟ ਦੇ ਸੰਤ੍ਰਿਪਤ ਘੋਲ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ ਕਿੰਨੇ ਗਰਾਮ ਪੋਟਾਸ਼ੀਅਮ ਨਾਈਟ੍ਰੇਟ ਦੀ ਲੋੜ ਹੋਵੇਗੀ ?
(ਅ) ਸੀਮਾ 353K ਤੇ ਪੋਟਾਸ਼ੀਅਮ ਕਲੋਰਾਈਡ ਦਾ ਇੱਕ ਸੰਤ੍ਰਿਪਤ ਘੋਲ ਤਿਆਰ ਕਰਦੀ ਹੈ ਅਤੇ ਉਸ ਘੋਲ ਨੂੰ ਕਮਰੇ ਦੇ ਤਾਪਮਾਨ ‘ਤੇ ਠੰਡਾ ਹੋਣ ਲਈ ਛੱਡਿਆ ਤਾਂ ਉਹ ਕੀ ਪ੍ਰੇਖਣ ਕਰੇਗੀ ? ਸਪੱਸ਼ਟ ਕਰੋ ।
(ੲ) 293K ਤੇ ਹਰੇਕ ਨਮਕ ਦੀ ਘੁਲਣਸ਼ੀਲਤਾ ਦੀ ਗਣਨਾ ਕਰੋ । ਇਸ ਤਾਪਮਾਨ ‘ਤੇ ਕਿਹੜਾ ਨਮਕ ਸਭ ਤੋਂ ਵੱਧ ਘੁਲਣਸ਼ੀਲ ਹੋਵੇਗਾ ?
(ਸ) ਤਾਪਮਾਨ ਵਿੱਚ ਪਰਿਵਰਤਨ ਨਾਲ ਨਮਕ ਦੀ ਘੁਲਣਸ਼ੀਲਤਾ ‘ ਤੇ ਕੀ ਪ੍ਰਭਾਵ ਪੈਂਦਾ ਹੈ ?
ਉੱਤਰ-
(ਉ) 100g ਪਾਣੀ ਵਿੱਚ 313K ਤੇ ਸੰਤ੍ਰਿਪਤ ਘੋਲ ਦੇ ਲਈ ਲੋੜੀਂਦਾ KNO₃ = 62g
50g ਪਾਣੀ ਵਿੱਚ 313K ਤੇ ਸੰਤ੍ਰਿਪਤ ਘੋਲ ਦੇ ਲਈ ਲੋੜੀਂਦਾ KNO₃ = \(\frac{62}{100}\) × 50 = 31g

(ਅ) 353 K ਤੇ KCl ਦੇ ਸੰਤ੍ਰਿਪਤ ਘੋਲ ਨੂੰ ਜਦੋਂ ਰੱਗਿਆ ਠੰਢਾ ਕਰਨ ਲਈ ਛੱਡ ਦੇਵੇਗੀ ਤਾਂ ਤਾਪਮਾਨ ਘੱਟ ਹੋਣ ਤੇ ਕ੍ਰਿਸਟਲੀਕਰਨ ਹੋ ਜਾਵੇਗਾ ਜਿਸ ਦੇ ਨਤੀਜੇ ਵਜੋਂ KCl ਦੇ ਕ੍ਰਿਸਟਲ ਬਣ ਜਾਣਗੇ ।

(ੲ) KNO₃ ਦੀ 100g ਪਾਣੀ ਵਿੱਚ ਘੁਲਣਸ਼ੀਲਤਾ = \(\frac{32}{100}\) × 100 = 32g
NaCI ਦੀ 100g ਪਾਣੀ ਵਿੱਚ ਘੁਲਣਸ਼ੀਲਤਾ = \(\frac{36}{100}\) × 100 = 36g
KCl ਦੀ 100g ਪਾਣੀ ਵਿੱਚ ਘੁਲਣਸ਼ੀਲਤਾ = \(\frac{35}{100}\) × 100 = 35g
NH₄Cl ਦੀ 100g ਪਾਣੀ ਵਿੱਚ ਘੁਲਣਸ਼ੀਲਤਾ = \(\frac{37}{100}\) × 100 = 37g
293K ਤੇ ਸਭ ਤੋਂ ਵੱਧ ਘੁਲਣਸ਼ੀਲਤਾ ਅਮੋਨੀਅਮ ਕਲੋਰਾਈਡ ਦੀ ਹੈ ।

(ਸ) ਤਾਪਮਾਨ ਵਿੱਚ ਪਰਿਵਰਤਨ ਨਾਲ ਲੂਣਾਂ ਦੀ ਘੁਲਣਸ਼ੀਲਤਾ ਪ੍ਰਭਾਵਿਤ ਹੁੰਦੀ ਹੈ । ਜਿਵੇਂ-ਜਿਵੇਂ ਤਾਪਮਾਨ ਵੱਧਦਾ ਹੈ ਉਸੇ ਤਰ੍ਹਾਂ ਲੂਣਾਂ ਦੀ ਘੁਲਣਸ਼ੀਲਤਾ ਵੱਧ ਜਾਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
ਹੇਠ ਲਿਖਿਆਂ ਦੀ ਉਦਾਹਰਨ ਸਹਿਤ ਵਿਆਖਿਆ ਕਰੋ :
(ੳ) ਸੰਤ੍ਰਿਪਤ ਘੋਲ
(ਅ) ਸ਼ੁੱਧ ਪਦਾਰਥ
(ੲ) ਕੋਲਾਇਡ
(ਸ) ਨਿਲੰਬਨ ।
ਉੱਤਰ-
(ੳ) ਸੰਤ੍ਰਿਪਤ ਘੋਲ – ਕਿਸੇ ਨਿਸਚਿਤ ਤਾਪਮਾਨ ‘ਤੇ ਜਦੋਂ ਘੋਲ ਵਿੱਚ ਘੁਲਿਤ ਪਦਾਰਥ ਨਹੀਂ ਘੁਲਦਾ ਹੈ ਤਾਂ ਉਸ ਨੂੰ ਸੰਤ੍ਰਿਪਤ ਘੋਲ ਕਹਿੰਦੇ ਹਨ ।

(ਅ) ਸ਼ੁੱਧ ਪਦਾਰਥ – ਸ਼ੁੱਧ ਪਦਾਰਥ ਉਹ ਹਨ ਜਿਨ੍ਹਾਂ ਦੇ ਸਿਰਫ਼ ਇਕੋ ਕਿਸਮ ਦੇ ਅਣੂ ਹਨ । ਸੁੱਧ ਪਦਾਰਥਾਂ ਵਿੱਚ ਭੌਤਿਕ ਅਤੇ ਰਸਾਇਣਿਕ ਗੁਣ ਹੁੰਦੇ ਹਨ | ਸਾਰੇ ਯੌਗਿਕ ਸ਼ੁੱਧ ਪਦਾਰਥ ਹਨ । ਉਦਾਹਰਨ-ਸਾਧਾਰਨ ਨਮਕ, ਚੀਨੀ, ਸੋਨਾ, ਤਾਂਬਾ, ਪਾਰਾ ਆਦਿ ।

(ੲ) ਕੋਲਾਇਡ – ਇਹ ਇਕ ਬਿਖਮਅੰਗੀ ਮਿਸ਼ਰਣ ਹੈ ਜਿਸ ਵਿੱਚ ਕਣਾਂ ਦਾ ਆਕਾਰ 1pm ਤੋਂ 100nm ਦੇ ਵਿੱਚ ਹੁੰਦਾ ਹੈ ਜਿਨ੍ਹਾਂ ਨੂੰ ਅੱਖਾਂ ਨਾਲ ਨਹੀਂ ਦੇਖਿਆ ਜਾ ਸਕਦਾ ਹੈ । ਇਹ ਕਣ ਇੰਨੇ ਵੱਡੇ ਆਕਾਰ ਦੇ ਹੁੰਦੇ ਹਨ ਕਿ ਪ੍ਰਕਾਸ਼ ਦੀਆਂ ਕਿਰਣਾਂ ਨੂੰ ਫੈਲਾਅ ਸਕਦੇ ਹਨ । ਇਹ ਕਣ ਤਲ ‘ਤੇ ਨਹੀਂ ਬੈਠਦੇ ਪਰ ਅਪਕੇਂਦਰੀਕਰਨ ਤਕਨੀਕ ਨਾਲ ਵੱਖ ਕੀਤੇ ਜਾ ਸਕਦੇ ਹਨ । ਉਦਾਹਰਨ-ਕੋਹਰਾ, ਬੱਦਲ, ਧੂੰਆਂ, ਦੁੱਧ, ਸਪੰਜ, ਜੈਲੀ, ਪਨੀਰ, ਮੱਖਣ ਆਦਿ ।

(ਸ) ਨਿਲੰਬਨ – ਇਹ ਬਿਖਮਅੰਗੀ ਘੋਲ ਹੈ ਜਿਸ ਵਿਚ ਠੋਸ, ਵ ਵਿੱਚ ਪਰਿਖੇਪਿਤ ਹੋ ਜਾਂਦਾ ਹੈ । ਇਸ ਵਿੱਚ ਘੁਲਿਤ ਪਦਾਰਥ ਦੇ ਕਣ ਘੁਲਦੇ ਨਹੀਂ ਹਨ ਬਲਕਿ ਮਾਧਿਅਮ ਦੀ ਸਮਸਟੀ ਵਿੱਚ ਨਿਲੰਬਿਤ ਰਹਿੰਦੇ ਹਨ । ਇਹਨਾਂ ਨੂੰ ਅੱਖਾਂ ਨਾਲ ਦੇਖਿਆ ਜਾ ਸਕਦਾ ਹੈ । ਛਾਣਨ ਵਿਧੀ ਨਾਲ ਇਹਨਾਂ ਨੂੰ ਮਿਸ਼ਰਨ ਤੋਂ ਵੱਖ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ; ਉਦਾਹਰਨ-ਪਾਣੀ ਵਿੱਚ ਚਾਕ ਪਾਉਡਰ ।

ਪ੍ਰਸ਼ਨ 5.
ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ਹਰ ਇੱਕ ਨੂੰ ਸਮਅੰਗੀ ਅਤੇ ਬਿਖਮਅੰਗੀ ਵਿੱਚ ਸ਼੍ਰੇਣੀਬੱਧ ਕਰੋ : ਸੋਡਾ ਪਾਣੀ, ਲੱਕੜੀ, ਬਰਫ਼, ਹਵਾ, ਮਿੱਟੀ, ਸਿਰਕਾ, ਫਿਲਟਰ ਕੀਤੀ ਹੋਈ ਚਾਹ ।
ਉੱਤਰ-
ਸੋਡਾ ਪਾਣੀ = ਸਮਅੰਗੀ
ਲੱਕੜੀ = ਬਿਖਮਅੰਗੀ
ਬਰਫ਼ = ਸਮਅੰਗੀ
ਹਵਾ = ਸਮਅੰਗੀ
ਮਿੱਟੀ = ਬਿਖਮਅੰਗੀ
ਸਿਰਕਾ = ਸਮਅੰਗੀ
ਫਿਲਟਰ ਕੀਤੀ ਹੋਈ ਚਾਹ = ਸਮਅੰਗੀ ।

ਸ਼ਨ 6.
ਤੁਸੀਂ ਕਿਵੇਂ ਪੁਸ਼ਟੀ ਕਰੋਗੇ ਕਿ ਦਿੱਤਾ ਹੋਇਆ ਰੰਗਹੀਣ ਵ ਸ਼ੁੱਧ ਪਾਣੀ ਹੈ ?
ਉੱਤਰ-
ਰੰਗਹੀਣ ਦ੍ਰਵ ਵਿੱਚ ਕਿਸੇ ਪ੍ਰਕਾਰ ਦੇ ਅੱਖਾਂ ਨਾਲ ਦਿਖਾਈ ਦੇਣ ਵਾਲੇ ਰੰਗ ਦੇ ਕਣ ਨਾ ਹੋਣ ਦੀ ਸਥਿਤੀ ਵਿੱਚ ਪਾਣੀ ਦੇ ਸ਼ੁੱਧ ਹੋਣ ਦੀ ਪੁਸ਼ਟੀ ਹੁੰਦੀ ਹੈ ਪਰ ਪਾਣੀ ਵਿੱਚ ਕਿਸੇ ਪ੍ਰਕਾਰ ਦਾ ਸਵਾਦ ਤੇ ਗੰਧ ਵੀ ਨਹੀਂ ਹੋਣੀ ਚਾਹੀਦੀ । ਇਸ 100°C ਜਾਂ 373 K ਤੇ ਉਬਲ ਜਾਣਾ ਚਾਹੀਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 7.
ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ਕਿਹੜੀਆਂ ਵਸਤੂਆਂ ਸ਼ੁੱਧ ਪਦਾਰਥ ਹਨ ?
(ੳ) ਬਰਫ਼,
(ਅ) ਦੁੱਧ,
(ੲ) ਲੋਹਾ,
(ਸ) ਹਾਈਡਰੋਕਲੋਰਿਕ ਐਸਿਡ,
(ਹ) ਕੈਲਸ਼ੀਅਮ ਆਂਕਸਾਈਡ,
(ਕ) ਪਾਰਾ
(ਖ) ਇੱਟ,
(ਗ) ਲੱਕੜੀ,
(ਘ) ਹਵਾ ।
ਉੱਤਰ-
ਲੋਹਾ, ਹਾਈਡਰੋਕਲੋਰਿਕ ਐਸਿਡ, ਪਾਰਾ, ਕੈਲਸ਼ੀਅਮ ਆਕਸਾਈਡ ।

ਪ੍ਰਸ਼ਨ 8.
ਹੇਠ ਲਿਖੇ ਮਿਸ਼ਰਣਾਂ ਵਿੱਚੋਂ ਘੋਲ ਦੀ ਪਹਿਚਾਣ ਕਰੋ-
(ੳ) ਮਿੱਟੀ
(ਅ) ਸਮੁੰਦਰੀ ਪਾਣੀ
(ੲ) ਹਵਾ
(ਸ) ਕੋਲਾ
(ਹ) ਸੋਡਾ ਪਾਣੀ ।
ਉੱਤਰ-
ਸਮੁੰਦਰੀ ਪਾਣੀ, ਹਵਾ, ਸੋਡਾ ਪਾਣੀ ।

ਪ੍ਰਸ਼ਨ 9.
ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ਕਿਹੜਾ ਟਿੰਡਲ ਪ੍ਰਭਾਵ ਨੂੰ ਦਰਸਾਏਗਾ ?
(ਉ) ਨਮਕ ਦਾ ਘੋਲ
(ਅ) ਦੁੱਧ
(ੲ) ਕਾਪਰ ਸਲਫੇਟ ਦਾ ਘੋਲ
(ਸ) ਸਟਾਰਚ ਦਾ ਘੋਲ ।
ਉੱਤਰ-
ਦੁੱਧ, ਸਟਾਰਚ ਦਾ ਘੋਲ ।

ਪ੍ਰਸ਼ਨ 10.
ਹੇਠ ਲਿਖਿਆਂ ਨੂੰ ਤੱਤ, ਯੋਗਿਕ ਅਤੇ ਮਿਸ਼ਰਣ ਵਿੱਚ ਸ਼੍ਰੇਣੀਬੱਧ ਕਰੋ
(ੳ) ਸੋਡੀਅਮ,
(ਅ) ਮਿੱਟੀ,
(ੲ) ਚੀਨੀ ਦਾ ਘੋਲ,
(ਸ) ਚਾਂਦੀ,
(ਹ) ਕੈਲਸ਼ੀਅਮ ਕਾਰਬੋਨੇਟ,
(ਕ) ਟਿਨ,
(ਖ) ਸਿਲੀਕਾਂਨ,
(ਗ) ਕੋਲਾ,
(ਘ) ਹਵਾ,
(੩) ਸਾਬਣ,
(ਚ) ਮੀਥੇਨ,
(ਛ) ਕਾਰਬਨ-ਡਾਈਆਕਸਾਈਡ,
(ਜ) ਖੂਨ ।
ਉੱਤਰ-
ਤੱਤ – ਸੋਡੀਅਮ, ਚਾਂਦੀ, ਟਿਨ, ਸਿਲੀਕਾਨ ।
ਯੌਗਿਕ – ਕੈਲਸ਼ੀਅਮ ਕਾਰਬੋਨੇਟ, ਮੀਥੇਨ, ਕਾਰਬਨ-ਡਾਈਆਕਸਾਈਡ ।
ਮਿਸ਼ਰਨ-ਮਿੱਟੀ, ਚੀਨੀ ਦਾ ਘੋਲ, ਕੋਲਾ, ਸਾਬਣ, ਹਵਾ, ਖੂਨ ।

ਪ੍ਰਸ਼ਨ 11.
ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ਕਿਹੜੇ-ਕਿਹੜੇ ਪਰਿਵਰਤਨ ਰਸਾਇਣਿਕ ਪਰਿਵਰਤਨ ਹਨ ?
(ੳ) ਪੌਦਿਆਂ ਦਾ ਵਧਨਾ
(ਅ) ਲੋਹੇ ਨੂੰ ਜੰਗ ਲੱਗਣਾ
(ੲ) ਲੋਹ ਚੂਰਣ ਅਤੇ ਰੇਤ ਨੂੰ ਮਿਲਾਉਣਾ
(ਸ) ਭੋਜਣ ਪਕਾਉਣਾ
(ਹ) ਭੋਜਨ ਦਾ ਪਾਚਨ
(ਕ) ਪਾਣੀ ਦਾ ਬਰਫ਼ ਬਣਨਾ
(ਖ) ਮੋਮਬੱਤੀ ਦਾ ਜਲਣਾ ।
ਉੱਤਰ-
ਲੋਹੇ ਨੂੰ ਜੰਗ ਲੱਗਣਾ, ਭੋਜਨ ਪਕਾਉਣਾ, ਭੋਜਨ ਦਾ ਪਾਚਨ, ਮੋਮਬੱਤੀ ਦਾ ਜਲਣਾ ।

Science Guide for Class 9 PSEB ਕੀ ਸਾਡੇ ਆਲੇ-ਦੁਆਲੇ ਦੇ ਪਦਾਰਥ ਸ਼ੁੱਧ ਹਨ? InText Questions and Answers

ਪਾਠ-ਪੁਸਤਕ ਦੇ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਉੱਤਰ

ਪ੍ਰਸ਼ਨ 1.
ਸ਼ੁੱਧ ਪਦਾਰਥ ਤੋਂ ਤੁਸੀਂ ਕੀ ਸਮਝਦੇ ਹੋ ?
ਉੱਤਰ-
ਸ਼ੁੱਧ ਪਦਾਰਥ – ਉਹ ਪਦਾਰਥ ਸ਼ੁੱਧ ਹੁੰਦੇ ਹਨ ਜਿਨ੍ਹਾਂ ਵਿੱਚ ਮੌਜੂਦ ਸਾਰੇ ਕਣ ਸਮਾਨ ਰਸਾਇਣਿਕ ਗੁਣਾਂ ਵਾਲੇ ਹੋਣ । ਸ਼ੁੱਧ ਪਦਾਰਥ ਵਿੱਚ ਸਦਾ ਹੀ ਇੱਕ ਪ੍ਰਕਾਰ ਦੇ ਕਣ ਹੁੰਦੇ ਹਨ , ਜਿਵੇਂ- ਸੋਨਾ, ਤਾਂਬਾ, ਸੋਡੀਅਮ ਕਲੋਰਾਈਡ, ਚੀਨੀ ਆਦਿ ।

ਪ੍ਰਸ਼ਨ 2.
ਸਮਅੰਗੀ ਅਤੇ ਬਿਖਮਅੰਗੀ ਮਿਸ਼ਰਣਾਂ ਵਿੱਚ ਅੰਤਰ ਦੱਸੋ ।
ਉੱਤਰ-
ਸਮਅੰਗੀ ਅਤੇ ਬਿਖਮਅੰਗੀ ਮਿਸ਼ਰਣਾਂ ਵਿੱਚ ਅੰਤਰ – ਸਮਅੰਗੀ ਮਿਸ਼ਰਣ ਦਾ ਰੂਪ, ਗੁਣ ਅਤੇ ਸੰਰਚਨਾ ਹਰ ਅਵਸਥਾ ਵਿੱਚ ਸਮਰੂਪ ਹੁੰਦਾ ਹੈ । ਬਿਖਮਅੰਗੀ ਮਿਸ਼ਰਣ ਦੇ ਘਟਕਾਂ ਦੇ ਭੌਤਿਕ ਗੁਣ ਇੱਕ-ਦੂਸਰੇ ਤੋਂ ਵੱਖ ਹੁੰਦੇ ਹਨ । ਜਲ ਵਿੱਚ ਨਮਕ ਅਤੇ ਜਲ ਵਿੱਚ ਚੀਨੀ ਸਮਅੰਗੀ ਮਿਸ਼ਰਣ ਦੇ ਉਦਾਹਰਨ ਹਨ । ਪਾਣੀ ਵਿੱਚ ਤੇਲ, ਨਮਕ ਵਿੱਚ ਗੰਧਕ, ਨਮਕ ਵਿੱਚ ਲੋਹੇ ਦੀ ਛਿੱਲਣ, ਰੇਤ ਵਿੱਚ ਨਮਕ, ਨਮਕ ਵਿੱਚ ਚੀਨੀ ਆਦਿ ਬਿਖਮਅੰਗੀ ਮਿਸ਼ਰਣ ਦੇ ਉਦਾਹਰਨ ਹਨ ।

ਪ੍ਰਸ਼ਨ 3.
ਉਦਾਹਰਨ ਸਹਿਤ ਸਮਅੰਗੀ ਅਤੇ ਬਿਖਮਅੰਗੀ ਮਿਸ਼ਰਣਾਂ ਵਿੱਚ ਅੰਤਰ ਦੱਸੋ ।
ਉੱਤਰ-

ਸਮਅੰਗੀ ਮਿਸ਼ਰਣ (Homogeneous Mixture)	ਬਿਖਮਅੰਗੀ ਮਿਸ਼ਰਣ (Heterogeneous Mixture)
(1) ਇਸ ਦੇ ਘਟਕ ਵਿੱਚ ਸਮਾਨ ਵੰਡੇ ਹੁੰਦੇ ਹਨ ।	(1) ਇਸਦੇ ਘਟਕ ਇੱਕ ਸਮਾਨ ਰੂਪ ਵਿੱਚ ਵੰਡੇ ਨਹੀਂ ਹੁੰਦੇ ।
(2) ਇਸ ਵਿੱਚ ਅੰਸ਼ਾਂ ਦੇ ਗੁਣ ਅਤੇ ਸੰਰਚਨਾ ਹਰ ਅਵਸਥਾ ਵਿੱਚ ਸਮਰੁਪ ਹੁੰਦੀ ਹੈ । ਉਦਾਹਰਨ-ਪਿੱਤਲ, ਕਾਂਸਾ, ਪਾਣੀ ਵਿੱਚ ਚੀਨੀ, ਐਲਕੋਹਲ ਵਿੱਚ ਪਾਣੀ, ਹਵਾ ਆਦਿ ।	(2) ਇਸ ਵਿੱਚ ਅੰਸ਼ਾਂ ਦੇ ਗੁਣ ਇੱਕ ਦੂਜੇ ਤੋਂ ਭਿੰਨ ਹੁੰਦੇ ਹਨ । ਉਦਾਹਰਨ-ਰੇਤ ਕਣ ਅਤੇ ਲੋਹ ਚੂਰਣ, ਰੇਤ+ਅਮੋਨੀਅਮ ਕਲੋਰਾਈਡ, ਪਾਣੀ ਵਿੱਚ ਚਾਕ ਪਾਣੀ ਵਿੱਚ ਤੇਲ ਆਦਿ ।

ਪ੍ਰਸ਼ਨ 4.
ਘੋਲ, ਨਿਲੰਬਨ ਅਤੇ ਕੋਲਾਇਡ ਇੱਕ ਦੂਜੇ ਤੋਂ ਕਿਵੇਂ ਭਿੰਨ ਹਨ ?
ਉੱਤਰ-

ਪ੍ਰਸ਼ਨ 5.
ਇੱਕ ਸੰਤ੍ਰਿਪਤ ਘੋਲ ਬਣਾਉਣ ਲਈ 36 ਗ੍ਰਾਮ ਸੋਡੀਅਮ ਕਲੋਰਾਈਡ ਨੂੰ 100 ਗ੍ਰਾਮ ਪਾਣੀ ਵਿੱਚ 293k ਤੇ ਘੋਲਿਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਤਾਪਮਾਨ ਤੇ ਇਸ ਦੀ ਸੰਘਣਤਾ ਪਤਾ ਕਰੋ ।
ਉੱਤਰ-
ਘੁਲਿਤ ਪਦਾਰਥ ਦਾ ਪੁੰਜ (ਸੋਡੀਅਮ ਕਲੋਰਾਈਡ = 36g
ਘੋਲਕ ਦਾ ਪੁੰਜ (ਪਾਣੀ) = 100g
ਘੋਲ ਦਾ ਪੁੰਜ = ਘੁਲਿਤ ਦਾ ਪੁੰਜ + ਘੋਲਕ ਦਾ ਪੁੰਜ
= 36g + 100g = 136g

= \(\frac{36}{136}\) × 100 = 26.47%

ਪ੍ਰਸ਼ਨ 6.
ਪੈਟਰੋਲ ਅਤੇ ਮਿੱਟੀ ਦਾ ਤੇਲ ਜੋ ਕਿ ਆਪਸ ਵਿੱਚ ਘੁਲਣਸ਼ੀਲ ਹਨ, ਦੇ ਮਿਸ਼ਰਣ ਨੂੰ ਤੁਸੀਂ ਕਿਵੇਂ ਨਿਖੋੜੇਗੇ ? ਪੈਟਰੋਲ ਅਤੇ ਮਿੱਟੀ ਦੇ ਤੇਲ ਦੇ ਉੱਬਾਲ ਦਰਜਿਆਂ ਵਿੱਚ 25° ਸੈ. ਤੋਂ ਵੱਧ ਅੰਤਰ ਹੈ ।
ਉੱਤਰ-
ਪੈਟਰੋਲ ਅਤੇ ਮਿੱਟੀ ਦੇ ਤੇਲ ਦੇ ਮਿਸ਼ਰਣ ਨੂੰ ਸਾਧਾਰਣ ਕਸ਼ੀਦਣ ਵਿਧੀ ਨਾਲ ਵੱਖ-ਵੱਖ ਕਰਾਂਗੇ ਕਿਉਂਕਿ ਦੋਵੇਂ ਵ ਬਗੈਰ ਅਪਘਟਨ ਦੇ ਉੱਬਲ ਜਾਣਗੇ । ਉਹਨਾਂ ਦੇ ਉੱਬਾਲ ਦਰਜੇ ਵਿੱਚ 25°C ਤੋਂ ਵੱਧ ਦਾ ਫਰਕ ਹੈ ।

ਪ੍ਰਸ਼ਨ 7.
ਨਿਖੇੜਨ ਦੀਆਂ ਆਮ ਵਿਧੀਆਂ ਦੇ ਨਾਂ ਦਿਓ-
(i) ਦਹੀਂ ਤੋਂ ਮੱਖਣ ।
(ii) ਸਮੁੰਦਰ ਦੇ ਪਾਣੀ ਤੋਂ ਨਮਕ ।
(iii) ਨਮਕ ਤੋਂ ਕਪੂਰ ।
ਉੱਤਰ-
(i) ਅਪਕੇਂਦਰਨ ।
(ii) ਕ੍ਰਿਸਟਲੀਕਰਨ ।
(iii) ਜੌਹਰ ਉਡਾਉਣਾ ।

ਪ੍ਰਸ਼ਨ 8.
ਕ੍ਰਿਸਟਲੀਕਰਣ ਵਿਧੀ ਦੇ ਨਾਲ ਕਿਸ ਤਰ੍ਹਾਂ ਦੇ ਮਿਸ਼ਰਣਾਂ ਦਾ ਨਿਖੇੜਨ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ?
ਉੱਤਰ-
ਕ੍ਰਿਸਟਲੀਕਰਨ ਵਿਧੀ ਦੁਆਰਾ ਠੋਸ ਪਦਾਰਥਾਂ ਵਿੱਚ ਰਲੀਆਂ ਅਸ਼ੁੱਧੀਆਂ ਨੂੰ ਦੂਰ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ । ਸਮੁੰਦਰੀ ਪਾਣੀ ਵਿੱਚ ਘੁਲੇ ਨਮਕ ਨੂੰ ਸ਼ੁੱਧ ਰੂਪ ਵਿੱਚ ਪ੍ਰਾਪਤ ਕਰਨ ਅਤੇ ਅਸ਼ੁੱਧ ਨਮੂਨੇ ਤੋਂ ਫਿਟਕਰੀ ਨੂੰ ਵੱਖ ਕਰਨ ਲਈ । ਕ੍ਰਿਸਟਲੀਕਰਣ ਦੀ ਵਰਤੋਂ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 9.
ਹੇਠ ਲਿਖਿਆਂ ਨੂੰ ਭੌਤਿਕ ਅਤੇ ਰਸਾਇਣਿਕ ਪਰਿਵਰਤਨਾਂ ਵਿੱਚ ਵਰਗੀਕ੍ਰਿਤ ਕਰੋ-
ਰੁੱਖਾਂ ਦਾ ਕੱਟਣਾ, ਮੱਖਣ ਦਾ ਇੱਕ ਬਰਤਨ ਵਿੱਚ ਪਿਘਲਣਾ, ਅਲਮਾਰੀ ਨੂੰ ਜੰਗ ਲੱਗਣਾ, ਪਾਣੀ ਦਾ ਉੱਬਲ ਕੇ ਵਾਸ਼ਪ ਬਣਨਾ, ਬਿਜਲੀ ਦਾ ਪਾਣੀ ਵਿੱਚੋਂ ਲੰਘਣਾ ਅਤੇ ਇਸ ਦਾ ਹਾਈਡਰੋਜਨ ਅਤੇ ਆਕਸੀਜਨ ਵਿੱਚ ਵਿਘਟਨ ਹੋਣਾ, ਪਾਣੀ ਵਿੱਚ ਸਧਾਰਨ ਨਮਕ ਦਾ ਘੁਲਣਾ, ਫਲਾਂ ਤੋਂ ਸਲਾਦ ਬਨਾਉਣਾ, ਲੱਕੜੀ ਅਤੇ ਕਾਗਜ਼ ਦਾ ਜਲਣਾ ।
ਉੱਤਰ-

1. ਰੁੱਖਾਂ ਦਾ ਕੱਟਣਾ-ਭੌਤਿਕ ਪਰਿਵਰਤਨ ।
2. ਮੱਖਣ ਦਾ ਇੱਕ ਬਰਤਨ ਵਿੱਚ ਪਿਘਲਣਾ-ਭੌਤਿਕ ਪਰਿਵਰਤਨ ।
3. ਅਲਮਾਰੀ ਨੂੰ ਜੰਗ ਲੱਗਣਾ-ਰਸਾਇਣਿਕ ਪਰਿਵਰਤਨ ।
4. ਪਾਣੀ ਦਾ ਉੱਬਲ ਕੇ ਵਾਸ਼ਪ ਬਣਨਾ-ਭੌਤਿਕ ਪਰਿਵਰਤਨ ।
5. ਬਿਜਲੀ ਦਾ ਪਾਣੀ ਵਿੱਚੋਂ ਲੰਘਣਾ ਇਸਦਾ ਹਾਈਡਰੋਜਨ ਅਤੇ ਆਕਸੀਜਨ ਵਿੱਚ ਵਿਘਟਨ ਹੋਣਾ-ਰਸਾਇਣਿਕ ਪਰਿਵਰਤਨ ।
6. ਪਾਣੀ ਵਿੱਚ ਸਾਧਾਰਨ ਨਮਕ ਦਾ ਘੁਲਣਾ-ਭੌਤਿਕ ਪਰਿਵਰਤਨ ।
7. ਫਲਾਂ ਤੋਂ ਸਲਾਦ ਬਨਾਉਣਾ-ਭੌਤਿਕ ਪਰਿਵਰਤਨ ।
8. ਲੱਕੜੀ ਅਤੇ ਕਾਗਜ਼ ਦਾ ਜਲਣਾ-ਰਸਾਇਣਿਕ ਪਰਿਵਰਤਨ ।

ਪ੍ਰਸ਼ਨ 10.
ਆਪਣੇ ਆਲੇ-ਦੁਆਲੇ ਦੀਆਂ ਵਸਤੂਆਂ ਨੂੰ ਸ਼ੁੱਧ ਪਦਾਰਥ ਜਾਂ ਮਿਸ਼ਰਣ ਵਿੱਚ ਵੰਡਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰੋ ।
ਉੱਤਰ-
ਸ਼ੁੱਧ ਪਦਾਰਥ – ਹਾਈਡੋਜਨ, ਤਾਂਬਾ, ਸੋਨਾ, ਨਮਕ, ਚੀਨੀ, ਪਾਣੀ, ਲੋਹਾ, ਚਾਂਦੀ ਆਦਿ ।
ਮਿਸ਼ਰਨ – ਸੋਡਾ ਵਾਟਰ, ਨਮਕ ਦਾ ਘੋਲ, ਸ਼ਰਬਤ, ਧੂੰਆਂ, ਆਈਸਕ੍ਰੀਮ, ਗੰਧਕ-ਲੋਹ ਚੂਰਣ ਦਾ ਮਿਸ਼ਰਣ, ਪਾਣੀ ਅਤੇ ਤੇਲ ਦਾ ਘੋਲ ।

Punjab State Board PSEB 11th Class Maths Book Solutions Chapter 10 Straight Lines Ex 10.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Maths Chapter 10 Straight Lines Ex 10.2

Question 1.
Write the equations for the x and y-axes.
Answer.
The y-coordinate of every point on the x-axis is 0.
Therefore, the equation of the x – axis is y = 0.
The x-coordinate of every point on the y – axis is 0.
Therefore, the equation of the y-axis is x = 0.

Question 2.
Find the equation of the line which passes through the point (- 4, 3) with slope \(\frac{1}{2}\).
Answer.
We know that the equation of the line passing through point (x₀, y₀), whose slope is m, is (y – y₀) = m (x – x₀).
Thus, the equation of the line passing through point (- 4, 3), whose slope is \(\frac{1}{2}\) is
(y – 3) = – (x + 4)
2 (y – 3) = x + 4
2y – 6 = x + 4
i.e., x – 2y + 10 = 0.

Question 3.
Find the equation of the line which passes through (0, 0) with slope m.
Answer.
We know that the equation of the line passing through point (x₀, y₀), whose slope is m, is
(y – y₀) = m (x – x₀)
Thus, the equation of the line passing through point (0, 0), whose slope is m is (y – 0) = m(x – 0)
i.e., y = mx.

Question 4.
Find the equation of the line which passes through (2, 2√3) and is inclined with the x-s’ at an angle of 75°.
Answer.
The slope of the line that inclines with the x-axis at an angle of 75° is m = tan75°
m = tan (45° + 30°)
= \(\frac{\tan 45^{\circ}+\tan 30^{\circ}}{1-\tan 45^{\circ} \tan 30^{\circ}}\)

= \(\frac{1+\frac{1}{\sqrt{3}}}{1-1 \cdot \frac{1}{\sqrt{3}}}\)

= \(\frac{\frac{\sqrt{3}+1}{\sqrt{3}}}{\frac{\sqrt{3}-1}{\sqrt{3}}}=\frac{\sqrt{3}+1}{\sqrt{3}-1}\)

We know that the equation of the line passing through point (x₀, y₀), whose slope is m, is (y – y₀) = m(x – x₀).
Thus, if a line passes though (2, 2√3) and inclines with the x-axis at an angle of 75°, then the equation of the line is given as
(y – 2√3) = (x – 2)
(y – 2√3) (√3 – 1) = (√3 + 1)(x – 2)
y(√3 – 1) – 2 √3 (√3 – 1) = x(√3 + 1) – 2 (√3 + 1)
(√3 + 1) x – (√3 – 1) y = 2√3 + 2 – 6 + 2√3
(√3 + 1) x – (√3 – 1) y = 4√3 – 4
i.e., (√3 + 1) x – (√3 – 1) y = 4(√3 – 1).

Question 5.
Find the equation of the line which intersects the x-axis at a distance of 3 units to the left of origin with slope – 2.
Answer.
It is known that if a line with slope m makes x-intercept d, then the equation of the line is given as y = m(x – d).
For the line intersecting the x-axis at a distance of 3 units to the left of the origin, d = – 3.
The slope of the line is given as m = – 2.
Thus, the required equation of the given line is
y = – 2 [x – (- 3)] = – 2x – 6
i.e., 2x + y + 6 = 0.

Question 6.
Find the equation of the line which intersects the y-axis at a distance of 2 units above the origin and makes an angle of 30° with the positive direction of the x-axis.
Answer.

The line intersect the 7-axis at distance of 2 units above the origin. It show that the line passes through (0, 2).
It makes an angle 30° with the positive direction of X – axis.
1 X
So, the slope of the line is = tan 30° = \(\frac{1}{\sqrt{3}}\)
Thus, the equation of straight line is
y – y₁ = m (x – x₁)
y – 2 = \(\frac{1}{\sqrt{3}}\) (x – 0)
\(\frac{x}{\sqrt{3}}\) – y + 2 = 0
x – √3y + 2√3 = 0.

Question 7.
Find the equation of the line which passes through the points (- 1, 1) and (2, – 4).
Answer.
Given points are A (x₁, y₁) = (- 1, 1) and B(x₂, y₂) = (2, – 4), then equation of line AB is
y – y₁ = \(\frac{y-{2}-y-{1}}{x-{2}-x-{1}}\) (x – x₁)
⇒ y – 1 = \(\frac{-4-1}{2+1}\) (x + 1)
[x₁ = – 1, y₁ = 1, x₂ = 2, y₂ = – 4]
⇒ y – 1 = – \(\frac{5}{3}\) (x + 1)
⇒ 3y – 3 = – 5x – 5
⇒ 5x + 3y + 2 = 0

Question 8.
Find the equation of the line which is at a perpendicular distance of 5 units from the origin and the angle made by the perpendicular with the positive x – axis is 30°.
Answer.
If p is the length of the normal from the origin to a line and A is the angle made by the normal with the positive direction of the x-axis, then the equation of the line is given by x cos A + y sin A = p
Here, p = 5 units and A = 30°
Thus, the required equation of the given line is x cos 30° + y sin 30° = 5
x \(\frac{\sqrt{3}}{2}\) + y . \(\frac{1}{2}\) = 5
i.e., √3x + y = 10.

Question 9.
The vertices of ∆PQR are P(2, 1), Q(- 2, 3) and R(4, 5). Find equation of the median through the vertex R.
Answer.
Since, median bisects the opposite sides i. e., S is the mid-point of PQ.
S = \(\left(\frac{\ddot{x}-{1}+x-{2}}{2}, \frac{y-{1}+y-{2}}{2}\right)\)

= \(\left(\frac{2-2}{2}, \frac{1+3}{2}\right)=\left(0, \frac{4}{2}\right)\)

= (0, 2)

y – y₁ = \(\frac{y-{2}-y-{1}}{x-{2}-x-{1}}\) (x – x₁)
⇒ y – 5 = \(\frac{2-5}{0-4}\) (x – 4)
[∵ x₁ = 2, y₁ = 1, x₁ = – 2, y₁ = 3]
⇒ y – 5 = \(\frac{-3}{-4}\) (x – 4)
4y – 20 = 3x – 12
⇒ 3x – 4y + 8 = 0

Question 10.
Find the equation of the line passing through (- 3, 5) and perpendicular to the line through the points (2, 5) and (- 3, 6).
Answer.
The slope of the line joining the points (2, 5) and (- 3, 6) is
m = \(\frac{6-5}{-3-2}=\frac{1}{-5}\)

We know that two non-vertical lines are perpendicular to each other if and only if their slopes are negative reciprocals of each other.

Therefore, slope of the line perpendicular to the line through the points (2, 5) and (- 3, 6)
= \(-\frac{1}{m}=-\frac{1}{\left(\frac{-1}{5}\right)}\) = 5

Now, the equation of the line passing through point (- 3, 5), whose slope is 5, is
(y – 5) = 5 (x + 3)
y – 5 = 5x + 15
i.e., 5x – y + 20 = 0.

Question 11.
A line perpendicular to the line segment joining the points (1, 0) and (2, 3) divides it in the ratio 1 : n. Find the equation of the line.
Answer.

Let the given points are A(1, 0) and B(2, 3).
Let the line PQ divide AB in the ratio 1 : n at R internally.
Then, coordinates of R = \(\left(\frac{1 \times x-{2}+n \times x-{1}}{1+n}, \frac{1 \times y-{2}+n \times y-{1}}{1+n}\right)\)

= \(\left(\frac{1 \times 2+n \times 1}{1+n}, \frac{1 \times 3+n \times 0}{1+n}\right)\)

[∵ x₁ = 1, y₁ = 0, x₂ = 2, y₂ = 3]

= \(\left(\frac{n+2}{n+1}, \frac{3}{1+n}\right)\)

Let the slope of the line is m.
Also, PQ ⊥ AB
∴ Slope of the line PQ × Slope of the line AB = – 1
⇒ m × \(\frac{y-{2}-y-{1}}{x-{2}-x-{1}}\) = – 1

⇒ m × \(\frac{3-0}{2-1}\) = – 1

[∵ x₁ = 1, y₁ = 0, x₂ = 2, y₂ = 2]

⇒ m × 3 = – 1
⇒ m = – \(\frac{1}{3}\)

Now, equation of line PQ y using y – y₀ = m (x – x₀)

y – \(\frac{3}{1+n}\) = \(\frac{-1}{3}\left(x-\frac{n+2}{n+1}\right)\)

[∵ R\(\left(\frac{n+2}{n+1}, \frac{3}{1+n}\right)\) = (x₁, y₁)

\(\frac{3(n+1) y-9}{1+n}=\frac{-x(n+1)+(n+2)}{n+1}\)

⇒ 3 (n + 1) y – 9 = – x (n + 1) + (n + 2)
⇒ x (n + 1) + 3 (n + 1) y = n + 2 + 9
⇒ x (n + 1) + 3 (n + 1) y = n + 11
Which is the required equation of line.

Question 12.
Find the equation of a line that cuts off equal intercepts on the coordinate axes and passes through the point (2, 3).
Answer.
The equation of a line in the intercept form is
\(\frac{x}{a}+\frac{y}{b}\) = 1 …………….(i)
Here, a and b are the intercepts on x and y axes respectively.
It is given that the line cuts off equal intercepts on both the axes.
This means that a = b.
Accordingly, equation (i) reduces to
\(\frac{x}{a}+\frac{y}{a}\) = 1
x + y = a ………………(ii)
Since the given line passes through point (2, 3), equation (ii) reduces to
2 + 3 = a
a = 5
On substituting the value of a in equation (ii), we obtain x + y = 5, which is the required equation of the line.

Question 13.
Find equation of the line passing through the point (2, 2) and cutting off intercepts on the axes whose sum is 9.
Answer.
The equation of a line in the intercept form is
\(\frac{x}{a}+\frac{y}{b}\) = 1 ……………(i)
Here, a and b are the intercepts on x and y axes respectively.
It is given that a + b = 9
⇒ b = 9 – a ………….. (ii)
From equations (i) and (ii), we obtain
\(\frac{x}{a}+\frac{y}{9-a}\) = 1 ………..(iii)

It is given that the line passes through point (2, 2).
Therefore, equation (iii) reduces to \(\frac{2}{a}+\frac{2}{9-a}\) = 1
⇒ \(2\left(\frac{1}{a}+\frac{1}{9-a}\right)\) = 1

⇒ \(2\left(\frac{9-a+a}{a(9-a)}\right)\) = 1

⇒ \(\frac{18}{9 a-a^{2}}\) = 1

⇒ 18 = 9a – a²
⇒ a² – 9a + 18 = 0
⇒ a² – 6a – 3a + 18 = 0
⇒ a (a – 6) – 3 (a – 6) = 0
⇒ (a – 6) (a – 3) = 0
⇒ a = 6 or a = 3
If a = 6 and b = 9 – 6 =3, then the equation of the line is \(\frac{x}{6}+\frac{y}{3}\) = 1
⇒ x + 2y – 6 = 0
If a = 3 and = 9 – 3 = 6, then the equation of the line is
\(\frac{x}{6}+\frac{y}{3}\) = 1
⇒ 2x + y – 6 = 0.

Question 14.
Find equation of the line through the point (0, 2) making an angle – with the positive x-axis. Also, find the equation of line 3 parallel to it and crossing the y-axis at a distance of 2 units below the origin.
Answer.

Slope of the line = tan \(\frac{2 \pi}{3}\)
tan (π – \(\frac{\pi}{3}\)) = tan \(\frac{\pi}{3}\) = – √3
Equation of the line AC with slope = – √3 and passing through the point D given by
y – 2 = – √3(x – 0)
⇒ √3x + y – 2 = 0
For beyond past, we take another line BD parallel to AC.
∴ Slope of the line BD = Slope of AC = – √3
BD is passing through the point D{0, – 2)
∴ Equation of BD is y + 2 = √3(x – 0)
⇒ √3x + y + 2 = 0
Hence, equation of AC and BD are,
√3x + y – 2 = 0 and √3x + y + 2 = 0.

Question 15.
The perpendicular from the origin to a line meets it at the point (- 2, 9), find the equation of the line.
Answer.
The slope of the line joining the origin (0, 0) and point (- 2, 9) is
m₁ = \(\frac{9-0}{-2-0}=-\frac{9}{2}\)

Accordingly, the slope of the line, perpendicular to the line joining the origin and point (- 2, 9) is
m₂ = \(-\frac{1}{m-{1}}=-\frac{1}{\left(-\frac{9}{2}\right)}=\frac{2}{9}\)

Now, the equation of the line passing through point (- 2, 9) and having a slope m2 is
(y – 9) = \(\frac{2}{9}\) (x + 2)
9y – 81 = 2x + 4
2x – 9y + 85 = 0.

Question 16.
The length L (in centimetre) of a copper rod is a linear function of its Celsius temperature C. In an experiment, if L = 124.942 when C = 20 and L = 125.134 when C = 110, express L in terms of C.
Answer.
Since, L is linear function of C.
L = a + bC …………….(i)
For L = 124.942, C = 20
124.942 = a + 20b ………………(ii)
For L = 125.134 C = 110
∴ 125.134 = a + 1106 ……………(iii)
Subtracting eq. (ii) from eq. (iii), we get
0. 192 = 90b
b = \(\frac{0.192}{90}\) = 0.00213
From eq. (ii),
124.942 = a + 20 × 0.00213 = a + 0.0426
a = 124.942 – 0.0426 = 124.8994
Hence from eq. (i) L in terms of C is
L = 124.8994 + 0.00213C.

Question 17.
The owner of a milk store finds that, he can sell 980 litres of milk each week at Rs. 14/litre and 1220 litres of milk each week at Rs. 16/litre. Assuming a linear relationship between selling price and demand, how many litres could he sell weekly at Rs. 17/litre?
Answer.
Let price and litre be denoted in ordered pair (x, y), where x denotes the ₹ per litre and y denotes the quantity of milk in litre.
Given, (14980) and (161220) are two points.
Let linear relations i. e., linear equation be
y – y₁ = \(\frac{y-{2}-y-{1}}{x-{2}-x-{1}}\) (x – x₁)

y – 980 = \(\frac{1220-980}{16-14}\) (x – 14)

y – 980 = \(\frac{240}{2}\) (x – 14)
[∵ x₁ = 14, y₁ = 980, x₂ = 16, y₂ = 1220]
⇒ y – 980 = 120 (x – 14)
⇒ y – 980 = 120x – 120 × 14
⇒ 120x – y = 1680 – 980
⇒ 120x – y = 700
When price JC = 17,
120 x 17 – y = 700
y = 2040 – 700 = 1340
He will sell weekly 1340 L milk at the rate of ₹ 172.

Question 18.
P(a, b) is the mid-point of a line segment between axes. Show that equation of the line is \(\frac{x}{a}+\frac{y}{b}\) = 2.
Answer.
Let AB be the line segment between the axes and let P(a, b) be its mid-point.

Let the coordinates of A and B be (0, y) and (x, 0) respectively.
Since P(a, b) is the mid-point of AB.
\(\left(\frac{0+x}{2}, \frac{y+0}{2}\right)\) = (a, b)

\(\left(\frac{x}{2}, \frac{y}{2}\right)\) = (a, b) and

\(\frac{x}{2}\) = a and \(\frac{y}{2}\) = b
x = 2a and y = 2b
Thus, the respectively coordinares of A and B are (0, 2b) and (2a, 0).
The equation of the line passing through points (0, 2b) and (2a, 0) is

(y – 2b) = \(=\frac{(0-2 b)}{(2 a-0)}\) (x – 0)

y – 2b = \(\frac{-2 b}{2 a}\) (x)

a (y – 2b) = – bx
ay – 2ab = – bx
i.e., bx + ay = 2ab
On dividing both sides by ab, we obtain
\(\frac{b x}{a b}+\frac{a y}{a b}=\frac{2 a b}{a b}\)

⇒ \(\frac{x}{a}+\frac{y}{b}\) = 2
Thus, the equation of the line is \(\frac{x}{a}+\frac{y}{b}\) = 2.

Question 19.
Point R (h, k) divides a line segment between the axes in the ratio 1 : 2. Find equation of the line.
Answer.

Let AB be the line segment between the axes such that point R(h, k) divides AB in the ratio 1 : 2.
Let the respective coordinates of A and B be (x, 0) and (0, y).
Since point R(h, k) divides AB in the ratio 1 : 2, according to the section formula,
(h, k) = \(=\left(\frac{1 \times 0+2 \times x}{1+2}, \frac{1 \times y+2 \times 0}{1+2}\right)\)

(h, k) = \(\left(\frac{2 x}{3}, \frac{y}{3}\right)\)

⇒ h = \(\frac{2 x}{3}\) and k = \(\frac{y}{3}\)
⇒ x = \(\frac{3 h}{2}\) and y = 3k

Therefore, the respective coordinates of A and B are (\(\frac{3 h}{2}\), o) and (0, 3k).

Now, the equation of line AB passing through points (\(\frac{3 h}{2}\), 0) and (0, 3k) is

(y – 0) = \(\frac{3 k-0}{0-\frac{3 h}{2}}\) (x – \(\frac{3 h}{2}\))

y = – \(\frac{2 k}{h}\) (x – \(\frac{3 h}{2}\))
hy = – 2kx + 3hk
i.e., 2kx + hy = 3hk
Thus, the required equation of the line is 2kx + hy = 3hk.

Question 20.
By using the concept of equation of a line, prove that the three points (3, 0), (- 2, – 2) and (8, 2) are collinear.
Answer.
In order to show that points (3, 0) (- 2, – 2) and (8, 2) are coimear, it suffices to show that the line passing through points (3, 0) and (- 2, – 2) also passes through point (8, 2).
The equation of the line passing through points (3, 0) and (- 2, – 2) is
(y – 0) = \(\frac{(-2-0)}{(-2-3)}\) (x – 3)

y = \(\frac{-2}{-5}\) (x – 3)
5y = 2x – 6
i.e., 2x – 5y = 6
It is observed that at x = 8 and y = 2,
5y = 2x – 6
i.e., 2x – 5y = 6
It is observed that at x = 8 and y = 2,
L.H.S. = 2 × 8 – 5 × 2
= 16 – 10 = 6 = R.H.S.
Therefore, the line passing through points (3, 0) and (- 2, – 2) also passes through point (8, 2).
Hence, points (3, 0), (- 2, – 2) and (8, 2) are collinear.

Punjab State Board PSEB 7th Class Science Book Solutions Chapter 13 ਗਤੀ ਅਤੇ ਸਮਾਂ Textbook Exercise Questions, and Answers.

PSEB Solutions for Class 7 Science Chapter 13 ਗਤੀ ਅਤੇ ਸਮਾਂ

PSEB 7th Class Science Guide ਗਤੀ ਅਤੇ ਸਮਾਂ Intext Questions and Answers

ਸੋਚੋ ਅਤੇ ਉੱਤਰ ਦਿਓ : (ਪੇਜ 157)

ਪ੍ਰਸ਼ਨ 1.
ਸਧਾਰਨ ਪੈਂਡੂਲਮ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਸਧਾਰਨ ਪੈਂਡੂਲਮ-ਇੱਕ ਧਾਗੇ ਨਾਲ ਬੰਨ੍ਹ ਕੇ ਕਿਸੇ ਸਥਿਰ ਥਾਂ ਤੋਂ ਲਟਕਾਏ ਗਏ ਭਾਰੇ ਪੁੰਜ (ਧਾਤੂ ਦੇ ਗੋਲੇ) ਨੂੰ ਸਧਾਰਨ ਪੈਂਡੂਲਮ ਆਖਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 2.
ਸਧਾਰਨ ਪੈਂਡੂਲਮ ਦੀ ਇੱਧਰ-ਉੱਧਰ ਦੀ ਗਤੀ ਨੂੰ ਕੀ ਆਖਦੇ ਹਨ ?
ਉੱਤਰ-
ਸਧਾਰਨ ਪੈਂਡੂਲਮ ਦੀ ਇੱਧਰ-ਉੱਧਰ ਦੀ ਗਤੀ ਨੂੰ ਡੋਲਨ ਗਤੀ ਆਖਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 3.
ਪੈਂਡੂਲਮ ਦੇ ਇੱਕ ਡੋਲਨ ਲਈ ਲੱਗੇ ਸਮੇਂ ਨੂੰ ………….. ਕਹਿੰਦੇ ਹਨ ।
ਉੱਤਰ-
ਆਵਰਤ ਕਾਲ ॥

ਪ੍ਰਸ਼ਨ 4.
ਪ੍ਰਤੀ ਇਕਾਈ ਸਮੇਂ ਵਿੱਚ ਕੀਤੀਆਂ ਡੋਲਨਾਂ ਦੀ ਸੰਖਿਆ ਨੂੰ …………. ਕਹਿੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਆਤੀ ।

ਸੋਚੋ ਅਤੇ ਉੱਤਰ ਦਿਓ : (ਪੇਜ 158)

ਪ੍ਰਸ਼ਨ 1.
ਅਸੀਂ ਵਿਰਾਮ ਘੜੀ ਨਾਲ ਕੀ ਮਾਪਦੇ ਹਾਂ ?
ਉੱਤਰ-
ਛੋਟੇ ਸਮਾਂ ਅੰਤਰਾਲ ਨੂੰ ਮਾਪਣ ਲਈ ਵਿਰਾਮ ਘੜੀ ਦੀ ਵਰਤੋਂ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਦੂਰੀ ਨੂੰ ਮਾਪਣ ਦੀ S.I. ਇਕਾਈ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਮੀਟਰ ।

PSEB 7th Class Science Guide ਗਤੀ ਅਤੇ ਸਮਾਂ Textbook Questions and Answers

1. ਖ਼ਾਲੀ ਸਥਾਨ ਭਰੋ-

(i) ਕਿਸੇ ਵਸਤੂ ਦੀ ਸਿੱਧੀ ਰੇਖਾ ਵਿੱਚ ਗਤੀ ਨੂੰ ………. ਗਤੀ ਆਖਦੇ ਹਨ ।
ਉੱਤਰ-
ਸਰਲ ਰੇਖੀ,

(ii) ਇੱਕ ਘੜੀ ਦੀ ਵਰਤੋਂ ………. ਮਾਪਣ ਲਈ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ।
ਉੱਤਰ-
ਸਮਾਂ,

(iii) ਇੱਕ ਸਮਾਨ ਗਤੀ ਲਈ ਤੈਅ ਕੀਤੀ ਦੂਰੀ ਅਤੇ ਲੱਗੇ ਸਮੇਂ ਵਿੱਚ ਬਣਾਇਆ ਗ੍ਰਾਫ਼ ਇੱਕ ………. ਰੇਖਾ ਹੈ ।
ਉੱਤਰ-
ਸਿੱਧੀ,

(iv) ਇੱਕ ਸਧਾਰਨ ਪੈਂਡੂਲਮ ਦੀ ਗਤੀ ਨੂੰ ………. ਗਤੀ ਆਖਦੇ ਹਨ ।
ਉੱਤਰ-
ਡੋਲਨ 1

2. ਹੇਠ ਲਿਖਿਆਂ ਲਈ ਠੀਕ ਜਾਂ ਗਲਤ ਲਿਖੋ

(i) ਪ੍ਰਤੀ ਇਕਾਈ ਸਮੇਂ ਵਿੱਚ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ ਨੂੰ ਚਾਲ ਆਖਦੇ ਹਨ ।
ਉੱਤਰ-
ਠੀਕ,

(ii) ਚਾਲ ਦੀ S1 ਇਕਾਈ Km/s ਹੈ ।
ਉੱਤਰ-
ਗ਼ਲਤ,

(iii) ਪੈਂਡੂਲਮ ਦੁਆਰਾ ਇੱਕ ਡੋਲਨ ਲਈ ਲਗਾਏ ਗਏ ਸਮੇਂ ਨੂੰ ਇਸਦਾ ਆਵਰਤ ਕਾਲ ਆਖਦੇ ਹਨ ।
ਉੱਤਰ-
ਠੀਕ,

(iv) ਚੱਲਦੇ ਹੋਏ ਵਾਹਨਾਂ ਦੀ ਗਤੀ ਮਾਪਣ ਲਈ ਵਰਤੇ ਜਾਂਦੇ ਯੰਤਰ ਨੂੰ ਸਪੀਡੋਮੀਟਰ ਆਖਦੇ ਹਨ ।
ਉੱਤਰ-
ਠੀਕ ।

3. ਕਾਲਮ ਮਿਲਾਨ ਕਰੋ –

ਉੱਤਰ

4. ਬਹੁ-ਵਿਕਲਪੀ ਪ੍ਰਸ਼ਨ

(i) ਹੇਠ ਦਿੱਤੇ ਵਿੱਚੋਂ ਕਿਹੜਾ ਦੂਰੀ-ਸਮਾਂ ਗ੍ਰਾਫ਼ ਵਸਤੂ ਦੀ ਵਿਰਾਮ ਅਵਸਥਾ ਨੂੰ ਦਰਸਾਉਂਦਾ ਹੈ ?

ਉੱਤਰ-
(ੲ) ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਦੂਰੀ-ਸਮਾਂ ਗ੍ਰਾਫ਼ X-ਧੁਰੇ (ਸਮਾਂ ਧੁਰੇ) ਦੇ ਸਮਾਨਾਂਤਰ ਇੱਕ ਸਿੱਧੀ ਰੇਖਾ ਹੁੰਦੀ ਹੈ ।

(ii) ਹੇਠ ਦਿੱਤੇ ਵਿੱਚੋਂ ਕਿਹੜੀ ਸਮੀਕਰਨ ਗਤੀ ਪਤਾ ਕਰਨ ਲਈ ਠੀਕ ਸੰਬੰਧ ਦਰਸਾਉਂਦੀ ਹੈ ?
(ਉ) ਚਾਲ = ਦੂਰੀ x ਸਮਾਂ
(ਆ) ਚਾਲ = ਦੂਰੀ/ਸਮਾਂ
(ਇ) ਚਾਲ = ਸਮਾਂ/ਦੂਰੀ
(ਸ) ਚਾਲ = 1/ਦੂਰੀ x ਸਮਾਂ ।
ਉੱਤਰ-
(ਅ) ਚਾਲ = ਦੂਰੀ/ਸਮਾਂ ।

(iii) ਸਧਾਰਨ ਪੈਂਡੂਲਮ ………….. ਗਤੀ ਦੀ ਉਦਾਹਰਣ ਹੈ ?

(ਉ) ਸਰਲ ਰੇਖੀ ਗਤੀ
(ਅ) ਡੋਲਨ ਗਤੀ
(ਇ) ਆਵਰਤੀ ਗਤੀ
(ਸ) ਚੱਕਰਾਕਾਰ ਗਤੀ ।
ਉੱਤਰ-
(ੲ) ਆਵਰਤੀ ਗਤੀ ।

(iv). ਇਕ ਕਾਰ 40 km/h ਦੀ ਚਾਲ ਨਾਲ 15 ਮਿੰਟ ਲਈ ਚਲਦੀ ਹੈ ਅਤੇ ਅਗਲੇ 15 ਮਿੰਟ ਲਈ ਉਸਦੀ ਚਾਲ 60 km/h ਹੋ ਜਾਂਦੀ ਹੈ | ਕਾਰ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਗਈ ਕੁੱਲ ਦੁਰੀ ਪਤਾ ਕਰੋ ।
(ਉ) 100 km
(ਅ) 25 km
(ਇ) 15 km
(ਸ) 10 km.
ਉੱਤਰ-
(ਅ) 25 km.

5. ਬਹੁਤ ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ

ਪ੍ਰਸ਼ਨ (i)
ਚਾਲ ਦੀ ਪਰਿਭਾਸ਼ਾ ਲਿਖੋ । ਇਸ ਦੀ S.I. ਇਕਾਈ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਚਾਲ-ਇਕਾਈ ਸਮੇਂ ਵਿੱਚ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ ਨੂੰ ਉਸ ਵਸਤੂ ਦੀ ਚਾਲ ਕਹਿੰਦੇ ਹਨ ।

ਇਕਾਈ-ਚਾਲ ਨੂੰ ਮਾਪਣ ਦੀ S.I. ਇਕਾਈ ਮੀਟਰ/ਸਕਿੰਟ (m/s) ਹੈ ।

ਪ੍ਰਸ਼ਨ (ii)
ਪੁਰਾਣੇ ਸਮੇਂ ਵਿੱਚ ਲੋਕ ਸਮਾਂ ਮਾਪਣ ਲਈ ਕਿਹੜੇ ਉਪਕਰਣਾਂ ਦੀ ਵਰਤੋਂ ਕਰਦੇ ਸਨ ?
ਉੱਤਰ-
ਪੁਰਾਣੇ ਸਮੇਂ ਵਿੱਚ ਲੋਕ ਕੁਦਰਤੀ ਘਟਨਾਵਾਂ ਦੁਆਰਾ ਸਮੇਂ ਦਾ ਮਾਪ ਕਰਦੇ ਸਨ । ਸਮਾਂ ਬੀਤਣ ਨਾਲ ਸਮਾਂ ਮਾਪਣ ਲਈ ਕੁੱਝ ਉਪਕਰਣਾਂ ਦੀ ਖੋਜ ਕੀਤੀ ਗਈ । ਉਨ੍ਹਾਂ ਵਿੱਚੋਂ ਕੁੱਝ ਹੇਠਾਂ ਦਿੱਤੇ ਗਏ ਹਨ-

• ਸੂਰਜੀ ਘੜੀ-ਸੂਰਜ ਦੀ ਸਥਿਤੀ ਵਿੱਚ ਪਰਿਵਰਤਨ ਕਾਰਨ ਪਰਛਾਵੇਂ ਦੀ ਸਥਿਤੀ ਵਿਚ ਪਰਿਵਰਤਨ ਨੂੰ ਸੂਰਜੀ ਘੜੀ ਦੁਆਰਾ ਮਾਪਿਆ ਜਾਂਦਾ ਹੈ ।
• ਰੇਤ ਘੜੀ-ਇਸ ਘੜੀ ਵਿੱਚ ਰੇਤ ਨੂੰ ਇੱਕ ਬਲਬ ਤੋਂ ਦੂਜੇ ਬਲਬ ਵਿੱਚ ਇੱਕ ਘੰਟੇ ਵੱਗਣੇ ਨੂੰ ਸਮਾਂ ਮਾਪਣ ਲਈ ਵਰਤਿਆ ਜਾਂਦਾ ਹੈ ।
• ਪਾਣੀ ਘੜੀ-ਇੱਕ ਬਰਤਨ ਤੋਂ ਦੂਜੇ ਬਰਤਨ ਵਿੱਚ ਖ਼ਾਸ ਸਮੇਂ ਵਿੱਚ ਪਾਣੀ ਦੇ ਵੱਗਣ ਨੂੰ ਸਮਾਂ ਮਾਪਣ ਲਈ ਵਰਤਿਆ ਜਾਂਦਾ ਹੈ ।
• ਪੈਂਡੂਲਮ-ਸਧਾਰਨ ਪੈਂਡੂਲਮ ਹਰੇਕ ਡੋਲਨ ਲਈ ਬਰਾਬਰ ਸਮਾਂ ਲੈਂਦਾ ਹੈ । ਇਸ ਕਾਲ ਸਮੇਂ ਨੂੰ ਆਵਰਤ ਕਾਲ ਕਹਿੰਦੇ ਹਨ । ਇਸ ਲਈ ਪੈਂਡੂਲਮ ਨੂੰ ਸਮਾਂ ਮਾਪਣ ਲਈ ਵਰਤਿਆ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ (iii)
ਇਹਨਾਂ ਦਾ ਮਾਪ ਪਤਾ ਕਰਨ ਲਈ ਵਰਤੇ ਜਾਂਦੇ ਉਪਕਰਣਾਂ ਦੇ ਨਾਂ ਲਿਖੋ ।
(ਉ) ਚੱਲਦੇ ਵਾਹਨ ਦੀ ਚਾਲ
(ਅ) ਵਾਹਨਾਂ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਦੂਰੀ ।
ਉੱਤਰ-
(ਉ) ਚੱਲਦੇ ਵਾਹਨ ਦੀ ਚਾਲ ਮਾਪਣ ਲਈ ਉਪਕਰਣ-ਸਪੀਡੋਮੀਟਰ ।
(ਅ) ਵਾਹਨਾਂ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਗਈ ਦੁਰੀ ਨੂੰ ਮਾਪਣ ਲਈ ਉਪਕਰਣ-ਓਡੋਮੀਟਰ ।

ਪ੍ਰਸ਼ਨ (iv)
ਗ੍ਰਾਫ਼ ਕੀ ਹੁੰਦਾ ਹੈ ? ਇਸ ਦੀਆਂ ਕਿਸਮਾਂ ਦੇ ਨਾਂ ਲਿਖੋ ।
ਉੱਤਰ-
ਗ੍ਰਾਫ਼-ਗ੍ਰਾਫ਼ ਇੱਕ ਮਾਤਰਾ ਦੀ ਦੂਸਰੀ ਮਾਤਰਾ ਨਾਲ ਤੁਲਨਾ ਨੂੰ ਚਿੱਤਰ ਰੂਪ ਵਿੱਚ ਦਰਸਾਉਂਦਾ ਹੈ । ਇੱਕ ਮਾਤਰਾ ਨੂੰ ਬਦਲਣ ਨਾਲ ਦੂਸਰੀ ਮਾਤਰਾ ਆਪਣੇ ਆਪ ਬਦਲ ਜਾਂਦੀ ਹੈ । ਗ੍ਰਾਫ਼ ਦੀਆਂ ਕਿਸਮਾਂ-ਫ਼ ਦੀਆਂ ਕਈ ਕਿਸਮਾਂ ਹੁੰਦੀਆਂ ਹਨ, ਜਿਵੇਂ –

1. ਰੇਖੀ ਫ਼,
2. ਛੜ ਗ੍ਰਾਫ਼,
3. ਪਾਈ ਚਾਰਟ ਜਾਂ ਚੱਕਰ ਗ੍ਰਾਫ਼ ॥

6. ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ

ਪ੍ਰਸ਼ਨ (i)
ਮੰਦ ਅਤੇ ਤੇਜ਼ ਗਤੀ ਵਿੱਚ ਅੰਤਰ ਦੱਸੋ । ਇਹਨਾਂ ਦੀਆਂ ਉਦਾਹਰਣਾਂ ਦਿਉ ।
ਉੱਤਰ-
ਮੰਦ ਗਤੀ-ਜੇ ਕੋਈ ਵਸਤੂ ਥੋੜੀ ਦੂਰੀ ਤੈਅ ਕਰਨ ਲਈ ਬਹੁਤ ਲੰਮਾ ਸਮਾਂ ਲਗਾਉਂਦੀ ਹੈ ਤਾਂ ਉਸ ਦੀ ਗਤੀ ਮੰਦ ਗਤੀ ਅਖਵਾਉਂਦੀ ਹੈ । ਉਦਾਹਰਣ-ਕੱਛੂ ਅਤੇ ਘੋਗਾ ਦੀ ਗਤੀ । ਤੇਜ਼ ਗਤੀ-ਜੇ ਕੋਈ ਵਸਤੁ ਉਸੀ ਦੁਰੀ ਨੂੰ ਤੈਅ ਕਰਨ ਲਈ ਘੱਟ ਸਮਾਂ ਲਗਾਉਂਦੀ ਹੈ ਤਾਂ ਉਸ ਦੀ ਗਤੀ ਤੇਜ਼ ਹੁੰਦੀ ਹੈ । ਉਦਾਹਰਣ-ਰੇਸਿੰਗ ਕਾਰ ਅਤੇ ਚੀਤੇ ਦੀ ਗਤੀ ।

ਪ੍ਰਸ਼ਨ (ii)
ਇੱਕ ਸਮਾਨ ਅਤੇ ਅਸਮਾਨ ਗਤੀਆਂ ਵਿੱਚ ਅੰਤਰ ਦੱਸੋ । ਇਹਨਾਂ ਦੀਆਂ ਉਦਾਹਰਣਾਂ ਦਿਉ ।
ਉੱਤਰ-
ਸਮਾਨ ਗਤੀ-ਜੇਕਰ ਕੋਈ ਵਸਤੁ ਬਰਾਬਰ ਸਮੇਂ ਵਿੱਚ ਬਰਾਬਰ ਦੂਰੀ ਤੈਅ ਕਰਦੀ ਹੈ ਭਾਵੇਂ ਕਾਲ ਅੰਤਰ ਕਿੰਨਾ ਵੀ ਛੋਟਾ ਕਿਉਂ ਨਾ ਹੋਵੇ, ਤਾਂ ਉਸ ਵਸਤੂ ਦੀ ਗਤੀ ਸਮਾਨ ਗਤੀ ਅਖਵਾਉਂਦੀ ਹੈ ।

ਉਦਾਹਰਣ-ਮੰਨ ਲਓ ਇੱਕ ਬੱਸ 10 km ਦੀ ਦੁਰੀ ਪਹਿਲੇ 15 ਮਿੰਟਾਂ ਵਿੱਚ ਤੈਅ ਕਰਦੀ ਹੈ ਅਤੇ ਅਗਲੇ 15 ਮਿੰਟਾਂ ਵਿੱਚ 10 Km ਦੀ ਦੁਰੀ, ਫਿਰ ਇਸ ਤੋਂ ਅਗਲੇ 15 ਮਿੰਟਾਂ ਵਿੱਚ ਵੀ 10 km ਦੀ ਦੂਰੀ ਤੈਅ ਕਰਦੀ ਹੈ, ਤਾਂ ਉਸ ਬੱਸ ਦੀ ਗਤੀ ਸਮਾਨ ਗਤੀ ਹੋਵੇਗੀ ।

ਅਸਮਾਨ ਗਤੀ-ਜੇਕਰ ਕੋਈ ਵਸਤੂ ਬਰਾਬਰ ਸਮੇਂ ਵਿੱਚ ਬਰਾਬਰ ਦੂਰੀ ਨਾ ਤੈਅ ਕਰੇ ਤਾਂ ਉਸ ਵਸਤੂ ਦੀ ਗਤੀ ਅਸਮਾਨ ਗਤੀ ਅਖਵਾਉਂਦੀ ਹੈ । ਉਦਾਹਰਣ-ਮੰਨ ਲਓ ਇੱਕ ਕਾਰ ਸਿੱਧੀ ਸੜਕ ‘ਤੇ 10 ਮਿੰਟਾਂ ਵਿੱਚ 25 km ਦੀ ਦੂਰੀ ਤੈਅ ਕਰਦੀ ਹੈ ਅਤੇ ਅਗਲੇ 10 ਮਿੰਟਾਂ ਵਿੱਚ 30 km ਅਤੇ ਇਸ ਤੋਂ ਅਗਲੇ 10 ਮਿੰਟਾਂ ਵਿੱਚ 20 km ਦੀ ਤੈਅ ਕਰਦੀ ਹੈ, ਤਾਂ ਉਸ ਕਾਰ ਦੀ ਗਤੀ ਅਸਮਾਨ ਗਤੀ ਹੋਵੇਗੀ ।

ਪ੍ਰਸ਼ਨ (iii)
ਅਜੈ ਆਪਣੇ ਘਰ ਤੋਂ 600 ਮੀਟਰ ਦੂਰ ਆਪਣੇ ਸਕੂਲ ਜਾਂਦਾ ਹੈ । ਜੇ ਉਸਨੂੰ ਆਪਣੇ ਘਰ ਤੋਂ ਪੈਦਲ ਸਕੂਲ ਤੱਕ ਜਾਣ ਵਿੱਚ 5 ਮਿੰਟ ਲੱਗਦੇ ਹੋਣ, ਤਾਂ ਉਸਦੀ ਚਾਲ ਮੀ./ਸੈਂ. ਵਿੱਚ ਪਤਾ ਕਰੋ ।
ਹੱਲ :
ਅਜੈ ਦੇ ਸਕੂਲ ਦੀ ਘਰ ਤੋਂ ਦੂਰੀ = 600 ਮੀਟਰ
ਸਕੂਲ ਤੋਂ ਘਰ ਦੀ ਦੂਰੀ ਤੈਅ ਕਰਨ ਵਿੱਚ ਲੱਗਿਆ ਸਮਾਂ = 5 ਮਿੰਟ
= 5 x 60 ਸਕਿੰਟ
= 300 ਸਕਿੰਟ

= 2 ਮੀ. /ਸੈਂ. ਉੱਤਰ

ਪ੍ਰਸ਼ਨ (iv)
ਦੋ ਸਟੇਸ਼ਨਾਂ ਵਿਚਕਾਰ 216 ਕਿਲੋਮੀਟਰ ਦੀ ਦੂਰੀ ਹੈ ।20 ਮੀ. /ਸੈਂ. ਦੀ ਚਾਲ ਨਾਲ ਚੱਲ ਰਹੀ ਇੱਕ ਰੇਲਗੱਡੀ ਕਿੰਨੇ ਘੰਟੇ ਵਿੱਚ ਇੱਕ ਸਟੇਸ਼ਨ ਤੋਂ ਦੂਜੇ ਸਟੇਸ਼ਨ ਤੱਕ ਪਹੁੰਚੇਗੀ ?
ਹੱਲ :
ਦੋ ਸਟੇਸ਼ਨਾਂ ਵਿਚਕਾਰ ਦੂਰੀ = 216 ਕਿਲੋਮੀਟਰ
ਰੇਲ ਗੱਡੀ ਦੀ ਚਾਲ = 20 ਮੀ. /ਸੈਂ.

ਦੋ ਸਟੇਸ਼ਨਾਂ ਵਿਚਕਾਰ ਤੈਅ ਕੀਤੀ ਦੂਰੀ ਨੂੰ ਲੱਗਾ ਸਮਾਂ =
= \(\frac{216}{72} \)
= 3 ਘੰਟੇ ਉੱਤਰ

ਪ੍ਰਸ਼ਨ (v)
ਇੱਕ ਸਧਾਰਨ ਪੈਂਡੂਲਮ 20 ਸਕਿੰਟ ਵਿੱਚ 50 ਡੋਲਨਾਂ ਪੂਰੀਆਂ ਕਰਦਾ ਹੈ । ਇਸ ਦਾ ਆਵਰਤ ਕਾਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ : ਸਧਾਰਨ ਪੈਂਡੂਲਮ ਦੇ ਡੋਲਨਾਂ ਦੀ ਸੰਖਿਆ = 50
50 ਡੋਲਨਾਂ ਨੂੰ ਪੂਰਾ ਕਰਨ ਲਈ ਲੱਗਾ ਸਮਾਂ = 20 ਸਕਿੰਟ
ਪੈਂਡੂਲਮ ਦਾ ਆਵਰਤ ਕਾਲ = ?
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ, ਆਵਰਤ ਕਾਲ = (1 ਡੋਲਨ ਨੂੰ ਲੱਗਾ ਸਮਾਂ)
= \(\frac{20}{50}\)
= \(\frac{2}{5}\) ਸਕਿੰਟ
= 0.4 ਸਕਿੰਟ ਉੱਤਰ

7. ਵੱਡੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ

ਪ੍ਰਸ਼ਨ (i)
ਇੱਕ ਸਧਾਰਨ ਪੈਂਡੂਲਮ ਦਾ ਆਵਰਤ ਕਾਲ ਪਤਾ ਕਰਨ ਦੀ ਵਿਧੀ ਲਿਖੋ ।
ਉੱਤਰ-
ਵਿਧੀ-ਚਿੱਤਰ ਵਿਚ ਦਿਖਾਏ ਅਨੁਸਾਰ ਲਗਭਗ 1 ਮੀਟਰ ਲੰਬੇ ਧਾਗੇ ਨਾਲ ਇੱਕ ਧਾਤੂ ਦੇ ਗੋਲੇ ਨੂੰ ਬੰਨ੍ਹ ਕੇ ਸਧਾਰਨ ਪੈਂਡੂਲਮ ਬਣਾਉ ॥ ਜੇ ਆਸ-ਪਾਸ ਕੋਈ ਪੱਖਾ ਚੱਲ ਰਿਹਾ ਹੈ ਤਾਂ ਉਸ ਨੂੰ ਬੰਦ ਕਰ ਦਿਓ । ਹੁਣ ਪੈਂਡੂਲਮ ਦੇ ਗੋਲੇ ਨੂੰ ਮੱਧ ਸਥਿਤੀ ਤੇ ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਆਉਣ ਦਿਉ । ਮੱਧ ਸਥਿਤੀ ਨੂੰ ਫ਼ਰਸ਼ ‘ਤੇ ਚਾਕ ਨਾਲ ਅੰਕਿਤ ਕਰੋ | ਪੈਂਡੂਲਮ ਦਾ ਆਵਰਤ ਕਾਲ ਮਾਪਣ ਲਈ ਇੱਕ ਵਿਰਾਮ ਘੜੀ ਜਾਂ ਮੋਬਾਈਲ ਜਾਂ ਹੱਥ ਘੜੀ ਲਓ । ਗੋਲੇ ਨੂੰ ਇੱਕ ਪਾਸੇ ਲਿਜਾਉ । ਧਿਆਨ ਰੱਖੋ ਕਿ ਧਾਗਾ ਖਿੱਚਿਆ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ । ਹੁਣ ਗੋਲੇ ਨੂੰ ਹੌਲੀ ਜਿਹੀ ਛੱਡ ਦਿਉ ।

ਜਦੋਂ ਗੋਲਾ ਅੰਤਿਮ ਸਥਿਤੀ ਤੇ ਹੋਵੇ ਤਾਂ ਵਿਰਾਮ ਘੜੀ ਨੂੰ ਸ਼ੁਰੂ ਕਰ ਦਿਉ । ਡੋਲਨਾਂ ਦੀ ਗਿਣਤੀ ਕਰੋ । ਪੈਂਡੂਲਮ ਦੁਆਰਾ 20 ਡੋਲਨਾਂ ਨੂੰ ਪੂਰਾ ਕਰਨ ਲਈ ਲਿਆ ਗਿਆ ਸਮਾਂ ਨੋਟ ਕਰੋ | ਆਪਣੇ ਨਿਰੀਖਣ ਨੂੰ ਦਿੱਤੀ ਗਈ ਸਾਰਣੀ ਵਿੱਚ ਨੋਟ ਕਰੋ | 20 ਡੋਲਨਾਂ ਲਈ ਲਏ ਗਏ ਸਮੇਂ ਨੂੰ ਡੋਲਨਾਂ ਦੀ ਗਿਣਤੀ (20) ਨਾਲ ਭਾਗ ਕਰੋ ਤਾਂ ਜੋ ਇੱਕ ਡੋਲਨ ਲਈ ਲੱਗਿਆ ਸਮਾਂ ਪਤਾ ਲੱਗ ਜਾਵੇਗਾ | ਪੈਂਡੂਲਮ ਦੁਆਰਾ ਇੱਕ ਡੋਲਨ ਲਈ ਲੱਗੇ ਸਮੇਂ ਨੂੰ ਇਸਦਾ ਆਵਰਤ ਕਾਲ ਆਖਦੇ ਹਨ । ਇਸਨੂੰ ਹਰਟਜ਼ (HZ) ਵਿੱਚ ਮਾਪਿਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਕਿਰਿਆ ਨੂੰ 3-4 ਵਾਰ ਦੁਹਰਾਉ ਅਤੇ ਹੇਠ ਦਿੱਤੀ ਸਾਰਣੀ ਵਿੱਚ ਨੋਟ ਕਰੋ ।

ਤੁਸੀਂ ਦੇਖੋਗੇ ਕਿ ਹਰ ਵਾਰ ਆਵਰਤ ਕਾਲ ਦਾ ਮਾਪ ਲਗਭਗ ਇੱਕੋ ਜਿਹਾ ਹੋਵੇਗਾ ।

ਪ੍ਰਸ਼ਨ (ii)
ਇੱਕ ਕਾਰ ਪਹਿਲੇ ਘੰਟੇ ਵਿੱਚ 60 ਕਿ. ਮੀ., ਦੂਜੇ ਘੰਟੇ ਵਿੱਚ 75 ਕਿ. ਮੀ., ਤੀਜੇ ਘੰਟੇ ਵਿੱਚ 55 ਕਿ. ਮੀ. ਅਤੇ ਚੌਥੇ ਘੰਟੇ ਵਿੱਚ 50 ਕਿ. ਮੀ. ਦੂਰੀ ਤੈਅ ਕਰਦੀ ਹੈ । ਕਾਰ ਦੀ ਗਤੀ ਲਈ ਦੂਰੀ-ਸਮਾਂ ਗ੍ਰਾਫ਼ ਬਣਾਉ ॥
(ੳ) ਪੂਰੇ ਸਫ਼ਰ ਲਈ ਕਾਰ ਦੀ ਚਾਲ ਪਤਾ ਕਰੋ ।
(ਅ) ਪਹਿਲੇ ਘੰਟੇ ਤੋਂ ਤੀਜੇ ਘੰਟੇ ਵਿਚਕਾਰ ਕਾਰ ਦੀ ਚਾਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ :

(ਉ)
ਪੂਰੇ ਸਫ਼ਰ ਵਿੱਚ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ = 60 ਕਿ.ਮੀ. +75 ਕਿ.ਮੀ. +55 ਕਿ.ਮੀ. +50 ਕਿ.ਮੀ.
= 240 ਕਿ.ਮੀ. ਕੁੱਲ ਲੱਗਿਆ ਸਮਾਂ = 4 ਘੰਟੇ

= 60 ਕਿ.ਮੀ. /ਘੰਟਾ ਉੱਤਰ

(ਅ) ਪਹਿਲੇ ਘੰਟੇ ਤੋਂ ਲੈ ਕੇ ਤੀਜੇ ਘੰਟੇ ਤੱਕ ਤੈਅ
1 ਕੀਤੀ ਗਈ ਦੁਰੀ = 75 ਕਿ.ਮੀ. + 55 ਕਿ.ਮੀ.
= 130 ਕਿ.ਮੀ.
ਸਮਾਂ = 2 ਘੰਟੇ
ਪਹਿਲੇ ਘੰਟੇ ਤੋਂ ਤੀਜੇ ਘੰਟੇ ਵਿਚਕਾਰ ਕਾਰ ਦੀ ਚਾਲ =
= 65 ਕਿ.ਮੀ. /ਘੰਟਾ ਉੱਤਰ

ਪ੍ਰਸ਼ਨ (iii)
ਚਿੱਤਰ ਵਿੱਚ ਦੋ ਵਾਹਨਾਂ A ਅਤੇ B ਦੀ ਗਤੀ ਲਈ ਦੂਰੀ-ਸਮਾਂ ਗ੍ਰਾਫ ਦਿੱਤਾ ਗਿਆ ਹੈ । ਦੋਹਾਂ ਵਿੱਚੋਂ ਕਿਸਦੀ ਚਾਲ ਜ਼ਿਆਦਾ ਹੈ ।

ਉੱਤਰ-
ਦੋਨੋਂ ਵਾਹਨਾਂ ਦੀ ਦੁਰੀ-ਸਮਾਂ ਗਾਫ਼ ਦੇ ਅਧਿਐਨ ਤੋਂ ਇਹ ਪਤਾ ਚਲਦਾ ਹੈ ਕਿ ਵਾਹਨ A ਲਈ ਦਰੀ ਅਤੇ ਸਮੇਂ ਦਾ ਅਨੁਪਾਤ ਵਾਹਨ B ਦੀ ਤੁਲਨਾ ਵਿੱਚ ਜ਼ਿਆਦਾ ਹੈ, ਇਸ ਲਈ A ਵਾਹਨ ਦੀ ਚਾਲ ਵਾਹਨ B ਦੇ ਮੁਕਾਬਲੇ ਵੱਧ ਹੈ ।

PSEB Solutions for Class 7 Science ਗਤੀ ਅਤੇ ਸਮਾਂ Important Questions and Answers

1. ਖ਼ਾਲੀ ਥਾਂਵਾਂ ਭਰੋ :

(i) ਕਿਸੇ ਵਸਤ ਦੁਆਰਾ ਇਕਾਈ ਸਮੇਂ ਵਿਚ ਤੈਅ ਕੀਤੀ ਗਈ ਦੁਰੀ ਨੂੰ ……………… ਆਖਦੇ ਹਨ ।
ਉੱਤਰ-
ਚਾਲ,

(ii) ਪੈਂਡੂਲਮ ਦੁਆਰਾ ਇੱਕ ਡੋਲਨ ਲਈ ਲੱਗੇ ਸਮੇਂ ਨੂੰ ਇਸ ਦਾ ………….. ਕਹਿੰਦੇ ਹਨ ।
ਉੱਤਰ-
ਆਵਰਤ ਕਾਲ,

(iii) ਵਾਹਨਾਂ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ ਮਾਪਣ ਲਈ ਵਰਤੇ ਜਾਣ ਵਾਲੇ ਯੰਤਰ ਨੂੰ ……….. ਕਹਿੰਦੇ ਹਨ ।
ਉੱਤਰ-
ਓਡੋਮੀਟਰ,

(iv) ਚਲਦੇ ਹੋਏ ਵਾਹਨਾਂ ਦੀ ਚਾਲ ਮਾਪਣ ਵਾਲੇ ਯੰਤਰ ਨੂੰ …………….. ਕਹਿੰਦੇ ਹਨ ।
ਉੱਤਰ-
ਸਪੀਡੋਮੀਟਰ,

(v) ਇੱਕ ਸਮਾਨ ਗਤੀ ਲਈ ਤੈਅ ਕੀਤੀ ਗਈ ਦੁਰੀ ਅਤੇ ਲੱਗੇ ਸਮੇਂ ਵਿੱਚ ਬਣਾਇਆ ਗਿਆ ਗਾਫ਼ :……….. ਹੈ ।
ਉੱਤਰ-
ਸਿੱਧੀ ਰੇਖਾ ॥

2. ਕਾਲਮ ‘ੴ’ ਦੇ ਕਥਨਾਂ ਦਾ ਕਾਲਮ “ਅ ਦੇ ਕਥਨਾਂ ਨਾਲ ਮਿਲਾ ਕਰੋ-

ਉੱਤਰ-

3. ਸਹੀ ਵਿਕਲਪ ਦੀ ਚੁਣੋ

(i) ਸਮੇਂ ਦਾ ਮੂਲ ਮਾਤਕ ਹੈ
(ਉ) ਮਿੰਟ
(ਅ) ਘੰਟਾ
(ੲ) ਸੈਕੰਡ
(ਸ) ਇਹਨਾਂ ਵਿੱਚੋਂ ਕੋਈ ਨਹੀਂ ।
ਉੱਤਰ-
(ੲ) ਸੈਕੰਡ ।

(ii) ਰੇਲਗੱਡੀ ਦੀ ਚਾਲ ਦਰਸਾਈ ਜਾਂਦੀ ਹੈ –
(ਉ) m/h
(ਅ) km/h
(ੲ) cm/h
(ਸ) mm/h.
ਉੱਤਰ-
(ਅ) km/h.

(iii) ਚਾਲ ਦਾ S.I. ਮਾਤ੍ਰ ਹੈ
(ਉ) m/s
(ਅ) km/s
(ੲ) cm/s
(ਸ) mm/s.
ਉੱਤਰ-
(ੳ) m/s.

(iv) ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ਕਿਹੜਾ ਸੰਬੰਧ ਸਹੀ ਹੈ ?
(ਉ) ਚਾਲ = ਦੂਰੀ x ਸਮਾਂ


(ਸ) ਇਹਨਾਂ ਵਿੱਚੋਂ ਕੋਈ ਨਹੀਂ ।
ਉੱਤਰ-

(v) ਗਤੀ ਜੋ ਇਕ ਸਮਾਨਾਂਤਰ ਸਮੇਂ ਦੇ ਬਾਅਦ ਆਪਣੇ ਆਪ ਨੂੰ ਦੁਹਰਾਉਂਦੀ ਹੈ –
(ਉ) ਦੋਲਨ ਗਤੀ .
(ਅ) ਆਵਰਤੀ ਗਤੀ
(ਇ) ਆਵਰਤ ਗਤੀ
(ਸ) ਇਹਨਾਂ ਵਿੱਚੋਂ ਕੋਈ ਵੀ ਨਹੀਂ ।
ਉੱਤਰ-
(ਅ) ਆਵਰਤੀ ਗਤੀ ॥

(vi) ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ ਨੂੰ ਮਾਪਣ ਵਾਲੀ ਯੁਕਤੀ ਹੈ –
(ਉ) ਚਾਲ ਮਾਪੀ
(ਅ) ਓਡੋਮੀਟਰ ਪਥਮਾਪੀ)
(ਈ) ਲੋਕ
(ਸ) ਇਹਨਾਂ ਵਿੱਚੋਂ ਕੋਈ ਨਹੀਂ ।
ਉੱਤਰ-
(ਅ) ਓਡੋਮੀਟਰ (ਪਥਮਾਪੀ) ।

(vii) ਸਰਲ ਲੋਕ ਦੁਆਰਾ ਇਕ ਦੋਲਨ ਪੂਰਾ ਕਰਨ ਵਿੱਚ ਲੱਗਾ ਸਮਾਂ ਹੈ –
(ੳ) ਆਵਰਤਕਾਲ
(ਅ) ਦੋਲਨ ਗਤੀ
(ੲ) ਸਮਾਂ ਚਾਲ
(ਸ) ਇਹਨਾਂ ਵਿੱਚੋਂ ਕੋਈ ਨਹੀਂ ।
ਉੱਤਰ-
(ੳ) ਆਵਰਤਕਾਲ ।

(viii) ਹੇਠ ਦਿਖਾਏ ਦੂਰੀ ਸਮਾਂ ਗਰਾਫਾਂ ਵਿੱਚੋਂ ਕਿਹੜਾ ਵਸਤੂ ਦੀ ਵਿਰਾਮ ਅਵਸਥਾ ਨੂੰ ਦਰਸਾਉਂਦਾ ਹੈ ?

(ਉ) (a)
(ਅ) (b)
(ਈ) (c)
(ਸ) ਇਨ੍ਹਾਂ ਵਿਚੋਂ ਕੋਈ ਨਹੀਂ ।
ਉੱਤਰ-
(ਉ) (a).

(ix) ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ਕਿਹੜਾ ਸੰਬੰਧ ਠੀਕ ਹੈ :
(ਉ) ਚਾਲ = ਦੂਰੀ x ਸਮਾਂ

(ੲ) ਚਾਲ = ਸਮਾਂ/ਦੂਰੀ

ਉੱਤਰ-

(x) ਚਾਲ ਦਾ ਮੂਲ ਮਾਤਕ ਹੈ :
(ਉ) km/min
(ਅ) /m/min.
(ਇ) km/hr.
(ਸ) m/s.
ਉੱਤਰ
(ਸ) m/s.

4. ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ਕਿਹੜਾ ਕਥਨ ਸਹੀ ਅਤੇ ਕਿਹੜਾ ਕਥਨ ਗ਼ਲਤ ਹੈ ?

(i) ਸਮੇਂ ਦਾ ਮੁਲ ਮਾਤਕ ਸੈਕੰਡ ਹੈ ।
(ii) ਹਰੇਕ ਵਸਤੁ ਇੱਕ ਸਮਾਨ ਚਾਲ ਨਾਲ ਗਤੀ ਕਰਦੀ ਹੈ ।
(iii) ਦੋ ਸ਼ਹਿਰਾਂ ਵਿਚਲੀ ਦੂਰੀ ਕਿਲੋਮੀਟਰਾਂ ਵਿੱਚ ਮਾਪੀ ਜਾਂਦੀ ਹੈ ।
(iv) ਕਿਸੇ ਦਿੱਤੇ ਗਏ ਪੈਂਡੂਲਮ ਦਾ ਆਵਰਤ ਕਾਲ ਇਕਸਮਾਨ ਨਹੀਂ ਹੁੰਦਾ ।
(v) ਰੇਲ ਗੱਡੀ ਦੀ ਚਾਲ m/h ਵਿੱਚ ਦਰਸਾਈ ਜਾਂਦੀ ਹੈ ।
ਉੱਤਰ-
(i) ਸਹੀ,
(ii) ਗ਼ਲਤ,
(iii) ਸਹੀ,
(iv) ਗਲਤ,
(v) ਗ਼ਲਤ ॥

5. ਬਹੁਤ ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ

ਪ੍ਰਸ਼ਨ 1.
ਦੂਰੀ ਤੈਅ ਕਰਨ ਦੀ ਦਰ ਕੀ ਅਖਵਾਉਂਦੀ ਹੈ-ਗਤੀ ਜਾਂ ਚਾਲ ?
ਉੱਤਰ-
ਚਾਲ ।

ਪ੍ਰਸ਼ਨ 2.
ਵਿਸਥਾਪਨ ਦੀ ਦਰ ਨੂੰ ਕੀ ਕਹਿੰਦੇ ਹਨ-ਗਤੀ ਜਾਂ ਚਾਲ ?
ਉੱਤਰ-
ਗਤੀ ।

ਪ੍ਰਸ਼ਨ 3.
ਸਤ ਚਾਲ ਦਾ ਸੂਤਰ ਕੀ ਹੈ ?
ਉੱਤਰ-

ਪ੍ਰਸ਼ਨ 4.
ਦੋ ਪ੍ਰਕਾਰ ਦੀਆਂ ਗਤੀਆਂ ਕਿਹੜੀਆਂ ਹਨ ?
ਉੱਤਰ-

• ਇੱਕ ਸਮਾਨ ਗਤੀ
• ਅਸਮਾਨ ਗਤੀ ।

ਪ੍ਰਸ਼ਨ 5.
ਘੜੀਆਂ ਦੀ ਚਾਲ ਕਿਸ ਗਤੀ ‘ਤੇ ਨਿਰਭਰ ਕਰਦੀ ਹੈ ?
ਉੱਤਰ-
ਤੇਲਨ ਗਤੀ ‘ਤੇ ।

ਪ੍ਰਸ਼ਨ 6.
ਸਮਾਂ ਅੰਤਰਾਲ ਨੂੰ ਮਾਪਣ ਲਈ ਕਿਸ ਯੰਤਰ ਦਾ ਉਪਯੋਗ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਘੜੀ ਦਾ ।

ਪ੍ਰਸ਼ਨ 7.
ਪੈਂਡੂਲਮ ਦੇ ਧਾਤਵੀ ਗੋਲੇ ਨੂੰ ਕੀ ਕਹਿੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਗੋਲਕ ।

ਪ੍ਰਸ਼ਨ 8. ਸਰਲ ਪੈਂਡੂਲਮ ਦੀ ਗਤੀ ਕਿਸ ਕਿਸਮ ਦੀ ਗਤੀ ਹੈ ?
ਉੱਤਰ-
ਆਵਰਤੀ ਗਤੀ ।

ਪ੍ਰਸ਼ਨ 9.
ਸਮੇਂ ਦਾ ਮੂਲ ਮਾਤ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਸੈਕਿੰਡ ।

ਪ੍ਰਸ਼ਨ 10.
ਸਮੇਂ ਦਾ ਵੱਡਾ ਮਾਤ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਮਿੰਟ ਅਤੇ ਘੰਟਾ ॥

ਪ੍ਰਸ਼ਨ 11.
ਓਡੋਮੀਟਰ ਕੀ ਕੰਮ ਆਉਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਓਡੋਮੀਟਰ-ਇਹ ਇੱਕ ਅਜਿਹੀ ਜੁਗਤ ਹੈ ਜਿਸ ਨਾਲ ਵਾਹਨ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ ਮਾਪੀ ਜਾਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 12.
ਸਪੀਡੋਮੀਟਰ ਕੀ ਕੰਮ ਕਰਦਾ ਹੈ ?
ਉੱਤਰ-
ਸਪੀਡੋਮੀਟਰ-ਇਸ ਦੁਆਰਾ ਵਾਹਨਾਂ ਦੀ ਚਾਲ (speed) ਮਾਪੀ ਜਾਂਦੀ ਹੈ । ਇਸ ਦੁਆਰਾ ਚਾਲ Kml ਵਿੱਚ ਮਾਪੀ ਜਾਂਦੀ ਹੈ ।

6. ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ ਨਾਲ

ਪ੍ਰਸ਼ਨ 1.
ਡੋਲਨ ਘੜੀਆਂ ਤੋਂ ਪਹਿਲਾਂ ਸਮਾਂ ਅੰਤਰਾਲ ਮਾਪਣ ਦੀ ਜੁਗਤ ਕਿਹੜੀ ਸੀ ?
ਉੱਤਰ-

• ਧੁੱਪ ਘੜੀ
• ਜਲ ਘੜੀ
• ਰੇਤ ਘੜੀ ।

ਪ੍ਰਸ਼ਨ 2.
ਗਾਫ਼ ਬਣਾਉਣ ਲਈ ਪੈਮਾਨੇ ਦੀ ਚੋਣ ਸਮੇਂ ਕਿਹੜੀਆਂ ਗੱਲਾਂ ਦਾ ਧਿਆਨ ਰੱਖਣਾ ਜ਼ਰੂਰੀ ਹੈ ?
ਉੱਤਰ-
ਗਾਫ਼ ਬਣਾਉਣ ਲਈ ਪੈਮਾਨੇ ਦੀ ਚੋਣ ਸਮੇਂ ਹੇਠ ਲਿਖੀਆਂ ਗੱਲਾਂ ਧਿਆਨ ਦੇਣ ਯੋਗ ਹਨ :

1. ਹਰੇਕ ਰਾਸ਼ੀ ਦੇ ਅਧਿਕਤਮ ਅਤੇ ਨਿਊਨਤਮ ਮਾਨ ਵਿੱਚ ਅੰਤਰ ।
2. ਹਰੇਕ ਰਾਸ਼ੀ ਦੇ ਮੱਧਮਾਨ ਦਾ ਅਨੁਮਾਨ ਹੋਣਾ ।
3. ਗਾਫ਼ ਪੇਪਰ ਦੇ ਵੱਧ ਤੋਂ ਵੱਧ ਭਾਗ ਦਾ ਉਪਯੋਗ ਕਰਨਾ ।

ਪ੍ਰਸ਼ਨ 3.
ਸਰਲ
ਪੈਂਡੂਲਮ ਕੀ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਸਰਲ ਪੈਂਡੂਲਮ-ਧਾਤੂ ਦੇ ਗੋਲੇ ਜਾਂ ਪੱਥਰ ਦੇ ਛੋਟੇ ਜਿਹੇ ਟੁੱਕੜੇ ਨੂੰ ਧਾਗੇ ਦੀ ਸਹਾਇਤਾ ਨਾਲ ਕਿਸੇ ਦ੍ਰਿੜੁ ਬਿੰਦੂ ਤੋਂ ਲਟਕਾਉਣ ਨਾਲ ਸਰਲ ਪੈਂਡੂਲਮ ਅਖਵਾਉਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
ਹੇਠ ਲਿਖੀਆਂ ਗਤੀਆਂ ਦਾ ਵਰਗੀਕਰਣ ਸਰਲ ਰੇਖੀ, ਗੋਲਾਕਾਰ ਅਤੇ ਡੋਲਨ ਗਤੀ ਵਿੱਚ ਕਰੋ :
(ਉ) ਦੌੜਦੇ ਸਮੇਂ ਤੁਹਾਡੇ ਹੱਥਾਂ ਦੀ ਗਤੀ
(ਅ) ਸਿੱਧੀ ਸੜਕ ‘ਤੇ ਗੱਡੀ ਨੂੰ ਖਿੱਚਦੇ ਘੋੜੇ ਦੀ ਗਤੀ
(ੲ) ‘‘ਮੈਰੀ ਗੋ ਰਾਉਂਡ’’ ਝੁਲੇ ਵਿੱਚ ਬੱਚੇ ਦੀ ਗਤੀ
(ਸ) ‘ਸੀ ਸਾ’ ਝੁਲੇ ਵਿੱਚ ਬੱਚੇ ਦੀ ਗਤੀ
(ਹ) ਬਿਜਲੀ ਘੰਟੀ ਦੇ ਹਥੋੜੇ ਦੀ ਗਤੀ
(ਕ) ਸਿੱਧੇ ਪੁਲ ‘ਤੇ ਰੇਲਗੱਡੀ ਦੀ ਗਤੀ ।
ਉੱਤਰ-
(ੳ) ਡੋਲਨ ਗਤੀ
(ਅ) ਸਰਲ ਰੇਖੀ ਗਤੀ
(ਈ) ਵਰਤੁਲ ਗਤੀ (ਚੱਕਰਾਕਾਰ ਗਤੀ ਜਾਂ ਗੋਲਾਕਾਰ ਗਤੀ)
(ਸ) ਡੋਲਨ ਗਤੀ
(ਹ) ਡੋਲਨ ਗਤੀ
(ਕ) ਸਰਲ ਰੇਖੀ ਗਤੀ ।

ਪ੍ਰਸ਼ਨ 5.
ਕੋਈ ਸਰਲ ਪੈਂਡੂਲਮ 20 ਡੋਲਨ ਪੂਰੇ ਕਰਨ ਵਿੱਚ 32 ਸੈਕਿੰਡ ਲੈਂਦਾ ਹੈ । ਪੈਂਡੂਲਮ ਦਾ ਆਵਰਤ ਕਾਲ ਕੀ ਹੈ ?
ਹੱਲ –
ਡੋਲਨਾਂ ਦੀ ਸੰਖਿਆ = 20 ਡੋਲਨ
20 ਡੋਲਨਾਂ ਨੂੰ ਪੂਰੇ ਕਰਨ ਲਈ ਲੱਗਿਆ ਸਮਾਂ = 32 ਸੈਕਿੰਡ

= \(\frac{32}{20}\)
= 1.6 ਸੈਕਿੰਡ ਉੱਤਰ

ਪ੍ਰਸ਼ਨ 6.
ਦੋ ਸਟੇਸ਼ਨਾਂ ਵਿਚਲੀ ਦੂਰੀ 200 km ਹੈ । ਕੋਈ ਰੇਲਗੱਡੀ ਇਸ ਦੂਰੀ ਨੂੰ ਤੈਅ ਕਰਨ ਵਿੱਚ 4 ਘੰਟੇ ਦਾ ਸਮਾਂ ਲੈਂਦੀ ਹੈ । ਰੇਲਗੱਡੀ ਦੀ ਚਾਲੇ ਪਤਾ ਕਰੋ ।
ਹੱਲ –
ਦੋ ਸਟੇਸ਼ਨਾਂ ਵਿਚਲੀ ਦੂਰੀ (S) = 200 km
200 km ਦੀ ਦੂਰੀ ਨੂੰ ਤੈਅ ਕਰਨ ਨੂੰ ਲੱਗਿਆ ਸਮਾਂ (t) = 4h

= \(\frac{200 \mathrm{~km}}{4 \mathrm{~h}}\)
= 50 km/h ਉੱਤਰ

ਪ੍ਰਸ਼ਨ 7.
ਸਲਮਾ ਆਪਣੇ ਘਰ ਤੋਂ ਸਾਈਕਲ ਤੇ ਸਕੂਲ ਪਹੁੰਚਣ ਵਿੱਚ 15 ਮਿੰਟ ਲੈਂਦੀ ਹੈ । ਜੇ ਸਾਈਕਲ ਦੀ ਚਾਲ 2 ms ਹੈ, ਤਾਂ ਘਰ ਤੋਂ ਸਕੂਲ ਦੀ ਦੂਰੀ ਪਤਾ ਕਰੋ ।
ਹੱਲ
ਲੱਗਿਆ ਸਮਾਂ (t) = 15 ਮਿੰਟ
= 15 x 60 ਸੈਕਿੰਡ
= 900 ਸੈਕਿੰਡ
ਸਾਈਕਲ ਦੀ ਚਾਲ (v) = 2 m/s
ਘਰ ਤੋਂ ਸਕੂਲ ਦੀ ਦੂਰੀ (S) = ?

ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ (S) = ਚਾਲ (v) X ਸਮਾਂ (t)
= 2 x 900
= 1800 m ਮੀਟਰ)
= \(\frac{1800}{1000}\)km
= 1.8 km ਉੱਤਰ

7. ਵੱਡੇ ਉੱਤਰ ਵਾਲਾ ਪ੍ਰਸ਼ਨ

ਪ੍ਰਸ਼ਨ-ਹੇਠ ਲਿਖਿਆਂ ਨੂੰ ਪਰਿਭਾਸ਼ਿਤ ਕਰੋ :
(i) ਆਵਰਤੀ ਗਤੀ
(ii) ਡੋਲਨ ਗਤੀ
(iii) ਇੱਕ ਡੋਲਨ
(iv) ਆਵਰਤ ਕਾਲ ।
ਉੱਤਰ-
(i) ਆਵਰਤੀ ਗਤੀ-ਉਹ ਗਤੀ ਜੋ ਇੱਕ ਸਮਾਨ ਸਮੇਂ ਅੰਤਰਾਲ ਮਗਰੋਂ ਦੁਹਰਾਉਂਦੀ ਹੈ, ਆਵਰਤ ਗਤੀ ਅਖਵਾਉਂਦੀ ਹੈ ।
(ii) ਡੋਲਨ ਗਤੀ-ਕਿਸੇ ਸਥਿਰ ਮੱਧ ਬਿੰਦੁ ਦੇ ਉੱਪਰ ਵਸਤੂ ਦੀ ਵਾਰ-ਵਾਰ ਦੁਹਰਾਈ ਜਾਣ ਵਾਲੀ ਗਤੀ ਡੋਲਨ ਗਤੀ ਹੁੰਦੀ ਹੈ ।
(iii) ਇੱਕ ਡੋਲਨ-ਵਸਤੁ ਦਾ ਵਾਰ-ਵਾਰ ਆਪਣੀ ਮੱਧ ਸਥਿਤੀ ਦੇ ਸੱਜੇ-ਖੱਬੇ ਜਾਂ ਅੱਗੇ-ਪਿੱਛੇ ਜਾਂ ਫਿਰ ਉੱਪਰ-ਹੇਠਾਂ ਗਤੀ ਕਰਨਾ ਡੋਲਨ ਕਹਾਉਂਦਾ ਹੈ । ਜਦੋਂ ਇਹ ਵਸਤੁ ਮੱਧ ਸਥਿਤੀ ਤੋਂ ਇੱਕ ਚਰਮ ਸੀਮਾਂ ਅਤੇ ਫਿਰ ਉੱਥੋਂ ਦੁਸਰੀ ਚਰਮ-ਸੀਮਾਂ ਅਤੇ ਬਾਅਦ ਵਿੱਚ ਮੱਧ ਸਥਿਤੀ ‘ਤੇ ਗਤੀ ਕਰਦੀ ਹੋਈ ਪਹੁੰਚ ਜਾਂਦੀ ਹੈ ਤਾਂ ਵਸਤੂ ਦੁਆਰਾ ਇੱਕ ਡੋਲਨ ਹੋ ਗਿਆ ਆਖਦੇ ਹਾਂ ।

(iv) ਆਵਰਤ ਕਾਲ- ਸਰਲ ਪੈਂਡੂਲਮ ਨੂੰ ਇੱਕ ਡੋਲਨ ਪੂਰਾ ਕਰਨ ਨੂੰ ਲੱਗਿਆ ਸਮਾਂ ਆਵਰਤ ਕਾਲ ਅਖਵਾਉਂਦਾ ਹੈ ।

Punjab State Board PSEB 9th Class Science Book Solutions Chapter 1 ਸਾਡੇ ਆਲੇ-ਦੁਆਲੇ ਦੇ ਪਦਾਰ Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Science Chapter 1 ਸਾਡੇ ਆਲੇ-ਦੁਆਲੇ ਦੇ ਪਦਾਰ

PSEB 9th Class Science Guide ਸਾਡੇ ਆਲੇ-ਦੁਆਲੇ ਦੇ ਪਦਾਰ Textbook Questions and Answers

ਅਭਿਆਸ ਦੇ ਪ੍ਰਸ਼ਨ

ਪ੍ਰਸ਼ਨ 1.
ਹੇਠ ਲਿਖੇ ਤਾਪਮਾਨਾਂ ਨੂੰ ਸੈਲਸੀਅਸ ਇਕਾਈ ਵਿੱਚ ਬਦਲੋ :
(ਉ) 293 K
(ਅ) 470 K.
ਉੱਤਰ-
(ੳ) 293 K = 293 – 273
= 20°C.

(ਅ) 470 K
= 470 – 273°C
= 197°C.

ਪ੍ਰਸ਼ਨ 2.
ਹੇਠ ਲਿਖੇ ਤਾਪਮਾਨਾਂ ਨੂੰ ਕੈਲਵਿਨ ਇਕਾਈ ਵਿੱਚ ਬਦਲੋ :
(ਉ) 25°C
(ਅ) 373°C
ਉੱਤਰ-
(ੳ) ਤਾਪਮਾਨ = 25°C .
= 25 + 273 = 298 K.

(ਅ) ਤਾਪਮਾਨ
= 373° C
= 373 + 273 = 646 K.

ਪ੍ਰਸ਼ਨ 3.
ਹੇਠ ਲਿਖੇ ਪ੍ਰੇਖਣਾਂ ਲਈ ਕਾਰਨ ਲਿਖੋ :
(ਉ) ਨੇਫਥਲੀਨ ਨੂੰ ਰੱਖਣ ਤੋਂ ਕੁਝ ਸਮੇਂ ਬਾਅਦ ਕੁਝ ਵੀ ਠੋਸ ਪਦਾਰਥ ਛੱਡੇ ਬਿਨਾਂ ਅਦਿੱਖ ਹੋ ਜਾਂਦੀ ਹੈ ।
(ਅ) ਸਾਨੂੰ ਇਤਰ ਦੀ ਖੁਸ਼ਬੂ ਬਹੁਤ ਦੂਰ ਬੈਠੇ ਹੋਏ ਹੀ ਪਹੁੰਚ ਜਾਂਦੀ ਹੈ ।
ਉੱਤਰ-
(ੳ) ਕਈ ਪਦਾਰਥ ਵ ਅਵਸਥਾ ਵਿੱਚ ਪਰਿਵਰਤਿਤ ਹੋਏ ਬਿਨਾਂ ਠੋਸ ਅਵਸਥਾ ਤੋਂ ਸਿੱਧੇ ਗੈਸ ਵਿੱਚ ਬਦਲ ਜਾਂਦੇ ਹਨ ਜਿਸ ਨੂੰ ਜੌਹਰ ਉਡਾਉਣ ਦੀ ਕਿਰਿਆ ਕਹਿੰਦੇ ਹਨ । ਨੇਫਥਾਲੀਨ ਦੀਆਂ ਗੋਲੀਆਂ ਇਸੇ ਪ੍ਰਕਿਰਿਆ ਕਾਰਨ ਬਿਨਾਂ ਕੁਝ ਵੀ ਠੋਸ ਪਦਾਰਥ ਛੱਡੇ ਅਦਿੱਖ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ।
ਅ ਪਦਾਰਥਾਂ ਦੇ ਕਣ ਲਗਾਤਰ ਗਤੀਸ਼ੀਲ ਹੁੰਦੇ ਹਨ । ਇਤਰ ਦੀ ਖੁਸ਼ਬੂ ਹਵਾ ਦੇ ਮਾਧਿਅਮ ਵਿੱਚ ਪਸਰਣ ਦੇ ਕਾਰਨ ਆਪਣੇ ਆਪ ਆਲੇ-ਦੁਆਲੇ ਦੇ ਵਾਤਾਵਰਨ ਵਿੱਚ ਫੈਲ ਜਾਂਦੀ ਹੈ ਜਿਸ ਕਾਰਨ ਉਸ ਨੂੰ ਕਈ ਮੀਟਰ ਦੂਰ ਤਕ ਸੁੰਘਿਆ ਜਾ ਸਕਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
ਹੇਠ ਲਿਖੇ ਪਦਾਰਥਾਂ ਨੂੰ ਉਨ੍ਹਾਂ ਦੇ ਕਣਾਂ ਦੇ ਵਿੱਚ ਵੱਧਦੇ ਹੋਏ ਆਕਰਸ਼ਣ ਦੇ ਅਨੁਸਾਰ ਤਰਤੀਬ ਵਿੱਚ ਕਰੋ :
(ਉ) ਪਾਣੀ
(ਅ) ਚੀਨੀ
(ੲ) ਆਕਸੀਜਨ ।
ਉੱਤਰ-
ਆਕਸੀਜਨ < ਪਾਣੀ < ਚੀਨੀ ।

ਪ੍ਰਸ਼ਨ 5.
ਹੇਠ ਲਿਖੇ ਤਾਪਮਾਨਾਂ ‘ਤੇ ਪਾਣੀ ਦੀ ਭੌਤਿਕ ਅਵਸਥਾ ਕੀ ਹੈ :
(ੳ) 25°C
(ਅ) 0°C
(ੲ) 100°C.
ਉੱਤਰ-
(ਉ) ਵ ਅਵਸਥਾ
(ਅ) ਠੋਸ ਅਵਸਥਾ
(ੲ) ਗੈਸੀ ਅਵਸਥਾ ।

ਪ੍ਰਸ਼ਨ 6.
ਪੁਸ਼ਟੀ ਲਈ ਕਾਰਣ ਦਿਓ :-
(ਉ) ਪਾਣੀ ਕਮਰੇ ਦੇ ਤਾਪਮਾਣ ‘ ਤੇ ਦੂਵ ਹੈ ।
(ਅ) ਲੋਹੇ ਦੀ ਅਲਮਾਰੀ ਕਮਰੇ ਦੇ ਤਾਪਮਾਨ ‘ਤੇ ਠੋਸ ਹੈ ?
ਉੱਤਰ-
(ੳ)

1. ਪਾਣੀ ਨੂੰ ਜਿਸ ਵੀ ਬਰਤਨ ਵਿਚ ਪਾਇਆ ਜਾਵੇ ਉਸ ਦਾ ਹੀ ਆਕਾਰ ਲੈ ਲੈਂਦਾ ਹੈ । ਕਮਰੇ ਦਾ ਤਾਪਮਾਨ ਪਾਣੀ ਦੇ ਉਬਾਲ ਦਰਜੇ ਤੋਂ ਘੱਟ ਅਤੇ ਜਮਾਵ ਦਰਜੇ ਤੋਂ ਵੱਧ ਹੈ ।
2. ਪਾਣੀ ਵੱਗਦਾ ਹੈ ਅਤੇ ਇਹ ਮਜ਼ਬੂਤ ਨਹੀਂ ਹੈ ।

(ਅ)

1. ਲੋਹੇ ਦੀ ਅਲਮਾਰੀ ਦਾ ਨਿਸਚਿਤ, ਸਪੱਸ਼ਟ ਸੀਮਾਵਾਂ ਅਤੇ ਸਥਿਰ ਆਇਤਨ ਹੁੰਦਾ ਹੈ ।
2. ਨਾਂ ਮਾਤਰ ਦਬੀਣਯੋਗਤਾ ਹੈ । ਕਮਰੇ ਦਾ ਤਾਪਮਾਨ ਲੋਹੇ ਦੇ ਉਬਾਲ ਦਰਜੇ ਤੋਂ ਘੱਟ ਅਤੇ ਪਿਘਲਣ ਦਰਜੇ ਤੋਂ ਵੱਧ ਹੈ | ਕਮਰੇ ਦੇ ਤਾਪਮਾਨ ਤੇ ਉਸਦੀ ਅਵਸਥਾ ਪਰਿਵਰਤਨ ਸੰਭਵ ਨਹੀਂ ਹੈ ਇਸ ਲਈ ਇਹ ਉਸ ਤਾਪਮਾਨ ਤੇ ਠੋਸ ਹੈ ।

ਪ੍ਰਸ਼ਨ 7.
273k ਤੇ ਬਰਫ਼ ਨੂੰ ਠੰਡਾ ਕਰਨ ਤੇ ਅਤੇ ਪਾਣੀ ਨੂੰ ਇਸੇ ਤਾਪਮਾਨ ਤੇ ਠੰਡਾ ਕਰਨ ਤੇ ਠੰਡਕ ਦਾ ਪ੍ਰਭਾਵ ਵਧੇਰੇ ਕਿਉਂ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
273K ਤੇ ਬਰਫ਼ ਇਸੇ ਤਾਪਮਾਨ ਤੇ ਪਾਣੀ ਦੀ ਤੁਲਨਾ ਵਿੱਚ ਸੰਗਲਨ ਦੀ ਗੁਪਤ ਤਾਪ ਊਰਜਾ ਦੇ ਕਾਰਨ ਵਧੇਰੇ ਪ੍ਰਭਾਵਸ਼ਾਲੀ ਹੁੰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 8.
ਉਬਲਦੇ ਹੋਏ ਪਾਣੀ ਜਾਂ ਭਾਫ਼ ਵਿੱਚੋਂ ਜਲਨ ਦੀ ਤੀਬਰਤਾ ਕਿਸ ਵਿੱਚ ਵਧੇਰੇ ਮਹਿਸੂਸ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਭਾਫ਼-ਜਦੋਂ ਪਾਣੀ 373K ਤੇ ਉਬਲਦਾ ਹੈ, ਤਾਂ 373K ਤੇ ਵਾਸ਼ਪ ਵਿੱਚ ਬਦਲਦਾ ਹੈ ਉਸ ਨੂੰ 536 ਕੈਲੋਰੀ/ ਗ੍ਰਾਮ ਤਾਪ ਦੀ ਲੋੜ ਹੁੰਦੀ ਹੈ । ਉਬਲਦੇ ਪਾਣੀ ਵਿੱਚ ਗੁਪਤ ਤਾਪ ਉਰਜਾ ਵੀ ਸ਼ਾਮਿਲ ਹੈ ।

ਪ੍ਰਸ਼ਨ 9.
ਹੇਠ ਲਿਖੇ ਚਿੱਤਰ ਦੇ ਲਈ ਉ, ਅ, ੲ, ਸ, ਹ ਅਤੇ ਕ ਦੀ ਅਵਸਥਾ ਪਰਿਵਰਤਨ ਨੂੰ ਨਾਂ ਦਿਓ :-

ਉੱਤਰ-
(ੳ) ਸੰਗਲਨ (Fusion)
(ਅ) ਵਾਸ਼ਪਣ (Oapourization)
(ੲ) ਸੰਘਣਨ (Condensation)
(ਸ) ਜੰਮਣਾ (Solidification)
(ਹ) ਜੌਹਰ ਉਡਾਉਣਾ (Sublimation ।

Science Guide for Class 9 PSEB ਸਾਡੇ ਆਲੇ-ਦੁਆਲੇ ਦੇ ਪਦਾਰ InText Questions and Answers

ਪਾਠ-ਪੁਸਤਕ ਦੇ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਉੱਤਰ

ਪ੍ਰਸ਼ਨ 1.
ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ਕਿਹੜੇ ਪਦਾਰਥ ਹਨ :
ਕੁਰਸੀ, ਹਵਾ, ਸੁਨੇਹ, ਗੰਧ, ਘਿਰਣਾ, ਬਦਾਮ, ਵਿਚਾਰ, ਠੰਡ, ਠੰਡਾ ਪਿਆਓ, ਇਤਰ ਦੀ ਗੰਧ ।
ਉੱਤਰ-
ਕੁਰਸੀ, ਹਵਾ, ਬਦਾਮ ਅਤੇ ਠੰਡਾ ਪਿਆਓ ਪਦਾਰਥ ਹਨ, ਕਿਉਂਕਿ ਇਹਨਾਂ ਦਾ ਪੰਜ ਹੁੰਦਾ ਹੈ ਤੇ ਇਹ ਸਥਾਨ ਘੇਰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 2.
ਹੇਠ ਲਿਖੇ ਪ੍ਰੇਖਣ ਦੇ ਕਾਰਨ ਦੱਸੋ :
ਗਰਮਾ-ਗਰਮ ਭੋਜਨ ਦੀ ਮਹਿਕ ਕਈ ਮੀਟਰ ਦੂਰ ਤੋਂ ਹੀ ਤੁਹਾਡੇ ਕੋਲ ਪਹੁੰਚ ਜਾਂਦੀ ਹੈ ਪਰ ਠੰਡੇ ਭੋਜਨ ਦੀ ਮਹਿਕ ਲੈਣ ਲਈ ਤੁਹਾਨੂੰ ਉਸ ਦੇ ਕੋਲ ਜਾਣਾ ਪੈਂਦਾ ਹੈ ।
ਉੱਤਰ-
ਗਰਮਾ-ਗਰਮ ਜਾਂ ਠੰਡਾ ਖਾਣਾ ਕਣਾਂ ਤੋਂ ਬਣਦਾ ਹੈ ਅਤੇ ਪਦਾਰਥ ਦੇ ਕਣ ਸਦਾ ਗਤੀਸ਼ੀਲ ਹੁੰਦੇ ਹਨ । ਉਹਨਾਂ ਵਿੱਚ ਵਿਸਰਣ ਹੁੰਦਾ ਹੈ । ਤਾਪਮਾਨ ਵੱਧਣ ਨਾਲ ਕਣਾਂ ਦੀ ਗਤੀ ਤੇਜ਼ ਹੋ ਜਾਂਦੀ ਹੈ । ਉਹਨਾਂ ਦੀ ਵਿਸਰਣ ਦੀ ਦਰ ਵੱਧ ਜਾਂਦੀ ਹੈ । ਗਰਮਾ-ਗਰਮ ਖਾਣੇ ਦੀ ਮਹਿਕ ਕਈ ਮੀਟਰ ਦੂਰ ਤੋਂ ਤੁਹਾਡੇ ਕੋਲ ਵਿਸਰਣ ਰਾਹੀਂ ਪਹੁੰਚ ਜਾਂਦੀ ਹੈ । ਦੂਜੇ ਪਾਸੇ ਭੋਜਨ ਠੰਡਾ ਹੋਣ ‘ਤੇ ਇਸਦੇ ਕਣਾਂ ਦਾ ਹਵਾ ਵਿੱਚ ਵਿਸਰਣ, ਲਗਪਗ ਨਾ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ । ਇਸ ਲਈ ਵਧੇਰੇ ਦੂਰੀ ‘ਤੇ ਠੰਡੇ ਭੋਜਨ ਦੀ ਮਹਿਕ ਨਹੀਂ ਆ ਪਾਉਂਦੀ ਅਤੇ ਸਾਨੂੰ ਭੋਜਨ ਦੇ ਨੇੜੇ ਜਾਣਾ ਪੈਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਸਵਿਮਿੰਗ ਪੂਲ ਵਿੱਚ ਗੋਤਾਖੋਰ ਪਾਣੀ ਕੱਟ ਲੈਂਦਾ ਹੈ ਇਸ ਨਾਲ ਪਦਾਰਥ ਦਾ ਕਿਹੜਾ ਗੁਣ ਖਿਤ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਸਵਿਮਿੰਗ ਪੂਲ ਵਿੱਚ ਗੋਤਾਖੋਰ ਪਾਣੀ ਨੂੰ ਕੱਟ ਲੈਂਦਾ ਹੈ ਕਿਉਂਕਿ ਪਾਣੀ ਦੇ ਕਣਾਂ ਵਿੱਚ ਅੰਤਰਾਅਣੂਕ ਬਲ ਕਾਰਜ ਕਰਦਾ ਹੈ ਜੋ ਕਣਾਂ ਨੂੰ ਇੱਕ ਨਾਲ ਰੱਖਦਾ ਹੈ । ਜਲ ਦੇ ਕਣਾਂ ਵਿੱਚ ਦੂਰੀ ਵਧੇਰੇ ਹੁੰਦੀ ਹੈ ਅਤੇ ਉਹਨਾਂ ਵਿੱਚ ਨਪੀੜਨ ਦਾ ਗੁਣ ਹੁੰਦਾ ਹੈ । ਸਵੀਮਿੰਗ ਪੂਲ ਵਿੱਚ ਗੋਤਾਖੋਰ ਜਦੋਂ ਪਾਣੀ ਨੂੰ ਆਪਣੇ ਹੱਥ ਨਾਲ ਧੱਕਦਾ ਹੈ ਤਾਂ ਪਾਣੀ ਦੇ ਅਣੂਆਂ ਵਿੱਚ ਆਕਰਸ਼ਣ ਬਲ ਘੱਟ ਹੋਣ ਦੇ ਕਾਰਨ ਉਹ ਪਾਣੀ ਨੂੰ ਕੱਟ ਸਕਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
ਪਦਾਰਥ ਦੇ ਕਣਾਂ ਦੀਆਂ ਕੀ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਹੁੰਦੀਆਂ ਹਨ ?
ਉੱਤਰ-
ਸਾਰੇ ਪਦਾਰਥ ਕਣਾਂ ਤੋਂ ਮਿਲਣ ‘ਤੇ ਬਣਦੇ ਹਨ । ਸਾਰੇ ਪਦਾਰਥਾਂ ਦੇ ਕਣ ਬਹੁਤ ਛੋਟੇ ਹੁੰਦੇ ਹਨ, ਇੰਨੇ ਛੋਟੇ ਹੁੰਦੇ ਹਨ ਕਿ ਉਹਨਾਂ ਦੇ ਛੋਟੇ ਆਕਾਰ ਦੀ ਅਸੀਂ ਕਲਪਨਾ ਵੀ ਨਹੀਂ ਕਰ ਸਕਦੇ । ਉਹਨਾਂ ਦੀਆਂ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਅੱਗੇ ਲਿਖੇ ਅਨੁਸਾਰ ਹਨ-

1. ਪਦਾਰਥ ਦੇ ਕਣਾਂ ਵਿੱਚ ਖ਼ਾਲੀ ਥਾਂਵਾਂ ਹੁੰਦੀਆਂ ਹਨ ।
2. ਪਦਾਰਥ ਦੇ ਕਣ ਲਗਾਤਾਰ ਗਤੀ ਕਰਦੇ ਰਹਿੰਦੇ ਹਨ ਉਹਨਾਂ ਵਿੱਚ ਗਤਿਜ ਊਰਜਾ ਹੁੰਦੀ ਹੈ ।
3. ਪਦਾਰਥ ਦੇ ਕਣ ਇੱਕ-ਦੂਸਰੇ ਨੂੰ ਆਕਰਸ਼ਿਤ ਕਰਦੇ ਹਨ । ਇਹ ਆਕਰਸ਼ਣ ਬਲ ਵੱਖ-ਵੱਖ ਪਦਾਰਥਾਂ ਵਿੱਚ ਵੱਖਵੱਖ ਹੁੰਦਾ ਹੈ ।
4. ਤਾਪਮਾਨ ਵਧਾਉਣ ਤੇ ਕਣਾਂ ਦੀ ਗਤਿਜ ਊਰਜਾ ਵੱਧ ਜਾਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 5.
ਕਿਸੇ ਪਦਾਰਥ ਦੇ ਇਕਾਈ ਆਇਤਨ ਦੇ ਪੁੰਜ ਨੂੰ ਘਣਤਾ ਕਹਿੰਦੇ ਹਨ । (ਘਣਤਾ = ਪੁੰਜ/ਆਇਤਨ ) ਵੱਧਦੀ ਹੋਈ ਘਣਤਾ ਦੇ ਕ੍ਰਮ ਵਿੱਚ ਹੇਠ ਲਿਖਿਆਂ ਨੂੰ ਦਰਸਾਓ :
ਹਵਾ, ਚਿਮਨੀ ਦਾ ਧੂੰਆਂ, ਸ਼ਹਿਦ, ਪਾਣੀ, ਚਾਕ, ਤੂੰ ਅਤੇ ਲੋਹਾ ।
ਉੱਤਰ-
ਚਿਮਨੀ ਦਾ ਧੂੰਆਂ, ਹਵਾ, ਨੂੰ, ਪਾਣੀ, ਸ਼ਹਿਦ, ਚਾਕ, ਲੋਹਾ ।

ਪ੍ਰਸ਼ਨ 6.
(ੳ) ਪਦਾਰਥ ਦੀਆਂ ਵੱਖ-ਵੱਖ ਅਵਸਥਾਵਾਂ ਦੇ ਗੁਣਾਂ ਵਿੱਚ ਹੋਣ ਵਾਲੇ ਅੰਤਰ ਨੂੰ ਸਾਰਣੀਬੱਧ ਕਰੋ ।
(ਅ) ਹੇਠ ਲਿਖਿਆਂ ‘ਤੇ ਟਿੱਪਣੀ ਕਰੋਨਿੱਗਰਤਾ, ਦਬੀਣਯੋਗਤਾ, ਤਰਲਤਾ, ਬਰਤਨ ਵਿੱਚ ਗੈਸ ਦਾ ਭਰਨਾ, ਆਕਾਰ, ਗਤਿਜ ਊਰਜਾ ਅਤੇ ਘਣਤਾ ।
ਉੱਤਰ-
(ੳ) ਪਦਾਰਥ ਦੀਆਂ ਵੱਖ-ਵੱਖ ਅਵਸਥਾਵਾਂ ਠੋਸ, ਵ ਅਤੇ ਗੈਸ ਹਨ ।
ਠੋਸ, ਦ੍ਰਵ ਅਤੇ ਗੈਸ ਵਿੱਚ ਅੰਤਰ-

(ਅ)
1. ਨਿੱਗਰਤਾ – ਨਿੱਗਰਤਾ ਠੋਸ ਪਦਾਰਥਾਂ ਦਾ ਗੁਣ ਹੈ । ਨਾਂ ਦੇ ਬਰਾਬਰ ਨਪੀੜਨ ਯੋਗਤਾ ਕਾਰਨ, ਇਹ ਬਾਹਰੀ ਬਲ ਲਗਾਉਣ ‘ਤੇ ਵੀ ਆਪਣੇ ਆਕਾਰ ਨੂੰ ਨਹੀਂ ਬਦਲਦੇ । ਠੋਸ ਪਦਾਰਥਾਂ ਵਿੱਚ ਆਕਰਸ਼ਣ ਬਲ ਦੇ ਕਾਰਨ ਮਜ਼ਬੂਤੀ ਵਧੇਰੇ ਹੁੰਦੀ ਹੈ । ਵ ਨੂੰ ਥੋੜ੍ਹਾ ਦਬਾਇਆ ਜਾ ਸਕਦਾ ਹੈ ਅਤੇ ਗੈਸ ਨੂੰ ਸਰਲਤਾ ਨਾਲ ਦਬਾਇਆ ਜਾ ਸਕਦਾ ਹੈ ।

2. ਦਬੀਣਯੋਗਤਾ – ਪਦਾਰਥਾਂ ਦਾ ਦਬੀਣਯੋਗਤਾ ਗੁਣ, ਉਹਨਾਂ ‘ਤੇ ਦਬਾਅ ਦੇ ਅਸਰ ਨੂੰ ਦੱਸਦਾ ਹੈ । ਜੇ ਪਦਾਰਥ ਨੂੰ ਬਾਹਰੀ ਦਬਾਅ ਨਾਲ ਦਬਾਇਆ ਨਹੀਂ ਜਾ ਸਕਦਾ ਤਾਂ ਉਸ ਦੀ ਦੁਬੀਣਯੋਗਤਾ ਨਾਂ ਦੇ ਬਰਾਬਰ ਹੋਵੇਗੀ । ਇਸ ਤੋਂ ਇਲਾਵਾ ਜੇ ਪਦਾਰਥ ਨੂੰ ਬਾਹਰੀ ਦਬਾਅ ਨਾਲ ਦਬਾਇਆ ਜਾ ਸਕਦਾ ਹੋਵੇ ਤਾਂ ਉਸਦੀ ਦਬੀਯੋਗਤਾ ਵਧੇਰੇ ਹੋਵੇਗੀ । ਦੂਜੇ ਸ਼ਬਦਾਂ ਵਿੱਚ ਦਬੀਯੋਗਤਾ ਪਦਾਰਥ ਦੇ ਆਇਤਨ ਨਾਲ ਸੰਬੰਧਿਤ ਹੁੰਦੀ ਹੈ । ਸਥਿਰ ਆਇਤਨ ਵਾਲੇ ਪਦਾਰਥਾਂ ਦੀ ਦਬੀਣਯੋਗਤਾ ਨਾ ਦੇ ਬਰਾਬਰ ਅਤੇ ਪਰਿਵਰਤਨਸ਼ੀਲ ਆਇਤਨ ਵਾਲੇ ਪਦਾਰਥਾਂ ਦੀ ਦਬੀਣਯੋਗਤਾ ਵੱਧ ਹੁੰਦੀ ਹੈ । ਠੋਸ ਪਦਾਰਥਾਂ ਨੂੰ ਬਾਹਰੀ ਬਲ ਦੁਆਰਾ ਦਬਾਇਆ ਨਹੀਂ ਜਾ ਸਕਦਾ ਅਤੇ ਇਹਨਾਂ ਦਾ ਆਇਤਨ ਵੀ ਨਿਸਚਿਤ ਹੁੰਦਾ ਹੈ । ਇਸ ਲਈ ਇਹਨਾਂ ਦੀ ਦਬੀਣਯੋਗਤਾ ਨਾ ਦੇ ਬਰਾਬਰ ਹੁੰਦੀ ਹੈ । ਵਾਂ ਦੀ ਦਬੀਣਯੋਗਤਾ ਠੋਸਾਂ ਤੋਂ ਵੱਧ ਹੁੰਦੀ ਹੈ ਅਤੇ ਗੈਸਾਂ ਦੀ ਦਬੀਣਯੋਗਤਾ ਸਭ ਤੋਂ ਵੱਧ ਹੁੰਦੀ ਹੈ । ਇਸੇ ਕਾਰਨ ਗੈਸਾਂ ਨੂੰ ਘੱਟ ਆਇਤਨ ਵਾਲੇ ਸਿਲੰਡਰਾਂ ਵਿੱਚ ਨਪੀੜਿਆ ਜਾ ਸਕਦਾ ਹੈ ।

3. ਤਰਲਤਾ – ਤਰਲਤਾ, ਤਰਲ ਪਦਾਰਥਾਂ ਦਾ ਗੁਣ ਹੈ ਜਿਨ੍ਹਾਂ ਦਾ ਨਿਸਚਿਤ ਆਕਾਰ ਨਹੀਂ ਹੁੰਦਾ ਪਰ ਨਿਸਚਿਤ ਆਇਤਨ ਜ਼ਰੂਰ ਹੁੰਦਾ ਹੈ । ਤਰਲਤਾ ਵੱਗਣ ਦੀ ਪ੍ਰਵਿਰਤੀ ਹੈ ਅਤੇ ਇਸ ਵਿੱਚ ਦਵ ਦਾ ਆਕਾਰ ਬਦਲਦਾ ਰਹਿੰਦਾ ਹੈ । ਠੋਸ ਬਿਲਕੁਲ ਨਹੀਂ ਵੱਗਦੇ ਪਰ ਗੈਸਾਂ ਸਾਰੀਆਂ ਦਿਸ਼ਾਵਾਂ ਵਿੱਚ ਵਗਦੀਆਂ ਹਨ ।

4. ਬਰਤਨ ਵਿੱਚ ਗੈਸ ਦਾ ਭਰਨਾ – ਗੈਸਾਂ ਦੇ ਕਣਾਂ ਵਿੱਚ ਅੰਤਰਾਣੁਕ ਬਲ ਨਾ ਦੇ ਬਰਾਬਰ ਹੋਣ ਕਰਕੇ ਦਬੀਣਯੋਗਤਾ ਬਹੁਤ ਜ਼ਿਆਦਾ ਹੁੰਦੀ ਹੈ, ਜਿਸ ਕਾਰਨ ਗੈਸ ਦੇ ਵਧੇਰੇ ਆਇਤਨ ਨੂੰ ਕਿਸੇ ਘੱਟ ਆਇਤਨ ਵਾਲੇ ਬਰਤਨ ਵਿੱਚ ਨਪੀੜਿਆ ਜਾ ਸਕਦਾ ਹੈ ਅਤੇ ਸਰਲਤਾ ਪੂਰਵਕ ਇੱਕ ਸਥਾਨ ਤੋਂ ਦੂਜੇ ਸਥਾਨ ਤਕ ਭੇਜਿਆ ਜਾ ਸਕਦਾ ਹੈ ।

5. ਆਕਾਰ – ਪਦਾਰਥ ਦੇ ਕਣਾਂ ਵਿੱਚ ਇੱਕ ਬਲ ਕਾਰਜ ਕਰਦਾ ਹੈ । ਇਹ ਬਲੇ ਕਣਾਂ ਨੂੰ ਇੱਕ ਸਾਰ ਰੱਖਦਾ ਹੈ ਅਤੇ ਵਸਤੂ ਨੂੰ ਆਕਾਰ ਪ੍ਰਦਾਨ ਕਰਦਾ ਹੈ । ਇਹ ਆਕਰਸ਼ਣ ਬਲ ਦਾ ਮੁੱਲ ਵੱਖ-ਵੱਖ ਪਦਾਰਥਾਂ ਵਿੱਚ ਵੱਖ-ਵੱਖ ਹੁੰਦੀ ਹੈ । ਠੋਸ ਪਦਾਰਥਾਂ ਦੇ ਕਣਾਂ ਵਿੱਚ ਅੰਤਰਾਅਲੁਕ ਬਲ ਵਧੇਰੇ ਹੁੰਦਾ ਹੈ, ਜਿਸ ਕਾਰਨ ਉਹਨਾਂ ਦਾ ਨਿਸਚਿਤ ਆਕਾਰ ਹੁੰਦਾ ਹੈ ਪਰ ਵਾਂ ਅਤੇ ਗੈਸਾਂ ਵਿੱਚ ਅਜਿਹਾ ਨਹੀਂ ਹੁੰਦਾ ।

6. ਗਤਿਜ ਉਰਜਾ – ਪਦਾਰਥਾਂ ਦੇ ਕਣ ਸਦਾ ਗਤੀਸ਼ੀਲ ਰਹਿੰਦੇ ਹਨ ਜਿਸ ਨੂੰ ਗਤਿਜ ਉਰਜਾ ਕਹਿੰਦੇ ਹਨ । ਤਾਪਮਾਨ ਦੇ ਵਧਣ ਨਾਲ ਕਣਾਂ ਦੀ ਗਤੀ ਤੇਜ਼ ਹੋ ਜਾਂਦੀ ਹੈ ਅਰਥਾਤ ਤਾਪਮਾਨ ਵਧਣ ਨਾਲ ਕਣਾਂ ਦੀ ਗਤਿਜ ਉਰਜਾ ਵੀ ਵੱਧ ਜਾਂਦੀ ਹੈ । ਠੋਸ ਵਿੱਚ ਵਧੇਰੇ ਗਤਿਜ ਊਰਜਾ ਨਹੀਂ ਹੁੰਦੀ । ਵ ਵਿੱਚ ਕੁਝ ਗਤਿਜ ਊਰਜਾ ਹੁੰਦੀ ਹੈ, ਪਰ ਗੈਸਾਂ ਵਿੱਚ ਬਹੁਤ ਜ਼ਿਆਦਾ ਗਤਿਜ ਊਰਜਾ ਹੁੰਦੀ ਹੈ ।

7. ਘਣਤਾ – ਕਿਸੇ ਵਸਤੂ ਦੀ ਘਣਤਾ ਪ੍ਰਤੀ ਇਕਾਈ ਆਇਤਨ ਦੇ ਪੁੰਜ ਦੇ ਬਰਾਬਰ ਹੁੰਦੀ ਹੈ ।

ਠੋਸ ਪਦਾਰਥਾਂ ਦੀ ਘਣਤਾ ਬਹੁਤ ਜ਼ਿਆਦਾ ਹੁੰਦੀ ਹੈ ; ਞ ਵਿੱਚ ਘੱਟ ਅਤੇ ਗੈਸਾਂ ਵਿੱਚ ਨਾਂ ਦੇ ਬਰਾਬਰ ਹੁੰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 7.
ਕਾਰਣ ਦੱਸੋ-
(ੳ) ਗੈਸ ਪੂਰੀ ਤਰ੍ਹਾਂ ਉਸ ਬਰਤਨ ਨੂੰ ਭਰ ਦਿੰਦੀ ਹੈ ਜਿਸ ਵਿੱਚ ਉਸ ਨੂੰ ਰੱਖਦੇ ਹਾਂ ।
(ਅ) ਗੈਸ ਬਰਤਨ ਦੀਆਂ ਦੀਵਾਰਾਂ ‘ਤੇ ਦਬਾਅ ਪਾਉਂਦੀ ਹੈ ।
(ੲ) ਲੱਕੜ ਦੀ ਮੇਜ਼ ਠੋਸ ਅਖਵਾਉਂਦੀ ਹੈ ।
(ਸ) ਹਵਾ ਵਿੱਚ ਅਸੀਂ ਅਸਾਨੀ ਨਾਲ ਆਪਣਾ ਹੱਥ ਚਲਾ ਸਕਦੇ ਹਾਂ, ਪਰ ਇੱਕ ਠੋਸ ਲੱਕੜੀ ਦੇ ਟੁਕੜੇ ਵਿੱਚ ਹੱਥ ਚਲਾਉਣ ਲਈ ਸਾਨੂੰ ਕਰਾਟੇ ਵਿੱਚ ਮਾਹਰ ਹੋਣਾ ਪਵੇਗਾ ।
ਉੱਤਰ-
(ੳ) ਗੈਸ ਦੇ ਕਣਾਂ ਦੀ ਸਥਿਤੀ ਬਹੁਤ ਢਿੱਲੀ ਹੁੰਦੀ ਹੈ ਤੇ ਉਹਨਾਂ ਵਿੱਚ ਖ਼ਾਲੀ ਸਥਾਨ ਵੀ ਬਹੁਤ ਹੁੰਦਾ ਹੈ । ਉਹਨਾਂ ਵਿੱਚ ਆਕਰਸ਼ਣ ਬਲ ਨਾਂ-ਮਾਤਰ ਹੁੰਦਾ ਹੈ ਅਤੇ ਉਹ ਤੀਬਰ ਗਤੀ ਨਾਲ ਸਾਰੀਆਂ ਦਿਸ਼ਾਵਾਂ ਵਿੱਚ ਇੱਧਰ-ਉੱਧਰ ਗਤੀ ਕਰ ਸਕਦੇ ਹਨ । ਇਹਨਾਂ ਦਾ ਨਿਸਚਿਤ ਆਇਤਨ ਵੀ ਨਹੀਂ ਹੁੰਦਾ, ਇਸ ਲਈ ਗੈਸ ਪੂਰੀ ਤਰ੍ਹਾਂ ਉਸ ਬਰਤਨ ਨੂੰ ਭਰ ਦਿੰਦੀ ਹੈ, ਜਿਸ ਵਿੱਚ ਇਸ ਨੂੰ ਰੱਖਿਆ ਜਾਂਦਾ ਹੈ ।

(ਅ) ਗੈਸ ਦੇ ਕਣਾਂ ਦੀ ਗਤੀ ਅਨਿਯਮਿਤ ਅਤੇ ਬਹੁਤ ਤੀਬਰ ਹੁੰਦੀ ਹੈ । ਇਸ ਅਨਿਯਮਿਤ ਗਤੀ ਦੇ ਕਾਰਨ ਇਹ ਕਣ ਆਪਸ ਵਿੱਚ ਬਰਤਨ ਦੀਆਂ ਦੀਵਾਰਾਂ ਨਾਲ ਟਕਰਾਉਂਦੇ ਹਨ । ਬਰਤਨ ਦੀ ਦੀਵਾਰ ਤੇ ਗੈਸ ਕਣਾਂ ਦੁਆਰਾ ਪ੍ਰਤੀ ਇਕਾਈ ਖੇਤਰ ‘ਤੇ ਲੱਗੇ ਬਲ ਦੇ ਕਾਰਨ ਦੀਵਾਰਾਂ ‘ਤੇ ਦਬਾਅ ਬਣਦਾ ਹੈ ।

(ੲ) ਲੱਕੜ ਦੀ ਮੇਜ਼ ਪਦਾਰਥ ਦੇ ਜਿਹੜੇ ਕਣਾਂ ਤੋਂ ਮਿਲ ਕੇ ਬਣੀ ਹੈ ਉਹਨਾਂ ਵਿੱਚ ਇੱਕ ਬਲ ਕਾਰਜ ਕਰਦਾ ਹੈ ਜੋ ਹੋਰ ਕਣਾਂ ਨੂੰ ਆਪਣੇ ਨਾਲ ਜੋੜ ਕੇ ਰੱਖਣ ਵਿੱਚ ਸਹਾਇਤਾ ਕਰਦਾ ਹੈ । ਨਿਸਚਿਤ ਆਕਾਰ, ਦਬੀਣਯੋਗਤਾ ਦੀ ਕਮੀ, ਸਪੱਸ਼ਟ ਸੀਮਾਵਾਂ ਅਤੇ ਸਥਿਰ ਆਇਤਨ ਦੇ ਕਾਰਨ ਇਹ ਠੋਸ ਕਹਾਉਂਦਾ ਹੈ । ਇਹ ਬਾਹਰੀ ਬਲ ਲੱਗਣ ਤੇ ਵੀ ਆਪਣੇ ਆਕਾਰ ਨੂੰ ਬਣਾਈ ਰੱਖਦਾ ਹੈ ।

(ਸ) ਪਦਾਰਥਾਂ ਦੇ ਕਣਾਂ ਵਿੱਚ ਆਕਰਸ਼ਣ ਬਲ ਹੁੰਦਾ ਹੈ ਜਿਸ ਦਾ ਮੁੱਲ ਵੱਖ-ਵੱਖ ਪਦਾਰਥਾਂ ਲਈ ਵੱਖ-ਵੱਖ ਹੁੰਦਾ ਹੈ । ਹਵਾ ਦੇ ਕਣਾਂ ਵਿੱਚ ਇਹ ਬਲ ਨਾਂ-ਮਾਤਰ ਹੀ ਹੁੰਦਾ ਹੈ ਜਿਸ ਕਾਰਨ ਇਸ ਦੇ ਕਣਾਂ ਵਿੱਚ ਸਥਾਨ ਬਣਾਇਆ ਜਾ ਸਕਦਾ ਹੈ ਅਰਥਾਤ ਹਵਾ ਵਿੱਚ ਅਸੀਂ ਆਪਣਾ ਹੱਥ ਸੌਖਿਆਂ ਚਲਾ ਸਕਦੇ ਹਾਂ, ਪਰ ਠੋਸ ਲੱਕੜੀ ਦੇ ਟੁਕੜੇ ਵਿੱਚ ਆਕਰਸ਼ਣ ਬਲ ਦਾ ਮੁੱਲ ਬਹੁਤ ਜ਼ਿਆਦਾ ਹੁੰਦਾ ਹੈ ਜਿਸ ਨਾਲ ਇਸ ਦੇ ਕਣ ਆਪਸ ਵਿੱਚ ਮਜ਼ਬੂਤੀ ਨਾਲ ਜੁੜੇ ਹੁੰਦੇ ਹਨ ਅਤੇ ਇਹਨਾਂ ਦੇ ਵਿੱਚ ਅਸੀਂ ਆਪਣਾ ਹੱਥ ਨਹੀਂ ਚਲਾ ਸਕਦੇ । ਲੱਕੜੀ ਦੇ ਟੁਕੜੇ ਵਿੱਚ ਹੱਥ ਚਲਾਉਣ ਲਈ ਸਾਨੂੰ ਕਰਾਟੇ ਕਲਾ ਵਿੱਚ ਮਾਹਰ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ਜਿਸ ਨਾਲ ਅਸੀਂ ਲੱਕੜੀ ਦੇ ਟੁਕੜੇ ਨੂੰ ਆਪਣੇ ਹੱਥ ਨਾਲ ਤੋੜ ਸਕਦੇ ਹਾਂ ।

ਪ੍ਰਸ਼ਨ 8.
ਆਮ ਤੌਰ ‘ਤੇ ਠੋਸ ਪਦਾਰਥ ਨਾਲੋਂ ਵਾਂ ਦੀ ਘਣਤਾ ਘੱਟ ਹੁੰਦੀ ਹੈ । ਪਰ ਤੁਸੀਂ ਬਰਫ਼ ਦੇ ਟੁਕੜੇ ਨੂੰ ਪਾਣੀ ਉੱਤੇ ਤੈਰਦੇ ਵੇਖਿਆ ਹੋਵੇਗਾ | ਪਤਾ ਕਰੋ ਅਜਿਹਾ ਕਿਉਂ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਬਹੁਤ ਸਾਰੀਆਂ ਵਸਤਾਂ ਗਰਮ ਹੋ ਕੇ ਫੈਲਦੀਆਂ ਹਨ । ਤਾਪਮਾਨ ਵਧਾਉਣ ਤੇ ਉਹਨਾਂ ਦੀ ਘਣਤਾ ਘੱਟਦੀ ਹੈ ਪਰ ਪਾਣੀ 0°C ਤੋਂ 4°C ਤਾਪਮਾਨ ਦੇ ਵਿੱਚ ਸੁੰਗੜਦਾ ਹੈ ਅਤੇ ਇਸ ਤੋਂ ਬਾਅਦ ਇਹ ਹੋਰ ਵਸਤੂਆਂ ਦੀ ਤਰ੍ਹਾਂ ਫੈਲਦਾ ਹੈ | ਪਾਣੀ ਦੀ ਵੱਧ ਤੋਂ ਵੱਧ ਘਣਤਾ 4°C ਤੇ 1g/cm³ ਹੁੰਦੀ ਹੈ । ਬਰਫ਼ ਦੀ ਘਣਤਾ ਪਾਣੀ ਨਾਲੋਂ ਘੱਟ ਹੈ ਇਸ ਲਈ ਇਹ ਪਾਣੀ ਦੇ ਤਲ `ਤੇ ਤੈਰਦੀ ਹੈ । ਇਹ ਦੇਖਿਆ ਗਿਆ ਹੈ ਕਿ 0.91 g ਪਾਣੀ 0°C ਤੇ 1 cm³ ਆਇਤਨ ਘੇਰਦਾ ਹੈ ਅਰਥਾਤ ਬਰਫ਼ ਦੀ ਘਣਤਾ 0.91g/cm³ ਹੁੰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 9.
ਹੇਠ ਲਿਖੇ ਤਾਪਮਾਨਾਂ ਨੂੰ ਸੈਲਸੀਅਸ ਵਿੱਚ ਬਦਲੋ :
(ਉ) 300 K
(ਅ) 573 K.
ਉੱਤਰ-
(ੳ) 300 K = 300 – 273
= 27°C

(ਅ) 573 K = 573 – 273
= 300°C

ਪ੍ਰਸ਼ਨ 10.
ਹੇਠ ਲਿਖੇ ਤਾਪਮਾਨ ਤੇ ਪਾਣੀ ਦੀ ਭੌਤਿਕ ਅਵਸਥਾ ਕੀ ਹੋਵੇਗੀ ?
(ਉ) 250°C
(ਅ) 100°C.
ਉੱਤਰ-
(ਉ) ਵਾਸ਼ਪ । ਸਾਰਾ ਪਾਣੀ ਭਾਫ਼ ਬਣ ਕੇ ਉੱਡ ਜਾਵੇਗਾ ।
(ਅ) ਪਾਣੀ ਉਬਲਣ ਲੱਗੇਗਾ । ਇਹ ਪਾਣੀ ਦਾ ਉਬਾਲ ਦਰਜਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 11.
ਕਿਸੇ ਵੀ ਪਦਾਰਥ ਦੀ ਅਵਸਥਾ ਪਰਿਵਰਤਨ ਦੇ ਦੌਰਾਨ ਤਾਪਮਾਨ ਸਥਿਰ ਕਿਉਂ ਰਹਿੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਕਿਸੇ ਵੀ ਪਦਾਰਥ ਦੀ ਅਵਸਥਾ ਪਰਿਵਰਤਨ ਦੇ ਦੌਰਾਨ ਸਥਿਰ ਰਹਿੰਦੀ ਹੈ । ਕਣਾਂ ਦੇ ਆਪਸੀ ਆਕਰਸ਼ਣ ਬਲ ਨੂੰ ਘਟਾਉਣ ਲਈ ਇਹ ਤਾਪ ਊਰਜਾ ਦੀ ਵਰਤੋਂ ਹੁੰਦੀ ਹੈ ਤੇ ਪਦਾਰਥ ਦੀ ਅਵਸਥਾ ਵਿੱਚ ਪਰਿਵਰਤਨ ਆ ਜਾਂਦਾ ਹੈ । ਤਾਪਮਾਨ ਵਿੱਚ ਵਾਧਾ ਦਿਖਾਏ ਬਿਨਾਂ ਹੀ ਪਦਾਰਥ ਤਾਪ ਊਰਜਾ ਨੂੰ ਸੋਖ ਲੈਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 12.
ਵਾਯੂਮੰਡਲੀ ਗੈਸਾਂ ਨੂੰ ਦ੍ਰਵ ਵਿੱਚ ਪਰਿਵਰਤਿਤ ਕਰਨ ਦੇ ਲਈ ਕੋਈ ਵਿਧੀ ਸੁਝਾਓ ।
ਉੱਤਰ-
ਵਾਯੂਮੰਡਲੀ ਗੈਸਾਂ ਨੂੰ ਕਿਸੇ ਬੰਦ ਬਰਤਨ ਵਿੱਚ ਬੰਦ ਕਰਕੇ ਦਬਾਅ ਵਧਾ ਕੇ ਅਤੇ ਤਾਪਮਾਨ ਘੱਟ ਕਰਕੇ ਇਸ ਨੂੰ ਤ੍ਰ ਵਿੱਚ ਬਦਲਿਆ ਜਾ ਸਕਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 13.
ਗਰਮ ਖੁਸ਼ਕ ਦਿਨ ਵਿੱਚ ਕੂਲਰ ਵਧੇਰੇ ਠੰਡ ਕਿਉਂ ਕਰਦਾ ਹੈ ?
ਉੱਤਰ-
ਗਰਮ ਖੁਸ਼ਕ ਦਿਨ ਵਿੱਚ ਤਾਪਮਾਨ ਵੱਧ ਜਾਣ ਕਾਰਨ ਵਧੇਰੇ ਕਣਾਂ ਨੂੰ ਗਤਿਜ ਊਰਜਾ ਮਿਲਦੀ ਹੈ । ਖ਼ੁਸ਼ਕ ਵਾਤਾਵਰਨ ਕਾਰਨ ਹਵਾ ਵਿੱਚ ਮੌਜੂਦ ਜਲ ਵਾਸ਼ਪ ਘੱਟ ਹੋ ਜਾਂਦੇ ਹਨ । ਹਵਾ ਵਿੱਚ ਜਲ ਕਣਾਂ ਦੀ ਮਾਤਰਾ ਘੱਟ ਹੋਣ ‘ਤੇ ਵਾਸ਼ਪੀਕਰਨ ਦੀ ਦਰ ਵੱਧ ਜਾਂਦੀ ਹੈ । ਵਾਸ਼ਪੀਕਰਨ ਤੋਂ ਠੰਡਕ ਪੈਦਾ ਹੁੰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 14.
ਗਰਮੀਆਂ ਵਿੱਚ ਘੜੇ ਦਾ ਪਾਣੀ ਠੰਡਾ ਕਿਉਂ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਮਿੱਟੀ ਦੇ ਬਣੇ ਘੜੇ ਵਿੱਚ ਛੋਟੇ-ਛੋਟੇ ਛੇਕ ਹੁੰਦੇ ਹਨ ਜਿਨ੍ਹਾਂ ਵਿੱਚੋਂ ਘੜੇ ਵਿੱਚ ਭਰਿਆ ਪਾਣੀ ਰਿਸ ਕੇ ਬਾਹਰ ਆ ਜਾਂਦਾ ਹੈ ਅਤੇ ਵਾਤਾਵਰਨ ਦੀ ਗਰਮ ਹਵਾ ਦੇ ਸੰਪਰਕ ਵਿੱਚ ਆ ਕੇ ਵਾਸ਼ਪੀਕ੍ਰਿਤ ਹੋ ਜਾਂਦਾ ਹੈ । ਪਾਣੀ ਦੇ ਵਾਸ਼ਪ ਵਿੱਚ ਬਦਲਣ ਲਈ ਲੋੜੀਂਦੀ ਤਾਪ ਉਰਜਾ ਘੜੇ ਦੇ ਅੰਦਰ ਵਾਲੇ ਪਾਣੀ ਤੋਂ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ । ਇਸ ਨਾਲ ਘੜੇ ਦੇ ਅੰਦਰ ਮੌਜੂਦ ਪਾਣੀ ਠੰਡਾ ਹੋ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 15.
ਐਸੀਟੋਨ/ਪੈਟਰੋਲ ਜਾਂ ਸੈਂਟ ਪਾਉਣ ‘ ਤੇ ਸਾਡੀ ਹਥੇਲੀ ਠੰਡੀ ਕਿਉਂ ਹੋ ਜਾਂਦੀ ਹੈ ?
ਉੱਤਰ-
ਐਸੀਟੋਨ/ਪੈਟਰੋਲ ਜਾਂ ਸੈਂਟ ਬਹੁਤ ਜਲਦੀ ਵਾਸ਼ਪੀੜਿਤ ਹੋ ਜਾਂਦੇ ਹਨ । ਜਦੋਂ ਇਹਨਾਂ ਪਦਾਰਥਾਂ ਨੂੰ ਹਥੇਲੀ ‘ਤੇ ਪਾਇਆ ਜਾਂਦਾ ਹੈ ਤਾਂ ਇਹਨਾਂ ਦੇ ਕਣ ਹਥੇਲੀ ਅਤੇ ਆਸ-ਪਾਸ ਦੇ ਵਾਤਵਰਨ ਤੋਂ ਉਰਜਾ ਪ੍ਰਾਪਤ ਕਰ ਲੈਂਦੇ ਹਨ ਅਤੇ ਵਾਸ਼ਪੀਕ੍ਰਿਤ ਹੋ ਜਾਂਦੇ ਹਨ । ਉਹਨਾਂ ਦੀ ਹਾਨੀ ਨਾਲ ਸਾਡੀ ਹਥੇਲੀ ਠੰਡੀ ਹੋ ਜਾਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 16.
ਕੱਪ ਦੀ ਬਜਾਏ ਪਲੇਟ ਵਿੱਚ ਅਸੀਂ ਗਰਮ ਦੁੱਧ ਜਾਂ ਚਾਹ ਜਲਦੀ ਕਿਉਂ ਪੀ ਲੈਂਦੇ ਹਾਂ ?
ਉੱਤਰ-
ਕੱਪ ਦੀ ਤੁਲਨਾ ਵਿੱਚ ਪਲੇਟ ਦੀ ਸਤ੍ਹਾ ਵੱਧ ਹੁੰਦੀ ਹੈ । ਪਲੇਟ ਦੀ ਸਤਾ ਵੱਧ ਹੋਣ ਕਾਰਨ ਇਸ ਵਿੱਚ ਭਰੇ ਦੁੱਧ ਜਾਂ ਚਾਹ ਦਾ ਵਾਸ਼ਪਣ ਵੱਧ ਹੁੰਦਾ ਹੈ । ਪਲੇਟ ਦੀ ਸਤਾ ਤੋਂ ਵਾਸ਼ਪਣ ਵੱਧ ਹੁੰਦਾ ਹੈ । ਪਲੇਟ ਦੀ ਸਤਹਿ ਤੋਂ ਵਾਸ਼ਪਣ ਵੱਧ ਹੋਣ ਨਾਲ ਦੁੱਧ ਅਤੇ ਚਾਹ ਜਲਦੀ ਠੰਡੇ ਹੋ ਜਾਂਦੇ ਹਨ । ਅਸੀਂ ਕੱਪ ਦੀ ਬਜਾਏ ਪਲੇਟ ਨਾਲ ਇਸ ਨੂੰ ਜਲਦੀ ਹੀ ਲੈਂਦੇ ਹੈ ।

ਪ੍ਰਸ਼ਨ 17.
ਗਰਮੀਆਂ ਵਿੱਚ ਸਾਨੂੰ ਕਿਸ ਕਿਸਮ ਦੇ ਕੱਪੜੇ ਪਹਿਨਣੇ ਚਾਹੀਦੇ ਹਨ ?
ਉੱਤਰ-
ਗਰਮੀਆਂ ਵਿੱਚ ਸਾਨੂੰ ਸੂਤੀ ਕੱਪੜੇ ਪਹਿਨਣੇ ਚਾਹੀਦੇ ਹਨ। ਸਰੀਰਕ ਪ੍ਰਕਿਰਿਆ ਦੇ ਕਾਰਨ ਗਰਮੀਆਂ ਵਿੱਚ ਪਸੀਨਾ ਵਧੇਰੇ ਆਉਂਦਾ ਹੈ, ਜਿਸ ਨਾਲ ਸਾਨੂੰ ਠੰਡਕ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ । ਪਸੀਨੇ ਦੇ ਵਾਸ਼ਪੀਕਰਨ ਦੇ ਦੌਰਾਨ ਪਸੀਨੇ ਦੇ ਕਣ ਸਾਡੇ ਸਰੀਰ ਜਾਂ ਆਸ-ਪਾਸ ਦੀ ਊਰਜਾ ਪ੍ਰਾਪਤ ਕਰਕੇ ਵਾਸ਼ਪ ਵਿੱਚ ਬਦਲ ਜਾਂਦੇ ਹਨ । ਵਾਸ਼ਪੀਕਰਨ ਦੀ ਗੁਪਤ ਤਾਪ ਉਰਜਾ ਦੇ ਬਰਾਬਰ ਤਾਪ ਊਰਜਾ ਸਾਡੇ ਸਰੀਰ ਵਿੱਚੋਂ ਸੋਖਿਤ ਹੋ ਜਾਂਦੀ ਹੈ, ਜਿਸ ਨਾਲ ਸਰੀਰ ਠੰਡਾ ਹੋ ਜਾਂਦਾ ਹੈ । ਕਿਉਂਕਿ ਸੂਤੀ ਕੱਪੜਿਆਂ ਵਿੱਚ ਪਾਣੀ ਦਾ ਸੋਖਣ ਵੱਧ ਹੁੰਦਾ ਹੈ, ਇਸ ਲਈ ਸਾਡਾ ਪਸੀਨਾ ਇਸ ਦੁਆਰਾ ਸੌਖ ਕੇ ਵਾਯੂਮੰਡਲ ਵਿੱਚ ਸੌਖਿਆਂ ਵਾਸ਼ਪੀਕ੍ਰਿਤ ਹੋ ਜਾਂਦਾ ਹੈ ।

Punjab State Board PSEB 7th Class Science Book Solutions Chapter 12 ਪੌਦਿਆਂ ਵਿੱਚ ਪ੍ਰਜਣਨ Textbook Exercise Questions, and Answers.

PSEB Solutions for Class 7 Science Chapter 12 ਪੌਦਿਆਂ ਵਿੱਚ ਪ੍ਰਜਣਨ

PSEB 7th Class Science Guide ਪੌਦਿਆਂ ਵਿੱਚ ਪ੍ਰਜਣਨ Intext Questions and Answers

ਸੋਚੋ ਅਤੇ ਉੱਤਰ ਦਿਓ : (ਪੇਜ 144)

ਪ੍ਰਸ਼ਨ 1.
ਪੁਨਰਜਣਨ (Regeneration) ਵਿਧੀ ਵਿੱਚ ਕੀ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਪੁਨਰਜਣਨ ਵਿਧੀ-ਇਸ ਵਿਧੀ ਵਿੱਚ ਜੀਵ (ਪੌਦੇ ਅਤੇ ਜੰਤ) ਆਪਣੇ ਆਪ ਦੀ ਮੁਰੰਮਤ ਕਰਦੇ ਹਨ ਜਾਂ ਫਿਰ ਟੁੱਟੇ-ਭੱਜੇ ਅੰਗਾਂ ਨੂੰ ਮੁੜ ਪੈਦਾ ਕਰਦੇ ਹਨ । ਇਸ ਤਰ੍ਹਾਂ ਉਹ ਆਪਣੇ ਪੁਰਾਣੇ ਜਾਂ ਮ੍ਰਿਤ ਸੈੱਲਾਂ ਦੀ ਥਾਂ ਨਵੇਂ ਸੈੱਲ ਬਣਦੇ ਹਨ । ਪੌਦਿਆਂ ਵਿੱਚ ਪੁਨਰਜਣਨ ਦੀ ਸਮਰੱਥਾ ਜੰਤੂਆਂ ਦੇ ਮੁਕਾਬਲੇ ਵਿੱਚ ਵੱਧ ਹੁੰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਦੋ-ਖੰਡਨ ਵਿਧੀ (Binary Fission) ਰਾਹੀਂ ਅਲਿੰਗੀ ਪ੍ਰਣਨ ਕਰਨ ਵਾਲੇ ਦੋ ਜੀਵਾਂ ਦੇ ਨਾਂ ਲਿਖੋ ।
ਉੱਤਰ-
ਦੋ-ਖੰਡਨ ਵਿਧੀ ਦੁਆਰਾ ਅਲਿੰਗੀ ਪ੍ਰਣਨ ਕਰਨ ਵਾਲੇ ਜੀਵ-

• ਕਾਈ,
• ਉੱਲੀ ।

PSEB 7th Class Science Guide ਪੌਦਿਆਂ ਵਿੱਚ ਪ੍ਰਜਣਨ Textbook Questions and Answers

1. ਖ਼ਾਲੀ ਥਾਂਵਾਂ ਭਰੋ

(i) ਪਰਾਗਕੋਸ਼ ਅਤੇ ਤੰਤੂ ਮਿਲ ਕੇ ਫੁੱਲ ਦਾ ……………. ਬਣਾਉਂਦੇ ਹਨ ।
ਉੱਤਰ-
ਪੁੰਕੇਸਰ,

(ii) …………… ਪ੍ਰਜਣਨ ਵਿੱਚ ਬੀਜ ਬਣਦੇ ਹਨ ।
ਉੱਤਰ-
ਦੋ-ਲਿੰਗੀ,

(iii) ਜਿਸ ਫੁੱਲ ਵਿੱਚ ਪੁੰਕੇਸਰ ਅਤੇ ਇਸਤਰੀ ਕੇਸਰ ਦੋਵੇਂ ਹੋਣ, ਉਸ ਫੁੱਲ ਨੂੰ …………..
ਉੱਤਰ-
ਦੋ-ਲਿੰਗੀ,

(iv) …………… ਅਲਿੰਗੀ ਪ੍ਰਜਣਨ ਦੀ ਇੱਕ ਵਿਧੀ ਹੈ ।
ਉੱਤਰ-
ਕਾਇਕ ਪ੍ਰਜਣਨ ॥

2. ਸਹੀ ਜਾਂ ਗਲਤ ਦੱਸੋ –

(i) ਖਮੀਰ ਵਿੱਚ ਲਿੰਗੀ ਅਤੇ ਅਲਿੰਗੀ ਢੰਗਾਂ ਨਾਲ ਪ੍ਰਜਣਨ ਹੁੰਦਾ ਹੈ ।
ਉੱਤਰ-
ਗਲਤ,

(ii) ਪਰਾਗਕਣ ਫੁੱਲ ਦੇ ਨਰ ਯੁਗਮਕ ਹੁੰਦੇ ਹਨ ।
ਉੱਤਰ-
ਸਹੀ,

(iii) ਅਦਰਕ ਇੱਕ ਤਣਾ ਹੈ ਜਿਸ ਵਿੱਚ ਗੰਢਾਂ ਅਤੇ ਅੰਤਰ ਗੰਢਾਂ ਹੁੰਦੀਆਂ ਹਨ ।
ਉੱਤਰ-
ਸਹੀ,

(iv) ਕਲਮਾਂ ਲਗਾਉਣਾ ਅਤੇ ਪਿਓਂਦ ਚੜ੍ਹਾਉਣਾ, ਪ੍ਰਜਣਨ ਦੇ ਕੁਦਰਤੀ ਢੰਗ ਹਨ ।
ਉੱਤਰ-
ਗਲਤ ।

3. ਕਾਲਮ ‘’ ਅਤੇ ‘ਅ’ ਦਾ ਮਿਲਾਨ ਕਰੋ

ਕਾਲਮ ‘ੳ’	ਕਾਲਮ ‘ਅ’
(i) ਸ਼ਕਰਕੰਦੀ	(ੳ) ਸੁਖਮ ਪ੍ਰਜਣਨ
(ii) ਆਲੂ	(ਅ) ਪੱਥਰ ਚੱਟ
(iii)  ਪੱਤਿਆਂ ਦੀਆਂ ਕਰੂੰਬਲਾਂ ਰਾਹੀਂ ਇਕ ਪ੍ਰਜਣਨ	(ਈ) ਬਨਾਉਟੀ ਪ੍ਰਜਣਨ
(iv) ਪਿਓਂਦ ਚੜ੍ਹਾਉਣੀ	(ਸ) ‘ ਖਮੀਰ .
(v) ਟਿਸ਼ੂ ਕਲਚਰ	(ਹ) ਸਪਾਈਰੋਗਾਇਰਾ
(vi) ਕਲੀ	(ਕ) ਫੁੱਲੀਆਂ ਜੜਾਂ
(vii) ਵਿਖੰਡਨ	(ਖ) ਗੰਢ (ਟਿਊਬਰ)

ਉੱਤਰ-

ਕਾਲਮ ‘ਉ’	ਕਾਲਮ “ਅ”
(i) ਸ਼ਕਰਕੰਦੀ	(ਕ) ਫੁੱਲੀਆਂ ਜੜਾਂ
(ii) ਆਲੂ	(ਖ) ਗੰਢ (ਟਿਊਬਰ)
(iii) ਪੱਤਿਆਂ ਦੀਆਂ ਕਰੂੰਬਲਾਂ	(ਅ) ਪੱਥਰ ਚੱਟ ਰਾਹੀਂ ਕਾਇੱਕ ਪ੍ਰਜਣਨ
(iv) ਪਿਓਂਦ ਚੜ੍ਹਾਉਣੀ	(ਇ) ਬਨਾਉਟੀ ਪ੍ਰਜਣਨ
(v) ਟਿਸ਼ੂ ਕਲਚਰ	(ਉ) ਸੁਖਮ ਪ੍ਰਜਣਨ
(vi) ਕਲੀ	(ਸ) ਖਮੀਰ
(vii) ਵਿਖੰਡਨ	(ਹ) ਸਪਾਈਰੋਗਾਇਰਾ ।

4. ਬਹੁਤ ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ

ਪ੍ਰਸ਼ਨ (i)
ਪ੍ਰਜਣਨ ਦੇ ਉਸ ਢੰਗ ਨੂੰ ਕੀ ਕਹਿੰਦੇ ਹਨ ਜਿਸ ਵਿੱਚ ਕੇਵਲ ਇੱਕ ਜਣਕ ਤੋਂ ਨਵੇਂ ਪੌਦੇ ਪੈਦਾ ਹੁੰਦੇ ਹਨ ?
ਉੱਤਰ-
(i) ਕਾਇਕ ਪ੍ਰਜਣਨ-ਕਲਮ ਲਗਾਉਣਾ, ਦਾਬ ਲਗਾਉਣਾ, ਟਿਸ਼ੂ ਕਲਚਰ ਬਨਾਉਟੀ ।

ਪ੍ਰਸ਼ਨ (ii)
ਫੁੱਲ ਦਾ ਕਿਹੜਾ ਭਾਗ ਫ਼ਲ ਬਣਦਾ ਹੈ ?
ਉੱਤਰ-
ਨਿਸ਼ੇਚਨ ਮਗਰੋਂ ਅੰਡਕੋਸ਼ ਫਲ ਬਣ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ (iii)
ਖਮੀਰ ਵਿਚ ਪ੍ਰਜਣਨ ਕਿਵੇਂ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਕਾਇਕ ਵਾਧੇ ਦਾ ਖਮੀਰ ਵਿੱਚ ਸਭ ਤੋਂ ਸਾਧਾਰਨ ਢੰਗ ਅਲਿੰਗੀ ਪ੍ਰਜਣਨ ਹੈ ਜਿੱਥੇ ਜਨਕ ਸੈੱਲ ’ਤੇ ਇੱਕ ਛੋਟੀ ਕਲੀ ਡਾਂਟਰ ਸੈੱਲ ਬਣਦੀ ਹੈ । ਜਨਕ ਸੈੱਲ ਟੁੱਟ ਕੇ ਡਾਂਟਰ ਨਿਊਕਲੀਅਸ ਬਣਾਉਂਦਾ ਹੈ ਜਿਹੜਾ ਡਾਂਟਰ ਸੈੱਲ ਵਿੱਚ ਚਲਾ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ (iv)
ਹਵਾ ਪਰਾਗਣ ਵਿੱਚ ਸਹਾਇਤਾ ਕਰਦੀ ਹੈ ? ਇੱਕ ਉਦਾਹਰਨ ਦਿਓ ।
ਉੱਤਰ-
ਜਦੋਂ ਪਰਾਗਕੋਸ਼ ਪੱਕ ਕੇ ਤਿਆਰ ਹੋ ਜਾਂਦੇ ਹਨ ਤਾਂ ਇਹ ਫਟ ਜਾਂਦੇ ਹਨ ਅਤੇ ਪਰਾਗਕਣ ਇਨ੍ਹਾਂ ਤੋਂ ਬਾਹਰ ਆ ਜਾਂਦੇ ਹਨ | ਪਰਾਗਕਣ ਬਹੁਤ ਹਲਕੇ ਹੁੰਦੇ ਹਨ । ਇਸ ਲਈ ਜਦੋਂ ਹਵਾ ਵੱਗਦੀ ਹੈ ਤਾਂ ਇਹ ਹਵਾ ਨਾਲ ਉੱਡ ਕੇ ਦੂਰ ਤੱਕ ਚਲੇ ਜਾਂਦੇ ਹਨ । ਇਹ ਪਰਾਗਕਣ ਉਸੇ ਪੌਦੇ ਦੇ ਦੋ ਫੁੱਲਾਂ ਦੇ ਜਾਂ ਉਸੇ ਪ੍ਰਜਾਤੀ ਦੇ ਦੂਜੇ ਫੁੱਲ ਦੇ ਇਸਤਰੀ ਕੇਸਰ ਦੀ ਪਰਾਗਕਣ ਹੀ ਤੱਕ ਪੁੱਜਦੇ ਹਨ ਜਿਸ ਤੋਂ ਪਰਾਗਣ-ਕਿਰਿਆ ਹੁੰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ (v)
ਫੁੱਲ ਦੇ ਲਿੰਗੀ ਭਾਗਾਂ ਦੇ ਨਾਂ ਲਿਖੋ ।
ਉੱਤਰ-
ਫੁੱਲ ਦੇ ਦੋ- ਗੀ ਭਾਗ-

• ਪੁੰਕੇਸਰ,
• ਇਸਤਰੀ ਕੇਸਰ ।

5. ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ

ਪ੍ਰਸ਼ਨ (i)
ਪੌਦਿਆਂ ਵਿੱਚ ਅਲਿੰਗੀ ਪ੍ਰਜਣਨ ਦੇ ਵੱਖ-ਵੱਖ ਢੰਗਾਂ ਦੇ ਨਾਂ ਲਿਖੋ ।
ਉੱਤਰ-
ਪੌਦਿਆਂ ਵਿੱਚ ਅਲਿੰਗੀ ਪ੍ਰਜਣਨ-ਅਲਿੰਗੀ ਪ੍ਰਜਣਨ ਅਜਿਹੀ ਵਿਧੀ ਹੈ, ਜਿਸ ਵਿਚ ਨਵੇਂ ਪੌਦੇ ਉਗਾਉਣ ਲਈ ਬੀਜਾਂ ਦੀ ਲੋੜ ਨਹੀਂ ਹੁੰਦੀ ਹੈ । ਇੱਕ ਹੀ ਜਣਕ ਤੋਂ ਨਵਾਂ ਪੰਦਾ ਤਿਆਰ ਹੋ ਜਾਂਦਾ ਹੈ | ਅਲਿੰਗੀ ਪ੍ਰਜਣਨ ਹੇਠ ਲਿਖੇ ਢੰਗਾਂ ਨਾਲ ਹੁੰਦਾ ਹੈ-

1. ਦੋ-ਖੰਡਨ ਵਿਧੀ
2. ਕਲੀਆਂ ਰਾਹੀਂ
3. ਵਿਖੰਡਨ
4. ਬੀਜਾਣੂਆਂ ਰਾਹੀਂ
5. ਪੁਨਰਜਣਨ ।

ਪ੍ਰਸ਼ਨ (ii)
ਪੌਦਿਆਂ ਵਿੱਚ ਬਨਾਉਟੀ ਪ੍ਰਜਣਨ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਪੌਦਿਆਂ ਵਿੱਚ ਬਨਾਉਟੀ ਪ੍ਰਜਣਨ-ਲਾਭਦਾਇਕ ਪੌਦਿਆਂ ਦੀ ਗਿਣਤੀ ‘ਚ ਵਾਧੇ ਲਈ ਕਾਇਕ ਪਜਣਨ ਦੇ ਬਨਾਉਟੀ ਢੰਗ ਅਪਣਾਏ ਜਾਂਦੇ ਹਨ | ਅਲਿੰਗੀ ਪ੍ਰਜਣਨ ਦੀ ਇਨ੍ਹਾਂ ਵਿਧੀਆਂ ਵਿੱਚ ਨਾ ਤਾਂ ਜਣਨ ਅੰਗ ਭਾਗ ਲੈਂਦਾ ਹੈ ਅਤੇ ਨਾ ਹੀ ਬੀਜ ਪੈਦਾ ਹੁੰਦਾ ਹੈ । ਇਸ ਬਣਾਉਟੀ ਪ੍ਰਜਣਨ ਵਿੱਚ ਜੜਾਂ, ਤਣੇ, ਟਹਿਣੀਆਂ ਜਾਂ ਪੱਤਿਆਂ ਰਾਹੀਂ ਨਵੇਂ ਪੌਦੇ ਪੈਦਾ ਹੁੰਦੇ ਹਨ ਕੁਝ ਬਨਾਉਟੀ ਢੰਗ ਹੇਠਾਂ ਦਿੱਤੇ ਗਏ ਹਨ-

• ਕਲਮ ਲਗਾਉਣਾ (ਤਣੇ ਅਤੇ ਜੜ੍ਹਾਂ ਦੀ ਕਲਮ),
• ਦਾਬ ਲਾਉਣਾ,
• ਪਿਓਂਦ,
• ਟਿਸ਼ੂ ਕਲਚਰ ।

ਪ੍ਰਸ਼ਨ (iii)
ਟਿਸ਼ੂ ਕਲਚਰ ਜਾਂ ਸੂਖਮ ਪ੍ਰਜਣਨ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਟਿਸ਼ੂ ਕਲਚਰ ਜਾਂ ਸੂਖਮ ਪ੍ਰਜਣਨ-ਇਸ ਵਿਧੀ ਵਿੱਚ ਪੌਦੇ ਦੀ ਟਹਿਣੀ ਦੇ ਸਿਖਰਲੇ ਨੁਕੀਲੇ ਭਾਗ ਵਿੱਚੋਂ ਟਿਸ਼ੂਆਂ ਦਾ ਕੁੱਝ ਪੰਜ ਲਿਆ ਜਾਂਦਾ ਹੈ ਕਿਉਂਕਿ ਇਸ ਵਿੱਚ ਤੇਜ਼ੀ ਨਾਲ ਵਿਭਾਜਿਤ ਹੋ ਰਹੇ ਘੱਟ ਵਿਕਸਿਤ ਅਤੇ ਅਣਵਿਭੇਦਿਤ ਸੈੱਲ ਹੁੰਦੇ ਹਨ । ਇਸ ਪੁੰਜ ਨੂੰ ਜ਼ਰੂਰੀ ਪੋਸ਼ਕਾਂ ਅਤੇ ਹਾਰਮੋਨਯੁਕਤ ਮਾਧਿਅਮ ਵਿੱਚ ਰੱਖਿਆ ਜਾਂਦਾ ਹੈ । ਇਹ ਟਿਸ਼ੂ ਇੱਕ ਅਣਵਿਭੇਦਿਤ ਪੁੰਜ ਵਿੱਚ ਵਿਕਸਿਤ ਹੋ ਜਾਂਦਾ ਹੈ । ਇਨ੍ਹਾਂ ਟਿਸ਼ੂਆਂ ਦਾ ਕੁੱਝ ਭਾਗ ਕਿਸੇ ਮਾਧਿਅਮ ਵਿਚ ਉਦੋਂ ਤੱਕ ਰੱਖਿਆ ਜਾਂਦਾ ਹੈ ਜਦੋਂ ਤੱਕ ਇਹ ਪੁੰਗਰਣ ਲੱਗ ਜਾਣ । ਇਨ੍ਹਾਂ ਪੁੰਗਰਾਂ (ਛੋਟੇ ਪੌਦਿਆਂ) ਨੂੰ ਗਿੱਲੀ ਮਿੱਟੀ ਵਿੱਚ ਉਗਾ ਲਿਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਵਿਧੀ ਨੂੰ ਸੂਖਮ ਪ੍ਰਸਾਰ ਵੀ ਆਖਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ (iv)
ਬੀਜ ਖਿਲਰਣ ਦੇ ਲਾਭ ਲਿਖੋ ।
ਉੱਤਰ-
ਬੀਜ ਖਿਲਰਣ ਦੇ ਲਾਭ-

1. ਬੀਜ ਖਿਲਰਣ ਨਾਲ ਪੌਦੇ ਜ਼ਿਆਦਾ ਖੇਤਰਾਂ ਵਿੱਚ ਫੈਲ ਜਾਂਦੇ ਹਨ ।
2. ਇੱਕ ਹੀ ਥਾਂ ‘ਤੇ ਪੌਦਿਆਂ ਦੇ ਸੰਘਣੇ ਹੋਣ ਦੀ ਸੰਭਾਵਨਾ ਘੱਟ ਜਾਂਦੀ ਹੈ ।
3. ਪੌਦਿਆਂ ਦੀ ਸਹੀ ਧੀ ਹੁੰਦੀ ਹੈ ਅਤੇ ਪੌਦਿਆਂ ਦਾ ਆਪਸ ਵਿੱਚ ਸੂਰਜ ਦੀ ਰੋਸ਼ਨੀ, ਪਾਣੀ ਅਤੇ ਖਣਿਜਾਂ ਦੀ ਪ੍ਰਾਪਤੀ ਲਈ ਮੁਕਾਬਲਾ ਘੱਟ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ (v)
ਪੁੰਗਰਨਾ ਕੀ ਹੈ ? ਪੁੰਗਰਨ ਲਈ ਜ਼ਰੂਰੀ ਹਾਲਤਾਂ ਕਿਹੜੀਆਂ ਹਨ ?
ਉੱਤਰ-
ਪੁੰਗਰਨਾ-ਸਿੱਲ੍ਹੀ ਮਿੱਟੀ ‘ਤੇ ਪਹੁੰਚ ਕੇ ਬੀਜ ਪਾਣੀ ਸੋਖ ਕੇ ਫੁੱਲ ਜਾਂਦੇ ਹਨ । ਹੁਣ ਭਰੂਣ ਪੁੰਗਰਨਾ ਸ਼ੁਰੂ ਕਰ ਦਿੰਦਾ ਹੈ ਅਤੇ ਇਸ ਦਾ ਰੈਡੀਕਲ (ਜੜ੍ਹ ਅੰਕੁਰ) ਮਿੱਟੀ ਅੰਦਰ ਧੱਸ ਜਾਂਦਾ ਹੈ ਅਤੇ ਜੜ੍ਹ ਬਣਦੀ ਹੈ ।ਤਣਾਂ ਅੰਕੁਰ (ਪਲਿਊਮਲ) ਉੱਪਰ ਹਵਾ ਵੱਲ ਵਧਦਾ ਹੈ ਅਤੇ ਪੱਤੇ ਨਿਕਲ ਆਉਂਦੇ ਹਨ । ਇਹ ਛੋਟੇ ਪੌਦੇ ਦਾ ਰੂਪ ਹੈ । ਪੁੰਗਰਨ ਲਈ ਜ਼ਰੂਰੀ ਹਾਲਤਾਂ-ਸਾਰੇ ਬੀਜਾਂ ਨੂੰ ਪੁੰਗਰਨ ਲਈ ਪਾਣੀ, ਆਕਸੀਜਨ (ਹਵਾ) ਅਤੇ ਉੱਚਿਤ ਤਾਪਮਾਨ ਦੀ ਲੋੜ ਹੁੰਦੀ ਹੈ । ਕੁੱਝ ਬੀਜਾਂ ਨੂੰ ਪ੍ਰਕਾਸ਼ ਦੀ ਸਹੀ ਮਾਤਰਾ ਦੀ ਵੀ ਲੋੜ ਹੁੰਦੀ ਹੈ ।

ਜਦੋਂ ਬੀਜ ਨੂੰ ਉੱਚਿਤ ਹਾਲਤਾਂ ਮਿਲਦੀਆਂ ਹਨ ਤਾਂ ਉਹ ਪਾਣੀ ਅਤੇ ਆਕਸੀਜਨ ਨੂੰ ਬਾਹਰਲੀ ਪਰਤ ਤੋਂ ਅੰਦਰ ਵੱਲ ਨੂੰ ਲਿਜਾ ਕੇ ਐਨਜਾਇਮ ਨੂੰ ਕਿਰਿਆਸ਼ੀਲ ਬਣਾਉਂਦਾ ਹੈ ਅਤੇ ਪੁੰਗਰਦਾ ਹੈ ਅਤੇ ਬੀਜ ਦੀ ਜੜ ਬਣਦੀ ਹੈ ਜੋ ਭੂਮੀ ਥੱਲਿਉਂ ਪਾਣੀ ਪਾਪਤ ਕਰਦਾ ਹੈ ਅਤੇ ਇਸ ਦਾ ਤਣਾ ਬਣਦਾ ਹੈ। ਜੋ ਉੱਪਰ ਹਵਾ ਵੱਲ ਨੂੰ ਵੱਧਦਾ ਹੈ ਅਤੇ ਤਣੇ ‘ਤੇ ਪੱਤੇ ਨਿਕਲ ਆਉਂਦੇ ਹਨ ਜਿਸ ਤੋਂ ਸੂਰਜ ਪ੍ਰਕਾਸ਼ ਵਿੱਚ ਭੋਜਨ ਬਣਾਉਂਦਾ ਹੈ।

6. ਵੱਡੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ

ਪ੍ਰਸ਼ਨ (i)
ਅਲਿੰਗੀ ਪ੍ਰਜਣਨ ਦੇ ਵੱਖ-ਵੱਖ ਢੰਗਾਂ ਦਾ ਉਦਾਹਰਨਾਂ ਸਹਿਤ ਵਰਣਨ ਕਰੋ ।
ਉੱਤਰ-
ਅਲਿੰਗੀ ਪ੍ਰਜਣਨ ਦੇ ਵੱਖ-ਵੱਖ ਢੰਗ ਨਵੇਂ ਜੀਵ-
1. ਦੋ-ਖੰਡਨ ਵਿਧੀ-ਇਹ ਅਲਿੰਗੀ ਪ੍ਰਜਣਨ ਦਾ ਆਮ ਢੰਗ ਹੈ ਜਿਸ ਵਿੱਚ ਇੱਕ ਜੀਵ, ਦੋ ਜੀਵਾਂ ਵਿੱਚ ਵੰਡਿਆ ਜਾਂਦਾ ਹੈ । ਇਹ ਪੌਦਿਆਂ ਅਤੇ ਕੁੱਝ ਇੱਕ ਸੈੱਲੀ ਜੀਵਾਂ ਜਿਵੇਂ ਉੱਲੀਆਂ, ਕੁਝ ਕਾਈਆਂ ਵਿੱਚ ਆਮ ਹੁੰਦਾ ਹੈ । ਪ੍ਰਜਣਨ ਦੀ ਇਸ ਵਿਧੀ ਵਿੱਚ ਜੀਵ ਦੋ ਬਰਾਬਰ ਭਾਗਾਂ ਵਿੱਚ ਵੰਡਿਆ ਜਾਂਦਾ ਹੈ । ਨਿਊਕਲੀਅਸ ਦੋ ਹਿੱਸਿਆਂ ਵਿੱਚ ਵੰਡਿਆ | ਜਣਕ ਜਾਂਦਾ ਹੈ ਅਤੇ ਦੋਵੇਂ ਭਾਗ ਵਿਕਸਿਤ ਹੋ ਕੇ ਦੋ ਨਵੇਂ ਜੀਵ ਨਵੇਂ ਜੀਵ ਉਤਪੰਨ ਕਰਦੇ ਹਨ ।

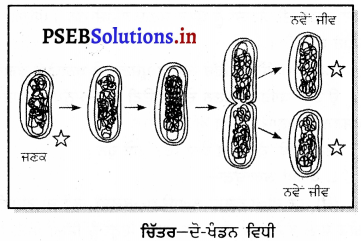
2. ਕਲੀਆਂ ਰਾਹੀਂ-ਅਜਿਹਾ ਪ੍ਰਜਣਨ ਹਾਈਡਰਾ ਵਿੱਚ ਦੇਖਿਆ ਜਾਂਦਾ ਹੈ । ਅਲਿੰਗੀ ਪ੍ਰਜਣਨ ਕਲੀਆਂ ਜਾਂ ਬੱਡ ਰਾਹੀਂ ਹੁੰਦਾ ਹੈ । ਜਣਕ ਪੌਦੇ (ਜੀਵ ਉੱਤੇ ਬਲਬ ਵਰਗੇ ਵਾਧੇ ਬਣਦੇ ਹਨ ਜਿਨ੍ਹਾਂ ਨੂੰ ਕਲੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ, ਇਹ ਕਲੀ ਆਪਣੇ ਆਪ ਨੂੰ ਮੁੱਖ ਪੌਦੇ ਤੋਂ ਵੱਖ ਕਰਕੇ ਇੱਕ ਨਵੇਂ ਪੌਦੇ ਵਿੱਚ ਵਿਕਸਿਤ ਹੁੰਦੀ ਹੈ ।

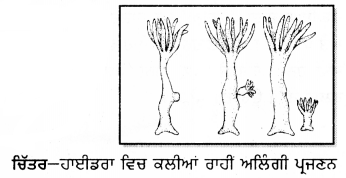
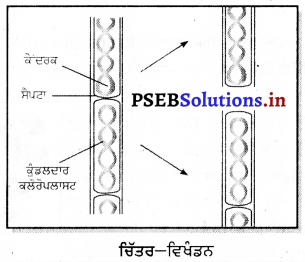
3. ਵਿਖੰਡਨ-ਇਹ ਛੱਪੜ, ਝੀਲਾਂ ਜਾਂ ਹੋਰ ਖੜੇ ਜਲ ਦੇ ਭੰਡਾਰਾਂ ਵਿੱਚ ਹਰੇ ਧੱਬਿਆਂ ਦੇ ਰੂਪ ਵਿੱਚ ਕੋਈ ਦਿਖਾਈ ਦਿੰਦੀ ਹੈ । ਜਦੋਂ ਭਰਪੂਰ ਮਾਤਰਾ ਵਿੱਚ ਪਾਣੀ ਅਤੇ ਪੋਸ਼ਣ ਉਪਲੱਬਧ ਹੁੰਦਾ ਹੈ ਤਾਂ ਵਿਖੰਡਨ ਵਿਧੀ ਰਾਹੀਂ ਇਹਨਾਂ ਦੀ ਗਿਣਤੀ ਵਿੱਚ ਵਾਧਾ ਹੁੰਦਾ ਹੈ । ਇਸ ਵਿਧੀ ਵਿੱਚ ਕੋਈ ਦੋ ਜਾਂ ਬਹੁਤੇ ਟੁਕੜਿਆਂ ਵਿੱਚ ਵੰਡੀ ਜਾਂਦੀ ਹੈ । ਹਰੇਕ ਟੁੱਕੜਾ ਪੂਰਨ ਕਾਈ ਵਿੱਚ ਵਿਕਸਿਤ ਹੋ ਜਾਂਦਾ ਹੈ । ਇਹ ਪ੍ਰਕਿਰਿਆ ਕਈ ਵਾਰ ਦੁਹਰਾਈ ਜਾਂਦੀ ਹੈ ।

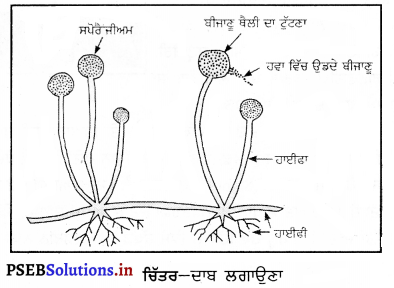
4. ਬੀਜਾਣੂਆਂ ਰਾਹੀਂ-ਬੀਜਾਣੂ ਬਹੁਤ ਛੋਟੇ, ਗੋਲ ਆਕਾਰ ਦੀਆਂ ਅਲਿੰਗੀ ਪ੍ਰਜਣਨ ਲਈ ਰਚਨਾਵਾਂ ਹੁੰਦੀਆਂ ਹਨ । ਬੀਜਾਣੂਆਂ ਦੀ ਬਾਹਰੀ ਪਰਤ ਸਖ਼ਤ ਹੁੰਦੀ ਹੈ ਅਤੇ ਇਹ ਹਵਾ ਵਿੱਚ ਲੰਬਾ ਸਮਾਂ ਰਹਿ ਸਕਦੇ ਹਨ | ਅਨੁਕੂਲ ਹਾਲਤਾਂ ਦੌਰਾਨ, ਹਰੇਕ ਬੀਜਾਣੂ ਪੁੰਗਰ ਕੇ ਇੱਕ ਨਵੇਂ ਜੀਵ ਦੇ ਰੂਪ ਵਿੱਚ ਵਿਕਸਿਤ ਹੋ ਜਾਂਦਾ ਹੈ । ਡਬਲ ਰੋਟੀ ਤੇ ਪੈਦਾ ਹੋਈ ਉੱਲੀ ਰਾਈਜ਼ੋਪਸ, ਬੀਜਾਆਂ ਰਾਹੀਂ ਅਲਿੰਗੀ ਪ੍ਰਜਣਨ ਨਾਲ ਪੈਦਾ ਹੁੰਦੀ ਹੈ । ਮੌਸ, ਫਰਨ ਵਰਗੇ ਪੌਦੇ ਵੀ ਬੀਜਾਣੂਆਂ ਰਾਹੀਂ ਪੈਦਾ ਹੁੰਦੇ ਹਨ ।

5. ਪੁਨਰ ਜਣਨ-ਜੀਵ ਕਿਸੇ ਨਾ ਕਿਸੇ ਰੂਪ ਵਿੱਚ ਆਪਣੇ ਟੱਟੇ-ਭੱਜੇ ਅੰਗ ਦੀ ਮੁਰੰਮਤ ਅਤੇ ਵਾਧਾ ਕਰਦਾ ਹੈ । ਪੁਰਾਣੇ ਜਾਂ ਮ੍ਰਿਤ ਸੈੱਲਾਂ ਦੀ ਥਾਂ ਨਵੇਂ ਸੈੱਲ ਬਣਾਉਂਦਾ ਹੈ । ਜੀਵਾਂ ਦੀ ਆਪਣੇ ਆਪ ਨੂੰ ਮੁਰੰਮਤ ਕਰਨ ਅਤੇ ਆਪਣੇ ਟੁੱਟੇ-ਭੱਜੇ ਅੰਗ ਮੁੜ ਪੈਦਾ ਕਰਨ ਦੀ ਯੋਗਤਾ ਨੂੰ ਪੁਨਰ ਜਣਨ ਕਹਿੰਦੇ ਹਨ । ਪੌਦਿਆਂ ਵਿੱਚ ਪੁਨਰ ਜਣਨ ਦੀ ਸਮਰੱਥਾ ਜੰਤੂਆਂ ਦੀ ਤੁਲਨਾ ਵਿੱਚ ਵਧੇਰੇ ਹੁੰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ (ii)
ਪੌਦਿਆਂ ਵਿੱਚ ਕਾਇਕ ਪ੍ਰਜਣਨ ਦੇ ਬਨਾਉਟੀ ਢੰਗਾਂ ਦਾ ਵਰਣਨ ਉਦਾਹਰਨਾਂ ਸਹਿਤ ਕਰੋ ।
ਉੱਤਰ-
ਕਾਇਕ ਪ੍ਰਜਣਨ ਦੇ ਬਨਾਉਟੀ ਢੰਗ-ਮਨੁੱਖ ਨੇ ਲਾਭਦਾਇਕ ਪੌਦਿਆਂ ਦੀ ਗਿਣਤੀ ਵਿੱਚ ਵਾਧੇ ਦੇ ਲਈ ਇਕ ਪ੍ਰਜਣਨ ਦੇ ਬਨਾਉਟੀ ਢੰਗ ਅਪਣਾਏ ਹਨ । ਇਨ੍ਹਾਂ ਵਿੱਚੋਂ ਕੁੱਝ ਢੰਗ ਹੇਠਾਂ ਦਿੱਤੇ ਗਏ ਹਨ-
1. ਕਲਮਾਂ ਲਗਾਉਣਾ-
(ਉ) ਤਣੇ ਦੀਆਂ ਕਲਮਾਂ ਲਗਾਉਣਾ-ਕਲਮਾਂ, ਤਣੇ ਜਾਂ ਟਹਿਣੀ ਦੇ ਗੰਢ ਵਾਲੇ ਛੋਟੇ ਭਾਗ ਹੁੰਦੇ ਹਨ, ਜਦੋਂ ਇਨ੍ਹਾਂ ਨੂੰ ਸਿੱਲ੍ਹੀ ਮਿੱਟੀ ਵਿੱਚ ਦਬਾਇਆ ਜਾਂਦਾ ਹੈ ਤਾਂ ਅਨੁਕੂਲ ਹਾਲਤਾਂ ਦੌਰਾਨ ਇਨ੍ਹਾਂ ਵਿੱਚ ਜਮ੍ਹਾਂ ਅਤੇ ਪੱਤੇ ਪੁੰਗਰ ਆਉਂਦੇ ਹਨ ਅਤੇ ਇਹ ਵੱਖਰੇ ਪੌਦੇ ਵਜੋਂ ਵਿਕਸਿਤ ਹੋ ਜਾਂਦੇ ਹਨ । ਬੋਗਨਵੇਲੀਆ, ਗੰਨਾ, ਕੈਕਟਸ ਅਤੇ ਗੁਲਾਬ ਆਦਿ ਕਲਮਾਂ ਰਾਹੀਂ ਉਗਾਏ ਜਾਂਦੇ ਹਨ ।

(ਅ) ਜੜ੍ਹਾਂ ਦੀਆਂ ਕਲਮਾਂ (Root Cuttings)-ਨਿੰਬੂ, ਇਮਲੀ ਵਰਗੇ ਪੌਦਿਆਂ ਦੀਆਂ ਜੜਾਂ ਦੇ ਟੋਟਿਆਂ ਨੂੰ ਜਦੋਂ ਸਿੱਲ੍ਹੀ ਮਿੱਟੀ ਵਿੱਚ ਦਬਾਇਆ ਜਾਂਦਾ ਹੈ ਤਾਂ ਇਹ ਨਵੇਂ ਪੌਦਿਆਂ ਵਿੱਚ ਵਿਕਸਿਤ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ।

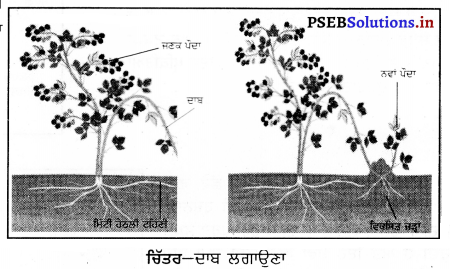
2. ਦਾਬ ਲਾਉਣਾ-ਪੌਦੇ ਦੀ ਇੱਕ ਟਹਿਣੀ ਨੂੰ ਮੋੜ ਕੇ ਮਿੱਟੀ ਵਿੱਚ ਦਬਾਇਆ ਜਾਂਦਾ ਹੈ । ਦੱਬੇ ਹੋਏ ਭਾਗ ਵਿੱਚ ਜੜ੍ਹਾਂ ਵਿਕਸਿਤ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ਅਤੇ ਇੱਕ ਸੁਤੰਤਰ ਪੌਦਾ ਤਿਆਰ ਹੋ ਜਾਂਦਾ ਹੈ ਕਿਉਂਕਿ ਇਸ ਟਹਿਣੀ ਦਾ ਉੱਪਰਲਾ ਸਿਰਾ ਪਹਿਲਾਂ ਹੀ ਹਵਾ ਵਿੱਚ । ਹੁੰਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਵਿਕਸਿਤ ਹੋਏ ਪੌਦੇ ਨੂੰ ਮੂਲ ਪੌਦੇ ਨਾਲੋਂ ਕੱਟ ਕੇ ਨਵੀਂ ਥਾਂ ‘ਤੇ ਉਗਾਇਆ ਜਾਂਦਾ ਹੈ । ਜੈਸਮੀਨ, ਸਟ੍ਰਾਬੈਰੀ, ਬੋਗਨਵੇਲੀਆ ਵਰਗੇ ਪੌਦੇ ਲੇਅਰਿੰਗ ਜਾਂ ਦਾਬ ਰਾਹੀਂ ਉਗਾਏ ਜਾਂਦੇ ਹਨ ।

3. ਪਿਓ-ਪਿਓਂਦ ਦੋ ਵੱਖ-ਵੱਖ ਪੌਦਿਆਂ ‘ਤੋਂ ਤਿਆਰ ਕੀਤੀ ਜਾਂਦੀ ਹੈ । ਇੱਕ ਪੌਦੇ ਦਾ ਜੜ੍ਹ ਵਾਲਾ ਹਿੱਸਾ ਤਣੇ ਸਮੇਤ ਚੁਣਿਆ ਜਾਂਦਾ ਹੈ ਜਿਸ ਨੂੰ ਮੁੱਢ (ਸਟਾਕ) ਕਹਿੰਦੇ ਹਨ ਜਦੋਂ ਕਿ ਦੂਜੇ ਪੌਦੇ ਲੋੜੀਂਦੇ ਗੁਣਾਂ ਵਾਲੇ) ਤੋਂ ਤਣੇ ਵਾਲਾ ਭਾਗ ਲਿਆ ਜਾਂਦਾ ਹੈ ਜਿਸ ਨੂੰ ਸ਼ਾਖਾ (Scion) ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਸ਼ਾਖਾ ਅਜਿਹੇ ਪੌਦੇ ਦੀ ਲਈ ਜਾਂਦੀ ਹੈ ਜਿਸਦੇ ਗੁਣਾਂ ਵਾਲਾ ਪੌਦਾ ਲੋੜੀਂਦਾ ਹੁੰਦਾ ਹੈ । ਮੁੱਢ ਅਤੇ ਸ਼ਾਖਾ ਦੋਵਾਂ ਨੂੰ ਤਿਰਛਾ ਕੱਟ ਕੇ ਆਹਮੋ-ਸਾਹਮਣੇ ਜੋੜਿਆ ਜਾਂਦਾ ਹੈ । ਫਿਰ ਦੋਵਾਂ ਸਿਰਿਆਂ ਨੂੰ ਘੁੱਟ ਕੇ ਬੰਨ੍ਹ ਦਿੱਤਾ ਜਾਦਾ ਹੈ । ਬੰਨ੍ਹੇ ਹੋਏ ਹਿੱਸੇ ਨੂੰ ਕਿਸੇ ਕੱਪੜੇ ਜਾਂ ਪਾਲੀਥੀਨ ਨਾਲ ਲਪੇਟ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ।

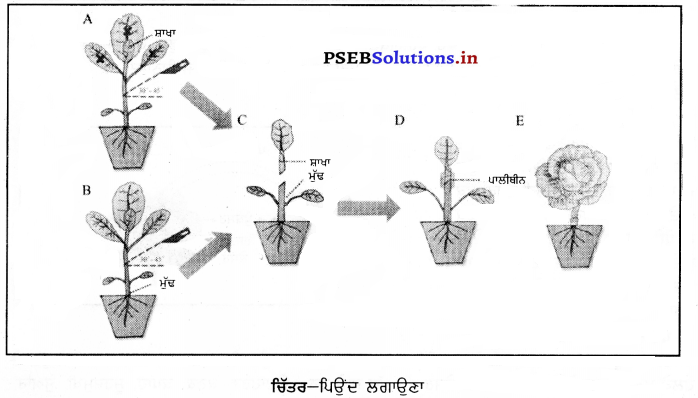
4. ਟਿਸ਼ੁ ਕਲਚਰ-ਇਸ ਵਿਧੀ ਵਿੱਚ ਪੌਦੇ ਦੀ ਟਹਿਣੀ ਦੇ ਸਿਖਰਲੇ ਨੁਕੀਲੇ ਭਾਗ ਵਿੱਚੋਂ ਇਸ਼ ਦਾ ਪੁੰਜ ਲਿਆ ਜਾਂਦਾ ਹੈ ਕਿਉਂਕਿ ਇਸ ਵਿੱਚ ਤੇਜ਼ੀ ਨਾਲ ਵਿਭਾਜਿਤ ਹੋ ਰਹੇ, ਘੱਟ ਵਿਕਸਿਤ ਜਣਕ ਪੌਦੇ ਤੋਂ ਅਤੇ ਅਣਵਿਭੇਦਿਤ ਸੈੱਲ ਹੁੰਦੇ ਹਨ । ਟਿਸ਼ੂ ਸੈਂਪਲ ਪੋਸ਼ਕ ਤੱਤਾਂ ਵਾਲੇ ਮਾਧਿਅਮ ਟਿਸ਼ੂ ਦੇ ਪੁੰਜ ਨੂੰ ਜ਼ਰੂਰੀ ਪੋਸ਼ਕਾਂ ਅਤੇ
ਵਿੱਚ ਰੱਖਿਆ ਟਿਸ਼ੂ ਸੈਂਪਲ ਹਾਰਮੋਨ ਯੁਕਤ ਮਾਧਿਅਮ ਵਿੱਚ ਰੱਖਿਆ ਜਾਂਦਾ ਹੈ । ਇਹ ਟਿਸ਼ ਇੱਕ ਅਣਵਿਭੇਦਿਤ ਪੁੰਜ ਵਿੱਚ ਵਿਕਸਿਤ ਹੁੰਦਾ ਹੈ । ਇਨ੍ਹਾਂ ਟਿਸ਼ੂਆਂ ਦਾ ਕੁੱਝ ਸੈਂਪਲ ਤੋਂ ਪਨੀਰੀ ਭਾਗ ਕਿਸੇ ਮਾਧਿਅਮ ਵਿੱਚ ਉਸ ਸਮੇਂ ਦਾ ਬਣਨਾ ਤੱਕ ਰੱਖਿਆ ਜਾਂਦਾ ਹੈ ਜਦ ਤੱਕ ਉਨ੍ਹਾਂ ਵਿੱਚੋਂ ਪੁੰਗਾਰਾਂ ਨਾ ਨਿਕਲ ਆਉਣ । ਇਨ੍ਹਾਂ ਪੁੰਗਾਰਾਂ (ਛੋਟੇ ਪੌਦਿਆਂ ਨੂੰ ਮਿੱਟੀ ਜਾਂ ਗਮਲੇ ਵਿੱਚ ਸਿੱਲੀ ਮਿੱਟੀ ਵਿੱਚ ਮਲੱੜ੍ਹ ਵਿੱਚ ਪਨੀਰੀ ਲਾਉਣਾ ਉਗਾਇਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਵਿਧੀ ਨੂੰ ਸੂਖਮ ਪ੍ਰਸਾਰ ਵੀ ਆਖਦੇ ਹਨ ।

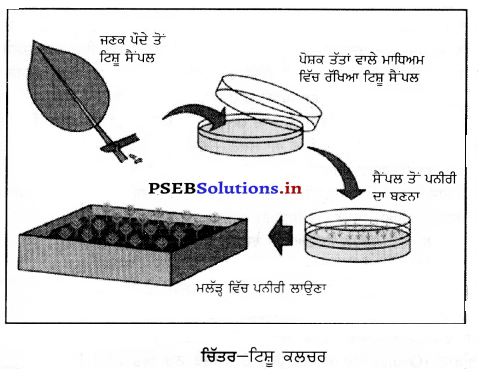
ਇਸ ਵਿਧੀ ਰਾਹੀਂ ਬਹੁਤ ਹੀ ਘੱਟ ਸਮੇਂ ਵਿੱਚ ਬਹੁਤ ਸਾਰੇ ਪੌਦੇ ਉਗਾਏ ਜਾ ਸਕਦੇ ਹਨ । ਇਸ ਤਕਨੀਕ ਦੀ ਵਰਤੋਂ ਬਿਮਾਰੀ-ਰਹਿਤ ਆਰਕਿਡ (Orchids), ਕਾਰਨੇਸ਼ਨ (Carnation), ਗਲੈਡੀਓਲਸ (Gladiolus), ਗੁਲਦਾਉਦੀ, ਆਲੂ, ਗੰਨਾ ਆਦਿ ਦੇ ਪੌਦੇ ਉਗਾਉਣ ਲਈ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ (iii)
ਪਰਾਗਣ ਕਿਰਿਆ ਕੀ ਹੈ ? ਦੋ ਤਰ੍ਹਾਂ ਦੀ ਪਰਾਗਣ ਕਿਰਿਆ ਕਿਹੜੀ ਹੈ ? ਪਰਾਗਣ ਦੇ ਵੱਖ-ਵੱਖ ਕਾਰਕਾਂ ਦਾ ਉਦਾਹਰਣ ਸਹਿਤ ਵਰਣਨ ਕਰੋ ।
ਉੱਤਰ-
ਪਰਾਗਣ (Pollination)-ਪੱਕੇ ਹੋਏ ਪਰਾਗਕਣਾਂ ਦਾ ਪਰਾਗਕੋਸ਼ ਤੋਂ ਪਰਾਗਕਣ ਹੀ (ਜਾਂ ਵਰਤਿਕਾਗਰ) ਤੱਕ ਸਥਾਨਅੰਤਰਣ, ਪਰਾਗਣ ਕਿਰਿਆ ਅਖਵਾਉਂਦਾ ਹੈ |ਪਰਾਗ ਕਣ ਹਲਕੇ ਹੁੰਦੇ ਹਨ ਇਸ ਲਈ ਇਹ ਹਵਾ, ਪਾਣੀ, ਕੀਟਾਂ ਜਾਂ ਜੰਤੂਆਂ ਰਾਹੀਂ ਦੂਰ-ਦੂਰ ਤੱਕ ਚਲੇ ਜਾਂਦੇ ਹਨ ਅਤੇ ਉਸੇ ਫੁੱਲ ਦੇ ਜਾਂ ਦੂਜੇ ਫੁੱਲ ਦੇ ਇਸਤਰੀ ਕੇਸਰ ਦੀ ਪਰਾਗਕਣ ਹੀ ਤੱਕ ਪੁੱਜਦੇ ਹਨ । ਪਰਾਗ ਕਣਾਂ ਦਾ ਪਰਾਗਕੋਸ਼ ਤੋਂ ਪਰਾਗਕਣ ਹੀ ਤੱਕ ਸਥਾਨੰਤਰਣ ਪਰਾਗਣ ਕਿਰਿਆ ਅਖਵਾਉਂਦਾ ਹੈ ।

ਪਰਾਗਣ ਦੀਆਂ ਕਿਸਮਾਂ-ਪਰਾਗਣ ਕਿਰਿਆ ਹੇਠ ਲਿਖੇ ਦੋ ਤਰ੍ਹਾਂ ਦੀ ਹੁੰਦੀ ਹੈ :
1. ਸਵੈ-ਪਰਾਗਣ-ਦੋ-ਲਿੰਗੀ ਫੁੱਲਾਂ ਵਿੱਚ ਪਰਾਗਕਣ, ਪਰਾਗਕੋਸ਼ ਵਿੱਚੋਂ ਜਦੋਂ ਉਸੇ ਫੁੱਲ ਦੇ ਇਸਤਰੀ ਕੇਸਰ ਦੀ ਪਰਾਗਕਣ ਹੀ ਤੱਕ ਜਾਂਦੇ ਹਨ ਤਾਂ ਇਸ ਕਿਰਿਆ ਨੂੰ ਸਵੈ-ਪਰਾਗਣ ਆਖਦੇ ਹਨ, ਕਿਉਂ ਜੋ ਇਨ੍ਹਾਂ ਦੀ ਜੀਨ ਰਚਨਾ ਸਮਾਨ ਹੁੰਦੀ ਹੈ । ਉਦਾਹਰਣ-ਬੈਂਗਣ, ਟਮਾਟਰ, ਸਰੋਂ ॥

2. ਪਰ-ਪਰਾਗਣ-ਪਰ-ਪਰਾਗਣ ਕਿਰਿਆ ਵਿੱਚ ਪਰਾਗਕਣ ਇੱਕ ਫੁੱਲ ਦੇ ਪਰ-ਪਰਾਗਣ ਪੁੰਕੇਸਰ (ਪਰਾਗ ਕੋਸ਼) ਤੋਂ ਕਿਸੇ ਦੂਸਰੇ ਫੁੱਲ ਦੀ ਪਰਾਗਕਣ ਬ੍ਰਾਹੀ (ਇਸਤਰੀ ਕੇਸਰ) ਤੱਕ ਜਾਂਦੇ ਹਨ | ਪਰ-ਪਰਾਗਣ ਕਿਰਿਆ ਇੱਕ ਪੁੰਕੇਸਰ ਹੀ ਪੌਦੇ ਦੇ ਦੋ ਫੁੱਲਾਂ ਜਾਂ ਉਸੇ ਪਜਾਤੀ ਦੇ ਦੋ ਇਸਤਰੀਂ ਪੌਦਿਆਂ ਦੇ ਫੁੱਲਾਂ ਵਿਚਕਾਰ ਹੁੰਦੀ ਹੈ । ਪੌਦਿਆਂ ਨੂੰ ਕੇਸਰ ਵਿੱਚ ਪਰ-ਪਰਾਗਣ ਹਵਾ, ਕੀਟ, ਪਾਣੀ ਅਤੇ ਜੰਤੂਆਂ ਦੁਆਰਾ ਹੁੰਦਾ ਹੈ ।

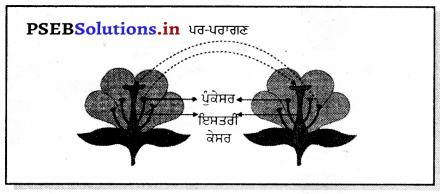
ਪਰਾਗਣ ਦੀਆਂ ਵੱਖ-ਵੱਖ ਵਿਧੀਆਂ –
1. ਹਵਾ ਦੁਆਰਾ ਪਰਾਗਣ-ਕਈ ਪੌਦਿਆਂ ਵਿੱਚ ਹਵਾ ਦੁਆਰਾ ਪਰਾਗਣ ਹੁੰਦਾ ਹੈ । ਤੇਜ਼ ਹਵਾ ਚੱਲਣ ਨਾਲ ਕਿਸੇ ਵੱਲ ਦੇ ਹਲਕੇ ਪਰਾਗਣ ਦੁਸਰੇ ਫੁੱਲ ਦੇ ਇਸਤਰੀ ਕੇਸਰ ਤੱਕ ਪੁੱਜ ਜਾਂਦੇ ਹਨ । ਉਦਾਹਰਣ-ਕਣਕ, ਕਪਾਹ, ਸੂਰਜਮੁਖੀ, ਜੁਆਰ, ਚੀੜ, ਕਕਰੋਂਦਾ, ਦੋ-ਫੱਲ, ਸੋਹਾਂਜਣੇ ਆਦਿ ।

2. ਕੀਟ ਦੁਆਰਾ ਪਰਾਗਣ-ਫੁੱਲਾਂ ਦੇ ਰੰਗ ਅਤੇ ਖ਼ੁਸ਼ਬੂ ਕਾਰਨ ਕੀਟ (ਤਿਤਲੀਆਂ ਅਤੇ ਭੌਰੇ) ਫੁੱਲਾਂ ਵੱਲ ਖਿੱਚੇ ਆਉਂਦੇ ਹਨ । ਇਨ੍ਹਾਂ ਫੁੱਲਾਂ ਤੇ ਇਸਤਰੀ ਕੈਸਰ ਆਮ ਤੌਰ ‘ਤੇ ਚਿਪਚਿਪੇ ਹੁੰਦੇ ਹਨ । ਜਦੋਂ ਕੀਟ ਇਨ੍ਹਾਂ ਫੁੱਲਾਂ ਤੇ ਆ ਕੇ ਬੈਠਦੇ ਹਨ ਤਾਂ ਉਨ੍ਹਾਂ ਦੇ ਪੈਰਾਂ ਅਤੇ ਖੰਭਾਂ ਨਾਲ ਪਰਾਗਕਣ ਚਿਪਕ ਜਾਂਦੇ ਹਨ । ਜਦੋਂ ਇਹ ਕੀਟ ਦੁਸਰੇ ਫੁੱਲ ‘ਤੇ ਜਾ ਕੇ ਬੈਠਦੇ ਹਨ ਤਾਂ ਉੱਥੇ ਇਸਤਰੀ ਕੇਸਰ ਤੇ ਪਰਾਗਕਣ ਛੱਡ ਦਿੰਦੇ ਹਨ । ਉਦਾਹਰਣ-ਅੰਜੀਰ, ਅੱਕ, ਗੂਲਰ ਆਦਿ ।

3. ਪਾਣੀ ਦੁਆਰਾ ਪਰਾਗਣ-ਪਾਣੀ ਵਿੱਚ ਉੱਗਣ ਵਾਲੇ ਪੌਦਿਆਂ ਦੇ ਫੁੱਲਾਂ ਦੇ ਪਰਾਗਕਣ ਪਾਣੀ ਨਾਲ ਵਹਿੰਦੇ ਹੋਏ ਦੂਜੇ ਫੁੱਲ ਦੇ ਇਸਤਰੀ ਕੇਸਰ ਤੱਕ ਪਹੁੰਚ ਜਾਂਦੇ ਹਨ ਕਿਉਂਕਿ ਪਰਾਗਕਣਾਂ ਦੀ ਘਣਤਾ ਇੰਨੀ ਹੁੰਦੀ ਹੈ ਕਿ ਉਹ ਪਾਣੀ ‘ਤੇ ਤੈਰਦੇ ਹਨ ਅਤੇ ਮਾਦਾ ਫੁੱਲ ਦੇ ਸੰਪਰਕ ਵਿੱਚ ਆ ਸਕਣ । ਉਦਾਹਰਣ-ਕਮਲ ਦਾ ਫੁੱਲ, ਜਲ-ਖਿੱਲੀ, ਵੈਲਸਨੇਰਿਆ ਆਦਿ ।

4. ਜੰਤੂਆਂ ਦੁਆਰਾ ਪਰਾਗਣ-ਕੁੱਝ ਪੌਦਿਆਂ ਵਿੱਚ ਪਰਾਗਣ ਪੰਛੀਆਂ, ਚਮਗਾਦੜਾਂ ਅਤੇ ਘੋਆਂ ਦੀ ਮਦਦ ਨਾਲ ਹੁੰਦਾ ਹੈ । ਉਦਾਹਰਣ- ਪਰਾਗਕਣ ਹੀ ਪਰਾਲੀ ਯੂਰੇਨਾ, ਜ਼ੈਂਬੀਅਮ ਸੈਮਲ, ਬਿਗੋਨੀਅਮ ਆਦਿ ।

ਪ੍ਰਸ਼ਨ (iv)
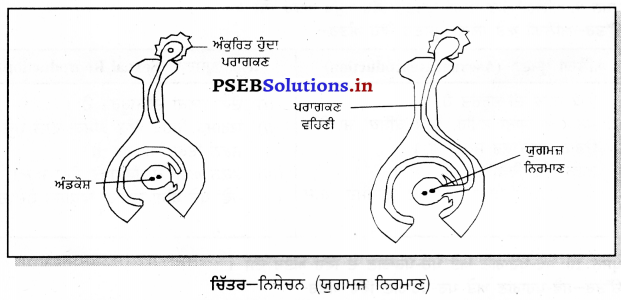
ਨਿਸ਼ੇਚਨ ਕਿਰਿਆ ਦਾ ਵਰਣਨ ਕਰੋ ।
ਉੱਤਰ-
ਨਿਸ਼ੇਚਨ ਕਿਰਿਆ-ਪਰਾਗਕਣਗਾਹੀ ‘ਤੇ ਪੁੱਜਣ ਤੋਂ ਬਾਅਦ ਧੁਰੀ ਕੇਂਦਰਕ ਪਰਾਗਕਣ ਵਿੱਚੋਂ ਇੱਕ ਛੋਟੀ ਜਿਹੀ ਟਿਊਬ ਨਿਕਲਦੀ ਹੈ, ਜਿਸਨੂੰ ਪਰਾਗਨਲੀ ਕਹਿੰਦੇ ਹਨ । ਇਹ ਇਸਤਰੀ ਕੇਸਰ ਦੀ ਪਰਾਗ ਵਹਿਣੀ ਜਾਂ ਵਰਤੀਕਾਗਰ ਵਿੱਚੋਂ ਹੋ ਕੇ ਅੰਡਕੋਸ਼ ਤੱਕ ਪੁੱਜਦੀ ਹੈ ਅਤੇ ਫਿਰ ਗੈਮੀਟੋਫਾਈਟ – ਅੰਡਾਣੁ (Ovule) ਵਿੱਚ ਦਾਖਲ ਹੁੰਦੀ ਹੈ । ਇੱਥੇ ਨਰ ਅਤੇ ਮਾਦਾ ਯੁਗਮ ਦਾ ਮੇਲ ਹੁੰਦਾ ਹੈ । ਨਰ ਯੁਗਮਕ ਅਤੇ ਮਾਦਾ ਯੁਗਮਕ ਦੇ । ਸ਼ੁਕਰਾਣੂ ਸੁਮੇਲ ਨੂੰ ਨਿਸ਼ਚਨ ਕਿਰਿਆ ਕਹਿੰਦੇ ਹਨ ।

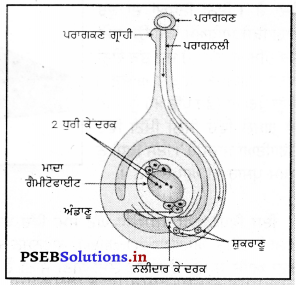
ਨਿਸ਼ੇਚਨ ਦੇ ਬਾਅਦ ਫੁੱਲ ਦੀਆਂ ਪੰਖੜੀਆਂ, ਪੁੰਕੇਸਰ, ਸਟਾਇਲ ਅਤੇ ਸਟਿਗਮਾ ਡਿਗ ਜਾਂਦੇ ਹਨ । ਬਾਹਰੀ ਦਲ ਸੁੱਕ ਜਾਂਦਾ ਹੈ ਅਤੇ ਅੰਡਕੋਸ਼ ਤੇ ਲੱਗਿਆ ਰਹਿੰਦਾ ਹੈ । ਅੰਡਕੋਸ਼ ਤੇਜ਼ੀ ਨਾਲ ਵਾਧਾ ਕਰਦਾ ਹੈ ਅਤੇ ਇਨ੍ਹਾਂ ਵਿੱਚ ਮੌਜੂਦ ਸੈੱਲ ਵਿਭਾਜਿਤ ਹੋ ਕੇ ਵਾਧਾ ਕਰਦੇ ਹਨ ਅਤੇ ਬੀਜ ਦਾ ਬਣਨਾ ਸ਼ੁਰੂ ਹੋ ਜਾਂਦਾ ਹੈ । ਬੀਜ ਵਿਚ ਇਕ ਭਰੂਣ ਹੁੰਦਾ ਹੈ । ਭਰੂਣ ਵਿਚ ਇੱਕ ਛੋਟੀ ਜੜ੍ਹ (ਮੂਲ ਜੜ੍ਹ), ਇੱਕ ਛੋਟਾ ਪ੍ਰੋਹ (ਕੁਰ) ਅਤੇ ਬੀਜ ਪੱਤਰ ਹੁੰਦੇ ਹਨ । ਬੀਜ ਪੱਤਰ ਵਿੱਚ ਭੋਜਨ ਸੰਚਿਤ ਰਹਿੰਦਾ ਹੈ । ਸਮੇਂ ਅਨੁਸਾਰ ਬੀਜ ਸਖ਼ਤ ਹੋ ਕੇ ਸੁੱਕ ਜਾਂਦਾ ਹੈ । ਇਹ ਬੀਜ ਪ੍ਰਤਿਕੂਲ ਹਾਲਤਾਂ ਵਿਚ ਜੀਵਤ ਰਹਿ ਸਕਦਾ ਹੈ । ਅੰਡਕੋਸ਼ ਦੀ ਦੀਵਾਰ ਵੀ ਸਖ਼ਤ ਹੋ ਸਕਦੀ ਹੈ ਅਤੇ ਇਕ ਫਲੀ ਬਣ ਜਾਂਦੀ ਹੈ ।ਨਿਸ਼ੇਚਨ ਦੇ ਬਾਅਦ ਸਾਰੇ ਅੰਡਕੋਸ਼ ਨੂੰ ਫਲ ਕਹਿੰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ (v)
ਫ਼ਲ ਅਤੇ ਬੀਜ ਬਣਨ ਦੀ ਪ੍ਰਕਿਰਿਆ ਦੇ ਵੱਖ-ਵੱਖ ਪੜਾਵਾਂ ਦਾ ਵਰਣਨ ਕਰੋ ।
ਉੱਤਰ-
ਫ਼ਲ ਅਤੇ ਬੀਜ ਦਾ ਬਣਨਾ ਨਿਸ਼ੇਚਨ ਤੋਂ ਬਾਅਦ ਫੁੱਲ ਵਿੱਚ ਹੇਠ ਲਿਖੇ ਬਦਲਾਵ ਆਉਂਦੇ ਹਨ-

1. ਨਿਸ਼ੇਚਨ ਮਗਰੋਂ ਅੰਡਕੋਸ਼, ਫਲ ਵਿੱਚ ਅਤੇ ਅੰਡਾਣੂ, ਬੀਜ ਵਿੱਚ ਪਰਿਵਰਤਿਤ ਹੋ ਜਾਂਦੇ ਹਨ । ਫੁੱਲ ਦੇ ਬਾਕੀ ਭਾਗ ਮੁਰਝਾ ਕੇ ਝੜ ਜਾਂਦੇ ਹਨ ।
2. ਬੀਜ ਇੱਕ ਵਿਕਸਿਤ ਅੰਡਾਣੂ ਹੁੰਦਾ ਹੈ ਜਿਸ ਵਿੱਚ ਭਰੁਣ ਅਤੇ ਪੋਸ਼ਣ ਮੌਜੂਦ ਹੁੰਦੇ ਹਨ । ਇਹ ਇੱਕ ਸੁਰੱਖਿਅਤ ਪਰਤ ਨਾਲ ਢੱਕਿਆ ਹੁੰਦਾ ਹੈ । ਜਿਸ ਨੂੰ ਬੀਜ ਦਾ ਛਿਲਕਾ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।
3. ਫਲ ਗੁੱਦੇਦਾਰ ਅਤੇ ਰਸ ਨਾਲ ਭਰੇ ਹੋਏ ਜਾਂ ਫਿਰ ਸੁੱਕੇ ਅਤੇ ਸਖ਼ਤ ਹੋ ਸਕਦੇ ਹਨ । ਅੰਬ, ਸੇਬ, ਸੰਤਰਾ, ਗੁੱਦੇਦਾਰ ਅਤੇ ਰਸ ਭਰੇ ਫ਼ਲ ਹੁੰਦੇ ਹਨ ਜਦ ਕਿ ਬਾਦਾਮ ਅਤੇ ਅਖ਼ਰੋਟ ਸੁੱਕੇ ਅਤੇ ਸਖ਼ਤ ਫ਼ਲ ਹੁੰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ (vi)
ਬੀਜਾਂ ਦਾ ਖਿਲਰਨਾ ਕੀ ਹੈ ? ਬੀਜ ਖਿਲਰਨ ਦੇ ਕੋਈ ਦੋ ਢੰਗਾਂ ਦਾ ਉਦਾਹਰਨਾਂ ਸਹਿਤ ਵਰਣਨ ਕਰੋ ।
ਉੱਤਰ-
ਬੀਜ ਦਾ ਖਿਲਰਨਾ-ਬੀਜ ਦਾ ਇੱਕ ਥਾਂ ਤੋਂ ਦੂਜੀ ਥਾਂ ਤੱਕ ਕਿਸੇ ਸਾਧਨ/ਕਾਰਕ-ਹਵਾ, ਪਾਣੀ, ਕੀਟ, ਪੰਛੀ, ਮਨੁੱਖਾਂ ਅਤੇ ਜੰਤੂਆਂ ਰਾਹੀਂ ਪਹੁੰਚਣਾ ਤਾਂ ਜੋ ਬੀਜ ਦੀ ਹੋਂਦ ਕਾਇਮ ਰਹੇ, ਬੀਜ ਦਾ ਖਿਲਰਨਾ ਅਖਵਾਉਂਦਾ ਹੈ ।
ਬੀਜ ਖਿਲਰਨ ਦੀਆਂ ਵਿਧੀਆਂ-

• ਹਵਾ ਨਾਲ ਖਿਲਾਰ,
• ਪਾਣੀ ਨਾਲ ਖਿਲਾਰ,
• ਜੰਤੂਆਂ ਦੁਆਰਾ ਖਿਲਾਰ,
• ਮਨੁੱਖਾਂ ਦੁਆਰਾ ਖਿਲਾਰ,
• ਵਿਸਫੋਟਕ ਪ੍ਰਕਿਰਿਆ ਦੁਆਰਾ ।

1. ਹਵਾ ਨਾਲ ਖਿਲਾਰ-ਹਵਾ ਨਾਲ ਖਿਲਰਨ ਵਾਲੇ ਬੀਜ ਛੋਟੇ ਅਤੇ ਹਲਕੇ ਹੁੰਦੇ ਹਨ । ਦੋਫਲ (Maple) ਅਤੇ ਸੋਹਾਂਜਣੇ (Drumsticks) ਦੇ ਬੀਜਾਂ ਦੇ ਖੰਭ ਹੁੰਦੇ ਹਨ । ਇਸ ਲਈ ਉਹ ਹਵਾ ਵਿੱਚ ਉੱਡ ਕੇ ਦੂਰ ਤੱਕ ਚਲੇ ਜਾਂਦੇ ਹਨ । ਘਾਹ ਦੇ ਹਲਕੇ ਬੀਜ, ਅੱਕ, ਕਕਰੌਦਾ, ਕਪਾਹ (Cotton) ਵਰਗੇ ਪੌਦਿਆਂ ਦੇ ਵਾਲਾਂ ਵਾਲੇ ਬੀਜ ਅਤੇ ਸੂਰਜ ਮੁਖੀ ਦੇ ਵਾਲਾਂ ਵਾਲੇ ਫ਼ਲ ਹਵਾ ਵਿੱਚ ਉੱਡ ਕੇ ਦੂਰ ਤੱਕ ਚਲੇ ਜਾਂਦੇ ਹਨ ।

2. ਪਾਣੀ ਨਾਲ ਖਿਲਾਰ-ਜਲ ਲਿੱਲੀ, ਕਮਲ ਅਤੇ ਨਾਰੀਅਲ ਦੇ ਫ਼ਲ ਅਤੇ ਬੀਜ ਪਾਣੀ ਉੱਤੇ ਤੈਰਦੇ ਰਹਿੰਦੇ ਹਨ । ਪਾਣੀ ਦੀਆਂ ਲਹਿਰਾਂ ਇਨ੍ਹਾਂ ਨੂੰ ਦੂਰ ਤੱਕ ਲੈ ਜਾਂਦੀਆਂ ਹਨ ।

PSEB Solutions for Class 7 Science ਜੰਤੂਆਂ ਅਤੇ ਪੌਦਿਆਂ ਵਿੱਚ ਪਰਿਵਹਨ Important Questions and Answers

1. ਖ਼ਾਲੀ ਥਾਂਵਾਂ ਭਰੋ

(i) ਜਨਕ ਪੌਦੇ ਦੇ ਭਾਗਾਂ ਤੋਂ ਨਵੇਂ ਪੌਦੇ ਦੇ ਬਣਨ ਦੀ ਪ੍ਰਕਿਰਿਆ ……… ਅਖਵਾਉਂਦੀ ਹੈ !
ਉੱਤਰ-
ਕਾਇਆ ਪ੍ਰਵਰਧਨ,

(ii) ਅਜਿਹੇ ਫੁੱਲਾਂ ਨੂੰ, ਜਿਨ੍ਹਾਂ ਵਿੱਚ ਸਿਰਫ਼ ਨਰ ਜਾਂ ਮਾਦਾ ਜਣਨ ਅੰਗ ਹੁੰਦੇ ਹਨ ……….. ਫੁੱਲ ਅਖਵਾਉਂਦੇ ਹਨ ।
ਉੱਤਰ-
ਇੱਕ ਲਿੰਗੀ ਫੁੱਲ,

(iii) ਪਰਾਗਕਣਾਂ ਦਾ ਉਸੇ ਫੁੱਲ ਜਾਂ ਕਿਸੇ ਹੋਰ ਪੌਦੇ ਦੇ ਹੋਰ ਫੁੱਲ ਦੇ ਪਰਾਗਕਣ ਹੀ ਉੱਤੇ ਸਥਾਨ-ਅੰਤਰਣ ਦੀ ਪ੍ਰਕਿਰਿਆ ……… ਅਖਵਾਉਂਦੀ ਹੈ ।
ਉੱਤਰ-
ਸਵੈ-ਪਰਾਗਣ,

(iv) ਨਰ ਅਤੇ ਮਾਦਾ ਯੁਗਮਤਾਂ ਦਾ ਯੁਗਮਨ ……… ਅਖਵਾਉਂਦਾ ਹੈ ।
ਉੱਤਰ-
ਨਿਸ਼ੇਚਨ,

(v) ਬੀਜ ਖਿੰਡਾਉਣਾ ……………….. ਅਤੇ ……… ਦੇ ਦੁਆਰਾ ਹੁੰਦਾ ਹੈ ।
ਉੱਤਰ-
ਪਾਣੀ, ਹਵਾ, ਜੰਤੂ ॥

2. ਕਾਲਮ ‘ੴ’ ਵਿੱਚ ਦਿੱਤੇ ਗਏ ਸ਼ਬਦਾਂ ਦਾ ਕਾਲਮ “ਅ” ਵਿੱਚ ਦਿੱਤੇ ਗਏ ਜੀਵਾਂ ਨਾਲ ਮਿਲਾਨ ਕਰੋ-

ਕਾਲਮ ‘A’	ਕਾਲਮ ‘B’
(ਉ) ਕਲੀ	(i) ਮੈਪਿਲ
ਅੱਖ	(ii) ਸਪਾਇਰੋਗਾ
(ਇ) ਖੰਡਨ	(iii) ਖ਼ਮੀਰ
(ਸ) ਖੰਡ	(iv) ਡਬਲ ਰੋਟੀ ਦੀ ਉੱਲੀ.
(ਹ) ਬੀਜਾਣੂ	(v) ਆਲੂ
	(vi) ਗੁਲਾਬ

ਉੱਤਰ-

ਕਾਲਮ ‘A’	ਕਾਲਮ ‘B’
(ਉ) ਕਲੀ	(iii) ਖ਼ਮੀਰ
(ਅ) ਅੱਖ	(v) ਆਲੂ
(ਇ) ਖੰਡਨ	(ii) ਸਪਾਇਰੋਗਾਇਰਾ
(ਸ) ਖੰਭ	(i) ਮੈਪਿਲ
(ਹ) ਬੀਜਾਣੂ	(iv) ਡਬਲ ਰੋਟੀ ਦੀ ਉੱਲੀ

3. ਸਹੀ ਵਿਕਲਪ ਚੁਣੋ

(i) ਮਾਤਾ-ਪਿਤਾ ਤੋਂ ਸੰਤਾਨ ਦੀ ਉਤਪੱਤੀ ਨੂੰ ਕੀ ਆਖਦੇ ਹਨ ?
(ਉ) ਪਰਿਵਹਿਣ
(ਅ) ਉਤਸਰਜਨ
(ੲ) ਪ੍ਰਜਣਨ
(ਸ) ਸਾਹਕਿਰਿਆ ।
ਉੱਤਰ-
(ੲ) ਪ੍ਰਜਣਨ ।

(ii) ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ਕਿਹੜਾ ਪੌਦੇ ਦਾ ਇਕ ਅੰਗ ਹੈ ?
(ਉ) ਤਣਾ
(ਅ) ਪੱਤੀ ।
(ਇ), ਜੜ੍ਹ
(ਸ) ਉਪਰੋਕਤ ਸਾਰੇ ।
ਉੱਤਰ-
(ਸ) ਉਪਰੋਕਤ ਸਾਰੇ ।

(iii) ਹੇਠ ਦਿੱਤਿਆਂ ਵਿੱਚੋਂ ਕਿਹੜਾ ਪੌਦੇ ਦਾ ਜਣਨ ਅੰਗ ਹੈ ?
(ਉ) ਜੜ੍ਹ
(ਅ) ਫੁੱਲ
(ਇ) ਪੱਤਾ
(ਸ) ਤਣਾ ।
ਉੱਤਰ-
(ਅ) ਫੁੱਲ ।

(iv) ਨਰ ਅਤੇ ਮਾਦਾ ਯੁਗਮਤਾਂ ਦੇ ਮੇਲ ਨੂੰ …… ਆਖਦੇ ਹਨ ।
(ਉ) ਨਿਸ਼ੇਚਨ
(ਅ) ਪਰਾਗਣ
(ਈ) ਯੁਗਮਨਜ਼
(ਸ) ਪ੍ਰਜਣਨ ॥
ਉੱਤਰ-
(ੳ) ਨਿਸ਼ੇਚਨ ।

(v) ਇੱਕ ਕੋਸ਼ੀ ਖਮੀਰ ਵਿੱਚ ਜਣਨ ਲਈ ਕਿਹੜੀ ਵਿਧੀ ਅਪਣਾਈ ਜਾਂਦੀ ਹੈ ?
(ੳ) ਖੰਡਨ
(ਅ) ਮੁਕੁਲਨ
(ਈ) ਬੀਜਾਣੂ ਨਿਰਮਾਣ
ਸ ਦੋ-ਖੰਡਨ ।
ਉੱਤਰ-
(ਅ) ਮੁਕੁਲਨ ॥

(vi) ਬਾਇਓਫਿਲਮ ਆਪਣੇ ………. ਭਾਗ ਦੁਆਰਾ ਜਣਨ ਕਰਦਾ ਹੈ –
(ਉ) ਪੱਤੀ
(ਆ) ਜੜ੍ਹ
(ਈ) ਤਣਾ
(ਸ) ਫਲ ।
ਉੱਤਰ-
(ਉ) ਪੱਤੀ ।

(vii) ਗੁਲਾਬ ਅਤੇ ਗੰਨੇ ਵਿੱਚ ਕਿਹੜੀ ਕਾਇਕ ਵਿਧੀ ਦੀ ਵਰਤੋਂ ਹੁੰਦੀ ਹੈ ?
(ਉ) ਖੰਡਨ
(ਅ) ਤੇ ਮੁਕੁਲਨ
(ਈ) ਦੋ-ਖੰਡਨ
(ਸ) ਕਲਮ ਲਗਾਉਣਾ ।
ਉੱਤਰ-
(ਸ) ਕਲਮ ਲਗਾਉਣਾ ।

4. ਹੇਠ ਦਿੱਤੇ ਕਥਨਾਂ ਵਿਚ ਕਿਹੜਾ ਕਥਨ ਸਹੀ ਹੈ ਅਤੇ ਕਿਹੜਾ ਗ਼ਲਤ –

(i) ਅਲਿੰਗੀ ਪ੍ਰਜਣਨ, ਲਿੰਗੀ ਪ੍ਰਜਣਨ ਦੇ ਮੁਕਾਬਲੇ ਬਹੁਤ ਆਮ ਹੈ ?
ਉੱਤਰ-
ਗ਼ਲਤ,

(ii) ਬੈਕਟੀਰੀਆ ਅਤੇ ਖ਼ਮੀਰ ਅਲਿੰਗੀ ਪ੍ਰਜਣਨ ਵਿਧੀ ਦੁਆਰਾ ਪ੍ਰਜਣਨ ਕਰਦੇ ਹਨ ।
ਉੱਤਰ-
ਸਹੀ,

(iii) ਬਹੁਤ ਸਾਰੇ ਜੀਵਾਂ ਵਿਚ ਪੁਨਰਜਣਨ ਦੀ ਸਮਰੱਥਾ ਕਿਸੇ ਨਾ ਕਿਸੇ ਵਿਧੀ ਦੁਆਰਾ ਹੁੰਦੀ ਹੈ ।
ਉੱਤਰ-
ਗ਼ਲਤ,

(iv) ਇੱਕ ਨਿਸ਼ਚਿਤ ਅੰਗ ਬੀਜ ਬਣਦਾ ਹੈ ।
ਉੱਤਰ-
ਸਹੀ ।

5. ਬਹੁਤ ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ

ਪ੍ਰਸ਼ਨ 1.
ਜਣਨ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਜਣਨ (Reproduction)-ਇਹ ਜੀਵਾਂ ਦਾ ਇੱਕ ਗੁਣ ਹੈ ਜਿਸਦੇ ਦੁਆਰਾ ਉਹ ਆਪਣੇ ਵਰਗੇ ਜੀਵ ਪੈਦਾ ਕਰ ਸਕਦੇ ਹਨ |

ਪ੍ਰਸ਼ਨ 2.
ਜਣਨ ਦਾ ਕੀ ਮੰਤਵ ਹੈ ?
ਉੱਤਰ-

• ਵੰਸ਼ ਨੂੰ ਵਧਾਉਣਾ
• ਜਾਤੀਆਂ ਦਾ ਨਿਰਮਾਣ ।

ਪ੍ਰਸ਼ਨ 3.
ਦੋ ਤਰ੍ਹਾਂ ਦੀਆਂ ਜਣਨ ਵਿਧੀਆਂ ਕਿਹੜੀਆਂ ਹਨ ?
ਉੱਤਰ-

1. ਲਿੰਗੀ ਜਣਨ
2. ਅਲਿੰਗੀ ਜਣਨ ।

ਪ੍ਰਸ਼ਨ 4.
ਪੌਦਿਆਂ ਵਿੱਚ ਵੱਖ-ਵੱਖ ਕਾਇਆ ਵਰਧਨ ਵਿਧੀਆਂ ਕਿਹੜੀਆਂ ਹਨ ?
ਉੱਤਰ-

• ਕਲਮ ਲਗਾ ਕੇ
• ਕਾਇਕ ਕਲੀਆਂ ਦਬਾ ਕੇ
• ਜੜ੍ਹ ਤੋਂ ।

ਪ੍ਰਸ਼ਨ 5.
ਗੁਲਾਬ ਅਤੇ ਗੰਨੇ ਵਿੱਚ ਕਿਹੜੀ ਕਾਇਆ ਪ੍ਰਵਰਧਨ ਵਿਧੀ ਦਾ ਉਪਯੋਗ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਕਲਮ ਲਗਾਉਣਾ ।

ਪ੍ਰਸ਼ਨ 6.
ਸਪਾਇਰੋਗਾਇਰਾ ਅਤੇ ਮਿਊਕਰ (Mucor) ਵਿੱਚ ਕਿਹੜੀ ਕਾਇਆ ਵਿਧੀ ਦਾ ਉਪਯੋਗ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਸਪਾਇਰੋਗਾਇਰਾ-ਖੰਡਨ ਮਿਉਕਰ-ਬੀਜਾਣੁ ਨਿਰਮਾਣ ।

ਪ੍ਰਸ਼ਨ 7.
ਬੋਗਨਵੇਲੀਆ ਅਤੇ ਪੁਦੀਨਾ ਵਿੱਚ ਅਲਿੰਗੀ ਜਣਨ ਕਿਵੇਂ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਬੋਗਨਵੇਲੀਆ-ਪੱਤਾ ਬਿਡਿੰਗ ਪੁਦੀਨਾ-ਜੜਾਂ ਮਿਲ ।

ਪ੍ਰਸ਼ਨ 8.
ਯੀਸਟ, ਸਪੰਜ ਅਤੇ ਹਾਈਡਾ ਵਿੱਚ ਅਲਿੰਗੀ ਜਣਨ ਕਿਵੇਂ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਤਿੰਨਾਂ ਵਿੱਚ ਬਡਿੰਗ ਵਿਧੀ ਨਾਲ ਜਣਨ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 9.
ਪਥਰਚੱਟ ਦਾ ਕਿਹੜਾ ਕਾਇਆ ਅੰਗ ਜਣਨ ਵਿੱਚ ਸਹਾਇਕ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਪੱਤੇ ।

ਪ੍ਰਸ਼ਨ 10.
ਇੱਕ-ਇੱਕ ਉਦਾਹਰਨ ਦਿਓ-ਕਾਇਆ ਜਣਨ-
(i) ਜੜ੍ਹ ਤੋਂ
(ii) ਤਣੇ ਤੋਂ ।
ਉੱਤਰ-
(i) ਜੜ੍ਹ ਨਾਲ ਕਾਇਆ ਜਣਨ-ਸ਼ਕਰਕੰਦੀ
(ii) ਤਣੇ ਨਾਲ ਕਾਇਆ ਜਣਨ-ਆਲੂ ।

ਪ੍ਰਸ਼ਨ 11.
ਪਰਾਗਣ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਪਰਾਗਣ (Pollination)-ਪਰਾਗਕਣਾਂ ਦਾ ਪਰਾਗਕਣ ਹੀ ਉੱਤੇ ਸਥਾਨ-ਅੰਤਰਣ ਪਰਾਗਣ ਅਖਵਾਉਂਦਾ ਹੈ ।

ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ

ਪ੍ਰਸ਼ਨ 1.
ਜਣਨ ਕੀ ਹੈ ? ਇਹ ਕਿੰਨੀ ਤਰ੍ਹਾਂ ਦਾ ਹੈ ?
ਉੱਤਰ-
ਜਣਨ (Reproduction)-ਸਾਰੇ ਜੀਵ ਜਿਹੜੇ ਇਸ ਧਰਤੀ ਉੱਤੇ ਪੈਦਾ ਹੋਏ ਹਨ ਉਨ੍ਹਾਂ ਦੇ ਜੀਵਨ ਦੀਆਂ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਹਨ; ਜਿਵੇਂ-ਜਣਨ, ਵਾਧਾ, ਜਣਨ, ਮੌਤ । ਜਣਨ-ਇਹ ਇਕ ਅਜਿਹੀ ਪ੍ਰਕਿਰਿਆ ਹੈ, ਜਿਸ ਵਿੱਚ ਜਾਤੀ ਪੀੜ੍ਹੀ ਦਰ ਪੀੜ੍ਹੀ ਵਾਧਾ ਕਰਦੀ ਹੈ । ਪੁਰਾਣੇ ਅਤੇ ਬੁੱਢੇ ਜੀਵਾਂ ਦੀ ਥਾਂ ਨਵੇਂ ਅਤੇ ਜਵਾਨ ਜੀਵ ਲੈ ਲੈਂਦੇ ਹਨ । ਜਣਨ ਦੋ ਤਰ੍ਹਾਂ ਦਾ ਹੁੰਦਾ ਹੈ :

• ਅਲਿੰਗੀ ਜਣਨ
• ਲਿੰਗੀ ਜਣਨ|

ਪ੍ਰਸ਼ਨ 2.
ਅਲਿੰਗੀ ਅਤੇ ਲਿੰਗੀ ਜਣਨ ਨੂੰ ਪਰਿਭਾਸ਼ਿਤ ਕਰੋ ।
ਉੱਤਰ-
ਅਲਿੰਗੀ ਜਣਨ-ਵਾਧੇ ਦੀ ਇਸ ਵਿਧੀ ਵਿੱਚ ਸੰਤਾਨ ਨਵਾਂ ਪੈਂਦਾ ਕਿਸੇ ਵੀ ਵਿਸ਼ੇਸ਼ ਜਾਂ ਕਾਇਆ ਭਾਗ ਤੋਂ ਉਤਪੰਨ ਹੋ ਸਕਦਾ ਹੈ । ਇਸ ਵਿੱਚ ਜਣਨ ਅੰਗ ਤੋਂ ਉਤਪੰਨ ਯੂਗਮਕਾਂ ਦਾ ਯੁਗਮਨ ਜ਼ਰੂਰੀ ਨਹੀਂ ਹੈ । ਲਿੰਗੀ ਜਣਨ-ਇਸ ਵਿਧੀ ਵਿੱਚ ਨਰ ਅਤੇ ਮਾਦਾ ਯੁਗਮਕਾਂ ਦੇ ਯੁਗਮਨ ਤੋਂ ਯੁਜ ਬਣਦਾ ਹੈ । ਇਸ ਵਿਧੀ ਦੇ ਦੋ ਭਾਗ ਹਨ :

• ਅਰਧ ਸੂਤਰੀ ਵਿਭਾਜਨ-ਇਸ ਵਿੱਚ ਗੁਣ ਸੂਤਰਾਂ ਦੀ ਸੰਖਿਆ ਅੱਧੀ ਹੋ ਜਾਂਦੀ ਹੈ ।
• ਨਿਸ਼ੇਚਨ-ਯੁਗਮਕਾਂ ਦੇ ਯੁਗਮਨ ਤੋਂ ਗੁਣ ਸੂਤਰਾਂ ਦੀ ਸੰਖਿਆ ਮੁੜ ਪੂਰੀ ਹੋ ਜਾਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਡਬਲਰੋਟੀ ਉੱਤੇ ਉੱਲੀ ਕਿੱਥੋਂ ਆਉਂਦੀ ਹੈ ?
ਉੱਤਰ-
ਉੱਲੀ ਦੇ ਬੀਜਾਣੂ ਹਵਾ ਵਿੱਚ ਮੌਜੂਦ ਹੁੰਦੇ ਹਨ । ਅਨੁਕੂਲਿਤ ਪਰਿਸਥਿਤੀਆਂ ਵਿੱਚ ਇਹ ਡਬਲਰੋਟੀ ਉੱਤੇ ਜੰਮ ਜਾਂਦੇ ਹਨ ਅਤੇ ਵਾਧਾ ਕਰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 4.
ਇਕ ਲਿੰਗੀ ਅਤੇ ਦੋ-ਲਿੰਗੀ ਫੁੱਲਾਂ ਦੇ ਉਦਾਹਰਨ ਦਿੰਦੇ ਹੋਏ ਪਰਿਭਾਸ਼ਾਵਾਂ ਲਿਖੋ ।
ਉੱਤਰ-
ਇਕ ਲਿੰਗੀ ਫੁੱਲ-ਅਜਿਹੇ ਫੁੱਲ ਜਿਸ ਵਿੱਚ ਅੰਡਪੁੰਜ ਅਤੇ ਪੁੰਕੇਸਰ ਵੱਖ-ਵੱਖ ਫੁੱਲਾਂ ਵਿੱਚ ਹੋਵੇ ਜਾਂ ਕੇਵਲ ਪੁੰਕੇਸਰ ਜਾਂ ਕੇਵਲ ਅੰਡ ਪੁੰਜ ਹੋਵੇ, ਉਨ੍ਹਾਂ ਨੂੰ ਇਕ ਲਿੰਗੀ ਫੁੱਲ ਕਹਿੰਦੇ ਹਨ । ਉਦਾਹਰਨ-ਮੱਕੀ, ਪਪੀਤਾ, ਤਰ । ਦੋ ਲਿੰਗੀ ਫੁੱਲ-ਇੱਕ ਹੀ ਫੁੱਲ ਵਿੱਚ ਦੋਵੇਂ ਅੰਡ ਪੁੰਜ ਅਤੇ ਪੁੰਕੇਸਰ ਦਾ ਹੋਣਾ, ਦੋ ਲਿੰਗੀ ਫੁੱਲ ਅਖਵਾਉਂਦਾ ਹੈ । ਉਦਾਹਰਨ-ਸਰੋਂ, ਗੁਲਾਬ ।

ਪ੍ਰਸ਼ਨ 5.
ਫੁੱਲ ਦੇ ਜਣਨ ਅੰਗਾਂ ਨੂੰ ਨਾਮਾਂਕਿਤ ਕਰੋ ।
ਉੱਤਰ-
ਫੁੱਲ ਦੇ ਜਣਨ ਅੰਗ :
(i) ਪੁੰਕੇਸਰ-ਇਸ ਵਿੱਚ ਇੱਕ ਲੰਬਾ ਤੰਤੂ ਅਤੇ ਇੱਕ ਪਰਾਗਕੋਸ਼ ਹੁੰਦਾ ਹੈ ਪਰਾਗਕੋਸ਼ ਵਿੱਚ ਪਰਾਗਕਣ ਹੁੰਦੇ ਹਨ | ਪਰਾਗਕਣ ਦੋ ਨਰ ਯੁਗਮ ਬਣਾਉਂਦੇ ਹਨ ।
(ii) ਅੰਡ ਪੁਜ-ਇਸ ਵਿੱਚ ਤਿੰਨ ਭਾਗ ਹੁੰਦੇ ਹਨ-

• ਪਰਾਗਕਣ ਹੀ,
• ਪਰਾਗਕਣ ਵਹਿਣੀ ਅਤੇ
• ਅੰਡਕੋਸ਼ ।

ਪਰਾਗਕਣ ਹੀ ਸਭ ਤੋਂ ਉੱਪਰ ਵਾਲਾ ਭਾਗ, ਪਰਾਗਕਣ ਵਹਿਣੀ ਇੱਕ ਸਿੱਧੀ ਨਲੀ ਵਰਗਾ ਭਾਗ ਹੈ ਅਤੇ ਅੰਡਕੋਸ਼ ਸਭ ਤੋਂ ਥੱਲੇ ਵਾਲਾ ਫੁੱਲਿਆ ਹੋਇਆ ਭਾਗ ਹੈ । ਬੀਜ ਅੰਡ ਬੀਜਦਾਨੀ ਵਿੱਚ ਹੁੰਦੇ ਹਨ । ਬੀਜ ਅੰਡ ਤੋਂ ਮਾਦਾ ਯੁਗਮਕ ਬਣਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 6.
ਬੀਜ ਅੰਡ ਅਤੇ ਅੰਡਕੋਸ਼ ਵਿੱਚ ਅੰਤਰ ਸਪੱਸ਼ਟ ਕਰੋ ।
ਉੱਤਰ-
ਬੀਜ ਅੰਡ (Ovule)-ਅੰਡਕੋਸ਼ ਦੀ ਇੱਕ ਸੰਰਚਨਾ, ਜਿਹੜੀ ਨਿਸ਼ੇਚਨ ਦੇ ਬਾਅਦ ਬੀਜ ਵਿੱਚ ਪਰਿਵਰਤਿਤ ਹੋ ਜਾਂਦੀ ਹੈ । ਬੀਜਦਾਨੀ (Ovary)-ਅੰਡ ਪੁੰਜ ਦੇ ਆਧਾਰ ਦਾ ਫੁੱਲਿਆ ਭਾਗ, ਜਿਸ ਵਿੱਚ ਬੀਜ ਅੰਡ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 7.
ਅਲਿੰਗੀ ਪ੍ਰਜਣਨ ਦੀਆਂ ਵੱਖ-ਵੱਖ ਵਿਧੀਆਂ ਦਾ ਵਰਣਨ ਕਰੋ । ਹਰੇਕ ਦੀ ਉਦਾਹਰਨ ਦਿਉ ।
ਉੱਤਰ-

• ਬਡਿੰਗ,
• ਖੰਡਨ,
• ਬੀਜਾਣੁ ਨਿਰਮਾਣ
• ਕਾਇਆ ਵਰਧਨ ।

(i) ਬਡੂੰਗ-ਸਪੰਜ ਅਤੇ ਹਾਈਡਾ ਵਿੱਚ ਆਮ ਤੌਰ ‘ਤੇ ਇਹੀ ਜਣਨ ਪ੍ਰਕਿਰਿਆ ਹੈ । ਇਸ ਪ੍ਰਕਿਰਿਆ ਵਿੱਚ ਜਨਕ ਪੌਦੇ ਤੇ ਇਕ ਨਵਾਂ ਪੌਦਾ ਵਿਕਸਿਤ ਹੁੰਦਾ ਹੈ । ਇਹ ਕੁੱਝ ਸਮੇਂ ਬਾਅਦ ਜਨਕ ਕੋਸ਼ਿਕਾ ਤੋਂ ਅਲੱਗ ਹੋ ਜਾਂਦਾ ਹੈ ਅਤੇ ਵਾਧਾ ਕਰਦਾ ਹੈ ।

(ii) ਖੰਡਨ-ਜਦੋਂ ਸ਼ੈਵਾਲ, ਫੀਤਾ ਕਿਰਮ, ਐਨੀਲਿਡਜ਼ ਅਤੇ ਚਪਟੇ ਕਿਰਮ ਦੋ ਜਾਂ ਜ਼ਿਆਦਾ ਖੰਡਾਂ ਵਿੱਚ ਵੰਡੇ ਜਾਂਦੇ ਹਨ ਅਤੇ ਹਰੇਕ ਖੰਡ ਨਵੇਂ ਜੀਵਾਂ ਵਿੱਚ ਵਾਧਾ ਕਰਦਾ ਹੈ, ਇਹ ਪ੍ਰਕਿਰਿਆ ਖੰਡਣ ਅਖਵਾਉਂਦੀ ਹੈ ।

(iii) ਬੀਜਾਣੂ ਨਿਰਮਾਣ-ਕਾਈ, ਮਿਉਕਰ ਆਦਿ ਬੀਜਾਣੂ ਪੈਦਾ ਕਰਦੇ ਹਨ, ਜੋ ਉੱਚ ਤਾਪ ਅਤੇ ਘੱਟ ਨਮੀਂ ਵਰਗੀਆਂ ਹਾਲਤਾਂ ਵਿੱਚ ਇੱਕ ਕਠੋਰ ਸਖ਼ਤ ਸੁਰੱਖਿਆਤਮਕ ਪਰਤ ਨਾਲ ਢੱਕੇ ਰਹਿੰਦੇ ਹਨ ਅਤੇ ਢੁੱਕਵੀਆਂ ਹਾਲਤਾਂ ਵਿੱਚ ਨਵੇਂ ਜੀਵ ਵਿਕਸਿਤ ਕਰਦੇ ਹਨ ।

(iv) ਕਾਇਆ ਪ੍ਰਵਰਧਨ-ਪੌਦੇ ਦਾ ਇੱਕ ਭਾਗ ਜੋ ਜਣਨ ਅੰਗ ਨਹੀਂ ਹੈ, ਨਵੇਂ ਪੌਦੇ ਵਿੱਚ ਵਿਕਸਿਤ ਹੋ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਇਸ ਵਿਧੀ ਨੂੰ ਕਾਇਆ ਪ੍ਰਵਰਧਨ ਆਖਦੇ ਹਨ । ਜਿਵੇਂ, ਗੁਲਾਬ ਦੀ ਕਲਮ ਨਵੇਂ ਪੌਦੇ ਦਾ ਨਿਰਮਾਣ ਕਰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 8.
ਪੌਦਿਆਂ ਵਿੱਚ ਲਿੰਗੀ-ਪ੍ਰਜਣਨ ਦੀ ਪ੍ਰਕਿਰਿਆ ਨੂੰ ਸਮਝਾਉ ।
ਉੱਤਰ-
ਪੌਦਿਆਂ ਵਿੱਚ ਲਿੰਗੀ ਪ੍ਰਜਣਨ-ਪੌਦਿਆਂ ਵਿੱਚ ਨਰ ਅਤੇ ਮਾਦਾ ਜਣਨ ਅੰਗ ਪੁੰਕੇਸਰ ਅਤੇ ਅੰਡ ਪੁੰਜ ਹਨ । ਪੁੰਕੇਸਰ, ਨਰ ਯੁਗਮਕ ਪੈਦਾ ਕਰਦਾ ਹੈ । ਅੰਡ ਪੁੰਜ, ਮਾਦਾ ਯੁਗਮਕ ਦਾ ਨਿਰਮਾਣ ਕਰਦੀ ਹੈ । ਇਹ ਦੋਵੇਂ ਜਣਨ ਅੰਗ ਇੱਕ ਹੀ ਜਾਂ ਵੱਖ-ਵੱਖ ਫੁੱਲਾਂ ਵਿੱਚ ਹੋ ਸਕਦੇ ਹਨ । ਪੌਦਿਆਂ ਵਿੱਚ ਲਿੰਗੀ ਜਣਨ ਬੀਜਾਂ ਦੁਆਰਾ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 9.
ਅਲਿੰਗੀ ਅਤੇ ਲਿੰਗੀ ਪ੍ਰਜਣਨ ਵਿੱਚ ਪ੍ਰਮੁੱਖ ਅੰਤਰ ਦੱਸੋ ।
ਉੱਤਰ-
ਅਲਿੰਗੀ ਅਤੇ ਲਿੰਗੀ ਪ੍ਰਜਣਨ ਵਿੱਚ ਅੰਤਰ –

ਅਲਿੰਗੀ ਪ੍ਰਜਣਨ (Asexual Reproduction)	ਲਿੰਗੀ ਪ੍ਰਜਣਨ (Sexual Reproduction)
(i) ਇੱਕ ਜਨਕ ਦੀ ਜ਼ਰੂਰਤ ਹੈ ।	(i) ਦੋਵੇਂ ਜਨਕਾਂ ਦੀ ਜ਼ਰੂਰਤ ਹੈ ।
(ii) ਜਨਕ ਦਾ ਸਾਰਾ ਸਰੀਰ, ਇੱਕ ਕੋਸ਼ਿਕਾ ਜਾਂ ਇੱਕ ਜਣਨ ਇਕਾਈਆਂ ਹਨ ।	(ii) ਯੁਗਮਕ ਜਿਹੜੇ ਇੱਕ ਕੋਸ਼ਿਕਾ ਵਾਲੇ ਹੁੰਦੇ ਹਨ ਉਭਾਰ ਜਣਨ ਕਰ ਸਕਦਾ ਹੈ ।
(iii) ਜਣਨ ਅੰਗ ਵਿਕਸਿਤ ਨਹੀਂ ਹੁੰਦੇ ।	(iii) ਜਣਨ ਅੰਗਾਂ ਦਾ ਵਿਕਸਿਤ ਹੋਣਾ ਜ਼ਰੂਰੀ ਹੈ ।
(iv) ਪੌਦੇ ਬੀਜਾਂ ਦੇ ਬਿਨਾਂ ਨਵੇਂ ਪੌਦੇ ਵਿਕਸਿਤ ਕਰਦੇ ਹਨ ।	(iv) ਨਵੇਂ ਪੌਦੇ ਬੀਜਾਂ ਦੁਆਰਾ ਵਿਕਸਿਤ ਹੁੰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 10.
ਸਵੈ-ਪਰਾਗਣ ਅਤੇ ਪਰ-ਪਰਾਗਣ ਦੇ ਵਿੱਚ ਅੰਤਰ ਦੱਸੋ ।
ਉੱਤਰ-
ਸਵੈ-ਪਰਾਗਣ ਅਤੇ ਪਰ-ਪਰਾਗਣ ਵਿੱਚ ਅੰਤਰ-

ਸਵੈ-ਪਰਾਗਣ (Self Pollinations)	ਪਰ-ਪਰਾਗਣ (Cross Pollinations)
(i) ਇਹ ਇੱਕ ਹੀ ਫੁੱਲ ਜਾਂ ਇੱਕ ਹੀ ਪੌਦੇ ਦੇ ਵੱਖ-ਵੱਖ ਫੁੱਲਾਂ ਵਿੱਚ ਹੁੰਦਾ ਹੈ ।	(i) ਇਹ ਦੋ ਫੁੱਲਾਂ ਦੇ ਵਿੱਚ ਹੋਣ ਵਾਲੀ ਕਿਰਿਆ ਹੈ ।
(ii) ਪਰਾਗਣ ਦੇ ਲਈ ਕਿਸੇ ਹੋਰ ਵਸਤੂ ਦੀ ਜ਼ਰੂਰਤ ਨਹੀਂ ।	(ii) ਪਰਾਗਣ ਸੰਪੂਰਨ ਕਰਨ ਦੇ ਲਈ ਹਵਾ, ਪਾਣੀ, ਜੰਤੂ ਆਦਿ ਕਾਰਕਾਂ ਦੀ ਜ਼ਰੂਰਤ ਹੁੰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 11.
ਫੁੱਲ ਵਿੱਚ ਨਿਸ਼ੇਚਨ ਦੀ ਪ੍ਰਕਿਰਿਆ ਕਿਸ ਤਰ੍ਹਾਂ ਪੂਰੀ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-

• ਪਰਾਗਕਣ ਦੁਆਰਾ ਫੁੱਲ ਦੇ ਪਰਾਗਕਣ ਹੀ ਉੱਤੇ ਪਰਾਗਕਣਾਂ ਦਾ ਸਥਾਨ-ਅੰਤਰਣ ਹੁੰਦਾ ਹੈ ।
• ਪਰਾਗਕਣ ਪਰਾਗਕਣ ਹੀ ਉੱਤੇ ਪਰਾਗ ਨਲੀ ਬਣਾਉਂਦੇ ਹਨ ਜਿਸ ਵਿੱਚ ਨਰ ਯੁਗਮਕ ਹੁੰਦੇ ਹਨ ।
• ਅੰਡ ਕੋਸ਼ ਵਾਧਾ ਕਰਦਾ ਹੈ ਅਤੇ ਵੱਡੀ ਮਾਦਾ ਕੋਸ਼ਿਕਾ ਦਾ ਰੂਪ ਲੈ ਲੈਂਦਾ ਹੈ ।
• ਇਹ ਕੋਸ਼ਿਕਾ ਅਰਧ ਸੂਤਰੀ ਵਿਭਾਜਨ ਤੋਂ ਚਾਰ ਬੀਜਾਣੂ ਬਣਾਉਂਦੀ ਹੈ ।
• ਇਨ੍ਹਾਂ ਵਿੱਚੋਂ ਇੱਕ ਵਿਕਸਿਤ ਹੋ ਕੇ ਭਰੁਣ ਥੈਲਾ ਬਣਾਉਂਦਾ ਹੈ ।
• ਨਰ ਯੁਗਮਕ ਅਤੇ ਮਾਦਾ ਯੁਗਮਕ ਦੇ ਸੰਜੋਗ ਤੋਂ ਯੁਗਮਜ ਬਣਦਾ ਹੈ । ਇਹ ਕਿਰਿਆ ਨਿਸ਼ੇਚਨ ਅਖਵਾਉਂਦੀ ਹੈ ।
• ਐਂਜੀਓਸਪਰਮਜ਼ ਵਿਚ ਦੋਹਰੀ ਨਿਸ਼ੇਚਨ ਕਿਰਿਆ ਹੁੰਦੀ ਹੈ ।

7. ਵੱਡੇ ਉੱਤਰ ਵਾਲਾ ਪ੍ਰਸ਼ਨ

ਪ੍ਰਸ਼ਨ-
ਪਰਾਗਣ ਤੋਂ ਲੈ ਕੇ ਬੀਜ ਬਣਨ ਦੀ ਪ੍ਰਕਿਰਿਆ ਦੇ ਵੱਖ-ਵੱਖ ਚਰਣਾਂ ਦਾ ਵਿਵਰਣ ਕਰੋ ।
ਉੱਤਰ-
ਪਰਾਗਕਣਾਂ ਦਾ ਪਰਾਗਕਣ ਹੀ ਉੱਤੇ ਸਥਾਨ-ਅੰਤਰਣ, ਪਰਾਗਣ ਅਖਵਾਉਂਦਾ ਹੈ । ਫੁੱਲ ਦੇ ਪੁੰਕੇਸਰ ਉੱਤੇ ਪਰਾਗਕੋਸ਼ ਹੁੰਦੇ ਹਨ, ਜਿਹੜੇ ਪਰਾਗਕਣਾਂ ਦਾ ਨਿਰਮਾਣ ਕਰਦੇ ਹਨ । ਅੰਡ ਪੁੰਜ ਦੇ ਤਿੰਨ ਭਾਗ ਹਨ-ਪਰਾਗਕਣ ਹੀ, ਪਰਾਗਕਣ ਵਹਿਣੀ ਬੀਜ ਦਾਨੀ | ਪਰਾਗਕਣ ਦੇ ਬਾਅਦ ਪਰਾਗਕਣਾਂ ਦੀ ਪਰਾਗ ਨਲੀ ਵਿਕਸਿਤ ਹੁੰਦੀ ਹੈ | ਪਰਾਗ ਨਲੀ ਵਿੱਚ ਕੇਂਦਰਕ ਦੋ ਕੇਂਦਰਕਾਂ ਵਿੱਚ ਵੰਡਿਆ ਜਾਂਦਾ ਹੈ । ਕਾਇਆ ਕੇਂਦਰਕ ਅਤੇ ਜਣਨ ਕੇਂਦਰਕ । ਜਣਨ ਕੇਂਦਰਕ ਦੋ ਨਵੇਂ ਯੁਗਮਤਾਂ ਦਾ ਨਿਰਮਾਣ ਕਰਦਾ ਹੈ । ਪਰਾਗ ਨਲੀ ਪਰਾਗਕਣ ਵਹਿਣੀ ਵਿੱਚੋਂ ਹੁੰਦੇ ਹੋਏ ਬੀਜਦਾਨੀ ਤਕ ਪਹੁੰਚਦੀ ਹੈ । ਇਕ ਨਰ ਯੁਗਮ ਬੀਜ ਅੰਡ ਨਾਲ ਯੁਗਮਨ ਕਰਕੇ ਯੁਗਮ ਬਣਾਉਂਦਾ ਹੈ ਤਾਂ ਦੂਸਰਾ ਨਰ ਯੁਗਮਕ ਦੋ ਧਰੁਵੀ ਕੇਂਦਰਕਾਂ ਤੋਂ ਯੁਗਮਨ ਕਰਕੇ ਕੇਂਦਰਕ ਬਣਾਉਂਦਾ ਹੈ ਜਿਹੜਾ ਐਂਡੋਸਪਰਮ (Endosperm) ਨੂੰ ਜਨਮ ਦਿੰਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਉੱਚ ਸਤਰ ਵਾਲ਼ੇ ਪੌਦਿਆਂ ਵਿੱਚ ਦੋਹਰੀ ਨਿਸ਼ੇਚਨ ਕਿਰਿਆ ਹੁੰਦੀ ਹੈ ।

ਨਿਸ਼ੇਚਨ ਦੇ ਬਾਅਦ ਬੀਜ ਦਾਨੀ ਫਲ ਵਿੱਚ ਵਿਕਸਿਤ ਹੋ ਜਾਂਦੀ ਹੈ ਅਤੇ ਫੁੱਲ ਦੇ ਬਾਕੀ ਭਾਗ ਮੁਰਝਾ ਕੇ ਡਿੱਗ ਜਾਂਦੇ ਹਨ । ਬੀਜ ਅੰਡ ਤੋਂ ਬੀਜ ਵਿਕਸਿਤ ਹੁੰਦੇ ਹਨ । ਬੀਜਾਂ ਵਿੱਚ ਭਰੂਣ ਹੁੰਦਾ ਹੈ ਜੋ ਸੁਰੱਖਿਆਤਮਕ ਬੀਜ ਪਰਤ ਦੇ ਅੰਦਰ ਰਹਿੰਦਾ ਹੈ । ਬੀਜ ਪਰਤ ਦੇ ਵਿੱਚ ਭੋਜਨ ਇਕੱਠਾ ਹੁੰਦਾ ਹੈ ।

Punjab State Board PSEB 11th Class Maths Book Solutions Chapter 10 Straight Lines Ex 10.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Maths Chapter 10 Straight Lines Ex 10.1

Question 1.
Draw a quadrilateral in the Cartesian plane, whose vertices are (- 4, 5), (0, 7), (5, – 5) and (- 4, – 2). Also find its area.
Answer.
Let ABCD be the given quadrilateral with vertices A (- 4, 5), B (0, 7), C (5 – 5), and D (- 4. – 2).
Then, by plotting A, B, C and D on the Cartesian plane and joining AB, BC, CD and DA the given quadrilateral can be drawn as

To find the area of quadrilateral ABCD, we draw one diagonal, say AC.
Accordingly, area (ABCD) = area (∆ABC) + area (∆ACD)
We know that the area of a triangle whose vertices are (x₁, y₁), (x₂, y₂) and (x₃, y₃) is \(\frac{1}{2}\) [x₁ (y₂ – y₃) + x₂ (y₃ – y₁) + x₃ (y₁ – y₂)]
Therefore, area of ∆ABC
= \(\frac{1}{2}\) |- 4 (7 + 5) + 0(- 5 – 5) + 5 (5 – 7)| unit²
= \(\frac{1}{2}\) |- 4 (12) + 5 (- 2)| unit²
= \(\frac{1}{2}\) |- 48 – 10| unit²
= \(\frac{1}{2}\) |- 58| unit²
= \(\frac{1}{2}\) × 58 unit²
= 29 unit²
Area of MCD = \(\frac{1}{2}\) |- 4 (- 5 + 2) + 5(- 2 – 5) ± (- 4) (5 + 5)| unit²
= \(\frac{1}{2}\) |- 4 (- 3) + 5 (- 7) – 4(10)| unit²
= \(\frac{1}{2}\) |12 – 35 – 40| unit²
= \(\frac{1}{2}\) |- 63| unit²
= \(\frac{63}{2}\) unit²
Thus, area (ABCD) = (29 + \(\frac{63}{2}\)) unit²
= \(\frac{58+63}{2}\) unit²
= \(\frac{121}{2}\) unit².

Question 2.
The base of an equilateral triangle with side 2a lies along the y-axis such that the mid point of the base is at the origin. Find vertices of the triangle.
Answer.

Let BC be the base of a triangle which lies on Y
Y-axis and third vertex may be A(h, 0) or A’.
Since, ∆ABC is an equilateral, then AB = BC.
∴ AB² = BC²
⇒ (h – 0)² + (0 – a²) = (2a)²
[∵ distance between two points (x₁, y₁) and (x₂, y₂)
= \(\left.\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\right]\)
For distance AB, (x₁, y₁) = (a, 0), (x₂, y₂) = (0, a)
h² + a² = 4a²
h² = 3a²
h = ± √3 a [taking square root]
Hence, the vertices of triangle are (√3a, 0), (0, a), (0,- a) or (- √3, a) (0, a), (0, – a).

Question 3.
Find the distance between P(x₁, y₁) and Q(x₂, y₂) when:
(i) PQ is parallel to the y – axis
(ii) PQ is parallel to the x-aLg.
Answer.

(i) When PQ is parallel to the Y-axis, it means the x-coordinates of P and Q are same i.e.,
x₁ = x₂.
∴ Distance between two points
PQ = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
= \(\sqrt{\left(x_{1}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
= \(\sqrt{\left(y_{2}-y_{1}\right)^{2}}=\left|y_{2}-y_{1}\right|\)

(ii)

When PQ is parallel to X-axis, it means y-coordinates of P and Q are same i.e., y₂ = y₁
∴ Distance between two points PQ = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)

= \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{1}-y_{1}\right)^{2}}\) [∵ y₂ = y₁]

= \(\sqrt{\left(x_{2}-x_{1}\right)^{2}}\)

= |x₂ – x₁|

Question 4.
Find a point on the x-axis, which is equidistance from the points (7, 6) and (3, 4).
Answer.
Let any point P on the X-axis is (x, 0) as for a point on X-axis y-coordinate is zero and the given points are A (7, 6) and B (3, 4).
Given, PA = PB
⇒ PA² = PB²
⇒ (x₁ – x₂)² + (y₁ – y₂)² = (x₁ – x₃)² + (y₁ – y₃)²
where x₁ = x, x₂ = 7, y₁ = 0, y₂ = 6, x₃ = 3, y₃ = 4
(x – 7)² + (0 – 6)² = (x – 3)² + (0 – 4)²
[∵ distance between two points = \(\left.\sqrt{\left(x_{1}-x_{2}\right)^{2}+\left(y_{1}-y_{2}\right)^{2}}\right]\)]
x² + 49 – 14x + 36 = x² + 9 – 6x + 16
⇒ – 14x + 6x = 25 – 36 – 49
⇒ – 8x = 25 – 85
⇒ Point P on X-axis = (\(\frac{15}{2}\), 0).

Question 5.
Find the slope of a line, which passes through the origin, and the mid-point of the line segment joining the points P(0, – 4) and B(8, 0).
Answer.

Given points are p (0, – 4) and Q (8, 0).
∴ x₁ = 0, y₁ = – 4, x₂ = 8, y₂ = 0
These points plotted in XY-plane are given below.
Mid-point of PQ is R = \(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)

= \(\left(\frac{0+8}{2}, \frac{-4+0}{2}\right)\) = (4, – 2)

∴ Slope of the OR = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)

= \(\frac{-2-0}{4-0}=\frac{-2}{4}=-\frac{1}{2}\)

[∵ x = 0, x₂ = 4, y₁ = 0, y₂ = – 2]

Question 6.
Without using the Pythagoras theorem show that the points (4, 4), (3, 5) and (- 1, – 1) are the vertices of a right angled triangle.
Answer.
In ∆ABC, we have
m₁ = Slope of AB = \(\frac{4-5}{4-3}\) = – 1 and
m₂ = Slope of AC = \(\frac{4-(-1)}{4-(-1)}\) = 1
Clearly, m₁ m₂ = – 1
This shows that AB is perpendicular to AC i. e.,
∠CAB = π/2
Hence, the given points are the vertices of a right-angled triangle.

Question 7.
Find the slope of the line, which makes an angle of 30° with the positive direction of y-axis measured anticlockwise.
Answer.
The line OP makes an angle of 30° with y-axis measured anticlockwise.

So OP makes an angle of 90° + 30° = 120° with positive direction of x-axis.
So, slope of OP = tan 120° = tan (180° – 60°) = – tan 60° = – √3.

Question 8.
Find the value of x for which the points (x, – 1), (2, 1) and (4, 5) are collinear.
Answer.
Given, points A (x, – 1), B (2, 1) and C (4, 5) are collinear.
Here, x₁ = x, y₁ = – 1, x₂ = 2, y₂ = 1, x₃ = 4 and y₃ = 5
∴ Slope of AB = Slope of BC
⇒ \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{y_{3}-y_{2}}{x_{3}-x_{2}}\)

⇒ \(\frac{1+1}{2-x}=\frac{5-1}{4-2}\)

⇒ \(\frac{2}{2-x}=\frac{4}{2}\)

⇒ 2 – x = 1
⇒ x = 2 – 1 = 1

Question 9.
Without using distance formula, show that points (- 2, – 1), (4, 0), (3, 3) and (- 3, 2) are vertices of a parallelogram.
Answer.
Let ABCD be a parallelogram, where vertices are

(x₁, y₁) → A (- 2, – 1),
(x₂, y₂) → B (4, 0),
(x₃, y₃) → C (3, 3) and
(x₄, y₄) → D (- 3, 2)
Mid-point of AC = \(\left(\frac{x_{1}+x_{3}}{2}, \frac{y_{1}+y_{3}}{2}\right)=\left(\frac{-2+3}{2}, \frac{-1+3}{2}\right)\)

= \(\left(\frac{1}{2}, \frac{2}{2}\right)=\left(\frac{1}{2}, 1\right)\)

[∵ mid-point of two points = \(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)]

Mid point of BD = \(\left(\frac{x_{2}+x_{4}}{2}, \frac{y_{2}+y_{4}}{2}\right)\)

= \(\left(\frac{4-3}{2}, \frac{0+2}{2}\right)=\left(\frac{1}{2}, 1\right)\)

∵ Mid-point of AC = Mid-point of BD

∴ ABCD is parallelogram.
Hence proved.

Question 10.
Find the angle between the xr-axis and the line joining the points (3, – 1) and (4, – 2).
Answer.
The slope of the line joining the points (3, – 1) and (4, – 2) is
m = \(\frac{-2-(-1)}{4-3}\)
= – 2 + 1 = – 1
Now, the inclination (θ) of the line joining the points (3, – 1) and (4, – 2) is given by tan θ = – 1
⇒ θ = (90° + 45°) = 135°
Thus, the angle between the x-axis and the line joining the points (3, – 1) and (4, – 2) is 135°.

Question 11.
The slope of a line is double of the slope of another line. If tangent of the angle between them is \(\frac{1}{3}\), find the slopes of the lines.
Answer.
Let m₁ and m be the slopes of the two given lines such that m₁ = 2m
We know that if 0 is the angle between the lines l₁ and l₂ with slopes m₁ and m₂ then
tan θ = \(\left|\frac{m_{2}-m_{1}}{1+m_{1} m_{2}}\right|\)
It is given that the tangent of the angle between the two lines is \(\frac{1}{3}\).
∴ \(\frac{1}{3}=\left|\frac{m-2 m}{1+(2 m) \cdot m}\right|\)

\(\frac{1}{3}=\left|\frac{-m}{1+2 m^{2}}\right|\)

\(\frac{1}{3}=\frac{-m}{1+2 m^{2}}\) or

\(\frac{1}{3}=-\left(\frac{-m}{1+2 m^{2}}\right)=\frac{m}{1+2 m^{2}}\)

Case I:

\(\frac{1}{3}=\frac{-m}{1+2 m^{2}}\)

⇒ 1 + 2 m² = – 3m
⇒ 2m + 3m + 1 = 0
⇒ 2m² + 2m + m + 1 = 0
⇒ (m + 1) (2m + 1) = 0
⇒ m = – 1 or m = – \(\frac{1}{2}\)
If m = – 1, then the slopes of the lines are – 1 and – 2.
If m = – \(\frac{1}{2}\), then the slopes of the lines are – \(\frac{1}{2}\) and – 1.

Case II:
\(\frac{1}{3}=\frac{m}{1+2 m^{2}}\)
⇒ 2m² + 1 = 3m
⇒ 2m² – 2m – m + 1 = 0
⇒ (m – 1) (2m – 1) = 0
⇒ m = 1 or m = \(\frac{1}{2}\)
If m = 1, then the slopes of the lines are 1 and 2.
If m = \(\frac{1}{2}\), then the slopes of the lines are \(\frac{1}{2}\) and 1.
Hence, the slopes of the lines are – 1 and – 2 or – \(\frac{1}{2}\) and – 1 or 1 and 2 or \(\frac{1}{2}\) and 1.

Question 12.
A line passes through (x₁, y₁) and (h, k). If slope of the line is m, show that k – y₁ = m (h – x₁).
Answer.
The slope of the line passing through (x₁, y₁) and (h, k) is \(\frac{k-y_{1}}{h-x_{1}}\).

It is given that the slope of the line is

∴ \(\frac{k-y_{1}}{h-x_{1}}\) = m
⇒ k – y₁ = m (h – x₁)
Hence, k – y₁ = m (h – x₁).

Question 13.
If three points (h, 0), (a, b) and (0, k) lie on a line, show that \(\frac{a}{\boldsymbol{h}}+\frac{b}{\boldsymbol{k}}\) = 1.
Answer.
If the points A (h, 0), B (a, b) and C (0, k) lie on a line, then
Slope of AB = Slope of BC
\(\frac{b-0}{a-h}=\frac{k-b}{0-a}\)

⇒ \(\frac{b}{a-h}=\frac{k-b}{-a}\)

⇒ – ab = (k – b) (a – h)
⇒ – ab = ka – kh – ab + bh
⇒ ka + bh = kh
On dividing both sides by kh, we obtain
\(\frac{k a}{k h}+\frac{b h}{k h}=\frac{k h}{k h}\)

\(\frac{a}{h}+\frac{b}{k}\) = 1

Hence \(\frac{a}{h}+\frac{b}{k}\) = 1.

Question 14.
Consider the given population and year graph. Find the slope of the line AB and uaing it, find what will be the peculation in the year 2010?

Answer.
Since line AB passes through points A(1985, 92) and B(1995, 97), its slope is = \(\frac{97-92}{1995-1985}=\frac{5}{10}=\frac{1}{2}\)

Let y be the population in the year 2010.
Then, according to the given graph, line AB must pass through point C (2010, y)
∴ Slope of AB = Slope of BC

⇒ \(\frac{1}{2}=\frac{y-97}{2010-1995}\)

⇒ \(\frac{1}{2}=\frac{y-97}{15}\)

⇒ \(\frac{15}{2}\) = y – 97
⇒ y – 97 = 7.5
⇒ y = 7.5 + 97 = 104.5
Thus, the slope of line AB is \(\frac{1}{2}\), while in the year 2010, the population will be 104.5 crores.

Punjab State Board PSEB 7th Class Science Book Solutions Chapter 16 ਪਾਣੀ: ਇੱਕ ਅਨਮੋਲ ਸਾਧਨ Textbook Exercise Questions, and Answers.

PSEB Solutions for Class 7 Science Chapter 16 ਪਾਣੀ: ਇੱਕ ਅਨਮੋਲ ਸਾਧਨ

PSEB 7th Class Science Guide ਪਾਣੀ : ਇੱਕ ਅਨਮੋਲ ਸਾਧਨ Intext Questions and Answers

ਸੋਚੋ ਅਤੇ ਉੱਤਰ ਦਿਓ : (ਪੇਜ 195)

ਪ੍ਰਸ਼ਨ 1.
ਅਜਿਹੀਆਂ ਤਿੰਨ ਗਤੀਵਿਧੀਆਂ ਲਿਖੋ ਜਿਨ੍ਹਾਂ ਦੌਰਾਨ ਸਭ ਤੋਂ ਵੱਧ ਪਾਣੀ ਬਰਬਾਦ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਤਿੰਨ ਗਤੀਵਿਧੀਆਂ ਜਿਨਾਂ ਦੌਰਾਨ ਪਾਣੀ ਦੀ ਬਰਬਾਦੀ ਹੁੰਦੀ ਹੈ

1. ਪਾਣੀ ਦੇ ਪਾਈਪ ਦਾ ਲੀਕ ਹੋਣਾ ।
2. ਬਰਤਨਾਂ ਨੂੰ ਵੱਗਦੇ ਪਾਣੀ ਨਾਲ ਧੋਣਾ ।
3. ਘੱਟ ਕੱਪੜਿਆਂ ਲਈ ਕੱਪੜੇ ਧੋਣ ਵਾਲੀ ਮਸ਼ੀਨ ਦੀ ਵਰਤੋਂ ਕਰਨਾ ।

ਪ੍ਰਸ਼ਨ 2.
ਕੀ ਸਾਨੂੰ ਪਾਣੀ ਦੀ ਬਰਬਾਦੀ ` ਤੇ ਕਾਬੂ ਪਾਉਣਾ ਚਾਹੀਦਾ ਹੈ ? ਜੇਕਰ ਹਾਂ, ਤਾਂ ਕਿਉਂ ?
ਉੱਤਰ-
ਸਾਨੂੰ ਪਾਣੀ ਦੀ ਬਰਬਾਦੀ ‘ਤੇ ਕਾਬੂ ਪਾਉਣਾ ਚਾਹੀਦਾ ਹੈ । ਪਾਣੀ ਦੀ ਵਰਤੋਂ ਘਟਾਉਣ ਨਾਲ ਪਾਣੀ ਨੂੰ ਸਾਫ਼ ਕਰਕੇ ਘਰਾਂ, ਵਪਾਰੀ ਸਥਾਨਾਂ, ਖੇਤੀ ਦੇ ਫਾਰਮਾਂ ਅਤੇ ਸਮਾਜਿਕ ਸੰਸਥਾਵਾਂ ਨੂੰ ਪਹੁੰਚਾਉਣ ਲਈ ਉਰਜਾ ਘੱਟ ਲਗਦੀ ਹੈ । ਅਜਿਹਾ ਕਰਨ ਨਾਲ ਪ੍ਰਦੂਸ਼ਣ ਵਿੱਚ ਕਮੀ ਹੁੰਦੀ ਹੈ ਅਤੇ ਈਂਧਣ ਦੀ ਵੀ ਬੱਚਤ ਹੁੰਦੀ ਹੈ । ਇਸ ਨਾਲ ਮਨੋਰੰਜਕ ਕਿਰਿਆਵਾਂ ਲਈ ਵੀ ਪਾਣੀ ਉਪਲੱਬਧ ਹੋ ਜਾਂਦਾ ਹੈ ।

ਸੋਚੋ ਅਤੇ ਉੱਤਰ ਦਿਓ : (ਪੇਜ 196 )

ਪ੍ਰਸ਼ਨ 1.
………. ਅਜਿਹੀ ਕਿਰਿਆ ਹੈ ਜਿਸ ਦੌਰਾਨ ਪਾਣੀ ਤਰਲ ਅਵਸਥਾ ਤੋਂ ਗੈਸ ਅਵਸਥਾ ਵਿੱਚ ਬਦਲਦਾ ਹੈ ।
ਉੱਤਰ-
ਵਾਸ਼ਪੀਕਰਨ ਅਜਿਹੀ ਕਿਰਿਆ ਹੈ ਜਿਸ ਦੌਰਾਨ ਪਾਣੀ ਤਰਲ ਅਵਸਥਾ ਤੋਂ ਗੈਸ ਅਵਸਥਾ ਵਿੱਚ ਬਦਲਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
………. ਅਜਿਹੀ ਕਿਰਿਆ ਹੈ ਜਿਸ ਦੌਰਾਨ ਪਾਣੀ ਗੈਸ ਅਵਸਥਾ ਤੋਂ ਤਰਲ ਅਵਸਥਾ ਵਿੱਚ ਬਦਲਦਾ ਹੈ ।
ਉੱਤਰ-
ਸੰਘਣਨ ਅਜਿਹੀ ਕਿਰਿਆ ਹੈ ਜਿਸ ਦੌਰਾਨ ਪਾਣੀ ਗੈਸ ਅਵਸਥਾ ਤੋਂ ਤਰਲ ਅਵਸਥਾ ਵਿੱਚ ਬਦਲਦਾ ਹੈ ।

ਸੋਚੋ ਅਤੇ ਉੱਤਰ ਦਿਓ : (ਪੇਜ 197)

ਪ੍ਰਸ਼ਨ 1.
ਕਿਹੜਾ ਬੀਕਰ ਧਰਤੀ ਹੇਠਲੇ ਪਾਣੀ ਨੂੰ ਦਰਸਾਉਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਬੀਕਰ ਵਿੱਚ ਲਿਆ ਗਿਆ ਪਾਣੀ ।

ਪ੍ਰਸ਼ਨ 2.
ਕਿਹੜਾ ਬੀਕਰ ਧਰਤੀ ਦੇ ਤਲ ਤੇ ਮੌਜੂਦ ਸਤਹੀ ਪਾਣੀ ਨੂੰ ਦਰਸਾਉਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਬੀਕਰ ‘ਸ’ ਵਿੱਚ ਲਿਆ ਗਿਆ ਪਾਣੀ ਧਰਤੀ ਦੇ ਤਲ ਤੇ ਸਤਹੀਂ ਪਾਣੀ ਨੂੰ ਦਰਸਾਉਂਦਾ ਹੈ ।

PSEB 7th Class Science Guide ਪਾਣੀ : ਇੱਕ ਅਨਮੋਲ ਸਾਧਨ Textbook Questions and Answers

1. ਖ਼ਾਲੀ ਥਾਂਵਾਂ ਭਰੋ

(i) ਜਿਹੜਾ ਪਾਣੀ ਅਸੀਂ ਪੀਂਦੇ ਹਾਂ ਉਹ ………. ਅਵਸਥਾ ਵਿੱਚ ਹੁੰਦਾ ਹੈ ।
ਉੱਤਰ-
ਤਰਲ,

(ii) ਪਾਣੀ ਦੇ ਮਿੱਟੀ ਵਿੱਚ ਰਿਸ ਕੇ ਜਾਣ ਦੀ ਕਿਰਿਆ ਨੂੰ ………. ਕਹਿੰਦੇ ਹਨ ।
ਉੱਤਰ-
ਇਨਫਿਲਟਰੇਸ਼ਨ,

(iii) ਭੌ-ਜਲ ਦੇ ਉੱਪਰਲੇ ਤਲ ਨੂੰ ………… ਕਹਿੰਦੇ ਹਨ ।
ਉੱਤਰ-
ਅਸੰਤ੍ਰਿਪਤ ਖੇਤਰ,

(iv) ………. ਦਾ ਅਰਥ ਹੈ ਪਾਣੀ ਦੀ ਹਰ ਸੰਭਵ ਵਧੀਆ ਢੰਗ ਨਾਲ ਵਰਤੋਂ ।
ਉੱਤਰ-
ਪ੍ਰਬੰਧਨ,

(v) ਕਿਸਾਨ …………. ਵਰਤ ਕੇ ਪਾਣੀ ਦੀ ਕਿਫਾਇਤੀ ਢੰਗ ਨਾਲ ਵਰਤੋਂ ਕਰ ਸਕਦੇ ਹਨ ।
ਉੱਤਰ-
ਤੁਪਕਾ ਸਿੰਚਾਈ ਪ੍ਰਣਾਲੀ ।

2. ਠੀਕ ਜਾਂ ਗਲਤ ਲਿਖੋ

(i) ਜਲ ਚੱਕਰ ਧਰਤੀ ਉੱਤੇ ਪਾਣੀ ਦੀ ਹੋਂਦ ਨੂੰ ਕਾਇਮ ਰੱਖਣ ਵਿੱਚ ਮਦਦ ਕਰਦਾ ਹੈ ।
ਉੱਤਰ-
ਠੀਕ,

(ii) ਧਰਤੀ ਉੱਤੇ ਮੌਜੂਦ ਕੁੱਲ ਪਾਣੀ ਦਾ ਲਗਭਗ 97% ਪਾਣੀ ਤਾਜ਼ਾ ਹੈ ।
ਉੱਤਰ-
ਗ਼ਲਤ,

(iii) ਪਾਣੀ ਦੀਆਂ ਲੀਕ ਕਰਦੀਆਂ ਪਾਈਪਾਂ ਅਤੇ ਟੂਟੀਆਂ ਦੀ ਛੇਤੀ ਮੁਰੰਮਤ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ ।
ਉੱਤਰ-
ਠੀਕ,

(iv) ਅਸੀਂ ਬੜੀ ਤੇਜ਼ੀ ਨਾਲ ਵਿਸ਼ਵ-ਪੱਧਰੀ ਜਲ ਸੰਕਟ ਵੱਲ ਵੱਧ ਰਹੇ ਹਾਂ ।
ਉੱਤਰ-
ਠੀਕ,

(v) ਬੁਰਸ਼ ਕਰਨ ਸਮੇਂ ਟੂਟੀ ਨੂੰ ਲਗਾਤਾਰ ਨਾ ਚਲਾਓ ।
ਉੱਤਰ-
ਠੀਕ ॥

3. ਕਾਲਮ ‘ਉ’ ਅਤੇ ਕਾਲਮ ‘ਅ’ ਦਾ ਮਿਲਾਣ ਕਰੋ

ਕਾਲਮ ‘ਉ’	ਕਾਲਮ ‘ਅ’
(i) ਬਰਫ਼	(ਉ) ਸਮੁੰਦਰ ਅਤੇ ਮਹਾਂਸਾਗਰ
(ii) ਖਾਰਾ ਪਾਣੀ	(ਅ) ਨਦੀਆਂ ਅਤੇ ਛੱਪੜ
(iii) ਤਾਜ਼ਾ ਪਾਣੀ	(ਇ) ਪਾਣੀ ਦੀ ਗੈਸੀ ਅਵਸਥਾ
(iv) ਜਲ ਵਾਸ਼ਪ	(ਸ) ਪਾਣੀ ਦਾ ਸਭ ਤੋਂ ਸ਼ੁੱਧ ਰੂਪ
(v) ਮੀਂਹ ਦਾ ਪਾਣੀ	(ਹ) ਪਾਣੀ ਦੀ ਠੋਸ ਅਵਸਥਾ ॥

ਉੱਤਰ

ਕਾਲਮ ‘ਉ’	ਕਾਲਮ ‘ਅ’
(i) ਬਰਫ਼	(ਹ) ਪਾਣੀ ਦੀ ਠੋਸ ਅਵਸਥਾ
(ii) ਖਾਰਾ ਪਾਣੀ	(ਉ) ਸਮੁੰਦਰ ਅਤੇ ਮਹਾਂਸਾਗਰ
(iii) ਤਾਜ਼ਾ ਪਾਣੀ	(ਸ) ਪਾਣੀ ਦਾ ਸਭ ਤੋਂ ਸ਼ੁੱਧ ਰੂਪ
(iv) ਜਲ ਵਾਸ਼ਪ	(ਇ), ਪਾਣੀ ਦੀ ਗੈਸੀ ਅਵਸਥਾ
(v) ਮੀਂਹ ਦਾ ਪਾਣੀ	(ਅ) ਨਦੀਆਂ ਅਤੇ ਛੱਪੜ ।

4. ਸਹੀ ਉੱਤਰ ਚੁਣੋ

(i) ਇਨ੍ਹਾਂ ਵਿੱਚੋਂ ਕਿਹੜਾ ਭੌ-ਜਲ ਦੇ ਘਟਣ ਲਈ ਜ਼ਿੰਮੇਵਾਰ ਹੈ ?
(ਉ) ਵੱਧਦੀ ਆਬਾਦੀ
(ਅ) ਵੱਧਦੇ ਉਦਯੋਗ
(ਇ) ਜੰਗਲਾਂ ਦੀ ਕਟਾਈ. .
(ਸ) ਇਹ ਸਾਰੇ ਹੀ ।
ਉੱਤਰ-
(ਸ) ਇਹ ਸਾਰੇ ਹੀ ।

(ii) ਪੰਜਾਬ ਜਲ ਸੰਭਾਲ ਕਾਨੂੰਨ ਇਸ ਸਾਲ ਪਾਸ ਹੋਇਆ
(ਉ) 2009
(ਆ) 2010
(ਇ) 2008
(ਸ) 2015.
ਉੱਤਰ-
(ਉ) 2009.

(iii) ਹਰ ਸਾਲ ਵਿਸ਼ਵ-ਜਲ ਦਿਵਸ ਮਨਾਇਆ ਜਾਂਦਾ ਹੈ
(ਉ) 22 ਅਪ੍ਰੈਲ
(ਆ) 24 ਮਾਰਚ
(ਈ) 22 ਮਾਰਚ .
(ਸ) 22 ਮਈ ॥
ਉੱਤਰ-
(ੲ) 22 ਮਾਰਚ ।

(iv) ਧਰਤੀ ਦੇ ਸਤਹੀ ਪਾਣੀ ਦਾ ਲਗਭਗ ………… ਪਾਣੀ ਸਮੁੰਦਰਾਂ ਅਤੇ ਮਹਾਂਸਾਗਰਾਂ ਵਿੱਚ ਹੈ ।
(ਉ) 75%
(ਅ) 71%
( 81% .
(ਸ) 29% .
ਉੱਤਰ-
(ਅ) 71%.

(v) ਸਾਨੂੰ ਟੂਟੀਆਂ ਚੱਲਦੀਆਂ ਕਦੋਂ ਨਹੀਂ ਰੱਖਣੀਆਂ ਚਾਹੀਦੀਆਂ ?
(ਉ) ਬੁਰਸ਼ ਕਰਦੇ ਸਮੇਂ ।
(ਅ ਸ਼ੇਵ ਕਰਦੇ ਸਮੇਂ
(ਇ) ਨਹਾਉਂਦੇ ਸਮੇਂ
(ਸ) ਇਹ ਸਾਰੇ ਹੀ ।
ਉੱਤਰ-
(ਸ) ਇਹ ਸਾਰੇ ਹੀ ।

5. ਬਹੁਤ ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ

ਪ੍ਰਸ਼ਨ (i)
ਭੌ-ਜਲ ਕੀ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਭੌ-ਜਲ-ਇਹ ਧਰਤੀ ਦੀ ਉੱਪਰਲੀ ਪਰਤ ਦੇ ਹੇਠਾਂ ਮਿੱਟੀ ਦੇ ਕਣਾਂ ਵਿੱਚ ਦੀਆਂ ਵਿੱਥਾਂ, ਟੁੱਟੀਆਂ ਚੱਟਾਨਾਂ ਅੰਦਰ ਇਕੱਠਾ ਹੋਇਆ ਪਾਣੀ ਹੈ । ਇਹ ਪਾਣੀ ਆਪਣੇ ਆਪ ਝਰਨੇ ਦੇ ਰੂਪ ਵਿੱਚ ਉੱਪਰ ਧਰਤੀ ‘ਤੇ ਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਪਾਣੀ ਨੂੰ ਟਿਊਬਵੈੱਲ ਰਾਹੀਂ ਧਰਤੀ ਦੀ ਸਤਹਿ ਉੱਪਰ ਲਿਆਇਆ ਜਾ ਸਕਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ (ii)
ਸਮੁੰਦਰਾਂ ਅਤੇ ਮਹਾਂਸਾਗਰਾਂ ਦਾ ਪਾਣੀ ਪੀਣ-ਯੋਗ ਕਿਉਂ ਨਹੀਂ ਹੁੰਦਾ ?
ਉੱਤਰ-
ਸਮੁੰਦਰਾਂ ਅਤੇ ਮਹਾਂਸਾਗਰਾਂ ਦਾ ਪਾਣੀ ਪੀਣ ਯੋਗ ਨਹੀਂ ਹੁੰਦਾ ਹੈ ਕਿਉਂਕਿ ਇਸ ਵਿੱਚ ਅਧਿਕ ਮਾਤਰਾ ਵਿੱਚ ਲੂਣ ਘੁਲਿਆ ਹੋਇਆ ਹੁੰਦਾ ਹੈ । ਇੱਕ ਲੀਟਰ ਸਮੁੰਦਰੀ ਪਾਣੀ ਵਿੱਚ 35 ਗ੍ਰਾਮ ਲੂਣ ਘੁਲੇ ਹੁੰਦੇ ਹਨ । ਇਸ ਪਾਣੀ ਨੂੰ ਪੀਣ ਨਾਲ ਨਿਰਜਲੀਕਰਨ, ਗੁਰਦੇ ਫੇਲ੍ਹ, ਬੇਹੋਸ਼ੀ ਅਤੇ ਮੌਤ ਵੀ ਹੋ ਸਕਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ (iii)
ਜਲਈ ਚੱਟਾਨੀ ਪਰਤਾਂ ਕੀ ਹੁੰਦੀਆਂ ਹਨ ?
ਉੱਤਰ-
ਜਲਈ ਚੱਟਾਨਾਂ ਪਰਤਾਂ-ਕਈ ਥਾਂਵਾਂ ‘ਤੇ ਵਾਟਰ ਟੇਬਲ ਤੋਂ ਵੀ ਹੇਠਾਂ ਸਖ਼ਤ ਚੱਟਾਨਾਂ ਦੀਆਂ ਪਰਤਾਂ ਹੁੰਦੀਆਂ ਹਨ ਜਿਨ੍ਹਾਂ ਵਿਚਕਾਰ ਭੌ-ਜਲ ਇਕੱਠਾ ਹੁੰਦਾ ਹੈ । ਇਨ੍ਹਾਂ ਚੱਟਾਨਾਂ ਦੀਆਂ ਪਰਤਾਂ ਨੂੰ ਜਲਈ ਚੱਟਾਨੀ ਪਰਤ ਕਹਿੰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ (iv)
ਪਾਣੀ ਦੀਆਂ ਤਿੰਨ ਅਵਸਥਾਵਾਂ ਕਿਹੜੀਆਂ ਹਨ ?
ਉੱਤਰ-
ਪਾਣੀ ਦੀਆਂ ਤਿੰਨ ਅਵਸਥਾਵਾਂ-

1. ਠੋਸ (ਬਰਫ਼ ਰੂਪ ਵਿੱਚ),
2. ਤਰਲ (ਸਧਾਰਨ ਪਾਣੀ) ਅਤੇ
3. ਗੈਸ ਵਾਸ਼ਪਾਂ ਦੇ ਰੂਪ ਵਿੱਚ) ।

ਪ੍ਰਸ਼ਨ (v)
ਭੌ-ਜਲ ਦੀ ਪ੍ਰਤੀਪੂਰਤੀ ਕਿਵੇਂ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਭੌ-ਜਲ ਦੀ ਪ੍ਰਤੀਪੂਰਤੀ-

• ਮੀਂਹ ਦੇ ਪਾਣੀ ਦੀ ਵਰਤੋਂ ਧਰਤੀ ਹੇਠਲੇ ਭੌ-ਜਲ ਦੀ ਪ੍ਰਤੀਪੂਰਤੀ ਲਈ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ ।
• ਖੇਤਾਂ ਵਿੱਚ ਕਿਸਾਨ, ਤੁਪਕਾ ਸਿੰਚਾਈ ਪ੍ਰਣਾਲੀ ਰਾਹੀਂ ਪਾਣੀ ਦੀ ਬੱਚਤ ਕਰ ਸਕਦੇ ਹਨ | ਅਜਿਹਾ ਕਰਨ ਨਾਲ ਵੀ ਭੌ-ਜਲ ਪ੍ਰਤੀਪੂਰਤੀ ਹੋ ਸਕਦੀ ਹੈ ।
• ਪ੍ਰਸ਼ਾਸਨਿਕ ਅਧਿਕਾਰੀ ਜਲ-ਸਪਲਾਈ ਦੀਆਂ ਪਾਈਪਾਂ ਵਿਚੋਂ ਜਲ ਰਿਸਾਵ ਰੋਕ ਨਾਲ ਭੌ-ਜਲ ਪ੍ਰਤੀਪੂਰਤੀ ਹੋ ਸਕਦੀ ਹੈ ।

6. ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ

ਪ੍ਰਸ਼ਨ (i)
ਕੁੱਝ ਅਜਿਹੀਆਂ ਮਨੁੱਖੀ-ਗਤੀਵਿਧੀਆਂ ਬਾਰੇ ਲਿਖੋ ਜਿਨ੍ਹਾਂ ਨਾਲ ਪਾਣੀ ਬਰਬਾਦ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਹੇਠਾਂ ਲਿਖੀਆਂ ਕੁੱਝ ਮਨੁੱਖੀ ਗਤੀਵਿਧੀਆਂ ਹਨ ਜਿਨ੍ਹਾਂ ਕਾਰਨ ਬਹੁਤ ਸਾਰਾ ਪਾਣੀ ਬਰਬਾਦ ਹੁੰਦਾ ਹੈ

• ਵੱਗਦੀ ਟੁਟੀ ਰੱਖ ਕੇ ਦੰਦ ਸਾਫ਼ ਕਰਨ ਲਈ ਬੁਰਸ਼ ਕਰਨਾ ਅਤੇ ਸ਼ੇਵ ਕਰਨਾ ।
• ਗਰਮੀਆਂ ਦੇ ਮੌਸਮ ਵਿੱਚ ਬਗੀਚੇ ਨੂੰ ਦੁਪਹਿਰ ਸਮੇਂ ਪਾਣੀ ਲਾਉਣਾ । ਜੇਕਰ ਤੜਕੇ 5 ਤੋਂ 7 ਵਜੇ ਵਿਚਕਾਰ ਪਾਣੀ ਲਗਾਇਆ ਜਾਵੇ ਤਾਂ ਪਾਣੀ ਦਾ ਵਾਸ਼ਪੀਕਰਨ ਘੱਟ ਹੋਵੇਗਾ ।
• ਰਸੋਈ ਦੇ ਬਰਤਨਾਂ ਨੂੰ ਚਲਦੀ ਟੂਟੀ ਹੇਠ ਸਾਫ਼ ਕਰਨ ਨਾਲ ਬਹੁਤ ਪਾਣੀ ਦੀ ਲੋੜ ਪਵੇਗੀ ।
• ਡਿਸ਼ਵਾਸ਼ਰ ਵਿੱਚ ਭਾਂਡੇ ਧੋਣਾ ਜਦੋਂ ਕਿ ਡਿਸ਼ਵਾਸ਼ਰ ਪੁਰੀ ਭਾਂਡਿਆਂ ਨਾਲ ਨਹੀਂ ਭਰੀ ਹੈ !
• ਕੱਪੜਿਆਂ ਨੂੰ ਧੋਣਾ ਜਦੋਂ ਕੱਪੜੇ ਧੋਣ ਵਾਲੀ ਮਸ਼ੀਨ ਕੱਪੜਿਆਂ ਨਾਲ ਪੂਰੀ ਭਰੀ ਹੋਈ ਨਹੀਂ ਹੈ ।
• ਵੱਗਦੇ ਪਾਣੀ ਦੀ ਟੂਟੀ ਹੇਠਾਂ ਬੈਠ ਕੇ ਨਹਾਉਣਾ ਜਾਂ ਫਿਰ ਲੰਮੇ ਸਮੇਂ ਲਈ ਫੁਹਾਰੇ ਥੱਲੇ ਬੈਠ ਕੇ ਨਹਾਉਣਾ ।

ਪ੍ਰਸ਼ਨ (ii)
ਤੁਸੀਂ ਬਗੀਚੇ ਵਿੱਚ ਪਾਣੀ ਦੀ ਖ਼ਪਤ ਕਿਵੇਂ ਘੱਟ ਕਰੋਗੇ ?
ਉੱਤਰ-
ਬਗੀਚੇ ਵਿੱਚ ਪਾਣੀ ਦੀ ਖ਼ਪਤ ਘੱਟ ਕਰਨਾ-

1. ਆਪਣੇ ਬਗੀਚੇ ਦੀ ਸਿੰਚਾਈ ਗਰਮੀਆਂ ਦੇ ਮੌਸਮ ਵਿੱਚ ਸਵੇਰੇਸਵੇਰੇ ਜਾਂ ਸ਼ਾਮ ਨੂੰ ਅਰਥਾਤ ਦੁਪਹਿਰ ਤੋਂ ਬਾਅਦ ਕਰਨ ਨਾਲ ਪਾਣੀ ਦੀ ਖ਼ਪਤ ਘੱਟ ਹੋ ਜਾਵੇਗੀ ਕਿਉਂਕਿ ਇਸ ਸਮੇਂ ਪਾਣੀ ਦੇ ਵਾਸ਼ਪ ਘੱਟ ਬਣਨਗੇ ।
2. ਬਗੀਚੇ ਦੀ ਸਿੰਚਾਈ ਤੁਪਕਾ ਸਿੰਚਾਈ ਪ੍ਰਣਾਲੀ ਜਾਂ ਸਪਿੰਕਲਰ ਨਾਲ ਕਰਾਂਗੇ ਜਿਸ ਤੋਂ ਪਾਣੀ ਓਨਾ ਹੀ ਲਗੇਗਾ ਜਿੰਨੀ ਇਸ ਨੂੰ ਲੋੜ ਹੈ ਅਰਥਾਤ ਪਾਣੀ ਦੀ ਬਰਬਾਦੀ ਵੀ ਨਹੀਂ ਹੋਵੇਗੀ ।

ਪ੍ਰਸ਼ਨ (iii)
ਪਾਣੀ ਸਾਡੇ ਲਈ ਕਿਵੇਂ ਮਹੱਤਵਪੂਰਨ ਹੈ ?
ਉੱਤਰ-
ਪਾਣੀ ਦੀ ਮਹੱਤਤਾ-ਧਰਤੀ ਦੇ ਸਭ ਤੋਂ ਮਹੱਤਵਪੂਰਨ ਸੋਤਾਂ ਵਿੱਚੋਂ ਇੱਕ ਪਾਣੀ ਹੈ । ਸਾਰੇ ਜੀਵਾਂ ਨੂੰ ਜਿਉਂਦੇ ਰਹਿਣ ਲਈ ਪਾਣੀ ਦੀ ਲੋੜ ਹੁੰਦੀ ਹੈ | ਪੀਣ ਤੋਂ ਇਲਾਵਾ ਮਨੁੱਖ ਨੂੰ ਖਾਣਾ ਬਣਾਉਣ ਲਈ, ਨਹਾਉਣ, ਕੱਪੜੇ ਧੋਣ, ਭਾਂਡੇ ਧੋਣ, ਦੰਦ ਸਾਫ਼ ਕਰਨ, ਘਰ ਅਤੇ ਹੋਰ ਥਾਂਵਾਂ ਸਾਫ਼ ਕਰਨ ਅਤੇ ਪੌਦਿਆਂ ਨੂੰ ਪਾਣੀ ਦੇਣ ਵਰਗੇ ਅਨੇਕਾਂ ਕਾਰਜਾਂ ਲਈ ਪਾਣੀ ਦੀ ਲੋੜ ਹੁੰਦੀ ਹੈ । ਪਾਣੀ ਦੀ ਵਰਤੋਂ ਕਰਕੇ ਬਿਜਲੀ ਪੈਦਾ ਕਰਨ ਲਈ, ਖੇਤੀਬਾੜੀ ਕਾਰਜਾਂ ਲਈ, ਉਪਯੋਗਾਂ ਵਿੱਚ ਕਈ ਸਾਮਾਨ ਤਿਆਰ ਕਰਨ ਲਈ, ਤੈਰਾਕੀ ਵਰਗੀਆਂ ਮਨੋਰੰਜਕ ਕਿਰਿਆਵਾਂ ਲਈ ਪਾਣੀ ਦੀ ਲੋੜ ਪੈਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ (iv)
ਮਨੁੱਖੀ ਵਸੋਂ ਦਾ ਵਾਧਾ ਭੌ-ਜਲ ਦੀ ਘਾਟ ਲਈ ਕਿਵੇਂ ਜ਼ਿੰਮੇਵਾਰ ਹੈ ?
ਉੱਤਰ-
ਮਨੁੱਖੀ ਵਸੋਂ ਦਾ ਵਾਧਾ ਭੌ-ਜਲ ਦੀ ਘਾਟ ਲਈ ਜ਼ਿੰਮੇਵਾਰ-ਮਨੁੱਖੀ ਆਬਾਦੀ ਬਹੁਤ ਤੇਜ਼ੀ ਨਾਲ ਵੱਧ ਰਹੀ ਹੈ । ਜਿਵੇਂ ਆਬਾਦੀ ਵੱਧਦੀ ਹੈ ਉਸ ਦੀਆਂ ਰੋਜ਼ਾਨਾ ਲੋੜਾਂ ਲਈ ਪਾਣੀ ਦੀ ਮੰਗ ਵੀ ਵੱਧਦੀ ਹੈ । ਅਕਸਰ ਧਰਤੀ ਹੇਠਲੇ ਪਾਣੀ ਦੀ ਵਰਤੋਂ ਘਰਾਂ, ਦੁਕਾਨਾਂ, ਦਫ਼ਤਰਾਂ, ਸੜਕਾਂ ਅਤੇ ਰੇਲ ਪਟੜੀਆਂ ਦੇ ਨਿਰਮਾਣ ਅਤੇ ਹੋਰ ਕਈ ਕੰਮਾਂ ਲਈ ਕੀਤੀ ਜਾਂਦੀ ਹੈ । ਅਜਿਹੇ ਨਿਰਮਾਣ ਨਾਲ ਮੀਂਹ ਦੇ ਪਾਣੀ ਦਾ ਧਰਤੀ ਹੇਠਾਂ ਰਿਸ ਕੇ ਜਾਣ ਵਾਲਾ ਖੇਤਰ ਵੀ ਘੱਟ ਜਾਂਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਅਸੀਂ ਧਰਤੀ ਹੇਠਲੇ ਪਾਣੀ ਦੀ ਖ਼ਪਤ ਹੀ ਨਹੀਂ ਕਰ ਰਹੇ ਸਗੋਂ ਧਰਤੀ ਹੇਠਾਂ ਰਿਸਣ ਵਾਲੇ ਪਾਣੀ ਨੂੰ ਵੀ ਘਟਾ ਰਹੇ ਹੁੰਦੇ ਹਾਂ ।

ਜਿਸ ਦਾ ਸਿੱਟਾ ਇਹ ਹੈ ਕਿ ਭੌ-ਜਲ ਪੱਧਰ ਹੇਠਾਂ ਡਿੱਗ ਜਾਂਦਾ ਹੈ ।ਵੱਧਦੀ ਆਬਾਦੀ ਦੀਆਂ ਲੋੜਾਂ ਪੂਰੀਆਂ ਕਰਨ ਲਈ ਵੱਧ ਤੋਂ ਵੱਧ ਉਦਯੋਗ ਸਥਾਪਤ ਕਰਨ ਦੀ ਲੋੜ ਹੁੰਦੀ ਹੈ ਜਿਸ ਤੋਂ ਧਰਤੀ ਹੇਠਲੇ ਪਾਣੀ ਦੀ ਜ਼ਿਆਦਾ ਵਰਤੋਂ ਕਰਦੇ ਹਾਂ ਜਿਸ ਨਾਲ ਭੌ-ਜਲ ਪੱਧਰ ਹੇਠਾਂ ਡਿੱਗਦਾ ਜਾਂਦਾ ਹੈ । ਵੱਧ ਰਹੀ ਆਬਾਦੀ ਦੀਆਂ ਲੋੜਾਂ ਪੂਰੀਆਂ ਕਰਨ ਲਈ ਰੁੱਖ ਕੱਟੇ ਜਾਂਦੇ ਹਨ ਜਿਸ ਨਾਲ ਜਲ-ਚੱਕਰ ਵਿਗੜ ਰਿਹਾ ਹੈ । ਇਹੀ ਕਾਰਨ ਹੈ ਕਿ ਧਰਤੀ ਹੇਠਾਂ ਰਿਸ ਕੇ ਜਾਣ ਵਾਲੇ ਪਾਣੀ ਦੀ ਮਾਤਰਾ ਵੀ ਘੱਟ ਰਹੀ ਹੈ ਅਤੇ ਭੌ-ਜਲ ਪੱਧਰ ਵੀ ਹੇਠਾਂ ਡਿੱਗ ਪੈਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ (v)
ਜੇ ਪੌਦਿਆਂ ਨੂੰ ਕੁੱਝ ਦਿਨ ਪਾਣੀ ਨਾ ਮਿਲੇ ਤਾਂ ਉਹ ਪਹਿਲਾਂ ਮੁਰਝਾਉਂਦੇ ਅਤੇ ਬਾਅਦ ਵਿੱਚ ਸੁੱਕ ਕਿਉਂ ਜਾਂਦੇ ਹਨ ?
ਉੱਤਰ-
ਕਈ ਦਿਨਾਂ ਤੋਂ ਬਾਅਦ ਜਦੋਂ ਵਰਖਾ ਨਹੀਂ ਹੋ ਰਹੀ ਇਕ ਗਰਮ ਦਿਹਾੜੇ ਜਿੰਨਾ ਪੌਦੇ ਨੂੰ ਪਾਣੀ ਮਿਲ ਰਿਹਾ ਹੈ ਉਸ ਤੋਂ ਵੱਧ ਉਸ ਤੋਂ ਵਾਸ਼ਪ ਉਤਸਰਜਨ ਕਾਰਨ ਨੁਕਸਾਨ ਹੋ ਰਿਹਾ ਹੈ । ਪੌਦੇ ਦੇ ਪੱਤਿਆਂ ਦੇ ਸੈੱਲਾਂ ਅਤੇ ਤਣੇ ਦਾ ਨਿਰਜਲੀਕਰਨ ਹੁੰਦਾ ਹੈ, ਜਿਸ ਤੋਂ ਉਹ ਪੌਦਾ ਸਿੱਧਾ ਨਾ ਰਹਿ ਕੇ ਮੁਰਝਾ ਜਾਂਦਾ ਹੈ ਅਤੇ ਕੁੱਝ ਸਮੇਂ ਬਾਅਦ ਵਿੱਚ ਮਰ ਜਾਂਦਾ ਹੈ !

7. ਵੱਡੇ ਉੱਤਰ ਵਾਲਾ ਪ੍ਰਸ਼ਨ

ਪ੍ਰਸ਼ਨ-ਤੁਸੀਂ ਪਾਣੀ ਦੀ ਸੰਭਾਲ ਲਈ ਕਿਹੜੇ ਕਦਮ ਚੁੱਕੋਗੇ ?
ਉੱਤਰ-
ਪਾਣੀ ਦੀ ਸੰਭਾਲ ਲਈ ਕਦਮ-ਅਸੀਂ ਹੇਠ ਲਿਖੇ ਕਦਮ ਚੁੱਕ ਕੇ ਪਾਣੀ ਦੀ ਬੱਚਤ ਕਰ ਸਕਦੇ ਹਾਂ

1. ਪਾਈਪਾਂ ਅਤੇ ਟੂਟੀਆਂ ਵਿਚੋਂ ਰਿਸਦੇ ਹੋਏ ਪਾਣੀ ਨੂੰ ਰੋਕ ਕੇ ।
2. ਦੰਦਾਂ ਨੂੰ ਬੁਰਸ਼ ਕਰਦੇ ਸਮੇਂ ਜਾਂ ਸ਼ੇਵ ਕਰਦੇ ਸਮੇਂ ਪਾਣੀ ਦੀਆਂ ਟੂਟੀਆਂ ਨੂੰ ਬੰਦ ਰੱਖ ਕੇ ।
3. ਫਰਸ਼ ਨੂੰ ਪਾਣੀ ਨਾਲ ਧੋਣ ਦੀ ਬਜਾਏ ਪੋਚਾ ਲਗਾ ਕੇ ਅਤੇ ਇਸ ਪ੍ਰਕਾਰ ਵਰਤੇ ਗਏ ਪਾਣੀ ਨੂੰ ਪੌਦਿਆਂ ਵਿੱਚ ਪਾਉਣ ਨਾਲ ਜਾਂ ਫਿਰ ਉਸ ਪਾਣੀ ਨੂੰ ਟਾਇਲਟ ਵਿੱਚ ਪਾਉਣ ਨਾਲ ।
4. ਸਬਜ਼ੀਆਂ ਅਤੇ ਫਲਾਂ ਨੂੰ ਵੱਗਦੀ ਟੂਟੀ ਹੇਠਾਂ ਧੋਣ ਦੀ ਬਜਾਏ ਵੱਡੇ ਬਰਤਨ ਵਿੱਚ ਪਾਣੀ ਪਾ ਕੇ ਧੋਣ ਨਾਲ ਅਤੇ ਬਾਅਦ ਵਿੱਚ ਇਸ ਪਾਣੀ ਨੂੰ ਪੌਦਿਆਂ ਵਿੱਚ ਪਾਉਣ ਨਾਲ ।
5. ਆਪਣੇ ਵਾਹਨ (ਕਾਰ ਜਾਂ ਸਕੂਟਰ) ਨੂੰ ਵੱਗਦੇ ਪਾਣੀ ਨਾਲ ਨਾ ਧੋਣ ਦੀ ਬਜਾਏ ਬਾਲਟੀ ਵਿੱਚ ਪਾਣੀ ਲੈ ਕੇ ਧੋਣ ਨਾਲ ।
6. ਮੀਂਹ ਦਾ ਪਾਣੀ ਇਕੱਠਾ ਕਰਕੇ ਉਸਦੀ ਭਿੰਨ ਕਾਰਜਾਂ ਲਈ ਵਰਤੋਂ ਕਰਕੇ ।
7. ਨਵੇਂ ਪੌਦਿਆਂ ਨੂੰ ਬਰਸਾਤ ਦੇ ਮੌਸਮ (ਰੁੱਤ) ਸਮੇਂ ਲਗਾਉਣ ਨਾਲ ।
8. ਲੋਕਾਂ ਨੂੰ ਪਾਣੀ ਦੀ ਸੰਭਾਲ ਬਾਰੇ ਜਾਗਰੂਕ ਕਰਕੇ, ਪਾਣੀ ਦੀ ਸੰਭਾਲ ਦੇ ਢੰਗਾਂ ਬਾਰੇ ਦੱਸਣ ਅਤੇ ਉਹਨਾਂ ਨੂੰ ਪਾਣੀ ਪ੍ਰਦੂਸ਼ਿਤ ਨਾ ਕਰਨ ਬਾਰੇ ਸੁਚੇਤ ਕਰ ਕੇ ।

PSEB Solutions for Class 7 Science ਪਾਣੀ : ਇੱਕ ਅਨਮੋਲ ਸਾਧਨ Important Questions and Answers

1. ਖ਼ਾਲੀ ਥਾਂਵਾਂ ਭਰੋ

(i) ਭੂਮੀ ਜਲ ਪ੍ਰਾਪਤ ਕਰਨ ਦੇ ਲਈ ………… ਅਤੇ …………. ਦੀ ਵਰਤੋਂ ਹੁੰਦੀ ਹੈ ।
ਉੱਤਰ-
ਟਿਊਬਵੈੱਲ, ਛਿਣ (ਬੋਰ-ਪਾਈਪ),

(ii) ਪਾਣੀ ਦੀਆਂ ਤਿੰਨ ਅਵਸਥਾਵਾਂ ……….. ਅਤੇ …………….. ਹਨ ।
ਉੱਤਰ-
ਠੋਸ, ਗੈਸ,

(iii) ਧਰਤੀ ਦੀ ਜਲ ਧਾਰਣ ਕਰਨ ਵਾਲੀ ਪਰਤ ……….. ਅਖਵਾਉਂਦੀ ਹੈ ।
ਉੱਤਰ-
ਭੂਮੀ ਜਲ ਪੱਧਰ,

(iv) ਧਰਤੀ ਅੰਦਰਲੇ ਖ਼ਾਲੀ ਸਥਾਨ ਨੂੰ ਪਾਣੀ ਦੇ ਰਿਸਾਵ ਨੂੰ ……………. ਕਹਿੰਦੇ ਹਨ ।
ਉੱਤਰ-
ਇਨਫਿਲਟਰੇਸ਼ਨ,

(v) ਮਨੁੱਖੀ ਸਰੀਰ ਦਾ …………… ਭਾਗ ਪਾਣੀ ਹੈ ।
ਉੱਤਰ-
70%,

(vi) ਧਰਤੀ ‘ਤੇ ਮੌਜੂਦ ਕੁੱਲ ਪਾਣੀ ਦਾ ਲਗਭਗ .. ………….. ਪ੍ਰਤੀਸ਼ਤ ਪਾਣੀ ਖਾਰਾ ਹੈ ।
ਉੱਤਰ-
97% |

2. ਕਾਲਮ ‘ਉਂ’ ਦੇ ਕਥਨਾਂ ਦਾ ਕਾਲਮ ‘ਅ’ ਦੇ ਕਥਨਾਂ ਨਾਲ ਮਿਲਾਨ ਕਰੋ –

ਕਾਲਮ ‘ਉਂ	ਕਾਲਮ ‘ਅ’
(i) ਭੌ-ਜਲ ਪੱਧਰ ਦਾ ਡਿੱਗਣਾ	(ੳ) ਖੇਤਾਂ ਵਿੱਚ ਕਿਸਾਨ ਪਾਣੀ ਦੀ ਬੱਚਤ ਕਰ ਸਕਦੇ ਹਨ
(ii) ਧਰਤੀ ‘ਤੇ ਪਾਣੀ ਦੀ ਕੁੱਲ ਮਾਤਰਾ ਕਾਇਮ ਰੱਖਦਾ	(ਅ) ਜਲਈ ਚੱਟਾਨੀ ਪਰਤ
(iii) ਤੁਪਕਾ ਸਿੰਚਾਈ ਪ੍ਰਣਾਲੀ	(ਇ) ਜਲ-ਚੱਕਰ
(iv) ਵਾਟਰ ਟੇਬਲ ਤੋਂ ਹੇਠਾਂ ਚੱਟਾਨਾਂ ਦੀਆਂ ਪਰਤਾਂ ਵਿਚਕਾਰ ਪਾਣੀ	(ਸ) ਵੱਧਦੀ ਆਬਾਦੀ, ਵੱਧਦੇ ਉਦਯੋਗ, ਜੰਗਲਾਂ ਦਾ ਕੱਟਣਾ ।

ਉੱਤਰ-

ਕਾਲਮ ‘ੳ’	ਕਾਲਮ ‘ਅ’
(i) ਭੌ-ਜਲ ਪੱਧਰ ਦਾ ਡਿੱਗਣਾ	(ਸ) ਵੱਧਦੀ ਆਬਾਦੀ, ਵੱਧਦੇ ਉਦਯੋਗ, ਜੰਗਲਾਂ ਦਾ ਕੱਟਣਾ
(ii) ਧਰਤੀ ‘ਤੇ ਪਾਣੀ ਦੀ ਕੁੱਲ ਮਾਤਰਾ ਕਾਇਮ ਰੱਖਣਾ	(ਈ) ਜਲ-ਚੱਕਰ
(iii) ਤੁਪਕਾ ਸਿੰਚਾਈ ਪ੍ਰਣਾਲੀ	(ੳ) ਖੇਤਾਂ ਵਿੱਚ ਕਿਸਾਨ ਪਾਣੀ ਦੀ ਬੱਚਤ ਕਰ ਸਕਦੇ ਹਨ
(iv) ਵਾਟਰ ਟੇਬਲ ਤੋਂ ਹੇਠਾਂ ਚੱਟਾਨਾਂ ਦੀਆਂ ਪਰਤਾਂ ਵਿਚਕਾਰ ਪਾਣੀ	(ਅ) ਜਲਈ ਚੱਟਾਨੀ ਪਰਤ |

3. ਸਹੀ ਵਿਕਲਪ ਚੁਣੋ

(i) ਪਾਣੀ ਦੀ ਕੁੱਲ ਮਾਤਰਾ ਕਿੱਥੇ ਸਥਿਰ ਹੁੰਦੀ ਹੈ ?
(ਉ) ਸੰਸਾਰ ਦੀਆਂ ਸਾਰੀਆਂ ਝੀਲਾਂ ਅਤੇ ਨਦੀਆਂ ਵਿੱਚ ਪਾਣੀ ਦੀ ਕੁੱਲ ਮਾਤਰਾ ਨਿਯਤ/ਸਥਿਰ ਰਹਿੰਦੀ ਹੈ ।
(ਅ) ਭੂਮੀ ਹੇਠ ਪਾਣੀ ਦੀ ਕੁੱਲ ਮਾਤਰਾ ਸਥਿਰ ਰਹਿੰਦੀ ਹੈ ।
(ਈ) ਸੰਸਾਰ ਦੇ ਸਮੁੰਦਰਾਂ ਅਤੇ ਮਹਾਂਸਾਗਰਾਂ ਵਿੱਚ ਪਾਣੀ ਦੀ ਕੁੱਲ ਮਾਤਰਾ ਸਥਿਰ ਹੈ ।
(ਸ) ਸੰਸਾਰ ਵਿੱਚ ਪਾਣੀ ਦੀ ਕੁੱਲ ਮਾਤਰਾ ਸਥਿਰ ਹੈ ।
ਉੱਤਰ-
(ਸ) ਸੰਸਾਰ ਵਿੱਚ ਪਾਣੀ ਦੀ ਕੁੱਲ ਮਾਤਰਾ ਸਥਿਰ ਹੈ ।

(ii) ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ਕਿਹੜਾ ਕਾਰਕ ਪਾਣੀ ਦੀ ਕਮੀ ਲਈ ਜ਼ਿੰਮੇਵਾਰ ਨਹੀਂ ਹੈ ?
(ਉ) ਉਦਯੋਗੀਕਰਣ ਵਿੱਚ ਵਾਧਾ
(ਅ) ਵਧਦੀ ਜਨਸੰਖਿਆ ।
(ਇ) ਬਹੁਤ ਜ਼ਿਆਦਾ ਵਰਖਾ
(ਸ) ਪਾਣੀ ਦੇ ਸਾਧਨਾਂ ਦਾ ਭੈੜਾ ਪ੍ਰਬੰਧ ।
ਉੱਤਰ-
(ਈ) ਬਹੁਤ ਜ਼ਿਆਦਾ ਵਰਖਾ ।

(iii) ਧਰਤੀ ਦੀ ਸਤਾ ਦਾ ਪ੍ਰਤੀਸ਼ਤ ਭਾਗ ਜਿਹੜਾ ਪਾਣੀ ਨਾਲ ਢੱਕਿਆ ਹੋਇਆ ਹੈ
(ਉ) 20%
(ਅ) 29
(ਈ) 71%
(ਸ) 30%
ਉੱਤਰ-
(ਈ) 71%.

(iv) ਦੁਨੀਆਂ ਦੇ ਕੁੱਲ ਤਾਜ਼ੇ ਪਾਣੀ ਦੀ ਪ੍ਰਤੀਸ਼ਤ ਮਾਤਰਾ ਮਨੁੱਖੀ ਵਰਤੋਂ ਲਈ ਉਪਲੱਬਧ ਹੈ ।
(ਉ) 0.003%
(ਅ) 1%
(ਇ) 71%
(ਸ) ਇਹਨਾਂ ਵਿੱਚੋਂ ਕੋਈ ਨਹੀਂ ।
ਉੱਤਰ-
(ਅ) 1%.

4. ਹੇਠ ਲਿਖੇ ਕਥਨ ਠੀਕ ਹਨ ਜਾਂ ਗਲਤ –

(i) ਭੁਮੀ ਜਲ ਸੰਸਾਰ ਭਰ ਦੀਆਂ ਨਦੀਆਂ ਅਤੇ ਝੀਲਾਂ ਵਿੱਚ ਮਿਲਣ ਵਾਲੇ ਪਾਣੀ ਤੋਂ ਬਹੁਤ ਜ਼ਿਆਦਾ ਹੈ ।
ਉੱਤਰ-
ਠੀਕ,

(ii) ਪਾਣੀ ਦੀ ਕਮੀ ਦੀ ਸਮੱਸਿਆ ਦਾ ਸਾਹਮਣਾ ਸਿਰਫ਼ ਪੇਂਡੂ ਖੇਤਰਾਂ ਦੇ ਨਿਵਾਸੀ ਕਰਦੇ ਹਨ ।
ਉੱਤਰ-
ਗ਼ਲਤ,

(iii) ਨਦੀਆਂ ਦਾ ਪਾਣੀ ਖੇਤਾਂ ਵਿੱਚ ਸਿੰਚਾਈ ਦਾ ਇਕ ਮਾਤਰ ਸੋਮਾ ਹੈ ।
ਉੱਤਰ-
ਗਲਤ,

(iv) ਵਰਖਾ ਸ਼ੁੱਧ ਪਾਣੀ ਦਾ ਇਕੱਲਾ ਸੋਮਾ ਹੈ ।
ਉੱਤਰ-
ਠੀਕ ।

5. ਬਹੁਤ ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ

ਪ੍ਰਸ਼ਨ 1.
ਸੰਸਾਰ ਵਿੱਚ ਜਲ ਕਿਨ੍ਹਾਂ ਥਾਂਵਾਂ ‘ਤੇ ਉਪਲੱਬਧ ਹੈ ?
ਉੱਤਰ-
ਮਹਾਂਸਾਗਰ ਅਤੇ ਸਮੁੰਦਰਾਂ ਵਿੱਚ ।

ਪ੍ਰਸ਼ਨ 2.
ਜਲ ਦੇ ਵਿਭਿੰਨ ਸਰੋਤਾਂ ਦੇ ਨਾਂ ਲਿਖੋ ।
ਉੱਤਰ-

• ਵਰਖਾ ਜਲ,
• ਖੂਹ,
•  ਨਦੀਆਂ,
• ਤਲਾਅ,
• ਝੀਲਾਂ,
• ਸਮੁੰਦਰ,
• ਮਹਾਂਸਾਗਰ ।

ਪ੍ਰਸ਼ਨ 3.
ਕਿਹੜਾ ਦਿਨ ਸੰਸਾਰ ਜਲ ਦਿਹਾੜੇ ਦੇ ਰੂਪ ਵਿੱਚ ਮਨਾਇਆ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
22 ਮਾਰਚ ਨੂੰ ।

ਪ੍ਰਸ਼ਨ 4.
ਜਲ ਦਿਵਸ ਦੀ ਕੀ ਮਹੱਤਤਾ ਹੈ ?
ਉੱਤਰ-
ਲੋਕਾਂ ਦਾ ਜਲ ਸੁਰੱਖਿਅਣ ਦੀ ਮਹੱਤਤਾ ਵੱਲ ਧਿਆਨ ਆਕਰਸ਼ਿਤ ਕਰਨਾ ।

ਪ੍ਰਸ਼ਨ 5.
ਕੀ ਪਾਣੀ ਹਰੇਕ ਜਗ੍ਹਾ ‘ਤੇ ਉਪਲੱਬਧ ਹੈ ?
ਉੱਤਰ-
ਨਹੀਂ, ਜਲ ਦੀ ਵੰਡ ਸੰਸਾਰ ਵਿੱਚ ਹਰ ਥਾਂ ‘ਤੇ ਇੱਕੋ ਜਿਹੀ ਨਹੀਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ 6.
ਜਲਵਾਸ਼ਪ ਕੀ ਹੁੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਪਾਣੀ ਦੇ ਗੈਸੀ ਰੂਪ ਨੂੰ ਜਲਵਾਸ਼ਪ ਕਹਿੰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 7.
ਸ਼ਹਿਰਾਂ ਵਿੱਚ ਪਾਣੀ ਦੀ ਸਪਲਾਈ ਕਿਵੇਂ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ?
ਉੱਤਰ-
ਪਾਈਪ ਦੇ ਵਿਸ਼ੇਸ਼ ਰੂਮ ਵਿੱਚ ਜਾਲ ਵਿਛਾ ਕੇ ।

ਪ੍ਰਸ਼ਨ 8.
ਭੂਮੀ ਜਲ ਸਤਰ ਕੀ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਭੂਮੀ ਹੇਠ ਵਰਖਾ ਦਾ ਪਾਣੀ ਰਿਸਾਅ ਹੋਣ ਕਾਰਨ ਚੱਟਾਨਾਂ ਦੇ ਉੱਪਰ ਅਤੇ ਖ਼ਾਲੀ ਥਾਂਵਾਂ ‘ਤੇ ਇਕੱਠਾ ਹੋ ਜਾਂਦਾ ਹੈ । ਇਸ ਇਕੱਠੇ ਹੋਏ ਪਾਣੀ ਦੀ ਉੱਪਰੀ ਪਰਤ ਨੂੰ ਭੁਮੀ ਜਲ ਸਤਰ ਆਖਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 9.
ਵਣ ਕਟਾਈ ਜਲ ਸਤਰ ਦੇ ਹੇਠਾਂ ਡਿੱਗਣ ਵਿੱਚ ਕਿਵੇਂ ਸਹਾਇਤਾ ਕਰਦਾ ਹੈ ?
ਉੱਤਰ-
ਵਣ ਕਟਾਈ ਕਾਰਨ ਪਾਣੀ ਦੇ ਰਿਸਾਅ ਦਾ ਖੇਤਰ ਘੱਟ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 10.
ਕੱਚੀ ਧਰਤੀ ਜਾਂ ਪੱਕੀ ਧਰਤੀ ਸਤਹਿ ਵਿੱਚੋਂ ਪਾਣੀ ਦਾ ਰਿਸਾਅ ਕਿਸ ਵਿੱਚ ਆਸਾਨੀ ਨਾਲ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਕੱਚੀ ਧਰਤੀ ਸਤਹਿ ਵਿੱਚ ।

ਪ੍ਰਸ਼ਨ 11.
ਮਾਰੂਥਲ ਰੇਗਿਸਤਾਨ ਕੀ ਹਨ ?
ਉੱਤਰ-
ਰੇਗਿਸਤਾਨ ਉਹ ਖੇਤਰ ਹੈ ਜਿੱਥੇ ਵਰਖਾ ਘੱਟ ਮਾਤਰਾ ਵਿੱਚ ਹੁੰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 12.
ਹੜ੍ਹ ਕਿਸ ਕਾਰਨਾਂ ਕਰਕੇ ਆਉਂਦੇ ਹਨ ?
ਉੱਤਰ-
ਜ਼ਿਆਦਾ ਵਰਖਾ ਹੋਣ ਕਾਰਨ ।

ਪ੍ਰਸ਼ਨ 13.
ਜਦੋਂ ਵਰਖਾ ਨਹੀਂ ਹੁੰਦੀ ਤਾਂ ਕੀ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਵਰਖਾ ਨਾ ਹੋਣ ਕਾਰਨ ਸੋਕਾ ਪੈ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 14.
ਸ਼ਹਿਰਾਂ ਵਿੱਚ ਕੀਮਤੀ ਪਾਣੀ ਦੇ ਨੁਕਸਾਨ ਨੂੰ ਰੋਕਣ ਵਿੱਚ ਕੌਣ ਜ਼ਿੰਮੇਵਾਰ ਹੈ ?
ਉੱਤਰ-
ਨਾਗਰਿਕ ਆਧਿਕਰਣ ।

ਪ੍ਰਸ਼ਨ 15.
NGO ਦਾ ਪੂਰਾ ਨਾਂ ਕੀ ਹੈ ?
ਉੱਤਰ-
NGO : ਗੈਰ ਸਰਕਾਰੀ ਸੰਗਠਨ (Non Government Organisation) ।

6. ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ

ਪ੍ਰਸ਼ਨ 1.
ਕੁਦਰਤ ਵਿੱਚ ਪਾਣੀ ਕਿੱਥੇ ਉਪਲੱਬਧ ਹੈ ?
ਉੱਤਰ-
ਧਰਤੀ ‘ਤੇ ਮਿਲਣ ਵਾਲੀਆਂ ਸਾਰੀਆਂ ਵਸਤੂਆਂ ਵਿੱਚੋਂ ਪਾਣੀ ਸਭ ਤੋਂ ਜ਼ਿਆਦਾ ਮਾਤਰਾ ਵਿੱਚ ਅਤੇ ਵਿਭਿੰਨ ਖੇਤਰਾਂ ਵਿੱਚ ਉਪਲੱਬਧ ਹੈ । ਇਹ ਪ੍ਰਕਿਰਤੀ ਵਿਚ ਹੇਠ ਲਿਖਿਆਂ ਥਾਂਵਾਂ ‘ਤੇ ਉਪਲੱਬਧ ਹੈ :

• ਖੂਹਾਂ, ਸਾਗਰਾਂ, ਝੀਲਾਂ, ਨਦੀਆਂ ਆਦਿ ਵਿੱਚ ।
• ਵਰਖਾ ਜਲ ਅਤੇ ਭੂਮੀ ਜਲ ਦੇ ਰੂਪ ਵਿੱਚ ।
• ਠੰਡੇ ਖੇਤਰਾਂ ਵਿੱਚ ਬਰਫ਼ ਅਤੇ ਹਿਮ ਦੇ ਰੂਪ ਵਿੱਚ ।
• ਵਾਯੂਮੰਡਲ ਵਿੱਚ ਜਲ ਵਾਸ਼ਪਾਂ ਦੇ ਰੂਪ ਵਿੱਚ |

ਪ੍ਰਸ਼ਨ 2.
ਵਰਖਾ ਜਲ ਸੰਹਿਣ ਕੀ ਹੈ ? ਇਸ ਦੀ ਕੀ ਲੋੜ ਹੈ ?
ਉੱਤਰ-
ਵਰਖਾ ਜਲ ਸੰਹਿਣ-ਵਰਖਾ ਦੇ ਪਾਣੀ ਨੂੰ ਵੱਡੇ ਤਲਾਅ ਜਾਂ ਖੁੱਲ੍ਹੇ ਖੇਤਰ ਵਿੱਚ ਇਕੱਠਾ ਕਰਨ ਦੀ ਪ੍ਰਕਿਰਿਆ ਨੂੰ ਵਰਖਾ ਜਲ ਸੰਹਿਣ ਕਹਿੰਦੇ ਹਨ ।
ਜ਼ਰੂਰਤ-

• ਪਾਣੀ ਦੀ ਉਪਲੱਬਧਤਾ ਵਧਾਉਣ ਲਈ ।
• ਪਾਣੀ ਦੀ ਘਾਟ ਸਮੇਂ ਇਸ ਪਾਣੀ ਦੀ ਵਰਤੋਂ ਲਈ !

ਪ੍ਰਸ਼ਨ 3.
ਜਲ ਦੇ ਨੁਕਸਾਨ ਲਈ ਜ਼ਿੰਮੇਵਾਰ ਕਿਹੜੇ ਕਾਰਨ ਹਨ ?
ਉੱਤਰ-

1. ਪਾਣੀ ਲਿਜਾਣ ਵਾਲੀਆਂ ਪਾਈਪਾਂ ਦਾ ਲੀਕ ਕਰਨਾ |
2. ਲੋੜ ਨਾ ਹੋਣ ਸਮੇਂ ਵੀ ਟੂਟੀਆਂ ਨੂੰ ਬੰਦ ਨਾ ਕਰਨਾ ।

ਪ੍ਰਸ਼ਨ 4.
ਜੇਕਰ ਪੌਦਿਆਂ ਨੂੰ ਕੁੱਝ ਦਿਨ ਪਾਣੀ ਨਾ ਦਿੱਤਾ ਜਾਵੇ ਤਾਂ ਪੌਦਿਆਂ ‘ਤੇ ਕੀ ਪ੍ਰਭਾਵ ਪਵੇਗਾ ?
ਉੱਤਰ-
ਜੇਕਰ ਪੌਦਿਆਂ ਨੂੰ ਕੁੱਝ ਦਿਨਾਂ ਲਈ ਪਾਣੀ ਨਾਲ ਸਿੰਚਾਈ ਨਹੀਂ ਕਰਾਂਗੇ, ਤਾਂ ਪੌਦੇ ਮੁਰਝਾ ਅਤੇ ਸੁੱਕ ਜਾਣਗੇ ।

7. ਵੱਡੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ

ਪ੍ਰਸ਼ਨ 1.
ਚਿੱਤਰ ਦੀ ਸਹਾਇਤਾ ਨਾਲ ਜਲ-ਚੱਕਰ ਪ੍ਰਕਿਰਿਆ ਨੂੰ ਸਮਝਾਓ ।
ਉੱਤਰ-
ਜਲ-ਚੱਕਰ-ਵੱਖ-ਵੱਖ ਕੁਦਰਤੀ ਵਿਧੀਆਂ ਦੁਆਰਾ ਧਰਤੀ ਉੱਤੇ ਪਾਣੀ ਦੀ ਲਗਾਤਾਰ ਉਪਲੱਬਧਤਾ ਬਣੀ ਰਹਿੰਦੀ ਹੈ । ਇਹ ਸਭ ਵਿਧੀਆਂ ਇਕੱਠੇ ਰੂਪ ਵਿੱਚ ਜਲ-ਚੱਕਰ ਦਾ ਨਿਰਮਾਣ ਕਰਦੀਆਂ ਹਨ । ਜਲ-ਚੱਕਰ ਦੌਰਾਨ ਪਾਣੀ ਆਪਣੀਆਂ ਤਿੰਨ ਅਵਸਥਾਵਾਂ-

• ਠੋਸ
• ਦਵ ਅਤੇ
• ਗੈਸ ਵਿੱਚੋਂ ਕਿਸੇ ਅਵਸਥਾ ਵਿੱਚ ਧਰਤੀ ਉੱਤੇ ਮਿਲ ਜਾਂਦਾ ਹੈ ।

ਧਰਤੀ ‘ਤੇ ਉਪਲੱਬਧ ਭੂਮੀ ਜਲ ਸਰੋਤਾਂ-ਸਮੁੰਦਰ, ਤਲਾਅ, ਨਦੀਆਂ, ਝੀਲਾਂ ਆਦਿ ਤੋਂ ਪਾਣੀ ਸੂਰਜ ਤੇ ਤਾਪ ਦੁਆਰਾ ਵਾਸ਼ਪ ਬਣ ਕੇ ਉੱਪਰ ਉੱਠਦਾ ਹੈ ਅਤੇ ਵਾਯੂਮੰਡਲ ਵਿੱਚ ਮੌਜੂਦ | ਰਹਿੰਦਾ ਹੈ । ਇਹ ਜਲ ਵਾਸ਼ਪ ਸੰਘਣਿਤ ਹੋ ਕੇ ਬੱਦਲ ਦਾ ਪਾਣੀ ਬਣਾਉਂਦੇ ਹਨ ਅਤੇ ਧਰਤੀ ਉੱਪਰ ਵਰਖਾ ਰੁਪ ਵਿੱਚ ਡਿੱਗਦੇ ਹਨ । ਠੋਸ ਅਵਸਥਾ ਵਿੱਚ , ਚਿੱਤਰ-ਜਲ-ਚੱਕਰ ਪਾਣੀ ਬਰਫ਼ ਅਤੇ ਹਿਮ ਦੇ ਰੂਪ ਵਿੱਚ ਧਰਤੀ ਦੇ ਧਰੁਵਾਂ ‘ਤੇ ਅਤੇ ਪਹਾੜਾਂ ‘ਤੇ ਗਲੇਸ਼ੀਅਰਾਂ ਦੇ ਰੂਪ ਵਿੱਚ ਹੁੰਦਾ ਹੈ । ਇਹ ਇਕੱਠਿਆਂ ਹੋ ਕੇ ਸਾਰੀ ਪ੍ਰਕਿਰਿਆ ਜਲ-ਚੱਕਰ ਦਾ ਨਿਰਮਾਣ ਕਰਦੀ ਹੈ ।

1. ਭੁਮੀ ਜਲ
2. ਵਾਸ਼ਪੀਕਰਨ
3. ਸੰਘਣਨ
4. ਬੱਦਲ
5. ਵਾਸ਼ਪ ਉਤਸਰਜਨ
6. ਵਰਖਾ ॥

ਪ੍ਰਸ਼ਨ 2.
ਭੁਮੀ ਜਲ ਪੱਧਰ ਦੇ ਨੀਵੇਂ ਹੋਣ ਲਈ ਜ਼ਿੰਮੇਵਾਰ ਕਾਰਕਾਂ ਨੂੰ ਸਮਝਾਓ ।
ਉੱਤਰ-
ਭੂਮੀ ਜਲ ਪੱਧਰ ਦੇ ਹੇਠਾਂ ਡਿੱਗਣ ਲਈ ਜ਼ਿੰਮੇਵਾਰ ਕਾਰਕ :

1. ਜਨਸੰਖਿਆ ਵਿੱਚ ਵਾਧਾ
2. ਉਦਯੋਗਿਕ ਅਤੇ ਖੇਤੀ ਗਤੀਵਿਧੀਆਂ
3. ਘੱਟ ਵਰਖਾ
4. ਜੰਗਲਾਂ ਦਾ ਕੱਟਣਾ
5. ਪਾਣੀ ਦੇ ਸੋਖਣ ਲਈ ਲੋੜੀਂਦੇ ਖੇਤਰ ਵਿੱਚ ਕਮੀ ਆਦਿ ਕੁੱਝ ਕਾਰਕ ਹਨ ਜੋ ਭੂਮੀ ਪੱਧਰ ਨੂੰ ਨੀਵੇਂ ਕਰਨ ਲਈ ਕੁੱਝ ਕਾਰਕ ਹਨ ।

1. ਜਨਸੰਖਿਆ ਵਿੱਚ ਵਾਧਾ-ਜਨਸੰਖਿਆ ਵਧਣ ਨਾਲ ਇਮਾਰਤਾਂ, ਦੁਕਾਨਾਂ, ਦਫ਼ਤਰਾਂ, ਸੜਕਾਂ ਅਤੇ ਹੋਰ ਕਈ ਸੰਸਥਾਨਾਂ ਦੇ ਨਿਰਮਾਣ ਦੀ ਮੰਗ ਵੱਧ ਜਾਂਦੀ ਹੈ । ਇਸ ਨਾਲ ਖੇਤੀਯੋਗ ਭੂਮੀ ਅਤੇ ਖੇਡਾਂ ਦੇ ਮੈਦਾਨ ਵਰਗੇ ਖੁੱਲ੍ਹੇ ਖੇਤਰਾਂ ਵਿੱਚ ਕਮੀ ਆ ਜਾਂਦੀ ਹੈ । ਇਸ ਕਾਰਨ ਭੂਮੀ ਵਿੱਚ ਵਰਖਾ ਦੇ ਪਾਣੀ ਦੀ ਸੋਖਣ ਦਰ ਘੱਟ ਜਾਂਦੀ ਹੈ । ਇਸ ਕਾਰਨ ਭੁਮੀ ਜਲ ਪੱਧਰ ਦਾ ਲਗਾਤਾਰ ਸੁਖਣਾਉਣ ਹੋ ਰਿਹਾ ਹੈ ।

2. ਵਧਦੇ ਉਦਯੋਗ-ਸਭ ਉਦਯੋਗਾਂ ਦੁਆਰਾ ਪਾਣੀ ਦੀ ਵਰਤੋਂ ਹੋ ਰਹੀ ਹੈ । ਵਰਤੋਂ ਵਿੱਚ ਆਉਣ ਵਾਲੀ ਹਰ ਚੀਜ਼ ਦੇ ਉਤਪਾਦਨ ਵਿੱਚ ਪਾਣੀ ਦੀ ਜ਼ਰੂਰਤ ਹੁੰਦੀ ਹੈ । ਵਧੇਰੇ ਉਦਯੋਗਾਂ ਦੁਆਰਾ ਵਰਤਿਆ ਜਾਣ ਵਾਲਾ ਪਾਣੀ ਭੂਮੀ ਵਿੱਚੋਂ ਕੱਢਿਆ ਜਾਂਦਾ ਹੈ ।

3. ਖੇਤੀ ਕਾਰਜ-ਬਹੁਤ ਸਾਰੇ ਕਿਸਾਨ ਫ਼ਸਲਾਂ ਦੀ ਸਿੰਚਾਈ ਦੇ ਲਈ ਵਰਖਾ ‘ਤੇ ਨਿਰਭਰ ਕਰਦੇ ਹਨ । ਅਨਿਯਮਿਤ ਵਰਖਾਂ ਦੇ ਕਾਰਨ ਪਾਣੀ ਦੀ ਉਪਲੱਬਧਤਾ ਵਿੱਚ ਕਮੀ ਹੋ ਜਾਂਦੀ ਹੈ । ਇਸ ਲਈ ਕਿਸਾਨਾਂ ਨੂੰ ਸਿੰਚਾਈ ਦੇ ਲਈ ਭੁਮੀ ਜਲ ਦੀ ਵਰਤੋਂ ਕਰਨੀ ਪੈਂਦੀ ਹੈ । ਜਨਸੰਖਿਆ ਦੇ ਵਾਧੇ ਕਾਰਨ ਖੇਤੀ ਦੇ ਲਈ ਭੁਮੀ ਜਲ ਦੀ ਵਰਤੋਂ ਦਿਨ-ਪ੍ਰਤੀ-ਦਿਨ ਵਧਦੀ ਜਾ ਰਹੀ ਹੈ । ਇਸ ਦੇ ਨਤੀਜੇ ਵਜੋਂ ਭੂਮੀ ਜਲ ਪੱਧਰ ਲਗਾਤਾਰ ਹੇਠਾਂ ਡਿੱਗਦਾ ਜਾ ਰਿਹਾ ਹੈ ।

4. ਪਾਣੀ ਦਾ ਮਾੜਾ ਪ੍ਰਬੰਧ-ਪਾਈਪਾਂ ਦੁਆਰਾ ਪਾਣੀ ਦੀ ਸਪਲਾਈ ਕਰਨ ਸਮੇਂ ਸਪਲਾਈ ਪਾਈਪਾਂ ਵਿੱਚ ਰਿਸਾਅ ਹੁੰਦਾ ਰਹਿੰਦਾ ਹੈ ਜਿਸ ਨਾਲ ਕਾਫ਼ੀ ਮਾਤਰਾ ਵਿੱਚ ਪਾਣੀ ਦਾ ਨੁਕਸਾਨ ਹੋ ਜਾਂਦਾ ਹੈ ਅਤੇ ਭੂਮੀ ਜਲ ਪੱਧਰ ਵਿੱਚ ਗਿਰਾਵਟ ਦਾ ਕਾਰਨ ਹੁੰਦਾ ਹੈ | ਮਾੜਾ ਪਾਣੀ ਪ੍ਰਬੰਧ ਜਾਂ ਬਰਬਾਦੀ ਵਿਅਕਤੀਗਤ ਪੱਧਰ ‘ਤੇ ਵੀ ਹੋ ਸਕਦੀ ਹੈ ਜਿਵੇਂ ਲੀਕ ਕਰ ਰਹੀਆਂ ਟੂਟੀਆਂ ਨੂੰ ਠੀਕ ਨਾ ਕਰਵਾਉਣ ਨਾਲ ਵੀ ਪਾਣੀ ਰਿਸਾਅ ਹੁੰਦਾ ਹੈ ।