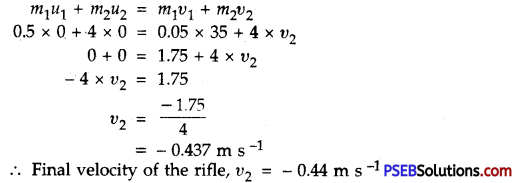Bhagya

Punjab State Board PSEB 10th Class Hindi Book Solutions Hindi Grammar vilom shabd विलोम शब्द Exercise Questions and Answers, Notes.

PSEB 10th Class Hindi Grammar विलोम शब्द

निम्नलिखित शब्दों के विलोम शब्द लिखिए

उत्तर:

निम्नलिखित बहुविकल्पी प्रश्नों के उत्तर एक सही विकल्प चुनकर लिखें.

प्रश्न 1.
असली का विलोम शब्द है
(क) निष्ठुर
(ख) अनुचित
(ग) नवीन
(घ) नकली।
उत्तर:
(घ) नकली

प्रश्न 2.
चेतन का विलोम शब्द है
(क) सुप्त
(ख) जड़
(ग) जागृत
(घ) निद्रा।
उत्तर:
(ख) जड़

प्रश्न 3.
कोमल का विलोम शब्द है
(क) निष्ठुर
(ख) निकृष्ट
(ग) कर्कश
(घ) अधम।
उत्तर:
(ग) कर्कश

प्रश्न 4.
सार्थक का विलोम शब्द है,
(क) व्यर्थ
(ख) निरर्थक
(ग) निर्गुण
(घ) क्षीण।
उत्तर:
(ख) निरर्थक

प्रश्न 5.
पूर्व का विलोम है, पश्चिम (हाँ या नहीं में उत्तर लिखें)
उत्तर:
हाँ

प्रश्न 6.
दानव का विलोम है, मानव (हाँ या नहीं में उत्तर लिखें)
उत्तर:
नहीं

प्रश्न 7.
भय का विलोम है, साहस (हाँ या नहीं में उत्तर लिखें)
उत्तर:
हाँ

प्रश्न 8.
ताप का विलोम है, शीत (सही या गलत लिखकर उत्तर दें)
उत्तर:
सही

प्रश्न 9.
पतन का विलोम है, गिरावट (सही या गलत लिखकर उत्तर दें)
उत्तर:
गलत

प्रश्न 10.
मिलन का विलोम है, विरह (सही या गलत लिख कर उत्तर दें)
उत्तर:
सही।

निम्नलिखित में से किसी एक शब्द का विलोम शब्द लिखिए

वर्ष
1. कंजूस, जिंदाबाद।
उत्तर:
कंजूस = दानी
जिंदाबाद = मुर्दाबाद।

2. हानि, ईमानदार।
उत्तर:
हानि = लाभ
ईमानदार = बेईमान।

3. निंदा, हार।
उत्तर:
निंदा = स्तुति
हार = जीत।

वर्ष
1. करीब, मित्र।
उत्तर:
करीब = दूर
मित्र = शत्रु।

2. आशा, मान
उत्तर:
आशा = निराशा
मान = अपमान।

3. विधवा, स्वस्थ।
उत्तर:
विधवा = सधवा
स्वस्थ = अस्वस्थ।

वर्ष
कंजूस, विस्तार।
उत्तर:
कंजूस = खर्चीला
विस्तार = संक्षेप।

प्रश्न 1.
विलोम शब्द किसे कहते हैं? उदाहरण सहित लिखिए।
उत्तर:
परस्पर विपरीत अर्थ का ज्ञान कराने वाले किसी शब्द को विलोम शब्द कहते हैं। इसे विपरीत या विलोमार्थी शब्द भी कहते हैं। उदाहरण-
(I) रीना सदा न्याय का पक्ष लेती है।
विलोम अर्थ-रीना सदा अन्याय का पक्ष लेती है।

(II) नीरज साधारण परिवार से संबंधित है।
विलोम अर्थ-नीरज असाधारण परिवार से संबंधित है।

(III) गली में एक व्यक्ति था।
विलोम अर्थ-गली में अनेक व्यक्ति थे।

(IV) गीताजंली का व्यवहार उचित था।
विलोम अर्थ-गीतांजली का व्यवहार अनुचित था।

(V) आप की यह हरकत पाक नहीं कहला सकती।
विलोम अर्थ-आप की यह हरकत नापाक नहीं कहला सकती।

प्रश्न 2.
विलोम शब्द किस-किस प्रकार बनाए जाते हैं? उदाहरण सहित लिखिए।
उत्तर:
विलोम शब्द प्रायः तीन प्रकार से बनाए जाते हैं-
(क) उपसर्ग के योग से
(ख) उपसर्ग बदलने से
(ग) विलोम शब्द मूल रूप से।
उदाहरण-
(क) उपसर्ग के योग सेइच्छा-अनिच्छा, साधारण-असाधारण, यश-अपयश, गुण-अवगुण, सुगंध-दुर्गंध, पसंद-नापसंद।
(ख) उपसर्ग बदलने से-साक्षर-निरक्षर, ईमानदार-बेईमानदार, स्वदेश-विदेश, संपन्न-विपन्न, अधुनातन-पुरातन, आयात-निर्यात।
(ग) विलोम शब्द मूल से-उदय-अस्त, आधुनिक-प्राचीन, उजड़ा-बसा, झगड़ा-समझौता, निकास-प्रवेश, दिवस-रात।

(क) उपसर्ग के योग से बने विलोम शब्द
(i) ‘अ’ उपसर्ग के योग से बने विलोम शब्द

(ii) ‘अन्’ उपसर्ग के योग से बने विलोम शब्द

(iii) ‘अप’ उपसर्ग के योग से बने विलोम शब्द

(iv) ‘अव’ उपसर्ग के योग से बने विलोम शब्द

(v) ‘कु’ उपसर्ग के योग से बने विलोम शब्द

(vi) ‘दुः/दुर्’ उपसर्ग के योग से बने विलोम शब्द

(vii) ‘ना’ उपसर्ग के योग से बने विलोम शब्द

(viii) ‘निः/निर्’ उपसर्ग के योग से बने विलोम शब्द

(ix) ‘पर’ उपसर्ग के योग से बने विलोम शब्द

(x) ‘प्रति’ उपसर्ग के योग से बने विलोम शब्द

(xi) ‘वि’ उपसर्ग के योग से बने विलोम शब्द

(xii) ‘बे’ उपसर्ग के योग से बने विलोम शब्द

कुछ विपरीत शब्द मूल रूप में ही प्रयुक्त होते हैं। जैसे-

Punjab State Board PSEB 9th Class Science Book Solutions Chapter 9 Force and Laws of Motion Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Science Chapter 9 Force and Laws of Motion

PSEB 9th Class Science Guide Force and Laws of Motion Textbook Questions and Answers

Question 1.
An object experiences a net zero external unbalanced force. Is it possible for the object to be travelling with a non-zero velocity? If yes, state the conditions that must be placed on the magnitude and direction of the velocity. If no, provide a reason.
Answer:
Yes, it is possible for an object to move with non-zero velocity even when net zero unbalanced force is experienced by it. In this situation the magnitude of velocity and direction will be same. As for example, in case of a rain drop falling freely with constant velocity, the weight of the drop is balanced by upthrust so to say the net unbalanced force on drop is zero.

Question 2.
When a carpet is beaten with a stick, the dust comes out of it? Explain.
Answer:
When a carpet is beaten with a stick, the carpet is set into motion while the dust particles due to inertia tend to remain at rest. In this way dust particles get detached from the carpet and come out of it.

Question 3.
Why is it advised to tie any luggage kept on the roof of a bus with rope?
Answer:
When a fast-moving bus suddenly takes a turn round a sharp bend then the luggage placed on the roof of a bus gets displaced. The reason for this is that the luggage tends to remain with linear motion while an unbalanced force is applied by the engine to change the direction of the bus so that the luggage kept at the roof of the bus gets displaced. So it is advised to tie the luggage with a rope on the roof of bus.

Question 4.
A batsman hits a cricket ball when then rolls on a level ground. After covering short distance, the ball comes to rest. The ball comes to a stop because
(a) the batsman did not hit the ball hard enough.
(b) velocity is proportional to the force exerted on the ball.
(c) there is a force on the ball opposing the motion.
(d) there is no unbalanced force on the ball so that ball would want to come to rest.
Answer:
(c) is correct. There is a force of friction on the ball in direction opposite to that of motion.

Question 5.
A truck starts from rest and rolls down a hill with constant acceleration. It travels a distance of 400 m in 20 s. Find its acceleration. Find the force on it if its mass is 7 metric tonnes. (1 tonne = 100 kg)
Solution:
Here initial velocity (u) = 0
Time (t) = 20 s
Distance (s) = 400 m
S = ut + \(\frac{1}{2}\)at²
400 = 0 × 30 + \(\frac{1}{2}\) × a × (20)²
400 = 0 + \(\frac{1}{2}\) × a × 20 × 20
400 = \(\frac{1}{2}\) × 20 × 20 × a
400 = 200 × a
or a = \(\frac{400}{200}\)
∴ a = 2ms^-2
Now mass of the truck(m) = 7 tonne
= 7 × 1000 kg
Acceleration (a) = 2ms^-2
But Force, F = m × a
= 7000 kg × 2 ms^-2
= 14000 kg – ms^-2
= 14000 N

Question 6.
A stone of 1 kg is thrown with a velocity of 20 m s^-1 across the frozen surface of a lake and comes to rest after travelling a distance of 50 m. What is the force of friction between the stone and the ice?
Solution:
Here, mass of stone (m) = 1 kg
Initial velocity of stone (u) = 20 ms^-1
Distance travelled by the stone (S) = 50 m
Final velocity of stone (υ) = 0 (at rest)
Force of friction between the stone and ice (F) = ?
Using υ² – u² = 2aS, we have
(0)² – (20)² = 2 × (a) × 50
– 20 × 20 = 100 × a
a = \(\frac{-20 \times 20}{100}\)
a = – 4 ms^-2
F = ma = 1 × (- 4)
F = – 4 N
Minus sign shows the force of friction is in direction opposite to direction of motion of stone.

Question 7.
A 8,000 kg engine pulls a train of 5 wagons, each of 2,000 kg along a horizontal track. If the engine exerts a force of 40,000 N and track offers a force of friction of 35,000 N, then calculate the
(a) net accelerating force;
(b) acceleration of the train; and
(c) force of wagon 1 on wagon 2.
Solution:
Mass of the engine = 8000 kg
Mass of 5 wagons = 5 × 2000 kg = 10,000 kg
∴ Total mass of engine and 5 wagons = 8000 kg + 10,000 kg = 18,000 kg
Total force of engine = 40,000 N
Frictional force offered by the track= 5000 N
(a) ∴ Net Accelerating Force (F) = Total force of engine – Frictional force of track
= 40,000 N – 5000 N = 35,000 N

(b) Acceleration of the train (a) = \(\frac{Accelerating force on rail(F)}{Mass of the train(m)}\)
= \(\frac{35000}{18000}\)
= \(\frac{35}{18}\)m^-2
= 1.94ms^-2

(c) Force exerted by wagon 1 on wagon 2 = Net Accelerating Force – Mass of wagon × Acceleration

= 35000 – 2000 × \(\frac{35}{18}\)
= 35000 – 3888.8
= 31111.2 N

Question 8.
An automobile vehicle has mass of 1,500 kg. What must be the force between vehicle and the road if vehicle is to be stopped with negative acceleration of 1.7 ms^-2?
Solution:
Here the mass of automobile (m) = 1500 kg
Acceleration of vehicle (a) = -1.7ms^-2
Frictional Force between road and vehicle (F) = ?
We know, F = m x a
= 15000 x (- 1.7)
= – 2550 N
∴ Backward frictional force (F) = 2550 N

Question 9.
What is the momentum of an object of mass m moving with velocity υ?
(a) (mυ)²; (b) mυ²; (c) \(\frac{1}{2}\)mυ², (d) mυ.
Answer:
(d) is correct. Momentum = mυ.

Question 10.
Using a horizontal force of 200 N, we intend to move a wooden cabinet across a floor with constant velocity. What is the friction force that will be exerted on the cabinet?
Answer:
When no acceleration is to be produced (i.e. body is to be moved with constant velocity), the net force has to be zero. Force of friction should be equal and opposite to the force applied i.e., force of friction has to be 200 N.

Question 11.
Two objects, each of mass 1.5 kg, are moving in the same straight line but in the opposite directions. The velocity of each object is 2.5 ms-1 before the collision during which they stick together. What will be the velocity of combined object after collision?
Solution:
Given, mass of the lirst object (m₁) – 1.5 kg
, and mass of the second object (m₂) = m1 = 1.5 kg
Initial velocity of the first object (u₁) = 2.5 ms^-1
Initial velocity of the second object (u₂) = – 2.5 ms^-1
(Since both the objects move in the direction opposite to each other therefore velocity of first object will be taken as positive and that of the other as negative.)
Suppose after collision the velocity of the combination of two objects is ‘υ’
∴ According to the law of conservation of momentum,
Total momentum before collision = Total momentum after collision
m₁u₁ + m₂u₂ = m₁υ + m₂υ
1.5 × 2.5 + 1.5 × (-2.5) = (1.5 × υ + 1.5 × υ)
1.5 [2.5 + (-2.5)] = (1.5 + 1.5) × υ
1.5 [2.5 – 2.5] = 3 × υ
1.5 × 0 = 3 × υ
0 = 3 × υ
∴ υ = 0 ms^-1
i. e. Both the objects will come to rest after collision.

Question 12.
According to the third law of motion when we push on an object, the object pushes back on us with an equal and opposite force. If the object is a massive truck parked along the road side, it will probably not move. A student justifies by answering that the two forces cancel each other. Comment on the logic and explain why the truck does not move.
Answer:
Student is justified. Friction is equal and opposite to force applied till the force applied crosses the force of limiting friction. When he applies a force slightly more than force of limiting friction, the truck will move. Till the truck moves uniformly, the force applied is exactly equal to force of friction at that instant.

Question 13.
A hockey ball of mass 200 g travelling at 10 ms^-1 is struck by a hockey stick so as to return it along its original path with a velocity at 5 ms^-1. Calculate the change in momentum occurred in the motion of hockey ball by the force applied by hockey stick.
Sol. Mass of the ball (m) = 200 g
= \(\frac{200}{1000}\)kg = 0.2 kg
Initial velocity of the ball (u) = 10 ms^-1
Final velocity of the ball (v) = – 5ms^-1
[∵ the direction of the ball is opposite to the first direction]
Change in momentum of the ball = Final momentum – Initial momentum.
= mυ – mu
= m (υ – u)
= 0.2 (- 5 – 10)
= 0.2 × (- 15)
= – 3.0 kg – ms^-1

Question 14.
A bullet of mass 10 kg travelling horizontally with a velocity of 150 ms^-1 strikes a stationary wooden block and come to rest in 0.03 s. Calculate the distance of penetration of the bullet into the block. Calculate the magnitude of force exerted by the wood in block in the bullet.
Solution:
Here, mass of the bullet (m) = 10 g = 0.01 kg
Initial velocity of the bullet (u) = 150 ms^-1
Final velocity of the bullet (υ) = 0
Time (t) = 0.03 s
We know, acceleration of the bullet (a) = \(\frac{v-u}{t}\)
= \(\frac{0-150}{0.03}\)
= – 5000 ms^-2

(a) Net force exerted by the wooden block on the bullet (F) = m × a
= 0.01 × (- 5000)
= 1 × (-50)
= -50N
∴ Magnitude of force = 50 N

(b) Distance covered by the bullet after penetration in the wooden block (S) = ?
using S = ut + \(\frac{1}{2}\)at²
= 15 × 0.03 + \(\frac{1}{2}\) × (- 5000) × (0.03)²
= 4.5 + (- 2.25)
= 4.5 – 2.25
S = 2.25 m

Question 15.
An object of mass 1 kg travelling in straight line with a velocity of 10 ms^-1 collides with it and sticks to a stationary wooden block of mass 5 kg. Then both move off together in the same straight line. Calculate the total momentum before the impact and just after the impact. Also calculate the velocity of combined object.
Solution:
Mass of the object (m₁) = 1 kg
Initial velocity of the object (u₁) = 10 ms^-1
Mass of the wooden block (m₂) = 5 kg
Initial velocity of the wooden block (u₂) = 0 [Wooden block at rest]
Suppose ‘υ’ is the velocity of the combination of the object and wooden block after collision
∴ Before collision total momentum of the object and block
= m₁u₁ + m₂u₂
= 1 × 10 + 5 × 0
= 10 + 0
= 10kg ms^-1 ……………… (i)
After collision. Total momentum of the object and block = m₁υ + m₂υ
= (m₁ + m₂) × υ
= (1 + 5) × υ
= 6υ kg m – ms ……… (ii)
According to the law of conservation of momentum,
Total momentum of the combinations before collision = Total momentum of the combination after collision 10 = 6υ
υ = \(\frac{10}{6}\)
∴ υ = \(\frac{5}{3}\) ms^-1
= 1.67 ms^-1
Substituting the value of υ in (ii) above
∴ Total momentum of the combination (after collision) = 6υ
= 6 × \(\frac{5}{3}\)
= 10kg – ms^-1

Question 16.
An object of mass 100 kg is accelerated uniformly from a velocity of 5 ms^-1 to 8 ms^-1 in 6s. Calculate the initial and final momentum of the object. Also find the force exerted on the object.
Solution:
Here, mass of the object (m) = 100kg
Initial velocity of the object (u) = 5ms^-1
Final velocity of the object (v) = 8ms^-1
Time interval (t) = 6s
Initial momentum of the object (p₁) = m × u
= 100 × 5 = 500 kg – ms^-1
Final momentum of the object (p₂) = m × υ
= 100 × 8 = 800 kg – ms^-1
Force acting on the object (F) = \(\frac{p_{2}-p_{1}}{t}\)
= \(\frac{(800-500) \mathrm{kg}-\mathrm{ms}^{-1}}{6 \mathrm{~s}}\)
= 50kg – ms^-2 = 50N

Question 17.
Akhtar, Kiran and Rahul were riding in a motor car that was moving with a high velocity on an express-way when an insect hit the windshield and got struck on wind-screen. Akhtar and Kiran started pondering over the situation. Kiran suggested that the insect suffered a greater change in momentum as compared to the change in momentum of motor car (because change in the velocity of insect was much more than that of motor car). Akhtar said that since the motor car was moving with a larger velocity, it exerted a larger force on the insect. As a result, the insect died. Rahul while putting in entirely new explanation said that both the motor car and the insect experienced the same force and same change in their momentum. Comment on these suggestions.
Answer:
I agree with Rahul’s explanation. According to law of conservation of momentum, during collision, the momentum of the system (insect and motor car) remains conserved. Therefore, both insect and motor car experience the same force and hence same change in momentum. The insect having smaller mass would suffer greater change in velocity as a result of this, it will crush the insect while the motor car does not suffer any noticeable change in velocity.

Question 18.
How much momentum will a dumbbell of mass 10 kg transfer to the floor if it falls from a height of 80 cm? Take its downward acceleration to be 10 ms^-2.
Solution:
Here, momentum of the dumb-bell (m) = 10 kg
Initial velocity of the bell (u) = 0 (at rest)
Distance covered by the bell (S) = (h) = 80 cm
= 0.80 m
Acceleration of the ball (a) = 10 ms^-2 (downward direction)
Let υ be the final velocity of the bell on reaching the ground.
Using υ² – u² = 2aS
υ² – (0)² = 2 × 10 × 0.80
υ² = 2 × 10 × 0.80
or υ² = 16
∴ Final velocity of the bell (υ) = \(\sqrt{16}\) = 4ms
Momentum transferred by the bell to the floor (p) = m × υ
= 10 × 4 = 40 kg – ms^-1

Science Guide for Class 9 PSEB Force and Laws of Motion InText Questions and Answers

Question 1.
Which of the following has more inertia:
(a) rubber ball and a stone of the same size?
(b) a bicycle and a train?
(c) a five rupees coin and a one-rupee coin?
Answer:
We know that mass of an object is the measure of its inertia. The more is the mass of an object, the more is its inertia hence.
(a) a stone of the same size has more inertia than a rubber ball.
(b) a train has more inertia than a bicycle.
(c) a ₹ 5 coin has more inertia than ₹ 1 coin because a ₹ 5 coin has more mass than a ₹ 1 coin.

Question 2.
In the following example, try to identify the number of times the velocity of the ball changes:
“A football player kicks a football to another player of his team who kicks the football towards the goal-keeper. The goal-keeper of opposite team collects the football and kicks it towards a player of his own team”. Also identify the agent supplying the force in each case.
Answer:
To push, to strike or to pull, all these activities act as a force for changing the velocity or for changing the direction of motion of the object. Therefore, in the above given example the velocity of ball changes four times.

1. First time the football player of first-team kicks the football to another player of his team and thus changes the velocity of the football.
2. In second time velocity changes when the second player kicks the football towards the goal-keeper of the opposite team and applies force on the ball.
3. Third time the goal-keeper pushes the ball and reduces its velocity to zero by applying force.
4. The goal-keeper now applies a force by kicking the football towards player of his team. In this case the force increases the velocity of the football.

Question 3.
Explain why some of the leaves may get detached from the tree if we vigorously shake its branch.
Answer:
Before shaking, the branch of the tree, both the branch and leaves were at rest. When we shake the branch of the tree, branch moves but the leaves remain at rest due to inertia of rest and get detached from the branch.

Question 4.
Why do you fall in the forward direction when a moving bus brakes to a stop and falls backward when it accelerates from rest?
Answer:
When the bus is moving, whole of our body is moving forward. When brakes are applied, the lower part of our body touching the bus (e.g., feet etc.) comes to rest and upper part of the body not touching the bus continue move forward due to inertia of motion and fall in forward direction.

When the bus suddenly starts and accelerates from rest, the lower part of our body starts moving forward (accelerating) along with the bus while upper part of our body tends to remain at rest due to inertia of rest and we fall backward.

Question 5.
If action is always equal to reaction, explain how a horse can pull a cart?
Answer:
According to Newton’s third law of motion “Action and Reaction are equal and opposite.”
The horse pulls (Action) the cart with some force in the forward direction and the cart applies equal force on the cart in the backward direction (Reaction). These two forces balance each other. When the horse pushes the ground with its feet in the backward direction with force P along OP it gets reaction R due to ground along OR in the upward direction.

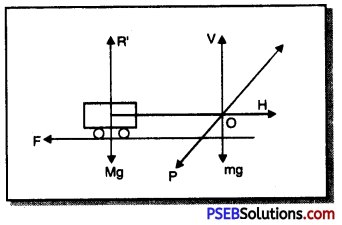
This force of reaction can be resolved into two rectangular components.
1. Vertical component ‘V’ which balances the weight mg of the horse and cart in the downward direction.
The horizontal component ‘H’ which helps to move the cart in the forward direction. The force of friction between wheels and ground acts in the backward direction but the horizontal component ‘H’ acts in the forward direction is more than the backward force of friction, it succeeds to move the cart forward.

Question 6.
Explain why is it difficult for a fireman to hold a hose, which ejects large amount of water at a high velocity?
Answer:
Water is ejected from rubber hose in forward direction with a force (action), it exerts an equal reaction on the hose in backward direction. Due to backward reaction, fire man finds it difficult to hold the hose.

Question 7.
From a rifle of mass 4 kg, a bullet df> mass 50 g is fired with an initial velocity of 35 m s^-1. Calculate the recoil velocity of the rifle.
Solution:
Mass of the bullet (m₁) = 50 g = 0.05 kg
Mass of the rifle (m₂) = 4 kg
Initial velocity of the bullet (u₁) = 0
Initial velocity of the rifle (u₂) = 0
Final velocity of the bullet (υ₁) = 35 m s^-1
Final velocity of the rifle (υ₂) = ?
According to the law of conservation of momentum,
Total initial momentum of bullet and rifle = Total final momentum of the bullet and rifle.

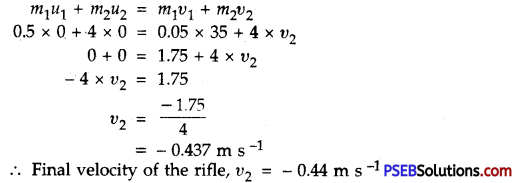
∴ Negative sign indicates that the rifle moves in a direction opposite to the direction of motion of the bullet.

Question 8.
Two objects of masses 100 g and 200 g are moving along the same line and direction with velocities of 2 ms^-1 and 1ms^-1 respectively. They collide and after the collision, the first object moves with a velocity of 1.67 m s^-1. Determine the velocity of the second object.
Solution:

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 1 Real Numbers Ex 1.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 1 Real Numbers Ex 1.1

Question 1.
Use Euclid’s division algorithm to find the HCF of:
(i) 135 and 225
(ii) 196 and 38220
(iii) 867 and 255.
Solution:
(i) By Euclid’s division Algorithm

Step 1.
Since 225 > 135,
we apply the division Lemma to 225 and 135,
we get 225 = 135 × 1 + 90

Step 2.
Since the remainder 90 ≠ 0,
we apply the division Lemma to 135 and 90,
we get 135 = 90 × 1 + 45

Step 3. Since the remainder 45 ≠ 0,
we apply the division Lemma to 90 and 45,
we get 90 = 45 × 2 + 0

Since the remainder has now become zero, so we stop procedure.
∵ divisor in the step 3 is 45
∵ HCF of 90 and 45 is 45
Hence, HCF of 135 and 225 is 45.

(ii) To find HCF of 196 and 38220
Step 1.
Since 38220 > 196,
we apply the division Lemma to 196 and 38220,
we get 38220 = 196 × 195 + 0
Since the remainder has now become zero so we stop the procedure.
∵ divisor in the step is 196
∵ HCF of 38220 and 196 is 196.
Hence, HCF of 38220 and 196 is 196.

(iii) To find HCF of 867 and 255
Step 1.
Since 867 > 255,
we apply the division Lemma to 867 and 255,
we get 867 = 255 × 3 + 102

Step 2.
Since remainder 102 ≠ 0,
we apply the divison Lemma to 255 and 102,
we get 255 = 102 × 2 + 51

Step 3.
Since remainder 51 ≠ 0,
we apply the division Lemma to 51 and 102, by taking 102 as division,
we get 102 = 51 × 2 + 0
Since the remainder has now become zero, so we stop the procedure.
∵ divisor in step 3 is 51.
HCF of 102 and 51 is 51.
Hence, HCF of 867 and 255 is 51.

Question 2.
Show that any positive odd integer is of the form 6q + 1 or 6q + 3 or 6q + 5, where q is some integer.
Solution:
Let a be any positive odd integer, we apply the division algorithm with a and b = 6.
Since 0 ≤ r < 6, the possible remainders are 0, 1, 2, 3, 4 and 5. i.e., a can be 6q or 6q + 1, or 6q + 2, or 6q + 3, or 6q + 4, or 6q + 5 where q is quotient. However, since a is odd ∵ a cannot be equal to 6q, 6q + 2, 6q + 4 ∵ all are divisible by 2. Therefore, any odd integer is of the form 6q + 1 or 6q + 3 or 6q + 5.

Question 3.
An army contingent of 616 members is to march behind an army band of 32 members in a parade. The two groups are to march in the same number of columns. What is the maximum number of columns in which they can march? Solution:
Total number of members in army = 616 and 32 (A band of two groups)
Since two groups are to march in same number of columns and we are to find out the maximum number of columns.
∴ Maximum Number of columns = HCF of 616 and 32
Step 1.
Since 616 > 32, we apply the division Lemma to 616 and 32, to get
616 = 32 × 19 + 8

Step 2.
Since the remainder 8 ≠ 0, we apply the division Lemma to 32 and 8, to get
32 = 8 × 4 + 0.
Since the remainder has now become zero
∵ divisor in the step is 8
∵ HCF of 616 and 32 is 8.
Hence, maximum number of columns in which they can march is 8.

Question 4.
Use Euclid’s division lemma to show that the square of any positive integer is either of the form 3m or 3m + 1 for some integer m.
[Hint. Let x be any positive integer then it is of the form 3q, 3q + 1 or 3q + 2. Now square each of these and show that they can be rewritten in the form 3m or 3m + L]
Solution:
Let x be any positive integer then it is of the form 3q, 3q + 1 or 3q + 2.
If x = 3 q
Squaring both sides,
(x)² = (3q)²
– 9q² = 3 (3q²) = 3m
where m = 3 q²
where m is also an integer
Hence x² = 3m ………… (1)
If x = 3q + 1
Squaring both sides,
x² = (3q + 1)²
x² = 9q² + 1 + 2 × 3q × 1
x² = 3 (3 q² + 2q) + 1
x² = 3m + 1 …. (2)
where m = 3q² + 2q where m is also an integer
From (1) and (2),
x² = 3m, 3m + 1
Hence, square of any positive integer is either of the form 3m or 3m + 1 for some integer m.

Question 5.
Use Euclid’s division lemma to show that the cube of any positive integer is of the form 9m, 9m + 1 or 9m + 8.
Solution:
Let x be any positive integer and b = 3
x = 3 q + r where q is quotient and r is remainder
If 0 ≤ r < 3
If r = 0 then x = 3 q
If r = 1 then x = 3q + 1
If r = 2 then x = 3q + 2
x is of the form 3q or 3q + 1 or 3q + 2
If x = 3q
Cubing both sides,
x³ = (3q)³
x³ = 27q³ = 9 (3q³) = 9m
where m = 3q³ and is an integer .
x³ = 9m ……….. (1)
If x = 3q + 1 cubing both sides,
x³ = (3 q +1)³
x³ = 27q³ + 27q² + 9q + 1
= 9 (3q³ + 3q² + q) + 1
= 9m + 1
where m = 3q³ + 3q² + q and is an integer
Again x³ = 9m + 1 …………. (2)
If x = 3q +2
Cubing both sides,
(x)³ = (3q + 2)²
= 27 q³ + 54 q² + 36q + 8
x³ = 9 (3 q³ + 6q² + 4q) + 8
x³ = 9m + 8 ………. (3)
where m = 3 q³ + 6q² + 4q
Again x³ = 9m + 8
From (1) (2), & (3), we find that
x³ can be of the form 9m, 9m + 1, 9m + 8.
Hence, x³ of any positive integer can be of he form 9m, 9m + 1 or 9m + 8

Punjab State Board PSEB 10th Class Hindi Book Solutions Hindi Grammar anek shabdon ke liye ek shabd अनेक शब्दों के लिए एक शब्द Exercise Questions and Answers, Notes.

PSEB 10th Class Hindi Grammar अनेक शब्दों के लिए एक शब्द

निम्नलिखित वाक्यांशों के लिए एक शब्द लिखिए

उत्तर:

निम्नलिखित बहुविकल्पी प्रश्नों के उत्तर एक सही विकल्प चुनकर लिखें

प्रश्न 1.
जो कहा न जा सके के लिए एक शब्द है-
(क) अकथ
(ख) अकहानीय
(ग) अगोचर
(घ) अनंत।
उत्तर:
(क) अकथ

प्रश्न 2.
जो देखा न जा सके के लिए एक शब्द है
(क) अमूर्त
(ख) अदृश्य
(ग) निराकार
(घ) निरंजन।
उत्तर:
(ख) अदृश्य

प्रश्न 3.
जो कभी न मरता हो के लिए एक शब्द है-
(क) अवध्य
(ख) अगम
(ग) अमर
(घ) अधोरी।
उत्तर:
(ग) अमर

प्रश्न 4.
जिसका आकार हो के लिए एक शब्द है,
(क) आर्कारी
(ख) साकार
(ग) सार्कारी
(घ) आर्कारीय।
उत्तर:
(ख) साकार

प्रश्न 5.
जो सब कुछ जानता हो के लिए एक शब्द है, अज्ञानी (हाँ या नहीं में उत्तर दीजिए)
उत्तर:
नहीं

प्रश्न 6.
जो ईश्वर को न मानता हो के लिए एक शब्द है, नास्तिक (सही या गलत लिखकर उत्तर दें)
उत्तर:
सही

प्रश्न 7.
जो प्रतिदिन होता हो के लिए एक शब्द है, दैनिक (सही या गलत लिखकर उत्तर दें)
उत्तर:
सही

प्रश्न 8.
जो आकाश में उड़ते हों के लिए एक शब्द है, नभीय (हाँ या नहीं में उत्तर दीजिए)
उत्तर:
नहीं

प्रश्न 9.
जिसके माता-पिता न हो के लिए एक शब्द है, अनादि (सही या ग़लत लिखकर उत्तर दें)
उत्तर:
गलत

प्रश्न 10.
पीछे-पीछे चलने वाला के लिए एक शब्द है, अनुगामी (हाँ या नहीं में उत्तर लिखें)
उत्तर:
हाँ।

बोर्ड परीक्षा में पूछे गए प्रश्न निम्नलिखित में से किसी एक वाक्यांश (अनेक शब्दों) के लिए एक शब्द लिखिए

वर्ष
डाक बाँटने वाला, आलोचना करने वाला।
उत्तर:
डाक बाँटने वाला = डाकिया
आलोचना करने वाला = आलोचक।

ईश्वर में विश्वास रखने वाला, वर्ष में एक बार होने वाला।
उत्तर:
ईश्वर में विश्वास रखने वाला = आस्तिक
वर्ष में एक बार होने वाला = वार्षिक।

उपकार को मानने वाला, कम खाने वाला।
उत्तर:
उपकार को मानने वाला = कृतज्ञ
कम खाने वाला = अल्पाहारी, मिताहारी।

वर्ष
समाज से संबंधित, देश से द्रोह करने वाला
उत्तर:
समाज से संबंधित = सामाजिक
देश से द्रोह करने वाला = देशद्रोही।

जिसका पार न हो, डाक बाँटने वाला।
उत्तर:
जिसका पार न हो = अपार
डाक बाँटने वाला = डाकिया।

गाँव में रहने वाला, कृषि कर्म करने वाला।
उत्तर:
गाँव में रहने वाला = ग्रामीण
कृषि कर्म करने वाला = कृषक।

वर्ष
पूर्वजों से प्राप्त हुई सम्पत्ति, जो नीति का ज्ञाता हो।
उत्तर:
पूर्वजों से प्राप्त हुई सम्पत्ति = पैतृक सम्पत्ति,
जो नीति का ज्ञाता हो = नीतिज्ञ।

प्रश्न 1.
वाक्यांश बोधक शब्द किसे कहते हैं?
उत्तर:
जो शब्द अनेक शब्दों के स्थान पर अकेले ही बोलने या लिखने के लिए प्रयोग में लाए जाते हैं उन्हें वाक्यांश बोधक शब्द कहते हैं, जैसे- कृतघ्न, सदाचारी, अवसरवादी, नास्तिक आदि।

प्रश्न 2.
अनेक शब्दों के लिए एक ही शब्द/वाक्यांश का प्रयोग भाषा में क्यों किया जाता है?
उत्तर:
अनेक शब्दों के लिए केवल एक ही शब्द/वाक्यांश का प्रयोग भाषा की सहजता, सुंदरता, संक्षिप्तता और प्रभावात्मकता को बढ़ाने के लिए किया जाता है। इससे कम-से-कम शब्दों में अधिक-से-अधिक भाव अभिव्यक्त किए जा सकते हैं। इसमें एक ही शब्द संपूर्ण वाक्य को अपने भीतर समेटे रहता है। उदाहरण-
जिसका जन्म न हो सके – अजन्मा
जिसके समान कोई दूसरा न हो – अद्वितीय
जिसका कोई शत्रु न हो – अजातशत्रु
बिना वेतन के काम करने वाला – अवैतनिक
विद्या ग्रहण करने वाला – विद्यार्थी’

अनेक शब्द/वाक्यांश के लिए एक शब्द के उदाहरण-

अनेक शब्द/वाक्यांश – एक शब्द
जहाँ पहुँचा न जा सके – अगम्य
अचानक होने वाली बात या घटना – आकस्मिक
अवसर के अनुसार बदल जाने वाला – अवसरवादी
अपना मतलब निकालने वाले – स्वार्थी, मतलबी
दूसरे के पीछे चलने वाला – ‘अनुयायी, अनुचर, अनुगामी
न करने योग्य – अकरणीय
आँखों के सामने होने वाला – प्रत्यक्ष
बिना वेतन काम करने वाला – अवैतनिक
आँखों के सामने न होने वाला – परोक्ष
कम जानने वाला – अल्पज्ञ
आलोचना करने वाला – आलोचक
तेज बुद्धि वाला – कुशाग्र बुद्धि
आगे या भविष्य की सोचने वाला – दूरदर्शी
बरे मार्ग पर चलने वाला – कुमार्गी
ईश्वर में विश्वास रखने वाला – आस्तिक
हानि को पूरा करना – क्षतिपूर्ति
ईश्वर में विश्वास न रखने वाला – नास्तिक
बड़ी इमारत के टूटे-फूटे भाग – खंडहर
उपकार को न मानने वाला – कृतज्ञ
चारों वेदों को जानने वाला – चतुर्वेदी
उपकार को न मानने वाला – कृतघ्न
बहुत समय तक बना रहने वाला – चिरस्थायी
ऊपर कहा गया – उपर्युक्त

जल में रहने वाला – जलचर
कम खाने वाला – अल्पाहारी, मिताहारी
जानने की इच्छा रखने वाला – जिज्ञासु
किसी विषय का विशेष ज्ञान रखने वाला – विशेषज्ञ
छोटा भाई – अनुज
कुछ जानने की इच्छा रखने वाला – जिज्ञासु
दूसरे देश से मँगाया जाना – आयात
जिसका आदि न हो – अनादि
उपजाऊ भूमि – उर्वरा
जिसका आचरण अच्छा हो – सदाचारी
उद्योग से संबंधित – औद्योगिक
किए हुए उपकार को मानने वाला – कृतघ्न
संध्या और रात्रि के बीच का समय – गोधूलि
आकाश को छूने वाला – गगनचुंबी
रोगी का इलाज करने वाला – चिकित्सक
जनता द्वारा चलाया जाने वाला राज – जनतंत्र
तीन मास में एक बार होने वाला – त्रैमासिक
बच्चों के लिए उपयोगी – बालोपयोगी
दूसरे के काम में हाथ डालना – हस्तक्षेप
अपना नाम स्वयं लिखना – हस्ताक्षर
जिसके हाथ में वीणा हो – वीणापति
जिसके पास लाखों रुपये हों – लखपति
जिसका इलाज न हो – लाइलाज
जिसका आचरण अच्छा हो – सदाचारी
जिसका आचरण बुरा हो – दुराचारी
जिसकी आत्मा महान् हो – महात्मा
जिसका कोई अर्थ हो। – सार्थक
जिसका मूल्य न आँका जा सके – अमूल्य
जिसका कोई अर्थ न हो – निरर्थक
जिसके हाथ में चक्र हो – चक्रपाणि
जिसका आकार न हो – निराकार
जिस पर उपकार किया गया हो – उपकृत
जिसका पार न हो – अपार
जिसका कोई स्वामी या नाथ न हो – अनाथ
जिसका भाग्य अच्छा न हो – अभागा, भाग्यहीन
जिसका जन्म न हो सके – अजन्मा
जिसकी परीक्षा ली जा रही हो – परीक्षार्थी
जिसका इलाज न हो सके – असाध्य
जिसकी आयु बड़ी लम्बी हो – दीर्घायु
जिसका विश्वास न किया जा सके – अविश्वसनीय
जिसकी बहुत अधिक चर्चा हो – बहुचर्चित
जिसका मन और ध्यान दूसरी तरफ़ हो – अन्यमनस्क
जिसकी कोई फीस न ली जाए – निःशुल्क
जिसका मूल्य न आँका जा सके – अमूल्य
जिसकी गिनती न की जा सके – अगणनीय
जिसका पति मर गया हो – विधवा
जिसका कोई शत्रु न हो – अजातशत्रु
जिसकी पत्नी मर गई हो – विधुर
जिसका पति जीवित हो – सधवा/सुहागिन
जिसे क्षमा न किया जा सके – अक्षम्य
जिसने ऋण चुका दिया हो – उऋण
जिसने अपनी इन्द्रियों पर विजय पा ली हो – जितेन्द्रिय
जिस पर अभियोग लगाया गया हो – अभियुक्त/प्रतिवादी
जो हाथ से लिखित हो – हस्तलिखित
जो कुछ न करता हो – अकर्मण्य
जो लोगों में प्रिय हो। – लोकप्रिय
जो सबसे आगे रहता हो – अग्रणी, अग्रगामी, अगग्रण्य
जो शरण में आया हो – शरणागत
जो अनुकरण करने योग्य हो – अनुकरणीय
जो सरलता से प्राप्त हो – सुलभ
जो धन का अपव्यय करता है – अपव्ययी
जो स्वयं सेवा करता हो – स्वयंसेवक
जो थोड़ा बोलता हो – अल्पभाषी/मितभाषी
जो वेतन के बिना काम करे – अवैतनिक
जो सदा रहे/जो कभी मरता न हो – अमर
जो देखा न जा सके – अदृश्य
जो कानून के विरुद्ध हो – अवैध

जो साथ-साथ पढ़ते हों – सहपाठी
जो सहन न किया जा सके – असह्य
जो थोड़ी देर पहले पैदा हुआ हो – नवजात
जो पहले न पढ़ा हो – अपठित
जो थोड़ा बोलता हो – मितभाषी
जो आँखों के सामने न हो – अप्रत्यक्ष
जो कम व्यय करता हो – मितव्ययी
जो परिचित न हो – अपरिचित
जो नियम के अनुसार न हो – अनियमित
जो केवल कहने और दिखाने के लिए हो – औपचारिक
जो बात कही ना सके – अकथनीय
जो कल्पना से परे हो – कल्पनातीत
जो पहले न पढ़ा हो – अपठित क
जो व्यक्ति अपनी बुराई के लिए प्रसिद्ध हो – ुख्यात
जो परिचित न हो – अपरिचित
जो निरंतर प्रत्यनशील रहे – कर्मठ
जो कभी तृप्त न हो – अतृप्त
जो पढ़ा-लिखा न हो – अनपढ़/निरक्षर
जो बात न कही गई हो – अनकही
जो उच्च कुल में पैदा हुआ हो – कुलीन
जो कार्य कष्ट से साध्य हो – कष्ट साध्य/दुःसाध्य
जो कड़वा बोलता हो – कटुभाषी
जो क्षमा करने योग्य हो। – क्षम्य
जो टुकड़े-टुकड़े हो गया हो – खंडित
जो छिपाने योग्य हो – गोपनीय
जो जन्म से अंधा हो – जन्मांध
जिसकी मीन/मछली जैसी आँखें हों – मीनाक्षी
जिसने यश प्राप्त किया है – यशस्वी
दूसरे लोक से संबंधित – पारलौकिक
मांस खाने वाला – मांसाहारी/समिषभोजी
युद्ध में स्थिर रहने वाला – युधिष्ठर
शक्ति के अनुसार – यथाशक्ति
अत्यंत सुंदर स्त्री – रूपसी
पत्तों से बनी कुटिया – पर्णकुटी
दिन में होने वाला – दैनिक
सप्ताह में एक बार होने वाला – साप्ताहिक
पंद्रह दिन में एक बार होने वाला – पाक्षिक
तीन मास में एक बार होने वाला – त्रैमासिक
वर्ष में एक बार होने वाला – वार्षिक
घूमने फिरने वाला – घुम्मकड़
देश से द्रोह करने वाला – देशद्रोही
छात्रों के रहने का स्थान – छात्रावास
दो कामों में से करने योग्य एक कार्य – वैकल्पिक
चारों वेदों को जानने वाला – चतुर्वेदी
नई चीज़ की खोज करने वाला – आविष्कारक
एक ही जाति के – सजातीय
परदेश में जाकर बस जाने वाला – प्रवासी
हिंसा करने वाला – हिंसक
पश्चिम से सम्बन्ध रखने वाला – पाश्चात्य
शक्ति का उपासक – शाक्त
पूर्वजों से प्राप्त हुई सम्पत्ति – पैतृक
संकट से ग्रस्त – संकटग्रस्त/विपन्न
प्रशंसा करने योग्य – प्रशंसनीय
समान अवस्था का – समवयस्क
बिना विचार किया हुआ विश्वास – अंधविश्वास
युगों से चला आने वाला – सनातन
समाज से संबंधित – सामाजिक
अच्छे चरित्र वाला – सच्चरित्र
सदा रहने वाला – शाश्वत

अपना मतलब निकालने वाला – स्वार्थी
सौ वर्षों का समूह – शताब्दी
साफ़-साफ़ कहने वाला – स्पष्टवादी
हित चाहने वाला – हितैषी, शुभेच्छु
सौतेली माँ – विमाता
जिसमें संदेह हो – संदिग्ध

Punjab State Board PSEB 10th Class Hindi Book Solutions Hindi Grammar samroopi bhinnarthak shabd समरूपी भिन्नार्थक शब्द Exercise Questions and Answers, Notes.

PSEB 10th Class Hindi Grammar समरूपी भिन्नार्थक शब्द

निम्नलिखित समरूपी भिन्नार्थक शब्द-युग्म का प्रयोग वाक्य में करके अर्थ स्पष्ट कीजिए-

उत्तर:

निम्नलिखित बहुविकल्पी प्रश्नों के उत्तर एक सही विकल्प चुनकर लिखिए

प्रश्न 1.
अचल-अचला के अर्थ हैं
(क) असमर्थ-अनुरक्त
(ख) पर्वत-पृथ्वी
(ग) साधन-साध्य
(घ) हिलना-डुलना।
उत्तर:
(ख) पर्वत-पृथ्वी

प्रश्न 2.
अनल-अनिल के अर्थ हैं
(क) आग-पानी
(ख) धूप-छाँव
(ग) आग-हवा
(घ) खट्टा-मीठा।
उत्तर:
(ग) आग-हवा

प्रश्न 3.
कुल-कूल के अर्थ हैं
(क) पूर्ण-अपूर्ण
(ख) वंश-किनारा
(ग) साधन-सहारा
(घ) पूरा-ठंडा।
उत्तर:
(ख) वंश-किनारा

प्रश्न 4.
चिर-चीर के अर्थ हैं
(क) देर-तट
(ख) चीरना-घाव
(ग) देरी-वस्त्र
(घ) चिड़ना-चीखना।
उत्तर:
(ग) देरी-वस्त्र

प्रश्न 5.
क्षिति-क्षति के अर्थ हैं-पृथ्वी-हानि (सही या गलत लिखकर उत्तर दें)
उत्तर:
सही

प्रश्न 6.
सुत-सूत के अर्थ हैं-पुत्र-सारथी (हाँ या नहीं लिख कर उत्तर दें)
उत्तर:
हाँ

प्रश्न 7.
तुरंग-तरंग के अर्थ हैं-मौज-मस्ती (हाँ या नहीं लिखकर उत्तर दें)
उत्तर:
नहीं

प्रश्न 8.
बलि-बली के अर्थ हैं-भेंट-बलवान (सही या गलत लिखकर उत्तर दें)
उत्तर:
सही

प्रश्न 9.
कर्म-क्रम के अर्थ हैं-काम-सिलसिला (हाँ या नहीं लिख कर उत्तर दें)
उत्तर:
हाँ

प्रश्न 10.
अंस-अंश के अर्थ हैं-हिस्सा-कंधा (सही या गलत लिखकर उत्तर दें)
उत्तर:
गलत।

निम्नलिखित में से किसी एक समरूपी भिन्नार्थक शब्द-युग्म का प्रयोग वाक्य में इस तरह करें ताकि उनका अर्थ स्पष्ट हो जाए-

वर्ष
1. असमान-आसमान, प्रणाम-प्रमाण।
उत्तर:
असमान = सुरेश उसके असमान है।
आसमान = आसमान में अनेक तारे हैं।
प्रणाम = पुत्र ने पिता को प्रणाम किया।
प्रमाण = प्रमाण के अभाव में आरोपी को आरोप मुक्त कर दिया गया।

2. उधार-उद्धार, प्रहार-परिहार।
उत्तर:
उधार = राम ने सुरेश को सौ रुपये उधार दिए।
उद्धार = सच्चे भक्त का उद्धार परमात्मा करते हैं।
प्रहार = गुंडे ने चाकू से दो प्रहार किए।
परिहार = स्वामी जी मोहमाया का परिहार कर चुके हैं।

3. राज-राज़, माँस-मास।
उत्तर:
राज = राजा अशोक ने भारत पर कई वर्षों तक राज किया।
राज़ = मुझे नरेश से राज़ की बात जाननी है।
माँस = शेर हिरण का माँस खा रहा था।
मास = दीपावली कार्तिक मास में मनाई जाती है।

वर्ष
1. गृह, ग्रह, धरा, धारा
उत्तर;
गृह = आपका गृह तो बड़ा भव्य है।
ग्रह = कुछ लोग शनि ग्रह को कष्टकारी मानते हैं।
धरा = यह धरा ही तो हमें अनाज प्रदान करती है।
धारा = गंगा की धारा देखने योग्य है।

2. सुत, सूत, मातृ, मात्र
उत्तर:
सुत = मेरा सुत भी अभी घर पहुंचा है।
सूत = आप तो बड़ा बारीक सूत कातते हैं।
मातृ’ = हमें जन्म देने वाली मातृ तो पूजनीय है।
मात्र = मेरी तो आपसे मिलने मात्र की इच्छा थी।

3. सूखी, सुखी, सास, साँस
उत्तर:
सूखी = इस सूखी धरती पर तो फसल नष्ट हो जाएगी।
सुखी = ईश्वर आपको सदा सुखी रखे।
सास = कल मेरी सास यहाँ आएगी।
साँस = रोगी की साँस मंद होती जा रही थी।

प्रश्न 1.
‘समरूपी भिन्नार्थक’ शब्द से क्या तात्पर्य है?
उत्तर:
विश्व-भर की सभी भाषाओं में कुछ ऐसे शब्द होते हैं जो उच्चारण में प्रायः समानता रखते हैं लेकिन उनके अर्थ में भिन्नता होती है। ऐसे शब्दों को समरूपी भिन्नार्थक शब्द कहते हैं। इन्हें श्रुतिसम भिन्नार्थक शब्द भी कहते हैं। इन शब्दों का प्रयोग अलग-अलग प्रसंगों में किया जाता है। जैसे-
(क) इत्र-सुगंधित पदार्थ
इतर-अन्य, दूसरा

(ख) गृह-घर
ग्रह-नक्षत्र

(ग) कृपण-कंजूस
कृपाण-तलवार

(घ) सुत-बेटा
सूत–सारथी/धागा

(ङ) ओर-तरफ
और-तथा

समरूपी भिन्नार्थक शब्दों के उदाहरण

Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 2 Fractions and Decimals Ex 2.5 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.5

1. Which is greater decimal number ?

Question (i).
0.9 or 0.4
Answer:
0.9 or 0.4
Here in 0.9 tenth place is greater than tenth place of 0.4.
9 > 4
∴ 0.9 > 0.4

Question (ii).
1.35 or 1.37
Answer:
1.35 or 1.37
Whole number parts of both number are equal
So, we have to compare decimal part
Also digits at tenths place are also equal.
Hundredths part of 1.37 is greater than hundredth the part of 1.35
∴ 1.37 > 1.35

Question (iii).
10.10 or 10.01
Answer:
10.10 or 10.01
Whole number parts of both numbers are equal
So, we have to compare decimal part
Tenths part of 10.10 is greater than tenths part of 10.01
∴ 10.10 > 10.01

Question (iv).
1735.101 or 1734.101
Answer:
1735.101 or 1734.101
Whole number part of 1735.101 is greater than whole number part of 1734.101
∴ 735.101 > 1734.101

Question (v).
0.8 or 0.88.
Answer:
0.8 or 0.88
Here tenths place in both the number is same and hundredths place in 0.88 is greater than the hundredths place in 0.8.
∴ 0.88 > 0.8

2. Write following decimal number in the expanded form :

Question (i).
40.38
Answer:
40.38 = 40 + 0 + .3+ .08
= 4 × 10 + 0 + 3 × \(\frac {1}{10}\) + 8 × \(\frac {1}{100}\)

Question (ii).
4.038
Answer:
4.038 = 4 + 0.0 + 0.03 + 0.008
4 + 0 × \(\frac {1}{10}\) + 3 × \(\frac {1}{100}\) + 8 × \(\frac {1}{1000}\)

Question (iii).
0.1038
Answer:
0.4038 = 0 + 0.4 + 0.00 + 0.003 + 0.0008
= 0 + 4 × \(\frac {1}{10}\) + 0 × \(\frac {1}{100}\) + 3 × \(\frac {1}{1000}\) + 8 × \(\frac {1}{10000}\)

Question (iv).
4.38.
Answer:
4.38 = 4 + 0.3 + 0.08
= 4 + 3 × \(\frac {1}{10}\) + 8 × \(\frac {1}{100}\)

3. Write the place value of 5 in the following decimal numbers :

Question (i).
17.56
Answer:
Place value of 5 in 17.56 = 0.5
= \(\frac {5}{10}\)

Question (ii).
1.253
Answer:
Place value of 5 in 1.253 = 0.05
= \(\frac {5}{100}\)

Question (iii).
10.25
Answer:
Place value of 5 in 10.25 = 0.05
= \(\frac {5}{100}\)

Question (iv).
5.62.
Answer:
Place value of 5 in 5.62 = 5

4. Express in rupees using decimals :

Question (i).
55 paise
Answer:
55 paise = ₹ \(\frac {55}{100}\)
= ₹ 0.55

Question (ii).
55 rupees 5 paise
Answer:
55 rupees 5 paise = 55 rupees + 5 paise
= ₹ 55 + ₹ \(\frac {5}{100}\)
= ₹ 55 + ₹ 0.5
= ₹ 55.05

Question (iii).
347 paise
Answer:
347 paise = ₹ \(\frac {347}{100}\)
= ₹ 3.47

Question (iv).
2 paise.
Answer:
2 paise = ₹ \(\frac {2}{100}\)
= ₹ 0.02.

5. Express in km :

Question (i).
350 m
Answer:
350 m = \(\frac {350}{1000}\) km
= 0.350 km
[Since 1000 m = 1 km,
∴ 1 m =\(\frac {1}{1000}\) km]

Question (ii).
4035 m
Answer:
4035 m = \(\frac {4035}{1000}\) km
= 4.035 km

Question (iii).
2 km 5 m
Answer:
2 km 5 m = 2 km + 5 m
= 2 km + \(\frac {5}{1000}\) km
= 2.05 km

6. Multiple Choice Questions :

Question (i).
Place value of 2 in 3.02 is :
(a) 2
(b) 20
(c) \(\frac {2}{10}\)
(d) \(\frac {2}{100}\)
Answer:
(d) \(\frac {2}{100}\)

Question (ii).
The correct ascending order of 0.7, 0.07, 7 is :
(a) 7 < 0.07 < 0.7
(b) 0.07 < 0.7 < 7
(c) 0.7 < 0.07 < 7
(d) 0.07 < 7 < 0.7.
Answer:
(b) 0.07 < 0.7 < 7

Question (iii).
Decimal expression of 5 kg 20 gram is :
(a) 5.2 kg
(b) 5.20 kg
(c) 5.02 kg
(d) None of these.
Answer:
(c) 5.02 kg

Question (iv).
Expanded form of 2.38 is
(a) 2 + \(\frac {38}{10}\)
(b) 2 + 3 + \(\frac {8}{10}\)
(c) \(\frac {238}{100}\)
(d) 2 + \(\frac {3}{10}\) + \(\frac {8}{100}\)
Answer:
(d) 2 + \(\frac {3}{10}\) + \(\frac {8}{100}\)

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 1 Real Numbers Ex 1.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 1 Real Numbers Ex 1.3

Question 1.
Prove that √5 is irrational.
Solution:
Let us suppose that √5 is rational so we can find integers r and s where s ≠ 0
such that √5 = \(\frac{r}{s}\)
Suppose r and s have some common factor other than 1, then divide r and s by the common factor to get :
√5 = \(\frac{a}{b}\) where a and b are coprime and b ≠ 0
b√5 = a
Squaring both sides,
⇒ (b√5)² = a²
⇒ b² (√5)² = a²
⇒ 5b² = a² …………..(1)
5 divides a².
By the theorem, if a prime number ‘p’ divides a² then ‘p’ divides a where a is positive integer
⇒ 5 divides a …………(2)
So a = 5c for some integer c.
Put the value of a in (1),
5b² = (5c)²
5b² = 25c²
b² = 5c²
or 5c² = b²
⇒ 5 divides b²
∵ if a prime number ‘p’ divides b², then p divides b ; where b is positive integer.
⇒ 5 divides b ………… (3)
From (2) and (3), a and b have at least 5 as common factor.
But this contradicts the fact that a and b are coprime i.e. no common factor other than 1.
∴ our supposition that √5 is rational wrong.
Hence √5 is irrational.

Question 2.
Prove that 3 + 2 √5 is irrational.
Solution:
Let us suppose that 3 + 2√5 is rational.
∴ we can find Co-Prime a and b, where a and b are integers and b ≠ 0
such that 3 + 2√5 = \(\frac{a}{b}\)

Since a and b both are integers,

∴ \(\frac{a-3 b}{2 b}=\frac{\text { (integer) }-3 \text { integer }}{2 \times \text { integer }}\) = rational number

Hence from (1), √5 is rational.
But this contradicts the fact that √5 is irrational.
∴ our supposition is wrong.
Hence 3 + 2√5 is irrational.

Question 3.
Prove that the following are irrationals :
(i) \(\frac{1}{\sqrt{2}}\)
(ii) 7√5
(iii) 6 + √2
Solution:
(i) Given that \(\frac{1}{\sqrt{2}}=\frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}}\)

\(\frac{1}{\sqrt{2}}=\frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}}\)

Let us suppose that \(\frac{\sqrt{2}}{2}\) is rational
∴ we can find co-prime integers a, b and b ≠ 0.

⇒ \(\frac{\sqrt{2}}{2}=\frac{a}{b}\)

⇒ √2 = \(\frac{2 a}{b}\) …………….(1)
because division of two integers is a rational number.
So \(\frac{2 a}{b}\) = rational number

∴ from (1), √2 is also a rational number, which contradicts the fact that J2 is irrational.
∴ our supposition is wrong.

Hence \(\frac{1}{\sqrt{2}}\) is irrational.

(ii) Given that 7√5
Let us suppose that 7^5 is rational
∴ we can find coprime integers a and b where b ≠ 0
such that 7√5 = \(\frac{a}{b}\)
⇒ 7b√5 = a
⇒ √5 = \(\frac{a}{7 b}\) ……………..(1)
Since a, 7 and b are integers, of two integers is a rational number.
i.e., \(\frac{a}{7 b}\) = rational number
∴ from (1)
√5 = rational number
which contradicts the fact that √5 is irrational number.
∴ Our supposition is wrong.
Hence 7√5 is irrational.

(iii) Given that 6 + √2
Let us suppose that 6 + √2 is rational
∴ we can find coprime integers a and b where b ≠ 0
such that 6 + √2 = \(\frac{a}{b}\)

∴ \(\frac{a}{b}\) – 6 = √2

or √2 = \(\frac{a-6 b}{b}\) ………………(1)
Since a and b are integers

∴ \(\frac{a-6 b}{b}=\frac{\text { integer }-6 \times \text { integer }}{\text { integer } \neq 0}\)

[∵ Subtraction of integers is also an integer]

= \(\frac{\text { integer }}{\text { integer } \neq 0}\) = rational number

[∵ Division of two integers is a rational number]

⇒ \(\frac{a-6 b}{b}\) = rational number

so from (1), √2 = rational number
which contradicts the fact that √2 is irrational number
∴ Our Supposition is wrong.
Hence 6 + √2 is irrational.

Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 2 Fractions and Decimals Ex 2.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.4

1. Find the reciprocal of each of the following fraction.
(i) \(\frac {2}{7}\)
(ii) \(\frac {3}{2}\)
(iii) \(\frac {5}{7}\)
(iv) \(\frac {1}{9}\)
(v) \(\frac {2}{3}\)
(vi) \(\frac {7}{8}\)
Answer:
(i) \(\frac {7}{2}\)
(ii) \(\frac {2}{3}\)
(iii) \(\frac {7}{5}\)
(iv) 9
(v) \(\frac {3}{2}\)
(vi) \(\frac {8}{7}\)

2. Solve the following (Division of a fraction by a non zero whole number)

Question (i).
\(\frac {19}{6}\) ÷ 10
Answer:
\(\frac {19}{6}\) ÷ 10
= \(\frac{19}{6} \times \frac{1}{10}\)
= \(\frac {19}{60}\)

Question (ii).
\(\frac {4}{9}\) ÷ 5
Answer:
\(\frac {4}{9}\) ÷ 5
= \(\frac{4}{9} \times \frac{1}{5}\)
= \(\frac {4}{45}\)

Question (iii).
\(\frac {8}{9}\) ÷ 8
Answer:
\(\frac {8}{9}\) ÷ 8
= \(\frac{8}{9} \times \frac{1}{8}\)
= \(\frac {1}{9}\)

Question (iv).
3\(\frac {1}{2}\) ÷ 4
Answer:
3\(\frac {1}{2}\) ÷ 4
= \(\frac{7}{2} \times \frac{1}{4}\)
= \(\frac {7}{8}\)

Question (v).
16\(\frac {1}{2}\) ÷ 5
Answer:
16\(\frac {1}{2}\) ÷ 5
= \(\frac{33}{2} \times \frac{1}{5}\)
= \(\frac {33}{10}\)
= 3\(\frac {3}{10}\)

Question (vi).
4\(\frac {1}{3}\) ÷ 3
Answer:
4\(\frac {1}{3}\) ÷ 3
= \(\frac{13}{3} \times \frac{1}{3}\)
= \(\frac {33}{9}\)
= 1\(\frac {4}{9}\)

3. Solve the following (Division of a whole number by a fraction)

Question (i).
8 ÷ \(\frac {7}{3}\)
Answer:
8 ÷ \(\frac {7}{3}\)
= 8 × \(\frac {3}{7}\)
= \(\frac {24}{7}\)
= 3\(\frac {3}{7}\)

Question (ii).
5 ÷ \(\frac {7}{5}\)
Answer:
5 ÷ \(\frac {7}{5}\)
= 5 × \(\frac {5}{7}\)
= \(\frac {25}{7}\)
= 3\(\frac {4}{7}\)

Question (iii).
4 ÷ \(\frac {8}{3}\)
Answer:
4 ÷ \(\frac {8}{3}\)
= 4 × \(\frac {3}{8}\)
= \(\frac {3}{2}\)
= 1\(\frac {1}{2}\)

Question (iv).
3 ÷ 2\(\frac {3}{5}\)
Answer:
3 ÷ 2\(\frac {3}{5}\)
= 3 ÷ \(\frac {13}{5}\)
= 3 × \(\frac {5}{13}\)
= \(\frac {15}{13}\)
= 1\(\frac {2}{13}\)

Question (v).
5 ÷ 3\(\frac {4}{7}\)
Answer:
5 ÷ 3\(\frac {4}{7}\)
= 5 ÷ 3\(\frac {25}{7}\)
= 5 × \(\frac {7}{25}\)
= \(\frac {7}{25}\)
= 1\(\frac {2}{5}\)

4. Solve the following (Division of a fraction by another fraction)

Question (i).
\(\frac{2}{3} \div \frac{10}{9}\)
Answer:
\(\frac{2}{3} \div \frac{10}{9}\)
= \(\frac{2}{3} \times \frac{9}{10}\)
= \(\frac {3}{5}\)

Question (ii).
\(\frac{4}{9} \div \frac{2}{3}\)
Answer:
\(\frac{4}{9} \div \frac{2}{3}\)
= \(\frac{4}{9} \times \frac{3}{2}\)
= \(\frac {2}{3}\)

Question (iii).
\(2 \frac{1}{2} \div \frac{3}{5}\)
Answer:
\(2 \frac{1}{2} \div \frac{3}{5}\)
= \(\frac{5}{2} \times \frac{5}{3}\)
= \(\frac {25}{6}\)
= 4\(\frac {1}{6}\)

Question (iv).
\(\frac{3}{7} \div 1 \frac{1}{5}\)
Answer:
\(\frac{3}{7} \div 1 \frac{1}{5}\)
= \(\frac{3}{7} \div \frac{6}{5}\)
= \(\frac{3}{7} \times \frac{5}{6}\)
= \(\frac {5}{14}\)

Question (v).
\(5 \frac{1}{2} \div 2 \frac{1}{5}\)
Answer:
\(5 \frac{1}{2} \div 2 \frac{1}{5}\)
= \(\frac{11}{2} \div \frac{11}{5}\)
= \(\frac{11}{2} \times \frac{5}{11}\)
= \(\frac {5}{2}\)
= 2\(\frac {1}{2}\)

Question (vi).
\(3 \frac{1}{5} \div 1 \frac{2}{3}\)
Answer:
\(3 \frac{1}{5} \div 1 \frac{2}{3}\)
\(\frac{16}{5} \div \frac{5}{3}\)
= \(\frac{16}{5} \times \frac{3}{5}\)
= \(\frac {48}{25}\)
= 1\(\frac {23}{25}\)

5. 11 small ropes are cut from 7\(\frac {1}{3}\) m long rope. Find the length of each of the small rope.
Solution:
Length of rope = 7\(\frac {1}{3}\) m = \(\frac {22}{3}\) m,
∴ Length of 11 small ropes = \(\frac {22}{3}\)m
Length of each small rope = \(\frac {22}{3}\)m ÷ 11
= \(\frac{22}{3} \times \frac{1}{11} \mathrm{~m}\)
= \(\frac {2}{3}\)m

6. Multiple choice questions :

Question (i).
Reciprocal of \(\frac {3}{4}\) is :
(a) \(\frac {3}{4}\)
(b) \(\frac {4}{3}\)
(c) 1
(d) none of these
Answer:
(b) \(\frac {4}{3}\)

Question (ii).
\(\frac{5}{7} \div \frac{7}{5}=?\)
(a) 1
(b) \(\frac {49}{25}\)
(c) \(\frac {25}{49}\)
(d) -1
Answer:
(c) \(\frac {25}{49}\)

Question (iii).
\(\frac{5}{7} \div \frac{5}{7}=?\)
(a) 1
(b) \(\frac {49}{25}\)
(c) \(\frac {25}{49}\)
(d) -1
Answer:
(a) 1

7.
Question (i).
The reciprocal of a proper fraction is an improper fraction (True/False)
Answer:
True

Question (ii).
The reciprocal of a whole number is always a whole number (True / False)
Answer:
False.