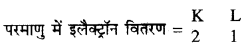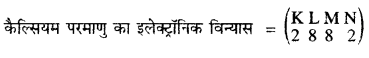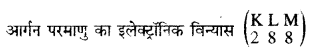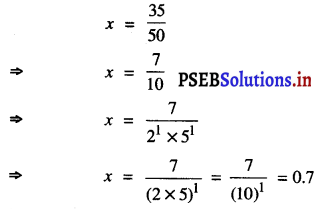Bhagya

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 2 बहुपद Ex 2.3 Textbook Exercise Questions and Answers

PSEB Solutions for Class 10 Maths Chapter 2 बहुपद Ex 2.3

प्रश्न 1.
विभाजन एल्गोरिथ्म का प्रयोग करके, निम्न में P(x) को g(x) से भाग देने पर भागफल तथा शेषफल ज्ञात कीजिए:
(i) P(x) = x³ – 3x² + 5x – 3, g(x) = x² – 2
(ii) P(x) = x⁴ – 3x² + 4x + 5, g(x) = x² + 1 – x
(iii) P(x) = x⁴ – 5x + 6, g(x) = 2 – x²
हल :
(i) दिया है कि p (x) = x³ – 3x² + 5x – 3 और g(x) = x² – 2

विभाजन एल्गोरिथ्म से, x³ – 3x² + 5x – 3
= (x – 3) (x² – 2) + (7x – 9)
अतः, भागफल = x – 3 और शेषफल = 7x – 9 उत्तर

(ii) दिया है कि p (x) = x⁴ – 3x² + 4x + 5 या p(x) = x⁴ + 0x³ – 3x² + 4x + 5
और g(x) = x² + 1 – x

विभाजन एल्गोरिथ्म से, x⁴ – 3x² + 4x + 5
= (x² + x – 3) (x² – x + 1) + 8
अतः, भागफल = x² + x – 3 और शेषफल = 8 उत्तर

(iii) दिया है कि p(x) = x – 5x + 6
p (x) = x⁴ + 0x³ + 0x² – 5x + 6
और g (x) = 2 – x²
या g (x) = – x² + 2

विभाजन एल्गोरिथ्म से,
x⁴ – 5x + 6 = (- x² – 2) (- x² + 2) + (- 5x + 10)
अतः भागफल = – x² – 2
शेषफल = – 5x + 10 उत्तर

प्रश्न 2.
पहले बहुपद से दूसरे बहुपद को भाग करके, जाँच कीजिए कि क्या प्रथम बहुपद द्वितीय बहुपद का एक गुणनखंड है :

(i) t² – 3, 2t⁴ + 3t³ – 2t² – 9t – 12
(ii) x² + 3x + 1, 3x⁴ + 5x³ – 7x² + 2x + 2
(iii) x³ – 3x + 1, x⁵ – 4x³ + x² + 3x + 1
हल :
(i)

∵ शेषफल शून्य नहीं है 41 -12
∴ विभाजन एल्गोरिथ्म से.
t² – 3, 2t⁴ + 3t³ – 2t² – 9t – 12 का गुणनखंड नहीं है। उत्तर

(ii)

∵ शेषफल शून्य है।
∴ विभाजन एल्गोरिथ्म से
x² + 3x + 1, 3x⁴ + 5x³ – 7x² + 2x + 2 का गुणनखंड है। उत्तर

(iii)

∵ शेषफल शून्य है।
∴ विभाजन एल्गोरिथ्म से
x³ – 3x + 1, x⁵ – 4x³ + x² + 3x + 1 का गुणनखंड हैं। उत्तर

प्रश्न 3.
3x⁴ + 6x³ – 2x⁴ – 10x – 5 के अन्य सभी शून्यक ज्ञात कीजिए, यदि इसके दो शून्यक और \(\sqrt{\frac{5}{3}}\) और \(-\sqrt{\frac{5}{3}}\) हैं।
हल :
दिया है कि दो शून्य हैं \(\sqrt{\frac{5}{3}}\) और \(-\sqrt{\frac{5}{3}}\) हैं।

∴ (x – \(\sqrt{\frac{5}{3}}\)) [x – (- \(\sqrt{\frac{5}{3}}\))] दिये गए बहु पद के गुणनखंड हैं।

या (x – \(\sqrt{\frac{5}{3}}\)) (x + \(\sqrt{\frac{5}{3}}\)) दिये गए बहुपद के गुणनखंड हैं।

या x² – \(\frac{5}{3}\) दिये गए बहु पद के गुणनखंड हैं।

दिये गए बहु पद और x² – \(\frac{5}{3}\) पर विभाजन एल्गोरिथ्म का प्रयोग करने पर,

∴ 3x⁴ + 6x³ – 2x⁴ – 10x – 5 = (x² – \(\frac{5}{3}\)) [3x² + 6x + 3]
S = 2, P = 1
= (x² – \(\frac{5}{3}\)) (3) [x² + 2x + 1]

= 3 (x² – \(\frac{5}{3}\)) [x² + x + x + 1]

= 3 (x² – \(\frac{5}{3}\)) [x (x + 1) + 1 (x + 1)]

= 3 (x² – \(\frac{5}{3}\)) (x + 1) (x + 1)
अब, बहुपद के अन्य शून्यक दिए गए हैं
x + 1 = 0 या x + 1 = 0
x = – 1 या x = – 1
∴ दी गई चार घात वाली बहुपद के शून्यक हैं :
\(\sqrt{\frac{5}{3}}\), – \(\sqrt{\frac{5}{3}}\), – 1, – 1 उत्तर

प्रश्न 4.
यदि x³ – 3x² + x + 2 को एक बहुपद g (x) से दिये गए बहुपद और .x-5 भाग देने पर, भागफल और शेषफल क्रमशः x – 2 और – 2x + 4 हैं, तो g (x) ज्ञात कीजिए :
हल :
मान लीजिए
p (x) = x³ – 3x² + x + 2
और q (x) = (x – 2)
और r (x) = – 2x + 4
दिए गए आँकड़ों की विभाजन एल्गोरिथ्म से तुलना करने पर हम प्राप्त करते हैं :
p (x) = g (x) . q (x) + r (x)
या p (x) – r (x) = g (x) . q (x)
या g (x) . q (x) = p (x) – r (x)
या g(x) = \(\frac{p(x)-r(x)}{q(x)}\)
भिन्न-भिन्न मान प्रतिस्थापित करने पर हम प्राप्त करते हैं :

∴ \(\frac{x^{3}-3 x^{2}+3 x-2}{x-2}\) = x² – x + 1
(1) और (2), से हम प्राप्त करते हैं g(x) = x² – x + 1 उत्तर.

प्रश्न 5.
बहुपदों p (x), g (x), q (x) और r (x) के ऐसे उदाहरण दीजिए जो विभाजन एल्गोरिथ्म को संतुष्ट करते हैं तथा
(i) घात p (x) = घात q (x)
(ii) घात q (x) = 0
(iii) घात q (x) = घात r (x)
हल :
(i) p(x)= 5x² – 5x + 10; g(x)= 5
q (x) = x² – x + 2; r (x) = 0

∴ विभाजन एल्गोरिथ्म से,
5x² – 5x + 10 = 5 (x² – x + 2) + 0
या p (x) = g (x) q (x) + r (x)
साथ ही, p (x) की घात = q (x) की घात = 2

(ii) मान लीजिए p (x) = 7x³ – 42x + 53;
g (x) = x³ – 6x + 7;
q(x) = 7;
r (x) = 4

∴ विभाजन एल्गोरिथ्म से 7x³ – 42x + 53 = 7 (x³ – 6x + 7) + 4
या p (x) = q (x) . g (x) + r (x)
साथ ही घात q (x) = 0

(iii) मान लीजिए p (x) = 4x³ + x² + 3x + 6
g(x) = x² + 3x + 1
q(x) = 4x – 11; r(x) = 32x + 17

∴ विभाजन एल्गोरिथ्म से 4x³ + x² + 3x + 6 = (4x – 11) (x² + 3x + 1) + (32x + 17)
या p (x) = q (x) . g (x) + r (x)
साथ ही घात q (x) = घात r (x)

Punjab State Board PSEB 9th Class Science Book Solutions Chapter 9 बल तथा गति के नियम Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Science Chapter 9 बल तथा गति के नियम

PSEB 9th Class Science Guide बल तथा गति के नियम Textbook Questions and Answers

प्रश्न 1.
कोई वस्तु शून्य बाह्य असंतुलित बल अनुभव करती है। क्या किसी भी वस्तु के लिए अशुन्य वेग से गति करना संभव है ? यदि हाँ, तो वस्तु के वेग के परिमाण एवं दिशा पर लगने वाली शर्तों का उल्लेख करें। यदि नहीं, तो कारण स्पष्ट करें।
उत्तर-
हाँ, किसी वस्तु के लिए कुछ वेग से गति करना संभव है, जबकि वह वस्तु बाह्य असंतुलित बल शून्य अनुभव कर रही हो। ऐसी अवस्था में वेग का परिमाण तथा दिशा समान रहेगी। उदाहरणार्थ, वर्षा के समय पानी की बूंद जब अचर वेग के साथ नीचे पृथ्वी की ओर गिरती है तो उस बूंद का भार तथा वायु का धकेल बल परस्पर एकदूसरे को संतुलित कर लेते हैं, अर्थात् पानी की बूंद पर परिणामी बल (नेट बल) शून्य होता है।

प्रश्न 2.
जब किसी छडी से एक दरी ( कार्पेट ) को पीटा जाता है, तो धूल के कण बाहर आ जाते हैं। स्पष्ट करें।
उत्तर-
जब हम दरी (कार्पेट) को छड़ी के साथ पीटते हैं तो दरी गति में आ जाती है जबकि धूल कण जड़त्व के कारण विराम अवस्था में बने रहते हैं। इस प्रकार धूल कण दरी (कार्पेट) से पृथक् होकर गिर जाते हैं।

प्रश्न 3.
बस की छत पर रखे सामान को रस्सी से क्यों बाँधा जाता है ?
उत्तर-
जब तीव्र गति से चल रही बस तीखे मोड़ पर गुड़ती है तो इसके छत पर रखा हुआ सामान एक ओर गिर (विस्थापित हो) जाता है। इसका कारण है कि सामान सरल रेखीय गति के साथ चलता रहना चाहता है जबकि बस की दिशा परिवर्तन के लिए ईंजन द्वारा असंतुलित बल लगाया जाता है तथा छत पर रखा सामान एक ओर खिसक जाता है।

प्रश्न 4.
किसी बल्लेबाज दवारा क्रिकेट की गेंद को मारने पर गेंद ज़मीन पर लुढ़कती है। कुछ दूरी चलने के पश्चात् गेंद रुक जाती है। गेंद रुकने के लिए धीमी होती है, क्योंकि
(a) बल्लेबाज ने गेंद को पर्याप्त प्रयास से हिट नहीं किया है।
(b) वेग गेंद पर लगाए गए बल के समानुपाती है।
(c) गेंद पर गति की दिशा के विपरीत एक बल कार्य कर रहा है।
(d) गेंद पर कोई असंतुलित बल कार्यरत नहीं है, अत: गेंद विरामावस्था में आने के लिए प्रयासरत है।
(सही विकल्प का चयन करें)
उत्तर-
(c) गेंद पर गति की दिशा के विपरीत एक बल कार्य कर रहा है।

प्रश्न 5.
एक टक विरामावस्था से किसी पहाड़ी से नीचे की ओर नियत त्वरण से लुढ़कना शुरू करता है। यह 20 s में 400 m की दूरी तय करता है। इसका त्वरण ज्ञात करें। अगर इसका द्रव्यमान 7 टन है तो इस पर लगने वाले बल की गणना करें। (1 टन = 1000 kg)।
हल-
यहां प्रारंभिक वेग (u) = 0
समय (t) = 20 s
दूरी (S) = 400 m
हम जानते हैं, S = ut + \(\frac {1}{2}\) at²
400 = 0 × 20 + \(\frac {1}{2}\) × a × (20)²
400 = 0 + \(\frac {1}{2}\) × a × 20 × 20
400 = 200a
या a = \(\frac{400}{200}\)
∴ a = 2 ms^-1
अब ट्रक का द्रव्यमान (m) = 7 टन
= 7 × 1000 kg
त्वरण (a) = 2 ms^-2
∴ बल, F = m × a
= 7000 kg × 2ms^-2
= 14000 kg m/s²
= 14000 N

प्रश्न 6.
1 kg द्रव्यमान के एक पत्थर को 20 ms^-1 के वेग से झील की जमी हुई सतह पर फेंका जाता है। पत्थर 50 m की दूरी तय करने के बाद रुक जाता है। पत्थर और बर्फ के बीच लगने वाले घर्षण बल की गणना करें।
हल-
यहाँ पत्थर का द्रव्यमान (m) = 1 kg
पत्थर का प्रारंभिक वेग (u) = 20 ms^-1
पत्थर द्वारा तय की गई दुरी (S) = 50 m
पत्थर का अंतिम वेग (v) = 0 (विराम अवस्था)
पत्थर तथा बर्फ में लगने वाला घर्षण बल (F) = ?
v² – u² = 2aS का प्रयोग करने पर
(0)² – (20)² = 2 × a × 50
-20 × 20 = 100 × a
या a = \(\frac{-20 \times 20}{100}\)
∴ a = -4 ms^-2
घर्षण बल, F = m × a
= 1 × (-4)
= -4 N

प्रश्न 7.
एक 8000 kg द्रव्यमान का रेल इंजन प्रति 2000 kg द्रव्यमान वाले पाँच डिब्बों को सीधी पटरी पर खींचता है। यदि इंजन 40000 N का बल आरोपित करता है तथा यदि पटरी 5000 N का घर्षण बल लगाती है, तो ज्ञात करें :
(a) नेट त्वरण बल,
(b) रेल का त्वरण तथा
(c) डिब्बे 1 द्वारा डिब्बे 2 पर लगाया गया बल।
हल-
इंजन का द्रव्यमान = 8000 kg 5
डिब्बों का द्रव्यमान = 5 × 2000 kg
= 10,000 kg
∴ इंजन तथा 5 डिब्बों का कुल द्रव्यमान = 8000 kg + 10,000 kg
= 18000 kg
इंजन द्वारा लगाया गया बल = 40000 N
पटरी द्वारा लगाया गया घर्षण बल = 5000 N

(a) नेट त्वरित बल = ईंजन का बल – पटरी का घर्षण बल
= 40000 N – 5000 N
= 35000 N

(b)
= \(\frac{35000}{18000}\)
= \(\frac{35}{18}\)
= 1.94 ms^-2

(c) पहले (1) डिब्बे द्वारा (2) दूसरे डिब्बे पर लगाया गया बल = नेट त्वरित बल – डिब्बे का द्रव्यमान × त्वरण

= 35000 – 2000 × \(\frac{35}{18}\)
= 35000 – 3888.8
= 31111.2N

प्रश्न 8.
एक गाड़ी का द्रव्यमान 1500 kg है। यदि गाड़ी को 1.7 ms^-2 के ऋणात्मक त्वरण (अवमंदन) के साथ विरामावस्था में लाना है, तो गाड़ी तथा सड़क के बीच लगने वाला बल कितना होगा ?
हल :
यहाँ गाड़ी का द्रव्यमान (m) = 1500 kg
त्वरण (a) = -1.7 ms^-2
घर्षण बल (F) = ?
हम जानते हैं, F = m × a
= 1500 × (-1.7)
= -2550 N
अर्थात् गाड़ी तथा सड़क के मध्य लगने वाला घर्षण बल 2550N है जिसकी दिशा गाड़ी की गति की दिशा के विपरीत है।

प्रश्न 9.
किसी m द्रव्यमान की वस्तु जिसका वेग । है का संवेग क्या होगा ?
(a) (mv)²
(b) mv²
(c) (1/2)mv²
(d) mv
(उपरोक्त में से सही विकल्प चुनें।)
उत्तर-
(d) mv.

प्रश्न 10.
हम एक लकड़ी के बक्से को 200 N बल लगाकर उसे नियत वेग से फ़र्श पर धकेलते हैं। बक्से पर लगने वाला घर्षण बल क्या होगा ?
उत्तर-
लकड़ी का बॉक्स उस अवस्था में स्थिर वेग से गति करेगा यदि नेट (परिणामी) बल शून्य होगा।
बॉक्स पर लगने वाला घर्षण बल = धकेल बल
= 200 N
परंतु इस घर्षण बल की दिशा बॉक्स की गति के विपरीत दिशा में होगा।

प्रश्न 11.
दो वस्तुएँ, प्रत्येक का द्रव्यमान 1.5 kg है, एक ही सीधी रेखा में एक-दूसरे के विपरीत दिशा में गति कर रही हैं। टकराने के पहले प्रत्येक का वेग 2.5 ms^-1 है। टकराने के बाद यदि दोनों एक-दूसरे से जुड़ जाती हैं, तब उनका सम्मिलित वेग क्या होगा ? ..
हल :
यहाँ, m₁ = m₂ = 1.5 kg
u₁ = 2.5 ms^-1, u₂ = -2.5 ms^-1
क्योंकि दोनों वस्तुएँ एक-दूसरे की विपरीत दिशा में जा रही हैं, इसलिए पहली वस्तु के वेग की दिशा धन तथा दूसरी वस्तु के वेग की दिशा को ऋण माना जाएगा।
मान लो टकराने के पश्चात् दोनों वस्तुओं के युग्म का वेग v है।
संवेग सरंक्षण नियमानुसार, टकराने से पहले दोनों वस्तुओं का कुल संवेग = टकराने के बाद कुल संवेग
m₁u₁ + m₂u₂ = m₁v + m₂v
m₁u₁ + m₂u₂ = (m₁ + m₂) × v
1.5 × 2.5 + 1.5 × (-2.5) = (1.5 + 1.5) × v
1.5 (2.5 – 2.5) = 3 × v
1.5 × 0 = 3 × v
0 = 3 × v
∴ v = 0 ms^-1

प्रश्न 12.
गति के तृतीय नियम के अनुसार जब हम किसी वस्तु को धक्का देते हैं, तो वस्तु उतने ही बल के साथ हमें भी विपरीत दिशा में धक्का देती है। यदि वह वस्तु एक ट्रक है जो सड़क के किनारे खड़ा है; संभवतः हमारे द्वारा बल आरोपित करने पर भी गतिशील नहीं हो पाएगा। एक विद्यार्थी इसे सही साबित करते हुए कहता है कि दोनों बल विपरीत एवं बराबर हैं जो एक-दूसरे को निरस्त कर देते हैं। इस तर्क पर अपने विचार दें और बताएँ कि ट्रक गतिशील क्यों नहीं हो पाता ?
उत्तर–
क्रिया तथा प्रतिक्रिया एक-दूसरे के समान तथा विपरीत होते हैं। ये एक-दूसरे को समाप्त (प्रभावहीन) नहीं करते हैं। जब हम एक भारी ट्रक को धक्का लगाते हैं,तो टायर तथा सड़क के मध्य घर्षण बल क्रिया करता है जो अत्यधिक मात्रा में होता है। इस कारण ट्रक गति नहीं करता है।

प्रश्न 13.
200 g द्रव्यमान की एक हॉकी की गेंद 10 ms^-1 की वेग से सीधी रेखा में चलती हुई 5 kg द्रव्यमान के लकड़ी के गुटके से संघट्ट करती है तथा उससे जुड़ जाती है। उसके बाद दोनों एक साथ उसी रेखा में गति करते हैं। संघट्ट के पहले और संघट्ट के बाद के कुल संवेगों की गणना करें। दोनों वस्तुओं की जुड़ी हुई अवस्था में वेग की गणना करें।
हल :
गेंद का द्रव्यमान (m) = 200g = 0.2 kg
गेंद का प्रारंभिक वेग (u) = 10 ms^-1
गेंद का अंतिम वेग (v) = -5 ms^-1 (∵ गेंद की दिशा पहली दिशा के विपरीत है।)
गेंद के संवेग में परिवर्तन = अंतिम संवेग – प्रारंभिक संवेग
= mv – mu
= m(v – u)
= 0.2 (-5 – 10)
= 0.2 × (-15)
= – 30 kg -ms^-1

प्रश्न 14.
10g. द्रव्यमान की एक गोली सीधी रेखा में 150 ms^-1 के वेग से चलकर एक लकड़ी के गुटके से टकराती है और 0.03 s के बाद रुक जाती है। गोली लकड़ी को कितनी दूरी तक भेदेगी ? लकड़ी के गुटके द्वारा गोली पर लगाए गए बल के परिमाण की गणना करें। हल :
यहाँ, गोली का द्रव्यमान (m) = 1g = 0.01 kg
गोली का प्रारंभिक वेग (u) = 150 ms^-1
गोली का अंतिम वेग (v) = 0
समय (t) = 0.03s
हम जानते हैं, गोली का प्रवेग (a) = \(\frac{v-u}{t}\)
= \(\frac{0-150}{0.03}\)
= -5000 ms^-1
लकड़ी के गुटके के भीतर घुसी गोली द्वारा तय की गई दूरी (S) = ?
सूत्र S = ut + \(\) at² का प्रयोग करके
S = 150 x 0.03 + \(\frac {1}{2}\) × (-5000) × (0.03)²
= 4.5 + (-2.25)
= 4.5 – 2.25
S = 2.25 m
प्रश्न 15.
एक वस्तु जिसका द्रव्यमान 1 kg है, 10 ms^-1 के वेग से एक सीधी रेखा में चलते हुए विरामावस्था में रखे 5 kg द्रव्यमान के एक लकड़ी के गुटके से टकराती है। उसके बाद दोनों साथ-साथ उसी सीधी रेखा में गति करते हैं। संघट्ट के पहले तथा बाद के कुल संवेगों की गणना करें। आपस में जुड़े हुए संयोजन के वेग की भी गणना करें।
हल :
वस्तु का द्रव्यमान (m₁) = 1 kg
वस्तु का प्रारंभिक वेग (u₁) = 10 ms^-1
लकड़ी के गुटके का द्रव्यमान (m₂) = 5 kg
लकड़ी के गुटके का प्रारंभिक वेग (u₂) = 0 (विराम अवस्था)
मान लो टकराने के पश्चात् वस्तु तथा गुटके के युग्म का अंतिम वेग है।
∴ टक्कर से पहले वस्तु तथा गुटके का कुल संवेग = m₁u₁ + m₂u₂
= 1 × 10 + 5 × 0
= 10 + 0
= 10 kg-ms^-1
टक्कर के पश्चात् युग्म (वस्तु तथा गुटके) का कुल संवेग = m₁v + m₂v
= (m₁ + m₂) × v
= (1 + 5) × v
= 6v kg-ms^-1
संवेग संरक्षण नियम अनुसार, टक्कर से पहले युग्म का कुल संवेग = टक्कर के पश्चात् युग्म का कुल संवेग
10 = 6v
∴ v = \(\frac{10}{6}[latex]
= [latex]\frac{5}{3}\) ms^-1 = 1.67 ms^-1
∴ टक्कर के पश्चात् युग्म का कुल संवेग = 6v
= 6 × \(\frac{5}{3}\)
= 10 kg – ms^-1

प्रश्न 16.
100 kg द्रव्यमान की एक वस्तु का वेग समान त्वरण से चलते हुए 6s में 5 ms^-1 से 8 ms^-1 हो जाता है। वस्तु के पहले और बाद के संवेगों की गणना करें। उस बल के परिमाण की गणना करें जो उस वस्तु पर आरोपित है।
हल :
यहाँ, वस्तु का द्रव्यमान (m) = 100 kg
वस्तु का प्रारंभिक वेग (u) = 5 ms^-1
वस्तु का अंतिम वेग (v) = 8 ms^-1
समय अंतराल (t) = 6s
वस्तु का प्रारंभिक संवेग (p) = m × u
= 100 × 5
= 500 kg-ms^-1
वस्तु का अंतिम संवेग (p₂) = m × v
= 100 × 8
= 800 kg-ms^-1
वस्तु पर लग रहा बल. F = \(\frac{p_{2}-p_{1}}{t}\)
= \(\frac{(800-500) \mathrm{kg}-\mathrm{ms}^{-1}}{6 \mathrm{~s}}\)
= 50 kg-ms^-2
= 50 N

प्रश्न 17.
अख्तर, किरण और राहुल किसी राजमार्ग पर बहुत तीव्र गति से चलती हुई कार में सवार हैं, अचानक उड़ता हुआ कोई कीड़ा, गाड़ी के सामने के शीशे से आ टकराया और वह शीशे से चिपक गया। अख़्तर और किरण इस स्थिति पर विवाद करते हैं। किरण का मानना है कि कीड़े के संवेग परिवर्तन का परिमाण कार के संवेग परिवर्तन के परिमाण की अपेक्षा बहुत अधिक है। (क्योंकि कीड़े के वेग में परिवर्तन का मान कार के वेग में परिवर्तन के मान से बहुत अधिक है।) अख़्तर ने कहा कि चूंकि कार का वेग बहुत अधिक था अतः कार ने कीड़े पर बहुत अधिक बल लगाया जिसके कारण कीड़े की मौत हो गई। राहुल ने एक नया तर्क देते हुए कहा कि कार तथा कीड़ा दोनों पर समान बल लगा और दोनों के संवेग में बराबर परिवर्तन हुआ। इन विचारों पर अपनी प्रतिक्रिया दें।
उत्तर-
राहुल का तर्क सही है। गति के तीसरे नियमानुसार क्रिया तथा प्रतिक्रिया समान तथा विपरीत होते हैं। इसलिए दोनों-कार तथा कीड़े पर समान मात्रा में बल लगेगा तथा दोनों में समान वेग परिवर्तन भी होगा। अब क्योंकि कीड़े का द्रव्यमान कार के द्रव्यमान की तुलना में अत्यधिक कम हैं, इसलिए कीड़े में हुआ संवेग परिवर्तन स्पष्ट दिखाई देता है। जड़त्व कम होने के कारण कीड़ा मर जाता है।

प्रश्न 18.
एक 10 kg द्रव्यमान की घंटी 80 cm की ऊँचाई से फ़र्श पर गिरी। इस अवस्था में घंटी द्वारा फ़र्श पर स्थानांतरित संवेग के मान की गणना करें। परिकलन में सरलता हेतु नीचे की ओर दिष्ट त्वरण का मान, 10 ms^-2 लें।
हल :
यहाँ, घंटी का द्रव्यमान (m) = 10 kg’
आरंभिक वेग (u) = 0 (विराम अवस्था)
तय की गई दूरी (S) = 80 cm
= 0.80 m
घंटी का त्वरण (a) = 10 ms^-2
मान लो पृथ्वी पर पहुँच कर घंटी का अंतिम वेग v है
∴ v² – u² = 2aS के प्रयोग से
v² – (0)² = 2 × 10 × 0.80
v² = 16
∴ घंटी का अंतिम वेग, v = \(\sqrt{16}\) = 4 ms^-1
घंटी द्वारा पृथ्वी को स्थानांतरित संवेग (p) = mv
= 10 × 4
= 40 kg – ms^-1

(a) ऊपर दी गई सारणी दर्शाती है कि गति त्वरित है तथा त्वरण समय के साथ-साथ एक समान रूप से बढ़ता है।
(b) क्योंकि त्वरण एक समान रूप से बढ़ रहा है, इसलिए वस्तु पर लग रहा बल भी समय के साथ समान रूप से बढ़ रहा है।

अतिरिक्त अभ्यास (Additional Exercises)

प्रश्न A1.
एक वस्तु की गति की अवस्था में दूरी समय सारणी निम्नवत् है:

समय (सेकंड)	दूरी (मीटर)
0	0
1	1
2	8
3	27
4	64
5	125
6	216
7	343

(a) त्वरण के बारे में आप क्या निष्कर्ष निकाल सकते हैं ? क्या यह नियत है ? बढ़ रहा है ? घट रहा है ? या शून्य है ?
(b) आप वस्तु पर लगने वाले बल के बारे में क्या निष्कर्ष निकाल सकते हैं ?
हल:

प्रश्न A2.
1200 kg द्रव्यमान की कार को एक समतल सड़क पर दो व्यक्ति समान वेग से धक्का देते हैं। उसी कार को तीन व्यक्तियों द्वारा धक्का देकर 0.2 ms-^-2का त्वरण उत्पन्न किया जाता है। कितने बल के साथ प्रत्येक व्यक्ति कार को धकेल पाते हैं। (मान लें कि सभी व्यक्ति समान पेशीय बल के साथ कार को धक्का देते हैं।)
हल :
यहाँ कार का द्रव्यमान (m) = 1200 kg
कार का त्वरण (a) = 0.2 ms^-2
पहले दो व्यक्तियों को धक्का देने से त्वरण = 0
स्पष्ट है कि जब तीसरा व्यक्ति कार को धक्का मारता है तो एक असंतुलित बल क्रिया करता है।
∴ तीसरे व्यक्ति द्वारा लगाया गया बल, F = m × a
= 1200 × 0.2
= 240 N
अब क्योंकि तीनों व्यक्ति पेशीय बल लगा कर कार को धकेलते हैं, इसलिए प्रत्येक व्यक्ति बल लगाता है = 240 N

प्रश्न A3.
500g द्रव्यमान के एक हथौड़े द्वारा 50 ms^-1 वेग से एक कील पर प्रहार किया जाता है। कील द्वारा हथौड़े को बहुत कम समय 0.01 s में ही रोक दिया जाता है। कील के द्वारा हथौड़े पर लगाए गए बल का परिकलन करें।
हल :
हथौड़े का द्रव्यमान (m) = 500g
= \(\frac{500}{1000}\) kg
= \(\frac{1}{2}\) kg
प्रारंभिक वेग (u) = 50 ms^-1
अंतिम वेग (v) = 0 ms^-1
समय (t) = 0.01s
बल (F) = ?
हम जानते हैं, v = u + at
0 = 50 + a × 0.01
-50 = a × \(\frac{1}{100}\)
∴ a = -50 × 100
= -5000 ms^-2
ऋणात्मक चिन्ह मंदन को दर्शाता है।
अब कील द्वारा हथौड़े पर लगाया गया बल (F) = m × a
= \(\frac{1}{2}\) × (-5000)
= -2500 N
∴ बल = 2500 N

प्रश्न A4.
एक 1200 kg द्रव्यमान की मोटरकार 90 km/h की वेग से एक सरल रेखा के अनुदिश चल रही है। उसका वेग बाहरी असंतुलित बल लगने के कारण 4s में घटकर 18 km/h हो जाता है। त्वरण और संवेग में परिवर्तन का परिकलन करें। लगने वाले बल के परिमाण का भी परिकलन करें।
हल :
यहाँ, कार का द्रव्यमान (m) = 1200 kg
समय (1) = 4s
कार का प्रारंभिक वेग (u) = 90 km/h
= \(\frac{90 \times 1000}{60 \times 60}\) m/s
= 25 ms^-1
कार का अंतिम वेग (v) = 18 km/h
= \(\frac{18 \times 1000 \mathrm{~m}}{60 \times 60 \mathrm{~s}}\)
= 5 ms^-1
कार का त्वरण (a) = ?
कार के संवेग में परिवर्तन = ?
कार पर लगने वाले बल का परिमाण (F) = ?
हम जानते हैं, v = u + at
5 = 25 + a x 4
-20 = 4a
∴ a = \(\frac{-20}{4}\)
= -5 ms^-2
कार के संवेग में परिवर्तन = अंतिम संवेग – प्रारंभिक संवेग
= mv – mu
= m (v – u)
= 1200 (5 – 25)
= 1200 × (-20)
= -24000 kg – ms^-1
= 24000 kg – ms^-1 की कमी उत्तर
परंतु F = m × a
= 1200 × 5
= 6000 N

Science Guide for Class 9 PSEB बल तथा गति के नियम InText Questions and Answers

पाठ्य-पुस्तक के प्रश्नों के उत्तर

प्रश्न 1.
निम्नलिखित में किस का जड़त्व अधिक है :
(a) एक रबर की गेंद एवं उसी आकार का पत्थर,
(b) एक साइकिल एवं एक रेलगाड़ी,
(c) पाँच रुपये का सिक्का एवं एक रुपये का सिक्का।
उत्तर-
हम जानते हैं कि किसी वस्तु का द्रव्यमान उसके जड़त्व का माप है, इसलिए जिस वस्तु का द्रव्यमान अधिक होगा उस वस्तु का जड़त्व भी अधिक होगा।
(a) गेंद के आकार वाले पत्थर का जड़त्व अधिक क्योंकि इसका द्रव्यमान गेंद के द्रव्यमान की अपेक्षा अधिक है।

(b) एक रेलगाड़ी का द्रव्यमान साइकिल के द्रव्यमान की तुलना से अधिक है इसलिए रेलगाड़ी का जड़त्व अधिक

(c) पाँच रुपये के सिक्के का जड़त्व एक रुपये के सिक्के से अधिक है क्योंकि पाँच रुपये के सिक्के का द्रव्यमान 1 रुपये के सिक्के की अपेक्षा अधिक है।

प्रश्न 2.
नीचे दिए गए उदाहरण में गेंद का वेग कितनी बार बदलता है, जानने का प्रयास करें :
“फुटबॉल का एक खिलाड़ी गेंद पर किक लगाकर गेंद को अपनी टीम के दूसरे खिलाड़ी के पास पहुँचाता है। दूसरा खिलाड़ी उस गेंद को किक लगाकर गोल की ओर पहुँचाने का प्रयास करता है। विपक्षी टीम का गोलकीपर गेंद को पकड़ता है और अपनी टीम के खिलाड़ी की ओर किक लगाता है।”
इसके साथ ही उस कारक की भी पहचान करें जो प्रत्येक अवस्था में बल प्रदान करता है।
उत्तर-
धक्का मारना, ठोकर लगानी, खींचना ये सभी क्रियाएँ वस्तु के वेग की मात्रा बदलने या गति की दिशा परिवर्तन के लिए बल के रूप में कार्य करती हैं। इसलिए ऊपर दी गई उदाहरण में गेंद का वेग तीन बार बदला है।

1. पहली बार प्रथम टीम के फुटबाल खिलाड़ी ने फुटबाल को किक (ठोकर) लगाकर गेंद के वेग में परिवर्तन किया।
2. द्वितीय बार उसी टीम के अन्य खिलाड़ी ने फुटबाल को किक (ठोकर) लगाकर गेंद में वेग परिवर्तन किया है।
3. तृतीय बार विरोधी टीम के गोलची ने फुटबाल को किक (ठोकर) लगाकर गेंद के वेग में परिवर्तन किया है।
   बल लगाने वाले कारक को मोटे अक्षरों में दिया गया है।

प्रश्न 3.
किसी पेड़ की शाखा को तीव्रता से हिलाने पर कुछ पत्तियाँ झड़ जाती हैं। क्यों ?
उत्तर-
टहनियों को हिलाने से पहले टहनियाँ तथा पत्ते दोनों विराम अवस्था में थे। हिलाने के फलस्वरूप टहिनयाँ गतिशील हो गईं जबकि पत्तियाँ विराम जड़त्व के कारण टहिनयों से अलग होकर नीचे गिर जाती हैं।

प्रश्न 4.
जब कोई गतिशील बस अचानक रुकती है तो आप आगे की ओर झुक जाते हैं और जब विरामावस्था से गतिशील होती है तो पीछे की ओर हो जाते हैं, क्यों ?
उत्तर-
जब गतिशील बस यकायक रुक जाती है तो हमारे शरीर का निचला भाग बस के संपर्क में होने से बस के साथ ही विराम अवस्था में आ जाता है, जबकि हमारे शरीर का ऊपर वाला भाग गतिशील रहने की प्रवृत्ति रखता है। इसलिए हम आगे की दिशा में गिर जाते हैं। जब बस अचानक त्वरित होती है तो हमारे शरीर का निचला भाग बस के संपर्क में होने से बस के साथ गतिशील हो जाता है, जबकि शरीर का ऊपरी भाग जड़त्व के कारण विराम अवस्था में रहने की प्रवृत्ति रखता है। इसलिए हम पीछे की ओर गिरते हैं।

प्रश्न 5.
यदि क्रिया सदैव प्रतिक्रिया के बराबर है तो स्पष्ट कीजिए कि घोड़ा गाड़ी को कैसे खींच पाता
है ?
उत्तर-
न्यूटन के गति के तीसरे नियम अनुसार, “क्रिया तथा प्रतिक्रिया सदैव समान तथा विपरीत दिशा में होते हैं।” घोड़ा-गाड़ी का बल (क्रिया) लगाकर आगे की ओर खींचता है। गाड़ी भी घोड़े को बल (प्रतिक्रिया) लगाकर (पीछे की) विपरीत दिशा में खींचती है। यह दोनों बल एक-दूसरे को संतुलित कर देते हैं। जब घोड़ा, गाड़ी को खींचता है तो वह अपने पैरों से पृथ्वी को पीछे की ओर धकेलता है। पृथ्वी की प्रतिक्रिया ऊपर की दिशा में कार्य करती है। इस प्रतिक्रिया बल को दो भागों में बाँटा जा सकता है। ऊपर की ओर लंबवत् दिशा में लगने वाला बल प्रतिक्रियात्मक बल घोड़े के भार को संतुलित करता है जबकि प्रतिक्रियात्मक बल का क्षितिज घटक गाड़ी को आगे की दिशा में गतिमान करता है। पृथ्वी तथा पहिए के मध्य घर्षण बल पीछे की दिशा में क्रिया करता है परंतु आगे की दिशा में लगने वाला बल घर्षण बल से अधिक होता है जिससे यह गाड़ी को गतिमान करने में सफल हो जाता है।

प्रश्न 6.
एक अग्निशमन कर्मचारी को तीव्र गति से बहुतायत मात्रा में पानी फेंकने वाली रबड़ की नली को पकड़ने में कठिनाई क्यों होती है ? स्पष्ट करें।
उत्तर-
रबड़ की नली में से पानी अत्यधिक बल (क्रिया) से बाहर निकलता है तथा उसी के समान बल (प्रतिक्रिया) को अग्निशमन कर्मचारी का हाथ अनुभव करता है। इसलिए उसे रबड़ की नली पकड़ने में असुविधा अनुभव होती है।

प्रश्न 7.
एक 50g द्रव्यमान की गोली 4kg द्रव्यमान, की रायफ़ल से 35 ms^-1 के प्रारंभिक वेग से छोड़ी जाती है। रायफल के प्रारंभिक प्रतिक्षेपित वेग की गणना कीजिए।
उत्तर-
गोली का द्रव्यमान (m₁) = 50 g = 0.05 kg
रायफल का द्रव्यमान (m₂) = 4 kg
गोली का प्रारंभिक वेग (u₁) = 0
रायफल का प्रारंभिक वेग (u₂) = 0
गोली का अंतिम वेग (v₁) = 35 ms^-1
रायफल का अंतिम वेग (v₂) = ?
संवेग संरक्षण के नियमानुसार, गोली तथा रायफ़ल का कुल प्रारंभिक संवेग = गोली तथा रायफल का कुल अंतिम संवेग
m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂
0.5 × 0 + 4 × 0 = 0.05 × 35 + 4 × v₂
0 + 0 = 1.75 + 4 × v₂
या -4 × v₂ = 1.75
v₂ = \(\frac{-1.75}{4}\)
= -0.437 ms^-1
= – 0.44 ms^-1
ऋणात्मक चिन्ह यह दर्शाता है कि रायफल के वेग की दिशा गोली के वेग की दिशा के विपरीत है।

प्रश्न 8.
100g और 200g द्रव्यमान की दो वस्तुएँ एक ही रेखा के अनुदिश एक ही दिशा में क्रमशः 2ms^-1 और 1ms^-1 के वेग से गति कर रही हैं। दोनों वस्तुएँ टकरा जाती हैं। टक्कर के पश्चात् प्रथम वस्तु का वेग 1.67 ^-1 हो जाता है, तो दूसरी वस्तु का वेग ज्ञात करें।
हल :
यहाँ, पहली वस्तु का द्रव्यमान (m₁) = 100g
= \(\frac{1}{10}\) kg
पहली वस्तु का प्रारंभिक वेग (u₁) = 2ms^-1
दूसरी वस्तु का द्रव्यमान (m₂) = 200g
= \(\frac{1}{5}\) kg
दूसरी वस्तु का प्रारंभिक वेग (u₂) = 1ms^-1
टकराने से पहले पहली वस्तु का प्रारंभिक संवेग = m₁ × u₁
= \(\frac{1}{10}\) × 2
= \(\frac{1}{5}\) kg – ms^-1
दूसरी वस्तु का प्रारंभिक संवेग = m₂ × u₂
= \(\frac{1}{5}\) × 1
= \(\frac{1}{5}\) kg -ms^-1
दोनों वस्तुओं का कुल प्रारंभिक संवेग = \(\frac{1}{5}+\frac{1}{5}\)
= \(\frac{2}{5}\)kg – ms^-1
टकराने के पश्चात् पहली वस्तु का अंतिम वेग (v₁) = 1.67 ms^-1
दूसरी वस्तु का अंतिम वेग (v₂) = ?
पहली वस्तु का अंतिम संवेग = m₁ × v₁
= \(\frac{1}{10}\) × 1.67
= 0.167 kg – ms^-1
दूसरी वस्तु का अंतिम वेग (v₂) = ?
दोनों वस्तुओं का कुल अंतिम संवेग = m₁ × v₁ + m₂ × v₂
= 0.167 + \(\frac{1}{5}\) × v₂
संवेग संरक्षण नियमानुसार
m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂
\(\frac{2}{5}\) = 0.167+ \(\frac{1}{5}\) × v₂
0.2 × v₂ = 0.4 – 0.167
0.2 × v₂ = 0.233
या v₂ = \(\frac{0.233}{0.2}\)
∴ v₂ = 0.116 ms^-1

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 2 बहुपद Ex 2.2 Textbook Exercise Questions and Answers

PSEB Solutions for Class 10 Maths Chapter 2 बहुपद Ex 2.2

प्रश्न 1.
निम्न द्विघात बहुपदों के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच के संबंध की अत: सत्यता की जाँच कीजिए :
(i) x² – 2x – 8
(ii) 4s² – 4s + 1
(iii) 6x² – 3 – 7x
(iv) 4u² + 8u
(v) t² – 15
(vi) 3x² – x – 4
हल :
(i) दी गई द्विघात बहुपद है x² – 2x – 8
S = – 2, P = – 8
= x² – 4x – 2x – 8
= x (x – 4) + 2 (x – 4)
= (x – 4) (x + 2)
x² – 2x – 8 का मान शून्य है
यदि (x – 4) = 0 या (x + 2) = 0
यदि x = 4 या x = – 2 इससे प्राप्त होता है
x² – 2x – 8 के शून्यक – 2 और 4 हैं। उत्तर
अब, शून्यकों का योग = (- 2) + (4) = 2

अतः शून्यकों तथा गुणांकों के बीच के संबंध का सत्यापन किया जाता है।

(ii) दी गई द्विघात बहुपद हैं
4s² – 4s + 1
= 4s² – 2s – 2s + 1
S = – 4, P = 4 × 1 = 4
= 2s (2s – 1) – 1(2s – 1)
= (2s – 1) (2s – 1)
4s² – 4s + 1 का मान शून्य है।
यदि (2s – 1) = 0 या (2s – 1) = 0
यदि s = \(\frac{1}{2}\) या s = \(\frac{1}{2}\)
अतः 4s² – 4s + 1 के शून्यक \(\frac{1}{2}\) और \(\frac{1}{2}\) हैं। उत्तर
अब शून्यकों का योग = \(\frac{1}{2}\) + \(\frac{1}{2}\) = 1
= \(\frac{-(-4)}{4}\)

अतः शून्यकों तथा गुणांकों के बीच के संबंध का सत्यापन किया जाता है।

(iii) दी गई द्विघात बहुपद हैं :
6x² – 3 – 7x
= 6x² – 7x – 3
S = – 7, P = 6 × – 3 = – 18
= 6x² – 9x + 2x – 3
= 3x (2x – 3) + 1 (2x – 3)
= (2x – 3) (3x + 1)
6x² – 3 – 7x का मान शून्य है
यदि (2x – 3) = 0 या 3x + 1 = 0
यदि x = \(\frac{3}{2}\) या \(-\frac{1}{3}\)
अतः 6x² – 7x – 3 के शून्यक \(\frac{3}{2}\) और \(-\frac{1}{3}\) हैं। उत्तर

अतः, शून्यकों तथा गुणांकों के बीच के संबंध को सत्यापित किया जाता है।

(iv) दी गई द्विघात बहुपद हैं :
4u² + 8u = 4u (u + 2)
4u² + 8u का मान शून्य है
यदि 4u = 0 या u + 2 = 0
यदि u = 0 या u = – 2
अतः, 4u² + 8u के शून्यक 0 और – 2 हैं। उत्तर
अब, शून्यकों का योग = 0 + (- 2)

अतः, शून्यकों तथा गुणांकों के बीच के संबंध का सत्यापन किया जाता है।

(v) दी गई द्विघात बहुपद हैं,
t² – 15
= t² – (√15)²
= (t – √15) (t + √15)
t² – 15 का मान शून्य है।
यदि t – √15 = 0 या t + √15 = 0
यदि t = √15 या t = – √15
अत: t² – 15 के शून्यक – √15 और √15 है। उत्तर
अब, शून्यकों का योग = – √15 + (√15)
= 0
= \(\frac{0}{1}\)

=

शून्यकों का गुणनफल = – (√15) (√15)
= – 15
= \(\frac{- 15}{1}\)

=

अतः, शून्यकों तथा गुणांकों के बीच के संबंध को सत्यापित किया जाता है।

(vi) दी गई द्विघात बहुपद हैं,
3x² – x – 4
= 3x² + 3x – 4x – 4
S = – 1, P = 3 × – 4 = – 12
= 3x (x + 1) – 4 (x + 1)
= (x + 1) (3x – 4) का मान शून्य है।
यदि (x + 1) = 0 या 3x – 4 = 0
यदि x = – 1 या x = \(\frac{4}{3}\)
अत 3x² – x – 4 के शून्यक – 1 और \(\frac{4}{3}\) है। उत्तर

अतः, शून्यकों तथा गुणांकों के बीच के संबंध को सत्यापित किया जाता है।

प्रश्न 2.
एक द्विघात बहुपद ज्ञात कीजिए, जिसके शून्यकों के योग तथा गुणनफल क्रमशः दी गई संख्याएँ हैं :
(i) \(\frac{1}{4}\), – 1
(ii) √2, \(\frac{1}{3}\)
(iii) 0, √5
(iv) 1, 1
(v) – \(\frac{1}{4}\), \(\frac{1}{4}\)
(vi) 4, 1
(iii) 0,15
हल :
(i) दिया गया है कि शून्यकों का योग तथा का गुणांक शून्यकों का गुणनफल क्रमशः \(\frac{1}{4}\) और – 1 है।
मान लीजिए कि ax² + bx + c एक द्विघात समीकरण है तथा α और β इसके शून्यक हैं।
∴ α + β = शून्यकों का योग = \(\frac{1}{4}\)
और αβ = शून्यकों का गुणनफल = – 1
अब, ax² + bx + c = k (x – α) (x – β)
जहाँ k कोई अचर है।
= k [x² – (α + β)x + αβ]
= k [x² – \(\frac{1}{4}\) x – 1]
k के भिन्न-भिन्न मानों के लिए, हम भिन्न-भिन्न द्विघात बहुपद प्राप्त करते हैं।

(ii) दिया गया है कि शून्यकों का योग तथा शून्यकों का का गुणनफल क्रमशः √2 और \(\frac{1}{3}\) है।
मान लीजिए कि ax² + bx + c एक द्विघात समीकरण तथा α और β इसके शून्यक हैं।
शून्यकों का गुणनफल = (-1) (4) है
∴ α + β = शून्यकों का योग = √2
और αβ = शून्यकों का गुणनफल = \(\frac{1}{3}\)
अब ax² + bx + c = k (x – α) (x – β)
जहाँ k कोई अचर है।
= k [x² – (α + β)x + αβ]
= k [x² – √2 x + \(\frac{1}{3}\)]
k के भिन्न-भिन्न मानों के लिए, हम भिन्न-भिन्न द्विघात बहुपद प्राप्त करते हैं।

(iii) दिया गया है कि शून्यकों का योग तथा शून्यकों का गुणनफल क्रमश: 0 और √5 है।
मान लीजिए कि ar- + bx + c एक द्विघात समीकरण है तथा α और β इसके शून्यक हैं।
∴ α + β = शून्यकों का योग = 0
और αβ = शून्यकों का गुणनफल = √5
अब, ax² + bx + c = k (x – α) (x – β)
जहाँ k कोई अचर है।
= k [x² – (α + β) x + αβ]
= k [x² – 0x + √5]
= k [x² + √5]
k के भिन्न-भिन्न मानों के लिए, हम भिन्न-भिन्न द्विघात बहुपद प्राप्त करते हैं।

(iv) दिया गया है कि शून्यकों का योग तथा शून्यकों का गुणनफल क्रमश: 1 और 1 है।
मान लीजिए कि ax² + bx + c एक द्विघात समीकरण है तथा α और β इसके शून्यक हैं।
∴ α + β = शून्यकों का योग = 1
और αβ = शून्यकों का गुणनफल = 1
अब, ax² + bx + c = k (x – α) (x – β)
जहाँ k कोई अचर है।
= k [x² – (α + β) x + αβ]
= k [x² – 1x + 1]
= k [x² – x + 1]
k के भिन्न-भिन्न मानों के लिए, हम भिन्न-भिन्न द्विघात बहुपद प्राप्त करते हैं।

(v) दिया गया है कि दी हुई बहुपद शून्यकों का योग तथा शून्यकों का गुणनफल क्रमश: \(-\frac{1}{4}\) और \(\frac{1}{4}\) है।
मान लीजिए कि ax² + bx + c एक द्विघात समीकरण है तथा α और β इसके शून्यक हैं।
∴ α + β = शून्यकों का योग = – \(\frac{1}{4}\)
और αβ = शून्यकों का गुणनफल = \(\frac{1}{4}\)
अब, ax² + bx + c = k (x – α) (x – β)
जहाँ k कोई अचर है।
= k [x² – (α + β) x + αβ]
= k [x² – \(\left(\frac{-1}{4}\right) x+\frac{1}{4}\)]
= k [x² + \(\frac{1}{4} x+\frac{1}{4}\)]
k के भिन्न-भिन्न मानों के लिए, हम भिन्न-भिन्न द्विघात बहुपद प्राप्त करते हैं।

(vi) दिया गया है कि दी गई बहुपद के शून्यकों का योग और शून्यकों का गुणनफल क्रमशः 4, 1 है।
मान लीजिए कि ax² + bx + c एक द्विघात बहुपद है k तथा α और β इसके शून्यक हैं।
∴ α + β = शून्यकों का योग = 4
और αβ = शून्यकों का गुणनफल = 1
अब, ax² + bx + c = k (x – α) (x – β)
जहाँ k कोई अचर है।
= k [x² – (α + β) x + αβ]
= k [x² – 4x + 1]
k के भिन्न-भिन्न मानों के लिए, हम भिन्न-भिन्न द्विघात बहुपद प्राप्त करते हैं।

Punjab State Board PSEB 9th Class Science Book Solutions Chapter 8 गति Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Science Chapter 8 गति

PSEB 9th Class Science Guide गति Textbook Questions and Answers

प्रश्न 1.
एक एथलीट वृत्तीय पथ, जिसका व्यास 200 m है, का एक चक्कर 40s में लगाता है। 2 min 20s के बाद वह कितनी दूरी तय करेगा और उसका विस्थापन क्या होगा ?
हल :

दिया है, वृत्तीय पथ का व्यास (d) = 200 m
∴ वृत्तीय पथ का अर्धव्यास = \(\frac{200}{2}\) = 100m
वृत्तीय पथ की लंबाई (ce) = 2πr
= 2 × \(\frac{22}{7}\) × 100
= \(\frac{4400}{7}\) m
1 चक्कर पूरा करने में लगा समय (t) = 40 s
कुल समय = 2 मिनट 20 सेकंड
= ( 2 × 60 + 20) सेकंड
= (120 + 20) सेकंड
= 140 सेकंड
40 s में तय की गई दूरी = \(\frac{4400 \mathrm{~m}}{7}\) (= 1 चक्कर की परिधि)
1 s में तय की गई दूरी = \(\frac{4400}{7 \times 40}\)
40 s में तय हुई दूरी = \(\frac{4400}{7 \times 40}\) × 140
= 2200 m
= \(\frac{1}{2}\) चक्कर की लंबाई
इसलिए गति के अंत में एथलीट \(\frac{1}{2}\) चक्कर लगाकर वृत्त के व्यास के दूसरे सामने वाले सिरे B पर पहुँचेगा।
∴ विस्थापन AB (मूल बिंदु तथा अंतिम बिंदु के मध्य की दूरी)
= 2200 m

प्रश्न 2.
300 m सरल रेखीय पथ पर जोसेफ़ जॉगिंग करता हुआ 2 min 30s में एक सिरे A से दूसरे सिरे B पर पहुंचता है और धूपकर 1 min में 100 m पीछे बिंदु C पर पहुँचता है। जोसेफ़ की औसत चाल और औसत वेग क्या होंगे ?
(a) सिरे A से सिरे B तक तथा
(b) सिरे A से सिरे C तक।
हल :

(a) सिरे A से सिरे B के बीच की लंबाई (AB) = 300 m
लगा समय (t) = 2 min 30 s
= (2 × 60 + 30) S
= (120 + 30)s
= 150 s
∴ औसत चाल = औसत वेग
=
= \(\frac{300 \mathrm{~m}}{150 \mathrm{~s}}\)
= 2 ms^-1

(b) A सिरे से सिरे B तक लंबाई + वापिस B से C तक की लंबाई
= AB + BC
= 300 m + 100 m
= 400 m
कुल समय = 2 min 30 s + 1 min
= 3 min 30 s
= (180 + 30)s
=210 s
औसत चाल = \(\frac{400 \mathrm{~m}}{210 \mathrm{~s}}\)
= \(\frac{40}{21}\) ms
= 1.9 ms^-1
औसत वेग = \(\frac{(300-100) \mathrm{m}}{210 \mathrm{~s}}\)
= \(\frac{200}{210}\)ms^-1
= \(\frac{20}{21}\) ms^-1
= 0. 95 ms^-1

प्रश्न 3.
अब्दुल गाड़ी से स्कूल जाने के क्रम में औसत चाल को 20 kmh^-1 पाता है। उसी रास्ते से लौटने के समय वहाँ भीड़ कम है और औसत चाल 30 kmh-1 है। अब्दुल की इस पूरी यात्रा में उसकी औसत चाल क्या है ?
हल :
मान लो घर से स्कूल की दरी = L
∴ घर से स्कूल तथा वापिस स्कूल से घर तक को दूरी = L + L = 2 L
स्कूल जाते समय औसत चाल (υ₂) = 200 kmh^-1
स्कल जाते समय औसत चाल (t₁) =
स्कूल से वापिस घर आते समय औसत चाल (v₂) = 30 kmh^-1
∴ स्कूल से वापिस घर आने में लगा समय (t₂) = \(\frac{\mathrm{L}}{v_{2}}\)
पूरे सफ़र के लिए लगा कुल समय = t₁ + t₂

= 24 Kmh^-1

प्रश्न 4.
कोई मोटरबोट झील में विरामावस्था से सरल रेखीय पथ पर 3.0 ms^-2 के नियत त्वरण से 8.0s तक चलती है। इस समय अंतराल में मोटरबोट कितनी दूरी तय करती है ?
हल :
यहाँ, प्रारंभिक वेग (u) = 0 (विरामावस्था)
त्वरण (a) = 3.0 ms^-2
समय (t) = 8.0 s
मोटरबोट द्वारा तय की गई दूरी (S) = ?
हम जानते हैं, S = ut + \(\frac{1}{2}\) at²
= 0 × 8 + \(\frac{1}{2}\) × 3 × (8)²
= 0 + \(\frac{1}{2}\) × 3 × 8 × 8
S = 96 m
अर्थात् मोटरबोट जितनी दूरी तय करती है = S = 96 m

प्रश्न 5.
किसी गाड़ी का चालक 52 km h^-1 की गति से चल रही कार में ब्रेक लगाता है तथा कार विपरीत दिशा में एकसमान दर से त्वरित होती है। कार 5 s में रुक जाती है। दूसरा चालक 30 kmh-1 की गति से चलती हुई दूसरी कार पर धीमे-धीमे ब्रेक लगाता है तथा 10s में रुक जाता है। एक ही ग्राफ पेपर पर दोनों कारों के लिये चाल-समय ग्राफ़ आलेखित करें। ब्रेक लगाने के पश्चात् दोनों में से कौन-सी कार अधिक दरी तक जाएगी ?
हल-

चित्र में दो कारों के चाल-समय ग्राफ़ AB तथा CD प्रदर्शित किए गए हैं जिनकी क्रमवार चाल 52 km h^-1 तथा 30 kmh^-1 है।
विरामावस्था में आने से पूर्व पहली कार द्वारा तय की गई दूरी = ΔAOB का क्षेत्रफल
= \(\frac{1}{2}\) × AO × OB
= \(\frac{1}{2}\) × (52 × \(\frac{5}{18}\)) × 5
= 36.1 m
विरामावस्था में आने से पूर्व दूसरी कार द्वारा तय की गई दूरी
= ΔCOD का क्षेत्रफल
= \(\frac{1}{2}\) × CO × OD
= \(\frac{1}{2}\) × (30 × \(\frac{5}{18}\)) × 10
= 47.2 m
इस तरह ब्रेक लगाने के पश्चात् दूसरी कार, पहली की तुलना में अधिक दूरी तय करेगी।

प्रश्न 6.
चित्र में तीन वस्तुओं A, B और C के दूरी-समय ग्राफ़ प्रदर्शित हैं। ग्राफ़ का अध्ययन करके निम्न प्रश्नों के उत्तर दीजिए :
(a) तीनों में से कौन सबसे तीव्र गति से गतिमान है ?
(b) क्या ये तीनों किसी भी समय सड़क के एक ही बिंदु पर होंगे ?
(c) जिस समय B, A से गुज़रती है उस समय तक C कितनी दूरी तय कर लेती है ?
(d) जिस समय B, C से गुजरती है तो उस समय तक यह कितनी दूरी तय कर लेती है ?

हल-

(a) A की चाल = P N की ढाल (Slope)
= \(\frac{10-6}{1.1-0}\)
= \(\frac{40}{11}\) = 3.63km h^-1
B की चाल = OM की ढाल (slope)
= \(\frac{6-0}{0.7-0}\)
= \(\frac{60}{7}\) = 8.57 km h^-1
C की चाल = QM की ढाल (slope)
= \(\frac{6-2}{0.7-0}\)
= \(\frac{40}{7}\) = 5.71 kmh^-1
क्योंकि वस्तु B की ढाल (Slope) सबसे अधिक है इसलिए यह सबसे तीव्र गति से चल रही है।

(b) क्योंकि तीनों के ग्राफ़ एक बिंदु पर नहीं काटते हैं इसलिए ये तीनों किसी समय भी सड़क पर एक बिंदु पर नहीं होंगे।

(c) जब B, N बिंदु पर A को मिलता है। (1.1 घंटा पर) तब उस समय C मूल बिंदु O से लगभग 9 km की दूरी पर होगी।

(d) B बिंदु M पर C को मिलती है, उस समय B 9 km की दूरी कर लेती है।

प्रश्न 7.
20 m की ऊँचाई से एक गेंद को गिराया जाता है। यदि उसका वेग 10 ms^-2 के एकसमान त्वरण की दर से बढ़ता है तो यह किस वेग से धरातल से टकराएगी ? कितने समय पश्चात् वह धरातल से टकराएगी ?
हल :
यहाँ u = 0
S = 20 m
a = g = 10 ms^-2
v = ?
v² – u² = 2 as का प्रयोग करने पर
v² – (0)² = 2 × 10 × 20
∴ v = \(\sqrt{400}\)
= \(\sqrt{20 \times 20}\)
= 20 ms^-1
अब v = 4 + at
20 = 0 + 10 + t
∴ t = \(\frac{20}{10}\)
t = 2s

प्रश्न 8.
किसी कार का चाल-समय ग्राफ़ चित्र में दर्शाया गया है।

(a) पहले 4 s में कार कितनी दूरी तय करती है ? इस अवधि में कार द्वारा तय की गई दूरी को ग्राफ़ में छायांकित क्षेत्र द्वारा दर्शाइए।
(b) ग्राफ़ का कौन-सा भाग कार की एकसमान गति को दर्शाता है ?
हल :
(a) X – अक्ष के 5 छोटे चिह्न = 2s
Y – अक्ष के 3 छोटे चिह्न – 2 ms^-1
∴ 15 छोटे वर्गों का क्षेत्रफल = 2 s × 2ms^-1
= 4 m
1 छोटे वर्ग का क्षेत्रफल = \(\frac{4}{15}\) m
0 से 5s के अंतर्गत चाल-समय ग्राफ़ का क्षेत्रफल
= 57 छोटे वर्ग + \(\frac{1}{2}\) × 6 छोटे वर्ग
= (57 + 3) वर्ग
= 60 छोटे वर्ग
कार द्वारा 4 सेकंड में तय हुई दूरी = 60 × \(\frac{4}{15}\) m
= 16 m

(b) 6 s पश्चात् कार की एकसमान गति है।

प्रश्न 9.
निम्नलिखित में से कौन-सी अवस्थाएँ संभव हैं तथा प्रत्येक के लिए एक उदाहरण दें:
(a) कोई वस्तु जिसका त्वरण नियत हो परंतु वेग शून्य हो।
(b) कोई वस्तु किसी निश्चित दिशा में गति कर रही हो तथा त्वरण उसके लंबवत् हो।
उत्तर-
(4) हाँ, यह स्थिति संभव है। जब किसी वस्तु को पृथ्वी तल से ऊपर की ओर फेंका जाता है तो अधिकतम ऊँचाई पर वस्तु का वेग शून्य होता है परंतु त्वरण स्थिर रहता है।

(b) हाँ, प्रक्षेप्य की अधिकतम ऊँचाई पर वेग क्षैतिज दिशा में होता है तथा त्वरण लंबवत् दिशा में जैसा कि चित्र में दिखाया गया है।

प्रश्न 10.
एक कृत्रिम उपग्रह 42250 km त्रिज्या की वृत्ताकार कक्षा में घूम रहा है। यदि वह 24 घंटे में पृथ्वी की परिक्रमा करता है तो उसकी चाल का परिकलन कीजिए।
हल :
कृत्रिम उपग्रह के वृत्ताकार पथ की त्रिज्या (r) = 42250 कि० मी०
पृथ्वी के केंद्र पर बना कोण (θ) = 2π रेडियन
पृथ्वी का एक चक्कर लगाने में उपग्रह द्वारा लिया गया समय (t) = 24 घंटे = 24 × 3600 सेकंड
= 86400 सेकंड
अत: कोणीय वेग (ω) = \(\frac{\theta}{\mathrm{t}}\)
= \(\frac{2 \pi}{86400}\) rad/s
उपग्रह का रैखिक वेग (v) = r × ω).
= 42250 × \(\frac{2 \pi}{86400}\) km/s
= \(\frac{42250 \times 2 \times 3.14}{86400}\) km/s
= 3.07 km/s

Science Guide for Class 9 PSEB गति InText Questions and Answers

पाठ्य-पुस्तक के प्रश्नों के उत्तर

प्रश्न 1.
एक वस्तु के द्वारा कुछ दूरी तय की गई। क्या इसका विस्थापन शून्य हो सकता है ? अगर हाँ, तो अपने उत्तर को उदाहरण के द्वारा समझाएँ।
उत्तर-
गति के दौरान विस्थापन की मात्रा शून्य (0) हो सकती है. यदि वह वस्तु गति करते हुए अपनी आरंभिक स्थिति में आ जाये। इस अवस्था में अंतिम स्थिति, आरंभिक स्थिति से मिल जाती है।

उदाहरणार्थ – मान लो एक वस्तु मूल बिंदु O से गति आरंभ करते हुये A बिंदु तक 60 km की दूरी तय करती है। यदि वह वस्तु गति करते हुए वापस A से O बिंदु पर आ जाए तो उस अवस्था में उसका विस्थापन शून्य (0) होगा।

परंतु वस्तु द्वारा तय की गई कुल दूरी = OA + AO
= 60 km + 60 km
= 120 km होगी।

प्रश्न 2.
एक किसान 10 m की भुजा वाले एक वर्गाकार खेत की सीमा पर 40s में चक्कर लगाता है। 2 मिनट (minute) 20 सेकंड (s) बाद किसान के विस्थापन का परिमाण क्या होगा?
हल :

खेत की सीमा (1 चक्कर) = AB + BC + CD + DA
– 10 m + 10m + 10m + 10m
= 40m
खेत की सीमा (40m) का 1 चक्कर लगाने में लगा समय = 40s
कुल समय = 2 मिनट 20 सेकंड = (2 × 60 + 20) सेकंड
= (120 + 20) सेकंड
= 140 सेकंड
किसान 3 चक्कर लगाने के लिए जो समय लगा = 3 × 40 सेकंड
= 120 सेकंड
3 पूरे चक्कर लगाने के बाद शेष समय = (140 – 120) सेकंड
= 20 सेकंड
∴ किसान 40 s में जो दूरी तय करता है = 40 m
∴ 1 s में जो दूरी तय करेगा = 1m
20s में जो दूरी तय करेगा = 20 m
अर्थात् A से गति आरंभ करता हुआ सीमा के साथ-साथ 3 चक्कर लगाकर 2 मिनट 20 सेकंड के पश्चात् C बिंदु पर पहुँच जाएगा।
विस्थापन की मात्रा = AC (मूल बिंदु और अंतिम बिंदु के मध्य न्यूनतम दूरी)
= \(\sqrt{A B^{2}+B C^{2}}\)
= \(\sqrt{(10)^{2}+(10)^{2}}\)
= \(\sqrt{100+100}\)
= \(\sqrt{200 \mathrm{~m}}\)
= \(\sqrt{100 \times 2 \mathrm{~m}}\)
= 10\(\sqrt{2 m}\)
= 10 × 1.414 m
= 14.14 m

प्रश्न 3.
विस्थापन के लिए निम्न में कौन सही है ?
(a) यह शून्य नहीं हो सकता है।
(b) इसका परिमाण वस्तु के द्वारा तय की गई दूरी से अधिक है।
उत्तर-
(a) तथा
(b) दोनों कथनों में से कोई भी सही नहीं है।

प्रश्न 4.
चाल एवं वेग में अंतर बताइए।
उत्तर-
चाल का पूर्ण रूप से व्यक्त करने के लिए केवल परिमाण (मात्रा) की आवश्यकता होती है, जबकि वेग को पूर्ण रूप से व्यक्त करने के लिए परिमाण (मात्रा) तथा दिशा दोनों का होना आवश्यक है। इसलिए चाल एक अदिश राशि है परंतु वेग एक सदिश राशि है। चाल सदैव धनात्मक होती है परंतु वेग धनात्मक तथा ऋणात्मक दोनों प्रकार की हो सकती है। चाल किसी वस्तु की इकाई समय में तय की गई दूरी होती है दूसरी ओर यदि इसके साथ दिशा का ज्ञान भी हो तो यह वेग कहलाता है। अर्थात् एक निश्चित दिशा में चाल को वेग कहते हैं।

प्रश्न 5.
किस अवस्था में किसी वस्तु के औसत वेग का परिमाण उसकी औसत चाल के बराबर होगा ?
उत्तर-

कुल लगा समय जब वस्तु एक सीधी रेखा में परिवर्तनशील गति के साथ एक दिशा में चलती है तो कुल तय की गई दूरी तथा विस्थापन दोनों के परिमाण बराबर होते हैं। इसलिए औसत चाल तथा औसत वेग बराबर होते हैं।

प्रश्न 6.
एक गाड़ी का ओडोमीटर क्या मापता है ?
उत्तर-
गाड़ी (स्वै चालित वाहन) का ओडोमीटर उस द्वारा तय की गई दूरी को मापता है।

प्रश्न 7.
जब वस्तु एकसमान गति में होती है तब इसका मार्ग कैसा दिखाई पड़ता है ?
उत्तर-
जब वस्तु एकसमान गति में होती है तब इसका मार्ग एक सीधी सरल रेखा होता है।

प्रश्न 8.
एक प्रयोग के दौरान, अंतरिक्षयान से एक सिग्नल को पृथ्वी पर पहुँचने में 5 मिनट का समय लगता है। पृथ्वी पर स्थित स्टेशन से उस अंतरिक्षयान की दूरी क्या है ?
(सिग्नल की चाल = प्रकाश की चाल = 3 × 10⁸ ms^-1)
हल :
सिग्नल को अंतरिक्षयान से पृथ्वी तक पहुँचने में लगा समय (t) = 5 मिनट
= 5 × 60 सेकंड
= 300 सेकंड
सिग्नल की चाल (v) = 3 × 10⁸ ms^-1
अंतरिक्षयान की पृथ्वी से दूरी (S) = ?
अंतरिक्षयान की पृथ्वी से दूरी (S) = सिग्नल की चाल (v) × लगा समय (t)
= 3 × 10⁸ × 300 = 3 × 108 × 3 × 10²
= 9 × 10⁸ × 10² = 9 × 10¹⁰ m

प्रश्न 9.
आप किसी वस्तु के बारे में कब कहेंगे कि,
(i) वह एक समान त्वरण से गति में है ?
(ii) वह असमान त्वरण से गति में है ?
उत्तर-
(i) जब कोई वस्तु सरल रेखा में चलती है तब इसका वेग समान समय अंतरालों में समान मात्रा से घटता और बढ़ता है, तब उस समय वह वस्तु एक समान त्वरण से गति करती हुई कहलाती है।

(i) जब किसी वस्तु का वेग असमान दर से परिवर्तित होता है, अर्थात् उस वस्तु का वेग समान समय अंतरालों में असमान मात्रा से घटता और बढ़ता है, तो उस अवस्था में वस्तु असमान त्वरण से गति करती हुई कहलाती है।

प्रश्न 10.
एक बस की गति 5 s में 80 kmh^-1 से घटकर 60 kmh^-1 हो जाती है। बस का त्वरण ज्ञात कीजिए।
हल :
बस का प्रारंभिक वेग (u) = 80 km h^-1
= 80 × \(\frac{5}{18}\) ms^-1
बस का अंतिम वेग (v) = 60 kmh^-1
60 × \(\frac{5}{18}\) ms^-1
लगा हुआ समय (t) = 5s [∵ 1kmh^-1 = \(\frac{5}{18}\) ms^-1]
बस का त्वरण (a) = ?

प्रश्न 11.
एक रेलगाड़ी स्टेशन से चलना प्रारंभ करती है और एकसमान त्वरण के साथ चलते हुए 10 मिनट में 40 kmh^-1 की चाल प्राप्त करती है। इसका त्वरण ज्ञात कीजिए।
हल :
रेलगाड़ी की आरंभिक चाल (u) = 0
रेलगाड़ी की अंतिम चाल (υ) = 40 kmh^-1
= 40 × \(\frac{5}{18}\) ms^-1
= \(\frac{100}{9}\)ms^-1
समय (t) = 10 मिनट
= 10 × 60 सेकंड
= 600 सेकंड
त्वरण (a) = 7

= 0.018 ms^-2

प्रश्न 12.
किसी वस्तु के एक समान व असमान गति के लिए समय-दूरी (x-t) ग्राफ़ की प्रकृति क्या होती है ?
उत्तर-
जब कोई वस्तु बराबर समय में बराबर दूरी तय करती है तब वह एक समान गति से चलती है अर्थात् इस अवस्था में वस्तु द्वारा तय की गई दूरी लगे हुए समय के सीधा अनुपात में होती है। इसलिये एक समान गति की वस्तु के लिए दूरी-समय (x-t) ग्राफ़ एक सरल रेखीय ग्राफ़ होता है।

किसी वस्तु की असमान गति के लिए दूरी-समय (x-t) ग्राफ किसी आकृति का वक्र-रेखीय ग्राफ़ हो सकता है क्योंकि यह वस्तु समान समय अंतरालों में असमान दूरी तय करती है।

प्रश्न 13.
किसी वस्तु की गति के विषय में आप क्या कह सकते हैं, जिसका दूरी-समय ग्राफ़ (x-t) समय अंक्ष के समानांतर एक सरल रेखा है ?
उत्तर-
वह वस्तु जिसका दूरी-समय (x-t) ग्राफ़ समय अक्ष के समानांतर एक सरल रेखा है, विराम अवस्था में होगी।

प्रश्न 14.
किसी वस्तु की गति के विषय में आप क्या कह सकते हैं, जिसका चाल-समय ग्राफ़ समय अक्ष के समानांतर एक सरल रेखा है।
उत्तर-
वह वस्तु जिसका चाल-समय (v-t) ग्राफ़ समय अक्ष के समानांतर सरल रेखा हो, एकसमान चाल से गतिमान होगी।

प्रश्न 15.
वेग-समय ग्राफ़ के नीचे के क्षेत्र से मापी गई राशि क्या होती है ?
उत्तर-
वेग-समय ग्राफ़ के नीचे घिरा हुए क्षेत्र द्वारा एक निश्चित समय में तय की गई दूरी मापता है।

प्रश्न 16.
कोई बस विरामावस्था से चलना प्रारंभ करती है तथा 2 मिनट तक 0.1 ms^-2 के एकसमान चरण से चलती है। परिकलन कीजिए,
(a) प्राप्त की गई चाल तथा
(b) तय की गई दूरी।
हल :
(i) बस का प्रारंभिक वेग (u) = 0 (विरामावस्था)
समय (t) = 2 मिनट
= 2 × 60 सेकंड
= 120 सेकंड
बस का अंतिम वेग (v) = ?
बस द्वारा तय की गई दूरी (S) = ?
हम जानते हैं, v = u + at
v = 0+ 0.1 × 120
v = 1 × 12
v = 12 ms^-1

(ii) अब v² – u² = 2 aS
(12²) – (0²) = 2 × 0.1 × 5
12 × 12 = 2 × 5
∴ S = \(\frac{12 \times 12}{2}\)
= \(\frac{144 \times 10}{2}\)
S = 720 m

प्रश्न 17.
कोई रेलगाड़ी 90 kmh^-1 के चाल से चल रही है। ब्रेक लगाए जाने पर वह – 0.5 ms^-2 का एकसमान त्वरण उत्पन्न करती है। रेलगाड़ी विरामावस्था में आने के पहले कितनी दूरी तय करेगी ?
हल :
रेलगाड़ी का प्रारंभिक वेग (u) = 90 kmh^-1
= 90 × \(\frac{5}{18}\) ms^-1
= 5 × 5ms^-1
= 25 ms^-1
त्वरण (a) = – 0.5 ms^-2
अंतिम वेग (v) = 0 (विरामावस्था)
रेलगाड़ी द्वारा तय की गई दूरी (S) = ?
हम जानते हैं, v² – u² = 2 aS
(0²) – (25²) = 2 × (-0.5) × 5
– 25 × 25 = – 1 × 5
या S = 25 × 25
∴ S = 625 m

प्रश्न 18.
एक ट्रॉली एक आनत तल पर 2 ms^-2 के त्वरण से नीचे जा रही है। गति प्रारंभ करने के 3 s के पश्चात् उसका वेग क्या होगा ? हल :
यहाँ ट्राली का आरंभिक वेग (u) = 0
त्वरण (a) = 2 ms^-2
समय (T) = 3s
ट्राली का अंतिम वेग (v) = ?
V = u + at समीकरण का प्रयोग करने पर
= 0 + 2 × 3
V = 6 ms^-1

प्रश्न 19.
एक रेसिंग कार का एकसमान त्वरण 4 ms^-2 है। गति प्रारंभ करने के 10 s के पश्चात् वह कितनी दूरी तय करेगी ?
हल :
रेसिंग कार का त्वरण (a) = 4 ms^-2
कार का आरंभिक वेग (u) = 0
समय (t) = 10s
कार द्वारा तय की गई दूरी (S) = ?
रेसिंग कार का अंतिम वेग (v) = ?
हम जानते हैं, v = u + at
v = 0 + 4 × 10
∴ v = 40 ms^-1
अब v² – u² = 2aS
(40²) – (0²) = 2 × 4 × S
40 × 40 = 8 × S
S = \(\frac{1600}{8}\)
∴ S = 200 m

प्रश्न 20.
किसी पत्थर को ऊर्ध्वाधर ऊपर की ओर 5 ms^-1 के वेग से फेंका जाता है। यदि गति के दौरान पत्थर का नीचे की ओर दिष्ट त्वरण 10 ms^-2 है, तो पत्थर के द्वारा कितनी ऊँचाई प्राप्त की गई तथा उसे वहाँ पहुँचने में कितना समय लगा ?
हल :
यहाँ, आरंभिक वेग (u) = 5 ms^-1
गुरुत्वात्वरण (a = g) = – 10 ms^-2
अंतिम वेग (v) = 0 (अधिकतम ऊँचाई पर पहुंचकर पत्थर विरामावस्था में आ जाता है)
समय (t) = ?
ऊँचाई (h = S) = ?
हम जानते हैं, v = u + gt
0 = 5 + (-10) × t
0 = 5 – 10t
या 10t = 5
∴ t = \(\frac{5}{10}\) = . 5 s
अब v² – u² = 2 gS
(0)² – (5)² = 2 × 10 × h
-5 × 5 = 20 × h
∴ h = \(\frac{-5 \times 5}{-20}\)
= \(\frac{25}{-20}\)
= \(\frac{5}{4}\)
∴ h = 1.25 m

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 2 बहुपद Ex 2.1 Textbook Exercise Questions and Answers

PSEB Solutions for Class 10 Maths Chapter 2 बहुपद Ex 2.1

प्रश्न 1.
किसी बहुपद p (x) के लिए, y = p(x) का ग्राफ नीचे आकृति में दिया है, प्रत्येक स्थिति में, p(x) के शून्यकों की संख्या ज्ञात कीजिए।]

हल :
किसी बहुपद p(x) के लिए, y = p(x) को ग्राफ नीचे आकृति में दिया है। प्रत्येक स्थिति में, p(x) के शून्यकों की संख्या नीचे दी गई है :

(i) ग्राफ से यह स्पष्ट है कि यह x-अक्ष को किसी भी बिंदु पर नहीं मिलता।
अतः इसका कोई भी शून्यक नहीं है।

(ii) ग्राफ से यह स्पष्ट है कि यह x-अक्ष को केवल एक बिंदु पर मिलता है।
अत: इसका एक शून्यक है।

(iii) ग्राफ से यह स्पष्ट है कि x-अक्ष को तीन बिंदुओं पर मिलता है।
अतः इसके शून्यकों की संख्या तीन है।

(iv) ग्राफ से यह स्पष्ट है कि यह x-अक्ष को दो बिंदुओं पर मिलता है।
अतः इसके शून्यकों की संख्या दो है।

(v) ग्राफ से यह स्पष्ट है कि यह x-अक्ष को चार | बिंदुओं पर मिलता है।
अतः इसके शून्यकों की संख्या चार है।

(vi) ग्राफ से यह स्पष्ट है कि यह x-अक्ष को तीन बिंदुओं पर मिलता है।
अतः इसके शून्यकों की संख्या तीन है।

Punjab State Board PSEB 9th Class Science Book Solutions Chapter 7 जीवों में विविधता Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Science Chapter 7 जीवों में विविधता

PSEB 9th Class Science Guide जीवों में विविधता Textbook Questions and Answers

प्रश्न 1.
जीवों के वर्गीकरण से क्या लाभ हैं ?
उत्तर-
जीवों के वर्गीकरण के लाभ-

1. यह विभिन्न प्रकार के जीवों के अध्ययन को सरल बनाता है।
2. यह सभी जीवों की एकदम स्पष्ट तस्वीर प्रदान करता है।
3. यह जीवों के विभिन्न समूहों के बीच संबंध के बारे में बतलाता है।
4. यह जीव विज्ञान की अन्य शाखाओं को आधार प्रदान करता है।
5. भूगोल का अध्ययन पूर्णतया पौधों तथा जंतुओं के वर्गीकरण पर आधारित है।
6. जीव विज्ञान की अन्य शाखाएं जैसे पारिस्थितिकी, कोशिका विज्ञान, कायिकी आदि का विकास वर्गीकरण के कारण ही संभव हुआ है।

प्रश्न 2.
वर्गीकरण में पदानुक्रम निर्धारण के लिए दो लक्षणों में से आप किस लक्षण का चयन करेंगे ?
उत्तर-
वर्गीकरण में पदानुक्रम निर्धारण के लिए कोशिकीय संरचना, पोषण के स्रोत और तरीके तथा शारीरिक संगठन को आधार बनाया गया है। प्रायः जीवों को उनकी शारीरिक संरचना और कार्य के आधार पर जाना जाता है। शारीरिक बनावट के लक्षण अन्य लक्षणों की तुलना में अधिक परिवर्तन लाते हैं। जब शारीरिक बनावट अस्तित्व में आती है तो यह शरीर में बाद में होने वाले परिवर्तनों को प्रभावित करती है। शरीर का संरचना के दौरान पहले दिखाई देने वाले लक्षणों को मूल लक्षण मानते हैं। वर्गीकरण के पदानुक्रम में जीवों को विभिन्न लक्षणों के आधार पर छोटे से छोटे समूहों में बांट कर आधारभूत इकाई तक पहुँचने में यह पद्धति अधिक सहायक है इसीलिए इसी का चयन ही श्रेष्ठ है। वर्गीकरण का अनक्रम है :
जगत → संघ → वर्ग → गण → कुल → वंश → जाति।

प्रश्न 3.
जीवों के पाँच जगत् के वर्गीकरण के आधार की व्याख्या कीजिए।
उत्तर-
व्हिटेकर ने सन् 1959 में जगत् के वर्गीकरण में पांच आधार स्थापित किए थे। वे हैं-मोनेरा, प्रोटिस्टा, फंजाई, प्लांटी और एनीमेलिया। इनका वर्गीकरण तीन
विशिष्टताओं पर आधारित है-
(I) कोशिकीय संरचना
(II) पोषण के स्रोत और तरीके
(III) शारीरिक संगठन

बाद में कार्ल बोस ने सन् 1977 में इसमें कुछ परिवर्तन किया था तथा मोनेरा किंगडम के आर्थीलैक्टेरिया और यूबैक्टेरिया भागों में विभाजित कर दिया था। वर्गीकरण की आधारभूत इकाई जाति (स्पीशीज़) को माना गया है क्योंकि एक ही जाति के जीवों के बाहय रूप से पर्याप्त समानता होती है। वृहिटेकर के दवारा वर्गीकृत पाँच जगत हैं-
(I) मोनेरा – इस वर्ग में उन एक कोशिकीय प्रोकेरियाटिक जीवों को स्थान दिया गया है जिनमें कोशिका भित्ति पाई जाती है। पोषण के आधार पर ये स्वपोषी या विषमपोषी दोनों हो सकते हैं। नीली हरी शैवाल, जीवाणु, माइक्रो प्लाज्मा आदि इस वर्ग के उदाहरण हैं।

(II) प्रोटिस्टा – इस वर्ग में उन एक कोशिक, यूकेरियोटिक जीवों को स्थान दिया जाता है जिनमें गमन के लिए सीलिया, फ्लैजेला नामक संरचनाएँ विद्यमान होती हैं। ये स्वपोषी और विषमपोषी दोनों प्रकार के होते हैं। एक कोशिक शैवाल, पैरामीशियम, डाइएटमस, प्रोटोजोवा, युग्लीना आदि इस वर्ग के उदाहरण हैं।

(III) फ्रंजाई – इन्हें मृत जीवी भी कहते हैं। ये विषमपोषी यूकेरियोटिक जीव सड़े-गले कार्बनिक पदार्थों पर निर्भर रहते हैं। इनमें से अनेक अपने जीवन में बहुकोशिक क्षमता पा लेते हैं। यीस्ट, मशरूम, पैंसीलियम आदि इनके उदाहरण हैं।

(IV) प्लांटी-इस वर्ग में बहुकोशिक यूकेरियोटिक जीवों को स्थान दिया जाता है जिनमें कोशिका भित्ति होती है। ये स्वपोषी हैं क्योंकि प्रकाश संश्लेषण विधि से ये अपना भोजन सूर्य के प्रकाश में क्लोरोफिल की सहायता से स्वयं तैयार करते हैं। सभी पेड़-पौधों को इसी वर्ग में रखा गया है। थैलोफाइटा, ब्रायेफ़ाइटा, टेरिडोफ़ाइटा, जिम्नोस्पर्म और एंजियोस्पर्म इसी के भाग हैं।

(V) एनीमेलिया – इस वर्ग में बहुकोशिकीय यूकेरियोटीक जीव को स्थान दिया जाता है। इनमें कोशिका भित्ति नहीं होती। इस वर्ग के जीव विषमपोषी होते हैं। सभी रीढ़धारी और अरीढ़धारी जंतु इसी वर्ग के उदाहरण हैं।

प्रश्न 4.
पादप जगत् के प्रमुख वर्ग कौन हैं ? इस वर्गीकरण का क्या आधार है ?
उत्तर-
पादप जगत् के प्रमुख वर्ग हैं-
(I) थैलोफाइटा
(II) ब्रायोफाइटा
(III) टेरिडोफाइटा
(IV) जिम्नोस्पर्म
(V) एंजियोस्पर्म।

इसके वर्गीकरण के आधार हैं-

1. पादप शरीर के प्रमुख घटकों का पूर्ण विकास और विभेदन।
2. पादप शरीर में जल तथा अन्य पदार्थों को संवहन करने वाले विशिष्ट ऊतकों की उपस्थिति।
3. पादप में बीज धारण करने की क्षमता।
4. फल में बीज की स्थिति।

प्रश्न 5.
जंतुओं और पौधों के वर्गीकरण के आधारों में मूल अंतर क्या है ?
उत्तर-
जंतुओं और पौधों के वर्गीकरण के आधारों में मूल अंतर-

पौधे (Plants)	जंतु (Animals)
(1) ये एक स्थान पर स्थिर रहते हैं।	(1) ये एक स्थान से दूसरे स्थान तक भ्रमण करते हैं।
(2) ये सूर्य के प्रकाश में प्रकाश-संश्लेषण द्वारा अपना भोजन स्वयं तैयार करते हैं।	(2) ये पौधों तथा अन्य जंतुओं से अपना भोजन प्राप्त करते हैं।
(3) इनमें अनिश्चित तथा लगातार वृद्धि होती है।	(3) इनमें वृद्धि कुछ विशेष आयु के पश्चात् रुक जाती है।
(4) इनमें पर्णहरित उपस्थित होता है।	(4) इनमें पर्णहरित नहीं होता।
(5) इनकी कोशिका भित्ति सेल्यूलोज की बनी होती है।	(5) इनकी कोशिका भित्ति नहीं होती।

प्रश्न 6.
वर्टीब्रेटा (कशेरुक प्राणी) को विभिन्न वर्गों में बांटने के आधार की व्याख्या कीजिए।
उत्तर-
वर्टीब्रेटा (कशेरुका प्राणी) में वास्तविक मेरुदंड और अंत: कंकाल होता है। उनमें पेशियों का वितरण और पेशियों का कंकाल से संबंध उन्हें चलने-फिरने में सहायक होता है। इनमें मस्तिष्क, हृदय, बाह्य त्वचा के अनेक स्तर, हीमोग्लोबिन, अस्थियां-उपस्थियां (Cartilages) आदि होते हैं। सभी कशेरुकाओं में निम्नलिखित लक्षण पाए जाते हैं-
(I) नोटोकार्ड
(II) कशेरुक दंड और मेरुरज्जु
(III) त्रिकोरिक शरीर
(IV) जोड़ीदार गलफड़
(V) देहगुहा
(VI) समतापी या असमतापी
(VII) अंडज या जरायुज
(VIII) हृदय में कक्षों की संख्या
(IX) क्लोम, त्वचा या फेफड़ों द्वारा श्वसन
(X) कवच रहित या कवच युक्त अंडे।

इनमें ऊतकों और अंगों का जटिल विभेदन पाया जाता है। इसीलिए इन्हें मत्स्य, जल, स्थल, चर, सरीसृप, पक्षी और स्तनधारी वर्गों में बांटा गया है।

Science Guide for Class 9 PSEB ऊतक InText Questions and Answers

पाठ्य-पुस्तक के प्रश्नों के उत्तर

प्रश्न 1.
हम जीवधारियों का वर्गीकरण क्यों करते हैं ?
उत्तर-
संसार में विभिन्न प्रकार के पौधे तथा जंतु पाए जाते हैं। इस में से कुछ जीवों की संरचना सरल तथा कुछ की जटिल होती है। उनके अध्ययन को सरल बनाने के लिए वर्गीकरण किया जाता है जो उनकी समानताओं और असमानताओं पर आधारित होता है।

प्रश्न 2.
अपने चारों ओर फैले जीव रूपों की विभिन्नता के तीन उदाहरण दें।
उत्तर-

1. अमीबा जैसे जीव सूक्ष्मदर्शी से ही देखे जा सकते हैं तो नीली व्हेल तीस मीटर तक लंबी होती है।
2. लाइकेन छोटे धब्बों के समान दिखाई देते हैं तो केलिफोर्निया के रेडवुड पेड़ 100 मीटर लंबे हैं।
3. मच्छर का जीवनकाल कुछ दिन का होता है तो कछुआ 300 वर्ष तक जीवित रह लेता है। सिकोया जैसे वृक्ष तो हजारों वर्ष तक जीवित रहते हैं।

प्रश्न 3.
जीवों के वर्गीकरण के लिए सर्वाधिक मूलभूत लक्षण क्या हो सकता है ?
(a) उनका निवास स्थान
(b) उनकी कोशिका संरचना।
उत्तर-
उनकी कोशिका संरचना।

प्रश्न 4.
जीवों के प्रारंभिक विभाजन के लिए किस मूल लक्षण को आधार बनाया गया ?
उत्तर-
जीवों के स्थल, जल और वायु में रहने के आधार पर।

प्रश्न 5.
किस आधार पर जंतुओं और वनस्पतियों को एक-दूसरे से भिन्न वर्ग में रखा जाता है ?
उत्तर-
जंतुओं को भोजन ग्रहण करने के अनुसार तथा वनस्पतियों को भोजन बनाने की क्षमता के अनुसार एक-दूसरे से भिन्न वर्ग में रखा जाता है।

प्रश्न 6.
आदिम जीव किन्हें कहते हैं ? ये तथाकथित उन्नत जीवों से किस प्रकार भिन्न हैं ?
उत्तर-
आदिम जीव पहले प्रकार के जीवों को कहते हैं। इनकी शारीरिक संरचना में तो खास परिवर्तन नहीं हुआ है पर तथाकथित उन्नत जीवों के समूहों में बदलाव हुआ है जो इन्हें उनसे भिन्न करता है।

प्रश्न 7.
क्या उन्नत जीव और जटिल जीव एक होते हैं ?
उत्तर-
हाँ, उन्नत जीव और जटिल जीव एक होते हैं क्योंकि विकास के दौरान जीवों में जटिलता की संभावना बनी रहती है।

प्रश्न 8.
मोनेरा अथवा प्रोटिस्टा जैसे जीवों के वर्गीकरण का मापदंड क्या है ?
उत्तर-
मोनेरा अथवा प्रोटिस्टा जैसे जीव एक कोशिकीय होते हैं। पोषण के स्तर पर ये स्वपोषी या विषमपोषी दोनों हो सकते हैं।

प्रश्न 9.
प्रकाश-संश्लेषण करने वाले एक कोशिक, यूकेरियोटीक जीव को आप किस जगत में रखेंगे ?
उत्तर-
एक कोशिक शैवाल।

प्रश्न 10.
वर्गीकरण के विभिन्न पदानुक्रमों में किस समूह में सर्वाधिक समान लक्षण वाले सबसे कम जीवों को और किस समूह में सबसे ज्यादा संख्या में जीवों को रखा जाएगा ?
उत्तर-
सबसे कम-जाति (स्पीशीज़)
सबसे ज्यादा-जगत् (किंगडम)।

प्रश्न 11.
सरलतम पौधों को किस वर्ग में रखा गया है ?
उत्तर-
थैलोफाइटा में।

प्रश्न 12.
टेरिडोफाइट और फ़ेनेरोगैम में क्या अंतर है ?
उत्तर-
टेरिडोफाइट में जड़, तना, पत्ती और संवहन ऊतक पाए जाते हैं। इसमें जननांग अप्रत्यक्ष होते हैं तथा बीज उत्पन्न करने की क्षमता नहीं होती पर फेनेरोगेम्स में जनन ऊतक पूर्ण विकसित और विभेदित होते हैं। जनन प्रक्रिया के पश्चात् बीज उत्पन्न करते हैं। बीज के अंदर भ्रूण के साथ संचित खाद्य पदार्थ होता है जिसका उपयोग भ्रूण के प्रारंभिक विकास और अंकुरण के समय होता है।

प्रश्न 13.
जिम्नोस्पर्म और एंजियोस्पर्म एक-दूसरे से किस प्रकार भिन्न हैं ?
उत्तर-
जिम्नोस्पर्म और एंजियोस्पर्म में अंतर-

जिम्नोस्पर्म (अनावृत्तबीजी)	एंजियोस्पर्म (आवृतबीजी)
1. इनके बीज नग्न होते हैं।	1. इनके बीज ढके हुए होते हैं।
2. इनके बीज फलों के द्वारा ढके हुए नहीं होते।	2. इनके बीज फलों के द्वारा ढके होते हैं।
3. यह बीज पाइन तथा साइकस पाए जाते हैं।	3. यह बीज गेहूं, मक्की आदि में पाए जाते हैं।
4. इनमें कोण (Cones) बनते हैं।	4. इनमें फूल बनते हैं।
5. इनमें साथी कोशिका नहीं होती।	5. इनमें साथी कोशिका होती है।
6. इनमें एकल निषेचन होता है।	6. इनमें दोहरा निषेचन होता है।
7. भ्रूणपोष निषेचन से पहले बनता है।	7. भ्रूणपोष निषेचन के बाद बनता है।

प्रश्न 14.
पोरीफ़ेरा और सिलेंटरेटा वर्ग के जंतुओं में क्या अंतर है ?
उत्तर-
पोरीफ़ेरा और सिलेंटरेटा वर्ग के जंतुओं में अंतर-

पोरीफेरा	सिलेंटरेटा
1. इनकी शारीरिक संरचना अति सरल होती है जिसमें ऊतकों का विभेदन नहीं होता।	1. इनका शारीरिक संगठन ऊतकीय स्तर का होता है।
2. इनके पूरे शरीर में अनेक छिद्र होते हैं।	2. इनके शरीर में देहगुहा पायी जाती है।
3. इनके शरीर में नाल प्रणाली होती है और शरीर कठोर आवरण से ढका रहता है।	3. इनका शरीर दो परतों (आंतरिक और बाह्य) से बना होता है।
4. ये अचर हैं तथा किसी आधार से चिपके रहते हैं।	4. ये मिल-जुल कर समूहों में एकाकी रहते हैं। कोरल समूह में रहते हैं तो हाइड्रा एकाकी रहता है।
5. ये स्थिर होते हैं और समूह में पाए जाते हैं।	5. ये चल होते हैं। अकेले या समूह में पाए जाते हैं।

प्रश्न 15.
एनीलिडा के जंतु, आर्थोपोडा के जंतुओं से किस प्रकार भिन्न हैं ?
उत्तर-
एनीलिडा के जंतु, आर्थोपोडा के जंतुओं में अंतर-

एनीलिडा	आर्थोपोडा
1. इनका शरीर द्विपार्श्व सममिति, त्रिकोरक और खंडयुक्त होता है।	1. इनमें द्विपार्श्व सममिति पाई जाती है और शरीर खंडयुक्त होता है।
2. इनकी देहगुहा में अंतरंग पाए जाते हैं।	2. इनमें खुला परिसंचरण तंत्र होता है जिस कारण देहगुहा रक्त से भरी रहती है। देहगुहा सीलोम की बजाय हीमोसील होता है।
3. इसके जीवों की संख्या कम है।	3. इस वर्ग में सबसे अधिक जीव हैं।
4. इनमें नेत्र नहीं होते।	4. इनमें संयुक्त नेत्र होते हैं।
5. आहार नली सीधी होती है।	5. आहार नली कुंडलित नलिका होती है।
6. ये एक लिंगी या द्विलिंगी होते हैं।	6. ये एक लिंगी होते हैं।
7. इनमें परिचलन शूक, चूसक या पैरोपोडिया के द्वारा होता है।	7. इनमें परिचलन संधियुक्त अंगों से होता है।
8. इनमें बाहरी कंकाल नहीं होता।	8. इनका बाह्य कंकाल काइटिन से बना होता है।

प्रश्न 16.
जल-स्थलचर और सरीसृप में क्या अंतर है ?
उत्तर-
जल स्थलचर और सरीसृप में अंतर-

जल स्थलचर	सरीसृप
1. इनकी त्वचा पर श्लेष्म ग्रंथियां होती हैं तथा शल्कों का अभाव होता है।	1. इनका शरीर श्लकों से ढका होता है।
2. इनमें बाह्य कंकाल नहीं होता।	2. इनमें हड्डियों से बना अंत:कंकाल होता है।
3. इनमें श्वसन गलफड़ों, त्वचा या फेफड़ों से होता है।	3. इनमें श्वसन फेफड़ों से होता है।
4. इनके हृदय में दो अलिंद और एक निलय होता है।	4. इसके हृदय में दो अलिंद और अपूर्ण रूप से बंटा हुआ निलय होता है।
5. ये सदा जल में अंडे देते हैं जो कवच रहित होते हैं।	5. ये स्थल पर कवच युक्त अंडे देते हैं।
6. ये जल और स्थल दोनों जगह रह सकते हैं।	6. ये प्रायः स्थल पर रहते हैं और रेंग कर चलते हैं।

प्रश्न 17.
पक्षी वर्ग और स्तनपायी वर्ग के जंतुओं में क्या अंतर है ?
उत्तर-
पक्षी वर्ग और स्तनधारी वर्ग के जंतुओं में अंतर-

पक्षी वर्ग	स्तनपायी वर्ग
1. इनमें लैंगिक दविरूपता स्पष्ट होती है और ये अंडे देते हैं।	1. ये संतान को जन्म देते हैं और इनमें दूध उत्पादन के लिए ग्रंथियां होती हैं। इकिडाना और प्लैटिपस अंडे देते हैं पर बच्चों को दूध पिलाते हैं।
2. इनका शरीर पंखों से ढंका होता है।	2. इनकी त्वचा पूर्ण या आंशिक रूप से बालों से ढकी होती है।
3. इनके आगे वाले पैर उड़ने के लिए पंखों में परिवर्तित हो जाते हैं।	3. इनमें पंख नहीं होते। चमगादड़ अपवाद है।
4. इन में कर्ण पल्लव तथा स्तन ग्रंथियां नहीं होतीं।	4. कर्ण पल्लव तथा स्तन ग्रंथियां होती हैं।
5. ये अंडज होते हैं।	5. ये जरायुज होते हैं।
6. जबड़े दाँत से रहित चोंच में बदल जाते हैं।	6. जबड़े दाँत युक्त होते हैं।

Punjab State Board PSEB 9th Class Science Book Solutions Chapter 6 ऊतक Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Science Chapter 6 ऊतक

PSEB 9th Class Science Guide ऊतक Textbook Questions and Answers

प्रश्न 1.
ऊतक को परिभाषित करें।
उत्तर-
एक समान उत्पत्ति, संरचना और कार्य करने वाली कोशिकाओं के समूह को ऊतक कहते हैं।

प्रश्न 2.
कितने प्रकार के तत्व मिलकर जाइलम ऊतक का निर्माण करते हैं ? उनके नाम बतायें।
उत्तर-
ज़ाइलम ऊतक का निर्माण चार प्रकार की अवयवों के मिलने से होता है, वे हैं-ट्रैकीड्स, वाहिका, ज़ाइलम पैरेंकाइमा और जाइलम फ़ाइबर्स।

प्रश्न 3.
पौधों में सरल ऊतक जटिल ऊतक से किस प्रकार भिन्न होते हैं ?
उत्तर-

सरल ऊतक (Simple Tissue)	जटिल ऊतक (Complex Tissue)
1. ये एक ही प्रकार की कोशिकाओं से निर्मित होते हैं। उदाहरण-पैरेंकाइमा, कालेंकाइमा और स्क्लेरेंकाइमा।	1. ये अनेक प्रकार की कोशिकाओं से मिलकर निर्मित होते हैं। उदाहरण-ज़ाइलम, फ्लोएम।
2. ये परत ऊतक के आधारीय पैकिंग का निर्माण करते हैं।	2. ये संवहन बंडल का निर्माण करते हैं।
3. ये पतली कोशिका भित्ति वाली सरल कोशिकाओं के बने होते हैं।	3. इनकी कोशिका भित्ति मोटी होती है।
4. ये जीवित कोशिकाएं हैं जो शिथिलता से जुड़ी होती हैं इसलिए इनकी कोशिकाओं के बीच काफ़ी जगह पाई जाती है।	4. जाइलम की अधिकांश कोशिकाएं मृत होती हैं तथा फ्लोएम में फ्लोयम रेशे मृत होते हैं। इनकी आकृति नालिकाएं या छिद्रित भित्ति वाली होती है।

प्रश्न 4.
कोशिका भित्ति के आधार पर पैरेंकाइमा, कॉलेंकाइमा और स्कैलेरेंकाइमा के बीच अंतर बताएं।
उत्तर-

पैरेंकाइमा	कॉलेंकाइमा	स्कैलेरेंकाइमा
1. इनमें कोशिका भित्ति पेक्टिन तथा सेल्यूलोज की बनी होती है।	1. इनमें कोशिका भित्ति पेक्टिन तथा सेल्यूलोज की बनी होती है।	1. इनमें कोशिका भित्ति लिजिनन की बनी होती है।
2. यह गोल, बारीक कोशिका भित्ति वाली कोशिकाओं से बना होता है।	2. यह बहुभुजी कोशिकाओं का बना होता है।	2. यह मोटी भित्ति वाली कोशि-काओं का बना होता है।

प्रश्न 5.
रंध्र के क्या कार्य हैं ?
उत्तर-
रंध्र वायुमंडल से गैसों का आदान-प्रदान करते हैं। वाष्पोत्सर्जन की क्रिया भी इन्हीं के द्वारा होती है।

प्रश्न 6.
तीनों प्रकार के पेशीय रेशों के चित्र बनाकर अंतर स्पष्ट करें।
उत्तर-
पेशीय ऊतक लंबी कोशिकाओं का बना होता है जिसे पेशीय रेशा भी कहते हैं। ये हमारे शरीर में गति के लिए उत्तरदायी होता है। ये तीन प्रकार के हैं-ऐच्छिक पेशी, अनैच्छिक पेशी और हृदय पेशी।

अंतर

ऐच्छिक पेशी	अनैच्छिक पेशी	हृदय पेशी
1. ये प्रायः अस्थियों से जुड़ी होती हैं।	1. ये आंख की पलकों, मूत्रवाहिनी और फेफड़ों की श्वसनी में होती हैं।	1. ये हृदय में पाई जाती है।
2. ये ऐच्छिक होती हैं।	2. ये अनैच्छिक होती हैं।	2. ये अनैच्छिक होती हैं।
3. इनमें गहरे तथा हल्के रंग की पटियां होती हैं। इसलिए इन्हें रेखित पेशियां भी कहते हैं।	3. इनमें गहरे तथा हल्के रंग की पटियां नहीं होती। इसीलिए इन्हें अरेखित पेशियां भी कहते हैं।	3. इनमें गहरे तथा हल्के रंग की पटियां नहीं होती।
4. ये लंबी, बेलनाकार, शाखारहित और और बहुनाभीय होती हैं।	4. ये लंबी, एक केंद्रकीय और बहु सिरे से नुकीली होती हैं।	4. ये बेलनाकार शाखाओं वाली बहु केंद्रकीय होती है।

प्रश्न 7.
कॉर्डिक ( हृदयक) पेशी का विशेष कार्य क्या है ?
उत्तर-
हृदयक पेशी का विशेष कार्य पूरे जीवन भर लयबद्ध होकर बिना थके हुए प्रसार और संकुचन करना है। इसी के परिणामस्वरूप रक्त सारे शरीर में गति करता है।

प्रश्न 8.
रेखित, अरेखित तथा कार्डियक ( हृदयक ) पेशियों में शरीर में स्थित कार्य और स्थान के आधार पर अंतर स्पष्ट करें।
उत्तर-

	रेखित पेशियां	अरेखित पेशियां	कार्डियक (हृदयक) पेशियां
शरीर में स्थिति स्थान	हाथ, पैर, अस्थियों से जुडी हुई।	आहारनली में भोजन का प्रवाह आँख की पलक, मूत्रवाहिनी, फेफड़ों की श्वसनी, रक्त नली का प्रसार एवं सकुंचन।	हृदय की दीवारों में पाई जाती हैं।
कार्य	शरीर को इच्छानुसार गति प्रदान करती है।	ये जंतु की इच्छा पर संचालित नहीं होती। पेशियां स्वयं इन की गति नियंत्रित करती हैं।	पेशियां स्वयं नियंत्रित करके के हृदय की धड़कन बनाए रखता हैं।

प्रश्न 9.
न्यूरॉन का एक चिह्नित चित्र बनायें।
उत्तर-
पाठ्य-पुस्तक के प्रश्नों के उत्तर के अंतर्गत प्रश्न संख्या 2 पृष्ठ संख्या 139 देखिए।

प्रश्न 10.
निम्नलिखित के नाम लिखें-
(अ)ऊतक जो मुँह के भीतर अस्तर का निर्माण करता है।
(ब) ऊतक जो मनुष्य की पेशियों को अस्थि से जोड़ता है।
(स) ऊतक जो पौधों में भोजन का संवहन करता है।
(द) ऊतक जो हमारे शरीर में वसा का संचय करता है।
(य) तरल आधात्री सहित संयोजी ऊतक,
(र) मस्तिष्क में स्थित ऊतक।
उत्तर-
(अ) शल्की एपिथीलियम (Squanous Epithelium)
(ब) कंडरा (Tendon)
(स) फ्लोएम (Phloem)
(द) वसामय ऊतक (Adipose Tissue)
(य) रक्त (Blood)
(र) न्यूरॉन (Neuron)।

प्रश्न 11.
निम्नलिखित में ऊतक के प्रकार की पहचान करें-
त्वचा, पौधे का वल्क, अस्थि, वृक्कीय नलिका अस्तर, संवहन बंडल।
उत्तर-
त्वचा – शल्की एपिथीलियम ऊतक
पौधे का वल्क – विभाज्योतक
अस्थि – अस्थि संयोजी ऊतक
वृक्कीय नलिका अस्तर – घनाकार एपिथीलियम
संवहन बंडल – जटिल ऊतक।

प्रश्न 12.
पैरेंकाइमा ऊतक किस क्षेत्र में स्थित होते हैं ? नाम बतायें।
उत्तर-
जब पैरेंकाइमा में क्लोरोफिल पाया जाता है, जिसके कारण प्रकाश-संश्लेषक की क्रिया संपन्न होती है तब इसे क्लोरेंकाइमा कहते हैं। जलीय पौधों में जब पैरेंकाइमा की कोशिकाओं में हवा भरी होती है और यह पौधों को तैरने के लिए उत्पलावन बल प्रदान करते हैं तब इसे एरेंकाइमा कहते हैं।

प्रश्न 13.
पौधों में एपीडर्मिस की क्या भूमिका है ?
उत्तर-
पौधों की कोशिकाओं की सबसे बाहरी परत एपीडर्मिस है। शुष्क स्थानों पर मिलने वाले पौधों में यह मोटी हो जाती है और पानी की हानि को कम कर उनकी रक्षा करती है। पौधों की पूरी सतह एपीडर्मिस से ढकी रहती हैं। इसलिए यह पौधों के सभी भागों की रक्षा करती है। इसके बाहर मोम जैसी जल प्रतिरोधी परत बनती है जो जल हानि के विरुद्ध यांत्रिक आघात तथा परजीवी कवक के प्रवेश से पौधों की रक्षा करती है। पत्तियों की एपीडर्मिस में छोटे-छोटे रंध्रों से वायुमंडल से गैसों का आदान-प्रदान होता है, इन्हीं से वाष्पोत्सर्जन क्रिया होती है। जड़ों की एपीडर्मल कोशिकाएं पानी सोखने का कार्य करती हैं । मरुस्थलीय पौधों के बाहरी सतह वाले एपीडर्मिस में रासायनिक पदार्थ क्यूटिन होता है जिस कारण पानी का वाष्प नहीं होता।

प्रश्न 14.
छाल (कॉर्क) किस प्रकार सुरक्षा ऊतक के रूप में कार्य करता है ?
उत्तर-
छाल (कॉर्क) पौधों के भीतर की कोशिकाओं की रक्षा करता है। इसका सुरक्षा ऊतक के रूप में कार्य रोधन तथा घातरोधत का है। जब वृक्ष की आयु बढ़ती है तो उस पर विभाज्योतक की पट्टी आ जाती है। बाहरी सतह की कोशिकाएं इससे अलग हो जाती हैं तथा पौधों पर बहुपरतों वाली मोटी कार्क का निर्माण करती है। यह मृत कोशिकाओं की होती है और बिना अंत:कोशिकीय स्थानों के होती है। इस पर सुबरिन नामक रसायन होता है जो हवा और पानी को प्रवेश नहीं करने देता।

प्रश्न 15.
निम्न दी गई तालिका को पूर्ण करें।

उत्तर-

Science Guide for Class 9 PSEB ऊतक InText Questions and Answers

पाठ्य-पुस्तक के प्रश्नों के उत्तर

प्रश्न 1.
ऊतक क्या हैं ?
उत्तर-
ऊतक समान उत्पत्ति, संरचना तथा कार्य करने वाली कोशिकाओं का एक समूह होता है।

प्रश्न 2.
बहुकोशिक जीवों में ऊतकों का क्या उपयोग है ?
उत्तर-
बहुकोशिकीय जीवों में लाखों कोशिकाएं होती हैं जो परस्पर मिलकर ऊतकों के रूप में विशेष कार्यों को संपन्न कराती हैं। मनुष्यों तथा पशु-पक्षियों में पेशिया इन्हीं से फैलती-सिकुड़ती हैं जिससे गति होती है, तंत्रिका से संदेशों का वहन होता है, रक्त ऑक्सीजन, भोजन, हारमोन तथा अपशिष्ट पदार्थों का वहन होता है। पौधों में भोजनपानी एक स्थान से दूसरे स्थान तक जाता है। ऊतक पेड़-पौधों को स्थिरता प्रदान करते हैं, उन्हें सहारा और मज़बूती देते हैं।

प्रश्न 3.
प्रकाश-संश्लेषण के लिए किस गैस की आवश्यकता होती है ?
उत्तर-
प्रकाश-संश्लेषण के लिए कार्बन डाइऑक्साइड गैस की आवश्यकता होती है।

प्रश्न 4.
पौधों में वाष्पोत्सर्जन के कार्यों का उल्लेख करें।
उत्तर-
पौधों के पत्तों में छोटे-छोटे छिद्र होते हैं जिन्हें स्टोमेटा कहते हैं। इन पर रक्षी कोशिकाएं होती हैं जो गैसों का आदान-प्रदान करती हैं। ये पृथ्वी से प्राप्त जल का वाष्पन करती हैं।
पौधों में वाष्पोत्सर्जन के उपयोग-

1. इससे पौधों में यांत्रिक रूतक सुदृढ़ होते हैं।
2. इसके खिंचाव के कारण पौधों में जल और खाद्य लवणों का संवहन होता है।
3. इससे जल पौधे के माध्यम से वायुमंडल में प्रवेश करता है जिससे पौधों का तापमान नहीं बढ़ पाता।
4. पौधे से अतिरिक्त जल का निष्कासन हो जाता है।

प्रश्न 5.
सरल ऊतकों के कितने प्रकार हैं ?
उत्तर-
सरल स्थायी ऊतक तीन प्रकार के हैं। वे हैं-पैरेंकाइमा (मृदुतक Parenchyma), कालेंकाइमा (स्थूल कोण ऊतक Collenchyma), स्क्ले रेंकाइमा (दृढ़ ऊतक Sclerenchyma)।

प्रश्न 6.
प्ररोह का शीर्षस्थ विभाज्योतक कहाँ पाया जाता है ?
उत्तर-
जड़ों और तनों की वृद्धि वाले भाग में पाया जाता है और यह इनकी लंबाई में वृद्धि करता है।

प्रश्न 7.
नारियल का रेशा किस ऊतक से बना होता है ? उत्तर-नारियल का रेशा स्क्लेरेंकाइमा ऊतक से बना होता है। प्रश्न 4. फ्लोएम के संघटक कौन-कौन से हैं ?
उत्तर-
चालनी नलिका, साथी कोशिका, फ्लोएम पैरेंकाइमा तथा फ्लोएम रेशे।

प्रश्न 8.
उस ऊतक का नाम बतायें जो हमारे शरीर में गति के लिए उत्तरदायी है।
उत्तर-
तंत्रिका और पेशीय ऊतकों का कार्यात्मक संयोजन हमारे शरीर में गति के लिए उत्तरदायी है।

प्रश्न 9.
न्यूरॉन देखने में कैसा लगता है ?
उत्तर-
तंत्रिका ऊतक की कोशिकाओं को न्यूरॉन कहते हैं । इन में कोशिकाओं केंद्रक तथा साइटोप्लाज़म होते हैं। इससे लंबे और पतले बालों जैसी शाखाएं निकली होती हैं। इसमें एक लंबा प्रवर्ध होता है जिसे एक्सॉन कहते हैं और बहुत सारी छोटी शाखा वाले प्रवों को डेंडराइट्स कहते हैं। एक न्यूरॉन एक मीटर लंबी हो सकती है।

प्रश्न 10.
हृदय पेशी के तीन लक्षणों को बतायें।
उत्तर-

1. हृदय पेशी अनैच्छिक पेशियों से बनती हैं। इन्हें कार्डिक (हृदयक) पेशी कहते हैं।
2. यह बेलनाकार, शाखाओं वाली और एक केंद्रकीय होती है।
3. यह जीवन भर लयबद्ध होकर प्रसार एवं संकुचन करती है।

प्रश्न 4.
एरीओलर ऊतक के क्या कार्य हैं ?
उत्तर-
एरीओलर ऊतक संयोजनी ऊतक, त्वचा और मांसपेशियों के बीच, रक्त नलिका के चारों ओर तथा नसों और अस्थि मज्जा में पाया जाता है। यह अंगों के भीतर की खाली जगह को भरता है तथा भीतरी अंगों को सहारा देता है। यह ऊतकों की मरम्मत करता है।

Punjab State Board PSEB 9th Class Science Book Solutions Chapter 5 जीवन की मौलिक इकाई Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Science Chapter 5 जीवन की मौलिक इकाई

PSEB 9th Class Science Guide जीवन की मौलिक इकाई Textbook Questions and Answers

प्रश्न 1.
पादप कोशिकाओं तथा जंतु कोशिकाओं में तुलना करो।
उत्तर-
पादप कोशिका तथा प्राणी (जंतु) कोशिका में अंतर

प्रश्न 2.
प्रोकैरियोटी कोशिकाएँ यूकैरियोटी कोशिकाओं से किस प्रकार भिन्न होती हैं ?
उत्तर-
प्रोकैरियोटी व यूकैरियोटी कोशिकाओं में भेद-

प्रोकैरियोटी कोशिका (Prokaryotic Cell)	यूकैरियोटी कोशिका (Eukaryotic Cell)
(1) ये प्राय छोटे आकार के होते हैं (1-10 μm)।	(1) ये प्रायः बड़े आकार के होते हैं (5-100 um)।
(2) इसमें झिल्लियों द्वारा घिरे कोशिकांग जैसे अंतः प्रदव्यी जालिका, गाल्जीकाय, लाइसोसोम, माइटोकांड्रिया आदि अनुपस्थित होते हैं।	(2) इन कोशिकाओं में झिल्लियों द्वारा घिरे सभी कोशिकांग पाए जाते हैं।
(3) इनमें राइबोसोम 70 S प्रकार के होते हैं।	(3) इनमें राइबोसोम 80 S प्रकार के होते हैं।
(4) इनमें गुण-सूत्र डी० एन० ए० के बने होते हैं तथा कोशिका द्रव्य में पाए जाते हैं।	(4) इनमें गुण-सूत्र डी० एन० ए० के बने होते हैं तथा केंद्रक कवक में पाए जाते हैं।
(5) इनमें गुण-सूत्र केंद्रक कला द्वारा घिरे हुए नहीं होते।	(5) इनमें गुण-सूत्र केंद्रक कला द्वारा घिरे हुए होते हैं।
(6) इसमें केंद्रिकाएं अनुपस्थित होती हैं।	(6) इसमें केंद्रिकाएं पाई जाती हैं।
(7) इसमें केवल एक गुण-सूत्र होता है।	(7) इसमें एक से अधिक गुण-सूत्र होते हैं।
(8) इसमें कोशिका विभाजन कलिका उत्पादन (budding) अथवा खंडन (fission) विधि द्वारा होता है।	(8) इसमें कोशिका विभाजन सूत्री (mitosis) अथवा अर्ध सूत्री (meiosis) विधि द्वारा होता है।

प्रश्न 3.
यदि प्लैज्मा झिल्ली फट जाए अथवा टूट जाए तो क्या होगा ?
उत्तर-
यदि प्लैज्मा झिल्ली फट जाए अथवा टूट जाए तो कोशिका अंगक लाइसोसोम फट जाएंगे और एंजाइम अपनी ही कोशिकाओं को पाचित कर लेंगे। ऐसी स्थिति में कोशिका का जीवित रहना कठिन हो जाएगा।

प्रश्न 4.
यदि गॉल्जी उपकरण न हो तो कोशिका के जीवन में क्या होगा ?
उत्तर-
यदि गॉल्जी उपकरण न हो अंतर्द्रव्यी जालिका (ER) में संश्लेषित पदार्थ कोशिका के बाहर तथा अंदर विभिन्न क्षेत्रों में नहीं आ पाएंगे। यह लाइसोसोम को बनाने में सहायक है जिससे कोशिका का अपशिष्ट निपटाया जाता है। गॉल्जी उपकरण के बिना पदार्थों का संचयन और रूपांतरण नहीं हो पाएगा।

प्रश्न 5.
कोशिका का कौन-सा अंगक बिजलीघर है ? और क्यों ?
उत्तर-
माइटोकांड्रिया कोशिका का बिजलीघर है। इसे कोशिका में भोजन पदार्थों के ऑक्सीकरण का स्थान माना जाता है। इसके श्वसन से पर्याप्त मात्रा में ऊर्जा मुक्त होती है। इसी कारण इसे कोशिका का ऊर्जा घर कह जाता है।

प्रश्न 6.
कोशिका झिल्ली को बनाने वाले लिपिड तथा प्रोटीन का संश्लेषण कहाँ होता है ?
उत्तर-
खुरदरी अंतर्द्रव्यी जालिका (RER) पर राइबोसोम लगे होते हैं जो प्रोटीन का संश्लेषण करते हैं। चिकनी अंतर्द्रव्यी जालिका (SER) लिपिड का संश्लेषण करती है।

प्रश्न 7.
अमीबा अपना भोजन कैसे प्राप्त करता है ?
उत्तर-
कोशिका झिल्ली में लचीलापन होता है जो अमीबा को बाह्य पर्यावरण से अपना भोज्य तथा अन्य पदार्थ ग्रहण करने में सहायता करता है। जिस प्रक्रिया से अमीबा अपना भोजन प्राप्त करता है, उसे एंडोसाइटोसिस कहते हैं। अमीबा जल में पाए जाने वाले सूक्ष्म जीवों को अपना आहार बनाता है। वह अपने भोजन को किसी भी सतह से कूटपाद के द्वारा ग्रहण कर लेता है। जब भोज्य पदार्थ उसके संपर्क में आता है तो वह अपने कूटपादों से उसे चारों ओर से घेर लेता है और वह प्यालेनुमा रचना के द्वारा करता है जिसे खाद्यधानी या रिक्तिका कहते हैं। इस तरह खाद्य पदार्थ

कोशिका द्रव्य में खाद्य के साथ खाद्यधानी कोशिका के भीतर एक थैली में बंद हो जाता है। अंतर्कोशिकीय पाचन प्रणाली से भोजन का पाचन एंजाइमों की सहायता से खाद्यधानी में होता है। पचा हुआ भोजन विसरण-प्रक्रिया से कोशिका द्रव्य में जाकर अवशोषित हो जाता है जिसे स्वांगीकरण कहते हैं । जो भोजन पच नहीं पाता वह शारीरिक सतह से खाद्य रिक्तिका के माध्यम से बाहर निकल जाता है। इसे बाहय क्षेपण कहते हैं।

प्रश्न 8.
परासरण क्या है ?
उत्तर-
परासरण – जल के अणुओं की गति जब वर्णात्मक पारगम्य झिल्ली के द्वारा हो तो उसे परासरण कहते हैं। प्लैज्मा झिल्ली से जल की गति जल में घुले पदार्थों की मात्रा के कारण प्रभावित होती है। जल के अणु वर्णात्मक पारगम्य झिल्ली से उच्च जल की सांद्रता से निम्न जल की सांद्रता की ओर जाते हैं। वर्णात्मक पारगम्य झिल्ली अपने छोटे-छोटे छिद्रों से जल अणुओं को पार गुजरने देती है पर घुलनशील पदार्थ के बड़े अणु इससे नहीं गुज़र पाते।

परागम्य झिल्ली परासरण प्रक्रिया की घटनाएं प्रायः तीन प्रकार की होती हैं-
(क) अल्पपरासरण – यदि कोशिका को तनु घोल माध्यम में रखा जाए तो जल परासरण विधि से जल कोशिका में चला जाता है। तनु घोल में नमक या चीनी या किसी अन्य लवण की मात्रा कम और जल की मात्रा ज्यादा होती है। जल के अणु कोशिका झिल्ली के दोनों ओर आने-जाने के लिए स्वतंत्र होते हैं पर कोशिका के भीतर जाने वाले जल की मात्रा कोशिका से बाहर आने वाले जल की मात्रा से अधिक होगी। इसका परिणाम यह होता है कि कोशिका फूलने लगती है। जल में डूबी किशमिश या खुबानी इसी कारण फूल जाती हैं।

(ख) सम परासरण – यदि कोशिका ऐसे माध्यम घोल में रखी जाए जिसमें बाहरी जल की सांद्रता कोशिका में विद्यमान जल की सांद्रता के बिल्कुल बराबर हो तो कोशिका झिल्ली से जल में से कोई शुद्ध गति नहीं होगी। जल कोशिका में आता-जाता है पर जल की जो मात्रा भीतर जाती है उतनी ही बाहर आ जाती है।

(ग) अति परासरण – यदि कोशिका के बाहर वाला घोल भीतर के घोल से सांद्र हो तो जल परासरण से कोशिका से बाहर आ जाएगा। इस स्थिति में कोशिका से ज्यादा जल बाहर आएगा और कम जल भीतर जाएगा।

प्रश्न 9.
निम्नलिखित परासरण प्रयोग करें
छिले हए आधे-आधे आलू के चार टुकड़े लो, इन चारों को खोखला करो जिससे कि आलू के कप बन जाएँ। इनमें से एक कप को उबले आलू में बनाना है। आलू के प्रत्येक कप को जल वाले बर्तन में रखो। अब
(a) कप ‘A’ को खाली रखो,
(b) कप ‘B’ में एक चम्मच चीनी डालो,
(c) कप ‘C’ में एक चम्मच नमक डालो तथा
(d) उबले आलू से बनाए गए कप ‘D’ में एक चम्मच चीनी डालो।
आलू के इन चारों कपों को दो घंटे तक रखने के पश्चात् उनका अवलोकन करो तथा निम्न प्रश्नों का उत्तर दो :
(i) ‘B’ तथा ‘C’ खाली भाग में जल क्यों एकत्र हो गया ? इसका वर्णन करो।
(ii) ‘A’ आलू इस प्रयोग के लिए क्यों महत्त्वपूर्ण है ?
(iii) ‘A’ तथा ‘D’ आलू के खाली भाग में जल एकत्र क्यों नहीं हुआ ? इसका वर्णन करो।
उत्तर-
छिले हुए कच्चे आलू से बने तीन तथा उबले हुए आलू से बने एक कप को चित्रानुसार जल से भरे बर्तन में रखो।

(i) B और C कप में जल एकत्रित हो गया। कच्चे आलू से बने दोनों कप वर्णात्मक पारगम्यता का कार्य करते हैं और जल परासरण विधि से जल खोखले आलुओं के भीतर चला गया। क्योंकि उनके भीतर चीनी और नमक विद्यमान थे। यह अल्पपरासरण का परिणाम है क्योंकि आलू के कपों के अंदर जाने वाले जल की मात्रा उससे बाहर आने वाले जल की मात्रा से अधिक थी।

(ii) ‘A’ आलू का कप कच्चे आलू से बना था जो वर्णानात्मक पारगम्य झिल्ली का कार्य करता है। भीतर से खाली होने के कारण जल में कोई शुद्ध गति नहीं हुई। यह नियंत्रण का कार्य करता है।

(iii) A और D कपों में जल एकत्रित नहीं हुआ क्योंकि दोनों में बाहरी जल की सांद्रता कपों में स्थित जल की सांद्रता के बराबर थी। जिस कारण परासरण नहीं होता। कप A कच्चे आलू का बना था और भीतर से खाली था पर कप D उबले आलू का था जिसमें एक चम्मच चीनी थी। उबला होने के कारण वह वर्णात्मक पारगम्य झिल्ली का कार्य नहीं करेगा। जिस कारण आलू के कपों से जल में कोई शुद्ध गति नहीं हो सकी।

Science Guide for Class 9 PSEB जीवन की मौलिक इकाई InText Questions and Answers

पाठ्य-पुस्तक के प्रश्नों के उत्तर

प्रश्न 1.
कोशिका की खोज किसने और कैसे की ?
उत्तर-
कोशिका की खोज रॉबर्ट हुक ने सन् 1665 में की थी। उन्होंने स्वनिर्मित सूक्ष्मदर्शी से कार्य की पतली काट को देखा था जिस में मधुमक्खी के छत्ते जैसी संरचना दिखाई दी थी। लेटिन भाषा में Cellulae (कोशिका) का अर्थ ‘छोटा कमरा’ है और यही नाम कोशिका के लिए प्रचलित हो गया था।

प्रश्न 2.
कोशिका को जीवन की संरचनात्मक व क्रियात्मक इकाई क्यों कहते हैं ?
उत्तर-
कोशिका की रचना अनेक कोशिकाओं से होती है। कोशिकाओं की आकृति और आकार उनके विशेष कार्यों के अनुरूप होते हैं। कोशिकांगों के कारण ही कोई कोशिका जीवित रहती है और अपने सभी कार्य करती है इसीलिए कोशिका को जीवन की संरचनात्मक और क्रियात्मक इकाई कहते हैं।

प्रश्न 3.
CO₂ तथा पानी जैसे पदार्थ कोशिका से कैसे अंदर तथा बाहर जाते हैं ? इस पर चर्चा करें।
उत्तर-
CO₂ तथा पानी जैसे पदार्थ कोशिका झिल्ली से आर-पार विसरण प्रक्रिया द्वारा आ-जा सकते हैं।

(i) CO₂ का बाहर जाना – CO₂ एक कोशीय अपशिष्ट है जिसे कोशिका से बाहर निकालना आवश्यक है। जब कोशिका में इसकी मात्रा बढ़ जाती है तो इसकी सांद्रता वातावरण में उपस्थित CO₂ की सांद्रता से बढ़ जाती है। जैसे ही कोशिका के भीतर और बाहर CO, की सांद्रता में अंतर आता है वैसे ही उच्च सांद्रता से निम्न सांद्रता की ओर विसरण द्वारा कोशिका से CO₂ बाहर निकल जाती है।

(ii) O₂ का भीतर जाना – जब कोशिका में ऑक्सीजन की सांद्रता कम हो जाती है तो वह बाहर से कोशिका में विसरण द्वारा भीतर चली जाती है।

(iii) पानी का भीतर तथा बाहर जाना – पानी भी विसरण के नियमों के अनुसार व्यवहार करता है। पानी के अणुओं की गति जब वर्णात्मक पारगम्य झिल्ली से होती है तो उसे परासरण कहते हैं । प्लैज्मा झिल्ली से पानी की गति पानी में घुले हुए पदार्थों की मात्रा के कारण प्रभावित होती है। वर्णात्मक पारगम्य झिल्ली से पानी के अणु उच्च पानी की सांद्रता से निम्न पानी की सांद्रता की तरफ गति करते हैं। यदि कोशिका को तनु विलयन वाले माध्यम में रखा जाए तो पानी अधिक मात्रा में होने के कारण परासरण विधि से कोशिका में चला जाएगा। पानी के अणु कोशिका झिल्ली के दोनों और आने-जाने के लिए स्वतंत्र होते हैं पर कोशिका के भीतर जाने वाले पानी की मात्रा कोशिका से बाहर आने वाले पानी की मात्रा से ज्यादा होगी, यदि कोशिका में पानी अधिक गया तो वह फूलने लगती है। यदि कोशिका को ऐसे माध्यम में रखा जाए जिसमें बाहरी पानी की सांद्रता कोशिका में विद्यमान पानी की सांद्रता के बराबर हो तो कोशिका झिल्ली से न पानी जाता है और न ही पानी आता है। यदि कोशिकाओं के बाहर वाला विलयन भीतर के घोल से सांद्र हो तो पानी परासरण से कोशिका से बाहर आ जाएगा जिस कारण कोशिका सिकुड़ जाएगी।

प्रश्न 4.
प्लैज्मा झिल्ली को वर्णात्मक पारगम्य झिल्ली क्यों कहते हैं ?
उत्तर-
लिपिड और प्रोटीन से बनी प्लैज़्मा झिल्ली लचीली होती है जो कोशिका के घटकों को बाहरी पर्यावरण से अलग करती है। यह कुछ पदार्थों को अंदर या बाहर आने-जाने देती है। यह अन्य पदार्थों की गति को भी रोकती है। विसरण प्रक्रिया से CO₂ तथा O₂ इसके आर-पार जा सकती है। जल के अणुओं की गति भी परासरण प्रक्रिया से होती है। चूंकि प्लैज्मा झिल्ली आवश्यक पदार्थों को उच्च सांद्रता से निम्न सांद्रता की ओर आने-जाने देती है इसलिए इसे वर्णात्मक पारगम्य झिल्ली कहते हैं।

प्रश्न 5.
क्या अब आप निम्नलिखित तालिका में दिए गए रिक्त स्थानों को भर सकते हैं, जिससे कि प्रोकैरियोटी तथा यूकैरियोटी कोशिकाओं में अंतर स्पष्ट हो सके :

प्रोकैरियोटी कोशिका	यूकैरियोटी कोशिका
1. आकार प्रायः छोटा (1-10 μm) 1 μm = 10-6m.	1. आकार प्रायः बड़ा (5-100 μm)
2. केंद्रकीय क्षेत्र : ………………….. और उसे ……….. कहते हैं।	2. केंद्रकीय क्षेत्र : सुस्पष्ट जो चारों ओर से केंद्रकीय झिल्ली से घिरा रहता है।
3. क्रोमोसोम : एक	3. क्रोमोसोम : एक से अधिक
4. झिल्ली युक्त कोशिका अंगक अनुपस्थित	4. …………………………

उत्तर-

प्रोकैरियोटी कोशिका	यूकैरियोटी कोशिका
1. आकार प्रायः छोटा (1-10 μm) 1μm = 10-6m.	1. आकार प्रायः बड़ा (5-100 μm)
2. केंद्रकीय क्षेत्र : अस्पष्ट केंद्रक क्षेत्र में केवल क्रोमैटिन पदार्थ होता है और उसे केंद्रकाय कहते हैं।	2. केंद्रकीय क्षेत्र : सुस्पष्ट जो चारों ओर से केंद्रकीय झिल्ली से घिरा रहता है।
3. क्रोमोसोम : एक	3. क्रोमोसोम : एक से अधिक
4. झिल्ली युक्त कोशिका अंगक अनुपस्थित।	4. केंद्रकीय झिल्ली तथा झिल्ली युक्त उपस्थित।

प्रश्न 6.
क्या आप दो ऐसे अंगकों का नाम बता सकते हैं जिनमें अपना आनुवंशिक पदार्थ होता है ?
उत्तर-
माइटोकाँड्रिया तथा प्लैस्टिड में अपना DNA अणु के रूप में होता है जिनमें कोशिका के निर्माण और संगठन की सभी आवश्यक सूचनाएं होती हैं।

प्रश्न 7.
यदि किसी कोशिका का संगठन किसी भौतिक अथवा रासायनिक प्रभाव के कारण नष्ट हो जाता है, तो क्या होगा ?
उत्तर-
यदि किसी कोशिका का संगठन किसी भौतिक या रासायनिक प्रभाव के कारण नष्ट हो जाता है तो कोशिका का अपशिष्ट निपटाने वाला तंत्र लाइसोसोम फट जाते हैं और एंजाइम अपनी ही कोशिकाओं को पाचित कर देते हैं।

प्रश्न 8.
लाइसोसोम को आत्मघाती थैली क्यों कहते हैं ?
उत्तर-
जब कोशिका क्षतिग्रस्त या मृत हो जाती है तो लाइसोसोम फट जाते हैं और एंजाइम अपनी ही कोशिकाओं को पचा लेते हैं इसलिए लाइसोसोम को ‘आत्मघाती थैली’ कहते हैं।

प्रश्न 9.
कोशिका के अंदर प्रोटीन का संश्लेषण कहाँ होता है ?
उत्तर-
कोशिका द्रव्य में राइबोसोम छोटे-छोटे कणों के रूप में अंतः प्रद्रव्यी जालिका के तल पर तथा केंद्रक झिल्ली के ऊपर मिलते हैं जो प्रोटीन का संश्लेषण करने में सहायक होते हैं।

Punjab State Board PSEB 9th Class Science Book Solutions Chapter 4 परमाणु की संरचना Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Science Chapter 4 परमाणु की संरचना

PSEB 9th Class Science Guide परमाणु की संरचना Textbook Questions and Answers

प्रश्न 1.
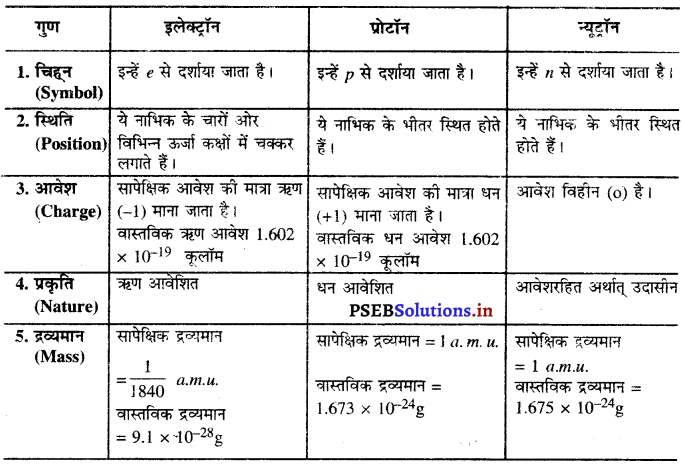
इलेक्ट्रॉन, प्रोटॉन और न्यूट्रॉन के गुणों की तुलना कीजिए।
उत्तर-
इलेक्ट्रॉन, प्रोटॉन तथा न्यूट्रॉन के गुणों की तुलना-

प्रश्न 2.
जे० जे० टॉमसन के परमाणु मॉडल की क्या सीमाएं हैं ?
उत्तर-
टॉमसन परमाणु मॉडल की सीमाएं – जे० जे० टॉमसन ने सुझाव दिया कि परमाणु का द्रव्यमान उसके अंदर स्थित प्रोटॉन तथा इलेक्ट्रॉन के फलस्वरूप होता है जोकि परमाणु के भीतर एक समान वितरित होते हैं जैसे क्रिसमस केक के अंदर ड्राइफ्रूट (मेवा) लगा रहता है।

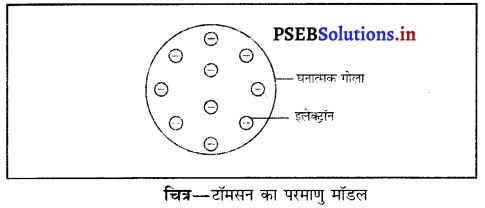
यह धारणा रदरफोर्ड के सुझाव से मेल नहीं खाती थी क्योंकि उसने कहा था कि परमाणु द्रव्यमान नाभिक के अंदर स्थित प्रोटॉनों तथा न्यूट्रॉनों के कारण होता है।

प्रश्न 3.
रदरफोर्ड के परमाणु मॉडल की क्या सीमाएं हैं ?
उत्तर-
रदरफोर्ड के परमाणु मॉडल की सीमाएं – रदरफोर्ड ने अपने परमाणु मॉडल में प्रस्तुत किया कि परमाणु का पूरा द्रव्यमान नाभिक में केंद्रित होता है। नाभिक धन आवेशित होता है जिसके चारों ओर इलेक्ट्रॉन विभिन्न ऊर्जा शैल में चक्कर लगाते हैं। ये ऋण आवेशित (इलेक्ट्रॉन) प्रवेगित कण चक्रीय गति करते हुए ऊर्जा विकसित करते हैं तथा ऊर्जा की हानि होने पर नाभिक में जा गिरते हैं ! इसका अभिप्राय यह हुआ कि परमाणु अस्थिर हैं जोकि सही नहीं है।

प्रश्न 4.
बोर के परमाणु मॉडल की व्याख्या कीजिए।
उत्तर-

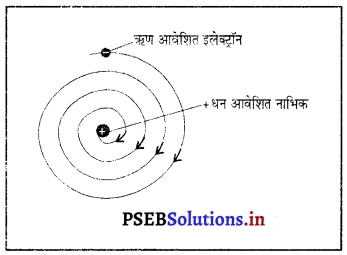
बोर का परमाणु मॉडल*
नीलस बोर ने परमाणु की संरचना के बारे निम्नलिखित मान्यताएं पेश की-

1. परमाणु का केंद्र धन आवेशित छोटा सा ठोस भाग होता है जिसे नाभिक (Nucleus) कहते हैं। नाभिक में प्रोटॉन तथा न्यूट्रॉन उपस्थित रहते हैं।
2. नाभिक का आयतन, परमाणु के आयतन की तुलना में बहुत छोटा होता है।
3. ऋण-आवेशित इलैक्ट्रॉन नाभिक के चारों तरफ कुछ निश्चित पथों (आर्बिट) में चक्कर लगाते रहते हैं जिन्हें इलेक्ट्रॉन के विविक्त आर्बिट (Discrete orbits) कहते हैं। जब इलेक्ट्रॉन विविक्त आर्बिट में चक्कर लगाते हैं तो उनकी ऊर्जा का विकिरण नहीं होता है।
4. जब इलेक्ट्रॉन चक्कर लगाते हुए एक ऊर्जा कोश से किसी दूसरे ऊर्जा कोश में छलांग लगाता है तो ऊर्जा परिवर्तन होता है।

प्रश्न 5.
इस अध्याय में दिए गए सभी परमाणु मॉडलों की तुलना कीजिए।
उत्तर-

विभिन्न परमाणु मॉडलों की तुलना-
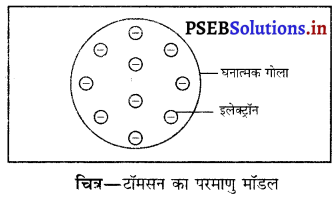
(i) टॉमसन का परमाणु मॉडल

1. डिस्चार्ज ट्यूब (विसर्जन नली) प्रयोग के आधार पर टॉमसन ने यह सुझाव दिया कि परमाणु विद्युतीय रूप से उदासीन है तथा इसके पूरे आयतन में इलेक्ट्रॉन समरूप फैले हुए हैं।
2. परमाणु धन आवेशित गोलाकार का बना होता है जिसमें इलेक्ट्रॉन धंसे रहते हैं।
3. परमाणु का आकार 10-10 मी० अथवा 1°A होता है।
4. परमाणु का द्रव्यमान समान रूप से पूर्ण क्षेत्र में फैला हुआ होता है।

(ii) रदरफोर्ड परमाणु मॉडल-

1. सोने की पन्नी से α-विकिरणों के प्रकीर्णन ने यह सुझाया कि नाभिक परमाणु का बहुत छोटा तथा ठोस भाग है जिसमें धन-आवेशित कण विदयमान होते हैं।
2. परमाणु के नाभिक का अर्धव्यास पूर्ण परमाणु के अद्धव्यास का 105 गुना होता है।
3. परमाणु में इलैक्ट्रॉन, नाभिक के इर्द-गिर्द विभिन्न कक्षाओं में तीव्र गति से चक्कर लगाते हैं।

(iii) नीलस बोर का परमाणु मॉडल-

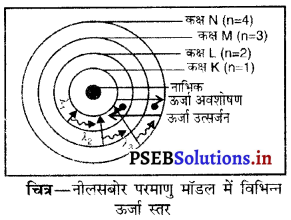
1. परमाणु का नाभिक इलेक्ट्रॉनों से घिरा रहता है।
2. नाभिक के इर्द-गिर्द इलेक्ट्रॉन निश्चित ऊर्जा स्तरों अथवा कोशों में चक्रीय गति करते हैं।
3. जब इलेक्ट्रॉन गति करते हुए एक कोश से दूसरे कोश में गिरता है तो ऊर्जा परिवर्तन होता है। (लाभ अथवा हानि) जो विविरणों के रूप में होता है तथा अंत में इलेक्ट्रॉन नाभिक में जा गिरता है। अर्थात् परमाणु अस्थिर है।

प्रश्न 6.
पहले अठारह तत्वों के विभिन्न कक्षों में इलैक्ट्रॉन वितरण के नियम को लिखिए।
उत्तर-
विभिन्न कोशों में इलैक्ट्रॉन वितरण – परमाणुओं के विभिन्न कक्षों में इलैक्ट्रॉन वितरण के लिए बोर तथा बरी ने निम्नलिखित नियम प्रतिपादित किए-

1. परमाणु के किसी कोश में उपस्थित अधिक-से-अधिक इलेक्ट्रॉनों की संख्या को 2n² सूत्र द्वारा दर्शाया जा सकता है, जहाँ n कोश अथवा ऊर्जा स्तर की संख्या है। भीतर से बाहर की ओर ऊर्जा स्तर के नाम क्रमश: K, L, M, ……. हैं।
2. बाह्यतम कोश में इलैक्ट्रॉनों की अधिकतम संख्या 8 हो सकती है।
3. बाह्यतम कोश से पहले कोश में 18 से अधिक इलेक्ट्रॉन नहीं हो सकते।
4. किसी परमाणु के दिए गए कोश में इलेक्ट्रॉन उस समय तक स्थान ग्रहण नहीं करते जब तक उससे अंदर वाला कोश पूरी तरह भर नहीं जाता है। अर्थात् कोश क्रमानुसार ही भरे जाते हैं।

प्रश्न 7.
सिलिकॉन और ऑक्सीजन का उदाहरण लेते हुए संयोजकता की परिभाषा दीजिए।
उत्तर-
किसी तत्व की संयोजक क्षमता को उस तत्व की संयोजकता कहते हैं। परमाणु के बाह्यतम कोश में उपस्थित इलेक्ट्रॉनों की संख्या उसकी संयोजकता बताती है। परंतु यदि बाह्यतम शैल में इलेक्ट्रॉन की संख्या उसकी अधिकतम क्षमता के समीप हो तो संयोजकता ज्ञात करने के लिए परमाणु के बाह्यतम कोश में उपस्थित इलेक्ट्रॉन संख्या को 8 में से घटा लिया जाता है।
सिलिकॉन – सिलिकॉन परमाणु में प्रोटॉनों की संख्या (p) = 14
∴ इलेक्ट्रॉनों की संख्या (e) = 14

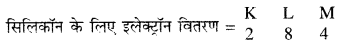
∴ सिलिकॉन परमाणु के बाह्यतम शैल में उपस्थित इलेक्ट्रॉनों की संख्या = 4
∴ सिलिकॉन की संयोजकता = 4
ऑक्सीजन
ऑक्सीजन परमाणु में प्रोटॉनों की संख्या (p) = 8
∴ इलेक्ट्रॉनों की संख्या (e) = 8

ऑक्सीजन के बाहयतम कोश में इलेक्ट्रॉनों की संख्या = 6
∴ ऑक्सीजन की संयोजकता = (8 – 6) = 2 है।

प्रश्न 8.
उदाहरण के साथ व्याख्या कीजिए-परमाणु संख्या, द्रव्यमान संख्या, समस्थानिक और समभारिक। समस्थानिकों के कोई दो उपयोग लिखिए।
उत्तर-
(i) परमाणु संख्या (Atomic Number) – किसी परमाणु के नाभिक में उपस्थित प्रोटॉनों की संख्या को उस परमाणु की परमाणु संख्या कहते हैं। उदाहरणार्थ मैग्नीशियम परमाणु के नाभिक 12 प्रोटॉन हैं।
इसलिए मैग्नीशियम की परमाणु संख्या 12 है। परमाणु संख्या को ‘z’ से दर्शाया जाता है ?
परमाणु संख्या (z) = प्रोटॉन संख्या (p) = इलैक्ट्रॉन संख्या (e)
इसी प्रकार कार्बन के परमाणु में 6 प्रोटॉन होते हैं।
∴ कार्बन की परमाणु संख्या (z) = 6

(ii) द्रव्यमान संख्या (Mass Number) – किसी तत्व के नाभिक में प्रोटॉन तथा न्यूट्रॉन जिन्हें इकट्ठा मिलाकर न्यूक्लीऑन कहते हैं, की कुल संख्या को द्रव्यमान संख्या कहते हैं । द्रव्यमान संख्या को ‘A’ से प्रदर्शित किया जाता है। द्रव्यमान संख्या (A) = नाभिक में उपस्थित प्रोटॉन की संख्या + नाभिक में उपस्थित न्यूट्रॉन की संख्या
उदाहरणार्थ, कार्बन के नाभिक में 6 प्रोटॉन तथा 6 न्यूट्रॉन उपस्थित होते हैं, इसलिए
कार्बन की द्रव्यमान संख्या A = p + n
= 6 + 6
= 12 है।

(ii) समस्थानिक (Isotopes) – एक ही तत्व के दो परमाणु जिनकी परमाणु संख्या एक समान है परंतु परमाणु द्रव्यमान भिन्न-भिन्न हो, उन्हें उस तत्व के समस्थानिक (Isotopes) कहते हैं।

उदाहरण के लिए क्लोरीन के दो समस्थानिक \({ }_{17}^{35} \mathrm{Cl}\) तथा \({ }_{17}^{37} \mathrm{Cl}\) हैं जिनकी परमाणु संख्या एक समान अर्थात् 17 है परंतु एक की परमाणु द्रव्यमान संख्या 35 और दूसरे की परमाण द्रव्यमान संख्या 37 है।

(iv) समभारिक (Isobars) – ऐसे तत्व जिनकी परमाणु संख्या भिन्न-भिन्न होती है परंतु द्रव्यमान संख्या एक समान होती हैं, उन्हें समभारिक कहते हैं। उदाहरणार्थ कैल्शियम की परमाणु संख्या 20 तथा आर्गान की परमाणु संख्या 18 है परन्तु इनकी द्रव्यमान संख्या 40 है जिस कारण इनमें इलैक्ट्रॉन की संख्या भिन्न-भिन्न होती है। इन तत्वों के रासायनिक गुण समान होते हैं। इन तत्वों में उपस्थित प्रोटॉन तथा न्यूट्रॉन की संख्या भिन्न होती है।

समस्थानिकों के उपयोग (Uses of Isotopes)-

1. कैंसर की चिकित्सा के लिए कोबाल्ट के समस्थानिक का उपयोग किया जाता है।
2. गॉयटर की चिकित्सा में आयोडीन के समस्थानिक का उपयोग किया जाता है।

प्रश्न 9.
Na⁺ के पूरी तरह भरे हुए K और L कोश होते हैं-व्याख्या कीजिए।
उत्तर-
किसी तत्व के परमाणु में इलेक्ट्रॉनों की संख्या उतनी ही होती है जितनी उस परमाणु के नाभिक में प्रोटॉन होते हैं। इलेक्ट्रॉन तथा प्रोटॉन पर विपरीत आवेश होता है जिसके परिणामस्वरूप परमाणु विद्युतीय उदासीन होता है। यदि उदासीन परमाणु में इलेक्ट्रॉन की वृद्धि होगी तो उसमें इकाई ऋण आवेश आ जायेगा। दूसरी ओर यदि उसमें से एक इलेक्ट्रॉन निकल जाता है तो वह इकाई धन आवेश ग्रहण कर लेगा। इसलिए इलेक्ट्रॉन का निकलना या संयोजित होने से ऐसे बने आवेशित कण को आयन कहते हैं।

सोडियम परमाणु विद्युतीय उदासीन है। इसमें 11 प्रोटॉन तथा 11 इलेक्ट्रॉन होते हैं। इन इलेक्ट्रॉनों का वितरण 2, 8, 1 है। अब उनमें से 1 इलेक्ट्रॉन निकलने से यह धन आवेशित सोडियम आयन बन जाता है।

सोडियम परमाणु (Na) – le e. → सोडियम आयन (Na⁺)
अथवा 11^-e – 1^-e → 10^-e
Na^O – 1^-e Na⁺
सोडियम आयन का इलेक्ट्रॉनिक विन्यास (2, 8) होगा।
अर्थात् इसमें K तथा L कोश पूर्ण रूप से भरे हुए होते हैं।

प्रश्न 10.
यदि ब्रोमीन परमाणु दो समस्थानिकों के [ \({ }_{35}^{79} \mathrm{Br}\)(49.7%) तथा \({ }_{35}^{81} \mathrm{Br}\) (50.3%) ] रूप में है तो ब्रोमीन परमाणु के औसत परमाणु द्रव्यमान की गणना कीजिए।
हल :
ब्रोमीन का समस्थानिक जिसका परमाणु द्रव्यमान 79 है = 49.7 %
∴ ब्रोमीन के परमाणु द्रव्यमान के लिए \({ }_{35}^{79} \mathrm{Br}\) का योगदान = \(\frac{79}{100}\) x 49.7
= 39.26u
ब्रोमीन का समस्थानिक जिसका परमाणु द्रव्यमान 81 है = 50.3 %
ब्रोमीन के परमाणु द्रव्यमान के लिए \({ }_{35}^{81} \mathrm{Br}\) का योगदान = \(\frac{50.3}{100}\) x 81
= 40.74 u
अब ब्रोमीन परमाणु का औसत परमाणु द्रव्यमान = 39.26 + 40.74 = 80.0 u

प्रश्न 11.
एक तत्व x का परमाणु द्रव्यमान 16.2 u है तो इस सैंपल में समस्थानिक \({ }_{8}^{16} x\) और \({ }_{8}^{18} x\) प्रतिशत क्या होगा ?
हल :
मान लो सैंपल में \({ }_{8}^{16} x\) की प्रतिशतता = y है
∴ सैंपल में \({ }_{8}^{18} x\) की प्रतिशतता = (100 – y)

16.2 x 100 = 1800 – 2 y
1620 = 1800 – 2y
2 y = 1800 – 1620
2 y = 180
∴ y = \(\frac{180}{2}\)
= 90
अर्थात् \({ }_{8}^{16} \mathrm{X}\) की प्रतिशतता = 90%
तथा \({ }_{8}^{18} \mathrm{X}\) की प्रतिशतता = 100 – 90
= 10%

प्रश्न 12.
यदि तत्व का Z = 3 तो तत्व की संयोजकता क्या होगी ? तत्व का नाम भी लिखिए।
हल :
तत्व की परमाणु संख्या को z से दर्शाया जाता है।
∴ तत्व की परमाणु संख्या = z = 3
अर्थात् तत्व के परमाणु में उपस्थित प्रोटॉनों की संख्या = इलैक्ट्रॉनों की संख्या = 3

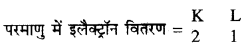
यह परमाणु लीथियम है तथा इसकी संयोजकता 1 है।

प्रश्न 13.
दो परमाणु स्पीशीज़ के केंद्रकों का संघटन नीचे दिया गया है-

X और Y की द्रव्यमान संख्या ज्ञात कीजिए। इन दोनों स्पीशीज़ में क्या संबंध है?
उत्तर-
X की द्रव्यमान संख्या = 6 + 6
= 12
Y की द्रव्यमान संख्या = 6 + 8
= 14
क्योंकि X तथा Y दोनों की परमाणु संख्या एक समान है परंतु इनकी द्रव्यमान संख्या भिन्न है इसलिए दोनों परमाणु एक ही तत्व के समस्थानिक 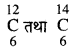हैं।

प्रश्न 14.
निम्नलिखित वक्तव्यों में गलत के लिए F और सही के लिए T लिखें।
(a) जे० जे० टॉमसन ने यह प्रस्तावित किया था कि परमाणु के केंद्रक में केवल न्यूक्लीयॉन्स होते हैं।
(b) एक इलेक्ट्रॉन और प्रोटॉन मिलकर न्यूट्रॉन का निर्माण करते हैं। इसलिए यह अनावेशित होता है।
(c) इलेक्ट्रॉन का द्रव्यमान प्रोटॉन से लगभग \(\frac{1}{2000}\) गुणा होता है।
(d) आयोडीन के समस्थानिक का इस्तेमाल टिंकचर आयोडीन बनाने में होता है।
उत्तर-
(a) False,
(b) False,
(c) True,
(d) TTrue.
प्रश्न संख्या 15, 16 तथा 17 में गलत के सामने (×) का चिह्न तथा सही के सामने (√) का चिह्न लगाएँ

प्रश्न 15.
रदरफोर्ड का अल्फा कण प्रकीर्णन प्रयोग किसकी खोज के लिए उत्तरदायी था-
(a) परमाणु केंद्रक
(b) इलैक्ट्रॉन
(c) प्रोटॉन
(d) न्यूट्रॉन।
उत्तर-
(a) परमाणु केंद्रक √
(b) ×
(c) ×
(d) ×.

प्रश्न 16.
एक तत्व के समस्थानिक में होते हैं-
(a) समान भौतिक गुण
(b) भिन्न रासायनिक गुण
(c) न्यूट्रॉनों के अलग-अलग संख्या
(d) भिन्न परमाणु संख्या।
उत्तर-
(a) ×
(b) ×
(c) न्यूट्रॉनों की अलग-अलग संख्या √
(d) ×

प्रश्न 17.
Cl^– आयन में संयोजकता इलैक्ट्रॉनों की संख्या है-
(a) 16
(b) 8
(c) 17
(d) 18.
उत्तर-
(a) ×
(b) 8 √
(c) ×
(d) ×.

प्रश्न 18.
सोडियम का सही इलैक्ट्रॉनिक विन्यास निम्न में से कौन-सा है ?
(a) 2, 8
(b) 8, 2.1
(c) 2. 1. 8
(d) 2. 8. 1.
उत्तर-
(a) ×
(b) ×
(c) ×
(d) 2, 8, 1√.

प्रश्न 19.
निम्नलिखित सारणी को पूरा कीजिए-

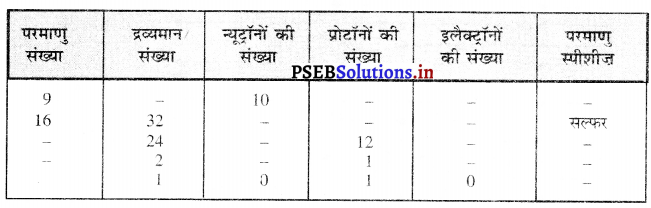
उत्तर-

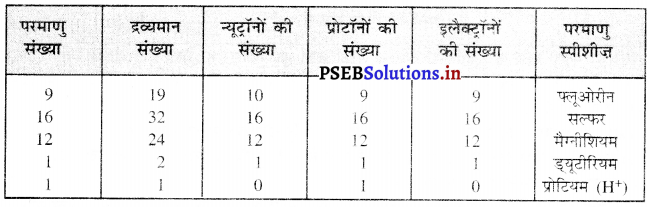
Science Guide for Class 9 PSEB परमाणु की संरचना InText Questions and Answers

पाठ्य-पुस्तक के प्रश्नों के उत्तर

प्रश्न 1.
केनाल किरणें क्या हैं ?
उत्तर-
केनाल किरणें (Canat Rays) – एनोड से उत्सर्जित होने वाली किरणें जब डिस्चार्ज टयब में गैस प्रयोग की जाती है, केनाल किरणें कहलाती हैं। ये धन आवेशित विकिरणें हैं जो ऐसे कणों से निर्मित होती हैं और जिनका द्रव्यमान, इलैक्ट्रॉन का 2000 गुना होता है परंतु इसका आवेश इलैक्ट्रॉन के आवेश से विपरीत होता है।

प्रश्न 2.
यदि किसी परमाणु में एक इलेक्ट्रॉन और एक प्रोटॉन है, तो उसमें कोई आवेश होगा या नहीं ?
उत्तर-
प्रत्येक प्रोटॉन का आवेश +1 तथा इलैक्ट्रॉन का आवेश -1 माना गया है। अब क्योंकि किसी परमाणु में एक प्रोटॉन तथा एक इलेक्ट्रॉन है जो परस्पर एक-दूसरे के आवेशों को संतुलित करते हैं। इसलिए इस परमाणु पर कोई परिणामी (नेट) आवेश नहीं होगा अर्थात् परमाणु विद्युतीय उदासीन होगा।

प्रश्न 3.
परमाणु उदासीन है, इस तथ्य को टॉमसन के मॉडल के आधार पर स्पष्ट कीजिए। उत्तर-टॉमसन का परमाणु मॉडल (Thomson’s Model of Atom)-

1. परमाणु धन आवेशित गोलाकार होता है तथा इलैक्ट्रॉन इसमें फँसे होते हैं जैसे क्रिसमस केक में मेवा लगा होता है।
2. ऋणात्मक तथा धनात्मक आवेश मात्रा में समान होते हैं जो एक-दूसरे को संतुलित करते हैं। इसलिए परमाणु विद्युतीय रूप से उदासीन (आवेश रहित) होता है।

प्रश्न 4.
रदरफोर्ड के परमाणु मॉडल के अनुसार नाभिक के परमाणु में कौन-सा अवपरमाणुक कण विद्यमान है ?
उत्तर-
रदरफोर्ड के परमाणु मॉडल अनुसार परमाणु का नाभिक (Nucleus) धन आवेशित होता है। परमाणु का लगभग सारा द्रव्यमान परमाणु के नाभिक में स्थित होता है तथा इलैक्ट्रॉन नाभिक के चारों ओर विभिन्न पथों (कक्षाओं) में चक्कर लगाते हैं। इसलिए परमाणु के नाभिक में अवपरमाणुक कण प्रोटॉन विद्यमान होता है।

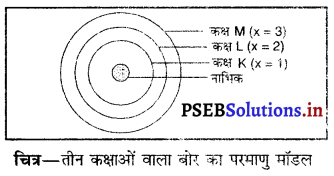
प्रश्न 5.
तीन कक्षाओं वाले बोर के परमाणु मॉडल का चित्र बनाइए।
उत्तर-

प्रश्न 6.
क्या अल्फा कणों का प्रकीर्णन प्रयोग सोने के अतिरिक्त दूसरी धातु के पन्नी से संभव होगा ?
उत्तर-
यदि अल्फा कणों का प्रकीर्णन प्रयोग सोने के अतिरिक्त किसी अन्य धातु की पन्नी से किया जाए तो वही परिणाम संभव होगा जो सोने की पन्नी के साथ हुआ था।

अंतर केवल इतना है कि सोना एक आघातवर्धनीय धातु है और इसे पीट कर पतलो चादर में बदला जा सकता है जबकि अन्य किसी धातु को इतना बारीक नहीं किया जा सकता है। यदि हम मोटी धातु की चादर का प्रयोग करेंगे तो अल्फा कण इससे टकराकर वापिस लौट आएंगे तथा हमें परमाणु के भीतर धन आवेशित प्रोटॉन की स्थिति का पक्का अनुमान नहीं होगा।

प्रश्न 7.
परमाणु के तीन अवपरमाणुक कणों के नाम लिखें।
उत्तर-
परमाणु के तीन अवपरमाणुक कण-परमाणु के निम्नलिखित तीन अवपरमाणुक कम हैं :-
(i) प्रोटॉन (₁P¹ )
(ii) इलेक्ट्रॉन (₀e^-1 )
(iii) न्यूट्रॉन (₁n⁰ )।

प्रश्न 8.
हीलियम परमाणु का परमाणु द्रव्यमान 4u है और उसके नाभिक में दो प्रोटॉन होते हैं। इसमें कितने न्यूट्रॉन होंगे ?
उत्तर-
हीलियम परमाणु में न्यूट्रॉनों की संख्या-किसी परमाणु का द्रव्यमान उसके नाभिक (Nucleus) में उपस्थित प्रोटॉन तथा न्यूट्रॉन के द्रव्यमानों के योग के कारण होता है : अब हीलियम परमाणु का परमाणु द्रव्यमान 4 u है तथा इसके नाभिक में 2 प्रोटॉन होते हैं और दो प्रोटॉनों का द्रव्यमान 20 है। इसलिए इसके नाभिक में (4 u -2u = 2u) द्रव्यमान न्यूट्रॉन की उपस्थिति के कारण है। क्योंकि 1 न्यूट्रॉन का द्रव्यमान 1 u होता है इसलिए नाभिक में 2 न्यूट्रॉन होंगे जो 2 u द्रव्यमान प्रदान करेंगे।
पाठ्य-पुस्तक के प्रश्नों के उत्तर

प्रश्न 9.
कार्बन और सोडियम के परमाणुओं के लिए इलैक्ट्रॉन-वितरण लिखिए।
उत्तर-
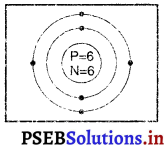
कार्बन परमाणु – कार्बन का परमाणु द्रव्यमान 12 है। इसलिए
इसमें प्रोटॉनों की संख्या (p) = 6 तथा इलैक्ट्रॉनों की संख्या (e) = 6 है।
कार्बन परमाणु में इलैक्ट्रॉन वितरण-
K-कोश में अधिकतम इलेक्ट्रॉनों की संख्या = 2
∴ L-कोश में इलेक्ट्रॉनों की संख्या = 4

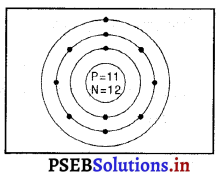
सोडियम परमाणु
सोडियम का परमाणु द्रव्यमान = 23 है, इसलिए सोडियम के परमाणु में प्रोटॉनों की संख्या (p) = 11 तथा इलेक्ट्रॉनों की संख्या (e) = 11 है।
सोडियम परमाणु में इलेक्ट्रॉनों का वितरण-
K-कोश में इलैक्ट्रॉनों की संख्या = 2
L-कोश में इलैक्ट्रॉनों की संख्या = 8
M-कोश में इलैक्ट्रॉनों की संख्या = 1

प्रश्न 10.
अगर किसी परमाणु का K और L कोश भरा है तो उस परमाणु में इलेक्ट्रॉनों की संख्या क्या होगी ?
उत्तर-
K-कोश भरा हुआ होने की परिस्थिति में इलेक्ट्रानों की कुल संख्या = 2
L-कोश पूरा भरा हुआ होने की अवस्था में इलेक्ट्रानों की संख्या = 8
∴ परमाणु में उपस्थित कुल इलैक्ट्रॉन = 2 + 8 = 10

प्रश्न 11.
क्लोरीन, सल्फर और मैग्नीशियम की परमाणु संख्या से आप संयोजकता कैसे प्राप्त करेंगे ?
उत्तर-
(i) क्लोरीन (Cl)-
क्लोरीन की परमाणु संख्या = 17
क्लोरीन के परमाणु में उपस्थित प्रोटॉनों की संख्या (p) = 17
इलेक्ट्रॉनों की संख्या (e) = 17

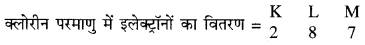
क्लोरीन परमाणु के बाह्यतम कोश में उपस्थित
इलेक्ट्रॉनों की संख्या = 7
∴ क्लोरीन की संयोजकता = 8 – 7
अर्थात् बाह्यतम कोश में अष्टक बनाने के लिए आवश्यक इलेक्ट्रॉन = 1

(ii) सल्फर (S)-
सल्फर की परमाणु संख्या = 16
सल्फर के परमाणु में उपस्थित प्रोटॉनों की संख्या (p) = 16
इलेक्ट्रॉनों की संख्या (e) = 16

सल्फर परमाणु के बाह्यतम कोश में उपस्थित इलेक्ट्रॉनों की संख्या = 6
बाह्यतम कोश में अष्टक (पूरा भरने) बनाने के लिए आवश्यक इलेक्ट्रॉन = 8 – 6 = 2
∴ सल्फर की संयोजकता = 2

(iii) मैग्नीशियम (Mg)-
मैग्नीशियम की परमाणु संख्या = 12
मैग्नीशियम के परमाणु में उपस्थित प्रोटॉनों की संख्या (p) = 12
इलेक्ट्रॉनों की संख्या (e) = 12

मैग्नीशियम के परमाणु के बाह्यतम कोश में उपस्थित इलेक्ट्रॉनों की संख्या
अर्थात् मैग्नीशियम परमाणु के बाह्यतम कोश को भरा होने के लिए जितने इलेक्ट्रॉन छोड़ने पड़ेंगे = 2
∴ मैग्नीशियम परमाणु की संयोजकता = 2

प्रश्न 12.
यदि किसी परमाणु में इलेक्ट्रॉनों की संख्या 8 है और प्रोटॉनों की संख्या भी 8 है, तब
(क) परमाणु की परमाणुक संख्या क्या होगी ?
(ख) परमाणु का क्या आवेश है ?
उत्तर-
(i) परमाणु की परमाणु संख्या = प्रोटॉनों की संख्या (p) = 8
∴ परमाणु में उपस्थित इलेक्ट्रॉन न्यूट्रॉनों की संख्या= 8
∴ परमाणु द्रव्यमान = प्रोटॉनों की संख्या + न्यूट्रॉनों की संख्या
= 8 + 8 = 16

(ii) परमाणु में उपस्थित इलेक्ट्रॉनों की संख्या = प्रोटॉनों की संख्या = 8
परमाणु पर उपस्थित आवेश = प्रोटॉनों की संख्या – इलेक्ट्रॉनों की संख्या
= 8 – 8
= 0
अर्थात् परमाणु आवेश विहीन है।

प्रश्न 13.
पाठ्य-पुस्तक की सारणी 4.1 की सहायता से ऑक्सीजन और सल्फर परमाणु की द्रव्यमान संख्या ज्ञात कीजिए।
उत्तर-
(i) ऑक्सीजन (O)
ऑक्सीजन परमाणु में उपस्थित प्रोटॉनों की संख्या (p) = 8
न्यूट्रॉनों की संख्या (n) = 8
∴ ऑक्सीजन परमाणु की परमाणु की द्रव्यमान संख्या = p + n
= 8 + 8
= 16

(ii) सल्फर (S)-
सल्फर के परमाणु में उपस्थित प्रोटॉनों की संख्या (p) = 16
न्यूट्रॉनों की संख्या (n) = 16
∴ सल्फर परमाणु की परमाणु द्रव्यमान संख्या = p + n
= 16 + 16
= 32

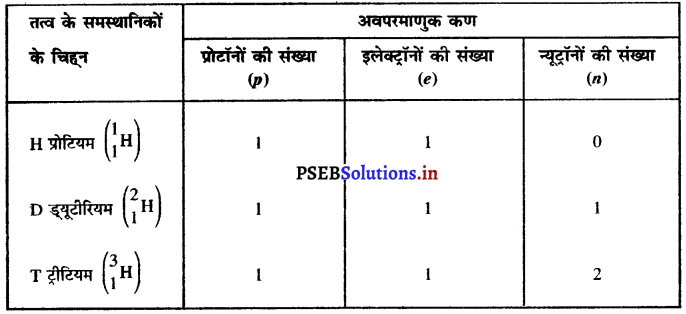
प्रश्न 14.
चिह्न H, D और T के लिए प्रत्येक में पाए जाने वाले तीन अवपरमाणुक कणों को सारणीबद्ध कीजिए।
उत्तर-
H, D और T चिह्न हाइड्रोजन के तीन समस्थानिक हैं जिनकी परमाणु संख्या 1 है परंतु परमाणु द्रव्यमान संख्या भिन्न-भिन्न है।

प्रश्न 15.
समस्थानिक और समभारिक के किसी एक युग्म का इलेक्ट्रॉनिक विन्यास लिखिए।
उत्तर-

(i) समस्थानिक (Isotopes) – क्लोरीन तत्व के दो समस्थानिक \({ }_{17}^{35} \mathrm{Cl}[latex] तथा [latex]{ }_{17}^{37} \mathrm{Cl}\) हैं। इन दोनों की परमाणु संख्या 17 है।
अब परमाणु संख्या = प्रोटॉनों की संख्या = इलेक्ट्रॉनों की संख्या = 17

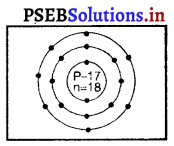
(ii) समभारिक (Isobars) – कैल्सियम \({ }_{20}^{40} \mathrm{C} a\) तथा आर्गन (\({ }_{18}^{40} \mathrm{~A} r\)) समभारिकों का युग्म है जिनका परमाणु द्रव्यमान एक समान 40 है परंतु १९ गाणु संख्या क्रमशः 20 और 18 भिन्न होने के कारण परमाणुओं का इलेक्ट्रॉन वितरण भी भिन्न होगा।

कैल्सियम (Ca)-
परमाणु द्रव्यमान संख्या = 40
अर्थात कैल्सियम के परमाणु में प्रोटॉनों की संख्या (p) = 20
इलैक्ट्रॉनों की संख्या (e) = 20 ……….(1)
परमाणु द्रव्यमान संख्या = n + p = 40 …………….(2)
∴ कैल्सियम के परमाणु में उपस्थित न्यूट्रॉनों की संख्या (n) = (2) – (1)
= 40 – 20
= 20

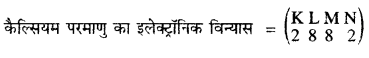
आर्गन (Ar) परमाणु संख्या = 18
अर्थात् आर्गन के परमाणु में प्रोटॉनों की संख्या (p) = इलैक्ट्रॉनों की संख्या (e) = 18 ………………. (1)
परमाणु द्रव्यमान संख्या = n + p = 40 ………………… (2)
∴ आर्गन परमाणु में उपस्थित न्यूट्रॉनों की संख्या (n)
= (2) – (1)
= 40 – 18
= 22

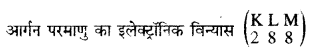
Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 1 वास्तविक संख्याएँ Ex 1.4 Textbook Exercise Questions and Answers

PSEB Solutions for Class 10 Maths Chapter 1 वास्तविक संख्याएँ 1.4

प्रश्न 1.
बिना लंबी विभाजन प्रक्रिया किए, बताइए कि निम्नलिखित परिमेय संख्याओं के दशमलव प्रसार सांत हैं या असांत आवर्ती हैं :
(i) \(\frac{13}{3125}\)

(ii) \(\frac{17}{8}\)

(iii) \(\frac{64}{455}\)

(iv) \(\frac{15}{1600}\)

(v) \(\frac{29}{343}\)

(vi) \(\frac{23}{2^{3} 5^{2}}\)

(vii) \(\frac{129}{2^{2} 5^{7} 7^{5}}\)

(viii) \(\frac{6}{15}\)

(ix) \(\frac{35}{50}\)

(x) \(\frac{77}{210}\)

हल :
(i) मान लीजिए x = \(\frac{13}{3125}\) ………………(1)
(1) की x = P से तुलना कीजिए,
यहाँ p = 13 और q = 3125
q के अभाज्य गुणनखंड = 3125 = 5 × 5 × 5 × 5
= 55 × 20
जोकि 2ⁿ × 5^m के रूप का है।
जहाँ n = 0, m = 5
जो ऋणोतर पूर्णांक हैं।
∴ x = \(\frac{13}{3125}\) का सांत दशमलव प्रसार है। उत्तर

(ii) मान लीजिए x = \(\frac{17}{8}\) ………….. (1)
(1) की x = \(\frac{p}{q}\) से तुलना कीजिए
यहाँ p = 17 और q = 8
q के अभाज्य गुणनखंड = 8 = 2 × 2 × 2 = 23
= 23 × 50
जोकि 2ⁿ × 5^m के रूप का है।
जहाँ n = 3 m = 0 है।
और ये ऋणेतर पूर्णांक हैं।
∴ x = \(\frac{17}{8}\)
जिसका दशमलव प्रसार सांत है। उत्तर

(iii) मान लीजिए x = \(\frac{64}{455}\) ……………. (1)
(1) की x = ” से तुलना कीजिए।
यहाँ p = 64, q = 455
q के अभाज्य गुणनखंड = 455 = 5 × 7 × 13
जोकि 2ⁿ × 5^m के रूप का नहीं है।
∴ x = \(\frac{64}{455}\) का दशमलव प्रसार असांत आवर्ती है।। उत्तर

(iv) मान लीजिए x = \(\frac{15}{1600}\) ……………..(1)
(1) की x = = के साथ तुलना कीजिए।
यहाँ p = 15 और q = 1600
q के अभाज्य गुणनखंड = 600
= 2 × 2 × 2 × 2 × 2 × 2 × 5 × 5
= 2⁶ × 5² .
जोकि 2ⁿ × 5^m, के रूप का है,
जहाँ n = 6, m = 2 और ये ऋणेतर पूर्णांक हैं।
∴ x = \(\frac{15}{1600}\) जिसका दशमलव प्रसार सांत है। उत्तर

(v) मान लीजिए x = \(\frac{29}{343}\) ……………(1)
(1) की x = \(\frac{p}{q}\) के साथ तुलना कीजिए।
यहाँ p = 29 और q = 343
q के अभाज्य गुणनखंड हैं = 343
= 7 × 7 × 7
= 7³
जोकि 2ⁿ × 5^m के रूप में नहीं है।
∴ x = \(\frac{29}{343}\) का दशमलव प्रसार असांत आवर्ती है। उत्तर

(vi) मान लीजिए x = \(\frac{23}{2^{3} 5^{2}}\) …………..(1)
(1) की x = 4 के साथ तुलना कीजिए।
यहाँ p = 23 और 4 = 2³5²
q के अभाज्य गुणनखंड = 2³5²
जोकि 2ⁿ × 5^m के रूप का है,
जहाँ n = 3, m = 2 और ये ऋणेतर पूर्णांक हैं।
∴ x = \(\frac{23}{2^{3} 5^{2}}\) का दशमलव प्रसार सांत है। उत्तर

(vii) मान लीजिए x = \(\frac{129}{2^{2} 5^{7} 7^{5}}\) ………………(1)
(1) की x = \(\frac{p}{q}\) के साथ तुलना कीजिए।
यहाँ p = 129 और q = 2² 5⁷ 7⁵
q के अभाज्य गुणनखंड = 2² 5⁷ 7⁵
जोकि 2ⁿ × 5^m के रूप में नहीं है।
∴ x = \(\frac{129}{2^{2} 5^{7} 7^{5}}\) का दशमलव प्रसार असांत आवर्ती है। उत्तर

(viii) मान लीजिए x = \(\frac{6}{15}=\frac{2}{5}\) ………….(1)
(1) की x = \(\frac{p}{q}\) के साथ से तुलना कीजिए।
यहाँ p = 2, q = 5
q के अभाज्य गुणनखंड हैं 5 = 2⁰ × 5¹
जोकि 2ⁿ × 5^m के रूप का है।
जहां n = 0, m = 1 और ये ऋणेतर पूर्णांक हैं।
∴ x = \(\frac{6}{15}\) का दशमलव प्रसार सांत है। उत्तर

(ix) मान लीजिए x = \(\frac{35}{50}=\frac{7}{10}\) ……………..(1)
(1) की x = \(\frac{p}{q}\) के साथ तुलना कीजिए।
यहाँ p = 7, q = 10
q के अभाज्य गुणनखंड हैं = 10 = 2 × 5 = 2¹ × 5¹
जहां 2ⁿ × 5^m के रूप का है,
जहाँ n = 1, m = 1 दोनों n और m ऋणेतर पूर्णांक हैं। .
∴ x = \(\frac{35}{50}\) का दशमलव प्रसार सांत है। उत्तर

(x) मान लीजिए x = \(\frac{77}{210}=\frac{11}{30}\)
(1) की. x = \(\frac{p}{q}\) के साथ तुलना कीजिए।
यहाँ p = 11, q = 30
q के अभाज्य गुणनखंड हैं = 30 = 2 × 3 × 5
जोकि 2ⁿ × 5^m के रूप में नहीं है।
∴ x = \(\frac{77}{210}\) का दशमलव प्रसार असांत आवर्ती है। उत्तर

प्रश्न 2.
ऊपर दिए गये प्रश्न में उन परिमेय संख्याओं के दशमलव प्रसारों को लिखिए जो सांत हैं।
हल :
(i) मान लीजिए x = \(\frac{13}{3125}\) ………….. (1)
(1) की x = \(\frac{p}{q}\) के साथ तुलना कीजिए
यहाँ p = 13, q = 3125
q के अभाज्य गुणनखंड = 3125 = 5 × 5 × 5 × 5 × 5
= 5⁵ × 2⁰
जोकि 2ⁿ × 5^m के रूप का है,
जहाँ n = 0, m = 5
∴ x = \(\frac{13}{3125}\) का दशमलव प्रसार सांत है। उत्तर

दशमलव के रूप में व्यक्त करना
x = \(\frac{13}{3125}=\frac{13}{5^{5} \times 2^{0}}\)

x = \(\frac{13 \times 2^{5}}{5^{5} \times 2^{5}}\)
[::: हम हर को 10 की कोई घात बनाने के लिए इसे 25 से गुणा और भाग करते हैं।] |

x = \(\frac{13 \times 32}{(2 \times 5)^{5}}\)

x = \(\frac{416}{(10)^{5}}=\frac{416}{100000}\)

x = 0.00416 उत्तर

(i) मान लीजिए x = \(\frac{17}{8}\)
(1) की x = \(\frac{p}{q}\) से तुलना कीजिए।
यहाँ p = 17, q = 8
q के अभाज्य गुणनखंड = 8 = 2 × 2 × 2
= 2³ × 5⁰
जोकि 2ⁿ × 5^m के रूप का है, जहाँ n = 3, m = 0 · और ये ऋणेतर पूर्णांक हैं।
∴ x = \(\frac{17}{8}\) को सांत दशमलव प्रसार के रूप में व्यक्त किया जा सकता है।

दशमलव के रूप में व्यक्त करना
x = \(\frac{17}{8}=\frac{17}{2^{3} \times 5^{0}}\)

x = \(\frac{17 \times 5^{3}}{2^{3} \times 5^{3}}\)
[हम हर को 10 की घात बनाने के लिए 53 से गुणा और भाग करते हैं।]

x = \(\frac{17 \times 125}{(2 \times 5)^{3}}\)

x = \(\frac{2125}{(10)^{3}}=\frac{2125}{1000}\)

x = 2.125
∴ \(\frac{17}{8}\) = 2.125 उत्तर .

(iii) मान लीजिए x = \(\frac{64}{455}\) ………….(1)
(1) की x = \(\frac{p}{q}\) से तुलना कीजिए
यहाँ p = 64, q = 455
q के अभाज्य गुणनखंड = 455 = 5 × 7 × 13
जोकि 2ⁿ × 5^m के रूप में नहीं है
∴ x = \(\frac{64}{455}\) का दशमलव प्रसार असांत आवर्ती है। उत्तर

(iv) मान लीजिए x = \(\frac{15}{1600}\) …………(1)
(1) की x = \(\frac{p}{q}\) से तुलना कीजिए।
यहाँ p = 15, q = 1600
q के अभाज्य गुणनखंड = 1600 = 2 × 2 × 2 × 2 × 2 × 2 × 5 × 5
= 2⁶ × 5²
जोकि 2ⁿ × 5^m के रूप का है,
जहाँ n = 6, m = 2 और ये ऋणेतर पूर्णांक हैं
∴ x = \(\frac{15}{1600}\) का सांत दशमलव प्रसार है।

दशमलव के रूप में व्यक्त करना

(v) मान लीजिए x = \(\frac{29}{343}\) …………. (1)
(1) की x = \(\frac{p}{q}\) से तुलना कीजिए
यहाँ p = 29 और q = 343 = 7 × 7 × 7 = 7³
जोकि 2ⁿ × 5^m के रूप में नहीं हैं।
∴ x = \(\frac{29}{343}\) का असांत आवर्ती दशमलव प्रसार होगा।

(vi) मान लीजिए x = \(\frac{23}{2^{3} 5^{2}}\) ………….. (1)
(1) की x = \(\frac{p}{q}\) से तुलना कीजिए
यहाँ p = 23 और q = 2³5²
q के अभाज्य गुणनखंड = 2³5²
जोकि 2ⁿ × 5^m के रूप का है,
जहाँ n = 3 और m = 2 और ये ऋणेतर पूर्णांक हैं।
∴ x = \(\frac{23}{2^{3} 5^{2}}\) का सांत दशमलव प्रसार है।

दशमलव के रूप में व्यक्त करना

(vii) मान लीजिए x = \(\frac{129}{2^{2} 5^{7} 7^{5}}\) ……….. (1)
(1) की x = \(\frac{p}{q}\) से तुलना कीजिए .
यहाँ p = 129 और 4 = 2² x 5⁷ x 7⁵
q के अभाज्य गुणनखंड = 2² x 5⁷ × 7⁵
जोकि 2ⁿ × 5^m के रूप में नहीं है।
∴ x = \(\frac{129}{2^{2} 5^{7} 7^{5}}\) का एक असांत आवर्ती दशमलव प्रसार है। उत्तर

(viii) मान लीजिए x = \(\frac{6}{15}=\frac{2}{5}\) ……………. (1)
(1) की x = \(\frac{p}{q}\) से तुलना कीजिए ।
यहाँ p = 2, q = 5
q के अभाज्य गुणनखंड = 5 = 2⁰ × 5¹
जोकि 2ⁿ × 5^m के रूप का है,
जहाँ n = 0, m = 1 है।
∴ x = \(\frac{6}{15}[/layex] का एक सांत दशमलव प्रसार है।

दशमलव के रूप में व्यक्त करना
x = [latex]\frac{6}{15}=\frac{2}{5}\)

x = \(\frac{2 \times 2^{1}}{2^{1} \times 5^{1}}=\frac{4}{10}\) = 0.4

दशमलव के रूप में,
x = \(\frac{6}{15}\) = 0.4.

(x) मान लीजिए x = \(\frac{35}{50}=\frac{7}{10}\) ………….. (1)
(1) की x = \(\frac{p}{q}\) से तुलना कीजिए।
यहाँ p = 7, q = 10
q के अभाज्य गुणनखंड = 10 = 2¹ × 5¹
जोकि 2ⁿ × 5^m के रूप का है,
जहाँ n = 1, m = 1
और n और m दोनों ऋणोतर पूर्णांक हैं।
∴ x = \(\frac{7}{10}\) का एक सांत दशमलव प्रसार है।

दशमलव के रूप में व्यक्त करना

अत: दशमलव रूप में,
x = 0.7.

(x) मान लीजिए x = \(\frac{77}{210}=\frac{11}{30}\) ……………..(1)
(1) की x = \(\frac{p}{q}\) से तुलना कीजिए।
यहाँ p = 11, q = 30
q के अभाज्य गुणनखंड = 30 = 2 × 3 × 5
जोकि 2ⁿ × 5^m के रूप में नहीं है
∴ x = \(\frac{77}{210}\) का असांत आवर्ती दशमलव प्रसार है। उत्तर

प्रश्न 3.
कुछ वास्तविक संख्याओं के दशमलव प्रसार नीचे दर्शाए गये हैं। प्रत्येक स्थिति के लिए निर्धारित कीजिए कि यह संख्या परिमेय संख्या है या नहीं। यदि यह परिमेय संख्या है और \(\frac{p}{q}\) के.रूप की है, तो के अभाज्य गुणनखंडों के बारे में आप क्या कह सकते हैं ?
(i) 43.123456789
(ii) 0.120120012000120000
(iii) \(43 . \overline{123456789}\)
हल :
(i) मान लीजिए x = 43.123456789 ……………(1)
संख्या से स्पष्ट है कि x एक परिमेय संख्या है।
अब संख्या में से दशमलव को हटा दीजिए
∴ x = \(\frac{43123456789}{1000000000}\)

x = \(\frac{43123456789}{10^{9}}\) ……………….(2)

(2) से x \(\frac{p}{q}\) के रूप की एक परिमेय संख्या है
जब p = 43123456789 और q = 10⁹
अब q के अभाज्य गुणनखंड = 10⁹ = (2 × 5)⁹
⇒ q के अभाज्य गुणनखंड 2⁹ × 5⁹ हैं। उत्तर

(ii) मान लीजिए x = 0.120120012000120000
संख्या से स्पष्ट है कि यह एक अपरिमेय संख्या है।

(iii) मान लीजिए x = \(43 . \overline{123456789}\) …. (1)
यह स्पष्ट है कि दी गई संख्या एक परिमेय संख्या है क्योंकि यह असांत और आवर्ती दशमलव है।

यह दर्शाने के लिए कि (i) P के रूप का है
(1) के दोनों पक्षों को 10⁹ से गुणा कीजिए
10⁹ x = 43123456789.123456789… …. (2)
(1) को (2) से घटाने पर हम प्राप्त करते हैं :

अतः, q के अभाज्य गुणनखंड 32 (12345679) हैं।