Bhagya

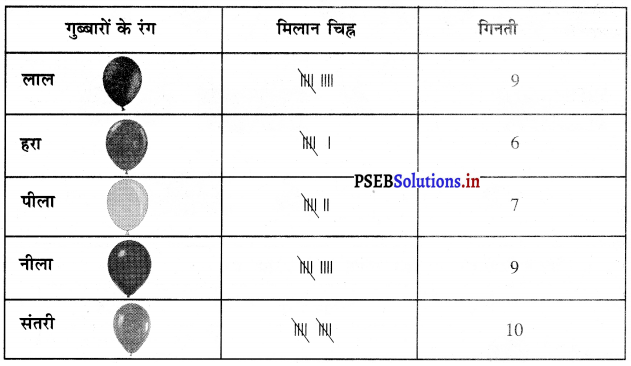
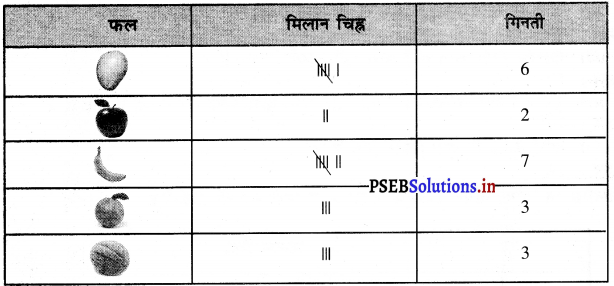
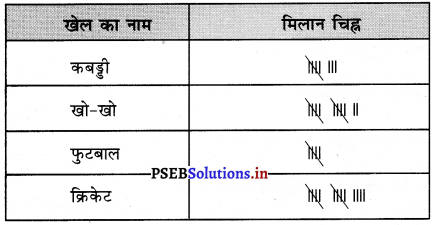
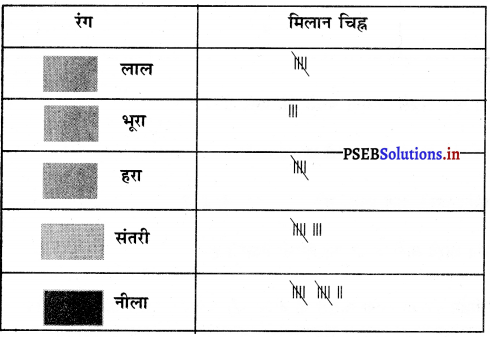
Punjab State Board PSEB 9th Class Science Book Solutions Chapter 2 क्या हमारे आस-पास के पदार्थ शुद्ध हैं Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Science Chapter 2 क्या हमारे आस-पास के पदार्थ शुद्ध हैं

PSEB 9th Class Science Guide क्या हमारे आस-पास के पदार्थ शुद्ध हैं Textbook Questions and Answers

प्रश्न 1.
निम्नलिखित को पृथक् करने के लिए आप किन विधियों को अपनायेंगे ?
(a) सोडियम क्लोराइड को जल के विलयन से पृथक् करने में।
(b) अमोनियम क्लोराइड को सोडियम क्लोराइड तथा अमोनियम क्लोराइड के मिश्रण से पृथक् करने में।
(c) धातु के छोटे टुकड़े को कार के इंजन आयल से पृथक करने में।
(d) दही से मक्खन निकालने के लिए।
(e) जल से तेल निकालने के लिए।
(f) चाय से पतियों को पृथक् करने में।
(g) बालू से लोहे की पिनों को पृथक् करने में।
(h) भूसे से गेहूँ के दानों को पृथक् करने में।
(i) पानी में तैरते हुए महीन मिट्टी के कण को पानी से अलग करने के लिए।
(j) पुष्प की पंखुड़ियों के निचोड़ से विभिन्न रंजकों को पृथक् करने में।
उत्तर-
(a) आसवन विधि/वाष्यण से
(b) ऊर्ध्वपातन विधि
(c) फिल्टरीकरण या छानन विधि
(d) अपकेंद्रण विधि
(e) पृथक्करण विधि (पृथक्कारो कीप विधि)
(f) छानन विधि
(g) चुंबकीय पृथक्करण विधि
(h) फटकन विधि
(i) फिल्टरीकरण या अपकेंद्रण विधि
(j) क्रोमैटोग्राफी।

प्रश्न 2.
चाय तैयार करने के लिए आप किन-किन चरणों का प्रयोग करेंगे। विलयन, विलायक, विलेय, घुलना, घुलनशील, अघुलनशील, घुलेय (फिल्ट्रेट) तथा अवशेष शब्दों का प्रयोग करें।
उत्तर-
विलयन का चयन – चाय बनाने के लिए जल आधारभूत विलयन के रूप में चुना जाता है जिसमें चाना और दूध विलेय के रूप में जल रूपी विलायक में सरलता से मिल सकते हैं।

क्वथन – जल को इतने तापमान तक गर्म किया जाता है कि वह क्वथनांक प्राप्त कर उबल जाए। उसमें घुलनशील चीनी और अघुलनशील चाय पत्ती आवश्यक मात्रा में डाल विलेय दूध में मिलाओ।

छानन – अघुलनशील चाय पत्नी को घुलेय पदार्थ मान कर छलनी से छानो। घुलनशीला चीनी और दूध वाय बनारे में प्रयुक्त हो जाएंगे। अवशेष रूप में चाय पत्ती को बाहर निकाल कर फिल्ट्रेट रूप में चाय प्राप्त कर लो ।

प्रश्न 3.
प्रज्ञा ने तीन अलग-अलग पदार्थों की घुलनशीलताओं को अलग-अलग तापमान पर जांचा और नीचे दिये गये आंकड़ों को प्राप्त किया। प्राप्त हुए परिणामों को 100 ग्राम जल में विलेय पदार्थ की मात्रा, जा संतृप्त विलयन बनाने हेतु पर्याप्त है, अग्रलिखित तालिका में दर्शाया गया है।

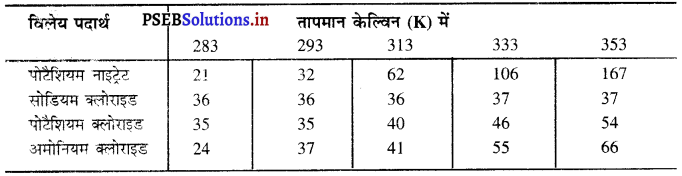
(a) 50 ग्राम जल में 313 K पर पोटैशियम नाइट्रेट के संतृप्त विलयन को प्राप्त करने हेतु कितने ग्राम पोटैशियम नाइट्रेट की आवश्यकता होगी ?
(b) प्रज्ञा 353 K पर पोटैशियम क्लोराइड का संतृप्त विलयन तैयार करती है और विलयन को कमरे के तापमान पर ठंडा होने के लिए छोड़ देती है। जब विलयन ठंडा होगा तो वह क्या अवलोकित करेगी ? स्पष्ट करें।
(c) 293 K पर प्रत्येक लवण की घुलनशीलता का परिकलन करें। इस तापमान पर कौन-सा लवण सबसे अधिक घुलनशील होगा ?
(d) तापमान के परिवर्तन में लवण की घुलनशीलता पर क्या प्रभाव पड़ता है ?
उत्तर-
(a) 100g जल में 313K पर संतृप्त विलयन के लिए आवश्यक KNO₃ = 62g
50g जल में 313K पर संतृप्त विलयन के लिए आवश्यक KNO₃ = \(\frac{62}{100}\) x 50 = 31g

(b) 353K पर KCI के संतृप्त विलयन को जब प्रज्ञा ठंडा करने के लिए छोड़ देगी तो तापमान कम होने पर क्रिस्टलीकरण हो जाएगा जिसके परिणामस्वरूप KCI के क्रिस्टल बन जाएंगे।

(c) KNO₃ की 100g जल में घुलनशीलता = \(\frac{32}{100}\) × 100 = 32g
NaCl की 100g जल में घुलनशीलता =\(\frac{36}{100}\) × 100 = 36g
KCl की 100g जल में घुलनशीलता = \(\frac{35}{100}\) × 100 = 35g
NH₄Cl की 100g जल में घुलनशीलता = \(\frac{37}{100}\) × 100 = 37g
293K पर सबसे अधिक घुलनशीलता अमोनियम क्लोराइड की है।

(d) तापमान में परिवर्तन से लवणों की घुलनशीलता प्रभावित होती है। जैसे-जैसे तापमान बढ़ता है वैसे-वैसे लवणों की घुलनशीलता बढ़ती जाती है।

प्रश्न 4.
निम्न की उदाहरण सहित व्याख्या करें :
(a) संतृप्त विलयन
(b) शुद्ध पदार्थ
(c) कोलाइड
(d) निलंबन।
उत्तर-
(a) संतृप्त विलयन – किसी निश्चित तापमान पर यदि विलयन में विलेय पदार्थ नहीं घुलता है तो उसे संतृप्त विलयन कहते हैं। भिन्न पदार्थों की भिन्न तापमानों पर विलयन क्षमता अलग-अलग होती है।

(b) शुद्ध पदार्थ – शुद्ध पदार्थ वह है जिसे केवल एक ही प्रकार के अणु हैं। शुद्ध पदार्थों में भौतिक तथा रासायनिक गुण होते हैं। सभी यौगिक शुद्ध पदार्थ हैं। उदाहरण-साधारण नमक, चीनी, सोना, तांबा, पारा आदि।

(c) कोलाइड – यह एक विषमांगी मिश्रण है जिसमें कणों का आकार 1 nm से 100 nm के बीच होता है जिन्हें आंखों से नहीं देखा जा सकता। ये कण इतने बड़े आकार के होते हैं कि प्रकाश की किरण को फैला सकें। ये कण तल पर नहीं बैठते लेकिन अपकेंद्रीकरण तकनीक से पृथक् किए जा सकते हैं। उदाहरण-कोहरा, बादल, धुआं, दूध, स्पंज, जेली, पनीर, मक्खन आदि।

(d) निलंबन – वह विषमांगी घोल जो ठोस द्रव में परिक्षेपित हो जाता है उसे निलंबन कहते हैं। इसमें विलेय पदार्थ कण घुलते नहीं हैं। बल्कि माध्यम की समष्टि में निलंबित रहते हैं। ये आंखों से देखे जा सकते हैं। छानन विधि से इन्हें मिश्रण से अलग किया जा सकता है। उदाहरण-जल में चाक पाऊडर।

प्रश्न 5.
निम्नलिखित में से प्रत्येक को समांगी और विषमांगी मिश्रणों में वर्गीकृत करें : सोडा-जल, लकड़ी, बर्फ, वायु, मिट्टी, सिरका, छनी हुई चाय।
उत्तर-
सोडा जल = समांगी
लकड़ी = विषमांगी
बर्फ = समांगी
वायु = समांगी
मिट्टी = विषमांगी
सिरका = समांगी
छनी हुई चाय = समांगी

समांगी प्रश्न 6.
आप किस प्रकार पुष्टि करेंगे कि दिया हुआ रंगहीन द्रव शुद्ध जल है ?
उत्तर-
रंगहीन द्रव में किसी प्रकार के आंखों से दिखाई देने वाले रंग के कण न होने की स्थिति में जल के शुद्ध होने की पुष्टि होती है लेकिन उसमें किसी प्रकार की गंध और स्वाद भी नहीं होना चाहिए। इसे 100°C या 373 K पर उबल जाना चाहिए।

प्रश्न 7.
निम्नलिखित में से कौन-सी वस्तु शुद्ध पदार्थ है ?
(a) बर्फ
(b) दूध
(c) लोहा
(d) हाइड्रोक्लोरिक अम्ल
(e) कैल्सियम ऑक्साइड
(f) पारा
(g) ईंट
(h) लकड़ी
(i) वायु।
उत्तर-
लोहा, हाइड्रोक्लोरिक अम्ल, पारा, कैल्शियम ऑक्साइड।

प्रश्न 8.
निम्नलिखित मिश्रणों में से विलयन की पहचान करें।
(a) मिट्टी
(b) समुद्री जल
(c) वायु
(d) कोयला
(e) सोडा जल।
उत्तर-
समुद्री जल, वायु, सोडा जल।

प्रश्न 9.
निम्नलिखित में से कौन टिंडल प्रभाव को प्रदर्शित करेगा ?
(a) नमक का घोल
(b) दूध
(c) कॉपर सल्फेट का विलयन
(d) स्टार्च विलयन।
उत्तर-
दुध, स्टार्च विलयन।

प्रश्न 10.
निम्नलिखित को तत्व यौगिक तथा मिश्रण में वर्गीकृत करें :-
(a) सोडियम
(b) मिट्टी
(c) चीनी का घोल
(d) चांदी
(e) कैल्सियम कार्बोनेट
(f) टिन
(g) सिलिकन
(h) कोयला
(i) वायु
(j) साबुन
(K) मीथेन
(l) कार्बन डाइऑक्साइड
(m) रक्त।
उत्तर-
तत्व = सोडियम, चांदी, टिन, सिलिकन
यौगिक = कैल्शियम कार्बोनेट, मिथेन, कार्बन डाइऑक्साइड
मिश्रण = मिट्टी, चीनी का घोल, कोयला, साबुन, वायु, रक्त।

प्रश्न 11.
निम्नलिखित में से कौन-से परिवर्तन रासायनिक हैं ?
(a) पौधों की वृद्धि
(b) लोहे में जंग लगना
(c) लोहे के चूर्ण और बालू को मिलाना
(d) खाना पकाना
(e) भोजन का पाचन
(1) जल से बर्फ बनना
(५) मोमबत्ती का जलना।
उत्तर-
लोहे में जंग लगना, खाना पकाना, भोजन का पाचन, मोमबत्ती का जलना।

Science Guide for Class 9 PSEB क्या हमारे आस-पास के पदार्थ शुद्ध हैं InText Questions and Answers

पाठ्य-पुस्तक के प्रश्नों के उत्तर

प्रश्न 1.
शुद्ध पदार्थ से आप क्या समझते हैं ?
उत्तर-
शुद्ध पदार्थ – वे पदार्थ शुद्ध कहलाते हैं जिनमें विद्यमान सभी कण समान रासायनिक प्रकृति के होते हैं। शुद्ध पदार्थ में सदा एक ही प्रकार के कण होते हैं ; जैसे-सोना, तांबा, सोडियम क्लोराइड, चीनी आदि।

प्रश्न 2.
समांगी और विषमांगी मिश्रणों में अंतर बताएं।।
उत्तर-
समांगी और विषमांगी मिश्रणों में अंतर – समांगी मिश्रण का रूप, गुण तथा संरचना हर अवस्था में समरूप होता है। विषमांगी मिश्रण के अंगों के भौतिक गुण एक-दूसरे से भिन्न होते हैं। जल में नमक और जल में चीनी समांगी मिश्रण के उदाहरण हैं। जल में तेल, नमक में गंधक, नमक में लोहे की छीलन, रेत में नमक, नमक में चीनी आदि विषमांगी मिश्रण के उदाहरण हैं।

प्रश्न 3.
उदाहरण के साथ समांगी एवं विषमांगी मिश्रणों में अंतर विभेद कीजिए। उत्तर-

उत्तरसमांगी मिश्रण	विषमांगी मिश्रण
(1) इसके अवयव एक समान बंटे होते हैं।	(1) इसके अवयव एक समान रूप में बंटे नहीं होते।
(2) इसमें अंशों के गुण तथा संरचना हर अवस्था में समरूप होती है। उदाहरण-पीतल, कांसा, पानी में चीनी, एल्कोहल में पानी, वायु आदि।	(2) इसमें अंशों के गुण एक-दूसरे से भिन्न होते हैं। उदाहरण-रेत कण और लोह चूर्ण, रेत + अमोनियम क्लोराइड, पानी में चॉक, पानी में तेल आदि।

प्रश्न 4.
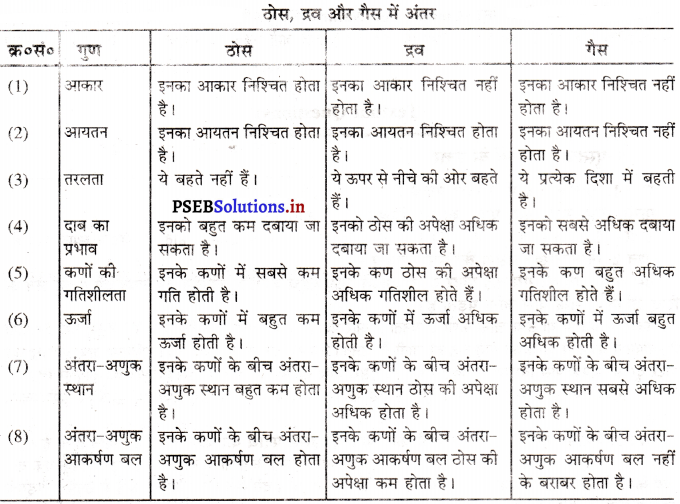
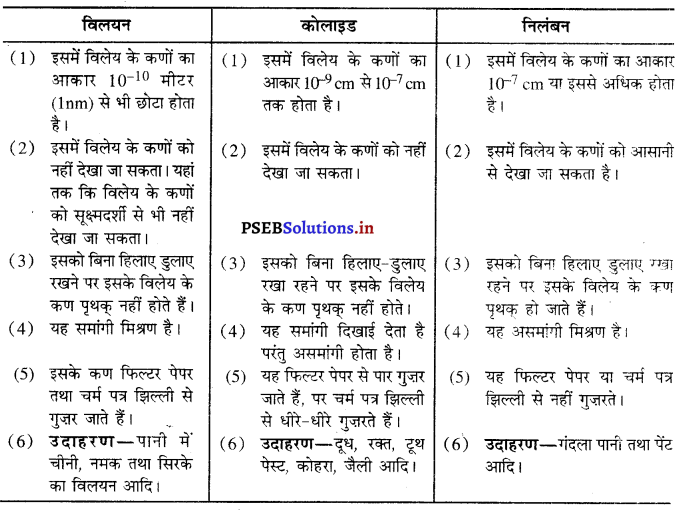
विलयन, निलंबन और कोलाइड एक-दूसरे से किस प्रकार भिन्न हैं ?
उत्तर-
विलयन, निलंबन और कोलाइड में भिन्नता-

प्रश्न 5.
एक संतृप्त विलयन बनाने के लिए 36g सोडियम क्लोराइड को 100g जल में 293K पर घोला जाता है। इस तापमान पर इसकी सांद्रता प्राप्त करें।
उत्तर-
विलेय पदार्थ का द्रव्यमान (सोडियम क्लोराइड) = 36g
विलायक का द्रव्यमान (जल) = 100g
विलयन का द्रव्यमान = विलेय पदार्थ का द्रव्यमान + विलायक का द्रव्यमान = 36g + 100g = 136g

= \(\frac{36}{136}\) x 100 = 26.47%

प्रश्न 6.
पेट्रोल और मिट्टी का तेल (Kerosene Oil) जोकि आपस में घुलनशील हैं, के मिश्रण को आप कैसे पृथक् करेंगे ? पेट्रोल तथा मिट्टी के तेल के क्वथनांकों में 25°C से अधिक का अंतराल है ?
उत्तर-
पेट्रोल और कैरोसीन के मिश्रण को साधारण आसवन विधि से अलग-अलग क । क्योंकि दोनों द्रव बिना अपघटन के उबल जाएंगे। उनके क्वथनांकों में 25°C के अधिक का अंतराल है।

प्रश्न 7.
पृथक करने की सामान्य विधियों के नाम दें-
(अ) दही से मक्खन
(ब) समुद्री जल से नमक
(स) नमक से कपूर।
उत्तर-
(अ) अपकेंद्रण
(ब) क्रिस्टलीकरण
(स) ऊर्ध्वपातन ।

प्रश्न 8.
क्रिस्टलीकरण विधि से किस प्रकार के मिश्रणों को पृथक् किया जा सकता है ?
उत्तर-
क्रिस्टलीकरण विधि से ठोस पदार्थों में मिली अशुद्धियों को दूर किया जा सकता है। समुद्री जल में घुले नमक को शुद्ध रूप में प्राप्त करने तथा अशुद्ध नमूने से फिटकरी को पृथक् करने के लिए क्रिस्टलीकरण का प्रयोग किया जाता है।

प्रश्न 9.
निम्न को रासायनिक और भौतिक परिवर्तनों में वर्गीकृत करें-
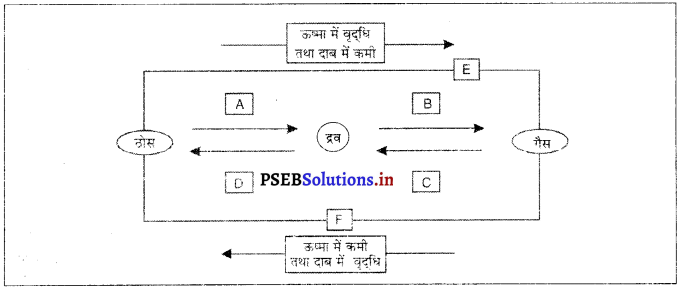
पेड़ों का काटना, मक्खन का एक बर्तन में पिघलना, अलमारी में जंग लगना, जल का उबल कर वाष्य बनना, विद्युत् तरंग का जल में प्रवाहित होना तथा उसका हाइड्रोजन और ऑक्सीजन गैसों में विघटित होना, जल में साधारण नमक का घुलना, फलों से सलाद बनाना, लकड़ी और कागज़ का जलना।
उत्तर-

1. पेड़ों का काटना = भौतिक परिवर्तन
2. मक्खन का एक बर्तन में पिघलना = भौतिक परिवर्तन
3. अलमारी में जंग लगना = रासायनिक परिवर्तन
4. जल का उबल कर वाष्प बनना = भौतिक परिवर्तन।
5. विद्युत तरंग का जल में प्रवाहित होना और उसका हाइड्रोजन और ऑक्सीजन गैसों में विघटित होना = रासायनिक परिवर्तन
6. जल में साधारण नमक का घुलना = भौतिक परिवर्तन
7. फलों से सलाद बनाना = भौतिक परिवर्तन
8. लकड़ी और कागज़ का जलना = रासायनिक परिवर्तन ।

प्रश्न 10.
अपने आस-पास की चीज़ों को शुद्ध पदार्थों या मिश्रण से अलग करने का प्रयत्न करें।
उत्तर-
शुद्ध पदार्थ – हाइड्रोजन, तांबा, सोना, नमक, चीनी, जल, लोहा, चांदी आदि।। मिश्रण-सोडा वाटर, नमक का घोल, शर्बत, धुवां, आइसक्रीम, गंधक-लोह चूर्ण का मिश्रण, जल और तेल का घोल।

This PSEB 9th Class Computer Notes Chapter 1 एम०एस० एक्सल (भाग-1) will help you in revision during exams.

PSEB 9th Class Computer Notes Chapter 1 एम०एस० एक्सल (भाग-1)

सैल को फारमेट करना-
किसी भी सैल के कंटेंट की अपनी आवश्यकता अनुसार दिखावट बदलने की प्रक्रिया को फारमेटिंग कहते हैं। इसमें टैक्सट का आकार, रंग, फोंट आदि बदला जाता है। नंबरों के फारमेट भी इसी के अंदर बदले जाते हैं। इसका उद्देश्य अपनी रिपोर्ट को सुंदर बनाने से होता है।

मर्ज तथा सैंटर
मर्ज तथा सैंटर वह सेवा है जिसके द्वारा दो या ज्यादा सैलों को पहले एक सैल में मर्ज किया जाता है तथा फिर उसके कंटेंट को सैंटर अलाइन किया जाता है। ये दोनों कार्य एक ही कमांड द्वारा किये जाते हैं। इस प्रक्रिया में सारे सैलों के कंटैंट इकट्ठे हो जाते हैं।
मर्ज करने के पग-सैलों को मर्ज करने के निम्न पग होते हैं –

1. सबसे पहले सैलों का चुनाव करें।
2. Home टैब पर क्लिक करें।
3. मर्ज तथा सैंटर बटन पर क्लिक करें। सारे सैल मर्ज हो जाएंगे तथा उनका डाटा सैंटर हो जाएगा।

नंबर ग्रुप
नंबर ग्रुप किसी भी सैल में नंबर को दिखाने के तरीके को परिभाषित करता है। एक्सल में विभिन्न प्रकार के नंबर फारमैट उपलब्ध हैं।

स्टाइल
सैल स्टाइल को सैल फारमैटिंग भी कहा जाता है। यह दो प्रकार की होती है

1. जनरल
2. कंडीशनल

इसका कार्य सैल की दिखावट में बदलाव करना होता है। कंडीशनल फारमेटिंग-कंडीशनल फारमेटिंग डाटा को फारमेट करने का एक ढंग है। इसमें डाटा को खास कंडीशन के आधार पर फारमेट किया जा सकता है। ये कंडीशन्ज़ यूजर की अपनी ज़रूरत के अनुसार होती है। यदि दी गई कंडीशन पूरी हो रही हो तो फारमेटिंग लागू हो जाती है अन्यथा वह फारमेटिंग लागू नहीं होती।

कंडीशनल फारमेटिंग नियम बनाने के पग निम्न हैं –

1. सबसे पहले सैल का चुनाव करें।
2. Format टैब पर क्लिक करें।
3. Conditional Formating पर क्लिक करें।
4. अपनी आवश्यकता अनुसार कंडीशन को डिफाइन करें।
5. OK पर क्लिक करें।

फारमेटिंग एज़ टेबल-सैल की एक रेंज को टेबल जैसे भी फारमेट कर सकते हैं। इसके लिए एक्सल में बने बनाए टेबल स्टाइल हैं। इसके लिए सूचना को टेबल रूप में फारमेट करना।

1. डाटा का चुनाव करें।
2. Home – Style ग्रुप – Format As table पर क्लिक करें।
3. अपनी ज़रूरत अनुसार स्टाइल चुनें।

सैल स्टाइल-सैल स्टाइल का अर्थ है-सैल के फोंट, रंग, बैकग्राऊंड आदि को फारमेट करना। यह यूजर द्वारा बनाए तथा पहले से परिभाषित हो सकते हैं।

सैल स्टाइल लागू करना

1. सैल का चुनाव करो।
2. Home – Style ग्रुप – Cell Styles का चुनाव करो।
3. अपनी आवश्यकता अनुसार स्टाइल चुनें।

सैल ग्रुप
एक्सल के रोअ तथा कॉलम के काट क्षेत्र को सैल कहते हैं। यह आयताकार आकृति होती है, एक्सल का सारा कार्य इसी में किया जाता है। इसी में टैक्सट, नंबर, फार्मूले तथा फंक्शन एंटर किये जाते हैं। नया सैल दाखिल करना

1. जहां सैल दाखिल करना है वहां का सैल चुनें।
2. Home – Cell ग्रुप – Insert वटन पर क्लिक करें।
3. एक डायलॉग वाक्स दिखाई देगा। ज़रूरत अनुसार विकल्प चुनें।

Shift Cell Right : मौजूदा सैल को दायें शिफ्ट करें।
Shift Cell Down : मौजूदा सैल को नीचे शिफ्ट करें।
Enter Row : सारी रोअ शिफ्ट कर नई रोअ दाखिल करें।
Enter Column : सारा कालम शिफ्ट कर नया कालम दाखिल करो।

सैल/रोअ/कालम डिलीट करना
ज़रूरत पड़ने पर हम सैल/रोअ या कॉलम डिलीट भी कर सकते हैं। इसके निम्न पग हैं

1. डिलीट करने वाले सैल/रोअ या कालम को सिलैक्ट करें।
2. Home – Cell ग्रुप – Delete ड्रापडाऊन में से उपयुक्त विकल्प चुनें।

वे विकल्प हैं-

• Delete Cells
• Delete Sheet Rows
• Delete Sheet Columns

3. एक डायलॉग बॉक्स दिखाई देगा। उसमें से आवश्यकता अनुसार विकल्प चुनें तथा OK बटन पर क्लिक करें।

नई वर्कशीट दाखिल करना
नई वर्कशीट दाखिल करने के लिए एक्सल विंडो के निचले भाग में उपलब्ध शीट बार पर उपलब्ध Insert Work Sheet बटन पर क्लिक करें या Shift + Fill कीअ दबाएं।

बर्कशीट डिलीट करना
वर्कशीट डिलीट करने के लिए वर्कशीट के नाम पर Right Click करके Delete का आप्शन चुनें।

सैल साइज
सैल का आकार उसकी चौड़ाई या ऊंचाई कम या ज्यादा करके बदला जा सकता है।

कॉलम की चौड़ाई बदलना
जिस कॉलम की चौड़ाई बदलनी हो उसके नाम तथा उसके अगले कॉलम के नाम के बीच माऊस ले जाएं। माऊस प्वाइंटर दो धारी हो जाएगा। माऊस बटन दबाकर ज़रूरत अनुसार खींचे। कॉलम की चौड़ाई बदल जाएगी।

रोअ की ऊंचाई बदलना
रोअ की ऊँचाई बदलने के लिए दो रोअ के नाम के बीच माऊस प्वाइंटर ले जाएं। वह दो धारी तीर बन जाएगा। ज़रूरत अनुसार ज्यादा या कम करें।

एडिटिंग
फार्मूला
फार्मूला एक्सल में किसी भी गणितीय फार्मूले का एक रूप होता है जिस प्रकार गणित में चरों तथा अचरों के मेल से फार्मूला बनता है, जिसका एक आऊटपुट प्राप्त होता है। इसी प्रकार, एक्सल में किसी खास गणना को करने के लिए चर,अचर तथा सैल मूल्यों का प्रयोग किया जाता है। इससे गणना का कार्य आसान तथा शीघ्र हो जाता है।
फार्मूला बनाने के पग-एक्सल में फार्मूला निम्न प्रकार से दाखिल किया जा सकता है-

1. उस सैल का चुनाव करें जहां फार्मूला दाखिल करना है।
2. बराबर ( = ) का निशान डालें।
3. फार्मूला टाइप करें।
4. एंटर कीअ दबाएं। फार्मूला दाखिल हो जाएगा।

सैल रैफरेसिंग
फार्मूले में सैल एडरैस वर्णन के तरीके को सैल रेफरेंसिंग कहते हैं।
यह तीन प्रकार की होती हैं
1. रिलेटिव रेफरेंसिंग
2. एबसोल्यूट रेफरेंसिंग
3. मिक्सड रेफरेंसिंग।

1. रिलेटिव रेफरेंसिंग-रिलेटिव रेफरेंसिंग वो रेफरेंसिंग होती है जो फार्मूला कापी करने से उसके अनुसार बदल जाती है।
2. एबसोल्यूट रेफरेंसिंग-जिस रेफरेंसिंग में फार्मूला कापी करने के साथ रेफरेंसिंग नहीं होता उस को एबसोल्यूट रेफरेंसिंग कहते हैं।
3. मिक्सड रेफरेसिंग-जिस रेफरेंसिंग में रिलेटिव और एबसोल्यूट दोनों तरह की रेफरेंसिंग का इस्तेमाल होता है, उस को मिक्सड रेफरेंसिंग कहते हैं।

फंक्शन
फंक्शन फार्मूले का ही उन्नत रूप है। फार्मूले हर बार टाइप करने पड़ते हैं तथा उनमें ग़लतियां भी हो जाती हैं। इनमें समय भी ज्यादा लगता है। बड़ा कार्य करने में फार्मूला भी बड़ा हो जाता है जिससे कार्य कठिन हो जाता है। फंक्शन एक्सल में बने बनाए फार्मूले होते हैं। जिन्हें एक खास नाम के अंदर स्टोर किया जाता है। उस नाम का प्रयोग करके फंक्शन का प्रयोग किया जा सकता है। इसमें अपरेटर बार-बार दाखिल नहीं करने पड़ते।

बेसिक फंक्शन दाखिल करने के पग एक्सल में बेसिक फंक्शन निम्न पग का प्रयोग करके दाखिल किया जा सकता है –

1. सबसे पहले सैल का चुनाव करें जहां फंक्शन दाखिल करनी है।
2. Formula टैब पर क्लिक करें।
3. Function बटन पर क्लिक करें।
4. आवश्यकता अनुसार फंक्शन ग्रुप तथा फंक्शन का चुनाव करें।
5. फंक्शन में प्रयोग होने वाले आर्गुमैंट दाखिल करें।
6. OK पर क्लिक करें। (फंक्शन दाखिल हो जाएगा।)

सोर्टिंग सोर्टिंग का अर्थ है-डाटा को ज़रूरत अनुसार क्रम बार करना। डाटा को बढ़ते या घटते क्रम में सोर्ट किया जा सकता है।
सोर्ट करने के पग

1. डाटा का चुनाव करें।
2. Date -Sort and Filter ग्रुप में Sort विकल्प चुनें।
3. डायलॉग वॉक्स में से सोर्ट करने का कॉलम, क्रम आदि चुनें तथा OK का बटन दबाएं।

डाटा फिल्टर
डाटा फिल्टर का अर्थ है-डाटा में से ज़रूरत का डाटा दिखाना तथा बाकी छुपाना। इससे बड़े डाटा पर काम करने में आसानी होती है।

डाटा फिल्टर के पग

1. डाटा की ऊपरी रोअ में क्लिक करें।
2. Date – Sort and Filter में Filter कमांड पर क्लिक करें।
3. हर हैडर रोअ सैल पर एक ऐरो दिखाई देगा।
4. किसी ऐरो पर क्लिक करें।
5. ज़रूरत अनुसार विकल्प चुनें।
6. OK बटन पर क्लिक करें।

फिल्टर क्लीयर करना
फिल्टर क्लीयर करने के लिए Data टैब पर Filter कमांड को बंद कर दें।

फाइंड एंड रिप्लेस
फाइंड एंड रिप्लेस का प्रयोग डाटा ढूंढने तथा उस को बदलने के लिए किया जाता है।

डाटा ढूंढना

1. Ctrl + F कीअ दबाएं। डायलॉग बॉक्स में जो ढूंढना है उसे टाइप करें।
2. ज़रूरत अनुसार अन्य विकल्प चुनें।
   जैसे- With in : Worksheet or Workbook

Search : By Row or By Column
Look in : फार्मूले, रिजल्ट आदि में से
Match Case : अक्षर बड़े छोटे भी मिलाने के लिए
Match Entire Cell Content : सारे सैल का कंटेंट मैच करने के लिए
3. Find बटन पर क्लिक करें।

डाटा रिप्लेस करना

1. Ctrl + H कीअ दबाएं।
2. डायलॉग बॉक्स में जो बदलना है वह टाइप करें तथा जिससे बदलना है उसे टाइप करें।
3. आवश्यकता अनुसार अन्य विकल्प चुनें।
4. Replace/Replace All बटन पर क्लिक करें।

Punjab State Board PSEB 9th Class Science Book Solutions Chapter 1 हमारे आस-पास के पदार्थ Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Science Chapter 1 हमारे आस-पास के पदार्थ

PSEB 9th Class Science Guide हमारे आस-पास के पदार्थ Textbook Questions and Answers

प्रश्न 1.
निम्नलिखित तापमान को सेल्सियस इकाई में परिवर्तित करें :
(a) 293K
(b) 470 K
उत्तर-
(a) 293 K = (293 – 273)
= 20°C

(b) 470 K = (470 – 273)°C
= 197°C

प्रश्न 2.
निम्नलिखित तापमान को केल्विन इकाई में परिवर्तित करें :
(a) 25°C
(b) 3730
उत्तर-
(a) तापमान = 25°C
= 25 + 273 = 298 K

(b) तापमान = 373°C
= 373 + 273 == 646 K

प्रश्न 3.
निम्नलिखित अवलोकनों हेतु के कारण लिखें :
(a) नैफ्थालीन को रखा रहने देने पर यह समय के साथ कुछ भी ठोस पदार्थ छोड़े बिना अदृश्य हो जाती है।
(b) हमें इत्र की गंध बहुत दूर बैठे हुए भी पहुंच जाती है।
उत्तर-
(a) अनेक पदार्थ द्रव अवस्था में परिवर्तित हुए बिना ठोस अवस्था से सीधे गैस में बदल जाते हैं जिसे ऊर्ध्वपातन कहते हैं। नेफ्थालीन की गोलियां इसी प्रक्रिया से बिना किसी ठोस को छोड़े लुप्त हो जाती हैं।

(b) पदार्थों के कण निरंतर गतिशील होते हैं। इत्र की सुगंध वायु के माध्यम से परासरण (विसरित) के कारण स्वयं आस-पास के वातावरण में फैल जाती है जिस कारण उसे कई मीटर दूर से भी सुंधा जा सकता है।

प्रश्न 4.
निम्नलिखित पदार्थों को उन के कणों के बीच बढ़ते हुए आकर्षण के अनुसार व्यवस्थित करें :
(a) जल
(b) चीनी
(c) ऑक्सीजन।
उत्तर-
ऑक्सीजन < जल < चीनी।

प्रश्न 5.
निम्नलिखित तापमानों पर जल की भौतिक अवस्था क्या है :
(a) 25°C
(b) 0°C
(c) 100°C?
उत्तर-
(अ) द्रव अवस्था
(ब) ठोस अवस्था
(स) उबलना (वाष्प)।

प्रश्न 6.
पुष्टि हेतु कारण दें:
(a) जल कमरे के ताप पर द्रव है।
(b) लोहे की अलमारी कमरे के ताप पर ठोस है।
उत्तर-
(a) (I) जल को जिस भी बर्तन में डाला जाए उसी का आकार ले लेता है। कमरे का तापमान जल के क्वथनांक से कम तथा हिमांक से अधिक है।
(II) जल बहता है और यह दृढ़ नहीं है।

(b) (I) लोहे की अलमारी की निश्चित, स्पष्ट सीमाएं और स्थिर आयतन है।
(II) नगण्य संपीड्यता है। कमरे का तापमान लोहे के क्वथनांक से कम और गलनांक से अधिक है। कमरे के तापमान पर उसका अवस्था परिवर्तन संभव नहीं है इसलिए वह उस तापमान पर ठोस है।

प्रश्न 7.
273 K पर बर्फ़ को ठंडा करने पर तथा जल को इसी तापमान पर ठंडा करने पर शीतलता का प्रभाव अधिक क्यों होता है ?
उत्तर-
273 K पर बर्फ इसी तापमान पर पानी की अपेक्षा संगलन की गुप्त ऊष्मा के कारण अधिक प्रभावशाली होती है।

प्रश्न 8.
उबलते हुए जल अथवा ताप में से जलने की तीव्रता किस में अधिक महसूस होती है ?
उत्तर-
भाप। जब जल 373 K पर उबलता है, तो 373 K वाष्प में बदलता है। उसे 536 कैलोरी/ग्राम ऊष्मा की आवश्यकता होती है। उबलते जल में गुप्त ऊष्मा भी सम्मिलित होती है।

प्रश्न 9.
निम्नलिखित चित्र के लिए A, B, C, D, E और F की व्यवस्था परिवर्तन को नामांकित करें-

उत्तर-
A – संगलन (Fusion)
B – वाष्पन (Vaporisation)
C – संघनन (Condensation)
D – जमना (Solidification)
E – ऊर्ध्वपातन (Sublimation)
F – ऊर्ध्वपातन (Sublimation)

Science Guide for Class 9 PSEB हमारे आस-पास के पदार्थ InText Questions and Answers

पाठ्य-पुस्तक के प्रश्नों के उत्तर

प्रश्न 1.
निम्नलिखित में से कौन पदार्थ हैं-
कुर्सी, वायु, स्नेह, गंध, घृणा, बादाम, विचार, शीत, शीतल पेय, इत्र की सुगंध।
उत्तर-
कुर्सी, वायु, बादाम और शीतल पेय पदार्थ हैं क्योंकि इन का द्रव्यमान होता है और ये स्थान घेरते हैं।

प्रश्न 2.
निम्नलिखित प्रेक्षण के कारण बताएँ-
गर्मा-गर्म खाने की गंध कई मीटर दूर से आपके पास पहुंच जाती है, लेकिन ठंडे खाने की महक लेने के लिए आपको उसके पास जाना पड़ता है।
उत्तर-
गर्मागर्म या ठंडा खाना कणों से बनता है और पदार्थ के कण सदा गतिशील होते हैं। उन में विसरण होता है। तापमान बढ़ने से कणों की गति तेज़ हो जाती है, उनकी विसरण की दर बढ़ जाती है। गर्मागर्म खाने की गंध कई मीटर दूर से आपके पास विसरण से पहुंच जाती है। दूसरी ओर खाना ठंडा होने पर इसके कणों का वायु में विसरण, लगभग नगण्य होता है। इसलिए अधिक दूरी पर ठंडे खाने की महक नहीं आ पाती तथा हमें खाने के समीप जाना पड़ता है।

प्रश्न 3.
स्वीमिंग पूल में गोताखोर पानी काट पाता है। इससे पदार्थ का कौन-सा गुण प्रेक्षित होता है?
उत्तर-
स्वीमिंग पूल में गोताखोर पानी को काट पाता है क्योंकि पानी के कणों के बीच अंतराअणुक नामक एक बल कार्य करता है जो कणों को एक साथ रखता है। जल के कणों के बीच दूरी अपेक्षाकृत अधिक होने से उनमें संपीड्यता का गुण होता है। स्वीमिंग पूल में गोताखोर जब पानी को अपने हाथों से धकेलता है तो पानी के अणुओं के मध्य आकर्षण बल कम होने के कारण वह पानी को काट पाता है।

प्रश्न 4.
पदार्थ के कणों की क्या विशेषताएं होती हैं? .
उत्तर-
प्रत्येक पदार्थ कणों के मिलने से बनता है। प्रत्येक पदार्थ के कण बहुत छोटे होते हैं इतने छोटे कि उन की छोटे आकार की हम कल्पना भी नहीं कर सकते। उनकी विशेषताएं निम्नलिखित हैं-

1. पदार्थ के कणों के बीच रिक्त स्थान होता है।
2. पदार्थ के कण निरंतर गतिशील होते हैं। उनमें गतिज ऊर्जा होती है।
3. पदार्थ के कण एक-दूसरे को आकर्षित करते हैं। यह आकर्षण बल अलग-अलग पदार्थों में अलग-अलग होता
4. तापमान बढ़ाने से कणों की गतिज ऊर्जा बढ़ जाती है।

प्रश्न 5.
किसी तत्त्व के द्रव्यमान प्रति इकाई आयतन को घनत्व कहते हैं। (घनत्व = )
बढ़ते हुए घनत्व के क्रम में निम्नलिखित को व्यवस्थित करें-
वायु, चिमनी का धुआं, शहद, जल, चॉक, रूई और लोहा।
उत्तर-
चिमनी का धुआं, वायु, रूई, जल, शहद, चॉक, लोहा।

प्रश्न 6.
(a) पदार्थ की विभिन्न अवस्थाओं के गुणों में होने वाले अंतर को सारणीबद्ध कीजिए।
(b) निम्नलिखित पर टिप्पणी कीजिए-दृढ़ता, संपीड्यता, तरलता, बर्तन में गैस का भरना, आकार, गतिज ऊर्जा एवं घनत्व।
उत्तर-
(a) पदार्थ की विभिन्न अवस्थाएँ ठोस, द्रव तथा गैस हैं। इनके मध्य अंतर निम्नलिखित हैं-

(b) 1 दृढ़ता – दृढ़ता ठोस पदार्थों का गुण है। नगण्य संपीड्यता के कारण वे बाह्य बल लगाने पर भी अपने आकार को नहीं बदलते। ये अपने आकार को दृढ़ता के गुण प्रदान करते हैं। ठोस पदार्थों में आकर्षण बल के कारण दृढ़ता अधिक होती है। द्रव को थोड़ा दबाया जा सकता है और गैस को सरलता से दबाया जा सकता है।

2. संपीड्यता – पदार्थों का संपीड्यता गुण, उन पर दाब के प्रभाव को व्यक्त करता है। यदि पदार्थ को बाह्य दाब के द्वारा दबाया नहीं जा सकता है तो उसकी संपीड्यता नगण्य होगी। इसके अतिरिक्त यदि पदार्थ को बाह्य दाब से दबाया जा सकता हो तो उसकी संपीड्यता अधिक होगी। दूसरे शब्दों में संपीड्यता पदार्थ के आयतन से संबंधित होती है। स्थिर आयतन वाले पदार्थों की संपीड्यता नगण्य तथा परिवर्तनशील आयतन वाले पदार्थों की संपीड्यता अधिक होती है। ठोस पदार्थों को बाह्य बल द्वारा दबाया नहीं जा सकता तथा इनका आयतन भी निश्चित होता है ; अतः इनकी संपीड्यता नगण्य होगी। द्रवों की संपीड्यता ठोसों से अधिक होती है तथा गैसों की संपीड्यता सर्वाधिक होती है। इसी कारण गैसों को कम आयतन वाले सिलिंडरों में संपीडित किया जा सकता है।

3. तरलता – तरलता तरल पदार्थों का गुण है जिनका निश्चित आकार नहीं होता पर निश्चित आयतन अवश्य होता है। तरलता बहने की प्रवृत्ति है और इसमें द्रव का आकार बदलता है। ठोस बिल्कुल नहीं बहते पर गैसें सब दिशाओं से बहती हैं।

4. बर्तन में गैस का भरना – गैसों के कणों में अंतराणुक बल क्षीण होने के कारण संपीड्यता बहुत अधिक होती है जिस कारण गैस के अत्यधिक आयतन को किसी कम आयतन वाले बर्तन में संपीडित किया जा सकता है और सरलतापूर्वक एक स्थान से दूसरे स्थान तक भेजा जा सकता है।

5. आकार – पदार्थ के कणों के बीच एक बल कार्य करता है। यह बल कणों को एक साथ रखता है और वस्तु को आकार प्रदान करता है। इस आकर्षण बल का सामर्थ्य प्रत्येक पदार्थ में अलग-अलग होता है। ठोस पदार्थों के कणों में अंतराणुक बल अधिक होता है जिस कारण उनका निश्चित आकार होता है पर द्रवों और गैसों में ऐसा नहीं होता।

6. गतिज ऊर्जा – पदार्थों के कण सदा गतिशील रहते हैं जिसे गतिज ऊर्जा कहते हैं। तापमान के बढ़ने से कणों की गति तेज़ हो जाती है अर्थात् तापमान बढ़ने से कणों की गतिज ऊर्जा भी बढ़ जाती है। ठोस में अधिक गतिज ऊर्जा नहीं होती। द्रव में कुछ गतिज ऊर्जा होती है, पर गैसों में उच्च गतिज ऊर्जा होती है।

7. घनत्व-किसी वस्तु का घनत्व प्रति एकांक आयतन के द्रव्यमान के बराबर होता है।

पदार्थ का आयतन ठोस पदार्थों का घनत्व उच्च होता है, द्रव में निम्न होता है, पर गैसों का घनत्व नगन्य होता है।

प्रश्न 7.
कारण बताएं-
(a) गैस पूरी तरह उस बर्तन को भर देती है, जिसमें इसे रखते हैं।
(b) गैस बर्तन की दीवारों पर दबाव डालती है।
(c) लकड़ी की मेज़ ठोस कहलाती है।
(d) हवा में हम आसानी से अपना हाथ चला सकते हैं लेकिन एक ठोस लकड़ी के टुकड़े में हाथ चलाने के लिए हमें कराटे में दक्ष होना पड़ेगा।
उत्तर-
(a) गैस में कणों को स्थिति बहुत ढीली होती है और उनके बीच रिक्त स्थान बहुत अधिक होते हैं। उनमें आकर्षण बल नगण्य के समान होता है और वे तीव्र गति से सभी दिशाओं में इधर-उधर गति कर सकते हैं। इनका निश्चित आयतन भी नहीं होता इसलिए गैस पूरी तरह उस बर्तन को भर देती है, जिसमें इसे रखा जाता है।

(b) गैस में कणों की गति अनियमित और अत्यधिक तीव्र होती है। इस अनियमित गति के कारण ये कण आपस में एवं बर्तन की दीवारों से टकराते हैं। बर्तन की दीवार पर गैस कणों द्वारा प्रति इकाई क्षेत्र पर लगे बल के कारण दीवारों पर दबाव बनता है।

(c) लकड़ी की मेज पदार्थ के जिन कणों से मिल कर बनती है उनके बीच एक बल कार्य करता है जो अन्य कणों को अपने साथ रखता है। निश्चित आकार, असंपीड्यता, स्पष्ट सीमाओं और स्थिर आयतन के कारण यह ठोस कहलाती है। यह बाह्य बल लगाने पर भी अपने आकार को बनाए रखती है।

(d) पदार्थ के कणों के मध्य आकर्षण बल होता है जिसकी सामर्थ्य भिन्न-भिन्न पदार्थों के लिए भिन्न-भिन्न होती है। हवा के कणों में यह बल्ल-सामर्थ्य नगण्य होती है जिससे इसके कणों के मध्य स्थान बनाया जा सकता है अर्थात् हवा के बीच में हम अपना हाथ आसानी से चला सकते हैं। परंतु ठोस लकड़ी के टुकड़े में आकर्षण बल-सामर्थ्य बहुत अधिक होती है जिससे इसके कण परस्पर दृढ़ता से जुड़े रहते हैं तथा इनके मध्य हम अपना हाथ नहीं चला सकते! लकड़ी के टुकड़े में हाथ चलाने के लिए हमें कराटे कला में निपुण होना चाहिए जिससे हम लकड़ी के टुकड़े को अपने हाथ से तोड़ सकते हैं।

प्रश्न 8.
सामान्यतया ठोस पदार्थ की अपेक्षा द्रवों का घनत्व कम होता है। लेकिन आपने बर्फ के टुकड़े को पानी में तैरते हुए देखा होगा पता लगाइए ऐसा क्यों होता है?
उत्तर-
अधिकांश वस्तुएं गर्म करने पर फैलती हैं। तापमान बढ़ने से उनका घनत्व घटता है पर पानी 0°C से 4°C तापमान के बीच सिकुड़ता है और इसके बाद यह अन्य वस्तुओं के समान फैलता है। पानी का अधिकतम घनत्व 4°C पर 1 g/cm3 है। बर्फ का घनत्व पानी से कम है इसलिए यह पानी के तल पर तैरती है। यह देखा गया है कि 0.91 g पानी (9°C पर 1 3 आयतन बेरता है अर्थात् बर्फ का घनत्व ) 91 g/cm3 होता है।

प्रश्न 9.
निम्नलिखित तापमान को सेल्सियस में बदलें।
(a) 300K
(b) 573 K
उत्तर-
(a) 300 K
300 -273 = 27°C

(b) 573K
573-273 = 300°C

प्रश्न 10.
निम्नलिखित तापमान पर पानी की भौतिक अवस्था क्या होगी?
(a) = 250°C
(b) = 100°C
उत्तर-
(a) वाष्प। सारा पानी भाप बन कर रड़ जाएगा।
(b) पानी उबलने लगेगा। जल का यही क्वथनांक है।

प्रश्न 11.
किसी भी पदार्थ की अवस्था परिवर्तन के दौरान स्थिर क्यों रहता है?
उत्तर-
किसी भी पदार्थ की अवस्था परिवर्तन के दौरान स्थिर रहती है। कणों के पारस्परिक आकर्षण बल को वशीभूत करके पदार्थ की अवस्था को बदलने में इस ऊष्मा का उपयोग होता है। तापमान में वृद्धि दिखाए बिना ही इस ऊष्मीय ऊर्जा को पदार्थ अवशोषित कर लेता है।

प्रश्न 12.
वायुमंडलीय गैसों को द्रव में परिवर्तन करने के लिए कोई विधि सुझाइए।
उत्तर-
वायुमंडलीय गैसों को किसी बंद बर्तन में बंद करके और दाब बढ़ा कर तथा तापमान कम कर के द्रव में बदला जा सकता है।

प्रश्न 13.
गर्म, शुष्क दिन में कूलर आंधक ठंडा क्यों करता है?
उत्तर-
गर्म, शुष्क दिन में तापमान बढ़ जाने से अधिक कणों को पर्याप्त गतिज ऊर्जा मिलती है। शुष्कता के कारण वायु में विद्यमान जलवाष्प कम हो जाते हैं। वायु में जल कणों की मात्रा कम होने से वाष्पीकरण की दर बढ़ जाती है। वाष्पीकरण से ठंडक उत्पन्न होती है।

प्रश्न 14.
गर्मियों में घड़े का जल ठंडा क्यों होता है ?
उत्तर-
मिट्टी से बने घड़े में छोटे-छोटे छिद्र (रध्र) होते हैं जिनमें से घड़े में भरा पानी रिसकर बाहर आ जाता है तथा वातावरण की गर्म वायु के संपर्क में आकर वाष्पीकृत हो जाता है। जल के वाष्प में परिवर्तित होने के लिए आवश्यक ऊष्मीय ऊर्जा घड़े के भीतर वाले जल से प्राप्त होती है। इससे घड़े के भीतर उपस्थित जल ठंडा हो जाता है।

प्रश्न 15.
ऐसीटोन/पेट्रोल या इत्र डालने पर हमारी हथेली ठंडी क्यों हो जाती है ?
उत्तर-
ऐसीटोन/पेट्रोल या इत्र शीघ्रता से वाष्पीकृत हो जाते हैं। जब इन पदार्थों को हथेली पर डाला जाता है तो इनके कण हथेली तथा आस-पास के वातावरण से ऊर्जा प्राप्त कर लेते हैं तथा वाष्पीकृत हो जाते हैं। ऊर्जा (ताप) के ह्रास से हमारी हथेली ठंडी हो जाती है।

प्रश्न 16.
कप की अपेक्षा प्लेट से हम गर्म दूध या चाय जल्दी क्यों पी लेते हैं ?
उत्तर-
कप की अपेक्षा प्लेट की सतह अधिक होती है। प्लेट की सतह अधिक होने के कारण इसमें भरे दूध या चाय का वाष्णन अधिक होता है। प्लेट की सतह से वाष्पन अधिक होने से दूध या बाय शीघ्रता से ठंडी हो जाती है और हम कप को अपेक्षा प्लेट से इसे जल्दी पी लेते हैं।

प्रश्न 17.
गर्मियों में हमें किस तरह के कपड़े पहनने चाहिए ?
उत्तर-
गर्मियों में हमें सूती कपड़े पहनने चाहिए। शारीरिक प्रक्रिया के कारण गर्मियों में पसीना अधिक आता है, जिससे हमें शीतलता प्राप्त होती है। पसीने के वाष्पीकरण के दौरान पसीने के कण हमारे शरीर या आस-पास से ऊर्जा प्राप्त करके वाष्प में बदल जाते हैं। वाष्पीकरण की प्रसुप्त ऊष्मा के बराबर ऊष्मीय ऊर्जा हमारे शरीर से अवशोषित हो जाती है जिससे शरीर शीतल हो जाता है। चूंकि सूती कपड़ों में जल का अवशोषण रोता है, इसलिए हमारा पसीना इसमें अवशोषित होकर वायुमंडल में आसानी से वाष्पीकृत हो जाता है।

Punjab State Board PSEB 3rd Class Maths Book Solutions Chapter 10 आंकड़े Textbook Exercise Questions and Answers

PSEB Solutions for Class 3 Maths Chapter 10 आंकड़े

पृष्ठ 197-198:

आओ करें:

प्रश्न 1.
नीचे दिया गया चित्र-ग्राफ स्कूल के विद्यार्थियों के मनपसंद कार्टून को दर्शा रहा है।

चित्र ग्राफ को पढ़कर निम्नलिखित प्रश्नों के उत्तर दो:
(i) बच्चों को कौन-सा कार्टून सबसे अधिक पसंद है ?
हल:
डोरा।

(ii) बच्चों को कौन-सा कार्टून कम पसंद है ?
हल:
मोटू पतलू।

(iii) डोरेमोन कार्टून पसंद करने वाले बच्चों की गिनती कितनी है ?
हल:
40.

(iv) कौन-से दो कार्टून बराबर बच्चों द्वारा पसंद किए जाते हैं ?
हल:
टॉम एंड जैरी तथा कृष्णा।

(v) छोटा भीम और मोटू पतलू कार्टून कितने बच्चों को पसंद है ?
हल:
50.

(vi) क्या उपरोक्त जानकारी को किसी और पैमाने में भी दर्शाया जा सकता है ?
हल:
हाँ।

पृष्ठ 198-199:

प्रश्न 2.
निम्नलिखित चित्र ग्राफ को पढ़ो और प्रश्नों के उत्तर दो:

(i) सबसे अधिक रन किसने बनाए और कितने ?
हल:
रोहित शर्मा ने सबसे अधिक 30 रन बनाये।

(ii) सबसे कम रन किसने बनाए और कितने ?
हल:
महेन्द्र सिंह धोनी ने सबसे कम 12 रन बनाए।

(iii) किन दो खिलाड़ियों ने बराबर रन बनाए और कितने ?
हल:
युवराज सिंह और शिखर धवन 18-18 रन।

(iv) शिखर धवन और विराट कोहली द्वारा कुल कितने रन बनाए गए ?
हल:
शिखर धवन और विराट कोहली द्वारा कुल 39 रन बनाए गए।

प्रश्न 3.
तीसरी कक्षा की गुरजोत के पेपरों में प्राप्त किए अंक निम्नलिखित अनुसार हैं:

इस जानकारी को चित्र संकेत, के रूप में अंकित करें। मान लो एक चित्र 10 अंकों को बताता है।
हल:

प्रश्न 4.
स्कूल की पाँच कक्षाएँ (पहली से पाँचवीं) को 5 फूलों की क्यारियों को संभालने की जिम्मेवारी दी गई है। प्रत्येक कक्षा को क्यारी में फूलों की गिनती निम्नलिखित सारणी में अंकित है:

इस जानकारी को चित्र के रूप में अंकित करें। मान लो = 2 फूल को दर्शाता है।
हल:

पृष्ठ 200

आओ करें:

1. मैथ किट की अलग-अलग आकृतियों को नीचे दिए बॉक्स में दर्शाया गया है

प्रश्न 1.
मिलान चिह्नों द्वारा उपरोक्त जानकारी को दर्शाया जाए:
हल:

प्रश्न 2.
आज तीसरी कक्षा के मनजीत सिंह का जन्मदिन है। सारी कक्षा के बच्चों ने इस अवसर पर कक्षा की एक दीवार को रंग-बिरंगे गुब्बारों से सजाया है।

मिलान चिह्न द्वारा पिछले पृष्ठ पर जानकारी दो दर्शाया जाए:

पता करो :
(i) कौन-से रंग के गुब्बारे सबसे अधिक है ?
उत्तर:
संतरी।

(ii) पीले रंग के गुब्बारों की गिनती कितनी है ?
उत्तर:
सात।

(ii) कुल गुब्बारों की गिनती कितनी है ?
उत्तर:
41

प्रश्न 3.
तीसरी कक्षा के बच्चों को उनके मनपसंद फलों के बारे में पूछा गया। बच्चों के मनपसंद फल इस प्रकार हैं:

मिलान चिह्न द्वारा पिछले पृष्ठ पर दी गई जानकारी को दर्शाया जाए :

पता करो:

(i) कौन-सा फल सबसे अधिक बच्चों को पसंद है ?
हल:
केला।

(ii) कौन-सा फल सबसे कम बच्चों को पसंद है ?
हल:
सेब।

(iii) केला पसंद करने वाले बच्चों की गिनती कितनी है ?
हल:
7.

(iv) सेब पसंद करने वाले बच्चों की गिनती कितनी है?
हल:
दो।

प्रश्न 4.
निम्नलिखित सारणी कक्षा तीसरी के बच्चों की मनपसंद खेलों को दर्शाती है।
हल:

पृष्ठ 204:

निम्नलिखित प्रश्नों के उत्तर :
(i) कौन-सी खेल को बच्चे अधिक पसंद करते हैं ?
हल:
क्रिकेट।

(ii) कौन-सी खेल को बच्चे कम पसंद करते हैं ?
हल:
फुटबाल।

(iii) खो-खो पसंद करने वाले बच्चों की गिनती कितनी हैं ?
हल:
12.

(iv) फुटबॉल और क्रिकेट खेलों को पसंद करने वाले बच्चों की गिनती कितनी हैं ?
हल:
19.

(v) तीसरी कक्षा के कुल कितने बच्चे हैं ?
हल:
39.

निम्नलिखित सारणी तीसरी कक्षा के बच्चों के मनपसंद रंगों को दर्शाती है:

पता करो:

(i) कौन-सा रंग सबसे अधिक बच्चों को पसंद है ?
हल:
नीला।

(ii) कौन-सा रंग सबसे कम बच्चों को पसंद है ?
हल:
भूरा।

(iii) लाल रंग कितने बच्चों को पसंद है ?
हल:
पाँच।

(iv) कौन-से दो रंग बराबर बच्चों को पसंद हैं ?
हल:
लाल, हरा।

(v) तीसरी कक्षा में कुल कितने बच्चे हैं ?
हल:
33.

पृष्ठ 207:

वर्कशीट:

(1)

(2) स्कूल के वार्षिक समारोह के लिए कक्षा तीसरी के चार बच्चों की तरफ से गुलदस्ता तैयार किया गया जिसे चित्र आलेख में दर्शाया गया है:

(i) जसप्रीत सिंह द्वारा गुलदस्ता बनाने के लिए 1 फूल का उपयोग किया गया।(✓ अथवा ×)
हल:
×.

(ii) संदीप द्वारा गुलदस्ता बनाने के लिए 20 फूल उपयोग किए गए। (✓ अथवा ×)
हल:
✓.

(iii) गुलदस्ता बनाने के लिए सबसे अधिक फूल संदीप द्वारा उपयोग किए गए।(✓ अथवा ×)
हल:
×.

(iv) गुलदस्ता बनाने के लिए 5 फूलों का उपयोग कौन-से बच्चे द्वारा किया गया ?
(a) जसप्रीत सिंह .
(b) हरप्रीत सिंह
(c) अमनदीप कौर
(d) संदीप।
हल:
(a) जसप्रीत सिंह।

(v) गुलदस्ता बनाने के लिए सभी बच्चों की ओर से कुल ……… फूल प्रयोग किए गए।
हल:
75.

(vi) गुलदस्ता बनाने के लिए कौन-से दो बच्चों की ओर से बराबर गिनती में फूल उपयोग किए गए ?
(a) जसप्रीत सिंह और हरप्रीत सिंह
(b) हरप्रीत सिंह और अमनदीप कौर
(c) अमनदीप कौर और संदीप
(d) हरप्रीत सिंह और संदीप।
हल:
(b) जसप्रीत सिंह और हरप्रीत सिंह।

(vii) अमनदीप कौर द्वारा उपयोग किए गए फूलों को मिलान चिह्न द्वारा कैसे दर्शाओगे ?

हल:

(viii) गुलदस्ता बनाने के लिए मिलान चिह्न किस बच्चे द्वारा बनाए गए ?
(a) अमनदीप कौर
(b) जसप्रीत सिंह
(c) संदीप
(d) हरप्रीत सिंह।
हल:
(c) संदीप।

(ix) उपरोक्त सारणी में = 5 फूलों को दर्शाता है ?
(✓ अथवा ×)
हल:
✓.

Punjab State Board PSEB 9th Class Computer Book Solutions Chapter 7 ई-गवर्नेस Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Computer Chapter 7 ई-गवर्नेस

Computer Guide for Class 9 PSEB ई-गवर्नेस Textbook Questions and Answers

1. बहुविकल्पीय प्रश्न-उत्तर

1. G2C का मतलब है-
(क) Government to Co-operation
(ख) Grievances to Co-operation
(ग) Government to Citizen
(घ) None of these.
उत्तर-
(ग) Government to Citizen.

2. G2G का मतलब है-
(क) Government to Government
(ख) Set to Go
(ग) Gather to Go
(घ) None of these.
उत्तर-
(क) Government to Government.

3. G2E का मतलब है-
(क) Grievance to employee
(ख) Government to employee
(ग) Government to environment
(घ) None of these.
उत्तर-
(ख) Government to employee.

4. G2B का मतलब है-
(क) Government to Banks
(a) Government to Businessmen
(ग) Government to Business
(घ) None of these.
उत्तर-
(ख) Government to Businessmen.

5. IRCTC का मतलब है-
(क) Indian Railway Catering and Tourism Co-operation Ltd.
(ख) Indian Runway Catering and Tourism Co-operation Ltd.
(ग) Indian Railway Catering and Travelling Co-operation Ltd.
(घ) Indian Railway Cargo and Tourism Co-operation Ltd.
उत्तर-
(क) Indian Railway Catering and Tourism Co-operation Ltd.

2. छोटे उत्तर वाले प्रश्न

प्रश्न 1.
ई-गवनेस क्या हैं ?
उत्तर-
ई-गवर्नेस का मतलब है कि सरकारी सेवाओं को आनलाइन करना। सरकार के कामकाज का आनलाइन होना।

प्रश्न 2.
ई-गवर्नेस के दो उद्देश्य कौन-से हैं ?
उत्तर

1. भिन्न-भिन्न आनलाइन सेवाओं का प्रयोग करके जनता की ज़रूरतों को आसानी से पूरा करना।
2. सरकारी प्रशासनिक काम-काज की पारदर्शी, उत्तरदेय और प्रभावशाली तरीके के साथ सेवाओं को उपलब्ध करवाना।

प्रश्न 3.
शहरी क्षेत्र में ई-गवर्नेस के कौन-कौन से काम होते हैं ?
उत्तर

1. सड़क सेवाओं के काम-काज जैसे-कच्चा आईसस बनना, गाड़ियों के टाइम-टेबल बनना।
2. बिल और टैक्स को आनलाइन जमा करवाना।
3. सड़क और सुरक्षा का प्रबंध करना।

प्रश्न 4.
गाँव क्षेत्र में ई-गवर्नेस कौन-कौन से काम करती है ?
उत्तर-
गाँव क्षेत्र में ई-गवर्नेस का बहुत अच्छा प्रभाव है। यहाँ पर खेती से संबंधित काम-काज से लेकर आम-सूचना के सारे काम ई-गवर्नेस ही करती है।

3. बड़े उत्तर वाले प्रश्न

प्रश्न 1.
एक अच्छी गवर्नेस की मुख्य विशेषताएं क्या हैं ?
उत्तर-
एक अच्छी गवर्नेस की मुख्य विशेषताएं निम्नलिखित हैं

1. अच्छी गवर्नेस में सभी सम्मिलित होते हैं। कोई भी आदमी जोकि किसी निर्णय द्वारा प्रभावित होता है या फैसला लेने की प्रक्रिया में भाग लेना चाहता है, में शामिल हो सकता है। यह कई ढंगों से जैसे कि किसी वर्ग के लोगों को जानकारी देनी और उनकी राय का पता लगाना, उनको सिफारिशों का मौका देना या कई बार उनको वास्तव में निर्णय करने के कार्य में शामिल कर लिया जा सकता है।
2. अच्छी गवर्नेस कानून का पालन करती है।
3. अच्छी गवर्नेस निर्णय करने और फैसले लागू करने में प्रभावशाली और कुशल होती है और कई प्रक्रियाओं द्वारा उपलब्ध लोगों, स्रोतों के अच्छे प्रयोग करके समाज की आवश्यकता अनुसार नतीजे प्राप्त करती है।
4. अच्छी गवर्नेस लिए गए फैसले के नतीजे के लिए जनता को उत्तरदायी होती है।
5. अच्छी गवर्नेस जनता की आवश्यकताओं को समय पर और ठीक ढंग से पूरा करने के लिए उत्तरदायी होती है।
6. अच्छी गवर्नैस पारदर्शी होती है, इससे अभिप्राय यह है कि जनता साफ-साफ यह देख सकती है कि कोई फैसला कैसे और क्यों लिया गया है।

प्रश्न 2.
ई-गवर्नेस के चार स्तंभ कौन-से हैं ?
उत्तर

1. संपर्क-लोगों को सरकार की सेवाओं से जोड़ने के लिए संपर्क की आवश्यकता होती है।
2. ज्ञान-ज्ञान का भाव है IT (Information Technology) का ज्ञान। सरकार अच्छे इंजीनियर को इस काम के लिए रखती है जो ई-गवर्नेस के काम को अच्छे से पूरा करते हैं।
3. डाटा-इंटरनैट पर सूचना को शेयर करने के लिए सरकार अपनी सेवाओं से संबंधित डाटाबेस का रख-रखाब करती है।
4. पैसा-सरकार की तरफ से अपनी सेवाओं को लागू करने के लिए लगाई गई राशि।

प्रश्न 3.
ई-गवर्नेस के चार मॉडल का विवरण करें।
उत्तर
1. सरकार से नागरिक-यह सरकार की उन सेवाओं के बारे में बताती है जो एक नागरिक प्रयोग करता है। इस मॉडल में नागरिक जिन सेवाओं का प्रयोग करना चाहते हैं, उस लिंक का प्रयोग करते हैं। इसका प्रयोग करके नागरिक आन लाइन पानी का बिल, बिजली और टैलीफोन आदि को जमा करवा सकता है।

2. सरकार से सरकार इस मॉडल में सरकार के बीच शेयर किये जाने वाली सेवाएं आती हैं। इसमें सरकार भिन्न-भिन्न प्रकार के राज्य के पुलिस विभाग शेयर किये जाने वाली सूचना और बजट से संबंधित काम शामिल है।

3. सरकार से व्यापारी-इसमें निजी क्षेत्र और सरकार के बीच रिश्ता और भी अच्छा होता है। यह व्यापारियों से सरकार और सरकार से व्यापारियों की बातचीत करने के लिए प्रयोग किया जाता है। इसमें टैक्स को इकट्ठा करना, पैकिंग वस्तुओं को मंजूर या न मंजूर करना आदि शामिल है।

4. सरकार से कर्मचारी-इस मॉडल में सरकार और इसके कर्मचारियों के बीच और अच्छे संबंधों के लिए काम करता है। इसके कर्मचारी सरकार के काम और कार्य प्रणाली की देखभाल करते हैं।

प्रश्न 4.
सेहत और शिक्षा के क्षेत्र में ई-गवर्नेस का क्या काम है ? विवरण करें।
उत्तर-
सेहत और शिक्षा के क्षेत्र में ई-गवस का बहुत महत्त्वपूर्ण योगदान है। इसमें सरकार शिक्षा के क्षेत्र और सेहत विभाग में क्या काम चल रहा है उसकी पूरी देखभाल करती है। इसमें सरकार इस बात को देखती है कि सेहत और शिक्षा के क्षेत्र में कितना सुधार हुआ है। यदि कोई सुधार हुआ है तो कितनी मात्रा में हुआ है।

प्रश्न 5.
ई-गवर्नेस का इतिहास और विकास का विवरण करें।
उत्तर-
भारत में ई-गवर्नेस 1970 में स्थापित की गई। उस समय सरकार ने इसको सुरक्षा के क्षेत्र, पैसे के लेन-देन की योजना के क्षेत्र में प्रयोग किया? सूचना और संचार टैकनोलॉजी का प्रयोग वोट, टैक्स, प्रशासन से संबंधित डाटे का प्रबंध करने के लिए किया जाता है। इसके बाद NIC-National Information Center की कोशिशों से सारे जिलों को आपस में जोड़ा गया।

साल 1990 की शुरुआत में ई-गवर्नेस ने सूचना टैकनोलॉजी का प्रयोग करके बहुत बड़े क्षेत्र में पहुंच गए और गांव क्षेत्र में पहुंचने की कोशिश की। पहले सरकार और नागरिक के बीच बात करने के लिए कार्यालय की ज़रूरत पड़ती थी। परन्तु सूचना और संचार के क्षेत्र में प्रगति आने से सरकारी काम और अच्छे तरीके से होने लगा। सूचना और संचार में ग्राहकों के लिए, सेवा केन्द्र को ढूंढना और भी संभव हो गया। यह केन्द्र सरकारी एजेंसी में ‘काऊंटर के रूप में या ग्राहकों के नजदीक सरकारी एजेंसी के बाहर भी हो सकते हैं।

PSEB 8th Class Computer Guide ई-गवर्नेस Important Questions and Answers

रिक्त स्थान भरें

1………….. से मतलब है कि सरकारी सेवाओं की ………….. .
उत्तर-
ई-गवर्नस, ऑनलाइन,

2. RSPCB का मतलब है
उत्तर-
Rajasthan State Pollution Control Board,

3. IRCTC का मतलब है ………….
उत्तर-
Indian Railway Catering and Tourism Co-operation Ltd.,

4. UIDAI से मतलब ……………..
उत्तर-
Unique Identification Authority of India,

5. HRTC का मतलब …………
उत्तर-
Himachal Road Transport Corporation Project,

6. E-Seva का भाव
उत्तर-
Electronic Seva, 6 ईगवनस,

7. सामाजिक कार्यों को करने के लिए प्रक्रियाओं के समूह को ………… कहा जाता है।
उत्तर-
सुविधा सेंटर,

8. सरकारी कार्यों को करने के लिए सरकार . ………… की प्रक्रिया का इस्तेमाल करती है।
उत्तर-
Single user Friendly Window Disposal Help line for Application,

9. सुविधा का अर्थ है ……………. ।
उत्तर-
सुविधा सेंटर,

10. एफीडेविट की तुरंत तसदीक …………….सेंटर में हो सकती है।
उत्तर-
रजिस्टरी,

11. वाहनों की ………. सुविधा सेंटर में हो सकती है।
उत्तर-
6.

12. आप …………….. में से किसी भी वक्त पैसे निकलवा सकते हैं।
उत्तर-
ATM.

सही या गलत बताइये-

1. i-tickets के प्रयोग से केवल ऑन लाइन रेलवे टिकट बुकिंग होती है।
उत्तर-
सही,

2. i-ticketing में टिकट बुकिंग 2 दिन पहले होनी जरूरी है।
उत्तर-
सही,

3. e-ticketing का प्रयोग तत्काल बुकिंग के लिए होता है।
उत्तर-
सही,

4. e-governance सुविधायें हासिल करने के लिए कम्प्यूटर का प्रयोग नहीं किया जाता।
उत्तर-
गलत,

5. ऑन लाइन बैंकिंग की मदद से एक खाते से दूसरे खाते में धन भेजना संभव है।
उत्तर-
सही,

6. i-tickets के प्रयोग से केवल ऑन लाइन रेलवे टिकट बुकिंग होती है।
उत्तर-
सही,

7. i-ticketing में टिकट बुकिंग 2 दिन पहले होनी जरूरी है।
उत्तर-
सही,

8. e-ticketing का प्रयोग तत्काल बुकिंग के लिए होता है।
उत्तर-
सही,

9. e-governance सुविधाएं हासिल करने के लिए कम्प्यूटर का प्रयोग नहीं किया जाता।
उत्तर-
गलत,

10. ऑन लाइन बैंकिंग की मदद से एक खाते से दूसरे खाते में धन भेजना संभव है।
उत्तर-
सही।

छोटे उत्तर वाले प्रश्न

प्रश्न 1.
E-Aadhar क्या है ?
उत्तर-
ई-आधार 12 अंकों का हर एक व्यक्ति के लिए पहचान नंबर है जोकि UIDAI का भारत सरकार लागू करती है। यह नंबर पूरे भारत में पहचान और पते का प्रमाण होता है।

प्रश्न 2.
आपदा प्रबंधन क्या है ?
उत्तर-
किसी भी सरकार के लिए आपदा/मुसीबत का सामना करना बहुत बड़ी बात होती है क्योंकि यह प्राकृतिक और किसी भी समय होने वाली घटना है। इस तरह की मुसीबत का सामना करने के लिए सरकार ने तथा कई राज्य सरकारों ने ई-गवर्नेस के बहुत-से क्षेत्र शुरू किये हैं।

प्रश्न 3.
ई-गवर्नेस से क्या अर्थ है?
उत्तर –
ई-गवर्नेस का अर्थ है सूचना तकनीक की मदद से नागरिकों और व्यापारियों को नई-से-नई व्यापारिक जानकारी देना और कार्यों को बढ़िया तरीके से उन को प्रदान करवाना।

प्रश्न 4.
ई-गवर्नस का प्रयोग (लाभ) बताइये।
उत्तर-

1. काम खर्च
2. तेज़ रफ्तार
3. कभी भी किसी भी समय।

प्रश्न 5.
ई-गवनैस की सेवा कौन-कौन से क्षेत्र प्रदान करता है?
उत्तर-

• बैंकों में
• हवाई जहाज और रेलवे की टिकट बुक करवाने में
• जन्म और मौत के सर्टीफिकेट जारी करने के लिए।

प्रश्न 6.
इंटरनेट बैंकिंग से भाव है?
उत्तर-
इस बैंकिंग के द्वारा हम इंटरनैट के द्वारा आम बैंकिंग सुविधाएं जैसे कि भुगतान (Payment), मनी ट्रांसफर (Money Transfer) और अकाऊंट बकाया (Account Balance) आदि काम 24 घंटे कर सकते हैं।

प्रश्न 7.
आन लाइन रेलवे और हाई टिकटिंग से क्या भाव है?
उत्तर-
इस तकनीक के द्वारा हम रेल गाड़ियों और हवाई उड़ानों की जानकारी पहले से ही प्राप्त कर सकते हैं और रेलवे और हवाई जहाज़ की टिकटें इंटरनेट के द्वारा घर बैठे बुक करवा सकते हैं।

प्रश्न 8.
भारती रेलवे की टिकटिंग प्रणालियों के नाम लिखें।
उत्तर-

1. आई-टिकटिंग (i-ticketing)
2. ई-टिकटिंग (e-ticketing)।

प्रश्न 9.
सुविधा सैंटर से क्या भाव है?
उत्तर-
इन सैंटरों में जनता की आम ज़रूरत में आने वाली सेवायें, सहूलतें प्रदान की जाती हैं, जैसे कि पासपोर्ट बनाने, राशन कार्ड बनाने, विवाह की रजिस्ट्रेशन।

प्रश्न 10.
JIT से आप क्या समझते हैं ?
उत्तर-
JIT से अर्थ है Just In Time, भाव जनता को उसी समय सुविधा प्रदान करवाना जिस समय वो यह सुविधा प्राप्त करना चाहता है जैसे कि ATM मशीनों के आ जाने से व्यक्ति किसी भी समय पैसे निकाल सकता है और यह 24 घंटे खुले रहते हैं और इनको ऑपरेट करने के लिए किसी भी व्यक्ति की ज़रूरत नहीं होती।

प्रश्न 11.
i-tickting क्या होती है ?
उत्तर-
आई-टिकटिंग (i-tickting) यह मुफ्त , web baised टिकटिंग सिस्टम है। इस प्रणाली में कस्टमर (Customer) को कम-से-कम 2 दिन पहले टिकट बुक करवानी पड़ती है और 2 या 3 दिन से अंदर टिकट घर पहुँचा दी जाती है।

प्रश्न 12.
E-tickting क्या होती है ?
उत्तर-
ई-टिकटिंग (E-tickting) यह एक आन लाइन (Online) टिकट है। इस टिकट को e-mail के द्वारा भेजा जा सकता है या (Printable Online) पर प्रिंट किया जा सकता है। ई-टिकटिंग गाड़ी के समय के चार्ट से हिसाब से बुक की जाती है। ई-टिकटिंग के लिए शिनास्ति सबूत जैसे कि Voter ID कार्ड, राशनकार्ड पासपोर्ट, PAN कार्ड या ड्राईविंग लाईसेंस आदि का विवरण देना पड़ता है। इस के बाद उसका एक प्रिंट लेकर और यात्रा करते समय यह प्रिंट और अपना ID सबूत साथ रखना चाहिये।

प्रश्न 13.
E-governance का क्या महत्त्व है?
उत्तर –

1. ई-गवर्नेस से कोई भी काम बड़ी तेज़ी, आसानी से कर सकते हैं। जिन कामों को बहुत ज्यादा समय लगता था, वही काम आज बड़ी आसानी और परंपरागत तरीकों से किया जा सकता है।
2. इस में लिखित, मौखिक, वीडियो और ऐनीमेशन तकनीकें शामिल हैं।
3. इसका खर्च परंपरागत साधनों के खर्च से बहुत कम होता है। पूरा सैट-आप स्थापित हो जाने से इसका रोज़ाना खर्चा बहुत कम होता है । सिर्फ शुरुआत के खर्चे ज्यादा हैं।
4. ई-गवर्नेस की मदद से हम भी कहीं भी किसी भी टाईम अपना काम कर सकते हैं जैसे हम किसी भी बैंक की वैब साईट से अपने अकाऊंट की जानकारी प्राप्त कर सकते हैं और बैंकों की नई स्कीमों की जानकारी प्राप्त कर सकते हैं।

प्रश्न 14.
सुविधा सैंटरों के कोई पाँच मुख्य उपयोगों का वर्णन करें ।
उत्तर-

1. इन सैंटरों में जनता की आम ज़रूरत में आने वाली सेवायें, सहूलतें प्रदान की जाती हैं।
2. हर सुविधा सैंटर में हैल्प-लाईन नंबर मौजूद हैं। कोई भी व्यक्ति टेलीफोन करके ज़रूरी जानकारी प्राप्त कर सकता है।
3. सेवाओं के लिए एक स्थान पर सारी ऐपलीकेशनज़ को जमा करवाना ।
4. जो भी नई स्कीम या तरीका हो उसकी जानकारी मौके पर उसी समय ही उपलब्ध हो जाती है।
5. सुविधा केंद्रों की कोरीयर (Courier) सर्विस भी बहुत तेज़ है जिस के द्वारा ज़रूरी कागजात अब 48 घंटों में व्यक्तियों के घर पहुंचा दिये जाते हैं।

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 1 वास्तविक संख्याएँ Ex 1.1 Textbook Exercise Questions and Answers

PSEB Solutions for Class 10 Maths Chapter 1 वास्तविक संख्याएँ Ex 1.1

प्रश्न 1.
निम्नलिखित संख्याओं का HCF ज्ञात करने के लिए यूक्लिड विभाजन एल्गोरिथ्म का प्रयोग कीजिए :
(i) 135 और 225
(ii) 196 और 38220
(iii) 867 और 255.
हल :
(i) यूक्लिड विभाजन एल्गोरिथ्म द्वारा,
चरण 1. क्योंकि 225 > 135, हम 225 और 135 पर यूक्लिड प्रमेयिका का प्रयोग करने पर, प्राप्त करते हैं।
225 = 135 × 1 + 90
चरण 2. क्योंकि शेषफल 90 # 0, है, इसलिए हम __135 और 90 पर यूक्लिड प्रमेयिका का प्रयोग करने पर, प्राप्त करते हैं।
135 = 90 × 1 + 45
चरण 3. क्योंकि शेषफल 45 # 0 है, इसलिए हम 90 और 45 पर यूक्लिड प्रमेयिका का प्रयोग करने पर, प्राप्त करते हैं।
90 = 45 × 2 + 0
क्योंकि शेषफल 0 प्राप्त हो गया है, इसलिए हम प्रक्रिया समाप्त करते हैं।
∵ चरण 3 में भाजक 45 है।
∵ 90 और 45 का HCF 45 है।
अतः, 135 और 225 का HCF 45 है। उत्तर

(ii) 196 और 38220 का HCF ज्ञात करना।
चरण 1. क्योंकि 38220 > 196 है, हम 196 और 38220 पर यूक्लिड प्रमेयिका का प्रयोग करने पर, प्राप्त करते हैं :
38220 = 196 × 195 + 0 क्योंकि शेषफल 0 प्राप्त हो गया है, इसलिए हम प्रक्रिया समाप्त करते हैं।
∵ इस चरण पर भाजक 196 है।
∴ 38220 और 196 का HCF 196 है।
अतः, 38220 और 196 का HCF 196 है। उत्तर

(iii) 867 और 255 का HCF ज्ञात करना।
चरण 1. क्योंकि 867 > 255 है, हम 867 और 255, पर यूक्लिड प्रमेयिका का प्रयोग करने पर प्राप्त करते हैं :
867 = 255 × 3 + 102
चरण 2. क्योंकि शेषफल 102 # 0 है, हम 255 और 102 पर यूक्लिड प्रमेयिका का प्रयोग करने पर प्राप्त करते हैं :
255 = 102 × 2 + 51
चरण 3. क्योंकि शेषफल 51 ≠ 0, है, हम 51 और 102, पर यूक्लिड प्रमेयिका का प्रयोग करने पर प्राप्त करते हैं :
102 = 51 × 2 + 0 क्योंकि शेषफल 0 प्राप्त हो गया है, इसलिए हम प्रक्रिया समाप्त करते हैं।
∵ चरण 3 का भाजक 51 है।
∴ 102 और 51 का HCF 51 है।
अतः, 867 और 255 का HCF 51 है। उत्तर

प्रश्न 2.
दर्शाइए कि कोई भी धनात्मक विषम पूर्णांक 6q + 1 या 6q + 3 या 6q + 5, के रूप का होता है, जहाँ १ कोई पूर्णांक है।
हल :
मान लीजिए a एक धनात्मक विषम पूर्णांक है। हम a और b = 6 के लिए विभाजन एल्गोरिथ्म का प्रयोग करते हैं।
चूँकि 0 < r < 6 है, इसलिए संभावित शेषफल अर्थात् 0, 1, 2, 3, 4 और 5 हैं। अर्थात् a संख्याओं 6q या 6q + 1, या 6q + 2, या 6q + 3, या 6q + 4, या 6q + 5 के रूप का हो सकता है जहाँ q भागफल है। चूँकि a एक विषम पूर्णांक है। ∴ यह 6q, 6q + 2, 6q + 4 के रूप का नहीं हो सकता।
∵ सभी 2 से विभाज्य हैं। इसलिए कोई भी धनात्मक विषम पूर्णांक 6q + 1 या 6q + 3 या 6q + 5 के रूप का होता है।

प्रश्न 3.
किसी परेड में 616 सदस्यों वाली एक सेना (आर्मी) की टुकड़ी को 32 सदस्यों वाले एक आर्मी बैंड के पीछे मार्च करना है। दोनों समूहों को समान संख्या वाले स्तंभों में मार्च करना है। उन स्तंभों की अधिकतम संख्या क्या है, जिसमें वे मार्च कर सकते है।
हल :
सेना में सदस्यों की कुल संख्या = 616 और 32 (दो समूहों का बैंड) क्योंकि दोनों समूहों को समान संख्या वाले स्तंभों में गप्त | मार्च करना है और हमने स्तंभों की अधिक सख्या ज्ञात | करनी है।
∴ स्तंभों की अधिकतम संख्या या = 616 और 32 का HCF
चरण 1. चूँकि 616 > 32, हम 616 और 32 को लेकर यूक्लिड प्रमेयिका का प्रयोग करके, हम प्राप्त करते हैं :
616 = 32 × 19 + 8
चरण 2. चूँकि शेषफल 8 ≠ 0, हम 32 और 8 को है, | लेकर यूक्लिड प्रमेयिका का प्रयोग करके, हम प्राप्त करते
32 = 8 × 4 + 0
क्योंकि अब शेषफल शून्य आ गया है।
∵ इस चरण में भाजक 8 है। …
∴ 616 और 32 का HCF 8
अतः, स्तंभों की अधिकतम संख्या जिसमें वे मार्च कर सकते हैं, 8 है। उत्तर

प्रश्न 4.
यूक्लिड विभाजन प्रमेयिका का प्रयोग करके दर्शाइए कि किसी धनात्मक पूर्णांक का वर्ग, किसी | पूर्णांक m के लिए 3m या 3m + 1 के रूप का होता है।
[संकेत : यह मान लीजिए x कोई धनात्मक पूर्णांक है।
तब, यह 3q, 3q + 1 या 34 + 2 के रूप में लिखा जा सकता है। इनमें से प्रत्येक का वर्ग कीजिए और दर्शाइए कि इन वर्गों को 3m या 3m + 1 के रूप में लिखा जा सकता है।
हल :
यदि x कोई धनात्मक पूर्णांक है, तब यह 3q, 3q + 1 या 3q + 2 के रूप का है। की
यदि x = 3q
दोनों ओर वर्ग करने पर,
(x)² = (34)²
9q² = 3 (3q²) = 3m
जहाँ m = 3q²
जहाँ m भी एक पूर्णांक है।
अतः = 3m …………….(1)
यदि x = 34 + 1
दोनों ओर वर्ग करने पर,
x² = (3q + 1)²
x² = 9q² + 1 + 2 x 3q x 1
x² = 3 (3q² + 2q) + 1
x² = 3m + 1 …………… (2)
जहाँ m = 3q² + 2q जहाँ m भी एक पूर्णांक है (1) और (2) से,
x² = 3m, 3m + 1
अतः, किसी धनात्मक पूर्णांक का वर्ग, किसी पूर्णांक m के लिए 3m या 3m + 1 के रूप का होता है।

प्रश्न 5.
यूक्लिड विभाजन प्रमेयिका का प्रयोग करके दर्शाइए कि किसी धनात्मक पूर्णांक का घन 9m, 9m + 1 या 9m + 8 के रूप का होता है।
हल :
मान लीजिए x कोई धनात्मक पूर्णांक है और b = 3 है।
x = 3q + r
जहाँ q भागफल है और r शेषफल है।
0 ≤ r < 3
यदि r = 0 तो x = 3q
यदि r = 1 तो x = 3q + 1
यदि r = 2 तो x = 3q + 2
x, 3q या 3q + 1 या 3q + 2 के रूप का है।
यदि x = 3q
दोनों ओर घन करने पर,
x³ = (3q)³
x³ = 27q³ = 9 (3q³) = 9q
जहाँ m = 3q³ और m एक पूर्णांक है।
x³ = 9m ……………….(1)
x = 3q + 1 दोनों ओर घन करने पर
x³ = (3q + 1)³
x = 27q³ + 27q² + 9q + 1)
= 9 (3q³ + 3q² + q) + 1
= 9m + 1
जहाँ m = 3q³ + 3q² + q और यह एक पूर्णांक है।
पुन: x³ = 9m + 1 ……………… (2)
यदि x = 3q + 2
दोनों ओर घन करने पर,
(x)³ = (3q + 2)²
= 27q³ + 54q² + 36q + 8
x³ = 9 (3q³ + 6q² + 4q) + 8
x³ = 9m + 8
जहाँ m = 3q³ + 6q² + 4q
पुनः x³ = 9m + 8 .
(1) और (2) से हम पाते हैं कि x³, 9m, 9m + 1, 9m + 8 के रूप का है।
अतः, x एक धनात्मक पूर्णांक है जो 9m या 9m + 1 या 9m + 8 के रूप का है।

Punjab State Board PSEB 3rd Class Maths Book Solutions Chapter 9 समय Textbook Exercise Questions and Answers

PSEB Solutions for Class 3 Maths Chapter 9 समय

पृष्ठ 179:

क्या आपको याद है ?
(A) सूरज कब निकलता है ?
उत्तर:
प्रातः

(B) पूरी छुट्टी कब होती है ?
उत्तर:
दोपहर

(C) गर्मियों की छुट्टियाँ किस महीने में होती हैं ?
उत्तर:
जून

(D) सप्ताह में कितने दिन होते हैं ?
उत्तर:
सात दिन

पृष्ठ 181:

आओ करें:

(1) मई महीने में कितने दिन हैं ?
(a) 28
(b) 29
(c) 30
(d) 31
उत्तर:
(d) 31

(2) 5 मई को कौन-सा दिन है ?
(a) सोमवार
(b) मंगलवार
(c) शनिवार
(d) शुक्रवार
उत्तर:
(c) शनिवार

(3) 28 मई को कौन-सा दिन है ?
(a) रविवार
(b) सोमवार
(c) वीरवार
(d) शनिवार
उत्तर:
(b) सोमवार

(4) मई महीने में पहले रविवार को कौन-सी तारीख है ?
(a) 1
(b) 2
(c) 5
(d) 6
उत्तर:
(d) 6

(5) मई महीने में पहले सोमवार को कौन-सी तारीख है ?
(a) 1
(b) 2
(c) 3
(d) 7
उत्तर:
(d) 7

(6) 31 मई को कौन-सा दिन है ?
(a) रविवार
(b) सोमवार
(c) वीरवार
(d) शनिवार
उत्तर:
(c) वीरवार

पृष्ठ 182:

प्रश्न 1.
कैलेंडर में देखो और सामने दिये खाने में तारीख भरो :
(क) 12 जून से 3 दिन बाद
हल:
15 जून

24 मई से 4 दिन बाद
हल:
28 मई

29 अप्रैल से 2 दिन बाद
हल:
1 मई

25 जनवरी से 10 दिन बाद
हल:
4 फरवरी

(ख) 20 जुलाई से 5 दिन पहले
हल:
15 जुलाई

12 जून से 2 दिन पहले
हल:
10 जून

6 मार्च से 3 दिन पहले
हल:
3 मार्च

5 अक्टूबर से 7 दिन पहले
हल:
28 सितंबर

पृष्ठ 183:

प्रश्न 2.
कैलेंडर देखो और बॉक्स में भरो :

(1) अक्टूबर महीने में कितने रविवार आते हैं ?
हल:
4

(2) 6 सितंबर को कौन-सा दिन है ?
हल:
वीरवार

(3) 25 अक्तूबर को कौन-सा दिन है ?
हल:
वीरवार

(4) आपका जन्म दिन कौन-से महीने हुआ ?
हल:
मई

(5) 18 मई को कौन सा दिन है ?
हल:
शुक्रवार

(6) मई महीने में कितने रविवार आए हैं ?
हल:
4

(7) अगस्त महीने में कितने वीरवार आए हैं ?
हल:
5

(8) पहली मई को कौन-सा दिन है ?
हल:
मंगलवार

(9) मई महीने का अंतिम दिन कौन-सा है ?
हल:
वीरवार

(10) फरवरी महीने में कितने दिन हैं ?
हल:
28

पृष्ठ 184:

आओ करें:

(1) घड़ी की बड़ी सूई हमें किसके बारे में बताती है?
हल:
मिनट

(2) घड़ी की सबसे छोटी सूई हमें किसके बारे में बताती है ?
हल:
घंटों

(3) घड़ी की सबसे बड़ी व तेज़ चलने वाली सूई हमें किसके बारे में बताती है ?
हल:
सैकिंड

पृष्ठ 185:

आओ करें:

प्रश्न 1.
घड़ी को देखो और समय लिखो :

हल:

पृष्ठ 186:

हल :

प्रश्न 2.
घड़ी के नीचे लिखे समय देखकर सूईयां बनाओ
हल:

प्रश्न 3.
बीच वाली घड़ी को देखकर बाएं व दाएं वाली घड़ियों में सही समय लिखो :
हल:

पृष्ठ 187:

प्रश्न 4.
समय देखो और मिलान करें :
हल :

पृष्ठ 188:

प्रश्न 1.
रिक्त स्थान भरो:
हल:
(a) एक साधारण साल में 365 दिन होते हैं।
(b) एक साल में 12 महीने होते हैं।
(c) एक सप्ताह में 7 दिन होते हैं।

प्रश्न 2.
निम्नलिखित प्रश्नों के उत्तर दें :
(a) अप्रैल महीने में कितने दिन होते हैं ?
हल:
30 दिन।

(b) मई महीने में कितने दिन होते हैं ?
हल:
31 दिन।

(c) आपका जन्म किस महीने में हुआ है ?
हल:
अपने जन्म का महीना लिखें।

प्रश्न 3.
घड़ी देखो और समय लिखो :

हल:

प्रश्न 4.
घड़ी के नीचे दिया समय देखकर सुइयाँ बनाओ :

हल:

Punjab State Board PSEB 9th Class Computer Book Solutions Chapter 6 इंटरनैट एप्लीकेशन Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Computer Chapter 6 इंटरनैट एप्लीकेशन

Computer Guide for Class 9 PSEB इंटरनैट एप्लीकेशन Textbook Questions and Answers

1. रिक्त स्थान भरें

1. Gmail ……………. की एक फ्री सेवा है।
(क) Yahoo
(ख) Google
(ग) Radiffmail
(घ) Hotmail.
उत्तर-
(ख) Google.

2. इंटरनैट पर प्रत्येक मशीन को एक विशिष्ट नंबर दिया जाता है। जिसे ………………………. कहते हैं।
(क) एडरैस
(ख) ई-मेल
(ग) D
(घ) IP एडरैस।
उत्तर-
(घ) IP एडरैस।

3. ……………………………. एक प्रकार का टैस्ट होता है जो पता लगाता है कि यूजर एक मनुष्य है कि नहीं।
(क) CAPTCHA
(ख) DERTSA
(ग) HEPTCHA
(घ) NEPHCA.
उत्तर-
(क) CAPTCHA.

4. …………………………….. एक प्रकार का मालवेयर होता है जो यूजर के कम्प्यूटर को बिना आज्ञा प्रयोग करने के लिए बनाया जाता है।
(क) स्पाईवेयर
(ख) टरोजन
(ग) मालवेयर
(घ) हॉरस।
उत्तर-
(ख) टरोजन।

5. TV तथा रेडियो इंटरनेट पर …………………….. मीडिया के उदाहरण हैं।
(क) स्ट्रीमिंग
(ख) लिमिटिड
(ग) आनलाइन
(घ) ऑफ़लाइन।
उत्तर-
(क) स्ट्रीमिंग।

2. सही या ग़लत बताएं

1. स्पाईवेयर एक ई-मेल धोखा है जिसमें ग़लत कार्य करने वाला व्यक्ति एक सही दिखने वाली ई-मेल भेजता है, जो हमारी निजी तथा वित्ती जानकारी इकट्ठी कर लेता है।
उत्तर-
ग़लत,

2. गूगल ड्राइव के साथ हम आनलाइन स्टोर तथा शेयर नहीं कर सकते।
उत्तर-
ग़लत,

3. एंटीवायरस साफ्टवेयर के साथ हम वायरस को सही कर सकते हैं।
उत्तर-
सही,

4. BCC में हम उन व्यक्तियों के पते टाइप करते हैं जिनको हम ई-मेल की एक कॉपी तो भेजते हैं पर दूसरे रिसीपटैंट को इसका पता नहीं चलता।
उत्तर-
सही,

5. डिजीटल सिगनेचर को बायोग्राफी के द्वारा बनाया तथा वेरीफाई किया जाता है।
उत्तर-
सही।

3. छोटे उत्तर वाले प्रश्न

प्रश्न 1.
CAPTCHA (कैपचा) कोड किसे कहते हैं ?
उत्तर-
CAPTCHA का पूरा नाम Completely Automated Public Thring Test to Tell Computer and Human Apart. यह एक प्रकार का टैस्ट होता है जो हमें बताता है कि यूजर मनुष्य है या नहीं। इसमें यूजर को कोई टैक्सट भरने के लिए दिया जाता है तथा उसे फिर चैक किया जाता है।

प्रश्न 2.
Google Apps से आप क्या समझते हैं ?
उत्तर-
Google Apps एक एप्लीकेशनज़ का सैट है जिसमें विभिन्न प्रयोग करने वाली एप्लीकेशनज़ हैं। यह सैट Google द्वारा बनाया गया है।

प्रश्न 3.
डिजीटल सिगनेचर क्या होता है ?
उत्तर-
डिजीटल सिगनेचर एक ऐसा कोड होता है जिसे इलेक्ट्रॉनिक ट्रांसफर होने वाली फाइल के साथ भेजा जाता है। इससे भेजने वाले की पहचान होती है।

प्रश्न 4.
ई-मेल भेजने का तरीका बताएँ।
उत्तर-
ई-मेल भेजने लिए सबसे पहले Compose पर क्लिक करें। फिर आपको ई-मेल भेजने का एंट्री फार्म नज़र आ जाएगा। To में पाने वाले का ई-मेल एडरैस टाइप करें, Subject भरें तथा संदेश टाइप करें।

प्रश्न 5.
डाऊनलोडिंग के बेसिक स्टैप लिखें।
उत्तर-

• लिंक पर क्लिक करें। (एक डायलाग बॉक्स दिखाई देगा।)
• Save या Open पर क्लिक करें।
• डाऊनलोड को Confirm करें।
• Open या Run पर क्लिक करें।

प्रश्न 6.
क्लाउड प्रिंटिंग क्या है ?
उत्तर-
कलाउड प्रिंटिंग वह प्रक्रिया है जिसमें किसी भी दस्तावेज को कलाउड नैटवर्क के साथ जुड़े किसी कम्प्यूटर पर से प्रिंट कर सकते हैं।

प्रश्न 7.
कोई चार एंटी वायरस के नाम बताओ।
उत्तर-

• Microsoft Essential
• Aura
• Avast
• Macafee.

4. बड़े उत्तर वाले प्रश्न

प्रश्न 1.
IP एडरैस क्या है ? व्याख्या करें।
उत्तर-
इंटरनैट से जुड़े प्रत्येक कम्प्यूटर को एक विशेष नंबर दिया जाता है जिसके द्वारा वह पहचाना जाता है। इस एडरैस या नाम को IP एडरैस कहते हैं। एक आई०पी० एडरैस में चार नंबर होते हैं जिनको (.) डाट द्वारा अलग किया जाता है। प्रत्येक नंबर 0 से 255 के बीच हो सकता है। ये चारों नंबर किसी खास नेटवर्क को दर्शाते हैं। 192.168.1.1 एक IP एडरैस की उदाहरण है। इस प्रकार इन सारे नंबरों का प्रयोग करके 4, 294, 967, 296 आई०पी० एडरैस बनाए जा सकते हैं। इंटरनैट पर कोई भी कम्प्यूटर एक आई०पी० एडरैस के नहीं हो सकते।

प्रश्न 2.
किन्हीं तीन गूगल एप्स का वर्णन करें।
उत्तर

1. गूगल कैलंडर-यह एक गूगल द्वारा बनाया गया टाइम मैनेजमैंट वैब एप्लीकेशन तथा मोबाइल एप्प है। उसके द्वारा हम अपने कार्य को रिकार्ड कर सकते हैं तथा यह हमें समय आने पर अलर्ट भी कर देता है। इसके लिए यूजर के पास Google अकाऊंट होना चाहिए।
2. गूगल मैप-गूगल मैप एक डैस्कटाप बैव मैपिंग सेवा है। इससे हमें सैटेलाइट इमेज, स्ट्रीट मैप, 360 डिग्री स्ट्रीट व्यू, मौजूदा ट्रैफिक कंडीशन, पब्लिक ट्रांसपोर्ट द्वारा यात्रा करना आदि जैसे विकल्प या सुविधाएं प्रदान की जाती हैं।

3. गूगल ट्रांसलेट-यह गूगल की एक फ्री सेवा है, जिसमें किसी एक भाषा से दूसरी भाषा में मशीनी ट्रांसलेशन की जा सकती है।

प्रश्न 3.
Gmail में ई-मेल अकाऊंट बनाने की प्रक्रिया का वर्णन करो।
उत्तर-
Gmail पर ई-मेल अकाऊंट बनाने के निम्न पग हैं

• अपना इंटरनैट ब्राऊजर खोलें।
• www.gmail.com एडरैस टाइप करें।
• Google का Sign in सैक्शन आ जाएगा।
• Create Account पर क्लिक करें।

एक नया पेज आएगा जिसमें हमसे कुछ बेसिक जानकारी पूछी जाती है। जैसे कि First name 711 Last name. Username जो आपका ई-मेल पता होगा। Password

Confirm Password Date of Birth Gender
Mobile Number.

सारी जानकारी भरने के बाद Next पर क्लिक करें तो ई-मेल अकाऊंट तैयार हो जाएगा।

प्रश्न 4.
Google Drive के लाभ बताएं।
उत्तर-
Google Drive के निम्न लाभ हैं-

1. Google Drive के साथ हम अपने दोस्तों, रिश्तेदारों आदि को जो गूगल ड्राइव प्रयोग करते हैं को अपनी फाइलें भेज सकते हैं।
2. इसके द्वारा फाइल वैब पर उपलब्ध हो जाती है, जिससे हम इसे कहीं भी देख सकते हैं।
3. गूगल ड्राइव एक मोबाइल एप्प भी है। इससे हम अपनी फाइलस को कहीं भी Smart Phone पर भी देख सकते हैं।
4. गूगल ड्राइव में एक बना बनाया सर्च इंजन भी होता है। इसके द्वारा हम अपनी फाइलों के कंटेंट को सर्च भी कर सकते हैं।
5. गूगल ड्राइव में ऑप्टीकल करैक्टर रैकोगनीशन सिस्टम भी है। इसे हम स्कैन किये दस्तावेज भी कुछ सर्च कर सकते हैं।
6. गूगल ड्राइव एक फ्री सेवा है, जब तक इसका ज्यादा बड़ा इस्तेमाल न किया जाए।

PSEB 8th Class Computer Guide इंटरनैट एप्लीकेशन Important Questions and Answers

रिक्त स्थान भरें-

1. ई-मेल से भाव है……….. ।
उत्तर-
इलैक्ट्रॉनिक मेल,

2. गूगल एप्प में …………, ………….. तथा ………….. एप्प है।
उत्तर-
ई-मेल, कैलंडर, मैप शीट,

3. गूगल ड्राइव में हम अपनी बड़ी फाइलें …………… कर सकते हैं।
उत्तर-
शेयर,

4. कलाऊड शब्द ………..के लिए प्रयोग किया जाता है।
उत्तर-
इंटरनेट,

5. ……… से कम्प्यूटर प्रोग्राम की फाइलों को नुकसान पहुंचाता है।
उत्तर-
वायरस।

सही या गलत बताइये-

1. E-mail, Microsoft का उत्पाद है।
उत्तर-
गलत,

2. हम इंटरनैट पर फाइल शेयर नहीं कर सकते।
उत्तर-
सही,

3. Google Drive पर डाटा कभी नष्ट नहीं होता।
उत्तर-
सही,

4. कम्प्यूटर में Cloud का अर्थ है बादल।
उत्तर-
गलत।

छोटे उत्तर वाले प्रश्न

प्रश्न 1.
ई-मेल से क्या अभिप्राय है ?
उत्तर-
ई-मेल का पूरा नाम इलैक्ट्रानिक मेल है। यह एक ऐसा तरीका है जिसमें संदेश भेजना, लिखना, पढ़ना तथा प्राप्त करना संभव है। यह इंटरनैट पर सबसे ज्यादा प्रयोग आने वाला साधन है।

प्रश्न 2.
Google+ क्या है?
उत्तर-
Google+ एक सोशल नेटवर्किंग का हिस्सा है। यह लगभग Facebook की तरह ही है। इसमें हम Facebook की तरह पोस्ट कर सकते हैं।

प्रश्न 3.
गूगल ड्राइव क्या है ?
उत्तर-
यह एक आनलाइन स्टोर करने की सेवा है। इसमें फाइलों को शेयर भी किया जा सकता है, इसकी शुरुआत 24 अप्रैल, 2012 को हुई। इसमें 5GB डाटा स्टोरेज स्पेस फ्री दी जाती है।

प्रश्न 4.
वायरस क्या होता है ?
उत्तर-
कम्प्यूटर वायरस एक कम्प्यूटर प्रोग्राम होता है जो दूसरे कम्प्यूटर प्रोग्राम में अपने आपको दोहराता है तथा हमारे हार्डवेयर तथा साफटवेयर को नुकसान पहुंचा सकता है।