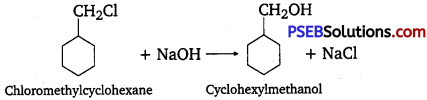
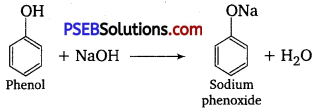
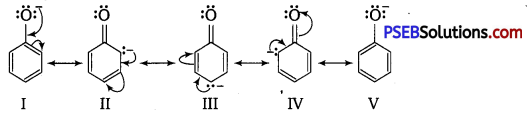
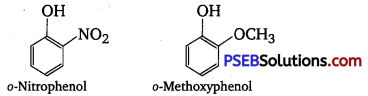
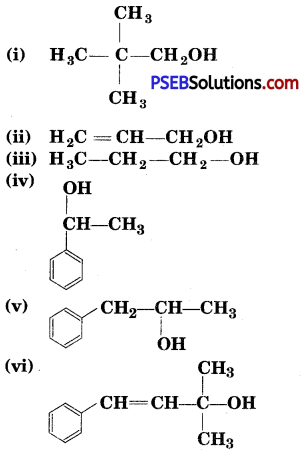
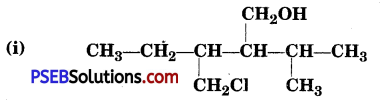
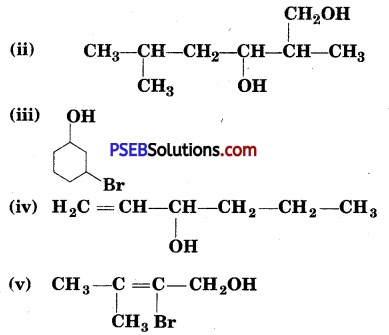
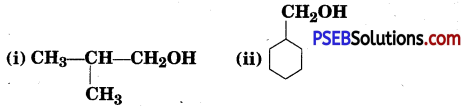
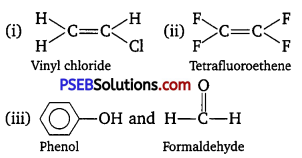
Punjab State Board PSEB 12th Class History Book Solutions Chapter 10 गुरु गोबिंद सिंह जी : खालसा पंथ की स्थापना, उनकी लड़ाइयाँ एवं व्यक्तित्व Textbook Exercise Questions and Answers.
PSEB Solutions for Class 12 History Chapter 10 गुरु गोबिंद सिंह जी : खालसा पंथ की स्थापना, उनकी लड़ाइयाँ एवं व्यक्तित्व
निबंधात्मक प्रश्न (Essay Type Questions)
गुरु गोबिंद सिंह जी का प्रारंभिक जीवन (Early life of Guru Gobind Singh Ji)
प्रश्न 1.
गुरु गोबिंद सिंह जी के आरंभिक जीवन के बारे में आप क्या जानते हैं ? व्याख्या करें।
(What do you know about the early life of Guru Gobind Singh Ji ? Explain.)
उत्तर-
गुरु गोबिंद सिंह जी न केवल पंजाब बल्कि संसार के महान् व्यक्तियों में से एक थे। सिख पंथ का जिस योग्यता एवं बुद्धिमता से गुरु गोबिंद सिंह जी ने नेतृत्व किया, उसकी इतिहास में कोई अन्य उदाहरण मिलनी बहुत ही मुश्किल है। खालसा पंथ की स्थापना के साथ ही उन्होंने सिख पंथ में नए युग का सूत्रपात किया। गुरु गोबिंद सिंह जी के आरंभिक जीवन का संक्षिप्त वर्णन इस प्रकार है—
1. जन्म और माता-पिता (Birth and Parentage) मात्र 9 वर्ष की आयु में अपने पिता जी को धर्म की रक्षा हेतु बलिदान देने की प्रेरणा देने वाले गुरु गोबिंद सिंह जी का जन्म 22 दिसंबर, 1666 ई० को पटना साहिब में हुआ था। आप गुरु तेग बहादुर जी के इकलौते पुत्र थे। आपकी माता जी का नाम गुजरी था। आपका आरंभिक नाम गोबिंद दास अथवा गोबिंद राय रखा गया। 1699 ई० में खालसा पंथ की स्थापना के पश्चात् आपका नाम गोबिंद सिंह पड़ गया था। गोबिंद दास के जन्म के समय एक मुस्लिम फकीर भीखण शाह ने यह भविष्यवाणी की थी, कि यह बालक बड़ा होकर महापुरुष बनेगा और यह भविष्यवाणी सत्य निकली।
2. बचपन (Childhood)—गोबिंद दास ने अपने बचपन के पहले 6 वर्ष पटना साहिब में ही व्यतीत किए। बचपन से ही गोबिंद दास में एक महान योद्धा के सभी गुण विद्यमान थे। वह तीरकमान तथा अन्य शस्त्रों से खेलते, अपने साथियों को दो गुटों में विभाजित करके उनमें कृत्रिम युद्ध करवाते। वह कई बार अपना दरबार लगाते तथा साथी बच्चों के झगड़ों के फैसले भी करते। उनके बचपन की अनेक घटनाओं से उनकी वीरता तथा बुद्धिमता की उदाहरण मिलती है। गुरु गोबिंद सिंह जी के नाबालिग काल में उनकी सरपरस्ती उनके मामा श्री कृपाल चंद जी ने की।
3. शिक्षा (Education)-1672 ई० में आप परिवार सहित चक्क नानकी (श्री आनंदपुर साहिब) आ गए। यहाँ पर आप की शिक्षा के लिए विशेष प्रबंध किया गया। आपने भाई साहिब चंद से गुरमुखी, पंडित हरिजस से संस्कृत और काज़ी पीर मुहम्मद से फ़ारसी और अरबी का ज्ञान प्राप्त किया। आपने घुड़सवारी और शस्त्र चलाने का प्रशिक्षण बजर सिंह नामी एक राजपूत से प्राप्त किया।
4. गुरुगद्दी की प्राप्ति (Assumption of Guruship)-औरंगज़ेब के अत्याचारों से तंग आकर कश्मीरी पंडितों का एक जत्था अपनी ‘दुःखभरी याचना लेकर गुरु तेग़ बहादुर जी के पास मई, 1675 ई० में श्री आनंदपुर साहिब पहुँचा। कश्मीरी पंडितों की गुहार तथा पुत्र की प्रेरणा पर धर्म की रक्षा हेतु गुरु तेग़ बहादुर जी ने अपना बलिदान देने का निश्चय किया। गुरु साहिब ने दिल्ली में अपनी शहीदी देने से पूर्व गोबिंद दास को अपना उत्तराधिकारी नियुक्त किए जाने की घोषणा की। इस प्रकार गोबिंद दास को सिख परंपरा के अनुसार 11 नवंबर, 1675 ई० को गुरुगद्दी पर बैठाया गया। इस तरह आप 9 वर्ष की आयु में सिखों के दशम गुरु बने। आप 1708 ई० तक गुरुगद्दी पर रहे।
5. सेना का संगठन (Army Organisation)-गुरुगद्दी पर विराजमान होने के शीघ्र पश्चात् गुरु साहिब ने यह घोषणा की कि जिस सिख के चार पुत्र हों, वह दो पुत्र गुरु साहिब की सेना में भर्ती करवाए। इसके साथ ही गुरु साहिब ने यह आदेश भी दिया कि सिख धन के स्थान पर घोड़े और शस्त्र भेंट करें। शीघ्र ही गुरु साहिब की सेना में बहुत-से सिख भर्ती हो गए और उनके पास बहुत-से शस्त्र और घोड़े भी एकत्रित हो गए। इन सब के पीछे गुरु साहिब का उद्देश्य मुग़ल साम्राज्य को टक्कर देना था।
6. शाही प्रतीक धारण करना (Adoption of Royal Symbols)-गुरु गोबिंद सिंह जी ने अपने दादा गुरु हरगोबिंद जी की भाँति शाही प्रतीकों को धारण करना आरंभ कर दिया। वह अपनी दस्तार में कलगी सजाने लग पड़े। उन्होंने सिंहासन और छत्र का प्रयोग करना आरंभ कर दिया। इनके अतिरिक्त गुरु साहिब ने एक विशेष नगाड़ा भी बनवाया, जिसका नाम रणजीत नगाड़ा रखा गया।
7. नाहन से निमंत्रण (Invitation from Nahan)-गुरु गोबिंद सिंह जी की सैनिक गतिविधियों के कारण कहलूर का शासक, भीम चंद गुरु साहिब से ईर्ष्या करने लग पड़ा था। गुरु साहिब अभी किसी भी प्रकार के सैनिक द्वंद्व में पड़ना नहीं चाहते थे। इसी समय नाहन के राजा, मेदनी प्रकाश ने उन्हें नाहन आने का निमंत्रण दिया। गुरु साहिब ने यह निमंत्रण तुरंत स्वीकार कर लिया और वह माखोवाल से अपने परिवार सहित नाहन चले गए। यहाँ पर गुरु साहिब ने एक दुर्ग का निर्माण करवाया, जिसका नाम पाऊँटा साहिब रखा गया।
8. पाऊँटा साहिब में गतिविधियाँ (Activities at Paonta Sahib)-गुरु साहिब ने पाऊँटा साहिब में सिखों को सैनिक प्रशिक्षण देना आरंभ कर दिया। उन्हें घुड़सवारी, तीर कमान और शस्त्रों का प्रयोग करने में निपुण बनाया गया। गुरु साहिब ने साढौरा के पीर बुद्ध शाह की सिफ़ारिश पर 500 पठानों को भी अपनी सेना में भर्ती कर लिया। पाऊँटा साहिब में ही गुरु गोबिंद सिंह जी ने बड़े उच्च कोटि के साहित्य की भी रचना की। गुरु साहिब ने अपने दरबार में 52 प्रसिद्ध कवियों को संरक्षण दिया हुआ था। इनमें सैनापत, नंद लाल, हंस राम एवं अनी राय प्रमुख थे। आपकी साहित्यिक रचना का उद्देश्य परमात्मा की प्रशंसा करना और सिखों में एक नया जोश उत्पन्न करना था। गुरु साहिब की साहित्यिक क्षेत्र में देन अद्वितीय थी।
पूर्व रवालसा एवं उत्तर रवालसा की लड़ाइयाँ (Battles of Pre-Khalsa and Post-Khalsa Period)
प्रश्न 2.
गुरु गोबिंद सिंह जी की पूर्व खालसा काल तथा उत्तर खालसा काल में लड़ी गई लड़ाइयों का संक्षिप्त वर्णन दो। (Give a brief account of Pre-Khalsa and Post-Khalsa battles of Guru Gobind Singh Ji.)
अथवा
गुरु गोबिंद सिंह जी के पूर्व खालसा काल तथा उत्तर खालसा काल की लड़ाइयों के क्या कारण थे ?
(What were the causes of the Pre-Khalsa and Post-Khalsa battles of Guru Gobind Singh Ji ?)
अथवा
गुरु गोबिंद सिंह जी की प्रसिद्ध लड़ाइयों का वर्णन करें। (Describe the important battles of Guru Gobind Singh Ji.)
उत्तर-
गुरुगद्दी पर विराजमान होते ही गुरु गोबिंद सिंह जी ने अपनी सैनिक गतिविधियाँ आरंभ कर दीं। गुरु जी की सैनिक गतिविधियों ने पहाड़ी राजाओं तथा मुग़लों को उनके विरुद्ध कर दिया। परिणामस्वरूप नौबत युद्ध तक आ गई। गुरु गोबिंद सिंह जी की पूर्व-खालसा तथा उत्तर-खालसा काल की लड़ाइयों का संक्षिप्त वर्णन इस प्रकार है—
1. भंगाणी की लड़ाई 1688 ई० (Battle of Bhangani 1688 A.D.)—गुरु.गोबिंद सिंह जी और पहाड़ी राजाओं के बीच प्रथम लड़ाई भंगाणी में हुई। इस लड़ाई के कई कारण उत्तरदायी थे। पहला, गुरु गोबिंद सिंह जी द्वारा पाऊँटा साहिब में सिखों को सैनिक प्रशिक्षण देने से पहाड़ी राजाओं में घबराहट उत्पन्न हो गई। दूसरा, गुरु गोबिंद सिंह जी मूर्ति-पूजा और जाति-प्रथा के विरुद्ध प्रचार करते थे। इसे पहाड़ी राजा अपने धर्म में हस्तक्षेप समझते थे। तीसरा, पहाड़ी राजाओं ने सिख संगतों द्वारा लाए जा रहे उपहारों को मार्ग में ही लूटना आरंभ कर दिया था। गुरु साहिब यह बात पसंद नहीं करते थे। चौथा, गुरु जी द्वारा भीम चंद को सफेद हाथी देने से इंकार करना था। पाँचवां, मुग़ल सरकार ने इन पहाड़ी राजाओं को गुरु साहिब के विरुद्ध कार्यवाई करने के लिए भड़काया। फलस्वरूप कहलूर के शासक भीम चंद और श्रीनगर के शासक फतह शाह के नेतृत्व में पहाड़ी राजाओं के गठबंधन ने गुरु साहिब पर भंगाणी नामक स्थान पर 22 सितंबर, 1688 ई० को आक्रमण कर दिया।
इस लड़ाई के आरंभ होने से पूर्व ही गुरु साहिब की सेना के पठान सैनिक गुरु साहिब को धोखा दे गए। ऐसे समय सढौरा का पीर बुद्ध शाह गुरु साहिब की सहायता के लिए अपने चार पुत्रों और 700 सैनिकों सहित रणभूमि में पहुँच गया। इस लड़ाई में गुरु हरगोबिंद साहिब की सुपुत्री बीबी वीरो के पाँच पुत्रों ने बहुत वीरता दिखाई। इस लड़ाई में पहाड़ी राजाओं के बहुत-से सैनिक और प्रसिद्ध नेता मारे गए। भीम चंद और फतह शाह युद्ध-भूमि से भाग गए। इस प्रकार गुरु गोबिंद सिंह जी ने इस लड़ाई में शानदार विजय प्राप्त की। इस विजय से गुरु साहिब की प्रतिष्ठा में काफ़ी वृद्धि हुई।
2. नादौन की लड़ाई 1690 ई० (Battle of Nadaun 1690 A.D.)-भंगाणी की लड़ाई के पश्चात् गुरु गोबिंद सिंह जी पुन: श्री आनंदपुर साहिब आ गए। इसी समय पहाड़ी राजाओं ने मुग़लों को दिया जाने वाला वार्षिक खिराज (कर) देना बंद कर दिया। जब औरंगज़ेब को इस संबंध में ज्ञात हुआ तो उसके आदेश पर जम्मू के सूबेदार, मीयाँ खाँ ने तुरंत अपने एक जरनैल, आलिफ खाँ के अंतर्गत मुग़लों की एक भारी सेना इन पहाड़ी राजाओं ने विरुद्ध भेजी। ऐसे समय में भीम चंद ने गुरु साहिब को सहायता के लिए निवेदन किया। गुरु साहिब ने यह निवेदन स्वीकार कर लिया। 20 मार्च, 1690 ई० को काँगड़ा के पास नादौन में भीम चंद और आलिफ खाँ की सेनाओं में लड़ाई आरंभ हुई। इस लड़ाई में गुरु साहिब और सिखों की वीरता के कारण आलिफ खाँ को पराजय का सामना करना पड़ा। इस प्रकार गुरु साहिब के सहयोग से भीम चंद और उसके साथी पहाड़ी राजाओं को विजय प्राप्त हुई।
3. खानजादा का अभियान 1694 ई० (Expedition of Khannada 1694 A.D.)-गुरु गोबिंद सिंह जी की बढ़ती हुई लोकप्रियता औरंगज़ेब के लिए चिंता का विषय बन गई। उसके आदेश पर लाहौर के सूबेदार, दिलावर खाँ ने अपने पुत्र खानजादा रुस्तम खाँ के अंतर्गत गुरु जी के विरुद्ध सेना भेजी। उसने रात्रि के अंधकार में आक्रमण करने की योजना बनाई। रुस्तम खाँ के आगमन का रात्रि को पहरा दे रहे सिख को पता चल गया। उसने फ़ौरन इसकी सूचना सिखों को दी। सिखों ने जैकारे की आवाज़ गुंजाई और गोलियाँ चलानी आरंभ की। परिणामस्वरूप, मुग़ल सैनिक बिना मुकाबला किए ही युद्ध के मैदान से भाग निकले।
4. कुछ सैनिक अभियान-1695-96 ई० (Some Military Expeditions 1695-96 A.D.)-169596 ई० में मुग़लों ने गुरु जी की शक्ति को कुचलने के लिए हुसैन खाँ, जुझार सिंह तथा शहजादा मुअज्जम के अधीन कुछ सैनिक अभियान भेजे। ये सभी अभियान किसी न किसी कारण असफल रहे तथा गुरु जी की शक्ति कायम रही।
5. श्री आनंदपुर साहिब की पहली लड़ाई 1701 ई० (First Battle of Sri Anandpur Sahib 1701 A.D.)-खालसा पंथ की स्थापना के बाद गुरु साहिब की बढ़ रही ख्याति के कारण पहाड़ी राजाओं में घबराहट पैदा हो गई। कहलूर के राजा भीम चंद, जिसकी रियासत में श्री आनंदपुर साहिब स्थित था, ने गुरु जी को श्री आनंदपुर साहिब छोड़ने के लिए कहा। गुरु जी ने ऐसा करने से इंकार कर दिया। इस पर भीम चंद ने कुछ पहाड़ी राजाओं से मिलकर 1701 ई० में श्री आनंदपुर साहिब के किले पर आक्रमण कर दिया। किले में सिखों की संख्या बहुत कम थी, फिर भी उन्होंने पहाड़ी राजाओं की सेनाओं का खूब डटकर सामना किया। जब पहाड़ी राजाओं ने देखा कि सफलता मिलने की कोई आशा नहीं है तो उन्होंने गुरु जी से संधि कर ली।
6. श्री आनंदपुर साहिब की दूसरी लड़ाई 1704 ई० (Second Battle of Sri Anandpur Sahib 1704 A.D.)-पहाड़ी राजाओं ने गुरु जी से प्रतिशोध लेने की खातिर मुग़ल सेनाओं से मिलकर मई, 1704 ई० में श्री आनंदपुर साहिब को दूसरी बार घेर लिया। घेरे की अवधि बहुत लंबी हो गई, जिस कारण दुर्ग के भीतर खाद्यसामग्री कम होनी आरंभ हो गई। इसलिए मुग़लों का मुकाबला करना कठिन हो गया। गुरु साहिब ने सिखों को कुछ और दिन संघर्ष जारी रखने को कहा। परंतु 40 सिख गुरु जी को बेदावा देकर दुर्ग छोड़ कर चले गए। दूसरी ओर शाही सेना भी बहुत परेशान थी। उन्होंने एक चाल चली। उन्होंने कुरान और गायों की कसम खाकर गुरु साहिब को विश्वास दिलाया कि यदि वे श्री आनंदपुर साहिब छोड़ दें तो उन्हें कोई क्षति नहीं पहुंचाई जायेगी। गुरु साहिब को इन कस्मों पर कोई विश्वास नहीं था, परंतु माता गुजरी और कुछ सिखों के निवेदन पर गुरु साहिब ने श्री आनंदपुर साहिब के दुर्ग को छोड़ दिया।
7. सरसा की लड़ाई 1704 ई० (Battle of the Sarsa 1704 A.D.)-श्री आनंदपुर साहिब छोड़ते ही मुग़ल सैनिकों ने गुरु जी पर फिर आक्रमण कर दिया। शाही सेना तथा सिखों में सरसा में लड़ाई हुई। इस लड़ाई में सिखों में भगदड़ मच गई। इसी भगदड़ में गुरु साहिब के छोटे साहिबजादे साहिबजादा जोरावर सिंह जी तथा साहिबजादा फतह सिंह जी और माता गुजरी जी उनसे बिछुड़ गए। गंगू जो गुरु साहिब का पुराना सेवक था, ने लालच में आकर उन्हें सरहिंद के नवाब वज़ीर खाँ को सौंप दिया। नवाब वज़ीर खाँ ने इन दोनों छोटे बालकों को 27 दिसंबर, 1704 ई० को दीवार में जीवित चिनवा दिया।
8. चमकौर साहिब की लड़ाई 1704 ई० (Battle of Chamkaur 1704 A.D.)—इसके उपरांत गुरु गोबिंद सिंह जी अपने 40 सिखों के साथ चमकौर साहिब पहुँचे। गुरु जी तथा उनके साथियों ने एक गढ़ी में शरण ली। मुग़ल सेना ने गढ़ी पर 22 दिसंबर, 1704 ई० को आक्रमण कर दिया। यह बड़ी जबरदस्त लड़ाई थी। इस लड़ाई में गुरु गोबिंद सिंह जी के दो बड़े साहिबजादों साहिबजादा अजीत सिंह जी तथा साहिबज़ादा जुझार सिंह जी ने अत्यंत वीरता का प्रदर्शन किया और अंततः लड़ते-लड़ते शहीद हो गये। जब पाँच सिख शेष रह गए तो उन्होंने खालसा पंथ के लिए गुरु साहिब से गढ़ी छोड़ देने की प्रार्थना की। गुरु जी ने इस प्रार्थना को सिख पंथ का आदेश समझकर अपने साथ तीन सिखों को लेकर गढ़ी छोड़ दी। गढ़ी को छोड़ने से पूर्व गुरु जी ने मुग़ल सेना को चुनौती दी तथा वे वहां से ताली बजाकर निकले।
9. गुरु जी माछीवाड़ा में (Guru Ji in Machhiwara)-गुरु जी चमकौर साहिब की लड़ाई के पश्चात् माछीवाड़ा के वनों में पहुँचे। यहाँ दो मुसलमान भाइयों नबी खाँ तथा गनी खाँ ने गुरु जी को एक पालकी में बिठा कर मुग़ल सैनिकों से उनकी रक्षा की। दीना कांगड़ नामक स्थान पर पहुँचने पर गुरु जी ने ज़फ़रनामा नामक फ़ारसी में एक चिट्ठी औरंगजेब को लिखी। इस चिट्ठी में गुरु जी ने बहुत निर्भीकता से औरंगजेब के अत्याचारों की आलोचना की।
10. खिदराना की लड़ाई 1705 ई० (Battle of Khidrana 1705 A.D.)-गुरु जी तथा मुग़ल सेना में लड़ी जाने वाली अंतिम निर्णायक लड़ाई खिदराना में हुई। 29 दिसंबर, 1705 ई० को सरहिंद के नवाब वज़ीर खाँ ने गुरु जी की सेना पर खिदराना के स्थान पर आक्रमण कर दिया। इस लड़ाई में सिखों ने बड़ी वीरता दिखाई और बड़ी शानदार विजय प्राप्त हुई। इसी लड़ाई में वे 40 सिख भी शहीद हो गए, जो श्री आनंदपुर साहिब की दूसरी लड़ाई में गुरु जी का साथ छोड़ गए थे। उनके अद्वितीय बलिदान से प्रभावित होकर गुरु साहिब ने उन्हें मुक्ति का वरदान दिया। इसी कारण खिदराना का नाम श्री मुक्तसर साहिब पड़ गया। प्रसिद्ध लेखक करतार सिंह के अनुसार,
“यह सच है कि वह (गुरु गोबिंद सिंह जी) मुग़ल साम्राज्य अथवा शक्ति को नष्ट न कर सके, परंतु इसे जड़ से हिलाकर रख दिया था।”1

प्रश्न 3.
गुरु गोबिंद सिंह जी के जीवन की उत्तर खालसा काल की मुख्य घटनाओं का वर्णन करें।
(Give a brief description of the events of the Post-Khalsa period of Guru Gobind Singh Ji.)
उत्तर-
1. श्री आनंदपुर साहिब की पहली लड़ाई 1701 ई० (First Battle of Sri Anandpur Sahib 1701 A.D.)-खालसा पंथ की स्थापना के बाद गुरु साहिब की बढ़ रही ख्याति के कारण पहाड़ी राजाओं में घबराहट पैदा हो गई। कहलूर के राजा भीम चंद, जिसकी रियासत में श्री आनंदपुर साहिब स्थित था, ने गुरु जी को श्री आनंदपुर साहिब छोड़ने के लिए कहा। गुरु जी ने ऐसा करने से इंकार कर दिया। इस पर भीम चंद ने कुछ पहाड़ी राजाओं से मिलकर 1701 ई० में श्री आनंदपुर साहिब के किले पर आक्रमण कर दिया। किले में सिखों की संख्या बहुत कम थी, फिर भी उन्होंने पहाड़ी राजाओं की सेनाओं का खूब डटकर सामना किया। जब पहाड़ी राजाओं ने देखा कि सफलता मिलने की कोई आशा नहीं है तो उन्होंने गुरु जी से संधि कर ली।
2. श्री आनंदपुर साहिब की दूसरी लड़ाई 1704 ई० (Second Battle of Sri Anandpur Sahib 1704 A.D.)-पहाड़ी राजाओं ने गुरु जी से प्रतिशोध लेने की खातिर मुग़ल सेनाओं से मिलकर मई, 1704 ई० में श्री आनंदपुर साहिब को दूसरी बार घेर लिया। घेरे की अवधि बहुत लंबी हो गई, जिस कारण दुर्ग के भीतर खाद्यसामग्री कम होनी आरंभ हो गई। इसलिए मुग़लों का मुकाबला करना कठिन हो गया। गुरु साहिब ने सिखों को कुछ और दिन संघर्ष जारी रखने को कहा। परंतु 40 सिख गुरु जी को बेदावा देकर दुर्ग छोड़ कर चले गए। दूसरी ओर शाही सेना भी बहुत परेशान थी। उन्होंने एक चाल चली। उन्होंने कुरान और गायों की कसम खाकर गुरु साहिब को विश्वास दिलाया कि यदि वे श्री आनंदपुर साहिब छोड़ दें तो उन्हें कोई क्षति नहीं पहुंचाई जायेगी। गुरु साहिब को इन कस्मों पर कोई विश्वास नहीं था, परंतु माता गुजरी और कुछ सिखों के निवेदन पर गुरु साहिब ने श्री आनंदपुर साहिब के दुर्ग को छोड़ दिया।
3. सरसा की लड़ाई 1704 ई० (Battle of the Sarsa 1704 A.D.)-श्री आनंदपुर साहिब छोड़ते ही मुग़ल सैनिकों ने गुरु जी पर फिर आक्रमण कर दिया। शाही सेना तथा सिखों में सरसा में लड़ाई हुई। इस लड़ाई में सिखों में भगदड़ मच गई। इसी भगदड़ में गुरु साहिब के छोटे साहिबजादे साहिबजादा जोरावर सिंह जी तथा साहिबजादा फतह सिंह जी और माता गुजरी जी उनसे बिछुड़ गए। गंगू जो गुरु साहिब का पुराना सेवक था, ने लालच में आकर उन्हें सरहिंद के नवाब वज़ीर खाँ को सौंप दिया। नवाब वज़ीर खाँ ने इन दोनों छोटे बालकों को 27 दिसंबर, 1704 ई० को दीवार में जीवित चिनवा दिया।
4. चमकौर साहिब की लड़ाई 1704 ई० (Battle of Chamkaur 1704 A.D.)—इसके उपरांत गुरु गोबिंद सिंह जी अपने 40 सिखों के साथ चमकौर साहिब पहुँचे। गुरु जी तथा उनके साथियों ने एक गढ़ी में शरण ली। मुग़ल सेना ने गढ़ी पर 22 दिसंबर, 1704 ई० को आक्रमण कर दिया। यह बड़ी जबरदस्त लड़ाई थी। इस लड़ाई में गुरु गोबिंद सिंह जी के दो बड़े साहिबजादों साहिबजादा अजीत सिंह जी तथा साहिबज़ादा जुझार सिंह जी ने अत्यंत वीरता का प्रदर्शन किया और अंततः लड़ते-लड़ते शहीद हो गये। जब पाँच सिख शेष रह गए तो उन्होंने खालसा पंथ के लिए गुरु साहिब से गढ़ी छोड़ देने की प्रार्थना की। गुरु जी ने इस प्रार्थना को सिख पंथ का आदेश समझकर अपने साथ तीन सिखों को लेकर गढ़ी छोड़ दी। गढ़ी को छोड़ने से पूर्व गुरु जी ने मुग़ल सेना को चुनौती दी तथा वे वहां से ताली बजाकर निकले।
5. गुरु जी माछीवाड़ा में (Guru Ji in Machhiwara)-गुरु जी चमकौर साहिब की लड़ाई के पश्चात् माछीवाड़ा के वनों में पहुँचे। यहाँ दो मुसलमान भाइयों नबी खाँ तथा गनी खाँ ने गुरु जी को एक पालकी में बिठा कर मुग़ल सैनिकों से उनकी रक्षा की। दीना कांगड़ नामक स्थान पर पहुँचने पर गुरु जी ने ज़फ़रनामा नामक फ़ारसी में एक चिट्ठी औरंगजेब को लिखी। इस चिट्ठी में गुरु जी ने बहुत निर्भीकता से औरंगजेब के अत्याचारों की आलोचना की।
6. खिदराना की लड़ाई 1705 ई० (Battle of Khidrana 1705 A.D.)-गुरु जी तथा मुग़ल सेना में लड़ी जाने वाली अंतिम निर्णायक लड़ाई खिदराना में हुई। 29 दिसंबर, 1705 ई० को सरहिंद के नवाब वज़ीर खाँ ने गुरु जी की सेना पर खिदराना के स्थान पर आक्रमण कर दिया। इस लड़ाई में सिखों ने बड़ी वीरता दिखाई और बड़ी शानदार विजय प्राप्त हुई। इसी लड़ाई में वे 40 सिख भी शहीद हो गए, जो श्री आनंदपुर साहिब की दूसरी लड़ाई में गुरु जी का साथ छोड़ गए थे। उनके अद्वितीय बलिदान से प्रभावित होकर गुरु साहिब ने उन्हें मुक्ति का वरदान दिया। इसी कारण खिदराना का नाम श्री मुक्तसर साहिब पड़ गया। प्रसिद्ध लेखक करतार सिंह के अनुसार,
“यह सच है कि वह (गुरु गोबिंद सिंह जी) मुग़ल साम्राज्य अथवा शक्ति को नष्ट न कर सके, परंतु इसे जड़ से हिलाकर रख दिया था।”1
1. “It is true that he did not actually uproot the Mughal empire or power, but he shook it violently to its very foundations.” Kartar Singh, Life of Guru Gobind Singh (Ludhiana : 1976) p. 222.
खालसा पंथ का सृजन (Creation of the Khalsa Panth)
प्रश्न 4.
1699 ई० में किन परिस्थितियों के कारण खालसा पंथ का सृजन किया गया ? इसका महत्त्व भी बताएँ।
(What were the circumstances that led to the creation of the Khalsa in 1699 A.D. ? Also point out its significance.)
अथवा
खालसा पंथ की स्थापना के क्या कारण थे ? इसकी ऐतिहासिक महत्ता ब्यान करें।
(What were the circumstances leading to the creation of the Khalsa ? Describe its historical importance.)
अथवा
गुरु गोबिंद सिंह जी द्वारा खालसा की स्थापना के कारणों की व्याख्या कीजिए।
(Describe the causes of the creation of the Khalsa by Guru Gobind Singh Ji.)
अथवा
गुरु गोबिंद सिंह जी द्वारा खालसा की स्थापना और उसके महत्त्व का वर्णन करो।
(Describe the creation of Khalsa by Guru Gobind Singh Ji. Also discuss its importance.)
अथवा
खालसा पंथ की स्थापना के कारण और महत्त्व का वर्णन करो। (Explain the reasons and importance of the creation of Khalsa Panth.)
अथवा
गुरु गोबिंद सिंह जी द्वारा खालसा की स्थापना का वर्णन कीजिए। इसके महत्त्व का भी मूल्यांकन करें। (Describe the creation of Khalsa by Guru Gobind Singh Ji. Examine its significance.)
अथवा
खालसा की स्थापना, मुख्य सिद्धांतों एवं महत्त्व के विषय में विस्तारपूर्वक चर्चा कीजिए।
(Discuss in detail the foundation, its main principles and significance of Khalsa.)
अथवा
खालसा की स्थापना के लिए सहायक कारण कौन-से थे ? इसके मुख्य सिद्धांतों तथा महत्त्व का अध्ययन कीजिए।
(What were the circumstances leading to the creation of Khalsa ? Study its main principles and significance.)
अथवा
खालसा पंथ की स्थापना के क्या कारण थे ? इसका क्या महत्त्व है ?
(What were the causes leading to the creation of the Khalsa Panth ? What are its significance ?)
अथवा
खालसा पंथ की स्थापना के कारण और महत्त्व बताएँ।
(Write down the causes and importance of the establishment to Khalsa Panth.)
उत्तर-
गुरु गोबिंद सिंह जी का सबसे महान कार्य 1699 ई० में वैसाखी वाले दिन खालसा पंथ का सृजन करना था। खालसा पंथ के सृजन को सिख इतिहास में एक नए युग का सूत्रपात माना जाता है। खालसा पंथ की स्थापना के कारण, उसकी स्थापना तथा उसके महत्त्व का विवरण निम्नलिखित अनुसार है। प्रसिद्ध लेखक हरबंस सिंह के अनुसार, “यह इतिहास का एक महान् रचनात्मक कार्य था जिसने लोगों के दिलों में क्रांतिकारी परिवर्तन लाए।”2
I. खालसा पंथ का सृजन क्यों किया गया ? (Why was The Khalsa Panth Created ?)
1. मुग़लों का अत्याचारी शासन (Tyrannical Rule of the Mughals)-जहाँगीर के काल से ही मुग़ल सिख संबंधों में तनाव उत्पन्न हो गया था। यह तनाव औरंगजेब के काल में सभी सीमाएँ पार कर चुका था। औरंगजेब ने हिंदुओं के कई प्रसिद्ध मंदिरों को गिरवा दिया था। उसने हिंदुओं की धार्मिक रस्मों पर प्रतिबंध लगा दिए तथा जज़िया कर को पुनः लागू कर दिया। उसने सिखों के गुरुद्वारों को गिराए जाने के भी आदेश दिए। उसने बड़ी संख्या में इस्लाम धर्म स्वीकार न करने वाले गैर-मुसलमानों की हत्या करवा दी। सबसे बढ़कर उसने गुरु तेग़ बहादुर जी को शहीद करवा दिया। अतः मुग़लों के इन बढ़ रहे अत्याचारों का अंत करने के लिए गुरु गोबिंद सिंह जी ने खालसा पंथ की स्थापना करने का निर्णय किया।
2. पहाड़ी राजाओं का विश्वासघात (Treachery of the Hill Chiefs)-गुरु जी मुग़लों के विरुद्ध संघर्ष के लिए पहाड़ी राजाओं को साथ लेना चाहते थे। परंतु गुरु जी इस बात से परिचित थे कि पहाड़ी राजाओं पर विश्वास नहीं किया जा सकता। इसलिए गुरु गोबिंद सिंह जी ने ऐसे सैनिकों को तैयार करने का निर्णय किया जो मुग़लों की शक्ति का सामना कर पाएँ। फलस्वरूप खालसा पंथ की स्थापना की गई।
3. जातीय बंधन (Shackles of the Caste System)-भारतीय समाज में जाति-प्रथा शताब्दियों से चली आ रही थी। फलस्वरूप समाज कई जातियों और उपजातियों में विभाजितं था। उच्च जाति के लोग निम्न जाति के लोगों के साथ बुरा व्यवहार करते थे। इस जाति-प्रथा ने भारतीय समाज को एक घुण की भाँति भीतर ही भीतर से खोखला बना दिया था। पूर्व हुए सभी गुरु साहिबान ने संगत और पंगत की संस्थाओं द्वारा जाति प्रथा को कड़ा आघात पहुँचाया था, किंतु यह अभी भी समाप्त नहीं हुई थी। गुरु गोबिंद सिंह जी एक ऐसे आदर्श समाज की स्थापना करना चाहते थे, जिसमें जाति-पाति का कोई स्थान न हो।
4. दोषपूर्ण मसंद प्रथा (Defective Masand System)-दोषपूर्ण मसंद प्रथा गुरु गोबिंद सिंह जी द्वारा खालसा पंथ की स्थापना का महत्त्वपूर्ण कारण बनी। समय के साथ-साथ मसंद अपने प्रारंभिक आदर्शों को भूल गए और बड़े भ्रष्टाचारी और अहंकारी बन गए। उन्होंने सिखों को लूटना आरंभ कर दिया। उनका कहना था कि वे गुरुओं को बनाने वाले हैं। बहुत से प्रभावशाली मसंदों ने अपनी अलग गुरुगद्दी स्थापित कर ली थी। गुरु गोबिंद सिंह जी ने इन मसंदों से छुटकारा पाने के लिए एक नए संगठन की स्थापना करने का निर्णय किया।
5. गुरुगद्दी का पैतृक होना (Hereditary Nature of Guruship)-गुरु अमरदास जी द्वारा गुरुगद्दी को पैतृक बना दिए जाने से भी अनेक समस्याएँ उत्पन्न हो गई थीं। जिसको भी गुरुगद्दी न मिली, उसने गुरु घर का विरोध करना आरंभ कर दिया। पृथी चंद, धीर मल्ल और रामराय ने तो गुरुगद्दी प्राप्त करने के लिए मुग़लों के साथ मिलकर कई षड्यंत्र भी रचे। इसलिए गुरु गोबिंद सिंह जी एक ऐसे समाज का निर्माण करना चाहते थे जिसमें धीर मल्लों और राम रायों जैसों के लिए कोई स्थान न हो।
6. गुरु गोबिंद सिंह जी का उद्देश्य (Mission of Guru Gobind Singh Ji)-गुरु गोबिंद सिंह जी ने ‘बचित्तर नाटक’ में लिखा है, कि उनके जीवन का उद्देश्य संसार में धर्म-प्रचार का कार्य करना और अत्याचारियों का विनाश करना है। अत्याचारियों के विनाश के लिए तलवार उठाना अत्यावश्यक है। अपने इस उद्देश्य की पूर्ति के लिए गुरु गोबिंद सिंह जी ने खालसा पंथ का सृजन किया। गुरु गोबिंद सिंह जी का कथन था,
हम यह काज जगत में आए।। धर्म हेतु गुरुदेव पठाए॥
जहाँ तहाँ तुम धर्म बिथारो।। दुष्ट देखियन पकड़ पछारो।।
2. “It was a grand creative deed of history which wrought revolutionary change in men’s minds.” Harbans Singh, Guru Gobind Singh (New Delhi : 1979) p. 50.
II. खालसा पंथ का सृजन कैसे किया गया ?
(How Khalsa was Created ?)
खालसा पंथ की स्थापना के लिए गुरु गोबिंद सिंह जी ने * 30 मार्च, 1699 ई० को बैसाखी वाले दिन श्री आनंदपुर साहिब में केसगढ़ नामक स्थान पर एक विशाल सम्मेलन का आयोजन किया। इस दीवान में 80,000 सिखों ने भाग लिया। जब लोगों ने अपना स्थान ग्रहण कर लिया तो गुरु जी मंच पर आए। उन्होंने म्यान से तलवार निकाल कर एकत्रित सिखों से कहा कि, “क्या आप में से कोई ऐसा सिख है जो धर्म के लिए अपना शीश भेंट करे ?” जब गुरु जी ने अपने शब्दों को तीन बार दोहराया तो भाई दया राम जी अपना बलिदान देने के लिए आगे आया। गुरु जी उसे पास ही एक तंबू में ले गए। कुछ समय के पश्चात् गुरु जी खून से भरी तलवार लेकर पुनः मंच पर आ गए। उन्होंने एक और सिख से बलिदान की माँग की। अब भाई धर्मदास जी आगे आया। इस क्रम को तीन बार और दोहराया गया। गुरु जी की आज्ञा का पालन करते हुए भाई मोहकम चंद जी, भाई साहिब चंद जी और भाई हिम्मत राय जी अपने बलिदानों के लिए उपस्थित हुए। गुरु जी उन्हें बारी-बारी से तंबू में ले जाते थे तथा खून से भरी तलवार लेकर लौटते थे। कुछ समय के पश्चात् गुरु जी ने इन पाँचों को केसरी रंग के कपड़े पहना कर स्टेज पर लाए। इस प्रकार गुरु गोबिंद सिंह जी ने ‘पाँच प्यारों का चुनाव किया। गुरु साहिब ने इन पाँच प्यारों को पहले खंडे का पाहुल छकाया और बाद में स्वयं इन प्यारों से अमृत छका। इसी कारण गुरु गोबिंद सिंह जी को ‘आपे गुरु चेला’ कहा जाता है। इस प्रकार खालसा पंथ का सृजन हुआ। गुरु गोबिंद सिंह जी का कथन था,
खालसा मेरो रूप है खास॥
खालसा में ही करु निवास।
III. खालसा पंथ के सिद्धांत (Principles of the Khalsa Panth)
गुरु गोबिंद सिंह जी ने खालसा की पालना के लिए कुछ विशेष नियम भी बनाए। कुछ प्रमुख नियमों का वर्णन निम्नलिखित अनुसार है—
- खालसा पंथ में सम्मिलित होने के लिए प्रत्येक व्यक्ति को ‘खंडे का पाहुल’ छकना होगा।
- खालसा ‘पाँच कक्कार’ अर्थात् केश, कंघा, कड़ा, कच्छहरा और कृपाण धारण करेगा।
- खालसा एक ईश्वर के अतिरिक्त किसी अन्य देवी-देवता की उपासना नहीं करेगा।
- खालसा पुरुष अपने नाम के साथ ‘सिंह’ और खालसा स्त्री ‘कौर’ शब्द का प्रयोग करेगी।
- खालसा जाति-प्रथा और ऊँच-नीच में विश्वास नहीं रखेगा।
- खालसा शस्त्र धारण करेगा और धर्म-युद्ध के लिए सदैव तैयार रहेगा।
- खालसा श्रम द्वारा अपनी आजीविका प्राप्त करेगा और अपनी आय का दशांश धर्म के लिए दान करेगा।
- खालसा प्रातः काल जागकर स्नान करने के पश्चात् गुरवाणी का पाठ करेगा।
- खालसा परस्पर भेंट के समय ‘वाहेगुरु’ जी का खालसा, वाहेगुरु जी की फ़तह कहेंगे।
- खालसा नशीले पदार्थों का सेवन, पर स्त्री गमन इत्यादि बुराइयों से कोसों दूर रहेगा।
- खालसा देश, धर्म की रक्षा के लिए अपना सब कुछ न्यौछावर करने के लिए सदैव तैयार रहेगा।
* विद्यार्थी यह बात विशेष तौर पर नोट करें कि खालसा की स्थापना के समय बैसाखी का दिवस 30 मार्च था। 1752 ई० में अंग्रेजों ने भारत में ग्रेगोरियन कैलेंडर को प्रचलित किया। अत: भारत में पूर्व प्रचलित विक्रमी कैलेंडर में 12 दिनों की बढ़ौतरी की गई। इस कारण आजकल बैसाखी सामान्य तौर पर 13 अप्रैल को मनाई जाती है।
IV. खालसा की सृजना का महत्त्व (Importance of the Creation of Khalsa)
1699 ई० में खालसा पंथ का सृजन न केवल पंजाब के इतिहास, बल्कि भारत के इतिहास में एक युग परिवर्तक घटना मानी जाती है। निस्संदेह, खालसा पंथ की स्थापना के बड़े दूरगामी परिणाम निकले।
1. सिखों की संख्या में वृद्धि (Increase in the number of Sikhs) खालसा पंथ की स्थापना के पश्चात् भारी संख्या में लोग इसमें शामिल होने लग पड़े। गुरु साहिब ने स्वयं हज़ारों सिखों को पाहुल छकाकर खालसा बनाया। इसके अतिरिक्त गुरु जी ने खालसा पंथ के किसी भी पाँच सिखों को अमृत छकाने का अधिकार देकर खालसा पंथ में आश्चर्यजनक रूप से वृद्धि की।
2. आदर्श समाज का निर्माण (Creation of an Ideal Society)-खालसा पंथ की स्थापना से एक आदर्श समाज का जन्म हुआ। खालसा पंथ में ऊँच-नीच के लिए कोई स्थान नहीं था। इसमें निम्न और पिछड़ी श्रेणियों को समानता का दर्जा दिया गया। खालसा समाज में अंध-विश्वासों तथा नशीले पदार्थों के सेवन करने के लिए कोई स्थान नहीं था। इस प्रकार गुरु जी ने खालसा पंथ को रच कर स्वस्थ समाज की रचना की। डॉक्टर इंद्रपाल सिंह के अनुसार,
“खालसा की महानता इस बात में है कि यह जाति एवं नस्ल की अपेक्षा मानव भाईचारे की बात करता है।”3
3. मसंद प्रथा एवं पंथ विरोधी संप्रदायों का अंत (End of Masand System and Sects which were against Panth)-मसंद प्रथा में आई कुरीतियाँ खालसा पंथ के निर्माण का एक प्रमुख कारण बनी थीं। इसलिए जब गुरु गोबिंद सिंह जी ने खालसा पंथ की स्थापना की, तो उसमें मसंदों को कोई स्थान नहीं दिया गया। गुरु जी ने सिखों को आदेश दिया, कि वे इनसे किसी प्रकार का कोई संबंध न रखें।
4. सिखों में नया जोश (New spirit among the Sikhs)-खालसा पंथ की स्थापना का सबसे महत्त्वपूर्ण परिणाम सिखों में एक नया जोश तथा शक्ति पैदा हुई। वे अपने आप को शेर के समान बहादुर समझने लग पड़े। उन्होंने अत्याचारियों के सम्मुख झुकने की अपेक्षा अब शस्त्र उठा लिए। उन्होंने मुग़लों और अफ़गानों से होने वाली लड़ाइयों में अद्वितीय वीरता और बलिदान के प्रमाण दिए।
5. निम्न जातियों के लोगों का उद्धार (Upliftment of the Downtrodden People)-खालसा पंथ की स्थापना निम्न जातियों के उद्धार का संदेश थी। इससे पूर्व निम्न जातियों के लोगों से बहुत दुर्व्यवहार किया जाता था। गुरु जी ने निम्न जाति के लोगों को खालसा पंथ में शामिल करके उन्हें उच्च जातियों के बराबर स्थान दिया। गुरु जी ने यह महान् पग उठाकर निम्न जाति के लोगों में एक नया जोश भरा। गुरु गोबिंद सिंह जी के नेतृत्व में वे महान् योद्धा सिद्ध हुए।
6. खालसा पंथ में लोकतंत्र (Democracy in The Khalsa Panth)-1699 ई० में खालसा पंथ की स्थापना के समय गुरु साहिब ने स्वयं पाँच प्यारों को उन्हें अमृतपान करवाने का निवेदन किया। ऐसा करना एक महान् क्रांतिकारी कदम था। गुरु साहिब ने यह घोषणा की थी कि कहीं भी पाँच खालसा एकत्रित होकर अन्य सिखों को अमृत छका सकते हैं। इस प्रकार गुरु साहिब ने सिखों में लोकतंत्र की भावना को प्रोत्साहित किया।
7. सिखों की राजनीतिक शक्ति का उत्थान (Rise of Political Power of the Sikhs)-खालसा पंथ की स्थापना के साथ ही सिखों की राजनीतिक शक्ति का भी उदय हुआ। असंख्य बलिदान के बाद वे पंजाब में अपनी स्वतंत्र मिसलें स्थापित करने में सफल हुए। तत्पश्चात् 19वीं शताब्दी में महाराजा रणजीत सिंह ने स्वतंत्र सिख-साम्राज्य की स्थापना की। इस प्रकार अंत में खालसों का स्वप्न साकार हुआ। अंत में हम डॉक्टर जी० एस० ढिल्लों के इन शब्दों से सहमत हैं,
“खालसा पंथ के सृजन को मानव इतिहास का एक आश्चर्यजनक कारनामा माना जा सकता है।”4
3. “The grandeur of Khalsa is that it is above all notions of caste and creed and speaks only of universal brotherhood.” Dr. Inderpal Singh, The Grandeur of Khalsa (Amritsar : 1999) p. 3.
4. “Creation of the Khalsa was a unique phenomenon in the annals of mankind.” Dr. G. S. Dhillon, Guru Gobind Singh and Creation of Khalsa (Amritsar : 1999) p.22.

गुरु गोबिंद सिंह जी का चरित्र तथा सफलताएँ (Character and Achievements of Guru Gobind Singh Ji)
प्रश्न 5.
गुरु गोबिंद सिंह जी के चरित्र एवं उपलब्धियों का वर्णन करें।
(Discuss the character and achievements of Guru Gobind Singh Ji.)
अथवा
गुरु गोबिंद सिंह जी के व्यक्तित्व का मूल्यांकन करें।
(Make an evaluation of the personality of Guru Gobind Singh Ji.)
अथवा
गुरु गोबिंद सिंह जी के बहु पक्षीय व्यक्तित्व की ऐतिहासिक उदाहरणों सहित व्याख्या करें। (Illustrate historically the multi-dimensional personality of Guru Gobind Singh Ji.).
अथवा
गुरु गोबिंद सिंह जी के एक मनुष्य, एक सैनिक और एक धार्मिक नेता के बारे में विस्तार से लिखो।
(Write in detail about Guru Gobind Singh Ji as a Man, as a Soldier and as a Religious Leader.)
अथवा
आप गुरु गोबिंद सिंह जी के एक मनुष्य, एक सैनिक, एक विद्वान् तथा एक धार्मिक नेता बारे क्या । जानते हैं ?
(What do you know about Guru Gobind Singh Ji as a man, as a Soldier, as a Scholar and as a Saint ?)
अथवा
गुरु गोबिंद सिंह जी के जीवन तथा उपलब्धियों का विवरण दें। (Give an account of the career and achievements of Guru Gobind Singh Ji.)
उत्तर-
गुरु गोबिंद सिंह जी के व्यक्तित्व में अनेक गुण थे। वह संपूर्ण मनुष्य, महान् योद्धा, अत्याचारियों के शत्रु, उच्चकोटि के कवि, समाज सुधारक, उत्तम संगठनकर्ता तथा महान् पैगंबर थे।
मनुष्य के रूप में
(As a Man)
1. शक्ल सूरत (Physical Appearance)-गुरु गोबिंद सिंह जी का व्यक्तित्व अत्यंत प्रभावशाली था। उनका कद लंबा, रंग गोरा तथा शरीर गठित था। उनका मुख मंडल भव्य था। वह बहुत मृदुभाषी थे। उनका पहरावा बहुत सुंदर होता था तथा वह सदैव शस्त्रों से सुसज्जित रहते थे। उनके संपर्क में आने वाला प्रत्येक व्यक्ति उनके जादुई व्यक्तित्व से बहुत प्रभावित होता था।
2. गृहस्थ जीवन (House Holder)-गुरु गोबिंद सिंह जी बड़े आज्ञाकारी पुत्र, विचारवान् पिता और आदर्श पति थे। उन्होंने अपनी माता जी की आज्ञा मानते हुए श्री आनंदपुर साहिब का किला खाली कर दिया था। इसके पश्चात् चाहे उन्हें भारी कष्टों का सामना करना पड़ा, परंतु उन्होंने कभी कोई शिकायत नहीं की। गुरु जी ने अपने पुत्रों को भी अत्याचारों का वीरता से सामना करने का सबक सिखाया।
3. उच्च चरित्र (High Character)-गुरु गोबिंद सिंह जी महान् चरित्र के स्वामी थे। झूठ, छल, कपट तो उन्हें छू भी न पाया था। युद्ध हो अथवा शाँति, उन्होंने कभी भी धैर्य नहीं छोड़ा था। वह स्त्रियों का बहुत सम्मान करते थे। वह प्रत्येक प्रकार के नशे के विरुद्ध थे। उन्होंने अपने सिखों को भी उच्च नैतिक जीवन व्यतीत करने के लिए प्रेरित किया।
4. कुर्बानी की प्रतिमा (Embodiment of Sacrifices)-गुरु गोबिंद सिंह जी कुर्बानी के पुंज थे। 9 वर्ष की आयु में उन्होंने अपने पिता गुरु तेग़ बहादुर जी को बलिदान के लिए प्रेरित किया। उन्होंने धर्म की रक्षा के लिए अपने जीवन के सभी सुख त्याग दिए। अन्याय के विरुद्ध लड़ते हुए गुरु जी के चारों साहिबजादों, माता तथा अनेक सिखों ने बलिदान दिए। ऐसा उदाहरण विश्व इतिहास में कहीं भी नहीं मिलता।
एक विद्वान् के रूप में
(As a Scholar)
गुरु गोबिंद सिंह जी एक उच्चकोटि के कवि तथा साहित्यकार थे। उन्हें अनेक भाषाओं जैसे अरबी, फ़ारसी, पंजाबी, हिंदी तथा संस्कृत आदि का ज्ञान था। ‘जापु साहिब’, ‘बचित्तर नाटक’, ‘ज़फ़रनामा’, ‘चंडी दी वार’ तथा ‘अकाल उस्तति’ आपकी प्रमुख रचनाएँ हैं। ये रचनाएँ संपूर्ण मानवता को स्वतंत्रता, भाईचारे, सामाजिक असमानता को दूर करने तथा अत्याचारों का मुकाबला करने की प्रेरणा देती हैं। इसके अतिरिक्त ये रचनाएँ आत्मा को शाँति भी प्रदान करती हैं। निस्संदेह ये रचनाएँ भक्ति एवं शक्ति के सुमेल का सुंदर उदाहरण हैं । आपने अपने दरबार में उच्चकोटि के 52 कवियों को आश्रय दिया हुआ था। इनमें से सैनापत, नंद लाल, गोपाल तथा उदै राय के नाम विशेष उल्लेखनीय हैं। विख्यात इतिहासकार दविंद्र कुमार का यह कथन बिल्कुल ठीक है।
“वह (गुरु गोबिंद सिंह जी) एक महान् कवि थे।”5
5. “He was a poet par excellence.” Devindra Kumar, Guru Gobind Singh’s Contribution to the Indian Literature, cited in, Guru Gobind Singh and Creation of Khalsa (Amritsar : 2000) p. 127.
योद्धा तथा सेनापति के रूप में (As a Warrior and General)
गुरु गोबिंद सिंह जी अपने समय के महान् योद्धा तथा सेनापति थे। वह घुड़सवारी, तीर चलाने तथा शस्त्र चलाने में बहुत प्रवीण थे। वह प्रत्येक युद्ध में अपने सैनिकों का नेतृत्व करते थे। गुरु जी ने लड़ाई में भी नैतिक सिद्धांतों का सदैव पालन किया। उन्होंने कभी भी रणभूमि से भाग रहे सिपाहियों तथा निहत्थों पर आक्रमण न किया। उनके तथा शत्रुओं के साधनों में आकाश-पाताल का अंतर था, फिर भी गुरु जी ने उनके विरुद्ध बड़ी शानदार सफलता प्राप्त की। उदाहरणस्वरूप गुरु जी ने भंगाणी की लड़ाई में, श्री आनंदपुर साहिब की प्रथम लड़ाई में, चमकौर साहिब की लड़ाई में तथा खिदराना की लड़ाई में कम सैनिकों तथा सीमित साधनों के होते हुए भी पहाड़ी राजाओं तथा मुग़लों के छक्के छुड़ा दिए थे। गुरु जी के सैनिक सदैव अपना बलिदान देने के लिए तैयार रहते थे।
धार्मिक नेता के रूप में (As a Religious Leader)
निस्संदेह गुरु गोबिंद सिंह जी.एक महान् धार्मिक नेता थे। गुरु जी ने अपने जीवन का अधिकाँश समय लड़ाइयों में व्यतीत किया, परंतु इन लड़ाइयों का उद्देश्य धर्म की रक्षा करना ही था। गुरु जी ने खालसा पंथ की स्थापना धार्मिक उद्देश्यों के लिए ही की थी। उन्होंने प्रत्येक सिख को यह आदेश दिया था कि वह सुबह उठकर स्नान के पश्चात् गुरुवाणी का पाठ करे। वह एक ईश्वर की ही पूजा करे तथा पवित्र जीवन व्यतीत करे। उनकी धार्मिक महानता का प्रमाण इस बात से मिलता है कि जब उन्हें साहिबजादों के बलिदान की सूचना दी गई तो झट खड़े होकर उन्होंने ईश्वर का धन्यवाद किया कि उनके पुत्रों के प्राण धर्म के लिए गए। डॉ० आई० बी० बैनर्जी के अनुसार,
“गुरु गोबिंद सिंह जी और चाहे जो कुछ भी थे, परंतु सब से पहले वह एक धार्मिक नेता थे।”6
6. “Whatever else he might have been, Guru Gobind Singh was first and foremost a great religious leader.” Dr. I. B. Banerjee, Evolution of the Khalsa (Calcutta : 1972) Vol. 2, p. 157.
समाज सुधारक के रूप में (As a Social Reformer)
गुरु गोबिंद सिंह जी एक महान समाज सुधारक भी थे। उन्होंने खालसा पंथ में निम्न जातियों के लोगों को भी उच्च जातियों के समान स्थान दिया। ऐसा करके गुरु जी ने शताब्दियों पुराने जाति-पाति के बंधनों को तोड़कर रख दिया। गुरु जी का कहना था, “मानस की जात सभै एकै पहिचानबो।” गुरु जी ने अपने सिखों को मादक पदार्थों से दूर रहने को कहा। उन्होंने सती तथा पर्दा प्रथा का जोरदार शब्दों में खंडन किया। इस प्रकार गुरु साहिब ने एक आदर्श समाज को जन्म दिया।
संगठनकर्ता के रूप में (As an Organiser)
गुरु गोबिंद सिंह जी उच्चकोटि के संगठनकर्ता थे। उस समय औरंगज़ेब का शासन था। वह ग़ैर-मुसलमानों के अस्तित्व को कभी सहन करने के लिए तैयार नहीं था। उसने गुरु तेग़ बहादुर जी को शहीद कर दिया था। सिखों में मसंद प्रथा बहुत भ्रष्ट हो गई थी। हिंदुओं में बहादुरी एवं आत्म-विश्वास की भावनाएँ खत्म हो चुकी थीं एवं
वे मुग़लों के अत्याचार सहने के अभ्यस्त हो चुके थे। पहाड़ी राजा अपने स्वार्थों के कारण मुग़ल सरकार से मिले हुए थे। ऐसे विरोधी तत्त्वों के रहते गुरु गोबिंद सिंह जी ने खालसा पंथ की स्थापना करके अपनी संगठन शक्ति का प्रमाण दिया। सचमुच यह एक महान् कार्य था। इसने लोगों में एक ऐसा जोश भरा जिसके आगे मुग़ल साम्राज्य को भी घुटने टेकने के लिए विवश होना पड़ा। अंत में हम प्रसिद्ध इतिहासकार प्रोफेसर मदनजीत कौर के इन शब्दों से सहमत हैं,
“गुरु गोबिंद सिंह जी के योगदान ने भारतीय इतिहास एवं विश्व सभ्यता के चित्रपट पर दूरगामी प्रभाव छोड़े।”7
7. “Guru Gobind Singh’s contributions had left imprints of deep impact on the canvas of Indian history and world civilisation.” Prof. Madanjit Kaur, Guru Gobind Singh and Creation of Khalsa (Amritsar : 2000) p. 1.

संक्षिप्त उत्तरों वाले प्रश्न (Short Answer Type Questions)
प्रश्न 1.
गुरुगद्दी पर बैठते समय गुरु गोबिंद सिंह.जी को किन कठिनाइयों का सामना करना पड़ा ?
(What difficulties were faced by Guru Gobind Singh Ji when he attained the Gurgaddi ?)
उत्तर-
- गुरु गोबिंद सिंह जी स्वयं बाल्यावस्था में थे। उनकी आयु केवल 9 वर्ष थी।
- मुग़ल सम्राट औरंगजेब बड़ा कट्टर सुन्नी मुसलमान था। वह इस्लाम के अतिरिक्त किसी अन्य धर्म के अस्तित्व को सहन करने को तैयार नहीं था।
- औरंगजेब के बढ़ते हुए अत्याचारों पर अंकुश लगाना आवश्यक था।
- उस समय मसंद बहुत भ्रष्ट हो चुके थे। उनसे निपटना आवश्यक था।
प्रश्न 2.
गुरु गोबिंद सिंह जी को किस प्रकार की शिक्षा दी गई ? (What kind of education was given to Guru Gobind Singh Ji ?)
उत्तर-
- गुरु गोबिंद सिंह जी ने साहित्यिक शिक्षा-भाई साहिब चंद से गुरमुखी, पंडित हरजस से संस्कृत, काजी पीर मुहम्मद से फ़ारसी तथा अरबी का ज्ञान प्राप्त किया।
- आप जी ने धार्मिक शिक्षा माता गुजरी जी एवं पिता गुरु तेग़ बहादुर जी से प्राप्त की।
- आप जी ने घुड़सवारी एवं हथियारों के प्रयोग संबंधी शिक्षा भाई बजर सिंह से प्राप्त की।
प्रश्न 3.
भीम चंद को श्री आनंदपुर साहिब में गुरु गोबिंद सिंह जी की मौजूदगी क्यों पसंद नहीं थी?
(Why did Bhim Chand not like the presence of Guru Gobind Singh Ji at Sri Anandpur Sahib ?)
उत्तर-
- भीम चंद श्री आनंदपुर साहिब में गुरु गोबिंद सिंह जी की प्रतिदिन बढ़ रही शक्ति को सहन करने को तैयार नहीं था।
- वह गुरु गोबिंद सिंह जी द्वारा श्री आनंदपुर साहिब में 1699 ई० में खालसा पंथ की स्थापना करने के कारण भड़क गया !
- भीम चंद ने गुरु गोबिंद सिंह जी को श्री आनंदपुर साहिब को छोड़ने का निर्देश दिया। किंतु गुरु साहिब ने ऐसा करने से इंकार कर दिया।

प्रश्न 4.
पाऊँटा साहिब का क्या महत्त्व है? (What is the importance of Paonta Sahib ?)
उत्तर-
1685 ई० में गुरु गोबिंद सिंह जी ने पाऊँटा साहिब नामक एक दुर्ग का निर्माण करवाया। पाऊँटा का अर्थ है पाँव रखने का स्थान अथवा ठहरने का स्थान। गुरु जी यहाँ 1685 ई० से 1688 ई० तक रहे। इस समय के दौरान गुरु जी ने सिखों में नवप्राण संचार करने तथा मुग़लों के अत्याचारी शासन का अंत करने का निर्णय किया। इस उद्देश्य से गुरु गोबिंद सिंह जी ने पाऊँटा साहिब में युद्ध एवं साहित्यिक गतिविधियों को एक नई दिशा प्रदान की।
प्रश्न 5.
भंगाणी की लड़ाई पर एक संक्षिप्त नोट लिखें। (Write a short note on the battle of Bhangani.)
अथवा
गुरु गोबिंद सिंह जी के भंगाणी युद्ध का वर्णन करें तथा इसका महत्त्व भी बताएँ। (Describe Guru Gobind Singh’s battle of Bhangani and also explain its importance.)
उत्तर-
भंगाणी के युद्ध के लिए कई कारण उत्तरदायी थे। गुरु गोबिंद सिंह जी की सैनिक तैयारियों से पहाड़ी राजाओं को अपनी स्वतंत्रता ख़तरे में अनुभव होने लगी। पहाड़ी राजा सिख संगतों को बहुत परेशान करते थे। मुग़ल सरकार भी इन पहाड़ी राजाओं को गुरु साहिब के विरुद्ध भड़का रही थी। फलस्वरूप कहलूर के शासक भीम चंद तथा श्रीनगर के शासक फ़तह शाह के नेतृत्व में पहाड़ी राजाओं ने 22 सितंबर, 1688 ई० को भंगाणी के स्थान पर गुरु गोबिंद सिंह जी की सेना पर आक्रमण कर दिया। इस युद्ध में सिखों की शानदार विजय हुई।
प्रश्न 6.
नादौन की लड़ाई पर एक संक्षिप्त नोट लिखें। (Write a short note on.the battle on Nadaun.)
उत्तर-
भंगाणी की लड़ाई में पराजय के बाद पहाड़ी राजाओं ने गुरु गोबिंद सिंह जी से मित्रता स्थापित कर ली थी। उन्होंने मुग़लों को वार्षिक खिराज (कर) भेजना बंद कर दिया। परिणामस्वरूप आलिफ खाँ के अधीन एक सेना पहाड़ी राजाओं के विरुद्ध भेजी गई। उसने 20 मार्च, 1690 ई० को पहाड़ी राजाओं के नेता भीम चंद की सेना पर नादौन में आक्रमण कर दिया। इस लड़ाई में गुरु गोबिंद सिंह जी ने भीम चंद का साथ दिया। इस-संयुक्त सेना ने मुग़ल सेना को परास्त कर दिया। आलिफ खाँ को युद्ध-भूमि से भागना पड़ा।

प्रश्न 7.
खालसा की स्थापना के कारणों की संक्षेप में व्याख्या कीजिए। (Give in brief the causes of the creation of Khalsa.)
अथवा
गुरु गोबिंद सिंह जी ने खालसा पंथ का सृजन क्यों किया?
(Why did Guru Gobind Singh Ji create the Khalsa ?)
अथवा
गुरु गोबिंद सिंह जी द्वारा खालसा पंथ की स्थापना के लिए उत्तरदायी मुख्य कारणों का संक्षिप्त में वर्णन कीजिए।
(Give a brief description of the circumstances responsible for the creation of Khalsa.)
अथवा
खालसा की स्थापना के लिए उत्तरदायी कोई तीन कारण लिखें। (Write any three causes that led to the creation of Khalsa.)
अथवा
(Write down the causes of the foundation of the Khalsa Panth ?)
उत्तर-
- मुग़लों के अत्याचार दिन-प्रतिदिन बढ़ते जा रहे थे। उन्होंने गैर-मुसलमानों को बलपूर्वक इस्लाम धर्म में सम्मिलित करना आरंभ कर दिया था।
- गुरु गोबिंद सिंह जी ऐसे समाज की स्थापना करना चाहते थे, जिसमें ऊँच-नीच के लिए कोई स्थान न हो।
- गुरु गोबिंद सिंह जी खालसा की स्थापना करके मसंद प्रथा का अंत करना चाहते थे।
प्रश्न 8.
खालसा पंथ की स्थापना कब, कहाँ और कैसे हुई ? (When, where and how was the Khalsa founded ?)
अथवा
खालसा की स्थापना पर संक्षिप्त नोट लिखें।
(Write a short note on the creation of Khalsa.)
अथवा
खालसा पंथ की सृजना कैसे की गई ?
(How was the Khalsa sect created ?)
उत्तर-
गुरु गोबिंद सिंह जी 30 मार्च, 1699 ई० को बैसाखी वाले दिन श्री आनंदपुर साहिब में केशगढ़ नामक स्थान पर एक विशाल सम्मेलन का आयोजन किया। गुरु जी ने म्यान से तलवार निकाली और एकत्रित सिखों को संबोधित किया, “क्या आप में से कोई ऐसा सिख है, जो धर्म के लिए अपना शीश भेंट करे ?” इस पर भाई दया राम जी अपना बलिदान देने के लिए आगे आया। गुरु जी के आदेश पर भाई धर्म दास जी, भाई मोहकम चंद जी, भाई साहिब चंद जी और भाई हिम्मत राय जी अपने बलिदानों के लिए उपस्थित हुए। इस प्रकार गुरु गोबिंद सिंह जी ने ‘पाँच प्यारों’ का चुनाव किया और खालसा पंथ की स्थापना की।
प्रश्न 9.
गुरु गोबिंद सिंह जी मसंदों के बारे में क्या कहते थे? (What does Guru Gobind Singh ji say about Masands ?)
उत्तर-
- मसंद बहुत भ्रष्टाचारी एवं बेपरवाह हो गए थे।
- वे बहुत लालची हो गए थे।
- वे बहुत व्याभीचारी हो गए थे।
- वे बहुत अभिमानी हो गए थे।

प्रश्न 10.
गुरु गोबिंद सिंह जी ने खालसा पंथ का सृजन कब किया और इसके मुख्य सिद्धांत क्या हैं ?
(When was the Khalsa created by Guru Gobind Singh Ji and what are its main principles ?)
अथवा
खालसा पंथ के मुख्य सिद्धांतों का वर्णन करो।
(Explain the main principles of the Khalsa.)
अथवा
गुरु गोबिंद सिंह जी द्वारा स्थापित किए गए ‘खालसा पंथ’ के मुख्य सिद्धांत लिखो।
(Write the main principles of the ‘Khalsa Panth’ founded by Guru Gobind Singh Ji.)
अथवा
खालसा पंथ के मुख्य सिद्धांत क्या थे ?
(What were the main principles of Khalsa Panth ?)
उत्तर-
- खालसा पंथ में सम्मिलित होने के लिए प्रत्येक को ‘खंडे का पाहल’ छकना पड़ेगा।
- प्रत्येक खालसा पुरुष अपने नाम के साथ ‘सिंह’ और खालसा स्त्री ‘कौर’ शब्द का प्रयोग करेगी।
- प्रत्येक खालसा एक ईश्वर की पूजा करेगा।
- प्रत्येक खालसा देश और धर्म की रक्षा के लिए सब कुछ न्यौछावर कर देगा।
प्रश्न 11.
खालसा पंथ की स्थापना के महत्त्व पर एक नोट लिखो। (Write a note on the importance of the Khalsa.)
अथवा
खालसा की स्थापना का क्या महत्त्व था? (What was the importance of the foundation of Khalsa ?)
अथवा
खालसा की स्थापना का क्या महत्त्व था?
(Study the importance of the creation of Khalsa.)
उत्तर-
- खालसा की स्थापना के पश्चात् लोग बड़ी संख्या में सिख धर्म में सम्मिलित होने लगे।
- खालसा की स्थापना से एक आदर्श समाज का जन्म हुआ।
- खालसा की स्थापना करके गुरु गोबिंद सिंह जी ने सिखों में नव प्राण फूंके।
- खालसा की स्थापना के कारण मसंद प्रथा का अंत हुआ।
- गुरु गोबिंद सिंह जी ने खालसा पंथ का सृजन करके एक स्वतंत्र कौम की स्थापना की।
प्रश्न 12.
श्री आनंदपुर साहिब की प्रथम लड़ाई पर एक संक्षिप्त नोट लिखें। (Write a brief note on the first battle of Sri Anandpur Sahib.)
उत्तर-
गुरु गोबिंद सिंह जी की बढ़ रही शक्ति के कारण पहाड़ी राजाओं के मन की शांति भंग हो गई। कहलूर के राजा भीम चंद ने गुरु जी को श्री आनंदपुर साहिब छोड़ने के लिए कहा। गुरु जी ने यह माँग मानने से इंकार कर दिया। उनका कहना था कि गुरु तेग़ बहादुर जी ने यह भूमि उचित मूल्य देकर खरीदी थी। इस पर भीम चंद ने पहाड़ी राजाओं से मिल कर 1701 ई० में श्री आनंदपुर साहिब के किले पर आक्रमण कर दिया। किले का घेरा कई दिनों तक जारी रहा। जब पहाड़ी राजाओं को कोई सफलता न मिली तो उन्होंने गुरु जी से संधि कर ली।

प्रश्न 13.
श्री आनंदपुर साहिब की दूसरी लड़ाई पर एक संक्षिप्त नोट लिखें। (Write a short note on the second battle of Sri Anandpur Sahib.)
उत्तर-
पहाड़ी राजाओं और मुग़ल सेना ने 1704 ई० में श्री आनंदपुर साहिब के दुर्ग पर दूसरी बार आक्रमण कर दिया। घेरे के लंबे हो जाने के कारण 40 सिख गुरु जी को बेदावा देकर दुर्ग छोड़कर चले गए। दूसरी ओर शाही सेना ने कुरान और गायों की कसम खाकर गुरु साहिब को विश्वास दिलाया कि यदि वे श्री आनंदपुर साहिब छोड़ दें तो उन्हें कोई क्षति नहीं पहुँचाई जायेगी। गुरु साहिब को इन झूठी कसमों पर कोई विश्वास नहीं था, परंतु माता गुजरी और कुछ अन्य सिखों के निवेदन पर गुरु साहिब ने 20 दिसंबर, 1704 ई० को श्री आनंदपुर साहिब के दुर्ग को छोड़ दिया।
प्रश्न 14.
चमकौर साहिब की लड़ाई का संक्षिप्त विवरण दीजिए। (Give a brief account of the battle of Chamkaur Sahib.)
उत्तर-
गुरु गोबिंद सिंह जी द्वारा आनंदपुर साहिब का किला छोड़ने के पश्चात् मुग़ल सेना ने उनका पीछा जारी रखा। गुरु साहिब ने चमकौर साहिब की एक कच्ची गढी में 40 सिखों सहित शरण ली। शीघ्र ही मुग़ल सैनिकों ने इस गढ़ी को घेर लिया। 22 दिसंबर, 1704 ई० में हुई चमकौर साहिब की यह लड़ाई बहुत घमासान लड़ाई थी। इस लड़ाई में गुरु गोबिंद सिंह जी के दो बड़े साहिबजादों अजीत सिंह तथा जुझार सिंह ने वीरता प्रदर्शित की और अंततः लड़ते-लड़ते शहीद हो गए।
प्रश्न 15.
खिदराना (श्री मुक्तसर साहिब) की लड़ाई पर एक संक्षिप्त नोट लिखो।
[Write a brief note on the battle of Khidrana (Sri Mukatsar Sahib.)]
अथवा
खिदराने का नाम श्री मुक्तसर साहिब कैसे पड़ा ? (How was Khidrana named Sri Mukatsar Sahib ?)
उत्तर-
सरहिंद के नवाब वजीर खाँ ने 29 दिसंबर, 1705 ई० को एक विशाल सेना के साथ गुरु जी की सेना पर खिदराना के स्थान पर आक्रमण कर दिया। इस लड़ाई में गुरु जी को शानदार विजय प्राप्त हुई। इस लड़ाई में वे 40 सिख भी लड़ते-लड़ते शहीद हो गए थे जो श्री आनंदपुर साहिब की दूसरी लड़ाई में गुरु जी का साथ छोड़ गए थे। उन 40 सिखों को गुरु,जी ने मुक्ति का वरदान दिया। उस समय से खिदराना श्री मुक्तसर साहिब के नाम से जाना जाता है।

प्रश्न 16.
गुरु गोबिंद सिंह जी ने सिख पंथ में सांप्रदायिक बँटवारे तथा बाह्य खतरों की समस्या को किस प्रकार हल किया ?
(How did Guru Gobind Singh Ji settle the sectarian divisions and external dangers to Sikhism ?)
उत्तर-
गुरु गोबिंद सिंह जी ने सिख पंथ में सांप्रदायिक बँटवारे तथा बाह्य. खतरों से निपटने के लिए 1699 ई० में खालसा पंथ की स्थापना की। गुरु जी ने इस बात की घोषणा की कि सारे सिख उनके ‘खालसा’ है और प्रत्यक्ष रूप से उनसे जुड़े हुए हैं । इस प्रकार मसंदों की मध्यस्थता समाप्त हो गई। मीणों, धीरमलियों, रामरइयों तथा हिंदालियों को सिख पंथ से निकाल दिया गया । बाह्य खतरों से निपटने के लिए गुरु जी ने सारे सिखों को शस्त्रधारी रहने का आदेश दिया।
प्रश्न 17.
गुरु गोबिंद सिंह जी की साहित्यिक सरगर्मियों के बारे में आप क्या जानते हैं ?
(What do you know about the literary activities of Guru Gobind Singh Ji ?)
अथवा
गुरु गोबिंद सिंह जी की साहित्यिक सरगर्मियों के बारे में बताइए।
(Describe the literary activities of Guru Gobind Singh Ji.)
अथवा
गुरु गोबिंद सिंह जी की साहित्यिक गतिविधियों पर रोशनी डालिए। (Evaluate the literary activities of Guru Gobind Singh Ji.).
उत्तर-
गुरु गोबिंद सिंह जी ने साहित्य के क्षेत्र में बहुत महत्त्वपूर्ण योगदान दिया। वह उच्चकोटि के कवि तथा साहित्यकार थे। गुरु साहिब ने अपनी रचनाओं में पंजाबी, हिंदी, फारसी, अरबी, संस्कृत आदि भाषाओं का प्रयोग किया। जाप साहिब, बचित्तर नाटक, ज़फ़रनामा, चंडी दी वार आपकी महान् रचनाएँ हैं। ये रचनाएँ आध्यात्मिक ज्ञान का भंडार हैं । आपकी रचनाओं से हमें अनेक ऐतिहासिक घटनाओं की जानकारी प्राप्त होती है। गुरु गोबिंद सिंह जी ने अपने दरबार में 52 उच्चकोटि के कवियों को संरक्षण दिया था।
प्रश्न 18.
ज़फ़रनामा क्या है ? इसके ऐतिहासिक महत्त्व का वर्णन करें।
(What is Zafarnama ? What is its historical importance ?)
अथवा
ज़फ़रनामा पर एक संक्षिप्त नोट लिखें ।
(Write a short note on Zafarnama.)
अथवा
गुरु गोबिंद सिंह जी द्वारा रचित ज़फ़रनामा के बारे में आप क्या जानते हैं ? (What do you know about the Zafarnama written by Guru Gobind Singh Ji ?)
उत्तर-
ज़फ़रनामा गुरु गोबिंद सिंह जी द्वारा औरंगजेब को फ़ारसी में लिखे गए एक पत्र का नाम है। इसे गुरु जी ने दीना कांगड़ नामक स्थान से लिखा था। इस पत्र में गुरु जी ने औरंगज़ेब तथा पहाड़ी राजाओं की ओर से कुरान की झूठी शपथ लेकर धोखा करने का वर्णन निर्भीकता से उल्लेख किया है। गुरु जी के इस पत्र को भाई दया सिंह जी ने औरंगज़ेब तक पहुँचाया था। इस पत्र का औरंगजेब पर बहुत गहरा प्रभाव पड़ा।

प्रश्न 19.
गुरु गोबिंद सिंह जी के सामाजिक सुधारों का इतिहास में क्या महत्व है ? (What is the importance of social reforms of Guru Gobind Singh Ji in History ?)
उत्तर-
गुरु गोबिंद सिंह जी खालसा पंथ की स्थापना करके समाज में एक क्रांति ला दी। इसमें सम्मिलित होने वाले निम्न जातियों के लोगों को भी उच्च जातियों के बराबर स्थान दिया गया। गुरु जी ने अपने अनुयायियों को शराब, भांग तथा अन्य मादक पदार्थों से दूर रहने के लिए कहा। गुरु जी ने सिखों को महिलाओं का पूर्ण सम्मान करने के लिए. कहा । मसंद प्रथा का अंत कर गुरु जी ने सिखों को उनके शोषण से बचाया।
प्रश्न 20.
“गुरु गोबिंद सिंह जी एक महान् संगठनकर्ता थे ।” क्या आप इस विचार से सहमत हैं ? (“Guru Gobind Singh Ji was a builder par-excellence”. Do you agree to this statement ?)
उत्तर-
गुरु गोबिंद सिंह जी उच्चकोटि के संगठनकर्ता थे। गुरु गोबिंद सिंह जी ने खालसा पंथ की स्थापना करके अपनी संगठन शक्ति का प्रमाण दिया। सचमुच यह एक महान कार्य था इसने लोगों में नया जोश उत्पन्न किया। वे महान् योद्धा बा गए और धर्म के नाम पर अपना सब कुछ न्योछावर करने को तैयार हो गए । उन्होंने तब तक सुख की साँस न ली जब तक पंजाब में से मुग़लों तथा अफ़गानों के शासन का अंत न कर लिया गया तथा पंजाब में एक स्वतंत्र सिख साम्राज्य की स्थापना न कर ली गई।
प्रश्न 21.
गुरु गोबिंद सिंह जी के व्यक्तित्व की मुख्य विशेषताएँ बताएँ । (Mention the main characteristics of Guru Gobind Singh Ji’s personality.)
उत्तर-
- गुरु गोबिंद सिंह जी बड़े उच्च चरित्र के स्वामी थे।
- गुरु गोबिंद सिंह जी एक उच्च कोटि के कवि तथा साहित्यकार थे।
- गुरु गोबिंद सिंह जी एक महान् समाज सुधारक थे।
- गुरु गोबिंद सिंह जी में एक महान् योद्धा तथा सेनापति के गुण विद्यमान थे।
- गुरु गोबिंद सिंह जी वीर तथा निडर थे। उन्होंने कभी भी अत्याचारियों से समझौता न किया।

वस्तुनिष्ठ प्रश्न (Objective Type Questions)
(i) एक शब्द से एक पंक्ति तक के उत्तर (Answer in One Word to One Sentence)
प्रश्न 1.
सिखों के दशम तथा अंतिम गुरु कौन थे ?
उत्तर-
गुरु गोबिंद सिंह जी।
प्रश्न 2.
गुरु गोबिंद सिंह जी का जन्म कब हुआ था ?
उत्तर-
22 दिसंबर, 1666 ई०।
प्रश्न 3.
गुरु गोबिंद सिंह जी का जन्म कहाँ हुआ था ?
उत्तर-
पटना साहिब।
प्रश्न 4.
गुरु गोबिंद सिंह जी की माता जी का नाम बताएँ ।
उत्तर-
गुजरी जी।

प्रश्न 5.
गुरु गोबिंद सिंह जी के पिता जी का क्या नाम था ?
उत्तर-
गुरु तेग़ बहादुर जी।
प्रश्न 6.
गुरु गोबिंद सिंह जी का प्रारंभिक नाम बताएँ।
उत्तर-
गोबिंद दास अथवा गोबिंद राय।
प्रश्न 7.
गुरु गोबिंद सिंह जी का बचपन कहाँ व्यतीत हुआ ?
उत्तर-
पटना साहिब।
प्रश्न 8.
गुरु गोबिंद सिंह जी ने गुरुगद्दी कब संभाली ?
उत्तर-
1675 ई० में।

प्रश्न 9.
गुरु गोबिंद सिंह जी के कितने साहिबजादे थे?
उत्तर-
चार।
प्रश्न 10.
गुरु गोबिंद सिंह जी के सबसे बड़े साहिबजादे का क्या नाम था?
उत्तर-
साहिबजादा अजीत सिंह।
प्रश्न 11.
गुरु गोबिंद सिंह जी के समय कहलूर (बिलासपुर) का शासक कौन था ?
उत्तर-
भीम चंद।
प्रश्न 12.
पाऊँटा साहिब से क्या अभिप्राय है ?
उत्तर-
पाँव रखने का स्थान अथवा ठहरने का स्थान।

प्रश्न 13.
गुरु गोबिंद सिंह जी के दरबार में कितने कवि थे ?
उत्तर-
52.
प्रश्न 14.
गुरु गोबिंद सिंह जी के किसी एक प्रसिद्ध कवि का नाम बताएँ
उत्तर-
सेनापत।
प्रश्न 15.
गुरु गोबिंद सिंह जी द्वारा बनाए गए नगारे का क्या नाम था ?
उत्तर-
रणजीत नगारा।
प्रश्न 16.
रणजीत नगारे को कब बजाया जाता है ?
उत्तर-
युद्ध को आरंभ करते समय, शिकार पर जाते समय तथा लंगर को आरंभ करते समय बजाया जाता है।

प्रश्न 17.
भीम चंद कौन था ?
उत्तर-
कहलूर का शासक।
प्रश्न 18.
गुरु गोबिंद सिंह जी और पहाड़ी राजाओं में कब प्रथम लड़ाई लड़ी गई थी ?
अथवा
भंगाणी की लड़ाई कब लड़ी गई ?
उत्तर-
1688 ई०।
प्रश्न 19.
गुरु गोबिंद सिंह जी किसके सहयोग से भंगाणी की लड़ाई विजित करने में सफल हुए ?
उत्तर-
पीर बुद्धू शाह।
प्रश्न 20.
नादौन की लड़ाई कब हुई थी?
उत्तर-
1690 ई०

प्रश्न 21.
श्री आनंदपुर साहिब का पहला नाम क्या था ?
उत्तर-
चक्क नानकी।
प्रश्न 22.
किस गुरु साहिब ने मसंद प्रथा का अंत किया था ?
उत्तर-
गुरु गोबिंद सिंह जी।
प्रश्न 23.
खालसा पंथ का सृजन किस गुरु ने किया था ?
उत्तर-
गुरु गोबिंद सिंह जी।
प्रश्न 24.
गुरु गोबिंद सिंह जी ने खालसा पंथ का सृजन कब किया गया था ?
उत्तर-
30 मार्च, 1699 ई०।

प्रश्न 25.
गुरु गोबिंद सिंह जी ने खालसा पंथ का सृजन कहाँ किया था?
उत्तर-
श्री आनंदपुर साहिब।
प्रश्न 26.
खालसा की स्थापना का कोई एक मुख्य कारण लिखें।
उत्तर-
मुगलों के अत्याचारों का सामना करने के लिए।
प्रश्न 27.
गुरु गोबिंद सिंह जी द्वारा सजाए गए किसी एक प्यारे का नाम बताएँ।
उत्तर-
भाई दया सिंह जी।
प्रश्न 28.
खंडे का पाहुल से क्या अभिप्राय है ?
उत्तर-
दोधारी खंडे द्वारा तैयार किया गया अमृत।

प्रश्न 29.
खालसा का कोई एक मुख्य सिद्धांत बताएँ।
उत्तर-
प्रत्येक खालसा एक ईश्वर के अतिरिक्त किसी अन्य देवी-देवता की पूजा नहीं करेगा।
प्रश्न 30.
गुरु गोबिंद सिंह जी ने प्रत्येक खालसा को कितने कक्कार धारण करने के लिए कहा ?
उत्तर-
पाँच।
प्रश्न 31.
खालसा की स्थापना का महत्त्व क्या था ?
उत्तर-
इसकी स्थापना से सिखों में एक नया जोश उत्पन्न हुआ।
प्रश्न 32.
श्री आनंदपुर साहिब की प्रथम लड़ाई कब हुई थी ?
उत्तर-
1701 ई०

प्रश्न 33.
श्री आनंदपुर साहिब की द्वितीय लड़ाई कब हुई थी?
उत्तर-
1704 ई०।
प्रश्न 34.
गुरु गोबिंद सिंह के दो छोटे साहिबजादों को कहाँ शहीद किया गया था ?
उत्तर-
सरहिंद।
प्रश्न 35.
गुरु गोबिंद सिंह जी के समय सरहिंद का फ़ौजदार कौन था ?
उत्तर-
वज़ीर खाँ।
प्रश्न 36.
गुरु गोबिंद सिंह जी के बड़े साहिबजादे किस लड़ाई में शहीद हुए थे ?
उत्तर-
चमकौर साहिब की लड़ाई में।

प्रश्न 37.
चमकौर साहिब की लड़ाई कब हुई ?
उत्तर-
22 दिसंबर, 1704 ई० को।
प्रश्न 38.
उन दो मुस्लिम भाइयों के नाम बताएँ जिन्होंने गुरु गोबिंद सिंह जी की माछीवाड़ा के वनों में सहायता की थी ?
अथवा
माछीवाड़ा के जंगलों में गुरु गोबिंद सिंह जी की जीवन रक्षा में उनके किन दो मुसलमान अनुयायियों ने सहायता की?
उत्तर-
नबी खाँ तथा गनी खाँ।
प्रश्न 39.
गुरु गोबिंद सिंह जी ने औरंगजेब को कौन-सी चिट्ठी लिखी थी ?
उत्तर-
ज़फ़रनामा (विजय पत्र)।
प्रश्न 40.
ज़फ़रनामा की रचना किसने की ?
उत्तर-
गुरु गोबिंद सिंह जी।

प्रश्न 41.
गुरु गोबिंद सिंह जी ने औरंगजेब को जफ़रनामा किस स्थान से लिखा था?
उत्तर-
दीना काँगड़।
प्रश्न 42.
ज़फ़रनामा को किस भाषा में लिखा गया था ?
उत्तर-
फारसी में।
प्रश्न 43.
गुरु गोबिंद सिंह जी तथा मुग़लों के मध्य लड़ी गई अंतिम लड़ाई कौन-सी थी ?
उत्तर-
खिदराना
प्रश्न 44.
खिदराना की लड़ाई कब लड़ी गई थी ?
उत्तर-
1705 ई०।

प्रश्न 45.
‘चाली मुक्ते’ कौन-सी लड़ाई से संबंध रखते हैं ?
उत्तर-
खिदराना की लड़ाई।
प्रश्न 46.
भाई महां सिंह कौन थे?
उत्तर-
भाई महां सिंह खिदराना के स्थान पर शहीदी प्राप्त करने वाले 40 सिखों के नेता थे।
प्रश्न 47.
भाई महां सिंह ने कहां शहीदी प्राप्त की थी ?
उत्तर-
खिदराना में।
प्रश्न 48.
भाई महां सिंह ने कब शहीदी प्राप्त की थी ?
उत्तर-
1705 ई० में।

प्रश्न 49.
खिदराना का आधुनिक नाम क्या है ?
उत्तर-
श्री मुक्तसर साहिब।
प्रश्न 50.
बचित्तर नाटक की रचना किसने की ?
उत्तर-
गुरु गोबिंद सिंह जी।
प्रश्न 51.
चंडी दी वार की रचना किसने की थी ?
उत्तर-गुरु गोबिंद सिंह जी ने।
प्रश्न 52.
भाई नंद लाल की रचना का नाम लिखें।
उत्तर-
दीवान-ए-गोआ।

प्रश्न 53.
नंद लाल कौन थे ?
उत्तर-
गुरु गोबिंद सिंह जी के दरबारी कवि।
प्रश्न 54.
गुरु की काशी किसे कहते हैं ?
उत्तर-
तलवंडी साबो को।
प्रश्न 55.
आदि ग्रंथ साहिब जी को किस गुरु ने गुरु ग्रंथ साहिब जी का दर्जा दिया ?
उत्तर-
गुरु गोबिंद सिंह जी।
प्रश्न 56.
गुरु गोबिंद सिंह जी कब ज्योति-जोत समाए ?
उत्तर-
7 अक्तूबर, 1708 ई०।

प्रश्न 57.
गुरु गोबिंद सिंह जी कहाँ ज्योति-जोत समाए ?
उत्तर-
नंदेड़।
(ii) रिक्त स्थान भरें (Fill in the Blanks)
प्रश्न 1.
गुरु गोबिंद सिंह जी सिखों के……..गुरु थे।
उत्तर-
(दशम)
प्रश्न 2.
गुरु गोबिंद सिंह जी का जन्म……..को हुआ।
उत्तर-
(22 दिसंबर, 1666 ई०)
प्रश्न 3.
गुरु गोबिंद सिंह का जन्म……..में हुआ।
उत्तर-
(पटना साहिब)

प्रश्न 4.
गुरु गोबिंद सिंह जी के पिता जी का नाम……..था।
उत्तर-
(गुरु तेग़ बहादुर जी)
प्रश्न 5.
गुरु गोबिंद सिंह जी की माता जी का नाम…….. था।
उत्तर-
(गुजरी)
प्रश्न 6.
गुरु गोबिंद सिंह जी ने बचपन में…………से गुरमुखी की शिक्षा प्राप्त की।
उत्तर-
(भाई साहिब चंद)
प्रश्न 7.
गुरु गोबिंद सिंह जी………में गुरुगद्दी पर बिराजमान हुए।
उत्तर-
(1675 ई०)

प्रश्न 8.
गुरु गोबिंद सिंह जी के…….साहिबजादे थे।
उत्तर-
(चार)
प्रश्न 9.
गुरु गोबिंद सिंह जी ने……..नगारा बनवाया।
उत्तर-
(रणजीत)
प्रश्न 10.
गुरु गोबिंद सिंह जी और पहाड़ी राजाओं के मध्य पहली लड़ाई……में हुई।
उत्तर-
(भंगाणी)
प्रश्न 11.
भंगाणी की लड़ाई……..में हुई।
उत्तर-
(1688 ई०)

प्रश्न 12.
नादौन की लड़ाई……में हुई।
उत्तर-
(1690 ई०)
प्रश्न 13.
गुरु गोबिंद सिंह जी ने खालसा का सृजन……….में किया।
उत्तर-
(1699 ई०)
प्रश्न 14.
गुरु गोबिंद सिंह जी ने खालसा का सृजन……..में किया।
उत्तर-
(श्री आनंदपुर साहिब)
प्रश्न 15.
गुरु गोबिंद सिंह जी के पहले प्यारे ……..थे।
उत्तर-
(भाई दया राम जी)

प्रश्न 16.
……में श्री आनंदपुर साहिब की पहली लड़ाई हुई।
उत्तर-
(1701 ई०)
प्रश्न 17.
…….. में श्री आनंदपुर साहिब की दूसरी लड़ाई हुई।
उत्तर-
(1704 ई०)
प्रश्न 18.
चमकौर साहिब की लड़ाई में गुरु गोबिंद सिंह जी के साहिबजादों……………….और………….ने शहीदी प्राप्त की।
उत्तर-
(अजीत सिंह, जुझार सिंह)
प्रश्न 19.
माछीवाड़ा के जंगलों में गुरु गोबिंद सिंह जी की दो मुसलमान भाईयों…….और…….ने बहुमूल्य सेवा की।
उत्तर-
(नबी खाँ, गनी खाँ)

प्रश्न 20.
गुरु गोबिंद सिंह जी को दीना काँगड़ से………नामक पत्र लिखा।
उत्तर-
(ज़फ़रनामा)
प्रश्न 21.
ज़फ़रनामा ……… भाषा में लिखा गया था।
उत्तर-
(फ़ारसी)
प्रश्न 22.
गुरु गोबिंद सिंह जी और मुग़लों के मध्य लड़ी गई अंतिम लड़ाई ……………..की लड़ाई थी।
उत्तर-
(खिदराना)
प्रश्न 23.
खिदराना की लड़ाई……में हुई।
उत्तर-
(1705 ई०)

प्रश्न 24.
चालीस मुक्ते…………….की लड़ाई से संबंधित थे।
उत्तर-
(खिदराना)
प्रश्न 25.
खिदराना का आधुनिक नाम……..है।
उत्तर-
(श्री मुक्तसर साहिब)
प्रश्न 26.
गुरु गोबिंद सिंह जी की आत्मकथा का नाम……है।
उत्तर-
(बचित्तर नाटक)
प्रश्न 27.
‘कृष्ण अवतार’ साहित्य की रचना ……….. ने की थी।
उत्तर-
(गुरु गोबिंद सिंह जी)

प्रश्न 28.
नंद लाल गुरु गोबिंद सिंह जी का……… था।
उत्तर-
(दरबारी कवि)
प्रश्न 29.
गुरु गोबिंद सिंह जी………में ज्योति ज्योत समा गए।
उत्तर-
(1708 ई०)
प्रश्न 30.
गुरु गोबिंद सिंह जी…….. नामक स्थान में ज्योति-ज्योत समा गए।
उत्तर-
(नंदेड़)
(iii) ठीक अथवा गलत (True or False)
नोट-निम्नलिखित में से ठीक अथवा गलत चुनें
प्रश्न 1.
गुरु गोबिंद सिंह जी सिखों के दसवें गुरु थे।
उत्तर-
ठीक

प्रश्न 2.
गुरु गोबिंद सिंह जी का जन्म 22 दिसंबर, 1666 ई० को हुआ।
उत्तर-
ठीक
प्रश्न 3.
गुरु गोबिंद सिंह जी के पिता जी का नाम गुरु तेग बहादुर जी था।
उत्तर-
ठीक
प्रश्न 4.
गुरु गोबिंद सिंह जी की माता जी का नाम गुजरी जी था।
उत्तर-
ठीक
प्रश्न 5.
गुरु गोबिंद सिंह जी का आरंभिक नाम गोबिंद राय था।
उत्तर-
ठीक

प्रश्न 6.
गुरु गोबिंद सिंह जी ने अपना बचपन पटना साहिब में व्यतीत किया था।
उत्तर-
ठीक
प्रश्न 7.
गुरु गोबिंद सिंह जी के घर पाँच साहिबजादों ने जन्म लिया था।
उत्तर-
गलत
प्रश्न 8.
गुरु गोबिंद सिंह जी के सबसे बड़े साहिबजादे का नाम अजीत सिंह था।
उत्तर-
ठीक
प्रश्न 9.
गुरु गोबिंद सिंह जी के दरबार के दो कवियों के नाम सेनापत और नंदलाल थे।
उत्तर-
ठीक

प्रश्न 10.
भंगाणी की लड़ाई 1688 ई० में लड़ी गई थी।
उत्तर-
ठीक
प्रश्न 11.
भंगाणी की लड़ाई में भीम चंद ने गुरु गोबिंद सिंह जी का सहयोग दिया था।
उत्तर-
गलत
प्रश्न 12.
गुरु गोबिंद सिंह जी और मुग़लों के मध्य नादौन की लड़ाई 1690 ई० में हुई थी।
उत्तर-
ठीक
प्रश्न 13.
1609 ई० में गुरु गोबिंद सिंह जी ने खालसा पंथ की स्थापना की।
उत्तर-
गलत

प्रश्न 14.
गुरु गोबिंद सिंह जी ने खालसा पंथ की सृजना के समय पाँच प्यारों का चुनाव किया।
उत्तर-
ठीक
प्रश्न 15.
गुरु गोबिंद सिंह जी ने पहले प्यारे के रूप में भाई धर्मदास जी को चुना।
उत्तर-
गलत
प्रश्न 16.
गुरु गोबिंद सिंह जी ने खालसा पंथ की सृजना के समय मसंद प्रथा का अंत किया।
उत्तर-
ठीक
प्रश्न 17.
श्री आनंदपुर साहिब की पहली लड़ाई 1701 ई० में हुई थी। .
उत्तर-
ठीक

प्रश्न 18.
श्री आनंदपुर साहिब की दूसरी लड़ाई 1706 ई० में हुई थी।
उत्तर-
गलत
प्रश्न 19.
चमकौर साहिब की लड़ाई 1704 ई० में हुई थी।
उत्तर-
ठीक
प्रश्न 20.
गुरु गोबिंद सिंह जी ने ज़फ़रनामा नामक चिट्ठी मुग़ल बादशाह शाहजहाँ को लिखी थी।
उत्तर-
गलत
प्रश्न 21.
गुरु गोबिंद सिंह जी ने ज़फ़रनामा को फ़ारसी भाषा में लिखा था।
उत्तर-
गलत

प्रश्न 22.
गुरु गोबिंद सिंह जी ने ज़फ़रनामा को दीना कांगड़ नामक स्थान से लिखा था ।
उत्तर-
ठीक
प्रश्न 23.
खिदराना की लड़ाई गुरु गोबिंद सिंह जी और मुग़लों के मध्य लड़ी जाने वाली अंतिम लड़ाई थी।
उत्तर-
ठीक
प्रश्न 24.
खिदराना की लड़ाई 1705 ई० में लड़ी गई।
उत्तर-
ठीक
प्रश्न 25.
खिदराना का आधुनिक नाम श्री मुक्तसर साहिब है।
उत्तर-
ठीक

प्रश्न 26.
गुरु गोबिंद सिंह जी की आत्म-कथा का नाम बचित्तर नाटक है।
उत्तर-
ठीक
प्रश्न 27.
गुरु गोबिंद सिंह जी 1707 ई० में ज्योति-ज्योत समाए थे।
उत्तर-
गलत
प्रश्न 28.
गुरु गोबिंद सिंह जी नंदेड़ में ज्योति-ज्योत समाए थे। ”
उत्तर-
ठीक

(iv) बहु-विकल्पीय प्रश्न (Multiple Choice Questions)
नोट-निम्नलिखित में से ठीक उत्तर का चयन कीजिए—
प्रश्न 1.
सिखों के दशम तथा अंतिम गुरु कौन थे ?
(i) गुरु हरगोबिंद जी
(ii) गुरु गोबिंद सिंह जी
(iii) गुरु तेग़ बहादुर जी
(iv) गुरु हर कृष्ण जी।
उत्तर-
(ii)
प्रश्न 2.
गुरु गोबिंद सिंह जी का जन्म कब हुआ ?
(i) 1646 ई० में |
(ii) 1656 ई० में
(iii) 1666 ई० में
(iv) 1676 ई० में।
उत्तर-
(iii)
प्रश्न 3.
गुरु गोबिंद सिंह जी का जन्म कहाँ हुआ ?
(i) पटना साहिब
(ii) गोइंदवाल साहिब
(iii) खडूर साहिब
(iv) श्री आनंदपुर साहिब।
उत्तर-
(i)

प्रश्न 4.
गुरु गोबिंद सिंह जी के पिता जी का क्या नाम था ?
(i) गुरु हरगोबिंद जी
(ii) गुरु हर राय जी
(iii) गुरु हर कृष्ण जी
(iv) गुरु तेग बहादुर जी।
उत्तर-
(iv)
प्रश्न 5.
गुरु गोबिंद सिंह जी की माता जी का क्या नाम था ?
(i) गुजरी
(i) नानकी
(iii) सुलक्खनी
(iv) खीवी।
उत्तर-
(i)
प्रश्न 6.
गुरु गोबिंद सिंह जी का प्रारंभिक नाम क्या था ?
(i) गोबिंद नाथ
(ii) गोबिंद दास
(iii) भाई जेठा जी
(iv) भाई लहणा जी।
उत्तर-
(ii)

प्रश्न 7.
गुरु गोबिंद सिंह जी के साहिबजादे कितने थे ?
(i) दो
(ii) तीन
(iii) चार
(iv) पाँच।
उत्तर-
(iii)
प्रश्न 8.
गुरु गोबिंद सिंह जी गुरुगद्दी पर कब विराजमान हुए ?
(i) 1666 ई० में
(ii) 1670 ई० में
(iii) 1672 ई० में
(iv) 1675 ई० में।
उत्तर-
(iv)
प्रश्न 9.
गुरु गोबिंद सिंह जी की साहित्यिक गतिविधियों का मुख्य केंद्र कौन-सा था ?
(i) सरहिंद
(ii) पाऊँटा साहिब
(iii) पटना साहिब
(iv) खडूर साहिब।
उत्तर-
(ii)

प्रश्न 10.
गुरु गोबिंद सिंह जी द्वारा बनाए गए नगारे का क्या नाम था ?
(i) रणजीत नगारा
(ii) नलवा नगारा
(iii) खालसा नगारा
(iv) पंथ नगारा।
उत्तर-
(i)
प्रश्न 11.
भीम चंद कौन था ?
(i) काँगड़ा का शासक
(ii) श्रीनगर का शासक
(iii) कहलूर का शासक
(iv) गुलेर का शासक।
उत्तर-
(iii)
प्रश्न 12.
भंगाणी की लड़ाई कब लड़ी गई ?
(i) 1686 ई० में
(ii) 1687 ई० में
(iii) 1688 ई० में
(iv) 1690 ई० में।
उत्तर-
(iii)

प्रश्न 13.
गुरु गोबिंद सिंह जी किसके सहयोग के साथ भंगाणी की लड़ाई में विजय रहे ?
(i) पीर बुद्धू शाह
(ii) संत मीयाँ मीर जी
(iii) पीर रहमत शाह
(iv) फतह शाह।
उत्तर-
(i)
प्रश्न 14.
नादौन की लड़ाई कब हुई ?
(i) 1688 ई० में
(i) 1690 ई० में
(iii) 1694 ई० में
(iv) 1695 ई० में।
उत्तर-
(ii)
प्रश्न 15.
किस गुरु साहिब ने मसंद प्रथा का अंत कर दिया ?
(i) गुरु अर्जन देव जी ने
(ii) गुरु हरगोबिंद जी ने
(iii) गुरु तेग़ बहादुर जी ने
(iv) गुरु गोबिंद सिंह जी ने।
उत्तर-
(iv)

प्रश्न 16.
खालसा पंथ की स्थापना किस गुरु ने की थी ?
(i) गुरु नानक देव जी ने
(ii) गुरु अर्जन देव जी ने
(iii) गुरु हरगोबिंद जी ने
(iv) गुरु गोबिंद सिंह जी ने।
उत्तर-
(iv)
प्रश्न 17.
गुरु गोबिंद सिंह जी ने खालसा पंथ की स्थापना कब की थी ?
(i) 1688 ई० में
(ii) 1690 ई० में
(iii) 1695 ई० में
(iv) 1699 ई० में।
उत्तर-
(iv)
प्रश्न 18.
गुरु गोबिंद सिंह जी ने खालसा पंथ की स्थापना कहाँ की थी ?
(i) अमृतसर
(ii) श्री आनंदपुर साहिब
(iii) कीरतपुर साहिब
(iv) गोइंदवाल साहिब।
उत्तर-
(ii)

प्रश्न 19.
गुरु गोबिंद सिंह जी द्वारा सजाया गया प्रथम प्यारा कौन था ?
(i) भाई दया राम जी
(ii) भाई साहिब चंद जी
(iii) भाई हिम्मत राय जी
(iv) भाई धर्म दास जी।
उत्तर-
(i)
प्रश्न 20.
खालसा की सृजना के समय गुरु गोबिंद सिंह जी ने हर खालसा को कितने कक्कार धारण करना जरूरी बताया ?
(i) दो
(ii) तीन
(iii) चार
(iv) पाँच।
उत्तर-
(iv)
प्रश्न 21.
श्री आनंदपुर साहिब की पहली लड़ाई कब हुई ?
(i) 1699 ई० में
(ii) 1701 ई० में
(iii) 1703 ई० में
(iv) 1704 ई० में।
उत्तर-
(ii)

प्रश्न 22.
श्री आनंदपुर साहिब की दूसरी लड़ाई कब हुई ?
(i) 1701 ई० में
(ii) 1702 ई० में
(iii) 1704 ई० में
(iv) 1705 ई० में।
उत्तर-
(iii)
प्रश्न 23.
किस लड़ाई में 40 सिख गुरु जी को बेदावा देकर चले गए ?
(i) भंगाणी की लड़ाई
(ii) श्री आनंदपुर साहिब की पहली लड़ाई
(iii) श्री आनंदपुर साहिब की दूसरी लड़ाई
(iv) चमकौर साहिब की लड़ाई।
उत्तर-
(iii)
प्रश्न 24.
चमकौर साहिब की लड़ाई कब हुई ?
(i) 1702 ई० में
(ii) 1703 ई० में
(iii) 1704 ई० में
(iv) 1706 ई० में।
उत्तर-
(iii)

प्रश्न 25.
गुरु गोबिंद सिंह जी के दो बड़े साहिबजादे किस लड़ाई में शहीद हुए ?
(i) खिदराना की लड़ाई में
(ii) चमकौर साहिब की लड़ाई में
(iii) श्री आनंदपुर साहिब की दूसरी लड़ाई में
(iv) भंगाणी की लड़ाई में।
उत्तर-
(ii)
प्रश्न 26.
गुरु गोबिंद सिंह जी ने औरंगजेब को कौन-सी चिट्ठी लिखी थी ?
(i) ज़फ़रनामा
(ii) शस्त्र नाममाला
(iii) बचित्तर नाटक
(iv) खत-ए-औरंगज़ेब।
उत्तर-
(i)
प्रश्न 27.
गुरु गोबिंद सिंह जी ने ज़फ़रनामा को किस भाषा में लिखा था ?
(i) हिंदी में
(ii) संस्कृत में
(iii) पंजाबी में
(iv) फ़ारसी में।
उत्तर-
(iv)

प्रश्न 28.
खिदराना की लड़ाई कब लड़ी गई ?
(i) 1703 ई० में
(ii) 1704 ई० में
(iii) 1705 ई० में
(iv) 1706 ई० में।
उत्तर-
(iii)
प्रश्न 29.
चाली मुक्ते कौन-सी लड़ाई के साथ संबंधित हैं ?
(i) चमकौर साहिब की लड़ाई के साथ
(ii) खिदराना की लड़ाई के साथ
(iii) श्री आनंदपुर साहिब की पहली लड़ाई के साथ
(iv) श्री आनंदपुर साहिब की दूसरी लड़ाई के साथ।
उत्तर-
(i)
प्रश्न 30.
श्री मुक्तसर साहिब किस नगर का नाम पड़ा ? ।
(i) भंगाणी का
(ii) माखोवाल का
(iii) खिदराना का
(iv) निर्मोह का।
उत्तर-
(iii)

प्रश्न 31.
बचित्तर नाटक किस गुरु साहिब की रचना है ?
(i) गुरु तेग़ बहादुर जी
(ii) गुरु गोबिंद सिंह जी
(iii) गुरु अर्जन देव जी
(iv) गुरु हर राय जी।
उत्तर-
(ii)
प्रश्न 32.
गुरु गोबिंद सिंह जी कब ज्योति-जोत समाए ?
(i) 1705 ई० में
(ii) 1706 ई० में
(iii) 1707 ई० में
(iv) 1708 ई० में।
उत्तर-
(iv)
प्रश्न 33
गुरु गोबिंद सिंह जी कहाँ ज्योति-जोत समाए ?
(i) खिदराना में
(ii) तलवंडी साबो में
(iii) नांदेड़ में ,
(iv) श्री आनंदपुर साहिब में।
उत्तर-
(iii)

Long Answer Type Question
प्रश्न 1.
गुरुगद्दी पर बैठते समय गुरु गोबिंद सिंह जी को किन कठिनाइयों का सामना करना पड़ा ?
(What difficulties were faced by Guru Gobind Singh Ji when he attained the Gurugaddi ?)
उत्तर-
1675 ई० में गुरुगद्दी पर बैठते समय गुरु गोबिंद सिंह जी को आंतरिक तथा बाह्य अनेकों कठिनाइयों का सामना करना पड़ा। प्रथम उस समय गुरु गोबिंद सिंह जी की आयु केवल 9 वर्ष थी परंतु उनके सामने पहाड़ जैसी चुनौतियाँ थीं। द्वितीय, उस समय मुग़ल सम्राट औरंगज़ेब का शासन था। वह बड़ा कट्टर सुन्नी मुसलमान था। वह इस्लाम के अतिरिक्त किसी अन्य धर्म के अस्तित्व को सहन करने को तैयार नहीं था। इसी कारण उसने गुरु तेग़ बहादुर जी को शहीद कर दिया। औरंगज़ेब के बढ़ते हुए अत्याचारों को नुकेल डालना आवश्यक था। तीसरा, पहाड़ी राजा अपने निहित स्वार्थों के कारण गुरु गोबिंद सिंह जी के विरुद्ध थे। चौथा, धीरमलिए तथा रामराइए गुरुगद्दी न मिलने के कारण गुरु साहिब के विरुद्ध षड्यंत्र रच रहे थे। पाँचवां, उस समय मसंद प्रणाली में अनेकों दोष आ गए थे। मसंद अब बहुत भ्रष्ट हो गए थे। वे सिखों को लूटने में प्रसन्नता अनुभव करते थे। छठा, उस समय हिंदू भी सदियों की गुलामी के कारण उत्साहहीन थे। परिणामस्वरूप सिखों को फिर से संगठित करने की आवश्यकता थी।
प्रश्न 2.
गुरु गोबिंद सिंह जी की किन्हीं छः लडाइयों का संक्षिप्त वर्णन करो। (Explain briefly any six battles of Guru Gobind Singh Ji.)
उत्तर-
1. भंगाणी की लड़ाई 1688 ई०-22 सितंबर, 1688 ई० को भंगाणी में गुरु गोबिंद सिंह जी की सेना पर पहाड़ी राजाओं ने आक्रमण कर दिया। इस लड़ाई में सढौरा के पीर बुद्ध शाह ने अपने सैनिकों सहित गुरु जी का साथ दिया। सिखों के जोश के सम्मुख पहाड़ी राजा युद्ध-भूमि छोड़ कर भागने के लिए विवश हो गए। इस विजय से सिखों का साहस बहुत बढ़ गया।
2. नादौन की लड़ाई 1690 ई०-भंगाणी की लड़ाई में पराजय के बाद पहाड़ी राजाओं ने गुरु गोबिंद सिंह जी से मित्रता स्थापित कर ली। उन्होंने मुग़लों को वार्षिक खिराज (कर) भेजना बंद कर दिया। अतैव आलिफ खाँ. के अधीन एक सेना पहाड़ी राजाओं के विरुद्ध भेजी गई। उसने 20 मार्च, 1690 ई० को पहाड़ी राजाओं के नेता भीम चंद की सेना पर नादौन में आक्रमण कर दिया। इस लड़ाई में गुरु गोबिंद सिंह जी ने भीम चंद का साथ दिया। इस संयुक्त सेना ने मुग़ल सेना को परास्त कर दिया। ..
3. श्री आनंदपुर साहिब की प्रथम लड़ाई 1701 ई०-1699 ई० में खालसा पंथ के सृजन के फलस्वरूप बड़ी संख्या में लोग सिख पंथ में शामिल होने लगे। गुरु जी की इस बढ़ती हुई शक्ति को देखकर कहलूर के शासक भीम चंद ने गुरु जी को श्री आनंदपुर साहिब का दुर्ग खाली करने के लिए कहा। गुरु जी के इंकार करने पर भीम चंद तथा उसके साथी पहाड़ी राजाओं ने 1701 ई० में श्री आनंदपुर साहिब के दुर्ग पर आक्रमण कर दिया। परंतु सफलता प्राप्त न होने के कारण पहाडी राजाओं ने गुरु जी के साथ संधि कर ली।
4. श्री आनंदपुर साहिब की द्वितीय लड़ाई 1704 ई०–पहाड़ी राजा गुरु गोबिंद सिंह जी से अपनी पराजय के अपमान का बदला लेना चाहते थे। इस उद्देश्य से उन्होंने मुग़ल सेनाओं से मिलकर 1704 ई० में श्री आनंदपुर साहिब के दुर्ग पर दूसरी बार आक्रमण कर दिया। सिखों ने दुर्ग के भीतर से इस सेना का डटकर सामना किया। सफलता न मिलती देखकर शाही सेनाओं ने एक चाल चली। उन्होंने झूठी सौगंध खाकर गुरु जी को कहा कि यदि वे दुर्ग छोड़ दें तो उन्हें कुछ नहीं कहा जाएगा। गुरु जी ने माता गुजरी जी तथा अन्य सिखों की विनती पर दुर्ग छोड़ने का निर्णय किया।
5. चमकौर साहिब की लड़ाई 1704 ई०-गुरु गोबिंद सिंह जी अपने 40 सिखों सहित चमकौर साहिब की गढ़ी में पहुँचे। वहाँ पहुँचते ही मुग़ल सैनिकों ने उन्हें घेर लिया। यहाँ बड़ी ही घमासान की लड़ाई हुई। इस लड़ाई में गुरु गोबिंद सिंह जी के दो बड़े साहिबजादों-साहिबजादा अजीत सिंह जी व साहिबजादा जुझार सिंह जी ने असंख्य मुसलमानों को यमलोक पहुँचा दिया और अंततः लड़ते-लड़ते शहीद हो गए।
6. खिदराना की लड़ाई 1705 ई०-29 दिसंबर, 1705 ई० को सरहिंद के नवाब वजीर खाँ ने विशाल सेना के साथ गुरु गोबिंद सिंह जी की सेना पर आक्रमण कर दिया। इस लड़ाई में सिखों ने मुग़ल सेना को कड़ी पराजय दी। इस लड़ाई में वह 40 सिख भी लड़ते-लड़ते शहीद हो गए थे जो श्री आनंदपुर साहिब की दूसरी लड़ाई में गुरु जी का साथ छोड़ गए थे। इस कारण गुरु जी द्वारा उन्हें मुक्ति का वर दिया। इस कारण खिदराना का नाम श्री मुक्तसर साहिब पड़ गया।
प्रश्न 3.
भंगाणी की लड़ाई पर एक संक्षिप्त नोट लिखें। (Write a short note on the battle of Bhangani.)
अथवा
गुरु गोबिंद सिंह जी के भंगाणी युद्ध का वर्णन करें तथा इसका महत्त्व भी बताएँ। (Describe Guru Gobind Singh’s battle of Bhangani and also explain its importance.)
उत्तर-
भंगाणी की लड़ाई गुरु गोबिंद सिंह जी तथा पहाड़ी राजाओं के बीच हुई प्रथम लड़ाई थी। यह लड़ाई 22 सितंबर, 1688 ई० में हुई थी। इस लड़ाई के लिए कई कारण उत्तरदायी थे। पहला, गुरु गोबिंद सिंह जी की चल रही सैनिक तैयारियों को देखकर पहाड़ी राजाओं में घबराहट फैल गई थी। उन्हें अपनी स्वतंत्रता ख़तरे में अनुभव होने लगी। दूसरा, गुरु गोबिंद सिंह जी के समाज-सुधार के कार्यों को पहाड़ी राजा अपने धर्म में हस्तक्षेप समझते थे। तीसरा, ये पहाड़ी राजा सिख संगतों को बहुत परेशान करते थे। चौथा, मुग़ल सरकार भी इन पहाडी राजाओं को गुरु साहिब के विरुद्ध कार्यवाही करने के लिए भड़का रही थी। पाँचवां, कहलूर का राजा भीम चंद गुरु साहिब से बहुत ईर्ष्या करता था। फलस्वरूप कहलूर के शासक भीम चंद तथा श्रीनगर के शासक फ़तह शाह के नेतृत्व में पहाड़ी राजाओं के एक गठबंधन ने 22 सितंबर, 1688 ई० में भंगाणी के स्थान पर गुरु गोबिंद सिंह जी की सेना पर आक्रमण कर दिया। इस लड़ाई में सढौरा के पीर बुद्ध शाह ने गुरु साहिब को सहायता दी। सिखों ने पहाड़ी राजाओं का डटकर सामना किया। इस लड़ाई में अंततः सिखों की विजय हुई। इस विजय के कारण सिखों का उत्साह बहुत बढ़ गया तथा गुरु साहिब की प्रसिद्धि दूर-दूर तक फैल गई। पहाड़ी राजाओं ने गुरु साहिब का विरोध छोड़कर उनसे मित्रता करने में ही अपनी भलाई समझी।

प्रश्न 4.
नादौन की लड़ाई पर एक संक्षिप्त नोट लिखें। (Write a short note on the battle of Nadaun.)
उत्तर-
भंगाणी की लड़ाई के पश्चात् गुरु गोबिंद सिंह जी पाऊँटा साहिब छोड़कर पुनः श्री आनंदपुर साहिब आ गए। अपनी स्थिति को दृढ़ करने के उद्देश्य से गुरु गोबिंद सिंह जी ने यहाँ पर आनंदगढ़, लोहगढ़, फतहगढ़ और केसगढ़ नामक चार दुर्गों का निर्माण करवाया। इस समय औरंगजेब दक्षिण के युद्धों में उलझा हुआ था। यह स्वर्ण अवसर देखकर पहाड़ी राजाओं ने मुग़लों को दिया जाने वाला वार्षिक खिराज (कर) देना बंद कर दिया। जब औरंगज़ेब को इस संबंध में ज्ञात हुआ तो उसने जम्मू के सूबेदार मीयाँ खाँ को इन पहाड़ी राजाओं को पाठ पढ़ाने का आदेश दिया। मीयाँ खाँ ने तुरंत अपने एक जरनैल आलिफ खाँ के अंतर्गत मुग़लों की एक भारी सेना इन पहाड़ी राजाओं के विरुद्ध कार्यवाही करने के लिए भेजी। ऐसे गंभीर समय में भीम चंद ने गुरु साहिब को सहायता के लिए निवेदन किया। गुरु साहिब ने यह निवेदन स्वीकार कर लिया और वे स्वयं अपने सिखों को साथ लेकर सहायता के लिए पहुंचे। 20 मई, 1690 ई० को काँगड़ा से लगभग 30 किलोमीटर दूर नादौन में भीम चंद और आलिफ खाँ की सेनाओं में लड़ाई आरंभ हुई। इस लड़ाई में काँगड़ा के राजा कृपाल चंद ने आलिफ खाँ का साथ दिया। इस लड़ाई में गुरु साहिब और उनके सिखों ने अपनी वीरता के ऐसे जौहर दिखाए कि आलिफ खाँ और उसके सैनिकों को रणभूमि से भागने के लिए विवश होना पड़ा। इस प्रकार गुरु साहिब के सहयोग से भीम चंद और उसके साथी पहाड़ी राजाओं को विजय प्राप्त हुई। इस लड़ाई के पश्चात् पहाड़ी राजाओं ने गुरु साहिब के साथ विश्वासघात किया और उन्होंने मुग़लों के साथ पुनः संधि कर ली।
प्रश्न 5.
खालसा पंथ की स्थापना के कारणों के बारे में चर्चा करें। (Give reasons for the creation of Khalsa Panth.)
अथवा
गुरु गोबिंद सिंह जी ने खालसा पंथ का सृजन क्यों किया ? (Why did Guru Gobind Singh create the Khalsa ?)
अथवा
गुरु गोबिंद सिंह जी द्वारा खालसा पंथ की स्थापना के लिए उत्तरदायी मुख्य कारणों का संक्षिप्त में वर्णन कीजिए। (Give a brief description of the circumstances responsible for the creation of Khalsa.)
अथवा
1699 ई० में खालसा की स्थापना के लिए कौन-से कारण उत्तरदायी थे? (What were the circumstances that led to the creation of Khalsa in 1699 A.D. ?)
उत्तर-
1. मुग़लों का अत्याचारी शासन औरंगजेब एक कट्टर सुन्नी बादशाह था। उसने हिंदुओं के कई प्रसिद्ध मंदिरों को गिरवा दिया था। उसने हिंदुओं की धार्मिक रस्मों पर प्रतिबंध लगा दिए तथा जज़िया कर को पुनः लागू कर दिया। उसने बड़ी संख्या में इस्लाम धर्म स्वीकार न करने वाले गैर-मुसलमानों की हत्या करवा दी। सबसे बढ़कर उसने गुरु तेग़ बहादुर जी को शहीद करवा दिया। अतः मुग़लों के इन बढ़ रहे अत्याचारों का अंत करने के लिए गुरु गोबिंद सिंह जी ने खालसा पंथ की स्थापना करने का निर्णय किया।
2. पहाड़ी राजाओं का विश्वासघात—गुरु जी मुग़लों के विरुद्ध संघर्ष के लिए पहाड़ी राजाओं को साथ लेना चाहते थे। परंतु गुरु जी इस बात से परिचित थे कि पहाड़ी राजाओं पर विश्वास नहीं किया जा सकता। इसलिए गुरु गोबिंद सिंह जी ने ऐसे सैनिकों को तैयार करने का निर्णय किया जो मुग़लों की शक्ति का सामना कर पाएँ। फलस्वरूप खालसा पंथ की स्थापना की गई।
3. जातीय बंधन भारतीय समाज में जाति-प्रथा शताब्दियों से चली आ रही थी। फलस्वरूप समाज कई जातियों और उपजातियों में विभाजित था। उच्च जाति के लोग निम्न जाति के लोगों के साथ बुरा व्यवहार करते थे। इस जाति-प्रथा ने भारतीय समाज को एक घुण की भाँति भीतर ही भीतर से खोखला बना दिया था। गुरु गोबिंद सिंह जी एक ऐसे आदर्श समाज की स्थापना करना चाहते थे, जिसमें जाति-पाति का कोई स्थान न हो।
4. दोषपूर्ण मसंद प्रथा—दोषपूर्ण मसंद प्रथा गुरु गोबिंद सिंह जी द्वारा खालसा पंथ की स्थापना का महत्त्वपूर्ण कारण बनी। समय के साथ-साथ मसंद अपने प्रारंभिक आदर्शों को भूल गए और बड़े भ्रष्टाचारी और अहंकारी बन गए। उन्होंने सिखों को लूटना आरंभ कर दिया। उनका कहना था कि वे गुरुओं को बनाने वाले हैं। बहुत-से प्रभावशाली मसंदों ने अपनी अलग गुरुगद्दी स्थापित कर ली थी। गुरु गोबिंद सिंह जी ने इन मसंदों से छुटकारा पाने के लिए एक नए संगठन की स्थापना करने का निर्णय किया।
5. गुरुगद्दी का पैतृक होना-गुरु अमरदास जी ने गुरुगद्दी को पैतृक बना दिया था। इसमें अनेक समस्याएँ उत्पन्न हो गई थीं। पृथी चंद, धीर मल और राम राय ने गुरुगद्दी प्राप्त करने के लिए सिख गुरुओं के लिए अनेक मुश्किलें उत्पन्न कर दी। इसलिए गुरु गोबिंद सिंह जी एक ऐसे समाज का निर्माण करना चाहते थे जिसमें मीणों, धीर मलों और राम राइयों के लिए कोई स्थान न हो।
6. गुरु गोबिंद सिंह जी का उद्देश्य-गुरु गोबिंद सिंह जी ने ‘बचित्तर नाटक’ में लिखा है, कि उनके जीवन का उद्देश्य संसार में धर्म-प्रचार का कार्य करना और अत्याचारियों का विनाश करना है। अत्याचारियों के विनाश के लिए तलवार उठाना अत्यावश्यक है। अपने इस उद्देश्य की पूर्ति के लिए गुरु गोबिंद सिंह जी ने खालसा पंथ का सृजन किया।

प्रश्न 6.
खालसा पंथ की स्थापना कब और कैसे हुई ?
(When and how was the Khalsa founded ?)
अथवा
खालसा की स्थापना पर संक्षिप्त नोट लिखें। (Write a short note on the creation of Khalsa.)
अथवा
गुरु गोबिंद सिंह जी ने ख़ालसा की स्थापना किस प्रकार की? (How Khalsa was created by Guru Gobind Singh Ji ?)
उत्तर-
गुरु गोबिंद सिंह जी ने 30 मार्च, 1699 ई० को बैसाखी वाले दिन श्री आनंदपुर साहिब में केसगढ़ नामक स्थान पर एक भारी दीवान सजाया। इस दीवान में 80,000 सिखों ने भाग लिया। जब सभी लोग बैठ गए तो गुरु जी मंच पर आए। उन्होंने म्यान से तलवार निकाली और एकत्रित सिखों को संबोधित किया, “क्या आप में से कोई ऐसा सिख है जो धर्म के लिए अपना शीश भेट करे ?” ये शब्द सुनकर दीवान में सन्नाटा छा गया। जब गुरु जी ने अपने शब्दों को तीन बार दोहराया तो भाई दया राम जी अपना बलिदान देने के लिए उपस्थित हुआ।
गुरु जी उसे पास ही एक तंबू में ले गए जहाँ उन्होंने दया राम को बिठाया और खून से भरी तलवार लेकर पुनः मंच पर आ गए। गुरु जी ने एक और सिख से बलिदान की मांग की। अब भाई धर्मदास जी उपस्थित हुआ। इस क्रम को तीन बार और दोहराया गया। गुरु जी की आज्ञा का पालन करते हुए भाई मोहकम चंद जी, भाई साहिब चंद जी और भाई हिम्मत राय जी अपने बलिदानों के लिए उपस्थित हुए। इस प्रकार गुरु गोबिंद सिंह जी ने ‘पाँच प्यारों’ का चुनाव किया। गुरु साहिब ने इन पाँच प्यारों को पहले खंडे का पाहुल पिलाया और बाद में स्वयं इन प्यारों से पाहुल पिया। इस प्रकार गुरु गोबिंद सिंह जी ने खालसा पंथ का सृजन किया।
प्रश्न 7.
गुरु गोबिंद सिंह जी ने खालसा पंथ का सृजन कब किया और इसके मुख्य सिद्धांत क्या हैं ?
(When was the Khalsa created by Guru Gobind Singh Ji and what are its main principles ?)
अथवा
खालसा पंथ के मुख्य सिद्धांतों का वर्णन करो। (Explain the main principles of the Khalsa.)
अथवा
गुरु गोबिंद सिंह जी द्वारा स्थापित किए गए ‘खालसा पंथ’ के मुख्य सिद्धांत लिखो। (Write the main principles of the ‘Khalsa Panth’ founded by Guru Gobind Singh Ji.)
उत्तर-
गुरु गोबिंद सिंह जी ने खालसा के सृजन के समय कुछ नए आदेश अथवा विशेष नियम बनाए थे। इन आदेशों का पालन करना प्रत्येक खालसा के लिए आवश्यक है। कुछ प्रमुख नियमों का वर्णन निम्नलिखित अनुसार है—
- खालसा पंथ में सम्मिलित होने के लिए प्रत्येक व्यक्ति के लिए ‘खंडे का पाहुल’ छकना आवश्यक है।
- प्रत्येक खालसा अपने नाम के साथ ‘सिंह’ और खालसा स्त्री ‘कौर’ शब्द का प्रयोग करेगी।
- प्रत्येक खालसा एक ईश्वर के अतिरिक्त किसी अन्य देवी-देवते की उपासना नहीं करेगा।
- प्रत्येक खालसा ‘पाँच कक्कार’ अर्थात् केश, कंघा, कड़ा, कच्छहरा और कृपाण पहनेगा।
- प्रत्येक खालसा देश, धर्म की रक्षा के लिए अपना सब कुछ न्यौछावर कर देगा।
- प्रत्येक खालसा प्रातःकाल जागकर स्नान करने के पश्चात् गुरुवाणी का पाठ करेगा।
- प्रत्येक खालसा श्रम द्वारा अपनी आजीविका प्राप्त करेगा और अपनी आय का दंशांश धर्म के लिए दान करेगा।
- प्रत्येक खालसा शस्त्र धारण करेगा और धर्म-युद्ध के लिए सदैव तैयार रहेगा।
- प्रत्येक खालसा परस्पर भेंट के समय वाहेगुरु जी का खालसा, वाहेगुरु जी की फ़तह’ कहेंगे।
- प्रत्येक खालसा सिगरेट, नशीले पदार्थों का सेवन, पर-स्त्री-गमन इत्यादि बुराइयों से कोसों दूर रहेगा।
- प्रत्येक खालसा जाति-प्रथा और ऊँच-नीच में विश्वास नहीं रखेगा।

प्रश्न 8.
खालसा पंथ की स्थापना के क्या महत्त्वपूर्ण प्रभाव पड़े ? (What were the important effects of the creation of Khalsa Panth ?)
अथवा
खालसा पंथ की स्थापना के सिख इतिहास में कौन से छः महत्त्वपूर्ण प्रभाव पड़े ?
(What were the six important effects of the creation of Khalsa in Sikh History ?)
अथवा
खालसा की स्थापना के महत्त्व का अध्ययन कीजिए। (Study the importance of the creation of Khalsa.)
उत्तर-
1699 ई० में खालसा पंथ का सृजन न केवल पंजाब के इतिहास, बल्कि भारत के इतिहास में एक युग परिवर्तक घटना मानी जाती है। निस्संदेह, खालसा पंथ की स्थापना के बड़े दूरगामी परिणाम निकले।
1. सिखों की संख्या में वृद्धि खालसा पंथ की स्थापना के पश्चात् भारी संख्या में लोग इसमें शामिल होने लग पड़े। गुरु साहिब ने स्वयं हज़ारों सिखों को पाहुल छकाकर खालसा बनाया। इसके अतिरिक्त गुरु जी ने खालसा पंथ के किसी भी पाँच सिखों को अमृत छकाने का अधिकार देकर खालसा पंथ में आश्चर्यजनक रूप से वृद्धि की।
2. आदर्श समाज का निर्माण-खालसा पंथ की स्थापना से एक आदर्श समाज का जन्म हुआ। खालसा पंथ में ऊँच-नीच के लिए कोई स्थान नहीं था। इसमें निम्न और पिछड़ी श्रेणियों को समानता का दर्जा दिया गया। खालसा समाज में अंध-विश्वासों तथा नशीले पदार्थों के सेवन करने के लिए कोई स्थान नहीं था। इस प्रकार गुरु जी ने खालसा पंथ को रच कर एक नए समाज की रचना की।
3. मसंद प्रथा एवं पंथ विरोधी संप्रदायों का अंत मसंद प्रथा में आई कुरीतियाँ खालसा पंथ के निर्माण का एक प्रमुख कारण बनी थीं। इसलिए जब गुरु गोबिंद सिंह जी ने खालसा पंथ की स्थापना की, तो उसमें मसंदों को कोई स्थान नहीं दिया गया। गुरु जी ने सिखों को आदेश दिया, कि वे इनसे किसी प्रकार का कोई संबंध न रखें।
4. निम्न जातियों के लोगों का उद्धार-खालसा पंथ की स्थापना निम्न जातियों के उद्धार का संदेश थी। इससे पूर्व निम्न जातियों के लोगों से बहुत दुर्व्यवहार किया जाता था। गुरु जी ने निम्न जाति के लोगों को खालसा पंथ में शामिल करके उन्हें उच्च जातियों के बराबर स्थान दिया। गुरु जी ने यह महान् पग उठाकर निम्न जाति के लोगों में एक नया जोश भरा। गुरु गोबिंद सिंह जी के नेतृत्व में वे महान् योद्धा सिद्ध हुए।
5. सिखों में नया जोश-खालसा पंथ की स्थापना ने सिखों में अद्वितीय जोश उत्पन्न किया। दुर्बल से दुर्बल सिख भी अब शेर बन गया। अत्याचारियों के सम्मुख झुकने की अपेक्षा अब उन्होंने शस्त्र उठा लिए। मुग़लों और अफ़गानों से होने वाली लड़ाइयों में सिखों ने अद्वितीय वीरता और बलिदान के प्रमाण दिए।
6. सिखों की राजनीतिक शक्ति का उत्थान-खालसा पंथ की स्थापना के साथ ही सिखों की राजनीतिक शक्ति का भी उदय हुआ। असंख्य बलिदान के बाद वे पंजाब में अपनी स्वतंत्र मिसलें स्थापित करने में सफल हुए। तत्पश्चात् 19वीं शताब्दी में महाराजा रणजीत सिंह ने स्वतंत्र सिख साम्राज्य की स्थापना की। इस प्रकार अंत में खालसों का स्वप्न साकार हुआ।
प्रश्न 9.
श्री आनंदपुर साहिब की प्रथम लड़ाई पर एक संक्षिप्त नोट लिखें। (Write a brief note on the first battle of Sri Anandpur Sahib.).
उत्तर-
1699 ई० में खालसा पंथ की स्थापना के पश्चात् भारी संख्या में लोग खालसा पंथ में सम्मिलित होने लगे थे। गुरु जी की दिन-प्रतिदिन बढ़ रही इस शक्ति के कारण पहाड़ी राजाओं के मन की शांति भंग हो गई थी। कहलूर के राजा भीम चंद, जिसकी रियासत में श्री आनंदपुर साहिब स्थित था, ने गुरु जी को श्री आनंदपुर साहिब छोड़ने के लिए कहा। गुरु जी ने यह माँग मानने से स्पष्ट इंकार कर दिया। उनका कहना था कि गुरु तेग़ बहादुर जी ने यह भूमि उचित मूल्य देकर क्रय की थी। इस पर भीम चंद ने कुछ अन्य पहाड़ी राजाओं से मिल कर 1701 ई० में श्री आनंदपुर साहिब के किले पर आक्रमण कर दिया। किले का घेरा कई दिनों तक जारी रहा। किले के भीतर यद्यपि सिखों की संख्या बहुत कम थी, फिर भी उन्होंने पहाड़ी राजाओं की सेनाओं का खूब डट कर सामना किया। जब पहाड़ी राजाओं को सफलता मिलने की कोई आशा न रही तो उन्होंने गुरु जी से संधि कर ली। यह संधि पहाड़ी राजाओं की एक चाल थी तथा वह अवसर देखकर गुरु गोबिंद सिंह जी पर एक ज़ोरदार आक्रमण करना चाहते थे।

प्रश्न 10.
श्री आनंदपुर साहिब की दूसरी लड़ाई पर एक संक्षिप्त नोट लिखें। (Write a short note on the second battle of Sri Anandpur Sahib.)
उत्तर-
पहाड़ी राजा गुरु गोबिंद सिंह जी से अपनी हुई निरंतर पराजयों के अपमान का प्रतिशोध लेना चाहते थे। इस उद्देश्य से उन्होंने मुग़ल सेनाओं से मिलकर मई, 1704 ई० में श्री आनंदपुर साहिब के दुर्ग पर दूसरी बार आक्रमण कर दिया। इस संयुक्त सेना ने दुर्ग के भीतर जाने के अनेक प्रयास किए, परंतु सिख योद्धाओं ने इन सभी प्रयासों को असफल बना दिया। घेरे के लंबे हो जाने के कारण दुर्ग के भीतर खाद्य-सामग्री कम होनी आरंभ हो गई। इसलिए सिखों के लिए अधिक समय तक लडाई को जारी रखना संभव नहीं था। अतः कुछ सिखों ने गुरु साहिब को श्री आनंदपुर साहिब का दुर्ग छोड़ने का निवेदन किया। गुरु साहिब ने सिखों को कुछ और दिन संघर्ष जारी रखने का परामर्श दिया। इस परामर्श को न मानते हुए 40 सिख गुरु जी को बेदावा देकर दुर्ग छोड़कर चले गए। दूसरी ओर इतने लंबे समय से घेरे के कारण शाही सेना भी बहुत परेशान थी। इसलिए उन्होंने एक चाल चली। उन्होंने कुरान और गायों की कसम खाकर गुरु साहिब को विश्वास दिलाया कि यदि वे श्री आनंदपुर साहिब को छोड़ दें तो उन्हें कोई क्षति नहीं पहुँचाई जायेगी। गुरु साहिब को इन झूठी कसमों पर कोई विश्वास नहीं था, परंतु माता गुजरी और कुछ अन्य सिखों के निवेदन पर गुरु साहिब ने 20 दिसंबर, 1704 ई० को आनंदपुर साहिब के दुर्ग को छोड़ दिया।
प्रश्न 11.
चमकौर साहिब की लड़ाई का संक्षिप्त विवरण दीजिए। (Give a brief account of the battle of Chamkaur Sahib.)
उत्तर-
गुरु गोबिंद सिंह जी द्वारा श्री आनंदपुर साहिब का दुर्ग छोड़ने के पश्चात् मुग़ल सेनाएँ बहुत तीव्रता से उनका पीछा कर रही थीं। गुरु साहिब ने चमकौर साहिब की एक कच्ची गढ़ी में 40 सिखों सहित शरण ली। 22 दिसंबर, 1704 ई० को हज़ारों की संख्या में मुग़ल सैनिकों ने इस गढ़ी को घेरे में ले लिया। चमकौर साहिब की यह लड़ाई बहुत घमासान लड़ाई थी। इस लड़ाई में गुरु गोबिंद सिंह के दो बड़े साहिबजादों-साहिबजादा अजीत सिंह जी तथा साहिबजादा जुझार सिंह जी ने वह वीरता प्रदर्शित की कि मुग़लों को दिन में तारे दिखाई देने लगे। उन्होंने असंख्य मुसलमानों को मृत्यु की गोद में सुलाया और अंततः लड़ते-लड़ते शहीद हो गए। चमकौर साहिब की उस लड़ाई में गुरु गोबिंद सिंह जी के अधीन जो वीरता सिखों ने दिखाई उसकी कोई अन्य उदाहरण मिलना बहुत कठिन है। पाँच,सिखों के अनुरोध पर गुरु गोबिंद सिंह जी ने चमकौर साहिब की गढ़ी को छोड़ दिया। गढ़ी छोड़ते समय गुरु जी ने मुग़ल सेना को ताली बजाकर ललकारा, परंतु वह गुरु साहिब का कुछ न बिगाड़ सकी।

प्रश्न 12.
खिदराना (श्री मुक्तसर साहिब) की लड़ाई पर एक संक्षिप्त नोट लिखो। [Write a brief note on the battle of Khidrana (Sri Mukatsar Sahib).]
उत्तर-
खिदराना की लड़ाई गुरु जी तथा मुग़ल सेना में लड़ी जाने वाली अंतिम निर्णायक लड़ाई थी। गुरु जी माछीवाड़ा के जंगलों में अनेक कठिनाइयाँ झेलते हुए खिदराना पहुँचे थे। जब मुग़लों को इस बात का पता चला तो सरहिंद के नवाब वज़ीर खाँ ने खिदराना में गुरु साहिब पर आक्रमण करने की योजना बनाई। उसने 29 दिसंबर, 1705 ई० को एक विशाल सेना के साथ गुरु जी की सेना पर खिदराना के स्थान पर आक्रमण कर दिया। इस लड़ाई में सिखों ने बड़ी वीरता दिखाई। उन्होंने मुग़ल सेना के ऐसे छक्के छुड़ाए कि वें युद्ध स्थल छोड़ कर भाग गए। इस प्रकार गुरु जी को अपनी इस अंतिम लड़ाई में बड़ी शानदार विजय प्राप्त हुई। इस लड़ाई में वह 40 सिख भी लड़ते-लड़ते शहीद हो गए थे जो श्री आनंदपुर साहिब की दूसरी लड़ाई में गुरु जी का साथ छोड़ गए थे। उनकी कुर्बानी से प्रभावित होकर और उनके नेता महा सिंह, जो जीवन की अंतिम सांसें ले रहा था की विनती को स्वीकार करके गुरु साहिब ने उनके द्वारा लिखे गए बेदावे को फाड़ दिया और उन्हें मुक्ति का वर दिया। इस कारण खिदराना का नाम श्री मुक्तसर साहिब पड़ गया।
प्रश्न 13.
गुरु गोबिंद सिंह जी ने सिख पंथ में सांप्रदायिक बंटवारे तथा बाह्य ख़तरों की समस्या को किस प्रकार हल किया ?
(How did Guru Gobind Singh Ji settle the sectarian divisions and external dangers to Sikhism ?)
उतर-
गुरु गोबिंद सिंह जी ने सिख पंथ में सांप्रदायिक बँटवारे तथा बाह्य ख़तरों से निपटने के लिए .1699 ई० में खालसा पंथ की स्थापना की। गुरु जी ने इस बात की घोषणा की कि सारे सिख उनके ‘खालसा’ हैं और प्रत्यक्ष रूप से उनसे जुड़े हुए हैं। इसलिए जो सिख प्रत्यक्ष रूप से गुरु जी के साथ नहीं जुड़ता था, उसे सिख नहीं माना जाता था। इस प्रकार मसंदों की मध्यस्थता समाप्त हो गई। मीणों, धीरमलियों, रामरइयों तथा हिंदालियों को सिख पंथ से निकाल दिया गया। बाह्य ख़तरों से निपटने के लिए गुरु जी ने सारे सिखों को शस्त्रधारी रहने का आदेश दिया। अपनी तथा अन्यों की रक्षा के लिए लड़ना सिखों का धर्म निश्चित किया गया। इस कारण सिख मुग़लों का डट कर सामना कर सके। इस प्रकार सिख पंथ एक नई शक्ति के रूप में उभर कर सामने आया।

प्रश्न 14.
गुरु गोबिंद सिंह जी की साहित्यिक सरगर्मियों के बारे में आप क्या जानते हैं ?
(What do you know about the literary activities of Guru Gobind Singh Ji ?)
अथवा
गुरु गोबिंद सिंह जी की साहित्यिक गतिविधियों के बारे में चर्चा करें। (Describe the literary activities of Guru Gobind Singh Ji.)
अथवा
गुरु गोबिंद सिंह जी की साहित्यिक उपलब्धियों का मूल्यांकन करें। (Evaluate the literary achievements of Guru Gobind Singh Ji.)
उत्तर-
साहित्य के क्षेत्र में गुरु गोबिंद सिंह जी का योगदान बहुत महत्त्वपूर्ण है। वह स्वयं उच्चकोटि के कवि तथा साहित्यकार थे। उनके द्वारा रचित अधिकाँश साहित्य सिरसा नदी में बह गया था। फिर भी जो साहित्य हम तक पहुँचा है, उससे आपके महान् विद्वान् होने का पर्याप्त प्रमाण मिलता है। गुरु साहिब ने अपनी रचनाओं में पंजाबी, हिंदी, फारसी, अरबी, संस्कृत आदि भाषाओं का प्रयोग किया। जापु साहिब, बचित्तर नाटक, ज़फरनामा, चंडी दी वार आप की महान् रचनाएँ हैं। इनमें आपने विभिन्न विषयों पर भरपूर प्रकाश डाला है। ये रचनाएँ आध्यात्मिक ज्ञान का भंडार हैं। इनसे हमें ऐतिहासिक घटनाओं की जानकारी भी प्राप्त होती है। आपकी ये रचनाएँ इतनी जोश से भरी हैं कि इन्हें पढ़ कर मुर्दा दिलों में भी जान आ जाती है। गुरु गोबिंद सिंह जी ने अपने दरबार में 52 उच्चकोटि के कवियों को संरक्षण दिया था। इन में से नंद लाल, सैनापत, गोपाल तथा उदै राय के नाम उल्लेखनीय हैं।
प्रश्न 15.
ज़फरनामा क्या है ?
(What is Zafarnama ?)
अथवा
ज़फरनामा पर एक संक्षिप्त नोट लिखें।
(Write a short note on Zafarnama.)
उत्तर-
ज़फरनामा गुरु गोबिंद सिंह जी द्वारा औरंगजेब को लिखे गए एक पत्र का नाम है। यह पत्र फ़ारसी में लिखा गया था। इसे गुरु जी ने दीना काँगड़ (फरीदकोट) नामक स्थान से लिखा था। इस पत्र में गुरु जी ने औरंगज़ेब का तथा पहाड़ी राजाओं तथा मुग़ल सेनापतियों की ओर से कुरान की झूठी शपथ लेकर भी गुरु जी से धोखा करने का उल्लेख बड़े साहस से किया है। गुरु गोबिंद सिंह जी लिखते हैं
“ऐ औरंगज़ेब तू झूठा दीनदार बना घूमता है, तुझ में तनिक भी सत्य नहीं, तुझे खुदा तथा मुहम्मद में कोई विश्वास नहीं। यह भी कोई वीरता नहीं कि हमारे 40 भूखे सिंहों पर तेरी लाखों की सेना आक्रमण करे। तू तथा तेरे सैन्य अधिकारी सभी मक्कार तथा कायर हैं। तुम झूठे तथा धोखेबाज़ हो। निस्संदेह तुम राजाओं के राजा तथा विख्यात सेनापति हो, परंतु तुम सच्चे धर्म से कोसों दूर हो। तुम्हारे मुँह में कुछ और है तो दिल में कुछ और।”
गुरु जी के इस पत्र का औरंगजेब के दिल पर बहुत गहरा प्रभाव पड़ा। उसने गुरु जी से भेंट का संदेश भेजा, परंतु गुरु जी अभी मार्ग में ही थे कि औरंगज़ेब की मृत्यु हो गई।

प्रश्न 16.
गुरु गोबिंद सिंह जी के सामाजिक सुधारों का इतिहास में क्या महत्त्व है ? (What is the importance of social reforms of Guru Gobind Singh Ji in History ?)
उत्तर-
गुरु गोबिंद सिंह जी के सामाजिक सुधार बहुत महत्त्वपूर्ण हैं। उन्होंने खालसा पंथ की स्थापना करके समाज में एक क्रांति ला दी। इसमें सम्मिलित होने वाले निम्न जातियों के लोगों को भी उच्च जातियों के बराबर लखनाय ह। स्थान दिया गया। ऐसा करके गुरु जी ने शताब्दियों से चले आ रहे जाति-पाति के बंधनों को तोड़ कर रख दिया। महिलाओं को भी अमृतपान करवा कर पुरुषों के बराबर दर्जा दिया। गुरु जी ने अपने अनुयायियों को शराब, भांग तथा अन्य मादक पदार्थों से दूर रहने के लिए कहा। गुरु जी ने नवजात लड़कियों को मार डालने वाले लोगों से कोई संबंध न रखने का आदेश दिया। गुरु साहिब ने सती प्रथा तथा पर्दा प्रथा का जोरदार शब्दों में खंडन किया। गुरु जी ने सिखों को महिलाओं का पूर्ण सम्मान करने के लिए कहा। मसंद प्रथा का अंत कर गुरु जी ने सिखों को उनके शोषण से बचाया। वास्तव में गुरु गोबिंद सिंह जी ने एक आदर्श समाज को जन्म दिया।
प्रश्न 17.
“गुरु गोबिंद सिंह जी एक महान् संगठनकर्ता थे।” क्या आप इस विचार से सहमत हैं ?
(“Guru Gobind Singh Ji was a builder par-excellence.” Do you agree to this statement ?)
उत्तर-
गुरु गोबिंद सिंह जी उच्चकोटि के संगठनकर्ता थे। उस समय औरंगजेब किसी भी लहर, विशेष रूप से सिख लहर को सहन करने के लिए तैयार नहीं थी। उसने गुरु तेग़ बहादुर जी को शहीद कर दिया था। सिखों में मसंद प्रथा बहुत भ्रष्ट हो गई थी। हिंदू बहुत समय से निरुत्साहित थे। पहाड़ी राजा अपने स्वार्थी हितों के कारण मुग़ल सरकार से मिले हुए थे। ऐसे विरोधी तत्त्वों के बावजूद गुरु गोबिंद सिंह जी ने खालसा पंथ की स्थापना करके अपनी संगठन शक्ति का प्रमाण दिया। सचमुच यह एक महान् कार्य था। इसने लोगों में नया जोश उत्पन्न किया। वे महान् योद्धा बन गए और धर्म के नाम पर अपना सब कुछ न्यौछावर करने को तैयार हो गए। उन्होंने तब तक सुख की सांस न ली जब तक पंजाब में से मुग़लों तथा अफ़गानों के शासन का अंत न कर लिया गया तथा पंजाब ‘ में एक स्वतंत्र सिख साम्राज्य की स्थापना न कर ली गईं।

प्रश्न 18.
गुरु गोबिंद सिंह जी के व्यक्तित्व की कोई छः विशेषताएँ बताएँ। (Mention any six characteristics of Guru Gobind Singh Ji’s personality.)
उत्तर-
गुरु गोबिंद सिंह जी विश्व के महान् व्यक्तियों में से एक थे। उनके व्यक्तित्व में अनेक गुण थे।
1. उच्च चरित्र-गुरु गोबिंद सिंह जी महान् चरित्र के स्वामी थे। झूठ, छल, कपट तो उन्हें छू भी न पाया था। युद्ध हो अथवा शाँति, उन्होंने कभी भी धैर्य नहीं छोड़ा था। वह स्त्रियों का बहुत सम्मान करते थे। वह प्रत्येक प्रकार के नशे के विरुद्ध थे। उन्होंने अपने सिखों को भी उच्च नैतिक जीवन व्यतीत करने के लिए प्रेरित किया।
2. कुर्बानी की प्रतिमा-गुरु गोबिंद सिंह जी कुर्बानी के पुंज थे। 9 वर्ष की आयु में उन्होंने अपने पिता गुरु तेग़ बहादुर जी को बलिदान के लिए प्रेरित किया। उन्होंने धर्म की रक्षा के लिए अपने जीवन के सभी सुख त्याग दिए। अन्याय के विरुद्ध लड़ते हुए गुरु जी के चारों साहिबजादों, माता जी तथा अनेक सिखों ने बलिदान दिए। ऐसा उदाहरण विश्व इतिहास में कहीं भी नहीं मिलता।
3. साहसी तथा वीर-गुरु गोबिंद सिंह जी शेरों की भाँति निडर तथा वीर थे। यद्यपि गुरु जी को अनेक कठिनाइयों का सामना करना पड़ा परंतु उन्होंने कभी भी अत्याचार से समझौता न किया।
4. एक विद्वान् के रूप में-गुरु गोबिंद सिंह जी एक उच्चकोटि के कवि तथा साहित्यकार थे। उन्हें अनेक भाषाओं जैसे अरबी, फारसी, पंजाबी, हिंदी तथा संस्कृत आदि का ज्ञान था। ‘जापु साहिब’, ‘बचित्तर नाटक’, ‘ज़फ़रनामा’, ‘चंडी दी वार’ तथा ‘अकाल उस्तति’ आपकी प्रमुख रचनाएँ हैं। ये रचनाएं संपूर्ण मानवता को स्वतंत्रता, भाईचारे, सामाजिक असमानता को दूर करने तथा अत्याचारों का मुकाबला करने की प्रेरणा देती हैं। आपने अपने दरबार में उच्चकोटि के 52 कवियों को आश्रय दिया हुआ था।
5. योद्धा तथा सेनापति के रूप में-गुरु गोबिंद सिंह जी अपने समय के महान योद्धा तथा सेनापति थे। वह घुड़सवारी, तीर चलाने तथा शस्त्र चलाने में बहुत प्रवीण थे। वह प्रत्येक युद्ध में अपने सैनिकों का नेतृत्व करते थे। गुरु जी ने लड़ाई में भी नैतिक सिद्धांतों का सदैव पालन किया। उन्होंने कभी भी रणभूमि से भाग रहे सिपाहियों तथा निहत्थों पर आक्रमण नहीं किया। उनके तथा शत्रुओं के साधनों में आकाश-पाताल का अंतर था, फिर भी गुरु जी ने उनके विरुद्ध बड़ी शानदार सफलता प्राप्त की।
Source Based Questions
नोट-निम्नलिखित अनुच्छेदों को ध्यानपूर्वक पढ़िए और उनके अंत में पूछे गए प्रश्नों का उत्तर दीजिए।
1
भंगाणी की लडाई गुरु गोबिंद सिंह जी तथा पहाडी राजाओं के बीच हई प्रथम लड़ाई थी। यह लड़ाई 22 सितंबर, 1688 ई० में हुई थी। इस लड़ाई के लिए कई कारण उत्तरदायी थे। पहला, गुरु गोबिंद सिंह जी की चल रही सैनिक तैयारियों को देखकर पहाड़ी राजाओं में घबराहट फैल गई थी। उन्हें अपनी स्वतंत्रता ख़तरे में अनुभव होने लगी। दूसरा, गुरु गोबिंद सिंह जी के समाज-सुधार के कार्यों को पहाड़ी राजा अपने धर्म में हस्तक्षेप समझते थे। तीसरा, ये पहाड़ी राजा सिख संगतों को बहुत तंग करते थे। चौथा, मुग़ल सरकार भी इन पहाड़ी राजाओं को गुरु साहिब के विरुद्ध कार्यवाही करने के लिए भड़का रही थी। पाँचवां, कहलूर का राजा भीम चंद गुरु साहिब से बहुत ईर्ष्या करता था। फलस्वरूप कहलूर के शासक भीम चंद तथा श्रीनगर के शासक फ़तह शाह के नेतृत्व में पहाड़ी राजाओं के एक गठबंधन ने 22 सितंबर, 1688 ई० में भंगाणी के स्थान पर गुरु गोबिंद सिंह जी की सेना पर आक्रमण कर दिया। इस लड़ाई में सढौरा के पीर बुद्ध शाह ने गुरु साहिब को सहायता दी। सिखों ने पहाड़ी राजाओं का डटकर सामना किया। इस लड़ाई में अंततः सिखों की विजय हुई। इस विजय के कारण सिखों का उत्साह बहुत बढ़ गया तथा गुरु साहिब की प्रसिद्धि दूर-दूर तक फैल गई। पहाड़ी राजाओं ने गुरु साहिब का विरोध छोड़कर उनसे मित्रता करने में ही अपनी भलाई समझी।
- गुरु गोबिंद सिंह जी तथा पहाड़ी राजाओं के मध्य लड़ी जाने वाली पहली लड़ाई कौन-सी थी
- भंगाणी की लड़ाई का कोई एक कारण लिखें।
- भंगाणी की लड़ाई कब हुई थी ?
- 1686 ई०
- 1687 ई०
- 1688 ई०
- 1699 ई०
- भंगाणी की लड़ाई में गुरु गोबिंद सिंह जी की सहायता किसने की थी ?
- भंगाणी की लड़ाई में सिखों की विजय का क्या परिणाम निकला ?
उत्तर-
- गुरु गोबिंद सिंह जी तथा पहाड़ी राजाओं के मध्य लड़ी जाने वाली पहली लड़ाई भंगाणी की लड़ाई थी।
- सिखों की तैयारियाँ देखकर पहाड़ी शासकों में घबराहट फैल गई थी।
- 1688 ई०।
- भंगाणी की लड़ाई में गुरु गोबिंद सिंह जी की सहायता सढौस के पीर बुद्ध शाह ने की थी।
- भंगाणी की लड़ाई में सिखों की विजय के कारण गुरु गोबिंद सिंह जी की प्रसिद्धि दूर-दूर तक फैल गई थी।

2
गुरु गोबिंद सिंह जी ने 1699 ई० को बैसाखी वाले दिन श्री आनंदपुर साहिब में एक भारी दीवान सजाया। इस दीवान में विभिन्न-विभिन्न स्थानों से लगभग 80,000 व्यक्तियों ने भाग लिया। जब सभी लोगों ने अपना स्थान ग्रहण कर लिया तो गुरु जी मंच पर आए। उन्होंने मयान से तलवार निकाली और कहा-क्या आप में से कोई ऐसा सिख है जो धर्म के लिए अपना शीश भेंट करें ? ये शब्द सुनकर दीवान में सन्नाटा छा गया। परंतु जब गुरु जी ने तीसरी बार दोहराया तो दयाराम जो कि जाति का खत्री था, वह अपना बलिदान देने के लिए आगे आया। गुरु जी उसे पास ही एक तंबू में ले गए तथा खून से भरी तलवार लेकर पुनः मंच पर आ गए। उन्होंने तंबू से बाहर आकर एक और शीश की माँग की। अब दिल्ली का एक जाट धर्म दास, गुरु साहिब के पास आया, गुरु जी उसे भी तंब में ले गए तथा खन से सनी तलवार लेकर बाहर आ गए। इसी प्रकार बारी-बारी गुरु जी ने अन्य तीन शीशों की माँग की। तीन शीश देने के लिए मोहकम चंद, साहिब चंद और हिम्मत राय बारी-बारी गुरु जी के पास आए। प्रत्येक व्यक्ति को गुरु जी तंबू में लेकर गए और नंगी तलवार लेकर जाते थे। बाद में गुरु जी ने इन पाँचों को अमृत छकाया। उन्हें पाँच प्यारे कंहा गया। उन्हें खंडे का पाहुल छकाया तथा बाद में स्वयं इन प्यारों से पाहुल छका। इस प्रकार वे गोबिंद राय से गोबिंद सिंह कहलाए। इन पाँच प्यारों को अमृत छकाने के पश्चात् खालसा का नाम दिया, जिसका अर्थ है-शुद्ध अर्थात् वे शुद्ध हो चुके हैं। उन्होंने कहा खालसा गुरु में है तथा गुरु खालसे में है। इस प्रकार गुरु गोबिंद जी आपे गुरु चेला कहलाए।
- खालसा शब्द से क्या भाव है ?
- गुरु जी को सबसे पहले शीश किसने भेंट किया ?
- शीश भेंट करने वालों को सामूहिक रूप में क्या नाम दिया गया ?
- ‘आपे गुरु चेला’ किसे कहा जाता है ?
- निम्नलिखित में से किसने धर्म के लिए शीश भेंट किया ?
- धर्म दास
- मोहकम चंद
- साहिब चंद
- उपरोक्त सभी।
उत्तर-
- खालसा शब्द से भाव है-शुद्ध।
- गुरु जी को सबसे पहले अपना शीश भाई दयाराम जी ने दिया।
- शीश भेंट करने वालों को सामूहिक रूप में पाँच प्यारों का नाम दिया।
- आपे गुरु चेला, गुरु गोबिंद सिंह जी को कहा जाता है।
- उपरोक्त सभी।
3
1699 ई० में खालसा पंथ की स्थापना के पश्चात् भारी संख्या में लोग खालसा पंथ में सम्मिलित होने लगे थे। गुरु जी की दिन-प्रतिदिन बढ़ रही इस शक्ति के कारण पहाड़ी राजाओं के मन की शांति भंग हो गई थी। कहलूर के राजा भीम चंद, जिसकी रियासत में श्री आनंदपुर साहिब स्थित था, ने गुरु जी को श्री आनंदपुर साहिब छोड़ने के लिए कहा। गुरु जी ने यह माँग मानने से स्पष्ट इंकार कर दिया। उनका कहना था कि गुरु तेग़ बहादुर जी ने यह भूमि उचित मूल्य देकर क्रय की थी। इस पर भीम चंद ने कुछ अन्य पहाड़ी राजाओं से मिलकर 1701 ई० में श्री आनंदपुर साहिब के किले पर आक्रमण कर दिया। किले का घेरा कई दिनों तक जारी रहा। किले के भीतर यद्यपि सिखों की संख्या बहत कम थी, फिर भी उन्होंने पहाड़ी राजाओं का खूब डटकर सामना किया। जब पहाड़ी राजाओं को सफलता मिलने की कोई आशा न रही तो उन्होंने गुरु जी से संधि कर ली। यह संधि पहाड़ी राजाओं की एक चाल थी।
- श्री आनंदपुर साहिब की पहली लड़ाई कब हुई ?
- भीम चंद कौन था ?
- श्री आनंदपुर साहिब की पहली लड़ाई का कोई एक कारण लिखें।
- भीम चंद ने कुछ अन्य पहाड़ी राजाओं से मिलकर …………. में श्री आनंदपुर साहिब के किले पर आक्रमण कर दिया।
- श्री आनंदपुर साहिब की पहली लड़ाई का क्या परिणाम निकला ?
उत्तर-
- श्री आनंदपुर साहिब की पहली लड़ाई 1701 ई० में हुई।
- भीम चंद कहलूर का शासक था।
- सिखों के बढ़ते हुए प्रभाव को पहाड़ी शासक सहन करने के लिए तैयार नहीं थे।
- 1701 ई०।
- पहाड़ी राजाओं ने गुरु गोबिंद सिंह जी के साथ संधि कर ली।

4
खिदराना की लड़ाई गुरु जी तथा मुग़ल सेना में लड़ी जाने वाली अंतिम निर्णायक लड़ाई थी। गुरु जी माछीवाड़ा के जंगलों में अनेक कठिनाइयाँ झेलते हुए खिदराना पहुँचे थे। जब मुग़लों को इस बात का पता चला तो सरहिंद के नवाब वज़ीर खाँ ने खिदराना में गुरु साहिब पर आक्रमण करने की योजना बनाई। उसने 29 दिसंबर, 1705 ई० को एक विशाल सेना के साथ गुरु जी की सेना पर खिदराना के स्थान पर आक्रमण कर दिया। इस लड़ाई में सिखों ने बड़ी वीरता दिखाई। उन्होंने मुग़ल सेना के ऐसे छक्के छुड़ाए कि वह युद्ध स्थल छोड़ कर भाग गए। इस प्रकार गुरु जी को अपनी इस अंतिम लड़ाई में बड़ी शानदार विजय प्राप्त हुई। इस लड़ाई में वह 40 सिख भी लड़ते-लड़ते शहीद हो गए थे जो श्री आनंदपुर साहिब की दूसरी लड़ाई में गुरु जी का साथ छोड़ गए थे। उनकी कुर्बानी से प्रभावित होकर और उनके नेता महा सिंह, जो जीवन की अंतिम साँसें ले रहा था, की विनती को स्वीकार करके गुरु साहिब ने उनके द्वारा लिखे गए बेदावे को फाड़ दिया और उन्हें मुक्ति का वर दिया। इस कारण खिदराना का नाम श्री मुक्तसर साहिब पड़ गया।
- गुरु गोबिंद सिंह जी तथा मुग़लों के मध्य होने वाली अंतिम लड़ाई कौन-सी थी ?
- सरहिंद का नवाब कौन था ?
- खिदराना की लड़ाई में किन सिखों ने शहीदी प्राप्त की थी ?
- खिदराना की लड़ाई कब हुई ?
- 1699 ई०
- 1701 ई०
- 1703 ई०
- 1705 ई०
- खिदराना का आधुनिक नाम क्या है ?
उत्तर-
- गुरु गोबिंद सिंह जी तथा मुग़लों के मध्य होने वाली अंतिम लड़ाई खिदराना की थी।
- सरहिंद का नवाब वज़ीर खाँ था। .
- खिंदराना की लड़ाई में वे 40 सिख शहीदी प्राप्त कर गए थे जो श्री आनंदपुर साहिब की दूसरी लड़ाई में गुरु गोबिंद सिंह जी का साथ छोड़ गए थे।
- 1705 ई०।
- खिदराना का आधुनिक नाम श्री मुक्तसर साहिब है।
5
गुरु गोबिंद सिंह जी एक उच्चकोटि के कवि तथा साहित्यकार थे। आपके द्वारा रचित अधिकाँश साहित्य सिरसा नदी में बह गया था फिर भी जो साहित्य हम तक पहुँचा है, उससे आपके महान् विद्वान् होने का प्रमाण मिलता है। गुरु जी ने अपनी रचनाओं में अरबी, फारसी, पंजाबी, हिंदी तथा संस्कृत. आदि भाषाओं का प्रयोग किया। ‘जापु साहिब’, ‘बचित्तर नाटक’, ‘ ज़फ़रनामा’, ‘चंडी दी वार’ तथा ‘अकाल उस्तति’ आपकी प्रमुख रचनाएँ हैं। आपने विभिन्न विषयों पर भरपूर प्रकाश डाला है। आपकी लेखन कला में वह जादू है कि इसे पढ़कर मृत-हृदयों में भी जान पड़ जाती है। आपकी रचनाएँ अंधेरे में भटक रहे मनुष्यों के लिए एक प्रकाश स्तंभ का कार्य करती हैं। इसमें संपूर्ण मानवता को स्वतंत्रता, भाईचारे, सामाजिक असमानता को दूर करने तथा अत्याचारों का डटकर मुकाबला करने की प्रेरणा दी गई है। इसके अतिरिक्त ये रचनाएँ आत्मा को शांति भी प्रदान करती हैं।
- गुरु गोबिंद सिंह जी की किन्हीं दो प्रसिद्ध रचनाओं के नाम लिखें।
- बचित्तर नाटक क्या है ?
- गुरु गोबिंद सिंह जी ने औरंगजेब को कौन-सा पत्र लिखा था ?
- जफ़रनामा में क्या वर्णन किया गया है ?
- औरंगज़ेब के अत्याचारों का
- औरंगज़ेब की दारा के साथ लड़ाई।
- औरंगजेब की धार्मिक नीति
- उपरोक्त सारे।
- गुरु गोबिंद सिंह जी के साहित्य की कोई एक विशेषता लिखें।
उत्तर-
- गुरु गोबिंद सिंह जी की दो प्रसिद्ध रचनाओं के नाम बचित्तर नाटक तथा जफ़रनामा हैं।
- बचित्तर नाटक गुरु गोबिंद सिंह जी की आत्मकथा का नाम है।
- गुरु गोबिंद सिंह जी ने औरंगजेब को जफ़रनामा नामक पत्र लिखा।
- औरंगजेब के अत्याचारों का।
- इसमें मानवता को आपसी भातृत्व का संदेश दिया गया है।
![]()
![]()


![]()
![]()

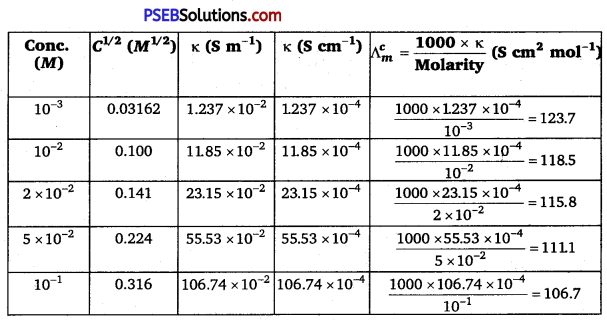
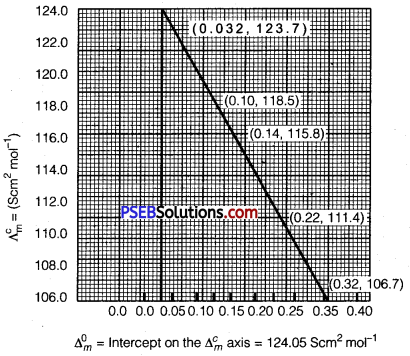
![]()
![]()

![]()

![]()

![]()

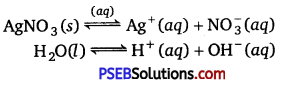
![]()


![]()
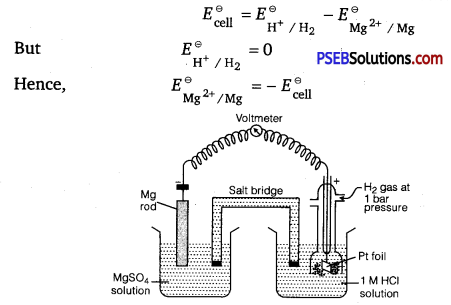
![]()

![]()
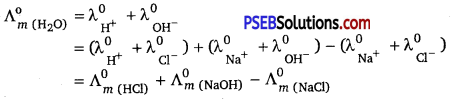
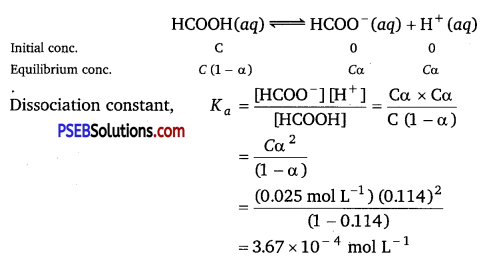
![]()
![]()
![]()