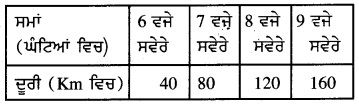
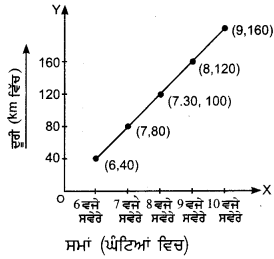
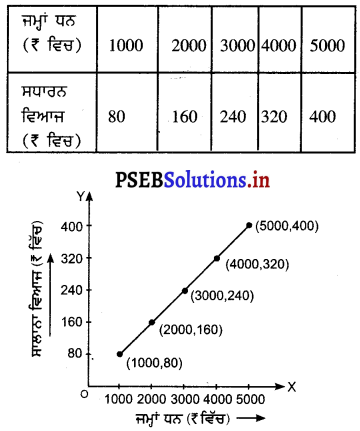
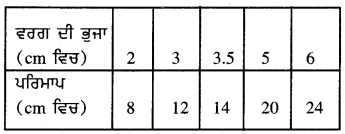
Punjab State Board PSEB 8th Class Science Book Solutions Chapter 3 ਸੰਸ਼ਲਿਸ਼ਤ ਰੇਸ਼ੇ ਅਤੇ ਪਲਾਸਟਿਕ Textbook Exercise Questions, and Answers.
PSEB Solutions for Class 8 Science Chapter 3 ਸੰਸ਼ਲਿਸ਼ਤ ਰੇਸ਼ੇ ਅਤੇ ਪਲਾਸਟਿਕ
PSEB 8th Class Science Guide ਸੰਸ਼ਲਿਸ਼ਤ ਰੇਸ਼ੇ ਅਤੇ ਪਲਾਸਟਿਕ Textbook Questions and Answers
ਪ੍ਰਸ਼ਨ 1. ਕੁੱਝ ਰੇਸ਼ੇ ਸੰਸ਼ਲਿਸ਼ਤ ਰੇਸ਼ੇ ਕਿਉਂ ਅਖਵਾਉਂਦੇ ਹਨ ?
ਉੱਤਰ-
ਕੁੱਝ ਰੇਸ਼ੇ ਸੰਸ਼ਲਿਸ਼ਤ ਅਖਵਾਉਂਦੇ ਹਨ ਕਿਉਂਕਿ ਇਹ ਕੁਦਰਤੀ ਤਾਂ ਦੁਆਰਾ ਪ੍ਰਾਪਤ ਨਹੀਂ ਹੁੰਦੇ । ਇਹਨਾਂ ਨੂੰ ਮਨੁੱਖਾਂ ਦੁਆਰਾ ਬਣਾਇਆ ਜਾਂਦਾ ਹੈ । ਸੰਸ਼ਲਿਸ਼ਤ ਰੇਸ਼ਿਆਂ ਦੀ ਕੱਚੀ ਸਾਮੱਗਰੀ ਪੇਟਰੋ-ਰਸਾਇਣਾਂ ਤੋਂ ਮਿਲਦੀ ਹੈ, ਜੋ ਖਥਰਾਟ ਬਾਲਣ, ਪੈਟਰੋਲੀਅਮ ਆਦਿ ਤੋਂ ਬਣਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 2.
ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ਕਿਹੜਾ ਕਥਨ ਸਹੀ ਹੈ ? ਰੇਯਾਨ ਇੱਕ ਸੰਸ਼ਸ਼ਤ ਰੇਸ਼ਾ ਨਹੀਂ ਹੈ, ਕਿਉਂਕਿ :
(ੳ) ਇਸਦਾ ਰੂਪ ਰੇਸ਼ਮ ਵਰਗਾ ਹੁੰਦਾ ਹੈ ।
(ਅ) ਇਸ ਨੂੰ ਲੱਕੜੀ ਦੀ ਪਲਪ ਤੋਂ ਤਿਆਰ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।
(ਈ) ਇਸਦੇ ਰੇਸ਼ਿਆਂ ਨੂੰ ਪ੍ਰਕਿਰਤਕ ਰੇਸ਼ਿਆਂ ਵਾਂਗ ਬੁਣਿਆ ਜਾ ਸਕਦਾ ਹੈ ।
ਉੱਤਰ-
(ਅ) ਇਸ ਨੂੰ ਲੱਕੜੀ ਦੀ ਪਲਪ ਤੋਂ ਤਿਆਰ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 3.
ਖ਼ਾਲੀ ਸਥਾਨ ਭਰੋ
(ੳ) ਸੰਸ਼ਲਿਸ਼ਤ ਰੇਸ਼ੇ ……… ਅਤੇ ………… ਰੇਸ਼ੇ ਵੀ ਅਖਵਾਉਂਦੇ ਹਨ ।
(ਅ) ਸੰਸ਼ਲਿਸ਼ਤ ਰੇਸ਼ੇ ਕੱਚੇ ਮਾਲ ਤੋਂ ਸੰਸ਼ਲਿਸ਼ਤ ਕੀਤੇ ਜਾਂਦੇ ਹਨ , ਜੋ ……….. ਅਖਵਾਉਂਦੇ ਹਨ ।
( ਸੰਸ਼ਸ਼ਤ ਰੇਸ਼ੇ ਵਾਂਗ ਪਲਾਸਟਿਕ ਵੀ ਇੱਕ ……….. ਹੈ ।
ਉੱਤਰ-
(ੳ) ਮਾਨਵ ਨਿਰਮਿਤ, ਬਣਾਉਟੀ ।
(ਅ) ਪੈਟਰੋਰਸਾਇਣ (ਈ ਸੰਸ਼ਲਿਸ਼ਤ ਰੇਸ਼ਾ ।
ਪ੍ਰਸ਼ਨ 4.
ਨਾਈਲਾਂਨ ਰੇਸ਼ਿਆਂ ਤੋਂ ਨਿਰਮਿਤ ਦੋ ਵਸਤਾਂ ਦੇ ਨਾਂ ਦੱਸੋ ਜੋ ਨਾਈਲਾਂਨ ਰੇਸ਼ੇ ਦੀ ਮਜ਼ਬੂਤੀ ਦਰਸਾਉਂਦੇ ਹੋਣ ।
ਉੱਤਰ-
ਪੈਰਾਸ਼ੂਟ, ਤੰਬੂ, ਰੱਸੇ|
ਪ੍ਰਸ਼ਨ 5.
ਭੋਜਨ ਪਦਾਰਥਾਂ ਨੂੰ ਭੰਡਾਰਨ ਕਰਨ ਦੇ ਲਈ ਪਲਾਸਟਿਕ ਬਰਤਨਾਂ ਦੀ ਵਰਤੋਂ ਦੇ ਤਿੰਨ ਪ੍ਰਮੁੱਖ ਲਾਭ ਦੱਸੋ ।
ਉੱਤਰ-
ਭੋਜਨ ਪਦਾਰਥਾਂ ਦੇ ਭੰਡਾਰਨ ਕਰਨ ਦੇ ਲਈ ਪਲਾਸਟਿਕ ਦੇ ਬਰਤਨਾਂ ਦੇ ਲਾਭ
- ਇਹ ਭੋਜਨ, ਪਾਣੀ ਅਤੇ ਹਵਾ ਨਾਲ ਕਿਰਿਆ ਨਹੀਂ ਕਰਦੇ ।
- ਇਹ ਮਜਬੂਤ ਤੇ ਹਲਕੇ ਹੁੰਦੇ ਹਨ ।
- ਇਹ ਵੱਖ-ਵੱਖ ਆਕਾਰ, ਰੂਪ ਅਤੇ ਰੰਗ ਵਿੱਚ ਮਿਲਦੇ ਹਨ ।
![]()
ਪ੍ਰਸ਼ਨ 6.
ਥਰਮੋਪਲਾਸਟਿਕ ਅਤੇ ਥਰਮੋਸੈਟਿੰਗ ਪਲਾਸਟਿਕ ਦੇ ਵਿੱਚ ਅੰਤਰ ਸਪੱਸ਼ਟ ਕਰੋ ।
ਉੱਤਰ-
ਬਰਮੋਪਲਾਸਟਿਕ ਅਤੇ ਥਰਮੋਸੈਟਿੰਗ ਪਲਾਸਟਿਕ ਦੇ ਵਿੱਚ ਅੰਤਰ-
| ਬਰਮੋਪਲਾਸਟਿਕ | ਬਰਮੋਸੈਟਿੰਗ ਪਲਾਸਟਿਕ |
| (i) ਇਹ ਆਸਾਨੀ ਨਾਲ ਮੁੜ ਸਕਦਾ ਹੈ । | (i) ਇਹ ਆਸਾਨੀ ਨਾਲ ਮੁੜ ਨਹੀਂ ਸਕਦਾ| |
| (ii) ਗਰਮ ਕਰਨ ਨਾਲ ਇਹਨਾਂ ਦਾ ਆਕਾਰ ਬਦਲ ਜਾਂਦਾ ਹੈ । | (ii) ਤਾਪ ਦਾ ਇਹਨਾਂ ਤੇ ਕੋਈ ਅਸਰ ਨਹੀਂ ਹੁੰਦਾ । |
| (iii) ਇਹਨਾਂ ਦੀ ਮੁੜ ਵਰਤੋਂ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ । | (iii) ਇਹਨਾਂ ਦੀ ਮੁੜ ਵਰਤੋਂ ਨਹੀਂ ਕੀਤੀ ਜਾ ਸਕਦੀ । |
| (iv) ਗਰਮ ਕਰਨ ਤੇ ਇਸ ਨੂੰ ਕਿਸੇ ਵੀ ਸਾਂਚੇ ਵਿੱਚ ਢਾਲਿਆ ਜਾ ਸਕਦਾ ਹੈ । ਉਦਾਹਰਨ-ਪੀ.ਵੀ.ਸੀ. (PVC), ਪਾਲੀਥੀਨ । | (iv) ਇਸ ਨੂੰ ਗਰਮ ਕਰਨ ਤੇ ਇੱਕੋ ਵਾਰ ਹੀ ਸਾਂਚੇ ਵਿੱਚ ਢਾਲਿਆ ਜਾ ਸਕਦਾ ਹੈ । ਉਦਾਹਰਨ-ਬੋਕੇਲਾਈਟ, ਮੈਲਾਮਾਈਨ । |
ਪ੍ਰਸ਼ਨ 7.
ਸਮਝਾਓ, ਥਰਮੋਸੈਟਿੰਗ ਪਲਾਸਟਿਕ ਤੋਂ ਹੇਠ ਲਿਖੇ ਕਿਉਂ ਬਣਾਏ ਜਾਂਦੇ ਹਨ
(ਉ) ਪਤੀਲੇ ਦਾ ਹੱਥਾ।
(ਅ) ਬਿਜਲੀ ਦੇ ਪਲੱਗ/ਸਵਿੱਚ/ਪਲੱਗ ਬੋਰਡ ।
ਉੱਤਰ-
(ੳ) ਪਤੀਲੇ ਦਾ ਹੱਥਾ-ਬਰਮੋਸੈਟਿੰਗ ਪਲਾਸਟਿਕ ਤੋਂ ਬਣਾਏ ਜਾਂਦੇ ਹਨ, ਕਿਉਂਕਿ ਪਲਾਸਟਿਕ ਬਿਜਲੀ ਦਾ ਕੁਚਾਲਕ ਹੈ, ਪਤੀਲੇ ਦਾ ਹੱਥਾ ਅੱਗ ਅਤੇ ਤਾਪ ਨੂੰ ਸਹਿ ਲੈਂਦਾ ਹੈ ।
(ਅ) ਬਿਜਲੀ ਪਲੱਗ/ਸਵਿੱਚ/ਪਲੱਗ ਬੋਰਡ ਆਦਿ ਨੂੰ ਥਰਮੋਸੈਟਿੰਗ ਪਲਾਸਟਿਕ ਤੋਂ ਬਣਾਇਆ ਜਾਂਦਾ ਹੈ ਕਿਉਂਕਿ ਇਹ ਪਲਾਸਟਿਕ ਬਿਜਲੀ ਦਾ ਕੁਚਾਲਕ ਹੈ ਅਤੇ ਟਿਕਾਊ ਹੁੰਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 8.
ਹੇਠ ਲਿਖੇ ਪਦਾਰਥਾਂ ਨੂੰ ‘‘ਦੁਬਾਰਾ ਚੱਕਰਿਤ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ’ ਅਤੇ ‘‘ਦੁਬਾਰਾ ਚੱਕਤ ਨਹੀਂ ਕੀਤੇ ਜਾ ਸਕਦੇ ਹਨ’ ਵਿੱਚ ਵਰਗੀਕ੍ਰਿਤ ਕਰੋ ਟੈਲੀਫ਼ੋਨ ਯੰਤਰ, ਪਲਾਸਟਿਕ ਖਿਡੌਣੇ, ਕੁੱਕਰ ਦੇ ਹੱਥੇ, ਸਮਾਨ ਲਿਆਉਣ ਵਾਲੇ ਥੈਲੇ, ਬਾਲ ਪੁਆਇੰਟ ਪੈਂਨ, ਪਲਾਸਟਿਕ ਦੀਆਂ ਕੌਲੀਆਂ, ਬਿਜਲੀ ਤਾਰਾਂ ਦੇ ਪਲਾਸਟਿਕ ਕਵਰ, ਪਲਾਸਟਿਕ ਦੀਆਂ ਕੁਰਸੀਆਂ, ਬਿਜਲੀ ਦੇ ਵਿੱਚ ।
ਉੱਤਰ-
ਦੁਬਾਰਾ ਚੱਕਰਿਤ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ-ਖਿਡੌਣੇ, ਸਮਾਨ ਲਿਆਉਣ ਵਾਲੇ ਥੈਲੇ, ਬਾਲ ਪੁਆਇੰਟ ਪੈਂਨ, ਪਲਾਸਟਿਕ ਦੇ ਕਟੋਰੇ, ਪਲਾਸਟਿਕ ਦੀਆਂ ਕੁਰਸੀਆਂ, ਬਿਜਲੀ ਤਾਰਾਂ ਦੇ ਪਲਾਸਟਿਕ ਕਵਰ । ਦੁਬਾਰਾ ਚੱਕਰਿਤ ਨਹੀਂ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ-ਟੈਲੀਫ਼ੋਨ ਯੰਤਰ, ਕੁੱਕਰ ਦੇ ਹੱਥੇ, ਬਿਜਲੀ ਸਵਿੱਚ ।
ਪ੍ਰਸ਼ਨ 9.
ਰਾਣਾ ਗਰਮੀਆਂ ਲਈ ਕਮੀਜ਼ਾਂ ਖਰੀਦਣਾ ਚਾਹੁੰਦਾ ਹੈ । ਉਸ ਨੂੰ ਸੂਤੀ ਕਮੀਜ਼ਾਂ ਖ਼ਰੀਦਣੀਆਂ ਚਾਹੀਦੀਆਂ ਹਨ ਜਾਂ ਸੰਸ਼ਲਿਸ਼ਤ ? ਕਾਰਣ ਸਹਿਤ ਰਾਣਾ ਨੂੰ ਸਲਾਹ ਦਿਓ ।
ਉੱਤਰ-
ਰਾਣੇ ਨੂੰ ਸੂਤੀ ਕਮੀਜ਼ਾਂ ਖ਼ਰੀਦਣੀਆਂ ਚਾਹੀਦੀਆਂ ਹਨ । ਕਿਉਂਕਿ
- ਸੂਤੀ ਕਮੀਜ਼ਾਂ ਵਿੱਚ ਛੇਕ ਹੁੰਦੇ ਹਨ ।
- ਸੂਤੀ ਕਮੀਜ਼ਾਂ ਪਸੀਨਾ ਸੋਖ ਕੇ ਸਰੀਰ ਨੂੰ ਸੁੱਕਾ ਰੱਖਦੀਆਂ ਹਨ ਜਦੋਂ ਕਿ ਸੰਸ਼ਲਿਸ਼ਤ ਕਮੀਜ਼ਾਂ ਨਾ ਤਾਂ ਪਸੀਨਾ ਸੋਖਦੀਆਂ ਹਨ ਅਤੇ ਨਾ ਹੀ ਛੇਕ ਯੁਕਤ ਹੁੰਦੀਆਂ ਹਨ ।
ਪ੍ਰਸ਼ਨ 10.
ਉਦਾਹਰਨ ਦੇ ਕੇ ਪ੍ਰਦਰਸ਼ਿਤ ਕਰੋ ਕਿ ਪਲਾਸਟਿਕ ਦਾ ਸੁਭਾਅ ਅਣ-ਖੋਰ ਹੈ ?
ਉੱਤਰ-
ਪਲਾਸਟਿਕ ਹਵਾ, ਪਾਣੀ ਆਦਿ ਨਾਲ ਕਿਰਿਆ ਨਹੀਂ ਕਰਦਾ ਇਸ ਲਈ ਇਹ ਗਲਦਾ|ਸੜਦਾ/ਖੁਰਦਾ ਨਹੀਂ ਹੈ ।
ਉਦਾਹਰਨ-
- ਵੱਖ-ਵੱਖ ਰਸਾਇਣ ਬੋਤਲਾਂ ਵਿੱਚ ਸਟੋਰ ਕੀਤੇ ਜਾਂਦੇ ਹਨ ।
- ਪਾਣੀ, ਪਲਾਸਟਿਕ ਦੀਆਂ ਬੋਤਲਾਂ ਵਿੱਚ ਰੱਖਿਆ ਜਾਂਦਾ ਹੈ ।
- ਆਚਾਰ ਅਤੇ ਭੋਜਨ ਪਦਾਰਥ ਪਲਾਸਟਿਕ ਦੇ ਬਰਤਨਾਂ ਵਿੱਚ ਭੰਡਾਰ ਕੀਤੇ ਜਾਂਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 11.
ਕੀ ਦੰਦ ਸਾਫ਼ ਕਰਨ ਵਾਲੇ ਬੁਰਸ਼ ਦੇ ਵਾਲ (ਬ੍ਰਿਸਟਲ ਅਤੇ ਹੱਥਾ ਇੱਕ ਹੀ ਪਦਾਰਥ ਦੇ ਬਣਨੇ ਚਾਹੀਦੇ ਹਨ ? ਆਪਣਾ ਉੱਤਰ ਸਪੱਸ਼ਟ ਕਰੋ ।
ਉੱਤਰ-
ਬਿਸਟਲ ਦੰਦਾਂ ਦੀ ਸਫ਼ਾਈ ਲਈ ਹਨ ਪਰ ਬੁਰਸ਼ ਦਾ ਹੈੱਡਲ ਸਹਾਰੇ ਲਈ ਹੁੰਦਾ ਹੈ । ਬ੍ਰਿਸਟਲ ਨਰਮ ਲਚਕੀਲੇ ਅਤੇ ਮਜ਼ਬੂਤ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ ਜਦੋਂ ਕਿ ਹੈਂਡਲ ਸਖ਼ਤ ਅਤੇ ਮਜ਼ਬੂਤ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ । ਇਸ ਲਈ ਬੁਰਸ਼ ਦਾ ਹੈਂਡਲ ਤੇ ਬ੍ਰਿਸਟਲ ਵੱਖ-ਵੱਖ ਪਦਾਰਥਾਂ ਦੇ ਬਣਾਉਣੇ ਚਾਹੀਦੇ ਹਨ !
ਪ੍ਰਸ਼ਨ 12.
“ਜਿੱਥੋਂ ਤੱਕ ਸੰਭਵ ਹੋ ਸਕੇ ਪਲਾਸਟਿਕ ਦੀ ਵਰਤੋਂ ਤੋਂ ਬਚੋਂ`ਇਸ ਕਥਨ ਤੇ ਸਲਾਹ ਦਿਓ ।
ਉੱਤਰ-
ਪਲਾਸਟਿਕ ਇੱਕ ਬਹੁਤ ਹੀ ਉਪਯੋਗੀ ਪਦਾਰਥ ਹੈ ਪਰ ਇਹ ਵਾਤਾਵਰਣ ਦਾ ਮਿੱਤਰ ਨਹੀਂ ਹੈ ਕਿਉਂਕਿ ਇਹ ਨਾ ਤਾਂ ਜਲਦੀ ਜਲਦਾ ਹੈ ਤੇ ਨਾ ਹੀ ਕੁਦਰਤੀ ਜੀਵਾਣੂਆਂ ਦੁਆਰਾ ਆਸਾਨੀ ਨਾਲ ਅਪਘਟਿਤ ਹੁੰਦਾ ਹੈ । ਵਾਤਾਵਰਣ ਨੂੰ ਸਾਫ਼ ਰੱਖਣ ਲਈ ਇਹਨਾਂ ਦੀ ਵਰਤੋਂ ਜਿੱਥੇ ਤੱਕ ਸੰਭਵ ਹੋਵੇ ਘੱਟ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 13.
ਕਾਲਮ (ਉ) ਦੇ ਪਦਾਂ ਦਾ ਕਾਲਮ (ਅ) ਵਿੱਚ ਦਿੱਤੇ ਗਏ ਵਾਕ ਖੰਡਾਂ ਨਾਲ ਸਹੀ ਮਿਲਾਨ ਕਰੋ –
| ਕਾਂਲਮ (ਉ) | ਕਾਂਲਮ (ਅ) |
| (1) ਪੱਲੀਐਸਟਰ | (ੳ) ਲੱਕੜੀ ਦੀ ਪਲਪ ਦੀ ਵਰਤੋਂ ਕਰਕੇ ਤਿਆਰ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । |
| (2) ਟੇਫ਼ਲਾਂਨ | (ਅ) ਪੈਰਾਸ਼ੂਟ ਅਤੇ ਜੁਰਾਬਾਂ ਬਣਾਉਣ ਵਿੱਚ ਵਰਤਿਆ ਜਾਂਦਾ ਹੈ । |
| (3) ਰੇਯਾਨ | (ਈ) ਨਾ ਚਿਪਕਣ ਵਾਲੇ ਭੋਜਨ ਬਣਾਉਣ ਵਾਲੇ ਬਰਤਨਾਂ ਦੇ ਨਿਰਮਾਣ ਵਰਤਿਆ ਜਾਂਦਾ ਹੈ । |
| (4) ਨਾਈਲਾਂਨ | (ਸ) ਕੱਪੜੇ ਵਿੱਚ ਆਸਾਨੀ ਨਾਲ ਵੱਟ ਨਹੀਂ ਪੈਂਦੇ | |
ਉੱਤਰ –
| ਕੱਲਮ (ਉ) | ਕਾਂਲਮ (ਅ) |
| (1) ਪਾਲੀਐਸਟਰ | (ਸ) ਕੱਪੜੇ ਵਿੱਚ ਆਸਾਨੀ ਨਾਲ ਵੱਟ ਨਹੀਂ ਪੈਂਦੇ । |
| (2) ਫ਼ਲਾਂਨ | (ਈ) ਨਾ ਚਿਪਕਣ ਵਾਲੇ ਭੋਜਨ ਬਣਾਉਣ ਵਾਲੇ ਬਰਤਨਾਂ ਦੇ ਨਿਰਮਾਣ ਵਰਤਿਆ ਜਾਂਦਾ ਹੈ। |
| (3) ਰੇਯਾਨ | (ੳ) ਲੱਕੜੀ ਦੀ ਪਲਪ ਦੀ ਵਰਤੋਂ ਕਰਕੇ ਤਿਆਰ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । |
| (4) ਨਾਈਲਾਂਨ | (ਅ) ਪੈਰਾਸ਼ੂਟ ਅਤੇ ਜ਼ੁਰਾਬਾਂ ਬਣਾਉਣ ਵਿੱਚ ਵਰਤਿਆ ਜਾਂਦਾ ਹੈ । |
ਪ੍ਰਸ਼ਨ 14.
‘‘ਸੰਬਲਿਸ਼ਤ ਰੇਸ਼ਿਆਂ ਦਾ ਉਦਯੋਗਿਕ ਨਿਰਮਾਣ ਅਸਲ ਵਿੱਚ ਜੰਗਲਾਂ ਦੇ ਸੁਰੱਖਿਅਣ ਵਿੱਚ ਸਹਾਇਕ ਹੋ ਰਿਹਾ ਹੈ ।’ ਟਿੱਪਣੀ ਕਰੋ ।
ਉੱਤਰ-
ਕੁਦਰਤੀ ਰੇਸ਼ੇ ਕੁਦਰਤੀ ਸ੍ਰੋਤਾਂ ਤੋਂ ਮਿਲਦੇ ਹਨ ਪਰੰਤੂ ਸੰਸ਼ਲਿਸ਼ਤ ਰੇਸ਼ੇ ਦੂਸਰੇ ਪਦਾਰਥਾਂ ਤੋਂ ਤਿਆਰ ਕੀਤੇ ਜਾਂਦੇ ਹਨ । ਇਸ ਲਈ ਸੰਸ਼ਸ਼ਤ ਰੇਸ਼ੇ ਕੁਦਰਤੀ ਉਪਜ ਤੇ ਨਿਰਭਰ ਨਹੀਂ ਕਰਦੇ । ਇਸ ਲਈ ਸੰਸ਼ਲਿਸ਼ਤ ਰੇਸ਼ਿਆਂ ਦਾ ਉਦਯੋਗਿਕ ਨਿਰਮਾਣ ਅਸਲ ਵਿੱਚ ਜੰਗਲਾਂ ਦੇ ਸੁਰੱਖਿਅਣ ਵਿੱਚ ਸਹਾਇਕ ਹੈ ।
ਪ੍ਰਸ਼ਨ 15.
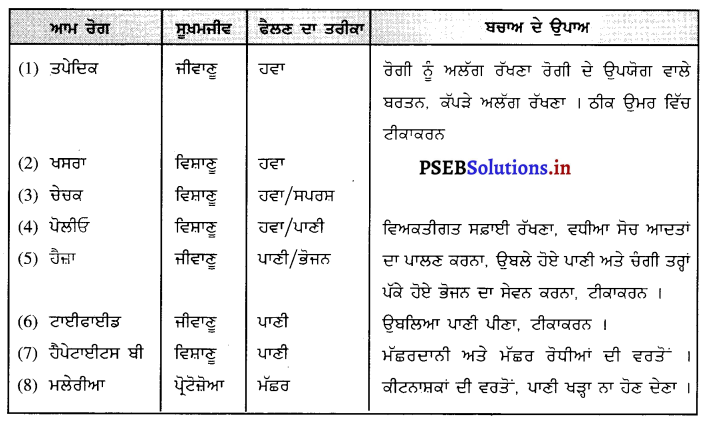
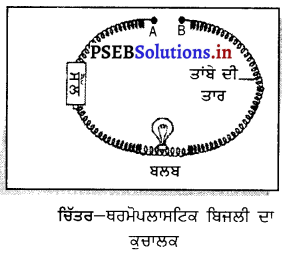
ਇਹ ਪ੍ਰਦਰਸ਼ਿਤ ਕਰਨ ਲਈ ਇੱਕ ਕਿਰਿਆ ਦਾ ਵਰਣਨ ਕਰੋ ਕਿ ਥਰਮੋਪਲਾਸਟਿਕ ਬਿਜਲੀ ਦਾ ਕੁਚਾਲਕ ਹੈ ।
ਉੱਤਰ-
ਕਿਰਿਆ-ਕੁੱਝ ਥਰਮੋਪਲਾਸਟਿਕ ਦੀਆਂ ਵਸਤੂਆਂ ਲਉ ਜਿਵੇਂ-ਪਾਲੀਥੀਨ, ਪੀ. ਵੀ. ਸੀ. ਨਾਈਲਾਂਨ, ਪਾਲੀਸਟਾਈਰੀਨ ਆਦਿ । ਚਿੱਤਰ ਵਿੱਚ ਦਰਸਾਏ ਪਰੀਪਥ ਨੂੰ ਪੂਰਾ ਕਰੋ ਅਤੇ ਦੋਨਾਂ ਟਰਮੀਨਲਾਂ ਦੇ ਵਿੱਚ ਨਾਈਲੱਨ ਦਾ ਟੁਕੜਾ ਰੱਖੋ । ਜੇ ਬਲਬ ਜਗ ਜਾਵੇ ਤਾਂ ਸਮਝ ਲਉ ਕਿ ਬਿਜਲੀ ਦਾ ਸੂਚਾਲਕ ਹੈ, ਨਹੀਂ ਤਾਂ ਕੁਚਾਲਕ । ਹੁਣ ਇਹ ਕਿਰਿਆ ਹੋਰ ਪਦਾਰਥਾਂ ਨਾਲ ਦੋਹਰਾਉ । ਸਾਰੇ ਪਦਾਰਥਾਂ ਨਾਲ ਬਲਬ ਜਗਦਾ ਨਹੀਂ ਹੈ । ਇਸ ਤੋਂ ਇਹ ਸਿੱਧ ਹੁੰਦਾ ਹੈ ਕਿ ਥਰਮੋਪਲਾਸਟਿਕ ਬਿਜਲੀ ਦਾ ਕੁਚਾਲਕ ਹੈ ॥
PSEB Solutions for Class 8 Science ਸੰਸ਼ਲਿਸ਼ਤ ਰੇਸ਼ੇ ਅਤੇ ਪਲਾਸਟਿਕ Important Questions and Answers
(A) ਬਹੁ-ਵਿਕਲਪੀ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ
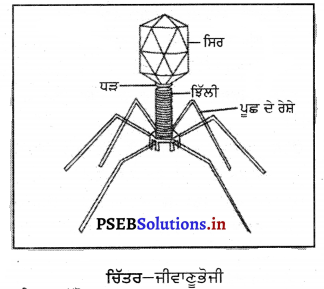
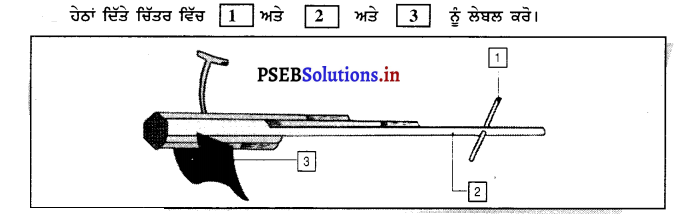
1. ਹੇਠਾਂ ਦਿੱਤੇ ਚਿੱਤਰ ਵਿਚ ਚਟਾਨ ਉੱਤੇ ਚੜ੍ਹਨ ਲਈ ਲੜਕਾ ਰੱਸੇ ਦੀ ਵਰਤੋਂ ਕਰਦਾ ਹੋਇਆ ਦਰਸਾਇਆ ਗਿਆ ਹੈ । ਦੱਸੋ ਇਹ ਰੱਸਾ ਕਿਸ ਪਦਾਰਥ ਦਾ ਬਣਿਆ ਹੋਇਆ ਉੱਚਿਤ ਹੁੰਦਾ ਹੈ ?

(ਉ) ਕਪਾਹ
(ਅ) ਉੱਨ
(ਈ) ਨਾਈਲਾਂਨ
(ਸ) ਇਹਨਾਂ ਵਿਚੋਂ ਕੋਈ ਵੀ ਨਹੀਂ ।
ਉੱਤਰ-
(ਈ) ਨਾਈਲਾਂਨ ।
2. ਹੇਠ ਲਿਖਿਆਂ ਵਿਚੋਂ ਕਿਹੜਾ ਬਣਾਉਟੀ ਰੇਸ਼ਮ ਕਹਾਉਂਦਾ ਹੈ ?
(ਉ) ਰਬੜ
(ਅ) ਟੈਫਲਾਨ
(ਈ) ਰੇਯਾਨ
(ਸ) ਪਾਲੀਥੀਨ ।
ਉੱਤਰ-
(ਈ) ਰੇਯਾਨ ।
3. ਪਾਲਿਸਟਰ ਦੇ ਕੱਪੜੇ ਬਣਾਉਣ ਲਈ ਵਰਤਿਆ ਜਾਂਦਾ ਹੈ
(ਉ) P.E.T.
(ਅ) ਐਲਿਕ
(ੲ) ਟੈਰੀਲੀਨ
(ਸ) ਇਨ੍ਹਾਂ ਵਿਚੋਂ ਕੋਈ ਵੀ ਨਹੀਂ ।
ਉੱਤਰ-
(ਈ) ਟੈਰੀਲੀਨ ।
![]()
4. ਅੱਜ ਕਲਾਸ ਵਿੱਚ ਪੜ੍ਹਾਈ ਦੌਰਾਨ ਨਿਸ਼ਾ ਨੂੰ ਪਤਾ ਲਗਾ ਕਿ ਇੱਕ ਅਜਿਹਾ ਪਲਾਸਟਿਕ ਹੈ ਜੋ ਗਰਮ ਕਰਨ ਤੇ ਆਪਣਾ ਰੂਪ ਬਦਲ ਲੈਂਦਾ ਹੈ । ਉਸ ਪਦਾਰਥ ਨੂੰ ਕੀ ਕਹਿੰਦੇ ਹਨ ?
(ਉ) ਪਲਾਸਟਿਕ
(ਅ ਥਰਮੋਪਲਾਸਟਿਕ
(ਈ) ਐਜ਼ਿਲਕ .
(ਸ) ਉਪਰੋਕਤ ਸਾਰੇ ।
ਉੱਤਰ-
(ਅ) ਥਰਮੋਪਲਾਸਟਿਕ ।
5. ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ਕਿਹੜਾ ਕੁਦਰਤੀ ਰੇਸ਼ਾ ਹੈ ?
(ਉ) ਰੇਆਨ
(ਅ) ਫੈਰੀਲੀਨ
(ਇ) ਉੱਨ
(ਸ) ਨਾਈਲਾਨ ।
ਉੱਤਰ-
(ਈ) ਉੱਨ ।
6. ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ਕਿਹੜਾ ਰੇਸ਼ਾ ਮਨੁੱਖ ਦੁਆਰਾ ਬਣਾਇਆ ਗਿਆ ਹੈ ?
(ੳ) ਕਪਾਹ
(ਅ) ਉੱਨ
(ਈ) ਰੇਆਨ
(ਸ) ਰੇਸ਼ਮ ।
ਉੱਤਰ-
(ਈ) ਰੇਆਨ ॥
7. ਇਹਨਾਂ ਵਿੱਚੋਂ ਕਿਹੜਾ ਜੈਵ-ਨਿਮਨੀਕਰਨੀ ਪਦਾਰਥ ਹੈ ?
(ਉ) ਧਾਤ
(ਅ) ਪਲਾਸਟਿਕ
(ਇ) ਕਾਗ਼ਜ਼
(ਸ) ਇਹ ਸਾਰੇ ਪਦਾਰਥ ।
ਉੱਤਰ-
(ਈ) ਕਾਗ਼ਜ਼ ।
8. ਥਰਮੋਪਲਾਸਟਿਕ ਦੀ ਕਿਹੜੀ ਕਿਸਮ ਤਾਪ ਅਤੇ ਬਿਜਲੀ ਦੀ ਕੁਚਾਲਕ ਹੈ ਜਿਸ ਦੀ ਵਰਤੋਂ ਸਵਿੱਚ ਬਣਾਉਣ ਲਈ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ?
(ਉ) ਨਾਈਲਾਂਨ
(ਅ) ਬੈਕੇਲਾਈਟ
(ਈ) ਮੈਲਾਮਾਈਨ
(ਸ) ਪਾਲੀਥੀਨ ।
ਉੱਤਰ-
(ਅ) ਬੈਕੇਲਾਈਟ ॥
9. ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ਕਿਹੜਾ ਥਰਮੋਪਲਾਸਟਿਕ ਹੈ ?
(ਉ) ਨਾਈਲਾਂਨ
(ਅ) ਪਾਲੀਥੀਨ
(ਈ) ਐਕਰਿਨਿਕ
(ਸ) ਬੈਕੇਲਾਈਟ ।
ਉੱਤਰ-
(ਸ) ਬੈਕੇਲਾਈਟ ।
10. ਸੰਸ਼ਲੇਸ਼ਿਤ ਰੇਸ਼ੇ ਛੋਟੀ ਇਕਾਈਆਂ ਦੇ ਮੇਲ ਤੋਂ ਬਣੇ ਹੁੰਦੇ ਹਨ, ਜਿਹਨਾਂ ਨੂੰ ਆਖਦੇ ਹਨ
(ਉ) ਸੈੱਲ .
(ਅ) ਅਣੂ
(ਈ) ਪਾਲੀਮਰ
(ਸ) ਇਹਨਾਂ ਵਿੱਚੋਂ ਕੋਈ ਨਹੀਂ ।
ਉੱਤਰ-
(ਅ) ਅਣੂ ।
11. ਸੈਰੀਕਲਚਰ ਹੇਠਾਂ ਦਿੱਤੇ ਜੀਵਾਂ ਵਿੱਚੋਂ ਕਿਸ ਜੀਵ ਦਾ ਪਾਲਣਾ ਹੈ
(ੳ) ਭੇਡ
(ਅ) ਬੱਕਰੀ
(ਈ) ਖਰਗੋਸ਼
(ਸ) ਰੇਸ਼ਮ ਕੀਟ ।
ਉੱਤਰ-
(ਸ) ਰੇਸ਼ਮ ਕੀਟ ।
12. ਕੁਦਰਤੀ ਰੇਸ਼ਾ ਹੈ
(ਉ) ਰੇਆਨ
(ਅ) ਨਾਈਲਾਂ
(ਇ) ਪਟਸਨ
(ਸ) ਪਾਲੀਸਟਰ ।
ਉੱਤਰ-
(ੲ) ਪਟਸਨ ।
13. ………. ਦਾ ਪਾਲਣਾ ਸੈਰੀਕਲਚਰ ਹੈ ।
(ੳ) ਭੇਡ .
(ਅ) ਬੱਕਰੀ
(ੲ) ਸ਼ਹਿਦ ਦੀ ਮੱਖੀ
(ਸ) ਰੇਸ਼ਮ ਦਾ ਕੀੜਾ ।
ਉੱਤਰ-
(ਸ) ਰੇਸ਼ਮ ਦਾ ਕੀੜਾ ।
ਬਹੁਤ ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ
ਪ੍ਰਸ਼ਨ 1.
ਕੁੱਝ ਕੁਦਰਤੀ ਰੇਸ਼ਿਆਂ ਦੇ ਨਾਂ ਲਿਖੋ ।
ਉੱਤਰ-
ਕਪਾਹ, ਉੱਨ, ਰੇਸ਼ਮ ।
ਪ੍ਰਸ਼ਨ 2.
ਇੱਕ ਕੁਦਰਤੀ ਬਹੁਲਕ ਦਾ ਨਾਂ ਲਿਖੋ ।
ਉੱਤਰ-
ਸੈਲੂਲੋਜ਼ ।
ਪ੍ਰਸ਼ਨ 3.
ਉਸ ਰੇਸ਼ੇ ਦਾ ਨਾਂ ਦੱਸੋ ਜੋ ਕਿ ਰੇਸ਼ਮ ਵਰਗਾ ਹੈ ਪਰ ਮਾਨਵ ਨਿਰਮਿਤ ਹੈ ।
ਉੱਤਰ-
ਰੇਆਂਨ ।
ਪ੍ਰਸ਼ਨ 4.
ਕਿਸ ਰੇਸ਼ੇ ਨਾਲ ਪੈਰਾਸ਼ੂਟ ਅਤੇ ਤੰਬੂ ਬਣਾਏ ਜਾਂਦੇ ਹਨ ?
ਉੱਤਰ-
ਨਾਈਲਾਨ ।
ਪ੍ਰਸ਼ਨ 5. PET ਕੀ ਹੈ ?
ਉੱਤਰ-
ਇਹ ਪਾਲੀਐਸਟਰ ਦੀ ਇੱਕ ਕਿਸਮ ਹੈ ਜਿਸਦੀ ਵਰਤੋਂ ਬੋਤਲਾਂ, ਬਰਤਨ, ਫ਼ਿਲਮ ਦੇ ਨਿਰਮਾਣ ਵਿੱਚ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 6.
ਪੈਰਾਸ਼ੂਟ ਅਤੇ ਚੱਟਾਨਾਂ ਤੇ ਚੜ੍ਹਨ ਵਾਲੇ ਰੱਸੇ ਨਾਇਲਾਨ ਦੇ ਕਿਉਂ ਬਣਾਏ ਜਾਂਦੇ ਹਨ ?
ਉੱਤਰ-
ਆਪਣੀ ਮਜ਼ਬੂਤੀ ਦੇ ਕਾਰਨ ।
ਪ੍ਰਸ਼ਨ 7.
ਪਲਾਸਟਿਕ ਦੀਆਂ ਕੁੱਝ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਪਲਾਸਟਿਕ ਵਿੱਚ ਪੁਨਰਚੱਕਰਣ, ਮੁੜ ਵਰਤੋਂ, ਰੰਗਣ, ਪਿਘਲਾਉਣ, ਸ਼ੀਟਾਂ ਅਤੇ ਤਾਰਾਂ ਬਣਾਉਣ ਵਾਲੇ ਗੁਣ ਹੁੰਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 8.
ਪਾਲੀਥੀਨ ਅਤੇ PVC ਕੀ ਹੈ ?
ਉੱਤਰ-
ਇਹ ਇੱਕ ਥਰਮੋਪਲਾਸਟਿਕ ਹੈ ।
ਪ੍ਰਸ਼ਨ 9.
ਬੈਕਲਾਈਟ ਕਿਹੜੇ ਪਲਾਸਟਿਕ ਦਾ ਉਦਾਹਰਨ ਹੈ ?
ਉੱਤਰ-
ਥਰਮੋਸੈਟਿੰਗ ਪਲਾਸਟਿਕ ।
ਪ੍ਰਸ਼ਨ 10.
ਟੇਫ਼ਲਾਨ ਕਿੱਥੇ ਵਰਤਿਆ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਟੇਫ਼ਲਾਨ ਦੀ ਵਰਤੋਂ ਨਾ-ਚਿਪਕਣ ਵਾਲੇ ਭੋਜਨ ਬਰਤਨ ਬਣਾਉਣ ਵਿੱਚ ਹੁੰਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 11.
ਥਰਮੋਪਲਾਸਟਿਕ ਦੀਆਂ ਦੋ ਉਦਾਹਰਨਾਂ ਦਿਓ ।
ਉੱਤਰ-
- ਪਾਲੀਥੀਨੇ
- ਪੀ.ਵੀ. ਸੀ. ॥
ਪ੍ਰਸ਼ਨ 12.
ਗਰਮ ਪਾਣੀ ਨਾਲ ਪਲਾਸਟਿਕ ਦੀਆਂ ਬੋਤਲਾਂ ਦਾ ਆਕਾਰ ਕਿਉਂ ਵਿਗੜ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਪਲਾਸਟਿਕ ਦੀਆਂ ਬੋਤਲਾਂ ਥਰਮੋਪਲਾਸਟਿਕ ਦੀਆਂ ਬਣੀਆਂ ਹੁੰਦੀਆਂ ਹਨ, ਜੋ ਗਰਮ ਹੋ ਕੇ ਪਿਘਲ ਜਾਂਦੀਆਂ ਹਨ ।
![]()
ਪ੍ਰਸ਼ਨ 13.
ਕਿਹੜਾ ਥਰਮੋਸੈਟਿੰਗ ਪਲਾਸਟਿਕ ਵਾਸ਼ਪਸ਼ੀਲ, ਊਸ਼ਮਾਰੋਧੀ ਅਤੇ ਅਗਨੀਪਰੂਫ਼ ਹੈ ?
ਉੱਤਰ-
ਮੇਲਾਮਾਈਨ ।
ਪ੍ਰਸ਼ਨ 14.
ਕਾਰਾਂ, ਜਹਾਜ਼ਾਂ ਆਦਿ ਵਿੱਚ ਧਾਤੂਆਂ ਦੀ ਜਗਾ ਪਲਾਸਟਿਕ ਕਿਉਂ ਵਰਤਿਆ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਕਿਉਂਕਿ ਇਹ ਧਾਤੂਆਂ ਦੀ ਤੁਲਨਾ ਵਿੱਚ ਹਲਕਾ ਹੁੰਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 15.
ਕੋਈ ਦੋ ਅਨਿਮਨਕਰਣੀ ਪਦਾਰਥਾਂ ਦੇ ਨਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
- ਪਲਾਸਟਿਕ
- ਧਾਤੂ ਦੇ ਬਰਤਨ ।
ਪ੍ਰਸ਼ਨ 16.
ਕੁਦਰਤੀ ਰੇਸ਼ਿਆਂ ਦੀ ਜਗ੍ਹਾ ਬਣਾਉਟੀ ਰੇਸ਼ਿਆਂ ਦੀ ਵਰਤੋਂ ਦੇ ਦੋ ਕਾਰਨ ਲਿਖੋ ।
ਉੱਤਰ-
- ਲੰਬੇ ਸਮੇਂ ਤੱਕ ਟਿਕਾਊਪਨ ਅਤੇ
- ਉਪਲੱਬਧਤਾ ।
ਪ੍ਰਸ਼ਨ 17.
ਨਿਮਨੀਕਰਨ ਪਦਾਰਥ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਨਿਮਨੀਕਰਨ-ਉਹ ਪਦਾਰਥ ਜਿਨ੍ਹਾਂ ਦਾ ਜੀਵਾਣੂਆਂ ਦੁਆਰਾ ਅਪਘਟਨ ਨਹੀਂ ਹੁੰਦਾ ਹੈ, ਉਹਨਾਂ ਨੂੰ ਨਿਮਨੀਕਰਨ (ਅਵਿਘਟਨਸ਼ੀਲ ਪਦਾਰਥ ਕਹਿੰਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 18.
4R ਸਿਧਾਂਤ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਵਰਤੋਂ ਘੱਟ ਕਰੋ (Reduce), ਦੁਬਾਰਾ ਵਰਤੋਂ ਕਰੋ (Reuse), ਦੁਬਾਰਾ ਚੱਕਰਿਤ ਕਰੋ (Recycle) ਅਤੇ ਦੁਬਾਰਾ ਪ੍ਰਾਪਤੀ ਕਰੋ (Recover) ॥
ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ
ਪ੍ਰਸ਼ਨ 1.
ਚਾਰ ਵਿਦਿਆਰਥੀਆਂ ਨੇ ਪਹਾੜ ਦੀ ਚੜ੍ਹਾਈ ਕਰਨ ਦਾ ਵਿਚਾਰ ਬਣਾਇਆ ਹੈ, ਉਹਨਾਂ ਨੇ ਹੇਠਾਂ ਵਿਖਾਏ ਟੇਬਲ ਅਨੁਸਾਰ ਰੱਸੀ ਦੀ ਚੋਣ ਕੀਤੀ ਹੈ। ਕਿਸ ਵਿਦਿਆਰਥੀ ਨੇ ਸਹੀ ਰੱਸੀ ਦੀ ਚੋਣ ਕੀਤੀ ਹੈ ਅਤੇ ਕਿਉਂ ?
| ਵਿਦਿਆਰਥੀ ਦਾ ਨਾਂ | ਰੱਸੀ |
| ਇੰਦਰਜੀਤ | ਸੂਤੀ |
| ਗੋਪਾਲ | ਰੇਸ਼ਮੀ |
| ਸਲੋਨੀ | ਨਾਇਲਾਨ |
| ਕਰਮਜੀਤ | ਉੱਨੀ |
ਉੱਤਰ-
ਸਲੋਨੀ ਨੇ ਸਹੀ ਰੱਸੀ ਦੀ ਚੋਣ ਕੀਤੀ ਹੈ, ਕਿਉਂ ਜੋ ਨਾਇਲਾਨ ਦੀ ਰੱਸੀ ਸੂਤੀ, ਰੇਸ਼ਮੀ ਅਤੇ ਊਨੀ ਦੇ ਮੁਕਾਬਲੇ ਵਧੇਰੇ ਮਜ਼ਬੂਤ ਹੈ।
ਪ੍ਰਸ਼ਨ 2.
ਹੇਠਾਂ ਦਿੱਤੀ ਸਾਰਣੀ ਨੂੰ ਰੇਸ਼ਿਆਂ ਦੀ ਕਿਸਮ ਲਿਖ ਕੇ ਪੂਰਾ ਕਰੋ ।
| ਰੇਸ਼ੇ ਦਾ ਨਾਂ | ਰੇਸ਼ੇ ਦੀ ਕਿਸਮ (ਕੁਦਰਤੀ/ਬਣਾਉਟੀ) |
| ਉੱਨ | |
| ਨਾਈਲਾਂਨ |
ਉੱਤਰ –
| ਰੇਸ਼ੇ ਦਾ ਨਾਂ | ਰੇਸ਼ੇ ਦੀ ਕਿਸਮ (ਕੁਦਰਤੀ/ਬਣਾਉਟੀ) |
| ਉੱਨ | ਕੁਦਰਤੀ |
| ਨਾਈਲਾਂਨ | ਬਣਾਉਟੀ |
ਪ੍ਰਸ਼ਨ 3.
ਬਹੁਲਕ ਪਾਲੀਮਰ) ਕੀ ਹੈ ?
ਉੱਤਰ-
ਬਹੁਲਕ- ਬਹੁਲਕ ਇੱਕ ਲੰਬੀ ਲੜੀ (ਵੱਡੀ ਏਕਲ) ਹੈ ਜਿਸ ਵਿੱਚ ਲੱਖਾਂ ਅਣੂ ਹੁੰਦੇ ਹਨ । ਇਹ ਰਸਾਇਣਿਕ ਪਦਾਰਥਾਂ ਦੀਆਂ ਛੋਟੀਆਂ ਇਕਾਈਆਂ ਦੇ ਮੇਲ ਤੋਂ ਬਣਦਾ ਹੈ । ਸੈਲੂਲੋਜ਼ ਕਪਾਹ ਦਾ ਕੁਦਰਤੀ ਬਹੁਲਕ ਹੈ । ਬਹੁਲਕ ਕੁਦਰਤ ਵਿੱਚ ਮਿਲਦਾ ਹੈ । ਉਦਾਹਰਨ ਵਜੋਂ, ਕਪਾਹ ਇੱਕ ਕੁਦਰਤੀ ਤੰਤੁ ਹੈ ਜੋ ਅਸਲ ਵਿੱਚ ਸੈਲੂਲੋਜ਼ ਹੈ । ਸੈਲੂਲੋਜ਼ ਵੱਡੀ ਸੰਖਿਆ ਵਿੱਚ ਗੁਲੂਕੋਜ਼ ਦੀਆਂ ਇਕਾਈਆਂ ਦੁਆਰਾ ਬਣਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 4.
ਸੰਸ਼ਲਿਸ਼ਤ ਰੇਸ਼ਾ ਕੀ ਹੈ ? ਸੰਸ਼ਸ਼ਤ ਰੇਸ਼ਿਆਂ ਦੇ ਉਦਾਹਰਨ ਦਿਉ ।
ਉੱਤਰ-
ਸ਼ੰਸ਼ਲਿਸ਼ਤ ਰੇਸ਼ਾ-ਕੁਦਰਤੀ ਰੇਸ਼ਿਆਂ ਤੋਂ ਵੱਖ ਰੇਸ਼ੇ ਜੋ ਮਨੁੱਖ ਦੁਆਰਾ ਨਿਰਮਿਤ ਕੀਤੇ ਜਾਂਦੇ ਹਨ, ਸੰਸ਼ਲਿਸ਼ਤ ਰੇਸ਼ੇ ਕਹਾਉਂਦੇ ਹਨ । ਇੱਕ ਸੰਸ਼ਸ਼ਤ ਰੇਸ਼ਾ ਛੋਟੀਆਂ ਇਕਾਈਆਂ ਨੂੰ ਜੋੜ ਕੇ ਬਣਾਈ ਗਈ ਲੜੀ ਹੈ । ਉਦਾਹਰਣ-ਆਨ, ਨਾਈਲਾਂਨ, ਪਾਲੀਸਟਰ, ਐਕ੍ਰਿਲਿਕ, ਟੈਰੀਲੀਨ ਆਦਿ ਸੰਸ਼ਲਿਸ਼ਤ ਰੇਸ਼ੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 5.
ਪਾਲੀਥੀਨ ਦੇ ਉਪਯੋਗ ਦੱਸੋ ।
ਉੱਤਰ-
ਪੱਲੀਥੀਨ ਦੇ ਉਪਯੋਗ-ਪਾਲੀਥੀਨ ਦੀਆਂ ਚਾਦਰਾਂ ਪੈਕਿੰਗ ਲਈ, ਥੈਲੇ ਦੁੱਧ ਦੀ ਪੈਕਿੰਗ ਲਈ, ਪਾਲੀਥੀਨ ਪਾਤਰ ਅਤੇ ਪਾਈਪਾਂ ਭੰਡਾਰਨ ਅਤੇ ਪਾਣੀ, ਤੇਲ ਜਾਂ ਦੂਸਰੇ ਪਦਾਰਥਾਂ ਦੇ ਸਥਾਨਾਂਤਰਨ ਦੇ ਲਈ ਵਰਤੋਂ ਵਿੱਚ ਆਉਂਦੇ ਹਨ | ਪਾਲੀਥੀਨ ਨੂੰ ਵਾਟਰ ਪਰੂਫ਼ (Water proof) ਦੇ ਵਜੋਂ ਵੀ ਵਰਤਿਆ ਜਾਂਦਾ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 6.
ਪੀ. ਵੀ. ਸੀ. (P.V.C.) ਦੇ ਕੁੱਝ ਉਪਯੋਗ ਲਿਖੋ ।
ਉੱਤਰ-
ਪੀ. ਵੀ. ਸੀ. ਦੇ ਉਪਯੋਗ-ਇਹ ਬੋਤਲਾਂ, ਫ਼ਰਸ਼ ਦੀਆਂ ਟਾਈਲਾਂ, ਰੇਨਕੋਟ, ਜੁੱਤੀਆਂ ਦੇ ਤਲੇ, ਸੈਂਡਲ, ਅਤੇ ਚਮੜੇ ਵਰਗੇ ਪਦਾਰਥ ਬਣਾਉਣ ਦੇ ਕੰਮ ਆਉਂਦਾ ਹੈ।
ਪ੍ਰਸ਼ਨ 7.
ਨਿਮਨੀਕ੍ਰਿਤ ਪਦਾਰਥ (Biodegradable) ਕੀ ਹੈ ?
ਉੱਤਰ-
ਨਿਮਨੀਤ ਪਦਾਰਥ-ਅਜਿਹੇ ਪਦਾਰਥ ਜੋ ਸੂਖ਼ਮ ਜੀਵਾਂ ਦੁਆਰਾ ਆਸਾਨੀ ਨਾਲ ਵਿਘਟਿਤ ਹੋ ਜਾਂਦੇ ਹਨ, ਨਿਮਨੀਕ੍ਰਿਤ ਪਦਾਰਥ ਕਹਾਉਂਦੇ ਹਨ । ਮਿਤੇ ਜੀਵਾਂ ਦੇ ਸਰੀਰ, ਮਾਨਵ ਮਲ-ਮੂਤਰ ਅਤੇ ਹੋਰ ਕਈ ਪਦਾਰਥ ਜੀਵਾਣੂਆਂ ਦੁਆਰਾ ਸਾਧਾਰਨ ਯੋਗਿਕਾਂ ਵਿੱਚ ਅਪਘਟਿਤ ਕੀਤੇ ਜਾਂਦੇ ਹਨ | ਅਜਿਹੇ ਪਦਾਰਥ ਨਿਮਨੀਕ੍ਰਿਤ ਕਹਾਉਂਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 8.
ਕੁਦਰਤੀ ਅਤੇ ਸੰਸ਼ਲਿਸ਼ਤ ਬਹੁਲਕ ਕੀ ਹੈ ?
ਉੱਤਰ-
- ਕੁਦਰਤੀ ਬਹੁਲਕ (Natural Polymer)-ਉਹ ਬਹੁਲਕ ਜੋ ਕੁਦਰਤ ਵਿੱਚ ਪੌਦਿਆਂ ਅਤੇ ਜੰਤੂਆਂ ਤੋਂ ਪ੍ਰਾਪਤ ਹੁੰਦੇ ਹਨ, ਕੁਦਰਤੀ ਬਹੁਲਕ ਕਹਾਉਂਦੇ ਹਨ, ਜਿਵੇਂ ਰਬੜ, ਸਟਾਰਚ, ਸੈਲੂਲੋਜ਼, ਪ੍ਰੋਟੀਨ ਆਦਿ ।
- ਸੰਸ਼ਸ਼ਤ ਬਹੁਲਕ (Synthetic Polymer)-ਉਹ ਬਹੁਲਕ ਜੋ ਕੁਦਰਤ ਵਿੱਚ ਉਪਲੱਬਧ ਨਹੀਂ ਹਨ ਅਤੇ ਜਿਨ੍ਹਾਂ ਨੂੰ ਪ੍ਰਯੋਗਸ਼ਾਲਾਵਾਂ ਵਿੱਚ ਤਿਆਰ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ, ਸੰਸ਼ਲਿਸ਼ਤ ਬਹੁਲਕ ਕਹਾਉਂਦੇ ਹਨ । ਇਹਨਾਂ ਨੂੰ ਮਾਨਵ ਨਿਰਮਿਤ ਬਹੁਲਕ ਵੀ ਕਹਿੰਦੇ ਹਨ , ਜਿਵੇਂ ਕਿ ਪਾਲੀਥੀਨ, ਪਾਲੀਵਿਨਾਈਲ ਕਲੋਰਾਈਡ, ਟੇਫ਼ਲਾਂਨ, ਬੈਕਲਾਈਟ ਆਦਿ ।
ਪ੍ਰਸ਼ਨ 9.
ਅੰਧਾ-ਧੁੰਦ ਅਸਾਵਧਾਨੀ ਨਾਲ ਸੁੱਟੇ ਗਏ ਪਲਾਸਟਿਕ ਪਾਲੀਥੀਨ ਬੈਗ ਕਿਸ ਪ੍ਰਕਾਰ ਜੰਤੂਆਂ ਦੇ ਲਈ ਹਾਨੀਕਾਰਕ ਹਨ ?
ਉੱਤਰ-
ਵਰਤੋਂ ਕਰਨ ਤੋਂ ਬਾਅਦ ਅਸਾਵਧਾਨੀ ਨਾਲ ਸੁੱਟੇ ਗਏ ਪਲਾਸਟਿਕ/ਪਾਲੀਥੀਨ ਦੇ ਲਿਫ਼ਾਫ਼ੇ ਅਤੇ ਬੈਗ ਅਵਾਰਾ ਜੰਤੂਆਂ ਦੁਆਰਾ ਨਿਗਲ ਲਏ ਜਾਂਦੇ ਹਨ । ਇਹ ਪਲਾਸਟਿਕ ਬੈਗ ਅਜੈਵ-ਵਿਘਟਨਕਾਰੀ ਪਦਾਰਥ ਤੋਂ ਬਣੇ ਹੁੰਦੇ ਹਨ ਜਿਸ ਨਾਲ ਉਹਨਾਂ ਦੀ ਸਾਹ ਨਲੀ ਜਾਂ ਤਾਂ ਬੰਦ ਹੋ ਜਾਂਦੀ ਹੈ ਜਾਂ ਫਿਰ ਪੇਟ ਵਿੱਚ ਇੱਕ ਪਰਤ ਬਣਾ ਲੈਂਦੀ ਹੈ ਜਿਸ ਨਾਲ ਉਹਨਾਂ ਦੀ ਮੌਤ ਹੋ ਜਾਂਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 10.
ਰਸੋਈ ਵਿੱਚ ਕੰਮ ਕਰਦੇ ਸਮੇਂ ਪੱਲੀਐਸਟਰ ਦੇ ਕੱਪੜੇ ਪਾਉਣ ਦਾ ਸੁਝਾਅ ਕਿਉਂ ਨਹੀਂ ਦਿੱਤਾ ਜਾਂਦਾ ?
ਉੱਤਰ-
ਪੱਲੀਐਸਟਰ ਇੱਕ ਸੰਸ਼ਲਿਸ਼ਤੇ ਰੇਸ਼ਾ ਹੈ । ਇਹ ਛੇਤੀ ਅੱਗ ਫੜ ਲੈਂਦਾ ਹੈ ਅਤੇ ਪਿਘਲ ਕੇ ਸਰੀਰ ਨਾਲ ਚਿਪਕ ਕੇ ਦਰਦ ਭਰੀ ਜਲਣ ਪੈਦਾ ਕਰਦਾ ਹੈ । ਇਸ ਲਈ ਰਸੋਈ ਵਿੱਚ ਕੰਮ ਕਰਦੇ ਸਮੇਂ ਪਾਲੀਐਸਟਰ ਦੇ ਕੱਪੜੇ ਨਾ ਪਾਉਣ ਦਾ ਸੁਝਾਅ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ।
ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ
ਪ੍ਰਸ਼ਨ 1.
ਅਧਿਆਪਕ ਨੇ ਮੁਕੇਸ਼ ਨੂੰ ਇਕੋ ਸਾਈਜ਼ ਦੇ ਦੋ ਟੁਕੜੇ ਜਿਨ੍ਹਾਂ ਵਿਚੋਂ ਇਕ ਕਿਰਤਕ ਰੇਸ਼ਿਆਂ ਤੋਂ ਬਣਿਆ ਅਤੇ ਦੂਜਾ ਟੁਕੜਾ ਸੰਸ਼ਲਿਸ਼ਟ ਰੇਸ਼ੇ ਤੋਂ ਬਣਿਆ ਹੋਇਆ ਦਿੱਤਾ । ਹੁਣ ਉਸ ਨੂੰ ਪਾਣੀ ਦੇ ਵੱਖ-ਵੱਖ ਮੱਗਾਂ ਵਿਚ ਉਨ੍ਹਾਂ ਟੁਕੜਿਆਂ ਨੂੰ ਡੁਬੋਣ ਲਈ ਕਿਹਾ | ਕੁੱਝ ਸਮੇਂ ਬਾਅਦ ਮੁਕੇਸ਼ ਨੂੰ ਉਨ੍ਹਾਂ ਟੁਕੜਿਆਂ ਨੂੰ ਬਾਹਰ ਕੱਢਣ ਲਈ ਅਤੇ ਫਿਰ ਧੁੱਪ ਵਿਚ ਖਿਲਾਰਣ ਲਈ ਕਿਹਾ । ਦੱਸੋ ਸੰਸ਼ਲਿਸ਼ਟ ਅਤੇ ਪ੍ਰਕਿਰਤਕ ਵਿਚੋਂ ਕਿਹੜਾ ਘੱਟ ਸਮੇਂ ਵਿਚ ਸੁੱਕਦਾ ਹੈ । ਆਪਣੇ ਉੱਤਰ ਦੀ ਪੁਸ਼ਟੀ ਲਈ ਕਾਰਨ ਵੀ ਦੱਸੋ ।

ਉੱਤਰ-
ਸੰਸ਼ਲਿਸ਼ਟ ਰੇਸ਼ੇ ਤੋਂ ਬਣਿਆ ਟੁਕੜਾ ਪ੍ਰਕਿਰਤਕ ਰੇਸ਼ੇ ਨਾਲ ਬਣੇ ਟੁਕੜੇ ਦੇ ਮੁਕਾਬਲੇ ਘੱਟ ਸਮੇਂ ਵਿਚ ਸੁੱਕ ਜਾਂਦਾ ਹੈ । ਇਸ ਦਾ ਕਾਰਨ ਇਹ ਹੈ ਕਿ ਸੰਸ਼ਲਿਸ਼ਟ ਰੇਸ਼ੇ, ਸੁਤੀ ਰੇਸ਼ੇ ਦੀ ਤੁਲਨਾ ਵਿਚ ਘੱਟ ਪਾਣੀ ਸੋਖਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 2.
ਕੂੜਾ-ਕਰਕਟ ਦੀਆਂ ਵਸਤੂਆਂ ਦਾ ਜੀਵਾਣੂਆਂ ਦੀ ਕਿਰਿਆ ਦੁਆਰਾ ਅਪਘਟਿਤ ਹੋਣ ਜਾਂ ਨਾ ਹੋਣ ਦੇ ਆਧਾਰ ਤੇ ਜੈਵ-ਵਿਘਟਨਸ਼ੀਲ ਅਤੇ ਅਜੈਵ ਵਿਘਟਨਸ਼ੀਲ ਵਿਚ ਵੰਡ ਕੇ ਹੇਠ ਦਿੱਤੀ ਸਾਰਣੀ ਨੂੰ ਪੂਰਾ ਕਰੋ ।
| ਕੂੜਾ-ਕਰਕਟ ਦੀਆਂ ਕਿਸਮਾਂ | ਜੈਵ-ਵਿਘਟਨਸ਼ੀਲ/ਅਜੈਵ-ਵਿਘਟਨਸ਼ੀਲ |
| ਸਬਜ਼ੀ ਅਤੇ ਫਲਾਂ ਦੇ ਛਿਲਕੇ | |
| ਲੱਕੜੀ | |
| ਪਲਾਸਟਿਕ ਦੀਆਂ ਥੈਲੀਆਂ |
ਉੱਤਰ-
| ਕੂੜਾ-ਕਰਕਟ ਦੀਆਂ ਕਿਸਮਾਂ | ਜੈਵ-ਵਿਘਟਨਸ਼ੀਲ|ਅਜੈਵ-ਵਿਘਟਨਸ਼ੀਲ |
| ਸਬਜ਼ੀ ਅਤੇ ਫਲਾਂ ਦੇ ਛਿਲਕੇ | ਜੈਵ-ਵਿਘਟਨਸ਼ੀਲ |
| ਲੱਕੜੀ | ਜੈਵ-ਵਿਘਟਨਸ਼ੀਲ |
| ਪਲਾਸਟਿਕ ਦੀਆਂ ਥੈਲੀਆਂ | ਅਜੈਵ-ਵਿਘਟਨਸ਼ੀਲ |
ਪ੍ਰਸ਼ਨ 3.
ਸੰਸ਼ਲਿਸ਼ਤ ਰੇਸ਼ਿਆਂ ਦੇ ਗੁਣ ਲਿਖੋ ਜਿਸ ਕਾਰਨ ਇਹ ਵੇਸਭੂਸ਼ਾ ਸਾਮਗਰੀ ਲਈ ਪ੍ਰਸਿੱਧ ਹਨ ।
ਉੱਤਰ-
ਸੰਸ਼ਲਿਸ਼ਤ ਰੇਸ਼ਿਆਂ ਦੇ ਗੁਣ-ਸੰਸ਼ਲਿਸ਼ਤ ਰੇਸ਼ਿਆਂ ਦੇ ਹੇਠ ਲਿਖੇ ਗੁਣ ਹਨ
- ਇਹ ਲੰਬੇ ਸਮੇਂ ਤੱਕ ਚੱਲਦੇ ਹਨ ।
- ਇਹਨਾਂ ਦੀ ਕੀਮਤ ਬਹੁਤ ਘੱਟ ਹੈ ।
- ਇਹ ਛੇਤੀ ਸੁੱਕ ਜਾਂਦੇ ਹਨ ।
- ਇਹ ਸੌਖਿਆਂ ਪ੍ਰਾਪਤ ਹੋ ਜਾਂਦੇ ਹਨ ।
- ਇਹਨਾਂ ਦੀ ਸੰਭਾਲ ਬਹੁਤ ਆਸਾਨ ਹੈ ।
- ਇਹਨਾਂ ਨੂੰ ਧੋਣਾ ਆਸਾਨ ਹੈ ਅਤੇ ਇਹਨਾਂ ਵਿੱਚ ਵੱਟ ਨਹੀਂ ਪੈਂਦੇ ! ਇਹਨਾਂ ਗੁਣਾਂ ਦੇ ਕਾਰਨ ਸੰਸ਼ਲਿਸ਼ਤ ਰੇਸ਼ੇ ਵੇਸ਼ਭੂਸ਼ਾ ਸਾਮੱਗਰੀ ਲਈ ਪ੍ਰਸਿੱਧ ਹਨ ।
ਪ੍ਰਸ਼ਨ 4.
ਕੀ ਹੁੰਦਾ ਹੈ ਜਦੋਂ ਬਣਾਵਟੀ ਰੇਸ਼ੇ ਜਿਵੇਂ ਨਾਈਲਾਂਨ, ਪਾਲੀਐਸਟਰ ਅਤੇ ਐਕ੍ਰਿਲਿਕ ਰੇਸ਼ੇ ਹਵਾ ਵਿੱਚ ਜਲਾਏ ਜਾਂਦੇ ਹਨ ?
ਉੱਤਰ-
ਵੱਖ-ਵੱਖ ਰੇਸ਼ਿਆਂ ਨੂੰ ਜਲਾਉਣ ਦੇ ਹੇਠ ਲਿਖੇ ਨਤੀਜੇ ਸਾਹਮਣੇ ਆਏ ਹਨ
- ਨਾਈਲਾਂਨ ਮੁਸ਼ਕਿਲ ਨਾਲ ਜਲਦਾ ਹੈ, ਅੱਗ ਲੱਗ ਜਾਂਦੀ ਹੈ ਤੇ ਰੇਸ਼ਾ ਸੁੰਗੜਦਾ ਹੈ, ਗੰਢ ਬਣਾਉਂਦੀ ਹੈ, ਵਾਲ ਜਲਾਉਣ ਵਰਗੀ ਗੰਧ ਦਿੰਦਾ ਹੈ ।
- ਪਾਲੀਐਸਟਰ ਨਾਈਲਾਂ ਦੀ ਤਰ੍ਹਾਂ ਸਮਾਨ ਗੁਣ ਹਨ, ਜਲਾਉਣ ਤੇ ਕਾਲਾ ਧੂੰਆਂ ਛੱਡਦਾ ਹੈ ।
- ਐਕ੍ਰਿਲਿਕ ਅੱਗ ਨਾਲ ਸੁੰਗੜ ਕੇ ਕਾਲੀ ਗੰਢ ਬਣਾਉਂਦਾ ਹੈ ਅਤੇ ਕਾਲੀ ਧੁੰਏਂ ਵਰਗੀ ਲਾਟ ਪੈਦਾ ਕਰਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 5.
ਪਲਾਸਟਿਕ ਪਦਾਰਥ ਜਿਵੇਂ ਪਾਲੀਥੀਨ ਦੀਆਂ ਕੁਦਰਤੀ ਪਦਾਰਥਾਂ ਤੋਂ ਵੱਖ ਕੁੱਝ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
- ਇਹ ਸਸਤਾ ਅਤੇ ਵਪਾਰਕ ਪੱਧਰ ਤੇ ਤਿਆਰ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ।
- ਇਹ ਭਾਰ ਵਿੱਚ ਹਲਕਾ ਹੁੰਦਾ ਹੈ ਅਤੇ ਆਸਾਨੀ ਨਾਲ ਇਸਦਾ ਸਥਾਨਾਂਤਰਨ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ।
- ਇਹ ਅਟੁੱਟ, ਨਾ ਗਲਣ-ਸੜਨ ਵਾਲਾ, ਮਜ਼ਬੂਤ ਅਤੇ ਲਚਕੀਲਾ ਹੁੰਦਾ ਹੈ ।
- ਇਹ ਆਸਾਨੀ ਨਾਲ ਸਾਂਚੇ ਵਿੱਚ ਢਾਲਿਆ ਜਾ ਸਕਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 6.
ਮਿਸ਼ਰਿਤ ਕੱਪੜਾ (Blended fabric) ਕੀ ਹੈ ? ਇਹ ਸੰਸ਼ਲਿਸ਼ਤ ਰੇਸ਼ਿਆਂ ਤੋਂ ਬਣੇ ਕੱਪੜਿਆਂ ਤੋਂ ਵੱਧ ਆਰਾਮਦਾਇਕ ਕਿਉਂ ਹੈ ?
ਉੱਤਰ-
ਮਿਸ਼ਰਿਤ ਕੱਪੜਾ (Blended fabric)- ਇਹ ਸੰਸ਼ਲਿਸ਼ਤ ਮਾਨਵ ਨਿਰਮਿਤ) ਅਤੇ ਕੁਦਰਤੀ ਰੇਸ਼ਿਆਂ ਦਾ ਮਿਸ਼ਰਣ ਹੈ । ਜਿਵੇਂ ਕਿ ਟੇਰੀਕਾਂਟ ਪਾਲੀਐਸਟਰ ਅਤੇ ਸੂਤੀ ਰੇਸ਼ਾ, ਟੈਰੀਟੂਲ ਆਦਿ ਸ਼ੁੱਧ ਸੰਸ਼ਲਿਸ਼ਤ ਰੇਸ਼ੇ ਪਸੀਨੇ ਨੂੰ ਚੰਗੀ ਤਰ੍ਹਾਂ ਸੋਖਦੇ ਨਹੀਂ ਹਨ । ਇਸ ਲਈ ਗਰਮੀਆਂ ਵਿੱਚ ਸਰੀਰ ਨਾਲ ਚਿਪਕ ਜਾਂਦੇ ਹਨ । ਕੁੱਝ ਸੰਸ਼ਲਿਸ਼ਤ ਰੇਸ਼ੇ ਜਲਦੀ ਅੱਗ ਫੜ ਲੈਂਦੇ ਹਨ । ਇਹਨਾਂ ਤਰੁੱਟੀਆਂ ਨੂੰ ਦੂਰ ਕਰਨ ਲਈ ਸੰਸ਼ਲਿਤ ਰੇਸ਼ੇ ਕੁਦਰਤੀ ਰੇਸ਼ਿਆਂ ਨਾਲ ਮਿਸ਼ਰਿਤ ਕਰਕੇ ਮਿਸ਼ਰਤ ਰੇਸ਼ੇ ਬਣਾਏ ਜਾਂਦੇ ਹਨ ।
![]()
ਪ੍ਰਸ਼ਨ 7.
ਪਲਾਸਟਿਕ ਸਾਮਗਰੀ ਦਾ ਘੱਟ ਪ੍ਰਯੋਗ ਕਰਨ ਦੇ ਕੁੱਝ ਤਰੀਕੇ ਸੁਝਾਓ ।
ਉੱਤਰ-
ਪਲਾਸਟਿਕ ਅਜੈਵ-ਅਪਘਟਕ ਹੈ ਇਸ ਲਈ ਵਾਤਾਵਰਨ ਦਾ ਮਿੱਤਰ ਨਹੀਂ ਹੈ । ਇਸ ਦੀ ਵਰਤੋਂ ਘੱਟ ਕਰਨ ਦਾ ਸਭ ਤੋਂ ਵਧੀਆ ਤਰੀਕਾ, 4R ਸਿਧਾਂਤ ਦੀ ਵਰਤੋਂ ਕਰਨਾ, ਜੋ ਇਸ ਤਰ੍ਹਾਂ ਹੈ
- Reduce – ਘੱਟ ਵਰਤੋਂ ਕਰੋ।
- Reuse – ਦੁਬਾਰਾ ਵਰਤੋਂ ਕਰੋ।
- Recycle – ਦੁਬਾਰਾ ਚੱਕਰਿਤ ਕਰੋ
- Recover – ਦੁਬਾਰਾ ਪ੍ਰਾਪਤ ਕਰੋ ।
ਪ੍ਰਸ਼ਨ 8.
ਪਲਾਸਟਿਕ ਪਦਾਰਥ ਦੀ ਵੱਧ ਵਰਤੋਂ ਕਿਸ ਤਰ੍ਹਾਂ ਵਾਤਾਵਰਨ ਅਤੇ ਸਮਾਜ ਦੇ ਲਈ ਹਾਨੀਕਾਰਕ ਹੈ ?
ਉੱਤਰ-
ਪਲਾਸਟਿਕ ਮਨੁੱਖ ਅਤੇ ਵਾਤਾਵਰਨ ਦੋਨਾਂ ਲਈ ਅੱਗੇ ਲਿਖੇ ਕਾਰਨਾਂ ਕਰਕੇ ਹਾਨੀਕਾਰਕ ਹੈ –
- ਕਿਉਂਕਿ ਪਲਾਸਟਿਕ ਪੈਟਰੋ-ਰਸਾਇਣਾਂ ਨਾਲ ਸੰਸ਼ਲਿਸ਼ਤ ਕੀਤਾ ਗਿਆ ਹੈ ਇਸ ਲਈ ਇਸਦੀ ਵੱਧ ਵਰਤੋਂਨਵਿਆਉਣਯੋਗ ਪੈਟਰੋ-ਰਸਾਇਣਾਂ ਦੇ ਸੀਮਤ ਭੰਡਾਰ ਨੂੰ ਖ਼ਤਮ ਕਰ ਦੇਵੇਗਾ ।
- ਪਲਾਸਟਿਕ ਅਜੈਵ-ਵਿਘਟਨਕਾਰੀ ਹੈ ਜੋ ਨਾਲੀਆਂ ਅਤੇ ਸੀਵਰੇਜ ਪ੍ਰਣਾਲੀ ਨੂੰ ਬੰਦ ਕਰ ਦਿੰਦਾ ਹੈ ਜੇ ਪ੍ਰਯੋਗ ਤੋਂ ਬਾਅਦ ਇਸਨੂੰ ਧਿਆਨਪੂਰਵਕ ਨਾ ਸੁੱਟਿਆ ਜਾਵੇ ।
- ਪਲਾਸਟਿਕ ਦਾ ਅਪੂਰਣ ਦਹਿਣ ਹੁੰਦਾ ਹੈ ਅਤੇ ਵੱਧ ਮਾਤਰਾ ਵਿੱਚ ਜ਼ਹਿਰੀਲਾ ਧੂੰਆਂ ਪੈਦਾ ਕਰਕੇ ਵਾਤਾਵਰਨ ਦੀ ਹਵਾ ਨੂੰ ਪ੍ਰਦੂਸ਼ਿਤ ਕਰਦਾ ਹੈ ।
- ਕਈ ਵਾਰ ਬੇਧਿਆਨੀ ਨਾਲ ਸੁੱਟੇ ਗਏ ਪਲਾਸਟਿਕ/ਪਾਲੀਥੀਨ ਜੰਤੂਆਂ ਦੁਆਰਾ ਨਿਗਲ ਲਿਆ ਜਾਂਦਾ ਹੈ ਜਿਸ ਦੇ ਸਿੱਟੇ ਵੱਜੋਂ ਮੌਤ ਹੋ ਜਾਂਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 9.
ਇੱਕ ਸਮਝਦਾਰ ਅਤੇ ਜ਼ਿੰਮੇਵਾਰ ਸ਼ਹਿਰੀ ਹੋਣ ਦੇ ਨਾਤੇ ਤੁਸੀਂ ਜਨਤਾ ਨੂੰ ਪਲਾਸਟਿਕ ਮੁਕਤ ਰੱਖਣ ਲਈ ਕੀ ਕਦਮ ਚੁੱਕੋਗੇ ?
ਉੱਤਰ-
- ਮੈਂ ਪਲਾਸਟਿਕ ਦੇ ਲਿਫ਼ਾਫ਼ੇ ਦੀ ਵਰਤੋਂ ਦੇ ਬਾਅਦ ਇਸਨੂੰ ਪਾਣੀ ਸ੍ਰੋਤ ਜਾਂ ਸੜਕ ਤੇ ਨਹੀਂ ਸੁੱਟਾਂਗਾ ।
- ਬਾਜ਼ਾਰ ਤੋਂ ਸਾਮਾਨ ਖ਼ਰੀਦਣ ਲਈ ਘਰ ਤੋਂ ਕੱਪੜੇ ਜਾਂ ਪਟਸਨ ਦਾ ਥੈਲਾ ਆਪਣੇ ਨਾਲ ਲੈ ਕੇ ਜਾਵਾਂਗਾ ! ਇੱਥੋਂ ਤੱਕ ਕਿ ਦੁਕਾਨਦਾਰ ਨੂੰ ਕਾਗਜ਼ ਦੇ ਲਿਫ਼ਾਫ਼ੇ ਵਿੱਚ ਪਾਉਣ ਲਈ ਮਜ਼ਬੂਰ ਕਰਾਂਗਾ ।
- ਪਲਾਸਟਿਕ ਤੋਂ ਬਣੇ ਹੋਏ ਲੰਚ ਬਾਕਸ ਦੇ ਸਥਾਨ ਤੇ ਸਟੀਲ ਦੇ ਡਿੱਬੇ ਦੀ ਵਰਤੋਂ ਕਰਾਂਗਾ |
ਪ੍ਰਸ਼ਨ 10.
ਨਾਈਲਾਂਨ ਰੇਸ਼ਿਆਂ ਦੇ ਚਾਰ ਮਹੱਤਵਪੂਰਨ ਗੁਣ ਅਤੇ ਉਪਯੋਗ ਲਿਖੋ ।
ਉੱਤਰ-
ਨਾਈਲਾਨ ਰੇਸ਼ਿਆਂ ਦੇ ਗੁਣ
- ਨਾਈਲਾਂਨ ਰੇਸ਼ੇ ਮਜ਼ਬੂਤ ਹਨ ।
- ਇਹ ਪਾਣੀ ਨੂੰ ਬਹੁਤ ਘੱਟ ਸੋਖਦੇ ਹਨ । ਇਸ ਲਈ ਬਹੁਤ ਜਲਦੀ ਸੁੱਕ ਜਾਂਦੇ ਹਨ ।
- ਨਾਈਲਾਂਨ ਦੇ ਕੱਪੜੇ ਵਿੱਚ ਸਿਲਵਟਾਂ ਨਹੀਂ ਪੈਂਦੀਆਂ ।
- ਇਹ ਵਧੇਰੇ ਟਿਕਾਊ ਹੈ ।
ਨਾਈਲਾਂਨ ਦੇ ਉਪਯੋਗ
- ਨਾਈਲਾਂ ਦੇ ਰੇਸ਼ੇ ਕਈ ਤਰ੍ਹਾਂ ਦੇ ਕੰਮਾਂ ਲਈ ਵਰਤੇ ਜਾਂਦੇ ਹਨ, ਜਿੱਥੇ ਮਜ਼ਬੂਤ ਰੇਸ਼ਿਆਂ ਦੀ ਲੋੜ ਹੁੰਦੀ ਹੈ ।
- ਇਸ ਨਾਲ ਪੈਰਾਸ਼ੂਟ, ਮੱਛੀ ਜਾਲ, ਟਾਇਰ ਦੇ ਪੱਟੇ, ਰੱਸੇ, ਜੁਰਾਬਾਂ ਅਤੇ ਹੋਰ ਕਈ ਕੱਪੜੇ ਬਣਾਏ ਜਾਂਦੇ ਹਨ ।
- ਨਾਈਲਾਂ ਨੂੰ ਉੱਨ ਦੇ ਨਾਲ ਮਿਲਾ ਕੇ ਦੇਰ ਤੱਕ ਰਹਿਣ ਵਾਲੇ ਰੇਸ਼ਿਆਂ ਦਾ ਨਿਰਮਾਣ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 11.
ਪਾਲੀਐਸਟਰ ਰੇਸ਼ਿਆਂ ਦੇ ਗੁਣ ਲਿਖੋ ।
ਉੱਤਰ-
ਪੱਲੀਐਸਟਰ ਰੇਸ਼ਿਆਂ ਦੇ ਗੁਣ
- ਇਹ ਸੂਤੀ, ਊਨੀ ਅਤੇ ਰੇਸ਼ਮੀ ਕੱਪੜਿਆਂ ਤੋਂ ਮਜ਼ਬੂਤ ਹਨ ।
- ਇਹ ਸੁੰਗੜਦੇ ਨਹੀਂ ।
- ਇਹ ਪਾਣੀ ਘੱਟ ਸੋਖਦੇ ਹਨ, ਇਸ ਲਈ ਜਲਦੀ ਸੁੱਕ ਜਾਂਦੇ ਹਨ ।
- ਇਹਨਾਂ ਵਿੱਚ ਵੱਟ ਨਹੀਂ ਪੈਂਦੇ ।
- ਸਾਧਾਰਨ ਰਸਾਇਣਾਂ ਤੋਂ ਇਹ ਪ੍ਰਭਾਵਿਤ ਨਹੀਂ ਹੁੰਦੇ ।
- ਇਹ ਹਲਕੇ ਅਤੇ ਆਕਰਸ਼ਕ ਵਿਖਾਈ ਹਨ ।
- ਇਹ ਸਾਧਾਰਨ ਘੋਲਕਾਂ ਵਿੱਚ ਅਘੁਲਣਸ਼ੀਲ ਹਨ ।
ਵੱਡੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ
ਪ੍ਰਸ਼ਨ 1.
ਹੇਠ ਲਿਖਿਆਂ ਦੇ ਉਪਯੋਗ ਲਿਖੋ
(ਉ) ਪੱਲੀਐਸਟਰ ਰੇਸ਼ਾ
(ਅ) ਟੇਫ਼ਲਾਨ
(ਇ) ਪਾਲੀਥੀਨ
(ਸ) ਪਾਲੀਪਰੋਪਾਈਲੀਨ
ਉੱਤਰ-
(ੳ) ਪਾਲੀਐਸਟਰ ਦੇ ਰੇਸ਼ਿਆਂ ਦੀ ਵਰਤੋਂ
- ਪਾਲੀਐਸਟਰ ਰੇਸ਼ੇ ਕੱਪੜਾ ਉਦਯੋਗ ਵਿੱਚ ਵਿਭਿੰਨ ਪ੍ਰਕਾਰ ਦੇ ਕੱਪੜੇ ਬਣਾਉਣ ਦੇ ਕੰਮ ਆਉਂਦੇ ਹਨ , ਜਿਵੇਂਸਾੜੀ, ਡਰੈਸ, ਪਰਦੇ ਆਦਿ ।
- ਪਾਲੀਐਸਟਰ ਰੇਸ਼ੇ, ਕੁਦਰਤੀ ਰੇਸ਼ਿਆਂ ਤੋਂ ਮਿਲਾ ਕੇ ਰੇਸ਼ੇ ਬਣਾਉਣ ਦੇ ਕੰਮ ਆਉਂਦੇ ਹਨ , ਜਿਵੇਂ-ਟੇਰੀਕਾਟ (ਸੂਤੀ ਨਾਲ), ਟੈਰੀਫੂਲ (ਉੱਨ ਦੇ ਨਾਲ
- ਇਸ ਨਾਲ ਕਿਸ਼ਤੀਆਂ ਦੀ ਪਤਵਾਰ ਬਣਾਈ ਜਾਂਦੀ ਹੈ ।
- ਇਸ ਨਾਲ ਪਾਣੀ ਦੀਆਂ ਟਿਊਬਾਂ (Hoses) ਬਣਦੀਆਂ ਹਨ, ਜਿਨ੍ਹਾਂ ਦੀ ਵਰਤੋਂ ਅੱਗ ਬੁਝਾਉਣ ਦੀ ਪ੍ਰਕਿਰਿਆ ਵਿੱਚ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ।
(ਅ) ਏਫ਼ਲਾਨ ਦੀ ਵਰਤੋਂ-
- ਇਸ ਨੂੰ ਨਾ ਚਿੱਪਕਣ ਵਾਲੇ ਭੋਜਨ ਬਣਾਉਣ ਵਾਲੇ ਪਾਤਰਾਂ ਵਿੱਚ ਵਰਤਿਆ ਜਾਂਦਾ ਹੈ ।
- ਇਸ ਨਾਲ ਸੀਲ ਅਤੇ ਗੈਸਕੇਟ ਬਣਾਈ ਜਾਂਦੀ ਹੈ ।
(ਇ) ਪਾਲੀਥੀਨ ਦੇ ਉਪਯੋਗ-
- ਇਸ ਨੂੰ ਥੈਲੇ, ਖਿਡੌਣੇ ਅਤੇ ਪਾਈਪ ਬਣਾਉਣ ਲਈ ਵਰਤਿਆ ਜਾਂਦਾ ਹੈ ।
- ਇਸ ਨਾਲ ਤਾਰਾਂ ਦਾ ਆਵਰਨ ਬਣਾਇਆ ਜਾਂਦਾ ਹੈ ਕਿਉਂਕਿ ਇਹ ਬਿਜਲੀ ਰੋਧਕ ਹੁੰਦਾ ਹੈ ।
(ਸ) ਪਾਲੀਪਰੋਪਾਈਲੀਨ ਦੇ ਉਪਯੋਗ-
- ਇਸ ਤੋਂ ਸੀਟ ਦੇ ਪੱਟੇ ਬਣਦੇ ਹਨ ।
- ਇਸ ਤੋਂ ਰੱਸੀਆਂ ਅਤੇ ਜਾਲ ਬਣਾਏ ਜਾਂਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 2.
ਪਲਾਸਟਿਕ ਕਿਸ ਨੂੰ ਕਹਿੰਦੇ ਹਨ ? ਇਸ ਦੀਆਂ ਵੱਖ-ਵੱਖ ਕਿਸਮਾਂ ਕਿਹੜੀਆਂ ਹਨ ? ਇਸਦੇ ਕਿਹੜੇ ਗੁਣ ਹਨ ਜੋ ਇਸ ਨੂੰ ਵਧੇਰੇ ਪਸੰਦ ਕਰਨ ਵਾਲਾ ਪਦਾਰਥ ਬਣਾ ਦਿੰਦੇ ਹਨ ? ਇਸ ਦੇ ਉਪਯੋਗ ਵੀ ਲਿਖੋ ।
ਉੱਤਰ-
ਪਲਾਸਟਿਕ-ਇਹ ਸੰਸ਼ਲਿਸ਼ਤ ਰੇਸ਼ੇ ਦੀ ਤਰ੍ਹਾਂ ਬਹੁਲਕ ਹੈ ! ਉਦਾਹਰਨ-ਪਾਲੀਥੀਨ । ਪਲਾਸਟਿਕ ਦੀਆਂ ਕਿਸਮਾਂ-ਸਾਰੇ ਕਿਸਮਾਂ ਦੇ ਪਲਾਸਟਿਕ ਵਿੱਚ ਇਕਾਈਆਂ ਦੀ ਸੰਰਚਨਾ ਇੱਕੋ ਜਿਹੀ ਨਹੀਂ ਹੁੰਦੀ । ਪਲਾਸਟਿਕ ਦੋ ਤਰ੍ਹਾਂ ਦੇ ਹੁੰਦੇ ਹਨ । ਇੱਕ ਜਿਨ੍ਹਾਂ ਵਿੱਚ ਇਕਾਈਆਂ ਦੀ ਸੰਰਚਨਾ ਸਰਲ ਰੇਖਾ ਵਿੱਚ ਹੁੰਦੀ ਹੈ ਅਤੇ ਦੂਸਰੀ ਕਿਸਮ ਵਿੱਚ ਸ ਜੋੜ ।
ਪਲਾਸਟਿਕ ਦੇ ਗੁਣ-
- ਪਲਾਸਟਿਕ ਤੇ ਹਵਾ ਅਤੇ ਪਾਣੀ ਦੀ ਕਿਰਿਆ ਨਹੀਂ ਹੁੰਦੀ ਮਤਲਬ ਹੈ ਕਿ ਇਹ ਅਕਿਰਿਆਸ਼ੀਲ ਅਤੇ ਅਖੁਰਣਸ਼ੀਲ ਸੁਭਾਅ ਦੇ ਹੁੰਦੇ ਹਨ ।
- ਪਲਾਸਟਿਕ ਹਲਕਾ, ਮਜ਼ਬੂਤ ਅਤੇ ਟਿਕਾਊ ਹੁੰਦਾ ਹੈ ।
- ਕੁੱਝ ਪਲਾਸਟਿਕਾਂ ਦੀ ਆਕ੍ਰਿਤੀ ਗਰਮ ਕਰਕੇ ਜਲਦੀ ਬਦਲੀ ਜਾ ਸਕਦੀ ਹੈ ਜਦੋਂਕਿ ਕੁੱਝ ਪਲਾਸਟਿਕ ਗਰਮ ਕਰਨ ਤੇ ਨਰਮ ਨਹੀਂ ਹੁੰਦੇ ਹਨ ।
- ਪਲਾਸਟਿਕ ਤਾਪ ਅਤੇ ਬਿਜਲੀ ਦੇ ਕੁਚਾਲਕ ਹਨ ।
![]()
ਪਲਾਸਟਿਕ ਦੇ ਉਪਯੋਗ –
- ਸਿਹਤ ਸੰਬੰਧੀ ਉਦਯੋਗ ਵਿੱਚ-ਪਲਾਸਟਿਕ ਆਮ ਕਰਕੇ ਸਿਹਤ ਸੰਬੰਧੀ ਉਦਯੋਗ ਵਿੱਚ ਦਵਾਈਆਂ ਦੀ ਪੈਕਿੰਗ ਅਤੇ ਜ਼ਖ਼ਮਾਂ ਤੇ ਟਾਂਕੇ ਲਗਾਉਣ ਲਈ ਧਾਗਾ, ਸਿਰਿੰਜ, ਡਾਕਟਰ ਦੇ ਦਸਤਾਨੇ ਅਤੇ ਕਈ ਯੰਤਰ ਬਣਾਉਣ ਵਿੱਚ ਵਰਤੋਂ ਵਿੱਚ ਆਉਂਦਾ ਹੈ ।
- ਰਸੋਈ ਦੇ ਬਰਤਣ ਬਣਾਉਣ ਵਿੱਚ-ਮਾਈਕਰੋ ਓਵਨ ਵਿੱਚ ਖਾਣਾ ਪਕਾਉਣ ਦੇ ਲਈ ਵਰਤੋਂ ਕੀਤੇ ਜਾਣ ਵਾਲੇ ਵਿਸ਼ੇਸ਼ ਬਰਤਨ ਪਲਾਸਟਿਕ ਤੋਂ ਬਣਾਏ ਜਾਂਦੇ ਹਨ ਜੋ ਵੱਧ ਤਾਪਮਾਨ ਸਹਿਣ ਕਰ ਸਕਦੇ ਹਨ ।
- ਟੇਫ਼ਲਾਨ ਜੋ ਇਕ ਤਰ੍ਹਾਂ ਦਾ ਪਲਾਸਟਿਕ ਹੈ ਜਿਸ ਤੋਂ ਨਾ-ਚਿਪਕਣ ਵਾਲੇ ਖਾਣਾ ਬਣਾਉਣ ਦੇ ਬਰਤਣ ਤਿਆਰ ਕੀਤੇ ਜਾਂਦੇ ਹਨ । ਇਹਨਾਂ ਤੇ ਤੇਲ ਅਤੇ ਪਾਣੀ ਨਹੀਂ ਚਿਪਕਦਾ ਹੈ ।
- ਫਾਇਰਮੈਨ ਦੀ ਪੋਸ਼ਾਕ ਦੇ ਅੰਦਰ ਮੈਲਾਮਾਈਨ ਪਲਾਸਟਿਕ ਦੀ ਤਹਿ ਬਣਾਈ ਜਾਂਦੀ ਹੈ । ਇਹ ਪੋਸ਼ਾਕ ਨੂੰ ਤਾਪ ਪ੍ਰਤੀਰੋਧਕ ਬਣਾ ਦਿੰਦਾ ਹੈ ।