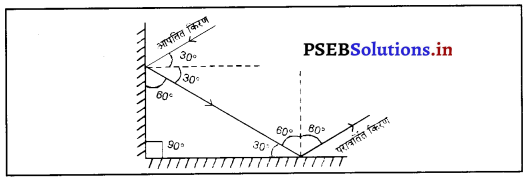
Punjab State Board PSEB 8th Class Science Book Solutions Chapter 12 Friction Textbook Exercise Questions and Answers.
PSEB Solutions for Class 8 Science Chapter 12 Friction
PSEB 8th Class Science Guide Friction Textbook Questions and Answers
Exercises
Question 1.
Fill in the blanks.
[a] Friction opposes the ………………… between the surfaces in contact with each other.
[b] Friction depends on ……………….. of surfaces.
[c] Friction produces ……………….
[d] Sprinkling of powder on the carrom board ……………….. friction.
[e] Sliding friction is ………………. than the static friction.
Answer:
(a) relative motion
(b) nature
(c) heat
(d) decreases
(e) less.
Question 2.
Four children were asked to arrange forces due to rolling, static and sliding frictions in decreasing order. Their arrangements are given below. Choose the correct arrangement.
[а] rolling, static, sliding
[b] rolling, sliding, static
[c] static, sliding, rolling
[d] sliding, static, rolling.
Answer:
(c) Static, sliding, rolling.
![]()
Question 3.
Alida runs her car on the dry marble floor, wet marble floor, newspaper and towel spread on the floor. The force of friction acting on the car on different surfaces in increasing order will be
(i) wet marble floor, dry marble floor, newspaper and towel.
(ii) newspaper, towel, dry marble floor, wet marble floor.
(iii) towel, newspaper, dry marble floor, wet marble floor.
(iv) wet marble floor, dry marble floor, towel, newspaper.
Answer:
(ii) Newspaper, towel, dry marble floor, wet-marble floor.
Question 4.
Supose your writing desk is tilted a little. A book kept on it starts sliding down. Show the direction of frictional force acting on it.
Answer:
Upward direction.
Question 5.
You spill a bucket of soapy water on a marble floor accidently. Would it make it easier or more difficult for you to walk on the floor ? Why ?
Answer:
Soapy water will make the walking more difficult.
Soapy floor acts as a smooth surface as it has no irregularities in it and soap is also very slippery in nature. So, when we walk on soapy floor, we do not have opposing force with the result we slip.
Question 6.
Explain why sportsmen use shoes with spikes.
Answer:
Sportsmen use shoes with spikes to get a better grip on the floor.
Question 7.
Iqbal has to push a lighter box and Seema has to push a similar heavier box on the same floor. Who will have to apply a larger force and why ?
Answer:
Seema will experience a more frictional force since heavier box applies greater pressure on the floor as compared to lighter box due to its weight.
Question 8.
Explain why sliding friction is less than static friction.
Answer:
When a body is at rest, then the force active between the two surfaces in contact is more due to irregularities on two surfaces locked into one another.
But when a body is moving or sliding, the contact points do not get enough time to lock into one another. So sliding friction is always less than’ static friction.
![]()
Question 9.
Give examples to show that friction is both a friend and a foe.
Answer:
Friction as a friend.
- We can write with a pen or pencil.
- Teacher is able to write with chalk on the blackboard.
- We walk on the floor.
- Fix a nail on the wall.
Friction as a foe.
- It weakens the materials.
- It produces heat in machines which damages the various parts.
- Stones on rubbing, produces fire.
Question 10.
Explain why objects moving in fluids must have special shapes.
Answer:
When objects move through fluids, they have to overcome friction acting on them. In this process, they lose energy. Efforts are made to minimize friction by giving special shapes to the moving objects.
PSEB Solutions for Class 8 Science Friction Important Questions and Answers
Multiple Choice Questions
Question 1.
While pushing a heavy box from one place to another in his house, Naresh noticed that it was difficult to take a stationary box from its resting position to moving position but it was easy to move that box with that speed. Why was it so ?
(a) Sliding friction is less than static friction
(b) Static friction is less than sliding friction
(c) The weight of the box decreases
(d) None of the above.
Answer:
(a) Sliding friction is less than static friction.
Question 2.
The moving ball on the floor stops after some time because ……………….. acts on it.
(a) magnetic force
(b) electrostatic force
(c) frictional force
(d) both electrostatic force and frictional force.
Answer:
(c) frictional force.
Question 3.
It is difficult to walk on wet floor because:
(a) frictional force increases
(b) frictional force decreases
(c) sometimes frictional force increases
(d) it is impossible to apply more muscular force
Answer:
(b) frictional force decreases.
Question 4.
You move a stone of glass on the cemented floor, marble floor, water, towel and on ice. The force of friction acting on the different surfaces in increasing order will be:
(a) cemented floor, water, towel, marble floor, ice
(b) marble floor, cemented floor, water, ice, towel
(c) ice, water, marble, towel, cemented floor
(d) water, ice, marble, cemented floor, towel
Answer:
(d) water, ice, marble, cemented floor, towel
![]()
Question 5.
Static friction works when:
(a) an attempt is made to bring an object from motion to rest form
(b) an attempt is made to bring an object from rest form to motion
(c) we do not want to bring any change in the situation of an object
(d) none of the above.
Answer:
(b) an attempt is made to bring an object from rest form to motion .
Question 6.
Rolling friction is:
(a) more than static friction
(b) equal to static friction
(c) less than static friction
(d) sometimes more than static friction and sometimes less than static friction.
Answer:
(c) less than static friction.
Question 7.
Four children were asked to arrange rolling, static and sliding frictions in decreasing order. Their arrangements are given below. Choose the correct arrangement.
(a) rolling, static, sliding
(b) rolling, sliding, static
(c) static, sliding, rolling
(d) sliding, static, rolling.
Answer:
(c) static, sliding, rolling
Question 8.
Alya runs her car on the dry marble floor, wet marble floor, newspaper and towel spread on the floor. The force of friction acting on the car on different surfaces in increasing order will be:
(a) wet marble floor, dry marble floor, newspaper and towel
(b) newspaper, towel, dry marble floor, wet marble floor
(c) towel, newspaper, dry marble floor, wet marble floor
(d) wet marble floor, dry marble floor, towel, newspaper.
Answer:
(a) wet marble floor, dry marble floor, newspaper and towel
Very Short Answer Type Questions
Question 1.
In which direction the force of friction acts ?
Answer:
It acts in a direction opposite to the direction in which the force is applied.
Question 2.
It is difficult to move a cycle along a road with its brakes on. Why ?
Answer:
Sliding friction is more than rolling friction.
![]()
Question 3.
Why a rolling ball stops after some time ?
Answer:
Due to opposing force of air and friction between the ball and the ground.
Question 4.
What is friction ?
Answer:
Friction.
It is the resistance offered to the movement of one material object against another when the two are in contact with each other.
Question 5.
Why are tyres made circular ?
Answer:
Rolling friction is less than sliding friction.
Question 6.
Friction is a self-adjusting force. Is it correct ?
Answer:
Till the body moves, forces of friction adjusts itself in such a way that it is equal and opposite to the applied force.
Question 7.
Which is more smooth : wet muddy or cemented floor ?
Answer:
Wet muddy floor.
Question 8.
What is a spring balance ?
Answer:
Spring balance. It is a device used to measure force dcting on an object.
![]()
Short Answer Type Questions
Question 1.
Why a horse has to apply more force to start a tonga than to keep it moving ?
Answer:
In the first few steps the horse has to do work against the force of friction as well as has to give acceleration (has to increase kinetic energy) to the tonga. After when it begins to move it has to work only against friction.
Question 2.
Give some examples of force of friction.
Answer:
The following are the examples of force of friction in our daily life.:
- A ball rolled inside a hall with smooth floor moves a longer distance than one on a rough ground, when both are rolled with the same initial velocity.
- A person walking inside a room, with polished tiles is afraid of slipping, especially when the tiles are wet.
- If talcum powder is spread on a carrom board the coins move easily and cover a longer distance.
- If a driver applies brakes, the moving vehicle stops.
Question 3.
Friction produces heat. How ?
Answer:
Friction produces heat. It can be shown by following examples-
- Rubbing hands together for few minutes makes our hand hot.
- Striking match stick produces fire by friction.
- Jar of a mixer becomes hot after when it is run for few minutes.
Question 4.
Out of the given two situations, which one will be easy to push the object and why ?

Answer:
In situation 1 it is easy to push the object because rolling friction is less than sliding friction.
Long Answer Type Questions
Question 1.
Define friction. What is the cause of friction ? Give factors affecting friction. Explain that friction is necessary evil.
Answer:
Friction.
It is the opposing force or retarding force; which is called into play when a body actually moves or tends to move over the surface of another body.
When an object is pushed with a small amount of force, it does not move at all. It means that the other surface on which object is lying exerts some force on the object which is in a direction opposite to our push. The opposing force is called friction.
Cause of friction.
Every surface, howsoever, consists of irregularities in the form of mounds and grooves. When one surface tends to move over the other surface, these irregularities get interlocked with one another and hence motion is opposed. This gives rise to frictional force. Thus, force of friction is due to roughness of the surface.
Factors affecting friction.
- Nature of two surfaces in contact.
- Area of contact.
- The normal force with which the two surfaces are pressed.
Friction is a necessary evil because it has both advantages and disadvantages.
Advantages of friction.
Friction plays a very important role in our daily life.
1. We can walk, run, climb up the mountains and the trees only due to friction. Steps of the stairs are made rough to increase friction and hence avoid slipping.
2. The moving vehicles can only be stopped by applying brakes. Due to lack of friction, it is very difficult to drive a vehicle out of mud. Tyres of the vehicles have special projections and depressions, so as to avoid slipping.
3. Belts and pulleys are capable of driving machine only because of friction.
4. If friction were absent, a knot could not be tied; a nail could not be fixed in the wood, the buildings would have tumbled down, the eatables could not be held in fingers and not chewed by the teeth. The clothes could not be stitched and the writing with pen was not possible.
Disadvantages of friction:
- It causes wear and tear.
- Efficiency of machines decreases due to loss of energy due to friction.
- Heat produced due to friction damages the machines.
This shows that friction is a necessary evil.
![]()
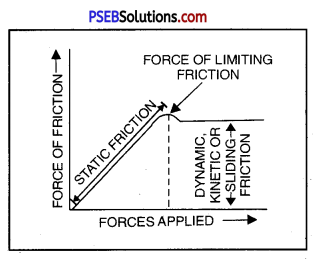
Question 2.
What is force of limiting friction and sliding friction?
Answer:
When no force is applied on a body, there is no force of friction acting on it and the body remains at rest. As you go on increasing applied force, force of friction increases by an equal amount upto a certain limit L. From O to L, the body remains at rest and force of friction is called force of static friction. If the force is slightly increased beyond L, the body starts sliding over the other body. This maximum force of friction which comes in to play is called force of limiting friction. Beyond L, the force of friction decreases a bit and the body starts sliding. This force of friction is called sliding, kinetic or dynamic friction.