Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 6 ਵਰਗ ਅਤੇ ਵਰਗਮੂਲ InText Questions and Answers.
PSEB 8th Class Maths Solutions Chapter 6 ਵਰਗ ਅਤੇ ਵਰਗਮੂਲ InText Questions
ਕੋਸ਼ਿਸ਼ ਕਰੋ :
ਪ੍ਰਸ਼ਨ 1.
ਦਿੱਤੀਆਂ ਗਈਆਂ ਸੰਖਿਆਵਾਂ ਦੇ ਵਿਚ ਮੌਜੂਦ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆਵਾਂ ਪਤਾ ਕਰੋ ।
(i) 30 ਅਤੇ 40
(ii) 50 ਅਤੇ 60.
ਹੱਲ:
(i) 30 ਅਤੇ 40 ਦੇ ਵਿਚ ਸੰਖਿਆ 36 ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਹੈ ।
(ii) 50 ਅਤੇ 60 ਵਿਚ ਕੋਈ ਵੀ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਨਹੀਂ ਹੈ ।
ਕੋਸ਼ਿਸ਼ ਕਰੋ :
ਪ੍ਰਸ਼ਨ 1.
ਕੀ ਅਸੀਂ ਕਹਿ ਸਕਦੇ ਹਾਂ ਕਿ ਹੇਠ ਲਿਖੀਆਂ ਸੰਖਿਆਵਾਂ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆਵਾਂ ਹਨ ? ਅਸੀਂ ਕਿਸ ਤਰ੍ਹਾਂ ਜਾਣਦੇ ਹਾਂ ?
(i) 1057
(ii) 23453
(iii) 7928
(iv) 222222
(v) 1069
(vi) 2061.
ਹੱਲ:
(i) 1057
1057 ਵਿਚ 7 ਇਸਦਾ ਇਕਾਈ ਦਾ ਅੰਕ ਹੈ ।
∴ 1057 ਪੂਰਨ ਵਰਗ ਨਹੀਂ ਹੈ ।
(ii) 23453
23453 ਵਿਚ 3 ਇਸਦਾ ਇਕਾਈ ਅੰਕ ਹੈ ।
∴ 23453 ਪੁਨ ਵਰਗ ਸੰਖਿਆ ਨਹੀਂ ਹੈ ।
(iii) 7928
7928 ਵਿਚ 8 ਇਸਦਾ ਇਕਾਈ ਦਾ ਅੰਕ ਹੈ ।
∴ 7928 ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਨਹੀਂ ਹੈ ।
(iv) 222222
222222 ਵਿਚ 2 ਇਸਦਾ ਇਕਾਈ ਦਾ ਅੰਕ ਹੈ ।
∴ 222222 ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਨਹੀਂ ਹੈ ।
(v) 1069 ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਨਹੀਂ ਹੈ ।
(vi) 2061 ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਨਹੀਂ ਹੈ ।
ਟਿੱਪਣੀ : 2, 3, 7 ਜਾਂ 8 ਵਿਚ ਖਤਮ ਹੋਣ ਵਾਲੀ ਸੰਖਿਆਵਾਂ ਕਦੇ ਵੀ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆਵਾਂ ਨਹੀਂ ਹੁੰਦੀਆਂ ।
ਪੰਜ ਇਸ ਤਰ੍ਹਾਂ ਦੀਆਂ ਸੰਖਿਆਵਾਂ ਲਿਖੋ ਜਿਸ ਦੇ ਇਕਾਈ ਸਥਾਨ ਨੂੰ ਦੇਖ ਕੇ ਤੁਸੀਂ ਦੱਸ ਸਕਦੇ ਹੋ ਕਿ ਇਹ ਸੰਖਿਆਵਾਂ ਵਰਗ ਸੰਖਿਆਵਾਂ ਨਹੀਂ ਹਨ ।
ਹੱਲ:
217, 168, 90, 4000, 143 ਆਦਿ ।

ਪ੍ਰਸ਼ਨ 2.
ਪੰਜ ਇਸ ਤਰ੍ਹਾਂ ਦੀਆਂ ਸੰਖਿਆਵਾਂ ਲਿਖੋ ਜਿਸ ਦੇ ਇਕਾਈ ਸਥਾਨ ਨੂੰ ਦੇਖ ਕੇ ਤੁਸੀਂ ਨਹੀਂ ਦੱਸ ਸਕਦੇ ਹੋ ਕਿ ਇਹ ਵਰਗ ਸੰਖਿਆਵਾਂ ਹਨ ਜਾਂ ਨਹੀਂ ਹਨ ।
ਹੱਲ:
82, 93, 187, 248, 4000 ਆਦਿ ।
ਕੋਸ਼ਿਸ਼ ਕਰੋ :
ਪ੍ਰਸ਼ਨ 1.
(123)2, (77)2, (82)2, (161)2, (109)2 ਵਿਚੋਂ ਕਿਹੜੀਆਂ ਸੰਖਿਆਵਾਂ ਅੰਕ 1’ਤੇ ਖ਼ਤਮ ਹੁੰਦੀਆਂ ਹਨ ?
ਹੱਲ:
(123)2 = 15129
(77)2 = 5929
(82)2 = 6724
(161)2 = 25921
(109)2 = 11881
ਇਸ ਲਈ (161)2 ਅਤੇ (109)2 ਅੰਕ 1 ਉੱਤੇ ਖ਼ਤਮ ਹੁੰਦੀ ਹੈ ।
ਕੋਸ਼ਿਸ਼ ਕਰੋ :
ਪ੍ਰਸ਼ਨ 1.
ਹੇਠਾਂ ਲਿਖੀਆਂ ਵਿਚ ਕਿਹੜੀਆਂ ਸੰਖਿਆਵਾਂ ਦੇ ਇਕਾਈ ਸਥਾਨ ‘ਤੇ 6 ਅੰਕ ਹੋਵੇਗਾ ?
(i) 192
(ii) 242
(iii) 262
(iv) 362
(v) 342
ਹੱਲ:
(i) 192 = 361
ਇਕਾਈ ਦਾ ਅੰਕ = 1
(ii) 242 = 576
ਇਕਾਈ ਦਾ ਅੰਕ = 6
(iii) 262 = 676
ਇਕਾਈ ਦਾ ਅੰਕ = 6
(iv) 362 = 1296
ਇਕਾਈ ਦਾ ਅੰਕ = 6
(v) 342 = 1156
ਇਕਾਈ ਦਾ ਅੰਕ = 6.

ਕੋਸ਼ਿਸ਼ ਕਰੋ :
ਪ੍ਰਸ਼ਨ 1.
ਹੇਠਾਂ ਲਿਖੀਆਂ ਸੰਖਿਆਵਾਂ ਦੇ ਵਰਗ ਕਰਨ ‘ਤੇ ਉਹਨਾਂ ਦੇ ਇਕਾਈ ਸਥਾਨ ‘ਤੇ ਕੀ ਹੋਵੇਗਾ ?
(i) 1234
(ii) 26387
(iii) 52698
(iv) 99880
(v) 21222
(vi) 9106.
ਹੱਲ:
(i) 1234
ਇਕਾਈ ਦਾ ਅੰਕ = 4
∴ ਇਕਾਈ ਅੰਕ ਦਾ ਵਰਗ = (4)2 = 16 ਸੰਖਿਆ ਦੇ ਵਰਗ ਦਾ ਇਕਾਈ ਅੰਕ = 6.
(ii) 26387
ਇਕਾਈ ਦਾ ਅੰਕ = 7.
∴ ਇਕਾਈ ਅੰਕ ਦਾ ਵਰਗ = (7)2 = 49 ਸੰਖਿਆ ਦੇ ਵਰਗ ਦਾ ਇਕਾਈ ਦਾ ਅੰਕ = 9.
(iii) 52698
ਇਕਾਈ ਦਾ ਅੰਕ = 8
∴ ਇਕਾਈ ਅੰਕ ਦਾ ਵਰਗ = (8)2 = 64 ਸੰਖਿਆ ਦੇ ਵਰਗ ਦਾ ਇਕਾਈ ਦਾ ਅੰਕ = 4
(iv) 99880
ਇਕਾਈ ਦਾ ਅੰਕ = 0
∴ ਇਕਾਈ ਅੰਕ ਦਾ ਵਰਗ = ਸੰਖਿਆ ਦੇ ਵਰਗ ਦਾ ਇਕਾਈ ਦਾ ਅੰਕ = 0.
(v) 21222
ਇਕਾਈ ਦਾ ਅੰਕ = 2
∴ ਇਕਾਈ ਅੰਕ ਦਾ ਵਰਗ = (2)2 = 4 ਸੰਖਿਆ ਦੇ ਵਰਗ ਦਾ ਇਕਾਈ ਦਾ ਅੰਕ = 4.
(vi) 9106
ਇਕਾਈ ਦਾ ਅੰਕ = 6
∴ ਇਕਾਈ ਅੰਕ ਦਾ ਵਰਗ = (6)2 = 36 ਸੰਖਿਆ ਦੇ ਵਰਗ ਦਾ ਇਕਾਈ ਦਾ ਅੰਕ = 6.
ਕੋਸ਼ਿਸ਼ ਕਰੋ :
ਪ੍ਰਸ਼ਨ 1.
ਹੇਠਾਂ ਲਿਖਿਆਂ ਵਿਚ ਕਿਹੜੀਆਂ ਸੰਖਿਆਵਾਂ ਦੇ ਵਰਗ ਟਾਂਕ ਸੰਖਿਆਵਾਂ/ਜਿਸਤ ਸੰਖਿਆਵਾਂ ਹੋਣਗੇ । ਕਿਉਂ ?
(i) 727
(ii) 158
(iii) 269
(iv) 1980.
ਹੱਲ:
(i) 727
ਕਿਉਂਕਿ ਸੰਖਿਆ 727 ਇਕ ਟਾਂਕ ਸੰਖਿਆ ਹੈ ।
∴ ਇਸਦਾ ਵਰਗ ਵੀ ਟਾਂਕ ਸੰਖਿਆ ਹੋਵੇਗਾ ।
(ii) 158
ਕਿਉਂਕਿ ਸੰਖਿਆ 158 ਇਕ ਜਿਸਤ ਸੰਖਿਆ ਹੈ ।
∴ ਇਸਦਾ ਵਰਗ ਵੀ ਜਿਸਤ ਸੰਖਿਆ ਹੋਵੇਗਾ ।
(iii) 269
ਕਿਉਂਕਿ ਸੰਖਿਆ 269 ਇਕ ਟਾਂਕ ਸੰਖਿਆ ਹੈ ।
∴ ਇਸਦਾ ਵਰਗ ਵੀ ਟਾਂਕ ਸੰਖਿਆ ਹੋਵੇਗਾ ।
(iv) 1980
ਕਿਉਂਕਿ ਸੰਖਿਆ 1980 ਵਿਚ ਇਕਾਈ ਦਾ ਅੰਕ 0 ਹੈ ਅਤੇ ਇਹ ਜਿਸਤ ਸੰਖਿਆ ਹੈ ।
∴ ਇਸਦੇ ਵਰਗ ਵਿਚ ਵੀ ਇਕਾਈ ਦਾ ਅੰਕ 0 ਹੋਵੇਗਾ ਅਤੇ ਇਹ ਜਿਸਤ ਸੰਖਿਆ ਹੋਵੇਗੀ ।
ਟਿੱਪਣੀ : (i) ਜਿਸਤ ਸੰਖਿਆ ਦਾ ਵਰਗ ਹਮੇਸ਼ਾਂ ਜਿਸਤ ਹੀ ਹੁੰਦਾ ਹੈ ।
(ii) ਟਾਂਕ ਸੰਖਿਆ ਦਾ ਵਰਗ ਹਮੇਸ਼ਾਂ ਟਾਂਕ ਹੀ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਹੇਠਾਂ ਲਿਖੀਆਂ ਸੰਖਿਆਵਾਂ ਦੇ ਵਰਗ ਵਿਚ ਸਿਫ਼ਰਾਂ ਦੀ ਸੰਖਿਆ ਕੀ ਹੋਵੇਗੀ ?
(i) 60
(ii) 400.
ਹੱਲ:
(i) (60)2 = 3600
∴ ਸਿਫ਼ਰਾਂ ਦੀ ਸੰਖਿਆ = 2.
(ii) (40)2 = 160000
∴ ਸਿਰਾਂ ਦੀ ਸੰਖਿਆ = 4.
ਕੋਸ਼ਿਸ਼ ਕਰੋ :
ਪ੍ਰਸ਼ਨ 1.
92 ਅਤੇ 102 ਦੇ ਵਿਚ ਕਿੰਨੀਆਂ ਪ੍ਰਾਕ੍ਰਿਤਕ ਸੰਖਿਆਵਾਂ ਹਨ ? 112 ਅਤੇ 122 ਦੇ ਵਿਚ ਵੀ ਪ੍ਰਾਕ੍ਰਿਤਕ ਸੰਖਿਆਵਾਂ ਦੀ ਸੰਖਿਆ ਦੱਸੋ ।
ਹੱਲ:
ਵਿਆਪਕ ਰੂਪ ਤੋਂ ਦੋ ਵਰਗ ਸੰਖਿਆਵਾਂ n ਅਤੇ (n + 1) ਦੇ ਵਿਚ 2 ਪ੍ਰਕਿਰਿਤਕ ਸੰਖਿਆਵਾਂ ਹਨ ।
ਅਰਥਾਤ (9)2 ਅਤੇ (9 + 1)2 = (10)2 ਦੇ ਵਿਚ
2n ਅਰਥਾਤ 2 (9) = (18) ਪ੍ਰਕਿਰਿਤਕ ਸੰਖਿਆਵਾਂ ਹਨ ।
ਅਰਥਾਤ 92 = 81.
ਅਤੇ 102 = 100.
(81), 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, (100).
112 ਅਤੇ 122 ਦੇ ਵਿਚ 2n ਅਰਥਾਤ 2 (11) = 22
ਕਿਰਿਤਕ ਸੰਖਿਆਵਾਂ ਹਨ ।
ਅਰਥਾਤ 112 = 121
ਅਤੇ 122 = 144
(121), 122, 123, 124, 125, 126, 17, 128, 129, 130, 131, 132, 133, 134, 135, 136, 137, 138, 139, 140, 141, 42, 143, (144).

ਪ੍ਰਸ਼ਨ 2.
ਹੇਠਾਂ ਲਿਖੀਆਂ ਸੰਖਿਆਵਾਂ ਦੇ ਜੋੜਿਆਂ ਦੇ ਵਿਚਲੀਆਂ ਸੰਖਿਆਵਾਂ ਦੱਸੋ ਜੋ ਵਰਗ ਸੰਖਿਆਵਾਂ ਨਹੀਂ ਹਨ ।
(i) (100)2 ਅਤੇ (101)2.
(ii) (90)2 ਅਤੇ (91)2
(iii) (1000)2 ਅਤੇ (1001)2.
ਹੱਲ:
ਵਿਆਪਕ ਰੂਪ ਤੋਂ ਦੋ ਵਰਗ. ਸੰਖਿਆਵਾਂ ਅਤੇ (n + 1) ਦੇ ਵਿਚ 2n ਸੰਖਿਆਵਾਂ ਹਨ ਜੋ ਵਰਗ ਸੰਖਿਆਵਾਂ ਨਹੀਂ ਹਨ ।
(i) (100)2 ਅਤੇ (100 + 1)2 = (101)2 ਦੇ ਵਿਚ
2n = 2 (100) = 200 ਸੰਖਿਆਵਾਂ ਹਨ ਜੋ ਵਰਗ ਸੰਖਿਆਵਾਂ ਨਹੀਂ ਹਨ ।
(ii) (90)2 ਅਤੇ (90 + 1)2 = (91)2 ਦੇ ਵਿਚ
2n = 2 (90) = 180 ਸੰਖਿਆਵਾਂ ਹਨ ਜੋ ਵਰਗ ਸੰਖਿਆਵਾਂ ਨਹੀਂ ਹਨ ।
(iii) (1000)2 ਅਤੇ (1001)2 ਦੇ ਵਿਚ ।
2n = 2 (1000) = 2000 ਸੰਖਿਆਵਾਂ ਹਨ ਜੋ ਵਰਗ ਸੰਖਿਆਵਾਂ ਨਹੀਂ ਹਨ ।
ਟਿੱਪਣੀ : ਪਹਿਲੀ ॥ ਟਾਂਕ ਪ੍ਰਾਕ੍ਰਿਤਕ ਸੰਖਿਆਵਾਂ ਦਾ ਜੋੜ n2 ਹੈ ।
ਅਰਥਾਤ ਜੇਕਰ ਇਕ ਸੰਖਿਆ, ਵਰਗ ਸੰਖਿਆ ਹੈ ਤਾਂ ਉਹ 1 ਤੋਂ ਸ਼ੁਰੂ ਹੋਣ ਵਾਲਾ ਕ੍ਰਮਵਾਰ ਟਾਂਕ ਸੰਖਿਆਵਾਂ ਦਾ ਜੋੜ ਹੈ ।
ਕੋਸ਼ਿਸ਼ ਕਰੋ :
ਪ੍ਰਸ਼ਨ 1.
ਹੇਠਾਂ ਲਿਖੀਆਂ ਸੰਖਿਆਵਾਂ ਵਿਚ, ਹਰੇਕ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਹੈ ਜਾਂ ਨਹੀਂ ?
(i) 121
(ii) 55
(iii) 81
(iv) 49
(v) 69
ਹੱਲ:
(i) 121
∴ 121 – 1 = 120
120 – 3 = 117 1
17 – 5 = 112
112 – 7 = 105
105 – 9 = 96
96 – 11 = 85
85 – 13 = 72
72 – 15 = 57
57 – 17 = 40
40 – 19 = 21
21 – 21 = 0
∴ 121 ਇਕ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਹੈ ।
(ii) 55
∴ 55 – 1 = 54
54 – 3 = 51
51 – 5 = 46.
46 – 7 = 39
39 – 9 = 30
30 – 11 = 19
19 – 13 = 6
6 – 15 = -9
∴ 55 ਇਕ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਨਹੀਂ ਹੈ ।
(iii) 81
∴ 81 – 1 = 80
80 – 3 = 77
77 – 5 = 72
72 – 7 = 65
65 – 9 = 56
56 – 11 = 45
45 – 13 = 32
32 – 15 = 17
17 – 17 = 0
∴ 81 ਇਕ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਹੈ ।
(iv) 49
∴ 49 – 1 = 48
48 – 3 = 45
45 – 5 = 40
40 – 7 = 33
33 – 9 = 24
24 – 11 = 13
13 – 13 = 0
∴ 49 ਇਕ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਹੈ ।
(v) 69
∴ 69 – 1 = 68
68 – 3 = 65
65 – 5 = 60
60 – 7 = 53
53 – 9 = 44
44 – 11 = 33
33 – 13 = 20
20 – 15 = 5
5 – 17 = – 12
∴ 69 ਇਕ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਨਹੀਂ ਹੈ ।
ਹੇਠਾਂ ਲਿਖੇ ਤਿਰੂਪ ਉੱਪਰ ਵਿਚਾਰ ਕਰੋ :
11 × 13 = 143 = 122 – 1
10 × 12 = 120 = 112 – 1
13 × 15 = 195 = 142 – 1
29 × 31 = 899 = 302 – 1
24 × 26 = 624 = 252 – 1
31 × 33 = 1023 = 322 – 1
49 × 51 = 2499 = 502 – 1
ਉੱਪਰ ਲਿਖੇ ਤਿਰੁਪ ਤੁਸੀਂ ਪਹਿਲੇ ਹੀ ਬੀਜਗਣਿਤ ਵਿਚ ਕਰ ਚੁੱਕੇ ਹੋ ਕਿ :
(a + b) × (a – b) = a2 – b2
⇒ 13 × 11
= (12 + 1) (12 – 1)
= 122 – 12
ਹੇਠਾਂ ਲਿਖੇ ਤਿਰੂਪ ਉੱਪਰ ਵਿਚਾਰ ਕਰੋ :
32 = 9 = 4 + 5
52 = 25 = 12 + 13
72 = 49 = 24 + 25
92 = 81 = 40 + 41
112 = 121 = 60 + 61
152 = 225 = 112 + 113.
ਅਰਥਾਤ ਅਸੀਂ ਕਿਸੇ ਵੀ ਟਾਂਕ ਸੰਖਿਆ ਦੇ ਵਰਗ ਤੋਂ ਦੋ ਲਗਾਤਾਰ ਧਨਾਤਮਕ ਸੰਪੂਰਨ ਸੰਖਿਆਵਾਂ ਦੇ ਜੋੜ ਦੇ ਰੂਪ ਵਿਚ ਦਰਸਾ ਸਕਦੇ ਹਾਂ ।

ਕੋਸ਼ਿਸ਼ ਕਰੋ :
ਪ੍ਰਸ਼ਨ 1.
ਹੇਠਾਂ ਲਿਖੀਆਂ ਸੰਖਿਆਵਾਂ ਨੂੰ ਦੋ ਲਗਾਤਾਰ ਧਨਾਤਮਕ ਸੰਪੂਰਨ ਸੰਖਿਆਵਾਂ ਦੇ ਜੋੜ ਦੇ ਰੂਪ ਵਿਚ ਲਿਖੋ :
(i) (21)2
(ii) (13)2
(iii) (11)2
(iv) (19)2.
ਹੱਲ:
(i) (21)2 = 441 = 220 + 221
(ii) (13)2 = 169 = 84 + 85
(iii) (11)2 = 121 = 60 + 61
(iv) (19)2 = 361 = 180 + 181
ਪ੍ਰਸ਼ਨ 2.
ਕੀ ਤੁਸੀਂ ਸੋਚ ਸਕਦੇ ਹੋ ਕਿ ਇਸਦਾ ਉਲਟ ਸੱਚ ਹੈ ਅਤੇ ਕੀ ਦੋ ਲਗਾਤਾਰ ਧਨਾਤਮਕ ਸੰਪੂਰਨ ਸੰਖਿਆਵਾਂ ਦਾ ਜੋੜ ਇਕ ਪੂਰਨ ਵਰਗ ਹੁੰਦਾ ਹੈ ? ਆਪਣੇ ਉੱਤਰ ਦੇ ਪੱਖ ਵਿਚ ਇਕ ਉਦਾਹਰਨ ਦਿਓ ।
ਹੱਲ:
ਨਹੀਂ, ਇਸਦਾ ਉਲਟ ਸਹੀ ਨਹੀਂ ਹੈ ।
ਉਦਾਹਰਨ : 11 ਅਤੇ 12 ਦਾ ਜੋੜ 23 ਹੈ ਜੋ ਇਕ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਨਹੀਂ ਹੈ ।
ਹੇਠਾਂ ਲਿਖੇ ਤੀਰੁਪ ਉਪਰ ਵਿਚਾਰ ਕਰੋ :
12 = 1
112 = 1 2 1
1112 = 1 2 3 2 1
11112 = 1 2 3 4 3 2 1
111112 = 1 2 3 4 5 4 3 2 1
1111112 = 1 2 3 4 5 6 5 4 3 2 1
11111112 = 1 2 3 4 5 6 7 6 5 4 3 2 1 ਆਦਿ ।

ਕੋਸ਼ਿਸ਼ ਕਰੋ :
ਪ੍ਰਸ਼ਨ 1.
ਉਪਰੋਕਤ ਪੈਟਰਨ ਦੀ ਵਰਤੋਂ ਕਰਦੇ ਹੋਏ ਵਰਗ ਸੰਖਿਆਵਾਂ ਲਿਖੋ :
(i) 1111112
(ii) 11111112
ਹੱਲ:
(i) 1111112 = 1 2 3 4 5 6 5 4 3 2 1
(ii) 11111112 = 1 2 3 4 5 6 7 6 5 4 3 2 1
ਇਕ ਹੋਰ ਰੋਚਕ ਪੈਟਰਨ
72 = 4
672 = 4 4 8 9
6672 = 4 4 4 8 8 9
66672 = 4 4 4 4 8 8 8 9
666672 = 4 4 4 4 4 8 8 8 8 9
6666672 = 4 4 4 4 4 4 8 8 8 8 8 9
ਕੋਸ਼ਿਸ਼ ਕਰੋ :
ਪ੍ਰਸ਼ਨ 1.
ਉਪਰੋਕਤ ਪੈਟਰਨ ਦੀ ਵਰਤੋਂ ਕਰਦੇ ਹੋਏ ਕੀ ਤੁਸੀਂ ਹੇਠ ਲਿਖੀਆਂ ਸੰਖਿਆਵਾਂ ਦਾ ਵਰਗ ਪਤਾ ਕਰ ਸਕਦੇ ਹੋ ?
(i) 66666672
(ii) 666666672
ਹੱਲ:
(i) 66666672 = 4 4 4 4 4 4 4 8 8 8 8 8 8 9
(ii) 666666672 = 4 4 4 4 4 4 4 4 8 8 8 8 8 8 8 9

ਕੋਸ਼ਿਸ਼ ਕਰੋ :
ਪ੍ਰਸ਼ਨ 1.
ਹੇਠਾਂ ਲਿਖੀਆਂ ਸੰਖਿਆਵਾਂ ਦਾ ਵਰਗ ਪਤਾ ਕਰੋ ਜਿਹਨਾਂ ਦਾ ਇਕਾਈ ਅੰਕ 5 ਹੈ ।
(i) 15
(ii) 95
(iii) 105
(iv) 205.
ਹੱਲ:
ਟਿੱਪਣੀ : ਇਕਾਈ ਦੀ ਥਾਂ ਉੱਤੇ ਅੰਕ 5 ਵਾਲੀ ਸੰਖਿਆਵਾਂ ਦਾ ਵਰਗ ਪਤਾ ਕਰਨ ਦੇ ਲਈ ਅਸੀਂ ਹੇਠਾਂ ਦਿੱਤੇ ਪੈਟਰਨ ਦੇ ਅਨੁਸਾਰ ਕਰਦੇ ਹਾਂ ।
(25)2 = 625 = (2 × 3) ਸੈਂਕੜਾ + 25
(35)2 = 1225 = (3 × 4) ਸੈਂਕੜਾ + 25
(752 = 5625 = (7 × 8) ਸੈਂਕੜਾ + 25
(125)2 = 15625 = (12 × 13) ਸੈਂਕੜਾ + 25.
(i) (15)2
∴ (15)2 = (1 × 2) ਸੈਂਕੜਾ + 25
= 200 + 25 = 225.
(ii) (95)2
∴ (95)2 = (9 × 10) ਸੈਂਕੜਾ + 25
= 9000 + 25 = 9025
(iii) (105)2
∴ (105)2 = (10 × 11) ਸੈਂਕੜੇ + 25
= 11000 + 25 = 11025
(iv) (205)2
∴ (205)2 = (20 × 21) ਸੈਂਕੜੇ + 25
= 42000 + 25 = 42025.
ਕੋਸ਼ਿਸ਼ ਕਰੋ :
ਪ੍ਰਸ਼ਨ 1.
(i) 112 = 121. 121 ਦਾ ਵਰਗਮੂਲ ਕੀ ਹੈ ?
(ii) 142 = 196. 196 ਦਾ ਵਰਗਮੂਲ ਕੀ ਹੈ ?
ਹੱਲ:
(i) 112 = 121 ; ਇਸ ਲਈ 121 ਦਾ ਵਰਗਮੂਲ 11 ਹੈ ।
(ii) 142 = 196 ; ਇਸ ਲਈ 196 ਦਾ ਵਰਗਮੂਲ 14 ਹੈ ।

ਸੋਚੋ, ਚਰਚਾ ਕਰੋ ਅਤੇ ਲਿਖੋ
ਪ੍ਰਸ਼ਨ 1.
(-1)2 = 1, ਕੀ 1 ਦਾ ਵਰਗਮੂਲ ਹੈ – 1 ?
ਹੱਲ:
ਹਾਂ, ਕਿਉਂਕਿ (1)2 = 1 ਅਤੇ (-1)2 = 1
ਅਸੀਂ ਕਹਿ ਸਕਦੇ ਹਾਂ ਕਿ 1 ਦਾ ਵਰਗਮੂਲ 1 ਅਤੇ – 1.
ਪ੍ਰਸ਼ਨ 2.
(-2)2 = 4 ਕੀ 4 ਦਾ ਵਰਗਮੂਲ ਹੈ – 2 ?
ਹੱਲ:
ਹਾਂ, 4 ਦਾ ਵਰਗਮੂਲ – 2 ਹੈ ।
ਪ੍ਰਸ਼ਨ 3.
(-9)2 = 81, ਕੀ 81 ਦਾ ਵਰਗਮੂਲ ਹੈ – 9 ?
ਹੱਲ:
ਹਾਂ ।

ਕੋਸ਼ਿਸ਼ ਕਰੋ :
ਪ੍ਰਸ਼ਨ 1.
1 ਤੋਂ ਸ਼ੁਰੂ ਕਰਕੇ ਕ੍ਰਮਵਾਰ ਟਾਂਕ ਪ੍ਰਾਕ੍ਰਿਤਕ ਸੰਖਿਆਵਾਂ ਨੂੰ ਘਟਾਉਣ ਨਾਲ ਪਤਾ ਕਰੋ ਕਿ ਹੇਠ ਲਿਖੀਆਂ ਸੰਖਿਆਵਾਂ ਪੂਰਨ ਵਰਗ ਹਨ ਜਾਂ ਨਹੀਂ ? ਜੇਕਰ ਕੋਈ ਸੰਖਿਆ ਪੂਰਨ ਵਰਗ ਹੈ ਤਾਂ ਇਸਦਾ ਵਰਗਮੁਲ ਪਤਾ ਕਰੋ ।
(i) 121
(ii) 55
(iii) 36
(iv) 49
(v) 9.
ਹੱਲ:
(i) 121
∴ 121 – 1 = 120
(ii) 120 – 3 = 117
(iii) 117 – 5 = 112
(iv) 112 – 7 = 105
(v) 105 – 9 = 96
(vi) 96 – 11 = 85
(vii) 85 – 13 = 72
(viii) 72 – 15 = 57
(ix) 57 – 17 = 40
(x) 40 – 19 = 21
(xi) 21 – 21 = 0
ਇੱਥੇ ਸਾਨੂੰ 11ਵਾਂ ਪਦ 0 ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
∴ \(\sqrt {121}\) = 11.
(ii) 55
(i) 55 – 1 = 54
(ii) 54 – 3 = 51
(iii) 51 – 5 = 46
(iv) 46 – 7 = 39
(v) 39 – 9 = 30
(vi) 30 – 11 = 19
(vii) 19 – 13 = 6
(viii) 6 – 15 = – 9
ਇੱਥੇ, ਬਾਰ-ਬਾਰ ਘਟਾਉਣ ਤੇ 0 ਪ੍ਰਾਪਤ ਨਹੀਂ ਹੁੰਦਾ ।
∴ 55 ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਨਹੀਂ ਹੈ ।
(iii) 36
(i) 36 – 1 = 35
(ii) 35 – 3 = 32
(iii) 32 – 5 = 27
(iv) 27 – 7 = 20
(v) 20 – 9 = 11
(vi) 11 – 11 = 0
ਇੱਥੇ ਸਾਨੂੰ 6ਵਾਂ ਪਦ 0 ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
∴ \(\sqrt {36}\) = 6.
(iv) 49
(i) 49 – 1 = 48
(ii) 48 – 3 = 45
(iii) 45 – 5 = 40
(iv) 40 – 7 = 33
(9) 33 – 9 = 24
(vi) 24 – 11 = 13
(vii) 13 – 13 = 0
∴ ਸਾਨੂੰ 7 ਵਾਂ ਪਦ 0 ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
∴ \(\sqrt {49}\) = 7.
(v) 90
(i) 90 – 1 = 89
(ii) 89 – 3 = 86
(iii) 86 – 5 = 81
(iv) 81 – 7 = 74
(v) 74 – 9 = 65
(vi) 65 – 11 = 54
(vii) 54 – 13 = 41
(viii) 41 – 15 = 26
(x) 26 – 17 = 9
(x) 9 – 19 = -10
ਇੱਥੇ, ਬਾਰ-ਬਾਰ ਘਟਾਉਣ ਤੇ 0 ਪ੍ਰਾਪਤ ਨਹੀਂ ਹੁੰਦਾ ਹੈ ।
∴ 90 ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਨਹੀਂ ਹੈ ।

ਸੋਚੋ, ਚਰਚਾ ਕਰੋ ਅਤੇ ਲਿਖੋ
ਪ੍ਰਸ਼ਨ 1.
ਕੀ ਅਸੀਂ ਕਹਿ ਸਕਦੇ ਹਾਂ ਕਿ ਇਕ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਵਿਚ ਜੇਕਰ n ਅੰਕ ਹੈ ਤਾਂ ਉਸਦੇ ਵਰਗਮੂਲ ਵਿਚ \(\frac{n}{1}\) ਅੰਕ ਹੋਣਗੇ ਜੇਕਰ n ਜਿਸਤ ਹੈ ਜਾਂ \(\frac{(n+1)}{2}\) ਹੋਣਗੇ ਜੇਕਰ ॥ ਟਾਂਕ ਹੈ ?
ਉੱਤਰ :
ਹਾਂ ।
ਕੋਸ਼ਿਸ਼ ਕਰੋ :
ਪ੍ਰਸ਼ਨ 1.
ਹੇਠਾਂ ਲਿਖੀਆਂ ਸੰਖਿਆਵਾਂ ਦੇ ਵਰਗਮੂਲ ਵਿਚ ਅੰਕਾਂ ਦੀ ਸੰਖਿਆ, ਵਰਗਮੂਲ ਪਤਾ ਕੀਤੇ ਬਿਨ੍ਹਾਂ ਪਤਾ ਕਰੋ ।
(i) 2560
(ii) 100000000
(iii) 36864.
ਹੱਲ:
(i) 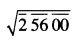
ਦਿੱਤੀ ਗਈ ਸੰਖਿਆ ਦੇ ਵਰਗਮੂਲ ਵਿਚ ਬਾਰ ਦੇ ਚਿੰਨ੍ਹਾਂ | ਦੀ ਸੰਖਿਆ 3 ਹੈ ।
∴ 25600 ਦੇ ਵਰਗਮੂਲ ਵਿਚ ਅੰਕਾਂ ਦੀ ਸੰਖਿਆ = 3
(ii) 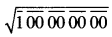
ਦਿੱਤੀ ਗਈ ਸੰਖਿਆ ਦੇ ਵਰਗਮੂਲ ਵਿਚ ਬਾਰ ਦੇ ਚਿੰਨ੍ਹਾਂ ਦੀ ਸੰਖਿਆ 5 ਹੈ ।
∴ 100000000 ਦੇ ਵਰਗਮੂਲ ਵਿਚ ਅੰਕਾਂ ਦੀ ਸੰਖਿਆ = 5 ਹੈ ।
(iii) 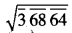
ਦਿੱਤੀ ਗਈ ਸੰਖਿਆ ਦੇ ਵਰਗਮੂਲ ਵਿਚ ਬਾਰ ਦੇ ਚਿੰਨ੍ਹਾਂ ਦੀ ਸੰਖਿਆ 3ਹੈ ।
∴ 36864 ਦੇ ਵਰਗਮੂਲ ਵਿਚ ਅੰਕਾਂ ਦੀ ਸੰਖਿਆ = 3

ਕੋਸ਼ਿਸ਼ ਕਰੋ :
ਪ੍ਰਸ਼ਨ 1.
ਹੇਠਾਂ ਲਿਖੀਆਂ ਸੰਖਿਆਵਾਂ ਦੇ ਨੇੜੇ ਤੋਂ ਨੇੜੇ ਪੂਰਨ ਸੰਖਿਆਵਾਂ ਦਾ ਅੰਦਾਜ਼ਾ ਲਗਾਓ :
(i) \(\sqrt {80}\)
(ii) \(\sqrt {1000}\)
(iii) \(\sqrt {350}\)
(iv) \(\sqrt {500}\)
ਹੱਲ:
(i) \(\sqrt {80}\)
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ ਕਿ ; 64 < 80 < 81
⇒ \(\sqrt {64}\) < \(\sqrt {80}\) < \(\sqrt {81}\)
⇒ 8 < \(\sqrt {80}\) < 9
ਕਿਉਂਕਿ 80, 64 ਦੀ ਤੁਲਨਾ 81 ਦੇ ਬਹੁਤ ਨੇੜੇ ਹੈ ।
∴ \(\sqrt {80}\) ≈ 9.
(ii) \(\sqrt {1000}\)
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ ਕਿ ; 961 < 1000 < 1024
⇒ \(\sqrt {961}\) < \(\sqrt {1000}\) < \(\sqrt {1024}\)
⇒ 31 < \(\sqrt {1000}\) < 32
ਕਿਉਂਕਿ 1000, 961 ਦੀ ਤੁਲਨਾ 1000 ਦੇ ਬਹੁਤ ਨੇੜੇ ਹੈ ।
∴ \(\sqrt {1000}\) ≈ 32.
(iii) \(\sqrt {350}\)
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ ਕਿ :
324 < 350 < 361
⇒ \(\sqrt {324}\) < \(\sqrt {350}\) < \(\sqrt {361}\)
⇒ 18 < \(\sqrt {350}\) < 19
ਕਿਉਂਕਿ 350, 324 ਦੀ ਤੁਲਨਾ 361 ਦੇ ਬਹੁਤ ਨੇੜੇ ਹੈ ।
∴ \(\sqrt {350}\) ≈ 19
(iv) \(\sqrt {500}\)
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ ਕਿ ;
484 < 500 < 529
⇒ \(\sqrt {484}\) < \(\sqrt {500}\) < \(\sqrt {529}\)
⇒ 22 < \(\sqrt {500}\) < 23
ਕਿਉਂਕਿ 500, 484 ਦੀ ਤੁਲਨਾ 529 ਦੇ ਬਹੁਤ ਨੇੜੇ ਹੈ ।
∴ \(\sqrt {500}\) ≈ 22.
![]()
![]()
![]()