Punjab State Board PSEB 9th Class Computer Book Solutions Chapter 5 एम०एस० अक्सैस से परिचय Textbook Exercise Questions and Answers.
PSEB Solutions for Class 9 Computer Chapter 5 एम०एस० अक्सैस से परिचय
Computer Guide for Class 9 PSEB एम०एस० अक्सैस से परिचय Textbook Questions and Answers
1. रिक्त स्थान भरें
1…………………… एक रिलेशन डाटाबेस मैनेजमैंट सिस्टम है।
(क) एक्सल
(ख) वर्ड
(ग) पॉवर पवाइंट
(घ) अक्सैस।
उत्तर-
(घ) अक्सैस।
2. …………… डाटाबेस का मुख्य अंग होता है।
(क) Queries
(ख) टेबल
(ग) Form
(घ) Modules.
उत्तर-
(ख) टेबल।
3. एक फील्ड एक तरह के …………………………….. का सैट होता है।
(क) डाटाबेस
(ख) टेबल
(ग) डाटा आइटम
(घ) फॉर्मज।
उत्तर-
(ग) डाटा आइटम।
4. Queries टेबल को बदलने. और …………………………….. करने के लिए प्रयोग की जाती हैं।
(क) संभालना, फार्म, अपडेट
(ख) काटना, टेबल बनाना, Queries अपडेट कापी करने
(ग) स्टोर करने, पेस्ट करने, कापी करने के लिए, रिपोर्ट बनाने
(घ) Queries तैयार करने, Modules रिपोर्ट बनाने।
उत्तर-
(क) संभालना, फार्म, अपडेट।

5. एक फील्ड के लिए खास सैटिंग ………………………………. कहलाती है।
(क) डाटाबेस
(ख) मैक्रो
(ग) डाटा टाइप
(घ) रिपोर्ट।
उत्तर-
(ग) डाटा टाइप।
2. छोटे उत्तर वाले प्रश्न
प्रश्न 1.
एम०एस० अक्सैस के Components के नाम बताएं।
उत्तर-
- टेबल,
- Queries,
- फार्म,
- रिपोर्ट,
- मैक्रो,
- Modules.
प्रश्न 2.
एम०एस० अक्सैस में कौन-कौन से डाटा टाइप प्रयोग किए जाते हैं ? ।
उत्तर-
- Text,
- नंबर,
- डेट/समय,
- हां/ना
- Currency,
- Auto Number,
- Memo,
- QLE object,
- Hyperlink,
- Calculated.
प्रश्न 3.
एम० एस० अक्सैस की विशेषताएं बताएं।
उत्तर-
- यह एक सुरक्षित डाटाबेस सिस्टम है।
- इस में हम अपने प्रयोग करने वाले डाटे को डाल सकते हैं।
- एम० एस० अक्सैस Multiuser का support करता है।
- यह बहुत सस्ता है। बाकी दूसरे बड़े सिस्टम में भी इसी तरह के फंक्शन प्रयोग किए जाते हैं।
प्रश्न 4.
रिकार्ड का क्या अर्थ है ?
उत्तर-
किसी एक आइटम से संबंधित कीमतों के सैट को रिकार्ड कहते हैं।
प्रश्न 5.
टेबल क्या होता है ? टेबल बनाने के अलग-अलग तरीके बताएं।
उत्तर-
किसी खास विषय के लिए इकट्ठा किया डाटा, टेबल कहलाता है। एक डाटाबेस में बहुत सारे टेबल होते हैं। टेबल बनाने के अलग-अलग तरीके इस प्रकार हैं-
- Create Table In Design View.
- Create Table In Wizard View.
- Create Table by Entering Data.
प्रश्न 6.
टेबल का क्या अर्थ है ?
उत्तर-
टेबल के बीच के डाटे को अपनी ज़रूरत अनुसार देखने और बदलने के लिए फार्म प्रयोग किए जाते हैं। User को टेबल के साथ जोड़ने के लिए फार्म सबसे अच्छा तरीका है।
प्रश्न 7.
रिपोर्ट क्या होती है ?
उत्तर-
यह टेबल या Queries के डाटे को दिखाने और छापने के लिए प्रयोग की जाती है। आप रिपोर्ट के बीच के डाटे को संपादन नहीं कर सकते।
3. बड़े उत्तर वाले प्रश्न
प्रश्न 1.
डाटाबेस डिजाइन के लिए आवश्यक दिशा निर्देश कौन-कौन से हैं ?
उत्तर-
डाटाबेस डिज़ाइन करने से पहले आप को कुछ दिशा निर्देश मानने पड़ेंगे। ये दिशा निर्देश आप को एक अच्छा डाटाबेस बनाने में मदद करेंगे-
- अपनी ज़रूरत अनुसार आप सभी फील्ड को ढूंढें जिन में आप की ज़रूरत के अनुसार जानकारी भरी जा सकती है।
- डाटाबेस को अच्छा बनाने के लिए डाटा के हर एक फील्ड को छोटे-छोटे महत्त्वपूर्ण हिस्से में बांटना चाहिए।
- ग्रुप के संबंधित फील्ड को टेबल में बनाएं।
- सभी टेबलों में एक मुख्य कुंजी लगाएं।
- टेबल में एक ऐसा फील्ड चाहिए जो आम हो।

प्रश्न 2.
Design View में टेबल कैसे बनाया जाता है ?
उत्तर
1. टेबल ग्रुप में कान्टेंट टैब पर टेबल बटन पर क्लिक करें। इससे एक नए खाली टेबल डाटाशीट में एक छोटी Window खुल जायेगी।
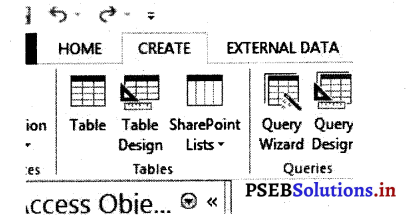
2. डाटे को डालते समय फील्ड भरना-डाटाशीट व्यू में डाटा Excel की वर्कशीट की तरह ही डाला जाता है। इसमें डाटा लगातार रोअज़ और कालम में दाखिल होता है। डाटाशीट व्यू में ऊपर दाईं (Left) तरफ क्लिक करें। जब भी कभी डाटाशीट व्यू में कोई नया कालम डालना होता है तो यह टेबल में एक नया फील्ड बना देता है। डाटाशीट व्यू में हर टेबल में अक्सैस अपने आप एक डाटाशीट के दाईं तरफ एक फील्ड बना देता है जिस को हम आई-डी (ID) कहते हैं। यह फील्ड अपने आप में प्राइमरी कीअ की तरह काम आता है।
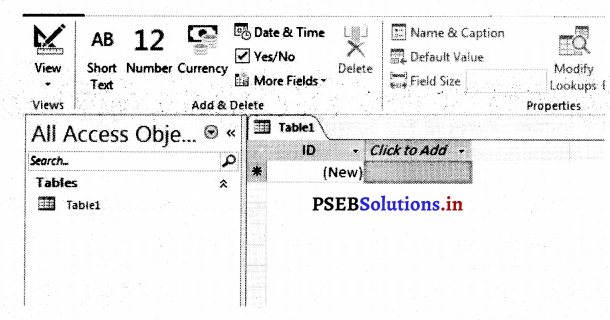
3. डाटा दाखिल करते समय फील्ड को भरना –
- Click to Add Column में पहले सैल पर क्लिक करो। इस के बाद अपने टेबल की आईटम में डाटा दाखिल करें। कालम में बाई (Right) तरफ जाने के लिए टैब (Tab) अथवा Enter कीअ को दबायें। अक्सैस अपने आप आई-डी फील्ड में 1 नंबर डाल देगा। जब भी हम कोई रोअज़ को सिलैक्ट करते हैं, वह अपने आप पैन्सिल में बदल जाता है। जब भी कोई रिकॉर्ड (Record) को डाला जाता है पर उस को सेव (Save) नहीं किया जाता है।
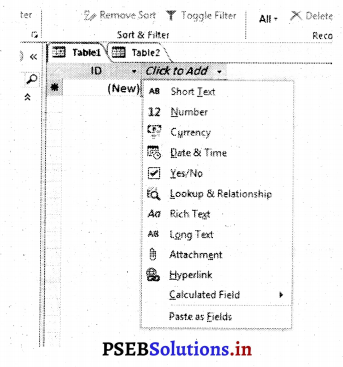
- रोअज़ आईकन में पैन्सिल पर क्लिक करें। इस तरह पहला रिकॉर्ड सेव (Save) हो जायेगा। जिसका नंबर 1 होगा। इस तरह आपका सारा रिकार्ड सेव (Save) हो जायेगा।
- इसी तरह आप डाटा आईटम डालते जाएं और Enter or Tab कीअ दबाते जायें।
(4) जब आप पहले रिकॉर्ड में डाटा दाखिल कर देते हैं तो आप रिकॉर्ड को सेव (Save) करने के लिए किसी भी रोअज़ पर क्लिक करें। आप जितना डाटा डालें उसके बाद टेबल को सेव कर लें।
प्रश्न 3.
डिज़ाइन दृश्य में टेबल कैसे तैयार किया जाता है ?
उत्तर-
जब भी आप डिज़ाइन दृश्य में टेबल बनाना चाहते हैं। आप को अपनी डाटाशीट पर बहुत ध्यान देना पड़ेगा। पहले हमें डिज़ाइन दृश्य में टेबल का ढांचा बनाना पड़ता है और बाद में डाटाशीट में जा कर डाटा को दाखिल करना पड़ता है।
डिज़ाइन दृश्य में पहले Object Window में दिए पेज़ नज़र आते हैं। उसमें पहला Field object पेज़ होता है जो window में दाईं तरफ होता है। इस का प्रयोग field name बताने के लिए और डाटा टाइप बनाने के लिए किया जाता है।
इस का दूसरा क्षेत्र है Property पेन है। यह window के नीचे दिखाई देता है जिस में फील्ड की प्रापर्टी के बारे में बताया जाता है। फील्ड प्रापर्टी में जो प्रापर्टीज़ होती है वह हमारी तरफ से दिए गए मूल्य पर निर्भर करती है। डिज़ाइन दृश्य में टेबल बनाने के स्टैप
- Create table में टेबल ग्रुप में टेबल डिज़ाइन बटन पर क्लिक करो। Object window में एक खाली टेबल आ जायेगा।
- फील्ड नेम कॉलम में पहले फील्ड नेम लिखें। फील्ड नेम 64 अंग्रेज़ी के अक्षर हो सकते हैं जिनमें लैटर, नंबर, स्पेस आदि हो सकते हैं।
- डाटा टाइप कॉलम में नीचे ऐरो पर क्लिक करें और लिस्ट में से डाटा टाइप चुनें।
- Description कॉलम में फील्ड की Description टाइप करें।
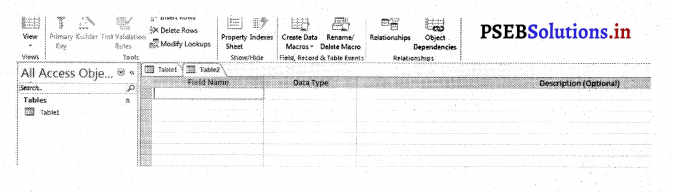
और फील्ड लेकर स्टैप 2 से 4 दुबारा करें। सारे फील्ड भरने के बाद टेबल को सेव करें।
प्रश्न 4.
फिल्टर क्या होता है ? इसको कैसे लगाया जाता है ?
उत्तर-
M.S. Access में फिल्टर एक ऐसा तरीका है जो आप को वही डाटा दिखाता है जिसकी आप को ज़रूरत होती है।
डाटा फिल्टर लगाने के स्टैप-
1. आप जिस फील्ड पर फिल्टर लगाना चाहते हैं, उस फील्ड के साथ के Drop down Arrow पर क्लिक करें। हम कक्षा के आधार पर फिल्टर लगाएं। क्योंकि हम पूरी कक्षा में उन विद्यार्थियों की सूची देखना चाहते हैं जो कि पास अथवा फेल हुए हैं।

2. एक चैक लिस्ट के साथ एक Drop down मीनू सामने आ जायेगे। फिल्टर के प्रणाम में चैक लगी हुई items ही दिखाई देगी। आगे लिखी हुई ऑप्शन पर आप फैसला कर सकते हो किस फिल्टर में आप कौन-सी आईटम ला सकते हो।
- किसी एक आईटम को एक समय सिलैक्ट या डीसिलैक्ट करने के लिए Check box पर क्लिक करें। यहाँ पर हम अकेले कक्षा में फिल्टर लगाना चाहते हैं और बाकी बची आप्शन को छोड़ देंगे।
- हर एक आईटम को फिल्टर लगाने के लिए सिलैक्ट आल पर क्लिक करें और दूसरी बार क्लिक करने पर सभी आईटम डी-सिलैक्ट हो जायेगी।
- ब्लैंक (Blank) पर क्लिक करने पर फिल्टर वही रिकॉर्ड सामने दिखाई देंगे जिस में कई फील्ड होंगे।
- OK पर क्लिक करके फिल्टर चालू हो जाएगा।

प्रश्न 5.
सोर्टिंग (Sorting) क्या है ? सोर्टिंग को आप अपने डॉक्यूमैंट पर कैसे लगायेंगे ?
उत्तर-
सोर्टिंग-आप डाटाबेस में जो रिकॉर्ड देखते हो वही नज़र आयेगा। जैसे कि सबसे पहला रिकॉर्ड और उसके बाद दूसरा रिकॉर्ड। इस तरह हम आसानी से स्क्रोल (Scroll) करके किसी भी रिकॉर्ड को ढूंढ़ सकते हैं। अक्सैस में रिकॉर्ड उनकी आई०डी० के आधार पर सोर्टिंग करता है। उदाहरण के लिए-कक्षा से संबंधित डाटाबेस को कई प्रकार से सोर्टिंग कर सकते हैं।
- विद्यार्थी को नतीजे, उनके नाम, अथवा नंबरों के आधार पर हम डाटे को शोर्ट (Sort) कर सकते
- रोल नंबर और नाम के आधार पर
- कक्षा के आधार पर
विद्यार्थी के टेबल को सोर्ट करने का तरीका :
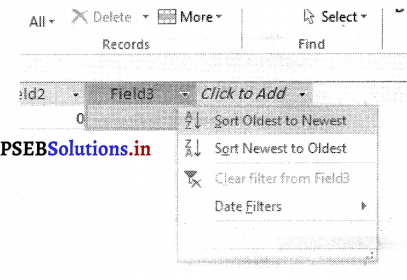
1. होम टैब टेबल पर क्लिक करें और सोर्टिंग और फिल्टर ग्रुप पर जायें।
2. फील्ड को सोर्ट करें। चढ़ते अथवा ढलते क्रम कमांड को सिलैक्ट करें।
- टैक्सट को A to Z और नंबर को छोटे से बड़े तक सोर्टिंग करने के चढ़ते क्रम को सिलैक्ट करें।
- चढ़ते क्रम को सिलैक्ट करें, जिससे टैक्सट Z to A और नंबर की बड़े से छोटे अंक पर सोर्टिंग करना चाहते हैं।
3. अब आप टेबल को सिलैक्ट करें फील्ड के अनुसार सिलैक्ट हो जायेगा।
प्रश्न 6.
एम०एस० अक्सैस में रिपोर्ट कैसे बनाई जाती है ?
उत्तर-
अक्सैस में रिपोर्ट आप को इकट्ठे किये डाटे की अपनी सुविधा अनुसार प्रिंट करने की सुविधा प्रधान करता है। आप अपने टेबल और Queries के आधार पर रिपोर्ट बना सकते हैं।
रिपोर्ट बनाने के कई तरीके हैं पर यहां पर हम विजार्ड के साथ रिपोर्ट बनायेंगे। रिपोर्ट बनाने का तरीका
- अपना डाटा बेस खोलें।
- Report टैब पर क्लिक करें।
- Create a Report by using wizard आप्शन पर क्लिक करें।

4. एक टेबल का चुनाव करें, जिस पर आधारित रिपोर्ट तैयार करनी है।
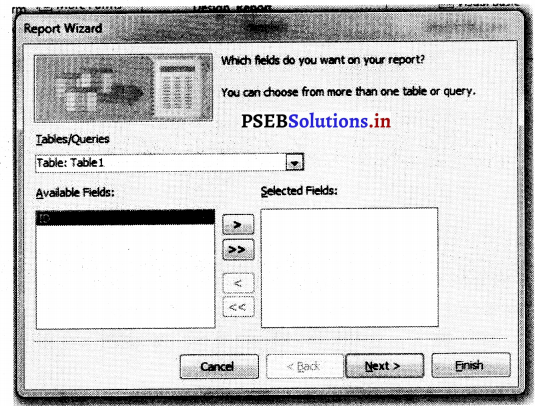
5. टेबल के बीच वाले फील्डस ज़रूरत के अनुसार चुनें।
6. Next बटन पर क्लिक करें।
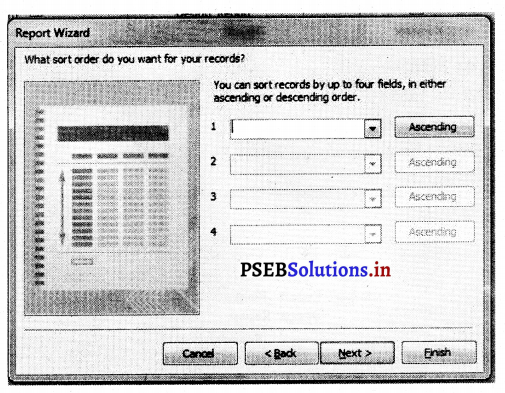
7. अपनी रिपोर्ट के लिए ज़रूरत अनुसार जानकारी दें और Next पर क्लिक करें।
8. फील्ड स्टोर करने के संबंध में जानकारी दें और Next बटन पर क्लिक करें।
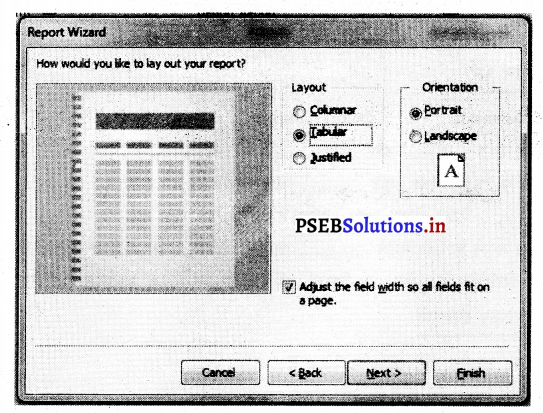
9. रिपोर्ट का ले आऊट निर्धारित करें और Next बटन पर क्लिक करें।
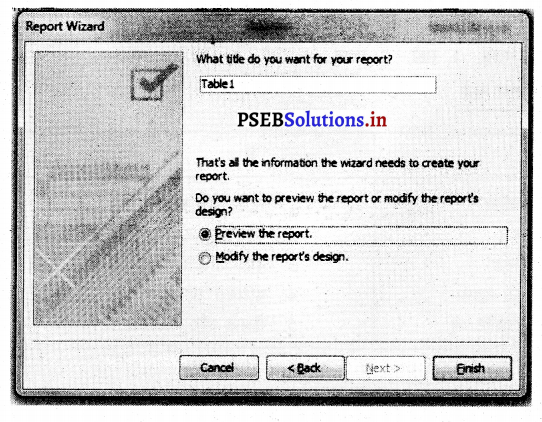
10. रिपोर्ट का स्टाइल चुनें।
11. First बटन पर क्लिक करें।
PSEB 8th Class Computer Guide एम०एस० अक्सैस से परिचय Important Questions and Answers
रिक्त स्थान भरें
1. एम०एस० अक्सैस ……………………………………….. मैनेजमैंट सिस्टम है।
उत्तर-
रिलेशनल डाटाबेस,
2. टेबल में डाटा ………………… और …………….. रखा जाता है।
उत्तर-
रिकार्ड, फील्ड,
3. अक्सैस में टैक्सट, नंबर आदि ………….. टाइप इस्तेमाल की जाती है।
उत्तर-
डाटा,
4. ………………….. टेबल बनाना बहुत आसन है।
उत्तर-
डाटाबेस,

5. डाटाबेस बनाने के लिए पहले ………… जाता है और फिर उस में डाटा दाखिल किया जाता है।
उत्तर-
टेबल बनाया।
सही या गलत बताइये-
1. एम०एस० अक्सैस एक स्प्रेडशीट पैकेज है।
उत्तर-
गलत,
2. अक्सैस में टेबल तीन ढंगों के द्वारा बनाया जा सकता है।
उत्तर-
सही,
3. टेबल में डाटा को सम्पादन (Edit) रखना संभव नहीं।
उत्तर-
गलत,
4. हम दो टेबलज़ के बीच में संबंध स्थापित कर सकते हैं।
उत्तर-
सही,
5. रिपोर्ट के बीच में डाटे को बदला नहीं जा सकता।
उत्तर-
सही,
6. डाटाबेस एक दूसरे से संबंधी रिकार्डज़ का इकट्ठ नहीं होता।
उत्तर-
गलत।
सही मिलान करें-
| A |
B |
| 1. अक्सैस |
1. स्टूडेंट रोल नंबर |
| 2. टेबल |
2. टैक्सट, नंबर, डेट एंड टाइम |
| 3. फील्ड |
3. डाटा दाखिल करवाने के लिए टेबल |
| 4. डाटा टाइप्स |
4. डाटाबेस साफ्टवेयर |
| 5. डाटाशीटव्यु |
5. रोअज़ और कॉलमज |
उत्तर-
| A |
B |
| 1. अक्सैस |
डाटाबेस साफ्टवेयर |
| 2. टेबल |
रोअज़ और कॉलमज़ |
| 3. फील्ड |
स्टूडेंट रोल नंबर |
| 4. डाटा टाइप्स |
टैक्सट, नंबर, डेट ऐंड टाइम |
| 5. डाटाशीट व्यू |
डाटा दाखिल करवाने के लिए टेबल। |
छोटे उत्तर वाले प्रश्न
प्रश्न 1.
टेबल बनाने के भिन्न-भिन्न तरीकों के नाम बताइये।
उत्तर-
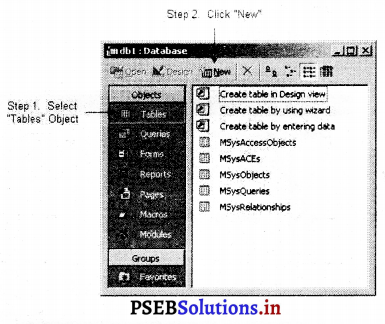
टेबल नीचे लिखे तीन तरीकों से बनाया जा सकता है
- डिज़ाइन व्यू के द्वारा
- विज़ार्ड के द्वारा
- डाटा ऐंटरी के द्वारा।
प्रश्न 2.
फार्म क्या होता है ?
उत्तर-
फार्म टेबल में डाटा एंटर करने का एक माध्यम है। इस में हम डाटे को अपनी ज़रूरत के अनुसार दिखा सकते हैं।
प्रश्न 3.
कोई 5 डाटा टाइप्स के नाम बताइये।
उत्तर-
डाटा टाइप्स नीचे लिखे प्रकार के हो सकते हैं –
- टैक्सट
- नंबर
- डेट/टाइप
- यैस/नौ
- मिमो
- करंसी
- आटो नंबर
- हाईपरलिंक।

प्रश्न 4.
कुएरीज़ क्या होती है ?
उत्तर-
कुएरीज़ टेबल से डाटा प्राप्त करने का साधन है। यह एक लाइन या स्टेटमैंट होती है जो DBMS को भेजी जाती है जिस का जवाब वो सूचना के रूप में देता है।
प्रश्न 5.
नई डाटाबेस फाइल बनाने का तरीका बताइये ।
उत्तर-
नई डाटाबेस फाइल नीचे लिखे तरीके से बनाई जा सकती है-
- File मीनू पर क्लिक करें।
- New → Blank Data Base पर क्लिक करें।
- डाटाबेस फाइल का नाम टाइप करें।
- Create बटन पर क्लिक करें। (डाटाबेस फाइल तैयार हो जायेगी)
प्रश्न 6.
अक्सैस में डाटा किस रूप में होता है ?
उत्तर-
टेबल।
प्रश्न 7.
एम० एस० अक्सैस को शुरू करने का तरीका क्या है ?
उत्तर-
Start → All Programme → Microsoft Office – MS-Access.
प्रश्न 8.
फील्ड क्या है ?
उत्तर-
फील्ड एक ही तरह के डाटा आईटम का सैट होता है। एक टेबल में बहुत फील्ड होते हैं। उदाहरणः विद्यार्थी का टेबल।
प्रश्न 9.
डाटा टाइप क्या है ?
उत्तर-
फील्ड की डाटा टाइप यह बताती है कि इसमें किस प्रकार का डाटा स्टोर किया जा सकता है। उदाहरण के लिए विद्यार्थी की माँ की डाटा टाइप Characters.
उत्तर-
माइक्रोसॉफ्ट अक्सैस एक डाटाबेस पैकेज है, जो अमरीका के माइक्रोसॉफ्ट कार्पोरेशन नामक कम्पनी द्वारा विकसित किए गए पैकेज माइक्रोसॉफ्ट ऑफिस (Microsoft Office) का एक भाग है। यह एक रिलेशनल डाटाबेस पैकेज है, जिसमें डाटा को सारणियों के रूप में रखा जाता है।
प्रश्न 11.
एम० एस० अक्सैस की मुख्य विशेषताएँ क्या हैं?
उत्तर-
एम० एस० अक्सैस में सभी प्रकार के डाटा को सारणियों में रखा जाता है। कोई सारणी किसी डाटा फील्ड के आधार पर अन्य सारणियों में सम्बन्धित हो सकती है। सारणियों में डाटा प्रविष्टि फार्म की सहायता से डाटा भरा और सुधारा जा सकता है। हम कुऐरियों द्वारा अपनी आवश्यकता का डाटा प्राप्त कर सकते हैं। सूचनाओं को रिपोर्टों में प्रस्तुत किया या छापा जा सकता है। एम० एस० अक्सैस में हम डाटा प्रविष्टि के समय ही डाटा की वैधता की जाँच कर सकते हैं।
प्रश्न 12.
एम० एस० अक्सैस में कोई सारणी क्या होती है?
उत्तर-
एम० एस० अक्सैस में कोई सारणी एक जैसे ढांचे वाले रिकार्डों का संग्रह होती है। प्रत्येक रिकार्ड में एक वस्तु के बारे में सूचनाएँ भरी जाती हैं। कोई रिकार्ड किसी वस्तु के बारे में कई डाटा फील्डों का संग्रह होता है। उदाहरण के लिए, यदि हम किसी कक्षा के विद्यार्थियों के बारे में एक सारणी बना रहे हैं, तो उसमें प्रत्येक विद्यार्थी के लिए एक रिकार्ड होगा। एक रिकार्ड में रॉल नं, नाम, पिता का नाम, जन्म तिथि, उम्र, लम्बाई , वज़न आदि डाटा फील्ड हो सकते हैं। किसी सारणी के सभी रिकार्डों में डाटा फील्ड एक जैसे और एक ही क्रम में होने चाहिए।
प्रश्न 13.
एम० एस० अक्सैस में कितने भिन्न-भिन्न डाटा टाइप उपलब्ध हैं?
उत्तर-
एम०एस० अक्सैस में कई डाटा टाइप उपलब्ध हैं। उनमें से मुख्य डाटा टाइप उनके आकार सहित निम्नलिखित हैं –
पाठ्य (Text) अधिकतम 255 चिन्हों तक
संख्या (Number) 1, 2, 4 या 8 बाइट
तारीख/समय (Date/Time) 8 बाईट
हाँ/नहीं (Yes/No 1 बिट
मेमो (Memo) 64000 चिह्नों तक
प्रश्न 14.
एम० एस० अक्सैस में कितने प्रकार के संख्यात्मक फील्ड स्टोर किये जा सकते हैं? उनके आकार का भी उल्लेख कीजिए।
उत्तर-
एम० एस० अक्सैस में निम्नलिखित प्रकार के संख्यात्मक फील्ड उपलब्ध हैं।
बाइट (Byte)- इनमें 0 से 255 तक प्राकृतिक संख्याओं को स्टोर कर सकते हैं। आकार 1 बाइट।
पूर्णांक (Integer)- इसमें -32768 से 32767 तक पूर्ण संख्याएँ स्टोर की जा सकती हैं। आकार 2 बाइट।
लम्बा पूर्णक (Long Integer)- इसमें -2147483648 से 2147483647 तक पूर्णांक स्टोर किए जा सकते हैं। आकार 4 बाइट।
सिंगल (Single)- इसमें 6 सार्थक अंकों तक की संख्याएँ स्टोर की जा सकती हैं, जिनका विस्तार3,402823×1034 से 3,402823×1038 तक होता है। आकार 4 बाइट।
डबल (Double)- इसमें 10 सार्थक अंकों तक की संख्याएँ स्टोर की जा सकती हैं, जिनका विस्तार -1.7976934862325×10304 से 1.7976934862323 x10308 तक होता है। इसका आकार 8 बाइट होता है। (यह डिफॉल्ट टाइप भी है।)

प्रश्न 15.
डाटा वैधता परीक्षण क्या होता है? यह कैसे किया जाता है ?
उत्तर-
डाटा वैधता परीक्षण किसी डाटा को डाटाबेस में जोड़ने से पहले उसके सही और सम्भव होने की जाँच करने की प्रक्रिया को कहा जाता है। यह मुख्यतः दो स्तरों पर किया जाता है- पहला, फील्ड स्तरीय और दूसरा, रिकार्ड स्तरीय। इन दोनों स्तरों के लिए, हम कुछ वैधता नियम तैयार करते हैं। यदि कोई डाटा किसी वैधता नियम पर खरा नहीं उतरता, तो उसे डाटाबेस में नहीं जोड़ा जाता और स्क्रीन पर उस डाटा को सही करने के लिए वैधता पाठ्य को चेतावनी के रूप में प्रदर्शित किया जाता है।
![]()
![]()












