Bhagya – Page 309 – PSEB Solutions

PSEB 8th Class Science Notes Chapter 7 पौधे एवं जंतुओं का संरक्षण

July 22, 2022 by Bhagya

This PSEB 8th Class Science Notes Chapter 7 पौधे एवं जंतुओं का संरक्षण will help you in revision during exams.

PSEB 8th Class Science Notes Chapter 7 पौधे एवं जंतुओं का संरक्षण

→ आजकल वनों को काटकर उस भूमि का उपयोग अन्य उद्देश्यों के लिए किया जा रहा है।

→ दावानल एवं भीषण सूखा भी वनोन्मूलन (deforestation) के प्राकृतिक कारक हैं।

→ वनोन्मूलन से पृथ्वी पर ताप एवं प्रदूषण के स्तर में वृद्धि होती है।

→ वनोन्मूलन से विश्व ऊष्मण, मृदा के गुणों में परिवर्तन, मृदा अपरदन का कारण, मृदा की जलधारण क्षमता में कमी आती है।

→ सरकार द्वारा वनों की सुरक्षा और संरक्षण हेतु नियम, विधियाँ और नीतियाँ बनाई गई हैं।

→ जैवमंडल पृथ्वी का वह भाग है जिसमें सजीव पाए जाते हैं अथवा जो जीवनयापन के योग्य हैं।

→ जैव विविधता से अभिप्राय है, पृथ्वी पर पाए जाने वाले विभिन्न जीवों की प्रजातियाँ, उनके पारस्परिक संबंध एवं पारस्परिक पर्यावरण से संबंध ।

→ जैवमंडल आरक्षित क्षेत्र विविधताओं के संरक्षण के लिए बनाए गए क्षेत्र हैं।

→ किसी विशेष क्षेत्र में पाए जाने वाले पेड़-पौधे उस क्षेत्र के ‘वनस्पतिजात’ एवं जीव-जंतु ‘प्राणिजात’ कहलाते हैं।

→ स्पीशीज़ सजीवों की समष्टि का वह समूह है, जो एक-दूसरे से अंतर्जनन करने में सक्षम होते हैं।

→ वे क्षेत्र जहाँ वन्य प्राणी (जंतु) सुरक्षित एवं संरक्षित रहते हैं, वन्यप्राणी अभ्यारण्य (Wild Life Sanctuaries) कहलाते हैं। यहाँ वन्य प्राणियों को सुरक्षा और रहने की उचित परिस्थितियाँ उपलब्ध करवाई जाती हैं।

→ कई सुरक्षित वन भी सुरक्षित नहीं रहे क्योंकि आस-पास के क्षेत्रों में रहने वाले लोग वनों का अतिक्रमण कर उन्हें नष्ट कर देते हैं।

→ राष्ट्रीय उद्यान (National Parks) उस क्षेत्र के वनस्पतिजाति, प्राणिजात, दृश्यभूमि तथा ऐतिहासिक वस्तुओं का संरक्षण करते हैं।

→ सतपुड़ा राष्ट्रीय उद्यान में सर्वोत्तम किस्म की टीक (सागौन) मिलती है।

→ 1 अप्रैल, 1973 में भारत सरकार द्वारा ‘प्रोजेक्ट टाइगर’ कानून बाघों के संरक्षण हेतु लागू हुआ।

→ संकटापन्न जंतु (Endangered Animals) वे जंतु हैं, जिनकी संख्या विलुप्त हो रही है।

→ पारितंत्र में सभी पौधे, जीव एवं सूक्ष्मजीव और अजैव घटक आते हैं।

→ ‘रेड डाटा पुस्तक’ एक ऐसी किताब है, जिसमें सभी संकटापन्न स्पीशीज़ का रिकार्ड रखा जाता है।

→ जलवायु में परिवर्तन के कारण प्रवासी पक्षी प्रत्येक वर्ष सुदूर क्षेत्रों से एक निश्चित समय पर उड़कर आते हैं।

→ कागज़ एक महत्त्वपूर्ण उत्पाद है, जो वनों से प्राप्त होता है अतः हमें कागज़ की बचत करनी चाहिए।

→ पुनर्वनरोपण (Reforestation) में काटे गए वृक्षों की कमी पूरी करने के उद्देश्य से नए वृक्षों का रोपण करना है।

→ जैव विविधता (Biodiversity)-पृथ्वी पर पाए जाने वाले विभिन्न जीवों की प्रजातियाँ, उनके पारस्परिक संबंध एवं पर्यावरण से संबंध से है।

→ वनोन्मूलन (Deforestration)-वनों का काटना।

→ मरुस्थलीकरण (Desertification)-उर्वर- भूमि का मृदा अपरदन के कारण अनउपजाऊ होना।

→ पारितंत्र (Ecosystem)-इसमें सभी पौधे, जीव एवं सूक्ष्मजीव और अजैव घटक आते हैं।

→ पुनर्वनरोपण (Reforestation)-पौधों का रोपण करना।

→ संकटापन्न स्पीशीज़ (Endangered Species)-वे जंतु हैं, जिनकी संख्या विलुप्त हो रही है।

→ प्राणिजात (Fauna)-किसी विशेष क्षेत्र में पाए जाने वाले जीव-जंतु प्राणिजात कहलाते हैं।

→ रेड डाटा पुस्तक (Red Data Book)-ऐसी किताब जिसमें सभी संकटापन्न स्पीशीज का रिकार्ड रखा जाता है।

→ विशेष क्षेत्री प्रजाति (Endemic Species)-जीवों की वह स्पीशीज जो किसी विशेष क्षेत्र में पाई जाती है।

→ वनस्पतिजात (Flora)-किसी विशेष क्षेत्र में पाए जाने वाले पौधे।

→ विलुप्त (Extinct)-वे जीव जो पृथ्वी से विलुप्त हो चुके हैं या जिनका अस्तित्व समाप्त हो चुका है।

→ प्रवास (Migration)-जीवनयापन हेतु कुछ स्पीशीज़ द्वारा अपने आवास से किसी निश्चित समय में बहुत दूर जाना।

→ अभ्यारण्य (Sanctuary)-वे क्षेत्र जहाँ वन्य प्राणी (जंतु) सुरक्षित एवं संरक्षित रहते हैं।

→ राष्ट्रीय उद्यान (National Park)-उस क्षेत्र के वनस्पतिजात, प्राणिजात, दृश्यभूमि तथा ऐतिहासिक वस्तुओं का संरक्षण करते हैं।

→ जैवमंडल आरक्षित क्षेत्र (Biosphere Reserve Area)-ये विविधताओं के संरक्षण के लिए बनाए क्षेत्र हैं।

PSEB 8th Class Science Notes Chapter 6 दहन और ज्वाला

July 22, 2022 by Bhagya

This PSEB 8th Class Science Notes Chapter 6 दहन और ज्वाला will help you in revision during exams.

PSEB 8th Class Science Notes Chapter 6 दहन और ज्वाला

→ विविध प्रयोजनों के लिए, विभिन्न प्रकार के ईंधनों का उपयोग होता है।

→ घरों में, उद्योगों में तथा वाहनों में विभिन्न प्रकार का ईंधन उपयोग होता है।

→ गोबर, लकड़ी, कोयला, काष्ठ कोयला, पेट्रोल, डीज़ल, प्राकृतिक गैस, एल० पी० जी० आदि विभिन्न ईंधन हैं।

→ कुछ पदार्थ ज्वाला के साथ जलते हैं और कुछ नहीं।

→ दहन, एक रासायनिक प्रक्रम है, जिसमें पदार्थ ऑक्सीजन के साथ अभिक्रिया कर ऊष्मा देते हैं।

→ ईंधन, वह पदार्थ है, जो जलने पर प्रकाश और ऊष्मा देता है।

→ भोजन, शरीर का ईंधन है।

→ ईंधनों को ठोस, तरल और गैसों में वर्गीकृत किया जाता है।

→ वे पदार्थ, जो जलने पर प्रकाश और ऊष्मा देते हैं, दाह्य पदार्थ कहलाते हैं।

→ वे पदार्थ, जो जलने पर ऑक्सीजन से अभिक्रिया नहीं कर सकते और न ही प्रकाश और ऊष्मा देते हैं। उन्हें अदाह्य पदार्थ (Non-combustible substances) कहते हैं।

→ लकड़ी, कागज़, मिट्टी का तेल, काष्ठ कोयला, माचिस की तीलियाँ, सब दाह्य पदार्थ (Combustible substance) हैं।

→ लोहे की कीलें, पत्थर के टुकड़े, काँच आदि अदाह्य पदार्थ हैं।

→ वह न्यूनतम ताप, जिस पर कोई पदार्थ जलने लगता है, उसका ज्वलन-ताप कहलाता है।

→ विभिन्न दाह्य पदार्थों को जलने के लिए विभिन्न ताप की आवश्यकता होती है।

→ ज्वलनशील पदार्थ वे पदार्थ हैं, जिनका ज्वलन-ताप बहुत कम होता है और जो ज्वाला के साथ जल्दी से आग पकड़ लेते हैं।

→ पेट्रोल, डीज़ल, एल० पी० जी०, एल्कोहल कुछ ज्वलनशील पदार्थों के उदाहरण हैं।

→ जंगल की आग बहुत खतरनाक होती है।

→ दहन के लिए ऑक्सीजन आवश्यक है।

→ आग उत्पन्न करने के लिए तीन आवश्यक परिस्थितियाँ हैं-

ऑक्सीजन की उपस्थिति
दहन पदार्थ की उपस्थिति
पदार्थ का निम्न ज्वलन ताप।

→ आग बुझाने के लिए इनमें से किसी एक आवश्यकता को दूर करना है।

→ आग बुझाने के लिए प्रायः जल का उपयोग किया जाता है, क्योंकि यह ज्वलन-ताप को कम कर देता है।

→ तेल और पेट्रोल में लगी आग बुझाने हेतु जल का उपयोग नहीं कर सकते, क्योंकि जल तेल से भारी होता है। यह तेल के नीचे चला जाता है और तेल ऊपर जलता रहता है।

→ जल विद्युत् का सुचालक है, इसलिए इसका उपयोग विद्युत् उपकरणों में लगी आग बुझाने हेतु नहीं किया जा सकता।

→ तरल ईंधनों अथवा विद्युत् से लगी आग बुझाने के लिए रेत/मिट्टी का उपयोग किया जाता है।

→ आग बुझाने के लिए, वायु का प्रवाह काटना या ईंधन का ताप कम करना अथवा दहन पदार्थ को दूर हटाना है।

→ विभिन्न प्रकार के अग्निशामक इस्तेमाल किए जाते हैं।

→ दहन की कई किस्में हैं, जैसे तीव्र दहन, स्वतः दहन और विस्फोट ।

→ ज्वाला, दहन के समय दहन पदार्थ से उत्पन्न वाष्पों से बनती है।

→ ज्वाला का नीला अदीप्त क्षेत्र का ताप सबसे अधिक है।

→ ज्वाला के दीप्त क्षेत्र में बिना जले कार्बन कण होते हैं।

→ ईंधन का उष्मीयमान 1 किलोग्राम के पूर्ण दहन से प्राप्त ऊष्मा ऊर्जा की मात्रा है।

→ उष्मीयमान की इकाई किलोजूल प्रति किलोग्राम है।

→ कोई भी ईंधन आदर्श ईंधन नहीं है।

→ ईंधनों के जलने से वायु प्रदूषण, स्वास्थ्य समस्याएँ, विश्व उष्मण, अम्लीय वर्षा आदि होते हैं।

→ पृथ्वी के वायुमंडल के ताप में धीमी वृद्धि विश्व उष्णन है।

→ सल्फर और नाइट्रोजन ऑक्साइड वर्षा में घुल कर अम्लीय वर्षा बनाते हैं। यह ऑक्साइड जीवाश्म ईंधन के जलने से उत्पन्न होते हैं।

→ अम्ल वर्षा उपजों, भवनों और मृदा के लिए हानिकारक है।

→ सी० एन० जी० एक साफ ईंधन है, क्योंकि यह वायु प्रदूषण नहीं फैलाते।

→ दहन (Combustion)-एक रासायनिक प्रक्रम है, जिसमें पदार्थ ऑक्सीजन के साथ अभिक्रिया कर ऊष्मा देते हैं।

→ दाहृय पदार्थ (Combustible Substance)-वे पदार्थ, जो जलने पर प्रकाश और ऊष्मा देते हैं, दाहय पदार्थ कहलाते हैं।

→ अदाह्य पदार्थ (Non Combustible Substance)-वे पदार्थ, जो जलने पर ऑक्सीजन से अभिक्रिया नहीं कर सकते और न ही प्रकाश और ऊष्मा देते हैं, उन्हें अदाह्य पदार्थ कहते हैं।

→ ज्वलन-ताप (Ignition Temperature)-वह न्यूनतम ताप, जिस पर कोई पदार्थ जलने लगता है।

→ ज्वलनशील पदार्थ (Combustible Substance)-वे पदार्थ, जिनका ज्वलन-ताप बहुत कम होता है और जल्दी से आग पकड़ लेते हैं।

→ अग्निशामक (Fire Extinguisher)-आग बुझाने का एक यंत्र।

→ ऊष्मीय मान (Calorific Value)-1 किलोग्राम पदार्थ के पूर्ण दहन के बाद प्राप्त ऊर्जा की मात्रा।

→ विश्व उष्णन (Global Warming)-पृथ्वी के वातावरण में धीमी ताप की वृद्धि।

PSEB 8th Class Science Notes Chapter 5 कोयला और पेट्रोलियम

July 22, 2022 by Bhagya

This PSEB 8th Class Science Notes Chapter 5 कोयला और पेट्रोलियम will help you in revision during exams.

PSEB 8th Class Science Notes Chapter 5 कोयला और पेट्रोलियम

→ मूलभूत आवश्यकताओं के लिए विभिन्न पदार्थ उपयोग में लाए जाते हैं।

→ दैनिक उपयोग में आने वाले पदार्थों का वर्गीकरण, प्राकृतिक और मानव-निर्मित में किया जाता है।

→ प्रकृति से मिले पदार्थों को प्राकृतिक संसाधन (Natural Resources) कहते हैं।

→ मृदा, जल, खनिज, पौधे और वन प्राकृतिक संसाधन हैं।

→ प्रकृति में उपलब्धता के आधार पर इन्हें अक्षय प्राकृतिक संसाधन (Inexhaustible Natural Resources) और समाप्त होने वाले प्राकृतिक संसाधन (Exhaustible Natural Resources) में किया गया है।

→ पदार्थ, जिनकी उपलब्धता प्रकृति में सीमित है और जो मनुष्य के क्रिया-क्लापों द्वारा खत्म किए जा सकते हैं, उन्हें समाप्त होने वाले संसाधन कहते हैं। कोयला, पेट्रोलियम और प्राकृतिक गैस समाप्त होने वाले संसाधन हैं।

→ सजीवों के अवशेषों से बने जीवाश्म ईंधनों में कोयला, पेट्रोलियम और प्राकृतिक गैस सम्मिलित हैं।

→ कोयला ठोस, काले रंग का पदार्थ ईंधन के रूप में उपयोग में आता है।

→ कोयला जलकर कार्बन डाइऑक्साइड पैदा करता है।

→ कोयले के भुनना प्रक्रमण से कोक, कोलतार और कोयला गैस उत्पन्न होती है।

→ कोक, एक कठोर, सरंध्र और काला पदार्थ है। यह कार्बन का शुद्ध रूप है।

→ कोलतार लगभग 200 पदार्थों का मिश्रण है। यह एक अप्रिय गंध वाला काला गाढ़ा द्रव है।

→ कोलतार, संश्लेषित रंग, औषधि, विस्फोटक, प्लास्टिक, सुगंध, पेंट, फोटोग्राफिक सामग्री, छत-निर्माण सामग्री, नैफ्थलीन की गोलियाँ आदि के लिए प्रारंभिक पदार्थ के रूप में काम आता है।

→ पेट्रोलियम, गहरे रंग का तेलीय द्रव है। इसकी अप्रिय-सी गंध है। यह कई विभिन्न संघटकों का मिश्रण है।

→ पेट्रोलियम के संघटकों में LPG, पेट्रोल, डीज़ल, केरोसीन, स्नेहक तेल, पैराफिन मोम, बिट्मन आदि होते हैं।

→ पेट्रोलियम के विभिन्न संघटकों को पृथक् करने का प्रक्रम परिष्करण (Refining) कहलाता है।

→ कोयले और पेट्रोलियम की मात्रा प्रकृति में सीमित है। इसलिए इनका न्यायोचित उपयोग करना चाहिए।

→ एल० पी० जी० (LPG) पेट्रोलियम गैस का तरल रूप है।

→ ईंधन (Fuel)-जलने पर ऊष्मा तथा प्रकाश ऊर्जा पैदा करने वाले पदार्थ।

→ जीवाश्म ईंधन (Fossil Fuel)-कुछ ज्वलनशील पदार्थ, जिनका निर्माण सजीवों के मृत अवशेषों से लाखों वर्ष पूर्व हुआ था।

→ कार्बनीकरण (Carbonisation)-मृत वनस्पति जो मृदा के नीचे दबी हुई है, उच्च ताप और दाब के कारण, धीमे प्रक्रम द्वारा कोयले में परिवर्तित होने के क्रम कार्बनीकरण कहते हैं।

→ कोयले का प्रक्रमण (Destructive Distillation of Coal)-कोयले को 1000°C ताप से अधिक पर गर्म करने के प्रक्रम को कोयले का प्रक्रमण कहते हैं।

→ परिष्करण (Refining)-पेट्रोलियम से विभिन्न प्रभाजों को पृथक् करने और अशुद्धियों को दूर करने के प्रक्रम को परिष्करण कहते हैं।

→ समाप्त होने वाले संसाधन (Exhaustible Resources)-वे संसाधन, जो मानव क्रिया-कलापों द्वारा धीरे-धीरे समाप्त हो रहे हैं, समाप्त होने वाले संसाधन अथवा सीमित प्राकृतिक संसाधन कहलाते हैं। उदाहरण, कोयला, पेट्रोलियम, प्राकृतिक गैस आदि।

→ अक्षय प्राकृतिक संसाधन (Inexhaustible Resources)-वे संसाधन जो मानव क्रिया-कलापों द्वारा समाप्त नहीं हो सकते, उन्हें अक्षय प्राकृतिक संसाधन अथवा असीमित प्राकृतिक संसाधन कहते हैं। उदाहरण-वायु, जल और सूर्य का प्रकाश आदि।

PSEB 8th Class Science Notes Chapter 4 पदार्थ : धातु और अधातु

July 22, 2022 by Bhagya

This PSEB 8th Class Science Notes Chapter 4 पदार्थ : धातु और अधातु will help you in revision during exams.

PSEB 8th Class Science Notes Chapter 4 पदार्थ : धातु और अधातु

→ पदार्थ को धातु या अधातु दो श्रेणियों में बांटा जा सकता है।

→ धातुएँ, अधातुओं से भौतिक और रासायनिक गुणों में भिन्न होते हैं।

→ धातु सामान्यतः चमकीले, कठोर, अधात्विक, आघातवर्धनीय और तन्य होते हैं। ये विदयुत् और ऊष्मा के चालक होते हैं। ये कक्ष ताप पर ठोस होते हैं। केवल पारा (Mercury) हो कक्ष ताप पर तरल है।

→ अधातु निष्प्रभ (बिना चमक) वाले होते हैं। ये विद्युत् और ऊष्मा के कुचालक, बिना आवाज़ वाले और भुरभुरे होते हैं। ये कक्ष ताप पर ठोस, तरल और गैसीय अवस्था में पाए जाते हैं। इनके गलनांक निम्न होते हैं।

→ धातुएँ ऑक्सीजन के साथ क्रिया करके क्षारीय ऑक्साइड बनाती है।

→ अधातुएँ ऑक्सीजन के साथ क्रिया करके अम्लीय ऑक्साइड बनाती है।

→ लोहा, पानी और वायु से क्रिया करके जंग लगाता है।

→ कुछ धातुएँ पानी के साथ अभिक्रिया करती हैं। सोडियम तीव्रता से ठंडे पानी के साथ अभिक्रिया करके सोडियम हाइड्रोऑक्साइड और हाइड्रोजन उत्पन्न करता है। सोना की भाप से भी अभिक्रिया नहीं होती।

→ सोडियम को मिट्टी के तेल में रखा जाता है।

→ फास्फोरस जल में रखा जाता है, क्योंकि यह वायु के साथ सक्रिय है।

→ अधातु पानी के साथ अभिक्रिया नहीं करते।

→ कुछ धातु अम्लों (हाइड्रोक्लोरिक अम्ल) के साथ अभिक्रिया करके हाइड्रोजन विस्थापित करती हैं। सोना, तांबा और चांदी पर हाइड्रोक्लोरिक अम्ल का कोई प्रभाव नहीं होता।

→ धातुओं की जल, वायु और अम्लों के साथ अभिक्रिया क्षमता के कारण अभिक्रियाशील श्रृंखला है-सोना, चांदी, तांबा, लोहा, जिंक, एल्यूमीनियम, मैग्नीशियम, और सोडियम।

→ अधिक अभिक्रियाशील धातु कम अभिक्रियाशील धातु का उसके धात्विक यौगिकों के जलीय विलयन में विस्थापित कर देती है।

→ हाइड्रोजन गैस ‘पॉप’ ध्वनि में जलती है।

→ धातुओं का उपयोग रसोई घर की वस्तुएँ में व्यापक रूप में होता है।

→ अधातुएँ भी काफ़ी उपयोग में आती हैं।

→ ऑक्सीजन जीवन के लिए अति आवश्यक है।

→ नाइट्रोजन का उपयोग उर्वरकों और पटाखों के निर्माण में होता है।

→ मानव शरीर को लोहा, मैग्नीशियम तथा सोडियम आदि की आवश्यकता रहती है।

→ आघातवर्धनीयता (Malleability)-धातुओं का गुण, जिसके कारण उन्हें हथौड़े से पीटकर शीट (चादर) में परिवर्तित किया जाता है।

→ तन्यता (Ductility)-धातुओं का वह गुण, जिससे उन्हें खींचकर तारों में परिवर्तित किया जा सकता है।

→ ध्वानिक (Sonorus)-धातुओं को टकराने पर उत्पन्न निनाद ध्वनि का गुण।

→ चमकीलापन (Lustre)-पदार्थों में चमकती सतह का गुण।

→ चालकता (Canductance)-धातुओं का गुण जिसके द्वारा विद्युत् या उष्मा एक सिरे से दूसरे सिरे तक पहुँचती है।

→ अम्लीय ऑक्साइड (Acidic Oxide)-अधातुओं के ऑक्साइड, जिन्हें जल में घोलकर अम्ल बनाते हैं।

→ क्षारीय ऑक्साइड (Basic Oxide)-धातुओं के ऑक्साइड, जो जल में घुलकर क्षार बनाते हैं।

PSEB 8th Class Science Notes Chapter 3 संश्लेषित रेशे और प्लास्टिक

July 22, 2022 by Bhagya

This PSEB 8th Class Science Notes Chapter 3 संश्लेषित रेशे और प्लास्टिक will help you in revision during exams.

PSEB 8th Class Science Notes Chapter 3 संश्लेषित रेशे और प्लास्टिक

→ रेशों से कपड़े बनते हैं।

→ तागों के मिलने से रेशे बनते हैं।

→ तागे कृत्रिम अथवा प्राकृतिक स्रोतों से प्राप्त हो सकते हैं।

→ संश्लेषित रेशों को मानव निर्मित अथवा कृत्रिम रेशे भी कहते हैं।

→ संश्लेषित अथवा कृत्रिम रेशे छोटी इकाइयों को जोड़कर बनायी गई एक लंबी श्रृंखला है। बहुत बड़ी शृंखला को बहुलक (पालीमर) कहते हैं।

→ सेलुलोज़ एक प्राकृतिक बहुलक है।

→ रेयॉन, नाइलॉन, पॉलिएस्टर अथवा ऐक्रिलिक मानव निर्मित रेशे हैं।

→ प्राकृतिक रेशों (कपास, रेशम आदि) के स्रोत पौधे और जंतु हैं।

→ कृत्रिम रेशों के स्रोत पौधे (लकड़ी) या जीवाश्म ईंधन (कोयला आदि) हैं।

→ नाइलॉन पहला पूर्ण संश्लेषित रेशा था।

→ विभिन्न रेशे अपनी प्रबलता, जल अवशोषण क्षमता, दहन प्रकृति, मूल्य, चिरस्थायित्व, उपलब्धता और रख-रखाव परिस्थितियों से पहचाने जाते हैं।

→ प्लास्टिक एक बहुलक है, जिसमें छोटी इकाइयाँ विभिन्न आकारों से जुड़ी हैं।

→ प्लास्टिक दो किस्म के हैं

थर्मोप्लास्टिक,
थर्मोसेटिंग प्लास्टिक।

→ पॉलिथीन भी एक प्रकार का प्लास्टिक है।

→ प्लास्टिक हल्का, मज़बूत, चिरस्थायी, जंगरहित, उष्मा और विद्युत् का रोधक है।

→ प्लास्टिक अपशिष्ट पर्यावरण हितैषी नहीं है। यह जैव अनिम्नीकरण प्रकृति का है। जलने पर यह विषैली गैसें उत्पन्न करता है, जो बदबू फैलाती हैं। भूमि पर डालने से, भूमि बंजर हो जाती है, क्योंकि इसका अपघटन जल्दी नहीं होता।

→ संश्लेषित अपशिष्ट के निस्तारण को 4R सिद्धांत (Reduce. Reuse. Recycle. Recover) को ध्यान में रखकर करना चाहिए।

→ मानव-निर्मित रेशे (Man made fibres)- मानव द्वारा बनाए गए रेशों को मानव निर्मित रेशे कहते हैं।

→ पॉलिमर (Polymer)-रसायने पदार्थों की एक जैसी छोटी इकाइयों से मिलकर बनी एक लंबी श्रृंखला अथवा एक जैसी छोटी इकाइयों से बनी बड़ी शृंखला।

→ रेयॉन (Rayon)-कृत्रिम रेशा जिसकी प्रकृति रेशम जैसी होती है इसे कृत्रिम रेशम भी कहते हैं।

→ पेट (PET)-पालिएस्टर की एक विशेष किस्म जिससे बोतलें, फिल्में, तारें, बर्तन आदि बनाए जाते हैं।

→ थर्मोप्लास्टिक (Thermoplastic)-प्लास्टिक की किस्म, जो गर्म होने पर अपना आकार बदल लेती है और आसानी से मुड़ सकती है, थर्मोप्लास्टिक कहलाती है।

→ थर्मोसैटिंग प्लास्टिक (Thermo Setting Plastic)-प्लास्टिक की किस्म, जो गर्म करने पर नर्म नहीं होती, थर्मोसैटिंग प्लास्टिक कहलाती है। इसे केवल एक ही बार साँचे में डाला जा सकता है।

PSEB 8th Class Science Notes Chapter 2 सूक्ष्मजीव : मित्र एवं शत्रु

July 22, 2022 by Bhagya

This PSEB 8th Class Science Notes Chapter 2 सूक्ष्मजीव : मित्र एवं शत्रु will help you in revision during exams.

PSEB 8th Class Science Notes Chapter 2 सूक्ष्मजीव : मित्र एवं शत्रु

→ सुक्ष्मजीव बहुत ही छोटे जीव हैं, जिन्हें केवल सूक्ष्मदर्शी (Microscope) द्वारा ही देखा जा सकता है।

→ सूक्ष्मजीव सभी प्रकार की परिस्थितियों में जीवित रह सकते हैं जैसे गर्म स्रोतों, बर्फीय जल, लवणीय जल, रेगिस्तानी मिट्टी और दलदली मिट्टी (marshy land)

→ सूक्ष्मजीवों का वर्गीकरण जीवाणु, कवक, प्रोटोज़ोआ, शैवाल और विषाणुओं में किया जाता है।

→ सूक्ष्मजीव सभी प्रकार के आवासों में पाए जाते हैं। प्रायः यह एक कोशिक होते हैं, पर कभी-कभी श्रृंखला अथवा समूह में भी पाए जाते हैं।

→ सूक्ष्मजीवों का हमारे जीवन में बहुत महत्त्व है।

→ जीवाणु हर जगह पाए जाते हैं और बहुत छोटे होते हैं।

→ जीवाणु के व्यास का आकार एक मिलीमीटर के एक हज़ारवें भाग का 1.25 गुणन है।

→ जीवाणु की तीन किस्में

छड़ नुमा,
गोल और
कुंडलीनुमा है।

→ जीवाणु, स्वपोषी अथवा परपोषी हो सकते हैं।

→ जीवाणु, कोशिका विखंडन अथवा विविखंडन से प्रजनन करते हैं।

→ शैवाल और जीवाणुओं में कई समानताएँ हैं।

→ साइनोबैक्टीरिया वातावरणी नाइट्रोजन को स्थिर कर मिट्टी की उपजाऊ शक्ति बढ़ाते हैं।

→ डायटम एक सूक्ष्म शैवाल है, जो झरनों, तलछटी और समुद्र में पाया जाता है।

→ कवक परजीवी तथा मृतजीवी होते हैं।

→ कुछ कवक खाद्य पदार्थ, चमड़ा, कागज़ और कपड़े को नष्ट करते हैं तो कुछ फसल और जानवरों के लिए घातक होते हैं।

→ खमीर (Yeast) एक कोशिक और परजीवी कवक है, जिसका उपयोग किण्वन (Fermentation) द्वारा बियर, शराब और दूसरे पेयजल बनाने में किया जाता है।

→ विषाणु (Virus) एक कोशिक मृतजीवी है जो कोशिका में गुणन करने की क्षमता रखता है।

→ प्रोटोज़ोआ (Protozoa) एक कोशीय सूक्ष्मजीव है जो पेचिश और मलेरिया जैसे रोग फैलाते हैं।

→ भोजन विषाक्तता (Food Poisoning) सूक्ष्मजीवों द्वारा नष्ट किए भोजन खाने से होती है।

→ भोजन पर वृद्धि करने वाले सूक्ष्मजीव विषैले पदार्थ उत्पन्न करते हैं।

→ भोजन के संरक्षण के मुख्य तरीके-रासायनिक तरीका जिसमें नमक मिलाना, चीनी मिलाना, तेल और सिरका मिलाना, गर्म और ठंडा करने की विधियाँ अपनाई जाती हैं।

→ प्रोटोज़ोआ (Protozoa)- यह एक कोशिक (Unicellular) सूक्ष्मजीव है, जो पेचिश और मलेरिया जैसे रोग फैलाते हैं।

→ कवक (Fungi)-कवक सूक्ष्मजीव पादप हैं जो हरे नहीं होते और खाद्य पदार्थों को संदूषित करते हैं।

→ विषाणु (Virus)-यह सूक्ष्मजीव सजीव और निर्जीव की सीमा रेखा पर है।

→ यह केवल पोषी (host) के शरीर में ही प्रजनन करते हैं।

→ जीवाणु (Bacteria)-यह सूक्ष्मजीव हर व्यापक जगह पर पाए जाते हैं और आकार में बहुत छोटे होते हैं। यह पोषण के आधार पर स्वपोषी और परपोषी हो सकते हैं।

→ खमीर (Yeast) खमीर एक कोशिक कवक है जो किण्वन द्वारा बियर, शराब और दूसरे पेय पदार्थ बनाने के काम आता है।

→ राइजोबियम (Rhizobium)-यह एक जीवाणु है जो नाइट्रोजन स्थिरीकरण में सहायक होता है। यह फलीदार पौधों की जड़ ग्रंथियों में पाया जाता है।

→ मिट्टी की उर्वरता (Soil Fertility)- मिट्टी में नाइट्रोजन पोषक तत्त्व की आपूर्ति ही मिट्टी की उर्वरता है। यह जीवाणु और नीले हरे शैवाल द्वारा होती है।

→ सूक्ष्मजीव (Microorganism)- बहुत छोटे जीव जिन्हें नंगी आँख द्वारा नहीं देखा जा सकता। इन्हें केवल सूक्ष्मदर्शी द्वारा ही देखा जा सकता है। यह सभी प्रकार के आवास में रहते हैं।

→ लैक्टोबेसिलस (Lactobacillus)-दूध में पाए जाने वाले जीवाणु, जो दही जमाने में सहायक होते हैं, लैक्टोबेसिलस कहलाते हैं।

→ वाहक (Carriers)-वाहक वे कीट या दूसरे जीव हैं जो रोग फैलाने वाले सूक्ष्मजीवों का संचारण करते हैं।

→ प्रतिरक्षी (Antibodies)-जब रोगाणु शरीर में प्रवेश करते हैं तो शरीर रोगाणुओं से लड़ने के लिए प्रतिरक्षी उत्पन्न करता है।

→ टीका (Vaccine)-यह मृत अथवा कमज़ोर सूक्ष्मजीव है जिन्हें स्वस्थ शरीर में प्रवेश कराया जाता है।

→ रोगाणु (Pathogen)-रोग फैलाने वाले सूक्ष्मजीव रोगाणु कहलाते हैं।

→ किण्वन (Fermentation)-चीनी को एल्कोहल में सूक्ष्मजीव खमीर द्वारा परिवर्तित करने की क्रिया किण्वन कहलाती है।

→ नाइट्रोजन स्थिरीकरण (Fixation of Nitrogen)-सूक्ष्मजीवों द्वारा वायुमंडलीय नाइट्रोजन को नाइट्राइट और नाइट्रेट में परिवर्तन करने की प्रक्रिया को नाइट्रोजन स्थिरीकरण कहते हैं। यह राइजोबियम जीवाणुओं द्वारा संभव होता है।

→ नाइट्रोजन चक्र (Nitrogen Cycle)-वायुमंडलीय नाइट्रोजन का स्थिरीकरण, नाइट्रीफिकेशन, डीनाइट्रीफिकेशन, आदि प्रक्रियाओं के बाद वापस नाइट्रोजन के रूप में वायुमंडल में प्रवेश करना ही नाइट्रोजन चक्र है।

PSEB 8th Class Science Notes Chapter 1 फसल उत्पादन एवं प्रबंध

July 22, 2022 by Bhagya

This PSEB 8th Class Science Notes Chapter 1 फसल उत्पादन एवं प्रबंध will help you in revision during exams.

PSEB 8th Class Science Notes Chapter 1 फसल उत्पादन एवं प्रबंध

→ खेत में पौधों को उगाना और देखभाल करना कृषि उत्पादन (Crop Yield) कहलाता है।

→ धन कमाने के लिए जो फसल उगाई जाती है, उसे नकदी फसल (Cash Crop) कहते हैं।

→ फसल के अतिरिक्त, सब्जियां, फल और फूल भी उगाए जाते हैं। यह हार्टीक्लचर (Horticulture) में आते हैं।

→ पौधों की उचित वृद्धि के लिए जल, ऑक्सीजन, सूर्य का प्रकाश और पोषक तत्त्व आवश्यक हैं।

→ कृषि उत्पादन में कुछ पद्धतियों का वैज्ञानिक ढंग से उपयोग होता है।

→ भूमि को नर्म और समतल करना मिट्टी तैयार करना अथवा जुताई कहलाता है। इससे जड़ें आसानी से मिट्टी में नीचे तक बढ़ती हैं।

→ पौधों को समय-समय पर पानी देने की विधि सिंचाई कहलाती है।

→ सिंचाई के साधन हैं-कुएं, ट्यूबवेल, तालाब, झीलें, नदियां, बाँध और नहरें।

→ सिंचाई की आधुनिक विधियां हैं-छिड़काव तंत्र और ड्रिप तंत्र।

→ बीज खेतों में हाथों द्वारा तथा सीड-ड्रिल द्वारा बोए जाते हैं।

→ पौध (Seedling) एक छोटा पौधा है। पौध को पौधशाला (नर्सरी) से खेत में रोपने को रोपण विधि कहते हैं।

→ ह्यूमस कार्बनिक पदार्थ से बनी मिट्टी की ऊपरी सतह है जो पौधों और पशुओं के अपशिष्ट के अपघटन से बनती है।

→ खाद पौधों और पशुओं के अपशिष्ट से तैयार की जाती है। उर्वरक एक रासायनिक मिश्रण है जिसमें पोटाशियम, नाइट्रोजन और फास्फोरस भरपूर उचित मात्रा में होते हैं। खाद और उर्वरक मिट्टी में पोषक तत्त्वों की पूर्ति करते हैं।

→ फसल के साथ उगने वाले अवांछित पौधे, खरपतवार कहलाते हैं। इन्हें खरपतवारनाशी छिड़क कर दूर किया जाता है।

→ कीट फसल को नुकसान पहुंचाते हैं। इन पर कीटनाशक का छिड़काव किया जाता है।

→ ऋतुओं के आधार पर फसलों के दो वर्ग हैं

रबी (Rabi) और
खरीफ (Kharif) ।

→ कटाई करते समय फसल को निकाला जाता है या काटा जाता है।

→ दानों को भूसे से अलग करने की विधि को थ्रेशिंग कहते हैं। फटकने (Winnowing) से दाने भूसे से अलग हो जाते हैं।

→ मिश्रित कृषि में दो या तीन फसलें एक ही खेत में इकट्ठी उगाई जाती हैं।

→ गाय, भैंस, पोल्टरी पक्षी और मछली का पालन माँस, अंडे और दूध जैसे खाद्य पदार्थों की प्राप्ति के लिए किया जाता है।

→ पालतू पशुओं को उचित भोजन, आवास एवं देखभाल की आवश्यकता होती है।

→ कटाई ऋतु के साथ कुछ विशेष पर्व जैसे पोंगल, वैसाखी, होली, दीवाली, नबान्या और बीहू जुड़े हुए हैं।

→ कृषि पद्धतियां (Agricultural Practices)- फसल उगाने के लिए किसान द्वारा सामयिक अवधि में अपनाए कई क्रिया-कलापों को कृषि पद्धतियां कहते हैं।

→ मिट्टी की तैयारी (Preparation of Soil)-फसल उगाने से पहले मिट्टी को पलटना, पोला बनाना और समतल करना पड़ता है। इसे जुताई कहते हैं।

→ बुआई (Sowing)-मिट्टी में बीज बोने की विधि को बुआई कहते हैं।

→ खाद और उर्वरक (Manures and Fertilizers)-वे कार्बनिक और रासायनिक पदार्थ जो फसल की अच्छी वृद्धि के लिए पोषकों के रूप में मिट्टी में मिलाए जाते हैं, खाद और उर्वरक कहलाते हैं।

→ सिंचाई (Irrigation)-पौधों की वृद्धि के लिए समय-समय पर पानी देने की विधि, सिंचाई कहलाती है।

→ कटाई (Harvesting)-पकने पर फसल काटने की विधि कटाई कहलाती है।

→ भंडारण (Storage)- फसल के दानों का बड़े-बड़े भंडार गृहों में भंडारण किया जाता है।

→ निराई (Weeding)-खरपतवार को खेत से बाहर निकालने की विधि निराई कहलाती है।

→ पशुपालन (Animal Husbandry)- पशुओं के उचित भोजन, आवास और देखभाल को पशुपालन कहते हैं।

→ साइलो (Silos)-बीजों का बड़े पैमाने पर भंडारण करने के लिए प्रयुक्त होने वाले बड़े पात्र, साइलो कहलाते हैं।

→ भंडार गृह (Granaries)-बड़े-बड़े खुले कमरे जहां अनाज के दानों को बड़े पैमाने पर सुरक्षित संभाल कर रखा जाता है।

→ थ्रेशिंग (Threshing)- भूसे से अनाज के दानों को पृथक् करने की विधि को थ्रेशिंग कहते हैं।

→ खरपतवार (Weeds)- अवांछित पौधे जो खेतों में अपने आप उग आते हैं, खरपतवार कहलाते हैं।

→ खरपतवारनाशी(Weedicides)-वे रसायन जो खरपतवारों को नष्ट करते हैं, खरपतवारनाशी कहलाते हैं।

PSEB 3rd Class Maths Solutions Chapter 8 माप

July 22, 2022 by Bhagya

Punjab State Board PSEB 3rd Class Maths Book Solutions Chapter 8 माप Textbook Exercise Questions and Answers

PSEB Solutions for Class 3 Maths Chapter 8 माप

पृष्ठ 162:

आओ करें:

प्रश्न 1.
लंबाई पता करो :

हल :

PSEB 3rd Class Maths Solutions Chapter 8 माप 1

पृष्ठ 163:

प्रश्न 2.
कुछ अन्य वस्तुएँ लेकर नीचे दी गई तालिका को पूरा करो :
हल :

PSEB 3rd Class Maths Solutions Chapter 8 माप 2

प्रश्न 3.
रेखा खंड की लंबाई माप कर सैंटीमीटर में लिखो :
हल :

PSEB 3rd Class Maths Solutions Chapter 8 माप 3

पृष्ठ 164:

आओ करें नीचे दी गई लंबाई के रेखा खंड खींचो :

(a) 5 सैं.मी.
(b) 8 सैं.मी.
(c) 6 सैं.मी.
(d) 10 सैं.मी.
(e) 2 सैं.मी…
(f) 7 सैं.मी.
(g) 9 सैं.मी.
(h) 12 सैं.मी.
हल :

PSEB 3rd Class Maths Solutions Chapter 8 माप 4

PSEB 3rd Class Maths Solutions Chapter 8 माप 5

प्रश्न 4.
₹ 100 के असली नोट की लंबाई और चौड़ाई पता करो :
हल :
असली ₹ 100 के नोट की लंबाई ……………… सैं.मी.
असली ₹ 100 के नोट की चौडाई …………….. सैं.मी.
हल : स्वयं कीजिए।

पृष्ठ 165:

आओ करें:

प्रश्न 1.
जोड़ करें:
हल :

PSEB 3rd Class Maths Solutions Chapter 8 माप 6

प्रश्न 2.
घटाव करो :
हल :

PSEB 3rd Class Maths Solutions Chapter 8 माप 7

प्रश्न 3.
स्कूल में लड़कियों को वर्दी के लिए कपड़ा दिया जाता है। सिमरन को कमीज के लिए 2 मीटर और सलवार के लिए 3 मीटर कपड़ा चाहिए। बताओ सिमरन को वर्दी के लिए कुल कितने मीटर कपड़ा चाहिए ?
हल :
कमीज के लिए कपड़ा = 2 मी.
सलवार के लिए कपड़ा = 3 मी.
सिमरन की वर्दी के लिए कुल कपड़ा = 5 मी.

PSEB 3rd Class Maths Solutions Chapter 8 माप 8

प्रश्न 4.
सतवीर सिंह का स्कूल उसके घर से 175 मीटर की दूरी पर है। उसके द्वारा एक दिन में घर से स्कूल आते व स्कूल से घर जाने में कितनी दरी तय की गई ?
हल :
घर से स्कूल की दूरी = 175 मी.
स्कूल आते व स्कूल से घर जाने में तय दूरी = 175 मी. + 175 मी. = 350 मी.
सतवीर द्वारा एक दिन में घर से स्कूल तथा स्कूल से घर जाने में कुल जितनी दूरी तय की गई = 350 मी.

PSEB 3rd Class Maths Solutions Chapter 8 माप 9

सतवीर ने कुल दूरी तय की = 3 5 0 मी.

प्रश्न 5.
सरोज ने एक फूल बनाने के लिए 75 सेंटीमीटर लाल रिब्बन व 60 सैंटीमीटर हरे रंग का रिब्बन लिया। फूल बनाने के लिए सरोज ने कितने सैंटीमीटर रिब्बन का उपयोग किया ?
हल :
लाल रिब्बन = 75 सें.मी.
हरा रिब्बन = 60 सैं.मी.
कुल रिब्बन = 135 सैं.मी.

PSEB 3rd Class Maths Solutions Chapter 8 माप 10

इसलिए, फूल बनाने के लिए 135 सें.मी. रिब्बन का उपयोग किया गया।

पृष्ठ 166:

भार:

क्या आपको याद है ?

प्रशन 1.
तुम्हारे एक हाथ में ज्यामैट्री बॉक्स है व दूसरे हाथ में पेंसिल है। कौन-सी चीज़ भारी लगेगी ?
हल :
ज्यामैट्री बॉक्स।

प्रशन 2.
तुम्हारे एक हाथ में पपीता है और दूसरे हाथ में बेर है। कौन-सी वस्तु भारी लेगीगी ?
हल :
पपीता।

प्रशन 3.
एक टोकरी में 20 आम हैं और दूसरी टोकरी में 20 बेर हैं। कौन-सी टोकरी में भार अधिक होगा ?
हल :
आम की टोकरी। |

पृष्ठ 168:

आओ करें:

प्रशन 1.
वस्तुओं के भार अनुसार सूई की स्थिति दर्शाओ :
हल :

PSEB 3rd Class Maths Solutions Chapter 8 माप 11

प्रशन 2.
भारी, हल्का या बराबर पता करो :
हल :

PSEB 3rd Class Maths Solutions Chapter 8 माप 12

पृष्ठ 169:

प्रशन 3.
नीचे दी वस्तओं को उनके भार के आधार पर हल्के से भारी क्रम में लिखो :
हल :

PSEB 3rd Class Maths Solutions Chapter 8 माप 13

प्रशन 4.
एक ईंट का भार 3 किलोग्राम है। नीचे दी गई वस्तुओं में से ईंट से भारी व हल्की वस्तुओं को चुनो और नीचे दी गई सारणी में लिखो :

PSEB 3rd Class Maths Solutions Chapter 8 माप 14

PSEB 3rd Class Maths Solutions Chapter 8 माप 15

हल:

PSEB 3rd Class Maths Solutions Chapter 8 माप 16

पृष्ठ 171:

आओ करें:

प्रशन 1.
जोड़ करो :
हल :

PSEB 3rd Class Maths Solutions Chapter 8 माप 17

प्रशन 2.
घटाव करो :
हल :

PSEB 3rd Class Maths Solutions Chapter 8 माप 18

प्रशन 3.
अमरीक सिंह ने एक दुकान से 25 किलोग्राम आटा और 8 किलोग्राम चीनी खरीदी, बताओ
उसने कितने किलोग्राम राशन खरीदा।
हल : अमरीक सिंह ने जितना आटा खरीदा = 25
किलोग्राम अमरीक सिंह ने जितनी चीनी खरीदी = 8
किलोग्राम कुल जितना राशन खरीदा = 33

PSEB 3rd Class Maths Solutions Chapter 8 माप 19

किलोग्राम इसलिए अमरीक सिंह ने कुल 33 किलोग्राम राशन खरीदा।

प्रशन 4.
शंकर सब्जी वाले ने सब्जी मंडी से 90 किलोग्राम आलू खरीदे। उसने 42 किलोग्राम आलू बेच दिए। बताओ उसके पास कितने किलोग्राम आलू बच गए ?
हल:
810 शंकर ने जितने आलू खरीदे = 90 किलोग्राम
जितने आलू बेच दिए = 42 किलोग्राम
जितने आलू बाकी बचे = 48 किलोग्राम

PSEB 3rd Class Maths Solutions Chapter 8 माप 20

इसलिए 48 किलोग्राम आलू बचे।

प्रशन 5.
एक सरकारी स्कूल में महीने के दौरान बने मिड-डे मील में 103 किलोग्राम गेहूँ और 98
किलोग्राम चावल का उपयोग हुआ। स्कूल में महीने के दौरान कितने अनाज का उपयोग हुआ ?
हल :
एक महीने में बने मिड-डे मील में गेहूँ का जितना उपयोग हुआ = 103 कि०ग्रा०
एक महीने में बने मिड-डे मील में चावल का जितना उपयोग हुआ = 98 कि०ग्रा०
एक महीने में बने मिड-डे मील का कुल उपयोग = 201 कि०ग्रा०

PSEB 3rd Class Maths Solutions Chapter 8 माप 21

इसलिए, स्कूल में बने महीने के दौरान 201 कि०ग्रा० अनाज का उपयोग हुआ।

पृष्ठ 172:

क्या आपको याद है ?

आयतन:
एक बोतल का आयतन 3 गिलास पानी के बराबर है तो :
हल:
(a) दो बोतलों का आयतन 6 गिलास पानी के बराबर होगा।
(b) तीन बोतलों का आयतन 9 गिलास पानी के बराबर होगा।
(c) चार बोतलों का आयतन 12 गिलास पानी के बराबर होगा।
(d) पाँच बोतलों का आयतन 15 गिलास पानी के बराबर होगा।
(e) छ: बोतलों का आयतन 18 गिलास पानी के बराबर होगा।

पृष्ठ 174:

आओ करें:

नीचे दी वस्तुओं को उनके आयतन के आधार पर कम से अधिक के क्रम में लिखो व खानों में 1 से 5 की संख्या लिखो :
हल :

PSEB 3rd Class Maths Solutions Chapter 8 माप 22

एक मग में एक लीटर पानी आता है, नीचे दी गई वस्तुओं में मग से कम व ज्यादा आयतन वाली वस्तुओं को चुनो :

PSEB 3rd Class Maths Solutions Chapter 8 माप 23

हल:

PSEB 3rd Class Maths Solutions Chapter 8 माप 24

अधिक, कम और बराबर पता करो :
हल:

पृष्ठ 175:

PSEB 3rd Class Maths Solutions Chapter 8 माप 25

नीचे दिए गए मापकों में दी गई मात्रा के अनुसार रंग भरो :
हल:

PSEB 3rd Class Maths Solutions Chapter 8 माप 26

प्रशन 5.
गिलास की मदद से कुछ बर्तन लेकर पता करो कि इनको कितने गिलासों में भरा जा सकता है:
हल:

PSEB 3rd Class Maths Solutions Chapter 8 माप 28

प्रशन 6.
उपरोक्त बर्तनों की भरपाई PSEB 3rd Class Maths Solutions Chapter 8 माप 29 की सहायता से भी पता करो।
हल :

PSEB 3rd Class Maths Solutions Chapter 8 माप 30

पृष्ठ 176:

आओ करें:

प्रशन 1.
जोड़ करो :
हल :

PSEB 3rd Class Maths Solutions Chapter 8 माप 31

प्रशन 2.
घटाव करो :
हल :

PSEB 3rd Class Maths Solutions Chapter 8 माप 34

पृष्ठ 177:

प्रशन 3.
श्रीमती देवकी रानी ने अपने घर के लिए 5 लीटर रिफाइंड तेल और 2 लीटर सरसों का तेल खरीदा। उसने कितना लीटर तेल खरीदा ?
हल :
श्रीमती देवकी रानी ने रिफाइंड तेल खरीदा = 5 लीटर
श्रीमती देवकी रानी ने सरसों तेल खरीदा = 2 लीटर
श्रीमती देवकी रानी ने कुल तेल खरीदा = 7 लीटर

PSEB 3rd Class Maths Solutions Chapter 8 माप 32

इसलिए श्रीमती देवकी रानी ने कुल 7 लीटर तेल खरीदा।

प्रशन 4.
एक परिवार के द्वारा एक दिन में 375 लीटर पानी का उपयोग किया गया। यदि टंकी में 500 लीटर पानी था तो अब टंकी मे कितने लीटर पानी है ?
हल :
टंकी में पानी = 500 लीटर
परिवार द्वारा एक दिन में उपयोग = 375 लीटर
टंकी में बचा पानी = 125 लीटर

PSEB 3rd Class Maths Solutions Chapter 8 माप 33

इसलिए, टंकी में अब 125 लीटर पानी है।

वर्कशीट:

सही उत्तर चुनकर (✓) का चिह्न लगाओ :

प्रशन 1.
1 मीटर में कितने सैंटीमीटर होते हैं ?
(a) 10 सैं.मी.
(b) 100 सैं.मी.
(c) 1000 सैं.मी.
(d) 10,000 सैं.मी.
हल :
(b) 100 सैं.मी.

प्रशन 2.
4 मीटर में कितने सैंटीमीटर होते हैं ?
(a) 3000 सैं.मी.
(b) 4000 सैं.मी.
(c) 400 सैं.मी.
(d) 40 सें.मी.
हल :
(c) 400 सैं.मी.

प्रशन 3.
पेंसिल की लंबाई 18 सैं.मी. और चॉक की लंबाई 6 सैं.मी. है। पेंसिल की लंबाई चॉक की लंबाई
से कितने सैं.मी. अधिक है ?
(a) 18 सैं.मी.
(b) 16 सैं.मी.
(c) 12 सैं.मी.
(d) 14 सैं.मी.
हल :
(c) 12 सैं.मी.

प्रशन 4.
पैन की लंबाई 12 सैं.मी. है। शॉपनर की लंबाई 2 सें.मी. है। पैन, शॉपनर से कितने सैं.मी. अधिक है ?
(a) 8 सैं.मी.
(b) 6 सैं.मी.
(c) 9 सैं.मी.
(d) 10 सैं.मी.
हल :
(d) 10 सैं.मी.

प्रशन 5.
रमन की माता जी ने सब्जी वाले से 5 कि०ग्राम आलू और 4 कि०ग्राम प्याज़ खरीदे। उसने कुल कितने कि०ग्राम सब्जी खरीदी ?
(a) 7 कि०ग्राम
(b) 9 कि०ग्राम
(c) 12 कि०ग्राम
(d) 8 कि०ग्राम
हल :
(b) 9 कि०ग्राम

प्रशन 6.
एक हलवाई एक दिन में 20 कि०ग्राम लड्डू बनाता है। वह 10 कि०ग्राम लड्डू बेच देता है। उसके पास कितने किलोग्राम लड्डू शेष हैं ?
(a) 5 कि०ग्राम
(b) 10 कि०ग्राम
(c) 20 कि०ग्राम
(d) 25 कि०ग्राम
हल :
(b) 10 कि०ग्राम

प्रशन 7.
एक बर्तन में 10 लीटर दूध है दूसरे बर्तन में 15 लीटर दूध है। बताओ दोनों बर्तनों में कितने लीटर दूध है ?
(a) 25 ली.
(b) 15 ली.
(c) 10 ली.
(d) 35 ली.
हल :
(a) 25 ली.

PSEB 8th Class Science Solutions Chapter 18 वायु तथा जल का प्रदूषण

July 22, 2022 by Bhagya

Punjab State Board PSEB 8th Class Science Book Solutions Chapter 18 वायु तथा जल का प्रदूषण Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Science Chapter 18 वायु तथा जल का प्रदूषण

PSEB 8th Class Science Guide वायु तथा जल का प्रदूषण Textbook Questions and Answers

अभ्यास

प्रश्न 1.
किन विभिन्न विधियों द्वारा जल का संदूषण होता है ?
उत्तर-
जल के संदूषित होने की विभिन्न विधियाँ हैं-

कपड़े धोने, नहाने और घर के अन्य कार्यों से।
सीवेज़ (Sewage) से।
उद्योग द्वारा फेंके गए जहरीले पदार्थों से।
कूड़ा-कर्कट और मृत शरीरों को पानी स्रोतों में फेंकने से।
उर्वरकों, कीटनाशकों, जीवनाशकों से।
खनिजों, धातुओं आदि के नदी तल पर बैठने से।

प्रश्न 2.
व्यक्तिगत स्तर पर आप वायु प्रदूषण को कम करने में कैसे सहायता कर सकते हैं ?
उत्तर-
व्यक्तिगत स्तर पर वायु प्रदूषण कम करने के उपाय-

वाहनों के उपयोग को कम करना और उसकी अच्छी तरह रख-रखाव करना। डीज़ल अथवा सीसा रहित पेट्रोल का उपयोग
करना।
पत्तों, टायरों आदि के जलाने पर रोक लगाना।
घरों के आस-पास पेड़-पौधे लगाना।
जन परिवहन का उपयोग करना।

प्रश्न 3.
स्वच्छ, पारदर्शी जल सदैव पीने योग्य होता है। टिप्पणी कीजिए।
उत्तर-
यह कथन सही नहीं है ! स्वच्छ, पारदर्शी जल देखने में साफ़ है, परंतु इसमें कई घुली हुई अशुद्धियाँ और सूक्ष्मजीव हो सकते हैं। ये सूक्ष्मजीव, रोगों के वाहक हो सकते हैं। इसलिए पीने योग्य जल साफ़, स्वच्छ, पारदर्शी, गंधरहित, सूक्ष्मजीवों रहित और घुली हुई अशुद्धियों रहित होना चाहिए। शुद्ध जल पाने का उत्तम तरीका उबालना है।

प्रश्न 4.
आप अपने शहर की नगरपालिका के सदस्य हैं। ऐसे उपायों की सूची बनाइए जिससे नगर के सभी निवासियों को स्वच्छ जल की आपूर्ति सुनिश्चित हो सके।
उत्तर-
शुद्ध जल पाने के उपायों की सूची-

उद्योगों के अपशिष्ट का जल स्रोतों में फेंकने से पहले उपचारित करना चाहिए।
सीवेज का भौतिक और रसायनों से उपचार करने के बाद जल स्रोतों में निष्कासित करना चाहिए।

प्रश्न 5.
शुद्ध वायु और प्रदूषित वायु में अंतर स्पष्ट कीजिए।
उत्तर-
शुद्ध वायु तथा प्रदूषित वायु में अंतर

शुद्ध वायु (Pure Air)	प्रदूषित वायु (Polluted air)
(i) वायु साफ़ और पारदर्शी है।	(i) वायु गंदी और पारभासी है।
(ii) धुआँ और धूलकण दिखाई नहीं देते।	(ii) धुआँ और धूलकणों की मात्रा अत्यधिक होती है।
(iii) कोई गंध नहीं होती।	(iii) दुर्गंध हो सकती है।
(iv) सूक्ष्मजीव अनुपस्थित होते हैं।	(iv) सूक्ष्मजीव उपस्थित होते हैं।

प्रश्न 6.
उन अवस्थाओं की व्याख्या कीजिए जिनसे अम्ल वर्षा होती है ? अम्ल वर्षा हमें कैसे प्रभावित करती
उत्तर-
अम्ल वर्षा (Acid Rain) – जीवाश्म ईंधनों के अपूर्ण जलने और अधातुओं के परिष्करण से निकली गैसें, जैसे-SO₂, SO₃, NO₂, N₂O आदि, जब जल में घुलती हैं, तो H₂SO₃, H₂SO₄, HNO₃, अम्ल बनाती हैं। यह अम्ल वर्षा के रूप में गिरते हैं, जिन्हें अम्ल वर्षा कहते हैं।

अम्ल वर्षा फसल, जंगली पौधों, स्टील, रेल पटरियों और विद्युत् उपकरणों को नष्ट करती है। यह गले, नाक और आँखों में जलन पैदा करती है।

प्रश्न 7.
निम्नलिखित में से कौन-सी पौधा-घर गैस नहीं है ?
(क) कार्बन डाइऑक्साइड
(ख) सल्फर डाइऑक्साइड
(ग) मेथैन
(घ) नाइट्रोजन।
उत्तर-
(घ) नाइट्रोजन।

प्रश्न 8.
पौधा-घर प्रभाव का अपने शब्दों में वर्णन कीजिए।
उत्तर-
पौधा-घर प्रभाव (Green House Effect) – वायुमंडल में कार्बन डाइऑक्साइड की थोड़ी मात्रा उपलब्ध है, जो प्रकाश संश्लेषण क्रिया में सहायक है। यह समुद्री जल में घुल कर कार्बोनेट बनाती है। यह पौधा-घर प्रभाव भी उत्पन्न करती है। पृथ्वी के वातावरण का गर्म होना, इसी के प्रभाव का कारण है। सूर्य से निकली किरणों में आरक्त और पराबैंगनी विकिरणें होती हैं। ओज़ोन परत, पराबैंगनी विकिरणों को अवशोषित कर लेती है, पर अवरक्त विकिरणे धरती पर पहुँचती हैं। इनमें से कुछ किरणें परावर्तित होती हैं। इन परावर्तित किरणों को CO₂ अवशोषित करती है और वातावरण को गर्म करती हैं, क्योंकि अवरक्त किरणों में गर्मी उत्पन्न करने का गुण है। चार गैसें जैसे-CO₂, जल कण (H₂O), ओज़ोन (O₃) तथा मिथेन (CH₄ ) अवरक्त किरणों को अवशोषित कर सकती है। इनमें से CO₂ ही चारों तरफ फैली है, इसलिए यही पौधा-घर प्रभाव के लिए उत्तरदायी है। यह शब्द शीशा घर से लिया गया है, जहाँ हरे पौधे रखे जाते हैं।

प्रश्न 9.
आपके द्वारा कक्षा में विश्व ऊष्णन के बारे में दिया जाने वाला संक्षिप्त भाषण लिखिए।
उत्तर-
विश्व ऊष्णन – जैसा कि नाम से ही स्पष्ट है, कि यह विश्व के तापमान में वृद्धि है। कुछ गैसें, जैसे CO₂ मैथेन, ओज़ोन इसके लिए उत्तरदायी हैं। इन गैसों की मात्रा वातावरण में धीरे-धीरे बढ़ रही है। यदि इसको समय पर नियंत्रित न किया गया, तो वातावरण में वृद्धि चारों तरफ समस्याएँ उत्पन्न कर देगी। जैसे-हिमपात पिघल जाएँगे, निम्न क्षेत्र डूब जाएँगे, वर्षा पर प्रभाव पड़ेगा। समुद्र तल ऊँचा उठेगा, जिससे कृषि, वन आदि और रहन-सहन पर प्रभाव पड़ेगा। इसलिए विश्व ऊष्णन को रोकने के लिए उचित और शीघ्र उपाय करने चाहिए।

प्रश्न 10.
ताजमहल की सुंदरता पर संकट का वर्णन कीजिए।
उत्तर-
ताज, दुनिया के सात अजूबों में से एक है। यह संगमरमर से बनी सफ़ेद इमारत है।
वायु प्रदूषण से इमारत को ख़तरा है। ताज का क्षेत्र सल्फर डाइऑक्साइड, नाइट्रोजन ऑक्साइड जैसी जहरीली गैसों से घिरा हुआ है। ये गैसें जीवाश्म ईंधन के अपूर्ण जलने से उत्पन्न होती हैं। ये गैसें वर्षा के जल में घुलकर अम्ल वर्षा बनाती हैं। यह अम्ल वर्षा, इमारत पर गिरती है, उसे घोलती और पीला करती है। यदि अम्ल वर्षा को न रोका गया तो एक दिन इमारत, गिर जाएगी या इसके पत्थर नष्ट हो जाएंगे।

प्रश्न 11.
जल में पोषकों के स्तर में वृद्धि किस प्रकार जल जीवों की उत्तरजीविता को प्रभावित करती है ?
उत्तर-
पोषकों (नाइट्रेट, फास्फेट) के स्तर की वृद्धि से जल में शैवाल (algae) की वृद्धि होती है। इस शैवाल के नष्ट होने पर अपघटित करने के लिए आक्सीजन की उपस्थिति आवश्यक है। इस कारण जल में आक्सीजन स्तर कम हो जाता है, जिससे जलीय जीवों की उत्तरजीविता प्रभावित होती है।

PSEB Solutions for Class 8 Science वायु तथा जल का प्रदूषण Important Questions and Answers

TYPE-I
अति लघु उत्तरात्मक प्रश्न

प्रश्न 1.
पर्यावरण की गुणवत्ता में कमी का उत्तरदायी कौन है ?
उत्तर-
मानव और उसकी गतिविधियाँ।

प्रश्न 2.
वातावरण की कौन-सी परिस्थितियाँ आजकल उपलब्ध नहीं हैं ?
उत्तर-
साफ़ आकाश, ताज़ी हवा, साफ़ जल आदि।

प्रश्न 3.
वायु के संघटक क्या हैं ?
उत्तर-
वायु के संघटक – वायु गैसों का मिश्रण है, जिसमें 78% नाइट्रोजन, 21% ऑक्सीजन, 1% अन्य गैसें। जैसे-कार्बन डाइऑक्साइड, कार्बन मोनोऑक्साइड, जल-कण, आर्गन, ओज़ोन, मैथेन आदि।

प्रश्न 4.
कौन-सा पदार्थ मुख्य वायु प्रदूषक है ?
उत्तर-
धुआँ।

प्रश्न 5.
धुएँ का मुख्य कारण है ?
उत्तर-
धुएँ का कारण-

वाहन
ईंधनों का जलना।

प्रश्न 6.
कुछ प्राकृतिक वायु प्रदूषकों के नाम लिखिए।
उत्तर-
धुआँ, धुल।

प्रश्न 7.
वायु प्रदूषण से कौन-सा रोग फैलता है ?
उत्तर-
श्वसन संबंधी रोग (Respiratory Problems)।

प्रश्न 8.
वाहनों से कौन-सी गैसें उत्सर्जित होती हैं ?
उत्तर-
कार्बन डाइऑक्साइड, कार्बन मोनोऑक्साइड, नाइट्रोजन ऑक्साइड, धुआँ आदि।

प्रश्न 9.
कौन-सी गैस रक्त में ऑक्सीजन ग्रहण करने की क्षमता को कम करती है ?
उत्तर-
कार्बन मोनोऑक्साइड (Carbon monoxide)।

प्रश्न 10.
धूम-कोहरा (Smog) क्या है ?
उत्तर-
स्मोग, धुआँ और धुंध का मिश्रण है।

प्रश्न 11.
श्वसन संबंधी कुछ समस्याओं के नाम लिखिए।
उत्तर-
श्वसन समस्याएँ-
दमा, खाँसी, बच्चों में छाती की छाँ-छाँ।

प्रश्न 12.
रेफ्रीजेनरेट्स, वातानुकूल, इत्रों में कौन-से रसायन उपयुक्त होते हैं ?
उत्तर-
क्लोरोफ्लोरो कार्बन।

प्रश्न 13.
क्लोरोफ्लोरो कार्बन के दुष्प्रभाव क्या हैं ?
उत्तर-
क्लोरोफ्लोरो (CFC) कार्बन ओज़ोन परत को नष्ट करते हैं।

प्रश्न 14.
ओज़ोन परत क्यों महत्त्वपूर्ण है ?
उत्तर-
यह पृथ्वी को सूर्य की UV किरणों से बचाती है।

प्रश्न 15.
वायु में निलंबित ठोस कणों के स्रोत क्या हैं ?
उत्तर-

वाहनों में पेट्रोल, डीज़ल आदि का जलना।
औद्योगिक प्रक्रियाएँ जैसे-स्टील उत्पादन और खाने खोदना।
शक्ति घर।

प्रश्न 16.
निलंबित ठोस कणों के दुष्प्रभाव क्या हैं ?
उत्तर-
दृष्टयता को कम करते हैं।

प्रश्न 17.
आगरे में स्थित ताज को कौन-से उद्योग अम्ल वर्षा से नष्ट करने में उत्तरदायी हैं ?
उत्तर-
रबड़ प्रक्रमण, स्वचालित वाहन, रसायन, मथुरा तेल परिष्करणी।

प्रश्न 18.
अम्ल-गैसें कौन-सी हैं ?
उत्तर-
सल्फर डाइऑक्साइड, सल्फर ट्राइऑक्साइड, नाइट्रस ऑक्साइड।

प्रश्न 19.
दो साफ़ ईंधनों के नाम लिखिए।
उत्तर-
CNG और LPG.

प्रश्न 20.
कौन-सी गैस सूर्य की विकिरणों को पकड़ कर पर्यावरण को गर्म करती है ?
उत्तर-
कार्बन डाइऑक्साइड।

प्रश्न 21.
कुछ पौधा-घर गैसों के नाम लिखिए।
उत्तर-
मैथेन, ओज़ोन, जल-कण, कार्बन डाइऑक्साइड।।

प्रश्न 22.
पौधा-घर प्रभाव कम करने के लिए कौन-सा अनुबंध किया है ?
उत्तर-
क्योटो प्रोटोकॉल (Kyoto Protocol) ।

प्रश्न 23.
कुछ वैकल्पिक ऊर्जा स्त्रोतों के नाम लिखिए।
उत्तर-
सूर्य ऊर्जा, जल शक्ति, पन ऊर्जा।

प्रश्न 24.
भारत में वन-महोत्सव कब मनाया जाता है ?
उत्तर-
प्रतिवर्ष जुलाई में।

प्रश्न 25.
सूखे पत्तों का क्या करना चाहिए ?
उत्तर-
सूखे पत्तों को कंपोस्ट गड्ढों में डालकर कंपोस्ट तैयार करनी चाहिए।

प्रश्न 26.
पानी के कौन-से गुणों में परिवर्तन होता है ?
उत्तर-
गंध, रंग तथा अम्लीयता।।

प्रश्न 27.
जल प्रदूषकों के नाम लिखिए।
उत्तर-
सीवेज़, ज़हरीले तत्व, कीटनाशक, खरपतवार नाशक आदि।

प्रश्न 28.
गंगा कार्य परियोजना कब आरंभ की गई ?
उत्तर-
सन् 1985 में।

प्रश्न 29.
गंगा नदी निर्जीव किन स्थानों पर है ?
उत्तर-
जिन स्थानों पर प्रदूषण स्तर अत्यधिक बढ़ने से, जल जीवन नष्ट हो गया है।

प्रश्न 30.
कौन-से शहर में गंगा अत्यधिक प्रदूषित है ? ।
उत्तर-
कानपुर में।

प्रश्न 31.
जल में ऑक्सीजन स्तर कम होने के क्या कारण हैं ?
उत्तर-
शैवाल की वृद्धि और मृत्यु।

प्रश्न 32.
कुछ जल वाहक रोगों के नाम लिखो।
उत्तर-
हैजा, टायफॉइड, पीलिया।

प्रश्न 33.
जल-वाहक सूक्ष्मजीव कौन-कौन से हैं ?
उत्तर-
जल-वाहक सूक्ष्मजीव – जीवाणु, विषाणु, कवक, मृतजीवी आदि।

प्रश्न 34.
पेयजल को परिभाषित करें।
उत्तर-
पेयजल-पीने योग्य जल को पेयजल कहते हैं।

प्रश्न 35.
पेयजल के गणों के बारे लिखो।
उत्तर-
रंगरहित, गंधरहित, घुलनशील, अशुद्धियों और सूक्ष्मजीवों के बिना।

प्रश्न 36.
जनसंख्या के कितने % को पेयजल उपलब्ध नहीं है ?
उत्तर-
25%.

प्रश्न 37.
एक आम प्रचलित घरेलू फिल्टर कौन-सा है ?
उत्तर-
कैंडल फिल्टर।

प्रश्न 38.
किस प्रक्रिया से जल में उपस्थित जीवाणु भर जाते हैं ?
उत्तर-
उबालने से।

प्रश्न 39.
कुछ रसायनों के नाम लिखिए जिनसे जल शुद्ध किया जाता है ?
उत्तर-
विरंजक चूर्ण अथवा क्लोरीन, ओज़ोन और आयोडीन गैस।

प्रश्न 40.
3R सिद्धांत क्या है ?
उत्तर-
3R सिद्धांत-कम उपयोग (Reduce), पुनः उपयोग (Reuse), पुनः चक्रण (Recycle)।

प्रश्न 41.
वाहित मल का उपचार क्यों करना चाहिए ?
उत्तर-
शुद्ध और साफ़ जल के लिए।

प्रश्न 42.
संदूषित जल पीने में क्या नुकसान है ?
उत्तर-
बीमारी का होना।

प्रश्न 43.
घरों में स्वच्छ जल की आपूर्ति के लिए कौन-सी संस्था उत्तरदायी है?
उत्तर-
नगर-निगम अथवा नगरपालिकाएँ।

प्रश्न 44.
क्या जल संरक्षण की आवश्यकता है ?
उत्तर-
हाँ।

TYPE-II
लघु उत्तरात्मक प्रश्न

प्रश्न 1.
वायु प्रदूषकों के दो उदाहरण लिखिए।
उत्तर-
वायु प्रदूषकों के उदाहरण-

सल्फर और नाइट्रोजन ऑक्साइड।
रेडियो ऐक्टिव कचरा।

प्रश्न 2.
वायु प्रदूषण के मुख्य स्रोत कौन-से हैं ?
उत्तर-
वायु प्रदूषण के मुख्य स्रोत-

उद्योग-कागज़ उद्योग, स्टील उद्योग, पेट्रोलियम परिष्करणशालाएँ और रसायन उद्योग।
वाहन
धुआँ।

प्रश्न 3.
वाहित मल (Sewage) क्या है ?
उत्तर-
वाहित मल – म्यूनिस्पिल और घरेलू अपशिष्ट का बहुत बड़ी मात्रा में उत्सर्जन वाहित मल कहलाता है। इसमें जैविक अपशिष्ट, जहरीले पदार्थ होते हैं जो कई कार्यविधियों को नुकसान पहुंचाते हैं।

प्रश्न 4.
वाहित मल-जल संदूषित जल क्यों कहलाता है ?
उत्तर-
वाहित मल-जल में मानव मल-मूत्र, कपड़े धोने का जल, औद्योगिक अपशिष्ट होते हैं। यह जल पीने के लिए अनोपयोगी है। इसमें ऑक्सीजन की कमी होती है। इसकी दुर्गंध होती है। यह कई रोगों का कारक है। इसलिए इसे संदूषित जल कहते हैं।

प्रश्न 5.
वायु प्रदूषणों को कैसे नियंत्रित किया जा सकता है ?
उत्तर-
वायु प्रदूषण नियंत्रित करने के उपाय-

जलनशील ठोस व्यर्थ भट्ठियों में जलाना चाहिए।
वाहनों में ईंधनों के पूर्ण जलने वाले ईंधनों जैसे डीज़ल आदि का प्रयोग करना चाहिए ताकि हानिकारक उत्पाद न बनें।
वनस्पति को अत्यधिक और अनावश्यक नहीं जलाना चाहिए।

प्रश्न 6.
नदी का प्रदूषण कैसे नियंत्रित किया जा सकता है ?
उत्तर-
नदी के प्रदूषण का नियंत्रण-

भौतिक और रासायनिक विधियों से वाहित मल का उपचार करके जलाशयों में गिराना चाहिए।
नदी के किनारों से रसायन उद्योग को दूर करना चाहिए और नए उद्योग लगाने में मनाही होनी चाहिए।

प्रश्न 7.
क्लोरोफ्लोरो कार्बन हानिकारक कैसे है ?
उत्तर-
क्लोरोफ्लोरो कार्बन वातावरण की ओज़ोन परत को क्षति पहुँचाते हैं। यह परत पृथ्वी पर रहने वाले जीवों की हानिकारक UV विकिरणों से रक्षा करती है।

प्रश्न 8.
कार्बन मोनोऑक्साइड जीवों पर क्या प्रभाव डालती है ?
उत्तर-
कार्बन मोनोऑक्साइड का जीवों पर प्रभाव-रक्त में उपस्थित हीमोग्लोबिन कार्बन मोनोऑक्साइड अवशोषित करती है, जिससे रक्त द्वारा ऑक्सीजन ग्रहण करने की शक्ति कम हो जाती है। ऑक्सीजन की आपूर्ति न होने से जीव की मृत्यु हो जाती है।

प्रश्न 9.
कौन-से धातु स्वास्थ्य के लिए हानिकारक हैं ?
उत्तर-
सीसा, आर्सेनिक, पारा।

प्रश्न 10.
वायु के मुख्य प्रदूषकों को चित्र द्वारा दर्शाओ।
उत्तर-
वायु प्रदूषक (Air Pollutants)।
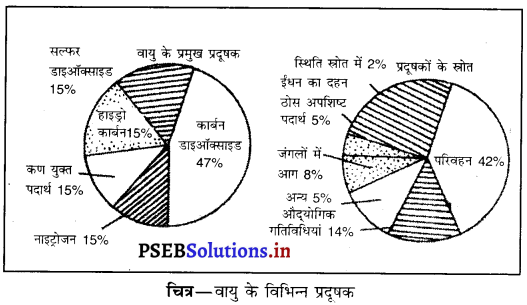
PSEB 8th Class Science Solutions Chapter 18 वायु तथा जल का प्रदूषण 1

प्रश्न 11.
पौधा-घर प्रभाव के हानिकारक प्रभाव लिखें।
उत्तर-
पौधा-घर प्रभाव के हानिकारक प्रभाव-
पौधा-घर प्रभाव से पृथ्वी के तापमान में वृद्धि होगी। इससे जीव-जंतुओं और मानवों का जीवन असुविधाजनक हो जाएगा।

वैज्ञानिकों ने अनुमान लगाया है, कि समुद्र तल 100 मी० ऊपर/बढ़ जाएगा। जब पौधा-घर प्रभाव से विश्व ऊष्णन में 3-6°C वृद्धि होगी। यदि ऐसा हुआ, तो तटीय क्षेत्र और कई द्वीप डूब जाएँगे और काफ़ी हानि होगी।

प्रश्न 12.
कानपुर में गंगा अत्यधिक संदूषित क्यों है ?
उत्तर-
कानपुर में गंगा में जल की मात्रा कम और गति धीमी है। लगभग 5000 उद्योग, अपने अपशिष्ट जहरीले पदार्थ नदी में विसर्जित करते हैं। लोग नदी में नहाते हैं, कपड़े धोते हैं, मल-मूत्र फेंकते हैं, फूल तथा पूजा सामग्री और प्लास्टिक थैले भी नदी में फेंकते हैं।

प्रश्न 13.
ओजोन परत हमारे लिए कैसे लाभदायक है ?
उत्तर-
वातावरण की ओजोन परत सभी जीवित वस्तुओं के लिए अत्यंत महत्त्वपूर्ण है। यह परत सूर्य से उत्सर्जित हानिकारक पराबैंगनी विकिरणों को अवशोषित कर लेती है। अन्यथा ये किरणें मानव और अन्य जंतुओं में त्वचा का कैंसर जैसे भयानक रोग उत्पन्न कर सकती हैं। ये पराबैंगनी किरणें फसलों के लिए भी हानिकारक होती हैं।

प्रश्न 14.
ओजोन परत की व्याख्या करो।
उत्तर-
ओज़ोन परत-हमारे वायुमंडल के समताप मंडल में पाई जाने वाली ओजोन, ओजोन परत के रूप में पाई जाती है जो हमें सूर्य की पराबैंगनी विकिरणों से सुरक्षा प्रदान करती है। फ्रिज, एयर कंडीशनर, प्लास्टिक फोम में एक जहरीले पदार्थ CFC (क्लोरोफ्लोरो कार्बन) का उपयोग होता है जो ओजोन परत को पतला कर देता है। इसे ओजोन परत ह्रास कहते हैं।

प्रश्न 15.
विश्व तापमान में वृद्धि से कौन-कौन सी समस्याएं पैदा हो सकती हैं ?
उत्तर-
विश्व तापमान से निम्नलिखित समस्याएँ उत्पन्न हो सकती हैं-

इससे गर्मियाँ खुश्क और गर्म हो जाएँगी। इसी प्रकार सर्दियाँ नमी वाली और अधिक ठंडी हो जाएँगी।
तापमान के बढ़ने से ग्लेशियर पिघल जाएँगे और समुद्र में जल का स्तर 2 फुट और बढ़ जाएगा।
जल की आपूर्ति प्रभावित हो जाएगी तथा व्यापक स्तर पर सूखा पड़ेगा।

प्रश्न 16.
गंगा के किनारे स्थित उद्योग धंधों ने गंगा को कैसे प्रदूषित करने का कार्य किया ?
उत्तर-
गंगा के किनारे बसे शहरों व नगरों में भारी संख्या में उद्योग स्थापित हैं। अकेले कानपुर में 5000 से अधिक औद्योगिक इकाइयाँ हैं जो गंगा में अपमार्जक चर्म के पेंट के उद्योगों का जहरीला अपशिष्ट, वाहित मल, कीटनाशक व कूड़ा कचरा आदि मिला रहे हैं। कागज़ की फैक्ट्रियाँ, चीनी मिलें व अन्य रासायनिक फैक्ट्रियाँ गंगा के जल में भारी मात्रा में अपशिष्ट मिलाकर दूषित कर रहे हैं।

प्रश्न 17.
सरकार ने गंगा जैसी पवित्र नदियों के जल की स्वच्छता बनाए रखने के लिए उद्योगों के लिए क्या निर्देश जारी किए हुए हैं ?
उत्तर-
तेल परिष्करणशालाएँ, वस्त्र व. चीनी मिलें, कागज़ फैक्ट्रियाँ व रासायनिक फैक्ट्रियाँ अपने औद्योगिक अपशिष्ट को सीधे नदियों में बहा देती हैं जिससे नदियों का जल विषैला होता जा रहा है इसे रोकने के लिए सरकार ने अधिनियम बनाए हैं। जिनके अनुसार उद्योगों को अपने यहाँ उत्पन्न अपशिष्टों को जल में प्रवाहित करने से पूर्व उपचारित करना आवश्यक है। परंतु अधिकतर उद्योग इन नियमों को अनुपालना नहीं कर रहे हैं।

TYPE -III
दीर्घ उत्तरात्मक प्रश्न

प्रश्न 1.
अपने चारों तरफ वायु प्रदूषण कम करने के आप क्या सुझाव देंगे ?
उत्तर-
वायु प्रदूषण कम करने के उपाय-

वैकल्पिक ऊर्जा के स्रोतों का उपयोग करना जो प्रदूषण न फैलाएँ जैसे-सौर ऊर्जा, पन ऊर्जा।
सीसा रहित ईंधन का उपयोग करके जैसे संपीड़ित प्राकृतिक गैस (CNG) का उपयोग कारों, बसों और ट्रकों में। वाहन नियमित रूप में प्रदूषण के लिए प्रेषित किए जाने चाहिए।
उद्योगों को घरों से दूर लगाना चाहिए और उनकी चिमनियों में फिल्टर होने चाहिए।
पेड़ वायु को शुद्ध करते हैं, इसलिए अधिक पेड़ लगाने चाहिए।
प्लास्टिक के थैलों की जगह कपड़े अथवा जूट के थैले उपयोग में लाने चाहिए।
पदार्थों का पुनः चक्रण जैसे-कागज़, धातु आदि करना चाहिए।
सूखे पत्ते, पेड़ों की शाखाएँ, कागज, कूड़े आदि को जलाना नहीं चाहिए क्योंकि धुआँ वायु प्रदूषण फैलाता है।
विद्युत् बचत करनी चाहिए।
ऐरोसाल जैसे पदार्थों के उपयोग में कमी लानी चाहिए क्योंकि यह पदार्थ वातावरण में कुछ मिनटों से कई वर्षों तक लटके रह सकते हैं। इनके आकार और भार पर सब निर्भर करता है जैसे–सुगंध आदि।
धूम्रपान से परहेज़ करना चाहिए और दूसरों को भी ऐसा करने की सलाह देनी चाहिए।

प्रश्न 2.
सीवेज़ जल प्रदूषण में कैसे उत्तरदायी है ?
उत्तर-
सीवेज़ को घरेलू और औद्योगिक अपशिष्ट में वर्गीकृत किया जा सकता है। घरेलू अपशिष्ट सीवेज़ का प्राथमिक स्रोत है। औद्योगिक अपशिष्ट भी जल संदूषण में मुख्य भूमिका निभाते हैं।

सीवेज से नदी, झील और समुद्र संदूषित होते हैं। संदूषित जल हैजा, टायफॉइड, पेचिश, पीलिया और त्वचा रोग जैसे संक्रमण रोगों का वाहक है।
सीवेज जल के अपघटन में ऑक्सीजन उपयोग में आती है जिससे जल में ऑक्सीजन की मात्रा में कमी आ जाती है। इस कमी के कारण जल जीवन प्रभावित होता है और मछलियों तथा अन्य जलीय जंतुओं के मृत्यु का कारण बनता है।
संदूषित जल पीने और खाना बनाने के उपयुक्त नहीं होता है। यह कृषि के लिए भी उपयुक्त नहीं होता।

प्रश्न 3.
वायु प्रदूषण पर संक्षिप्त नोट लिखें।
उत्तर-
वायु प्रदूषण – वायु प्राकृतिक और मानव क्रियाओं द्वारा शुद्ध नहीं रही। वायु के जैविक, भौतिक और रासायनिक गुणों में अवांछनीय परिवर्तनों को वायु प्रदूषण कहते हैं। वे पदार्थ जो वायु प्रदूषण के उत्तरदायी हैं, वायु प्रदूषक कहलाते हैं। मुख्य प्रदूषक कार्बन डाइऑक्साइड, कार्बन मोनोऑक्साइड, सल्फर डाइऑक्साइड, नाइट्रोजन के ऑक्साइड और निलंबित ठोस कण हैं। वायु प्रदूषण के मानव पर अत्यधिक दुष्प्रभाव हैं। यह कच्चे माल, औद्योगिक प्रक्रियाओं, रहन-सहन और सांस्कृतिक संपदा जैसे ऐतिहासिक इमारतों को प्रभावित करता है। यह जीवन के लिए घातक सिद्ध हो रहा है।

प्रश्न 4.
अम्ल गैसों को परिभाषित करें। उदाहरण दें। क्या इसका प्रभाव आप नयी बनी संगमरमर की इमारतों में देख सकते हो ?
उत्तर-
वे गैसें जो जल में घुलकर अम्ल बनाती हैं, अम्ल गैसें कहलाती हैं।
उदाहरण – सल्फर डाइऑक्साइड (SO₂ नाइट्रोजन डाइऑक्साइड (NO₂).
संगमरमर इमारत पर प्रभाव – वातावरण में पाई जाने वाली SO₂ और NO₂ जल से क्रिया करके अम्ल बनाती है।
PSEB 8th Class Science Solutions Chapter 18 वायु तथा जल का प्रदूषण 2

यह अम्ल वर्षा के जल के साथ इमारतों पर गिरते हैं । अम्ल-युक्त इस वर्षा को अम्ल वर्षा कहते हैं। अम्ल संगमरमर (CaCO₃) पत्थर को नष्ट करते हैं।
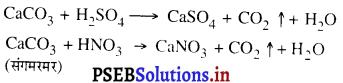
PSEB 8th Class Science Solutions Chapter 18 वायु तथा जल का प्रदूषण 3
इस तरह अम्ल वर्षा संगमरमर की इमारतों को क्षति पहुँचाती है।

प्रश्न 5.
ओज़ोन ह्रास (Ozone depletion) (Ozone depletion) का वर्णन करें।
उत्तर-
ओज़ोन ह्रास (Ozone depletion) – ओज़ोन परत पृथ्वी की सुरक्षा परत है। मानव क्रियाओं द्वारा उत्पन्न CFC ओजोन परत का ह्रास हो रहा है जिससे UV विकिरणें धरती पर पहुँच रही हैं। यही ओजोन ह्रास है।

ओज़ोन ह्रास के प्रभाव-

UV विकिरणें, त्वचा कैंसर और आँखों के रोगों को फैला रही हैं।
ये किरणें, मानव शरीर में प्रतिरक्षी तंत्र को प्रभावित करती हैं।
विश्व वर्षा को प्रभावित करती है।
पर्यावरणीय दुर्घटनाएँ जैसे-बाढ़, खाद्य पदार्थों में कमी आदि के लिए उत्तरदायी।

प्रश्न 6.
जल संदूषण के स्रोतों की व्याख्या करो।
उत्तर-
जल संदूषण के स्रोत :-
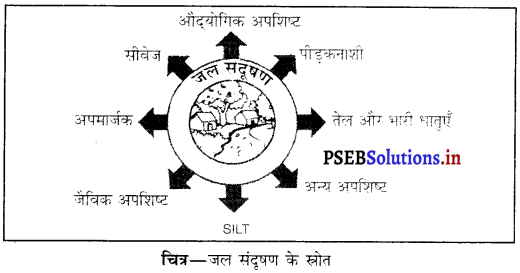
PSEB 8th Class Science Solutions Chapter 18 वायु तथा जल का प्रदूषण 4
(क) घरेलू अपशिष्ट – इसमें शामिल हैं-
(a) मानव और जंतु का मल-मूत्र
(b) जैविक पदार्थ (खाद्य पदार्थों)
(c) अपमार्जक
(d) जीवाणु।

(ख) औद्योगिक अपशिष्ट – औद्योगिक अपशिष्टों में भारी धातुएँ जैसे-पारा, सीसा, कॉपर, ऑर्सेनिक, कैडमियम हो सकते हैं जिन्हें नदी, झीलों, तालाबों में फेंक दिया जाता है।

(ग) पीड़कनाशी और उर्वरक – खेतों से पानी अपने साथ उर्वरक, पीड़कनाशी, कीटनाशी आदि कई रसायन जलाशयों तक बहा ले जाता है। DDT जैसे पीड़कनाशी अनिम्नकरणीय पदार्थ हैं।

(घ) जल ऊष्मा – मानव कार्यविधियों द्वारा पानी के ताप की वृदधि जल ऊप्मा कहलाती है। ऊष्मीय शक्ति घर आदि गर्म जल जलाशयों में बहा देते हैं जिससे जलाशयों के जल अचानक गर्म हो जाते हैं और जलीय जीवन पर दुष्प्रभाव डालते हैं।

PSEB 9th Class Computer Solutions Chapter 4 डी०बी०एम०एस० से परिचय

July 22, 2022 by Bhagya

Punjab State Board PSEB 9th Class Computer Book Solutions Chapter 4 डी०बी०एम०एस० से परिचय Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Computer Chapter 4 डी०बी०एम०एस० से परिचय

Computer Guide for Class 9 PSEB डी०बी०एम०एस० से परिचय Textbook Questions and Answers

1. रिक्त स्थान भरें

1. डी० बी० एम० एस० का पूरा नाम ………….. है।
(क) डाटाबेस मैनेजर सिस्टम
(ख) डाटाबेस मैनेजिंग सिस्टम
(ग) डाटाबेस मैनेजमैंट सिस्टम
(घ) डाटाबेस मैसजर सॉफ्टवेयर।
उत्तर-
(ग) डाटाबेस मैनेजमैंट सिस्टम।

2. डाटाबेस को संभालने की ज़िम्मेदारी ………………………….. की होती है।
(क) डाटाबेस मास्टर
(ख) डाटाबेस एडमिनिस्ट्रेटर
(ग) यूज़र
(घ) आम व्यक्ति।
उत्तर-
(ख) डाटाबेस एडमिनिस्ट्रेटर।

3. प्रोसैसिंग के बाद डाटा ……………………. में बदल जाता है।
(क) डाटाबेस
(ख) सूचना
(ग) एन०टी०टी०
(घ) सॉफ्टवेयर।
उत्तर-
(ख) सूचना।

4. एक-दूसरे से सम्बन्धित समूह को ………………………… तैयार करते हैं।
(क) डाटाबेस
(ख) डी०बी०एम०एस०
(ग) डी०बी०ए०
(घ) फाइल प्रोसैसिंग सिस्टम।
उत्तर-
(घ) फाइल प्रोसैसिंग सिस्टम।

5. एक ही डाटाबेस की एक ही जैसे डाटा की स्टोर करने की प्रक्रिया का डाटा ……………………………. होती है।
(क) इंटीग्रीटी
(ख) रिडुयनसी
(ग) आवजैक्स
(घ) फौरन की।
उत्तर-
(ख) रिडुयन.सी।

6. …………………………….. एक विल्क्षण की होती है।
(क) प्राइमरी की
(ख) फौरन की
(ग) इलैक्ट्रोनिक की
(घ) डाटाबेस की।
उत्तर-
(क) प्राइमरी की।

2. पूरे नाम बताओ

1. DBA
2. DBMS
3. SQL
उत्तर-
1. DBA-डाटाबेस एडमिनिस्ट्रेटर
2. DBMS-डाटाबेस मैनेजमैंट सिस्टम
3. SQL-सट्रक्चर कुएरी लेंगुएज़।

3. छोटे उत्तर वाले प्रश्न

प्रश्न 1.
डाटाबेस से क्या अभिप्राय है ?
उत्तर-
डाटाबेस व्यवस्थित सूचनाओं का समूह होता है जो कम्प्यूटर में स्टोर होता है। डाटाबेस से यूज़र सूचना भी प्राप्त कर सकता है।

प्रश्न 2.
सम्बन्ध कौन-कौन से होते हैं ?
उत्तर-

एक से एक (1-1)
एक से अनेक (1-M)
अनेक से अनेक (M-M).

प्रश्न 3.
भिन्न-भिन्न प्रकार के डी० बी० ए० के नाम बताओ।
उत्तर-

एडमिनिस्ट्रेटर डी० बी० ए०
डिवेलपमेंट डी० बी० ए०
आर्किटैक्ट डी० बी० ए०
वेयर हाऊस डी० बी० ए०।

प्रश्न 4.
SQL क्या हैं ?
उत्तर-
यह एक हाई लैवल भाषा है जो रिलेशनल डाटाबेस में डाटा को संभालने, नियंत्रण करने, बदलने के लिए प्रयोग की जाती है।

प्रश्न 5.
कीज़ कितने प्रकार की होती हैं ?
उत्तर-

सुपर कीअ
कैंडीडेंट कीअ
प्राइमरी कीअ
कंपोजिट कीअ
फौरन की।

4. बड़े उत्तर वाले प्रश्न

प्रश्न 1.
नारमलाइज़ेशन के बारे बताओ। यह कितनी प्रकार की होती है ?
उत्तर-
नारमलाइज़ेशन एक वैज्ञानिक विधि है जिसके द्वारा टेबल को आसान तरीके से यूज़र को समझने योग्य रूप में बदला जा सकता है। टेबल में रिडुयनडेंसी को कम करने के लिए और डाटाबेस इनकनसिसटैंसी को कम करने और अपने डाटाबेस को मज़बूत करने के लिए आगे कुछ पग दिये हैं।

सब टेबल में एक आइडेंटीफाईर ज़रूरी होना चाहिए।
सब टेबल में एक टाइप का एन०टी०टी० स्टोर होना चाहिए।
नल वैल्यू को कम-से-कम स्टोर करना चाहिए।
वैलयूज़ बार-बार कम आनी चाहिए।

आमतौर पर नारमल फारमज़ पांच होती है।

First Normal Form (INF)
Second Normal Form (2NF)
Third Normal Form (3NF)
Fourth Normal Form (4NF)
Boyce coded Normal Form (BCNF).

प्रश्न 2.
फाइल प्रोसैसिंग सिस्टम क्या है ? इसके लाभ तथा हानियां क्या हैं ?
उत्तर-
कम्प्यूटर आने से पहले सारी सूचना कागज़ों के ऊपर स्टोर की जाती थी। जब सब सूचना ढूँढ़नी हो तो कागज़ को देखना होता था।
फाइल प्रोसैसिंग सिस्टम के लाभफाइल प्रोसैसिंग सिस्टम में निम्नलिखित लाभ हैं :

तकनीकी जानकारी की आवश्यकता नहीं-फाइल प्रोसैसिंग सिस्टम में किसी भी प्रकार की खास कम्प्यूटर या साफ्टवेयर की जानकारी की आवश्यकता नहीं होती। .
कम डाटा में आसानी-फाइल प्रोसैसिंग सिस्टम में कम डाटा के साथ काम करने में आसानी होती है।
समझने में आसानी-फाइल प्रोसैसिंग सिस्टम में डाटा की स्ट्रक्चर को समझना डी०वी०एम०एस० से आसान होता है।
सस्ता-फाइल प्रोसैसिंग सिस्टम की कीमत कम होती है।
सरल-फाइल प्रोसैसिंग सिस्टम सरल होता है।
फालतू हार्डवेयर की आवश्यकता नहीं-आम करके फाइल प्रोसैसिंग सिस्टम में किसी हार्डवेयर की आवश्यकता नहीं होती।
आसान जगह बदली-फाइल प्रोसैसिंग सिस्टम में डाटा की आसानी से जगह बदली जा सकती है। सिर्फ फाइलें कापी तथा पेस्ट ही करनी होती हैं।

फाइल प्रोसैसिंग सिस्टम के हानियांफाइल प्रोसैसिंग सिस्टम में निम्नलिखित हानियां हैं :
डाटामैपिंग अकसैस-सब संबंधित सूचना को अलग-अलग फाइल में स्टोर करना होता है पर इनमें किसी भी प्रकार की मैपिंग नहीं होती है।

डाटा रिडुयनहुँसी-डुपलीकेट डाटा को वैलिडेट करने के लिए फाइल सिस्टम में कोई भी तरीका नहीं होता है। फाइल सिस्टम में डुपलीकेट डाटा को संभाला नहीं जा सकता। क्योंकि इससे स्पेस घटती है जिससे डाटा को हमेशा संभाल के रखने में मुश्किल होती है। इससे डाटाबेस संभाल सकते हैं।

डाटा डिपेंडेंस-फाइल में डाटा एक विशेष प्रकार से स्टोर किया जाता है ; जैसे कि टैब, कोमा या सैमीकालम जब फाइल का फारमैट बदल दिया जाए। वह फाइल प्रोसैस करने के लिए पूरा प्रोग्राम बदलना पड़ेगा। सारा डाटा खराब हो जाएगा। क्योंकि बहुत प्रोग्राम फाइल का प्रयोग करते हैं। इससे फाइलों का प्रयोग काफी मुश्किल हो जाता है।

डाटा इनकनसिसटेंसी-एक ही प्रकार के डाटा की भिन्न कापियों में कोई अंतर नहीं होना चाहिए। इस प्रकार के डाटा को इनकनसिसटैंसी कहते हैं। इसका कारण है कि फाइल की सही सूची नहीं बनी होती जिसके कारण डाटा की एक जैसी कापी नहीं होती है।

सुरक्षा-हर फाइल को पासवर्ड लागकर सुरक्षित किया जाता है। परंतु अगर फाइल में से हम कोई रिकार्ड देखते हैं जैसे कि किसी भी यूज़र ने अपना नतीजा देखना हो तो यह फाइल प्रोसैसिंग सिस्टम में बहुत मुश्किल होता है।

प्रश्न 3.
DBMS क्या है ? इसकी लाभ तथा हानियां बताओ।
उत्तर-
DBMS का पूरा नाम डाटाबेस मैनेजमैंट सिस्टम है। यह एक सॉफ्टवेयर होता है। जो यूज़र को डाटाबेस बनाने, संभाल कर रखने, कन्ट्रोल करने और देखने की आज्ञा देता है। DBMS वास्तव में प्रोग्रामों का एक समूह है जो यूज़र को स्टोर करने, बदलने और डाटाबेस में से संक्षेप सूचना निकालने की स्वीकृति देता है।
DBMS के लाभ-

यह अधिकता को कंट्रोल करता है।
डाटा का मॉडल बनाया जा सकता है।
डाटा की साझेदारी की जा सकती है।
अशुद्धता लागू होती है।
इसका उचित स्तर होता है।
इसे बिना आज्ञा कोई व्यक्ति नहीं चला सकता और न ही देख सकता है।
निजी ज़रूरतों से लेकर उद्योगों की ज़रूरतें पूरी करता है।
इससे ज़्यादा यूज़र इकट्ठे कार्य कर सकते हैं।
इसमें बैकअप की यूटिलिटी भी होती है।

हानियां

यह जटिल होता है।
इसका छोटे कम्प्यूटर पर उच्च स्तर पर प्रयोग नहीं हो सकता।
खराब होने का खतरा अधिक होता है।
आकार काफ़ी बड़ा होता है।
इसका मूल्य काफ़ी अधिक होता है।
अतिरिक्त हार्डवेयर की ज़रूरत पड़ती है।
परिवर्तन का मूल्य काफ़ी अधिक होता है।

प्रश्न 4.
एन० टी० टी० क्या होता है ? इसकी किस्मों के बारे में बताएं।
उत्तर-
वह चीज़ जिसकी जानकारी हम डाटा के रूप में डाटाबेस में स्टोर करते हैं। उसे एन० टी० टी० कहते हैं।

एन० टी० टी० किस्में1. कमज़ोर एन० टी० टी०-यह एक ऐसी एन० टी० टी० है। जो आपके एट्रीब्यूट्स से अलग नहीं पहचानी जा सकती।
बढ़िया एन० टी० टी०- इस में प्राइमरी कीअ लगी होती है। यह एन० टी० टी० बढ़िया से जान सकते हैं। यह डाटा से अलग हो जाती है।

प्रश्न 5.
डाटा मॉडल क्या होता है ? इस के भागों के बारे में बताएं।
उत्तर-
डाटा मॉडल वह तरीका है जो हमें डाटाबेस स्ट्रक्चर के बारे में जानकारी देता है। यह तीन प्रकार के होते हैं।
1. ऑब्जैकट ओरीऐंटिड मॉडल-यह लाइन दर लाइन डाटा का वर्णन करते हैं। यह पाँच प्रकार के होते हैं।

बाइनरी मॉडल
फंकशन मॉडल
एन० टी० टी० रिलेशनशिप
ऑब्जैकट ओरऐंटिड मॉडल
सिमेटिक डाटा मॉडल।

2. रिकार्ड बेस लॉजीकल मॉडल-यह लाइन दर लाइन डाटा का वर्णन करते हैं। पर यह एक फारमैट का प्रयोग करते हैं। इसमें हर एक रिकार्ड के अपने एट्रीब्यूट्स और फील्डस होते हैं, जिसे एक निश्चित अधिकार होता है। यह तीन प्रकार के होते हैं।

नेटवर्क मॉडल
रिलेशनल मॉडल
हैरारीकल मॉडल।

3. फिजीकल डाटा मॉडल-फिजीकल डाटा मॉडल का प्रयोग डाटाबेस में से नीचे लेवल के डाटा का वर्णन करने के लिए किया जाता है।
यह इस प्रकार है-

एन० टी० टी०-यह डाटाबेस के अलग-अलग वस्तु के बारे में जानकारी देता है।
एट्रीब्यूट-यह प्रयोगकर्ता के नाम, पता आदि के एन० टी० टी० के बारे में जानकारी देता है।
एन० टी० टी० सेट-यह एन० टी० टी० सैट और एट्रीब्यूट सुमेल से बनता है। इसमें अलग-अलग ऐन० टी० टी० और एट्रीब्यूट स्टोर की जाती है।
रिलेशनशिप-हम जिस भी एन० टी० टी० का प्रयोग कर सकते हैं। वह आपसी डाटाबेस में किसी अन्य एन० टी० टी० से भी जुड़ी हो सकती है। इसी को रिलेशनशिप या संबंध कहते हैं।

PSEB 8th Class Computer Guide डी०बी०एम०एस० से परिचय Important Questions and Answers

रिक्त स्थान भरें

1. प्रोसैस के बाद डाटा …………….. में बदल जाता है।
उत्तर-
सूचना,

2. ………. एक बहुत सारे डाटा का समूह है।
उत्तर-
रिकार्ड,

3. ……………… सिस्टम में डाटा की फाइलों के रूप में संभाला जाता है।
उत्तर-
कम्प्यूट्रीकृत डाटाबेस,

4. एक-दूसरे के साथ सम्बन्धित रिकार्ड के समूह को ……………… कहा जाता है।
उत्तर-
फाइल,

5. फाइल प्रोसैसिंग में ……………… के अवसर अधिक है।
उत्तर-
डुप्लीकेसी,

6. ……………… व्यक्ति या व्यक्तियों का समूह है जो डाटाबेस प्रणाली का नियंत्रण करता है।
उत्तर-
डाटाबेस, एडमिनिस्ट्रेटर।

सही या गलत बताइये

1. प्रोसैस (प्रक्रिया) किये डाटा को सूचना कहा जाता है।
उत्तर-
सही,

2. डाटाबेस में सुरक्षा और प्रबन्ध करने के गुण होते हैं।
उत्तर-
सही,

3. DBMS को सम्भालने की ज़िम्मेवारी DBA की नहीं।
उत्तर-
गलत,

4. एक दूसरे से सम्बन्धित डाटा आइटम के समूह को रिकार्ड कहा जाता है।
उत्तर-
सही,

5. सम्बन्धित डाटा आइटम के समूह को फाइल कहा जाता है।
उत्तर-
गलत।

पूरे नाम बताइये

1. DBA
2. DBMS
उत्तर-
1. DBA-Data Base Administrator
2. DBMS-Data Base Management System

छोटे उत्तर वाले प्रश्न

प्रश्न 1.
डाटा और इनफॉरमेशन क्या होता है ?
उत्तर-
डाटा-डाटा कच्चे पदार्थ होते हैं जिन पर कम्प्यूटर प्रोग्राम काम करते हैं। इनफॉरमेशन-प्रोसैस किये गए डाटा को इनफॉरमेशन कहते हैं।

प्रश्न 2.
डाटा बेस एप्लीकेशन का प्रयोग कहां होता है ?
उत्तर-

इसके प्रयोग से बैंकों के अकाऊंट्स की संभाल की जाती है।
एयरलाइन रिज़रवेशन और एनफॉरमेशन शेडयूल के लिए।
संस्था की महीने वार स्टेटमैंट बनाने के लिए।
दूर-संचार के लिए।

प्रश्न 3.
डाटा रिडुयन.सी क्या होता है ?
उत्तर-
किसी डाटाबेस में एक ही प्रकार के डाटा को बार-बार स्टोर करने की स्थिति को डाटा रिडुयन.सी कहते हैं।

प्रश्न 4.
एन० टी० टी० रिलेशनशिप डायाग्राम क्या है ?
उत्तर-
E-R Diagram एक ऐसा तरीका है जिसके साथ हम किसे भी Entity को बताने वाले । Atributes को लाजिकली दर्शा सकते हैं।
PSEB 9th Class Computer Solutions Chapter 4 डी०बी०एम०एस० से परिचय 1

प्रश्न 5.
डाटा (Data) क्या होता है ?
उत्तर-
कच्चे तथ्यों, अंकों, अक्षरों, शब्दों आदि के इकट्ठ को डाटा कहा जाता है। इनका अपने आप में कोई अर्थ नहीं होता।

प्रश्न 6.
सूचना (Information) क्या होती है ?
उत्तर-
प्रोसैसड डाटे को सूचना कहा जाता है। जब हम डाटे की अपनी ज़रूरत अनुसार किसी खास रूप में ढाल देते हैं, उसको सूचना कहा जाता है।

प्रश्न 7.
डाटाबेस (Database) से क्या भाव है ? ।
उत्तर-
सम्बन्धित सूचनाओं का वो इकट्ठ जो एक नाम के नीचे सम्भाला जाता है, उस को डाटाबेस कहते हैं।

प्रश्न 8.
डाटाबेस में कौन-कौन से काम किये जाते हैं ?
उत्तर-
डाटाबेस में नीचे दिये गये काम किये जाते हैं-

डाटे को स्टोर करना।
डाटे से सूचना तैयार करना।
स्टोर की सूचना को दोबारा प्राप्त करना।
सूचना को बदलना।
अनावश्यक सूचना को डिलीट करना।
सूचना को आवश्यक क्रम में लगाना।
सूचनाओं के मेल से नई सूचना तैयार करना।

प्रश्न 9.
DBMS के लाभ बताइये।
उत्तर-
DBMS के निम्नलिखित लाभ हैं

यह अधिकता को नहीं होने देता।
यह डाटे को अजोड़ रखता है।
इस में डाटे की साझेदारी की जा सकती है।
इस का उचित स्तर होता है।
इस में डाटा सुरक्षित रहता है।
यह सभी की ज़रूरतें पूरी करता है।
यह बैकअप की रिकवरी की सुविधा प्रदान करता है।
इस में अखण्डता की सुविधा होती है।

प्रश्न 10.
निम्नलिखित पर नोट लिखें
1. सम्बन्धों की किस्में
2. रिकार्ड
3. फाईल
4. DBA
5. प्राइमरी
6. फौरन की
7. एक से एक सम्बन्ध।
उत्तर
1. सम्बन्धों की किस्में-सम्बन्ध दो या ज़्यादा टेबलों में आपसी सम्बन्ध को दर्शाता है। यह सम्बन्ध अलग-अलग फील्डज़ में होते हैं। यह सम्बन्ध तीन प्रकार के होते हैं-

एक से एक सम्बन्ध
एक से अनेक सम्बन्ध
अनेक से अनेक सम्बन्ध

एक से एक सम्बन्ध-इस में एक टेबल की एक रो का दूजे टेबल की एक रो से सम्बन्ध होता है।
एक से अनेक सम्बन्ध-इस में एक टेबल की एक रो का दूसरे टेबल की एक से ज्यादा रोअज़ से सम्बन्ध होता है।
अनेक से अनेक सम्बन्ध-इस में एक टेबल की एक से ज्यादा रोअज़ का दूसरे टेबल की एक से ज्यादा रोअ से सम्बन्ध होता है।

2. रिकार्ड-एक दूसरे से सम्बन्धित डाटा आइटम के समूह को रिकार्ड कहा जाता है। यह एक टेबल की एक रोअ होती है, जिसमें सारे फील्डज़ की कीमतें शामिल होती हैं। ये सभी कीमतें मिल कर एक रिकार्ड बनाती हैं।

3. फाईल-जब सम्बन्धित जानकारी को एक नाम के नीचे सम्भाला जाता है तो उस को फाईल कहते हैं। यह एक दूसरे से सम्बन्धित रिकार्डज़ का समूह होती हैं।

4. DBADBA का पूरा नाम है डाटाबेस एडमनिस्ट्रेटर (Database Administrator)। इस को डाटाबेस प्रबन्धक भी कहा जाता है। यह उन व्यक्तियों का समूह होता है जो डाटाबेस प्रणाली को नियन्त्रित करते हैं। इसका सभी डाटाबेस पर कण्ट्रोल होता है।

5. प्राइमरी कीअ-किसी टेबल में वो फील्ड या फील्डों का समूह जो अपने आप में विलक्षण होता है, प्राइमरी कीअ कहलाता है। इस कीअ का इस्तेमाल करके टेबल के किसी भी रिकार्ड की प्राप्ति की जा सकती है।

6. फौरन कीअ-वो कीअ जो किसी अन्य टेबल कीअ प्राइमरी की होती है, को पहले टेबल कीअ फौरन कीअ कहा जाता है। यह दो टेबलों में सम्बन्ध स्थापित करती है।

7. एक से एक सम्बन्ध-एक से एक सम्बन्ध वो होता है, जिस में एक टेबल के एक रिकार्ड का किसी दूसरे टेबल की एक ही रिकार्ड से सम्बन्ध होता है।

प्रश्न 11.
डाटाबेस क्या होता है ? साधारण डाटा फाइलों से यह कैसे अधिक उपयोगी है ?
उत्तर-
कोई डाटाबेस आपस में सम्बन्धित डाटा का ऐसा संग्रह होता है, जो एक व्यवस्थित रूप से एक इकाई की तरह एक ही स्थान पर स्टोर किया जाता है। यह साधारण डाटा फाइलों से बहुत अधिक उपयोगी है, क्योंकि हम अपनी आवश्यक सूचनाएँ कई फाइलों को एक साथ मिलाकर प्राप्त कर सकते हैं।

प्रश्न 12.
डाटाबेस बनाने के क्या लाभ हैं ?
उत्तर-
डाटाबेस बनाने के कई लाभ होते हैं, जिनमें से कुछ निम्न प्रकार हैं

डाटा के दोहराव में कमी
कई उपयोगकर्ताओं के बीच डाटा का साझा
डाटा की पूर्णता (Integrity)
डाटा का मानकीकरण (Standardization)
बेहतर डाटा सुरक्षा।