Bhagya

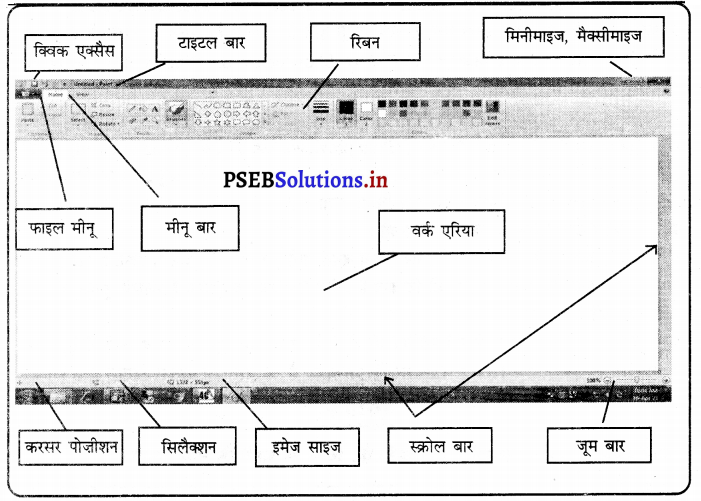
Punjab State Board PSEB 7th Class Science Book Solutions Chapter 2 जंतुओं में पोषण Textbook Exercise Questions and Answers.

PSEB Solutions for Class 7 Science Chapter 2 जंतुओं में पोषण

PSEB 7th Class Science Guide जंतुओं में पोषण Textbook Questions and Answers

1. खाली स्थानों की पूर्ति कीजिए :-

(i) जो जंतु पौधे तथा जन्तु दोनों को खा लेते हैं, उन्हें …………………. कहते हैं।
उत्तर-
सर्वाहारी

(ii) मनुष्य में भोजन का …………………….. मुख में ही आरंभ हो जाता है और ……………………….. में पूर्ण होता है।
उत्तर-
पाचन, छोटी आंत

(iii) ……………………. मनुष्य के शरीर की सबसे बड़ी ग्रंथि है।
उत्तर-
यकृत (जिगर)

(iv) बृहदांत्र में अनपचे भोजन में से ……………………. और ……………………. अवशोषित किए जाते हैं।
उत्तर-
फालतू पानी, नमक (लवण)।

2. नीचे लिखे वाक्यों में सही या गलत बताइए :-

(i) जीभ भोजन को लार के साथ मिलाने में सहायता करती है।
उत्तर-
सही

(ii) मनुष्य में पाचन क्रिया अमाशय में पूरी हो जाती है।
उत्तर-
ग़लत

(iii) जुगाली करने वाले जन्तुओं को रूमीनेंट कहते हैं।
उत्तर-
सही

(iv) अमीबा कृत्रिम पाँवों/पादाभ की सहायता से भोजन झपटता है।
उत्तर-
ग़लत

3. सही विकल्पों का मिलान करो :-

कॉलम ‘क’	कॉलम ‘ख’
(i) जुगाली करने वाला/रूमीनेंट	(क) पित्त
(ii) कार्बोहाइड्रेट	(ख) अनपचा भोजन जमा होता है
(ii) पित्ताशय	(ग) ग्लूकोस
(iv) क्षुदांत्र	(घ) गाय
(v) मल-नली	(ङ) भोजन का पाचन पूर्ण होता है।

उत्तर-

कॉलम ‘क	कॉलम ‘ख’
(i) जुगाली करने वाला/रूमीनेंट	(घ) गाय
(ii) कार्बोहाइड्रेट	(ग) ग्लूकोस
(ii) पित्ताशय	(क) पित्त
(iv) क्षुदांत्र	(ङ) भोजन का पाचन पूर्ण होता है
(v) मल-नली	(ख) अनपचा भोजन जमा होता है

4. सही विकल्प चुनें :-

प्रश्न (i)
जो जन्तु केवल पौधे खाते हैं :
(क) मांसाहारी
(ख) शाकाहारी
(ग) सर्वाहारी
(घ) मृतजीवी।
उत्तर-
(ख) शाकाहारी।

प्रश्न (ii)
कोशिका से बाहर पाचन होता है-
(क) परजीवी
(ख) मांसाहारी
(ग) मृतजीवी
(घ) शाकाहारी।
उत्तर-
(ग) मृतजीवी।

प्रश्न (iii)
जंतु द्वारा शरीर के अंदर भोजन ग्रहण करने की क्रिया कहलाती है-
(क) भोजन ग्रहण
(ख) पाचन
(ग) अवशोषण
(घ) मल त्याग।
उत्तर-
(क) भोजन ग्रहण।

प्रश्न (iv)
यकृत का रिसाव है-
(क) प्रोटीन
(ख) पित्त रस
(ग) कार्बोहाइड्रेट
(घ) लार।
उत्तर-
(ख) पित्त रस।

प्रश्न (v)
अमीबा में पोषण है-
(क) परजीवी
(ख) प्राणीवत
(ग) मृतजीवी ।
(घ) स्वांगीकरण।
उत्तर-
(ख) प्राणीवत।

5. लघूत्तर प्रश्न :-

प्रश्न (i)
प्राणीवत पोषण क्या है ?
उत्तर-
प्राणीवत पोषण – इस प्रकार के पोषण के दौरान जटिल भोजन शरीर के भीतर ले जाते हैं तथा फिर इसे एन्जाइमों की सहायता से साधारण घुलनशील यौगिकों में विभाजित किया जाता है। जिसे शरीर द्वारा इसका अवशोषण कर लिया जाता है। जैसे-अमीबा, मनुष्य आदि।

प्रश्न (ii)
अवशोषण से क्या अभिप्राय है ? ।
उत्तर-
अवशोषण – इस क्रिया में पचे हुए भोजन को छोटी आंत की दीवारों द्वारा अवशोषित कर लिया जाता है। इसके बाद पचा हुआ भोजन रुधिर वाहिकाओं में चला जाता है। छोटी आंत की अंदरूनी दीवार पर बड़ी गिनती में उंगली जैसे उभरे हुए आकार होते हैं, जिनको रस-अंकुर या विली (Villi) कहते हैं। यह रस अंकुर आंत के अवशोषण क्षेत्र को बढ़ा देते हैं।

प्रश्न (iii)
स्वांगीकरण की परिभाषा लिखो।
उत्तर-
स्वांगीकरण – आंतों द्वारा अवशोषित किया भोजन रुधिर वाहिकाओं द्वारा रक्त द्वारा शरीर के भिन्न-भिन्न भागों तक पहुँच जाता है। इसे स्वांगीकरण कहते हैं।

प्रश्न (iv)
भोजन नली के भागों के नाम लिखो।
उत्तर-
पाचन नली के भाग-

1. मुख गुहिका
2. भोजन नली
3. पेट
4. छोटी आंत
5. बड़ी आंत
6. रैक्टम
7. मल द्वार।

6. निबंधात्मक प्रश्न :-

प्रश्न (i)
दूध के दाँत एवं स्थायी दाँतों से क्या भाव है ?
उत्तर-
दूध के दाँत – मनुष्य के जीवन काल के दौरान दाँतों के दो सैट विकसित होते हैं। पहला सैट 20 छोटे दाँतों का होता है। जिन्हें दूध के दाँत भी कहते हैं। यह बाल अवस्था के दौरान आते हैं और 06 से 08 साल की उम्र के दौरान टूट जाते हैं।

स्थायी दाँत – 6 से 8 साल की उम्र के दौरान दूध के दाँतों के गिरने के बाद स्थायी दाँत (32) आते हैं। स्थायी दाँत 50 से 60 साल की उम्र तक गिरने आरंभ हो जाते हैं।

प्रश्न (ii)
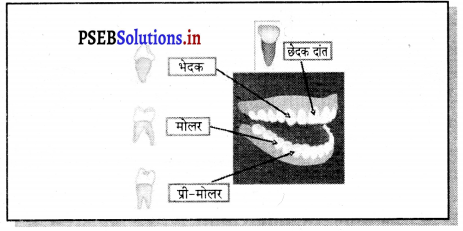
मनुष्य में पाए जाने वाले चार प्रकार के दाँत तथा उनके कार्य लिखो।
उत्तर-
मनुष्य में पाए जाने वाले चार प्रकार के दाँत तथा उनके कार्य – मनुष्य में चार प्रकार के दाँत होते हैं जो निम्न लिखे गए हैं

दाँत की किस्में	दाँतों के कार्य
1. छेदक/कृन्तक (Incisors)	यह भोजन को काटने के लिए प्रयोग होते हैं।
2. भेदक/ रदनक (Canines)	यह फोड़ने के लिए प्रयोग होते हैं।
3. अग्र चर्वणक (Premolars)	यह दाँत भोजन चबाने तथा पीसने के लिए प्रयोग होते हैं।
4. चर्वणक/बुद्धि के दाँत (Molars)	यह भी भोजन को पीसने के लिए प्रयोग होते हैं।

प्रश्न (iii)
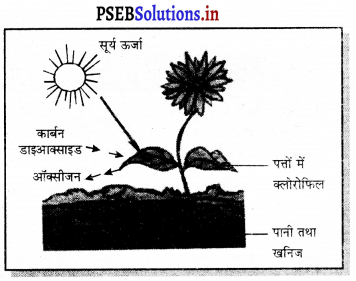
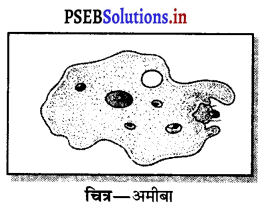
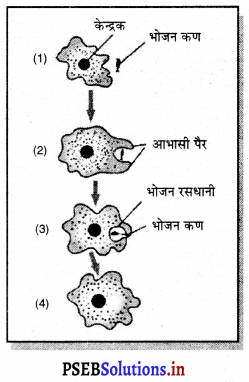
चित्र की सहायता से अमीबा में पोषण का वर्णन करो।
उत्तर-
अमीबा में पोषण – अमीबा एक कोशिका (सैली) सूक्ष्मजीव है। इसके बाहर कोशिका झिल्ली होती है। यह आभासी पैरों में चलता है। यह उंगली जैसी रचनाएँ होती हैं जो गति करने में तथा अमीबे के संपर्क में आए भोजन को पकड़ने में सहायता करती हैं। भोजन प्राप्ति के दौरान भोजन के आस-पास दोनों आभासी पैरों के बीच की झिल्ली द्रवित हो जाती है तथा भोजन का कण, भोजन वैक्यूल में बदल जाता है तथा इसके अंदर पाचक रसों का रिसाव होता है जिसमें पोषक अवशोषित कर लिए जाते हैं। अनपचे भोजन कण अमीबा के शरीर में ऐसी ही प्रक्रिया द्वारा त्याग दिए जाते हैं।

प्रश्न (iv)
नीचे लिखे चित्रों को अंकित करें ।

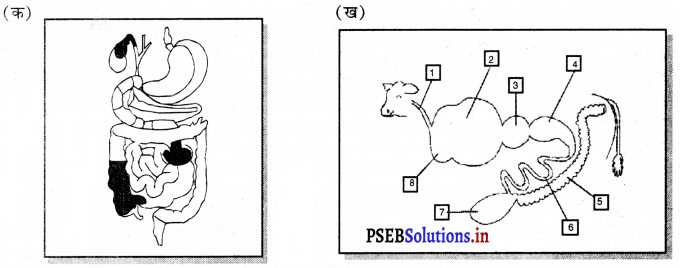
उत्तर-

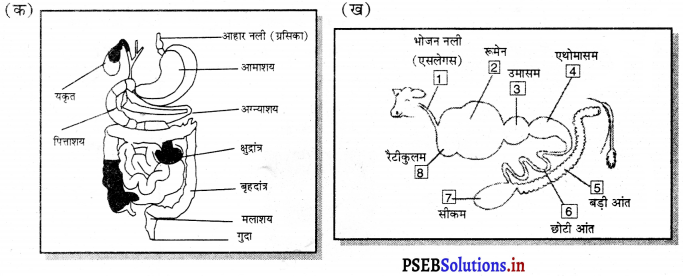
Science Guide for Class 7 PSEB जंतुओं में पोषण Intext Questions and Answers

सोचें तथा उत्तर दें :- (पेज 12)

प्रश्न 1.
मुख में लार ग्रंथियों द्वारा रिसने वाले घोल का नाम बताइए।
उत्तर-
मुख में लार ग्रंथियों द्वारा छोड़े गए रस का नाम ‘लार रस’ है।

प्रश्न 2.
आयोडीन का घोल स्टार्च के ऊपर डालने पर क्या परिवर्तन पाया जाता है ?
उत्तर-
आयोडीन का घोल स्टार्च में मिलाने से आयोडीन के घोल का रंग जामनी अथवा नीला हो जाता है।

प्रश्न 3.
मुख में पाचन के बाद स्टार्च किस में परिवर्तित हो जाता है ?
उत्तर-
मुख में लार ग्रंथियों द्वारा लार रस छोड़ा जाता है जिसमें एसाइलेज़ नाम का एन्जाइम होता है। यह एन्ज़ाइम स्टार्च को शर्करा (ग्लूकोज़) में बदल देता है।

सोचें तथा उत्तर दें :- (पेज 13)

प्रश्न 1.
भोजन को काटने वाले दाँत का नाम लिखो।
उत्तर-
काटने वाले दाँतों को तीखे दाँत भी कहा जाता है।

प्रश्न 2.
किस आयु तक अग्रदाढ़ें या दाढ़ें नहीं होती?
उत्तर-
50 साल या इस से अधिक उम्र के व्यक्तियों में अग्रदाढ़ें या दाढें टूटनी आरंभ हो जाती हैं।

प्रश्न 3.
प्रौढ़ व्यक्ति के मुख में अधिक से अधिक कितने दाँत होते हैं ?
उत्तर-
30 साल की उम्र वाले वयस्क के मुख में सभी प्रकार के (कुल 32 दाँत) होते हैं।

सोचें तथा उत्तर दें :- (पेज 14)

प्रश्न 1.
जीभ के किस क्षेत्र से खट्टा स्वाद अनुभव होता है ?
उत्तर-
जीभ के अगले भाग से आरंभ होकर \(\frac{3}{4}\) भाग अर्थात् मध्य से थोड़ा-सा पीछे खट्टा स्वाद अनुभव होता है।

प्रश्न 2.
जीभ के अगले क्षेत्र में कड़वा स्वाद अनुभव क्यों नहीं होता ?
उत्तर-
जीभ का अगला भाग सभी ओर गति करने के लिए स्वतन्त्र होता है तथा यह भाग केवल भोजन को चबाने तथा लार मिलाने में सहायता करता है। जीभ पर चार ग्रंथियां मीठा, नमकीन, खट्टा तथा कड़वा होती हैं। जीभ के अगले हिस्से में केवल मीठे स्वाद का ही अनुभव होता है जबकि जीभ के अंतिम भाग में कड़वे स्वाद का अनुभव होता है।

PSEB Solutions for Class 7 Science जंतुओं में पोषण Important Questions and Answers

वस्तुनिष्ठ प्रश्न

प्रश्न 1.
रिक्त स्थानों की पूर्ति कीजिए-

(क) मानव पाचन के मुख्य चरण …………………, …………………, ……………….., …………………, एवं ………………. हैं।
उत्तर-
अंतर्ग्रहण, पाचन, अवशोषण, स्वांगीकरण, निष्कासन

(ख) मानव शरीर की सबसे बड़ी ग्रंथि का नाम ……………………… है।
उत्तर-
यकृत

(ग) आमाशय में हाइड्रोक्लोरिक अम्ल एवं ……………………. का स्राव होता है, जो भोजन पर किया करते हैं।
उत्तर-
पाचक रस

(घ) क्षुद्रांत्र की आंतरिक भित्ति पर अँगुली के समान अनेक उभार होते हैं, जो ………………. कहलाते हैं।
उत्तर-
दीर्घ रोम

(च) अमीबा अपने भोजन का पाचन ……………………. में करता है।
उत्तर-
खाद्य धानी।

प्रश्न 2.
सत्य एवं असत्य कथनों को चिह्नित कीजिए।

(i) मंड का पाचन आमाशय से प्रारंभ होता है।
उत्तर-
असत्य

(ii) जीभ लाला-ग्रंथि को भोजन के साथ मिलाने में सहायता करती है।
उत्तर-
सत्य

(iii) पित्ताशय में पित्त रस अस्थायी रूप से भंडारित होता है।
उत्तर-
सत्य

(iv) रूमिनेंट निगली हुई घास को अपने मुख में वापस लाकर धीरे-धीरे चबाते रहते हैं।
उत्तर-
सत्य

प्रश्न 3.
कॉलम A में दिए गए कथनों का मिलान कॉलम B में दिए गए कथनों से कीजिए।

कॉलम A- खाद्य घटक	कॉलम B-पाचन के उत्पाद
कार्बोहाइड्रेट्स	वसा अम्ल एवं ग्लिसरॉल
प्रोटीन	शर्करा
वसा	ऐमीनो अम्ल

उत्तर-

कॉलम A- खाद्य घटक	कॉलम B-पाचन के उत्पाद
कार्बोहाइड्रेट्स	शर्करा
प्रोटीन	ऐमीनो अम्ल
वसा	वसा अम्ल एवं ग्लिसरॉल

प्रश्न 4.
सही विकल्प चुनें-

(i) जटिल खाद्य पदार्थों के सरल पदार्थों में परिवर्तित होने को क्या कहते हैं ?
(क) स्वांगीकरण
(ख) अंतर्ग्रहण
(ग) पाचन
(घ) बहिक्षेपण।
उत्तर-
(ग) पाचन।

(ii) मानव की सबसे बड़ी पाचन ग्रंथि का नाम क्या है ?
(क) लार
(ख) अग्न्याशय
(ग) यकृत
(घ) आंत्र।
उत्तर-
(ग) यकृत।

(iii) आमाशय में कौन-सा अम्ल जीवाणुओं को मारता है ?
(क) सल्फ्यूरिक
(ख) नाइट्रिक
(ग) हाइड्रोक्लोरिक
(घ) फास्फोरिक।
उत्तर-
(ग) हाइड्रोक्लोरिक।

(iv) निम्न पशुओं में से किसमें रूमेन पाया जाता है ?
(क) गाय
(ख) कुत्ता
(ग) शेर
(घ) चीता।
उत्तर-
(क) गाय।

(v) क्षुद्रांत्र की लंबाई कितनी होती है ?
(क) 10.5 मीटर
(ख) 4 मीटर
(ग) 3 मीटर
(घ) 7.5 मीटर।
उत्तर-
(घ) 7.5 मीटर।

(vi) पाचन नली में भोजन की गति है-
(क) चलन
(ख) पंपिंग
(ग) संकुचन (पेरीस्टालसिस) ।
(घ) फिसलना।
उत्तर-
(ग) संकुचन (पेरीस्टालसिस)

(vii) सबसे सरल कार्बोहाइड्रेट कौन-सा है ?
(क) ग्लूकोस
(ख) सुक्रोस
(ग) स्टार्च
(घ) उपरोक्त सभी।
उत्तर-
(क) ग्लूकोस।

(viii) लार कहाँ पैदा होती है ?
(क) आमाशय
(ख) पित्ताशय
(ग) लार ग्रंथि
(घ) इनमें से कोई नहीं।
उत्तर-
(ग) लार ग्रंथि

अति लघु उत्तरात्मक प्रश्न

प्रश्न 1.
आहारनली क्या है?
उत्तर-
आहारनली – मुख-गुहिका, ग्रास-नली, आमाशय, क्षुद्रांत्र, बृहदांत्र, मलाशय आदि भागों के समूह को आहारनली कहते हैं।

प्रश्न 2.
मानव की पाचक ग्रंथियों के नाम लिखो।
उत्तर-
लार-ग्रंथि, यकृत, अग्न्याशय।

प्रश्न 3.
पाचक तंत्र के विभिन्न अंश कौन-कौन से हैं?
उत्तर-
पाचक रस और आहार नली।

प्रश्न 4.
अस्थायी अथवा दुग्ध-दाँत कब गिर जाते हैं ?
उत्तर-
छ: से आठ वर्ष की आयु तक।

प्रश्न 5.
क्षुद्रांत्र की कितनी लंबाई है?
उत्तर-
7.5 मीटर (लगभग)

प्रश्न 6.
बृहदांत्र कितनी लंबी होती है?
उत्तर-
1.5 मीटर।

प्रश्न 7.
विभिन्न प्रकार के दाँतों के नाम लिखिए।
उत्तर-

1. कर्तन,
2. रुदनक,
3. अग्रचवर्णक तथा
4. चवर्णक।

प्रश्न 8.
काटने व दशन के लिए कौन-से दाँत हैं ?
उत्तर-
कर्तन दाँत।

प्रश्न 9.
चीरने (वेधन) और फाड़ने का काम कौन-से दाँतों द्वारा किया जाता है?
उत्तर-
रुदनक दाँत।

प्रश्न 10.
अग्रचवर्णक और चवर्णक के क्या कार्य हैं ?
उत्तर-
चबाना और पीसना।

प्रश्न 11.
जीभ क्या है?
उत्तर-
जीभ – जीभ, एक माँसल पेशीय अंग है जो मुख गुहिका के अधर तल में पीछे की ओर जुड़ी होती है।

प्रश्न 12.
जीभ स्वाद कैसे चखती है?
उत्तर-
स्वाद कलिकाओं की मदद से।

प्रश्न 13.
दंत क्षय के उत्तरदायी पदार्थो के नाम लिखें।
उत्तर-
चॉकलेट, ठंडे पेय, चीनी युक्त मिठाइयाँ।

प्रश्न 14.
आमाशय में कौन-सा अम्ल जीवाणुओं को मारता है?
उत्तर-
हाइड्रोक्लोरिक अम्ल।

लघु उत्तरात्मक प्रश्न

प्रश्न 1.
रसांकुर क्या है ? वह कहां मिलते हैं तथा उनके क्या कार्य हैं ?
उत्तर-
रसांकुर (Villi) – अंगुलियों के समान उभरी हुई संरचनाएं जो छोटी आंत की आंतरिक भित्ति में होती हैं। रसांकुर कहलाती है।
रसांकुर छोटी आंतों में पाया जाता है। इसका मुख्य कार्य पचे हुए भोजन को अवशोषित करना है।

प्रश्न 2.
पित्त रस कहां बनता है। यह भोजन के किस घटक के पाचन में मदद करता है ?
उत्तर-
पित्त रस जिगर में निर्मित होता है तथा पित्ते में अस्थायी रूप से इकट्ठा होता है। इसका मुख्य कार्य चर्बी का पाचन करना है।

प्रश्न 3.
उस कार्बोहाइड्रेट का नाम लिखें जिसका पाचन रूमीनैंट द्वारा किया जाता है परन्तु मनुष्य द्वारा नहीं। इसका कारण बताएं।
उत्तर-
सैलूलोज का पाचन रूमीनैंट द्वारा आसानी से हो सकता है। सैलूलोज को पचाने में एक प्रकार के जीवाणु सहायक होते हैं जो रूमीनैंट में छोटी तथा बड़ी आंतों के मध्य एक थैली जैसी संरचना में पाये जाते हैं।

प्रश्न 4.
क्या कारण है कि हमें ग्लूकोज़ के द्वारा ऊर्जा तुरंत मिलती है ?
उत्तर-
ग्लूकोज़ कार्बोहाइड्रेट का एक सरल रूप है जिस को शरीर आसानी से अवशोषित कर लेता है। ये लहु में आसानी से घुल जाता है तथा तुरंत ऊर्जा प्रदान करता है।

प्रश्न 5.
आहार नाल के कौन-से भाग द्वारा निम्न क्रियाएँ संपादित होती हैं ?
(i) घचे भोजन का अवशोषण
(ii) भोजन को चबाना ………………… ।
(iii) जीवाणु नष्ट करना ……………….. ।
(iv) भोजन का संपूर्ण पाचन …………………………… ।
(v) मल का निर्माण ………………… ।
उत्तर-
(i) क्षुद्रांत्र
(ii) मुँह गुहिका
(iii) आमाशय
(iv) क्षुद्रांत्र
(v) बृहदांत्र ।

प्रश्न 6.
मानव एवं अमीबा के पोषण में कोई एक समानता एवं एक अंतर लिखिए।
उत्तर-
मानव और अमीबा के पाचन में समानताएँ-
(क) आहार का अवशोषण
(ख) ऊर्जा का निर्मोचन

मानव और अमीबा के पाचन में असमानताएँ – मानवों में एक विकसित पाचन तंत्र होता है जबकि अमीबा में केवल खाद्यधानी होती है।

प्रश्न 7.
क्या हम केवल हरी सब्जियों/घास का भोजन कर जीवन निर्वाह कर सकते हैं? चर्चा कीजिए।
उत्तर-
हरी सब्जियों/घास पर जीवन निर्वाह – कच्ची हरी सब्जियाँ, लवण, सेलूलोज, जल और विटामिन के स्रोत हैं। इनके अतिरिक्त शरीर को कार्बोहाइड्रेट्स, वसा और प्रोटीन भी चाहिए। इसलिए केवल हरी सब्जियों/घास पर जीवन निर्वाह करना मुश्किल है।

प्रश्न 8.
पाचन क्रिया क्या है तथा इसके मुख्य उद्देश्य क्या हैं ?
उत्तर-
पाचन – जटिल पदार्थों का सरल पदार्थों में टूटना या परिवर्तित होना विघटन कहलाता है और यह पाचन क्रिया है।
पाचन क्रिया के उद्देश्य-

1. बड़े कणों का छोटे कणों मे टूटना ताकि झिल्ली में से गुजर सकें।
2. अघुलनशील पदार्थों का घुलनशील पदार्थों में बदलना ताकि घोल के रूप में सभी जगह पहुंच सकें।
3. जटिल भोजन पदार्थों का सरल पदार्थों में परिवर्तित होना ताकि कोशिकाओं द्वारा शोषित किया जा सके।

प्रश्न 9.
दंत खोड (गुहिका) क्या है तथा यह क्यों होती है ?
उत्तर-
दंत खोड (गुहिका) – बहुत ज्यादा मीठी वस्तुएं खाने से तथा दांतों की सफाई न रखने से हम जीवाणुओं को निमंत्रण देते हैं जो हमारे दांतों को नुकसान पहुंचाते हैं। अगर हम दांतों की सफाई नहीं रखते तो भोजन के कण दांतों में फंसे रह जाते हैं। जिन पर हमला करके वैक्टीरिया इन भोजन कणों का अपघटन करना शुरू कर देते हैं। जिसके कारण तेजाब पैदा होता है। यह तेज़ाब दांतों के इनैमल को नष्ट कर देता है तथा दांतों में खोड़ों का कारण बनता है। इसलिए हमें भोजन तथा मीठा खाने के बाद हमेशा दांत साफ करने चाहिए।

दीर्घ उत्तरात्मक प्रश्न

प्रश्न 1.
मानव के पाचन तंत्र की व्याख्या करें।
उत्तर-
मानव पाचन तंत्र – मानव के पाचक तंत्र के मुख्य अंग निम्नलिखित हैं-
मुँह – यह आहार नली का पहला भाग है। इसमें जीभ, दाँत और लार-ग्रंथियाँ होती हैं। जीभ स्वाद का अनुभव करती है। लार ग्रंथियाँ लार पैदा करती हैं, जो भोजन को नर्म बनाती हैं। दाँत भोजन को छोटे टुकड़ों में काटते हैं।

ग्रास-नली – यह एक गोलाकार नली मुँह से आमाशय तक जाती है। इसका काम भोजन को मुँह से आमाशय तक ले जाना है।

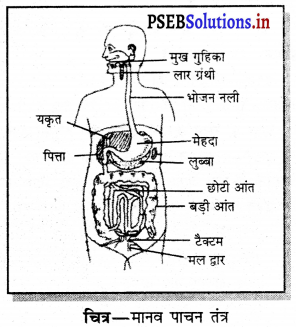
आमाशय – यह एक U आकृति का थैलीनुमा भाग है, जिसका कार्य भोजन को पचे रूप में परिवर्तन करना है। इसमें हानिकारक जीवाणु भी नष्ट होते हैं।

क्षुद्रांत्र – यह एक 7.5 मीटर लंबी कुंडलित नली है। भोजन का पूरा अवशोषण इसमें होता है। इसमें यकृत और अग्न्याशय के रस आकर मिलते हैं।

बृहदांत्र – यह अनपचे भोजन में से जल का अवशोषण करती है। इसके निचले हिस्से में मल और अनपचा भोजन अस्थायी रूप से संग्रहित होते हैं। फिर गुदा द्वारा शरीर से बाहर फेंके जाते हैं।

प्रश्न 2.
जुगाली करने की प्रक्रिया क्या है। जुगाली करने वाले पशुओं में पाचन कैसे होता है ? समझाएं।
उत्तर-
घास खाने वाले पशु जुगाली करते हैं तथा इनको रूमीनैंट कहते हैं। गाय, भैंस, ऊंट तथा हिरण रूमीनेंट की कुछ उदाहरण हैं इनका यकृत चार खानों वाला होता है। पहला खाना रूमेन होता है जो मेहदे का सब से बड़ा भाग होता है । जंतु पहले भोजन को निगल लेता है तथा उसको रूमेन में जमा कर लेता है। यहां भोजन का अंशक पाचन होता है इस अधपचे भोजन को कड्ड कहते हैं। बाद में यह कड्डू जंतु के मुंह में गोलों के रूप मे आ जाता है तथा जंतु इसे धीरे-धीरे चबाता रहता है इस प्रक्रिया को जुगाली करना कहते हैं। ऐसे जंतुओं को जुगाली करने वाले या रूमीनैंट कहते हैं।

जुगाली करते समय भोजन का सैलूलोज साधारण यौगिकों में टूट जाता है। फिर यह बाकी तीन दिन खानों में तरल रूप में पचता है रूमीनैंट जंतुओं की भोजन नली की छोटी आंत तथा बड़ों आंत के अंदर थैलीनमा रचना होती है जिसको सीकम कहते हैं जहां कुछ बैकटीरिया होते हैं। जो घास फूस के पाचन में सहायक होते हैं।

Punjab State Board PSEB 6th Class Computer Book Solutions Chapter 5 एम एस पेंट (भाग-2) Textbook Exercise Questions and Answers.

PSEB Solutions for Class 6 Computer Science Chapter 5 एम एस पेंट (भाग-2)

Computer Guide for Class 6 PSEB एम एस पेंट (भाग-2) Textbook Questions and Answers

1. रिक्त स्थान भरो।

(i) क्लिप बोर्ड मीनू में तीन ऑप्शन होते हैं। कट, कापी तथा ………
(क) पेस्ट
(ख) मूव
(ग) क्लोज
(घ) जूम।
उत्तर-
(क) पेस्ट

(ii) सबसे ऊपरी बटन जो डायमंड शेप के बीच लाइन होती है उसको ……. टूल कहते हैं।
(क) पेस्ट
(ख) कट
(ग) कापी
(घ) क्रोप।
उत्तर-
(घ) क्रोप।

(iii) ……….. टूल पेंटागन ड्रा करने में प्रयोग होता है।
(क) त्रिभुज
(ख) आयत
(ग) पेंटागन
(घ) हैक्सागन।
उत्तर-
(ग) पेंटागन

(iv) इरेज़र टूल की मदद से हम माऊस का ………. बटन दबा कर तस्वीर मिटा सकते हैं।
(क) दायां
(ख) बायां
(ग) स्क्रोल
(घ) कोई नहीं।
उत्तर-
(ख) बायां

(v) अगर हम माऊस का ………. बटन दबाते हैं तो कलर 1-2 का प्रयोग होता है।
(क) बायां
(ख) दायां
(ग) स्क्रोल
(घ) कोई नहीं।
उत्तर-
(ख) दायां

2. बहुत छोटे उत्तरों वाले प्रश्न

प्रश्न 1.
किस टूल का प्रयोग करके वर्ग बनाया जा सकता है ?
उत्तर-
रैक्टेंगल टूल का प्रयोग करके।

प्रश्न 2.
किस टूल का प्रयोग करके तस्वीर के किसी भाग को मिटाया जा सकता है ?
उत्तर-
इरेज़र टूल का प्रयोग करके।

प्रश्न 3.
किस टूल का प्रयोग तस्वीर को बड़ा करके देखने के लिए किया जाता है ?
उत्तर-
जूम टूल को।

प्रश्न 4.
किस टूल का प्रयोग स्वतंत्र लाइनर लगाने के लिए किया जाता है ?
उत्तर-
पेंसिल टूल का।

प्रश्न 5.
किस टूल का प्रयोग ड्राइंग में टैक्सट शामिल करने के लिए किया जाता है ?
उत्तर-
टैक्सट टूल का।

3. छोटे उत्तरों वाले प्रश्न

प्रश्न 1.
क्लिप बोर्ड मीनू में कौन-कौन से विकल्प उपलब्ध होते हैं ?
उत्तर-
क्लिप बोर्ड मीनू में नीचे दिए तीन उपलब्ध होते हैं

1. कट
2. कॉपी
3. पेस्ट।

प्रश्न 2.
क्रॉप विकल्प के बारे में लिखो।
उत्तर-
क्रॉप विकल्प का प्रयोग अपनी तस्वीर को क्रॉप करने के लिए किया जाता है। यह एक डायमंड कार का बटन होता है। इसके बीच एक लाइन लगी होती है। इसके द्वारा चुनाव किया गया हिस्सा ही सेव होता है। बाकी सारा हिस्सा कट जाता है।

प्रश्न 3.
टूल्स मीनू में मौजूद टूल्स के नाम लिखो।
उत्तर-
टूल्स मीनू में नीचे लिखे टूल्स उपलब्ध होते हैं –

1. पेंसिल टूल
2. फिल विद कलर टूल
3. टैक्सट टूल
4. इरेज़र टूल
5. कलर पिकर
6. मैग्नी फायर।

प्रश्न 4.
साइज टूल क्या होता है ?
उत्तर-
साइज टूल ऐसा टूल होता है जिसकी सहायता से पेंट में ब्रश पेंसिल तथा इरेज़र का आकार बदला जा सकता है। यह टूल ब्रश पेंसिल तथा इरेज़र टूल सिलेक्ट करने के बाद ही एक्टिव होता है।

प्रश्न 5.
ब्रश के बारे में लिखो।
उत्तर-
ब्रश टूल की सहायता से अपनी तस्वीर में विभिन्न मोटाई की तथा विभिन्न टेक्सचर की लाइनें दाखिल की जा सकती हैं। ब्रश टूल हमें विभिन्न प्रकार के टेक्सचर भी प्रदान करता है।

प्रश्न 6.
होम टैब रिबन में मौजूद ग्रुप के नाम लिखो।
उत्तर-
होम टैब रिबन में नीचे दिए गए ग्रुप मौजूद होते हैं –

1. क्लिप बोर्ड
2. इमेज
3. टूल्स
4. ब्रश
5. शेप
6. साइज
7. कलर।

4. बड़े उत्तरों वाले प्रश्न

प्रश्न 1.
एम एस पेंट में कलर टूल की व्याख्या करें।
उत्तर-
रिबन के कलर सैक्शन के तीन भाग होते हैं –
1. बॉक्स जो एक्टिव कलर दिखाते हैं कलर 1 तथा कलर 2
2. कलर पैलेट
3. एडिट कलर बटन

1. कलर बॉक्स
कलर 1-यह फोर कलर होता है। शुरू में यह काला होता है।
कलर 2-यह बैकग्राऊंड कलर होता है। शुरू में यह सफेद होता है।

2. कलर पैलेट-जब हम तस्वीर बनाते हैं तो कलर पैलेट की दो लाइनें मौजूदा रंग को दिखाती हैं। नीचे वाली लाइन हमारे बनाए कलर दिखाती हैं। पेंट बंद करने के बाद हमारे द्वारा बनाए – कलर खत्म हो जाते हैं।

3. एडिट कलर-यह हमें एडिट कलर डायलाग बाक्स में ले जाता है।

इसमें हम किसी भी कलर को चुन कर Add to Custom Colours बटन पर क्लिक कर सकते हैं। इसमें हर बार सिर्फ एक ही रंग शामिल किया जा सकता है। अन्य रंग शामिल करने के लिए हमें दोबारा इस डायलाग बॉक्स में आना पड़ेगा और प्रत्येक बार, एक रंग ही शामिल किया जा सकता है।

प्रश्न 2.
टैक्सट टूल क्या होता है ? टैक्सट को किस प्रकार फॉर्मेट किया जाता है ?
उत्तर-
टैक्सट टूल का प्रयोग अपनी तस्वीर में टैक्सट लिखने के लिए किया जाता है। टैक्सट टूल का प्रयोग करने के लिए पहले टैक्सट टूल के ऊपर क्लिक करो। करसर एक बार में बदल जाएगा करसर को तस्वीर पर खींचते हुए एक बॉक्स ड्रा करो अब इस बॉक्स में अपनी ज़रूरत अनुसार टाइप किया जा सकता है। जब सारा टाइप हो जाए तब इस बॉक्स से बाहर कहीं भी क्लिक करके टाइपिंग बंद की जा सकती है। टाइप करते समय इस टैक्सट बॉक्स से बाहर लिखाई नहीं करना चाहिए।

टैक्सट को फॉर्मेट करना-टैक्सट को फॉर्मेट करने के लिए नीचे दिए स्टेप प्रयोग किए जाते हैं –

1. टाइप किए गए टैक्सट को सिलेक्ट करो।
2. Font बॉक्स के अंत में दिखाए गए ऐरो के ऊपर क्लिक करो इससे पाठ की एक सूची दिखाई देगा।
3. बिना माऊस बटन दबाएं अपने करसर को इस सूची में ऊपर नीचे घुमाओ अपनी पसंद अनुसार अपना फोंट का चुनाव करो तथा उस पर क्लिक करो।
4. फोंट लिस्ट बंद हो जाएगी तथा हमारे सिलेक्ट किए हुए टैक्सट पर वह फॉर्म अप्लाई हो जाएगा।
5. इस प्रक्रिया को हम दोबारा प्रयोग करके दूसरे टैक्सट को फॉर्मेट कर सकते हैं।
6. हम बैकग्राऊंड को भी ट्रांसपेरेंट से उपेक यहाँ opaque ट्रांसपेरेंट बना सकते हैं।
7. हम कलर एक तथा कलर दो भी बदल सकते हैं।

अगर हम टैक्सट के अंत में एंटर की दबाते हैं तो टैक्सट बॉक्स अगली एलाइन इंसर्ट कर देता है। हम टैक्सट बॉक्स को अपनी तस्वीर के अंदर खींचकर बड़ा या छोटा भी कर सकते हैं। किसी नए टैक्सट को टैक्सट बॉक्स के अंदर नहीं रखा जा सकता। किसी स्थान पर नया टैक्सट टाइप करने के लिए पहले करसर को उस स्थान पर ले जाना पड़ता है इसके लिए ऐरो कीस का प्रयोग किया जाता है। स्पेस की का प्रयोग करके सेंट्रल एलाइन भी किया जा सकता है।

हम एक ही टैक्सट बॉक्स में विभिन्न प्रकार के रंग साइज तथा फोंट का प्रयोग कर सकते हैं। अपने टैक्सट में हम जो बदलाव करते हैं वह सिर्फ सिलेक्ट किए गए टैक्सट पर ही अप्लाई होता है। जब हमारा कार्य पूरा हो जाता है तो टैक्सट बॉक्स के बाहर कहीं भी क्लिक करने से टैक्सट बॉक्स गायब हो जाता है तथा फिर इसको दोबारा एडिट नहीं किया जा सकता। अब यह टैक्सट तस्वीर का एक हिस्सा बन जाता है।

एक्टिविटी
नीचे दिए टूलज़ के नाम लिखो

उत्तर-
1. पैसिल
2. फिल विद कलर
3. टैक्सट
4. इरेज़र
5. कलर पिकर
6. मैगनीफाइर।

निम्न शेपस के नाम बताओ।

उत्तर-
1. त्रिभुज (Triangle)
2. आयत (Rectangle)
3. ओवल (Oval)
4. पेंटागन (Pentagon)
5. हैक्सागन (Hexagon)
6. डायमंड (Diamond)।

PSEB 6th Class Computer Guide एम एस पेंट से जान-पहचान Important Questions and Answers

रिक्त स्थान भरें

(i) होम टैब रिबन ………. के नीचे होता है।
(क) मीनू वार
(ख) स्टेटस वार
(ग) वर्क एरिया
(घ) स्क्रोल बार।
उत्तर-
(क) मीनू वार

(ii) …….. का प्रयोग तस्वीर का हिस्सा मिटाने के लिए किया जाता है।
(क) कलर
(ख) सिलैक्ट
(ग) इरेज़र।
(घ) पैंसिल।
उत्तर-
(ग) इरेज़र।

(iii) क्रोप बटन की शेप ….. की तरह होती है।
(क) डायमंड
(ख) पेंटागन
(ग) वर्ग।
(घ) आयत।
उत्तर-
(क) डायमंड

(iv) पेंटागन की ……. भुजाएं होती हैं।
(क) 2
(ख) 3
(ग) 7
(घ) 5.
उत्तर-
(घ) 5.

बहुत छोटे उत्तरों वाले प्रश्न

प्रश्न 1.
क्लिप बोर्ड में कौन-से ऑप्शन होते हैं ?
उत्तर-
कट, कापी तथा पेस्ट।

प्रश्न 2.
सिलैक्शन में कौन-कौन से ऑप्शन होते हैं ?
उत्तर-
Crop, Resize तथा Rotate Flip.

प्रश्न 3.
फिल विद कलर क्या होता है ?
उत्तर-
फिल विद कलर के साथ किसी क्षेत्र में एक रंग भरा जा सकता है।

छोटे उत्तरों वाले प्रश्न

प्रश्न 1.
फ्री फॉर्म सिलैक्शन की ज़रूरत कब पड़ती है ?
उत्तर-
फ्री फॉर्म सिलैक्शन की ज़रूरत तब पड़ती है जब हमें उस स्थान पर कार्य करना हो जो कई वस्तुओं से घिरा हो तथा हम उन वस्तुओं को शामिल नहीं करना चाहते।

प्रश्न 2.
क्रोप बटन के बारे में जानकारी दो।
उत्तर-
सिलैक्शन ऑप्शन के सबसे ऊपर जो बटन होता है उसे क्रोप बटन कहा जाता है। इसका प्रयोग तस्वीरों को क्रोप करने के लिए किया जाता है।

प्रश्न 3.
इनवर्ट कलर ऑप्शन क्या करता है ?
उत्तर-
इनवर्ट कलर ऑप्शन एक काले रंग के मास्क में सफेद अक्षरों से लिखने का कार्य करता है ताकि टैक्सर शानदार नज़र आए।

प्रश्न 4.
पैंसिल टूल किस प्रकार कार्य करता है ?
उत्तर-
पैंसिल टूल का प्रयोग लाइनें लगाने के लिए किया जाता है या फिर इसका प्रयोग जूम इनमें टैक्सट एडिट करने के लिए किया जाता है।

प्रश्न 5.
मैगनीफायर टूल के बारे में बताओ।
उत्तर-
मैगनीफायर टूल का प्रयोग तस्वीर को जूम इन करने के लिए किया जाता है। इसके साथ तस्वीर को नज़दीक से देखा जा सकता है।

प्रश्न 6.
होम टैब रिबन क्या होता है ?
उत्तर-
होम टैब रिबन पेंट का एक मुख्य रिबन होता है। यह रिबन में पेंट विंडो के बीच मीनू बार के नीचे दिखाई देता है इस क्लिप बोर्ड इमेज टूल्स ब्रश सेप साईज तथा कलर मीनू मौजूद होते हैं।

प्रश्न 7.
होम टैब रिबन के मुख्य भागों के नाम लिखो।
उत्तर-
होम टैब रिबन के मुख्य भाग क्लिप बोर्ड, इमेज, टूल्स, ब्रश, शेप, साईज तथा कलर मीनू होते हैं ।

प्रश्न 8.
टूल्स में मौजूद टूल्स के नाम लिखो।
उत्तर-
टूल्स मीनू में नीचे दिए टूल्स मौजूद होते हैं –

• पैंसिल टूल
• फिल विद कलर
• टैक्सट टूल
• इरेज़र टूल
• कलर पिकर
• मैग्नी फायर टूल
• ब्रश।

प्रश्न 9.
साइज टूल क्या होता है?
उत्तर-
साइज टूल वह टूल होता है जिसकी मदद से ब्रश इरेजर या पेंसिल की मोटाई का चुनाव किया जाता है।

प्रश्न 10.
ब्रश के बारे में बताओ।
उत्तर-
ब्रश एक ऐसा टूल है जिसकी सहायता से विभिन्न प्रकार के टेक्सचर तथा मोटाई की लाइनें बनाई जा सकती हैं।

Punjab State Board PSEB 7th Class Science Book Solutions Chapter 1 पादपों में पोषण Textbook Exercise Questions and Answers.

PSEB Solutions for Class 7 Science Chapter 1 पादपों में पोषण

PSEB 7th Class Science Guide पादपों में पोषण Textbook Questions and Answers

1. खाली स्थानों की पूर्ति कीजिए :-

(i) किसी जीव द्वारा भोजन ग्रहण करने तथा इसके उपयोग करने को ……………………. कहते हैं।
उत्तर-
पोषण

(ii) पत्तों के नीचे के सूक्ष्मछिद्रों के द्वारा प्रकाश संश्लेषण के लिए हवा से …………………….. ली जाती है।
उत्तर-
कार्बनडाइऑक्साइड

(iii) प्रकाश संश्लेषण का पहला उत्पाद …………………………… है।
उत्तर-
ग्लुकोज़ (कार्बोहाइड्रेट्स)

(iv) जो पादप, दूसरों द्वारा तैयार किए भोजन पर निर्भर करते हैं, उन्हें ……………………… कहते हैं।
उत्तर-
परपोषी।

2. नीचे लिखे वाक्यों में सही या गलत बताइए :-

(i) कार्बोहाइड्रेट्स भोजन का आवश्यक घटक नहीं है।
उत्तर-
ग़लत

(ii) सभी हरे पादप स्वपोषी होते हैं।
उत्तर-
सही

(iii) एक ऐसा जीव है जिसमें पादप तथा जन्तुओं दोनों के गुण होते हैं।
उत्तर-
सही

(iv) प्रकाश-संश्लेषण के लिए सौर प्रकाश आवश्यक नहीं।
उत्तर-
ग़लत

3. सही विकल्पों का मिलान करो :-

कॉलम ‘क’	कॉलम ‘ख’
(i) खुंभ (agaricus)	(क) पत्ते
(ii) राइजोबियम	(ख) परजीवी
(iii) क्लोरोफिल	(ग) मृतजीवी
(iv) अमरबेल	(घ) फलीदार पादप।

उत्तर-

कॉलम ‘क’	कॉलम ‘ख’
(i) खुंभ (agaricus)	(ग) मृतजीवी
(ii) राइजोबियम	(घ) फलीदार पादप
(iii) क्लोरोफिल	(क) पत्ते
(iv) अमरबेल	(ख) परजीवी।

4. सही विकल्प चुनें :-

प्रश्न (i)
ऐसा सूक्ष्मजीव, जो हवा की नाइट्रोजन को मृदा में स्थिर करता है-
(क) अमरबेल
(ख) खुंब (मशरूम)
(ग) राइजोबियम
(घ) क्लोरोफिल।
उत्तर-
(ग) राइजोबियम।

प्रश्न (ii)
जो जीव अपना भोजन स्वयं तैयार नहीं कर सकते एवं अपने भोजन के लिए दूसरों पर निर्भर करते है-
(क) स्वपोषी
(ख) परपोषी
(ग) पोषक तत्त्व
(घ) खनिज।
उत्तर-
(ख) परपोषी।

प्रश्न (iii)
पादपों का भोजन का कारखाना है-
(क) पत्ता
(ख) तना
(ग) जड़
(घ) फूल।
उत्तर-
(क) पत्ता।

प्रश्न (iv)
इनमें से मृतजीवी है-
(क) राइजोबियम
(ख) खुंभ (agaricus)
(ग) अमरबेल
(घ) प्रोटीन।
उत्तर-
(ख) खुंभ।

5. अति लघूत्तर प्रश्न :-

प्रश्न (i)
पोषण की परिभाषा लिखें।
उत्तर-
पोषण – जीव द्वारा भोजन प्राप्त करना तथा उसके प्रयोग को पोषण कहते हैं। सभी जीवों के लिए एक जैसा भोजन नहीं होता।

प्रश्न (ii)
प्रकाश-संश्लेषण क्रिया क्या होती है ?
उत्तर-
प्रकाश संश्लेषण – यह एक ऐसी क्रिया है जिसमें पौधों द्वारा भोजन (कार्बोहाइड्रेट्स) का निर्माण होता है। इस क्रिया के दौरान सौर-ऊर्जा, प्रकाश ऊर्जा तथा पौधों के हरे रंग का पदार्थ (क्लोरोफिल वर्णक) की मौजूदगी में कार्बन डाइऑक्साइड तथा जल को
कार्बन ग्लूकोज़ (सरल कार्बोहाइड्रेट्स) में परिवर्तित किया जाता है।

इस क्रिया द्वारा हरे पौधे प्रकाश ऊर्जा को रासायनिक क्लोरोफिल ऊर्जा में परिवर्तित करते हैं।

प्रश्न (iii)
प्रकाश-संश्लेषण के लिए आवश्यक सामग्री का नाम लिखें।
उत्तर-
प्रकाश संश्लेषण के लिए आवश्यक सामग्री-

1. कार्बन-डाइऑक्साइड
2. पानी
3. सौर प्रकाश ऊर्जा।

प्रश्न (iv)
कीटभक्षी पौधे क्या होते हैं ?
उत्तर-
कीटभक्षी पौधे – ऐसे पौधे जिनके अंदर जीवों को पकड़ने तथा हज़म करने की प्रणाली मौजूद होती है, कीटभक्षी पौधे कहलाते हैं; जैसे-पिचर प्लांट। कीटों को पकड़ने के लिए पौधे के पत्तों के आकार घड़े के रूप में रूपांतरित होते हैं।

6. लघूत्तर प्रश्न :-

प्रश्न (i)
परजीवी पोषण से आप क्या समझते हो ?
उत्तर-
परजीवी पोषण – ऐसा पोषण जिसमें परजीवी जीव दूसरे जीव को हानि पहुँचा कर उससे अपना भोजन प्राप्त करते हैं, परजीवी पोषण कहलाता है।

प्रश्न (ii)
सहजीवन/सहजीवी संबंध का वर्णन करो।
उत्तर-
सहजीवी संबंध – दो भिन्न-भिन्न जीव एक-दूसरे के साथ सह-संबंध में रहते हैं तथा अपने पोषण के लिए एक-दूसरे पर निर्भर रहते हैं, इसे सहजीवी संबंध कहते हैं। इस प्रकार के संबंध में दोनों जीवों को एक-दूसरे से लाभ होता है। जैसे कि कई पौधों की जड़ों पर कवक पाये जाते हैं।

काई (कवक) – यह पौधे की जड़ों से पोषण प्राप्त करती है और बदले में पौधे को धरती में से पानी तथा लत्रण अवशोषित करने में सहायता करती है। लाइकेन तथा कवक सहजीवी संबंधों का एक अच्छा उदाहरण है। यहाँ काई (कवक) धरती में से पानी अवशोषित करते है और बदले में काई (कवक) प्रकाश संश्लेषण क्रिया द्वारा भोजन उपलब्ध करवाती है।

प्रश्न (iii)
घटपर्णी पादप कीड़ों को कैसे पकड़ता है ?
उत्तर-
घड़ा-बूटी (पिचर-प्लांट) पौधा कीटों को पकड़ने के लिए अपने पत्ते घड़े जैसी रचनाओं में परिवर्तित करता है। इस घड़े जैसी रचना के मुँह के नीचे की ओर मुड़े हुए बाल होते हैं। जब कोई कीट इस पर बैठता है तो वह नीचे की ओर फिसल जाता है। वह दोबारा ऊपर नहीं चढ़ पाता है तथा घड़े के अंदर के तल पर गिर जाता है। तल के ऊपर उपस्थित पाचक रसों से उस कीट का पाचन हो जाता है।

7. निबंधात्मक प्रश्न :-

प्रश्न (i)
मृदा में पोषकों की पूर्ति कैसे होती है ?
चित्र-घड़ा-बूटी
उत्तर-
मृदा में पोषकों की पुनः पूर्ति – पौधे मिट्टी में से पानी, लवण तथा पोषक तत्त्व अवशोषित करते रहते हैं जिस कारण मिट्टी में पोषकों की कमी हो जाती है। मिट्टी में इन पोषकों की पूर्ति समय-समय पर करनी चाहिए ताकि मिट्टी में उपजाऊ शक्ति बनी रहे। किसान आम तौर पर मिट्टी में मैन्योर तथा रासायनिक खाद (जिसमें एक से अधिक पोषक तत्त्व होते हैं), मिला कर इन पोषकों की कमी को दोबारा पूरा करते हैं।
जंगलों में विघटकों, पत्तों तथा जन्तुओं की बची सरल अणुओं के विघटन से पोषकों की पूर्ति करते रहते हैं।

प्रश्न (ii)
पोषकों से क्या अभिप्राय है ? पादपों में पोषण की भिन्न-भिन्न विधियों का वर्णन करो।
उत्तर-
पोषक – कार्बोहाइड्रेट्स, वसा, प्रोटीन, विटामिन तथा लवण भोजन के मुख्य अंश हैं। यह शरीर के निर्माण तथा वृद्धि के लिए सहायक होते हैं तथा इन्हें पोषक तत्त्व कहते हैं।

पोषण के विभिन्न ढंग-पौधों (पादपों) में पोषण की दो विधियाँ मुख्य हैं-
(i) स्वपोषी पोषण
(ii) विषमपोषी पोषण

(i) स्वपोषी पोषण – जो पौधे सरल पदार्थों से अपना भोजन स्वयं तैयार करते हैं उन्हें स्वपोषी कहा जाता है। ऐसे पौधों के भोजन तैयार करने की विधि को स्वपोषी पोषण कहते हैं। सारे हरे पौधे स्वपोषी होते हैं। इस विधि में पौधों में मौजूद हरे रंग का वर्णक क्लोरोफिल हवा से कार्बन-डाइऑक्साइड तथा पानी लेकर सौर प्रकाश ऊर्जा की उपस्थिति में कार्बोहाइड्रेट के रूप में भोजन बनाते हैं। इस क्रिया को प्रकाश संश्लेषण कहते हैं। उदाहरण-सारे हरे पौधे।

(ii) परपोषी पोषण – कुछ पौधे ऐसे होते हैं जिनमें हरे रंग का वर्णक (क्लोरोफिल) नहीं होता है तथा वह अपना भोजन स्वयं तैयार नहीं कर सकते जिस कारण वह भोजन के लिए दूसरे पौधों द्वारा तैयार किए भोजन पर निर्भर करते हैं। ऐसे पौधों को विषमपोषी पौधे कहते हैं तथा भोजन प्राप्त करने के इस ढंग को विषमपोषण कहते हैं। विषमपोषी उदाहरण–अमरबेल।

PSEB Solutions for Class 7 Science पादपों में पोषण Important Questions and Answers

वस्तुनिष्ठ प्रश्न

प्रश्न 1.
रिक्त स्थानों की पूर्ति कीजिए-

(क) क्योंकि हरे पादप अपना भोजन स्वयं बनाते हैं, इसलिए उन्हें …………………….. कहते हैं।
उत्तर-
स्वपोषी

(ख) पादपों द्वारा संश्लेषित भोजन का भंडारण ………………………. के रूप में किया जाता है।
उत्तर-
मंड (स्टार्च)

(ग) प्रकाश संश्लेषण के प्रक्रम में जिस वर्णक द्वारा सौर ऊर्जा संग्रहित की जाती है, उसे ……………………….. कहते हैं।
उत्तर-
क्लोरोफिल

(घ) प्रकाश संश्लेषण में पादप वायुमंडल से …………………. लेते हैं तथा ………………….. का उत्पादन करते हैं।
उत्तर-
कार्बन डाइऑक्साइड, ऑक्सीजन।

प्रश्न 2.
निम्नलिखित कथनों में से ठीक/गलत बताएं-

(i) प्रकाश संश्लेषण में कार्बन डाइऑक्साइड मुक्त होती है।
उत्तर-
ग़लत

(ii) ऐसे पौधे जो अपना भोजन स्वयं संश्लेषण करते हैं, मृतजीवी कहलाते हैं।
उत्तर-
ग़लत

(iii) प्रकाश संश्लेषण का उत्पाद प्रोटीन नहीं है।
उत्तर-
ग़लत

(iv) प्रकाश संश्लेषण में सूर्य ऊर्जा का रासायनिक ऊर्जा में रूपांतरण हो जाता है।
उत्तर-
ठीक ।

प्रश्न 3.
कॉलम A में दिए गए शब्दों का मिलान कॉलम B के शब्दों से कीजिए-

कॉलम A	कॉलम B
(क) क्लोरोफिल	(i) जीवाणु
(ख) नाइट्रोजन	(ii) परपोषित
(ग) अमरबेल	(iii) घटपर्णी (पिचर पादप)
(घ) जंतु	(iv) पत्ते
(च) कीटभक्षी	(v) परजीवी

उत्तर-

कॉलम A	कॉलम B
(क) क्लोरोफिल	(iv) पत्ते
(ख) नाइट्रोजन	(i) जीवाणु
(ग) अमरबेल	(v) परजीवी
(घ) जंतु	(ii) परपोषित
(च) कीटभक्षी	(iii) घटपर्णी (पिचर पादप)।

प्रश्न 4.
सही विकल्प चुनें-

(i) वे जीव जो अपने भोजन के लिए दूसरे जीवों पर निर्भर करते हैं, क्या कहलाते हैं ?
(क) सहजीवी
(ख) परजीवी
(ग) स्वपोषी
(घ) मृतजीवी।
उत्तर-
(ख) परजीवी।

(ii) रंध्र प्रायः पौधे के किस भाग में पाए जाते हैं ?
(क) जड़
(ख) तना
(ग) पत्ते
(घ) फूल।
उत्तर-
(ग) पत्ते।

(iii) प्रकाश संश्लेषण में कौन-सी गैस मुक्त होती है ?
(क) ऑक्सीजन
(ख) कार्बन डाइऑक्साइड
(ग) नाइट्रोजन
(घ) हाइड्रोजन।
उत्तर-
(क) ऑक्सीजन।

(iv) सजीवों की इकाई को क्या कहते हैं ?
(क) अंग
(ख) अंग प्रणाली
(ग) सैल
(घ) उत्तक।
उत्तर-
(ग) सैल।

(v) सजीवों में ऊर्जा का चरम स्रोत क्या है ?
(क) चंद्रमा
(ख) सूर्य
(ग) तारे
(घ) ग्रह।
उत्तर-
(ख) सूर्य।

(vi) एक खाने योग्य कवक है।
(क) शैवाल
(ख) जीवाणु
(ग) राइज़ोपस
(घ) मशरूम।
उत्तर-
(घ) मशरूम।

(vii) पादप निम्न में से किस अंग द्वारा साँस लेते हैं ?
(क) ऐपिडर्मिस
(ख) झली
(ग) स्टोमेटा
(घ) मूल रोम।
उत्तर-(ग) स्टोमेटा।

(vii) तालाबों में पानी पर हरे रंग के धागों जैसी संरचनाओं को क्या कहते हैं ?
(क) फंगस
(ख) शैवाल
(ग) अमीबा
(घ) पैरामीशियम।
उत्तर-
(ख) शैवाल।

(ix) पौधे के किस भाग द्वारा प्रकाश संश्लेषण के लिए हवा में से कार्बनडाइऑक्साइड ली जाती है ?
(क) मूलरोम
(ख) स्टोमैटा (रंध्र)
(ग) पत्ता शिराएँ
(घ) सैपल।
उत्तर-
(ख) स्टोमैटा (रंध्र)।

(x) वायुमंडल में मुख्य रूप में जिस भाग द्वारा पौधे कार्बनडाइऑक्साइड प्राप्त करते हैं। वह है-
(क) जड़
(ख) तना
(ग) फूल
(घ) पत्ते।
उत्तर-
(घ) पत्ते।

अति लघु उत्तरात्मक प्रश्न

प्रश्न 1.
पोषकों के नाम लिखो ।
उत्तर-
पोषक – कार्बोहाइड्रेट्स, विटामिन, वसा, प्रोटीन, लवण।

प्रश्न 2.
पादप खाद्य पदार्थों को कैसे संश्लेषित करते हैं ?
उत्तर-
पादप खाद्य पदार्थों को कार्बनडाइऑक्साइड, जल और सूर्य प्रकाश से क्लोरोफिल की उपस्थिति में संश्लेषित करते हैं। इस प्रक्रम को प्रकाश संश्लेषण क्रिया कहते हैं।

प्रश्न 3.
विभिन्न पोषण विधियों के नाम लिखिए।
उत्तर-
स्वपोषी, विषमपोशी (परपोषी, मृतजीवी, परजीवी)।

प्रश्न 4.
पत्तियों पर पाए जाने वाले छोटे-छोटे छिद्रों को क्या कहते हैं ?
उत्तर-
रंध्र (Stomata)।

प्रश्न 5.
पत्तियों में क्लोरोफिल का क्या कार्य है?
उत्तर-
क्लोरोफिल, सौर प्रकाश की ऊर्जा को संग्रहित करते हैं।

प्रश्न 6.
सजीवों में ऊर्जा का मुख्य स्रोत क्या है ?
उत्तर-
सूर्य ऊर्जा का मुख्य स्रोत है।

प्रश्न 7.
प्रकाश-संश्लेषण प्रक्रम के उत्पाद क्या हैं ?
उत्तर-
कार्बोहाइड्रेट्स और ऑक्सीजन।

प्रश्न 8.
पत्तियों के अतिरिक्त पादप के अन्य भागों के नाम लिखिए जो प्रकाश-संश्लेषण में भाग लेते हैं ?
उत्तर-
हरे तने और हरी शाखाएँ।

प्रश्न 9.
हरी पत्तियों के अतिरिक्त किन रंगों की पत्तियाँ पादपों में पाई जाती हैं ?
उत्तर-
लाल तथा भूरे रंग की पत्तियाँ।

प्रश्न 10.
शैवाल क्या है?
उत्तर-
शैवाल – तालाबों या ठहरे पानी में हरे अवपंकी (काई जैसा पादप) ही शैवाल है।

प्रश्न 11.
क्या शैवाल खाद्य संश्लेषण करते हैं ? कैसे?
उत्तर-
हाँ, क्योंकि उनमें क्लोरोफिल नाम का हरा वर्णक पाया जाता है।

प्रश्न 12.
कार्बोहाइड्रेट्स कौन-कौन से तत्वों से बनते हैं ?
उत्तर-
कार्बन, हाइड्रोजन और ऑक्सीजन।

प्रश्न 13.
कोई चार मानवी परजीवियों के नाम बताएं।
उत्तर-

1. मच्छर,
2. जूं,
3. खटमल,
4. जोंक।

प्रश्न 14.
एक आहारीय (कवक) का नाम लिखें।
उत्तर-
खुंभ (मशरूम)।

प्रश्न 15.
कवक कहां उगती है ?
उत्तर-
नमी तथा वर्षा वाले स्थान पर।

लघु उत्तरात्मक प्रश्न

प्रश्न 1.
निम्न कथनों से संबद्ध पारिभाषिक शब्द बनाइए-
(क) दुर्बल तने वाला परजीवी पादप
(ख) एक पादप जिसमें स्वपोषण एवं विषमपोषण दोनों ही प्रणालियां पाई जाती हैं।
(ग) वे रंध्र, जिनके द्वारा पत्तियों में गैसों का आदान-प्रदान (विनिमय) होता है।
उत्तर-
(क) अमरबेल (Cuscutta)
(ख) घटपर्णी (Pitcher plant)
(ग) रंध्र (Stomata)।

प्रश्न 2.
स्वपोषी और विषमपोषी पोषण में अंतर स्पष्ट करें।
उत्तर-
स्वपोषी और विषमपोषी पोषण में अंतर-

स्वपोषी (Autotrophs)	विषमपोषी (Heterotrophs)
ये सजीव सूर्य की रोशनी में अपना भोजन स्वयं तैयार करते हैं।	ये सजीव अपना भोजन पादपों या अन्य जीवों से प्राप्त करते हैं।
उदाहरण-हरे पादप, नीली हरित शैवाल।	उदाहरण-परजीवी, कवक, जीवाणु, जंतु।

प्रश्न 3.
रंगदार पत्तियाँ हरी नहीं होती फिर भी प्रकाश संश्लेषण प्रक्रम में सहायक होती हैं। क्यों?
उत्तर-
रंगदार पत्तियाँ (लाल, भूरी) में हरा वर्णक क्लोरोफिल होता है परंतु दूसरे रंग हरे रंग को प्रच्छादित (दबा) कर देते हैं। क्लोरोफिल के अस्तित्व कारण रंगदार पत्ते प्रकाश संश्लेषण प्रक्रिया में सहायक होते हैं।

प्रश्न 4.
काई (कवक) कहाँ उगती है ?
उत्तर-
नमी तथा वर्षा वाले स्थान पर।

प्रश्न 5.
लाइकेन सहजीवी संबंध कैसे दर्शाते हैं?
उत्तर-
लाइकेन में दो भागीदार होते हैं-एक शैवाल और दूसरा कवक। कवक आवास, जल एवं पोषक शैवाल को देता है जबकि शैवाल प्रकाश-संश्लेषण प्रक्रम से प्राप्त खाद्य पदार्थ कवक को देता है। इस तरह दोनों सहजीवी संबंध दर्शाते हैं।

प्रश्न 6.
राइजोबियम तथा पौधों का परजीवी संबंध बताएं।
उत्तर-
राइजोबियम एक बैक्टीरिया है जो फलीदार पौधों की जड़ों पर मौजूद गांठों में रहता है। यह हवा में मौजूद नाइट्रोजन को प्रयोग योग्य बना देता है। जिसका प्रयोग पौधे द्वारा किया जाता है तथा बदले में पौधे इस बैक्टीरिया को आश्रय तथा भोजन प्रदान करते हैं।

प्रश्न 7.
परजीवी, सहजीवी संबंध और मृतजीवी से क्या अभिप्राय है? प्रत्येक का एक उदाहरण दीजिए।
उत्तर-

1. परजीवी – वे पादप और जंतु जो अपने भोजन के लिए सजीव परपोषी पर निर्भर करते हैं इन्हें परजीवी कहते हैं। उदाहरण-अमरबेल, कवक, जीवाणु आदि।
2. सहजीवी संबंध – यह एक ऐसा प्रबंध है जिसमें दोनों सजीवों को लाभ होता है। एक जीव आवास, जल और पोषक तत्व उपलब्ध कराता है जबकि दूसरा जीव खाद्य पदार्थ संश्लिष्ट करता है। उदाहरण-लाइकेन।
3. मृतजीवी – वे जीव जो मृत एवं विघटनकारी वस्तुओं पर पनपते हैं और अपना भोजन प्राप्त करते हैं, मृतजीवी कहलाते हैं। उदाहरण-जीवाणु, कवक।

प्रश्न 8.
परजीवी एवं मृतजीवी में अंतर स्पष्ट कीजिए।
उत्तर-
परजीवी और मृतजीवी में अंतर-

परजीवी (Parasites)	मृतजीवी (Saprophytes)
(1) ये जीव दूसरे सजीवों पर खाद्य के लिए निर्भर होते हैं।	(1) ये जीव मृत पदार्थों से अपनी खाद्य सामग्री प्राप्त करते हैं।
(2) ये पोषण के लिए कुछ विशेष अंग विकसित करते हैं। उदाहरण-अमरबेल, फीताकृमि, गोलकृमि।	(2) ये कुछ एंजाइमों का रिसाव करते हैं जो भोजन को विलयन में परिवर्तित कर देते हैं। उदाहरण-कवक, जीवाणु।

प्रश्न 9.
स्वपोषी पोषण के लिए आवश्यक परिस्थितियाँ तथा इसके मूल तथा उप-उत्पाद क्या हैं?
उत्तर-
स्वपोषी पोषण के लिए प्रकाश संश्लेषण आवश्यक है जिसके लिए आवश्यक स्थितियाँ हैं-

1. सूर्य प्रकाश
2. क्लोरोफिल (हरा वर्णक)
3. कार्बनडाइऑक्साइड तथा
4. जल।

मूल उत्पाद – प्रकाश संश्लेषण क्रिया के मूल उत्पाद ऑक्सीजन गैस तथा ग्लूकोज़ हैं। ग्लूकोज़ को बाद में स्टार्च के रूप में जमा किया जाता है। उप-उत्पाद- इस प्रक्रिया के सह अथवा उप-उत्पाद हैं-जल तथा ऑक्सीजन ।

दीर्य उत्तरात्मक प्रश्न

प्रश्न 1.
सहजीवी संबंध दोनों भागीदारों के लिए लाभदायक है। स्पष्ट कीजिए।
उत्तर-
वह संबंध जो दोनों भागीदारों के लिए लाभदायक हो, सहजीवी संबंध कहलाता है।
लाइकेन जैसे पादपों में, कवक और शैवाल भागीदार दोनों होते हैं। कवक, हरित वर्णक रहित है। यह शैवाल को आवास, जल एवं लवण उपलब्ध कराता है जबकि शैवाल हरित वर्णक होने के कारण कवक के लिए खाद्य पदार्थ संश्लेषित करता है जिसे कवक को उपलब्ध कराता है। इस तरह दोनों एक दूसरे पर निर्भर करते हैं।

Punjab State Board PSEB 6th Class Computer Book Solutions Chapter 4 एम एस पेंट से जान-पहचान Textbook Exercise Questions and Answers.

PSEB Solutions for Class 6 Computer Science Chapter 4 एम एस पेंट से जान-पहचान

Computer Guide for Class 6 PSEB एम एस पेंट से जान-पहचान Textbook Questions and Answers

1. रिक्त स्थान भरें

(i) पेंट विंडो के सबसे ऊपर ……….. बार मौजूद होता है।
(क) टाइटल बार
(ख) स्टेटस बार
(ग) स्क्रोल बार
(घ) टास्कबार।
उत्तर-
(क) टाइटल बार

(ii) ………… टूलबार पहले से ही टाइटल बार में मौजूद होता है। उसकी पोजीशन हम टाइटल बार में ऊपर या नीचे बदल सकते हैं।
(क) क्विक एक्सैस बार
(ख) स्टेटस बार
(ग) स्क्रोल बार
(घ) उपरोक्त सभी।
उत्तर-
(क) क्विक एक्सैस बार

(iii) मीनू बार के बायें तरफ सबसे पहले ………… बटन होता है।
(क) पेंट
(ख) हैल्प
(ग) क्लोज़
(घ) मिनीमाइज़।
उत्तर-
(क) पेंट

(iv) स्क्रोल बार स्क्रीन को घुमाने के लिए प्रयोग होता है। यह ………. प्रकार का होता है।
(क) दो
(ख) तीन
(ग) चार
(घ) पांच।
उत्तर-
(क) दो

(v) ………. ऑप्शन की मदद हम एक तस्वीर की एक कापी दूसरे नाम से सेव कर सकते हैं।
(क) सेव ऐज़
(ख) ओपन
(ग) न्यू
(घ) एग्ज़िट।
उत्तर-
(क) सेव ऐज़|

2. निम्न कार्यों के लिए शार्टकट कीअज़ बताएं ।

(i) नई फाइल बनाने के लिए
(ii) पहले से बनी फाइल खोलने के लिए
(iii) फाइल को सेव करने के लिए
(iv) फाइल प्रिंट करने के लिए
(v) अन-डू (UNDO) करने के लिए
(vi) री-डू (REDO) या रिपीट (REPEAT) करने के लिए
उत्तर-
(i) Ctrl + N
(ii) Ctrl +O
(ii) Ctrl + S
(iv) Ctrl + P
(v) Ctrl + Z
(vi) Ctrl + Y.

3. छोटे उत्तरों वाले प्रश्न

प्रश्न 1.
पेंट क्या है?
उत्तर-
पेंट एक साफ्टवेयर है जिसका प्रयोग तस्वीरें बनाने के लिए किया जाता है। यह माइक्रोसाफ्ट कंपनी का उत्पाद है।

प्रश्न 2.
एम. एस. पेंट किस प्रकार शुरू किया जाता है ?
उत्तर-
पेंट शुरू करने के लिए निम्न स्टैप करो

1. Start पर क्लिक करें।
2. All Programs पर क्लिक करो।
3. Accessories पर क्लिक करो।
4. Paint पर क्लिक करो।

प्रश्न 3.
पेंट विंडो के भागों के नाम लिखो।
उत्तर-
पेंट विंडो के भागों के निम्नलिखित नाम होते हैं –

1. टाइटल बार
2. क्विक एक्सेस बार
3. मीनू बार
4. स्क्रोल बार
5. स्टेटस बार
6. वर्क ऐरिया।

प्रश्न 4.
वर्क ऐरिया क्या होता है ?
उत्तर-
पेंट में काम करने वाले स्थान को वर्क ऐरिया कहते हैं। इस स्थान पर हम तस्वीरें बना सकते हैं।

प्रश्न 5.
सेव कमांड का प्रयोग बताएं।
उत्तर-
सेव कमांड का प्रयोग पेंट में अपने द्वारा किए गए कार्य को किसी फाइल के नाम के साथ सेव करने के लिए किया जाता है। एक बार सेव करने के बाद उस फाइल को दोबारा सेव करने के लिए भी इसी कमांड का प्रयोग किया जाता है।

प्रश्न 6.
स्क्रोल बार की श्रेणियों के नाम लिखो।
उत्तर-
1. होरीजोंटल स्क्रोल बार
2. वर्टीकल स्क्रोल बार।

4. बड़े उत्तरों वाले प्रश्न

प्रश्न 1.
क्विक एक्सैस टूलबार क्या होता है? इसके बारे में विस्तार से बताएं।
उत्तर-
क्विक एक्सैस टूलबार वह टूलबार होता है जो ज्यादा प्रयोग आने वाली कमांडों को दर्शाता है ताकि इन्हें जल्दी से चलाया जा सके। आमतौर पर इनमें चार बटन होते हैं-सेव, अनडू, रीडू तथा कस्टमाइज। आम तौर पर यह टाइटल बार के बायें तरफ होते हैं। पर इनको रिबन के नीचे भी लाया जा सकता है। इसके लिए कस्टमाइज़ आइकन पर क्लिक कर Show below the Ribbon ऑप्शन पर क्लिक करना पड़ता है।

क्विक एक्सैस टूलबार में अन्य ऑप्शन भी शामिल किये जा सकते हैं। जैसे कि न्यू (New), ओपन (Open), सेव (Save), प्रिंट (Print), प्रिंट प्रीव्यू (Print preview), सेंड इन ईमेल (Send in email) आदि। हम रिबन की वस्तुओं को भी इस में शामिल कर सकते हैं। इसके लिए उस वस्तु को राइट क्लिक कर Add to Quick Toolbar ऑप्शन का चुनाव किया जाता है।

प्रश्न 2.
होम टैब रिबन के बारे में बताओ।
उत्तर-
सारे टूलज, शोपस, कलर पैलेट तथा अन्य बहुत सारी कमांडों को रिबन में इकट्ठा किया जाता है। होम टैब भी इसी प्रकार कई कमांड को दिखाता है। होम टैब रिबन वह होता है जिसमें टूलज, शोपस, ब्रुश तथा रंगों को चुना जाता है। इसमें रिबन को मिनीमाइज करने की ऑप्शन भी होती है। अगर हम इस का चुनाव करते हैं तो रिबन गायब हो जाता है। अगर हम Home Tab पर क्लिक करते हैं तो यह फिर वापस दिखाई देता है। एक्टीविटी आओ हमने जो पढ़ा है उसकी दुहराई करें। पेंट विंडो के भागों के नाम लिखो।

PSEB 6th Class Computer Guide एम एस पेंट से जान-पहचान Important Questions and Answers

रिक्त स्थान भरें

(i) स्क्रोल बार ……….. प्रकार के होते हैं।
(क) 1
(ख) 2
(ग) 3
(घ) 4.
उत्तर-
(ख) 2

(ii) तस्वीरें …….. में बनाई जाती हैं।
(क) रिबन
(ख) टैब
(ग) वर्क एरिया
(घ) टाइटल बार।
उत्तर-
(ग) वर्क एरिया

(iii) पेंट विंडो के सबसे ऊपर ………… होता है।
(क) स्टेटस बार
(ख) टाइटल बार
(ग) मीनू बार
(घ) रिबन।
उत्तर-
(ख) टाइटल बार

(iv) कमांडज़ ……….. बटन में होती है।
(क) मिनीमाइज
(ख) पेंट
(ग) कलोज
(घ) स्टेटस बार।
उत्तर-
(ख) पेंट।

निम्न कार्यों के लिए शार्टकट कीअज़ बताएं –

निम्नलिखित कामों की शार्टकट की बताएं –
1. मदद लेने के लिए
2. पेंट बंद करने के लिए।
उत्तर-
1. F₁
2. Alt + F₄.

छोटे उत्तरों वाले प्रश्न

प्रश्न 1.
क्विक एक्सैस टूल बार क्या होती है ?
उत्तर-
क्विक एक्सैस टूल बार वह टूल बार होता है जो ज़्यादा प्रयोग आने वाली कमांडों के बटन को दर्शाता है।

प्रश्न 2.
क्विक एक्सैस टूलबार में आइटमज़ हटाने के लिए किस ऑप्शन का प्रयोग किया जाता है ?
उत्तर-
Remove from Quick Access Toolbar.

प्रश्न 3.
पेंट बटन क्या होता है?
उत्तर-
मीनू बार के बायें तरफ पेंट बटन होता है। इस पर क्लिक करने से कई कमांड दिखाई देती हैं।

प्रश्न 4.
स्क्रोल बार का प्रयोग किस लिए किया जाता है ?
उत्तर-
तस्वीर को स्क्रोल करने के लिए।

Punjab State Board PSEB 6th Class Computer Book Solutions Chapter 3 कम्प्यूटर के आधारभूत कार्य Textbook Exercise Questions and Answers.

PSEB Solutions for Class 6 Computer Science Chapter 3 कम्प्यूटर के आधारभूत कार्य

Computer Guide for Class 6 PSEB कम्प्यूटर के आधारभूत कार्य Textbook Questions and Answers

1. सही उत्तर का चुनाव करें।

(i) कम्प्यूटर पर लॉग-इन के बाद दिखाई देने वाली स्क्रीन को क्या कहा जाता है ?
(क) स्टार्ट मेन्यू (Start Menu)
(ख) डैस्कटाप (Desktop)
(ग) टास्कबार (Taskbar)
(घ) इनमें से कोई नहीं।
उत्तर-
(ख) डैस्कटाप (Desktop)

(ii) डिलीट की गई फाइलें कैसे प्राप्त की जा सकती हैं ?
(क) माई कम्प्यूटर (My Computer)
(ख) नैटवर्क (Network)
(ग) रीसाइकिल बिन (Recycle bin)
(घ) उपरोक्त सभी।
उत्तर-
(ग) रीसाइकिल बिन (Recycle bin)

(iii) विंडो का कौन-सा भाग स्क्रीन पर हर समय नज़र आता रहता है जब हम और एप्लीकेशनज़ का प्रयोग कर रहे होते हैं ?
(क) रीसाइकिल बिन (Recycle bin)
(ख) डैस्कटाप (Desktop)
(ग) टास्कबार (Taskbar)
(घ) इनमें से कोई नहीं।
उत्तर-
(ग) टास्कबार (Taskbar)

(iv) कौन-सा आपरेटिंग सिस्टम का उदाहरण है ?
(क) विंडो (Windows)
(ख) एंड्रायड (Android)
(ग) डॉस (DOS)
(घ) उपरोक्त सभी।
उत्तर-
(घ) उपरोक्त सभी।

(v) किसी भी फाइल को खोलने के लिए हम किस पर डबल क्लिक कर सकते हैं ?
(क) संबंधित फाइल (File itself)
(ख) फाइल का शार्टकट (Shortcut of file)
(ग) दोनों क तथा ख
(घ) इनमें से कोई नहीं।
उत्तर-
(ग) दोनों क तथा ख

2. छोटे उत्तरों वाले प्रश्न

प्रश्न 1.
किसी तीन विंडो एप्लीकेशनों के नाम लिखें।
उत्तर-
तीन विंडो एप्लीकेशनों के नाम निम्नलिखित हैं

1. नोट पैड
2. वर्ड पैड
3. कैलकुलेटर।

प्रश्न 2.
किसी तीन आइकनों के नाम लिखो।
उत्तर-
तीन आइकनों के नाम निम्नलिखित हैं

1. माई कम्प्यूटर
2. नेटवर्क
3. रीसाइकिल बिन।

प्रश्न 3.
डैस्कटॉप के भागों के नाम लिखें।
उत्तर-
डैस्कटॉप के निम्नलिखित तीन भाग होते हैं

1. आइकनज़ (Icons)
2. टास्कबार (Taskbar)
3. शॉर्टकट (Shortcut)

प्रश्न 4.
डैस्कटॉप क्या होता है?
उत्तर-
बूटिंग तथा लागइन के बाद जो पहली स्क्रीन नज़र आती है उसको डैस्कटॉप कहते हैं। डैस्कटॉप पर टॉस्कबार, आइकन तथा स्टार्ट बटन होता है।

3. बड़े उत्तरों वाले प्रश्न

प्रश्न 1.
आपरेटिंग सिस्टम क्या है ? अलग-अलग आपरेटिंग सिस्टम की उदाहरन सहित व्याख्या करें।
उत्तर-
आपरेटिंग सिस्टम वह सिस्टम सॉफ्टवेयर होता है जो कम्प्यूटर हार्डवेयर के साथ संपर्क करने तथा आपरेट करने के योग्य बनाता है। यह कम्प्यूटर तथा उसमें पड़े सॉफ्टवेयर को चलाता है। यह कम्प्यूटर से संबंधित महत्त्वपूर्ण कार्य करता है। यह अनधिकृत पहुंच को भी रोकता है।
आपरेटिंग की परिभाषा (Definition of Operating System)-आपरेटिंग सिस्टम वह सॉफ्टवेयर होता है जो कम्प्यूटर हार्डवेयर को सॉफ्टवेयर के साथ संपर्क करने तथा अपडेट करने के योग्य बनाता है।
1. विंडोज़ (Windows) विंडोज़ एक महत्त्वपूर्ण ऑपरेटिंग सिस्टम है। यह GUI (ग्राफ्किल यूज़र इंटरफेस) किस्म का होता है। विंडोज़ की मदद से हम कम्प्यूटर का प्रोग्राम चला सकते हैं। कम्प्यूटर पर हम जब कोई प्रोग्राम खोलते हैं, तो वो एक फ्रेम में नज़र आता है। इस फ्रेम को विंडोज़ कहते हैं। विंडोज़ माइक्रोसॉफ्ट कम्पनी का उत्पादन है। इसी कारण इसको माइक्रोसॉफ्ट विंडोज़ भी कहा जाता है।

2. डॉस (DOS)-डॉस का पूरा नाम डिस्क ऑपरेटिंग सिस्टम है यह ऑपरेटिंग सिस्टम माइक्रोसॉफ्ट कंपनी द्वारा तैयार किया गया था। यह एक करैक्टर आधारित इंटरफ़ेस प्रदान करता है यह ‘ऑपरेटिंग सिस्टम ज्यादा शक्तिशाली ऑपरेटिंग सिस्टम नहीं था। इसमें कार्य करना भी आसान नहीं था। इसमें कार्य करने के लिए यूज़र को विभिन्न कमांड टाइप करनी पड़ती थी तथा उसे इन कमांडज़ को याद भी रखना पड़ता था। यह ऑपरेटिंग सिस्टम छोटी मशीनों जिनमें कम मेमोरी तथा कम स्पीड होती थी उनके लिए बनाया गया था। इस ऑपरेटिंग सिस्टम का मुख्य कार्य डिस्क पर फाइलों को संभालना होता था। आजकल यह ऑपरेटिंग सिस्टम प्रयोग में नहीं लाया जाता।

3. एंड्रॉयड ऑपरेटिंग सिस्टम (Android Operating System) एंड्रॉयड ऑपरेटिंग सिस्टम एक मोबाइल ऑपरेटिंग सिस्टम है यह ऑपरेटिंग सिस्टम गूगल कंपनी द्वारा तैयार किया गया है। यह ऑपरेटिंग सिस्टम मुख्य रूप से यंत्रों के लिए तैयार किया गया है जिनमें टचस्क्रीन का प्रयोग होता है जैसे कि स्मार्टफोन तथा टेबलेट। इस ऑपरेटिंग सिस्टम में अपनी उंगली का प्रयोग करके विभिन्न कमांडों तथा अन्य विकल्प का चुनाव कर सकता है। आजकल ज्यादातर मोबाइल फोन में एंड्रॉयड ऑपरेटिंग सिस्टम का ही प्रयोग होता है। आजकल एंड्रॉयड ऑपरेटिंग सिस्टम आधारित टेलीविज़न, कार तथा घड़ियां भी आ रही हैं प्रत्येक प्रकार के यंत्र में एक विभिन्न इंटरफ़ेस होता है यह ऑपरेटिंग सिस्टम चलाने में काफी आसान होता है। इसमें आइकन तथा बहुत बढ़िया विकल्प भी दिए गए हैं।

प्रश्न 2.
टास्कबार क्या है ? इसके विभिन्न कार्यों के बारे में जानकारी दें।
उत्तर-
टास्कबार डैस्कटॉप के सबसे नीचे वाले हिस्से पर होती है। यह एक लम्बी पट्टी की तरह होती है। इसके बायें हाथ पर स्टार्ट बटन होता है और दायें हाथ पर टाइम नज़र आता है। जब कोई प्रोग्राम चलता है तो उसका एक बटन इस पर बन जाता है। इसके अलावा भी इस पर कुछ और बटन होते हैं और Quick Launch bar भी होता है। टास्कबार में उपरोक्त सभी भागों का अपना-अपना कार्य होता है-
1. स्टार्ट बटन (Start Button)-स्टार्ट बटन की मदद से किसी भी प्रोग्राम को चलाया जा . सकता है। यह टास्कबार के ऊपर सबसे पहले स्थित होता है। इसका आइकन होता है। इसके ऊपर विंडो को लोगो बना होता है।

2. क्विक लांच आइकॉन (Quick Launch Bar)-किसी भी प्रोग्राम को जल्दी चलाने के लिए यहां रखा जा सकता है।

3. सिस्टम ट्रेअ (System Tray)-यह टास्कबार के दाएं तरफ होती है। इसके ऊपर एक छोटा आइकन लगा होता है जो कि हमें आसानी से कार्य करने में जैसे-फैक्स, माडम, आवाज़ आदि तक पहुंचने में मदद करता है।

4. नोटीफिकेशन एरिया (Notification Area)-इसमें सारे नोटीफिकेशन दिखाई देते हैं।

5. डेट एण्ड टाइम (Date and Clock)-यहां पर समय तथा तारीख दिखाई देती है।

6. एक्टिव प्रोग्राम (Active Programs)-टास्कबार के इस भाग में सभी चल रहे प्रोग्राम नज़र आते हैं तथा हम इनमें से किसी भी प्रोग्राम तक पहुंच कर सकते हैं।

प्रश्न 3.
आइकन से आपका क्या अभिप्राय है ? किसी तीन डैस्कटॉप आइकनों की व्याख्या करें।
उत्तर-
डैस्कटॉप पर नज़र आने वाली छोटी तस्वीरों को आइकन कहते हैं। ये बटन की तरह काम करते हैं। आइकन फाइल तथा फोल्डर दिखाते हैं इन पर डबल क्लिक करके सम्बन्धित प्रोग्राम चल पड़ता है।

1. माई कम्प्यूटर (My Computer)-माई कम्प्यूटर की मदद से हम अपने कम्प्यूटर की सभी चीजें देख सकते हैं। इनमें फाइल, फोल्डर तथा ड्राइव होते हैं।
2. नैटवर्क (Network)-इस आइकन की मदद से हम अपने कम्प्यूटर से जुड़े बाकी कम्प्यूटर को देख सकते हैं।
3. यूज़र फाइल (User Files)-इस फोल्डर में यूज़र द्वारा तैयार तथा डाऊनलोड की गई फाइलें दिखाई देती हैं।

प्रश्न 4.
कम्प्यूटर सिस्टम बंद करने की विभिन्न ऑप्शनों की व्याख्या करें।
उत्तर-
कम्प्यूटर सिस्टम को बंद करने के विकल्प निम्न अनुसार हैं –
1. स्लीप (Sleep)-जब कम्प्यूटर को स्लीप मोड में डाला जाता है तब इसकी पावर सप्लाई को चालू रखा जाता है। इस मोड़ के दौरान कम्प्यूटर की पावर लाइट टिमटिमाती रहती है। यह टिमटिमाती लाइट दर्शाती है कि कम्प्यूटर स्लीप मोड में है तथा यूज़र पावर बटन दबाकर कम्प्यूटर दोबारा शुरू कर सकते हैं।

2. शट डाउन (Shut Down)-शटडाउन विकल्प का प्रयोग तब किया जाता है जब कम्प्यूटर के सारे भाग बंद करने होते हैं। इसमें किसी भी भाग की पावर सप्लाई नहीं चल रही होती। कम्प्यूटर को शटडाउन करने के बाद हम कम्प्यूटर की मेन पावर सप्लाई बंद कर सकते हैं। इस प्रोसेस को पूरा होने में कुछ समय लग जाता है तथा इस दौरान यूज़र को इंतज़ार करना पड़ता है।

3. लॉग ऑफ (Log Off)-कई बार एक कम्प्यूटर पर कई यूज़र कार्य करते हैं। हम अपना डाटा बाकी दूसरों से सुरक्षित रख सकते हैं। जब हम अपना कार्य कर लेते हैं तथा कम्प्यूटर को छोड़ना चाहते हैं पर साथ ही अन्य दूसरों के लिए उसे चालू ही रहने देना चाहते हैं तब हम अपने कम्प्यूटर को चालू कर सकते हैं। इस स्थिति में लॉग इन करने वाली क्रीम कम्प्यूटर पर दिखाई देने लगती है।

4. रीस्टार्ट (Restart)-रीस्टार्ट का प्रयोग कम्प्यूटर को बंद करके दोबारा शुरू करने के लिए किया जाता है। इस विकल्प का प्रयोग तब किया जाता है जब हम अपने कंप्यूटर पर कोई प्रोग्राम इंस्टॉल करते हैं तथा वह प्रोग्राम शुरू होने के लिए कम्प्यूटर को दोबारा शुरू करने को कहता है। इसका प्रयोग तब भी किया जाता है जब सिस्टम में कोई बदलाव किया जाता है। रीस्टार्ट विकल्प पर क्लिक करने के बाद कम्प्यूटर बंद हो जाता है तथा फिर से ही शुरू हो जाता है।

एक्टीविटी
निम्न दिए आइकनों के नाम लिखें :

उत्तर –
1. नौट पैड
2. एम.एस.पेंट
3. कैलकुलेटर
4. माई कम्प्यूटर
5. नेटवर्क
6. रीसाइकिल बिन
7. स्टार्ट बटन।

PSEB 6th Class Computer Guide कम्प्यूटर के आधारभूत कार्य Important Questions and Answers

रिक्त स्थान भरें।
(i) कम्प्यूटर की प्रथम स्क्रीन ( पहले से खुली) को ……….. कहा जाता है।
(क) माई नैटवर्क
(ख) आइकॉन
(ग) डैस्कटाप
(घ) रीसाइकिल बिन।
उत्तर-
(ग) डैस्कटाप

(ii) डैस्कटाप के नीचे लेटवीं बार को ……… कहा जाता है।
(क) टाइटल बार
(ख) स्टेटस बार
(ग) टास्कबार
(घ) स्क्रोल बार।
उत्तर-
(ग) टास्कबार

(iii) विंडो की ऊपर नज़र आती बार को ………. कहा जाता है।
(क) टाइटल बार
(ख) स्टेटस बार
(ग) टास्कबार
(घ) स्क्रोल बार।
उत्तर-
(क) टाइटल बार

(iv) मिटाई हुई फॉइलें ……. में चली जाती हैं।
(क) माई नैटवर्क
(ख) माई डाक्यूमैंट
(ग) माई कम्प्यूटर
(घ) रीसाइकिल बिन।
उत्तर-
(घ) रीसाइकिल बिन।

(v) ………… बटन का उपयोग विंडो को बन्द करने के लिए किया जाता है।
(क) मिनीमाइज़
(ख) मैक्सीमाइज़
(ग) क्लोज़
(घ) स्टार्ट।
उत्तर-
(ग) क्लोज़ |

छोटे उत्तरों वाले प्रश्न

प्रश्न 1.
आपरेटिंग सिस्टम क्या होता है ?
उत्तर-
आपरेटिंग सिस्टम वह सिस्टम साफ्टवेयर होता है जो यूज़र तथा कम्प्यूटर के बीच एक माध्यम या इंटरफेम का कार्य करता है।

प्रश्न 2.
विंडोज़ क्या है ?
उत्तर-
विंडोज़ एक आपरेटिंग सिस्टम है जो माइक्रोसाफ्ट कंपनी का उत्पाद है। यह एक GUI टाइप का आपरेटिंग सिस्टम है।

प्रश्न 3.
डैस्कटाप क्या होता है ?
उत्तर-
कम्प्यूटर ऑन करने के बाद जो स्क्रीन हमारे सामने आती है, उसे डैस्कटाप कहते हैं। इस पर कई आइकन्ज़ होते हैं।

प्रश्न 4.
आइकनज़ क्या होते हैं? कोई तीन आइकनज़ के नाम लिखो।
उत्तर-
आइकनज़ एक छोटी सी चित्रनुमा वस्तु होती है, जो किसी फाइल या फोल्डर को बताती है। कम्प्यूटर, री-साईकिल बिन, तथा नैटवर्क तीन आइकनज़ के नाम हैं।

प्रश्न 5.
विंडोज़ के अलग-अलग भागों के नाम लिखो।
उत्तर-
विंडोज़ के अलग-अलग भाग निम्नलिखित हैं –

1. टाइटल बार,
2. मेन्यू बार,
3. टूल बार,
4. स्क्रोल बार,
5. बार्डर।

प्रश्न 6.
टास्कबार के शो डैस्कटाप बटन के बारे में बताओ।
उत्तर-
शो डैस्कटाप एक आयताकार बटन होता है जो टास्कबार के दायें तरफ होता है। शो डैस्कटाप बटन के द्वारा हम सभी खुली विंजोज़ को मिनीमाइज़ कर डेस्कटाप देख सकते हैं। इस पर दोबारा क्लिक करके सारी विंडोज़ को दोबारा बड़ा किया जा सकता है।

प्रश्न 7.
हम कम्प्यूटर को किस प्रकार बंद कर सकते हैं ?
उत्तर-
कम्प्यूटर को बंद करने के लिए निम्न स्टैप करें –

1. Start बटन पर क्लिक करें। (Start मेन्यू खुलेगा)
2. Shut down पर क्लिक करें। (कम्प्यूटर अपने आप बंद हो जाएगा।)