Punjab State Board PSEB 6th Class Punjabi Book Solutions Chapter 6 ਬਾਬਾ ਬੁੱਢਾ ਜੀ Textbook Exercise Questions and Answers.
PSEB Solutions for Class 6 Punjabi Chapter 6 ਬਾਬਾ ਬੁੱਢਾ ਜੀ (1st Language)
Punjabi Guide for Class 6 PSEB ਬਾਬਾ ਬੁੱਢਾ ਜੀ Textbook Questions and Answers
ਬਾਬਾ ਬੁੱਢਾ ਜੀ ਪਾਠ-ਅਭਿਆਸ
1. ਦੱਸੋ :
(ਉ) ਬੂੜੇ ਨਾਂ ਦਾ ਬਾਲਕ ਕੀ ਕਰਦਾ ਹੁੰਦਾ ਸੀ?
ਉੱਤਰ :
ਬੂੜਾ ਸਾਰਾ ਦਿਨ ਗਊਆਂ ਦਾ ਵੱਗ ਚਾਰਦਾ ਹੁੰਦਾ ਸੀ।
(ਅ) ਬੂੜਾ ਉਦਾਸ ਕਿਉਂ ਰਹਿੰਦਾ ਸੀ?
ਉੱਤਰ :
ਬੁੜਾ ਇਸ ਕਰਕੇ ਉਦਾਸ ਰਹਿੰਦਾ ਸੀ ਕਿਉਂਕਿ ਉਸ ਨੂੰ ਹਰ ਵੇਲੇ ਮੌਤ ਦਾ ਡਰ ਰਹਿੰਦਾ ਸੀ।

(ੲ) ਗੁਰੂ ਸਾਹਿਬ ਨੇ ਬੂੜੇ ਨੂੰ ਕਿਸ ਚੀਜ਼ ਦੀ ਦਾਤ ਬਖ਼ਸ਼ੀ ਅਤੇ ਉਸ ਦਾ ਕੀ ਨਾਂ ਰੱਖਿਆ?
ਉੱਤਰ :
ਗੁਰੂ ਸਾਹਿਬ ਨੇ ਬੂੜੇ ਨੂੰ ਗੁਰਸਿੱਖੀ ਦੀ ਦਾਤ ਬਖ਼ਸ਼ੀ ਤੇ ਉਸ ਦਾ ਨਾਂ ਬਾਬਾ ਬੁੱਢਾ ਰੱਖ ਦਿੱਤਾ ਬੂ।
(ਸ) ਬਾਬਾ ਬੁੱਢਾ ਜੀ ਨੇ ਛੇਵੇਂ ਗੁਰੂ ਤੇ ਉਹਨਾਂ ਦੇ ਬੱਚਿਆਂ ਨੂੰ ਕਿਸ ਪ੍ਰਕਾਰ ਦੀ ਸਿੱਖਿਆ ਦਿੱਤੀ ਸੀ?
ਉੱਤਰ :
ਨੇ ਛੇਵੇਂ ਗੁਰੂ ਜੀ ਤੇ ਉਨਾਂ ਦੇ ਬੱਚਿਆਂ ਨੂੰ ਪੜ੍ਹਾਈ-ਲਿਖਾਈ ਦੇ ਨਾਲ ਸ਼ਸਤਰ-ਵਿੱਦਿਆ ਦੀ ਸਿੱਖਿਆ ਦਿੱਤੀ !
(ਹ) ਬਾਬਾ ਬੁੱਢਾ ਜੀ ਨੇ ਮਾਤਾ ਗੰਗਾ ਜੀ ਨੂੰ ਕੀ ਅਸੀਸ ਦਿੱਤੀ?
ਉੱਤਰ :
ਨੇ ਮਾਤਾ ਗੰਗਾ ਜੀ ਨੂੰ ਅਸੀਸ ਦਿੱਤੀ ਕਿ ਉਨ੍ਹਾਂ ਦੇ ਘਰ ਅਜਿਹਾ ਪੁੱਤਰ ਜਨਮ ਲਵੇਗਾ, ਜਿਹੜਾ ਦੁਸ਼ਮਣਾਂ ਦੇ ਇਸੇ ਤਰ੍ਹਾਂ ਸਿਰ ਭੰਨੇਗਾ, ਜਿਸ ਤਰ੍ਹਾਂ ਉਨ੍ਹਾਂ ਗੰਢਾ ਭੰਨਿਆ ਹੈ।
(ਕ) ਬਾਬਾ ਬੁੱਢਾ ਜੀ ਨੇ ਹਰਿਮੰਦਰ ਸਾਹਿਬ ਵਿਖੇ ਕਿਸ ਪ੍ਰਕਾਰ ਦੀ ਸੇਵਾ ਕੀਤੀ?
ਉੱਤਰ :
ਨੇ ਹਰਿਮੰਦਰ ਸਾਹਿਬ ਵਿਚ ਪਹਿਲੇ ਗ੍ਰੰਥੀ ਦੀ ਸੇਵਾ ਕੀਤੀ।

2. ਹੇਠ ਲਿਖੇ ਸ਼ਬਦਾਂ ਨੂੰ ਵਾਕਾਂ ਵਿੱਚ ਵਰਤੋ :
ਵੱਗ, ਅਡੋਲ, ਅਨੋਖਾ, ਆਦਰ, ਤਕਾਲਾਂ, ਸੁਲਝਿਆ, ਮਸ਼ਹੂਰ
ਉੱਤਰ :
- ਵੱਗ (ਗਊਆਂ ਦਾ ਇਕੱਠ)-ਵਾਗੀ ਗਊਆਂ ਦਾ ਵੱਗ ਚਾਰ ਰਿਹਾ ਹੈ।
- ਅਡੋਲ ਜੋ ਡੋਲੇ ਨਾ)-ਗੁਰੂ ਜੀ ਅਡੋਲ ਸਮਾਧੀ ਲਾਈ ਬੈਠੇ ਸਨ।
- ਅਨੋਖਾ (ਜੋ ਸਭ ਤੋਂ ਵੱਖਰਾ ਹੋਵੇ)-ਸਾਹਮਣੇ ਅਨੋਖਾ ਕੁਦਰਤੀ ਨਜ਼ਾਰਾ ਦਿਖਾਈ ਦੇ ਰਿਹਾ ਹੈ।
- ਆਦਰ ਸਤਿਕਾਰ-ਬੱਚਿਆਂ ਨੂੰ ਵੱਡਿਆਂ ਦਾ ਆਦਰ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ।
- ਤਰਕਾਲਾਂ (ਸ਼ਾਮ ਦਾ ਵੇਲਾ)-ਤਰਕਾਲਾਂ ਪੈ ਗਈਆਂ ਤੇ ਸੂਰਜ ਡੁੱਬ ਗਿਆ।
- ਸੁਲਝਿਆ (ਸਮਝਦਾਰ, ਗਿਆਨਵਾਨ)-ਪ੍ਰਿੰ: ਸੰਤ ਸਿੰਘ ਸੇਖੋਂ ਇਕ ਸੁਲਝਿਆ ਹੋਇਆ ਵਿਦਵਾਨ ਸੀ।
- ਮਸ਼ਹੂਰ ਪ੍ਰਸਿੱਧ)-ਪੁਸਤਕਾਂ ਦੀ ਦੁਨੀਆ ਵਿਚ ਐੱਮ. ਬੀ. ਡੀ. ਦਾ ਨਾਂ ਬਹੁਤ ਮਸ਼ਹੂਰ ਹੈ।
- ਸਮਾਧੀ ਅੱਖਾਂ ਮੀਟ ਕੇ ਧਿਆਨ ਟਿਕਾਉਣਾ)-ਸਾਧੂ ਸਮਾਧੀ ਵਿਚ ਲੀਨ ਸੀ।
- ਅੰਤਰ-ਧਿਆਨ-ਸਮਾਧੀ ਦੀ ਹਾਲਤ ਵਿਚ-ਗੁਰੁ ਜੀ ਅੰਤਰ-ਧਿਆਨ ਹੋ ਕੇ ਬੈਠੇ ਸਨ
- ਸ਼ਰਨ (ਆਸਰਾ)-ਭਾਈ ਘਨਈਆ ਜੀ ਗੁਰੁ ਤੇਗ ਬਹਾਦਰ ਜੀ ਦੀ ਸ਼ਰਨ ਵਿਚ ਪੁੱਜੇ।
- ਸ਼ਾਨ-ਸ਼ੌਕਤ ਸ਼ਾਨ ਨਾਲ-ਇਸ ਰੱਜੇ-ਪੁੱਜੇ ਪਰਿਵਾਰ ਦੇ ਬੰਦੇ ਬੜੀ ਸ਼ਾਨ-ਸ਼ੌਕਤ ਨਾਲ ਰਹਿੰਦੇ ਹਨ।
- ਅਸੀਸ ਸ਼ੁੱਭ ਇੱਛਾ-ਬੁੱਢੀ ਮਾਈ ਨੇ ਬੱਚੇ ਨੂੰ ਅਸੀਸ ਦਿੱਤੀ, “ਜੁਗ-ਜੁਗ ਜੀਓ ਤੇ ਜੁਆਨੀਆਂ ਮਾਣੋ !
- ਪ੍ਰਕਾਸ਼ (ਚਾਨਣ, ਗੁਰੂ ਗ੍ਰੰਥ ਸਾਹਿਬ ਜੀ ਦੀ ਖੁੱਲ੍ਹੀ ਹੋਈ ਬੀੜ)-ਇਸ ਗੁਰਦੁਆਰੇ ਵਿਚ ਹਰ ਰੋਜ਼ ਸਵੇਰੇ 4 ਵਜੇ ਗੁਰੂ ਗ੍ਰੰਥ ਸਾਹਿਬ ਜੀ ਦਾ ਪ੍ਰਕਾਸ਼ ਹੁੰਦਾ ਹੈ।
3. ਹੇਠ ਲਿਖੇ ਸ਼ਬਦ ਕਿਸ ਨੇ, ਕਿਸ ਨੂੰ ਕਹੇ :
(ੳ) “ਗੁਰੂ ਜੀ! ਮੈਨੂੰ ਸਾਰਾ ਵਕਤ ਮੌਤ ਦਾ ਡਰ ਰਹਿੰਦਾ ਹੈ। ਮੈਨੂੰ ਰਾਤ ਨੂੰ ਵੀ ਚੰਗੀ ਤਰ੍ਹਾਂ ਨੀਂਦ ਨਹੀਂ ਆਉਂਦੀ।
(ਅ) “ਹੇ ਬਾਲਕ ! ਤੂੰ ਤਾਂ ਬੁੱਢਿਆਂ ਵਾਲੀਆਂ ਗੱਲਾਂ ਕਰਦਾ ਹੈਂ। ਤੂੰ ਤਾਂ ਅਜੇ ਬਾਲ ਏ। ਤੇਰਾ ਨਾਂ ਕੀ ਹੈ।
(ੲ) “ਤੂੰ ਬੂੜਾ ਨਹੀਂ, ਬੁੱਢਾ ਹੈਂ। ਹੇ ਬੁੱਢੇ ਬਾਲਕ ! ਤੈਨੂੰ ਰੱਬ ਨੇ ਉੱਚੇ ਕੰਮ ਸੌਂਪੇ ਨੇ।”
(ਸ) “ਜੇ ਕਿਸੇ ਕੋਲੋਂ ਅਸੀਸ ਲੈਣ ਜਾਣਾ ਹੋਵੇ ਤਾਂ ਇਸ ਤਰ੍ਹਾਂ ਰਥਾਂ ਵਿੱਚ ਚੜ੍ਹ ਕੇ ਨਹੀਂ ਜਾਈਦਾ।”
(ਹ) “ਤੇਰੇ ਘਰ ਵਿੱਚ ਇਹੋ-ਜਿਹਾ ਪੁੱਤਰ ਜਨਮ ਲਵੇਗਾ ਜਿਹੜਾ ਇਸੇ ਤਰ੍ਹਾਂ ਦੁਸ਼ਮਣਾਂ ਤੇ ਸਿਰ ਭੰਨੇਗਾ।”
ਉੱਤਰ :
(ੳ) ਬੂੜੇ ਨੇ ਗੁਰੂ ਨਾਨਕ ਦੇਵ ਜੀ ਨੂੰ ਕਹੇ।
(ਅ) ਗੁਰੂ ਨਾਨਕ ਦੇਵ ਜੀ ਨੇ ਬੂੜੇ ਨੂੰ ਕਹੇ।
(ਈ) ਗੁਰੂ ਨਾਨਕ ਦੇਵ ਜੀ ਨੇ ਬੂੜੇ ਨੂੰ ਕਹੇ !
(ਸ) ਗੁਰੂ ਅਰਜਨ ਦੇਵ ਜੀ ਨੇ ਆਪਣੀ ਸੁਪਤਨੀ ਮਾਤਾ ਗੰਗਾ ਜੀ ਨੂੰ ਕਹੇ।
(ਹ) ਨੇ ਮਾਤਾ ਗੰਗਾ ਜੀ ਨੂੰ ਕਹੇ।

ਵਿਆਕਰਨ :
ਗੁਰੂ ਜੀ ਨੇ ਉਸ ਨੂੰ ਗੁਰਸਿੱਖੀ ਦੀ ਦਾਤ ਬਖ਼ਸ਼ੀ ਤੇ ਉਸ ਦਾ ਨਾਂ ‘ਬਾਬਾ ਬੁੱਢਾ’ ਰੱਖ ਦਿੱਤਾ। ਬਾਬਾ ਬੁੱਢਾ । ਜੀ ਪੂਰਨ ਗੁਰਸਿੱਖ ਹੋਏ। ਛੇਵੇਂ ਹਰਿਗੋਬਿੰਦ ਜੀ ਤੱਕ ਮਨੁੱਖੀ ਜਾਮੇ ਵਿੱਚ ਰਹੇ। ਗੁਰੂ-ਘਰ ਦੀ ਬੜੀ ਸੇਵਾ ਕੀਤੀ। ਜਦੋਂ ਅੰਮ੍ਰਿਤਸਰ ਵਿਖੇ ਹਰਿਮੰਦਰ ਸਾਹਿਬ ਬਣਿਆ ਤਾਂ ਉਸ ਦੀ ਉਸਾਰੀ ਵਿੱਚ ਬਾਬਾ ਬੁੱਢਾ ਜੀ ਨੇ ਬਹੁਤ ਸੇਵਾ ਕੀਤੀ। ਦਰਬਾਰ ਸਾਹਿਬ ਦੀ ਡਿਓੜੀ ਤੋਂ ਅੰਦਰ ਪਰਿਕਰਮਾ ਵਿੱਚ ਵੜਦਿਆਂ ਹੀ ਸਾਮਣੇ ਬਾਬਾ ਬੁੱਢਾ ਜੀ ਦੀ ਬੇਰੀ ਹੈ।
ਉੱਪਰ ਦਿੱਤੇ ਪੈਰੇ ਵਿੱਚੋਂ ਆਮ ਨਾਂਵ ਅਤੇ ਖ਼ਾਸ ਨਾਂਵ ਚੁਣ ਕੇ ਆਪਣੀ ਕਾਪੀ ਵਿੱਚ ਲਿਖੋ।
ਉੱਤਰ :
ਆਮ ਨਾਂਵ-ਗੁਰੁ ਜੀ, ਡਿਉਢੀ, ਪਰਕਰਮਾ !
ਖ਼ਾਸ ਨਾਂਵ-, ਗੁਰੂ ਹਰਗੋਬਿੰਦ ਨੂੰ, ਅੰਮ੍ਰਿਤਸਰ, ਹਰਿਮੰਦਰ ਸਾਹਿਬ, ਦਰਬਾਰ ਸਾਹਿਬ, ਬੇਰੀ।
ਅਧਿਆਪਕ ਲਈ :
ਅਧਿਆਪਕ ਵਿਦਿਆਰਥੀਆਂ ਨੂੰ ਦੱਸੇਗਾ ਕਿ ਸ੍ਰੀ ਗੁਰੂ ਨਾਨਕ ਦੇਵ ਜੀ ਨੇ ਬਾਲਕ ਬੂੜੇ ਨੂੰ ਬੁੱਢਾ ਇਸ ਲਈ ਕਿਹਾ ਕਿਉਂਕਿ ਉਹ ਬਚਪਨ ‘ਚ ਹੁੰਦਿਆਂ ਹੋਇਆਂ ਵੀ ਬੜੀਆਂ ਸੂਝ ਭਰੀਆਂ ਤੇ ਦਲੀਲ ਭਰਪੂਰ ਗੱਲਾਂ ਕਰਦਾ ਸੀ।
PSEB 6th Class Punjabi Guide ਬਾਬਾ ਬੁੱਢਾ ਜੀ Important Questions and Answers
ਪ੍ਰਸ਼ਨ –
ਪਾਠ ਦਾ ਸਾਰ ਆਪਣੇ ਸ਼ਬਦਾਂ ਵਿਚ ਲਿਖੋ।
ਉੱਤਰ :
ਬੂੜਾ ਨਾਂ ਦਾ ਇਕ ਬਾਲਕ ਗਊਆਂ ਚਾਰਦਾ ਹੁੰਦਾ ਸੀ। ਉਹ ਬਹੁਤ ਸੁਲਝਿਆ ਹੋਇਆ ਬਾਲਕ ਸੀ। ਰਾਵੀ ਦੇ ਕੰਢੇ ਗਉਆਂ ਚਾਰਦਿਆਂ ਉਸ ਨੇ ਗੁਰੂ ਨਾਨਕ ਦੇਵ ਜੀ ਨੂੰ ਅਡੋਲ ਸਮਾਧੀ ਲਾਈ ਬੈਠਿਆਂ ਦੇਖਿਆ। ਬੁੜਾ ਨੇੜੇ ਦੇ ਖੂਹ ਤੋਂ ਪਾਣੀ ਦੀ ਇਕ ਟਿੰਡ ਖੋਲ ਕੇ ਲਿਆਇਆ ! ਦੂਜੀ ਕੋਰੀ ਟਿੰਡ ਵਿਚ ਉਸ ਨੇ ਗਾਂ ਦਾ ਦੁੱਧ ਚੋ ਲਿਆ ਤੇ ਦੋਹਾਂ ਟਿੰਡਾਂ ਨੂੰ ਗੁਰੂ ਜੀ ਦੇ ਅੱਗੇ ਰੱਖ ਕੇ ਚਰਨੀਂ ਢਹਿ ਪਿਆ।
ਗੁਰੂ ਜੀ ਨੇ ਬੂੜੇ ਨੂੰ ਪੁੱਛਿਆ ਕਿ ਉਹ ਕੀ ਚਾਹੁੰਦਾ ਹੈ। ਬੂੜੇ ਨੇ ਉੱਤਰ ਦਿੱਤਾ ਕਿ ਉਸਨੂੰ ਮੌਤ ਤੋਂ ਬਹੁਤ ਡਰ ਲਗਦਾ ਹੈ। ਗੁਰੂ ਜੀ ਨੇ ਕਿਹਾ ਕਿ ਉਹ ਤਾਂ ਅਜੇ ਬਾਲਕ ਹੈ। ਉਸ ਦੇ ਮਨ ਵਿਚ ਕਿਸ ਨੇ ਅਜਿਹੀਆਂ ਗੱਲਾਂ ਪਾਈਆਂ ਹਨ?
ਬੁੜੇ ਨੇ ਦੱਸਿਆ ਕਿ ਇਕ ਦਿਨ ਉਸ ਦੀ ਮਾਂ ਅੱਗ ਬਾਲ ਰਹੀ ਸੀ, ਤਾਂ ਉਸ ਨੇ ਦੇਖਿਆ ਕਿ ਪਹਿਲਾਂ ਉਸਨੇ ਛੋਟੀਆਂ ਲੱਕੜੀਆਂ ਲਾਈਆਂ ਤੇ ਫਿਰ ਵੱਡੀਆਂ ਪਹਿਲਾਂ ਛੋਟੀਆਂ ਲੱਕੜੀਆਂ ਬਲੀਆਂ ਤੇ ਫਿਰ ਪਿੱਛੋਂ ਵੱਡੀਆਂ ਨੂੰ ਅੱਗ ਲੱਗੀ ਤੇ ਉਸ ਦੇ ਮਨ ਵਿਚ ਡਰ ਪੈਦਾ ਹੋ ਗਿਆ ਕਿ ਜਿਵੇਂ ਛੋਟੀਆਂ ਲੱਕੜੀਆਂ ਨੂੰ ਪਹਿਲਾਂ ਅੱਗ ਲੱਗੀ ਹੈ। ਇਸੇ ਤਰ੍ਹਾਂ ਉਹ ਵੀ ਕਿਤੇ ਛੋਟੀ ਉਮਰ ਵਿਚ ਹੀ ਨਾ ਮਰ ਜਾਵੇ। ਇਕ ਹੋਰ ਘਟਨਾ ਨੇ ਵੀ ਉਸ ਦੇ ਮਨ ਉੱਤੇ ਡੂੰਘਾ ਅਸਰ ਕੀਤਾ। ਕੁੱਝ ਚਿਰ ਪਹਿਲਾਂ ਇਕ ਦੁਸ਼ਮਣ ਦਲ ਆਇਆ, ਤਾਂ ਉ ਆਪਣੀਆਂ ਘੋੜੀਆਂ ਲਈ ਖੇਤ ਵਿਚੋਂ ਕੱਚੀ-ਪੱਕੀ ਸਾਰੀ ਫ਼ਸਲ ਵੱਢ ਲਈ ਡਾਢਿਆਂ ਅੱਗੇ ਕਿਸੇ ਦੀ ਪੇਸ਼ ਨਾ ਗਈ।
ਇਸੇ ਤਰ੍ਹਾਂ ਜੇਕਰ ਉਸ ਨੂੰ ਜਮ ਹੁਣੇ ਲੈਣ ਆ ਜਾਣ, ਤਾਂ ਉਹ ਕੀ ਕਰ ਸਕਦਾ ਹੈ। ਇਸ ਕਰਕੇ ਉਹ ਚਾਹੁੰਦਾ ਹੈ ਕਿ ਉਹ ਕੋਈ ਅਜਿਹਾ ਕੰਮ ਕਰੇ, ਜਿਸ ਨਾਲ ਮਨ ਸ਼ਾਂਤ ਰਹੇ। ਉਹ ਚਾਹੁੰਦਾ ਹੈ ਕਿ ਉਹ ਉਸ ਨੂੰ ਆਪਣੀ ਸ਼ਰਨ ਵਿਚ ਲੈ ਲੈਣ। ਗੁਰੂ ਨੇ ਕਿਹਾ ਕਿ ਤੂੰ ਅਜੇ ਬਾਲਕ ਹੈਂ, ਪਰ ਗੱਲਾਂ ਬੁੱਢਿਆਂ ਵਾਲੀਆਂ ਕਰਦਾ ਹੈਂ। ਗੁਰੂ ਜੀ ਦੇ ਪੁੱਛਣ ਤੇ ਜਦੋਂ ਉਸ ਨੇ ਆਪਣਾ ਨਾਂ ਬੂੜਾ ਦੱਸਿਆ, ਤਾਂ ਗੁਰੂ ਜੀ ਨੇ ਕਿਹਾ ਕਿ ਉਹ ਬੁੜਾ ਨਹੀਂ, ਸਗੋਂ ਬੁੱਢਾ ਹੈ। ਤੈਨੂੰ ਰੱਬ ਨੇ ਉੱਚੇ ਕੰਮ ਸੌਂਪੇ ਹਨ।
ਤੂੰ ਰੱਬ ਨਾਲ ਆਪਣਾ ਧਿਆਨ ਜੋੜ ਰੱਖ। ਇਸ ਨਾਲ ਤੇਰੇ ਮਨ ਦੇ ਸਾਰੇ ਡਰ ਦੂਰ ਹੋ ਜਾਣਗੇ। ਗੁਰੂ ਜੀ ਨੇ ਉਸ ਨੂੰ ਗੁਰਸਿੱਖੀ ਦੀ ਦਾਤ ਬਖ਼ਸ਼ੀ ਅਤੇ ਉਸ ਦਾ ਨਾਂ ਬਾਬਾ ਬੁੱਢਾ ਰੱਖ ਦਿੱਤਾ ਉਹ ਛੇਵੇਂ ਗੁਰੂ ਹਰਗੋਬਿੰਦ ਜੀ ਤਕ ਮਨੁੱਖੀ ਜਾਮੇ ਵਿਚ ਰਹੇ। ਉਨ੍ਹਾਂ ਹਰਿਮੰਦਰ ਸਾਹਿਬ ਦੀ ਉਸਾਰੀ ਸਮੇਂ ਬਹੁਤ ਸੇਵਾ ਕੀਤੀ। ਦਰਬਾਰ ਸਾਹਿਬ ਦੀ ਡਿਉਢੀ ਤੋਂ ਅੰਦਰ ਪਰਕਰਮਾ ਵਿਚ ਵੜਦਿਆਂ ਹੀ ਸਾਹਮਣੇ ਦੀ ਬੇਰੀ ਹੈ। ਦੂਜੀ ਪਾਤਸ਼ਾਹੀ ਛੇਵੀਂ ਪਾਤਸ਼ਾਹੀ ਤਕ ਗੁਰਿਆਈ ਦਾ ਤਿਲਕ ਲਾਉਣ ਦਾ ਕੰਮ ਨੇ ਹੀ ਕੀਤਾ ਛੇਵੇਂ ਗੁਰੂ ਜੀ ਨੂੰ ਪੜ੍ਹਾਈ-ਲਿਖਾਈ ਤੇ ਸ਼ਸਤਰ ਵਿੱਦਿਆ ਵੀ ਇਨ੍ਹਾਂ ਨੇ ਹੀ ਸਿਖਾਈ ( ਗੁਰੂ ਹਰਗੋਬਿੰਦ ਜੀ ਦੇ ਬੱਚਿਆਂ ਨੂੰ ਆਪ ਨੇ ਹੀ ਸਿੱਖਿਆ ਦਿੱਤੀ।

ਆਪ ਬੜੀ ਨਿਮਰਤਾ ਦੇ ਮਾਲਕ ਸਨ। ਇਕ ਵਾਰੀ ਗੁਰੂ ਅਰਜਨ ਦੇਵ ਜੀ ਦੀ ਸੁਪਤਨੀ ਮਾਤਾ ਗੰਗਾ ਜੀ ਨੇ ਗੁਰੂ ਜੀ ਤੋਂ ਪੁੱਤਰ ਦੀ ਦਾਤ ਮੰਗੀ। ਗੁਰੂ ਜੀ ਨੇ ਉਨ੍ਹਾਂ ਨੂੰ ਤੋਂ ਅਸੀਸ ਲੈਣ ਲਈ ਕਿਹਾ ਮਾਤਾ ਜੀ ਸਵੇਰੇ ਉੱਠ ਕੇ ਤਿਆਰ ਹੋਏ।ਉਹ ਦੁੱਧ, ਮੱਖਣ ਤੇ ਹੋਰ ਚੀਜ਼ਾਂ ਲੈ ਕੇ ਨੌਕਰਾਣੀਆਂ ਨਾਲ ਰੱਥ ਉੱਤੇ ਚੜ੍ਹ ਕੇ ਬਾਬਾ ਜੀ ਵਲ ਚਲ ਪਏ ਬਾਬਾ ਜੀ ਨੇ ਦੂਰੋਂ ਧੂੜ ਉਡਦੀ ਦੇਖੀ ਤੇ ਨੇੜੇ ਆਉਣ ਤੇ ਬੋਲੇ, ” ਅੱਜ ਗੁਰੂ ਦੇ ਮਹਿਲਾਂ ਨੂੰ ਕੀ ਭਾਜੜ ਪਈ ਹੈ?” ਮਾਤਾ ਜੀ ਖ਼ਾਲੀ ਝੋਲੀ ਵਾਪਸ ਆ ਗਏ।
ਮਾਤਾ ਜੀ ਨੇ ਸਾਰੀ ਵਿਥਿਆ ਗੁਰੂ ਜੀ ਨੂੰ ਸੁਣਾਈ, ਤਾਂ ਗੁਰੂ ਜੀ ਨੇ ਕਿਹਾ ਕਿ ਅਸੀਸ ਲੈਣ ਲਈ ਰੱਥਾਂ ਉੱਤੇ ਚੜ੍ਹ ਕੇ ਨਹੀਂ, ਸਗੋਂ ਨੰਗੇ ਪੈਰੀਂ ਜਾ ਕੇ ਨਿਮਰਤਾ ਨਾਲ ਕੁੱਝ ਮੰਗੀਦਾ ਹੈ। ਦੂਜੇ ਦਿਨ ਮਾਤਾ ਜੀ ਨੇ ਸਵੇਰੇ ਉੱਠ ਕੇ ਇਸ਼ਨਾਨ ਕੀਤਾ। ਦੁੱਧ ਰਿੜਕ ਕੇ ਮੱਖਣ ਕੱਢਿਆ ਤੇ ਮਿੱਸੇ ਪਰਸ਼ਾਦੇ ਤਿਆਰ ਕੀਤੇ। ਉਹ ਸਾਰਾ ਕੁੱਝ ਸਿਰ ਤੇ ਰੱਖ ਕੇ ਨੰਗੇ ਪੈਰੀਂ ਅਰਦਾਸਾਂ ਕਰਦੇ ਹੋਏ ਕੋਲ ਪਹੁੰਚੇ। ਬਾਬਾ ਜੀ ਨੇ ਆਦਰ ਨਾਲ ਬਿਠਾਇਆ ਤੇ ਭੋਜਨ ਛਕਿਆ ਬਾਬਾ ਜੀ ਮਾਤਾ ਜੀ ਦੇ ਦਿਲ ਦੀ ਗੱਲ ਬੁੱਝ ਗਏ ਸਨ।
ਉਨ੍ਹਾਂ ਇਕ ਗੰਢਾ ਲੈ ਕੇ ਮੁੱਕੀ ਮਾਰ ਕੇ ਭੰਨਿਆ ਤੇ ਕਿਹਾ, “ਤੇਰੇ ਘਰ ਇਹੋ ਜਿਹਾ ਪੁੱਤਰ ਜਨਮ ਲਵੇਗਾ, ਜੋ ਇਸੇ ਤਰ੍ਹਾਂ ਦੁਸ਼ਮਣਾਂ ਦੇ ਸਿਰ ਭੰਨੇਗਾ ਮਾਤਾ ਜੀ ਇਹ ਸੁਣ ਕੇ ਪ੍ਰਸੰਨ ਹੋ ਕੇ ਘਰ ਆ ਗਏ। ਜਦੋਂ ਸ੍ਰੀ ਗੁਰੁ ਗ੍ਰੰਥ ਜੀ ਸਾਹਿਬ ਦੀ ਪਹਿਲੀ ਬੀੜ ਤਿਆਰ ਹੋਈ, ਤਾਂ ਉਸ ਦਾ ਪਹਿਲਾ ਪ੍ਰਕਾਸ਼ ਦਰਬਾਰ ਸਾਹਿਬ ਸ੍ਰੀ ਹਰਿਮੰਦਰ ਸਾਹਿਬ ਵਿਚ ਕੀਤਾ ਗਿਆ ਤੇ ਗੁਰੂ ਅਰਜਨ ਦੇਵ ਜੀ ਨੇ ਨੂੰ ਪਹਿਲਾ ਥੀ ਥਾਪਿਆ।
ਸਵਾ ਸੌ ਸਾਲ ਉਮਰ ਭੋਗ ਕੇ ਗੁਰੂ ਹਰਿਗੋਬਿੰਦ ਸਿੰਘ ਜੀ ਦੇ ਸਮੇਂ ਪਿੰਡ ਰਾਮਦਾਸ ਵਿਚ ਚਲਾਣਾ ਕਰ ਗਏ। ਗੁਰੂ ਜੀ ਨੇ ਆਪਣੇ ਹੱਥੀਂ ਉਨ੍ਹਾਂ ਦਾ ਸਸਕਾਰ ਕੀਤਾ। ਉਸ ਜਗ੍ਹਾ ਉੱਤੇ ਇਸ ਸਮੇਂ ਸੁੰਦਰ ਤੇ ਇਤਿਹਾਸਿਕ ਗੁਰਦੁਆਰਾ ਬਣ ਚੁੱਕਾ ਹੈ, ਜਿਹੜਾ ਸੱਚਖੰਡ ਦੇ ਨਾਂ ਨਾਲ ਮਸ਼ਹੂਰ ਹੈ।
ਔਖੇ ਸ਼ਬਦਾਂ ਦੇ ਅਰਥ-ਬਣਾਂ-ਜੰਗਲਾਂ ਵਾਗੀਆਂ – ਗਊ ਸੁਲਝਿਆ – ਸਪੱਸ਼ਟ ਵਿਚਾਰਾਂ ਵਾਲਾ, ਸੂਝਵਾਨ ! ਤਬੇਲਾ ਘੋੜੇ ਪਸ਼) ਬੰਨ੍ਹਣ ਦੀ ਥਾਂ। ਅਡੋਲ – ਜੋ ਡੋਲੇ ਨਾ, ਦਿੜ੍ਹ ਸਮਾਧੀ – ਅੰਤਰ-ਧਿਆਨ ਹੋਣਾ ( ਅਨੋਖਾ – ਸਾਰਿਆਂ ਤੋਂ ਵੱਖਰਾ, ਨਿਰਾਲਾ 1 ਨੂਰ – ਚਾਨਣ 1 ਬਲੀਆਂ – ਲੰਮੀਆਂ ਗੋਲ ਲੱਕੜੀਆਂ ਘਾਵੇ – ਜ਼ਖ਼ਮ } ਡਾਢਿਆਂ – ਜ਼ੋਰਾਵਰਾਂ। ਜਮ – ਜਮਦੂਤ, ਜੋ ਮਰਨ ਸਮੇਂ ਮਨੁੱਖ ਨੂੰ ਲੈਣ ਆਉਂਦੇ ਹਨ ਪ੍ਰਕਾਸ਼ – ਗੁਰੂ ਗ੍ਰੰਥ ਸਾਹਿਬ ਜੀ ਦੀ ਬੀੜ ਨੂੰ ਖੋਲ੍ਹ ਕੇ ਸਥਾਪਿਤ ਕਰਨਾ।
1. ਪਾਠ-ਅਭਿਆਸ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ
ਪਸ਼ਨ 1.
ਹੇਠ ਲਿਖੇ ਵਾਕਾਂ ਵਿਚਲੀਆਂ ਖ਼ਾਲੀ ਥਾਂਵਾਂ ਵਿਚ ਢੁੱਕਵੇਂ ਸ਼ਬਦ ਭਰੋ
(ਉ) ਬੂੜੇ ਨਾਂ ਦਾ ਇਕ ਬਾਲਕ ……………………………………. ਚਰਾਉਂਦਾ ਹੁੰਦਾ ਸੀ।
(ਅ) ਬੂੜਾ ਬੜਾ ……………………………………. ਹੋਇਆ ਬਾਲਕ ਸੀ।
(ਈ) ਮੈਨੂੰ ਸਾਰਾ ਵਕਤ ……………………………………. ਦਾ ਡਰ ਰਹਿੰਦਾ ਹੈ।
(ਸ) ਅੱਗੇ ਕਿਸੇ ਦੀ ਪੇਸ਼ ਨਾ ਗਈ। ਤੂੰ ਤਾਂ ……………………………………. ਵਾਲੀਆਂ ਗੱਲਾਂ ਕਰਦਾ ਹੈ :
(ਕ) ਤੂੰ ਬੁੜਾ ਨਹੀਂ ……………………………………. ਹੈਂ।
(ਖ) ਦੂਜੀ ਪਾਤਸ਼ਾਹੀ ਤੋਂ ……………………………………. ਪਾਤਸ਼ਾਹੀ ਤਕ ਤਿਲਕ ਲਗਾਉਣ ਦਾ ਕੰਮ ਨੇ ਕੀ ਕੀਤਾ।
(ਗ) ਗੁਰੂ ਅਰਜਨ ਦੇਵ ਜੀ ਨੇ ਨੂੰ ਪਹਿਲਾ ……………………………………. ਥਾਪਿਆ ਸੀ !
ਉੱਤਰ :
(ਉ) ਗਊਆਂ
(ਅ) ਸੁਲਝਿਆ
(ਈ) ਮੌਤ
(ਸ) ਡਾਢਿਆਂ,
(ਹ) ਬੁੱਢਿਆਂ
(ਕ) ਬੁੱਢਾ,
(ਖ) ਛੇਵੀਂ,
(ਗ) ਗ੍ਰੰਥੀ।

2. ਪੈਰਿਆਂ ਸੰਬੰਧੀ ਪ੍ਰਸ਼ਨ
ਪ੍ਰਸ਼ਨ 1.
ਹੇਠ ਦਿੱਤੇ ਪੈਰੇ ਨੂੰ ਪੜੋ ਅਤੇ ਹੇਠਾਂ ਦਿੱਤੇ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਬਹੁਵਿਕਲਪੀ ਉੱਤਰਾਂ ਵਿੱਚੋਂ ਸਹੀ ਉੱਤਰ ਚੁਣੋ –
ਬੂੜਾ ਨਾਂ ਦਾ ਇੱਕ ਬਾਲਕ ਗਊਆਂ ਚਰਾਉਂਦਾ ਫਿਰਦਾ ਸੀ। ਬਣਾਂ ਵਿੱਚ ਸਾਰਾ ਦਿਨ ਵਾਗੀਆਂ ਵਾਂਗ ਫਿਰਦਾ ਰਹਿੰਦਾ। ਤ੍ਰਿਕਾਲਾਂ ਪੈਂਦੀਆਂ ਤਾਂ ਵੱਗ ਨੂੰ ਹਿੱਕ ਕੇ ਘਰ ਵਲ ਲੈ ਜਾਂਦਾ। ਬੂੜਾ ਬੜਾ ਸੁਲਝਿਆ ਹੋਇਆ ਬਾਲਕ ਸੀ। ਸ਼ੁਰੂ ਤੋਂ ਹੀ ਡੂੰਘੀਆਂ ਸੋਚਾਂ ਸੋਚਦਾ ਸੀ। ਇੱਕ ਦਿਨ ਗਊਆਂ ਚਰਾਉਂਦੇ-ਚਰਾਉਂਦੇ ਨੇ ਰਾਵੀ ਦੇ ਕਿਨਾਰੇ ਗੁਰੂ ਨਾਨਕ ਦੇਵ ਜੀ ਨੂੰ ਅੰਤਰ ਧਿਆਨ ਬੈਠਿਆਂ ਵੇਖਿਆ ਗਊਆਂ ਚਰਾਉਂਦਾ ਘੜੀ-ਮੁੜੀ ਉੱਧਰ ਫੇਰਾ ਮਾਰਦਾ ਤੇ ਵੇਖਦਾ ਕਿ ਇੱਕ ਮਹਾਤਮਾ ਉਸੇ ਤਰ੍ਹਾਂ ਅਡੋਲ ਸਮਾਧੀ ਲਾਈ ਬੈਠੇ ਹਨ।
ਚਿਹਰੇ ਉੱਤੇ ਅਨੋਖਾ ਨੂਰ ਹੈ। ਬੂੜੇ ਦੇ ਮਨ ਵਿੱਚ ਪਤਾ ਨਹੀਂ ਕੀ ਖ਼ਿਆਲ ਆਇਆ। ਉਹ ਨੇੜੇ ਹੀ ਖੂਹ ਵਿੱਚ ਉੱਤਰ ਕੇ ਪਾਣੀ ਦੀ ਇੱਕ ਟਿੰਡ ਖੋਲ੍ਹ ਕੇ ਲਿਆਇਆ। ਇੱਕ ਹੋਰ ਸਾਫ਼ ਟਿੰਡ ਵਿੱਚ ਗਾਂ ਦਾ ਦੁੱਧ ਚੋ ਲਿਆਇਆ ਤੇ ਦੋਹਾਂ ਟਿੰਡਾਂ ਨੂੰ ਗੁਰੂ ਜੀ ਅੱਗੇ ਰੱਖ ਕੇ ਚਰਨੀਂ ਢਹਿ ਪਿਆ ਗੁਰੂ ਜੀ ਮੁਸਕਰਾ ਕੇ ਪੁੱਛਣ ਲੱਗੇ, “ਹੇ ਬਾਲਕ ! ਤੈਨੂੰ ਕੀ ਚਾਹੀਦਾ ਹੈ? ਬੜਾ ਉਦਾਸ ਦਿਸ ਰਿਹਾ ਹੈਂ।’ ਬੂੜਾ ਕਹਿਣ ਲੱਗਾ, “ਗੁਰੂ ਜੀ। ਮੈਨੂੰ ਸਾਰਾ ਵਕਤ ਮੌਤ ਦਾ ਡਰ ਰਹਿੰਦਾ ਹੈ। ਮੈਨੂੰ ਰਾਤ ਨੂੰ ਵੀ ਚੰਗੀ ਤਰ੍ਹਾਂ ਨੀਂਦ ਨਹੀਂ ਆਉਂਦੀ।”
1. ਬੂੜਾ ਕੀ ਚਰਾਉਂਦਾ ਸੀ?
(ੳ) ਮੱਝਾਂ
(ਅ) ਗਊਆਂ
(ਈ) ਘੋੜੇ
(ਸ) ਬੱਕਰੀਆਂ।
ਉੱਤਰ :
(ਅ) ਗਊਆਂ
2. ਬੁੜਾ ਸਾਰਾ ਦਿਨ ਕਿੱਥੇ ਵਾਗੀਆਂ ਵਾਂਗ ਫਿਰਦਾ ਰਹਿੰਦਾ ਸੀ?
(ਉ) ਬਣਾਂ ਵਿਚ
(ਆ) ਬੰਜਰਾਂ ਵਿਚ
(ਈ) ਚਰਾਗਾਹਾਂ ਵਿਚ
(ਸ) ਬਾਗਾਂ ਵਿਚ
ਉੱਤਰ :
(ਉ) ਬਣਾਂ ਵਿਚ
3. ਬੂੜਾ ਤ੍ਰਿਕਾਲਾਂ ਵੇਲੇ ਕਿਸਨੂੰ ਹਿੱਕ ਕੇ ਘਰ ਲੈ ਆਉਂਦਾ ਸੀ?
(ਉ) ਵੱਗ
(ਅ) ਚੌਣਾ
(ਈ) ਇੱਜੜ
(ਸ) ਝੰਡ।
ਉੱਤਰ :
(ਉ) ਵੱਗ
4. ਬੁੜਾ ਕਿਹੋ ਜਿਹਾ ਬਾਲਕ ਸੀ?
(ਉ) ਗੰਭੀਰ
(ਅ) ਸੁਲਝਿਆ ਹੋਇਆ
(ਇ) ਵਿਹਲੜ
(ਸ) ਮਨਮਤੀਆ !
ਉੱਤਰ :
(ਅ) ਸੁਲਝਿਆ ਹੋਇਆ

5. ਅੰਤਰ-ਧਿਆਨ ਹੋ ਕੇ ਕੌਣ ਬੈਠਾ ਸੀ?
ਜਾਂ
ਅਨੋਖਾ ਨੂਰ ਕਿਸਦੇ ਚਿਹਰੇ ਉੱਤੇ ਸੀ?
(ਉ) ਬੂੜਾ
(ਅ) ਗੁਰੁ ਨਾਨਕ ਦੇਵ ਜੀ।
(ਇ) ਬਾਬਾ ਬੁੱਢਾ ਜੀ
(ਸ) ਭਾਈ ਮਰਦਾਨਾ।
ਉੱਤਰ :
(ਅ) ਗੁਰੁ ਨਾਨਕ ਦੇਵ ਜੀ।
6. ਬੂੜੇ ਨੇ ਗੁਰੂ ਜੀ ਨੂੰ ਕਿਸ ਨਦੀ ਦੇ ਕਿਨਾਰੇ ਸਮਾਧੀ ਵਿਚ ਦੇਖਿਆ ਸੀ?
(ਉ) ਸਿੰਧ
(ਅ) ਸਤਲੁਜ
(ਈ) ਰਾਵੀ
(ਸ) ਬਿਆਸ॥
ਉੱਤਰ :
(ਈ) ਰਾਵੀ
7. ਬੂੜਾ ਪਾਣੀ ਤੇ ਦੁੱਧ ਕਿਸ ਚੀਜ਼ ਵਿਚ ਲਿਆਇਆ?
(ਉ) ਟਿੰਡਾਂ ਵਿਚ
(ਅ) ਗੜਬੀਆਂ ਵਿਚ
(ਈ) ਪਤੀਲਿਆਂ ਵਿਚ
(ਸ) ਬਾਲਟੀਆਂ ਵਿੱਚ।
ਉੱਤਰ :
(ਉ) ਟਿੰਡਾਂ ਵਿਚ
9. ਬੁੜਾ ਕਿਹੋ ਜਿਹੀ ਹਾਲਤ ਵਿਚ ਦਿਖਾਈ ਦਿੱਤਾ?
(ਉ) ਖ਼ੁਸ਼
(ਅ) ਉਦਾਸ
(ਈ) ਉਤਸ਼ਾਹਿਤ
(ਸ) ਹੌਸਲੇ ਵਿਚ ਹੀ
ਉੱਤਰ :
(ਅ) ਉਦਾਸ

9. ਬੂੜੇ ਨੂੰ ਹਰ ਵਕਤ ਕਿਸ ਚੀਜ਼ ਦਾ ਡਰ ਰਹਿੰਦਾ ਸੀ?
(ਉ) ਚੋਰੀ
(ਅ) ਦਾਅ ਬਘਿਆੜਾਂ ਦਾ
(ਏ) ਸੱਪਾਂ ਦਾ
(ਸ) ਮੌਤ ਦਾ।
ਉੱਤਰ :
(ਸ) ਮੌਤ ਦਾ।
ਪ੍ਰਸ਼ਨ 2.
(i) ਉਪਰੋਕਤ ਪੈਰੇ ਵਿੱਚੋਂ ਕੋਈ ਪੰਜ ਨਾਂਵ ਸ਼ਬਦ ਚੁਣੋ।
(ii) ਉਪਰੋਕਤ ਪੈਰੇ ਵਿੱਚੋਂ ਪੜਨਾਂਵ ਸ਼ਬਦ ਚੁਣੋ।
(iii) ਉਪਰੋਕਤ ਪੈਰੇ ਵਿੱਚੋਂ ਕੋਈ ਪੰਜ ਵਿਸ਼ੇਸ਼ਣ ਸ਼ਬਦ ਚੁਣੋ।
(iv) ਉਪਰੋਕਤ ਪੈਰੇ ਵਿੱਚੋਂ ਕੋਈ ਪੰਜ ਕਿਰਿਆ ਸ਼ਬਦ ਚੁਣੋ।
ਉੱਤਰ :
(i) ਬੂੜੇ, ਬਾਲਕ, ਗਊਆਂ, ਦਿਨ, ਰਾਵੀ ਨੂੰ
(ii) ਕੀ, ਉਹ, ਮੈਨੂੰ
(iii) ਇਕ, ਸਾਰਾ, ਬੜਾ, ਡੂੰਘੀਆਂ, ਦੋਹਾਂ।
(iv) ਫਿਰਦਾ ਰਹਿੰਦਾ, ਜਾਂਦਾ, ਸੋਚਦਾ ਸੀ, ਵੇਖਿਆ, ਆਇਆ !
ਪ੍ਰਸ਼ਨ 3.
ਉਪਰੋਕਤ ਪੈਰੇ ਵਿੱਚੋਂ ਹੇਠ ਲਿਖੇ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਸਹੀ ਵਿਕਲਪ ਚੁਣੋ
(i) ਬਾਲਕ ਸ਼ਬਦ ਦਾ ਲਿੰਗ ਚੁਣੋ
(ਉ) ਬਾਲੀ
(ਅ) ਬਾਲਿਕਾ
(ਏ) ਬਾਲ
(ਸ) ਬਾਲਾ।
ਉੱਤਰ :
(ਅ) ਬਾਲਿਕਾ
(ii) ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ਕਿਹੜਾ ਸ਼ਬਦ ਵਿਸ਼ੇਸ਼ਣ ਹੈ?
(ਉ) ਘੜੀ-ਮੁੜੀ
(ਅ) ਦੁੱਧ
(ਈ) ਤੇ ਡੂੰਘੀਆਂ
(ਸ) ਵਕਤ।
ਉੱਤਰ :
(ਈ) ਤੇ ਡੂੰਘੀਆਂ

(iii) ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ‘ਬਣਾਂ ਸ਼ਬਦ ਦਾ ਸਮਾਨਾਰਥਕ ਸ਼ਬਦ ਕਿਹੜਾ ਹੈ?
(ਉ) ਬਣਾਂ
(ਅ) ਥਣਾਂ
(ਈ) ਜੰਗਲਾਂ
(ਸ) ਸੰਗਲਾਂ।
ਉੱਤਰ :
(ਈ) ਜੰਗਲਾਂ
ਪ੍ਰਸ਼ਨ 4.
ਉਪਰੋਕਤ ਪੈਰੇ ਵਿੱਚੋਂ ਹੇਠ ਲਿਖੇ ਵਿਸਰਾਮ ਚਿੰਨ੍ਹ ਲਿਖੋ
(i) ਡੰਡੀ
(ii) ਕਾਮਾ
(iii) ਛੁੱਟ-ਮਰੋੜੀ
(iv) ਦੋਹਰੇ ਪੁੱਠੇ ਕਾਮੇ
(v) ਪ੍ਰਸ਼ਨਿਕ ਚਿੰਨ੍ਹ
(vi) ਵਿਸਮਿਕ ਚਿੰਨ੍ਹ
ਉੱਤਰ :
(i) ਡੰਡੀ ( । )
(ii) ਕਾਮਾ (,)
(iii) ਛੁੱਟ ਮਰੋੜੀ (‘)
(iv) ਦੋਹਰੇ ਪੁੱਠੇ ਕਾਮੇ (” “)
(v) ਪ੍ਰਸ਼ਨਿਕ ਚਿੰਨ੍ਹ (?)
(vi) ਵਿਸਮਿਕ ਚਿੰਨ੍ਹ (!)
ਪ੍ਰਸ਼ਨ 5.
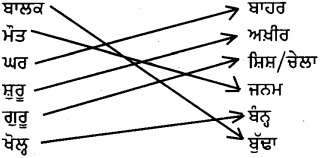
ਉਪਰੋਕਤ ਪੈਰੇ ਵਿੱਚੋਂ ਵਿਰੋਧੀ ਸ਼ਬਦਾਂ ਦਾ ਸਹੀ ਮਿਲਾਨ ਕਰੋ :

ਉੱਤਰ :

ਪ੍ਰਸ਼ਨ 2.
ਹੇਠ ਲਿਖੇ ਪੈਰੇ ਨੂੰ ਪੜੋ ਅਤੇ ਅੱਗੇ ਦਿੱਤੇ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਬਹੁਵਿਕਲਪੀ ਉੱਤਰ ਵਿੱਚੋਂ ਸਹੀ ਉੱਤਰ ਚੁਣ ਕੇ ਲਿਖੋ ਗੁਰੂ ਸਾਹਿਬ ਨੇ ਕਿਹਾ, “ਹੇ ਬਾਲਕ। ਤੂੰ ਤਾਂ ਬੁੱਢਿਆਂ ਵਾਲੀਆਂ ਗੱਲਾਂ ਕਰਦਾ ਹੈਂ। ਤੂੰ ਤਾਂ ਅਜੇ ਬਾਲ ਏਂ। ਤੇਰਾਂ ਨਾਂ ਕੀ ਹੈ?’’ ‘‘ਜੀ, ਮੈਨੂੰ ਬੁੜਾ ਕਹਿੰਦੇ ਹਨ।’’ ਬਾਲਕ ਨੇ ਉੱਤਰ ਦਿੱਤਾ ਗੁਰੂ ਜੀ ਕਹਿਣ ਲੱਗੇ, “ਤੂੰ ਬੂੜਾ ਨਹੀਂ, ਬੁੱਢਾ ਹੈਂ। ਹੇ ਬੁੱਢੇ ਬਾਲਕ ! ਤੈਨੂੰ ਰੱਬ ਨੇ ਉੱਚੇ ਕੰਮ ਸੌਂਪੇ ਨੇ। ਤੂੰ ਆਪਣਾ ਧਿਆਨ ਪਰਮੇਸ਼ਰ ਨਾਲ ਜੋੜੀ ਰੱਖੀ। ਇਸ ਤਰ੍ਹਾਂ ਮਨ ਦੇ ਸਾਰੇ ਡਰ ਦੂਰ ਹੋ ਜਾਂਦੇ ਹਨ।
ਗੁਰੂ ਜੀ ਨੇ ਉਸ ਨੂੰ ਗੁਰਸਿੱਖੀ ਦੀ ਦਾਤ ਬਖ਼ਸ਼ੀ ਤੇ ਉਸ ਦਾ ਨਾਂ “ਬਾਬਾ ਬੁੱਢਾ’ ਰੱਖ ਦਿੱਤਾ ਪੂਰਨ ਗੁਰਸਿੱਖ ਹੋਏ। ਉਹ ਛੇਵੇਂ ਗੁਰੂ ਹਰਿਗੋਬਿੰਦ ਜੀ ਤੱਕ ਮਨੁੱਖੀ ਜਾਮੇ ਵਿੱਚ ਰਹੇ। ਗੁਰੂ-ਘਰ ਦੀ ਬੜੀ ਸੇਵਾ ਕੀਤੀ। ਜਦੋਂ ਅੰਮ੍ਰਿਤਸਰ ਵਿਖੇ ਹਰਿਮੰਦਰ ਸਾਹਿਬ ਬਣਿਆ, ਤਾਂ ਉਸ ਦੀ ਉਸਾਰੀ ਵਿੱਚ ਨੇ ਬਹੁਤ ਸੇਵਾ ਕੀਤੀ ਦਰਬਾਰ ਸਾਹਿਬ ਦੀ ਡਿਓੜੀ ਤੋਂ ਅੰਦਰ ਪਰਿਕਰਮਾ ਵਿੱਚ ਵੜਦਿਆਂ ਹੀ ਸਾਮਣੇ ਦੀ ਬੇਰੀ ਹੈ। ਦੂਜੀ ਪਾਤਸ਼ਾਹੀ ਤੋਂ ਲੈ ਕੇ ਛੇਵੀਂ ਤੱਕ ਗੁਰਿਆਈ ਦਾ ਤਿਲਕ ਲਾਉਣ ਦਾ ਕੰਮ ਨੇ ਹੀ ਕੀਤਾ। ਛੇਵੇਂ ਗੁਰੂ ਜੀ ਨੂੰ ਪੜ੍ਹਾਈ ਲਿਖਾਈ ਤੇ ਸ਼ਸਤਰ ਵਿੱਦਿਆ ਇਹਨਾਂ ਨੇ ਹੀ ਸਿਖਾਈ ਤੇ ਅੱਗੋਂ ਹਰਿਗੋਬਿੰਦ ਜੀ ਦੇ ਬੱਚਿਆਂ ਨੂੰ ਸਿੱਖਿਆ ਦਿੰਦੇ ਰਹੇ।
1. ਬਾਲਕ ਕਿਹੋ ਜਿਹੀਆਂ ਗੱਲਾਂ ਕਰ ਰਿਹਾ ਸੀ?
(ਉ) ਨਿਆਣੀਆਂ
(ਅ) ਅਣਜਾਣੀਆਂ
(ਈ) ਬੁੱਢਿਆਂ ਵਾਲੀਆਂ
(ਸ) ਜਵਾਨਾਂ ਵਾਲੀਆਂ
ਉੱਤਰ :
(ਈ) ਬੁੱਢਿਆਂ ਵਾਲੀਆਂ
2. ਬਾਲਕ ਦਾ ਨਾਂ ਕੀ ਸੀ?
(ਉ) ਬੁੱਢਾ
(ਅ) ਬੱਚਾ
(ਈ) ਬੁੜਾ
(ਸ) ਕੂੜਾ।
ਉੱਤਰ :
(ਈ) ਬੁੜਾ
3. ਗੁਰੂ ਜੀ ਨੇ ਬੂੜੇ ਦਾ ਨਾਂ ਕੀ ਰੱਖਿਆ?
(ਉ) ਬਾਬਾ ਬਾਲਕ
(ਅ) ਬਾਬਾ ਬੁੜਾ
(ਏ) ਬਾਬਾ ਬੁੱਢਾ
(ਸ) ਬਾਬਾ ਸਿਆਣਾ
ਉੱਤਰ :
(ਏ) ਬਾਬਾ ਬੁੱਢਾ

4. ਗੁਰੂ ਜੀ ਨੇ ਬੂੜੇ ਨੂੰ ਕਿਹੜੀ ਦਾਤ ਬਖ਼ਸ਼ੀ?
(ਉ) ਸੰਤਾਨ ਦੀ .
(ਅ) ਗੁਰਸਿੱਖੀ ਦੀ
(ਇ) ਇਸੇਵਾ ਦੀ
(ਸ) ਧਨ-ਦੌਲਤ ਦੀ।
ਉੱਤਰ :
(ਅ) ਗੁਰਸਿੱਖੀ ਦੀ
5. ਕਿਹੋ-ਜਿਹੇ ਗੁਰਸਿੱਖ ਬਣੇ?
(ਉ) ਪੂਰਨ
(ਅ) ਅਪੂਰਨ
(ਈ) ਅੱਧੇ-ਅਧੂਰੇ
(ਸ) ਚੰਗੇ।
ਉੱਤਰ :
(ਉ) ਪੂਰਨ
6. ਕਿਸ ਗੁਰੂ ਤੱਕ ਮਨੁੱਖੀ ਜਾਮੇ ਵਿਚ ਰਹੇ?
(ੳ) ਗੁਰੂ ਅੰਗਦ ਦੇਵ ਜੀ
(ਅ) ਗੁਰੂ ਰਾਮਦਾਸ ਜੀ
(ਈ) ਗੁਰੂ ਹਰਗੋਬਿੰਦ ਜੀ
(ਸ) ਗੁਰੂ ਗੋਬਿੰਦ ਸਿੰਘ ਜੀ।
ਉੱਤਰ :
(ਈ) ਗੁਰੂ ਹਰਗੋਬਿੰਦ ਜੀ
7. ਨੇ ਕਿਸ ਇਮਾਰਤ ਦੀ ਉਸਾਰੀ ਵਿਚ ਬਹੁਤ ਸੇਵਾ ਕੀਤੀ?
(ਉ) ਸ੍ਰੀ ਹਰਿਮੰਦਰ ਸਾਹਿਬ
(ਅ) ਤੇ ਅਕਾਲ ਤਖ਼ਤ ਸਾਹਿਬ
(ਈ) ਸ਼ਹੀਦ ਬੁੰਗਾ .
(ਸ) ਰਾਮਗੜ੍ਹੀਆ ਬੂੰ।
ਉੱਤਰ :
(ਉ) ਸ੍ਰੀ ਹਰਿਮੰਦਰ ਸਾਹਿਬ

8. ਸ੍ਰੀ ਦਰਬਾਰ ਸਾਹਿਬ ਦੀ ਪਰਿਕ੍ਰਮਾ ਵਿਚ ਨਾਲ ਸੰਬੰਧਿਤ ਕੀ ਹੈ?
(ਉ) ਬੇਰੀ
(ਆ) ਪਿੱਪਲ
(ਇ) ਫਲਾਹ
(ਸ) ਜੰਡ।
ਉੱਤਰ :
(ਉ) ਬੇਰੀ
9. ਦੂਜੀ ਪਾਤਸ਼ਾਹੀ ਤੋਂ ਛੇਵੀਂ ਪਾਤਸ਼ਾਹੀ ਤੱਕ ਗੁਰਿਆਈ ਦਾ ਤਿਲਕ ਲਾਉਣ ਦਾ ਕੰਮ ਕਿਸ ਨੇ ਕੀਤਾ?
(ੳ) ਗੁਰੂ ਸਾਹਿਬਾਨ ਨੇ ਆਪ
(ਅ) ਨੇ
(ਈ) ਭਾਈ ਗੁਰਦਾਸ ਜੀ ਨੇ
(ਸ) ਭਾਈ ਬੰਨੋ ਜੀ ਨੇ।
ਉੱਤਰ :
(ਅ) ਨੇ
10. ਨੇ ਕਿਸ ਗੁਰੂ ਸਾਹਿਬ ਨੂੰ ਸ਼ਸਤਰ ਵਿੱਦਿਆ ਦਿੱਤੀ?
(ਉ) ਗੁਰੂ ਅੰਗਦ ਦੇਵ
(ਅ) ਗੁਰੂ ਹਰਗੋਬਿੰਦ ਜੀ
(ਇ) ਗੁਰੂ ਤੇਗ ਬਹਾਦਰ ਜੀ
(ਸ) ਗੁਰੂ ਗੋਬਿੰਦ ਸਿੰਘ ਜੀ।
ਉੱਤਰ :
(ਅ) ਗੁਰੂ ਹਰਗੋਬਿੰਦ ਜੀ
ਪ੍ਰਸ਼ਨ 2.
(i) ਉਪਰੋਕਤ ਪੈਰੇ ਵਿੱਚੋਂ ਕੋਈ ਪੰਜ ਨਾਂਵ ਸ਼ਬਦ ਚੁਣੋ।
(ii) ਉਪਰੋਕਤ ਪੇਰੇ ਵਿੱਚੋਂ ਕੋਈ ਪੰਜ ਪੜਨਾਂਵ ਸ਼ਬਦ ਚੁਣੋ।
(ii) ਉਪਰੋਕਤ ਪੈਰੇ ਵਿੱਚੋਂ ਕੋਈ ਪੰਜ ਵਿਸ਼ੇਸ਼ਣ ਸ਼ਬਦ ਚੁਣੋ।
(iv) ਉਪਰੋਕਤ ਪੈਰੇ ਵਿੱਚੋਂ ਕੋਈ ਪੰਜ ਕਿਰਿਆ ਸ਼ਬਦ ਚੁਣੋ।
ਉੱਤਰ :
(i) ਬਾਲਕ, ਬੂੜਾ, ਕੰਮ, ਗੁਰਸਿੱਖੀ, ਸ੍ਰੀ ਹਰਿਮੰਦਰ ਸਾਹਿਬ।
(ii) ਤੂੰ, ਕੀ, ਤੈਨੂੰ, ਉਸ, ਇਹਨਾਂ।
(iii) ਉੱਚੇ, ਸਾਰੇ, ਪੂਰਨ, ਬੜੀ, ਬਹੁਤ !
(iv) ਕਿਹਾ, ਕਰਦਾ ਹੈਂ, ਹੋ ਜਾਂਦੇ ਹਨ, ਕੀਤਾ, ਰਹੇ।

ਪ੍ਰਸ਼ਨ 3.
ਉਪਰੋਕਤ ਪੈਰੇ ਵਿੱਚੋਂ ਹੇਠ ਲਿਖੇ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਸਹੀ ਵਿਕਲਪ ਚੁਣੋ
(i) ‘ਬੁੱਢਾ ਸ਼ਬਦ ਦਾ ਲਿੰਗ ਬਦਲੋ
(ਉ) ਬੂੜੀ,
(ਆ) ਬੁਢਾਪਾ
(ਈ) ਬੁੱਢੀ
(ਸ) ਬੁੜੀ ਨੂੰ
ਉੱਤਰ :
(ਈ) ਬੁੱਢੀ
(ii) ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ਵਿਸ਼ੇਸ਼ਣ ਕਿਹੜਾ ਹੈ?
(ਉ) ਸਾਹਮਣੇ
(ਅ) ਬੜੀ
(ਇ) ਇਸੇਵਾ
(ਸ) ਇਹਨਾਂ।
ਉੱਤਰ :
(ਅ) ਬੜੀ
(iii) “ਪਰਮੇਸ਼ਰ ਦਾ ਸਮਾਨਾਰਥੀ ਸ਼ਬਦ ਕਿਹੜਾ ਹੈ?
(ਉ) ਮਾਤਮਾ
(ਅ) ਪਰਮੇਸ਼ਵਰ
(ਈ) ਗੁਰੂ
(ਸ) ਸ਼ਬਦ।
ਉੱਤਰ :
(ਅ) ਪਰਮੇਸ਼ਵਰ
ਪ੍ਰਸ਼ਨ 4.
ਉਪਰੋਕਤ ਪੈਰੇ ਵਿੱਚੋਂ ਹੇਠ ਲਿਖੇ ਵਿਸਰਾਮ ਚਿੰਨ੍ਹ ਲਿਖੋ-
(i) ਡੰਡੀ
(ii) ਕਾਮਾ
(iii) ਪ੍ਰਸ਼ਨਿਕ ਚਿੰਨ੍ਹ
(iv) ਜੋੜਨੀ
(v) ਦੋਹਰੇ ਪੁੱਠੇ-ਕਾਮੇ
(iv) ਇਕਹਿਰੇ ਪੁੱਠੇ-ਕਾਮੇ
ਉੱਤਰ :
(i) ਡੰਡੀ (।)
(ii) ਕਾਮਾ (,)
(ii) ਪ੍ਰਸ਼ਨਿਕ ਚਿੰਨ੍ਹ (?)
(iv) ਜੋੜਨੀ (-)
(v) ਦੋਹਰੇ ਪੁੱਠੇ ਕਾਮੇ (” “)
(vi) ਇਕਹਿਰੇ ਪੁੱਠੇ ਕਾਮੇ (‘ ‘)

ਪ੍ਰਸ਼ਨ 5.
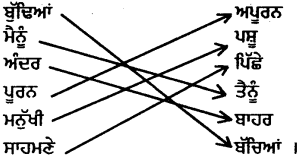
ਉਪਰੋਕਤ ਪੈਰੇ ਵਿਚੋਂ ਵਿਰੋਧੀ ਸ਼ਬਦਾਂ ਦਾ ਸਹੀ ਮਿਲਾਨ ਕਰੋ :

ਉੱਤਰ :

![]()
![]()