Prasanna

Punjab State Board PSEB 7th Class Home Science Book Solutions Chapter 4 खाना बनाने के सिद्धान्त Textbook Exercise Questions and Answers.

PSEB Solutions for Class 7 Home Science Chapter 4 खाना बनाने के सिद्धान्त

PSEB 7th Class Home Science Guide खाना बनाने के सिद्धान्त Textbook Questions and Answers

वस्तुनिष्ठ प्रश्न

प्रश्न 1.
भोजन ज्यादा देर पकाने से क्या नष्ट हो जाता है?
उत्तर-
विटामिन तथा खनिज लवण।

प्रश्न 2.
फलों और सब्जियों का पतला छिलका उतारने की सलाह क्यों दी जाती है?
उत्तर-
छिलकों के बिल्कुल नीचे ही विटामिन तथा खनिज लवण होते हैं, इसलिए मोटा छिलका उतारने से ये नष्ट हो जाते हैं।

प्रश्न 3.
डिब्बाबंद भोजन खरीदते समय हमें किस बात का ध्यान रखना चाहिए?
उत्तर-
डिब्बा फूला हुआ था पिचका हुआ न हो।

प्रश्न 4.
खाने वाले सोडे का प्रयोग भोजन पकाने में क्यों वर्जित है?
उत्तर-
इससे विटामिन तथा खनिज लवण नष्ट हो जाते हैं।

लघूत्तर प्रश्न

प्रश्न 1.
भोजन पकाते समय किन-किन बातों का ध्यान रखना चाहिए?
उत्तर-
भोजन पकाते समय निम्नलिखित बातों का ध्यान रखना चाहिए

1. चोकर सहित आटे का प्रयोग करना चाहिए इसमें विटामिन पाया जाता है। रोटी सेंकने से कम-से-कम आधा घण्टा पहले ही आटा गूंध कर स्वच्छ गीले कपड़े से ढक कर रखें।
2. चावल पकाने से पूर्व बार-बार न धोयें, इससे खनिज लवण और विटामिन नष्ट हो जाते हैं।
3. भोजन सदैव स्वच्छ बर्तन में ही पकाना चाहिए।
4. गृहिणी को अपने हाथ और नाखून साफ़ रखने चाहिए।
5. रसोईघर में प्रयोग आने वाले कपड़े, जैसे-तौलिया, नेपकिन, झाड़न, पोंछा आदि स्वच्छ होना चाहिए।
6. बर्तनों को खुला नहीं छोड़ना चाहिए, इससे कीड़े-मकौड़े का भोजन में गिरने का डर रहता है।
7. दाल, सब्जी में पानी केवल उतना ही डालना चाहिए जिससे भोजन पक जाए।
   अधिक पानी डालकर फिर फेंकने से बहुत-से खनिज लवण एवं विटामिन नष्ट हो जाते हैं।
8. भोजन धीमी आँच पर पकाना चाहिए; भाप द्वारा पकाना सबसे उत्तम होता है इसके लिए प्रेशर कुकर का प्रयोग करना चाहिए।
9. भोजन को ढक्कनदार बर्तन में पकाना चाहिए।
10. दूध को धीमी आँच पर न उबालकर तेज़ आँच पर उबालना चाहिए।
11. मांस व अण्डे को बहुत अधिक नहीं पकाना चाहिए।
12. भोजन पकाते समय सोडे का प्रयोग नहीं करना चाहिए; इससे विटामिन B नष्ट हो जाते हैं।
13. भोजन में अधिक मसालों का प्रयोग नहीं करना चाहिए। अधिक मिर्च, मसाले व घी के प्रयोग से व्यक्ति का स्वास्थ्य खराब हो जाता है।
14. भोजन पकाने के पश्चात् परोसने में देर न करें। पके हुए भोजन को पुनः गर्म करना ठीक नहीं होता है।

प्रश्न 2.
भोजन पकाते समय निजी सफ़ाई से क्या भाव है?
उत्तर-
भोजन पकाते समय निजी सफ़ाई से भाव निम्नलिखित हैं

1. जिन लोगों को जुकाम, गला खराब, खाँसी, फ्लू, फोड़े आदि हों उन्हें खाना पकाने का काम नहीं करना चाहिए।
2. खाना पकाते समय हाथ और नाखून हमेशा साफ़ होना चाहिए। कपड़े भी साफ़ होने चाहिएं और बालों को अच्छी तरह बाँधकर रखना चाहिए।
3. कच्चे मीट, मछली, सब्जियों और फलों के छिलकों को हाथ लगाने से पहले हाथ अच्छी तरह धो लेने चाहिए।
4. भोजन को चलाते समय कड़छी या चम्मच का इस्तेमाल करना चाहिए। जहाँ तक हो सके भोजन को हाथ नहीं लगाना चाहिए।
5. खाना बनाते समय अगर छींक या खाँसी आने लगे तो मुँह को ढक लेना चाहिए।
6. जिस चम्मच के साथ खाने का स्वाद देखना हो उसको फिर धोकर इस्तेमाल करना चाहिए।

प्रश्न 3.
रसोई और बर्तनों की सफ़ाई कैसे करनी चाहिए?
उत्तर-
रसोई तथा बर्तनों की सफाई निम्नलिखित ढंग से करनी चाहिए

1. रसोईघर के दरवाजों और खिड़कियों पर जाली लगी होनी चाहिए ताकि मक्खी, मच्छर, आदि अन्दर न आ सके।
2. रसोईघर की सफ़ाई हर रोज़ खाना खाने के बाद जूठे बर्तनों को साफ़ करने के बाद करनी चाहिए। दिन में एक बार रसोई को अच्छी तरह साफ़ करना चाहिए। सप्ताह में एक बार जाले उतार कर दीवारों को साफ़ करना चाहिए और साल में एक बार या दो बार सफेदी करनी चाहिए।
3. खाना पकाने वाले बर्तनों को प्रत्येक बार इस्तेमाल करने के बाद अच्छी तरह साफ़ करना चाहिए। मीट काटने के बाद चाकू को धो लेना चाहिए।
4. बर्तनों या शैल्फ जहां कच्छा मीट, मुर्गा या मछली रखी हो वहां दूसरी खाने की वस्तु रखने से पहले उसे अच्छी तरह साफ़ करना चाहिए।
5. जूठे बर्तनों को साफ़ बर्तनों से अलग रखना चाहिए।
6. जूठे बर्तनों को धोने के लिए गर्म पानी और साबुन या डिटरजेन्ट का इस्तेमाल करना चाहिए। इससे बर्तन साफ़ और कीटाणुरहित हो जाते हैं। बर्तनों को धोकर अगर धूप में सुखाया जाए तो इनमें चमक आ जाती है।

निबन्धात्मक प्रश्न

प्रश्न 1.
खाना पकाने के सिद्धान्त लिखो।
उत्तर-
खाना पकाने के निम्नलिखित सिद्धान्त हैं

1. खाना पकाते समय सब्जियों के छिलके उतारने चाहिएं।
2. इनको ज्यादा नहीं धोना और न ही ज्यादा देर तक भिगोकर रखना चाहिए।
3. भोजन को हमेशा ढककर पकाना चाहिए।
4. जिस पानी में भोजन पकाया जाए उसे फेंकना नहीं चाहिए।
5. भोजन को धूप में नहीं रखना चाहिए और भोजन पकाते समय सोडा नहीं डालना चाहिए।
6. सब्जियों को बहुत छोटे-छोटे टुकड़ों में नहीं काटना चाहिए।

प्रश्न 2.
भोजन खरीदते समय कौन-कौन सी बातों का ध्यान रखना चाहिए?
उत्तर-
भोजन खरीदते समय निम्नलिखित बातों का ध्यान रखना चाहिए

1. भोजन ऐसे स्थानों से खरीदना चाहिए जहां सफ़ाई का पूरा ध्यान रखा जाता हो। जिस बाज़ार में मक्खियां, मच्छर या दूसरे कीड़े-मकौड़े और चूहे आदि हों, वहाँ से भोजन की कोई वस्तु नहीं खरीदनी चाहिए।
2. बेचने वाले दुकानदार साफ़ होने चाहिएं, उसके कपड़े साफ़ हों और सेहत अच्छी हो। अगर उनको खाँसी या जुकाम लगा हो तो उससे खाने की वस्तु नहीं खरीदनी चाहिए।
3. मीट खरीदते समय यह देखना ज़रूरी है कि जानवर बीमार न हो और साथ ही उस पर डॉक्टर की मोहर भी लगी होनी चाहिए।
4. डिब्बे में बन्द वस्तु खरीदते समय यह देख लेना चाहिए कि डिब्बा फूला हुआ या चिपका हुआ न हो। फूले हुए डिब्बे में बैक्टीरिया होते हैं। जहाँ तक सम्भव हो सके डिब्बे किसी अच्छी फ़र्म के बने ही इस्तेमाल करने चाहिए।
5. फल और सब्जियाँ गली-सड़ी नहीं होनी चाहिए। (6) दालें, चावल, आटे आदि में कीड़े या सुसरी नहीं होनी चाहिए।
6. दूध और दूध से बनी वस्तुएँ ताजी होनी चाहिएँ और उनसे खट्टी महक नहीं आनी चाहिए।
7. कटे हुए फल-सब्जियाँ, जिन पर धूल पड़ी होने का सन्देह हो या उन पर मक्खियां बैठी हों, नहीं खरीदनी चाहिए।
8. पका हुआ भोजन खरीदना हो तो उसकी सफ़ाई के बारे में पूरी जाँच-पड़ताल कर लेनी चाहिए।
9. भोजन की चीजें लाने के बाद सूखी चीज़ों को सूखे डिब्बों में भरकर रसोई की अलमारी या स्टोर में रख देना चाहिए।

प्रश्न 3.
रसोई की सफ़ाई से क्या अभिप्राय है?
उत्तर-
रसोईघर के प्रत्येक स्थान को धो-पोंछकर साफ़ करना चाहिए। भोजन समाप्त होने के बाद बची हुई खाद्य-सामग्री को दूसरे स्वच्छ बर्तनों में रखकर जालीदार अलमारी . या रेफ्रीजरेटर में रख देना चाहिए। जूठे बर्तनों को साफ़ करने के स्थान पर ही साफ़ किया जाना चाहिए। भोजन पकाने तथा परोसने के स्थान को पहले गीले तथा फिर सूखे कपड़े से पोंछकर स्वच्छ करना चाहिए। बर्तनों को साफ़ करके यथास्थान व्यवस्थित करना चाहिए। नल, फर्श, सिंक आदि को साफ़ करके सूखा रखने का प्रयत्न करना चाहिए। रसोईघर की चौकी, तख्त, मेज, कुर्सी की सफाई भी प्रतिदिन की जानी चाहिए तथा फर्श को भी पानी से प्रतिदिन सींक को झाडू या कूची से रगड़कर धोना चाहिए।

प्रश्न 4.
भोजन घर लाने के बाद ताज़ी और सूखी चीज़ों की सम्भाल आप कैसे करोगे?
उत्तर-
भोजन की चीजें घर लाने के बाद सूखी चीज़ों को सूखे डिब्बों में भरकर रसोई की अलमारी या स्टोर में रख देना चाहिए। ताजी सब्जियों और फलों को फ्रिज या किसी अन्य ठण्डी जगह पर रखना चाहिए। मीट लाने के बाद अगर फ्रिज़ हो तो उसको सबसे ठण्डे खाने में रखना चाहिए। अगर ऐसा न हो सके तो उसे जल्दी ही पका लेना चाहिए।
दूध को हमेशा उबालकर जाली के साथ ढककर रखना चाहिए। अगर फ्रिज़ हो तो उसमें रखना चाहिए नहीं तो ठण्डी जगह का पानी दूध वाले बर्तन में रखना चाहिए।

Home Science Guide for Class 7 PSEB खाना बनाने के सिद्धान्त Important Questions and Answers

अति छोटे उत्तर वाले प्रश्न

प्रश्न 1.
भोज्य पदार्थ को पकाने का मुख्य उद्देश्य क्या है?
उत्तर-
भोजन को पचने योग्य बनाना।

प्रश्न 2.
प्रोटीन पर पकाने का क्या प्रभाव पड़ता है?
उत्तर-
प्रोटीन पकाने पर सुपाच्य (पचने योग्य) हो जाती है तथा तरल प्रोटीन ठोस रूप में बदल जाती है।

प्रश्न 3.
कार्बोहाइड्रेट्स पर पकाने का क्या प्रभाव पड़ता है?
उत्तर-
पकाने से कार्बोहाइड्रेट्स पचने योग्य तथा मीठे हो जाते हैं।

प्रश्न 4.
पकाने का वसा पर क्या प्रभाव पड़ता है?
उत्तर-
पकाने से वसा पिघलती है और सुपाच्य बन जाती है।

प्रश्न 5.
सब्जी पकाने का मुख्य अभिप्राय क्या है?
उत्तर-
सब्जी के सैलुलोज को मुलायम करना तथा श्वेतसार कणों को फुलाकर जिलेटिन के रूप में परिवर्तित करना।

प्रश्न 6.
किन खनिज तत्त्वों पर ताप का प्रभाव बहुत कम पड़ता है?
उत्तर-
कैल्शियम तथा लोहे पर।

प्रश्न 7.
कैरोटीन पकाने पर नष्ट क्यों नहीं होता?
उत्तर-
क्योंकि यह जल में घुलनशील नहीं है।

प्रश्न 8.
भोजन पकाने से विटामिन ‘बी’ तथा ‘सी’ प्रायः नष्ट क्यों हो जाते हैं?
उत्तर-
जल में घुलनशील होने तथा ताप द्वारा नष्ट हो जाने के कारण।

प्रश्न 9.
शक्कर को गर्म करने पर क्या प्रभाव पड़ता है?
उत्तर-
शक्कर को गर्म करने पर वह भूरे रंग का हो जाता है। इसको अधिक गर्म करने पर काले रंग का हो जाता है।

प्रश्न 10.
कौन-से पदार्थ पेट में अधिक वायु बनाते हैं?
उत्तर-
कच्चे सलाद पेट में अधिक वायु बनाते हैं।

छोटे उत्तर वाले प्रश्न

प्रश्न 1.
रसोईघर के लिए निम्नलिखित केन्द्रों की व्यवस्था आप कैसी करेंगी?
(क) तैयारी केन्द्र,
(ख) खाना पकाने व परोसने का केन्द्र।
उत्तर-
(क) तैयारी केन्द्र-खाना पकाने से पूर्व खाद्य पदार्थों की तैयारी करनी पड़ती है। इनमें दाल-चावल चुनना व धोना, साग-सब्जी धोना व काटना, आटा छानना, गूंधना आदि जैसे कार्य रहते हैं। कार्य करने के लिए शेल्फों की ऊँचाई गृहिणी की लम्बाई के अनुसार उचित होनी चाहिए जिससे गृहिणी को कार्य करने में असुविधा न हो। इन शेल्फों के नीचे तथा ऊपर अलमारियों में भोजन की तैयारी में उपयोग में आने वाले उपकरण आटा, दालें आदि संग्रहीत करके रखी जा सकती हैं।

(ख) खाना पकाने व परोसने का केन्द्र-भोजन पकाने के लिए जिन वस्तुओं की आवश्यकता होती है, उन्हें ऐसे स्थान पर रखना चाहिए, जिससे गृहिणी को अधिक दौड़ धूप न करनी पड़े। भोजन पकाने के केन्द्र के निकट ही एक ऐसा स्थान या अलमारी हो जिसमें सभी मसालों से भरी शीशियां, घी, तेल तथा पकाने के बर्तन हों।

भोजन पकाने के बाद भोजन परोसना सबसे महत्त्वपूर्ण कार्य है। भोजन दो प्रकार से परोसा जाता है-भारतीय शैली तथा विदेशी शैली।
भारतीय शैली में खाना थाली एवं कटोरियों में परोसकर प्रायः रसोईघर में चौकी पर रखा जाता है और व्यक्ति पटरे पर बैठकर खाता है। विदेशी शैली में खाना डोंगों में भरकर मेज़ पर लगाया जाता है और व्यक्ति इच्छानुसार स्वयं परोसकर खाता है।

प्रश्न 2.
रसोईघर के बर्तनों की धुलाई व सफ़ाई के उत्तम प्रबन्ध के लिए किन किन बातों का ध्यान रखना चाहिए?
उत्तर-
जूठे तथा भोजन पकाए हुए बर्तनों को साफ़ करने के लिए एक निश्चित स्थान होना चाहिए। बर्तन साफ़ करने के केन्द्र के पास सिंक की व्यवस्था अवश्य होनी चाहिए। सिंक के पास एक ओर गंदे बर्तन तथा दूसरी ओर धुले बर्तन रखने के लिए शेल्फ होने चाहिएं। सिंक कभी कोने में नहीं होना चाहिए। इस केन्द्र में विम, छनी हुई राख, सर्फ, मिट्टी, ब्रश, स्पंज तथा झाडू आदि रखने की व्यवस्था होनी चाहिए।

एक शब्द में उत्तर दें

प्रश्न 1.
सब्ज़ियाँ तथा फलों के छिलकों के बिल्कुल नीचे ………….. तथा ……………. होते हैं।
उत्तर-
विटामिन, खनिज लवण।

प्रश्न 2.
……… सहित आटे का प्रयोग करना चाहिए इसमें विटामिन ‘बी’ होता है।
उत्तर-
चोकर।

प्रश्न 3.
श्वेतसार के कण पकाने पर फूल जाते हैं तथा किस रूप में परिवर्तित होते हैं?
उत्तर-
जिलेटिन।

प्रश्न 4.
कैरोटीन …………. में घुलनशील नहीं है।
उत्तर-
जल।

प्रश्न 5.
अधिक गर्म करने पर शक्कर कैसी हो जाती है?
उत्तर-
काली।

प्रश्न 6.
गर्म करने से तरल प्रोटीन ……. रूप में बदल जाता है।
उत्तर-
ठोस।

प्रश्न 7.
भोजन को …………….. सेंक पर पकाना चाहिए।
उत्तर-
मध्यम।

खाना बनाने के सिद्धान्त PSEB 7th Class Home Science Notes

• सब्जियों और फलों के छिलकों के बिल्कुल नीचे ही विटामिन और खनिज लवण होते हैं।
• अधिक देर तक खाना पकाने से भी विटामिन और खनिज लवण नष्ट हो जाते हैं। इसलिए भोजन उतनी देर तक ही पकाना
• चाहिए जब तक वह गल कर पचने योग्य न हो जाए।
• कुछ विटामिन और खनिज लवण पानी में घुल जाते हैं। इसलिए सब्जियों को धोने के बाद ही काटना चाहिए।
• जिन लोगों को जुकाम, गला खराब, खांसी, फ्लू, फोड़े आदि हों उन्हें खाना पकाने का काम नहीं करना चाहिए।
• खाना पकाते समय हाथ और नाखून हमेशा साफ़ होने चाहिए।
• भोजन को हिलाते समय कड़छी या चम्मच का इस्तेमाल करना चाहिए।
• रसोईघर के दरवाजों और खिड़कियों पर जाली लगी होनी चाहिए ताकि मक्खी, मच्छर आदि अन्दर न आ सकें।
• खाना पकाने वाले बर्तनों को प्रतिदिन इस्तेमाल करने के बाद अच्छी तरह साफ़ करना चाहिए।
• जूठे बर्तनों को साफ़ बर्तनों से अलग रखना चाहिए।
• जूठे बर्तनों को धोने के लिए गर्म पानी, साबुन या डिटरजेन्ट का इस्तेमाल करना चाहिए।

Punjab State Board PSEB 8th Class Home Science Book Solutions Chapter 5 कार्यात्मक फर्नीचर Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Home Science Chapter 5 कार्यात्मक फर्नीचर

PSEB 8th Class Home Science Guide कार्यात्मक फर्नीचर Textbook Questions and Answers

प्रश्न 1.
कार्यात्मक फर्नीचर से क्या भाव है ?
उत्तर-
जो फर्नीचर किसी खास काम के लिए इस्तेमाल किया जाता हो।

प्रश्न 2.
सोने वाले कमरे में आरामदायक फर्नीचर होना चाहिए। बताओ क्यों ?
उत्तर-
सोने वाले कमरे में आरामदायक फर्नीचर होना चाहिए क्योंकि उठने-बैठने तथा सोने में कष्टदायक न हो।

प्रश्न 3.
कार्यात्मक फर्नीचर कितनी प्रकार का होता है ?
उत्तर-
दो प्रकार का-

1. कार्यात्मक,
2. केवल सजावटी।

प्रश्न 4.
मेज़ के ऊपर सनमाइका लगाने का क्या लाभ है ?
उत्तर-
मेज़ के ऊपरी भाग पर सनमाइका लगाने से मेज़ साफ़ करना आसान रहता है।

प्रश्न 5.
किस प्रकार की लकड़ी फर्नीचर के लिए सबसे अच्छी रहती है ?
उत्तर-
टीक, महोगनी, गुलाब और अखरोट की लकड़ी फर्नीचर के लिए सबसे अच्छी रहती है।

प्रश्न 6.
पलंग का आम माप क्या होता है और बच्चों के लिए कैसा पलंग हो सकता
उत्तर-
पलंग का साधारण माप \(2 \frac{1}{2}\) से \(3 \frac{1}{2}\) तक चौड़ा और \(6 \frac{1}{2}\) फुट तक लम्बा होता है।
बच्चों के लिए छोटी चारपाई हो सकती है। इसका माप 4′ × 2′ होता है।

प्रश्न 7.
पढ़ाई वाले मेज़ का आम माप क्या होता है ?
उत्तर-
पढ़ाई वाले मेज़ का साधारण माप \(2 \frac{1}{2}\) फुट × 4 फुट और ऊँचाई \(2 \frac{1}{2}\) फुट हो सकती है।

प्रश्न 8.
पढ़ाई वाले मेज़ पर कार्य करते समय किस प्रकार की कुर्सी का प्रयोग करना चाहिए ?
उत्तर-
पढ़ाई वाले मेज़ पर काम करते समय कुर्सी सीधी पीठ वाली और बाजू वाली प्रयोग करनी चाहिए।

लघूत्तर प्रश्न

प्रश्न 1.
भारतीय मौसम के अनुसार किस तरह का फर्नीचर होना चाहिए ?
उत्तर-
भारतीय मौसम के अनुसार निम्नलिखित तरह का फर्नीचर होना चाहिए

1. फर्नीचर नए डिज़ाइन का हो।
2. फर्नीचर कमरे के आकार का हो।
3. फर्नीचर आर्थिक दृष्टि से मितव्ययी हो।
4. फर्नीचर स्थान की दृष्टि से मितव्ययी हो।
5. फर्नीचर कमरे के लिए उपयोगी हो।
6. फर्नीचर मज़बूत व टिकाऊ हो।
7. फर्नीचर उपयोगी और सुन्दर होने के साथ-साथ आरामदायक हो।
8. फर्नीचर उठाने-धरने में सुविधाजनक हो।
9. फर्नीचर सदैव अच्छे कारीगर द्वारा बना हो।

प्रश्न 2.
बैठने वाले और खाने वाले कमरों में कौन-कौन सा फर्नीचर होना ज़रूरी है ?
उत्तर-
बैठने वाले कमरों में फर्नीचर-सोफासेट, गद्देदार, कुर्सियाँ, मेज़, कॉफी टेबल,सेन्टर टेबल और आराम कुर्सियाँ। खाने वाले कमरों में फर्नीचर- भोजन की मेज़, कुर्सियाँ, परोसने की मेज़, साइड बोर्ड ट्राली (पहिए वाली मेज़)।

प्रश्न 3.
पढ़ाई वाले कमरे की आवश्यकता क्यों समझी जाती है ? इसमें किस तरह का फर्नीचर होना चाहिए ?
उत्तर-
शिक्षा के प्रसार से हमारे देश में भी पश्चिमी देशों की तरह पढ़ाई वाले कमरे की आवश्यकता है जिसमें बच्चों की पढ़ाई सही ढंग से हो सके। पढ़ाई वाले कमरे का फर्नीचर-पढ़ने वाला मेज़, कुर्सी, पुस्तकों की अलमारी आदि होनी चाहिएँ। मेज़ का आम माप 2^1/2 फुट × 4 फुट और ऊँचाई 272 फुट होती है। लेकिन मेज़ इससे लम्बा और चौड़ा भी हो सकता है। मेज़ इतना बड़ा होना चाहिए कि उस पर लैम्प, पुस्तकें, शब्दकोष, पेन, पेंसिलें आदि आसानी से आ सकें। अगर टाइपराइटर रखने की जगह हो सके तो और भी अच्छा है। कुर्सी सीधी पीठ वाली और बाजू वाली होनी चाहिए। इसकी सीट बेंत की या गद्देदार होनी चाहिए। यदि टाइपराइटर का प्रबन्ध हो तो कुर्सी पहियों वाली होनी चाहिए ताकि आवश्यकता पड़ने पर इसको टाइपराइटर की तरफ़ या मेज़ की तरफ़ घुमाया जा सके। पुस्तकों के लिए शैल्फ़ वाली अलमारी इस कमरे में होनी चाहिए। हमारे देश के मौसम के अनुसार शीशे वाली अलमारी होनी चाहिए क्योंकि मिट्टी, धूल से पुस्तकों को सुरक्षित रखा जा सके।

प्रश्न 4.
लकड़ी के फर्नीचर की किस तरह देखभाल करोगे ? ।
उत्तर-
लकड़ी के फर्नीचर की देखभाल के लिए निम्नलिखित बातों का ध्यान रखना चाहिए

1. फर्नीचर की सफ़ाई प्रतिदिन की जानी चाहिए।
2. फर्नीचर को बहुत सावधानी से एक स्थान से दूसरे स्थान तक ले जाना चाहिए।
3. फर्नीचर को खींचना या घसीटना नहीं चाहिए। फर्नीचर को रगड़ लगने से भी बचाना चाहिए।
4. फर्नीचर पर किसी प्रकार की खाने की वस्तु न गिरे, यदि गिर भी जाए तो उसे तत्काल साफ़ कर देना चाहिए नहीं तो दाग-धब्बे पड़ने का डर रहता है।

प्रश्न 5.
गद्देदार और चमड़े के फर्नीचर को किस तरह साफ़ करोगे ?
उत्तर-
गद्देदार और चमड़े के फर्नीचर को साफ़ करने के लिए निम्नलिखित बातों का ध्यान रखना चाहिए

1. प्रतिदिन साफ़ कपड़े से झाड़ना चाहिए।
2. कभी-कभी पानी में नर्म साबुन का घोल बनाकर कपड़े के साथ घोल लगाकर चमड़े और रेक्सीन को साफ़ करना चाहिए।
3. साफ़ करने के बाद पॉलिश करना चाहिए ताकि चमड़ा नरम हो जाए और कटे नहीं।

प्रश्न 6.
बैंत के फर्नीचर का क्या लाभ और हानियाँ हैं ?
उत्तर-
बैंत के फर्नीचर से निम्नलिखित लाभ हैं-

1. बैंत का फर्नीचर लकड़ी से हल्का होता है।
2. यह लकड़ी के फर्नीचर की अपेक्षा आसानी से बाहर निकाला जा सकता है।
3. यह लकड़ी के फर्नीचर से सस्ता होता है।

बैंत के फर्नीचर की सफ़ाई-

1. बैंत वाले फर्नीचर को रोज़ कपड़े या ब्रुश से साफ़ करना चाहिए।
2. बैंत वाले फर्नीचर को नमक के पानी से साफ़ करना चाहिए।

हानियाँ-

1. इस फर्नीचर को कुत्तों, बिल्लियों से बचाना पड़ता है।
2. यह लम्बे समय तक चलने योग्य नहीं होता।

प्रश्न 7.
मीनाकारी वाले फर्नीचर के क्या लाभ और हानियाँ हैं ?
उत्तर-
लाभ-

1. मीनाकारी फर्नीचर देखने में सुन्दर होता है।
2. इससे कमरा आकर्षक लगता है।

हानियाँ-

1. हमारे यहाँ तेज़ हवा चलती है जिस कारण मीनाकारी फर्नीचर पर धूलमिट्टी की परतें जम जाती हैं।
2. इस फर्नीचर की आसानी से सही सफ़ाई नहीं होती।
3. सफ़ाई न होने से यह अनाकर्षक दिखायी देने लगता है।

प्रश्न 8.
फर्नीचर पर घी, तेल, पेंट और लुक आदि के दाग कैसे दूर किये जा सकते
उत्तर-
फर्नीचर पर लगे घी, तेल, पेंट तथा तारकोल आदि के धब्बे निम्नलिखित ढंग से दूर किये जा सकते हैं

1. तरल पदार्थों को किसी साफ़ कपड़े से पोंछ देना चाहिए।
2. चिकने और चिपकने वाले दागों के लिए गुनगुने पानी का इस्तेमाल करना चाहिए। आवश्यकता हो तो किसी नरम साबुन का इस्तेमाल करना चाहिए। लकड़ी को अधिक गीला नहीं करना चाहिए।
3. यदि लकड़ी पर कोई गर्म बर्तन रखा जाए तो भी उस पर दाग पड़ जाते हैं। इस तरह के दाग पर कुछ दिन थोड़ा सा युक्लिप्टस का तेल या पीतल का पॉलिश लगाकर अच्छी तरह रगड़ना चाहिए। 8-10 दस दिनों के बाद दाग उतर जाएगा।
4. पेन्ट या रोगन के दाग के लिए मैथिलेटिड स्पिरिट इस्तेमाल में लानी चाहिए और फर्नीचर पर पॉलिश करनी चाहिए।
5. स्याही के दाग के लिए ऑग्जैलिक तेज़ाब का हल्का घोल इस्तेमाल करना चाहिए।
6. रगड़ के निशानों को दूर करने के लिए उबालकर ठंडा किया अलसी का तेल इस्तेमाल करना चाहिए।

निबन्धात्मक प्रश्न

प्रश्न 1.
फर्नीचर का चुनाव करते समय कौन-कौन सी बातों का ध्यान रखना आवश्यक है ?
उत्तर-
फर्नीचर के चुनाव में निम्नलिखित बातों पर ध्यान देना आवश्यक है
(1) उपयोगिता,
(2) सुन्दरता,
(3) डिज़ाइन,
(4) आरामदेही,
(5) मूल्य,
(6) मज़बूती,
(7) आकार।
1. उपयोगिता-केवल उपयोगी फर्नीचर का ही चुनाव करना चाहिए। अनुपयोगी फर्नीचर कितना ही सुन्दर क्यों न हो, वह हमारे लिए कोई महत्त्व नहीं रखता।

2. सुन्दरता-फर्नीचर आकर्षक व सन्तोषजनक होना चाहिए। सामान्य नियमों का पालन करते हुए सुन्दरता पर ध्यान देना चाहिए।

3. बनावट (डिज़ाइन)-मकान की बनावट के अनुसार फर्नीचर आधुनिक, सादा या पुराने डिज़ाइन का हो सकता है। आधुनिक मकान में पुराने डिज़ाइन का फर्नीचर शोभा नहीं देता। आधुनिक मकान का सभी फर्नीचर आधुनिक ही होना चाहिए।

4. आरामदेही-फर्नीचर की विशेषता उसका आरामदेह होना है। उठने-बैठने तथा सोने में कष्ट देने वाले फर्नीचर कितने ही सुन्दर क्यों न हों, बेकार होते हैं।

5. मूल्य-घर की आर्थिक स्थिति तथा फर्नीचर के मूल्य में तालमेल होना चाहिए। अपनी आर्थिक स्थिति से बाहर निकलकर खर्च करना बुद्धिमानी नहीं है। बहुत सस्ता फर्नीचर भी नहीं खरीदना चाहिए क्योंकि वह टिकाऊ नहीं हो सकता।

6. मज़बूती-फर्नीचर सुन्दर होने के साथ-साथ मज़बूत भी होना चाहिए। चीड की लकड़ी का फर्नीचर शीघ्र टूट जाता है। सागवान व शीशम की लकड़ी का फर्नीचर मज़बूत होता है। स्टील या लोहे के फर्नीचर में चादर की मज़बूती का ध्यान रखना चाहिए।

7. आकार- फर्नीचर का चुनाव कमरे के आकार के आधार पर ही करना चाहिए। छोटे कमरों में छोटे आकार का फर्नीचर और बड़े कमरों में बड़े आकार का फर्नीचर ही उपयुक्त रहता है।

प्रश्न 2.
लकड़ी के फर्नीचर पर रगड़ के निशानों को कैसे दूर कर सकते हैं ?
उत्तर-
लकड़ी के फर्नीचर पर रगड़ के निशानों को दूर करने के लिए अलसी का तेल उबालकर ठंडा करके प्रयोग किया जाता है।

Home Science Guide for Class 8 PSEB कार्यात्मक फर्नीचर Important Questions and Answers

I. बहुविकल्पी प्रश्न

प्रश्न 1.
ग़लत तथ्य हैं
(क) बैंत का फर्नीचर लकड़ी से हल्का होता है।
(ख) पढ़ाई वाली मेज़ 4 फुट ऊंची होती है।
(ग) सजावटी फर्नीचर केवल सजावट के लिए होता है।
(घ) सभी ठीक।
उत्तर-
(ख) पढ़ाई वाली मेज़ 4 फुट ऊंची होती है।

प्रश्न 2.
ठीक तथ्य है
(क) फर्नीचर दो प्रकार का होता है।
(ख) सब से अच्छा फर्नीचर लकड़ी का होता है।
(ग) फर्नीचर आराम दायक होना चाहिए।
(घ) सभी ठीक।
उत्तर-
(घ) सभी ठीक।

प्रश्न 3.
ठीक तथ्य है
(क) बैंत वाले फर्नीचर को नमक वाले पानी से साफ करना चाहिए।
(ख) मीनाकारी वाले फर्नीचर से कमरा आकर्षक लगता है।
(ग) बैंत का फर्नीचर लकड़ी के फर्नीचर से सस्ता होता है।
(घ) सभी ठीक।
उत्तर-
(घ) सभी ठीक।

II. ठीक/गलत बताएं

1. पुराने फर्नीचर भारी तथा नक्काशीदार होते हैं।
2. फर्नीचर का चयन कमरे के रंग, आकार अनुसार करें।
3. देवदार, अखरोट की लकड़ी हल्की होती है।
4. बहु-उद्देशीय फर्नीचर कम स्थान लेता है।

उत्तर-

1. ✓
2. ✓
3. ✓
4.  ✓

III. रिक्त स्थान भरें

1. फर्नीचर का चयन कमरे के ……………….. के अनुसार करें।
2. पढ़ाई वाले कमरे में कुर्सी ………………. तथा बाजू वाली होनी चाहिए।
3. मेज़ के ऊपर ……………….. लगा होना चाहिए।
4. लकड़ी के फर्नीचर पर रगड़ दूर करने के लिए …… का तेल प्रयोग करें।
5. स्याही के दाग़ दूर करने के लिए ……………….. प्रयोग करें।

उत्तर-

1. रंग, आकार,
2. सीधी पीठ वाली,
3. सनमाईका,
4. अलसी,
5. आग्जैलिक तेज़ाब।

IV. एक शब्द में उत्तर दें

प्रश्न 1.
सबसे अच्छा फर्नीचर किसका होता है ?
उत्तर-
लकड़ी का।

प्रश्न 2.
जो फर्नीचर बार-बार हटाये या खिसकाये जाएं, वे किस प्रकार की लकड़ी के बने होते हैं ?
उत्तर-
हल्की लकड़ी (देवदार, अखरोट) आदि के।

प्रश्न 3.
बच्चों के फर्नीचर किसके बने होने चाहिएँ ?
उत्तर-
बेंत के।

प्रश्न 4.
पुराने फर्नीचर किस प्रकार के होते हैं ?
उत्तर-
भारी और नक्काशीदार।

प्रश्न 5.
आधुनिक फर्नीचर कैसे होते हैं तथा इनके डिज़ाइन क्या हैं ? .
उत्तर-
हल्के तथा तरल डिज़ाइन वाले।

अति लघु उत्तरीय प्रश्न

प्रश्न 1.
फर्नीचर के अन्तर्गत कौन-कौन सी वस्तुएँ आती हैं ?
उत्तर-
मेज़, कुर्सी, पलंग, चौकी, तिपाई, सोफा, मूढा, बुक-रैक, अलमारी आदि।

प्रश्न 2.
फर्नीचर कितने प्रकार का होता है ?
उत्तर-

1. लकड़ी का,
2. बेंत का,
3. गद्देदार का,
4. लोहे का,
5. कामचलाऊ,
6. अलंकृत, तथा
7. स्थान बचाऊ या फोल्डिंग।

प्रश्न 3.
फर्नीचर किस किस्म की लकड़ी का हो सकता है ?
उत्तर-
फर्नीचर लकड़ी मज़बूत और अच्छी तरह पकी हुई लकड़ी का हो सकता है।

प्रश्न 4.
कार्यात्मक फर्नीचर से क्या तात्पर्य है ?
उत्तर-
जो फर्नीचर किसी खास काम के लिए प्रयोग किया जाता हो।

प्रश्न 5.
फर्नीचर के दो आवश्यक गुण बताओ।
उत्तर-

1. आरामदायकता,
2. मज़बूती।

प्रश्न 6.
बैठक में क्या-क्या फर्नीचर होता है ?
उत्तर-
सोफासेट, गद्देदार, कुर्सियाँ, मेज़, कॉफी टेबत, केन्टर टेबल और आराम कुर्सियाँ ।

प्रश्न 7.
भोजन कक्ष में इस्तेमाल होने वाला फीस कौन-सा होता है ?
उत्तर-
भोजन की मेज़, कुर्सियाँ, परोसने की मेज़, साइड छोर्ड ट्राली (पहिये वाली मेज़)।

प्रश्न 8.
सोने के कमरे का फर्नीचर बताओ।
उत्तर-
सिंगल या डबल बैड, साइड मेज़, ड्रेसर खानों सहित, ड्रेसिंग टेबल, लोहे या लकड़ी की अलमारी, आराम कुर्सी।।

प्रश्न 9.
फर्नीचर खरीदते समय कौन-सी आवश्यक बातें ध्यान में रखनी चाहिएँ ?
उत्तर-

1. उपयोगिता,
2. सुन्दरता,
3. डिज़ाइन,
4. मूल्य,
5. आरामदायकता,
6. मज़बूती,
7. आकार, तथा
8. परिवार के सदस्यों की रुचि।

प्रश्न 10.
फर्नीचर के मुख्य लाभ क्या हैं ?
उत्तर-

1. घर में उठने-बैठने के लिए,
2. शरीर को आराम पहुँचाने के लिए,
3. काम करने में सुविधा प्रदान करना,
4. घर की सजावट,
5. सामाजिक एवं आर्थिक स्थिति का परिचय तथा
6. वस्तुओं की सुरक्षा।

प्रश्न 11.
फर्नीचर बनाने में प्रायः कौन-कौन सी लकड़ी का प्रयोग किया जाता है ?
उत्तर-
देवदार, आबनूस, शीशम, आम, सागवान, अखरोट, चीड़ आदि।

प्रश्न 12.
बेंत से कौन-से फर्नीचर बनाए जाते हैं ?
उत्तर-
मोटी बेंत से कुर्सी,सोफा, मेज़ और मूढ़े बनाये जाते हैं।

प्रश्न 13.
बेंत के फर्नीचर किस स्थान के लिए अधिक उपयोगी होते हैं ?
उत्तर-
बगीचे, बरामदे और आँगन के लिए। बच्चों के कमरों में भी ऐसे फर्नीचर उचित रहते हैं।

प्रश्न 14.
अच्छे फर्नीचर की क्या विशेषता होती है ?
उत्तर-
अच्छा फर्नीचर उपयोगी, मज़बूत, नये डिज़ाइन का, कम कीमत का तथा आरामदेह होता है।

प्रश्न 15.
फर्नीचर का चुनाव करते समय कमरे के आकार का क्या महत्त्व है ?
उत्तर-
फर्नीचर कमरे के आकार के अनुसार ही होना चाहिए। जैसे छोटे कमरे में अधिक या बड़े आकार के फर्नीचर से कमरा भरा लगेगा तथा चलने फिरने की जगह भी नहीं रहेगी।

प्रश्न 16.
सजावटी फर्नीचर से क्या भाव है ?
उत्तर-
ऐसा फर्नीचर घर की सजावट के लिए प्रयोग होता है। इस फर्नीचर पर नक्काशीदार खुदाई की होती है।

लघ उत्तरीय प्रश्न

प्रश्न 1.
फर्नीचर से क्या अभिप्राय है ?
उत्तर-
फर्नीचर’ शब्द से अभिप्राय ऐसे सामान से है जो प्रतिदिन उठने-बैठने, आराम करने, विभिन्न वस्तुओं को सुरक्षित रखने आदि के काम आता है। इसके अन्तर्गत कुर्सी, मेज़, सोफा, मूढा, तिपाई, पलंग, तख्त, चारपाई, डोली, बेंच, बुक-रैक तथा अलमारी आदि भी फर्नीचर में आते हैं।

प्रश्न 2.
घर में फर्नीचर का क्या महत्त्व है ?
उत्तर-
घर में फर्नीचर का महत्त्व निम्नलिखित प्रकार है-

1. फर्नीचर घर की आन्तरिक सजावट के लिए आवश्यक है।
2. फर्नीचर से व्यक्ति की मान-मर्यादा और प्रतिष्ठा को बढ़ावा मिलता है।
3. घर में सुसज्जित फर्नीचर से परिवार के व्यक्तित्व की झलक दिखाई देती है।
4. वस्तुओं को सुरक्षित रखने एवं कार्यों को सुविधापूर्वक करने के लिए भी फर्नीचर अत्यन्त आवश्यक है।

प्रश्न 3.
फर्नीचर कितने प्रकार का होता है ?
उत्तर-
फर्नीचर का विभाजन तीन प्रकार से किया जा सकता है-
(1) फर्नीचर किस वस्तु का बना है ?
(2) कीमत के आधार पर।
(3) उपयोगिता के आधार पर।

1. फर्नीचर किस वस्तु का बना है ?
   • लकड़ी का फर्नीचर।
   • बेंत का फर्नीचर।
   • बाँस का फर्नीचर।
   • गद्देदार फर्नीचर।
   • लोहे का फर्नीचर।
   • एल्यूमिनियम का फर्नीचर।
2.  कीमत के आधार पर-
   • कम लागत का फर्नीचर।
   • मध्यम लागत का फीचर।
   • उच्च लागत का फर्नीचर।
3. उपयोगिता के आधार पर-
   • बैठने के लिए फर्नीचर।
   • मध्यम लागत का फर्नीचर।
   • कार्य सम्पादन के लिए फर्नीचर।
   • सामान को सुरक्षित रखने के लिए फर्नीचर।

प्रश्न 4.
लकड़ी के फर्नीचर पर पॉलिश के सामान्य नियम क्या हैं ?
उत्तर-

1. पॉलिश या वार्निश लगाने से पूर्व फर्नीचर पर पड़े धूल कण तथा गन्दगी को मुलायम झाड़न से पोंछकर साफ़ कर देना चाहिए।
2. फर्नीचर को गुनगुने पानी से या सोडे से धोने पर ऊपरी मैल तथा धब्बे छूट जाते हैं।
3. पूरा फर्नीचर एक साथ गीला नहीं करना चाहिए। थोड़ा-थोड़ा भाग गीला करके साफ़ करते जाना चाहिए।
4. पॉलिश लगाने अथवा चमकाने के पूर्व लकड़ी को पूर्णतः सूख जाना चाहिए।
5. फर्नीचर पर चमक लाने के लिए साफ़ और मुलायम कपड़े से अधिक ज़ोर देकर जल्दी-जल्दी रगड़ना चाहिए।

प्रश्न 5.
फर्नीचर खरीदते समय आप किन-किन बातों का ध्यान रखोगी ?
उत्तर-

1. फर्नीचर नए डिज़ाइन का हो।
2. फर्नीचर कमरे के आकार के अनुरूप हो।
3. फर्नीचर आर्थिक दृष्टि से मितव्ययी हो।
4. फर्नीचर स्थान की दृष्टि से मितव्ययी हो।
5. फर्नीचर कमरे के लिए उपयोगी हो।
6. फर्नीचर मज़बूत व टिकाऊ हो।
7. फर्नीचर उपयोगी और सुन्दर होने के साथ-साथ आरामदायक हो।
8. फर्नीचर एक स्थान से दूसरे स्थान पर ले जाने में सुविधाजनक हो।
9. फर्नीचर सदैव अच्छे कारीगर द्वारा बना हो।

प्रश्न 6.
फर्नीचर की देखभाल के नियम बताइए।
उत्तर-
फर्नीचर की देखभाल के लिए निम्नलिखित नियमों का पालन करना चाहिए-

1. फर्नीचर पर गद्दियों तथा कवर आदि का प्रयोग करना चाहिए।
2. फर्नीचर की टूट-फूट होने पर उसकी मरम्मत तुरन्त करवानी चाहिए।
3. फर्नीचर को रोज़ सूखे कपड़े से पोंछकर साफ़ रखना चाहिए।
4. नक्काशीदार फर्नीचर को ब्रुश के प्रयोग से साफ़ रखना चाहिए।
5. फर्नीचर को नमी या धूप के स्थान पर नहीं रखना चाहिए।
6. आवश्यकता अनुभव होने पर फर्नीचर की पॉलिश करवानी चाहिए।
7. फर्नीचर उठाते या सरकाते समय सावधानी बरतनी चाहिए।

प्रश्न 7.
बहुउद्देशीय स्थान-बचाऊ की क्या उपयोगिता है ?
उत्तर-
बहुउद्देशीय स्थान-बचाऊ फर्नीचर फोल्डिंग (मुड़ने वाला) फर्नीचर होता है, जैसे सोफा-कम-बैड, फोल्डिंग कुर्सियाँ, मशीन कवर-कम-टेबल आदि। छोटे घरों में इसकी बहुत उपयोगिता होती है-

1. यह स्थान कम घेरता है।
2. फोल्डिंग सोफे को रात्रि में खोलकर पलंग का काम लिया जा सकता है।
3. रात्रि में फोल्डिंग कुर्सियों व मेज़ आदि को फोल्ड करके रख देने से छोटे घर में स्थान की समस्या हल हो जाती है।
4. तबादले के समय सामान एक स्थान से दूसरे स्थान पर ले जाने में सुविधा रहती है।

प्रश्न 8.
मुख्य प्रकार के फर्नीचर तथा उनके उदाहरण बताओ।
उत्तर-

1. लकड़ी का फर्नीचर-कुर्सी, मेज़, पलंग, चौकी,तख्त, अलमारी आदि।
2. बेंत का फर्नीचर-कुर्सी, मेज़, सोफा, मूढ़े आदि।
3. गद्देदार फर्नीचर-सोफा, गद्देदार, कुर्सियाँ आदि।
4. लोहे का फर्नीचर-फोल्डिंग टेबल, कुर्सियाँ, अलमारियाँ, रैकं आदि।
5. अलंकृत फर्नीचर- नक्काशीदार फर्नीचर।
6. काम चलाऊ फर्नीचर-बॉक्स पर गद्दी, बिछाकर बेंच के रूप में, लकड़ी की पेटियों की बुक-रैक, क्रॉकरी तथा बर्तन रखने की अलमारी आदि।

प्रश्न 9.
घर में कौन-कौन से फर्नीचर प्रयोग में लाये जाते हैं ?
उत्तर-
घर में निम्नलिखित फर्नीचर प्रयोग में लाए जाते हैं-

1. सोफासेट-लकड़ी का, स्प्रिंग वाला गद्देदार, फोम रबड़ का, बेंत का या फोल्डिंग।
2. कुर्सियाँ-साधारण, ड्राइंग रूम के लिए, भोजन कक्ष के लिए, अध्ययन कक्ष के लिए फोल्डिंग कुर्सी तथा आराम कुर्सियाँ।
3. मेज़-बैठक के लिए केन्द्रीय मेज़, बगल वाली मेज़, कोने वाली मेज़ व कॉफी मेज़, खाने की मेज़ (डाइनिंग टेबल), श्रृंगार मेज़, पढ़ने की मेज़।
4.  चारपाई तथा पलंग।
5. तख्त और दीवान।
6. अलमारियाँ-दीवार में बनी, लकड़ी की, स्टील की तथा रैक।
7. शो केस।
8. वॉल केबिनेट।

प्रश्न 10.
‘महँगा रोए एक बार सस्ता रोए बार-बार’ पर टिप्पणी दो।
उत्तर-
घर के उपयोग की कुछ वस्तुएँ ऐसी होती हैं जिन्हें जीवन में प्रायः एक-दो बार ही खरीदा जाता है, जैसे-मकान, टी० वी०, फ्रिज़, फर्नीचर आदि। ऐसी वस्तुएँ जब खरीदी जाती हैं तब उनके मूल्य की ओर इतना ध्यान न देकर उनकी मज़बूती, आरामदेहता तथा बनावट की ओर अधिक ध्यान दिया जाता है। कुछ लोग नासमझी में सस्ती वस्तुएँ खरीद तो लेते हैं, परन्तु उनके खराब होने या टूट जाने पर उन्हें दूसरी बार या कई बार खरीदना पड़ता है। तात्पर्य यह है कि एक ही बार सोच-समझकर अधिक पैसे खर्च कर अच्छी चीज़ खरीदना या कम पैसे खर्च कर सस्ती चीज़ कई बार खरीदना, इन दोनों बातों के आधार पर ही यह कथन है कि ‘महँगा रोए एक बार’ ‘सस्ता रोए बार-बार’।

दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
विभिन्न प्रकार के फर्नीचर का वर्णन कीजिए।
उत्तर-
फर्नीचर विभिन्न प्रकार के होते हैं जो निम्नलिखित हैं-
1. लकड़ी का फर्नीचर-लकड़ी का फर्नीचर हल्का होता है। यह धूप तथा पानी से खराब हो जाता है। घरों में काम आने वाला अधिकतर फर्नीचर, जैसे-मेज़, कुर्सी, पलंग, अलमारी, चौकी आदि प्रायः लकड़ी का ही बना होता है। इस प्रकार के फर्नीचर देवदार, शीशम, आम, सागवान, अखरोट, चीड़, आबनूस आदि लकड़ी के बनते हैं। फर्नीचर की कीमत लकड़ी पर निर्भर करती है। सागवान तथा शीशम का फर्नीचर सुदृढ़, आकर्षक, भारी एवं मज़बूत होता है। आजकल पर्ती लकड़ी (प्लाइवुड) का फर्नीचर भी बनाया जाता है।

2. बेंत का फर्नीचर-बेंत का फर्नीचर विभिन्न रंगों का तथा हल्का होता है। बेंत का फर्नीचर मज़बूत नहीं होता। यह देखी में सुन्दर लगता है। बच्चों के कमरों में इस प्रकार का फर्नीचर उपयोगी होता है। बेंत का फर्नीचर बगीचे, बरामदे तथा आँगन के लिए भी उपयोगी होता है। लकड़ी की कुर्सी में भी बेंत का जाल बुना जा सकता है। मोटी बेंत द्वारा कुर्सी, मेज़, सोफा, मूढ़े आदि बनाये जाते हैं।

3. गद्देदार फर्नीचर-गद्देदार फर्नीचर, जैसे-सोफासेट, गद्देदार कुर्सियाँ, तिपाई आदि लकड़ी या धातु के ढाँचे में जूट, नारियल के रेशे, रूई तथा भूसा आदि भरकर तथा स्प्रिंग डालकर बनाए जाते हैं। इन्हें ऊपर से चमड़े, रेक्सीन या प्लास्टिक से ढका जाता है। गद्दों में फोम, रबर, डनलप का प्रयोग भी किया जाता है। ये टिकाऊ तथा आरामदायक होता है।

4. स्टील या लोहे का फर्नीचर-स्टील या लोहे का फर्नीचर प्रायः लोहे की चादरों तथा खोखले पाइप से बनाया जाता है। लोहे का फर्नीचर हल्का तथा मज़बूत होता है। इस पर आसानी से रंग चढ़ाया जा सकता है। इसमें सीलन तथा कीड़े-मकोड़े नहीं घुस सकते। इससे बनी कुर्सियों में गद्दों का तथा गद्दों पर रेक्सीन व चमड़े का कवर लगाया जाता है। इसके अन्तर्गत मुड़ने वाला (फोल्डिंग) फर्नीचर भी आता है। सुरक्षा की दृष्टि से मूल्यवान वस्तुओं को रखने के लिए स्टील की पेटियाँ तथा अलमारियाँ काम में लाई जाती हैं।

5. बाँस का फर्नीचर-बाँस से सोफासेट, गोल एवं चौकोर कुर्सियाँ, मेज़, मूढ़े आदि बनाए जाते हैं। ये अधिक सस्ते होते हैं तथा इन पर पॉलिश की जा सकती है। ये अधिक हल्के होते हैं।

6. एल्यूमीनियम का फर्नीचर-आजकल एल्यूमीनियम की बनी नलियों के फ्रेम वाले फर्नीचर प्रचलित हो गए हैं। कुर्सियों, स्टूलों, मेज़ों और पलंगों के फ्रेम एल्यूमीनियम के बनने लगे हैं। ये सस्ते और हल्के होते हैं। इन पर नायलॉन की तारों और निवाड़ की बुनाई होती है।

7. कामचलाऊ फर्नीचर-धन की कमी के कारण उपलब्ध सामग्री को फर्नीचर के रूप में प्रयोग किया जा सकता है, जैसे सामान की पेटी पर गद्दी तथा चादर बिछाकर बेंच का काम लिया जा सकता है। कम दामों में लकड़ी की पेटियाँ खरीदकर उनसे बुक-रैक, क्रॉकरी तथा बर्तन रखने की अलमारी बनायी जा सकती है।

8. अलंकृत फर्नीचर-कुछ फर्नीचर नक्काशीदार खुदाई किए हुए भी बनाया जाता है। इस प्रकार के फर्नीचर पर धूल-मिट्टी की पर्ते जम जाती है। इस फर्नीचर की आसानी से सही सफ़ाई नहीं हो पाती। सफ़ाई न होने से यह अनाकर्षक दिखायी देने लगता है।

9. आधुनिक स्थानबचाऊ बहुउद्देशीय फर्नीचर-आज बड़े-बड़े शहरों जैसे मुम्बई, कोलकाता, दिल्ली आदि में स्थान की कमी के कारण आधुनिक स्थानबचाऊ फर्नीचर का उपयोग किया जाता है। स्थानबचाऊ बहुउद्देशीय फर्नीचर फोल्डिंग होता है, जैसे सोफाकम-बैड जिसे दिन में सोफे के रूप में तथा रात्रि में उसे खोलकर बिस्तर के रूप में प्रयोग किया जा सकता है। सिलाई मशीनें भी इस तरह की होती हैं जिसमें आवश्यकतानुसार पहिया लगाकर चौकोर मेज़ के रूप में प्रयोग किया जाता है। आजकल विभिन्न प्रकार के फोल्डिंग, मेज़, कुर्सी, पलंग बनाये जाते हैं जो बन्द करके रखे जा सकते हैं।

प्रश्न 2.
आप घर में अलग-अलग प्रकार के फर्नीचर की देखभाल कैसे करेंगे ?
उत्तर-
स्वयं करें।

कार्यात्मक फर्नीचर PSEB 8th Class Home Science Notes

• फर्नीचर दो प्रकार के होते हैं-कार्यात्मक और सजावट वाले।
• कार्यात्मक फर्नीचर वह होता है जिसका अलग-अलग काम हो।
• सजावटी फर्नीचर केवल सजावट के लिए होता है।
• फर्नीचर खरीदते समय डिज़ाइन का ध्यान रखना बहुत आवश्यक है।
• सबसे अच्छा फर्नीचर लकड़ी का होता है।
• फर्नीचर के जोड़ मज़बूत होने चाहिएँ।
• फर्नीचर आरामदेह होना चाहिए।
• लकड़ी के फर्नीचर को प्रतिदिन बड़े ध्यान से साफ़ करना चाहिए।
• लकड़ी के फर्नीचर पर कोई चीज़ गिर जाए तो उसको वहीं सूखने नहीं देना चाहिए। उसको उसी समय साफ़ कर देना चाहिए।
• चिकने और चिपकने वाले दागों के लिए गुनगुने पानी का इस्तेमाल करना चाहिए।
• पेंट या रोगन के दाग के लिए मैथिलेटिड स्पिरिट इस्तेमाल में लानी चाहिए और फर्नीचर पर पॉलिश करनी चाहिए।
• साल में एक दो बार फर्नीचर को अच्छी तरह साफ़ करके पॉलिश करना चाहिए।
• चाय, कॉफी, कलों के रस के दागों के लिए पानी में थोड़ा-सा नरम साबुन घोलकर कपड़े के साथ साफ़ करना चाहिए।
• गद्देदार फर्नीचर को आवश्यकतानुसार ड्राइक्लीन करवाना चाहिए।
•  बेंत वाले फर्नीचर को नमक वाले पानी से साफ़ करना चाहिए।

Punjab State Board PSEB 12th Class History Book Solutions Chapter 8 गुरु हर राय जी और गुरु हर कृष्ण जी Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 History Chapter 8 गुरु हर राय जी और गुरु हर कृष्ण जी

निबंधात्मक प्रश्न (Essay Type Questions)

गुरु हर राय जी (Guru Har Rai Ji)

प्रश्न 1.
गुरु हर राय जी के जीवन और उपलब्धियों के संबंध में आप क्या जानते हैं ? (What do you know about Guru Har Rai Ji’s early career and achievements ?)
उत्तर-
गुरु हर राय जी सिखों के सातवें गुरु थे। उनके गुरुकाल (1645 से 1661 ई०) को सिख पंथ का शांतिकाल कहा जा सकता है। गुरु हर राय जी के आरंभिक जीवन तथा उनके अधीन सिख पंथ के विकास का संक्षिप्त वर्णन इस प्रकार है—
1. जन्म तथा माता-पिता (Birth and Parentage)-गुरु हर राय जी का जन्म 30 जनवरी, 1630 ई० को कीरतपुर साहिब नामक स्थान पर हुआ। उनके माता जी का नाम बीबी निहाल कौर था। आप गुरु हरगोबिंद जी के पौत्र तथा बाबा गुरदित्ता जी के पुत्र थे।

2. बाल्यकाल तथा विवाह (Childhood and Marriage)-आप बाल्यकाल से ही शाँत प्रकृति, मृदुभाषी तथा दयालु स्वभाव के थे। कहते हैं कि एक बार हर राय जी बाग में सैर कर रहे थे। उनके चोले से लग जाने से कुछ फूल झड़ गए। यह देखकर आपकी आँखों में आँसू आ गए। आप किसी का भी दुःख सहन नहीं कर सकते थे।
आपका विवाह अनूप शहर (यू० पी०) के दया राम जी की सुपुत्री सुलक्खनी जी से हुआ। आपके घर दो पुत्रों राम राय तथा हर कृष्ण ने जन्म लिया।

3. गुरुगद्दी की प्राप्ति (Assumption of Guruship)-गुरु हरगोबिंद जी के पाँच पुत्र थे। बाबा गुरदित्ता, अणि राय तथा अटल राय अपने पिता के जीवन काल में स्वर्गवास को चुके थे। शेष दो में से सूरजमल का सांसारिक मामलों की ओर आवश्यकता से अधिक झुकाव था तथा तेग़ बहादुर जी का बिल्कुल नहीं। इसलिए गुरु हरगोबिंद जी ने बाबा गुरदित्ता के छोटे पुत्र हर राय जी को अपना उत्तराधिकारी बनाया। आप 8 मार्च, 1645 ई० को गुरुगद्दी पर विराजमान हुए। इस प्रकार आप सिखों के सातवें गुरु बने।

4. गुरु हर राय जी के समय में सिख धर्म का विकास (Development of Sikhism under Guru Har Rai Ji)—आप 1645 ई० से 1661 ई० तक गुरुगद्दी पर विराजमान रहे। आपने सिख धर्म के प्रचार के लिए तीन मुख्य केंद्र स्थापित किए जिन्हें ‘बख्शीशें’ कहा जाता था। पहली बख्शीश एक संन्यासी गिरि की थी जिसकी भक्ति से प्रसन्न होकर गुरु साहिब ने उसका नाम भक्त भगवान रख दिया। उसने पूर्वी भारत में सिख धर्म के बहुत-से केंद्र स्थापित किए। इनमें पटना, बरेली तथा राजगिरी के केंद्र प्रसिद्ध हैं। दूसरी बख्शीश सुथरा शाह की थी। उसे सिख धर्म के प्रचार के लिए दिल्ली भेजा गया। तीसरी बख्शीश भाई फेरु की थी। उनको राजस्थान भेजा गया था। इसी प्रकार भाई नत्था जी को ढाका, भाई जोधा जी को मुलतान भेजा गया तथा आप स्वयं पंजाब के कई स्थानों जैसे जालंधर, करतारपुर, हकीमपुर, गुरदासपुर, अमृतसर, पटियाला, अंबाला तथा हिसार आदि गए।

5. फूल को आशीर्वाद (Blessing to Phool)-एक दिन काला नामक श्रद्धालु अपने भतीजों संदली तथा फूल को गुरु जी के दर्शन हेतु ले आया। उनकी शोचनीय हालत को देखते हुए गुरु साहिब ने उन्हें आशीर्वाद दिया कि एक दिन वे बहुत धनी बनेंगे। गुरु जी की यह भविष्यवाणी सत्य निकली। फूल की संतान ने फूलकिया मिसल की स्थापना की।

6. राजकुमार दारा की सहायता (Help to Prince Dara)-गुरु हर राय जी के समय दारा शिकोह पंजाब का गवर्नर था। वह औरंगज़ेब का बड़ा भाई था। सत्ता प्राप्त करने के प्रयास में औरंगज़ेब ने उसे विष दे दिया। इस कारण वह बहुत बीमार हो गया। उसने गुरु साहिब से आशीर्वाद माँगा। गुरु साहिब ने अमूल्य जड़ी-बूटियाँ देकर दारा की चिकित्सा की। इस कारण वह गुरु साहिब का आभारी हो गया। वह प्रायः उनके दर्शन के लिए आया करता।

7. गुरु हर राय जी को दिल्ली बुलाया गया (Guru Har Rai Ji was summoned to Delhi)औरंगज़ेब को संदेह था कि गुरु ग्रंथ साहिब में कुछ श्लोक इस्लाम धर्म के विरुद्ध हैं। इस बात की पुष्टि के लिए उसने आपको अपने दरबार में उपस्थित होने के लिए कहा। गुरु साहिब ने अपने पुत्र रामराय को औरंगजेब के पास भेजा। औरंगजेब ने ‘आसा दी वार’ में से एक पंक्ति की ओर संकेत करते हुए उससे पूछा कि इसमें मुसलमानों का विरोध क्यों किया गया है। यह पंक्ति थी,
मिटी मुसलमान की पेडै पई कुम्हिआर॥
घड़ भाँडे इटा कीआ जलदी करे पुकार॥
इसका अर्थ था मुसलमान की मिट्टी कुम्हार के घमट्टे में चली जाएगी जो इससे बर्तन तथा ईंटें बनाएगा। जैसेजैसे वह जलेगी तैसे-तैसे मिट्टी चिल्लाएगी। औरंगज़ेब के क्रोध से बचने के लिए रामराय ने कहा कि इस पंक्ति में भूल से बेईमान शब्द की अपेक्षा मुसलमान शब्द लिखा गया है। गुरु ग्रंथ साहिब के इस अपमान के कारण आपने रामराय को गुरुगद्दी से वंचित कर दिया।

8. उत्तराधिकारी की नियुक्ति (Nomination of the Successor)—गुरु हर राय जी ने ज्योति-जोत समाने से पूर्व आपने गुरुगद्दी अपने छोटे पुत्र हर कृष्ण को सौंप दी। 6 अक्तूबर, 1661 ई० को गुरु हर राय जी ज्योति जोत समा गए।

9. गुरु हर राय जी के कार्यों का मूल्याँकन (Estimate of the works of Guru Har Rai Ji)-गुरु हर राय जी हालाँकि अल्प आयु में ही ज्योति-जोत समा गए परंतु उन्होंने सिख पंथ के विकास में अमूल्य योगदान दिया। आप जी ने माझा, दोआबा और मालवा में सिख धर्म का प्रचार किया। आपने संगत और पंगत की मर्यादा को पूरी तेजी के साथ जारी रखा। आपके दवाखाने से बिना किसी भेद-भाव के निःशुल्क चिकित्सा और सेवा प्रदान की जाती थी। इस प्रकार आपने सिख धर्म के विकास में महत्त्वपूर्ण योगदान दिया।

गुरु हर कृष्ण जी (Guru Har Krishan Ji)

प्रश्न 2.
गुरु हर कृष्ण जी के समय सिख पंथ के हुए विकास का संक्षिप्त वर्णन करें।
(Give a brief account of Development of Sikhism during the pontificate of Guru Har Kishan Ji.)
उत्तर-
गुरु हर कृष्ण जी सिख इतिहास में बाल गुरु के नाम से जाने जाते हैं। वे 1661 ई० से लेकर 1664 ई० तक गुरुगद्दी पर विराजमान रहे। उनके अधीन सिख पंथ में हुए विकास का वर्णन निम्नलिखित अनुसार है—
1. जन्म और माता-पिता (Birth and Parents)-गुरु हर कृष्ण जी का जन्म 7 जुलाई, 1656 ई० में कीरतपुर साहिब में हुआ। आप गुरु हर राय साहिब के छोटे पुत्र थे। आप जी की माता का नाम सुलक्खनी जी था। रामराय आपके बड़े भाई थे।

2. गुरुगद्दी की प्राप्ति (Assumption of Guruship)-गुरु हर राय जी ने अपने बड़े पुत्र राम राय को उसकी अयोग्यता के कारण गुरुगद्दी से वंचित कर दिया था । 1661 ई० को गुरु हर राय जी ने हर कृष्ण जी को गुरुगद्दी सौंप दी। उस समय हर कृष्ण जी की आयु मात्र 5 वर्ष थी। इस कारण इतिहास में आपको बाल गुरु के नाम से याद किया जाता है। यद्यपि आप उम्र में बहुत छोटे थे पर फिर भी आप बहुत उच्च प्रतिभा के स्वामी थे। आप में अद्वितीय सेवा भावना, बड़ों के प्रति मान-सम्मान, मीठा बोलना, दूसरों के प्रति सहानुभूति तथा अटूट भक्तिभावना इत्यादि के गुण कूट-कूट कर भरे हुए थे। इन गुणों के कारण ही गुरु हर राय जी ने आपको गुरुगद्दी सौंपी। इस प्रकार आप सिखों के आठवें गुरु बने। आप 1664 ई० तक गुरुगद्दी पर विराजमान रहे।

3. राम राय का विरोध (Opposition of Ram Rai)-राम राय गुरु हर राय जी का बड़ा पुत्र होने के कारण गुरु साहिब के पश्चात् गुरुगद्दी का अधिकारी स्वयं को समझता था, परंतु गुरु हर राय जी उसे पहले ही गुरुगद्दी से वंचित कर चुके थे। जब उसे ज्ञात हुआ कि गुरुगद्दी हर कृष्ण जी को सौंपी गई है तो वह यह बात सहन न कर सका। उसने गद्दी हथियाने के लिए षड्यंत्र रचने आरंभ कर दिए। उसने बहुत-से बेईमान और स्वार्थी मसंदों को अपने साथ मिला लिया। इन मसंदों द्वारा उसने यह घोषणा करवाई कि वास्तविक गुरु राम राय हैं और सभी सिख उसी – अपना गुरु मानें परंतु वह उसमें सफल न हो पाया। फिर उसने औरंगजेब से सहायता लेने का प्रयास किया। औरंगजेब ने गुरु साहिब को दिल्ली बुलाया ताकि दोनों गुटों की बात सुनकर वह अपना निर्णय दे सके।

4. गुरु साहिब का दिल्ली जाना (Guru Sahib’s Visit to Delhi)—गुरु साहिब को दिल्ली लाने का कार्य औरंगज़ेब ने राजा जय सिंह को सौंपा। राजा जय सिंह ने अपने दीवान परस राम को गुरु जी के पास भेजा। गुरु जी ने औरंगजेब से मिलने और दिल्ली जाने से इंकार कर दिया, परंतु परस राम के यह कहने पर कि दिल्ली की संगतें गुरु साहिब के दर्शनों के लिए बेताब हैं, गुरु साहिब ने दिल्ली जाना तो स्वीकार कर लिया, परंतु औरंगजेब से भेंट करने से इंकार कर दिया। आप 1664 ई० में दिल्ली चले गए और राजा जय सिंह के घर निवास करने के लिए मान गए। गुरु साहिब की औरंगजेब से भेंट हुई अथवा नहीं, इस संबंध में इतिहासकारों में बहुत मतभेद पाए जाते हैं।

5. ज्योति-जोत समाना (Immersed in Eternal Light)—उन दिनों दिल्ली में चेचक और हैजा फैला हुआ था। गुरु हर कृष्ण जी ने यहाँ बीमारों, निर्धनों और लावारिसों की तन, मन और धन से अथक सेवा की। चेचक और हैज़े के सैंकड़ों रोगियों को ठीक किया, परंतु इस भयंकर बीमारी का आप स्वयं भी शिकार हो गए। यह बीमारी उनके लिए घातक सिद्ध हुई। उन्हें बहुत गंभीर अवस्था में देखते हुए श्रद्धालुओं ने प्रश्न किया कि आपके पश्चात् उनका नेतृत्व कौन करेगा तो आप ने एक नारियल मंगवाया। नारियल और पाँच पैसे रखकर माथा टेका और “बाबा बकाला” का उच्चारण करते हुए 30 मार्च, 1664 ई० को दिल्ली में ज्योति-जोत समा गए। आपकी याद में यहाँ गुरुद्वारा बाला साहिब का निर्माण किया गया है।

गुरु हर कृष्ण जी ने कोई अढ़ाई वर्ष के लगभग गुरुगद्दी संभाली और गुरु के रूप में आपने सभी कर्त्तव्य बड़ी सूझ-बूझ से निभाए। आप इतनी कम आयु में भी तीक्ष्ण बुद्धि, उच्च विचार और अलौकिक ज्ञान के स्वामी थे।

संक्षिप्त उत्तरों वाले प्रश्न (Short Answer Type Questions)

प्रश्न 1.
सिख पंथ के विकास में गुरु हर राय जी का गुरुकाल क्यों महत्त्वपूर्ण है ?
(Why is pontificate of Guru Har Rai Ji considered important in the development of Sikhism ?).
अथवा
गुरु हर राय जी पर एक संक्षिप्त नोट लिखें।
(Write a short note on Guru Har Rai Ji.)
अथवा
सिख धर्म में गुरु हर राय जी का क्या योगदान है ?
(What is the contribution of Guru Har Rai Ji for the development of Sikh religion ?)
अथवा
गुरु हर राय जी के जीवन एवं कार्यों के बारे में संक्षेप में लिखें। (Write in short about the life and works of Guru Har Rai Ji.)
उत्तर-
सिखों के सातवें गुरु, गुरु हर राय जी का जन्म 30 जनवरी, 1630 ई० को कीरतपुर साहिब में हुआ था। आप बचपन से ही साधू स्वभाव के थे। 1645 ई० से लेकर 1661 ई० तक गुरुगद्दी पर विराजमान रहे। उनका गुरुकाल सिख धर्म के शांतिपूर्वक विकास का काल था। गुरु हर राय साहिब ने सिख धर्म का प्रचार करने के लिए पंजाब के कई स्थानों का भ्रमण किया। इसके अतिरिक्त गुरु साहिब ने पंजाब से बाहर अपने प्रचारक भेजे। परिणामस्वरूप सिख धर्म का काफ़ी प्रसार हुआ। गुरु जी ने अपने छोटे पुत्र हर कृष्ण को अपना उत्तराधिकारी नियुक्त किया।

प्रश्न 2.
धीरमल संबंधी एक संक्षिप्त नोट लिखें।
(Write a short note about Dhirmal.)
उत्तर-
धीरमल गुरु हर राय जी का बड़ा भाई था। वह चिरकाल से गुरुगद्दी प्राप्त करने का प्रयत्न कर रहा था। जब धीर मल को यह समाचार. मिला कि सिख संगतों ने तेग़ बहादुर जी को अपना गुरु मान लिया है तो उसके क्रोध की कोई सीमा न रही। उसने शींह नामक एक मसंद के साथ मिल कर गुरु जी की हत्या का षड्यंत्र रचा। शीह के साथियों ने गुरु साहिब के घर का बहुत-सा सामान लूट लिया। बाद में धीरमल तथा शींह द्वारा क्षमा याचना करने पर गुरु साहिब ने उन्हें क्षमा कर दिया।

प्रश्न 3.
गुरु हर कृष्ण जी पर एक संक्षिप्त नोट लिखें। उनको बाल गुरु क्यों कहा जाता है?
(Write a brief note on Guru Har Krishsn Ji. Why is He called Bal Guru ?)
अथवा
सिख धर्म में गुरु हर कृष्ण जी का क्या योगदान था ?
(What was the contribution of Guru Har Krishan Ji in the development of Sikhism ?)
अथवा
गुरु हर कृष्ण जी पर संक्षेप नोट लिखो। (Write a short note on Guru Har Krishan Ji.)
उत्तर-
सिखों के आठवें गुरु, गुरु हर कृष्ण जी गुरु हर राय जी के छोटे पुत्र थे। वह 1661 ई० में गुरुगद्दी पर विराजमान हुए। उस समय उनकी आयु केवल पाँच वर्ष थी। इस कारण उनको ‘बाल गुरु’ के नाम से याद किया जाता है। गुरु हर कृष्ण जी के बड़े भाई राम राय के उकसाने पर औरंगजेब ने गुरु साहिब को दिल्ली आने का आदेश दिया। गुरु साहिब 1664 ई० में दिल्ली गए। उन दिनों दिल्ली में भयानक चेचक एवं हैजा फैला हुआ था। गुरु जी ने वहाँ पर बीमारों की अथक सेवा की। वह 30 मार्च, 1664 ई० को ज्योति-जोत समा गए।

वस्तुनिष्ठ प्रश्न (Objective Type Questions)

(i) एक शब्द से एक पंक्ति तक के उत्तर (Answer in One Word to One Sentence)

प्रश्न 1.
गुरु हरगोबिंद जी के उत्तराधिकारी कौन थे ?
अथवा
गुरु हरगोबिंद जी ने किसको अपना उत्तराधिकारी बनाया ?
उत्तर-
गुरु हर राय जी।

प्रश्न 2.
गुरु हर राय जी का जन्म कहाँ हुआ था ?
उत्तर-
कीरतपुर साहिब।

प्रश्न 3.
गुरु हर राय जी के.पिता जी का नाम बताएँ।
उत्तर-
बाबा गुरदित्ता जी।

प्रश्न 4.
सिखों के सातवें गुरु कौन थे ?
अथवा
सातवें सिख गुरु का क्या नाम था ?
उत्तर-
गुर हर राय जी।

प्रश्न 5.
गुरु हर राय जी कब गुरुगद्दी पर आसीन हुए ?
उत्तर-
1645 ई०

प्रश्न 6.
दारा शिकोह कौन था ?
उत्तर-
शाहजहाँ का सबसे बड़ा पुत्र।

प्रश्न 7.
गुरु हर राय जी ने सिख धर्म के प्रचार के लिए काबुल किसे भेजा था ?
उत्तर-
भाई गोंदा जी को।

प्रश्न 8.
गुरु हर राय जी ने सिख धर्म के प्रचार के लिए ढाका किसे भेजा था ?
उत्तर-
भाई नत्था जी को।

प्रश्न 9.
गुरु हर राय जी कब ज्योति-जोत समाए ?
उत्तर-
1661 ई०।

प्रश्न 10.
सिखों के आठवें गुरु कौन थे ?
उत्तर-
गुरु हर कृष्ण जी।

प्रश्न 11.
गुरु हर कृष्ण जी का जन्म कहाँ हुआ?
उत्तर-
कीरतपुर साहिब।

प्रश्न 12.
गुरु हर कृष्ण जी का जन्म कब हुआ था?
उत्तर-
7 जुलाई, 1656 ई०।

प्रश्न 13.
गुरु हर कृष्ण जी गुरुगद्दी पर कब बैठे ?
उत्तर-
1661 ई०।

प्रश्न 14.
सिखों के बाल गुरु कौन थे ?
उत्तर-
गुरु हर कृष्ण जी।

प्रश्न 15.
गुरु हर कृष्ण जी का गुरुकाल बताएँ।
उत्तर-
1661 ई० से 1664 ई०

प्रश्न 16.
गुरुगद्दी पर बैठने के पश्चात् गुरु हर कृष्ण जी को किसके विरोध का सामना करना पड़ा ?
उत्तर-
राम राय के

प्रश्न 17.
गुरु हर कृष्ण जी कब ज्योति-जोत समाए ?
उत्तर-
1664 ई०

प्रश्न 18.
गुरु हर कृष्ण जी कहाँ ज्योति-जोत समाए थे ?
उत्तर-
दिल्ली।

(ii) रिक्त स्थान भरें (Fill in the Blanks)

प्रश्न 1.
…………… सिखों के सातवें गुरु थे।
उत्तर-
(गुरु हर राय जी)

प्रश्न 2.
गुरु हर राय जी का जन्म …………… में हुआ।
उत्तर-
(1630 ई०)

प्रश्न 3.
गुरु हर राय जी का जन्म …………. नाम के स्थान पर हुआ।
उत्तर-
(कीरतपुर साहिब)

प्रश्न 4.
गुरु हर राय जी के पिता का नाम …………. था।
उत्तर-
(बाबा गुरदित्ता जी)

प्रश्न 5.
गुरु हर राय जी ……………. में गुरुगद्दी पर बैठे। .
उत्तर-
(1645 ई०)

प्रश्न 6.
……………. सिखों के आठवें गुरु थे।
उत्तर-
(गुरु हर कृष्ण जी)

प्रश्न 7.
गुरु हर कृष्ण जी ……………. में गुरुगद्दी पर बैठे।
उत्तर-
(1661 ई०)

प्रश्न 8.
गुरु हर कृष्ण जी दिल्ली में ………… के बंगले में ठहरे।
उत्तर-
(राजा जय सिंह)

प्रश्न 9.
………… को बाल गुरु के नाम से याद किया जाता है।
उत्तर-
(गुरु हर कृष्ण जी)

(ii) ठीक अथवा गलत (True or False)

नोट-निम्नलिखित में से ठीक अथवा गलत चुनें।

प्रश्न 1.
गुरु हर राय जी सिखों के सातवें गुरु थे।
उत्तर-
ठीक

प्रश्न 2.
गुरु हर राय जी का जन्म 1630 ई० में हुआ था।
उत्तर-
ठीक

प्रश्न 3.
गुरु हर राय जी के पिता जी का नाम बाबा बुड्डा जी था।
उत्तर-
गलत

प्रश्न 4.
गुरु हर राय जी की माता जी का नाम बीबी निहाल कौर था।
उत्तर-
ठीक

प्रश्न 5.
गुरु हर राय जी 1661 ई० में गुरुगद्दी पर बिराजमान हुए।
उत्तर-
गलत

प्रश्न 6.
गुरु हर कृष्ण जी सिखों के आठवें गुरु थे।
उत्तर-
ठीक

प्रश्न 7.
गुरु हर कृष्ण जी को बाल गुरु के नाम से भी जाना जाता है।
उत्तर-
ठीक

प्रश्न 8.
गुरु हर कृष्ण जी 1664 ई० में ज्योति-ज्योत समाए।
उत्तर-
ठीक

(iv) बहु-विकल्पीय प्रश्न (Multiple Choice Questions):

नोट-निम्नलिखित में से ठीक उत्तर का चयन कीजिए

प्रश्न 1.
सिखों के सातवें गुरु कौन थे ?
(i) गुरु हरगोबिंद जी
(ii) गुरु हर राय जी
(iii) गुरु हर कृष्ण जी
(iv) गुरु तेग़ बहादुर जी।
उत्तर-
(ii)

प्रश्न 2.
गुरु हर राय जी का जन्म कब हुआ ?
(i) 1627 ई० में
(ii) 1628 ई० में
(iii) 1629 ई० में
(iv) 1630 ई० में।
उत्तर-
(iv)

प्रश्न 3.
गुरु हर राय जी के पिता जी का क्या नाम था ?
(i) गुरदित्ता जी
(ii) अटल राय जी
(ii) अणि राय जी
(iv) सूरजमल जी।
उत्तर-
(i)

प्रश्न 4.
गुरु हर राय जी गुरुगद्दी पर कब बैठे ?
(i) 1635 ई० में
(ii) 1637 ई० में
(ii) 1645 ई० में ,
(iv) 1655 ई० में।
उत्तर-
(iii)

प्रश्न 5.
दारा शिकोह कौन था ?
(i) शाहजहाँ का बड़ा बेटा
(ii) शाहजहाँ का छोटा बेटा
(iii) जहाँगीर का बड़ा बेटा
(iv) औरंगज़ेब का बड़ा बेटा।
उत्तर-
(i)

प्रश्न 6.
गुरु हर राय जी ने अपना उत्तराधिकारी किसको नियुक्त किया ?
(i) हर कृष्ण जी को
(ii) तेग़ बहादुर जी को
(iii) राम राय को
(iv) गुरदित्ता जी को।
उत्तर-
(i)

प्रश्न 7.
गुरु हर राय जी कब ज्योति-जोत समाए थे ?
(i) 1645 ई० में
(ii). 1660 ई० में
(iii) 1661 ई० में
(iv) 1664 ई० में।
उत्तर-
(iii)

प्रश्न 8.
सिखों के आठवें गुरु कौन थे ?
(i) गुरु हर कृष्ण जी
(ii) गुरु तेग बहादुर जी
(iii) गुरु हर राय जी
(iv) गुरु गोबिंद सिंह जी।
उत्तर-
(i)

प्रश्न 9.
गुरु हर कृष्ण जी का जन्म कब हुआ ?
(i) 1630 ई० में
(ii) 1635 ई० में
(iii) 1636 ई० में
(iv) 1656 ई० में।
उत्तर-
(iv)

प्रश्न 10.
गुरु हर कृष्ण जी के पिता जी कौन थे ?
(i) गुरु हरगोबिंद साहिब जी
(ii) गुरु हर राय जी
(iii) बाबा गुरदित्ता जी
(iv) बाबा बुड्डा जी।
उत्तर-
(ii)

प्रश्न 11.
सिख इतिहास में ‘बाल गुरु’ के नाम से किसको जाना जाता है ?
(i) गुरु रामदास जी को
(ii) गुरु हर राय जी को
(iii) गुरु हर कृष्ण जी को
(iv) गुरु गोबिंद सिंह जी को।
उत्तर-
(iii)

प्रश्न 12.
गुरु हर कृष्ण जी गुरुगद्दी पर कब विराजमान हुए ?
(i) 1645 ई० में
(ii) 1656 ई० में
(iii) 1661 ई० में
(iv) 1664 ई० में।
उत्तर-
(iii)

प्रश्न 13.
गुरु हर कृष्ण जी कब ज्योति-जोत समाए ?
(i) 1661 ई० में
(ii) 1662 ई० में
(iii) 1663 ई० में
(iv) 1664 ई० में।
उत्तर-
(iv)

प्रश्न 14.
गुरु हर कृष्ण जी कहाँ ज्योति-जोत समाए ?
(i) लाहौर
(ii) दिल्ली
(iii) मुलतान
(iv) जालंधर
उत्तर-
(ii)

Long Answer Type Question

प्रश्न 1.
सिख पंथ के विकास में गुरु हर राय जी का समय क्यों महत्त्वपूर्ण है ?
(Why is pontificate of Guru Har Rai Ji considered important in the development of Sikhism ?).
अथवा
गुरु हर राय जी पर एक संक्षिप्त नोट लिखें।
(Write a short note on Guru Har Rai Ji.)
अथवा
गुरु हर राय जी के बारे में आप क्या जानते हैं ?
(What do you know about Guru Har Rai Ji ?)
उत्तर-
गुरु हर राय जी 1645 ई० से 1661 ई० तक गुरुगद्दी पर विराजमान रहे। इस समय के दौरान उन्होंने सिख धर्म के विकास के लिए निम्नलिखित कार्य किए—
1. गुरु हर राय जी के समय में सिख धर्म का विकास-गुरु हर राय जी ने सिख धर्म के प्रचार के लिए तीन मुख्य केंद्र स्थापित किए जिन्हें ‘बख्शीशें’ कहा जाता था। भगत,गिरि को पूर्वी भारत, सुथरा शाह को दिल्ली, भाई फेरू को राजस्थान, भाई नत्था जी को ढाका, भाई जोधा जी को मुलतान भेजा गया तथा आपने स्वयं पंजाब के कई स्थानों का भ्रमण किया। इस कारण सिख पंथ का बहुत प्रसार हुआ।

2. फूल को आशीर्वाद-एक दिन काला नामक श्रद्धालु अपने भतीजों संदली तथा फूल को गुरु हर राय जी के दर्शन हेतु ले आया। उनकी शोचनीय हालत को देखते हुए गुरु साहिब ने उन्हें आशीर्वाद दिया कि एक दिन वे बहुत धनी बनेंगे। गुरु जी की यह भविष्यवाणी सत्य निकली। फूल ने फूलकिया मिसल की स्थापना की।

3. राजकुमार दारा की सहायता-गुरु हर राय जी के समय दारा शिकोह पंजाब का गवर्नर था। वह औरंगजेब का बड़ा भाई था। सत्ता प्राप्त करने के प्रयास में औरंगज़ेब ने उसे विष दे दिया। इस कारण वह बहुत बीमार हो गया। उसने गुरु साहिब से आशीर्वाद माँगा। गुरु साहिब ने अमूल्य जड़ी-बूटियाँ देकर दारा की चिकित्सा की। इस कारण वह गुरु साहिब का आभारी हो गया। वह प्रायः उनके दर्शन के लिए आने लगा।

4. गुरु हर राय साहिब को दिल्ली बुलाया गया-औरंगज़ेब को संदेह था कि गुरु ग्रंथ साहिब में कुछ श्लोक इस्लाम धर्म के विरुद्ध हैं। इस बात की पुष्टि के लिए उसने गुरु हर राय जी को अपने दरबार में उपस्थित होने के लिए कहा। गुरु साहिब ने अपने पुत्र रामराय को औरंगजेब के पास भेजा। गुरुवाणी की ग़लत व्याख्या के कारण आपने रामराय को गुरुगद्दी से वंचित कर दिया।

5. उत्तराधिकारी की नियुक्ति-गुरु हर राय जी ने अपने ज्योति-जोत समाने से पूर्व गुरुगद्दी अपने छोटे पुत्र हरकृष्ण को सौंप दी। गुरु हर राय जी 6 अक्तूबर, 1661 ई० को कीरतपुर साहिब में ज्योति-जोत समा गए।

प्रश्न 2.
धीरमल संबंधी एक संक्षिप्त नोट लिखें। (Write a short note about Dhirmal.)
उत्तर-
धीरमल गुरु हर राय जी का बड़ा भाई था। वह चिरकाल से गुरुगद्दी प्राप्त करने का प्रयत्न कर रहा था। बकाला में जो विभिन्न 22 मंजियाँ स्थापित हुईं उनमें से एक धीरमल की भी थी। जब धीरमल को यह समाचार मिला कि सिख संगतों ने तेग़ बहादुर जी को अपना गुरु मान लिया है तो उसके क्रोध की कोई सीमा न रही। उसने शीह नामक एक मसंद के साथ मिल कर गुरु जी की हत्या का षड्यंत्र रचा। एक दिन शींह तथा उसके सशस्त्र गुंडों ने गुरु जी पर आक्रमण कर दिया। इस आक्रमण के समय गुरु जी के कंधे में गोली लगी जिससे वह घायल हो गए, परंतु वह शाँत बने रहे। शीह के साथियों ने गुरु साहिब के घर का बहुत-सा सामान लूट लिया। इस घटना से सिख रोष से भर उठे तथा उन्होंने मक्खन शाह के नेतृत्व में धीरमल के घर पर आक्रमण कर दिया। वह न केवल धीरमल तथा शींह को पकड़ कर गुरु जी के पास लाए अपितु गुरु जी का लूटा हुआ सामान भी वापस ले आए। धीरमल तथा शींह द्वारा क्षमा याचना करने पर गुरु साहिब ने उन्हें क्षमा कर दिया।

प्रश्न 3.
गुरु हरकृष्ण जी पर एक संक्षिप्त नोट लिखें। उनको बाल गुरु क्यों कहा जाता है ? (Write a brief note on Guru Har Krishan Ji. Why is he called Bal Guru ?)
अथवा
गुरु हरकृष्ण जी पर संक्षेप नोट लिखो। (Write a short note on Guru Har Krishan Ji.)
अथवा
गुरु हरकृष्ण जी के बारे में विस्तारपूर्वक वर्णन करें।
(Explain in detail about Guru Har Krishan Ji.)
उत्तर-
गुरु हरकृष्ण जी सिखों के आठवें गुरु थे। आपके गुरुगद्दी के समय (1661-1664 ई०) सिख पंथ के विकास का संक्षिप्त वर्णन निम्नलिखित अनुसार है—
1. गुरुगद्दी की प्राप्ति-गुरु हर राय जी ने अपने बड़े पुत्र रामराय को उसकी अयोग्यता के कारण गुरुगद्दी से वंचित कर दिया था। 1661 ई० को गुरु हर राय जी ने हरकृष्ण जी को गुरुगद्दी सौंप दी। उस समय हरकृष्ण साहिब की आयु मात्र 5 वर्ष थी। इस कारण इतिहास में आपको बाल गुरु के नाम से याद किया जाता है। आप सिखों के आठवें गुरु बने। आप 1664 ई० तक गुरुगद्दी पर विराजमान रहे।

2. रामराय का विरोध-रामराय गुरु हर राय जी का बड़ा पुत्र होने के कारण गुरु साहिब के पश्चात् गुरुगद्दी का अधिकारी स्वयं को समझता था, परंतु गुरु हर राय जी उसे पहले ही गुरुगद्दी से वंचित कर चुके थे। जब उसे ज्ञात हुआ कि गुरुगद्दी हरकृष्ण साहिब को सौंपी गई है तो वह यह बात सहन न कर सका। उसने गद्दी हथियाने के लिए षड्यंत्र रचने आरंभ कर दिए।

3. गुरु हरकृष्ण जी का दिल्ली जाना-गुरु हरकृष्ण जी को दिल्ली लाने का कार्य औरंगज़ेब ने राजा जय सिंह को सौंपा। राजा जय सिंह ने अपने दीवान परस राम को गुरु जी के पास भेजा। गुरु जी ने औरंगज़ेब से मिलने और दिल्ली जाने से इंकार कर दिया, परंतु परस राम के यह कहने पर कि दिल्ली की संगतें गुरु साहिब के दर्शनों के लिए बेताब हैं, गुरु साहिब ने दिल्ली जाना तो स्वीकार कर लिया, परंतु औरंगज़ेब से भेंट करने से इंकार कर दिया। आप 1664 ई० में दिल्ली चले गए और राजा जय सिंह के घर निवास करने के लिए मान गए। गुरु साहिब की औरंगज़ेब से भेंट हुई अथवा नहीं, इस संबंध में इतिहासकारों में बहुत मतभेद पाए जाते हैं।

4. ज्योति-जोत समाना-उन दिनों दिल्ली में चेचक और हैजा फैला हुआ था। गुरु हरकृष्ण जी ने यहाँ बीमारों, निर्धनों और अनाथों की तन, मन और धन से अथक सेवा की। परंतु इस भयंकर बीमारी का आप स्वयं भी शिकार हो गए। आप 30 मार्च, 1664 ई० को दिल्ली में ज्योति-जोत समा गए। आपकी याद में यहाँ गुरुद्वारा बाला साहिब का निर्माण किया गया है।

Source Based Questions

नोट-निम्नलिखित अनुच्छेदों को ध्यानपूर्वक पढ़िए और उनके अंत में पूछे गए प्रश्नों का उत्तर दीजिए।
1
गुरु हर राय जी 1645 ई० से लेकर 1661 ई० तक गुरुगद्दी पर आसीन रहे। उनकी गुरुगद्दी का समय सिख इतिहास में शाँति का काल कहा जा सकता है। गुरु हर राय साहिब जी सिख धर्म का प्रचार करने के लिए पंजाब के कई स्थानों पर जैसे जालंधर, अमृतसर, करतारपुर, गुरदासपुर, फिरोज़पुर, पटियाला, अंबाला, करनाल और हिसार इत्यादि स्थानों पर गए। इसके अतिरिक्त गुरु साहिब ने पंजाब से बाहर अपने प्रचारक भेजे। अपने प्रचार दौरे के दौरान गुरु साहिब ने अपने एक श्रद्धालु फूल को यह आशीर्वाद दिया कि उसकी संतान शासन करेगी। गुरु साहिब की यह भविष्यवाणी सत्य निकली। गुरु हर राय जी ने अपने छोटे पुत्र हर कृष्ण जी को अपना उत्तराधिकारी नियुक्त किया।

1. गुरु हर राय जी गुरुगद्दी पर कब बैठे थे ?
2. गुरु हर राय जी सिख धर्म का प्रचार करने के लिए पंजाब के कौन-से स्थानों पर गए ? किन्हीं दो के नाम बताएँ।
3. गुरु हर राय जी ने अपने किस श्रद्धालु को यह वरदान दिया कि उसकी संतान राज करेगी?
4. गुरु हर राय जी ने अपना उत्तराधिकारी किसे नियुक्त किया ?
5. शाहजहाँ के बड़े पुत्र का क्या नाम था ?
   • दारा
   • शुज़ा
   • औरंगजेब
   • मुराद।

उत्तर-

1. गुरु हर राय जी 1645 ई० में गुरुगद्दी पर बैठे थे।
2. गुरु हर राय जी सिख धर्म का प्रचार करने के लिए पंजाब में जालंधर तथा अमृतसर में गए।
3. गुरु हर राय जी ने अपने एक श्रद्धालु फूल को यह आर्शीवाद दिया कि उसकी सन्तान राज करेगी।
4. गुरु हर राय जी ने हर कृष्ण जी को अपना उत्तराधिकारी नियुक्त किया।
5. दारा।

2
गुरु हर कृष्ण जी गुरु हर राय जी के छोटे पुत्र थे। वह 1661 ई० में गुरगद्दी पर बैठे। वह सिखों के आठवें गुरु थे। जिस समय वह गुरुगद्दी पर बैठे तो उस समय उनकी आयु केवल पाँच वर्ष थी। इस कारण उनको ‘बाल गुरु’ के नाम से स्मरण किया जाता है। गुरु हरकृष्ण जी के बड़े भाई राम राय ने आप जी को गुरुगद्दी दिए जाने का कट्टर विरोध किया, क्योंकि वह अपने आपको गुरुगद्दी का वास्तविक अधिकारी मानता था। जब वह अपनी कुटिल चालों में सफल न हो सका तो उसने औरंगजेब से सहायता माँगी। इस संबंध में औरंगज़ेब ने गुरु साहिब को दिल्ली आने का आदेश दिया। गुरु साहिब 1664 ई० में दिल्ली गए। वहाँ वह राजा जय सिंह के यहाँ ठहरे। उन दिनों दिल्ली में भयानक चेचक एवं हैजा फैला हुआ था। गुरु जी ने इन बीमारों, ग़रीबों एवं अनाथों की भरसक सेवा की।

1. सिखों के आठवें गुरु कौन थे ?
2. गुरु हर कृष्ण जी …………. में गुरुगद्दी पर बैठे थे।
3. गुरु हर कृष्ण जी को बाल गुरु क्यों कहा जाता है ?
4. राम राय कौन था ?
5. गुरु हर कृष्ण जी ने दिल्ली में कौन-सी सेवा निभाई ?

उत्तर-

1. सिखों के आठवें गुरु हर कृष्ण जी थे।
2. 1661 ई०।
3. क्योंकि गुरुगद्दी पर बैठते समय उनकी आयु केवल 5 वर्ष की थी।
4. राम राय गुरु हर कृष्ण जी का बड़ा भाई था।
5. गुरु हर कृष्ण जी जिस समय दिल्ली में थे उस समय वहाँ चेचक तथा हैज़ा नामक बीमारियाँ फैली हुई थीं। गुरु जी ने इन बीमारों, ग़रीबों तथा अनाथों की बहुत सेवा की।

Punjab State Board PSEB 12th Class Geography Book Solutions Chapter 7 परिवहन/यातायात, संचार तथा व्यापार Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Geography Chapter 7 परिवहन/यातायात, संचार तथा व्यापार

PSEB 12th Class Geography Guide परिवहन/यातायात, संचार तथा व्यापार Textbook Questions and Answers

प्रश्न 1. निम्नलिखित प्रश्नों के उत्तर एक वाक्य में दें:

प्रश्न 1.
यातायात प्रबंध को मुख्य रूप में कौन-सी किस्मों में विभाजित किया जाता है ?
उत्तर-
यातायात प्रबंध को मुख्य रूप में इन किस्मों में विभाजित किया जाता है-

• स्थल मार्ग यातायात।
• जल मार्ग यातायात।
• वायु मार्ग यातायात।

प्रश्न 2.
स्थल मार्ग यातायात की कौन-सी तीन किस्में होती हैं ?
उत्तर-
स्थल मार्ग यातायात की सड़कें, रेलवे तथा पाइप लाइन तीन मुख्य किस्में होती हैं।

प्रश्न 3.
कौन-से राज्य भारत के दोनों गलियारा (सड़कों) योजनाओं में संभेद हैं ?
उत्तर-
उत्तर प्रदेश तथा मध्य प्रदेश दोनों गलियारा योजनाओं में संभेद राज्य हैं।

प्रश्न 4.
रेल गेज कौन-सी किस्मों की होती हैं ?
उत्तर-
भारतीय रेल गेजों की निम्नलिखित तीन किस्में होती हैं-

• चौड़ी गेज (Broad Gauge)
• मीटर गेज (Metre Gauge)
• perluf 1757 (Narrow Gauge).

प्रश्न 5.
विश्व की प्रथम रेलवे लाइन कब बिछाई गई ?
उत्तर-
विश्व की प्रथम रेलवे लाइन सन 1863 से 1869 में अमेरिका में बिछाई गई।

प्रश्न 6.
ट्रांस साइबेरियाई रेलवे लाइन कहा तक हैं ?
उत्तर-
ट्रांस साइबेरियाई रेलवे लाइन मास्को से रूस के पर्व में ब्लादिवोस्तोक तक हैं।

प्रश्न 7.
भारत में कितने रेलवे गलियारे हैं ?
उत्तर-
भारत में 2014 के बजट के अनुसार 9 रेलवे गलियारे हैं।

प्रश्न 8.
IRCTC का पूरा नाम क्या है ?
उनर-
IRCTC का पूरा नाम इण्डियन कैटरिंग एंड टूरिज्म कार्पोरेशन लिमिटेड है।

प्रश्न 9.
भारत में कितने जल मार्गों को राष्ट्रीय स्तर के माना जाता है ?
उत्तर-
भारत में 10 जल मार्गों को राष्ट्रीय स्तर के माना जाता है।

प्रश्न 10.
उत्तरी अमेरिका की कोई दो बड़ी झीलों के नाम लिखो।
उत्तर-
उत्तरी अमेरिका की बड़ी झीलें हैं-सुपीरियर, मिशिगन, हायरन, एरी, ओटारियो तथा सेंट लॉरेस।

प्रश्न 11.
भारत की पहली वायु सेवा कब शुरू हुई तथा कहां तक थी ?
उत्तर-
भारत की पहली वायु सेवा 1911 में शुरू हुई तथा इसका इलाहाबाद से नैनी तक, 10 कि०मी० की दूरी के लिए वायु डाक का प्रयोग किया गया।

प्रश्न 12.
पंजाब के कौन-से दो अंतर्राष्ट्रीय हवाई अड्डे हैं ?
उत्तर-
पंजाब में अंतर्राष्ट्रीय हवाई अड्डे अमृतसर तथा मोहाली में हैं।

प्रश्न 13.
TAPI पाइप लाइन का पूरा नाम लिखो।
उत्तर-
तुर्कमेनिस्तान-अफ़गानिस्तान-पाकिस्तान-भारत पाइप लाइन।

प्रश्न 14.
संचार की कौन सी प्रमुख किस्में हैं ?
उत्तर-
संचार की मुख्य किस्में हैं-

• व्यक्तिगत संचार
• जन संचार।

प्रश्न 15.
GATT का पूरा नाम क्या है ?
उत्तर-
जनरल ऐग्रीमैंट ओन टैरिफज एंड ट्रेड। (शुल्क तथा व्यापार पर समझौते)।

प्रश्न 2. निम्नलिखित प्रश्नों के उत्तर चार पंक्तियों में दें: .

प्रश्न 1.
भारत की ग्रामीण सड़क योजना से पहचान करवाओ।
उत्तर-
इस योजना का उद्देश्य ग्रामीण क्षेत्रों में सड़कों का विकास करना है तथा ऐसा करके कम से कम 1500 व्यक्तियों की तथा इससे अधिक जनसंख्या वाले गांवों को आपस में सड़क मार्ग के साथ जोड़ा जाता है। यह सड़कें इस प्रकार बनाई जाती हैं कि हर प्रकार की मौसमी मुसीबतों को सहन कर सकें।

प्रश्न 2.
सूबाई सड़क मार्ग क्या होते हैं ?
उत्तर-
जब किसी राज्य में व्यापारिक तथा भारी यात्री यातायात के लिए सड़कें बनाई जाए, वह राज्य सड़क मार्ग होते हैं। यह सड़कें जो कि आर्थिक कारवाई की नब्ज़ मानी जाती हैं, जिला मुख्य केंद्रों को राज्यों की राजधानियों के राष्ट्रीय शाहमार्ग के साथ मिलाती हैं।

प्रश्न 3.
‘सुनहरी चतुर्भुज’ कौन से शहरों को आपस में जोड़ती हैं ?
उत्तर-
‘सुनहरी चतुर्भुज’ भारत के अहमदाबाद, भुवनेश्वर, जयपुर, कानपुर, पुणे, सूरत, नैलूर विजयवाड़ा, गंटूर तथा बंगलुरु इत्यादि शहरों को आपस में जोड़ती हैं।

प्रश्न 4.
19वीं सदी के अंत तक भारत में कौन-से तीन रेलवे-मार्ग बने हैं ?
उत्तर-
19वीं सदी के अंत तक भारत में कोलकाता, मुंबई तथा चेन्नई तीन प्रमुख नये रेलवे-मार्ग बने हैं।

प्रश्न 5.
कोलकाता कौन-कौन से रेलवे जोनों का मुख्यालय है ?
उत्तर-
कोलकाता पूर्वी रेलवे तथा मैट्रो रेलवे जोनों का मुख्यालय है।

प्रश्न 6.
कैनेडियन पैसेफ़िक रेलवे क्या है ?
उत्तर-
कैनेडियन पैसेफिक रेलवे, पार महाद्वीप रेल मार्ग की एक उदाहरण है जो कि उत्तरी अमेरिका महाद्वीप में कैनेडा के नागरिकों की सेवा कर रहा है इसका कुछ हिस्सा संयुक्त राज्य अमेरिका में भी निकलता है। इस मार्ग का निर्माण 1881 में शुरू हुआ था तथा अभी तक विस्तार चल रहा है।

प्रश्न 7.
डाइमंड चतुर्भुज कौन-से राज्यों को छू पाएगी?
उत्तर-
डाइमंड चतुर्भुज उत्तर प्रदेश, राजस्थान, महाराष्ट्र, गुजरात, दिल्ली, हरियाणा, आन्ध्र प्रदेश, तेलंगाना, कर्नाटक, बिहार, उड़ीसा, झारखण्ड तथा पश्चिमी बंगाल राज्यों को छू पाएगी।

प्रश्न 8.
दिल्ली आगरा रेल गलियारा से पहचान करवाओ।
उत्तर-
दिल्ली आगरा रेल गलियारा का उद्घाटन 5 अप्रैल, 2016 में हुआ है। दिल्ली से आगरा तक 160 किलोमीटर प्रति घंटा की रफ़्तार के साथ आगरा गतिमान ऐक्सप्रैस चलाई गई।

प्रश्न 9.
भारत में आंतरिक जल यातायात कौन-से दरियाओं में होती है ?
उत्तर-
भारत में आंतरिक जल यातायात के अनुकूल दरिया हैं-गंगा, भगीरथी, हुगली, ब्रह्मपुत्र, महानदी, कृष्णा, जुयारी, काली, शरावति, नेर्तावति इत्यादि।

प्रश्न 10.
व्यक्तिगत संचार के साधन कौन-कौन से हैं ?
उत्तर-
व्यक्तिगत संचार के प्रमुख साधन हैं-

• डाक सेवाएं
• ई-मेल सेवा
• फैक्स संदेश
• टैलीफोन
• कोरियर सेवा
• कम्प्यूटर या सैलफोन सेवाएं।

प्रश्न 3. निम्नलिखित प्रश्नों के उत्तर 10-12 पंक्तियों में दें:

प्रश्न 1.
भारत के उत्तर दक्षिण तथा पूर्व-पश्चिम गलियारा प्रोजैक्टों से पहचान करवाओ।
उत्तर-
भारत के उत्तर-दक्षिण तथा पूर्व-पश्चिम गलियारा प्रोजैक्टों का मुख्य उद्देश्य देश के हर कोने तक बढ़िया सड़क-मार्गों का जाल बिछाने का है। इस योजना की देख-रेख की पूरी ज़िम्मेदारी नैशनल हाईवे अथॉरिटी ऑफ इंडिया के अंतर्गत की गई जो कि केंद्रीय सड़क यातायात तथा शाहमार्ग मंत्रालय के अंतर्गत काम कर रही है। इस प्रकल्प का मुख्य उद्देश्य चार से छः मार्गी, कुल 7300 कि०मी० लंबी सड़क का निर्माण करने से है जो उत्तर से दक्षिण की तरफ श्रीनगर से कन्या कुमारी, पूर्व से पश्चिम की तरफ पोरबंदर से सिलचर तक बनाना था। उत्तर-दक्षिण गलियारा जो कि श्रीनगर से कन्या-कुमारी तक है, इसकी लंबाई 4000 कि०मी० है तथा यह कोची के साथ जुड़ता है। पूर्व-पश्चिम गलियारा जो कि पोरबंदर से सिलचर तक है इसकी लंबाई 3300 किलोमीटर है। यह दोनों सड़क मार्ग गलियारे 17 राज्यों को छूते हैं। जो हैं-जम्मू तथा कश्मीर, पंजाब, हरियाणा, दिल्ली, उत्तर प्रदेश, मध्य प्रदेश, महाराष्ट्र, तेलंगाना, आन्ध्र प्रदेश, कर्नाटक, तमिलनाडु, केरल, गुजरात, राजस्थान, बिहार, पश्चिमी बंगाल तथा असम। यहां यह भी है कि उत्तर-दक्षिण तथा पूर्व-पश्चिम गलियारे बनाने के लिए सिर्फ राष्ट्रीय शाहमार्ग ही प्रयोग किये जाते हैं। उत्तर प्रदेश का झाँसी प्रदेश वह रेलवे जंक्शन है जहाँ सड़क गलियारे आपस में काटते हैं।

प्रश्न 2.
सुनहरी चतुर्भुज सड़क मार्ग योजना पर नोट लिखो।
उत्तर-
सुनहरी चतुर्भुज, राष्ट्रीय शाहमार्ग विकास प्रकल्प के अधीन भारत में सम्पूर्ण होने वाली सबसे बड़ी सड़क निर्माण योजना है। इसका प्रबंध भी राष्ट्रीय शाहमार्ग अथॉरिटी के अंतर्गत ही था। यह दुनिया की पांचवीं बड़ी सड़क निर्माण योजना है। यह योजना साल 2001 में प्रधानमंत्री श्री अटल बिहारी वाजपेयी द्वारा प्रारंभ की गई जो 2012 में सम्पूर्ण होनी थी। इस प्रकल्प में भारत के चार महानगरों दिल्ली, मुंबई, चेन्नई तथा कोलकाता को आपस में मिसाली सड़क-मार्ग के साथ जोड़े जाने की एक योजना है जो कि रेखा-गणितिक आकृति होने के कारण तथा चतुर्भुज का आकार होने के कारण सुनहरी चतुर्भुज कहलाती है। इस योजना से जुड़े सड़क-मार्ग के साथ कुछ बड़े शहर लगते हैं जैसे बंगलूरु, अहमदाबाद, जयपुर, भुवनेश्वर, कानपुर, पुणे, सूरत, नैलूर, विजयवाड़ा तथा गंटूर। इस सुनहरी चतुर्भुज की लंबाई 5846 कि०मी० है तथा इसके अंतर्गत चार तथा छः मार्गी ऐक्सप्रेस हाईवे बनाए गए हैं। इस चतुर्भुज का शाहमार्ग देश के 13 राज्यों में से निकलता है तथा सबसे अधिक हिस्सा आंध्र प्रदेश में है तथा सबसे कम हिस्सा दिल्ली में पड़ता है।

प्रश्न 3.
भारतीय रेलवे नीति के मुख्य उद्देश्य क्या हैं ? लिखो ?
उत्तर-
भारतीय रेलवे नीति के मुख्य उद्देश्य निम्नलिखित हैं-

1. रेलवे मार्गों की लंबाई बढ़ाना।
2. गेज का परिवर्तन भाव सौड़ी मीटर गेज को चौड़ी लाइन में बदलता।
3. रेल मार्ग का बिजलीकरण करना।
4. रेल प्रबंध की कार्य कुशलता में सुधार करना।
5. पुराने भाप के इंजनों तथा डीज़ल इंजनों को बदल कर बिजली इंजन प्रयोग में लाने।
6. सिगनल संचार तकनीक को सुधारना।
7. मुसाफ़िरों के लिए अच्छी सुविधाएं उपलब्ध करवाना।
8. यात्री किराया में स्थिरता लाना।
9. ऊंची रफ़्तार की गाड़ियों को चलाना।
10. रेलवे कार्य के लिए कंप्यूटर प्रयोग में लाना।

प्रश्न 4.
भारतीय रेलवे जोनों पर नोट लिखो।
उत्तर-
स्वतन्त्रता के पश्चात् भारतीय रेल प्रबंध को भारतीय रेलवे बोर्ड ने 6 जोनों में विभाजित किया था जो थेउत्तरी खंड, पश्चिमी खंड, पूर्वी खंड, मध्यम खंड, दक्षिणी खंड तथा उत्तर-पूर्वी खंड परंतु बाद में सन् 1958 से 1960 तक तीन अन्य खंड बना दिए गए जिस के साथ रेलवे के कुल 9 जोन बन गए तथा लगभग तीन दहाकों के पश्चात् रेलवे में अब 18 जोन हैं, जो ये हैंक्रम संख्या

रेलवे जोन — मुख्यालय

1. उत्तरी रेलवे — नई दिल्ली
2. उत्तर-पूर्वी रेलवे — गोरखपुर
3. उत्तर-पूर्वी फ्रंटीयर — मालीगाऊ (गुवाहाटी)
4. पूर्वी रेलवे — कोलकाता
5. दक्षिणी-पूर्वी रेलवे — बिलासपुर
6. दक्षिणी-मध्यम रेलवे — सिकंद्राबाद
7. दक्षिणी रेलवे — चेन्नई
8. मध्य रेलवे — मुंबई
9. पश्चिमी रेलवे — मुंबई
10. दक्षिणी-पश्चिमी रेलवे — हुँबली
11. उत्तर-पश्चिमी रेलवे — जयपुर
12. पश्चिमी-मध्यम रेलवे — जबलपुर
13. उत्तरी-मध्यम रेलवे  – इलाहाबाद
14. दक्षिणी-पूर्वी मध्यम रेलवे — बिलासपुर
15. पूर्वी तटवर्ती — भुवनेश्वर
16. पूर्वी रेलवे मध्यम रेलवे — हाजीपुर  मध्यम रेलवे
17. कोंकण रेलवे — नई दिल्ली
18. मैट्रो रेलवे — कोलकाताइलाहाबाद

प्रश्न 5.
अन्तर्राष्ट्रीय व्यापार के आधार क्या हो सकते हैं ? भारत की दरामद तथा बरामद पर नोट लिखो।
उत्तर-
अन्तर्राष्ट्रीय व्यापार के आधार-

• प्राकृतिक साधनों के अस्तित्व में फर्क।
• मांग तथा पूर्ति में अंतर।
• तकनीकी विकास में अंतर।
• जलवायु तथा आर्थिक विकास में अंतर।
• व्यापारिक देशों की जंग तथा अमन के हालात।
• व्यापारिक नीतियां तथा देशों के बीच आपसी राजनीतिक संबंध

भारत की दरामद तथा बरामद-भारत में उत्पादन किया गया फालतू सामान बेच दिया जाता है तथा जिसकी आवश्यकता होती है वह सामान खरीद लिया जाता है जो सामान बेचा जाता है उसको बरामद तथा जो सामान खरीदा जाता है उसे दरामद कहते हैं। भारत खनिज ईंधन, खनिज तेल, मोम, जैविक रसायन, फार्मेसी उत्पादन, गेहूं से बनी वस्तुएं, अनाज, बिजली की मशीनरी, कपास से सूती कपड़ा, प्लास्टिक/कहवा, मसाले इत्यादि का बरामद करता है तथा पैट्रोल, खनिज, मशीनरी, खाद्य, लोहा तथा इस्पात, मोती तथा कीमती पत्थर, सोना तथा चांदी, रसायन, दवाइयां फाईबर इत्यादि दरामद की जाती हैं।

प्रश्न 6.
भारत के अन्तर्राष्ट्रीय हवाई अड्डों तथा प्रमुख बंदरगाहों के नाम लिखो।
उत्तर-
भारत के अन्तर्राष्ट्रीय हवाई अड्डे-भारत के प्रमुख हवाई अड्डे निम्नलिखित हैं-

भारतीय बंदरगाहें-कांडला, पोरबंदर, सूरत, पणजी, मर्मागाओ, मंगलौर, कोची, तूतीकोरन, नागापट्नम, चेन्नई, ईनौर, मछलीपटनम, काकीनाड़ा, विशाखापटनम, पाराद्वीप, हलदिया प्रमुख बंदरगाहें हैं।

प्रश्न 7.
व्यक्तिगत संचार तथा जन संचार की आपसी तुलना करो।
उत्तर-
व्यक्तिगत संचार –

1. जब दो व्यक्ति या दो से अधिक व्यक्ति आमने सामने होकर किसी साधन की सहायता के साथ अपनी भावनाओं, विचारों तथा संदेशों को बांटना व्यक्तिगत संचार कहलाता है।
2. ऐसे संचार में दोनों पक्ष एक दूसरे से परिचित होते हैं।
3. इसमें कुछ साधनों का प्रयोग किया जाता है जैसे- डाक सेवाएं, ई-मेल, फैक्स, टैलीफोन, कोरियर, कंप्यूटर इत्यादि।

जन संचार-

1. जब कोई संदेश एक बड़ी गिनती में लोगों के साथ बाँटा जाता है उसको जन संचार कहते हैं।
2. संचार पक्ष में शामिल लोग एक-दूसरे से परिचित नहीं होते।
3. जन संचार में कुछ साधन प्रयोग किए जाते हैं जैसे-जनतक ऐलान, रेडियो, टी०वी०, सिनेमा,अख़बार, सैटेलाईट, इंटरनैट संचार इत्यादि।

प्रश्न 8.
कांडला-बठिंडा पाइप लाइन पर नोट लिखो।
उत्तर-
कांडला-बठिंडा पाइप लाइन ऑयल कार्पोरेशन (IOC) की ओर बठिंडा के तेल शोधक कारखाने को कच्चा तेल पहुँचाने के लिए 1443 किलोमीटर लंबी पाइप लाइन 2392 करोड़ रुपए खर्च कर बिछाने की योजना बनाई गई थी। इस योजना का पहला चरण जो कांडला से सागानौर तक था। 1996 में पूरा हो गया तथा मई 1996 में सागानोर से पानीपत तथा जून 1996 में पानीपत से बठिंडा तक का चरण पूरा कर दिया गया था। इस प्रकल्प का अगला चरण शुरू कर दिया गया जो कि चल रहा है। यह बठिंडा-जम्मू-श्रीनगर गैस पाइप लाइन बिछाने का है। इस प्रकल्प के पूरा होने से जम्मू तथा कश्मीर को हर समय रसोई गैस की सप्लाई मिल सकेगी। इसलिए यह प्रकल्प जम्मू कश्मीर सूबे के लिए विशेष महत्त्व रखता है।

प्रश्न 9.
भारतीय राष्ट्रीय जल मार्गों पर नोट लिखो।
उत्तर-
भारतीय राष्ट्रीय जल मार्ग-भारत में 10 मार्गों को राष्ट्रीय जल-मार्ग का दर्जा हासिल है। यह हैं-

1. गंगा, हल्दिया तथा इलाहाबाद के बीच।
2. ब्रह्मपुत्र, सेतिया तथा युबड़ी के बीच।
3. पश्चिमी उटी नहर, कोल्लम से कोटापुर्म के बीच।
4. केरल में चंपाकारा नहर के साथ का क्षेत्र।
5. केरल में उद्योगमंडल नहर के साथ का क्षेत्र।
6. ब्रह्मनी नदी तलचर से धर्मरा तक।
7. काकीनाड़ा से पांडिचेरी तक।
8. गोदावरी नदी में भदराचलम से राजामुंदरी तक।
9. कृष्णा नदी में वज़ीरावाद से विजयवाड़ा तक।
10. लखीमपुर से भंग तक।

प्रश्न 10.
भारतीय वायु यातायात से पहचान करवाओ।
उत्तर-
भारत जैसे बड़े तथा घनी जनसंख्या वाले देश के लिए वायु यातायात का बहुत महत्त्व है। भारत में वायु यातायात का आरंभ 1911 के साल में हुआ जब इलाहाबाद से लेकर नैनी तक, 10 कि०मी० की दूरी के साथ वायु डाक सेवा का प्रयोग किया गया था। इसके बाद कई वायु अड्डे भी बनाये गए तथा फलाईंग क्लब भी बनाए गए जिसके साथ वायु यातायात को प्रोत्साहन मिला। देश की आज़ादी के बाद तथा विभाजन समय (1947) भारत में चार वायु सेवाएं हैं-टाटा सन्ज लिमिटेड, इण्डियन नैशनल एयरवेज़, एयर सर्विसज़ आफ इंडिया तथा डैकन एयरवेज तथा 1951 में चार कंपनियां भारत में वायु सेवाएं लाने के काम में जुट गई। बाद में इन कंपनियों की मलकियत सरकार ने अपने हाथों में ले ली तथा दो कार्पोरेशनें बना दीं। एयर इंडिया जो अन्तर्राष्ट्रीय उड़ानों के लिए थी तथा दूसरी इण्डियन एयर लाइन्ज़ घरेलु उड़ानों के लिए थी।

प्रश्न 4. निम्नलिखित प्रश्नों के उत्तर 20 पंक्तियों में दो :

प्रश्न 1.
भारत की अलग-अलग सड़क योजनाओं से पहचान करवाओ।
उत्तर-
किसी भी देश में सड़कों के लिए विशेष स्थान होता है। लोगों तथा समान को एक स्थान से दूसरे स्थान तक पहुँचाने के लिए सड़कों का ही प्रयोग किया जाता है। इसके अलावा सड़क यातायात अन्य यातायात के साधनों से सबसे सस्ता है। सड़क मार्गों का जाल फैलाने के लिए कई सड़क योजनाओं को बनाया गया है। जैसे-

1. नागपुर योजना (Nagpur Plan)-यह योजना भारत में सड़कों के प्रसार के लिए 1943 में बनाई गई थी।
इस योजना के अधीन देश की मुख्य सड़कों तथा आम सड़कों तथा अन्य सड़कों की लंबाई भी बढ़ती गई।

2. बीस वर्षीय योजना (Twenty Year Plan)-इस योजना की शुरुआत 1961 में हुई। इस योजना का मुख्य उद्देश्य देश में सड़कों की कुल लंबाई 6 लाख 56 हजार किलोमीटर से बढ़ाकर 10 लाख 60 हज़ार किलोमीटर तक करना था तथा सड़क घनत्व भी प्रति 100 कि०मी० रकबे में 32 कि०मी० करना था। इस योजना को पूरा करने के लिए 20 सालों का समय तय किया गया।

3. ग्रामीण सड़क योजना (The Rural Road Development Plan)-इस योजना का मुख्य उद्देश्य ग्रामीण क्षेत्रों के बीच सड़कों का विकास करके कम-से-कम 1500 व्यक्तियों की तथा इससे अधिक आबादी वाले गाँवों को आपस में सड़क मार्गों के साथ जोड़ना था। यह सड़कें इस तरह बनाई जाती हैं कि मौसमी कठिनाइयों को सहन कर सके।

4. बी०ओ०टी० (निर्माण, उपयोग तथा हवाले करो) (Built, Operate and Transfer Scheme)-इस योजना में प्राइवेट बिल्डरों तथा ठेकेदारों को सड़कों तथा पुलों का निर्माण करने के लिए ठेके दिए गए थे तथा यह सहमति भी दी गई कि यह अपना निर्माण सड़क से जाने वाले वाहनों के चालकों से सीमित किए समय के लिए टोल टैक्स इकट्ठा करना तथा फिर सड़कों को सरकार के हवाले कर देना। यह योजना एक सफल योजना रही तथा देश के कई हिस्सों में इस योजना को सफलता हासिल हुई।

5. केंद्रीय सड़क फंड (Central Road Fund)-इस फंड के साथ संबंधित एक्ट दिसंबर 2000 में लागू किया गया था। इस एक्ट के अनुसार सड़कों का विकास पैट्रोल तथा डीज़ल पर लगे टैक्स तथा कस्टम कर को इकट्ठा करके किया जाएगा।

प्रश्न 2.
नए राष्ट्रीय शाहमार्ग अंकण योजना पर विस्तार सहित नोट लिखो।
उत्तर-
राष्ट्रीय शाह मार्ग अंकण योजना एक नई अंकण योजना थी। भारत में यह मार्ग प्रबंध भारत सरकार की एजेन्सियों की तरफ से चलाया तथा संभाला गया है। राष्ट्रीय शाह मार्ग की लंबाई जून 2016 तक एक लाख 87 किलोमीटर थी। इनमें लगभग 26,200 किलोमीटर शाहमार्ग 4 मार्ग तथा बाकी 2 मार्ग हैं। केंद्रीय सरकार के तय किए उद्देश्य के मुताबिक सन् 2017 से हर रोज 30 कि०मी० शाह मार्ग विकसित किए जाए तथा नए विकास के लिए लुक तथा कोयले की बजाए सीमेंट का प्रयोग किया जाए। हाल ही में कई सड़क मार्गों को राष्ट्रीय मार्ग घोषित किया गया है। अब बड़े क्षेत्रों तथा शहरों के इधर-उधर बाईपास बनाये जा रहे हैं, ताकि शाह मार्गों पर यातायात का बहाव बिना रोक-टोक के निरंतर चलता रहे। इन शाहमार्ग का विकास तेजी से हो रहा है। 2004 से 2014 के समय में शाह मार्ग में सिर्फ 18,000 कि०मी० की वृद्धि हुई है।

भारतीय सड़क यातायात तथा हाईवेज़ मंत्रालय ने 28 अप्रैल, 2010 को एक नोटीफिकेशन निकाला तथा इसमें राष्ट्रीय शाहमार्ग को नए अंकों का प्रबंध दिया। यह नया नम्बर राष्ट्रीय शाहमार्ग के भौगोलिक क्षेत्र का ज्ञान हमें करवाता है। अब पूर्व से पश्चिम दिशा की तरफ जा रहे सारे शाहमार्ग का क्रम पहचान अंक टांक अंक हैं जिन की शुरुआत उत्तर में हो रही है तथा जैसे-जैसे हम दक्षिण दिशा की ओर जाते हैं क्रम अंक में वृद्धि होनी शुरू हो जाती है तथा जैसे ही विस्तार अंक में वृद्धि होगी, शाहमार्ग पहचान अंक कम होता चला जाएगा, विस्तार अंक के कम होने के साथ पहचान अंक में वृद्धि होगी।

उदाहरण के तौर पर राष्ट्रीय शाहमार्ग नंबर 1 जम्मू कश्मीर में है तथा नंबर 87 तमिलनाडु में है। अब इससे पता चलता है कि उत्तर-दक्षिण दिशा की ओर जाते शाहमार्ग का क्रम पहचान अंक जिस्त है तथा इसकी शुरुआत पूर्व में होकर पश्चिम की ओर जाते समय बढ़ती है। जैसे ही लंबकार अंक कम होगा तब शाहमार्ग पहचान अंक के वृद्धि होगी तथा लंबकार अंक बढ़ेगा तो शाहमार्ग पहचान अंक कम हो जाएगा। जैसे कि राष्ट्रीय शाहमार्ग नंबर-2 उत्तर-पूर्वी राज्यों में पड़ता है तथा नंबर 68 राजस्थान से गुजरात की ओर जा रहा है।

राष्ट्रीय शाहमार्ग की एक और विशेषता यह है कि प्रमुख राष्ट्रीय शाहमार्गों का पहचान अंक एकहरा, दोहरा होता है परंतु उनमें निकल रहे अगले शाहमार्ग के पहचान अंक तीहरे होते हैं, भाव सैंकड़ों में होते हैं। जहाँ यह भी वर्णन योग्य है कि नई अंकण योजना में सिर्फ पुराने शाहमार्गों के अंक ही नहीं बदले गए, बल्कि मार्गों का सारा प्रबंध दुबारा से किया गया है, जैसे कि राष्ट्रीय शाहमार्ग नंबर 27 जो पोरबंदर से सिलचर तक है तथा पूर्व से पश्चिमी गलियारा है। कितने ही पुराने राष्ट्रीय शाहमार्ग को हर मार्ग आपस में जोड़ रहा है। आज के नये प्रबंध के अनुसार अब देश में 218 राष्ट्रीय शाहमार्ग हैं तथा 78 प्रमुख शाहमार्ग तथा 140 राष्ट्रीय मार्ग है जो शाह राज्यों में ही निकल रहे हैं। इन को ऑफ सूट हाईवेज कहा जाता है। इन ऑफ सूट हाईवेज की पहचान अंक सैंकड़ों में हुआ है तथा अधिक पहचान अंक का ईकाई अंक दिशा निर्धारण करता है, जैसे कि यह इकाई अंक टांक हैं, तो शाहमार्ग में निकला मार्ग भी पूर्व-पश्चिम दिशा में है तथा यह अंक इकाई है, जिस्त हैं तब शाहमार्ग में निकला मार्ग भी उत्तर-दक्षिण दिशा में है।

प्रश्न 3.
पार-महाद्वीपीय रेलवे जालों से पहचान करवाओ।
उत्तर-
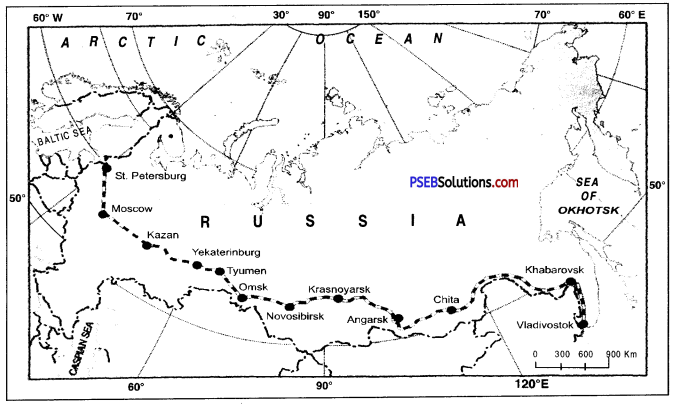
पार-महाद्वीपीय रेलवे मार्ग लंबी दूरी तय करने वाले रेल मार्ग हैं। इन रेल-मार्गों का जाल ऐसा है जो कि महाद्वीप की सारी भूमि को पार करके दूसरे महासागर के साथ लगते महाद्वीप के सिरे तक पहुंच जाता है। पार-महाद्वीप रेल-मार्गों का इतिहास आज से तकरीबन 150 साल पुराना है। संसार की सबसे पहली रेल लाईन 1863 से 1869 के बीच अमेरिका में पसारी गई जो कि यू०एस०ए० में से गुजरती हुई अंध-महासागर के तट पर होती हुई प्रशांत महासागर तक 1776 मील का रास्ता तय करती थी। संसार में और भी कई पार-महाद्वीप रेल मार्गों का निर्माण हुआ है जो कि बहुत बड़ी संख्या में मुसाफिरों तथा माल को एक स्थान से दूसरे स्थान तक पहुंचाने के लिए जाने गए। ट्रांस साइबेरियाई रेल मार्ग मास्को से रूस के पूर्व के तरफ वलादिवोस्तोक तक 9,289 किलोमीटर लंबा है तथा इसका निर्माण 1891 से 1916 तक के समय हुआ था। इस की कई शाखाएं हैं जो मास्को से इस मार्ग की सहायता के साथ चीन, मंगोलिया तथा उत्तरी कोरिया से जोड़ती हैं। इस मार्ग का विस्तार अभी भी चल रहा है।

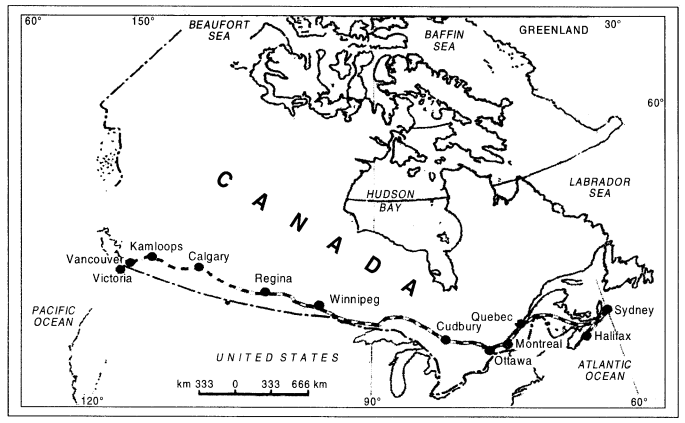
कैनेडियन पैसेफिक रेल-मार्ग-रेलवे मार्ग की यह एक बहुत अच्छी उदाहरण हैं। यह रेल मार्ग कनाडा में पूर्वी भाग में हैलीफैक्स से चलकर पश्चिमी में बैन्कूवर तक पहुंचता है। यह रेल मार्ग दुर्ग पर्वत क्षेत्रों में से गुजरता है। इस रेल मार्ग से लकड़ी, खनिज पदार्थ, गेहूँ व लोहे का परिवहन होता है। इस मार्ग का निर्माण 1881 में शुरू किया गया तथा अभी तक इसका विस्तार हो रहा है।

पार ऑस्ट्रेलिया रेलवे मार्ग-यह रेलवे मार्ग पोर्ट ओगस्ता से लेकर कालगुरली तक फैला है। इसका काम 1917 में पूरा हो गया था यह रेल-मार्ग ऑस्ट्रेलिया के पूर्व से पश्चिमी सिरो को आपस में मिलाता है। ब्रिसबेन से बारस्ता सिडनी-मैलबोरन-ऐडिलेड इस मार्ग पथ तक पहुँचता है। इसके निर्माण के समय से ही इसमें तीन गेजों का उपयोग किया गया था जिस कारण इसकी शुरुआत तक का सफर सच हो गया। बाद में 1970 के साल में इसको एक रेलवे गेज में बदला गया। आज के समय सिडनी पथ के बीच वाले रेलवे मार्ग को इण्डिन पैसेफिक रूट कहते हैं।

पनामा कैनाल रेलवे-यह रेलवे मार्ग पनामा नहर के समांतर चलता है तथा मध्य अमेरिका में अंध महासागर के तट से प्रशांत महासागर के तट तक चली जाती है जो कि 77 कि०मी० तक लंबी है। अंध महासागर के शहर कोलेन से प्रशांत महासागर के शहर बल्लबरा तक का रेलवे मार्ग ज्यादा लंबा तो नहीं परंतु यह मार्ग विश्व के बड़े महासागरों को मिलाता है जिस कारण इसका महत्त्व काफी बढ़ गया है। यह रेल मार्ग मुसाफिरों तथा माल को एक स्थान से दूसरे स्थान तक पहुंचाता है।

दक्षिणी अमेरिका में पार इण्डियन तथा पार ऐमेजीयन रेलवे प्रकल्प हैं। अफ्रीकन यूनियन ऑफ रेलवेज़ भी अफ्रीका में पार-महाद्वीपी रेल प्रकल्प बनाने की योजना बना रहे हैं।

भारत का रेलवे नैटवर्क दुनिया का सबसे बड़ा नैटवर्क है, जो कि हर रोज 1 करोड़ 80 लाख यात्रियों को तथा 20 लाख टन माल को एक स्थान से दूसरे स्थान पर पहुँचाया जाता है। ऐसा विस्तृत रेल प्रबंध ही भारतीय रेलवे कहलाता हैं।

प्रश्न 4.
देश की तेज रफ़्तार शाही गाड़ियों से पहचान करवाओ।
उत्तर-
रेल के द्वारा सफर बाकी यातायात के साधनों से सस्ता तथा अधिक आरामदायक होता है। भारत में रेल मार्गों का महत्त्व बढ़ रहा है क्योंकि देश में सफर को आसान बनाने के लिए तेज़ रफ़्तार गाड़ियों को चलाया जा रहा है। ताकि समय की बचत की जा सके। सरकार इस तरफ काफी मेहनत कर रही है देश में पहले ही कुछ तेज़ रफ़्तार गाड़ियां हैं। जिनमें से मुख्य हैं

1. नयी दिल्ली-आगरा गतिमान ऐक्सप्रैस, रफ़्तार 160 कि०मी०/घंटा।
2. नयी दिल्ली-भोपाल शताब्दी एक्सप्रैस, इसकी रफ़्तार 91 कि०मी०/घंटा है।
3. मुंबई-नई दिल्ली राजधानी एक्सप्रैस, इसकी रफ़्तार 90.46 कि०मी०/घंटा है।
4. सियालदा-नई दिल्ली दुरंतो एक्सप्रैस, इसकी रफ्तार 91.0 कि०मी० प्रति घंटा है।
5. नयी दिल्ली-कानपुर शताब्दी एक्सप्रैस, इसकी रफ़्तार 89.63 कि०मी०/घंटा है ।
6. नयी दिल्ली-हावड़ा, दुरांतो एक्सप्रैस, इसकी रफ़्तार 88.21 कि०मी०/घंटा है।
7. नयी दिल्ली-हावड़ा, दुरांतो ऐक्सप्रैस, इसकी रफ्तार 87.06 कि०मी०/घंटा है।
8. नयी दिल्ली-इलाहाबाद, दुरांतो ऐक्सप्रैस, इसकी रफ़्तार 86.85 कि०मी०/घंटा है।
9. सियालदा-नयी दिल्ली राजधानी ऐकस्प्रेस, इसकी रफ़्तार 87.06 कि०मी०/घंटा है।
10. निजामुद्दीन-बांद्रा गरीब रथ, इसकी रफ्तार 82.80 कि०मी० प्रति घंटा।

तेज़ रेल गाड़ियों के अलग देश में रेल गाड़ी की एक और सहूलियत भी है जिसमें सफर शाही सुविधाओं से लैस होता है। इनको लग्ज़री गाड़ियां कहते हैं। इनका प्रबंध इण्डियन रेलवे कैटरिंग एंड टूरिज्म कार्पोरेशन लिमिटड (IRCTC) द्वारा किया गया। कुछ शाही गाड़ियों की सूची निम्नलिखित है-

I. महाराजा ऐक्सप्रैस-यह ऐक्सप्रैस देश के सैलानी महत्त्व रखने वाले स्थानों की शाही सैर करवाती है।
II. पैलेस ऑन वहील्ज़-यह ऐक्सप्रैस राजस्थान के सबसे बढ़िया सैलानी स्थानों की शाही सैर करवाती है।
III. द डैकन उड़ीसी-यह ऐक्सप्रैस शाही ढंग से दक्षिणी भारत की सैर करवाती है।
IV. रॉयल राजस्थान ऑन व्हील्स-यह हमें भारत की संस्कृति की शाही यात्रा करवाती है।
V. रॉयल ओरिएंट ट्रेन-यह रेलवे हमें मध्य भारत की शाही सैर करवाती है।
VI. गोल्डन चैरीयट- यह रेल हमें महाराष्ट्र तथा गुजरात की शाही सैर करवाती है।
VII. फैरी कुईन ऐक्सप्रैस-यह हमें राजस्थान तथा अलवर तथा सरिसका की यात्रा करवाती है।

प्रश्न 5.
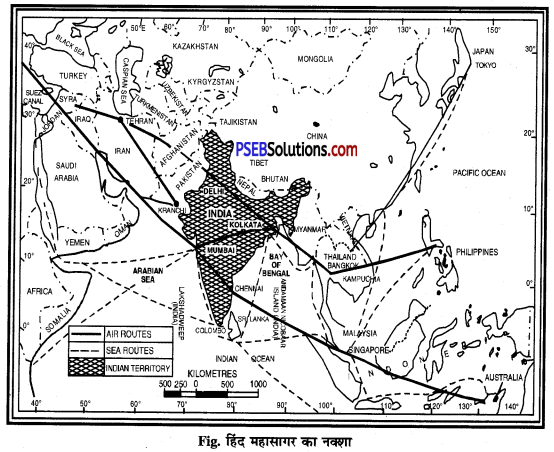
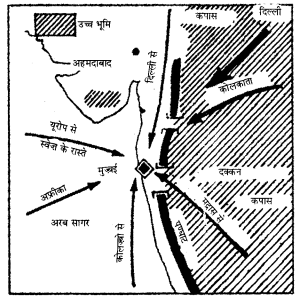
संसार के प्रमुख समुद्री मार्गों पर नोट लिखो।
उत्तर-
संसार में व्यापार का एक बड़ा हिस्सा समुद्री मार्गों के द्वारा किया जाता है। समुद्री जहाजों की सहायता से भारी तथा आवश्यक चीज़ों को एक स्थान से दूसरे स्थान तक पहुँचाया जाता है। यह स्थान बदली का एक सस्ता ढंग है। संसार में व्यापार अलग-अलग समुद्री मार्गों द्वारा किया जाता है तथा व्यापार के लिए छोटे मार्ग को चुना जाता है। संसार के प्रसिद्ध समुद्री मार्ग निम्नलिखित हैं-

1. उत्तरी अंध-महासागरीय मार्ग (North Atlantic Route)- यह समुद्री मार्ग विश्व में सबसे अधिक उपयोग किया जाता है तथा इसके द्वारा ही संसार का आधे से ज्यादा समुद्री व्यापार हो रहा है। इस क्षेत्र की मुख्य व्यापारिक बंदरगाहें हैं-रॉटरडैम, एंटवर्प, लंडन, बोस्टन, न्यूयॉर्क, फिलाडेल्फिया हैं।

2. केप ऑफ़ गुड होप (Cape of Good Hope)-यह समुद्री मार्ग अमेरिका महाद्वीप के दक्षिणी हिस्से से लेकर आशा अंतरीप हिस्से के आस-पास घूमता है।

3. भू-मध्य सागरीय स्वेज़ ऐशियाई मार्ग (The Mediterranean-SuejAsiatic Route)—यह मार्ग ऐशियाई तथा यूरोपीय देश को स्वेज़ नहर की सहायता से आपस में जोड़ता है।

4. पनामा नहर मार्ग (Panama Canal Route)-यह मार्ग अंध-महासागर तथा प्रशांत महासागर को आपस में मिलाता है तथा प्रशांत महासागर द्वार कहलाता है।

5. दक्षिणी अंध महासागरीय मार्ग (South Atlantic Route)-यूरोप के पश्चिमी देशों को अंध महासागर के रास्ते की सहायता के साथ दक्षिणी अमेरिका के पूर्वी उटी क्षेत्रों से मिलाकर व्यापार का मौका दिया जाता है।

6. पार प्रशांत-मार्ग (The Transpacific Route)-इस मार्ग का मुख्य केंद्र हवाई टापू में स्थित है।

Geography Guide for Class 12 PSEB परिवहन/यातायात, संचार तथा व्यापार Important Questions and Answers

I. वस्तुनिष्ठ प्रश्नोत्तर (Objective Type Question Answers)

A. बहु-विकल्पी प्रश्न :

प्रश्न 1.
भारत में सबसे लंबा राष्ट्रीय महामार्ग कौन-सा है ?
(A) NH
(B) NHS
(C) NH
(D) NHA
उत्तर-
(C) NH

प्रश्न 2.
संसार में सबसे लंबा रेलमार्ग कौन-सा है ?
(A) यूनियन पैसिफ़िक
(B) कैनेडियन नैशनल
(C) ट्रांस साइबेरियन
(D) ट्रांस इण्डियन।
उत्तर-
(C) ट्रांस साइबेरियन

प्रश्न 3.
ट्रांस साइबेरियन रेलमार्ग के पूर्वी छोर पर स्थित स्टेशन है ?
(A) हनोई
(B) शंघाई
(C) टोकियो
(D) ब्लाडी वास्टेक।
उत्तर-
(D) ब्लाडी वास्टेक।

प्रश्न 4.
भारतीय रेलवे सिस्टम को कितने रेलवे जोन में विभाजित किया है ?
(A) 9
(B) 16
(C) 14
(D) 12.
उत्तर-
(B) 16

प्रश्न 5.
निम्नलिखित में से कौन-सी स्थल मार्ग यातायात की किस्म नहीं है :
(A) सड़कें
(B) रेलें
(C) पाइप लाइनें
(D) हवाई अड्डा।
उत्तर-
(C) पाइप लाइनें

प्रश्न 6.
राष्ट्रीय मार्गों का निर्माण तथा देखभाल कौन करता है ?
(A) केंद्र सरकार
(B) ज़िला सरकार
(C) बी०ओ०टी०
(D) NHAY.
उत्तर-
(A) केंद्र सरकार

प्रश्न 7.
यमुना एक्सप्रेस हाईवे किस के हवाले है ?
(A) नोएडा तथा आगरा
(B) आगरा तथा दिल्ली
(C) दिल्ली तथा हिमाचल
(D) दिल्ली तथा पंजाब।
उत्तर-
(A) नोएडा तथा आगरा

प्रश्न 8.
सुनहरी चतुर्भुज सड़क मार्ग प्रकल्प में निम्नलिखित महानगरी में किसको शामिल नहीं किया जाता ?
(A) दिल्ली
(B) मुंबई
(C) अहमदाबाद
(D) चेन्नई।
उत्तर-
(C) अहमदाबाद

प्रश्न 9.
भारत सरकार के सड़क यातायात मंत्रालय के 28 अप्रैल, 2010 के नोटिफिकेशन में राष्ट्रीय शाहमार्ग को क्या प्रदान किया गया ?
(A) नई सड़कें
(B) नए अंक
(C) नए मार्ग
(D) सड़कों की मुरम्मत।
उत्तर-
(B) नए अंक

प्रश्न 10.
देश में पहली रेल यात्रा मुंबई से थाने तक की गई :
(A) 1853
(B) 1854
(C) 1865
(D) 1868.
उत्तर-
(A) 1853

प्रश्न 11.
दूसरी रेलवे लाइन जो कोलकाता से रानीगंज तक थी यह कब बिछाई गई ?
(A) 1853
(B) 1854
(C) 1870
(D) 1865.
उत्तर-
(B) 1854

प्रश्न 12.
1950-51 के अंत तक रेलवे लाइनों की लंबाई कितनी थी ?
(A) 53,596 कि०मी०
(B) 53,000 कि०मी०
(C) 58,000 कि०मी०
(D) 60,000 कि०मी० ।
उत्तर-
(A) 53,596 कि०मी०

प्रश्न 13.
उत्तर पूर्वी रेलवे जोन का मुख्यालय कहां पर है ?
(A) गोरखपुर
(B) दिल्ली
(C) आगरा
(D) कोलकाता।
उत्तर-
(A) गोरखपुर

प्रश्न 14.
संसार की पहली रेलवे अमेरिका में कब बिछाई गई ?
(A) 1863 से 1869
(B) 1865-66
(C) 1870-75
(D) 1870-71.
उत्तर-
(A) 1863 से 1869

प्रश्न 15.
मध्य अमेरिका में कौन-सी नहर अंध-महासागर के तट तक जाती है ?
(A) पिली का
(B) पनामा
(C) राईन
(D) वूलर।
उत्तर-
(B) पनामा

प्रश्न 16.
साल 2014 के बजट अनुसार देश में कितने अर्ध तेज रेल गलियारे स्थापित किये जाते थे ?
(A) 9
(B) 10
(C) 6
(D) 5.
उत्तर-
(A) 9

प्रश्न 17.
निम्नलिखित में से कौन-सी लग्ज़री गाड़ी की उदाहरण नहीं है ?
(A) महाराजा ऐक्सप्रैस
(B) हावड़ा दुरांतो ऐक्सप्रेस
(C) पैलेस ऑन वहीक्लज़
(D) गोल्डन चैरीअट।
उत्तर-
(B) हावड़ा दुरांतो ऐक्सप्रेस

प्रश्न 18.
भारत में हवाई यातायात का प्रारंभ किस साल में हुआ ?
(A) 1910
(B) 1911
(C) 1921
(D) 1922.
उत्तर-
(B) 1911

प्रश्न 19.
संचार की प्रमुख कितनी किस्में हैं ?
(A) 2
(B) 1
(C) 3
(D) 4.
उत्तर-
(A) 2

प्रश्न 20.
भारत निम्नलिखित में कौन-सी चीज़ों की दरामद नहीं करता ?
(A) पैट्रोल
(B) खनिज
(C) लोहा तथा इस्पात
(D) गेहूँ।
उत्तर-
(D) गेहूँ।

B. खाली स्थान भरें :

1. यातायात सुविधाओं को मुख्य रूप में …………. भागों में बांटा जाता है।
2. नागपुर योजना ………………… के साल में बनाई गई।
3. देश में यातायात का बहाव संभव बनाने के लिए . ……………. नाम से शाह मार्ग का निर्माण किया गया।
4. सन् 1871 तक तीन प्रमुख शहरों कोलकाता, ………………….. तथा …………………. रेल तंत्र द्वारा आपस में जोड़े गए।
5. भारतीय रेल तीन गेज चौड़ी, सौड़ी तथा ……………… गेज में बांटी जाती हैं।
6. एशिया तथा यूरोप के देशों को .. ……………. नहर की सहायता के साथ आपस में मिलाया गया।
उत्तर-

1. तीन,
2. 1943,
3. एक्सप्रेस हाईवेज,
4. मुंबई, चेन्नई,
5. मीटर,
6. स्वेज।

C. निम्नलिखित कथन सही (√) हैं या गलत (x):

1. बीस वर्षीय योजना 1961 में आरंभ की गई।
2. पूर्व पश्चिमी गलियारा राजस्थान से पोरबंदर तक है।
3. सुनहरी चतुर्भुज दुनिया की पाँचवीं सबसे बड़ी सड़क योजना है।
4. देश में रेल-तंत्र विकसित करने का एक उद्देश्य था सिगनल संचार तकनीक में सुधार करना।
5. गोल्डन चैरीअट महाराष्ट्र और गुजरात की शाही सैर करवाती है।
उत्तर-

1. सही
2. गलत,
3. सही,
4. सही,
5. सही।

II. एक शब्द /एक पंक्ति वाले प्रश्नोत्तर (One Word/Line Question Answers) :

प्रश्न 1.
ट्रशरी व्यवसाय क्या है ?
उत्तर-
जो सेवाएं प्रदान करते हैं।

प्रश्न 2.
परिवहन साधनों के तीन प्रकार बताएं।
उत्तर-
जल-मार्ग, थल मार्ग, हवाई-मार्ग।

प्रश्न 3.
भारतीय सड़क मार्ग की लंबाई बताओ।
उत्तर-
18 लाख कि०मी०।

प्रश्न 4.
स्वर्ण चतुर्भुज से क्या अभिप्राय है ?
उत्तर-
राष्ट्रीय मार्गों का जाल जो दिल्ली, मुंबई, चेन्नई, कोलकाता को जोड़ता है।

प्रश्न 5.
ट्रांस साईबेरियन रेलमार्ग कौन-से स्थानों को जोड़ता है ?
उत्तर-
वलादिवोस्तक और सेंट पीटरसबर्ग।

प्रश्न 6.
संसार में सबसे लंबा रेलमार्ग कौन-सा है ?
उत्तर-
ट्रांस साईबेरियन रेलमार्ग 8800 कि०मी० लंबा है।

प्रश्न 7.
भारत में रेलमार्गों की कुल लंबाई बताओ।
उत्तर-
63000 कि०मी०।

प्रश्न 8.
संसार के दो अंदरूनी जलमार्गों के नाम बताओ।
उत्तर-
राइन नदी और महान झीलें।

प्रश्न 9.
अंध-महासागर पर दो बंदरगाहें बताओ।
उत्तर-
लंदन और न्यूयार्क।

प्रश्न 10.
स्वेज नहर किन सागरों को जोड़ती है ?
उत्तर-
लाल सागर और रूम सागर।

प्रश्न 11.
पनामा नहर किन सागरों को जोड़ती है ?
उत्तर-
अंध महासागर और प्रशांत महासागर।

प्रश्न 12.
भारत के पश्चिमी तट पर दो बंदरगाहों के नाम बताओ।
उत्तर-
कांडला और मुंबई।

प्रश्न 13.
थल-मार्ग के यातायात प्रबंध की तीन किस्में बताओ।
उत्तर-
सड़कें, पाइप लाइन और रेल।

प्रश्न 14.
पहली रेल यात्रा कब और कहाँ तक की गई ?
उत्तर-
1853 में मुंबई से थाने तक।

प्रश्न 15.
लग्ज़री गाड़ियों का प्रबंध किसके अधीन है ?
उत्तर-
भारतीय रेलवे कैटरिंग और टूरिज्म कार्पोरेशन लिमिटेड।

प्रश्न 16.
राष्ट्रीय यातायात नीति कमेटी के अनुसार कितने जल मार्गों को राष्ट्रीय जलमार्ग ऐलान किया गया ?
उत्तर-
10 जल मार्गों को।

प्रश्न 17.
ऐयरपोर्ट्स अथारिटी ऑफ इण्डिया की ओर से दी जाने वाली जानकारी/सूचना के अनुसार कितने अंतर्राष्ट्रीय और घरेलू हवाई अड्डे हैं ?
उत्तर-
30 अंतर्राष्ट्रीय और 400 घरेलू हवाई अड्डे हैं।

प्रश्न 18.
संसार में सबसे लंबी कच्चे तेल की पाइप लाइन कहाँ बिछाई गई ?
उत्तर-
उत्तरी अमेरिका में।

प्रश्न 19.
TAPI पाइप लाइन किस ओर से विकसित की गई ?
उत्तर-
एशियाई विकास बैंक।

प्रश्न 20.
संचार की मुख्य किस्में बताओ।
उत्तर-
व्यक्तिगत और जन-संचार।

प्रश्न 21.
व्यापार से आपका क्या भाव है ?
उत्तर-
वस्तुओं और सेवाओं की खरीदो-फरोख्त की क्रिया को व्यापार कहा जाता है।

प्रश्न 22.
भारत की ओर से बरामद की जाने वाली वस्तुओं के नाम बताओ।
उत्तर-
खनिज तेल, मोम, ईंधन, जैविक रसायन, फार्मेसी, उत्पादन, कनक/गेहूँ से बनी वस्तुएँ।

प्रश्न 23.
भारत की मुख्य चार बंदरगाहों के नाम बताओ।
उत्तर-
मैंगलोर, कोची, सूरत, पणजी।

प्रश्न 24.
आलमी व्यापार संगठन क्या है ?
उत्तर-
यह एक अंतर-सरकारी संस्था है, जो अंतर्राष्ट्रीय व्यापार को क्रमबद्ध करती है और अलग-अलग देशों के मध्य व्यापारिक नियमावली निश्चित करती है।

अति लघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
यातायात सविधाओं को कौन-से वर्गों में वर्गीकृत किया जाता है ?
उत्तर-
यातायात सुविधाओं को निम्नलिखित वर्गों में वर्गीकृत किया जाता है-

1. स्थल मार्ग यातायात
2. जल मार्ग यातायात
3. वायु मार्ग यातायात।

प्रश्न 2.
यातायात के साधन कौन-से ज़रूरी तत्त्वों पर निर्भर करता है ?
उत्तर-
यातायात के साधन के विकास में कई तत्त्वों का योगदान रहता है। यातायात मार्ग का निर्धारण आवश्यक है। वाहन तथा ऊर्जा के साधन परिवहन मार्गों पर प्रभाव डालते हैं। स्थल आकृति, मौसम परिवहन साधनों को प्रभावित करते हैं। आर्थिक विकास में कच्चे माल की प्राप्ति परिवहन के लिए आवश्यक तत्त्व है।

प्रश्न 3.
अंतर-महाद्वीपी रेल-मार्ग किसे कहते हैं ? उदाहरण दो।
उत्तर-
अंतर महाद्वीपीय रेल-मार्ग उन रेल मार्गों को कहते हैं जो महाद्वीप के एक किनारे को दूसरे किनारे से जोड़ते हैं। यह रेल-मार्ग महाद्वीप के उल्ट तटों पर स्थित स्थानों को जोड़ते हैं। ट्रांस साइबेरियाई रेल-मार्ग तथा ट्रांस कैनेडियन रेल मार्ग इसकी दो उदाहरण हैं।

प्रश्न 4.
रेलमार्ग किन हिस्सों में बनाये जाते हैं ?
उत्तर-

• रेलमार्ग हमेशा मैदानी समतल हिस्सों में बनाये जाते हैं।
• रेल मार्ग हमेशा घनी जनसंख्या वाले प्रदेशों तथा आर्थिक रूप में विकसित प्रदेशों में बनाये जाते हैं।
• बंदरगाहों को देश के आंतरिक हिस्सों से जोड़ने के लिए रेलमार्गों का निर्माण किया जाता है।

प्रश्न 5.
भारत के सीमावर्ती सड़क मार्ग बताओ।
उत्तर-
भारत के सीमावर्ती प्रदेशों में सड़कों का निर्माण करने के लिए सीमा सड़क बोर्ड की सन् 1960 में स्थापना की गई। भारत में सीमा निकट प्रदेशों में 27,000 कि०मी० लंबी पक्की सड़कें बनाई गई हैं। जिन में मनाली से लेह तक मुख्य सड़क है। इस सड़क की औसत ऊंचाई 4270 मीटर है।

प्रश्न 6.
संसार के मुख्य समुद्री मार्गों का महत्त्व बताओ।
उत्तर-
यातायात के साधनों में समुद्री यातायात सबसे सस्ता तथा महत्त्वपूर्ण साधन है। संसार का अधिकतर व्यापार समुद्री मार्ग के द्वारा होता है। जब बहुत सारे जहाज एक निश्चित मार्गों पर चलते हैं, तब उसे समुद्री मार्ग कहते हैं।

प्रश्न 7.
भारतीय रेल-मार्गों की अलग-अलग आकार की पटरियां बताओ।
उत्तर-
भारत में रेल मार्ग तीन तरह के हैं:

1. चौड़ी पटरी (Broad Gauge)-1.68 मीटर चौड़ी।
2. छोटी पटरी (Metre Gauge)-1 मीटर चौड़ाई।
3. तंग पटरी (Narrow Gauge)-0.68 मीटर चौड़ाई।

प्रश्न 8.
पनामा नहर की महत्ता बताओ।
उत्तर-
इस नहर के निर्माण के साथ अंध-महासागर के मध्य दूरी कम हो गई है। इससे पहले जहाज़ दक्षिणी अमेरिका के केप हारन का चक्कर ला कर जाते हैं। इस नहर से सबसे अधिक लाभ संयुक्त राज्य अमेरिका को हुआ है। इसके पश्चिमी तथा पूर्वी तटों के मध्य दूरी कम हो गई है। संयुक्त राज्य अमेरिका के पूर्वीतट से आस्ट्रेलिया, न्यूजीलैंड, दक्षिणी अमेरिका, जापान की बंदरगाहों की दूरी कम हो गई है। इस नहर द्वारा यूरोप को कोई विशेष लाभ नहीं है।

प्रश्न 9.
HBJ गैस पाइप लाइन का वर्णन करो।
उत्तर-
भारत में गैस परिवहन के लिए हजीरा-विजयपुर-जगदीशपुर पाइप लाइन बनाई गई है। यह पाइप लाइन 1700 किलोमीटर लंबी है। यह पाइप लाइन गुजरात, मध्य प्रदेश, राजस्थान, उत्तर प्रदेश राज्यों से गुजरती है। इस गैस के साथ विजयपुर, सवाई माधोपुर, जगदीशपुर, शाहजहांपुर, अंबाला तथा बबराला में खाद बनाने की योजना है।

प्रश्न 10.
व्यक्तिगत संचार से आपका क्या अर्थ है ?
उत्तर-
जब दो या दो से ज्यादा व्यक्ति आमने-सामने होकर या किसी साधन का उपयोग करके कोई जानकारी, विचार संदेश आपस में आदान-प्रदान करें उसे व्यक्तिगत संचार कहते हैं। ऐसे संचार के साधनों में व्यक्ति आपस में एक-दूसरे से पहचान करवाते हैं। मुख्य साधन हैं-डाक सेवाएं, टैलीफोन, ई-मेल इत्यादि।

प्रश्न 11.
राष्ट्रीय व्यापार के कोई चार आधार लिखो।
उत्तर-
राष्ट्रीय व्यापार के आधार निम्नलिखित हैं-

• मांग तथा पूर्ति में अंतर।
• प्राकृतिक साधनों के अस्तित्व में अंतर।
• माल के मूल्यों में अंतर।
• व्यापारिक नीतियां।

प्रश्न 12.
आलमी व्यापार संगठन (World Trade Organization) क्या हैं ?
उत्तर-
आलमी व्यापार संगठन पहली बार जनवरी, 1995 को मराकेश समझौते द्वारा अस्तित्व में आया। जिस में संसार के 123 देशों ने हस्ताक्षर किए तथा शुल्क और व्यापार पर सामान्य समझौता (General Agreement on Tarrifism and Trade) का अंत कर दिया। इस संगठन का मुख्य दफ्तर जनेवा में है। खासकर व्यापारिक मसलों का समाधान तथा नियमों को लागू इस द्वारा ही किया जाता है। यह संगठन आलमी व्यापार स्तर को सुधार से राष्ट्रीय व्यापार को ज्यादा महत्त्वपूर्ण बना रहा है।

प्रश्न 13.
NNB पाइप लाइन का वर्णन करो।
उत्तर-
NNB नाहरकटिया नानूमती बरोनी पाइप लाइन देश की पहली पाइप लाइन है जो कि नाहरकटिया के तेल के कुओं से नानूमती तक कच्चा तेल पहुँचाने के लिए बिछाई गई थी तथा बाद में यह पाइप लाइन बरोनी तक बढ़ा दी गई। इसकी लंबाई 1167 कि०मी० है तथा अब इसको उत्तर प्रदेश के कानपुर शहर तक बढ़ा दिया गया है। इस NNB पाइप लाइन का काम 1962 तक शुरू हो गया था जब तक कि बरोनी तक का भाग 1964 में शुरू किया गया।

प्रश्न 14.
उत्तरी अंध महासागरी मार्ग पर नोट लिखो।
उत्तर-
यह संसार के प्रमुख समुद्री मार्गों में एक है। यह जल-मार्ग संसार का सबसे अधिक उपयोग में आने वाला जल मार्ग है। इस जल मार्ग के द्वारा आधे से अधिक समुद्री व्यापार किया जा रहा है। उत्तरी अंध महासागर मार्ग की प्रमुख बंदरगाहें हैं-रॉटरडैम, फिलाडेल्फिया, ऐंटवर्प, लंदन, न्यूयॉर्क, बोस्टन इत्यादि हैं।

प्रश्न 15.
जल-मार्गी यातायात को कौन-से दो भागों में विभाजित किया जाता है ?
उत्तर-
जल मार्गी यातायात को मुख्य रूप में दो भागों में विभाजित किया जाता है :

1. आंतरिक जल मार्ग
2. समुद्री जल मार्ग।

प्रश्न 16.
सड़क मार्गों का जाल बिछाने के लिए कौन-सी योजनाएं देश में चल रही हैं ?
उत्तर-
सड़क मार्गों का जाल बिछाने के लिए मुख्य योजनाएं हैं :

• नागपुर योजना
• बीस वर्षीय योजना
• ग्रामीण सड़क योजना
• बी०ओ०टी०
• केंद्रीय सड़क फंड।

प्रश्न 17.
सड़क यातायात आसान क्यों है ?
उत्तर-
स्थल यातायात का मुख्य साधन सड़कें हैं। यह एक सस्ता तथा तेज़ यातायात का साधन है। सड़कें खेतों को फैक्ट्रियों के साथ तथा वस्तुओं को विक्रेताओं तथा खरीददारों तक पहुँचाने का एक साधन है। सड़कें असमतल तथा ऊँचे-नीचे स्थानों पर भी बनाई जा सकती हैं। घनी यूरोपीय सड़कें उन देशों के विकास का एक मुख्य साधन हैं।

प्रश्न 18.
पनामा नहर की मुख्य विशेषताएं बताओ।
उत्तर-
पनामा नहर-

1. यह पनामा के स्थान पर स्थित है तथा U.S.A. का इस पर अधिकार है।
2. इस नहर से निकलने वाले जहाजों पर टैक्स कम लगाया जाता है।
3. इसके कारण अंध महासागर तथा प्रशांत महासागर के बीच दूरी कम हो गई।
4. यह नहर संयुक्त राज्य अमेरिका के लिए बहुत उपयोगी है क्योंकि इस कारण अब जहाजों को केप होरन तक नहीं जाना पड़ता।

प्रश्न 19.
सड़क मार्गों के क्या दोष हैं ?
उत्तर-

1. सड़क मार्ग महंगे हैं।
2. इनसे वायु प्रदूषण होता है।
3. अधिक दूरी तक भारी वस्तुओं का परिवहन नहीं होता।
4. दुर्घटनाएं प्रतिदिन बढ़ रही हैं।

लघु उत्तरीय प्रश्न (Short Answer Type Questions)

प्रश्न 1.
परिवहन के विभिन्न साधनों के प्रकार बताओ।
उत्तर-
परिवहन के विभिन्न साधनों के प्रकार हैं-

1. स्थल परिवहन
2. जल परिवहन
3. वायु परिवहन।

स्थल परिवहन में सड़कें, रेलें तथा पाइप लाइनें शामिल हैं। जल परिवहन के मुख्य रूप हैं-

1. आंतरिक मार्ग
2. समुद्री मार्ग।

वायु परिवहन में वायुयान सेवाएं गिनी जाती हैं।

प्रश्न 2.
ग्रामीण सड़कें तथा ज़िला सड़कों में अंतर स्पष्ट करो।
उत्तर-
ग्रामीण सड़कें-

1. यह सड़कें गाँव को जिले से जोड़ती हैं।
2. ग्रामीण सड़कें अकसर समतल तथा स्थाई नहीं होती।
3. इन सड़कों में काफी मोड़ आते हैं जिन पर भारी वाहन नहीं चल सकते।

जिला सड़कें-

1. यह सड़कें कस्बे, बड़े गांवों तथा जिला केंद्रों को आपस में जोड़ती हैं।
2. यह सड़कें अकसर स्थाई होती हैं।
3. यहां पर मोड़ ज्यादा नहीं होते तथा अक्सर भारी वाहन चलते हैं।

प्रश्न 3.
भारतीय सड़कों की मुख्य विशेषताएं बताओ।
उत्तर-
भारतीय सड़कों की विशेषताएं निम्नलिखित हैं-

• भारत में पक्की सड़कों की लंबाई 8 लाख 88 हजार कि०मी० है।
• भारत में कच्ची सड़कों की लंबाई 9 लाख 55 हजार कि०मी० है।
• भारत में हर 100 वर्ग किलोमीटर के पीछे 48 किलोमीटर सड़कें हैं जहां पर हर एक लाख लोगों के पीछे 293 किलोमीटर सड़कें हैं।
• देश में राष्ट्रीय राज मार्गों की लंबाई 313558 किलोमीटर है।
• इन सड़कों पर लगभग 37 लाख मोटर गाड़ियां चलती हैं।
• भारतीय सड़कों को हर साल ₹ 1580 करोड़ की आमदन होती है।
• भारत का 30% सामान सड़कों के द्वारा परिवहन किया जाता है।

प्रश्न 4.
रेल मार्गों के विकास का क्या महत्त्व है ?
उत्तर-
स्थलीय परिवहन में रेल-मार्ग एक महत्त्वपूर्ण साधन है। आधुनिक युग में देश में आर्थिक, सामाजिक तथा राजनीतिक दृष्टि से रेलों का बड़ा महत्त्व है।
महत्त्व-

1. रेल-मार्ग किसी क्षेत्र के खनिज पदार्थों के विकास में सहायता करते हैं।
2. रेल मार्ग औद्योगिक क्षेत्र में कच्चे माल तथा तैयार माल के वितरण में सहायता करते हैं।
3. रेल मार्ग व्यापार को उन्नत करते हैं।
4. रेल मार्ग राजनीतिक एकता व स्थिरता लाने में योगदान देते हैं।
5. रेल मार्ग संकट काल में सहायता कार्यों में महत्त्वपूर्ण हैं।
6. कम जनसंख्या वाले प्रदेशों में रेलमार्ग-जनसंख्या वृद्धि का आधार बनते हैं।
7. लंबी-लंबी दूरियों को जोड़ने में रेलों ने महत्त्वपूर्ण भूमिका निभाई है। वास्तव में रेल मार्गों के विकास में मानव ने दूरी और समय पर विजय प्राप्त कर ली है।

प्रश्न 5.
आंतरिक जल मार्गों का क्या महत्त्व है ?
उत्तर-
जल मार्ग दो प्रकार के हैं-आंतरिक तथा महासागरी मार्ग। अंतर्राष्ट्रीय व्यापार के लिए समुद्री मार्गों का प्रयोग किया जाता है। किसी देश के प्रादेशिक व्यापार के लिए नदियां, नहरें, झीलों का आंतरिक जलमार्गों के रूप में प्रयोग किया जाता है। __मनुष्य प्राचीन काल से ही नदियों तथा नहरों का यातायात के लिए प्रयोग करता आया है। आजकल विकसित देशों में आंतरिक जल मार्गों को बड़े पैमाने पर उपयोग किया जाता है। कृषि तथा उद्योगों के विकास में आंतरिक जल मार्ग महत्त्वपूर्ण हैं।

प्रश्न 6.
गोल्डन कुआर्डीलेटरल या सुनहरी चतुर्भुज से आपका क्या भाव है ?
उत्तर-
गोल्डन कुआर्डीलेटर भारत में बनाई गई पहली सड़क निर्माण योजना है जो कि राष्ट्रीय शाहमार्ग विकास प्रकल्प के तहत शुरू की गई। इसको संसार की पाँचवीं बड़ी सड़क निर्माण योजना का दर्जा हासिल है। इस प्रकल्प में भारत के चार प्रसिद्ध महानगरों दिल्ली, मुंबई, चेन्नई तथा कोलकाता को आपस में मिलाये जाने की योजना है जोकि एक चतुर्भुज की आकृति लेती है जिस के कारण इसको सुनहरी चतुर्भुज भी कहते हैं। इस सड़क योजना से जुड़े बड़े शहर हैं-अहमदाबाद, बैंगलोर, भुवनेश्वर, जयपुर, कानपुर, पुणे, सूरत, नैलूर, विजयवाड़ा तथा गंटूर। इस चतुर्भुज की कुल लंबाई 5846 किलोमीटर है तथा इसके अधीन चार तथा छः मार्गी ऐक्सप्रेस हाईवे निर्मित किए गए हैं। इस योजना का शाहमार्ग देश 13 राज्यों में से गुजरता है तथा इन 13 राज्यों में आन्ध्र प्रदेश में सबसे अधिक तथा दिल्ली में सबसे कम भाग पड़ता है। इस प्रकल्प के कारण औद्योगिक व्यापार को प्रोत्साहन मिला है।

प्रश्न 7.
डाइमंड कुआर्डिलेटरल का वर्णन करो।
उत्तर-
डाइमंड कुआर्डिलेटरल भारत के प्रसिद्ध महानगरों (दिल्ली, मुंबई, कोलकाता तथा चेन्नई) को आपस में तेज रफ़्तार से चलने वाली रेल गाड़ियों के साथ जोड़ने की योजना को कहते हैं। यह सड़क योजना सुनहरी चतुर्भुज जैसी ही है। देश के रेल तंत्र को आरामदायक बनाने तथा इसमें सुधार लाने के लिए तेज रफ्तार रेल गाड़ियों तथा बुलेट ट्रेन जैसी गाड़ियों को चलाया गया जिस प्रकल्प में यह रेल गाड़ियां चलाई गई, उसको डायमंड कुआर्डीलेटरल प्रकल्प कहते हैं। इस रेल मार्ग द्वारा कई बड़े शहर आपस में जुड़ गए जैसे-उत्तर प्रदेश, राजस्थान, महाराष्ट्र, गुजरात, दिल्ली, हरियाणा, आन्ध्र प्रदेश, तेलंगाना, तमिलनाडु, कर्नाटक, केरल, बिहार, उड़ीसा, झारखण्ड तथा पश्चिमी बंगाल इत्यादि राज्यों में से गुजरते हैं। यहाँ बिजली की सुविधा भी है क्योंकि यह मार्ग चौड़ी गेज वाले हैं। इन रेलों की रफ्तार 250 किलोमीटर प्रति घंटा की होगी जब कि रेल गाड़ियों 320 कि०मी० प्रति घंटा की रफ्तार से दौड़ेगी।

प्रश्न 8.
समुद्री मार्गों की महत्ता बताओ।
उत्तर-
यातायात के साधनों में समुद्री यातायात सबसे सस्ता तथा महत्त्वपूर्ण साधन है। विश्व का ज्यादातर व्यापार समुद्री मार्गों द्वारा होता है। जब बहुत सारे जहाज़ एक निश्चित मार्ग से चलते हैं तब उसे समुद्री मार्ग कहते हैं।

समुद्री मार्गों की महत्ता (Importance of Ocean Routes)-

• यह सबसे सस्ता यातायात का साधन है।
• यह प्राकृतिक मार्ग है। समुद्र में मार्ग बनाने में कुछ खर्च नहीं होता।
• जहाजों को चलाने के लिए कोयला या पैट्रोल कम खर्च होता है।
• समुद्री मार्ग असल में अंतर्राष्ट्रीय मार्ग हैं, क्योंकि सारे महासागर एक-दूसरे से मिले हैं।
• ‘इन मार्गों पर जहाजों की कम दुर्घटना होती है।
• इन मार्गों द्वारा दूर-दूर के देशों के आपसी सम्पर्क बढ़े हैं।
• इन मार्गों द्वारा अंतर्राष्ट्रीय व्यापार में वृद्धि होती हैं।

प्रश्न 9.
जन संचार के साधनों का वर्णन करो।
उत्तर-
जब हम बडी गिनती में लोगों तक कोई संदेश या विचार पहुँचाना चाहते हैं या जनता के साथ बांटना चाहते हैं तो उसे जन संचार कहते हैं। ऐसा संचार कई प्रकार के साधनों द्वारा किया जाता है। जिसमें व्यक्तिगत संचार की तरह पक्ष एक-दूसरे से परिचित नहीं होता। जनसंचार के प्रमुख साधन हैं-

1. जनतक घोषणा, रैली इत्यादि।
2. रेडियो, टेलीविज़न।
3. अख़बारें, रसाले, मैगज़ीन ।
4. सिनेमा।
5. कंप्यूटर की सहायता से ही जनतक सूचना।
6. इंटरनैट संचार।
7. औजू सैट।

प्रश्न 10.
व्यापार से आपका क्या अर्थ है ? इसकी किस्में बताओ।
उत्तर-
वस्तुओं को बेचने तथा खरीदने को व्यापार कहते हैं या किसी वस्तु के लेन-देन को व्यापार कहते हैं। यह खरीददार तथा विक्रेता के बीच की अदायगी की क्रिया है। व्यापार मुख्य रूप में दो प्रकार का होता है-

1. निजी व्यापार।
2. राष्ट्रीय व्यापार।

प्रश्न 11.
राष्ट्रीय व्यापार तथा इसके क्या कारण हैं ?
उत्तर-
जब व्यापार/बेच-खरीद/लेन-देन राष्ट्रीय स्तर पर होता है, तब उसे राष्ट्रीय व्यापार कहते हैं। अगर कोई देश अपने देश की सीमाओं से बाहर कोई व्यापार लेन-देन करता है उसको अंतर्राष्ट्रीय व्यापार कहते हैं। राष्ट्रीय व्यापार के कारण निम्नलिखित हैं-

• किसी देश में प्राकृतिक साधनों की कमी।
• देश में वस्तुओं की मांग तथा पूर्ति में अंतर।
• तकनीकी साधनों की कमी के कारण कई बार वस्तुओं को दूसरे देश से मंगवाना पड़ता है।
• भौगोलिक भिन्नता।
• आर्थिक विकास में कमी।
• व्यापारिक देशों में जंग तथा अमन शांति के हालात।
• व्यापारिक नीतियां।
• देश के आपसी संबंध।

प्रश्न 12.
भारतीय आयात तथा निर्यात पर नोट लिखो।
उत्तर-
उत्पादित फालतू सामान को जब किसी और देश में बेचा जाता है तब उसे निर्यात कहते हैं तथा स्रोतों की कमी के कारण जब किसी देश से स्रोतों को खरीदा जाता है तो उसे आयात कहते हैं।

भारतीय निर्यात-भारत खनिज तेल, खनिज मोम, जैविक रसायन, फार्मेसी उत्पादन, गेहूँ से बनी वस्तुओं, अनाज, बिजली की मशीनरी, कपास के सूती कपड़े, काहवा, चाय, मसाले इत्यादि बाकी देशों को निर्यात करता है।
भारतीय आयात-भारत पैट्रोल, खनिज मशीनरी, खाद्य, लोहा तथा इस्पात, मोती, कीमती पत्थर, सोना, चांदी, खुराकी तेल, रसायन, दवाइयां, कागज़ फाईबर इत्यादि दूसरे देशों से आयात करता है।

प्रश्न 13.
आलमी व्यापार संगठन (WTO) पर नोट लिखो।
उत्तर-
सन् 1995 में गैट का रूप बदलकर विश्व व्यापार संगठन बनाया गया। यह जनेवा में एक स्थायी संगठन के रूप में कार्यरत है तथा यह व्यापारिक झगड़ों का निपटारा भी करता है। यह संगठन सेवाओं के व्यापार को भी नियंत्रित करता है। किंतु इसे अभी भी महत्त्वपूर्ण कर रहित नियंत्रणों जैसे निर्यात निषेध, निरीक्षण की आवश्यकता, स्वास्थ्य एवं सुरक्षा स्तरों तथा आयात लाइसेंस व्यवस्था जिनसे आयात प्रभावित होना है, को सम्मिलित करना शेष है। आलमी व्यापार संगठन में 123 देशों ने हस्ताक्षर करके जनरल एग्रीमैंट का खात्मा कर दिया है। इस प्रकार आलमी व्यापार संगठन राष्ट्रीय व्यापार को अच्छा तथा महत्त्वपूर्ण बना देता है

निबंधात्मक प्रश्न (Essay Type Questions)

प्रश्न 1.
यातायात से आपका क्या भाव है ? देश में प्रशासकीय प्रबंध के आधार पर सड़कों का वर्गीकरण करो तथा सड़क-मार्गों का जाल बिछाने के लिए बनाई योजनाओं के बारे में विस्तार से चर्चा करो।
या
भारतीय सड़कों के विकास का वर्णन करो।
उत्तर-
यातायात-मनुष्य, जानवरों तथा वस्तुओं को एक स्थान से दूसरे स्थान तक पहुँचाने को या वस्तुओं के परिवहन को यातायात कहते हैं। यातायात के मुख्य वर्ग हैं

1. स्थल-मार्ग यातायात।
2. जल-मार्ग यातायात।
3. वायु-मार्ग यातायात।

सड़कों का प्रशासकीय प्रबंध के आधार पर वर्गीकरण-प्रशासकीय प्रबंध के आधार पर सड़कों का वर्गीकरण निम्नलिखित किया गया है –
1. ग्रामीण सड़कें (Rural Roads)—जो सड़कें गाँव को जिले की सड़कों से मिलाती हैं, ग्रामीण सड़कें कहलाती हैं। इन सड़कों में मोड़ काफी होते हैं यहाँ बहुत भारी वाहनों को काफी मुश्किलों का सामना करना पड़ता है।

2. जिला सड़कें (District Roads)—यह सड़कें जिले की सड़कों, कस्बे तथा बड़े गाँवों को आपस में जोड़ती हैं। इन सड़कों की देखभाल जिला परिषद् तथा आम जनता की ज़िम्मेदारी होती है।

3. राज्य मार्ग (State Highways) राज्य के व्यापार तथा भारी यात्री यातायात की किस्म राज्य मार्गों के अधीन आती है। यह सड़कें आर्थिकता की मुख्य इकाई होती हैं, सड़कों के मुख्य केंद्रों को राज्य की राजधानियों तथा राष्ट्रीय शाहमार्गों के साथ मिलाती हैं।

4. राष्ट्रीय शाह मार्ग (National Highways)-राष्ट्रीय शाहमार्गों की देख-भाल की ज़िम्मेदारी केंद्रीय सरकार की होती है। भारत में राष्ट्रीय शाहमार्ग एथॉरिटी इन मार्गों की देख-रेख करती है। यह सड़कें देश के सारे कोनों तक फैली हुई हैं।

5. सीमान्त इलाकों की सड़के (Border Roads)-इन सड़कों की देख-भाल की ज़िम्मेदारी सीमान्त सड़क संगठन के अंतर्गत आती है।

सड़क योजनाएं-सड़कें किसी देश के विकास की रीढ़ की हड्डी हैं। यह वस्तुओं, मनुष्य, जानवरों, स्रोतों इत्यादि के परिवहन में अहम् तथा महत्त्वपूर्ण भूमिका अदा करती हैं। इसके अलावा इन सड़कों द्वारा सफर करना आसान तथा आरामदायक भी होता है। सड़कों का अच्छा तथा सड़क-मार्गों का जाल बिछाने के लिए कई योजनाएं देश अंदर चल रही हैं।

1. नागपुर योजना (Nagpur Plan)-नागपुर योजना सन् 1943 में भारत में सड़कें बिछाने के लिए बनाई गई। इस योजना में देश की प्रमुख सड़कों के अलावा और आम सड़कों की लंबाई भी बढ़ाई गई।

2. बीस वर्षीय योजना (Twenty Year Plan)-इस योजना की शुरुआत 1961 में हुई। इस योजना का उद्देश्य देश में सड़कों की लंबाई 6 लाख 56 कि०मी० से बढ़ाकर 10 लाख 60 हज़ार कि०मी० तक करना था तथा इसके लिए समय 20 साल तय किया गया।

3. ग्रामीण सड़क विकास योजना (The Rural Road Development Scheme)-इस योजना का मुख्य उद्देश्य ग्रामीण इलाकों में सड़कों का विकास करना था।

4. बी०ओ०टी० योजना (Build, Operate and Transfer Scheme)-इस योजना में प्राईवेट बिल्डरों तथा
ठेकेदारों को सड़कें तथा पुलों का निर्माण करने के लिए ठेके दिए गए तथा इज़ाजत दी गई कि वह निर्माण की गई सड़क पर गुजरने वाले वाहनों के चालकों से टोल टैक्स ले सकेंगे तथा बाद में सड़क भारत सरकार के हवाले कर देंगे।

5. केन्द्रीय सड़क फंड (Cential Road Fund)-इस फंड को दिसम्बर 2000 में शुरू किया गया। इसके अनुसार पैट्रोल तथा डीज़ल पर टैक्स तथा कस्टम ड्यूटी लगाकर इकट्ठा किया पैसा सड़कों के विकास पर लगाया जाएगा। भारत में प्राचीन काल से ही सड़कों की महत्ता रही हैं। शेरशाह सूरी ने जी०टी०रोड के राष्ट्रीय राजमार्ग का निर्माण किया। आजादी के बाद 10 वर्षीय नागपुर योजना के अधीन सड़कों के विकास की योजना बनाई गई। भारत की मुख्य सड़कें निम्न हैं।

राष्ट्रीय मार्ग (National Highways)

• ग्रैंड ट्रंक रोड (Grand Trunk Road)-कोलकाता से अमृतसर तक है। इसको शेरशाह सूरी मार्ग भी कहा जाता है।
• दिल्ली-मुंबई रोड।
• कोलकाता-मुंबई रोड।
• मुंबई-चेन्नई रोड।
• ग्रेट दक्षिण रोड।
• कोलकाता-चेन्नई रोड।
• पठानकोट- श्रीनगर रोड।
• भारत की सीमावर्ती प्रदेशों में सड़कों का निर्माण करने के लिए सीमा सड़क बोर्ड को सन् 1960 में स्थापित किया गया। भारत में सीमान्त प्रदेशों में 7000 कि०मी० लम्बी पक्की सड़कें बनायी गई हैं। जिनमें मनाली से लेकर लेह तक मुख्य सड़कें हैं। इस सड़क की औसत ऊंचाई 4270 मीटर है।

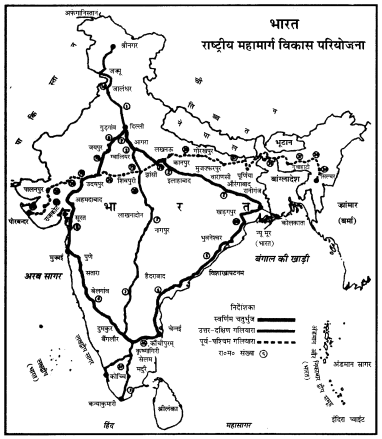
प्रश्न 2.
संसार के प्रमुख रेल मार्गों की स्थिति तथा महत्त्व का वर्णन करो।
उत्तर-
स्थल यातायात में रेलवे सबसे अधिक महत्त्वपूर्ण साधन है। सन् 1819 में भाप के इंजन की खोज के साथ रेल के यातायात का प्रारंभ ग्रेट ब्रिटेन में हुआ। आधुनिक युग में किसी देश में आर्थिक, सामाजिक तथा राजनीतिक दृष्टि से रेलवे का बड़ा महत्त्व है।

महत्त्व-

• रेलमार्ग किसी क्षेत्र के खनिज पदार्थों के विकास में सहायता करते हैं।
• रेलमार्ग औद्योगिक क्षेत्र में कच्चे माल तथा तैयार माल के वितरण में सहायता करते हैं।
• रेलमार्ग व्यापार को उन्नत करते हैं।
• रेलमार्ग राजनीतिक एकता व स्थिरता लाने में योगदान देते हैं।
• रेलमार्ग संकट काल में सहायता कार्यों में महत्त्वपूर्ण हैं।
• कम जनसंख्या वाले प्रदेशों में रेल-मार्ग जनसंख्या वृद्धि का आधार बनते हैं।
• लम्बी-लम्बी दूरियों को जोड़ने में रेलों ने महत्त्वपूर्ण भूमिका निभाई हैं। वास्तव में रेल-मार्गों के विकास से मानव ने दूरी और समय पर विजय प्राप्त कर ली है।

रेलमार्गों की स्तिति के तत्त्व (Factors of Location),

1. अधिक जनसंख्या हो।
2. समतल मैदानी धरातल हो।
3. औद्योगिक तथा व्यापारिक विकास अधिक हो।
4. खनिज पदार्थ के अधिक भंडार हो।
5. तकनीकी ज्ञान प्राप्त हो।

संसार के मुख्य रेलमार्ग (Major Railways) रेलमार्गों की सबसे अधिक लंबाई संयुक्त राज्य अमेरिका में हैं। कई देशों में मोटर, सड़कें तथा जल मार्गों के अधिक विकास के कारण रेलमार्ग कम हैं।

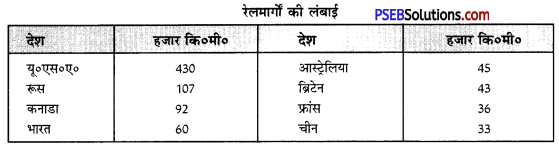
ट्रांस-साइबेरियन रेलमार्ग-यह रेलमार्ग 9289 कि०मी० लम्बा है तथा संसार में सबसे लम्बा रेलमार्ग है। यह रेल मार्ग साइबेरिया तथा यूराल प्रदेश के आर्थिक तथा औद्योगिक विकास का आधार है। यह एक अन्तः महाद्वीपीय मार्ग है। यह रेल-मार्ग पश्चिम में बाल्टिक सागर पर स्थित सेंट पीटर्जसवर्ग बन्दरगाह के पूर्व में प्रशान्त महासागर पर स्थित ब्लाडीवोस्टक बन्दरगाह को जोड़ता है। इस रेल-मार्ग के मुख्य स्टेशन मास्को, रंयाजन, कुइबाशेव चेलिया बिन्सक, ओमस्क, नीवी सिबीरस्क, चीता इकूटस्क तथा खाबारीवस्क हैं । इस रेलमार्ग द्वारा कोयला, तेल, लकड़ी, खनिज, कृषि उत्पाद, मशीनरी तथा औद्योगिक उत्पादों का आदान-प्रदान पूर्व से पश्चिम को होता है।

2. कैनेडियन पैसेफिक रेलमार्ग-कनाडा का पूर्व-पश्चिम में अधिक विस्तार है। यह रेलमार्ग कनाडा में पूर्वी भाग में हैली फैक्स से चलकर पश्चिम में बेन्कूवर तक पहुंचता है। यह रेलमार्ग दुर्गम पर्वत क्षेत्रों में से गुजरता है। इस रेलमार्ग से लकड़ी, खनिज पदार्थ, गेहूं व लोहे का परिवहन होता है। कैनेडियन पैसेफिक रेल-मार्ग की लम्बाई 7050 किलोमीटर हैं। इस मार्ग पर सेंटजॉन मांट्रिगल, ओटावा, विनीपेग इत्यादि नगर स्थित है। यह रेल-मार्ग क्यूबेक मांट्रियल के औद्योगिक क्षेत्र को कोणधारी वनों तथा प्रेयरीज के गेहूं से जोड़ता हैं। इस प्रकार यह रेल मार्ग राजनीतिक तथा आर्थिक रूप से एकता स्थापित करता है।

3. संयुक्त राज्य अमेरिका के रेलमार्ग संयुक्त राज्य अमेरिका के पूर्वी भाग में रेलवे का अधिक विकास हुआ है। पश्चिम में जनसंख्या कम है। यहां शुष्क जलवायु तथा पर्वतीय भागों के कारण रेलमार्ग कम हैं। यह रेलमार्ग देश के पश्चिमी तथा पूर्वी क्षेत्रों को आपस में मिलाता है। देश के मध्यवर्ती क्षेत्र की कृषि तथा खनिज क्षेत्रों के लिए यह बहुत योग्य सिद्ध हुए हैं। इस देश में मुख्य महाद्वीप रेलमार्ग निम्नलिखित हैं।

• उत्तरी पैसेफिक रेलमार्ग-यह मार्ग शिकागो से होकर सेंटपाल पोर्टलैंड तक जाता है।
• दक्षिणी पैसेफिक रेलमार्ग-यह रेलमार्ग पश्चिम में लॉस एंजिलस तक जाता है।
• महान् उत्तरी रेलमार्ग-यह रेलमार्ग सुपीरियर झील के तट से डिओलब में होकर सीटल तक जाता है।
• यूनियन पैसेफिक रेलमार्ग-यह रेलमार्ग एटलांटिक तट से लेकर न्यूयॉर्क और फिर यहां से शिकागो, उमाहा, सान फ्रांसिस्को तथा प्रशांत महासागर तट तक जाता है। शिकागो संसार का सबसे बड़ा रेलकेंद्र है।

4. केप काहिरा रेलमार्ग-यह रेलमार्ग अफ्रीका के दक्षिणी किनारे को उत्तरी किनारे से जोड़ता है। यह मार्ग केपटाऊन से प्रारम्भ होकर काहिरा तक है। इस मार्ग के मध्य में कई कठिनाइयां हैं जैसे सहारा मरुस्थल, ऊंचे पर्वत, जल प्रपात इत्यादि। इन प्रतिबन्धों के कारण रेलमार्ग पूरा नहीं हो सका। यह रेल मार्ग केपटाऊन से शुरू होकर किंबरले से जाइरे देश में बोकामा तक है। इसके पीछे विक्टोरिया झील तक सड़क या रेलमार्ग की सुविधा है। इसके आगे नील नदी के किनारे खरतूम तक सड़क मार्ग है। इसके आगे काहिरा तक रेलमार्ग है। इस रेलमार्ग के विकास के साथ अफ्रीका महाद्वीप के कई क्षेत्रों में खनिज पदार्थ तथा कृषि पदार्थों के निर्यात में भी वृद्धि हुई है।

5. ट्रांस एण्डियन रेलमार्ग (Trans Andean Railway)-यह रेलमार्ग दक्षिणी अमेरिका से चिली के वालप्रेसो नगर तथा अजेन्टाइना के ब्यूनस आयर्स नगर को मिलाता है। यह रेलमार्ग एण्डीज पर्वतों को 3485 मीटर की ऊंचाई से पार करके उस्पलाटा दर्रे तथा सुरंगों से गुजरता है। यह पम्पास के कृषि तथा पशुपालन क्षेत्रों को चिली के खनिज तथा फल उत्पादन क्षेत्र से जोड़ता है।

6. दिल्ली-लंदन-मार्ग (Delhi London Railway)—इस मार्ग के साथ यूरोप तथा एशिया के महाद्वीपों को मिलाने की योजना है। यह प्रकल्प आर्थिक तथा सामाजिक कमिशन के अधीन है। इस मार्ग पर कई देशों में इस योजना को पूरा करने के प्रयास किये जा रहे हैं ताकि लंदन को इण्डोनेशिया से मिलाया जा सके। यह भारत से पश्चिम की तरफ पाकिस्तान मध्य पूर्व (इरान, इराक, तुर्की) से यूरोप तक जाएगा। कई राजनीतिक बंदिशों के कारण कई स्थानों पर जैसे बर्मा-बंगला देश में यह काम सफल नहीं हो सका है। इस मार्ग पर तुर्की के पास बासकोर्स में इंग्लैंड चैनल के रास्ते समुद्र पार करना पड़ेगा तथा नावों का प्रयोग करना पड़ेगा। इण्डोनेशिया से लंदन तक यह यात्रा 15 दिनों में पूरी की जाएगी।

7. भारतीय रेलमार्ग (Indian Railway) परिवहन के साधनों में रेलों का महत्त्व सबसे अधिक है। 1853 ई० में भारत में प्रथम रेल लाइन 32 कि०मी० लम्बी मुम्बई से थाना स्टेशन तक बनाई गई। भारतीय रेलवे की मुख्य विशेषताएं निम्नलिखित हैं-

1. 1. भारतीय रेल-मार्ग एशिया का सबसे लम्बा रेलमार्ग है।
   2. भारतीय रेल-मार्ग 62211 कि०मी० लम्बा है।
   3. विश्व में भारत का चौथा स्थान है।
   4. भारतीय रेलों मे 18 लाख कर्मचारी काम करते हैं।
   5. प्रतिदिन 12670 रेलगाड़ियां लगभग 13 लाख कि०मी० दूरी पर चलती हैं तथा 7100 रेलवे स्टेशन हैं।
   6. प्रतिदिन लगभग 350 करोड़ यात्री यात्रा करते हैं तथा 22 करोड़ टन भार ढोया जाता है।
   7. भारतीय रेलों में 8000 करोड़ रुपए की पूंजी लगी हुई है तथा प्रतिवर्ष 21,000 करोड़ रुपए की आय होती है।
   8. भारतीय रेलों में 11,000 रेल इंजन, 38,000 सवारी डिब्बों तथा 4 लाख सामान ढोने वाले डिब्बे हैं।
   9. भारत में 80% सामान तथा 70% यात्री रेलों द्वारा ही ले जाए जाते हैं।

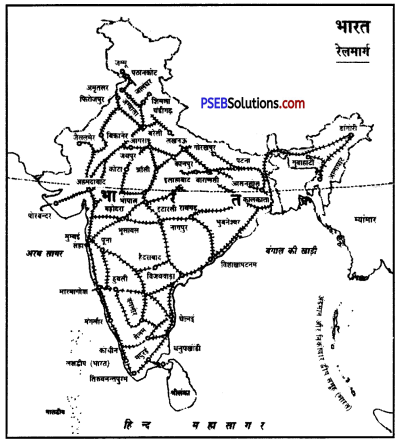
1. 1. भारतीय रेलों का अधिक विस्तार उत्तरी भारत के समतल मैदान में है।
   2. भारत में जम्मू कश्मीर, पूर्वी क्षेत्र, पश्चिमी घाट, छोटा नागपुर पठार तथा थार के मरुस्थल में रेलमार्ग कम
   3. दक्षिणी भारत में पथरीली, ऊंची-नीची भूमि के कारण, छोटी-छोटी नदियों पर जगह जगह पुल बनाने की असुविधा है।
   4. अब भारतीय रेलों पर 3454 डीजल इंजन तथा 1533 बिजली के इंजन 4950 भाप इंजन हैं।

1. 1. लगभग 9100 किलोमीटर लम्बे रेलमार्ग पर बिजली से चलने वाली गाड़ियां दौड़ती हैं। भारत में रेलमार्ग तीन प्रकार के हैं –

(i) चौड़ी पटरी (Broad Gauge)-1.68 मीटर चौड़ाई।
(ii) छोटी पटरी (Metre Gauge)-1 मीटर चौड़ाई।
(iii) तंग पटरी (Narrow Gauge)-0.68 मीटर चौड़ाई है।

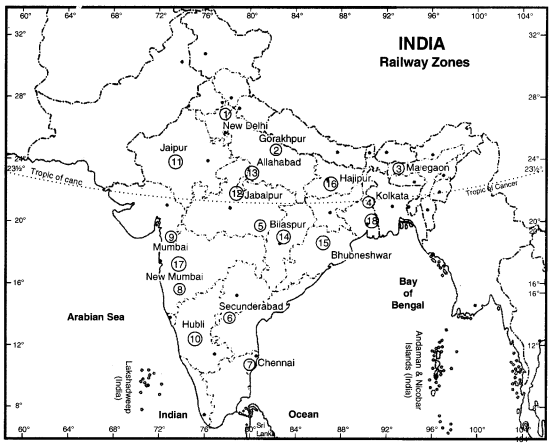
रेल क्षेत्र (Railway Zones)—अच्छे प्रबंध के लिए भारतीय रेलों में अलग-अलग तरह से विभाजित किया गया है। भारत में 1958 से 1966 तक भारतीय रेलवे के कुल 9 क्षेत्र थे। लगभग तीन दहाकों के बाद यही रेल प्रबंध जारी रहा पर अब भारतीय रेलवे के कुल 18 क्षेत्र हैं, जो इस प्रकार हैं –

रेल क्षेत्र — प्रमुख कार्यालय

1. उत्तरी रेलवे — नई दिल्ली
2. उत्तरी-पूर्वी रेलवे — गोरखपुर
3. उत्तर पूर्वी सीमान्त रेलवे — मालीगाऊ (गुवाहाटी)
4. पूर्वी रेलवे — कोलकाता
5. दक्षिणी-पूर्वी रेलवे — बिलासपुर (छत्तीसगढ़)
6. दक्षिण-मध्य रेलवे — सिकंदराबाद
7. दक्षिणी रेलवे — चेन्नई
8. मध्य रेलवे — मुंबई
9. पश्चिमी रेलवे — मुंबई
10. दक्षिण-पश्चिमी रेलवे — हुबली (बंगलौर)
11. उत्तर पश्चिमी रेलवे — जयपुर
12. पश्चिमी मध्य रेलवे — जबलपुर
13. उत्तर मध्य रेलवे — इलाहाबाद
14. दक्षिण-पूर्वी मध्य रेलवे — बिलासपुर
15. पूर्व तटवर्ती रेलवे — भुवनेश्वर
16. पूर्व मध्य रेलवे — हाजीपुर
17. कोंकण रेलवे — न्यू दिल्ली
18. मैट्रो रेलवे — कोलकाता।

प्रश्न 3.
जल यातायात तथा जल मार्ग यातायात की किस्में बताओ। विश्व के मुख्य समुद्री मार्गों का विस्तार सहित वर्णन करो।
उत्तर-
यातायात के साधनों में समुद्री यातायात सबसे सस्ता तथा महत्त्वपूर्ण साधन है। विश्व का अधिकतर व्यापार समुद्री मार्ग के द्वारा होता है। जब बहुत सारे जहाज़ एक निश्चित मार्ग पर चलते हैं तब उसे समुद्री मार्ग कहते हैं।
समुद्री मार्गों का महत्त्व (Importance of Ocean Routes)-

• यह सबसे सस्ता यातायात का साधन है।
• यह प्राकृतिक मार्ग है। समुद्र में मार्ग बनाने में कुछ खर्च नहीं होता।
• जहाजों को चलाने के लिए कोयला तथा पैट्रोल कम खर्च होता है।
• समुद्री मार्ग असलियत में अंतर्राष्ट्रीय मार्ग है क्योंकि सारे महामार्ग एक दूसरे से मिले हैं।
• इन मार्गों पर जहाजों की दुर्घटनाएं कम होती हैं।
• इन मार्गों द्वारा दूर दूर देशों के आपसी सम्पर्क बढ़ जाते हैं।
• इन मार्गों द्वारा अंतर्राष्ट्रीय व्यापार में भी वृद्धि होती है।

समुद्री मार्गों को प्रभावित करने वाले तत्व (Factors influencing the Ocean Routes) अधिकतर समुद्री मार्ग महान् चक्कर के अनुसार कम दूरी के कारण बनाये जाते हैं। जल मार्ग हिंद तोदियों से बचा कर बनाये जाते हैं। समुद्री मार्ग तूफानी क्षेत्रों तथा कोहरे से दूर होते हैं। समुद्री मार्गों में ईंधन के लिए कोयला, तेल तथा परिवहन के लिए माल ज्यादा प्राप्त हो।

जल मार्गों की किस्में-जल मार्ग मुख्य रूप में दो तरह के होते हैं-

1. आंतरिक जलमार्ग
2. समुद्री जलमार्ग

1. आंतरिक जलमार्ग-किसी देश या पृथ्वी पर स्थित जल साधनों, झीलों, नहरों इत्यादि के द्वारा यातायात को आंतरिक जलमार्गी यातायात कहते हैं। किसी देश के प्रादेशिक व्यापार के लिए नदियां, नहरें तथा झीलों का आन्तरिक जल मार्गों के रूप में प्रयोग किया जाता है। मनुष्य प्राचीन काल से ही नदियों तथा नहरों का यातायात के लिए प्रयोग करता आया है। आजकल विकसित देशों में आंतरिक जल-मार्गों का बड़े पैमाने पर प्रयोग किया जाता है। कृषि तथा उद्योगों के विकास में आंतरिक जल-मार्ग महत्त्वपूर्ण है। आन्तरिक जल मार्गों पर कई तत्वों का प्रभाव पड़ता है। नदियों तथा नहरों में जल अधिक मात्रा में हों, जल का प्रवाह सारा साल लगातार तथा सीधा होना चाहिए। अधिक ढाल जल प्राप्त अधिक घुमाव तथा रेत के जमाव से यातायात में बाधाएं उत्पन्न हो जाती हैं। शीतकाल में नदियां हिम से जमनी नहीं चाहिए।

प्रमुख आंतरिक जलमार्ग-

1. फ्रांस में सीन तथा रीन नदियां यातायात के लिए प्रयोग की जाती हैं।
2. पश्चिमी जर्मनी में राईन (Rhine) नदी सबसे महत्त्वपूर्ण जल मार्ग है। यह नदी पश्चिमी जर्मनी के व्यापार की जीवनरेखा है। इस नदी द्वारा रूहर घाटी से खनिज पदार्थों का परिवहन किया जाता है।
3. यूरोप में कई अन्य नदियां, डैन्यूब, वेसर, ऐल्ब, ओडर, विसबूला भी महत्त्वपूर्ण जल मार्ग हैं।
4. रूस में वोल्गा, नीपर नदियां यातायात के साधन के रूप में प्रयोग की जाती हैं।
5. उत्तरी अमेरिका में महान झीलें तथा मिसीसिपी नदी तथा सेंट लारेंस जल-मार्ग महत्त्वपूर्ण है।
6. भारत में गंगा तथा ब्रह्मपुत्र नदी, चीन में यंगसी नदी तथा बर्मा में इरावती नदी महत्त्वपूर्ण भीतरी जल-मार्ग हैं।
7. दक्षिणी अमेरिका में अमेज़न नदी से तट से 1600 कि०मी० अन्दर तक जहाज़ चलाए जा सकते हैं। परन्तु कम जनसंख्या तथा पिछड़ेपन के कारण इस घाटी में इस जल-मार्ग का महत्त्व कम है।
8. अफ्रीका में नील, नाईजर, कांगो तथा जैम्बजी नदियां जल प्रपातों के कारण अधिक उपयोगी नहीं हैं।
9. संसार में कई देशों में नहरें भी यातायात के साधन के रूप में प्रयोग की जाती हैं। पश्चिमी जर्मनी में कील नहर और राईन नहर, रूस में वोल्गा-वाल्टिक नहर, उत्तरी अमेरिका में हडसन-मोहाक नहर, इंग्लैण्ड में मानचेस्टर, लिवरपूल नहर, भारत में बकिंघम नहर यातायात के लिए महत्त्वपूर्ण हैं।

II. समद्री जलमार्ग- अन्तर्राष्ट्रीय व्यापार मुख्यतः समुद्री मार्ग द्वारा ही होता है। स्थल मार्ग की अधिकता के कारण मुख्य समुद्री मार्ग मध्य अक्षांशों में स्थित हैं। संसार के मुख्य समुद्री मार्ग निम्नलिखित हैं-

1. उत्तरी अन्ध महासागरीय मार्ग (North Atlantic Route) यह संसार का सब से अधिक उपयोग किया जाने वाला समुद्री मार्ग है। यह मार्ग 40° – 50° उत्तर अक्षांशों में यूरोप तथा उत्तरी अमेरिका के बीच स्थित हैं। यह संसार का सबसे व्यस्ततम व्यापारिक मार्ग है। संसार के 75% जलयान इस मार्ग पर चलते हैं। संसार के आधे से अधिक बन्दरगाह इस मार्ग पर स्थित हैं। इस मार्ग के किनारों पर यूरोप तथा उत्तरी अमेरिका के उन्नत औद्योगिक प्रदेश हैं। इसलिए संसार का 25% व्यापार इसी मार्ग से होता है। यह मार्ग महान् वृत्त है। इस पर कोयला व तेल की सुविधाएं हैं। संसार के गहरे, सुरक्षित बन्दरगाह हैं। यहां बड़े-बड़े शिपयार्ड स्थित हैं। परन्तु न्यूयार्क के निकट रेतीले, तट, न्यूफाउण्डलैंड के निकट कोहरा व हिमखण्ड की कठिनाइयां हैं। यूरोप की ओर लन्दन/लिवरपूल, ग्लासगो, ओसलो, हैम्बर्ग, रोटरडम, लिस्बन प्रमुख बन्दरगाह हैं।

2. स्वेज नहर मार्ग (Suez Canal Route)—यह सागर रूम सागर तथा लाल सागर को जोड़ने वाली स्वेज नहर के कारण महत्त्वपूर्ण मार्ग है। यह संसार का दूसरा बड़ा मार्ग है। इसे सबसे अधिक लम्बा मार्ग होने के कारण ग्रांड ट्रंक मार्ग भी कहते हैं। इस मार्ग पर संसार की घनी जनसंख्या वाले प्रदेश स्थित हैं। इस मार्ग पर कोयला व तेल की सुविधाएं प्राप्त हैं। इस मार्ग के कारण यूरोप तथा एशिया के लगभग 81000 किलोमीटर की दूरी कम हो गई है। इस नहर द्वारा इंग्लैंड के साम्राज्य व व्यापार को बहुत सुरक्षा प्राप्त थी। इसे ब्रिटिश साम्राज्य की जीवन रेखा भी कहा जाता है। रूम सागर व लाल सागर को पार करने के पश्चात् इसकी तीन शाखाएं हो

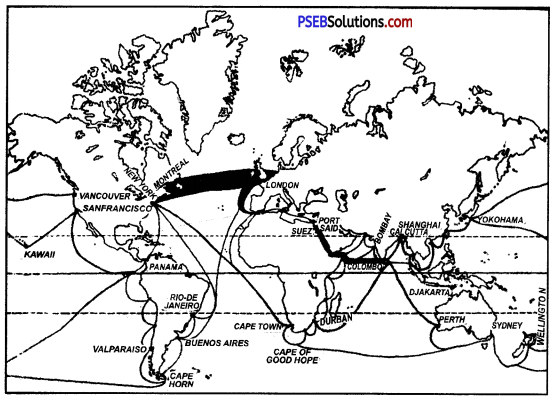
जाती हैं। अफ्रीका, ऑस्ट्रेलिया तथा एशिया की ओर लन्दन, लिवरपूल, मोर्सेल्ज, लिस्बन, नेपल्स, सिकन्दरिया प्रमुख बन्दरगाह हैं। लंदन, कराची, मुंबई, कोलकाता, चेन्नई, कोलम्बो, रंगून, सिंगापुर, हांगकांग, शंघाई योकोहामा, मेलबोर्न, विलिंगटन प्रमुख बंदरगाह हैं।

3. पनामा नहर मार्ग (Panama Canal Route)-अन्ध महासागर तथा प्रशांत महासागर को मिलाने वाली
पनामा नहर के 1914 में निर्माण होने से इस मार्ग का महत्त्व बढ़ गया है। इस मार्ग का विशेष महत्त्व संयुक्त ‘राज्य अमेरिका, ऑस्ट्रेलिया तथा न्यूज़ीलैंड को है। इस मार्ग के खुल जाने के कारण दक्षिणी अमेरिका के Cape Horn का चक्कर लगाने की आवश्यकता नहीं रही। इस प्रकार अमेरिका के पूर्वी तथा पश्चिमी तटों के बीच 10,000 किलोमीटर की दूरी कम हो गई। आकलैंड, वालपरेसी, लॉस ऐंजल्स, सानफ्रांसिस्को, बैनकूवर तथा प्रिंस रूपर्ट प्रमुख बन्दरगाह हैं। किंगस्टन हवाना, रियो-डी-जैनेरो, पनामा, न्यू ओरलियनज प्रमुख बन्दरगाह हैं।

4. आशा अन्तरीप मार्ग (Cope of Good Hope Route)—यह एक प्राचीन समुद्री मार्ग है। 1498 में वास्को डी-गामा ने इस मार्ग की खोज की। स्वेज नहर के बन्द हो जाने के कारण इस मार्ग का महत्त्व बढ़ गया है। यह मार्ग दक्षिणी अफ्रीका, ऑस्ट्रेलिया व न्यूज़ीलैंड के लिए महत्त्वपूर्ण है। इस मार्ग पर कोयला व तेल की सुविधाएं प्राप्त हैं। यह मार्ग स्वेज़ मार्ग की अपेक्षा सस्ता व ठण्डा है तथा बड़े-बड़े जहाज इस मार्ग पर गुज़र सकते हैं। लंदन, लिवरपूल, लिस्बन, लागोस, मानचेस्टर इत्यादि यूरोप की बन्दरगाहें हैं।

5. प्रशान्त महासागरीय मार्ग (Trans-Pacific Route)—यह मार्ग एशिया तथा अमेरिका महाद्वीपों को मिलाता है। यह मार्ग कम महत्त्वपूर्ण है। इस मार्ग की लम्बाई बहुत अधिक है तथा इसके किनारों पर कम उन्नत प्रदेश हैं। इस मार्ग पर हिमशिलाओं का अभाव है। इस मार्ग की कई शाखाएं होनोलूलू नामक स्थान पर मिलती हैं। योकोहामा, हांगकांग, शंघाई, मनीला, बेंकूवर, प्रिंस, रूपर्ट, सानफ्रांसिस्को, लास ऐंजल्स प्रमुख बन्दरगाह हैं।

6. दक्षिणी अन्ध महासागरीय मार्ग (South Atlantic Route)-यह मार्ग दक्षिणी अमेरिका तथा यूरोप के देशों को मिलाता है। ब्राज़ील के केप सन रोके से आगे इस मार्ग के दो भाग हो जाते हैं। यह यूरोप की तथा दूसरा अमेरिका की ओर यहां दक्षिणी अफ्रीका से आने वाले मार्ग भी मिलते हैं। उत्तर की ओर यूरोप तथा उत्तरी अमेरिका के प्रसिद्ध बन्दरगाह तथा दक्षिण की ओर व्यूनस आयर्स, मोण्टी वीडियो, रियो-डी-जेनेरो, बहियां, सैन्टाज़ हैं।

प्रश्न 4.
भारत की प्रमुख बन्दरगाहों का वर्णन करो। उनकी स्थिति, विशेषताएं तथा व्यापारिक महत्त्व बताएं।
उत्तर-
समुद्र पत्तन समुद्र के किनारे जहाजों के ठहरने के स्थान होते हैं। इनके द्वारा किसी देश का विदेशी व्यापार होता है। एक आदर्श बन्दरगाह के लिए कटी फटी तट रेखा, अधिक गहरा जल, सम्पन्न पृष्ठ-भूमि, उत्तम जलवायु तथा समुद्र मार्गों पर स्थित होना आवश्यक है। भारत की तट रेखा 61,00 किलोमीटर लम्बी है। इस तट रेखा पर अच्छी बन्दरगाहों की कमी है। केवल 10 प्रमुख बन्दरगाहें, 22 मध्यम बन्दरगाहें तथा 145 छोटी बन्दरगाहें हैं।

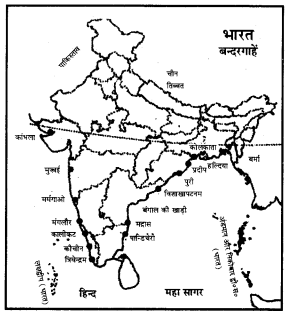
भारत की प्रमुख बन्दरगाहें-भारत के पश्चिमी तट पर कांडला, मुम्बई, मारमगाओ तथा कोचीन प्रमुख बन्दरगाहें हैं। पूर्वी तट पर कोलकाता पाराद्वीप, विशाखापट्टनम तथा चेन्नई प्रमुख बन्दरगाहें हैं। मंगलौर तथा तूतीकोरन का बड़े बन्दरगाहों के रूप में विस्तार किया जा रहा है। भारत की प्रमुख बन्दरगाहों का उल्लेख इस प्रकार है।

(क) पश्चिमी तट की बन्दरगाहें

1. कांडला (Kandla)-

(i) स्थिति (Location)—यह बन्दरगाह खाड़ी कच्छ (Gulf of Kutch) के शीर्ष (Head) पर स्थित है।
(ii) विशेषताएं (Characteristics)
(a) यह एक सुरक्षित व प्राकृतिक बन्दरगाह है।
(b) इसकी पृष्ठ-भूमि बहुत विशाल तथा सम्पन्न है, उसमें समस्त उत्तर-पश्चिमी भारत के उपजाऊ प्रदेश हैं।

(c) समुद्र की गहराई 10 मीटर से अधिक है।
(d) यहां बड़े-बड़े जहाजों के ठहरने की सुविधाएं हैं।
(e) यह स्थान स्वेज़ (Suez) समुद्री मार्ग पर स्थित है।
(f) यह बन्दरगाह कराची की बन्दरगाह का स्थान लेगी।

(iii) व्यापार (Trade)
(a) आयात (Imports)—सूती कपड़ा, सीमेंट, मशीनें तथा दवाइयां।
(b) निर्यात (Exports)-सूती कपड़ा, सीमेंट, अभ्रक, तिलहन, नमक।

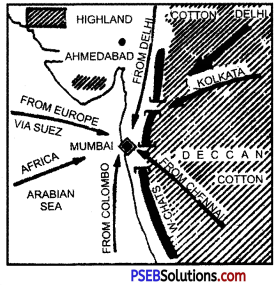
2. मुम्बई (Mumbai)

(i) स्थिति (Location)-यह बन्दरगाह पश्चिमी तट के मध्य भाग पर एक छोटे-से टापू पर स्थित है। यह टापू एक पुल द्वारा स्थल से मिला हुआ है।

(ii) विशेषताएं (Characteristics)
(a) यह भारत की सबसे बड़ी प्राकृतिक व सुरक्षित बन्दरगाह है।
(b) स्वेज़ मार्ग पर स्थित होने के कारण यूरोप (Europe) के निकट स्थित है।
(c) इसी पृष्ठ-भूमि में काली मिट्टी का कपास क्षेत्र तथा उन्नत औद्योगिक प्रदेश है।
(d) अधिक गहरा जल होने के कारण बड़े-बड़े जहाज़ ठहर सकते हैं, परन्तु यहां कोयले की कमी है।
(e) यहां पांच डॉको (Docks) में उत्तम गोदामों की व्यवस्था है।
(f) यह भारत की सबसे बड़ी बन्दरगाह है।
(g) इसे भारत का सिंहद्वार (Gateway of India) भी कहते हैं। यह महाराष्ट्र की राजधानी है। यहां ट्राम्बे में भाभा अणु शक्ति केन्द्र, मैरीन ड्राइव, इण्डिया गेट तथा ऐलीफेंटा गुफाएं दर्शनीय स्थान हैं। यह भारतीय जल-सेना का प्रमुख केन्द्र हैं।

(iii) व्यापार (Trade)-

(a) आयात (Import) मशीनरी, पैट्रोल, कोयला, कागज़ कच्ची फिल्में।
(b) निर्यात (Exports)-सूती कपड़ा, तिलहन, मैंगनीज, चमड़ा, तम्बाकू।

3. मारमगाओ (Marmago)
(i) स्थिति (Location)—यह बन्दरगाह पश्चिम तट गोआ (Goa) में स्थित है।
(ii) विशेषताएं (Characteristics)
(a) यह एक प्राकृतिक बन्दरगाह है।
(b) इसकी पृष्ठ-भूमि में महाराष्ट्र तथा कर्नाटक प्रदेश के पश्चिमी भाग हैं।
(c) इसमें 50 के लगभग जहाज़ खड़े हो सकते हैं।
(iii) 214P (Trade)—
(a) आयात (Imports)-खाद्यान्न, रासायनिक खाद, मशीनें, खनिज तेल।
(b) निर्यात (Exports)–नारियल, मूंगफली, मैंगनीज़, खनिज, लोहा।

4. कोचीन (Cochin)
(i) स्थिति (Location) यह बन्दरगाह मालबार तट पर केरल प्रदेश में पाल घाट दर्रे के सामने स्थित हैं।
(ii) विशेषताएँ (Characteristics)-
(a) यह बन्दरगाह एक लैगून झील (Lagoon) के किनारे स्थित होने के कारण सुरक्षित और प्राकृतिक बन्दरगाह है।
(b) इसकी पृष्ठ-भूमि में नीलगिरि का बागानी कृषि क्षेत्र तथा कोयम्बटूर का औद्योगिक प्रदेश स्थित है।
(c) यह जल-मार्ग द्वारा पृष्ठ-भूमि से मिला हुआ है।
(d) यह पूर्वी एशिया तथा ऑस्ट्रेलिया के जलमार्गों पर स्थित है।
(e) भारत का दूसरा पोत निर्माण केन्द्र (Shipyard) यहां पर है।
(iii) व्यापार (Trade)-
(a) आयात (Imports)-चावल, कोयला, पैट्रोल, रसायन, मशीनरी।
(b) निर्यात (Exports)-कहवा, चाय, काजू, गर्म मसाले, नारियल, इलायची, रबड़ सूती कपड़ा।

(ख) पूर्वी तट की बन्दरगाहें
1. कोलकाता (Kolkata)(i) स्थिति (Location)—यह एक नदी पत्तन (Riverport) है। यह खाड़ी बंगाल में गंगा के डेल्टा प्रदेश पर हुगली नदी के बाएं किनारे पर तट से 120 किलोमीटर भीतर स्थित है।
(ii) विशेषताएं (Characteristics)-
(a) इनकी पृष्ठ-भूमि बहुत विशाल तथा सम्पन्न है जिसमें गंगा घाटी का कृषि क्षेत्र, छोटा नागपुर का खनिज व उद्योग क्षेत्र तथा बंगाल, असम का चाय और पटसन क्षेत्र शामिल हैं।
(b) यह दूर पूर्व में जापान तथा अमेरिका के जल-मार्ग पर स्थित है।

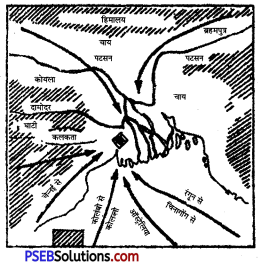
(c) परन्तु यह एक कृत्रिम बन्दरगाह है तथा गहरी नदी है।
(d) प्रति वर्ष नदियों की रेत और मिट्टी हटाने के लिए काफ़ी खर्च करना पड़ता है।
(e) जहाज़ केवल ज्वार-भाटा के समय ही आ जा सकते हैं। बड़े जहाजों को 70 किलोमीटर दूर
डायमण्ड हारबर (Diamond Harbour) में ही रुक जाना पड़ता है। () इस बन्दरगाह के विस्तार के लिए हल्दिया (Haldia) नामक स्थान पर एक विशाल पत्तन का निर्माण
किया जा रहा है। यह भारत की दूसरी बड़ी बन्दरगाह है।

(iii) व्यापार (Trade)-
(a) आयात (Imports)—मोटरें, पेट्रोल, रबड़, चावल, मशीनरी।
(b) निर्यात (Exports)—पटसन, चाय, खनिज लोहा, कोयला, चीनी, अभ्रक।

2. विशाखापट्टनम (Vishakhapatnam)-
(i) स्थिति (Location)—यह बन्दरगाह पूर्वी तट पर कोलकाता और चेन्नई के मध्य स्थित है।
(ii) fagtuang (Characteristics)

(a) डाल्फिन नोज (Dalphin-Nose) नाम की कठोर चट्टानों से घिरे होने के कारण यह एक सुरक्षित व प्राकृतिक बन्दरगाह है।
(b) इसकी पृष्ठ-भूमि में लोहा, कोयला तथा मैंगनीज़ का महत्त्वपूर्ण खनिज क्षेत्र है।
(c) यहां तेल, कोयला, ईंधन आदि सुलभ हैं।
(d) भारत का जहाज़ बनाने का सबसे बड़ा कारखाना यहां पर स्थित है।
(e) यह भारत की तीसरी प्रमुख बन्दरगाह है।

(ii) व्यापार (Trade)-
(a) आयात (Imports)-मशीनरी, चावल, पैट्रोल, खाद्यान्न।
(b) निर्यात (Exports)-मैंगनीज़, लोहा, तिलहन, चमड़ा, लाख, तम्बाकू।

3. पारादीप (Paradip)
(i) स्थिति (Location)—यह बन्दरगाह खाड़ी बंगाल में कटक से 160 किलोमीटर दूर स्थित है।
(ii) विशेषताएं (Characteristics)-

(a) यह एक नवीनतम बन्दरगाह है।
(b) यह एक सुरक्षित व प्राकृतिक बन्दरगाह है।
(c) पानी की अधिक गहराई के कारण यहां बड़े-बड़े जहाज़ ठहर सकते हैं।
(d) इसकी पृष्ठभूमि में उड़ीसा का विशाल खनिज क्षेत्र है।
(e) उड़ीसा के खनिज पदार्थों के निर्यात के लिए इस बन्दरगाह का विशेष महत्त्व है।

(iii) व्यापार (Trade)-

(a) निर्यात (Exports)-जापान का लोहा, मैंगनीज़, अभ्रक आदि खनिज पदार्थ ।
(b) आयात (Imports)-मशीनरी, तेल, चावल।

4. चेन्नई (Chennai)
(i) स्थिति (Location)—यह बन्दरगाह तमिलनाडु राज्य में कोरोमण्डल तट पर स्थित है।
(ii) विशेषताएं (Characteristics)-
(a) यह एक कृत्रिम बन्दरगाह है।
(b) कंकरीट की दो मोटी जल-तोड़ दीवारें (Break waters) बनाकर यह सुरक्षित बन्दरगाह बनाई गई है।
(c) इसकी पृष्ठभूमि में एक उपजाऊ कृषि क्षेत्र तथा औद्योगिक प्रदेश है।
(d) यहां कोयले की कमी है।

(iii) व्यापार (Trade)-
(a) आयात (Imports)-चावल, कोयला, मशीनरी, पैट्रोल, लोहा, इस्पात।
(b) निर्यात (Exports)-चाय, कहवा, गर्म मसाले, तिलहन, चमड़ा, रबड़।

प्रश्न 5.
स्वेज़ नहर के भौगोलिक, आर्थिक तथा सैनिक महत्त्व का वर्णन करो।
उत्तर-
स्वेज नहर (Suez Canal)

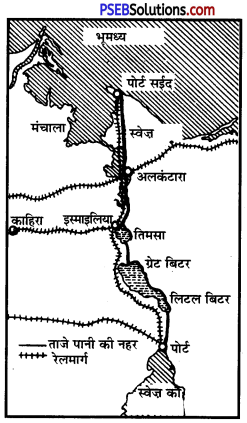
1. स्थिति (Location)-स्वेज़ नहर संसार की सबसे बड़ी जहाज़ी नहर (Navigation Canal) है। यह नहर अरब गणराज्य (U.A.R.) में स्थित है। यह नहर स्वेज़ के स्थलडमरू मध्य (Suez Isthmus) को काट कर बनाई गई है।

2. इतिहास (History)—इस नहर का निर्माण एक फ्रांसीसी इन्जीनियर फटनेण्ड डी लैसैप्स (Ferdinand De Lesseps) की देख-रेख में सन् 1859 ई० में शुरू हुआ। इस निर्माण में लगभग 10 वर्ष लगे। इस नहर को 17 नवम्बर, 1869 को चालू किया गया। इसके निर्माण काल में 1 लाख 20 हज़ार मजदूरों की जानें गईं। इस नहर के निर्माण पर 180 लाख पौंड खर्च हुए। इस नहर का निर्माण स्वेज नहर कम्पनी (Suez Canal Company) द्वारा किया गया। इस कम्पनी के अधिकतर हिस्से (Shares) फ्रांस तथा इंग्लैंड के थे। इस प्रकार इस नहर पर इंग्लैंड तथा फ्रांस का अधिकार था। यह नहर 99 वर्षों के पट्टे पर दी गई थी। परन्तु मिस्र के राष्ट्रपति कर्नल नासिर ने 26 जुलाई, 1956 को इस नहर के राष्ट्रीयकरण की घोषणा कर दी। 1967 में मिस्र व इज़राइल में युद्ध हुआ तथा नहर स्वेज़ जहाजों के लिए बन्द हो गई। 1975 में स्वेज़ नहर पुनः खुल गई है।

3. सागर तथा बन्दरगाह (Sea And Ports)—यह नहर रक्त सागर (Red Sea) तथा रूम सागर (Mediterranean Sea) को मिलाती है। रूम सागर की ओर पोर्ट सईद (Port Said) तथा रक्त सागर की ओर पोट स्वेज़ (Port Suez) की बन्दरगाह है। इस नहर की कुल लम्बाई 162 किलोमीटर, चौड़ाई 60 से 65 मीटर तक तथा कमसे-कम गहराई 10 मीटर है। यह नहर पूरी लम्बाई में समुद्र तल पर बनी है।

इस नहर के मार्ग में नमकीन पानी की तीन झीलें हैं-

1. लिटिल बिटर झील (Little Bitter Lake)
2. ग्रेट बिटर झील (Great Bitter Lake)
3. टिमशाह झील (Timshah Lake) ।

इस नहर को पार करने में 12 घण्टे लग जाते हैं। जहाज़ औसत रूप से 14 किलोमीटर प्रति घण्टा की गति से चलते हैं। कम चौड़ाई के कारण एक साथ दो जहाज़ गुज़र सकते हैं। इसलिए एक जहाज़ को झील में ठहरा लिया जाता है।

4. महत्त्व (Importance)-

• यह मार्ग संसार की घनी जनसंख्या वाले मध्य क्षेत्र में से गुज़रता है।
• इस मार्ग पर बहुत अधिक देश स्थित हैं जिनके द्वारा विभिन्न वस्तुओं का व्यापार होता है।
• इस मार्ग पर ईंधन के लिए कोयला व तेल मिल जाते हैं।
• इस मार्ग पर छोटे-छोटे कई मार्ग मिल जाते हैं।
• इस मार्ग पर कई उत्तम बन्दरगाह स्थित हैं।
• यह नहर तीन महाद्वीपों के केन्द्र पर स्थित है। (It is located at the crossroads of three continents) यहां यूरोप, अफ्रीका तथा एशिया महाद्वीप के मार्ग निकलते हैं।
• इस नहर द्वारा इंग्लैंड के साम्राज्य तथा व्यापार की रक्षा होती है। इसलिए इसे ब्रिटिश साम्राज्य की जीवन रेखा (Life Line of British Empire) भी कहते हैं।
• इस नहर के खुल जाने से दक्षिणी अफ्रीका का चक्कर काटकर आने-जाने की आवश्यकता नहीं रही।

5. व्यापारिक महत्त्व (Commercial Importance)-इस नहर के बन जाने से यूरोप तथा एशिया सुदूर पूर्व के बीच दूरी काफ़ी कम हो गई। कई देशों की दूरी की बचत निम्नलिखित है –

स्थान से	स्थान तक	दूरी की बचत
1. लन्दन	खाड़ी फारस	8800 किलोमीटर
2. लन्दन	मुम्बई	8000 किलोमीटर
3. लन्दन	सिंगापुर	6000 किलोमीटर
4. लन्दन	मम्बासा	4800 किलोमीटर
5. लन्दन	जकार्ता	1500 किलोमीटर
6. लन्दन	सिडनी	6000 किलोमीटर
7. न्यूयार्क	मुम्बई	4000 किलोमीटर
8. न्यूयार्क	हांगकांग	8800 किलोमीटर

 

6. व्यापार (Trade)-इस नहर के कारण एशिया तथा यूरोप के बीच व्यापार अधिक हो गया है। नहर को चौड़ा व गहरा करने के कारण अब औसत रूप से 87 जहाज़ प्रतिदिन गुज़र सकते हैं। 1976 में इस नहर में लगभग 20,000 जहाजों ने प्रवेश किया। इस मार्ग पर संसार का 25% व्यापार होता है। इसमें से अधिकतर जहाज़ ब्रिटेन को जाते हैं। 70% जहाज़ तेल वाहक जहाज़ (Oil Tankers) होते हैं। इस मार्ग से यूरोप को कच्चे माल (Raw Materials) जाते हैं तथा यूरोप से तैयार माल व मशीनरी एशिया को भेजी जाती है। एशिया की ओर से कपास, पटसन, चाय, चीनी, काहवा, गेहूं, तेल, ऊन, मांस, डेयरी पदार्थ, रेशम, रबड़, चावल, तांबा, तम्बाकू, चमड़ा आदि पदार्थ यूरोप को भेजे जाते हैं। इस नहर द्वारा भारत का 60% निर्यात तथा 70% आयात व्यापार होता था। परन्तु अब यह व्यापार आशा अन्तरीप मार्ग से होता है।

7. त्रुटियां (Drawbacks)-इस नहर में निम्नलिखित त्रुटियां भी हैं-

• यह नहर कम चौड़ी व कम गहरी है। इसलिए बड़े-बड़े आधुनिक जहाज़ तथा बड़े-बड़े तेल वाहक जहाज़ (Oil Tankers) नहीं गुज़र सकते हैं।
• एक पक्षीय यातायात होने के कारण नहर पार करने में समय अधिक लगता है।
• यह मार्ग बहुत महंगा है। जहाज़ों से बहुत अधिक चुंगी कर (Taxes) वसूल किया जाता है।
• दोनों ओर से मरुस्थल की रेत उड़-उड़ कर नहर में गिरती है। इसे साफ करने पर बहुत व्यय करना पड़ता है।

8. भविष्य (Future)-स्वेज़ नहर पर आधुनिक सुविधाएं प्रदान करने की योजना है। कई बार म्रिस-इज़राइल
झगड़े के कारण यह नहर बन्द रही है। परन्तु अब संसार का अधिकतर व्यापार आशा अन्तरीप मार्ग पर तेज़ जहाज़ों से होने लग पड़ा है। भविष्य में स्वेज नहर इतनी महत्त्वपूर्ण नहीं होगी। (It will not be the same old romantic Suez Canal.)

प्रश्न 6.
पनामा नहर के भौगोलिक, आर्थिक व राजनीतिक महत्त्व का वर्णन करो।
उत्तर-
पनामा नहर (Panama Canal)-
1. स्थिति (Location)-यह नहर मध्य अमेरिका (Central America) के पनामा गणराज्य में स्थित है। यह नहर पनामा स्थल डमरू मध्य (Panama Isthmus) को काटकर बनाई गई है।

2. इतिहास (History)-स्वेज़ नहर की सफलता को देखकर पनामा नहर के निर्माण की योजना बनाई गई।
1882 ई० में फर्डिनेण्ड-डी-लैसैप्स ने इस नहर का निर्माण कार्य आरम्भ किया परन्तु पीले ज्वर तथा मलेरिया के कारण हजारों श्रमिक मर गए। अतः यह प्रयत्न असफल रहा। उसके पश्चात् सन् 1904 में संयुक्त राज्य (U.S.A.) सरकार ने इस नहर का निर्माण आरम्भ किया। यह नहर दस वर्ष में 15 अगस्त 1914 को बन कर तैयार हुई। इसके निर्माण पर 712 करोड़ पौंड खर्च हुए। यह नहर संयुक्त राज्य के अधीन है। इस नहर के निर्माण में कई कठिनाइयों का सामना करना पड़ा था। इसलिए नहर का सफलतापूर्वक निर्माण आधुनिक विज्ञान की बहुत बड़ी सफलता है। (“The construction of Panama Canal was a great feat of Engineering.”) इस नहर का निर्माण दो खाड़ियों (Bays), एक कृत्रिम झील (Artifical Lake), एक प्राकृतिक झील (Natural Lake) तथा तीन द्वार प्रणालियों (Lock Systems) द्वारा किया गया है। इस नहर का तल समुद्र तल के समान नहीं है। इसका निर्माण कुलबेरा (Culbera) नामक पहाड़ी को काट कर किया गया है। गातुन (Gatun) नामक कृत्रिम झील बनाई गई हैं। इस नहर में तीन स्थानों पर फाटक बनाए गए हैं।

1. गातुन (Gatun) द्वार।
2. पैड्रो मिग्वल (Padromiguel) द्वार।
3. मिरा फ्लोर्स (Miraflore) द्वार।

इन द्वारों को खोलकर जल-स्तर समान किया जाता है। फिर जलयान ऊपर चढ़ाए या नीचे गाटुन बाँध उतारे जाते हैं।
यह दोहरी द्वार प्रणाली (Double Lock System) है जिससे एक ही समय में दोनों ओर यातायात सम्भव है। इस प्रकार जहाज़ों को इस नहर में 45 मीटर तक ऊपर चढ़ना या नीचे उतरना पड़ता है। इस नहर को चार्जेस (Charges) नदी द्वारा जल-विद्युत प्रदान की जाती है जिसके प्रकाश व जलयानों को खींचने की शक्ति मिलती है।

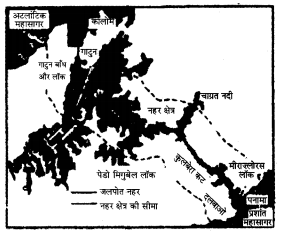
3. सागर तथा बन्दरगाह (Seas and Ports)—यह नहर प्रशान्त महासागर (Pacific Ocean) तथा अन्ध महासागर (Atlantic Ocean) को मिलाती है। इसे प्रशान्त महासागर का द्वार (Gateway of the Pacific) भी कहते हैं। प्रशान्त तट पर पनामा (Panama) तथा अन्धमहासागर तट पर कालोन (Colon) के बन्दरगाह हैं। यह नहर 8.16 किलोमीटर लम्बी, 12 मीटर गहरी तथा 90 से 300 मीटर चौड़ी है। इस नहर को पार करने में 8 घण्टे लगते हैं। इस नहर में से बड़े-बड़े जहाज़ नहीं गुज़र सकते।

4. महत्त्व (Importance)-(1) इस नहर के निर्माण से अन्ध महासागर तथा प्रशान्त महासागर के बीच दूरी कम हो गई है। (Panama Canal has changed the element of distance in geography of transport.”) इससे पहले दक्षिणी अमेरिका के (सिरे) केप हार्न (Cape Horn) का चक्कर लगा कर जाते थे। इस नहर से सबसे अधिक लाभ संयुक्त राज्य अमेरिका (U.S.A.) को हुआ है। इसके पश्चिमी व पूर्वी तट से ऑस्ट्रेलिया, न्यूजीलैंड, दक्षिणी अमेरिका, जापान की बन्दरगाहों की दूरी कम हो गई है। इस नहर के द्वारा यूरोप को कोई विशेष लाभ नहीं है। कई देशों की दूरी की बचत इस प्रकार है –

स्थान से	स्थान तक	दूरी की बचत
1. न्यूयार्क	सान फ्रांसिस्को	1300 किलोमीटर
2. न्यूयार्क	सिडनी	6000 किलोमीटर
3. न्यूयार्क	हांगकांग	7000 किलोमीटर
4. न्यूयार्क	वालपरेसो	6800 किलोमीटर
5. न्यूयार्क	टोकियो	6000 किलोमीटर
6. न्यूयार्क	सिडनी	700 किलोमीटर
7. न्यूयार्क	सान फ्रांसिस्को	9000 किलोमीटर

(2) इस नहर के कारण पश्चिमी द्वीप समूह (West Indies) का महत्त्व बढ़ गया है।
(3) इस नहर के कारण संयुक्त राज्य संकट के समय एक ही नौ-सेना (Navy) से पश्चिमी व पूर्वी तट की रक्षा कर सकता है।

5. व्यापार (Trade)-इस नहर द्वारा व्यापार में बहुत वृद्धि हुई है। औसत रूप से प्रतिदिन 50 जहाज़ गुजरते हैं।
प्रति वर्ष लगभग 15,000 जहाज़ प्रवेश करते हैं। अन्ध महासागर से प्रशान्त महासागर की ओर अधिक व्यापार होता है। पूर्व की ओर से संयुक्त राज्य व यूरोप से शिल्पी वस्तुएं, खनिज पदार्थ, तेल, मशीनें, दवाइयां, सूती व ऊनी कपड़ा भेजा जाता है। पश्चिमी की ओर से डेयरी पदार्थ, मांस, रेशम, रबड़, चाय, तम्बाकू, नारियल, शोरा, तांबा भेजा जाता है।

6. त्रुटियां (Drawbacks)-इस मार्ग में निम्नलिखित दोष –

1. इस नहर में बड़े-बड़े जहाज़ नहीं गुज़र सकते।
2. द्वार प्रणाली के कारण काफ़ी असुविधा रहती है।
3. इस मार्ग पर बन्दरगाह बहुत कम हैं।
4. इस नहर के साथ के देश उन्नत नहीं हैं।

7. भविष्य (Future)-दक्षिणी अमेरिका के देश बड़ी तेज़ी से उन्नति कर रहे हैं। इनके विकास के कारण इस मार्ग पर व्यापार बढ़ेगा।

प्रश्न 7.
भारतीय में तेल तथा गैस पाइप लाइनों की विस्तार से व्याख्या करो।
उत्तर-
पाइप लाइन भी परिवहन का एक महत्त्वपूर्ण साधन है। इस साधन के द्वारा खास कर तरल पदार्थों का परिवहन किया जाता है। इन पाइप लाइनों की सहायता से तरल पदार्थ जैसे तेल तथा गैस को एक स्थान से दूसरे स्थान तक पहुंचाया जाता है। इन पाइप लाइनों की सहायता से कोयले को भी तरल पदार्थ के रूप में एक जगह से दूसरी जगह पहुँचाया जाता है। पाइप लाइन द्वारा लेकर जाए जाने वाले स्रोत हैं-पैट्रोलियम तथा पैट्रोलियम से बने पदार्थ, प्राकृतिक गैस, जैविक ईंधन इस तरीके से एक स्थान से दूसरे स्थान पर पहुंचाये जाते हैं। पंप स्टेशनों को तेल पाइपों के द्वारा ही चलाया जाता है। इसी प्रकार बहुत सारे प्राकृतिक पदार्थों को तरल रूप में तबदील करके इनको पाइप लाइनों के द्वारा एक स्थान से दूसरे स्थान तक पहुंचाया जाता है।

कुछ प्रमुख राष्ट्रीय पाइप लाइनें हैं-
1. तुर्कमेनिस्तान अफगानिस्तान-पाकिस्तान भारत (TAPI पाइप लाइन)-इस पाइप लाइन का विकास एशियाई विकास बैंक द्वारा किया गया तथा यह प्राकृतिक गैस पाइप लाइन है। यह पाइप लाइन, तुर्कमेनिस्तान, अफगानिस्तान तथा पाकिस्तान में से गुजरती है। इस प्रकल्प का प्रारम्भ 13 दिसंबर, 2015 में किया गया तथा 2019 तक पूरी करने की योजना बनाई गई है। इस पाइप लाइन की दिशा उत्तर से दक्षिण तक है। इसकी कुल लंबाई 1814 कि०मी० बनती है।

2. हजीरा-विजयपुर-जगदीशपुर ( HBJ) पाइप लाइन-यह पाइप लाइन मध्य प्रदेश के मध्य में स्थित विजयपुर या विजैपुर दोनों नामों से पहचानी जाती है। इसलिए इसको HBJ या HVJ कहते हैं। यह पाइप लाइन गैस अथॉरिटी ऑफ इण्डिया की तरफ से बिछाई गयी। इस प्रकल्प का प्रारम्भ 1986 में किया गया तथा 1997 में पूरा हो गया। भारत में गैस परिवर्तन के लिए हजीरा-विजयपुर, जगदीशपुर पाइप लाइन बनाई गई। यह पाइप लाइन 1700 किलोमीटर लम्बी है। यह पाइप लाइन गुजरात, मध्य प्रदेश, राजस्थान, उत्तर प्रदेश राज्यों में से गुजरती है। इस गैस से विजयपुर, सवाई माधोपुर, जगदीशपुर, शाहजहांपुर, अंबाला, बथराला खाद बनाने की योजना है।

3. नाहरकटिया-नानूमती-बरौनी पाइप लाइन-NNB देश की ऐसी पहली पाइप लाइन है जो कि नाहरकटिया के तेल के कुओं से नानूमती (असम) तक कच्चा तेल पहुंचाने के लिए बिछाई गई थी तथा इसके बाद बरौनी (बिहार) तक इसको बढ़ा दिया गया है। इस पाइप लाइन की लम्बाई 1167 किलोमीटर है तथा अब तक इसको उत्तर प्रदेश के शहर कानपुर तक बढ़ा दिया गया है। इस पाइप लाइन ने 1962 तक अपना काम आरम्भ कर लिया था तथा इसका बरौनी का भाग 1964 तक क्रियाशील हुआ।

4. जामनगर लोनी LPG पाइप लाइन-यह पाइप लाइन गैस अथॉरिटी ऑफ इंडिया लिमिटेड (GAIL) की तरफ 1250 करोड़ की लागत से तैयार की गई है। यह पाइप लाइन 1269 किलोमीटर लम्बी है। यह भारत के गुजरात, राजस्थान, हरियाणा तथा उत्तर प्रदेश इत्यादि राज्यों में से गुजरती है। यह पाइप लाइन दुनिया की सबसे लम्बी पाइप लाइन है तथा यह पाइप लाइन 3 लाख एल० पी०जी० सिलिंडरों जितनी गैस हर रोज़ 1269 कि०मी० की दूरी तक लेकर जाती है। पाइप लाइन द्वारा इस काम के लिए 500 करोड़ रुपये की बचत होती हैं।

5. कांडला-बठिंडा पाइप लाइन-कांडला-बठिंडा पाइप लाइन इण्डियन आयल कार्पोरेशन (IOC) की तरफ
से बठिंडा के तेल शोधक कारखाने को कच्चा तेल पहुंचाने के लिए 2392 करोड़ रुपये के खर्च से तैयार किये गए थे। इस पाइप लाइन की लम्बाई 1443 किलोमीटर है। इस योजना का पहला चरण कांडला से लेकर सांगानौर तक था। यह चरण 1996 में पूरा हो गया था। इस पाइप लाइन का अगला चरण जारी है। यह चरण बठिंडा-जम्मू-श्रीनगर तक गैस पाइप लाइन बिछाने का है।

प्रश्न 8.
भारतीय वायुमार्ग यातायात का वर्णन करो तथा राष्ट्रीय हवाई अड्डों की जानकारी दो।
उत्तर-
आधुनिक समय में वायुमार्ग यातायात सबसे अधिक तीव्रगामी यातायात है। यह यातायात लम्बे सफर के लिए बहुत लाभदायक है। आज के समय में संसार भर में वायु यातायात उपलब्ध है। भारतीय घनी आबादी वाले देशों में वायुमार्ग मौजूद है। भारत में वायु यातायात का प्रारम्भ 1911 में हुआ। इसके बाद भारत में कई हवाई अड्डों का निर्माण हो गया। संसार में वायु मार्गों का विकास प्रथम विश्व युद्ध के पश्चात् हुआ। इसमें मार्गों के निर्माण पर खर्च नहीं होता केवल हवाई अड्डों का निर्माण करना पड़ता है। 1947 में देश की आजादी के समय चार मुख्य कंपनियों के द्वारा ही हवाई यातायात शुरू किया। ये कंपनियां थीं टाटा-सन्ज लिमिटेड, इण्डियन नैशनल एयरवेज़, एयर सर्विस आफ इंडिया तथा डैकन ऐयरवेज़। 1951 तक 4 और कंपनियों ने भारत में हवाई यातायात के लिए काम शुरू कर दिया। इसके बाद कंपनियों का स्वामित्व भारत सरकार ने अपने अधिकार क्षेत्र में ले लिया तथा दो कॉर्पोरेशनें बना दीं। एयर इंडिया तथा इण्डियन एयरलाइन्ज/परंतु आज ये कॉर्पोरेशनें एक ही हो चुकी हैं।

Airports Authority of India की तरफ से दी गई जानकारी से पता चलता है कि 30 राष्ट्रीय हवाई अड्डे हैं तथा 400 के करीब घरेलू हवाई अड्डे हैं, जबकि विदेशी कंपनियों के जहाजों को सिर्फ राष्ट्रीय हवाई अड्डों से ही उड़ानें भरने की अनुमति है।

पंजाब में इस समय दो राष्ट्रीय हवाई अड्डे हैं जो अमृतसर तथा मोहाली में हैं तथा पंजाब में राष्ट्रीय हवाई अड्डों के अलावा बठिंडा, साहनेवाल, पटियाला तथा पठानकोट में घरेलू हवाई अड्डे हैं।

यू०एस०ए०, यूरोप तथा आसियान की विदेशी कंपनियों को भारत में उड़ानों को भरने की मन्जूरी दिए जाने के बाद कई प्राइवेट कंपनियों ने जिनमें एयरवेज, स्पाइस जैट, गो इंडिगो, किंग फिशर, विस्तारा इत्यादि के जहाज़ भी अब भारत के देशी तथा विदेशी उड़ानें चला रहे हैं।

संसार में हवाई मार्गों का विकास विश्वयुद्ध के बाद हुआ। आजकल इसका बहुत बड़ा महत्त्व है। यह एक तेज़ गति वाला साधन है। इस में मार्गों के निर्माण में कोई खर्च नहीं होता। इससे पर्वतों, विशाल महासागरों व मरुस्थलों के पार पहुँचा जा सकता है। जहां दूसरे साधन नहीं पहुँच सकते। विभिन्न संस्कृतियों के बड़े-बड़े नगरों के वायुमार्गों द्वारा जुड़े होने से अंतर्राष्ट्रीय भावना का विकास होता है।

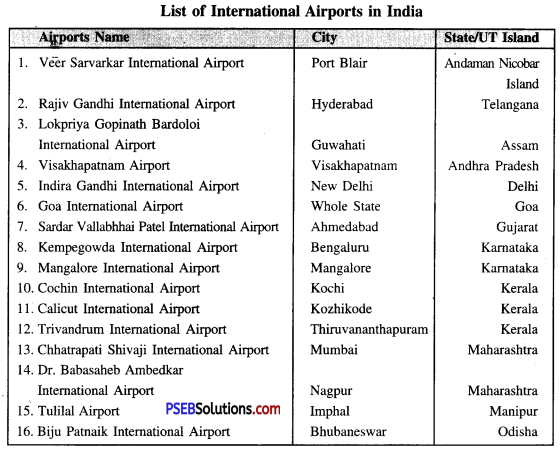
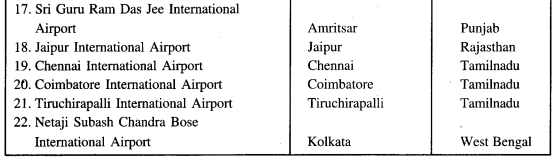
वायु मार्गों के गुण तथा दोष-
संसार के वायु मार्गों का विकास पहले विश्व युद्ध के पश्चात् हुआ। आजकल इसका बहुत बड़ा महत्त्व है। यह एक तीव्रगामी साधन है। इसमें मार्गों के निर्माण पर कोई खर्च नहीं होता। केवल हवाई अड्डों का निर्माण करना पड़ता है। इससे पर्वतों, विशाल महासागरों व मरुस्थलों के पार पहुंचा जा सकता है। जहाँ दूसरे साधन नहीं पहुँच सकते। विभिन्न संस्कृतियों के बड़े-बड़े नगरों के वायु मार्गों द्वारा जुड़े होने में अंतर्राष्ट्रीय भावना का विकास होता है।
परंतु इस साधन पर व्यय बहुत होता है। इसका व्यापारिक महत्त्व भी अधिक नहीं है। वायुयानों द्वारा यात्रियों, डाक व शीघ्र खराब होने वाले पदार्थों का परिवहन होता है।

प्रश्न 9.
व्यापार से आपका क्या भाव है ? इसकी किस्मों का विस्तार से वर्णन करो।
उत्तर-
वस्तुओं की क्रय-विक्रय/लेन-देन/खरीद-वेच को व्यापार कहते हैं। यह व्यापार की क्रिया खरीददार तथा विक्रेता के बीच का लेन-देन होता है। व्यापार मुख्य रूप में दो प्रकार का होता है।

1. निजी व्यापार-जो व्यापार निजी तौर पर या दो या अधिक लोगों के मध्य होता है वह छोटे स्तर का व्यापार होता है।
2. राष्ट्रीय स्तर का व्यापार-इस प्रकार के व्यापार में वस्तुओं को खरीदना बेचना राष्ट्रीय स्तर पर होता है। ज्यादातर राष्ट्रीय सीमाओं या इलाकों के पार किया व्यापार राष्ट्रीय व्यापार कहलाता है। राष्ट्रीय व्यापार करने के कई कारण हैं-

1. किसी देश में प्राकृतिक साधनों की कमी।
2. देश में वस्तुओं की मांग तथा पूर्ति में अंतर।
3. तकनीकी साधनों की कमी कारण कई बार वस्तुएं किसी अन्य देश से मंगवानी पड़ती हैं।
4. भौगोलिक भिन्नता के कारण स्रोतों में अंतर आ जाता है।
5. व्यापारिक नीति तथा आर्थिक विकास में अंतर।
6. देशों के आपसी संबंध।

विश्व व्यापार संगठन (WTO)- सन् 1995 में गैट का रूप बदलकर विश्व व्यापार संगठन बनाया गया। यह जेनेवा में एक स्थायी संगठन के रूप में कार्यरत है तथा यह व्यापारिक झगड़ों का निपटारा भी करता है। यह संगठन सेवाओं के व्यापार को भी नियंत्रित करता है, किंतु इसे अभी भी महत्त्वपूर्ण कर रहित नियंत्रणों जैसे निर्यात निषेध, निरीक्षण की आवश्यकता, स्वास्थ्य एवं सुरक्षा स्तरों तथा आयात लाइसैंस व्यवस्था, जिनसे आयात प्रभावित होता है, को सम्मिलित करना शेष है।

भारत सरकार की तरफ से Indian Institute of Foreign Trade की स्थापना की गयी है। इन संस्था की स्थापना 1963 में की गयी। यह भारत के पहले 10 चोटी के व्यापारिक तथा कारोबारी आदारों में एक संस्था है। इस संस्था के आदारे नई दिल्ली तथा कोलकाता में मौजूद है।
मौजूदा समय में 120 से अधिक क्षेत्र व्यापार संगठन संसार का 52% व्यापार कंट्रोल कर रहे हैं।

परिवहन/यातायात, संचार तथा व्यापार PSEB 12th Class Geography Notes

• वस्तुओं तथा यात्रियों को एक स्थान से दूसरे स्थान तक पहुँचाने को यातायात कहते हैं। किसी भी देश के ।
  विकास के लिए यातायात से संबंधित गतिविधियां एक अहम भूमिका निभाती हैं। यातायात सुविधाओं को | मुख्य रूप में तीन वर्गों में विभाजित किया जाता है-
  • स्थल मार्ग यातायात
  • जल मार्ग यातायात
  • वायु मार्ग यातायात
• स्थल मार्ग यातायात में सड़कें तथा रेलवे प्रारंभिक यातायात के साधन हैं।
• भारतीय यातायात का तंत्र एक विशाल प्रसार है। 1950-51 में कुल स्थल मार्ग 4 लाख किलोमीटर था जो कि 2007-08 में 33.1 लाख कि०मी० तक पहुँच गया।
• सड़कों का जाल पसारने के लिए कई योजनाएं, जैसे कि नागपुर पलान बीस वर्षीय, ग्रामीण सड़क विकास योजना, बी०ओ०टी० केंद्रीय सड़क फंड इत्यादि देश में चल रही हैं।
• सड़कों में ग्रामीण सड़कें, जिला, राज्य, राष्ट्रीय शाह मार्ग इत्यादि वर्गों में वर्गीकृत किया जाता है।
• उत्तर-दक्षिण तथा पूर्व-पश्चिम गलियारा प्रोजैक्ट देश के हर कोने तक बढ़िया सड़क-मार्गों का जाल | पसारने के लिए बनाया गया। इस योजना की देख-रेख की ज़िम्मेदारी राष्ट्रीय हाईवे एथारिटी ऑफ इंडिया के सुपुर्द की गई।
• भारत में राष्ट्रीय शाहमार्ग प्रबंध, भारत सरकार की एजैन्सी की ओर से चलाया तथा संभाला जाता है।
• भारतीय रेलवे तीन गेज पर गाड़ियां चलाती हैं-चौड़ी गेज पटरी, मीटर गेज पटरी तथा संकीर्ण गेज पटरी।
• भारतीय रेलवे के कुल 18 ज़ोन हैं।
•  संसार की पहली रेलवे लाइन 1863 से 1869 के बीच अमेरिका में बिछाई गई।
• ट्रांस साइबेरियाई रेल मार्ग मास्को से रूस के पूर्व में व्लादिवोस्तोक तक 9,289 किलोमीटर लंबा है। यह विश्व का सबसे लंबा रेल मार्ग है।
• स्वेज नहर लाल सागर तथा रोम सागरों को आपस में जोड़ती है।
• पनामा नहर अंधमहानगरों दिल्ली, मुंबई, कोलकाता, चेन्नई को तेज़ी से चलने वाली रेल गाड़ी के तंत्र जोड़ने की योजना को डायमंड चतुर्भुज कहते हैं।
• भारत में अर्ध तेज़ रफ़्तार रेलवे गलियारे हैं।
• पाइप लाइन द्वारा तरल गैसीय पदार्थों की स्थान बदली की जाती है।
• जब हम अपने विचारों, संदेश, भावनाओं को लिखकर या बोलकर दूसरों तक पहुँचाते हैं, उसे संचार कहते हैं। इसके दो मुख्य प्रकार हैं-
  • व्यक्तिगत संचार,
  •  जन-संचार।
• यातायात-वस्तुओं तथा मनुष्य को एक स्थान से दूसरे स्थान तक पहुँचाने को यातायात कहते हैं।
• यातायात के साधनों की किस्में-यातायात के साधनों को मुख्य रूप में तीन किस्मों में विभाजित किया जाता ‘ है-स्थल, जल तथा वायु मार्ग।
• राष्ट्रीय शाह मार्ग-राष्ट्रीय मार्गों का निर्माण तथा देखभाल भारत की केंद्र सरकार करती है। इस तरह की सड़कें राज्यों की राजधानियों, बंदरगाहों और नामवर तथा महत्त्वपूर्ण शहरों को आपस में मिलाती हैं।
• सुनहरी चतुर्भुज सड़क मार्ग-इस प्रोजैक्ट में भारत के चार महानगर दिल्ली, मुंबई, चेन्नई तथा कोलकाता को सड़क-मार्ग से जोड़ा गया है तथा इसका चतुर्भुज आकार होने के कारण इसको चतुर्भुज मार्ग कहते हैं।
• बंदरगाह-भारत में 12 मुख्य बंदरगाहें हैं।
• जलमार्गों की किस्में-
  • आंतरिक जल मार्ग
  • समुद्री जल मार्ग।
• संचार-जब हम अपने संदेश, भाव, विचारों को लिखकर या बोलकर पहुँचाते हैं इस क्रिया को संचार कहते हैं।
• संचार की किस्में-
  • व्यक्तिगत संचार
  • जन संचार।
• व्यापार-वस्तु को बेचने तथा खरीदने की क्रिया को व्यापार कहते हैं।
• भारत में ईंधन, खनिज तेल, खनिज मोम, जैविक रसायन फार्मेसी उत्पादन तथा चीजें निर्यात (बरामद) की जाती हैं। पैट्रोल, खनिज, मशीनरी, खादें, लोहा इस्पात, मोती के कीमती पत्थर, सोना-चांदी, खुराकी तेल, कागज़, दवाइयां, फर्नीचर इत्यादि का आयात (दरामद) किया जाता है।

Punjab State Board PSEB 12th Class Political Science Book Solutions Chapter 5 उदारवाद Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Political Science Chapter 5 उदारवाद

दीर्घ उत्तरीय प्रश्न-

प्रश्न 1.
उदारवाद क्या है ? इसके मुख्य सिद्धान्तों का वर्णन कीजिए। (What is Liberalism ? Discuss its main principles.)
अथवा
उदारवाद की परिभाषा दीजिए तथा इसके मुख्य सिद्धान्तों का वर्णन कीजिए। (Define Liberalism and Explain its basic principles.)
अथवा
उदारवाद की परिभाषा बताइए और इसकी मुख्य विशेषताओं की व्याख्या कीजिए। (Define Liberalism and discuss its main characteristics.)
उत्तर-
उदारवाद आधुनिक युग की एक महत्त्वपूर्ण विचारधारा है। यूरोपीय देशों पर इस विचारधारा का बहुत गहरा प्रभाव पड़ा है। परन्तु उदारवाद की एक निश्चित परिभाषा देना अति कठिन कार्य है। इसका कारण यह है कि उदारवाद एक निश्चित और क्रमबद्ध विचारधारा नहीं है। उदारवाद किसी एक विचारक की देन नहीं है और न ही इसका किसी एक युग के साथ सम्बन्ध है। यह एक ऐसी व्यापक विचारधारा है जिसमें अनेक विद्वानों के विचार और आदर्श शामिल हैं और जो समय के साथ-साथ परिवर्तित होते रहे हैं। लॉक और लॉस्की तक और आगे भी इसका क्रम चलता जा रहा है तथा इसका कोई अन्त नहीं है। अत: उदारवाद को सीमाओं में बांधना एक कठिन कार्य है। लॉस्की (Laski) ने ठीक ही कहा है, “उदारवाद की व्याख्या करना या परिभाषा देना सरल कार्य नहीं है क्योंकि यह कुछ सिद्धान्तों का समूहमात्र ही नहीं है बल्कि मस्तिष्क में रहने वाला विचार भी है।”

उदारवाद से सम्बन्धित गलत धारणाएं-उदारवाद के अर्थ को समझने के लिए यह जानना अति आवश्यक है कि उदारवाद क्या नहीं है ?

1. उदारवाद अनुदारवाद का उल्टा नहीं है-कुछ लोग उदारवाद को अनुदारवाद (Conservatism) का उल्टा मानते हैं। अनुदारवाद परिवर्तनों और सुधार का विरोध करने वाली विचारधारा है। परन्तु उदारवाद ने 19वीं शताब्दी तक उन सभी संस्थाओं, कानूनों और प्रथाओं का विरोध किया जिनमें राजा, सामन्तों और वर्ग के विशेषाधिकारों की रक्षा होती थी। इस प्रकार उदारवादियों ने क्रान्तिकारी परिवर्तनों का जोरों से समर्थन किया। किन्तु आज जब साम्यवादी पूंजीवाद को समाप्त करने की बाद करते हैं तो उदारवादी उनका विरोध करते हैं। एल्बर्ट बिजबोर्ड (Albert Weisbord) ने ठीक ही कहा है, “विरोधात्मक रूप में पूरे इतिहास में उदारवादियों ने क्रान्ति को प्रारम्भ किया है और फिर इसके विरोध में संघर्ष किया है।”

2. उदारवाद व्यक्तिवाद नहीं है-कुछ व्यक्ति उदारवाद को व्यक्तिवाद का पर्यायवाची मानते हैं जोकि पूर्णतः सत्य नहीं है। निःसन्देह व्यक्तिवाद उदारवाद की आधारशिला है परन्तु दोनों एक ही चीज़ नहीं है। सेबाइन (Sabine) ने इन दोनों में भिन्नता को स्पष्ट करते हुए कहा है, “19वीं शताब्दी के तीसरे चरण के अन्त तक इन दोनों में कोई विशेष भेद नहीं था, क्योंकि उस समय तक ये दोनों विचारधाराएं व्यक्ति के जीवन में राज्य के हस्तक्षेप की विरोधी थीं, लेकिन बाद
में स्थिति बदल गई और उदारवाद में काफ़ी परिवर्तन आ गया। इसका रूप सकारात्मक हो गया है। उदारवाद व्यक्ति के स्थान पर सामाजिक हित को महत्त्व देने लगा है। यहां तक कि जन-कल्याण के लक्ष्य को पूरा करने के लिए व्यक्तियों के जीवन में हस्तक्षेप करना या उस पर नियन्त्रण करना राज्य का आवश्यक कार्य बन गया है।”

3. उदारवाद और लोकतन्त्र एक नहीं है-कुछ विद्वान् लोकतन्त्र को ही उदारवाद मानते हैं जो कि ठीक नहीं है। यद्यपि उदारवाद और लोकतन्त्र में गहरा सम्बन्ध है, परन्तु दोनों एक ही नहीं है। उदारवाद व्यक्ति की स्वतन्त्रता पर जोर देता है जबकि लोकतन्त्र समानता को महत्त्व देता है। उदारवाद वास्तव में लोकतन्त्र से कुछ अधिक है।

उदारवाद का सही अर्थ-उदारवाद को अंग्रेजी में ‘लिबरलिज्म’ (Liberalism) कहते हैं। इस शब्द की उत्पत्ति लैटिन भाषा के शब्द ‘लिबरलिस’ (Liberalis) से हुई है जिसका शाब्दिक अर्थ है-स्वतन्त्र व्यक्ति (Free man) । इस सिद्धान्त का सार यही है कि व्यक्ति को स्वतन्त्रता मिले जिससे वह अपने व्यक्तित्व का विकास तथा उसकी अभिव्यक्ति कर सके। इनसाइक्लोपीडिया ब्रिटेनिका (Encyclopaedia Britainica) के अनुसार, “उदारवाद के सारे विचार का सार स्वतन्त्रता का सिद्धान्त है, इसके अतिरिक्त स्वतन्त्रता का विचार इसका समूल है।” मैकगवर्न (Macgovern) के शब्दों में, “एक राजनीतिक सिद्धान्त के रूप में उदारवाद दो पृथक् तत्त्वों का मिश्रण है। इनमें से एक तत्त्व लोकतन्त्र है और दूसरा है व्यक्तिवाद।” (“Liberalism as a political creed is compound of two separate elements. One of these is democracy, the other is individualism.”) उदारवाद एक तरफ लोकतन्त्रीय व्यवस्था का समर्थन करता है और दूसरी ओर व्यक्ति को अपने व्यक्तित्व के विकास के लिए पूर्ण अवसर देना चाहता है। उदारवाद व्यक्ति को ही समस्त मानवीय व्यवस्था का केन्द्र मानता है। सारटोरी (Sartori) ने उदारवाद की सरल परिभाषा दी है। उसके शब्दों में, “साधारण शब्दों में उदारवाद व्यक्तिगत स्वतन्त्रता, न्यायिक सुरक्षा तथा संवैधानिक राज्य का सिद्धान्त व व्यवहार है।” (“In simple words liberalism is the theory. and practice of individual liberty, Judicial defence and constitutional state.”)

बट्रेण्ड रसल (Bertand Russel) के अनुसार, “उदारवादी विचारधारा व्यवहार में जियो और जीने दो, सहनशील तथा स्वतन्त्रता जिस सीमा तक सार्वजनिक व्यवस्था आज्ञा दे तथा राजनीतिक मामलों में कट्टरता का अभाव है।”
हैलोवेल (Hallowell) ने उदारवाद का अर्थ निम्नलिखित विश्वासों में अंकित किया है-

• मनुष्य के व्यक्तित्व का सर्वोच्च मूल तथा सभी व्यक्तियों की आध्यात्मिक समानता।
• व्यक्ति की इच्छा की स्वतन्त्रता।
• व्यक्ति की भलाई व दृढ़ विवेकशीलता।
• जीवन, स्वतन्त्रता तथा सम्पत्ति के अधिकारों का अस्तित्व।
• व्यक्ति के प्राकृतिक अधिकारों को सुरक्षित बनाए रखने के उद्देश्य से पारस्परिक सहमति द्वारा राज्य की रचना।
• व्यक्ति तथा राज्य के बीच प्रसंविदापूर्ण सम्बन्ध ; आदि समझौते की शर्तों का उल्लंघन हो तो व्यक्ति को राज्य के विरुद्ध विद्रोह करने का अधिकार है।
• सामाजिक नियन्त्रण के यन्त्र के रूप में कानून का प्रशासकीय आदेश से ऊपर होना।
• व्यक्ति को राजनीतिक, सामाजिक, आर्थिक, मानसिक और धार्मिक आदि सभी क्षेत्रों में स्वतन्त्रता है और उसे स्वतन्त्र होना चाहिए।
• विवेक पर आश्रित एक सर्वोच्च यथार्थ का अस्तित्व जिसे व्यक्ति के अन्त:करण व चिन्तन द्वारा प्राप्त किया जा सके।
  उदारवाद के मुख्य सिद्धान्त या विशेषताएं-

यद्यपि उदारवाद अनेक विचारधाराओं का सम्मिश्रिण है, फिर भी इसके कुछ सर्वमान्य मौलिक सिद्धान्त हैं, जिनमें मुख्य निम्नलिखित हैं-

1. मानवीय विवेक में आस्था (Faith in Human Reason)-उदारवाद का मूल सिद्धान्त मानवीय बुद्धि और विवेक में आस्था है। मध्य युग में यूरोप के अनेक देशों में ईसाइयत ने मनुष्य की बुद्धि को कठोर बन्धनों में जकड़ रखा था और वह धर्म, ईश्वर तथा पोप को ही सब कुछ मानता था। परन्तु नवजागरण ने इन बन्धनों को तोड़ दिया और मनुष्य को विवेक द्वारा विश्व की संस्थाओं को समझने के लिए कहा। 17वीं तथा 18वीं शताब्दी में जॉन लॉक और टॉमस पेन जैसे उदारवादियों ने इस बात पर बल दिया कि मनुष्य को किसी भी ऐसे सिद्धान्त, कानून या परम्परा को नहीं मानना चाहिए जिसकी उपयोगिता बुद्धि से सिद्ध न होती हो। टॉमस पेन ने रूढ़िवादी परम्पराओं को चुनौती देते हुए कहा है, “मेरा अपना मन ही मेरा चर्च है।” इस प्रकार उदारवाद भावना के स्थान पर विवेक को महत्त्व देता है।

2. इतिहास तथा परम्परा का विरोध (Opposition of History and Tradition)—मध्य युग में अन्धविश्वास और रूढ़िवादी परम्पराओं का बोलबाला था। उदारवाद अन्धविश्वासों और रूढ़ियों के विरुद्ध विद्रोह था। उदारवादियों ने इस बात पर जोर दिया कि उन्हीं संस्थाओं, सिद्धान्तों तथा कानूनों इत्यादि को स्वीकार किया जाए तो विवेक के साथ संगत हों। इंग्लैण्ड के उपयोगितावादी उदारवादियों ने उँपयोगिता के आधार पर पहले से चली आ रही व्यवस्था और परम्पराओं का खण्डन किया। उदारवाद के प्रभाव के कारण ही इंग्लैण्ड, अमेरिका और फ्रांस में क्रान्तियां हुईं। परन्तु उदारवाद सदा ही विद्यमान व्यवस्था का विरोधी नहीं रहा है और आज तो वह व्यवस्था को समाप्त करने के बिल्कुल पक्ष में नहीं है।

3. मानवीय स्वतन्त्रता का पोषक (Supporter of Human Freedom)-उदारवाद का मूल सिद्धान्त है कि मनुष्य जन्म से ही स्वतन्त्र है और स्वतन्त्रता उसका प्राकृतिक एवं जन्मसिद्ध अधिकार है। स्वतन्त्रता का अभिप्राय यह है कि मनुष्य के जीवन पर किसी स्वेच्छाचारी सत्ता का नियन्त्रण न हो और उसे अपने विवेक के अनुसार आचरण करने की स्वतन्त्रता हो। लॉस्की (Laski) के अनुसार, “उदारवाद का स्वतन्त्रता से सीधा सम्बन्ध है क्योंकि इसका जन्म समाज के किसी वर्ग के द्वारा जन्म अथवा धर्म पर आधारित विशेषाधिकारों का विरोध करने के लिए हुआ है।”

4. राज्य का उद्देश्य मनुष्य के व्यक्तित्व का विकास करना है (The purpose of the State is to develop the personality of the individual)-उदारवादियों के अनुसार, व्यक्ति के विकास में ही राज्य व समाज का विकास है और व्यक्ति की भलाई में राज्य की भलाई है। इसलिए राज्य का उद्देश्य मनुष्य के व्यक्तित्व का विकास करना है।

5. व्यक्ति साध्य तथा राज्य साधन (Man is the End, State is the Mean)-उदारवादी व्यक्ति को साध्य और राज्य को साधन मानते हैं। मानवीय संस्थाएं और समुदाय व्यक्ति के लिए बने हैं। इसलिए राज्य का कार्य व्यक्ति की सेवा करना है। वह सेवक है, स्वामी नहीं। व्यक्ति के उद्देश्य की पूर्ति करना ही राज्य का उद्देश्य है। उदारवादी आदर्शवादियों के इस कथन में विश्वास नहीं करते कि समाज व्यक्तियों की एक उच्च नैतिक संस्था है। आधुनिक उदारवादी व्यक्ति और समाज के हित में सामंजस्य स्थापित करते हैं और दोनों को एक-दूसरे का पूरक मानते हैं न कि विरोधी।

6. राज्य कृत्रिम संस्था है (State is an Artificial institution)-उदारवादी राज्य को ईश्वरीय या प्राकृतिक संस्था नहीं मानते बल्कि वे राज्य को कृत्रिम संस्था मानते हैं। उनके मतानुसार राज्य का निर्माण व्यक्तियों ने अपने विशेष आवश्यकताओं की पूर्ति के लिए किया है। यदि राज्य व्यक्तियों की आवश्यकताओं को पूरा नहीं करता तो व्यक्तियों को यह अधिकार प्राप्त है कि वह राज्य और समाज के संगठन में आवश्यकतानुसार परिवर्तन कर सके।

7. व्यक्ति के प्राकृतिक अधिकारों की धारणा में विश्वास (Belief in the concept of Natural Rights of Man)-उदारवाद व्यक्ति के प्राकृतिक अधिकारों में विश्वास करता है। प्राकृतिक अधिकार वह अधिकार है जो व्यक्ति को जन्म से प्राप्त होते हैं। लॉक के अनुसार, जीवन, स्वतन्त्रता और सम्पत्ति के अधिकार प्रमुख प्राकृतिक अधिकार हैं। राज्य एवं समाज प्राकृतिक अधिकारों का उल्लंघन नहीं कर सकते। राज्य का परम कर्तव्य प्राकृतिक अधिकारों की रक्षा करना है।

8. धर्म-निरपेक्षता में विश्वास (Faith in Secularism) मध्य युग में चर्च का व्यक्ति के जीवन पर पूरा नियन्त्रण था। उदारवादियों ने धर्म के विशेषाधिकारों का विरोध किया तथा व्यक्ति की धार्मिक स्वतन्त्रता पर बल दिया। उदारवादियों ने धार्मिक संस्थाओं को राज्य से अलग रखने की बात कही और सभी व्यक्तियों को समान रूप से धर्म की स्वतन्त्रता देने पर बल दिया। उदारवाद के अनुसार, धर्म व्यक्ति का व्यक्तिगत मामला है और राज्य को व्यक्तिगत धर्म में हस्तक्षेप नहीं करना चाहिए।

9. लोकतन्त्र का समर्थन (Support of Democracy)-लोकतन्त्र उदारवाद का अभिन्न अंग है। उदारवाद का जन्म ही स्वेच्छाचारी शासन के विरुद्ध प्रतिक्रिया के रूप में हुआ और लोकतन्त्र उदारवाद का मूल तत्त्व है। उदारवाद लोक प्रभुसत्ता में विश्वास रखता है। उदारवाद के अनुसार मनुष्य स्वतन्त्र पैदा हुआ है, इसलिए उस पर शासन उसकी सहमति से होना चाहिए। व्यक्ति को अधिकार तभी प्राप्त हो सकते हैं यदि ‘लोकतान्त्रिक शासन प्रणाली हो और व्यक्ति को शासन के निर्माण में अधिकार प्राप्त हों। इसलिए उदारवाद का निर्वाचित संसद्, वयस्क मताधिकार, प्रेस की स्वतन्त्रता एवं निष्पक्ष न्यायालय में पूर्ण विश्वास है।

10. संवैधानिक शासन (Constitutional Government)-उदारवाद का उदय निरंकुश एवं स्वेच्छाचारी शासन की प्रतिक्रिया के रूप में हुआ। इसलिए उदारवाद निरंकुश शासन का विरोधी है। उदारवाद सीमित सरकार अर्थात् सरकार की सीमित शक्तियों का समर्थन करता है। यदि शासक मनमानी करता है या अपनी शक्तियों का दुरुपयोग करता है तो जनता को ऐसे शासक के विरुद्ध विद्रोह करने का अधिकार है। लॉक ने इंग्लैण्ड की 1688 की क्रान्ति का समर्थन किया।

11.बहसमुदाय समाज में विश्वास (Belief in Pluralistic Society)-उदारवादियों के अनुसार, मनुष्य अपनी आवश्यकताओं की पूर्ति के लिए अनेक समुदायों की स्थापना करता है। समाज में अनेक समुदाय होते हैं और राज्य भी एक समुदाय है। राज्य विभिन्न समुदायों में सामंजस्य स्थापित करते है। व्यक्ति के जीवन के कई पहलू हैं जो राज्य के कार्य-क्षेत्र से बाहर हैं। कई समुदाय जैसे परिवार राज्य से अधिक प्राकृतिक और मौलिक है। लॉस्की और मैकाइवर ने बहु-समुदाय समाज की धारणा पर विशेष बल दिया।

12. अन्तर्राष्ट्रीय और विश्व-शान्ति में विश्वास (Faith in Internationalism and World Peace)उदारवाद ‘जियो और जीने दो’ के सिद्धान्त पर आधारित है। यह विश्व-शान्ति तथा विश्व-बन्धुत्व के आदर्श में विश्वास करता है। प्रत्येक राष्ट्र को धीरे-धीरे शान्तिपूर्वक प्रगति करनी चाहिए और उसे अन्य राष्ट्रों की प्रगति में सहायता करनी चाहिए। प्रत्येक राष्ट्र को दूसरे राष्ट्र की अखण्डता एवं सीमा का आदर करना चाहिए और किसी राष्ट्र को दूसरे के विरुद्ध शक्ति का प्रयोग नहीं करना चाहिए। अन्तर्राष्ट्रीय समस्याओं का हल अन्तर्राष्ट्रीय कानून और शान्तिपूर्वक साधनों द्वारा होना चाहिए।

प्रश्न 2.
उदारवाद के मुख्य सिद्धान्तों का वर्णन करो। (Explain the main Principles of Liberalism.)
अथवा
उदारवाद के मूल सिद्धान्तों की विवेचना करो। (Discuss the Fundamental Principles of Liberalism.)
उत्तर-
यद्यपि उदारवाद अनेक विचारधाराओं का सम्मिश्रिण है, फिर भी इसके कुछ सर्वमान्य मौलिक सिद्धान्त हैं, जिनमें मुख्य निम्नलिखित हैं-

1. मानवीय विवेक में आस्था (Faith in Human Reason)-उदारवाद का मूल सिद्धान्त मानवीय बुद्धि और विवेक में आस्था है। मध्य युग में यूरोप के अनेक देशों में ईसाइयत ने मनुष्य की बुद्धि को कठोर बन्धनों में जकड़ रखा था और वह धर्म, ईश्वर तथा पोप को ही सब कुछ मानता था। परन्तु नवजागरण ने इन बन्धनों को तोड़ दिया और मनुष्य को विवेक द्वारा विश्व की संस्थाओं को समझने के लिए कहा। 17वीं तथा 18वीं शताब्दी में जॉन लॉक और टॉमस पेन जैसे उदारवादियों ने इस बात पर बल दिया कि मनुष्य को किसी भी ऐसे सिद्धान्त, कानून या परम्परा को नहीं मानना चाहिए जिसकी उपयोगिता बुद्धि से सिद्ध न होती हो। टॉमस पेन ने रूढ़िवादी परम्पराओं को चुनौती देते हुए कहा है, “मेरा अपना मन ही मेरा चर्च है।” इस प्रकार उदारवाद भावना के स्थान पर विवेक को महत्त्व देता है।

2. इतिहास तथा परम्परा का विरोध (Opposition of History and Tradition)—मध्य युग में अन्धविश्वास और रूढ़िवादी परम्पराओं का बोलबाला था। उदारवाद अन्धविश्वासों और रूढ़ियों के विरुद्ध विद्रोह था। उदारवादियों ने इस बात पर जोर दिया कि उन्हीं संस्थाओं, सिद्धान्तों तथा कानूनों इत्यादि को स्वीकार किया जाए तो विवेक के साथ संगत हों। इंग्लैण्ड के उपयोगितावादी उदारवादियों ने उँपयोगिता के आधार पर पहले से चली आ रही व्यवस्था और परम्पराओं का खण्डन किया। उदारवाद के प्रभाव के कारण ही इंग्लैण्ड, अमेरिका और फ्रांस में क्रान्तियां हुईं। परन्तु उदारवाद सदा ही विद्यमान व्यवस्था का विरोधी नहीं रहा है और आज तो वह व्यवस्था को समाप्त करने के बिल्कुल पक्ष में नहीं है।

3. मानवीय स्वतन्त्रता का पोषक (Supporter of Human Freedom)-उदारवाद का मूल सिद्धान्त है कि मनुष्य जन्म से ही स्वतन्त्र है और स्वतन्त्रता उसका प्राकृतिक एवं जन्मसिद्ध अधिकार है। स्वतन्त्रता का अभिप्राय यह है कि मनुष्य के जीवन पर किसी स्वेच्छाचारी सत्ता का नियन्त्रण न हो और उसे अपने विवेक के अनुसार आचरण करने की स्वतन्त्रता हो। लॉस्की (Laski) के अनुसार, “उदारवाद का स्वतन्त्रता से सीधा सम्बन्ध है क्योंकि इसका जन्म समाज के किसी वर्ग के द्वारा जन्म अथवा धर्म पर आधारित विशेषाधिकारों का विरोध करने के लिए हुआ है।”

4. राज्य का उद्देश्य मनुष्य के व्यक्तित्व का विकास करना है (The purpose of the State is to develop the personality of the individual)-उदारवादियों के अनुसार, व्यक्ति के विकास में ही राज्य व समाज का विकास है और व्यक्ति की भलाई में राज्य की भलाई है। इसलिए राज्य का उद्देश्य मनुष्य के व्यक्तित्व का विकास करना है।

5. व्यक्ति साध्य तथा राज्य साधन (Man is the End, State is the Mean)-उदारवादी व्यक्ति को साध्य और राज्य को साधन मानते हैं। मानवीय संस्थाएं और समुदाय व्यक्ति के लिए बने हैं। इसलिए राज्य का कार्य व्यक्ति की सेवा करना है। वह सेवक है, स्वामी नहीं। व्यक्ति के उद्देश्य की पूर्ति करना ही राज्य का उद्देश्य है। उदारवादी आदर्शवादियों के इस कथन में विश्वास नहीं करते कि समाज व्यक्तियों की एक उच्च नैतिक संस्था है। आधुनिक उदारवादी व्यक्ति और समाज के हित में सामंजस्य स्थापित करते हैं और दोनों को एक-दूसरे का पूरक मानते हैं न कि विरोधी।

6. राज्य कृत्रिम संस्था है (State is an Artificial institution)-उदारवादी राज्य को ईश्वरीय या प्राकृतिक संस्था नहीं मानते बल्कि वे राज्य को कृत्रिम संस्था मानते हैं। उनके मतानुसार राज्य का निर्माण व्यक्तियों ने अपने विशेष आवश्यकताओं की पूर्ति के लिए किया है। यदि राज्य व्यक्तियों की आवश्यकताओं को पूरा नहीं करता तो व्यक्तियों को यह अधिकार प्राप्त है कि वह राज्य और समाज के संगठन में आवश्यकतानुसार परिवर्तन कर सके।

7. व्यक्ति के प्राकृतिक अधिकारों की धारणा में विश्वास (Belief in the concept of Natural Rights of Man)-उदारवाद व्यक्ति के प्राकृतिक अधिकारों में विश्वास करता है। प्राकृतिक अधिकार वह अधिकार है जो व्यक्ति को जन्म से प्राप्त होते हैं। लॉक के अनुसार, जीवन, स्वतन्त्रता और सम्पत्ति के अधिकार प्रमुख प्राकृतिक अधिकार हैं। राज्य एवं समाज प्राकृतिक अधिकारों का उल्लंघन नहीं कर सकते। राज्य का परम कर्तव्य प्राकृतिक अधिकारों की रक्षा करना है।

8. धर्म-निरपेक्षता में विश्वास (Faith in Secularism) मध्य युग में चर्च का व्यक्ति के जीवन पर पूरा नियन्त्रण था। उदारवादियों ने धर्म के विशेषाधिकारों का विरोध किया तथा व्यक्ति की धार्मिक स्वतन्त्रता पर बल दिया। उदारवादियों ने धार्मिक संस्थाओं को राज्य से अलग रखने की बात कही और सभी व्यक्तियों को समान रूप से धर्म की स्वतन्त्रता देने पर बल दिया। उदारवाद के अनुसार, धर्म व्यक्ति का व्यक्तिगत मामला है और राज्य को व्यक्तिगत धर्म में हस्तक्षेप नहीं करना चाहिए।

9. लोकतन्त्र का समर्थन (Support of Democracy)-लोकतन्त्र उदारवाद का अभिन्न अंग है। उदारवाद का जन्म ही स्वेच्छाचारी शासन के विरुद्ध प्रतिक्रिया के रूप में हुआ और लोकतन्त्र उदारवाद का मूल तत्त्व है। उदारवाद लोक प्रभुसत्ता में विश्वास रखता है। उदारवाद के अनुसार मनुष्य स्वतन्त्र पैदा हुआ है, इसलिए उस पर शासन उसकी सहमति से होना चाहिए। व्यक्ति को अधिकार तभी प्राप्त हो सकते हैं यदि ‘लोकतान्त्रिक शासन प्रणाली हो और व्यक्ति को शासन के निर्माण में अधिकार प्राप्त हों। इसलिए उदारवाद का निर्वाचित संसद्, वयस्क मताधिकार, प्रेस की स्वतन्त्रता एवं निष्पक्ष न्यायालय में पूर्ण विश्वास है।

10. संवैधानिक शासन (Constitutional Government)-उदारवाद का उदय निरंकुश एवं स्वेच्छाचारी शासन की प्रतिक्रिया के रूप में हुआ। इसलिए उदारवाद निरंकुश शासन का विरोधी है। उदारवाद सीमित सरकार अर्थात् सरकार की सीमित शक्तियों का समर्थन करता है। यदि शासक मनमानी करता है या अपनी शक्तियों का दुरुपयोग करता है तो जनता को ऐसे शासक के विरुद्ध विद्रोह करने का अधिकार है। लॉक ने इंग्लैण्ड की 1688 की क्रान्ति का समर्थन किया।

11.बहसमुदाय समाज में विश्वास (Belief in Pluralistic Society)-उदारवादियों के अनुसार, मनुष्य अपनी आवश्यकताओं की पूर्ति के लिए अनेक समुदायों की स्थापना करता है। समाज में अनेक समुदाय होते हैं और राज्य भी एक समुदाय है। राज्य विभिन्न समुदायों में सामंजस्य स्थापित करते है। व्यक्ति के जीवन के कई पहलू हैं जो राज्य के कार्य-क्षेत्र से बाहर हैं। कई समुदाय जैसे परिवार राज्य से अधिक प्राकृतिक और मौलिक है। लॉस्की और मैकाइवर ने बहु-समुदाय समाज की धारणा पर विशेष बल दिया।

12. अन्तर्राष्ट्रीय और विश्व-शान्ति में विश्वास (Faith in Internationalism and World Peace)उदारवाद ‘जियो और जीने दो’ के सिद्धान्त पर आधारित है। यह विश्व-शान्ति तथा विश्व-बन्धुत्व के आदर्श में विश्वास करता है। प्रत्येक राष्ट्र को धीरे-धीरे शान्तिपूर्वक प्रगति करनी चाहिए और उसे अन्य राष्ट्रों की प्रगति में सहायता करनी चाहिए। प्रत्येक राष्ट्र को दूसरे राष्ट्र की अखण्डता एवं सीमा का आदर करना चाहिए और किसी राष्ट्र को दूसरे के विरुद्ध शक्ति का प्रयोग नहीं करना चाहिए। अन्तर्राष्ट्रीय समस्याओं का हल अन्तर्राष्ट्रीय कानून और शान्तिपूर्वक साधनों द्वारा होना चाहिए।

प्रश्न 3.
पुरातन उदारवाद तथा समकालीन उदारवाद में मुख्य अन्तर बताइए।
(Distinguish between Classical Liberalism and Contemporary Liberalism)
अथवा
परम्परावादी उदारवाद तथा समकालीन उदारवाद में अन्तर की व्याख्या कीजिए।
(Explain differences between Classical Liberalism and Modern Liberalism.)
उत्तर-
शास्त्रीय उदारवाद तथा समकालीन उदारवाद में भेद का निम्नलिखित प्रकार से वर्णन किया जाता है-

1. व्यक्तिवाद के सम्बन्ध में अन्तर-शास्त्रीय उदारवाद व्यक्तिवाद का समर्थन करता है, और कई विद्वान् उदारवाद और व्यक्तिवाद को एक ही मानते हैं, परन्तु समकालीन उदारवाद व्यक्तिवाद का खण्डन करता है। शास्त्रीय उदारवाद का आरम्भ ‘व्यक्ति’ से होता है, परन्तु समकालीन उदारवाद का आरम्भ ‘समूह’ तथा ‘संस्था’ से होता है।

2. प्राकृतिक अधिकारों के सम्बन्ध में अन्तर–शास्त्रीय उदारवाद व्यक्ति को प्राप्त प्राकृतिक अधिकारों का समर्थन करता है। शास्त्रीय उदारवाद के अनुसार जीवन, स्वतन्त्रता तथा सम्पत्ति के आधार प्राकृतिक अधिकार हैं। समकालीन उदारवाद व्यक्ति के अधिकारों को समाज की देन मानते हैं तथा उसे वह अधिकार देने का समर्थन करता है जो व्यक्तिगत तथा सामाजिक हित में है।

3. स्वतन्त्रता के सम्बन्ध में अन्तर-शास्त्रीय उदारवाद स्वतन्त्रता के नकारात्मक रूप पर बल देता है जबकि समकालीन उदारवाद स्वतन्त्रता के सकारात्मक रूप पर बल देता है। अत: जहां शास्त्रीय उदारवाद स्वतन्त्रता और राज्य के कार्य करने की शक्ति को परस्पर विरोधी मानता है, वहीं समकालीन उदारवाद स्वतन्त्रता और राज्य के कार्य करने की शक्ति को परस्पर विरोधी न मानकर सहयोगी मानता है।

4. राज्य के कार्यों के सम्बन्ध में अन्तर-शास्त्रीय उदारवाद इस बात पर बल देता है कि राज्य को कम-से-कम कार्य करने चाहिएं जबकि समकालीन उदारवाद इस बात पर बल देता है कि राज्य को सार्वजनिक कल्याण के लिए काम करने चाहिएं। शास्त्रीय उदारवाद राज्य को सीमित कार्य करने के लिए कहता है जबकि समकालीन उदारवाद राज्य को सभी तरह के कल्याणकारी कार्य करने के लिए कहता है। समकालीन उदारवाद व्यक्ति के विकास के लिए सभी तरह के कार्यों को करने के लिए राज्य को कहता है।

5. राज्य के सम्बन्ध में अन्तर-शास्त्रीय उदारवाद राज्य को एक आवश्यक बुराई मानता है। इसके अनुसार मनुष्य के सर्वांगीण विकास में मुख्य बाधा राज्य ही है, और राज्य के रहते व्यक्ति अपना पूर्ण विकास नहीं कर सकता। इसके विपरीत समकालीन उदारवाद राज्य को एक आवश्यक बुराई न मानकर प्राकृतिक और नैतिक संस्था मानता है। समकालीन उदारवादियों के अळुसार राज्य समस्त वर्गों के हितों को ध्यान में रखकर ही कार्य करता है।

6. दृष्टिकोण के सम्बन्ध में अन्तर-शास्त्रीय उदारवाद अपने दृष्टिकोण में सुधारवादी है जबकि समकालीन उदारवादी यथास्थिति को बनाए रखने के समर्थक हैं।

7. स्वतन्त्र व्यापार एवं पूंजीवाद के सम्बन्ध में अन्तर-शास्त्रीय उदारवाद स्वतन्त्र व्यापार तथा पूंजीवाद का समर्थन करता है जबकि समकालीन उदारवाद पूंजीवाद पर अंकुश लगाए जाने का समर्थन करता है। शास्त्रीय उदारवाद, राज्य को अर्थ-व्यवस्था को नियमित करने की शक्ति देने के विरुद्ध है जबकि समकालीन उदारवाद राज्य की हस्तक्षेप की नीति का समर्थन करता है। समकालीन उदारवाद श्रमिकों के हितों के लिए और सामाजिक कल्याण के लिए व्यापार और उद्योगों को नियन्त्रित करने के पक्ष में है। इसके अनुसार स्वतन्त्र व्यापार एवं अनियन्त्रित प्रतियोगिता ग़रीब को और ग़रीब एवं अमीर को और अमीर बना देती है।

8. विचारधारा के आधार पर अन्तर–शास्त्रीय उदारवाद मध्य वर्ग की एक राजनीतिक विचारधारा है जबकि समकालीन उदारवाद शक्ति-सम्पन्न पूंजीवादी वर्ग की विचारधारा है।

9. राज्य के हस्तक्षेप की नीति के सम्बन्ध में अन्तर-शास्त्रीय उदारवाद आर्थिक क्षेत्र में राज्य के हस्तक्षेप के विरुद्ध है। शास्त्रीय उदारवाद आर्थिक क्षेत्र में व्यक्ति को पूर्ण स्वतन्त्रता देने के पक्ष में है, परन्तु समकालीन उदारवाद । आर्थिक क्षेत्र में राज्य के हस्तक्षेप का समर्थन करता है।

प्रश्न 4.
उदारवाद का शाब्दिक अर्थ बताते हुए, समकालीन (आधुनिक) उदारवाद की चार विशेषताएं बताओ।
(Give the verbal meaning of the word Liberalism and explain four features of contemporary Liberalism.).
उत्तर-
उदारवाद का अर्थ-इसके लिए प्रश्न नं. 1 देखें।
समकालीन (आधुनिक) उदारवाद की विशेषताएं-जे० एस० मिल, ग्रीन, लॉस्की आदि विद्वान् समकालीन उदारवाद के मुख्य समर्थक माने जाते हैं। इसकी मुख्य विशेषताएं निम्नलिखित हैं-

1. प्राकृतिक अधिकारों का खण्डन-समकालीन उदारवादियों ने प्राकृतिक अधिकारों का खण्डन किया है और अधिकारों को समाज की देन माना है। समकालीन उदारवाद उन अधिकारों का समर्थन करता है जो व्यक्तिगत तथा सामूहिक हित में हों।.

2. राज्य के कल्याणकारी कार्य-समकालीन उदारवाद राज्य के कार्यों को सीमित नहीं करता है। समकालीन उदारवाद के अनुसार राज्य को सार्वजनिक कल्याण के लिए सभी कार्य करने चाहिए। लॉस्की ने राज्य को अधिकतम भलाई करने वाली सामाजिक संस्था माना जाता है। जो राज्य जनता की भलाई का जितना अधिक कार्य करता है वह उतना ही अच्छा होता है।

3. स्वतन्त्रता के सकारात्मक रूप का समर्थन-समकालीन उदारवाद स्वतन्त्रता के सकारात्मक रूप पर बल देता है। स्वतन्त्रता का अर्थ है-बन्धनों का अभाव। राज्य लोगों के कल्याण के लिए व्यक्तिगत स्वतन्त्रता पर प्रतिबन्ध लगा सकता है। समकालीन उदारवाद के अनुसार स्वतन्त्रता का अर्थ उन कार्यों को करने की स्वतन्त्रता है जो कार्य करने योग्य हैं।

4. मानवीय स्वतन्त्रता का पोषक-उदारवाद का मूल सिद्धान्त है कि मनुष्य जन्म से ही स्वतन्त्र है और.स्वतन्त्रता उसका प्राकृतिक एवं जन्म सिद्ध अधिकार है। स्वतन्त्रता का अभिप्राय यह है कि मनुष्य के जीवन पर किसे स्वेच्छाचारी सत्ता का नियन्त्रण न हो और उसे अपने विवेक के अनुसार आचरण करने की स्वतन्त्रता हो।

लघु उत्तरीय प्रश्न-

प्रश्न 1.
उदारवाद के शाब्दिक अर्थों की व्याख्या कीजिए।
अथवा
उदारवाद से आपका क्या अभिप्राय है ?
उत्तर-
उदारवाद आधुनिक युग की एक महत्त्वपूर्ण विचारधारा है। उदारवाद को अंग्रेज़ी में लिबरलिज्म’ (Liberalism) कहते हैं। इस शब्द की उत्पत्ति लैटिन भाषा के शब्द ‘लिबरलिस’ से हुई है जिसका शाब्दिक अर्थ है-स्वतन्त्र व्यक्ति। इस सिद्धान्त का सार यही है कि व्यक्ति को स्वतन्त्रता मिले जिससे वह अपने व्यक्तित्व का विकास तथा उसकी अभिव्यक्ति कर सके। उदारवाद एक ऐसी व्यापक विचारधारा है जिसमें अनेक विद्वानों के विचार और आदर्श शामिल हैं और जो समय के साथ-साथ परिवर्तित होते रहते हैं। उदारवाद एक तरफ लोकतान्त्रिक व्यवस्था का समर्थन करता है और दूसरी तरफ व्यक्ति को अपने व्यक्तित्व के विकास के लिए पूरे अवसर देना चाहता है। उदारवाद व्यक्ति को ही समस्त मानवीय व्यवस्था का केन्द्र मानता है।

प्रश्न 2.
उदारवाद की कोई चार परिभाषाएं दें।
अथवा उदारवाद की कोई भी दो परिभाषाएं लिखें।
उत्तर-

• इन्साइक्लोपीडिया ब्रिटेनिका के अनुसार, “उदारवाद के सारे विचार का सार स्वतन्त्रता का सिद्धान्त है। इसके अतिरिक्त स्वतन्त्रता का विचार इसका मूल है।”
• मैकगर्वन के शब्दों में, “एक राजनीतिक सिद्धान्त के रूप में उदारवाद दो पृथक् तत्त्वों का मिश्रण है। इनमें से एक तत्त्व लोकतन्त्र है और दूसरा व्यक्तिवाद है।”..
• सारटोरी के अनुसार, “साधारण शब्दों में उदारवाद व्यक्तिगत स्वतन्त्रता, न्यायिक सुरक्षा तथा संवैधानिक राज्य का सिद्धान्त व व्यवहार है।”
• बट्रेण्ड रसल के अनुसार, “उदारवादी विचारधारा व्यवहार में जियो और जीने दो, सहनशील तथा स्वतन्त्रता जिस सीमा तक सार्वजनिक व्यवस्था आज्ञा दे तथा राजनीतिक मामलों में कट्टरता का अभाव है।”

प्रश्न 3.
परम्परागत उदारवाद किसे कहते हैं ?
अथवा
परम्परावादी उदारवाद क्या है ?
उत्तर-
शास्त्रीय उदारवाद (परम्परावादी उदारवाद) अपने प्रारम्भिक रूप में व्यक्तिवाद के निकट रहा है। शास्त्रीय उदारवाद को व्यक्तिवाद का दूसरा नाम कहा जा सकता है। लॉक ने व्यक्तिगत स्वतन्त्रता तथा सीमित राज्य के सिद्धान्त पर बल दिया है। लॉक द्वारा प्रस्तुत यह सिद्धान्त शास्त्रीय उदारवाद की आधारशिला माना जाता है। शास्त्रीय उदारवाद मानव व्यक्तित्व के असीम मूल्य तथा व्यक्तियों की आध्यात्मिक समानता में विश्वास रखता है। शास्त्रीय उदारवाद व्यक्ति के प्राकृतिक अधिकारों का समर्थन करता है। शास्त्रीय उदारवाद ने विशेषकर जीवन, स्वतन्त्रता तथा सम्पत्ति के अधिकार पर बल दिया है। शास्त्रीय उदारवाद राज्य को एक आवश्यक बुराई मानता है। इसके अनुसार वह सरकार सबसे अच्छी है जो कम-से-कम शासन करे। शास्त्रीय उदारवाद राज्य के कार्यों को सीमित करने पर बल देता है। शास्त्रीय उदारवादियों के मतानुसार राज्य का अधिक हस्तक्षेप व्यक्ति की स्वतन्त्रता को कम कर देता है। शास्त्रीय उदारवाद खुली प्रतियोगिता, स्वतन्त्र व्यापार तथा पूंजीवाद का समर्थन करता है।

प्रश्न 4.
परम्परावादी उदारवाद की कोई चार विशेषताएं लिखें।
उत्तर-
परम्परावादी उदारवाद की मुख्य विशेषताएं निम्नलिखित हैं-

• राज्य एक आवश्यक बुराई है-परम्परावादी उदारवाद राज्य को एक आवश्यक बुराई मानता है। इसके अनुसार वह सरकार सबसे अच्छी है जो कम-से-कम शासन करे।
• राज्य के न्यूनतम कार्य-परम्परावादी उदारवाद राज्य को कम-से-कम कार्य देने के पक्ष में है। परम्परावादी उदारवादियों के मतानुसार राज्य का कार्य केवल जीवन तथा सम्पत्ति की रक्षा करना और अपराधियों को दण्ड देना ही है। राज्य की शिक्षा, कृषि, व्यापार इत्यादि कार्य नहीं करने चाहिए।
• मानव की स्वतन्त्रता-परम्परावादी उदारवाद मानव की स्वतन्त्रता का महान् समर्थक है। इसके अनुसार व्यक्ति को जीवन के हर क्षेत्र में स्वतन्त्रता प्राप्त होनी चाहिए। स्वतन्त्रता का अर्थ बन्धनों का अभाव माना गया है।
• परम्परागत उदारवाद खुली प्रतियोगिता का समर्थन करता है।

प्रश्न 5.
समकालीन उदारवाद किसे कहते हैं ?
अथवा
समकालीन उदारवाद क्या है ?
उत्तर-
जे० एस० मिल, ग्रीन, लॉस्की आदि विद्वान् समकालीन उदारवाद के मुख्य समर्थक माने जाते हैं। समकालीन उदारवाद ने प्राकृतिक अधिकारों का खण्डन किया और अधिकारों को समाज की देन माना है। समकालीन उदारवाद उन अधिकारों का समर्थन करता है जो व्यक्तिगत तथा सामूहिक हित में हों। समकालीन उदारवाद ने खुली प्रतियोगिता का विरोध किया है। समकालीन उदारवाद राज्य को अधिक कार्य देने के पक्ष में है ताकि समस्त जनता का कल्याण हो सके। समकालीन उदारवाद स्वतन्त्रता और कानून में विरोध नहीं मानता बल्कि कानून को स्वतन्त्रता का संरक्षक मानता है। समकालीन उदारवाद ने सकारात्मक स्वतन्त्रता का समर्थन किया है।

प्रश्न 6.
समकालीन उदारवाद की कोई चार विशेषताएं लिखें।
उत्तर-
जे० एस० मिल, ग्रीन, लॉस्की आदि विद्वान् समकालीन उदारवाद के मुख्य समर्थक माने जाते हैं। इसकी मुख्य विशेषताएं निम्नलिखित हैं
1. प्राकृतिक अधिकारों का खण्डन-समकालीन उदारवादियों ने प्राकृतिक अधिकारों का खण्डन किया है और अधिकारों को समाज की देन माना है। समकालीन उदारवाद उन अधिकारों का समर्थन करता है जो व्यक्तिगत तथा सामूहिक हित में हों।

2. राज्य के कल्याणकारी कार्य-समकालीन उदारवाद राज्य के कार्यों को सीमित नहीं करता है। समकालीन उदारवाद के अनुसार राज्य को सार्वजनिक कल्याण के लिए सभी कार्य करने चाहिए। लॉस्की ने राज्य को अधिकतम भलाई करने वाली सामाजिक संस्था माना है। जो राज्य जनता की भलाई का जितना अधिक कार्य करता है वह उतना ही अच्छा होता है।

3. स्वतन्त्रता के सकारात्मक रूप का समर्थन–समकालीन उदारवाद स्वतन्त्रता के सकारात्मक रूप पर बल देता है। स्वतन्त्रता का अर्थ है-बन्धनों का अभाव। राज्य लोगों के कल्याण के लिए व्यक्तिगत स्वतन्त्रता पर प्रतिबन्ध लगा सकता है। समकालीन उदारवाद के अनुसार स्वतन्त्रता का अर्थ उन कार्यों को करने की स्वतन्त्रता है जो कार्य करने योग्य है।

4. समकालीन उदारवाद आर्थिक क्षेत्र में राज्य के हस्तक्षेप का समर्थन करता है।

प्रश्न 7.
पुरातन उदारवाद और समकालीन उदारवाद में चार अन्तर लिखो।
उत्तर-
शास्त्रीय उदारवाद तथा समकालीन उदारवाद में निम्नलिखित अन्तर पाए जाते हैं-

• शास्त्रीय उदारवाद का आरम्भ ‘व्यक्ति’ से होता है, परन्तु समकालीन उदारवाद का आरम्भ ‘समूह’ तथा ‘संस्था’ से होता है।
• शास्त्रीय उदारवाद व्यक्ति को प्राप्त प्राकृतिक अधिकारों का समर्थन करता है। समकालीन उदारवाद व्यक्ति के
  अधिकारों को समाज की देन मानता है तथा उसे वह अधिकार देने का समर्थन करता है है जो व्यक्तिगत तथा सामाजिक हित में हैं।
• शास्त्रीय उदारवाद स्वतन्त्रता के नकारात्मक रूप पर बल देता है जबकि समकालीन उदारवाद स्वतन्त्रता के सकारात्मक रूप पर बल देता है।
• शास्त्रीय उदारवाद राज्य को एक आवश्यक बुराई मानता है जबकि समकालीन उदारवाद राज्य को एक आवश्यक बुराई न मानकर प्राकृतिक और नैतिक संस्था मानता है।

प्रश्न 8.
उदारवाद के चार सिद्धान्तों का वर्णन करो।
उत्तर-
उदारवाद आधुनिक युग की एक महत्त्वपूर्ण विचारधारा है। उदारवाद के मूल सिद्धान्त निम्नलिखित हैं-

• मानवीय स्वतन्त्रता का पोषक-उदारवाद का मूल सिद्धान्त है कि मनुष्य जन्म से ही स्वतन्त्र है और स्वतन्त्रता उसका प्राकृतिक एवं जन्मसिद्ध अधिकार है। स्वतन्त्रता का अभिप्राय यह है कि मनुष्य के जीवन पर किसी स्वेच्छाचारी सत्ता का नियन्त्रण न हो और उसे अपने विवेक के अनुसार आचरण करने की स्वतन्त्रता हो।
• राज्य का उद्देश्य मनुष्य के व्यक्तित्व का विकास करना है-उदारवादियों के अनुसार व्यक्ति के विकास में राज्य व समाज का विकास है और व्यक्ति की भलाई में राज्य की भलाई है। इसलिए राज्य का उद्देश्य मनुष्य के व्यक्तित्व का विकास करना है।
• व्यक्ति साध्य तथा राज्य साधन-उदारवादी व्यक्ति को साध्य और राज्य को साधन मानते हैं। मानवीय संस्थाएं और समुदाय व्यक्ति के लिए बने हैं। इसलिए राज्य का कार्य व्यक्ति की सेवा करना है। वह सेवक है, स्वामी नहीं। व्यक्ति के उद्देश्य की पूर्ति करना ही राज्य का उद्देश्य है।
• उदारवाद का निर्वाचित संसद, वयस्क मताधिकार, प्रैस की स्वतन्त्रता एवं निष्पक्ष न्यायालय में पूर्ण विश्वास है।

प्रश्न 9.
उदारवाद के विरोध में चार तर्क लिखो।
उत्तर-

• मनुष्य केवल स्वार्थी नहीं है- उदारवादी विशेषकर बैन्थम जैसे उदारवादियों ने मनुष्य को स्वार्थी माना है। परन्तु यह धारणा ग़लत है। कोई भी व्यक्ति पूरी तरह न तो स्वार्थी है और न ही परमार्थी।
• राज्य एक आवश्यक बुराई नहीं है-अनेक उदारवादियों ने राज्य को एक आवश्यक बुराई माना है, जोकि ठीक नहीं है। राज्य बुराई नहीं है। यह मनुष्य की सामाजिक चेतना की स्वाभाविक अभिव्यक्ति है।
• अस्पष्ट धारणा-उदारवाद की विचारधारा स्पष्ट नहीं है। इसकी निश्चित परिभाषा नहीं की जा सकती और न ही इसके सिद्धान्तों पर सभी उदारवादी सहमत हैं।
• राज्य की अयोग्यता का तर्क उचित नहीं है।

अति लघु उत्तरीय प्रश्न-

प्रश्न 1.
उदारवाद के शाब्दिक अर्थ का वर्णन कीजिए।
उत्तर-
उदारवाद आधुनिक युग की एक महत्त्वपूर्ण विचारधारा है। उदारवाद को अंग्रेजी में ‘लिबरलिज्म’ (Liberalism) कहते हैं। इस शब्द की उत्पत्ति लैटिन भाषा के शब्द ‘लिबरलिस’ से हुई है जिसका शाब्दिक अर्थ है-स्वतन्त्र व्यक्ति। इस सिद्धान्त का सार यही है कि व्यक्ति को स्वतन्त्रता मिले जिससे वह अपने व्यक्तित्व का विकास तथा उसकी अभिव्यक्ति कर सके।

प्रश्न 2.
उदारवाद की दो परिभाषाएं दें।
उत्तर-

• इन्साइक्लोपीडिया ब्रिटेनिका के अनुसार, उदारवाद के सारे विचार का सार स्वतन्त्रता का सिद्धान्त है। इसके अतिरिक्त स्वतन्त्रता का विचार इसका मूल है।
• मैकग्वन के शब्दों में, “एक राजनीतिक सिद्धान्त के रूप में उदारवाद दो पृथक् तत्त्वों का मिश्रण है। इसमें से एक तत्त्व लोकतन्त्र है दूसरा व्यक्तिवाद है।”

प्रश्न 3.
परम्परावादी उद्गारवाद क्या है ?
उत्तर-
परम्परागत (शास्त्रीय) उदारवाद मानव व्यक्तित्व के असीम मूल्य तथा व्यक्तियों की आध्यात्मिक समानता में विश्वास रखता है। शास्त्रीय उदारवाद व्यक्ति के प्राकृतिक अधिकारों का समर्थन करता है। शास्त्रीय उदारवाद ने विशेषकर जीवन, स्वतन्त्रता तथा सम्पत्ति के अधिकार पर बल दिया है। शास्त्रीय उदारवाद राज्य को एक आवश्यक बुराई मानता है।

प्रश्न 4.
समकालीन उदारवाद क्या है ?
उत्तर-
समकालीन उदारवाद उन अधिकारों का समर्थन करता है जो व्यक्तिगत तथा सामूहिक हित में हों। समकालीन उदारवाद ने खुली प्रतियोगिता का विरोध किया है। समकालीन उदारवाद राज्य को अधिक कार्य देने के पक्ष में है ताकि समस्त जनता का कल्याण हो सके।

प्रश्न 5.
शास्त्रीय उदारवाद तथा समकालीन उदारवाद में दो अन्तर करें।
उत्तर-

• शास्त्रीय उदारवाद का आरम्भ ‘व्यक्ति’ से होता है, परन्तु समकालीन उदारवाद का आरम्भ ‘समूह’ तथा ‘संस्था’ से होता है।
• शास्त्रीय उदारवाद व्यक्ति को प्राप्त प्राकृतिक अधिकारों का समर्थन करता है। समकालीन उदारवाद व्यक्ति के अधिकारों को समाज की देन मानता है तथा उसे वह अधिकार देने का समर्थन करता है जो व्यक्तिगत तथा सामाजिक हित में हैं।

प्रश्न 6.
उदारवाद के कोई दो सिद्धान्त लिखो।
उत्तर-

• मानवीय स्वतन्त्रता का पोषक-उदारवाद का मूल सिद्धान्त है कि मनुष्य जन्म से ही स्वतन्त्र है और स्वतन्त्रता उसका प्राकृतिक एवं जन्मसिद्ध अधिकार है।
• राज्य का उद्देश्य मनुष्य के व्यक्तित्व का विकास करना है-उदारवादियों के अनुसार व्यक्ति के विकास में राज्य व समाज का विकास है और व्यक्ति की भलाई में राज्य की भलाई है। इसलिए राज्य का उद्देश्य मनुष्य के व्यक्तित्व का विकास करना है।

वस्तुनिष्ठ प्रश्न-

प्रश्न I. एक शब्द/वाक्य वाले प्रश्न उत्तर

प्रश्न 1.
Liberalism शब्द की उत्पत्ति किस भाषा से हुई है ?
उत्तर-
Liberalism शब्द की उत्पत्ति लैटिन भाषा से हुई है।

प्रश्न 2.
किस विद्वान ने ‘स्वतन्त्रता पर निबन्ध’ पस्तक लिखी ?
उत्तर-
‘स्वतन्त्रता पर निबन्ध’ पुस्तक जे० एस० मिल ने लिखी।

प्रश्न 3.
उदारवाद का अंग्रेज़ी रूप क्या है ?
उत्तर-
उदारवाद का अंग्रेज़ी रूप Liberalism है।

प्रश्न 4.
Liberalism शब्द की उत्पत्ति लैटिन भाषा के किस शब्द से हुई है ?
उत्तर-
Liberalism शब्द की उत्पत्ति लैटिन भाषा के लिबरलिस शब्द से हुई है।

प्रश्न 5.
उदारवाद शब्द का मूल क्या है?
उत्तर-
उदारवाद शब्द का मूल स्वतन्त्र व्यक्ति है।

प्रश्न 6.
उदारवाद के कितने रूप हैं ?
उत्तर-
उदारवाद के दो रूप हैं।

प्रश्न 7.
उदारवाद के कोई दो रूपों के नाम लिखें।
अथवा
उदारवाद के दो रूप लिखें।
उत्तर-
(1) शास्त्रीय उदारवाद
(2) समकालीन उदारवाद।

प्रश्न 8.
उदारवाद के कोई एक व्याख्याकार का नाम लिखो।
उत्तर-
लॉस्की।

प्रश्न 9.
उदारवाद की एक परिभाषा लिखें।
उत्तर-
सारटोरी के अनुसार, “सामान्य शब्दों में उदारवाद व्यक्तिगत स्वतन्त्रता, न्यायिक सुरक्षा तथा संवैधानिक राज्य का सिद्धान्त तथा व्यवहार है।”

प्रश्न 10.
उदारवाद के अर्थ लिखो।
उत्तर-
उदरवाद का अर्थ है, कि व्यक्ति को स्वतन्त्रता मिले, जिससे वह अपने व्यक्तित्व का विकास तथा उसकी अभिव्यक्ति कर सके।

प्रश्न 11.
समकालीन या आधुनिक उदारवाद से आपका क्या अभिप्राय है ?
अथवा
समकालीन उदारवाद से क्या भाव है ?
उत्तर-
समकालीन उदारवाद उन अधिकारों का समर्थन करता है, जो व्यक्तिगत तथा सामूहिक हित में हो, यह सकारात्मक स्वतन्त्रता का समर्थन करता है।

प्रश्न 12.
परम्परावादी उदारवाद से क्या अभिप्राय है ?
उत्तर-
परम्परावादी उदारवाद मानव व्यक्तित्व के असीम मूल्यों तथा व्यक्तियों की आध्यात्मिक समानता में विश्वास रखता है, यह व्यक्ति के प्राकृतिक अधिकारों का समर्थन करता है।

प्रश्न II. खाली स्थान भरें-

1. उदारवाद ………… का उल्टा नहीं है।
2. उदारवाद ………… नहीं है।
3. उदारवाद व्यक्ति की स्वतन्त्रता पर जोर देता है, जबकि लोकतन्त्र ……….. को महत्त्व देता है।
4. उदारवाद को अंग्रेजी में ………… कहते हैं। ।
5. Liberalism शब्द की उत्पत्ति ………… भाषा के शब्द से हुई है।
उत्तर-

1. अनुदारवाद
2. व्यक्तिवाद
3. समानता
4. Liberalism
5. लैटिन।

प्रश्न III. निम्नलिखित वाक्यों में से सही एवं ग़लत का चुनाव करें-

1. शास्त्रीय उदारवाद व्यक्तिवाद का दूसरा नाम कहा जा सकता है।
2. जॉन लॉक एक प्रसिद्ध अमेरिकन राजनीतिक विद्वान् थे।
3. जॉन लॉक ने लेवियाथान नामक पुस्तक लिखी।
4. लॉक के अनुसार जीवन का अधिकार, स्वतन्त्रता का अधिकार एवं सम्पत्ति का अधिकार मनुष्य के प्राकृतिक अधिकार हैं।
5. एडम स्मिथ ने आर्थिक आधार पर राज्य के कार्यों को सीमित किया और व्यक्ति के कार्यों में राज्य के हस्तक्षेप को अनुचित माना।
उत्तर-

1. सही
2. ग़लत
3. ग़लत
4. सही
5. सही।

प्रश्न IV. बहुविकल्पीय प्रश्न-

प्रश्न 1.
यह कथन किसका है कि, “उदारवाद की व्याख्या करना या परिभाषा देना सरल कार्य नहीं है, क्योंकि यह कुछ सिद्धान्तों का समूह नहीं है, बल्कि मस्तिष्क में रहने वाला विचार है।”
(क) लॉस्की
(ख) विलोबी
(ग) टी० एच० ग्रीन
(घ) लासवैल।
उत्तर-
(क) लॉस्की

प्रश्न 2.
हेलोवेल ने उदारवाद का अर्थ किस प्रकार प्रकट किया है ?
(क) व्यक्ति की इच्छा की स्वतन्त्रता
(ख) व्यक्ति की भलाई एवं दृढ़ विवेकशीलता
(ग) जीवन, स्वतन्त्रता तथा सम्पत्ति के अधिकारों का अस्तित्व
(घ) उपरोक्त सभी।
उत्तर-
(घ) उपरोक्त सभी।

प्रश्न 3.
निम्न में से उदारवाद का सिद्धान्त है-
(क) मानवीय विवेक में आस्था
(ख) इतिहास एवं परम्परा का विरोध
(ग) मानवीय स्वतन्त्रता का पोषक
(घ) उपरोक्त सभी।
उत्तर-
(घ) उपरोक्त सभी।

प्रश्न 4.
जॉन लॉक किस देश का राजनीतिक विद्वान् था ?
(क) भारत
(ख) अमेरिका
(ग) इंग्लैण्ड
(घ) जर्मनी।
उत्तर-
(ग) इंग्लैण्ड

प्रश्न 5.
शास्त्रीय उदारवाद की विशेषता है-
(क) व्यक्ति की सर्वोच्च महानता
(ख) व्यक्ति साध्य और राज्य साधन
(ग) राज्य एक आवश्यक बुराई है
(घ) उपरोक्त सभी।
उत्तर-
(घ) उपरोक्त सभी।

Punjab State Board PSEB 10th Class Welcome Life Book Solutions Chapter 6 संतुलित भावुक विकास Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Welcome Life Chapter 6 संतुलित भावुक विकास

PSEB 10th Class Welcome Life Guide संतुलित भावुक विकास Textbook Questions and Answers

नोट-इस अध्याय के कोई पाठ्य प्रश्न नहीं हैं।

पाठ पर आधारित प्रश्न

मेरी भावनाओं की सूझ

नीचे दिए खाके में कुछ भावनाएं दी गई हैं। इस तालिका को पूरा करके आप अपनी भावनाओं की संवेदनशीलता का अंदाजा लगा सकते हो —

मुझे खुशी होती है जब …………

1. कोई मेरे काम की तारीफ करता है।
2. मेरे दोस्त मेरे साथ खेलते हैं।
3. मेरा परिणाम बहुत अच्छा आता है।

मुझे दुःख होता है जब …………

1. कोई मेरे बारे में गलत बोलता है।
2. कोई मेरी पीठ पीछे मेरी निंदा करता है।
3. जब मेरी मेहनत का नतीजा अच्छा नहीं आता है।

मुझे डर लगता हैं जब …………

1. शिक्षक को कोई मेरे बारे में कुछ गलत कहता है।
2. मेरे पेपर अच्छे नहीं होते और बुरा परिणाम आना हो।

मुझे नफरत हैं जब …………
कोई मेरी पीठ पीछे बात करके मुझे बदनाम करता है और सामने बोलने की हिम्मत नहीं करता।

मुझे गर्व महसूस होता है जब …………
मेरी मेहनत का अच्छा परिणाम आता है और हर कोई मेरा सम्मान करता है।

मैं निराश हो जाता हूँ जब ………….
मेरी मेहनत के बावजूद, परिणाम उम्मीद के मुताबिक नहीं आता।

मुझे सहानुभूति होती है जब ……..
मेरे दोस्तों को कम अंक मिलते हैं और मैं अपने आस-पास बहुत सारे गरीब लोगों को देखता हूँ।

मुझे विश्‍वास है कि जब …………
हर कोई मुझसे कहता है कि यदि इस बार नहीं तो अगली बार परिणाम बेहतर होंगे क्योंकि मेहनत व्यर्थ नहीं जाती है।

सकारात्मक भावनाएं

नकारात्मक भावनाएं

सहपाठियों से विचार करने की कला

(क) अपने दोस्तों के नाम लिखो।
1. ……………….. 2. ……………… 3. ………………..
(ख) आप अपने दोस्तों से कितनी बार नाराज होते हैं?
कभी नहीं/अक्सर/कभी कभी।
(ग) आप अपने दोस्तों के साथ नाराज़गी से कितनी देर के बाद खेलना फिर से शुरू करते ैं?
(घ) अपने साथियों को खुश करने के लिए आप क्या प्रयास करते हैं?
उत्तर-
(क) क, ख, ग …….।
(ख) कभी-कभी।
(ग) थोड़ी देर बाद जब आक्रोश दूर हो जाता है।
(घ) मैं उन्हें टहलने के लिए बाहर ले जाता हूँ और साथ में बैठकर कुछ खा लेता हूँ। इसका बिल का भुगतान करता हूँ।

मान लीजिए आपका एक दोस्त एक दिन आपके साथ कैंटीन जाता है। आप चाय और समोसे का ऑर्डर करते हैं लेकिन वह केवल चाय लेता है, समोसे की कीमत पूछने के बाद। ऐसी स्थिति में आप क्या करेंगे? उत्तर-इस स्थिति में मैं उसे एक समोसा खरीद दूंगा और हम एक साथ समोसा खाएंगे।
आपकी कक्षा में एक छात्र बिना नाश्ता किए स्कूल में आ गया है। वह अपना टिफिन-बॉक्स भी नहीं लाया। आप उसके लिए क्या करेंगे ? उत्तर-मैं उसके साथ अपना टिफिन साझा करूँगा और कहूंगा कि वह चिंता न करे। हम उसके साथ हैं।

Welcome Life Guide for Class 10 PSEB संतुलित भावुक विकास Important Questions and Answers

वस्तुनिष्ठ प्रश्न

(क) बहुविकल्पीय प्रश्न

प्रश्न 1.
भावनाओं पर नियंत्रण नहीं रखने से किस पर बुरा प्रभाव पड़ता है?
(a) मानसिक स्वास्थ्य
(b) पारिवारिक संबंध
(c) सामाजिक संबंध
(d) उपरोक्त सभी।
उत्तर-
(d) उपरोक्त सभी।

प्रश्न 2.
बुरे प्रभावों से बचने के लिए हमें क्या करना चाहिए?
(a) भावनाओं को खुलकर व्यक्त करना चाहिए
(b) भावनाओं को नियंत्रण में रखना चाहिए
(c) कोई भावनाएं नहीं होनी चाहिए
(d) इनमें से कोई नहीं।
उत्तर-
(b) भावनाओं को नियंत्रण में रखना चाहिए।

प्रश्न 3.
इनमें से कौन-सा एक सकारात्मक भाव है?
(a) खुशी
(b) उदासी
(c) ईर्ष्या
(d) निराशा।
उत्तर-
(a) खुशी।

प्रश्न 4.
इनमें से कौन-सा एक नकारात्मक भाव है?
(a) दुःख
(b) गौरव
(c) सहानुभूति
(d) प्यार!
उत्तर-
(a) दुःख।

प्रश्न 5.
निम्नलिखित में से सकारात्मक भावना चुनें
(a) गर्व
(b) विश्वास
(c) सहानुभूति
(d) उपरोक्त सभी।
उत्तर-
(d) उपरोक्त सभी।

प्रश्न 6.
नकारात्मक भावना का पता करो।
(a) दुःख
(b) चिंता
(c) डर
(d) ये सभी।
उत्तर-
(d) ये सभी।

(ख) खाली स्थान भरें

1. ………… लिखना एक अच्छी आदत है।
2. गर्व करना एक ………………… भावना है।
3. ईर्ष्या करना एक …………………. भावना है।
4. हमें अपनी ………………… को काबू में रखना चाहिए।
5. डायरी एक महत्त्वपूर्ण ………………… बन जाती है।

उत्तर-

1. डायरी,
2. सकारात्मक,
3. नकारात्मक,
4. भावनाएं,
5. दस्तावेज़।

(ग) सही/ग़लत चुनें

1. हमें भावनाओं को नियंत्रण में रखना चाहिए।
2. खुशी व्यक्त करना नकारात्मक भावना है।
3. बेचैनी और भय सकारात्मक भावनाएं हैं।
4. हमें डायरी लिखने की आदत नहीं डालनी चाहिए।
5. भावनाओं को व्यक्त करने की एक सीमा होनी चाहिए।

उत्तर-

1. सही,
2. ग़लत,
3. ग़लत,
4. ग़लत,
5. सही।

(घ) कॉलम से मेल करे

कॉलम I — कॉलम II
(a) उत्तेजना (जोश) — (i) नकारात्मक भाव
(b) भावनाओं पर नियंत्रण — (ii) सकारात्मक भाव
(c) क्रोध — (iii) अच्छी आदतें
(d) विश्वास (iv) भावना
(e) डायरी लिखना — (v) भाव व्यक्त करना।
उत्तर-
कॉलम I — कॉलम II
(a) उत्तेजना (जोश) — (iv) भावना
(b) भावनाओं पर नियंत्रण — (v) भाव व्यक्त करना
(c) क्रोध — (i) नकारात्मक भाव
(d) विश्वास — (ii) सकारात्मक भाव
(e) डायरी लिखना — (iii) अच्छी आदतें

अति लघु उत्तरीय प्रश्न

प्रश्न 1.
भावनाओं के संतुलन से क्या अभिप्राय है?
उत्तर-
इसका मतलब है कि हमें पता होना चाहिए कि कब और कितनी भावनाओं को व्यक्त करना है।

प्रश्न 2.
भावनाओं को नियंत्रण करने की आवश्यकता क्यों है?
उत्तर-
यदि हम अपनी भावनाओं को नियंत्रित नहीं करेंगे, तो हमें कई नुकसान हो सकते हैं।

प्रश्न 3.
हमारे पास किस प्रकार की भावनाएं होती हैं?
उत्तर-
भय, सुख, दुःख, हैरानी, पश्चाताप, विश्वास, प्रेम इत्यादि।

प्रश्न 4.
भावनाओं को नियंत्रित न करने से क्या हानि है?
उत्तर-
यह हमारे मानसिक स्वास्थ्य, पारिवारिक संबंधों और सामाजिक संबंधों पर बुरा असर डाल सकता है।

प्रश्न 5.
भावनाओं को व्यक्त करने के लिए क्या ज़रूरी है?
उत्तर-
भावनाओं को व्यक्त करने की निश्चित सीमा होनी चाहिए।

प्रश्न 6.
डायरी लिखने से क्या फायदा है?
उत्तर-
इससे हम अपने अच्छे पलों को सहेज सकते हैं जो हमारे जीवन में आए हैं।

लघु उत्तरीय प्रश्न

प्रश्न 1.
भावनाओं को व्यक्त करने पर एक नोट लिखो।
उत्तर-
हमारे पास बहुत सारी भावनाएँ हैं जैसे कि भय, चिंता, घबराहट, खुशी, प्यार इत्यादि। भावनाओं को नियंत्रण में रखना बहुत आवश्यक है अन्यथा हमें इसके परिणाम, भुगतने होंगे। यदि भावनाएं नियंत्रण से बाहर हो जाएंगी, तो इससे हमारे स्वास्थ्य, सामाजिक संबंधों और पारिवारिक संबंधों पर बुरा प्रभाव हो सकता है। इसलिए उन्हें नियंत्रण में रखना आवश्यक है। इसके साथ-साथ हमें यह भी सीखना चाहिए कि भावुक होकर हम कोई ऐसी गलती न कर बैठें जिससे हमें बाद में पश्चाताप हो।

प्रश्न 2.
तस्वीर की मदद से सकारात्मक भावनाएं दिखाएं।
उत्तर-

प्रश्न 3.
तस्वीर की मदद से नकारात्मक भावनाएं दिखाएं।
उत्तर-

प्रश्न 4.
हमें डायरी लिखने की आदत क्यों होनी चाहिए?
उत्तर-
डायरी लिखना एक अच्छी आदत है क्योंकि इसमें हम अपनी जिंदगी के वह पल संभाल सकते हैं जो हमारी जिंदगी में बीते हैं। हम खुश होते हैं जब हम अपनी डायरी से अपने पुरानी यादों को याद करते हैं। डायरी हमारे लिए एक महत्त्वपूर्ण दस्तावेज़ बन जाती है। इसीलिए सबको डायरी लिखने की आदत डालनी चाहिए और इसे जिंदगी का एक अहम हिस्सा बनाना चाहिए।

दीर्घ उत्तरीय प्रश्न

प्रश्न-हम इस अध्याय से क्या सीखते हैं ? विस्तार से बताएं।
उत्तर-

1. हर व्यक्ति की बहुत सी भावनाएँ होती हैं जिनको वे समय-समय पर व्यक्त करते हैं।
2. सकारात्मक भावनाओं में हम गर्व, विश्वास, प्यार, खुशी इत्यादि को शामिल करते हैं। नकारात्मक भावनाओं में हम गुस्सा शर्म, ईर्ष्या, डर इत्यादि को शामिल करते हैं।
3. हमें अपनी भावनाओं को नियंत्रित करने की आवश्यकता है अन्यथा हमारे मानसिक, पारिवारिक और सामाजिक रिश्तों पर उनका हानिकारक प्रभाव पड़ता है।
4. हमें अपनी भावनाओं को सोच-समझ कर व्यक्त करना चाहिए ताकि किसी और को गुस्सा न आए। इसलिए, भावनाओं का संतुलन रखना महत्त्वपूर्ण है।
5. हमें डायरी लिखने की आदत डालनी चाहिए और अपनी भावनाओं को केवल डायरी में व्यक्त करना चाहिए।
6. डायरी एक अनमोल दस्तावेज़ बन जाती है जिसे हम अपनी पुरानी यादों को ताज़ा करने के लिए कभी भी पढ़ सकते हैं।

संतुलित भावुक विकास PSEB 10th Class Welcome Life Notes

• हर व्यक्ति के पास बहुत सारी भावनाएं होती हैं जैसे कि खुशी, दुःख बेचैनी, घबराहट, डर इत्यादि। इन भावनाओं पर नियंत्रण रखना आवश्यक है नहीं तो वे हानिकारक साबित हो सकती हैं।
• यदि हम अपनी भावनाओं को नियंत्रित नहीं करते, तो हम भावुक होकर ऐसी गलती कर बैठेंगे, जिससे हमें बाद में पश्चाताप होगा।
• यदि हम स्वयं में स्वयं-मूल्यांकन की भावना विकसित करते हैं, तो हम बेहतर नागरिक बन सकते हैं। इस तरह की भावनाएँ हमारे जीवन में बहुत महत्त्वपूर्ण भूमिका निभाती हैं।
• हमें अपनी भावनाओं का संतुलन रखना चाहिए और उन्हें एक निश्चित सीमा तक ही व्यक्त करना चाहिए।
• हमारे पास कुछ सकारात्मक और कुछ नकारात्मक भावनाएँ हैं और उन्हें ठीक से समन्वित करने की आवश्यकता है।
• नकारात्मक भावनाओं से छुटकारा पाकर सकारात्मक भावनाओं के प्रति अधिक झुकाव होना चाहिए।
• दोस्तों के बीच घूमने की प्रवृत्ति होनी चाहिए होती भी है। यह हमें उनके करीब जाने और हमारी भावनाओं को उनके साथ साझा करने की अनुमति देता है। ऐसा करने से डिप्रेशन या तनाव जैसी समस्याओं से बेचा जा सकता है।
• बहुत से लोग डायरी लिखना पसंद करते हैं और यह एक बहुत अच्छी आदत है। डायरी में हम अपने दैनिक जीवन के अच्छे या बुरे पल लिख सकते हैं। यह डायरी बाद में हमारे जीवन का एक वैध दस्तावेज बन जाती है।

Punjab State Board PSEB 11th Class Geography Book Solutions Chapter 10 हिंद महासागर की स्थिति का भू-राजनीति के पक्ष से महत्त्व Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Geography Chapter 10 हिंद महासागर की स्थिति का भू-राजनीति के पक्ष से महत्त्व

PSEB 11th Class Geography Guide हिंद महासागर की स्थिति का भू-राजनीति के पक्ष से महत्त्व Textbook Questions and Answers

वस्तुनिष्ठ प्रश्न तु (Objective Type Questions)

नीचे लिखे प्रश्नों के उत्तर 2-4 शब्दों में दें-

प्रश्न 1.
हिंद महासागर का विस्तार बताएँ।
उत्तर-
7 करोड़ 80 लाख वर्ग किलोमीटर।

प्रश्न 2.
हिंद महासागर विश्व के महासमुद्री क्षेत्र का कितने प्रतिशत है ?
उत्तर-
20.9%.

प्रश्न 3.
कौन-से महाद्वीप हिंद महासागर के तटों को छूते हैं ?
उत्तर-
एशिया, अफ्रीका और ऑस्ट्रेलिया।

प्रश्न 4.
हिंद महासागर के पश्चिम की ओर के किन्हीं दो छोटे सागरों के नाम बताएँ।
उत्तर-
लाल सागर और अरब सागर।

प्रश्न 5.
हिंद महासागर में मिलने वाली धातुओं की गाँठें बताएँ।
उत्तर-
मैंगनीज़, तांबा और कोबाल्ट।

प्रश्न 6.
हिंद महासागर के तट पर मिलने वाले तेल क्षेत्र बताएँ।
उत्तर-
खाड़ी कच्छ, खंबात की खाड़ी, मुंबई हाई।

अति लघु उत्तरात्मक प्रश्न – (Very Short Answer Type Questions)

नीचे लिखे प्रश्नों के उत्तर 2-3 वाक्यों में दें-

प्रश्न 1.
भू-राजनीति से क्या अभिप्राय है ?
उत्तर-
राष्ट्रीय संबंधों के बारे में भूगोल के योगदान और विश्लेषण के तरीके को भू-राजनीति कहते हैं।

प्रश्न 2.
कौन-से देशांतर हिंद महासागर की सीमाएँ हैं ?
उत्तर-
दक्षिणी गोलार्द्ध में कैपटाऊन का लंबकार 18°82′ पूर्व हिंद महासागर को भौगोलिक पक्ष से अंध महासागर से और तस्मानिया प्रायद्वीप का दक्षिण-पूर्वी लंबकार 147° पूर्व, प्रशांत महासागर से अलग करता है।

प्रश्न 3.
हिंद महासागर को ‘ग्रेट रेस बेस’ क्यों कहते हैं ?
उत्तर-
भू-राजनीतिक महत्ता के कारण सभी बड़ी शक्तियाँ इस क्षेत्र पर कब्जा करने में लगी हुई हैं।

प्रश्न 4.
हिंद महासागर को ‘तृतीय विश्व का हृदय’ क्यों कहते हैं ?
उत्तर-
पूर्वी भागों को तृतीय विश्व या ‘तीसरी दुनिया’ कहा जाता है। इस क्षेत्र में हिंद महासागर एक अंतर्राष्ट्रीय व्यापारिक मार्ग है, इसलिए इस महत्त्वपूर्ण व्यापारिक मार्ग के कारण इसे ‘तृतीय विश्व का हृदय’ कहा जाता है।

लघु उत्तरात्मक प्रश्न । (Short Answer Type Questions)

नीचे लिखे प्रश्नों के उत्तर 60-80 शब्दों में दें-

प्रश्न 1.
हिंद महासागर की उसके पड़ोसी देशों के साथ सीमाएँ बताएँ।’ .
उत्तर-
विश्व के तीन महाद्वीपों एशिया, अफ्रीका और ऑस्ट्रेलिया के तटीय किनारे इस महाद्वीप को छूते हैं, जबकि यह महासागर अपने उत्तर की ओर एशियाई धरती से बंद है, परंतु दक्षिण की ओर इसका खुला प्रसार है। अंतर्राष्ट्रीय हाइड्रोग्राफिक ऑर्गेनाइजेशन (आई० एच० ओ०) अंटार्कटिका के तट को हिंद महासागर का दक्षिणी सिरा मानती है। विश्व की कुल तट रेखा का 40% भाग हिंद महासागर के तटों को छूता है।

प्रश्न 2.
हिंद महासागर के पास वाले कम गहरे सागरों के नाम बताएँ।
उत्तर-
हिंद महासागर में कई ऐसे कम गहरे सागर शामिल हैं, जो पास वाले तटीय क्षेत्रों को छूते हैं। इनमें मैलागासी सागर, लक्षद्वीप सागर, लाल सागर, अदन की खाड़ी, अरब की खाड़ी, ओमान की खाड़ी, अरब सागर, पाक जलडमरू, सुवा सागर, तिमौर सागर, अराफरा सागर, कारपैंटरिया की खाड़ी के टोर जलडमरू, ऐगज़माऊथ खाड़ी, ऑस्ट्रेलियाई धुंडी, स्पैंसर खाड़ी और बास जलडमरू आदि शामिल हैं।

प्रश्न 3.
हिंद महासागर के आस-पास कितने देश हैं ?
उत्तर-
हिंद महासागर के आस-पास 38 + 15 + 15 देश पड़ते हैं, जो हिंद महासागरीय रिम ऐसोसिएशन (Indian Ocean Rim Association) की ओर से संगठित हैं। इनमें अफ्रीका के 13, मध्य पूर्व (Middle East) के 11, दक्षिणी एशिया के 5, दक्षिण-पूर्वी एशिया के 5, पूर्वी तिमोर, ऑस्ट्रेलिया और फ्रांस तथा बर्तानिया के कब्जे वाले क्षेत्र शामिल हैं।

प्रश्न 4.
हिंद महासागर में अलग-अलग संकरे मार्ग बताएँ।
उत्तर-
हिंद महासागर में पड़ते अंतर्राष्ट्रीय व्यापार मार्गों में कम-से-कम 7 संकरे मार्ग आते हैं-

1. मोजंबिक चैनल,
2. बाब-अल-मेंडर,
3. सुएज़ या स्वेज़ नदी,
4. स्ट्रेट ऑफ होरमूज,
5. मलाका स्ट्रेट,
6. सूंदा स्ट्रेट,
7. लोबोक स्ट्रेट।

निबंधात्मक प्रश्न (Essay Type Questions)

नीचे लिखे प्रश्नों के उत्तर 150-250 शब्दों में दें-

प्रश्न 1.
हिंद महासागर के नक्शे और विशेषताएँ बताएँ।
उत्तर-
हिंद महासागर का उत्तरी क्षेत्र ऐतिहासिक और कार्य शैली के पक्ष से बहुत महत्त्वपूर्ण माना जाता है क्योंकि यह पूर्वी और पश्चिमी भागों से कई सँकरे जल डमरुओं (Straits) से जुड़ा हुआ है। पश्चिम में लाल सागर और अरब की खाड़ी तथा पूर्व में मलाका जल डमरू, तिमौर सागर और अराफरा सागर इसके अंग हैं।

विशेषताएं-हिंद महासागर की अपनी अलग विलक्षण विशेषताएँ हैं-

1. सुदूर दक्षिणी भाग को छोड़कर बाकी सारे महासागर का जल न केवल गर्म और शांत है, बल्कि यहाँ बहती हवाओं का वेग भी अनुमान से बहुत अधिक भटकता नहीं।
2. सर्दी और गर्मी की बदलती ऋतु में हवाओं की बदलती दिशा, हवाओं के वेग द्वारा गहराई वाले सागरों में जहाज़रानी को आसान कर देती है।
3. हिंद महासागर में किसी विरोधी (विपरीत) धारा का प्रवाह भी नहीं है।
4. ‘रोरिंग फोर्टीज़’ नामक पश्चिमी वायु, जो 40° दक्षिण की ओर चलती है, गुड होप जल डमरू से ऑस्ट्रेलिया के पश्चिमी तट तक सागरीय जहाजरानी में बहुत सहायक सिद्ध होती है।

प्रश्न 2.
हिंद महासागरों के प्राकृतिक साधनों का वर्णन करें।
उत्तर-
हिंद महासागर विभिन्न प्राकृतिक साधनों से भरपूर है, जिनमें से कुछ इस प्रकार हैं-
1. समुद्री समूह-समुद्री समूह में रेत, बजरी और शैल (खोल) के समूह मिलते हैं, जो किसी-न-किसी रूप में निर्माण कार्यों के लिए प्रयोग किए जाते हैं। ये समूह महाद्वीपीय शैल्फों पर मिलते हैं।

2. प्लेसर-प्लेसर समूहों में मिलने वाले वे खनिज हैं, जो सागरीय रेत और बजरी में मिलते हैं। ये भारी और लचकीले रासायनिक विशेषताओं वाले खनिज होते हैं, जो खनिज पदार्थों के अपरदन के कारण सागरीय जल में शामिल हो जाते हैं। इन खनिजों में सोना, टिन, प्लास्टिक, टाइटेनियम, मैग्नेटाइट (लोहा), जिरकोनियम बोरियम और रत्न आदि शामिल हैं।

3. बहु-धात्वीय गाँठे-समुद्र में ऐसी गाँठें भी मिलती हैं, जो अनेक धातुओं के मिश्रण से बनी होती हैं। हिंद महासागर में मैंगनीज़, तांबा, गिल्ट (निकल) और कोबाल्ट आदि धातुओं का मिश्रण अधिक मात्रा में पाया जाता है।

4. मैंगनीज़ गाँठे-ये धात्वीय गाँठें सबसे पहले 1872-76 के दौरान चैलेंजर की वैज्ञानिक यात्रा के दौरान खोजी गई, परंतु इनका खोज कार्य 1950 के दशक के अंत में ही आरंभ किया जा सका। संयुक्त राष्ट्र ने भारत को हिंद महासागर के डेढ़ लाख वर्ग किलोमीटर क्षेत्र में से ही बहु धात्वीय गाँठे निकालने की अनुमति दी है। हिंद महासागर की गोद में फास्फेट, बेरीयम सल्फेट, तांबा, कोबाल्ट, कच्चा लोहा, बॉक्साइट, सल्फर आदि भी मिलता है। मैंगनीज़ की गाँठे समुद्री फर्श पर सतह से 2 से 6100 मीटर की गहराई तक मिलती हैं।

5. तेल और गैस-हिंद महासागर की महाद्वीपीय शैल्फ खनिज तेल से भरपूर है। वर्तमान समय में, कुल तेल और गैस के उत्पादन का लगभग आधा हिस्सा सागरीय भंडारों से आता है और 75 से अधिक देश समुद्रों में से तेल और गैस उत्पन्न करते हैं। भारत के नज़दीकी क्षेत्र कच्छ की शैल्फ, खंबात की खाड़ी और मुंबई हाई खनिज तेल उत्पादन के लिए प्रसिद्ध क्षेत्र हैं, जबकि आंध्र प्रदेश के तट से परे समुद्र में स्थित कृष्णा-गोदावरी बेसिन प्राकृतिक गैस के बड़े स्रोत के रूप में प्रसिद्ध है। विश्व-भर में खनिज तेल और गैस के उत्पादन के लिए अरब की खाड़ी सबसे अधिक महत्त्वपूर्ण है। इस खाड़ी की विशेषता यह भी है कि यह सागर से थोड़ा हटकर है। कम गहरी है और आने वाली कठिनाइयाँ भी कम हैं। सऊदी अरब, कुवैत, बहरीन, कतार, संयुक्त अरब अमीरात (यू०ए०ई०), इरान और इराक इस खाड़ी से सबसे अधिक लाभ लेने वाले देश हैं।

प्रश्न 3.
हिंद महासागर की भू-राजनीति और समस्याएँ बताएँ।
उत्तर-
भू-राजनीति (Geo-Politics)-हिंद महासागर की भू-राजनीति कुछ प्राथमिक बिंदुओं के आस-पास घूमती है, जोकि इस प्रकार हैं-

1. ऋतु परिवर्तन
2. ध्रुवीकरण और उत्जीविता समीकरण
3. प्राकृतिक संसाधनों का विकास
4. आर्थिक विकास पर बेरोक आपूर्ति तंत्र

समस्याएँ-

1. हिंद महासागर के सभी क्षेत्रों में व्यापारिक जहाज़रानी पर डकैतियाँ।
2. व्यापक साधनों का विकास, विशेष रूप से खनिज तेल, प्राकृतिक गैस, खनिज पदार्थों और मछलियों के रूप में फैली आर्थिकता के पक्ष।
3. हिंद महासागर के निकट के तटीय क्षेत्रों में, समुद्री जल में बंदरगाहों के निर्माण पर राजनीतिक और वित्तीय परिणाम।
4. क्षेत्रीय और गैर-क्षेत्रीय देशों की ओर से हिंद महासागर में जल-सेना शक्ति का प्रदर्शन।

प्रश्न 4.
चीन की ‘स्टरिंग ऑफ पर्लज’ कूटनीति का वर्णन करें।
उत्तर-
स्टरिंग ऑफ पर्लज़ (String of Pearls) वास्तव में चीन की ओर से अपने खनिज तेल के व्यापार को सुरक्षा प्रदान करने के लिए यह एक राजनीतिक युक्ति है। चीन अपने बढ़ रहे भू-राजनीतिक प्रभाव को समर्थ बनाने के लिए कूटनीति संबंधों द्वारा सुरक्षा-शक्ति को ही ताकतवर नहीं बना रहा, बल्कि अपनी बंदरगाहों और हवाई अड्डों की सुरक्षा की ओर भी विशेष ध्यान दे रहा है। चीन की यह कोशिश दक्षिण चीन सागर से स्वेज़ नदी तक प्रसार करने की है, जिसमें मलाका स्ट्रेट, स्ट्रेट ऑफ होरमूज़, अरब की खाड़ी और लाल सागर सहित सारे हिंद महासागर में अड्डे बनाना शामिल है। चीन का ‘स्टरिंग ऑफ पर्लज़’ इन व्यापारिक समुद्री भागों में से होकर गुजरता है और भविष्य में एशियाई ऊर्जा स्रोतों तक पहुँचने का सपना देखता है।

भारत ने सन् 1971 से 1999 तक मलाका स्ट्रेट पर पाबंदी लगाकर चीन और पाकिस्तान के बीच पनपते स्वतंत्र समुद्री संबंधों पर रोक लगा दी थी। ‘स्टरिंग ऑफ पर्लज़’ की नीति वास्तव में चीन की ओर से हिंद महासागर में हर . प्रकार के व्यापारिक संबंधों को बिना मानव हस्तक्षेप के और भारत के स्वतंत्र अस्तित्व’ को प्रभाव मुक्त करने के लिए अपनाई है। यद्यपि चीन का मानना है, “हम सभी का महासागर पर समान रूप से अधिकार है, इस पर किसी एक का अधिकार नहीं है। हम किसी सैनिक शक्ति का प्रदर्शन नहीं करेंगे और न ही किसी ताकत का प्रदर्शन करेंगे और न ही किसी अन्य देश के साथ ईर्ष्या को बढ़ावा देंगे।”

पर्लज़ (चीनी अड्डे)

1. हांगकांग (विस्तृत प्रशासकीय क्षेत्र)
2. हैनान का टापू (टांगकिंग की खाड़ी)
3. वूडी टापू
4. स्पार्टा टापू (छ: देश-चीन, वियतनाम, ताईवान, मलेशिया, फिलीपाइन्ज़ और बरुनी के अधीन)
5. कैमपोंग सोम
6. कराह ईस्थमस-थाईलैंड
7. म्यांमार के कोको टापू
8. म्यांमार का तटीय शहर सितवें
9. बांग्लादेश में चिट्टागांग
10. श्रीलंका में हंबनटोटा
11. मालद्वीप में हाराओ अतोल
12. पाकिस्तान (बलोचिस्तान) में गवाडर
13. ईराक में अल-अहदाब
14. कीनिया में लामू
15. सूडान में उत्तरी बंदरगाह (North Port)

प्रश्न 5.
भारत की ओर से चीन की ‘स्टरिंग ऑफ पर्लज़’ नीति का क्या जवाब दिया गया ?
उत्तर-
भारतीय जल सेना और भारतीय जल सैनिक राजनीतियों/कूटनीतियों के पक्ष को सामने रखते हुए सन् 2007 में एक दस्तावेज़ ‘इंडियन मेरीटाईम डॉक्टरिन’ जारी किया, जिसमें भारतीय जल सेना ने ‘स्ट्रेट ऑफ होरमूज़’ से ‘मलाका स्ट्रेट’ तक भारतीय जल सेना की भरपूर गतिविधियों की बात की गई। इस दस्तावेज़ में अंतर्राष्ट्रीय समुद्री व्यापारिक मार्गों की पुलिस की देख-रेख और तंग समुद्री मार्गों पर पूर्ण नियंत्रण की बात की गई। पिछले दो दशकों के दौरान भारत ने अपनी विदेश नीति के अंतर्गत हिंद महासागर के आस-पास के देशों में अपने हितों का विशेष ध्यान रखते हुए मारीशस, मालदीव, सिसली और मैडगास्कर के द्वीपीय देशों और दक्षिणी अफ्रीका, तंजानिया और मोजम्बिक आदि देशों के साथ अपने संबंधों में प्रसार किया है।

भारतीय जल सेना के पास अति आधुनिक हाइड्रोग्राफिक (जल सर्वेक्षण और चित्रकारी) कैडर है, जिसमें पूरे उपकरणों से युक्त सर्वेक्षणीय समुद्री जहाज़, कई सर्वेक्षणीय किश्तियाँ, देहरादून में विश्व-स्तर के इलैक्ट्रॉनिक चार्ट तैयार करने की सुविधा और गोवा में एक हाइड्रोग्राफिक प्रशिक्षण स्कूल है। चीन की तरह ही भारत अपनी ऊर्जा प्राप्त करने के लिए खनिज तेल के आयात पर निर्भर करता है। भारत का 89% के लगभग खनिज तेल समुद्री जहाज़ के मार्ग से भारत तक पहुँचता है, जो भारत की कुल ऊर्जा की ज़रूरतों की 33% पूर्ति करता है। इसलिए प्रमुख समुद्री मार्गों की सुरक्षा सबसे अहम् आर्थिक ज़रूरत बन जाती है। इतिहास साक्षी है कि भारत शुरू से ही हिंद महासागर में डकैती और आतंकी कार्रवाइयों का सदा से ही तीखा विरोधी रहा है।

प्रश्न 6.
महासागरों संबंधी बनाए गए U.N.O. के कानूनों का वर्णन करें।
उत्तर-
महासागरों संबंधी कानूनों के बारे में संयुक्त राष्ट्रीय सम्मेलन (UNCOLS)—सन् 1972 से 1982 तक सागरों संबंधी अंतर्राष्ट्रीय नियमावली और कानून बनाने हेतु संयुक्त राष्ट्र की ओर से करवाए गए सम्मेलनों के दौरान तीसरे सम्मेलन के सम्मुख आए अंतर्राष्ट्रीय समझौते को समुद्री सम्मेलनों का कानून भी कह दिया जाता है। इस कानून के अंतर्गत विश्व-भर के महासागरों की पूर्ति करने हेतु राष्ट्रों के अधिकार और कर्तव्य तय कर दिए गए हैं, वित्तीय कार्यवाही के लिए नियमावली बना दी गई है और समुद्री प्राकृतिक साधनों के प्रबंध के लिए अनिवार्य आदेश जारी कर दिए गए हैं। यू० एन० कोल्ज़ (UNCOLS) सन् 1994 में लागू हुआ और इस सम्मेलन में अगस्त 2014 में, 165 देश और यूरोपीय संघ शामिल हुए। सम्मेलन के दौरान कई नियम भी लागू किए गए, जिनमें से महत्त्वपूर्ण थे-सीमा निर्धारण, जहाजरानी नियम, द्वीप समूहों के अधिकार-क्षेत्र और यातायात नियम, विशेष आर्थिक क्षेत्र (EEZ), महाद्वीपीय शैल्फ की सीमाएँ, समुद्री फर्श पर खनन के नियम, समुद्री पर्यावरण की सुरक्षा, विज्ञान अन्वेषण और झगड़ों के निपटारे संबंधी नियम। सम्मेलन के दौरान कई क्षेत्रों में सीमाएँ निर्धारित की गई हैं या परिभाषित की गईं।

1. बेस लाइन-निम्न जल रेखा या वह सीधी रेखा, जो गहरे तटीय क्षेत्रों में चट्टानी भित्तियों को जोड़ती है।

2. आंतरिक (Internal) जल-क्षेत्र-तट के निकट का वह जल-क्षेत्र जो बेस लाइन और तट के बीच हो। इस क्षेत्र के लिए संबंधित देश ही नियम तय करता है, लागू करता है और यहाँ के साधनों का प्रयोग करता है। विदेशी जहाजों और किश्तियों को किसी भी अन्य देश के आंतरिक जल-क्षेत्र में आने-जाने की आज्ञा नहीं होती।

3. क्षेत्रीय (Territorial) जल-क्षेत्र-बेस लाइन से 12 नाटीकल मील (सड़क के 22 किलोमीटर या 14 मील) तक का क्षेत्र क्षेत्रीय जल-क्षेत्र होता है जिसके बारे में तटीय देश को नियम-कानून बनाने का अधिकार होता है और वह प्राकृतिक साधनों का प्रयोग भी कर सकता है। शांतमयी ढंग से गुजरने वाले विदेशी जहाज़ों और किश्तियों को भी इस क्षेत्र में से गुज़रने की अनुमति होती है, जबकि युद्ध नीति रखने वाले महत्त्वपूर्ण स्ट्रेटों (जल-डमरुओं) में से गुजरने वाले युद्धपोतक नावों को आज्ञा लेनी पड़ती है।

4. टापू-समूह (आरकीपिलाजिक) जल-क्षेत्र-सम्मेलन के दौरान द्वीप समूही जल-क्षेत्र की परिभाषा चौथे भाग (अध्याय) में दी गई, जिसमें किसी देश को अपनी क्षेत्रीय सीमा निर्धारित करने के लिए आधार भी परिभाषित किए गए। द्वीप-समूहों में से सबसे बाहरी द्वीप के सबसे बाहरी भागों को जोड़ती एक बेस लाइन खींच ली जाती है और इस रेखा के अंदर आते जल-क्षेत्र को द्वीप-समूह जल-क्षेत्र का नाम दिया जाता है। किसी भी देश को अपने इस जल-क्षेत्र संबंधी संपूर्ण प्रभुसत्ता प्राप्त होती है।

5. निकटवर्ती (Contiguous) जल-क्षेत्र-किसी भी तट से 12 नाटीकल मील (22 किलोमीटर) की सीमा से आगे 12 नाटीकल मील की सीमा तक के जल-क्षेत्र को निकटवर्ती जल-क्षेत्र माना जाता है। इस क्षेत्र में कोई भी देश चार विषयों-निर्यात शुल्क, शुल्क निर्धारण, आवास नियम और प्रदूषण संबंधी अपने नियम लागू कर
सकता है।

6. विशेष आर्थिक क्षेत्र (Exclusive Economic Zone)-किसी भी देश की बेस लाइन से आगे, क्षेत्रीय जल-क्षेत्र में और आगे 200 नाटीकल मील (370 किलोमीटर या 230 मील) तक का जल-क्षेत्र विशेष आर्थिक क्षेत्र होता है, जहाँ के प्राकृतिक साधनों के प्रयोग के सभी अधिकार तटीय देशों के पास सुरक्षित होते हैं।

7. महाद्वीपीय शैल्फ (Continental Shelf)—महाद्वीपीय शैल्फ को किसी भी थल-क्षेत्र का प्राकृतिक विस्तार माना जाता है, जोकि भू-क्षेत्र से महाद्वीपीय तट के बाहरी सिरे तक या फिर 200 नाटीकल मील किलोमीटर) में से जो अधिक हो, तक माना जाता है। किसी स्थान पर यदि महाद्वीपीय शैल्फ कम हो तो उसका जल-क्षेत्र 200 नाटीकल मील तक माना ही जाएगा।

8. समुद्री कानून संबंधी अंतर्राष्ट्रीय ट्रिब्यूनल (आई० ई० एल० ओ० एस०)-यह ट्रिब्यूनल नियम-कानूनों की व्यवस्था के अतिरिक्त मछली पकड़ने संबंधी नियमों और विशेषकर समुद्री वातावरण के झगड़ों के निपटारे संबंधी कार्य करता है।

9. अंतर्राष्ट्रीय समुद्री थल अथॉरिटी (International Sea-Bed Authority – I.S.A) – missing अधिकारित जल-क्षेत्र से बाहर के क्षेत्र, जोकि अंतर्राष्ट्रीय समुद्री थल का क्षेत्र माना जाता है, में खनिज पदार्थों संबंधी और अन्य नियंत्रण अथवा संगठन के लिए अंतर-सरकारी टीम तैयार की गई है, जिसे अंतर्राष्ट्रीय समुद्री थल अथॉरिटी के नाम से जाना जाता है।

Punjab State Board PSEB 6th Class Home Science Book Solutions Chapter 8 व्यक्तिगत स्वास्थ्य विज्ञान Textbook Exercise Questions and Answers.

PSEB Solutions for Class 6 Home Science Chapter 8 व्यक्तिगत स्वास्थ्य विज्ञान

PSEB 6th Class Home Science Guide व्यक्तिगत स्वास्थ्य विज्ञान Textbook Questions and Answers

प्रश्न 1.
स्वास्थ्य क्या है ?
उत्तर-
मनुष्य के शरीर की रोग-रहित दिशा ही स्वास्थ्य है।

प्रश्न 2.
आँखों के लिए कौन-सा विटामिन महत्त्वपूर्ण है ?
उत्तर-
विटामिन ‘ऐ’।

प्रश्न 3.
दाँतों के लिए भोजन के कौन-से तत्त्व महत्त्वपूर्ण हैं ?
उत्तर-
कैल्शियम, विटामिन डी, फास्फोरस।

प्रश्न 4.
खाना खाने के बाद कैसे फल खाने चाहिए ?
उत्तर-
ताजे तथा तेजाबी अंश वाले रसदार फल ।

प्रश्न 5.
आँखों को नीरोग रखने के लिए क्या करना चाहिए ?
उत्तर-
आँखों को धुआँ, धूल, धूप तथा तेज़ रोशनी से बचाना चाहिए।

लघूत्तर प्रश्न

प्रश्न 1.
आँखों की सम्भाल करनी क्यों आवश्यक है ?
उत्तर-
आँखें हमारे शरीर में अत्यन्त ही महत्त्वपूर्ण अंग हैं। इनसे ही हम विभिन्न वस्तुओं को देख सकते हैं। इसलिए यह कहावत कि ‘आँखें हैं तो जहान है’ कही जाती है। इनकी संभाल के लिए निम्नलिखित उपाय किए जाने चाहिएं –

1. आँखों को बाहर की गन्दगी जैसे धूल-मिट्टी, कूड़ा-करकट, कीट-पतंगे आदि से बचाना चाहिए। कुछ धूल तथा जीवाणु तो आँख के द्वारा बाहर निकल जाते हैं। यदि किसी कारण से आँखों में कुछ गिर जाए तो उसको नार्मल सेलाइन या साफ़ जल से धो डालना चाहिए।
2. मुंह तथा आँखों को कई बार धोने तथा पोंछने से सफ़ाई होती है।
3. गन्दे हाथों से अथवा गन्दे रूमाल से आँखों को नहीं पोंछना चाहिए, न ही इन्हें रगड़ना या मलना चाहिए।
4. तौलिया, साबुन, बाल्टी, मग तथा मुँह पोंछने का कपड़ा जिनका उपयोग दूसरे व्यक्ति करते हों, प्रयोग नहीं करना चाहिए। विशेषकर दुखती आँखों वाले व्यक्ति का।
5. आँखों को तेज़ धूप, चकाचौंध अथवा तेज़ रोशनी से बचाना चाहिए। इसके लिए धूप के चश्मे आदि का प्रयोग किया जा सकता है।
6. कम प्रकाश में लिखना-पढ़ना अथवा कोई महीन काम करना आँखों के लिए घातक सिद्ध हो सकता है।
7. आँखों की विभिन्न बीमारियों जैसे-रोहे इत्यादि से आँखों को बचाना चाहिए और यदि इनमें से कोई रोग हो तो तुरन्त ही नेत्र-विशेषज्ञ की सलाह लेनी चाहिए।

प्रश्न 2.
काम करते समय रोशनी किस तरफ से आनी चाहिए ?
उत्तर-
काम करते समय रोशनी ठीक और बाएँ हाथ की ओर से आनी चाहिए, बाएँ हाथ से काम करने वालों के लिए यह रोशनी दाईं ओर से आनी चाहिए।

प्रश्न 3.
आँखों के व्यायाम के बारे में आप क्या जानते हो ? लिखो।
उत्तर-
प्रत्येक दिन सुबह उठकर ताजे पानी से आँखों को धोना चाहिए और ठण्डे पानी के हल्के-हल्के छींटे मारने चाहिएं। पुतली बाएँ से दाएँ, दाएँ से बाएँ, ऊपर से नीचे और नीचे से ऊपर की तरफ़ बार-बार घुमाना चाहिए। इस व्यायाम में आँखें रुकनी नहीं चाहिएं।

प्रश्न 4.
यदि दाँत ठीक तरह साफ़ न किए जाएं तो क्या होता है ?
उत्तर-
यदि दाँतों को अच्छी तरह साफ़ न किया जाए तो भोजन के कण दाँतों के खोलों में इकट्ठे हो जाते हैं। इससे दाँत कमजोर होने लगते हैं। जीवाणुओं के प्रभाव से ये भोजन कण सड़ते हैं और एक अम्ल बनाते हैं जिनसे दाँतों में सड़न उत्पन्न होने लगती है और पाचन-क्रिया भी खराब हो जाती है। मसूड़ों पर भी बुरा प्रभाव पड़ता है।

प्रश्न 5.
मिठाइयां, निशास्ते वाला भोजन और तेज़ गंध वाली चीजें और पान क्यों अधिक नहीं खाने चाहिएं ?
उत्तर–
दाँतों के लिए अधिक मिठाइयां, निशास्ते वाला भोजन जैसे मैदे की बनी चीजें दाँतों से चिपक जाती हैं। तेज़ गंध वाली चीज़ों को खाने से मुँह में गंध आ जाती है, जैसेलहसुन, प्याज, मछली आदि। अधिक पान खाने से दाँत मैले, कुचैले और काले हो जाते हैं और दाँतों पर निकोटीन की तरह जम जाती है। इससे दाँतों को नुक़सान होता है।

प्रश्न 6.
नाखून गन्दे क्यों नहीं रखने चाहिएं और इन्हें कैसे साफ़ रख सकते हों, लिखो।
उत्तर-
नाखूनों के अन्दर किसी प्रकार की गन्दगी नहीं होनी चाहिए क्योंकि भोजन के साथ इनमें उपस्थित रोगों के कीटाणु, जीवाणु आदि आहार नाल में पहुंचकर विकार उत्पन्न करेंगे। इसी कारण कई बार बच्चों की पाचन-क्रिया खराब हो जाती है और छोटी उम्र में बच्चों को दस्त लग जाते हैं और उल्टियां आने लगती हैं। सप्ताह में एक बार नाखून ज़रूर काटने चाहिएं।

प्रश्न 7.
कम रोशनी में क्यों नहीं पढ़ना चाहिए ?
उत्तर-
कम रोशनी में पढ़ने से आँखों पर दबाव पड़ता है इसलिए नहीं पढ़ना चाहिए।

प्रश्न 8.
नहाने से पहले मालिश क्यों करनी चाहिए ?
उत्तर-
नहाने से पहले मालिश इसलिए करनी चाहिए कि शरीर स्वस्थ और सुन्दर बने।

प्रश्न 9.
सिगरेट पीने से दाँतों पर किस वस्तु की परत जम जाती है ?
उत्तर-
निकोटीन की।

प्रश्न 10.
दाँत काले हो जाने के क्या कारण हैं ?
उत्तर-
नसवार रगड़ने, पान खाने और सिगरेट पीने से दाँत काले हो जाते हैं।

प्रश्न 11.
दाँतों का रंग सफ़ेद क्यों होता है ?
उत्तर-
दाँतों का रंग सफ़ेद इनैमल के कारण होता है।

प्रश्न 12.
‘आँखें गईं जहान गया’ से क्या भाव है ?
उत्तर-
इसका भाव यह है कि आँखों के बिना सचमुच ही यह संसार अंधकारमय है। यदि आँखें काम न करें तो दुनिया के ये सभी दृश्य व्यर्थ हैं।

प्रश्न 13.
आँखों के लिए कौन-सा विटामिन महत्त्वपूर्ण हैं ?
उत्तर-
विटामिन ‘ए’।

प्रश्न 14.
भोजन के कौन-से तत्त्व दाँतों के लिए महत्त्वपूर्ण हैं ?
उत्तर-
कैल्शियम, विटामिन ‘डी’ और फॉस्फोरस।

प्रश्न 15.
प्रत्येक व्यक्ति को अपने कपड़े तथा तौलिया अलग क्यों रखने चाहिए?
उत्तर-
प्रत्येक व्यक्ति को अपने कपड़े तथा तौलिया अलग-अलग रखने चाहिए क्योंकि एक साथ रखने पर छूत की बीमारी फैलने का भय रहता है जैसे-आँखों का रोग, खाज, खुजली, दाद आदि।

निबन्धात्मक प्रश्न अब

प्रश्न 1.
दाँत कैसे साफ़ और स्वस्थ रखे जा सकते हैं ?
उत्तर-
1. प्रत्येक भोजन करने के बाद दाँतों को अच्छी प्रकार साफ़ करना चाहिए। कुल्ली करके दाँतों में फंसे भोजन कण निकाल देने चाहिएं।

2. हर सुबह व रात्रि को सोने से पूर्व दाँतों को उँगली या दन्त ब्रुश से मन्जन या पेस्ट की सहायता से साफ़ करना चाहिए। ऐसा करने से दाँतों को रोगमुक्त रखा जा सकता है। दन्त ब्रुश बहुत बड़े बालों का नहीं होना चाहिए अन्यथा मसूड़ों में घाव होने की सम्भावना रहती है।

3. बचपन से ही दाँतों की सफ़ाई की उचित विधि की शिक्षा देनी चाहिए। दाँतों को सब ओर से, दाँतों के भीतर व बाहर आदि भोजन चबाने वाले ऊपर व नीचे के भागों को नियमपूर्वक साफ़ करना आवश्यक है।

4. दाँतों को तिनकों या सुई से कुरेदना नहीं चाहिए।

5. दन्त चिकित्सक से बच्चों के दाँतों का नियमित निरीक्षण करवाना चाहिए।

6. दाँतों की स्वस्थता के लिए उपयुक्त भोजन की आवश्यकता होती है। इससे निम्नलिखित लाभ होते हैं –
(i) दाँतों की सुदृढ़ता शरीर के सामान्य स्वास्थ्य पर बहुत निर्भर करती है। शरीर के उचित स्वास्थ्य के लिए उपयुक्त भोजन आवश्यक होता है। प्रोटीन, कैल्शियम, फॉस्फोरस तथा विटामिन ‘C’ व ‘D’ दाँतों के निर्माण व स्वास्थ्य में महत्त्वपूर्ण योगदान देते हैं। भोजन में इन तत्त्वों की कमी दाँतों के स्वास्थ्य को बिगाड़ती है। अतः हमें अपने आहार में इन तत्त्वों का विशेष ध्यान रखना चाहिए।

(ii) कच्चे फल व सब्जियाँ चबा-चबाकर खाने से मसूड़ों को व्यायाम का अवसर मिलता है जिससे वे स्वस्थ बने रहते हैं।

(iii) मिठाइयां, मीठी व चिपकने वाली चॉकलेट, टॉफी, लॉलीपॉप आदि बहुत कम खाना चाहिए। मीठी वस्तुएं खाने के पश्चात् मुँह को कुल्ला करके साफ़ करना अत्यन्त आवश्यक है।

(iv) गरम भोजन के तुरन्त बाद ठण्डा पानी या पेय नहीं लेना चाहिए।

प्रश्न 2.
स्नान के बारे में आप जो भी जानते हो विस्तार से लिखो।
उत्तर-
निरोग जीवन और व्यक्तिगत सफ़ाई के लिए स्नान बहुत ज़रूरी है। विशेष कर कान के पिछले भाग, बगले या जाँघों की सफाई करनी ज़रूरी है नहीं तो बदबू आने लगती है। काम करने से कई कोशिकाएं मरने के बाद चमड़ी पर इकट्ठी हो जाती हैं। इसको स्नान करके दूर करना ज़रूरी है। यदि पसीना बाहर निकलना रुक जाए तो गुर्दे अपना काम ठीक तरह से नहीं कर सकते।

स्नान से शारीरिक ताप भी ठीक रहता है। गर्मियों में खुश्की, फोड़े, फुसियाँ, पित्त आदि हो जाते हैं और गर्मी शरीर को झुलसाती है। ठीक तरह से स्नान करके त्वचा साफ़ रखने से ऐसे रोग नहीं होते। गर्मी में शारीरिक तापमान बढ़ जाता है। स्नान पर खुली हवा में बैठने से शारीरिक तापमान में गर्मी के कारण वृद्धि नहीं होती। यदि हो सके तो स्नान करते समय शरीर की सखी मालिश भी करनी चाहिए। मालिश करने से रक्त का दौरा तेज़ होता है। इससे रक्त साफ़ और शुद्ध होकर बहने लगता है।

हमें सप्ताह में एक बार सिर को मालिश करके बाल अच्छी तरह धो लेने चाहिएं। सुबह का समय स्नान के लिए सबसे अच्छा होता है। यदि हम स्नान नहीं करेंगे या सिर अच्छी तरह साफ़ नहीं करेंगे तो बालों में जुएँ पड़ जाएंगी इससे सिर की खोपड़ी कमजोर हो जाती है और सारा दिन खुजलाने के लिए एक हाथ सिर में ही रहता है। कुछ लोग गर्मियों में ठीक तरह से स्नान नहीं करते। वे अपना शरीर साफ़ नहीं करते। अतः उनके कपड़ों और शरीर पर भी जुएँ पड़ जाती हैं। ऐसे व्यक्ति के पास कोई भी नहीं बैठ सकता।

सर्दियों में गर्म पानी से स्नान करना चाहिए। इससे गर्मी मिलती है और शक्ति संचार होता है। खेलने के बाद गर्म पानी से स्नान करना चाहिए नहीं तो सर्द-गर्म होने का खतरा रहता है। लेकिन स्वस्थ और बलवान मनुष्य ठण्डे पानी से ही स्नान करते हैं। इससे ताजगी और प्रसन्नता की भावना पैदा होती है।

खाना खाने और थक जाने के पश्चात् स्नान करना ठीक नहीं रहता। ठण्डे देशों में भाप स्नान भी किया जाता है।

प्रश्न 3.
आँखों की सम्भाल कैसे करनी चाहिए ?
उत्तर-
कहते हैं आँख है तो जहान है क्योंकि इनसे ही हम संसार को देख सकते हैं। इनकी सम्भाल के लिए निम्न उपाय किए जाने चाहिएं –

1. आँखों को बाहरी गंदगी, जैसे धूल-मिट्टी, कूड़ा-करकट, कीट-पतंगों आदि से बचाना चाहिए। गन्दी आँखें दुखने लगती हैं। यदि किसी कारण से आँखों में कुछ गिर जाए, तो साफ़ जल से धोकर निकाल देना चाहिए।
2. गन्दे हाथों से अथवा गन्दे रूमाल से आँखों को नहीं पोंछना चाहिए।
3. आँखों को रगड़ना या मलना नहीं चाहिए।
4. आँखों को तेज़ धूप, चकाचौंध अथवा तेज़ रोशनी से बचाना चाहिए। इसके लिए धूप के चश्मे आदि का प्रयोग किया जा सकता है।
5. कम प्रकाश में लिखना-पढ़ना अथवा कोई महीन काम नहीं करना चाहिए।
6. आँखों में तकलीफ होने पर नेत्र-चिकित्सक की राय लेनी चाहिए।

Home Science Guide for Class 6 PSEB व्यक्तिगत स्वास्थ्य विज्ञान Important Questions and Answers

अति छोटे उत्तर वाले प्रश्न

प्रश्न 1.
शरीर-क्रिया विज्ञान में स्वास्थ्य की परिभाषा क्या होगी ?
उत्तर-
कोशिकाओं, अंगों व तन्त्रों की स्वाभाविक क्रियाशीलता को स्वास्थ्य कहते हैं।

प्रश्न 2.
WHO के विचार से स्वास्थ्य क्या है ?
उत्तर-
WHO (विश्व स्वास्थ्य संगठन) के विचार से स्वास्थ्य में मनुष्य का सम्पूर्ण शारीरिक, मानसिक व संवेगात्मक कल्याण निहित है।

प्रश्न 3.
जीवन में सुखी रहने के लिए क्या आवश्यक है ?
उत्तर-
शरीर का स्वस्थ और शक्तिशाली होना।

प्रश्न 4.
त्वचा को नियमित रूप से साफ़ करना आवश्यक क्यों है ?
उत्तर-
त्वचा से पसीना और अपशिष्ट पदार्थ बाहर निकलते हैं। यदि त्वचा को साफ़ नहीं किया जाता है तो मैल जम जाता है जिसके कारण त्वचा के छिद्र बंद हो जाते हैं, इसलिए त्वचा को नियमित रूप से साफ़ करना आवश्यक है।

प्रश्न 5.
दाँतों को साफ़ करना आवश्यक क्यों है ?
उत्तर–
दाँतों को खोखले होने से, गिरने से, दर्द होने से बचाने के लिए दाँतों को साफ करना आवश्यक है।

प्रश्न 6.
कानों में सलाई या तिनका क्यों नहीं फेरना चाहिए ?
उत्तर-
कानों में सलाई या तिनका फेरने से कान में घाव हो जाते हैं और पर्दा भी फट सकता है। इसलिए कानों में सलाई नहीं फेरनी चाहिए।

प्रश्न 7.
कान का संक्रमण होने पर इसका इलाज तुरन्त क्यों करवाना चाहिए ?
उत्तर-
कान का संक्रमण होने पर यदि इसका इलाज न करवाया जाए तो यह दिमाग़ तक नुकसान पहुंचा सकता है। इसलिए इसका इलाज तुरन्त करवा लेना चाहिए।

प्रश्न 8.
धूप सेंकने से क्या लाभ होता है ?
उत्तर-
धूप सेंकने से शरीर में विटामिन ‘D’ उत्पन्न होता है।

प्रश्न 9.
किस समय की धूप स्वास्थ्य के लिए लाभदायक होती है ?
उत्तर-
प्रायः शीतकाल में प्रात:काल की धूप।

प्रश्न 10.
घर में धूप का आना किसलिए आवश्यक है ?
उत्तर-
धूप जीवाणुओं को नष्ट करती है।

प्रश्न 11.
गूढ़ निद्रा शरीर के लिए क्यों आवश्यक है ?
उत्तर-
शरीर की थकावट दूर करने के लिए।

प्रश्न 12.
नियमित व्यायाम व उत्तम आसन शरीर के लिए क्यों आवश्यक है ?
उत्तर-
शरीर को सुन्दर, सुगठित व स्वस्थ रखने के लिए।

प्रश्न 13.
दाँतों को केरीज रोग से बचाने के लिए क्या उपाय किए जाने चाहिएं ?
उत्तर-

1. भोजन के बाद कुल्ला करना चाहिए।
2. दाँतों को अँगुली से साफ़ करना चाहिए।

प्रश्न 14.
दाँतों का केरीज रोग क्या होता है ?
उत्तर–
दाँतों में कार्बोहाइड्रेट युक्त तथा मीठे पदार्थों के सड़ने से जीवाणुओं की क्रिया से एसिड बनता है जो दाँतों के एनेमल को क्षीण कर देता है।

प्रश्न 15.
पायरिया रोग के क्या लक्षण हैं ?
उत्तर-

1. मसूड़े सूजने लगते हैं,
2. मसूड़ों में पीड़ा होती है,
3. मसूड़ों से दाँत अलग होने लगते हैं,
4. मुँह से दुर्गन्ध आती है।

प्रश्न 16.
स्वस्थ बाल कैसे होते हैं ?
उत्तर-
चमकीले और साफ़।

प्रश्न 17.
स्वस्थ आँखें कैसी होती हैं ?
उत्तर-
चौकन्नी, साफ़ और मलविहीन।

प्रश्न 18.
स्वस्थ त्वचा की क्या पहचान है ?
उत्तर-
चिकनी, ठोस और जगह पर होती है।

प्रश्न 19.
स्वस्थ नाक की क्या पहचान है ?
उत्तर-
साफ़ और सांस लेती हुई होती है।

प्रश्न 20.
स्वस्थ मुख और होंठ कैसे होते हैं ?
उत्तर-
स्वस्थ मुख प्रसन्न और आनन्दित तथा स्वस्थ होंठ लाल और गीले होते हैं।

प्रश्न 21.
स्वस्थ गला किसे कहते हैं ?
उत्तर-
साफ़, गीला तथा बाधा विहीन गले को।

प्रश्न 22.
स्वस्थ दाँत कैसे होते हैं ?
उत्तर-
साफ, सही और कष्टविहीन।

प्रश्न 23.
स्वस्थ मसूड़े कैसे होने चाहिएं ?
उत्तर-
ठोस तथा लाल।

प्रश्न 24.
स्वस्थ तथा अस्वस्थ हाथ में क्या अन्तर होता है ?
उत्तर-
हाथ की हथेलियाँ लाल होने पर स्वस्थ तथा पीली होने पर अस्वस्थ मानी जाती हैं।

प्रश्न 25.
सोने से पहले कोई परिश्रम या अधिक दौड़ भाग का काम क्यों नहीं करना चाहिए ?
उत्तर-
इससे निद्रा अच्छी नहीं आती।

प्रश्न 26.
छुट्टी वाले दिन क्या कार्य करने चाहिए ?
उत्तर-
हल्के और मनोरंजक कार्य करने चाहिएं।

छोटे उत्तर वाले प्रश्न

प्रश्न 1.
व्यायाम शरीर के लिए क्यों आवश्यक है ?
उत्तर-
व्यायाम हमारे स्वास्थ्य के लिए तथा शरीर को निरोग रखने के लिए अत्यन्त आवश्यक है। इसके विभिन्न कारण हैं –

1. व्यायाम करने से भोजन शीघ्र पच जाता है था भूख खुलकर लगती है।
2. व्यायाम करने से शरीर की गन्दगी शीघ्र बाहर निकल जाती है।
3. व्यायाम करने से शरीर की मांसपेशियां मज़बूत हो जाती हैं जिससे शरीर मजबूत होता है।
4. व्यायाम करने से शरीर के सब अंग खुल जाते हैं। फेफड़े बड़े हो जाते हैं। श्वास की क्रिया तेजी से होती है।
5. रक्त शुद्ध हो जाता है।
6. व्यायाम करने से अधिक शुद्ध रक्त मिलता है जिससे वह तरोताज़ा रहता है।
7. रोग रोधन क्षमता बढ़ जाती है।

प्रश्न 2.
व्यायाम के सामान्य नियम क्या हैं ?
उत्तर-
व्यायाम (Exercise) करते समय व्यायाम के नियमों का पालन करना चाहिए। व्यायाम के नियम निम्नलिखित हैं –

1. व्यायाम शुद्ध वायु तथा खुले स्थान पर करना चाहिए।
2. व्यायाम बीमारी से तुरन्त उठने, भोजन के पश्चात् अथवा चिन्ता की दिशा में नहीं करना चाहिए।
3. व्यायाम आयु तथा स्वास्थ्य के आधार पर करना चाहिए।
4. व्यायाम को धीरे-धीरे बढ़ाइए। एकदम अधिक व्यायाम नहीं करना चाहिए।
5. व्यायाम के तुरन्त बाद जल नहीं पीना चाहिए और न ही नहाना चाहिए।
6. व्यायाम करते समय सर्दी से बचने के लिए शरीर पर कोई ढीला वस्त्र अवश्य रहना चाहिए।
7. मस्तिष्क के कार्य करने वालों के लिए सैर करना, हल्की दौड़, ओस पर चलना ही उचित व्यायाम है।
8. पेट के रोगियों को झुकने वाले व्यायाम करने चाहिएं।
9. व्यायाम करते समय मुख से सांस नहीं लेना चाहिए।

प्रश्न 3.
नियमित स्नान के क्या लाभ हैं ?
उत्तर-
नियमित स्नान से शरीर को निम्न लाभ होते हैं –

1. त्वचा की स्वच्छता होती है।
2. रोमकूपों के मुँह खुल जाते हैं।
3. ठण्डे पानी से नहाने से त्वचा के तापमान को सामान्य बनाने के लिए रक्त अधिक मात्रा में तथा तीव्र गति से त्वचा की ओर प्रवाहित होता है।
4. नहाने के बाद तौलिए से शरीर रगड़ने से रक्त संचरण उत्तम होता है।
5. स्नान से हानिकारक पदार्थों तथा रोगाणुओं से मुक्ति मिलती है।
6. धुलकर बह जाने से पसीने की दुर्गन्ध जाती रहती है।

बड़े उत्तर वाले प्रश्न

प्रश्न 1.
विश्राम और निद्रा से स्वास्थ्य को क्या लाभ होता है ?
उत्तर-
विश्राम और निद्रा से स्वास्थ्य को लाभ-विश्राम नितान्त आवश्यक होता है। हम जो भी शारीरिक अथवा मानसिक कार्य करते हैं, उससे हमारे शरीर में थकान आ जाती है। वास्तव में, शारीरिक परिश्रम करते समय हमारे शरीर में अनेक विषैले पदार्थ एकत्र हो जाते हैं। ये पदार्थ ही हमारी माँसपेशियों को थकाते हैं। इसके अतिरिक्त कार्य करते समय हमारे शरीर के ऊतक अधिक टूटते-फूटते रहते हैं। कार्य करते समय इनकी मरम्मत नहीं हो पाती। अतः शरीर के स्वास्थ्य के लिए इन ऊतकों की मरम्मत तथा विषैले पदार्थों का बाहर निकलना अनिवार्य होता है। इन क्रियाओं के लिये विश्राम आवश्यक होता है।

विश्राम का सबसे उत्तम उपाय नींद है। नींद व्यक्ति के लिए वरदान है। निद्रा के समय हमारे शरीर में कार्य करने के परिणामस्वरूप हुई टूट-फूट ठीक हो जाती है तथा शरीर नई शक्ति अर्जित कर लेता है। पर्याप्त नींद ले लेने से व्यक्ति एकदम तरोताज़ा एवं स्वस्थ हो जाता है। नींद के समय हमारे शरीर के सभी अंगों को आराम मिलता है। इस समय हमारी नाड़ी एवं श्वास की गति भी कुछ मन्द हो जाती है तथा रक्तचाप भी घट जाता है, अतः सम्बन्धित अंगों को भी कुछ आराम मिलता है। यदि किसी व्यक्ति को पर्याप्त नींद नहीं आती तो उसका स्वास्थ्य बिगड़ जाता है। नींद के अभाव में व्यक्ति दुर्बल हो जाता है, स्वभाव में चिड़चिड़ाहट आ जाती है तथा चेहरे पर उदासी छा जाती है।

प्रश्न 2.
स्नान करने का महत्त्व स्पष्ट करें। किन देशों में नहाने का महत्त्व है ?
उत्तर-
स्वयं करें।

एक शब्द में उत्तर दें

प्रश्न 1.
दाँतों के किसी रोग का नाम बताओ।
उत्तर-
केरीज़।

प्रश्न 2.
आँख गई ……………….. गया।
उत्तर-
जहान।

प्रश्न 3.
ठण्डे देश में …………………… स्नान भी किया जाता है।
उत्तर-
भाप।

प्रश्न 4.
निरोगी जीवन के लिए …………………… बहुत आवश्यक है।
उत्तर-
स्नान।

प्रश्न 5.
खेलने के बाद ………………………. से नहाना चाहिए।
उत्तर-
गर्म पानी।

प्रश्न 6.
शारीरिक या मानसिक कार्य करने से क्या होता है ?
उत्तर-
थकावट।

प्रश्न 7.
डैनटीन के अन्दर एक खोल होता है उसे क्या कहते हैं ?
उत्तर-
पलम खोल।

प्रश्न 8.
हमारे नाखून सफेद क्यों हो जाते हैं ?
उत्तर-
कैल्शियम, लोहे या खनिज पदार्थों की कमी के कारण।

व्यक्तिगत स्वास्थ्य विज्ञान PSEB 6th Class Home Science Notes

• व्यक्तिगत स्वास्थ्य विज्ञान वह विज्ञान है जो हमारे शरीर को स्वस्थ एवं सुचालित रखने में हमारी सहायता करता है।
• निरोग और बलिष्ठ मनुष्य ही देश की उन्नति में सहायता कर सकते हैं।
• स्वस्थ और स्वच्छ रहने के लिए यह आवश्यक है कि हम अपने शरीर को स्वच्छ रखें और उसकी उचित देखभाल करें।
• आँखें हमारे शरीर की बहुत ही महत्त्वपूर्ण और नाजुक अंग हैं। इनकी देखभाल बहुत ज़रूरी है। बड़ों का कहना है कि “आँखें गईं जहान गया।”
• आँखों की स्वस्थता के लिए विटामिन ‘ए’ बहुत ज़रूरी है।
• आँखों का दुखना एक छूत की बीमारी है।
• आँखों के रोगी को अपना तौलिया, रूमाल और अन्य कपड़े दूसरों से अलग रखने चाहिएं।
• मध्यम रोशनी में बारीक अक्षर पढ़ने से, सूर्यास्त के समय सिलाई-कढाई का काम करने से आँखों पर काफ़ी दबाव पड़ता है।
• जब कभी रात के समय काम करना हो तो रोशनी ठीक और बाएँ हाथ की ओर होनी चाहिए, लेकिन बाएँ हाथ से काम करने वालों के लिए यह रोशनी दाईं ओर से आनी चाहिए।
• प्रत्येक दिन सुबह उठकर ताजे पानी से आँखों को धोना चाहिए और ठण्डे पानी के हल्के-हल्के छींटे मारने चाहिएं।
• यदि आँखों पर दबाव पड़ने वाला काम अधिक देर तक करना पड़े तो थोड़ी देर बाद कुछ पलों के लिए आँखों को धीरे से बन्द कर लेना चाहिए। इससे आँखों को आराम मिलता है।
• दाँत मनुष्य की सुन्दरता को बढ़ाते हैं।
• भोजन का सही स्वाद लेने के लिए दाँत बहुत ज़रूरी हैं।
• यदि दाँतों को अच्छी तरह साफ़ न किया जाए तो भोजन का कुछ भाग दाँतों के खोलों में इकट्ठा हो जाता है। जिससे दाँतों में कई प्रकार की बीमारियाँ हो जाती है।
• खाना खाने के बाद गर्म या नमक मिले पानी या लाल दवाई से घोल के साथ कुल्ली करना लाभदायक है।
• दाँतों को दिन में कम-से-कम दो बार ब्रुश या दातुन से साफ़ करना चाहिए।
• दाँतों से सख्त चीजें जैसे बादाम, अखरोट आदि नहीं तोड़ने चाहिएं।
• छोटे बच्चे जब दाँत निकाल रहे हों तो उनके भोजन में विटामिन ‘डी’, कैल्शियम और फॉस्फोरस की मात्रा का ध्यान रखना चाहिए।
• कैल्शियम, विटामिन ‘डी’ और फॉस्फोरस की कमी के कारण दंतासिन नामक रोग हो जाता है।
• साफ़ नाखून हाथों की सुन्दरता को बढ़ा देते हैं।
• गन्दे हाथों से तैयार किया और खाया भोजन कई बीमारियाँ पैदा करता है, जैसे बदहज़मी, जी मितलाना, दस्त लगना, उल्टी आना आदि।
• नींबू काटकर नाखूनों पर रगड़ने से चमक आ जाती है।
• हमारे शरीर में विटामिन या किसी खनिज पदार्थ की कमी हो जाने से नाखून सफ़ेद हो जाते हैं या उन पर सफ़ेद निशान पड़ जाते हैं।
• पसीने की ग्रंथियों से पसीना बाहर निकलता है।
• नहाने से शारीरिक ताप भी ठीक रहता है।
• सुबह का समय स्नान के लिए सबसे अच्छा होता है।
• सर्दियों में गर्म पानी से स्नान करने पर गर्मी मिलती है।
• ठण्डे देशों में भाप स्नान भी किया जाता है।

Punjab State Board PSEB 6th Class Social Science Book Solutions History Chapter 15 गुप्त साम्राज्य Textbook Exercise Questions and Answers.

PSEB Solutions for Class 6 Social Science History Chapter 15 गुप्त साम्राज्य

SST Guide for Class 6 PSEB गुप्त साम्राज्य Textbook Questions and Answers

I. निम्नलिखित प्रश्नों के उत्तर दीजिए

प्रश्न 1.
समुद्रगुप्त की विजयों का वर्णन करें।
उत्तर-
समुद्रगुप्त एक महान् विजेता था। उसकी प्रमुख विजयों का वर्णन इस प्रकार है –
1. समुद्रगुप्त ने सबसे पहले उत्तरी भारत के तीन राजाओं को हराया और उनके राज्य . को गुप्त साम्राज्य में मिला लिया।

2. समुद्रगुप्त की सबसे बड़ी विजय दक्षिणी भारत की विजय थी। उसने दक्षिण के 12 राजाओं को हराया। परन्तु उनके द्वारा अधीनता स्वीकार करने पर उसने उनके राज्य लौटा दिए।

3. कुछ जंगली जातियों ने राज्य में अशांति फैला रखी थी। ये जातियां आमतौर पर उड़ीसा के जंगलों में रहती थीं। समुद्रगुप्त ने इन जातियों को युद्ध में हरा कर शान्ति स्थापित की।

वास्तव में समुद्रगुप्त ने फ्रांस के शासक तथा सेनापति नेपोलियन की तरह अनेक प्रदेशों पर विजय प्राप्त की। इसलिए उसे भारत का नेपोलियन भी कहा जाता है।

प्रश्न 2.
चन्द्रगुप्त विक्रमादित्य के बारे में आप क्या जानते हैं?
उत्तर-
चन्द्रगुप्त विक्रमादित्य समुद्रगुप्त का पुत्र था। उसे चन्द्रगुप्त द्वितीय भी कहा जाता है। वह गुप्त वंश का एक प्रतापी राजा था। उसने लगभग 380 ई० से 412 ई० तक राज्य किया।

1. उसने पश्चिमी भारत के शकों को हराया। उसने अपनी सैनिक शक्ति द्वारा अपने साम्राज्य को अरब सागर तक बढ़ाया तथा सौराष्ट्र और काठियावाड़ को जीता।
2. उसने दिल्ली में कुतुबमीनार के समीप लोहे का विशाल स्तम्भ बनवाया, जिस पर लिखे लेख में उसकी सफलताओं का वर्णन है।
3. उसने कला तथा साहित्य को प्रोत्साहन दिया। उसके दरबार में नौ विद्वान् थे जिन्हें ‘नवरत्न’ कहा जाता था।
4. वह धार्मिक दृष्टि से बहुत सहनशील था। वह स्वयं भगवान् विष्णु का भक्त था लेकिन वह सभी धर्मों का सम्मान करता था।
5. उसने बड़ी मात्रा में सोने, चांदी तथा तांबे के सिक्के चलाए।
6. उसके शासन काल में ही चीनी यात्री फाह्यान भारत आया था।
7. चन्द्रगुप्त द्वितीय ने विक्रमादित्य की उपाधि धारण की थी, जिसका अर्थ है ‘वीरता का सूर्य’।

प्रश्न 3.
कालिदास के बारे में एक नोट लिखें।
उत्तर-
कालिदास संस्कृत के एक प्रसिद्ध कवि थे। वह गुप्त सम्राट चन्द्रगुप्त विक्रमादित्य के दरबार के ‘नवरत्नों’ में से एक थे। उन्होंने बहुत-से नाटकों तथा कविताओं की रचना की। शकुन्तला, रघुवंश, कुमारसम्भव तथा मेघदूत आदि उनकी अमर रचनाएं हैं। शकुन्तला नाटक संसार भर में प्रसिद्ध है।

प्रश्न 4.
गुप्तकाल में आर्थिक जीवन के बारे में आप क्या जानते हैं?
उत्तर-
गुप्तकाल में आर्थिक जीवन बहुत समृद्ध था।

1. कर बहुत कम थे तथा दैनिक आवश्यकताओं की वस्तुएं बहुत सस्ती थीं। आम लोग इन्हें ख़रीदने के लिए कौड़ियों अथवा तांबे के सिक्कों का प्रयोग करते थे। लेकिन इस काल में सबसे अधिक सोने के सिक्के चलाए गए। ऐसे सिक्कों को दीनार कहते थे।
2. लोगों का मुख्य व्यवसाय कृषि था। कई प्रकार के अनाजों के अतिरिक्त फलों, तथा तेल-बीजों की कृषि भी की जाती थी।
3. देशी तथा विदेशी, दोनों प्रकार का व्यापार उन्नत था। भारत के दक्षिण-पूर्वी एशिया, चीन, मध्य एशिया तथा यूरोपीय देशों के साथ व्यापारिक सम्बन्ध थे।
4. साहूकारों, व्यापारियों तथा उत्पादकों के अपने-अपने संगठन थे, जिन्हें श्रेणी अथवा निगम कहा जाता था।
5. पशु-पालन तथा औद्योगिक-धन्धे अन्य प्रसिद्ध व्यवसाय थे।

प्रश्न 5.
गुप्तकाल को भारत का ‘स्वर्ण युग’ क्यों कहते हैं?
उत्तर-
गुप्तकाल में जीवन के प्रत्येक क्षेत्र में बहुत उन्नति हुई थी, जिस कारण इसे भारत का ‘स्वर्ण युग’ कहा जाता है।

1. गुप्त साम्राज्य का शासन प्रबन्ध बहुत उत्तम था। राजा मन्त्रियों तथा अधिकारियों की सहायता से शासन चलाता था।
2. लोग समृद्ध, सुखी तथा ईमानदार थे। कर बहुत कम थे। दैनिक प्रयोग की चीजें बहुत सस्ती थीं। इस काल में सोने के सिक्के बड़ी मात्रा में चलाए गए।
3. कृषि तथा व्यापार का बहुत विकास हुआ था।
4. गुप्तकाल में उच्चकोटि के साहित्य तथा कला की रचना हुई। साहित्यकारों तथा कलाकारों को राजाओं का संरक्षण प्राप्त था।
5. सभी धर्मों का सम्मान किया जाता था। चाहे गुप्त राजा स्वयं हिन्दू धर्म को मानते थे लेकिन वे सभी धर्मों के लोगों के साथ सम्मानपूर्वक व्यवहार करते थे।सभी लोगों को पूर्ण धार्मिक स्वतन्त्रता प्राप्त थी।
6. गुप्तकाल में विज्ञान तथा तकनीकी का बहुत विकास हुआ था। आर्यभट्ट, वराहमिहिर, ब्रह्मगुप्त तथा बाणभट्ट इस काल के प्रसिद्ध वैज्ञानिक थे।
7. शिक्षा के क्षेत्र में भी बहुत विकास हुआ था। ब्राह्मण तथा भिक्षु अध्यापक होते थे जो आमतौर पर मन्दिरों तथा मठों में शिक्षा देते थे। तक्षशिला, सारनाथ तथा नालन्दा गुप्तकाल के विश्वविद्यालय थे।
8. गुप्तकाल में भारतीय संस्कृति तथा सभ्यता का विदेशों में प्रचार किया गया।

II. रिक्त स्थानों की पूर्ति करें

1. समुद्रगुप्त एक ………….. एवं ………….. था।
2. कालिदास द्वारा लिखित नाटक …………. तथा काव्य ……….. बहुत प्रसिद्ध हैं।
3. चन्द्रगुप्त द्वितीय ने बड़ी संख्या में ……….. और ……… के सिक्के जारी . किए।
4. गुप्त साम्राज्य कई प्रांतों में बंटा हुआ था जिन्हें ………. कहा जाता है।
5. (गुप्तकाल में) जिलों को …………… कहते थे।

उत्तर-

1. महान् योद्धा, शासक
2. सोने, चांदी
3. भुक्ति
4. विषय
5. शकुंतला, मेघदूत।

III. सही जोड़े बनायें

1. आर्यवर्त – (क) पंजाब
2. मुद्रक – (ख) उत्तरी भारत
3. लौह स्तम्भ – (ग) एक अधिकारी
4. कुमारामात्य – (घ) दिल्ली

उत्तर-सही जोड़े

1. आर्यवर्त – उत्तरी भारत
2. मुद्रक – पंजाब
3. लौह स्तम्भ – दिल्ली
4. कुमारामात्य – एक अधिकारी

IV. सही (✓) अथवा ग़लत (✗) बताएं

1. महाराज गुप्त प्रथम गुप्त राजा था।
2. विक्रमादित्य ने समुद्रगुप्त की उपाधि धारण की थी।
3. योद्येय दक्षिण भारत पर राज्य करते थे।
4. फाह्यान यूनानी लेखक था।
5. गुप्तों ने सोने के सिक्के जारी किए।
6. आर्यभट्ट एक प्रसिद्ध वैज्ञानिक था।

उत्तर-

1. (✓)
2. (✗)
3. (✗)
4. (✗)
5. (✓)
6. (✓)

PSEB 6th Class Social Science Guide गुप्त साम्राज्य Important Questions and Answers

कम से कम शब्दों में उत्तर वाले प्रश्न

प्रश्न 1.
गुप्तवंश के पहले महान् शासक चन्द्रगुप्त प्रथम ने एक लिच्छवी राजकुमारी से विवाह किया था। उसका क्या नाम था?
उत्तर-
कुमार देवी।

प्रश्न 2.
समुद्रगुप्त की उपलब्धियों से जुड़े इलाहाबाद स्तंभ लेख का लेखक कौन था?
उत्तर-
हरिषेण।

प्रश्न 3.
महरौली में कुतुबमीनार के समीप लौह स्तम्भ इतिहास में किस राजवंश के काल में बना था?
उत्तर-
गुप्त वंश।

बहु-विकल्पीय प्रश्न

प्रश्न 1.
गुप्तवंश के पतन में निम्न में से किन आक्रमणकारियों की विशेष भूमिका रही?
(क) ह्यूण
(ख) मंगोल
(ग) आर्य।
उत्तर-
(क) ह्यूण

प्रश्न 2.
अजन्ता की गुफ़ाएं अपनी किस विशेषता के लिए प्रसिद्ध हैं?
(क) सुंदर भित्ति-चित्र
(ख) हिन्दू देवी-देवताओं की मूर्तियां
(ग) विशाल तोरण द्वार।
उत्तर-
(क) सुंदर भित्ति-चित्र

प्रश्न 3.
कालिदास ने मेघदूत तथा शकुंतला जैसे प्रसिद्ध ग्रंथों की रचना की। वह निम्न में से किस भाषा का कवि था?
(क) ब्रज
(ख) संस्कृत
(ग) पालि।
उत्तर-
(ख) संस्कृत

अति लघ उत्तरीय प्रश्न

प्रश्न 1.
गुप्त वंश की जानकारी देने वाले चार स्रोतों के नाम लिखें।
उत्तर-
गुप्त वंश की जानकारी देने वाले चार स्रोत हैं –

1. पुराण,
2. कालिदास के नाटक,
3. चीनी यात्री फाह्यान का वृत्तान्त,
4. अभिलेख।

प्रश्न 2.
गुप्त वंश का प्रथम स्वतन्त्र राजा कौन था?
उत्तर-
गुप्त वंश का प्रथम स्वतन्त्र राजा चन्द्रगुप्त प्रथम था।

प्रश्न 3.
चन्द्रगुप्त प्रथम ने कौन-से राज्यवंश के साथ वैवाहिक सम्बन्ध बनाए?
उत्तर-
चन्द्रगुप्त प्रथम ने लिच्छवी वंश के साथ वैवाहिक सम्बन्ध बनाए।

प्रश्न 4.
चन्द्रगुप्त प्रथम का राज्यकाल बताएं।
उत्तर-
चन्द्रगुप्त प्रथम का राज्यकाल 320 ई० से 335 ई० तक था।

प्रश्न 5.
समुद्रगुप्त राजगद्दी पर कब बैठा?
उत्तर-
समुद्रगुप्त 335 ई० में राजगद्दी पर बैठा।

प्रश्न 6.
समुद्रगुप्त ने कौन-से नाग राजाओं को पराजित किया?
उत्तर-
समुद्रगुप्त ने जिन नाग राजाओं को पराजित किया उनके नाम थे-अच्युत नाग, नागसेन तथा गणपति नाग।

प्रश्न 7.
भारत का नेपोलियन किस राजा को कहा जाता है?
उत्तर-
समुद्रगुप्त को भारत का नेपोलियन कहा जाता है।

प्रश्न 8.
समुद्रगुप्त ने कौन-से विदेशी राजा के साथ मित्रता स्थापित की?
उत्तर-
समुद्रगुप्त ने श्रीलंका के राजा मेघवर्मन के साथ मित्रता स्थापित की।

प्रश्न 9.
चन्द्रगुप्त विक्रमादित्य का राज्यकाल बताएं।
उत्तर-
चन्द्रगुप्त विक्रमादित्य का राज्यकाल 380 ई० से 415 ई० तक था।

प्रश्न 10.
पंचतन्त्र के लेखक का क्या नाम था?
उत्तर-
पंचतन्त्र का लेखक विष्णु शर्मा था।

लघु उत्तरीय प्रश्न

प्रश्न 1.
चन्द्रगुप्त प्रथम की विजयों के बारे में लिखें।
उत्तर-
चन्द्रगुप्त प्रथम ने लिच्छवी वंश की राजकुमारी कुमार देवी से विवाह किया। लिच्छवी वंश राजनीतिक रूप से शक्तिशाली था। इस वंश की सहायता से चन्द्रगुप्त प्रथम ने मगध, बिहार तथा इलाहाबाद के समीपवर्ती प्रदेशों को जीत लिया। उसने अपने नाम पर एक संवत् भी चलाया।

प्रश्न 2.
समुद्रगुप्त की कला के क्षेत्र में क्या देन थी?
उत्तर-
समुद्रगुप्त ने कला तथा साहित्य को पूर्ण सुरक्षा दी। उसको संगीत से बड़ा लगाव था। उसके राज्य के कुछ सिक्कों पर उसको वीणा बजाते हुए दिखाया गया है। हरिषेन उसका दरबारी कवि था।

प्रश्न 3.
गुप्तकाल की वैज्ञानिक उन्नति का ब्योरा दीजिए।
उत्तर-
गुप्तकाल में विज्ञान के क्षेत्र में बहुत उन्नति हुई। आर्यभट्ट इस काल का प्रसिद्ध ज्योतिषी तथा गणित का विद्वान् था। उसने संसार को शून्य, सूर्य ग्रहण तथा चन्द्र ग्रहण की जानकारी दी। ब्रह्मगुप्त गणित तथा बीज गणित का विद्वान् था। वराहमिहिर वनस्पति विज्ञान । तथा भूगोल का विद्वान् था।

प्रश्न 4.
समुद्रगुप्त की दक्षिण विजयों का वर्णन करें।
उत्तर-
समुद्रगुप्त की सबसे महान् विजय दक्षिणी भारत की विजय थी। उसने दक्षिण – भारत के 12 राजाओं को पराजित किया । उसने उत्तरी भारत में सभी जीते हुए प्रदेशों को अपने राज्य में मिला लिया, परन्तु दक्षिण भारत के सभी विजित प्रदेश उसने वहां के राजाओं को लौटा दिए। उनसे वह केवल कर वसूल करता रहा।

प्रश्न 5.
चन्द्रगुप्त द्वितीय के दूसरे देशों के साथ सम्बन्धों की जानकारी दें।
उत्तर-
चन्द्रगुप्त ने एक शक्तिशाली साम्राज्य की स्थापना करके विक्रमादित्य की उपाधि धारण की। उसने अपने साम्राज्य को दृढ़ करने के लिए पड़ोसी राजाओं के साथ वैवाहिक सम्बन्ध स्थापित किए। उसने अपनी पुत्री प्रभावती का विवाह वाकाटक राज्य के राजकुमार रुद्रसेन द्वितीय के साथ किया। परन्तु दुर्भाग्य से रुद्रसेन द्वितीय की शीघ्र ही मृत्यु हो गई। अतः चन्द्रगुप्त ने प्रभावती तथा अपने अवयस्क दोहतों की वाकाटक राज्य को सम्भालने में सहायता की। चन्द्रगुप्त की इस नीति के कारण वाकाटक राज्य की जनता चन्द्रगुप्त की आभारी हो गई। गुप्त राजाओं के कुन्तल के कांदव शासक की पुत्रियों से भी विवाह हुए। इस प्रकार चन्द्रगुप्त द्वितीय ने अपनी शक्ति को और भी दृढ़ कर लिया।

निबन्धात्मक प्रश्न

प्रश्न 1.
फाह्यान के वृत्तांत का संक्षिप्त वर्णन कीजिए।
उत्तर-
फाह्यान एक चीनी यात्री था। वह चन्द्रगुप्त विक्रमादित्य के शासनकाल में भारत आया। वह भारत में बौद्ध तीर्थ स्थानों की यात्रा करने तथा बौद्ध ग्रन्थों की खोज के लिए भारत आया था। उसने अपने वृत्तांत में निम्नलिखित बातों का वर्णन किया है –

1. चन्द्रगुप्त विक्रमादित्य के शासन के बारे में-फाह्यान ने चन्द्रगुप्त विक्रमादित्य के उदारवादी राज्य प्रबन्ध का वर्णन किया है। वह लिखता है कि दण्ड नर्म थे, फिर भी अपराध नहीं होते थे। सड़कें सुरक्षित थीं। राज्य प्रबन्ध को सुचारु रूप से चलाने के लिए साम्राज्य को प्रान्तों में बांटा हुआ था। प्रान्तों का प्रबन्ध गर्वनरों के हाथ में था।

2. लोगों के बारे में-फाह्यान के अनुसार गुप्त साम्राज्य में लोग समृद्ध, ईमानदार तथा अच्छे नागरिक थे। वे कानून का पालन करते थे। उनका नैतिक जीवन ऊंचा था। लोग मुख्य रूप में शाकाहारी थे। चण्डालों को घृणा की दृष्टि से देखा जाता था। इसलिए वे नगर से बाहर रहते थे।

3. धर्म के बारे में – फाह्यान के वृत्तांत से पता चलता है कि गुप्तकाल में बौद्ध धर्म बहुत विकसित था। लेकिन गुप्त शासक स्वयं हिन्दू धर्म को मानते थे। वे विष्णु के पुजारी थे। लेकिन वे दूसरे धर्मों के प्रति उदारवादी थे।

प्रश्न 2.
गुप्तकाल के साहित्य की जानकारी दीजिए।
उत्तर-
गुप्तकाल में राज दरबार की भाषा संस्कृत थी। इसलिए संस्कृत भाषा तथा साहित्य ने इस काल में विशेष उन्नति की।

1. इस काल के प्रसिद्ध लेखक कालिदास ने संस्कृत भाषा में अनेक नाटक तथा कविताएं लिखीं। शकुन्तला, रघुवंश, मेघदूत तथा ऋतुसंहार उनके द्वारा रचित मुख्य नाटक हैं। कालिदास, चन्द्रगुप्त द्वितीय के नवरत्नों में से एक थे। उन्हें भारतीय शेक्सपीयर भी कहा जाता है।
2. समुद्रगुप्त के समय हरिषेन एक प्रसिद्ध साहित्यकार था।
3. विष्णु शर्मा का पंचतन्त्र, विशाखादत्त का मुद्राराक्षस तथा अमर सिंह का अमरकोष भी संस्कृत भाषा की अनमोल रचनाएं हैं।
4. गुप्तकाल में नालन्दा, सारनाथ, तक्षशिला, पाटलिपुत्र, बनारस, मथुरा आदि शिक्षा के महत्त्वपूर्ण केन्द्र थे। इन केन्द्रों में साहित्य, धर्म, दर्शन, वेदों आदि की शिक्षा दी जाती थी।

Punjab State Board PSEB 10th Class Home Science Book Solutions Chapter 3 आस-पास की सफ़ाई Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Home Science Chapter 3 आस-पास की सफ़ाई

PSEB 10th Class Home Science Guide आस-पास की सफ़ाई Textbook Questions and Answers

वस्तुनिष्ठ प्रश्न

प्रश्न 1.
आस-पास की सफ़ाई से आप क्या समझते हैं?
उत्तर-
आस-पास से अभिप्राय घर का इर्द-गिर्द है जिसमें गली, पार्क और शैड शामिल किए जा सकते हैं। घर की भीतरी सफ़ाई के साथ-साथ आस-पास की सफ़ाई को इर्द-गिर्द की सफ़ाई कहा जाता है।

प्रश्न 2.
घरेलू कूड़े में कौन-कौन सी वस्तुएं होती हैं?
उत्तर-
घर में वस्तुओं का प्रयोग करते समय कूड़े-कर्कट का पैदा होना स्वाभाविक है। इस कूड़े-कर्कट में हम रसोई की जूठन, राख, फल और सब्जियों के छिलके, गत्ते के डिब्बे, पोलीथीन के लिफाफे, कागज़-पत्र आदि शामिल होते हैं।

प्रश्न 3.
आस-पास की सफ़ाई का क्या महत्त्व है?
उत्तर-
घर को साफ़ रखने के लिए घर के आस-पास की सफ़ाई होना बहुत आवश्यक है। घर के आस-पास की सफ़ाई के कई लाभ हैं।
साफ़ सुथरा आस-पास हमें बदबू और गन्दगी से बचाकर रखता है। कीड़े-मकौड़े पैदा नहीं होते। पानी और भूमि के प्रदूषण का डर नहीं रहता और आए गए को भी साफ़सुथरा स्थान अच्छा लगता है।

प्रश्न 4.
घर की नालियां साफ़ करना क्यों ज़रूरी है?
उत्तर-
घर की सफ़ाई तभी ठीक रह सकती है यदि घर में फालतू पानी का निकास ठीक हो। आजकल बड़े शहरों में तो भूमिगत (Underground) सीवरेज़ का प्रबन्ध हो चुका है, परन्तु गाँवों और कस्बों में फालतू पानी के निकास को ठीक रखने के लिए नालियों की रोज़ाना सफ़ाई आवश्यक है।

प्रश्न 5.
मल-मूत्र को ठिकाने लगाना सबसे जरूरी है, क्यों?
उत्तर-
मल-मूत्र को ठिकाने लगाने का कार्य सबसे महत्त्वपूर्ण है क्योंकि मल-मूत्र में हानिकारक बैक्टीरिया, वाइरस और जीवाणु होते हैं यदि इसको जल्दी ठिकाने न लगाया जाए तो बीमारियां फैलने का खतरा रहता है। कई बीमारियां जैसे टाइफाइड, हैज़ा और आंतों के रोग हो सकते हैं।

छोटे उत्तर वाले प्रश्न

प्रश्न 6.
घर के कूड़े-कर्कट को कितने भागों में बांटा जा सकता है तथा इसका निपटारा कैसे करना चाहिए?
उत्तर-
घर के कूड़े-कर्कट को सम्भालना घर की सफ़ाई के लिए बहुत महत्त्वपूर्ण है। घर के कूड़े-कर्कट को हम चार भागों में विभाजित कर सकते हैं-

1. फलों सब्जियों के छिलके और रसोई का कूड़ा-कर्कट आदि को सम्भालने के लिए एक मज़बूत कूड़ेदान होना चाहिए जिस पर ढक्कन हो और दोनों ओर कुण्डे लगे हों ताकि इसको आसानी से उठाया जा सके। इस कूड़ेदान को ऐसे स्थान पर रखना चाहिए जहां से तेज़ हवा से कूड़ा न उड़े और न ही वर्षा का पानी पड़ सके। इस कूड़े को रोज़ाना निपटाना आवश्यक है।
2. आंगन और बगीची में झाड़ लगाते समय निकला कूड़ा, टूटी हुई वस्तुओं के टुकड़े और गुसलखाने का कूड़ा-कर्कट घर के कूड़े की दूसरी किस्म है । इसको भी किसी ढोल या कूड़ेदान में इकट्ठा करना आवश्यक है।
3. जिस घर में पशु हों उसमें गोबर, बचा हुआ चारा, घर में काफ़ी कूड़ा-कर्कट पैदा करता है, इसको रोज़ाना सम्भालना चाहिए, पशुओं के गोबर से गोबर गैस भी बनाई जा सकती है और इसके उपले बनाकर भी प्रयोग किए जा सकते हैं।
4. घर में मानवीय मल-मूत्र को ठिकाने लगाने के कार्य मुश्किल और महत्त्वपूर्ण हैं। यदि घर में फ्लश सिस्टम न हो तो मानवीय मल-मूत्र द्वारा बीमारियां फैलने का डर बना रहता है। इसलिए मानवीय मल-मूत्र जल्दी से जल्दी ठिकाने लगाने का पक्का प्रबन्ध होना चाहिए।

प्रश्न 7.
कूड़े को जलाया क्यों जाता है?
उत्तर-
वातावरण की सफाई के लिए कूड़े-कर्कट का निपटारा करना बहुत आवश्यक है। वैसे तो कूड़े के निपटारे के लिए कई ढंग हैं, परन्तु कूड़े को जलाना सब से अच्छा समझा जाता है। कूड़े-कर्कट को इकट्ठा करके खुले स्थान पर आग लगा कर नष्ट किया जा सकता है, परन्तु कूड़े को जलाने का सबसे बढ़िया ढंग भट्ठी बनाकर उसमें कूड़े को जलाना है, इस प्रकार कूड़ा भी नष्ट हो जाता है और धुआं भी चिमनी द्वारा ऊपर चला जाता है और वातावरण भी साफ़-सुथरा रहता है।

प्रश्न 8.
कूड़े-कर्कट से खाद कैसे बनाई जाती है? इसका क्या लाभ है?
अथवा
कूड़े से खाद किस प्रकार बनाई जाती है और इससे नीची जगह को कैसे भरा जाता है?
उत्तर-
कड़े-कर्कट को खाद में परिवर्तित कर देना सदियों पुराना लाभदायक ढंग है। इस ढंग से मल-मूत्र और कूड़ा कर्कट को विशेष प्रकार के गड्ढों में भर कर ऊपर सूखी मिट्टी डालकर ढक दिया जाता है। इस तरह कई गड्ढे भर लिए जाते हैं। गर्मियों के दिनों में कभी-कभी पानी फेंका जाता है। 4-6 महीनों के पश्चात् यह कूड़ा-कर्कट खाद में परिवर्तित हो जाता है।

कूड़े-कर्कट को खाद में परिवर्तित कर लेना बहुत लाभदायक ढंग है। बहुत कम मेहनत से कूड़ा केवल सम्भाला ही नहीं जाता बल्कि उसको खाद में परिवर्तित करके फ़सलों, सब्जियों आदि में प्रयोग किया जाता है, जिससे फ़सलें भी अच्छी होती हैं।

प्रश्न 9.
कूड़े-कर्कट से गड्ढे भरने का स्वास्थ्य पर क्या प्रभाव होता है?
उत्तर-
कूड़े-कर्कट से खुले गड्ढे भरने से मानवीय स्वास्थ्य पर बुरा प्रभाव पड़ता है। यदि कूड़े-कर्कट को गड्ढे में डाल कर ऊपर से ढका न जाए तो जब कूड़ा गल जाता है उससे चारों ओर बदबू फैलती है। कई तरह के बैक्टीरिया और अन्य कीड़े-मकौड़े भी पैदा हो जाते हैं। इससे पूरा वातावरण दूषित हो जाता है और आस-पास रहते लोग कई बीमारियों का शिकार हो जाते हैं। इसके अतिरिक्त वर्षा के पानी के साथ मिलकर यह कूड़ा-कर्कट धरती निचले पानी को प्रदूषित कर देता है। इसलिए खुले गड्ढों में कूड़ाकर्कट फेंकने से मानवीय स्वास्थ्य पर बुरा प्रभाव पड़ता है।

प्रश्न 10.
कूड़े का निपटारा करने के ढंगों के नाम लिखो।
उत्तर-
कूड़े के निपटारे की निम्नलिखित विधियां हैं

1. भट्ठी में जलाना
2. गड्ढों को भरना
3. खाद बनाना
4. छांटना।

प्रश्न 11.
गन्दगी का स्वास्थ्य पर क्या प्रभाव पड़ता है?
उत्तर-
देखें अन्य महत्त्वपूर्ण प्रश्नों में।

निबन्धात्मक प्रश्न

प्रश्न 12.
कूड़े-कर्कट को ठिकाने लगाने की विधियों का वर्णन करें।
उत्तर-
देखें अन्य महत्त्वपूर्ण प्रश्नों में।

प्रश्न 13.
आस-पास की सफ़ाई क्यों आवश्यक है? इसके लिए क्या-क्या करना चाहिए?
उत्तर-
घर की सफ़ाई परिवार के सदस्यों के स्वास्थ्य के लिये घर के आस-पास की सफ़ाई से प्रत्यक्ष रूप से जुड़ी हुई है। इसलिए परिवार के सदस्यों को बीमारियों से बचाने के लिए घर की सफ़ाई के साथ-साथ घर के आस-पास की सफ़ाई का भी ध्यान रखना चाहिए। घर के आस-पास की गन्दगी कई प्रकार के कीड़े-मकौड़े, बैक्टीरिया, मक्खी, मच्छर पैदा करने में सहायक होती है। इनसे मलेरिया, दस्त, टाइफाइड, फ्लू आदि बीमारियां लग सकती हैं और आस-पास की सफ़ाई करके हम काफ़ी हद तक इन बीमारियों से बच सकते हैं। इसके अतिरिक्त घर का साफ़-सुथरा आस-पास आए गए मेहमानों को सुन्दर लगता है और मेहमान भी खुश हो कर मिलने आते हैं। यदि घर के आस-पास गन्दगी होगी तो कोई सफ़ाई पसन्द मित्र और रिश्तेदार आप को मिलने आने से झिझकते हैं। इसलिए घर के आस-पास की गन्दगी परिवार का सामाजिक स्तर कम करती है।

आस-पास की सफ़ाई के लिए क्या करना चाहिए?

1. पानी के सही नियम का प्रबन्ध-गाँव और उन शहरों, कस्बों में जहां भूमिगत सीवरेज का प्रबन्ध नहीं है। घर के पानी से आस-पास प्रदूषित होता है क्योंकि खाना बनाना, बर्तन साफ़ करने, नहाना, पशुओं को साफ़ रखने के लिए, आंगन को साफ़ रखने के लिए पानी की अधिक मात्रा में आवश्यकता होती है और यदि इसका निकास ठीक न हो तो यह पानी घर के किसी कोने या घर के बाहर गली या किसी गड़े में इकट्ठा होता रहता है। इकट्ठा हुआ पानी केवल बदबू ही नहीं फैलाता बल्कि मच्छर, मक्खियों
और अन्य कीटाणुओं का जन्म स्थान बन जाता है जिससे कई बीमारियां फैलती हैं। इसलिए घर के पानी का सही निकास करके और बाहर नालियों की सफाई करके हम काफ़ी हद तक आस-पास को साफ़ रख सकते हैं।

2. गलियों की सफाई करके-प्रायः यह देखने में आता है कि अधिकतर लोग अपना फर्ज केवल घर के अन्दर को साफ़ करना ही समझते हैं या घर का कूड़ा-कर्कट बाहर गली में फेंक देते हैं। इससे केवल गली में ही गन्दगी नहीं फैलती बल्कि पूरा वातावरण ही दूषित हो जाता है। इसलिए घर के बाहर गली को घर का भाग समझ कर ही सफ़ाई करनी चाहिए।

3. घर के आस-पास पड़े खाली स्थान साफ़ करके-कई बार घरों के आसपास खाली स्थान पड़े होते हैं, जिसमें घास-फूस पैदा हो जाता है, गड्ढों में पानी भर जाता है, झाड़ियां पैदा हो जाती हैं, अन्धेरे में कई लोग जंगल पानी जाने लगते हैं। इस तरह गन्दगी बढ़ती जाती है और यह गन्दगी कई तरह की बीमारियों का कारण बनती है। ऐसे इलाके में बने खूबसूरत घर भी गन्दे लगते हैं। इसलिए ऐसे इलाके के निवासियों को खाली पड़े स्थान की सफ़ाई रखने की कोशिश करनी चाहिए। ऐसे स्थान में घास-फूस काट कर बच्चों के खेलने के लिए जगह बन सकती है या घास, फूल, पौधे लगा कर इसको खूबसूरत पार्क में परिवर्तित किया जाता है।

4. मुहल्ले के बच्चों को सफ़ाई प्रति चेतन करके-बच्चों को सफ़ाई प्रति चेतन करके बच्चों को घर के आस-पास की सफ़ाई करने के लिए लगाया जा सकता है। यह तर्जुबा कई समाज सेवी जत्थेबंदियां सफलतापूर्वक कर चुकी हैं। बच्चे आदर्शवादी और शक्ति भरपूर होते हैं। बस थोड़ी सी सीध देने और उत्साहित करने से वह घरों के आस-पास की सफ़ाई आसानी से कर सकते हैं। इसके अतिरिक्त मुहल्ला निवासी पैसे इकट्ठे करके भी मज़दूरों से सफ़ाई करवा सकते हैं।
इसलिए उपरोक्त ढंगों को अपना कर घर का आस-पास साफ़-सुथरा रखा जा सकता है जो केवल सुन्दर ही नहीं लगता बल्कि स्वास्थ्य के लिए भी लाभदायक रहता है।

Home Science Guide for Class 10 PSEB आस-पास की सफ़ाई Important Questions and Answers

अति लघु उत्तरीय प्रश्न

प्रश्न 1.
आसपास की सफ़ाई किसे कहते हैं?
उत्तर-
घर के आसपास की सफ़ाई को।

प्रश्न 2.
घरेलू कूड़े में क्या कुछ होता है?
उत्तर-
रसोई की जूठन, फल, सब्जियों के छिलके आदि।

प्रश्न 3.
पाखानों की उचित सफ़ाई न की जाए तो कौन-से रोग हो सकते हैं?
उत्तर-
टाईफाईड, हैजा।

प्रश्न 4.
नालियों को साफ रखने के लिए यह कैसी होनी चाहिए?
उत्तर-
पक्की होनी चाहिए।

प्रश्न 5.
कूड़े से खाद कितने दिनों में तैयार हो सकती है?
उत्तर-
4-6 महीनों में।

प्रश्न 6.
कूड़े के निपटारे के ढंग बताओ।
उत्तर-
भट्ठी में जलाना, गड्ढों को भरना, खाद बनाना, छांटना।

प्रश्न 7.
री साईकल करने वाले कूड़े में क्या कुछ आता है?
उत्तर-
टूटा कांच, चीनी का सामान, प्लास्टिक का सामान, रद्दी कागज़ आदि।

प्रश्न 8.
खाद किस प्रकार के कूड़े से बनाई जा सकती है?
उत्तर-
वनस्पति कूड़े-कर्कट से।

प्रश्न 9.
कूड़े के निपटारे के दो ढंग बताओ।
उत्तर-
भट्ठी में जलाना, गड्डों को भरना।

प्रश्न 10.
घरेलू कूड़े में क्या कुछ होता है?
उत्तर-
देखें उपरोक्त प्रश्नों में।

लघु उत्तरीय प्रश्न

प्रश्न 1.
कूड़े-कर्कट को ठिकाने लगाने से पहले छांटना क्यों ज़रूरी है?
उत्तर-
कूड़े-कर्कट को ठिकाने लगाने से पहले छांटना इसलिये ज़रूरी है कि कूड़े के बीच चीज़ों को प्रयोग में लाया जा सके। जैसे-

1. कूड़े में से कोयले, अर्द्ध जले कोयले, पत्थर-गीटे अलग करके प्रयोग में लाये जा सकते हैं।
2. सब्जियों के छिलकों से खाद बनाई जा सकती है। कुछ चीजें कबाड़ियों को बेचकर पैसे कमाए जा सकते हैं।

प्रश्न 2.
कूड़े का अन्तिम निपटारा खाद बनाकर कैसे किया जाता है?
उत्तर-
स्वयं उत्तर दें।

प्रश्न 3.
कूड़े का अन्तिम निपटारा कैसे किया जाता है? विस्तार में बताएं।
उत्तर-
स्वयं उत्तर दें।

प्रश्न 4.
आस-पास की सफ़ाई क्यों ज़रूरी है?
उत्तर-
स्वयं उत्तर दें।

प्रश्न 5.
घर की नालियों की सफाई कैसे की जाती है?
उत्तर-
नालियों को साफ़-सुथरा रखने के लिए इनका पक्का होना आवश्यक है और इनकी ढलान इस तरह होनी चाहिए कि पानी आसानी से निकल सके। इनमें समय-समय पर कीटनाशक दवाइयां डालते रहना चाहिए ताकि मक्खी मच्छर पैदा न हों।

दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
आस-पास की सफ़ाई का हमारे स्वास्थ्य पर क्या प्रभाव पड़ता है?
उत्तर-
परिवार के सदस्यों को स्वस्थ रखने के लिए घर की सफ़ाई के साथ-साथ घर के आस-पास की सफ़ाई करना भी बहुत आवश्यक है। यदि घर का इर्द-गिर्द साफ़ नहीं होगा तो गन्दी हवा मक्खी मच्छर घर के अन्दर आएंगे। घर के निकट ईंटें, लकड़ियां, उपले या कूड़े के ढेर नहीं होने चाहिएं। इन पर मक्खी मच्छर तो पैदा होते ही हैं। इसके साथ-साथ और अन्य खतरनाक जीव भी इसमें जाकर अपना स्थान बना लेते हैं। कई बार यह जानलेवा भी साबित हो जाते हैं। इसलिए इस बात का विशेष ध्यान रखना चाहिए कि घर के इर्द-गिर्द कूड़े कर्कट के ढेर न हों, पानी खड़ा न हो और घास-फूस न उगा हो ताकि घर का आस-पास साफ़-सुथरा रह सके।

प्रश्न 2.
आस-पास की गन्दगी का मानवीय स्वास्थ्य पर क्या प्रभाव पड़ता है?
अथवा
गन्दे वातावरण में रहने का क्या नुकसान है?
उत्तर-
आस-पास की गन्दगी का हमारे स्वास्थ्य पर सीधा प्रभाव पड़ता है। गन्दे वातावरण में रहने के निम्नलिखित नुकसान हैं —

1. कीटाणुओं का पैदा होना-घर के इर्द-गिर्द गन्दगी होने के कारण कई बीमारियों के कीटाणु पैदा हो जाते हैं जिनसे कई बीमारियां जैसे तपेदिक, हैजा, टाइफाइड जैसे हानिकारक कीटाणु हमारे स्वास्थ्य को खराब कर सकते हैं।
2. बदबू-गन्दगी और कूड़े-कर्कट के ढेरों में कुछ समय के पश्चात् बदबू आनी शुरू हो जाती है जो इर्द-गिर्द की वायु को दूषित करती हुई कई बीमारियों का कारण बनती है।
3. कीड़े-मकौड़ों की उत्पत्ति-कूड़े-कर्कट में मक्खियां और मच्छर अनेकों प्रकार के कीड़े-मकौड़े पैदा होते हैं, जो हमारे स्वास्थ्य पर काफ़ी प्रभाव डालते हैं। मच्छर से मलेरिया फैल सकता है और मक्खियां भी हैजा, टाइफाइड आदि रोगों को फैलाती हैं।
4. पानी का प्रदूषण-लगातार पड़ी रहने वाली गन्दगी के ढेर वर्षा के पानी में घुलकर धरती निचले पानी को भी दूषित करती है जिसका मानवीय स्वास्थ्य पर हानिकारक प्रभाव पड़ता है।
5. धूल और मिट्टी-यदि हम घर का इर्द-गिर्द साफ़ नहीं करते तो धूल और मिट्टी से घर भर जाता है जिससे फेफड़ों का रोग, दमा और कई प्रकार के चमड़ी के रोग भी हो सकते हैं।

प्रश्न 3.
घर के आस-पास को साफ़ रखने के लिए कूड़े का अन्तिम निपटारा किस तरह करना चाहिए?
अथवा
कूड़े-कर्कट को ठिकाने लगाने की विधियों का वर्णन करें।
उत्तर-
आस-पास को साफ़ रखने के लिए कूड़े-कर्कट को इस तरह ठिकाने लगाना चाहिए जिससे रोज़ाना लोगों को कोई परेशानी पैदा न हो। गाँवों में रहने वाले लोग जानते हैं कि पशुओं के गोबर और कूड़े को गड्ढों में भरकर खाद बनाई जाती है जो बाद में फ़सलों के काम आती है। इस तरह कूड़े-कर्कट को सही ढंग से ठिकाने लगाया जा सकता है। कूड़े-कर्कट को निम्नलिखित ढंगों से ठिकाने लगाया जा सकता है —

1. भट्ठी में जलाना-यह ढंग सबसे अच्छा समझा जाता है। परन्तु कूड़े-कर्कट को एक विशेष भट्ठी में ही जलाया जाता है शेष केवल राख ही बचती है। कूड़े को जलाने के लिए पक्की भट्ठी बनाई जाती है। इसके निकट एक चबूतरा होना चाहिए जहां कि शहर से लाया गया कूड़ा-कर्कट रखा जा सके। भट्ठी में एक रास्ते द्वारा थोड़ा-थोड़ा करके कूड़ा भट्ठी में फेंका जाता है। इस तरह करने से धुआं चिमनी द्वारा बाहर निकल जाता है।
2. निम्न स्थान को भरना-प्रत्येक शहर में या गांव में नीचे इलाके होते हैं जिनमें कूड़ा-कर्कट भरकर ठिकाने लगाया जाता है। कूड़ा-कर्कट कुछ देर पड़ा रहता है। धीरे-धीरे यह कूड़ा-कर्कट गल-सड़ कर दब जाता है फिर इस पर और कूड़ा-कर्कट फेंक दिया जाता है। इस तरह धीरे-धीरे सड़क आदि के बराबर आ जाता है फिर उस पर थोड़ी मिट्टी डालकर समतल कर दिया जाता है। इस तरह करने से स्थान साफ़सुथरा हो जाता है।
3. खाद बनानी-कूड़े-कर्कट को खाद में परिवर्तित करना सदियों पुराना ढंग है। इस ढंग से मानवीय और पशुओं का मल-मूत्र और घर का अन्य कूड़ा-कर्कट एक गहरे गड्ढे में दबाकर खाद बनाई जाती है जो फ़सलों के प्रयोग में लाई जाती है। यह कूड़ाकर्कट सम्भालने का सबसे बढ़िया ढंग है।
4. छांटना-कूड़े-कर्कट को सम्भालने से पहले उसको तीन भागों में बांट लिया जाता है
   1. कोयले, अर्द्ध जले कोयले, पत्थर गीटे, बट्टे आदि अलग करके ईंटें बनाने के लिए प्रयोग किया जाता है।
   2. वनस्पति कूड़ा-कर्कट जैसे फल सब्जियों के छिलके रसोई की जूठन आदि को अलग कर खाद बनाई जा सकती है।
   3. टूटे हुए कांच, चीनी, मिट्टी के बर्तन, प्लास्टिक के सामान को दोबारा प्रयोग कर लिया जा सकता है।
      उपरोक्त ढंगों को प्रयोग करने से कूड़े-कर्कट को सम्भाल लिया जाता है और कूड़े-कर्कट का लाभदायक प्रयोग भी किया जा सकता है।

प्रश्न 4.
कूड़े को भट्ठी में किस प्रकार जलाया जाता है?
उत्तर-
देखें उपरोक्त प्रश्नों के उत्तर में।

वस्तनिष्ठ प्रश्न

I. रिक्त स्थान भरें

1. घर के कूड़े-कर्कट को ……………. में नहीं फेंकना चाहिए।
2. कूड़े से खाद ………………. महीनों में बन जाती है।
3. खाद ………………. कूड़े-कर्कट से बनती है।

उत्तर-

1. गली,
2. 4 से 6,
3. वनस्पति।

II. ठीक/ग़लत बताएं

1. वातावरण की सफ़ाई के लिए कूड़े-कर्कट का निपटारा करना आवश्यक है।
2. कूड़े-कर्कट से खुले खड्डे भरने से मानवीय स्वास्थ्य पर बुरा प्रभाव नहीं पड़ता
3. घरेलू कूड़े का भाग है-रसोई की जूठन, फ़ल तथा सब्जियों के छिलके।

उत्तर-

1. ठीक,
2. ग़लत,
3. ठीक।

III. बहुविकल्पीय प्रश्न

प्रश्न 1.
निम्न में ठीक है
(क) कूड़े-कर्कट को खाद में बदल लेना लाभदायक है।
(ख) कूड़ा-कर्कट को खुले खड्डे में न भरें।
(ग) कूड़े के निपटारे के लिए भट्ठी में जलाना भी एक ढंग है।
(घ) सभी ठीक।
उत्तर-
(घ) सभी ठीक।

प्रश्न 2.
गंदे वातावरण से निम्नलिखित हानियां हैं
(क) कीटाणु पैदा होते हैं
(ख) बदबू पैदा होती है
(ग) पानी प्रदूषित होता है
(घ) सभी ठीक।
उत्तर-
(घ) सभी ठीक।

आस-पास की सफ़ाई 10th Class Home Science Notes

1. घर के इर्द-गिर्द की सफाई को आस-पास की सफ़ाई कहा जाता है।
2. घर की नालियों की सफाई के बिना घर साफ़ नहीं रह सकता।
3. घर के आस-पास की सफ़ाई हमें बीसों बीमारियों से बचाती है।
4. घर के कूड़े-कर्कट को गली में नहीं फेंकना चाहिए।
5. कूड़े-कर्कट को सही ढंग से ही निपटाना चाहिए।
6. घर के आस-पास गंदगी जमा नहीं होने देनी चाहिए।
7. घर के आस-पास की सफ़ाई से परिवार का सामाजिक स्तर बढ़ता है।

परिवार के सदस्यों को खुश और तन्दुरुस्त रखने के लिए सफ़ाई रखनी आवश्यक है। घर जितना चाहे बढ़िया बना हो परन्तु यदि उसमें सफाई न हो तो अच्छा नहीं लगता। घर की गन्दगी बीमारियों को बुलावा देती है। परन्तु घर की सफ़ाई भी तभी रह सकती है यदि आस-पास भी साफ़ हो। इसलिए घर की सफ़ाई के साथ-साथ आस-पास की सफ़ाई का भी ध्यान रखना चाहिए।