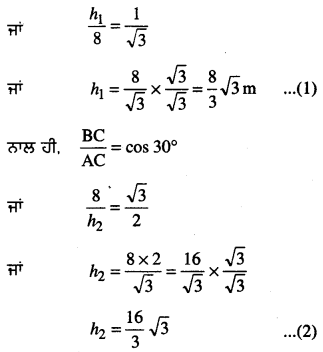Punjab State Board PSEB 7th Class Punjabi Book Solutions Punjabi Rachana Lekha Rachana ਰਚਨਾ ਲੇਖ-ਰਚਨਾ Textbook Exercise Questions and Answers.
PSEB 7th Class Punjabi Rachana ਲੇਖ-ਰਚਨਾ (1st Language)
1. ਗੁਰੂ ਨਾਨਕ ਦੇਵ ਜੀ
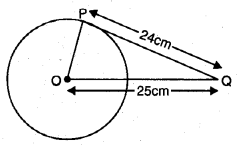
ਗੁਰੂ ਨਾਨਕ ਦੇਵ ਜੀ ਸਿੱਖ ਧਰਮ ਦੇ ਮੋਢੀ ਸਨ। ਆਪ ਦਾ ਜਨਮ 15 ਅਪਰੈਲ, 1469 ਈ: ਨੂੰ ਰਾਏ ਭੋਇ ਦੀ ਤਲਵੰਡੀ (ਅੱਜ – ਕਲ੍ਹ ਨਨਕਾਣਾ ਸਾਹਿਬ, ਪਾਕਿਸਤਾਨ) ਵਿਚ ਹੋਇਆ। ਉੱਬ ਸਿੱਖਾਂ ਵਿਚ ਪ੍ਰਚਲਿਤ ਰਵਾਇਤ ਅਨੁਸਾਰ ਆਪ ਦਾ ਜਨਮ ਕੱਤਕ ਦੀ ਪੂਰਨਮਾਸ਼ੀ ਨੂੰ ਮਨਾਇਆ ਜਾਂਦਾ ਹੈ। ਆਪ ਦੇ ਪਿਤਾ ਜੀ ਦਾ ਨਾਂ ਮਹਿਤਾ ਕਾਲੂ ਅਤੇ ਮਾਤਾ ਜੀ ਦਾ ਨਾਂ ਤ੍ਰਿਪਤਾ ਸੀ !
ਜਿਸ ਸਮੇਂ ਆਪ ਸੰਸਾਰ ਵਿਚ ਆਏ, ਉਸ ਸਮੇਂ ਹਰ ਪਾਸੇ ਜਬਰ – ਜ਼ੁਲਮ ਹੋ ਰਿਹਾ ਸੀ। ਹਰ ਪਾਸੇ ਪਾਖੰਡ ਤੇ ਅਨਿਆਂ ਪ੍ਰਧਾਨ ਸੀ।
ਸੱਤ ਸਾਲ ਦੀ ਉਮਰ ਵਿਚ ਆਪ ਨੂੰ ਪਾਂਧੇ ਕੋਲ ਪੜ੍ਹਨ ਲਈ ਭੇਜਿਆ ਗਿਆ। ਆਪ ਨੇ ਆਪਣੇ ਵਿਚਾਰ ਦੱਸ ਕੇ ਪਾਂਧੇ ਨੂੰ ਨਿਹਾਲ ਕੀਤਾ ਜਵਾਨ ਹੋਣ ‘ਤੇ ਆਪ ਦਾ ਮਨ ਘਰ ਦੇ ਕੰਮਾਂ ਵਿਚ ਨਾ ਲੱਗਾ। ਪਿਤਾ ਮਹਿਤਾ ਕਾਲੂ ਨੇ ਆਪ ਨੂੰ ਆਪ ਦੀ ਭੈਣ ਬੇਬੇ ਨਾਨਕੀ ਕੋਲ ਸੁਲਤਾਨਪੁਰ ਭੇਜ ਦਿੱਤਾ ਇੱਥੇ ਆਪ ਨੇ ਨਵਾਬ ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਦਾ ਮੋਦੀਖਾਨਾ ਚਲਾਇਆ। ਸੁਲਤਾਨਪੁਰ ਵਿਚ ਹੀ ਇਕ ਦਿਨ ਆਪ ਵੇਈਂ ਨਦੀ ਵਿਚ ਇਸ਼ਨਾਨ ਕਰਨ ਗਏ ਤੇ ਤਿੰਨ ਦਿਨ ਅਲੋਪ ਰਹੇ।
ਇਸ ਸਮੇਂ ਆਪ ਨੂੰ ਨਿਰੰਕਾਰ ਵਲੋਂ ਸੰਸਾਰ ਦਾ ਕਲਿਆਣ ਕਰਨ ਦਾ ਸੁਨੇਹਾ ਪ੍ਰਾਪਤ ਹੋਇਆ ਇਸ ਤੋਂ ਪਿੱਛੋਂ ਆਪ ਨੇ ਸੰਸਾਰ ਨੂੰ ਤਾਰਨ ਲਈ ਪੂਰਬ, ਦੱਖਣ, ਉੱਤਰ ਤੇ ਪੱਛਮ ਦੀਆਂ ਚਾਰ ਉਦਾਸੀਆਂ ਕੀਤੀਆਂ ਤੇ ਸੰਸਾਰ ਨੂੰ ਸੱਚ ਦਾ ਉਪਦੇਸ਼ ਦਿੱਤਾ। ਆਪ ਹਿੰਦੂਆਂ ਦੇ ਗੁਰੂ ਤੇ ਮੁਸਲਮਾਨਾਂ ਦੇ ਪੀਰ ਕਹਾਏ।
ਆਪ ਨੇ ਬਹੁਤ ਸਾਰੀ ਬਾਣੀ ਰਚੀ। ਆਪ ਨੇ ਆਪਣੀ ਗੱਦੀ ਦਾ ਵਾਰਸ ਭਾਈ ਲਹਿਣਾ ਜੀ ਨੂੰ ਗੁਰੂ ਅੰਗਦ ਦੇਵ ਨਾਂ ਨਾਲ ਸੁਸ਼ੋਭਿਤ ਕਰਕੇ ਚੁਣਿਆ। 22 ਸਤੰਬਰ, 1539 ਈ: ਨੂੰ ਆਪ ਕਰਤਾਰਪੁਰ ਵਿਚ ਜੋਤੀ – ਜੋਤ ਸਮਾ ਗਏ।

2. ਗੁਰੂ ਗੋਬਿੰਦ ਸਿੰਘ ਜੀ
ਗੁਰੂ ਗੋਬਿੰਦ ਸਿੰਘ ਜੀ ਸਿੱਖਾਂ ਦੇ ਦਸਵੇਂ ਗੁਰੂ ਹੋਏ ਹਨ ਆਪ ਦਾ ਜਨਮ 1666 ਈ: ਵਿਚ ਪਟਨਾ ਸ਼ਹਿਰ ਵਿਖੇ ਮਾਤਾ ਗੁਜਰੀ ਜੀ ਦੀ ਕੁੱਖੋਂ ਹੋਇਆ। ਗੁਰੂ ਤੇਗ਼ ਬਹਾਦਰ ਜੀ ਆਪ ਦੇ ਪਿਤਾ ਸਨ। ਬਚਪਨ ਵਿਚ ਆਪ ਆਪਣੇ ਹਾਣੀਆਂ ਨਾਲ ਕਈ ਤਰਾਂ ਦੇ ਚੋਜ ਕਰਦੇ ਰਹਿੰਦੇ ਸਨ। 1672 ਈ: ਵਿਚ ਆਪ ਦੇ ਪਿਤਾ ਜੀ ਪਟਨੇ ਤੋਂ ਆਨੰਦਪੁਰ ਸਾਹਿਬ ਆ ਗਏ। ਇੱਥੇ ਆਪ ਨੇ ਸ਼ਸਤਰ ਵਿੱਦਿਆ ਤੇ ਧਾਰਮਿਕ ਵਿੱਦਿਆ ਪ੍ਰਾਪਤ ਕੀਤੀ। ਮੁਗ਼ਲ ਬਾਦਸ਼ਾਹ ਔਰੰਗਜ਼ੇਬ ਨੇ ਹਿੰਦੂ ਧਰਮ ਨੂੰ ਖ਼ਤਮ ਕਰਨ ਲਈ ਅੱਤ ਚੁੱਕੀ ਹੋਈ ਸੀ।
ਕਸ਼ਮੀਰੀ ਪੰਡਤ ਦੁਖੀ ਹੋ ਕੇ ਗੁਰੂ ਤੇਗ਼ ਬਹਾਦਰ ਸਾਹਿਬ ਕੋਲ ਸਹਾਇਤਾ ਲਈ ਫ਼ਰਿਆਦ ਲੈ ਕੇ ਆਏ। ਉਸ ਸਮੇਂ ਆਪ ਕੇਵਲ 9 ਸਾਲਾਂ ਦੇ ਸਨ ਆਪ ਨੇ ਆਪਣੇ ਪਿਤਾ ਜੀ ਨੂੰ ਔਰੰਗਾਂਜ਼ੇਬ ਦੇ ਜ਼ੁਲਮਾਂ ਵਿਰੁੱਧ ਕੁਰਬਾਨੀ ਦੇਣ ਲਈ ਦਿੱਲੀ ਭੇਜਿਆ ਪਿਤਾ ਜੀ ਦੀ ਸ਼ਹੀਦੀ ਪਿੱਛੋਂ ਆਪ ਨੇ ਕੌਮ ਨੂੰ ਇਕ – ਮੁੱਠ ਕਰ ਕੇ ਸ਼ਸਤਰ ਵਿੱਦਿਆ ਦੇਣੀ ਸ਼ੁਰੂ ਕੀਤੀ।
1699 ਈ: ਵਿਚ ਵਿਸਾਖੀ ਵਾਲੇ ਦਿਨ ਆਪ ਨੇ ਖ਼ਾਲਸਾ ਪੰਥ ਸਾਜਿਆ ਤੇ ਅੰਮ੍ਰਿਤ ਦੀ ਦਾਤ ਬਖ਼ਸ਼ੀ। ਇਸ ਪਿੱਛੋਂ ਗੁਰੂ ਜੀ ਨੂੰ ਪਹਾੜੀ ਰਾਜਿਆਂ ਤੇ ਮੁਗ਼ਲ ਫ਼ੌਜਾਂ ਨਾਲ ਕਈ ਲੜਾਈਆਂ ਲੜਨੀਆਂ ਪਈਆਂ। ਆਪ ਦੇ ਦੁਸ਼ਮਣਾਂ ਨੂੰ ਹਰ ਥਾਂ ਹਾਰ ਦਾ ਮੂੰਹ ਦੇਖਣਾ ਪਿਆ ਆਪ ਦੇ ਦੋ ਛੋਟੇ ਸਾਹਿਬਜ਼ਾਦਿਆਂ ਨੂੰ ਸਰਹੰਦ ਦੇ ਨਵਾਬ ਨੇ ਨੀਹਾਂ ਵਿਚ ਚਿਣਵਾ ਦਿੱਤਾ। ਦੋ ਵੱਡੇ ਸਾਹਿਬਜ਼ਾਦੇ ਚਮਕੌਰ ਦੀ ਜੰਗ ਵਿਚ ਸ਼ਹੀਦ ਹੋ ਗਏ।
ਅੰਤ ਆਪ ਨੰਦੇੜ ਪੁੱਜੇ। 1708 ਈ: ਵਿਚ ਆਪ ਇੱਥੇ ਹੀ ਜੋਤੀ – ਜੋਤ ਸਮਾ ਗਏ।
3. ਮਹਾਤਮਾ ਗਾਂਧੀ
ਮਹਾਤਮਾ ਗਾਂਧੀ ਭਾਰਤ ਦੇ ਰਾਸ਼ਟਰ – ਪਿਤਾ ਸਨ। ਆਪ ਨੇ ਭਾਰਤ ਦੀ ਅਜ਼ਾਦੀ ਲਈ ਘੋਲ ਕੀਤਾ ਆਪ ਅਹਿੰਸਾ ਦੇ ਅਵਤਾਰ ਸਨ। ਆਪ ਦਾ ਜਨਮ 2 ਅਕਤੂਬਰ, 1869 ਈ: ਨੂੰ ਪੋਰਬੰਦਰ (ਕਾਠੀਆਵਾੜ), ਗੁਜਰਾਤ ਵਿਚ ਹੋਇਆ। ਆਪ ਦਾ ਪੂਰਾ ਨਾਂ ਮੋਹਨ ਦਾਸ ਕਰਮ ਚੰਦ ਗਾਂਧੀ ਸੀ। ਆਪ ਸਦਾ ਸੱਚ ਬੋਲਦੇ ਸਨ ਤੇ ਮਾਤਾ – ਪਿਤਾ ਦੀ ਆਗਿਆ ਦਾ ਪਾਲਣ ਕਰਦੇ ਸਨ 1 ਦੇਸ਼ ਵਿਚ ਬੀ. ਏ. ਪਾਸ ਕਰ ਕੇ ਆਪ ਨੇ ਵਲਾਇਤ ਤੋਂ ਬੈਰਿਸਟਰੀ ਦੀ ਡਿਗਰੀ ਪ੍ਰਾਪਤ ਕੀਤੀ।
ਆਪ ਦੇ ਮਨ ਵਿਚ ਦੇਸ਼ – ਪਿਆਰ ਠਾਠਾਂ ਮਾਰ ਰਿਹਾ ਸੀ। ਆਪ ਨੇ ਭਾਰਤ ਨੂੰ ਅਜ਼ਾਦ ਕਰਾਉਣ ਦਾ ਨਿਸਚਾ ਕਰ ਲਿਆ ਆਪ ਨੇ ਕਾਂਗਰਸ ਪਾਰਟੀ ਦੀ ਵਾਗ – ਡੋਰ ਸੰਭਾਲ ਕੇ ਅੰਗਰੇਜ਼ਾਂ ਵਿਰੁੱਧ ਪੀ ਰੂ ਕੀਤਾ ਤੇ ਨਾ – ਮਿਲਵਰਤਨ ਲਹਿਰ ਤੇ ਹੋਰ ਲਹਿਰਾਂ ਚਲਾਈਆਂ। ਗਾਂਧੀ ਜੀ ਕਈ ਵਾਰ ਜੇਲ ਗਏ 1930 ਈ: ਵਿਚ ਆਪ ਨੇ ਲੁਣ ਦਾ ਸਤਿਆਗ੍ਰਹਿ ਕੀਤਾ 1942 ਈ: ਵਿਚ ਆਪ ਨੇ ਅੰਗਰੇਜ਼ਾਂ ਵਿਰੁੱਧ ‘ਭਾਰਤ ਛੱਡੋ’ ਲਹਿਰ ਚਲਾਈ।
ਅੰਤ ਅੰਗਰੇਜ਼ਾਂ ਨੇ ਮਜਬੂਰ ਹੋ ਕੇ 15 ਅਗਸਤ, 1947 ਈ: ਨੂੰ ਹਥਿਆਰ ਸੁੱਟ ਦਿੱਤੇ ਅਤੇ ਭਾਰਤ ਨੂੰ ਅਜ਼ਾਦ ਕਰ ਦਿੱਤਾ ਇਸ ਸਮੇਂ ਦੇਸ਼ ਦੀ ਵੰਡ ਕਾਰਨ ਹੋਏ ਫ਼ਿਰਕੂ – ਫ਼ਸਾਦਾਂ ਨੂੰ ਦੇਖ ਕੇ ਆਪ ਬਹੁਤ ਦੁਖੀ ਹੋਏ।
ਆਪ ਅਛੂਤ – ਉਧਾਰ ਦੇ ਬਹੁਤ ਹਾਮੀ ਸਨ ਅਤੇ ਆਪ ਨੇ ਜਾਤ – ਪਾਤ ਤੇ ਛੂਤ – ਛਾਤ ਦੇ ਭੇਦ – ਭਾਵ ਨੂੰ ਖ਼ਤਮ ਕਰਨ ਲਈ ਸਿਰ – ਤੋੜ ਯਤਨ ਕੀਤੇ। 30 ਜਨਵਰੀ, 1948 ਈ: ਨੂੰ ਹਤਿਆਰੇ ਨੱਥੂ ਰਾਮ ਗੌਡਸੇ ਨੇ ਗੋਲੀਆਂ ਮਾਰ ਕੇ ਆਪ ਨੂੰ ਸ਼ਹੀਦ ਕਰ ਦਿੱਤਾ।

4. ਪੰਡਿਤ ਜਵਾਹਰ ਲਾਲ ਨਹਿਰੂ
ਪੰਡਿਤ ਜਵਾਹਰ ਲਾਲ ਨਹਿਰੂ ਦਾ ਜਨਮ 14 ਨਵੰਬਰ, 1889 ਈ: ਨੂੰ ਅਲਾਹਾਬਾਦ ਵਿਚ ਉੱਘੇ ਵਕੀਲ ਤੇ ਦੇਸ਼ – ਭਗਤ ਪੰਡਿਤ ਮੋਤੀ ਲਾਲ ਨਹਿਰੂ ਦੇ ਘਰ ਹੋਇਆ। ਆਪ ਨੇ ਇੰਗਲੈਂਡ ਤੋਂ ਬੈਰਿਸਟਰੀ ਦੀ ਡਿਗਰੀ ਪ੍ਰਾਪਤ ਕੀਤੀ। ਇੰਗਲੈਂਡ ਤੋਂ ਵਾਪਸ ਪਰਤ ਕੇ ਆਪ ਭਾਰਤ ਦੀ ਅਜ਼ਾਦੀ ਦੀ ਲਹਿਰ ਵਿਚ ਹਿੱਸਾ ਲੈਣ ਲੱਗੇ।
1920 ਈ: ਵਿਚ ਜਦੋਂ ਗਾਂਧੀ ਜੀ ਨੇ ਨਾ – ਮਿਲਵਰਤਨ ਲਹਿਰ ਚਲਾਈ, ਤਾਂ ਨਹਿਰੂ ਜੀ ਨੇ ਪਰਿਵਾਰ ਸਮੇਤ ਇਸ ਲਹਿਰ ਵਿਚ ਹਿੱਸਾ ਲਿਆ 1930 ਈ: ਵਿਚ ਪੰਡਿਤ ਨਹਿਰੂ ਕਾਂਗਰਸ ਪਾਰਟੀ ਦੇ ਪ੍ਰਧਾਨ ਚੁਣੇ ਗਏ ਆਪ ਕਈ ਵਾਰ ਜੇਲ੍ਹ ਗਏ।
ਅੰਤ 15 ਅਗਸਤ, 1947 ਈ: ਨੂੰ ਭਾਰਤ ਅਜ਼ਾਦ ਹੋ ਗਿਆ ਭਾਰਤ ਦੇ ਦੋ ਟੋਟੇ ਹੋ ਗਏ। ਆਪ ਅਜ਼ਾਦ ਭਾਰਤ ਦੇ ਪਹਿਲੇ ਪ੍ਰਧਾਨ ਮੰਤਰੀ ਬਣੇ।
ਪੰਡਿਤ ਨਹਿਰੂ ਦੀ ਅਗਵਾਈ ਹੇਠ ਭਾਰਤ ਨੇ ਬਹੁਤ ਤੰਰੱਕੀ ਕੀਤੀ। ਆਪ ਨੇ ਹਰ ਇਕ ਦੇਸ਼ ਨਾਲ ਮਿੱਤਰਤਾ ਵਧਾਈ। ਆਪ ਜੰਗ ਦੇ ਵਿਰੋਧੀ ਅਤੇ ਸ਼ਾਂਤੀ ਦੇ ਪੁਜਾਰੀ ਸਨ।
ਪੰਡਿਤ ਨਹਿਰੂ ਦੇ ਦਿਲ ਵਿਚ ਦੇਸ਼ – ਵਾਸੀਆਂ ਨਾਲ ਅਥਾਹ ਪਿਆਰ ਸੀ। ਬੱਚੇ ਉਨ੍ਹਾਂ ਨੂੰ ‘ਚਾਚਾ ਨਹਿਰੂ’ ਆਖ ਕੇ ਪੁਕਾਰਦੇ ਸਨ। ਭਾਰਤ ਵਾਸੀਆਂ ਦਾ ਇਹ ਹਰਮਨ – ਪਿਆਰਾ ਨੇਤਾ 27 ਮਈ, 1964 ਨੂੰ ਦਿਲ ਦੀ ਧੜਕਣ ਬੰਦ ਹੋਣ ਨਾਲ ਅੱਖਾਂ ਮੀਟ ਗਿਆ।
5. ਸ਼ਹੀਦ ਸ: ਭਗਤ ਸਿੰਘ
ਸ: ਭਗਤ ਸਿੰਘ ਭਾਰਤ ਦੀ ਅਜ਼ਾਦੀ ਦੇ ਇਤਿਹਾਸ ਦਾ ਸਿਰਲੱਥ ਯੋਧਾ ਸੀ। ਉਸ ਦਾ ਪਿਤਾ ਸ: ਕਿਸ਼ਨ ਸਿੰਘ ਕਾਂਗਰਸ ਦਾ ਉੱਘਾ ਲੀਡਰ ਸੀ। ਸ: ਅਜੀਤ ਸਿੰਘ ਜਲਾਵਤਨ ਉਸ ਦਾ ਚਾਚਾ ਸੀ। ਉਸ ਦਾ ਜਨਮ 28 ਸਤੰਬਰ, 1907 ਈ: ਨੂੰ ਚੱਕ ਨੰਬਰ 105, ਜ਼ਿਲ੍ਹਾ ਲਾਇਲਪੁਰ ਵਿਚ ਹੋਇਆ ਖਟਕੜ ਕਲਾਂ (ਜ਼ਿਲ੍ਹਾ ਜਲੰਧਰ) ਉਸ ਦਾ ਜੱਦੀ ਪਿੰਡ ਸੀ।
ਬਚਪਨ ਵਿਚ ਜਲ੍ਹਿਆਂ ਵਾਲੇ ਬਾਗ ਦੇ ਖੂਨੀ ਕਾਂਡ ਨੇ ਉਸ ਦੇ ਮਨ ਉੱਪਰ ਡੂੰਘਾ ਅਸਰ ਪਾਇਆ। 1925 ਵਿਚ ਭਗਤ ਸਿੰਘ, ਸੁਖਦੇਵ, ਭਗਵਤੀ ਚਰਨ ਤੇ ਧਨਵੰਤੀ ਆਦਿ ਨੇ “ਨੌਜਵਾਨ ਭਾਰਤ ਸਭਾ’ ਬਣਾਈ ਤੇ ਅੰਗਰੇਜ਼ਾਂ ਵਿਰੁੱਧ ਘੋਲ ਆਰੰਭ ਕਰ ਦਿੱਤਾ।
ਸ: ਭਗਤ ਸਿੰਘ ਤੇ ਉਸ ਦੇ ਸਾਥੀਆਂ ਨੇ ਲਾਲਾ ਲਾਜਪਤ ਰਾਏ ਦੇ ਕਤਲ ਦਾ ਬਦਲਾ ਲੈਣ ਲਈ ਸਾਂਡਰਸ ਨੂੰ ਮਾਰਿਆ। ਇਸ ਪਿੱਛੋਂ 8 ਅਪਰੈਲ, 1929 ਨੂੰ ਭਗਤ ਸਿੰਘ ਤੇ ਬੀ. ਕੇ. ਦੱਤ ਨੇ ਧਮਾਕੇ ਵਾਲੇ ਦੋ ਬੰਬ ਅਸੈਂਬਲੀ ਹਾਲ ਵਿਚ ਸੁੱਟੇ ਤੇ “ਇਨਕਲਾਬ ਜ਼ਿੰਦਾਬਾਦ’ ਦੇ ਨਾਅਰੇ ਲਾਉਂਦਿਆਂ ਗ੍ਰਿਫ਼ਤਾਰੀ ਦੇ ਦਿੱਤੀ।
ਸਰਕਾਰ ਨੇ ਮੁਕੱਦਮੇ ਦਾ ਡਰਾਮਾ ਰਚ ਕੇ ਬੰਬ ਸੁੱਟਣ ਦੇ ਦੋਸ਼ ਵਿਚ ਭਗਤ ਸਿੰਘ ਤੇ ਬੀ. ਕੇ. ਦੱਤ ਨੂੰ ਉਮਰ ਕੈਦ ਦੀ ਸਜ਼ਾ ਦਿੱਤੀ। ਸਾਂਡਰਸ ਦੇ ਕਤਲ ਦੇ ਦੋਸ਼ ਵਿਚ ਅਦਾਲਤ ਨੇ 7 ਅਕਤੂਬਰ, 1930 ਨੂੰ ਭਗਤ ਸਿੰਘ, ਸੁਖਦੇਵ ਤੇ ਰਾਜਗੁਰੂ ਨੂੰ ਫਾਂਸੀ ਦੀ ਸਜ਼ਾ ਸੁਣਾਈ। ਇਸ ਸਮੇਂ ਗਾਂਧੀ ਜੀ ਦਾ ਲੂਣ ਦਾ ਮੋਰਚਾ ਚਲ ਰਿਹਾ ਸੀ ਲੋਕ ਬੜੇ ਜੋਸ਼ ਵਿਚ ਸਨ।

ਅੰਗਰੇਜ਼ ਸਰਕਾਰ ਨੇ ਲੋਕਾਂ ਤੋਂ ਡਰਦਿਆਂ 23 ਮਾਰਚ, 1931 ਨੂੰ ਰਾਤ ਵੇਲੇ ਹੀ ਭਗਤ ਸਿੰਘ ਤੇ ਉਸਦੇ ਦੋਹਾਂ ਸਾਥੀਆਂ ਨੂੰ ਫਾਂਸੀ ਲਾਇਆ ਤੇ ਲੋਥਾਂ ਵਾਰਸਾਂ ਦੇ ਹਵਾਲੇ ਕਰਨ ਦੀ ਥਾਂ ਪਿਛਲੇ ਚੋਰ ਦਰਵਾਜ਼ੇ ਥਾਣੀ ਕੱਢ ਕੇ ਫ਼ਿਰੋਜ਼ਪੁਰ ਲੈ ਗਏ। ਤਿੰਨਾਂ ਦੀ ਇਕੱਠੀ ਚਿਖਾ ਬਣਾ ਕੇ ਤੇ ਮਿੱਟੀ ਦਾ ਤੇਲ ਪਾ ਕੇ ਅੱਗ ਲਾ ਦਿੱਤੀ। ਅੱਧਸੜੀਆਂ ਲਾਸ਼ਾਂ ਪੁਲਿਸ ਨੇ ਦਰਿਆ ਸਤਲੁਜ ਵਿਚ ਰੋੜ੍ਹ ਦਿੱਤੀਆਂ।
ਭਗਤ ਸਿੰਘ ਤੇ ਉਸ ਦੇ ਸਾਥੀਆਂ ਦੀ ਇਸ ਕੁਰਬਾਨੀ ਨੇ ਸਾਰੇ ਦੇਸ਼ ਨੂੰ ਜਗਾ ਦਿੱਤਾ ਤੇ ਲੋਕ ਅੰਗਰੇਜ਼ਾਂ ਨੂੰ ਭਾਰਤ ਵਿਚੋਂ ਕੱਢਣ ਲਈ ਹੋਰ ਵੀ ਜ਼ੋਰ ਨਾਲ ਘੋਲ ਕਰਨ ਲੱਗੇ। ਅੰਤ 15 ਅਗਸਤ, 1947 ਨੂੰ ਅਜਿਹੇ ਸਿਰਲੱਥ ਸੂਰਮਿਆਂ ਦੀਆਂ ਕੁਰਬਾਨੀਆਂ ਸਦਕਾ ਭਾਰਤ ਅਜ਼ਾਦ ਹੋ ਗਿਆ।
6. ਦੀਵਾਲੀ
ਦੀਵਾਲੀ ਭਾਰਤ ਦਾ ਇਕ ਪ੍ਰਸਿੱਧ ਤਿਉਹਾਰ ਹੈ। ਇਹ ਹਰ ਸਾਲ ਕੱਤਕ ਦੀ ਮੱਸਿਆ ਨੂੰ ਮਨਾਇਆ ਜਾਂਦਾ ਹੈ। ਇਸ ਤੋਂ ਕੁੱਝ ਦਿਨ ਪਹਿਲਾਂ ਲੋਕ ਆਪਣੇ ਘਰਾਂ ਦੀ ਸਫ਼ਾਈ ਕਰਦੇ ਹਨ। ਉਹ ਆਪਣੇ ਮਕਾਨਾਂ ਨੂੰ ਸਫ਼ੈਦੀ ਤੇ ਰੰਗ – ਰੋਗਨ ਕਰਾਉਂਦੇ ਅਤੇ ਸ਼ਿੰਗਾਰਦੇ ਹਨ। ਇਸ ਤਿਉਹਾਰ ਦਾ ਸੰਬੰਧ ਉਸ ਦਿਨ ਨਾਲ ਹੈ, ਜਦੋਂ ਸ੍ਰੀ ਰਾਮਚੰਦਰ ਜੀ 14 ਸਾਲਾਂ ਦਾ ਬਨਵਾਸ ਕੱਟ ਕੇ ਤੇ ਰਾਵਣ ਨੂੰ ਮਾਰ ਕੇ ਵਾਪਸ ਅਯੁੱਧਿਆ ਪਹੁੰਚੇ ਸਨ ਉਸ ਦਿਨ ਲੋਕਾਂ ਨੇ ਖ਼ੁਸ਼ੀ ਵਿਚ ਦੀਪਮਾਲਾ ਕੀਤੀ ਸੀ।
ਉਸੇ ਦਿਨ ਦੀ ਯਾਦ ਵਿਚ ਅੱਜ ਵੀ ਇਹ ਤਿਉਹਾਰ ਮਨਾਇਆ ਜਾਂਦਾ ਹੈ। ਇਸ ਦਿਨ ਸਿੱਖਾਂ ਦੇ ਛੇਵੇਂ ਗੁਰੂ ਹਰਿਗੋਬਿੰਦ ਸਾਹਿਬ ਜਹਾਂਗੀਰ ਦੀ ਨਜ਼ਰਬੰਦੀ ਤੋਂ ਰਿਹਾ ਹੋ ਕੇ ਆਏ ਸਨ। ਪੰਜਾਬ ਵਿਚ ਅੰਮ੍ਰਿਤਸਰ ਦੀ ਦੀਵਾਲੀ ਦੇਖਣ ਯੋਗ ਹੁੰਦੀ ਹੈ। ਦੀਵਾਲੀ ਵਾਲੇ ਦਿਨ ਲੋਕਾਂ ਵਿਚ ਬੜਾ ਚਾ ਤੇ ਉਮਾਹ ਹੁੰਦਾ ਹੈ। ਲੋਕ ਪਟਾਕੇ, ਸਜਾਵਟ, ਪੂਜਾ ਦਾ ਸਮਾਨ ਤੇ ਮਠਿਆਈਆਂ ਖ਼ਰੀਦਦੇ ਹਨ ਅਤੇ ਇਕ – ਦੂਜੇ ਨੂੰ ਮਠਿਆਈਆਂ ਤੇ ਤੋਹਫ਼ੇ ਦੇ ਕੇ ਦੀਵਾਲੀ ਦੀਆਂ ਸ਼ੁੱਭ – ਇੱਛਾਵਾਂ ਦਿੰਦੇ ਹਨ ਹਨੇਰਾ ਹੋਣ ਤੇ ਲੋਕ ਆਪਣੇ ਘਰਾਂ ਵਿਚ ਦੀਪਮਾਲਾ ਕਰਦੇ ਹਨ।
ਚਾਰੇ ਪਾਸਿਓਂ ਪਟਾਕੇ ਚੱਲਣ ਦੀਆਂ ਅਵਾਜ਼ਾਂ ਆਉਂਦੀਆਂ ਹਨ ਅਸਮਾਨ ਵਲ ਚੜ੍ਹ ਰਹੀਆਂ ਆਤਸ਼ਬਾਜ਼ੀਆਂ ਤੇ ਹਵਾਈਆਂ ਕੜਕਵੀਂ ਆਵਾਜ਼ ਨਾਲ ਫਟਦੀਆਂ ਤੇ ਅੱਗ ਦੇ ਫੁੱਲਾਂ ਦੀ ਵਰਖਾ ਕਰਦੀਆਂ ਹੋਈਆਂ ਵਾਤਾਵਰਨ ਨੂੰ ਬਹੁਤ ਹੀ ਦਿਲ – ਖਿੱਚਵਾਂ ਬਣਾ ਦਿੰਦੀਆਂ ਹਨ।
ਲੋਕ ਰਾਤ ਭਰ ਲੱਛਮੀ ਦੀ ਪੂਜਾ ਕਰਦੇ ਹਨ ਤੇ ਦਰਵਾਜ਼ੇ ਖੁੱਲ੍ਹੇ ਰੱਖਦੇ ਹਨ, ਤਾਂ ਜੋ ਲੱਛਮੀ ਉਨ੍ਹਾਂ ਦੇ ਘਰ ਫੇਰਾ ਪਾ ਸਕੇ। ਦੀਵਾਲੀ ਦੀ ਰਾਤ ਨੂੰ ਕਈ ਲੋਕ ਸ਼ਰਾਬ ਪੀਂਦੇ, ਜੂਆ ਖੇਡਦੇ ਤੇ ਟੂਣੇ ਆਦਿ ਕਰਦੇ ਹਨ। ਸਾਨੂੰ ਇਨ੍ਹਾਂ ਬੁਰਾਈਆਂ ਨੂੰ ਦੂਰ ਕਰਨ ਲਈ ਯਤਨ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ਤੇ ਦੀਵਾਲੀ ਦੇ ਤਿਉਹਾਰ ਨੂੰ ਵੱਧ ਤੋਂ ਵੱਧ ਪਵਿੱਤਰ ਬਣਾਉਣਾ ਚਾਹੀਦਾ ਹੈ।

7. ਦੁਸਹਿਰਾ
ਦੁਸਹਿਰਾ ਭਾਰਤ ਦਾ ਇਕ ਬਹੁਤ ਪੁਰਾਣਾ ਤਿਉਹਾਰ ਹੈ। ਇਹ ਦੀਵਾਲੀ ਤੋਂ 20 ਦਿਨ ਪਹਿਲਾਂ ਮਨਾਇਆ ਜਾਂਦਾ ਹੈ।
ਦੁਸਹਿਰੇ ਦਾ ਤਿਉਹਾਰ ਉਸ ਦਿਨ ਦੀ ਯਾਦ ਵਿਚ ਮਨਾਇਆ ਜਾਂਦਾ ਹੈ, ਜਦੋਂ ਸ੍ਰੀ ਰਾਮ ਚੰਦਰ ਜੀ ਨੇ ਲੰਕਾ ਦੇ ਰਾਜੇ ਰਾਵਣ ਨੂੰ ਮਾਰ ਕੇ ਆਪਣੀ ਪਤਨੀ ਸੀਤਾ ਜੀ ਨੂੰ ਮੁੜ ਪ੍ਰਾਪਤ ਕੀਤਾ ਸੀ। ਦੁਸਹਿਰੇ ਤੋਂ ਪਹਿਲਾਂ ਨੌਂ ਨਰਾਤੇ ਹੁੰਦੇ ਹਨ। ਇਨ੍ਹਾਂ ਦਿਨਾਂ ਵਿਚ ਰਾਤ ਨੂੰ ਸ਼ਹਿਰਾਂ ਵਿਚ ਥਾਂ – ਥਾਂ ਰਾਮ – ਲੀਲ੍ਹਾ ਹੁੰਦੀ ਹੈ। ਲੋਕ ਬੜੇ ਉਮਾਹ ਤੇ ਸ਼ਰਧਾ ਨਾਲ ਰਾਮ – ਲੀਲ੍ਹਾ ਵੇਖਣ ਜਾਂਦੇ ਹਨ। ਦਿਨ ਸਮੇਂ ਬਜ਼ਾਰਾਂ ਵਿਚ ਰਾਮ – ਲੀਲ੍ਹਾ ਦੀਆਂ ਝਾਕੀਆਂ ਵੀ ਨਿਕਲਦੀਆਂ ਹਨ।
ਦਸਵੀਂ ਵਾਲੇ ਦਿਨ ਕਿਸੇ ਖੁੱਲੇ ਥਾਂ ਵਿਚ ਰਾਵਣ, ਮੇਘਨਾਦ ਅਤੇ ਕੁੰਭਕਰਨ ਦੇ ਕਾਗ਼ਜ਼ਾਂ ਤੇ ਬਾਂਸਾਂ ਦੇ ਬਣੇ ਪੁਤਲੇ ਗੱਡ ਦਿੱਤੇ ਜਾਂਦੇ ਹਨ। ਦੂਰ – ਨੇੜੇ ਦੇ ਲੋਕ ਰਾਵਣ ਦੇ ਸਾੜਨ ਦਾ ਦ੍ਰਿਸ਼ ਦੇਖਣ ਲਈ ਟੁੱਟ ਪੈਂਦੇ ਹਨ। ਲੋਕ ਪੰਡਾਲ ਵਿਚ ਚਲ ਰਹੀ ਆਤਸ਼ਬਾਜ਼ੀ ਤੇ ਠਾਹ – ਠਾਹ ਚਲਦੇ ਪਟਾਕਿਆਂ ਦਾ ਆਨੰਦ ਲੈਂਦੇ ਹਨ। ਰਾਮ – ਲੀਲਾ ਦੀ ਅੰਤਮ ਝਾਕੀ ਪੇਸ਼ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ਤੇ ਰਾਵਣ, ਸ੍ਰੀ ਰਾਮਚੰਦਰ ਹੱਥੋਂ ਮਾਰਿਆ ਜਾਂਦਾ ਹੈ। ਇਸ ਸਮੇਂ ਸੂਰਜ ਛਿਪਣ ਵਾਲਾ ਹੁੰਦਾ ਹੈ।
ਰਾਵਣ ਸਮੇਤ ਸਾਰੇ ਪੁਤਲਿਆਂ ਨੂੰ ਅੱਗ ਲਾ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ। ਇਸ ਸਮੇਂ ਲੋਕਾਂ ਵਿਚ ਹਫ਼ੜਾ – ਦਫੜੀ ਮਚ ਜਾਂਦੀ ਹੈ ਤੇ ਉਹ ਘਰਾਂ ਵਲ ਚਲ ਪੈਂਦੇ ਹਨ। ਕਈ ਲੋਕ ਰਾਵਣ ਦੇ ਪੁਤਲੇ ਦੇ ਅੱਧ – ਜਲੇ ਬਾਂਸ ਵੀ ਚੁੱਕ ਕੇ ਨਾਲ ਲੈ ਜਾਂਦੇ ਹਨ। ਵਾਪਸੀ ‘ਤੇ ਲੋਕ ਬਜ਼ਾਰਾਂ ਵਿਚੋਂ ਲੰਘਦੇ ਹੋਏ ਮਠਿਆਈਆਂ ਦੀਆਂ ਦੁਕਾਨਾਂ ਦੁਆਲੇ ਭੀੜਾਂ ਪਾ ਲੈਂਦੇ ਹਨ ਤੇ ਮਨ ਭਾਉਂਦੀਆਂ ਮਠਿਆਈਆਂ ਖ਼ਰੀਦ ਕੇ ਘਰਾਂ ਨੂੰ ਜਾਂਦੇ ਹਨ। ਫਿਰ ਰਾਤੀਂ ਖਾ – ਪੀ ਕੇ ਸੌਂਦੇ ਹਨ। ਇਸ ਪ੍ਰਕਾਰ ਦੁਸਹਿਰਾ ਮਨ – ਪਰਚਾਵੇ ਦਾ ਇਕ ਤਿਉਹਾਰ ਹੈ। ਇਹ ਭਾਰਤੀ ਲੋਕਾਂ ਦੇ ਆਪਣੇ ਧਾਰਮਿਕ ਤੇ ਇਤਿਹਾਸਕ ਵਿਰਸੇ ਪ੍ਰਤੀ ਸਤਿਕਾਰ ਨੂੰ ਪ੍ਰਗਟ ਕਰਦਾ ਹੈ।
8. ਬਸੰਤ ਰੁੱਤ
ਭਾਰਤ ਰੁੱਤਾਂ ਦਾ ਦੇਸ਼ ਹੈ। ਸਾਰੀਆਂ ਰੁੱਤਾਂ ਵਿਚੋਂ ਬਸੰਤ ਸਭ ਤੋਂ ਹਰਮਨ – ਪਿਆਰੀ ਰੁੱਤ ਹੈ। ਇਹ ਖੁੱਲੀ ਤੇ ਨਿੱਘੀ ਰੁੱਤ ਹੈ। ਇਸ ਨਾਲ ਸਰਦੀ ਦਾ ਅੰਤ ਹੋ ਜਾਂਦਾ ਹੈ। ਇਸ ਦਾ ਆਰੰਭ ਬਸੰਤ – ਪੰਚਮੀ ਦੇ ਤਿਉਹਾਰ ਨਾਲ ਹੁੰਦਾ ਹੈ।
ਬਸੰਤ – ਪੰਚਮੀ ਦੇ ਦਿਨ ਥਾਂ – ਥਾਂ ਮੇਲੇ ਲੱਗਦੇ ਹਨ। ਖਿਡੌਣਿਆਂ ਤੇ ਮਠਿਆਈਆਂ ਦੀਆਂ ਦੁਕਾਨਾਂ ਸਜਦੀਆਂ ਹਨ। ਲੋਕ ਬਸੰਤੀ ਰੰਗ ਦੇ ਕੱਪੜੇ ਪਾਉਂਦੇ ਹਨ ਘਰ – ਘਰ ਬਸੰਤੀ ਹਲਵਾ, ਚਾਵਲ ਅਤੇ ਕੇਸਰੀ ਰੰਗ ਦੀ ਖੀਰ ਬਣਾਈ ਜਾਂਦੀ ਹੈ। ਬੱਚੇ ਅਤੇ ਜਵਾਨ ਪਤੰਗਬਾਜ਼ੀਆਂ ਕਰਦੇ ਹਨ। ਮੇਲਿਆਂ ਵਿਚ ਪਹਿਲਵਾਨਾਂ ਦੀਆਂ ਕੁਸ਼ਤੀਆਂ ਅਤੇ ਹੋਰ ਖੇਡਾਂ – ਤਮਾਸ਼ਿਆਂ ਦਾ ਪ੍ਰਬੰਧ ਕੀਤਾ ਜਾਂਦਾ ਹੈ। ਇਸ ਦਿਨ ਦਾ ਸੰਬੰਧ ਬਾਲ ਹਕੀਕਤ ਰਾਏ ਧਰਮੀ ਦੀ ਸ਼ਹੀਦੀ ਨਾਲ ਵੀ ਹੈ।
ਇਸ ਦਿਨ ਉਸ ਵੀਰ ਨੂੰ ਆਪਣੇ ਧਰਮ ਵਿਚ ਪੱਕਾ ਰਹਿਣ ਕਰਕੇ ਮੌਤ ਦੇ ਘਾਟ ਉਤਾਰ ਦਿੱਤਾ ਗਿਆ ਸੀ। ਇਹ ਰੁੱਤ ਬਹੁਤ ਹੀ ਸੁਹਾਵਣੀ ਹੁੰਦੀ ਹੈ। ਇਹ ਨਿੱਘੀ ਤੇ ਮਨ – ਭਾਉਣੀ ਹੁੰਦੀ ਹੈ। ਜੀਵ – ਜੰਤੂਆਂ ਅਤੇ ਪੌਦਿਆਂ ਵਿਚ ਨਵੇਂ ਜੀਵਨ ਦਾ ਸੰਚਾਰ ਹੁੰਦਾ ਹੈ। ਸਰੋਂ ਦੇ ਬਸੰਤੀ ਰੰਗ ਦੇ ਫੁੱਲਾਂ ਨਾਲ ਭਰਿਆ ਹੋਇਆ ਆਲਾ – ਦੁਆਲਾ ਇਸ ਤਰ੍ਹਾਂ ਲਗਦਾ ਹੈ, ਜਿਵੇਂ ਕੁਦਰਤ ਆਪ ਪੀਲੇ ਗਹਿਣੇ ਪਹਿਨ ਕੇ ਬਸੰਤ ਦਾ ਤਿਉਹਾਰ ਮਨਾ ਰਹੀ ਹੋਵੇ।
ਇਹ ਰੁੱਤ ਮਨੁੱਖ ਦੀ ਸਿਹਤ ਨੂੰ ਵਧਾਉਣ ਵਿਚ ਵੀ ਸਹਾਇਤਾ ਕਰਦੀ ਹੈ। ਇਸ ਰੁੱਤ ਵਿਚ ਚੰਗੀ ਖ਼ੁਰਾਕ ਖਾਣੀ ਚਾਹੀਦੀ ਹੈ ਤੇ ਕਸਰਤ ਆਦਿ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ।

9. ਵਰਖਾ ਰੁੱਤ
ਜਾਂ
ਬਰਸਾਤ ਦੀ ਰੁੱਤ
ਪੰਜਾਬ ਦੀਆਂ ਰੁੱਤਾਂ – ਪੰਜਾਬ ਇਕ ਬਹੁ – ਰੁੱਤਾ ਦੇਸ਼ ਹੈ। ਇੱਥੇ ਹਰ ਦੋ ਮਹੀਨਿਆਂ ਮਗਰੋਂ ਰੁੱਤ ਬਦਲ ਜਾਂਦੀ ਹੈ। ਇਸ ਕਰਕੇ ਇੱਥੇ ਸਾਲ ਵਿਚ ਛੇ ਰੁੱਤਾਂ ਆਉਂਦੀਆਂ ਹਨ। ਇਹ ਰੁੱਤਾਂ ਹਨ – ਬਸੰਤ ਰੁੱਤ, ਗਰਮ ਰੁੱਤ, ਵਰਖਾ ਰੁੱਤ, ਸਰਦ ਰੁੱਤ, ਪਤਝੜ ਰੁੱਤ ਤੇ ਸੀਤ ਰੁੱਤ। ਇਹ ਸਾਰੀਆਂ ਰੁੱਤਾਂ ਆਪੋ – ਆਪਣੀ ਥਾਂ ਬਹੁਤ ਹੀ ਮਹੱਤਵਪੂਰਨ ਹਨ ਪਰੰਤੂ ਇਨ੍ਹਾਂ ਵਿਚੋਂ ਵਧੇਰੇ ਹਰਮਨ – ਪਿਆਰੀਆਂ ਰੁੱਤਾਂ ਬਸੰਤ ਰੁੱਤ ਤੇ ਵਰਖਾ ਰੁੱਤ ਹਨ।
ਵਰਖਾ ਰੁੱਤ ਦਾ ਵਾਤਾਵਰਨ – ਵਰਖਾ ਰੁੱਤ ਦਾ ਆਰੰਭ ਜੂਨ ਮਹੀਨੇ ਦੇ ਅੰਤ ਵਿਚ ਹੁੰਦਾ ਹੈ, ਜਦੋਂ ਗਰਮੀ ਦੀ ਰੁੱਤ ਆਪਣੇ ਸਿਖ਼ਰ ‘ਤੇ ਪੁੱਜ ਚੁੱਕੀ ਹੁੰਦੀ ਹੈ। ਸੂਰਜ ਅਸਮਾਨ ਤੋਂ ਅੱਗ ਵਰ੍ਹਾ ਰਿਹਾ ਹੁੰਦਾ ਹੈ ਤੇ ਧਰਤੀ ਭੱਠੀ ਵਾਂਗ ਤਪ ਰਹੀ ਹੁੰਦੀ ਹੈ। ਇਸ ਮਹੀਨੇ ਵਿਚ ਬੰਦੇ ਤਾਂ ਕੀ, ਸਗੋਂ ਧਰਤੀ ਦੇ ਸਾਰੇ ਜੀਵ ਤੇ ਪਸ਼ੂ – ਪੰਛੀ ਗਰਮੀ ਤੋਂ ਤੰਗ ਆਏ ਮੀਂਹ ਦੀ ਮੰਗ ਕਰ ਰਹੇ ਹੁੰਦੇ ਹਨ। ਜੂਨ ਮਹੀਨੇ ਦੇ ਅੰਤ ਵਿਚ ਵਗਦੀ ਲੁ ਇਕ ਦਮ ਠੰਢੀ ਹਵਾ ਵਿਚ ਬਦਲ ਜਾਂਦੀ ਹੈ ਤੇ ਅਸਮਾਨ ਉੱਪਰ ਬੱਦਲ ਘਨਘੋਰਾਂ ਪਾਉਣ ਲੱਗ ਪੈਂਦੇ ਹਨ ਪਹਿਲਾਂ ਕਿਣਮਿਣ ਹੁੰਦੀ ਹੈ ਤੇ ਫਿਰ ਮੋਹਲੇਧਾਰ ਮੀਂਹ ਆਰੰਭ ਹੋ ਜਾਂਦਾ ਹੈ ਤੇ ਘੜੀਆਂ ਵਿਚ ਹੀ ਚਾਰੇ ਪਾਸੇ ਜਲ – ਥਲ ਹੋਇਆ ਦਿਖਾਈ ਦਿੰਦਾ ਹੈ।
ਇਸ ਤੋਂ ਮਗਰੋਂ ਹਰ ਰੋਜ਼ ਅਸਮਾਨ ਉੱਪਰ ਬੱਦਲ ਮੰਡਲਾਉਂਦੇ ਰਹਿੰਦੇ ਹਨ। ਦਿਨ ਨੂੰ ਸੂਰਜ ਤੇ ਰਾਤ ਨੂੰ ਚੰਦ ਉਨ੍ਹਾਂ ਵਿਚ ਲੁਕਣ – ਮੀਟੀ ਖੇਡਦਾ ਹੈ। ਮੀਂਹ ਦਾ ਕੋਈ ਵੇਲਾ ਨਹੀਂ ਹੁੰਦਾ ਮਾੜਾ ਜਿਹਾ ਹੁੱਸੜ ਹੁੰਦਾ ਹੈ ਤੇ ਬੱਸ ਕੁੱਝ ਪਲਾਂ ਮਗਰੋਂ ਹੀ ਬੱਦਲ ਗੜਗੜਾਹਟ ਪਾਉਣ ਲਗਦਾ ਹੈ। ਮੀਂਹ ਪੈਣ ਨਾਲ ਬਨਸਪਤੀ ਹਰੀ – ਭਰੀ ਹੋ ਜਾਂਦੀ ਹੈ ਅੰਬ ਤੇ ਜਾਮਣੁ ਰਸ ਜਾਂਦੇ ਹਨ। ਕੋਇਲ ਦੀ ਕੁ – ਕੁ ਬੰਦ ਹੋ ਜਾਂਦੀ ਹੈ ਤੇ ਛੱਪੜਾਂ, ਟੋਭਿਆਂ ਦੇ ਕੰਢਿਆਂ ਉੱਪਰ ਡੱਡੂ ਗੁੜੈ – ਗੁੜੈ ਕਰਨ ਲਗਦੇ ਹਨ।
ਮੱਛਰਾਂ ਤੇ ਮੱਖੀਆਂ ਦੀ ਭਰਮਾਰ ਹੋ ਜਾਂਦੀ ਹੈ। ਸੱਪ, ਅਲੂਏਂ ਤੇ ਹੋਰ ਅਨੇਕਾਂ ਪ੍ਰਕਾਰ ਦੇ ਕੀੜੇ – ਪਤੰਗੇ, ਘੁਮਿਆਰ ਤੇ ਚੀਚ – ਵਹੁਟੀਆਂ ਘੁੰਮਣ ਹਨ। ਖੱਬਲ ਘਾਹ ਦੀਆਂ ਹਰੀਆਂ ਤਿੜਾਂ ਤੇ ਅਨੇਕਾਂ ਪ੍ਰਕਾਰ ਦੇ ਹੋਰ ਹਰੇ ਪੌਦਿਆਂ ਨਾਲ ਧਰਤੀ ਕੱਜੀ ਜਾਂਦੀ ਹੈ। ਸਾਉਣ – ਭਾਦੋਂ ਦੇ ਦੋ ਮਹੀਨੇ ਅਜਿਹਾ ਲੁਭਾਉਣਾ ਵਾਤਾਵਰਨ ਪਸਰਿਆ ਰਹਿੰਦਾ ਹੈ। ਕੁੜੀਆਂ ਬਾਗਾਂ ਵਿਚ ਪੀਂਘਾਂ ਝੂਟਦੀਆਂ ਹਨ, ਤੀਆਂ ਲਗਦੀਆਂ ਹਨ ਤੇ ਗਿੱਧੇ ਮਚਦੇ ਹਨ ਪੰਜਾਬੀ ਸੱਭਿਆਚਾਰ ਤੇ ਇਸ ਕੁਦਰਤੀ ਵਾਤਾਵਰਨ ਦਾ ਚਿਤਰਨ ਧਨੀ ਰਾਮ ਚਾਤ੍ਰਿਕ ਨੇ ਆਪਣੀ ਕਵਿਤਾ ਵਿਚ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਕੀਤਾ ਹੈ –
ਸਾਉਣ ਮਾਹ ਝੜੀਆਂ ਗਰਮੀ ਝਾੜ ਸੁੱਟੀ,
ਧਰਤੀ ਪੁੰਗਰੀ ਟਹਿਕੀਆਂ ਡਾਲੀਆਂ ਨੇ।
ਰਾਹ ਰੋਕ ਲਏ ਛੱਪੜਾਂ ਟੋਭਿਆਂ ਨੇ,
ਨਦੀ ਨਾਲਿਆਂ ਜੂਹਾਂ ਹੁੰਘਾਲੀਆਂ ਨੇ।
ਵਰਖਾ ਧਰਤੀ ਲਈ ਪਰਮਾਤਮਾ ਦੀ ਇਕ ਮਹਾਨ ਬਖ਼ਸ਼ਿਸ਼ ਹੈ। ਇਹ ਸਭ ਜੀਵਾਂ ਤੇ ਬਨਸਪਤੀ ਦੇ ਜੀਵਨ ਦਾ ਅਧਾਰ ਹੈ। ਇਸ ਤੋਂ ਪ੍ਰਾਪਤ ਹੋਇਆ ਪਾਣੀ ਜੀਵਾਂ ਤੇ ਬਨਸਪਤੀ ਦੇ ਜੀਵਨ ਦਾ ਮੁੱਖ ਅਧਾਰ ਬਣਦਾ ਹੈ। ਇਹੋ ਪਾਣੀ ਹੀ ਜ਼ਮੀਨ ਵਿਚ ਰਚ ਕੇ ਸਾਰਾ ਸਾਲ ਖੂਹਾਂ, ਨਲਕਿਆਂ ਤੇ ਟਿਊਬਵੈੱਲਾਂ ਰਾਹੀਂ ਖੇਤਾਂ, ਮਨੁੱਖਾਂ ਤੇ ਜੀਵਾਂ ਦੀ ਪਾਣੀ ਦੀ ਲੋੜ ਪੂਰੀ ਕਰਦਾ ਹੈ। ਜੇ ਵਰਖਾ ਨਾ ਹੋਵੇ, ਤਾਂ ਸੂਰਜ ਦੀ ਗਰਮੀ ਨਾਲ ਸਭ ਕੁੱਝ ਸੁੱਕ ਜਾਵੇ ਤੇ ਧਰਤੀ ਤੋਂ ਜ਼ਿੰਦਗੀ ਨਸ਼ਟ ਹੋ ਜਾਵੇ। ਇਸ ਕਰਕੇ ਅੱਡੀਆਂ ਰਗੜ – ਰਗੜ ਕੇ ਮੀਂਹ ਦੀ ਮੰਗ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ਤੇ ਕਿਹਾ ਜਾਂਦਾ ਹੈ –

ਰੱਬਾ ਰੱਬਾ ਮੀਂਹ ਵਰਾ, ਸਾਡੀ ਕੋਠੀ ਦਾਣੇ ਪਾ।
10. ਮੇਰਾ ਮਨ – ਭਾਉਂਦਾ ਅਧਿਆਪਕ
ਜਾਂ
ਸਾਡਾ ਮੁੱਖ ਅਧਿਆਪਕ
ਉਂਝ ਤਾਂ ਸਾਡੇ ਸਕੂਲ ਦੇ ਸਾਰੇ ਅਧਿਆਪਕ ਹੀ ਬੜੇ ਸਤਿਕਾਰਯੋਗ ਹਨ, ਪਰ ਮੇਰਾ ਮਨ – ਭਾਉਂਦਾ ਅਧਿਆਪਕ ਸਾਡਾ ਮੁੱਖ ਅਧਿਆਪਕ ਹੈ। ਉਨ੍ਹਾਂ ਦਾ ਨਾਂ ਸ: ਹਰਜਿੰਦਰ ਸਿੰਘ ਹੈ। ਉਨ੍ਹਾਂ ਨੇ ਐੱਮ. ਏ., ਬੀ. ਐੱਡ. ਤਕ ਵਿੱਦਿਆ ਹਾਸਲ ਕੀਤੀ ਹੋਈ ਹੈ। ਉਹ ਸਾਨੂੰ ਹਿਸਾਬ ਪੜ੍ਹਾਉਂਦੇ ਹਨ। ਉਨ੍ਹਾਂ ਵਿਚ ਸਭ ਤੋਂ ਵੱਡੀ ਵਿਸ਼ੇਸ਼ਤਾ ਉਨ੍ਹਾਂ ਦੇ ਪੜ੍ਹਾਉਣ ਦਾ ਢੰਗ ਹੈ। ਉਨ੍ਹਾਂ ਦੀ ਪੜ੍ਹਾਈ ਇਕ – ਇਕ ਚੀਜ਼ ਵਿਦਿਆਰਥੀਆਂ ਨੂੰ ਚੰਗੀ ਤਰ੍ਹਾਂ ਯਾਦ ਹੋ ਜਾਂਦੀ ਹੈ।
ਉਹ ਔਖੇ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਤਰੀਕਿਆਂ ਨੂੰ ਸਮਝਾਉਣ ਲਈ ਬੜੇ ਸਰਲ ਅਤੇ ਸੌਖੇ ਢੰਗਾਂ ਦੀ ਵਰਤੋਂ ਕਰਦੇ ਹਨ ! ਉਹ ਵਿਦਿਆਰਥੀਆਂ ਨਾਲ ਬਹੁਤ ਪਿਆਰ ਕਰਦੇ ਹਨ। ਉਹ ਕਿਸੇ ਵਿਦਿਆਰਥੀ ਨੂੰ ਕੋਈ ਚੀਜ਼ ਸਮਝ ਨਾ ਆਉਣ ‘ਤੇ ਉਸ ਨੂੰ ਮਾਰਦੇ – ਕੁੱਟਦੇ ਨਹੀਂ, ਸਗੋਂ ਪਿਆਰ ਤੇ ਹਮਦਰਦੀ ਨਾਲ ਵਾਰ – ਵਾਰ ਸਮਝਾਉਂਦੇ ਹਨ। ਇਸ ਦੇ ਨਾਲ ਹੀ ਸਾਡੇ ਮੁੱਖ ਅਧਿਆਪਕ ਸਾਹਿਬ ਨੇ ਸਕੂਲ ਵਿਚ ਵਿਦਿਆਰਥੀਆਂ ਨੂੰ ਡਿਸਿਪਲਨ ਵਿਚ ਰਹਿਣ ਦੀ ਚੰਗੀ ਸਿੱਖਿਆ ਦਿੱਤੀ ਹੈ।
ਉਹ ਵਿਦਿਆਰਥੀ ਜੀਵਨ ਵਿਚ ਖੇਡਾਂ ਦੀ ਮਹਾਨਤਾ ਨੂੰ ਵੀ ਸਪੱਸ਼ਟ ਕਰਦੇ ਹਨ। ਉਹ ਵਿਦਿਆਰਥੀਆਂ ਨੂੰ ਸਿਖਾਉਂਦੇ ਹਨ ਕਿ ਉਨ੍ਹਾਂ ਨੂੰ ਮਾਤਾ – ਪਿਤਾ ਤੇ ਅਧਿਆਪਕਾਂ ਦਾ ਸਤਿਕਾਰ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ। ਮੁੱਖ ਅਧਿਆਪਕ ਸਾਹਿਬ ਹਰ ਰੋਜ਼ ਸਮੇਂ ਸਿਰ ਸਕੂਲ ਪੁੱਜਦੇ ਤੇ ਪ੍ਰਾਰਥਨਾ ਵਿਚ ਸ਼ਾਮਲ ਹੁੰਦੇ ਹਨ। ਉਹ ਸਾਡੀ ਕਲਾਸ ਦੇ ਇੰਚਾਰਜ ਵੀ ਹਨ ਉਹ ਚੰਗੇ ਤਕੜੇ ਸਰੀਰ ਦੇ ਮਾਲਕ ਹਨ।ਉਹ ਹਰ ਇਕ ਨਾਲ ਮਿੱਤਰਤਾ ਤੇ ਪਿਆਰ ਰੱਖਦੇ ਹਨ ਸਕੂਲ ਦੇ ਸਾਰੇ ਅਧਿਆਪਕ ਉਨ੍ਹਾਂ ਦੇ ਹੁਕਮਾਂ ਦੀ ਪ ਤਣਾ ਕਰਦੇ ਹਨ। ਉਨ੍ਹਾਂ ਦੀਆਂ ਕਲਾਸਾਂ ਦੇ ਨਤੀਜੇ ਹਰ ਸਾਲ ਸ਼ਾਨਦਾਰ ਆਉਂਦੇ ਹਨ। ਇਸ ਕਰਕੇ ਉਹ ਮੇਰੇ ਮਨ – ਭਾਉਂਦੇ ਅਧਿਆਪਕ ਹਨ।
11. ਸਵੇਰ ਦੀ ਸੈਰ।
ਸਵੇਰ ਦੀ ਸੈਰ ਹਰ ਉਮਰ ਦੇ ਵਿਅਕਤੀ ਲਈ ਲਾਭਦਾਇਕ ਹੈ। ਇਹ ਇਕ ਪ੍ਰਕਾਰ ਦੀ ਹਲਕੀ ਕਸਰਤ ਹੈ, ਜਿਸ ਤੋਂ ਸਰੀਰ ਨੂੰ ਬਹੁਮੁੱਲਾ ਲਾਭ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ। ਜਿਨ੍ਹਾਂ ਲੋਕਾਂ ਦੇ ਸਰੀਰ ਵਿਚ ਖੇਡਾਂ ਖੇਡਣ ਜਾਂ ਭਾਰੀ ਕਸਰਤ ਕਰਨ ਦੀ ਸ਼ਕਤੀ ਨਹੀਂ ਹੁੰਦੀ, ਉਨ੍ਹਾਂ ਲਈ ਸੈਰ ਬੜੀ ਗੁਣਕਾਰੀ ਸਾਬਤ ਹੁੰਦੀ ਹੈ। ਇਹ ਚੰਗੇ ਰਿਸ਼ਟ – ਪੁਸ਼ਟ ਵਿਅਕਤੀ ਦੇ ਜੀਵਨ ਵਿਚ ਵੀ ਭਾਰੀ ਮਹਾਨਤਾ ਰੱਖਦੀ ਹੈ। ਸਵੇਰ ਦੀ ਸੈਰ ਸੂਰਜ ਚੜ੍ਹਨ ਤੋਂ ਪਹਿਲਾਂ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ। ਇਸ ਸਮੇਂ ਸਾਡੇ ਫੇਫੜਿਆਂ ਨੂੰ ਤਾਜ਼ੀ ਅਤੇ ਖੁੱਲ੍ਹੀ ਹਵਾ ਮਿਲਦੀ ਹੈ, ਜੋ ਸਾਡੀ ਸਰੀਰਕ ਅਤੇ ਮਾਨਸਿਕ ਅਰੋਗਤਾ ਲਈ ਬਹੁਤ ਹੀ ਲਾਭਦਾਇਕ ਸਿੱਧ ਹੁੰਦੀ ਹੈ। ਇਸ ਨਾਲ ਸਾਡੇ ਸਰੀਰ ਦੇ ਹਰ ਇਕ ਅੰਗ ਨੂੰ ਲਾਭ ਪਹੁੰਚਦਾ ਹੈ। ਇਸ ਨਾਲ ਸਰੀਰ ਵਿਚ ਚੁਸਤੀ ਤੇ ਦਿਮਾਗ਼ ਵਿਚ ਫੁਰਤੀ ਪੈਦਾ ਹੁੰਦੀ ਅਤੇ ਅੱਖਾਂ ਦੀ ਰੌਸ਼ਨੀ ਤੇਜ਼ ਹੁੰਦੀ ਹੈ।
ਸਵੇਰ ਦੀ ਸੈਰ ਨਾਲ ਸਾਡੀ ਉਮਰ ਲੰਮੀ ਹੁੰਦੀ ਹੈ। ਇਸ ਨਾਲ ਸਾਡਾ ਸਰੀਰ ਕਈ ਬਿਮਾਰੀਆਂ ਤੋਂ ਬਚਿਆ ਰਹਿੰਦਾ ਹੈ। ਇਸ ਨਾਲ ਸਾਡੀ ਭੁੱਖ ਵਧਦੀ ਹੈ ਤੇ ਪਾਚਨ – ਸ਼ਕਤੀ ਤੇਜ਼ ਹੁੰਦੀ ਹੈ। ਜਿਹੜੇ ਹਰ ਰੋਜ਼ ਸੈਰ ਨਹੀਂ ਕਰਦੇ, ਉਹ ਕਿਸੇ ਨਾ ਕਿਸੇ ਬਿਮਾਰੀ ਦੇ ਸਹਿਜੇ ਹੀ ਸ਼ਿਕਾਰ ਹੋ ਜਾਂਦੇ ਹਨ ਸੈਰ ਉੱਤੇ ਮਨੁੱਖ ਦਾ ਕੋਈ ਮੁੱਲ ਨਹੀਂ ਲਗਦਾ ਪਰ ਇਹ ਸਰੀਰ ਨੂੰ ਇੰਨੇ ਫ਼ਾਇਦੇ ਦਿੰਦੀ ਹੈ, ਜੋ ਕੀਮਤੀ ਤੋਂ ਕੀਮਤੀ ਖੁਰਾਕ ਜਾਂ ਦੁਆਈ ਵੀ ਨਹੀਂ ਦੇ ਸਕਦੀ ਹੈ।
ਵਿਦਿਆਰਥੀ, ਜੋ ਸਾਰਾ ਦਿਨ ਕਿਤਾਬਾਂ ਨਾਲ ਮੱਥਾ ਮਾਰਦਾ ਹੈ, ਉਸ ਲਈ ਇਹ ਬਹੁਤ ਹੀ ਜ਼ਰੂਰੀ ਹੈ। ਇਹ ਉਸ ਦੇ ਦਿਮਾਗ਼ ਦੀ ਥਕਾਵਟ ਲਾਹ ਕੇ ਉਸ ਨੂੰ ਤਾਜ਼ਗੀ ਬਖਸ਼ਦੀ ਹੈ। ਇਸ ਨਾਲ ਉਸ ਦੀ ਬੁੱਧੀ ਤੇਜ਼ ਹੁੰਦੀ ਹੈ ਤੇ ਯਾਦ ਕਰਨ ਦੀ ਸ਼ਕਤੀ ਵਧਦੀ ਹੈ ; ਇਸ ਕਰਕੇ ਵਿਦਿਆਰਥੀਆਂ ਨੂੰ ਹਰ ਰੋਜ਼ ਸੈਰ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ।

12. ਲੋਹੜੀ ਦਾ ਤਿਉਹਾਰ
ਪੰਜਾਬ ਦਾ ਜੀਵਨ ਮੇਲਿਆਂ ਅਤੇ ਤਿਉਹਾਰਾਂ ਨਾਲ ਭਰਪੂਰ ਹੈ। ਸਾਲ ਵਿਚ ਸ਼ਾਇਦ ਹੀ ਕੋਈ ਅਜਿਹਾ ਮਹੀਨਾ ਹੋਵੇਗਾ, ਜਿਸ ਵਿਚ ਕੋਈ ਨਾ ਕੋਈ ਤਿਉਹਾਰ ਨਾ ਆਉਂਦਾ ਹੋਵੇ। ਲੋਹੜੀ ਵੀ ਪੰਜਾਬ ਦਾ ਇਕ ਖ਼ੁਸ਼ੀਆਂ ਭਰਿਆ ਤਿਉਹਾਰ ਹੈ, ਜੋ ਜਨਵਰੀ ਮਹੀਨੇ ਵਿਚ ਮਾਘੀ ਤੋਂ ਇਕ ਦਿਨ ਪਹਿਲਾਂ ਮਨਾਇਆ ਜਾਂਦਾ ਹੈ।
ਲੋਹੜੀ ਦੇ ਤਿਉਹਾਰ ਦੀ ਪਰੰਪਰਾ ਬਹੁਤ ਪੁਰਾਣੀ ਹੈ। ਵੈਦਿਕ ਕਾਲ ਵਿਚ ਵੀ ਰਿਸ਼ੀ ਲੋਕ ਦੇਵਤਿਆਂ ਨੂੰ ਖ਼ੁਸ਼ ਕਰਨ ਲਈ ਹਵਨ ਕਰਦੇ ਸਨ। ਇਸ ਧਾਰਮਿਕ ਕੰਮ ਵਿਚ ਪਰਿਵਾਰ ਦੇ ਬੰਦੇ ਹਵਨ ਵਿਚ ਘਿਓ, ਸ਼ਹਿਦ, ਤਿਲ ਅਤੇ ਗੁੜ ਆਦਿ ਪਾਉਂਦੇ ਸਨ। ਇਸ ਤਿਉਹਾਰ ਨਾਲ ਬਹੁਤ ਸਾਰੀਆਂ ਕਥਾਵਾਂ ਵੀ ਜੋੜੀਆਂ ਜਾਂਦੀਆਂ ਹਨ। ਇਕ ਕਥਾ ਅਨੁਸਾਰ ਲੋਹੜੀ ਦੇਵੀ ਨੇ ਇਕ ਅੱਤਿਆਚਾਰੀ ਰਾਕਸ਼ ਨੂੰ ਮਾਰਿਆ ਤੇ ਉਸ ਦੇਵੀ ਦੀ ਯਾਦ ਵਿਚ ਇਹ ਤਿਉਹਾਰ ਮਨਾਇਆ ਜਾਂਦਾ ਹੈ।
ਇਸ ਤਿਉਹਾਰ ਦਾ ਸੰਬੰਧ ਪੌਰਾਣਿਕ ਕਥਾ ‘ਸਤੀ – ਦਹਿਨ’ ਨਾਲ ਵੀ ਜੋੜਿਆ ਜਾਂਦਾ ਹੈ। ਇਸ ਤੋਂ ਬਿਨਾਂ ਇਸ ਨਾਲ ਇਕ ਹੋਰ ਲੋਕ – ਕਥਾ ਵੀ ਸੰਬੰਧਿਤ ਹੈ, ਜੋ ਇਸ ਪ੍ਰਕਾਰ ਹੈ। ਕਿਸੇ ਗ਼ਰੀਬ ਬਾਹਮਣ ਦੀ ਸੁੰਦਰੀ ਨਾਂ ਦੀ ਧੀ ਸੀ। ਬਾਹਮਣ ਨੇ ਉਸ ਦੀ ਕੁੜਮਾਈ ਇਕ ਥਾਂ ਪੱਕੀ ਕਰ ਦਿੱਤੀ, ਪਰੰਤੂ ਉੱਥੋਂ ਦੇ ਦੁਸ਼ਟ ਹਾਕਮ ਨੇ ਕੁੜੀ ਦੀ ਸੁੰਦਰਤਾ ਬਾਰੇ ਸੁਣ ਕੇ ਉਸ ਨੂੰ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਠਾਣ ਲਈ। ਇਹ ਸੁਣ ਕੇ ਕੁੜੀ ਦੇ ਬਾਪ ਨੇ ਮੁੰਡੇ ਵਾਲਿਆਂ ਨੂੰ ਕਿਹਾ ਕਿ ਉਹ ਕੁੜੀ ਨੂੰ ਵਿਆਹ ਤੋਂ ਪਹਿਲਾਂ ਹੀ ਆਪਣੇ ਘਰ ਲੈ ਜਾਣ, ਪਰ ਮੁੰਡੇ ਵਾਲੇ ਡਰ ਗਏ।
ਜਦੋਂ ਕੁੜੀ ਦਾ ਬਾਪ ਨਿਰਾਸ਼ ਹੋ ਕੇ ਵਾਪਸ ਜਾ ਰਿਹਾ ਸੀ, ਤਾਂ ਰਸਤੇ ਵਿਚ ਉਸ ਨੂੰ ਦੁੱਲਾ ਭੱਟੀ ਡਾਕੂ ਮਿਲਿਆ ਬਾਹਮਣ ਦੀ ਰਾਮ – ਕਹਾਣੀ ਸੁਣ ਕੇ ਉਸ ਨੇ ਉਸ ਨੂੰ ਮੱਦਦ ਕਰਨ ਤੇ ਉਸ ਦੀ ਧੀ ਨੂੰ ਆਪਣੀ ਧੀ ਬਣਾ ਕੇ ਵਿਹਾਉਣ ਦਾ ਭਰੋਸਾ ਦਿੱਤਾ। ਉਹ ਮੁੰਡੇ ਵਾਲਿਆਂ ਦੇ ਘਰ ਗਿਆ ਤੇ ਪਿੰਡ ਦੇ ਸਾਰਿਆਂ ਬੰਦਿਆਂ ਨੂੰ ਮਿਲ ਕੇ ਉਸ ਨੇ ਰਾਤ ਵੇਲੇ ਜੰਗਲ ਨੂੰ ਅੱਗ ਲਾ ਕੇ ਕੁੜੀ ਦਾ ਵਿਆਹ ਕਰ ਦਿੱਤਾ। ਗ਼ਰੀਬ ਬ੍ਰਾਹਮਣ ਦੀ ਧੀ ਦੇ ਕੱਪੜੇ ਵਿਆਹ ਸਮੇਂ ਵੀ ਫਟੇ – ਪੁਰਾਣੇ ਸਨ। ਦੁੱਲੇ ਭੱਟੀ ਦੇ ਕੋਲ ਉਸ ਸਮੇਂ ਕੇਵਲ ਸ਼ੱਕਰ ਸੀ।ਉਸਨੇ ਉਹ ਸ਼ੱਕਰ ਹੀ ਕੁੜੀ ਦੀ ਝੋਲੀ ਵਿਚ ਸ਼ਗਨ ਵਜੋਂ ਪਾਈ ਮਗਰੋਂ ਇਸ ਘਟਨਾ ਦੀ ਯਾਦ ਵਿਚ ਇਹ ਤਿਉਹਾਰ ਅੱਗ ਬਾਲ ਕੇ ਮਨਾਇਆ ਜਾਣ ਲੱਗਾ।
ਲੋਹੜੀ ਦਾ ਦਿਨ ਆਉਣ ਤੋਂ ਕੁੱਝ ਦਿਨ ਪਹਿਲਾਂ ਹੀ ਗਲੀਆਂ ਵਿਚ ਮੁੰਡਿਆਂ – ਕੁੜੀਆਂ ਦੀਆਂ ਢਾਣੀਆਂ ਗੀਤ ਗਾਉਂਦੀਆਂ ਹੋਈਆਂ ਲੋਹੜੀ ਮੰਗਦੀਆਂ ਫਿਰਦੀਆਂ ਹਨ। ਕੋਈ ਉਨ੍ਹਾਂ ਨੂੰ ਦਾਣੇ ਦਿੰਦਾ ਹੈ, ਕੋਈ ਗੁੜ, ਕੋਈ ਪਾਥੀਆਂ ਅਤੇ ਕੋਈ ਪੈਸੇ। ਲੋਹੜੀ ਮੰਗਣ ਵਾਲੀਆਂ ਟੋਲੀਆਂ ਦੇ ਗਲੀਆਂ ਵਿਚ ਗੀਤ ਗੂੰਜਦੇ ਹਨ –
ਸੁੰਦਰ, ਮੁੰਦਰੀਏ ਹੋ,
ਤੇਰਾ ਕੌਣ ਵਿਚਾਰਾ ? ਹੋ।
ਦੁੱਲਾ ਭੱਟੀ ਵਾਲਾ, ਹੋ।
ਦੁੱਲੇ ਦੀ ਧੀ ਵਿਆਹੀ, ਹੋ।
ਸੇਰ ਸ਼ੱਕਰ ਪਾਈ, ਹੋ।
ਕੁੜੀ ਦਾ ਬੋਝਾ ਪਾਟਾ, ਹੋ।
ਜੀਵੇ ਕੁੜੀ ਦਾ ਚਾਚਾ, ਹੋ।
ਲੰਬੜਦਾਰ ਸਦਾਏ, ਹੋ।
ਗਿਣ ਗਿਣ ਪੌਲੇ ਲਾਏ, ਹੋ।
ਇਕ ਪੌਲਾ ਰਹਿ ਗਿਆ, ਸਿਪਾਹੀ ਫੜ ਕੇ ਲੈ ਗਿਆ।
ਇਸ ਦਿਨ ਭਰਾ ਭੈਣ ਲਈ ਲੋਹੜੀ ਲੈ ਕੇ ਜਾਂਦੇ ਹਨ। ਉਹ ਪਿੰਨੀਆਂ ਤੇ ਖਾਣ – ਪੀਣ ਦੇ ਹੋਰ ਸਮਾਨ ਸਹਿਤ ਕੋਈ ਹੋਰ ਸੁਗਾਤ ਵੀ ਭੈਣ ਦੇ ਘਰ ਪੁਚਾਉਂਦੇ ਹਨ।
ਜਿਨ੍ਹਾਂ ਘਰਾਂ ਵਿਚ ਬੀਤੇ ਸਾਲ ਵਿਚ ਮੁੰਡੇ ਨੇ ਜਨਮ ਲਿਆ ਹੁੰਦਾ ਹੈ, ਉਸ ਘਰ ਵਿਚ ਵਿਸ਼ੇਸ਼ ਰੌਣਕਾਂ ਹੁੰਦੀਆਂ ਹਨ। ਇਸ ਘਰ ਦੀਆਂ ਇਸਤਰੀਆਂ ਸਾਰੇ ਮੁਹੱਲੇ ਵਿਚ ਮੁੰਡੇ ਦੀ ਲੋਹੜੀ ਵੰਡਦੀਆਂ ਹਨ, ਜਿਸ ਵਿਚ ਗੁੜ, ਮੁੰਗਫਲੀ ਤੇ ਰਿਉੜੀਆਂ ਆਦਿ ਸ਼ਾਮਲ ਹੁੰਦੀਆਂ ਹਨ ਸਾਰਾ ਦਿਨ ਉਸ ਘਰ ਵਿਚ ਲੋਹੜੀ ਮੰਗਣ ਵਾਲੇ ਮੁੰਡਿਆਂ – ਕੁੜੀਆਂ ਦੇ ਗੀਤਾਂ ਦੀਆਂ ਰੌਣਕਾਂ ਲੱਗੀਆਂ ਰਹਿੰਦੀਆਂ ਹਨ ! ਰਾਤ ਵੇਲੇ ਵੱਡੇ ਵੀ ਇਨ੍ਹਾਂ ਰੌਣਕਾਂ ਵਿਚ ਸ਼ਾਮਲ ਹੋ ਜਾਂਦੇ ਹਨ।
ਖੁੱਲ੍ਹੇ ਵਿਹੜੇ ਵਿਚ ਲੱਕੜਾਂ ਤੇ ਪਾਥੀਆਂ ਇਕੱਠੀਆਂ ਕਰ ਕੇ ਵੱਡੀ ਧੂਣੀ ਲਾਈ ਜਾਂਦੀ ਹੈ। ਕਈ ਇਸਤਰੀਆਂ ਘਰ ਵਿਚ ਮੁੰਡਾ ਹੋਣ ਦੀ ਖ਼ੁਸ਼ੀ ਧੂਣੀ ਵਿਚ ਆਪਣਾ ਚਰਖਾ ਵੀ ਬਾਲ ਦਿੰਦੀਆਂ ਹਨ। ਇਸਤਰੀਆਂ ਤੇ ਮਰਦ ਰਾਤ ਦੇਰ ਤਕ ਧੂਣੀ ਸੇਕਦੇ ਹੋਏ ਰਿਉੜੀਆਂ, ਮੂੰਗਫਲੀ, ਭੁੱਗਾ ਆਦਿ ਖਾਂਦੇ ਹਨ ਤੇ ਧੂਣੀ ਵਿਚ ਤਿਲਚੌਲੀ ਆਦਿ ਸੁੱਟਦੇ ਹਨ ਅੱਧੀ ਰਾਤ ਤੋਂ ਪਿੱਛੋਂ ਧੂਣੀ ਦੀ ਅੱਗ ਦੇ ਠੰਢੀ ਪੈਣ ਤਕ ਇਹ ਮਹਿਫ਼ਲ ਲੱਗੀ ਰਹਿੰਦੀ ਹੈ।

13. ਅੱਖੀਂ ਡਿੱਠਾ ਮੈਚ
मां
ਫੁੱਟਬਾਲ ਦਾ ਮੈਚ
ਐਤਵਾਰ ਦਾ ਦਿਨ ਸੀ। ਪਿਛਲੇ ਦੋ ਦਿਨਾਂ ਤੋਂ ਲਾਇਲਪੁਰ ਖ਼ਾਲਸਾ ਸੀਨੀਅਰ ਸੈਕੰਡਰੀ ਸਕੂਲ, ਜਲੰਧਰ ਦੇ ਖੇਡ ਦੇ ਮੈਦਾਨ ਵਿਚ ਫੁੱਟਬਾਲ ਦੇ ਮੈਚ ਹੋ ਰਹੇ ਸਨ ਫਾਈਨਲ ਮੈਚ ਸਾਡੇ ਸਕੂਲ (ਗੌਰਮਿੰਟ ਸੀਨੀਅਰ ਸੈਕੰਡਰੀ ਸਕੂਲ, ਟਾਊਨ ਹਾਲ, ਅੰਮ੍ਰਿਤਸਰ) ਦੀ ਟੀਮ ਅਤੇ ਦੁਆਬਾ ਸੀਨੀਅਰ ਸੈਕੰਡਰੀ ਸਕੂਲ, ਜਲੰਧਰ ਦੀ ਟੀਮ ਵਿਚਕਾਰ ਖੇਡਿਆ ਜਾਣਾ ਸੀ।
ਸ਼ਾਮ ਦੇ ਚਾਰ ਵਜੇ ਖਿਡਾਰੀ ਖੇਡ ਦੇ ਮੈਦਾਨ ਵਿਚ ਆ ਗਏ। ਰੈਫ਼ਰੀ ਨੇ ਠੀਕ ਸਮੇਂ ‘ਤੇ ਵਿਸਲ ਵਜਾਈ ਅਤੇ ਦੋਵੇਂ ਟੀਮਾਂ ਮੈਚ ਖੇਡਣ ਲਈ ਤਿਆਰ ਹੋ ਗਈਆਂ ਸਾਡੀ ਟੀਮ ਦਾ ਕੈਪਟਨ ਸਰਦੂਲ ਸਿੰਘ ਅਤੇ ਦੁਆਬਾ ਸਕੂਲ ਦੀ ਟੀਮ ਦਾ ਕੈਪਟਨ ਕਰਮ ਚੰਦ ਸੀ ਟਾਸ ਸਾਡੇ ਸਕੂਲ ਦੀ ਟੀਮ ਨੇ ਜਿੱਤਿਆ ਸਾਰੇ ਖਿਡਾਰੀ ਖੇਡ ਦੇ ਮੈਦਾਨ ਵਿਚ ਖਿੰਡ ਗਏ ਤੇ ਉਨ੍ਹਾਂ ਨੇ ਆਪਣੀਆਂ ਪੁਜ਼ੀਸ਼ਨਾਂ ਸੰਭਾਲ ਲਈਆਂ।
ਰੈਫ਼ਰੀ ਦੀ ਵਿਸਲ ਨਾਲ ਅੱਖ ਫ਼ਰਕਣ ਦੇ ਸਮੇਂ ਵਿਚ ਹੀ ਖੇਡ ਆਰੰਭ ਹੋ ਗਈ। ਮੈਚ ਦੇਖਣ ਵਾਲਿਆਂ ਦੀ ਗਿਣਤੀ 5 ਹਜ਼ਾਰ ਤੋਂ ਵੀ ਜ਼ਿਆਦਾ ਸੀ ਪਹਿਲਾਂ ਤਾਂ 15 ਕੁ ਮਿੰਟ ਸਾਡੀ ਟੀਮ ਖੂਬ ਅੜੀ ਰਹੀ, ਪਰ ਦੁਆਬਾ ਹਾਈ ਸਕੂਲ ਦੇ ਫਾਰਵਰਡਾਂ ਨੇ ਬਾਲ ਨੂੰ ਸਾਡੇ ਗਲਾਂ ਵਲ ਹੀ ਰੱਖਿਆ ਸਾਡਾ ਬਿੱਲਾ ਰਾਈਟ – ਆਉਟ ਖੇਡਦਾ ਸੀ। ਜਦੋਂ ਬਾਲ ਉਸ ਕੋਲ ਆਇਆ, ਤਾਂ ਉਹ ਜਲਦੀ ਹੀ ਮੈਦਾਨ ਦੀ ਹੱਦ ਦੇ ਨਾਲ – ਨਾਲ ਉਨ੍ਹਾਂ ਦੇ ਗੋਲਾਂ ਪਾਸ ਪੁੱਜ ਗਿਆ।
ਉਸ ਨੇ ਬਾਲ ਕੈਪਟਨ ਸਰਦੂਲ ਸਿੰਘ ਨੂੰ ਦਿੱਤਾ ਹੀ ਸੀ ਕਿ ਉਨ੍ਹਾਂ ਦੇ ਫੁੱਲ – ਬੈਕਾਂ ਨੇ ਉਸ ਪਾਸੋਂ ਬਾਲ ਲੈ ਲਿਆ ਤੇ ਇੰਨੀ ਜ਼ੋਰ ਦੀ ਕਿੱਕ ਮਾਰੀ ਕਿ ਬਾਲ ਮੁੜ ਸਾਡੇ ਗੋਲਾਂ ਵਿਚ ਆ ਗਿਆ, ਪਰ ਸਾਡਾ ਗੋਲਕੀਪਰ ਬਹੁਤ ਚੌਕੰਨਾ ਸੀ ਬਾਲ ਉਸ ਦੇ ਪਾਸ ਪੁੱਜਾ ਹੀ ਸੀ ਕਿ ਉਸ ਨੇ ਰੋਕ ਲਿਆ ਅਚਾਨਕ ਹੀ ਅੱਧੇ ਸਮੇਂ ਦੀ ਵਿਸਲ ਵੱਜ ਗਈ। ਕੁੱਝ ਮਿੰਟਾਂ ਮਗਰੋਂ ਖੇਡ ਦੂਜੀ ਵਾਰ ਆਰੰਭ ਹੋਈ। ਉਨ੍ਹਾਂ ਦੇ ਖੱਬੇ – ਆਊਟ ਨੇ ਅਜਿਹੀ ਕਿੱਕ ਮਾਰੀ ਕਿ ਬਾਲ ਉਨ੍ਹਾਂ ਦੇ ਕੈਪਟਨ ਪਾਸ ਪੁੱਜ ਗਿਆ।
ਦਰਸ਼ਕਾਂ ਨੇ ਤਾੜੀਆਂ ਵਜਾਈਆਂ ਅਚਾਨਕ ਹੀ ਬਾਲ ਸਾਡੇ ਫੱਲ – ਬੈਕ ਕੋਲੋਂ ਹੁੰਦਾ ਹੋਇਆ ਸਾਡੇ ਗੋਲਾਂ ਕੋਲ ਜਾ ਪੁੱਜਾ। ਗੋਲਚੀ ਦੇ ਬਹੁਤ ਯਤਨ ਕਰਨ ‘ਤੇ ਵੀ ਸਾਡੇ ਸਿਰ ਇਕ ਗੋਲ ਹੋ ਗਿਆ। ਹੁਣ ਉਨ੍ਹਾਂ ਦੀ ਚੜ੍ਹ ਬਹੁਤ ਜ਼ਿਆਦਾ ਮਚ ਗਈ।
ਸਮਾਂ ਕੇਵਲ 10 ਮਿੰਟ ਹੀ ਰਹਿ ਗਿਆ ਸਾਡੇ ਕੈਪਟਨ ਨੇ ਬਾਲ ਉਨ੍ਹਾਂ ਦੇ ਦੋ ਖਿਡਾਰੀਆਂ ਵਿਚੋਂ ਕੱਢ ਕੇ ਰਾਈਟ – ਆਉਟ ਨੂੰ ਦਿੱਤਾ। ਉਸ ਨੇ ਨੁੱਕਰ ਉੱਤੇ ਜਾ ਕੇ ਅਜਿਹੀ ਕਿੱਕ ਮਾਰੀ ਕਿ ਗੋਲ ਉਤਾਰ ਦਿੱਤਾ।
ਇਸ ਵੇਲੇ ਖੇਡ ਬਹੁਤ ਗਰਮਜ਼ੋਸ਼ੀ ਨਾਲ ਖੇਡੀ ਜਾ ਰਹੀ ਸੀ ਅਚਾਨਕ ਬਾਲ ਸਾਡੇ ਗੋਲਾਂ ਵਿਚ ਪੁੱਜ ਗਿਆ। ਜੇਕਰ ਸਾਡਾ ਗੋਲਚੀ ਚੁਸਤੀ ਨਾ ਦਿਖਾਉਂਦਾ, ਤਾਂ ਗੋਲ ਹੋ ਜਾਂਦਾ। ਇਸ ਪਿੱਛੋਂ ਸਾਡੇ ਕੈਪਟਨ ਨੇ ਸੈਂਟਰ ਵਿਚੋਂ ਅਜਿਹੀ ਕਿੱਕ ਮਾਰੀ ਕਿ ਉਨ੍ਹਾਂ ਦੇ ਗੋਲਚੀ ਨੇ ਰੋਕ ਤਾਂ ਲਈ, ਪਰੰਤੁ ਬਾਲ ਖਿਸਕ ਕੇ ਗੋਲਾਂ ਵਿਚੋਂ ਲੰਘ ਗਿਆ ਰੈਫ਼ਰੀ ਨੇ ਵਿਸਲ ਮਾਰ ਕੇ ਗੋਲ ਦਾ ਐਲਾਨ ਕਰ ਦਿੱਤਾ। ਇਕ ਮਿੰਟ ਮਗਰੋਂ ਹੀ ਖੇਡ ਸਮਾਪਤ ਹੋ ਗਈ। ਅਸੀਂ ਮੈਚ ਜਿੱਤ ਗਏ। ਇਹ ਮੈਚ ਜਿੱਤ ਕੇ ਅਸੀਂ ਜ਼ਿਲ੍ਹੇ ਵਿਚੋਂ ਪਹਿਲੇ ਨੰਬਰ ਤੇ ਰਹੇ।

14. ਸਿਨਮੇ ਦੇ ਲਾਭ ਤੇ ਹਾਨੀਆਂ
ਸਿਨਮਾ ਵਰਤਮਾਨ ਮਨੁੱਖੀ ਜੀਵਨ ਦਾ ਇਕ ਮਹੱਤਵਪੂਰਨ ਅੰਗ ਹੈ ! ਉਂਝ ਹੁਣ ਘਰ – ਘਰ ਟੈਲੀਵਿਯਨ ਦੇ ਆਉਣ ਨਾਲ ਇਸ ਦੀ ਲੋਕ – ਪ੍ਰਿਅਤਾ ਪਹਿਲਾਂ ਜਿੰਨੀ ਨਹੀਂ ਰਹੀ ਪਰ ਫਿਰ ਵੀ ਲੋਕ ਸਿਨਮਾ ਦੇਖਣ ਜਾਂਦੇ ਹਨ। ਇਸ ਦੇ ਬਹੁਤ ਸਾਰੇ ਲਾਭ ਵੀ ਹਨ ਤੇ ਨੁਕਸਾਨ ਵੀ। ਇਸ ਦੇ ਲਾਭ ਹੇਠਾਂ ਲਿਖੇ ਹਨ ਸਿਨਮੇ ਦਾ ਸਭ ਤੋਂ ਵੱਡਾ ਲਾਭ ਇਹ ਹੈ ਕਿ ਇਹ ਲੋਕਾਂ ਦੇ ਦਿਲ – ਪਰਚਾਵੇ ਦਾ ਸਭ ਤੋਂ ਵਧੀਆ ਤੇ ਸਸਤਾ ਸਾਧਨ ਹੈ।
ਦਿਨ ਭਰ ਦਾ ਕੰਮ ਨਾਲ ਥੱਕਿਆ – ਟੁੱਟਿਆ ਬੰਦਾ ਸਿਨਮੇ ਵਿਚ ਜਾ ਕੇ ਭਿੰਨ – ਭਿੰਨ ਪ੍ਰਕਾਰ ਦੀਆਂ ਫ਼ਿਲਮਾਂ, ਨਾਚਾਂ, ਗਾਣਿਆਂ, ਹਸਾਉਣੇ ਤੇ ਰੁਆਉਣੇ ਦ੍ਰਿਸ਼ਾਂ, ਮਾਰ – ਕੁਟਾਈ ਤੇ ਕੁਦਰਤੀ ਦ੍ਰਿਸ਼ਾਂ ਨਾਲ ਆਪਣਾ ਮਨ ਪਰਚਾ ਲੈਂਦਾ ਹੈ। ਸਿਨਮੇ ਦਾ ਦੂਜਾ ਵੱਡਾ ਲਾਭ ਇਹ ਹੈ ਕਿ ਇਸ ਰਾਹੀਂ ਅਸੀਂ ਭਿੰਨ – ਭਿੰਨ ਪ੍ਰਕਾਰ ਦੀ ਜਾਣਕਾਰੀ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ ਇਸ ਤੋਂ ਬਿਨਾਂ ਸਿਨਮੇ ਰਾਹੀਂ ਖੇਤੀਬਾੜੀ, ਸਿਹਤ, ਪਰਿਵਾਰ ਭਲਾਈ, ਸੁਰੱਖਿਆ ਤੇ ਵਿੱਦਿਆ ਦੇ ਮਹਿਕਮੇ ਲੋਕਾਂ ਨੂੰ ਭਿੰਨ – ਭਿੰਨ ਪ੍ਰਕਾਰ ਦੀ ਜਾਣਕਾਰੀ ਦਿੰਦੇ ਹਨ।
ਸਿਨਮੇ ਦਾ ਦੇਸ਼ ਦੀ ਵਿੱਦਿਅਕ ਉੱਨਤੀ ਵਿਚ ਕਾਫ਼ੀ ਹਿੱਸਾ ਹੈ। ਸਿਨਮੇ ਰਾਹੀਂ ਵਿਦਿਆਰਥੀਆਂ ਨੂੰ ਕਾਫ਼ੀ ਲਾਭ ਪੁਚਾਇਆ ਜਾ ਸਕਦਾ ਹੈ।
ਸਿਨਮੇ ਤੋਂ ਵਪਾਰੀ ਲੋਕ ਵੀ ਖੂਬ ਲਾਭ ਉਠਾਉਂਦੇ ਹਨ। ਉਹ ਆਪਣੀਆਂ ਚੀਜ਼ਾਂ ਦੀ ਸਿਨਮੇ ਰਾਹੀਂ ਮਸ਼ਹੂਰੀ ਕਰ ਕੇ ਲਾਭ ਉਠਾਉਂਦੇ ਹਨ।
ਸਿਨਮੇ ਦਾ ਇਕ ਹੋਰ ਲਾਭ ਇਹ ਵੀ ਹੈ ਕਿ ਫ਼ਿਲਮ ਸਨਅਤ ਅਤੇ ਸਿਨਮਾਘਰਾਂ ਵਿਚ ਸੈਂਕੜੇ ਲੋਕ ਕੰਮ ਕਰ ਕੇ ਆਪਣੇ ਪੇਟ ਪਾਲ ਰਹੇ ਹਨ।
ਜਿੱਥੇ ਸਿਨਮੇ ਦੇ ਇੰਨੇ ਲਾਭ ਹਨ, ਉੱਥੇ ਇਸ ਦੀਆਂ ਹਾਨੀਆਂ ਵੀ ਹਨ ਇਸ ਦਾ ਸਭ ਤੋਂ ਵੱਡਾ ਨੁਕਸਾਨ ਇਹ ਹੈ ਕਿ ਅਸ਼ਲੀਲ ਫ਼ਿਲਮਾਂ ਦਾ ਨੌਜਵਾਨਾਂ ਦੇ ਆਚਰਨ ਉੱਪਰ ਬਹੁਤ ਬੁਰਾ ਅਸਰ ਪੈਂਦਾ ਹੈ। ਨੌਜਵਾਨ ਤੇ ਮੁਟਿਆਰਾਂ ਇਨ੍ਹਾਂ ਨੂੰ ਦੇਖ ਕੇ ਫ਼ੈਸ਼ਨ – ਪ੍ਰਸਤੀ ਵਲ ਪੈ ਜਾਂਦੇ ਹਨ ਤੇ ਜੀਵਨ ਦੇ ਅਸਲ ਮੰਤਵ ਨੂੰ ਭੁੱਲ ਜਾਂਦੇ ਹਨ, ਪਰ ਹੁਣ ਇਸ ਦੋਸ਼ ਵਿਚ ਟੀ. ਵੀ. ਸਿਨਮੇ ਨਾਲੋਂ ਅੱਗੇ ਨਿਕਲ ਗਿਆ ਹੈ। ਸਿਨਮੇ ਉੱਪਰ ਤਾਂ ਸੈਂਸਰ ਬੋਰਡ ਬੈਠਾ ਹੈ, ਪਰ ਟੀ.ਵੀ. ਦੀਆਂ ਲਗਾਮਾਂ ਵਧੇਰੇ ਖੁੱਲ੍ਹੀਆਂ ਹਨ ਤੇ ਉਹ ਦੇਖਿਆ ਵੀ ਘਰ – ਘਰ ਜਾਂਦਾ ਹੈ। ਬਹੁਤਾ ਸਿਨਮਾ ਵੇਖਣ ਨਾਲ ਟੀ.ਵੀ. ਸਕਰੀਨ ਵਾਂਗ ਹੀ ਸਿਨਮੇ ਦੇ ਪਰਦੇ ਉੱਪਰ ਪੈ ਰਹੀ ਤੇਜ਼ ਰੌਸ਼ਨੀ ਦਾ ਮਨੁੱਖੀ ਨਜ਼ਰ ਉੱਪਰ ਬੁਰਾ ਅਸਰ ਪੈਂਦਾ ਹੈ।
ਮੁੱਕਦੀ ਗੱਲ ਇਹ ਹੈ ਕਿ ਸਿਨਮਾ ਦਿਲ – ਪਰਚਾਵੇ ਦਾ ਵਧੀਆ ਤੇ ਸਸਤਾ ਸਾਧਨ ਹੈ, ਪਰ ਇਸ ਦੀਆਂ ਹਾਨੀਆਂ ਨੂੰ ਦੂਰ ਕਰਨ ਵਲ ਸਰਕਾਰ ਨੂੰ ਧਿਆਨ ਦੇਣਾ ਚਾਹੀਦਾ ਹੈ।
15. ਅਖ਼ਬਾਰਾਂ ਦੇ ਲਾਭ – ਹਾਨੀਆਂ
ਅਖ਼ਬਾਰਾਂ ਵਰਤਮਾਨ ਜੀਵਨ ਦਾ ਮਹੱਤਵਪੂਰਨ ਅੰਗ ਹਨ। ਆਦਮੀ ਨੂੰ ਸਵੇਰੇ ਉੱਠਦਿਆਂ ਹੀ ਇਹ ਆਪਣੇ ਰਸ ਵਿਚ ਕੀਲ ਲੈਂਦੀਆਂ ਹਨ। ਅਖ਼ਬਾਰਾਂ ਤੋਂ ਸਾਨੂੰ ਬਹੁਤ ਸਾਰੇ ਲਾਭ ਹਨ, ਜੋ ਹੇਠ ਲਿਖੇ ਹਨ ਅਖ਼ਬਾਰਾਂ ਦਾ ਸਾਨੂੰ ਸਭ ਤੋਂ ਵੱਡਾ ਲਾਭ ਇਹ ਹੈ ਕਿ ਇਹ ਸਵੇਰੇ ਉੱਠਦਿਆਂ ਹੀ ਸਾਨੂੰ ਦੁਨੀਆ ਭਰ ਦੀਆਂ ਖ਼ਬਰਾਂ ਲਿਆ ਦਿੰਦੀਆਂ ਹਨ ਅਸੀਂ ਘਰ ਬੈਠੇ – ਬਿਠਾਏ ਸੰਸਾਰ ਭਰ ਦੇ ਹਾਲਾਤਾਂ ਤੋਂ ਜਾਣੂ ਹੋ ਜਾਂਦੇ ਹਾਂ ਸਾਨੂੰ ਪਤਾ ਲਗ ਜਾਂਦਾ ਹੈ ਕਿ ਕਿੱਥੇ ਹੜਤਾਲ ਹੋਈ ਹੈ, ਜਿੱਥੇ ਪੁਲਿਸ ਨੇ ਲਾਠੀ – ਗੋਲੀ ਚਲਾਈ ਹੈ ਤੇ ਕਿੱਥੇ ਦੁਰਘਟਨਾਵਾਂ ਹੋਈਆਂ ਹਨ।
ਅਖ਼ਬਾਰਾਂ ਤੋਂ ਅਸੀਂ ਭਿੰਨ – ਭਿੰਨ ਪ੍ਰਕਾਰ ਦੀ ਜਾਣਕਾਰੀ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ। ਇਹ ਸੂਚਨਾ – ਸੰਚਾਰ ਦਾ ਪ੍ਰਮੁੱਖ ਸਾਧਨ ਹੈ, ਜਿਸ ਤੋਂ ਅਸੀਂ ਖੇਤੀ – ਬਾੜੀ, ਵਿੱਦਿਆ, ਸਿਹਤ ਤੇ ਆਪਣੇ ਸੱਭਿਆਚਾਰ ਨੂੰ ਉੱਨਤ ਕਰਨ ਲਈ ਕਾਫ਼ੀ ਲਾਭ ਪ੍ਰਾਪਤ ਕਰ ਸਕਦੇ ਹਾਂ। ਇਨ੍ਹਾਂ ਨੂੰ ਪੜ੍ਹਨ ਨਾਲ ਮਨੁੱਖ ਦੇ ਗਿਆਨ ਵਿਚ ਬਹੁਪੱਖੀ ਵਾਧਾ ਹੁੰਦਾ ਹੈ। ਇਸ ਤੋਂ ਇਲਾਵਾ ਅਖ਼ਬਾਰਾਂ ਵਿਚ ਭਿੰਨ – ਭਿੰਨ ਅਦਾਰਿਆਂ ਵਲੋਂ ਆਪਣੀਆਂ ਚੀਜ਼ਾਂ ਤੇ ਪ੍ਰੋਗਰਾਮਾਂ ਬਾਰੇ ਇਸ਼ਤਿਹਾਰ ਦਿੱਤੇ ਜਾਂਦੇ ਹਨ, ਜਿਨ੍ਹਾਂ ਤੋਂ ਅਸੀਂ ਕਾਫ਼ੀ ਲਾਭ ਉਠਾ ਸਕਦੇ ਹਾਂ ਅਸੀਂ ਅਖ਼ਬਾਰਾਂ ਵਿਚੋਂ ਰੁਜ਼ਗਾਰ ਲਈ ਖ਼ਾਲੀ ਥਾਂਵਾਂ ਦੀ ਜਾਣਕਾਰੀ ਵੀ ਪ੍ਰਾਪਤ ਕਰ ਸਕਦੇ ਹਾਂ।
ਮਨੁੱਖ ਦੇ ਦਿਲ – ਪਰਚਾਵੇ ਲਈ ਅਖ਼ਬਾਰਾਂ ਵਿਚ ਬਹੁਤ ਕੁੱਝ ਹੁੰਦਾ ਹੈ। ਇਸ ਵਿਚ ਸਾਹਿਤ, ਲੋਕ – ਸਾਹਿਤ, ਫ਼ਿਲਮਾਂ, ਚੁਟਕਲਿਆਂ, ਭਿੰਨ – ਭਿੰਨ ਵਿਸ਼ਿਆਂ ਸੰਬੰਧੀ ਗੰਭੀਰ ਲੇਖਾਂ ਤੇ ਜੀਵਨ ਦੇ ਹੋਰ ਬਹੁਤ ਸਾਰੇ ਪੱਖਾਂ ਬਾਰੇ ਅਗਵਾਈ ਕਰਨ ਵਾਲੀ ਬਹੁਮੁੱਲੀ ਜਾਣਕਾਰੀ ਹੁੰਦੀ ਹੈ। ਅਖ਼ਬਾਰਾਂ ਵਿਚੋਂ ਅਸੀਂ ਦਿਲ – ਪਰਚਾਵੇ ਦੇ ਸਾਧਨਾਂ ਫ਼ਿਲਮਾਂ, ਰੇਡੀਓ ਤੇ ਟੈਲੀਵਿਜ਼ਨ ਦੇ ਪ੍ਰੋਗਰਾਮਾਂ ਬਾਰੇ ਵੀ ਜਾਣਕਾਰੀ ਪ੍ਰਾਪਤ ਕਰ ਸਕਦੇ ਹਾਂ।

ਪੁਰਾਣੀਆਂ ਅਖ਼ਬਾਰਾਂ ਬੇਕਾਰ ਨਹੀਂ ਜਾਂਦੀਆਂ, ਸਗੋਂ ਇਨ੍ਹਾਂ ਦੇ ਕਾਗ਼ਜ਼ ਨੂੰ ਰੱਦੀ ਦੇ ਰੂਪ ਵਿਚ ਵੇਚ ਕੇ ਪੈਸੇ ਵੱਟ ਲਏ ਜਾਂਦੇ ਹਨ। ਅਖ਼ਬਾਰਾਂ ਇੰਨਾ ਲਾਭ ਪਹੁੰਚਾਉਣ ਤੋਂ ਇਲਾਵਾ ਕਈ ਵਾਰ ਸਮਾਜ ਨੂੰ ਨੁਕਸਾਨ ਵੀ ਪੁਚਾਉਂਦੀਆਂ ਹਨ। ਸਭ ਤੋਂ ਹਾਨੀਕਾਰਕ ਗੱਲ ਇਨ੍ਹਾਂ ਵਿਚ ਭੜਕਾਊ ਖ਼ਬਰਾਂ ਦਾ ਛਪਣਾ ਹੈ। ਕਈ ਵਾਰ ਖ਼ੁਦਗਰਜ਼ ਤੇ ਸਵਾਰਥੀ ਹੱਥਾਂ ਵਿਚ ਚਲ ਰਹੀਆਂ ਅਖ਼ਬਾਰਾਂ ਝੂਠੀਆਂ ਖ਼ਬਰਾਂ ਛਾਪ ਕੇ ਸਮਾਜਿਕ ਵਾਤਾਵਰਨ ਨੂੰ ਗੰਧਲਾ ਕਰਦੀਆਂ ਹਨ।
ਅਖ਼ਬਾਰਾਂ ਵਿਚ ਅਸ਼ਲੀਲ ਫੋਟੋਆਂ ਤੇ ਮਨ – ਘੜਤ ਕਹਾਣੀਆਂ ਦਾ ਛਪਣਾ ਨੌਜਵਾਨਾਂ ਦੇ ਆਚਰਨ ‘ਤੇ ਬੁਰਾ ਅਸਰ ਪਾਉਂਦਾ ਹੈ।
ਅੰਤ ਵਿਚ ਅਸੀਂ ਕਹਿ ਸਕਦੇ ਹਾਂ ਕਿ ਅਖ਼ਬਾਰਾਂ ਕੁੱਝ ਹਾਨੀਆਂ ਦੇ ਬਾਵਜੂਦ ਸਾਡੇ ਜੀਵਨ ਲਈ ਬਹੁਤ ਲਾਭਦਾਇਕ ਹਨ।
16. ਵਿਗਿਆਨ ਦੇ ਚਮਤਕਾਰ
20ਵੀਂ ਸਦੀ ਨੂੰ ਵਿਗਿਆਨ ਦਾ ਯੁਗ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ਤੇ ਇਹ ਆਪਣੀਆਂ ਕਾਢਾਂ ਤੇ ਖੋਜਾਂ ਨਾਲ ਮਨੁੱਖੀ ਜੀਵਨ ਵਿਚ ਕ੍ਰਾਂਤੀਕਾਰੀ ਤਬਦੀਲੀਆਂ ਲਿਆਉਂਦਾ ਹੋਇਆ ਅੱਜ 21ਵੀਂ ਸਦੀ ਵਿਚ ਪ੍ਰਵੇਸ਼ ਕਰ ਚੁੱਕਾ ਹੈ। ਵਿਗਿਆਨ ਦੀਆਂ ਕਾਢਾਂ ਨੇ ਸਾਡੇ ਹਰ ਪ੍ਰਕਾਰ ਦੇ ਜੀਵਨ ਵਿਚ ਨਵਾਂ ਪਲਟਾ ਲੈ ਆਂਦਾ ਹੈ ! ਇਸ ਨੇ ਜਿੱਥੇ ਬਹੁਤ ਸਾਰੀਆਂ ਲਾਭਦਾਇਕ ਕਾਢਾਂ ਕੱਢ ਕੇ ਮਨੁੱਖ ਨੂੰ ਸੁਖ ਦਿੱਤਾ ਹੈ, ਉੱਥੇ ਇਸ ਨੇ ਐਟਮ ਤੇ ਹਾਈਡਰੋਜਨ ਬੰਬਾਂ ਜਿਹੇ ਭਿਆਨਕ ਹਥਿਆਰ ਬਣਾ ਕੇ ਤੇ ਵਾਤਾਵਰਨ ਨੂੰ ਪਲੀਤ ਕਰ ਕੇ ਧਰਤੀ ਉੱਤੇ ਮਨੁੱਖ ਸਮੇਤ ਸਮੁੱਚੇ ਜੀਵਾਂ ਤੇ ਬਨਸਪਤੀ ਦੀ ਹੋਂਦ ਲਈ ਖ਼ਤਰਾ ਪੈਦਾ ਕਰ ਦਿੱਤਾ ਹੈ।
ਵਿਗਿਆਨ ਦੀਆਂ ਮਾਰੂ ਕਾਢਾਂ ਤੇ ਦੇਣਾਂ ਦੇ ਉਲਟ ਉਸਾਰੂ ਕਾਢਾਂ ਨੇ ਸਾਡੇ ਰੋਜ਼ਾਨਾ ਜੀਵਨ ਨੂੰ ਬੜੇ ਸੁਖ, ਅਰਾਮ ਅਤੇ ਲਾਭ ਪਹੁੰਚਾ ਕੇ ਇਸ ਵਿਚ ਤੇਜ਼ੀ ਲੈ ਆਂਦੀ ਹੈ। ਇਨ੍ਹਾਂ ਵਿਚੋਂ ਵਿਗਿਆਨ ਦੀ ਸਭ ਤੋਂ ਮਹੱਤਵਪੂਰਨ ਕਾਢ ਬਿਜਲੀ ਹੈ। ਸਾਡੇ ਜੀਵਨ ਦੇ ਬਹੁਤੇ ਕੰਮ ਇਸੇ ਨਾਲ ਚਲਦੇ ਹਨ। ਇਹ ਸਾਡੇ ਘਰਾਂ ਵਿਚ ਰੌਸ਼ਨੀ ਕਰਦੀ ਹੈ, ਪੱਖੇ ਚਲਾਉਂਦੀ ਹੈ, ਖਾਣਾ ਬਣਾਉਣ ਵਿਚ ਸਹਾਇਤਾ ਕਰਦੀ ਹੈ, ਕੱਪੜੇ ਐੱਸ ਕਰਨ ਵਿਚ ਮੱਦਦ ਦਿੰਦੀ ਹੈ। ਗਰਮੀਆਂ ਵਿਚ ਕਮਰਿਆਂ ਨੂੰ ਠੰਢੇ ਕਰਨ ਤੇ ਸਰਦੀਆਂ ਵਿਚ ਕਮਰਿਆਂ ਨੂੰ ਗਰਮ ਕਰਨ ਵਿਚ ਮੱਦਦ ਦਿੰਦੀ ਹੈ। ਇਹੋ ਹੀ ਕਾਰਖ਼ਾਨੇ ਚਲਾਉਂਦੀ ਹੈ, ਜਿੱਥੇ ਬਹੁਤ ਸਾਰਾ ਉਤਪਾਦਨ ਹੁੰਦਾ ਹੈ। ਇਹੋ ਹੀ ਕੰਪਿਊਟਰ, ਫੋਟੋ – ਸਟੇਟ ਤੇ ਰੋਬੋਟ ਆਦਿ ਚਲਾਉਂਦੀ ਹੈ।
ਵਿਗਿਆਨ ਦੀ ਦੂਜੀ ਮਹੱਤਵਪੂਰਨ ਕਾਢ ਆਵਾਜਾਈ ਦੇ ਮਸ਼ੀਨੀ ਸਾਧਨਾਂ ਦੀ ਹੈ, ਜਿਨ੍ਹਾਂ ਵਿਚ ਸਕੂਟਰ, ਮੋਟਰ – ਸਾਈਕਲ, ਮੋਟਰਾਂ, ਕਾਰਾਂ, ਗੱਡੀਆਂ ਤੇ ਹਵਾਈ ਜਹਾਜ਼ ਸ਼ਾਮਲ ਹਨ। ਇਹ ਸਾਧਨ ਸਾਨੂੰ ਬਹੁਤ ਥੋੜੇ ਸਮੇਂ ਵਿਚ ਤੇ ਘੱਟ ਖ਼ਰਚ ਨਾਲ ਇਕ ਥਾਂ ਤੋਂ ਦੂਜੀ ਥਾਂ ‘ਤੇ ਪੁਚਾ ਦਿੰਦੇ ਹਨ। ਇਨ੍ਹਾਂ ਤੋਂ ਬਿਨਾਂ ਸਾਡਾ ਵਰਤਮਾਨ ਜੀਵਨ ਇਕ ਘੜੀ ਵੀ ਨਹੀਂ ਚਲ ਸਕਦਾ ਇਸ ਦੇ ਨਾਲ ਹੀ ਵਿਗਿਆਨ ਦੀ ਮਹੱਤਵਪੂਰਨ ਕਾਢ ਸੰਚਾਰ ਦੇ ਸਾਧਨਾਂ ਦੀ ਹੈ, ਜਿਨ੍ਹਾਂ ਵਿਚ ਟੈਲੀਫ਼ੋਨ, ਵਾਇਰਲੈਂਸ, ਰੇਡੀਓ, ਟੈਲੀਵਿਜ਼ਨ, ਮੋਬਾਇਲ ਫ਼ੋਨ ਤੇ ਈ – ਮੇਲ ਸ਼ਾਮਲ ਹਨ।ਇਨ੍ਹਾਂ ਰਾਹੀਂ ਅਸੀਂ ਘਰ ਬੈਠਿਆਂ ਹੀ ਦੂਰ – ਦੂਰ ਤਕ ਸੁਨੇਹੇ ਭੇਜ ਸਕਦੇ ਹਾਂ।
ਵਿਗਿਆਨ ਨੇ ਬਹੁਤ ਸਾਰੇ ਮਨ – ਪਰਚਾਵੇ ਦੇ ਸਾਧਨ ਵੀ ਵਿਕਸਿਤ ਕੀਤੇ; ਜਿਵੇਂ ਰੇਡੀਓ, ਟਾਂਜ਼ਿਸਟਰ, ਟੈਲੀਵਿਯਨ, ਸਿਨੇਮਾ, ਵੀ.ਡੀ.ਓ. ਗੇਮਾਂ, ਕੰਪਿਊਟਰ, ਸੀ. ਡੀ. ਪਲੇਅਰ, ਕੈਸਟ ਪਲੇਅਰ ਆਦਿ ਸ਼ਾਮਲ ਹਨ। ਵਿਗਿਆਨ ਦੀ ਕਾਢ ਕੰਪਿਉਟਰ ਨੇ ਅਜੋਕੇ ਯੁਗ ਵਿਚ ਇਨਕਲਾਬ ਲੈ ਆਂਦਾ ਹੈ। ਕੰਪਿਉਟਰ ਇਕ ਤਰ੍ਹਾਂ ਦਾ ਮਨੁੱਖੀ ਦਿਮਾਗ ਹੈ, ਜੋ ਬਹੁਤ ਹੀ ਤੇਜ਼ੀ ਅਤੇ ਸੁਯੋਗਤਾ ਨਾਲ ਮਨੁੱਖੀ ਦਿਮਾਗ਼ ਵਾਲੇ ਸਾਰੇ ਕੰਮ ਕਰਦਾ ਹੈ।
ਕੰਪਿਊਟਰ ਦੀ ਵਰਤੋਂ ਵੱਡੇ – ਵੱਡੇ ਉਤਪਾਦਨ ਕੇਂਦਰਾਂ, ਵਪਾਰਕ ਅਦਾਰਿਆਂ, ਦਫ਼ਤਰਾਂ ਤੇ ਘਰਾਂ, ਗੱਲ ਕੀ ਜੀਵਨ ਦੇ ਹਰ ਖੇਤਰ ਵਿੱਚ ਹੁੰਦੀ ਹੈ। ਇਸ ਨਾਲ ਕੰਮ – ਕਾਰ ਵਿਚ ਬਹੁਤ ਤੇਜ਼ੀ ਆ ਗਈ ਹੈ। ਇਹ ਵਿਗਿਆਨੀਆਂ, ਡਾਕਟਰਾਂ ਤੇ ਕਲਾਕਾਰਾਂ ਦੇ ਕੰਮਾਂ ਵਿਚ ਵੀ ਸ਼ਾਮਲ ਹੁੰਦਾ ਹੈ। ਇੰਟਰਨੈੱਟ ਰਾਹੀਂ ਇਸ ਨੇ ਸਾਰੀ ਦੁਨੀਆ ਲਈ ਗਿਆਨ, ਜਾਣਕਾਰੀ ਅਤੇ ਭਿੰਨ – ਭਿੰਨ ਸੇਵਾਵਾਂ ਦੇ ਭੰਡਾਰ ਖੋਲ੍ਹਣ ਦੇ ਨਾਲ – ਨਾਲ ਬਹੁਪੱਖੀ ਆਪਸੀ ਸੰਚਾਰ ਵਿਚ ਭਾਰੀ ਤੇਜ਼ੀ ਲੈ ਆਂਦੀ ਹੈ। ਕੰਪਿਊਟਰੀਕ੍ਰਿਤ ਰੋਬੋਟ ਮਨੁੱਖ ਵਾਂਗ ਬਹੁਤ ਸਾਰੇ ਔਖੇ ਤੇ ਜ਼ੋਖ਼ਮ ਭਰੇ ਕੰਮ ਲੰਮਾ ਸਮਾਂ ਬਿਨਾਂ ਅੱਕੇ – ਥੱਕੇ ਕਰ ਸਕਦਾ ਹੈ।
ਵਿਗਿਆਨ ਨੇ ਮਨੁੱਖੀ ਸਰੀਰ ਦੇ ਰੋਗਾਂ ਨੂੰ ਯੰਤਰਾਂ ਤੇ ਦਵਾਈਆਂ ਨਾਲ ਬਹੁਤ ਹੱਦ ਤਕ ਕਾਬੂ ਕਰ ਲਿਆ ਹੈ। ਵਿਗਿਆਨ ਨੇ ਖਾਦਾਂ ਤੇ ਕੀੜੇਮਾਰ ਦਵਾਈਆਂ ਨਾਲ ਫ਼ਸਲਾਂ ਦੀ ਉਪਜ ਵੀ ਵਧਾਈ ਹੈ। ਲਗਪਗ ਹਰ ਖੇਤਰ ਵਿਚ ਕੰਮ ਕਰਨ ਲਈ ਨਵੀਂ ਤਕਨੀਕ ਨਾਲ ਬਣੀਆਂ ਮਸ਼ੀਨਾਂ ਮਿਲ ਜਾਂਦੀਆਂ ਹਨ। ਇਸਦੇ ਨਾਲ ਹੀ ਇਸਨੇ ਮਨੁੱਖੀ ਜੀਵਨ ਵਿਚੋਂ ਅੰਧ – ਵਿਸ਼ਵਾਸਾਂ ਦਾ ਬਿਸਤਰਾ ਗੋਲ ਕਰ ਕੇ ਉਸਨੂੰ ਵਿਗਿਆਨਿਕ ਲੀਹਾਂ ਉੱਤੇ ਤੋਰ ਦਿੱਤਾ ਹੈ। ਇਸ ਪ੍ਰਕਾਰ ਵਿਗਿਆਨ ਦੀਆਂ ਕਾਢਾਂ ਦੀ ਸਾਡੇ ਰੋਜ਼ਾਨਾ ਜੀਵਨ ਵਿਚ ਬਹੁਤ ਮਹਾਨਤਾ ਹੈ ਤੇ ਇਨ੍ਹਾਂ ਨੇ ਸਾਡੇ ਰੋਜ਼ਾਨਾ ਜੀਵਨ ਵਿਚ ਤੇਜ਼ੀ, ਸੁਖ ਤੇ ਅਰਾਮ ਲਿਆਂਦਾ ਹੈ।

17. ਵਿਸਾਖੀ ਦਾ ਅੱਖੀਂ ਡਿੱਠਾ ਮੇਲਾ
ਵਿਸਾਖੀ ਦਾ ਤਿਉਹਾਰ ਹਰ ਸਾਲ 13 ਅਪਰੈਲ ਨੂੰ ਭਾਰਤ ਭਰ ਵਿਚ ਮਨਾਇਆ ਜਾਂਦਾ ਹੈ। ਇਹ ਤਿਉਹਾਰ ਹਾੜੀ ਦੀ ਫ਼ਸਲ ਦੇ ਪੱਕਣ ਦੀ ਖ਼ੁਸ਼ੀ ਵਿਚ ਮਨਾਇਆ ਜਾਂਦਾ ਹੈ।
ਵਿਸਾਖੀ ਦੇ ਤਿਉਹਾਰ ਨੂੰ ਮਨਾਉਣ ਲਈ ਸਾਡੇ ਪਿੰਡ ਤੋਂ ਦੋ ਮੀਲ ਦੀ ਵਿੱਥ ‘ਤੇ ਭਾਰੀ ਮੇਲਾ ਲਗਦਾ ਹੈ। ਐਤਕੀਂ ਮੈਂ ਆਪਣੇ ਪਿਤਾ ਜੀ ਨਾਲ ਵਿਸਾਖੀ ਦਾ ਇਹ ਮੇਲਾ ਵੇਖਣ ਲਈ ਗਿਆ ਰਸਤੇ ਵਿਚ ਮੇਰੇ ਪਿਤਾ ਜੀ ਨੇ ਮੈਨੂੰ ਦੱਸਿਆ ਕਿ ਇਸ ਮਹਾਨ ਦਿਨ ਉੱਤੇ ਗੁਰੂ ਗੋਬਿੰਦ ਸਿੰਘ ਜੀ ਨੇ ਆਨੰਦਪੁਰ ਸਾਹਿਬ ਵਿਚ ਖ਼ਾਲਸਾ ਪੰਥ ਦੀ ਸਾਜਨਾ ਕੀਤੀ ਸੀ। ਇਸੇ ਦਿਨ ਹੀ ਜ਼ਾਲਮ ਅੰਗਰੇਜ਼ ਜਨਰਲ ਡਾਇਰ ਨੇ ਜਲ੍ਹਿਆਂ ਵਾਲੇ ਬਾਗ਼ ਅੰਮ੍ਰਿਤਸਰ ਵਿਚ ਨਿਹੱਥੇ ਲੋਕਾਂ ਉੱਪਰ ਗੋਲੀ ਚਲਾਈ ਸੀ।
ਹੁਣ ਅਸੀਂ ਮੇਲੇ ਵਿਚ ਪਹੁੰਚ ਗਏ। ਮੇਲੇ ਵਿਚ ਕਾਫ਼ੀ ਭੀੜ – ਭੜੱਕਾ ਅਤੇ ਰੌਲਾ – ਰੱਪਾ ਸੀ ਆਲੇ – ਦੁਆਲੇ ਮਠਿਆਈਆਂ ਤੇ ਖਿਡੌਣਿਆਂ ਦੀਆਂ ਦੁਕਾਨਾਂ ਸਜੀਆਂ ਹੋਈਆਂ ਸਨ। ਇਧਰ – ਉਧਰ ਖੇਡਾਂ – ਤਮਾਸ਼ਿਆਂ ਦੇ ਪੰਡਾਲ ਲੱਗੇ ਹੋਏ ਸਨ। ਅਸੀਂ ਇਕ ਦੁਕਾਨ ‘ਤੇ ਬੈਠ ਕੇ ਤੱਤੀਆਂ – ਤੱਤੀਆਂ ਜਲੇਬੀਆਂ ਖਾਧੀਆਂ। ਫਿਰ ਅਸੀਂ ਇਕ ਥਾਂ ਚਾਟ ਖਾਧੀ ਤੇ ਫਿਰ ਕੁੱਝ ਦੇਰ ਮਗਰੋਂ ਮਾਈ ਬੁੱਢੀ ਦਾ ਝਾਟਾ ਤੇ ਫਿਰ ਆਈਸਕ੍ਰੀਮ : ਮੇਲੇ ਵਿਚ ਇਸਤਰੀਆਂ ਤੇ ਬੱਚੇ ਪੰਘੂੜੇ ਝੂਟ ਰਹੇ ਸਨ।
ਮੈਂ ਵੀ ਪੰਘੂੜੇ ਵਿਚ ਝੂਟੇ ਲਏ ਤੇ ਫਿਰ ਜਾਦੂ ਦੇ ਖੇਲ ਦੇਖੇ। ਅਸੀਂ ਇਕ ਸਰਕਸ ਵੀ ਦੇਖੀ, ਜਿਸ ਵਿਚ ਮਨੁੱਖਾਂ ਤੇ ਪਸ਼ੂਆਂ ਦੇ ਅਦਭੁਤ ਕਰਤੱਬ ਦਿਖਾਏ ਗਏ। ਇੰਨੇ ਨੂੰ ਸੂਰਜ ਛਿਪ ਰਿਹਾ ਸੀ। ਮੇਲੇ ਵਿਚ ਇਕ ਪਾਸੇ ਕੁੱਝ ਲੋਕਾਂ ਵਿਚ ਲੜਾਈ ਹੋ ਪਈ। ਮੇਰੇ ਪਿਤਾ ਜੀ ਨੇ ਮੈਨੂੰ ਨਾਲ ਲੈ ਕੇ ਛੇਤੀ – ਛੇਤੀ ਪਿੰਡ ਦਾ ਰਸਤਾ ਫੜ ਲਿਆ। ਕਾਫ਼ੀ ਹਨੇਰੇ ਹੋਏ ਅਸੀਂ ਘਰ ਪਹੁੰਚੇ।
ਮੇਰੇ ਸਕੂਲ ਦਾ ਨਾਂ ਖ਼ਾਲਸਾ ਸੀਨੀਅਰ ਸੈਕੰਡਰੀ ਸਕੂਲ ਹੈ। ਇਹ ਜਲੰਧਰ ਸ਼ਹਿਰ ਵਿਚ ਨਕੋਦਰ ਰੋਡ ਉੱਤੇ ਸਥਿਤ ਹੈ। ਇਸ ਸਕੂਲ ਦੀ ਇਮਾਰਤ ਬਹੁਤ ਵੱਡੀ ਹੈ। ਇਸ ਦੇ 25 ਤੋਂ ਵੱਧ ਵੱਡੇ ਕਮਰੇ ਹਨ। ਇਕ ਵੱਡਾ ਹਾਲ ਹੈ। ਇਸ ਵਿਚ ਸਾਇੰਸ ਦੇ ਵਿਦਿਆਰਥੀਆਂ ਲਈ ਹਰ ਪੱਖ ਤੋਂ ਸੰਪੂਰਨ ਪ੍ਰਯੋਗਸ਼ਾਲਾਵਾਂ ਬਣੀਆਂ ਹੋਈਆਂ ਹਨ। ਇਸ ਵਿਚ ਇਕ ਵੱਡੀ ਲਾਇਬਰੇਰੀ ਵੀ ਹੈ। ਇਸ ਸਕੂਲ ਵਿਚ 800 ਵਿਦਿਆਰਥੀ ਪੜ੍ਹਦੇ ਹਨ। ਉਨ੍ਹਾਂ ਨੂੰ ਪੜ੍ਹਾਉਣ ਲਈ 25 ਅਧਿਆਪਕ ਹਨ। ਇੱਥੋਂ ਦੇ ਮੁੱਖ ਅਧਿਆਪਕ ਸਾਹਿਬ ਬੜੇ ਲਾਇਕ ਤੇ ਤਜਰਬੇਕਾਰ ਹਨ।
18. ਮੇਰਾ ਸਕੂਲ
ਇਸ ਸਕੂਲ ਦੀ ਸਭ ਤੋਂ ਵੱਡੀ ਵਿਸ਼ੇਸ਼ਤਾ ਇਸ ਵਿਚ ਵਿਦਿਆਰਥੀਆਂ ਦੁਆਰਾ ਅਨੁਸ਼ਾਸਨ ਦੀ ਪਾਲਣਾ ਹੈ। ਅਧਿਆਪਕ ਅਤੇ ਵਿਦਿਆਰਥੀ ਸਮੇਂ ਸਿਰ ਸਕੂਲ ਪੁੱਜਦੇ ਹਨ ਅਧਿਆਪਕ ਪੂਰੀ ਮਿਹਨਤ ਨਾਲ ਪੜ੍ਹਾਉਂਦੇ ਹਨ ਤੇ ਉਹ ਵਿਦਿਆਰਥੀਆਂ ਨਾਲ ਨਿੱਜੀ ਸੰਬੰਧ ਪੈਦਾ ਕਰ ਕੇ ਉਨ੍ਹਾਂ ਦੀਆਂ ਪੜ੍ਹਾਈ ਸੰਬੰਧੀ ਮੁਸ਼ਕਿਲਾਂ ਨੂੰ ਦੂਰ ਕਰਦੇ ਹਨ। ਉਹ ਬੜੇ ਤਜਰਬੇਕਾਰ ਤੇ ਆਪਣੇ – ਆਪਣੇ ਵਿਸ਼ੇ ਵਿਚ ਨਿਪੁੰਨ ਹਨ। ਇਹ ਉਨ੍ਹਾਂ ਦੀ ਮਿਹਨਤ ਦਾ ਹੀ ਸਿੱਟਾ ਹੈ ਕਿ ਇਸ ਸਕੂਲ ਦੇ ਨਤੀਜੇ ਹਰ ਸਾਲ ਚੰਗੇ ਰਹਿੰਦੇ ਹਨ।
ਇਸ ਸਕੂਲ ਦਾ ਬਗੀਚਾ ਹਰਾ – ਭਰਾ ਤੇ ਫੁੱਲਾਂ ਨਾਲ ਲੱਦਿਆ ਪਿਆ ਹੈ। ਇਸ ਸਕੂਲ ਦੀ ਬਿਲਡਿੰਗ ਨਵੀਂ ਹੈ, ਜਿਸ ਵਿਚ ਕਮਰੇ ਖੁੱਲ੍ਹੇ ਤੇ ਹਵਾਦਾਰ ਹਨ। ਇਸ ਸਕੂਲ ਕੋਲ ਹਾਕੀ, ਫੁੱਟਬਾਲ, ਬਾਸਕਟਬਾਲ ਤੇ ਕ੍ਰਿਕਟ ਖੇਡਣ ਲਈ ਖੁੱਲੀਆਂ ਤੇ ਪੱਧਰੀਆਂ ਗਰਾਊਂਡਾਂ ਹਨ। ਮੈਂ ਆਪਣੇ ਇਸ ਸਕੂਲ ਨੂੰ ਬਹੁਤ ਪਿਆਰ ਕਰਦਾ ਹਾਂ।
19. ਮੇਰਾ ਮਿੱਤਰ
ਅਰਸ਼ਦੀਪ ਮੇਰਾ ਮਿੱਤਰ ਹੈ। ਉਹ ਮੇਰਾ ਸਹਿਪਾਠੀ ਹੈ। ਅਸੀਂ ਦੋਵੇਂ ਸੱਤਵੀਂ ਜਮਾਤ ਵਿਚ ਪੜ੍ਹਦੇ ਹਾਂ। ਅਸੀਂ ਦੋਵੇਂ ਇੱਕੋ ਡੈਸਕ ਉੱਤੇ ਬੈਠਦੇ ਹਾਂ ਅਸੀਂ ਦੋਵੇਂ ਵੱਧ ਤੋਂ ਵੱਧ ਸਮਾਂ ਇਕੱਠੇ ਰਹਿੰਦੇ ਹਾਂ। ਰਾਤ ਨੂੰ ਅਸੀਂ ਇਕੱਠੇ ਪੜ੍ਹਦੇ ਹਾਂ ! ਉਸ ਦੇ ਮਾਤਾ – ਪਿਤਾ ਬਹੁਤ ਨੇਕ ਵਿਅਕਤੀ ਹਨ। ਉਸ ਦਾ ਪਿਤਾ ਇਕ ਡਾਕਟਰ ਹੈ। ਉਸ ਦੀ ਮਾਤਾ ਇਕ ਸਕੂਲ ਵਿਚ ਅਧਿਆਪਕਾ ਹੈ। ਮੇਰਾ ਮਿੱਤਰ ਪੜ੍ਹਾਈ ਵਿਚ ਬਹੁਤ ਹੁਸ਼ਿਆਰ ਹੈ। ਉਹ ਹਰ ਸਾਲ ਕਲਾਸ ਵਿਚੋਂ ਅੱਵਲ ਰਹਿੰਦਾ ਹੈ ਤੇ ਇਨਾਮ ਪ੍ਰਾਪਤ ਕਰਦਾ ਹੈ।
ਉਹ ਹਿਸਾਬ ਅਤੇ ਅੰਗਰੇਜ਼ੀ ਵਿਚ ਬਹੁਤ ਹੀ ਹੁਸ਼ਿਆਰ ਹੈ। ਉਹ ਫ਼ਜ਼ੂਲ – ਖ਼ਰਚੀ ਨਹੀਂ ਕਰਦਾ। ਉਹ ਆਪਣੇ ਜੇਬ – ਖ਼ਰਚ ਵਿਚੋਂ ਬਚਾਏ ਪੈਸਿਆਂ ਨਾਲ ਗ਼ਰੀਬ ਵਿਦਿਆਰਥੀਆਂ ਦੀ ਮੱਦਦ ਕਰਦਾ ਹੈ। ਸਕੂਲ ਤੋਂ ਘਰ ਆ ਕੇ ਉਹ ਪਹਿਲਾਂ ਸਕੂਲ ਦਾ ਸਾਰਾ ਕੰਮ ਮੁਕਾਉਂਦਾ ਹੈ। ਉਹ ਕਿਤਾਬੀ ਕੀੜਾ ਨਹੀਂ। ਉਹ ਹਰ ਰੋਜ਼ ਫੁੱਟਬਾਲ ਖੇਡਣ ਜਾਂਦਾ ਹੈ। ਉਹ ਇਕ ਨੇਕ ਤੇ ਵਫ਼ਾਦਾਰ ਮਿੱਤਰ ਹੈ। ਉਸ ਦਾ ਸਰੀਰ ਸੁੰਦਰ ਅਤੇ ਤਕੜਾ ਹੈ। ਉਹ ਹਰ ਸਮੇਂ ਮੇਰੀ ਸਹਾਇਤਾ ਕਰਨ ਲਈ ਤਿਆਰ ਰਹਿੰਦਾ ਹੈ। ਸਕੂਲ ਦੇ ਸਾਰੇ ਅਧਿਆਪਕ ਅਤੇ ਮੁੱਖ ਅਧਿਆਪਕ ਸਾਹਿਬ ਉਸ ਨੂੰ ਬਹੁਤ ਪਿਆਰ ਕਰਦੇ ਹਨ। ਮੈਨੂੰ ਆਪਣੇ ਇਸ ਮਿੱਤਰ ਉੱਤੇ ਬਹੁਤ ਮਾਣ ਹੈ।

20. ਟੈਲੀਵਿਜ਼ਨ ਦੇ ਲਾਭ ਤੇ ਹਾਨੀਆਂ
ਟੈਲੀਵਿਜ਼ਨ ਦੂਰਦਰਸ਼ਨ ਆਧੁਨਿਕ ਵਿਗਿਆਨ ਦੀ ਇਕ ਅਦਭੁਤ ਕਾਢ ਹੈ। ਇਸ ਵਿਚ ਰੇਡੀਓ ਅਤੇ ਸਿਨੇਮਾ ਦੋਹਾਂ ਦੇ ਗੁਣ ਸਮੋਏ ਪਏ ਹਨ ਤੇ ਇਸ ਦਾ ਵਰਤਮਾਨ ਦਿਲ – ਪਰਚਾਵੇ ਦੇ ਸਾਧਨਾਂ ਵਿਚ ਆਪਣਾ ਮੌਲਿਕ ਤੇ ਵਿਸ਼ੇਸ਼ ਸਥਾਨ ਹੈ। ਭਾਰਤ ਵਿਚ ਸਭ ਤੋਂ ਪਹਿਲਾ ਟੈਲੀਵਿਜ਼ਨ ਇਕ ਨੁਮਾਇਸ਼ ਵਿਚ ਆਇਆ ਸੀ ਅਕਤੂਬਰ, 1959 ਵਿਚ ਡਾ: ਰਜਿੰਦਰ ਪ੍ਰਸ਼ਾਦ ਨੇ ਦਿੱਲੀ ਵਿਖੇ ਆਕਾਸ਼ਵਾਣੀ ਦੇ ਟੈਲੀਵਿਜ਼ਨ ਵਿਭਾਗ ਦਾ ਉਦਘਾਟਨ ਕੀਤਾ। ਫਿਰ ਇਸ ਦਾ ਦੇਸ਼ ਦੇ ਹੋਰਨਾਂ ਭਾਗਾਂ ਵਿਚ ਵਿਕਾਸ ਹੋਇਆ।
ਮਗਰੋਂ ਉਪ – ਗ੍ਰਹਿਆਂ ਦੀ ਮੱਦਦ ਨਾਲ ਭਾਰਤ ਦੇ ਟੈਲੀਵਿਜ਼ਨ ਪ੍ਰਸਾਰਨ ਨੂੰ ਦੂਰ – ਦੂਰ ਦੀਆਂ ਥਾਵਾਂ ਉੱਤੇ ਭੇਜਣਾ ਸੰਭਵ ਹੋ ਗਿਆ ਹੈ ਤੇ ਇਸ ਤਰ੍ਹਾਂ ਭਾਰਤ ਵਿੱਚ ਟੈਲੀਵਿਜ਼ਨ ਦਿਨੋ – ਦਿਨ ਵਿਕਸਿਤ ਹੋ ਰਿਹਾ ਹੈ। ਅੱਜ – ਕੱਲ੍ਹ ਤਾਂ 80 – 90 ਦੇ ਲਗਪਗ ਕੇਬਲ ਟੀ.ਵੀ. ਪ੍ਰਸਾਰਨ ਵੀ ਸ਼ੁਰੂ ਹੋ ਚੁੱਕੇ ਹਨ।
ਟੈਲੀਵਿਜ਼ਨ ਦੇ ਵਰਤਮਾਨ ਮਨੁੱਖ ਨੂੰ ਬਹੁਤ ਲਾਭ ਹਨ, ਜੋ ਕਿ ਹੇਠ ਲਿਖੇ ਹਨ
ਉੱਪਰ ਦੱਸੇ ਅਨੁਸਾਰ ਟੈਲੀਵਿਜ਼ਨ ਵਰਤਮਾਨ ਮਨੁੱਖ ਦੇ ਮਨੋਰੰਜਨ ਦਾ ਪ੍ਰਮੁੱਖ ਸਾਧਨ ਹੈ। ਘਰ ਬੈਠੇ ਹੀ ਅਸੀਂ ਨਵੀਆਂ – ਪਰਾਣੀਆਂ ਫ਼ਿਲਮਾਂ, ਨਾਟਕ, ਚਲ ਰਹੇ ਮੈਚ, ਭਾਸ਼ਨ, ਨਾਚ, ਗਾਣੇ ਦੇਖਦੇ ਤੇ ਸੁਣਦੇ ਹਾਂ ਤੇ ਇਸ ਪ੍ਰਕਾਰ ਆਪਣਾ ਮਨ ਪਰਚਾਉਂਦੇ ਹਾਂ। ਟੈਲੀਵਿਜ਼ਨ ਉੱਤੇ ਹਰ ਉਮਰ, ਹਰ ਵਰਗ ਤੇ ਹਰ ਰੁਚੀ ਦੇ ਵਿਅਕਤੀ ਲਈ ਮਨੋਰੰਜਨ ਦੀ ਸਾਮਗਰੀ ਪੇਸ਼ ਕੀਤੀ ਜਾਂਦੀ ਹੈ।
ਟੈਲੀਵਿਜ਼ਨ ਦਾ ਅਗਲਾ ਵੱਡਾ ਲਾਭ ਇਹ ਹੈ ਕਿ ਇਸ ਰਾਹੀਂ ਸਾਨੂੰ ਭਿੰਨ – ਭਿੰਨ ਵਿਸ਼ਿਆਂ ਤੇ ਮੁਸਲਿਮ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ। ਇਸ ਰਾਹੀਂ ਸਾਨੂੰ ਗਿਆਨ – ਵਿਗਿਆਨ ਦੀਆਂ ਖੋਜਾਂ, ਇਤਿਹਾਸ, ਮਿਥਿਹਾਸ, ਵਣਜ – ਵਪਾਰ, ਵਿੱਦਿਆ, ਕਾਨੂੰਨ, ਚਿਕਿੱਤਸਾ – ਵਿਗਿਆਨ, ਸਿਹਤ – ਵਿਗਿਆਨ, ਭਿੰਨ – ਭਿੰਨ ਪ੍ਰਕਾਰ ਦੇ ਪਕਵਾਨ ਬਣਾਉਣ, ਫ਼ੈਸ਼ਨ, ਧਰਤੀ ਦੇ ਵੱਖ – ਵੱਖ ਖਿੱਤਿਆਂ ਵਿਚ ਰਹਿਣ ਵਾਲੇ ਲੋਕਾਂ, ਜੰਗਲੀ ਪਸ਼ੂਆਂ ਤੇ ਸਮੁੰਦਰੀ ਜੀਵਾਂ, ਗੁਪਤਚਰਾਂ ਦੇ ਕੰਮਾਂ ਤੇ ਪ੍ਰਾਪਤੀਆਂ ਅਤੇ ਬਹੁਤ ਸਾਰੀਆਂ ਹੋਰ ਅਣਦੇਖੀਆਂ ਤੇ ਅਚੰਭੇਪੁਰਨ ਕਾਢਾਂ, ਖੋਜਾਂ, ਸਥਾਨਾਂ ਤੇ ਹੋਂਦਾਂ ਬਾਰੇ ਜਾਣਕਾਰੀ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ, ਜਿਸ ਨਾਲ ਦਿਲ – ਪਰਚਾਵੇ ਨਾਲ ਸਾਡਾ ਬੌਧਿਕ ਵਿਕਾਸ ਵੀ ਹੁੰਦਾ ਹੈ।
ਟੈਲੀਵਿਜ਼ਨ ਦਾ ਤੀਜਾ ਵੱਡਾ ਲਾਭ ਵਪਾਰਕ ਅਦਾਰਿਆਂ ਨੂੰ ਹੈ। ਇਸ ਰਾਹੀਂ ਵਪਾਰੀ ਲੋਕ ਆਪਣੇ ਮਾਲ ਦੀ ਮਸ਼ਹੂਰੀ ਕਰ ਕੇ ਲਾਭ ਕਮਾਉਂਦੇ ਹਨ।
ਇਸ ਦਾ ਚੌਥਾ ਵੱਡਾ ਲਾਭ ਤਾਜ਼ੀਆਂ ਵਾਪਰੀਆਂ ਘਟਨਾਵਾਂ ਦੀ ਜਾਣਕਾਰੀ ਦੇਣਾ ਹੈ। ਇਸ ਸੰਬੰਧੀ ਤਾਂ ਬਹੁਤ ਸਾਰੇ ਵਿਸ਼ੇਸ਼ ਚੈਨਲ ਰਾਤ – ਦਿਨ ਖ਼ਬਰਾਂ ਦਾ ਚਲ – ਚਿਤਰਾਂ ਰਾਹੀਂ ਪ੍ਰਸਾਰਨ ਕਰਦੇ ਰਹਿੰਦੇ ਹਨ।
ਇਸ ਦਾ ਅਗਲਾ ਵੱਡਾ ਲਾਭ ਇਹ ਹੈ ਕਿ ਟੈਲੀਵਿਜ਼ਨ ਸਟੇਸ਼ਨਾਂ ਉੱਤੇ ਬਹੁਤ ਸਾਰੇ ਲੋਕਾਂ ਨੂੰ ਰੁਜ਼ਗਾਰ ਮਿਲਦਾ ਹੈ ਤੇ ਨਾਲ ਹੀ ਕਲਾਕਾਰ ਧਨ ਨਾਲ ਮਾਲਾ – ਮਾਲ ਹੁੰਦੇ ਹਨ।
ਜਿੱਥੇ ਟੈਲੀਵਿਜ਼ਨ ਦੇ ਬਹੁਤ ਸਾਰੇ ਲਾਭ ਹਨ, ਉੱਥੇ ਇਸ ਦੀਆਂ ਕੁੱਝ ਹਾਨੀਆਂ ਵੀ ਹਨ। ਇਸ ਦੀ ਸਭ ਤੋਂ ਵੱਡੀ ਹਾਨੀ ਇਹ ਹੈ ਕਿ ਇਹ ਸੁਆਦਲੇ ਤੇ ਵੰਨ – ਸੁਵੰਨੇ ਪ੍ਰੋਗਰਾਮ ਪੇਸ਼ ਕਰ ਕੇ ਮਨੁੱਖ ਦਾ ਬਹੁਤ ਸਾਰਾ ਸਮਾਂ ਨਸ਼ਟ ਕਰਦਾ ਹੈ। ਟੈਲੀਵਿਜ਼ਨ ਨੇ ਗਲੀਆਂ – ਮੁਹੱਲਿਆਂ ਵਿਚ ਰੌਲੇ – ਰੱਪੇ ਨੂੰ ਵੀ ਵਧਾਇਆ ਹੈ।
ਕੇਬਲ ਟੀ. ਵੀ. ਦੇ ਪਸਾਰ ਰਾਹੀਂ ਟੈਲੀਵਿਜ਼ਨ ਨੇ ਸਾਡੇ ਸਭਿਆਚਾਰ ਉੱਤੇ ਮਾਰੂ ਹਮਲਾ ਬੋਲਿਆ ਹੈ, ਫਲਸਰੂਪ ਇਸ ਦਾ ਤੇਜ਼ੀ ਨਾਲ ਪੱਛਮੀਕਰਨ ਹੋ ਰਿਹਾ ਹੈ। ਵੱਖ – ਵੱਖ ਕੰਪਨੀਆਂ ਟੈਲੀਵਿਜ਼ਨ ਉੱਤੇ ਆਪਣੇ ਨਾਲ ਸੰਬੰਧੀ ਕੂੜ – ਪ੍ਰਚਾਰ ਤੇ ਇਸ਼ਤਿਹਾਰਬਾਜ਼ੀ ਕਰ ਕੇ ਜਿੱਥੇ ਲੋਕਾਂ ਤੋਂ ਪੈਸੇ ਬਟੋਰਦੀਆਂ ਹਨ, ਉੱਥੇ ਉਨ੍ਹਾਂ ਦੇ ਖਾਣ – ਪੀਣ ਤੇ ਰਹਿਣ – ਸਹਿਣ ਦੀਆਂ ਆਦਤਾਂ ਨੂੰ ਵੀ ਬਦਲ ਰਹੀਆਂ ਹਨ। ਕਈ ਵਾਰ ਫ਼ਿਲਮਾਂ ਤੇ ਲੜੀਵਾਰ ਨਾਟਕਾਂ ਵਿਚਲੇ ਸ਼ ਇੰਨੇ ਨੰਗੇਜ਼ਵਾਦੀ ਹੁੰਦੇ ਹਨ ਕਿ ਸਾਉ ਲੋਕ ਉਨ੍ਹਾਂ ਨੂੰ ਆਪਣੇ ਪਰਿਵਾਰ ਵਿਚ ਬੈਠ ਕੇ ਦੇਖ ਨਹੀਂ ਸਕਦੇ। ਇਸ ਤੋਂ ਇਲਾਵਾ ਟੈਲੀਵਿਜ਼ਨ ਸਕਰੀਨ ਦੀ ਤੇਜ਼ ਰੌਸ਼ਨੀ ਤੇ ਰੇਡਿਆਈ ਕਿਰਨਾਂ ਅੱਖਾਂ ਦੀ ਨਜ਼ਰ ਉੱਪਰ ਬੁਰਾ ਅਸਰ ਪਾਉਂਦੀਆਂ ਹਨ।

ਟੈਲੀਵਿਜ਼ਨ ਨੇ ਲੋਕਾਂ ਦੇ ਸਮਾਜਿਕ ਜੀਵਨ ਉੱਪਰ ਬਹੁਤ ਬੁਰਾ ਅਸਰ ਪਾਇਆ ਹੈ। ਲੋਕ ਸ਼ਾਮ ਵੇਲੇ ਇਕ – ਦੂਜੇ ਦੇ ਘਰ ਜਾਣਾ ਤੇ ਮਿਲਣਾ – ਗਿਲਣਾ ਛੱਡ ਕੇ ਆਪਣੇ ਘਰ ਵਿਚ ਟੈਲੀਵਿਜ਼ਨ ਦੇ ਮੋਹਰੇ ਬੈਠਣਾ ਵਧੇਰੇ ਪਸੰਦ ਕਰਦੇ ਹਨ। ਜਦੋਂ ਮਿੱਤਰ ਜਾਂ ਗੁਆਂਢੀ ਦੂਸਰੇ ਦੇ ਘਰ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਉਸ ਨੂੰ ਰੰਗ ਵਿਚ ਭੰਗ ਪਾਉਣ ਵਾਲਾ ਸਮਝਿਆ ਜਾਂਦਾ ਹੈ। ਉਪਰੋਕਤ ਸਾਰੀ ਚਰਚਾ ਤੋਂ ਅਸੀਂ ਇਸ ਸਿੱਟੇ ‘ਤੇ ਪੁੱਜਦੇ ਹਾਂ ਕਿ ਟੈਲੀਵਿਜ਼ਨ ਆਧੁਨਿਕ ਵਿਗਿਆਨ ਦੀ ਇਕ ਅਦਭੁਤ ਕਾਢ ਹੈ।
ਇਸ ਦੇ ਵਿਕਾਸ ਤੋਂ ਬਿਨਾਂ ਵਰਤਮਾਨ ਸਭਿਆਚਾਰ ਉੱਨਤੀ ਨਹੀਂ ਕਰ ਸਕਦਾ। ਇਹ ਵਰਤਮਾਨ ਮਨੁੱਖਾਂ ਦੇ ਮਨ – ਪਰਚਾਵੇ ਤੇ ਜੀਵਨ ਦੀਆਂ ਹੋਰ ਲੋੜਾਂ ਪੂਰੀਆਂ ਕਰਨ ਦਾ ਜ਼ਰੂਰੀ ਸਾਧਨ ਹੈ। ਇਸ ਦੇ ਪ੍ਰੋਗਰਾਮ ਦਾ ਪ੍ਰਬੰਧ ਕਰਨ ਵਾਲੇ ਵਿਅਕਤੀਆਂ ਤੇ ਸਰਕਾਰ ਨੂੰ ਚਾਹੀਦਾ ਹੈ ਕਿ ਉਹ ਇਸ ਨੂੰ ਵੱਧ ਤੋਂ ਵੱਧ ਉਸਾਰੂ ਰੋਲ ਅਦਾ ਕਰਨ ਦੇ ਯੋਗ ਬਣਾਉਣ।
21. ਪਹਾੜ ਦੀ ਸੈਰ
ਵਿਦਿਆਰਥੀ ਜੀਵਨ ਵਿਚ ਭਿੰਨ – ਭਿੰਨ ਸਥਾਨਾਂ ਦੀ ਯਾਤਰਾ ਤੇ ਸੈਰ ਦਾ ਮਹੱਤਵਪੂਰਨ ਸਥਾਨ ਹੈ। ਵਿਦਿਆਰਥੀ ਇਨ੍ਹਾਂ ਤੋਂ ਬਹੁਪੱਖੀ ਜਾਣਕਾਰੀ ਪ੍ਰਾਪਤ ਕਰਦਾ ਹੈ ਤੇ ਇਸ ਨਾਲ ਉਸ ਦੀ ਸਿੱਖਿਆ ਨੂੰ ਇਕ ਹੁਲਾਰਾ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ। ਪਿਛਲੇ ਸਾਲ ਮੈਂ ਗਰਮੀਆਂ ਦੀਆਂ ਛੁੱਟੀਆਂ ਵਿਚ ਆਪਣੇ ਕੁੱਝ ਸਹਿਪਾਠੀਆਂ ਨਾਲ ਕਸ਼ਮੀਰ ਦੀ ਸੈਰ ਕਰਨ ਲਈ ਗਿਆ। ਅਸੀਂ ਸਾਰੇ ਬੱਸ ਵਿਚ ਬੈਠ ਕੇ ਪਹਿਲਾਂ ਜੰਮੂ ਪੁੱਜੇ ਤੇ ਅਗਲੇ ਦਿਨ ਬੱਸ ਵਿਚ ਸਵਾਰ ਹੋ ਕੇ ਸ੍ਰੀਨਗਰ ਵੱਲ ਚਲ ਪਏ।
ਆਲੇ – ਦੁਆਲੇ ਦੇ ਪਹਾੜ ਝਾੜੀਆਂ ਤੇ ਜੰਗਲੀ ਪੌਦਿਆਂ ਨਾਲ ਭਰੇ ਹੋਏ ਸਨ। ਜਿਉਂ – ਜਿਉਂ ਅਸੀਂ ਅੱਗੇ ਵਧਦੇ ਗਏ, ਪਹਾੜ ਉੱਚੇ ਹੁੰਦੇ ਗਏ ਪਹਾੜ ਚੀਲਾਂ ਤੇ ਦੇਵਦਾਰਾਂ ਨਾਲ ਲੱਦੇ ਹੋਏ ਸਨ ਕਈ ਥਾਂਵਾਂ ‘ਤੇ ਪਹਾੜੀ ਆਬਸ਼ਾਰਾਂ ਵਿਚੋਂ ਪਾਣੀ ਡਿਗ ਰਿਹਾ ਸੀ। ਬੱਸ ਉੱਚੀਆਂ – ਨੀਵੀਆਂ ਅਤੇ ਵਲ ਖਾਂਦੀਆਂ ਸੜਕਾਂ ਤੋਂ ਲੰਘਦੀ ਹੋਈ ਅੱਗੇ ਜਾ ਰਹੀ ਸੀ। ਰਾਤ ਨੂੰ ਸਵਾ ਸੱਤ ਵਜੇ ਅਸੀਂ ਸ੍ਰੀਨਗਰ ਪਹੁੰਚ ਗਏ !
ਦੂਜੇ ਦਿਨ ਅਸੀਂ ਸਾਰੇ ਸਾਥੀ ਬੱਸ ਵਿਚ ਸਵਾਰ ਹੋ ਕੇ ਟਾਂਗਮਰਗ ਪਹੁੰਚੇ। ਇੱਥੋਂ ਅਸੀਂ ਗੁਲਮਰਗ ਤੋਂ ਖਿਲਮਰਗ ਦੀ ਸੈਰ ਕਰਨ ਲਈ ਨਿਕਲੇ। ਇੱਥੋਂ ਗੁਲਮਰਗ ਅੱਠ ਕਿਲੋਮੀਟਰ ਦੂਰ ਹੈ ਅਸੀਂ ਗੁਲਮਰਗ ਤਕ ਪੈਦਲ ਤੁਰ ਕੇ ਜਾਣ ਤੇ ਪਹਾੜ ਦੀ ਸੈਰ ਦਾ ਆਨੰਦ ਮਾਣਨ ਦਾ ਫ਼ੈਸਲਾ ਕੀਤਾ ਅਸੀਂ ਸਾਰੇ ਬੜੀ ਖ਼ੁਸ਼ੀ – ਖੁਸ਼ੀ, ਹੱਸਦੇ – ਨੱਚਦੇ, ਗਾਉਂਦੇ ਤੇ ਹੁਸੀਨ ਕੁਦਰਤੀ ਨਜ਼ਾਰਿਆਂ ਦਾ ਆਨੰਦ ਮਾਣਦੇ ਹੋਏ ਆਪਣਾ ਪੰਧ ਮੁਕਾ ਰਹੇ ਸਾਂ। ਇੱਥੋਂ ਦੇ ਪਹਾੜ ਸਾਲ, ਚੀਲ ਤੇ ਦਿਉਦਾਰਾਂ ਨਾਲ ਭਰੇ ਪਏ ਹਨ ਪਹਾੜ ਦੇ ਦੂਜੇ ਪਾਸੇ ਡੂੰਘੀਆਂ ਪਤਾਲਾਂ ਤਕ ਪਹੁੰਚਦੀਆਂ ਖੱਡਾਂ ਹਨ।
ਥੋੜ੍ਹੀ ਦੇਰ ਮਗਰੋਂ ਅਸੀਂ ਗੁਲਮਰਗ ਪੁੱਜੇ। ਇੱਥੇ ਇਕ ਛੋਟਾ ਜਿਹਾ ਕੁਦਰਤੀ ਸੁੰਦਰਤਾ ਨਾਲ ਭਰਿਆ ਮੈਦਾਨ ਹੈ, ਜਿਸ ਵਿਚ ਚਸ਼ਮੇ ਵਗਦੇ ਹਨ ਤੇ ਉੱਚੀਆਂ ਚੀਲਾਂ ਤੇ ਦਿਉਦਾਰਾਂ ਦੀਆਂ ‘ਸੰਘਣੀਆਂ ਤੇ ਲੰਮੀਆਂ ਕਤਾਰਾਂ ਨੇ ਆਲੇ – ਦੁਆਲੇ ਨੂੰ ਬਹੁਤ ਹੀ ਹੁਸੀਨ ਤੇ ਦਿਲ – ਖਿੱਚਵਾਂ ਬਣਾ ਦਿੱਤਾ ਹੈ। ਗੁਲਮਰਗ ਤੋਂ ਅਸੀਂ ਘੋੜਿਆਂ ਉੱਤੇ ਬੈਠੇ ਤੇ ਉਨ੍ਹਾਂ ਨੂੰ ਭਜਾਉਂਦੇ ਹੋਏ ਖਿਲਮਰਗ ਪੁੱਜੇ। ਇਹ ਥਾਂ ਸਮੁੰਦਰ ਤੋਂ 11000 ਫੁੱਟ ਉੱਚੀ ਹੈ। ਇੱਥੇ ਬਰਫ਼ ਜੰਮੀ ਹੋਈ ਸੀ।
ਅਸੀਂ ਬਰਫ਼ ਵਿਚ ਕੁਦਾੜੀਆਂ ਮਾਰਨ ਲੱਗੇ ਤੇ ਉਸ ਨੂੰ ਚੁੱਕ – ਚੁੱਕ ਕੇ ਇਕ – ਦੂਜੇ ਉੱਤੇ ਸੁੱਟਣ ਲੱਗੇ। ਕੁੱਝ ਸਮਾਂ ਅਸੀਂ ਇੱਥੇ ਠਹਿਰੇ ਤੇ ਫਿਰ ਵਾਪਸ ਗੁਲਮਰਗ ਵਿਚੋਂ ਹੁੰਦੇ ਹੋਏ ਟਾਂਗਮਾਰਗ ਪਹੁੰਚੇ। ਰਾਤ ਅਸੀਂ ਮੁੜ ਸ੍ਰੀਨਗਰ ਆ ਠਹਿਰੇ। ਇਸ ਤੋਂ ਬਿਨਾਂ ਅਸੀਂ ਕਸ਼ਮੀਰ ਦੇ ਹੋਰਨਾਂ ਵੇਖਣ ਯੋਗ ਸਥਾਨਾਂ ਡਲ ਝੀਲ, ਨਿਸ਼ਾਤ ਬਾਗ਼, ਕੁੱਕੜ ਨਾਗ, ਇੱਛਾਬਲ, ਅਵਾਂਤੀਪੁਰੇ ਦੇ ਖੰਡਰ, ਪਹਿਲਗਾਮ ਤੇ ਚੰਦਨਵਾੜੀ ਦੇ ਹੁਸੀਨ ਨਜ਼ਾਰੇ ਵੀ ਦੇਖੇ। ਇਸ ਪ੍ਰਕਾਰ ਦਸ ਦਿਨ ਕਸ਼ਮੀਰ ਦੇ ਪਹਾੜਾਂ ਦੀ ਸੈਰ ਕਰਨ ਪਿੱਛੋਂ ਅਸੀਂ ਵਾਪਸ ਪਰਤ ਆਏ।

22. ਮੇਰੇ ਮਾਤਾ ਜੀ
ਪੋ: ਮੋਹਨ ਸਿੰਘ ਨੇ ਸੱਚ ਕਿਹਾ ਹੈ
ਮਾਂ ਵਰਗਾ ਘਣਛਾਵਾਂ ਬੂਟਾ, ਮੈਨੂੰ ਨਜ਼ਰ ਨਾ ਆਏ।
ਲੈ ਕੇ ਇਸ ਤੋਂ ਛਾਂ ਉਧਾਰੀ, ਰੱਬ ਨੇ ਸੁਰਗ ਬਣਾਏ।
ਬਾਕੀ ਕੁੱਲ ਦੁਨੀਆਂ ਦੇ ਬੂਟੇ ਜੜ੍ਹ ਸੁੱਕਿਆਂ ਮੁਰਝਾਂਦੇ।
ਐਪਰ ਫੁੱਲਾਂ ਦੇ ਮੁਰਝਾਇਆਂ, ਇਹ ਬੂਟਾ ਸੁੱਕ ਜਾਏ।
ਸੰਸਾਰ ਭਰ ਦੇ ਚਿੰਤਕਾਂ ਨੇ ਮਾਂ ਦੀ ਮਹਿਮਾ ਗਾਈ ਹੈ ਮਾਂ ਦਾ ਰਿਸ਼ਤਾ ਸਭ ਤੋਂ ਪਵਿੱਤਰ ਤੇ ਉੱਚਾ – ਸੁੱਚਾ ਹੈ। ਸੰਸਾਰ ਵਿਚ ਬੰਦੇ ਦੀ ਮਾਂ ਦੇ ਬਰਾਬਰ ਹੋਰ ਕੋਈ ਨਹੀਂ ਹੋ ਸਕਦਾ, ਜਿਹੜੀ ਕਿ ਉਸਨੂੰ ਜਨਮ ਦਿੰਦੀ ਹੈ, ਪਾਲਦੀ ਹੈ, ਤੁਰਨਾ ਤੇ ਬੋਲਣਾ ਸਿਖਾਉਂਦੀ ਹੈ ਤੇ ਸੰਸਾਰ ਵਿਚ ਜਿਉਣ ਦੇ ਯੋਗ ਬਣਾਉਂਦੀ ਹੈ।
ਮੇਰੇ ਮਾਤਾ ਜੀ ਵੀ ਮੈਨੂੰ ਬਹੁਤ ਪਿਆਰੇ ਹਨ। ਉਨ੍ਹਾਂ ਦਾ ਨਾਂ ਸ੍ਰੀਮਤੀ ਮਨਜੀਤ ਕੌਰ ਹੈ। ਉਨ੍ਹਾਂ ਦੀ ਉਮਰ 35 ਸਾਲਾਂ ਦੀ ਹੈ। ਉਹ ਬੀ. ਏ., ਬੀ. ਐੱਡ. ਪਾਸ ਹਨ ਅਤੇ ਉਹ ਇਕ ਸੀਨੀਅਰ ਸੈਕੰਡਰੀ ਸਕੂਲ ਵਿਚ ਅਧਿਆਪਕ ਲੱਗੇ ਹੋਏ ਹਨ। ਉਹ ਸਕੂਲ ਵਿਚ ਅੰਗਰੇਜ਼ੀ ਅਤੇ ਸੋਸ਼ਲ ਸਟੱਡੀ ਪੜ੍ਹਾਉਂਦੇ ਹਨ। ਉਹ ਆਪਣੇ ਸਕੂਲ ਵਿਚ ਬਹੁਤ ਹੀ ਹਰਮਨ – ਪਿਆਰੇ ਹਨ ਉਹ ਸਵੇਰੇ ਉੱਠਦੇ ਹਨ ਤੇ ਹਰ ਰੋਜ਼ ਇਸ਼ਨਾਨ ਕਰਦੇ ਹਨ। ਉਹ ਹਰ ਰੋਜ਼ ਸਵੇਰੇ ‘ਜਪੁਜੀ ਸਾਹਿਬ’ ਦਾ ਪਾਠ ਕਰਦੇ ਹਨ।
ਸ਼ਾਮ ਵੇਲੇ ਉਹ ਰਹਿਰਾਸ ਸਾਹਿਬ ਦਾ ਪਾਠ ਕਰਦੇ ਹਨ। ਉਹ ਸਦਾ ਸਾਫ਼ – ਸੁਥਰੇ ਕੱਪੜੇ ਪਹਿਨਦੇ ਹਨ। ਉਹ ਚੰਗੇ ਖਾਣੇ ਬਣਾਉਂਦੇ ਹਨ। ਉਹ ਘਰ ਦਾ ਸਾਰਾ ਕੰਮ ਆਪ ਕਰਦੇ ਹਨ। ਉਹ ਸਦਾ ਕੰਮ ਵਿਚ ਜੁੱਟੇ ਰਹਿੰਦੇ ਹਨ। ਉਨ੍ਹਾਂ ਦਾ ਸੁਭਾ ਬਹੁਤ ਚੰਗਾ ਹੈ। ਉਹ ਸਦਾ ਖੁਸ਼ ਰਹਿੰਦੇ ਹਨ। ਉਨ੍ਹਾਂ ਦੇ ਚਿਹਰੇ ਉੱਤੇ ਅਨੋਖੀ ਚਮਕ ਤੇ ਖਿੱਚ ਕਾਇਮ ਰਹਿੰਦੀ ਹੈ ! ਉਹ ਸਾਨੂੰ ਸਭ ਨੂੰ ਬਹੁਤ ਪਿਆਰ ਕਰਦੇ ਹਨ। ਅਸੀਂ ਸਭ ਉਨ੍ਹਾਂ ਦਾ ਬਹੁਤ ਸਤਿਕਾਰ ਕਰਦੇ ਹਾਂ।
ਗਲੀ – ਗੁਆਂਢ ਵਿਚ ਉਨ੍ਹਾਂ ਦਾ ਬਹੁਤ ਸਤਿਕਾਰ ਹੈ। ਉਹ ਮੁਹੱਲੇ ਦੀ ਇਸਤਰੀ ਸਭਾ ਦੇ ਪ੍ਰਧਾਨ ਹਨ। ਲੋਕ ਆਪਣੇ ਘਰਾਂ ਦੇ ਕੰਮਾਂ ਵਿਚ ਉਨ੍ਹਾਂ ਦੀ ਸਲਾਹ ਲੈਂਦੇ ਹਨ।
ਮੇਰੇ ਮਾਤਾ ਜੀ ਦਾ ਫੁੱਲਾਂ ਤੇ ਪੌਦਿਆਂ ਨਾਲ ਬਹੁਤ ਪਿਆਰ ਹੈ। ਉਨ੍ਹਾਂ ਨੇ ਘਰ ਵਿਚ ਕਿਆਰੀਆਂ ਅਤੇ ਗਮਲਿਆਂ ਵਿਚ ਬਹੁਤ ਸਾਰੇ ਰੰਗ – ਬਰੰਗੇ ਪੱਤਿਆਂ ਤੇ ਫੁੱਲਾਂ ਦੇ ਬੂਟੇ ਲਾਏ ਹੋਏ ਹਨ। ਦੋ – ਤਿੰਨ ਮਹੀਨਿਆਂ ਬਾਅਦ ਮੌਸਮੀ ਫੁੱਲਾਂ ਦੀ ਪਨੀਰੀ ਆਪ ਤਿਆਰ ਕਰਕੇ ਪੌਦੇ ਤਿਆਰ ਕਰਦੇ ਹਨ। ਉਹ ਪੌਦਿਆਂ ਨੂੰ ਆਪ ਪਾਣੀ ਦਿੰਦੇ ਹਨ। ਉਨ੍ਹਾਂ ਦੀ ਇਸ ਲਗਨ ਸਦਕਾ ਸਾਡਾ ਘਰ ਫੁੱਲਾਂ ਨਾਲ ਭਰਿਆ ਰਹਿੰਦਾ ਹੈ। ਫੁੱਲਾਂ ਤੋਂ ਇਲਾਵਾ ਉਹ ਕਿਆਰੀਆਂ ਵਿਚ ਕਈ ਪ੍ਰਕਾਰ ਦੀਆਂ ਸਬਜ਼ੀਆਂ ਵੀ ਲਾਉਂਦੇ ਹਨ ਸਾਡੇ ਘਰ ਦੀ ਰਸੋਈ ਵਿਚ ਉਨ੍ਹਾਂ ਦੇ ਹੱਥਾਂ ਦੀਆਂ ਪਾਲੀਆਂ ਸਬਜ਼ੀਆਂ ਹੀ ਬਣਦੀਆਂ ਹਨ।
ਮੇਰੇ ਮਾਤਾ ਜੀ ਮੈਨੂੰ ਤੇ ਮੇਰੀ ਛੋਟੀ ਭੈਣ ਦੀ ਸਿਹਤ ਤੇ ਪੜ੍ਹਾਈ ਦਾ ਬਹੁਤ ਖ਼ਿਆਲ ਰੱਖਦੇ ਹਨ। ਉਹ ਪਿਤਾ ਜੀ ਨਾਲ ਕਦੇ ਕੌੜਾ ਨਹੀਂ ਬੋਲਦੇ ਤੇ ਨਾ ਹੀ ਹੋਰ ਕਿਸੇ ਨਾਲ ਉਨ੍ਹਾਂ ਨੂੰ ਗੁੱਸਾ ਬਹੁਤ ਘੱਟ ਆਉਂਦਾ ਹੈ। ਇਸ ਪ੍ਰਕਾਰ ਮੇਰੇ ਮਾਤਾ ਜੀ ਇਕ ਆਦਰਸ਼ ਇਸਤਰੀ ਹੈ।
23. ਪੰਦਰਾਂ ਅਗਸਤ
ਭਾਰਤ ਲੰਮਾ ਸਮਾਂ ਗੁਲਾਮੀ ਦੀਆਂ ਜ਼ੰਜੀਰਾਂ ਵਿਚ ਜਕੜਿਆ ਰਿਹਾ ਹੈ। ਇਸ ਨੂੰ ਲਗਪਗ 100 ਸਾਲ ਵਿਦੇਸ਼ੀਆਂ ਦੀ ਗੁਲਾਮੀ ਦਾ ਦੁੱਖ ਕੱਟਣਾ ਪਿਆ ਹੈ। ਸਮੇਂ – ਸਮੇਂ ਦੇਸ਼ ਭਰ ਵਿਚੋਂ ਵਿਦੇਸ਼ੀ ਹਮਲਾਵਰਾਂ ਦੇ ਜਬਰ – ਜ਼ੁਲਮ ਤੇ ਅਨਿਆਂ ਵਿਰੁੱਧ ਅਵਾਜ਼ ਉੱਠਦੀ ਰਹੀ ਹੈ ਤੇ ਕੁੱਝ ਰਾਜੇ – ਮਹਾਰਾਜੇ ਤੇ ਲੋਕ – ਆਗੂ ਇਸ ਵਿਰੁੱਧ ਹਥਿਆਰਬੰਦ ਸੰਘਰਸ਼ ਕਰਦੇ ਰਹੇ ਹਨ। ਵਿਦੇਸ਼ੀ ਪਠਾਣਾਂ ਤੇ ਮੁਗ਼ਲਾਂ ਦੀ ਗੁਲਾਮੀ ਵਿਰੁੱਧ ਰਾਣਾ ਪ੍ਰਤਾਪ, ਸ਼ਿਵਾ ਜੀ ਤੇ ਗੁਰੂ ਗੋਬਿੰਦ ਸਿੰਘ ਜੀ ਦੁਆਰਾ ਕੀਤੀਆਂ ਕੁਰਬਾਨੀਆਂ ਭਰੇ ਸੰਘਰਸ਼ਾਂ ਨੂੰ ਕੌਣ ਭੁੱਲ ਸਕਦਾ ਹੈ ?
ਵਿਦੇਸ਼ੀ ਪਠਾਣ ਤੇ ਮੁਗਲ ਤਾਂ ਭਾਰਤ ਵਿਚ ਆ ਕੇ ਭਾਰਤ – ਵਾਸੀ ਹੀ ਬਣ ਕੇ ਰਹਿ ਗਏ, ਜਿਸ ਕਰਕੇ ਭਾਰਤ ਦੇ ਲੋਕਾਂ ਨੇ ਗੁਲਾਮੀ ਦੇ ਦੁੱਖ ਨੂੰ ਬਹੁਤਾ ਅੰਗਰੇਜ਼ੀ ਰਾਜ ਵਿਚ ਹੀ ਮਹਿਸੂਸ ਕੀਤਾ ਪੰਜਾਬ, ਬੰਗਾਲ ਤੇ ਮਹਾਂਰਾਸ਼ਟਰ ਆਦਿ ਭਾਰਤ ਦੇ ਸਮੁੱਚੇ ਦੇਸ਼ਾਂ ਵਿਚੋਂ ਉੱਠੇ ਦੇਸ਼ – ਭਗਤਾਂ ਨੇ ਅੰਗਰੇਜ਼ੀ ਰਾਜ ਨੂੰ ਖ਼ਤਮ ਕਰਨ ਤੇ ਸੁਤੰਤਰਤਾ ਪ੍ਰਾਪਤੀ ਲਈ ਅਕਹਿ ਕਸ਼ਟ ਸਹਿ ਕੇ ਕੁਰਬਾਨੀਆਂ ਦਿੱਤੀਆਂ ਇਸ ਸੰਬੰਧ ਵਿਚ ਨਾਮਧਾਰੀ ਲਹਿਰ, “ਪਗੜੀ ਸੰਭਾਲ ਜੱਟਾ’ ਲਹਿਰ, ਗਦਰ ਲਹਿਰ, ਕਾਂਗਰਸ ਪਾਰਟੀ, ਬੱਬਰ ਅਕਾਲੀ ਲਹਿਰ, ਨੌਜਵਾਨ ਭਾਰਤ ਸਭਾ, ਅਜ਼ਾਦ ਹਿੰਦ ਫ਼ੌਜ ਤੇ ਦੇਸ਼ ਭਰ ਦੀਆਂ ਹੋਰ ਬਹੁਤ ਸਾਰੀਆਂ ਦੇਸ਼ – ਭਗਤ ਲਹਿਰਾਂ ਵਿਚ ਹਿੱਸਾ ਲੈ ਰਹੇ ਨੌਜਵਾਨਾਂ ਨੇ ਬੇਮਿਸਾਲ ਕੁਰਬਾਨੀਆਂ ਦਿੱਤੀਆਂ। ਕਰਤਾਰ ਸਿੰਘ ਸਰਾਭਾ, ਸ: ਅਜੀਤ ਸਿੰਘ, ਗੰਗਾਧਰ ਤਿਲਕ ਸ਼ਹੀਦ ਭਗਤ ਸਿੰਘ, ਮਹਾਤਮਾ ਗਾਂਧੀ, ਲਾਲਾ ਲਾਜਪਤ ਰਾਏ, ਜਵਾਹਰ ਲਾਲ ਨਹਿਰੂ ਤੇ ਨੇਤਾ ਜੀ ਸੁਭਾਸ਼ ਚੰਦਰ ਬੋਸ ਆਦਿ ਅਜ਼ਾਦੀ ਦੀ ਲਹਿਰ ਦੇ ਪ੍ਰਸਿੱਧ ਆਗੂ ਹੋਏ ਹਨ, ਜਿਨ੍ਹਾਂ ਨੇ ਸਾਰੇ ਹਿੰਦੁਸਤਾਨ ਵਿਚ ਧੁੰਮਾ ਦਿੱਤਾ – “ਸੁਤੰਤਰਤਾ ਸਾਡਾ ਜਮਾਂਦਰੂ ਅਧਿਕਾਰ ਹੈ ਅਤੇ ਅਸੀਂ ਇਸ ਨੂੰ ਲੈ ਕੇ ਰਹਾਂਗੇ। ਸ਼ਹੀਦ ਭਗਤ ਸਿੰਘ, ਰਾਜਗੁਰੂ ਤੇ ਸੁਖਦੇਵ ਵਰਗੇ ਸੂਰਮੇ ਬੜੇ ਚਾ ਨਾਲੇ ਗਾਉਂਦੇ –

ਸਰ ਫ਼ਰੋਸ਼ੀ ਕੀ ਤਮੰਨਾ ਅਬ ਹਮਾਰੇ ਦਿਲ ਮੇਂ ਹੈ।
ਦੇਖਨਾ ਹੈ ਜ਼ੋਰ ਕਿਤਨਾ ਬਾਜ਼ੂਏ ਕਾਤਿਲ ਮੇਂ ਹੈ।
ਅੰਤ ਦੇਸ਼ – ਭਗਤਾਂ ਦੀਆਂ ਸ਼ਹੀਦੀਆਂ ਤੇ ਕੁਰਬਾਨੀਆਂ ਰਾਹੀਂ ਡੁੱਲ੍ਹਿਆ ਖੂਨ ਬਿਰਥਾ ਨਾ ਗਿਆ 15 ਅਗਸਤ, 1947 ਈ: ਨੂੰ ਅੰਗਰੇਜ਼ ਭਾਰਤ ਛੱਡ ਕੇ ਚਲੇ ਗਏ ਤੇ ਸਮੁੱਚੇ ਭਾਰਤ – ਵਾਸੀਆਂ ਨੂੰ ਅਜ਼ਾਦ ਵਾਤਾਵਰਨ ਵਿਚ ਵਿਚਰਨ ਦਾ ਮੌਕਾ ਪ੍ਰਾਪਤ ਹੋਇਆ ਪਰਤੰਤਰਤਾ ਦੀ ਰਾਤ ਬੀਤ ਗਈ ਤੇ ਸੁਤੰਤਰਤਾ ਦੀਆਂ ਸੁਨਹਿਰੀ ਕਿਰਨਾਂ ਖਿਲਾਰਦਾ ਸੂਰਜ ਨਿਕਲ ਆਇਆ। ਇਸ ਪ੍ਰਕਾਰ 15 ਅਗਸਤ ਦਾ ਦਿਨ ਸਮੁੱਚੇ ਭਾਰਤ – ਵਾਸੀਆਂ ਲਈ ਗੌਰਵ ਭਰਿਆ ਦਿਨ ਹੈ। ਇਸ ਦੇ ਪਿੱਛੇ ਸੰਘਰਸ਼ ਭਰੇ ਤੇ ਖੂਨ – ਰੰਗੇ ਇਤਿਹਾਸ ਦੀ ਇਕ ਲੰਮੀ ਕਹਾਣੀ ਹੈ। ਹਰ ਸਾਲ ਭਾਰਤ – ਵਾਸੀ ਇਸ ਦਿਨ ਨੂੰ ਇਕ ਤਿਉਹਾਰ ਵਾਂਗ ਬੜੇ ਚਾ ਤੇ ਉਮਾਹ ਨਾਲ ਮਨਾਉਂਦੇ ਹਨ।
ਇਸ ਦਿਨ ਸਵੇਰੇ ਦੇਸ਼ ਦੇ ਪ੍ਰਧਾਨ ਮੰਤਰੀ ਲਾਲ ਕਿਲ੍ਹੇ ਉੱਪਰ ਤਿਰੰਗਾ ਝੰਡਾ ਝੁਲਾਉਂਦੇ ਹਨ। ਰਾਸ਼ਟਰੀ ਗੀਤ ਗਾਇਆ ਜਾਂਦਾ ਹੈ। ਉਹ ਅਜ਼ਾਦੀ ਦੇ ਯੋਧਿਆਂ ਨੂੰ ਸ਼ਰਧਾਂਜਲੀਆਂ ਭੇਟਾ ਕਰਦੇ ਹੋਏ ਕੌਮ ਦੇ ਨਾਂ ਸੰਦੇਸ਼ ਪ੍ਰਸਾਰਿਤ ਕਰਦੇ ਹਨ। ਸਾਰੇ ਦੇਸ਼ – ਵਾਸੀ ਟੈਲੀਵਿਜ਼ਨ ਉੱਪਰ ਇਸ ਪ੍ਰੋਗਰਾਮ ਨੂੰ ਦੇਖਦੇ ਹਨ ਰਾਜਧਾਨੀ ਤੋਂ ਇਲਾਵਾ ਦੇਸ਼ ਭਰ ਵਿਚ ਭਿੰਨ – ਭਿੰਨ ਦੇਸ਼ਾਂ ਦੀਆਂ ਰਾਜਧਾਨੀਆਂ ਤੇ ਨਗਰਾਂ ਵਿਚ ਇਸ ਨੂੰ ਮਨਾਉਣ ਲਈ ਪ੍ਰੋਗਰਾਮ ਬਣਾਏ ਜਾਂਦੇ ਹਨ ਦੇਸ਼ਾਂ ਦੇ ਮੁੱਖ ਮੰਤਰੀ, ਦੂਸਰੇ ਮੰਤਰੀ ਤੇ ਜ਼ਿਲ੍ਹਾ ਅਧਿਕਾਰੀ ਭਿੰਨ – ਭਿੰਨ ਮਿੱਥੇ ਥਾਂਵਾਂ ਉੱਪਰ ਤਿਰੰਗਾ ਝੰਡਾ ਲਹਿਰਾਉਣ ਦੀ ਰਸਮ ਅਦਾ ਕਰਦੇ ਹਨ ਹਵਾਈ ਜਹਾਜ਼ ਫੁੱਲਾਂ ਦੀ ਵਰਖਾ ਕਰਦੇ ਹਨ ਅਜ਼ਾਦੀ ਦੇ ਯੋਧਿਆਂ ਤੇ ਸ਼ਹੀਦਾਂ ਨੂੰ ਸ਼ਰਧਾਂਜਲੀਆਂ ਭੇਟ ਕੀਤੀਆਂ ਜਾਂਦੀਆਂ ਹਨ ਉਨ੍ਹਾਂ ਦੀਆਂ ਸਮਾਧੀਆਂ ਤੇ ਫੋਟੋਆਂ ਉੱਤੇ ਫੁੱਲਾਂ ਦੇ ਹਾਰ ਪਾਏ ਜਾਂਦੇ ਹਨ।
ਫਿਰ ਸ਼ਹਿਰ ਵਿਚ ਪੁਲਿਸ ਦੀਆਂ ਟੁਕੜੀਆਂ ਤੇ ਸਕੂਲਾਂ ਦੇ ਬੱਚਿਆਂ ਦੁਆਰਾ ਜਲੂਸ ਕੱਢਿਆ ਜਾਂਦਾ ਹੈ। ਢੋਲ ਤੇ ਨਗਾਰੇ ਵਜਾਏ ਜਾਂਦੇ ਹਨ। ਲੋਕ ਮਠਿਆਈਆਂ ਵੰਡਦੇ ਹਨ। ਸ਼ਾਮ ਨੂੰ ਰਾਜਧਾਨੀ ਨਵੀਂ ਦਿੱਲੀ, ਦੇਸ਼ਕ ਰਾਜਧਾਨੀਆਂ ਤੇ ਸ਼ਹਿਰਾਂ ਵਿਚ ਦੀਪਮਾਲਾ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ਅਤੇ ਆਤਸ਼ਬਾਜ਼ੀ ਚਲਾਈ ਜਾਂਦੀ ਹੈ। ਸੜਕਾਂ ਤੇ ਬਜ਼ਾਰ ਰੌਸ਼ਨੀਆਂ ਨਾਲ ਡੁੱਲ੍ਹ – ਡੁੱਲ੍ਹ ਪੈਂਦੇ ਹਨ।
ਇਸ ਪ੍ਰਕਾਰ 15 ਅਗਸਤ ਦਾ ਦਿਨ ਭਾਰਤ ਦੇ ਇਤਿਹਾਸ ਵਿਚ ਬਹੁਤ ਮਹੱਤਵਪੂਰਨ ਹੈ। ਭਾਰਤੀਆਂ ਨੂੰ ਇਹ ਦਿਨ ਬੇਅੰਤ ਕੁਰਬਾਨੀਆਂ ਤੇ ਸੈਂਕੜੇ ਸ਼ਹੀਦੀਆਂ ਪਿੱਛੋਂ ਪ੍ਰਾਪਤ ਹੋਇਆ ਹੈ ਅੱਜ ਸਾਡਾ ਕਰਤੱਵ ਹੈ ਕਿ ਅਸੀਂ ਭਾਰਤ ਦੀ ਅਜ਼ਾਦੀ ਨੂੰ ਕਾਇਮ ਰੱਖਣ ਲਈ ਆਪਣਾ ਤਨ, ਮਨ ਤੇ ਧਨ ਕੁਰਬਾਨ ਕਰਨ ਲਈ ਤਿਆਰ ਰਹੀਏ ਤੇ ਇੱਥੇ ਪਸਰ ਰਹੇ ਭ੍ਰਿਸ਼ਟਾਚਾਰ ਤੇ ਕੱਟੜਵਾਦ ਵਿਰੁੱਧ ਇਕ ਜ਼ੋਰਦਾਰ ਜੰਗ ਛੇੜੀਏ।
24. ਛੱਬੀ ਜਨਵਰੀ
ਜਾਂ
ਗਣਤੰਤਰਤਾ ਦਿਵਸ
26 ਜਨਵਰੀ ਦਾ ਦਿਨ ਭਾਰਤ ਦੀ ਅਜ਼ਾਦੀ ਦੇ ਇਤਿਹਾਸ ਤੇ ਅਜ਼ਾਦੀ ਮਿਲਣ ਤੋਂ ਪਿੱਛੋਂ ਦੇ ਇਤਿਹਾਸ ਵਿਚ ਮਹੱਤਵਪੂਰਨ ਸਥਾਨ ਰੱਖਦਾ ਹੈ। ਜਦੋਂ ਭਾਰਤ ਵਿਚ ਅਜ਼ਾਦੀ ਦਾ ਅੰਦੋਲਨ ਚਲ ਰਿਹਾ ਸੀ, ਤਾਂ 31 ਦਸੰਬਰ, 1929 ਈ: ਨੂੰ ਕਾਂਗਰਸ ਪਾਰਟੀ ਨੇ ਲਾਹੌਰ ਵਿਖੇ ਹੋਏ ਆਪਣੇ ਸਾਲਾਨਾ ਸਮਾਗਮ ਵਿਚ ਇਕ ਮਤੇ ਰਾਹੀਂ ਅੰਗਰੇਜ਼ਾਂ ਤੋਂ ਪੂਰਨ ਅਜ਼ਾਦੀ ਦੀ ਮੰਗ ਕੀਤੀ ਤੇ ਨਾਲ ਹੀ ਹਰ ਸਾਲ 26 ਜਨਵਰੀ ਨੂੰ ਭਾਰਤ ਦੀ ਅਜ਼ਾਦੀ ਦਾ ਦਿਨ ਮਨਾਉਣ ਦਾ ਫ਼ੈਸਲਾ ਕੀਤਾ ਉਸ ਦਿਨ ਤੋਂ ਲੈ ਕੇ ਭਾਰਤ ਦੇ ਅਜ਼ਾਦ ਹੋਣ ਤਕ ਇਹ ਦਿਨ ਪੂਰਨ ਅਜ਼ਾਦੀ ਦੀ ਮੰਗ ਨੂੰ ਲੈ ਕੇ ਮਨਾਇਆ ਜਾਂਦਾ ਰਿਹਾ। ਅੰਤ 15 ਅਗਸਤ, 1947 ਈ: ਨੂੰ ਭਾਰਤ ਅਜ਼ਾਦ ਹੋ ਗਿਆ।
ਫਿਰ ਸੁਤੰਤਰ ਭਾਰਤ ਦਾ ਸੰਵਿਧਾਨ ਬਣਾਉਣ ਦਾ ਕੰਮ ਸ਼ੁਰੂ ਹੋਇਆਂ। 26 ਜਨਵਰੀ, 1950 ਈ: ਨੂੰ ਭਾਰਤ ਦਾ ਸੰਵਿਧਾਨ ਲਾਗੂ ਹੋਇਆ, ਜਿਸ ਰਾਹੀਂ ਭਾਰਤ ਨੂੰ ਸੁਤੰਤਰ ਤੇ ਖ਼ੁਦਮੁਖ਼ਤਾਰ ਗਣਤੰਤਰ ਦਾ ਦਰਜਾ ਦਿੰਦਿਆਂ ਇੱਥੇ ਲੋਕ – ਰਾਜ ਕਾਇਮ ਕਰਨ ਦਾ ਐਲਾਨ ਕੀਤਾ ਗਿਆ ਅਤੇ ਭਾਰਤ – ਵਾਸੀਆਂ ਨੂੰ ਬੋਲਣ, ਲਿਖਣ, ਤੁਰਨ – ਫਿਰਨ, ਜਾਇਦਾਦ ਬਣਾਉਣ ਤੇ ਵੋਟਾਂ ਪਾਉਣ ਦੇ ਬੁਨਿਆਦੀ ਅਧਿਕਾਰ ਦਿੱਤੇ ਗਏ। ਇਸ ਸੰਵਿਧਾਨ ਅਨੁਸਾਰ ਅੱਜ ਤਕ ਭਾਰਤ ਵਿਚ ਰਾਜ – ਕਾਜ ਚਲਾਇਆ ਜਾ ਰਿਹਾ ਹੈ।
ਇਸ ਪ੍ਰਕਾਰ 26 ਜਨਵਰੀ ਦਾ ਦਿਨ ਭਾਰਤੀ ਲੋਕਾਂ ਲਈ ਬਹੁਤ ਹੀ ਮਹਾਨਤਾ ਭਰਿਆ ਦਿਨ ਹੈ। ਹਰ ਸਾਲ ਸਾਰੇ ਭਾਰਤੀ ਇਸ ਦਿਨ ਨੂੰ ਬੜੇ ਉਤਸ਼ਾਹ ਨਾਲ ਮਨਾਉਂਦੇ ਹਨ। ਇਸ ਤੋਂ ਇਕ ਦਿਨ ਪਹਿਲਾਂ ਰਾਸ਼ਟਰਪਤੀ ਜੀ ਰੇਡੀਓ ਤੇ ਟੈਲੀਵਿਜ਼ਨ ਤੋਂ ਕੌਮ ਦੇ ਨਾਂ ਆਪਣਾ ਸੁਨੇਹਾ ਪ੍ਰਸਾਰਿਤ ਕਰਦੇ ਹਨ। ਇਸ ਦਿਨ ਸਵੇਰੇ ਨਵੀਂ ਦਿੱਲੀ ਵਿਚ ਰਾਸ਼ਟਰਪਤੀ ਜੀ ਵਿਜੈ ਚੌਂਕ ਵਿਖੇ ਝੰਡਾ ਲਹਿਰਾਉਣ ਮਗਰੋਂ ਤਿੰਨਾਂ ਫ਼ੌਜਾਂ ਦੇ ਯੂਨਿਟਾਂ ਤੋਂ ਸਲਾਮੀ ਲੈਂਦੇ ਹਨ। ਇਸ ਸਮੇਂ ਦੇਸ਼ ਦੀ ਫ਼ੌਜੀ ਸ਼ਕਤੀ ਅਤੇ ਵਿਗਿਆਨਿਕ ਤੇ ਸੱਨਅਤੀ ਖੇਤਰਾਂ ਵਿਚ ਤਰੱਕੀ ਦਾ ਭਾਰੀ ਪ੍ਰਦਰਸ਼ਨ ਕੀਤਾ ਜਾਂਦਾ ਹੈ। ਲੋਕ ਦੂਰੋਂ – ਦੂਰੋਂ ਦਿੱਲੀ ਵਿਚ 26 ਜਨਵਰੀ ਦੀਆਂ ਰੌਣਕਾਂ ਦੇਖਣ ਆਉਂਦੇ ਹਨ।

ਇਸ ਸਮੇਂ ਫ਼ੌਜ, ਪੁਲਿਸ, ਸਕੂਲਾਂ – ਕਾਲਜਾਂ ਦੇ ਮੁੰਡਿਆਂ – ਕੁੜੀਆਂ ਅਤੇ ਸਕਾਊਟਾਂ ਵਲੋਂ ਸਾਰੇ ਸ਼ਹਿਰ ਵਿਚ ਜਲੂਸ ਕੱਢਿਆ ਜਾਂਦਾ ਹੈ। ਫ਼ੌਜ ਤੇ ਪੁਲਿਸ ਆਪਣੇ ਨਾਲ ਹਥਿਆਰ ਲੈ ਕੇ ਚਲਦੀ ਹੈ। ਜਲੂਸ ਤੇ ਆਲਾ – ਦੁਆਲਾ ਤਿਰੰਗੇ ਝੰਡਿਆਂ ਨਾਲ ਸਜਿਆ ਹੁੰਦਾ ਹੈ। ਹਵਾਈ ਜਹਾਜ਼ ਫੁੱਲਾਂ ਦੀ ਵਰਖਾ ਕਰਦੇ ਹਨ। ਭਾਰਤ ਦੇ ਕੋਨੇ – ਕੋਨੇ ਵਿਚੋਂ ਲੋਕ – ਨਾਚ ਨੱਚਣ ਵਾਲੀਆਂ ਟੋਲੀਆਂ ਆਉਂਦੀਆਂ ਹਨ ਤੇ ਉਹ ਨੈਸ਼ਨਲ ਸਟੇਡੀਅਮ ਦੇ ਵਿਸ਼ਾਲ ਮੰਚ ਉੱਤੇ ਆਪਣੇ ਨਾਚ ਪੇਸ਼ ਕਰਦੀਆਂ ਹਨ। ਲੱਖਾਂ ਦਰਸ਼ਕ ਇਨ੍ਹਾਂ ਨਾਚਾਂ ਦਾ ਆਨੰਦ ਮਾਣਦੇ ਹਨ। ਸਾਰਾ ਦਿਨ ਰਾਜਧਾਨੀ ਵਿਚ ਚਹਿਲ – ਪਹਿਲ ਰਹਿੰਦੀ ਹੈ। ਇਨ੍ਹਾਂ ਰੌਣਕਾਂ ਵਿਚ ਵਿਦੇਸ਼ੀ ਪ੍ਰਾਹੁਣੇ ਵੀ ਭਾਗ ਲੈਂਦੇ ਹਨ।
ਰਾਤ ਨੂੰ ਆਤਸ਼ਬਾਜ਼ੀ ਤੇ ਪਟਾਕਿਆਂ ਨਾਲ ਇਸ ਦਿਨ ਦੀਆਂ ਖੁਸ਼ੀਆਂ ਵਿਚ ਵਾਧਾ ਕੀਤਾ ਜਾਂਦਾ ਹੈ। ਇਸ ਤੋਂ ਬਿਨਾਂ ਦੇਸ਼ ਦੇ ਹੋਰ ਵੱਡੇ – ਵੱਡੇ ਸ਼ਹਿਰਾਂ ਤੇ ਦੇਸ਼ਾਂ ਦੀਆਂ ਰਾਜਧਾਨੀਆਂ ਵਿਚ ਮੁੱਖ ਮੰਤਰੀ, ਮੰਤਰੀ ਤੇ ਸਰਕਾਰੀ ਅਫ਼ਸਰ ਝੰਡਾ ਝੁਲਾਉਣ ਦੀ ਰਸਮ ਅਦਾ ਕਰਦੇ ਹਨ। ਇਸ ਸਮੇਂ ਜਹਾਜ਼ ਫੁੱਲਾਂ ਦੀ ਵਰਖਾ ਕਰਦੇ ਹਨ। ਇਨ੍ਹਾਂ ਸਮਾਗਮਾਂ ਵਿਚ ਲੋਕ ਬੜੇ ਉਤਸ਼ਾਹ ਨਾਲ ਪੁੱਜਦੇ ਹਨ। ਇਸ ਸਮੇਂ ਵਜ਼ੀਰਾਂ, ਸਰਕਾਰੀ ਅਫ਼ਸਰਾਂ ਤੇ ਹੋਰਨਾਂ ਲੀਡਰਾਂ ਦੇ ਭਾਸ਼ਨ ਵੀ ਹੁੰਦੇ ਹਨ, ਜੋ ਜਨਤਾ ਨੂੰ ਇਸ ਦਿਨ ਦੀ ਮਹਾਨਤਾ ਤੋਂ ਜਾਣੂ ਕਰਾ ਕੇ ਉਨ੍ਹਾਂ ਵਿਚ ਦੇਸ਼ – ਭਗਤੀ ਤੇ ਲੋਕ – ਰਾਜ ਪ੍ਰਤੀ ਸਤਿਕਾਰ ਦੀ ਭਾਵਨਾ ਪੈਦਾ ਕਰਦੇ ਹਨ। ਇਸ ਦਿਨ ਸ਼ਹਿਰਾਂ ਵਿਚ ਵੱਡੇ – ਵੱਡੇ ਜਲੂਸ ਵੀ ਕੱਢੇ ਜਾਂਦੇ ਹਨ।
ਇਸ ਪ੍ਰਕਾਰ 26 ਜਨਵਰੀ ਦਾ ਦਿਨ ਭਾਰਤ ਦੇ ਇਤਿਹਾਸ ਵਿਚ ਭਾਰੀ ਮਹੱਤਤਾ ਰੱਖਦਾ ਹੈ।
25. ਅਸੀਂ ਪਿਕਨਿਕ ‘ਤੇ ਗਏ
ਪਿਛਲੇ ਸ਼ਨਿਚਰਵਾਰ ਅਸੀਂ ਸਤਲੁਜ ਦਰਿਆ ਦੇ ਕੰਢੇ ਪਿਕਨਿਕ ਲਈ ਗਏ। ਇਸ ਵਿਚ ਸਾਡੀ ਕਲਾਸ ਦੇ ਦਸ ਮੁੰਡੇ ਸ਼ਾਮਲ ਸਨ। ਇਸ ਲਈ ਮੈਂ ਆਪਣੇ ਘਰੋਂ ਗੈਸ ਦਾ ਛੋਟਾ ਸਿਲੰਡਰ ਤੇ ਛੋਟਾ ਚੁੱਲ੍ਹਾ ਲੈ ਗਿਆ। ਮਨਜੀਤ ਨੇ ਪਤੀਲੀ, ਕੱਪ – ਪਲੇਟਾਂ ਤੇ ਚਾਹ ਬਣਾਉਣ ਦਾ ਸਮਾਨ ਲੈ ਲਿਆ। ਗੁਰਜੀਤ ਦੀ ਮੰਮੀ ਨੇ ਸਾਨੂੰ ਪਕੌੜੇ ਬਣਾਉਣ ਲਈ ਤੇਲ, ਵੇਸਣ, ਪਾਲਕ – ਪਿਆਜ਼ ਤੇ ਲੂਣ – ਮਸਾਲਾ ਆਦਿ ਦੇ ਦਿੱਤਾ ਅਸੀਂ ਕੁੱਝ ਪਲਾਸਟਿਕ ਦੇ ਕੱਪ ਤੇ ਪਲੇਟਾਂ ਲੈ ਲਈਆਂ। ਇਸ ਦੇ ਨਾਲ ਬਿਸਕੁਟਾਂ ਦੇ ਕੁੱਝ ਪੈਕਟ ਵੀ ਲੈ ਲਏ। ਸਤਲੁਜ ਦਰਿਆ ਸਾਡੇ ਪਿੰਡਾਂ ਪੰਦਰਾਂ ਕਿਲੋਮੀਟਰ ਸੀ। ਅਸੀਂ ਸਾਰੇ ਉੱਤੇ ਸਮਾਨ ਰੱਖ ਕੇ ਚਲ ਪਏ।
ਦਰਿਆ ਦੇ ਕੰਢੇ ਪਹੁੰਚ ਕੇ ਅਸੀਂ ਇਕ ਸਾਫ਼ – ਸੁਥਰੀ ਥਾਂ ਚੁਣ ਲਈ ਤੇ ਉੱਥੇ ਬੈਠ ਗਏ। ਸਾਡੇ ਵਿਚੋਂ ਸਭ ਨੂੰ ਤਰਨਾ ਆਉਂਦਾ ਸੀ ਅਸੀਂ ਸਭ ਨੇ ਕੱਪੜੇ ਲਾਹ ਕੇ ਕੰਢੇ ਉੱਤੇ ਰੱਖ ਦਿੱਤੇ ਤੇ ਇਕ ਘੰਟਾ ਖੂਬ ਤਾਰੀਆਂ ਲਾਉਂਦੇ ਰਹੇ। ਇੰਨੇ ਨੂੰ ਸਾਨੂੰ ਇਕ ਕਿਸ਼ਤੀ ਦਿਸ ਪਈ ! ਮਲਾਹ ਮੱਛੀਆਂ ਫੜ ਰਿਹਾ ਸੀ। ਅਸੀਂ ਉਸਨੂੰ ਬੇਨਤੀ ਕੀਤੀ, ਤਾਂ ਉਹ ਸਾਡੇ ਵਿਚੋਂ ਤਿੰਨਾਂ – ਤਿੰਨਾਂ ਨੂੰ ਕਿਸ਼ਤੀ ਵਿਚ ਬਿਠਾ ਕੇ ਘੁੰਮਾਉਣਾ ਮੰਨ ਗਿਆ ਅਸੀਂ ਤਿੰਨ – ਤਿੰਨ ਗਰੁੱਪ ਬਣਾ ਕੇ ਪੰਦਰਾਂ – ਪੰਦਰਾਂ ਵਿਚ ਕਿਸ਼ਤੀ ਵਿਚ ਚੜ੍ਹ ਕੇ ਦਰਿਆ ਦਾ ਆਨੰਦ ਮਾਣਿਆ ਸਾਡੇ ਵਿਚੋਂ ਕੁੱਝ ਨੇ ਆਪ ਚੱਪੂ ਚਲਾਏ ਤੇ ਇਕ – ਦੋ ਨੇ ਮੱਛੀਆਂ ਲਈ ਭੰਡੀ ਵੀ ਲਾਈ। ਫਿਰ ਸਾਨੂੰ ਭੁੱਖ ਲੱਗ ਗਈ।
ਦਰਿਆ ਤੋਂ ਬਾਹਰ ਆ ਕੇ ਮੈਂ ਨੇੜੇ ਦੇ ਗੈਸਟ ਹਾਊਸ ਵਿਚ ਜਾ ਕੇ ਪਾਣੀ ਦੀ ਬਾਲਟੀ ਲੈ ਆਂਦੀ ਤੇ ਮੈਂ ਗੈਸ ਦਾ ਚੁੱਲ੍ਹਾ ਬਾਲ ਦਿੱਤਾ ਗੁਰਜੀਤ ਨੇ ਕੜਾਹੀ ਉੱਤੇ ਰੱਖ ਕੇ ਤੇਲ ਗਰਮ ਕਰਨਾ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤਾ। ਬਲਵੀਰ ਨੇ ਕੁੱਝ ਵੇਸਣ ਵਿਚ ਪਾਲਕ ਤੇ ਕੁੱਝ ਵਿਚ ਪਿਆਜ਼ ਮਿਲਾ ਕੇ ਘੋਲ ਤਿਆਰ ਕਰ ਲਿਆ ਤੇ ਪਕੌੜੇ ਤਲਣ ਲੱਗਾ। ਉਹ ਗਰਮ – ਗਰਮ ਪਕੌੜੇ ਕੱਢ ਰਿਹਾ ਸੀ ਤੇ ਅਸੀਂ ਖਾ ਰਹੇ ਸੀ। ਫਿਰ ਅਸੀਂ ਚਾਹ ਬਣਾਈ ਤੇ ਉਸ ਨਾਲ ਬਿਸਕੁਟ ਖਾਧੇ। ਇਸ ਪਿੱਛੋਂ ਅਸੀਂ ਸਾਰੇ ਗੋਲ ਘੇਰਾ ਬਣਾ ਕੇ ਬੈਠ ਗਏ। ਰਾਕੇਸ਼ ਨੇ ਲਤੀਫ਼ੇ ਸੁਣਾ – ਸੁਣਾ ਕੇ ਸਾਨੂੰ ਖੂਬ ਹਸਾਇਆ। ਜੋਤੀ ਤੇ ਮਿੱਕੀ ਨੇ ਗੀਤ ਸੁਣਾਏ ! ਹਰਦੀਪ ਨੇ ਕੁੱਝ ਮੰਤਰੀਆਂ ਤੇ ਐਕਟਰਾਂ ਦੀਆਂ ਨਕਲਾਂ ਲਾ ਕੇ ਖੂਬ ਹਸਾਇਆ।
ਇਸ ਤਰ੍ਹਾਂ ਤਿੰਨ – ਚਾਰ ਘੰਟੇ ਪਿਕਨਿਕ ਦਾ ਮਜ਼ਾ ਲੈਣ ਮਗਰੋਂ ਅਸੀਂ ਘਰ ਪਰਤ ਆਏ !

26. ਟਰੈਫਿਕ ਸਪਤਾਹ
ਸਾਡੇ ਸ਼ਹਿਰ ਵਿਚ ਪੁਲਿਸ ਵਲੋਂ ਬੀਤੇ 1 ਜਨਵਰੀ ਤੋਂ 7 ਜਨਵਰੀ ਤਕ ਟਰੈਫ਼ਿਕ ਸਪਤਾਹ ਮਨਾਇਆ ਗਿਆ ਸਾਰੇ ਸ਼ਹਿਰ ਵਿਚ ਟਰੈਫ਼ਿਕ ਨਿਯਮਾਂ ਦੀ ਪਾਲਣਾ ਸੰਬੰਧੀ ਚਿੱਟੇ ਰੰਗ ਦੇ ਬੈਨਰ ਲੱਗੇ ਹੋਏ ਸਨ। ਟਰੈਫ਼ਿਕ ਦੇ ਸਿਪਾਹੀ ਆਪਣੇ ਹੱਥਾਂ ਉੱਤੇ ਚਿੱਟੇ ਰੰਗ ਦੇ ਦਸਤਾਨੇ ਪਾਈ ਥਾਂ – ਥਾਂ ਸਰਗਰਮ ਦਿਖਾਈ ਦੇ ਰਹੇ ਸਨ। ਭਿੰਨ – ਭਿੰਨ ਸਕੂਲਾਂ ਦੇ ਵਿਦਿਆਰਥੀਆਂ ਨੂੰ ਵੀ ਇਸ ਮੁਹਿੰਮ ਵਿਚ ਸ਼ਾਮਿਲ ਕੀਤਾ ਗਿਆ ਸੀ ਤੇ ਉਹ ਵੀ ਹੱਥਾਂ ਵਿਚ ਬੈਨਰ ਫੜ ਕੇ ਤੇ ਟੋਲੀਆਂ ਬਣਾ ਕੇ ਸੜਕਾਂ ਉੱਤੇ ਤੁਰ ਰਹੇ ਸਨ। ਇਹ ਸਾਲ ਦਾ ਉਹ ਹਫ਼ਤਾ ਸੀ, ਜਿਸ ਵਿਚ ਲੋਕਾਂ ਨੂੰ ਟਰੈਫ਼ਿਕ ਨਿਯਮਾਂ ਤੇ ਉਨ੍ਹਾਂ ਦੀ ਪਾਲਣਾ ਸੰਬੰਧੀ ਸੁਚੇਤ ਕੀਤਾ ਜਾ ਰਿਹਾ ਸੀ।
ਇਸ ਉਦੇਸ਼ ਦੀ ਪ੍ਰਾਪਤੀ ਲਈ ਥਾਂ – ਥਾਂ ਵਰਕਸ਼ਾਪਾਂ, ਡਰਾਈਵਿੰਗ ਟੈਸਟਾਂ, ਲੈਕਚਰਾਂ ਤੇ ਭਾਸ਼ਨ – ਮੁਕਾਬਲਿਆਂ ਦੇ ਆਯੋਜਨ ਵੀ ਕੀਤੇ ਜਾ ਰਹੇ ਸਨ। ਇਸੇ ਲੜੀ ਵਿਚ ਸਾਡੇ ਸਕੂਲ ਵਿਚ ਵੀ ਵਿਦਿਆਰਥੀਆਂ ਨੂੰ ਟਰੈਫ਼ਿਕ ਨਿਯਮਾਂ ਸੰਬੰਧੀ ਜਾਗਰੂਕ ਕਰਨ ਲਈ ਇਕ ਅੰਤਰ – ਸਕੂਲ ਭਾਸ਼ਨ ਮੁਕਾਬਲਾ ਹੋ ਰਿਹਾ ਸੀ। ਇਸ ਵਿਚ ਮੁੱਖ ਮਹਿਮਾਨ ਸਾਡੇ ਇਲਾਕੇ ਦੇ ਪੁਲਿਸ ਸਟੇਸ਼ਨ ਦੇ ਟਰੈਫ਼ਿਕ – ਇਨਸਪੈਕਟਰ ਸਨ। ਭਾਸ਼ਨ ਮੁਕਾਬਲੇ ਵਿਚ ਹਿੱਸਾ ਲੈਣ ਵਾਲੇ ਵਕਤਿਆਂ ਨੇ ਸਰੋਤਿਆਂ ਨੂੰ ਭਾਰਤ ਵਿਚ ਸੜਕਾਂ ਉੱਤੇ ਦਿਨੋ – ਦਿਨ ਵਧ ਰਹੇ ਹਾਦਸਿਆਂ, ਅਜਾਈਂ ਜਾਂਦੀਆਂ ਜਾਨਾਂ ਤੇ ਅਪੰਗ ਹੋਣ ਵਾਲੇ ਵਿਅਕਤੀਆਂ ਦੀ ਲੂੰ ਕੰਡੇ ਕਰਨ ਵਾਲੀ ਗਿਣਤੀ ਬਾਰੇ ਦੱਸਦਿਆਂ ਟਰੈਫ਼ਿਕ ਨਿਯਮਾਂ ਦੀ ਉਲੰਘਣਾ, ਟਰੈਫ਼ਿਕ ਨਿਯਮਾਂ ਨੂੰ ਇਸ ਸੰਬੰਧ ਵਿਚ ਪੁਲਿਸ ਅਤੇ ਨੇਤਾ ਲੋਕਾਂ ਦੀ ਕਾਰਗੁਜ਼ਾਰੀ ਬਾਰੇ ਕਾਫ਼ੀ ਚਾਨਣਾ ਪਾਇਆ।
ਉਨ੍ਹਾਂ ਦਿਨੋ – ਦਿਨ ਤਰ੍ਹਾਂ – ਤਰ੍ਹਾਂ ਦੇ ਵਾਹਨਾਂ ਤੇ ਸੜਕਾਂ ਦੀ ਮੰਦੀ ਹਾਲਤ ਬਾਰੇ ਵੀ ਆਪਣੇ – ਆਪਣੇ ਵਿਚਾਰ ਰੱਖੇ। ਮੁੱਖ ਮਹਿਮਾਨ ਟਰੈਫ਼ਿਕ ਇਨਸਪੈਕਟਰ ਨੇ ਆਪਣੇ ਭਾਸ਼ਨ ਵਿਚ ਵਿਦਿਆਰਥੀਆਂ ਨੂੰ ਦੱਸਿਆ ਕਿ ਉਨ੍ਹਾਂ ਦੀ ਆਪਣੀ ਸੁਰੱਖਿਆ ਲਈ ਤੇ ਆਵਾਜਾਈ ਨੂੰ ਨਿਰਵਿਘਨ ਚਲਦਾ ਰੱਖਣ ਲਈ ਟਰੈਫ਼ਿਕ ਨਿਯਮਾਂ ਦੀ ਪਾਲਣਾ ਬਹੁਤ ਜ਼ਰੂਰੀ ਹੈ।
ਉਨ੍ਹਾਂ ਡਰਾਈਵਿੰਗ ਸਿੱਖਣ, ਲਾਈਸੈਂਸ ਪ੍ਰਾਪਤ ਕਰਨ, ਟਰੈਫ਼ਿਕ ਨਿਯਮਾਂ ਦੀ ਪਾਲਣਾ ਕਰਨ ਤੇ ਪਾਰਕਿੰਗ ਆਦਿ ਸੰਬੰਧੀ ਵਿਦਿਆਰਥੀਆਂ ਨੂੰ ਬਹੁਤ ਸਾਰੀ ਜਾਣਕਾਰੀ ਦਿੱਤੀ। ਉਨ੍ਹਾਂ ਇਹ ਵੀ ਕਿਹਾ ਕਿ ਟਰੈਫ਼ਿਕ ਨਿਯਮਾਂ ਦੀ ਪਾਲਣਾ ਵਿਚ ਪੁਲਿਸ ਸੱਚੇ ਦਿਲੋਂ ਉਨ੍ਹਾਂ ਦੇ ਨਾਲ ਹੈ ਤੇ ਆਮ ਲੋਕਾਂ ਦਾ ਇਸ ਵਿਚ ਸਹਿਯੋਗ ਬਹੁਤ ਜ਼ਰੂਰੀ ਹੈ। ਇਸ ਲਈ ਸਾਡਾ ਸਭ ਦਾ ਫ਼ਰਜ਼ ਹੈ ਕਿ ਆਪਣੀ ਸੁਰੱਖਿਆ, ਆਵਾਜਾਈ ਨੂੰ ਨਿਰਵਿਘਨ ਚਲਦਾ ਰੱਖਣ ਤੇ ਦੇਸ਼ ਦੀ ਤਰੱਕੀ ਦੀ ਰਫ਼ਤਾਰ ਨੂੰ ਤੇਜ਼ ਰੱਖਣ ਲਈ ਟਰੈਫ਼ਿਕ ਨਿਯਮਾਂ ਦੀ ਪਾਲਣਾ ਕਰੀਏ।
ਅੰਤ ਵਿਚ ਸਾਡੇ ਮੁੱਖ ਅਧਿਆਪਕ ਸਾਹਿਬ ਨੇ ਮੁੱਖ ਮਹਿਮਾਨ ਦਾ ਧੰਨਵਾਦ ਕਰਦਿਆਂ ਤੇ ਭਾਸ਼ਨ ਮੁਕਾਬਲੇ ਵਿਚ ਭਾਗ ਲੈਣ ਵਾਲੇ ਵਿਦਿਆਰਥੀਆਂ ਤੇ ਆਪਣੇ ਸਕੂਲ ਦੇ ਵਿਦਿਆਰਥੀਆਂ ਦੁਆਰਾ ਟਰੈਫ਼ਿਕ ਸਪਤਾਹ ਵਿਚ ਹਿੱਸਾ ਲੈਣ ਉੱਤੇ ਖ਼ੁਸ਼ੀ ਪ੍ਰਗਟ ਕਰਦਿਆਂ ਦੱਸਿਆ ਕਿ ਕਿਸ ਤਰ੍ਹਾਂ ਆਵਾਜਾਈ ਨੂੰ ਸੁਚਾਰੂ ਢੰਗ ਨਾਲ ਚਲਾਉਣ ਲਈ ਟਰੈਫ਼ਿਕ ਨਿਯਮਾਂ ਦੀ ਪਾਲਣਾ ਦੇ ਨਾਲ ਦਿਨੋ – ਦਿਨ ਵਧ ਰਹੇ ਵਾਹਨਾਂ ਤੇ ਆਵਾਜਾਈ ਲਈ ਚੰਗੀਆਂ ਸੜਕਾਂ, ਟਰੈਫ਼ਿਕ ਲਾਈਟਾਂ ਦਾ ਚੰਗੀ ਹਾਲਤ ਵਿਚ ਹੋਣਾ, ਟਰੈਫ਼ਿਕ ਨਿਯਮਾਂ ਦੀ ਉਲੰਘਣਾ ਕਰਨ ਵਾਲੇ ਵਿਰੁੱਧ ਪੁਲਿਸ ਦਾ ਬੇਲਿਹਾਜ਼ ਹੋਣਾ, ਪੈਦਲਾਂ ਲਈ ਜ਼ੈਬਰਾ ਕਰਾਸਿੰਗ ਤੇ ਫੁੱਟਪਾਥਾਂ ਦੇ ਹੋਣ ਤੋਂ ਇਲਾਵਾ ਟਰੈਫ਼ਿਕ ਭੀੜਾਂ ਨੂੰ ਰੋਕਣ ਲਈ ਥਾਂ – ਥਾਂ ਫਲਾਈਓਵਰਾਂ ਦਾ ਬਣੇ ਹੋਣਾ ਵੀ ਜ਼ਰੂਰੀ ਹੈ। ਅੰਤ ਵਿਚ ਉਨ੍ਹਾਂ ਆਸ ਪ੍ਰਗਟ ਕੀਤੀ ਕਿ ਇਸ ਟਰੈਫ਼ਿਕ ਸਪਤਾਹ ਤੋਂ ਬਹੁਤ ਸਾਰੇ ਲੋਕ ਟਰੈਫ਼ਿਕ ਨਿਯਮਾਂ ਸੰਬੰਧੀ ਜਾਗਰੂਕ ਹੋਏ ਹੋਣਗੇ ਤੇ ਅੱਗੋਂ ਸ਼ਹਿਰ ਵਿਚ ਟਰੈਫ਼ਿਕ ਦੀ ਸਮੱਸਿਆ ਬਹੁਤ ਹੱਦ ਤਕ ਘੱਟ ਜਾਵੇਗੀ।

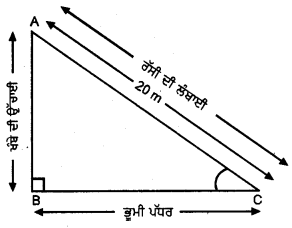
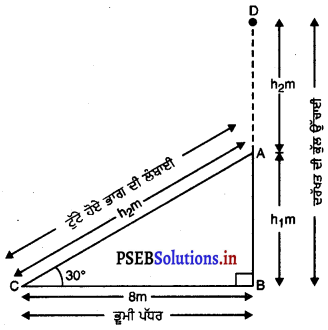
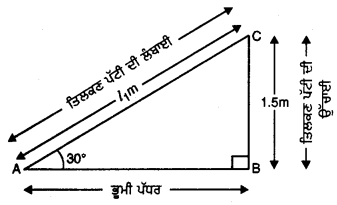
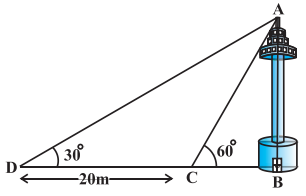
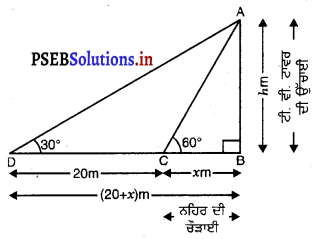
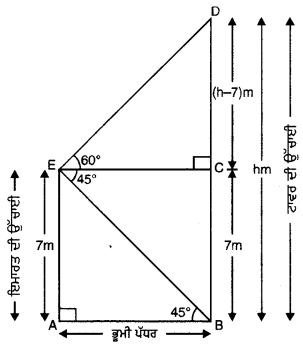
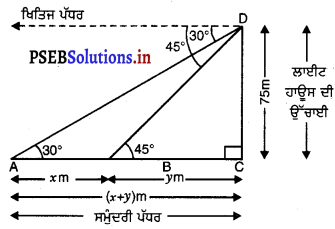
27. ਗਰਮੀ ਦੀ ਰੁੱਤ
ਪੰਜਾਬ ਬਹੁਰੰਗੀਆਂ ਰੁੱਤਾਂ ਦਾ ਦੇਸ਼ ਹੈ। ਇਸ ਵਿਚ ਮੌਸਮ ਕਈ ਰੰਗ ਦਿਖਾਉਂਦਾ ਹੈ। ਇਸ ਵਿਚ ਅਤਿ ਦੀ ਸਰਦੀ ਵੀ ਪੈਂਦੀ ਹੈ ਤੇ ਅੱਤ ਦੀ ਗਰਮੀ ਵੀ। ਗਰਮੀ ਸਰਦੀ ਤੋਂ ਬਿਨਾਂ ਬਰਸਾਤ, ਪੱਤਝੜ ਤੇ ਬਸੰਤ ਇੱਥੋਂ ਦੀਆਂ ਹੋਰ ਪ੍ਰਸਿੱਧ ਰੁੱਤਾਂ ਹਨ।
ਗਰਮੀ ਦੀ ਰੁੱਤ ਦਾ ਆਰੰਭ ਬਸੰਤ ਰੁੱਤ ਦੇ ਬੀਤਣ ਨਾਲ ਹੀ ਹੋ ਜਾਂਦਾ ਹੈ। ਪੰਜਾਬ ਵਿਚ ਜੇਠ – ਹਾੜ੍ਹ ਅਰਥਾਤ ਮਈ ਜੂਨ ਗਰਮੀ ਦੇ ਮਹੀਨੇ ਮੰਨੇ ਜਾਂਦੇ ਹਨ। ਇਨ੍ਹਾਂ ਮਹੀਨਿਆਂ ਵਿਚ ਪੰਜਾਬ ਵਿਚ ਅਤਿ ਦੀ ਗਰਮੀ ਪੈਂਦੀ ਹੈ। ਸੂਰਜ ਅਸਮਾਨ ਵਿਚ ਸਿਖਰ ਉੱਤੇ ਪੁੱਜ ਜਾਂਦਾ ਹੈ ਤੇ ਅੱਗ ਵਰਾਉਂਦਾ ਹੈ।
ਸਿਖਰ ਦੁਪਹਿਰੇ ਜੇਠ ਦੀ, ਵਰੁਨ ਪਏ ਅੰਗਿਆਰ॥
ਲੋਆਂ ਵਾਓ ਵਰੋਲਿਆਂ, ਰਾਹੀਂ ਲਏ ਖਲਾਰ।
ਲੋਹ ਤਪੇ ਜਿਉਂ ਪਿਥਵੀ, ਭਖ ਲਵਣ ਅਸਮਾਨ !
ਪਸ਼ੂਆਂ ਜੀਭਾਂ ਸੁੱਟੀਆਂ, ਪੰਛੀ ਭੁੱਜਦੇ ਜਾਣ।
ਗਰਮੀ ਦੀ ਰੁੱਤ ਦਾ ਪਹਿਲਾ ਐਕਟ ਵਿਸਾਖ ਅਰਥਾਤ ਅਪਰੈਲ ਦੇ ਅੱਧ ਤੋਂ ਸ਼ੁਰੂ ਹੋ ਜਾਂਦਾ ਹੈ। ਮਈ – ਜੂਨ ਵਿਚ ਇਹ ਸਿਖਰ ਉੱਤੇ ਪੁੱਜ ਜਾਂਦਾ ਹੈ। ਧੁੱਪ, ਗਰਮੀ, ਹਨੇਰੀ ਤੇ ਲੂ ਇਸ ਦੇ ਪਾਤਰ ਹਨ। ਜੁਲਾਈ – ਅਗਸਤ ਵਿਚ ਮੀਂਹ ਪੈਣ ਨਾਲ ਗਰਮੀ ਘਟਣ ਲਗਦੀ ਹੈ ਤੇ ਸਤੰਬਰ ਵਿਚ ਇਸ ਦਾ ਅੰਤ ਹੋ ਜਾਂਦਾ ਹੈ। ਇਨ੍ਹਾਂ ਦਿਨਾਂ ਵਿਚ ਦਿਨ ਵੱਡੇ ਤੇ ਰਾਤਾਂ ਛੋਟੀਆਂ ਹੁੰਦੀਆਂ ਹਨ। ਦਿਨੇ ਧਰਤੀ ਤਪਦੇ ਸੂਰਜ ਦੀ ਗਰਮੀ ਨੂੰ ਜਜ਼ਬ ਕਰਦੀ ਹੈ, ਪਰ ਰਾਤ ਛੋਟੀ ਹੋਣ ਕਰਕੇ ਉਹ ਗਰਮੀ ਘੱਟ ਖਾਰਜ ਕਰਦੀ ਹੈ, ਇਸ ਕਰਕੇ ਗਰਮੀ ਜਮਾਂ ਹੋਣ ਨਾਲ ਅੰਦਰ – ਬਾਹਰ ਤਪਣ ਲਗਦੇ ਹਨ ਜੂਨ ਵਿਚ ਗਰਮੀ ਦਾ ਤਾਪਮਾਨ ਕਈ ਵਾਰੀ 48° ਸੈਲਸੀਅਸ ਤਕ ਪਹੁੰਚ ਜਾਂਦਾ ਹੈ।
ਲੋਕਾਂ ਨੂੰ ਰੁੱਖਾਂ ਦੀਆਂ ਠੰਢੀਆਂ ਛਾਂਵਾਂ, ਪੱਖਿਆਂ, ਕੂਲਰਾਂ ਤੇ ਏਅਰ ਕੰਡੀਸ਼ਨਰਾਂ ਦਾ ਸਹਾਰਾ ਲੈਣਾ ਪੈਂਦਾ ਹੈ। ਬਾਹਰ ਧੁੱਪ ਵਿਚ ਨਿਕਲਣਾ ਬਹੁਤ ਔਖਾ ਹੁੰਦਾ ਹੈ। ਸਿਰ ਨੂੰ ਪੱਗ, ਪਰਨੇ ਜਾਂ ਟੋਪੀ ਨਾਲ ਢੱਕਣ ਜਾਂ ਛਤਰੀ ਲੈਣ ਨਾਲ ਹੀ ਕੁੱਝ ਚੈਨ ਮਿਲਦਾ ਹੈ ਪਾਣੀ ਪੀ – ਪੀ ਕੇ ਪਿਆਸ ਨਹੀਂ ਬੁਝਦੀ। ਲੋਕ ਘੜੇ, ਕੁਲਰ ਜਾਂ ਫਰਿਜ਼ ਦਾ ਠੰਢਾ ਪਾਣੀ ਪੀਂਦੇ ਹਨ। ਕਈ ਲੋਕ ਸ਼ਰਬਤ, ਸ਼ਕੰਜਵੀ, ਲੱਸੀ, ਸੱਤ ਜਾਂ ਸ਼ਰਦਾਈ ਦੀ ਵਰਤੋਂ ਵੀ ਕਰਦੇ ਹਨ।
ਇਸ ਤੋਂ ਬਿਨਾਂ ਗਰਮੀ ਤੋਂ ਬਚਣ ਲਈ ਕੋਕਾ ਕੋਲਾ, ਪੈਪਸੀ ਜਾਂ ਹੋਰ ਸੋਢੇ ਦੀਆਂ ਬੋਤਲਾਂ ਪੀਤੀਆਂ ਜਾਂਦੀਆਂ ਹਨ ਅਤੇ ਆਈਸ ਕ੍ਰੀਮ ਤੇ ਕੁਲਫੀਆਂ ਖਾਧੀਆਂ ਜਾਂਦੀਆਂ ਹਨ। ਵਿਹੜੇ ਤੇ ਕਮਰੇ ਠੰਢੇ ਰੱਖਣ ਲਈ ਪਾਣੀ ਦਾ ਛਿੜਕਾ ਕੀਤਾ ਜਾਂਦਾ ਹੈ। ਦਿਨ ਵਿਚ ਦੋ ਜਾਂ ਤਿੰਨ ਵਾਰੀ ਠੰਢੇ ਪਾਣੀ ਨਾਲ ਇਸ਼ਨਾਨ ਕੀਤਾ ਜਾਂਦਾ ਹੈ।
ਗਰਮੀ ਦੀ ਰੁੱਤ ਤੋਂ ਤੰਗ ਆਏ ਲੋਕ ਮੀਂਹ ਮੰਗਦੇ ਹਨ। ਜਿਸ ਦਿਨ ਕਿਤੇ ਇੰਦਰ ਦੇਵਤੇ ਦੀ ਮਿਹਰ ਹੁੰਦੀ ਹੈ, ਲੋਕ ਬਹੁਤ ਖ਼ੁਸ਼ ਹੁੰਦੇ ਹਨ। ਮੀਂਹ ਪੈਣ ਨਾਲ ਤਪਸ਼ ਜ਼ਰੂਰ ਘਟ ਜਾਂਦੀ ਹੈ, ਪਰ ਸਰੀਰ ਵਿਚੋਂ ਪਸੀਨੇ ਦੇ ਹੜ ਵਗਣ ਲਗਦੇ ਹਨ। ਗਰਮੀ ਦੀ ਰੁੱਤ ਵਿਚ ਧੁੱਪ ਦੀਆਂ ਸਿੱਧੀਆਂ ਕਿਰਨਾਂ ਪੈਣ ਨਾਲ ਕਈ ਲੋਕ ਸਨ – ਸਟਰੋਕ ਨਾਲ ਮੌਤ ਦੇ ਸ਼ਿਕਾਰ ਹੋ ਜਾਂਦੇ ਹਨ ਕਈ ਸਿਰ ਦਰਦ ਤੇ ਅੱਖਾਂ ਦੇ ਰੋਗਾਂ ਦੇ ਸ਼ਿਕਾਰ ਵੀ ਹੋ ਜਾਂਦੇ ਹਨ। ਸਾਨੂੰ ਗਰਮੀ ਤੋਂ ਬਚਣ ਲਈ ਕੁੱਝ ਉਪਾ ਜ਼ਰੂਰ ਕਰਨੇ ਚਾਹੀਦੇ ਹਨ।
ਇਸ ਮੌਸਮ ਵਿਚ ਲੂਣ ਮਿਲਿਆ ਨਿੰਬੂ – ਪਾਣੀ ਵਧੇਰੇ ਲਾਭਦਾਇਕ ਰਹਿੰਦਾ ਹੈ। ਸਾਨੂੰ ਇਹ ਵੀ ਯਾਦ ਰੱਖਣਾ ਚਾਹੀਦਾ ਹੈ ਕਿ ਸੂਰਜ ਦੀ ਗਰਮੀ ਧਰਤੀ ਦੇ ਜੀਵਾਂ ਤੇ ਬਨਸਪਤੀ ਲਈ ਇਕ ਵਰਦਾਨ ਹੈ। ਇਸ ਤੋਂ ਬਿਨਾਂ ਧਰਤੀ ਉੱਪਰ ਜੀਵਨ ਦੀ ਹੋਂਦ ਸੰਭਵ ਨਹੀਂ !

28. ਸਾਡਾ ਰਾਸ਼ਟਰੀ ਪੰਛੀ – ਮੋਰ
ਮੋਰ ਸਾਡਾ ਰਾਸ਼ਟਰੀ ਪੰਛੀ ਹੈ। ਇਹ ਸੁੰਦਰਤਾ, ਸ਼ਿਸ਼ਟਤਾ ਅਤੇ ਰਹੱਸ ਦਾ ਚਿੰਨ ਹੈ। ਭਾਰਤ ਵਿਚ 1972 ਵਿਚ ਇਕ ਐਕਟ ਰਾਹੀਂ ਇਸਨੂੰ ਮਾਰਨ ਜਾਂ ਕੈਦ ਕਰ ਕੇ ਰੱਖਣ ਉੱਤੇ ਪੂਰੀ ਪਾਬੰਦੀ ਲਾਈ ਗਈ ਹੈ।
ਮੋਰ ਬੜਾ ਸੁੰਦਰ ਪੰਛੀ ਹੈ। ਇਸ ਦੇ ਸਿਰ ਉੱਪਰ ਸੁੰਦਰ ਕਲਗੀ ਹੁੰਦੀ ਹੈ। ਇਸ ਦੀ ਛੋਟੀ ਜਿਹੀ ਚੁੰਝ ਤੇ ਨੀਲੇ ਰੰਗ ਦੀ ਲੰਮੀ ਧੌਣ ਹੁੰਦੀ ਹੈ। ਇਸ ਦੇ ਲੰਮੇ – ਲੰਮੇ ਪਰ ਹੁੰਦੇ ਹਨ ਪਰਾਂ ਦਾ ਚਮਕੀਲਾ ਰੰਗ, ਨੀਲਾ, ਕਾਲਾ ਤੇ ਸੁਨਹਿਰੀ ਹੁੰਦਾ ਹੈ। ਹਰੇਕ ਪਰ ਦੇ ਸਿਰੇ ਉੱਤੇ ਇਨ੍ਹਾਂ ਹੀ ਮਿਲੇ – ਜੁਲੇ ਰੰਗਾਂ ਦਾ ਇਕ ਸੁੰਦਰ ਗੋਲ ਜਿਹਾ ਚੱਕਰ ਹੁੰਦਾ ਹੈ। ਕ੍ਰਿਸ਼ਨ ਜੀ ਨੇ ਮੋਰ ਮੁਕਟ ਰਾਹੀਂ ਇਸ ਨੂੰ ਗੌਰਵ ਬਖ਼ਸ਼ਿਆ ਹੈ।
ਮੋਰ ਖੇਤਾਂ ਵਿਚ ਜਾਂ ਰੁੱਖਾਂ ਦੀ ਓਟ ਵਿਚ ਆਪਣੇ ਪਰ ਫੈਲਾ ਕੇ ਪੈਲ ਪਾਉਂਦਾ ਹੈ। ਉਸ ਦੇ ਪਰ ਪੱਖੇ ਵਰਗੇ ਲਗਦੇ ਹਨ। ਪੈਲ ਪਾਉਂਦਿਆਂ ਉਹ ਮਸਤੀ ਵਿਚ ਨੱਚਦਾ ਹੈ। ਇਹ ਦ੍ਰਿਸ਼ ਬੜਾ ਲੁਭਾਉਣਾ ਹੁੰਦਾ ਹੈ। ਜੇਕਰ ਪੈਲ ਪਾਉਂਦੇ ਮੋਰ ਦੇ ਕੋਲ ਜਾਵੇ, ਤਾਂ ਉਹ ਪੈਲ ਪਾਉਣੀ ਬੰਦ ਕਰ ਕੇ ਲੁਕ ਜਾਂਦਾ ਹੈ।
ਮੋਰ ਆਪਣੇ ਲੰਮੇ ਤੇ ਭਾਰੇ ਪਰਾਂ ਕਰਕੇ ਲੰਮੀ ਉਡਾਰੀ ਨਹੀਂ ਮਾਰ ਸਕਦਾ ਮੋਰਨੀ ਦੇ ਪਰ ਨਹੀਂ ਹੁੰਦੇ। ਮੋਰ – ਮੋਰਨੀ ਨਾਲੋਂ ਇਸੇ ਤਰ੍ਹਾਂ ਹੀ ਵਧੇਰੇ ਸੁੰਦਰ ਹੁੰਦਾ ਹੈ, ਜਿਸ ਤਰ੍ਹਾਂ ਕੁੱਕੜ – ਕੁਕੜੀ ਨਾਲੋਂ ਮੋਰ – ਮੋਰਨੀ ਕੁੱਕੜ – ਕੁਕੜੀ ਵਾਂਗ ਆਪਣੇ ਪਰਿਵਾਰ ਨਾਲ ਰਹਿੰਦੇ ਹਨ।
ਮੋਰ ਸੁਤੰਤਰਤਾ ਨਾਲ ਰਹਿਣਾ ਪਸੰਦ ਕਰਦਾ ਹੈ। ਪਿੰਜਰੇ ਜਾਂ ਕਮਰੇ ਵਿਚ ਕੈਦ ਕੀਤੇ ਜਾਣ ਨਾਲ ਉਹ ਕੁੱਝ ਦਿਨਾਂ ਵਿਚ ਹੀ ਮਰ ਜਾਂਦਾ ਹੈ। ਉਸ ਦੀ ਡੀਲ – ਡੌਲ ਤੋਂ ਪਤਾ ਲਗਦਾ ਹੈ ਕਿ ਉਸ ਨੂੰ ਆਪਣੇ ਸ਼ੈਮਾਨ ਦੀ ਬਹੁਤ ਸੂਝ ਹੁੰਦੀ ਹੈ। ਕਿਹਾ ਜਾਂਦਾ ਹੈ ਕਿ ਉਹ ਆਪਣੇ ਭੱਦੇ ਪੈਰਾਂ ਵਲ ਵੇਖ ਕੇ ਝੂਰਦਾ ਹੈ।
ਮੋਰ ਆਮ ਕਰਕੇ ਸੰਘਣੇ ਰੁੱਖਾਂ ਵਿਚ ਰਹਿੰਦਾ ਹੈ। ਫ਼ਸਲਾਂ, ਘਾਹ ਦੇ ਮੈਦਾਨਾਂ ਤੇ ਨਹਿਰ ਦੇ ਕੰਢਿਆਂ ਦੇ ਨੇੜੇ ਤੁਰਨਾ – ਫਿਰਨਾ ਪਸੰਦ ਕਰਦਾ ਹੈ। ਇਹ ਬੱਦਲਾਂ ਨੂੰ ਦੇਖ ਕੇ ਨੱਚਦਾ ਤੇ ਪੈਲਾਂ ਪਾਉਂਦਾ ਹੈ। ਇਹ ਮੀਂਹ ਵਿਚ ਨੱਚ, ਟੱਪ ਅਤੇ ਨਹਾ ਕੇ ਬੜਾ ਖੁਸ਼ ਹੁੰਦਾ ਹੈ।
ਮੋਰ ਸਾਡਾ ਮਿੱਤਰ ਪੰਛੀ ਹੈ। ਇਹ ਹਾਨੀਕਾਰਕ ਕੀੜਿਆਂ ਨੂੰ ਖਾ ਜਾਂਦਾ ਹੈ। ਇਹ ਸੱਪ ਦਾ ਬੜਾ ਵੈਰੀ ਹੈ ਤੇ ਉਸ ਨੂੰ ਮਾਰ ਦਿੰਦਾ ਹੈ। ਸੱਪ ਮੋਰ ਤੋਂ ਬਹੁਤ ਡਰਦਾ ਹੈ ਮੋਰ ਦੀ ਅਵਾਜ਼ ਸੁਣ ਕੇ ਸੱਪ ਬਾਹਰ ਨਹੀਂ ਨਿਕਲਦਾ। ਮੋਰ ਦੇ ਖੰਭਾਂ ਦੇ ਚੌਰ ਬਣਾਏ ਜਾਂਦੇ ਹਨ ਜੋ ਮੰਦਰਾਂ, ਗੁਰਦੁਆਰਿਆਂ ਤੇ ਪੂਜਾ – ਸਥਾਨਾਂ ਉੱਤੇ ਵਰਤੇ ਜਾਂਦੇ ਹਨ। ਕਹਿੰਦੇ ਹਨ ਕਿ ਮੋਰ ਦੇ ਪਰਾਂ ਦੀ ਹਵਾ ਕਈ ਰੋਗਾਂ ਨੂੰ ਠੀਕ ਕਰਦੀ ਹੈ।
ਜੋਗੀ ਤੇ ਮਾਂਦਰੀ ਲੋਕ ਚੌਰ ਦੀ ਵਰਤੋਂ ਨਾਲ ਰੋਗ ਨੂੰ ਝਾੜਦੇ ਹਨ ਕਈ ਚਿਤਰਾਂ ਵਿਚ ਰਾਜੇ – ਰਾਣੀਆਂ ਨੂੰ ਉਨ੍ਹਾਂ ਦੇ ਦਾਸ – ਦਾਸੀਆਂ ਮੋਰਾਂ ਦੇ ਖੰਭਾਂ ਦੇ ਚੌਰ ਨਾਲ ਹਵਾ ਝੱਲ ਰਹੇ ਹੁੰਦੇ ਹਨ। ਕਈ ਚਿਰਾਂ ਵਿਚ ਮੋਰ ਦੇ ਮੂੰਹ ਵਿਚ ਸੱਪ ਹੁੰਦਾ ਹੈ। ਇਸ ਪ੍ਰਕਾਰ ਮੋਰ ਦਾ ਸੰਬੰਧ ਜਨ – ਜੀਵਨ ਨਾਲ ਜੁੜਿਆ ਹੋਇਆ ਹੈ। ਇਸੇ ਕਰਕੇ ਮੋਰ ਨੂੰ ਸਾਡਾ ਰਾਸ਼ਟਰੀ ਪੰਛੀ ਮੰਨਿਆ ਗਿਆ ਹੈ। ਇਸ ਦਾ ਸ਼ਿਕਾਰ ਕਰਨ ਦੀ ਆਗਿਆ ਨਹੀਂ। ਸਾਨੂੰ ਇਸ ਉੱਤੇ ਮਾਣ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ।

29. ਸਾਡਾ ਰਾਸ਼ਟਰੀ ਝੰਡਾ – ਤਿਰੰਗਾ
ਸਾਡਾ ਰਾਸ਼ਟਰੀ ਝੰਡਾ ਤਿਰੰਗਾ ਹੈ। ਇਸਨੂੰ ਇਸਦੀ ਵਰਤਮਾਨ ਸ਼ਕਲ ਵਿਚ 15 ਅਗਸਤ, 1947 ਵਾਲੇ ਦਿਨ ਅਜ਼ਾਦੀ ਪ੍ਰਾਪਤ ਹੋਣ ਤੋਂ 24 ਦਿਨ ਪਹਿਲਾਂ ਭਾਰਤ ਵਿਚ 22 ਜੁਲਾਈ, 1947 ਨੂੰ ਸੰਵਿਧਾਨ ਸਭਾ ਦੀ ਹੋਈ ਐਡਹਾਕ ਮੀਟਿੰਗ ਵਿਚ ਪ੍ਰਵਾਨ ਕੀਤਾ ਗਿਆ ਸੀ। ਇਸ ਤੋਂ ਪਿੱਛੋਂ 15 ਅਗਸਤ, 1947 ਤੋਂ ਲੈ ਕੇ 26 ਜਨਵਰੀ, 1950 ਭਾਰਤ ਦੇ ਗਣਤੰਤਰਤਾ ਦਿਵਸ ਤਕ ਇਸਨੂੰ ਡੋਮੀਨੀਅਨ ਆਫ਼ ਇੰਡੀਆ ਦੇ ਕੌਮੀ ਝੰਡੇ ਵਜੋਂ ਅਪਣਾਇਆ ਗਿਆ ਸੀ।
ਇਹ ਝੰਡਾ ਇੰਡੀਅਨ ਨੈਸ਼ਨਲ ਕਾਂਗਰਸ ਦੇ ਝੰਡੇ ਉੱਤੇ ਆਧਾਰਿਤ ਸੀ, ਜਿਸਦਾ ਡਿਜ਼ਾਈਨ ਪਿੰਗਾਲੀ ਵੈਨਕਾਇਆ ਨਾਂ ਦੇ ਇਕ ਵਿਦਵਾਨ ਨੇ ਕੀਤਾ ਸੀ। ਉਂਝ ਭਾਰਤ ਦੀ ਅਜ਼ਾਦੀ ਲਈ 1913 – 14 ਵਿਚ ਸੰਘਰਸ਼ ਕਰਨ ਵਾਲੀ ਗ਼ਦਰ ਪਾਰਟੀ ਦਾ ਝੰਡਾ ਵੀ ਤਿੰਨ – ਰੰਗਾਂ ਹੀ ਸੀ।
ਇਸ ਝੰਡੇ ਦੇ ਤਿੰਨ ਰੰਗ ਹਨ – ਕੇਸਰੀ, ਚਿੱਟਾ ਤੇ ਹਰਾ। ਇਸ ਦਾ ਕੇਸਰੀ ਰੰਗ ਸਭ ਤੋਂ ਉੱਪਰ ਹੁੰਦਾ ਹੈ, ਚਿੱਟਾ ਵਿਚਕਾਰ ਤੇ ਹਰਾ ਸਭ ਤੋਂ ਥੱਲੇ। ਚਿੱਟੇ ਦੇ ਵਿਚਕਾਰ ਉਸਦੀ ਚੌੜਾਈ ਦੇ ਨੇਵੀ ਬਲਿਊ ਰੰਗ ਅਸ਼ੋਕ ਚੱਕਰ ਦਾ ਚਿੰਨ੍ਹ ਹੁੰਦਾ ਹੈ, ਜਿਸਨੂੰ ਸਾਰਨਾਥ ਵਿਚ ਬਣੇ ਅਸ਼ੋਕ ਦੇ ਥੰਮ ਤੋਂ ਲਿਆ ਗਿਆ ਹੈ।
ਇਸ ਵਿਚਲਾ ਕੇਸਰੀ ਰੰਗ ਕੁਰਬਾਨੀ ਦਾ, ਚਿੱਟਾ ਰੰਗ ਅਮਨ ਦਾ ਤੇ ਹਰਾ ਰੰਗ ਖ਼ੁਸ਼ਹਾਲੀ ਦਾ ਪ੍ਰਤੀਕ ਹੈ। ਅਸ਼ੋਕ ਚੱਕਰ ਵਿਕਾਸ ਤੇ ਤਰੱਕੀ ਦਾ ਚਿੰਨ੍ਹ ਹੈ। ਇਹ ਝੰਡਾ ਭਾਰਤ ਦੀਆਂ ਫ਼ੌਜਾਂ ਦਾ ਜੰਗੀ ਝੰਡਾ ਵੀ ਹੈ ਅਤੇ ਇਹ ਫ਼ੌਜੀ ਕੇਂਦਰਾਂ ਉੱਤੇ ਬੁਲਾਇਆ ਜਾਂਦਾ ਹੈ। ਇਹ ਹੱਥ ਦੇ ਕੱਤੇ ਖੱਦਰ ਦਾ ਬਣਿਆ ਹੁੰਦਾ ਹੈ।
26 ਜਨਵਰੀ ਨੂੰ ਗਣਤੰਤਰਤਾ ਦਿਵਸ ਉੱਤੇ ਰਾਸ਼ਟਰਪਤੀ ਇਸਨੂੰ ਝੁਲਾਉਂਦੇ ਹਨ ਤੇ ਤਿੰਨਾਂ ਫ਼ੌਜਾਂ ਦੇ ਯੂਨਿਟਾਂ ਵਲੋਂ ਇਸਨੂੰ ਸਲਾਮੀ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ। 15 ਅਗਸਤ ਸੁਤੰਤਰਤਾ ਦਿਵਸ ਦੇ ਮੌਕੇ ‘ਤੇ ਪ੍ਰਧਾਨ ਮੰਤਰੀ ਇਸਨੂੰ ਲਾਲ ਕਿਲ੍ਹੇ ਉੱਤੇ ਝੁਲਾਉਂਦੇ ਹਨ। ਇਸ ਝੰਡੇ ਨੂੰ ਝੁਲਾਉਣ ਮਗਰੋਂ ਭਾਰਤ ਦਾ ਕੌਮੀ ਗੀਤ ‘ਜਨ ਗਨ ਮਨ….’ ਗਾਇਆ ਜਾਂਦਾ ਹੈ ਤੇ ਸਭ ਸਾਵਧਾਨ ਹੋ ਕੇ ਖੜੇ ਹੋ ਜਾਂਦੇ ਹਨ।
ਇੰਡੀਅਨ ਫਲੈਗ ਕੋਡ ਦੁਆਰਾ ਇਸ ਝੰਡੇ ਦੀ ਉੱਚਾਈ ਤੇ ਚੌੜਾਈ ਨਿਸਚਿਤ ਹੈ ਤੇ ਨਾਲ ਹੀ ਇਸਨੂੰ ਝੁਲਾਉਣ ਦੇ ਨਿਯਮ ਅਤੇ ਉਤਾਰਨ ਦੇ ਨਿਯਮ ਵੀ ਨਿਰਧਾਰਿਤ ਹਨ। ਜਦੋਂ ਕਿਸੇ ਵੱਡੇ ਨੇਤਾ ਦੀ ਮੌਤ ਹੋ ਜਾਂਦੀ ਹੈ, ਤਾਂ ਇਸਨੂੰ ਝੁਕਾ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ। ਤਿਰੰਗੇ ਝੰਡੇ ਦੇ ਸਤਿਕਾਰ ਤੇ ਮਹੱਤਤਾ ਨੂੰ ਪ੍ਰਗਟ ਕਰਨ ਲਈ ਬਹੁਤ ਸਾਰੇ ਕਵੀਆਂ ਨੇ ਗੀਤ ਲਿਖੇ ਹਨ ; ਜਿਵੇਂ –
ਝੰਡਿਆ ਤਿਰੰਗਿਆ ਨਿਰਾਲੀ ਤੇਰੀ ਸ਼ਾਨ ਏ।
ਸਾਰੇ ਦੇਸ਼ ਵਾਸੀਆਂ ਨੂੰ ਤੇਰੇ ਉੱਤੇ ਮਾਣ ਏ।
ਇਕ ਇਕ ਤਾਰ ਤੇਰੀ ਜਾਪੇ ਮੂੰਹੋਂ ਬੋਲਦੀ।
ਮੁੱਲ ਹੈ ਅਜ਼ਾਦੀ ਸਦਾ ਲਹੂਆਂ ਨਾਲ ਤੋਲਦੀ।
ਉੱਚਾ ਸਾਡਾ ਅੰਬਰਾਂ ‘ਤੇ ਝੂਲਦਾ ਨਿਸ਼ਾਨ ਏ।
ਝੰਡਿਆ ਤਿਰੰਗਿਆ ਨਿਰਾਲੀ ਤੇਰੀ ਸ਼ਾਨ ਏ। ਇਸ ਪ੍ਰਕਾਰ ਸਾਡਾ ਝੰਡਾ ਮਹਾਨ ਹੈ। ਇਹ ਸਦਾ ਉੱਚਾ ਰਹੇ। ਇਹ ਭਾਰਤ ਵਾਸੀਆਂ ਦੀ ਆਨ – ਸ਼ਾਨ ਦਾ ਪ੍ਰਤੀਕ ਹੈ। ਸਾਨੂੰ ਇਸ ਉੱਪਰ ਮਾਣ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ।

30. ਅੱਖੀਂ ਡਿੱਠੇ ਵਿਆਹ ਦਾ ਹਾਲ
ਪਿਛਲੇ ਐਤਵਾਰ ਮੇਰੇ ਮਿੱਤਰ ਦੇ ਵੱਡੇ ਭਰਾ ਦਾ ਵਿਆਹ ਸੀ। ਉਸ ਦੀ ਬਰਾਤ ਸਾਡੇ ਸ਼ਹਿਰ ਤੋਂ ਕੋਈ 20 ਕੁ ਕਿਲੋਮੀਟਰ ਦੁਰ ਫਗਵਾੜੇ ਵਿਚ ਜਾਣੀ ਸੀ। ਮੈਂ ਵੀ ਉਸ ਬਰਾਤ ਵਿਚ ਸ਼ਾਮਿਲ ਸਾਂ। ਬਰਾਤ ਦੇ 50 ਕੁ ਆਦਮੀ ਸਨ ਅਸੀਂ ਸਾਰੇ ਸਵੇਰ ਦੇ 10 ਕੁ ਵਜੇ ਬੱਸ ਵਿਚ ਸਵਾਰ ਹੋ ਕੇ ਚੱਲ ਪਏ। ਕੁੱਝ ਬਰਾਤੀ ਪੰਜ – ਛੇ ਕਾਰਾਂ ਵਿਚ ਸਵਾਰ ਸਨ। ਸਿਹਰਿਆਂ ਨਾਲ ਸਜੇ ਲਾੜੇ ਦੀ ਫੁੱਲਾਂ ਨਾਲ ਸ਼ਿੰਗਾਰੀ ਕਾਰ ਸਭ ਤੋਂ ਅੱਗੇ ਸੀ। ਸਵੇਰ ਦੇ ਕੋਈ 11 ਕੁ ਵਜੇ ਅਸੀਂ ਮਿੱਥੇ ਪ੍ਰੋਗਰਾਮ ਅਨੁਸਾਰ ਫਗਵਾੜੇ ਪਹੁੰਚੇ ਤੇ ਸ਼ਹਿਰ ਦੇ ਅੰਦਰ ਇਕ ਥਾਂ ਬਣੇ ਮੈਰਿਜ ਪੈਲਿਸ ਦੇ ਅੱਗੇ ਜਾ ਰੁਕੇ।
ਸਾਰੇ ਬਰਾਤੀ ਬੱਸ ਤੇ ਕਾਰਾਂ ਵਿਚੋਂ ਉਤਰੇ ਤੇ ਮਿਲਣੀ ਲਈ ਖੜ੍ਹੇ ਹੋ ਗਏ। ਲੜਕੀ ਵਾਲਿਆਂ ਦੇ ਰਿਸ਼ਤੇਦਾਰਾਂ ਤੇ ਸੰਬੰਧੀਆਂ ਨੇ ਸ਼ਬਦ ਪੜੇ ਤੇ ਅਰਦਾਸ ਕਰਨ ਪਿੱਛੋਂ ਮਿਲਣੀਆਂ ਹੋਈਆਂ ਪਹਿਲੀ ਮਿਲਣੀ ਸੁਰਿੰਦਰ ਦੇ ਪਿਤਾ ਅਤੇ ਲੜਕੀ ਦੇ ਪਿਤਾ ਦੀ ਸੀ।ਫਿਰ ਮਾਮਿਆਂ, ਚਾਚਿਆਂ ਤੇ ਭਰਾਵਾਂ ਤੋਂ ਇਲਾਵਾ ਹੋਰ ਸੰਬੰਧੀਆਂ ਦੀਆਂ ਮਿਲਣੀਆਂ ਹੋਈਆਂ। ਲੜਕੀ ਵਾਲਿਆਂ ਨੇ ਮਿਲਣੀ ਕਰਨ ਵਾਲੇ ਸੰਬੰਧੀਆਂ ਨੂੰ ਕੰਬਲ ਦਿੱਤੇ ਪਰ ਸੁਰਿੰਦਰ ਦੇ ਪਿਤਾ ਤੇ ਮਾਮੇ ਨੂੰ ਸੋਨੇ ਦੀਆਂ ਮੁੰਦਰੀਆਂ ਪਹਿਨਾਈਆਂ ਗਈਆਂ ਵੀਡੀਓ ਕੈਮਰਾ ਨਾਲੋ – ਨਾਲ ਫ਼ਿਲਮ ਬਣਾ ਰਿਹਾ ਸੀ।
ਮਿਲਣੀ ਤੋਂ ਮਗਰੋਂ ਕੁੜੀਆਂ ਮੈਰਿਜ ਪੈਲਿਸ ਦੇ ਮੁੱਖ ਦੁਆਰ ਨੂੰ ਰਿਬਨ ਬੰਨ੍ਹ ਕੇ ਰੋਕ ਕੇ ਖੜ੍ਹੀਆਂ ਹੋ ਗਈਆਂ ਕਾਫ਼ੀ ਹਾਸੇ – ਮਖੌਲ ਭਰੇ ਤਕਰਾਰ ਪਿੱਛੋਂ ਲਾੜੇ ਨੇ 100 ਰੁਪਏ ਦਿੱਤੇ ਤੇ ਅੱਗੇ ਲੰਘਣ ਦਿੱਤਾ ਗਿਆ। ਇਸ ਸਮੇਂ ਲਾੜੇ ਦੇ ਕੁੱਝ ਚਲੇ ਮਿੱਤਰਾਂ ਨੇ ਰਾਹ ਰੋਕ ਕੇ ਖੜੀਆਂ ਸਾਲੀਆਂ ਉੱਤੇ ਵੱਖ – ਵੱਖ ਸਪਰੇਆਂ ਦੀ ਬਛਾੜ ਕੀਤੀ, ਜਿਸ ਨੇ ਕਈਆਂ ਦਾ ਝੈ ਝੱਗ ਨਾਲ ਭਰ ਦਿੱਤੇ ਤੇ ਕਈਆਂ ਨੂੰ ਕੱਚੇ ਜਿਹੇ ਰੱਸਿਆਂ ਵਿਚ ਲਪੇਟ ਦਿੱਤਾ। ਕੁੱਝ ਸਪਰੇ ਖ਼ੁਸ਼ਬੂ ਖਿਲਾਰਨ ਵਾਲੇ ਵੀ ਸਨ।
ਫਿਰ ਸਾਰੇ ਬਰਾਤੀ ਸਾਹਮਣੇ ਮੇਜ਼ਾਂ ਉੱਤੇ ਲੱਗੇ ਨਾਸ਼ਤੇ ਤੇ ਹੋਰ ਪਕਵਾਨਾਂ ਦੇ ਸਟਾਲਾਂ ਵਲ ਵਧੇ। ਹਰ ਕੋਈ ਪਲੇਟ ਚਮਚਾ ਮਨ ਭਾਉਂਦੇ ਪਕਵਾਨ ਖਾਣ ਲੱਗਾ। ਇਨਾਂ ਵਿਚ ਬਹੁਤ ਕੁੱਝ ਸ਼ਾਕਾਹਾਰੀ ਤੇ ਮਾਸਾਹਾਰੀ ਸ਼ਾਮਿਲ ਸੀ। ਦਸ – ਬਾਰਾਂ ਸੁਨੈਕਸਾਂ ਦੇ ਸਟਾਲ ਸਨ। ਕਿਸੇ ਪਾਸੇ ਸਾਫ਼ਟ ਡਰਿੰਕ ਦੇ ਸਟਾਲ ਤੇ ਕਿਸੇ ਪਾਸੇ ਕਾਫ਼ੀ, ਚਾਹ ਤੇ ਕੇਸਰੀ ਦੁੱਧ ਤੋਂ ਇਲਾਵਾ ਮਠਿਆਈਆਂ, ਨੂਡਲਾਂ, ਗੋਲ – ਗੱਪਿਆਂ, ਚਾਟਾਂ ਤੇ ਕਈ ਪ੍ਰਕਾਰ ਦੇ ਜੂਸਾਂ ਦੇ ਸਟਾਲ ਸਨ।
ਇਸ ਪਿੱਛੋਂ ਗੁਰਦੁਆਰੇ ਵਿਚ ਲਾਵਾਂ ਹੋਈਆਂ। ਇਸ ਸਮੇਂ ਬਹੁਤੇ ਬਰਾਤੀ ਮੈਰਿਜ ਪੈਲਿਸ ਵਿਚ ਬੈਠੇ ਰਹੇ ਤੇ ਸਾਹਮਣੇ ਗਾਇਕ – ਟੋਲੀ ਵੱਲੋਂ ਪੇਸ਼ ਕੀਤੇ ਜਾ ਰਹੇ ਗਾਣਿਆਂ ਤੇ ਨੱਚਦੀਆਂ ਕੁੜੀਆਂ ਦੇ ਪ੍ਰੋਗਰਾਮ ਨੂੰ ਦੇਖਦੇ ਰਹੇ ਅਤੇ ਨਾਲ – ਨਾਲ ਖਾਂਦੇ – ਪੀਂਦੇ ਵੀ ਰਹੇ।
ਲਾਵਾਂ ਪਿੱਛੋਂ ਲਾੜੇ – ਲਾੜੀ ਨੂੰ ਲਿਆ ਕੇ ਸਭ ਦੇ ਸਾਹਮਣੇ ਸਟੇਜ ਦੇ ਇਕ ਪਾਸੇ ਲੱਗੀਆਂ ਸ਼ਾਹੀ ਕੁਰਸੀਆਂ ਉੱਤੇ ਬਿਠਾ ਦਿੱਤਾ ਗਿਆ ਲੜਕੀ ਗਹਿਣਿਆਂ ਨਾਲ ਸਜੀ ਹੋਈ ਸੀ ਸਭ ਰਿਸ਼ਤੇਦਾਰ ਵਾਰੋ – ਵਾਰੀ ਸ਼ਗਨ ਪਾਉਣ ਲੱਗੇ। ਵੀ.ਡੀ.ਓ. ਰਾਹੀਂ ਨਾਲੋ – ਨਾਲ ਫੋਟੋਗ੍ਰਾਫ਼ੀ ਹੋ ਰਹੀ ਸੀ।ਉੱਧਰ ਕੁੱਝ ਬਰਾਤੀ ਵਰਤਾਈ ਜਾ ਰਹੀ ਸ਼ਰਾਬ ਪੀ – ਪੀ ਕੇ ਭੰਗੜਾ ਪਾਉਣ ਲੱਗ ਪਏ ਸਨ। ਕੁੱਝ ਕੁੜੀਆਂ ਵੀ ਇਸ ਨਾਚ ਵਿਚ ਸ਼ਾਮਿਲ ਹੋ ਗਈਆਂ।
ਫਿਰ ਦੁਪਹਿਰ ਤੋਂ ਪਿੱਛੋਂ ਦਾ ਖਾਣਾ ਆਰੰਭ ਹੋ ਗਿਆ, ਜਿਸ ਵਿਚ ਬਹੁਤ ਕਿਸਮਾਂ ਦੇ ਸੂਪ, ਸ਼ਾਕਾਹਾਰੀ ਤੇ ਮਾਸਾਹਾਰੀ ਭੋਜਨ, ਕਈ ਪ੍ਰਕਾਰ ਦੇ ਸਲਾਦ, ਆਈਸ ਕ੍ਰੀਮਾਂ ਤੇ ਮਠਿਆਈਆਂ ਸ਼ਾਮਿਲ ਸਨ। ਉੱਧਰ ਨਾਲ – ਨਾਲ ਭੰਗੜਾ ਪੈ ਰਿਹਾ ਸੀ ਤੇ ਵਾਰਨੇ ਹੋ ਰਹੇ ਸਨ ਗਾਇਕ ਟੋਲੀ ਦਾ ਮੁਖੀ ਬਖ਼ਸ਼ੇ ਜਾ ਰਹੇ ਵੇਲਾਂ ਦੇ ਨੋਟ ਸੰਭਾਲੀ ਜਾ ਰਿਹਾ ਸੀ ਇਕ – ਦੋ ਸ਼ਰਾਬੀਆਂ ਨੇ ਨਿੱਕੀਆਂ – ਮੋਟੀਆਂ ਸ਼ਰਾਰਤਾਂ ਵੀ ਕੀਤੀਆਂ।

ਸਭ ਤੋਂ ਮਗਰੋਂ ਲਾੜੇ – ਲਾੜੀ ਸਮੇਤ ਉਨ੍ਹਾਂ ਦੇ ਨਜ਼ਦੀਕੀ ਰਿਸ਼ਤੇਦਾਰਾਂ ਨੇ ਇਕ ਟੇਬਲ ਉੱਤੇ ਬੈਠ ਕੇ ਰੋਟੀ ਖਾਧੀ। ਖਾਣਾ ਖਾਣ ਮਗਰੋਂ ਸੁਰਿੰਦਰ ਦੇ ਪਿਤਾ ਨੇ ਵਰੀ ਦਾ ਕੀਮਤੀ ਸਮਾਨ ਦਿਖਾਇਆ ਤੇ ਫਿਰ ਕੁੜੀ ਵਾਲਿਆਂ ਨੇ ਦਾਜ ॥ ਅੰਤ ਕੁੜੀ ਨੂੰ ਤੋਰ ਦਿੱਤਾ ਗਿਆ। ਤੁਰਨ ਸਮੇਂ ਸੁਰਿੰਦਰ ਦੇ ਪਿਤਾ ਨੇ ਜੋੜੀ ਉੱਪਰੋਂ ਪੈਸੇ ਸੁੱਟੇ। ਇਹ ਸਾਰਾ ਕੁੱਝ ਦੇਖ ਕੇ ਮੇਰਾ ਮਨ ਬੜਾ ਹੈਰਾਨ ਹੋ ਰਿਹਾ ਸੀ ਕਿ ਸਾਡਾ ਸਮਾਜ ਵਿਆਹਾਂ ਉੱਪਰ ਕਿਸ ਤਰ੍ਹਾਂ ਫ਼ਜ਼ੂਲ – ਖ਼ਰਚੀ ਕਰਦਾ ਹੈ ਤੇ ਰੁਪਏ ਨੂੰ ਉਸਾਰੂ ਕੰਮਾਂ ਵਿਚ ਲਾਉਣ ਦੀ ਬਜਾਏ ਅਜਿਹੀਆਂ ਰਸਮਾਂ ਉੱਪਰ ਰੋੜਦਾ ਹੈ। ਵਿਆਹਾਂ ਵਿਚ ਮਹਿੰਗੇ ਮੈਰਿਜ ਪੈਲਿਸਾਂ, ਹੋਟਲਾਂ ਤੇ ਨੱਚਣ – ਗਾਉਣ ਵਾਲਿਆਂ ਦੀ ਕੋਈ ਲੋੜ ਨਹੀਂ।
ਵਿਆਹ ਸਮੇਂ ਸ਼ਰਾਬ ਪੀਣ ਦੀ ਕੋਈ ਵੀ ਪ੍ਰਸੰਸਾ ਨਹੀਂ ਕਰ ਸਕਦਾ ਕਿਉਂਕਿ ਸ਼ਰਾਬੀ ਆਪਣੇ ਹੋਸ਼ – ਹਵਾਸ ਗੁਆ ਕੇ ਰੰਗ ਵਿਚ ਭੰਗ ਪਾ ਦਿੰਦੇ ਹਨ। ਇਸ ਕਰਕੇ ਵਿਆਹ ਹਰ ਤਰ੍ਹਾਂ ਦੇ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ। ਸ਼ਾਮੀਂ 7 ਵਜੇ ਅਸੀਂ ਵਾਪਸ ਘਰ ਪਹੁੰਚ ਗਏ ! ਵਹੁਟੀ ਨੂੰ ਕਾਰ ਵਿਚੋਂ ਉਤਾਰ ਕੇ ਘਰ ਲਿਆਂਦਾ ਗਿਆ ਸੱਸ ਨੇ ਪਾਣੀ ਵਾਰ ਕੇ ਪੀਤਾ ਵਹੁਟੀ ਤੇ ਲਾੜੇ ਦੇ ਘਰ ਪਹੁੰਚਣ ਮਗਰੋਂ ਸਾਰੇ ਜਾਂਦੀ ਤੇ ਹੋਰ ਪ੍ਰਾਹੁਣੇ ਆਪਣੇ – ਆਪਣੇ ਘਰਾਂ ਨੂੰ ਖਿਸਕਣ ਲੱਗੇ।
31. ਡਾਕੀਆ
ਡਾਕੀਆ ਸਾਡੇ ਜੀਵਨ ਦੇ ਹਰ ਖੇਤਰ ਵਿਚ ਮਹੱਤਵਪੂਰਨ ਸਥਾਨ ਰੱਖਦਾ ਹੈ। ਉਸ ਦੀ ਹਰ ਘਰ, ਹਰ ਦਫ਼ਤਰ ਤੇ ਹਰ ਸਥਾਨ ਉੱਤੇ ਉਡੀਕ ਕੀਤੀ ਜਾਂਦੀ ਹੈ। ਉਹ ਸਾਡੇ ਘਰਾਂ ਵਿਚ ਮਿੱਤਰਾਂ ਅਤੇ ਸੰਬੰਧੀਆਂ ਦੀਆਂ ਚਿੱਠੀਆਂ ਲੈ ਕੇ ਆਉਂਦਾ ਹੈ। ਉਹ ਘਰਾਂ ਤੇ ਦਫ਼ਤਰਾਂ ਵਿਚ ਨਿੱਜੀ, ਸਰਕਾਰੀ ਤੇ ਵਪਾਰਕ ਚਿੱਠੀਆਂ, ਰਜਿਸਟਰੀਆਂ, ਪਾਰਸਲ ਤੇ ਮਨੀਆਰਡਰ ਪੁਚਾਉਂਦਾ ਹੈ। ਉਸ ਦੀ ਹਰ ਥਾਂ ਉੱਤੇ ਤੀਬਰਤਾ ਨਾਲ ਉਡੀਕ ਕੀਤੀ ਜਾਂਦੀ ਹੈ। ਉਸ ਨੂੰ ਦੇਖ ਕੇ ਆਮ ਕਰਕੇ ਹਰ ਇਕ ਦਾ ਚਿਹਰਾ ਖਿੜ੍ਹ ਜਾਂਦਾ ਹੈ।
ਇਕ ਥਾਂ ਤੋਂ ਦੂਜੀ ਥਾਂ ਸੁਨੇਹੇ ਪੁਚਾਉਣ ਦਾ ਕੰਮ ਤਾਂ ਬਹੁਤ ਪੁਰਾਣਾ ਹੈ। ਸੁਨੇਹਾ ਪੁਚਾਉਣ ਲਈ ਅੱਜ – ਕਲ੍ਹ ਟੈਲੀਫੋਨ, ਕੋਰੀਅਰ, ਮੋਬਾਈਲ ਫੋਨ ਤੇ ਇੰਟਰਨੈੱਟ ਦੀ ਵਰਤੋਂ ਵੀ ਹੁੰਦੀ ਹੈ ਤੇ ਇਨ੍ਹਾਂ ਰਾਹੀਂ ਸੁਨੇਹੇ ਝਟਪਟ ਪਹੁੰਚ ਜਾਂਦੇ ਹਨ। ਪਰ ਸਾਡੇ ਹੱਥਾਂ ਨਾਲ ਲਿਖਿਆ ਸੁਨੇਹਾ ਕੇਵਲ ਡਾਕੀਆ ਹੀ ਦੂਜਿਆਂ ਤਕ ਪੁਚਾਉਂਦਾ ਹੈ। ਇਸ ਪ੍ਰਕਾਰ ਡਾਕੀਏ ਦੀ ਸਾਡੇ ਜੀਵਨ ਵਿਚ ਭਾਰੀ ਤੇ ਸਦੀਵੀ ਮਹਾਨਤਾ ਹੈ।
ਡਾਕੀਆ ਸਰਕਾਰੀ ਮੁਲਾਜ਼ਮ ਹੈ। ਉਹ ਖ਼ਾਕੀ ਵਰਦੀ ਪਾਉਂਦਾ ਹੈ। ਉਸ ਦੇ ਸਾਈਕਲ ਦੀ ਟੋਕਰੀ ਵਿਚ ਚਿੱਠੀਆਂ ਤੇ ਰਜਿਸਟਰੀਆਂ ਹੁੰਦੀਆਂ ਹਨ। ਉਸ ਦੇ ਬੈਗ ਵਿਚ ਮਨੀਆਰਡਰਾਂ ਦੇ ਪੈਸੇ ਤੇ ਪਾਰਸਲ ਹੁੰਦੇ ਹਨ। ਉਹ ਦੋ ਵਾਰੀ ਡਾਕ ਵੰਡਣ ਲਈ ਜਾਂਦਾ ਹੈ। ਉਸ ਦੀ ਤਨਖ਼ਾਹ ਬਹੁਤੀ ਨਹੀਂ ਹੁੰਦੀ, ਪਰ ਉਹ ਇਕ ਈਮਾਨਦਾਰ ਆਦਮੀ ਹੁੰਦਾ ਹੈ। ਉਹ ਹਰ ਅਮੀਰ – ਗਰੀਬ ਤੇ ਹਰ ਖ਼ੁਸ਼ੀ – ਗਮੀ ਵਿਚ ਘਿਰੇ ਬੰਦੇ ਦੀ ਆਸ ਹੁੰਦਾ ਹੈ। ਇਸ ਪ੍ਰਕਾਰ ਉਹ ਹਰ ਥਾਂ ਹਰਮਨ – ਪਿਆਰਾ ਬਣਿਆ ਰਹਿੰਦਾ ਹੈ।
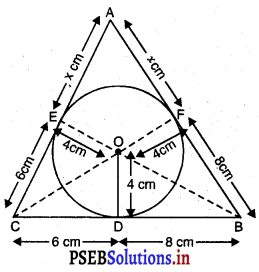
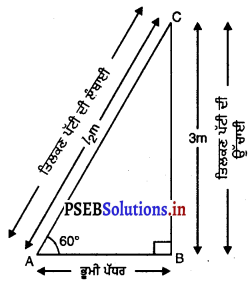
32. ਕਿਸੇ ਕਾਮੇ ਦੇ ਜੀਵਨ ਦਾ ਇਕ ਦਿਨ
ਮੈਂ ਇਕ ਕਾਮਾ ਹਾਂ। ਮੈਨੂੰ ਮਜ਼ਦੂਰ ਵੀ ਕਹਿੰਦੇ ਹਨ। ਮੈਂ ਦਿਹਾੜੀ ਉੱਤੇ ਕੰਮ ਕਰਦਾ ਹਾਂ। ਮੈਂ ਆਮ ਕਰਕੇ ਮਕਾਨ ਬਣਾਉਣ ਦੇ ਕੰਮਾਂ ਵਿਚ ਸਹਾਇਤਾ ਕਰਦਾ ਹਾਂ। ਮੈਂ ਇੱਟਾਂ ਵੀ ਢੋਂਦਾ ਹਾਂ। ਸੀਮਿੰਟ ਅਤੇ ਰੇਤ ਮਿਲਾ ਕੇ ਮਸਾਲਾ ਵੀ ਬਣਾਉਂਦਾ ਹਾਂ ਪਾਣੀ ਨਾਲ ਤਰਾਈ ਵੀ ਕਰਦਾ ਹਾਂ ਅਤੇ ਮਿੱਟੀ ਵੀ ਪੁੱਟਦਾ ਹਾਂ।
ਅੱਜ ਮੈਂ ਸਵੇਰੇ – ਸਵੇਰੇ ਮਜ਼ਦੂਰਾਂ ਤੇ ਮਿਸਤਰੀਆਂ ਦੇ ਅੱਡੇ ਉੱਪਰ ਖੜ੍ਹਾ ਕਿਸੇ ਕੰਮ ਕਰਾਉਣ ਵਾਲੇ ਦੀ ਉਡੀਕ ਕਰ ਰਿਹਾ ਸਾਂ। ਇੰਨੇ ਨੂੰ ਇਕ ਬਾਬੂ ਆ ਗਿਆ। ਉਸ ਦੇ ਦੁਆਲੇ ਬਹੁਤ ਸਾਰੇ ਮਜ਼ਦੂਰਾਂ ਨੇ ਝੁਰਮੁਟ ਪਾ ਲਿਆ। ਉਨ੍ਹਾਂ ਵਿਚ ਮੈਂ ਵੀ ਖੜਾ ਸਾਂ। ਮੈਂ ਪਿਛਲੇ ਤਿੰਨ ਦਿਨਾਂ ਤੋਂ ਵਿਹਲਾ ਸਾਂ। ਜੇਕਰ ਮੈਨੂੰ ਅੱਜ ਵੀ ਕੋਈ ਕੰਮ ਨਾ ਮਿਲਦਾ, ਤਾਂ ਅੱਜ ਰਾਤ ਨੂੰ ਮੇਰੇ ਘਰ ਰੋਟੀ ਪੱਕਣੀ ਔਖੀ ਹੋ ਜਾਣੀ ਸੀ। ਮੇਰੀ ਛੋਟੀ ਧੀ ਨੂੰ ਬੁਖ਼ਾਰ ਸੀ। ਮੈਂ ਉਸ ਲਈ ਦਵਾਈ ਵੀ ਲਿਆਉਣੀ ਸੀ ॥
ਬਾਬੂ ਨੇ ਪੁੱਛਿਆ ਕਿ ਕਿੰਨੀ ਦਿਹਾੜੀ ਲਵੋਗੇ ? ਤਿੰਨ – ਚਾਰ ਇਕੱਠੇ ਬੋਲ ਪਏ, 200 ਰੁਪਏ।’ ਬਾਬੂ ਨੇ ਕਿਹਾ, “ਮੈਂ ਤਾਂ 180 ਹੀ ਦੇਵਾਂਗਾ, ਜਿਸ ਦੀ ਮਰਜ਼ੀ ਹੋਵੇ ਚਲ ਪਏ !” ਮੈਂ 180 ਰੁਪਏ ਲੈਣੇ ਮਨਜ਼ੂਰ ਕਰ ਕੇ ਉਸ ਨਾਲ ਤੁਰ ਪਿਆ। ਥੋੜੀ ਦੂਰ ਉਸ ਦੀ ਕੋਠੀ ਬਣ ਰਹੀ ਸੀ। ਮੈਨੂੰ ਉਸ ਨੇ ਰੋੜੀ ਕੁੱਟਣ ਦੇ ਕੰਮ ਉੱਤੇ ਲਾ ਦਿੱਤਾ। ਮੈਂ ਆਪਣੀਆਂ ਉਂਗਲੀਆਂ ਨੂੰ ਸੱਟਾਂ ਤੋਂ ਬਚਾਉਣ ਲਈ ਪੱਟੀਆਂ ਬੰਨ੍ਹ ਕੇ ਹਥੌੜੇ ਨਾਲ ਰੋੜੀ ਕੁੱਟਣ ਲੱਗ ਪਿਆ।

ਥੋੜ੍ਹੀ ਦੇਰ ਮਗਰੋਂ ਉਹ ਬਾਬੂ ਆਇਆ ਤੇ ਬੜੇ ਗੁੱਸੇ ਨਾਲ ਕਹਿਣ ਲੱਗਾ, “ਤੂੰ ਕੰਮ ਬੜਾ ਹੌਲੀ ਕਰਦਾ ਹੈਂ, ਪਰ ਰੁਪਏ 180 ਮੰਗਦਾ ਹੈਂ।” ਮੈਂ ਕਿਹਾ, “ਜੀ ਦਿਹਾੜੀ ਤਾਂ 180 ਹੀ ਲਵਾਂਗਾ।” ਇਹ ਗੱਲ ਕਰਦਿਆਂ ਹਥੌੜਾ ਮੇਰੀਆਂ ਉਂਗਲੀਆਂ ਉੱਤੇ ਜਾ ਵੱਜਾ ਤੇ ਇਕ ਉਂਗਲੀ ਵਿਚੋਂ ਖੂਨ ਵਹਿਣ ਲੱਗਾ ਮੈਨੂੰ ਕਾਫ਼ੀ ਦਰਦ ਹੋ ਰਹੀ ਸੀ, ਪਰ ਉੱਥੇ ਸੁਣਨ ਵਾਲਾ ਕੌਣ ਸੀ ? ਮੈਂ ਪਾਣੀ ਪੀਤਾ ਤੇ ਫਿਰ ਪੱਟੀਆਂ ਬੰਨ੍ਹ ਕੇ ਰੋੜੀ ਕੁੱਟਦਾ ਰਿਹਾ। ਇਕ ਵਾਰੀ ਫਿਰ ਬਾਬੂ ਨੇ ਮੇਰੇ ਕੰਮ ਹੌਲੀ ਕਰਨ ਦੀ ਸ਼ਿਕਾਇਤ ਕੀਤੀ।
ਦੁਪਹਿਰੇ ਉਸ ਨੇ ਮੈਨੂੰ ਚੁਕੰਨਾ ਕੀਤਾ ਕਿ ਮੈਂ ਅੱਧੇ ਘੰਟੇ ਤੋਂ ਵੱਧ ਛੁੱਟੀ ਨਾ ਕਰਾਂ। ਸ਼ਾਮ ਤਕ ਮੇਰਾ ਮੁੰਹ ਸਿਰ ਘੱਟੇ ਨਾਲ। ਤੇ ਹੱਥ ਸੱਟਾਂ ਨਾਲ ਭਰ ਗਏ ਸਨ। 51 ਵਜੇ ਬਾਬੂ ਨੇ ਮਸਾਂ – ਮਸਾਂ 180 ਰੁਪਏ ਦਿੱਤੇ ਤੇ ਮੈਂ ਸੁਖ ਦਾ ਸਾਹ ਲੈ ਕੇ ਘਰ ਪੁੱਜਾ। ਇਸ ਸਮੇਂ ਮੇਰਾ ਸਰੀਰ ਥਕੇਵੇਂ ਤੇ ਸੱਟਾਂ ਨਾਲ ਦੁੱਖ ਰਿਹਾ ਸੀ, ਪਰ ਬੱਚੀ ਦੇ ਬੁਖ਼ਾਰ ਨੇ ਮੈਨੂੰ ਸਭ ਕੁੱਝ ਭੁਲਾ ਦਿੱਤਾ।
33. ਰੁੱਖਾਂ ਦੇ ਲਾਭ
ਰੁੱਖਾਂ ਦੀ ਸਾਡੇ ਜੀਵਨ ਵਿਚ ਬਹੁਤ ਮਹਾਨਤਾ ਹੈ ਮਨੁੱਖਾਂ ਸਮੇਤ ਜਿੰਨੇ ਜੀਵ ਧਰਤੀ ਉੱਤੇ ਵਸਦੇ ਹਨ, ਉਨ੍ਹਾਂ ਦਾ ਜੀਵਨ ਰੁੱਖਾਂ ਦੇ ਸਹਾਰੇ ਹੀ ਹੈ। ਜੇਕਰ ਰੁੱਖ ਨਾ ਹੋਣ ਤਾਂ ਜੀਵਾਂ ਨੂੰ ਇਕ ਪਲ ਲਈ ਵੀ ਜਿਊਣਾ ਔਖਾ ਹੋ ਜਾਵੇ। ਇਹ ਸਾਡੀ ‘ਕੁਲੀ ਗੁੱਲੀ ਤੇ ਜੁੱਲੀ ਦੀਆਂ ਤਿੰਨੇ ਮੁੱਖ ਲੋੜਾਂ ਪੂਰੀਆਂ ਕਰਦੇ ਹਨ। ਇਹ ਸਾਨੂੰ ਨਾ ਕੇਵਲ ਫਲ ਤੇ ਲੱਕੜੀ ਹੀ ਦਿੰਦੇ ਹਨ, ਸਗੋਂ ਸਾਨੂੰ ਭੋਜਨ ਤੋਂ ਜ਼ਰੂਰੀ ਚੀਜ਼ ਆਕਸੀਜਨ ਦਿੰਦੇ ਹਨ, ਜਿਸ ਤੋਂ ਬਿਨਾਂ ਬੰਦਾ ਇਕ ਮਿੰਟ ਵੀ ਨਹੀਂ ਕੱਢ ਸਕਦਾ।
ਸਭ ਤੋਂ ਪਹਿਲੀ ਗੱਲ ਇਹ ਹੈ ਕਿ ਮਨੁੱਖ ਨੂੰ ਜਿਉਂਦੇ ਰਹਿਣ ਲਈ ਭੋਜਨ ਦੀ ਲੋੜ ਹੈ। ਭੋਜਨ ਲਈ ਫਲ, ਅੰਨ, ਖੰਡ, ਘਿਓ – ਦੁੱਧ, ਸਬਜ਼ੀਆਂ ਆਦਿ ਸਭ ਕੁੱਝ ਸਾਨੂੰ ਰੁੱਖਾਂ ਦੀ ਬਦੌਲਤ ਹੀ ਪ੍ਰਾਪਤ ਹੁੰਦੇ ਹਨ ਫਲ ਤੇ ਸਬਜ਼ੀਆਂ ਤਾਂ ਰੁੱਖ ਸਿੱਧੇ ਤੌਰ ਤੇ ਦਿੰਦੇ ਹਨ, ਪਰੰਤੂ ਭੇਡਾਂ, ਬੱਕਰੀਆਂ ਤੇ ਹੋਰ ਪਸ਼ੂ ਇਨ੍ਹਾਂ ਦੇ ਪੱਤੇ ਖਾ ਕੇ ਹੀ ਸਾਨੂੰ ਦੁੱਧ ਦਿੰਦੇ ਹਨ, ਜਿਸ ਤੋਂ ਦਹੀਂ, ਲੱਸੀ, ਮੱਖਣ ਤੇ ਪਨੀਰ ਪ੍ਰਾਪਤ ਹੁੰਦੇ ਹਨ ਬਾਕੀ ਖਾਣ ਦੀਆਂ ਚੀਜ਼ਾਂ ਵੀ ਰੁੱਖਾਂ ਤੇ ਪੌਦਿਆਂ ਤੋਂ ਹੀ ਪ੍ਰਾਪਤ ਹੁੰਦੀਆਂ ਹਨ ਸ਼ਹਿਤੂਤ ਦੇ ਰੁੱਖਾਂ ਤੇ ਪਲਣ ਵਾਲਾ ਰੇਸ਼ਮ ਦਾ ਕੀੜਾ ਸਾਨੂੰ ਰੇਸ਼ਮ ਦਿੰਦਾ ਹੈ, ਜਿਸ ਤੋਂ ਸਾਡੇ ਲਈ ਕੀਮਤੀ ਕੱਪੜਾ ਬਣਦਾ ਹੈ।
ਸਾਡੇ ਸਿਰਾਂ ਨੂੰ ਢੱਕਣ ਲਈ ਮਕਾਨ ਬਣਾਉਣ ਲਈ ਵੀ ਸਾਨੂੰ ਲੱਕੜੀ ਦੀ ਜ਼ਰੂਰਤ ਪੈਂਦੀ ਹੈ, ਜੋ ਕਿ ਸਾਨੂੰ ਰੁੱਖਾਂ ਤੋਂ ਹੀ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ। ਸਾਡੇ ਘਰਾਂ ਵਿਚ ਪਿਆ ਵਧੀਆ ਤੇ ਹੰਢਣਸਾਰ ਫ਼ਰਨੀਚਰ ਵੀ ਰੁੱਖਾਂ ਦੀ ਲੱਕੜੀ ਤੋਂ ਹੀ ਤਿਆਰ ਹੁੰਦਾ ਹੈ। ਇਸ ਤੋਂ ਇਲਾਵਾ ਧੁੱਪ ਤੇ ਮੀਂਹ ਤੋਂ ਵੀ ਸਾਨੂੰ ਰੁੱਖ ਹੀ ਬਚਾਉਂਦੇ ਹਨ। ਰੁੱਖ ਸਾਡੇ ਸਾਹ ਲੈਣ ਲਈ ਹਵਾ ਨੂੰ ਸਾਫ਼ ਕਰਦੇ ਹਨ, ਜੋ ਕਿ ਸਾਡੇ ਜੀਵਨ ਦਾ ਆਧਾਰ ਹੈ। ਜੇਕਰ ਰੁੱਖ ਘੱਟ ਜਾਣ ਜਾਂ ਨਾ ਹੋਣ ਤਾਂ ਅਸ਼ੁੱਧ ਹਵਾ ਨਾਲ ਸਾਡਾ ਸਰੀਰ ਭਿਆਨਕ ਬਿਮਾਰੀਆਂ ਦਾ ਸ਼ਿਕਾਰ ਹੋ ਜਾਵੇ ਤੇ ਅੱਡੀਆਂ ਰਗੜ – ਰਗੜ ਕੇ ਮਰੇ।
ਇਹ ਜੀਵਾਂ ਦੇ ਸਾਹ ਵਿਚੋਂ ਨਿਕਲੀ ਗੰਦੀ ਹਵਾ ਵਿਚੋਂ ਕਾਰਬਨ – ਡਾਇਆਕਸਾਈਡ ਨੂੰ ਚੂਸ ਕੇ ਆਕਸੀਜਨ ਛੱਡਦੇ ਕਿ ਜੀਵਾਂ ਦੇ ਸਾਹ ਲੈਣ ਤੇ ਜਿਉਣ ਲਈ ਜ਼ਰੂਰੀ ਹੈ। ਇਹ ਸਾਡੇ ਲਈ ਵਰਖਾ ਦਾ ਕਾਰਨ ਵੀ ਬਣਦੇ ਹਨ ਤੇ ਉਪਜਾਊ ਮਿੱਟੀ ਨੂੰ ਰੁੜ੍ਹਨ ਤੋਂ ਵੀ ਬਚਾਉਂਦੇ ਹਨ। ਰੁੱਖਾਂ ਦੇ ਪੱਤੇ ਤੇ ਹੋਰ ਹਿੱਸੇ ਗਲ – ਸੜ ਕੇ ਖਾਦ ਬਣ ਜਾਂਦੇ ਹਨ, ਜੋ ਕਿ ਹੋਰਨਾਂ ਪੌਦਿਆਂ ਦੀ ਖ਼ੁਰਾਕ ਬਣਦੀ ਹੈ। ਇਸ ਨਾਲ ਭਿੰਨ – ਭਿੰਨ ਪ੍ਰਕਾਰ ਦੇ ਅੰਨ, ਸਬਜ਼ੀਆਂ, ਦਾਲਾਂ ਤੇ ਫਲ ਪੈਦਾ ਹੁੰਦੇ ਹਨ। ਰੁੱਖਾਂ ਦੇ ਪੱਤਿਆਂ, ਫੁੱਲਾਂ, ਛਿੱਲਾਂ ਤੇ ਜੜ੍ਹਾਂ ਤੋਂ ਬਹੁਤ ਸਾਰੀਆਂ ਦਵਾਈਆਂ ਬਣਦੀਆਂ ਹਨ। ਨਿੰਮ, ਪਿੱਪਲ, ਬੋਹੜ, ਸਿਨਕੋਨਾ, ਅਸ਼ੋਕ, ਅਮਲਤਾਸ ਤੇ ਬਿੱਲ ਅਜਿਹੇ ਹੀ ਰੁੱਖ ਹਨ।
ਰੁੱਖ ਸਾਨੂੰ ਬਹੁਤ ਸਾਰੇ ਫਲ ਸਵਾਦੀ ਤੇ ਰਸੀਲੇ ਫਲ ਦਿੰਦੇ ਹਨ। ਇਨ੍ਹਾਂ ਤੋਂ ਪ੍ਰਾਪਤ ਕੇਲਿਆਂ, ਸੰਤਰਿਆਂ, ਅੰਬਾਂ, ਸੇਬਾਂ, ਅੰਗੂਰਾਂ, ਨਾਸ਼ਪਾਤੀਆਂ, ਨਿੰਬੂਆਂ, ਬਦਾਮਾਂ ਤੇ ਖੁਰਮਾਨੀਆਂ ਤੋਂ ਬਿਨਾਂ ਸਾਡਾ ਭੋਜਨ ਬੇਸੁਆਦ ਹੋ ਕੇ ਰਹਿ ਜਾਵੇ !

ਰੁੱਖ ਸਾਡੇ ਆਲੇ – ਦੁਆਲੇ ਨੂੰ ਸੁੰਦਰ ਵੀ ਬਣਾਉਂਦੇ ਹਨ। ਇਨ੍ਹਾਂ ਦੇ ਫੁੱਲ ਦਿਲ ਨੂੰ ਖਿੱਚਦੇ ਹਨ ਤੇ ਮਹਿਕਾਂ ਖਿਲਾਰਦੇ ਹਨ। ਇਨ੍ਹਾਂ ਦੇ ਫੁੱਲਾਂ ਤੋਂ ਸਾਨੂੰ ਸ਼ਹਿਦ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ।
ਇਸ ਪ੍ਰਕਾਰ ਰੁੱਖਾਂ ਦੀ ਸਾਡੇ ਜੀਵਨ ਵਿਚ ਬਹੁਤ ਮਹਾਨਤਾ ਹੈ। ਇਹ ਸਾਡੇ ਜੀਵਨ ਦਾ ਆਧਾਰ ਹਨ ਸਾਨੂੰ ਇਨ੍ਹਾਂ ਨੂੰ ਵੱਢਣਾ ਨਹੀਂ ਚਾਹੀਦਾ ਤੇ ਇਨ੍ਹਾਂ ਨੂੰ ਵੱਧ ਤੋਂ ਵੱਧ ਲਾ ਕੇ ਇਨ੍ਹਾਂ ਦੀ ਪਾਲਣਾ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ।
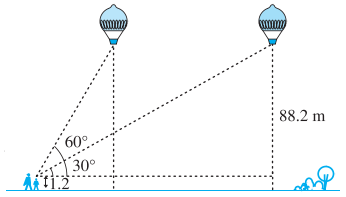
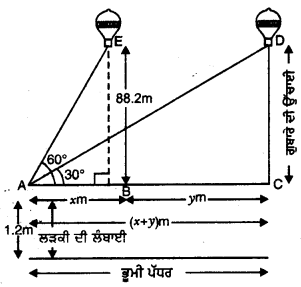
34. ਸਾਡੇ ਸਕੂਲ ਦੀ ਵਿੱਦਿਅਕ ਯਾਤਰਾ
ਬੀਤੇ 24 ਜੂਨ ਨੂੰ ਸਾਡੇ ਸਕੂਲ ਤੋਂ ਇਤਿਹਾਸ ਦੇ ਅਧਿਆਪਕ ਸਾਹਿਬ ਦੀ ਅਗਵਾਈ ਹੇਠ 10 ਵਿਦਿਆਰਥੀਆਂ ਦਾ ਇਕ ਗਰੁੱਪ ਭਾਖੜਾ ਡੈਮ ਦੀ ਸੈਰ ਕਰਨ ਲਈ ਗਿਆ ਅਸੀਂ ਇਕ ਸਕਾਰਪੀਓ ਗੱਡੀ ਕਿਰਾਏ ਉੱਤੇ ਲਈ ਤੇ ਹੁਸ਼ਿਆਰਪੁਰ ਤੋਂ ਹੁੰਦੇ ਹੋਏ ਪਹਾੜੀ ਸੜਕ ਉੱਪਰ ਪੈ ਗਏ ਤੇ ਦੋ ਕੁ ਘੰਟਿਆਂ ਵਿਚ ਨੰਗਲ ਪਾਰ ਕਰ ਗਏ। ਕੁੱਝ ਦੂਰ ਅੱਗੇ ਜਾ ਕੇ ਸਾਨੂੰ ਭਾਖੜਾ ਡੈਮ ਦੁਰੋਂ ਦਿਸਣ ਲੱਗ ਪਿਆ ਅਖੀਰ ਅਸੀਂ ਹਰੇ – ਭਰੇ ਉਸ ਥਾਂ ਉੱਤੇ ਪਹੁੰਚ ਗਏ, ਜਿੱਥੇ ਸਤਲੁਜ ਇਹ ਬੰਨ ਬਣਿਆ ਹੋਇਆ ਹੈ।
ਇੱਥੇ ਸਕਿਉਰਿਟੀ ਵਾਲਿਆਂ ਨੇ ਸਾਨੂੰ ਚੈੱਕ ਕੀਤਾ ਤੇ ਅੱਗੇ ਜਾਣ ਦਿੱਤਾ। ਡੈਮ ਦੇ ਉੱਤੇ ਕੇ ਅਧਿਆਪਕ ਜੀ ਨੇ ਸਾਨੂੰ ਦੱਸਣਾ ਸ਼ੁਰੂ ਕੀਤਾ ਕਿ ਇਹ ਏਸ਼ੀਆ ਦਾ ਸਭ ਤੋਂ ਉੱਚਾ ਬੰਨ ਹੈ ਤੇ ਕਾ ਹੈ ਤੇ ਭਾਰਤ ਵਿਚ ਬਣਿਆ ਇਹ ਇੰਨਾ ਪੱਕਾ ਬੰਨ੍ਹ ਹੈ ਕਿ ਇਸ ਉੱਪਰ ਭੂਚਾਲ, ਹੜ੍ਹ ਜਾਂ ਕਿਸੇ ਤੋੜ – ਫੋੜ ਦਾ ਅਸਰ ਨਹੀਂ ਹੋ ਸਕਦਾ। ਇਹ ਸਮੁੰਦਰ ਦੇ ਤਲ ਤੋਂ 225.55 ਮੀਟਰ ਉੱਚਾ ਹੈ। ਇਸ ਦੀ ਲੰਬਾਈ 518 ਮੀ: ਹੈ ਅਤੇ ਇਸ ਉੱਤੇ ਬਣੀ ਸੜਕ ਦੀ ਚੌੜਾਈ 304.84 ਮੀਟਰ ਹੈ। ਇਸ ਦੇ ਪਰਲੇ ਪਾਸੇ ਬਹੁਤ ਸਾਰੇ ਪਿੰਡਾਂ ਨੂੰ ਉਜਾੜ ਕੇ ਪਾਣੀ ਦੀ ਇਕ ਵੱਡੀ ਝੀਲ ਬਣਾਈ ਗਈ ਹੈ। ਜਿਸ ਵਿਚ 96210 ਲੱਖ ਕਿਊਬਿਕ ਮੀਟਰ ਪਾਣੀ ਇਕੱਠਾ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ਤੇ ਇਸ ਝੀਲ ਦਾ ਨਾਂ ਗੋਬਿੰਦ ਸਾਗਰ ਹੈ।
ਜੇਕਰ ਇਹ ਬੰਨ੍ਹ ਕਿਸੇ ਤਰ੍ਹਾਂ ਟੁੱਟ ਜਾਵੇ, ਤਾਂ ਇਹ ਚੰਡੀਗੜ੍ਹ, ਪੰਜਾਬ, ਹਰਿਆਣੇ ਤੇ ਦਿੱਲੀ ਦੇ ਕੁੱਝ ਹਿੱਸੇ ਨੂੰ ਪੂਰੀ ਤਰ੍ਹਾਂ ਰੋੜ ਸਕਦਾ ਹੈ ਸਾਡੇ ਅਧਿਆਪਕ ਜੀ ਜਦੋਂ ਇਹ ਦੱਸ ਰਹੇ ਸਨ ਤੇ ਵਿਸ਼ਾਲ ਝੀਲ ਵੱਲ ਦੇਖ ਕੇ ਸਾਡਾ ਮਨ ਹੈਰਾਨ ਹੋ ਰਿਹਾ ਸੀ।
ਅਧਿਆਪਕ ਜੀ ਨੇ ਦੱਸਿਆ ਕਿ ਇਸ ਬੰਨ ਦਾ ਉਦਘਾਟਨ ਕਰਨ ਸਮੇਂ ਭਾਰਤ ਦੇ ਪ੍ਰਧਾਨ ਮੰਤਰੀ ਜਵਾਹਰ ਲਾਲ ਨਹਿਰੂ ਨੇ ਇਸ ਨੂੰ ‘ਭਾਰਤ ਦੇ ਪੁਨਰ – ਉਥਾਨ ਦਾ ਮੰਦਰ ਕਿਹਾ ਸੀ। ਅਸੀਂ ਫਿਰ ਤੁਰ ਕੇ ਇਸ ਡੈਮ ਨੂੰ ਵੇਖ ਰਹੇ ਸਾਂ ਬਹੁਤ ਸਾਰੇ ਹੋਰ ਯਾਤਰੀ ਵੀ ਉੱਥੇ ਆਏ ਹੋਏ ਸਨ ਕਈ ਪਿਕਨਿਕ ਮਨਾ ਰਹੇ ਸਨ। ਕੁੱਝ ਕਿਸ਼ਤੀਆਂ ਵਿਚ ਸੈਰ ਵੀ ਕਰ ਰਹੇ ਸਨ।
ਅਧਿਆਪਕ ਜੀ ਨੇ ਦੱਸਿਆ ਕਿ ਇਸ ਦਾ ਕੰਟਰੋਲ ਭਾਖੜਾ ਮੈਨਜਮੈਂਟ ਬੋਰਡ ਕੋਲ ਹੈ। ਇਸ ਬੰਨ ਨਾਲ ਦਰਿਆ ਦੇ ਪਾਣੀ ਨੂੰ ਰੋਕ ਕੇ ਮੈਦਾਨੀ ਤੇ ਰੇਗਸਤਾਨੀ ਇਲਾਕੇ ਨੂੰ ਸਿੰਜਣ ਲਈ ਬਹੁਤ ਸਾਰੀਆਂ ਨਹਿਰਾਂ ਕੱਢੀਆਂ ਹਨ ਤੇ ਟਰਬਾਈਨਾਂ ਚਲਾ ਕੇ ਬਿਜਲੀ ਪੈਦਾ ਕੀਤੀ ਗਈ ਹੈ, ਜਿਸ ਨਾਲ ਭਾਰਤ ਅੰਨ ਦੀ ਲੋੜ ਵਿਚ ਸ਼ੈ – ਨਿਰਭਰ ਹੋਇਆ ਹੈ ਤੇ ਬਿਜਲੀ ਨਾਲ ਸ਼ਹਿਰ ਤੇ ਪਿੰਡ ਜਗਮਗਾ ਉੱਠੇ ਹਨ ਤੇ ਉਦਯੋਗਾਂ ਨੂੰ ਖੂਬ ਹੁਲਾਰਾ ਮਿਲਿਆ ਹੈ।
ਇਸ ਤਰ੍ਹਾਂ ਕੋਈ ਤਿੰਨ ਘੰਟੇ ਉੱਥੇ ਗੁਜ਼ਾਰਨ ਮਗਰੋਂ ਅਸੀਂ ਵਾਪਸ ਪਰਤ ਆਏ।

35. ਰੇਲਵੇ ਸਟੇਸ਼ਨ ਦਾ ਦ੍ਰਿਸ਼
ਸਟੇਸ਼ਨ ਉੱਤੇ ਪਹੁੰਚਣਾ – ਐਤਕੀਂ ਗਰਮੀਆਂ ਦੀਆਂ ਛੁੱਟੀਆਂ ਵਿਚ ਮੈਂ ਆਪਣੇ ਪਿਤਾ ਜੀ ਨਾਲ ਦਿੱਲੀ ਜਾਣ ਲਈ ਤਿਆਰ ਹੋ ਗਿਆ ਘਰੋਂ ਬਾਹਰ ਨਿਕਲ ਕੇ ਅਸੀਂ ਆਟੋ ਰਿਕਸ਼ਾ ਲਿਆ ਤੇ ਰੇਲਵੇ ਸਟੇਸ਼ਨ ਵਲ ਚਲ ਪਏ। ਪੰਦਰਾਂ ਮਿੰਟਾਂ ਵਿਚ ਅਸੀਂ ਰੇਲਵੇ ਸਟੇਸ਼ਨ ਦੇ ਬਾਹਰ ਪੁੱਜ ਗਏ ਆਟੋ ਰਿਕਸ਼ੇ ਵਾਲੇ ਨੂੰ ਪੈਸੇ ਦੇ ਕੇ ਅਸੀਂ ਪਹਿਲਾਂ ਮੁਸਾਫ਼ਰਖ਼ਾਨੇ ਵਿਚ ਪੁੱਜੇ।
ਮੁਸਾਫ਼ਰਖ਼ਾਨੇ ਦਾ ਦ੍ਰਿਸ਼ – ਮੁਸਾਫ਼ਰਖ਼ਾਨੇ ਵਿਚ ਬਹੁਤ ਭੀੜ ਸੀ ਉੱਥੇ ਬਹੁਤ ਸਾਰੇ ਲੋਕ ਆ – ਜਾ ਰਹੇ ਸਨ। ਕੁੱਝ ਬੰਦੇ ਕਤਾਰਾਂ ਬਣਾ ਕੇ ਟਿਕਟਾਂ ਲੈਣ ਲਈ ਖਿੜਕੀਆਂ ਅੱਗੇ ਖੜ੍ਹੇ ਸਨ ! ਕੁੱਝ ਖਿੜਕੀਆਂ ਉੱਤੇ ਅਗਾਊਂ ਬੁਕਿੰਗ ਹੋ ਰਹੀ ਸੀ। ਇਕ ਪਾਸੇ ਪਹਿਲੇ ਦਰਜੇ ਦੀ ਬੁਕਿੰਗ ਦੀ ਖਿੜਕੀ ਸੀ।
ਪਲੇਟਫਾਰਮ ਦ੍ਰਿਸ਼ – – ਮੇਰੇ ਪਿਤਾ ਜੀ ਨੇ ਦੋ ਦਿਨ ਪਹਿਲਾਂ ਹੀ ਸੁਪਰ ਫ਼ਾਸਟ ਦੀਆਂ ਸੀਟਾਂ ਰਿਜ਼ਰਵ ਕਰਾ ਲਈਆਂ ਸਨ, ਇਸ ਕਰਕੇ ਅਸੀਂ ਮੁਸਾਫ਼ਰਖਾਨੇ ਵਿਚੋਂ ਹੁੰਦੇ ਹੋਏ ਸਿੱਧੇ ਪਲੇਟਫ਼ਾਰਮ ਉੱਤੇ ਜਾ ਪੁੱਜੇ। ਕੁੱਝ ਲੋਕਾਂ ਨੇ ਆਪਣਾ ਸਮਾਨ ਲਾਲ ਵਰਦੀ ਵਾਲੇ ਕੁਲੀਆਂ ਨੂੰ ਚੁਕਵਾਇਆ ਹੋਇਆ ਸੀ। ਸਾਡੇ ਕੋਲ ਬਹੁਤਾ ਭਾਰ ਨਹੀਂ ਸੀ। , ਪਲੇਟਫ਼ਾਰਮ ਨੰਬਰ ਦੋ – ਸਾਡੀ ਗੱਡੀ ਪਲੇਟਫ਼ਾਰਮ ਨੰਬਰ ਦੋ ਤੋਂ ਚੱਲਣੀ ਸੀ।ਉੱਥੇ ਪਹੁੰਚਣ ਲਈ ਸਾਨੂੰ ਲਾਈਨਾਂ ਉੱਤੋਂ ਦੀ ਬਣਿਆ ਪੁਲ ਪਾਰ ਕਰਨਾ ਪਿਆ।
ਗੱਡੀ ਆਉਣ ਵਿਚ ਅਜੇ ਦਸ ਕੁ ਮਿੰਟ ਦਾ ਸਮਾਂ ਸੀ। ਪਲੇਟਫ਼ਾਰਮ ਉੱਤੇ ਬੜੀ ਭੀੜ ਤੇ ਚਹਿਲ – ਪਹਿਲ ਸੀ। ਲੋਕ ਤੇਜ਼ੀ ਨਾਲ ਇਧਰ – ਉਧਰ ਜਾ ਰਹੇ ਸਨ। ਕੁੱਝ ਲੋਕ ਸਮਾਨ ਹੇਠਾਂ ਰੱਖ ਕੇ ਖੜ੍ਹੇ ਸਨ ਤੇ ਕੁੱਝ ਬੈਂਚਾਂ ਉੱਤੇ ਬੈਠੇ ਸਨ। ਕੁੱਝ ਕੁਲੀ ਸਮਾਨ ਚੁੱਕੀ ਆ ਰਹੇਂ ਸਨ। ਕਿਤੇ – ਕਿਤੇ ਪੁਲਿਸ ਦੇ ਸਿਪਾਹੀ ਵੀ ਦਿਖਾਈ ਦੇ ਰਹੇ ਸਨ। ਪਲੇਟ
ਹ, ਪਕੌੜਿਆਂ, ਛੋਲੇ – ਭਰਿਆਂ, ਚਾਵਲ – ਛੋਲਿਆਂ, ਕੋਲਡ ਡਰਿੰਕਸ ਅਤੇ ਅਖ਼ਬਾਰਾਂ ਤੇ ਮੈਗਜ਼ੀਨਾਂ ਦੇ ਸਟਾਲ ਲੱਗੇ ਹੋਏ ਸਨ, ਜਿੱਥੋਂ ਲੋਕ ਲੋੜ ਅਨੁਸਾਰ ਚੀਜ਼ਾਂ ਖ਼ਰੀਦ ਰਹੇ ਸਨ।
ਮੇਰੇ ਪਿਤਾ ਜੀ ਨੇ ਇਕ ਬੋਰਡ ਉੱਤੇ ਆਪਣੀ ਰਿਜ਼ਰਵੇਸ਼ਨ ਬਾਰੇ ਪੜ੍ਹਿਆ ਤੇ ਫਿਰ ਕੁਲੀ ਨੂੰ ਪੁੱਛਿਆ ਕਿ ਸਾਡਾ ਡੱਬਾ ਨੰਬਰ ਕਿੱਥੇ ਕੁ ਰੁਕੇਗਾ। ਉਸ ਦੇ ਕਹਿਣ ਅਨੁਸਾਰ ਅਸੀਂ ਪਲੇਟਫ਼ਾਰਮ ਉੱਤੇ ਲੱਗੀ ਘੜੀ ਤੋਂ ਅੱਗੇ ਚਲੇ ਗਏ।ਇੱਥੇ ਅਸੀਂ ਪਾਣੀ ਦੀ ਇਕ ਬੋਤਲ ਲੈ ਕੇ ਆਪਣੇ ਬੈਗ ਵਿਚ ਪਾ ਲਈ। ਸਿਗਨਲ ਨੀਵਾਂ ਹੋਣਾ – ਇੰਨੇ ਨੂੰ ਲਾਊਡ ਸਪੀਕਰ ਉੱਤੇ ਗੱਡੀ ਦੇ ਆਉਣ ਦੀ ਸੂਚਨਾ ਮਿਲੀ। ਮੇਰੇ ਪਿਤਾ ਜੀ ਨੇ ਮੈਨੂੰ ਦੱਸਿਆ ਕਿ ਔਹ ਸਿਗਨਲ ਹੋ ਗਿਆ ਹੈ ਤੇ ਗੱਡੀ ਆ ਰਹੀ ਹੈ।
ਗੱਡੀ ਦਾ ਆਉਣਾ – ਬੱਸ ਦੋ ਕੁ ਮਿੰਟਾਂ ਬਾਅਦ ਹੀ ਗੱਡੀ ਪਲੇਟਫ਼ਾਰਮ ਉੱਤੇ ਆ ਗਈ ਤੇ ਹੌਲੇ – ਹੌਲੇ ਰੁਕ ਗਈ। ਗੱਡੀ ਵਿਚ ਸਵਾਰ ਹੋਣਾ – ਸਾਡਾ ਡੱਬਾ ਜ਼ਰਾ ਹੋਰ ਅੱਗੇ ਜਾ ਕੇ ਰੁਕਿਆ। ਮੇਰੇ ਪਿਤਾ ਜੀ ਅਟੈਚੀਕੇਸ ਚੁੱਕ ਕੇ ਤੇ ਮੇਰਾ ਹੱਥ ਫੜ ਕੇ ਫਟਾ – ਫਟ ਡੱਬੇ ਕੋਲ ਪੁੱਜੇ ਤੇ ਫਿਰ ਦਰਵਾਜ਼ੇ ਦੀ ਭੀੜ ਨੂੰ ਚੀਰਦੇ ਹੋਏ ਡੱਬੇ ਵਿਚ ਦਾਖ਼ਲ ਹੋ ਗਏ। ਸਾਡੀਆਂ ਸੀਟਾਂ ਵਿਚਕਾਰ ਜਿਹੇ ਸਨ। ਉਨ੍ਹਾਂ ਉੱਤੇ ਦੋ ਬੰਦੇ ਪਹਿਲਾਂ ਹੀ ਬੈਠੇ ਸਨ। ਮੇਰੇ ਪਿਤਾ ਜੀ ਦੇ ਕਹਿਣ ‘ਤੇ ਉਨ੍ਹਾਂ ਸੀਟਾਂ ਖ਼ਾਲੀ ਕਰ ਦਿੱਤੀਆਂ ਅਤੇ ਅਸੀਂ ਬੈਠ ਗਏ। ਇਸ ਤੋਂ ਦੋ – ਤਿੰਨ ਮਿੰਟ ਮਗਰੋਂ ਹੀ ਗੱਡੀ ਚਲ ਪਈ ਤੇ ਮੈਂ ਗੱਡੀ ਦੇ ਸਫ਼ਰ ਦਾ ਆਨੰਦ ਲੈਣ ਲੱਗਾ।
36. ਪੰਜਾਬ ਦਾ ਇਤਿਹਾਸਿਕ ਸ਼ਹਿਰ – ਅੰਮ੍ਰਿਤਸਰ
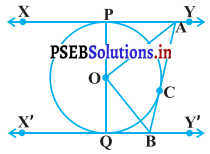
ਅੰਮ੍ਰਿਤਸਰ ਪੰਜਾਬ ਦਾ ਇਕ ਮਹੱਤਵਪੂਰਨ ਸ਼ਹਿਰ ਹੈ। ਇਸ ਸ਼ਹਿਰ ਬਾਰੇ ਕਿਹਾ ਗਿਆ ਹੈ “ਅੰਮ੍ਰਿਤਸਰ ਸਿਫਤੀ ਦਾ ਘਰ। ਇਹ ਇਕ ਪੁਰਾਤਨ ਧਾਰਮਿਕ ਸ਼ਹਿਰ ਹੈ ਪਰ ਇਸ ਦੇ ਨਾਲ ਹੀ ਇਹ ਇਕ ਬਹੁਤ ਵੱਡਾ ਵਪਾਰਕ ਕੇਂਦਰ ਵੀ ਹੈ। ਅੰਮ੍ਰਿਤਸਰ ਦਾ ਅਸਲ ਮਹੱਤਵ ਇੱਥੇ ਸਿੱਖਾਂ ਦੇ ਸਭ ਤੋਂ ਵੱਡੇ ਤੀਰਥ ਸ੍ਰੀ ਹਰਿਮੰਦਰ ਸਾਹਿਬ ਦਾ ਹੋਣਾ ਹੈ। ਇਹ ਸ਼ਹਿਰ ਪਾਕਿਸਤਾਨ ਦੀ ਸਰਹੱਦ ਤੋਂ ਕੇਵਲ 24 ਕਿਲੋਮੀਟਰ ਉਰੇ ਪੂਰਬ ਵਲ ਸਥਿਤ ਹੈ।

ਇਸ ਸ਼ਹਿਰ ਦਾ ਇਤਿਹਾਸ ਕਾਫ਼ੀ ਪੁਰਾਣਾ ਹੈ ਪਹਿਲਾ ਗੁਰੂ ਅਮਰਦਾਸ ਜੀ ਦੀ ਆਗਿਆ ਅਨੁਸਾਰ ਗੁਰੁ ਰਾਮਦਾਸ ਜੀ ਨੇ ਸੰਮਤ 1621 (1663 ਈ:) ਵਿਚ ਇਕ ਤਾਲ ਖ਼ਦਵਾਇਆ, ਜਿਸ ਨੂੰ ਮਗਰੋਂ ਗੁਰੂ ਅਰਜਨ ਦੇਵ ਰਨ ਸੰਮਤ 1645 ਵਿਚ ਸੰਪੂਰਨ ਕਰਕੇ ਇਸ ਦਾ ਨਾਂ ਸੰਤੋਖਸਰ ਰੱਖਿਆ। ਸੰਮਤ 1631 (1573 ਈ:) ਵਿਚ ਗੁਰੂ ਅਮਰਦਾਸ ਜੀ ਦੀ ਆਗਿਆ ਅਨੁਸਾਰ ਹੀ ਇਕ ਪਿੰਡ ਬੰਨਿਆ ਗਿਆ ਤੇ ਆਪਣੇ ਰਹਿਣ ਲਈ ਮਕਾਨ ਬਣਵਾਏ, ਜੋ ‘ਗੁਰੂ ਕੇ ਮਹਿਲ’ ਨਾਂ ਨਾਲ ਪ੍ਰਸਿੱਧ ਹਨ। ਉਸ ਦੇ ਚੜ੍ਹਦੇ ਪਾਸੇ ਦੁਖ ਭੰਜਨੀ ਬੇਰੀ ਦੇ ਕੋਲ ਸੰਮਤ 1634 ਵਿਚ ਇਕ ਤਾਲ ਖ਼ੁਦਵਾਇਆ, ਜਿਸ ਨੂੰ ਗੁਰੂ ਅਰਜਨ ਦੇਵ ਜੀ ਨੇ ਸੰਪੂਰਨ ਕੀਤਾ ਤੇ ਚਾਰੇ ਪਾਸਿਓਂ ਵਪਾਰੀ ਤੇ ਕਿਰਤੀ ਲੋਕ ਵਸਾ ਕੇ ਇਸਦਾ ਨਾਂ ਰਾਮਦਾਸਪੁਰ ਰੱਖਿਆ।
ਸੰਮਤ 1643 ਵਿਚ ਸਰੋਵਰ ਨੂੰ ਪੱਕਾ ਕਰਨ ਦਾ ਕੰਮ ਆਰੰਭ ਹੋਇਆ ਤੇ ਇਸ ਸ਼ਹਿਰ ਦਾ ਨਾਂ ਅੰਮ੍ਰਿਤਸਰ ਰੱਖਿਆ ਗਿਆ 1 ਮਾਘ 1645 ਵਿਚ ਗੁਰੂ ਅਰਜਨ ਦੇਵ ਜੀ ਨੇ ਸ੍ਰੀ ਹਰਿਮੰਦਰ ਸਾਹਿਬ ਦੀ ਨੀਂਹ ਰੱਖੀ ਅਤੇ ਇਮਾਰਤ ਨੂੰ ਪੂਰੀ ਕਰਨ ਮਗਰੋਂ ਸੰਮਤ 1661 ਵਿਚ ਇੱਥੇ ਸ੍ਰੀ ਗੁਰੂ ਗ੍ਰੰਥ ਸਾਹਿਬ ਦਾ ਪ੍ਰਕਾਸ਼ ਕੀਤਾ।
ਇਤਿਹਾਸਿਕ ਤੌਰ ‘ਤੇ ਇਸ ਸ਼ਹਿਰ ਨੇ ਬਹੁਤ ਸਾਰੇ ਉਤਾਰ – ਚੜ੍ਹਾਅ ਅਤੇ ਦੁਖਾਂਤ ਦੇਖੇ ਹਨ ਪਰੰਤੂ ਇਸ ਦੇ ਬਾਵਜੂਦ ਇੱਥੇ ਸ੍ਰੀ ਹਰਿਮੰਦਰ ਸਾਹਿਬ ਸਭ ਦੀ ਸ਼ਰਧਾ ਦਾ ਕੇਂਦਰ ਹੈ ਅਤੇ ਇਹ ਘੁੱਗ ਵਸਦਾ ਹੈ। ਇੱਥੇ ਬਹੁਤ ਸਾਰੇ ਵਪਾਰੀ ਲੋਕ ਰਹਿੰਦੇ ਹਨ, ਜੋ ਕਿ ਕੱਪੜੇ ਅਤੇ ਸੋਨੇ ਚਾਂਦੀ ਦੇ ਗਹਿਣਿਆਂ ਦਾ ਵਪਾਰ ਕਰਦੇ ਹਨ। ਇਹ ਸ਼ਹਿਰ ਭਿੰਨ – ਭਿੰਨ ਪ੍ਰਕਾਰ ਦੇ ਸੁਆਦਲੇ ਤੇ ਚਟਪਟੇ ਖਾਣਿਆਂ ਲਈ ਬਹੁਤ ਮਸ਼ਹੂਰ ਹੈ। ਇੱਥੋਂ ਦੇ ਪਾਪੜ – ਵੜੀਆਂ, ਕੁਲਚੇ ਅਤੇ ਲੱਸੀ ਬਹੁਤ ਮਸ਼ਹੂਰ ਹੈ।
ਇਸ ਸ਼ਹਿਰ ਵਿਚ ਹਿੰਦੂਆਂ ਅਤੇ ਸਿੱਖਾਂ ਦੇ ਬਹੁਤ ਸਾਰੇ ਧਾਰਮਿਕ ਅਸਥਾਨ ਹਨ। ਸ੍ਰੀ ਹਰਿਮੰਦਰ ਸਾਹਿਬ ਇੱਥੋਂ ਦਾ ਹੀ ਨਹੀਂ, ਸਗੋਂ ਸੰਸਾਰ ਭਰ ਦਾ ਸਰਵਉੱਚ ਧਾਰਮਿਕ ਸਥਾਨ ਹੈ, ਜਿਸ ਦੀ ਇਮਾਰਤ ਉੱਤੇ ਸੋਨਾ ਚੜ੍ਹਿਆ ਹੋਇਆ ਹੈ। ਅਕਾਲ ਤਖ਼ਤ ਮੀਰੀ – ਪੀਰੀ ਦਾ ਕੇਂਦਰ ਹੈ। ਇਸ ਤੋਂ ਇਲਾਵਾ ਗੁਰਦੁਆਰਾ ਸੰਤੋਖਸਰ, ਗੁਰਦੁਆਰਾ ਅਟੱਲ ਸਾਹਿਬ, ਗੁਰਦੁਆਰਾ ਸ਼ਹੀਦਾਂ, ਕੌਲਸਰ, ਗੁਰੂ ਕੇ ਮਹਿਲ ਤੇ ਗੁਰਦੁਆਰਾ ਥੜ੍ਹਾ ਸਾਹਿਬ ਸਿੱਖਾਂ ਦੇ ਧਰਮ ਅਸਥਾਨ ਹਨ।
ਦੁਰਗਿਆਣਾ ਮੰਦਰ ਤੇ ਸਤਿ ਨਰਾਇਣ ਦਾ ਮੰਦਰ ਹਿੰਦੂਆਂ ਦੇ ਧਰਮ ਅਸਥਾਨ ਹਨ। ਇੱਥੇ ਸ੍ਰੀ ਗੁਰੂ ਹਰਗੋਬਿੰਦ ਜੀ ਦਾ ਤਿਆਰ ਕਰਾਇਆ ਕਿਲ੍ਹਾ ਲੋਹਗੜ੍ਹ ਵੀ ਹੈ ਤੇ ਅਕਾਲੀ ਫੂਲਾ ਸਿੰਘ ਬੁਰੀ ਤੋਂ ਇਲਾਵਾ ਰਾਮਗੜ੍ਹੀਆ ਮਿਸਲ ਨਾਲ ਸੰਬੰਧਿਤ ਬੁੰਗੇ ਵੀ ਹਨ।
ਇੱਥੇ ਹੀ ਦੇਸ਼ ਦੀ ਅਜ਼ਾਦੀ ਨਾਲ ਸੰਬੰਧਿਤ ਪ੍ਰਸਿੱਧ ਜਲਿਆਂ ਵਾਲਾ ਬਾਗ਼ ਹੈ, ਜਿੱਥੇ ਅੰਗਰੇਜ਼ ਜਨਰਲ ਡਾਇਰ ਨੇ 13 ਅਪ੍ਰੈਲ, 1919 ਨੂੰ ਨਿਹੱਥੇ ਦੇਸ਼ – ਭਗਤਾਂ ਦੇ ਖੂਨ ਦੀ ਹੋਲੀ ਖੇਡਦਿਆਂ ਸੈਂਕੜਿਆਂ ਨੂੰ ਗੋਲੀਆਂ ਨਾਲ ਭੁੰਨ ਦਿੱਤਾ। ਇੱਥੇ ਸ਼ਹੀਦਾਂ ਦੀ ਯਾਦ ਵਿਚ ਇਕ ਮੀਨਾਰ ਬਣਿਆ ਹੋਇਆ ਹੈ। ਅੰਮ੍ਰਿਤਸਰ ਬਹੁਤ ਵੱਡਾ ਵਿੱਦਿਅਕ ਕੇਂਦਰ ਵੀ ਹੈ। ਇੱਥੇ ਪੰਜਾਬ ਦਾ ਪੁਰਾਤਨ ਆਲੀਸ਼ਾਨ ਖ਼ਾਲਸਾ ਕਾਲਜ ਸਥਿਤ ਹੈ ਤੇ ਹੋਰ ਬਹੁਤ ਸਾਰੇ ਡਿਗਰੀ ਕਾਲਜ ਵੀ। ਇੱਥੇ ਇਕ ਮੈਡੀਕਲ ਕਾਲਜ ਵੀ ਹੈ ਤੇ ਗੁਰੂ ਨਾਨਕ ਦੇਵ ਜੀ ਯੂਨੀਵਰਸਿਟੀ ਵੀ।
ਇੱਥੇ ਅੰਗਰੇਜ਼ਾਂ ਦੇ ਸਮੇਂ ਦਾ ਕੰਪਨੀ ਬਾਗ਼ ਵੀ ਹੈ, ਜਿਸ ਦਾ ਅੱਜ – ਕਲ੍ਹ ਨਾਂ ਨਹਿਰੂ ਬਾਗ਼ ਹੈ। ਇੱਥੇ ਹੀ ਮਹਾਰਾਜਾ ਰਣਜੀਤ ਸਿੰਘ ਨਾਲ ਸੰਬੰਧਿਤ ਬਾਰਾਦਰੀ ਵੀ ਹੈ।
ਇਹ ਪੰਜਾਬ ਦਾ ਬੇਸ਼ੱਕ ਪੁਰਾਤਨ ਸ਼ਹਿਰ ਹੈ, ਪਰ ਇਹ ਸਾਰੀਆਂ ਨਵੀਨਤਾਵਾਂ ਨਾਲ ਭਰਪੂਰ ਹੈ। ਇਹ ਲਾਹੌਰ ਦੇ ਨਾਲ ਮਾਝੀ ਉਪਭਾਸ਼ਾ ਦਾ ਕੇਂਦਰ ਹੈ ਤੇ ਇੱਥੋਂ ਦੀ ਬੋਲੀ ਪੰਜਾਬ ਦੀ ਟਕਸਾਲੀ ਭਾਸ਼ਾ ਦਾ ਧੁਰਾ ਹੈ।
ਸਮੁੱਚੇ ਤੌਰ ‘ਤੇ ਅੰਮ੍ਰਿਤਸਰ ਪੰਜਾਬ ਦਾ ਇਤਿਹਾਸਿਕ, ਧਾਰਮਿਕ ਤੇ ਵਪਾਰਕ ਮਹੱਤਤਾ ਵਾਲਾ ਸ਼ਹਿਰ ਹੈ।

37. ਖੇਡਾਂ ਦਾ ਮਹੱਤਵ
ਜਾਂ
ਵਿਦਿਆਰਥੀ ਅਤੇ ਖੇਡਾਂ
ਖੇਡਾਂ ਤੇ ਮਨੁੱਖੀ ਜੀਵਨ – ਖੇਡਾਂ ਦੀ ਮਨੁੱਖੀ ਜੀਵਨ ਵਿਚ ਬਹੁਤ ਮਹਾਨਤਾ ਹੈ। ਇਨ੍ਹਾਂ ਦੀ ਸਾਡੇ ਸਰੀਰ ਨੂੰ ਇਸੇ ਪ੍ਰਕਾਰ ਹੀ ਜ਼ਰੂਰਤ ਹੈ, ਜਿਵੇਂ ਸਾਨੂੰ ਖੁਰਾਕ, ਹਵਾ ਤੇ ਪਾਣੀ ਆਦਿ ਦੀ ਜ਼ਰੂਰਤ ਹੈ। ਜਿੱਥੇ ਸਰੀਰ ਨੂੰ ਤੰਦਰੁਸਤ ਰੱਖਣ ਲਈ ਖ਼ੁਰਾਕ ਆਪਣਾ ਹਿੱਸਾ ਪਾਉਂਦੀ ਹੈ, ਉੱਥੇ ਖੇਡਾਂ ਵੀ ਸਾਡੇ ਸਰੀਰ ਨੂੰ ਖੁਰਾਕ ਦਾ ਵੱਧ ਤੋਂ ਵੱਧ ਲਾਭ ਉਠਾਉਣ ਦੇ ਯੋਗ ਬਣਾਉਂਦੀਆਂ ਹਨ। ਇਹ ਸਾਡੇ ਦਿਨ ਭਰ ਦੇ ਦਿਮਾਗੀ ਅਤੇ ਸਰੀਰਕ ਥਕੇਵੇਂ ਨੂੰ ਦੂਰ ਕਰ ਦਿੰਦੀਆਂ ਹਨ ਤੇ ਸਾਡੇ ਸਰੀਰ ਵਿਚ ਤਾਜ਼ਗੀ ਤੇ ਫੁਰਤੀ ਪੈਦਾ ਕਰਦੀਆਂ ਹਨ।
ਉੱਨਤ ਕੌਮਾਂ ਤੇ ਖੇਡਾਂ – ਸੰਸਾਰ ਦੀਆਂ ਉੱਨਤ ਕੌਮਾਂ ਖੇਡਾਂ ਦੀ ਮਹਾਨਤਾ ਨੂੰ ਚੰਗੀ ਤਰ੍ਹਾਂ ਸਮਝਦੀਆਂ ਹਨ, ਇਸੇ ਕਰਕੇ ਹੀ ਉਹ ਜੀਵਨ ਦੇ ਹਰ ਖੇਤਰ ਵਿਚ ਖੇਡਾਂ ਨੂੰ ਵੱਧ ਤੋਂ ਵੱਧ ਮਹੱਤਤਾ ਦਿੰਦੀਆਂ ਹਨ। ਉੱਨਤ ਦੇਸ਼ਾਂ ਵਿਚ ਖੇਡਾਂ ਦਾ ਪ੍ਰਬੰਧ ਕੇਵਲ ਵਿਦਿਆਰਥੀਆਂ ਜਾਂ ਨੌਜਵਾਨਾਂ ਲਈ ਹੀ ਨਹੀਂ, ਸਗੋਂ ਵਡੇਰੀ ਉਮਰ ਦੇ ਵਿਅਕਤੀਆਂ ਤੇ ਬੱਚਿਆਂ ਲਈ ਵੀ ਹੈ। ਖੇਡਾਂ ਅਤੇ ਸਰੀਰਕ ਸਿਹਤ – ਖੇਡਾਂ ਸਾਡੇ ਸਰੀਰ ਨੂੰ ਅਰੋਗ ਤੇ ਤਕੜਾ ਰੱਖਣ ਵਿਚ ਭਾਰੀ ਹਿੱਸਾ ਪਾਉਂਦੀਆਂ ਹਨ ਖੇਡਾਂ ਵਿਚ ਹਿੱਸਾ ਲੈਣ ਨਾਲ ਸਾਡੇ ਸਰੀਰ ਵਿਚ ਖੂਨ ਦਾ ਦੌਰਾ ਤੇਜ਼ ਹੁੰਦਾ ਹੈ।
ਫੇਫੜਿਆਂ ਨੂੰ ਤਾਜ਼ੀ ਹਵਾ ਮਿਲਦੀ ਹੈ ਤੇ ਪਾਚਨ – ਸ਼ਕਤੀ ਤੇਜ਼ ਹੁੰਦੀ ਹੈ। ਰੋਜ਼ ਖੇਡਾਂ ਵਿਚ ਹਿੱਸਾ ਲੈਣ ਵਾਲੇ ਮਨੁੱਖਾਂ ਦਾ ਸਰੀਰ ਅਰੋਗ ਰਹਿੰਦਾ ਹੈ ਤੇ ਉਨ੍ਹਾਂ ਦੇ ਅੰਦਰ ਬਿਮਾਰੀਆਂ ਦਾ ਮੁਕਾਬਲਾ ਕਰਨ ਦੀ ਸ਼ਕਤੀ ਪੈਦਾ ਹੁੰਦੀ ਹੈ। ਖੇਡਾਂ ਵਿਚ ਭਾਗ ਲੈਣ ਵਾਲਿਆਂ ਦੇ ਸਰੀਰ ਵਿਚ ਹਮੇਸ਼ਾ ਚੁਸਤੀ ਤੇ ਤਾਜ਼ਗੀ ਰਹਿੰਦੀ ਹੈ ਤੇ ਉਨ੍ਹਾਂ ਦਾ ਚਿਹਰਾ ਖਿੜਿਆ ਰਹਿੰਦਾ ਹੈ।
ਖੇਡਾਂ ਅਤੇ ਮਾਨਸਿਕ ਸਿਹਤ – ਸਰੀਰ ਦੇ ਅਰੋਗ ਰਹਿਣ ਨਾਲ ਮਨੁੱਖ ਆਪਣੇ ਦਿਮਾਗ਼ ਤੋਂ ਵੀ ਵੱਧ ਤੋਂ ਵੱਧ ਲਾਭ ਉਠਾ ਸਕਦਾ ਹੈ। ਖੇਡਾਂ ਨਾਲ ਦਿਮਾਗ਼ ਦੀ ਗ੍ਰਹਿਣ ਕਰਨ ਦੀ ਸ਼ਕਤੀ ਵਧਦੀ ਹੈ। ਇਨ੍ਹਾਂ ਨਾਲ ਦਿਮਾਗ਼ ਤਾਜ਼ਾ ਤੇ ਚੁਸਤ ਰਹਿੰਦਾ ਹੈ। ਇਨ੍ਹਾਂ ਤੋਂ ਬਿਨਾਂ ਨਿਰੇ ਕਿਤਾਬੀ ਕੀੜੇ ਜ਼ਿੰਦਗੀ ਦੀ ਦੌੜ ਵਿਚ ਪਿੱਛੇ ਰਹਿ ਜਾਂਦੇ ਹਨ।
ਆਚਰਨ ਦੀ ਉਸਾਰੀ – ਸਰੀਰਕ ਅਤੇ ਦਿਮਾਗੀ ਅਰੋਗਤਾ ਤੋਂ ਬਿਨਾਂ ਖੇਡਾਂ ਮਨੁੱਖ ਦੇ ਆਚਰਨ ਦੀ ਉਸਾਰੀ ਵੀ ਕਰਦੀਆਂ ਹਨ। ਜਦੋਂ ਅਸੀਂ ਦੂਜਿਆਂ ਨਾਲ ਮਿਲ ਕੇ ਖੇਡਦੇ ਹਾਂ, ਤਾਂ ਸਾਡੇ ਵਿਚ ਇਕ – ਦੂਸਰੇ ਦੀ ਸਹਾਇਤਾ ਕਰਨ, ਕਿਸੇ ਨਾਲ ਵਧੀਕੀ ਨਾ ਕਰਨ, ਆਪਣੀ ਗ਼ਲਤੀ ਨੂੰ ਮੰਨ ਲੈਣ, ਧੋਖਾ ਨਾ ਕਰਨ, ਆਗੂ ਦਾ ਹੁਕਮ ਮੰਨਣ, ਆਪਣੀ ਜਿੱਤ ਲਈ ਜ਼ੋਰ ਲਾਉਣ, ਨੇਮਾਂ ਦੀ ਪਾਲਣਾ ਕਰਨ ਤੇ ਮਿਲ ਕੇ ਚੱਲਣ ਦੇ ਗੁਣ ਪੈਦਾ ਹੁੰਦੇ ਹਨ।
ਮਨੁੱਖੀ ਮਨ ਵਿਚ ਟਿਕਾਓ ਪੈਦਾ ਕਰਨਾ – ਖੇਡਾਂ ਮਨੁੱਖੀ ਮਨ ਵਿਚ ਟਿਕਾਓ ਤੇ ਇਕਾਗਰਤਾ ਪੈਦਾ ਕਰਦੀਆਂ ਹਨ ਖੇਡਾਂ ਵਿਚ ਲੱਗ ਕੇ ਮਨੁੱਖ ਸੰਸਾਰਕ ਝੰਜਟਾਂ ਨੂੰ ਭੁੱਲ ਕੇ ਫ਼ਿਕਰਾਂ ਤੇ ਮਾਨਸਿਕ ਤਣਾਓ ਤੋਂ ਮੁਕਤ ਹੋ ਜਾਂਦਾ ਹੈ। ਇਸ ਕਰਕੇ ਖੇਡਾਂ ਦੀ ਭਾਰੀ ਮਨੋਵਿਗਿਆਨਿਕ ਮਹਾਨਤਾ ਹੈ।
ਦਿਲ – ਪਰਚਾਵੇ ਦਾ ਸਾਧਨ – ਖੇਡਾਂ ਦਿਲ – ਪਰਚਾਵੇ ਦਾ ਇਕ ਬਹੁਤ ਵਧੀਆ ਸਾਧਨ ਹਨ। ਇਨ੍ਹਾਂ ਨਾਲ ਮਨੁੱਖੀ ਮਨ ਵਿਚ ਖ਼ੁਸ਼ੀ ਨੱਚਦੀ ਹੈ। ਉਸ ਨੂੰ ਕਈ ਮੌਕਿਆਂ ਤੇ ਖੁੱਲ੍ਹ ਕੇ ਹੱਸਣ ਦਾ ਮੌਕਾ ਮਿਲਦਾ ਹੈ। ਇਸ ਤਰ੍ਹਾਂ ਉਸ ਦਾ ਮਨ ਖਿੜ੍ਹਦਾ ਹੈ। ਖੇਡਾਂ ਸਰੀਰ ਰੂਪੀ ਮਸ਼ੀਨ ਲਈ ਤੇਲ ਦਾ ਕੰਮ ਕਰਦੀਆਂ ਹਨ। ਖਿੜਿਆ ਮਨ ਤੇ ਅਰੋਗ ਸਰੀਰ ਆਲੇ – ਦੁਆਲੇ ਵਿਚ ਮਹਿਕ ਖਿਲਾਰਦਾ ਹੈ ! ਆਸ਼ਾਵਾਦ ਜਗਾਉਣਾ – ਖੇਡਾਂ ਵਿਚ ਭਾਗ ਲੈਣ ਵਾਲਾ ਮਨੁੱਖ ਜੀਵਨ ਦੀ ਖੇਡ ਨੂੰ ਦਲੇਰੀ ਨਾਲ ਖੇਡਦਾ ਹੈ। ਉਹ ਕਿਸੇ ਥਾਂ ਇਕ ਵਾਰ ਹਾਰ ਖਾ ਕੇ ਨਿਰਾਸ਼ ਨਹੀਂ ਹੁੰਦਾ, ਸਗੋਂ ਆਸ਼ਾਵਾਦੀ ਰਹਿੰਦਾ ਹੈ।
ਖੇਡਾਂ ਲਈ ਸਮੇਂ ਦੀ ਠੀਕ ਵਰਤੋਂ – ਸਾਨੂੰ ਇਹ ਗੱਲ ਨਹੀਂ ਭੁੱਲਣੀ ਚਾਹੀਦੀ ਕਿ ਖੇਡਾਂ ਨੂੰ ਨਿਸਚਿਤ ਸਮਾਂ ਹੀ ਦੇਣਾ ਚਾਹੀਦਾ ਹੈ। ਹਰ ਸਮੇਂ ਖੇਡਾਂ ਵਿਚ ਹੀ ਨਹੀਂ ਲੱਗੇ ਰਹਿਣਾ ਚਾਹੀਦਾ ਕਿਉਂਕਿ ਇਸ ਤਰ੍ਹਾਂ ਅਸੀਂ ਆਪਣੀਆਂ ਹੋਰਨਾਂ ਜ਼ਿੰਮੇਵਾਰੀਆਂ ਨੂੰ ਸਫਲਤਾ ਨਾਲ ਨਹੀਂ ਨਿਭਾ ਸਕਾਂਗੇ। ਇਸ ਲਈ ਸਾਨੂੰ ਯਾਦ ਰੱਖਣਾ ਚਾਹੀਦਾ ਹੈ ਕਿ “ਖੇਡਾਂ ਜੀਵਨ ਲਈ ਹਨ, ਨਾ ਕਿ ਜੀਵਨ ਖੇਡਾਂ ਲਈ।

38. ਰੰਗਾਂ ਦਾ ਤਿਉਹਾਰ ਹੋਲੀ
ਜਾਣ – ਪਛਾਣ – ਹੋਲੀ ਦਾ ਤਿਉਹਾਰ ਸਾਡੇ ਦੇਸ਼ ਵਿਚ ਵਿਸ਼ੇਸ਼ ਮਹਾਨਤਾ ਰੱਖਦਾ ਹੈ। ਇਹ ਤਿਉਹਾਰ ਭਾਰਤ ਦੇ ਮੁੱਖ ਤਿਉਹਾਰਾਂ ਵਿਚੋਂ ਇਕ ਹੈ। ਹੋਲੀ ਦੇ ਆਉਣ ਨਾਲ ਮਨੁੱਖ ਸਭ ਵਿਤਕਰੇ ਤੇ ਵੈਰ – ਵਿਰੋਧ ਭੁਲਾ ਕੇ ਦੂਜਿਆਂ ਨੂੰ ਖ਼ੁਸ਼ੀ ਵਿਚ ਭਾਈਵਾਲ ਬਣਾਉਣ ਲਈ ਤਤਪਰ ਹੋ ਉੱਠਦਾ ਹੈ ਤੇ ਹਰ ਇਕ ਨਾਲ ਮਿੱਤਰਾਂ ਵਾਂਗ ਹੱਸਦਾ – ਖੇਡਦਾ ਤੇ ਖ਼ੁਸ਼ੀਆਂ ਮਨਾਉਂਦਾ ਹੈ।
ਸੁਹਾਵਣੀ ਰੁੱਤ – ਹਰ ਸਾਲ ਜਦੋਂ ਇਹ ਤਿਉਹਾਰ ਆਉਂਦਾ ਹੈ, ਤਾਂ ਅਸੀਂ ਆਪਣੇ ਮਿੱਤਰਾਂ ਤੇ ਸੰਬੰਧੀਆਂ ਨਾਲ ਮਿਲ ਕੇ ਖ਼ਬ ਹੋਲੀ ਖੇਡਦੇ ਹਾਂ। ਹੋਲੀ ਦਾ ਤਿਉਹਾਰ ਉਸ ਮੌਸਮ ਵਿਚ ਆਉਂਦਾ ਹੈ, ਜਦੋਂ ਸਰਦੀ ਦਿਨੋ – ਦਿਨ ਅਲੋਪ ਹੋ ਰਹੀ ਹੁੰਦੀ ਹੈ ਤੇ ਗਰਮੀ ਵਧਦੀ ਜਾਂਦੀ ਹੈ। ਬਸੰਤ ਰੁੱਤ ਹੋਣ ਕਰਕੇ ਹਰ ਪਾਸੇ ਦਰੱਖ਼ਤਾਂ, ਬੂਟਿਆਂ ਤੇ ਛੋਟੇ ਪੌਦਿਆਂ ਉੱਤੇ ਹਰਿਆਵਲ ਛਾ ਰਹੀ ਹੁੰਦੀ ਹੈ ਥਾਂ – ਥਾਂ ਰੰਗ – ਬਰੰਗੇ ਫੁੱਲ ਖਿੜ੍ਹ ਰਹੇ ਹੁੰਦੇ ਹਨ। ਇਨ੍ਹਾਂ ਦਿਨਾਂ ਵਿਚ ਛੋਲਿਆਂ ਨੂੰ ਡੰਡੇ ਲੱਗ ਜਾਂਦੇ ਹਨ ਤੇ ਉਨ੍ਹਾਂ ਦੀਆਂ ਹੋਲਾਂ ਖਾਣ ਲਈ ਹਰ ਇਕ ਦੇ ਮੂੰਹ ਵਿਚ ਪਾਣੀ ਭਰ ਆਉਂਦਾ ਹੈ। ਸ਼ਾਇਦ ਛੋਲਿਆਂ ਦੀਆਂ ਹੋਲਾਂ ਦਾ ਨਾਂ ਵੀ ਹੋਲੀ ਤੋਂ ਹੀ ਪਿਆ ਹੈ।
ਇਤਿਹਾਸਿਕ ਪਿਛੋਕੜ – ਮੇਰੇ ਪਿਤਾ ਜੀ ਨੇ ਮੈਨੂੰ ਦੱਸਿਆ ਕਿ ਹੋਲੀ ਦਾ ਸੰਬੰਧ ਕ੍ਰਿਸ਼ਨ ਜੀ ਦੁਆਰਾ ਪੂਤਨਾ ਦਾਈ ਨੂੰ ਮਾਰਨ ਮਗਰੋਂ ਗੋਪੀਆਂ ਨਾਲ ਰੰਗ ਦੀ ਹੋਲੀ ਖੇਡ ਕੇ ਖੁਸ਼ੀ ਮਨਾਉਣ ਦੇ ਨਾਲ ਜੋੜਿਆ ਜਾਂਦਾ ਹੈ। ਪਰ ਕਈ ਲੋਕਾਂ ਦੁਆਰਾ ਹੋਲੀ ਦੇ ਤਿਉਹਾਰ ਦਾ ਇਤਿਹਾਸਿਕ ਪਿਛੋਕੜ ਪ੍ਰਹਿਲਾਦ ਦੀ ਭੂਆ ਹੋਲਿਕਾ ਨਾਲ ਜੋੜਿਆ ਜਾਂਦਾ ਹੈ। ਹੋਲਿਕਾ ਨੂੰ ਅੱਗ ਵਿਚ ਨਾ ਸੜਨ ਦਾ ਵਰਦਾਨ ਮਿਲਿਆ ਹੋਇਆ ਸੀ। ਉਹ ਪ੍ਰਹਿਲਾਦ ਨੂੰ ਚੁੱਕ ਕੇ ਅੱਗ ਵਿਚ ਬੈਠ ਗਈ। ਸਿੱਟੇ ਵਜੋਂ ਹਿਲਾਦ ਬਚ ਗਿਆ, ਪਰੰਤੂ ਹੋਲਿਕਾ ਸੜ ਕੇ ਮਰ ਗਈ। ਕਿਹਾ ਜਾਂਦਾ ਹੈ ਕਿ ਇਹ ਤਿਉਹਾਰ ਉਸ ਦਿਨ ਤੋਂ ਹੀ ਮਨਾਇਆ ਜਾਂਦਾ ਹੈ।
ਹੋਲੀ ਦਾ ਤਿਉਹਾਰ ਬਹੁਤਾ ਕਰਕੇ ਹਿੰਦੂਆਂ ਵਿਚ ਮਨਾਇਆ ਜਾਂਦਾ ਹੈ। ਸਿੱਖ ਇਸ ਤੋਂ ਅਗਲੇ ਦਿਨ ਹੋਲਾ ਮਨਾਉਂਦੇ ਹਨ ਆਨੰਦਪੁਰ ਸਾਹਿਬ ਦਾ ਹੋਲਾ – ਮਹੱਲਾ ਬਹੁਤ ਪ੍ਰਸਿੱਧ ਹੈ।
ਰੰਗ ਸੁੱਟਣ ਦੀ ਖੇਡ – ਹੋਲੀ ਵਾਲੇ ਦਿਨ ਮੈਂ ਅਜੇ ਸਵੇਰੇ ਉੱਠ ਕੇ ਨਹਾ ਧੋ ਕੇ ਕੱਪੜੇ ਪਾਏ ਹੀ ਸਨ ਕਿ ਸਿਰ ਤੋਂ ਪੈਰਾਂ ਤਕ ਰੰਗ ਨਾਲ ਭਰੇ ਹੋਏ ਮੇਰੇ ਕੁੱਝ ਮਿੱਤਰ ਤੇ ਉਨ੍ਹਾਂ ਦੀਆਂ ਭੈਣਾਂ ਰੰਗਾਂ ਦੇ ਲਿਫ਼ਾਫੇ ਚੁੱਕੀ ਆ ਪੁੱਜੇ। ਹੁਣ ਕੋਈ ਮੇਰੇ ਮੂੰਹ ਉੱਤੇ ਰੰਗ ਸੁੱਟ ਰਿਹਾ ਸੀ, ਕੋਈ ਮੇਰੇ ਸਿਰ ਉੱਤੇ ਤੇ ਕੋਈ ਮੇਰੇ ਕੱਪੜਿਆਂ ਉੱਤੇ ! ਜਦੋਂ ਉਹ ਮੇਰੇ ਉੱਪਰ ਰੰਗ ਸੁੱਟ ਤੇ ਮਲ ਰਹੇ ਸਨ, ਤਾਂ ਸਾਡੇ ਘਰ ਦੇ ਬਾਕੀ ਮੈਂਬਰਾਂ ਨੇ ਆਪਣੇ ਹੱਥਾਂ ਵਿਚ ਰੰਗਾਂ ਦੇ ਲਿਫ਼ਾਫੇ ਫੜ ਕੇ ਉਨ੍ਹਾਂ ਨੂੰ ਰੰਗਣਾ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤਾ।
ਇੰਨੇ ਨੂੰ ਮੈਂ ਵੀ ਆਪਣੇ ਹੱਥਾਂ ਵਿਚ ਰੰਗ ਦਾ ਲਿਫ਼ਾਫਾ ਫੜ ਕੇ ਉਨ੍ਹਾਂ ਉੱਪਰ ਰੰਗ ਧੂੜਨਾ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤਾ। ਇਸ ਤੋਂ ਮਗਰੋਂ ਅਸੀਂ ਸਾਰੇ ਮਿਲ ਕੇ ਦੂਜੀ ਗਲੀ ਵਿਚ ਰਹਿੰਦੇ ਇਕ ਹੋਰ ਮਿੱਤਰ ਵਲ ਤੁਰੇ, ਪਰ ਉਹ ਸਾਨੂੰ ਰਸਤੇ ਵਿਚ ਹੀ ਕੁੱਝ ਹੋਰ ਮਿੱਤਰਾਂ ਨਾਲ ਹੋਲੀ ਖੇਡਦਾ ਮਿਲ ਪਿਆ। ਸਾਡੇ ਦੋਹਾਂ ਗਰੁੱਪਾਂ ਨੇ ਇਕ – ਦੂਜੇ ਉੱਪਰ ਰੰਗ ਸੁੱਟ – ਸੁੱਟ ਕੇ ਖੂਬ ਦਿਲ ਦੀਆਂ ਲਾਹੀਆਂ ਇਸ ਸਮੇਂ ਮੇਰੇ ਉੱਪਰ ਇਕ ਰੁੱਸੇ ਹੋਏ ਮਿੱਤਰ ਨੇ ਰੰਗ ਸੁੱਟਿਆ ਤੇ ਮੈਂ ਉਸ ਉੱਪਰ ਰੰਗ ਸੁੱਟ ਦਿੱਤਾ।
ਬੱਸ ਇੰਨੇ ਨਾਲ ਹੀ ਸਾਡੀ ਮੰਨ – ਮਨਉੜੀ ਹੋ ਗਈ ਸਾਡੇ ਇਕ ਸਾਥੀ ਨੇ ਇਕ ਚਿਟ ਕੱਪੜੀਏ ਸਕੂਟਰ ਸਵਾਰ ਉੱਪਰ ਰੰਗ ਸੁੱਟਿਆ, ਜਿਸ ਤੇ ਅਸੀਂ ਸਾਰਿਆਂ ਨੇ ਉਸ ਨੂੰ ਵਰਜਿਆ ਕਿ ਉਹ ਕਿਸੇ ਓਪਰੇ ਉੱਪਰ ਰੰਗ ਨਾ ਸੁੱਟੇ। ਰਸਤੇ ਵਿਚ ਅਸੀਂ ਕੁੱਝ ਬੱਚਿਆਂ ਨੂੰ ਪਿਚਕਾਰੀਆਂ ਵਿਚ ਰੰਗਦਾਰ ਪਾਣੀ ਭਰ ਕੇ ਇਕ – ਦੂਜੇ ਉੱਪਰ ਸੁੱਟਦਿਆਂ ਦੇਖਿਆ ਅਸੀਂ ਉਨ੍ਹਾਂ ਨਾਲ ਵੀ ਹੋਲੀ ਦਾ ਆਨੰਦ ਮਾਣਿਆ। ਸਾਡਾ ਇਕ ਮਿੱਤਰ ਅਚਾਨਕ ਸਾਡੇ ਕਾਬ ਆ ਗਿਆ।
ਉਸ ਨੇ ਸਾਫ਼ ਤੇ ਸੰਦਰ ਕੱਪੜੇ ਪਾਏ ਹੋਏ ਸਨ, ਪਰ ਅਸੀਂ ਉਸ ਦਾ ਜ਼ਰਾ ਲਿਹਾਜ਼ ਨਾ ਕੀਤਾ, ਜਿਸ ‘ਤੇ ਉਹ ਗੁੱਸੇ ਵਿਚ ਆ ਗਿਆ, ਪਰ ਜਦੋਂ ਅਸੀਂ ਉਸ ਨੂੰ ਦੱਸਿਆ ਕਿ ਹੋਲੀ ਤਾਂ ਸਾਡੇ ਵੱਡੇ – ਵੱਡੇ ਨੇਤਾ ਵੀ ਖੇਡਦੇ ਹਨ ਤੇ ਇਸ ਵਿਚ ਪ੍ਰਧਾਨ ਮੰਤਰੀ, ਰਾਸ਼ਟਰਪਤੀ ਤੇ ਵਿਦੇਸ਼ੀ ਪ੍ਰਾਹੁਣੇ ਵੀ ਸ਼ਾਮਲ ਹੁੰਦੇ ਹਨ, ਤਾਂ ਉਸ ਦਾ ਗੁੱਸਾ ਠੰਢਾ ਹੋ ਗਿਆ ਤੇ ਉਹ ਵੀ ਰੰਗ ਲੈ ਕੇ ਸਾਡੇ ਨਾਲ ਹੋਲੀ ਖੇਡਣ ਲੱਗ ਪਿਆ।
ਰਾਗ – ਰੰਗ – ਵਾਪਸ ਆ ਕੇ ਅਸੀਂ ਆਪਣੇ ਘਰ ਹੋਲਿਕਾ ਜਲਾਈ ਤੇ ਪ੍ਰਹਿਲਾਦ ਭਗਤ ਨੂੰ ਯਾਦ ਕਰ ਕੇ ਪ੍ਰਭੂ ਦੇ ਗੁਣ ਗਾਏ। ਰਾਤ ਨੂੰ ਅਸੀਂ ਇਕ ਸੰਗੀਤ ਸਮਾਰੋਹ ਦਾ ਪ੍ਰਬੰਧ ਕੀਤਾ।

ਸਾਰ – ਅੰਸ਼ – ਇਸ ਪ੍ਰਕਾਰ ਹੋਲੀ ਇਕ ਖੁਸ਼ੀਆਂ ਭਰਿਆ ਤਿਉਹਾਰ ਹੈ ਤੇ ਇਹ ਵੈਰ – ਵਿਰੋਧ ਮਿਟਾਉਣ ਤੇ ਮਿੱਤਰ ਭਾਵ ਪੈਦਾ ਕਰਨ ਵਿਚ ਕਾਫ਼ੀ ਸਹਾਇਕ ਹੈ।
39. ਪੰਜਾਬ ਦੀ ਲੋਕ – ਗਾਇਕਾ – ਸੁਰਿੰਦਰ ਕੌਰ
(ਨੋਟ – ਦੇਖੋ ਪੰਜਾਬੀ ਪੁਸਤਕ – 7 ਵਾਲੇ ਭਾਗ ਵਿਚ ਪਾਠ 3 ਦਾ ਸਾਰ)
40. ਬਾਬਾ ਬੰਦਾ ਸਿੰਘ ਬਹਾਦਰ
(ਨੋਟ – ਦੇਖੋ ਪੰਜਾਬੀ ਪੁਸਤਕ – 7 ਵਾਲੇ ਭਾਗ ਵਿਚ ਪਾਠ 11 ਦਾ ਸਾਰ)
41. ਕਰਤਾਰ ਸਿੰਘ ਸਰਾਭਾ
(ਨੋਟ – ਦੇਖੋ ਪੰਜਾਬੀ ਪੁਸਤਕ – 7 ਵਾਲੇ ਭਾਗ ਵਿਚ ਪਾਠ 14 ਦਾ ਸਾਰ)
42. ਲਾਲਾ ਲਾਜਪਤ ਰਾਏ
(ਨੋਟ – ਦੇਖੋ ਪੰਜਾਬੀ ਪੁਸਤਕ – 7 ਵਾਲੇ ਭਾਗ ਵਿਚ ਪਾਠ 17 ਦਾ ਸਾਰ)
43. ਪੁਲਾੜ – ਯਾਤਰੀ – ਸੁਨੀਤਾ ਵਿਲੀਅਮਜ਼
(ਨੋਟ – ਦੇਖੋ ਪੰਜਾਬੀ ਪੁਸਤਕ – 7 ਵਾਲੇ ਭਾਗ ਵਿਚ ਪਾਠ 21 ਦਾ ਸਾਰ
44. ਵਿਰਾਸਤ – ਏ – ਖ਼ਾਲਸਾ
(ਨੋਟ – ਦੇਖੋ ਪੰਜਾਬੀ ਪੁਸਤਕ – 7 ਵਾਲੇ ਭਾਗ ਵਿਚ ਪਾਠ 22 ਦਾ ਸਾਰ)
45. ਮੈਂ ਇਸ ਸਾਲ ਕੀ ਕਰਾਂਗਾ
ਇਸ ਸਾਲ ਮੈਂ ਛੇਵੀਂ ਪਾਸ ਕਰ ਕੇ ਸੱਤਵੀਂ ਵਿਚ ਦਾਖ਼ਲ ਹੋਇਆ ਹਾਂ। ਇਸ ਕਰਕੇ ਇਸ ਸਾਲ ਦਾ ਮੇਰੇ ਲਈ ਸਭ ਤੋਂ ਮਹੱਤਵਪੂਰਨ ਕੰਮ ਪਹਿਲਾਂ ਵਾਂਗ ਹੀ ਚੰਗੇ ਨੰਬਰ ਲੈ ਕੇ ਸੱਤਵੀਂ ਪਾਸ ਕਰਨਾ ਹੈ। ਇਸ ਮੰਤਵ ਲਈ ਮੈਂ ਹੁਣ ਤੋਂ ਹੀ ਆਪਣੀ ਪੜ੍ਹਾਈ ਵਲ ਧਿਆਨ ਦੇਣ ਦਾ ਫ਼ੈਸਲਾ ਕੀਤਾ ਹੈ। ਛੇਵੀਂ ਜਮਾਤ ਤਕ ਦੀ ਪੜ੍ਹਾਈ ਕਰਦਿਆਂ ਮੈਂ ਇਹੋ ਮਹਿਸੂਸ ਕੀਤਾ ਹੈ ਕਿ ਜਿੰਨੀ ਬਹੁਤੀ ਮਿਹਨਤ ਕਰੋ, ਪ੍ਰੀਖਿਆ ਵਿਚ ਓਨੇ ਹੀ ਚੰਗੇ ਨੰਬਰ ਆਉਂਦੇ ਹਨ।
ਇਸ ਕਰਕੇ ਮੈਂ ਇਸ ਗੱਲ ਨੂੰ ਸਭ ਤੋਂ ਵੱਧ ਮਹੱਤਵ ਦੇਣਾ ਸ਼ੁਰੂ ਕੀਤਾ ਹੈ ਕਿ ਕਲਾਸ ਵਿਚ ਪੜ੍ਹਾ ਰਹੇ ਅਧਿਆਪਕ ਦੀ ਗੱਲ ਨੂੰ ਮਨ ਪੂਰੀ ਤਰ੍ਹਾਂ ਇਕਾਗਰ ਕਰ ਕੇ ਸੁਣਿਆ ਜਾਵੇ। ਜੇਕਰ ਇਸ ਤਰ੍ਹਾਂ ਕੀਤਾ ਜਾਵੇ, ਤਾਂ ਅਧਿਆਪਕ ਦੁਆਰਾ ਪੜ੍ਹਾਏ ਜਾ ਰਹੇ ਪਾਠ ਤੇ ਸਮਝਾਈਆਂ ਗਈਆਂ ਗੱਲਾਂ ਨਾਲੋ ਨਾਲ ਹੀ ਯਾਦ ਹੋ ਜਾਂਦੀਆਂ ਹਨ।
ਇਸ ਕਰਕੇ ਇਸ ਸਾਲ ਦੀ ਕਲਾਸ ਰੂਮ ਵਿਚਲੀ ਪੜ੍ਹਾਈ ਵਿਚ ਮੈਂ ਅਧਿਆਪਕਾਂ ਦੀ ਗੱਲ ਨੂੰ ਧਿਆਨ ਨਾਲ ਸੁਣ ਕੇ ਸਮਝਣ ਤੇ ਮਨ ਵਿਚ ਵਸਾਉਣ ਦਾ ਯਤਨ ਕਰਾਂਗਾ, ਤਾਂ ਜੋ ਮੇਰੀ ਪੜਾਈ ਨਾਲੋ ਨਾਲ ਹੁੰਦੀ ਰਹੇ ਤੇ ਮੈਂ ਕਿਸੇ ਗੱਲ ਵਿਚ ਪਛੜਾਂ ਨਾ। ਇਸ ਤੋਂ ਇਲਾਵਾ ਮੈਂ ਆਪਣੀ ਦੋਸਤੀ ਵੀ ਚੰਗੇ ਤੇ ਹੁਸ਼ਿਆਰ ਮੁੰਡਿਆਂ ਨਾਲ ਰੱਖਾਂਗਾ, ਤਾਂ ਜੋ ਮੇਰੇ ਚਰਿੱਤਰ ਵਿਚ ਕਿਸੇ ਤਰ੍ਹਾਂ ਦੀ ਗਿਰਾਵਟ ਤੇ ਭਟਕਣ ਨਾ ਆਵੇ ਤੇ ਮੇਰਾ ਦਿਮਾਗੀ ਵਿਕਾਸ ਲਗਾਤਾਰ ਹੁੰਦਾ ਰਹੇ।

ਆਪਣੀ ਪੜ੍ਹਾਈ ਵਿਚ ਪੂਰੀ ਮੁਹਾਰਤ ਹਾਸਲ ਕਰਨ ਲਈ ਮੈਂ ਟੈਲੀਵਿਯਨ ਦੇ ਫ਼ਜ਼ੂਲ ਕਿਸਮ ਦੇ ਪ੍ਰੋਗਰਾਮ ਦੇਖਣ ਤੇ ਮੋਬਾਈਲ ਫੋਨ ਦੀ ਦੁਰਵਰਤੋਂ ਕਰਨ ਤੋਂ ਵੀ ਬਚੇ ਰਹਿਣ ਦਾ ਯਤਨ ਕਰਾਂਗਾ, ਪਰ ਮੈਂ ਆਪਣੀ ਸਿਹਤ ਦਾ ਪੂਰਾ – ਪੂਰਾ ਧਿਆਨ ਰੱਖਾਂਗਾ ਕਹਿੰਦੇ ਹਨ ਕਿ ਅਰੋਗ ਸਰੀਰ ਵਿਚ ਹੀ ਅਰੋਗ ਮਨ ਵਸਦਾ ਹੈ। ਇਸ ਲਈ ਮੈਂ ਸਰੀਰਕ ਕਸਰਤ ਤੇ ਯੋਗ ਆਸਣ ਅਪਣਾਉਣ ਤੋਂ ਇਲਾਵਾ ਆਪਣੀ ਮਨ – ਪਸੰਦ ਕਬੱਡੀ ਖੇਡ ਵੀ ਖੇਡਦਾ ਰਹਾਂਗਾ ਕਬੱਡੀ ਇਕ ਸੰਪੂਰਨ ਖੇਡ ਹੈ।
ਇਸ ਵਿਚ ਭਿੰਨ – ਭਿੰਨ ਖੇਡਾਂ ਦੇ ਗੁਣ ਇਕੋ ਥਾਂ ਸਮੋਏ ਮਿਲਦੇ ਹਨ ਇਸ ਵਿਚ ਸਰੀਰਕ ਤਕੜਾਈ ਦਾ ਪ੍ਰਦਰਸ਼ਨ, ਦੌੜਾਂ, ਦਮ, ਛਾਲਾਂ, ਕੁਸ਼ਤੀ, ਵੀਣੀ ਫੜਨਾ, ਘੋਲ – ਘੁਮਾਣੇ, ਝਕਾਨੀਆਂ ਤੇ ਦਾਓ – ਪੇਚ ਸਭ ਕੁੱਝ ਸ਼ਾਮਿਲ ਹੈ। ਕਬੱਡੀ ਖੇਡਣ ਵਾਲੇ ਨੂੰ ਹੋਰ ਕੋਈ ਖੇਡ ਖੇਡਣ ਦੀ ਲੋੜ ਨਹੀਂ ਰਹੀ ਰਹਿੰਦੀ। ਇਸ ਨਾਲ ਸਰੀਰ ਦਾ ਸੰਪੂਰਨ ਵਿਕਾਸ ਹੁੰਦਾ ਹੈ। ਦਿਮਾਗ਼ ਤੇਜ਼ ਤੇ ਫੁਰਤੀਲਾ ਬਣਦਾ ਹੈ। ਇਸ ਸਾਲ ਮੈਂ ਪਿਛਲੇ ਸਾਲ ਵਾਂਗ ਹੀ ਆਪਣੇ ਸਕੂਲ ਦੀ ਕਬੱਡੀ ਵਿਚ ਆਪਣਾ ਮੁਹਰਲਾ ਸਥਾਨ ਬਣਾਈ ਰੱਖਾਂਗਾ ਤੇ ਹੋਰਨਾਂ ਥਾਂਵਾਂ ਤੇ ਹੋਏ ਮੁਕਾਬਲਿਆਂ ਵਿਚ ਆਪਣੇ ਇਕ ਵਧੀਆ ਖਿਡਾਰੀ ਹੋਣ ਦੇ ਪ੍ਰਮਾਣ ਦਿੰਦਾ ਰਹਾਂਗਾ।
ਇਸ ਤੋਂ ਇਲਾਵਾ ਮੈਂ ਵਾਤਾਵਰਨ ਦੀ ਸੰਭਾਲ ਤੇ ਸਫ਼ਾਈ ਵਿਚ ਹਿੱਸਾ ਪਾਉਣ ਲਈ ਆਪਣੇ ਘਰ, ਸਕੂਲ ਤੇ ਗਲੀ – ਮੁਹੱਲੇ ਵਿਚ ਸਫ਼ਾਈ ਦੀ ਰੁਚੀ ਪੈਦਾ ਕਰਨ ਲਈ ਵਧ – ਚੜ੍ਹ ਕੇ ਹਿੱਸਾ ਪਾਵਾਂਗਾ। ਮੈਂ ਆਪਣੇ ਜਨਮ ਦਿਨ 10 ਅਕਤੂਬਰ ਦੇ ਦਿਨ ਘੱਟੋ – ਘੱਟ ਇਕ ਰੁੱਖ ਜ਼ਰੂਰ ਲਾਵਾਂਗਾ ਤੇ ਫਿਰ ਉਸਦੀ ਪਾਲਣਾ ਵਲ ਵੀ ਧਿਆਨ ਦੇਵਾਂਗਾ।
ਇਸ ਸਾਲ ਵਿਚ ਮੈਂ ਆਪਣੇ ਆਪ ਨੂੰ ਮਾਤਾ – ਪਿਤਾ ਤੇ ਅਧਿਆਪਕਾਂ ਦਾ ਆਦਰ – ਸਤਿਕਾਰ ਕਰਨ ਵਾਲੇ, ਹੱਥੀਂ ਕੰਮ ਤੋਂ ਜੀ ਨਾ ਚਰਾਉਣ ਵਾਲੇ, ਖ਼ਦਗਰਜ਼ੀ ਤੋਂ ਦੂਰ ਰਹਿਣ ਵਾਲੇ, ਲੋੜਵੰਦਾਂ ਦੀ ਸਹਾਇਤਾ ਕਰਨ ਵਾਲੇ ਤੇ ਨੈਤਿਕ ਦੇ ਧਾਰਨੀ ਲੜਕੇ ਦੇ ਰੂਪ ਵਿਚ ਪੇਸ਼ ਕਰਦਿਆਂ ਇਕ ਆਦਰਸ਼ ਵਿਦਿਆਰਥੀ ਨੌਜਵਾਨ ਦੇ ਰੂਪ ਵਿਚ ਉੱਭਰ ਕੇ ਸਾਹਮਣੇ ਆਵਾਂਗਾ ਬੱਸ ਇਹੋ ਹੀ ਮੇਰਾ ਟੀਚਾ ਹੈ, ਤਾਂ ਜੋ ਮੈਂ ਵੱਡਾ ਹੋ ਕੇ ਇਕ ਨੇਕ ਇਨਸਾਨ ਬਣ ਸਕਾਂ।
46. ਸਾਡੇ ਪਿੰਡ
ਭਾਰਤ ਪਿੰਡਾਂ ਦਾ ਦੇਸ਼ ਹੈ। ਇਸਦੀ ਬਹੁਤੀ ਅਬਾਦੀ ਪਿੰਡਾਂ ਵਿਚ ਵਸਦੀ ਹੈ। ਅੱਜ ਤੋਂ ਪੰਜਾਹ ਕੁ ਸਾਲ ਪਹਿਲਾਂ ਸਾਡੇ ਪਿੰਡ ਬਹੁਤ ਪਛੜੇ ਹੋਏ ਸਨ। ਨਾ ਉੱਥੇ ਪੱਕੀਆਂ ਸੜਕਾਂ ਸਨ, ਨਾ ਆਵਾਜਾਈ ਦੇ ਮਸ਼ੀਨੀ ਸਾਧਨ ਤੇ ਨਾ ਹੀ ਬਿਜਲੀ। ਪਰੰਤੂ ਸਾਡੇ ਵਰਤਮਾਨ ਪਿੰਡ ਸ਼ਹਿਰਾਂ ਤੋਂ ਕਿਸੇ ਤਰ੍ਹਾਂ ਵੀ ਘੱਟ ਨਹੀਂ, ਸਗੋਂ ਖੁੱਲ੍ਹੀ ਤੇ ਤਾਜ਼ੀ ਹਵਾ ਅਤੇ ਸ਼ੁੱਧ ਦੁੱਧ, ਦਹੀਂ ਤੇ ਅੰਨ ਵਿਚ ਉਹ ਸ਼ਹਿਰਾਂ ਤੋਂ ਅੱਗੇ ਹਨ। ਅੱਜ ਪਿੰਡਾਂ ਵਿਚ ਸੜਕਾਂ ਦਾ ਜਾਲ ਵਿਛ ਚੁੱਕਾ ਹੈ ਤੇ ਉਨ੍ਹਾਂ ਉੱਤੇ ਆਵਾਜਾਈ ਦੇ ਹਰ ਪ੍ਰਕਾਰ ਦੇ ਸਾਧਨ ਦੌੜਦੇ ਫਿਰਦੇ ਹਨ ਅੱਜ ਕਾਰਾਂ, ਬੱਸਾਂ, ਸਕੂਟਰ, ਮੋਟਰ ਸਾਈਕਲ ਆਮ ਲੋਕਾਂ ਕੋਲ ਹਨ।
ਘਰਾਂ ਵਿਚ ਟੈਲੀਫੋਨ ਹਨ ਤੇ ਹੱਥਾਂ ਵਿਚ ਮੋਬਾਈਲ ਫੋਨ ਡਾਕਟਰੀ ਸਹਾਇਤਾ ਵੀ ਹਰ ਪਿੰਡ ਦੇ ਨੇੜੇ ਹੀ ਮਿਲ ਜਾਂਦੀ ਹੈ ਅੱਜ ਸਾਡੇ ਪਿੰਡ ਵਿੱਦਿਅਕ ਸੰਸਥਾਵਾਂ ਨਾਲ ਭਰਪੂਰ ਹਨ। ਪਿੰਡ ਵਿਚ ਪ੍ਰਾਇਮਰੀ ਸਕੂਲ, ਮਿਡਲ ਸਕੂਲ, ਹਾਈ ਸਕੂਲ, ਸੀਨੀਅਰ ਸੈਕੰਡਰੀ ਸਕੂਲ, ਪਬਲਿਕ ਸਕੂਲ, ਕਾਲਜ ਤੇ ਭਿੰਨ – ਭਿੰਨ ਕਿੱਤਿਆਂ ਵਿਚ ਸਿਖਲਾਈ ਦੇਣ ਵਾਲੀਆਂ ਸੰਸਥਾਵਾਂ ਮੌਜੂਦ ਹਨ, ਜਿਸ ਕਾਰਨ ਪਿੰਡਾਂ ਵਿਚ ਅਨਪੜ੍ਹਤਾ ਤੇਜ਼ੀ ਨਾਲ ਖ਼ਤਮ ਹੋ ਰਹੀ ਹੈ ਤੇ ਪੜ੍ਹੇ – ਲਿਖੇ ਮੁੰਡੇ ਤੇ ਕੁੜੀਆਂ ਅੱਗੇ ਵੱਧ ਕੇ ਕੌਮਾਂਤਰੀ ਖੇਤਰ ਵਿਚ ਮਾਰਾਂ ਮਾਰਦੇ ਹੋਏ ਉੱਚੇ ਆਹੁਦੇ ਪ੍ਰਾਪਤ ਕਰਨ ਦੇ ਨਾਲ ਵੱਡੇ – ਵੱਡੇ ਕਾਰੋਬਾਰ ਵੀ ਚਲਾਉਣ ਲੱਗੇ ਹਨ।
ਪਿੰਡਾਂ ਵਿਚ ਸਰਕਾਰ ਵਲੋਂ ਥਾਂ – ਥਾਂ ਸਿਹਤ ਸਹੂਲਤਾਂ ਦੇਣ ਵਾਲੀਆਂ ਡਿਸਪੈਂਸਰੀਆਂ ਖੋਲ੍ਹ ਦਿੱਤੀਆਂ ਹਨ ਥਾਂ – ਥਾਂ ਸਿਖਲਾਈ ਪ੍ਰਾਪਤ ਡਾਕਟਰ ਆਪਣੇ ਨਿੱਜੀ ਕਲੀਨਿਕ ਖੋਲ੍ਹ ਕੇ ਲੋਕਾਂ ਨੂੰ ਡਾਕਟਰੀ ਸਹੂਲਤਾਂ ਪ੍ਰਦਾਨ ਕਰ ਰਹੇ ਹਨ। ਇਸ ਨਾਲ ਪਿੰਡਾਂ ਵਿਚ ਬਹੁਤ ਸਾਰੇ ਰੋਗਾਂ ਦਾ ਖ਼ਾਤਮਾ ਹੋ ਗਿਆ ਹੈ ਤੇ ਲੋਕ ਤੇ ਬੱਚੇ ਅਣਆਈ ਮੌਤ ਦੇ ਮੂੰਹ ਵਿਚ ਪੈਣ ਤੋਂ ਬਚ ਗਏ ਹਨ ਅਜੋਕੇ ਪਿੰਡਾਂ ਵਿਚ ਪਹਿਲਾਂ ਨਾਲੋਂ ਸਫ਼ਾਈ ਵੀ ਵਧੇਰੇ ਹੈ। ਲੋਕਾਂ ਨੇ ਆਪਣੇ ਘਰਾਂ ਵਿਚ ਫਲੱਸ਼ਾਂ ਬਣਵਾ ਲਈਆਂ ਹਨ ਤੇ ਘਰਾਂ ਦਾ ਪਾਣੀ ਅੰਡਰ – ਗਰਾਊਂਡ ਨਾਲੀਆਂ ਵਿਚ ਜਾਣ ਲੱਗਾ ਹੈ, ਜਿਸ ਕਰਕੇ ਮੱਖੀਆਂ, ਮੱਛਰ ਵੀ ਘੱਟ ਹੋ ਗਏ ਹਨ। ਪਿੰਡਾਂ ਵਿਚ ਜਿੱਥੇ ਗੰਦੇ ਪਾਣੀ ਦੇ ਨਿਕਾਸ ਦੇ ਪ੍ਰਬੰਧ ਠੀਕ ਹੋ ਗਏ ਹਨ, ਉੱਥੇ ਪੀਣ ਲਈ ਵੀ ਸੁਥਰਾ ਪਾਣੀ ਦੇਣ ਦੇ ਪ੍ਰਬੰਧ ਕੀਤੇ ਗਏ ਹਨ।

ਪਿੰਡਾਂ ਵਿਚ ਪੰਚਾਇਤਾਂ ਬਹੁਤ ਜ਼ਿੰਮੇਵਾਰੀ ਨਾਲ ਕੰਮ ਕਰਦੀਆਂ ਹਨ। ਉਹ ਪਿੰਡਾਂ ਵਿਚ ਹੋਣ ਵਾਲੇ ਛੋਟੇ – ਮੋਟੇ ਝਗੜਿਆਂ ਨੂੰ ਵੀ ਨਿਬੇੜਦੀਆਂ ਹਨ ਤੇ ਪਿੰਡ ਵਿਚ ਪ੍ਰੇਮ – ਪਿਆਰ ਪੈਦਾ ਕਰਨ ਦੇ ਨਾਲ ਗਲੀਆਂ ਦੀ ਸਫ਼ਾਈ ਦੇ ਪ੍ਰਬੰਧ ਤੇ ਰੌਸ਼ਨੀ ਦੇ ਪ੍ਰਬੰਧ ਨੂੰ ਠੀਕ ਰੱਖਣ ਦਾ ਕੰਮ ਵੀ ਕਰਦੀਆਂ ਹਨ। ਕਈ ਪਿੰਡਾਂ ਵਿਚ ਉਦਯੋਗਿਕ ਇਕਾਈਆਂ ਵੀ ਕਾਇਮ ਹੋਈਆਂ ਹਨ, ਜੋ ਬੇਰੁਜ਼ਗਾਰ ਲੋਕਾਂ ਲਈ ਰੁਜ਼ਗਾਰ ਦੇ ਮੌਕੇ ਪੈਦਾ ਕਰਦੀਆਂ ਹਨ, ਜਿਸ ਨਾਲ ਖ਼ੁਸ਼ਹਾਲੀ ਤੇ ਵਿਕਾਸ ਵਿਚ ਵਾਧਾ ਹੁੰਦਾ ਪਿੰਡਾਂ ਦੀਆਂ ਔਰਤਾਂ ਹੁਣ ਅਨਪੜ੍ਹ ਨਹੀਂ ਤੇ ਨਾ ਹੀ ਸਿਰਫ਼ ਘਰਾਂ ਦੇ ਕੰਮ ਕਰਦੀਆਂ ਹਨ।ਉਹ ਕਈ ਪ੍ਰਕਾਰ ਦੀਆਂ ਨਿਗਾਂ ਪ੍ਰਾਪਤ ਕਰ ਕੇ ਤੇ ਨੌਕਰੀਆਂ ਉੱਤੇ ਲੱਗ ਕੇ ਆਪਣੇ ਪੈਰਾਂ ਉੱਤੇ ਖੜ੍ਹੀਆਂ ਹੋ ਰਹੀਆਂ ਹਨ।
ਪਿੰਡਾਂ ਦਾ ਜੀਵਨ ਸਰਲ ਤੇ ਰੰਗੀਨੀਆਂ ਭਰਪੂਰ ਹੈ। ਇੱਥੇ ਵਸਣ ਵਾਲਾ ਕੁਦਰਤ ਦੀ ਗੋਦੀ ਦਾ ਨਿੱਘ ਮਾਣਦਾ ਹੈ। ਇਨ੍ਹਾਂ ਵਿਚ ਸ਼ਹਿਰਾਂ ਨਾਲੋਂ ਪ੍ਰਦੂਸ਼ਣ ਘੱਟ ਹੈ। ਪਿੰਡਾਂ ਵਿਚ ਹੋ ਰਹੀ ਬਹੁਪੱਖੀ ਤਰੱਕੀ ਨੂੰ ਦੇਖ ਕੇ ਜਾਪਦਾ ਹੈ ਕਿ ਉਹ ਸਮਾਂ ਨੇੜੇ ਹੀ ਹੈ, ਜਦੋਂ ਪਿੰਡਾਂ ਤੇ ਸ਼ਹਿਰਾਂ ਦੇ ਜੀਵਨ ਵਿਚ ਬਹੁਤਾ ਫ਼ਰਕ ਨਹੀਂ ਰਹਿ ਜਾਵੇਗਾ।
47. ਮੋਬਾਈਲ ਫੋਨ ਦੀ ਲੋਕ – ਪ੍ਰਿਅਤਾ
ਮੋਬਾਈਲ ਫੋਨ ਵਰਤਮਾਨ ਸੰਸਾਰ ਵਿਚ ਸੂਚਨਾ – ਸੰਚਾਰ ਦਾ ਸਭ ਤੋਂ ਹਰਮਨ – ਪਿਆਰਾ ਸਾਧਨ ਬਣ ਗਿਆ ਹੈ। ਅੱਜ ਦੁਨੀਆ ਦੀ ਸਾਢੇ 7 ਅਰਬ ਅਬਾਦੀ ਵਿਚੋਂ ਸਾਢੇ 6 ਅਰਬ ਲੋਕ ਮੋਬਾਈਲ ਫੋਨ ਦੀ ਵਰਤੋਂ ਕਰ ਰਹੇ ਹਨ। ਭਾਰਤ ਵਿਚ ਇਸ ਸਮੇਂ ਮੋਬਾਈਲ ਫੋਨ ਦੀ ਵਰਤੋਂ ਕਰਨ ਵਾਲੇ ਲੋਕਾਂ ਦੀ ਗਿਣਤੀ ਇਕ ਅਰਬ ਤੋਂ ਉੱਪਰ ਹੈ ਅਤੇ ਇਹ ਦਿਨੋ – ਦਿਨ ਤੇਜ਼ੀ ਨਾਲ ਵਧ ਰਹੀ ਹੈ।
ਆਓ ਜ਼ਰਾ ਦੇਖੀਏ ਇਸ ਦੇ ਲਾਭ ਕੀ ਹਨ ?
ਉੱਪਰ ਦੱਸੇ ਅਨੁਸਾਰ ਮੋਬਾਈਲ ਫੋਨ ਦਾ ਸਭ ਤੋਂ ਵੱਡਾ ਲਾਭ ਤਟਫਟ ਸੂਚਨਾ – ਸੰਚਾਰ ਦਾ ਸਾਧਨ ਹੋਣਾ ਹੈ ਤੁਸੀਂ ਭਾਵੇਂ ਕਿੱਤੇ ਵੀ ਅਤੇ ਕਿਸੇ ਵੀ ਹਾਲਤ ਵਿਚ ਹੋਵੋ, ਇਹ ਨਾ ਕੇਵਲ ਤੁਹਾਡੀ ਗੱਲ ਜਾਂ ਸੰਦੇਸ਼ ਨੂੰ ਮਿੰਟਾਂ – ਸਕਿੰਟਾਂ ਵਿਚ ਦੁਨੀਆ ਦੇ ਕਿਸੇ ਥਾਂ ਵੀ ਕਿਸੇ ਵੀ ਹਾਲਤ ਵਿਚ ਮੌਜੂਦ ਤੁਹਾਡੇ ਮਿੱਤਰ – ਪਿਆਰੇ, ਸਨੇਹੀ – ਰਿਸ਼ਤੇਦਾਰ ਜਾਂ ਵਪਾਰਕ ਸੰਬੰਧੀ ਤਕ ਪੁਚਾ ਸਕਦਾ ਹੈ, ਸਗੋਂ ਉਸ ਦਾ ਉੱਤਰ ਵੀ ਨਾਲੋ – ਨਾਲ ਤੁਹਾਡੇ ਤਕ ਪੁਚਾ ਦਿੰਦਾ ਹੈ।
ਮੋਬਾਈਲ ਫੋਨ ਦਾ ਦੂਜਾ ਵੱਡਾ ਲਾਭ ਸੂਚਨਾ – ਸੰਚਾਰ ਵਿਚ ਤੇਜ਼ੀ ਆਉਣ ਦਾ ਹੀ ਸਿੱਟਾ ਹੈ। ਇਸ ਤੇਜ਼ੀ ਨਾਲ ਜਿੱਥੇ ਸਾਡੇ ਪਰਿਵਾਰਿਕ, ਸਮਾਜਿਕ, ਆਰਥਿਕ ਤੇ ਰਾਜਨੀਤਿਕ ਜੀਵਨ ਵਿਚ ਸਾਡੀ ਕਿਰਿਆਤਮਕਤਾ ਨੂੰ ਹੁਲਾਰਾ ਮਿਲਦਾ ਹੈ, ਉੱਥੇ ਨਾਲ ਹੀ ਵਪਾਰਕ ਤੇ ਆਰਥਿਕ ਖੇਤਰ ਵਿਚ ਉਤਪਾਦਨ, ਖ਼ਰੀਦ – ਫਰੋਖਤ, ਮੰਗ – ਪੂਰਤੀ, ਦੇਣ – ਲੈਣ, ਭੁਗਤਾਨ ਅਤੇ ਕਾਨੂੰਨ – ਵਿਵਸਥਾ ਦੇ ਸੁਧਾਰ ਵਿਚ ਗਤੀ ਆਉਣ ਨਾਲ ਵਿਕਾਸ ਦੀ ਦਰ ਤੇਜ਼ ਹੁੰਦੀ ਹੈ, ਜਿਸ ਦੇ ਸਿੱਟੇ ਵਜੋਂ ਖ਼ੁਸ਼ਹਾਲੀ ਵਧਦੀ ਹੈ ਤੇ ਜੀਵਨ – ਪੱਧਰ ਉੱਚਾ ਹੁੰਦਾ ਹੈ।
ਮੋਬਾਈਲ ਫੋਨ ਦਾ ਤੀਜਾ ਲਾਭ ਇਸ ਦਾ ਦਿਲ – ਪਰਚਾਵੇ ਦਾ ਸਾਧਨ ਹੋਣਾ ਹੈ। ਮੋਬਾਈਲ ਫੋਨ ਜੇਬ ਵਿਚ ਹੁੰਦਿਆਂ ਸਾਨੂੰ ਇਕੱਲ ਦਾ ਬਹੁਤਾ ਅਹਿਸਾਸ ਨਹੀਂ ਹੁੰਦਾ। ਇਸ ਨਾਲ ਜਿੱਥੇ ਅਸੀਂ ਆਪਣੀ ਇਕੱਲ ਨੂੰ ਤੋੜਨ ਲਈ ਕਿਸੇ ਵੀ ਮਨ – ਭਾਉਂਦੇ ਵਿਅਕਤੀ ਨਾਲ ਗੱਲਾਂ ਕਰ ਸਕਦੇ ਹਾਂ, ਉੱਥੇ ਅਸੀਂ ਇੰਟਰਨੈੱਟ, ਈ. ਮੇਲ, ਫੇਸਬੁੱਕ, ਟਵਿੱਟਰ ਤੇ ਵੱਟਸੈਪ ਮੋਬਾਈਲ, ਐੱਮ. ਪੀ. 3, ਰੇਡੀਓ, ਟੈਲੀਵਿਯਨ, ਕੈਮਰੇ ਤੇ ਵੀ. ਡੀ. ਓ. ਗੋਮਾਂ ਦੀ ਵਰਤੋਂ ਕਰ ਕੇ ਆਪਣਾ ਦਿਲ – ਪਰਚਾਵਾ ਕਰਨ ਦੇ ਨਾਲ ਆਪਣੀ ਜਾਣਕਾਰੀ ਤੇ ਗਿਆਨ ਵਿਚ ਵੀ ਵਾਧਾ ਕਰ ਸਕਦੇ ਹਾਂ।

ਮੋਬਾਈਲ ਫੋਨ ਦਾ ਅਗਲਾ ਵੱਡਾ ਲਾਭ ਵਪਾਰਕ ਅਦਾਰਿਆਂ ਨੂੰ ਹੈ। ਮੋਬਾਈਲ ਫੋਨ ਉਤਪਾਦਕ ਕੰਪਨੀਆਂ ਭਿੰਨ – ਭਿੰਨ ਪ੍ਰਕਾਰ ਦੇ ਨਵੇਂ – ਨਵੇਂ ਦਿਲ – ਖਿੱਚਵੇਂ ਮਾਡਲਾਂ ਨੂੰ ਮਾਰਕਿਟ ਵਿਚ ਪਰੋਸ ਕੇ ਤੇ ਇਸ ਸੰਚਾਰ ਸਾਧਨ ਦੀ ਸੇਵਾ ਮੁਹੱਈਆ ਕਰਾਉਣ ਵਾਲੀਆਂ ਕੰਪਨੀਆਂ ਭਿੰਨ – ਭਿੰਨ ਪ੍ਰਕਾਰ ਦੀਆਂ ਸਕੀਮਾਂ ਤੇ ਪੈਕਿਜਾਂ ਨਾਲ ਮੋਬਾਈਲ ਫੋਨਾਂ ਨੂੰ ਆਮ ਲੋਕਾਂ ਦੀ ਖ਼ਰੀਦ – ਸ਼ਕਤੀ ਦੇ ਅਨੁਕੂਲ ਬਣਾਉਂਦੀਆਂ ਹੋਈਆਂ ਖ਼ਪਤਕਾਰਾਂ ਦੀ ਗਿਣਤੀ ਵਧਾ ਕੇ ਅਰਬਾਂ ਰੁਪਏ ਕਮਾ ਰਹੀਆਂ ਹਨ।
ਮੋਬਾਈਲ ਫੋਨ ਦਾ ਲਾਭ ਜੁਰਮਾਂ ਦੀ ਪੜਤਾਲ ਕਰਨ ਵਿਚ ਪੁਲਿਸ ਤੇ ਹੋਰਨਾਂ ਗੁਪਤਚਰ ਏਜੰਸੀਆਂ ਨੂੰ ਵੀ ਹੋਇਆ ਹੈ। ਫਲਸਰੂਪ ਉਹ ਇਸ ਵਿਚ ਮੌਜੂਦ ਕਾਲਾਂ ਦੇ ਰਿਕਾਰਡ ਬਹੁਤ ਸਾਰੇ ਮੁਜਰਮਾਂ ਤੇ ਉਨ੍ਹਾਂ ਦੇ ਸਾਥੀਆਂ ਦੇ ਲੁਕਵੇਂ ਥਾਂ – ਟਿਕਾਣੇ ਲੱਭ ਕੇ ਉਨ੍ਹਾਂ ਵਿਰੁੱਧ ਕਾਰਵਾਈ ਕਰਨ ਦੇ ਸਮਰੱਥ ਹੋਈਆਂ ਹਨ ਮੋਬਾਈਲ ਫੋਨ ਉੱਤੇ ਪ੍ਰਾਪਤ ਐੱਸ. ਐੱਮ. ਐੱਸ. ਦੀ ਸਹੂਲਤ, ਜਿੱਥੇ ਲੋਕਾਂ ਨੂੰ ਇਕ – ਦੂਜੇ ਨਾਲ ਕਈ ਪ੍ਰਕਾਰ ਦਾ ਸੰਚਾਰ ਕਰਨ ਅਤੇ ਆਪਸ ਵਿਚ ਲਤੀਫ਼ੇ ਤੇ ਦਿਲ – ਲਗੀਆਂ ਦੇ ਆਦਾਨ – ਪ੍ਰਦਾਨ ਕਰ ਕੇ ਮਨ ਨੂੰ ਤਣਾਓ – ਮੁਕਤ ਕਰਨ ਦਾ ਪਦਾਰਥ ਮੁਹੱਈਆ ਕਰਦੀ ਹੈ, ਉੱਥੇ ਨਾਲ ਹੀ ਉਨ੍ਹਾਂ ਦੀ ਟੈਲੀਵਿਯਨ ਵਿਚ ਦਿਖਾਏ ਜਾ ਰਹੇ ਕਈ ਤਰ੍ਹਾਂ ਦੇ ਮੁਕਾਬਲਿਆਂ ਵਿਚ ਸ਼ਮੂਲੀਅਤ ਕਰ ਕੇ ਉਨ੍ਹਾਂ ਅੰਦਰ ਮੁਕਾਬਲੇਬਾਜ਼ੀ ਦੀ ਭਾਵਨਾ, ਆਸ਼ਾਵਾਦ ਤੇ ਜਗਿਆਸਾ ਨੂੰ ਵੀ ਮਘਾਉਂਦੀ ਹੈ, ਜਿਸ ਨਾਲ ਜ਼ਿੰਦਗੀ ਵਿਚ ਰਸ ਪੈਦਾ ਹੁੰਦਾ ਹੈ ਤੇ ਬਹੁਤ ਸਾਰੇ ਲੋਕਾਂ, ਖ਼ਾਸ ਕਰ ਕਲਾਕਾਰਾਂ ਨੂੰ ਪਦਾਰਥਕ ਲਾਭਾਂ ਦੇ ਨਾਲ – ਨਾਲ ਲੋਕ – ਮਕਬੂਲੀਅਤ ਵੀ ਹਾਸਲ ਹੁੰਦੀ ਹੈ।
ਮੋਬਾਈਲ ਫੋਨ ਇਨ੍ਹਾਂ ਬਹੁਤ ਸਾਰੇ ਲਾਭਾਂ ਦੇ ਨਾਲ ਅਜੋਕੇ ਸਮਾਜ ਨੂੰ ਬਹੁਤ ਸਾਰੇ ਨੁਕਸਾਨ ਵੀ ਪੁਚਾ ਰਿਹਾ ਹੈ, ਜਿਨ੍ਹਾਂ ਦਾ ਲੇਖਾ – ਜੋਖਾ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਹੈ :
ਮੋਬਾਈਲ ਫੋਨ ਦਾ ਸਭ ਤੋਂ ਵੱਡਾ ਨੁਕਸਾਨ ਇਸ ਦਾ ਸਮਾਜ – ਵਿਰੋਧੀ, ਗੁੰਡਾ ਅਨਸਰਾਂ ਤੇ ਕਪਟੀ ਲੋਕਾਂ ਦੇ ਹੱਥਾਂ ਵਿਚ ਹੋਣਾ ਹੈ। ਸੂਚਨਾ ਦਾ ਤੇਜ਼, ਨਿੱਜੀ, ਸਰਲ ਤੇ ਸੌਖਾ ਸਾਧਨ ਹੋਣ ਕਰਕੇ ਇਸ ਨਾਲ ਬਹੁਤ ਸਾਰੇ ਸਮਾਜ ਵਿਰੋਧੀ ਅਤੇ ਛਲ – ਕਪਟ, ਬਲੈਕ – ਮੇਲ ਤੇ ਧੋਖੇ ਭਰੇ ਕੰਮਾਂ ਨੂੰ ਨੇਪਰੇ ਚਾੜ੍ਹਿਆ ਜਾਂਦਾ ਹੈ। ਅੱਜ – ਕਲ੍ਹ ਕੋਈ ਵੀ ਵੱਡਾ ਜੁਰਮ ਚੋਰੀ, ਡਾਕਾ, ਅਗਵਾਂ – ਕਾਂਡ ਜਾਂ ਅੱਤਵਾਦੀ ਕਾਰਵਾਈ ਇਸ ਦੀ ਵਰਤੋਂ ਤੋਂ ਬਿਨਾਂ ਸਿਰੇ ਨਹੀਂ ਚੜ੍ਹੀ ਹੁੰਦੀ।
ਇਸਦੇ ਨਾਲ ਹੀ ਨੌਜਵਾਨ ਮੁੰਡੇ – ਕੁੜੀਆਂ, ਖ਼ਾਸ ਕਰ ਵਿਦਿਆਰਥੀਆਂ ਅਤੇ ਵਿਹਲੜਾਂ ਨੂੰ ਇਸ ਦੀ ਜ਼ਰੂਰਤ ਨਹੀਂ ਪਰ ਇਸ ਦੀ ਸਭ ਤੋਂ ਵੱਧ ਵਰਤੋਂ ਸਕੂਲਾਂ – ਕਾਲਜਾਂ ਵਿਚ ਪੜ੍ਹਦੇ ਮੁੰਡੇ – ਕੁੜੀਆਂ ਹੀ ਕਰ ਰਹੇ ਹਨ। ਇਨ੍ਹਾਂ ਰਾਹੀਂ ਬਾਲਗਾਂ ਤੇ ਨਾਬਾਲਗਾਂ ਵਿਚ ਅਸ਼ਲੀਲ ਸਮੱਗਰੀ ਦੇ ਆਦਾਨ – ਪ੍ਰਦਾਨੇ ਦਾ ਸਿਲਸਿਲਾ ਚਲਦਾ ਰਹਿੰਦਾ ਹੈ। ਕਾਲਜਾਂ ਵਿਚ ਵੀ ਕੈਮਰੇ ਵਾਲੇ ਮੋਬਾਈਲ ਫੋਨ ਅਤੇ ਐੱਮ. ਐੱਮ. ਐੱਸ. ਦੀ ਲਚਰਤਾ ਭਰੀ ਵਰਤੋਂ ਬਾਰੇ ਖ਼ਬਰਾਂ ਆਉਂਦੀਆਂ ਰਹਿੰਦੀਆਂ ਹਨ। ਇਸ ਕਰਕੇ ਇੱਥੇ ਇਹ ਗੱਲ ਕਹਿਣੀ ਗ਼ਲਤ ਨਹੀਂ ਕਿ ਇਸ ਦੀ ਸਕੂਲ ਟਾਈਮ ਵਿਚ ਵਰਤੋਂ ਉੱਤੇ ਬਿਲਕੁਲ ਪਾਬੰਦੀ ਲੱਗਣੀ ਚਾਹੀਦੀ ਹੈ।
ਮੋਬਾਈਲ ਫੋਨ ਦਾ ਅਗਲਾ ਵੱਡਾ ਨੁਕਸਾਨ ਸਿਹਤ ਸੰਬੰਧੀ ਹੈ। ਮੋਬਾਈਲ ਫੋਨ ਦੇ ਹੈੱਡ – ਸੈਂਟ ਅਤੇ ਸਟੇਸ਼ਨ ਟਾਵਰ ਵਰਗੇ ਐਨਟੀਨਾ ਵਿਚੋਂ ਨਿਕਲਦੀ ਰੇਡੀਓ ਕਿਉਂ ਸੀ ਰੇਡੀਏਸ਼ਨ ਸੰਬੰਧੀ ਹੋਈ ਖੋਜ ਨੇ ਸਰੀਰ ਉੱਤੇ ਪੈਂਦੇ ਇਸ ਦੇ ਬੁਰੇ ਅਸਰਾਂ ਦਾ ਜ਼ਿਕਰ ਕੀਤਾ ਹੈ। ਮੋਬਾਈਲ ਫੋਨ ਦਾ ਇਕ ਹੋਰ ਨੁਕਸਾਨ ਇਹ ਹੈ ਕਿ ਇਸ ਦੇ ਨਿੱਤ ਵਿਕਸਿਤ ਹੋ ਰਹੇ ਨਵੇਂ ਮਾਡਲਾਂ ਤੇ ਇਨ੍ਹਾਂ ਦੀ ਵਰਤੋਂ ਉੱਪਰ ਹੋ ਰਹੇ ਖ਼ਰਚੇ ਦਾ ਬੇਸ਼ੱਕ ਉੱਪਰਲੇ ਤਬਕੇ ਉੱਪਰ ਕੋਈ ਅਸਰ ਨਹੀਂ ਪੈਂਦਾ, ਪਰੰਤੂ ਹੇਠਲੀ ਮੱਧ ਸ਼੍ਰੇਣੀ ਤੇ ਆਮ ਲੋਕਾਂ ਦੀਆਂ ਜੇਬਾਂ ਉੱਪਰ ਬਹੁਤ ਬੁਰਾ ਅਸਰ ਪੈ ਰਿਹਾ ਹੈ।
ਜਿੱਥੇ ਹੈੱਡ – ਸੈੱਟ ਬਣਾਉਣ ਵਾਲੀਆਂ ਕੰਪਨੀਆਂ ਨਵੇਂ – ਨਵੇਂ ਤੇ ਬਹੁਮੰਤਵੀ ਮਾਡਲਾਂ ਨਾਲ ਆਮ ਲੋਕਾਂ ਨੂੰ ਪੁਰਾਣੇ ਮਾਡਲ ਦੇ ਹੈੱਡ – ਸੈੱਟਾਂ ਦੀ ਥਾਂ ਨਵੇਂ ਮਾਡਲ ਖ਼ਰੀਦਣ ਲਈ ਉਕਸਾ ਰਹੀਆਂ ਹਨ, ਉੱਥੇ ਮੋਬਾਈਲ ਫੋਨ ਸੰਚਾਰ ਪ੍ਰਦਾਨ ਕਰਨ ਵਾਲੀਆਂ ਕੰਪਨੀਆਂ ਨਵੀਆਂ – ਨਵੀਆਂ ਸਕੀਮਾਂ ਤੇ ਪੈਕਿਜਾਂ ਤੋਂ ਇਲਾਵਾ ਤਰ੍ਹਾਂ – ਤਰ੍ਹਾਂ ਦੀਆਂ ਰਿੰਗ – ਟੋਨਾਂ ਬਣਾ ਕੇ, ਐੱਸ. ਐੱਮ. ਐੱਸ. ਤੇ ਐੱਮ. ਐੱਮ. ਐੱਸ. ਰਾਹੀਂ ਲੱਚਰ ਤੇ ਅਭੱਦਰ ਲਤੀਫ਼ੇ, ਤਸਵੀਰਾਂ, ਕਈ ਪ੍ਰਕਾਰ ਦੇ ਛਲਾਊ ਮੁਕਾਬਲੇ ਪਰੋਸ ਕੇ ਤੇ ਖ਼ਪਤਕਾਰਾਂ ਤੋਂ ਕਰੋੜਾਂ ਰੁਪਏ ਬਟੋਰ ਰਹੀਆਂ ਹਨ।

ਮੋਬਾਈਲ ਫੋਨ ਦਾ ਇਕ ਹੋਰ ਵੱਡਾ ਨੁਕਸਾਨ ਇਹ ਹੈ ਕਿ ਜਦੋਂ ਸਭਾ, ਸੰਗਤ, ਕਲਾਸ, ਸਮਾਗਮ ਜਾਂ ਕਾਨਫਰੰਸ ਵਿਚ ਬੈਠੇ ਕਿਸੇ ਬੰਦੇ ਦੀ ਜੇਬ ਵਿਚ ਇਸ ਦੀ ਘੰਟੀ ਵੱਜਦੀ ਹੈ, ਤਾਂ ਸਭ ਦਾ ਧਿਆਨ ਉਚਾਟ ਹੋ ਜਾਂਦਾ ਹੈ।
ਇਸ ਦਾ ਇਕ ਹੋਰ ਗੰਭੀਰ ਨੁਕਸਾਨ ਇਸ ਦੀ ਵਰਤੋਂ ਕਰਨ ਵਾਲਿਆਂ ਦੀ ਆਪਣੀ ਬੇਪਰਵਾਹੀ ਤੇ ਮੂਰਖਤਾ ਕਰਕੇ ਪੈਦਾ ਹੁੰਦਾ ਹੈ। ਕਈ ਲੋਕ ਕਾਰ, ਕਟਰ, ਮੋਟਰ ਸਾਈਕਲ ਜਾਂ ਸਾਈਕਲ ਉੱਤੇ ਜਾਂਦਿਆਂ ਮੋਬਾਈ ਕੇ ਤੇ ਕੰਨ ਹੇਠ ਦਬਾ ਕੇ ਗੱਲਾਂ ਕਰਦੇ ਜਾਂਦੇ ਹਨ। ਇਸ ਨਾਲ ਦੁਰਘਟਨਾਵਾਂ ਦਾ ਖ਼ਤਰਾ ਹਰ ਵੇਲੇ ਬਣਿਆ ਰਹਿੰਦਾ ਹੈ।
ਬੇਸ਼ੱਕ ਉੱਪਰ ਅਸੀਂ ਮੋਬਾਈਲ ਫੋਨ ਦੇ ਫ਼ਾਇਦਿਆਂ ਨਾਲ ਇਸ ਦੇ ਬਹੁਤ ਸਾਰੇ ਨੁਕਸਾਨ ਵੀ ਗਿਣਾਏ ਹਨ ਪਰ ਇਸ ਵਿਚ ਕੋਈ ਸ਼ੱਕ ਨਹੀਂ ਕਿ ਇਹ ਦਿਨੋ – ਦਿਨ ਹਰਮਨ – ਪਿਆਰਾ ਹੋ ਰਿਹਾ ਹੈ ਤੇ ਲੋਕ ਇਸ ਦੇ ਖ਼ਤਰਿਆਂ ਦੀ ਪ੍ਰਵਾਹ ਨਾ ਕਰਦੇ ਹੋਏ ਇਸ ਨੂੰ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ ਤਤਪਰ ਰਹਿੰਦੇ ਹਨ।
48. ਵਾਤਾਵਰਨ ਦਿਵਸ
ਸੰਯੁਕਤ ਰਾਸ਼ਟਰ ਵਾਤਾਵਰਨ ਪ੍ਰੋਗਰਾਮ ਦੀ ਸਰਪ੍ਰਸਤੀ ਹੇਠ ਹਰ ਸਾਲ ਪੰਜ ਜੂਨ ਦਾ ਦਿਨ ਵਿਸ਼ਵ ਵਾਤਾਵਰਨ ਦਿਵਸ ਵਜੋਂ ਮਨਾਇਆ ਜਾਂਦਾ ਹੈ। ਇਸ ਦਾ ਮੰਤਵ ਵਿਸ਼ਵ ਭਰ ਵਿਚ ਕੁਦਰਤ ਅਤੇ ਧਰਤੀ ਨੂੰ ਬਚਾਉਣ ਲਈ ਚੇਤਨਾ ਪੈਦਾ ਕਰਨਾ ਹੈ। ਇਹ ਸੰਯੁਕਤ ਰਾਸ਼ਟਰ ਵਲੋਂ ਧਰਤੀ ਉਤਲੇ ਵਾਤਾਵਰਨ ਨੂੰ ਬਚਾਉਣ ਲਈ ਉਪਰਾਲੇ ਕਰਨ ਸੰਬੰਧੀ ਜਾਗ੍ਰਿਤੀ ਪੈਦਾ ਕਰਨ ਵਾਲਾ ਬਹੁਤ ਹੀ ਮਹੱਤਵਪੂਰਨ ਦਿਵਸ ਹੈ। ਇਸਦਾ ਆਰੰਭ 1974 ਵਿਚ ਹੋਇਆ ਸੀ ਅਤੇ ਹੁਣ ਇਹ ਇਕ ਵਿਸ਼ਵਵਿਆਪੀ ਲਹਿਰ ਬਣ ਕੇ ਹਰ ਸਾਲ ਲਗਪਗ 100 ਦੇਸ਼ਾਂ ਵਿਚ ਮਨਾਇਆ ਜਾਣ ਲੱਗਾ ਹੈ !
ਸੰਯੁਕਤ ਰਾਸ਼ਟਰ ਦੇ ਇਸ ਪ੍ਰੋਗਰਾਮ ਨੂੰ ਸਫਲ ਬਣਾਉਣ ਲਈ ਸੰਸਾਰ ਦੀਆਂ ਪ੍ਰਸਿੱਧ ਹਸਤੀਆਂ ਅਤੇ ਮੀਡੀਆ ਇਸ ਦੇ ਪਰਚਾਰ ਲਈ ਵਧ – ਚੜ੍ਹ ਕੇ ਹਿੱਸਾ ਪਾਉਂਦੇ ਹਨ ਉਨ੍ਹਾਂ ਵਲੋਂ ਸੰਸਾਰ ਭਰ ਦੇ ਲੋਕਾਂ ਨੂੰ ਵਾਤਾਵਰਨ ਨੂੰ ਬਚਾਉਣ ਦੇ ਕਾਰਜ ਵਿਚ ਹਿੱਸਾ ਪਾਉਣ ਲਈ ਉਤਸਾਹਿਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ। ਇਸੇ ਉਦੇਸ਼ ਦੀ ਪੂਰਤੀ ਵਿਚ ਹਿੱਸਾ ਪਾਉਂਦਿਆਂ ਸਾਡੇ ਪ੍ਰਧਾਨ ਮੰਤਰੀ ਨੇ 5 ਜੂਨ, 2015 ਨੂੰ ਆਪਣੀ ਸਰਕਾਰੀ ਰਿਹਾਇਸ਼ ਵਿਖੇ ਰੁੱਖ ਲਾਏ ਸਨ ਤੇ ਸਮੁੱਚੇ ਦੇਸ਼ ਵਾਸੀਆਂ ਨੂੰ ਅਜਿਹਾ ਕਰਨ ਲਈ ਪ੍ਰੇਰਦਿਆਂ ਵਾਤਾਵਰਨ ਨੂੰ ਸੂਛ ਬਣਾਉਣ ਦਾ ਪੈਗਾਮ ਦਿੱਤਾ ਸੀ। ਉਨ੍ਹਾਂ ਦੇ ‘ਛ ਭਾਰਤ’ ਨਾਅਰੇ ਦਾ ਵੀ ਇਸ ਦਿਸ਼ਾ ਵਲ ਹੀ ਇਕ – ਕਦਮ ਹੈ।
ਅੱਜ ਸਮੁੱਚੇ ਸੰਸਾਰ ਵਿਚ ਵਾਤਾਵਰਨ ਇੰਨਾ ਗੰਧਲਾ ਹੋ ਚੁੱਕਾ ਹੈ ਕਿ ਇਸ ਨਾਲ ਮਨੁੱਖ ਸਮੇਤ ਧਰਤੀ ਉੱਤੇ ਸਮੁੱਚੇ ਜੀਵ – ਜਗਤ ਦੀ ਹੋਂਦ ਖ਼ਤਰੇ ਵਿਚ ਪੈ ਗਈ ਤੇ ਆਵਾਜਾਈ ਦੇ ਸਾਧਨਾਂ ‘ਤੇ ਥਰਮਲ ਪਲਾਂਟਾਂ ਵਿਚੋਂ ਨਿਕਰ ਪ੍ਰਮਾਣੂ ਧਮਾਕਿਆਂ ਨੇ ਹਵਾ ਨੂੰ ਜ਼ਹਿਰਾਂ ਨਾਲ ਭਰ ਦਿੱਤਾ ਹੈ, ਜਿਸ ਕਾਰਨ ਮਨੁੱਖਾਂ ਤੇ ਜੀਵਾਂ ਨੂੰ ਸਾਹ ਲੈਣ ਲਈ ਸ਼ੁੱਧ ਆਕਸੀਜਨ ਨਹੀਂ ਮਿਲਦੀ। ਰੁੱਖਾਂ ਦੀ ਕਟਾਈ ਕਰਨ ਨਾਲ ਜੰਗਲ ਘਟ ਰਹੇ ਹਨ। ਫਲਸਰੂਪ ਕਾਰਬਨ – ਡਾਇਆਕਸਾਈਡ ਨੂੰ ਆਕਸੀਜਨ ਵਿਚ ਬਦਲਣ ਵਾਲੇ ਕੁਦਰਤੀ ਸਾਧਨਾਂ ਦੇ ਘਟਣ ਨਾਲ ਧਰਤੀ ਉੱਤੇ ਕਾਰਬਨ – ਡਾਇਆਕਸਾਈਡ ਦੀ ਮਾਤਰਾ ਵਧ ਰਹੀ ਹੈ, ਜਿਸਦੇ ਸਿੱਟੇ ਵਜੋਂ ਧਰਤੀ ਦਾ ਤਾਪਮਾਨ ਵਧ ਰਿਹਾ ਹੈ।
ਗਲੇਸ਼ੀਅਰ ਪਿਘਲ ਰਹੇ ਹਨ ਤੇ ਸਮੁੰਦਰਾਂ ਦਾ ਪਾਣੀ ਵਧ ਰਿਹਾ ਹੈ। ਇਸ ਨਾਲ ਸਮੁੰਦਰਾਂ ਦੇ ਕੰਢੇ ਵਸੇ ਸ਼ਹਿਰਾਂ ਲਈ ਖ਼ਤਰਾ ਪੈਦਾ ਹੋ ਗਿਆ ਹੈ। ਕਾਰਬਨ – ਡਾਇਆਕਸਾਈਡ ਬੱਦਲਾਂ ਵਿਚ ਮਿਲ ਕੇ ਤੇਜ਼ਾਬੀ ਵਰਖਾ ਦਾ ਕਾਰਨ ਬਣ ਰਹੀ ਹੈ, ਜਿਸ ਨਾਲ ਨਾ ਕੇਵਲ ਧਰਤੀ ਦੀ ਬਨਸਪਤੀ ਤੇ ਜੀਵ ਹੀ ਪ੍ਰਭਾਵਿਤ ਹੋ ਰਹੇ ਹਨ, ਸਗੋਂ ਪਾਣੀ ਦੇ ਜੀਵਾਂ ਦੀ ਜ਼ਿੰਦਗੀ ਵੀ ਖ਼ਤਰੇ ਵਿਚ ਪੈ ਗਈ ਹੈ। ਸੀਵਰੇਜ ਤੇ ਕਾਰਖ਼ਾਨਿਆਂ ਦੇ ਪਾਣੀ ਦਰਿਆਵਾਂ ਤੇ ਸਮੁੰਦਰਾਂ ਵਿਚ ਰੋੜ ਦੇਣ ਨਾਲ ਸਾਫ਼ ਪਾਣੀ ਦੇ ਸੋਮੇ ਖ਼ਤਮ ਹੋ ਰਹੇ ਹਨ।

ਭਿੰਨ – ਭਿੰਨ ਪ੍ਰਕਾਰ ਦੀਆਂ ਗੈਸਾਂ ਨੇ ਧਰਤੀ ਦੇ ਜੀਵਾਂ ਨੂੰ ਸੂਰਜ ਦੀਆਂ ਪਰਾਬੈਂਗਣੀ ਕਿਰਨਾਂ ਤੋਂ ਬਚਾਉਣ ਵਾਲੀ ਓਜ਼ੋਨ ਗੈਸ ਦੀ ਪਰਤ ਨੂੰ ਨਸ਼ਟ ਕਰਨਾ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤਾ ਹੈ ਧਰਤੀ ਉੱਤੇ ਖਿਲਰੇ ਕੂੜੇ, ਕੀੜੇਮਾਰ ਦਵਾਈਆਂ ਤੇ ਰਸਾਇਣਿਕ ਖਾਦਾਂ ਨੇ ਖੇਤਾਂ ਦੀ ਮਿੱਟੀ, ਧਰਤੀ ਹੇਠਲੇ ਪਾਣੀ ਤੇ ਧਰਤੀ ਉੱਪਰ ਉਪਜਣ ਵਾਲੀਆਂ ਫ਼ਸਲਾਂ, ਫਲਾਂ, ਸਬਜ਼ੀਆਂ ਤੇ ਅੰਨ ਨੂੰ ਜ਼ਹਿਰੀਲੇ ਬਣਾ ਦਿੱਤਾ ਹੈ। ਸ਼ੋਰ ਪ੍ਰਦੂਸ਼ਣ ਤੇ ਬਿਜਲ – ਚੁੰਬਕੀ ਕਿਰਨਾਂ ਦੇ ਵਿਕੀਰਨੇ ਨੇ ਸਾਡੀ ਧਰਤੀ ਤੇ ਆਲੇ – ਦੁਆਲੇ ਦੇ ਵਾਤਾਵਰਨ ਨੂੰ ਮਨੁੱਖ ਤੇ ਜੀਵਾਂ ਦੇ ਰਹਿਣ – ਯੋਗ ਛੱਡਿਆ ਹੀ ਨਹੀਂ। ਫਲਸਰੂਪ ਬਹੁਤ ਸਾਰੇ ਪਸ਼ੂ – ਪੰਛੀ ਤੇ ਰੁੱਖ – ਬੂਟੇ ਅਲੋਪ ਹੋ ਗਏ ਹਨ। ਨਵੀਆਂ – ਨਵੀਆਂ ਭਿਆਨਕ ਬਿਮਾਰੀਆਂ ਪੈਦਾ ਹੋ ਰਹੀਆਂ ਹਨ ਮੌਸਮ ਵਿਗੜ ਰਹੇ ਹਨ ਜੇਕਰ ਇਹ ਵਿਗਾੜ ਇਸੇ ਤਰ੍ਹਾਂ ਵਧਦਾ ਗਿਆ, ਤਾਂ ਇਕ ਦਿਨ ਧਰਤੀ ਉੱਤੋਂ ਮਨੁੱਖਾਂ ਸਮੇਤ ਸਾਰੇ ਜੀਵ – ਜਗਤ ਦਾ ਨਾਸ਼ ਹੋ ਜਾਵੇਗਾ।
ਇਸੇ ਸਥਿਤੀ ਨੂੰ ਭਾਂਪਦਿਆਂ ਹੀ ਸੰਯੁਕਤ ਰਾਸ਼ਟਰ ਸੰਘ ਨੇ ਇਸ ਪ੍ਰਕਿਰਿਆ ਨੂੰ ਰੋਕਣ ਦੇ ਉਪਰਾਲੇ ਆਰੰਭੇ ਹਨ ਤੇ ਵਿਸ਼ਵ ਵਾਤਾਵਰਨ ਦਿਵਸ ਨੂੰ ਮਨਾਉਣਾ ਉਸਦਾ ਇਸ ਦਿਸ਼ਾ ਵਲ ਮਹੱਤਵਪੂਰਨ ਕਦਮ ਹੈ। ਇਹ ਦਿਵਸ ਸਾਨੂੰ ਹਰ ਸਾਲ ਯਾਦ ਕਰਾਉਂਦਾ ਹੈ ਕਿ ਸਾਨੂੰ ਆਪਣੇ ਵਾਤਾਵਰਨ ਨੂੰ ਵਿਗੜਨ ਤੋਂ ਬਚਾਉਣਾ ਚਾਹੀਦਾ ਹੈ ਤੇ ਇਸਨੂੰ ਪਲੀਤ ਕਰਨ ਵਾਲੇ ਕਾਰਕਾਂ ਨੂੰ ਘਟਾਉਣਾ ਚਾਹੀਦਾ ਹੈ। ਇਸ ਲਈ ਸਾਨੂੰ ਰੁੱਖ ਕੱਟਣੇ ਨਹੀਂ ਚਾਹੀਦੇ, ਸਗੋਂ ਲਾਉਣੇ ਚਾਹੀਦੇ ਹਨ : ਧੂੰਆਂ ਪੈਦਾ ਕਰਨ ਵਾਲੇ ਵਾਹਨਾਂ ਦੀ ਵਰਤੋਂ ਘੱਟ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ ਤੇ ਆਰਗੈਨਿਕ ਖੇਤੀ ਨੂੰ ਉਤਸ਼ਾਹਿਤ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ। ਸਾਨੂੰ ਸ਼ੋਰ ਘਟਾਉਣ ਤੇ ਕੁੜੇ ਦੀ ਸਾਂਭ – ਸੰਭਾਲ ਕਰਨ ਵਲ ਵੀ ਵਿਸ਼ੇਸ਼ ਧਿਆਨ ਦੇਣਾ ਚਾਹੀਦਾ ਹੈ, ਤਾਂ ਹੀ ਵਿਸ਼ਵ ਵਾਤਾਵਰਨ ਦਿਵਸ ਦਾ ਉਦੇਸ਼ ਪੂਰਾ ਹੋ ਸਕੇਗਾ।
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()