Punjab State Board PSEB 9th Class Social Science Book Solutions Geography Chapter 3b पंजाब : जलतन्त्र Exercise Questions and Answers.
PSEB Solutions for Class 9 Social Science Geography Chapter 3b पंजाब : जलतन्त्र
SST Guide for Class 9 PSEB पंजाब : जलतन्त्र Textbook Questions and Answers
(क) नक्शा कार्य (Map Work):
प्रश्न 1.
पंजाब के रेखाचित्र में दिखाएं :
(i) रावी, ब्यास, सतलुज तथा घग्गर
(ii) कोई चार नहरें
(iii) कोई चार चो।
उत्तर-
यह प्रश्न विद्यार्थी MBD Map Master की सहायता से स्वयं करें।
प्रश्न 2.
नदियों का प्रदूषण कैसे रोका जाए, इस विषय पर कक्षा में अध्यापक से चर्चा करें।
उत्तर-
यह प्रश्न विद्यार्थी स्वयं करें।

प्रश्न 3.
अपने समीप नदी या नहर में हो रहे प्रदूषण के लिए अध्यापक व अधिकारियों को सूचना दें।
उत्तर-
यह प्रश्न विद्यार्थी स्वयं करें।
PSEB 9th Class SST Solutions Geography Chapter 3a भारत : जलप्रवाह
(ख) निम्न वस्तुनिष्ठ प्रश्नों के उत्तर दें:
प्रश्न 1.
कौन-सी नदी का उद्गम स्थान मान सरोवर के पास रक्षताल झील है ?
(i) घग्गर
(ii) ब्यास
(iii) सतलुज
(iv) ब्रह्मपुत्र।
उत्तर-
(iii) सतलुज।
प्रश्न 2.
पंजाब में कितनी नदियां हैं-
(i) तीन
(ii) चार
(iii) पाँच
(iv) आठ।
उत्तर-(i) तीन।
प्रश्न 3.
रणजीत सागर अथवा थीन डैम का निर्माण कौन-सी नदी पर हुआ है ?
(i) ब्यास
(ii) रावी
(iii) सतलुज
(iv) इनमें से कोई नहीं।
उत्तर-
(ii) रावी।
प्रश्न 4.
भंगी और बाशा चोअ कौन-से जिले में पड़ते हैं ?
(i) फिरोज़पुर
(ii) गुरदासपुर
(iii) होशियारपुर
(iv) कोई भी नहीं।
उत्तर-
(iii) होशियारपुर।
प्रश्न 5.
कौन-सा कथन गलत है और कौन-सा सही है
(i) रावी, ब्यास व सतलुज बारामारसी नदियां हैं।
(ii) काली बेई व पावर्ती, ब्यास की सहायक नदियां हैं।
(iii) प्राकृतिक जल का शुद्धतम रूप वर्षा का जल है। .
(iv) पंजाब में 10 हैडवर्क्स तथा 20,786 किलोमीटर नहरें हैं।
उत्तर-
- सही,
- सही,
- सही,
- गलत।
प्रश्न 6.
बिस्त दोआब में बिस्त से क्या अभिप्राय है ?
उत्तर-
ब्यास तथा सतलुज दरियाओं के पहले शब्दों ‘बि’ तथा ‘सत’ को मिला. कर बिस्त शब्द बना है।

प्रश्न 7.
हरीके झील से राजस्थान को पानी ले जाने वाली दो नहरें कौन-कौन सी हैं ?
उत्तर-
राजस्थान फीडर नहर जिसे इंदिरा गांधी कमांड नहर भी कहा जाता है।
प्रश्न 8.
पंजाब की कौन-सी नहर हरियाणा को जल प्रदान करती है ?
उत्तर-
घग्गर नदी।
प्रश्न 9.
अपर बारी दोआब नहर का स्त्रोत क्या है ?
उत्तर-
माधोपुर हैडवर्कस।
प्रश्न 10.
पौंग डैम का निर्माण कौन-सी नदी पर किया गया है ?
उत्तर-
ब्यास दरिया।
(ग) प्रश्नों के संक्षेप उत्तर दें:
प्रश्न 1.
ब्यास व रावी की सहायक नदियों की सारणी बनाएं।
उत्तर-
व्यास-ब्यास की सहायक नदियां हैं-सुकन्तरी, पार्वती, सोहां, उहल तथा काली बेईं।
रावी-ऊज, सक्की किरन नाला रावी की प्रमुख नदियां हैं।
प्रश्न 2.
चोअ क्या होते हैं ? किन्हीं चार के नाम लिखें।
उत्तर-
चोअ छोटी मौसमी नदियां होती हैं जो वर्षा की ऋतु में पानी से पूर्णतया भर जाती हैं। बहुत सी चौएं कटारधार तथा सोलहासिंगी पहाड़ियों से शुरू होती हैं। पंजाब के कण्डी क्षेत्र में बहुत सी मौसमी चौएं हैं। बाणा चोअ, टोसां चोअ, बलाचौर चोअ, गढ़शंकर चोअ, नरियाला चोअ, मैली चोअ इत्यादि कुछ प्रमुख चौ हैं।
प्रश्न 3.
पंजाब के नदी, नहरों के प्रदूषण से अवगत करवायें।
उत्तर-
जब पानी में अनावश्यक वस्तुएं मिला दी जाती हैं जिस से पानी प्रयोग करने लायक नहीं रहता, इसे जल प्रदूषण कहते हैं। इसमें कोई शंका नहीं है कि पंजाब की सभी नदियों तथा नहरों में काफ़ी अधिक जल प्रदूषण है। भारत सरकार के कई विभागों तथा मन्त्रालयों का भी मानना है कि पंजाब की नहरों में काफ़ी अधिक जल प्रदूषण है तथा इनमें खतरनाक ज़हर भर रहा है। यह ज़हर पानी की सहायता से हमारी भोजन प्रणाली में पहुँच रहा है तथा लोग इससे खतरनाक बिमारियों का शिकार हो रहे हैं। उदाहरण के लिए बुड्ढा नाला पूर्णतया तेजाबी हो चुका है। हमें सभी नदियों को बचाने की आवश्यकता है ताकि हम पानी के साथ-साथ अपने जीवन को बचा कर रख सकें।
(घ) निम्न प्रश्नों के विस्तृत उत्तर दें
प्रश्न 1.
सतलुज नदी, उस पर बनाये डैमों तथा उसकी सहायक नदियों की जानकारी दें।
उत्तर-
सतलुज नदी तिब्बत में 4630 मीटर की ऊँचाई पर स्थित मानसरोवर झील से रक्षताल नामक स्थान से शुरू होता है। जब यह हिमालय पर्वत को पार कर रहा होता है तो गहरी खाइयां बनाता है। सतलुज मैदानों में भाखड़ा में दाखिल होता है तथा यहां ही भाखड़ा डैम बनाया गया है। नंगल से सतलुज दरिया दक्षिण दिशा की तरफ बढ़ता है तथा जब यह रोपड़ पहुँचता है तो इसमें सुआं, सरसा नदियां, मौसमी चोअ मिल जाते हैं। फिरोजपुर जिले में यह हरीके पत्तण से 60 किलोमीटर की दूरी पर स्थित सुलेमानकी नामक स्थान से पाकिस्तान में चला जाता है। सतलुज दरिया पर भाखड़ा बाँध के साथ-साथ कोटला बाँध, नाथपा झाखड़ी तथा नंगल बाँध भी बनाए गए हैं। सुआं, ब्यास तथा चिट्टी बेईं सतलुज की सहायक नदियां हैं। मक्खु में गिद्दड़ पिण्डी तथा चिट्टी बेईं सतलुज में मिल जाती है। सतलुज दरिया पर कई बाँधों के साथ-साथ रोपड़ तथा हरीके हैडवर्क्स भी बनाए गए हैं।

प्रश्न 2.
पंजाब के नहर प्रबन्ध के विषय में लिखें। इससे कृषि को क्या लाभ हैं ?
उत्तर-
पंजाब की अधिकतर जनता कृषि या इससे संबंधित कार्यों में लगी हुई है तथा पंजाब में ही 1960 के दशक में हरित क्रान्ति की शुरूआत हुई। हरित क्रान्ति में सिंचाई की बहुत बड़ी भूमिका थी क्योंकि किसान फसलों की सिंचाई के लिए केवल वर्षा पर निर्भर नहीं रह सकता। इस कारण पंजाब ने समय-समय पर अपनी नहरी व्यवस्था को काफी विकसित किया। पंजाब में 14500 किलोमीटर लंबी नहरें तथा 5 हैडवर्क्स हैं। यहां 10 नहरें भी हैं जिनके नाम हैंसरहिन्द नहर, अपर बारी दोआब नहर, बिस्त दोआब नहर, भाखड़ा मेन लाइन नहर, फिरोज़पुर/सरहिन्द फीडर प्रबन्ध, कश्मीर नहर, मक्खु, नहर, शाह नहर, राजस्थान फीडर तथा बीकानेर नहर। इन 10 नहरों में से 8 नहरों का वर्णन इस प्रकार है-
| नहर |
उत्पात का स्थान |
लंबाई |
| 1. भाखड़ा मेन लाइन |
नंगल बैराज |
161.36 कि०मी० |
| 2. राजस्थान फीडर |
हरीके हैडवर्क्स |
149.53 कि०मी० |
| 3. सरहिन्द फीडर II |
हरीके हैडवर्क्स |
136.53 कि०मी० |
| 4. सरहिन्द |
रोपड़ हैडवर्क्स |
59.44 कि०मी० |
| 5. बिस्त दोआब |
रोपड़ हैडवर्क्स |
43.00 कि०मी० |
| 6. अपर बारी दोआब |
माधोपुर हैडवर्क्स |
42.35 कि०मी० |
| 7. पूर्वी नहर |
हुसैनीवाला हैडवर्क्स |
8.02 कि०मी० |
| 8. शाह नहर |
मुकेरियां हाईडल चैनल |
2.23 कि०मी० |
कृषि को लाभ-इस नहरी व्यवस्था से पंजाब की कृषि को काफी लाभ हुआ जिसका वर्णन इस प्रकार है-
- इन नहरों से पंजाब की कृषि को सारा साल पानी मिलता रहता है।
- सिंचाई के साधन बढ़ने से किसान साल में दो या अधिक फसलें उगाने में सफल हो गए हैं।
- अधिक फसलें उगाने से किसानों को काफ़ी फायदा हुआ है तथा उनकी आय भी बढ़ गई है।
- दरियाओं तथा नहरों पर डैम बना कर पानी को रोका गया ताकि वर्षा न होने की स्थिति में किसानों तक पानी पहुँचाया जा सके।
- डैमों से बिजली तैयार की गई जिससे उद्योगों तथा घरों को 24 घण्टे बिजली प्राप्त हुई।
प्रश्न 3.
पंजाब के चोअ और रौअ कौन-कौन से हैं ? विस्तत नोट लिखें।
उत्तर-
चौएं छोटी छोटी वर्षा पर आधारित तथा मौसमी नदियां होती हैं जो वर्षा के मौसम में पानी से भर जाती हैं। पंजाब में एक कण्डी क्षेत्र है जहां बहुत-सी चौएं मौजूद हैं। इनमें से कई चौओं का जन्म कटारधार तथा सेलासिंगी की पहाड़ियों में होता है। जब वर्षा आती है तो इन चौओं में पानी भर जाता है। पंजाब सरकार ने इनमें से कई चौओं को बंद करने में सफलता प्राप्त कर ली है तथा इनमें आने वाले वर्षा के पानी को कृषि अथवा अन्य कार्यों के लिए प्रयोग किया जा रहा है।
होशियारपुर जिले के दक्षिण पश्चिम में 93 चौएं मौजूद हैं जिनमें से बहुत से काली बेईं तथा चिट्टी बेईं में जाकर मिल जाते हैं। होशियारपुर में बहुत से चौएं हैं जिनमें कुछ काफी प्रमुख हैं जैसे कि टोसां चौ, बणा चौ, गढ़शंकर चौ, बलाचौर चौ, मैली चौ, नरियाला चौ, नंगल शहीदां चौ, गोंदपुर चौ, दसूहा चौ इत्यादि। इन पर नियन्त्रण रखने के लिए पंजाब सरकार ने कण्डी क्षेत्र विकास (Kandi Area Development) को भी शुरू किया है। पंजाब में कुछ बरसाती नाले भी हैं जैसे कि पटियाला की राव, जैंतिया देवी की रौ, बुड्ढ़ा नाला इत्यादि।
PSEB 9th Class Social Science Guide पंजाब : जलतन्त्र Important Questions and Answers
बहुविकल्पीय प्रश्न (Multiple Choice Questions)
प्रश्न 1.
पंजाब कौन-से दो शब्दों से मिलकर बना है ?
(क) पंज + आब
(ख) पंजा + आहब
(ग) पंज + अहाब
(घ) पं + जाहब।
उत्तर-
(क) पंज + आब

प्रश्न 2.
अब पंजाब में कितने दरिया हैं ?
(क) दो
(ख) तीन
(ग) चार
(घ) पाँच।
उत्तर-
(ख) तीन
प्रश्न 3.
इनमें से कौन-सा मौसमी दरिया है ?
(क) घग्गर
(ख) सकी किरन
(ग) काली बेई
(घ) उपर्युक्त सभी।
उत्तर-
(घ) उपर्युक्त सभी।
प्रश्न 4.
इनमें से कौन-सा बारहमासी दरिया है ?
(क) रावी
(ख) ब्यास
(ग) सतलुज
(घ) उपर्युक्त सभी।
उत्तर-
(घ) उपर्युक्त सभी।
प्रश्न 5.
रणजीत सागर डैम किस दरिया पर बना है ?
(क) रावी
(ख) सतलुज
(ग) ब्यास
(घ) चिनाब।
उत्तर-
(क) रावी
प्रश्न 6.
पौंग डैम किस दरिया पर बना है ?
(क) रावी
(ख) सतलुज
(ग) ब्यास
(घ) जेहलम।
उत्तर-
(ग) ब्यास

प्रश्न 7.
होशियारपुर में कितने चौएं हैं ?
(क) 70
(ख) 93
(ग) 84
(घ) 54.
उत्तर-
(ख) 93
रिक्त स्थान की पूर्ति करें (Fill in the Blanks)
1. सन् …………. में भारत तथा पाकिस्तान के विभाजन का सबसे बड़ा नुकसान …….. को हुआ।
2. रावी, ब्यास तथा सतलुज ……….. दरिया हैं।
3. रणजीत सागर डैम का कार्य ………… में पूर्ण हुआ था।
4. सुकन्तरी ………. की प्रमुख सहायक नदी है।
5. ………… किसी समय सरस्वती नदी का हिस्सा थी।
उत्तर-
- 1947, पंजाब,
- बारहमासी,
- 2001,
- ब्यास,
- घग्गर
सही/ग़लत (True/False)
1. जेहलम, चिनाब तथा सिन्धु पाकिस्तान वाले पंजाब में रह गए।
2. रावी ककझ मंझ नाम के स्थान पर पाकिस्तान में प्रवेश करता है।
3. रणजीत सागर डैम से 1600 वाट बिजली उत्पन्न होती है।
4. ब्यास दरिया पर पौंग डैम बनाया गया है।
5. रावी दरिया से राजस्थान फीडर नहर निकाली गई है।
उत्तर-
- ✓
- ✓
- ✗
- ✓
- ✗
अति लघु उत्तरों वाले प्रश्न।।
प्रश्न 1.
पंजाब शब्द का क्या अर्थ है ?
उत्तर-
पंजाब शब्द दो शब्दों ‘पंज-आब’ से मिलकर बना है जिसका अर्थ है पाँच दरियाओं की धरती।
प्रश्न 2.
1947 के पश्चात् कौन-से दरिया पंजाब में रह गए।
उत्तर-
सतलुज, रावी तथा ब्यास।
प्रश्न 3.
1947 के पश्चात् कौन-से दरिया पाकिस्तान वाले पंजाब में चले गए ?
उत्तर-
जेहलम, चिनाब तथा सिन्धु।
प्रश्न 4.
बारहमासी दरिया कौन-से होते हैं ?
उत्तर-
वह दरिया जिनमें सम्पूर्ण वर्ष पानी रहता है उन्हें बारहमासी दरिया कहते हैं।
प्रश्न 5.
बारहमासी दरियाओं में सम्पूर्ण वर्ष पानी कहां से आता है ?
उत्तर-
बारहमासी दरियाओं में पहाड़ों से पिघली बर्फ का पानी सम्पूर्ण वर्ष आता रहता है।

प्रश्न 6.
पंजाब के कुछ मौसमी दरियाओं के नाम लिखो।
उत्तर-
घग्गर, काली बेईं, चिट्टी बेईं, ऊज, चक्की खड्ड, स्वात इत्यादि।
प्रश्न 7.
किन्हीं दो अवशेषी दरियाओं के नाम लिखें।
उत्तर-
बुड्डा नाला तथा सक्की किरन नाला।
प्रश्न 8.
रावी दरिया का जन्म कहां पर होता है ?
उत्तर-
रावी दरिया कुल्लू की पहाड़ियों में स्थित रोहतांग दर्रे के उत्तर में 4116 मीटर की ऊंचाई से शुरू होता है।
प्रश्न 9.
रावी दरिया पर कौन-सा डैम बनाया गया है तथा इसमें से कौन-सी नहर निकाली गई है ?
उत्तर-
रावी दरिया पर रणजीत सागर डैम बनाया गया है तथा इससे अपर बारी दोआब नहर निकाली गई है।
प्रश्न 10.
रावी दरिया पर कौन-से हैडवर्क्स बनाए गए हैं ?
उत्तर-
शाहपुर कण्डी के नज़दीक धाना या बसन्तपुर, कटारधार, माधोपुर हैडवर्क्स तथा माधोपुर ब्यास लिंक पर कठुआ फीडर।
प्रश्न 11.
रणजीत सागर डैम के बारे में बताएं।
उत्तर-
यह रावी दरिया पर बनाया गया डैम है जिससे 600 मेगावाट बिजली पैदा होती है। यह 1981 में शुरू हुआ था तथा मार्च 2011 में इसका कार्य पूर्ण हुआ था।
प्रश्न 12.
ब्यास दरिया कहां से निकलता है ?
उत्तर-
ब्यास दरिया ब्यास कुण्ड से निकलता है जो हिमाचल प्रदेश में रोहतांग दर्रे के पास 4060 मीटर की ऊंचाई पर स्थित है।
प्रश्न 13.
व्यास दरिया पर कौन-से डैम बनाए गए हैं ?
उत्तर-
हिमाचल प्रदेश में पंडोह तथा पंजाब में पौंग डैम।
प्रश्न 14.
ब्यास से कौन सी नहर निकाली गई है ?
उत्तर-
ब्यास से राजस्थान फीडर नहर निकाली गई है जिसे इंदिरा गांधी कमांड नहर का नाम भी दिया गया है।

प्रश्न 15.
ब्यास की सहायक नदियों के नाम लिखें।
उत्तर–
पार्वती, सुकन्तरी, सौहां, उम्मन तथा काली बेईं।
प्रश्न 16.
सतलुज दरिया कहां पर शुरू होता है ?
उत्तर-
सतलुज दरिया तिब्बत में मानसरोवर झील के नज़दीक स्थित रक्षताल से शुरू होता है।
प्रश्न 17.
सतलुज दरिया कहां पर पाकिस्तान में प्रवेश करता है ?
उत्तर-
सतलुज दरिया फिरोज़पुर में सुलेमान की नामक स्थान से पाकिस्तान में प्रवेश करता है।
प्रश्न 18.
सतलुज दरिया पर कौन-से डैम बनाए गए हैं ?
उत्तर-
नाथपा झाखड़ी, नंगल डैम, कौटला डैम।
प्रश्न 19.
घग्गर किस प्रकार की नदी है ?
उत्तर-
घग्गर दक्षिणी पंजाब में बहने वाली एक मौसमी नदी है ।
प्रश्न 20.
घग्गर कहां से निकलती है ?
उत्तर-
घग्गर नदी सिरमौर की पहाड़ियों से निकलती है।
प्रश्न 21.
पंजाब के किस क्षेत्र में बहुत से चोअ मिलते हैं ?
उत्तर-
कण्डी क्षेत्र में।
प्रश्न 22.
चोअ क्या होता है ?
उत्तर-
चोअ एक छोटी सी नदी होती है जो वर्षा के मौसम में पानी से भर जाती है।
प्रश्न 23.
पंजाब के किस जिले में बहुत से चोअ हैं ?
उत्तर-
होशियारपुर जिले में।
प्रश्न 24.
पंजाब की नहरों की लंबाई बताएं।
उत्तर-
पंजाब की नहरों की लंबाई 14500 किलोमीटर है।
प्रश्न 25.
पंजाब की सबसे लंबी नहर कौन-सी है ?
उत्तर-
भाखड़ा मेन लाइन जिसकी लंबाई 161.36 किलोमीटर है।
प्रश्न 26.
कौन-सा दरिया किसी समय सरस्वती नदी का सहायक होता था ?
उत्तर-
घग्गर दरिया किसी समय सरस्वती नदी का सहायक होता था।

लघु उत्तरों वाले प्रश्न
प्रश्न 1.
पंजाब के जलतन्त्र के बारे में बताएं।
उत्तर-
पंजाब दो शब्द ‘पंज’ तथा ‘आब’ से मिलकर बना है जिसका अर्थ है पाँच दरियाओं की धरती। पंजाब में 1947 से पहले कई दरिया होते थे परन्तु देशों के विभाजन के कारण जेहलम, चिनाब, सिन्धु तथा बहुत सी नदियां पाकिस्तान में चली गईं। अब पंजाब में केवल तीन दरिया रावी, ब्यास तथा सतलुज ही हैं। यह तीनों दरिया बारहमासी हैं जिनमें पहाड़ों की बर्फ पिघलने के कारण सारा साल पानी रहता है। यहां बहुत से मौसमी दरिया भी हैं जैसे कि घग्गर, ऊज, काली बेईं, चिट्टी बेईं, स्वान, नूरपुर बेदी चोअ इत्यादि। यहां अवशेषी दरिया, जैसे कि बुड्ढा नाला तथा सक्की किरन नाला भी मिलते हैं।
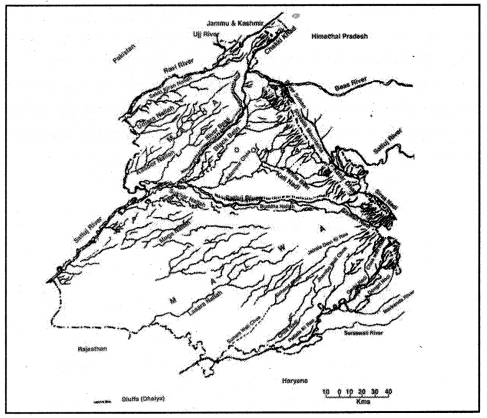
प्रश्न 2.
रावी की सहायक नदियों के बारे में बताएं।
उत्तर-
जब रावी दरिया माधोपुर पहुँचता है तो इसमें कई सहायक नदियां आकर मिल जाती हैं। इनमें सबसे महत्त्वपूर्ण ऊज नदी है। इसके साथ ही सक्की किरन नाला रावी के साथ-साथ चलता है तथा भारत और पाकिस्तान की सरहद पर इसमें मिल जाता है। रावी दरिया पर चार हैडवर्क्स भी बनाए गए हैं जिनके नाम हैं माधोपुर ब्यास लिंक पर कठुआ फीडर, शाहपुर कण्डी के नज़दीक धाना या बसन्तपुर, माधोपुर हैडवर्क्स तथा कटारधार।
प्रश्न 3.
ब्यास दरिया की सहायक नदियों के बारे में बताएं।
उत्तर-
सुकन्तरी-उग्मन, पारबती, काली बेईं तथा सौहां ब्यास की कुछ सहायक नदियां हैं। तलवाड़ा पहुँच कर सौहां ब्यास में मिल जाती हैं। हरीके के नज़दीक काली बेईं होशियारपुर तथा कपूरथला से होते हुए ब्यास में मिल जाती है। ब्यास दरिया पर पौंग डैम तथा पंडोह डैम को भी बनाया गया है।
प्रश्न 4.
घग्गर पर एक नोट लिखें।
उत्तर-
पंजाब में काफी पहले सरस्वती नदी बहती थी तथा घग्गर भी उसका ही हिस्सा थी। परन्तु अब घग्गर एक मौसमी नदी है जो दक्षिण पंजाब में बहती है। यह सिरमौर की पहाड़ियों से निकलती है। मुबारकपुर नाम के स्थान पर यह मैदानी इलाकों में आ जाती है। इसके पश्चात् यह पटियाला, घनौर तथा हरियाणा के इलाकों को पार करती हैं। इसके पश्चात् यह राजस्थान के रेगिस्तान में जाकर खत्म हो जाती है।
दीर्घ उत्तर वाला प्रश्न
प्रश्न-रावी दरिया पर एक नोट लिखें।
उत्तर-रावी पंजाब का एक बारहमासी दरिया है जिसमें सारा साल पानी रहता है क्योंकि पहाड़ों की बर्फ पिघलने के कारण इसमें लगातार पानी आता रहता है। रावी दरिया कुल्लू की पहाड़ियों में रोहतांग दर्रे के उत्तर से शुरू होता है जिसकी ऊंचाई 4116 मीटर है। रावी दरिया अपने आरंभिक स्थान (Place of Origin) से लगातार बहते हुए धौलाधार तथा पीर पंजाल की पहाड़ियों को पार करता है तथा वहां बनी हुई गतॊ (Depressions) से बहते हुए चम्बा तथा डलहौजी को पार करता है। पठानकोट में माधोपुर नाम के स्थान पर यह मैदानों में प्रवेश कर जाता है। रावी के ऊपर रणजीत सागर डैम तथा थीन डैम बनाए गए हैं तथा इनके लिए माधोपुर हैडवर्क्स बनाया गया है। यहां से अपर बारी दोआब नहर भी निकाली गई है। इसके पश्चात् रावी दरिया पठानकोट, गुरदासपुर तथा अमृतसर जिलों में से निकलता है। यह भारत व पाकिस्तान की सरहद निश्चित करता है। कलझ मंझ नाम के स्थान पर यह पाकिस्तान में चला जाता है। पाकिस्तान में यह सिधानी नाम के स्थान पर चिनाब में मिल जाता है। ऊज नदी तथा सक्की किरन वाला रावी की प्रमुख सहायक नदियां हैं।